RESEARCH ARTICLE

A principled methodology for comparing
relatedness measures for clustering publications

开放访问

杂志

Ludo Waltman1

, Kevin W. Boyack2

, Giovanni Colavizza3

, and Nees Jan van Eck1

1Centre for Science and Technology Studies, 莱顿大学, 荷兰人
2SciTech Strategies, 公司, Albuquerque, NM, 美国
3University of Amsterdam, 荷兰人

关键词: 准确性, citation relation, clustering, relatedness measure, textual similarity

抽象的

There are many different relatedness measures, based for instance on citation relations or
textual similarity, that can be used to cluster scientific publications. We propose a principled
methodology for evaluating the accuracy of clustering solutions obtained using these
relatedness measures. We formally show that the proposed methodology has an important
consistency property. The empirical analyses that we present are based on publications in the
fields of cell biology, condensed matter physics, and economics. Using the BM25 text-based
relatedness measure as the evaluation criterion, we find that bibliographic coupling relations
yield more accurate clustering solutions than direct citation relations and cocitation relations.
The so-called extended direct citation approach performs similarly to or slightly better than
bibliographic coupling in terms of the accuracy of the resulting clustering solutions. 另一个
way around, using a citation-based relatedness measure as evaluation criterion, BM25 turns
out to yield more accurate clustering solutions than other text-based relatedness measures.

引文: Waltman, L。, Boyack, K. W.,
Colavizza, G。, & van Eck, 氮. J. (2020). A
principled methodology for comparing
relatedness measures for clustering
出版物. Quantitative Science
学习, 1(2), 691–713. https://doi.org/
10.1162/qss_a_00035

DOI:
https://doi.org/10.1162/qss_a_00035

已收到: 21 一月 2019
公认: 28 八月 2019

通讯作者
Ludo Waltman
waltmanlr@cwts.leidenuniv.nl

处理编辑器:
Vincent Larivière

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

介绍

Clustering of scientific publications is an important problem in the field of bibliometrics.
Bibliometricians have employed many different clustering techniques (例如, Gläser,
Scharnhorst, & Glänzel, 2017; Šubelj, Van Eck, & Waltman, 2016). 此外, 他们有
used various different relatedness measures to cluster publications. These relatedness mea-
sures are typically based on either citation relations (例如, direct citation relations, bibliographic
coupling relations, or cocitation relations) or textual similarity, or sometimes a combination of
the two.

Which relatedness measure yields the most accurate clustering of publications? Two per-
spectives can be taken on this question. One perspective is that there is no absolute notion of
准确性 (例如, Gläser et al., 2017). Following this perspective, each relatedness measure
yields clustering solutions that are accurate in their own right, and it is not meaningful to
ask whether one clustering solution is more accurate than another one. 例如, 不同的
citation-based and text-based relatedness measures each emphasize different aspects of the
way in which publications relate to each other, and the corresponding clustering solutions
each provide a legitimate viewpoint on the organization of the scientific literature. 另一个
perspective is that for some purposes it is useful, and perhaps even necessary, to assume the
existence of an absolute notion of accuracy (例如, Klavans & Boyack, 2017). When this

版权: © 2020 Ludo Waltman,
Kevin W. Boyack, Giovanni Colavizza,
and Nees Jan van Eck. Published under
a Creative Commons Attribution 4.0
国际的 (抄送 4.0) 执照.

麻省理工学院出版社

Comparing relatedness measures for clustering publications

perspective is taken, 有可能的, at least in principle, to say that some relatedness measures
yield more accurate clustering solutions than others.

We believe that both perspectives are useful. From a purely conceptual point of view, 这
first perspective is probably the more satisfactory one. 然而, from a more applied point of
看法, the second perspective is highly important. In many practical applications, users expect
to be provided with a single clustering of publications. Users typically have some intuitive idea
of accuracy and, based on this idea of accuracy, they expect the clustering provided to them to
be as accurate as possible. 在本文中, we take this applied viewpoint and therefore focus on
the second perspective.

Identifying the relatedness measure that yields the most accurate clustering of publications
is challenging because of the lack of a ground truth. There is no perfect classification of pub-
lications that can be used to evaluate the accuracy of different clustering solutions. 对于在-
姿态, suppose we study the degree to which a clustering solution resembles an existing
classification of publications (例如, Haunschild, Schier, 等人。, 2018). The difficulty then is that
it is not clear how discrepancies between the clustering solution and the existing classification
should be interpreted. Such discrepancies could indicate shortcomings of the clustering solu-
的, but they could equally well reflect problems of the existing classification.

As an alternative, the accuracy of clustering solutions can be evaluated by domain experts
who assess the quality of different clustering solutions in a specific scientific domain (例如,
Šubelj et al., 2016). This approach has the difficulty that it is hard to find a sufficiently large
number of experts who are willing to spend a considerable amount of time making a detailed
assessment of the quality of different clustering solutions. 而且, the knowledge of experts
will often be restricted to relatively small domains, and it will be unclear to what extent the
conclusions drawn by experts generalize to other domains.

在本文中, we take a large-scale data-driven approach to compare different relatedness
measures based on which publications can be clustered. The basic idea is to cluster publica-
tions based on a number of different relatedness measures and to use another more or less
independent relatedness measure as a benchmark for evaluating the accuracy of the clustering
solutions. This approach has already been used extensively in a series of papers by Kevin
Boyack, Dick Klavans, and colleagues. They compared different citation-based relatedness
措施 (Boyack & Klavans, 2010; Klavans & Boyack, 2017), including relatedness measures
that take advantage of full-text data (Boyack, 小的, & Klavans, 2013), as well as different text-
based relatedness measures (Boyack, 纽曼, 等人。, 2011). To evaluate the accuracy of clus-
tering solutions, they used grant data, textual similarity (Boyack & Klavans, 2010; Boyack
等人。, 2011, 2013), and more recently also the reference lists of “authoritative” publications,
defined as publications with at least 100 参考 (Klavans & Boyack, 2017).1

Our aim in this paper is to introduce a principled methodology for performing analyses
similar to those mentioned above. We restrict ourselves to the use of one specific clustering
技术, namely the technique introduced in the bibliometric literature by Waltman and
Van Eck (2012), but we allow the use of any measure of the relatedness of publications. 为了
two relatedness measures A and B, our proposed methodology offers a principled way to eval-
uate the accuracy of clustering solutions obtained using the two measures, where a third

1 In a somewhat different context, the idea of evaluating two systems using a third more or less independent
system as the evaluation criterion was explored by Li and Ruiz-Castillo (2013). These authors were interested
in evaluating two classification systems for calculating field-normalized citation impact statistics, 和他们
proposed using a third independent classification system to perform the evaluation.

Quantitative Science Studies

692

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Comparing relatedness measures for clustering publications

relatedness measure C is used as the evaluation criterion. Unlike approaches taken in earlier
文件, our methodology has an important consistency property.

This paper is organized as follows. In section 2, we introduce our methodology for evalu-
ating the accuracy of clustering solutions obtained using different relatedness measures. 在
部分 3, we discuss the relatedness measures that we consider in our analyses. We report
the results of the analyses in section 4. We present comparisons of different citation-based and
text-based relatedness measures that can be used to cluster publications. Our analyses are
based on publications in the fields of cell biology, condensed matter physics, and economics.
We summarize our conclusions in section 5.

2. METHODOLOGY

To introduce our methodology for evaluating the accuracy of clustering solutions obtained
using different relatedness measures, we first discuss the quality function that we use to cluster
出版物. We then explain how we evaluate the accuracy of a clustering solution and
analyze the consistency of our evaluation framework. 最后, we discuss the importance of
using an independent evaluation criterion.

2.1. Quality Function for Clustering Publications

≥ 0 denote the relatedness of publications i and j (和
Consider a set of N publications. Let rX
ij
2 {1, 2, ……} denote
i = 1, ……, N and j = 1, ……, 氮 ) based on relatedness measure X, and let cX
我
the cluster to which publication i is assigned when publications are clustered based on
relatedness measure X.

Publications are assigned to clusters by maximizing a quality function. We focus on the

quality function of Waltman and Van Eck (2012). This quality function is given by

Q ¼

我;j

(西德:2)
I cX
我

(西德:3)

(西德:2)
rX
ij

(西德:3)
;

− γ

¼ cX
j

(1)

i = cX

where I(cX

j ) equals 1 if cX

j and 0 否则, and where γ ≥ 0 denotes a so-called
resolution parameter. The higher the value of this parameter, the larger the number of clusters
that will be obtained. 因此, the resolution parameter γ determines the granularity of the clus-
tering. An appropriate value for this parameter can be chosen based on the specific purpose
for which a clustering of publications is intended to be used. For some purposes it may be
desirable to have a highly granular clustering, while for other purposes a less granular cluster-
ing may be preferable. Sjögårde and Ahlgren (2018, 2020) proposed approaches for choosing
the value of the resolution parameter γ that allow clusters to be interpreted as research topics
or specialties.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The quality function in Eq. (1) can also be written as

Q ¼

我;j

(西德:2)
I cX
我

(西德:3)
rX
ij

− γ

(西德:4) (西德:5)2;
sX
k

¼ cX
j

where sX

k denotes the number of publications assigned to cluster k; 那是,

(西德:4)
I cX
我

我

(西德:5)
:

¼ k

sX
k

(2)

(3)

We also refer to sX

k as the size of cluster k.

In the network science literature, the above quality function was proposed by Traag, 货车
Dooren, and Nesterov (2011), who referred to it as the constant Potts model. The quality func-
tion is closely related to the well-known modularity function introduced by Newman and

Quantitative Science Studies

693

Comparing relatedness measures for clustering publications

Girvan (2004) and Newman (2004). 然而, as shown by Traag et al. (2011), it has the im-
portant advantage that it does not suffer from the so-called resolution limit problem (Fortunato
& Barthélemy, 2007). Waltman and Van Eck (2012) introduced the above quality function in
the bibliometric literature. In the field of bibliometrics, the quality function has been used by,
除其他外, Boyack and Klavans (2014), Klavans and Boyack (2017), Perianes-Rodriguez
and Ruiz-Castillo (2017), Ruiz-Castillo and Waltman (2015), Sjögårde and Ahlgren (2018,
2020), 小的, Boyack, and Klavans (2014), and Van Eck and Waltman (2014).

2.2. Evaluating the Accuracy of a Clustering Solution

Suppose that we have three relatedness measures A, 乙, 和C, and suppose also that we have
used relatedness measures A and B to cluster a set of publications. 此外, suppose that
we want to use relatedness measure C to evaluate the accuracy of the clustering solutions
obtained using relatedness measures A and B. One way in which this could be done is by
using relatedness measure C to obtain a third clustering solution and by comparing the clus-
tering solutions obtained using relatedness measures A and B with this third clustering solu-
的. A large number of methods have been proposed for comparing clustering solutions (例如,
Fortunato, 2010). 然而, we do not take this approach. In order to have a consistent eval-
uation framework (参见部分 2.3), we evaluate the accuracy of the clustering solutions ob-
tained using relatedness measures A and B based directly on relatedness measure C, not on a
clustering solution obtained using this relatedness measure.

Let AX|C denote the accuracy of a clustering solution obtained using relatedness measure X
(with X = A or X = B), where the accuracy is evaluated using relatedness measure C. We define
AX|C as

AXjC ¼ 1
氮

(西德:2)
I cX
我

我;j

(西德:3)
rC
ij

¼ cX
j

(4)

The clustering solution obtained using relatedness measure A is considered to be more accu-
rate than the clustering solution obtained using relatedness measure B if AA|C > AB|C, 和
反过来.

The above approach for evaluating the accuracy of a clustering solution favors less granular
solutions over more granular ones. Of all possible clustering solutions, the least granular so-
lution is the one in which all publications belong to the same cluster. According to Eq. (4), 这
least granular clustering solution always has the highest possible accuracy. There can be no
other clustering solution with higher accuracy. In order to perform meaningful comparisons,
Eq. (4) should be used only for comparing clustering solutions that have the same granularity.

How do we determine whether two clustering solutions have the same granularity? 我们
could require that both clustering solutions have been obtained using the same value for
the resolution parameter γ. 或者, we could require that both clustering solutions con-
sist of the same number of clusters. We do not take either of these approaches. 反而, 我们
require that the sum of the squared cluster sizes is the same for two clustering solutions. 在
也就是说, two clustering solutions obtained using relatedness measures A and B have the
same granularity if

(西德:4)

(西德:5)2 ¼

sA
k

(西德:4) (西德:5)2:
sB
我

我

(5)

If Eq. (5) is satisfied, Eq. (4) can be used to compare in an unbiased way the clustering solutions
obtained using relatedness measures A and B. 另一方面, if Eq. (5) is not satisfied, A
comparison based on Eq. (4) will be biased in favor of the less granular clustering solution. 在

Quantitative Science Studies

694

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Comparing relatedness measures for clustering publications

实践, obtaining two clustering solutions that satisfy Eq. (5) typically will not be easy. 为了
both clustering solutions, it may require a significant amount of trial and error with different
values of the resolution parameter γ. 到底, it may turn out that Eq. (5) can be satisfied only
大约, not exactly. We will return to this issue in section 4.3.

A conceptual motivation for the evaluation framework introduced in this subsection is pre-
sented in Appendix A.1. This motivation is based on an analogy with the evaluation of the
accuracy of different indicators that provide estimates of values drawn from a probability
分配.

2.3. Consistency of the Evaluation Framework

The choice of the accuracy measure defined in Eq. (4) and the granularity condition presented
in Eq. (5) may seem quite arbitrary. 然而, provided we use the quality function defined in
Eq. (1), this choice has an important justification. Suppose that the accuracy of clustering so-
lutions is evaluated using some relatedness measure X. Our choice of the accuracy measure in
Eq. (4) and the granularity condition in Eq. (5) then guarantees that of all possible clustering
solutions of a certain granularity the solution obtained using relatedness measure X will be the
most accurate one. 换句话说, it is guaranteed that AX|X ≥ AY|X for any relatedness measure
是. This is a fundamental consistency property that we believe should be satisfied by any sound
framework for evaluating the accuracy of clustering solutions obtained using different related-
ness measures.

认为, 例如, that we have three clustering solutions, all of the same granularity:
one obtained based on direct citation relations between publications, another obtained based
on bibliographic coupling relations, and a third obtained based on cocitation relations.
Suppose also that the accuracy of the clustering solutions is evaluated based on direct citation
关系. It would then be a rather odd outcome if the clustering solution obtained based on
bibliographic coupling or cocitation relations turned out to be more accurate than the solution
obtained based on direct citation relations. In our evaluation framework, it is guaranteed that
there can be no such inconsistent outcomes. When the accuracy of clustering solutions is eval-
uated based on direct citation relations, the clustering solution obtained based on direct cita-
tion relations will always be the most accurate one. We refer to Appendix B for a formal
analysis of this important consistency property. The appendix also provides an example of
an inconsistent evaluation framework.

2.4.

Independent Evaluation Criterion

As already mentioned in section 1, the approach that we take in this paper is to cluster pub-
lications based on a number of different relatedness measures and to use another more or less
independent relatedness measure to evaluate the accuracy of the clustering solutions. 我们的
idea is to consider different relatedness measures as different proxies of the same underlying
notion of relatedness. This underlying notion of relatedness, which may be referred to as the
“true” relatedness of publications, cannot be directly observed. It can only be approximated.
Given the notion of the true relatedness of publications, each relatedness measure provides
both signal and noise. To the extent that a relatedness measure approximates the true related-
ness of publications, it provides signal. For the rest, it provides noise. We consider two relat-
edness measures to be independent if their noise is uncorrelated. 例如, a citation-based
measure and a text-based relatedness measure may be considered independent. They are both
嘈杂, but in quite different ways. 另一方面, two citation-based relatedness measures
may not be considered independent. Both relatedness measures can be expected to be

Quantitative Science Studies

695

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Comparing relatedness measures for clustering publications

affected by similar types of noise: 例如, noise caused by the fact that the authors of a
publication cite a specific reference while some other reference would have been more
相关的.

在本文中, we use a text-based relatedness measure to evaluate the accuracy of different
clustering solutions obtained using citation-based relatedness measures, and conversely we
use a citation-based relatedness measure to evaluate the accuracy of different clustering solu-
tions obtained using text-based relatedness measures. 重要的, we are not interested in
evaluating citation-based clustering solutions using a citation-based relatedness measure or
text-based clustering solutions using a text-based relatedness measure. Such evaluations are
of little interest because the relatedness measure used for evaluation is not sufficiently indepen-
dent of the relatedness measures being evaluated. 例如, when direct citation relations
are used to evaluate the accuracy of different clustering solutions obtained using citation-based
relatedness measures, the clustering solution obtained based on direct citation relations will be
the most accurate one. The evaluation simply shows that the clustering solution obtained
based on direct citation relations is best aligned with an evaluation criterion based on direct
citation relations, which of course is not surprising. This illustrates the importance of using an
independent evaluation criterion. The more the relatedness measure used for evaluation can
be considered to be independent of the relatedness measures being evaluated, the more infor-
mative the evaluation will be.

In Appendix A.2, we provide a further demonstration of the importance of using an inde-

pendent evaluation criterion.

3. RELATEDNESS MEASURES

We now discuss the relatedness measures that we consider in this paper. We first discuss re-
latedness measures based on citation relations, followed by relatedness measures based on
textual similarity. We also discuss the so-called top M relatedness approach as well as the idea
of normalized relatedness measures.

3.1. Citation-Based Relatedness Measures

Below we discuss a number of citation-based approaches for determining the pairwise relat-
edness for a set of N publications. We use cij to indicate whether publication i cites publication
j (cij = 1) 或不 (cij = 0).

The relatedness of publications i and j based on direct citation relations is given by

(西德:4)
¼ max cij; cji

(西德:5)

rDC
ij

(6)

因此, rDC

ij = 1 if publication i cites publication j or the other way around and rDC

ij = 0 if neither

publication cites the other.

The relatedness of publications i and j based on bibliographic coupling relations equals the

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

number of common references in the two publications. This can be written as

rBC
ij

cikcjk

;

(7)

where the summation extends over all publications in the database that we use, not only over
the N publications for which we aim to determine their pairwise relatedness.

As is well known, cocitation can be seen as the opposite of bibliographic coupling. 这
relatedness of publications i and j based on cocitation relations equals the number of

Quantitative Science Studies

696

Comparing relatedness measures for clustering publications

publications in which publications i and j are both cited. In mathematical terms,

rCC
ij

ckickj

;

(8)

where the summation again extends over all publications in the database that we use.

The above approaches for determining the relatedness of publications may also be com-

bined. This results in

rDC−BC−CC
ij

¼ αrDC
ij

þ rBC
ij

þ rCC
ij

;

(9)

where α denotes a parameter that determines the weight of direct citation relations relative to
bibliographic coupling and cocitation relations. A direct citation relation may be consid-
ered a stronger signal of the relatedness of two publications than a bibliographic coupling
or cocitation relation (Waltman & Van Eck, 2012), and therefore one may want to give more
weight to a direct citation relation than to the two other types of relations. This can be
achieved by setting α to a value above 1. The idea of combining different types of citation-
based relations is not new. This idea was also explored by Small (1997) and Persson (2010).

In addition to the above citation-based approaches for determining the relatedness of pub-
lications, we also consider a so-called extended direct citation approach. Like the ordinary di-
rect citation approach, the extended direct citation approach takes into account only direct
citation relations between publications. 然而, direct citation relations are considered not
just within the set of N focal publications but within an extended set of publications. 此外
to the N focal publications, the extended set of publications includes all publications in our
database that have a direct citation relation with at least two focal publications. (Publications
that have a direct citation relation with only one focal publication are not considered because
they do not contribute to improving the clustering of the focal publications.) The technical de-
tails of the extended direct citation approach are somewhat complex. These details are dis-
cussed in Appendix C. We note that an approach similar to our extended direct citation
approach was also used by Boyack and Klavans (2014) and Klavans and Boyack (2017).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

3.2. Text-Based Relatedness Measures

We consider two text-based approaches for determining the relatedness of publications. 我们
use oil to denote the number of occurrences of term l in publication i. To count the number of
occurrences of a term in a publication, only the title and abstract of the publication are con-
sidered, not the full text. Part-of-speech tagging is applied to the title and abstract of the pub-
lication to identify nouns and adjectives. The part-of-speech tagging algorithm provided by the
Apache OpenNLP 1.5.2 library is used. A term is defined as a sequence of nouns and adjec-
特维斯, with the last word in the sequence being a noun. No distinction is made between sin-
gular and plural nouns, so neural network and neural networks are regarded as the same term.
此外, shorter terms embedded in longer terms are not counted. 例如, if a pub-
lication contains the term artificial neural network, this is counted as an occurrence of artificial
neural network but not as an occurrence of neural network or network. 最后, no stop word
list is used, so there are no terms that are excluded from being counted.

A straightforward text-based measure of the relatedness of publications i and j is given by

rCT
ij

(西德:4)

我

oilojlP
kokl

(西德:5)β

(10)

We refer to this as relatedness based on common terms. The denominator in Eq. (10) aims to
reduce the influence of frequently occurring terms. The parameter β in the denominator

Quantitative Science Studies

697

Comparing relatedness measures for clustering publications

determines the extent to which the influence of these terms is reduced. If β = 0, no reduction in
the influence of frequently occurring terms takes place. 另一方面, if β = 1, 流感-
ence of frequently occurring terms is strongly reduced, following a so-called fractional
counting approach (Perianes-Rodriguez, Waltman, & Van Eck, 2016).

Boyack et al. (2011) identified BM25 as one of the most accurate text-based relatedness
measures for clustering publications. We therefore also include BM25 in our analysis.
BM25 originates from the field of information retrieval, where it is used to determine the rel-
evance of a document for a search query (Sparck Jones, 沃克, & 罗伯逊, 2000A, 2000乙).
Following Boyack et al. (2011), we use BM25 as a text-based measure of the relatedness of
出版物. The BM25 relatedness measure is defined as

rBM25
ij

我

ð
I oil

> 0

ÞIDFl

ð
(西德:2)

ojl k1 þ 1
Þ
þ k1 1 − b þ b dj
(西德:1)
d

(西德:3) ;

ojl

(11)

(西德:1)
d denote, 分别, 这
where I(oil > 0) equals 1 if oil > 0 和 0 otherwise and where dj and
length of publication j and the average length of all N publications. We define the length of a
publication as the total number of occurrences of terms in the publication. This results in

di ¼

油

和

我

d ¼ 1
(西德:1)
氮

我

的:

IDFl in (11) denotes the inverse document frequency of term l, which we define as

IDFl

¼ log

N − nl þ 0:5
þ 0:5

;

where nl denotes the number of publications in which term l occurs, 那是,

ð
I oil

> 0

Þ:

我

(12)

(13)

(14)

The BM25 relatedness measure in Eq. (11) depends on the parameters k1 and b. 下列的
Boyack et al. (2011), we set these parameters to values of 2 和 0.75, 分别. 不像
all other relatedness measures that we consider in this paper, the BM25 relatedness measure
is not symmetrical. 换句话说, rBM25

does not need to be equal to rBM25

3.3. Top M Relatedness Approach

Our interest focuses on large-scale clustering analyses that may involve hundreds of thousands
or even millions of publications. These analyses impose significant challenges in terms of com-
puting time and memory requirements. 尤其, in these analyses, it may not be feasible
to store all nonzero relatedness values in the main memory of the computer that is used.

To deal with this problem, we use the top M relatedness approach. This approach is quite
similar to the idea of similarity filtering typically used by Kevin Boyack and Dick Klavans (例如,
Boyack & Klavans, 2010; Boyack et al., 2011). In the top M relatedness approach, only the top
M strongest relations per publication are kept (ties are broken randomly). The remaining rela-
tions are discarded. We use erX
ij to denote the relatedness of publications i and j based on re-
latedness measure X after discarding relations that are not in the top M per publication. 这
means that erX
ij if publication j is among the M publications that are most strongly related to
publication i and that erX
ij = 0 否则. Relatedness of a publication with itself is ignored.
因此, erX

ij = 0 if i = j. 一般来说, erX

ij will not be symmetrical.

ij = rX

Quantitative Science Studies

698

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Comparing relatedness measures for clustering publications

In most of the analyses presented in this paper, we use a value of 20 for M, although we
also explore alternative values. We apply the top M relatedness approach to all our relatedness
measures except for the measures based on (extended) direct citation relations. As pointed out
by Waltman and Van Eck (2012), the use of direct citation relations has the advantage of re-
quiring only a relatively limited amount of computer memory, and therefore there is no need
to use the top M relatedness approach when working with direct citation relations. Applying
the top M relatedness approach in the case of direct citation relations would also be problem-
atic, because all relations are equally strong, making it difficult to decide which relations to
keep and which ones to discard. 因此, in the case of direct citation relations, we simply have
erDC
ij = rDC
ij

for all publications i and j.

3.4. Normalization of Relatedness Measures

We also normalize all relatedness measures. The normalized relatedness of publication i with
publication j equals the relatedness of publication i with publication j divided by the total re-
latedness of publication i with all publications. 因此, the normalized relatedness of publica-
tion i with publication j based on relatedness measure X is given by

rX
ij

erX
ijP
erX
ik
k

(15)

This normalization was also used by Waltman and Van Eck (2012). The idea of the normal-
ization is that the relatedness values of publications in different fields of science should be of
the same order of magnitude, so that clusters in different fields will be of similar size. 没有
the normalization, citation-based relatedness values for instance can be expected to be much
higher in the life sciences than in the social sciences. In a clustering analysis that involves both
publications in the life sciences and publications in the social sciences, this would result in life
sciences clusters being systematically larger than social sciences clusters. The normalization in
Eq. (15) can be used to correct for such differences between fields. The normalization also has
the advantage that, regardless of the choice of relatedness measure, a specific value of the
resolution parameter γ will always yield clustering solutions that have approximately the same
granularity.

All results presented in the next section are based on normalized relatedness measures.

4. 结果

We start the discussion of the results of our analyses by explaining the data collection and the
way in which publications were clustered. We then introduce the idea of granularity-accuracy
plots. 下一个, we present a comparison of different citation-based relatedness measures that can
be used to cluster publications. This is followed by a comparison of different text-based relat-
edness measures.

4.1. Data Collection

Data was collected from the Web of Science (WoS) 数据库. We used the in-house version of
the WoS database available at the Centre for Science and Technology Studies at Leiden
大学. This version of the database includes the Science Citation Index Expanded, 这
Social Sciences Citation Index, and the Arts & Humanities Citation Index.

Like in our earlier work (例如, Klavans & Boyack, 2017; Waltman & Van Eck, 2012), 我们的
final interest is in clustering all publications available in the database that we use, 没有
restricting ourselves to certain fields of science. 然而, to keep the analyses presented in

Quantitative Science Studies

699

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Comparing relatedness measures for clustering publications

this paper manageable, we restricted ourselves to three specific fields. We selected all publi-
cations of the document types article and review that appeared in the period 2007–2016 in
journals belonging to the WoS subject categories Cell biology, Physics, condensed matter, 和
经济学. Our aim was to cover three broad scientific domains, namely the life sciences, 这
物理科学, and the social sciences. The subject categories Cell biology, Physics, 骗局-
densed matter, and Economics were chosen because they cover these three domains and be-
cause they are relatively large in terms of the number of publications they include. The number
of publications is 252,954 in cell biology, 272,935 in condensed matter physics, 和 172,690
在经济学中.

The relatedness measures discussed in section 3 were calculated for the selected publica-
系统蒸发散. Two comments need to be made. 第一的, in determining bibliographic coupling relations
between publications, only common references to publications indexed in our WoS database
were considered. This database includes publications starting from 1980. Common references
to nonindexed publications (例如, 图书, conference proceedings publications, and PhD theses)
were not taken into account. Nonindexed publications were not considered in the extended
direct citation approach either. 第二, when we collected the data in Spring 2017, our data-
base included a limited number of publications from 2017. These publications were not used in
determining cocitation relations between publications. They also were not considered in the
extended direct citation approach.

桌子 1 reports for each of the three fields of science that we analyze and for each of the
relatedness measures that we consider the average number of relations per publication and the
percentage of publications that have no relations at all. The average number of relations per
publication was calculated after applying the top M relatedness approach (except for DC and
EDC; 参见部分 3.3). 桌子 1 shows that in the case of DC and especially CC a quite high
percentage of the publications have no relations. This can be expected to have a negative
effect on the accuracy of clustering solutions obtained using these relatedness measures, 自从
publications without relations cannot be properly clustered.

桌子 1. The average number of relations per publication (ANR) and the percentage of publications
without relations (PWR) for different fields of science and different citation-based and text-based
relatedness measures

直流

DC-BC-CC (α = 1)

DC-BC-CC (α = 5)

EDC

BM25

CT (β = 0.0)

CT (β = 0.5)

CT (β = 1.0)

Cell biology
PWR
8.5%

ANR
11.3

32.4

25.7

32.3

31.6

69.0

31.7

38.1

31.0

26.3

0.5%

13.5%

0.4%

0.3%

0.0%

Condensed matter physics

经济学

ANR
7.5

31.3

19.6

31.3

30.5

39.5

32.0

38.6

29.6

26.8

PWR
12.3%

1.0%

20.0%

0.7%

0.3%

ANR
8.0

30.6

PWR
11.0%

4.3%

16.9

30.7%

30.9

29.8

24.2

32.1

38.5

30.3

27.0

2.7%

2.6%

0.2%

700

Quantitative Science Studies

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Comparing relatedness measures for clustering publications

4.2. Clustering of Publications

For each of our three fields (cell biology, condensed matter physics, and economics), the se-
lected publications were clustered based on each of our relatedness measures. Clustering was
performed by maximizing the quality function presented in Eq. (1). To maximize the quality
function, we used an iterative variant (Waltman & Van Eck, 2013) of the well-known Louvain
algorithm (Blondel, Guillaume, 等人。, 2008). Five iterations of the algorithm were performed.
此外, to speed up the algorithm, we employed ideas similar to the pruning idea of
Ozaki, Tezuka, and Inaba (2016) and the prioritization idea of Bae, Halperin, 等人. (2017).
Our algorithm is a predecessor of the recently introduced Leiden algorithm (Traag,
Waltman, & Van Eck, 2019), which was not yet available when we carried out our analyses.
一般来说, our algorithm will not be able to find the global maximum of the quality function,
but it can be expected to get close to the global maximum.

Different levels of granularity were considered. For each relatedness measure, 我们得到了
10 clustering solutions, each of them for a different value of the resolution parameter γ. 这
following values of γ were used: 0.00001, 0.00002, 0.00005, 0.0001, 0.0002, 0.0005, 0.001,
0.002, 0.005, 和 0.01. Because of the normalization discussed in section 3.4, 相同
values of γ could be used for all relatedness measures. Without normalization, different values
of γ would need to be used for each of the relatedness measures.

4.3. Granularity-Accuracy Plots

A difficulty of the evaluation framework presented in section 2.2 is the requirement that the
clustering solutions being compared have exactly the same granularity. This requirement,
which is formalized in the condition in Eq. (5), is hard to meet in practice. Clustering solutions
obtained using different relatedness measures but the same value of the resolution parameter γ
will approximately satisfy Eq. (5), but the condition normally will not be satisfied exactly.

To deal with this problem, we propose a graphical approach based on the idea of granularity-
准确性 (遗传算法) plots. Using a GA plot, relatedness measures can be compared despite differ-
ences in granularity between clustering solutions. The horizontal axis in a GA plot represents
the granularity of a clustering solution. We define the granularity of a clustering solution ob-
tained using relatedness measure X as

磷

氮
(西德:4) (西德:5)
k sX
k

(16)

Two clustering solutions that have the same granularity according to Eq. (16) indeed satisfy the
condition in Eq. (5). The vertical axis in a GA plot represents the accuracy of a clustering solu-
tion as defined in Eq. (4). Clustering solutions are plotted in a GA plot based on their granularity
and accuracy. Lines are drawn between clustering solutions obtained using the same related-
ness measure but different values of the resolution parameter γ. We use a logarithmic scale for
both the horizontal and the vertical axis in a GA plot.

In the interpretation of a GA plot, one should be aware that for any relatedness measure an
increase in granularity will always cause a decrease in accuracy. This is a mathematical ne-
cessity in our evaluation framework, and therefore it is not something one should be con-
cerned about. A GA plot can be interpreted by comparing the accuracy of different
relatedness measures at a specific level of granularity. As explained above, clustering solutions
obtained using different relatedness measures normally do not have exactly the same granu-
larity. 然而, in a GA plot, lines are drawn between different clustering solutions obtained
using the same relatedness measure, providing interpolations between these solutions. Based

Quantitative Science Studies

701

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Comparing relatedness measures for clustering publications

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

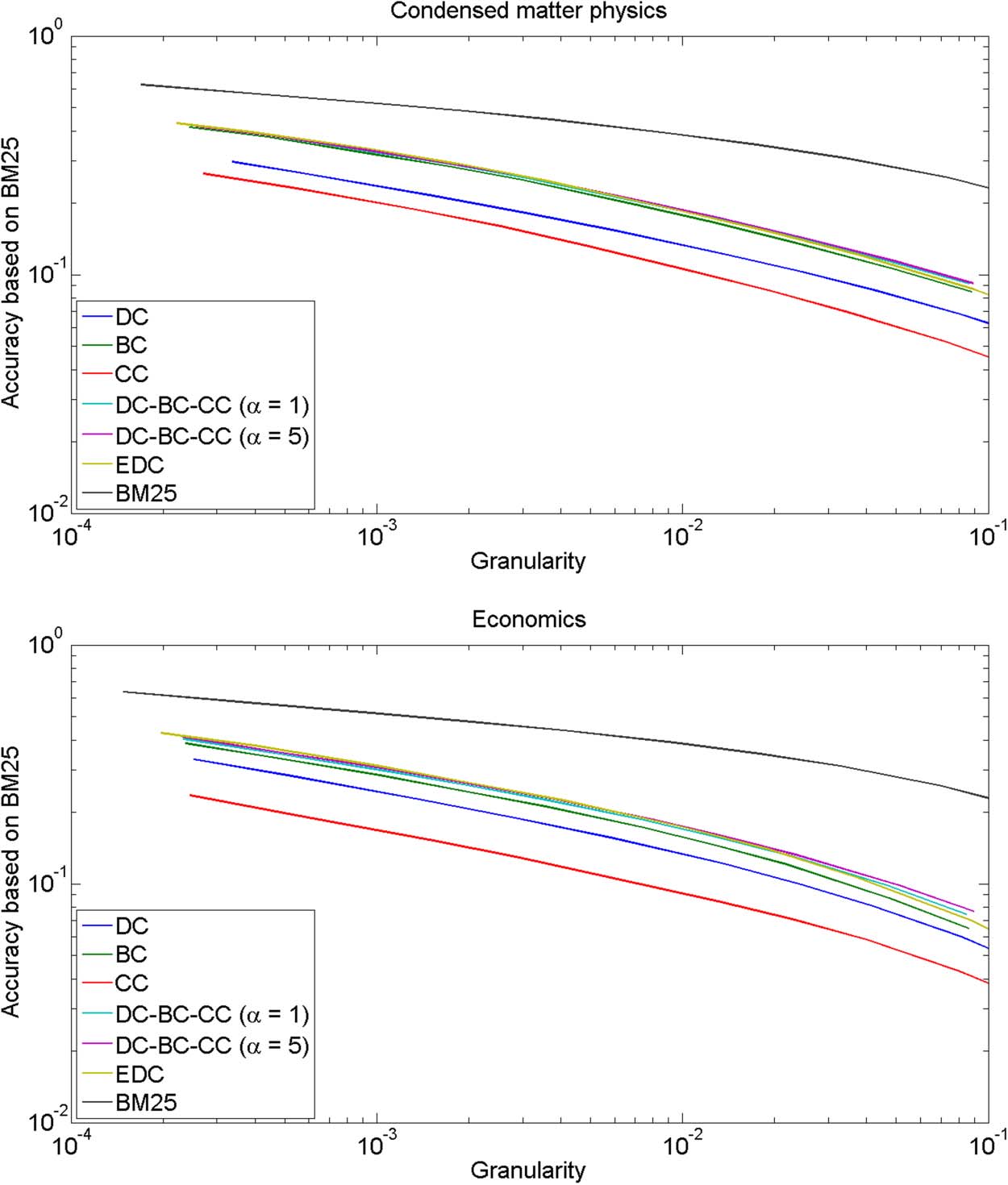
数字 1. GA plots for comparing citation-based relatedness measures. The BM25 text-based re-
latedness measure is used as the evaluation criterion.

on such interpolations, the accuracy of different relatedness measures can be compared at a
specific level of granularity. These comparisons can be performed at different levels of gran-
独特性. Sometimes different levels of granularity will yield inconsistent results, 和, for in-
姿态, relatedness measure A outperforming relatedness measure B at one level of
granularity and the opposite outcome at another level of granularity. 在其他情况下, consistent
results will be obtained at all levels of granularity. 例如, relatedness measure C may
consistently outperform relatedness measure D, regardless of the level of granularity.

In the next two subsections, GA plots will be used to compare different citation-based and

text-based relatedness measures.

4.4. Comparison of Citation-Based Relatedness Measures

For each of our three fields (cell biology, condensed matter physics, and economics), 数字 1
presents a GA plot for comparing the DC, BC, CC, DC-BC-CC, and EDC citation-based relat-
edness measures discussed in section 3.1. In the case of the DC-BC-CC relatedness measure,
two values of the parameter α are considered: α = 1 and α = 5. The BM25 text-based related-
ness measure discussed in section 3.2 is used as the evaluation criterion. The results obtained
when this relatedness measure is used to cluster publications are also included in the GA plots.

Quantitative Science Studies

702

Comparing relatedness measures for clustering publications

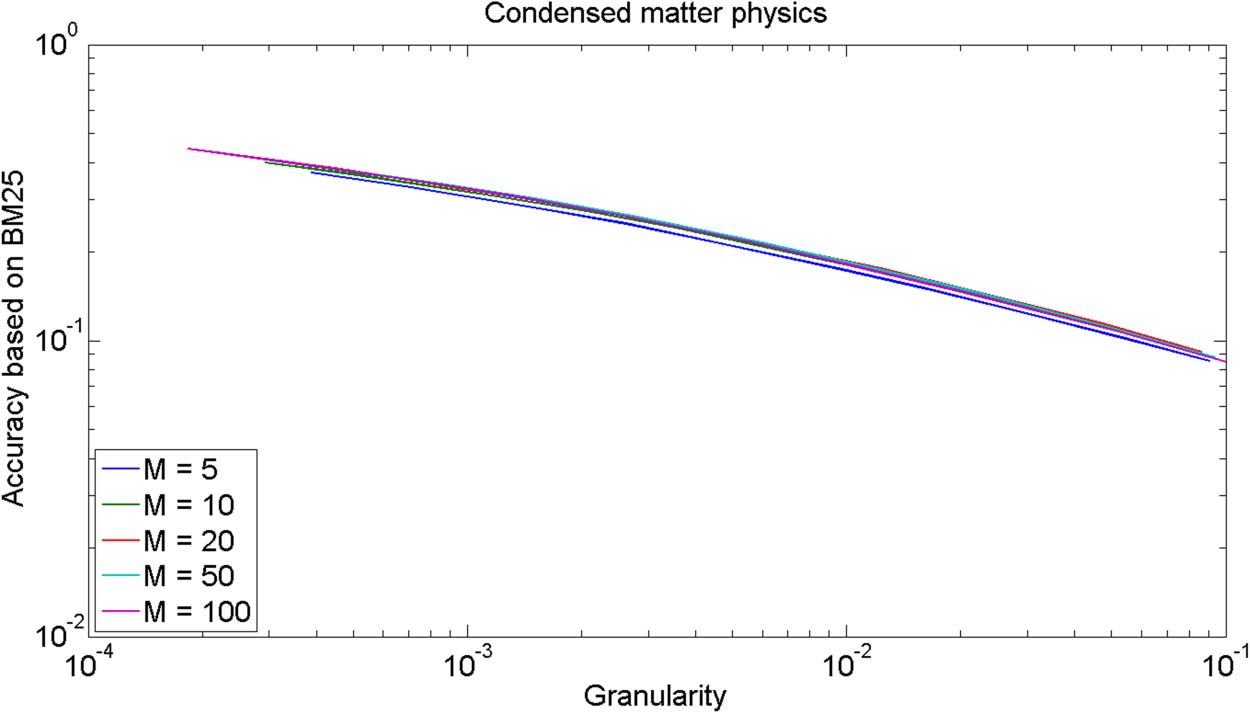
数字 2. GA plot for comparing the DC-BC-CC citation-based relatedness measure (with α = 1)
for different values of the parameter M of the top M relatedness approach. The BM25 text-based
relatedness measure is used as the evaluation criterion.

These results provide an upper bound for the results that can be obtained using the citation-
based relatedness measures. (回忆部分 2.3 that the highest possible accuracy is ob-
tained when publications are clustered based on the same relatedness measure that is also
used as the evaluation criterion.) All relatedness measures (except for DC and EDC; 参见部分
3.3) use a value of 20 for the parameter M of the top M relatedness approach.

To interpret the GA plots in Figure 1, it is important to have some understanding of the
meaning of the different levels of granularity. For each of our three fields, a clustering solution
consists of several hundreds of significant clusters when the granularity is around 0.001, 在哪里
we define a significant cluster as a cluster that includes at least 10 出版物. A granularity
大约 0.01 corresponds to several thousands of significant clusters.

As can be seen in Figure 1, the results obtained for cell biology, condensed matter physics,
and economics are similar. Using BM25 as the evaluation criterion, CC has the worst perfor-
mance of all citation-based relatedness measures. This is not surprising. Uncited publications
have no cocitation relations with other publications and therefore cannot be properly clus-
tered. 桌子 1 shows that in all three fields the percentage of publications without cocitation
relations is quite high. This is an important explanation of the bad performance of CC, 这是
in line with recent results of Klavans and Boyack (2017). DC outperforms CC, but is outper-
formed by all other citation-based relatedness measures. The performance of DC is especially
weak in cell biology. The disappointing performance of DC in all three fields is an important
finding, in particular given the increasing popularity of DC in recent years. BC, DC-BC-CC,
and EDC all perform about equally well. DC-BC-CC and EDC seem to slightly outperform BC,
but the difference is tiny, especially in cell biology and condensed matter physics. 同样地,
there is hardly any difference between the parameter values α = 1 and α = 5 for DC-BC-CC.
Our finding that BC and EDC perform about equally well differs from the results of Klavans and
Boyack, who found that an approach similar to EDC significantly outperforms BC. Our results are
based on a more principled evaluation framework and a different evaluation criterion than the re-
sults of Klavans and Boyack, which most likely explains why our findings are different from theirs.

To test the sensitivity of our results to the value of the parameter M of the top M relat-
edness approach, 数字 2 presents a GA plot in which the DC-BC-CC citation-based relat-
edness measure (with α = 1) is compared for different values of M. The BM25 text-based

Quantitative Science Studies

703

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Comparing relatedness measures for clustering publications

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 3. GA plots for comparing text-based relatedness measures. The DC-BC-CC citation-based
relatedness measure (with α = 1) is used as the evaluation criterion.

relatedness measure is again used as the evaluation criterion. Only the field of condensed
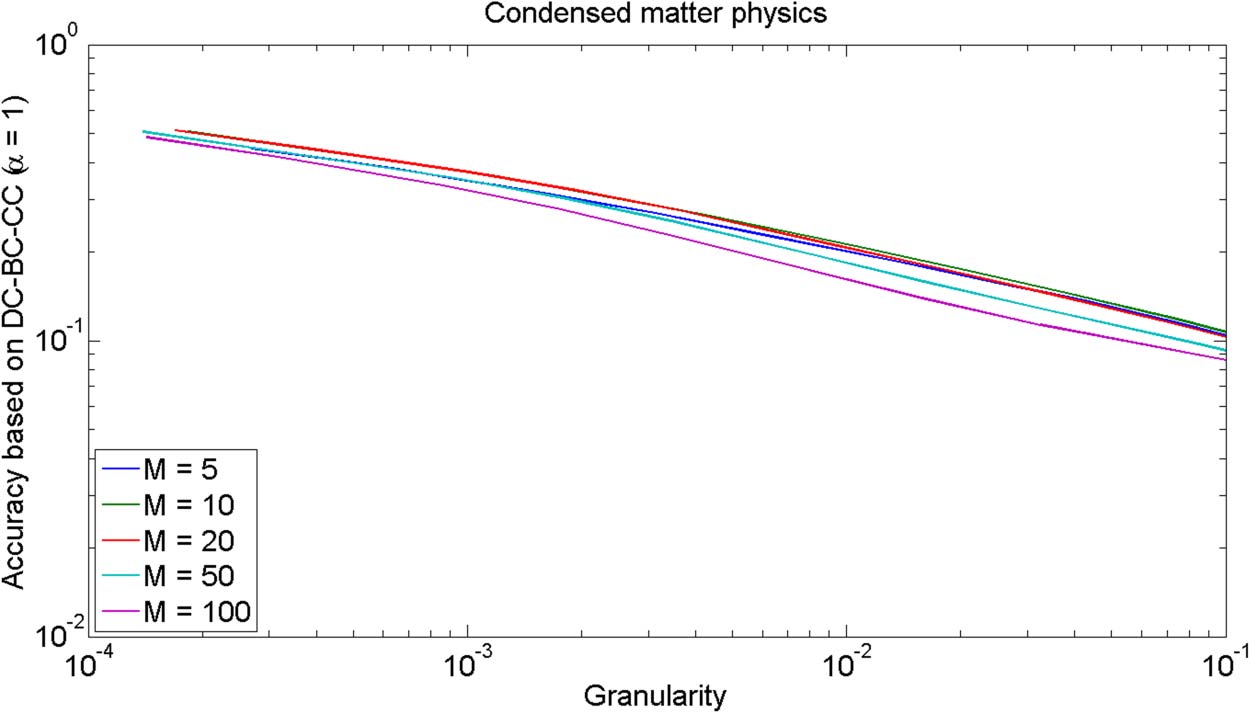
matter physics is considered. As can be seen in Figure 2, our results are rather insensitive to
the value of M.

Quantitative Science Studies

704

Comparing relatedness measures for clustering publications

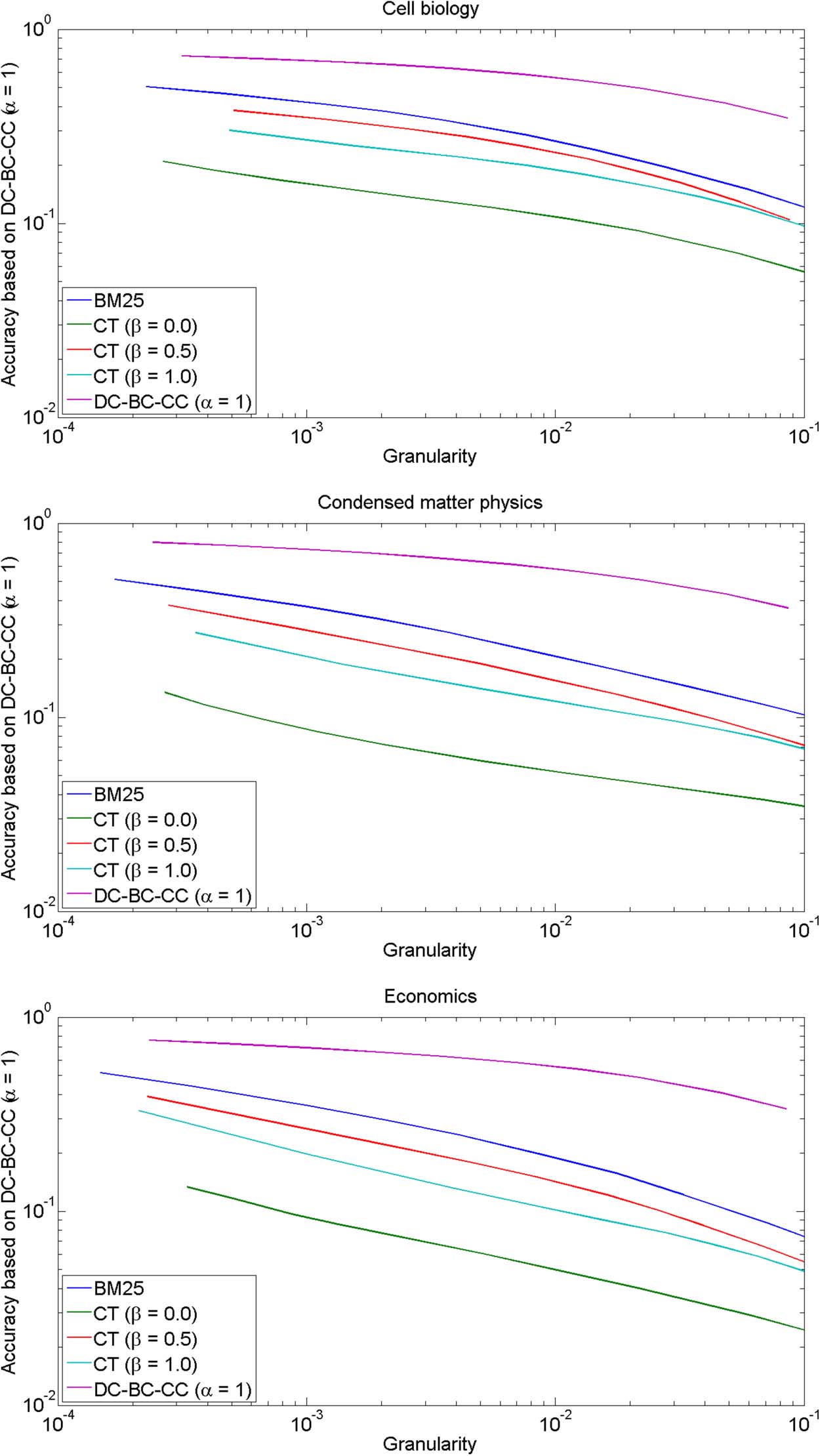
数字 4. GA plot for comparing the BM25 text-based relatedness measure for different values of
the parameter M of the top M relatedness approach. The DC-BC-CC citation-based relatedness
措施 (with α = 1) is used as the evaluation criterion.

We also tested the sensitivity of our results to the choice of the text-based relatedness mea-
sure that is used as the evaluation criterion. The results turned out to be insensitive to this
选择. Replacing BM25 by CT (with β = 0.5) yielded very similar results (not shown).

4.5. Comparison of Text-Based Relatedness Measures

数字 3 presents GA plots for comparing the BM25 and CT text-based relatedness measures
discussed in section 3.2. In the case of the CT relatedness measure, three values of the param-
eter β are considered: β = 0.0, β = 0.5, and β = 1.0. The DC-BC-CC citation-based relatedness
measure discussed in section 3.1 (with α = 1) is used as the evaluation criterion. Results ob-
tained when this relatedness measure is used to cluster publications are also included in the
GA plots. These results provide an upper bound for the results that can be obtained using the
text-based relatedness measures. All relatedness measures use a value of 20 for the parameter
M of the top M relatedness approach.

The results presented in Figure 3 for cell biology, condensed matter physics, and economics
非常相似. Using DC-BC-CC as the evaluation criterion, BM25 outperforms CT, 看待-
less of the value of the parameter β. The good performance of BM25 is in agreement with the
results of Boyack et al. (2011). By far the worst performance is obtained when CT is used with
the parameter value β = 0.0. This confirms the importance of reducing the influence of fre-
quently occurring terms. 然而, CT with the parameter value β = 0.5 outperforms CT with
the parameter value β = 1.0. 因此, the influence of frequently occurring terms should not be
reduced too strongly.

To test the sensitivity of our results to the value of the parameter M of the top M relatedness
方法, 数字 4 presents a GA plot in which the BM25 text-based relatedness measure is
compared for different values of M, using the DC-BC-CC citation-based relatedness measure
(with α = 1) as the evaluation criterion. Only the field of condensed matter physics is consid-
埃雷德. 有趣的是, and perhaps surprisingly, the highest values of M (IE。, 米= 50 and M = 100)
are outperformed by lower values of M. 因此, while the highest values of M require most
computing time and most computer memory, they yield the lowest accuracy. The highest ac-
curacy is obtained for M = 10 or M = 20. In line with the approach taken by Boyack et al.

Quantitative Science Studies

705

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Comparing relatedness measures for clustering publications

(2011), it therefore seems sufficient to keep only the 10 或者 20 strongest relations per
出版物.

We also tested the sensitivity of our results to the choice of the citation-based relatedness
measure that is used as the evaluation criterion. The results turned out to be insensitive to this
选择. Replacing DC-BC-CC (with α = 1) by CC yielded very similar results (not shown).

5. 结论

The problem of clustering scientific publications involves significant conceptual and method-
ological challenges. We have introduced a principled methodology for evaluating the accu-
racy of clustering solutions obtained using different relatedness measures. Our methodology
can be applied to evaluate the accuracy of clustering solutions obtained using two relatedness
measures A and B, where a third relatedness measure C is used as the evaluation criterion.
Preferably, relatedness measure C should be as independent as possible from relatedness mea-
sures A and B. Relatedness measures A and B, 例如, may be citation-based relatedness
措施, and relatedness measure C may be a text-based relatedness measure (or the other
way around).

The empirical results that we have presented are based on a large-scale analysis of publi-
cations in the fields of cell biology, condensed matter physics, and economics indexed in the
WoS database. We have used our proposed methodology, complemented with a graphical
approach based on so-called GA plots, to compare different citation-based relatedness mea-
sures that can be used to cluster publications. Using the BM25 text-based relatedness measure
as the evaluation criterion, we have found that cocitation relations and direct citation relations
yield less accurate clustering solutions than a number of other citation-based relatedness mea-
确定. Bibliographic coupling relations, possibly combined with direct citation relations and
cocitation relations, can be used to obtain more accurate clustering solutions. The so-called
extended direct citation approach yields clustering solutions with an accuracy that is similar to
or even somewhat higher than the accuracy of clustering solutions obtained using bibliogra-
phic coupling relations. We note that our analyses have been restricted to individual fields of
科学. In an analysis that covers all fields of science and a long period of time, 差异
between the ordinary direct citation approach and the extended direct citation approach can
be expected to be much smaller. We have also compared different text-based relatedness
measures using a citation-based relatedness measure (obtained by combining direct citation
关系, bibliographic coupling relations, and cocitation relations) as the evaluation criterion.
BM25 has turned out to yield more accurate clustering solutions than the other text-based
relatedness measures that we have studied.

We have also analyzed the use of the so-called top M relatedness approach. 这种方法
can be used to reduce the amount of computing time and computer memory needed to cluster
出版物. We have found that the use of the top M relatedness approach does not decrease
the accuracy of clustering solutions. 实际上, in the case of text-based relatedness measures, 这
accuracy of clustering solutions may even increase.

在本文中, we have adopted the perspective that it is useful to assume the existence of an
absolute notion of accuracy. Given the lack of a ground truth, the accuracy of a clustering
solution cannot be directly measured. 然而, by assuming the existence of an absolute no-
tion of accuracy, our methodology allows the accuracy of a clustering solution to be evaluated
in an indirect way. An alternative perspective is that there is no absolute notion of accuracy
and that it is not meaningful to ask whether one clustering solution is more accurate than an-
other one (例如, Gläser et al., 2017). 从这个角度来看, clustering solutions obtained using

Quantitative Science Studies

706

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Comparing relatedness measures for clustering publications

different relatedness measures each provide a legitimate viewpoint on the organization of the
scientific literature. We fully acknowledge the value of this alternative perspective, 和我们
recognize the need to better understand how clustering solutions obtained using different re-
latedness measures offer complementary viewpoints. 尽管如此, from an applied point of
view focused on practical applications, we believe that there is a need to evaluate the accu-
racy of clustering solutions obtained using different relatedness measures and to identify the
relatedness measures that yield the most accurate clustering solutions. This motivates our
choice to make the assumption of the existence of an absolute notion of accuracy. For those
who consider this assumption to be problematic, we would like to suggest that the results pro-
vided by our methodology could be given an alternative interpretation that does not depend
on this assumption. Instead of interpreting the results in terms of accuracy, they could be inter-
preted in terms of the degree to which different relatedness measures yield similar clustering
solutions.

The most obvious direction for future research is to apply our methodology to a broader set
of relatedness measures. Examples include relatedness measures based on full-text data, grant
数据, and keyword data (例如, MeSH terms). Some of this work is already ongoing (Boyack &
Klavans, 2018).

致谢

The authors would like to thank Dick Klavans, Vincent Traag, and two reviewers for their help-
ful comments.

作者贡献
Ludo Waltman: 概念化, 形式分析, 方法, 软件, Writing—original
草稿. Kevin W. Boyack: 概念化, 方法, Writing—review & 编辑.
Giovanni Colavizza: 概念化, 方法, Writing—review & 编辑. Nees Jan
van Eck: 概念化, 方法, Writing—review & 编辑.

COMPETING INTERESTS

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

The authors use clustering approaches similar to those discussed in this paper in commercial
applications.

资金信息

Part of this research was conducted when Giovanni Colavizza was affiliated with the Digital
Humanities Laboratory, École Polytechnique Fédérale de Lausanne, 瑞士. 乔万尼
Colavizza was in part supported by a Swiss National Fund grant (number P1ELP2_168489).

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

DATA AVAILABILITY

The data used in this paper were obtained from the WoS database produced by Clarivate
Analytics. Due to license restrictions, the data cannot be made openly available. To obtain
WoS, please contact Clarivate Analytics (https://clarivate.com/products/web-of-science).

参考

Bae, S.-H., Halperin, D ., 西方, J. D ., Rosvall, M。, & 豪, 乙.
(2017). Scalable and efficient flow-based community detection
for large-scale graph analysis. ACM Transactions on Knowledge
Discovery from Data, 11(3), 32.

Blondel, V. D ., Guillaume, J.-L., 兰比奥特, R。, & Lefebvre, 乙.
(2008). Fast unfolding of communities in large networks.
Journal of Statistical Mechanics: Theory and Experiment, 10,
P10008.

Quantitative Science Studies

707

Comparing relatedness measures for clustering publications

Boyack, K. W., & Klavans, 右. (2010). Co-citation analysis, biblio-
graphic coupling, and direct citation: Which citation approach
represents the research front most accurately? Journal of the
American Society for Information Science and Technology, 61
(12), 2389–2404.

Boyack, K. W., & Klavans, 右. (2014). Including cited non-source
items in a large-scale map of science: What difference does it
制作? Journal of Informetrics, 8(3), 569–580.

Boyack, K. W., & Klavans, 右. (2018). Accurately identifying topics
using text: Mapping PubMed. 在R中. Costas, 时间. Franssen, & A.
Yegros-Yegros (编辑。), Proceedings of the 23rd International
Conference on Science and Technology Indicators, PP. 107–115.
Leiden, 荷兰人.

Boyack, K. W., 纽曼, D ., Duhon, 右. J。, Klavans, R。, Patek, M。,
Biberstine, J. R。, …… & Börner, K. (2011). Clustering more than two
million biomedical publications: Comparing the accuracies of
nine text-based similarity approaches. PLOS ONE, 6(3), e18029.
Boyack, K. W., 小的, H。, & Klavans, 右. (2013). Improving the ac-
curacy of co-citation clustering using full text. Journal of the
American Society for Information Science and Technology,
64(9), 1759–1767.

Fortunato, S. (2010). Community detection in graphs. Physics

报告, 486(3–5), 75–174.

Fortunato, S。, & Barthélemy, 中号. (2007). Resolution limit in commu-
nity detection. 美国国家科学院院刊
美利坚合众国, 104(1), 36–41.

Gläser, J。, Scharnhorst, A。, & Glänzel, 瓦. (2017). Same data—different
结果? Towards a comparative approach to the identification of
thematic structures in science. Scientometrics, 111(2), 981–998.
Haunschild, R。, Schier, H。, 马克思, W., & Bornmann, L. (2018).
Algorithmically generated subject categories based on citation
关系: An empirical micro study using papers on overall water
splitting. Journal of Informetrics, 12(2), 436–447.

Klavans, R。, & Boyack, K. 瓦. (2017). Which type of citation anal-
ysis generates the most accurate taxonomy of scientific and tech-
nical knowledge? Journal of the Association for Information
Science and Technology, 68(4), 984–998.

李, Y。, & Ruiz-Castillo, J. (2013). The comparison of normalization
procedures based on different classification systems. 杂志
Informetrics, 7(4), 945–958.

纽曼, 中号. 乙. J. (2004). Fast algorithm for detecting community

structure in networks. Physical Review E, 69(6), 066133.

纽曼, 中号. 乙. J。, & Girvan, 中号. (2004). Finding and evaluating com-
munity structure in networks. Physical Review E, 69(2), 026113.
Ozaki, N。, Tezuka, H。, & Inaba, 中号. (2016). A simple acceleration
method for the Louvain algorithm. International Journal of
Computer and Electrical Engineering, 8(3), 207–218.

Perianes-Rodriguez, A。, & Ruiz-Castillo, J. (2017). A comparison of
the Web of Science and publication-level classification systems
of science. Journal of Informetrics, 11(1), 32–45.

Perianes-Rodriguez, A。, Waltman, L。, & Van Eck, 氮. J. (2016).
Constructing bibliometric networks: A comparison between
full and fractional counting. Journal of Informetrics, 10(4),
1178–1195.

Persson, 氧. (2010). Identifying research themes with weighted di-

rect citation links. Journal of Informetrics, 4(3), 415–422.

Ruiz-Castillo,

J。, & Waltman, L.

(2015). Field-normalized cita-
tion impact indicators using algorithmically constructed clas-
Informetrics, 9(1),
sification systems of science.
102–117.

杂志

Sjögårde, P。, & Ahlgren, 磷. (2018). Granularity of algorithmically
constructed publication-level classifications of research publica-
系统蒸发散: Identification of topics. Journal of Informetrics, 12(1),
133–152.

Sjögårde, P。, & Ahlgren, 磷. (2020). Granularity of algorithmically
constructed publication-level classifications of research publica-
系统蒸发散: Identification of specialties. Quantitative Science Studies, 1
(1), 207–238.

小的, H. (1997). Update on science mapping: Creating large doc-

ument spaces. Scientometrics, 38(2), 275–293.

小的, H。, Boyack, K. W., Klavans, 右. (2014). Identifying emerg-
ing topics in science and technology. Research Policy, 43(8),
1450–1467.

Sparck Jones, K., 沃克, S。, & 罗伯逊, S. 乙. (2000A). A probabilistic
model of information retrieval: Development and comparative
实验: 部分 1. Information Processing and Management,
36(6), 779–808.

Sparck Jones, K., 沃克, S。, & 罗伯逊, S. 乙. (2000乙). A probabilistic
model of information retrieval: Development and comparative
实验: 部分 2. Information Processing and Management,
36(6), 809–840.

Šubelj, L。, Van Eck, 氮. J。, & Waltman, L. (2016). Clustering scien-
tific publications based on citation relations: A systematic com-
parison of different methods. PLOS ONE, 11(4), e0154404.

Traag, V. A。, Van Dooren, P。, & Nesterov, 是. (2011). Narrow scope
for resolution-limit-free community detection. Physical Review E,
84(1), 016114.

Traag, V. A。, Waltman, L。, & Van Eck, 氮. J. (2019). From Louvain to
Leiden: Guaranteeing well-connected communities. Scientific
报告, 9, 5233.

Van Eck, 氮. J。, & Waltman, L. (2014). CitNetExplorer: A new soft-
ware tool for analyzing and visualizing citation networks. 杂志
of Informetrics, 8(4), 802–823.

Waltman, L。, & Van Eck, 氮. J. (2012). A new methodology for con-
structing a publication-level classification system of science.
Journal of the American Society for Information Science and
技术, 63(12), 2378–2392.

Waltman, L。, & Van Eck, 氮. J. (2013). A smart local moving algo-
rithm for large-scale modularity-based community detection.
European Physical Journal B, 86(11), 471.

Quantitative Science Studies

708

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Comparing relatedness measures for clustering publications

APPENDIX A: MOTIVATION FOR THE EVALUATION FRAMEWORK

In this appendix, we present a conceptual motivation for the framework introduced in section
2 for evaluating the accuracy of clustering solutions obtained using different relatedness mea-
确定. The motivation is based on an analogy with the evaluation of the accuracy of different
indicators that provide estimates of values drawn from a probability distribution. 我们用这个
analogy because the evaluation of the accuracy of different indicators can be analyzed in a
more precise way than the evaluation of the accuracy of clustering solutions obtained using
different relatedness measures.

A.1. Evaluating Two Indicators Using a Third Indicator

氮, vB

1 , ……, vB

1 , ……, vA

Suppose N values v1, ……, vN have been drawn from a standard normal distribution. These values
cannot be observed directly. 然而, we have available three indicators A, 乙, and C that pro-
vide estimates of the values v1, ……, vN. Let the estimates provided by the indicators A, 乙, and C be
1 , ……, vC
denoted by vA
氮, 分别. Suppose we need to choose
between the use of indicator A or indicator B. We therefore want to know which of these two
indicators is more accurate. Since the values v1, ……, vN cannot be observed directly, we cannot
1, ……, vB
evaluate the accuracy of indicators A and B by comparing the estimates vA
氮
with the true values v1, ……, vN. 然而, if indicator C can be assumed to be independent of
indicators A and B (see Appendix A.2 for a further discussion of this assumption), it is possible to
use indicator C to evaluate the accuracy of indicators A and B. This can be seen as follows.

氮, and vC

1 , ……, vA

N and vB

Suppose the estimates provided by indicators A, 乙, and C are given by

ﬃﬃﬃﬃﬃ
aA

vi þ

ﬃﬃﬃﬃﬃ
aB

vi þ

ﬃﬃﬃﬃﬃ
aC

vi þ

vA
我

vB
我

vC
我

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
1 − aA
ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
1 − aB
ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
1 − aC

;

eA
我

;

eB
我

;

eC
我

(A1)

(A2)

(A3)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

where αA, αB, αC 2 [0, 1] denote the accuracy of indicators A, 乙, and C and where eA
我 , 和
eC
i have been independently drawn from a standard normal distribution. Eqs. (A1), (A2), 和
(A3) imply that the estimates provided by indicators A, 乙, and C follow a standard normal
分配. Because eA
i have been independently drawn, we say that indicators
A, 乙, and C are independent of each other.
B or α

A < α B. To determine this, we calculate the mean squared difference between the estimates provided by indicators A and C and between the estimates provided by indicators B and C. This yields We want to know whether α i , and eC A > A

我 , eB

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

MSDAC ¼ 1
氮

MSDBC ¼ 1
氮

(西德:4)

我

(西德:4)

我

(西德:5)2;

(西德:5)2:

vA
我

− vC
我

vB
我

− vC
我

If N is infinitely large, standard results from probability theory can be used to show that
MSDAC ¼ 2 - 2

;

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
aAaC
ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
aBaC

MSDBC ¼ 2 - 2

(A4)

(A5)

(A6)

(A7)

Based on Eqs. (A6) 和 (A7), if MSDAC < MSDBC, then αA > αB. 反过来, if MSDAC >

Quantitative Science Studies

709

Comparing relatedness measures for clustering publications

MSDBC, then αA < αB. This shows that indicator C can be used to evaluate the accuracy of indicators A and B and to determine which of the two indicators is more accurate. Moreover, this is possible even if indicator C itself has a low (but nonzero) accuracy, perhaps much lower than the accuracy of indicators A and B. We have now demonstrated how an indicator C can be used to evaluate the accuracy of indicators A and B. The idea of the evaluation framework presented in section 2 is similar, but instead of indicators we consider relatedness measures and clustering solutions obtained using these relatedness measures. We use a relatedness measure C to evaluate the accuracy of clus- tering solutions obtained using relatedness measures A and B. Relatedness measures A and B, for instance, could be two citation-based measures, such as a measure based on direct citation relations and a measure based on bibliographic coupling relations, while relatedness measure C could be a text-based measure, such as a measure based on BM25. If relatedness measure C can be assumed to be (approximately) independent of relatedness measures A and B, it can be used to evaluate the accuracy of clustering solutions obtained using relatedness measures A and B. This is possible even if relatedness measure C itself has a lower accuracy than related- ness measures A and B. A.2. Independence Assumption l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . ¼ In Appendix A.1, we relied on the assumption that indicator C is independent of indicators A and B. We now demonstrate the importance of this assumption. To do so, we drop the assump- tion and we allow for a dependence between indicators A and C. Rather than by Eq. (A3), suppose estimates provided by indicator C are given by ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ p ð ÞaC þ dACaA 1 − dAC vC i 2 [0, 1] denotes the dependence between indicators A and C. If dAC = 0, there is no where dAC dependence between indicators A and C and Eq. (A8) reduces to Eq. (A3). On the other hand, if dAC = 1, there is a full dependence between indicators A and C. The indicators then provide identical estimates, and Eq. (A8) therefore reduces to Eq. (A1). Eq. (A8) implies that the estimates provided by indicator C follow a standard normal distribution and that there is no dependence between indicators B and C. p ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ ð Þ ð Þ 1 − aC 1 − dAC ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ Þ ð dAC 1 − aA eA i vi þ (A8) eC i p þ ; Based on Eqs. (A1), (A2), and (A8), it can be shown that MSDAC ¼ 2 − 2 p ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ aAaAC ð 1 − aA Þ; − 2 p p ﬃﬃﬃﬃﬃﬃﬃﬃ dAC ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ aBaAC ; MSDBC ¼ 2 − 2 where ð aAC ¼ 1 − dAC ÞaC þ dACaA: (A9) (A10) (A11) / e d u q s s / a r t i c e - p d l f / / / / 1 2 6 9 1 1 8 8 5 7 8 3 q s s _ a _ 0 0 0 3 5 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 As expected, if dAC = 0, Eqs. (A9) and (A10) reduce to Eqs. (A6) and (A7). It follows from Eqs. (A9) and (A10) that MSDBC < MSDAC if and only if aB > aA þ dAC
aAC

ð
1 − aA

Þ2 þ 2

ﬃﬃﬃﬃﬃﬃﬃﬃ
dAC
aAC

ﬃﬃﬃﬃﬃ
aA

1 − aA
ð

Þ:

(A12)

If dAC > 0 and α
A < 1, the sum of the second and the third term in the right-hand side of Eq. (A12) is positive. It is then possible that the inequality in Eq. (A12) is not satisfied even though αB > αA. 因此, it is possible that MSDBC > MSDAC, even though αB > αA. Indicator C then
gives the incorrect impression that indicator A is more accurate than indicator B. This is due to
the dependence between indicators A and C. The higher the dependence dAC, the more likely

Quantitative Science Studies

710

Comparing relatedness measures for clustering publications

indicator C is to give the incorrect impression that indicator A is more accurate than indicator
乙. In the extreme case in which dAC = 1, it is even impossible for indicator B to be considered
more accurate than indicator A.

We have now demonstrated the importance of the independence assumption when an in-
dicator C is used to evaluate the accuracy of indicators A and B. In the evaluation framework
presented in section 2, the independence assumption has a similar importance. When a relat-
edness measure C is used to evaluate the accuracy of clustering solutions obtained using re-
latedness measures A and B, it is important that relatedness measure C is (大约)
independent of relatedness measures A and B. 例如, if there is a dependence between
relatedness measures A and C, evaluations performed using relatedness measure C will be
biased in favor of clustering solutions obtained using relatedness measure A.

APPENDIX B: CONSISTENT AND INCONSISTENT EVALUATION FRAMEWORKS

In this appendix, we formally show the consistency of the evaluation framework proposed

in section 2. We also present an example of an inconsistent evaluation framework.

B.1. Consistency of the Proposed Evaluation Framework

1, ……, cX

Consider two relatedness measures X and Y. Suppose that we have obtained a clustering so-
lution cX
N for relatedness measure X by maximizing the quality function in Eq. (2) 使用
the resolution parameter γX. 此外, we have obtained a clustering solution cY
N for
relatedness measure Y by maximizing the same quality function using the resolution parameter
γY. Suppose also that the two clustering solutions satisfy the condition in Eq. (5). 因此, 这
two clustering solutions have the same granularity. When the accuracy of the two clustering
solutions is evaluated using relatedness measure X, it is guaranteed that the clustering solution
obtained using relatedness measure X will be more accurate than the clustering solution ob-
tained using relatedness measure Y. 更确切地说, it is guaranteed that AX|X ≥ AY|X, where AX|X
and AY|X denote the accuracy of the two clustering solutions according to the accuracy measure
in Eq. (4). This result shows the consistency of our evaluation framework.

1 , ……, cY

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d

我

F
/

1
2
6
9
1
1
8
8
5
7
8
3
q
s
s
_
A
_
0
0
0
3
5
p
d

To prove the above result, suppose that AX|X < AY|X. It then follows from Eq. (4) that X i;j (cid:2) I cX i (cid:3) ¼ cX j < rX ij X i;j (cid:2) I cY i (cid:3) rX ij : ¼ cY j The granularity condition in Eq. (5) states that (cid:4) (cid:5)2 ¼ sX k X k X l (cid:4) (cid:5)2: sY l Table B.1. Relatedness of publications according to relatedness measure X P1 P2 P3 P4 P5 P6 P1 2 2 1 1 1 P2 2 2 1 1 1 P3 2 2 1 1 1 P4 1 1 1 2 2 P5 1 1 1 2 2 Quantitative Science Studies f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 (B1) (B2) P6 1 1 1 2 2 711 Comparing relatedness measures for clustering publications Table B.2. Relatedness of publications according to relatedness measure Y P1 P2 P3 P4 P5 P6 P1 2 2 2 2 1 P2 2 2 2 2 1 P3 2 2 2 2 1 P4 2 2 2 2 1 P5 2 2 2 2 1 P6 1 1 1 1 1 Eqs. (B1) and (B2) imply that (cid:3) X rX ij (cid:2) I cX i ¼ cX j i;j − γX X k (cid:4) (cid:5)2 < sX k X i;j (cid:2) I cY i (cid:3) ¼ cY j rX ij − γX X l (cid:4) (cid:5)2: sY l (B3) It now follows from Eqs. (2) and (B3) that cY N offers a higher quality clustering solution for relatedness measure X and resolution parameter γX than cX N . However, this is not possible, since cX N is defined as the clustering solution that maximizes Eq. (2) for relatedness measure X and resolution parameter γX. We therefore have a contradiction. This proves that AX|X ≥ AY|X. 1 , …, cX 1 , …, cX 1, …, cY A minor qualification needs to be made. In practice, heuristic algorithms are usually used to maximize the quality function in Eq. (2). There is no guarantee that these algorithms are able to find the global maximum of the quality function (see section 4.2). In exceptional cases, this might cause the consistency of our evaluation framework to be violated. B.2. Example of an Inconsistent Evaluation Framework Consider an evaluation framework in which clustering solutions are compared using Eq. (4) subject to a granularity condition requiring that clustering solutions consist of the same num- ber of clusters. This granularity condition, which was used by Klavans and Boyack (2017), replaces the granularity condition in Eq. (5). The following example shows that this evaluation framework is inconsistent. Suppose we have six publications, labeled P1 to P6. Consider two relatedness measures X and Y. Tables B.1 and B.2 show the relatedness of the six publications according to relatedness measures X and Y, respectively. Suppose that the resolution parameter γ is set to a value of 1.1. For relatedness measure X, maximization of the quality function in Eq. (2) then yields two clus- ters, one consisting of publications P1 to P3 and the other consisting of publications P4 to P6. For relatedness measure Y, we also obtain two clusters, one consisting of publications P1 to P5 and the other consisting only of publication P6. Since the two clustering solutions both consist of two clusters, our granularity condition is satisfied. Based on Eq. (4), we now compare the two clustering solutions. Using relatedness measure Y to evaluate the accuracy of the clustering solutions, we obtain AX|Y = 10/3 and AY|Y = 20/3. Hence, as we would intuitively expect, according to relatedness measure Y, the clustering so- lution obtained using relatedness measure Y is more accurate than that obtained using relat- edness measure X. Let us now use relatedness measure X to evaluate the accuracy of the clustering solutions. This yields AX|X = 4 and AY|X = 28/6. In other words, we obtain the Quantitative Science Studies 712 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 6 9 1 1 8 8 5 7 8 3 q s s _ a _ 0 0 0 3 5 p d / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Comparing relatedness measures for clustering publications counterintuitive result that, according to relatedness measure X, the clustering solution obtained using relatedness measure X is less accurate than the one obtained using relatedness measure Y. This shows the inconsistency of our evaluation framework. APPENDIX C: EXTENDED DIRECT CITATION APPROACH In this appendix, we discuss the technical details of the extended direct citation approach introduced in section 3.1. Our aim is to cluster publications 1, …, N. We refer to these publications as our focal pub- lications. To cluster the focal publications, we also consider publications N + 1, …, NEXT. Each of these nonfocal publications has a direct citation relation with at least two focal publications. For i = 1, …, N and j = 1, …, NEXT, the relatedness of publications i and j in the extended direct citation approach is given by (cid:4) (cid:5) rij ¼ max cij; cji ; (C1) where cij indicates whether publication i cites publication j (cij = 1) or not (cij = 0). Following the ideas presented in section 3.4, for i = 1, …, N and j = 1, …, NEXT, the nor- malized relatedness of publication i with publication j in the extended direct citation approach equals rij ¼ rijP krik : (C2) To accommodate the nonfocal publications N + 1, …, NEXT, the quality function in Eq. (1) needs to be adjusted. In the extended direct citation approach, publications 1, …, NEXT are assigned to clusters c1, …, cNEXT by maximizing the quality function Q ¼ X N i¼1 h X (cid:4) I ci ¼ cj (cid:5) (cid:4) rij − γ (cid:5) þ X NEXT j¼N þ 1 (cid:4) I ci ¼ cj (cid:5) rij N j¼1 i : (C3) The nonfocal publications are treated in a special way in Eq. (C3). The costs and benefits of assigning a publication to a cluster are different for the nonfocal publications than for the focal ones. On the one hand, there is no cost in assigning a nonfocal publication to a cluster. To see this, notice that there is no subtraction of γ in the second term within the square brackets in Eq. (C3). On the other hand, nonfocal publications do not yield benefits in the same way as focal publications do. To see this, notice that the outer summation in Eq. (C3) extends only over the focal publications. The nonfocal publications are not included in this summation. After the quality function in Eq. (C3) has been maximized, we discard the cluster assign- ments cN+1, …, cNEXT of the nonfocal publications, since we are interested only in the cluster assignments c1, …, cN of the focal publications. Quantitative Science Studies 713 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 6 9 1 1 8 8 5 7 8 3 q s s _ a _ 0 0 0 3 5 p d / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 RESEARCH ARTICLE image

下载pdf