研究
Infant functional networks are modulated by state
of consciousness and circadian rhythm
Rachel J. Smith1
, Ehsan Alipourjeddi1, Cristal Garner2, Amy L. Maser3,
丹尼尔·W. Shrey2,4, and Beth A. Lopour1
1Department of Biomedical Engineering, 加州大学, 尔湾, CA, 美国
2Division of Neurology, Children’s Hospital of Orange County, Orange, CA, 美国
3心理学系, Children’s Hospital of Orange County, Orange, CA, 美国
4Department of Pediatrics, 加州大学, 尔湾, 尔湾, CA, 美国
开放访问
杂志
关键词: Functional connectivity, Graph theory, Cross-correlation, Electroencephalography,
Resting-state networks, Pediatrics
抽象的
Functional connectivity networks are valuable tools for studying development, 认识,
and disease in the infant brain. In adults, such networks are modulated by the state of
consciousness and the circadian rhythm; 然而, it is unknown if infant brain networks
exhibit similar variation, given the unique temporal properties of infant sleep and circadian
patterning. To address this, we analyzed functional connectivity networks calculated from
long-term EEG recordings (average duration 20.8 小时) 从 19 healthy infants. Networks were
subject specific, as intersubject correlations between weighted adjacency matrices were
低的. 然而, within individual subjects, both sleep and wake networks were stable over
时间, with stronger functional connectivity during sleep than wakefulness. Principal
component analysis revealed the presence of two dominant networks; visual sleep scoring
confirmed that these corresponded to sleep and wakefulness. 最后, we found that network
strength, 程度, clustering coefficient, and path length significantly varied with time of day,
when measured in either wakefulness or sleep at the group level. 一起, these results
suggest that modulation of healthy functional networks occurs over ~24 hr and is robust
and repeatable. Accounting for such temporal periodicities may improve the physiological
interpretation and use of functional connectivity analysis to investigate brain function in
health and disease.
作者总结
In adults, functional connectivity networks are modulated by the state of consciousness and
the circadian rhythm. We investigated whether infant brain networks exhibited similar
variations, given the unique temporal properties of infant sleep and circadian patterning.
Functional connectivity networks were calculated from ~24-hr EEG recordings from 19
healthy infants. We found that networks were subject specific and exhibited stronger
connections during sleep compared to wakefulness. Within subjects, both sleep and wake
networks reoccurred over time. 然而, network strength, 程度, clustering coefficient,
and path length significantly varied with time of day, when measured in either wakefulness
or sleep at the group level. 一起, these results suggest that modulation of healthy infant
functional networks occurs over 24-hr periods and is robust and repeatable.
引文: 史密斯, 右. J。, Alipourjeddi, E.,
Garner, C。, Maser, A. L。, Shrey, D. L. W.,
& Lopour, 乙. A. (2021). Infant functional
networks are modulated by state of
consciousness and circadian rhythm.
网络神经科学, 5(2), 614–630.
https://doi.org/10.1162/netn_a_00194
DOI:
https://doi.org/10.1162/netn_a_00194
支持信息:
https://doi.org/10.1162/netn_a_00194
已收到: 28 八月 2020
公认: 22 行进 2021
通讯作者:
Beth A. Lopour
beth.lopour@uci.edu
处理编辑器:
Mark Kramer
版权: © 2021
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
A
_
0
0
1
9
4
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
Infant:
A pediatric subject typically between
3 和 12 months of age.
State of consciousness:
The subject’s level of awareness;
这里, we specifically study the states
of wakefulness and sleep.
Ultradian periodicities:
Fluctuations in network
characteristics with periods greater
比 1 hr and less than 24 小时, 例如
the sleep cycle.
介绍
Measurements of functional connectivity in the infant brain can provide valuable insight into
neural development, 认识, 和疾病. Much of our knowledge of infant brain networks
comes from functional magnetic resonance imaging (功能磁共振成像) 学习 (Gao et al., 2017), but EEG is
increasingly being used to probe such questions, as it has the advantage of sampling functional
networks with high temporal resolution for long periods of time. 例如, EEG-based func-
tional networks reflect the network segregation that occurs during prenatal development, 和
newborns exhibiting network hubs in the frontal and parieto-occipital lobes (Omidvarnia et al.,
2014; Tóth et al., 2017). These networks evolve slowly throughout childhood, with unique
frequency-specific connectivity for infants, toddlers, 孩子们, and adolescents (Chu et al.,
2014). EEG-based functional networks are also associated with cognitive functions, such as sus-
tained infant attention (Xie, Mallin, & Richards, 2019), and network oscillations during sleep are
correlated with motor, 语言, and social development in toddlers (页, Lustenberger, &
Fröhlich, 2018). As a marker of disease, functional connectivity analysis has been used to char-
acterize infantile epilepsy (Shrey et al., 2018) and predict the onset of autism spectrum disorder
(Righi et al., 2014).
To accurately assess these functional networks, the subject’s state of consciousness must be
经过考虑的. In adults, functional networks measured during wakefulness exhibited higher den-
sity and lower clustering coefficient than those measured during sleep (Chu et al., 2012), 这样的
that networks during sleep exhibit small-world properties (Ferri et al., 2008). 相比之下, 婴儿
networks exhibit greater strength during sleep compared to wakefulness, for both healthy sub-
jects and those with epilepsy (史密斯等人。, 2020). 而且, the network characteristics are a
function of the specific sleep stage. In newborns, studies found that strong, short-range func-
tional connections are concentrated in the occipital lobe during active sleep, with more broadly
distributed long-distance connections predominating during quiet sleep (Tokariev et al., 2019;
Tokariev, Vanhatalo, & 崇拜, 2016). Despite the widespread accessibility of EEG and its broad
use in the young, no prior studies of infant sleep networks have included analysis of overnight EEG
录音. Most have relied on short clips, ~3–20 min in duration, recorded during daytime sleep.
Only one study (史密斯等人。, 2020) included a direct comparison of networks during sleep and
wakefulness. Filling this knowledge gap is critical for understanding the role that functional net-
works play in health and disease.
Beyond the characteristics associated with each discrete state of consciousness, features of
the EEG exhibit periodicities over a range of timescales. Ultradian periodicities in EEG signal
特征, such as frequency band power, have been well studied in adults (Aeschbach et al.,
1999; Kaiser, 2008). It is known that EEG-based functional networks are stable when measured
over several minutes in sleep or wakefulness, despite the rapid visual variability of the time series
(Chapeton, Inati, & Zaghloul, 2017; Kramer et al., 2011). 然而, functional networks based
on intracranial EEG exhibit strong circadian modulation of graph theoretical measures, 例如
the clustering coefficient and path length (Geier, Lehnertz, & Bialonski, 2015; Kuhnert, Elger, &
Lehnertz, 2010). This is emerging as a promising marker to aid in seizure prediction, as oscillations
in functional network properties over hours and days have been shown to correlate to seizure on-
set in patients with epilepsy (Anastasiadou et al., 2016; Baud et al., 2018; Karoly et al., 2017;
Kuhnert et al., 2010; Mitsis et al., 2020). 然而, ultradian and circadian periodicities of infant
functional networks have yet to be studied. Given that infant sleep cycles are quite distinct from
adult sleep patterns, in both electrographic appearance and circadian patterning, the networks
may exhibit modulation over timescales that are less than 24 小时, or not at all. These unknown
temporal periodicities have the potential to further confound the study of infant brain networks.
网络神经科学
615
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
A
_
0
0
1
9
4
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
We hypothesize that both the state of consciousness and the time of day will significantly
impact spontaneous functional networks in infants. 所以, our overall goal is to use ~24-hr
EEG recordings from healthy subjects to disentangle these effects so they can be accounted for
in future studies. 要做到这一点, we take advantage of the noncircadian infant sleep cycle, 哪个
allows us to record periods of wakefulness and sleep during both the day and the night. 我们
first describe the functional networks associated with sleep and wake states, assess the inter-
subject variability in those state-specific networks, and identify graph theoretical measures that
separate the two states. Then we show that measurement of each sleep or wake network is
stable and repeatable within an individual subject. 最后, we show circadian variation in func-
tional connectivity strength and graph theoretical measures when assessed at the group level.
This work increases our understanding of the infant brain’s physiological fluctuations in func-
tional connectivity, which has the potential to act as a baseline for investigations of develop-
蒙特, 认识, 和疾病.
方法
Subject Recruitment and EEG Recording
This prospective study was approved by the Institutional Review Board of the Children’s
Hospital of Orange County. Subjects were recruited and consented from June 2017 到
二月 2019 and underwent overnight long-term video EEG recording to rule out a form
of pediatric epilepsy called infantile spasms. If the infant was not diagnosed with infantile
spasms, they were classified as a control subject. Clinical data were collected at the time of
enrollment. Subjects were deemed “healthy” controls if they (A) exhibited a normal EEG re-
cording, (乙) did not receive a diagnosis of epilepsy, (C) had no known neurological conditions,
和 (d) were developmentally normal for age (as assessed with the Vineland Adaptive
Behavior Scales, 3rd Edition, Sparrow, Cicchetti, & Saulnier 2016). Nineteen channels of
EEG data were sampled at 200 Hz with impedances below 5 kΩ.
A certified sleep technologist at the Children’s Hospital of Orange County manually delin-
eated time periods of wakefulness, rapid eye movement (REM) 睡觉, and non-REM sleep
阶段 (N1, N2, N3) in all EEG recordings in accordance with the American Academy of
Sleep Medicine guidelines. For our analysis, time periods of sleep and wakefulness were sep-
arated based on these markings. For comparison with automatic sleep staging (参见部分
Recurrence of Network States and Correspondence to Manual Sleep Staging), we combined
N1, N2, N3, and REM sleep stages into one “sleep” category.
EEG Preprocessing
EEG data were re-referenced offline to the common average. To be effective, this referencing
scheme relies on substantial coverage of the head by electrodes; in adults, this may imply the
use of high-density EEG. 然而, infant heads are significantly smaller than those of adults,
thus providing more extensive coverage than is usually possible with 19 electrodes. 在阿迪-
的, the connectivity measure used here (cross-correlation measured at nonzero time lags; 看
section Functional Connectivity) was found to be minimally affected by the choice of refer-
恩斯, with common average, bipolar, and common referencing schemes providing similar re-
苏丹 (Anastasiadou et al., 2019).
Artifactual time periods were identified with an automatic extreme value artifact detector,
similar to previously published methods (Durka et al., 2003; Moretti et al., 2003).
具体来说, to identify artifacts we broadband bandpass filtered the data (1.5–40 Hz,
Butterworth filter, chosen to match the settings of clinical EEG viewing/analysis), subtracted
Sleep staging:
Visual categorization of EEG into
wakefulness, rapid eye movement
(REM) 睡觉, and non-REM sleep
stages 1–3; also called sleep scoring.
Cross-correlation:
Bivariate, amplitude-based
synchronization measure, calculated
as the dot product of two EEG signals
as one signal is shifted in time.
网络神经科学
616
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
A
_
0
0
1
9
4
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
the mean from each channel, and calculated the standard deviation of each zero-mean time
系列. Artifacts were defined as time points in which the absolute value of the voltage exceeded
a threshold of 7.5 standard deviations above the mean value in any single channel. We chose
this threshold because it resulted in the best correspondence between automatically detected
and visually identified artifacts in a previous dataset (史密斯等人。, 2017). To ensure that the entire
artifact was marked, a buffer of 0.9 s was added to both sides of each contiguous set of time
points containing extreme amplitude values. Data recorded during EEG impedance checks were
also marked as artifact. For the connectivity analysis, a broadband bandpass filter was applied to
the raw, re-referenced data (0.5–55 Hz, Butterworth filter). One-second epochs that contained
artifactual data were removed from all channels after filtering.
Functional Connectivity
We calculated functional connectivity networks via cross-correlation using the method devel-
oped by Kramer et al. (2009) and Chu et al. (2012) and previously applied to infant EEG data
(Shrey et al., 2018). We chose cross-correlation because it is a simple bivariate measure that is
highly sensitive to linear changes in EEG activity (大卫, Cosmelli, & 弗里斯顿, 2004; Jalili,
Barzegaran, & Knyazeva, 2014) and has been shown to be comparable to other measures
of synchronization (Jalili et al., 2014; Quian Quiroga et al., 2002). Although cross-correlation
is generally insensitive to nonlinear interactions in the EEG, we opted for this rapid and
straightforward linear measure of synchronization because no nonlinear metric has been
shown to reliably measure actual changes in coupling strength while discounting spurious in-
creases in synchronization due to changes in other signal properties (David et al., 2004;
Pereda et al., 2001).
The functional connectivity calculation was performed as described in Shrey et al. (2018);
we briefly summarize it here. Data were divided into 1-s epochs, and the EEG signals in each
epoch (one from each channel) were normalized to have zero-mean and unit variance. 为了
each epoch, we calculated the cross-correlation between every pair of channels and identified
the maximum of the absolute value of the cross-correlation. Epochs in which the maximal
cross-correlation value occurred at zero time lag were excluded, as they were likely a result
of volume conduction (Chu et al., 2012). A partial correlation with the common average ref-
erence time series was performed to test whether the reference induced the correlation mea-
sured between the channels (Shrey et al., 2018). If there was a large difference between the
partial correlation and the correlation value between the channels, the measured correlation
was presumed to have resulted from referencing artifact and the epoch was removed from
further analysis (Supporting Information Table S1). Z-values were calculated for the nonartifac-
tual epochs by dividing the Fisher-transformed correlation coefficient value by the estimated
标准差, taking the autocorrelation of each channel epoch into account (Chu et al.,
2012; Kramer et al., 2009). This method nullifies the autocorrelation component of the time
series that would produce spurious correlations. The z-values were compared to a baseline
distribution created via permutation resampling. Permutation resampling was performed by
selecting two random 1-s epochs of data from the time series that were separated by at least
1 s, calculating the max cross-correlation between the channels, and iterating this procedure
500 次 (Nichols & Holmes, 2003). The standardized correlation values from all iterations
were sorted and the threshold of significance was defined as the value corresponding to the
95th percentile of the distribution for each electrode pair. For each epoch, correlation values
between channel pairs that exceeded this threshold value were deemed to be significant, 和
these connections were assigned a value of one; connections that did not exceed this
网络神经科学
617
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
A
_
0
0
1
9
4
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
threshold were assigned a value of zero. Thus for p EEG channels, the output of the connec-
tivity calculation for each epoch was a binary matrix of dimension p × p.
Across epochs, connectivity data were stored in a three-dimensional array Q, 哪里的
binary value at position Q(我, j, k) represented the connection between electrode i and electrode
j in epoch k. Then the overall connection strength between two channels was calculated as the
fraction of time series epochs in which there was a significant connection between them. 为了
wakefulness, this calculation used the Nw binary connectivity matrices that coincided with
times of wakefulness, based on manual sleep staging. For sleep, the Ns epochs marked as sleep
(N1, N2, N3, and REM) were used. Because Nw and Ns were unequal for each subject, 我们
performed a bootstrapping procedure. For each iteration, we randomly sampled 11,000
纪元 (Nsamp) with replacement from each sleep/wake state; we chose 11,000 epochs be-
cause this was the shortest duration of a single sleep/wake state over all patients. We used
those values to calculate functional connectivity networks associated with wakefulness, Qm
w ,
and sleep, Qm
w(我, j) =
s (我, j) = (1/Nsamp) (西德:1)k2sleep Q(我, j, k). We performed this calculation
(1/Nsamp) (西德:1)k2wake Q(我, j, k) and Qm
为了 1,000 iterations and then averaged to obtain the wakefulness network Qw and the sleep net-
n¼1 Qm
work Qs for each subject, where Qw(我, j) = (1/1,000)
s .
We evaluated network strength by applying a proportional threshold to the connectivity values
(Garrison et al., 2015). 具体来说, we calculated the average of the strongest 10% of connec-
tions in the wakefulness and sleep networks. The Benjamini–Hochberg procedure was used to
correct for multiple comparisons where applicable (Benjamini & Hochberg, 1995).
s . This constituted one iteration, denoted by the superscript m. 具体来说, Qm
w and Qs(我, j) = (1/1,000)
m¼1 Qm
P1;000
P1;000
Network strength:
Amount of synchronization between
节点, here defined as the
percentage of 1-s epochs in which
two nodes are significantly
连接的.
Graph Theoretical Measures
Studies of functional connectivity are often augmented by complex network analysis because
it provides easily computable measures with biophysiological significance (鲁比诺夫 & 斯波恩斯,
2010). We computed three weighted graph theoretical measures that summarize the functional
connectivity networks computed in this study. 第一的, we calculated the degree for each node by
summing the weights of the connections incident to that node (布莫尔 & 斯波恩斯, 2009;
鲁比诺夫 & 斯波恩斯, 2010). The degree is related to our measurement of network strength,
which is an important marker for distinguishing sleep and wakefulness (史密斯等人。, 2020)
and can also be an indicator of pathological networks (Shrey et al., 2018). 然而, 这
weighted calculation of degree has an advantage over strength, as it does not require a thresh-
old to binarize the network. 第二, the clustering coefficient is defined as the fraction of a
node’s neighbors that are also neighbors of each other and is thought to quantify the level of
functional segregation in the brain network (鲁比诺夫 & 斯波恩斯, 2010; Watts & Strogatz, 1998).
In the weighted network case, the clustering coefficient is derived from the “intensity” and
“coherence” of a subgraph using measures of its geometric and arithmetic mean (Onnela
等人。, 2005). Before calculating the clustering coefficient, we normalized the adjacency matrix
by dividing each element by the maximum connection value in the network (Antoniou &
Tsompa, 2008; Onnela et al., 2005). 第三, we computed the shortest path length, 哪个重新-
ports the minimum sum of the edge “lengths” for a path from one node to another (Antoniou &
Tsompa, 2008; 鲁比诺夫 & 斯波恩斯, 2010; 斯塔姆 & Reijneveld, 2007). In our case, because we
assume that information flow will increase with higher connection values, we defined the edge
lengths as the inverse of the edge weights. 因此, the minimum sum of these inverse edge
weights maximizes the connectivity strength between each pair of electrodes (鲁比诺夫 &
斯波恩斯, 2010). The shortest path length is one of the most common metrics to assess functional
一体化 (鲁比诺夫 & 斯波恩斯, 2010). Similar to the clustering coefficient calculation, 我们
网络神经科学
618
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
A
_
0
0
1
9
4
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
normalized the adjacency matrix before computing the inverse and determining the shortest
paths between nodes in the network (Antoniou & Tsompa, 2008; Onnela et al., 2005).
We chose these measures because the clustering coefficient and characteristic path length
have previously been used to characterize the newborn and infant brain (Omidvarnia et al.,
2014; Tymofiyeva et al., 2012). Clustering coefficients decrease in lower frequency bands and
increase in higher frequency bands during development (Chu et al., 2014; Omidvarnia et al.,
2014; Tymofiyeva et al., 2012). Path length increases and clustering coefficients decrease with
sustained attention in infants (Xie et al., 2019), and the ratio between the clustering coefficient
and path length indicates that the infant brain exhibits small-world properties (Gao et al.,
2011; Tymofiyeva et al., 2012). 而且, changes in brain state affect graph theoretical mea-
sures in adults, with higher clustering coefficients (Chu et al., 2012) and greater small-
worldness (Ferri et al., 2008) during sleep. 重要的, such global graph characteristics
can be robustly measured in infant EEG, as indicated by a test-retest reliability study (van
der Velde, Haartsen, & Kemner 2019), making them suitable for our analysis.
Time-Varying Functional Connectivity Measurement
To analyze time-varying changes in the functional connections, we averaged the binary p × p
matrices across windows of successive epochs. Let Qn represent the p × p matrix averaged
over a window of n 1-s epochs. The value of Qn(我, j ) indicates the proportion of epochs in
which the connection between channel i and channel j was significant, analogous to the
values of Qw and Qs for wakefulness and sleep, 分别. For our analysis, we calculated
Q300, the averaged connectivity matrix in a window of 300 s, and this window was shifted in
30-s increments (90% 重叠). We chose a window size of 300 s because networks were
shown to be stable over this amount of time in two separate studies (Chu et al., 2012;
Shrey et al., 2018).
Recurrence of Network States and Correspondence to Manual Sleep Staging
We hypothesized that different brain states (例如, sleep or wakefulness) would be associated
with different functional networks and that the functional network associated with a single
state would be relatively consistent over time. 所以, we used principal component anal-
分析 (PCA) to identify the set of functional networks that accounted for a majority of the var-
iance over time, assuming that state transitions would be the greatest source of this variance.
This also let us assess how many network states occurred in the data and whether the states
recurred over time.
To perform PCA on the functional connectivity networks over time, we first calculated Q300
in 300-s windows with 90% 重叠, as described in section Time-Varying Functional
Connectivity Measurement. We then placed the values for all unique connections in Q300
(171 channel pairs in total, 排除自连接) into a column vector c and normalized
it to have zero-mean and unit variance. We concatenated p successive vectors, where p de-
notes the number of windows that were available in the dataset, into matrix C and subtracted
the mean from each row to ensure that the distribution of connections for each channel pair
was zero-mean. We performed PCA on these normalized functional connectivity time series C
to ascertain the latent networks that explained the most variance in the data. We then calcu-
lated the time course of the first principal component, which represents the relative weight
assigned to that component as a function of time.
Once the network states were identified, we determined their physiological significance by
comparing them to visual sleep staging of the EEG. We hypothesized that there would be
Principal component analysis:
Dimensionality reduction technique
based on the eigendecomposition of
the covariance matrix.
网络神经科学
619
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
A
_
0
0
1
9
4
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
Gaussian mixture model:
Parametric model that assumes the
data can be represented by a
weighted sum of a finite number of
Gaussian distributions.
Network stability:
Variability of the functional
network within a single state of
consciousness; stable networks are
highly correlated over time.
transitions between two different states, likely representing wakefulness and sleep, so we fit a
two-component Gaussian mixture model (GMM) to the principal component time series. 我们
then calculated normalized probability distribution functions (PDFs) for the two GMM distri-
butions. The threshold to separate the states was defined as the intersection of the two PDFs.
To avoid finding intersections at the extreme tails of the distributions, we calculated the PDF
ratio and identified the index where this ratio was closest to 1:
(西德:2)
(西德:4)
(西德:2)
(西德:2)
−1
(西德:2)
thresholdIndex ¼ min PDF1
PDF2
(西德:2)
(西德:3)
(西德:2)
(西德:2)
(西德:2)
:
The principal component value associated with this index was the threshold that best distin-
guished the two states. We used this value to separate the networks from all time points into
two states, and we compared these results to visual sleep scoring done by a certified EEG sleep
technician.
Calculation of Network Stability
We assessed network stability of the functional connectivity measurement by performing 2-D
correlations between independent average connectivity networks during wakefulness or sleep.
We first concatenated all epochs during sleep (Ns) or wakefulness (Nw) and then calculated
Ns/n or Nw/n sequential, nonoverlapping measurements of Qn where n is the size of the win-
dow. Then a 2-D correlation was calculated between each successive measurement of Qn
and this was repeated for window sizes n ranging from 10 s to 200 s. The mean of the cor-
relation values was recorded for each window size for each subject. The mean and 95% 骗局-
fidence interval of the average correlation coefficient values for all subjects were then plotted
as a function of n.
Calculation of Circadian Changes in Functional Networks
最后, we investigated whether there were circadian modulations in the functional connectiv-
ity networks. For this analysis, sleep and wakefulness were analyzed separately based on man-
ual EEG sleep scoring. For both wakefulness and sleep, we calculated four metrics (平均值
network strength and the three graph theoretical measures) as a function of time using Q300
(see section Time-Varying Functional Connectivity Measurement). 下一个, the values of each of
these four metrics were associated with the 24-hr (circadian) clock time corresponding to the
beginning of their Q300 epoch. We did this for each subject in the dataset, thereby obtaining a
distribution of values across subjects for each of the 1,440 circadian time points (every minute
on a 24-hr clock). We then calculated the mean across all subjects for each 1-min block of
时间; if there were less than five data points in the 1-min block, the data were considered
insufficient and that time point was discarded. To assess statistical significance, we aggregated
all data points from 11 AM to 1 PM as the “daytime” distribution and we aggregated all data
points from 11 PM to 1 AM as the “nighttime” distribution. Similar to the sampling methods
used in section Functional Connectivity, we randomly selected observations with replacement
from the daytime and nighttime periods for 1,000 迭代. With each iteration, we calculated
the difference between the means of the distributions (daytime compared to nighttime), 和
we tested whether the confidence interval of the resulting difference distribution included 0.
结果
Subject Demographics
总共, 19 healthy subjects (15 女性, 4 males) were recruited for the study between June
2017 and February 2019, and all were included in our analysis. The mean age of the subjects
网络神经科学
620
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
A
_
0
0
1
9
4
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
曾是 6.3 月 (+/- 3.1 月, 标准差). The recordings lasted 20.8 hr on average
(+/- 7.8 小时, 标准差). Recording durations are listed for every subject in Supporting
Information Table S2.
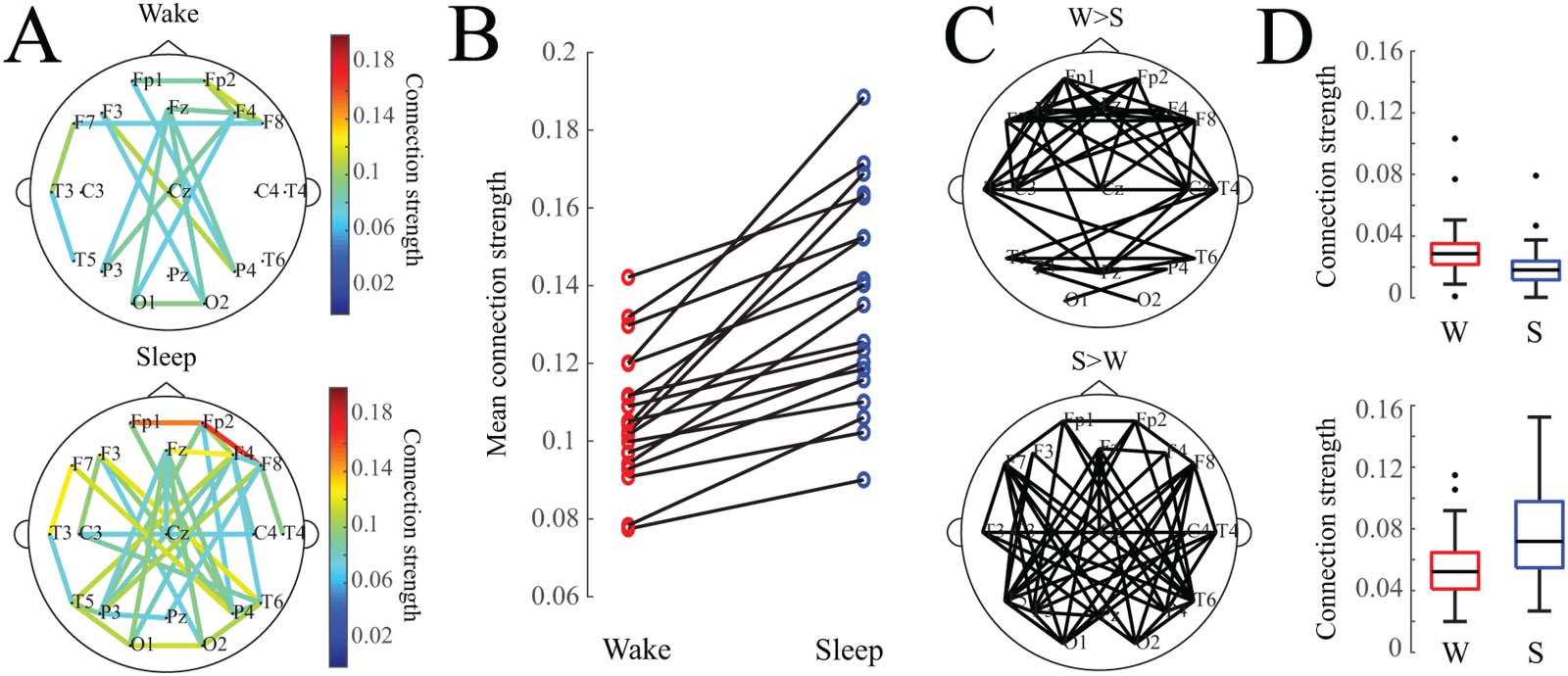
Sleep Is Associated with Stronger Functional Connections
Sleep was associated with stronger functional connections, as evidenced by the averaged con-
nectivity networks Qw and Qs across all subjects (Figure 1A) and the individual subject results
(Figure 1B). We also tested whether specific connection pairs were consistently stronger in
wakefulness or sleep; 去做这个, we compared the distribution of connection strengths for
one electrode pair during wakefulness to the distribution during sleep in a pairwise fashion
(n = 19 subjects). 在 48 的 171 possible connections, wakefulness revealed stronger con-
nectivity values (Figure 1C, 顶部) (two-tailed Wilcoxon sign-rank test, adjusted via Benjamini–
Hochberg procedure, adj. p < 0.05). In 55 of the 171 possible connections, sleep connectivity
values were significantly stronger than wakefulness (Figure 1C, bottom) (two-tailed Wilcoxon
sign-rank test, adjusted via Benjamini–Hochberg procedure, adj. p < 0.05). The strongest con-
nections in the averaged network were typically associated with sleep rather than wakefulness;
although a number of connections were statistically stronger during wakefulness than sleep,
these connections were typically weak, with strengths <0.04 (Figure 1D).
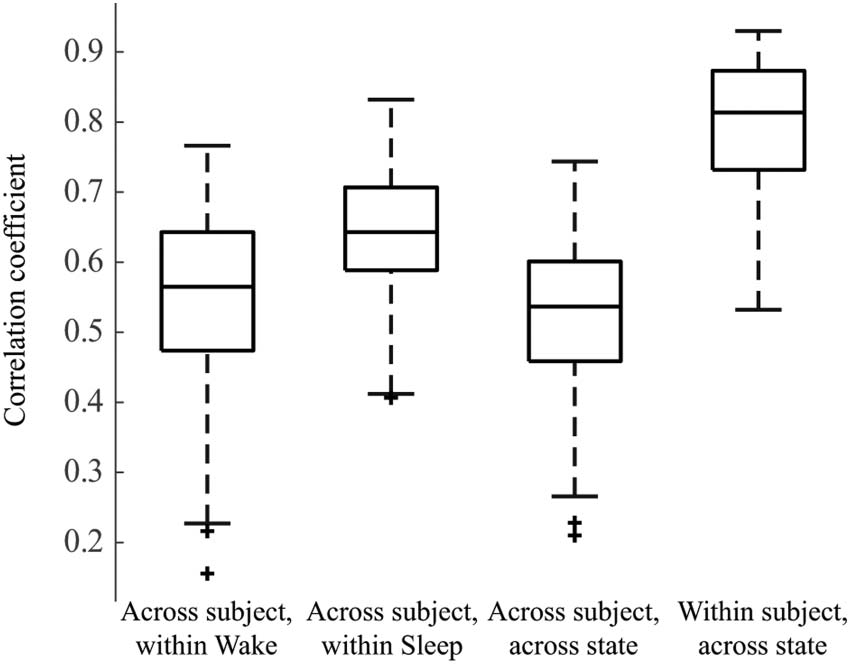
Functional Network Structures Are Subject Specific
We then measured the similarity of the functional connectivity network structure within and
across subjects, as well as within and across sleep/wake states (Figure 2). Across all subjects,
the within-sleep distribution of correlation coefficients was statistically significantly higher
than the within-wakefulness distribution, and both were significantly higher than the across-
state distribution ( Wilcoxon rank-sum test, p < 0.05). However, Cohen’s effect size value
between the within-wakefulness and across-state distributions suggested low practical signif-
icance (d = 0.233). All effect sizes are reported in Supporting Information Table S3. Within-
subject across-state correlations (e.g., comparing subject 1 sleep to subject 1 wakefulness)
were higher than across-subject within-state correlations (e.g., comparing sleep networks
(A) Average functional connectivity networks for wakefulness and sleep. For visualization, an edge is drawn if the connection value
Figure 1.
exceeds an absolute threshold of 0.075. (B) Mean connection strength for individual subjects (calculated as the average strength of the stron-
gest 10% of connections) is higher during sleep. (C) Network maps showing connections that were statistically significantly greater in wake-
fulness (top) or sleep (bottom). (D) Box plots of mean connection strength for connections that were significantly different between wakefulness
and sleep (shown in subfigure C).
Network Neuroscience
621
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
Figure 2. Box plot showing 2-D correlations within and across weighted connectivity matrices for
each subject. We first compared networks across subjects within a state, for example, Subject 1
Wake to Subject 2 Wake, and the analogous comparisons during sleep; n = 171 observations each.
Then we compared across subjects and across states, for example, Subject 1 Wake to Subject 2
Sleep; n = 171 observations. Lastly, we calculated the 2-D correlation between the sleep and wake
networks within single subjects, for example, Subject 1 Wake to Subject 1 Sleep; n = 19 observa-
tions. All distributions are statistically significantly different from one another ( Wilcoxon rank-sum
test, p < 0.05).
across all subjects). This indicates that, while state-specific functional network structure com-
monalities are seen across subjects, the network structures are also patient-specific.
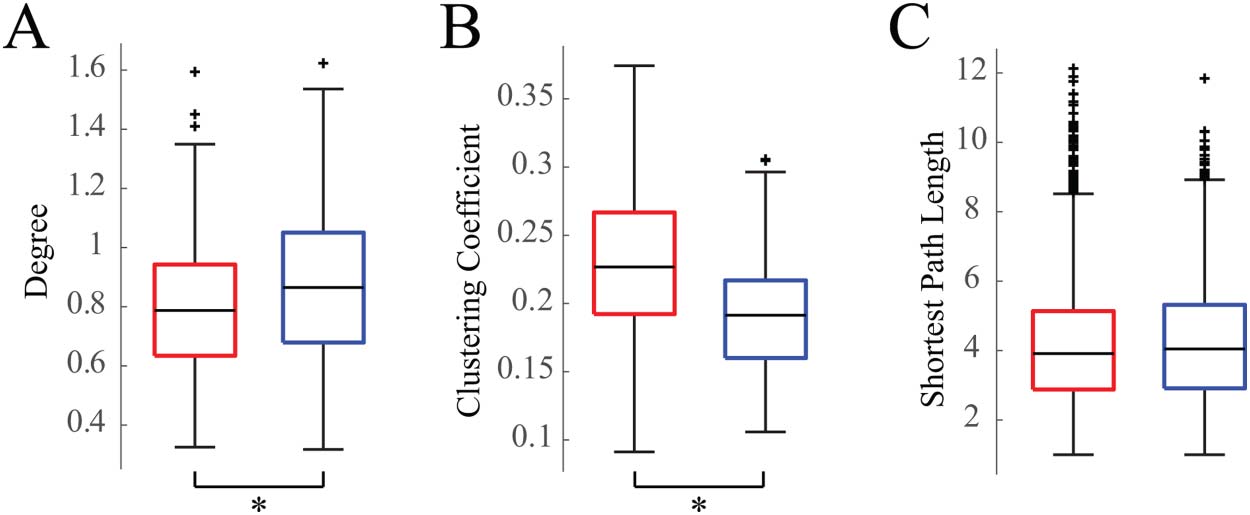
Network Structure Is More Segregated During Wakefulness
We calculated three standard weighted graph theoretical measures on the average functional
connectivity maps for sleep and wakefulness for each subject. Consistent with our finding that
networks tended to be stronger during sleep than during wakefulness, the node degree was
significantly greater in sleep than in wakefulness (Figure 3A) ( Wilcoxon rank-sum test, p <
0.05, Cohen’s d = 0.34). The clustering coefficient was significantly greater in wakefulness
compared to sleep (Figure 3B) ( Wilcoxon rank-sum test, p < 0.05, Cohen’s d = 0.78).
Lastly, we found that the shortest average path length was not significantly different between
sleep and wakefulness (Figure 3C) ( Wilcoxon rank-sum test, p < 0.05, Cohen’s d = 0.03).
Figure 3. Box plots of weighted graph theoretical measures. (A) Degree, (B) clustering coefficients,
and (C) shortest path lengths of wakefulness (red) and sleep (blue) networks for all 19 subjects.
Asterisk denotes p values less than 0.05.
Network Neuroscience
622
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
Figure 4. Stability of functional connectivity networks in wakefulness (red) and sleep (blue). We
calculated the 2-D correlation between independent averaged connectivity networks from windows
of data of varying size. We found that sleep exhibited more stable networks, with nonoverlapping
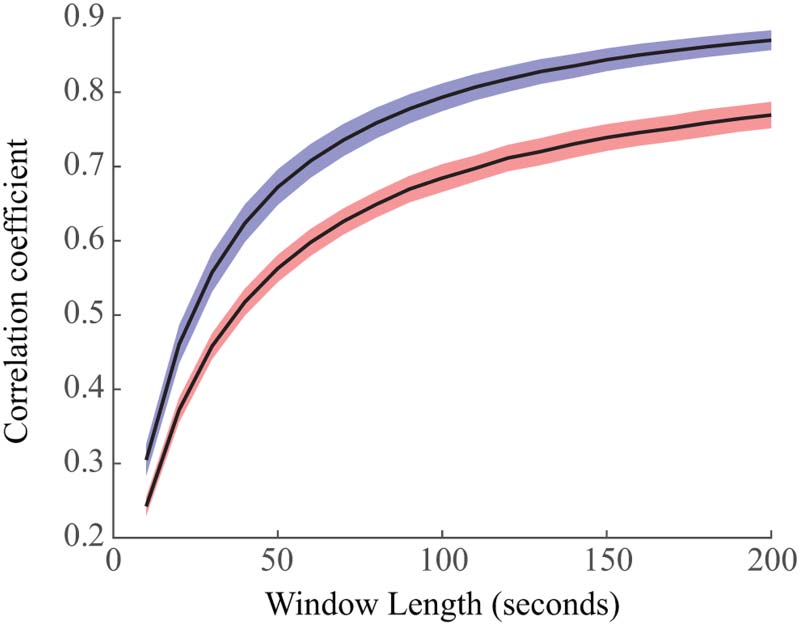
confidence intervals for the means for all window sizes.
Functional Networks Are More Stable in Sleep Than Wakefulness
We then calculated the stability of each subject’s functional connectivity networks within a
given brain state (Figure 4). Here, stability was assessed using the correlation coefficient be-
tween networks calculated from independent windows of data. Higher correlation coefficients
indicated greater similarity between networks and thus, higher stability. For each subject, we
calculated the mean correlation coefficient for each window size and then calculated the 95%
confidence interval for the mean correlation coefficients across all subjects. We found that
sleep networks were significantly more stable than networks derived from EEG during wake-
fulness (Figure 4). The confidence intervals for the mean of the stability distributions did not
overlap for any window size, indicating statistical significance over all tested window sizes.
Functional Networks Associated with Sleep and Wakefulness Recur over Hours and Days
Our analysis thus far has shown that an individual subject’s functional network remains stable
throughout each period of wakefulness or sleep. However, this analysis did not test whether
the networks recur, that is, whether the functional network of one sleep period matches that of
another sleep period within the same person. To address this, we used PCA to determine the
latent variable that described the most variance in the connectivity data; we hypothesized that
this variance would be due to transitions between wakefulness and sleep. If the networks re-
main stable for each state over multiple sleep/wake cycles, the time series of the first principal
component, which signifies the weight of that component in the functional connectivity time
series, should oscillate between two values.
We performed PCA on all functional connectivity network time series as outlined in section
Recurrence of Network States and Correspondence to Manual Sleep Staging. A representative
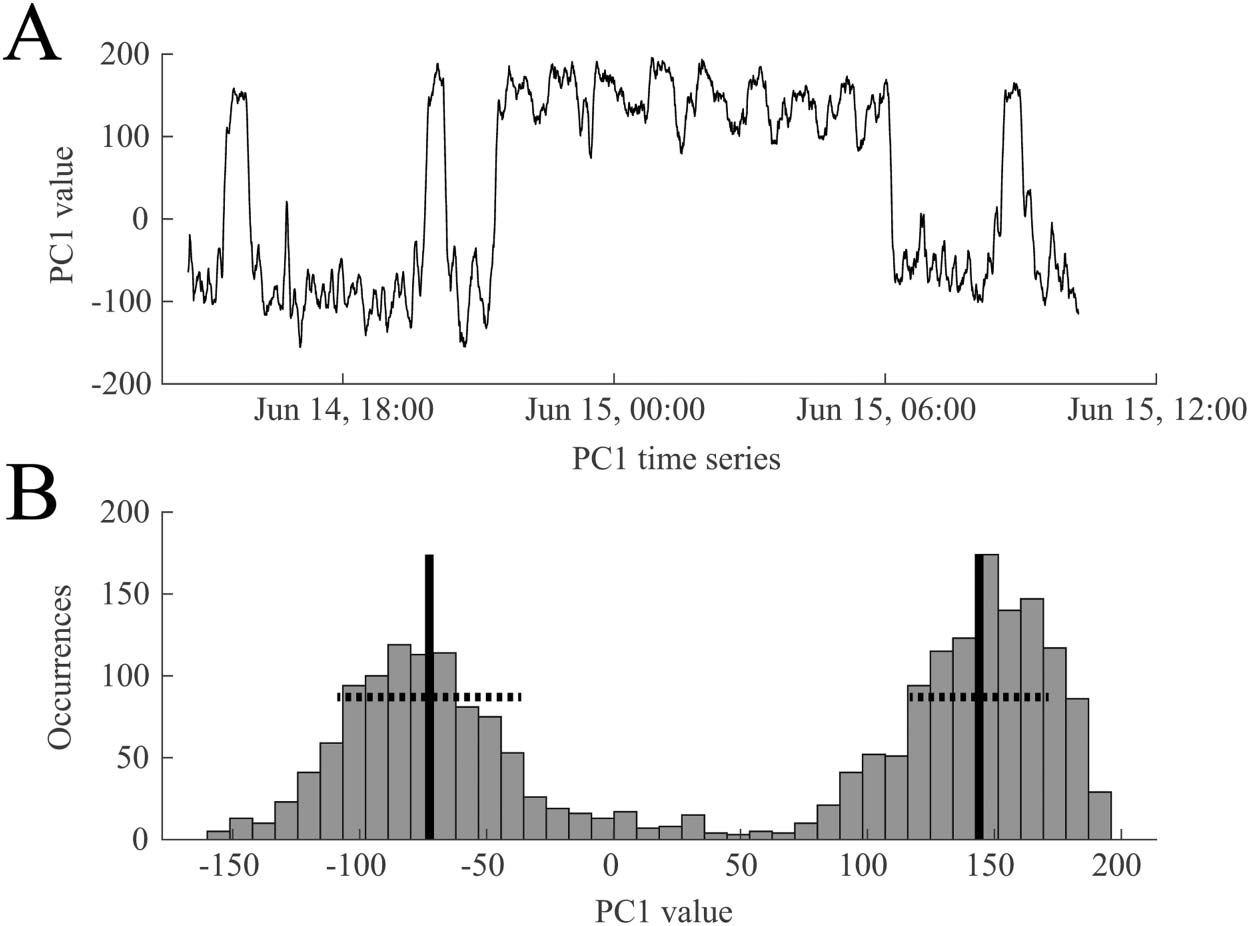
example of a time series from the first principal component (PC1) is shown in Figure 5A, dem-
onstrating the bimodal nature of the signal. This suggests that the brain is switching between
two functional network states over the course of 1 day. This was also reflected in the histogram
of the first principal component, which we fit with a two-component GMM (Figure 5B).
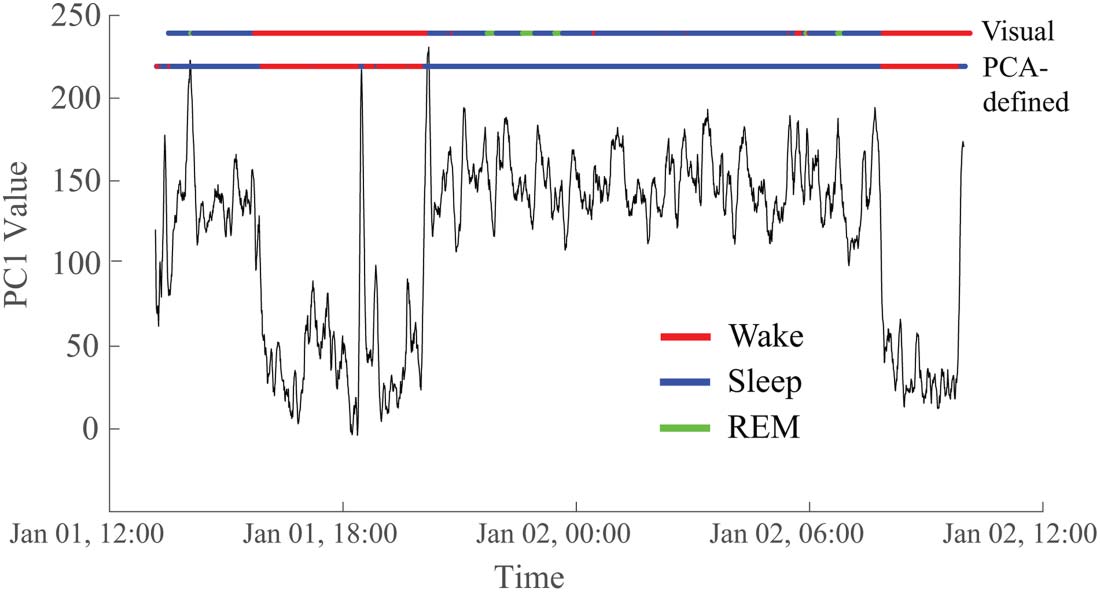
To determine whether the two reoccurring states evident in the PCA results corresponded
to wakefulness and sleep, we compared the GMM output to visual sleep staging (Figure 6).
We found a high correspondence between the two states uncovered via PCA (defined by a
Network Neuroscience
623
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
Figure 5. A representative example of the time course of the first principal component (PC1), re-
flecting how much weight is assigned to PC1 in the functional connectivity time series. (A) PC1
oscillates between two states during ~18 hr of EEG data. (B) The bimodal nature of PC1 is reflected
in its histogram. A two-component Gaussian mixture model was derived from these values and used
to classify the two states. The black vertical lines indicate the means of the two distributions, and the
dashed horizontal lines denote one standard deviation. Data are from Subject 1.
threshold applied to the GMM) and the visually identified sleep and wake stages. Across
subjects, the median percentage of correspondence was 91.2% (Supporting Information
Table S4), confirming our hypothesis that the PCA-determined states reflected wakefulness
and sleep.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. The two states derived from the PC1 time series correspond to visually marked sleep and
wakefulness in the EEG. In this representative example, the correspondence is 95.1%. The top hor-
izontal line (“Visual”) is colored to indicate the sleep/wake state based on visual markings. Red
indicates the subject is awake, blue is non-REM sleep, and green is REM sleep. The bottom hori-
zontal line (“PCA-defined”) reflects the values of the first principal component after thresholding
based on the Gaussian mixture model, with red representing wakefulness and blue representing
sleep. Data are from Subject 5.
Network Neuroscience
624
Circadian dynamics in infant functional connectivity networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
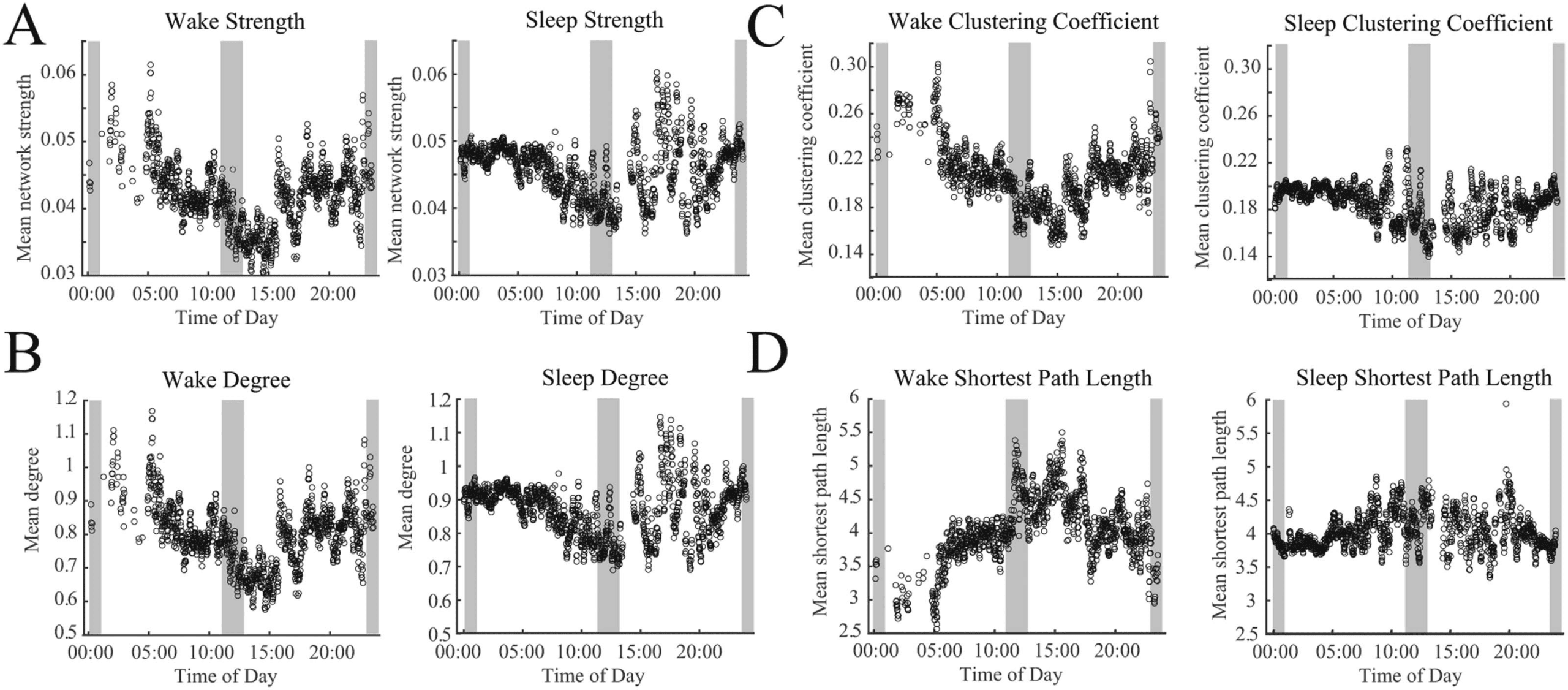
Figure 7. Circadian patterns emerge in both wakefulness and sleep for network strength and graph theoretical metrics. Twenty-four hour
periodicities are shown for (A) the network strength, defined as the mean of all connections, (B) network degree, (C) clustering coefficient,
and (D) the shortest path length. Each subfigure shows data recorded during wakefulness (left) and sleep (right). Gray shaded regions mark
daytime (11:00–13:00) and nighttime (23:00–01:00) hours.
EEG Functional Networks Exhibit Circadian Variation
When subjects were awake, the mean network strength was significantly decreased during the
daytime and was increased at nighttime (Figure 7A; 95% confidence interval does not include
0). Similar patterns were seen for the network degree (Figure 7B) and the clustering coefficient
(Figure 7C). The shortest path length showed the opposite trend (Figure 7D). Similar patterns
were observed using data collected when subjects were sleeping, although the modulation
over 24 hr was less dramatic. However, all trends in graph theoretical measures were signif-
icantly different between daytime and nighttime hours (Figure 7B–7D; 95% confidence inter-
val does not include 0). This indicated that, in addition to the significant differences between
sleep and wake functional networks, the time of day modulated the network within each state.
We noted that the sleep measurements during the daytime exhibited high amounts of vari-
ability, and, in general, there was higher variance in the measurements when subjects were
asleep during the daytime or awake at nighttime. However, this may be partially due to the
low number of data points in some time periods, as the high variance did not occur when there
were a large number of data points in the 1-min windows (Supporting Information Figure S1). A
larger cohort or more EEG data per subject would be needed to robustly quantify this variance.
DISCUSSION
In this study, we report characteristics of functional connectivity networks based on long-term EEG
recordings from 19 healthy infants. We first showed that functional connectivity networks associ-
ated with sleep and wakefulness exhibited statistically significant differences both in strength and
structure. We also showed that, although sleep and wakefulness were associated with stable net-
works, those networks were highly individualized. Within-subject comparisons of sleep to wake-
fulness were more similar than comparisons across subjects within the same state of
Network Neuroscience
625
Circadian dynamics in infant functional connectivity networks
Topology metrics:
Graph theoretical measurements of
network characteristics, such as
degree, clustering coefficient, and
shortest path length.
consciousness. Furthermore, state-specific networks recurred over multiple periods of sleep and
wakefulness within each subject, as revealed by the correspondence of PCA-derived networks to
visual sleep scoring. Lastly, we showed that circadian rhythms significantly modulated network
properties in a relatively stereotyped fashion. This suggests that the time of day during which a
recording is obtained may significantly impact measurements of functional connectivity, which
bears relevance for both cognitive and clinical studies involving functional networks.
The analysis of infant EEG, which is visually distinct from adult EEG, is a unique aspect of
this study. The vast majority of EEG functional connectivity studies focus on healthy adult data
(Stevens, 2009); thus, this study fills a critical need by reporting basic characteristics of healthy
EEG-based functional networks as a baseline for studying conditions specific to the
neonatal/infant period, including early-onset epilepsies and neurodevelopmental conditions
(Righi et al., 2014; Shrey et al., 2018). Infant EEG poses unique advantages and disadvantages
in comparison with adult recordings. On one hand, it enables study of circadian dynamics and
network characteristics separately for sleep and wakefulness because infant sleep cycles do
not always coincide with diurnal rhythms. On the other hand, the EEG patterns associated with
sleep and wakefulness in infant EEG rapidly evolve as the infant grows and develops. Wakeful
background activity in infant EEG is slower than adult EEG, and rhythms become faster with
age (Fisch, 1999; Rowan & Tolunsky, 2003). The emergence of critical patterns, such as the
posterior dominant rhythm and the mu rhythm, occurs at around 3 and 4–6 months of age,
respectively (Laoprasert, 2011; Stern, 2005). Moreover, the structural connectivity in the infant
brain is constantly changing and developing (Barkovich et al., 2006; Tymofiyeva et al., 2012),
whereas structural connectivity in adults is relatively static. This age dependence could partially
explain the subject-specific nature of the networks observed in our study, but we found no sig-
nificant correlations in our strength and topology metrics (Supporting Information Figure S2),
and subject-specific networks were also reported in adults (Chu et al., 2012). While researchers
have advanced the study of the relationship between structure and function in the brain (Pernice
et al., 2011; Ponten et al., 2010), further work is needed to examine this relationship in the
developing brain. Overall, we expect that the functional connections underlying infant neural
activity will differ from adults.
We found that functional networks were stronger during sleep than wakefulness, and they
were less clustered when the subject was awake (Burroughs et al., 2014; Kuhnert et al., 2010;
Mitsis et al., 2020). The networks were significantly stronger during sleep when compared to
wakefulness in all subjects (Figure 1B); however, we note that the effects of thresholding net-
works, even with a proportional threshold, is an active area of research and will require further
investigation (Chapeton et al., 2017; Garrison et al., 2015). To reduce the bias introduced by
thresholding the network graphs, we calculated graph theoretic properties of the networks on
the weighted adjacency matrices. The degree was significantly higher in the functional net-
works derived from sleep, consistent with our finding of overall stronger networks in sleep.
The clustering coefficient of the normalized networks was higher in awake networks, indicat-
ing greater functional segregation during wakefulness (Rubinov & Sporns, 2010; Watts &
Strogatz, 1998). Interestingly, the shortest path length, calculated as the inverse of the normal-
ized connection strength, was not significantly different between the two states, indicating sim-
ilar levels of functional integration in wakefulness and sleep (Watts & Strogatz, 1998).
We found that the awake and sleep networks were more similar within a single subject than
the awake or asleep networks across subjects. The subject-specific nature of these functional
networks was also described in a long-term intracranial EEG study in adults (Kramer et al.,
2011), as well as in a previous study by our group in a cohort of pediatric epilepsy patients
(Shrey et al., 2018). This may indicate a need for a paradigm shift in the analysis of functional
Network Neuroscience
626
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
connectivity networks. Most functional network studies have focused on finding common net-
works and pathways that facilitate specific functions or the resting state. However, the unique-
ness of functional networks has become a recent area of investigation in the fMRI community
and may deserve further attention in EEG functional network analysis (Chapeton et al., 2017;
Chen et al., 2008; D’Esposito, 2019; Dubois & Adolphs, 2016; Fingelkurts & Fingelkurts,
2011; Finn et al., 2020; Gonzalez-Castillo et al., 2015; Kramer et al., 2011). A comparison
of functional connectivity networks may require attention to both elements: the common path-
ways underlying the activity of interest, as well as the individuality of the subject’s unique func-
tional network.
The stability of functional connectivity networks in EEG is a function of the timescale used to
measure them. We found that the binary connectivity matrices in 1-s epochs were highly variable,
but stable networks were identified over the course of 200–500 s (Chu et al., 2012; Shrey et al.,
2018). However, these networks become unstable again at the timescale of hours due to brain
state transitions and circadian rhythms. This multilevel stability is assumed in our study, but further
investigation is needed to define characteristic timescales of stability in functional connectivity
networks in the human brain (Kuhnert et al., 2010). This is perhaps related to the concept that
EEG amplitude modulations do not have a characteristic scale and exhibit a fractal nature
(Hardstone et al., 2012; Linkenkaer-Hansen et al., 2001; Smith et al., 2017). This fractal nature
may be transferred to functional networks (Lehnertz et al., 2017), mathematically suggesting that
brain activity is changing in an organized way that may not have a characteristic timescale.
Several limitations of our study should be addressed in future investigations of healthy func-
tional connectivity networks. First, our EEG recordings were an average of 20.8 hr, and a lim-
ited number of recordings were longer than 24 hr. Thus, circadian patterns were assessed on
the group level rather than an individual level. Future studies could include longer, multiday
EEG recordings to analyze true subject-specific assessments of circadian patterns. Second, we
used an automatic algorithm to remove artifacts in our data, as it was infeasible to visually
confirm all artifacts due to the long recording durations. Therefore, some artifacts may have
escaped detection/removal while other artifact-free data may have been erroneously removed.
This could have contributed to the differences seen in the wake and sleep networks because
artifacts are more frequent during wakefulness; on the other hand, the results reported here
mirror those obtained with visually marked artifacts (Shrey et al., 2018). Lastly, although there
are many advantages to analyzing data from a cohort of infants, the limited age range reduces
the generalizability to other pediatric populations, and we did not have enough subjects to
discern network properties specific to each age or developmental stage. Note, though, that
a preliminary analysis revealed no modulation in strength or topology metrics as a function
of age (Supporting Information Figure S2). Future studies should increase the number of sub-
jects and broaden the age range.
The importance of this study lies in generating functional connectivity networks derived
from ~24-hr recordings of normal EEG data in infants. In addition to imparting knowledge
of how physiological functional networks are modulated throughout the day and within wak-
ing and sleep states, this will facilitate understanding of changes in network topology due to
pediatric diseases such as epilepsy and autism (Righi et al., 2014; Shrey et al., 2018). Seizure
forecasting in epilepsy has largely relied on prediction of seizure onset with several minutes of
data, but it has been shown that modulations in functional networks due to physiological pro-
cesses such as waking and sleeping can mask “pre-seizure” changes (Kuhnert et al., 2010;
Mitsis et al., 2020; Schelter et al., 2011). Accounting for these physiological fluctuations in
seizure prediction models may improve their accuracy and ultimately improve care for patients
suffering from epilepsy.
Network Neuroscience
627
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
ACKNOWLEDGMENTS
The authors thank the EEG technologists at the Children’s Hospital of Orange County (CHOC)
for their help in acquiring the EEG data. The authors also thank Dr. Michael Nunez and Derek
Hu for helpful discussions regarding the manuscript. This study was funded by a CHOC PSF
Tithe grant.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00194.
AUTHOR CONTRIBUTIONS
Rachel June Smith: Conceptualization; Data curation; Formal analysis; Investigation;
Methodology; Project administration; Software; Writing – original draft. Ehsan Alipourjeddi:
Data curation; Formal analysis; Investigation; Software; Writing – review & editing. Cristal
Garner: Data curation. Amy L. Maser: Data curation. Daniel W. Shrey: Conceptualization;
Data curation; Funding acquisition; Methodology; Supervision; Writing – review & editing.
Beth A. Lopour: Conceptualization; Funding acquisition; Investigation; Methodology;
Project administration; Resources; Supervision; Writing – review & editing.
FUNDING INFORMATION
Daniel W. Shrey, Children’s Hospital of Orange County, Award ID: PSF Tithe Grant.
REFERENCES
Aeschbach, D., Matthews, J. R., Postolache, T. T., Jackson, M. A.,
Giesen, H. A., & Wehr, T. A. (1999). Two circadian rhythms in
the human electroencephalogram during wakefulness. American
Journal of Physiology, 277(6), 1771–1779. https://doi.org/10
.1152/ajpregu.1999.277.6.R1771, PubMed: 10600925
Anastasiadou, M., Hadjipapas, A., Christodoulakis, M.,
Papathanasiou, E. S., Papacostas, S. S., & Mitsis, G. D. (2016).
Epileptic seizure onset correlates with long term EEG functional
brain network properties. Proceedings of the Annual
International Conference of the IEEE Engineering in Medicine
and Biology Society, EMBS, 2016-Octob, 2822–2825. https://
doi.org/10.1109/EMBC.2016.7591317
Anastasiadou, M. N., Christodoulakis, M., Papathanasiou, E. S.,
Papacostas, S. S., Hadjipapas, A., & Mitsis, G. D. (2019).
Graph theoretical characteristics of EEG-based functional brain
networks in patients with epilepsy: The effect of reference choice
and volume conduction. Frontiers in Neuroscience, 13(March),
1–18. https://doi.org/10.3389/fnins.2019.00221, PubMed:
30949021
Antoniou, I. E., & Tsompa, E. T. (2008). Statistical analysis of
weighted networks. Discrete Dynamics in Nature and Society,
2008. https://doi.org/10.1155/2008/375452
Barkovich, A. J., Miller, S. P., Bartha, A., Newton, N., Hamrick, S. E. G.,
Mukherjee, P., … Vigneron, D. B. (2006). MR imaging, MR
spectroscopy, and diffusion tensor imaging of sequential studies in
neonates with encephalopathy. American Journal of Neuroradiology,
27(3), 533–547, PubMed: 16551990
Baud, M. O., Kleen, J. K., Mirro, E. A., Andrechak, J. C., King-
Stephens, D., Chang, E. F., & Rao, V. R. (2018). Multi-day rhythms
modulate seizure risk in epilepsy. Nature Communications, 9(1),
1–10. https://doi.org/10.1038/s41467-017-02577-y, PubMed:
29311566
Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discov-
ery rate: A practical and powerful approach to multiple testing.
Journal of the Royal Statistical Society. Series B, 57(1), 289–300.
https://doi.org/10.1111/j.2517-6161.1995.tb02031.x
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038
/nrn2575, PubMed: 19190637
Burroughs, S. A., Morse, R. P., Mott, S. H., & Holmes, G. L. (2014).
Brain connectivity in West syndrome. Seizure: European Journal
of Epilepsy, 23(7), 576–579. https://doi.org/10.1016/j.seizure
.2014.03.016, PubMed: 24794162
Chapeton, J. I., Inati, S. K., & Zaghloul, K. A. (2017). Stable func-
tional networks exhibit consistent timing in the human brain.
Brain, 140(3), 628–640. https://doi.org/10.1093/brain/aww337,
PubMed: 28364547
Chen, A. C. N., Feng, W., Zhao, H., Yin, Y., & Wang, P. (2008).
EEG default mode network in the human brain: Spectral regional
field powers. NeuroImage, 41(2), 561–574. https://doi.org/10
.1016/j.neuroimage.2007.12.064, PubMed: 18403217
Chu, C. J., Leahy, J., Pathmanathan, J., Kramer, M. A., & Cash, S. S.
(2014). The maturation of cortical sleep rhythms and networks
Network Neuroscience
628
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
over early development. Clinical Neurophysiology, 125(7),
1360–1370. https://doi.org/10.1016/j.clinph.2013.11.028,
PubMed: 24418219
Chu, C. J., Kramer, M. A., Pathmanathan, J., Bianchi, M. T.,
Westover, M. B., Wizon, L., & Cash, S. S. (2012). Emergence
of stable functional networks in long-term human electroenceph-
alography. The Journal of Neuroscience, 32(8), 2703–2713.
https://doi.org/10.1523/ JNEUROSCI.5669-11.2012, PubMed:
22357854
D’Esposito, M. (2019). Are individual differences in human brain
organization measured with functional MRI meaningful?
Proceedings of the National Academy of Sciences of the
United States of America, 116(45), 22432–22434. https://doi.org
.org/10.1073/pnas.1915982116, PubMed: 31619565
David, O., Cosmelli, D., & Friston, K. J. (2004). Evaluation of differ-
ent measures of functional connectivity using a neural mass
model. NeuroImage, 21(2), 659–673. https://doi.org/10.1016/j
.neuroimage.2003.10.006, PubMed: 14980568
Dubois, J., & Adolphs, R. (2016). Building a science of individual
differences from fMRI. Trends in Cognitive Sciences, 20(6),
425–443. https://doi.org/10.1016/j.physbeh.2017.03.040,
PubMed: 28363838
Durka, P. J., Klekowicz, H., Blinowska, K. J., Szelenberger, W., &
Niemcewicz, S. (2003). A simple system for detection of EEG ar-
tifacts in polysomnographic recordings. IEEE Transactions on
Biomedical Engineering, 50(4), 526–528. https://doi.org/10
.1109/TBME.2003.809476, PubMed: 12723066
Ferri, R., Rundo, F., Bruni, O., Terzano, M. G., & Stam, C. J. (2008).
The functional connectivity of different EEG bands moves to-
wards small-world network organization during sleep. Clinical
Neurophysiology, 119(9), 2026–2036. https://doi.org/10.1016/j
.clinph.2008.04.294, PubMed: 18571469
Fingelkurts, A. A., & Fingelkurts, A. A. (2011). Persistent operational
synchrony within brain default-mode network and self-
processing operations in healthy subjects. Brain and Cognition,
75(2), 79–90. https://doi.org/10.1016/j.bandc.2010.11.015,
PubMed: 21172727
Finn, E. S., Glerean, E., Khojandi, A. Y., Nielson, D., Molfese, P. J.,
Handwerker, D. A., & Bandettini, P. A. (2020). Idiosynchrony:
From shared responses to individual differences during naturalis-
tic neuroimaging. NeuroImage, 215(April), 116828. https://doi
.org/10.1016/j.neuroimage.2020.116828, PubMed: 32276065
Fisch, B. J. (1999). Fisch and Spehlmann’s EEG primer: Basic prin-
ciples of digital and analog EEG (3rd ed.). Elsevier.
Gao, W., Gilmore, J. H., Giovanello, K. S., Smith, J. K., Shen, D.,
Zhu, H., & Lin, W. (2011). Temporal and spatial evolution of
brain network topology during the first two years of life. PLoS
ONE, 6(9). https://doi.org/10.1371/journal.pone.0025278,
PubMed: 21966479
Gao, W., Lin, W., Grewen, K., & Gilmore, J. H. (2017). Functional
connectivity of the infant human brain: Plastic and modifiable.
Neuroscientist, 23(2), 169–184. https://doi.org/10.1177
/1073858416635986, PubMed: 26929236
Garrison, K. A., Scheinost, D., Finn, E. S., Shen, X., & Constable, R. T.
(2015). The (in)stability of functional brain network measures
across thresholds. NeuroImage, 118, 651–661. https://doi.org/10
.1016/j.neuroimage.2015.05.046, PubMed: 26021218
Geier, C., Lehnertz, K., & Bialonski, S. (2015). Time-dependent
degree-degree correlations in epileptic brain networks: From assor-
tative to dissortative mixing. Frontiers in Human Neuroscience,
9(August), 1–11. https://doi.org/10.3389/fnhum.2015.00462,
PubMed: 26347641
Gonzalez-Castillo, J., Hoy, C. W., Handwerker, D. A., Robinson,
M. E., Buchanan, L. C., Saad, Z. S., & Bandettini, P. A. (2015).
Tracking ongoing cognition in individuals using brief, whole-
brain functional connectivity patterns. Proceedings of the
National Academy of Sciences of the United States of America,
112(28), 8762–8767. https://doi.org/10.1073/pnas.1501242112,
PubMed: 26124112
Hardstone, R., Poil, S. S., Schiavone, G., Jansen, R., Nikulin, V. V.,
Mansvelder, H. D., & Linkenkaer-Hansen, K. (2012). Detrended
fluctuation analysis: A scale-free view on neuronal oscillations.
Frontiers in Physiology, 3(450), 75–87. https://doi.org/10.3389
/fphys.2012.00450, PubMed: 23226132
Jalili, M., Barzegaran, E., & Knyazeva, M. G. (2014). Synchronization
of EEG: Bivariate and multivariate measures. IEEE Transactions on
Neural Systems and Rehabilitation Engineering, 22(2), 212–221.
https://doi.org/10.1109/ TNSRE.2013.2289899, PubMed:
24216751
Kaiser, D. (2008). Ultradian and circadian effects in electroenceph-
alography activity. Biofeedback, 36(4), 148.
Karoly, P. J., Ung, H., Grayden, D. B., Kuhlmann, L., Leyde, K.,
Cook, M. J., & Freestone, D. R. (2017). The circadian profile of
epilepsy improves seizure forecasting. Brain, 140(8), 2169–2182.
https://doi.org/10.1093/brain/awx173, PubMed: 28899023
Kramer, M. A., Eden, U. T., Lepage, K. Q., Kolaczyk, E. D., Bianchi,
M. T., & Cash, S. S. (2011). Emergence of persistent networks in
long-term intracranial EEG recordings. Journal of Neuroscience,
31(44), 15757–15767. https://doi.org/10.1523/JNEUROSCI.2287
-11.2011, PubMed: 22049419
Kramer, M. A., Eden, U. T., Cash, S. S., & Kolaczyk, E. D. (2009).
Network interference with confidence from multivariate time se-
ries. Physical Review E, 79(6). https://doi.org/10.1103/PhysRevE
.79.061916, PubMed: 19658533
Kuhnert, M. T., Elger, C. E., & Lehnertz, K. (2010). Long-term variabil-
ity of global statistical properties of epileptic brain networks. Chaos,
20(4). https://doi.org/10.1063/1.3504998, PubMed: 21198096
Laoprasert, P. (2011). Atlas of pediatric EEG (1st ed.). McGraw-Hill.
Lehnertz, K., Geier, C., Rings, T., & Stahn, K. (2017). Capturing
time-varying brain dynamics. EPJ Nonlinear Biomedical
Physics, 5, 2. https://doi.org/10.1051/epjnbp/2017001
Linkenkaer-Hansen, K., Nikouline, V. V, Palva, J. M., & Ilmoniemi,
R. J. (2001). Long-range temporal correlations and scaling behavior
in human brain oscillations. The Journal of Neuroscience, 21(4),
1370–1377. https://doi.org/10.1002/anie.201106423, PubMed:
22170851
Mitsis, G. D., Anastasiadou, M. N., Christodoulakis, M.,
Papathanasiou, E. S., Papacostas, S. S., & Hadjipapas, A.
(2020). Functional brain networks of patients with epilepsy ex-
hibit pronounced multiscale periodicities, which correlate with
seizure onset. Human Brain Mapping, 41(8), 2059–2076.
https://doi.org/10.1002/hbm.24930, PubMed: 31977145
Moretti, D. V., Babiloni, F., Carducci, F., Cincotti, F., Remondini,
E., Rossini, P. M., … Babiloni, C. (2003). Computerized
Network Neuroscience
629
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
processing of EEG-EOG-EMG artifacts for multi-centric studies in
EEG oscillations and event-related potentials. International
Journal of Psychophysiology, 47(3), 199–216. https://doi.org
/10.1016/S0167-8760(02)00153-8, PubMed: 12663065
Nichols, T., & Holmes, A. (2003). Nonparametric permutation tests for
functional neuroimaging. Human Brain Function, 25(August 1999),
887–910. https://doi.org/10.1016/B978-012264841-0/50048-2
Omidvarnia, A., Fransson, P., Metsäranta, M., & Vanhatalo, S.
(2014). Functional bimodality in the brain networks of preterm
and term human newborns. Cerebral Cortex, 24(10), 2657–2668.
https://doi.org/10.1093/cercor/bht120, PubMed: 23650289
Onnela, J. P., Saramäki, J., Kertész, J., & Kaski, K. (2005). Intensity
and coherence of motifs in weighted complex networks. Physical
Review E - Statistical, Nonlinear, and Soft Matter Physics, 71(6),
1–4. https://doi.org/10.1103/ PhysRevE.71.065103, PubMed:
16089800
Page, J., Lustenberger, C., & Fröhlich, F. (2018). Social, motor, and
cognitive development through the lens of sleep network dynam-
ics in infants and toddlers between 12 and 30 months of age.
Sleep, 41(4), 1–10. https://doi.org/10.1093/sleep/zsy024,
PubMed: 29506060
Pereda, E., Rial, R., Gamundi, A., & González, J. (2001).
Assessment of changing interdependencies between human
electroencephalograms using nonlinear methods. Physica D:
Nonlinear Phenomena, 148(1–2), 147–158. https://doi.org/10
.1016/S0167-2789(00)00190-1
Pernice, V., Staude, B., Cardanobile, S., & Rotter, S. (2011). How
structure determines correlations in neuronal networks. PLoS
Computational Biology, 7(5). https://doi.org/10.1371/journal
.pcbi.1002059, PubMed: 21625580
Ponten, S. C., Daffertshofer, A., Hillebrand, A., & Stam, C. J. (2010).
The relationship between structural and functional connectivity:
Graph theoretical analysis of an EEG neural mass model.
NeuroImage, 52, 985–994. https://doi.org/10.1016/j.neuroimage
.2009.10.049, PubMed: 19853665
Quian Quiroga, R., Kraskov, A., Kreuz, T., & Grassberger, P.
(2002). Performance of different synchronization measures in
real data: A case study on electroencephalographic signals.
Physical Review E - Statistical Physics, Plasmas, Fluids, and
Related Interdisciplinary Topics, 65(4), 14. https://doi.org/10
.1103/PhysRevE.65.041903, PubMed: 12005869
Righi, G., Tierney, A. L., Tager-Flusberg, H., & Nelson, C. A. (2014).
Functional connectivity in the first year of life in infants at risk for
autism spectrum disorder: An EEG study. PLoS ONE, 9(8), 1–8.
https://doi.org/10.1371/journal.pone.0105176, PubMed: 25140874
Rowan, A. J., & Tolunsky, E. (2003). Primer of EEG with a mini-atlas.
Butterworth-Heinemann.
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52,
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Schelter, B., Feldwisch-Drentrup, H., Ihle, M., Schulze-Bonhage,
A., & Timmer, J. (2011). Seizure prediction in epilepsy: From
circadian concepts via probabilistic forecasting to statistical
evaluation. Proceedings of the Annual International Conference
of the IEEE Engineering in Medicine and Biology Society, EMBS,
1624–1627. https://doi.org/10.1109/ IEMBS.2011.6090469,
PubMed: 22254634
Shrey, D. W., Kim McManus, O., Rajaraman, R., Ombao, H., Hussain,
S. A., & Lopour, B. A. (2018). Strength and stability of EEG functional
connectivity predict treatment response in infants with epileptic
spasms. Clinical Neurophysiology, 129(10), 2137–2148. https://
doi.org/10.1016/j.clinph.2018.07.017, PubMed: 30114662
Smith, R. J., Sugijoto, A., Rismanchi, N., Hussain, S. A., Shrey, D. W.,
& Lopour, B. A. (2017). Long-range temporal correlations reflect
treatment response in the electroencephalogram of patients with
infantile spasms. Brain Topography, 30(6). https://doi.org/10.1007
/s10548-017-0588-5, PubMed: 28905146
Smith, R. J., Hu, D. K., Shrey, D. W., Rajaraman, R., Hussain, S. A.,
& Lopour, B. A. (2020). Computational characteristics of interic-
tal EEG as objective markers of epileptic spasms. BioRxiv. https://
doi.org/10.1101/2020.11.13.380691
Sparrow, S. S., Cicchetti, D. V., & Saulnier, C. A. (2016). Vineland
adaptive behavior scales (3rd ed.). Pearson.
Stam, C. J., & Reijneveld, J. C. (2007). Graph theoretical analysis of com-
plex networks in the brain. Nonlinear Biomedical Physics, 1(3), 1–19.
https://doi.org/10.1186/1753-4631-1-3, PubMed: 17908336
Stern, J. M. (2005). Atlas of EEG patterns (2nd ed.). Lippincott
Williams & Wilkins.
Stevens, M. C. (2009). The developmental cognitive neuroscience of
functional connectivity. Brain and Cognition, 70(1), 1–12. https://
doi.org/10.1016/j.bandc.2008.12.009, PubMed: 19185406
Tokariev, A., Roberts, J. A., Zalesky, A., Zhao, X., Vanhatalo, S.,
Breakspear, M., & Cocchi, L. (2019). Large-scale brain modes
reorganize between infant sleep states and carry prognostic infor-
mation for preterms. Nature Communications, 10(1). https://doi
.org/10.1038/s41467-019-10467-8, PubMed: 31197175
Tokariev, A., Vanhatalo, S., & Palva, J. M. (2016). Analysis of infant
cortical synchrony is constrained by the number of recording
electrodes and the recording montage. Clinical Neurophysiology,
127(1), 310–323. https://doi.org/10.1016/j.clinph.2015.04.291,
PubMed: 26122070
Tóth, B., Urbán, G., Háden, G. P., Márk, M., Török, M., Stam, C. J.,
& Winkler, I. (2017). Large-scale network organization of EEG
functional connectivity in newborn infants. Human Brain
Mapping, 38(8), 4019–4033. https://doi.org/10.1002/ hbm
.23645, PubMed: 28488308
Tymofiyeva, O., Hess, C. P., Ziv, E., Tian, N., Bonifacio, S. L.,
McQuillen, P. S., … Xu, D. (2012). Towards the “baby connec-
tome”: Mapping the structural connectivity of the newborn brain.
PLoS ONE, 7(2). https://doi.org/10.1371/journal.pone.0031029,
PubMed: 22347423
ven der Velde, B., Haartsen, R., & Kemner, C. (2019). Test-retest reli-
ability of EEG network characteristics in infants. Brain and Behavior,
9(5), 1–10. https://doi.org/10.1002/brb3.1269, PubMed: 30912271
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of
“small-world” networks. Nature, 393(6684), 440–442. https://
doi.org/10.1038/30918, PubMed: 9623998
Xie, W., Mallin, B. M., & Richards, J. E. (2019). Development of
brain functional connectivity and its relation to infant sustained
attention in the first year of life. Developmental Science, 22(1),
1–18. https://doi.org/10.1111/desc.12703, PubMed: 29968370
Network Neuroscience
630
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3