研究 - 麻省理工学院人工智能研究专业

研究

Large-scale network dynamics of beta-band
oscillations underlie auditory perceptual
决策

Mohsen Alavash1,2, Christoph Daube2, Malte Wöstmann1,2,
Alex Brandmeyer2, and Jonas Obleser1,2

1心理学系, University of Lübeck, 德国
2Max Planck Research Group “Auditory Cognition,” Max Planck Institute for Human Cognitive and
Brain Sciences, 莱比锡, 德国

关键词: Network dynamics, Perceptual decision, Oscillation, 乙二醇, Functional connectivity

开放访问

杂志

抽象的

Perceptual decisions vary in the speed at which we make them. Evidence suggests
that translating sensory information into perceptual decisions relies on distributed
interacting neural populations, with decision speed hinging on power modulations of
the neural oscillations. Yet the dependence of perceptual decisions on the large-scale
network organization of coupled neural oscillations has remained elusive. We measured
magnetoencephalographic signals in human listeners who judged acoustic stimuli composed
of carefully titrated clouds of tone sweeps. These stimuli were used in two task contexts,
in which the participants judged the overall pitch or direction of the tone sweeps. 我们
traced the large-scale network dynamics of the source-projected neural oscillations on a
trial-by-trial basis using power-envelope correlations and graph-theoretical network
发现. In both tasks, faster decisions were predicted by higher segregation and lower
integration of coupled beta-band (~16–28 Hz) oscillations. We also uncovered the brain
network states that promoted faster decisions in either lower-order auditory or higher-order
control brain areas. Speciﬁcally, decision speed in judging the tone sweep direction
critically relied on the nodal network conﬁgurations of anterior temporal, cingulate,
and middle frontal cortices. Our ﬁndings suggest that global network communication
during perceptual decision-making is implemented in the human brain by large-scale
couplings between beta-band neural oscillations.

作者总结

The speed at which we make perceptual decisions varies. This translation of sensory
information into perceptual decisions hinges on dynamic changes in neural oscillatory
活动. 然而, the large-scale neural-network embodiment supporting perceptual
decision-making is unclear. We addressed this question by experimenting two auditory
perceptual decision-making situations. Using graph-theoretical network discovery, 我们
traced the large-scale network dynamics of coupled neural oscillations to uncover the
brain network states that support the speed of auditory perceptual decisions. 我们发现
that higher network segregation of coupled beta-band oscillations supports faster auditory
perceptual decisions over trials. 而且, when auditory perceptual decisions are relatively
difﬁcult, the decision speed beneﬁts from higher segregation of frontal cortical areas, 但
lower segregation and greater integration of auditory cortical areas.

引文: Alavash, M。, Daube, C。,
Wöstmann, M。, Brandmeyer, A。, &
Obleser, J. (2017). Large-scale network
dynamics of beta-band oscillations
underlie auditory perceptual
决策. 网络
神经科学, 1(2), 166–191.
https://doi.org/10.1162/netn_a_00009

DOI:
https://doi.org/10.1162/netn_a_00009

支持信息:
http://www.mitpressjournals.org/doi/
suppl/10.1162/netn_a_00009

已收到: 19 十二月 2016
公认: 1 行进 2017

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
Mohsen Alavash
mohsen.alavash@uni-luebeck.de

处理编辑器:
奥拉夫·斯波恩斯

版权: © 2017
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

1
2
1
6
6
1
0
9
1
9
3
1
n
e
n
_
A
_
0
0
0
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Brain network states and auditory perceptual decision-making

Neural oscillation:
A rhythmic voltage ﬂuctuation
generated by the electrical activity of
neuronal populations and
characterized by its dominant
频率

Large-scale network:
A network comprising widely
distributed nodes showing short- 和
long-distance associations

Perceptual decision-making:
Evaluation—often implicit—of
sensory information in order to arrive
at a behaviorally relevant decision

Topology:
The wiring diagram of a set of
interacting elements, representing
how their associations are organized
as a whole

Network modularity:
Segregation of a network into groups
of partner nodes showing dense
intraconnections but sparse
interconnections

Network integration:
The capacity of a network to
combine distributed information
across its nodes, often characterized
by global network efﬁciency

Functional connectivity:
Statistical dependency between
time-varying brain activities

Contemporary neuroscience is departing from a focus solely on regional brain activations,
toward emphasizing the network organization of brain function. This view recognizes the
large-scale interactions between distributed cortical areas as the biological basis of behav-
ior and cognition (Misic & 斯波恩斯, 2016; 斯波恩斯, 2014). A more mechanistic view holds
frequency-speciﬁc neural oscillations to be relevant to both behavior and cognition (Buzsaki
& Draguhn, 2004; 恩格尔, 格尔洛夫, 希尔格塔格, & 诺尔特, 2013). How the large-scale network or-
ganization of interacting neural oscillations (S. 崇拜 & 崇拜, 2012; 西格尔, 唐纳, & 恩格尔,
2012)—in particular,
temporal network dynamics (Kopell, Gritton, Whittington, &
克莱默, 2014; Shine et al., 2016)—relate to perception and cognition is poorly understood,
然而. Here we investigated the dependence of auditory perceptual decision-making in
humans on spectrally, temporally, and topologically resolved large-scale brain networks.

他们的

Accumulating evidence suggests that frequency-speciﬁc neural oscillations are key to pro-
cessing sensory information (de Pesters et al., 2016; Hanslmayr, 总的, Klimesch, & 夏皮罗,
2011; J. 中号. 崇拜, 数量, 库拉谢卡尔, & 崇拜, 2010). 例如, previous studies indi-
cate that attentional modulation of cortical excitability in sensory regions is reﬂected in oscil-
latory alpha power (~8–10 Hz) under visual (詹森 & Mazaheri, 2010; Lange, Oostenveld, &
薯条, 2013; Lou, 李, Philiastides, & Sajda, 2014) or auditory tasks (穆勒 & 魏兹, 2012;
Strauß, Wöstmann, & Obleser, 2014; 魏兹, 穆勒, Jatzev, & Bertrand, 2014; Wöstmann,
Herrmann, Maess, & Obleser, 2016). 此外, it has been shown that audiovisual per-
ception relies on synchronized cortical networks within beta (~20 Hz) 和伽玛 (~80 Hz)
乐队 (希普, 恩格尔, & 西格尔, 2011). 最近, studies have begun to explore more speciﬁ-
cally whether modulations in neural oscillations arise from lower-order sensory or higher-order
control areas (Friese et al., 2016; Kayser, McNair, & Kayser, 2016; 公园, Ince, Schyns, Thut, &
总的, 2015; 萨达吉亚尼 & Klenschmidt, 2016). 这里, on the basis of localization of neuro-
physiological sources (希勒布兰德, 辛格, Holliday, Furlong, & 巴恩斯, 2005), 我们探索了
large-scale network organization of interacting neural oscillations during auditory processing.

Speciﬁcally, we asked how the network topology

of coupled neural oscillations
(Bassett et al., 2009) relates to the listeners’ perceptual decisions.
In a previous magneto-
encephalography (乙二醇) 学习, Nicol and colleagues (2012) measured the synchronization of
brain gamma-band (33–64 Hz) responses in an auditory mismatch-negativity paradigm. 他们
found that deviant stimuli were associated with increases in local network clustering in left
temporal sensors within the immediate response period. Building upon prestimulus hemody-
namic responses, 萨达吉亚尼, 波琳娜, 克莱因施密特, and D’Esposito (2015) recently suggested
higher modularity of brain networks as a proxy for perceiving near-threshold auditory tones.
而且, it has been shown that higher global integration of brain networks measured from
prestimulus high-alpha band MEG responses precedes the detection of near-threshold stimuli
(Leske et al., 2015; 魏兹, Wuhle et al., 2014). 总共, brain network correlates of auditory
perception have been observed on different topological scales.

Naturally, the cortical networks involved in processing sensory information require context-
sensitive conﬁgurations, as well as moment-to-moment reconﬁgurations to fulﬁll dynamic
task adjustments (Bassett, Meyer-Lindenberg, Achard, Duke, & 布莫尔, 2006). This leads
the neural coactivations, which shape the brain’s functional connectivity, to diverge from
their underlying structural connectivity (Marrelec, Messe, Giron, & Rudrauf, 2016; Misic et al.,
2016; 公园 & 弗里斯顿, 2013). 像这样, the estimation of functional connectivity, when collapsed
随着时间的推移, overemphasizes structural connectivity (蜂蜜, Kotter, Breakspear, & 斯波恩斯, 2007;
沉, 和记黄埔, Bezgin, Everling, & McIntosh, 2015) and disregards the temporal dy-
namics of large-scale brain network topology (克林格尔巴赫, McIntosh, 里特尔, Jirsa, & 德科,

网络神经科学

167

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

1
2
1
6
6
1
0
9
1
9
3
1
n
e
n
_
A
_
0
0
0
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Brain network states and auditory perceptual decision-making

Graph-theoretical network analysis:
Mathematical formalization aimed at
studying systems of interacting
元素 (节点) with pair-wise
协会 (连接)

Acoustic texture:
An auditory object composed of a
dense overlay of multiple,
frequency-modulated tone sweeps

2015; 扎莱斯基, 假如, Cocchi, Gollo, & Breakspear, 2014). 然而, these dynamics have
to behavior during challenging motor or cognitive tasks (Alavash,
been found relevant
Thiel, & Giessing, 2016;
Bassett et al., 2013; Braun et al., 2015; Chai, Mattar, 空白的,
Fedorenko, & Bassett, 2016).

所以, to ﬁnd the neural network substrate of auditory perceptual decision-making,
we adopted the framework of dynamic brain networks (Calhoun, 磨坊主, Pearlson, & Adali,
2014; 德科, 托诺尼, 博利, & 克林格尔巴赫, 2015) and merged this with neural oscillations to
uncover frequency-speciﬁc brain network states. Our method is based on both a previously
established technique to estimate large-scale neural
interactions in source space (希普,
Hawellek, 科尔贝塔, 西格尔, & 恩格尔, 2012) and graph-theoretical network analysis (布莫尔
& 斯波恩斯, 2009).

We applied this approach to MEG signals measured from human listeners who made per-
ceptual decisions on brief acoustic textures under two distinct task sets. The acoustic textures
consisted of densely layered tone sweeps that varied in their overall pitch (high or low) 还有
as in the proportion of coherent tones in terms of sweep direction (up or down; Figure 1A).
Using the identical set of stimuli, two auditory paradigms with distinct decision contexts were
designed to deliver challenging perceptual decision-making tasks (Figure 1B). 像这样, 印度人-
viduals’ perceptual decision accuracy and speed ﬂuctuated on a trial-by-trial basis (Figure 1C).
This allowed us to investigate the relation between frequency-speciﬁc brain network states
and trial-by-trial decision-making performance (数字 2). 自从, under each of the two per-
ceptual decision-making tasks, subjects focused on a different acoustic feature of an identical
set of auditory stimuli, two dynamic network proﬁles were expected. 第一的, we anticipated that
the brain network states responsible for the cortico-cortical communication (mainly fronto-
颞) involved in common for both of the tasks would predict decision-making per-
formance. 第二, we expected that any task-speciﬁc brain network states emerging from
auditory association or higher-order decision areas would differentially predict performance
in either of the tasks.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

1
2
1
6
6
1
0
9
1
9
3
1
n
e
n
_
A
_
0
0
0
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

结果

Auditory Perceptual Decision-Making Performance

The participants judged the overall pitch or sweep direction of the acoustic texture stimuli
and showed accuracies around 70%, as we had intended from use of the adaptive-tracking
procedure (average accuracies ± SEMs: pitch task = 76% ± 1.1, direction task = 70% ± 2.1;
−1] ± SEMs: pitch task = 1.8 ± 0.1, direction task = 1.7 ± 0.1).
mean decision speed [s
The bootstrap Kolmogorov–Smirnov test revealed that the distributions of the behavioral mea-
sures did not signiﬁcantly deviate from a normal distribution (准确性: pitch task p = 0.8,
direction task p = 0.1; decision speed: pitch task p = 0.8, direction task p = 0.5). 尽管
our experimental efforts to equate the difﬁculties of both tasks, analysis of variance (ANOVA)
revealed main effects of task for both accuracy [F(1, 19) = 6, p = 0.024, η2
= 0.05] 和
G
= 0.01]. Participants showed signiﬁcantly
decision speed [F(1, 19) = 9.9, p = 0.005, η2
G
lower accuracy in the direction task than in the pitch task (exact permutation test for a paired
测试; p = 0.02). 此外, the decision speed was signiﬁcantly lower in the direction task
than in the pitch task (p = 0.004). The experimental manipulation of the pitch of the acoustic
textures yielded signiﬁcant effects of stimulus spectral center on both accuracy [F(3, 57) = 64,
p = 2e−16, η2
= 0.02]. 然而,
G
stimulus coherence had a signiﬁcant effect only on accuracy [F(3, 57) = 45.3, p = 4e−15,
= 0.12]. Across participants, we found a signiﬁcant positive correlation between decision
η2
G

= 0.18] and decision speed [F(3, 57) = 30, p = 9e−12, η2
G

网络神经科学

168

Brain network states and auditory perceptual decision-making

(A) Auditory stimuli used to design the tasks. 每个
数字 1. Experimental stimuli and tasks.
cell represents an acoustic texture, which can be viewed as a pattern of sound sweeps whose fre-
quency increases or decreases over time. Each texture stimulus had a duration of 400 ms and
consisted of 72 frequency-modulated (FM) sweeps of 100-ms duration. The stimuli were titrated
along two dimensions: overall coherence and spectral center. For a given stimulus, a variable pro-
portion (25–100%) of the sweeps were assigned the same frequency slope (连贯性)—that is,
their frequency went up or down at the same rate over time. The rest of the sweeps had a randomly
assigned slope. 此外, each stimulus had one of eight spectral centers relative to a mean center
频率. (乙) Two auditory perceptual decision-making tasks, namely pitch and direction discrimi-
国家, were designed using the identical acoustic stimuli. During the pitch task, the subjects judged
the overall pitch of the stimuli (low or high). In the direction task, they were asked to report the
overall direction (up or down) in which the frequencies of the stimuli were changing (增加
or decreasing) 随着时间的推移. Subjects had 3 s at maximum to press one of two response buttons
to report their perceptual decision.
In each task, the decision labels for the left-hand and right-
hand buttons (indicated by “1”/“2”) were randomized across trials and shown after stimulus pre-
sentation within the response window. There were eight blocks per task, and the order of the
tasks alternated from one block to another. (C) Exemplary trial-by-trial auditory perceptual decision
准确性 (moving average of four trials applied to correct/incorrect responses) and decision speed
−1). Before the actual tasks, adaptive perceptual tracking was used to tailor the
([响应时间]
two tasks per participant, so that their overall accuracies converged at ~70%. This led individuals’
decision accuracies and speeds to ﬂuctuate over trials. Note that for the purpose of the regression
分析 (see Materials and Methods), the trial-wise estimates of accuracy and speed were ﬁrst rank-
transformed and then normalized (IE。, z-scored). Exemplary data are shown for a representative
participant in the pitch task, second block.

speed in the pitch task and decision speed in the direction task (Spearman’s ρ = 0.9, p =
5e −6). 然而, the correlation between the accuracies in the two tasks was not signiﬁcant
(ρ = 0.2, p = 0.47).

The correlation between the trial-by-trial estimates of decision accuracy or speed and the
trial-by-trial acoustic features of the stimuli was tested using a two-level regression analy-
姐姐 (see Materials and Methods). We found a signiﬁcant positive correlation between deci-
sion speed and stimulus coherence in the direction task (average regression weights ± SEMs:
0.045 ± 0.012; one-sample exact permutation test: p = 9e −4). The trial-by-trial estimates
of decision accuracy in the direction task also showed a signiﬁcant positive correlation with
the coherence of the stimuli (average regression weights ± SEMs: 0.087 ± 0.01, p = 2e −6).
A signiﬁcant negative correlation emerged between decision accuracy in the pitch task and
stimulus coherence (average regression weight ± SEM: −0.022 ± 0.01, p = 0.03).

网络神经科学

169

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

1
2
1
6
6
1
0
9
1
9
3
1
n
e
n
_
A
_
0
0
0
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Brain network states and auditory perceptual decision-making

来源
locations

mean functional connectivity

1.7

.05

e
r
哦
C
s
z

–1.7

–1

0
power corr.

mean local network eﬃciency

1.7

.07

e
r
哦
C
s
z

–1.7

network modularity

1.7

e
r
哦
C
s
z

–1.7

global network eﬃciency

我

t
哦
p
哦
哦
G
我
C
A

我

s
C
A
e

我

e
r
哦
C
s
z

1.7

–.08

–1.7

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

1
2
1
6
6
1
0
9
1
9
3
1
n
e
n
_
A
_
0
0
0
0
9
p
d

审判

128
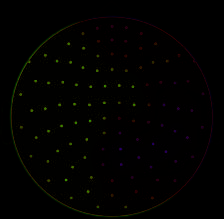
数字 2. Trial-by-trial dynamics of brain functional connectivity and network topology. To inves-
tigate the relation between the frequency-speciﬁc brain network states and decision-making perfor-
曼斯, all-to-all power-envelope correlations (source connectivity matrix; top left) and whole-brain
graph-theoretical network metrics were estimated at 10% of the network density (see Materials and
方法). This analysis was done at each frequency within 1–32 Hz, and per trial in the course of
each pitch and direction task. The temporal graph-theoretical metrics captured brain network states
on the local (local efﬁciency), intermediate (模块化), and global (global efﬁciency) scales of
network topology. The yellow-shaded ovals in brain graphs illustrate the topological scale at which
each network metric is measured. Global efﬁciency (bottom graph) is inversely related to the sum
of shortest path lengths (例如, orange path) between every pair of nodes. Mean local efﬁciency
(top graph) is equivalent to global efﬁciency computed on the direct neighbors of each node
(例如, the orange node), which is then averaged over all nodes. 模块化 (middle graph) 的-
scribes the segregation of partner nodes into relatively dense groups (这里, the orange nodes forming
four modules), which are sparsely interconnected. For the purpose of the regression analysis (看
Materials and Methods), the trial-wise estimates of network metrics were ﬁrst rank-transformed
and then normalized (IE。, z-scored). Exemplary data are shown for a representative subject, 作为
in Figure 1C.

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

网络神经科学

170

Brain network states and auditory perceptual decision-making

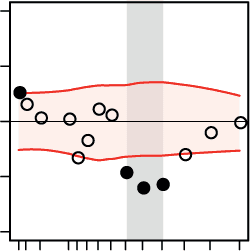
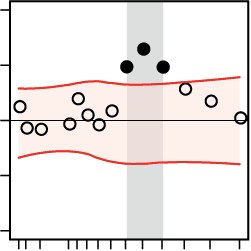
Neural Oscillatory Power During Auditory Perceptual Decision-Making

We investigated power perturbations in the MEG oscillatory signal while subjects listened to
the acoustic textures and judged either their overall pitch or sweep direction. As is illustrated in
数字 3, MEG oscillatory alpha (~8–13 Hz) power was increased relative to the baseline inter-
val (–0.5 to 0 s) just after stimulus presentation. 此外, during and after stimulus presen-
tation but before the response prompt (0 到 1 s), we observed left-lateralized decrease in MEG
oscillatory power in the low- and mid-beta band (~14–24 Hz) relative to the baseline interval.
The above perturbations in alpha and beta bands were similarly observed in both the pitch and
direction tasks (Figures 3A and 3B, ﬁrst two panels) and are well in line with previous studies
on the neural substrates of perceptual decision-making (唐纳, 西格尔, 薯条, & 恩格尔, 2009;
Haegens et al., 2011; 凯莉 & O’Connell, 2015; O’Connell, Dockree, & 凯莉, 2012). 最后,
as expected, there was strong, motor-related suppression in the MEG oscillatory power rela-
tive to baseline within the time interval when the subjects manually reported their perceptual

A Pitch task

]
z
H

[
y
C
n
e
你
q
e
r
F

27.8

24.2
21.1
18.3
16
13.9

10.5
8

–.5

1.5

刺激

response
迅速的

时间 [s]

B Direction task

27.8

24.2
21.1
18.3
16
13.9

]
z
H

[
y
C
n
e
你
q
e
r
F

10.5
8

–.5

1.5

刺激

response
迅速的

时间 [s]

–1

–2

–1

–2

]
乙
d
[

r
e
w
哦
p

]
乙
d
[

r
e
w
哦
p

–.2

–.4

–.6

]
乙
d
[

r
e
w
哦
p

–.2

–.4

–.6

]
乙
d
[

r
e
w
哦
p

decision speed ~ source power

solid: p<.05 i t h g e w n o i s s e r g e r n a e m 1 . 0 1 – . 1 4 8 12 18 24 32 frequency [Hz] decision speed ~ source power solid: p<.05 i t h g e w n o i s s e r g e r n a e m 1 . 0 1 – . 1 4 8 12 18 24 frequency [Hz] 32 non-parametric conﬁdence interval 0-1s, 8-32 Hz 0-1s, 8-32 Hz Figure 3. Dynamics of neural oscillatory power under each auditory task and their relation to the speed of perceptual decisions. (Left) Spectrotemporal representations of the epoched signals during (A) the pitch task and (B) the direction task were estimated and averaged over trials, 102 com- bined gradiometer sensors, and all subjects (N = 20). Whereas an increase in oscillatory alpha (8–13 Hz) power was observed time-locked to the auditory stimulation relative to the baseline interval (–0.5 to 0 s), there was a decrease in oscillatory power within the low- and mid-beta bands (14–24 Hz) during the time window in which participants listened to the stimuli (0 to 1 s). (Middle) The topographical maps show the broadband baseline-corrected oscillatory power (8–32 Hz) from stimulus onset to the onset of the response prompt (0–1 s). Note that within this time period, the subjects were not yet aware of the mapping between the decision labels (pitch task: high/low; direction task: up/down) and the left-hand/right-hand response buttons, since the mapping was randomized across trials. (Right) Results from the regression analysis. The relation between the ongoing power of neural oscillations and decision speed was investigated by means of linear regressions in which the trial-by-trial decision speed was predicted by the oscillatory power of source signals. In the course of both auditory tasks, faster perceptual decisions were nega- tively correlated with the ongoing oscillatory power of source signals within the alpha and beta bands. The black circles show normalized regression weights averaged over subjects at each fre- quency. The horizontal shaded regions show 95% conﬁdence intervals of the null mean regression weights generated by circularly shifting the behavioral responses across trials (corrected for mul- tiple comparisons across frequency bins using the false-coverage statement rate [FCR]; p < 0.05). Network Neuroscience 171 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making decision following the response prompt (Pfurtscheller & Lopes da Silva, 1999). This perturba- tion was widely distributed within the alpha and beta bands (8–32 Hz; Figures 3A and 3B, ﬁrst panels). Since the aim of this study was to ﬁnd the relation between frequency-speciﬁc brain net- work states and auditory perceptual decision-making on a trial-by-trial basis, we next focused on trial-by-trial ﬂuctuations in the power of the source-projected signals. Toward this end, we implemented a general linear model (GLM) per participant, whereby the time series estimates of trial-by-trial decision accuracy or speed (Figure 1C) were predicted by the baseline-corrected power of the whole-brain source-projected signals. We found signiﬁcant negative correlations between decision speed during either the pitch or direction task and ongoing neural oscillatory power within the alpha and beta bands (8–32 Hz; Figures 3A and 3B, third panels). These results indicate that, during both the pitch and direction tasks, a stronger decrease in neural oscillatory power relative to the baseline interval correlated with faster perceptual decisions. However, we found no signiﬁcant correlation between decision accuracy and the ongoing oscillatory power of the source-projected signals. Whole-Brain Network Dynamics of Beta-Band Oscillations Predict Decision Speed The aim of this study was to ﬁnd the frequency-speciﬁc brain network states underlying individuals’ perceptual decision-making in the course of judging auditory stimuli. The audi- tory stimuli were identical but were presented in two distinct task sets—that is, either judging the overall pitch or the overall direction of frequency-modulated tone sweeps. To predict trial-by-trial decision-making performance from the ongoing brain network states, we imple- mented a linear regression model in which the time series estimates of trial-by-trial decision accuracy or speed (Figure 1C) were predicted by temporal graph-theoretical network metrics (Figure 2). 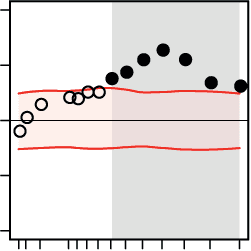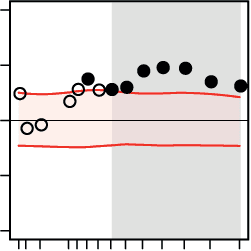On the whole-brain level, for both the pitch and direction tasks, we found signiﬁcant cor- relations between decision speed, on the one hand, and the functional connectivity and topol- ogy of dynamic brain networks, on the other hand (Figure 4). These correlations peaked within the beta-band range (Figure 4, solid points). The signiﬁcant correlations indicate that, for both the pitch and direction tasks, higher local efﬁciency but lower global efﬁciency of large- scale brain networks supported faster perceptual decisions (Figure 4, second and last columns, respectively). In addition, higher segregation of brain network modules predicted faster per- ceptual decisions in both tasks (Figure 4, third column). More speciﬁcally, we found positive correlations between the mean functional connectivity of dynamic brain networks and decision speed in both the pitch and direction task within the frequency range of 16 to 28 Hz (Figure 4, ﬁrst column). In both tasks, faster perceptual decisions about the acoustic textures were accompanied by increases in the mean functional connectivity of dynamic brain networks over trials. This effect was not limited to functional connectivity, but was also reﬂected in the topology of dynamic brain networks. On the local scale of network topology, higher mean local efﬁciency of dynamic brain networks within the frequency range of 16 to 28 Hz predicted faster decisions in both tasks over trials (Figure 4, second column). Moreover, on the intermediate level of network topology, higher modularity of dynamic brain networks at the same frequencies also predicted faster decisions in both tasks (Figure 4, third column). Finally, on the global scale of network topology, faster decisions were predicted by decreases in global network efﬁciency at frequencies ranging from 18 to 21 Hz Network efﬁciency: A graph-theoretical measure inversely related to the average length of the shortest paths existing between network nodes Network Neuroscience 172 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making A Regression of decision speed during pitch task on brain network dynamics source locations topological scale –1 0 power corr. mean functional connectivity 1 mean local network eﬃciency network modularity global network eﬃciency i t h g e w n o i s s e r g e r n a e m 1 . 0 1 – . 1 4 8 12 18 24 frequency [Hz] i t h g e w n o i s s e r g e r n a e m 1 . 0 1 – . 32 1 4 8 12 18 24 frequency [Hz] i t h g e w n o i s s e r g e r n a e m 1 . 0 1 – . 32 1 4 8 12 18 24 frequency [Hz] i t h g e w n o i s s e r g e r n a e m 1 . 0 1 – . 32 1 4 8 12 18 24 frequency [Hz] 32 non-parametric conﬁdence interval (solid: p<.05) B Regression of decision speed during direction task on brain network dynamics mean functional connectivity mean local network eﬃciency network modularity global network eﬃciency i t h g e w n o i s s e r g e r n a e m 1 . 0 1 – . 1 4 8 12 18 24 frequency [Hz] i t h g e w n o i s s e r g e r n a e m 1 . 0 1 – . 32 1 4 8 12 18 24 frequency [Hz] i t h g e w n o i s s e r g e r n a e m 1 . 0 1 – . 32 1 4 8 12 18 24 frequency [Hz] i t h g e w n o i s s e r g e r n a e m 1 . 0 1 – . 32 1 4 8 12 18 24 frequency [Hz] 32 non-parametric conﬁdence interval (solid: p<.05) Figure 4. Whole-brain network dynamics of beta-band oscillations predicted decision speed. The relation between the ongoing dynamics of large-scale brain networks and perceptual decisions on auditory stimuli was investigated by means of linear regressions in which trial-by-trial decision speed was predicted by temporal graph-theoretical network metrics. This analysis was done sep- arately for each (A) pitch and (B) direction task, at frequencies ranging from 1 to 32 Hz. In the course of both auditory tasks, faster perceptual decisions positively correlated with the ongoing local efﬁciency (second column) and modular segregation (third column) of brain networks built upon beta-band oscillations. However, higher global integration showed the opposite effect (fourth column). Black circles indicate the mean regression weights averaged over subjects at each fre- quency. Horizontal shaded regions show 95% conﬁdence intervals of the null mean regression weights generated by circularly shifting the behavioral responses across trials (corrected for mul- tiple comparisons across frequency bins using the false-coverage statement rate; p < 0.05). The graphs at top provide schematic illustrations of graph-theoretical metrics capturing brain network states at the local (local efﬁciency), intermediate (modularity), and global (global efﬁciency) scales of topology. The yellow shaded ovals illustrate the topological scale at which each network metric is measured. (Figure 4, fourth column). Note that we did not observe any signiﬁcant correlation between the trial-by-trial estimates of decision accuracy and brain network metrics in either of the tasks. The analysis of neurobehavioral correlations was based on estimating all-to-all source con- nectivity per trial, which covered the time points from −0.5 to 1.5 s in steps of 0.05 s. To further investigate possible predictions from pre- or poststimulus dynamic network states, we applied the same analyses to the data measured during the prestimulus interval (−0.85 to 0 s) or the poststimulus interval (0 to +1 s) separately. In addition, to examine the extent to which our results might merely reﬂect neural processes involved in giving manual responses after the response prompt (see Figure 3), we also analyzed the mid-beta-band (16–28 Hz) power Network Neuroscience 173 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making correlations using only the data measured during the response window (+1 to +1.5 s). None of these analyses revealed consistent signiﬁcant correlations with the speed of auditory per- ceptual decisions (Alavash, Daube, Wöstmann, Brandmeyer, & Obleser, 2017, Figure S1). To test the task speciﬁcity of the correlations between a given network diagnostic and trial- by-trial decision accuracy or speed, we also computed mean differences in the regression weights. We found no signiﬁcant difference between the two tasks in predicting decision accuracy or speed from the ongoing dynamics of network topology on the whole-brain level. In addition, to investigate the possible lead/lag relationship between brain network states and trial-by-trial decision-making performance, we computed the cross-correlations between behavioral time series, on the one hand, and the dynamics of brain networks, on the other hand. This analysis replicated signiﬁcant neurobehavioral correlations that peaked at a zero trial lag (Alavash et al., 2017, Figure S2). We also considered the possible effect of graph thresholding at 10% of network density on dynamic functional connectivity. Toward this aim, we derived the power-envelope coupling strength without thresholding the temporal graphs, and subsequently used raw trial-by-trial measures of functional connectivity in the linear regression analysis. The results were consis- tent with our main ﬁnding: faster perceptual decisions were positively correlated with power- envelope coupling between beta-band neural oscillations (Alavash et al., 2017, Figure S4). This ﬁnding suggests that the functional connectivity dynamics of beta-band oscillations are not diminished by ﬁxing the connection density of the temporal brain graphs at 10%. More- over, our results were also present when brain graphs were thresholded at 5% of network density (Alavash et al., 2017, Figure S8). Finally, to dissociate network from power effects, we implemented a linear regression analysis by adding the trial-by-trial estimates of source power as an additional regressor in the model. This analysis revealed that the network dynam- ics of beta-band oscillatory power predicted trial-by-trial decision speed over and above the oscillatory source power (Alavash et al., 2017, Figure S5). In an additional analysis, we investigated the dependence of trial-by-trial network metrics on trial-by-trial acoustic features (i.e., spectral center and stimulus coherence) by means of separate linear regression models (consistent with the main analysis). In each model, we treated the trial-by-trial acoustic features as the dependent variable and tested the signif- icance of the mean regression weights averaged over subjects. On the whole-brain level, we did not observe any consistent signiﬁcant correlation between brain network metrics and acoustic features in either of the tasks (Alavash et al., 2017, Figure S7). In addition, our main ﬁnding—the brain–behavior relation observed on the whole-brain level—was still present when we did not control for the acoustic features of the trial-by-trial stimuli in our regres- sion model. These ﬁndings together suggest that the large-scale network organization of cou- pled beta-band oscillations during auditory perceptual decision-making is not globally altered by the external perturbation induced by stimuli. The global conﬁguration of brain networks, rather, is organized according to the decision goal in light of which the auditory stimuli need to be evaluated. Overall, our ﬁndings show that the dynamics of brain functional connectivity predict trial-by-trial ﬂuctuations in the speed at which auditory perceptual decisions are made and executed. More importantly, faster decisions positively correlated with the ongoing local clustering and modular segregation of large-scale brain networks over trials. At the same time, faster decisions were also predictable from a decrease in the global integration of dynamic brain networks. Brain network correlates of auditory perceptual decision-making were found Network Neuroscience 174 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making only for decision speed and were similar across both task sets. Additionally, our ﬁndings were speciﬁc to the mid-beta band (~20 Hz) of neural oscillations and were only observed when neural oscillatory responses within both the pre- and poststimulus intervals were used to estimate the trial-by-trial brain network states. Regional Network States of Beta-Band Oscillations Predict Decision Speed The participants judged identical acoustic stimuli under two distinct task sets. Therefore, we not only expected similar network states to correlate with auditory perceptual decision-making in both tasks (mainly associated with frontotemporal cortical communication), but also antic- ipated ﬁnding task-speciﬁc network states (potentially emerging from auditory association or higher-order decision areas). On the whole-brain level, we found no signiﬁcant difference between the two tasks in predicting the trial-by-trial speed or accuracy of auditory perceptual decisions from the ongoing dynamics of brain networks. However, the regional properties of large-scale brain networks could still predict decision speed speciﬁcally in either the pitch or the direction task, or in both, but in different directions. Thus, we aimed to investigate the regional network states that would differentially predict the speed of auditory perceptual decisions during the pitch versus the direction task. 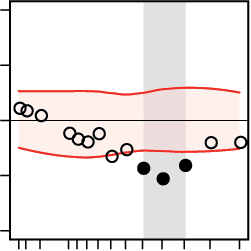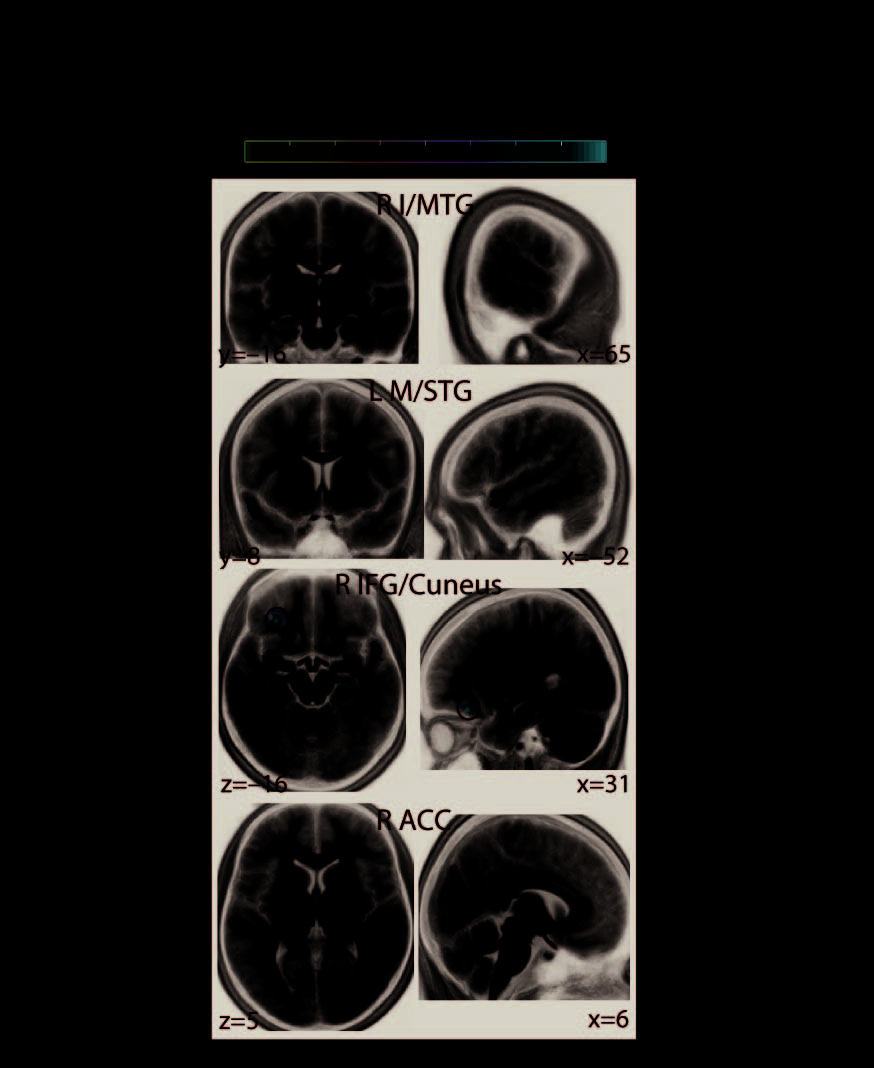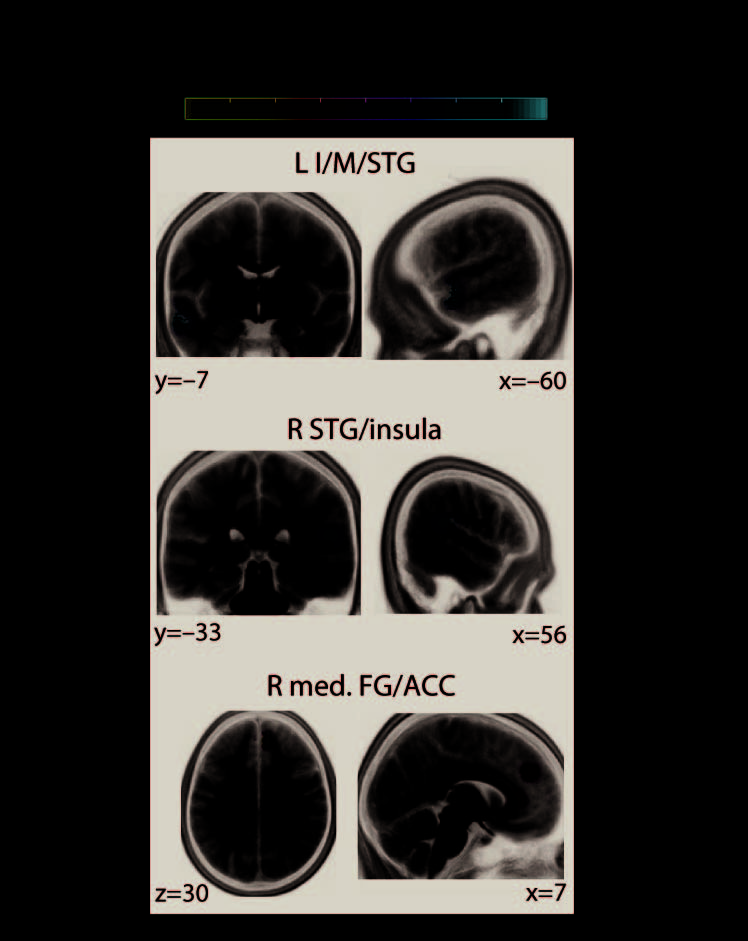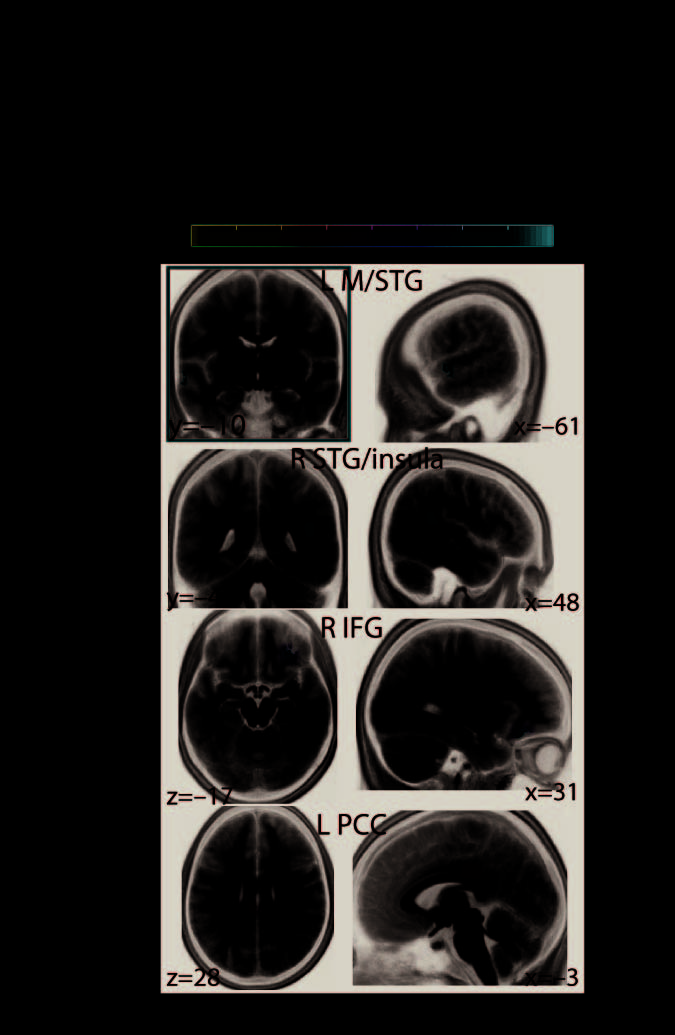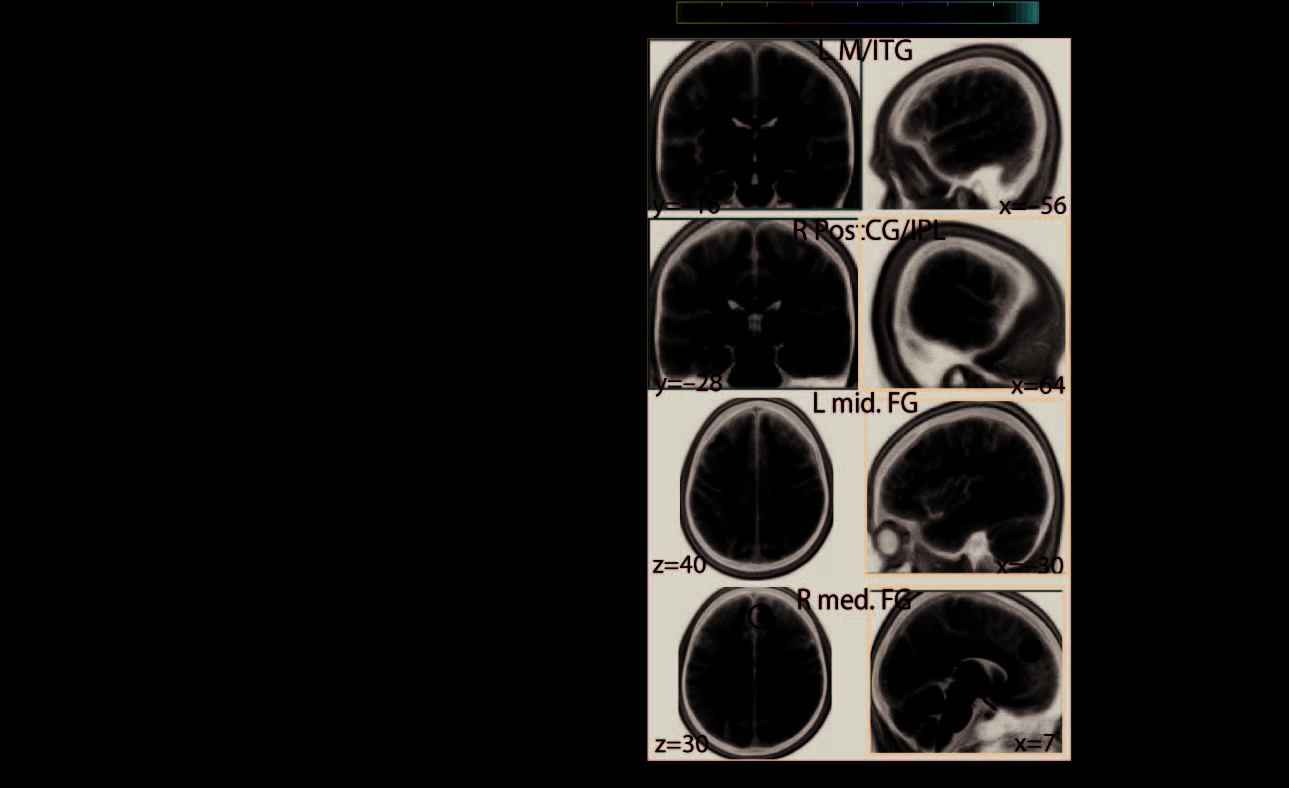Figure 5 gives a comprehensive overview of all differential network effects found at the regional level of large-scale brain networks. These maps show signiﬁcant differential cor- relations at cortical source locations. Four regional network properties were analyzed (see Alavash et al., 2017): (A) nodal connectivity (also known as nodal strength), (B) local efﬁciency, (C) modular segregation (also known as the within-module z-score), and (D) nodal efﬁciency. First, the connectivity of two network nodes (i.e., MEG source locations) located within the left and right temporal gyri showed signiﬁcant differential correlations with decision speed during the pitch task in contrast to the direction task (Figure 5A, ﬁrst and second rows). Lower connectivity at these locations—overlapping with middle and superior divisions of the left and right temporal cortices, respectively—predicted faster auditory perceptual decisions specif- ically during the direction task. Also, lower connectivity of a network node in right inferior frontal gyrus predicted faster decisions during the direction task (Figure 5A, third row), whereas lower connectivity of a node overlapping with left posterior cingulate cortex predicted faster perceptual decisions during the pitch task (Figure 5A, last row). Second, lower local efﬁciency of left middle/inferior temporal gyri speciﬁcally predicted faster decisions during the direction task (Figure 5B, ﬁrst row). These faster decisions, however, were concurrent with an increase in local efﬁciency of the left middle and right medial frontal cortices (Figure 5B, last two rows). 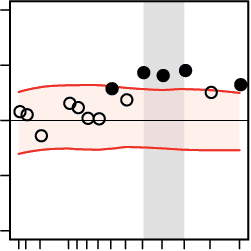Third, the modular segregation of certain network nodes within left and right auditory and frontal cortices showed correlations with decision speed speciﬁcally during the direction task (Figure 5C). More precisely, when subjects judged the overall direction of the frequency- modulated tone sweeps faster, two source locations within bilateral auditory cortices showed decreases in their modular segregation (Figure 5C, ﬁrst two rows). Notably, higher modular segregation of a source location within right anterior cingulate predicted faster decisions during the direction task (Figure 5C; last row). Finally, we found strong correlations between decision speed during the direction task and the integration of three nodes within left auditory cortex into the whole-brain network (Figure 5D). This result emerged from the lower nodal efﬁciency of three source locations Network Neuroscience 175 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . 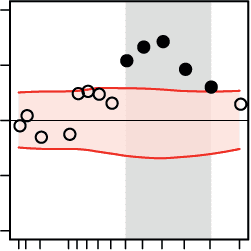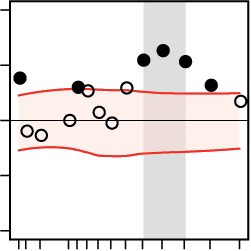t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making A Regression of decision speed on nodal connectivity diﬀ. in reg. weight (pitch – direction) –.08 0 .08 lower nodal connectivity predicts faster decisions *** –.05 * –.05 * r 0 0 higher nodal connectivity predicts faster decisions .05 .05 –.05 0 .05 ** –.05 0 .05 C Regression of decision speed on modular network segregation diﬀ. in reg. weight (pitch – direction) 0 –.08 .08 lower modular segregation predicts faster decisions ** r higher modular segregation predicts faster decisions –.05 0 .05 ** –.05 0 .05 * * * –.05 0 .05 ** –.05 0 .05 I F G C u n e u s B Regression of decision speed on local network eﬃciency higher local eﬃciency predicts faster decisions diﬀ. in reg. weight (pitch – direction) 0 –.08 .08 r lower local eﬃciency predicts faster decisions ** –.05 0 .05 –.05 0 .05 ** ** –.05 0 .05 ** –.05 0 .05 D Regression of decision speed on nodal network eﬃciency higher nodal eﬃciency predicts faster decisions diﬀ. in reg. weight (pitch – direction) 0 –.08 .08 r lower nodal eﬃciency predicts faster decisions *** G T M *** ** G T I G T S –.05 0 .05 S T G * i n s u a l * –.05 0 .05 * A C C 0 .05 G F . d e m * –.05 pitch task direction task * p<.05 ** p<.01 *** p<.001 Figure 5. Cortical regions where the network states of beta-band oscillations differentially pre- dicted decision speed during the pitch versus the direction task. At the regional level of large- scale brain networks, we aimed at ﬁnding task-speciﬁc correlations between the ongoing dynamics of regional network metrics and trial-by-trial decision speed. The analysis was focused on four regional network properties: (A) nodal connectivity, (B) local efﬁciency, (C) modular segregation (within-module z-score), and (D) nodal efﬁciency. The direction task (green bars), as compared to the pitch task (rose bars), showed stronger correlations with the network properties of sources within temporal and frontal cortices. Within auditory cortex, decreases in local network efﬁciency (B, ﬁrst row), modular segregation (C, ﬁrst two rows), and nodal efﬁciency (D, ﬁrst row) supported faster decisions during the direction task. Within the frontal cortex, increases in local efﬁciency (B, last two rows) and module segregation (C, last row) correlated with faster decisions during the direction task. To create the color brain maps for each network metric and source location, the mean regression weights obtained from the direction task data were subtracted from the mean regression weights obtained from the pitch task data. The difference was considered signiﬁcant if it did not cover the 95% conﬁdence interval of the null distribution generated from shifting the behavioral responses (corrected for the number of source locations using the false coverage state- ment rate; p < 0.05). Bar plots show the task-speciﬁc mean regression weights (r) whose signiﬁcance was tested against zero by means of one-sample permutation tests with 10,000 repetitions (error bars indicate SEMs). L and R abbreviate the left and right brain hemispheres, respectively, and [x, y, z] values indicate MNI coordinates (in millimeters). I/M/STG, inferior/middle/superior temporal gyrus; A/PCC, anterior/posterior cingulate cortex; I/mid./med. FG, inferior/middle/medial frontal gyrus; IPL, inferior parietal lobule. Network Neuroscience 176 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making overlapping with left inferior, middle, and superior temporal gyri, and was speciﬁc to the direction task. The correlation between decision speed during the direction task and the nodal efﬁciency of brain networks was not limited to these regions within auditory cortex: higher nodal efﬁciency of a source location in right anterior cingulate cortex also predicted faster deci- sions during the direction task (Figure 5D, faster perceptual decisions during the pitch task correlated with higher nodal efﬁciency of right superior tem- poral gyrus and insula (Figure 5D, second row). In contrast, last row). We also investigated the contributions of regional network states to the results observed on the whole-brain level shown in Figure 4. Toward this end, we implemented the same analysis we had done on the whole-brain level, but used a regional network metric extracted per source location over trials as a predictor. This analysis was conducted independently per pitch and direction task. We found signiﬁcant correlations between the ongoing dynamics of brain regional network metrics and the trial-by-trial speed of auditory perceptual decisions in both the pitch and direction tasks (nondifferential effects; Alavash et al., 2017, Figure S3). These results were in good agreement with the direction of the correlations observed on the whole-brain level (Figure 4). In brief, higher local network efﬁciency, modular segregation, and nodal network efﬁciency of the source locations predominantly within bilateral sensorimotor and parietal cortices predicted faster decisions in both tasks. However, decrease in all of the regional network metrics in source locations predominantly within auditory cortex supported faster decisions, which was more evident in the case of the direction task. Taken together, the results obtained at the regional level of whole-brain networks point to stronger correlations between brain network states and the speed of perceptual decisions during the direction than during the pitch task. These predictions emerged from auditory and frontal cortices. Among these predictions, the stronger ones (signiﬁcance levels of p < 0.01) converged on decreases in the nodal connectivity, local network efﬁciency, modular segre- gation, and nodal network efﬁciency of regions within auditory cortex. Within the frontal cortex, however, faster decisions during the direction task were predicted by increases in local network efﬁciency and modular segregation. DISCUSSION A time- and frequency-resolved analysis of large-scale brain networks during auditory per- ceptual decision-making unveiled two main results: For both the pitch and direction tasks and on the whole-brain level, faster decisions were predicted by higher local efﬁciency and modular segregation, but lower global integration of coupled beta-band oscillations. On the regional level, the results of our task-differential analysis revealed that the relatively more dif- ﬁcult direction task relied critically on speciﬁc network conﬁgurations of temporal and frontal regions. We discuss these results in terms of neural oscillations and complex brain networks. Further elaboration is provided in the Supplementary Discussion (Alavash et al., 2017). Network Dynamics of Beta-Band Oscillations Predict Decision Speed Oscillations are key to neural communication (Adrian, 1944; Buzsaki & Draguhn, 2004; Fries, 2015; Schroeder & Lakatos, 2009). Although most studies on neural oscillations aim to uncover mechanisms for dynamic excitation, inhibition, and synchrony (Jensen & Mazaheri, 2010; Keitel & Gross, 2016; Singer & Gray, 1995; Womelsdorf et al., 2007), fewer studies have focused on long-range synchronizations between distributed cortical areas (e.g., Doesburg, Green, McDonald, & Ward, 2009; Donner & Siegel, 2011; Hanslmayr, Staresina, Network Neuroscience 177 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making & Bowman, 2016; Varela, Lachaux, Rodriguez, & Martinerie, 2001). Here we measured cou- pling between the power envelopes of MEG source signals, which has been shown to underlie global network communication across the cortex (Siegel et al., 2012). The temporal network dynamics of these large-scale interactions predicted the speed of auditory perceptual deci- sions, which was speciﬁc to brain networks tuned at the mid-beta band of neural oscillations, centered around 20 Hz. Beta-band oscillations have classically been associated with sensorimotor functions (Aumann & Prut, 2015; Brovelli et al., 2004; Crone, Miglioretti, Gordon, & Lesser, 1998) and are attenuated during voluntary movements or motor imagery (Pfurtscheller, 2001; Pfurtscheller & Lopes da Silva, 1999; Turella et al., 2016). In our study, faster decisions nega- tively correlated with the power of neural oscillations within the alpha and beta bands. How- ever, the network effect was speciﬁc to the mid-beta band. We argue that this network effect is a manifestation of large-scale neural couplings underlying auditory processing and man- ual responding. The results of our control analysis suggest that motor actions per se can- not explain all of the correlations we found on the whole-brain level. In this analysis, we used the mid-beta-band data within the period when subjects manually reported their judg- ments. We observed positive correlations only between decision speed and local network efﬁciency (Alavash et al., 2017, Figure S1). Knowing that local network efﬁciency is related to nodal clustering (Rubinov & Sporns, 2010), this effect might be due to local beta-band desyn- chronization coherently occurring within sensorimotor cortex, thereby forming dense clusters with high local efﬁciency. Besides our control analysis, we also investigated pre- and post- stimulus effects (Alavash et al., 2017, Figure S1), which did not reveal consistent signiﬁcant effects. These ﬁndings together highlight one very important question: what neural dynamics account for predicting decision speed from brain network states? We here used the correlation between band-limited power envelopes as a functional con- nectivity measure, and had to choose a certain length for the trial-wise time windows; this is a key parameter in dynamic network analysis (Hutchison et al., 2013) and is related to the frequency content of the underlying signal. Perhaps the length of the above-mentioned time windows (used in control analyses) not long enough to estimate correlations between beta- band power envelopes per trial. Power envelopes evolve within longer time windows than do their underlying carrier frequencies (Siegel et al., 2012). Beta-band power envelopes ﬂuctuate slowly at frequencies below 0.3 Hz (Engel et al., 2013), and therefore their dynamic coupling is estimated better when a time window of ~3 s (in our case, one trial) is used. Accordingly, our control analysis could not entirely preclude the effect of sensorimotor beta-band desynchron- zation in our main ﬁndings. Within the last 500 ms of a trial concurrent with planning and executing a manual response, the power envelope of a ~20-Hz oscillation can be moderately modulated due to the suppression in its underlying carrier. Thus, the trial-wise power-envelope correlations likely reﬂect the neural couplings underlying perceptual decision-making (from –0.5 to +1 s) and the neural underpinning of manual responses given after the response prompt (from +1 to 1.5 s). Indeed, the effects we found on the regional level support the involvement of auditory, sensorimotor, and frontal cortices in predicting decision speed (Alavash et al., 2017, Figure S2). However, the sluggish dynamics of beta-band power envelopes makes it difﬁcult to dissociate the network states arising from perceptual decision processes from those related to manual responses. Moreover, previous work on the timing of perceptual decision-making has suggested that, in sensorimotor tasks, a decision is already represented in motor areas before a behav- ioral response is generated (de Lange, Rahnev, Donner, & Lau, 2013; Gold & Shadlen, 2007; Network Neuroscience 178 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making Kelly & O’Connell, 2015). Speciﬁcally, a decision variable undergoes a dynamic process through which the accumulated sensory evidence is integrated over time until the action is executed (Schroeder, Wilson, Radman, Scharfman, & Lakatos, 2010; Wyart, de Gardelle, Scholl, & Summerﬁeld, 2012). Several studies across different sensory modalities have asso- ciated modulations in beta-band activity with the temporal evolution of perceptual decisions (Senkowski, Molholm, Gomez-Ramirez, & Foxe, 2006). For example, Donner et al. (2007; Donner et al., 2009) reported frontoparietal beta-band activity that was predictive of accu- racy during a visual motion detection task, and that only occurred during the decision period of the trials. Accordingly, in Siegel, Engel, and Donner (2011) the authors provided two possible interpretations for these observations: the maintenance and accumulation of sensory evidence during decision formation, or the maintenance of the sensorimotor mapping rule between the accumulated sensory evidence and action (see Engel & Fries, 2010, for an elaboration). Additionally, a study by O’Connell et al. (2012) demonstrated that, during target detection tasks in different sensory modalities, left-hemisphere beta power was modulated by a reduc- tion in the stimulus contrast, and this gradual modulation predicted trial-by-trial reaction times. Finally, the role of beta-band oscillations in decision-making has been supported by animal studies (Haegens et al., 2011; Heekeren, Marrett, & Ungerleider, 2008) and computa- tional modeling (Mostert, Kok, & de Lange, 2015; Sherman et al., 2016). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 In sum, and in good agreement with previous accounts (Donner & Siegel, 2011; Hipp et al., 2011), we found that large-scale network interactions mediated by the power of beta-band oscillations are crucial for perceptual decision-making. Our ﬁndings draw a direct link be- tween the dynamic network organization of coupled neural oscillations at ~20 Hz and the trial-by-trial speed of auditory perceptual decisions, built up from early perception to execut- ing manual responses. Network States of Frontotemporal Regions Supporting Auditory Perceptual Decisions Our task-differential analyses at the regional level suggest that the arguably more difﬁcult direction task, in comparison to the pitch task, relied critically on speciﬁc network conﬁg- urations of beta-band oscillations. The differences we found in nodal network topology across the two tasks were speciﬁc to MEG sources located within the temporal and frontal cortices. Within the vicinity of auditory cortex, effects in support of faster decisions during the direction task converged toward decreases in the (i) nodal connectivity, (ii) local efﬁciency, (iii) modular segregation, and (iv) nodal efﬁciency of source locations mostly overlapping with the anterior division of left superior temporal cortex. Within frontal cortex, however, increases in (i) the local efﬁciency of left middle and medial frontal gyri and (ii) the modular segregation of right anterior cingulate predicted faster decisions during the direction task. One pattern forged of these results is that faster decisions during a particularly challenging auditory perceptual task are accompanied by an increase in the network segregation of frontal regions, and that this segregation supports higher-order decision-related processes. Theoreti- cally, high local clustering of neighbor nodes is associated with high efﬁciency in local infor- mation transfer and fault tolerance (Achard & Bullmore, 2007), indicating how well neighbor nodes can still communicate when the target node (in our case, a frontal region) is removed. As such, when making a perceptual decision is relatively difﬁcult (i.e., the direction task), the decision process beneﬁts from a more autonomous network conﬁguration of frontal regions. The critical frontal regions in perceptual decision-making has been supported by previous animal studies on local ﬁeld potentials (LFPs), in which frontal cortex involvement of Network Neuroscience 179 Brain network states and auditory perceptual decision-making responses were found to selectively encode auditory stimulus features (Fritz, David, Radtke- Schuller, Yin, & Shamma, 2010) or to show higher synchrony in the beta band (19–40 Hz) as a cortical representation of a task’s rules (Antzoulatos & Miller, 2016; Buschman, Denovellis, Diogo, Bullock, & Miller, 2012). Additionally, in the visual domain it has been shown that top-down control of attention is mediated by higher coherence between frontal and pari- etal LFPs in the beta band (22–34 Hz; Buschman & Miller, 2007). Recently, Stanley et al. (2016) found that higher local synchrony between LFPs over lateral prefrontal cortex within 16–20 Hz predicted stimulus categorization. Finally, a casual role for frontal cortex in percep- tual decision-making was recently proposed by Rahnev, Nee, Riddle, Larson, and D’Esposito (2016). In contrast to what we observed in frontal regions, network states concurrent with less clustered and less segregated auditory regions were found to speed up decisions during the direction task. One possibility is that during these states brain networks were more inte- grated (the opposite pole of segregation). However, we did not ﬁnd signiﬁcant correlations between decision speed and so-called module participation (Guimerà & Nunes Amaral, 2005), a well-established nodal metric that is quantiﬁed on the basis of intermodular connectivity and is attributed to network integration and hubs (Sporns, 2013; Sporns, Honey, & Kötter, 2007; van den Heuvel & Sporns, 2013). Accordingly, the decreases in the clustering and segregation of auditory regions are likely due to pruning of some short-range (intramodular) connections. This local network reconﬁguration might be necessary in order to remove direct connections and instead establish longer paths through intermediate critical nodes, thereby supporting the decision process. We also note that faster decisions during the direction task were predicted by a decrease in the nodal efﬁciency of left auditory regions. This was perhaps due to the emergence of longer paths between these regions and other network nodes and the pruning of long-range shortcuts. This globally less-efﬁcient and more-distributed information routing might be nec- essary to support perceptual decisions for the more difﬁcult direction task. Indeed, a study by Siegel, Buschman, and Miller (2015) suggested that, during a sensorimotor decision task, information was not restricted to speciﬁc cortical regions, but instead was distributed across graded specialized cortical regions. In addition, and relevant to frequency-speciﬁc distributed information routing, a study by Weisz, Wuhle et al. (2014) demonstrated that, during con- scious perception, brain networks tuned at 17 Hz get more globally integrated through shorter communication paths. To conclude, the present study suggests that the large-scale network organization of coupled neural oscillations at ~20 Hz (the beta band) underlies how quickly momentary auditory per- ceptual decisions are made and executed. Thus, global communication in brain networks dur- ing perceptual decision-making is likely implemented by neural oscillations at around 20 Hz. During auditory perceptual decision-making, this dynamic global communication appears as complex network interactions between beta-band neural oscillations evolving within lower- order auditory and higher-order control areas. MATERIALS AND METHODS Participants Twenty healthy, right-handed volunteers (15 females, ﬁve males; age range 20–32 years, mean ± SD age = 26.2 ± 3.35 years) participated in the study. None of the participants reported any neurological diseases or hearing problems. Ethical approval was obtained from Network Neuroscience 180 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making the local ethics committee of the University of Leipzig. All procedures were carried out with written informed consent of the participants and in accordance with the principles of the Declaration of Helsinki. Volunteers received monetary compensation for participating in the study. Stimuli Two auditory task sets were designed that used identical stimuli consisting of variable acoustic textures (see, e.g., Overath et al., 2010, or the “cloud of tones” in Znamenskiy & Zador, 2013) of 400 ms duration (Figure 1A). Each stimulus consisted of 72 frequency-modulated sine tone ramps, or sweeps, of 100 ms duration. The starting time points and frequencies of the individ- ual sweeps were uniformly distributed across time and log frequency. Their frequency slopes spanned ±3.3 octaves per second. For manipulation of the spectral center (low vs. high), the acoustic textures had one of eight spectral centers relative to a mean center frequency of 707.1 Hz. More speciﬁcally, the textures could deviate ±2, 1, 0.5, or 0.25 semitones from the center frequency. Their spectral centers were approximately 630, 667, 687, 697, 717, 728, 749, and 794 Hz. For manipulation of the spectral coherence, a variable proportion (25%, 50%, 75%, or 100%) of the sweeps were assigned the same frequency slope; that is, they were “coherent” with one another. The rest of the sweeps had randomly assigned slopes. Tasks The participants had to judge one feature of the auditory stimuli under two distinct task sets (Figure 1B). The feature was either the overall spectral center of the sweeps in the acoustic texture (the “pitch” feature: high or low) or the overall direction of the individual sweeps (the “direction” feature: up or down). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t Trials started with a white ﬁxation cross that appeared on a black background at the center of a back-projection screen. After a prestimulus interval of 1 s (with no time jitter), an acoustic texture was presented. Then the participants gave a delayed response to the auditory stimulus. This means that 0.6 s after the offset of the acoustic texture, the participants were visually prompted by the decision labels for the left- and right-hand response buttons (see Figure 1B). During the response window, the ﬁxation cross was replaced by a question mark, asking for the subject’s perceptual decision. The response to the previous trial was immediately followed (with no time jitter) by the presentation of the ﬁxation cross for the subsequent trial. f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 To prevent systematic effects of motor preparation, the mapping of the high/low and up/down labels to the two response buttons was randomized across trials. Participants had 3 s at max- imum to respond before the experiment would automatically proceed to the next trial. As in all MEG studies from the Leipzig Max Planck center (e.g., Wöstmann et al., 2016), the audi- tory stimuli were presented via a nonmagnetic, echo-free stimulus delivery system with almost linear frequency characteristics in the critical range of 200–4000 Hz. On a separate session before MEG recording, adaptive perceptual tracking was conducted with feedback so that each participant’s average accuracy converged at ~70% in each task. This was done to avoid ceiling or ﬂoor effects, and to assure that the two tasks were challenging enough. Network Neuroscience 181 Brain network states and auditory perceptual decision-making At the recording session, the participants completed eight task blocks, each consisting of 128 trials (~8 min). The two auditory paradigms, namely the pitch task and the direction task, alternated from block to block, and the initial task was randomized across the participants. Each block contained two trials of each possible combination of direction (two levels), coher- ence (four levels), and spectral center (eight levels). Subjects were presented two blocks at the beginning to familiarize them with the stimuli and the tasks. The last six blocks were used for data acquisition, resulting in a total of 384 trials per task for each subject. Between the blocks, participants were given self-paced breaks. Analysis of Behavioral Data The performance of the subjects was measured using the average proportions of correct re- −1). Decision speed sponses (i.e., accuracy) and decision speed (deﬁned as [response time] was calculated relative to the onset of the response prompt (see Figure 1B) and was used as a proxy for the difﬁculty of perceptual decision-making during each task. Trials on which no response was given were discarded from the analysis. To estimate the dynamic pattern of decision accuracy over trials, a moving-average pro- cedure was applied to the trial-by-trial binary responses (i.e., correct = 1, incorrect = 0; rectangular window with unit height and a length of four trials). The choice of the window size was guided by a recent study by Alavash et al. (2016), in which the strongest dynamic coupling of hemodynamic brain networks and behavioral accuracy emerged within time windows of ~16 s (four trials, in our case). To capture trial-by-trial ﬂuctuations in decision speed, we used inverse response times on trials in which a decision (correct or incorrect) was given. The procedures above gave us time series estimates of decision accuracy and speed over trials per subject (Figure 1C). To test the correlations between the trial-by-trial estimates of decision accuracy or speed and the trial-by-trial acoustic features (i.e., spectral center and percent coherence) of the auditory stimuli, we used a two-level general linear model (GLM). In this model, the time series estimates of decision accuracy or speed were predicted by an acoustic feature. Since the positively skewed distribution of response times can violate the normality assumption underlying the general linear model (Baayen & Milin, 2010), the dependent variable and the regressors were ﬁrst rank-transformed and then normalized (i.e., z-scored) before estimating the regression models (Cohen & Cavanagh, 2011). MEG Data Acquisition and Preprocessing MEG responses were recorded using a 306-channel Neuromag Vectorview system (Elekta, Helsinki, Finland) in an electromagnetically shielded room (Vacuumschmelze, Hanau, Germany) at a sampling rate of 1,000 Hz with a bandwidth of 330 Hz DC. Movement of each participant’s head relative to the MEG sensors was monitored by means of ﬁve head- position measurement coils. An electroencephalogram from 64 scalp electrodes (Ag/AgCl) was recorded but not analyzed in this study. The raw MEG data were ﬁrst subjected to the Maxﬁlter software to suppress any disturb- ing magnetic interference using the signal space separation method (Taulu, Kajola, & Simola, 2004). Next, the data were corrected for head movements and scanned for intervals during which channels were static or ﬂat. Subsequently, signals recorded from 204 planar gradi- ometer sensors at 102 locations were fed into the following steps, which were implemented Network Neuroscience 182 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making in MATLAB (version 2015a; MathWorks, Natick, MA, USA) using the Fieldtrip toolbox (Oostenveld, Fries, Maris, & Schoffelen, 2011) and other custom scripts. The signals were high-pass-ﬁltered at 0.5 Hz (ﬁnite impulse response [FIR] ﬁlter, sync window, order 6,000, zero-phase ﬁltering) and low-pass-ﬁltered at 140 Hz (FIR ﬁlter, sync window, order 44, zero-phase ﬁltering). Next, epochs from −1 to +2 s around the onset of the acoustic textures were extracted and down-sampled to 500 Hz. Independent component analysis was employed to exclude artifactual components con- taining heart, eye, or muscle activity. Then the single-trial sensor data were visually inspected to exclude trials that still contained eye blinks or movements, muscle activity, static or ﬂat intervals, signal jumps, or drifts, or that had a range larger than 300 pT/m (mean number of rejected trials ± SEM: 29.4 ± 4). Time-Frequency Analysis of MEG Sensor Data To analyze the induced perturbation of the MEG signal power during trials, spectrotemporal estimates of the sensor signals were obtained within −0.5 to 1.5 s (relative to the onset of the acoustic textures), at frequencies ranging from 8 to 32 Hz on a logarithmic scale (Morlet’s wavelets; number of cycles = 6). The logarithms of the squared magnitudes of the wavelet coefﬁcients were then baseline-corrected relative to the power of the signals within −0.5 to 0 s. Source Projection of MEG Sensor Data Individual forward head models were created on the basis of each participant’s T1-weighted magnetic resonance image (3–T Magnetom Trio, Siemens, Germany). The anatomical images were segmented using Freesurfer and coregistered to the MEG coordinates using the MNE software (http://martinos.org/mne). The ﬁt of approximately 200 digitized head surface points (Polhemus Fastrak 3D digitizer) to the reconstructed head surface was optimized using the iterative closest-point algorithm after the manual identiﬁcation of anatomical landmarks (nasion, left, and right preauricular points). The individual segmented and coregistered ana- tomical images were spatially normalized to the standard stereotaxic Montreal Neurological Institute space. The inverses of these operations were applied to a 12-mm grid created in the template brain in order to obtain subject-speciﬁc grids in the standard space (1,781 inside- brain source locations separated by 12 mm distance). To obtain the physical relation between the sources and sensors for all grid points, single- shell volume conduction models (Nolte, 2003) were constructed using the individual seg- mented anatomical images. The weakest of three dipole orientations per grid point was removed. Next, a linearly constrained minimum-variance beam-forming approach (Van Veen, Van Drongelen, Yuchtman, & Suzuki, 1997) was implemented. Spatial adaptive ﬁlters were generated by ﬁrst concatenating all single-trial signals into one time series per subject, and then computing the covariance matrices using these time series. The regularization param- eter was set to 7% and the singular-value decomposition approach was used to estimate the dominant dipole orientation independently per grid point. Finally, the single-trial sensor data from −1 to +2 s around the onset of the acoustic textures were multiplied by the spa- tial ﬁlters, and the results were treated as trial-wise source-projected signals in the subsequent analyses. Network Neuroscience 183 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making Time-Frequency Analysis of Source-Projected Signals Time–frequency representations of the source-projected signals were derived using Morlet’s wavelets based on multiplication in the frequency domain. As in Hipp et al. (2012), the spec- tral band-width of the wavelets was set at 0.5 octaves (number of cycles = 6). The center frequencies were spaced logarithmically using base 2, with exponents ranging from 3 to 5 in In addition, we included three lower frequencies at 1, 2, and 4 Hz in order steps of 0.25. to thoroughly investigate the neurobehavioral correlations within the range 1–32 Hz. Note that since our analysis was done for each trial (see below), to capture the low-frequency os- cillations per trial the time–frequency estimations at 1, 2, and 4 Hz were accomplished by mirror-symmetric extension of the source signals to the left and right. For the main analysis, time points from −0.5 to 1.5 s (relative to the onset of the acoustic textures), in steps of 0.05 s, were used to extract complex-valued spectrotemporal estimates of the source-projected signals per trial (41 data points). For analysis of the prestimulus interval, time points from −0.85 to 0 s (relative to the onset of the acoustic textures) were used. For analysis of the poststimulus interval, we analyzed the time points from the onset of the acous- tic textures up to +1 s, during which the participants listened to the auditory stimuli but did not manually give their responses. Additionally, since the power of beta-band oscillations is known to be related to the preparation and execution of movements (Aumann & Prut, 2015; Brovelli et al., 2004; Crone et al., 1998), we performed one control analysis. That is, we ana- lyzed the data within the response window (+1 to +1.5 s relative to the onset of the acoustic textures) at frequencies within the beta band (16–28 Hz). This analysis was aimed at inves- tigating possible effects arising from the neural processes involved in the button press rather than in auditory perceptual decision-making. The results of these analyses are summarized in supplementary Figure S1. Correlation Between Ongoing Neural Oscillatory Power and Auditory Perceptual Decision-Making On a trial-by-trial basis, in order to predict individuals’ decision-making performance from the ongoing power of the source-projected signals over trials, we implemented a two-level GLM approach. First, at the single-subject level, time series estimates of trial-by-trial decision accuracy or speed (Figure 1C) were predicted by the baseline-corrected power of the whole- brain source-projected signals over trials, while controlling for effects of the acoustic fea- tures (i.e., spectral center and percent coherence). For this analysis, the time points from −0.5 to 1.5 s (relative to the onset of the acoustic textures), in steps of 0.05 s, were used to extract complex-valued spectrotemporal estimates of the source-projected signals per trial. Subsequently, for each pitch and direction task, separate GLMs were constructed. This procedure was applied to the data obtained from each participant at each frequency of neural-oscillatory power (1–32 Hz). To account for the normality assumption underlying the GLM (Baayen & Milin, 2010), the dependent variable and the predictors were ﬁrst rank- transformed and then normalized (i.e., z-scored) before estimating the regression models (Cohen & Cavanagh, 2011). Finally, the regression weights obtained from the ﬁt of each GLM per task were averaged over participants at each frequency and statistically compared with a null distribution of mean regression weights. Power Envelope Correlations and Functional Connectivity Analysis The power envelope of a band-limited oscillatory signal is the squared magnitude of the time–frequency signal following wavelet decomposition. To assess frequency-speciﬁc neural Network Neuroscience 184 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making interactions, we computed Pearson’s correlations between the log-transformed powers of all pairs of sources per trial (Figure 2). This analysis was done at each frequency within the range 1–32 Hz. To eliminate the trivial common covariation in power measured from the same sources, we used the orthogonalization approach proposed by Hipp et al. (2012) prior to computing the power correlations (see Alavash et al., 2017). This approach has been suggested and used to circumvent overestimation of instantaneous short-distance correlations, which can otherwise occur due to magnetic ﬁeld propagation (Mehrkanoon, Breakspear, Britz, & Boonstra, 2014; Siems, Pape, Hipp, & Siegel, 2016). The procedure above gave us frequency-speciﬁc N-by-N functional connectivity matrices (where N denotes the number of source locations) per subject and trial, for each pitch and direction task (Figure 2). Building Dynamic Brain Networks To construct brain graphs from the functional connectivity matrices, different approaches have been suggested and used (Fornito, Zalesky, & Breakspear, 2013; Garrison, Scheinost, Finn, Shen, & Constable, 2015; van Wijk, Stam, & Daffertshofer, 2010). One way is to con- struct brain graphs over different network densities by including links in the graph according to the ranks of their absolute correlation values (Alexander-Bloch et al., 2010; Ginestet, Nichols, In our study, to make the brain graphs comparable in terms Bullmore, & Simmons, 2011). of size across subjects and trials, the number of links in each brain graph per trial was ﬁxed at 10% of the network density. The choice of the density threshold was based on previous work demonstrating that the brain network correlates of behavior are observed within a low-density range of network connections (Achard & Bullmore, 2007; Alavash, Hilgetag, Thiel, & Giessing, 2015; Alavash et al., 2016; Giessing, Thiel, Alexander-Bloch, Patel, & Bullmore, 2013; Godwin, Barry, & Marois, 2015). However, to assure that the results were not speciﬁc to one network density, we repeated our analysis at 5% of the network density, and have summarized these results in supplementary Figure S8. Subsequently, binary undirected brain graphs were built, from which graph-theoretical network metrics were extracted per trial (Figure 2). The mean functional connectivity was estimated as the mean of the upper-diagonal correlation values within the sparse temporal connectivity matrices. Network Diagnostics Three key topological properties were estimated per trial: mean local efﬁciency, network modularity, and global network efﬁciency. These graph-theoretical metrics were used to cap- ture dynamic patterns of functional integration and segregation on the local, intermediate, and global scales of network topology, respectively (Figure 2). For each graph-theoretical metric, we computed a global network diagnostic that collapsed the metric into a single measure on the whole-brain level, and a regional diagnostic characterizing the same metric but for a cer- tain cortical source location. The regional network diagnostics were therefore used to localize the cortical regions contributing to the network integration or segregation measured on the whole-brain level. First, we used nodal connectivity (also known as nodal strength) as the regional measure of mean functional connectivity. Second, local efﬁciency was computed within each source’s neighborhood graph as the regional measure of mean local efﬁciency. Network Neuroscience 185 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making Third, module segregation (which was quantiﬁed using the “within-module zscore”) was used to measure the strength of the membership of a given source in its network module. Finally, nodal efﬁciency was measured to capture the integration of a given source into the entire network (see supplementary information, Alavash et al., 2017, for details). Correlation Between Brain Network Dynamics and Auditory Perceptual Decision-Making To predict trial-by-trial perceptual decision-making performance from the ongoing brain net- work states, we employed the same regression approach we had used for predicting perfor- mance from the brain’s ongoing oscillatory power. That is, we implemented a GLM in which time series estimates of trial-by-trial decision accuracy or speed (Figure 1C) were predicted by the graph-theoretical network metrics over trials (Figure 2), while controlling for effects of the acoustic features (i.e., the spectral center and percent coherence). For each network diagnostic, a separate GLM was constructed. Thus, each model consisted of three regressors together with a constant term. Since the statistical distribution of the temporal brain network metrics is not necessarily normal, the dependent variable and the predictors were ﬁrst rank-transformed and then normalized (i.e., z-scored) before estimating the regression model (Cohen & Cavanagh, 2011). This procedure was applied separately to the data obtained from each pitch and direc- tion task, subject, and frequency of neural oscillatory power. Finally, the normalized regression weights obtained from the ﬁt of each GLM per task were averaged over participants at each frequency and statistically compared with a null distribution of mean regression weights. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 To measure the task speciﬁcity of the correlations between a given network diagnostic and either trial-by-trial decision accuracy or speed, we also computed the mean difference between the regression weights β obtained from each GLM model—that is, mean(β − β ). pitch dir Statistical Analysis Behavioral data. Mean decision speeds and average accuracies were compared between the different task and stimulus conditions by means of an analysis of variance (ANOVA) for re- peated measures, using Task (pitch, direction), Coherence (four levels), and Spectral Center (four levels) as within-subjects factors. We used generalized eta-squared (η2 G; Bakeman, 2005) as the effect size statistic. Prior to the ANOVA, the distributions of the behavioral measures across participants were statistically analyzed by means of bootstrap Kolmogorov–Smirnov tests with 10,000 repetitions to ensure that the data derived from a normally distributed popu- lation. The bootstrap Kolmogorov–Smirnov test, unlike the traditional Kolmogorov–Smirnov test, allows for the presence of ties in the data (Sekhon, 2007). The behavioral measures (i.e., mean decision speed and average accuracies) were compared between the pitch and direction tasks using exact permutation tests for paired samples. The correlations between each of the behavioral measures across the two tasks were tested using the rank-based non- parametric Spearman’s ρ correlation (Spearman, 1904) with 10,000 permutations applied to the correlation coefﬁcients (Pesarin & Salmaso, 2010). To test the correlation between the trial-by-trial estimates of decision accuracy or speed and the trial-by-trial acoustic features of the stimuli, a two-level GLM was applied separately to each pitch and direction task per subject. The regression weights obtained from the ﬁt of each GLM were averaged over par- ticipants and statistically tested against zero using one-sample exact permutation tests. To predict trial-by-trial perceptual decision accuracy or speed Neurobehavioral correlations. from the ongoing brain oscillatory power or network states, we implemented a two-level GLM Network Neuroscience 186 Brain network states and auditory perceptual decision-making approach. The regression weights obtained from the ﬁt of each GLM were averaged over participants at each frequency and statistically compared with a null distribution. The null distribution was generated using a randomization procedure in which the trial-by-trial binary responses or decision speeds were circularly shifted 350 times (the number of trials remained after preprocessing in every subject) over trials, per task and per subject. Circular shifting pre- serves the autocorrelation structure inherent to the time series (e.g., the trial-by-trial sequential correlation in response times; Baayen & Milin, 2010), and thus has the advantage over random shufﬂing. For the circularly shifted behavioral responses, we conducted the same analysis steps we had done for the empirical behavioral data. To statistically test the signiﬁcance of the neu- robehavioral correlations, the observed mean regression weight was compared with the null distribution generated from the randomization procedure at each frequency. The observed mean regression weight was considered signiﬁcant if it was higher than the 97.5th percentile or lower than 2.5th percentile of the null distribution (upper and lower bounds of the horizontal shading in Figures 3 and 4). At the regional level of the brain networks, we tested whether the time Regional analysis. series estimates of decision-making performance under each pitch and direction task differen- tially correlated with the regional diagnostics of the brain networks (see Alavash et al., 2017). Toward this end, the mean regression weights obtained from the direction task data were sub- tracted from the mean regression weights obtained from the pitch task data. The signiﬁcance of the difference between the correlations was statistically tested using a null distribution of the difference in mean regression weights generated from circularly shifting the behavioral responses. We also investigated the regional network states per pitch and direction task sepa- rately. Toward this end, we implemented the same analysis we had done on the whole-brain level, but used a regional network property estimated per source location over trials. The results of this analysis are summarized in supplementary Figure S2. For all statistical tests (i.e., inference on the behavioral and brain- Signiﬁcance thresholds. network effects) we used p < 0.05 (two-sided) as the threshold of signiﬁcance. For the anal- ysis on the whole-brain level, in order to correct for the multiple comparisons entailed by the number of frequency bins (14), we implemented a correction method suggested by Benjamini and Yekutieli (2005) and used by Obleser, Leaver, Vanmeter, and Rauschecker In this method, called the “false coverage statement (2010) and Obleser and Weisz (2012). rate” (FCR), we ﬁrst selected those frequencies at which the observed mean regression weight did not cover the null distribution at the conﬁdence level of 95%. In a second correction pass, we (re)constructed the FCR-corrected conﬁdence intervals for these selected frequencies at a level of 1 − Fs × q , where Fs is the number of selected frequencies at the ﬁrst pass, Ft is the Ft total number of frequency bins tested, and q is the tolerated rate for false coverage state- ments, here 0.05. The FCR correction procedure yields inﬂated, and thus more conservative conﬁdence limits (bounds of the horizontal shading in Figure 3). To correct for the multi- ple comparisons entailed by the regional analysis, we used the same procedure to adjust the conﬁdence limits according to the number of source locations (1,781). ACKNOWLEDGMENTS This research was supported by the Max Planck Society (through a Max Planck Research Group grant to J.O.) and the European Research Council (ERC Consolidator AUDADAPT, Grant No. 646696 to J.O.). Yvonne Wolff and Burkhard Maess helped acquire the MEG data. Network Neuroscience 187 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making AUTHOR CONTRIBUTIONS Mohsen Alavash: Conceptualization; Formal analysis; Investigation; Methodology; Visualization; Writing – original draft; Writing – review & editing Christoph Daube: Data curation; Formal analysis; Visualization; Writing – review & editing Malte Wöstmann: Conceptualization; Methodology; Writing – review & editing Alex Brandmeyer: Conceptualization; Data curation; Methodology; Visualization; Writing – review & editing Jonas Obleser: Conceptualization; Funding acquisition; Methodology; Project administration; Resources; Supervision; Writing – review & editing REFERENCES Achard, S., & Bullmore, E. (2007). Efﬁciency and cost of eco- nomical brain functional networks. PLoS Computational Biology, e17, 3. Adrian, E. (1944). Brain rhythms. Nature, 153, 360–362. Alavash, M., Daube, C., Wöstmann, M., Brandmeyer, A., & Obleser, J. (2017). Supplemental material for “large-scale network dy- namics of beta-band oscillations underlie auditory perceptual decision-making.”. Network Neuroscience, 1(2). doi:10.1162/ netn_a_00009 Alavash, M., Hilgetag, C. C., Thiel, C. M., & Giessing, C. (2015). Persistency and ﬂexibility of complex brain networks underlie dual-task interference. Human Brain Mapping, 36, 3542–3562. Alavash, M., Thiel, C. M., & Giessing, C. (2016). Dynamic coupling of complex brain networks and dual-task behavior. NeuroImage, 129, 233–246. Alexander-Bloch, A. F., Gogtay, N., Meunier, D., Birn, R., Clasen, L., Lalonde, F., . . . Bullmore, E. T. (2010). Disrupted modularity and local connectivity of brain functional networks in childhood- onset schizophrenia. Frontiers in Systems Neuroscience, 4, 147. Antzoulatos, E. G., & Miller, E. K. (2016). Synchronous beta rhythms of frontoparietal networks support only behaviorally relevant representations. eLife, 5, e17822. Aumann, T. D., & Prut, Y. (2015). Do sensorimotor beta-oscillations maintain muscle synergy representations in primary motor cortex? Trends in Neurosciences, 38, 77–85. Baayen, R. H., & Milin, P. (2010). Analyzing reaction times. Inter- national Journal of Psychological Research, 3, 12–28. Bakeman, R. (2005). Recommended effect size statistics for repeated measures designs. Behavior Research Methods, 37, 379–384. Bassett, D. S., Bullmore, E. T., Meyer-Lindenberg, A., Apud, J. A., Weinberger, D. R., & Coppola, R. (2009). Cognitive ﬁtness of cost-efﬁcient brain functional networks. Proceedings of the National Academy of Sciences, 106, 11747–11752. Bassett, D. S., Meyer-Lindenberg, A., Achard, S., Duke, T., & Bullmore, E. (2006). Adaptive reconﬁguration of fractal small- world human brain functional networks. Proceedings of the National Academy of Sciences, 103, 19518–19523. Bassett, D. S., Wymbs, N. F., Rombach, M. P., Porter, M. A., Mucha, P. J., & Grafton, S. T. (2013). Task-based core-periphery organ- ization of human brain dynamics. PLoS Computational Biology, 9, e1003171. Benjamini, Y., & Yekutieli, D. (2005). False discovery rate-adjusted multiple conﬁdence intervals for selected parameters. Journal of the Acoustical Society of America, 100, 71–81. Braun, U., Schäfer, A., Walter, H., Erk, S., Romanczuk-Seiferth, N., (2015). Dynamic reconﬁguration Haddad, L., . . . Bassett, D. of frontal brain networks during executive cognition in humans. Proceedings of the National Academy of Sciences, 112, 11678–11683. Brovelli, A., Ding, M., Ledberg, A., Chen, Y., Nakamura, R., & Bressler, S. L. (2004). Beta oscillations in a large-scale sensori- motor cortical network: Directional inﬂuences revealed by Proceedings of the National Academy of granger causality. Sciences, 101, 9849–9854. Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph theoretical analysis of structural and functional systems. Nature Reviews Neuroscience, 10, 186–198. Buschman, T. J., Denovellis, E. L., Diogo, C., Bullock, D., & Miller, E. K. Synchronous oscillatory neural ensembles for rules in the prefrontal cortex. Neuron, 76, 838–846. (2012). Buschman, T. J., & Miller, E. K. (2007). Top-down versus bottom- up control of attention in the prefrontal and posterior parietal cortices. Science, 315, 1860–1862. Buzsaki, G., & Draguhn, A. (2004). Neuronal oscillations in cortical networks. Science, 304, 1926–1929. Calhoun, V. D., Miller, R., Pearlson, G., & Adali, T. (2014). The chronnectome: Time-varying connectivity networks as the next frontier in fmri data discovery. Neuron, 84, 262–274. Chai, L. R., Mattar, M. G., Blank, I. A., Fedorenko, E., & Bassett, (2016). Functional network dynamics of the language D. S. system. Cerebral Cortex, 26, 4148–4159. doi:10.1093/cercor/ bhw238 Cohen, M. X., & Cavanagh, J. F. (2011). Single-trial regression eluci- dates the role of prefrontal theta oscillations in response conﬂict. Frontiers in Psychology, 2, 30. Crone, N., Miglioretti, D., Gordon, B., & Lesser, R. (1998). Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis: II. Event-related syn- chronization in the gamma band. Brain, 121, 2301–2315. de Lange, F. P., Rahnev, D. A., Donner, T. H., & Lau, H. (2013). Prestimulus oscillatory activity over motor cortex reﬂects percep- tual expectations. Journal of Neuroscience, 33, 1400–1410. Network Neuroscience 188 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making de Pesters, A., Coon, W. G., Brunner, P., Gunduz, A., Ritaccio, A. L., Brunet, N. M., . . . Schalk, G. (2016). Alpha power indexes task- related networks on large and small scales: A multimodal ecog study in humans and a non-human primate. NeuroImage, 134, 122–31. Deco, G., Tononi, G., Boly, M., & Kringelbach, M. L. (2015). Rethinking segregation and integration: Contributions of whole- brain modelling. Nature Reviews Neuroscience, 16, 430–439. Doesburg, S. M., Green, J. J., McDonald, J. J., & Ward, L. M. (2009). inhibition to long-range integration: a functional dissociation of alpha-band synchronization across cortical scales in visuospatial attention. Brain Research, 1303, 97–110. From local Donner, T. H., & Siegel, M. (2011). A framework for local cortical oscillation patterns. Trends in Cognitive Sciences, 15, 191–199. Donner, T. H., Siegel, M., Fries, P., & Engel, A. K. (2009). Buildup of choice-predictive activity in human motor cortex during per- ceptual decision making. Current Biology, 19, 1581–1585. Donner, T. H., Siegel, M., Oostenveld, R., Fries, P., Bauer, M., & Engel, A. K. (2007). Population activity in the human dorsal pathway predicts the accuracy of visual motion detection. Jour- nal of Neurophysiology, 98, 345–359. Engel, A. K., & Fries, P. (2010). Beta-band oscillations—signalling the status quo? Current Opinion in Neurobiology, 20, 156–165. (2013). In- trinsic coupling modes: Multiscale interactions in ongoing brain activity. Neuron, 80, 867–886. Engel, A. K., Gerloff, C., Hilgetag, C. C., & Nolte, G. Fornito, A., Zalesky, A., & Breakspear, M. (2013). Graph analysis of the human connectome: Promise, progress, and pitfalls. Neu- roImage, 80, 426–444. Fries, P. (2015). Rhythms for cognition: Communication through coherence. Neuron, 88, 220–235. Friese, U., Daume, J., Goschl, F., Konig, P., Wang, P., & Engel, A. K. (2016). Oscillatory brain activity during multisensory attention reﬂects activation, disinhibition, and cognitive control. Scientiﬁc Reports, 6, 32775. Fritz, J. B., David, S. V., Radtke-Schuller, S., Yin, P., & Shamma, S. A. (2010). Adaptive, behaviorally gated, persistent encod- ing of task-relevant auditory information in ferret frontal cortex. Nature Neuroscience, 13, 1011–1019. Garrison, K. A., Scheinost, D., Finn, E. S., Shen, X., & Constable, R. T. (2015). The (in)stability of functional brain network mea- sures across thresholds. NeuroImage, 118, 651–661. Giessing, C., Thiel, C. M., Alexander-Bloch, A. F., Patel, A. X., & Bullmore, E. T. (2013). Human brain functional network changes associated with enhanced and impaired attentional task perfor- mance. Journal of Neuroscience, 33, 5903–5914. Ginestet, C. E., Nichols, T. E., Bullmore, E. T., & Simmons, A. (2011). Brain network analysis: Separating cost from topology using cost-integration. PLoS ONE, 6, e21570. Godwin, D., Barry, R. L., & Marois, R. (2015). Breakdown of the brain’s functional network modularity with awareness. Proceedings of the National Academy of Sciences, 112, 3799–3804. Gold, J. I., & Shadlen, M. N. (2007). The neural basis of decision making. Annual Review of Neuroscience, 30, 535–574. Guimerà, R., & Nunes Amaral, L. A. (2005). Functional cartography of complex metabolic networks. Nature, 433, 895–900. doi:10. 1038/nature03288 Haegens, S., Nácher, V., Hernández, A., Luna, R., Jensen, O., & Romo, R. (2011). Beta oscillations in the monkey sensorimotor network reﬂect somatosensory decision making. Proceedings of the National Academy of Sciences, 108, 10708–10713. Hanslmayr, S., Gross, J., Klimesch, W., & Shapiro, K. L. (2011). The role of alpha oscillations in temporal attention. Brain Research Reviews, 67, 331–343. Hanslmayr, S., Staresina, B. P., & Bowman, H. (2016). Oscil- lations and episodic memory: Addressing the synchroniza- tion/desynchronization conundrum. Trends in Neurosciences, 39, 16–25. Heekeren, H. R., Marrett, S., & Ungerleider, L. G. (2008). The neural systems that mediate human perceptual decision making. Nature Reviews Neuroscience, 9, 467–479. Hillebrand, A., Singh, K. D., Holliday, I. E., Furlong, P. L., & Barnes, G. R. (2005). A new approach to neuroimaging with magneto- encephalography. Human Brain Mapping, 25, 199–211. Hipp, J. F., Engel, A. K., & Siegel, M. (2011). Oscillatory syn- chronization in large-scale cortical networks predicts perception. Neuron, 69, 387–396. Hipp, J. F., Hawellek, D. J., Corbetta, M., Siegel, M., & Engel, A. K. (2012). Large-scale cortical correlation structure of spontaneous oscillatory activity. Nature Neuroscience, 15, 884–890. Honey, C. J., Kotter, R., Breakspear, M., & Sporns, O. (2007). Net- work structure of cerebral cortex shapes functional connectivity on multiple time scales. Proceedings of the National Academy of Sciences, 104, 10240–10245. Hutchison R. M., Womelsdorf T., Allen E. A., Bandettini P. A., Calhoun V. D., Corbetta M., Della Penna S., Duyn J. H., Glover G. H., Gonzalez-Castillo J., Handwerker D. A., Keilholz S., Kiviniemi V., Leopold D. A., de Pasquale F., Sporns O., Walter M., & Chang C. (2013). Dynamic functional connectivity: Promise, issues, and interpretations. NeuroImage, 80, 360–378. Jensen, O., & Mazaheri, A. (2010). Shaping functional architecture by oscillatory alpha activity: Gating by inhibition. Frontiers in Human Neuroscience, 4, 186. Kayser, S. J., McNair, S. W., & Kayser, C. (2016). Prestimulus inﬂu- ences on auditory perception from sensory representations and decision processes. Proceedings of the National Academy of Sciences, 113, 4842–4847. (2016). Individual human brain areas can be identiﬁed from their characteristic spectral activation ﬁnger- prints. PLoS Biology, 14, e1002498. Keitel, A., & Gross, J. Kelly, S. P., & O’Connell, R. G. (2015). The neural processes under- lying perceptual decision making in humans: recent progress and future directions. Journal of Physiology, 109, 27–37. Kopell, N. J., Gritton, H. J., Whittington, M. A., & Kramer, M. A. (2014). Beyond the connectome: The dynome. Neuron, 83, 1319–1328. Network Neuroscience 189 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making Kringelbach, M. L., McIntosh, A. R., Ritter, P., Jirsa, V. K., & Deco, G. (2015). The rediscovery of slowness: Exploring the timing of cognition. Trends in Cognitive Sciences, 19, 616–628. Lange, J., Oostenveld, R., & Fries, P. (2013). Reduced occipital alpha power indexes enhanced excitability rather than im- Journal of Neuroscience, 33, proved visual perception. 3212–3220. Leske, S., Ruhnau, P., Frey, J., Lithari, C., Muller, N., Hartmann, T., & Weisz, N. (2015). Prestimulus network integration of auditory cortex predisposes near-threshold perception independently of local excitability. Cerebral Cortex, 25, 4898–907. Lou, B., Li, Y., Philiastides, M. G., & Sajda, P. (2014). Prestimulus alpha power predicts ﬁdelity of sensory encoding in perceptual decision making. NeuroImage, 87, 242–251. Marrelec, G., Messe, A., Giron, A., & Rudrauf, D. (2016). Func- tional connectivity’s degenerate view of brain computation. PLoS Computational Biology, 12, e1005031. Mehrkanoon, S., Breakspear, M., Britz, J., & Boonstra, T. W. (2014). Intrinsic coupling modes in source-reconstructed electro- encephalography. Brain Connectivity, 4, 812–825. Misic, B., Betzel, R. F., de Reus, M. A., van den Heuvel, M. P., Berman, M. G., McIntosh, A. R., & Sporns, O. (2016). Network- level structure-function relationships in human neocortex. Cere- bral Cortex, 26, 3285–3296. Misic, B., & Sporns, O. (2016). From regions to connections and networks: New bridges between brain and behavior. Current Opinion in Neurobiology, 40, 1–7. Mostert, P., Kok, P., & de Lange, F. P. (2015). Dissociating sensory from decision processes in human perceptual decision making. Scientiﬁc Reports, 5, 18253. Müller, N., & Weisz, N. (2012). Lateralized auditory cortical alpha band activity and interregional connectivity pattern Cerebral Cortex, 22, reﬂect anticipation of target sounds. 1604–1613. Nicol, R. M., Chapman, S. C., Vertes, P. E., Nathan, P. J., Smith, M. L., Shtyrov, Y., & Bullmore, E. T. (2012). Fast reconﬁguration of high-frequency brain networks in response to surprising changes in auditory input. Journal of Neurophysiology, 107, 1421–1430. (2003). The magnetic lead ﬁeld theorem in the quasi- static approximation and its use for magnetoencephalography forward calculation in realistic volume conductors. Physics in Medicine and Biology, 48. Nolte, G. Obleser, J., Leaver, A. M., Vanmeter, J., & Rauschecker, J. P. (2010). Segregation of vowels and consonants in human auditory cortex: Evidence for distributed hierarchical organization. Frontiers in Psychology, 1, 232. Obleser, J., & Weisz, N. (2012). Suppressed alpha oscillations predict intelligibility of speech and its acoustic details. Cerebral Cortex, 22, 2466–2477. O’Connell, R. G., Dockree, P. M., & Kelly, S. P. (2012). A supramodal accumulation-to-bound signal that determines perceptual decisions in humans. Nature Neuroscience, 15, 1729–1735. Oostenveld, R., Fries, P., Maris, E., & Schoffelen, J. M. (2011). Fieldtrip: Open source software for advanced analysis of MEG., EEG, and invasive electrophysiological data. Computational Intelligence and Neuroscience, 2011, 156869. Overath, T., Kumar, S., Stewart, L., von Kriegstein, K., Cusack, R., Rees, A., & Grifﬁths, T. D. (2010). Cortical mechanisms for the Journal of segregation and representation of acoustic textures. Neuroscience, 30, 2070–2076. Palva, J. M., Monto, S., Kulashekhar, S., & Palva, S. (2010). Neuronal synchrony reveals working memory networks and predicts individual memory capacity. Proceedings of the National Academy of Sciences, 107, 7580–7585. Palva, S., & Palva, J. M. (2012). Discovering oscillatory interaction networks with M/EEG: Challenges and breakthroughs. Trends in Cognitive Sciences, 16, 219–230. Park, H., Ince, R. A., Schyns, P. G., Thut, G., & Gross, J. (2015). Frontal top-down signals increase coupling of auditory low- frequency oscillations to continuous speech in human listeners. Current Biology, 25, 1649–1653. Park, H. J., & Friston, K. (2013). Structural and functional brain net- works: From connections to cognition. Science, 342, 1238411. Pesarin, F., & Salmaso, L. (2010). The permutation testing approach: A review. Statistica, 70, 481–509. Pfurtscheller, G. (2001). Functional brain imaging based on erd/ers. Vision Research, 41, 1257–1260. Pfurtscheller, G., & Lopes da Silva, F. H. (1999). Event-related EEG/MEG synchronization and desynchronization: Basic princi- ples. Clinical Neurophysiology, 110, 1842–1857. Rahnev, D., Nee, D. E., Riddle, J., Larson, A. S., & D’Esposito, M. (2016). Causal evidence for frontal cortex organization for per- ceptual decision making. Proceedings of the National Academy of Sciences, 113, 6059–6064. Rubinov, M., & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52, 1059–1069. Sadaghiani, S., & Kleinschmidt, A. (2016). Brain networks and alpha-oscillations: Structural and functional foundations of cog- nitive control. Trends in Cognitive Sciences, 20, 805–817. Sadaghiani, S., Poline, J. B., Kleinschmidt, A., & D’Esposito, M. (2015). Ongoing dynamics in large-scale functional connectiv- ity predict perception. Proceedings of the National Academy of Sciences, 112, 8463–8468. Schroeder, C. E., & Lakatos, P. (2009). Low-frequency neuronal oscillations as instruments of sensory selection. Trends in Neu- rosciences, 32, 9–18. Schroeder, C. E., Wilson, D. A., Radman, T., Scharfman, H., & (2010). Dynamics of active sensing and perceptual Lakatos, P. selection. Current Opinion in Neurobiology, 20, 172–176. Sekhon, J. (2007). Multivariate and propensity score matching soft- ware with automated balance optimization: The matching pack- Journal of Statistical Software, 42(7), 1–52. doi:10. age for R. 18637/jss.v042.i07 Senkowski, D., Molholm, S., Gomez-Ramirez, M., & Foxe, J. J. (2006). Oscillatory beta activity predicts response speed dur- ing a multisensory audiovisual reaction time task: A high-density electrical mapping study. Cerebral Cortex, 16, 1556–1565. Shen, K., Hutchison, R. M., Bezgin, G., Everling, S., & McIntosh, A. R. (2015). Network structure shapes spontaneous Network Neuroscience 190 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Brain network states and auditory perceptual decision-making functional connectivity dynamics. Journal of Neuroscience, 35, 5579–5588. Sherman, M. A., Lee, S., Law, R., Haegens, S., Thorn, C. A., (2016). Neural Hamalainen, M. S., Moore, C. I., Jones, S. R. mechanisms of transient neocortical beta rhythms: Converging evidence from humans, computational modeling, monkeys, and mice. Proceedings of the National Academy of Sciences, 113, E4885–E4894. doi:10.1073/pnas.1604135113 Shine, J. M., Bissett, P. G., Bell, P. T., Koyejo, O., Balsters, J. H., Gorgolewski, K. J., Moodie, C. A., Poldrack, R. A. (2016). The dynamics of functional brain networks: Integrated network states during cognitive task performance. Neuron, 92, 1–11. Siegel, M., Buschman, T. J., & Miller, E. K. (2015). Cortical in- formation ﬂow during ﬂexible sensorimotor decisions. Science, 348, 1352–1355. doi:10.1126/science.aab0551 Siegel, M., Donner, T. H., & Engel, A. K. (2012). Spectral ﬁn- gerprints of large-scale neuronal interactions. Nature Reviews Neuroscience, 13, 121–134. Siegel, M., Engel, A. K., & Donner, T. H. (2011). Cortical network dynamics of perceptual decision-making in the human brain. Frontiers in Human Neuroscience, 5, 21. Siems, M., Pape, A. A., Hipp, J. F., & Siegel, M. (2016). Measur- ing the cortical correlation structure of spontaneous oscillatory activity with EEG and MEG. NeuroImage, 129, 345–355. Singer, W., & Gray, C. M. (1995). Visual feature integration and the temporal correlation hypothesis. Annual Review of Neuro- science, 18, 555–586. Spearman, C. (1904). The proof and measurement of association between two things. The American Journal of Psychology, 15, 72–101. Sporns, O. (2013). Network attributes for segregation and integra- tion in the human brain. Current Opinion in Neurobiology, 23, 162–171. Sporns, O. (2014). Contributions and challenges for network models in cognitive neuroscience. Nature Neuroscience, 17, 652–660. (2007). Sporns, O., Honey, C. J., & Kötter, R. Identiﬁcation and classiﬁcation of hubs in brain networks. PLoS ONE, 17, e1049. Stanley, D. A., Roy, J. E., Aoi, M. C., Kopell, N. J., & Miller E. K. (2016). Low-beta oscillations turn up the gain during category judgments. Cerebral Cortex, 1–15 Advance online publication. doi:10.1093/cercos/bhw356 Taulu, S., Kajola, M., & Simola, J. (2004). Suppression of inter- ference and artifacts by the signal space separation method. Brain Topography, 16, 269–275. Turella, L., Tucciarelli, R., Oosterhof, N. N., Weisz, N., Rumiati, R., & Lingnau, A. (2016). Beta band modulations underlie ac- tion representations for movement planning. NeuroImage, 136, 197–207. van den Heuvel, M. P., & Sporns, O. (2013). Network hubs in the human brain. Trends in Cognitive Sciences, 17, 683–696. Van Veen, B. D., Van Drongelen, W., Yuchtman, M., & Suzuki, A. (1997). Localization of brain electrical activity via linearly con- strained minimum variance spatial ﬁltering. IEEE Transactions on Biomedical Engineering, 44, 867–880. doi:10.1109/10.623056 van Wijk, B. C. M., Stam, C. J., & Daffertshofer, A. (2010). Com- paring brain networks of different size and connectivity density using graph theory. PLoS ONE, 5, e13701. Varela, F., Lachaux, J., Rodriguez, E., & Martinerie, J. (2001). The brain web: Phase synchronization and large-scale integration. Nature Reviews Neuroscience, 2, 229–239. Weisz, N., Muller, N., Jatzev, S., & Bertrand, O. (2014a). Oscilla- tory alpha modulations in right auditory regions reﬂect the valid- ity of acoustic cues in an auditory spatial attention task. Cerebral Cortex, 24, 2579–2590. Weisz, N., Wuhle, A., Monittola, G., Demarchi, G., Frey, J., Popov, T., & Braun, C. (2014b). Prestimulus oscillatory power and connectivity patterns predispose conscious somatosensory per- ception. Proceedings of the National Academy of Sciences, 111, e417–425. Womelsdorf, T., Schoffelen, J. M., Oostenveld, R., Singer, W., Desimone, R., Engel, A. K., & Fries, P. (2007). Modulation of neu- ronal interactions through neuronal synchronization. Science, 316, 1609–1612. Wöstmann, M., Herrmann, B., Maess, B., & Obleser, J. (2016). Spatiotemporal dynamics of auditory attention synchronize with speech. Proceedings of the National Academy of Sciences, 113, 3873–3878. Wyart, V., de Gardelle, V., Scholl, J., & Summerﬁeld, C. (2012). Rhythmic ﬂuctuations in evidence accumulation during decision making in the human brain. Neuron, 76, 847–858. Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., & Breakspear, M. (2014). Time-resolved resting-state brain networks. Proceedings of the National Academy of Sciences, 111, 10341–10346. Strauß, A., Wöstmann, M., & Obleser, J. (2014). Cortical alpha oscillations as a tool for auditory selective inhibition. Frontiers in Human Neuroscience, 8, 350. Znamenskiy, P., & Zador, A. M. (2013). Corticostriatal neurons in auditory cortex drive decisions during auditory discrimination. Nature, 497, 482–485. Network Neuroscience 191 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 2 1 6 6 1 0 9 1 9 3 1 n e n _ a _ 0 0 0 0 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 研究形象

下载pdf