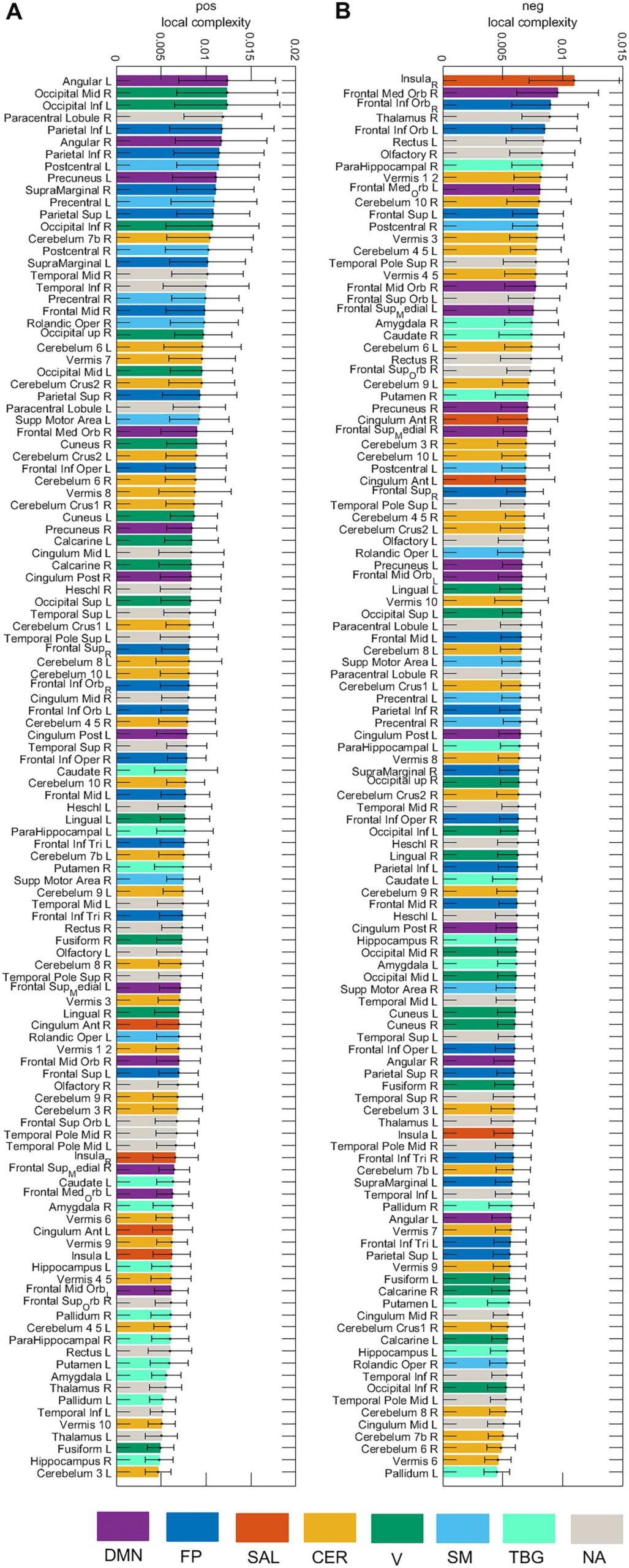研究 - 麻省理工学院人工智能研究专业

研究

Estimation of global and local complexities of
brain networks: A random walks approach

Roberto C. Sotero1,2,3, Lazaro M. Sanchez-Rodriguez1,2,
Narges Moradi1,2,3, and Mehdy Dousty4,5

1Hotchkiss Brain Institute, University of Calgary, AB, 加拿大
2放射科, University of Calgary, AB, 加拿大
3Biomedical Engineering Graduate Program, University of Calgary, AB, 加拿大
4Institute of Biomaterials and Biomedical Engineering, 多伦多大学, 在, 加拿大
5KITE, Toronto Rehab, University Health Network, 多伦多, 在, 加拿大

开放访问

杂志

关键词: Network complexity, Local complexity, Random walk, Sample entropy, Resting-state
网络

抽象的

The complexity of brain activity has been observed at many spatial scales and has been
proposed to differentiate between mental states and disorders. Here we introduced a new
measure of (全球的) network complexity, constructed as the sum of the complexities of its
节点 (IE。, local complexity). The complexity of each node is obtained by comparing the
sample entropy of the time series generated by the movement of a random walker on the
network resulting from removing the node and its connections, with the sample entropy of
the time series obtained from a regular lattice (ordered state) and a random network
(disordered state). We studied the complexity of fMRI-based resting-state networks. 我们
found that positively correlated (pos) networks comprising only the positive functional
connections have higher complexity than anticorrelation (neg) 网络 (comprising the
negative connections) and the network consisting of the absolute value of all connections
(abs). We also observed a signiﬁcant correlation between complexity and the strength of
functional connectivity in the pos network. Our results suggest that the pos network is related
to the information processing in the brain and that functional connectivity studies should
analyze pos and neg networks separately instead of the abs network, as is commonly done.

作者总结

Current measures of network complexity fail to capture the structural and functional diversity
of brain networks, in which hierarchies of linked communities span across several spatial
scales, from cortical minicolumns to large-scale networks. In this paper we use random
walks processes to obtain a time series reﬂecting the complex structure of brain networks and
use this time series to construct measures of local and global complexity. We found that
complexity is signiﬁcantly correlated to the strength of the connections in the positively
correlated brain network, being stronger at the global than at the local scale.

介绍

The development of a quantitative measure of complexity has proven difﬁcult because of the
variety of systems that may be labeled as “complex.” In the case of the complexity of networks,
perhaps the most popular approach has been the use of information-based measures (Bonchev
& Buck, 2005; Dehmer & Barbarini, 2009). The basic principle to construct these measures

引文: Sotero, 右. C。, Sanchez-
罗德里格斯, L. M。, Moradi, N。, & Dousty,
中号. (2020). Estimation of global and
local complexities of brain networks: A
random walks approach. 网络
神经科学, 4(3), 575–594. https://
doi.org/10.1162/netn_a_00138

DOI:
https://doi.org/10.1162/netn_a_00138

支持信息:
https://doi.org/10.1162/netn_a_00138

已收到: 15 八月 2019
公认: 23 行进 2020

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
Roberto C. Sotero
roberto.soterodiaz@ucalgary.ca

处理编辑器:
Bratislav Misic

版权: © 2020
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
7
5
1
8
6
7
3
8
1
n
e
n
_
A
_
0
0
1
3
8
p
d

乙
y
G
你
e
s
t

哦
n
0
9
S
e
p
e
米
乙
e
r
2
0
2
3

Complexity of brain networks

Random Walk:
A succession of random steps along
some mathematical space.

Functional connectivity:
Statistical dependencies between the
time series of different brain areas.

Global signal:
The mean time course computed
over all voxels within the brain. 这是
used a normalization factor for
removing the effects of global
variations in fMRI data.

Pearson correlation:
A number between −1 and 1 那
indicates the strength of the linear
relationship between two variables.

网络神经科学

is to select an arbitrary graph invariant X, partitioned as X1, . . . , XN. Probabilities can be
inferred for each partition using the entities pi = Xi/ ∑N
i=1 pi = 1.
The information content of the graph is then computed using the Shannon formula (Shannon,
1948): H = ∑N
i=1 pilog (pi). Another important deﬁnition of complexity was proposed by
Kolmogorov (1968). The Kolmogorov complexity of a network is the length of the shortest
computer program that produces the network as output. Although Kolmogorov complexity is
uncomputable it can be approximated to a degree that allows its practical use (李 & Vitányi,
2008).

i=1 Xi since it holds that ∑N

The measures of complexity described above assume it to be a monotonically increasing
function of disorder. 然而, complexity can also be deﬁned as a monotonically increasing
function of order, as shown by McShea (1991), who found that the morphological complexity
of organisms changed with the level of self-organization, and the latter with order. 最后,
complexity can be deﬁned as a convex function of disorder; 那是, a quantity that attains
a minimum for both completely ordered and completely disordered systems, and a maxi-
mum at some intermediate level of disorder or order (López-Ruiz, Mancini, & Calbet, 1995;
Shiner, Davison, & Landsberg, 1999; 托诺尼, Edelman, & 斯波恩斯, 1998). 这里, we adopt this
latter notion by assuming that network complexity achieves a minimum for regular lattice (RL)
网络 (Watts & Strogatz, 1998) and random networks, also known as Erdös–Rényi (ER)
网络 (Erdös & Rényi, 1959).

In addition to the global complexity of the brain network, in this work we are interested in
computing the local complexities (a measure for each of the different brain areas), 这样
the global complexity of the network is the sum of the local ones; 那是, the complexity of the
system is the sum of the complexity of its parts. To estimate the complexities, we let random
walkers diffuse on the network and construct time series of the strengths of the nodes (脑
地区) visited by each of the walkers. The sample entropy (SampEn) (Richman & Moorman,
2000) of the time series is then calculated. Local complexities are obtained by iteratively re-
moving a node and all its connections, constructing the time series from the walker movement
in the resulting network, computing the SampEn, and comparing this value to the average
value obtained from 1,000 ER and 1,000 RL networks with the same degree distribution and
connections strengths.

Functional connectivity in the brain is deﬁned as the synchronization of neurophysiological
events among anatomically separated brain areas (弗里斯顿, Jezzard, & 车工, 1994). Biswal,
Yetkin, Haughton, and Hyde (1995) were the ﬁrst to report that during resting state the pri-
mary motor regions in the left and right hemispheres were positively correlated. Later studies
identiﬁed positive correlations between regions that are now known to comprise the default
mode network (DMN) (巴克纳, Andrews-Hanna, & Schacter, 2008; Raichle, 斯奈德, 权力,
Gusnard, & 舒尔曼, 2001). In addition to the reported correlated networks, anticorrelated
networks have also been reported by several studies (狐狸, 张, 斯奈德, & Raichle, 2009;
Gopinath, Krishnamurthy, Cabanban, & Crosson, 2015; 梁, 国王, & 张, 2012). 铝-
though anticorrelations have been attributed to the global signal removal, recent studies sug-
gest a physiological basis (Fox et al., 2009; Kazeminejad & Sotero, 2019). 为此原因, 在
this paper we computed three different functional connectivity matrices for each subject by
using the Pearson correlation between the resting-state functional magnetic resonance imag-
英 (功能磁共振成像) signals recorded from each of the 116 brain areas considered. A matrix consisting
of the absolute value of all connections (denoted as abs), a matrix consisting of only the posi-
tive connections (denoted as pos) representing the positively correlated network, and a matrix
comprising the absolute value of only the negative connections (denoted as neg) representing
the anticorrelation network. We then compute the local complexities of the 116 brain areas,

576

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
7
5
1
8
6
7
3
8
1
n
e
n
_
A
_
0
0
1
3
8
p
d

乙
y
G
你
e
s
t

哦
n
0
9
S
e
p
e
米
乙
e
r
2
0
2
3

Complexity of brain networks

Functional magnetic resonance
成像 (功能磁共振成像):
Detect changes in blood oxygenation
and ﬂow that occur in response to
neuronal activity.

Network integration:
The combination of information
exclusive to specialized brain
地区.

Network segregation:
Processes occur separately in groups
of interconnected populations or
地区.

as well as the global complexities of the entire brain network, and seven known functional
networks of the brain (Sedeño et al., 2016): default mode network (DMN), 额顶叶 (FP),
salience (SAL), sensorimotor (SM), visual (V), cerebellar (CER), and temporo-basal-ganglial
(TBG) 网络. Our results show that the pos network has higher global complexity than
the neg and abs networks. We also found that the link between complexity and functional
connectivity is stronger for the pos network than for neg network, and changes with the spatial
scale for the pos network, being stronger at the global scale than at the local scale. 还, 在里面
pos network global complexity was strongly correlated to the network integration and segrega-
的, whereas neg and abs were not signiﬁcantly correlated with integration and segregation.
Our results suggest that the pos network is related to the information processing in the brain
network and should be used for functional connectivity analysis instead of the abs network.

方法

Data Acquisition and Preprocessing

We requested and received access to data collected by NIH Human Connectome Project
(HCP) for the purpose of scientiﬁc investigation and agreed to their open-access terms of use.
The resting-state fMRI dataset of 89 subjects from the HCP (https://db.humanconnectome.org)
(Van Essen et al., 2013) was used in this research. The HCP consent procedure was approved
by the Washington University institutional review board. For more information see Van Essen
等人. (2013). Each subject was involved in four runs of 15 minutes each using a 3 T Siemens
scanner while their eyes were open and had a relaxed ﬁxation on a projected bright cross-hair
on a dark background. The data were acquired with 2.0-mm isotropic voxels for 72 slices, TR =
0.72 s, = 33.1 多发性硬化症, 1,200 frames per run, 0.58-ms echo spacing, 和 2,290 Hz/Px bandwidth
(Moeller et al., 2010). 所以, the fMRI data were acquired with a spatial resolution of 2 ×
2 × 2 mm and a temporal resolution of 0.72 s, using multibands accelerated echo-planar
imaging to generate a high quality and the most robust fMRI data. The fMRI data were spa-
tially preprocessed to remove spatial artifacts produced by head motion, B0 distortions, 和
gradient nonlinearities (Jovicich et al., 2006). Since comparison of fMRI images across sub-
jects and studies is possible when the images have been transformed from the subject’s native
volume space to the Montreal Neurological Institute (MNI) 空间, fMRI images were wrapped
and aligned into the MNI space with FSL’s FLIRT 12 DOF afﬁne and then an FNIRT nonlin-
ear registration (詹金森, 栏干, 布雷迪, & 史密斯, 2002) was performed. In this study, 这
MNI-152-2mm atlas (Mazziotta et al., 2001) was utilized for fMRI data registration.

Construction of Functional Connectivity Matrices

The peak voxel in each region, 那是, the voxel of maximal activation, was selected by com-
puting the root-mean-square for each voxel’s fMRI signal over all time.
It has been shown
that the peak voxel provides the best effect of any voxel in the region of interest (ROI) (Sharot,
Delgado, & Phelps, 2004). 此外, the peak voxel activity correlates better with evoked
scalp electrical potentials than the average activity across the ROI. This means that the peak
voxel represents the ROI’s activity better than other choices (Arthurs & Boniface, 2003). 这
peak voxel in each region is determined using previously published Talairach coordinates
(after conversion to MNI coordinates and using Automated Anatomical Labeling (AAL) 116
atlas) (Fox et al., 2005). The resulting signal was ﬁltered to keep only low-frequency ﬂuctu-
ations (0.01–0.08 Hz) (严 & Zang, 2010). 最后, the global signal (IE。, the average of the
fMRI signals over the whole brain (Moradi, Dousty, & Sotero, 2019)) was regressed out.

网络神经科学

577

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
7
5
1
8
6
7
3
8
1
n
e
n
_
A
_
0
0
1
3
8
p
d

乙
y
G
你
e
s
t

哦
n
0
9
S
e
p
e
米
乙
e
r
2
0
2
3

Complexity of brain networks

We then computed the Pearson correlation between all possible pairs of time series, cre-
ating a 116 × 116 functional connectivity matrix for each subject.
In all cases p values
were corrected by means of a multiple comparison analysis based on the false discovery rate
(Benjamini & Hochberg, 1995). Three different networks were obtained from this matrix. A
network consisting of the absolute value of all connections (denoted as abs) which is the most
commonly used in fMRI connectivity studies (Meier et al., 2016; Meszlényi, Hermann, Buza,
Gál, & Vidnyánszky, 2017; Salvador et al., 2005), a network consisting of only the positive
连接 (denoted as pos), and a network comprising the absolute value of only the nega-
tive connections (denoted as neg).

Construction of Anatomical Connectivity Matrices

The HCP preprocessed diffusion data and the structural preprocessed data were used to
compute the structural connectivity for each subject. The preprocessed steps in HCP were
conducted by using FSL and Freesurfer softwares (Sotiropoulos et al., 2013). 下列
describes the preprocessing steps for the DTI data. Six diffusion series were used to normalize
the intensity of mean b0 images. Several algorithms implemented in FSL were used to remove
distortions, 那是, the TOPUP algorithm to remove the echo planner distortion and the EDDY
algorithm to correct the Eddy current-induced distortions and subject motion. The registration
was done by using the FLIRT and FreeSurfer’s Bbregister algorithms (Sotiropoulos et al., 2013).
The T1W images were parcellated with the IBASPM toolbox (Alemán-Gómez, Melie-Garcia,
& Valdés-Hernández, 2006) into AAL 116. The MRtrix toolbox was used to perform diffusion-
weighted MRI white matter tractography by using constrained spherical deconvolution and
a probabilistic streamlines algorithm (图尔尼耶, 卡拉曼特, & 康纳利, 2012). A weighted
structural connectivity matrix was obtained after eliminating volume and ﬁber length biases
(Tournier et al., 2012).

Construction of the Time Series of the Random Walker’s Movements on the Connectivity Matrix

We ﬁrst consider an unweighted network consisting of N nodes. We place a large number
K (K ≫ N) of random walkers onto this network. 在每个时间步, the walkers move ran-
domly (with the same probability) between the nodes that are directly linked to each other.
We allow the walkers to perform T time steps. As a walker visits a node, we record the degree
of the node. 因此, after T time steps, we obtain K time series reﬂecting different realizations
of the random walker’s movement on the network. Nodes with high degree (枢纽) will appear
more frequently in the series than nodes with low degree.

In the case of weighted networks, such as the functional connectivity matrix representing
the brain network, the routing strategy is a biased random walker, where the motion of a
random walker located at a given node is biased according to the weights of the connections
to the neighboring nodes (张, Shan, & 陈, 2013). Speciﬁcally, the transition probability
pij from brain area i to brain area j is given by pij = wij/ ∑N
j=1 wij, where wij is the weight
of the connection from area i to area j (Sotero, Sanchez-Rodriguez, Dousty, Iturria-Medina,
& Sanchez-Bornot, 2019). We then construct a time series with the strengths of the nodes i
visited by the walker: stri = ∑N

j=1 wij.

Computing the Entropy of the Time Series

In this paper we use sample entropy (SampEn) (Richman & Moorman, 2000) to estimate the
complexity of the time series of the diffusion of the random walker in the network. SampEn
improved from approximate entropy (ApEn) (Pincus, 1991) by reducing the bias caused by

网络神经科学

578

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
7
5
1
8
6
7
3
8
1
n
e
n
_
A
_
0
0
1
3
8
p
d

乙
y
G
你
e
s
t

哦
n
0
9
S
e
p
e
米
乙
e
r
2
0
2
3

Complexity of brain networks

self-matching. For a time series x(我), 1 ≤ i ≤ N, of ﬁnite length N, we ﬁrst reconstitute the
N − m + 1 vectors Xm(我) following the form:

Xm(我) = {X(我), X(我 + 1), . . . , X (我 + 米 - 1)} ,

(1)

i = 1, 2, . . . , N − m + 1

where m is the embedding dimension, 那是, the minimum dimension required to recon-
struct the phase space of the time series (曹, 1997). SampEn is the negative logarithm of the
probability that if two sets of simultaneous data points of length m have distance smaller than
the tolerance r, then two sets of simultaneous data points of length m + 1 also have distance
smaller than r. 从数学上来说, we start by deﬁning the probability Gm
我 (r) that any vector
Xm(j) is within distance r of Xm(我):

我 (r) =

N − m + 1 ∑N − m + 1

j = 1

dm
ij − r

(西德:16)

(西德:17)

where dm

ij is the distance between the vectors Xm(我) and Xm(j), deﬁned as:

dm
ij = max (|X(我 + k) − x (j − k)|) ,
k = 0, 1, . . . , 米

When the embedding dimension is m, the total number of template matches is:

Bm(r) =

1
N − m

∑N − m

i = 1 Gm

我 (r)

(2)

(3)

(4)

相似地, when the embedding dimension is m + 1, the total number of template matches is:

是(r) =

1
N − m

∑N − m

i = 1 Gm + 1

我

(r)

最后, the SampEn of the time series is estimated by:

SampEn(r, 米, 氮) = −ln

是(r)
Bm(r) (西德:19)

(西德:18)

(5)

(6)

For all calculations, we take the value of m to be 2 and the value of r to be 0.2 std, where std is
the standard deviation of the time series which should be taken over a large dataset (Delgado-
Bonal & Marshak, 2019). Supporting Information Figure S1 shows the sample entropy of the
time series constructed with the strengths of the nodes visited by a random walker released on
an ER network (N= 100) for different values of the length of the time series. We see that for
series comprising more than 23,000 points there is no signiﬁcant change in the sample entropy
when the length is increased. Based on this simulation, we chose a length of 25,000 点
for all calculations of the entropy.

Computing Local Complexities and Global Complexity

We propose to obtain local complexities ci by (1) iteratively removing a node and all its con-
连接, (2) constructing the time series from the random walker diffusion in the resulting
网络, 和 (3) computing the SampEn of the time series obtained in the previous step. 为了
node i, the resulting SampEn is labeled as H6=i. Then we compare this entropy to the aver-
age SampEn (computed following the same procedure outlined before) 的 1,000 ER ( ¯HER) 和
1,000 RL networks ( ¯HRL) of the same size (i.e, N − 1) and connections strengths taken from
the original matrix. The local complexity is the percent this comparison is of the square of the

网络神经科学

579

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
7
5
1
8
6
7
3
8
1
n
e
n
_
A
_
0
0
1
3
8
p
d

乙
y
G
你
e
s
t

哦
n
0
9
S
e
p
e
米
乙
e
r
2
0
2
3

Complexity of brain networks

entropy of the original matrix (H), multiplied by the probability (pi) of the appearance of the
node in the time series:

ci = 100pi (西德:12)
(西德:12)

(西德:0)

H6=i − ¯HER

H6=i − ¯HRL

H2
(西德:1) (西德:0)

(西德:1)(西德:12)
(西德:12)

(7)

Note that the connection strengths of the 1,000 ER and 1,000 RL networks used to compute
¯HER and ¯HRL in Equation 7 are generated using a probability density function estimated from
the original matrix by means of a kernel density estimator (Bowman & Azzalini, 1997) 作为
implemented by Matlab’s function “ksdensity.” In the case of the functional and anatomical
brain connectivity data, we construct a vector with the nonzero strengths from all subjects and
use as input to the ksdensity function.

数字 1 shows the steps described above for computing the local complexities. The global

complexity of the network C is then computed as the sum of the local complexities:

C = ∑N

i = 1 词

(8)

Measures of Network Integration and Segregation

Segregation and integration are two complementary phenomena that coexist in the brain. Seg-
regation is the ability for specialized processing to occur within densely interconnected groups
of areas, whereas integration is the ability to rapidly combine specialized information from dis-
tributed areas (鲁比诺夫 & 斯波恩斯, 2010). Complex networks present both high integration and

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
7
5
1
8
6
7
3
8
1
n
e
n
_
A
_
0
0
1
3
8
p
d

乙
y
G
你
e
s
t

哦
n
0
9
S
e
p
e
米
乙
e
r
2
0
2
3

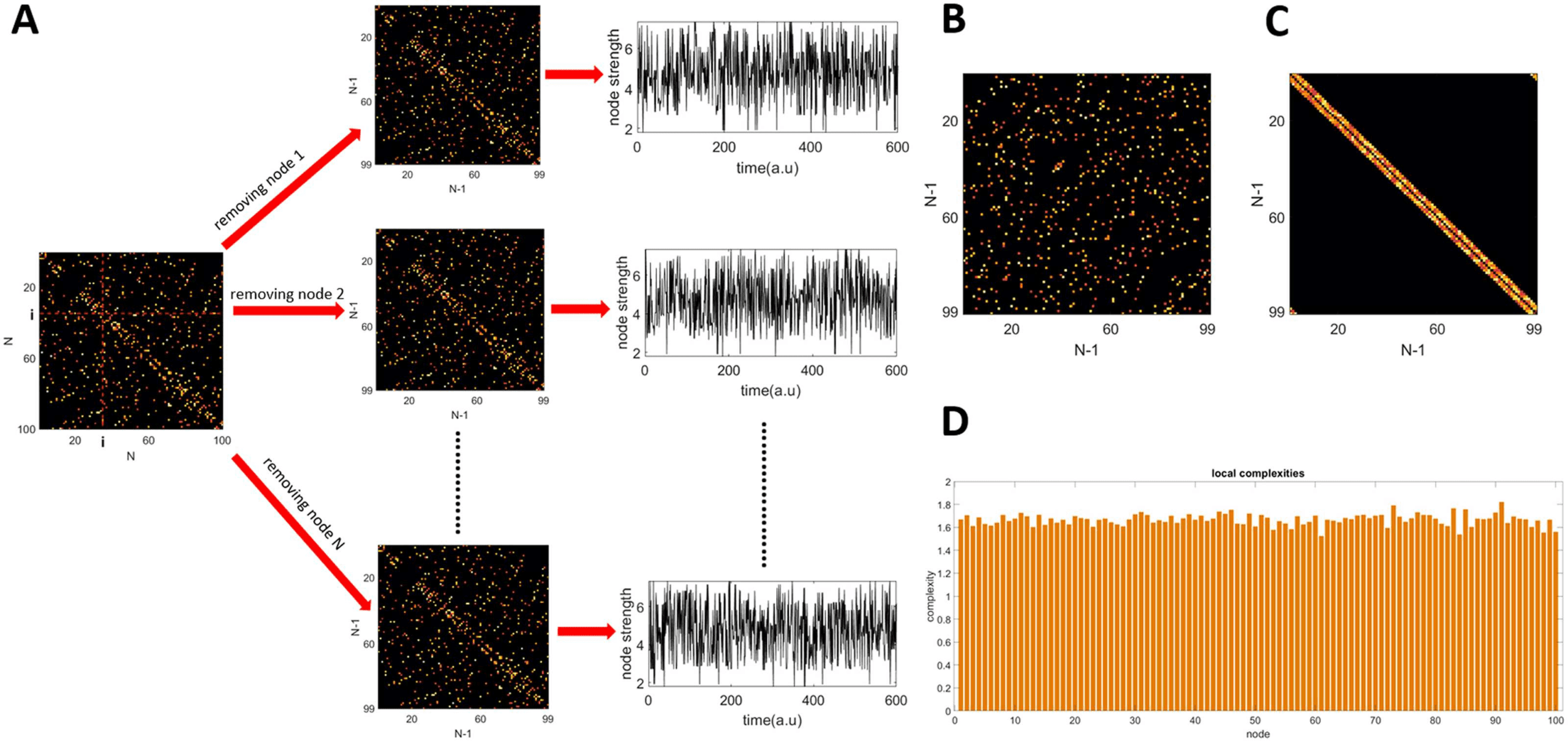
数字 1. Methodology for computing local complexities. (A) Given a connectivity matrix of size N, each node is removed iteratively and a
new matrix of size (N − 1) × (N − 1) is obtained. Then a time series of node strengths is constructed from the diffusion of a random walker in
the new matrix. (乙) A random network of size (N − 1) × (N − 1) with the same average degree and strengths as the matrices obtained in A. (C)
A regular network of size (N − 1) × (N − 1) with the same average degree and strengths as the matrices obtained in A. (D) Local complexities.

网络神经科学

580

Complexity of brain networks

Clustering coefﬁcient:
Ratio between existing and possible
number of triangle motifs in a
网络. Measure of network
segregation.

Global efﬁciency:
Measures how efﬁciently the
information is exchanged in the
网络. Measure of network
一体化.

Erdös–Rényi network:
A random graph where each possible
edge has the same probability of
existing.

Small-world network:
Network with high clustering
coefﬁcient and short average path
length.

segregation (托诺尼, 斯波恩斯, & Edelman, 1994). The clustering coefﬁcient
is a measure of
segregation, whereas global efﬁciency (Latora & Marchiori, 2001) is a measure of integration.

Since the network is weighted, the weighted version of the complex network measurements
needs to be applied. Let A = {amn} be the directed adjacency matrix (阿尔伯特 & 巴拉巴斯, 2002)
of the network (amn = 1 when there is a connection from m to n, amn = 0 否则). Let also
m be the total degree of node m, and d↔
dtot
m = ∑m6=n amnanm. The local clustering coefﬁcient
of node m for weighted networks is (Fagiolo, 2007):

瓦 +

W T

Cm =

(西德:16)
2 [dtot
米 (dtot
乙

(西德:17)
米 - 1) − 2d↔
米 ]

乙

毫米

W = W1/3, 和

瓦 +
在哪里
然后, C = ∑m Cm is used as a measure of segregation.
乙

W T

毫米

(西德:16)

(西德:17)

乙

is the mth element of the main diagonal of

(9)

(西德:17)

瓦 +

W T

(西德:16)

乙

The second measure we are going to compute is the global efﬁciency, calculated as (Latora

& Marchiori, 2001; 鲁比诺夫 & 斯波恩斯, 2010):

E =

1
氮 (N − 1)

−1

∑i6=j

~lij
(西德:16)

(西德:17)

(10)

where ~lij is the shortest weighted path length from i to j.

结果

Global Complexity of Simulated Complex Networks

As stated before, the goal of this work is to propose a new measure of structural complexity
that is useful for brain networks. To demonstrate the usefulness of the quantity we deﬁned, 我们
start by measuring how changes in the underlying network structure affect the observed values
of global complexity. 为此, we devised a scenario in which the network gradually
transforms from the perfectly orderly state (regular lattice network) to a completely random
状态 (Erdös–Rényi network).
Following Equations 7 和 8 we expect complexity to have a
minimum at these states. Network states different from these minimums would have a mixture
of order and disorder and thus were modeled using the small-world model (Watts & Strogatz,
1998). In this model, nodes of the network are placed on a regular k-dimensional grid and
each node is connected to m of its nearest neighbors, producing a regular lattice of nodes with
equal degrees. 然后, with probability p, each connection is randomly rewired. The RL network
corresponds to the value p = 0. When p > 0, edge rewiring is applied, and this changes the
degree distribution of nodes. On the other end of the spectrum is the ER model (Erdös &
Rényi, 1959), obtained when p = 1, in which there is no connectivity pattern between nodes.
In between, small-world networks, obtained for values 0 < p < 1, present high clustering and short path length (Watts & Strogatz, 1998). Graph theoretical studies of mammalian cortical networks recreated from tract tracing ex- periments demonstrated that the cat and macaque interareal anatomical networks share sim- ilar SW properties of short path length and high clustering (Hilgetag & Kaiser, 2004; Sporns & Zwi, 2004). Additionally, studies of anatomical and functional connectivity networks es- timated from human neuroimaging data also found SW characteristics (Bassett & Bullmore, 2006; Salvador et al., 2005). To simulate RL, SW, and ER networks we use Matlab’s function WattsStrogatz.m, which has as inputs the parameters k and p. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d t . 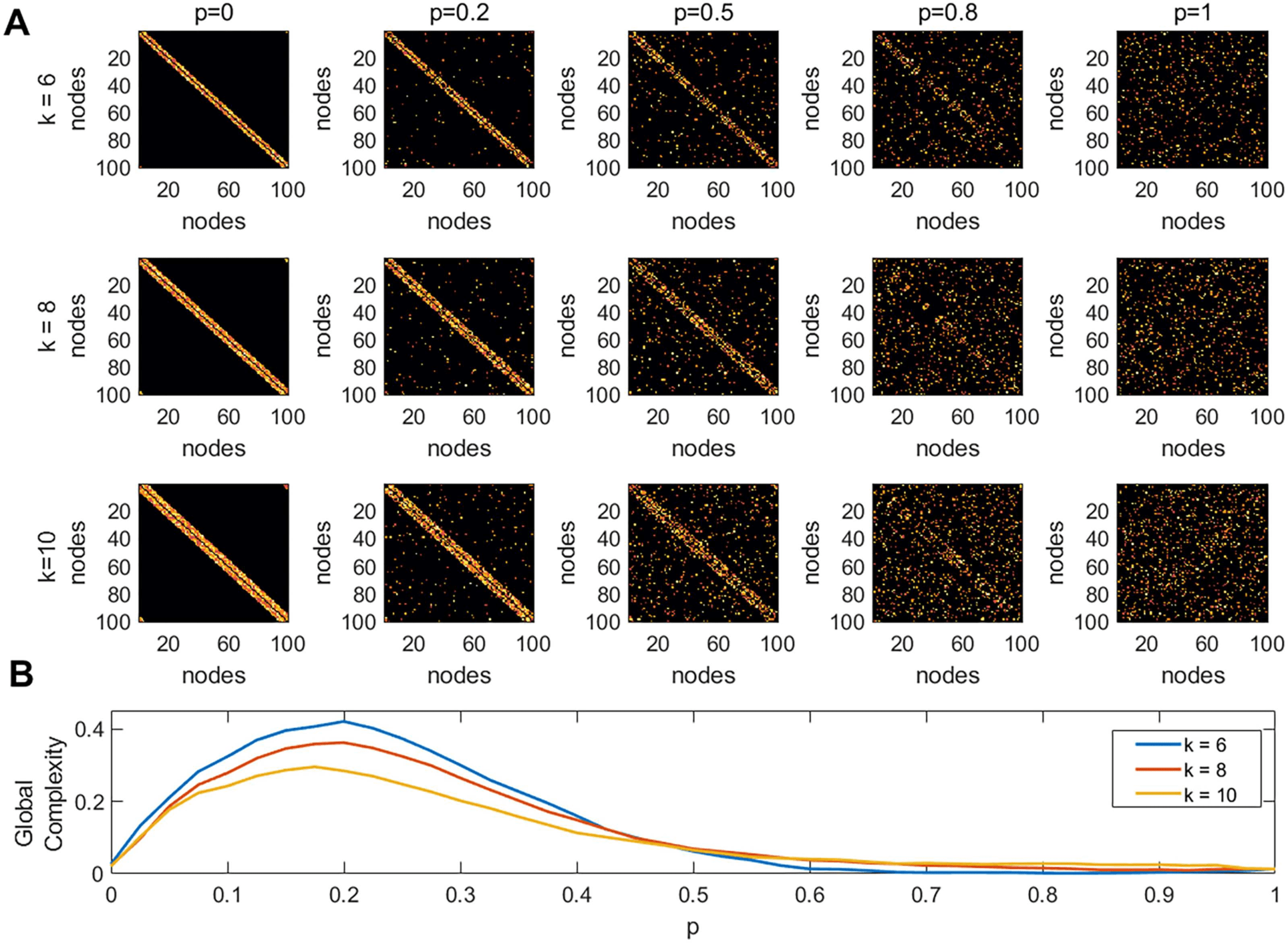f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Network Neuroscience 581 Complexity of brain networks Figure 2. Global complexity of simulated networks. (A) All networks have the same size N = 100, and were simulated using the Watts and Strogatz algorithm for creating small-world networks. The inputs to the model are the rewiring probability p, and mean node degree k. (B) Global complexity as a function of the rewiring probability p. Figure 2A shows examples of matrices of size N = 100, for ﬁve different values of the rewiring probability p, and three values of the mean node degree k. The weights in the net- work were generated from a uniform random distribution with values between 0 and 1. We then placed 104 random walkers onto these networks. The steps for estimating the global com- plexity of the network are presented in Figure 1 and described in detail in the Methods section. Figure 2B shows the global complexity of a network as a function of the rewiring probability p. Three different values of the average node degree were used k = 6, 8, 10. The results show that for a ﬁxed network size the maximum global complexity decreases with the increase of k (the network gets denser). Additionally, the probability at which the peak in complexity was achieved, also decreased with the increase of k. 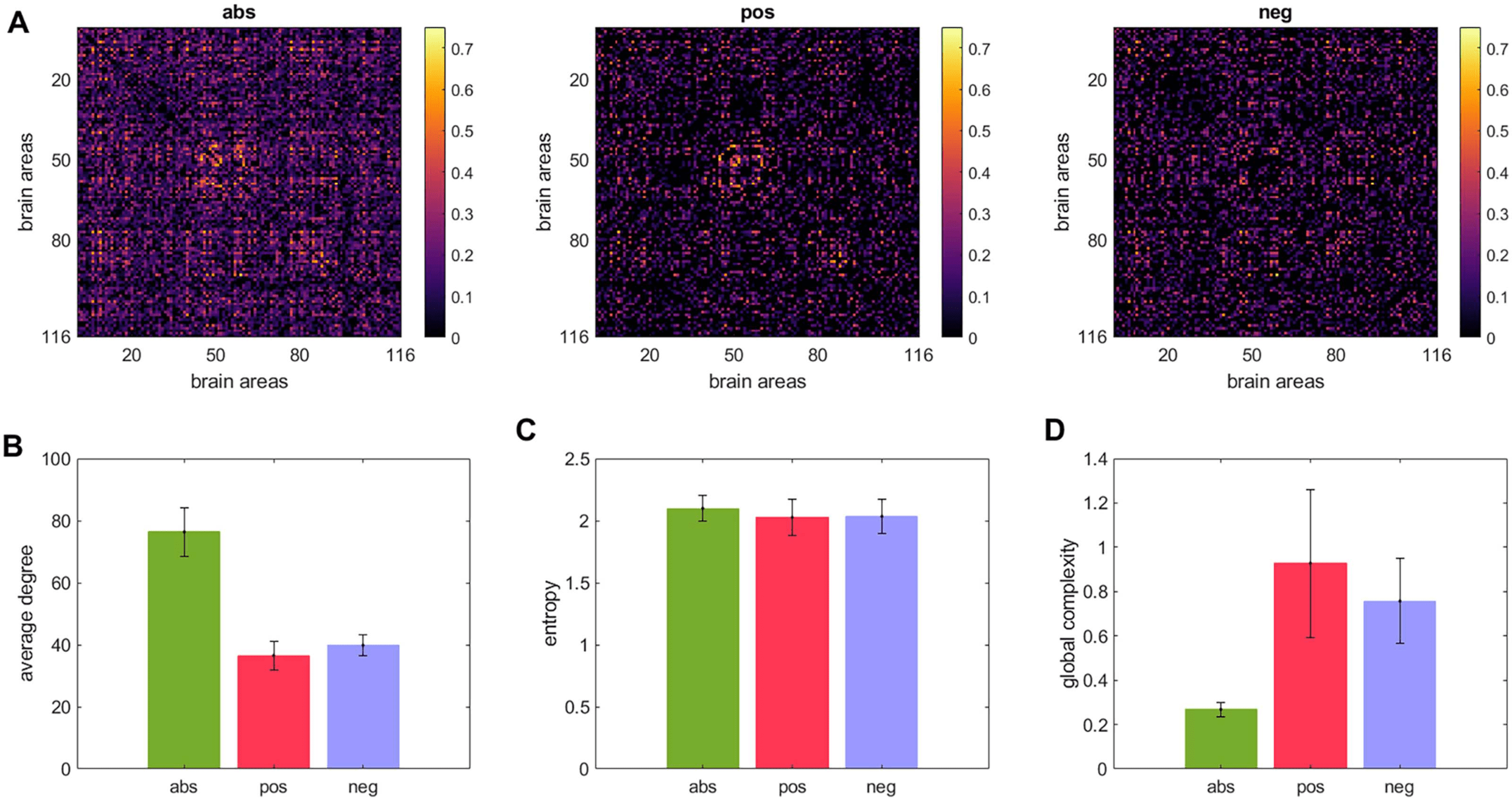Complexity Analysis of Large-Scale Human Brain Networks Figure 3A displays the abs, pos, and neg matrices for one subject. Figure 3B shows the node degree of the three matrices average across all subjects, Figure 3C shows their entropy, and Figure 3D their global complexity. Our results show that the pos matrices are sparser than the neg matrices but have approximately the same entropy. This combination results in the pos network having a higher global complexity than the neg matrices. The abs matrices presented the lowest global complexity of the three cases. Note that the density of connections by itself is not a predictor of the global complexity of the network. If the raw fMRI data includes more positive correlations than negative, which is common, then we expect that removing the global signal increases negative correlations. This is veriﬁed by the increase in the density of negative correlations and the decrease in the density of positive correlations (Supporting Information Figure S2A) when removing the global signal. The average weights of the connections follow the same trend (Supporting Information Figure S2B). This seems to indicate that the spatial complexity of the network is linked to its density. However, our results indicate this is not the Network Neuroscience 582 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d t . f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Complexity of brain networks Figure 3. Global complexity of the entire brain network. (A) A matrix consisting of the absolute value of all connections (denoted as abs), a matrix consisting of only the positive connections (de- noted as pos), and a matrix comprising the absolute value of only the negative connections (denoted as neg). (B) Node degree averaged across subjects. (C) Entropy averaged across subjects. (D) global complexity averaged across subjects. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d t . f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 case. Supporting Information Table S1 shows the correlation between global complexity and network density for the abs, pos, and neg cases. As we can see, the only signiﬁcant correlation (r = 0.59) was obtained for the pos case when removing the global signal; in all the other cases the correlations were small and nonsigniﬁcant. 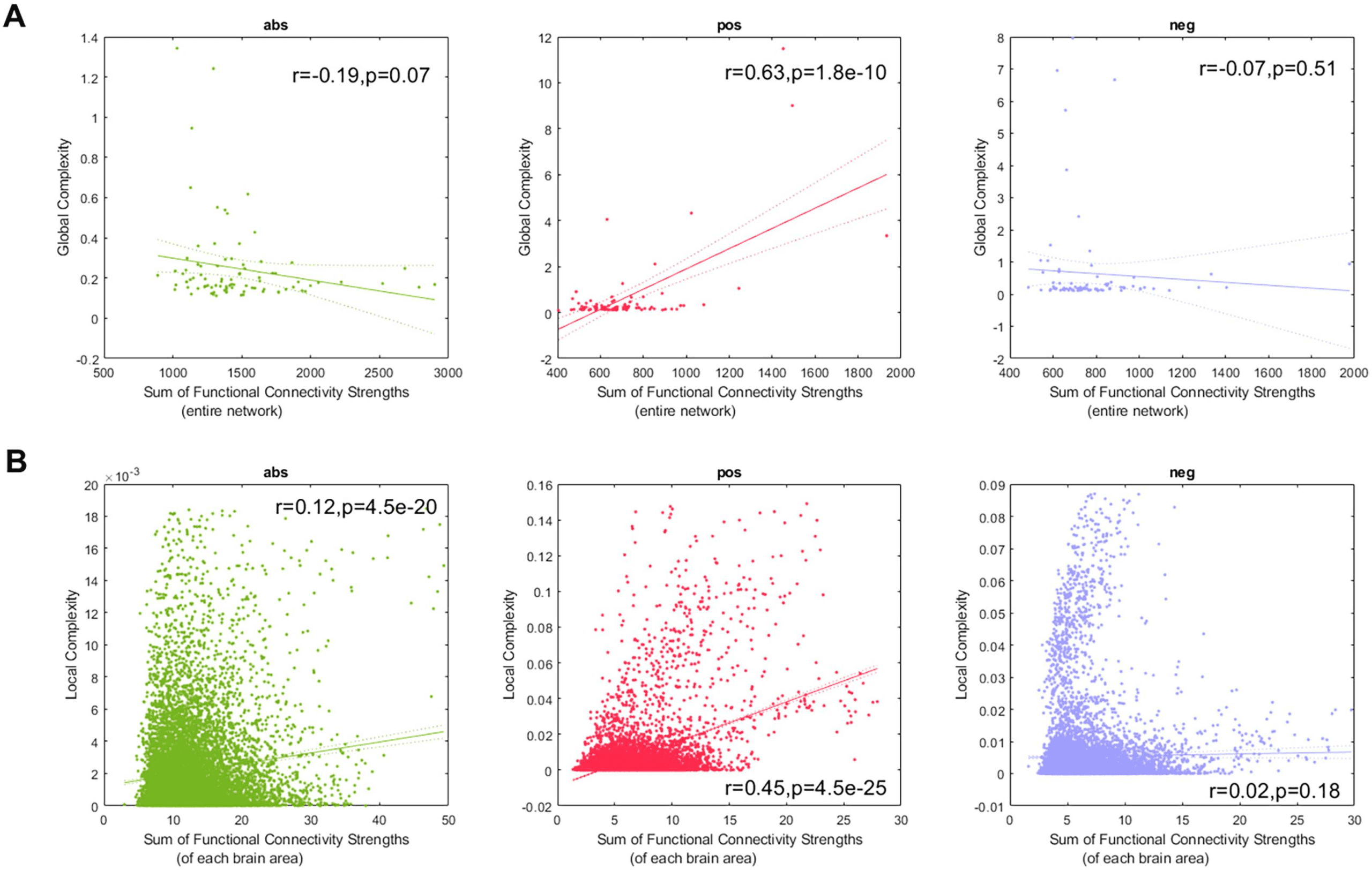Figure 4A shows the linear ﬁts between the global complexity and the sum of the functional connectivity strengths (SFCS) of the entire brain network for the abs, pos, and neg cases. We found that for the pos case, there is a strong correlation (r = 0.63, p < 0.05) between global complexity and SFCS. The anticorrelation network (r = −0.07, p = 0.51) and the abs network (r = −0.19, p = 0.07) were not signiﬁcantly correlated with SFCS. We also computed the linear ﬁts between local complexities and the SFCS of each brain area (Figure 4B). We found that for the pos case the link between complexity and functional connectivity was signiﬁcantly weaker at the local scale (r = 0.45, p < 0.05) compared with the global scale (Figure 4A). For the anticorrelation network there was no link at the local scale (r = 0.02, p = 0.18), while we found a weak correlation for the abs case (r = 0.12, p < 0.05). In the analysis involving local complexities, the large number of samples (we consider all subjects and all brain areas resulting in a maximum of 89 × 116 = 10, 324 points) allows us to compute the mutual information (MI) (Cover & Thomas, 2006) between local complexities and SFCS, which was not feasible for the analysis involving global complexities where we only had 89 data points. The advantage of using MI is that it is model free and can estimate nonlinear interactions, which are not possible to detect using the linear analysis presented in Figure 4. We computed MI with the MATLAB toolbox for the analysis of neuroscience data developed by Timme and Lapish (2018). A signiﬁcant value was attached to the MI by using a surrogate data approach (Pereda, Quiroga, & Bhattacharya, 2005). We created surrogate data by randomly shufﬂing the local complexity series 1,000 times. For each new surrogate series, we computed its MI with the SFCS series. We then calculated the mean and the standard deviation of the MI surrogates and used the MI value obtained from the original signals to construct a Z-score. The results (Supporting Information Table S2) show that both pos and neg networks present a Mutual information: Quantiﬁes the reduction in uncertainty about one random variable through observing another variable. Network Neuroscience 583 Complexity of brain networks l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d . t f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Figure 4. Link between complexity and connectivity. (A) Global complexity versus the sum of functional connectivity strengths for all subjects, resulting in a maximum of 89 points. (B) local complexities versus the sum of functional connectivity strengths, for all subjects and brain areas, resulting in a maximum of 89 × 116 = 10,324 points. The abs, pos, and neg networks appear in that order from left to right. In all panels, points outside of the percentiles 5 and 95 were classiﬁed as outliers and were removed. signiﬁcant statistical dependence between local complexity and SFCS, being the dependence for the pos network more than 10 times stronger than the dependence for neg networks. 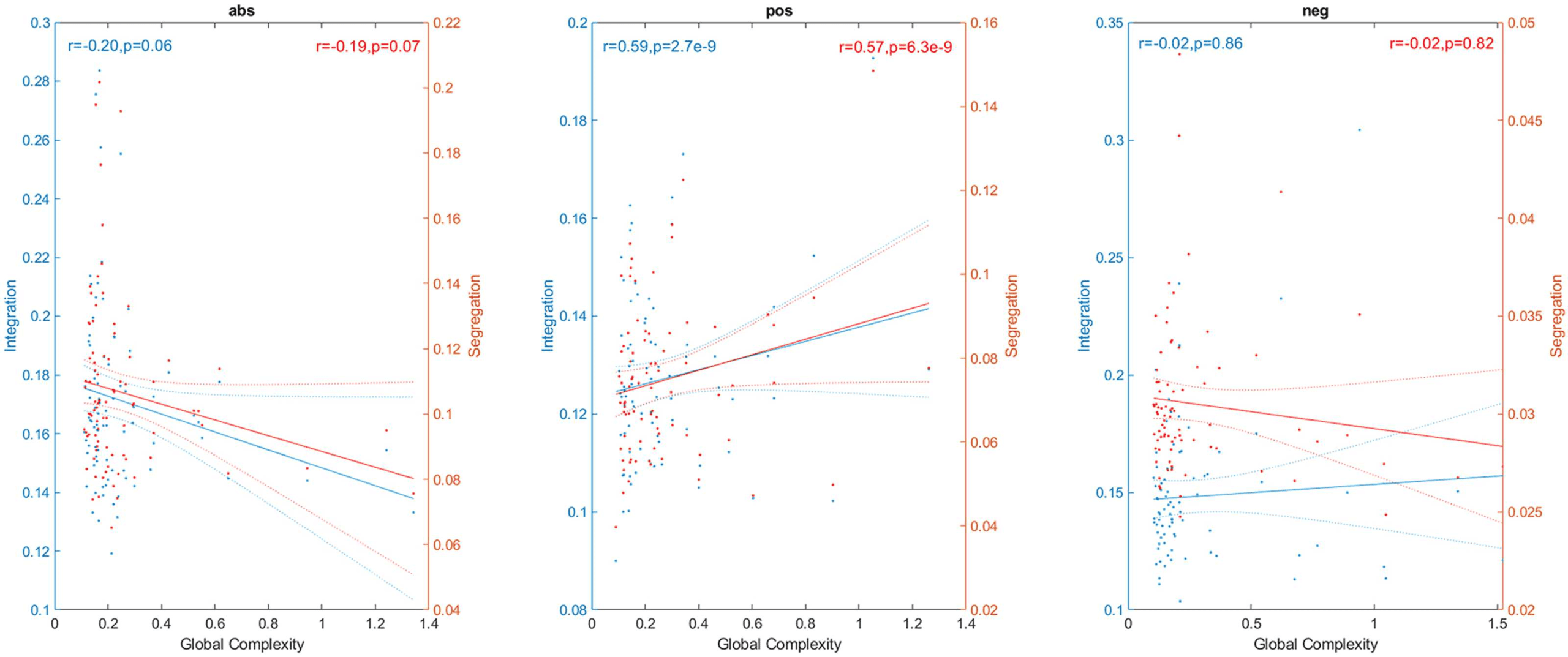Complex networks are expected to present high values of both integration and segregation. Thus, we also explored the link between them and global complexity (Figure 5). Integration and segregation were estimated using the global efﬁciency and average clustering coefﬁcient of the network, respectively (Sporns, 2013). We found strong correlations between global complexity and both integration (r = 0.59, p < 0.05) and segregation (r = 0.57, p < 0.05) for the pos network, and no signiﬁcant correlations for the neg case (r = −0.02, p = 0.86 for integration, and r = −0.02, p = 0.82 for segregation). Correlations were negative for the abs case (r = −0.20, p = 0.06 for the correlation with integration and r = −0.19, p = 0.07 for the correlation with segregation). Although nonsigniﬁcant, the p values were close to the p = 0.05 threshold. These negative correlations are counterintuitive, since we expect that a complex network has both high values of integration and segregation, and as we increase the complexity of the network those topological values should also increase. Network Neuroscience 584 Complexity of brain networks l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . Figure 5. Link between global complexity and integration (blue) and segregation (red). Points outside of the percentiles 5 and 95 were classiﬁed as outliers and were removed. 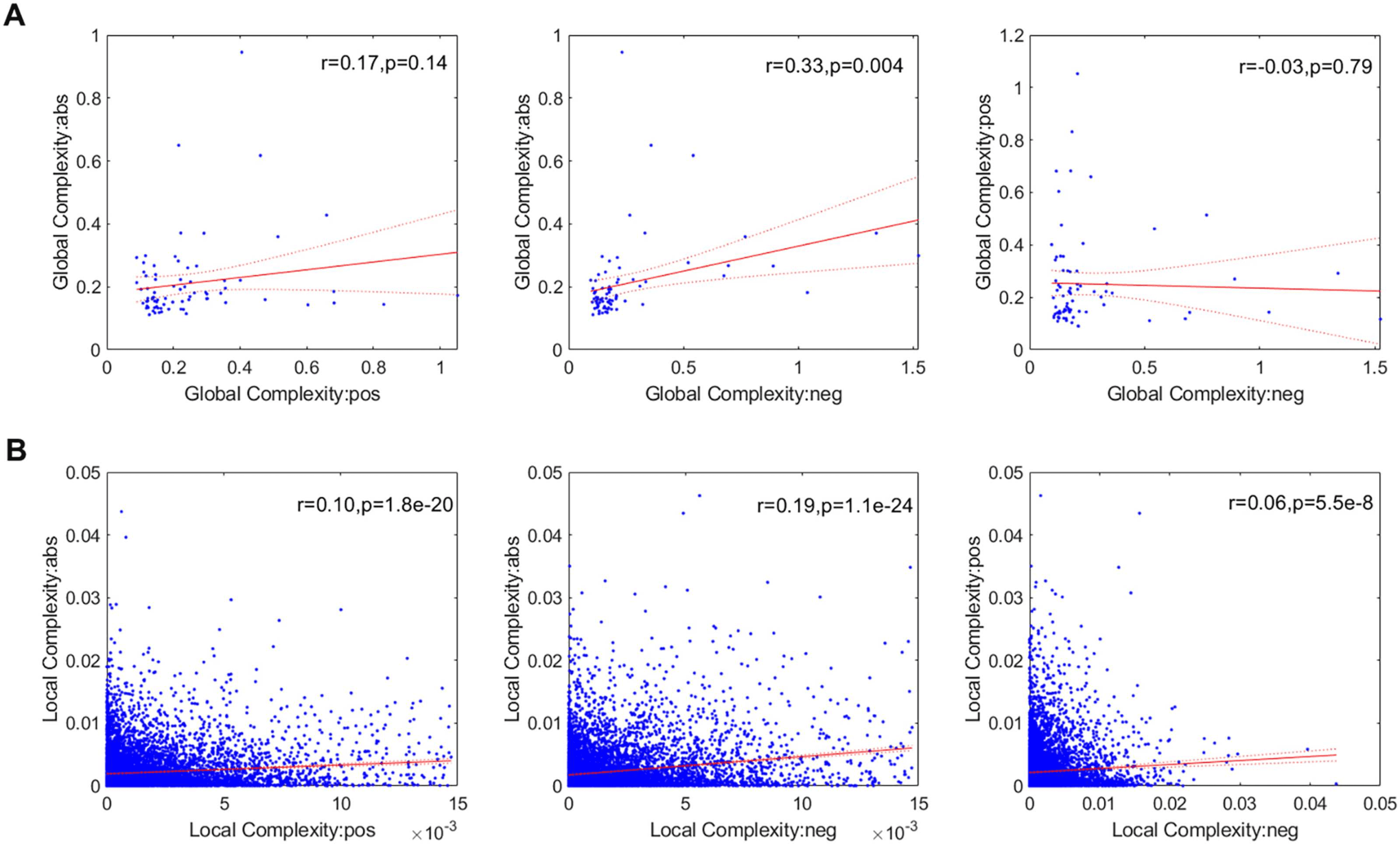We also investigated the link between the three network types at the global (Figure 6A) and local scales (Figure 6B), ﬁnding that the pos and neg networks are not signiﬁcantly correlated at any spatial scale. Figure 7 presents the local complexity of the 116 brain areas for the pos and neg cases. Seven resting-state networks (Sedeño et al., 2016) were considered (DMN, FP, SAL, CER, V, / / t e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d t . f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Figure 6. Link between the three network types (abs, pos, and neg) at the global (A) and local (B) scales. Points outside of the percentiles 5 and 95 were classiﬁed as outliers and were removed. Network Neuroscience 585 Complexity of brain networks l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d . t f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Figure 7. Local complexity of the 116 brain areas for the pos and neg cases. Seven resting-state networks (see Supporting Information Table S3) are represented through different colors: default mode network (DMN), fronto-parietal (FP), salience (SAL), sensorimotor (SM), visual (V), cerebellar (CER), and temporo-basal-ganglial (TBG) networks. The gray color represents areas not assigned (NA) to any of these networks. Network Neuroscience 586 Complexity of brain networks Anatomical connectivity: Network of structural (synaptic) connections linking sets of neurons, neuronal populations, or brain areas. SM, TGB) as well as areas that were not allocated to a network (NA). In the pos case, the area with the highest complexity belongs to the DMN (Angular L), whereas for the neg case, the area belongs to the salience network (Insula R). 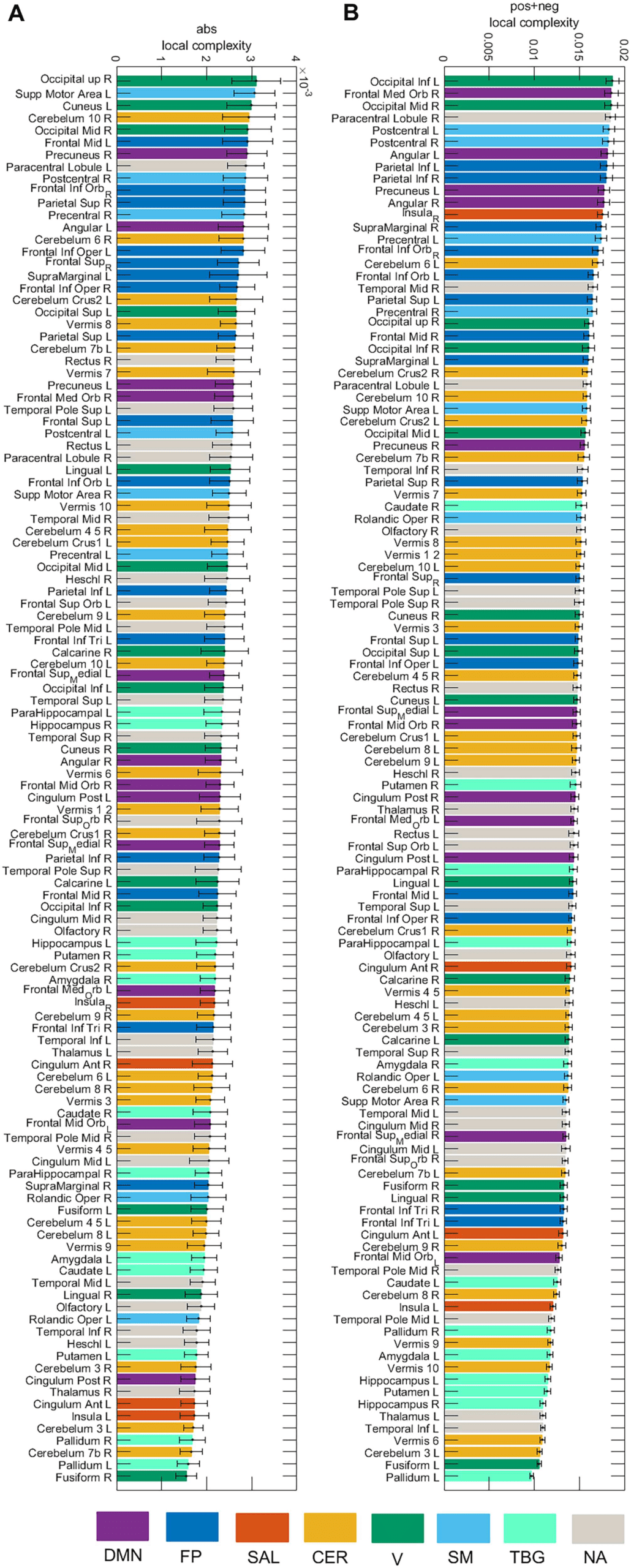Figure 8 displays the local complexity for the abs case and the sum of the complexities of the neg and pos case (neg+pos). In the abs case, the highest complexity was obtained for the Occipital_Sup_R, while the Occipital_Inf_L presented the highest complexity for the neg+pos case. 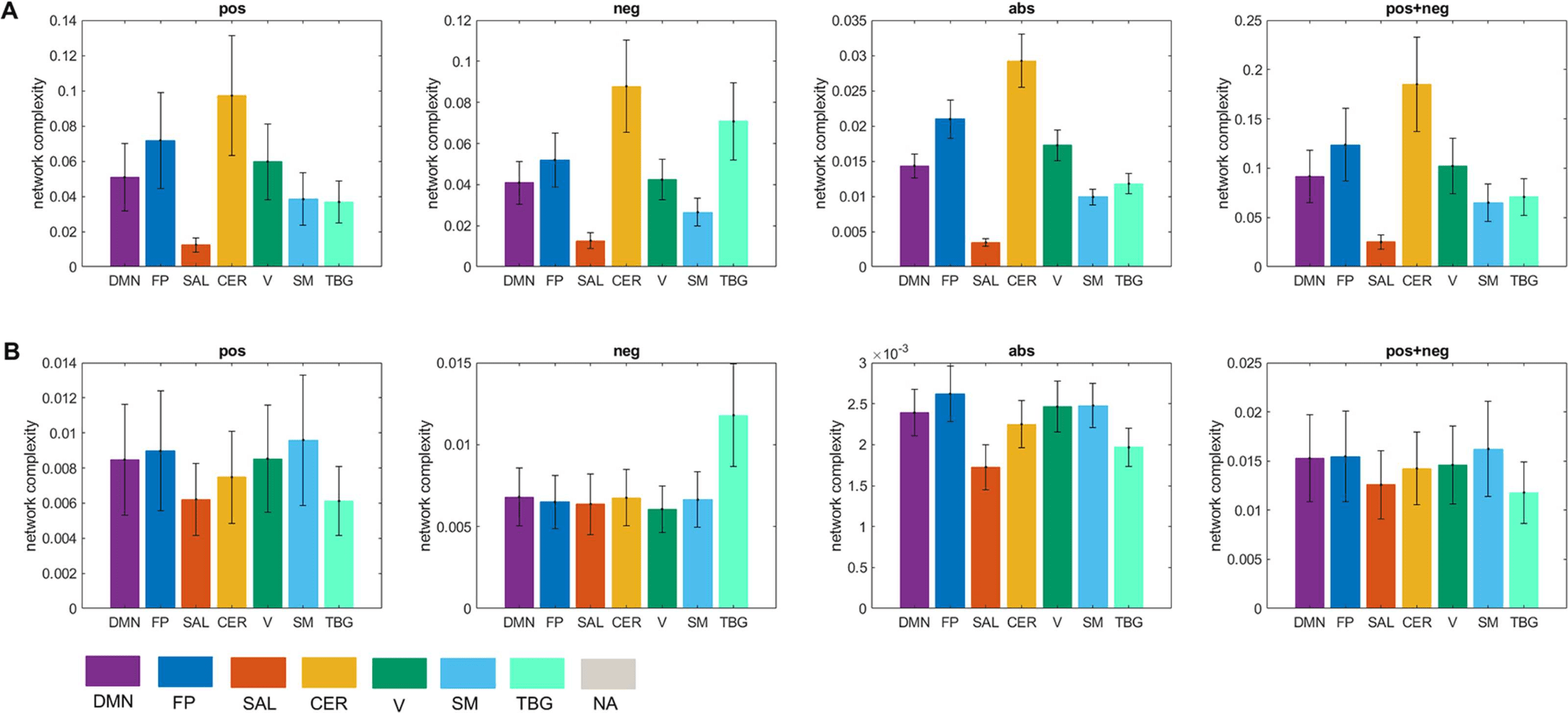We computed the global complexity of the seven resting-state networks (Figure 9A). We found that the network with the highest complexity for all cases was the cerebellar network, while the network with the lowest complexity was the salience network. The DMN, FP, CER, V, and SM networks presented more complexity in the pos than in the neg case, while the SAL and TGB networks were more complex in the neg case. When interpreting this result we need to be aware of the fact that since the global complexity of the network is computed as the sum of the local complexities (Equation 8), networks comprising few brain areas (as is the case of the salience network) will have a low value of global complexity provided that the difference in the values of the local complexities is not high (see Figures 7 and 8). To account for this issue, we also divided the global complexity of each network by the number of areas in each network (Figure 9B). As a result, although the average contribution of the areas in the salience network to the network complexity is still the lowest among the seven resting-state networks for the pos case, it is the areas in the visual network the ones with the lowest contribution in the neg case. 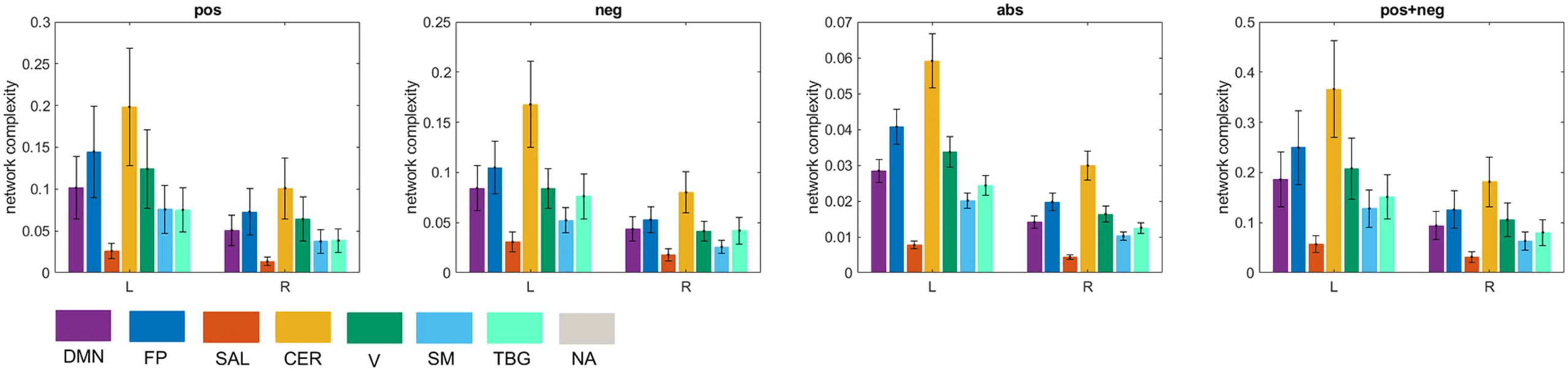Along these lines, hemispherical differences can be investigated as well. Previous studies have found interhemispheric asymmetry in brain connectivity during resting state (Medvedev, 2014). We found that the left hemisphere was signiﬁcantly more complex than the right hemi- sphere for the seven resting-state networks (Figure 10). The results presented above were obtained in connectivity matrices obtained from fMRI signals where the global signal was removed. For comparison, we also computed the global and local complexities of the networks constructed from fMRI data without global signal re- gression. Supporting Information Figure S3 shows the local complexity of the 116 brain areas for the pos and neg cases, while Supporting Information Figure S4 shows the complexities for the abs and pos+neg cases. When comparing these results to the global signal regression case (Figures 7 and 8), we found that the rank of areas with high complexity changed completely. Additionally, we also computed the correlation between global complexity and the integration and segregation of the abs, pos, and neg networks. Our results show that while there is a strong correlation between these topological measures and global complexity when the global signal is regressed out (Figure 5) for the pos case, no signiﬁcant correlation exists when the global signal is present (Supporting Information Figure S5). Previously, we have focused on the complexity of fMRI-based brain networks. For compari- son, we also analyzed the complexity of the anatomical network underlying brain activity. For this, the anatomical connectivity matrix of each subject was computed using the HCP pre- processed diffusion data (see Methods). Supporting Information Figure S6 shows the average anatomical connectivity across all subjects. Supporting Information Figure S7 shows the com- plexity of the 116 areas. Most of the top-ranked areas according to complexity values belong to the TBG network. Additionally, the global complexity of the anatomical matrix was not sig- niﬁcantly correlated to the integration and segregation of the network (Supporting Information Figure S8). Network Neuroscience 587 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d . t f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Complexity of brain networks l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d t . f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Figure 8. Local complexity of the 116 brain areas for the abs and pos+neg cases. Seven resting- state networks (see Supporting Information Table S3) are represented through different colors: default mode network (DMN), fronto-parietal (FP), salience (SAL), sensorimotor (SM), visual (V), cerebellar (CER), and temporo-basal-ganglial (TBG) networks. The gray color represents areas not assigned (NA) to any of these networks. Network Neuroscience 588 Complexity of brain networks Figure 9. Network complexity. (A) Global complexity of seven resting-state networks. (B) Global complexity divided by the number of areas in each network. Seven resting-state networks (see Supporting Information Table S3) are represented through different colors: default mode network (DMN), fronto-parietal (FP), salience (SAL), sensorimotor (SM), visual (V), cerebellar (CER), and temporo-basal-ganglial (TBG) networks. The gray color represents areas not assigned (NA) to any of these networks. Figure 10. Interhemispheric asymmetry of global complexity. L = left hemisphere R = right hemi- sphere. Seven resting-state networks (see Supporting Information Table S3) are represented through different colors: default mode network (DMN), fronto-parietal (FP), salience (SAL), sensorimotor (SM), visual (V), cerebellar (CER), and temporo-basal-ganglial (TBG) networks. The gray color rep- resents areas not assigned (NA) to any of these networks. DISCUSSION In this study, the complexity of each node in a network (i.e., local complexity) was computed using an index that compares the sample entropy of the time series generated by the movement of a random walker on the network, resulting from removing the node and its connections, to the sample entropy of the time series obtained from a regular lattice (the ordered state) and an Erdös–Rényi network (disordered state). Then, the network (global) complexity was constructed as the sum of the complexities of its nodes. Our simulations demonstrated that our measure of complexity (Equations 7 and 8), achieves a minimum for the regular lattice and Erdös–Rényi networks, and a maximum at some intermediate state, representing a small-world network with both order and disorder characteristics (Figure 2). The rationale behind the use of random walks is that diffusion processes are capable of uncovering the large-scale topological structure of complex networks (Noh & Rieger, 2004; Simonsen, Astrup Eriksen, Maslov, & Sneppen, 2004; Skardal & Adhikari, 2018). For instance, random walks are the basis of Infomap (Rosvall & Bergstrom, 2008), a popular method for Network Neuroscience 589 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d . t f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Complexity of brain networks detecting community structure in complex networks. Past studies of anatomical and functional brain connectivity have found interlinked communities that form a partly decomposable modu- lar architecture (Ashourvan, Telesford, Verstynen, Vettel, & Bassett, 2019; Meunier, Lambiotte, Fornito, Ersche, & Bullmore, 2009). Such architectures are hallmarks of complex systems and are thought to be of fundamental importance for understanding mental processing and cog- nition (Bola & Borchardt, 2016). In the brain, hierarchies of linked communities span several levels including brain regions, functional circuits, and large-scale networks. This structural diversity cannot be captured by previous structural complexity measures relying mainly on Shannon entropy (Shannon, 1948), but can be probed using random walks (Rosvall & Bergstrom, 2008). Once we constructed the time series of the random walker’s movement in the network, we needed a measure to estimate its complexity. There is a diversity of complexity measures based on different entropy deﬁnitions, such as Shannon entropy (Shannon, 1948), Tsallis en- tropy (Tsallis, 1988), spectral entropy (Inouye et al., 1991), wavelet entropy (Rosso et al., 2001), approximate entropy (Pincus, 1991), sample entropy (Richman & Moorman, 2000), fuzzy en- tropy (Chen, Wang, Xie, & Yu, 2007), and permutation entropy (Bandt & Pompe, 2002). In this work we selected sample entropy as it quantiﬁes the amount of regularity and unpre- dictability of ﬂuctuations in a time series (Richman & Moorman, 2000). This is important be- cause of the presence of communities in brain networks (Ashourvan et al., 2019; Meunier et al., 2009), which will result in repetitive patterns of nodes in the time series of the random walker’s movement (Fortunato & Hric, 2016; Sanchez-Rodriguez, Iturria-Medina, Mouches, & Sotero, 2019). On the other hand, this same community structure will result in a random walker’s movement that can be decomposed into different oscillatory modes (or temporal scales). This is because the random walker will spend considerable time in large communities (reﬂected in slow modes) and signiﬁcantly less time in smaller clusters (reﬂected in fast modes). These multiple temporal scales are not considered in the sample entropy method, which is based on a single temporal scale. To address this issue in future works, we propose to use the multi- scale entropy method (Costa, Goldberger, & Peng, 2005), which computes sample entropy at shorter and longer timescales, and the quantiﬁcation of the overall entropy of the time series is computed as the sum of the entropy values over all individual timescales. Our study of brain complexity found interhemispheric asymmetry, where the left hemi- sphere was signiﬁcantly more complex than the right hemisphere, for all the seven brain networks explored. Previous studies have also found interhemispheric asymmetry in brain connectivity during resting state. For instance, a recent study used near-infrared spectroscopy signals to estimated functional connectivity matrices (Medvedev, 2014). Their results revealed signiﬁcantly stronger and denser connectivity patterns in the right hemisphere in most subjects. This denser pattern of connections in the right hemisphere compared with the left hemisphere can lead to a lower structural complexity if it is not accompanied with a signiﬁcant increase in the entropy of the network. Thus, the balance between the entropy of the network and its density determines the network’s complexity. This was exempliﬁed in Figure 3 where we found that the entropy of the positive network and the anticorrelated network were essentially the same, but the positive network was sparser, which resulted in it being more complex than the anticorrelated network. Finally, we found that the complexity of the pos network is correlated to functional con- nectivity between the brain areas comprising the network, as well as to the integration and segregation of the network, suggesting the pos network is related to the information process- ing in the brain. On the other hand, the neg network presented a weaker (although statistically signiﬁcant) nonlinear dependence between local complexity and functional connectivity than Network Neuroscience 590 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d t . f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Complexity of brain networks the pos network. Although weaker than the pos case, this dependence should not be neglected. For example, a recent study has shown that the inclusion of anticorrelations improved the per- formance of a support vector machine model for classifying autism spectrum disorder by using fMRI-based functional connectivity data (Kazeminejad & Sotero, 2019). Based on these re- sults, we suggest that functional connectivity studies should analyze pos and neg networks separately, instead of the abs network as is commonly done. ACKNOWLEDGMENTS Data were provided, in part, by the Human Connectome Project, WU-Minn Consortium (Prin- cipal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657), funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research, and by the McDonnell Center for Systems Neuroscience at Washington University. SUPPORTING INFORMATION Supporting Information for this article is available at https://doi.org/10.1162/netn_a_00138. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d . t f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 AUTHOR CONTRIBUTIONS Roberto Sotero: Conceptualization; Formal analysis; Funding acquisition; Investigation; Method- ology; Project administration; Resources; Software; Supervision; Validation; Visualization; Writing - Original Draft. Lazaro M. Sanchez-Rodriguez: Conceptualization; Methodology; Software; Writing - Original Draft. Narges Moradi: Data curation; Software; Writing - Original Draft. Mehdy Dousty: Data curation; Software; Writing - Original Draft. FUNDING INFORMATION Roberto Sotero, Canadian Network for Research and Innovation in Machining Technology, Natural Sciences and Engineering Research Council of Canada (http://dx.doi.org/10.13039/ 501100002790), Award ID: RGPIN-2015-05966. REFERENCES Albert, R., & Barabási, A.-L. Statistical mechanics of complex networks. Statistical Mechanics of Complex Networks. https://doi.org/10.1103/RevModPhys.74.47 (2002). the 12th Annual Meeting of Alemán-Gómez, Y., Melie-Garcia, L., & Valdés-Hernández, P. A. (2006). IBASPM: Toolbox for automatic parcellation of brain struc- the Or- tures. Proceedings of ganization for Human Brain Mapping, Florence, June 11–15. NeuroImage, 27(1). Arthurs, O. J., & Boniface, S. J. (2003). What aspect of the fMRI BOLD signal best reﬂects the underlying electrophysiology in human somatosensory cortex? Clinical Neurophysiology: Ofﬁ- cial Journal of the International Federation of Clinical Neurophysi- ology, 114(7), 1203–1209. Retrieved from http://www.ncbi.nlm. nih.gov/pubmed/12842716 Italy, Ashourvan, A., Telesford, Q. K., Verstynen, T., Vettel, J. M., & Bassett, D. S. (2019). Multi-scale detection of hierarchical com- munity architecture in structural and functional brain networks. PLoS One, 14(5), e0215520. https://doi.org/10.1371/journal.pone. 0215520 Bandt, C., & Pompe, B. (2002). Permutation entropy: A natural com- plexity measure for time series. Physical Review Letters, 88(17), 174102. https://doi.org/10.1103/PhysRevLett.88.174102 Bassett, D. S., & Bullmore, E. (2006). Small-world brain net- works. The Neuroscientist, 12(6), 512–523. https://doi.org/10. 1177/1073858406293182 Benjamini, Y., & Hochberg, Y. (1995). Controlling the false dis- covery rate: A practical and powerful approach to multiple Journal of the Royal Statistical Society. Series B. Re- testing. trieved from http://engr.case.edu/ray_soumya/mlrg/controlling_ fdr_benjamini95.pdf Biswal, B., Yetkin, F. Z., Haughton, V. M., & Hyde, J. S. (1995). Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magnetic Resonance in Medicine, Network Neuroscience 591 Complexity of brain networks 34(4), 537–541. Retrieved from http://www.ncbi.nlm.nih.gov/ pubmed/8524021 Bola, M., & Borchardt, V. (2016). Cognitive processing involves the whole-brain network’s func- dynamic reorganization of Journal of Neuroscience, 36(13), tional community structure. 3633–3635. https://doi.org/10.1523/JNEUROSCI.0106-16.2016 Bonchev, D., & Buck, G. A. (2005). Quantitative measures of network complexity. In Complexity in chemistry, biology, and ecology. (pp. 191—235). Boston, MA: Springer US. https://doi.org/10. 1007/0-387-25871-X_5 Bowman, A. W., & Azzalini, A. (1997). Applied smoothing tech- niques for data analysis: the kernel approach with S-Plus illustra- tions. Oxford, UK: Clarendon Press. Buckner, R. L., Andrews-Hanna, J. R., & Schacter, D. L. (2008). The brain’s default network. Annals of the New York Academy of Sciences, 1124(1), 1–38. https://doi.org/10.1196/annals.1440.011 (1997). Practical method for determining the minimum embedding dimension of a scalar time series. Physica D: Nonlin- ear Phenomena, 110(1–2), 43–50.https://doi.org/10.1016/S0167- 2789(97)00118-8 Cao, L. Costa, M., Goldberger, A. L., & Peng, C. K. (2005). Multiscale en- tropy analysis of biological signals. Physical Review, E - Statistical, Nonlinear, and Soft Matter Physics, 71(2), 021906. https://doi. org/10.1103/PhysRevE.71.021906 Cover, T. M., & Thomas, J. A. (2006). Elements of information theory. Wiley-Interscience. Retrieved from https://www.wiley. com/en-us/Elements+of+Information+Theory%2C+2nd+Edition- p-9780471241959 Dehmer, M., Barbarini, N., Varmuza, K., & Graber, A. (2009). A large scale analysis of information-theoretic network complexity measures using chemical structures. PLoS One, 4(12), e8057. https://doi.org/10.1371/journal.pone.0008057 Delgado-Bonal, A., & Marshak, A. (2019). Approximate entropy and sample entropy: A comprehensive tutorial. Entropy, 21(6), 541. https://doi.org/10.3390/e21060541 Erdös, & Rényi, A. (1959). On random graphs, I. Publicationes Mathematicae (Debrecen), 6. Fagiolo, G. (2007). Clustering in complex directed networks. Phys- ical Review E - Statistical, Nonlinear, and Soft Matter Physics. https://doi.org/10.1103/PhysRevE.76.026107 Fortunato, S., & Hric, D. (2016). Community detection in net- works: A user guide. Physics Reports, 659, 1–44. https://doi.org/ 10.1016/J.PHYSREP.2016.09.002 Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen, D. C., & Raichle, M. E. (2005). The human brain is intrinsically orga- nized into dynamic, anticorrelated functional networks. Proceed- ings of the National Academy of Sciences of the United States of America, 102(27), 9673–9678. https://doi.org/10.1073/pnas. 0504136102 Fox, M. D., Zhang, D., Snyder, A. Z., & Raichle, M. E. (2009). The global signal and observed anticorrelated resting state brain net- works. Journal of Neurophysiology, 101(6), 3270–3283. https:// doi.org/10.1152/jn.90777.2008 Friston, K. J., Jezzard, P., & Turner, R. (1994). Analysis of functional MRI time-series. Human Brain Mapping, 1(2), 153–171. https:// doi.org/10.1002/hbm.460010207 Gopinath, K., Krishnamurthy, V., Cabanban, R., & Crosson, B. A. (2015). Hubs of anticorrelation in high-resolution resting-state functional connectivity network architecture. Brain Connectiv- ity, 5(5), 267–275. https://doi.org/10.1089/brain.2014.0323 Hilgetag, C. C., & Kaiser, M. (2004). Clustered organization of cor- tical connectivity. Neuroinformatics, 2(3), 353–360. https://doi. org/10.1385/NI:2:3:353 Inouye, T., Shinosaki, K., Sakamoto, H., Toi, S., Ukai, S., Iyama, A., . . . Hirano, M. (1991). Quantiﬁcation of EEG irregularity by use of the entropy of the power spectrum. Electroencephalography and Clinical Neurophysiology, 79(3), 204–210. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/1714811 Jenkinson, M., Bannister, P., Brady, M., & Smith, S. Im- proved optimization for the robust and accurate linear registra- tion and motion correction of brain images. NeuroImage, 17(2), 825–841. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/ 12377157 (2002). Jovicich, J., Czanner, S., Greve, D., Haley, E., van der Kouwe, A., Gollub, R., . . . Dale, A. (2006). Reliability in multi-site structural MRI studies: effects of gradient non-linearity correction on phan- tom and human data. NeuroImage, 30(2), 436–443. https://doi. org/10.1016/j.neuroimage.2005.09.046 Kolmogorov, A. N. Kazeminejad, A., & Sotero, R. (2019). The importance of anti- correlations in graph theory based classiﬁcation of autism spec- trum disorder. BioRxiv, 557512. https://doi.org/10.1101/557512 (1968). Three approaches to the quantita- International Journal of Com- tive deﬁnition of information. puter Mathematics, 2(1–4), 157–168. https://doi.org/10.1080/ 00207166808803030 Latora, V., & Marchiori, M. (2001). Efﬁcient behavior of small- world networks. Physical Review Letters. https://doi.org/10.1103/ PhysRevLett.87.198701 Li, M., & Vitaìnyi, P. M. B. (2008). An introduction to Kolmogorov complexity and its applications. Berlin: Springer. Liang, Z., King, J., & Zhang, N. (2012). Anticorrelated resting-state functional connectivity in awake rat brain. NeuroImage, 59(2), 1190–1199. https://doi.org/10.1016/j.neuroimage.2011.08.009 (1995). A statistical measure of complexity. Physics Letters A, 209(5–6), 321–326. https://doi.org/10.1016/0375-9601(95)00867-5 López-Ruiz, R., Mancini, H. L., & Calbet, X. Mazziotta, J., Toga, A., Evans, A., Fox, P., Lancaster, J., Zilles, K., . . . Mazoyer, B. (2001). A four-dimensional probabilistic atlas of the human brain. Journal of the American Medical Informatics Association: JAMIA, 8(5), 401–430. Retrieved from http://www. ncbi.nlm.nih.gov/pubmed/11522763 McShea, D. W. (1991). Complexity and evolution: What everybody knows. Biology & Philosophy, 6(3), 303–324. https://doi.org/10. 1007/BF00132234 Medvedev, A. V. (2014). Does the resting state connectivity have hemispheric asymmetry? A near-infrared spectroscopy study. NeuroImage, 85 Pt 1(01), 400–407. https://doi.org/10.1016/j. neuroimage.2013.05.092 Meier, J., Tewarie, P., Hillebrand, A., Douw, L., van Dijk, B. W., Stufﬂebeam, S. M., . . . Van Mieghem, P. (2016). A mapping between structural and functional brain networks. Brain Connec- tivity, 6(4), 298–311. https://doi.org/10.1089/brain.2015.0408 Network Neuroscience 592 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d . t f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Complexity of brain networks Meszlényi, R. J., Hermann, P., Buza, K., Gál, V., & Vidnyánszky, Z. (2017). Resting state fMRI functional connectivity analysis using dynamic time warping. Frontiers in Neuroscience, 11, 75. https://doi.org/10.3389/fnins.2017.00075 Meunier, D., Lambiotte, R., Fornito, A., Ersche, K., & Bullmore, E. T. (2009). Hierarchical modularity in human brain functional net- works. Frontiers in Neuroinformatics, 3, 37. https://doi.org/10. 3389/neuro.11.037.2009 Moeller, S., Yacoub, E., Olman, C. A., Auerbach, E., Strupp, J., Harel, N., . . . U˘gurbil, K. (2010). Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magnetic Resonance in Medicine, 63(5), 1144–1153. https://doi. org/10.1002/mrm.22361 Moradi, N., Dousty, M., & Sotero, R. C. (2019). Spatiotemporal empirical mode decomposition of resting-state fMRI signals: Ap- plication to global signal regression. Frontiers in Neuroscience, 13(JUL), 736. https://doi.org/10.3389/fnins.2019.00736 Noh, J. D., & Rieger, H. (2004). Random walks on complex net- works. Physical Review Letters, 92(11), 118701. https://doi.org/ 10.1103/PhysRevLett.92.118701 Pereda, E., Quiroga, R. Q., & Bhattacharya, J. (2005). Nonlinear multivariate analysis of neurophysiological signals. Progress in Neurobiology. https://doi.org/10.1016/j.pneurobio.2005.10.003 Pincus, S. M. (1991). Approximate entropy as a measure of system complexity. Proceedings of the National Academy of Sciences of the United States of America, 88(6), 2297–2301. https://doi.org/ 10.1073/PNAS.88.6.2297 Raichle, M. E., MacLeod, A. M., Snyder, A. Z., Powers, W. J., (2001). A default mode of Gusnard, D. A., & Shulman, G. L. brain function. Proceedings of the National Academy of Sciences of the United States of America, 98(2), 676–682. https://doi.org/ 10.1073/pnas.98.2.676 Richman, J. S., & Moorman, J. R. (2000). Physiological time- series analysis using approximate entropy and sample entropy. American Journal of Physiology-Heart and Circulatory Physiol- ogy, 278(6), H2039–H2049. https://doi.org/10.1152/ajpheart. 2000.278.6.H2039 Rosso, O. A., Blanco, S., Yordanova, J., Kolev, V., Figliola, A., (2001). Wavelet entropy: A new Schürmann, M., & Ba¸sar, E. tool for analysis of short duration brain electrical signals. Journal of Neuroscience Methods, 105(1), 65–75. Retrieved from http:// www.ncbi.nlm.nih.gov/pubmed/11166367 Rosvall, M., & Bergstrom, C. T. (2008). Maps of random walks on complex networks reveal community structure. Proceed- ings of the National Academy of Sciences of the United States of America, 105(4), 1118–1123. https://doi.org/10.1073/pnas. 0706851105 Rubinov, M., & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52(3), 1059–1069. https://doi.org/10.1016/J.NEUROIMAGE.2009.10. 003 Salvador, R., Suckling, J., Coleman, M. R., Pickard, J. D., Menon, D., & Bullmore, E. (2005). Neurophysiological ar- chitecture of functional magnetic resonance images of human brain. Cerebral Cortex, 15(9), 1332–1342. https://doi.org/10. 1093/cercor/bhi016 Sanchez-Rodriguez, L. M., Iturria-Medina, Y. M., Mouches, P., & Sotero, R. C. (2019). A method for multiscale community detection in brain networks. BioRxiv Neuroscience, 743732. https://doi.org/10.1101/743732 Sedeño, L., Couto, B., García-Cordero, I., Melloni, M., Baez, S., Morales Sepúlveda, J. P., . . . Ibanez, A. (2016). Brain network organization and social executive performance in frontotemporal dementia. Journal of the International Neuropsychological Soci- ety, 22(2), 250–262.https://doi.org/10.1017/S1355617715000703 Shannon, C. E. (1948). A mathematical theory of communication. Bell System Technical Journal, 27(3), 379–423. https://doi.org/ 10.1002/j.1538-7305.1948.tb01338.x Sharot, T., Delgado, M. R., & Phelps, E. A. (2004). How emotion en- hances the feeling of remembering. Nature Neuroscience, 7(12), 1376–1380. https://doi.org/10.1038/nn1353 Shiner, J. S., Davison, M. & Landsberg, P. T. (1999). Landsberg, P. T Simple measure for complexity. Physical Review E, 59(2), 1459–1464. https://doi.org/10.1103/PhysRevE.59.1459 Simonsen, I., Astrup Eriksen, K., Maslov, S., & Sneppen, K. (2004). Diffusion on complex networks: A way to probe their large- scale topological structures. Physica A: Statistical Mechanics and Its Applications, 336(1–2), 163–173. https://doi.org/10.1016/J. PHYSA.2004.01.021 Skardal, P. S., & Adhikari, S. (2018). Dynamics of nonlinear ran- dom walks on complex networks. Journal of Nonlinear Science, 1–26. https://doi.org/10.1007/s00332-018-9521-7 Sotero, R. C., Sanchez-Rodriguez, L. M., Dousty, M., Iturria- Medina, Y., & Sanchez-Bornot, J. M. (2019). Cross-frequency in- teractions during information ﬂow in complex brain networks are facilitated by scale-free properties. Frontiers in Physics, 7(JULY), 107. https://doi.org/10.3389/fphy.2019.00107 Sotiropoulos, S. N., Jbabdi, S., Xu, J., Andersson, J. L., Moeller, S., Auerbach, E. J., . . . , Behrens, T. E. J. (2013). Advances in diffu- sion MRI acquisition and processing in the Human Connectome Project. NeuroImage, 80, 125–143. https://doi.org/10.1016/j. neuroimage.2013.05.057 Sporns, O. (2013). Network attributes for segregation and inte- gration in the human brain. Current Opinion in Neurobiology, 23(2), 162–171. https://doi.org/10.1016/j.conb.2012.11.015 Sporns, O., & Zwi, J. D. (2004). The small world of the cerebral cor- tex. Neuroinformatics, 2(2), 145–162. https://doi.org/10.1385/ NI:2:2:145 Timme, N. M., & Lapish, C. (2018). A tutorial for information the- ory in neuroscience. ENeuro. https://doi.org/10.1523/ENEURO. 0052-18.2018 Tononi, G., Edelman, G. M., & Sporns, O. (1998). Complexity and coherency: Integrating information in the brain. Trends in Cog- nitive Sciences, 2(12), 474–484. https://doi.org/10.1016/S1364- 6613(98)01259-5 Tononi, G., Sporns, O., & Edelman, G. M. (1994). A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proceedings of the National Academy of Sciences of the United States of America, 91(11), 5033–5037. https://doi.org/10.1073/pnas.91.11.5033 Tournier, J.-D., Calamante, F., & Connelly, A. (2012). MRtrix: Diffu- sion tractography in crossing ﬁber regions. International Journal of Imaging Systems and Technology, 22(1), 53–66. https://doi. org/10.1002/ima.22005 Network Neuroscience 593 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d t . f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Complexity of brain networks Tsallis, C. (1988). Possible generalization of Boltzmann-Gibbs statis- tics. Journal of Statistical Physics, 52(1–2), 479–487. https://doi. org/10.1007/BF01016429 Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E. J., Yacoub, E., Ugurbil, K., & WU-Minn HCP Consortium. (2013). The WU-Minn Human Connectome Project: An overview. Neu- roImage, 80, 62–79. https://doi.org/10.1016/j.neuroimage.2013. 05.041 Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small- world’ networks. Nature, 393(6684), 440–442. https://doi.org/ 10.1038/30918 Weiting Chen, Zhizhong Wang, Hongbo Xie, & Wangxin Yu. (2007). Characterization of surface EMG signal based on fuzzy entropy. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 15(2), 266–272. https://doi.org/10.1109/TNSRE. 2007.897025 Yan, C., & Zang, Y. (2010). DPARSF: A MATLAB toolbox for “pipeline” data analysis of resting-state fMRI. Frontiers in System Neuroscience, 4, 13. https://doi.org/10.3389/fnsys.2010.00013 Zhang, Z., Shan, T., & Chen, G. (2013). Random walks on weighted networks. Physical Review E, 87(1), 012112. https://doi.org/10. 1103/PhysRevE.87.012112 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 3 5 7 5 1 8 6 7 3 8 1 n e n _ a _ 0 0 1 3 8 p d . t f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 Network Neuroscience 594 研究形象

下载pdf