研究
The sensitivity of network statistics to incomplete
electrode sampling on intracranial EEG
艾琳·C. Conrad1,2,∗, 约翰·M. Bernabei2,3,∗, Lohith G. Kini2,3, Preya Shah2,3, Fadi Mikhail1,2,
Ammar Kheder4, 拉塞尔·T. Shinohara5,6,7, 凯瑟琳A. Davis1,2,
Danielle S. Bassett1,3,8,9,10, and Brian Litt1,2,3,11
1神经内科, Hospital of the University of Pennsylvania, 费城, PA, 美国
2Center for Neuroengineering and Therapeutics, 宾夕法尼亚大学, 费城, PA, 美国
3Department of Bioengineering, School of Engineering and Applied Science, 宾夕法尼亚大学, 费城, PA, 美国
4神经内科, Emory University, 亚特兰大, 遗传算法, 美国
5生物统计学系, 流行病学, 和信息学, 宾夕法尼亚大学, 费城, PA, 美国
6宾夕法尼亚大学成像与可视化统计中心, 宾夕法尼亚大学, 费城, PA, 美国
7生物医学图像计算与分析中心, 宾夕法尼亚大学, 费城, PA, 美国
8Department of Electrical and Systems Engineering, School of Engineering and Applied Science, 宾夕法尼亚大学,
费城, PA, 美国
9Department of Physics and Astronomy, College of Arts and Sciences, 宾夕法尼亚大学, 费城, PA, 美国
10Department of Psychiatry, Hospital of the University of Pennsylvania, 费城, PA, 美国
11Department of Neurosurgery, Hospital of the University of Pennsylvania, 费城, PA, 美国
*这些作者的贡献同等.
关键词:
Reliability, Jackknife subsampling
颅内脑电图, Electrocorticography, Network model, Graph theory, Epilepsy,
抽象的
Network neuroscience applied to epilepsy holds promise to map pathological networks,
localize seizure generators, and inform targeted interventions to control seizures. 然而,
incomplete sampling of the epileptic brain because of sparse placement of intracranial
electrodes may affect model results. In this study, we evaluate the sensitivity of several
published network measures to incomplete spatial sampling and propose an algorithm using
network subsampling to determine confidence in model results. We retrospectively evaluated
intracranial EEG data from 28 patients implanted with grid, strip, and depth electrodes
during evaluation for epilepsy surgery. We recalculated global and local network metrics
after randomly and systematically removing subsets of intracranial EEG electrode contacts.
We found that sensitivity to incomplete sampling varied significantly across network metrics.
This sensitivity was largely independent of whether seizure onset zone contacts were targeted
or spared from removal. We present an algorithm using random subsampling to compute
patient-specific confidence intervals for network localizations. Our findings highlight the
difference in robustness between commonly used network metrics and provide tools to
assess confidence in intracranial network localization. We present these techniques as an
important step toward translating personalized network models of seizures into rigorous,
quantitative approaches to invasive therapy.
作者总结
Network neuroscience applied to epileptic brains seeks to identify pathological neural
connections that promote and maintain seizures, and holds promise to guide surgical
planning in patients with intractable epilepsy. 然而, sampling of the epileptic network in
intracranial EEG recording is limited by the choice of where to place intracranial electrodes,
which is highly variable within and between epilepsy centers. The effect of incomplete
spatial sampling generated by sparse electrode placement on network statistics is unknown.
这里, we determine the sensitivity of several network statistics to incomplete spatial
开放访问
杂志
引文: 康拉德, 乙. C。, Bernabei, J. M。,
Kini, L. G。, Shah, P。, Mikhail, F。, Kheder,
A。, . . . 一点, 乙. (2020). The sensitivity of
network statistics to incomplete
electrode sampling on intracranial
EEG. 网络神经科学, 4(2),
484–506. https://doi.org/10.1162/
netn_a_00131
DOI:
https://doi.org/10.1162/netn_a_00131
支持信息:
https://doi.org/10.1162/netn_a_00131
https://github.com/erinconrad/network-
subsets
已收到: 1 十一月 2019
公认: 10 二月 2020
利益争夺: See Conflict of
Interest statement
通讯作者:
艾琳·C. 康拉德
erin.conrad@uphs.upenn.edu
处理编辑器:
Daniele Marinazzo
版权: © 2020
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
A
_
0
0
1
3
1
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
Network node:
A discrete region in a network,
connected to other regions (节点)
via edges.
Node strength:
A nodal metric that represents the
sum of the weights of the
connections to the node of interest.
Eigenvector centrality:
A nodal metric that represents
the sum of connection weights to
the node of interest, weighted
by the eigenvector centrality
of the connected nodes.
Betweenness centrality:
A nodal metric calculating the
fraction of all shortest paths in a
network that pass through a node of
兴趣.
Clustering coefficient:
A nodal metric that measures the
tendency of a node to cluster into
tight groups.
Control centrality:
A nodal metric that represents the
change in synchronizability that
occurs with removal of a node of
兴趣.
Global metric:
Metrics in network neuroscience
representing a property of the overall
网络.
Global efficiency:
A global metric that is thought to
represent how easily information is
transmitted through a network.
Synchronizability:
A global metric that quantifies the
stability of the fully synchronous
network state.
Transitivity:
A global metric that is thought to
represent the degree to which nodes
in a graph tend to cluster together.
sampling, and we propose a method using electrode subsampling to determine
patient-specific confidence intervals in network model predictions.
介绍
Epilepsy is a significant cause of disability worldwide, particularly among the one third of
patients whose seizures cannot be controlled by medications (Kwan, Schachter, & Brodie,
2011; Wiebe, Eliasziw, Bellhouse, & Fallahay, 1999). While these patients may benefit from
surgery or implanted devices, many continue to experience seizures after invasive therapies
(恩格尔, 1996; Englot, Birk, & 张, 2017; Noe et al., 2013; Wiebe, Blume, Girvin, & Eliasziw,
2001). One reason for this persistence of seizure activity may be the difficulty in localizing
seizure-generating brain regions, the drivers of complex epileptic brain dynamics.
Clinicians and scientists now agree that epilepsy is in part a disease of brain networks
(克莱默 & 现金, 2012). Driven by clinical observations, scientists have applied formal mod-
els from network theory to better understand seizure dynamics and target therapy (Bassett,
Zurn, & 金子, 2018).
在这些模型中, the brain is discretized into regions represented by
network nodes, while network edges are used to represent their structural or functional con-
nectivity. Network theory applied to epilepsy employs a wide variety of metrics to understand
seizure generation and control, including node strength (Proix, Bartolomei, Guye, & Jirsa,
2017), eigenvector centrality (Burns et al., 2014), betweenness centrality (威尔克, Worrell, &
他, 2011), clustering coefficient (Liao et al., 2010), and control centrality (Khambhati, 戴维斯,
Lucas, 一点, & Bassett, 2016; Kini et al., 2019), as well as global metrics including global ef-
ficiency (Pedersen, Omidvarnia, Walz, & Jackson, 2015), synchronizability (Khambhati et al.,
2016), and transitivity (Paldino, 张, Chu, & Golriz, 2017). Collectively, these network
measures have been used to predict neuronal firing as seizures begin and spread, track seizure
progression, identify the seizure onset zone, and predict surgical outcome (Burns et al., 2014;
弗莱彻 & Wennekers, 2018; Panzica, Varotto, Rotondi, Spreafico, & Franceschetti, 2013;
Ponten, Bartolomei, & 斯塔姆, 2007; Sinha et al., 2017; Wilke et al., 2011).
When using invasive sensors such as intracranial EEG (脑电图) to estimate functional con-
nectivity, sampling from the full brain is impossible, and the network measures available for
In fields outside of
modeling depend on the location and number of electrodes implanted.
epilepsy, missing data are known to affect the results of network analyses (阿尔伯特, 阿尔伯特, &
Nakarado, 2004; 阿尔伯特, Jeong, & 巴拉巴斯, 2000; Guimerà & Sales-Pardo, 2009; Lü & 周,
2011). The effect of missing data on network models and clinical care in epilepsy has not been
rigorously explored. While network models have potential to add rigor to clinical decision-
制作, their application may be limited by uncertainty in estimated network metrics and the
unknown interaction between that uncertainty and sparse brain sampling. In this study we seek
to rigorously assess the extent to which different network metrics are sensitive to intracranial
electrode sampling. Our goal is not to determine which, 如果有的话, network statistic correctly lo-
calizes the seizure onset zone or predicts surgical outcome, as this important work is currently
under way by several groups (Kini et al., 2019; Proix, Jirsa, Bartolomei, Guye, & Truccolo,
2018; Shah, Bernabei, 等人。, 2018; Sinha et al., 2017, 2019). 相当, our goal is to determine
(A) whether and how incomplete spatial sampling affects the practical utility of network statis-
抽动症, 和 (乙) how sensitivity to spatial sampling can estimate patient-specific uncertainty in
network model predictions. This computational work is a vital first step to deploying network
models as an adjunct to clinical decision-making.
网络神经科学
485
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
A
_
0
0
1
3
1
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
颅内脑电图:
Electroencephalogram (EEG) 在
which electrodes are placed inside
the skull, either on top of the brain
surface (grid and strip electrodes) 或者
in the brain (depth electrodes).
Reliability:
A statistical measure of the
consistency of a metric, defined as
the variance of the true metric
divided by the total variance, 在哪里
the total variance is the sum of the
variance of the true metric and the
variance of the error.
Jackknife subsampling:
A subsampling technique (also called
jackknife resampling) in which a
random subset of observations is
removed and this is repeated many
times in order to obtain estimates of
sample variance.
材料和方法
Summary
We use a high-quality dataset that has been included in multiple network studies in epilepsy
(Khambhati et al., 2015, 2016; Kini et al., 2019; Sinha et al., 2017) and is publicly available
at www.IEEG.org. We randomly eliminate nodes from functional networks to simulate the
uncertainty consequent to variable sampling of brain regions by iEEG and to determine the
reliability of different network metrics within and across patients. Based upon the assumption
that the main drivers of epilepsy network behavior might localize to an epileptogenic region,
we ask to what extent electrode contacts far away from the seizure onset zone impact the
estimated values of various network metrics, and whether subsampling that targets the seizure
onset zone disproportionately affects network statistics compared with subsampling that spares
the seizure onset zone. We then randomly remove nodes by jackknife subsampling in order
to derive patient-specific estimates of confidence in network statistics.
Patient Selection, Intracranial EEG Recording, and Electrode Localization
All patients gave written informed consent in accordance with the Institutional Review Board
of the Hospital of the University of Pennsylvania (HUP) and the Mayo Clinic in Rochester.
此外, all patients consented to publishing their full-length iEEG recordings on the pub-
lic web portal IEEG.org (Wagenaar, Brinkmann, Ives, Worrell, & 一点, 2013). This study was
performed in accordance with the Declaration of Helsinki.
A total of 28 patients with drug-resistant epilepsy underwent iEEG recording during presur-
gical evaluation at HUP or the Mayo Clinic. Electrode configurations (Ad Tech Medical Instru-
评论, Racine, WI) consisted of linear cortical strips and two-dimensional cortical grid arrays
(2.3-mm diameter with 10-mm intercontact spacing), and linear depth electrodes (1.1-mm di-
ameter with 10-mm intercontact spacing). EEG signals were recorded at a sampling frequency
的 512 Hz at HUP and 500 Hz at Mayo Clinic. All electrode and EEG recording systems were
FDA approved and are commercially available.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
A
_
0
0
1
3
1
p
d
.
t
Each patient underwent MPRAGE T1-weighted magnetic resonance imaging (MRI) on a 3T
Siemens Magnetom Trio scanner (Siemens, Erlangen, 德国) prior to electrode implanta-
的, and they also underwent spiral CT imaging (Siemens, Erlangen, 德国) after electrode
implantation. We cross-referenced the CT images with a surgical cartoon map to localize
electrode coordinates (Wu et al., 2011). To segment the resection zone, we registered the
preimplant MRI to postresection imaging and the postimplant CT using the Advanced Nor-
malization Toolkit (ANTs; Avants et al., 2011). We utilized a random forest classifier with
ITK-SNAP to semiautomatically estimate the resection zone and identify electrodes overlying
resected cortex (Yushkevich et al., 2006).
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Seizures were identified clinically and confirmed in a clinical case conference discussion.
Board-certified epileptologists (Fadi Mikhail, Ammar Kheder, Kathryn Davis, and Brian Litt)
then reviewed the seizures and identified the earliest electrographic change (EEC; Litt et al.,
2001) and the electrode contacts of seizure onset (identified using the clinical standard for
recognizing the electrode contact with the EEC) for each seizure. We performed our primary
analysis on the first seizure identified for each patient. For patients with more than one seizure
(N= 26), we also performed the analysis on the second seizure to assess the sensitivity of our
results to the choice of seizure. For patients with three or more seizures (N= 23), we also
performed the analysis on the patient’s last seizure in order to evaluate more temporally distant
seizures, given evidence that temporally clustered seizures may have similar dynamics, 和
EEC:
Earliest electrographic change, 这
first appreciable EEG change during
a seizure.
网络神经科学
486
Effect of incomplete spatial sampling on epilepsy network statistics
given the possibility that earlier seizures may be atypical because of postimplantation effect
(Schroeder et al., 2019; Sun, Arcot Desai, Tcheng, & 莫雷尔, 2018). One patient (HUP111)
had two separate electrode implantations, and we analyzed both implantations separately.
Calculating Functional Networks
We examined 1-s time windows (sampled at 512 Hz at HUP and 500 Hz at Mayo Clinic) 在
each of the following time periods: 10 s prior to the EEC, 5 s prior to the EEC, at the EEC, 5 s
after the EEC, 和 10 s after the EEC. We chose 1-s time windows so as to have sufficient data
to perform coherence calculations and because of the validation of this time window in prior
出版物 (Khambhati et al., 2016; Kini et al., 2019; Kramer et al., 2011). To determine
the sensitivity of our results to this choice, we repeated this analysis with time windows of
2 s. We performed our primary analysis on the time period at the EEC given evidence for
changes in network parameters that occur at the EEC (Khambhati et al., 2015, 2016). We then
repeated the analysis for each other time window in order to assess the sensitivity of our results
to the choice of time period, and given the evidence that both interictal networks and post-
EEC networks localize the seizure onset zone (Burns et al., 2014; Shah, Bernabei, 等人。, 2018).
A common average reference was applied to iEEG signals to remove common sources of
noise. Data were filtered using an elliptic bandpass filter with cutoff frequencies of 5 赫兹和
115 赫兹, as well as a 60-Hz notch filter to remove power line noise. Signals were prewhitened
using a continuous autoregressive model to account for slow dynamics and to accentuate
higher frequencies known to be involved in seizure dynamics. This also enhanced local neural
population dynamics in order to minimize the effect of signal mixing (Arbabshirani et al., 2014;
Khambhati et al., 2015; Towle, Carder, Khorasani, & Lindberg, 1999). For each 1-s window, 我们
constructed functional networks in which iEEG electrode contacts represented network nodes.
Edges were weighted by multitaper coherence, which estimates the correlation between two
electrode contact signals in the frequency domain and is frequently used to calculate functional
networks in neuroscience publications (Khambhati et al., 2016; 米特拉 & Pesaran, 1999; 韦斯
等人。, 2015). We calculated coherence in the high gamma frequency band (95–105 Hz),
which we chose because of its importance in seizure propagation and spread (Khambhati et al.,
2016). We also repeated the analysis in beta (15–25 Hz) to assess the sensitivity of our results
to the choice of frequency band, and in acknowledgment of the fact that the beta frequency
is also thought to be important in epileptic networks (Bettus et al., 2011). This separation of
the data resulted in an adjacency matrix for each frequency band representing a network with
undirected, weighted edges for each patient, where each row and each column represented
an electrode contact, and each matrix element represented the signal coherence between the
two contacts.
To determine the sensitivity of our results to the choice of network density, we also per-
formed weight-based thresholding in which we set matrix elements below a weight w to 0,
where w was tuned for each patient to achieve a network density of 0.5 (in addition to the
unthresholded network).
Network Metrics
For each functional network, we calculated several global and nodal network metrics, 选择的
because of their importance in graph theory and their use in recent epilepsy publications as
如上所述. The global metrics were synchronizability, global efficiency, and transitivity.
The nodal metrics were node strength, control centrality, clustering coefficient, eigenvector
centrality, and betweenness centrality. The methods for calculating these metrics have been
487
Functional coherence:
A method of constructing functional
networks that estimates the
correlation between two electrode
contact signals in the frequency
domain.
Nodal metrics:
Metrics in network neuroscience
measuring the importance of
individual nodes.
网络神经科学
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
A
_
0
0
1
3
1
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
previously described, and we briefly summarize each below. We specifically describe their
calculations for an undirected, weighted network. We calculated each using the Brain Con-
nectivity Toolbox (鲁比诺夫 & 斯波恩斯, 2010), or using custom code for synchronizability and
control centrality (Khambhati et al., 2016).
Global metrics. Global efficiency is a global measure that is thought to represent how easily
information travels throughout the network (Latora & Marchiori, 2001). It is defined as
E =
1
氮(N − 1)
∑i6=j
1
σij
,
where E is global efficiency, N is the number of nodes, and σij is the shortest weighted path
length between node i and node j, for example estimated using Dijkstra’s algorithm (Dijkstra,
1959). A high global efficiency is thought to reflect a greater ease of information transfer
throughout the network (Bassett et al., 2009). Path lengths were weighted by the inverse of the
values of the adjacency matrix, to reflect the fact that information is thought to be transferred
more readily along stronger edges (Opsahl, Agneessens, & Skvoretz, 2010).
Synchronizability is a global metric that quantifies the stability of the fully synchronous
network state (Boccaletti, Latora, Moreno, Chavez, & Hwang, 2006; Schindler, Bialonski,
Horstmann, Elger, & Lehnertz, 2008) and has been shown to predict seizure generalization
(Khambhati et al., 2016). It is calculated by first computing the weighted Laplacian L = D − A
as the difference between the node strength matrix D and the adjacency matrix A. Synchro-
nizability is then obtained by the equation Sync = λ2
, where Sync is synchronizability, λ2
λmax
is the second smallest eigenvalue of the Laplacian, and λmax is the largest eigenvalue. Greater
synchronizability reflects a smaller spread between eigenvalues, which suggests greater ease
for a network to synchronize its dynamics.
Transitivity is another global measure that represents the degree to which nodes in a
graph tend to cluster together (Holland & Leinhardt, 1971; Opsahl & Panzarasa, 2009; Watts
& Strogatz, 1998). It is defined as
T =
∑ τ∆
∑ τ
,
where T is transitivity, ∑ τ∆ is the sum of the weights of closed triplets, and ∑ τ is the sum of
the weights of all triplets. A triplet is defined as a set of three nodes connected by either two
or three edges. A closed triplet, more specifically, is a set of three nodes connected by three
边缘. Higher transitivity implies that nodes tend to cluster together into exclusive groups.
Nodal metrics. Node strength represents the total strength of connections involving a partic-
ular node (假如, 扎莱斯基, & 布莫尔, 2016), and is defined as
si = ∑N
j=1 Aij,
in which si is the strength of node i, Aij is the adjacency matrix element containing the edge
weight between node j and node i, and N is the number of nodes. A high node strength
implies that the total weight of its connected edges is large. Eigenvector centrality is a simi-
lar nodal measure that weights individual node influence by the relative influence of each of
its connected nodes (弗莱彻 & Wennekers, 2018; 纽曼, 2008). It is specifically defined
as λ = Ax, where x is the vector containing the eigenvector centrality of each node, A is
网络神经科学
488
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
A
_
0
0
1
3
1
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
the adjacency matrix, and λ is the largest eigenvalue of the matrix (which results in nonneg-
ative eigenvector centralities). A high eigenvector centrality implies that a node is strongly
connected to nodes that themselves are highly connected.
Betweenness centrality is a nodal metric that is closely related to the global metric global
efficiency and measures the fraction of all shortest paths in the network that pass through a
given node (弗里曼, 1977). It is defined as
bi = ∑h6=i6=j
σhj(我)
σhj
,
where bi is the betweenness centrality of node i, σhj(我) is the number of shortest paths from
node h to node j that pass through node i, and σhj is the total weighted path length between
node h and node j. A high betweenness centrality suggests that the node acts as a central node
in the shortest paths between many other nodes. The path lengths were weighted by the inverse
of the values of the adjacency matrix as described above.
Control centrality is a local metric that measures the effect of each node on synchronizabil-
性. It is defined as ci = Syncnew−Syncold
, where ci is the control centrality of node i, Syncold
is the original synchronizability, and Syncnew is the synchronizability of the network with the
node removed (Khambhati et al., 2016). Negative control centrality nodes are synchronizing,
whereas positive control centrality nodes are desynchronizing.
Syncold
Clustering coefficient is the nodal extension of transitivity that measures the amount of
interaction between local triplets (Barrat, Barthélemy, & Vespignani, 2007). It is calculated by
cli = 2 ∑k,j
, in which A is the adjacency matrix edge weight and v is the number
of neighbors. Higher clustering coefficients reflect greater clustering of the node into tight
团体.
(Aik Aij Ak j)1/3
v(v−1)
Network Subsampling
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
A
_
0
0
1
3
1
p
d
t
.
To determine the sensitivity of network metrics to spatial sampling, we randomly identified
electrode contacts for removal in each patient. We removed the rows and columns corre-
sponding to these electrode contacts from the adjacency matrix representing the network.
We recalculated each of the network metrics above. We performed this analysis removing
20%, 40%, 60%, 和 80% of randomly selected electrode contacts. We repeated this process
1,000 times for each removal percentage to obtain a distribution of new metrics in the randomly
subsampled network (数字 1).
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Determining Metric Reliability
时间 + σ2
X = σ2
乙, and σ2
T is the variance of the true scores, σ2
To determine the stability of each network metric to subsampling, we calculated the reliability
σ2
for each removal percentage (Davidshofer & 墨菲, 2005). Reliability is defined as R =
时间
σ2
X
where σ2
E is the variance of the
错误, and σ2
X is the total variance. We defined the variance of the error to be the variance
of the subsampled metric across the 1,000 random subsamples, averaged across electrode
contacts in the case of nodal metrics. For nodal metrics, we defined the variance in the true
scores to be the variance of the subsampled metric across electrode contacts, 平均超过
all permutations.
In the case of global metrics, we defined the variance in the true scores
to be the variance in the subsampled metric across patients, averaged over all permutations.
Reliability is constrained to be between 0 和 1, 在哪里 1 indicates that no variance is due
,
网络神经科学
489
Effect of incomplete spatial sampling on epilepsy network statistics
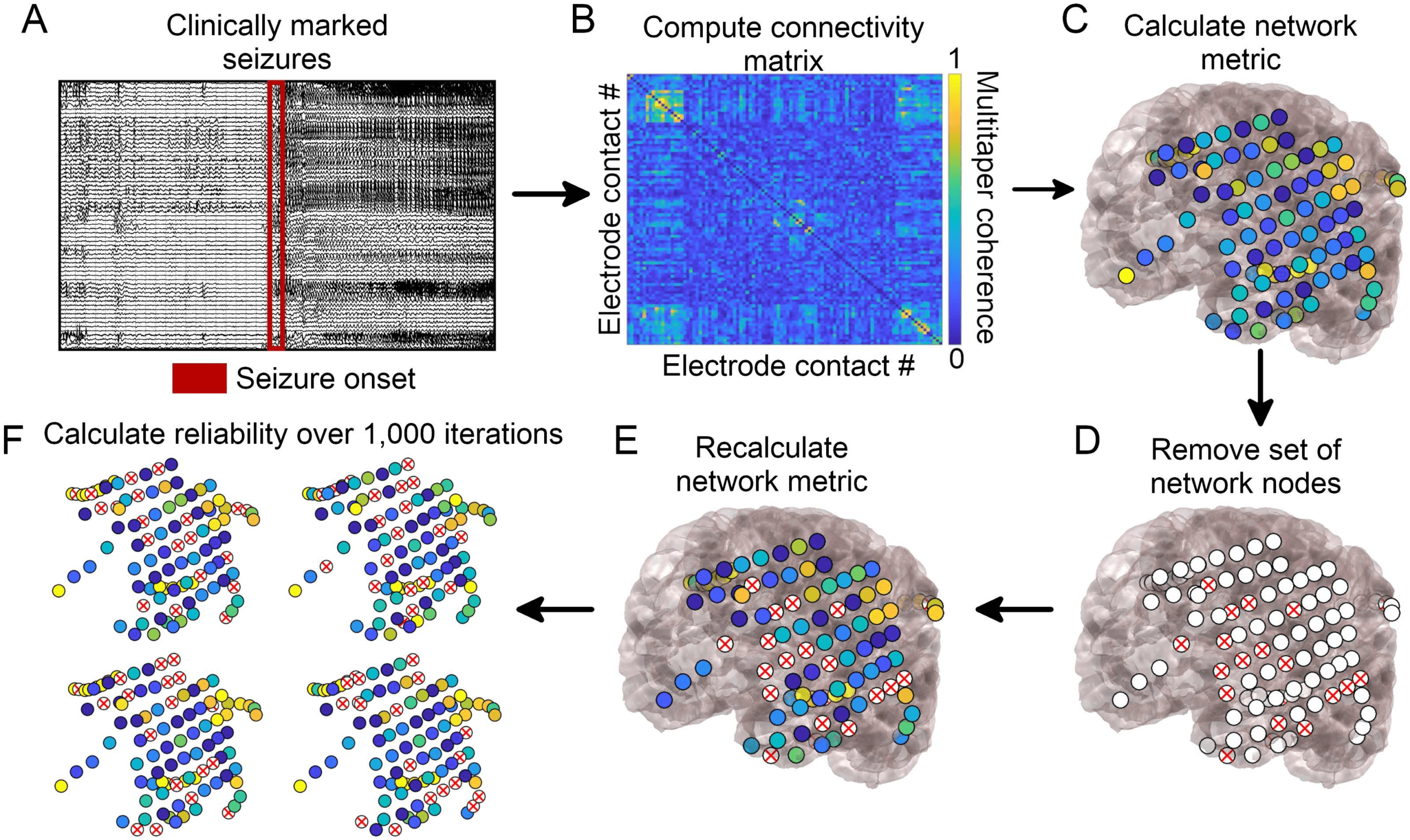
数字 1. Network generation and subsampling methods. (A) Seizure onset times were marked by
a board-certified epileptologist. (乙) Multitaper coherence of a 1-s interval of EEG signal at seizure
onset was used to create a functional adjacency matrix. (C) Network metrics were calculated using
the adjacency matrix with all nodes included.
(D) A subset of nodes were removed to simulate
the effect of leaving out electrodes. (乙) Network metrics were recalculated from the subsampled
网络. (F) This process was repeated over 1,000 iterations and the reliability of each metric was
quantified.
to random subsampling, 0 indicates that all variance is due to random subsampling, 和 0.5
indicates that the variance due to random subsampling equals the variance of the true metric.
The goal of the reliability measure is to compare how much metrics vary across subsamples
relative to how much they vary across patients (in the case of global metrics) or electrode
contacts within the patient (in the case of nodal metrics). Lower reliabilities suggest that the
variance across subsamples is higher than that across patients (global metrics) or electrode
contacts (nodal metrics), suggesting that minor changes in electrode configurations could result
in different orderings of highest-to-lowest metric values, thus decreasing our confidence in the
结果. Of note, we calculated the variance in the true scores in the subsampled networks,
rather than the original network, to avoid a bias in which some network metrics (such as node
strength) have larger values and larger variances across electrodes in larger networks, resulting
in paradoxically higher reliabilities when removing more electrodes.
To determine whether some metrics were more robust to subsampling than others, we com-
pared the metric reliability across all patients for the 20% removal percentage using separate
Friedman tests, one for global metrics and one for nodal metrics (α = 0.05; 弗里德曼, 1937).
In the case of significant Friedman test results, we performed post hoc Dunn-Šidák multiple
comparisons tests to identify significant differences between individual metrics (Dunn, 1964;
Šidák, 1967). We also determined the reliability of metrics for removal percentages other than
20%, which we report in our Supporting Information. We repeated this analysis for beta band
连贯性, alternate times relative to the EEC, removal of contiguous rather than random elec-
trode contacts, alternate network densities, alternate time windows for calculating coherence,
and different seizures, which we also report in our Supporting Information.
网络神经科学
490
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
A
_
0
0
1
3
1
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
As an additional test of network stability to subsampling for nodal metrics, we calculated
the Spearman rank correlation of the vector of nodal metrics across electrodes between the
original network and each of the 1,000 subsampled metrics. We obtained the mean of the rank
correlation across all 1,000 subsamples as a measure of the average correlation between the
original set of nodal metrics and the subsampled metrics. We compared the metric rank cor-
relations across all patients for the 20% removal percentage using a Friedman test (α = 0.05),
performing post hoc Dunn-Šidák multiple comparisons tests to identify significant differences
between individual metrics in the case of significant Friedman test results.
We then determined whether there was a relationship between the network reliability and
the number of electrode contacts comprising the original network. We obtained the reliability
for each patient and each nodal and global metric at the 20% removal percentage of random
electrode contacts, using the EEC time period and gamma band coherence. For each metric,
we correlated the reliability with the original number of electrode contacts in the patient’s
network using Spearman rank correlation. We performed Bonferroni correction as we were
testing eight network metrics, yielding an α of 0.05/8 = 0.00625.
Influence of Seizure Onset Zone on Network Reliability
We next hypothesized that ictal network metrics may be more affected by removing electrode
contacts near the seizure onset zone, as these contacts may have a stronger influence on epilep-
tic networks. 为了测试这个, we again subsampled the network, this time systematically removing
each electrode contact and its N − 1 nearest neighbors, where N was equal to 20% of the total
number of contacts in the network (we also calculated it for other removal percentages and
report these results in our Supporting Information). We recalculated each of the global and
nodal metrics in this systematically subsampled network. We obtained a measure of agree-
ment between the original metric and the new metric in the subsampled network. For nodal
指标, the agreement measure a was defined as the Spearman’s rank correlation coefficient
across electrode contacts between the original and subsampled metric. For global metrics, 这
agreement measure was defined as the negative of the absolute value of the relative difference
between the two metrics
a = −
(西德:12)
(西德:12)
(西德:12)
(西德:12)
metricnew − metricold
metricold
(西德:12)
(西德:12)
(西德:12)
(西德:12)
.
The global agreement a was equal to 0 when there was perfect agreement between the new
and original metric, and was increasingly negative with larger absolute differences.
To test whether there was larger metric agreement when the removed electrode contacts
were further from the seizure onset zone, we obtained the Spearman’s rank correlation coef-
ficient between the agreement measure a with the distance between the centroid of the re-
moved electrode contacts and the centroid of the seizure onset zone. We obtained the Fisher’s
transformation of the rank coefficient for each patient, which is equal to the inverse hyperbolic
tangent of the rank coefficient, in order to transform the coefficients to a variable whose dis-
tribution is approximately normal (Fisher, 1915). We aggregated these transformed rank co-
efficients across patients and performed a two-sided one-sample t test to determine whether
the mean coefficient was significantly different from 0. We performed this test for each of the
global and nodal metrics. We performed Bonferroni correction as we were testing eight net-
work metrics, yielding an α of 0.05/8 = 0.00625.
As an additional test of the hypothesis that removing seizure onset zone electrodes dispro-
portionately affects network statistics, we performed two additional subsampling methods: A
网络神经科学
491
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
A
_
0
0
1
3
1
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
seizure onset zone-targeted subsampling and a seizure onset zone-sparing subsampling. 在里面
seizure onset zone-targeted subsampling, we identified all electrodes forming the clinician-
defined seizure onset zone and we removed all of these and only these electrodes.
在里面
seizure onset zone-sparing subsampling, we identified a randomly selected subset of elec-
特罗德斯, equal in number to the number of seizure onset zone electrodes, but excluding the
seizure onset zone (in one patient, Study022, the number of seizure onset electrodes was more
than half of the total number of electrodes, and in this case we removed all other electrodes
for the seizure onset zone-sparing subsampling). We repeated the seizure onset zone-sparing
subsampling 1,000 次. For each subsampling, we again calculated the agreement, A, 是-
tween the original and subsampled network statistics, where a is defined above for both global
and nodal metrics. We took the mean agreement across all 1,000 subsamples in the case of
seizure onset zone-sparing subsampling. We compared the mean seizure onset zone-sparing
agreement and the seizure onset zone-targeted agreement with a two-sided paired t test to de-
termine whether the metric agreement when subsampling using a seizure onset zone-sparing
method was significantly different from that using a seizure onset zone-targeted method. 我们
performed this test for each of the global and nodal metrics. We performed Bonferroni correc-
tion as we tested eight network metrics, yielding an α of 0.05/8 = 0.00625.
As an alternative approach, we also calculated for each patient the percentage of seizure
onset zone-sparing agreements that were higher than the seizure onset zone-targeted agree-
蒙特. We performed a one-sample two-sided t test to determine whether the mean percentile
was significantly different from 50% (under the null hypothesis that if the seizure onset zone
contacts were not of particular importance to the network metrics, half of patients would be
expected to have higher seizure onset zone-sparing versus seizure onset zone-targeting agree-
评论), using a Bonferroni correction for eight network metrics (α = 0.00625). Of note, 那里
were six patients for whom the number of seizure onset zone electrode contacts was large rela-
tive to the total number of electrode contacts (approaching half ), and so for these patients there
was likely a high interdependence between the 1,000 seizure onset zone-sparing subsamples.
We expect that this makes this analysis less conservative than our primary analysis above.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
A
_
0
0
1
3
1
p
d
t
.
We repeated the seizure onset zone analyses restricting analysis to patients with good (在-
ternational League Against Epilepsy, ILAE = 1) 结果 (N= 13 患者), as it is possible
that in the poor-outcome patients, the clinician-defined seizure onset zone did not accurately
capture seizure generators. We also repeated these analyses using the electrodes overlying the
resected area of cortex, rather than the seizure onset zone, while restricting analysis to ILAE
1 outcome patients, under the assumption that the resected cortex in these good-outcome
patients likely overlaps with seizure generators.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Deriving Patient-Specific Confidence in Network Results Using Jackknife Subsampling
We next utilized a jackknife subsampling method to generate patient-specific estimates in the
confidence of the results of network analyses. Jackknife estimation is a method of sampling
without replacement to derive statistical estimates (Quenouille, 1949, 1956; Tukey, 1958). 它
applies the same subsampling technique from our earlier analyses, but with the aim of obtain-
ing patient-specific confidence rather than metric-specific reliabilities. Our goal was to deter-
mine how much a network result would be expected to change if a small number of electrode
contacts had not been present. We randomly removed 20% of electrode contacts, recalculated
the network statistic of interest for the random subsample, and repeated this process for 1,000
迭代. We chose a 20% removal percentage for this analysis to simulate minor variability
in electrode implantation strategy. For each of the nodal metrics, we identified the electrode
网络神经科学
492
Effect of incomplete spatial sampling on epilepsy network statistics
contact with the maximal metric value (minimal value for control centrality) in each of the
1,000 迭代. We identified the electrode contacts comprising 95% of all occurrences of
the maximal metric value across the 1,000 迭代. We called this set of contacts the 95%
jackknife confidence contact set. We also identified the 95% confidence contact set of the min-
imum regional control centrality, defined as the locations of an electrode contact and its N − 1
nearest neighbors, where N equals the number of resected electrode contacts that produces
the largest negative change in synchronizability when removed. Regional control centrality
attempts to identify a region of a defined size—rather than a single electrode contact—with
the largest control centrality, and thus a potential site for resection (Kini et al., 2019). A larger
95% jackknife confidence set of electrode contacts implies greater sensitivity of the identity
of the electrode contact with the maximal metric value to spatial subsampling, suggesting
lower confidence in the patient-specific network result. For global metrics, we performed this
method to obtain the 95% jackknife confidence interval for the value of the metric for a given
病人, which was the interval containing 95% of all values obtained with jackknife subsam-
pling. A larger 95% jackknife confidence interval for global metrics implies greater sensitivity
of the global network statistic to spatial subsampling, suggesting lower confidence in the global
network value. The runtime for the jackknife subsampling algorithm (1,000 迭代) 对全部
metrics at a single time and frequency band was approximately ten minutes per patient when
performed in MATLAB R2018a on an Intel Xeon processor (CPU E5-2698 v3 @ 2.30 GHz).
Statistical Analysis
All analyses were performed on MATLAB R2018a (The MathWorks, Natick). Specific analyses
are discussed in the four preceding sections, 多于.
结果
Patient and Electrode Information
Patients had a variety of clinical histories, electrode configurations, pathologies, and clinical
结果 (Supplemental Table 1). 有 28 患者 (13 女性), one of whom had
two temporally distinct implantations, which were separately analyzed. The average age at
implantation was 33.9 年 (range 5–57). The mean number of electrode contacts was 77
(range 16–118). The mean number of seizures was 6.8 (range 1–36). The median ILAE outcome
score at 2 years was 2 (range 1–5).
Stability of Metrics to Random Subsampling
For all network measures, reliability to subsampling decreased as more electrode contacts were
已删除. The stability of network measures to subsampling varied across patients (数字 2).
The mean reliability was R = 0.92 for synchronizability, R = 0.98 for global efficiency, 和
R = 0.98 for transitivity, averaged over all patients when a random sample of 20% of electrode
contacts was removed. 相比之下, when a contiguous sample of 20% of electrode contacts
was removed, the mean reliabilities were lower, with R = 0.85 for synchronizability, R = 0.92
for global efficiency, and R = 0.93 for transitivity. The reliability to random electrode contact
2 = 36.5, p <
removal was significantly different between global metrics (Friedman test: χ2
0.001). Synchronizability was significantly less reliable than either global efficiency or transi-
tivity (post hoc Dunn-Šidák multiple comparison test: t = −3.02, p = 0.008 compared with
global efficiency and t = −6.04, p < 0.001 compared with transitivity). Global efficiency was
also significantly less reliable than transitivity (t = −3.02, p = 0.008). The reliability for global
efficiency was slightly lower than that for transitivity for 26 out of 29 patient implantations.
Network Neuroscience
493
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
Figure 2. Reliability of network metrics to incomplete sampling. (A) Reliability of nodal measures,
averaged across all patients, when different percentages of electrodes were removed. (B) Reliability
of global measures, averaged across all patients, when different percentages of electrodes were
removed. Error bars show the standard deviation of the reliability across patients. All data shown are
for the EEC of first seizure, high gamma coherence, and random electrode removal. For all measures,
reliability decreased as more electrodes were removed. Patients are heterogeneous in the reliability
of their network measures, and certain network measures exhibit higher reliability than others.
However, for two implantations the reliability for global efficiency was substantially larger,
explaining why global efficiency and transitivity have similar means despite global efficiency
having significantly lower reliability by ordinal statistics.
For nodal measures, the mean reliability was R = 0.84 for control centrality, R = 0.96 for
node strength, R = 0.88 for betweenness centrality, R = 0.97 for eigenvector centrality, and
R = 0.95 for clustering coefficient, averaged over all patients when 20% of electrode contacts
were randomly removed (again, mean reliabilities were lower with contiguous removal, R =
0.82 for control centrality, R = 0.95 for node strength, R = 0.88 for betweenness centrality,
R = 0.94 for eigenvector centrality, and R = 0.91 for clustering coefficient). The reliability
4 = 107.9, p < 0.001). Control
differed significantly between nodal measures (Friedman test: χ2
centrality was less reliable than node strength (post hoc Dunn-Šidák test: t = −6.73, p <
0.001), eigenvector centrality (t = −8.64, p < 0.001), and clustering coefficient (t = −3.99,
p = 0.001) but was not significantly different from betweenness centrality (t = −1.00, p =
0.979). Node strength was also significantly more reliable than betweenness centrality (t =
5.73, p < 0.001) but did not differ significantly from eigenvector centrality (t = −1.91, p =
0.439) or clustering coefficient (t = 2.74, p = 0.060). Betweenness centrality was significantly
less reliable than both eigenvector centrality (t = −7.64, p < 0.001) and clustering coefficient
(t = −2.99, p = 0.028). Eigenvector centrality was more reliable than clustering coefficient
(t = 4.65, p < 0.001).
When we examined the time periods 10 s before, 5 s before, 5 s after, and 10 s after the
EEC (as opposed to the second at the EEC), synchronizability continued to have the lowest
reliability of the global metrics. Control centrality continued to have the lowest reliability of
the nodal metrics, and eigenvector centrality and node strength continued to have the highest
reliabilities. The pattern remained when we examined beta frequency coherence rather than
high gamma frequency coherence, when we removed contiguous as opposed to random sets
Network Neuroscience
494
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
of electrode contacts, when we examined the second seizure or the last seizure rather than
the first seizure, when we thresholded the network weights to achieve a network density of
0.5, and when we used a 2-s time window for coherence calculations rather than a 1-s win-
dow (Supplemental Table 2). When we instead removed 40% or 60% of electrode contacts,
control centrality and synchronizability continued to have the lowest reliability of nodal and
global metrics, respectively, and node strength and eigenvector centrality continued to have
the highest nodal metric reliabilities. When we removed 80% of electrode contacts, clustering
coefficient instead demonstrated the lowest nodal metric reliability, and otherwise the pattern
was unchanged (Supplemental Table 3).
For nodal metrics, the Spearman rank correlation between the original and subsampled met
ric revealed the same ranking of metric robustness as with our primary approach. The mean
Spearman rank correlation between the original metric and the subsampled metric, averaged
across all subsamplings and all patients when 20% of electrode contacts were randomly re-
moved, was ρ = 0.84 ± 0.08 for control centrality, ρ = 0.97 ± 0.02 for node strength, ρ = 0.91 ±
0.03 for betweenness centrality, ρ = 0.98 ± 0.02 for eigenvector centrality, and ρ = 0.97 ± 0.02
for clustering coefficient. The Spearman rank correlation significantly differed across nodal
4 = 99.5, p < 0.001). The Spearman rank correlation between the
metrics (Friedman test: χ2
original and subsampled control centrality metric was significantly lower than that for node
strength (post hoc Dunn-Šidák test: t = −5.81, p < 0.001), eigenvector centrality (t = −8.64,
p < 0.001), and clustering coefficient (t = −5.98, p < 0.001). The Spearman rank correlation
between the original and subsampled node strength metric was significantly higher than that
for betweenness centrality (t = 4.24, p < 0.001) and significantly lower than that for eigenvec-
tor centrality (t = −2.82, p = 0.046). The Spearman rank correlation between the original and
subsampled betweenness centrality metric was significantly lower than that for eigenvector
centrality (t = −7.06, p < 0.001) and for clustering coefficient (t = −4.40, p < 0.001). The
comparisons between control centrality and betweenness centrality (t = −1.58, p = −0.704),
node strength and clustering coefficient (t = −0.17, p = 1.00), and eigenvector centrality and
clustering coefficient (t = 2.66, p = 0.076) were not significant.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
.
t
We next examined the relationship between robustness to electrode contact subsampling
and the number of electrode contacts in the original network. Among global measures, there
was a significant positive relationship between reliability and number of contacts for synchro-
nizability (Spearman rank correlation: r27 = 0.68, p < 0.001), but not for global efficiency
(r27 = 0.20, p = 0.299) or transitivity (r27 = 0.22, p = 0.260). Among nodal measures,
clustering coefficient (r27 = 0.53, p = 0.003) demonstrated a significant positive relation-
ship, and relationships for control centrality (r27 = −0.12, p = 0.551), node strength (r27 =
0.45, p = 0.015), betweenness centrality (r27 = 0.38, p = 0.043), and eigenvector centrality
(r27 = 0.44, p = 0.016) were nonsignificant (α = 0.00625, Bonferroni correction for eight
measures). This pattern of findings suggests that, at least for synchronizability and clustering
coefficient, patients with more electrode contacts implanted were less vulnerable to incom-
plete spatial sampling.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Influence of Seizure Onset Zone on Sensitivity of Network Statistics to Subsampling
There was no significant association between metric agreement and distance of the removed
electrode contacts from the seizure onset zone for any metric (one-sample two-sided t test:
control centrality, t = 0.80, p = 0.433; node strength, t = 1.25, p = 0.222; betweenness
centrality, t = −0.95, p = 0.352; eigenvector centrality, t = 1.02, p = 0.318; clustering
coefficient, t = 1.23, p = 0.230; synchronizability, t = −0.26, p = 0.793; global efficiency,
Network Neuroscience
495
Effect of incomplete spatial sampling on epilepsy network statistics
t = 0.74, p = 0.469; transitivity, t = 0.37, p = 0.717). This pattern of findings implies that
all metrics are equally sensitive to removing electrode contacts near versus distant from the
seizure onset zone (Figure 3). This result was invariant to the choice of peri-ictal time window,
choice of frequency band, choice of seizure, exclusion of non-ILAE 1 outcome patients, use
of resection zone rather than seizure onset zone (excluding non-ILAE 1 patients), choice of
network density, and choice of time window (Supplemental Table 4) as well as to the choice
of removal percentage (Supplemental Table 5).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
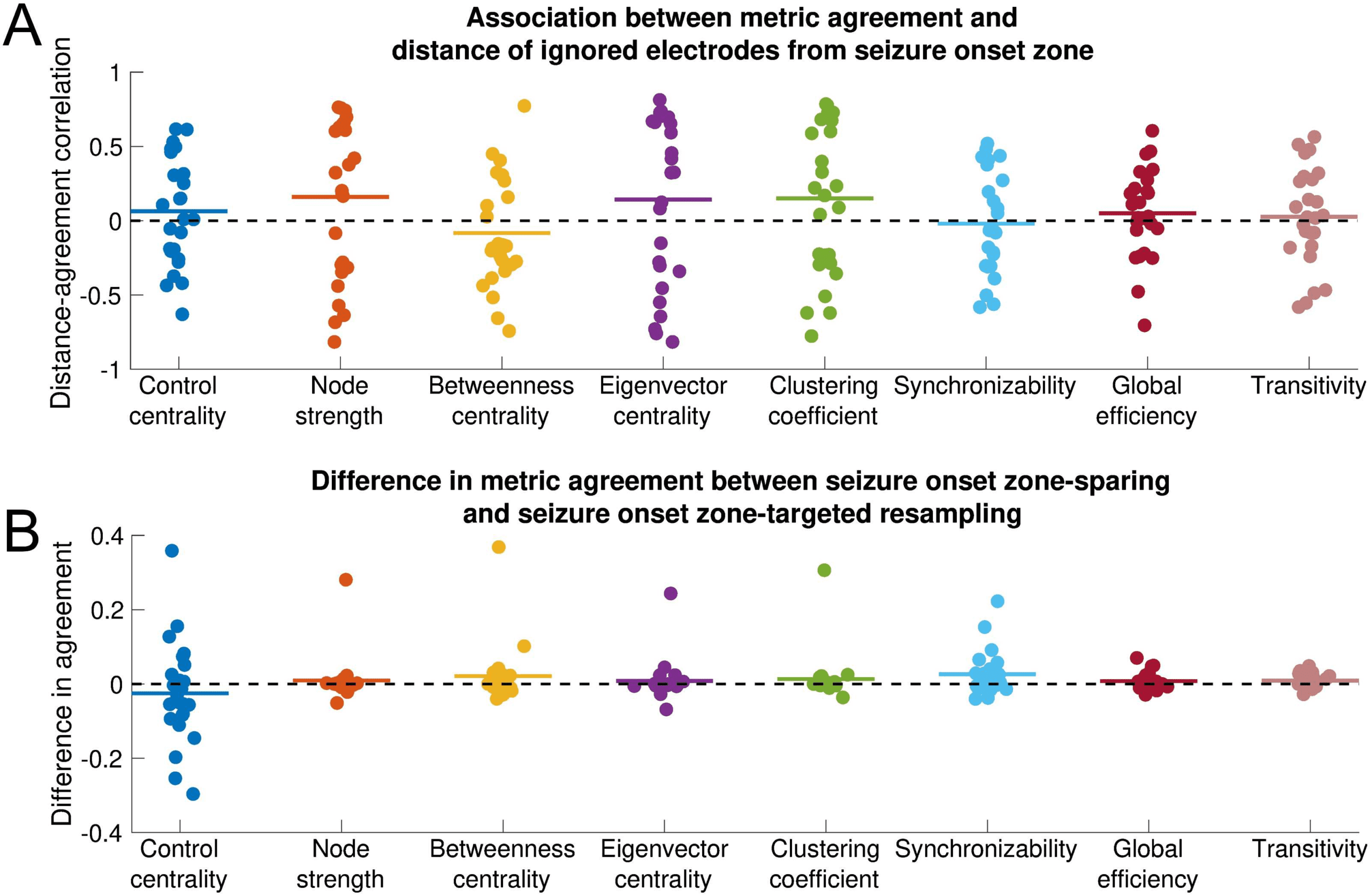
Influence of seizure onset zone on sensitivity of network statistics to subsampling. Each
Figure 3.
nodal and global metric is shown. All data shown are for the EEC of first seizure and high gamma
coherence. (A) Association between metric agreement and distance of ignored electrode contacts
from the seizure onset zone. Each point represents the patient-specific Spearman rank correla-
tion coefficient between the metric agreement and the distance of the ignored electrodes from the
seizure onset zone. The metric agreement is defined for nodal metrics as the Spearman rank cor-
relation coefficient between the original metric and the metric obtained from subsampling, and for
global metrics as the negative absolute value of the relative difference between the original and
subsampled metric. Horizontal lines show the average distance-agreement association across pa-
tients. No distance-agreement association was significantly different from 0 (two-sided one-sample
t test, α = 0.05/8 for Bonferroni correction), signifying that all metrics are equally vulnerable to
incomplete sampling near versus distant from the seizure onset zone. (B) Difference in metric agree-
ment between seizure onset zone-sparing and seizure onset zone-targeted subsampling. Each point
represents the patient-specific difference in metric agreement between subsampling that spares the
seizure onset zone electrode contacts and subsampling that targets the seizure onset zone elec-
trode contacts. Positive values indicate that sparing the seizure onset zone from removal yields a
higher agreement with the original network statistic than does targeting the seizure onset zone for
removal. Horizontal lines show the average difference in metric agreement across patients. No
difference in agreement was significantly different from 0 (two-sided one-sample t test, α = 0.05/8
for Bonferroni correction), signifying that metrics are equally vulnerable to subsampling that spares
versus targets the seizure onset zone. However, there was nonsignificantly higher transitivity metric
agreement when the seizure onset zone was spared. The horizontal position of individual points
was determined by random jitter to improve readability.
Network Neuroscience
496
Effect of incomplete spatial sampling on epilepsy network statistics
When we compare metric agreement removing all seizure onset zone electrode contacts
as opposed to removing only non-seizure onset zone electrode contacts, there was again no
significant difference in metric agreement between the seizure onset zone-sparing and seizure
onset zone-targeted approach for any metric (paired two-sided t test: control centrality t =
−0.99, p = 0.331; node strength, t = 0.84, p = 0.408; betweenness centrality, t = 1.43, p =
0.167; eigenvector centrality, t = 0.81, p = 0.424; clustering coefficient, t = 1.10, p = 0.283;
synchronizability, t = 2.33, p = 0.028; global efficiency, t = 1.74, p = 0.095; transitivity, t =
2.65, p = 0.014; α = 0.00625, Bonferonni correction for eight metrics). These findings suggest
that sparing versus targeting seizure onset zone electrode contacts for removal has equivalent
effects on most network statistics. Across conditions, transitivity generally displayed the largest
differences between seizure onset zone-sparing agreement and seizure onset zone-targeted
agreement, although these differences were significant only for the EEC + 10-s condition, the
second seizure, and 50% network density (Supplemental Table 6). To determine whether the
trend in transitivity perturbation was to increase or decrease network transitivity, we obtained
the signed relative difference (as opposed to the metric agreement, which is unsigned) between
the subsampled and the original transitivity measure, and compared this for the seizure onset
zone-sparing and seizure onset zone-targeted subsampling methods. The relative difference
in transitivity was nonsignificantly higher (more positive) when seizure onset zone-targeted
subsampling was performed, which persisted across all time periods, frequency bands, and
the second seizure (Supplemental Table 6, two-sided paired t test, α = 0.00625, Bonferonni
correction for eight metrics). This suggests that removing seizure onset zone electrode contacts
may disproportionately increase transitivity (although this result was nonsignificant for most
conditions).
When we used the approach calculating the percentage of seizure onset zone-sparing agree-
ments larger than the seizure onset zone-targeted agreement, we found that the seizure onset
zone-sparing agreement was significantly higher than the seizure onset zone-targeted agree-
ment for both synchronizability (one sample two-sided t test, t = 3.72, p = 0.001) and tran-
sitivity (t = 3.04, p = 0.005) with no significant difference for other measures (Supplemental
Table 6). The directions of these results were the same as those seen in the above analysis.
However, given the dependence between seizure onset zone-sparing subsamples discussed in
the Methods section, we believe that this analysis is less conservative than our primary analysis
above.
Jackknife Confidence Intervals
Both nodal and global metrics varied across patients with respect to jackknife confidence in-
tervals produced by subsampling (Figure 4A–C). The median and range for the number of
electrode contacts accounting for 95% of all jackknife instances of the maximum nodal metric
(minimum for control centrality) was 3 (range 2–5) for node strength, 4 (3–9) for betweenness
centrality, 3 (2–5) for eigenvector centrality, 3 (2–5) for clustering coefficient, and 9 (4–22)
for control centrality. The median number of electrode contacts accounting for 95% of all
jackknife instances of the minimum regional control centrality (where the set of electrode con-
tacts with minimum regional control centrality is the set, equal in number to the number of
resected electrode contacts, that together produces the largest negative change in synchroniz-
ability when removed) was 48 (range 12–93). The median ratio between this number and the
number of electrode contacts forming the true minimum regional control centrality set was 4.0
(range 1.6–16.0; Figure 4D). Regarding global metrics, the median width of the 95% jackknife
confidence interval was 0.094 (range 0.045–0.192) for synchronizability, 0.016 (range 0.006–
0.058) for global efficiency, and 0.012 (range 0.004–0.062) for transitivity (Figure 4E). These
Network Neuroscience
497
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
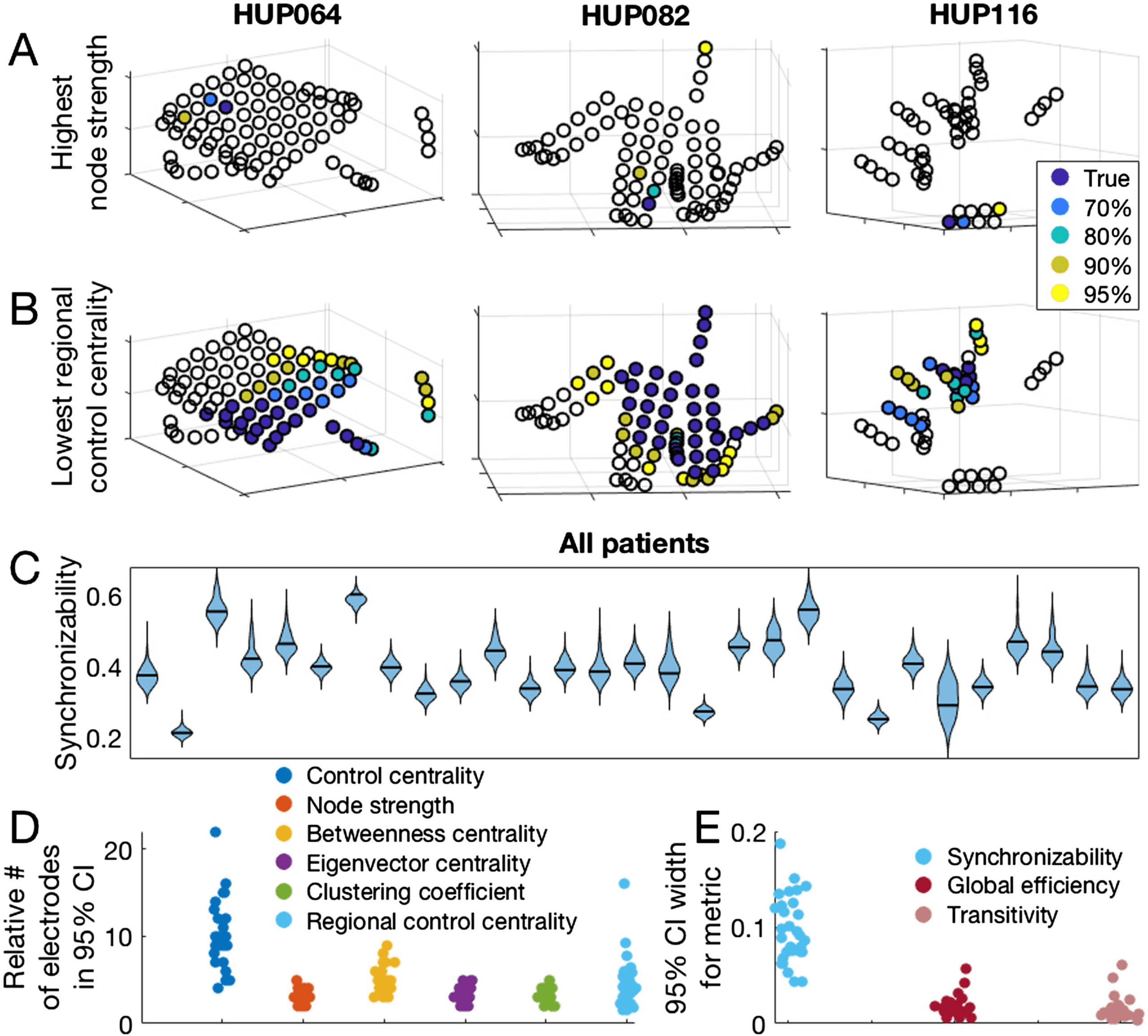
Figure 4.
Jackknife subsampling to estimate confidence regarding network metric values. (A) The
location of the electrode with the highest node strength, as well as the electrodes accounting for
various percentages of highest node strength occurrences in 1,000 random jackknife subsampling
networks for three example patients. (B) The location of the most synchronizing region (which is
the region with the lowest regional control centrality), and the regions accounting for various per-
centages of the most synchronizing region occurrences in 1,000 random jackknife subsampling
networks for three patients. (C) Patient-specific synchronizability distributions across subsamples.
Each separate violin represents a patient and shows the distribution of synchronizability values ob-
tained across 1,000 random jackknife subsamples. Horizontal black lines show the original value
in the non-subsampled network. (D) Number of electrodes forming the 95% jackknife confidence
electrode set for each nodal metric, for all patients. For each nodal metric, each dot shows the
patient-specific number of electrodes accounting for 95% of all occurrences of the maximum (min-
imum for control centrality and regional control centrality) metric value in 1,000 random jackknife
subsampling networks. For regional control centrality, this number is divided by the number of elec-
trodes forming the minimum regional control centrality in the original non-subsampled network to
obtain a ratio. (E) Width of the 95% jackknife confidence interval for each global metric, for all
patients. For each global metric, each dot shows the patient-specific width of the 95% jackknife
confidence interval of the metric value across 1,000 random subsamples.
In D and E, the hori-
zontal position of individual points was determined by random jitter to improve readability. This
figure demonstrates the variability in confidence of network theory results across patients that can
be revealed by jackknife subsampling.
results demonstrate the heterogeneity among patients in the level of confidence in estimated
network statistics that can be revealed by the jackknife algorithm. The locations of electrode
contacts with the maximum or minimum metric values, as well as the results of jackknife
subsampling, varied somewhat across time periods, choice of frequency band for coherence,
Network Neuroscience
498
Effect of incomplete spatial sampling on epilepsy network statistics
seizure, network density, and time window for coherence calculations (Supplemental Figure 1,
Supplemental Table 7).
DISCUSSION
Handling missing data is a long-standing problem in science in general and is particularly
problematic in network science, where a missing node may limit our understanding of the
entire network (Guimerà & Sales-Pardo, 2009). In social networks, missing data can dramati-
cally alter network statistics (Albert et al., 2000, 2004; Kossinets, 2006). In the field of neuro-
science, Jalili demonstrated that global efficiency of scalp EEG-based functional networks in
healthy individuals was highly sensitive to the removal of certain nodes (Jalili, 2015). To our
knowledge, this is the first study examining the reliability of network statistics in the epileptic
brain and in iEEG data. We determined that network measures differ in robustness to spa-
tial subsampling, and that the sensitivity to sampling does not depend on the distance from
the seizure onset zone. We also found that more extensive implants were more robust to
subsampling. Finally, we developed and applied an algorithm using jackknife subsampling
of electrode contacts to estimate confidence in nodal and global statistics in patient brain
networks.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Functional Network Metrics Exhibit Differential Reliability Under Spatial Subsampling
Metric reliability for all network measures decreased with a greater degree of missing data,
which has previously been reported in social networks (Kossinets, 2006; Smith & Moody,
2013). Among examined nodal metrics, node strength and eigenvector centrality were most re-
liable and control centrality was least reliable; among the global metrics we tested, transitivity
was most reliable and synchronizability was least reliable. The difference in reliability across
metrics reflects, in part, the underlying sensitivity of each metric to graph topology. Prior stud-
ies in social networks have also observed that node strength is more robust to subsampling than
betweenness centrality (Costenbader & Valente, 2003; Galaskiewicz, 1991; Smith & Moody,
2013). The relative robustness of node strength and eigenvector centrality compared with other
nodal measures may reflect that metrics that primarily incorporate immediate connections to
the node of interest are less sensitive to subsampling than metrics that more strongly weigh
multistep connections. The preserved ordinality of network metric reliability across most pa-
tients, timescales, and frequency bands suggests that this result is generalizable. Clinically,
applying network statistics that are more robust to spatial sampling may be preferable in cases
in which the electrode coverage of important regions is uncertain. The ability of each metric
to capture network behavior must be weighed against its spatial reliability if such personalized
models are to be translated clinically.
Sensitivity to incomplete sampling depends somewhat on the number of electrode con-
tacts forming the original implantation. Although synchronizability and clustering coefficient
were the only global and nodal measures, respectively, to demonstrate a significant positive
relationship between number of electrode contacts and metric reliability, all other measures
except control centrality demonstrated nonsignificant positive relationships. This pattern of
findings suggests that for most network measures, greater robustness can be achieved in part
through more extensive electrode coverage. This agrees with work finding that more exten-
sive electrode coverage results in better predictions of surgical outcome (Wang et al., 2019).
Mechanistically, this may imply that random subsampling is less likely to remove important
hubs in larger networks. Alternatively, perhaps information about missing nodes and edges
can be inferred from the remaining components of the network, which is facilitated by a larger
Network Neuroscience
499
Effect of incomplete spatial sampling on epilepsy network statistics
starting network. Clinically, this suggests that implanting a greater number of electrode con-
tacts may increase our confidence in network statistics. This benefit would have to be weighed
against the risks of more extensive coverage, including hemorrhage and infection (Mullin et al.,
2016). Network metrics were generally more sensitive to contiguous removal than to random
removal of electrodes. This may reflect spatial correlation of brain signals, such that informa-
tion from a missing electrode contact may be more easily inferred from remaining neighbor
contacts (Betzel et al., 2019; Lagarde et al., 2018). Alternatively, removing contiguous con-
tacts may increase the probability of removing the entire set of critical electrode contacts
that are needed to localize seizure generators. The analysis removing contiguous electrode
contacts may better approximate the clinical scenario of leaving out an entire electrode
or region from sampling, whereas the analysis removing random contacts better simulates
choosing sparser network coverage. Consideration of which type of “missed coverage”
applies in a given clinical context will inform how strongly that missing coverage may affect
network results.
One limitation of the reliability measure as an approximation of metric robustness to
subsampling is that nodal network metrics and their variances across subsampling are not
normally distributed, and so the reliability measure may be disproportionately influenced by
electrode contacts with more extreme values. The fact that nodal metrics had the same dif-
ferential ordering in robustness to subsampling as measured by Spearman rank correlation
between the original and subsampled metric supports the validity of the ordering of nodal
metric reliabilities.
Metric Sensitivity to Incomplete Sampling Is Independent of Distance From the Seizure Onset Zone
All metrics tested were equally sensitive to removing nodes in close or far proximity from the
clinician-defined seizure onset zone. Most metrics were also equally sensitive to subsampling
that targeted removal of the complete seizure onset zone and subsampling that spared the
seizure onset zone. This may be because the seizure-generating network is a relatively small
subset of the full peri-ictal network, and thus perturbation of the seizure-generating network
has a small effect on the network as a whole. These results are practically concerning in the
case of metrics with lower reliability to spatial subsampling, such as control centrality and
synchronizability, because placement of electrodes in the network periphery away from clini-
cal zones of interest is often variable across patients and across epilepsy centers. To increase
the clinical confidence in the results of these network measures, the incomplete network may
be supplemented using structural connectivity data and atlas-based approaches (Betzel et al.,
2017; Fan, Li, Yu, & Jiang, 2016; Greicius, Supekar, Menon, & Dougherty, 2009; Liao et al.,
2011; Reddy et al., 2018; Shah, Bassett, et al., 2018). Network theory also proposes several
methods of predicting missing links (Guimerà & Sales-Pardo, 2009; Lü, Pan, Zhou, Zhang,
& Stanley, 2015; Lü & Zhou, 2011; Pan, Zhou, Lü, & Hu, 2016). The finding of nonsignifi-
cantly increased sensitivity of the transitivity measure to removing the entire seizure onset zone,
along with a disproportionate increase in transitivity when seizure onset zone electrodes are
removed, may reflect a tendency of nodes in the seizure onset zone to form widespread net-
work connections peri-ictally. Practically, this finding also suggests that transitivity—and more
specifically, subsampling-induced change in transitivity—is a promising measure to identify
electrodes overlying the seizure onset zone. Of note, the seizure onset zone-targeted versus
sparing subsampling method introduces a potential bias in that removing the seizure onset
zone as opposed to random non-seizure onset zone electrodes disproportionately targets elec-
trodes that are spatially clustered together.
If anything, we would expect this bias to act to
decrease transitivity when seizure onset zone electrodes are removed, as we might expect
Network Neuroscience
500
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
electrodes in close proximity to have a higher within-group clustering and thus increase the
overall transitivity of the network.
A limitation of this analysis is that clinical methods for identifying the seizure onset zone
are imperfect, and so the clinician-defined seizure onset zone may not capture actual seizure
generators. When redefining the hypothesized site of seizure generation as the resection zone
(for good-outcome patients) we also found no difference in removing nodes in close or distant
proximity from the resection zone. However, it is possible that neither method accurately
captured true seizure generators.
Jackknife Network Subsampling Generates Confidence Intervals for Virtual Resection
Prior work has used global and nodal network measures to stratify surgical candidates and to
select nodes for resection (Lopes et al., 2017; Shah, Bernabei, et al., 2018; Sinha et al., 2017;
Tomlinson, Porter, & Marsh, 2017). Here we provide a simple algorithm to augment these
methods by determining patient-specific confidence in the robustness of estimated statistics
to small perturbations in spatial sampling. Similar resampling-based approaches have been
used in social networks (Duval, Christensen, & Spahiu, 2010; Lusseau, Whitehead, & Gero,
2008; Ohara, Saito, Kimura, & Motoda, 2014), in gene expression data (de Matos Simoes
& Emmert-Streib, 2012), and in resting fMRI data of healthy subjects (Cheng et al., 2017).
The heterogeneity in confidence across patients may be used to stratify patients into those for
whom enough information of the epileptic network is captured to accurately use personalized
network models and those for whom models are likely to be inaccurate because of implantation
strategy. In this study we do not claim to identify the ideal network model among the many
published studies. The jackknife subsampling method may be easily applied to any of these
network models.
Methodological Limitations and Future Directions
Our method of network subsampling can examine how networks change only with the re-
moval of electrode contacts, and not upon the addition of contacts. For an intracranial EEG
study that has parsimoniously captured seizure onset and spread, using our statistical sub-
sampling method may miss critical electrode contacts and thus erroneously characterize the
network as unreliable. However, for those patients who have very clear seizure onset and prop-
agation, personalized network models of epilepsy may not be required to guide surgical plan-
ning. An additional limitation is that our measure of nodal metric similarity—the Spearman
rank correlation—may not capture how network model predictions practically change with
subsampling. It is conceivable that a network metric would demonstrate low reliability to sub-
sampling as defined in this paper, but still generate consistent predictions about the optimal site
of surgical intervention depending on how these predictions are formed. Different groups have
proposed different methods to direct surgical targeting using network statistics (Kini et al.,
2019; Proix et al., 2018; Shah, Bernabei, et al., 2018; Sinha et al., 2017, 2019), and our
proposed subsampling method can be used to test the sensitivity of any targeting predictions
to incomplete spatial sampling, similar to the jackknife procedure described in the section
above.
The jackknife analysis results varied somewhat across time, frequency band, and choice of
seizure, reflecting the different states of the network. These observations underscore the fact
that spatial sampling is one of several sources of bias of the network statistics. Further explo-
ration of the sensitivity of network statistics to the choice of seizure, time, and frequency band
will be necessary for useful clinical implementation. Also, additional steps toward translating
Network Neuroscience
501
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
this work into clinical care will require expanding our dataset to include larger numbers of
patients, stereo EEG implantations, and those treated with focal laser ablation and perhaps
brain stimulation devices.
While in this study we implemented only data-driven metrics that describe underlying net-
work properties, there is significant interest in fitting generative models of neural population
dynamics to brain networks. One such example, the Epileptor model (Jirsa, Stacey, Quilichini,
Ivanov, & Bernard, 2014), is a neural mass model that describes many relevant epileptic dy-
namics and is currently under study as a clinical trial in Europe to guide epilepsy surgery (Proix
et al., 2018). Our network subsampling approach may also be used for generative neurophys-
iologic models and gives confidence to their clinical utility.
Conclusions
The field of network science provides a promising set of tools for understanding epilepsy dy-
namics and for surgical planning. However, the robustness of empirical estimates of network
statistics to incomplete electrode sampling is not well understood. We have shown variabil-
ity across network measures in robustness to incomplete sampling. Network measures are
equally vulnerable to removing electrode contacts near versus distant from the seizure onset
zone, and to removing electrode contacts within the seizure onset zone versus an equivalent
number of non-seizure onset zone electrode contacts. Robustness to incomplete sampling is
highly heterogeneous across patients, and jackknife subsampling is a simple algorithm to ob-
tain patient-specific confidence in the results of network statistics. The choice of individual
network models should be based upon the intended application and on the clinical certainty
that important seizure generators have been sampled by intracranial implants.
DATA AVAILABILITY
All EEG records and annotations are available on the International Epilepsy Electrophysiology
Portal (https://www.ieeg.org; Kini, Davis, & Wagenaar, 2016; Wagenaar et al., 2013). All code
is available on GitHub (https://github.com/erinconrad/network-subsets; Conrad & Bernabei,
2019). We include an example script and an associated example dataset in a single patient
to demonstrate usage of the code base. We do not publicly host network adjacency matrices
because of file size, but will share them with readers upon request.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00131.
AUTHOR CONTRIBUTIONS
Erin Conrad: Conceptualization; Formal analysis; Methodology; Writing - Original Draft. John
Bernabei: Conceptualization; Formal analysis; Methodology; Writing - Original Draft; Writing -
Review & Editing. Lohith Kini: Data curation; Formal analysis; Writing - Review & Editing.
Preya Shah: Conceptualization; Writing - Review & Editing. Fadi Mikhail: Data curation.
Ammar Kheder: Data curation. Russell Shinohara: Formal analysis; Writing - Review & Editing.
Kathryn Davis: Conceptualization; Supervision; Writing - Review & Editing. Danielle Bassett:
Conceptualization; Supervision; Writing - Review & Editing. Brian Litt: Supervision; Writing -
Review & Editing.
Network Neuroscience
502
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
FUNDING INFORMATION
Brian Litt, National Institute of Neurological Disorders and Stroke (http://dx.doi.org/10.13039/
100000065), Award ID: R01-NS099348-01. Kathryn Davis, National Institute of Neurological
Disorders and Stroke (http://dx.doi.org/10.13039/100000065), Award ID: R01-NS099348-01.
Danielle Bassett, National Institute of Neurological Disorders and Stroke (http://dx.doi.org/
10.13039/100000065), Award ID: R01-NS099348-01. Brian Litt, National Institute of Neuro-
logical Disorders and Stroke (http://dx.doi.org/10.13039/100000065), Award ID: 1-T32-NS-
091006-01. Fadi Mikhail, National Institute of Neurological Disorders and Stroke (http://
dx.doi.org/10.13039/100000065), Award ID: 1-T32-NS-091006-01. Erin Conrad, National
Institute of Neurological Disorders and Stroke (http://dx.doi.org/10.13039/100000065), Award
ID: R25-NS065745. Kathryn Davis, National Institute of Neurological Disorders and Stroke
(http://dx.doi.org/10.13039/100000065), Award ID: K23 NS073801. Brian Litt, Mirowski Fam-
ily Foundation. Brian Litt, Neil and Barbara Smit. Brian Litt, Jonathan Rothberg. Kathryn Davis,
Thornton Foundation. Danielle Bassett, Alfred P. Sloan Foundation (http://dx.doi.org/10.13039/
100000879). Danielle Bassett, John D. and Catherine T. MacArthur Foundation (http://dx.doi.
org/10.13039/100000870). Russell Shinohara, National Institutes of Health (http://dx.doi.org/
10.13039/100000002), Award ID: R01MH112845. Russell Shinohara, National Institutes of
Health (http://dx.doi.org/10.13039/100000002), Award ID: R01NS060910. Danielle Bassett,
ISI Foundation. Russell Shinohara, National Multiple Sclerosis Society. Russell Shinohara,
Race to Erase MS. Fadi Mikhail, the Institute of Translational Medicine and Therapeutics
(ITMAT) of the Perelman School of Medicine at the University of Pennsylvania.
COMPETING INTERESTS
Erin Conrad has received consulting income from Ceribell. Russell Shinohara has received
consulting income and has served on a scientific advisory board for Genentech/Roche, and
has received income for editorial/reviewership duties from the American Medical Association
and Research Square.
REFERENCES
Albert, R., Albert, I., & Nakarado, G. L. (2004). Structural vulner-
ability of the North American power grid. Physical Review. E,
Statistical, Nonlinear, and Soft Matter Physics, 69(2), 025103.
Albert, R., Jeong, H., & Barabási, A.-L. (2000). Error and attack tol-
erance of complex networks. Nature, 406(6794), 378–382.
Arbabshirani, M. R., Damaraju, E., Phlypo, R., Plis, S., Allen, E.,
Ma, S., . . . Calhoun, V. D. (2014). Impact of autocorrelation on
functional connectivity. NeuroImage, 102(Pt. 2), 294–308.
Avants, B. B., Tustison, N. J., Song, G., Cook, P. A., Klein, A., &
Gee, J. C. (2011). A reproducible evaluation of ANTs similarity
metric performance in brain image registration. NeuroImage, 54,
2033–2044.
Barrat, A., Barthélemy, M., & Vespignani, A. (2007). The architec-
ture of complex weighted networks: Measurements and mod-
els. In G. Caldarelli & A. Vespignani (Eds.), Large scale structure
and dynamics of complex networks (pp. 67–92). Hackensack, NJ:
World Scientific Publishing.
Bassett, D. S., Bullmore, E. T., Meyer-Lindenberg, A., Apud, J. A.,
Weinberger, D. R., & Coppola, R.
(2009). Cognitive fitness
of cost-efficient brain functional networks. Proceedings of the
National Academy of Sciences, 106(28), 11747–11752.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Bassett, D. S., Zurn, P., & Gold, J. I. (2018). On the nature and use of
models in network neuroscience. Nature Reviews Neuroscience,
19(9), 566–578.
Bettus, G., Ranjeva, J.-P., Wendling, F., Bénar, C. G., Confort-
Gouny, S., Régis, J., . . . Guye, M. (2011). Interictal functional
connectivity of human epileptic networks assessed by intracere-
bral EEG and BOLD signal fluctuations. PloS ONE, 6(5), e20071.
Betzel, R. F., Medaglia, J. D., Kahn, A. E., Soffer, J., Schonhaut, D. R.,
& Bassett, D. S. (2017). Inter-regional ECoG correlations pre-
dicted by communication dynamics, geometry, and correlated
gene expression. arXiv:1706.06088
Betzel, R. F., Medaglia, J. D., Kahn, A. E., Soffer, J., Schonhaut,
D. R., & Bassett, D. S. (2019). Structural, geometric and genetic
factors predict interregional brain connectivity patterns probed
by electrocorticography. Nature Biomedical Engineering, 3(11),
902–916.
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., & Hwang, D.
(2006). Complex networks: Structure and dynamics. Physics Re-
ports, 424(4–5), 175–308.
Burns, S. P., Santaniello, S., Yaffe, R. B., Jouny, C. C., Crone,
N. E., Bergey, G. K., . . . Sarma, S. V. (2014). Network dynamics
of the brain and influence of the epileptic seizure onset zone.
Network Neuroscience
503
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
t
.
Effect of incomplete spatial sampling on epilepsy network statistics
Proceedings of the National Academy of Sciences, 111(49),
E5321–E5330.
Cheng, H., Li, A., Koenigsberger, A. A., Huang, C., Wang, Y.,
Sheng, J., & Newman, S. D. (2017). Pseudo-bootstrap network
analysis—An application in functional connectivity fingerprint-
ing. Frontiers in Human Neuroscience, 11, 1153.
Conrad, E., & Bernabei, J. (2019). Network subsets analysis, GitHub,
https://github.com/erinconrad/network-subsets
Costenbader, E., & Valente, T. W. (2003). The stability of centrality
measures when networks are sampled. Social Networks, 25(4),
283–307.
Davidshofer, K. R., & Murphy, C. O. (2005). Psychological testing:
Principles and applications. Upper Saddle River, NJ: Pearson/
Prentice Hall.
de Matos Simoes, R., & Emmert-Streib, F. (2012). Bagging statistical
network inference from large-scale gene expression data. PloS
ONE, 7(3), e33624.
Dijkstra, E. W. (1959). A note on two problems in connexion with
graphs. Numerische Mathematik, 1(1), 269–271.
Dunn, O. J. (1964). Multiple comparisons using rank sums. Tech-
nometrics: A Journal of Statistics for the Physical, Chemical, and
Engineering Sciences, 6(3), 241–252.
Duval, R. D., Christensen, K., & Spahiu, A. (2010). Bootstrapping
a terrorist network. Conference of Southern Illinois University
Carbondale. Political Networks Conference. http://www.academia.
edu/download/31009775/viewcontent.pdf
Guimerà, R., & Sales-Pardo, M. (2009). Missing and spurious inter-
actions and the reconstruction of complex networks. Proceedings
of the National Academy of Sciences, 106(52), 22073–22078.
Holland, P. W., & Leinhardt, S.
(1971). Transitivity in struc-
tural models of small groups. Comparative Group Studies, 2(2),
107–124.
Jalili, M. (2015). Resiliency of EEG-based brain functional networks.
PloS ONE, 10(8), e0135333.
Jirsa, V. K., Stacey, W. C., Quilichini, P. P., Ivanov, A. I., & Bernard,
C. (2014). On the nature of seizure dynamics. Brain, 137(8),
2210–2230.
Khambhati, A. N., Davis, K. A., Lucas, T. H., Litt, B., & Bassett,
D. S. (2016). Virtual cortical resection reveals push-pull network
control preceding seizure evolution. Neuron, 91(5), 1170–1182.
Khambhati, A. N., Davis, K. A., Oommen, B. S., Chen, S. H.,
Lucas, T. H., Litt, B., & Bassett, D. S. (2015). Dynamic network
drivers of seizure generation, propagation and termination in hu-
man neocortical epilepsy. PLoS Computational Biology, 11(12),
e1004608.
Kini, L. G., Bernabei, J. M., Mikhail, F., Hadar, P., Shah, P., Khambhati,
A. N., . . . Litt, B. (2019). Virtual resection predicts surgical out-
come for drug-resistant epilepsy. Brain. https://doi.org/10.1093/
brain/awz303
Kini, L. G., Davis, K. A., & Wagenaar, J. B. (2016). Data integra-
tion: Combined imaging and electrophysiology data in the cloud.
NeuroImage, 124(Pt. B), 1175–1181.
Kossinets, G. (2006). Effects of missing data in social networks.
Engel, J., Jr. (1996). Surgery for seizures. New England Journal of
Social Networks, 28(3), 247–268.
Medicine, 334(10), 647–652.
Englot, D. J., Birk, H., & Chang, E. F. (2017). Seizure outcomes in
nonresective epilepsy surgery: An update. Neurosurgical Review,
40(2), 181–194.
Fan, L., Li, H., Yu, S., & Jiang, T. (2016). Human Brainnetome
Atlas and its potential applications in brain-inspired comput-
ing. In K. Amunts, L. Grandinetti, T. Lippert, & N. Petkov (Eds.),
BrainComp (pp. 1–14). Cham, Switzerland: Springer.
Fisher, R. A. (1915). Frequency distribution of the values of the cor-
relation coefficient in samples from an indefinitely large popula-
tion. Biometrika, 10(4), 507–521.
Fletcher, J. M., & Wennekers, T. (2018). From structure to activity:
Using centrality measures to predict neuronal activity. Interna-
tional Journal of Neural Systems, 28(2), 1750013.
Fornito, A., Zalesky, A., & Bullmore, E. (2016). Fundamentals
of brain network analysis. Amsterdam, Netherlands: Academic
Press.
Freeman, L. C. (1977). A set of measures of centrality based on
betweenness. Sociometry, 40(1), 35–41.
Friedman, M. (1937). The use of ranks to avoid the assumption
of normality implicit in the analysis of variance. Journal of the
American Statistical Association, 32(200), 675–701.
J.
Galaskiewicz,
(1991). Estimating point centrality using dif-
ferent network sampling techniques. Social Networks, 13(4),
347–386.
Greicius, M. D., Supekar, K., Menon, V., & Dougherty, R. F. (2009).
Resting-state functional connectivity reflects structural con-
nectivity in the default mode network. Cerebral Cortex, 19(1),
72–78.
Kramer, M. A., & Cash, S. S. (2012). Epilepsy as a disorder of cortical
network organization. The Neuroscientist, 18(4), 360–372.
Kramer, M. A., Eden, U. T., Lepage, K. Q., Kolaczyk, E. D., Bianchi,
M. T., & Cash, S. S. (2011). Emergence of persistent networks in
long-term intracranial EEG recordings. Journal of Neuroscience,
31(44), 15757–15767.
Kwan, P., Schachter, S. C., & Brodie, M. J. (2011). Drug-resistant
epilepsy. New England Journal of Medicine, 365(10), 919–926.
Lagarde, S., Roehri, N., Lambert, I., Trebuchon, A., McGonigal,
A., Carron, R., . . . Bartolomei, F. (2018). Interictal stereotactic-
EEG functional connectivity in refractory focal epilepsies. Brain,
141(10), 2966–2980.
Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world
networks. Physical Review Letters, 87(19), 198701.
Liao, W., Zhang, Z., Pan, Z., Mantini, D., Ding, J., Duan, X., . . .
Chen, H. (2010). Altered functional connectivity and small-world
in mesial temporal lobe epilepsy. PloS ONE, 5(1), e8525.
Liao, W., Zhang, Z., Pan, Z., Mantini, D., Ding, J., Duan, X.,
. . . Chen, H. (2011). Default mode network abnormalities in
mesial temporal lobe epilepsy: A study combining fMRI and DTI.
Human Brain Mapping, 32(6), 883–895.
Litt, B., Esteller, R., Echauz, J., Alessandro, M. D., Shor, R., Henry, T.,
. . . Vachtsevanos, G. (2001). Seizure precursors may begin hours
in advance of temporal lobe seizures: A report of five patients.
Neuron, 29(4), 51–64.
Lopes, M. A., Richardson, M. P., Abela, E., Rummel, C., Schindler,
K., Goodfellow, M., & Terry, J. R. (2017). An optimal strategy for
epilepsy surgery: Disruption of the rich-club? PLoS Computa-
tional Biology, 13(8), e1005637.
Network Neuroscience
504
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
Lü, L., Pan, L., Zhou, T., Zhang, Y.-C., & Stanley, H. E. (2015). To-
ward link predictability of complex networks. Proceedings of
the National Academy of Sciences, 112(8), 2325–2330.
Lü, L., & Zhou, T. (2011). Link prediction in complex networks:
A survey. Physica A: Statistical Mechanics and Its Applications,
390(6), 1150–1170.
Lusseau, D., Whitehead, H., & Gero, S. (2008). Incorporating uncer-
tainty into the study of animal social networks. Animal Behaviour,
75(5), 1809–1815.
Mitra, P. P., & Pesaran, B. (1999). Analysis of dynamic brain imaging
data. Biophysical Journal, 76(2), 691–708.
Mullin, J. P., Shriver, M., Alomar, S., Najm, I., Bulacio, J., Chauvel,
P., & Gonzalez-Martinez, J. (2016). Is SEEG safe? A system-
atic review and meta-analysis of stereo-electroencephalography-
related complications. Epilepsia, 57(3), 386–401.
Newman, M. E. J. (2008). Mathematics of networks. In S. Durlauf &
L. Blume (Eds.), New Palgrave dictionary of economics (pp. 1–8).
New York, NY: Palgrave Macmillan.
Noe, K., Sulc, V., Wong-Kisiel, L., Wirrell, E., Van Gompel, J. J.,
Wetjen, N., . . . Worrell, G. A. (2013). Long-term outcomes after
nonlesional extratemporal lobe epilepsy surgery. JAMA Neurol-
ogy, 70(8), 1003–1008.
Ohara, K., Saito, K., Kimura, M., & Motoda, H. (2014). Resampling-
based framework for estimating node centrality of large social
network. In S. Džeroski, P. Panov, D. Kocev, & L. Todorovski
(Eds.), Lecture notes in computer science (pp. 228–239). Cham,
Switzerland: Springer.
Opsahl, T., Agneessens, F., & Skvoretz, J. (2010). Node centrality
in weighted networks: Generalizing degree and shortest paths.
Social Networks, 32(3), 245–251.
Opsahl, T., & Panzarasa, P. (2009). Clustering in weighted networks.
Social Networks, 31(2), 155–163.
Paldino, M. J., Zhang, W., Chu, Z. D., & Golriz, F. (2017). Metrics
of brain network architecture capture the impact of disease in
children with epilepsy. NeuroImage: Clinical, 13, 201–208.
Pan, L., Zhou, T., Lü, L., & Hu, C.-K. (2016). Predicting missing links
and identifying spurious links via likelihood analysis. Scientific
Reports, 6, 22955.
Panzica, F., Varotto, G., Rotondi, F., Spreafico, R., & Franceschetti,
S. (2013). Identification of the epileptogenic zone from stereo-
EEG signals: A connectivity-graph theory approach. Frontiers in
Neurology, 4, 175.
Pedersen, M., Omidvarnia, A. H., Walz, J. M., & Jackson, G. D.
(2015). Increased segregation of brain networks in focal epi-
lepsy: An fMRI graph theory finding. NeuroImage: Clinical, 8,
536–542.
Ponten, S. C., Bartolomei, F., & Stam, C. J. (2007). Small-world net-
works and epilepsy: Graph theoretical analysis of intracerebrally
recorded mesial temporal lobe seizures. Clinical Neurophysiol-
ogy, 118(4), 918–927.
Proix, T., Bartolomei, F., Guye, M., & Jirsa, V. K. (2017). Individual
brain structure and modelling predict seizure propagation. Brain,
140(3), 641–654.
Proix, T., Jirsa, V. K., Bartolomei, F., Guye, M., & Truccolo, W.
(2018). Predicting the spatiotemporal diversity of seizure prop-
agation and termination in human focal epilepsy. Nature Com-
munications, 9(1), 1088.
Quenouille, M. H. (1949). Problems in plane sampling. Annals of
Mathematical Statistics, 20(3), 355–375.
Quenouille, M. H. (1956). Notes on bias in estimation. Biometrika,
43(3/4), 353–360.
Reddy, P. G., Betzel, R. F., Khambhati, A. N., Shah, P., Kini, L.,
Litt, B., . . . Bassett, D. S. (2018). Genetic and neuroanatomi-
cal support for functional brain network dynamics in epilepsy.
arXiv:1809.03934
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069.
Schindler, K. A., Bialonski, S., Horstmann, M.-T., Elger, C. E., &
Lehnertz, K. (2008). Evolving functional network properties and
synchronizability during human epileptic seizures. Chaos, 18(3),
033119.
Schroeder, G. M., Diehl, B., Chowdhury, F. A., Duncan, J. S., de
Tisi, J., Trevelyan, A. J., . . . Wang, Y. (2019). Seizure pathways
change on circadian and slower timescales in individual patients
with focal epilepsy. https://doi.org/10.1101/661371
Shah, P., Bassett, D. S., Wisse, L. E. M., Detre, J. A., Stein, J. M.,
Yushkevich, P. A., . . . Das, S. R. (2018). Mapping the structural
and functional network architecture of the medial temporal lobe
using 7T MRI. Human Brain Mapping, 39(2), 851–865.
Shah, P., Bernabei, J., Kini, L., Ashourvan, A., Boccanfuso, J.,
Archer, R., . . . Litt, B. (2018). High interictal connectivity within
the resection zone is associated with favorable post-surgical out-
comes in focal epilepsy patients. bioRxiv:459008
Šidák, Z. (1967). Rectangular confidence regions for the means of
multivariate normal distributions. Journal of the American Statis-
tical Association, 62(318), 626–633.
Sinha, N., Dauwels, J., Kaiser, M., Cash, S. S., Brandon Westover,
M., Wang, Y., & Taylor, P. N. (2017). Predicting neurosurgical out-
comes in focal epilepsy patients using computational modelling.
Brain, 140(2), 319–332.
Sinha, N., Wang, Y., da Silva, N. M., Miserocchi, A., McEvoy, A. W.,
de Tisi, J., . . . Taylor, P. N. (2019). Node abnormality predicts
seizure outcome and relates to long-term relapse after epilepsy
surgery. bioRxiv:747725
Smith, J. A., & Moody, J. (2013). Structural effects of network sam-
pling coverage I: Nodes missing at random. Social Networks,
35(4).
Sun, F. T., Arcot Desai, S., Tcheng, T. K., & Morrell, M. J. (2018).
Changes in the electrocorticogram after implantation of intracra-
nial electrodes in humans: The implant effect. Clinical Neuro-
physiology, 129(3), 676–686.
Tomlinson, S. B., Porter, B. E., & Marsh, E. D. (2017). Interictal
network synchrony and local heterogeneity predict epilepsy
surgery outcome among pediatric patients. Epilepsia, 58(3),
402–411.
Towle, V. L., Carder, R. K., Khorasani, L., & Lindberg, D. (1999).
Journal of Clinical
Electrocorticographic coherence patterns.
Neurophysiology, 16(6), 528–547.
Tukey, J. (1958). Bias and confidence in not quite large samples.
Annals of Mathematical Statistics, 29, 614.
Wagenaar, J. B., Brinkmann, B. H., Ives, Z., Worrell, G. A., & Litt,
B. (2013). A multimodal platform for cloud-based collaborative
Network Neuroscience
505
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Effect of incomplete spatial sampling on epilepsy network statistics
research. 2013 6th International IEEE/EMBS Conference on Neu-
ral Engineering (NER), 1386–1389.
Wang, Y., Sinha, N., Schroeder, G. M., Ramaraju, S., McEvoy, A. W.,
Miserocchi, A., . . . Taylor, P. N. (2019). Interictal intracranial
EEG for predicting surgical success: The importance of space and
time. arXiv:1909.07932
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-
world” networks. Nature, 393(6684), 440–442.
Weiss, S. A., Lemesiou, A., Connors, R., Banks, G. P., McKhann,
G. M., Goodman, R. R., . . . Schevon, C. A. (2015). Seizure lo-
calization using ictal phase-locked high gamma: A retrospective
surgical outcome study. Neurology, 84(23), 2320–2328.
Wiebe, S., Blume, W. T., Girvin, J. P., & Eliasziw, M. (2001). A ran-
domized, controlled trial of surgery for temporal-lobe epilepsy.
New England Journal of Medicine, 345(5), 311–318.
Wiebe, S., Eliasziw, M., Bellhouse, D. R., & Fallahay, C. (1999). Bur-
den of epilepsy: The Ontario Health Survey. Canadian Journal of
Neurological Sciences, 26(4), 263–270.
Wilke, C., Worrell, G., & He, B. (2011). Graph analysis of epilepto-
genic networks in human partial epilepsy. Epilepsia, 52(1), 84–93.
Wu, J., Davis, K., Azarion, A., Zheng, Y., Wang, H., Litt, B., &
Gee, J. (2011). Brain parcellation aids in electrode localization
in epileptic patients. In C. A. Linte, J. T. Moore, E. C. S. Chen, &
D. R. Holmes (Eds.), Lecture notes in computer science. Berlin,
Germany: Springer. https://link.springer.com/chapter/10.1007/
978-3-642-32630-1_13
Yushkevich, P. A., Piven, J., Hazlett, H. C., Smith, R. G., Ho, S., Gee,
J. C., & Gerig, G. (2006). User-guided 3D active contour segmen-
tation of anatomical structures: Significantly improved efficiency
and reliability. NeuroImage, 31, 1116–1128.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
8
4
1
8
6
6
6
6
1
n
e
n
_
a
_
0
0
1
3
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
506