研究 - 麻省理工学院人工智能研究专业

研究

扩散MRI纤维束成像的比较
皮质-皮质的组织学追踪
雪貂大脑的结构连接

席琳·德莱特1,2,3, 阿诺·梅西2, 利-安妮·戴尔2, 奥菲莉·福贝1,
卡佳豪雅1.4, 伯努瓦·拉拉特5, 塞巴斯蒂安·梅里奥5, 让-弗朗索瓦·曼金5,
伊莎贝尔·雷洛6, 胡安·罗梅罗之路6, 维克多·博雷尔6,

罗伯托·托罗1.7, 和克劳斯·C. 希尔格塔格

2,8

1人类遗传学和认知功能单位, 巴斯德研究所, UMR 3571, 法国国家科学研究中心, 巴黎, 法国
2计算神经科学研究所, 艾彭多夫大学医学中心, 汉堡大学, 汉堡, 德国
3巴黎狄德罗大学, 巴黎索邦大学, 巴黎, 法国
4神经心理学系, 马克斯·普朗克人类认知和脑科学研究所, 莱比锡, 德国
5神经旋转, 欧洲原子能委员会, 巴黎萨克雷大学, 伊维特河畔吉夫, 法国
6发育神经生物学单位, 神经科学研究所, 科学研究高级委员会,
米格尔·埃尔南德斯大学, 阿利坎特的圣琼, 西班牙
7研究与跨学科中心 (显色指数), 巴黎笛卡尔大学, 巴黎, 法国
8健康科学系, 波士顿大学, 波士顿, 嘛, 美国

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
A
_
0
0
0
9
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

关键词: 验证, 弥散磁共振成像, 纤维束成像术, 纤维束追踪, 结构连接, 雪貂

抽象的

大脑的解剖连接是网络神经科学的中心焦点. 弥散磁共振成像
纤维束成像提供了研究体内脑纤维结构的独特机会
并且无创地. 然而, 其可靠性仍备受争议. 这里, 我们探索了
扩散 MRI 纤维束成像匹配侵入性解剖纤维束追踪连接的能力
雪貂大脑的数据. 我们还研究了几种最先进技术的影响
与地面真实连接数据匹配的纤维束成像算法. 纤维束追踪
连接数据是通过逆行示踪剂注射到枕骨中获得的, 顶叶,
和成年雪貂的颞叶皮质. 我们发现投影的相对密度
从解剖学实验中确定的结果与所有估计值高度相关
研究的扩散纤维束成像算法 (Spearman 的 rho 范围为 0.67 到 0.91),
虽然很小, 纤维束成像算法中出现了不显着的变化.
这些结果与在小鼠和猴子中报告的结果相当, 增加
对扩散 MRI 纤维束成像结果的信心. 而且, 我们的结果提供了一些见解
纤维束成像算法的灵敏度和特异性的变化, 并因此进入
选择一种算法相对于另一种算法的影响.

作者总结

在本文中，我们使用束追踪数据作为黄金标准来验证扩散 MRI 的使用
纤维束成像用于推断雪貂大脑的结构连接以及评估
几种最先进的纤维束成像算法对推断连接的影响. 我们
发现扩散 MRI 纤维束成像和纤维束追踪之间存在高度对应性，几乎不需要
探索的算法之间的差异. 我们的结论是，扩散 MRI 纤维束成像
提供了对可以使用的结构连接的有价值的全脑估计
进一步解剖, 发展性的, 和雪貂大脑的计算研究.

开放访问

杂志

引文: 德莱特雷, C。, 大量的, A。, 戴尔,
洛杉矶。, 富贝特, 奥。, 豪雅, K., 放牧, B.,
. . . 希尔格塔格, C. C. (2019). 比较
扩散 MRI 纤维束成像之间
和组织学追踪
皮质-皮质结构连接
在雪貂的大脑中. 网络
神经科学, 3(4), 1038–1050.
https://doi.org/10.1162/netn_a_00098

DOI:
https://doi.org/10.1162/netn_a_00098

支持信息:
https://doi.org/10.1162/netn_a_00098
https://github.com/神经解剖学/
Ferret扩散轨迹追踪比较

已收到: 22 一月 2019
公认: 23 可能 2019

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
克劳斯·C. 希尔格塔格
c.hilgetag@uke.de

处理编辑器:
奥拉夫·斯波恩斯

版权: © 2019
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

比较雪貂大脑中的纤维束成像和纤维束追踪

结构连接:
物理或解剖学网络
连接神经元的连接
合奏团通常被称为
脑连接组.

弥散磁共振成像:
MRI 序列量化
水分子的方向
扩散.

纤维束成像术:
用于重建的技术
大脑白质连接
基于扩散MRI.

介绍

大脑功能是通过空间分布的大规模网络的通信产生的
底层结构连接架构 (恩格尔, 格尔洛夫, 希尔格塔格, & 诺尔特, 2013; 坎德尔,
施瓦茨, 杰塞尔, 海豹树, & 哈德斯佩斯, 2012; 公园 & 弗里斯顿, 2013; 瓦雷拉, 拉绍,
罗德里格斯, & 马蒂内里, 2001). 结构连通性的系统分析揭示了
大脑网络的特征, 包括模块的存在, 枢纽, 及更高
有序拓扑性质, 认为支持有效的信息处理 (斯波恩斯, 2010).
而且, 结构连接被认为是受到各种影响的神经基质
病理状况, 例如阿尔茨海默病和精神分裂症谱系障碍
(假如 & 布莫尔, 2015). 所以, 大脑结构连接的可靠估计是
对于增进我们对大脑功能网络基础的理解至关重要.

扩散 MRI 纤维束成像是推断大脑结构连接性的间接方法
来自受轴突纤维结构约束的水分子的布朗运动
(约里森, 德科托, 森, & 利曼斯, 2017). 因此, 它提供了独特的机会
调查, 体内和非侵入性, 完整或改变的大脑的结构连接,
例如中风的情况 (维瑟等人。, 2018), 大脑发育的纵向分析
(哈格曼等人。, 2010), 或在子宫内获得产前大脑结构 (卡斯普里安等人。,
2008). 然而, 扩散 MRI 纤维束成像正确标测结构的可靠性
联系仍然备受争议 (琼斯, 克诺舍, & 车工, 2013; 托马斯等人。, 2014).
所以, 验证似乎是评估当前方法和识别的关键步骤
改进的新视角 (德尔比, 无辜者, 贝克, & 伦德尔, 2018).

少数研究设计了基准以探讨差异的可靠性-
MRI纤维束成像 (席林等人。, 2018). 例如, 使用组成的虚拟数据集
通过扩散 MRI 纤维束成像重建的已知纤维束作为基本事实, 的准确度
在人体中评估了大量最先进的纤维束成像算法 (迈尔-海因
等人。, 2017). 结果显示, 对于所有算法, 他们有能力恢复大部分现有的-
荷兰国际集团捆绑, 但同时也暴露了一个变数, 但实质性的, 误报数. 相似地
萨瓦尔, 你的兄弟, & 扎莱斯基 (2018) 比较确定性和概率性拖拉机-
具有数字生成模型的图形算法并得出权衡
根据纤维束成像算法的类型在灵敏度和特异性之间做出选择.
虽然这些研究提供了对广泛范围的特异性和敏感性的初步估计
纤维束成像算法, 使用的基本事实基于扩散 MRI 纤维束成像
或数字生成，从而, 人们可以辩论他们的现实主义.

纤维束追踪:
侵入性神经科学技术
用于确定路径
神经元实体之间通过
将染料注入大脑区域.

顺行追踪:
绘制神经网络图谱的技术
注射部位的连接
(细胞体) 到投影目标,
标记突触末端.

逆行追踪:
绘制神经网络图谱的技术
通过标记来源进行连接
(细胞体) 的神经元投射到
注射部位 (突触).

迄今为止, 评估结构性大脑连接的黄金标准是由tract提供的-
追踪实验, 物理调查, 在细胞水平, 的相对数量
使用病毒将某个区域与大脑其他部分连接起来, 细菌, 或生物素化葡聚糖
代理人 (比兹利, 低的, 节点, & 国王, 2015; 丢弃, 斯波恩斯, & 斯旺森, 2015; 马尔可夫等人。,
2014; 辛格等人。, 2015). 这些试剂充当顺行或逆行示踪剂. 这样的
解剖连接的组织学追踪提供了方向和层流信息-
逆行追踪的情况下, 组织学追踪还可以量化
预测的变化.
投影中轴突的数量, 因为每个标记的投射神经元提供一个轴突.
在猕猴身上进行的研究 (阿扎巴赫特等人。, 2015; 多纳休等人。, 2016; 席林, 内斯,
等人。, 2019; 张等人。, 2018), 松鼠猴 (Gao et al., 2013; 席林, 高, 等人。,
2019), 猪 (克诺舍, 安旺德, 利普特罗特, & 德尔比, 2015), 老鼠 (卡拉布雷塞, 巴德, 科弗,
齐, & 约翰逊, 2015), 和老鼠 (辛克等人。, 2018) 探索了之间的关系
纤维束追踪实验和纤维束成像. 全面的, 这些研究表明扩散
MRI 纤维束成像可以很好地估计大脑结构连接. 很少的探索

网络神经科学

1039

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
A
_
0
0
0
9
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

比较雪貂大脑中的纤维束成像和纤维束追踪

已经对不同纤维束成像方法可用于估计的能力进行了研究
结构连接权重 (Gao et al., 2013). 以往的研究主要集中在
纤维束成像算法通过以下方式正确估计白质通路的能力
体素重叠 (克诺舍等人。, 2015), 或关于可检测性 (存在或不存在) 的
连接 (辛克等人。, 2018), 或两者 (席林, 高, 等人。, 2019; 席林, 内斯, 等人。,
2019).

雪貂的大脑在出生后开始折叠, 并在大约 1 时达到成人折叠模式
月龄. 所以, 雪貂是一种广泛用于研究大脑折叠的动物模型-
英 (巴尼特等人。, 2009; 冯, 克莱顿, 张, 冈本, & 贝利, 2013). 此外,
这些哺乳动物表现出复杂的行为, 住房便宜, 并有一个短暂的孕期-
化期限以及有限的寿命, 使它们成为有吸引力的“全寿命模型”
(狐狸, 1998). 最近建立了广泛的雪貂纤维追踪连接数据 (看
戴尔, 无辜者, 希尔格塔格, & 马槽, 2019A, 2019乙, 2019C) 使得比较成为可能
与纤维束成像方法报告的解剖皮质连接. 因此, 现在
研究旨在使用雪貂作为动物模型来评估六种扩散轨迹的性能-
断层扫描算法与枕骨组织学束追踪数据的比较, 顶叶,
和雪貂的颞叶皮质. 全面的, 我们的结果表明，扩散 MRI 纤维束成像
提供雪貂大脑结构连接的统计显着性估计, 虽然
不同的纤维束成像算法在灵敏度和特异性方面存在差异.

材料和方法

雪貂大脑图谱

我们使用了基于 Bizley 的后皮质图集的分割 & 国王 (2009). 这
分区方案是在扩散 MRI 空间中的左半球上手动绘制的-
使用在线工具 BrainBox (豪雅, 戈什, 英镑, & 旅游, 2016, http://Brainbox.pasteur.fr/).
区域追踪数据可用 17, 18, 19, 21 (枕叶视觉区域); 20a和20b
合并的 (颞视区); 和 PPr 和 PPc (顶叶视觉区). 见图 1A.

扩散 MRI 数据

使用小动物离体获得高分辨率 MRI 7 特斯拉使用 MRI 扫描仪
(神经旋转, 萨克雷, 法国). 这些收购是事后进行的，以减少
运动伪影并提高灵敏度 (福尔摩斯等人。, 2017). 大脑已获得
来自 2 个月大的雪貂. 这只雪貂因过量服用戊巴比妥而被安乐死
经心灌注 0.9% 盐水溶液并用磷酸盐缓冲液进行后固定 4%
多聚甲醛 (粉煤灰). 提取后, 大脑被存储在 4
C 在一个 4% PFA溶液
直到 MRI 采集. 所有程序均得到动物护理机构的批准
米格尔·埃尔南德斯大学和 CSIC 的使用和使用委员会 (高级理事会
科学研究), 阿利坎特, 西班牙.

○

大脑被转移到 0.01 M磷酸盐缓冲盐水 (公共广播公司) 解决方案
补液 24 MRI 采集前 hr. MRI 采集前不久, 大脑样本
被转移到充满非质子液体的塑料管中 (氟惰性) 以免
可能引起磁敏伪影的空气-组织界面, 以及避免折叠 MRI
由于来自成像场之外的质子液体的质子信号而产生的伪影
看法 (麦克罗比, 摩尔, & 格雷夫斯, 2017). 然后将管子放置在专用支架中
发射/接收 MRI 体积射频线圈的中间. 温度稳定性为
通过调节室温以及梯度线圈的冷却来确保, 用水

网络神经科学

1040

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
A
_
0
0
0
9
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

比较雪貂大脑中的纤维束成像和纤维束追踪

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
A
_
0
0
0
9
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

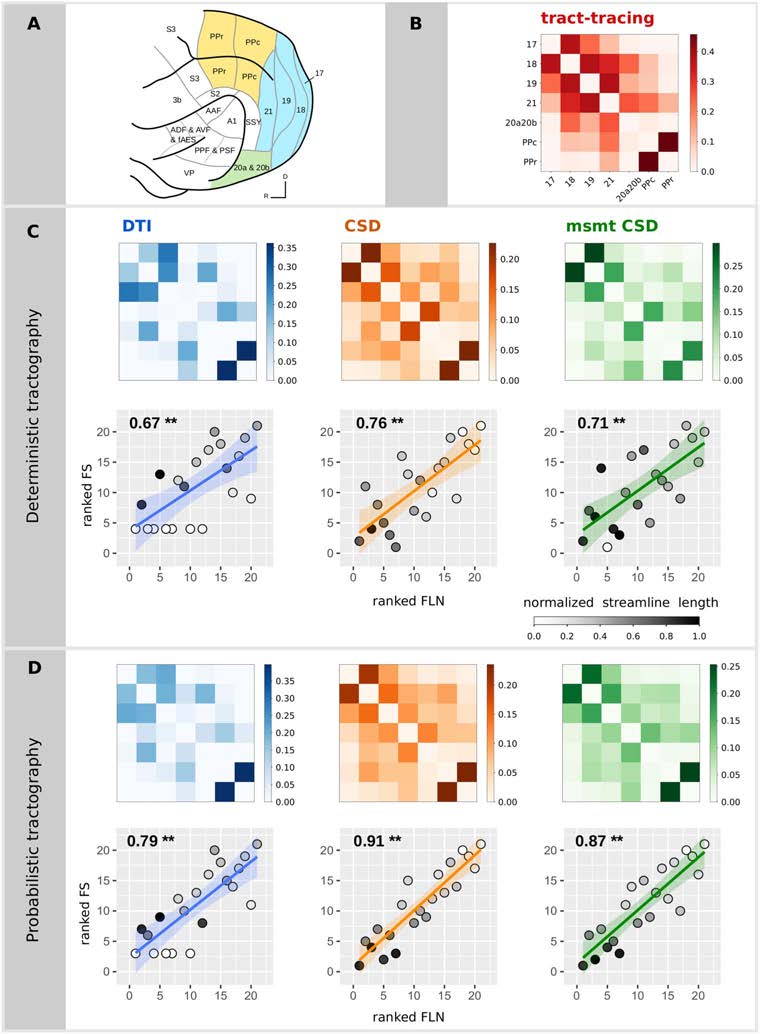
数字 1. 扩散 MRI 纤维束成像与纤维束追踪实验之间的关系.
(A)
根据 Bizley 和 King 分区的雪貂大脑图谱 (图改编自 Bizley &
国王, 2009). 比较研究感兴趣的区域是那些有颜色的区域. 颜色代码为
不同的视觉大脑区域: 后顶叶 (黄色的), 枕骨 (蓝色的), 和颞叶皮质
(绿色的).
(乙) 基于束追踪实验的结构连接矩阵, 权重在哪里
代表标记神经元的分数 (FLN). 结构连接矩阵估计
确定性的 (C) 和概率的 (D) 纤维束成像算法和相关的散点图
排名 FLN vs. FS排名. 散点图中的每个点对应于之间的连接
一对用于追踪结果的区域 (横坐标) 和扩散结果 (纵坐标). 排名中的
连接的权重允许将斯皮尔曼的 rho 可视化为拟合曲线的斜率.
平均流线长度的灰色代码 (通过最大流线标准化的值
所有算法的长度). P值小于 0.001 表示为 **.

网络神经科学

1041

比较雪貂大脑中的纤维束成像和纤维束追踪

C在磁铁最内部不断流动. 平衡

○

在 16
样品的温度为 20

○

使用多层多回波采集高分辨率 T2 加权 MRI 数据 (中小微企业)
序列与 18 回声时间和 0.12 mm 各向同性体素. 获取扩散 MRI 数据
使用多切片 2-D 自旋回波分段 DTI-EPI 序列 (4 细分市场) 以及以下内容
参数: TR = 40 s; = 32 多发性硬化症; 矩阵大小= 160 × 120 × 80; 0.24 mm 各向同性体素;
200 扩散加权方向，b = 4,000 秒/毫米2; 和 10 b0 在se 的开头-
序列, 扩散梯度持续时间= 5 ms 和扩散梯度分离 = 17 多发性硬化症. 谢谢
与临床扫描仪相比具有更强的梯度, b值可以达到 4,000 秒/毫米2, 在-
确保强大的扩散权重，从而提高对各向异性的敏感性，同时
保持回波时间足够短以节省信噪比 (信噪比) 并限制 EPI 畸变-
系统蒸发散. b 值为 4,000 s/mm2 之前已被证明是一个很好的折衷方案
解开交叉纤维以进行离体成像 (迪尔比等人。, 2011). 引入的噪声由
高扩散权重通过高角分辨率来平衡. 这 200 方向
生成为均匀分布在球体上的非共线方向 (哈桑, 派克,
& 亚历山大, 2001). 空间分辨率被选为可用的最高分辨率
扫描仪以实现良好的信噪比，同时保持合理的采集时间. 我们
获得的信噪比为 4.2, 测量为大脑中信号平均值之间的比率
和背景信号的标准偏差. 总采集时间
扩散 MRI 序列大约是 37 小时.

预处理

第一的, 使用以下命令将 MRI 数据从 2dseq Bruker 格式转换为标准 NIFTI 格式
bruker2nifti 脚本的修改版本 (原版: https://github.com/SebastianoF/
用户2nifti; 修改版本: https://github.com/neuroanatomy/bruker2nifti). 对于有限的
卷数, Bruker 常规图像重新校正 EPI 轨迹的效果不佳-
构造函数, 这导致音量嘈杂. 为了排除这些卷, 扩散-
其平均信号的加权方向 2 远离标准差
所有卷的全球平均值均经过目视检查并删除. 三出 200
按照此标准删除了卷. 主要完成了预处理步骤
使用 MRtrix3 函数并包含局部主成分分析 (LPCA) 德努瓦-
英 (维拉特等人。, 2016), 吉布斯振铃校正 (凯尔纳, 迪塔尔, 基谢列夫, & 旅行过, 2016),
基于FSL的涡流校正 (安德森 & 索蒂罗普洛斯, 2016; 詹金森, 贝克曼,
贝伦斯, 伍尔里奇, & 史密斯, 2012), 和B1场不均匀性校正 (塔斯蒂森等人。,
2010). 从高分辨率 T2 图像中手动分割脑掩模, 为了
获得脑沟和脑回的精确轮廓. 使用线性变换进行空间归一化-
使用以下方法计算高分辨率 T2 体积和扩散 MRI 数据之间的关系
调情工具 (詹金森, 栏干, 布雷迪, & 史密斯, 2002), 并且脑罩被注册到
扩散空间.

纤维束成像术

我们评估了不同纤维束成像方法可靠地重建结构的能力
由束追踪实验提供的连接. 我们考虑了三个本地模型:
(A) 扩散张量 (DT) 模型; (乙) 纤维取向分布 (是) 估计与
约束球形反卷积 (可持续发展委员会) 使用tournier算法 (图尔尼耶, 卡拉曼特,
& 康纳利, 2013); 和 (C) 使用多壳多组织 CSD 估计 FOD (msmt CSD) 我们-
dhollander 算法, 它提供了组织特异性的无监督估计

1042

扩散张量模型 (DT):
数学模型表示
扩散方向
水分子呈椭球体
(或雪茄).

纤维取向分布 (是):
复杂的数学模型
代表纤维的方向
人群中可能含有
多方向.

约束球形反卷积
(可持续发展委员会):
高阶数学模型
允许推断纤维
取向分布.

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
A
_
0
0
0
9
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

比较雪貂大脑中的纤维束成像和纤维束追踪

响应函数. msmt CSD 使用 WM/CSF 室模型进行
(约里森, 图尔尼耶, 多霍兰德, 康纳利, & 西贝尔斯, 2014). 三种纤维束描记术中的每一种
然后将模型与确定性和概率性跟踪算法配对. 确定-
使用欧拉积分执行基于 istic DT 的跟踪 (张量_It; 贝斯, 帕耶维奇,
皮尔保利, 杜达, & 阿尔德鲁比, 2000), 而基于 DT 的概率跟踪则使用 bootstrapping
(张量_概率; 琼斯, 2008). 根据 FOD 峰值进行基于 CSD 的纤维束成像
要么确定性地 (SD_STREAM; 图尔尼耶, 卡拉曼特, & 康纳利, 2012) 或可能-
抽搐地 (外来物2; 图尔尼耶, 卡拉曼特, & 康纳利, 2010). 球谐阶为 8 曾是
用于基于 CSD 的估计. 在整个大脑中追踪了一百万条流线
MRtrix3推荐的参数: 步长 0.024 毫米 (0.12 iFOD2 毫米), 角度
90
对于iFOD2), 最小流线长度 1.2 毫米, 最大长度 2.4 厘米.
在脑罩内的随机位置产生流线种子，直到定义的
已达到流线数量. 防止流线穿过沟, 大脑
mask 被用作停止标准.

每个体素 (45

○

基于纤维束成像的连通性矩阵

使用 num 从纤维束成像结果中提取结构连接矩阵-
连接区域对的流线的误码率. 连接矩阵可在
支持信息. 报告区域之间平均纤维长度的矩阵是
还计算了. 然后, 使用分数标度对结构连接矩阵进行归一化-
英, 这样，区域对之间的流线数量除以
连接到每个区域的流线计数, 排除自连接 (多纳休
等人。, 2016). 权重代表流线的分数 (FS).

所有 MRI 数据分析均使用 MRtrix3 软件进行 (http://www.mrtrix.org/),
以及 Python 的自定义脚本 (http://www.python.org), 包括 Python 包 Nipype
(戈尔戈莱夫斯基等人。, 2011), 尼巴贝尔 (布雷特等人。, 2018), 和 NumPy (奥利芬特, 2015). 一切
脚本和数据可在以下 GitHub 存储库中获取: 德莱特雷 & 旅游 (2019).

解剖束追踪数据

来自成年雪貂解剖束追踪实验的结构连接数据 (的
2 年龄) 从 Dell 等人获得. (2019A, 2019乙, 2019C). 实验考试-
确定区域的皮质-皮质和皮质-丘脑连接 17, 18, 19, 和 21 (奥西普-
视觉皮层), PPc和PPr (顶后视皮层), 以及20a和20b (颞
视觉皮层) 在成年雪貂中通过逆行生物素化右旋糖酐胺示踪剂 (商业发展局).
通过逆行束追踪, 神经元投射是从轴突末端追踪到的-
餐饮区域 17, 18, 19, 21, 聚丙烯酸酯, 聚丙稀, 20A, 和20b (注射部位) 一个半球到
神经元的细胞体, 位于不同的大脑区域和两个大脑半球.
因此, 注射的大脑区域被定义为目标区域, 和大脑区域
标记为 BDA 阳性的细胞体被定义为源区域. 骗局-
然后通过获得一小部分标记的神经元来量化连接 (FLN) 价值; 参考
戴尔等人. (2019A, 2019乙, 2019C) 实验过程的详细解释.
此外, 为了本研究的目的, 我们只考虑同侧投影和广告-
调整连接矩阵和 FLN 值以排除对侧投影, 为了
专注于边缘完整的子网络.

基于束追踪的连接矩阵

从左半球组装结构连接矩阵，使得权重
代表区域对之间逆行标记神经元的数量. 这提供了

网络神经科学

1043

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
A
_
0
0
0
9
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

比较雪貂大脑中的纤维束成像和纤维束追踪

不对称的我们 (指导的) 矩阵指示示踪剂注射部位的投影.
使用标记神经元的分数对权重进行归一化 (FLN), 拉的数量-
源区域中的标记神经元除以源区域中标记神经元的总数
注射区 (马尔可夫等人。, 2014). 考虑到弥散 MRI 纤维束成像并不
提供有关连接方向性的信息, 束追踪矩阵也是
通过平均两个方向的 FLN 值进行对称化.

统计分析

相关系数用于量化扩散 MRI 纤维束成像的程度
匹配的纤维束追踪数据. 此后, 为了表征纤维束成像的能力
映射结构权重, 追踪数据中最强的联系逐渐
从两个来源中删除 (纤维束描记术和纤维束追踪), 相关系数为
然后计算剩余的连接.
同样的方式, 我们还计算了正确的-
排除最弱的束追踪连接时的关系系数. 这样的探索
使我们能够探究相关系数值是否主要由强
连接, 与短距离连接相关，并且统计上更有可能
被检测到. 相比之下, 弱连接或长距离连接更有可能是虚假连接 (错误的
积极的一面). 为了处理结构连通性值的对数正态分布
扩散 MRI 纤维束成像和纤维束追踪实验, 我们计算了非-
参数斯皮尔曼相关系数或皮尔逊相关系数
对数变换后的值 (FLN 和 FS). 为了应对断线的情况-
执行对数变换时的蒸发散, 皮尔逊相关系数, 全部是生的
流线和标记神经元的计数 (正常化之前) 增加了
1. 置信区间是使用自举法计算的，置信水平为 95%. 在
添加, 我们在回归欧几里得时计算了部分 Spearman 相关性
我们皮质区域质心之间的距离. 我们首先将关系建模为-
将 FLN 和 FS 值的对数与每对之间的欧氏距离进行补间
皮质区域并提取其残差. FLN 和 FS 的残差为
使用斯皮尔曼相关系数进行相关.

量化纤维束描记术正确检测现有纤维束追踪连接的能力,
我们计算了基本的分类性能指标: 灵敏度, 特异性, 和精度.
灵敏度量化了检测真实连接的能力, 同时特异性
估计某个数量在避免错误检测方面的表现. 平均精度量化了如何
许多积极检测到的连接都是相关的. 束追踪结构连接
矩阵逐渐阈值化和二值化，保持最强的给定比例
重量, 从 0.1 到 0.9 一步一步地 0.1 (鲁比诺夫 & 斯波恩斯, 2010) 为了建立一系列
接收者操作特征以及精确度和召回率曲线. 绩效衡量标准
然后对每个阈值进行平均作为汇总统计.

使用 R 进行统计分析 (https://www.R-project.org/) 和Python

使用 scikit-learn 包 (加雷塔 & 蒙切基, 2013).

结果

扩散 MRI 纤维束成像的结构连接评估结果均为高度阳性
−3;
与追踪数据相关 (Spearman 的 rho 范围为 0.67 到 0.91, 所有p < 10 see Table 1 and Figure 1). Probabilistic tractography algorithms increased the correlation val- ues obtained with deterministic tractography. The DT model was not able to recover all the connections found in tract-tracing data for both deterministic (7 connections) and probabilistic Network Neuroscience 1044 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 3 8 1 8 6 6 7 6 1 n e n _ a _ 0 0 0 9 8 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Comparing tractography and tract-tracing in the ferret brain Table 1. Correlations between diffusion MRI tractography and tract-tracing experiments. Undirected tract-tracing matrix Directed tract-tracing matrix Spearman Pearson Spearman Pearson Deterministic DTI CSD 0.67 ** [0.44–0.94] 0.69 ** [0.37–0.86] 0.50 * [0.22–0.82] 0.48 * [0.07–0.75] 0.76 ** [0.56–1.00] 0.68 ** [0.36–0.86] 0.62 * [0.36–0.93] 0.53 * [0.13–0.78] msmt CSD 0.71 ** [0.50–0.98] 0.71 ** [0.40–0.87] 0.57 * [0.22–0.94] 0.55 ** [0.16–0.79] Probabilistic DTI CSD 0.79 ** [0.65–0.99] 0.78 ** [0.53–0.90] 0.67 ** [0.49–0.91] 0.63 ** [0.27–0.83] 0.91 ** [0.83–1.00] 0.88 ** [0.73–0.95] 0.77 ** [0.56–1.00] 0.69 ** [0.38–0.86] msmt CSD 0.87 ** [0.76–1.00] 0.89 ** [0.76–0.95] 0.70 ** [0.46–0.98] 0.67 ** [0.33–0.85] P values smaller than 0.001 are indicated by ** and p values inferior to 0.05 by *. (5 connections) tractography, as shown by the white circles that correspond to connections that were not found by the diffusion MRI tractography (lowest rank), and hence the average stream- line length of these connections is 0 (white circles; Figures 1C and 1D). The 95% conﬁdence intervals for the relative predictive power of the different tractography algorithms overlapped, suggesting an absence of statistically signiﬁcant differences. Consistent results were observed when using the Pearson correlation coefﬁcient (Table 1; and Supplementary Figure 1, Support- ing Information). Spearman correlations were decreased after regressing out the Euclidean distance. Partial Spearman correlation values were no longer statistically signiﬁcant for deterministic tractogra- phy (DTI: r = 0.36, p = 0.10; CSD: r = 0.39, p = 0.09; msmt CSD: r = 0.40, p = 0.07). How- ever, for probabilistic tractography correlations remained statistically signiﬁcant (DTI: r = 0.54, p < 0.05; CSD: r = 0.66, p < 0.05; msmt CSD: r = 0.77, p < 0.05); see Supplementary Figure 8 (Supporting Information). Consistent results were observed when using the Pearson correla- tion coefﬁcient (Supplementary Table 1, Supporting Information). 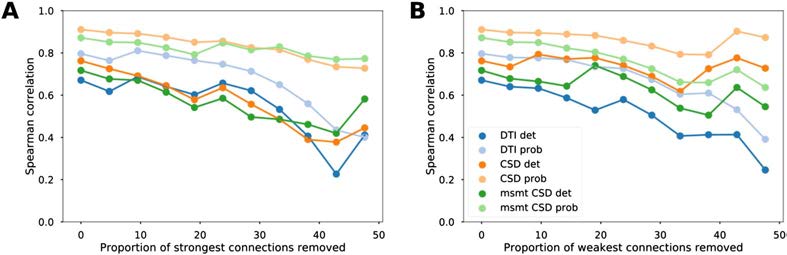We then tested the inﬂuence of strong and weak connections on the relationship be- tween diffusion MRI tractography and tract-tracing data. Structural connectivity estimates from diffusion MRI tractography remained highly positively correlated to tract-tracing data after progressive removal of 25% of the strongest connections and similarly after removal of the weakest connections (Figure 2 and Supplementary Figure 2, Supporting Information, for Figure 2. Reliability of the association between diffusion MRI tractography and tract-tracing data. Evolution of the Spearman correlation values between tract-tracing and diffusion MRI tractography data as a function of the proportion of strongest (A) and weakest (B) connections removed for the different tractography algorithms. Network Neuroscience 1045 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 3 8 1 8 6 6 7 6 1 n e n _ a _ 0 0 0 9 8 p d t . 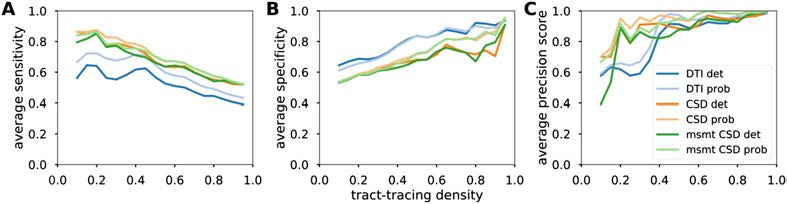/ f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Comparing tractography and tract-tracing in the ferret brain Figure 3. Detection performance of diffusion MRI tractography algorithms. Averaged sensitivity (A), speciﬁcity (B), and precision (C) as a function of the tract-tracing density. Pearson correlations). These results show that the correlations between diffusion tractography and tract-tracing were not primarily driven by connections most likely to be recovered by dif- fusion tractography because of their topographic proximity or their strength (strong weights). Similarly, we observed that the correlations were not affected by the weakest connections, which are generally more sensitive to noise (leading to false positives); otherwise there would have been an increase in correlation values. Measures of sensitivity/speciﬁcity/precision give an indication of the detectability of the con- nections. Our results were averaged and plotted as a function of the proportion of tract-tracing connections (Figure 3). CSD-based algorithms had generally higher sensitivity and precision compared with the diffusion tensor model, while tensor-based tractography had slightly higher speciﬁcity. All analyses were also performed comparing tractography with the directed structural con- nectivity from tract-tracing. We found decreased yet still statistically signiﬁcant associations (see Table 1; Supplementary Figures 3 to 7, Supporting Information). DISCUSSION l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 3 8 1 8 6 6 7 6 1 n e n _ a _ 0 0 0 9 8 p d . / t In the present study, we investigated the ability of different diffusion MRI tractography algo- rithms to reliably map ferret brain structural connectivity as retrieved from invasive tract-tracing experiments. We found that structural connectivity estimates from tractography were highly correlated with tract-tracing data. The different algorithms presented small, nonsigniﬁcant variations. Our ﬁndings in the ferret results from previous studies in the monkey (Donahue et al., 2016) and the mouse (Calabrese et al., 2015) as well as results using manganese tracing in the pig (Knösche et al., 2015). Overall, these ﬁndings enhance our conﬁdence in diffusion MRI tractography as a powerful tool for exploring the structural connectional architecture of the brain. f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 We obtained estimates of the reliability of six different tractography algorithms with regard to tract-tracing data for the same cortical areas of the ferret brain. CSD-based algorithms pre- sented the highest degree of concordance with tract-tracing data, and DT-based algorithms the least. However, the differences in correlation values did not appear to be statistically signiﬁ- cant, as suggested by the overlapping 95% conﬁdence intervals. High concordance with no particular algorithm outperforming the others was also reported when matching tract pathways from tractography and manganese tracing for a set of tractography algorithms (Knösche et al., 2015). Comparable overall correlations of the weighted connections have been obtained in the macaque brain, with a Spearman’s correlation of 0.59 (Donahue et al., 2016). However, here we report little effect of the strongest/weakest connections in the correlation values. The Network Neuroscience 1046 Comparing tractography and tract-tracing in the ferret brain gradual decrease of our correlations indicated that our correlations were not ampliﬁed by the weight of strong connections or underestimated by a high amount of false positives stemming from weak connections. In addition, we showed high detection performance values across algorithms. Consistent with the correlation analysis, we observed higher performances for CSD-based algorithms in terms of precision. Also consistent with prior studies, DT-based re- sults appeared to give slightly higher speciﬁcity than CSD-based algorithms, to the detriment of their sensitivity (Knösche et al., 2015; Sarwar et al., 2018). Such results are likely due to the lower ability of diffusion tensor models to resolve complex ﬁber geometries (Maier-Hein et al., 2017; Zalesky et al., 2016). Our correlations were decreased and no longer statistically signiﬁcant after regressing out distance, for deterministic tractography. Similar results have been reported in the macaque, where correlations decreased from r = 0.59 to r = 0.22 after regressing out the distance effects (Donahue et al., 2016). Tractography’s ability to recover tracts is expected to decrease as a function of the distance because of technical biases (e.g., in probabilistic tractography, the probability to follow a given path drops exponentially with distance). Thus, it has been shown that structural connectivity estimates from diffusion MRI tractography are highly related to their lengths (Liptrot, Sidaros, & Dyrby, 2014; Roberts et al., 2016). On the other hand, distance is a biological principle for the preferential connection between two brain areas (Hilgetag, Medalla, Beul, & Barbas, 2016). As such, it remains challenging to disentangle these two factors from tractography outputs. Our regions can also be considered as neighbors relative to the whole-brain size as they are all located in the occipital, parietal, and temporal lobes of one hemisphere. This proximity could have inﬂated our correlations beneﬁting from the ability of tractography and tract-tracing to more accurately recover connections from neighboring areas. In any case, the correlations in which distance was regressed out, which corrects for both effects of distance (proximity and remoteness), maintain statistically signiﬁcant correlations for all probabilistic tractography algorithms (especially based on CSD). Our results showed a high correlation between diffusion MRI tractography and tract-tracing data; however, we note the limitations in our methodology. First, the two datasets had different origins (i.e., the tract-tracing and tractography were not performed in the same animal) and the sample sizes were very small. Although the ferrets could all be considered mature in terms of brain development (Jackson, Peduzzi, & Hickey, 1989; Neal et al., 2007), the ferret used for the MR imaging was only 2 months old, while the animals used in tract-tracing were around 2 years old. This may have increased interindividual variability and induced a bias in our cortical parcellations: Although the sulcal and gyral patterns (used for cortical parcellation of MRI data, in relation to Bizley & King, 2009) are unchanged after postnatal week 4, the ferret brain is still undergoing maturation and growth in all brain structures. The ferret brain growth reaches a plateau at postnatal week 24; however, the differences due to age should be only minor because the cortical architecture at 2 months of age resembles that at adult age (Jackson et al., 1989; Neal et al., 2007). Similarly, the cortex continues to undergo rostrocaudal expansion until postnatal week 24, after which the ferret brain reaches its adult size; however, previous studies have showed no signiﬁcant changes of MRI-measured indices (Barnette et al., 2009; Neal et al., 2007). Although the brain of a 2-month-old ferret is structurally similar to that of an adult brain, it still undergoes functional differentiation and pruning of connections, which could result in a minor shift in the placement of our cortical cytoarchitectonic parcellations, and such parcellations can be observed only in histological sections and not in MRI scans. Second, tract-tracing experiments, despite considered as ground truth, are not exempted from limitations, such as the creation of false positives and false negatives, speciﬁcity of tracer Network Neuroscience 1047 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 3 8 1 8 6 6 7 6 1 n e n _ a _ 0 0 0 9 8 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Comparing tractography and tract-tracing in the ferret brain and antibody used, spillage of tracer, and passive diffusion (Heimer & Robards, 2013; Köbbert et al., 2000; Zaborszky, Wouterlood, & Lanciego, 2006). In addition, in this study we con- sidered only the retrograde connections that are easier to quantify and neglected anterograde tracing results. In sum, this study allowed us to validate structural connectivity estimates from diffusion MRI tractography by comparison with tract-tracing data in the ferret brain, and it provided an estimation of the performance of three diffusion tractography algorithms, namely DT, CSD, and msmt CSD, using both deterministic and probabilistic tracking. Generally, the currently available connectivity data for the ferret are quite limited; therefore, whole-brain tractography based on diffusion imaging can provide an initial, worthwhile estimate of structural connectiv- ity that can be used for further anatomical, developmental, and computational studies of the ferret brain. SUPPORTING INFORMATION Supporting information for this article is available at https://doi.org/10.1162/netn_a_00098. AUTHOR CONTRIBUTIONS Céline Delettre: Conceptualization; Data curation; Formal analysis; Methodology; Software; Writing – Original Draft; Writing – Review & Editing. Arnaud Messé: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Validation; Writing – Original Draft; Writing – Review & Editing. Leigh-Anne Dell: Data curation; Investigation; Methodology; Writing – Original Draft; Writing – Review & Editing. Ophélie Foubet: Data curation; Re- sources. Katja Heuer: Software. Benoit Larrat: Investigation; Resources; Writing – Review & Editing. Sebastien Meriaux: Jean-Francois Mangin: Concep- Investigation; Resources. Isabel Reillo: Project administration; Resources. Camino de Juan tualization; Resources. Romero: Project administration; Resources. Victor Borrell: Project administration; Resources. Roberto Toro: Conceptualization; Funding acquisition; Investigation; Project administration; Resources; Software; Supervision; Writing – Original Draft; Writing – Review & Editing. Claus C. Hilgetag: Conceptualization; Funding acquisition; Investigation; Project administration; Re- sources; Supervision; Writing – Original Draft; Writing – Review & Editing. FUNDING INFORMATION Claus C. Hilgetag, Deutsche Forschungsgemeinschaft (http://dx.doi.org/10.13039/501100001659), Award ID: SFB 936/A1/Z3 and SPP 2041 / HI 1286/6-1. Claus C. Hilgetag, Human Brain Project, Award ID: HBP-SGA2 (785907)/ SGA2. Roberto Toro, Agence Nationale de la Recherche (http://dx.doi.org/10.13039/501100001665), Award ID: ANR-15-HBPR-0005. REFERENCES Andersson, J. L. R., & Sotiropoulos, S. N. (2016). An integrated ap- proach to correction for off-resonance effects and subject move- ment in diffusion MR imaging. NeuroImage, 125, 1063–1078. Azadbakht, H., Parkes, L. M., Haroon, H. A., Augath, M., Logothetis, N. K., de Crespigny, A., J. M. (2015). Validation of high-resolution tractography against in vivo tracing in the macaque visual cortex. Cerebral Cortex, 25(11), 4299–4309. . Parker, G. . . Barnette, A. R., Neil, J. J., Kroenke, C. D., Grifﬁth, J. L., Epstein, A. A., Bayly, P. V., . . . Inder, T. E. (2009). Characterization of brain development in the ferret via MRI. Pediatric Research, 66(1), 80–84. Basser, P. J., Pajevic, S., Pierpaoli, C., Duda, J., & Aldroubi, A. (2000). In vivo ﬁber tractography using DT-MRI data. Magnetic Resonance in Medicine, 44(4), 625–632. Bizley, J. K., Bajo, V. M., Nodal, F. R., & King, A. J. (2015). Cortico- Journal of cortical connectivity within ferret auditory cortex. Comparative Neurology, 523(15), 2187–2210. Bizley, J. K., & King, A. J. (2009). Visual inﬂuences on ferret auditory cortex. Hearing Research, 258(1–2), 55–63. Network Neuroscience 1048 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 3 8 1 8 6 6 7 6 1 n e n _ a _ 0 0 0 9 8 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Comparing tractography and tract-tracing in the ferret brain Bota, M., Sporns, O., & Swanson, L. W. (2015). Architecture of the cerebral cortical association connectome underlying cogni- tion. Proceedings of the National Academy of Sciences, 112(16), E2093–E2101. Brett, M., Hanke, M., Markiewicz, C., Côté, M. -A., McCarthy, P., Ghosh, S., . . . Basile. (2018). Nipy/nibabel: 2.3.0. https://doi. org/10.5281/zenodo.1287921 Calabrese, E., Badea, A., Cofer, G., Qi, Y., & Johnson, G. A. (2015). A diffusion MRI tractography connectome of the mouse brain and comparison with neuronal tracer data. Cerebral Cortex, 25(11), 4628–4637. Delettre, C., & Toro, R. (2019). A comparison between diffusion tractography and tract tracing in ferrets. GitHub. https://github. com/neuroanatomy/FerretDiffusionTractTracingComparison Dell, L.-A., Innocenti, G. M., Hilgetag, C. C., & Manger, P. R. (2019a). Cortical and thalamic connectivity of occipital visual cortical areas 17, 18, 19 and 21 of the domestic ferret (Mustela putorius furo). Journal of Comparative Neurology. https://doi.org/ 10.1002/cne.24631 Dell, L.-A., Innocenti, G. M., Hilgetag, C. C., & Manger, P. R. (2019b). Cortical and thalamic connectivity of posterior parietal visual cortical areas PPc and PPr of the domestic ferret (Mustela putorius furo). Journal of Comparative Neurology. https://doi.org/ 10.1002/cne.24630 Dell, L.-A., Innocenti, G. M., Hilgetag, C. C., & Manger, P. R. (2019c). Cortical and thalamic connectivity of temporal visual cortical areas 20a and 20b of the domestic ferret (Mustela puto- rius furo). Journal of Comparative Neurology. https://doi.org/10. 1101/492728 Donahue, C. J., Sotiropoulos, S. N., Jbabdi, S., Hernandez- Fernandez, M., Behrens, T. E., Dyrby, T. B., . . . Glasser, M. F. (2016). Using diffusion tractography to predict cortical connec- tion strength and distance: A quantitative comparison with trac- ers in the monkey. Journal of Neuroscience, 36(25), 6758–6770. Dyrby, T. B., Baaré, W. F. C., Alexander, D. C., Jelsing, J., Garde, E., & Søgaard, L. V. (2011). An ex vivo imaging pipeline for produc- ing high-quality and high-resolution diffusion-weighted imaging datasets. Human Brain Mapping, 32(4), 544–563. Dyrby, T. B., Innocenti, G. M., Bech, M., & Lundell, H. (2018). Val- idation strategies for the interpretation of microstructure imag- ing using diffusion MRI. NeuroImage. https://doi.org/10.1016/j. neuroimage.2018.06.049 Engel, A. K., Gerloff, C., Hilgetag, C. C., & Nolte, G. (2013). In- trinsic coupling modes: Multiscale interactions in ongoing brain activity. Neuron, 80(4), 867–886. Feng, Y., Clayton, E. H., Chang, Y., Okamoto, R. J., & Bayly, P. V. (2013). Viscoelastic properties of the ferret brain measured in vivo at multiple frequencies by magnetic resonance elastography. Journal of Biomechanics, 46(5), 863–870. Fornito, A., & Bullmore, E. T. (2015). Connectomics: A new paradigm for understanding brain disease. European Neuropsy- chopharmacology, 25(5), 733–748. Fox, J. G. Blackwell. (1998). Biology and diseases of the ferret. Wiley- Gao, Y., Choe, A. S., Stepniewska, I., Li, X., Avison, M. J., & Anderson, A. W. (2013). Validation of DTI tractography-based measures of primary motor area connectivity in the squirrel monkey brain. PLoS ONE. https://doi.org/10.1371/journal.pone. 0075065 Garreta, R., & Moncecchi, G. (2013). Learning scikit-learn: Machine learning in python. Packt Publishing. Gorgolewski, K., Burns, C. D., Madison, C., Clark, D., Halchenko, Y. O., Waskom, M. L., & Ghosh, S. S. (2011). Nipype: A ﬂexible, lightweight and extensible neuroimaging data processing frame- work in Python. Frontiers in Neuroinformatics, 5, 13. Hagmann, P., Sporns, O., Madan, N., Cammoun, L., Pienaar, R., Wedeen, V. J., . . . Grant, P. E. (2010). White matter matura- tion reshapes structural connectivity in the late developing hu- man brain. Proceedings of the National Academy of Sciences, 107(44), 19067–19072. Hasan, K. M., Parker, D. L., & Alexander, A. L. (2001). Comparison of gradient encoding schemes for diffusion-tensor MRI. Journal of Magnetic Resonance Imaging, 13(5), 769–780. Heimer, L., & Robards, M. J. (2013). Neuroanatomical tract-tracing methods. Springer Science & Business Media. Heuer, K., Ghosh, S., Sterling, A. R., & Toro, R. (2016). Open neu- roimaging laboratory. Research Ideas and Outcomes, 2, e9113. Hilgetag, C. C., Medalla, M., Beul, S. F., & Barbas, H. (2016). The primate connectome in context: Principles of connections of the cortical visual system. NeuroImage, 134, 685–702. Holmes, H. E., Powell, N. M., Ma, D., Ismail, O., Harrison, I. F., Wells, J. A., . . . Lythgoe, M. F. (2017). Comparison of in vivo and ex vivo MRI for the detection of structural abnormalities in a mouse model of tauopathy. Frontiers in Neuroinformatics, 11, 20. Jackson, C. A., Peduzzi, J. D., & Hickey, T. L. (1989). Visual cor- tex development in the ferret. I. Genesis and migration of visual cortical neurons. Journal of Neuroscience, 9(4), 1242–1253. Jenkinson, M., Bannister, P., Brady, M., & Smith, S. (2002). Im- proved optimization for the robust and accurate linear registra- tion and motion correction of brain images. NeuroImage, 17(2), 825–841. Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W., & Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790. Jeurissen, B., Descoteaux, M., Mori, S., & Leemans, A. (2017). Dif- fusion MRI ﬁber tractography of the brain. NMR in Biomedicine. https://doi.org/10.1002/nbm.3785 Jeurissen, B., Tournier, J.-D., Dhollander, T., Connelly, A., & Sijbers, J. (2014). Multi-tissue constrained spherical deconvo- lution for improved analysis of multi-shell diffusion MRI data. NeuroImage, 103, 411–426. Jones, D. K. (2008). Tractography gone wild: Probabilistic ﬁbre tracking using the wild bootstrap with diffusion tensor MRI. IEEE Transactions on Medical Imaging, 27(9), 1268–1274. Jones, D. K., Knösche, T. R., & Turner, R. (2013). White matter in- tegrity, ﬁber count, and other fallacies: The do’s and don’ts of diffusion MRI. NeuroImage, 73, 239–254. Kandel, E., Schwartz, J., Jessell, T., Siegelbaum, S., & Hudspeth, A. J. (2012). Principles of neural science (5th ed.). McGraw-Hill Professional. Kasprian, G., Brugger, P. C., Weber, M., Krssák, M., Krampl, E., Herold, C., & Prayer, D. (2008). In utero tractography of fetal white matter development. NeuroImage, 43(2), 213–224. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 3 8 1 8 6 6 7 6 1 n e n _ a _ 0 0 0 9 8 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network Neuroscience 1049 Comparing tractography and tract-tracing in the ferret brain Kellner, E., Dhital, B., Kiselev, V. G., & Reisert, M. (2016). Gibbs- ringing artifact removal based on local subvoxel-shifts. Magnetic Resonance in Medicine, 76(5), 1574–1581. Knösche, T. R., Anwander, A., Liptrot, M., & Dyrby, T. B. (2015). Validation of tractography: Comparison with manganese tracing. Human Brain Mapping, 36(10), 4116–4134. Köbbert, C., Apps, R., Bechmann, I., Lanciego, J. L., Mey, J., & Thanos, S. (2000). Current concepts in neuroanatomical tracing. Progress in Neurobiology, 62(4), 327–351. Liptrot, M. G., Sidaros, K., & Dyrby, T. B. (2014). Addressing the path-length-dependency confound in white matter tract segmen- tation. PLoS ONE, 9(5), e96247. Maier-Hein, K. H., Neher, P. F., Houde, J.-C., Côté, M.-A., Garyfallidis, E., Zhong, J., . . . Descoteaux, M. (2017). The chal- lenge of mapping the human connectome based on diffusion tractography. Nature Communications, 8(1), 1349. Markov, N. T., Vezoli, J., Chameau, P., Falchier, A., Quilodran, R., Huissoud, C., . . . Kennedy, H.(2014). Anatomy of hierarchy: Feedforward and feedback pathways in macaque visual cortex. Journal of Comparative Neurology, 522(1), 225–259. McRobbie, D. W., Moore, E. A., & Graves, M. J. (2017). MRI from picture to proton. https://doi.org/10.1017/9781107706958 Neal, J., Takahashi, M., Silva, M., Tiao, G., Walsh, C. A., & Sheen, V. L. (2007). Insights into the gyriﬁcation of developing fer- ret brain by magnetic resonance imaging. Journal of Anatomy, 210(1), 66–77. Oliphant, T. (2015). Guide to NumPy (2nd ed.). CreateSpace. Park, H.-J., & Friston, K. (2013). Structural and functional brain networks: From connections to cognition. Science, 342(6158), 1238411. Roberts, J. A., Perry, A., Lord, A. R., Roberts, G., Mitchell, P. B., Smith, R. E., . . . Breakspear, M. (2016). The contribution of geometry to the human connectome. NeuroImage, 124(Pt. A), 379–393. Rubinov, M., & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52(3), 1059–1069. Sarwar, T., Ramamohanarao, K., & Zalesky, A. (2018). Mapping connectomes with diffusion MRI: Deterministic or probabilistic tractography? Magnetic Resonance in Medicine. https://doi.org/ 10.1002/mrm.27471 Schilling, K. G., Daducci, A., Maier-Hein, K., Poupon, C., Houde, J. C., Nath, V., . . . Descoteaux, M. (2018). Challenges in diffusion MRI tractography: Lessons learned from interna- tional benchmark competitions. Magnetic Resonance Imaging, 57, 194–209. Schilling, K. G., Gao, Y., Stepniewska, I., Janve, V., Landman, B. A., & Anderson, A. W. (2019). Anatomical accuracy of standard- practice tractography algorithms in the motor system: A histolog- ical validation in the squirrel monkey brain. Magnetic Resonance Imaging, 55, 7–25. Schilling, K. G., Nath, V., Hansen, C., Parvathaneni, P., Blaber, J., Gao, Y., . . . Landman, B. A. (2019). Limits to anatomical accuracy of diffusion tractography using modern approaches. NeuroImage, 185, 1–11. Sinke, M. R. T., Otte, W. M., Christiaens, D., Schmitt, O., Leemans, A., van der Toorn, A., . . . Dijkhuizen, R. M. (2018). Diffusion MRI-based cortical connectome reconstruction: Dependency on tractography procedures and neuroanatomical characteristics. Brain Structure and Function, 223(5), 2269–2285. Sporns, O. (2010). Networks of the brain. MIT Press. Thomas, C., Ye, F. Q., Irfanoglu, M. O., Modi, P., Saleem, K. S., Leopold, D. A., & Pierpaoli, C. (2014). Anatomical accuracy of brain connections derived from diffusion MRI tractography is inherently limited. Proceedings of the National Academy of Sci- ences, 111(46), 16574–16579. Tournier, J.-D., Calamante, F., & Connelly, A. (2010). Improved probabilistic streamlines tractography by 2nd order integra- tion over ﬁbre orientation distributions. Paper presented at the ISMRM, Proceedings of the International Society for Magnetic Resonance in Medicine. Tournier, J.-D., Calamante, F., & Connelly, A. (2012). MRtrix: Diffu- sion tractography in crossing ﬁber regions. International Journal of Imaging Systems and Technology, 22(1), 53–66. Tournier, J.-D., Calamante, F., & Connelly, A. (2013). Determina- tion of the appropriate b value and number of gradient directions for high-angular-resolution diffusion-weighted imaging. NMR in Biomedicine, 26(12), 1775–1786. Tustison, N. J., Avants, B. B., Cook, P. A., Zheng, Y., Egan, A., Yushkevich, P. A., & Gee, J. C. (2010). N4ITK: Improved N3 bias correction. IEEE Transactions on Medical Imaging, 29(6), 1310–1320. Varela, F., Lachaux, J. P., Rodriguez, E., & Martinerie, J. (2001). The brainweb: Phase synchronization and large-scale integra- tion. Nature Reviews Neuroscience, 2(4), 229–239. Veraart, J., Novikov, D. S., Christiaens, D., Ades-Aron, B., Sijbers, J., & Fieremans, E. (2016). Denoising of diffusion MRI using random matrix theory. NeuroImage, 142, 394–406. Visser, M. M., Yassi, N., Campbell, B. C. V., Desmond, P. M., Davis, S. M., Spratt, N., . . . Bivard, A. (2018). White matter degenera- tion after ischemic stroke: A longitudinal diffusion tensor imag- ing study. Journal of Neuroimaging. https://doi.org/10.1111/jon. 12556 Zaborszky, L., Wouterlood, F. G., & Lanciego, J. L. (2006). Neu- roanatomical tract-tracing: Molecules, neurons, and systems. Springer Science & Business Media. Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., van den Heuvel, M. P., & Breakspear, M. (2016). Connectome sensitivity or speci- ﬁcity: Which is more important? NeuroImage, 142, 407–420. Zhang, T., Kong, J., Jing, K., Chen, H., Jiang, X., Li, L., . . . Liu, T. (2018). Optimization of macaque brain DMRI connectome by neuron tracing and myelin stain data. Computerized Medical Imaging and Graphics, 69, 9–20. Zingg, B., Hintiryan, H., Gou, L., Song, M. Y., Bay, M., Bienkowski, M. S., . . .Dong, H.-W. (2015). Neural networks of the mouse neocortex. Annals of Neurosciences, 22(4), . https://doi.org/10. 5214/ans.0972.7531.220409 Network Neuroscience 1050 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 3 8 1 8 6 6 7 6 1 n e n _ a _ 0 0 0 9 8 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 研究形象

下载pdf