研究
Functional control of electrophysiological
network architecture using direct
neurostimulation in humans
Ankit N. Khambhati
罗伯特·E. 总的
1
, Ari E. Kahn
10
1,3,9
, Barbara C. Jobst
15
11
Gregory Worrell
Richard Gorniak
, Sarah Seger
, Sandhitsu R. 这
5
7
Timothy H. Lucas
5
, 凯瑟琳A. 戴维斯
, Bradley C. Lega
15
, 乔尔·M. 斯坦因
14
17
, Julia Costantini
, Youssef Ezzyat
, Ethan A. Solomon
1
4
, Sameer A. Sheth
, Kareem A. Zaghloul
12
16
1
,
16
, Shennan Weiss
8
, Daniel S. Rizzuto
, Michael R. Sperling
4
, 迈克尔·J. Kahana
4
, Joseph I. Tracy
, and Danielle S. Bassett
16
13
,
1,2,5,6
1Department of Bioengineering, 宾夕法尼亚大学, 费城, PA, 美国
2Department of Electrical and Systems Engineering, 宾夕法尼亚大学, 费城, PA, 美国
3Department of Neuroscience, 宾夕法尼亚大学, 费城, PA, 美国
4心理学系, 宾夕法尼亚大学, 费城, PA, 美国
5神经内科, Hospital of the University of Pennsylvania, 费城, PA, 美国
6Department of Physics & Astronomy, 宾夕法尼亚大学, 费城, PA, 美国
7Department of Neurosurgery, Hospital of the University of Pennsylvania, 费城, PA, 美国
8放射科, Hospital of the University of Pennsylvania, 费城, PA, 美国
9Human Research and Engineering Directorate, 我们. Army Research Laboratory, Aberdeen, 医学博士, 美国
10Department of Neurosurgery, Emory University Hospital, 亚特兰大, 遗传算法, 美国
11神经内科, Dartmouth-Hitchcock Medical Center, Lebanon, NH, 美国
12Department of Neurosurgery, Baylor College of Medicine, Houston, TX, 美国
13Surgical Neurology Branch, 美国国立卫生研究院, Bethesda, 医学博士, 美国
14神经内科, Mayo Clinic, 罗切斯特, 明尼苏达州, 美国
15Department of Neurosurgery, University of Texas, Southwestern Medical Center, 达拉斯, TX, 美国
16神经内科, Thomas Jefferson University Hospital, 费城, PA, 美国
17放射科, Thomas Jefferson University Hospital, 费城, PA, 美国
关键词: Neurostimulation, Electrocorticography, Structural controllability, Reconfiguration
抽象的
Chronically implantable neurostimulation devices are becoming a clinically viable option
for treating patients with neurological disease and psychiatric disorders. Neurostimulation
offers the ability to probe and manipulate distributed networks of interacting brain areas
in dysfunctional circuits. 这里, we use tools from network control theory to examine the
dynamic reconfiguration of functionally interacting neuronal ensembles during targeted
neurostimulation of cortical and subcortical brain structures. By integrating multimodal
intracranial recordings and diffusion-weighted imaging from patients with drug-resistant
epilepsy, we test hypothesized structural and functional rules that predict altered patterns of
synchronized local field potentials. We demonstrate the ability to predictably reconfigure
functional interactions depending on stimulation strength and location. Stimulation of areas
with structurally weak connections largely modulates the functional hubness of downstream
areas and concurrently propels the brain towards more difficult-to-reach dynamical states.
By using focal perturbations to bridge large-scale structure, function, and markers of
行为, our findings suggest that stimulation may be tuned to influence different scales
of network interactions driving cognition.
作者总结
Brain stimulation devices capable of perturbing the physiological state of neural systems are
rapidly gaining popularity for their potential to treat neurological and psychiatric disease.
A root problem is that underlying dysfunction spans a large-scale network of brain regions,
,
,
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
A
_
0
0
0
8
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
开放访问
杂志
引文: Khambhati, A. N。, Kahn, A. E.,
Costantini, J。, Ezzyat, Y。, Solomon, 乙. A。,
总的, 右. E., . . . Bassett, D. S. (2019).
Functional control of
electrophysiological network
architecture using direct
neurostimulation in humans. 网络
神经科学, 3(3), 848–877.
https://doi.org/10.1162/netn_a_00089
DOI:
https://doi.org/10.1162/netn_a_00089
支持信息:
https://doi.org/10.1162/netn_a_00089
已收到: 2 一月 2019
公认: 14 四月 2019
利益争夺: 作者有
声明不存在竞争利益
存在.
通讯作者:
Danielle S. Bassett
dsb@seas.upenn.edu
处理编辑器:
Alex Fornito
版权: © 2019
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
Functional control of brain networks using direct neurostimulation
requiring the ability to control the complex interactions between multiple brain areas.
这里, we use tools from network control theory to examine the dynamic reconfiguration of
functionally interacting neuronal ensembles during targeted neurostimulation of cortical and
subcortical brain structures. We demonstrate the ability to predictably reconfigure patterns
of interactions between functional brain areas by modulating the strength and location of
stimulation. Our findings have high significance for designing stimulation protocols capable
of modulating distributed neural circuits in the human brain.
介绍
Novel neurotechnologies capable of perturbing the physiological state of neural systems are
rapidly gaining popularity for their potential to treat neurological disease and psychiatric dis-
orders (Stacey & 一点, 2008). Chronically implantable devices that stimulate the human brain
are clinically approved to treat Parkinson’s disease, essential tremor, dystonia, epilepsy, 和
obsessive-compulsive disorder and have been investigated for major depressive disorder and
Tourette syndrome (Lozano & Lipsman, 2013). Recent human studies have investigated the
ability for direct stimulation of cortical and subcortical structures to modulate biomarkers of
记忆 (Ezzyat et al., 2017; Inman et al., 2017), visual perception (Rangarajan et al., 2014;
Winawer & Parvizi, 2016), language production (张, Kurteff, & Wilson, 2017), somatosen-
sory perception (Muller et al., 2018), sensorimotor function (瓦. 王等人。, 2013), and subjec-
tive experience (促进 & Parvizi, 2017). While neurostimulation is a promising interventional
approach to modulate brain state, current practices of calibrating where, 什么时候, and how to
stimulate the brain are “open-loop” and limited in efficacy—relying on manual and periodic
tuning of device parameters to optimize therapy (莫雷尔, 2011). Automated, “closed-loop”
approaches would augment the capability of current stimulation devices to dynamically ad-
just parameters based on the physiological state of the brain network, monitored in real time
(Stanslaski et al., 2012). Undoubtedly, the translational prospect of neurostimulation to ma-
nipulate brain networks that generate abnormal rhythms, dysrhythmias, or bursts of activity
associated with dysfunction is promising. 然而, critical gaps in knowledge hinder the
development of a robust control policy for next-generation implantable devices.
How does the architecture of the neural system mediate the effect of neurostimulation on
neurophysiology and behavior? Network control theory (Pasqualetti, Zampieri, & Bullo, 2014)
provides a mathematical framework for mapping the influence of a control signal on the dy-
namics of an interconnected system. When combined with graph modeling tools from network
神经科学 (Bassett & 斯波恩斯, 2017), where nodes represent discrete brain regions and edges
represent the structural connections between brain regions, control theoretic approaches can
elucidate how the brain’s structural architecture of white matter fiber pathways shapes its abil-
ity to navigate through a repertoire of dynamical states (Gu et al., 2015). Theoretical rules of
controllability prescribe the trajectories through state space elicited by a given control signal
(贝策尔, Gu, Medaglia, Pasqualetti, & Bassett, 2016; Gu et al., 2017, 2015), and begin to ex-
plain why one brain network may be more or less influential on brain dynamics than another
(Kim et al., 2018). Recent efforts to test control theoretic predictions of the relationship between
controllability and brain activity have relied on in silico models in which neuronal ensembles
are interlinked by structural connections measured by human neuroimaging (Muldoon et al.,
2016). Despite the promising convergence between theory and model simulation, empirical
stimulation data bridging network control and neurophysiology are lacking.
849
Direct neurostimulation:
Delivery of electrical pulses to
electrodes located on the surface or
in deep structures of the brain.
Control policy:
Rules for when, 在哪里, 以及如何
inputs should be delivered to a
dynamical system to reach the
desired target state.
Network control theory:
Framework to model changes in the
state of a complex system under
constraints prescribed by the
structure of that system.
图形:
Mathematical representation of a
network consisting of nodes as brain
regions and edges as structural or
functional connections between
地区.
Controllability:
Ability to steer a dynamical system
from its current state towards a
desired target state over a finite time
horizon.
网络神经科学
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
A
_
0
0
0
8
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
Coherence:
Functional communication capacity
(连接性) between two brain
regions based on phase alignment of
their oscillatory activity at a specific
频率.
Network control theory accounts for the structural connections that convey modulated brain
activity to downstream regions in the network; 然而, it does not account for the functional
rules that govern whether communication between brain regions can occur at a specific point
in time. At the millimeter scale, synchronous oscillations in the local field potential are thought
to actively gate the transfer of information across the network (Bonnefond, Kastner, & 詹森,
2017; Buzsáki et al., 2012; Canolty & 骑士, 2010; 薯条, 2015; Schalk, 2015) and are com-
monly observed during higher order cognitive processing (Buzsáki, 2006). A functional (而不是
结构性的) network representation of the coherence between different ensembles of neurons may
capture dynamical states of communication (德科 & 克林格尔巴赫, 2016; Hutchison et al.,
2013). The neurophysiologic interpretation of these states can depend on the measured frequency
range of the functional network (Bassett, Meyer-Lindenberg, Achard, Duke, & 布莫尔, 2006;
Solomon et al., 2017), which in turn implicates certain types of cells interacting over specific
spatial scales (Kopell, Ermentrout, Whittington, & Traub, 2000). Prior studies have examined
how these functional networks may reconfigure during higher order cognitive functions such
as learning new skills (Bassett ,Wymbs et al., 2011; Bassett et al., 2013; Bassett, 哪个, Wymbs,
& Grafton, 2015; Mattar, Cole, Thompson-Schill, & Bassett, 2015), forming memories (布劳恩
等人。, 2015), attending to the environment (Shine, Koyejo, & Poldrack, 2016), 和加工
语言 (Chai, Mattar, 空白的, Fedorenko, & Bassett, 2016). Complimentary work also posits
that reconfiguration of functional networks may underlie neurophysiological abnormalities in
patients with epilepsy (Khambhati et al., 2017, 2015), schizophrenia (Bassett, 纳尔逊, Mueller,
Camchong, & Lim, 2012; Braun et al., 2016), Parkinson’s disease (Olde Dubbelink et al., 2014;
Sang et al., 2015), and stroke (Grefkes & Fink, 2011; L. 王等人。, 2010). While these studies
explain changes in functional network reconfiguration when the brain is perturbed en masse,
a rigorously quantified map of functional network reconfiguration due to controlled, focal per-
turbation has not been attained.
Here we seek to elucidate the network control principles by which neurostimulation can
alter function and behavior based on constraints prescribed by structural connectivity and
spontaneous functional interactions. We measure the electrocorticogram (ECoG) 在 94 药品-
resistant epilepsy patients undergoing neurostimulation (Figure 1A–B), and we construct
structural networks from diffusion imaging data acquired in the same individuals. We also con-
struct functional networks before and after individual stimulation trials using multitaper coher-
ence between sensors (Prieto, 派克, & Vernon, 2009) in distinct frequency bands (Khambhati,
Davisa, Lucas, 一点, & Bassett, 2016; Kramer et al., 2011 (Figure 1C), and we define brain state
before and after stimulation using a previously validated biomarker of memory (Ezzyat et al.,
2017). We test four hypotheses. 第一的, we hypothesize that the strength and location of stimula-
tion can differentially drive two separate modes of global versus local control over functional
建筑学 (Muldoon et al., 2016). 直观地, stimulation to functional hubs—nodes that tend
to interact strongly with the rest of the network—may have swiftly attenuated effects due to sig-
nal dispersion across many downstream regions, while stimulation to nonhubs may have more
localized and targeted effects. 第二, we hypothesize that regions with strong baseline func-
tional interaction with the stimulation site are more likely to exhibit altered hub properties
following stimulation than brain regions with weak functional interaction with the stimula-
tion site, indicating a functional conduit of stimulation. 第三, based on prior data (贝策尔,
Medaglia, Kahn, 等人。, 2017), we hypothesize that these functional interactions—particularly
in high-frequency bands—colocalize with structural white matter networks (Figure 1D). 第四,
we hypothesize that neurostimulation directed towards modal control points (Gu et al., 2015;
Pasqualetti et al., 2014), which tend to be structural nonhubs of a patient’s white matter network
thereby minimizing signal dispersion, facilitate a stronger shift in dynamical state associated
with memory encoding, a function that is altered in patients with epilepsy (Aarts, Binnie, Smit,
网络神经科学
850
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
A
_
0
0
0
8
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
A
_
0
0
0
8
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
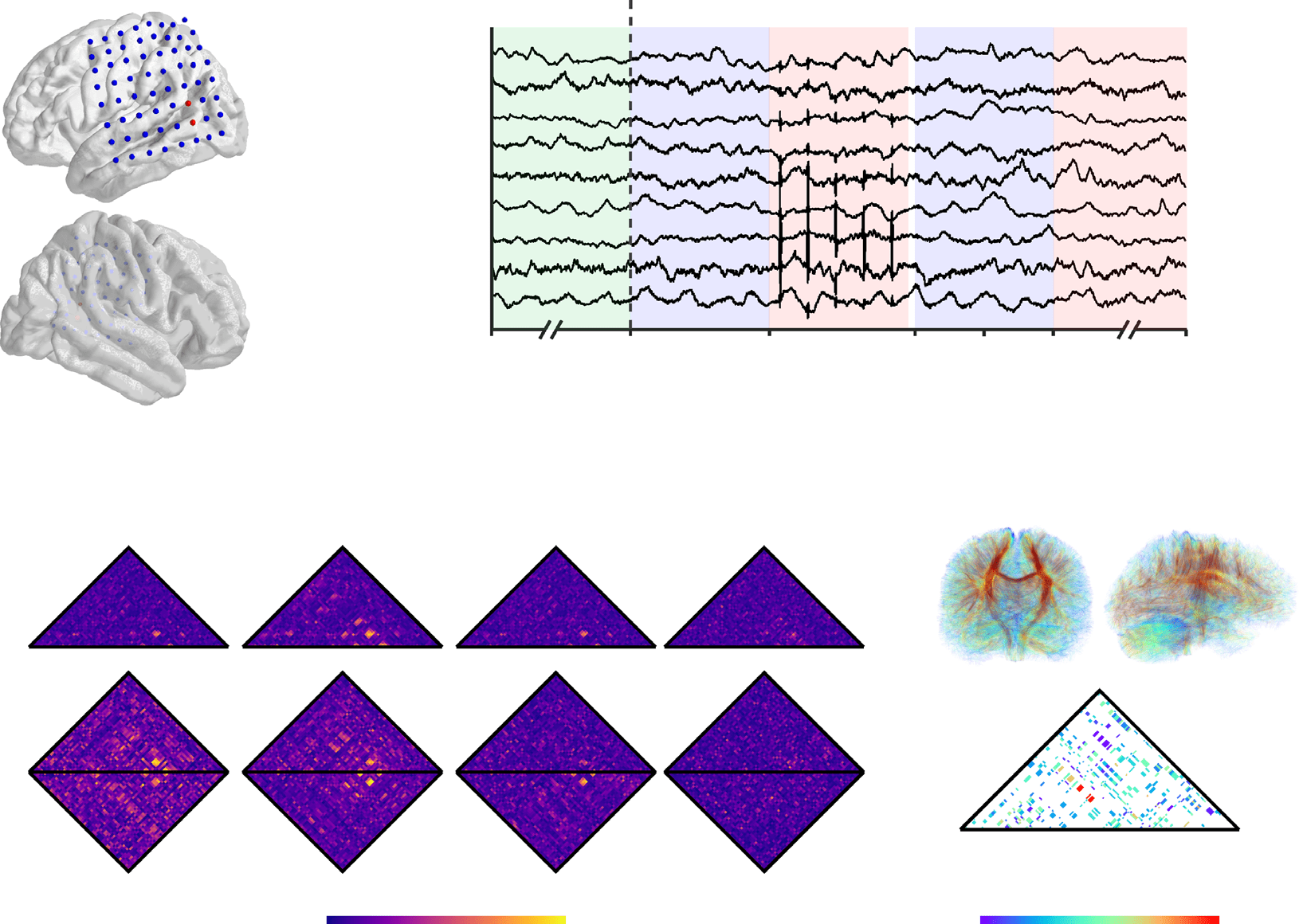
数字 1. Measuring network response to targeted, intracranial neurostimulation. (A) We record the electrocorticogram (ECoG) 在 94 患者
with drug-resistant epilepsy across 8 clinical institutions using intracranial sensors implanted in cortical and subcortical brain structures. 到
evoke a network response, we stimulate adjacent electrode pairs using a charge-balanced, biphasic current source with a square waveform
of variable amplitude, 频率, and duration. (乙) For each experimental session, we select a stimulation location and collect the following
epochs of ECoG activity: (我) 30 seconds of baseline activity before any stimulation is given, (二) one half-second of activity before a stimulation
审判, 和 (三、) two consecutive and nonoverlapping half-second windows of activity after a stimulation trial. A stimulation trial is defined by
a combination of pulse frequency, 振幅, and duration, and consecutive stimulation trials are separated by an inter-stimulation interval
drawn from a uniform random distribution ranging from 2.75 s to 3.25 s. (C) We measure the impact of neurostimulation on functional network
architecture by constructing dynamic graph models in which intracranial sensors are represented by nodes and the functional interactions
between intracranial sensors are represented by edges. To infer functional interactions, we calculate the multitaper coherence between each
pair of ECoG signals in nonoverlapping, half-second time windows for each baseline epoch, pre-stimulation epoch, and post-stimulation epoch
in the following four frequency bands: (我) alpha/theta (5−15 Hz), (二) beta (15−25 Hz), (三、) low gamma (30−40 Hz), 和 (四号) high gamma (95–
105 赫兹) (Khambhati et al., 2016; Kramer et al., 2011). (D) To examine how structural connectivity constrains functional network reconfiguration
to neurostimulation, we also construct a static graph model of the brain’s structural network by applying deterministic tractography to each
subject’s diffusion-weighted imaging data.
& Wilkins, 1984; Holmes & Lenck-Santini, 2006; Uhlhaas & 歌手, 2006). Collectively, 这些
analyses will supply a roadmap of the impact of neurostimulation on network physiology, 我-
diated by network structure, and provide fundamental mechanistic insight into the influence
of neurostimulation on behavioral state.
方法
Study Cohort
Ninety-four patients undergoing intracranial EEG monitoring as part of clinical treatment for
drug-resistant epilepsy were included in this study. Data were collected as part of a multicenter
网络神经科学
851
Functional control of brain networks using direct neurostimulation
project designed to assess the effects of electrical stimulation on memory-related brain func-
的. Data analyzed in this study were collected at the following centers: Thomas Jefferson Uni-
versity Hospital (N= 23), University of Texas Southwestern (N= 23), Mayo Clinic (N= 17),
美国国立卫生研究院 (N= 11), Dartmouth-Hitchcock Medical Center (N= 9), Hospi-
tal of the University of Pennsylvania (N= 6), Columbia University Medical Center (N= 4),
and Emory University Hospital (N= 1). The research protocol was approved by the institu-
tional review board at each hospital and informed consent was obtained from each participant.
Anatomical Localization of Intracranial Electrodes
Patients undergoing surgical treatment for medically refractory epilepsy believed to be of neo-
cortical origin underwent implantation of intracranial electrodes to localize the seizure onset
zone. These procedures were applied after presurgical evaluation with scalp EEG recording
of ictal epochs, MRI, PET, and neuropsychological testing suggested that focal cortical re-
section may be a therapeutic option. Patients were then deemed candidates for implantation
of intracranial electrodes to better define epileptic networks. Electrode configurations spanned
the surface of the cortex (linear and two-dimensional arrays, each sensor is 2.3 mm diameter
spaced 10 mm apart) and subcortical depth (each sensor is 1.5–10 mm apart). All electrode
configurations were planned by a multidisciplinary team of neurologists and neurosurgeons
at each of the eight medical centers.
Electrodes were anatomically localized using separate processing pipelines for surface and
depth electrodes. To localize depth electrodes we first labeled hippocampal subfields and
medial temporal lobe cortices in a pre-implant, 2 mm thick, coronal T2-weighted MRI using
the automatic segmentation of hippocampal subfields (ASHS) multiatlas segmentation method
(Yushkevich et al., 2015). We additionally used whole-brain segmentation to localize depth
electrodes not in medial temporal lobe cortices. We next coregistered a postimplant CT with
the preimplant MRI using advanced normalization tools (ANTs; Avants, 爱泼斯坦, Grossman, &
Gee, 2009). Electrodes visible in the CT were then localized within subregions of the medial
temporal lobe by a pair of neuroradiologists with expertise in medial temporal lobe anatomy.
The neuroradiologists performed quality checks on the output of the ASHS/ANTs pipeline. 到
localize subdural electrodes, we first extracted the cortical surface from a pre-implant, volu-
metric, T1-weighted MRI using FreeSurfer (Fischl et al., 2004). We next coregistered and local-
ized subdural electrodes to cortical regions using an energy minimization algorithm (Dykstra
等人。, 2012). For patient imaging in which automatic localization failed, the neuroradiologists
performed manual localization of the electrodes.
Electrophysiological Data Acquisition and Stimulation Mapping Protocol
The electrocorticogram (ECoG) was recorded and digitized at 500 赫兹, 512 赫兹, 1,000 赫兹,
1,024 赫兹, 或者 2,000 Hz depending on clinical considerations at each medical center. 信号
were recorded using a referential montage with the reference electrode, chosen by the clinical
team, distant to the site of seizure onset.
To study the response of the electrocorticogram to neurostimulation, we used a mapping
procedure in which stimulation was delivered to cortical and subcortical brain regions. Patients
were not instructed to engage in any other task before or during stimulation. Prior to the start
of each mapping session, we selected a pair of adjacent electrodes for stimulation by prior-
itizing electrodes in brain regions thought to be associated with memory function. For each
mapping session, we selected a new stimulation site and patients underwent one or several
mapping sessions depending on their availability for testing and the monitoring needs of the
网络神经科学
852
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
A
_
0
0
0
8
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
clinicians. Prior to the start of a mapping session, we recorded 30 s of ECoG activity as a
baseline epoch. During a mapping session, we performed several stimulation trials in which
a single trial consisted of the following epochs: (A) a half-second pre-stimulation epoch, (乙)
a stimulation epoch with variable duration, two consecutive and nonoverlapping half-second
post-stimulation epochs, and an inter-stimulation epoch with variable duration. During each
stimulation trial, we delivered stimulation using charge-balanced, biphasic, rectangular pulses
with a pulse width of 600 μs and combinations of the following parameters: pulse frequency
(10, 25, 50, 100, 200 赫兹), pulse amplitude (maximum safe amplitude minus 0, 0.5, 1 mA;
range of 0.125–3.0 mA across subjects), stimulation duration (250, 500, 1,000 多发性硬化症), and inter-
stimulation interval (2,750–3,250 ms). These stimulation parameter ranges were chosen to be
well below the accepted safety limits for charge density (Shannon, 1992) and ECoG was con-
tinuously monitored for afterdischarges by a trained neurologist.
We will now describe a typical stimulation experimental session in further detail. In a sin-
gle session, stimulation location was kept constant across trials, and in each trial stimulation
参数 (pulse frequency, pulse amplitude, and duration) were each separately drawn uni-
formly at random from the aforementioned list of parameters. This procedure produced 45
possible parameter combinations. The sampling distribution of parameter combinations was
consistent across patients; 然而, the number of trials in a given session differed based on a
number of factors in the hospital setting of the Epilepsy Monitoring Unit, including patient fa-
tigue, availability, and willingness to participate. 一般来说, across 94 participants we con-
ducted an average of 3 ± 2 experimental sessions (unique stimulation locations), 和每
session we conducted an average of 1, 655 ± 697 trials—more than 36 times the number of
possible parameter combinations. We confirmed that the full parameter space was sampled
within a session.
To eliminate confounding effects of stimulation on signal quality and saturation, we dis-
regarded ECoG data collected during the stimulation epoch and the 100 ms following stim-
ulation offset. We also employ a conservative electrode screening procedure, in which we
discard nonstimulated channels that exhibit evidence of stimulation-related artifact. Specifi-
卡莉, before re-referencing to a common average reference, we use a paired t test to compare
the distribution of mean signal amplitude during the pre-stimulation epoch to the distribution
of mean signal amplitude during the post-stimulation epoch, for each electrode across stimu-
lation trials. Using a Bonferroni uncorrected p-value threshold of 0.05, we discard electrodes
that exhibit significantly elevated raw, mean signal amplitude during each stimulation session.
We analyzed ECoG data collected during the baseline, pre-stimulation, and post-stimulation
纪元. The post-stimulation epoch following 100 ms of a buffer period was split into two
consecutive and nonoverlapping segments, 0.5 s in duration to assess delayed effects of
stimulation—we refer to the first segment as the 100-ms response and the second segment
as the 600-ms response. Because of the time constraints on experimentation in the hospi-
tal setting of the Epilepsy Monitoring Unit, we utilized the 30 s of ECoG activity recorded
before the start of a stimulation session as an indicator of the patient’s baseline state. To quan-
tify the difference between the stimulation-induced effect on network topology in contrast to
the spontaneous effects over the passage of time, we constructed a surrogate distribution of
stimulation “trials” from the baseline period by sampling-with-replacement time windows
equal in duration to the true stimulation trials. 换句话说, the surrogate distribution con-
sisted of the same number of trials as the number of trials conducted during the stimulation
session, and each surrogate baseline trial was associated with a true stimulation trial and was
网络神经科学
853
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
A
_
0
0
0
8
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
constructed from the same duration of baseline data as its corresponding stimulation trial. 这
sampling scheme was used to mitigate the limited baseline data that were available for analysis.
Constructing Frequency-Based Functional Brain Networks
ECoG signals were divided into 0.5s, nonoverlapping, time windows—the pre-stimulation
epoch consisted of one time window per stimulation trial, and the post-stimulation epoch
consisted of two time windows per stimulation trial (100−600 ms post-stimulation and 600−
1,100 ms post-stimulation). We applied a common average reference to the artifact-free ECoG
signal before constructing functional networks (Burns, Santaniello, Yaffe, Jouny, & Crone, 2014;
Khambhati et al., 2016; Kramer et al., 2010, 2011; Towle, Carder, Khorasani, & Lindberg, 1999).
To measure functional interactions between ECoG signals in each time window, we com-
puted spectral coherence, which is a measure of correlation between the power spectra of two
signals within a frequency range. Prior studies have shown that coherence is largely indepen-
dent of the shape of the power spectrum in ECoG signals (Bullock et al., 1995A, 1995乙; Towle
等人。, 1999), and underlies different forms of synchronous interactions between neural popu-
lations (Kopell et al., 2000). We constructed functional networks in each time window using
multitaper coherence estimation, which defines a graph edge between electrode pairs (图形
节点) as the power spectral similarity of signal activity over a specific frequency band. 我们
applied the mtspec Python implementation (Prieto et al., 2009) of multitaper coherence es-
timation with time-bandwidth product of five and eight tapers in accord with related studies
(Kramer et al., 2011). This procedure resulted in a symmetric adjacency matrix A(t, F ) 和
size N × N, where N is the number of network nodes, or electrode sensors, t is the time win-
dow, and f is the frequency band. In this study, we examined network activity in the following
four frequency bands: α/θ (5–15 Hz), β (15–25 Hz), low γ (30–40 Hz), and high γ (95–105 Hz).
These frequency ranges cover traditional oscillatory classes and have been previously exam-
ined for their network topology (Khambhati et al., 2016; Kramer et al., 2011).
An alternate representation of the symmetric, square adjacency matrix A(t, F ) is a config-
uration vector ˆA(t, F ), which tabulates all N × N pairwise interactions. Because of symme-
try of the adjacency matrix, we unravel the upper triangle of A, resulting in the weights of
E = N(N−1)
functional interactions. 因此, ˆA(t, F ) is a vector of size E.
2
Node strength:
Measure of global influence, 或者
hubness, of a node based on its
average connectivity to all other
network nodes.
Metrics of Functional Network Topology
In this study, we investigated the effect of neurostimulation on functional network architecture
at the scale of network nodes and at the scale of network edges. At the node scale, we first
quantified the change in the node strength—a measure of functional “hubness”—of individual
network nodes. Specifically, we computed the node strength as ki(t, F ) = 1
N−1 ∑j∈N Aij(t, F ),
where k is the strength of node i and Aij is the edge weight between nodes i and j. Based on the
time-dependent set of node strengths in the network, we computed the change in the mean
of node strengths between time windows and the change in the variance of node strengths
between time windows. To assess the magnitude of change in node strength for a node between
time windows tn and tm, we calculated Δki(tn,米, F ) = abs(ki(tm, F ) − ki(tn, F )).
At the edge scale, we quantified the amount of change in the configurational pattern of the
network edges, or coherences, as described previously in Khambhati et al. (2015). Specifically,
we computed the configuration similarity between configuration vectors ˆA(tn, F ) and ˆA(tm, F ),
where tn and tm are two different time windows, using the Pearson correlation test statistic. 二
网络神经科学
854
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
A
_
0
0
0
8
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
vectors with a Pearson correlation value closer to 0 are more dissimilar in their configurational
pattern of network edges than two vectors with a Pearson correlation value closer to 1.
For the stimulation epoch, we computed global and local network metrics between the
pre-stimulation time window and the post-stimulation time window of a stimulation trial. 为了
the baseline epoch, we computed global and local network metrics between time windows
separated by an equal length of time as the duration of stimulations in the associated stimula-
tion session.
Diffusion-Weighted Imaging Acquisition and Preprocessing
We collected diffusion-weighted imaging data for a subset of patients from Thomas Jefferson
University Hospital (N= 11) and Hospital of the University of Pennsylvania (N= 3) 和
validated our analysis of the functional network response to neurostimulation.
All scans at Thomas Jefferson University Hospital were acquired with a 3T Philips Achieva
with an 8-channel head coil using an echo-planar diffusion-weighted technique. The diffusion
and TE/TR = 98/7,251 多发性硬化症. The matrix
scan was 62-directional with a b-value of 3,000 s/mm
size was 96 × 96 and the slice number was 52. The field of view was 230 × 230 毫米
和
the slice thickness 2.5 毫米. Acquisition time was 496 s per DTI scan.
2
2
All scans at the Hospital of the University of Pennsylvania were acquired with a 3T Siemens
Tim Trio with a 32-channel head coil using an echo-planar diffusion-weighted technique. 这
and TE/TR = 117/4,180 多发性硬化症.
diffusion scan was 116-directional with a b-value of 2,000 s/mm
The matrix size was 96 × 96 and the slice number was 92. The field of view was 210 ×
and the slice thickness 1.5 毫米. Acquisition time was 506 s per DTI scan.
210 毫米
2
2
Based on recent evidence that diffusion imaging is highly sensitive to subject movement
(Yendiki, Koldewyn, Kakunoori, Kanwisher, & 菲舍尔, 2014) and to directional eddy currents
(Jezzard, Barnett, & 皮尔保利, 1998), we processed data using the FMRIB Software Library
(詹金森, 贝克曼, 贝伦斯, 伍尔里奇, & 史密斯, 2012). We first created individual masks of
the patient brain using BET (史密斯, 2002). We next simultaneously corrected for motion effects
and eddy current distortions by applying the EDDY correction tool (安德森 & 索蒂罗普洛斯,
2016) to the diffusion scans and a b = 0 image collected at the beginning of the scan.
We next reconstructed orientation density functions (ODFs) of the diffusion imaging in
each voxel. Specifically, we used DSI Studio (http://www.dsi-studio.labsolver.org) and gen-
eralized q-sampling imaging (GQI; Yeh, 威登, & Tseng, 2010) to compute the quantitative
anisotropy (QA; Yeh, Verstynen, 王, Fernández-Miranda, & Tseng, 2013) in each voxel. 到
conduct fiber tractography on the reconstructed diffusion images, we used DSI Studio to gener-
吃 1,000,000 streamlines with a maximum turning angle of 35
(Bassett, 棕色的, 德什潘德,
卡尔森, & Grafton, 2011) and a maximum length of 500 毫米 (Cieslak & Grafton, 2014). 我们
next used the streamlines to define the structural brain network at the two following spatial res-
olutions of the Lausanne atlas included in the Connectome Mapping Toolkit (Cammoun et al.,
2012) consistent with previous work (Bassett, 棕色的, 等人。, 2011; Bassett et al., 2010; Gu
等人。, 2017, 2015; Hermundstad et al., 2013, 2014; Muldoon et al., 2016): (A) at the fine
scale we divided the brain into N = 1, 015 cortical and subcortical regions of interest (ROIs)
(average ROI volume 1.56 ± 0.06 厘米
), 和 (乙) at the coarse scale we divided the brain into
N= 234 cortical and subcortical ROIs (average ROI volume 6.78 ± 0.02 厘米
). We summarized
these measurements in a symmetric and weighted structural adjacency matrix S whose entries
○
3
3
网络神经科学
855
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
A
_
0
0
0
8
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
Sij reflect the structural connectivity (quantitative anisotropy) between region i and region j,
separately for the fine-scale and coarse-scale parcellation.
We localized electrodes in native subject T1-weighted MRI space to the Lausanne anatom-
ical space by using ANTs (Avants et al., 2009) to register the subject’s T1 image to the subject’s
扩散 0 image via affine transformation and also to register the subject’s T1 image to MNI
空间 (also native Lausanne space) using a nonlinear warp.
Metrics of Structural Controllability
To study the architectural constraints of the structural brain network with the functional net-
work response to neurostimulation, we adopted a control theoretic approach known as net-
work controllability. 简单地说, the controllability of a networked system refers to its ability to be
driven to specific dynamical states upon external input (Kalman, 1963). Recent research efforts
have made substantial progress in the development of quantitative heuristics to characterize
different strategies for control (Pasqualetti et al., 2014; Pequito et al., 2016). These approaches
are now being applied to brain imaging data to understand how structural brain network topol-
ogy constrains function and behavior (Betzel et al., 2016; Gu et al., 2017, 2015; Kim et al.,
2018; Tang et al., 2017).
In line with these prior studies, we employ a simplified noise-free linear discrete-time and
time-invariant model of network dynamics:
X(t + 1) = Ax(t) + BKuK(t),
(1)
where x : R≥0 → RN
describes the state (IE。, voltage, firing rate, BOLD signal) of brain regions
随着时间的推移. 因此, the state vector x has length N, where N is the number of brain regions in the
connectome parcellation, and the value of xi describes the brain activity state of that region.
The diagonal elements of the matrix A satsify Aii = 0. Prior to calculating controllability
价值观, we divide A by 1 + ξ0(A), where ξ0(A) is the largest singular value of A. The input
matrix BK identifies the control point K in the brain, where K = k1, …, km and
BK = [ek1
· · · ekm
],
(2)
and ei denotes the i-th canonical vector of dimension N. The input uK : R≥0 → R M
the control strategy.
denotes
One control strategy that we investigate in this study is modal controllability—the ability of
a network region to feasibly control all the dynamical modes of a system (Pasqualetti et al.,
2014). To calculate the modal controllability of an anatomical brain region, we first computed
the eigenvector matrix V = [vij] of the structural network adjacency matrix S—intuitively, vij
encodes the ability to control the j-th dynamical mode from region i (Kailath, 1980). Based
on our previous work, we defined φi = ∑j∈N(1 − λ2
ij as a scaled measure of the con-
trollability of all N dynamical modes λ1(S), . . . , λN(S) from brain region i (Gu et al., 2015;
Muldoon et al., 2016; Pasqualetti et al., 2014; Tang et al., 2017). Brain regions with high modal
controllability are versatile in their ability to control all dynamical modes of the network, 和
j (S))v2
网络神经科学
856
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
A
_
0
0
0
8
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
brain regions with low modal controllability are specific in their ability to control a subset of
dynamical modes of the network.
To provide additional insight into the topological properties of structural control points,
we evaluated the structural “hubness” of each brain region by computing the structural node
strength as ki = 1
N−1 ∑j∈N Sij—similar to the calculation for functional node strength specified
早些时候.
Mapping Intracranial Electrodes to Anatomical Brain Regions
To relate structural controllability to functional network topology of the stimulated electrodes,
we first computed metrics of the structural network topology for 234 或者 1015 brain regions
defined by the Lausanne anatomical parcellation. The advantage of computing these mea-
sures using the anatomical parcellation is the ability to account for whole-brain structural
连接性, including areas that are not directly sampled by the intracranial electrodes. 我们
next assigned intracranial electrodes to the Lausanne brain regions based on a nearest voxel
方法. Specifically, we identified the voxel closest to the electrode and assigned the elec-
trode to the brain region containing that voxel. Based on this assignment, we associated values
of each structural network metric to the intracranial electrodes.
Detection of Brain States Associated With Memory Encoding
We examined stimulation-driven changes in dynamical brain state using a classifier of neural
activity associated with memory encoding processes that was previously validated on data
collected during behavioral experimentation with the same patients recruited in this study
(Ezzyat et al., 2017; Kragel et al., 2017). 简单地说, in these prior studies a logistic regression
classifier was trained to discriminate memory encoding-related changes in spectral power in
eight logarithmically spaced frequency bands across intracranial electrodes that are predictive
of whether a word was later remembered or forgotten during a free-recall task (Ezzyat et al.,
2017; Kragel et al., 2017). In this study, we evaluated the trained memory encoding state
classifier on task-free stimulation data of the same patients by measuring spectral power during
the pre-stimulation epoch and the post-stimulation epoch, and by computing the change in
probability of good memory encoding state for each stimulation trial. We next calculated the
average change in probability of good memory encoding state across all stimulation trials of
each stimulation mapping session of each patient. These data allowed us to assess the putative
effects of different dimensions of the stimulation parameter space on previously validated,
neural biomarkers of cognitive function, specifically on memory encoding.
结果
Neurostimulation Drives Localized and Distributed Functional Network Reconfiguration
We first ask the question, “How does neurostimulation alter the architecture of functional brain
网络?” Based on recent theoretical insights on the costs of forming and breaking connec-
tions in structural and functional brain networks (Achard & 布莫尔, 2007; 贝策尔, Medaglia,
Papadopoulos, 等人。, 2017; 布莫尔 & 斯波恩斯, 2012), we expect stimulation to heteroge-
neously affect existing coherent interactions, strengthening some and weakening others. To test
these expectations, we study the average change in the following three measures of network
topology across stimulation trials per patient: two at the topological scale of nodes and one at
the topological scale of edges (图2A). At the node scale, we first compute the strength, 或者
average coherence, for each network node during the pre-stim epoch and post-stim epoch for
each of the four coherence frequency bands. We next examine the change in the mean of node
Memory encoding state:
Pattern of brain activity associated
with the likelihood that a subject has
successfully encoded a word into
their episodic memory.
网络神经科学
857
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
A
_
0
0
0
8
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
A
_
0
0
0
8
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 2. Control of frequency-specific functional network topology. (A) Does stimulation induce
network reconfiguration at the scale of network nodes or at the scale of network edges? Shown here
are different forms of network reconfiguration: two forms at the node scale and one form at the edge
规模. At the node scale, stimulation may increase or decrease the overall functional interactions of
a node with other nodes in the network, resulting in a change in the mean of node strengths and/or
a change in the variance, or heterogeneity, of node strengths in the network. At the edge scale,
stimulation may alter the configurational pattern of functional interactions underlying functional
network topology. We measure edge scale change by computing a configuration similarity metric
(Khambhati et al., 2015) of the pattern of network coherences between the pre-stim trial and the
post-stim trial; values near 1 (或者 0) imply a lesser (or greater) change in network configuration. (B–D)
The change in network topology due to stimulation is compared with the change in network topol-
ogy due to passive changes in the brain’s internal state by subtracting the change at baseline from the
stimulation-induced change—each plot point reflects the average of this difference across all trials
during a single stimulation session. (乙) Difference in the change in mean of node strengths between
stim epochs and baseline epochs. Change in the mean of node strengths is significantly greater
during stimulation epochs than baseline epochs in the alpha/theta band (p < 0.01, corrected).
(C) Difference in the change in variance of node strengths between stim epochs and baseline epochs.
Change in the variance of node strengths is significantly greater during stimulation epochs than
baseline epochs in the alpha/theta band (p < 0.001, corrected). Stimulation alters low-frequency
organization of the functional network at the scale of network nodes. (D) Difference in the con-
figuration similarity of network edges between stim epochs and baseline epochs. Reconfiguration
of functional interactions is significantly greater during stimulation epochs than baseline epochs in
the high gamma band (p < 0.001, corrected). Stimulation alters high-frequency organization of the
functional network at the scale of network edges. Each observation is the average across epochs
within a stimulation session of a single subject. Solid lines represent the median, and dashed lines
represent the first and third quartiles. *p < 0.05, **p < 0.01, ***p < 0.001.
strengths and the change in the variance of node strengths between the pre-stim epoch and the
post-stim epoch. Intuitively, a change in the mean of node strengths quantifies the likelihood
that nodes exhibit greater frequency-specific functional interaction following stimulation, and
a change in the variance of node strengths quantifies the likelihood that nodes exhibit greater
heterogeneity in their degree of functional interaction with other nodes in the network. At
Network Neuroscience
858
Functional control of brain networks using direct neurostimulation
the edge scale, we compute the configuration similarity (Khambhati et al., 2015): a Pearson
correlation between the vector of coherence weights during the pre-stim epoch and the vec-
tor of coherence weights during the post-stim epoch. Similarity values near 0 imply a greater
change in the configuration of network coherences, and values near 1 imply a lesser change in
the configuration of network coherences. We confirmed that the topological measurements at
the node scale capture different reconfiguration phenomenon than the topological measure-
ments at the edge scale by observing weak relationships between changes in the mean and
variance of node strengths to configuration similarity (Supporting Information: Figure 1-1).
Next, we test our expectation that stimulation heterogeneously affects existing coherent in-
teractions, strengthening some and weakening others, by comparing the change in network
topology measures during stimulation trials to passive changes in network topology that occur
during the baseline period before the stimulation session begins. We first study changes in
the mean and variance of node strengths between the pre-stim epoch and post-stim epoch for
each of the four coherence frequency bands (Figure 2B,C). Using a Wilcoxon rank-sum test,
Bonferroni correction for multiple comparisons, and effect size based on rank correlation, we
examine whether node-level changes in the network 100 ms after stimulation offset are any
greater than passive changes observed over an equal duration of spontaneous activity at base-
line, before any stimulation, across stimulation sessions over subjects. We find that stimulation
leads to a significantly greater change in the mean of node strengths than expected at base-
line in the alpha/theta band (Z(247) = 11, 448, p = 0.001, rank correlation = 0.63) and to
a nonsignificant change in the beta band (Z(247) = 14, 006, p = 0.68), in the low gamma
band (Z(247) = 13, 131, p = 0.13), and in the high gamma band (Z(247) = 14, 883, p = 1.0).
We also find that stimulation leads to a significantly greater change in the variance of node
strengths than expected at baseline in the alpha/theta band (Z(247) = 10, 660, p = 0.0001,
rank correlation = 0.65) and to a non-significant change in the beta band (Z(247) = 13, 422,
p = 0.24), in the low gamma band (Z(247) = 14, 137, p = 0.84), and in the high gamma band
(Z(247) = 14, 086, p = 0.76). We find that these effects indeed persist and possibly strengthen
in the beta band and low gamma band at least 600 ms after stimulation offset (Supporting
Information: Figure 2-1b, c). These results demonstrate that stimulation amenably alters func-
tional network organization in lower alpha/theta band frequencies (5–15 Hz) at the node scale.
Specifically, we observe that nodes generally exhibit an increase in low-frequency interaction
following neurostimulation. However, changes in node strengths are also heterogeneously dis-
tributed across nodes in the network.
We next ask whether stimulation may still alter functional network topology at the edge
scale. Using a Wilcoxon rank-sum test and Bonferroni correction for multiple comparisons,
we examine whether configurational changes in the network edges 100 ms after stimulation
offset are any greater than the passive change observed over an equal duration of spontaneous
activity at baseline, before any stimulation, across stimulation sessions over subjects. We find
that stimulation leads to a significantly lower configuration similarity (greater reconfiguration)
than expected at baseline in the high gamma band (Z(247) = 9, 252, p = 2.3 × 10−6
, rank
correlation = 0.70) and to a nonsignificant change in the alpha/theta band (Z(247) = 13, 543,
p = 1.0), in the beta band (Z(247) = 12, 820, p = 1.0), and in the low gamma band (Z(247) =
13, 502, p = 1.0). We find that these effects indeed persist at least 600 ms after stimulation offset
(Supporting Information: Figure 2-1d). These results demonstrate that stimulation amenably
alters functional network organization in high gamma band frequencies (95–105 Hz) at the
edge scale. Specifically, we observe that functional interactions undergo a change in their
configurational pattern in high frequencies following neurostimulation.
Network Neuroscience
859
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
Input Intensity Differentially Modulates Topological Scale of Functional Network Response
Building on our observations of a complex, frequency-dependent network response to stimula-
tion, we next ask, “Do properties of the stimulation signal, such as amplitude, pulse frequency,
and duration, influence the extent of functional network reconfiguration?” There is a funda-
mental gap in knowledge of how different parameters of direct brain stimulation influence
brain networks—delaying the therapeutic benefits of stimulation in the treatment of neurologi-
cal and neuropsychiatric disorders by several months or years (Crowell, Garlow, Riva-Posse, &
Mayberg, 2015; Fisher, 2011; Nair & Morrell, 2017). To understand how stimulation parameters
influence functional network reconfiguration, we draw stimulation parameters from a prede-
fined list, uniformly at random, for each consecutive trial (Figure 3A), and we compute the
stimulation intensity as the product between the three parameters (Figure 3B). Based on prior
observations of a relationship between stimulation intensity and volume of tissue activated
(Butson & McIntyre, 2008), we hypothesize that stronger stimulation input into the functional
network will lead to more widespread change in functional architecture than weaker stimula-
tion input, presumably by penetrating the network along short axonal fibers in the gray matter
and long myelinated fibers in the white matter.
To test this hypothesis, we first compute a within-session Spearman’s ρ correlation between
stimulation intensity and the three measures of functional network reconfiguration (change in
mean of node strengths, change in variance of node strengths, and configuration similarity) for
the four coherence frequency bands (Figure 3C–E). Using a one-sample t test, Bonferroni cor-
rection for multiple comparisons, and effect size based on Cohen’s d we test whether increasing
stimulation intensity drives greater node-level changes in the network 100 ms after stimulation
offset (Figure 3C, D). We find that greater stimulation intensity leads to a significant decrease in
the mean of node strengths in the high gamma band (t(247) = −6.5, p = 7.0 × 10−9
, Cohen’s
d = 0.41), and to a nonsignificant change in the alpha/theta band (t(247) = 1.6, p = 1.0),
beta band (t(247) = 0.2, p = 1.0), and low gamma band (t(247) = −2.0, p = 0.53). We also
find that greater stimulation intensity leads to a significant decrease in the variance of node
strengths in the high gamma band (t(247) = −5.9, p = 7.5 × 10−5
, Cohen’s d = 0.40), and
to a nonsignificant change in the alpha/theta band (t(247) = 1.2, p = 1.0), in the beta band
(t(247) = −0.7, p = 1.0), and in the low gamma band (t(247) = −1.6, p = 1.0). We find that
these effects indeed persist in the high gamma band at least 600 ms after stimulation offset
(Supporting Information: Figure 3-1c, d). Our results indicate a robust dependence of high-
frequency functional reorganization at the scale of network nodes on stimulation strength.
Specifically, greater stimulation intensity disrupts and decreases cohesive node-level interac-
tions in high-frequency bands. We did not observe a similar disruption in node-level architec-
ture in the lower frequency bands.
Logically, we next ask whether stimulation intensity similarly alters the edge-level architec-
ture of the network. Using a one-sample t test and Bonferroni correction for multiple compar-
isons, we test whether increasing stimulation intensity drives greater configurational change in
the network edges 100 ms after stimulation offset (Figure 3E). We find that greater stimulation
intensity leads to a significant decrease in the configuration similarity (greater reconfiguration)
in the high gamma band (t(247) = −2.8, p = 0.04, Cohen’s d = 0.18), and to a nonsignificant
change in the alpha/theta band (t(247) = −2.8, p = 0.06), in the beta band (t(247) = −1.6,
p = 1.0), and in the low gamma band (t(247) = −1.2, p = 1.0). We find that these effects
dissipate 600 ms after stimulation offset (Supporting Information: Figure 3-1e). Our results indi-
cate that greater stimulation intensity drives greater reconfiguration of the functional topology
in high-frequency bands. Additionally, stimulation strength only explains immediate edge-level
Network Neuroscience
860
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Edge reconfiguration:
Alteration in the spatial arrangement
of connections in a dynamic
network.
Figure 3. Dose-dependent response of network reconfiguration to stimulation. (A) To examine the
effect of stimulation intensity on network reconfiguration, we vary the amplitude, pulse frequency,
and duration of the square-wave input. (B) We quantify the total input intensity delivered during
a stimulation trial as the product between the amplitude, pulse frequency, and duration. Here, we
show the three-dimensional plane of input parameters that contribute to the overall stimulation
intensity. (C) Distribution of correlations between the stimulation intensity and the change in mean of
node strengths. Correlations are significantly negative in the low gamma band (p < 0.05, corrected)
and in the high gamma band (p < 0.001, corrected). (D) Distribution of correlations between the
stimulation intensity and the change in variance of node strengths. Correlations are significantly
negative in the high gamma band (p < 0.001, corrected). Greater stimulation intensity decreases
node-level interactions in high-frequency networks and leads to a more homogenous distribution of
node strengths in the network. (E) Distribution of correlations between the stimulation intensity and
the configuration similarity. Correlations are significantly negative in the alpha/theta band (p < 0.01,
corrected) and in the high gamma band (p < 0.05, corrected). Greater stimulation intensity leads
to lower configuration similarity (greater edge reconfiguration) in both the low-frequency and the
high-frequency networks. For high-frequency networks, the extent of edge-level reconfiguration may
subserve a finer scale mechanism for node-level alterations in functional network topology. Each
observation is the correlation across trials within a stimulation session of a single subject. Solid
lines represent the median, and dashed lines represent the first and third quantiles. *p < 0.05,
**p < 0.01, ***p < 0.001.
reconfiguration of network topology and does not exhibit a relationship with later stage edge-
level reconfiguration.
Lastly, we asked whether the observed changes in network topology were primarily driven
by any single dimension of the stimulation parameter space (trial duration, pulse amplitude,
pulse frequency). In contrast to stimulation duration and stimulation amplitude, we observed
that changes in the frequency of stimulation significantly drives altered network topology at
the node level and at the edge level (Supporting Information: Figure 3-2g–i). Specifically, faster
stimulation frequencies may disrupt high-frequency coherence between network nodes, by
presumably redistributing coherent edges across the network and reducing the variance in
node strengths. Conversely, slower stimulation frequencies may increase node strengths in
Network Neuroscience
861
Functional control of brain networks using direct neurostimulation
high-frequency networks by driving less topological reconfiguration of the network edges and
simply reinforcing existing functional interactions.
Stimulation of Baseline Hubs Versus Nonhubs Has Differential Effects on the Network
We next build upon our analysis of the influence of stimulation parameters on functional net-
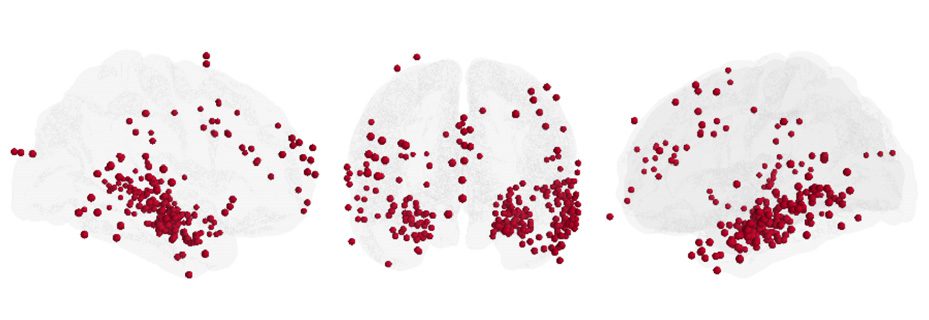
work topology by similarly investigating the role of 248 unique stimulation locations over
94 subjects in the functional brain network (83 depth locations and 165 surface locations,
Figure 4A; see Supporting Information, Figure 4-1, for regional distribution of stimulation lo-
cation). We specifically ask, “Do functional hubs drive more widespread reconfiguration of
the functional network than functionally isolated brain areas?” To answer this question, we
measure the node strength as the mean coherence of the stimulation node to all other nodes
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Functional hubs constrain topological response to stimulation. (A) Distribution of 248
stimulation locations sampled across 94 subjects. (B) To examine the effect of stimulation location
on the reconfiguration of functional network topology, we measure the node strength of the stimu-
lation region during the baseline epoch—before any stimulation is delivered—for each coherence
frequency band. Intuitively, nodes with low strength (left) tend to be functionally isolated and ex-
hibit weak coherence with the other nodes in the network, while nodes with high strength (right)
tend to be functional hubs and exhibit strong coherence with the other nodes in the network. We
expect that stimulation of strong functional hubs will lead to a homogenous change in network
topology, and we conversely expect that stimulation of weak functional hubs will lead to a het-
erogenous change in network topology. (C) Correlation between the stimulation node strength and
the change in mean of node strengths. We find no significant relationship between the stimulation
node strength and the change in mean of node strengths in any frequency band. (D) Correlation
between the stimulation node strength and the change in variance of node strengths. We find no
significant relationship between the stimulation node strength and the change in variance of node
strengths. (E) Correlation between the stimulation node strength and the configuration similarity.
Correlations are significantly positive in the low gamma band (p < 0.05, corrected) and in the high
gamma band (p < 0.001, corrected). Greater stimulation node strength leads to greater configura-
tion similarity (lower edge reconfiguration) in high-frequency networks. Correlations are computed
over stimulation sessions across subjects. *p < 0.05, **p < 0.01, ***p < 0.001.
Network Neuroscience
862
Functional control of brain networks using direct neurostimulation
at baseline. We hypothesize that stimulation of a stronger functional hub will lead to greater
dispersion of input intensity throughout the network, driving a homogenous network response;
stimulation of a weaker functional hub will lead to more targeted dispersion of input intensity
to a subset of network nodes, driving a heterogenous network response (Figure 4B).
To test this hypothesis, we first compute a Spearman’s ρ correlation between baseline node
strength of the stimulation region and the average of each of the three measures of func-
tional network reconfiguration (change in the mean of node strengths, change in the variance
of node strengths, and the configuration similarity) for the four coherence frequency bands
(Figure 4C–E). Using a Bonferroni correction for multiple comparisons, we test whether greater
node strength of the stimulation region drives greater node-level changes in the network 100 ms
after stimulation offset, over stimulation sessions across subjects (Figure 4C, D). We find that
stimulation node strength does not significantly influence the mean of node strengths in the
alpha/theta band (ρ(246) = −0.02, p = 1.0), in the beta band (ρ(246) = −0.02, p = 1.0), in
the low gamma band (ρ(246) = −0.06, p = 1.0), or in the high gamma band (ρ(246) = −0.03,
p = 1.0). We also find that the stimulation node does not significantly influence the vari-
ance of node strengths in the alpha/theta band (ρ(246) = −0.05, p = 1.0), in the beta band
(ρ(246) = −0.03, p = 1.0), in the low gamma band (ρ(246) = −0.14, p = 0.09), or in the high
gamma band (ρ(246 = −0.11, p = 0.3). We also do not observe these effects after 600 ms
following stimulation offset (Supporting Information: Figure 4-2c, d). Our results indicate that
baseline node strength does not play an influential role in altering large-scale organization of
network nodes.
We next ask whether the strength of the stimulation node can differentially drive reconfig-
uration of edge-level architecture of the network. Using a Bonferroni correction for multiple
comparisons, we test whether greater node strength of the stimulation region drives greater
configurational change in the network edges 100 ms after stimulation offset, over stimulation
sessions across subjects (Figure 4E). We find that greater stimulation node strength leads to a
significantly greater configuration similarity (lower reconfiguration) in the low gamma band
(ρ(246) = 0.17, p = 0.03) and in the high gamma band (ρ(246) = 0.58, p = 2.2 × 10−22
),
and to a nonsignificant change in the alpha/theta band (ρ(246) = 0.01, p = 1.0) and in the
beta band (ρ(246) = 0.13, p = 0.2). We find that these effects persist in the low gamma
band and in the high gamma band, and that they strengthen in the beta band at least 600
ms after stimulation offset (Supporting Information: Figure 4-1e). These results suggest that the
functional topology of the stimulation region significantly impacts the pattern of coherent in-
teractions in low and high gamma coherence frequency bands. Specifically, stimulation of
weaker functional hubs tends to drive a greater change in the pattern of coherent interactions
in low gamma networks and in high gamma networks. We find that a location-based rule for
using stimulation to control the distributed reconfiguration of functional interactions is most
robust for high gamma networks thought to reflect activity associated with synaptic input and
short-range interactions.
Combined with our earlier findings on the negative relationship between stimulation in-
tensity and edge reconfiguration, our findings suggest that stimulation of stronger functional
hubs may lead to greater attenuation of the stimulation intensity and drive less edge-level re-
configuration than stimulation of weaker functional hubs. Another possible explanation for our
findings is that stronger coherent interactions between stimulated hub nodes and the remaining
nodes in the network mechanistically constrain the network response to stimulation—which
we assess next.
Network Neuroscience
863
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
Baseline Coherence of Stimulation Target With Other Regions Constrains Future Network Response
Our findings in the previous section point to an important role of the baseline functional net-
work in constraining the network response to stimulation. Logically, a stimulation node that
exhibits stronger coherence with one set of brain regions may be more likely to convey the
stimulation input to these brain regions than to another set of brain regions with which it ex-
hibits weaker coherence. We therefore next test the hypothesis that the baseline coherence
between the stimulation node and a downstream node predicts the probability that the down-
stream node will be evoked during a stimulation trial (Figure 5A). In other words, a stronger
baseline coherence between the stimulation node and the downstream node may facilitate a
greater magnitude change in the node strength of the downstream node.
To address this hypothesis, we first compute the within-session mean and variance of the
magnitude change in node strength. For each session, we next compute the Spearman’s ρ
correlation between the set of baseline coherence values between the stimulation node and
the downstream nodes and the mean of the magnitude changes in node strength of each
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Predicting downstream modulation of regional coherence. (A) We hypothesize that the
baseline strength of coherent interactions between the stimulation node (red) and network nodes
away from the stimulation node (black) predicts the likelihood that these downstream nodes will
be evoked because of stimulation. Intuitively, a weak baseline coherence between the stimulation
node and a downstream network node is less likely to modulate the mean coherence of the down-
stream node (left), and a strong baseline coherence between the stimulation node and a downstream
network node is more likely to modulate the mean coherence of the downstream node (right). To
test this hypothesis, we first quantify the magnitude change in node strength within each stimulation
session. We next compute Spearman’s ρ correlation between the mean (and variance) of change in
downstream node strength across stimulation trials and the baseline coherence between the stimula-
tion node and the downstream nodes. (B) Distribution of correlations between the mean of change
in downstream node strength and the baseline coherence between the stimulation node and the
downstream nodes, for each of the four coherence frequency bands. We find a significantly positive
correlation in the alpha/theta band (p < 0.01, corrected), in the beta band (p < 0.001, corrected),
and in the low gamma band (p < 0.001, corrected). These results suggest that baseline functional
network topology involving the stimulation node predicts downstream modulation in node strength.
(C) Distribution of correlations between the variance of change in downstream node strength and
the baseline coherence between the stimulation node and the downstream nodes. We find a sig-
nificantly positive correlation in the beta band (p < 0.001, corrected) and in the low gamma band
(p < 0.001, corrected). These results suggest that baseline functional network topology involving the
stimulation node predicts the flexibility with which a downstream node may alter its interactions
with other nodes in the network. Each observation is the correlation within a stimulation session
of a single subject. Solid lines represent the median, and dashed lines represent the first and third
quantiles. *p < 0.05, **p < 0.01, ***p < 0.001.
Network Neuroscience
864
Functional control of brain networks using direct neurostimulation
downstream node (Figure 5B). Intuitively, positive correlation values imply that stronger base-
line coherence between the stimulation node and the downstream nodes predicts greater mag-
nitude change in node strength across stimulation epochs. Using a Wilcoxon rank-sum test,
Bonferroni correction for multiple comparisons, and effect size based on rank correlation, we
find a significant positive correlation values in the alpha/theta band (Z(247) = 4, 986, p =
0.003, rank correlation = 0.84), in the beta band (Z(247) = 2, 092, p = 5.4 × 10−15
, rank
correlation = 0.93), in the low gamma band (Z(247) = 2, 355, p = 1.4 × 10−13
, rank correla-
tion = 0.92), and we find a nonsignificant positive trend in the high gamma band (Z(247) =
5, 928, p = 0.19). We also assess the Spearman’s ρ correlation between the set of baseline
coherence values between the stimulation node and the downstream nodes and the variance
of the magnitude changes in node strength of each downstream node (Figure 5B). We find a
significantly positive correlation in the beta band (Z(247) = 2, 721, p = 9.9 × 0−11
, rank cor-
relation = 0.91) and in the low gamma band (Z(247) = 2, 997, p = 2.0 × 10−10
, rank
correlation = 0.90), and we find a nonsignificant positive trend in the alpha/theta band
(Z(247) = 5, 993, p = 0.24) and in the high gamma band (Z(247) = 6, 340, p = 0.72).
We find that these effects persist in the alpha/theta band, in the beta band, and in the low
gamma band and strengthen in the high gamma band at least 600 ms after stimulation offset
(Supporting Information: Figure 5-1b,c).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Our findings are consistent with the hypothesis that the baseline functional network topol-
ogy involving the stimulation node may be used to predict the downstream network regions
that are most influenced by stimulation. We also find that this predictive capacity is dependent
on the frequency band of the coherent measurement: The likelihood of modulating the coher-
ent interactions of a downstream node is less predictable for higher frequencies. This finding
suggests that the direct coherence between a stimulation node and a downstream node may
be more influential in conveying stimulation input to the downstream node for lower coher-
ence frequency bands. Our analysis highlights a putative mechanism of node-level flexibility,
or the ability for a network region to dynamically alter its level of interaction with other re-
gions in the network. Specifically, stronger baseline coherence between the stimulation node
and a downstream node tends to predict greater variability with which the downstream node
changes its level of interaction with the rest of the network within a stimulation session. Such
a rule can guide more principled targeting of network structures to amenably drive flexible
reconfiguration of the functional network.
Unifying Stimulation and Functional Reconfiguration With Network Control Theory
We lastly seek to integrate our observations on stimulation-driven reconfiguration of functional
brain networks with first principles theory. Network control theory provides a mathematical
framework to model changes in the state of a complex system under a set of constraints pre-
scribed by the structure of that system (Pasqualetti et al., 2014; Yan et al., 2017). For brain
networks, network control theory offers an opportunity to model the logical progression of
a stimulus input into an anatomically defined structural brain network, the traversal of that
input through the network, the resulting change in interregional communication, and an ac-
companying shift in the dynamical state of the brain that accommodates a change in behavior
(Figure 6A; Gu et al., 2017, 2015; Kim et al., 2018; Muldoon et al., 2016; Pequito et al.,
2016). The structural topology of the network may confer important control properties to a
complex system such as modal controllability, which enables a system to move from its cur-
rent dynamical state to more difficult-to-reach dynamical states through an efficient expen-
diture of energy resources (Ashourvan, Gu, Mattar, Vettel, & Bassett, 2017; Gu et al., 2015;
Pasqualetti et al., 2014). Recent theoretical inquiry into the relationship between brain structure
Network Neuroscience
865
Functional control of brain networks using direct neurostimulation
Modal controller:
Network node that facilitates
energetically challenging state
transitions and is defined based
on its rigid structural connectivity
with other network nodes.
and function during stimulation posited that stimulation of the structural brain network’s modal
controllers may drive a heterogenous change in functional architecture (Muldoon et al., 2016).
However, experimental evidence linking the network control theoretic model to brain stimu-
lation and its influence on functional architecture and dynamical brain state via the structural
brain network is lacking.
In this study, we have so far shown that stimulation drives a rich and complex functional
network response that is dependent on the stimulation input intensity and the stimulation in-
put location. While the input intensity drives the magnitude of functional reconfiguration, the
baseline coherence of the input location constrains the spatial specificity of the functional
reconfiguration. Yet, how does baseline network topology in the vicinity of the stimulation
region relate to the modal control strategy put forth by structural control theory? To answer
this question, we construct structural brain networks by applying deterministic tractography to
diffusion-weighted imaging data that are parcellated into 1,015 anatomically defined, cortical
and subcortical regions of interest (Cammoun et al., 2012) in a subset of 14 participants (see
Methods; the other participants did not have diffusion-weighted imaging data). We next assign
the intracranial ECoG sensors for a subject to their nearest anatomical ROI based on the short-
est spatial distance between a sensor and the ROI centroids. We then measure the structural
connectivity between anatomical ROIs and the modal controllability of each anatomical ROI
in the structural network, and we assign these values to the intracranial sensors based on their
proximity to the nearest ROI.
To establish a clear relation between structural connectivity and baseline functional con-
nectivity (measured by coherence), we calculate the Pearson correlation between the pattern
of structural connections and the pattern of baseline coherent interactions between intracra-
nial sensors, for each coherence frequency band and each subject (Figure 6B). This proce-
dure is conducted separately for connections that span the same hemisphere of the brain
(intra-hemispheric connections) and for connections that span opposing hemispheres of the
brain (inter-hemispheric connections), and correlation values are subsequently z-scored us-
ing the Fisher transformation. Using a one-sample t test, we test the null hypothesis that
the z-transformed correlation between structural connectivity and functional connectivity is
equal to 0. For intra-hemispheric connections, we observe significant negative correlation be-
tween structural connectivity and baseline coherence in the low gamma band (t(13) = −3.0,
p = 0.04, corrected) and in the high gamma band (t(13) = −3.6, p = 0.01, corrected),
and non-significant negative trends in the alpha/theta band (t(13) = −1.5, p = 0.64, cor-
rected) and in the beta band (t(13) = −1.8, p = 0.34, corrected). For inter-hemispheric
connections, we observe nonsignificant positive trends between structural connectivity and
baseline coherence in the alpha/theta band (t(13) = −0.7, p = 0.48, corrected), in the beta
band (t(13) = 0.9, p = 0.37, corrected), in the low gamma band (t(13) = 0.9, p = 0.39,
corrected), and in the high gamma band (t(13) = 0.8, p = 0.44, corrected). Generally,
inter-hemispheric connections exhibited positive trends between structural connectivity and
ECoG functional connectivity, while intra-hemispheric connections exhibited negative trends
between structural connectivity and ECoG functional connectivity. This observed relationship
was stronger at the finer scale parcellation of the brain than at the coarser scale parcellation
(Supporting Information: Figure 6-1). Our results imply that weaker structural connections be-
tween brain regions within the same hemisphere are generally associated with stronger coher-
ent interactions in higher frequency bands, which typically reflect local, bottom-up processing
associated with synaptic input. This divergent relationship can be explained by an expectedly
strong coherence between brain regions that are in close proximity to one another, which
Network Neuroscience
866
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Using neurostimulation to bridge structure, function, and behavior. (A) Network control theory can model dynamical state changes
due to external input and structural constraints on the system. Consider a stimulation input to the structural brain network (left). This input would
evoke a functional response constrained by the architecture of the structural network (middle) and shift the brain from one state to another
state (right). Previous studies posit that structural topology of the input region—modal controllability—may relate to the energy required to
move between different dynamical states (Gu et al., 2015; Pasqualetti et al., 2014). Specifically, stronger modal controllers may lead to more
distant transitions across an energy landscape than weaker modal controllers (right). Here, we demonstrate a link between stimulation of the
structural brain network, the evoked functional network response, and changes in dynamical state associated with behavior. Briefly, we use a
previously published biomarker of brain state based on a logistic regression-based classifier of neural activity associated with positive memory
encoding (Ezzyat et al., 2017). (B) Distribution of Fisher z-transformed correlations between structural connectivity from DTI and baseline
coherence from ECoG, across subjects. Distributions are subdivided by inter-hemispheric and intra-hemispheric connections and coherence
frequency band. We find a significant negative correlation between structural connectivity and baseline functional connectivity in the low and
high gamma bands (p < 0.05, corrected) for intra-hemispheric connections; we observed nonsignificant positive trends between structural
connectivity and baseline functional connectivity for inter-hemispheric connections. (C) Correlation between the modal controllability of the
stimulated brain region and the average functional configuration similarity across stimulation sessions. We find a significant positive correlation
in the beta band (p < 0.01, corrected), in the low gamma band (p < 0.01, corrected), and in the high gamma band (p < 0.01, corrected).
This result implies that stimulation of modal controllers leads to less network-wide reconfiguration of functional interactions. (D) We find
a significant positive correlation between the average change in classifier likelihood of positive memory encoding state during stimulation
trials and the modal controllability of stimulated nodes based on the structural brain network (p < 0.05). This result implies that stimulation
of structural brain regions that are more capable of pushing the brain to difficult-to-reach dynamical states is associated with an increased
likelihood of reaching a positive memory encoding state after stimulation. *p < 0.05, **p < 0.01, ***p < 0.001.
are more likely to be weakly linked by structural U-shaped white matter fibers (Schmahmann
et al., 2007).
Based on the result
that structural connectivity weakly constrains baseline coherent
interactions between brain regions, we ask whether a control strategy motivated by modal control-
lability of the structural brain network predicts stimulation-driven reconfiguration of the func-
tional network topology. To answer this question, we first calculate the modal controllability for
Network Neuroscience
867
Functional control of brain networks using direct neurostimulation
the brain region in each stimulation session across subjects. We next compute the Spearman’s
ρ correlation between modal controllability of the stimulated brain region and the average,
within-session configuration similarity. Using Bonferroni correction for multiple comparisons,
we find a significant positive correlation between modal controllability and configuration sim-
ilarity in the beta band ( ρ(24) = 0.61, p = 0.003), in the low gamma band ( ρ(24) = 0.65,
p = 0.001), and in the high gamma band ( ρ(24) = 0.59, p = 0.005), and we find a nonsignif-
icant positive trend in the alpha/theta band ( ρ(24) = 0.47, p = 0.05). These effects persist
at least 600 ms after stimulation offset (Supporting Information: Figure 6-2a). These results
imply that stimulation of stronger modal controllers drives lower reconfiguration of the coher-
ent interactions in the functional network. To contextualize these findings, we draw upon the
well-established positive relationship between modal controllability and structurally isolated
brain regions (Gu et al., 2015). By targetting strong modal controllers in the structural brain
network, stimulation modulates structurally isolated brain areas and drives lower functional
reconfiguration than stimulation of weak modal controllers in structurally connected brain
areas.
Notably, our results demonstrate a complex and frequency-specific link between structural
topology and functional topology—weak structural connections tend to span between brain
areas with stronger, high-frequency functional interactions, and stimulation of modal con-
trollers in structurally isolated brain regions tends to limit the extent of functional network
reconfiguration. Combined with earlier findings, we put forth a putative sequence of physio-
logical events associated with modal control in which stimulation of strong modal controllers
activates strong, local functional hubs that drive less functional reconfiguration of network-
wide edges (Figure 4E) and greater change in the node strengths of functionally connected,
downstream brain regions (Figure 5B). In contrast, stimulation of weak modal controllers acti-
vates weaker, functionally isolated regions that drive distributed functional reconfiguration of
network-wide edges (Figure 4E). While these findings establish a link between network con-
trol and functional reconfiguration, they do not establish a link between network control and
changes in dynamical brain state.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
t
.
To experimentally examine the relationship between the modal controllability of the stimu-
lation region and the shift in dynamical brain state following stimulation, we leverage a previ-
ously documented and validated binary classifier of neural activity into good and poor episodic
memory encoding states (Ezzyat et al., 2017). Specifically, we first train the classifier to dis-
criminate between successful and unsuccessful word recall trials during a delayed free recall
task using features based on spectral power of ECoG activity. We next evaluate the classifier on
ECoG activity during the pre-stim epoch and the post-stim epoch of each stimulation trial and
compute the change in probability of being in a good memory encoding state. We calculate
the correlation between the modal controllability of the stimulation region and the average,
within-session change in probability of being in a good memory state over stimulation trials
(Figure 6D). We find a significant positive correlation (Pearson’s r(17) = 0.49, p = 0.03).
These findings imply that the push towards better memory encoding states is associated with
stimulation of strong modal controllers that are theoretically positioned to push the brain to
more energetically unfavorable and distant brain states.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Collectively, our study reveals a link between brain structure and brain function that is
grounded in network control theory. Using the network control framework, we uncover the
important role of stimulation on reconfiguration of functional architecture that accounts for
anatomical constraints on network dynamics via the topology of structural network connectiv-
ity. We find that brain networks may use a modal control strategy during transitions between
Network Neuroscience
868
Functional control of brain networks using direct neurostimulation
difficult-to-reach dynamical states, which is associated with a reconfiguration in the localized
coherence of individual network nodes to the broader functional brain network.
DISCUSSION
Here, we addressed the hypothesis that direct stimulation of cortical and subcortical struc-
tures alters the architecture of functional brain networks and shifts the dynamical brain state in
accord with control strategies identified by applying tools from network control theory to elec-
trophysiological and structural brain imaging data. In human epilepsy patients, we measured
coherent patterns of ECoG activity thought to underlie coordinated functional interactions, and
we mapped how these interactions vary with neurostimulation parameters. We observed that
stimulation drives two modes of functional reconfiguration: The first mode involves distributed
changes in the pattern of functional interactions across the network, and the second mode
involves preferentially localized changes in the functional interactions associated with select
brain regions. Notably, the mode of reconfiguration may be strategically selected based on the
strength and location of stimulation. When we stimulated brain regions with weak structural
connections to the rest of the network, we tended to invoke a modal control strategy marked
by a modulation of the functional hubness of downstream brain regions and a large change in
dynamical brain state.
Predictors of Functional Reconfiguration: Implications for Brain Network Control
The field of network neuroscience has long sought to understand how the rigid and inter-
connected anatomy of the structural brain network shapes interactions amongst functionally
specialized brain areas, which may change from moment to moment and drive cognition and
behavior (Hermundstad et al., 2013, 2014; Miši´c et al., 2016; Park & Friston, 2013). Tools from
network control theory (Liu, Slotine, & Barabasi, 2011; Pasqualetti et al., 2014; Tang & Bassett,
2017) have enabled researchers to identify controllability rules that prescribe how the dynam-
ical state of a neural system can change based solely on the structural topology of the system
(Betzel et al., 2016; Gu et al., 2017, 2015; Kim et al., 2018; Tang et al., 2017; Yan et al., 2017).
Structural controllability rules account for network interactions that can occur, but they do not
account for finer scale functional constraints that dictate whether these interactions will occur
at a point in time (Liu et al., 2011; Tang & Bassett, 2017). Previous studies have incorporated
these functional constraints into the study of network control by using neurophysiologically
inspired dynamical mean-field models (Jirsa et al., 2017; Muldoon et al., 2016; Taylor et al.,
2015), which require estimation of biologically plausible parameters.
In contrast to these studies, we used a data-driven, perturbative approach for inferring rules
of functional network reconfiguration. By focally stimulating brain tissue at the millimeter
scale, we mapped changes in the statistical interdependencies between brain regions. We
note that there is a subtle distinction in the statistical methods used here to measure bidrec-
tional, synchronized interactions and statistical methods used elsewhere to measure directed,
effective functional interactions (Battaglia, Witt, Wolf, & Geisel, 2012; Friston, 2011; Lepage,
Ching, & Kramer, 2013). We found that the observed change in statistical interdependency
can be predicted by baseline levels measured before any stimulation is delivered. That is, a
brain region that exhibits a strong, spontaneous functional interaction with the stimulated brain
region is more likely to be modulated during stimulation than a brain region with a weak, spon-
taneous functional interaction with the stimulated brain region. In the long-standing debate re-
garding the validity of functional network models to explain causal dynamics (Jonas & Kording,
2017), these data provide compelling evidence in favor of a mechanism in which the functional
Network Neuroscience
869
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
network may causally convey the influence of stimulation on one brain region to other strongly
interacting brain regions. Our findings implicate a strategy for the functional control of brain
networks in which (a) stimulation of functionally isolated brain regions leads to spatially focal
and strong downstream functional reconfiguration, and (b) stimulation of functionally hub-like
brain regions leads to spatially diffuse and weak downstream functional reconfiguration.
To relate rules for functional control to theoretical predictions from structural controllabil-
ity, we bridged electrophysiological data with structural brain imaging data. Confirming results
from prior studies on controllability in healthy subjects (Gu et al., 2015; Tang et al., 2017), in
epilepsy subjects we found that brain regions with structurally weak connections tend to be
strong modal controllers, which facilitate more difficult transitions in brain state. Stimulations
of structurally weak modal control points lead to strong, local change of functional architecture
in a mean-field model of neuron population dynamics (Muldoon et al., 2016). In contrast, here
we demonstrated that stimulation of modal control points leads to widespread, weak change
in functional architecture because of the presence of strong functional hubs in the stimulated
brain regions. We identified two potential explanations for the distinction between the model
simulation and our empirical observations. First, the in silico model assumes identical bio-
physical parameters across different neuronal ensembles distributed across the brain network,
which may limit the reproducibility of detailed spatial and temporal dynamics that would other-
wise be expressed in vivo and measured by intracranial ECoG sensors. Second, the in silico
model accounts for structural connectivity between neuronal ensembles using diffusion imag-
ing, which measures white matter fiber pathways spanning long distances but does not capture
gray matter pathways spanning short distances (Thomas et al., 2014) and synaptic microarchi-
tecture responsible for plasticity over varying time scales (Song, Miller, & Abbott, 2000). When
combined with additional data demonstrating a moderate relationship between white matter
connectivity and correlated ECoG dynamics (Betzel, Medaglia, Kahn, et al., 2017), our find-
ings suggest that non–white matter structural connectivity and other physiological factors may
contribute to the reconfiguration of functional network architecture.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
Physiological Interpretations of Altered Functional Topology
Neuronal synchronization is purported to play a crucial role in facilitating interareal commu-
nication between ensembles of neurons (Bonnefond et al., 2017; Buzsáki et al., 2012; Canolty
& Knight, 2010; Fries, 2015; Schalk, 2015). Fries (2015) proposed that rhythmic oscillations in
the local field potential give rise to states of excitability depending on the temporal position
during an oscillatory cycle—two different ensembles of neurons are able to reliably transfer
information between one another when they are mutually excitable, or exhibit oscillations
that are in-phase. Equally important to communication is the frequency of the oscillation—
higher frequency bands (γ) are thought to facilitate communication of bottom-up input over
short distances, and lower frequency bands (θ, α, β) are thought to facilitate communication
of top-down processes over long distances (Fries, 2015; Kopell et al., 2000).
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Notably, we found that stimulation parameters may be tuned to selectively modulate dif-
ferent regions and spatial extents of the functional network. Stimulation intensity tends to pro-
vide greater control over reconfiguration of lower frequency networks, and stimulation location
tends to provide greater control over reconfiguration of higher frequency networks. Specifically,
we observed that the strength of the stimulation input has a greater effect on functional recon-
figuration in lower frequency bands than in higher frequency bands, suggesting that stimulation
parameters such as amplitude, pulse frequency, and duration may play an important role in
the modulation of long-range, top-down functional interactions. We speculate that a stronger
Network Neuroscience
870
Functional control of brain networks using direct neurostimulation
stimulation input may be more likely to penetrate wider spatial extent of cortex and heteroge-
nously modulate network excitability at low frequencies (Fries, 2015). We also observed that
the location of the stimulation input has a greater effect on functional reconfiguration in higher
frequency bands than in lower frequency bands, suggesting that the hubness of the stimu-
lated brain region may play an important role in the modulation of short-range, bottom-up
functional
that brain regions involved in bottom-up
communication associated with broadly conveying sensory input to higher order cortices might
also be more sensitive to modulations via stimulation than brain regions involved in top-down
communication.
Intuitively, we expect
interactions.
Methodological Considerations and Future Work
We chose to perform a network analysis of intracranial data during neurostimulation, rather
than a univariate analysis of individual activations. Our decision enabled us to examine the
influence of neurostimulation on the distributed and interconnected physiology of the human
brain, which is in line with previous in silico modeling work (Muldoon et al., 2016). Several
notable studies have teased apart the effective connectivity between brain regions using neuro-
stimulation to generate cortico-cortico evoked potentials (CCEPs; Keller, Honey, Entz, et al.,
2014; Keller, Honey, Me, et al., 2014; Matsumoto et al., 2004), and have more recently pre-
dicted where CCEPs might occur using a combination of repetitive low-frequency stimulation
and baseline connectivity (Keller et al., 2018). In a departure from these studies on effective
connectivity, we test the novel hypothesis that neurostimulation can predictively perturb inter-
areal statistical dependencies underlying distributed brain function. Our study is motivated by
recent hypotheses regarding the role of coherent synchronization in neuronal communication.
With the maturation of network analysis tools that enable simultaneous tracking of dynamic
network architecture and dynamic activity (Murphy et al., 2016), we envision future studies
where we investigate the potential for neurostimulation to selectively modulate brain activity
or perturb functional network architecture.
We also chose to examine static changes in the functional network architecture aggregated
over many repeated trials of neurostimulation. This approach allowed us to examine the ability
of stimulation to drive network reconfiguration within each subject, and to evaluate the statisti-
cal robustness of effects across subjects. Generally, we find medium to large effect sizes on the
order of 0.4–0.9. The advantage of our chosen approach is that the effects of stimulation are
assessed separately for each patient, which enabled us to account for an individual’s stereo-
typed network topology while examining generalized rules that predict the network effects of
stimulation. We can thus address questions such as, “Are some brain regions more likely to
change their functional interactions than other brain regions?” and “How are these brain re-
gions associated with the stimulated brain region?” In future studies, we aim to understand
how stimulation influences the functional brain network from one moment in time to the next,
as a function of brain state. For instance, does stimulation during the beginning of a coherent
oscillatory cycle influence network architecture differently than stimulation during the middle
of a coherent oscillatory cycle? This temporal mapping could inform control strategies to steer
functional brain network reconfiguration in real time.
One important question regarding the neural adaptation effects of stimulation is beyond the
scope of this analysis and remains unanswered: “How long do stimulation-induced changes
to the network last?” An answer to this valuable question could support therapeutic applica-
tions of direct stimulation by reducing the need to stimulate the brain for long periods of time at
high intensity—potentially improving safety, efficacy, and longevity of chronically implantable
Network Neuroscience
871
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
devices (Fisher, 2011; Stacey & Litt, 2008). The adaptation question will be addressed in a fu-
ture study by introducing longer periods of rest between consecutive stimulation trials and
quantifying the duration of connectivity changes. A related consideration of this study is that
a sham condition was not included during the stimulation session and changes in functional
network architecture were instead compared with passive changes in network architecture at
baseline. Indeed, a dedicated sham condition during stimulation would be able to dissoci-
ate the effects of stimulation from natural fluctation in the brain’s internal dynamics. Previous
studies have emphasized that sham stimulation may be more effective at assessing behavioral,
“placebo” effects of stimulation than quantifying neural effects, given the biophysical differ-
ences between external input from a current source in comparison to spontaneous fluctuation
of endogenous neural activity (Duecker & Sack, 2015). In this study, we enforced a fairer com-
parative condition to understand neural effects of stimulation by parameterically titrating the
dose of stimulation via current amplitude, frequency, and duration—all likely inducing a more
similar biophysical change to neural tissue than a sham condition with zero current deliv-
ery. Furthermore, stimulation trials were made blind to the patient, trial durations were kept
short (below 1 s), and the start of a stimulation trial was randomly jittered to mitigate neural
expectation of stimulation timing.
Approaches for recording and interrogating intracranial electrophysiology are inherently
limited by spatial coverage of the ECoG sensors, which is determined during the management
of a patient’s epilepsy. This sampling bias leads to a varied representation of the functional
brain network between individual patients. While it is not yet possible to record from the
entirety of the human brain using ECoG, we mitigated this shortcoming by taking key steps
in our analysis. First, we used a statistically robust approach for characterizing the network
impact of stimulation in individual patients. We computed separate measures of topology for
each patient’s functional brain network, which enabled us to account for individual variability
in sensor placement and physiological state. Our data demonstrated a set of functional rules
for network reconfiguration that fundamentally depend on topological characteristics of the
stimulated brain area that can vary within and between patients. Second, we used a large
dataset consisting of 94 epilepsy patients, allowing us to account for a range of individual
variability in functional brain network architecture that is often not possible in studies of human
electrophysiology.
CONCLUSIONS
Here we mapped the impact of targeted neurostimulation on distributed functional architecture
in the human brain. We demonstrated that network physiology can be predictably altered
based on control theoretic rules that account for structural and functional organization of the
brain network. Our results provide a causal, quantified description of the influence of structure
and function on dynamical brain state. Our findings have significant translational implications
in strategizing stimulation-based therapy based on a combination of behavioral biomarkers
and neurophysiology.
ACKNOWLEDGMENTS
We thank Blackrock Microsystems for providing neural recording and stimulation equipment.
The views, opinions, and/or findings contained in this material are those of the authors and
should not be interpreted as representing the official views or policies of the Department of
Defense, the U.S. government, or any of the funding agencies.
Network Neuroscience
872
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
AUTHOR CONTRIBUTIONS
Ankit N. Khambhati: Conceptualization; Formal analysis; Investigation; Methodology; Software;
Validation; Visualization; Writing – Original Draft; Writing – Review & Editing. Ari E. Kahn:
Methodology. Julia Costantini: Formal analysis; Software. Youssef Ezzyat: Conceptualization;
Data curation. Ethan A. Solomon: Conceptualization; Data curation. Robert E. Gross: Data cu-
ration. Barbara C. Jobst: Data curation. Sameer A. Sheth: Data curation. Kareem A. Zaghloul:
Data curation. Gregory Worrell: Data curation. Sarah Seger: Data curation. Bradley C. Lega:
Data curation. Shennan Weiss: Data curation. Michael R. Sperling: Data curation. Richard
Gorniak: Data curation. Sandhitsu R. Das: Data curation; Methodology; Software. Joel M. Stein:
Data curation; Methodology; Software. Daniel S. Rizzuto: Data curation; Project administra-
tion. Michael J. Kahana: Data curation; Funding acquisition; Project administration; Resources.
Timothy H. Lucas: Data curation. Kathryn A. Davis: Data curation. Joseph I. Tracy: Data cura-
tion. Danielle S. Bassett: Conceptualization; Funding acquisition; Methodology; Project
administration; Resources; Supervision; Writing - Original Draft; Writing - Review & Editing.
FUNDING INFORMATION
Danielle S. Bassett,
John D. and Catherine T. MacArthur Foundation (http://dx.doi.org/
10.13039/100000870). Danielle S. Bassett, Alfred P. Sloan Foundation (http://dx.doi.org/
10.13039/100000879). Danielle S. Bassett, Army Research Laboratory (http://dx.doi.org/10.
13039/100006754), Award ID: W911NF-10-2-0022. Danielle S. Bassett, Army Research
Laboratory (http://dx.doi.org/10.13039/100006754), Award ID: W911NF-14-1-0679. Danielle
Institutes of Health (http://dx.doi.org/10.13039/
S. Bassett, Foundation for the National
100000009), Award ID: 2-R01-DC-009209-11. Danielle S. Bassett, Foundation for the Na-
tional Institutes of Health (http://dx.doi.org/10.13039/100000009), Award ID: 1R01HD086888-01.
Danielle S. Bassett, Foundation for the National
Institutes of Health (http://dx.doi.org/
10.13039/100000009), Award ID: R01-MH107235. Danielle S. Bassett, Foundation for the Na-
tional Institutes of Health (http://dx.doi.org/10.13039/100000009), Award ID: R01-MH107703.
Danielle S. Bassett, Foundation for the National Institutes of Health (http://dx.doi.org/10.13039/
100000009), Award ID: R21-M MH-106799. Danielle S. Bassett, U.S. Naval Research Labo-
ratory (http://dx.doi.org/10.13039/100009917). Danielle S. Bassett, National Science Foun-
dation (http://dx.doi.org/10.13039/100000001), Award ID: BCS-1441502. Danielle S. Bassett,
National Science Foundation (http://dx.doi.org/10.13039/100000001), Award ID: CAREER
PHY-1554488. Danielle S. Bassett, National Science Foundation (http://dx.doi.org/10.13039/
100000001), Award ID: BCS-1631550. Michael J.Kahana, Defense Advanced Research Projects
Agency (http://dx.doi.org/10.13039/100000185), Award ID: N66001-14-2-4032.
REFERENCES
Aarts, J. H., Binnie, C. D., Smit, A. M., & Wilkins, A. J. (1984). Selec-
tive cognitive impairment during focal and generalized epilepti-
form EEG activity. Brain, 107(Pt. 1), 293–308.
Achard, S., & Bullmore, E. (2007). Efficiency and cost of economi-
cal brain functional networks. PLoS Computational Biology, 3(2),
e17. https://doi.org/10.1371/journal.pcbi.0030017
Andersson, J. L., & Sotiropoulos, S. N. (2016). An integrated ap-
proach to correction for off-resonance effects and subject move-
ment in diffusion MR imaging. NeuroImage, 125, 1063–1078.
https://doi.org/10.1016/j.neuroimage.2015.10.019
in the human brain connectome. NeuroImage, 157, 364–380.
https://doi.org/10.1016/j.neuroimage.2017.05.067
Avants, B. B., Epstein, C. L., Grossman, M., & Gee, J. C. (2009). Sym-
metric diffeomorphic image registration with cross-correlation:
Evaluating automated labeling of elderly and neurodegenerative
brain. Medical Image Analysis, 12(1), 26–41.
Bassett, D. S., Brown, J. A., Deshpande, V., Carlson, J. M., & Grafton,
S. T. (2011). Conserved and variable architecture of human white
matter connectivity. NeuroImage, 54(2), 1262–1279. https://doi.
org/10.1016/j.neuroimage.2010.09.006
Ashourvan, A., Gu, S., Mattar, M. G., Vettel, J. M., & Bassett, D. S.
(2017). The energy landscape underpinning module dynamics
Bassett, D. S., Greenfield, D. L., Meyer-Lindenberg, A., Weinberger,
D. R., Moore, S. W., & Bullmore, E. T. (2010). Efficient physical
Network Neuroscience
873
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
embedding of topologically complex information processing net-
works in brains and computer circuits. PLoS Computational Biol-
ogy, 6(4). https://doi.org/10.1371/journal.pcbi.1000748
Bassett, D. S., Meyer-Lindenberg, A., Achard, S., Duke, T., &
Bullmore, E. (2006). Adaptive reconfiguration of fractal small-
world human brain functional networks. Proceedings of the
National Academy of Sciences, 103(51), 19518–19523.
Bassett, D. S., Nelson, B. G., Mueller, B. A., Camchong, J., & Lim,
K. O. (2012). Altered resting state complexity in schizophre-
nia. NeuroImage, 59(3), 2196–2207. https://doi.org/10.1016/
j.neuroimage.2011.10.002
Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353–364. https://doi.org/10.1038/nn.4502
Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson,
J. M., & Grafton, S. T. (2011). Dynamic reconfiguration of hu-
man brain networks during learning. Proceedings of the National
Academy of Sciences, 108(18), 7641–7646. https://doi.org/
10.1073/pnas.1018985108
Bassett, D. S., Wymbs, N. F., Rombach, M. P., Porter, M. A., Mucha,
P. J., & Grafton, S. T. (2013). Task-based core-periphery organi-
zation of human brain dynamics. PLoS Computational Biology,
9(9), e1003171. https://doi.org/10.1371/journal.pcbi.1003171
Bassett, D. S., Yang, M., Wymbs, N. F., & Grafton, S. T. (2015).
Learning-induced autonomy of sensorimotor systems. Nature
Neuroscience, 18(5), 744–751. https://doi.org/10.1038/nn.3993
Battaglia, D., Witt, A., Wolf, F., & Geisel, T. (2012). Dynamic ef-
fective connectivity of inter-areal brain circuits. PLoS Computa-
tional Biology, 8(3), 1–20. https://doi.org/10.1371/journal.pcbi.
1002438
Betzel, R. F., Gu, S., Medaglia, J. D., Pasqualetti, F., & Bassett, D. S.
(2016). Optimally controlling the human connectome: The role of
network topology. Scientific Reports, 6. doi: 10.1038/srep30770
Betzel, R. F., Medaglia, J. D., Kahn, A. E., Soffer, J., Schonhaut, D. R.,
& Bassett, D. S. (2017). Inter-regional ECoG correlations pre-
dicted by communication dynamics, geometry, and correlated
gene expression. arXiv:1706.06088, 1–36.
Betzel, R. F., Medaglia, J. D., Papadopoulos, L., Baum, G. L., Gur,
R. C., Gur, R. E., . . . Bassett, D. S. (2017). The modular organi-
zation of human anatomical brain networks: Accounting for the
cost of wiring. Network Neuroscience, 1(1), 1–45. https://doi.
org/10.1162/netn
Bonnefond, M., Kastner, S., & Jensen, O.
(2017). Communi-
cation between brain areas based on nested oscillations.
Neuro, 4(2), ENEURO.0153–16.2017. https://doi.org/10.1523/
ENEURO.0153-16.2017
Braun, U., Schäfer, A., Bassett, D. S., Rausch, F., Schweiger, J. I.,
Bilek, E., & Erk, S.
(2016). Dynamic brain network recon-
figuration as a potential schizophrenia genetic risk mechanism
modulated by NMDA receptor function. Proceedings of the
National Academy of Sciences, 113(44). https://doi.org/10.1073/
pnas.1608819113
Braun, U., Schäfer, A., Walter, H., Erk, S., Romanczuk-Seiferth, N.,
Haddad, L., . . . Bassett, D. S. (2015). Dynamic reconfiguration
of frontal brain networks during executive cognition in humans.
Proceedings of the National Academy of Sciences, 112(37),
11678–11683. https://doi.org/10.1073/pnas.1422487112
Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(May), 336–349.
https://doi.org/10.1038/nrn3214
Bullock, T. H., McClune, M. C., Achimowicz, J. Z., Iragui-Madoz,
V. J., Duckrow, R. B., & Spencer, S. S. (1995a). EEG coherence
has structure in the millimeter domain: Subdural and hippocam-
pal recordings from epileptic patients. Electroencephalography
and Clinical Neurophysiology, 95(3), 161–177. https://doi.org/
10.1016/0013-4694(95)93347-A
Bullock, T. H., McClune, M. C., Achimowicz, J. Z., Iragui-Madoz,
V. J., Duckrow, R. B., & Spencer, S. S. (1995b). Temporal fluctu-
ations in coherence of brain waves. Proceedings of the National
Academy of Sciences, 92(25), 11568–11572. https://doi.org/
10.1073/pnas.92.25.11568
Burns, S. P., Santaniello, S., Yaffe, R. B., Jouny, C. C., & Crone,
N. E. (2014). Network dynamics of the brain and influence of
the epileptic seizure onset zone. Proceedings of the National
Academy of Sciences, 111(49), E5321–5330. https://doi.org/
10.1073/pnas.1401752111
Butson, C. R., & McIntyre, C. C. (2008). Current steering to con-
trol the volume of tissue activated during deep brain stimulation.
Brain Stimulation, 1(1), 7–15. https://doi.org/10.1016/j.brs.2007.
08.004.Current
Buzsáki, G. (2006). Rhythms of the brain. Oxford, United Kingdom:
Oxford University Press. https://doi.org/10.1093/acprof:oso/
9780195301069.001.0001
Buzsáki, G., Anastassiou, C. A., Koch, C., Buzsaki, G., Anastassiou,
C. A., & Koch, C. (2012). The origin of extracellular fields and
currents–EEG, ECoG, LFP and spikes. Nature Reviews. Neuro-
science, 13(6), 407–420. https://doi.org/10.1038/nrn3241
Cammoun, L., Gigandet, X., Meskaldji, D., Thiran, J. P., Sporns, O.,
Do, K. Q., . . . Hagmann, P. (2012). Mapping the human con-
nectome at multiple scales with diffusion spectrum MRI. Journal
of Neuroscience Methods, 203(2), 386–397. https://doi.org/10.
1016/j.jneumeth.2011.09.031
Canolty, R. T., & Knight, R. T.
(2010). The functional role of
cross-frequency coupling. Trends in Cognitive Sciences, 14(11),
506–515. https://doi.org/10.1016/j.tics.2010.09.001
Chai, L. R., Mattar, M. G., Blank, I. A., Fedorenko, E., & Bassett,
D. S. (2016). Functional network dynamics of the language sys-
tem. Cerebral Cortex, 26, 112. https://doi.org/10.1093/cercor/
bhw238
Chang, E. F., Kurteff, G., & Wilson, S. M. (2017). Selective inter-
ference with syntactic encoding during sentence production by
direct electrocortical stimulation of the inferior frontal gyrus.
Journal of Cognitive Neuroscience, Early access, 1–11.
Cieslak, M., & Grafton, S. T. (2014). Local termination pattern analy-
sis: A tool for comparing white matter morphology. Brain Imaging
and Behavior, 8(2), 292–299. https://doi.org/10.1007/s11682-
013-9254-z
Crowell, A. L., Garlow, S. J., Riva-Posse, P., & Mayberg, H. S. (2015).
Characterizing the therapeutic response to deep brain stimula-
tion for treatment-resistant depression: A single center long-term
perspective. Frontiers in Integrative Neuroscience, 9, 41.
Deco, G., & Kringelbach, M. L.
(2016). Metastability and co-
herence: Extending the communication through coherence hy-
pothesis using a whole-brain computational perspective. Trends
Network Neuroscience
874
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
in Neurosciences, 39(3), 125–135. https://doi.org/10.1016/j.tins.
2016.01.001
Duecker, F., & Sack, A. T. (2015). Rethinking the role of sham TMS.
Frontiers in Psychology, 6, 210.
Dykstra, A. R., Chan, A. M., Quinn, B. T., Zepeda, R., Keller,
C. J., Cormier, J., . . . Cash, S. S. (2012). Individualized localiza-
tion and cortical surface-based registration of intracranial elec-
trodes. NeuroImage, 59(4), 3563–3570. https://doi.org/10.1016/
j.neuroimage.2011.11.046.Individualized
Ezzyat, Y., Kragel, J. E., Burke, J. F., Levy, D. F., Lyalenko, A., Wanda,
P., . . . Kahana, M. J. (2017). Direct brain stimulation modulates
encoding states and memory performance in humans. Current
Biology, 27(9), 1251–1258. https://doi.org/10.1016/j.cub.2017.
03.028
Fischl, B., Kouwe, A. V. D., Destrieux, C., Halgren, E., Ségonne, F.,
Salat, D. H., . . . Dale, A. M. (2004). Automatically parcellating
the human cerebral cortex. Cerebral Cortex, 14(1), 11–22. https://
doi.org/10.1093/cercor/bhg087
Fisher, R. S. (2011). Neurostimulation for epilepsy: Do we know the
best stimulation parameters? Epilepsy Currents, 11(6), 203–204.
Foster, B. L., & Parvizi, J. (2017). Direct cortical stimulation of hu-
man posteromedial cortex. Neurology, 88(7), 685–691. https://
doi.org/10.1212/WNL.0000000000003607
Fries, P. (2015). Rhythms for cognition: Communication through
coherence. Neuron, 88(1), 220–235. https://doi.org/10.1016/
j.neuron.2015.09.034
Friston, K. J. K. (2011). Functional and effective connectivity: A re-
view. Brain Connectivity, 1(1), 13–36. https://doi.org/10.1089/
brain.2011.0008
Grefkes, C., & Fink, G. R. (2011). Reorganization of cerebral net-
works after stroke: New insights from neuroimaging with con-
nectivity approaches. Brain, 134(5), 1264–1276. https://doi.org/
10.1093/brain/awr033
Gu, S., Betzel, R. F., Cieslak, M., Delio, P. R., Grafton, S. T.,
Pasqualetti, F., & Bassett, D. S.
trajectories
of brain state transitions. NeuroImage, 148(January), 305–317.
https://doi.org/10.1016/j.neuroimage.2017.01.003
(2017). Optimal
Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Yu, A. B.,
Kahn, A. E., . . . Bassett, D. S. (2015). Controllability of structural
brain networks. Nature Communications, 6, 8414. https://doi.org/
10.1038/ncomms9414
Hermundstad, A. M., Bassett, D. S., Brown, K. S., Aminoff, E. M.,
Clewett, D., Freeman, S., . . . Carlson, J. (2013). Structural
foundations of resting-state and task-based functional connec-
tivity in the human brain. Proceedings of the National Academy
of Sciences, 110(15), 6169–6174. https://doi.org/10.1073/pnas.
1219562110
Hermundstad, A. M., Brown, K. S., Bassett, D. S., Aminoff, E. M.,
Frithsen, A., Johnson, A., . . . Carlson, J. M. (2014). Structurally
constrained relationships between cognitive states in the hu-
man brain. PLoS Computational Biology, 10(5). https://doi.org/
10.1371/journal.pcbi.1003591
Holmes, G. L., & Lenck-Santini, P. P. (2006). Role of interictal
epileptiform abnormalities in cognitive impairment. Epilepsy and
Behavior, 8(3), 504–515. https://doi.org/10.1016/j.yebeh.2005.
11.014
Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini,
P. A., Calhoun, V. D., Corbetta, M., . . . Chang, C. (2013).
Dynamic functional connectivity: Promise, issues, and inter-
pretations. NeuroImage, 80, 360–378. https://doi.org/10.1016/
j.neuroimage.2013.05.079
Inman, C. S., Manns, J. R., Bijanki, K. R., Bass, D. I., Hamann, S.,
Drane, D. L., . . . Willie, J. T. (2017). Direct electrical stimula-
tion of the amygdala enhances declarative memory in humans.
Proceedings of the National Academy of Sciences, 1–6. http://dx.
doi.org/10.1159/000478281
Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W.,
& Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790. https://
doi.org/10.1016/j.neuroimage.2011.09.015
Jezzard, P., Barnett, A. S., & Pierpaoli, C. (1998). Characterization
of and correction for eddy current artifacts in echo planar diffu-
sion imaging. Magnetic Resonance in Medicine, 39(5), 801–812.
https://doi.org/10.1002/mrm.1910390518
Jirsa, V. K., Proix, T., Perdikis, D., Woodman, M. M., Wang, H.,
Gonzalez-Martinez, J., . . . Bartolomei, F. (2017). The virtual
epileptic patient: Individualized whole-brain models of epilepsy
spread. NeuroImage, 145, 377–388. https://doi.org/10.1016/
j.neuroimage.2016.04.049
Jonas, E., & Kording, K. P. (2017). Could a neuroscientist under-
stand a microprocessor? PLoS Computational Biology, 13(1), 1–24.
https://doi.org/10.1371/journal.pcbi.1005268
Kailath, T. (1980). Linear systems (Vol. 156). Englewood Cliffs, NJ:
Prentice-Hall.
Kalman, R. E. (1963). Mathematical description of linear dynamical
systems. Journal of the Society for Industrial and Applied Mathe-
matics, Series A: Control, 1(2), 152–192. https://doi.org/10.1137/
0301010
Keller, C. J., Honey, C. J., Entz, L., Bickel, S., Groppe, D. M., Toth,
E., . . . Mehta, A. D. (2014). Corticocortical evoked potentials re-
veal projectors and integrators in human brain networks. Journal
of Neuroscience, 34(27), 9152–9163. https://doi.org/10.1523/
JNEUROSCI.4289-13.2014
Keller, C. J., Honey, C. J., Me, P., Entz, L., Ulbert, I., & Mehta, A. D.
(2014). Mapping human brain networks with cortico-cortical
evoked potentials. Philosophical Transactions of the Royal Soci-
ety B, 369, 1–14.
Keller, C. J., Huang, Y., Herrero, J. L., Fini, M. E., Du, V., Lado, F. A.,
. . . Mehta, A. D. (2018). Induction and quantification of excitabil-
ity changes in human cortical networks. Journal of Neuroscience,
38(23), 5384–5398.
Khambhati, A. N., Bassett, D. S., Oommen, B. S., Chen, S. H.,
Lucas, T. H., Davis, K. A., & Liit, B. (2017). Recurring functional
interactions predict network architecture of interictal and ictal
states in neocortical epilepsy. eNeuro, 4(1). https://doi.org/10.
1523/ENEURO.0091-16.2017
Khambhati, A. N., Davis, K. A., Lucas, T. H., Litt, B., & Bassett,
D. S. (2016). Virtual cortical resection reveals push-pull network
control preceding seizure evolution. Neuron, 91(5), 1170–1182.
https://doi.org/10.1016/j.neuron.2016.07.039
Khambhati, A. N., Davis, K. A., Oommen, B. S., Chen, S. H.,
Lucas, T. H., Litt, B., & Bassett, D. S. (2015). Dynamic network
drivers of seizure generation, propagation and termination in
Network Neuroscience
875
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
human neocortical epilepsy. PLOS Computational Biology, 11(12),
e1004608. https://doi.org/10.1371/journal.pcbi.1004608
Kim, J. Z., Soffer, J. M., Kahn, A. E., Vettel, J. M., Pasqualetti, F., &
(2018). Role of graph architecture in controlling
Bassett, D. S.
dynamical networks with applications to neural systems. Nature
Physics, 14, 91–98.
Kopell, N., Ermentrout, G. B., Whittington, M. A., & Traub, R. D.
(2000). Gamma rhythms and beta rhythms have different syn-
chronization properties. Proceedings of the National Academy
of Sciences, 97(4), 1867–1872. https://doi.org/10.1073/pnas.97.
4.1867
Kragel, J. E., Ezzyat, Y., Sperling, M. R., Gorniak, R., Worrell, G. A.,
Berry, B. M., . . . Kahana, M. J. (2017). Similar patterns of
neural activity predict memory function during encoding and
retrieval. NeuroImage, 155(February), 60–71. https://doi.org/
10.1016/j.neuroimage.2017.03.042
Kramer, M. A., Eden, U. T., Kolaczyk, E. D., Zepeda, R., Eskandar,
E. N., & Cash, S. S. (2010). Coalescence and fragmentation of
cortical networks during focal seizures. Journal of Neuroscience,
30(30), 10076–10085. https://doi.org/10.1523/JNEUROSCI.6309-
09.2010
Kramer, M. A., Eden, U. T., Lepage, K. Q., Kolaczyk, E. D.,
Bianchi, M. T., & Cash, S. S. (2011). Emergence of persistent
networks in long-term intracranial EEG recordings. Journal of
Neuroscience, 31(44), 15757–15767. https://doi.org/10.1523/
JNEUROSCI.2287-11.2011
Lepage, K. Q., Ching, S., & Kramer, M. A. (2013). Inferring evoked
Journal of
brain connectivity through adaptive perturbation.
Computational Neuroscience, 34(2), 303–318. https://doi.org/
10.1007/s10827-012-0422-8
Liu, Y.-Y., Slotine, J.-J., & Barabasi, A.-L. (2011). Controllability of
complex networks. Nature, 473(7346), 167–173.
Lozano, A. M., & Lipsman, N. (2013). Probing and regulating dys-
functional circuits using deep brain stimulation. Neuron, 77(3),
406–424. https://doi.org/10.1016/j.neuron.2013.01.020
Matsumoto, R., Nair, D. R., LaPresto, E., Najm, I., Bingaman, W.,
Shibasaki, H., & Lüder, H. O. (2004). Functional connectivity in
the human language system: A cortico-cortical evoked potential
study. Brain, 127(10), 2316–2330. https://doi.org/10.1093/brain/
awh246
Mattar, M. G., Cole, M. W., Thompson-Schill, S. L., & Bassett,
D. S. (2015). A functional cartography of cognitive systems. PLoS
Computational Biology, 11(12), 1–26. https://doi.org/10.1371/
journal.pcbi.1004533
Miši´c, B., Betzel, R. F., de Reus, M. A., van den Heuvel, M. P.,
Berman, M. G., McIntosh, A. R., & Sporns, O. (2016). Network-
level structure-function relationships in human neocortex. Cere-
bral Cortex, 26(7), 3285–3296. https://doi.org/10.1093/cercor/
bhw089
Morrell, M. J. (2011). Responsive cortical stimulation for the treatment
of medically intractable partial epilepsy. Neurology, 77(13),
1295–1304. https://doi.org/10.1212/WNL.0b013e3182302056
Muldoon, S. F., Pasqualetti, F., Gu, S., Cieslak, M., Grafton, S. T.,
Vettel, J. M., & Bassett, D. S. (2016). Stimulation-based control
of dynamic brain networks. PLoS Computational Biology, 12(9).
https://doi.org/10.1109/TAC.2015.2496191
Muller, L., Rolston, J. D., Fox, N. P., Knowlton, R., Rao, V. R., &
Chang, E. F. (2018). Direct electrical stimulation of human cor-
tex evokes high gamma activity that predicts conscious somato-
sensory perception. Journal of Neural Engineering, 15(2), 026015.
Murphy, A. C., Gu, S., Khambhati, A. N., Wymbs, N. F., Grafton,
S. T., Satterthwaite, T. D., & Basset, D. S. (2016). Explicitly
linking regional activation and function connectivity: Commu-
nity structure of weighted networks with continuous annotation.
arXiv:1611.07962.
Nair, D., & Morrell, M. (2017). Long-term safety and efficacy of re-
sponsive brain stimulation in adults with medically intractable
partial onset seizures (S21.004). Neurology, 88(Suppl. 16).
Olde Dubbelink, K. T. E., Hillebrand, A., Stoffers, D., Deijen, J. B.,
Twisk, J. W. R., Stam, C. J., & Berendse, H. W. (2014). Disrupted
brain network topology in Parkinson’s disease: A longitudinal
magnetoencephalography study. Brain, 137(1), 197–207. https://
doi.org/10.1093/brain/awt316
Park, H. J., & Friston, K. (2013). Structural and functional brain
networks: From connections to cognition. Science, 342(6158),
1238411. https://doi.org/10.1093/brain/awt316
Pasqualetti, F., Zampieri, S., & Bullo, F. (2014). Controllability met-
rics and algorithms for complex networks. IEEE Transactions
on Control of Network Systems, 1(1), 40–52. https://doi.org/
10.1109/ACC.2014.6858621
Pequito, S., Khambhati, A. N., Pappas, G. J., Siljak, D. D., Bassett,
D. S., & Litt, B. (2016). Structural analysis and design of dynamic-
flow networks: Implications into the brain dynamics. In American
Control Conference.
Prieto, G. A., Parker, R. L., & Vernon, F. L. (2009). A Fortran
90 library for multitaper spectrum analysis. Computers and
Geosciences, 35(8), 1701–1710. https://doi.org/10.1016/j.cageo.
2008.06.007
Rangarajan, V., Hermes, D., Foster, B. L., Weiner, K. S., Jacques,
C., Grill-Spector, K., & Parvizi, J. (2014). Electrical stimulation of
the left and right human fusiform gyrus causes different effects
in conscious face perception. Journal of Neuroscience, 34(38),
12828–12836. https://doi.org/10.1523/JNEUROSCI.0527-14.2014
Sang, L., Zhang, J., Wang, L., Zhang, J., Zhang, Y., Li, P., . . . Qiu,
M. (2015). Alteration of brain functional networks in early-stage
Parkinson’s disease: A resting-state fMRI study. PLoS ONE, 10(10),
1–19. https://doi.org/10.1371/journal.pone.0141815
Schalk, G. (2015). A general framework for dynamic cortical func-
tion: The function-through-biased-oscillations (FBO) hypothesis.
Frontiers in Human Neuroscience, 9(June), 1–10. https://doi.org/
10.3389/fnhum.2015.00352
J., & Weeden, V.
Schmahmann, J. D., Pandya, D. N., Wang, R., Dai, G., D’arceuil,
(2007). Asso-
H. E., de Crespigny, A.
ciation fibre pathways of the brain: Parallel observations from
diffusion spectrum imaging and autoradiography. Brain, 130(3),
630–653.
Shannon, R. V.
(1992). A model of safe levels for electrical
stimulation. IEEE Transactions on Biomedical Engineering, 39(4),
424–426. https://doi.org/10.1109/10.126616
J.
Shine, J. M., Koyejo, O., & Poldrack, R. A. (2016). Temporal meta-
states are associated with differential patterns of time-resolved
connectivity, network topology, and attention. Proceedings of the
National Academy Sciences, 113(35), 9888–9891.
Smith, S. M.
(2002). Fast
robust automated brain extraction.
Human Brain Mapping, 17(3), 143–155. https://doi.org/10.1002/
hbm.10062
Network Neuroscience
876
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional control of brain networks using direct neurostimulation
Solomon, E. A., Kragel, J. E., Sperling, M. R., Sharan, A., Worrell,
G. A., Kucewicz, M., . . . Branch, S. N. (2017). Widespread theta
synchrony and high-frequency desynchronization underlies en-
hanced cognition. Nature Communications, 8. https://doi.org/
10.1038/s41467-017-01763-2
Song, S., Miller, K. D., & Abbott, L. F. (2000). Competitive Hebbian
synaptic plasticity.
learning through spike-time dependent
Nature Neuroscience, 3(9), 919–926.
Stacey, W. C., & Litt, B. (2008). Technology insight: Neuroengineer-
ing and epilepsy-designing devices for seizure control. Nature
clinical practice. Neurology, 4(4), 190–201. https://doi.org/10.
1038/ncpneuro0750
Stanslaski, S., Afshar, P., Cong, P., Giftakis, J., Stypulkowski, P.,
Carlson, D., . . . Denison, T. (2012). Design and validation of a
fully implantable, chronic, closed-loop neuromodulation device
IEEE Transactions on
with concurrent sensing and stimulation.
Neural Systems and Rehabilitation Engineering, 20(4), 410–421.
https://doi.org/10.1109/TNSRE.2012.2183617
Tang, E., & Bassett, D. S. (2017). Control of dynamics in brain net-
works. arXiv:1701.01531, 1–21.
Tang, E., Giusti, C., Baum, G. L., Gu, S., Pollock, E., Kahn, A. E.,
. . . Basset, D. S. (2017). Developmental increases in white mat-
ter network controllability support a growing diversity of brain
dynamics. Nature Communications, 8(1), 1252.
Taylor, P. N., Thomas, J., Sinha, N., Dauwels, J., Kaiser, M., Thesen,
T., & Ruth, J. (2015). Optimal control based seizure abatement
using patient derived connectivity. Frontiers in Neuroscience,
9(June), 1–10. https://doi.org/10.3389/fnins.2015.00202
Thomas, C., Ye, F. Q., Irfanoglu, M. O., Modi, P., Saleem, K. S.,
Leopold, D. A., & Pierpaoli, C. (2014). Anatomical accuracy
of brain connections derived from diffusion MRI tractography
is inherently limited. Proceedings of the National Academy of
Sciences, 111(46), 16574–16579. https://doi.org/10.1073/pnas.
1405672111
Towle, V. L., Carder, R. K., Khorasani, L., & Lindberg, D.
(1999). Electrocorticographic coherence patterns. Journal of Clin-
ical Neurophysiology, 16(6), 528–547. https://doi.org/10.1097/
00004691-199911000-00005
Uhlhaas, P. J., & Singer, W. (2006). Neural synchrony in brain disor-
ders: Relevance for cognitive dysfunctions and pathophysiology.
Neuron, 52(1), 155–168. https://doi.org/10.1016/j.neuron.2006.
09.020
Wang, W., Collinger,
J. L., Degenhart, A. D., Tyler-Kabara,
E. C., Schwartz, A. B., Moran, D. W., . . . Boninger, M. L.
(2013). An electrocorticographic brain interface in an individual
with tetraplegia. PLoS ONE, 8(2), 1–8. https://doi.org/10.1371/
journal.pone.0055344
Wang, L., Yu, C., Chen, H., Qin, W., He, Y., Fan, F., . . . Zhu, C.
(2010). Dynamic functional reorganization of the motor execu-
tion network after stroke. Brain, 133(4), 1224–1238. https://doi.
org/10.1093/brain/awq043
Winawer, J., & Parvizi, J. (2016). Linking electrical stimulation
of human primary visual cortex, size of affected cortical area,
neuronal responses, and subjective experience. Neuron, 92(6),
1213–1219. https://doi.org/10.1016/j.neuron.2016.11.008
Yan, G., Vértes, P. E., Towlson, E. K., Chew, Y. L., Walker, D. S.,
Schafer, W. R., & Barabási, A. L. (2017). Network control princi-
ples predict neuron function in the Caenorhabditis elegans con-
nectome. Nature, 550(7677), 519–523. https://doi.org/10.1038/
nature24056
Yeh, F. C., Verstynen, T. D., Wang, Y., Fernández-Miranda, J. C.,
& Tseng, W. Y. I. (2013). Deterministic diffusion fiber tracking
improved by quantitative anisotropy. PLoS ONE, 8(11), 1–16.
https://doi.org/10.1371/journal.pone.0080713
IEEE Transactions on Medical
Yeh, F.-C., Wedeen, V. J., & Tseng, W.-Y. I. (2010). Generalized
Imaging,
q-sampling imaging.
29(9), 1626–1635. https://doi.org/10.1109/TMI.2010.2045126
Yendiki, A., Koldewyn, K., Kakunoori, S., Kanwisher, N., & Fischl, B.
(2014). Spurios group differences due to head motion in a diffu-
sion MRI study. Neuroimage, 88, 79–90. https://doi.org/10.1111/
obr.12065.Variation
Yushkevich, P. A., Pluta, J. B., Wang, H., Xie, L., Ding, S.-L., Gertje,
E. C., . . . Wolk, D. A. (2015). Automated volumetry and regional
thickness analysis of hippocampal subfields and medial tempo-
ral cortical structures in mild cognitive impairment. Human Brain
Mapping, 36(1), 258–287. https://doi.org/10.1002/hbm.22627.
Automated
Network Neuroscience
877
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
8
4
8
1
0
9
2
4
4
0
n
e
n
_
a
_
0
0
0
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3