研究 - 麻省理工学院人工智能研究专业

研究

Centralized and distributed cognitive task
processing in the human connectome

Enrico Amico1,2, Alex Arenas

3, and Joaquín Goñi1,2,4

1School of Industrial Engineering, Purdue University, West-Lafayette, 在, 美国
2Purdue Institute for Integrative Neuroscience, Purdue University, West-Lafayette, 在, 美国
3Departament d’Enginyeria Informàtica i Matemàtiques, Universitat Rovira i Virgili, Tarragona, 西班牙
4Weldon School of Biomedical Engineering, Purdue University, West-Lafayette, 在, 美国

关键词: Brain connectomics, Functional connectivity, Network science, Information theory,
Cognitive task processing

开放访问

杂志

抽象的

A key question in modern neuroscience is how cognitive changes in a human brain can be
quantiﬁed and captured by functional connectivity (FC). A systematic approach to measure
pairwise functional distance at different brain states is lacking. This would provide a
straightforward way to quantify differences in cognitive processing across tasks; 还, 它会
help in relating these differences in task-based FCs to the underlying structural network. 这里
we propose a framework, based on the concept of Jensen-Shannon divergence, to map the
task-rest connectivity distance between tasks and resting-state FC. We show how this
information theoretical measure allows for quantifying connectivity changes in distributed
and centralized processing in functional networks. We study resting state and seven tasks
from the Human Connectome Project dataset to obtain the most distant links across tasks.
We investigate how these changes are associated with different functional brain networks,
and use the proposed measure to infer changes in the information-processing regimes.
此外, we show how the FC distance from resting state is shaped by structural
连接性, and to what extent this relationship depends on the task. This framework
provides a well-grounded mathematical quantiﬁcation of connectivity changes associated
with cognitive processing in large-scale brain networks.

作者总结

A key question in modern neuroscience is how cognitive changes in a human brain can be
quantiﬁed and captured by functional connectivity (FC). Here we propose a framework,
based on Jensen-Shannon divergence, to deﬁne “connectivity distance” and to infer about
brain network reconﬁguration across different tasks with respect to resting state, 并
explore changes in centralized and distributed processing in FCs.

Three functional networks (dorsal attention, frontoparietal and DMN) showed major changes
in distributed processing and minor changes in centralized processing. Changes in
centralized processing depend on the underlying structural connectivity weights and
structural path “hiddenness.”

These ﬁndings suggest that the cognitive “switch” between resting state and task states is a
complex interplay between maximally and minimally distant functional connections, 和
underlying structure.

引文: Amico, E., Arenas, A。, & 戈尼,
J. (2019). Centralized and distributed
cognitive task processing in the human
connectome. 网络神经科学,
3(2), 455–474. https://doi.org/
10.1162/netn_a_00072

DOI:
https://doi.org/10.1162/netn_a_00072

支持信息:
https://doi.org/10.1162/netn_a_00072
https://engineering.purdue.edu/
ComplexityLab

已收到: 31 一月 2018
公认: 24 九月 2018

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
Joaquín Goñi
jgonicor@purdue.edu

处理编辑器:
Danielle Bassett

版权: © 2018
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Cognitive task processing in the human connectome

网络:
An ordered pair formed by a set of
nodes and a set of edges (哪个
represent connections between
pairs of nodes). Nodes are usually
represented by circles, 然而
edges are represented by lines or
arcs connecting pairs of nodes.

Diffusion-weighted imaging (DWI):
A form of magnetic resonance
成像 (MRI) technique based on
measuring the random Brownian
motion of water molecules within
a voxel based on sampling 3D
方向. This technique allows for
estimating white matter streamlines
and ﬁber bundles connecting brain
地区.

纤维束成像术:
Computational reconstruction
procedure that may be used to
obtain, from DWI data, 白色的
matter streamlines or ﬁber tracts
connecting different brain regions.

Functional magnetic resonance
成像 (功能磁共振成像):
A noninvasive technique that
estimates brain activity by detecting
changes associated with blood ﬂow.
The rationale of this technique relies
on the fact that there is a positive
association between cerebral blood
ﬂow and neuronal activation.

Connectome or structural
连接性 (SC) 矩阵:
A network representation of the
physical connections in the brain.
Nodes represent brain regions,
whereas edges represent physical
connections of pairs of brain
regions through the white matter.
Weights typically denote the density
or the integrity of the connections.

介绍

The progress in neuroimaging methodologies in recent years, together with the rise of pub-
licly available datasets (Van Essen, 史密斯, 等人。, 2013; Van Essen, Ugurbil, 等人。, 2012), 有
boosted research on quantitative analysis of brain connectivity patterns based on network sci-
恩斯. The intuition of modeling the brain as a network (Bassett & 布莫尔, 2006; 布莫尔
& 斯波恩斯, 2009; 假如, 扎莱斯基, & 布莫尔, 2016; 斯波恩斯, 2011) has rapidly expanded into
the scientiﬁc area denominated brain connectomics (假如, 扎莱斯基, & Breakspear, 2015;
Fornito et al., 2016). In brain network models, nodes correspond to gray matter regions (基于
on brain atlases or parcellations), while links or edges correspond to structural or functional
连接. Structural connections are estimated from diffusion-weighted imaging (碧涵,
2003; 图尔尼耶, 森, & 利曼斯, 2011) data by modeling white matter pathways through
tractography algorithms (右. 乙. 史密斯, 图尔尼耶, 卡拉曼特, & 康纳利, 2012, 2015; 图尔尼耶,
卡拉曼特, & 康纳利, 2012). Functional connections represent statistical dependencies be-
tween brain region time series while subjects are either at rest or performing a task during
functional MRI (功能磁共振成像) sessions (van den Heuvel & Hulshoff Pol, 2010). These functional asso-
ciations are usually measured via correlations among fMRI time series to study functional con-
nectivity (FC) in the human brain (狐狸 & Raichle, 2007; van den Heuvel & Hulshoff Pol, 2010).

These recent advances have led the brain connectivity community to start exploring and
quantify differences between resting-state FCs and task-based FCs (Cole, Bassett, 力量, Braver,
& 彼得森, 2014; Cole et al., 2013; Cole & 施耐德, 2007; Gonzalez-Castillo et al., 2012;
Gratton, 劳曼, Gordon, Adeyemo, & 彼得森, 2016; 克里宁, 杨, & 巴克纳, 2014).
Some of the main lines of research in this direction involved whole-brain network similar-
ity analyses on the intrinsic and task-evoked network architecture of human connectome
(Cole et al., 2014); the mapping of cortical hubs and brain region for adaptive task control
(so-called cognitive control network (Cole et al., 2013; Cole & 施耐德, 2007); and the in-
vestigation of activity ﬂow from resting-state FCs to infer brain regions that carry diverse cog-
nitive task information (Cole et al., 2013; Ito et al., 2017). Despite all these efforts in trying to
characterize connectivity differences between resting-state and task activity in brain networks,
a systematic analysis on how to measure pairwise (IE。, at the level of FC links) “cognitive dis-
tance” between these different functional states is still lacking. Such a methodology would pro-
vide a straightforward way to quantify differences in cognitive processing across tasks; 还, 它
would help in relating these local differences in task-based FCs to the underlying structural net-
work architecture, another exciting avenue for the brain connectomics community (Fukushima
等人。, 2018; Hermundstad et al., 2013; Hermundstad et al., 2014; Medaglia et al., 2018; Miši´c
等人。, 2016; see also our recent work, Amico & 戈尼, 2018).

Here we propose a framework, based on Jensen-Shannon (JS) 分歧 (Brit & Harremos,
2009; Cover & 托马斯, 2012), to map the “cognitive distance” between task and resting-state
functional connections. We show how this simple measure allows for quantifying the amount
of changes in distributed and centralized processing in human functional networks.

We use resting-state and seven different task sessions from the Human Connectome Project
(HCP) database to obtain the most JS-distant edges across tasks. We study how these changes
across tasks are associated with different functional brain networks, and use the proposed
measure to infer modiﬁcations in the information-processing regimes of these networks. 毛皮-
瑟莫雷, we show how cognitive distance is shaped by the brain structural architecture and
the level of nestedness of axonal pathways, and to what extent this relationship depends on the
任务. We conclude by discussing the new insights offered by this approach, as well as potential
applications and future directions.

网络神经科学

456

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Cognitive task processing in the human connectome

Jensen-Shannon divergence:
In probability theory and statistics,
the Jensen-Shannon divergence
is a method of measuring the
dissimilarity between two probability
分布. The square root of the
Jensen-Shannon divergence is a
metric often referred to as Jensen-
Shannon distance.

方法

数据集

The fMRI dataset used in this work is from the publicly available Human Connectome Project
(HCP, http://www.humanconnectome.org/ ), Release Q3. Per HCP protocol, all subjects gave
written informed consent to the Human Connectome Project consortium. Below is the full
description of the acquisition protocol and processing steps.

HCP: Functional Data

We assessed the 100 unrelated subjects (54 女性, 46 males, mean age = 29.1 年, 标准差=
3.7 年) as provided at the HCP 900 subjects data release (Van Essen, 史密斯, 等人。, 2013;
Van Essen, Ugurbil, 等人。, 2012). This subset of subjects provided by HCP ensures that they
are not family relatives. This criterion was crucial to exclude the need of family-structure co-
variables in our analyses as well as possible identiﬁability confounds. The fMRI resting-state
runs were acquired in separate sessions on two different days (HCP ﬁlenames: rfMRI_REST1
and rfMRI_REST2), with two different acquisitions (left to right or LR, and right to left or RL)
per day (Glasser et al., 2013; S. 中号. 史密斯等人。, 2013). The seven fMRI tasks were gam-
bling (tfMRI_GAMBLING), relational (tfMRI_RELATIONAL), 社会的 (tfMRI_SOCIAL), 在职的
记忆 (tfMRI_WM), motor (tfMRI_MOTOR), 语言 (tfMRI_LANGUAGE, including both a
story-listening and an arithmetic task), and emotion (tfMRI_EMOTION). The working memory,
gambling, and motor tasks were acquired on the ﬁrst day, and the other tasks were acquired
on the second day (Barch et al., 2013; Van Essen, 史密斯, 等人。, 2013). The HCP scanning
protocol was approved by the local Institutional Review Board at Washington University in
英石. 路易斯. For all sessions, data from both the left-right (LR) and right-left (RL) phase-encoding
runs were averaged to calculate connectivity matrices. This operation was done for all seven
fMRI tasks. Full details on the HCP dataset have been published previously (Glasser et al.,
2013; S. 中号. 史密斯等人。, 2013; Van Essen, Ugurbil, 等人。, 2012).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

HCP: Structural Data

We used DWI runs from the same 100 unrelated subjects of the HCP 900 subjects data re-
租 (Van Essen, 史密斯, 等人。, 2013; Van Essen, Ugurbil, 等人。, 2012). The diffusion acquisi-
tion protocol is covered in detail elsewhere (Glasser et al., 2013; Sotiropoulos et al., 2013;
Uurbil et al., 2013). Below we mention the main characteristics. Very high-resolution acqui-
地点 (1.25 mm isotropic) were obtained by using a StejskalTanner (monopolar) (Stejskal &
Tanner, 1965) diffusion-encoding scheme. Sampling in q-space was performed by including
three shells at b = 1, 000, 2, 000, 和 3, 000 秒/毫米2. For each shell corresponding to 90 扩散
gradient directions and ﬁve reference volumes ( b = 0) were obtained, with the phase-encoding
direction reversed for each pair (IE。, LR and RL pairs). Directions were optimized within and
across shells (IE。, staggered) to maximize angular coverage using the approach of Caruyer et al.
(2011; http://www-sop.inria.fr/members/Emmanuel.Caruyer/q-space-sampling.php), and form
a total of 270 noncollinear directions for each phase-encoding direction. Correction for EPI
and eddy current-induced distortions in the diffusion data was based on manipulation of the
acquisitions so that a given distortion manifests itself differently in different images (安德森,
Skare, & Ashburner, 2003). To ensure better correspondence between the phase-encoding re-
versed pairs, the whole set of diffusion-weighted (DW) volumes is acquired in six separate
系列. These series were grouped into three pairs, and within each pair the two series
contained the same DW directions but with reversed phase-encoding (IE。, a series of Mi

网络神经科学

457

Cognitive task processing in the human connectome

DW volumes with RL phase-encoding is followed by a series of Mi volumes with LR phase-
encoding, where i = [1, 2, 3]).

Brain atlas. We employed a cortical parcellation into 360 brain regions as recently proposed
by Glasser et al. (2016). For completeness, 14 subcortical regions were added, as provided
by the HCP release (ﬁlename Atlas_ROI2.nii.gz). 这样做, this ﬁle was converted from NIFTI
to CIFTI format by using the HCP workbench software (Glasser et al., 2013; Marcus et al., 2011;
http://www.humanconnectome.org/software/connectome-workbench.html, command -cifti-
create-label).

HCP Preprocessing: Functional Data

The HCP functional preprocessing pipeline (Glasser et al., 2013; S. 中号. 史密斯等人。, 2013)
was used for the employed dataset. This pipeline included artifact removal, motion correction,
and registration to standard space. Full details on the pipeline can be found in Glasser et al.
(2013) 和S. 中号. Smith et al. (2013). The main steps were spatial (最小的) preprocessing,
in both volumetric and grayordinate forms (IE。, where brain locations are stored as surface
vertices; S. 中号. 史密斯等人。, 2013); weak high-pass temporal ﬁltering (>2,000 s full width at
half maximum) applied to both forms, achieving slow drift removal; MELODIC ICA (詹金森,
贝克曼, 贝伦斯, 伍尔里奇, & 史密斯, 2012) applied to volumetric data; and artifact com-
ponents identiﬁed using FIX (Salimi-Khorshidi et al., 2014). Artifacts and motion-related time
courses were regressed out (IE。, the six rigid-body parameter time series, their backwards-
looking temporal derivatives, plus all 12 resulting regressors squared) of both volumetric and
grayordinate data (S. 中号. 史密斯等人。, 2013).

For the resting-state fMRI data, we also added the following steps: global gray matter signal
was regressed out of the voxel time courses (Power et al., 2014); a bandpass ﬁrst-order But-
terworth ﬁlter in forward and reverse directions [0.001 赫兹, 0.08 赫兹] (Power et al., 2014) 曾是
applied (MATLAB functions butter and ﬁltﬁlt); and the voxel time courses were z-scored and
then averaged per brain region, excluding outlier time points outside of 3 标准差
from the mean, using the workbench software (workbench command -cifti-parcellate). For task
fMRI data, we applied the same above-mentioned steps but we opted for a more liberal band-
pass ﬁlter [0.001 赫兹, 0.25 赫兹], since it is still unclear the connection between different tasks
and optimal frequency ranges (Cole et al., 2014).

Pearson correlation coefﬁcients between pairs of nodal time courses were calculated
(MATLAB command corr), resulting in a symmetric connectivity matrix for each fMRI session
of each subject. In this paper we will refer to this matrix as functional connectivity matrix or
functional connectome (FC). As aforementioned, data from both the left-right (LR) and right-
左边 (RL) phase-encoding runs were averaged to calculate individual functional connectomes
in each fMRI session. Functional connectivity matrices were kept in its signed weighted form,
hence neither thresholded nor binarized. 最后, the resulting individual functional connec-
tivity matrices were ordered (rows and columns) according to seven functional cortical sub-
网络 (FNs) as proposed by Yeo and colleagues (Yeo et al., 2011). 这样做, for each brain
region in the Glasser atlas, the FN-membership (as a percentage) to each of the seven functional
网络 (sum of the membership vector being equal to 1) was calculated. 最后, each brain
region was assigned to the most highly present FN. For completeness, an eighth subnetwork
包括 14 HCP subcortical regions was added (as analogously done in recent papers;
Amico & 戈尼, 2018; Amico et al., 2017).

Functional connectome/connectivity
(FC) 矩阵:
A network representation of the
functional coupling between brain
地区. Such coupling is usually
measured by quantifying the
statistical dependencies between
time series of brain regions (例如,
pairwise Pearson’s correlation,
mutual information) as obtained by
functional magnetic resonance
成像 (功能磁共振成像).

网络神经科学

458

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Cognitive task processing in the human connectome

HCP Preprocessing: Structural Data

The HCP DWI data were processed following the MRtrix3 (Tournier et al., 2011) guidelines
(http://mrtrix.readthedocs.io/en/latest/tutorials/hcp_connectome.html). 总之, we ﬁrst
generated a tissue-segmented image appropriate for anatomically constrained tractography
(ACT; 右. 乙. 史密斯等人。, 2012; MRtrix command 5ttgen); we then estimated the multi-shell,
multi-tissue response function (Christiaens et al., 2015; MRtrix command dwi2response
msmt_5tt) and performed the multi-shell, multi-tissue constrained spherical deconvolution
(约里森, 图尔尼耶, 多霍兰德, 康纳利, & 西贝尔斯, 2014; MRtrix dwi2fod msmt_csd). 后-
wards, we generated the initial tractogram (MRtrix command tckgen, 10 million streamlines,
maximum tract length = 250, FA cutoff = 0.06) and applied the successor of spherical-
deconvolution informed ﬁltering of tractograms (SIFT2; 右. 乙. 史密斯等人。, 2015) 方法论
(MRtrix command tcksift2). Both SIFT (右. 乙. 史密斯, 图尔尼耶, 卡拉曼特, & 康纳利, 2013)
and SIFT2 (右. 乙. 史密斯等人。, 2015) methods provide more biologically meaningful estimates
of structural connection density. SIFT2 allows for a more logically direct and computationally
efﬁcient solution to the streamlines connectivity quantiﬁcation problem: By determining an
appropriate cross-sectional area multiplier for each streamline rather than removing stream-
lines altogether, measures of ﬁber connectivity are obtained while making use of the complete
streamlines reconstruction (右. 乙. 史密斯等人。, 2015). 最后, we mapped the SIFT2 outputted
streamlines onto the 374 chosen brain regions (360 from the Glasser et al., 2016, brain atlas
加 14 subcortical regions; see the Brain Atlas section) to produce a structural connectome
(MRtrix command tck2connectome). 最后, a log10 transformation (Fornito et al., 2016) 曾是
applied on the structural connectomes (SC; IE。, the anatomical networks) to better account
for differences at different magnitudes. In consequence, SC values ranged between 0 和 5 在
this dataset.

Jensen-Shannon Distance on Functional Edges

The Jensen-Shannon divergence is a method commonly used to measure dissimilar-
ities between two probability distributions (Brit & Harremos, 2009; Cover & 托马斯, 2012;
De Domenico, 尼科西亚, Arenas, & Latora, 2015). In the case of two discrete probability distri-
butions P and Q, the Jensen-Shannon divergence (JSD) is deﬁned by

JSD(磷||问) = 1
2

DKL(磷||中号) + 1
2

DKL(问||中号),

(1)

where M = 1
2
For two discrete probability distributions P and Q, it is deﬁned by

(磷 + 问) and DKL is the Kullback-Leibler divergence (Cover & 托马斯, 2012).

DKL(磷||问) = − ∑
我

磷(我) 日志

问(我)
磷(我) .

(2)

For the particular case of measuring the dissimilarity between two probability distributions P
and Q, the Jensen-Shannon divergence is bounded between 0 和 1, given that one uses the
根据 2 logarithm:

0 ≤ JSD(磷||问) ≤ 1.

(3)

It has been shown that the square root of the Jensen-Shannon divergence is a well-deﬁned
distance metric (Endres & Schindelin, 2003; Österreicher &Vajda, 2003), often referred to as
“Jensen-Shannon distance”:

(西德:2)

JSdist(磷||问) =

JSD(磷||问).

(4)

459

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Cognitive task processing in the human connectome

We used the JSdist to map “connectivity distance” between resting-state and task sessions.
Here we assume resting state to be the “cognitive baseline,” and we measured the JSdist link
to link from every task FCs to resting-state FCs. Below follows a detailed description of the
procedure (see also the scheme at Figure 1). 第一的, for every edge in a functional connectome,
we extracted the corresponding individual values (在......之外 100 HCP subjects, we picked 50
subjects for resting-state FCs and 50 different subjects for the task FCs). In this study, this resulted
in having two vectors with 50 元素, one for each resting-state edge and one for each
edge in the task FCs whose JS distance is to be evaluated. These vectors represent Pearson’s
correlation distributions of connectivity values across all subjects in the cohort. 第二, 我们
transform these two Pearson’s distributions into discrete probability distributions. We sampled
这 [−1, 1] Pearson’s range via uniform binning (bin width = 0.2), and counted the likelihood
of occurrence of the connectivity values in each bin. 最后, the JSdist between these two
probability distributions was computed for every edge and HCP task considered in this study.
This edgewise functional connectivity distance from resting state can be seen as a task-speciﬁc
connectivity distance. 那是, how far the distribution of values is in a speciﬁc task with respect
to the resting-state FC baseline.

The Jensen-Shannon distance as deﬁned above is thought for the general case where the
two distributions P and Q come from different data samples (例如, different subjects). 这不是

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

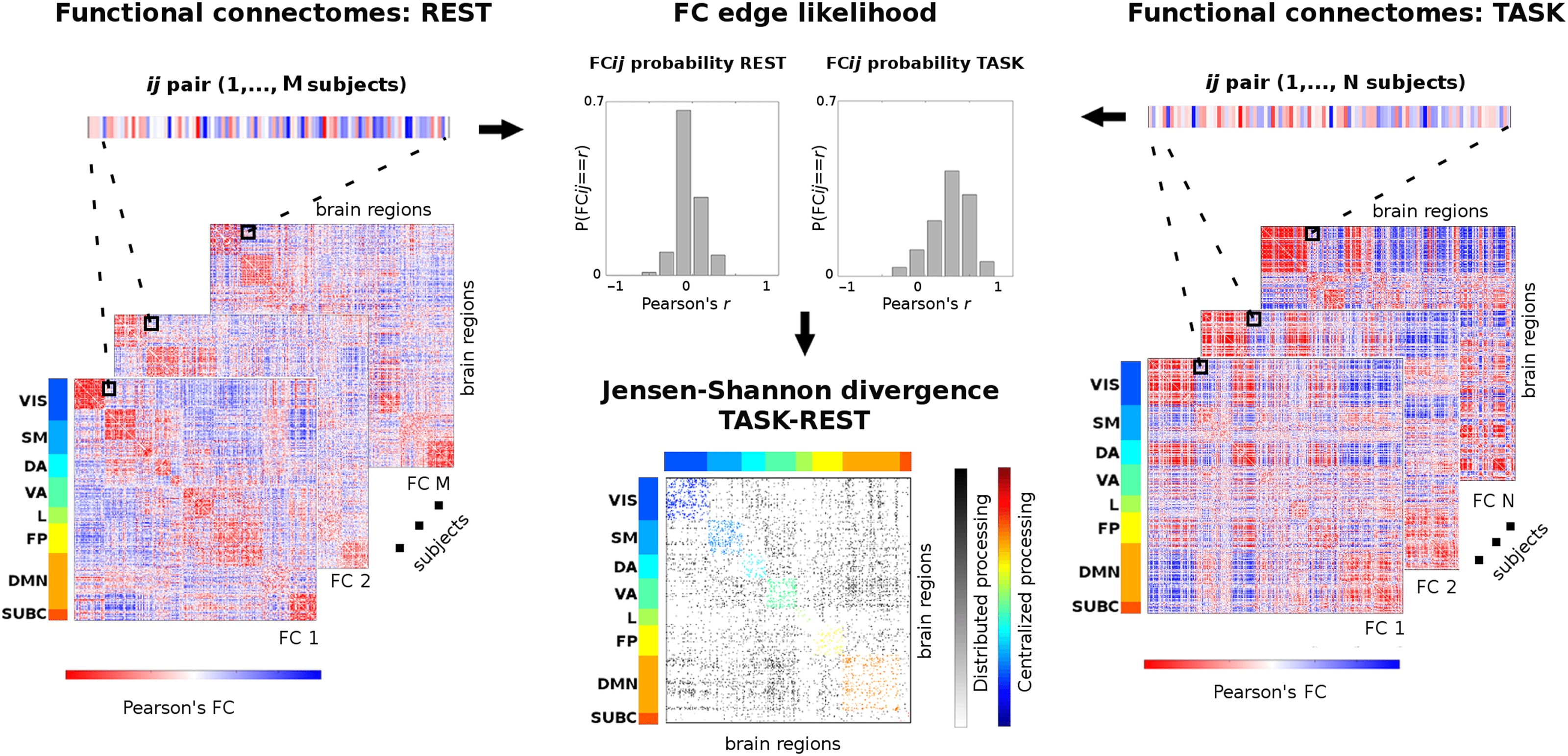
数字 1. Workﬂow scheme for task-rest connectivity distance (unpaired). This scheme summarizes the procedure to measure edgewise dis-
tance from two cohorts of (M and N) functional connectomes (FCs) at rest (左边) to a task-based one (正确的). 第一的, an edge ij is extracted from
集合, for both the resting-state and task-based FCs; these two vectors of M and N connectivity values are then transformed into probability
分布 (center top); ﬁnally, the Jensen-Shannon distance for these two edgewise probabilities is computed (center bottom). Iterating this
procedure over all possible ij pairs gives a Jensen-Shannon (JS) matrix of local distance in task FCs with respect to the REST baseline. 这
JS matrix is ordered by the seven functional networks (FNs): visual (VIS), somatomotor (SM), dorsal attention (DA), ventral attention (VA),
limbic (L), frontoparietal (FP), and default mode network (DMN). An eighth subcortical network (SUBC) is added for completeness. 之内-
network most distant edges are color coded according to FNs. Between-network most distant edges are in gray scale. This method allows for
quantifying the changes between centralized (within-network) 并分布式 (between-network) processing when a speciﬁc task is performed
with respect to the resting-state baseline.

网络神经科学

460

Cognitive task processing in the human connectome

dist

the most proper assessment in situations (like in the HCP data) where repeated measurements
from same subjects are available, allowing for paired comparisons between FCs. To cover the
necessity of that, we extended the concept of Jensen-Shannon distance by proposing a “paired”
version of JSdist, namely JSpaired
, as follows. Similarly to JSdist, for every edge in a functional
connectome, we extract the corresponding individual values. Then we take the element-wise
difference between the two vectors, where subjects are indexed in the same order. Such a
difference vector is then used to obtain distribution P([−2, 2] 范围, with uniform binning size
的 0.1). We then compare P against a “null” distribution Q, which is probability 1 at the bin
包括 0 价值, 和 0 for all other bins. Such Q distribution reﬂects the expectation
of having no difference between repeated measurements. Deviations of P with respect to Q
on functional edges reﬂect individual changes (in any direction and/or magnitude) 之间
repeated measurements on subjects. 最后, we iterate this procedure for every edge and task
to compute JSpaired

dist

Centralized and Distributed Processing in Functional Connectomes
The aforementioned procedure produced 374 × 374 (IE。, number of regions in the employed
brain atlas) JSdist matrices per each task. 下一个, we sought to relate the proposed connectivity
distance measure with changes in functional processing across functional networks (FNs). 到
do so, we ﬁrst thresholded the JSdist matrices based on the 95th percentile of the entire JSdist
distribution of values across all tasks, to select only the most distant links from resting state (看
数字 2). 下一个, we quantify the amount of change in each of the eight functional FNs (看到
HCP Preprocessing: Functional Data section for details on the chosen FNs) by counting the
number of edges that survived the threshold divided by the total number of edges present in
each FN. We can then formalize changes in centralized processing (CP), for each functional
network k, 作为

CPk =

(西德:2)JSdist(我, j)
W Nk(我, j) ,

∑
我,j∈W Nk
∑
我,j∈W Nk

(5)

在哪里 (西德:3)JSdist is the binary version of the JSdist matrix thresholded at the 95 percentile (1 为了
surviving edges, 0 别处) for a speciﬁc task, and W Nk
is a binary matrix of the same size
作为 (西德:3)JSdist, 和 1 if an edge falls within functional network k, 和 0 别处. 相似地, 一
can quantify changes in distributed processing (DP) 作为

DPkl =

(西德:2)JSdist(我, j)
BNkl(我, j) ,

∑
我,j∈BNkl
∑
我,j∈BNkl

(6)

where now BNkl
functional networks k, 我, 和 0 别处.

is a binary matrix of the same size as (西德:3)JSdist, 和 1 if an edge falls between

因此, for each one of the eight functional networks considered here (see the HCP Prepro-
cessing: Functional Data section for details), one can obtain one value of CP and seven values
of DP (considering all pairwise FN interactions), for a speciﬁc task. These values provide an
estimate of the density of the most connectivity distant functional links across, 之内, 和

网络神经科学

461

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Cognitive task processing in the human connectome

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

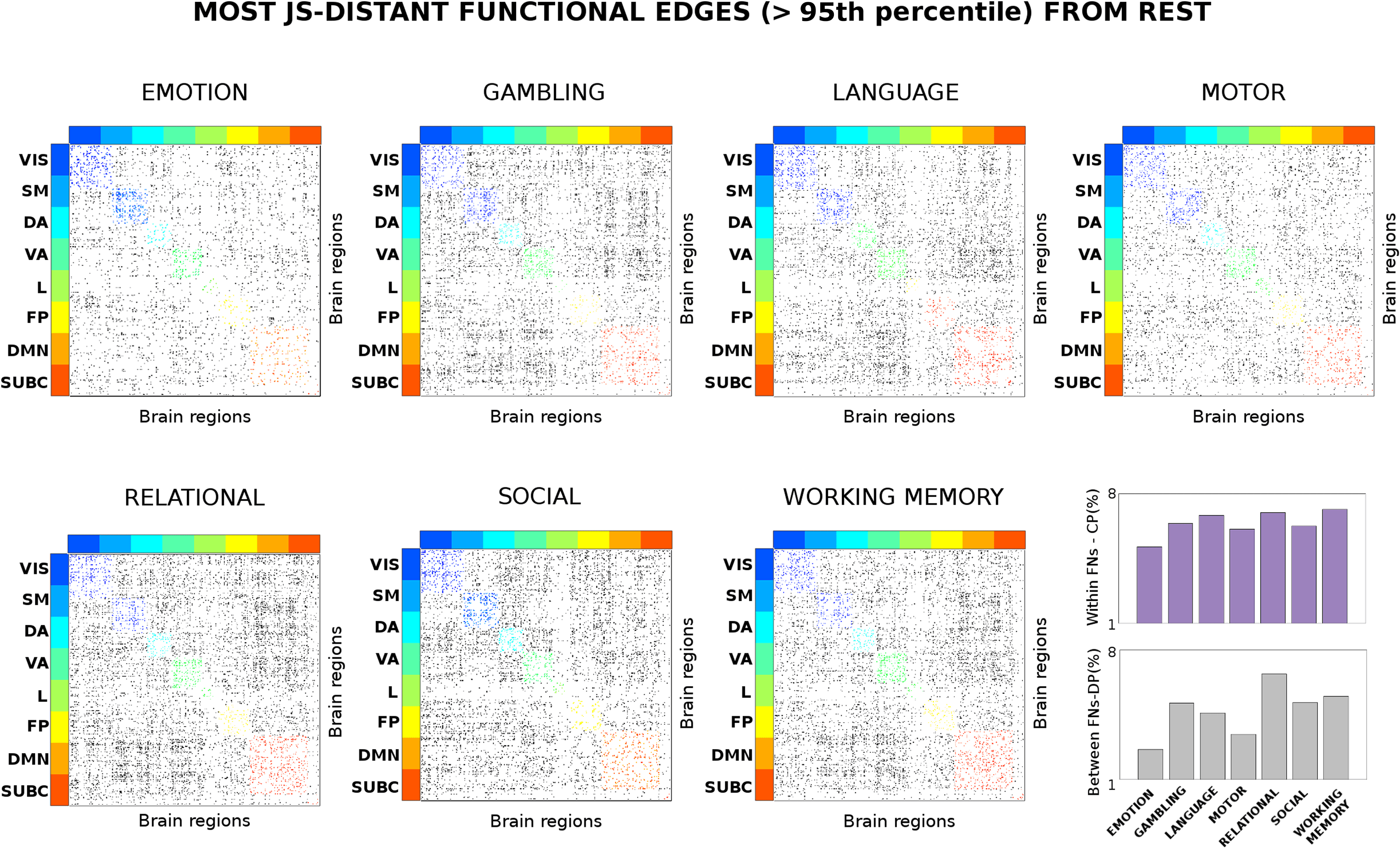
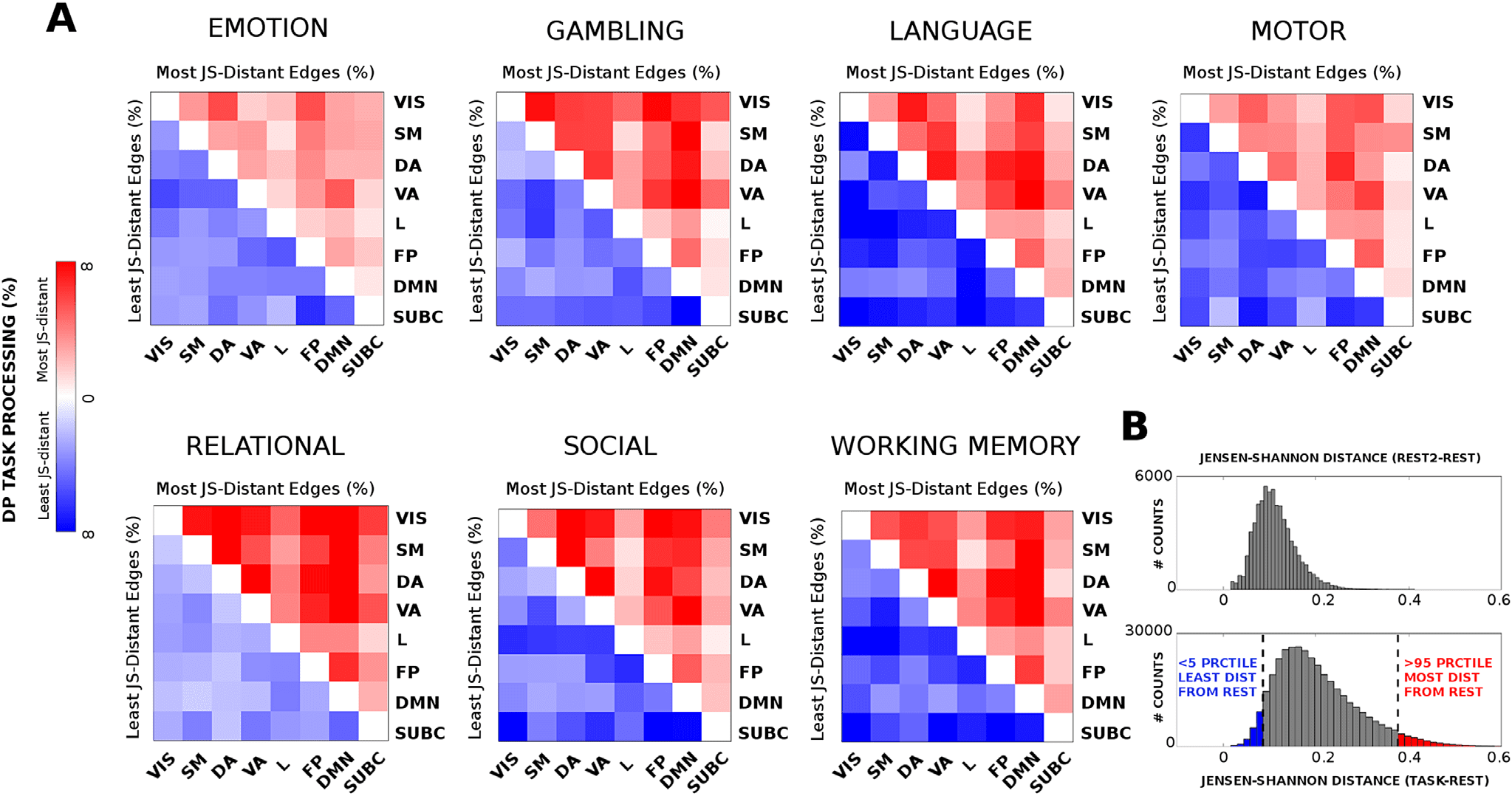
数字 2. Connectivity distance across different tasks. Evaluation of the most distant functional links (in terms of Jensen-Shannon [JS] distance;
参见方法) across seven different task sessions. The JS matrices were thresholded at the 95th percentile of the distribution of JS values across
the seven tasks. The JS matrices were then ordered by seven functional networks (FNs; Yeo et al., 2011); visual (VIS), somatomotor (SM), dorsal
注意力 (DA), ventral attention (VA), limbic (L), frontoparietal (FP), and default mode network (DMN). An eight subcortical network (SUBC)
was added for completeness. The edges surviving the threshold corresponding to within-FN connections are color-coded accordingly. Edges
corresponding to between-FN connections are depicted in gray scale. Note how the connectivity distance depends on the task: 在某些情况下
within-FN connectivity is more recruited (IE。, for the emotion task), in other between-FN connections are the most distant (IE。, relational
任务). The bottom-right bar plots depict the average percentage of within-FN most distant edges, IE。, centralized processing (CP, violet bars)
and the average percentage of between-FN edges, 那是, distributed processing (DP, gray bars) across the different tasks.

between FN connectivity. 那是, the amount of local changes in distributed and centralized
processing in each FN from baseline, deﬁned as resting-state functional connectivity.

Bandpass Filter Evaluation on Centralized and Distributed Processing Analysis

In order to check whether the different bandpass ranges applied for resting state and task had
an impact on centralized and distributed processing in FCs, we applied the same (liberal,
IE。, [0.001赫兹, 0.25赫兹]) bandpass ﬁlter onto resting-state data. We then evaluated changes
in centralized and distributed processing after the new bandpass, and checked the similarity
with the “standard” bandpass results by computing the cosine similarity between the vectors
deﬁned by centralized and distributed processing coordinates. Cosine similarity is a measure
of similarity between two nonzero vectors of an inner product space that measure the angle
它们之间. 这里, each vector represents a point in the state space deﬁned by centralized
and distributed processing.

网络神经科学

462

Cognitive task processing in the human connectome

Null Model Evaluation for Connectivity Distance Analysis

To validate the JSdist results in functional connectomes, we tested the same approach on
randomized counterparts (or “surrogates”) of the original data. 这样做, we employed the
amplitude adjusted fourier transform (AAFT) surrogates method (Schreiber & Schmitz, 2000)
to obtain data random surrogates. Starting from the 374 fMRI time series (one per brain region
in the atlas; see also the Brain Atlas section), we generated AAFT fMRI time series surrogates as
proposed in (Schreiber & Schmitz, 2000). This method aims to build surrogate time series that
preserve the amplitude distribution and the power spectrum of the original data (Schreiber &
Schmitz, 2000).

For each of the seven HCP tasks and resting state, we computed 100 surrogate versions of
the functional connectivity matrices, and then evaluated the number of nonzero elements in
(西德:3)JSdistsurrogate for each of the 100 realizations. This provided null distributions (one per task) 为了
the connectivity distance measure, which allowed us to test whether the results obtained on
the original FCs were statistically signiﬁcant.

最后, in order to test the signiﬁcance of differences between pairs of (highly structured)
correlation matrices, we also employed a permutation test that preserved intact the correlation
structure of the FC matrices but randomly permuted the task/rest labels, computed the JS dis-
tance on the permuted data, and then evaluated the number of JS edges per task surviving the
95% threshold based on the original data.

Estimation of Functional Connectivity Distance Associations with Structural Connectomes

下一个, we sought to assess the role of structural connections in the connectivity distance of func-
tional links across all seven tasks. In order to do so, we divided the group-averaged structural
连接性 (SC) 重量 (see the HCP Preprocessing: Structural Data section for details on SC
计算) into ﬁve different percentile intervals {0−20; 20−40; 40−60; 60−80; 80−100}. 我们
then counted the average number of most distant edges (IE。, the nonzero elements of (西德:3)JSdist)
falling in each of the ﬁve percentile intervals, for each of the seven HCP tasks. This provides
an estimate on the relationship between structural connections and connectivity distance and
whether it depends on the speciﬁc task being performed. We also tested whether centralized
and distributed processing depend on the “nestedness” or “hiddenness” of the structural path-
方法, as measured by search information (Goñi et al., 2014; Rosvall, Grönlund, Minnhagen,
& Sneppen, 2005; Trusina, Rosvall, & Sneppen, 2005). Search information (和) quantiﬁes the
accessibility or hiddenness of the shortest path between a source node and a target node within
the network by measuring the amount of knowledge or information in bits needed to access
the path (Goñi et al., 2014; Rosvall et al., 2005; Trusina et al., 2005; Wirsich et al., 2016) 这
more nested the shortest path is between two brain regions ij, the higher its SI value; 骗局-
versely, the less hidden or integrated the path, the lower its SI value. Similarly to the exper-
iment performed on SC weights, we again divided the group-average SI range of values into
ﬁve different percentile intervals: {0−20; 20−40; 40−60; 60−80; 80−100}. 最后, we counted
the average number of most distant edges (IE。, the nonzero elements of (西德:3)JSdist) falling in each
of the ﬁve SI percentile intervals, for each of the seven HCP tasks. This provides an estimate on
the relationship between structural “hiddenness” and connectivity distance and its associations
with the speciﬁc task being performed. For both SC weights and SI, the signiﬁcance of the asso-
ciations with centralized and distributed processing was assessed through one-way analysis of
方差 (ANOVA; Hogg & Ledolter, 1987; MATLAB command anova1), with “observations”
being centralized and distributed processing values for the seven tasks, and “groups” being the
ﬁve percentile intervals described above.

Search information:
A measurement that quantiﬁes the
accessibility or hiddenness of the
shortest path between a source
node and a target node within the
network by measuring the amount
of knowledge or information
(expressed in bits) needed to
access that exact path.

网络神经科学

463

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Cognitive task processing in the human connectome

结果

Metric:
In mathematics, a metric or distance
function is a function that deﬁnes a
distance between each pair of
elements of a set and satisﬁes the
properties of nonnegativity, 身份
of indiscernibles, symmetry, 和
triangle inequality. A set with a
metric is called a metric space.

The dataset used for this study consisted of functional data from the 100 unrelated subjects in
the Q3 release of the HCP (Van Essen, 史密斯, 等人。, 2013; Van Essen, Ugurbil, 等人。, 2012).
We deﬁned the “connectivity distance” between task FC links and resting-state FC links as the
edgewise Jensen-Shannon distance (JSdist) between resting-state FCs and task FCs (see also
the scheme at Figure 1). This metric quantiﬁes the connectivity distance of a functional link
recruited in a task with respect to its correspondent “usage” in resting state. For each of the
seven HCP tasks (see Methods for details), we computed the corresponding JSdist and JSpaired
matrices, and extracted the most connectivity distant edges (≥ 95 percentile distribution of
JSdist and JSpaired
values across all tasks). 数字 2 shows the results corresponding to JSdist
(unpaired, all different subjects for resting-state and task FCs), and Figure S1 (Amico, Arenas,
& 戈尼, 2019) summarizes the results for JSpaired
(paired, same subjects for resting-state and
dist
task FCs). Please also see the Jensen-Shannon Distance on Functional Edges section for details.

dist

尤其, the results obtained are signiﬁcantly different from the same analyses performed
在 100 realizations of surrogate data built from the fMRI time series considered in this study
(Figure S2 and Table S1, Amico et al., 2019); see the Null Models Evaluation for Connectivity
Distance Analysis section for details). 此外, with the only exception of motor versus
emotion for absolute frame displacement, no signiﬁcant differences were observed in frame-
wise displacement estimates (p < 0.01, double-sided t test between task pairs). This included absolute frame displacement (root mean squared, HCP ﬁlename Abs_RMS) and relative frame l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 4 5 5 1 0 9 2 6 0 0 n e n _ a _ 0 0 0 7 2 p d . 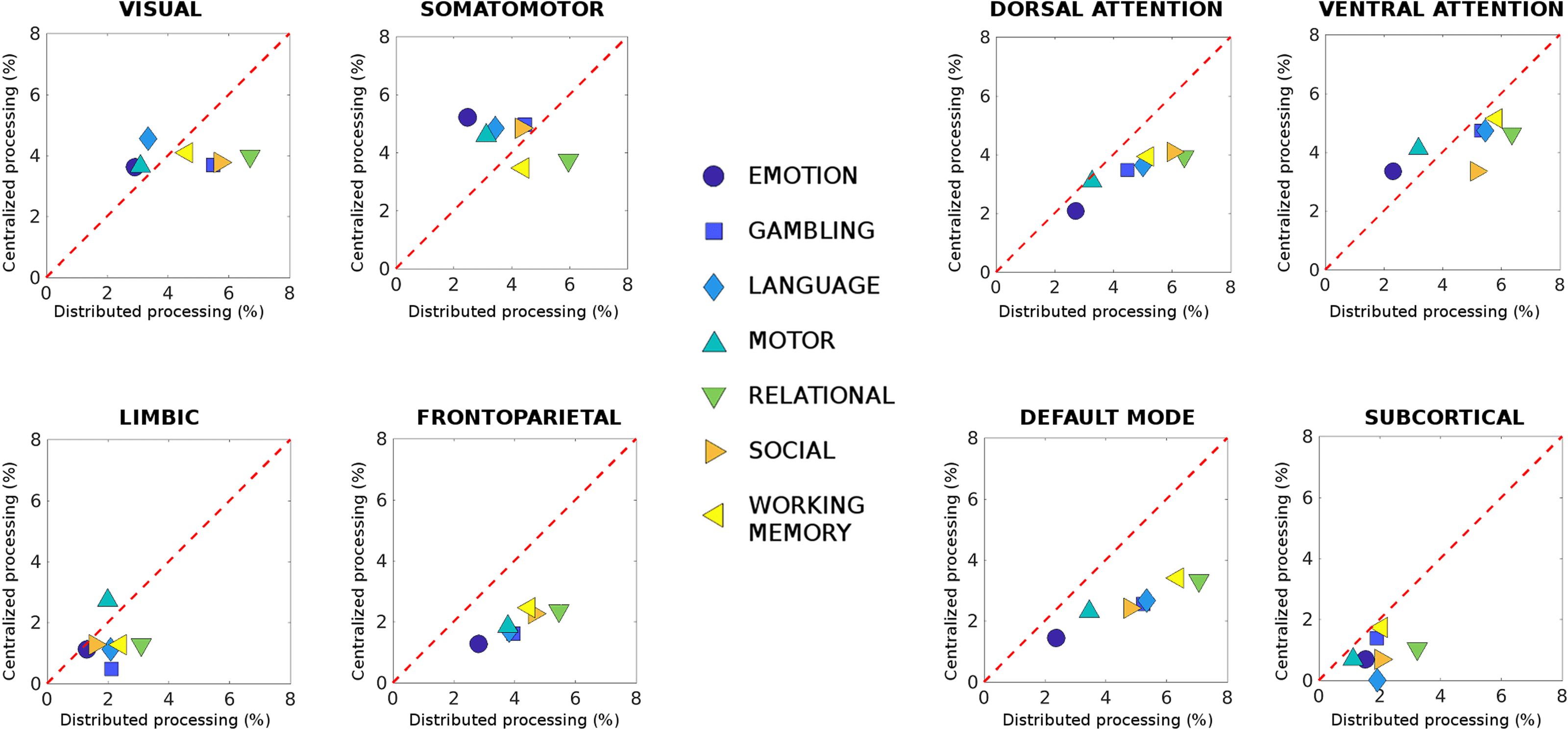t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 3. Centralized and distributed task processing in functional connectomes. Each plot shows differences in centralized versus distrib- uted processing (see Methods) for each of the seven functional networks (FNs; visual, somatomotor, dorsal and ventral attention, limbic, frontoparietal, and DMN; Yeo et al., 2011) and subcortical network, for all seven different HCP tasks. The difference in centralized processing with respect to resting state was deﬁned as the number of most Jensen-Shannon (JS) distant edges within-FN divided by the total number of edges in the FN (reported as percentage). Similarly, deviations from distributed processing in resting state were deﬁned as the number of most JS-distant edges between FN divided by the total number of between-FN connections. Note how FP and DMN networks deviate from rest mainly in the amount of distributed processing, that is, between-FN connectivity. Network Neuroscience 464 Cognitive task processing in the human connectome displacement (root mean squared, HCP ﬁlename Rel_RMS). These ﬁndings suggest that head motion is not biasing rest to task JS distances depicted in Figure 2 and Figure S1 (Amico et al., 2019). Interestingly, the level of distance from resting state seems to be associated with the speciﬁc task (Figure 2). For some tasks, the within-functional network links are more distant, that is, more involved (e.g., for the emotion and motor tasks); in others the between-FN connections are the most distant ones (i.e., relational or working memory tasks). The dichotomy between intra-network (i.e., centralized) and inter-network (i.e., distributed) distance led us to quan- tify the changes in centralized and distributed processing in task FCs (Figure 3; also see the Centralized and Distributed Processing in Functional Connectomes section). Note how, for three functional networks—dorsal, frontoparietal, and default mode—there is a clear demarcation between centralized and distributed processing, for all seven tasks evalu- ated (Figure 3). This indicates that the functional connections between these networks get more distant from rest when they are recruited in a task. Furthermore, with the exception of limbic and subcortical networks, where little difference in centralized and distributed processing can be observed (Figure 3), in all the other FNs (i.e., visual, somatomotor, and ventral attention) there is balance between intra- and inter-network processing. This trade-off seems to depend on the task at hand (slightly more centralized in some, more distributed in others; Figure 3). Note that these different distributions of centralized and distributed processing across tasks are not related to the different bandpass applied for rest and task data, since very similar results were obtained when the same (liberal, i.e., [0.001Hz, 0.25Hz]) bandpass parameters were applied onto resting-state data; (see Figure S3 in the supporting information, Amico et al., 2019). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 5 5 1 0 9 2 6 0 0 n e n _ a _ 0 0 0 7 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 4. Least and most distant edges per functional network across tasks. (A) Heat maps, for all seven fMRI tasks evaluated, showing the most (red, upper triangular) and least (blue, lower triangular) distributed processing (DP) values between pairs of functional networks with respect to REST. (B) Top: distribution of JS-distance values when comparing REST2 session to the baseline REST session. Bottom: distribution of Jensen-Shannon distance values across the seven tasks evaluated. The tails of the histogram are highlighted in blue (least distant edges, < 5th percentile) and red (most distant edges, > 95th percentile).

网络神经科学

465

Cognitive task processing in the human connectome

When looking at JS-distance differences between functional networks across tasks, 任务-
speciﬁc patterns may be observed (see Figure 4A). 例如, relational tasks exhibit a
whole-brain tendency to get more distant from rest (IE。, higher general distributional process-
英); emotion or motor tasks are among the least distant from rest; whereas some other tasks
(例如, language or social) display a more specialized distributed processing across functional
networks combining most and least distant functional edges. The histogram of the distribution
of JS-distance values across all tasks gives more insights on the cognitive distance task-rest:
there is a general tendency to be different from REST. 然而, some edges (< 5%, Figure 4B, blue bars) stay almost unchanged with respect to REST conﬁguration; others (> 95%, Figure 4B,
red bars) switch to more distant values, allowing for the cognitive reconﬁguration of the sys-
TEM. Note that the JS distance does not depend on the baseline (IE。, REST FCs) magnitude of
the correlations, as the average correlation between JS-values and median REST FC correlation
values across tasks is −0.006 ± 0.026. 重要的, no single edge survived to the 95th per-
centile threshold after permutation testing of the TASK-REST labels (see Methods for details;
Figure S4, Amico et al., 2019). Analogously, 少于 1% of REST2-REST edges survived to
that same threshold (Figure 4B). 全面的, these analyses indicate that the conservative thresh-
old chosen will depict actual task-rest FC changes.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

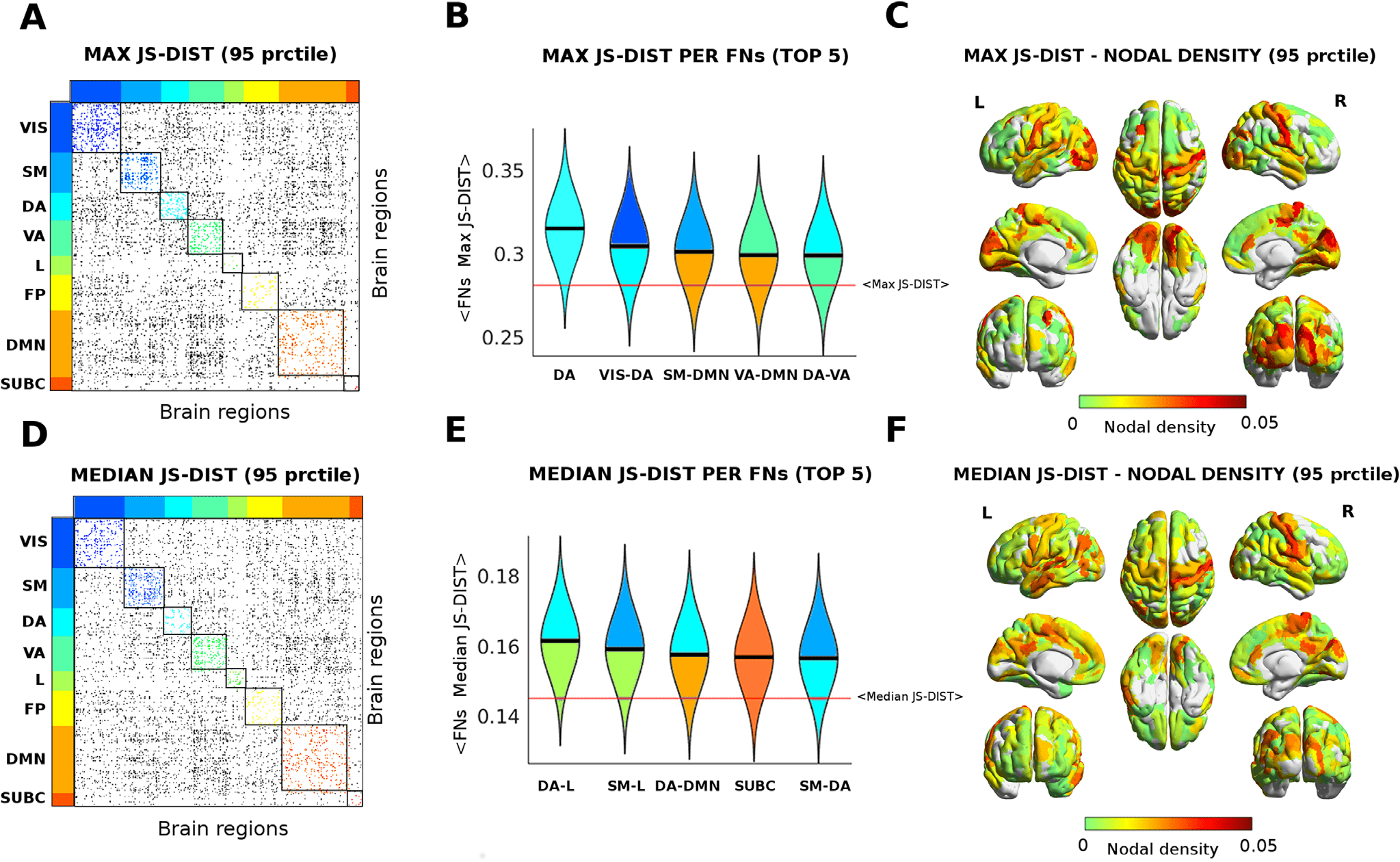
数字 5. Functional reconﬁguration via Jensen-Shannon distance. (A–D) Edgewise max (A) and median (D) Jensen-Shannon distance across
all tasks (thresholded by 95th percentiles for max and for median). The colored dots depict JS values within FNs; gray dots indicate signiﬁcant
JS-distant edges between FNs. (B–E) Violin plot of edgewise JS distance (max and median) for the top ﬁve FNs and FN interactions. Within-FNs
are color coded accordingly (as in A–D), while between-FNs are color coded using the colors of the two FNs involved. Solid black lines depict
median values of each distribution; solid red lines indicate the whole-brain median value of max and median distributions. (C–F) Brain render
of max and median JS distances as nodal density per region. The strength per brain region computed as sum of JS distance (max and median)
for functional edges above the 95 percentile threshold divided by the total number of brain regions.

网络神经科学

466

Cognitive task processing in the human connectome

The results in Figure 4 display the extent to which JS distance is sensitive to different levels
of functional reconﬁguration (Krienen et al., 2014; Schultz & Cole, 2016; Shine et al., 2016)
for different functional networks across different tasks. Hence we decided to explore further
on this, and evaluated the edgewise maximum and median JS distance across all tasks. 这
would provide an overall summary of the main edges and functional networks involved in the
cognitive switch across the seven tasks (见图 5). Notice that median and max give two
different “ﬂavors” of brain network reconﬁguration: The median tells us how far, 一般,
brain regions (and functional networks) change when subjects perform tasks. The max tells us
what are the most distant values, hence the highest achieved functional reconﬁguration for a
brain region across the seven different tasks under study.

In order to determine whether changes in task processing are related to the underlying
structural connectivity, we ﬁrst evaluated the relationship between connectivity distance in
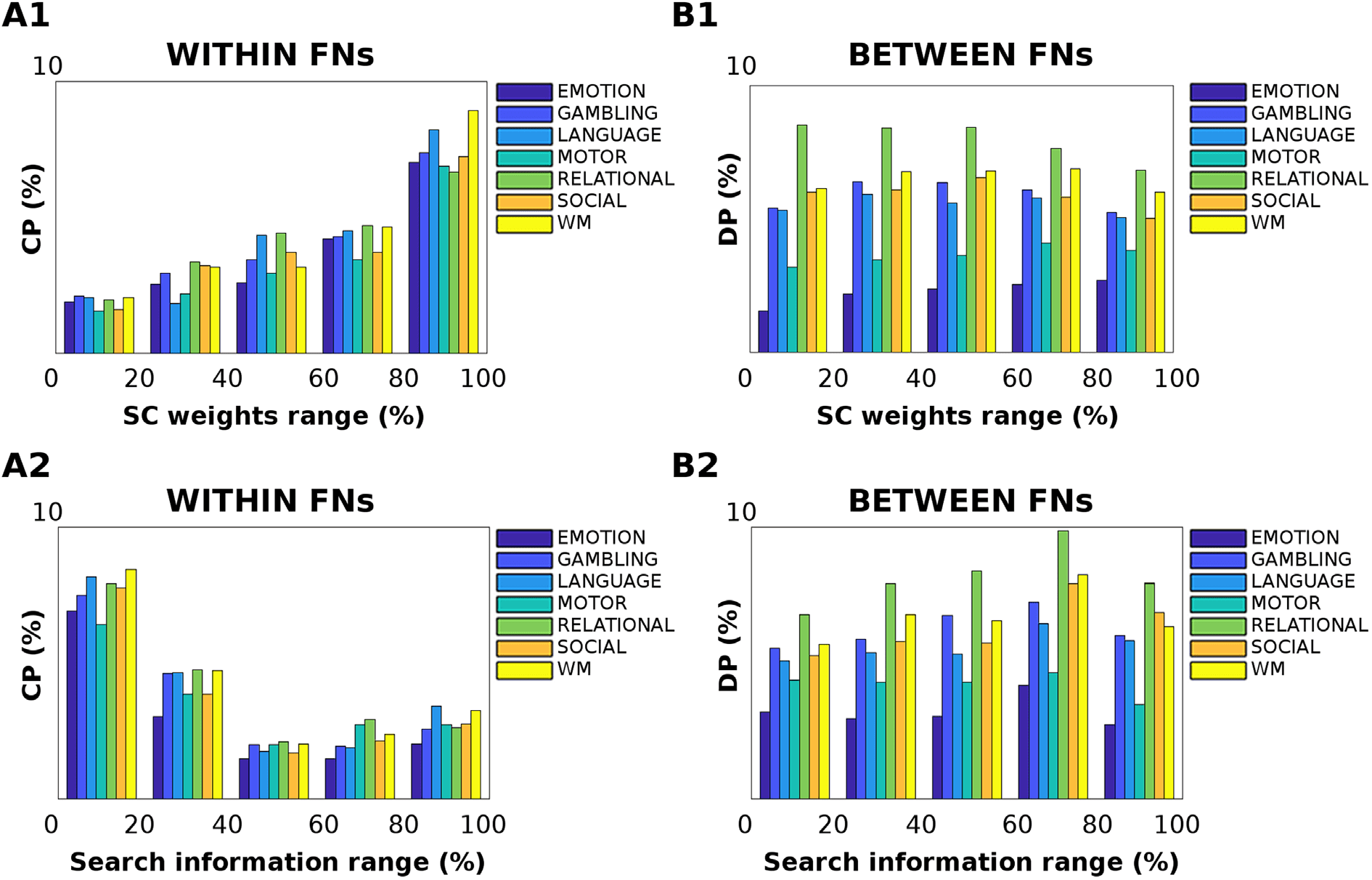
each task and structural connectivity weights (数字 6, A1–B1). 有趣的是, a signiﬁcant
trend arises for all tasks between centralized processing and number of tracts (one-way ANOVA

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 6. Effect of structural pathways on centralized and distributed processing changes. (A1–B1) The relationship between the anatomical
connections and Jensen-Shannon distance was evaluated across the seven different tasks. The bar plots show the percentage of centralized
加工 (CP) within functional networks (FNs, A1) and distributed processing (DP) between FNs (B1), per ﬁve different percentile ranges
of structural connectivity weights: 0−20, 20−40, 40−60, 60−80, and 80−100. The percentile range was extracted from the group-averaged
structural connectome. Note how, for within-FN connections (A1), the change in centralized processing signiﬁcantly correlates with the
−20); 反过来, 底层的
strength of structural connections across all tasks (one-way ANOVA F = 163.39, d f = 4, p = 6.62 · 10
structural connectivity does not play a major role in distributed processing changes (one-way ANOVA F = 1.11, d f = 4, p = 0.37). (A2–B2)
The effect of structural path accessibility (as measured by search information; 参见方法) on centralized and distributed processing was
tested across the seven different tasks, per ﬁve different percentile intervals of search information: 0−20, 20−40, 40−60, 60−80, and 80−100.
The percentile range was extracted from the group-averaged search information matrix. 尤其, changes in centralized processing (A2) 是
−18); 反过来, 不
signiﬁcantly associated with low values of search information (one-way ANOVA F = 131.75, d f = 4, p = 1.41 · 10
signiﬁcant association between SI and distributed processing changes was found (one-way ANOVA F = 1.85, d f = 4, p = 0.14).

网络神经科学

467

Cognitive task processing in the human connectome

−20, 数字 6, A1). 那是, the more structurally connected
F = 163.39, d f = 4, p = 6.62 · 10
two regions are within a functional network, the higher the number of centralized processing
edges recruited in a task. Notice how this trend is general and independent from the task, 甚至
the magnitude of this linear association between structure and function depends on the task at
手 (数字 6, A1). 另一方面, when looking at changes in distributed processing, 那
是, for edges involved in between-functional network connectivity, no signiﬁcant associations
with structural connectivity were observed (one-way ANOVA F = 1.11, d f = 4, p = 0.37,
数字 6, B1).

We then dug deeper into the relationship between task processing and structural connec-
tome by evaluating the level of hiddenness or accessibility of a structural path, as measured by
search information (Goñi et al., 2014; see also the Estimation of Functional Connectivity Dis-
tance Associations with Structural Connectomes section for details), and testing its association
with changes in cognitive task processing (数字 6, A2–B2). 有趣的是, the hiddenness of
structural paths appears to be inversely related to changes in centralized processing (one-way
−18, 数字 6, A2). 那是, the more “isolated” the
ANOVA F = 131.75, d f = 4, p = 1.41 · 10
structural pathway between two brain regions within a functional network, the higher will be
its recruitment in a task. The more nested or integrated the path, the less distant the centralized
processing with respect to resting state (数字 6, A2). No signiﬁcant associations were found
when looking at changes in distributed processing versus search information range of values
(one-way ANOVA F = 1.85, d f = 4, p = 0.14, 见图 6, B2).

讨论

Cognitive brain network mapping (Cole et al., 2013; Cole & 施耐德, 2007; Finn et al., 2017;
Krienen et al., 2014), or the analysis of brain network features underlying task performance
and cognitive control (Cole et al., 2014; Finn et al., 2017; Gratton et al., 2016; Khambhati,
Medaglia, Karuza, Thompson-Schill, & Bassett, 2018; Tavor et al., 2016), is a recent and ex-
citing new line of investigation in brain connectomics. While the general intrinsic common
architecture between resting-state and task-based functional patterns has been explored (Cole
等人。, 2014), still very little is known about task connectivity distances and their associa-
tions with information processing (Cole, Ito, Bassett, & Schultz, 2016; Cole & 施耐德, 2007;
Ito et al., 2017). 此外, an even more intricate question relates to the relationship be-
tween the different task-based FC scenarios and the underlying structural connectivity (Amico
& 戈尼, 2018; Fukushima et al., 2018; Hermundstad et al., 2013; Hermundstad et al., 2014;
Miši´c et al., 2016).

Here we addressed these questions by proposing a novel methodology in neuroscience,
rooted to the concept of Jensen-Shannon divergence (Brit & Harremos, 2009; De Domenico
等人。, 2015), to measure task-based pairwise functional distance with respect to the “cognitive
baseline” deﬁned by resting-state FCs (数字 1). This framework may also be seen from a
multilayer perspective, with the ground layer being resting-state FCs and top layers deﬁned
by the multiple task-based different connectivity scenarios. The distance deﬁned here can be
thought as interlayer coupling, or as the amount of cognitive processing necessary to make the
“cognitive switch” from the resting-state ground layer to the top task-based functional layers.
The JS divergence has several advantages: it is a nonparametric test, does not assume any form
of distribution, and allows for quantifying ﬁne-grained changes between two distributions. 作为
shown in Figure S5 (Amico et al., 2019), there were a large number of functional edges for
which REST or TASK FC distributions did not pass a normality test.

网络神经科学

468

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Cognitive task processing in the human connectome

The work presented here complements the aforementioned recent studies on cognitive map-
平, where the resting-state scaffolding was usually used to infer or also predict task changes
in connectivity (Cole et al., 2014; Cole et al., 2016; Ito et al., 2017; Tavor et al., 2016). 这里
we evaluate and investigate the pairwise distance task-rest, and use it to map speciﬁc changes
dictated by the task at hand. This adds up to previous studies in that it improves our under-
standing of how edge speciﬁc is the cognitive switch, and its level of recruitment (in terms of
“connectivity distance”), as well as in terms of centralized and distributed processing changes
in functional networks (数字 2).

We exploited this new concept of connectivity distance to infer about the level of recruit-
ment of an edge or of a functional network (数字 2). 尤其, the connectivity distant patterns
present in the original data were signiﬁcantly different from the ones obtained by surrogate data
built from the original fMRI time series (Figure S2 and Table S1, Amico et al., 2019) or from the
ones obtained by randomly shufﬂing rest-task FCs. 的确, the more distant a functional net-
work is in a specific task, the more different its recruitment with respect to resting state, 因此,
the more changes in cognitive information processing that functional subsystem will undergo.
This intuition led us to explore the concept of centralized and distributed processing in large-
scale functional networks, which we deﬁned as the difference between intra- (IE。, 集中)
and inter- (IE。, 分散式) network connectivity (数字 3). 有趣的是, three functional net-
作品 (dorsal attention, frontoparietal, and DMN) showed major changes in distributed pro-
cessing and very minor changes in centralized processing, for all seven tasks evaluated with
respect to resting state (数字 3). This is in line with recent ﬁndings showing that frontoparietal
and attentional areas appear to be the more ﬂexible for cognitive control and task performance
(Cole et al., 2013; Cole & 施耐德, 2007; Krienen et al., 2014; Shine et al., 2016).

The fact that these networks and the DMN, which is well known to play a major role in
resting state (Greicius, Krasnow, Reiss, & Menon, 2003; Raichle, 2015; Raichle et al., 2001),
change mainly in terms of intercommunication when transitioning to task is also noteworthy.
This ﬁnding goes along with the concept of integration of information between neural sub-
系统 (托诺尼, 斯波恩斯, & Edelman, 1994) and also with our recent ﬁndings on the associa-
tion between FP-DMN disconnectivity and degradation in arousal and levels of consciousness
(Amico et al., 2017). Possibly, the more demanding the task, the more the cross-talk between
FP, DMN, attentional networks, and the rest of the brain might be needed to achieve the
proper amount of cognitive processing or “brain network reconﬁguration” (Krienen et al., 2014;
Schultz & Cole, 2016).

We further investigated on the concept of brain network reconﬁguration across tasks, 经过
evaluating most and least distant functional edges between functional networks (数字 4).
有趣的是, some tasks seem to require extremely distant interactions between FNs (例如,
relational), and other tasks require speciﬁc subsets of FN interactions (例如, 语言, 在职的
记忆). The investigation of the max and median nodal JSdist centrality (数字 5) across tasks
added more information on the complex scenario depicted in Figure 4. Dorsal and occipital
regions seem to be the ones that are generally more distant from rest when engaged in a task
(数字 5, A–C). 另一方面, somatomotor and dorsal areas seem to be the ones that
achieve the largest reconﬁguration (IE。, maximal JSdist from resting state) across the seven
tasks evaluated (数字 5, D–F).

合在一起, these ﬁndings suggest that the cognitive “switch” between resting-state and
task states is more than a general shift in terms of functional links, but rather a complex interplay
between maximally distant and minimally distant functional connections (数字 4, 数字 5). 这

网络神经科学

469

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Cognitive task processing in the human connectome

is in line with recent studies investigating the complex reconﬁguration of brain networks during
任务 (Bassett et al., 2013; Khambhati et al., 2018; Krienen et al., 2014; Shine et al., 2016).

Another major question relates to how these changes in cognitive processing are shaped or
determined by the underlying structural architecture of a human brain. Very few studies so far
have tried to elucidate the relationship between cognitive changes and axonal pathways, 任何一个
for localized cortical subsystems (例如, fusiform gyrus; Saygin et al., 2012) or for a speciﬁc task
(例如, visual stimuli; Osher et al., 2015), or at the whole-brain level (Hermundstad et al., 2013;
Hermundstad et al., 2014; Miši´c et al., 2016). In a recent work we tackled this problem from
a whole-brain network perspective, by means of an ICA-based approach to extract the main
“hybrid” functional-structural connectivity features sensitive to cognitive changes across seven
different tasks (Amico & 戈尼, 2018).

Here we took this investigation one step further by assessing functional connectivity dis-
tance associations with respect to the underlying structural connectivity weights (数字 6).
有趣的是, for changes in centralized processing, the relationship with structural connectivity
is linear (数字 6, A1). 那是, when the cognitive processing involves mainly within-network
连接性, the higher the ﬁber strength is between two regions, the more distant they will
是. 尽管如此, this relationship is not present when looking at distributed processing link-to-
link effects (数字 6, B1). Previous ﬁndings reported that between-network connectivity links
can play a key role in the creation of more complex cognitive regimes (Fukushima et al., 2018;
Hermundstad et al., 2013; Hermundstad et al., 2014; Miši´c et al., 2016). The cross-talk be-
tween functional networks might bring the brain network up to a more integrated level, allow-
ing for a more dynamic and distributed cognitive processing, that ultimately deviates far from
the static underlying boundaries given by the structural ﬁber tracts.

为了检验这个假设, we evaluated the relationship between changes in distributed and
centralized processing and structural path “hiddenness” or accessibility, as measured by search
信息 (Goñi et al., 2014; see also the Estimation of Functional Connectivity Distance
Associations with Structural Connectomes section). 尤其, when looking at centralized pro-
cessing deviations from rest, these two quantities appear to be inversely related (数字 6, A2,
B2). The less integrated the path is between two regions within a functional network, the higher
the value in centralized processing, the more integrated the structural pathways, and the less
centralized activity (数字 6, A2).

These ﬁndings corroborate the hypothesis on the integration segregation in the human brain
(Tononi et al., 1994). They are also in line with our ﬁndings on the importance of cross-talking
between functional networks for task changes (Amico & 戈尼, 2018), which can be summa-
rized as follows: For a human brain to make a cognitive switch, a delicate interplay between
centralized and distributed processing is necessary. The centralized activity within functional
subsystems is shaped by brain structure. 而且, the more isolated the shortest path con-
necting two centralized brain regions is, the higher the level of task processing (数字 4).
然而, in order to achieve proper cognitive complexity for the task at hand, an appropriate
level of distributed processing and subsequent integration between these subsystems is needed:
The level of cross-talking and structural integration will depend on the speciﬁc task at hand
(数字 2, 数字 4) and on the functional subnetwork involved (数字 3), with no signiﬁcant
function-structure associations (数字 4).

This study has several limitations. The framework presented here is based on the quan-
tiﬁcation of distances between estimations of functional connectivity data. The accuracy and
representativity of the estimate JS distance will be subject to the quantity and quality of the fMRI

网络神经科学

470

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Cognitive task processing in the human connectome

data as well as the processing steps. Further studies should explore how different aspects of the
data and subsequent processing may have an impact in the JS-distance quantiﬁcations, 包括-
ing number of subjects, duration of the REST and TASK fMRI sessions, spatiotemporal limita-
tions on fMRI data, and motion regressors included, 除其他外. Analogously, our ﬁndings
associating SC properties (weights and search information on SC shortest paths) with JS dis-
tance may also be, to some extent, sensitive to diffusion tractography user-deﬁned free param-
埃特斯. The effect of different brain atlases (here we used the one proposed by Glasser et al.
(2016)) and functional network organization (here we used the one proposed by Yeo et al.
(2011)) on the centralized and processing changes should be explored. Because of the way it
is deﬁned, the measure does not allow for individualized connectivity distance patterns. 如何-
曾经, future studies could explore to what extent individual FCs can be predicted by group-wise
changes in centralized and distributed processing, or use the information on the most distant
link at the group level to select the most meaningful pairwise connectivity for the task at hand.
Another potentially promising application of this methodology may be related to measuring JS
divergence at the single-subject level with dynamic functional connectivity. 在这种情况下, 这
different FCs would be given by the FC snapshots obtained from sliding the FC window along
the same subject acquisition during resting state and a speciﬁc task (as opposed to the slices
being subjects as depicted in Figure 1 of this paper).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

It is also important to remark on the importance of introducing a well-deﬁned distance met-
ric (IE。, JSdist) in the functional connectome domain, as we propose in this work. This can open
several promising new lines of research in brain connectomics in terms of topological analysis
of the connectivity domain, and of the deﬁnition of metrizable spaces where to map cogni-
tive changes in brain functional networks. 最后, the simplicity of the methodology allows
for its applicability in the clinical domain, where it could be employed to measure connectiv-
ity distance between “healthy” and “diseased” populations (例如, Alzheimer’s, schizophrenia,
coma), or to determine task-rest distance in situations where the cognitive switch is damaged
or disrupted (例如, in autism or similar neurological disorders).

综上所述, we have reported a new methodology that aims at capturing the functional
differences between different tasks when compared with resting state. The methodology based
on the Jensen-Shannon distance is promising, and has been proved to discern between cen-
tralized and distributed activity across brain areas for different tasks. These results pave the
way to the usage of this framework in other experiments, and to the development of a new
information theoretical framework for the analysis of functional and structural connectomes.

致谢

Data were provided [部分地] by the Human Connectome Project, WU-Minn Consortium (prin-
cipal investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657), funded by the 16
NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; 并由
the McDonnell Center for Systems Neuroscience at Washington University.

SUPPORTING INFORMATION

The code used for computing Jensen-Shannon distance in functional connectomes will be made
available on the CONNplexity lab website (https://engineering.purdue.edu/ConnplexityLab).

作者贡献

Enrico Amico: 概念化; 数据管理; 形式分析; 调查; Writing –
original draft; 写作——复习 & 编辑. Alex Arenas: 概念化; 方法;

网络神经科学

471

Cognitive task processing in the human connectome

监督; 写作——复习 & 编辑. Joaquín Goñi: 概念化; 调查;
方法; 项目管理; 监督; 验证; Writing – original draft;
写作——复习 & 编辑.

资金信息

Joaquín Goñi, 美国国立卫生研究院 (http://dx.doi.org/10.13039/100000002), 奖
ID: R01EB022574. Joaquín Goñi, 美国国立卫生研究院 (http://dx.doi.org/10.13039/
100000002), 奖项ID: R01MH108467. Joaquín Goñi, Indiana Clinical and Translational
Sciences Institute (http://dx.doi.org/10.13039/100006975), 奖项ID: UL1TR001108. Alex
Arenas, Ministerio de Economía y Competitividad (http://dx.doi.org/10.13039/501100003329),
奖项ID: FIS2015-71582-C2-1. Alex Arenas, Institució Catalana de Recerca i Estudis Avançats
(http://dx.doi.org/10.13039/501100003741). Alex Arenas, 詹姆斯·S. McDonnell Foundation,
(http://dx.doi.org/10.13039/100000913), 奖项ID: 220020325.

参考

Amico, E., Arenas, A。, & 戈尼, J. (2019). Supporting information
for “Centralized and distributed cognitive task processing in the
human connectome.” Network Neuroscience, 3(2), 455–474.
https://doi.org/10.1162/netn_a_00072

Amico, E., & 戈尼, J. (2018). Mapping hybrid functional-structural
connectivity traits in the human connectome. Network Neuro-
科学, 2(3), 306–322. https://doi.org/10.1162/netn_a_00049
Amico, E., Marinazzo, D ., Di Perri, C。, Heine, L。, Annen, J。, Martial,
C。, . . . Goi, J. (2017). Mapping the functional connectome traits
of levels of consciousness. 神经影像, 148, 201–211. https://
doi.org/10.1016/j.neuroimage.2017.01.020

安德森, J. L. R。, Skare, S。, & Ashburner, J. (2003). How to correct
susceptibility distortions in spin-echo echo-planar images: Appli-
cation to diffusion tensor imaging. 神经影像, 20(2), 870–888.
https://doi.org/10.1016/S1053-8119(03)00336-7

Barch, D. M。, 伯吉斯, G. C。, Harms, 中号. P。, 彼得森, S. E.,
施拉加尔, 乙. L。, 科尔贝塔, M。, . . . Van Essen, D. C. (2013). Func-
tion in the human connectome: Task-fMRI and individual differ-
ences in behavior. 神经影像, 80, 169–189. https://doi.org/10.
1016/j.neuroimage.2013.05.033

Bassett, D. S。, & 布莫尔, 乙. (2006). Small-world brain networks.

The Neuroscientist, 12(6), 512–523.

Bassett, D. S。, Wymbs, 氮. F。, Rombach, 中号. P。, Porter, 中号. A。, Mucha,
磷. J。, & Grafton, S. 时间. (2013). Task-based core-periphery organ-
ization of human brain dynamics. 公共科学图书馆计算生物学,
9(9), e1003171.

碧涵, D. L. (2003). Looking into the functional architecture of the
brain with diffusion MRI. 自然评论神经科学, 4(6), 469.
Brit, J。, & Harremos, 磷. (2009). Properties of classical and quantum
Jensen-Shannon divergence. Physical Review A, 79(5), 052311.
https://doi.org/10.1103/PhysRevA.79.052311

布莫尔, E., & 斯波恩斯, 氧. (2009). 复杂的大脑网络: 图形
结构和功能系统的理论分析. 自然
评论神经科学, 10(3), 186–198. https://doi.org/10.1038/
nrn2575

Caruyer, E., Cheng, J。, Lenglet, C。, Sapiro, G。, Jiang, T。, & Deriche,
右. (2011). Optimal design of multiple Q-shells experiments for
diffusion MRI. https://hal.inria.fr/inria-00617663/文档

Christiaens, D ., 旅行过, M。, 多霍兰德, T。, Sunaert, S。, Suetens,
P。, & Maes, F. (2015). Global tractography of multi-shell diffusion-
weighted imaging data using a multi-tissue model. Neuro-
图像, 123, 89–101. https://doi.org/10.1016/j.neuroimage.2015.
08.008

Cole, 中号. W., Bassett, D. S。, 力量, J. D ., Braver, 时间. S。, & 彼得森,
S. 乙. (2014). Intrinsic and task-evoked network architectures of
the human brain. 神经元, 83(1), 238–251. https://doi.org/10.
1016/j.neuron.2014.05.014

Cole, 中号. W., Ito, T。, Bassett, D. S。, & Schultz, D. H. (2016). Activity
ﬂow over resting-state networks shapes cognitive task activations.
自然神经科学, 19(12), 1718.

Cole, 中号. W., Reynolds, J. R。, 力量, J. D ., Repovs, G。, Anticevic,
A。, & Braver, 时间. S. (2013). Multi-task connectivity reveals ﬂexi-
ble hubs for adaptive task control. 自然神经科学, 16(9),
1348. https://doi.org/10.1038/nn.3470

Cole, 中号. W., & 施耐德, 瓦. (2007). The cognitive control net-
工作: Integrated cortical regions with dissociable functions. Neuro-
图像, 37(1), 343–360. https://doi.org/10.1016/j.neuroimage.
2007.03.071

Cover, 时间. M。, & 托马斯, J. A. (2012). Elements of information
理论. 霍博肯, 新泽西州: 约翰·威利 & Sons. (Google-Books-ID:
VWq5GG6ycxMC)

De Domenico, 中号. D ., 尼科西亚, 五、, Arenas, A。, & Latora, V. (2015).
Structural reducibility of multilayer networks. Nature Communi-
阳离子, 6, 6864. https://doi.org/10.1038/ncomms7864

Endres, D. M。, & Schindelin, J. 乙. (2003). A new metric for probabil-
ity distributions. IEEE Transactions on Information Theory, 49(7),
1858–1860.

芬恩, 乙. S。, Scheinost, D ., 芬恩, D. M。, 沉, X。, Papademetris, X。,
& Constable, 右. 时间. (2017). Can brain state be manipulated to
emphasize individual differences in functional connectivity?
神经影像, 160, 140–151.

假如, A。, 扎莱斯基, A。, & Breakspear, 中号. (2015). The connectomics
of brain disorders. 自然评论神经科学, 16(3), 159–172.
https://doi.org/10.1038/nrn3901

假如, A。, 扎莱斯基, A。, & 布莫尔, 乙. (2016). Fundamentals of

brain network analysis. 伦敦: 学术出版社.

网络神经科学

472

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Cognitive task processing in the human connectome

狐狸, 中号. D ., & Raichle, 中号. 乙. (2007). Spontaneous ﬂuctuations
in brain activity observed with functional magnetic resonance
成像. 自然评论神经科学, 8(9), 700–711. https://
doi.org/10.1038/nrn2201

Fukushima, M。, 贝策尔, 右. F。, 他, Y。, van den Heuvel, 中号. P。, Zuo,
X.-N., & 斯波恩斯, 氧. (2018). Structure–function relationships dur-
ing segregated and integrated network states of human brain
功能连接. Brain Structure and Function, 223(3),
1091–1106.

Glasser, 中号. F。, Coalson, 时间. S。, 罗宾逊, 乙. C。, Hacker, C. D .,
Harwell, J。, Yacoub, E., . . . Van Essen, D. C. (2016). 一个多-
modal parcellation of human cerebral cortex. 自然, 536(7615),
171–178. https://doi.org/10.1038/nature18933

Glasser, 中号. F。, 索蒂罗普洛斯, S. N。, Wilson, J. A。, Coalson, 时间. S。,
菲舍尔, B., 安德森, J. L。, . . .
詹金森, 中号. (2013). 这
minimal preprocessing pipelines for the Human Connectome
项目. 神经影像, 80, 105–124. https://doi.org/10.1016/
j.neuroimage.2013.04.127

戈尼,

J。, van den Heuvel, 中号. P。, Avena-Koenigsberger, A。,
de Mendizabal, 氮. 五、, 贝策尔, 右. F。, Griffa, A。, . . . 斯波恩斯, 氧.
(2014). Resting-brain functional connectivity predicted by ana-
lytic measures of network communication. 诉讼程序
美国国家科学院, 111(2), 833–838. https://doi.org/
10.1073/pnas.1315529111

Gonzalez-Castillo, J。, Saad, Z. S。, Handwerker, D. A。, Inati, S. J。,
Brenowitz, N。, & Bandettini, 磷. A. (2012). Whole-brain, 时间-
locked activation with simple tasks revealed using massive av-
eraging and model-free analysis. 国家会议录
Academy of Sciences, 109(14), 5487–5492.

Gratton, C。, 劳曼, 时间. 奥。, Gordon, 乙. M。, Adeyemo, B., &
彼得森, S. 乙. (2016). Evidence for two independent factors that
modify brain networks to meet task goals. Cell Reports, 17(5),
1276–1288.

Greicius, 中号. D ., Krasnow, B., Reiss, A. L。, & Menon, V. (2003).
Functional connectivity in the resting brain: A network analy-
sis of the default mode hypothesis. 国家会议录
Academy of Sciences, 100(1), 253–258. https://doi.org/10.1073/
普纳斯.0135058100

Hermundstad, A. M。, Bassett, D. S。, 棕色的, K. S。, Aminoff, 乙. M。,
Clewett, D ., 弗里曼, S。, . . . 卡尔森, J. 中号. (2013). 结构性
foundations of resting-state and task-based functional connectiv-
ity in the human brain. 美国国家科学院院刊
科学, 110(15), 6169–6174.

Hermundstad, A. M。, 棕色的, K. S。, Bassett, D. S。, Aminoff, 乙. M。,
Frithsen, A。, 约翰逊, A。, . . . 卡尔森, J. 中号. (2014). 结构上
constrained relationships between cognitive states in the human
脑. 公共科学图书馆计算生物学, 10(5), e1003591.

Hogg, 右. 五、, & Ledolter, J. (1987). Engineering statistics. Macmillan.
Ito, T。, 库尔卡尼, K. R。, Schultz, D. H。, Mill, 右. D ., 陈, 右. H。,
Solomyak, L. 我。, & Cole, 中号. 瓦. (2017). Cognitive task informa-
tion is transferred between brain regions via resting-state net-
work topology. Nature Communications, 8(1), 1027. https://土井.
org/10.1038/s41467-017-01000-w

詹金森, M。, 贝克曼, C. F。, 贝伦斯, 时间. 乙. J。, 伍尔里奇, 中号. W.,
& 史密斯, S. 中号. (2012). FSL. 神经影像, 62(2), 782–790. https://
doi.org/10.1016/j.neuroimage.2011.09.015

约里森, B., 图尔尼耶,
J.

J.-D., 多霍兰德, T。, 康纳利, A。, &
西贝尔斯,
(2014). Multi-tissue constrained spherical decon-
volution for improved analysis of multi-shell diffusion MRI
数据. 神经影像, 103, 411–426. https://doi.org/10.1016/
j.neuroimage.2014.07.061
Khambhati, A. N。, Medaglia,

J. D ., Karuza, 乙. A。, 汤普森-
Schill, S. L。, & Bassett, D. S. (2018). Subgraphs of functional
brain networks identify dynamical constraints of cognitive con-
控制. PLOS Computational Biology, 14(7), 1–33. https://doi.org/
10.1371/journal.pcbi.1006234

克里宁, F. M。, 杨, 乙. T。, & 巴克纳, 右. L. (2014). Reconﬁgurable
task-dependent functional coupling modes cluster around a core
functional architecture. Philosophical Transactions of the Royal
Society of London B: Biological Sciences, 369(1653), 20130526.
马库斯, D ., Harwell, J。, Olsen, T。, 霍奇, M。, Glasser, M。, 事先的,
Informatics and data mining
F。, . . . Van Essen, D.
the Human Connectome Project.
tools and strategies for
神经信息学前沿, 5. https://doi.org/10.3389/fninf.
2011.00004

(2011).

Medaglia, J. D ., 黄, W., Karuza, 乙. A。, Kelkar, A。, 汤普森-
Schill, S. L。, Ribeiro, A。, & Bassett, D. S. (2018). Functional
alignment with anatomical networks is associated with cognitive
ﬂexibility. Nature Human Behaviour, 2(2), 156.

Miši´c, B., 贝策尔, 右. F。, De Reus, 中号. A。, van den Heuvel, 中号. P。,
Berman, 中号. G。, McIntosh, A. R。, & 斯波恩斯, 氧. (2016). 网络-
level structure-function relationships in human neocortex. Cere-
bral Cortex, 26(7), 3285–3296.

Osher, D. E., Saxe, 右. R。, Koldewyn, K., Gabrieli, J. D ., Kanwisher,
N。, & Saygin, Z. 中号. (2015). Structural connectivity ﬁngerprints
predict cortical selectivity for multiple visual categories across
cortex. 大脑皮层, 26(4), 1668–1683.

Österreicher, F。, & Vajda, 我. (2003). A new class of metric diver-
gences on probability spaces and its applicability in statistics.
Annals of the Institute of Statistical Mathematics, 55(3), 639–653.
力量, J. D ., 米特拉, A。, 劳曼, 时间. 奥。, 斯奈德, A. Z。, 施拉加尔,
乙. L。, & 彼得森, S. 乙. (2014). Methods to detect, characterize,
and remove motion artifact in resting state fMRI. 神经影像, 84,
320–341. https://doi.org/10.1016/j.neuroimage.2013.08.048
Raichle, 中号. 乙. (2015). The brain’s default mode network. Annual Re-
view of Neuroscience, 38(1), 433–447. https://doi.org/10.1146/
annurev-neuro-071013-014030

Raichle, 中号. E., MacLeod, A. M。, 斯奈德, A. Z。, 权力, 瓦. J。,
Gusnard, D. A。, & 舒尔曼, G. L. (2001). A default mode
of brain function. 美国国家科学院院刊-
恩塞斯, 98(2), 676–682. https://doi.org/10.1073/pnas.98.2.676

Rosvall, M。, Grönlund, A。, Minnhagen, P。, & Sneppen, K.

(2005).

Searchability of networks. Physical Review E, 72(4), 046117.
Salimi-Khorshidi, G。, Douaud, G。, 贝克曼, C. F。, Glasser, 中号. F。,
Griffanti, L。, & 史密斯, S. 中号. (2014). Automatic denoising of func-
tional MRI data: Combining independent component analysis
and hierarchical fusion of classiﬁers. 神经影像, 90, 449–468.
https://doi.org/10.1016/j.neuroimage.2013.11.046

Saygin, Z. M。, Osher, D. E., Koldewyn, K., Reynolds, G。, Gabrieli,
J. D ., & Saxe, 右. 右. (2012). Anatomical connectivity patterns pre-
dict face selectivity in the fusiform gyrus. 自然神经科学,
15(2), 321.

网络神经科学

473

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
2
4
5
5
1
0
9
2
6
0
0
n
e
n
_
A
_
0
0
0
7
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Cognitive task processing in the human connectome

Schreiber, T。, & Schmitz, A. (2000). Surrogate time series. Physica
D: Nonlinear Phenomena, 142(3), 346–382. https://doi.org/10.
1016/S0167-2789(00)00043-9
Schultz, D. H。, & Cole, 中号. 瓦.

(2016). Higher intelligence is
associated with less task-related brain network reconﬁguration.
神经科学杂志, 36(33), 8551–8561.

Shine, J. M。, Bissett, 磷. G。, 钟, 磷. T。, Koyejo, 奥。, Balsters, J. H。,
Gorgolewski, K. J。, . . . Poldrack, 右. A. (2016). The dynamics
of functional brain networks: Integrated network states during
cognitive task performance. 神经元, 92(2), 544–554.

史密斯, 右. E., 图尔尼耶, J.-D., 卡拉曼特, F。, & 康纳利, A. (2012).
Anatomically constrained tractography: Improved diffusion MRI
streamlines tractography through effective use of anatomical
信息. 神经影像, 62(3), 1924–1938. https://doi.org/10.
1016/j.neuroimage.2012.06.005

史密斯, 右. E., 图尔尼耶,

J.-D., 卡拉曼特, F。, & 康纳利, A.
(2013). SIFT: Spherical-deconvolution informed ﬁltering of
tractograms. 神经影像, 67, 298–312. https://doi.org/10.1016/
j.neuroimage.2012.11.049

史密斯, 右. E., 图尔尼耶,

J.-D., 卡拉曼特, F。, & 康纳利, A.
(2015). SIFT2: Enabling dense quantitative assessment of
brain white matter connectivity using streamlines tractography.
神经影像, 119, 338–351. https://doi.org/10.1016/j.neuroimage.
2015.06.092

史密斯, S. M。, 贝克曼, C. F。, 安德森, J。, 奥尔巴赫, 乙. J。,
Bijsterbosch, J。, Douaud, G。, . . . Glasser, 中号. F. (2013). Resting-
state fMRI in the Human Connectome Project. 神经影像, 80,
144–168. https://doi.org/10.1016/j.neuroimage.2013.05.039
索蒂罗普洛斯, S. N。, Jbabdi, S。, 徐, J。, 安德森, J. L。, Moeller,
S。, 奥尔巴赫, 乙. J。, . . . 贝伦斯, 时间. 乙. J. (2013). 进展
diffusion MRI acquisition and processing in the Human Con-
nectome Project. 神经影像, 80, 125–143. https://doi.org/10.
1016/j.neuroimage.2013.05.057

斯波恩斯, 氧. (2011). The human connectome: A complex network.
Annals of the New York Academy of Sciences, 1224(1), 109–125.
https://doi.org/10.1111/j.1749-6632.2010.05888.x

Stejskal, 乙. 奥。, & Tanner, J. 乙. (1965). Spin diffusion measurements:
Spin echoes in the presence of a time-dependent ﬁeld gradient.
Journal of Chemical Physics, 42(1), 288–292. https://doi.org/10.
1063/1.1695690

Tavor, 我。, 琼斯, 氧. P。, 火星, 右. B., 史密斯, S. M。, 贝伦斯, 时间. E., &
Jbabdi, S. (2016). Task-free MRI predicts individual differences

in brain activity during task performance. 科学, 352(6282),
216–220. https://doi.org/10.1126/science.aad8127

托诺尼, G。, 斯波恩斯, 奥。, & Edelman, G. 中号. (1994). A measure for brain
复杂: Relating functional segregation and integration in the
nervous system. 美国国家科学院院刊,
91(11), 5033–5037. http://www.pnas.org/content/91/11/5033
图尔尼耶, J.-D., 卡拉曼特, F。, & 康纳利, A. (2012). MRtrix: Diffu-
sion tractography in crossing ﬁber regions. International Journal
of Imaging Systems and Technology, 22(1), 53–66. https://土井.
org/10.1002/ima.22005

图尔尼耶, J.-D., 森, S。, & 利曼斯, A. (2011). Diffusion tensor
imaging and beyond. Magnetic Resonance in Medicine, 65(6),
1532–1556. https://doi.org/10.1002/mrm.22924

Trusina, A。, Rosvall, M。, & Sneppen, K. (2005). 沟通
boundaries in networks. 物理评论快报, 94(23), 238701.
Uurbil, K., 徐, J。, 奥尔巴赫, 乙. J。, Moeller, S。, Vu, A. T。, Duarte-
Carvajalino, J. M。, . . . Yacoub, 乙. (2013). Pushing spatial and
temporal resolution for functional and diffusion MRI in the Hu-
man Connectome Project. 神经影像, 80, 80–104. https://土井.
org/10.1016/j.neuroimage.2013.05.012

van den Heuvel, 中号. P。, & Hulshoff Pol, H. 乙. (2010). Exploring the
brain network: A review on resting-state fMRI functional connec-
活力. European Neuropsychopharmacology, 20(8), 519–534.
https://doi.org/10.1016/j.euroneuro.2010.03.008

Van Essen, D. C。, 史密斯, S. M。, Barch, D. M。, 贝伦斯, 时间. 乙. J。,
Yacoub, E., & Ugurbil, K. (2013). The WU-Minn Human Con-
nectome Project: 概述. 神经影像, 80, 62–79. https://
doi.org/10.1016/j.neuroimage.2013.05.041

Van Essen, D. C。, Ugurbil, K., 奥尔巴赫, E., Barch, D ., 贝伦斯,
时间. 乙. J。, Bucholz, R。, . . . Wu-Minn HCP Consortium (2012).
The Human Connectome Project: A data acquisition perspec-
主动的. 神经影像, 62(4), 2222–2231. https://doi.org/10.1016/
j.neuroimage.2012.02.018

Wirsich, J。, Perry, A。, Ridley, B., Proix, T。, Golos, M。, Bénar, C。,
. . . Guye, 中号. (2016). Whole-brain analytic measures of network
communication reveal increased structure-function correlation
in right temporal lobe epilepsy. 神经影像: Clinical, 11, 707–718.
杨, 乙. 时间. T。, 克里宁, F. M。, 墓, J。, 肥皂, 中号. R。, 军队,
D ., 霍林斯黑德, M。, .
. . 巴克纳, 右. L. (2011). The orga-
nization of the human cerebral cortex estimated by intrinsic
神经生理学杂志, 106(3),
功能连接.
1125–1165. https://doi.org/10.1152/jn.00338.2011