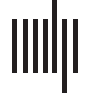研究
Regions of Interest as nodes of dynamic
functional brain networks
Elisa Ryyppö
1
, Enrico Glerean
2,3
, Elvira Brattico
4
, Jari Saramäki
1
, and Onerva Korhonen
1,3
1计算机科学系, School of Science, Aalto University, Espoo, 芬兰
2Turku PET Centre, 图尔库大学, 图尔库, 芬兰
3Department of Neuroscience and Biomedical Engineering, School of Science, Aalto University, Espoo, 芬兰
4Center for Music in the Brain, Department of Clinical Medicine, Aarhus University, and The Royal Academy of Music
Aarhus/Aalborg, 丹麦
关键词: Dynamic brain networks, Node definition, Functional homogeneity, Neighborhood
周转, Region of Interest, Functional magnetic resonance imaging
开放访问
杂志
抽象的
The properties of functional brain networks strongly depend on how their nodes are chosen.
Commonly, nodes are defined by Regions of Interest (罗伊斯), predetermined groupings of
fMRI measurement voxels. 较早, we demonstrated that the functional homogeneity of ROIs,
captured by their spatial consistency, varies widely across ROIs in commonly used brain
atlases. 这里, we ask how ROIs behave as nodes of dynamic brain networks. 为此,
we use two measures: spatiotemporal consistency measures changes in spatial consistency
across time and network turnover quantifies the changes in the local network structure
around an ROI. We find that spatial consistency varies non-uniformly in space and time,
which is reflected in the variation of spatiotemporal consistency across ROIs. 此外,
we see time-dependent changes in the network neighborhoods of the ROIs, reflected in
high network turnover. Network turnover is nonuniformly distributed across ROIs: 罗伊斯
with high spatiotemporal consistency have low network turnover. 最后, we reveal that
there is rich voxel-level correlation structure inside ROIs. Because the internal structure and
the connectivity of ROIs vary in time, the common approach of using static node definitions
may be surprisingly inaccurate. 所以, network neuroscience would greatly benefit
from node definition strategies tailored for dynamical networks.
作者总结
利益区域 (罗伊斯) are often used as the nodes of functional brain networks.
ROIs consist of several fMRI measurement voxels that are assumed to be functionally
homogeneous, 那是, behave similarly. 较早, we showed that the assumption of similar
voxel dynamics is not always true: functional homogeneity varies widely across ROIs. 在这个
纸, we demonstrate that functional homogeneity changes in time. These changes are
connected to changes in local network structure around ROIs, which suggests that an ROI’s
functional homogeneity may reflect its role in the network. 最后, we show that there is rich,
time-dependent structure of voxel-level connectivity inside ROIs. This leads us to ask if the
dynamic brain networks can be described by any set of static ROIs.
介绍
在 1909, Korbinian Brodmann published the results of his seminal work: maps of brain areas
with different cytoarchitectures. His results were among the first to suggest that the brain does
引文: Ryyppö, E., Glerean, E.,
Brattico, E., Saramäki, J。, & 科尔霍宁,
氧. (2018). Regions of Interest as nodes
of dynamic functional brain networks.
网络神经科学, 2(4), 513–535.
https://doi.org/10.1162/netn_a_00047
DOI:
https://doi.org/10.1162/netn_a_00047
已收到: 4 十月 2017
公认: 6 二月 2018
利益争夺: 作者有
声明不存在竞争利益
存在.
通讯作者:
Onerva Korhonen
onerva.korhonen@gmail.com
处理编辑器:
奥拉夫·斯波恩斯
版权: © 2018
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
A
_
0
0
0
4
7
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
ROIs and dynamic functional brain networks
not process information as an undivided entity. 反而, cognitive tasks are distributed among
specialized brain areas. Since Brodmann’s time, the neuroscientific community has reached
consensus on the distributed nature of brain function (see Wig, 施拉加尔, & 彼得森 (2011)
进行审查). Information processing in the brain is based on the balance between segrega-
tion and integration: there are clusters with strong internal connections and weak long-range
connectivity between them (弗里斯顿, 1994; 斯波恩斯, 2013乙; 托诺尼, 斯波恩斯, & 爱德曼, 1994).
Because of the crucial role of connectivity in the brain function, it is natural to model
the brain as a network. In a network model of the brain, the nodes represent brain areas and
the links represent the anatomical or functional connections between the nodes (巴塞特 &
斯波恩斯, 2017; 斯波恩斯, 2013A, 2013乙; Wig et al., 2011). Network neuroscience has unveiled
several important features of the structure and function of the human brain. For reviews,
看, 例如, Bassett and Sporns (2017), Betzel and Bassett (2017), 斯波恩斯 (2013A), 和
Wig et al. (2011).
Networks of the brain vary across people and in time. Structural and functional brain net-
works have been reported to differ between people, in particular between diseased sub-
jects and healthy controls, and to change across the lifespan (巴塞特 & 布莫尔, 2009; 陈,
Alhazmi, 公园, Savalia, & 假发, 2017; Papo, Zanin, Pineda-Pardo, Boccaletti, & Buldú, 2014;
斯波恩斯, 2013乙). Functional brain networks vary on shorter timescales too, 例如, 和
different cognitive tasks (Bassett et al., 2011; Braun et al., 2015; Göttlich, 叶, 罗德里格斯-
Fornells, 硬币, & Krämer, 2017; 蜂蜜, Kötter, 断裂, & 斯波恩斯, 2007). 然而, 这
traditional tools of connectivity analysis cannot capture this time variation: there is still a lack
of appropriate methods for understanding the dynamics of brain networks.
There are two questions of fundamental importance for functional brain networks: what do
the nodes represent, and how are their links defined? The common approach is to use Regions
of Interest (罗伊斯) as the nodes. ROIs are collections of fMRI measurement voxels defined on the
basis of anatomy, connectivity profiles, or function (进行审查, see de Reus & Van den Heuvel,
2013). The BOLD time series of each voxel follows the changes in the voxel’s level of activity.
To arrive at a time series that represents an entire ROI, its voxel time series are typically aver-
老化. 然后, the weights of the links between ROIs are quantified with some similarity measure
of their time series, such as the commonly used Pearson correlation coefficient.
The ROI time series are typically taken as accurate representations of the dynamics of the
voxels within the ROI. 最后, a minimum requirement for an ROI to be reasonably
defined is its functional homogeneity: each of the voxels should have similar dynamics.
在
我们以前的工作 (科尔霍宁, Saarimäki, Glerean, Sams, & Saramäki, 2017), we have used
the concept of spatial consistency for quantifying this functional homogeneity. 我们发现
spatial consistency varies widely across ROIs in the commonly used parcellations, 指示
that the assumption of functional homogeneity does not hold for all ROIs in functional brain
网络.
There are two possible reasons for low spatial consistency. 第一的, it is possible that it indicates
technical problems in the investigated parcellations: although functionally homogeneous re-
gions may exist in the brain, the parcellations are not able to capture these regions. 第二,
spatial consistency may vary in time: averaging over periods of extremely low and moderately
high consistency would yield low values of average consistency. In Korhonen et al. (2017), 我们
speculated that the variation of spatial consistency between ROIs may not be just a technical
Functional homogeneity:
Every voxel of an ROI is performing
some particular function and
therefore has (大致) 相似的
动力学, yielding strongly
correlated voxel time series.
网络神经科学
514
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
A
_
0
0
0
4
7
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
ROIs and dynamic functional brain networks
Turnover:
Differences between a node’s sets of
neighbors in two consecutive time
windows.
issue that can be overcome by some sophisticated parcellation scheme. 反而, it may carry
cognitive meaning and be related to changes in the ROIs’ activation, 例如.
In the present work, we generalize the investigation of spatial consistency into dynamic
brain networks. We explore how spatial consistency varies in time, and ask how its varia-
tion relates to changes in the local network structure around ROIs. 为此, we use two
措施: spatiotemporal consistency quantifies temporal changes in spatial consistency, 和
network turnover measures the amount of turnover in a node’s network neighborhood across
时间. We use in-house data collected from 13 healthy subjects during free music listening and
resting-state data of 28 healthy subjects from the Autism Brain Imaging Data Exchange (ABIDE)
倡议 (Di Martino et al., 2014). The in-house dataset is a subset of a larger dataset that has
been earlier partially described in Alluri et al. (2015, 2017) and Burunat et al. (2015).
With these data, we show that the ROIs exhibit varying levels of spatiotemporal consistency,
which indicates that their spatial consistency indeed changes in time. 此外, 重要的
turnover takes place in the neighborhoods of many ROIs. Network turnover is high especially
for ROIs with low spatiotemporal consistency. Looking at the constituent voxels of ROIs in
细节, we see that ROIs often have rich internal correlation structure that varies in time.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
A
_
0
0
0
4
7
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
These results indicate that the topology of functional brain networks changes continuously
on short timescales, which should be taken into account in brain network studies. 此外,
the significant temporal variation of functional homogeneity may suggest that new, dynamical
ways of defining nodes are required for creating an accurate network model of the brain.
重要的, the variation of functional homogeneity should not be seen as a technical issue
that should be eliminated with some parcellation approach, but a phenomenon that carries
cognitive meaning and that should be taken into account in the analysis of dynamic functional
连接性.
结果
Spatial Consistency of ROIs Varies Across Time
Using predefined ROIs as nodes of functional brain networks is based on the assumption
of functional homogeneity: all voxels within an ROI are assumed to have similar dynamics
that can be accurately represented by the ROI time series. To test this assumption, we cal-
culated the distribution of spatial consistency for five commonly used parcellations of the
脑: connectivity-based Brainnetome atlas and Craddock 200/400 parcellations as well as
two anatomical atlases: HarvardOxford (HO) and Automated Anatomical Labeling (AAL). Spa-
tial consistency is defined as the average Pearson correlation coefficient between the voxel
time series in a ROI (参见方程 2). The results are in concordance with our earlier ob-
服务 (Korhonen et al., 2017): although the maximum spatial consistency is moderately
高的 (Brainnetome: φspatial = 0.53, HO: φspatial = 0.53, AAL: φspatial = 0.34, Craddock
200: φspatial = 0.55, Craddock 400: φspatial = 0.65), the distribution of spatial consistency
is broad and peaks at low values (Brainnetome: φspatial = 0.12, HO: φspatial = 0.083, AAL:
φspatial = 0.083, Craddock 200: φspatial = 0.12, Craddock 400: φspatial = 0.15) (图1A). 为了
Brainnetome or Craddock 200/400, there is no significant correlation between ROI size in vox-
els and spatial consistency (Brainnetome: Pearson correlation coefficient r = 0.10, p = 0.12,
Figure 4A; Craddock 200: r = −8.31 × 10−4
, p = 0.991; Craddock 400: r = 0.031, p = 0.538).
For AAL and HO, there is a weak but significant correlation between ROI size and spatial con-
sistency (AAL: r = −0.32, p = 4.13 × 10−4
). The spatial
; HO: r = −0.33, p = 8.62 × 10−5
网络神经科学
515
ROIs and dynamic functional brain networks
Static spatial consistency:
A measure of functional
homogeneity; defined as the mean
intra-ROI Pearson correlation
coefficient calculated over whole
voxel time series.
Sliding windows:
A set of time windows defined so that
subsequent windows overlap with
彼此.
数字 1. The distribution of spatial consistency over ROIs indicates variation in functional homo-
geneity. (A) Distributions of static spatial consistency for the five parcellations investigated. (乙) 迪斯-
tributions of spatial consistency calculated separately for five time windows of 80 samples for the
Brainnetome ROIs. There is no visible difference between the distributions. All distributions have
been calculated from the pooled data of 13 主题. For AAL, HO, and Craddock 200/400 看
Supporting Information Figure S1 (Ryyppö et al., 2018).
consistency investigated here was calculated over the whole measurement time series; 我们将
from here on refer to it as static spatial consistency.
At least two different scenarios can explain the low values of static spatial consistency.
一方面, the voxels in an ROI may just have uncorrelated dynamics across the whole
measurement time series. 另一方面, a moderately low level of correlation between
the voxel time series may result from changes in the overall pattern, 例如, there may be
periods of highly correlated activity and periods of no correlations at all. In the latter scenario,
one would obtain time-dependent changes in spatial consistency by dividing the measurement
time series into shorter time windows. 所以, we divided the measurement time series into
five sliding windows of 80 samples each, 和 50% overlap between consecutive windows,
and investigated the spatial consistency separately for each time window.
We found no visible difference between distributions of spatial consistency calculated in
different time windows (图1B). One could assume that decreasing the time window length
and the overlap between consecutive windows would cause the spatial consistency distribu-
tions to differ more between windows. 然而, decreasing the window length to 50 样品
and the overlap to 25% did not induce more variation between time windows (数据未显示).
另一方面, increasing the overlap to the largest possible value, window length – 1, 做过
not affect the distributions of spatial consistency either (see Supporting Information Figure S29,
Ryyppö, Glerean, Brattico, Saramäki, & 科尔霍宁, 2018).
At the level of single ROIs, 然而, the situation is different. The spatial consistency of most
ROIs changes between time windows, and the largest relative changes in spatial consistency
are around 30% (图2A). These changes have a nonrandom spatial distribution and seem
to occur in clusters larger than simple ROIs. This is visible, 例如, as the drop in spatial
consistency of the frontal regions between the time windows 2 和 3. A possible reason for
the similar behavior of spatially close ROIs is their assumed functional similarity; 尤其,
ROIs belonging to the same functional subsystem of the brain may be expected to behave
similarly in terms of spatial consistency.
Similar time-dependent changes also take place in the spatial consistency ranks of ROIs
(数据未显示), demonstrating that the observations cannot be explained by changes in the
网络神经科学
516
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
A
_
0
0
0
4
7
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
ROIs and dynamic functional brain networks
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
A
_
0
0
0
4
7
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
数字 2. Spatial consistency of ROIs varies between time windows. (A) Relative changes of spa-
tial consistency between consecutive time windows. Changes in spatial consistency are nonran-
domly distributed in time, meaning that changes between different time windows are not similar.
此外, the changes show strong spatial correlations: the spatial consistency of anatomically
adjacent ROIs tends to change in the same way. The location of nodes in the visualization is de-
termined by a two-dimensional projection of the anatomical coordinates of the Brainnetome ROI
centroids. The visualization follows the neurological convention: the right hemisphere is on the
right and the frontal areas in the upper part of the visualization. (乙) Spatiotemporal consistency of
the Brainnetome ROIs on the brain surface. As one may expect based on A, spatiotemporal con-
sistency has a nonrandom anatomical distribution and shows strong spatial correlations. All results
are averages over 13 主题. Grayscale areas are not included in the present study (白质
and cerebellum). For AAL, HO, and Craddock 200/400, see Supporting Information Figures S2, S3,
S4, and S5 (Ryyppö et al., 2018).
overall level of spatial consistency. Note that in ROIs with small spatial consistency, even large
relative changes may be rather small in the absolute sense; therefore the distributions of spatial
consistency obtained in different time windows are almost identical at lower consistency values
(见图1B), although we see relative changes in consistency of almost every ROI. At higher
consistency values, large relative changes are larger in the absolute sense as well. 所以,
distributions obtained in different time windows differ more from each other.
In order to quantify the amount of temporal variation in spatial consistency, we defined the
spatiotemporal consistency as the inverse of the averaged relative change of spatial consistency
across time windows (参见方程 3). 换句话说, spatiotemporal consistency is a static
measure that tells how stable the ROI’s spatial consistency is over time windows on average.
Spatiotemporal consistency is not anatomically uniform (图2B), and identity of the ROIs
with the highest and lowest spatiotemporal consistency varies largely across subjects. 这
intersubject difference is partly explained by technical issues. The investigated parcellations
网络神经科学
517
ROIs and dynamic functional brain networks
have been defined at the group level, and they match differently with the individual anatomy
and brain function of different subjects. 另一方面, differences in spatiotemporal con-
sistency may also reflect the different cognitive responses of different subjects during free music
listening.
The Brainnetome ROIs with the highest average spatiotemporal consistency include the right
cuneus (5_3), 左下额回 (6_4), right occipital gyrus (4_3), right superior occipital
回 (2_1), and right inferior parietal lobule (6_2). In AAL, among the ROIs with the highest
average spatiotemporal consistency are the left medial orbitofrontal cortex, right cerebellar
区域 6, 左中间回, right insula, and left gyrus rectus. In HO, the ROIs with
the highest average spatiotemporal consistency include the right supracalcarine cortex, 左边
frontal pole, anterior division of left superior temporal gyrus, right angular gyrus, and posterior
division of right middle temporal gyrus. In Craddock 200/400, ROI boundaries do not respect
anatomical landmarks, and the ROIs are referred to only by numbers. For the location of the
Craddock 200/400 ROIs with the highest and lowest average spatiotemporal consistency, 这
reader is referred to Supporting Information Figures S18 and S19 (Ryyppö et al., 2018).
In Brainnetome, the ROIs with the lowest average spatiotemporal consistency are the right
parahippocampal gyrus (6_5 and 6_2), right paracentral lobule (2_1), and left postcentral
回 (4_4 and 4_2).
In AAL, the ROIs with the lowest average spatiotemporal consistency
include the left cerebellar area 4_5, right supplementary motor area, left paracentral lobule,
right parahippocampal gyrus, and right thalamus. In HO, the ROIs with the lowest average
spatiotemporal consistency include the right hippocampus, posterior division of right parahip-
pocampal gyrus, right precentral gyrus, right thalamus, and brain stem.
In all investigated
atlases, many subcortical areas are among the ROIs with low spatiotemporal consistency. 我们
will discuss possible reasons for this later in this article.
As one possible explanation for the variation of spatiotemporal consistency across ROIs,
we found a weak but significant correlation between the ROI size and the spatiotemporal
consistency in the Brainnetome atlas (r = 0.24, p = 1.37 × 10−4
; see Figure 4B). In AAL, HO,
or Craddock atlases, there is no significant correlation between the spatiotemporal consistency
and ROI size (AAL: r = 0.16, p = 0.0963; HO: r = −0.025, p = 0.770; Craddock 200: r =
0.028, p = 0.698, Craddock 400: r = 0.014, p = 0.780). The lack of correlation in the Craddock
parcellations is not surprising: these parcellations aim at minimizing the variation of ROI sizes,
and they have clearly smaller SDs of ROI size than the other parcellations investigated. 那里
are a few possible reasons for why we observe a correlation in the Brainnettome but not in AAL
or HO. 第一的, Brainnetome contains more ROIs than AAL or HO. 第二, unlike Brainnetome,
AAL and HO contain the cerebellum where ROIs are small because of anatomical reasons,
but they do not have systematically higher values of spatiotemporal consistency than the ROIs
of the cerebral cortex. 最后, in AAL and HO the ROI size is negatively correlated with static
spatial consistency; this is not the case for Brainnetome. 另一方面, in all atlases, 罗伊斯
with high static spatial consistency tend to have high spatiotemporal consistency as well (看
以下). 因为这, one would expect to see a negative correlation between ROI size and
spatiotemporal consistency in HO and AAL. This negative correlation may have masked the
positive correlation obtained for the Brainnetome atlas.
A sliding window with a one time frame shift is commonly used for studying dynamic func-
tional connectivity (Keilholz, Caballero-Gaudes, 乐队, 德科, & Calhoun, 2017). 在这个
方法, the overlap between consecutive time windows is as large as possible: window
length −1.
在我们的情况下, 然而, this large an overlap would hide the changes in local
网络神经科学
518
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
A
_
0
0
0
4
7
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
ROIs and dynamic functional brain networks
network structure. It would also lead to extremely low values of network turnover (见下文).
然而, we investigated how the 1 TR shift would affect the observed values of spatiotem-
poral consistency in the Brainnetome parcellation. 正如预期的那样, 使用 1 TR shift sliding
window moved the distribution of spatiotemporal consistency slightly to the right (distribu-
tion peaking at φst = 3.1 vs φst = 4.9; see Supporting Information Figure S29B, Ryyppö et al.,
2018): as the overlap between consecutive time series increases, there is less room for changes
in spatial consistency. 然而, 这 1 TR shift approach did not affect the overall shape of the
distribution of spatiotemporal consistency, and low values of spatiotemporal consistency that
indicate large relative changes in spatial consistency are observed with this approach too.
Subject motion is known to possibly affect the structure of functional brain networks (力量,
巴恩斯, 斯奈德, 施拉加尔, & 彼得森, 2012). 所以, one may ask if the temporal variation
in spatial consistency is of genuine neurophysiological origin or if it could be explained by
motion artifacts. To answer this, we investigated the temporal correlation between the mean
framewise displacement (fd) and the spatial consistency concatenated across subjects. 如何-
曾经, they did not correlate significantly for any ROI in any of the investigated atlases. 这
correlation between the static spatial consistency and the mean FD over subjects was not sig-
nificant neither.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
A
_
0
0
0
4
7
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Temporal fluctuations in functional connectivity of the brain may underlie changes in cogni-
tive processing (Cocchi et al., 2017). We found a significant correlation between time-resolved
功能连接 (Cocchi et al., 2017; 扎莱斯基, 假如, 厨师, Gollo, & 断裂,
2014) and spatial consistency for some ROIs of Brainnetome and HO. For further details, 这
reader is referred to Supporting Information Results (Ryyppö et al., 2018).
In the present article, we investigate five atlases: Brainnetome, Craddock 200/400, AAL,
and HO. Despite the differences between these atlases, we obtained highly similar results for
所有人. In the main article, we concentrate on the results obtained with the Brainnetome
atlas; for detailed results and visualizations for the Craddock 200/400, AAL, and HO atlases,
the reader is referred to Supporting Information Results (Ryyppö et al., 2018).
To verify that the results generalize, we repeated all analyses for a second, 独立的
dataset from the ABIDE I initiative (Di Martino et al., 2014). The results obtained using the
ABIDE data were very similar to those reported here; full details can be found in the Supporting
Information Results (Ryyppö et al., 2018).
Network neighborhoods of nodes change in time
The structure of functional brain networks is known to change in time. For an individual node,
this means that the local structure around the node, that is the identity of its neighbors, 可能
改变. This change can be quantified in terms of the Jaccard index between the node’s sets of
neighbors in consecutive time windows. We defined an ROI’s closest neighborhood as its 35
most strongly linked neighbors and investigated the Jaccard index. 的确, we found signifi-
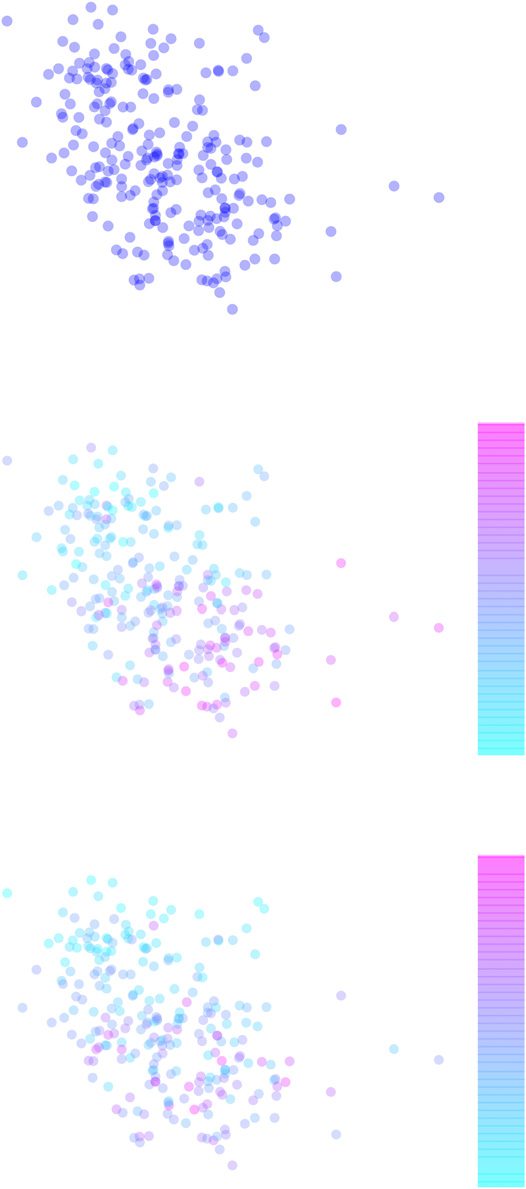
cant changes in ROIs’ neighborhoods in time (图3a). ROIs with the highest neighborhood
turnover may change up to 75% of their closest neighbors between two time windows, 克雷尔-
sponding to a Jaccard index of 0.25. Even the ROIs with the most stable neighborhoods only
reach a Jaccard index value of 0.55, meaning that half of their closest neighborhood changes
between consecutive time windows. 用于比较, shuffling the weights of 5% of randomly
chosen links in the full network for 1000 times yields an average Jaccard index of 0.89±0.062
(mean±SD).
Jaccard index:
A measure of similarity between two
套; defined as the proportion of
intersection of the sets to their union.
Closest neighborhood:
The set of nodes most strongly
connected to the focal node; 这里,
the size of the closest neighborhood
是 35.
网络神经科学
519
ROIs and dynamic functional brain networks
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
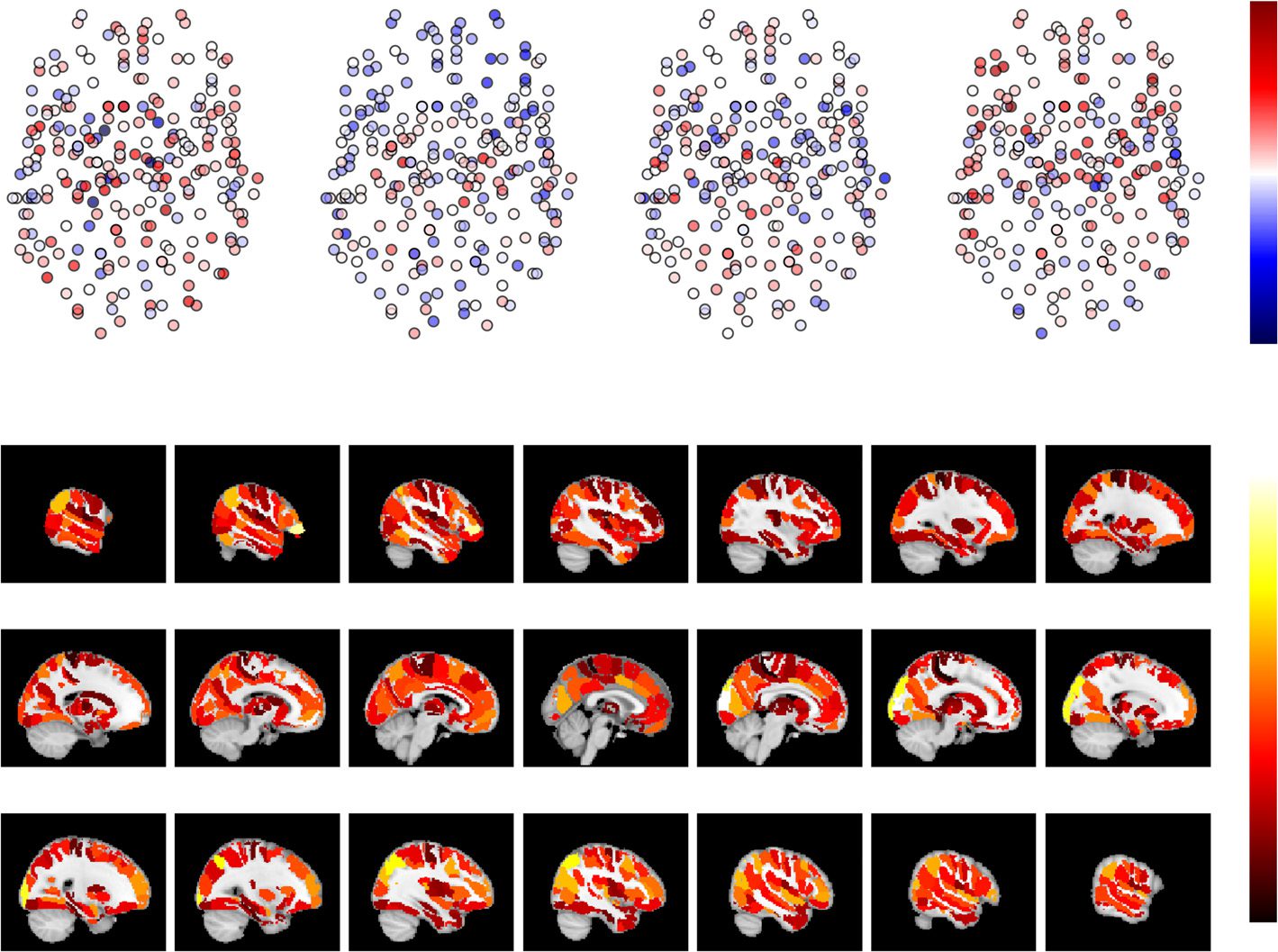
数字 3. There is strong neighborhood turnover in dynamic functional brain networks. (A) 这
Jaccard index between consecutive time windows. Values of the Jaccard index are nonuniformly
distributed in space and show strong spatial correlations: adjacent ROIs show similar values. Node
locations are as in Figure 2. (乙) Network turnover on the brain surface in the Brainnetome atlas.
High network turnover of subcortical ROIs as compared with cortical ROIs is particularly visible.
Jaccard index values and network turnovers have been averaged over 13 主题. For AAL, HO,
and Craddock 200/400, see Supporting Information Figures S6, S7, S8, and S9 (Ryyppö et al., 2018).
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
A
_
0
0
0
4
7
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
The spatial distribution of the Jaccard index over the ROIs appears stable in time. In partic-
他们是, subcortical ROIs have clearly lower Jaccard index values than cortical ROIs independent
of the time window pair investigated. We will discuss possible reasons for this later.
Network turnover, defined as the complement of the mean Jaccard index of the ROI’s
neighborhood over time (参见方程 4), quantifies the overall tendency of the neighborhood
to change in time. Like spatiotemporal consistency, network turnover varies between ROIs
(Figure 3B). As expected because of their low Jaccard index values, subcortical ROIs have
higher network turnover than cortical ROIs. Network turnover is spatially strongly correlated:
anatomically adjacent ROIs tend to have similar values of network turnover.
The Brainnetome ROIs that have the highest average network turnover include the left and
right parahippocampal gyrus (6_5), left thalamus (8_2), and right and left inferior temporal
回 (7_1). In AAL, these include vermis 9, the left caudate nucleus, left cerebellar area 3, 版本-
mis 1_2, and right olfactory cortex. In HO, the ROIs with the highest average network turnover
include the right and left pallidum, anterior division of left temporal fusiform cortex, vermis
X, and vermis VIIIb. For the Craddock 200/400 ROIs with the highest and lowest network
周转, the reader is referred to Supporting Information Figures S18 and S19 (Ryyppö et al.,
2018). There is some variation in the identity of the highest network turnover ROIs across sub-
项目; 然而, subcortical areas tend to have high network turnover in all subjects.
网络神经科学
520
ROIs and dynamic functional brain networks
Identity of ROIs with the lowest network turnover vary a lot across subjects. The ROIs with
the lowest average network turnover include in Brainnetome the left occipital gyrus (4_1),
左中间回 (4_1), right superior occipital gyrus (2_2), and left superior frontal
回 (7_7 and 7_3). In AAL, they include the right fusiform cortex, right cerebellar area 6,
right superior occipital gyrus, 左角回, and right middle occipital gyrus. In HO, 这
low average network turnover ROIs include the left frontal pole, left middle frontal gyrus, 左边
角回, left paracingulate gyrus, and left cuneal cortex.
; AAL: r = −0.42, p (西德:2) 10-5
In addition to spatial variation, we found significant negative correlation between an ROI’s
size and network turnover (Brainnetome: r = −0.60, p (西德:2) 10-5
; HO: r = −0.30, p = 4.02 ×
10-4
; Craddock 200: r = −0.21, p = 0.00232; Craddock 400:
r = −0.41, p (西德:2) 10-5
; Figure 4C). This correlation is most probably dominated by the very
high network turnover values of the subcortical ROIs that, for anatomical reasons, tend to be
smaller than cortical ROIs. In the AAL and HO atlases, the correlation may have been partly
shadowed by the lower number of ROIs and the presence of cerebellar ROIs that are small but
do not have systematically lower network turnover values than ROIs of the cerebral cortex.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
A
_
0
0
0
4
7
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
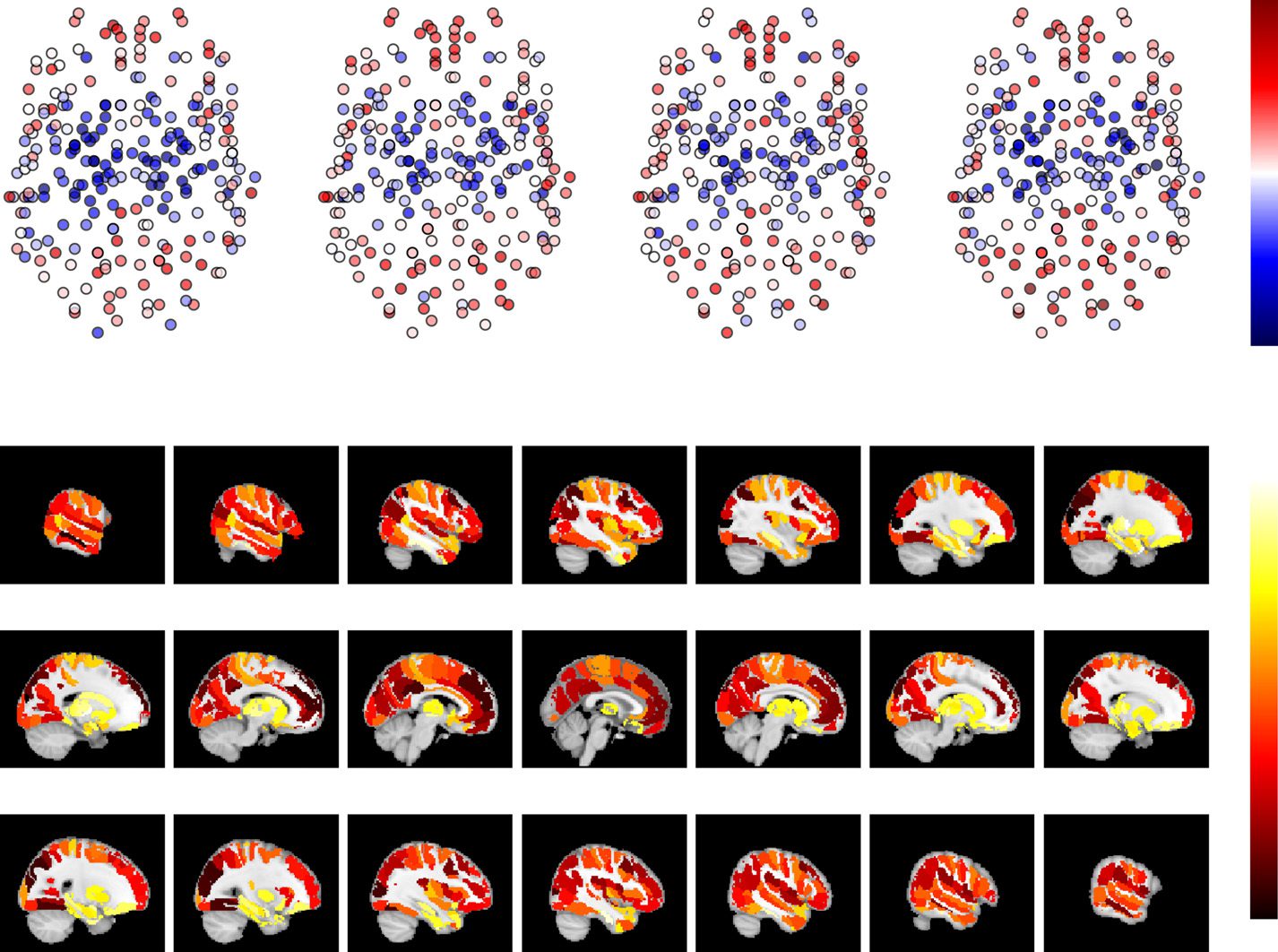
数字 4. Relationship of the sizes of the Brainnetome ROIs to their spatial and spatiotemporal
consistency and network turnover. (A) Static spatial consistency does not correlate with ROI size.
(乙) There is a weak positive correlation between spatiotemporal consistency and ROI size.
(C) Network turnover and ROI size are clearly negatively correlated. Data have been averaged over
13 主题. The solid red lines show bin averages; binning has been done on the basis of ROI
尺寸. For AAL, HO, and Craddock 200/400, see Supporting Information Figures S10 and S11 (Ryyppö
等人。, 2018).
网络神经科学
521
ROIs and dynamic functional brain networks
ROIs with the Highest Spatiotemporal Consistency Have the Lowest Turnover in Their Neighborhood
下一个, we asked how spatiotemporal consistency and network turnover relate to each other. 在
the group level, 那是, averaging the spatiotemporal consistencies and turnovers over subjects,
we found a significant negative correlation between these measures (Brainnetome: r = −0.42,
p (西德:2) 10-5
; Craddock 200:
r = −0.46, p (西德:2) 10-5
) (图5A). 换句话说,
ROIs with the highest spatiotemporal consistency have the lowest amount of turnover in their
街区. These ROIs also have the highest static spatial consistency (图5b).
; Craddock 400: r = −0.42, p (西德:2) 10-5
; AAL: r = −0.38, p = 2.08 × 10−5
; HO: r = −0.44, p (西德:2) 10-5
The correlation between spatiotemporal consistency and network turnover was also visible,
albeit weaker, at the level of single subjects (Brainnetome: 重要的 [p < 0.05] negative
correlation for 6 subjects, negative but nonsignificant correlation for 5 subjects, nonsignificant
positive correlation for 1 subject; HO: significant negative correlation for 7 subjects, negative
but nonsignificant correlation for 5 subjects, nonsignificant positive correlation for 1 subject;
AAL: significant negative correlation for 4 subjects, negative but nonsignificant correlation for
5 subjects, nonsignificant positive correlation for 4 subjects). A plausible reason for the weaker
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
a
_
0
0
0
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Spatial and spatiotemporal consistency and network turnover depend on each other.
A) Spatiotemporal consistency is negatively correlated with network turnover. B) ROIs with the high-
est static spatial consistency also have the highest spatiotemporal consistency and lowest network
turnover. C) Largest ROIs tend to have highest spatial and spatiotemporal consistency and lowest
network turnover in the Brainnetome atlas. Data have been averaged over 13 subjects. For AAL,
HO, and Craddock 200/400, see Supporting Information Figures S12, S13, S14, and S15 (Ryyppö
et al., 2018).
Network Neuroscience
522
ROIs and dynamic functional brain networks
and less significant correlations obtained for AAL is the number of data points: AAL contains
fewer ROIs (116) than Brainnetome (246) or HO (138), which may have made it more difficult
to obtain a significant correlation.
The connectivity profiles of ROIs with low network turnover change only little between
time windows and they resemble the connectivity profiles obtained over the whole time series.
Therefore, ROIs with low network turnover should have stronger links in the networks extracted
from the whole time series. As low-turnover ROIs tend to have high static spatial consistency, it
is not too surprising that we found a correlation between static spatial consistency and degree in
networks extracted from the whole time series. At 2.5% density, this correlation was significant
; AAL: r = 0.31, p (cid:2) 10−5
for all investigated parcellations (Brainnetome: r = 0.48, p (cid:2) 10−5
;
; Craddock 200: r = 0.50, p (cid:2) 10−5
HO: r = 0.41, p (cid:2) 10−5
; Craddock 400: r = 0.57,
p (cid:2) 10−5
). The correlation remained significant also for higher network densities; the highest
density where the correlation was present varied between parcellations (Brainnetome: d =
45.0, r = 0.037, p = 0.0368; AAL: d = 10.0, r = 0.11, p (cid:2) 10−5
; HO: d = 10.0, r = 0.057,
p = 0.0155; Craddock 200: d = 30.0, r = 0.058, p = 0.00309; Craddock 400: d = 40.0,
r = 0.0603, p = 1.67 × 10−5
).
In Brainnetome, the ROIs with the highest spatiotemporal consistency and lowest net-
work turnover tend to be larger than ROIs with lower spatiotemporal consistency and higher
network turnover (Figure 5C). This is as one may expect based on the correlations between
spatiotemporal consistency and ROI size, and network turnover and ROI size (Figure 4B and C).
In AAL, HO, and Craddock 200/400, this relationship is less clear (see Supporting Information
Figures S12C, S13C, S14C, and S15C, Ryyppö et al., 2018).
The relationship between spatiotemporal consistency and network turnover strongly depends
on how we define spatiotemporal consistency. The definition given in Equation 3 measures
relative changes in spatial consistency. To get a more complete picture, we also investigated
an alternative definition of spatiotemporal consistency that measures absolute changes. For
details, the reader is referred to the reader is referred to Supporting Information Results (Ryyppö
et al., 2018).
ROIs Can Be Divided into Two Extreme Groups on the Basis of Consistency and Turnover,
and These Match with Cortical and Subcortical Regions
So far, we have investigated the relationship between spatiotemporal consistency and network
turnover at the population level. Next, we asked which specific ROIs are the ones with the
highest and lowest values of spatiotemporal consistency and network turnover. To this end,
we obtained two groups of extreme ROIs by applying principal component analysis (PCA) in
the space spanned by spatiotemporal consistency and network turnover. The extreme groups
contain the five ROIs with the largest and smallest projected coordinates on the first principal
component. ROIs of the first group have high spatiotemporal consistency and low network
turnover, and ROIs of the second group have lower spatiotemporal consistency and high net-
work turnover (Figure 6). As the PCA has only two degrees of freedom, the extreme groups
could in principle have been defined by visual inspection alone; the main reason for applying
PCA was to avoid subjectivity and to ensure that the extreme groups are defined similarly in
all investigated parcellations.
In Brainnetome, the first group contains the right cuneus (5_3), right superior occipital gyrus
(2_1), left inferior frontal gyrus (6_4), right inferior parietal lobule (6_2) and left occipital gyrus
(4_1). The AAL ROIs of this group are the right cerebellar area 6, left medial orbitofrontal cortex,
Network Neuroscience
523
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
a
_
0
0
0
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
ROIs and dynamic functional brain networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
a
_
0
0
0
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
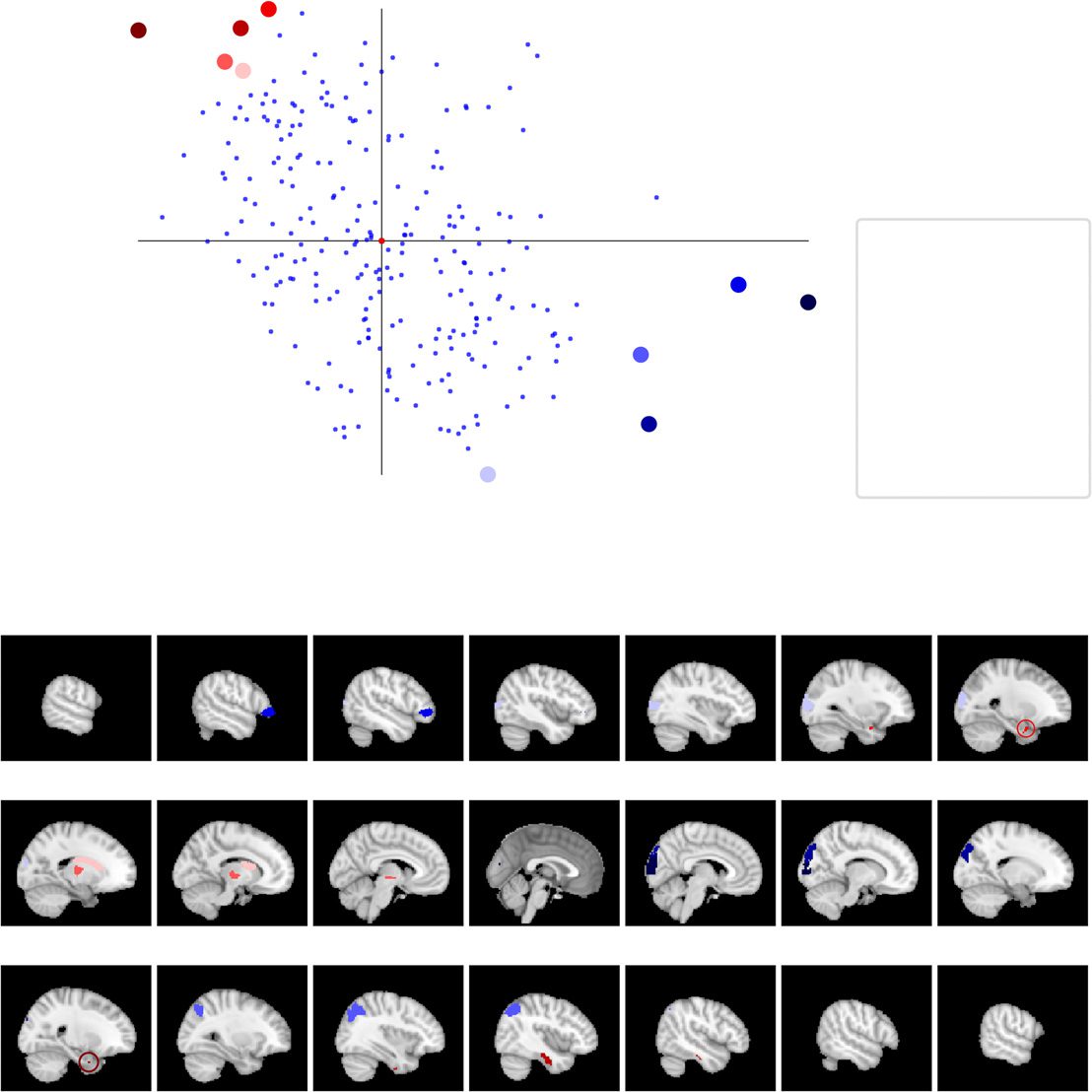
Figure 6. Extreme ROIs in terms of spatiotemporal consistency and network turnover. (A) Location
of extreme ROIs in the space spanned by spatiotemporal consistency and network turnover. The
blue and red groups have been chosen with the help of PCA (see text). The ROIs in the blue group
have high spatiotemporal consistency and low network turnover, whereas the ROIs in the red group
have low spatiotemporal consistency and high network turnover. The internal voxel-level connec-
tivity of ROIs marked with a square is investigated in detail; see Figure 7. (B) Location of extreme
ROIs on the brain surface. L: left; R: right; Cun: cuneus; sOcG: superior occipital gyrus; IFG: infe-
rior frontal gyrus; IPL: inferior parietal lobule; OcG: occipital gurys; Str: striatum; Tha: thalamus;
PhG: parahippocampal gyrus; ITG: inferior temporal gyrus. For AAL, HO, and Craddock 200/400,
see Supporting Information Figures S16, S17, S18, and S19 (Ryyppö et al., 2018).
right superior occipital gurys, left angular gyrus and right middle occipital gyrus. In HO, this
group comprises the left frontal pole, right and left supracalcarine cortex, left middle frontal
gyrus and right angular gyrus. For Craddock 200/400 ROIs belonging to the extreme groups,
the reader is referred to Supporting Information Figures S18 and S19 (Ryyppö et al., 2018).
The second group, that is, the ROIs with low spatiotemporal consistency and high network
turnover, contains in Brainnetome the left and right parahippocampal gyrus (6_5), right inferior
temporal gyrus (7_1), left thalamus (8_8) and left striatum (6_5). The AAL ROIs that belong to
this group are the right globus pallidum, left paracentral lobule, right olfactory cortex, right
cerebellar area 9 and Vermis 1_2. In HO, this group contains the right and left pallidum, brain
stem, right hippocampus, and right thalamus. In all five parcellations, most ROIs of this group
are relatively small areas located deep in the brain. Because of the location, the signal-to-noise
ratio (SNR) of the fMRI measurement tends to be low for these areas. This may at least partially
explain their low spatiotemporal consistency and may also limit the accuracy of estimating
their network connectivity, leading to noisy closest neighborhoods and high turnover.
The sets of extreme ROIs in different parcellations are not the same, but this is to be ex-
pected. First, the ROIs of different parcellations have different shapes, sizes, and locations.
Network Neuroscience
524
ROIs and dynamic functional brain networks
Second, there are many ROIs with spatiotemporal consistency and network turnover that are
rather close to those of the five most extreme ROIs; this hard threshold is of course arbitrary.
Nontrivial, Dynamic Voxel-Level Structure Occurs within ROIs
From both groups of extreme ROIs, we selected two ROIs for a more detailed investigation.
We chose the most extreme ROIs that were not exceptionally small or too large for the visual-
ization discussed below. In Brainnetome, the selected ROIs were the left inferior frontal gyrus
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
a
_
0
0
0
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. The internal connectivity structure of ROIs is visible in the voxel-level correlation matrices of their internal connections. This
internal structure changes in time. The upper two rows display matrices for high-spatiotemporal-consistency-low-network-turnover ROIs,
and the two lower rows those for low-spatiotemporal-consistency-high-network-turnover ROIs. To order the voxels within each ROI, voxels
were assigned to communities with the generalized Louvain method for multiplex networks, and then the Hamming distance between these
community assignments was used to find the optimal leaf order of the hierarchical clustering tree (Jeub et al., 2011–2017; Mucha et al., 2010).
The order of voxels is same in all time windows. Data of one representative subject are shown here. L: left; R: right; IFG: inferior frontal
gyrus; sOcG: superior occipital gyrus; Str: striatum; Tha:
thalamus. For AAL, HO, and Craddock 200/400, see Supporting Information
Figures S20 and S21 (Ryyppö et al., 2018).
Network Neuroscience
525
ROIs and dynamic functional brain networks
(6_4) and right superior occipital gyrus (2_1) from the high-spatiotemporal-consistency-low-
network-turnover group and the left striatum (6_5) and left thalamus (8_8) from the opposite
group. We calculated voxel-level correlation matrices to reveal the internal correlation struc-
ture inside these ROIs (Figure 7).
The two groups are visibly different in terms of their correlation matrices: the overall cor-
relation level is clearly higher for ROIs with high spatiotemporal consistency than for ROIs
with low spatiotemporal consistency. The voxel-level correlations are not, however, uniformly
distributed. Instead, a division into several internally highly correlated subareas is visible inside
ROIs with high spatiotemporal consistency and ROIs with low spatiotemporal consistency.
This internal structure of ROIs is seen to change in time. In the right superior occipital gyrus
that has high spatial and spatiotemporal consistency, the voxels are uniformly correlated across
the whole ROI in time windows 1 and 2 but separate into two clusters between time windows
2 and 3. Similarly, the left thalamus that has low spatial and spatiotemporal consistency shows
time-dependent internal cluster structure.
The internal structure of ROIs may affect their spatiotemporal consistency and static spatial
consistency in several ways. For example, stable internal structure should manifest itself as
high spatiotemporal consistency, because the average voxel-level correlation does not change
in time. Fewer and larger subareas lead to larger amounts of correlated voxels within the ROI
and should therefore be associated with higher static spatial consistency. On the other hand, a
large number of small subareas should lead to low static spatial consistency, as should a total
lack of internal structure.
DISCUSSION
Functional Homogeneity of ROIs Varies in Time
The use of ROIs as nodes of fMRI brain networks assumes functional homogeneity: each of
the ROI’s voxels is thought to have similar dynamics, and therefore the ROI time series is con-
sidered as an accurate representation of the voxel-level dynamics. Earlier (Korhonen et al.,
2017), we have shown that this assumption does not hold for the ROIs of commonly used
parcellations. To this end, we used spatial consistency, a measure of functional homogeneity
defined as the mean Pearson correlation coefficient between voxel time series inside an ROI.
Functional homogeneity is often considered as a static ROI property. However, functional
brain networks change in time, even on short timescales (Bassett et al., 2011; Göttlich et al.,
2017; Honey et al., 2007). Here, we investigated the temporal behavior of spatial consistency.
We divided fMRI data measured during a free music listening task into time windows and cal-
culated the relative change in spatial consistency between them. For quantifying the temporal
variation in spatial consistency, we introduced spatiotemporal consistency as the inverse of the
mean relative change in spatial consistency over time windows (see Equation 3). We found
that spatial consistency changes significantly in time, the largest relative changes being up to
30%, resulting in low spatiotemporal consistency.
The concept of dynamic functional connectivity has been recently debated among the
neuroscientific community. Although many studies have reported time-dependent changes
in the structure of functional brain networks (Bassett et al., 2011; Cocchi et al., 2017; Honey
et al., 2007; Zalesky et al., 2014), the neurophysiological meaning of these changes is not fully
understood (Keilholz et al., 2017; Preti, Bolton, & Van De Ville, 2016). An fMRI measurement
is always only a single realization of the underlying stochastic process, and it may therefore
Network Neuroscience
526
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
a
_
0
0
0
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
ROIs and dynamic functional brain networks
show connectivity fluctuations even if the underlying process is stationary (Liegeois, Laumann,
Snyder, Zhou, & Yeo, 2017). However, obtaining multiple realizations of the exact same pro-
cess is impossible; the measurements of different subjects as well as the measurements of same
subject at different times are different processes (Liegeois et al., 2017). Therefore, it is hard to
construct a proper null model for evaluating the statistical significance of dynamic functional
connectivity (Liegeois et al., 2017; Miller, Adali, Levin-Schwartz, & Calhoun, 2017). We do
not use a stationary null model in the present study, similarly to many other studies.
If one wants to investigate in detail whether the observed changes in spatial consistency
are meaningful, two different paths can be taken. First, testing the results against a statistically
rigorous null model would ensure their significance. Second, the neurophysiological meaning
of spatiotemporal consistency could be addressed by comparing consistencies obtained for
data measured during rest and during different tasks: obtaining similar changes in response
to a common stimulus in a group of subjects can be considered as indicative of some real
underlying mechanism, even if no formal null model is applied.
Functionally Homogeneous and Inhomogeneous ROIs Have Both Turnover in Their
Network Neighborhoods
The structure of functional brain networks changes with cognitive tasks (Braun et al., 2015;
Chan et al., 2017; Göttlich et al., 2017), and increased local connectivity can be associated
with increased activity and cognitive demand (Hearne, Cocchi, Zalesky, & Mattingley, 2017;
Jiang & Zuo, 2016; Zang, Jiang, Lu, He, & Tian, 2004). If the temporal variation in spatial con-
sistency is related to changes in brain function, one would expect to see simultaneous changes
in network structure as well. Indeed, there was clear turnover in the closest neighborhoods of
ROIs, “closest” being defined as the 35 most strongly connected neighbors. This turnover was
lower for ROIs with high spatial and spatiotemporal consistency; however, even these ROIs
changed up to half of their closest neighbors between consecutive time windows. This indi-
cates that the local structure of functional brain networks truly changes on short time scales.
Furthermore, the network turnover investigated here only quantifies the changes in the identi-
ties of the closest neighbors, but does not take into account changes in connection strengths
within the closest neighborhood. Therefore, prominent changes may take place in the ranks
of the closest neighbors of even an ROI with moderately low network turnover.
We saw that network turnover varies across ROIs. One may speculate about how this vari-
ation may relate to the ROIs’ different functional roles. It is possible that some ROIs need a
diverse and varying set of connections for performing their cognitive tasks, whereas others re-
quire a stable set of neighbors. However, there may be a more straightforward explanation for
the variation in network turnover. The ROIs with the highest network turnover are subcortical
and cerebellar areas that also have low spatiotemporal and spatial consistency. The SNR of the
signals originating from these ROIs is known to be low in fMRI measurements (Glasser et al.,
2016). This may partially explain their low spatiotemporal and spatial consistency, and also
suggests that their connectivity may be inaccurately mapped. Therefore, their extreme network
turnover may be partially explained by measurement noise.
We obtained temporal changes in both the spatial consistency and the closest neighbor-
hoods of ROIs. However, we did not investigate the exact timing of these changes. If neighbor-
hood turnover and variation in spatial consistency are both caused by changes in brain activity,
these changes should be more or less simultaneous. This would result in a temporal correlation
between the variation of spatial consistency and the neighborhood turnover. The datasets used
in the present study—free music listening and resting state—may not necessarily be optimal
Network Neuroscience
527
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
a
_
0
0
0
4
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
ROIs and dynamic functional brain networks
for this kind of investigation. Cognitive responses to the music may differ between subjects,
and in the resting-state subjects are instructed to let their mind wander uncontrolled. A more
detailed investigation of the connection between spatial consistency and turnover would re-
quire a dataset with more control on the timing of putative activity changes. This could be
achieved with the traditional block design, where stimuli are repeated at set intervals and the
timeline is divided into blocks (see, e.g., Tie et al., 2009). However, the shortness of the blocks
is problematic from the viewpoint of network studies: reliable estimation of a functional brain
network requires time series significantly longer than typical block lengths.
The Internal Structure of an ROI May Relate to Its Functional Role
Functional networks are constructed using only the averaged ROI time series, and the only
feature that is used in any subsequent analysis is the ROI’s location on the brain surface. At the
same time, their size, shape, and in particular internal connectivity are typically ignored. This
view of ROIs as featureless entities may, however, be largely oversimplified. We found rich,
time-dependent structure of voxel-level correlations inside ROIs. Considering the complexity
of the brain and the small number of ROIs and their connections to which this complexity is
reduced, this is not surprising at all.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
a
_
0
0
0
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The ROIs that we investigated have very different looking internal structures. These are not
necessarily reflected in their consistency measures; in Figure 7 the two uppermost ROIs have
high spatiotemporal consistency, but their correlation matrices display different kinds of struc-
tures. The same applies to the two low-consistency bottom rows.
Why do ROIs have different kinds of internal structures? A plausible hypothesis is that the
correlation structure inside an ROI relates to an ROI’s functional role. Let us consider local
and connector hubs (Bullmore & Sporns, 2009; Guimerà & Amaral, 2005) as an example.
Local hub nodes are central in their local network modules and have only few connections to
nodes outside of their own module, whereas connector hubs act as bridges between different
modules. So, could one separate local and connector hubs from each other in terms of their
internal structure? Local hubs are connected only to a relatively stable neighborhood; one
might expect that the voxel-level correlation distribution inside them is relatively uniform, and
periods of high and low voxel-level correlations reflect changes in the activity of the ROI.
Connector hubs, on the other hand, need to be able to connect to several different network
modules; an internal structure of diverse subareas could help in this.
Can Brain Networks Be Modelled by Static Nodes?
When ROIs are used as nodes of functional brain networks, the brain is assumed to contain
a set of static functional areas. An optimal parcellation of the brain then maps to these areas,
resulting in functionally homogeneous ROIs.
If the static-area assumption holds, low func-
tional homogeneity of ROIs then only tells about inaccuracies in ROI definitions, which can
be corrected by a more accurate parcellation scheme.
Time-dependent changes have been reported in the module structure of functional brain
networks at the ROI level (Khambhati, Sizemore, Betzel, & Bassett, in press). Our results
suggest that similar changes also occur in the voxel-level correlation structure inside ROIs.
The dynamically changing internal connectivity of ROIs appears to challenge the assumption
of static functional areas. Because the ROIs of multiple different parcellations have a time-
varying structure, it seems plausible that the changing internal connectivity is not a technical
Instead, it may be a genuine
issue that can be fixed by an elaborate parcellation scheme.
Network Neuroscience
528
ROIs and dynamic functional brain networks
feature and related to how the brain works. If so, it may even be impossible to define ROIs in
a way that would make them persistently homogeneous.
Many problems caused by the functional inhomogeneity of ROIs can be overcome by using
fMRI measurement voxels as nodes of brain networks (Fornito, Zalesky, & Breakspear, 2013;
Hayasaka & Laurienti, 2010). However, there is evidence for existence of functional areas
larger than single voxels (Shen, Tokoglu, Papademetris, & Constable, 2013; Wig et al., 2011),
which motivates investigating brain networks above the level of voxels as well. For example,
Preti & Van De Ville (2017) have suggested an approach for parcellating the brain based on
the dynamic connectivity of voxels; these parcels would be an interesting option for defining
network nodes. Similarly, the negative correlation we observed between network turnover and
spatial consistency could be used for defining ROIs: defining ROIs as clusters of voxels that
have minimal network turnover should produce ROIs with reasonable spatial consistency.
An optimal network model of the brain should measure the dynamic connectivity between
In the
clusters of voxels and also quantify the changing internal structure of these clusters.
coarse-graining approach by Kujala et al. (2016), self-links are used to model changes in inter-
nal connectivity. As long as static sets of nodes are used to model the time-dependent connec-
tivity of the human brain, outcomes of brain network analysis may be surprisingly inaccurate.
Therefore, network neuroscience would greatly benefit from node definition strategies tailored
for dynamic networks.
MATERIALS AND METHODS
Subjects
fMRI data of 13 subjects (7 women, 6 men, age 28.70 ± 10.17 years, mean ± SD, 1 left-handed,
12 right-handed) were used in the present study. The data were collected as a part of a study of
functional connectivity during music listening, containing both musicians and non-musicians
freely listening to music, and have been earlier described in Alluri et al. (2015, 2017) and
Burunat et al. (2015). For the present study, we used the parts of the dataset that were readily
available at the Department of Neuroscience and Biomedical Engineering, Aalto University.
The subjects used in the present study were considered as non-musicians, that is, they had no
formal musical training.
All participants signed an informed consent on arrival to the laboratory and received com-
pensation for the use of their time. All experimental procedures for this study, included in the
broad research protocol termed Tunteet, were approved by the Coordinating Ethics Commit-
tee of the Hospital District of Helsinki and Uusimaa (the approval number 315/13/03/00/11,
obtained on March 11, 2012). All procedures were conducted in agreement with the ethical
principles of the Declaration of Helsinki.
Data Acquisition
Functional magnetic resonance imaging (fMRI) data were acquired using a 3T MAGNETOM
Skyra scanner (Siemens Healthcare, Erlangen, Germany) and a standard 32-channel head-neck
coil in the AMI Centre (Aalto Neuroimaging, Aalto University, Espoo, Finland). A T2*-weighted
whole-brain EPI sequence was measured with the following parameters: TR = 2 s, 33 oblique
, voxel size = 3×3×4 mm
slices, TE = 32 ms, flip angle = 75
, matrix
size = 64 × 64. T1-weighted structural magnetic resonance images (MRI) were acquired with
the following parameters: 176 slices, FOV = 256×256 mm
, matrix size = 256 × 256, slice
thickness = 1 mm.
, FOV = 192 × 192 mm
◦
3
2
2
Network Neuroscience
529
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
a
_
0
0
0
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
ROIs and dynamic functional brain networks
During the measurement, subjects were instructed to fix their gaze on the screen and ac-
tively listen to a musical stimulus (Adios, Nonino by Astor Piazzolla) via MR-compatible insert
earphones. Foam was used to suppress the noise caused by the imaging gradients. Duration
of the stimulus, and therefore of the measured time series, was 8.13 min (244 samples).
The data were preprocessed with FSL software (www.fmrib.ox.ac.uk,
Preprocessing of the data.
version 5.0.9) and custom in-house MATLAB code (BRAMILA pipeline v2.0, available at
https://version.aalto.fi/gitlab/BML/bramila) following the standard fMRI preprocessing steps.
This included EPI slice time correction as well as head motion correction using MCFLIRT.
The data were coregistered to the Montreal Neurological Institute (MNI) 152 2 mm standard
template using FLIRT two-step procedure where the EPI volumes were first registered to the
anatomical image of participants brain (9 degrees of freedom) and the participants anatomical
image was then registered to the standard template (12 degrees of freedom). No spatial smooth-
ing was applied, but a 240-sec-long cubic Savitzky-Golay filter (Çukur, Nishimoto, Huth, &
Gallant, 2013) was used to remove scanner drift, and the BOLD time series were filtered using
a Butterworth bandpass filter at 0.01–0.08 Hz. For increased control of motion and physio-
logical artifacts, 24 motion-related regressors, signal from deep white matter, ventricles and
cerebrospinal fluid were regressed out of the BOLD time series (Power et al., 2014).
Voxels with over 70% of their variance explained by motion or signal from tissues other
than the grey matter were removed from the analysis.
Regions of Interest
After preprocessing, we divided the cortex, subcortical areas, and cerebellum into ROIs. We
used ROIs from five commonly-used parcellations:
the connectivity-based Brainnetome
atlas and Craddock 200/400 atlases as well as the anatomical Automated Anatomical Labeling
(AAL) and HarvardOxford (HO) atlases. To build the group-level mask for each of the parcella-
tions, we used the subject-wise analysis masks obtained as a part of the preprocessing pipeline
to account for individual differences in anatomy, and included in the group-level mask only
voxels that were present in the analysis masks of all subjects. Voxel-wise time series were ex-
tracted for each ROI, and ROI-wise time series were obtained as an average of these voxel-wise
time series within each ROI:
XI(t) =
1
Ni
∑
i∈I
xi(t),
(1)
where XI(t) is the time series of the focal ROI I, NI is its size defined as the number of
constituent voxels, xi(t) is the time series of voxel i, and summation is over voxels i in the
focal ROI.
Some of the parcellations used in this study, in particular AAL and Craddock 200/400, are
known to show rather low mean functional homogeneity across ROIs (Gordon et al., 2014).
However, the ROIs of these parcellations are commonly used as nodes of functional brain
networks, and therefore we have chosen to include them in our study.
The Brainnetome atlas (Fan et al., 2016) is based on combination of struc-
Brainnetome atlas.
tural and functional connectivity measured by multimodal imaging techniques. In the present
study, we used 246 Brainnetome ROIs. Of these, 210 ROIs were located in the cerebral cor-
tex, while 36 ROIs covered subcortical gray matter. Note that the Brainnetome atlas does not
include cerebellar ROIs.
Network Neuroscience
530
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
a
_
0
0
0
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
ROIs and dynamic functional brain networks
Size of the Brainnetome ROIs varied between 6 and 1,102 with a median of 414. Mean
ROI size was 424.02±222.76 (mean±SD).
James,
The connectivity-based Craddock parcellations
Craddock 200/400.
Holtzheimer, Hu, & Mayberg, 2012a) have been obtained by applying a two-level normalized
cut spectral clusteringalgorithm on the voxel-level resting-state connectivity matrix. In the present
study, we investigate the Craddock 200 and Craddock 400 parcellations that contain 200 and
392 ROIs, respectively, covering the cerebral cortex, subcortical areas, and cerebellum.
(Craddock,
The sizes of the Craddock 200 ROIs varied between 202 and 1,239 with a median of 706.5.
The mean ROI size was 689.96±168.12 (mean±SD). The sizes of the Craddock 400 ROIs
varied between 56 and 600 with a median of 354.5. The mean ROI size was 352.02±88.787
(mean±SD).
AAL (Tzourio-Mazoyer et al., 2002) is an anatomical
Automated Anatomical Labeling atlas.
atlas that has been obtained by parcellating a spatially normalized high-resolution single-
subject structural volume based on the main sulci. After the parcellation, each ROI has been
automatically associated with a label. We used 116 AAL ROIs, 90 of which were located in
the cerebral cortex, 8 in the subcortical gray matter, and 18 in the cerebellum.
Size of the AAL ROIs varied between 44 and 4,370 with a median of 1,158.5 and a mean
of 1,366.01±929.64.
The HO atlas (http://neuro.debian.net/pkgs/fsl-harvard-oxford-atlases.
HarvardOxford atlas.
html; Desikan et al., 2006) is a probabilistic atlas, where the brain is divided into ROIs based
on macroanatomical boundaries. We used HO ROIs at the probability level of 30%, meaning
that each voxel belonged to the ROI it is associated with in 30% or more of the subjects used
to construct the atlas. We used 138 HO ROIs, out of which 96 were located in the cerebral
cortex, 15 covered subcortical gray matter, and 27 were located in the cerebellum. Note that
one of the cerebellar ROIs of the HO atlas (Vermis Crus I) is not defined at the probability level
of 30%. Therefore, this ROI is not included in the present study.
Size of the HO ROIs varied between 28 and 5,578 with a median of 633.5 and a mean of
915.63±921.83 (mean±SD).
Network Extraction
To construct the dynamic functional brain networks, the time series were divided into time
windows of 80 samples. This corresponds to a duration of 160 s. The consecutive time windows
had an overlap of 50%. This resulted in a total of five time windows along the duration of the
scan.
The window length was selected so that we were able to investigate the changes of spatial
consistency and local network structure (see below) across as many windows as possible, but
the values of spatial consistency were not affected by the short window length. The window
length that we used was selected so that further increasing it did not increase the value of
spatial consistency obtained in the window (see Supporting Information Methods, Ryyppö
et al., 2018, for details on selecting the window length). It has been suggested that the time
window length should be equal or larger than 1/ fmin where fmin is the lowest signal frequency
present in the data (Leonardi & Van De Ville, 2015; Shakil, Billings, Keilholz, & Lee, 2017;
Network Neuroscience
531
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
5
1
3
1
0
9
2
2
5
9
n
e
n
_
a
_
0
0
0
4
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
ROIs and dynamic functional brain networks
Shakil, Keilholz, & Lee, 2015); the selected window length fulfills this condition. Furthermore,
time windows of similar length have been used for constructing dynamic brain networks in the
literature (Bassett et al., 2011, 2013).
We computed the ROI-level adjacency matrix A separately in each of the time windows.
The elements AI J of the adjacency matrix quantified the connectivity between ROIs I and J,
defined as Pearson correlation coefficient between their ROI time series. The diagonal of the
adjacency matrix was set to zero in order to remove self-links. No thresholding of the correla-
tion values was performed at this stage.
Spatial and Spatiotemporal Consistency
For quantifying the functional homogeneity of the ROIs, we used spatial consistency that we
have introduced in Korhonen et al. (2017). The spatial consistency φspatial(I) of ROI I is defined
as the mean Pearson correlation coefficient between the time series of voxels within the ROI:
φspatial(I) =
1
NI (NI − 1) ∑
i,i(cid:5)∈I
C(xi(t), xi(cid:5) (t)),
(2)
where voxels i and i(cid:5)
belong to ROI I and C denotes the Pearson correlation coefficient.
We calculated spatial consistency of all ROIs separately in each time window. For quanti-
fying the variation of spatial consistency across time, we defined spatiotemporal consistency
for ROI I as
φst =
2 ∑t