研究 - 麻省理工学院人工智能研究专业

研究

Comparing individual and group-level simulated
neurophysiological brain connectivity using
the Jansen and Rit neural mass model

S. D. Kulik1,3,4

, L. Douw1,3, 乙. van Dellen5, 中号. D. Steenwijk1,4, J. J. G. Geurts1,4,

C. J. Stam2, A. Hillebrand2, 中号. 中号. Schoonheim1,4, 和P. Tewarie2

1Amsterdam UMC, Vrije Universiteit Amsterdam, Department of Anatomy & 神经科学,
Amsterdam Neuroscience, Amsterdam The Netherlands
2Amsterdam UMC, Vrije Universiteit Amsterdam, Department of Neurology and Department of Clinical
Neurophysiology and MEG Center, Amsterdam Neuroscience, Amsterdam The Netherlands
3Amsterdam UMC, Vrije Universiteit Amsterdam, Brain Tumour Center Amsterdam, 阿姆斯特丹, 荷兰人
4Amsterdam UMC, Vrije Universiteit Amsterdam, MS Center Amsterdam, 阿姆斯特丹, 荷兰人
5University Medical Center Utrecht, Department of Psychiatry, Brain Center, 乌得勒支, 荷兰人

关键词: Computational modeling, 脑磁图, Functional connectivity,
Individual prediction

抽象的

Computational models are often used to assess how functional connectivity (FC) 图案
emerge from neuronal population dynamics and anatomical brain connections. It remains
unclear whether the commonly used group-averaged data can predict individual FC
图案. The Jansen and Rit neural mass model was employed, where masses were coupled
using individual structural connectivity (SC). Simulated FC was correlated to individual
magnetoencephalography-derived empirical FC. FC was estimated using phase-based (phase
lag index (PLI), phase locking value (PLV)), and amplitude-based (amplitude envelope
correlation (AEC)) metrics to analyze their goodness of fit for individual predictions. 个人
FC predictions were compared against group-averaged FC predictions, and we tested whether
SC of a different participant could equally well predict participants’ FC patterns. The AEC
provided a better match between individually simulated and empirical FC than phase-based
指标. Correlations between simulated and empirical FC were higher using individual
SC compared to group-averaged SC. Using SC from other participants resulted in similar
correlations between simulated and empirical FC compared to using participants’ own SC.
This work underlines the added value of FC simulations using individual instead of group-
averaged SC for this particular computational model and could aid in a better understanding of
mechanisms underlying individual functional network trajectories.

作者总结

Employing the Jansen and Rit neural mass model, we simulated individual FC by using
individual SC. The AEC, one of the applied FC metrics, proved to give the highest correlations
between simulated and empirical FC. 还, individual SC as compared to group-averaged
SC provided higher correlations between simulated and empirical FC. 然而, using SC
from other participants resulted in similar correlations between simulated and empirical FC
compared to using participants’ own SC. 重要的, this work underlines the value of
individual SC as compared to group-averaged SC to simulate FC. The insights obtained from

开放访问

杂志

引文: Kulik, S. D ., Douw, L。, van
Dellen, E., Steenwijk, 中号. D ., Guerts,
J. J. G。, 斯塔姆, C. J。, 希勒布兰德, A。,
Schoonheim, 中号. M。, & Tewarie, 磷.
(2023). Comparing individual and
group-level simulated neurophysiological
brain connectivity using the Jansen
and Rit neural mass model. 网络
神经科学, 7(3), 950–965. https://土井
.org/10.1162/netn_a_00303

DOI:
https://doi.org/10.1162/netn_a_00303

支持信息:
https://doi.org/10.1162/netn_a_00303

已收到: 25 七月 2022
公认: 24 十二月 2022

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
Shanna D. Kulik
s.kulik@amsterdamumc.nl

处理编辑器:
Pedro Valdes-Sosa

版权: © 2023
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
3
9
5
0
2
1
5
4
8
2
8
n
e
n
_
A
_
0
0
3
0
3
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Individualized modeling of brain connectivity

Functional connectivity:
Statistical interdependencies
between time series that describe
activity measurements.

Computational model:
Model to simulate brain activity
based on empirically derived
structural information, a coupling
function and a local model.

结构连接:
Estimation of white matter tracts
physically interconnect brain regions
based on diffusion measurements.

Neural mass:
Mean-field description of a
population of neurons with usually a
restricted number of state variables
for each population.

this work might lead to a better understanding of mechanisms underlying individual functional
network trajectories.

介绍

The brain is a complex network of brain regions that display interregional communication, 那
是, so-called functional connectivity (FC). FC is defined by statistical interdependencies
between time series of brain activity (弗里斯顿, 2011). In case of neurophysiological data, FC
can be estimated from either the phase or amplitude of neuronal oscillations (西格尔等人。,
2012; Siems & 西格尔, 2020). Disruption of the FC patterns are known to be clinically relevant
in neurological (斯塔姆, 2014) and psychiatric disorders (Hallett et al., 2020). 计算型
models are often used to gain insight into mechanisms that result in disrupted patterns of
FC. Using this approach, the impact of pathology at the neuronal population level or at the
level of structural connections on FC can be assessed and used to make predictions of empir-
ical FC patterns. Especially individualized prediction of disease trajectories (Douw et al., 2019)
are important in this context. 然而, so far mainly group-averaged structural connectivity
(SC) and FC have been used, and it remains an open question whether individual predictions
of FC are feasible, even in healthy conditions.

Computational modeling of brain activity and FC can be approached using so-called neural
mass modeling (Deco et al., 2008). Neural mass models assume a mean ensemble activity of
neurons that reduces the number of dimensions and allows multiple interacting local popula-
系统蒸发散 (Breakspear, 2017). A neural mass corresponds to activity within a brain region, 和
masses can be coupled using empirically measured structural connections, 导致
whole-brain network simulations. A well-known model that is known to generate physiolog-
ically accurate brain activity (Aburn et al., 2012) was developed by Lopes da Silva et al. (1974)
and further improved by Jansen and Rit (Jansen & Rit, 1995). The Jansen and Rit model is able
to produce oscillatory activity in the alpha band, 那是, the dominant rhythm in resting-state
neurophysiological data. Usage of this model can be justified by the fact that its dynamical
properties have been thoroughly investigated and are well understood (Grimbert & Faugeras,
2006; Spiegler et al., 2011).

迄今为止, computational modeling of empirical neurophysiological connectivity is mainly
based on group-averaged SC as input to neural mass models (Abeysuriya et al., 2018; Cabral
等人。, 2014; Deco et al., 2017; Hadida et al., 2018; Moon et al., 2015; O’Neill et al., 2018;
Tewarie et al., 2014; Tewarie et al., 2019A). One previous study on structure-function relation-
ships compared individually simulated and empirically derived FC, based on electroenceph-
alography (EEG) 数据 (Finger et al., 2016). This study showed moderate to strong correlations
between individually simulated and empirical FC by using a simple autoregressive model. FC
was calculated with different phase-based FC metrics. Finger and colleagues tested the spec-
ificity of using individual SC by correlating individually simulated FC with either the corre-
sponding empirical FC matrices, or with empirical FC matrices of other participants, and found
no significant differences between the two approaches. This finding could be supported by a
recent functional magnetic resonance imaging (MRI) 学习 (Zimmermann et al., 2019) where it
was found that the correspondence between empirical SC and FC in many participants was
limited due to the small variability between participants in SC compared with the larger var-
iability in FC, perhaps indicating that structural data is not specific enough to simulate FC
accurately. Despite the relevance of previous work (Finger et al., 2016), we argue that the

网络神经科学

951

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
3
9
5
0
2
1
5
4
8
2
8
n
e
n
_
A
_
0
0
3
0
3
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Individualized modeling of brain connectivity

乙二醇:
脑磁图; 记录
the magnetic fields produced by
electrical currents generated by
神经群体.

dMRI:
Specific MRI sequence that quantifies
the diffusion of water molecules in
different directions, which can be
used for probabilistic tractography.

纤维束成像术:
Method for tracking the trajectory of
the axonal pathways that exploits
the anisotropy of the diffusion MRI
signal.

feasibility of individual predictions of FC should be retested in an independent dataset and
should be tested using both amplitude- and phase-based metrics for FC, as recent work suggest
that both phase and amplitude could encode complementary information (Siems & 西格尔,
2020). 然而, this observation has not been reproduced in an independent dataset. 在
添加, we will extend previous work by including more participants, making use of
脑磁图 (乙二醇) instead of EEG data and applying different FC metrics.

In the current work, we investigated how well individual empirical FC can be approximated
by simulating an estimate of FC based on an individual’s own SC. We analyzed both
振幅- and phase-based metrics in this context, calculated from MEG data. To put our
results into perspective, we compared our results of individual simulations with FC approxi-
mations based on group-averaged SC and individual predictions based on nonmatched
empirical SC.

方法

参加者

Forty healthy participants (37.5% 男人, 年龄 50.7 ± 6.1 年) from the Amsterdam multiple
sclerosis cohort were included (Eijlers et al., 2018). We only included participants who under-
went both diffusion MRI (dMRI) and magnetoencephalography recordings. Approval was
obtained from the institutional ethics review board of the VU University Medical Center,
and participants gave written, informed consent prior to participation.

Empirical Structural Data: 弥散磁共振成像

Individually weighted dMRI matrices were obtained to describe the SC between the neural
masses. dMRI matrices were calculated with probabilistic tractography as described previously
(Meijer et al., 2020). 简而言之, participants were scanned on a 3 T scanner (GE signa HDxt),
using an eight-channel phased-array head coil. For volumetric measurements, a 3D T1-
weighted inversion-prepared fast-spoiled gradient recall sequence (repetition time 7.8 多发性硬化症,
echo time 3 多发性硬化症, inversion time 450 多发性硬化症, flip angle 12°, sagittal 1.0-mm sections, 0.94 ×
0.94 mm2 in-plane resolution) was taken into account. A diffusion-weighted imaging
顺序 (dMRI) was applied covering the entire brain using five volumes without directional
weighting (IE。, b = 0 秒/毫米2) 和 30 volumes with noncollinear diffusion gradients (echo
planar imaging (EPI), b = 1,000 秒/毫米2, repetition time 13,000 多发性硬化症, echo time 91 多发性硬化症, flip angle
90°, 2.4-mm contiguous axial slices, 2 × 2 mm2 in-plane resolution). 随后, the FMRIB
Diffusion Toolbox (part of FSL 5) was performed using eddy current distortion correction. 下一个,
using the fiber orientation distribution (是), probabilistic tractography was applied using
MRtrix 3.0 (Tournier et al., 2012). In this model, N streamlines are reconstructed by randomly
putting seeds in white matter and using constrained spherical deconvolution to estimate the
local FOD (Tournier et al., 2007). 这 30 noncollinear diffusion directions in the data were
adjusted by restricting the maximum spherical harmonic order (lmax) 到 6. 然后, for each par-
ticipant, a random seeding of 100 million fibers within the brain mask was applied to perform
whole-brain probabilistic tractography. Probabilistic tractography was applied because it is
frequently used due to its low sensitivity for false positives (Maier-Hein et al., 2017).

Cortical gray matter regions were defined by processing the 3D T1-weighted image of each
participant with the FreeSurfer 5.3 pipeline. The automated anatomical labeling (AAL) atlas
(Tzourio-Mazoyer et al., 2002) was used to define 78 cortical regions (Gong et al., 2009)
on the native cortical surface. Structural networks were constructed by considering regions
as nodes and the number of fibers between pairs of nodes as links. We performed

网络神经科学

952

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
3
9
5
0
2
1
5
4
8
2
8
n
e
n
_
A
_
0
0
3
0
3
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Individualized modeling of brain connectivity

normalization of elements in the SC matrices. For each individual SC matrix, link weights that
exceeded 1.5 * IQR (interquartile range) above the third quartile (Q3 + 1.5 * IQR) were set to
that value, to make sure that very high values would not disproportionally influence the
simulations. 随后, the weighted SC matrices were rescaled to the range [0 1].

Empirical Functional Data: 脑磁图

Acquisition and preprocessing of the MEG data was performed as described previously (Derks
等人。, 2018). 简而言之, eyes-closed, resting-state measurements of 5 min were used. Measure-
ments were performed in a magnetically shielded room ( Vacuum Schmelze GmbH, Hanau,
德国) with a 306-channel whole-head MEG system (Elekta Neuromag Oy, Helsinki, Fin-
土地). Data were sampled at 1250 赫兹, and a high-pass filter (0.1 赫兹) and anti-aliasing filter
(410 赫兹) were employed online. The extended Signal Space Separation method (xSSS) (van
Klink et al., 2017) was applied to identify malfunctioning channels. Additional malfunctioning
channels were identified using visual inspection (SK, LD). We then applied the temporal exten-
sion of SSS in MaxFilter software (Elekta Neuromag Oy, version 2.2.15) on the raw data for
artifact removal (Taulu & Simola, 2006). Malfunctioning channels than were identified using
xSSS or visual inspection were excluded for tSSS analysis. The head position relative to the
MEG sensors was recorded continuously with the signals from four or five head-localization
coils. The head-localization coil positions and outline of the participants scalp were digitized
using a 3D digitizer (3Space Fastrak, Polhemus, Colchester, VT, 美国). Each participant’s scalp
surface was coregistered to their structural MRI using a surface-matching procedure. 亚塞-
经常地, the coregistered MRI was spatially normalized to a template MRI. Centroid voxels
(Hillebrand et al., 2016) 的 78 cortical regions of the AAL atlas, the same as was used
for the SC, were selected for further analyses after inverse transformation to the participant’s
coregistered MRI. A single best fitting sphere was fitted to the outline of the scalp as obtained
from the coregistered MRI and used as a volume conductor model for the beamformer
方法 (希勒布兰德 & 巴恩斯, 2005; Hillebrand et al., 2005). An atlas-based scalar beam-
former implementation (Elekta Neuromag Oy, version 2.1.28), similar to Synthetic Aperture
Magnetometry (罗宾逊 & Vrba, 1999), was applied to project MEG data from sensor level
to source space (Hillebrand et al., 2012). The beamformer weights were based on the data
covariance matrix and the forward solution (lead field) of a dipolar source at the voxel
地点. Orientation of the sources was estimated based on singular value decomposition
(Sekihara et al., 2006). The broadband (0.5–48 Hz) time series of the 78 centroids were pro-
jected through the normalized (Cheyne et al., 2007) broadband beamformer weights for each
target voxel (IE。, centroid voxel). From these time series, for each participant, the maximum
amount of artifact free data, 那是, 26 consecutive epochs of 6.55 s (8,192 样品), 是
分析过的 (Liuzzi et al., 2017). Time series were digitally band-pass filtered in the alpha band
(8–13 Hz) using a fast Fourier transform, after which all bins outside the passbands were set to
零, and an inverse Fourier transform was performed (implemented using in house script in
MATLAB (version 2018b, MathWorks, Natick, 嘛, 美国)). 随后, FC was calculated
using different FC metrics (see section Simulated and Empirical Functional Connectivity). 全部
the analyses in the current work were performed in MATLAB using in house scripts (see https://
github.com/multinetlab-amsterdam/projects/tree/master/modelling_paper_2021).

Simulated Functional Data: Network of Neural Masses

We considered a network of coupled neural masses with network size N = 78. Each node
(neural mass) corresponded to a cortical region of the AAL atlas. Link weights (number of
streamlines) were derived from an individual’s weighted SC matrix. We used the Jansen and

网络神经科学

953

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
3
9
5
0
2
1
5
4
8
2
8
n
e
n
_
A
_
0
0
3
0
3
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Individualized modeling of brain connectivity

Rit model as described in Grimbert and Faugeras (2006) to model a single neural mass. 这
model allows for simulation of fluctuations in the synaptic membrane potential of a neuronal
人口 (Jansen & Rit, 1995). Each mass consists of three populations (pyramidal popula-
的, and excitatory and inhibitory neuronal populations) (see Figure 1A). The Jansen and Rit
model is optimized to generate alpha oscillations. 简而言之, each neuronal population is
described by a second-order ordinary differential equation that models modulations in the
mean membrane potential due to the mean incoming firing rate from the same population
and from other populations in the neural mass. Incoming mean firing rates are obtained by
a nonlinear sigmoid function that transforms the mean membrane potential to a mean firing
速度 (Jansen & Rit, 1995). Uncorrelated Gaussian noise was fed to the pyramidal population
仅有的. The three interconnected neuronal populations were connected using the coupling

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
3
9
5
0
2
1
5
4
8
2
8
n
e
n
_
A
_
0
0
3
0
3
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

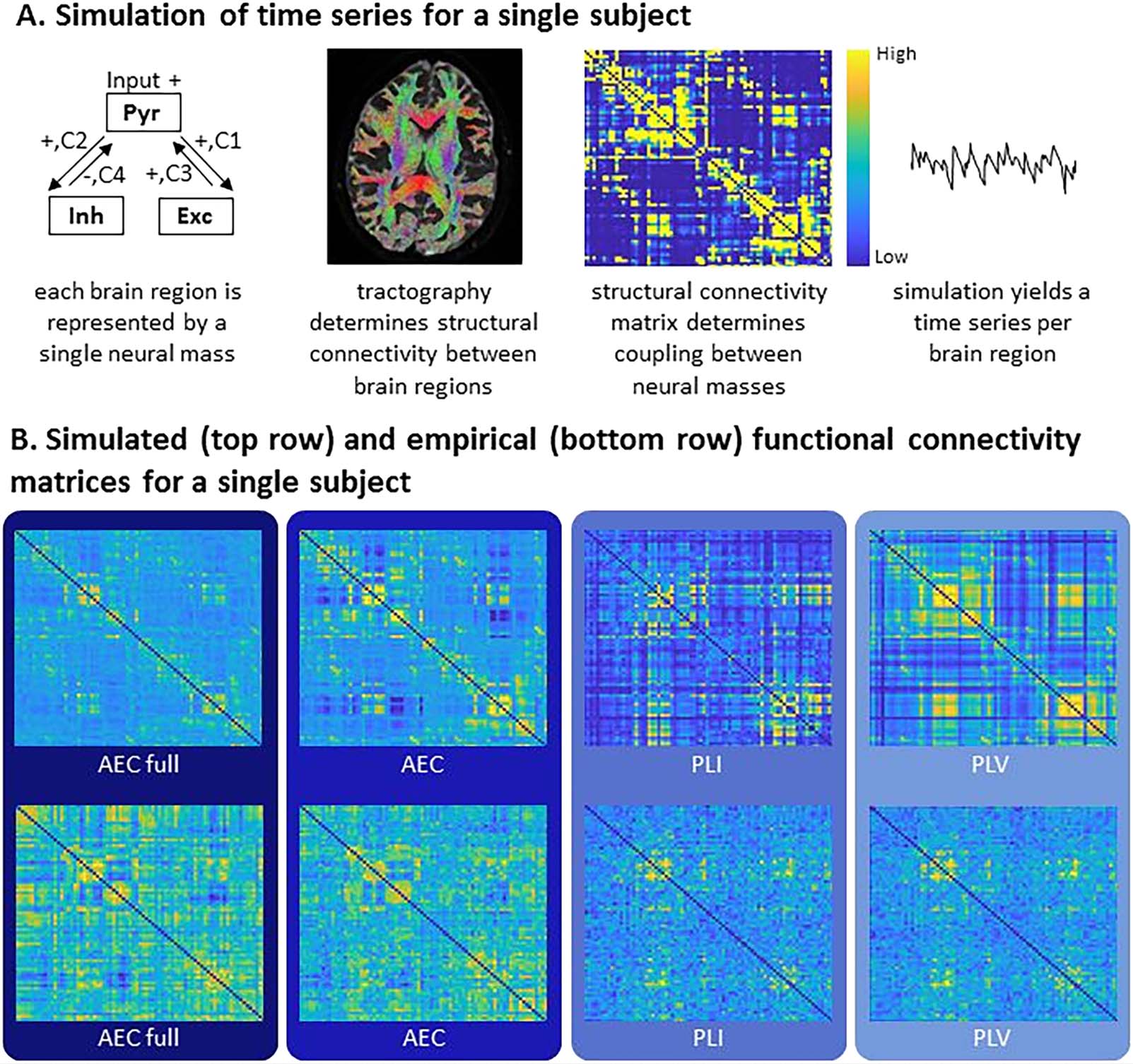
数字 1. Overview of the applied methods. (A) 左边: overview of the Jansen and Rit model reflecting the connections between the pyramidal
(Pyr), inhibitory (Inh), and excitatory (Exc) 人口. Individual weighted structural connectivity, computed by probabilistic tractography
using MRTrix, was used as input to the Jansen and Rit model to connect the neural masses. Each neural mass, reflecting a brain region, 亲-
duces MEG-like time series. (乙) Exemplar simulated and empirical weighted functional connectivity matrices for one participant. Cold colors
represent low connectivity and warmer colors represent high connectivity (this also applies to the structural connectivity matrix). For both
simulated and empirical data, FC was estimated between all pairs of regions using different FC metrics. AEC = amplitude envelope correlation;
AEC full = AEC calculated over the full time series (epochs concatenated), AEC, calculated over epochs; PLI = phase lag index, calculated over
纪元; PLV = phase locking value, calculated over epochs. AEC full, AEC, and PLV were corrected for signal leakage in the empirical data, 不是
in the simulated data. PLI inherently corrects for signal leakage and therefore corrects in both empirical and simulated data. For each partic-
ipant and per connectivity metric, a correlation between the simulated and empirical FC was performed.

网络神经科学

954

Individualized modeling of brain connectivity

桌子 1.

Parameters and values included in the model (based on Grimbert & Faugeras, 2006)

范围
C1, C2, C3, C4

意义
Average number of synapses between populations

Value
135 * [1 0.8 0.25 0.25]

Beta_E

Beta_I

乙

theta

Conduction velocity

时间

磷

Time scale for excitatory population

Time scale for inhibitory population

Average excitatory synaptic gain

Average inhibitory synaptic gain

Threshold of sigmoid

Slope of sigmoid

Amplitude of sigmoid

Sample frequency

Integration time step

Observation time

External input to each of the neural masses

100 多发性硬化症

50 多发性硬化症

3.25

5 s−1

0.56 mV−1

6 mV

10 m/s

1250 赫兹

0.0001

20 s

150

Coupling

Coupling between the neural masses

[0.1:0.012:0.292]

价值观 (C1, C2, C3, C4) (数字 1 和表 1). These values represent the average number of
synaptic connections between each population. Connectivity between the neural masses was
implemented exactly the same as in Forrester et al. (2020), and the same parameters were used
as in Grimbert and Faugeras (2006). A fourth order stochastic Runge–Kutta method (汉森 &
Penland, 2006) was used to numerically solve the coupled differential equations of the model.

Each neural mass receives external input (磷) that corresponds to external sources or activity
from neighboring populations (Ableidinger et al., 2017). The external input was set to P = 150
for all neural masses. For the global coupling parameter, which determines the coupling
between all neural masses, we used the interval [0.1, 0.292], with a discrete step size of
0.012. As explained in more detail later, this range was used to scan the parameter space
in order to obtain the coupling value for every individual that optimized the goodness of fit
between simulated and empirical FC matrices. We included distance dependent delays
between nodes based on the Euclidian distance between centroids in the AAL atlas divided
by the conduction velocity. 见表 1 for an overview of all model parameters. We ran the
model for each global coupling value to generate time series of neuronal activity. For each run,
the time series were band-pass filtered in the alpha band (8–13 Hz) in the same way as for
empirical data, and FC was calculated using different FC metrics (see section Simulated and
Empirical Functional Connectivity). To obtain robust results and to minimize the stochastic
effect of the model’s stochastic differential equations, the model was run 20 times per subject,
and subsequently FC values were averaged over the 20 runs.

Simulated and Empirical Functional Connectivity

Three FC metrics were calculated that capture either amplitude-based connectivity or phase-
based connectivity: the amplitude envelope correlation (AEC) (布鲁克斯等人。, 2011; Bruns

网络神经科学

955

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
3
9
5
0
2
1
5
4
8
2
8
n
e
n
_
A
_
0
0
3
0
3
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Individualized modeling of brain connectivity

等人。, 2000; 希普等人。, 2012), the phase lag index (PLI) (Stam et al., 2007), and the phase
locking value (PLV) (Lachaux et al., 1999). The AEC quantifies amplitude-based connectivity
between two time series, whereas the PLI and PLV are both metrics of phase synchronization.
The main difference between the latter two metrics is that the PLI inherently is insensitive to
zero-lag phase differences and thereby reduces the effect of primary signal leakage. Prior to FC
estimation, we first band-pass filtered the data in the alpha band (8–13 Hz) followed by cor-
rection for signal leakage. 进一步来说, we applied pairwise orthogonalization in order to
correct for signal leakage only in empirical data and only for metrics that are inherently sen-
sitive to signal leakage (AEC and PLV). To calculate the AEC, the amplitude envelopes were
obtained from the analytical signal after a Hilbert transformation of the band-pass filtered
orthogonalized time series, and the correlations between the amplitude envelopes of pairs
of time series were computed. For the empirical data, the AEC was calculated in two different
方法: (1) AEC: the data were divided into epochs (6.55 s), and AEC computed for every epoch.
The AEC was subsequently averaged over epochs; (2) AEC full: AEC was computed for the
entire time series, after concatenating all epochs. To calculate the PLI and the PLV, the instan-
taneous phases were obtained from the same analytical signal after the Hilbert transformation.
The PLI and PLV were both calculated for every epoch (6.55 s) and subsequently averaged
over epochs. For the simulated data, for each FC metric, the FC matrices were averaged over
这 20 runs per coupling value.

Similarity Between Simulated and Participant-Specific Empirical Functional Connectivity Using

Individual Structural Connectivity
We computed a Spearman rank correlation ( ρ) between simulated and empirical FC matrices
for every global coupling value to quantify the match between simulated and individual
empirical FC. 要做到这一点, the upper triangular part of the matrices were vectorized and subse-
quently correlated between simulated and empirical FC. Spearman correlations were applied
since the distribution of FC values for most metrics was typically non-Gaussian. For all statis-
tical tests performed, values of p < 0.05 were considered to be significant. Simulations were performed with the individual SC matrix as input to the neural mass models. The highest Spearman correlation within the coupling range [0.1, 0.292] was considered to be the best fit with the empirical FC, further referred to as the maximum correlation per participant, and calculated per FC metric. If the coupling value corresponding to the maximum correlation was at the end of the coupling range (i.e., coupling = 0.292), we extended the coupling range to 0.4, with a step size of 0.012, to test whether that coupling range would result in higher correlation values for that individual. Subsequently, the maximum correlation for the range [0.1, 0.4] was determined. Upon determining the optimal coupling per subject, the same parameters were used for all subsequent analyses. A Wilcoxon signed rank test was subsequently performed to compare the maximum corre- lations between FC metrics. The FC metric that resulted in the highest maximum correlations at the group level was selected for further analyses. Differences between coupling values corresponding to the maximum correlations for the different FC metrics were tested with Friedman’s test. Similarity Between Simulated and Participant-Specific Empirical Functional Connectivity Using Group- Averaged Structural Connectivity We subsequently tested whether the individual SC as input to the model outperformed simu- lations based on the group-averaged SC. We therefore used the average SC as input to the model and correlated the resulting simulated FC for the range of coupling values, with the Network Neuroscience 956 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 3 9 5 0 2 1 5 4 8 2 8 n e n _ a _ 0 0 3 0 3 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Individualized modeling of brain connectivity individual empirical FC, using a Spearman correlation. As reference, we also predicted group- averaged FC based on simulations with the group-averaged SC as input. The group-averaged SC and FC matrices were obtained by averaging SC and FC matrices across all participants, respectively. Next, in the group-averaged weighted SC, outliers were removed and normaliza- tion of the matrix was applied as described in section Empirical Structural Data: Diffusion MRI. All subsequent steps to calculate the match between simulated and empirical FC were as described in section Similarity Between Simulated and Participant-Specific Empirical Func- tional Connectivity Using Individual SC. Simulated Versus Empirical Functional Connectivity in Matched Versus Nonmatched Participants In a subsequent analysis, we tested whether the predictions of individual empirical FC based on participants’ own SC matrix were specific. We tested the null hypothesis that prediction of empirical FC for a given participant based on simulated FC with the SC of another participant as input to the simulations would lead to an equally well prediction. To this end, we correlated the individually simulated FC matrices, based on that participant’s optimized coupling param- eter, to empirical FC matrices from other participants. We then compared the Spearman cor- relations between simulated and empirical FC for matched versus nonmatched data. To test whether participant’s own maximum correlation (matched data) was higher compared to the correlations obtained with all other participants’ empirical data (nonmatched data), these correlations were ranked per participant. Subsequently, if the participant’s own maximum correlation would fall within the highest 97.5% of this ranking, it was considered to be signif- icantly higher compared to the correlations to other participants. For all previously described analyses, no corrections for multiple comparisons were performed. RESULTS Exemplar time series and power spectrum of simulated data for one participant are shown in Supporting Information Figure S1. Examples of simulated and empirical FC matrices of the same participant are shown in Figure 1B. Similarity Between Individually Simulated and Empirical Functional Connectivity The similarity between the individually simulated and individual empirical FC was calculated for each of the FC metrics for the range of coupling values. 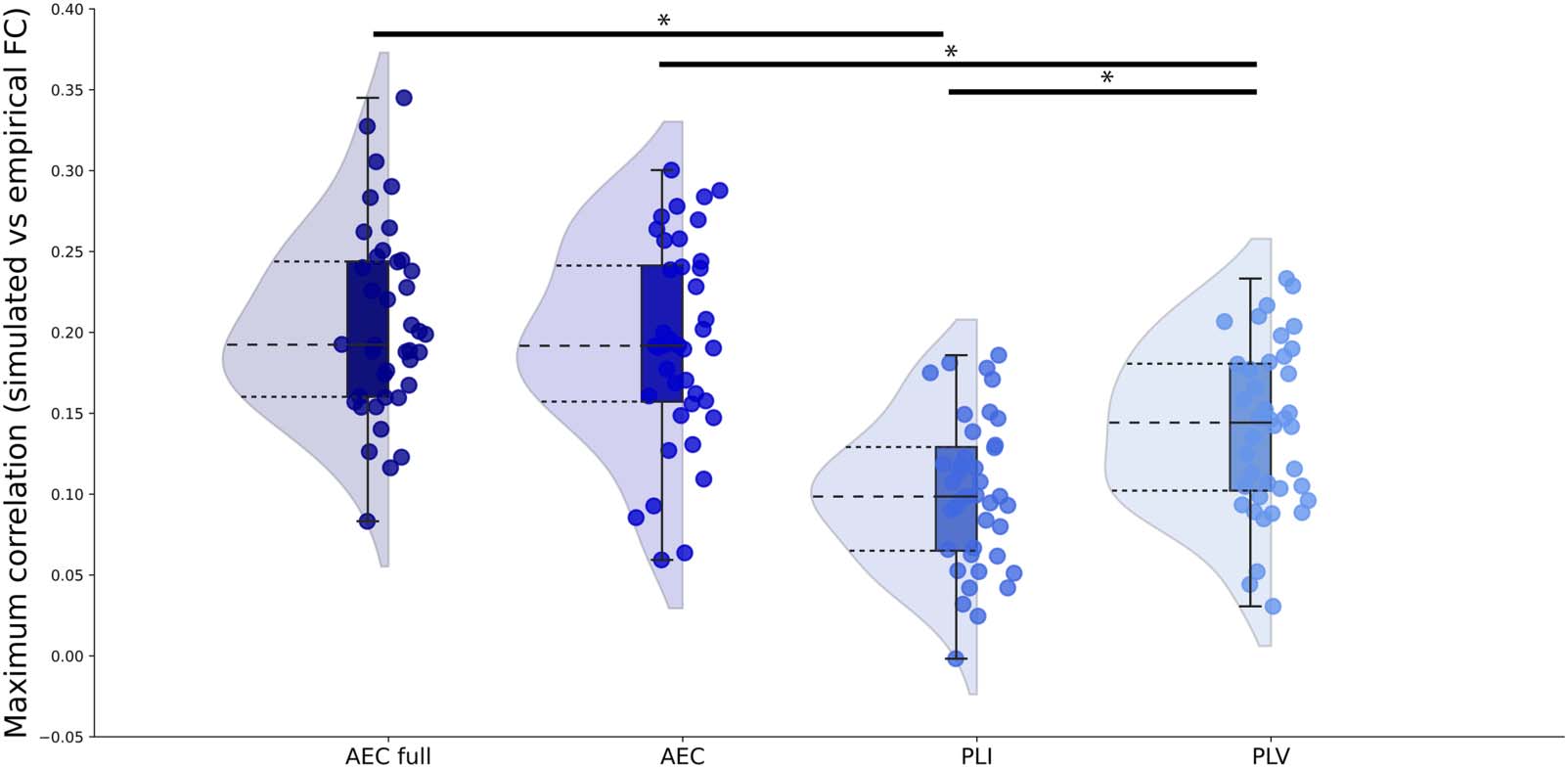The resulting individual maximum correlation values between simulated and empirical FC are shown in Figure 2 for each FC metric. The median of the maximum correlations for each FC metric were AEC full 0.19, AEC 0.19, PLI 0.10, and PLV 0.14. All of these maximum correlations between simulated and empirical FC for the AEC full and AEC were statistically significant (for all participants with AEC full p < 0.001; for all participants with AEC: p < 0.01). For the PLI and PLV, correlations between the simulated and empirical FC were statistically significant for most participants (PLI: p < 0.005; PLV: p < 0.01), except for three (PLI) and two (PLV) participants. 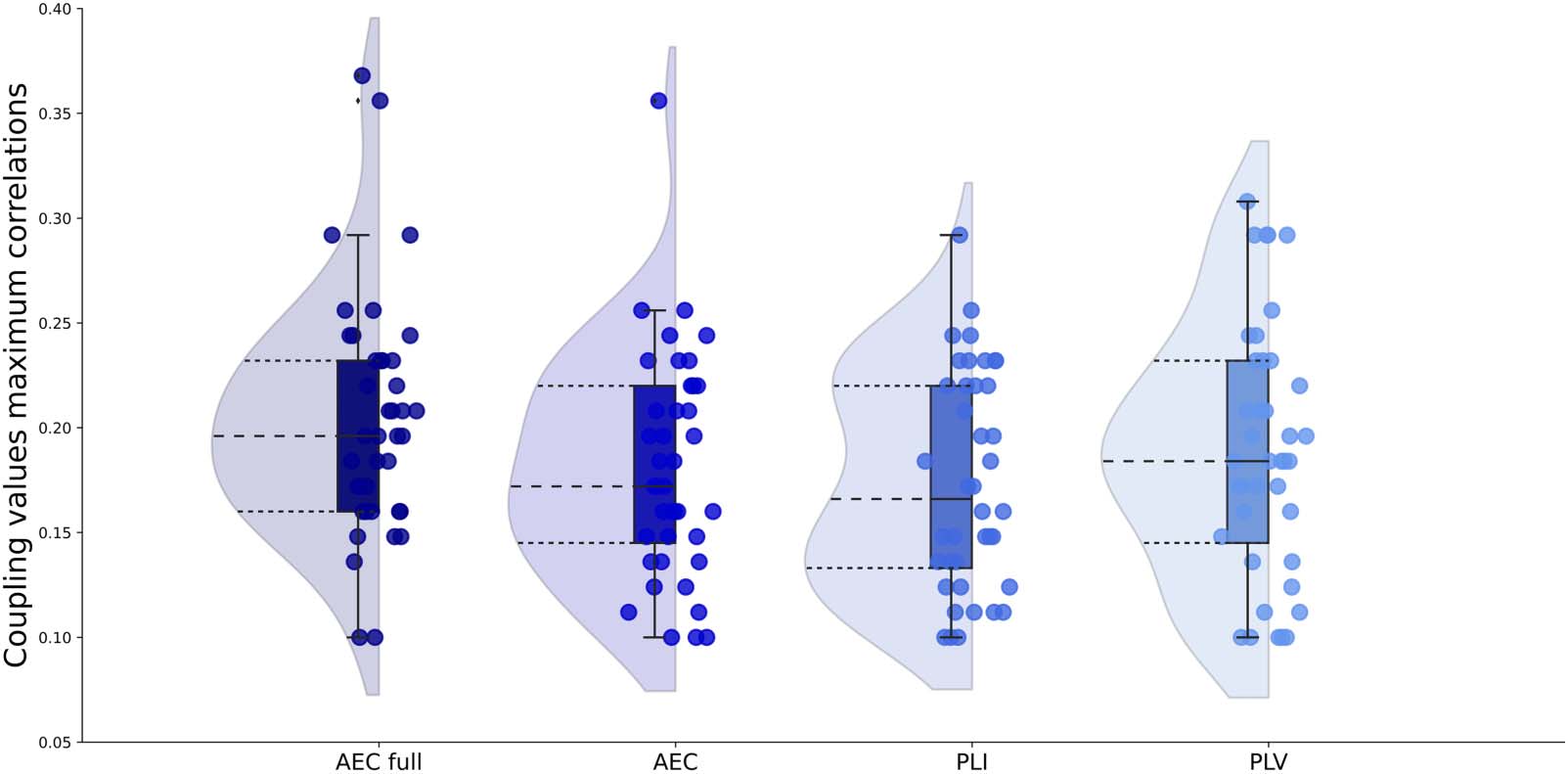The coupling values corresponding to the maximum correlation between simulated and empirical FC for each participant and each FC metric are displayed in Figure 3 and Supporting Information Table S1. Coupling values corresponding to the maximum correlations did not differ between metrics ( χ2 = 5.09, p = 0.17). We compared individual maximum correlations between FC metrics. There was no signif- icant difference between the AEC full and the AEC ( W = 505, p = 0.20). AEC full showed significantly higher maximum correlations than the PLI ( W = 804, p < 0.001), and the PLV ( W = 722, p < 0.001). The AEC also showed significantly higher maximum correlations Network Neuroscience 957 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 3 9 5 0 2 1 5 4 8 2 8 n e n _ a _ 0 0 3 0 3 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Individualized modeling of brain connectivity Figure 2. Maximum correlations between simulated and empirical FC. Rain cloud figures showing the maximum correlations between sim- ulated and empirical FC for each FC metric. Both amplitude- and phase-based FC metrics were included: amplitude envelope correlation (AEC); AEC full refers to AEC computed over the full time series, phase lag index (PLI), phase locking value (PLV). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 3 9 5 0 2 1 5 4 8 2 8 n e n _ a _ 0 0 3 0 3 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 compared to both the PLI ( W = 787, p < 0.001) and the PLV ( W = 699, p < 0.001). Finally, the PLI performed significantly worse than the PLV ( W = 28, p < 0.001) in terms of maximum correlations between simulated and empirical FC at the individual level. Since the use of the AEC full and AEC resulted in significant better predictions of individual empirical FC, we continued using only these metrics for further analyses. Additionally, we analyzed the similarity between the strongest connections of the individ- ually simulated and empirical data. A detailed description of this analyses can be found in the Supporting Information. For the AEC, maximal correlations between the strongest connections of simulated and empirical data showed to be significantly higher compared to the maximal correlations when the full matrices were taken into account ( W = 205, p = 0.006, see Figure S2). Figure 3. Optimal global coupling values for all FC metrics. Optimized global coupling values between neural masses as determined by the maximum correlation between simulated and empirical FC for each FC metric. AEC = amplitude envelope correlation (AEC); AEC full = AEC computed over the full time series; PLI = phase lag index; PLV = phase locking value. 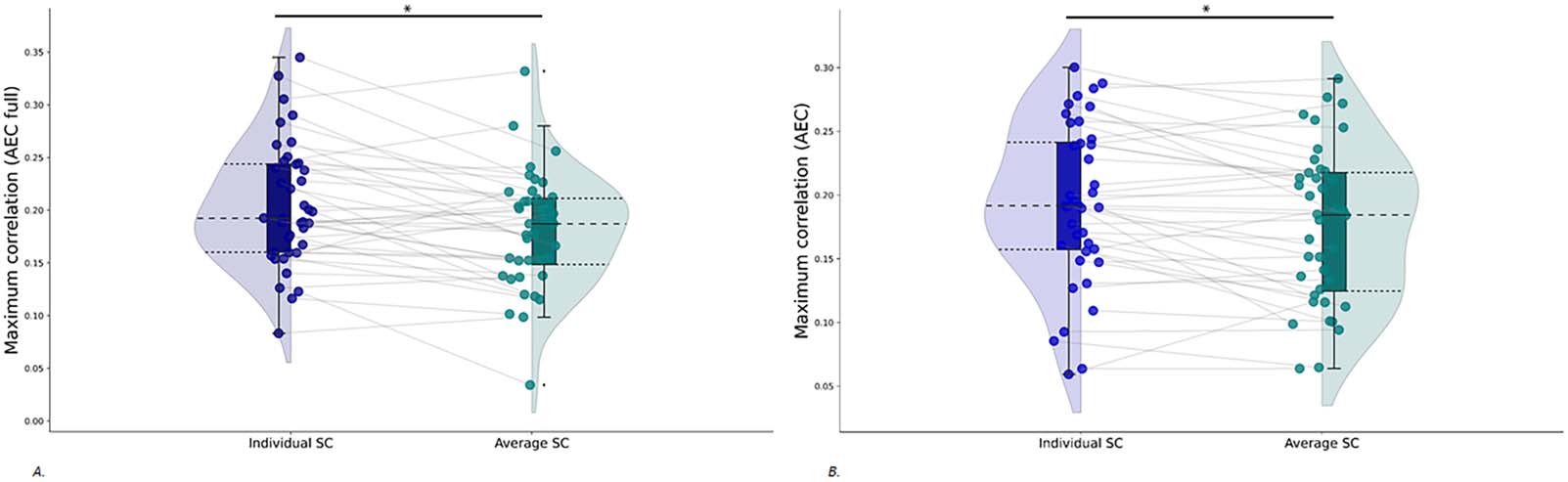Network Neuroscience 958 Individualized modeling of brain connectivity Figure 4. Paired rain cloud figures containing the maximum correlations, for all coupling values, between simulated and empirical FC. Gray lines between the dots connect one participant for simulations with the individual SC matrices as input to the model (blue rain clouds) and simulations with the group-averaged SC matrix as input to the model (green rain clouds). (A) FC calculated with the AEC full. (B) FC calculated with the AEC. AEC = amplitude envelope correlation (AEC); AEC full = AEC computed over the full time series. Similarity Between Simulated Functional Connectivity and Empirical Function Connectivity Using Group-Averaged Structural Connectivity We next predicted individual empirical FC (AEC full and AEC) based on simulations with the group-averaged SC as input. The match between simulated and individual empirical FC was better for simulations with the individual SC as input compared to simulations with the group- averaged SC as input, for both the AEC full ( W = 185, p = 0.003) and AEC ( W = 200, p = 0.005; see Figure 4). Results further show a median of the maximum correlations of 0.19 for both the AEC full and AEC. There was no significant difference between the maximum corre- lations for these two FC metrics ( W = 462, p = 0.5). We also computed a correlation between simulations with group-averaged SC and group- averaged FC, which showed a significant correlation between the two (AEC full: r = 0.40, p < 0.001 and AEC: r = 0.36, p < 0.001). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 3 9 5 0 2 1 5 4 8 2 8 n e n _ a _ 0 0 3 0 3 p d . 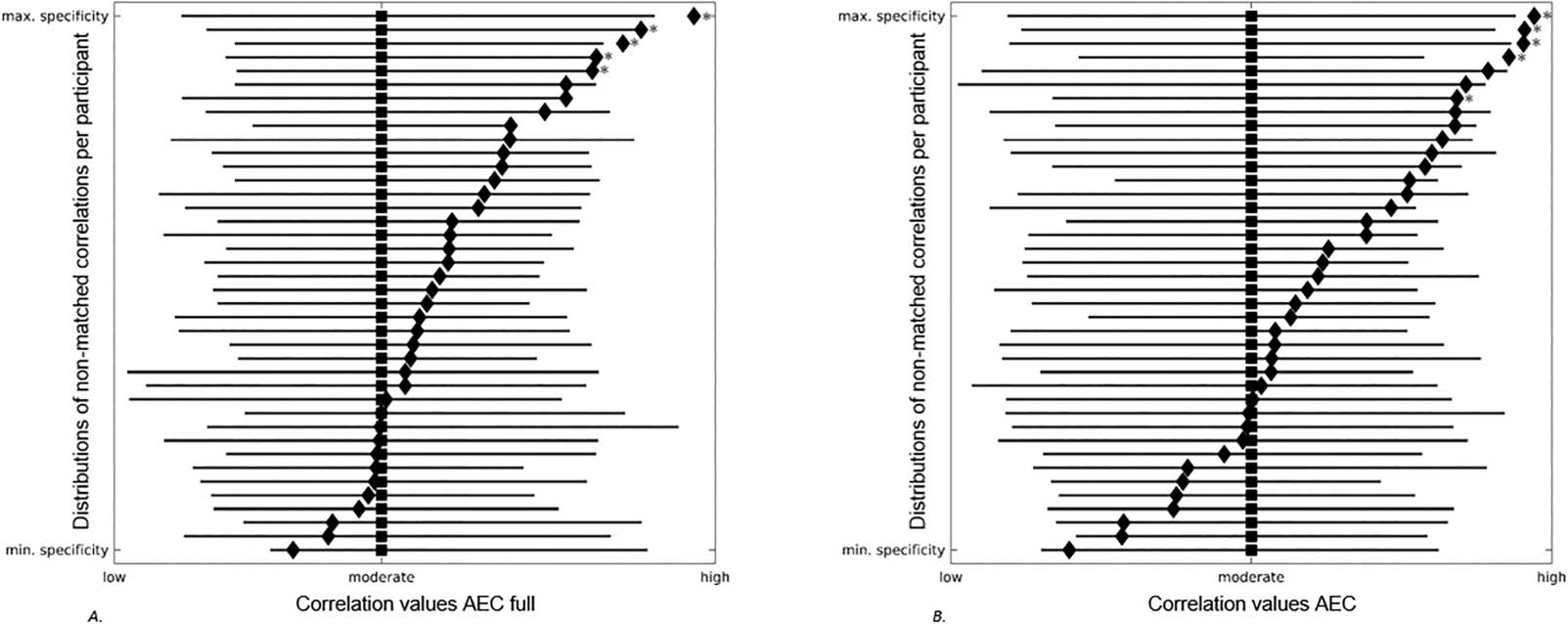t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Forest plots showing the distributions of nonmatched correlations per participant. Gray lines correspond to correlation distributions Figure 5. (low-moderate-high) between a participants’ own simulated FC and all other participants’ empirical FC. Black squares denote median values of these distributions. Black diamonds correspond to the correlation between a participants’ own simulated and empirical FC. Gray stars display the correlations between participants’ own simulated and empirical FC that were significantly higher compared to correlations between participants’ own simulated FC and all other participants’ empirical FC. Participants are ranked based on the distance between their own correlation value and the median of all other correlation values, indicating the range between minimum and maximum specificity of participants’ own correlation values. (A) AEC full. (B) AEC. AEC = amplitude envelope correlation; AEC full = AEC computed over the full time series. Network Neuroscience 959 Individualized modeling of brain connectivity Similarity Between Simulated Versus Empirical Functional Connectivity in Nonmatched Versus Matched Participants Next, we analyzed whether empirical FC of a given participant could be equally well pre- dicted by simulated FC on the basis of another participant’s SC matrix. We correlated individ- ually simulated FC to the empirical FC of all other participants. For both the AEC full and the AEC, in 5 out of the 40 participants, participants’ own individual correlation was significantly higher compared to the correlations with all other participants (see Figure 5). DISCUSSION The main aim of this study was to assess the feasibility and accuracy of modeling individual empirical FC using individual empirical SC matrices. We found moderate correlations between simulated and empirical FC using the amplitude-based AEC, while the phase-based metrics (PLI and PLV) performed significantly worse. Using individual SC, instead of group-averaged SC, improved the correlation between simulated and individual empirical FC significantly. However, correlations between individually simulated FC and other participant’s empirical FC were in general not significantly lower than between the matched pair of FC patterns. The FC simulations using individual SC outperformed simulations based on group-averaged SC, indicating increased precision modeling of brain activity and FC when incorporating par- ticipants’ own structural network. These findings are corroborated by Aerts and colleagues (Aerts et al., 2018), who simulated fMRI data in brain tumor patients using The Virtual Brain. Individually optimized model parameters also resulted in improved accuracy of individually simulated FC. However, when correlating an individual’s simulated FC to the empirical FC of other participants, we found correlations that were comparable to matched simulated and empirical individual FC. Although this finding is in line with earlier work (Finger et al., 2016), it remains unclear whether simulated FC can be attributed to a specific individual. It would be useful for future work to explore the causes of this apparent aspecificity. A recent study reported on subject specific MEG FC patterns, also known as functional fingerprints (Da Silva Castanheira et al., 2021). Future studies could look into such fingerprints in repeated MEG measurements over time, both between and within participants. The variation that is present between and within participants in the match between simulated and empirical FC could increase our understanding of whether the simulated or empirical FC is underlying the aspecificity that we found. A second main result of this study is the clear difference between amplitude- and phase- based metrics in the correlations between individually simulated and empirical FC. The AEC full and AEC outperformed the PLI and PLV, while the PLV performed better in comparison to the PLI. These findings partly corroborate earlier work in which only phase-based metrics were considered (Finger et al., 2016), also showing better performance for the PLV in comparison to PLI. It is, however, important to note that Finger and colleagues used FC metrics both corrected and uncorrected for signal leakage. Although signal leakage is known to cause spurious cor- relations between nearby sources (Gross et al., 2013), the previously mentioned study cor- rected their empirical data dependent on the FC metric. Since leakage is not present in our simulated data, we therefore chose not to perform leakage correction to our simulated data, but only to the empirical data. Important to note here, however, is that the PLI inherently cor- rects for leakage and therefore is corrected in both our simulated and empirical data. The difference in the performance of phase- and amplitude-based metrics could relate to the consistency levels of the FC metrics. In the alpha band, the AEC has been shown to be more consistent in repeated empirical measurements from the same participants, hypothetically Network Neuroscience 960 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 3 9 5 0 2 1 5 4 8 2 8 n e n _ a _ 0 0 3 0 3 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Individualized modeling of brain connectivity since phase-based metrics are more susceptible to noise (Colclough et al., 2016; Tewarie et al., 2019b). If noise indeed underlies the poorer performance of phase-based FC metrics in indi- vidual simulations, including more data, that is, including 10- instead of 5-min recordings, might improve results with these metrics (Liuzzi et al., 2017). Additionally, previous research including EEG data of patients with Alzheimer’s disease found higher reproducibility of the PLI in the theta band, while the AEC was more consistent in the alpha and beta frequency bands (Briels et al., 2020). This work could indicate that consistency of FC metrics might be frequency dependent in empirical data, an aspect that we did not take into account by only analyzing our data in the alpha frequency band. We found moderate (r = 0.19 on average) correlations between individually simulated FC and individual empirical FC, which is lower than obtained by Finger and colleagues (average correlation of 0.53). However, direct comparison of these correlation values is not straightfor- ward due to the many methodological differences between their study and ours. Nevertheless, several factors may have contributed to these results. The quality of both the empirical SC and FC matrices could have influenced the correlation strengths that we found. Regarding SC, trac- tography is known to underestimate the presence of interhemispheric fibers, which strongly influences modeling results (Messe et al., 2015). The tractography method we used is the cur- rent standard in the field and takes care of false positives (Maier-Hein et al., 2018). Nonethe- less, future studies may investigate whether increasing the quality of the SC matrices, for instance, by improving scanner hardware, diffusion sequences, duration of scans, or the trac- tography methods, could enhance modeling accuracy. Furthermore, MEG data is known to be susceptible to noise caused by environmental, instrumental and biological factors. Although we only included MEG data that was visually free from artifacts, noise may still have been present in the individual FC matrices. In an additional analysis we only took the strongest con- nections of the simulated and empirical FC into account (Figure S2), thereby decreasing the noise of the included connections. For the AEC, the resulting match between simulated and empirical FC was higher compared to taking the full matrices into account. Furthermore, func- tional connections can also occur where there are few or no structural connections, possibly explained by indirect connections and interregional distance (Meier et al., 2016; Robinson, 2012). This means that even small variations in SC can support many different FC patterns, which makes the interdependence between them complicated (Popovych et al., 2019). Addi- tionally, by correcting the empirical data for signal leakage, true zero-lag interactions are also removed, which might have been present in the simulated data, causing a decrease in agree- ment between simulated and empirical data. Computational models that use average SC as an input have been frequently applied so far (Abeysuriya et al., 2018; Cabral et al., 2014; Deco et al., 2017; Hadida et al., 2018; Moon et al., 2015; O’Neill et al., 2018; Tewarie et al., 2014, 2019a), but hamper further tailoring of such models to individuals, particularly in the setting of neurological disease modeling. Pre- viously, damage that reflects different diseases, has been modeled with advanced computa- tional models (Aerts et al., 2020; de Haan et al., 2012; Tewarie et al., 2018; van Dellen et al., 2013), but these disease models have not yet been applied to individual data. Such tailored disease models could elucidate mechanisms underlying functional network trajecto- ries (Douw et al., 2019) in neurological disease, for instance, modeling the impact of focal lesions on global network dysfunction and cognitive decline. Of relevance to future computational work in health and disease, one of the limitations of our work is that we have limited our analysis to prediction of individual FC matrices and did not take into account any local aspects of the simulated data, for example, power spectral density in different brain regions. Future work using advanced and novel spectral graph based Network Neuroscience 961 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 3 9 5 0 2 1 5 4 8 2 8 n e n _ a _ 0 0 3 0 3 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Individualized modeling of brain connectivity theory of neuronal oscillations could include both prediction of individual FC and first order regional power spectra (Raj et al., 2020; Verma et al., 2022). Relevant other limitations that may have played a role in the moderate fit between the simulated and empirical data in our study and the literature on how well computational modeling recapitulates empirical data relate to general confounders of MEG measurements, such as head motion, respiration, car- diac artifacts, mind wandering, and such. Although we visually inspected our data for large artifacts and used a common tool to remove such confounders from the empirical data, remaining features could have lowered the correlation with the simulated data. To conclude, we show that simulated FC best relates to individual empirical FC when using the individual SC as input to our implementation of the Jansen-Rit model, compared to the use of group-averaged SC at least. This work therefore underlines a first step toward individual FC modeling. ACKNOWLEDGMENTS The authors thank Lucas Breedt for his help with the creation of the rain cloud figures. SUPPORTING INFORMATION Supporting information for this article is available at https://doi.org/10.1162/netn_a_00303. AUTHOR CONTRIBUTIONS Shanna Kulik: Conceptualization; Formal analysis; Investigation; Methodology; Visualization; Writing – original draft; Writing – review & editing. L. Douw: Conceptualization; Formal analysis; Methodology; Supervision; Visualization; Writing – original draft; Writing – review & editing. E. van Dellen: Conceptualization; Methodology; Supervision; Writing – original draft; Writing – review & editing. M. D. Steenwijk: Data curation; Software; Writing – original draft; Writing – review & editing. J. J. G. Geurts: Supervision; Writing – original draft; Writing – review & editing. C. J. Stam: Writing – original draft; Writing – review & editing. Arjan Hillebrand: Data curation; Writing – original draft; Writing – review & editing. Menno Schoonheim: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Supervision; Visualization; Writing – original draft; Writing – review & editing. Prejaas Tewarie: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Software; Supervision; Visualization; Writing – original draft; Writing – review & editing. FUNDING INFORMATION Menno M. Schoonheim, ZonMW Vidi grant, Award ID: 09150172010056. REFERENCES Abeysuriya, R. G., Hadida, J., Sotiropoulos, S. N., Jbabdi, S., Becker, R., Hunt, B. A. E., Brookes, M. J., & Woolrich, M. W. (2018). A biophysical model of dynamic balancing of excitation and inhibition in fast oscillatory large-scale networks. PLoS Computional Biology, 14(2), e1006007. https://doi.org/10.1371 /journal.pcbi.1006007, PubMed: 29474352 Ableidinger, M., Buckwar, E., & Hinterleitner, H. (2017). A stochastic version of the Jansen and Rit neural mass model: Analysis and numerics. Journal of Mathematical Neuroscience, 7(1), 8. https://doi.org/10.1186/s13408-017-0046-4, PubMed: 28791604 Aburn, M. J., Holmes, C. A., Roberts, J. A., Boonstra, T. W., & Breakspear, M. (2012). Critical fluctuations in cortical models near instability. Frontiers in Physiology, 3, 331. https://doi.org /10.3389/fphys.2012.00331, PubMed: 22952464 Aerts, H., Schirner, M., Dhollander, T., Jeurissen, B., Achten, E., Van Roost, D., Ritter, P., & Marinazzo, D. (2020). Modeling brain dynamics after tumor resection using The Virtual Brain. Network Neuroscience 962 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 3 9 5 0 2 1 5 4 8 2 8 n e n _ a _ 0 0 3 0 3 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Individualized modeling of brain connectivity NeuroImage, 213, 116738. https://doi.org/10.1016/j.neuroimage .2020.116738, PubMed: 32194282 Aerts, H., Schirner, M., Jeurissen, B., Van Roost, D., Achten, E., Ritter, P., & Marinazzo, D. (2018). Modeling brain dynamics in brain tumor patients using The Virtual Brain. eNeuro, 5(3). https://doi .org/10.1523/ENEURO.0083-18.2018, PubMed: 29911173 Breakspear, M. (2017). Dynamic models of large-scale brain activity. Nature Neuroscience, 20(3), 340–352. https://doi.org/10.1038/nn .4497, PubMed: 28230845 Briels, C. T., Schoonhoven, D. N., Stam, C. J., de Waal, H., Scheltens, P., & Gouw, A. A. (2020). Reproducibility of EEG functional con- nectivity in Alzheimer’s disease. Alzheimer’s Research & Therapy, 12(1), 68. https://doi.org/10.1186/s13195-020-00632-3, PubMed: 32493476 Brookes, M. J., Woolrich, M., Luckhoo, H., Price, D., Hale, J. R., Stephenson, M. C., Barnes, G. R., Smith, S. M., & Morris, P. G. (2011). Investigating the electrophysiological basis of resting state networks using magnetoencephalography. Proceedings of the National Academy of Sciences, 108(40), 16783–16788. https:// doi.org/10.1073/pnas.1112685108, PubMed: 21930901 Bruns, A., Eckhorn, R., Jokeit, H., & Ebner, A. (2000). Amplitude envelope correlation detects coupling among incoherent brain signals. Neuroreport, 11(7), 1509–1514. https://doi.org/10.1097 /00001756-200005150-00029, PubMed: 10841367 Cabral, J., Luckhoo, H., Woolrich, M., Joensson, M., Mohseni, H., Baker, A., Kringelbach, M. L., & Deco, G. (2014). Exploring mechanisms of spontaneous functional connectivity in MEG: How delayed network interactions lead to structured amplitude envelopes of band-pass filtered oscillations. NeuroImage, 90, 423–435. https://doi.org/10.1016/j.neuroimage.2013.11.047, PubMed: 24321555 Cheyne, D., Bostan, A. C., Gaetz, W., & Pang, E. W. (2007). Event- related beamforming: A robust method for presurgical functional mapping using MEG. Clinical Neurophysiology, 118(8), 1691–1704. https://doi.org/10.1016/j.clinph.2007.05.064, PubMed: 17587643 Colclough, G. L., Woolrich, M. W., Tewarie, P. K., Brookes, M. J., Quinn, A. J., & Smith, S. M. (2016). How reliable are MEG resting-state connectivity metrics? NeuroImage, 138, 284–293. https://doi.org/10.1016/j.neuroimage.2016.05.070, PubMed: 27262239 Da Silva Castanheira, J., Orozco, H. D., Misic, B., & Baillet, S. (2021). MEG, myself and I: Individual identification from neuro- physiological brain activity. bioRxiv. https://doi.org/10.1101 /2021.02.18.431803 de Haan, W., Mott, K., van Straaten, E. C., Scheltens, P., & Stam, C. J. (2012). Activity dependent degeneration explains hub vulnerability in Alzheimer’s disease. PLoS Computational Biology, 8(8), e1002582. https://doi.org/10.1371/journal.pcbi .1002582, PubMed: 22915996 Deco, G., Cabral, J., Woolrich, M. W., Stevner, A. B. A., van Hartevelt, T. J., & Kringelbach, M. L. (2017). Single or multiple frequency generators in on-going brain activity: A mechanistic whole-brain model of empirical MEG data. NeuroImage, 152, 538–550. https:// doi.org/10.1016/j.neuroimage.2017.03.023, PubMed: 28315461 Deco, G., Jirsa, V. K., Robinson, P. A., Breakspear, M., & Friston, K. (2008). The dynamic brain: From spiking neurons to neural masses and cortical fields. PLoS Computational Biology, 4(8), e1000092. https://doi.org/10.1371/journal.pcbi.1000092, PubMed: 18769680 Derks, J., Wesseling, P., Carbo, E. W. S., Hillebrand, A., van Dellen, E., de Witt Hamer, P. C., Klein, M., Schenk, G. J., Geurts, J. J. G., Reijneveld, J. C., & Douw, L. (2018). Oscillatory brain activity associates with neuroligin-3 expression and predicts progression free survival in patients with diffuse glioma. Journal of Neuro- oncology, 140(2), 403–412. https://doi.org/10.1007/s11060-018 -2967-5, PubMed: 30094719 Douw, L., van Dellen, E., Gouw, A. A., Griffa, A., de Haan, W., van den Heuvel, M., Hillebrand, A., Van Mieghem, P., Nissen, I. A., Otte, W. M., Reijmer, Y. D., Schoonheim, M. M., Senden, M., van Straaten, E. C. W., Tijms, B. M., Tewarie, P., & Stam, C. J. (2019). The road ahead in clinical network neuroscience. Network Neu- roscience, 3(4), 969–993. https://doi.org/10.1162/netn_a_00103, PubMed: 31637334 Eijlers, A. J. C., van Geest, Q., Dekker, I., Steenwijk, M. D., Meijer, K. A., Hulst, H. E., Barkhof, F., Uitdehaag, B. M. J., Schoonheim, M. M., & Geurts, J. J. G. (2018). Predicting cognitive decline in multiple sclerosis: A 5-year follow-up study. Brain, 141(9), 2605–2618. https://doi.org/10.1093/ brain/awy202, PubMed: 30169585 Finger, H., Bonstrup, M., Cheng, B., Messe, A., Hilgetag, C., Thomalla, G., Gerloff, C., & Konig, P. (2016). Modeling of large-scale functional brain networks based on structural con- nectivity from DTI: Comparison with EEG derived phase cou- pling networks and evaluation of alternative methods along the modeling path. PLoS Computational Biology, 12(8), e1005025. https://doi.org/10.1371/journal.pcbi.1005025, PubMed: 27504629 Forrester, M., Crofts, J. J., Sotiropoulos, S. N., Coombes, S., & O’Dea, R. D. (2020). The role of node dynamics in shaping emergent functional connectivity patterns in the brain. Network Neuroscience, 4(2), 467–483. https://doi.org/10.1162/netn_a _00130, PubMed: 32537537 Friston, K. J. (2011). Functional and effective connectivity: A review. Brain Connectivity, 1(1), 13–36. https://doi.org/10.1089 /brain.2011.0008, PubMed: 22432952 Gong, G., He, Y., Concha, L., Lebel, C., Gross, D. W., Evans, A. C., & Beaulieu, C. (2009). Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography. Cerebral Cortex, 19(3), 524–536. https://doi.org/10 .1093/cercor/bhn102, PubMed: 18567609 Grimbert, F., & Faugeras, O. (2006). Bifurcation analysis of Jansen’s neural mass model. Neural Computation, 18(12), 3052–3068. https://doi.org/10.1162/neco.2006.18.12.3052, PubMed: 17052158 Gross, J., Baillet, S., Barnes, G. R., Henson, R. N., Hillebrand, A., Jensen, O., Jerbi, K., Litvak, V., Maess, B., Oostenveld, R., Parkkonen, L., Taylor, J. R., van Wassenhove, V., Wibral, M., & Schoffelen, J. M. (2013). Good practice for conducting and reporting MEG research. NeuroImage, 65, 349–363. https://doi .org/10.1016/j.neuroimage.2012.10.001, PubMed: 23046981 Hadida, J., Sotiropoulos, S. N., Abeysuriya, R. G., Woolrich, M. W., & Jbabdi, S. (2018). Bayesian optimisation of large-scale bio- physical networks. NeuroImage, 174, 219–236. https://doi.org /10.1016/j.neuroimage.2018.02.063, PubMed: 29518570 Hallett, M., de Haan, W., Deco, G., Dengler, R., Di Iorio, R., Gallea, C., Gerloff, C., Grefkes, C., Helmich, R. C., Kringelbach, Network Neuroscience 963 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 3 9 5 0 2 1 5 4 8 2 8 n e n _ a _ 0 0 3 0 3 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Individualized modeling of brain connectivity M. L., Miraglia, F., Rektor, I., Strycek, O., Vecchio, F., Volz, L. J., Wu, T., & Rossini, P. M. (2020). Human brain connectivity: Clinical applications for clinical neurophysiology. Clinical Neu- rophysiology, 131(7), 1621–1651. https://doi.org/10.1016/j .clinph.2020.03.031, PubMed: 32417703 Hansen, J. A., & Penland, C. (2006). Efficient approximate techniques for integrating stochastic differential equations. Monthly Weather Review, 134(10), 3006–3014. https://doi.org/10.1175/MWR3192.1 Hillebrand, A., & Barnes, G. R. (2005). Beamformer analysis of MEG data. International Review of Neurobiology, 68, 149–171. https:// doi.org/10.1016/S0074-7742(05)68006-3, PubMed: 16443013 Hillebrand, A., Barnes, G. R., Bosboom, J. L., Berendse, H. W., & Stam, C. J. (2012). Frequency-dependent functional connectivity within resting-state networks: An atlas-based MEG beamformer solution. NeuroImage, 59(4), 3909–3921. https://doi.org/10 .1016/j.neuroimage.2011.11.005, PubMed: 22122866 Hillebrand, A., Singh, K. D., Holliday, I. E., Furlong, P. L., & Barnes, G. R. (2005). A new approach to neuroimaging with magnetoen- cephalography. Human Brain Mapping, 25(2), 199–211. https:// doi.org/10.1002/hbm.20102, PubMed: 15846771 Hillebrand, A., Tewarie, P., van Dellen, E., Yu, M., Carbo, E. W., Douw, L., Gouw, A. A., van Straaten, E. C., & Stam, C. J. (2016). Direction of information flow in large-scale resting-state networks is frequency-dependent. Proceedings of the National Academy of Sciences, 113(14), 3867–3872. https://doi.org/10 .1073/pnas.1515657113, PubMed: 27001844 Hipp, J. F., Hawellek, D. J., Corbetta, M., Siegel, M., & Engel, A. K. (2012). Large-scale cortical correlation structure of spontaneous oscillatory activity. Nature Neuroscience, 15(6), 884–890. https:// doi.org/10.1038/nn.3101, PubMed: 22561454 Jansen, B. H., & Rit, V. G. (1995). Electroencephalogram and visual evoked potential generation in a mathematical model of coupled cortical columns. Biological Cybernetics, 73(4), 357–366. https:// doi.org/10.1007/BF00199471, PubMed: 7578475 Lachaux, J.-P., Rodriguez, E., Martinerie, J., & Varela, F. J. (1999). Measuring phase synchrony in brain signals. Human Brain Mapping, 8(4), 194–208. https://doi.org/10.1002/(SICI)1097-0193 (1999)8:4<194::AID-HBM4>3.0.一氧化碳;2-C, 考研: 10619414
Liuzzi, L。, Gascoyne, L. E., Tewarie, 磷. K., Barratt, 乙. L。, Boto, E., &
布鲁克斯, 中号. J. (2017). Optimising experimental design for MEG
resting state functional connectivity measurement. 神经影像,
155, 565–576. https://doi.org/10.1016/j.neuroimage.2016.11
.064, 考研: 27903441

Lopes da Silva, F. H。, Hoeks, A。, Smits, H。, & Zetterberg, L. H.
(1974). Model of brain rhythmic activity. Kybernetik, 15,
27–37. https://doi.org/10.1007/BF00270757, 考研: 4853232
迈尔-海因, K. H。, Neher, 磷. F。, Houde, J. C。, Cote, 中号. A。, Garyfallidis,
E., Zhong, J。, Chamberland, M。, Yeh, F. C。, 林, 是. C。, 吉, Q.,
Reddick, 瓦. E., Glass, J. 奥。, 陈, D. Q., 冯, Y。, 高, C。,
吴, Y。, Ma, J。, 他, R。, 李, Q., … Descoteaux, 中号. (2017). 查尔-
lenge of mapping the human connectome based on diffusion
tractography. Nature Communications, 8(1), 1349. https://土井
.org/10.1038/s41467-017-01285-x, 考研: 29116093

迈尔-海因, L。, Eisenmann, M。, Reinke, A。, Onogur, S。, Stankovic,
M。, Scholz, P。, Arbel, T。, Bogunovic, H。, Bradley, A. P。, Carass, A。,
Feldmann, C。, Frangi, A. F。, Full, 磷. M。, van Ginneken, B.,
Hanbury, A。, Honauer, K., Kozubek, M。, Landman, 乙. A。, März,
K., … Kopp-Schneider, A. (2018). Why rankings of biomedical

image analysis competitions should be interpreted with care.
Nature Communications, 9(1), 5217. https://doi.org/10.1038
/s41467-018-07619-7, 考研: 30523263

Meier, J。, Tewarie, P。, 希勒布兰德, A。, Douw, L。, van Dijk, 乙. W.,
Stufflebeam, S. M。, & Van Mieghem, 磷. (2016). A mapping between
structural and functional brain networks. Brain Connectivity, 6(4),
298–311. https://doi.org/10.1089/ brain.2015.0408, 考研:
26860437

Meijer, K. A。, Steenwijk, 中号. D ., Douw, L。, Schoonheim, 中号. M。, &
Geurts, J. J. G. (2020). Long-range connections are more severely
damaged and relevant for cognition in multiple sclerosis. Brain,
143(1), 150–160. https://doi.org/10.1093/brain/awz355, 考研:
31730165

Messe, A。, Rudrauf, D ., Giron, A。, & Marrelec, G. (2015). Predicting
functional connectivity from structural connectivity via computa-
tional models using MRI: An extensive comparison study. Neuro-
图像, 111, 65–75. https://doi.org/10.1016/j.neuroimage.2015
.02.001, 考研: 25682944

Moon, J.-Y., 李, U。, Blain-Moraes, S。, & Mashour, G. A. (2015).
General relationship of global topology, local dynamics, 和
directionality in large-scale brain networks. 公共科学图书馆计算
生物学, 11(4), e1004225. https://doi.org/10.1371/journal.pcbi
.1004225, 考研: 25874700

奥尼尔, G. C。, Tewarie, P。, Vidaurre, D ., Liuzzi, L。, 伍尔里奇,
中号. W., & 布鲁克斯, 中号. J. (2018). Dynamics of large-scale electro-
physiological networks: A technical review. 神经影像, 180(Pt B),
559–576. https://doi.org/10.1016/j.neuroimage.2017.10.003,
考研: 28988134

Popovych, 氧. 五、, Manos, T。, Hoffstaedter, F。, & Eickhoff, S. 乙.
(2019). What can computational models contribute to neuroim-
aging data analytics? Frontiers in Systems Neuroscience, 12, 68.
https://doi.org/10.3389/fnsys.2018.00068, 考研: 30687028
Raj, A。, Cai, C。, Xie, X。, Palacios, E., 欧文, J。, Mukherjee, P。, &
Nagarajan, S. (2020). Spectral graph theory of brain oscillations.
人脑图谱, 41(11), 2980–2998. https://doi.org/10
.1002/hbm.24991, 考研: 32202027

罗宾逊, 磷. A. (2012). Interrelating anatomical, effective, 和
functional brain connectivity using propagators and neural field
理论. Physical Review E: Statistical, Nonlinear, and Soft Matter
Physics, 85(1 Pt 1), 011912. https://doi.org/10.1103/PhysRevE.85
.011912, 考研: 22400596

罗宾逊, S. E., & Vrba, J. (1999). Functional neuroimaging by
synthetic aperture magnetometry (SAM). In Recent advances in
biomagnetism (PP. 302–305). Sendai, 日本: Tohoku University
按.

Sekihara, K., Hild, K. E., 2ND, & Nagarajan, S. S. (2006). A novel
adaptive beamformer for MEG source reconstruction effective
when large background brain activities exist. IEEE Transactions
on Biomedical Engineering, 53(9), 1755–1764. https://doi.org
/10.1109/TBME.2006.878119, 考研: 16941831

西格尔, M。, 唐纳, 时间. H。, & 恩格尔, A. K. (2012). Spectral finger-
prints of large-scale neuronal interactions. Nature Reviews Neu-
roscience, 13(2), 121–134. https://doi.org/10.1038/nrn3137,
考研: 22233726

Siems, M。, & 西格尔, 中号. (2020). Dissociated neuronal phase- 和
amplitude-coupling patterns in the human brain. 神经影像,
209, 116538. https://doi.org/10.1016/j.neuroimage.2020.116538,
考研: 31935522

网络神经科学

964

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
3
9
5
0
2
1
5
4
8
2
8
n
e
n
_
A
_
0
0
3
0
3
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Individualized modeling of brain connectivity

Spiegler, A。, 克诺舍, 时间. R。, Schwab, K., Haueisen, J。, & Atay, F. 中号.
(2011). Modeling brain resonance phenomena using a neural
mass model. 公共科学图书馆计算生物学, 7(12), e1002298.
https://doi.org/10.1371/journal.pcbi.1002298, 考研:
22215992

斯塔姆, C. J. (2014). Modern network science of neurological disor-
德斯. 自然评论神经科学, 15(10), 683–695. https://土井
.org/10.1038/nrn3801, 考研: 25186238

斯塔姆, C. J。, 诺尔特, G。, & Daffertshofer, A. (2007). Phase lag index:
Assessment of functional connectivity from multi channel EEG
and MEG with diminished bias from common sources. 人类
Brain Mapping, 28(11), 1178–1193. https://doi.org/10.1002
/hbm.20346, 考研: 17266107

Taulu, S。, & Simola, J. (2006). Spatiotemporal signal space sepa-
ration method for rejecting nearby interference in MEG mea-
surements. Physics in Medicine & 生物学, 51(7), 1759–1768.
https://doi.org/10.1088/0031-9155/51/7/008, 考研:
16552102

Tewarie, P。, Abeysuriya, R。, Byrne, Á., 奥尼尔, G. C。, 索蒂罗普洛斯,
S. N。, 布鲁克斯, 中号. J。, & Coombes, S. (2019A). How do spatially
distinct frequency specific MEG networks emerge from one
underlying structural connectome? The role of the structural
eigenmodes. 神经影像, 186, 211–220. https://doi.org/10
.1016/j.neuroimage.2018.10.079, 考研: 30399418

Tewarie, P。, 希勒布兰德, A。, van Dellen, E., Schoonheim, 中号. M。,
Barkhof, F。, Polman, C. H。, Beaulieu, C。, 锣, G。, van Dijk,
乙. W., & 斯塔姆, C. J. (2014). Structural degree predicts functional
network connectivity: A multimodal resting-state fMRI and MEG
学习. 神经影像, 97, 296–307. https://doi.org/10.1016/j
.neuroimage.2014.04.038, 考研: 24769185

Tewarie, P。, Liuzzi, L。, 奥尼尔, G. C。, 奎因, A. J。, Griffa, A。,
伍尔里奇, 中号. W., 斯塔姆, C. J。, 希勒布兰德, A。, & 布鲁克斯, 中号. J.
(2019乙). Tracking dynamic brain networks using high temporal
resolution MEG measures of functional connectivity. Neuro-
图像, 200, 38–50. https://doi.org/10.1016/j.neuroimage.2019
.06.006, 考研: 31207339

Tewarie, P。, Steenwijk, 中号. D ., 布鲁克斯, 中号. J。, Uitdehaag, 乙. 中号. J。,
Geurts, J. J. G。, 斯塔姆, C. J。, & Schoonheim, 中号. 中号. (2018).

Explaining the heterogeneity of functional connectivity findings
in multiple sclerosis: An empirically informed modeling study.
人脑图谱, 39(6), 2541–2548. https://doi.org/10
.1002/hbm.24020, 考研: 29468785

图尔尼耶, J. D ., 卡拉曼特, F。, & 康纳利, A. (2007). Robust deter-
mination of the fibre orientation distribution in diffusion MRI:
Non-negativity constrained super-resolved spherical deconvolu-
的. 神经影像, 35(4), 1459–1472. https://doi.org/10.1016/j
.neuroimage.2007.02.016, 考研: 17379540

图尔尼耶, J. D ., 卡拉曼特, F。, & 康纳利, A. (2012). MRtrix:
Diffusion tractography in crossing fiber regions. 国际的
Journal of Imaging Systems and Technology, 22(1), 53–66.
https://doi.org/10.1002/ima.22005

Tzourio-Mazoyer, N。, Landeau, B., Papathanassiou, D ., Crivello, F。,
Etard, 奥。, Delcroix, N。, Mazoyer, B., & Joliot, 中号. (2002). 汽车-
mated anatomical labeling of activations in SPM using a macro-
scopic anatomical parcellation of the MNI MRI single-subject
脑. 神经影像, 15(1), 273–289. https://doi.org/10.1006
/nimg.2001.0978, 考研: 11771995

van Dellen, E., 希勒布兰德, A。, Douw, L。, Heimans, J. J。, Reijneveld,
J. C。, & 斯塔姆, C. J. (2013). Local polymorphic delta activity in
cortical lesions causes global decreases in functional connectivity.
神经影像, 83, 524–532. https://doi.org/10.1016/j.neuroimage
.2013.06.009, 考研: 23769919

van Klink, N。, van Rosmalen, F。, Nenonen, J。, Burnos, S。, Helle, L。,
Taulu, S。, Furlong, 磷. L。, Zijlmans, M。, & 希勒布兰德, A. (2017).
Automatic detection and visualisation of MEG ripple oscillations
in epilepsy. 神经影像: Clinical, 15, 689–701. https://doi.org
/10.1016/j.nicl.2017.06.024, 考研: 28702346

Verma, P。, Nagarajan, S。, & Raj, A. (2022). Spectral graph theory of
brain oscillations—Revisited and improved. 神经影像, 249,
118919. https://doi.org/10.1016/j.neuroimage.2022.118919,
考研: 35051584

Zimmermann, J。, Griffiths, J。, Schirner, M。, 里特尔, P。, & McIntosh,
A. 右. (2019). Subject specificity of the correlation between
large-scale structural and functional connectivity. Network Neu-
roscience, 3(1), 90–106. https://doi.org/10.1162/netn_a_00055,
考研: 30793075