研究
An information-theoretic analysis of
resting-state versus task fMRI
Julia Tuominen1,2
, Karsten Specht1,3,4
, Liucija Vaisvilaite1,3
, and Peter Zeidman5
1Department of Biological and Medical Psychology, University of Bergen, 卑尔根, Norway
2Department of Global Public Health and Primary Care, University of Bergen, 卑尔根, Norway
3Mohn Medical Imaging and Visualization Centre, Haukeland University Hospital, 卑尔根, Norway
4教育部, The Arctic University of Norway UiT, Tromsø, Norway
5Wellcome Centre for Human Neuroimaging, UCL Institute of Neurology, 伦敦大学学院, 伦敦, 英国
关键词: Bayesian data comparison, Effective connectivity, Resting-state, Task fMRI, Data quality
开放访问
杂志
抽象的
Resting-state fMRI is an increasingly popular alternative to task-based fMRI. 然而, a formal
quantification of the amount of information provided by resting-state fMRI as opposed to active task
conditions about neural responses is lacking. We conducted a systematic comparison of the quality
of inferences derived from a resting-state and a task fMRI paradigm by means of Bayesian Data
比较. In this framework, data quality is formally quantified in information-theoretic terms
as the precision and amount of information provided by the data on the parameters of interest.
Parameters of effective connectivity, estimated from the cross-spectral densities of resting-state-
and task time series by means of dynamic causal modelling (DCM), were subjected to the analysis.
Data from 50 individuals undergoing resting-state and a Theory-of-Mind task were compared, 两个都
datasets provided by the Human Connectome Project. A threshold of very strong evidence was
reached in favour of the Theory-of-Mind task (>10 bits or natural units) regarding information gain,
which could be attributed to the active task condition eliciting stronger effective connectivity.
Extending these analyses to other tasks and cognitive systems will reveal whether the superior
informative value of task-based fMRI observed here is case specific or a more general trend.
作者总结
The ongoing replication crisis in neuroscience and the concurrent “paradigm shift” from
task-based to resting-state fMRI raises a question about the relative quality of the data obtained
from these imaging paradigms. We compared parameters of intrinsic effective connectivity
estimated from resting-state and Theory-of-Mind datasets. The much weaker connectivity
and consequent lower information gain of the resting condition was notable as the network
was specified based on connectivity patterns observed under rest and consisted of regions
associated with the default mode network, which is characterized by being active during rest.
These results support the assumption that the resting connectivity of the default mode network
may reflect physiological rather than neural processes, and that the neural system in question
better lends itself to investigation under an active task condition.
介绍
In functional magnetic resonance imaging (功能磁共振成像) 研究, the shift from functional localiza-
tion to functional and effective connectivity as the primary object of investigation has been
引文: Tuominen, J。, Specht, K.,
Vaisvilaite, L。, & Zeidman, 磷. (2023).
An information-theoretic analysis of
resting-state versus task fMRI. 网络
神经科学, 7(2), 769–786. https://土井
.org/10.1162/netn_a_00302
DOI:
https://doi.org/10.1162/netn_a_00302
支持信息:
https://doi.org/10.1162/netn_a_00302
已收到: 9 六月 2022
公认: 6 一月 2023
利益争夺: 作者有
声明不存在竞争利益
存在.
通讯作者:
Julia Tuominen
julia.tuominen@uib.no
处理编辑器:
奥拉夫·斯波恩斯
版权: © 2023
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
A
_
0
0
3
0
2
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Resting-state versus task fMRI
Effective connectivity:
Causal influence directed from one
brain region to another.
Intrinsic functional connectivity:
Consistent temporospatial
correlations among brain regions that
emerge in the absence of
experimental perturbation.
Entropy:
Amount of disorder or randomness in
a system, or in statistical terms, lack
of information associated with
probability distributions.
Bayesian data comparison (BDC):
Method to systematically compare
the quality of two or more datasets
based on information theory.
Dynamic causal modelling (DCM):
A generative model of effective
connectivity that incorporates
information on the hemodynamic
response and a model of
unobservable neural dynamics.
naturally accompanied by a so-called “paradigm shift” in the design of imaging protocols
(Raichle, 2009). Resting-state fMRI (rs-fMRI) has become an attractive alternative to task-based
功能磁共振成像 (t-fMRI) due to ease and efficiency of acquisition (Dubois & Adolphs, 2016; Leuthardt
等人。, 2015), and because the intrinsic functional connectivity of the brain can be investigated
without a known timeline of experimental events (Cole et al., 2014). 然而, research questions
posed in the context of t-fMRI are not restricted to those pertaining to functional localization.
Both functional and effective connectivity can be and are being studied under different task
状况, revealing temporally coherent networks congruent with those observed in rest
(Calhoun et al., 2008; Cole et al., 2014; Kieliba et al., 2019; 史密斯等人。, 2009). 此外,
clinically relevant individual differences have been demonstrated to be preserved across rest
and different active tasks (Mwansisya et al., 2017; Schurz et al., 2015). Followingly, 这 (dys)
function of a given neural system can be investigated under both imaging paradigms, 哪个
makes inquiries into the relative quality of the obtained data highly relevant.
Studies that have compared the performance of t-fMRI to rs-fMRI data suggest the superi-
ority of t-fMRI in measures such as predictive accuracy and reliability (Finn et al., 2017; Frässle
& Stephan, 2022; Gaut et al., 2019; Greene et al., 2018; Kristo et al., 2014; McCormick et al.,
2022; Noble et al., 2019; Rosazza et al., 2014; Specht et al., 2003; 王等人。, 2017; 韦伯
等人。, 2013; Xie et al., 2018; Yoo et al., 2018). Performance in such measures is of increasing
importance given the growing interest in applying fMRI in the identification of disease bio-
markers and in individualized treatment approaches (布鲁克斯 & Vizueta, 2014; Carter et al.,
2008; McDermott et al., 2018). In clinical applications the measurement of activation strength,
such as the strength of between-region coupling, becomes particularly important, which intro-
duces additional demands on data quality (Specht, 2020).
In this study the question about data quality was formulated as to whether rs- or t-fMRI data
provide more information about neural responses, the relative precision with which we can infer
the strength of individual connection parameters, as well as the ability to distinguish between
different neural network architectures. These can be formally assessed with an information-
theoretic approach in terms of reduction in entropy. The present question could therefore be
tackled using Bayesian data comparison (BDC), an analysis framework introduced by Zeidman
等人. (2019C) that draws on Bayesian statistics to measure movement from prior to posterior
distributions afforded by the data. Neural responses, defined as the rate of change in the activity
of neural populations in units of s−1 (赫兹), cannot be directly observed using BOLD fMRI but can
only be inferred under a parameterized generative model. 所以, BDC was here applied in
the context of dynamic causal modelling (DCM) to obtain parameters of effective connectivity,
which is simply the contribution of one population’s neural response towards another’s. 我们的
research question can formally be stated as: how much more information do we have about
the unknown parameters governing neural responses after observing each kind of data.
The data quality indices obtained from BDC have been demonstrated to be positively cor-
related with signal-to-noise ratio (信噪比), a metric commonly used to quantify the quality of
fMRI data (Bennett & 磨坊主, 2010; Welvaert & Rosseel, 2013; Zeidman et al., 2019C). 如何-
曾经, unlike SNR that is insensitive to the feature of interest in connectivity studies, 现在
indices measure data quality in relation to the studied connectivity parameters. 因此, BDC
enables an analysis of data quality beyond that indicated by SNR or the relative amount of
之内- and between-individual variability, which is typically quantified in studies of reliability
and predictive accuracy.
We envisage that comparing the performance of several datasets in the context of a partic-
ular network model would be especially useful in clinical settings, where the focus shifts from
网络神经科学
770
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
A
_
0
0
3
0
2
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Resting-state versus task fMRI
Theory-of-mind (ToM):
Mental function involving social-
cognitive and self-referential
流程.
Default mode network (DMN):
Medial fronto-parietal network that
deactivates to a range of cognitive
tasks and activates during rest and to
tasks requiring self-referential
加工.
identifying the affected neural system to optimizing the imaging paradigm under which to best
measure its function. We hypothesized that perturbations of a neural network by external stim-
uli, which evoke cognitive processes supported by that network, will facilitate the estimation
of effective connectivity parameters and lead to better performance in terms of the above-
mentioned quality indices. We used data from the Human Connectome Project (Van Essen
等人。, 2013), which is particularly suitable for the present purpose due to being acquired under
both resting-state and different task conditions using the same acquisition protocol and the
same set of subjects, in addition to coming from a quality-assured, open data source.
材料和方法
The Data
We employed the minimally preprocessed data provided by the Human Connectome Project
(HCP). The sample consisted of 50 subjects in total, 23 males and 27 females between the ages
22 和 35, selected from the predefined subset of 100 unrelated subjects of the Young Adult
dataset. Informed consent was obtained from the subjects both upon initial screening and at
the beginning of the scanning session (Van Essen et al., 2013). The present study did not neces-
sitate the use of data from siblings or twins, or biological data from HCP Restricted Data,
which are considered more sensitive and are available only through a separate application
过程 (Van Essen et al., 2013). 此外, the results will be reported only at the group
等级, such that any risk of identification should be minimal. The authors of the present study
have agreed to the Open Access Data Use Terms of HCP, and the Norwegian Regional Com-
mittees for Medical and Health Research Ethics (REK) approved the use of HCP data in the
project “When Default is not Default,” of which the present study is part of (REK West: 31972).
HCP provides data on the same subjects undergoing two rs-fMRI sessions and seven t-fMRI
sessions. The different tasks have been demonstrated to recruit a wide range of well-
characterized neural systems efficiently and reliably (Barch et al., 2013). For the current anal-
分析, we selected a social cognition task adapted from the ones developed by Castelli et al.
(2000) and Wheatley et al. (2007). It consists of social animation stimuli in the form of video
clips of geometrical objects moving either randomly or in a biologically meaningful pattern,
which were rated online by the participants based on whether they were perceived to involve
social interaction. The cognitive processes deliberately evoked by this type of task, 集体地
known as the Theory-of-Mind (ToM), are suggested to occur spontaneously during rest. 相似的
to other tasks engaging such “self-referential” processes, it has been observed to activate parts
of the default mode network (DMN) (Andreasen et al., 1995; 火星等人。, 2012; Schilbach
等人。, 2008; Spreng & Grady, 2010; Spreng et al., 2009). It was therefore particularly interest-
ing to compare data from this task, hereafter referred to as the ToM task, to data from a rs-fMRI
session for the same group of subjects.
In HCP, fast sampling with TR of 720 ms and TE of 33 ms is used (Glasser et al., 2013). A
detailed account of the image acquisition protocol and the HCP minimal preprocessing pipe-
line can be found in Van Essen et al. (2012) and Glasser et al. (2013). Due to the specific image
acquisition protocol employed in HCP there were two runs of each imaging condition, scanned
with reversed phase encoding directions (Van Essen et al., 2013). For simplicity, in our analysis
we included only data from Run 2 of the ToM task scanned in the left-right direction, 组成
of three clips of social interaction and two clips of random movement. Each run started with a
countdown of 8 s, and the duration of each animation clip was 20 s, 其次是 3 s for a behav-
ioural response and a 15-s fixation block. One complete run therefore lasted for 3 min and 27 s.
Data from a resting-state (RS) session carried out on the same day was utilized to avoid possible
网络神经科学
771
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
A
_
0
0
3
0
2
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Resting-state versus task fMRI
differences in the two datasets arising from factors fluctuating on a daily basis. For the sake of
一致性, we utilized the preprocessed datasets in which ICA-based denoising has not been
applied, as this option is available only for rs-fMRI data. 再次, data acquired with the left-right
scanning direction was employed, which was always the first run. The duration of the run was
14 min 33 s. In the RS condition the participants were requested to lie with their eyes open and
fixated on a white cross on a dark background, to think of nothing particular, and not to fall
asleep (史密斯等人。, 2013). The use of concatenated images across the opposite scanning direc-
tions was assessed to potentially increase overall data quality but to greatly complicate the pre-
paratory data processing without changing the relative quality of the two datasets. As our main
interest was in the relative and not in the absolute data quality, only the images acquired with
one scanning direction were included in the analysis.
Preparatory Analyses
The minimally preprocessed data were smoothed with an 8-mm Gaussian kernel, using SPM-12
(v7771) in MATLAB 2019a. 此后, a standard univariate general linear model (GLM) 曾是
conducted on the ToM data. In the first-level GLM analysis a design matrix was specified, 哪个
included the countdown, block, response, and fixation times specified above. The default
options of microtime resolution and onset of 16 和 18, 高通滤波器 128 s and canonical
hemodynamic response function (HRF) convolution model were applied, 和 12 移动-
ment parameters (翻译, rotation, and their derivatives) were included as covariates in
the design matrix. Countdown, fixation, and response times were included as regressors in
order to obtain a map of activation specific to viewing social stimuli. A contrast between blocks
of socially meaningful movement and blocks of random movement (Social > Random) 曾是
defined. In the second-level group analysis a one-sample t test was calculated for this contrast
to identify regions specifically and significantly responsive to social interaction. The results
were exported as a binary mask to be used at the subsequent stages of the analysis.
An independent component analysis (ICA) was conducted on the RS dataset with the pur-
pose of identifying a component that best corresponds to the activation map obtained from the
preceding GLM analysis, thereby thought to reflect the intrinsic connectivity of regions associ-
ated with ToM processes. The RS images were also smoothed in SPM-12 with an 8-mm smooth-
ing kernel before importing the files to the GIFT-toolbox v3.0b in MATLAB 2019a, 哪里的
ICA was performed. 的数量 42 成分, advocated in some sources (Kiviniemi
等人。, 2009), was considered high enough not to result in wide, functionally heterogeneous
networks but neither in overly circumscribed within-region networks. The default algorithm
Infomax was applied. The stability of the derived components was analysed with ICASSO that
repeated the analysis 10 次. The spatial configurations of the components were individually
reconstructed and sorted according to their spatial overlap with the binary mask extracted from
the GLM analysis of ToM data. This allowed us to identify a RS independent component that
best overlapped with the ToM activation map. The reconstructed maps of this component from
each subject were imported to SPM-12, where a one-sample t test was conducted to obtain a
group-level spatial map of significant clusters. The coordinates of five most significant clusters
were used as nodes in the following DCM analysis. These five clusters are listed in Table 1.
Main Analysis
Time series extraction. While the time courses of the ToM task were directly extracted from the
preparatory individual first-level GLM analysis, the RS data needed some further processing.
The RS time series was reduced from the original scanning length of 14 min 33 s to the same
length as the ToM task, 那是 3 min and 27 s. This ensured a more formal comparison of data
网络神经科学
772
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
A
_
0
0
3
0
2
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Resting-state versus task fMRI
DCM for cross-spectral densities
(csd-DCM):
Estimates effective connectivity from
correlations in amplitudes and phase
delays of fMRI time series, 适用的
to both resting-state and task fMRI
数据.
桌子 1. Coordinates of the DCM nodes extracted from the best matching independent component
Label
R angular gyrus
R superior temporal sulcus
R/L precuneus
R temporal pole
R fusiform gyrus
X
56
54
4
50
44
MNI1
y
−50
−46
−54
−6
−50
z
20
6
60
−18
−20
T-value
30.94
25.24
13.23
12.44
7.01
笔记. R = Right, L = Left. FWE correction at p < 0.05 and cluster level 20 were used.
1 Montreal Neurological Institute brain coordinates.
quality not influenced by the accumulation of signal across time, which is known to increase
SNR. As an additional analysis, we compared ToM data also to the full-length RS data, as this is
more consistent with the typical application of rs-fMRI. First, a dummy GLM was set up to
extract time series from the RS data, followed by another GLM in which the 12 movement
regressors and signals from white matter [0, −24, −33] and cerebrospinal fluid [0, −40, −5]
were used to regress out further noise related to motion, scanner, and physiological processes
(Weissenbacher et al., 2009). The same high-pass filter as for the ToM data analysis was
applied. Time series for the five nodes were extracted by centring spherical regions with a
radius of 8 mm on their coordinates, from which the first principal eigenvariate of all voxels
within the sphere, centred on the peak voxel, summarized the time series of a given node. The
time series were mean corrected. Motion correction and time series extraction proceeded in a
similar manner for ToM data.
Dynamic causal modelling. The measures of data quality applied here depend on both the effi-
ciency of the selected tasks for inducing effective connectivity among the regions of interest,
and the efficiency of the model for inferring the presence of those effects. As our focus was
comparing tasks, we kept the model as consistent as possible across datasets by using the same
forward model with the same regions of interest and connectivity architectures.
We employed DCM for cross-spectral densities (csd-DCM) in SPM-12 to invert a neural
network model consisting of the nodes identified at the preparatory stage of the analysis (Razi
et al., 2015). This was done separately for RS and ToM data, which produced subject-specific
estimates of intrinsic effective connectivity. DCM for CSD was used due to it being applicable
to both t-fMRI and rs-fMRI data (Friston et al., 2014), although this version of DCM does not
allow the testing of condition-specific modulations on effective connectivity (i.e., no B matrix).
However, this is not relevant for the present study, where the t-fMRI data only included a single
experimental factor (social vs. random movement). Therefore, only the blocks of social stimuli
were included as driving input through the fusiform gyrus (C matrix) when modelling connec-
tivity during the ToM task. The quality indices were based on the invariant connectivity (A
matrix) of the respective dataset.
We allowed all connections between the regions to be informed by the data. In the within-
subject (DCM) and between-subject (parametric empirical Bayes, PEB) models, priors on
parameters were left at their default values, as supplied with the SPM12 software. Priors at
the within-subject subject level are detailed in table 3 of Zeidman et al. (2019a) and priors
at the between-subject level are detailed in appendices 1 and 2 of Zeidman et al. (2019b).
The most important parameters in the DCM neural model for the analyses presented were
Network Neuroscience
773
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Resting-state versus task fMRI
those forming the region-by-region effective connectivity matrix (matrix A). To briefly reprise,
this was multivariate normal prior, where the connection from region j to region i had the
probability density Aij ∼ N(0, 1/64). This is referred to as a shrinkage prior, because in the
absence of evidence to the contrary, it assumes no connectivity (0 Hz) among regions.
Bayesian data comparison. The subject-specific effective connectivity parameters were subjected
to the BDC analysis pipeline (spm_dcm_bdc.m, revision 7495) in SPM-12. Whereas standard
statistics based on likelihood ratios are used to compare the evidence for different models fitted
to the same data (e.g., F tests, Bayes factors), these statistics cannot be used to compare models
fitted to different data. The BDC procedure works around this by evaluating which dataset affords
the greatest precision or confidence about the model parameters and the models themselves.
Ideally, one would follow standard statistical procedure for Bayesian hypothesis testing, which
is to evaluate the log evidence ln P(y|mi) for each model of interest mi, and then compare them
by computing the log Bayes factor. For two models, the log Bayes factor is simply the difference
in log evidences, ln P(y|m1) − ln P(y|m2). However, this assumes that the data y are the same for
each model, which precludes the use of the Bayes factor for comparing models fitted to different
datasets. To address this, the log evidence (and its free energy approximation used here) can be
decomposed into the difference between the model’s accuracy and complexity:
lnP yjmi
ð
ð
Þ ¼ lnP yjθ; mi
h
Þ
p θjy;mi
ð
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
accuracy
Þ
i
½
ð
− KL P θjy; m
(cid:2)
Þ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
complexity
Þ‖P θjmð
In words, the accuracy is the expected log likelihood (the probability of observing the data under
the model after estimating the parameters), which would not be meaningful to compare across
datasets. The complexity, also called the relative entropy, describes how far the parameters have
diverged from their prior expectations. This is quantified by the Kullback–Leibler (KL) diver-
gence, also called the relative entropy, which is a measure of difference between two probability
distributions (Joyce, 2011):
h
(cid:3)
DKL P β ið ÞjY ið Þ
(cid:4)
i
(cid:3)
(cid:4)∥P β ið Þ
This quality index considers the prior and posterior expected values of the parameters (μ ið Þ
0 , (cid:2)(i ))
and the covariance matrices ((cid:1) ið Þ
0 , (cid:1)(i )), which determines the effective number of independent
parameters that the data can support (Zeidman et al., 2019c). This measures how much infor-
mation has been gained after observing the data and has natural units (nats), which enable a
convenient comparison between datasets. For this reason, it is used in BDC as the basis for com-
paring how much has been learnt from each dataset. A difference between 1.1 and 3 nats can be
described as positive evidence in favour of one dataset over another, a difference between 3 and
5 nats as strong evidence, and differences beyond that indicate very strong evidence (akin to a
Bayes Factor; Kass & Raftery, 1995).
The central steps of BDC are as follows. First, connection parameters are estimated for each
subject and are then optimized after obtaining the average connectivity of the group (empirical
Bayes). In more detail, for each subject s and dataset i, a generative model of fMRI data is specified:
(cid:3)
vec Y i;sð
Þ
(cid:4)
(cid:3)
¼ f θ i;sð
(cid:4)
Þ
þ (cid:3) i;sð
Þ
where Y is a matrix of fMRI timeseries data, the vec(·) operator converts a matrix to a vector, f is a
model (here, an fMRI DCM), θ is a vector of connection parameters and (cid:3) are the residuals. Model
fitting is then performed for each subject, to obtain a posterior probability distribution over the
parameters, P(θ(i,s)|Y (i,s)), as well as score for the quality of the model, the log evidence, which
Network Neuroscience
774
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Resting-state versus task fMRI
Parameter certainty:
Encodes variance and covariance
among parameters, defined as
negative entropy of the covariance
matrix.
Information gain:
Relative entropy, that is, reduction
in uncertainty after seeing the data
relative to the uncertainty before
seeing the data.
is approximated by the free energy F (i,s) ≈ ln P(Y (i,s)). All subjects’ models are then reestimated,
using the group-average connection parameters (across all subjects and both datasets) as priors.
This reestimation procedure can “rescue” any subjects whose parameters have fallen into different
local optima.
Next, the optimized subject-specific connectivity parameters are summarized at the group
level, separately for each dataset, using a hierarchical PEB model. This Bayesian scheme pro-
vides an estimated probability distribution over the group-average connectivity parameters as
well as a score for the quality of the complete hierarchical model—the free energy—for each
dataset. These two outputs—the group-level parameters and the free energy—form the basis
for the comparisons that follow. More formally, for each dataset i = h1, 2i and subject s, we
have a hierarchical model:
ð
Level 2
Þ θ ið Þ ¼ X β ið Þ þ E ið Þ
ð
Level 1
(cid:3)
Þ vec Y i;sð
(cid:4)
Þ
(cid:4)
(cid:3)
¼ f θ i;sð
Þ
þ (cid:3) i;sð
Þ
where θ(i ) is a vector of all subjects’ connection parameters, the design matrix X encodes any
between-subjects effects, β are the parameters encoding the group-average connectivity and the
effects of any covariates on the connections, and E is the unexplained between-subjects variabil-
ity. Constraints are imposed on the group-level parameters through a prior probability distribu-
tion, P(β(i )) = N(μ ið Þ
0 ). Estimating the model supplies a posterior probability distribution over
the group-level connection parameters, informed by all subjects, which is multivariate normal
P(β(i)|Y (i)) = N(μ(i), (cid:1)(i)), as well as the overall free energy of the hierarchical model F (i ) ≈ ln P(Y (i )).
0 , (cid:1) ið Þ
Three statistics are then computed in order to compare the hierarchical models fitted to the
different datasets, referred to as (1) parameter certainty, (2) information gain over parameters
and (3) information gain over models.
The parameter certainty is the confidence with which the connection parameters have been
estimated at the group level. It is a function of the posterior covariance matrix (cid:1)(i ), which
encodes the uncertainty or variance of each parameter on its leading diagonal, and the covari-
ance among parameters on the off-diagonal entries. The covariance determines the extent to
which parameters can be distinguished from each other, which is important when testing
hypotheses that consist of several parameters being estimated simultaneously. The parameter
certainty S(i ) is defined as the negative entropy of the covariance matrix:
S ið Þ ¼ −0:5 ln 2πe(cid:1) ið Þ
(cid:5)
(cid:5)
(cid:5)
(cid:5)
The dataset with highest negative entropy affords greater reduction in uncertainty, measured
in nats.
The information gain over parameters scores the reduction in uncertainty after seeing the
data relative to the uncertainty before seeing the data. It quantifies how far the parameters have
changed from prior beliefs P(β (i )) to the posterior beliefs P(β (i )|Y (i )), that is, the relative entropy
as explained above.
Finally, information gain over models indicates the ability to discriminate between models
and to identify the optimal one (Zeidman et al., 2019c). In BDC, a model space consisting of
equally plausible but difficult to distinguish models is formed, by switching on or off particular
connections in the neural network. In the current case, only the A matrix from the DCM
models served as input for the BDC procedure. The models are assigned equal prior probabil-
ities, forming a discrete prior probability distribution over models. The posterior probability of
Network Neuroscience
775
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Resting-state versus task fMRI
each model is calculated, and the KL-divergence between the prior and posterior probability
distributions is computed (Zeidman et al., 2019c). The less uniformly the posterior probability
is distributed among the models (i.e., the more that some models are favoured over others), the
higher KL-divergence, indicating better discrimination among models and greater information
gain over the model structure (see Formula S1). An analytic approach for rapidly approximat-
ing the posteriors and model evidence called Bayesian model reduction (BMR) is used to
reduce computation time (Friston et al., 2016).
In summary, the BDC procedure involves fitting models (DCMs) to each subject’s fMRI data,
then taking the model parameters from all subjects up to the group level and fitting a GLM for
each dataset under consideration. The parameters of each GLM quantifies the group-average
connectivity, which are used to compute the statistics described above.
An additional step originally proposed in the BDC pipeline by Zeidman et al. (2019c) was
not applied here. They used BMR to prune away any redundant parameters that do not con-
tribute to model evidence at the group-level GLM. It results in one parsimonious model
informed equally by all datasets, the parameters of which are used to reestimate individual-
level connections. In this study, BDC was conducted on a fully connected model by turning off
the BMR function. This was done because the network structure may differ under rs- and
t-fMRI and fitting the data to a model that represents a compromise between the two imaging
conditions might have unpredictable effects on the rest of the analysis.
RESULTS
The comparison between the ToM activation map obtained with the GLM and the 42 RS inde-
pendent components obtained with the ICA identified one component that covered a substan-
tial part of the ToM activation map. A spatial map of this component and the ToM activation
map are displayed in Figure 1. The activation peaks of the ToM task can be found in the Sup-
porting Information (Table S1). The five most significant regions identified with the group-level
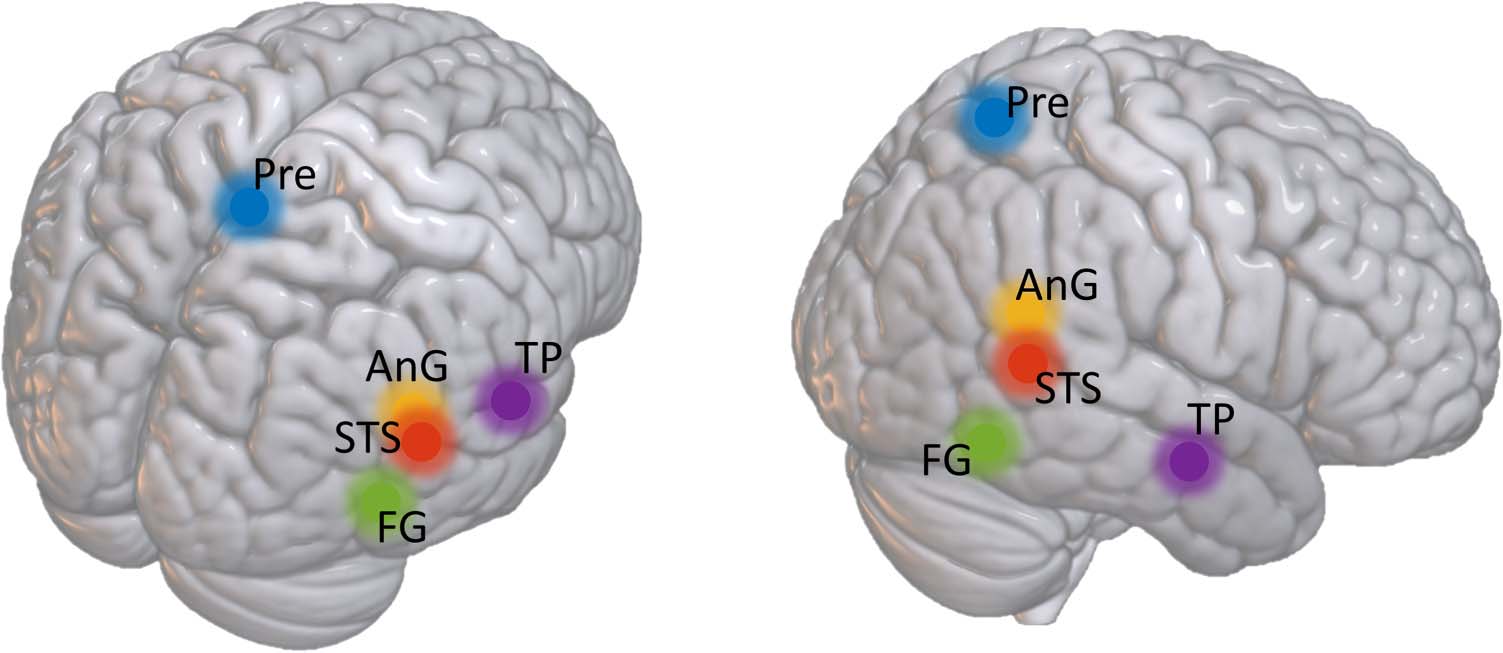
one-sample t test on the RS component were located in the right superior temporal sulcus
(rSTS), (bilateral) precuneus, right angular gyrus (rAnG), right temporal pole (rTP), and right
fusiform gyrus (rFG). The MNI coordinates of their cluster peaks are summarized in Table 1
and approximate locations are displayed in Figure 2.
The patterns of effective connectivity among the five nodes during the ToM task and during
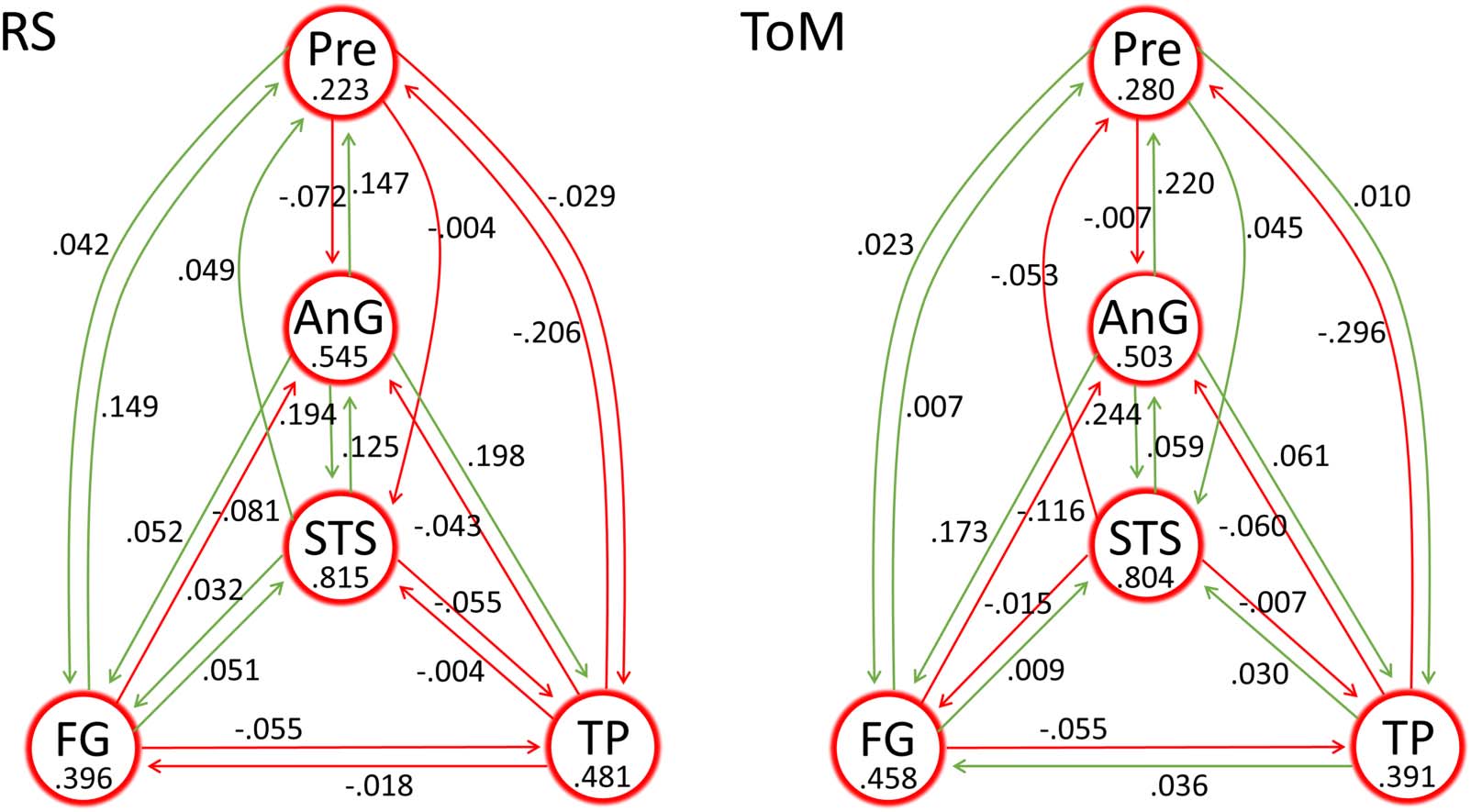
RS, directly after model inversion conducted independently on the two datasets, are displayed
in Figure 3. Six out of 20 between-region connections displayed reversed direction of activity
in terms of excitation and inhibition across the datasets. Activity within all five regions had
stronger self-inhibition than the default value (−0.5 Hz) in both datasets.
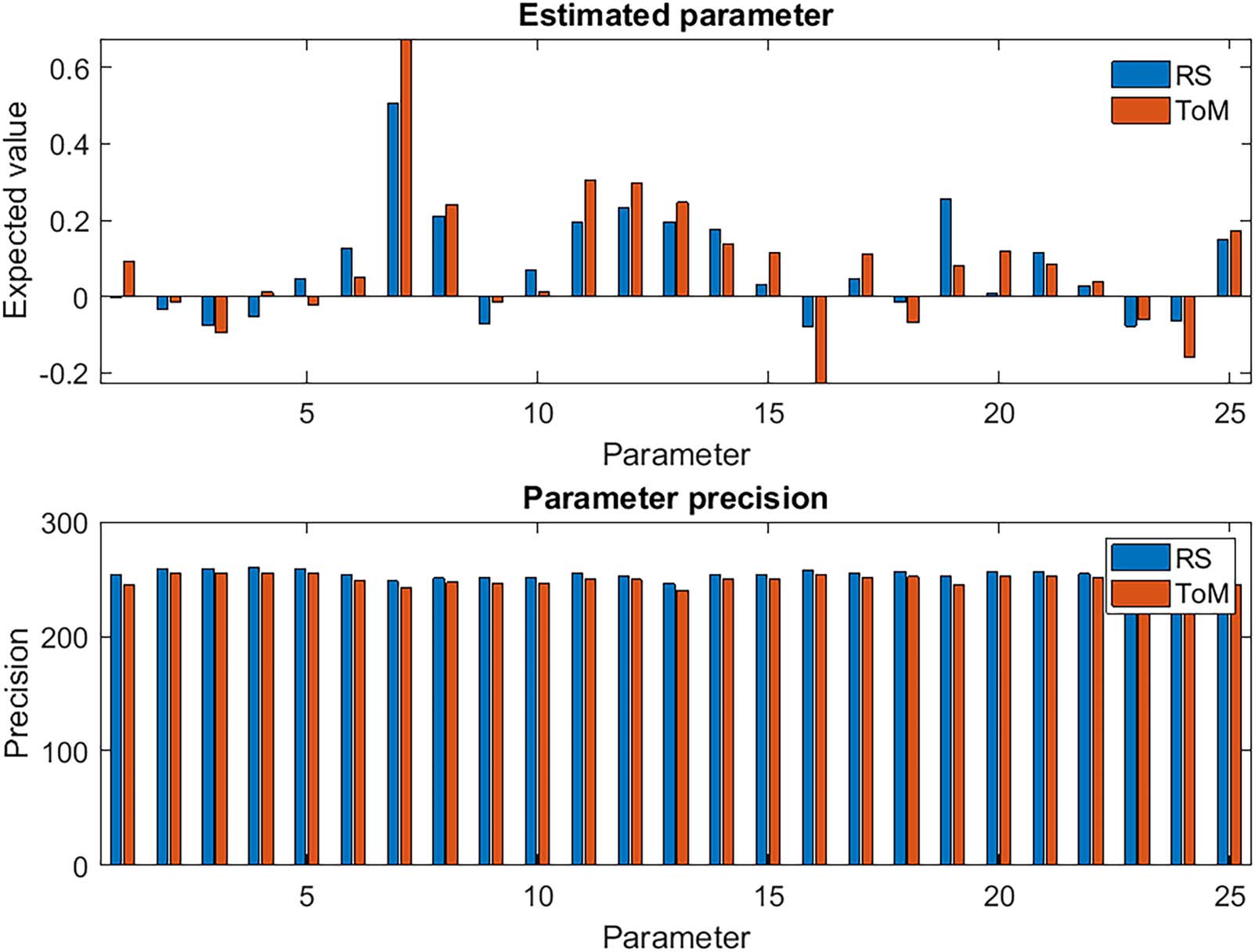
The connectivity parameters, after being reestimated with priors based on both datasets, are
displayed in the upper graph of Figure 4. Although the sign and relative amplitude of the
parameters is generally consistent between the two datasets, the majority of the connections
in the ToM condition moved further from the default value of zero compared to RS, which
indicates stronger connections in the ToM condition.
(cid:6)
The parameter-specific precisions across the 25 within- and between-region connections,
that is, our confidence about the connection strengths after seeing the data, are displayed in
the lower plot of Figure 4. These precisions are defined as the inverse of the posterior variance
−1. It is apparent that the precisions were consistent across connections and were
diag
slightly higher in the RS condition than the ToM condition. The information-theoretic analyses
that follow quantify whether these differences across datasets were nontrivial.
(cid:1)(i )
(cid:7)
Network Neuroscience
776
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Resting-state versus task fMRI
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
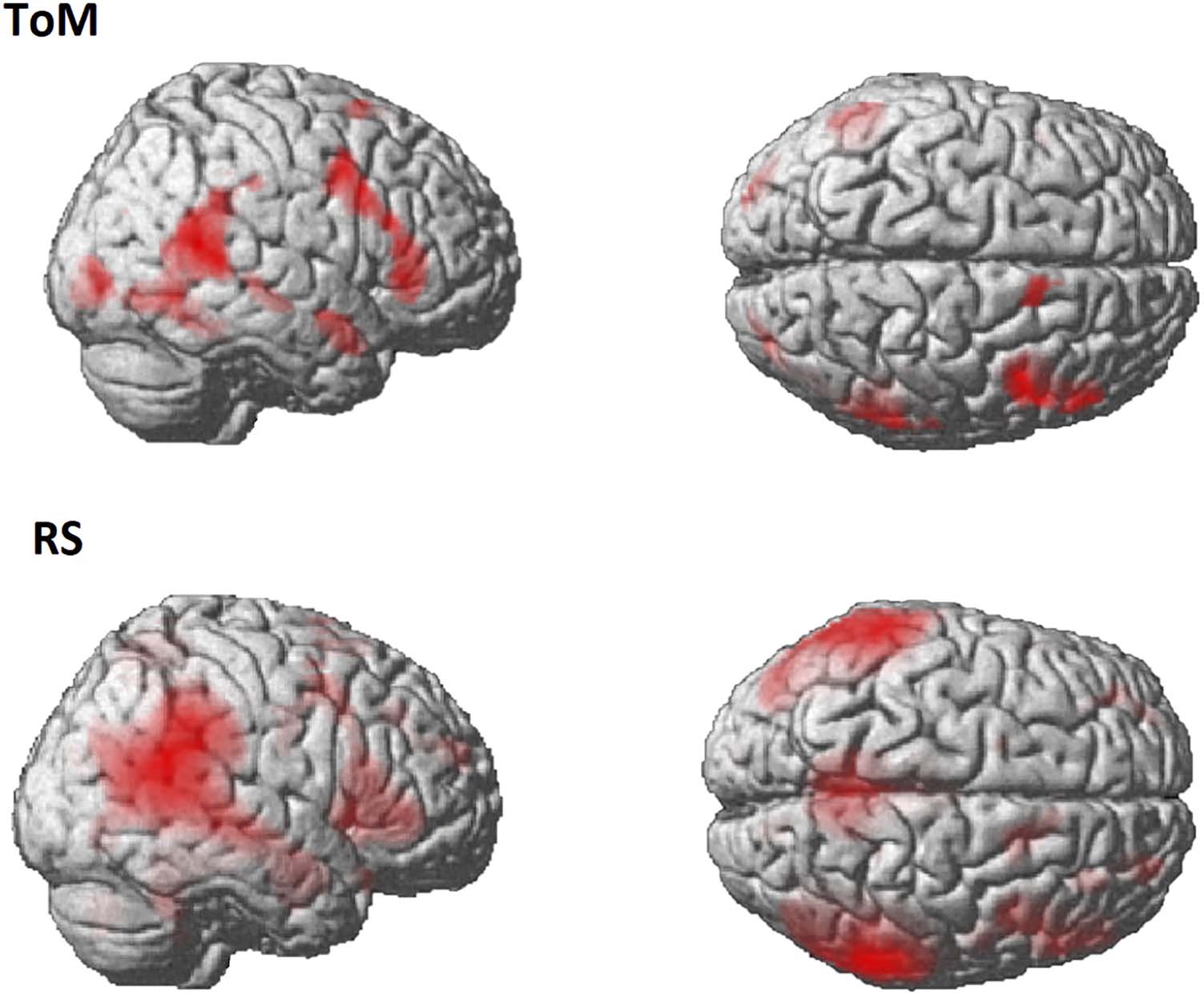
Figure 1. Activation map for the contrast Social > Random in the ToM task and the independent RS
component that best overlapped with that map, both displayed with p(FWE) < 0.05 and cluster level 20.
We summarised the estimated precision of the parameters across connections in terms of
the parameter certainty, that is, the negative entropy, which also accounts for covariance
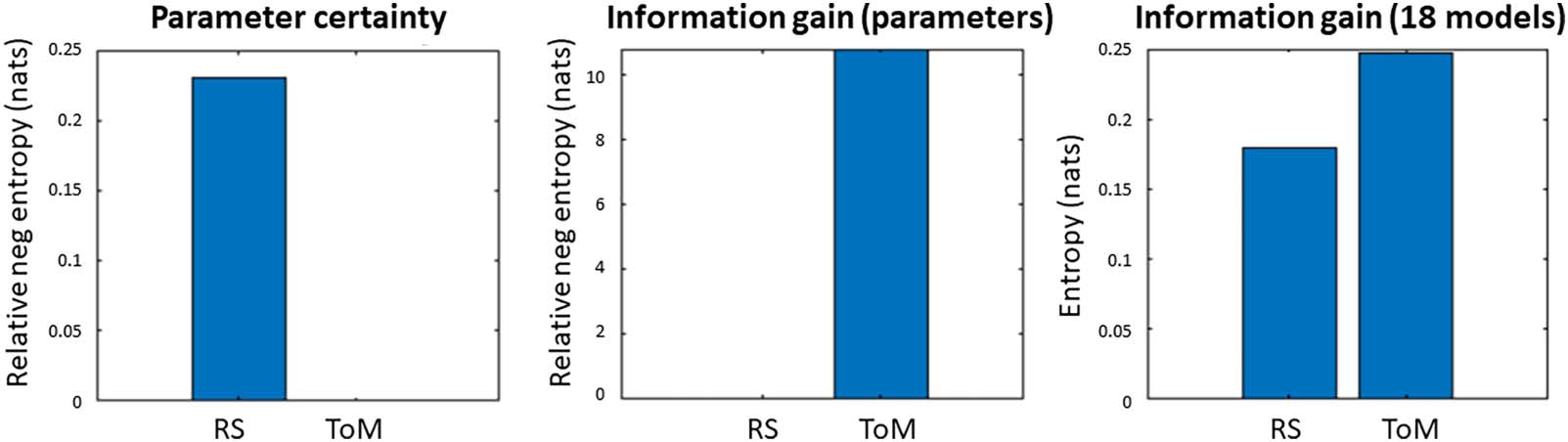
between the parameters. This was 0.23 nats in favour of the RS dataset (left panel of
Figure 5). This difference is trivially small and not large enough to count as positive evidence
towards either condition. Thus, both conditions provided a similar level of confidence about
the estimated values of the parameters.
The information gain over parameters, that is, the relative entropy from the priors to the
posteriors, quantifies how much has been learnt by performing the experiment in units of nats.
Figure 2. Approximate locations of the five nodes included in the csd-DCM.
Network Neuroscience
777
Resting-state versus task fMRI
Effective connectivity during RS and ToM. The values for between-region connections are in units of Hz whereas self-connections
Figure 3.
are unitless log-scaling values. Green and red colours represent excitatory and inhibitory connectivity, respectively. For the self-connections,
positive values indicate more self-inhibition than the default value of −0.5 Hz, indicated with red circles.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Estimated connectivity parameters. The parameters form a multivariate normal distribution with expected values illustrated in the
Figure 4.
top plot and precisions illustrated in the bottom plot. The parameters are ordered according to outgoing connections from precuneus (bars
1–5), STS (bars 6–10), AnG (bars 11–15), TP (bars 15–19), and FG (bars 20–25). The parameters for between-region connections are rate
constants with units of Hz (s−1), whereas the self-connections are unitless log-scaling parameters, which control the level of inhibition in each
region. Precision is the reciprocal of variance; therefore, the units are the reciprocal of the (squared) units of the parameters.
Network Neuroscience
778
Resting-state versus task fMRI
Figure 5. Parameter certainty and information gain over parameters and models in units of nats. The first two indices, parameter certainty and
information gain over parameters, are negative entropies in units of nats, which are presented relative to the worst performing dataset (by
subtracting the negative entropy of the best performing dataset from that of the worst performing dataset). The third index displays the amount
of information gained with model comparison, separately for both datasets. Note the difference in scales—there was little difference in the
parameter certainty (left) or information gain over models (right), but there was a large difference in the information gain over parameters
(middle).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
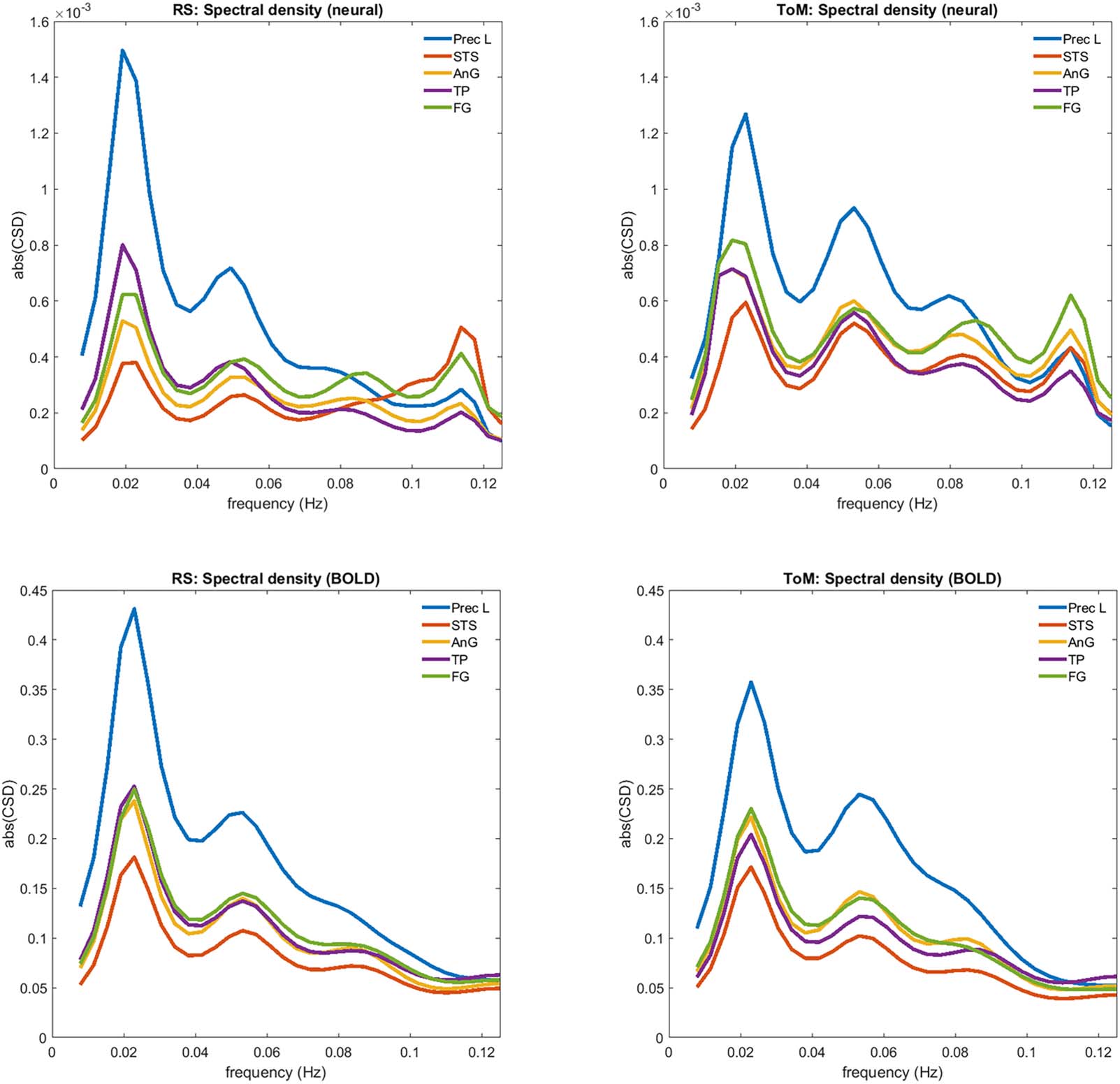
Figure 6. The subject-averaged power spectrum of each region corresponding to the estimated neural parameters (above) and the observed
BOLD response (below) during RS and ToM. The numbers from DCM.Hs were averaged and plotted against DCM.Hz. The y-axis corresponds
to power and x-axis to frequency.
Network Neuroscience
779
Resting-state versus task fMRI
The difference in information gain between ToM and RS was above 10 nats and qualifies as
very strong evidence in favour of t-fMRI (middle panel of Figure 5). Repeating the comparison
using the full-length RS dataset did not noticeably change the relative information gain, which
remained above 10 nats in favour of ToM (Figure S1). There was even a small decrease in the
relative parameter certainty that was previously slightly more in favour of RS.
Information gain depends on both the estimated strength of the connections and the preci-
sion of these estimates. As the precisions did not differ meaningfully between the two datasets
(as quantified by the parameter certainty measure), the higher information gain connected to
the ToM data was primarily driven by the stronger connection strengths. This is also evinced by
the subject-averaged power spectrum of the estimated neural parameters associated with the
datasets (Figure 6), which reveal higher amplitudes across different frequency bands and
across most of the brain regions during the ToM task. More specifically, AnG and fusiform
gyrus (FG) display higher amplitudes in the ToM condition across all frequency bands,
whereas precuneus and temporal pole (TP) display lower amplitudes only at the lowest fre-
quency and superior temporal sulcus (STS) at the highest frequency. The power spectrum of
the observed BOLD response did not differ much between the datasets, except for the lowest
frequency that showed higher amplitudes in most of the regions in the RS dataset.
The right panel of Figure 5 displays the information gained by comparing several equally
plausible model structures. This analysis assessed whether ToM or RS data could best discrim-
inate 18 difficult to disambiguate connectivity models. The information gain over model struc-
ture was 0.18 nats for RS and 0.25 nats for ToM. Both the amount of information gained after
model comparison and the difference between the datasets in this index were negligible and
do not count as evidence in favour of one or the other dataset.
DISCUSSION
The relative merits of using an active task versus a passive task (rest) for eliciting measurable
neural responses was assessed by conducting a systematic comparison of t-fMRI and rs-fMRI
data, in information-theoretic terms. A social cognitive task evoking ToM processes served as
the t-fMRI condition, which was chosen on the grounds of having previously demonstrated
to activate brain regions attributed to the DMN (Andreasen et al., 1995; Mars et al., 2012;
Schilbach et al., 2008; Spreng & Grady, 2010; Spreng et al., 2009). Parameters of effective
connectivity derived by means of csd-DCM were subjected to the analysis.
Activation peaks of a group-level GLM across each individual’s reconstructed RS compo-
nent were defined as DCM regions or nodes. The RS component was derived by means of ICA
and selected based on its overlap with the ToM activation map. The nodes were located in
rSTS, bilateral precuneus, rAnG, rTP, and rFG, each of which have been attributed to the DMN
in earlier research (Greicius et al., 2003; Mars et al., 2012; Uddin et al., 2009). None of the
core hubs of DMN in the middle frontal and cingulate regions were found significantly active
in the current ToM task. To specifically target these regions, other ToM tasks such as false
belief, trait judgement, autobiographical memory, or mind-in-the-eyes tasks could be consid-
ered (Andrews-Hanna et al., 2014; Schurz et al., 2014; Spreng et al., 2009).
Results from BDC show that the ToM task condition contributed significantly more informa-
tion about the effective connectivity of the network model investigated here, compared to RS.
The difference in information gain between the two datasets can be described as very strong
evidence in favour of t-fMRI. Information gain depends on how far the parameters have moved
from their prior expectation (zero) after seeing the data, as well as the confidence with which
Network Neuroscience
780
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Resting-state versus task fMRI
they could be estimated (their precision). In this case, the precisions of individual parameters
were similar between the two datasets, but most of the connections were notably stronger in
the ToM condition. This means that the higher information gain in the ToM task was primarily
due to the stronger effective connectivity that it elicited compared to RS. Our results therefore
demonstrate that the ToM task elicited stronger and more readily detectable effective connec-
tivity than RS among regions associated with DMN. Connectivity strength has also been found
to positively correlate with test-retest reliability in effective and functional connectivity mea-
sures (Frässle & Stephan, 2022; Noble et al., 2019).
A useful feature of DCM is that it discriminates between neural and haemodynamic com-
ponents by modelling both separately to generate the observed signal, which enables the infer-
ence of connectivity parameters controlling hidden or latent neural activity (Friston et al.,
2003, 2014). As the fMRI signal is an indirect measure of neural activity dependent on the
level of blood oxygenation (Buxton, 2013), there are concerns that some patterns of connec-
tivity are physiological rather than neural in origin (Ekstrom, 2010; Kelly et al., 2012; Lurie
et al., 2020). Discerning the neural signal from physiological and background noise is more
challenging in rs-fMRI compared to t-fMRI due to the lack of a control condition and a refer-
ence point provided by a time line of brain activity. Also, the slowly fluctuating neural activity
measured in rs-fMRI may occupy the same frequency bands as noise (Birn et al., 2008; Dubois
& Adolphs, 2016; Liu, 2016; Reid et al., 2019), and a considerable amount of rs-fMRI signal
reliability and variability can be attributed to different noise sources (Almgren et al., 2020; Birn
et al., 2014; Sjuls & Specht, 2022; Vaisvilaite et al., 2022; Wise et al., 2004; Yang et al., 2015).
Consequently, the neural basis of the rs-fMRI signal and its relation to cognition and behaviour
are a matter of uncertainty and there is a risk of confounding by physiological variables.
The results of the present analysis lend further support to this possibility, given the much
lower information gain connected to rs-fMRI relative to t-fMRI. This is especially notable in
light of two features of the present study: first, the specific network model investigated in this
analysis consisted of regions associated with DMN, a network thought to be active during rest.
Second, the nodes of the DCM were located around peak coordinates of a rs-fMRI component,
where only the choice of the specific component was guided by the ToM activation map,
hence the analysis was more biased in favour of the RS condition. The power spectra in
Figure 6 further emphasize the possible confounding by physiological variables when inves-
tigating connectivity in rs-fMRI data. Despite the notably higher amplitudes in the neural
power spectrum of the t-fMRI data, differences in the observed BOLD power spectrum
between rs- and t-fMRI are almost indiscernible.
The lower information gain observed with rs-fMRI data may also partly be attributable to the
effect of noise correction based on signal from white matter and cerebrospinal fluid. As men-
tioned earlier, physiological noise may occupy the same frequency bands as the low-
frequency RS activity (Liu, 2016), and regressing them out from the signal may also remove
some of the signal of interest. A recent study demonstrated that global noise regression
reduced information gain but increased information certainty over effective connectivity
parameters (Almgren et al., 2020). It is in accordance with the higher information gain con-
nected to t-fMRI in our study, however, with the difference that global signal regression is a
more radical noise correction method than the one applied in the present analysis. It also
accords with the slightly higher certainty connected to rs-fMRI, which again is explicable
by the decreased within and between variance observed with such noise correction methods
(Birn et al., 2014). Physiological noise and noise correction are fundamental issues in fMRI
data analysis, and the effect of different methods of noise correction on both t-fMRI and rs-
fMRI data can be further investigated with the present information-theoretic approach.
Network Neuroscience
781
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Resting-state versus task fMRI
The final quality index, that of model discrimination ability, was low for both datasets, and
information gain over model structure was not significantly different across the datasets. This
statistic quantifies how readily similar models can be distinguished, where the models differ
only in whether particular connections are switched on or off (by setting permissive or restric-
tive priors on those connections respectively). One likely explanation is that switching on or
off individual connections in the model made only a small difference in the model evidence
(free energy), due to covariance among the parameters. This may have been compounded by
the short length of the time series subjected to DCM analysis, relative to the number of param-
eters in the model. Thus, finding sufficiently strong evidence for switching off any individual
connection would be difficult.
It is important to note that alternative approaches to group-level analysis of rs-fMRI data
may result in different peak coordinates when specifying nodes for DCM. The influence of
such data analysis choices on information value is an important topic to cover in future stud-
ies. Furthermore, due to our interest in quantifying information value in the context of a net-
work underlying ToM processes, we selected the rs-fMRI component that most closely
matched activation patterns during the ToM condition. This means that there may have existed
other partly overlapping rs-fMRI components with higher information value. Thus, our conclu-
sions pertain only to this particular network, and not the informative value of rs-fMRI in gen-
eral. More general statements about rs-fMRI will require extensive work that covers different
cognitive systems and networks, as well as several alternative tasks. When considering the
clinical utility of the imaging protocol, suitability of the task for the given patient population
must be considered and similar analyses repeated on patient data. Furthermore, the superiority
of the task fMRI data was here demonstrated with csd-DCM, and the results cannot be directly
generalized to other models or analysis methods.
CONCLUSION
The main finding of the present study is that a social cognition task (ToM) gave rise to more
informative inferences about the effective connectivity of regions of the DMN than was
enabled by rs-fMRI. The ToM task elicited stronger connections among regions compared
to rs-fMRI, causing an increase in the measured information gain. The brain regions we
examined were identified based on their activation during rs-fMRI, thus even for brain regions
typically associated with activation during rest, there is a compelling argument for using an
experimentally controlled task such as ToM to investigate them. Higher information gain due
to stronger effective connectivity is an advantage in situations where the detectability of a
network and reliability of the connectivity parameters are crucial, such as in clinical contexts.
The present results therefore speak for an active task condition, such as the ToM task, to be
preferred over rs-fMRI when investigating the (dys)function of the associated neural system.
The strength of DCM is that it discriminates between neural and physiological sources of
signal. The present results are therefore of interest also from a theoretical point of view,
with the much weaker connectivity observed during rest supporting the assumption that
the resting functional connectivity of DMN to a large part reflects physiological rather than
neural processes.
With this study we wanted to demonstrate the utility of the BDC framework for the present
issue and it should be considered a starting point for such analyses. The present investigation
may be extended to neural networks underlying other cognitive and affective domains
according to current theoretical and clinical research questions where the development of a
suitable imaging paradigm is of interest.
Network Neuroscience
782
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Resting-state versus task fMRI
ACKNOWLEDGMENTS
Data were provided by the Human Connectome Project, WU-Minn Consortium (Principal
Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16
National Institutes of Health and Centers that support the NIH Blueprint for Neuroscience
Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00302. All
data were obtained from the Human Connectome Project database (ConnectomeDB) and are
available to investigators upon application. Analysis scripts used here are available from
https://github.com/picusacademicus/RSvsToM.
AUTHOR CONTRIBUTIONS
Julia Axiina Tuominen: Conceptualization; Formal analysis; Investigation; Methodology;
Supervision; Validation; Visualization; Writing – original draft; Writing – review & editing.
Karsten Specht: Conceptualization; Formal analysis; Funding acquisition; Investigation;
Methodology; Project administration; Supervision; Validation; Visualization; Writing – review
& editing. Liucija Vaisvilaite: Conceptualization; Investigation; Supervision; Writing – review
& editing. Peter Zeidman: Conceptualization; Methodology; Software; Validation; Writing –
review & editing.
FUNDING INFORMATION
Karsten Specht, Norges Forskningsråd (https://dx.doi.org/10.13039/501100005416), Award ID:
276044.
REFERENCES
Almgren, H., Van de Steen, F., Razi, A., Friston, K., & Marinazzo, D.
(2020). The effect of global signal regression on DCM estimates
of noise and effective connectivity from resting state fMRI. Neu-
roImage, 208, 116435. https://doi.org/10.1016/j.neuroimage
.2019.116435, PubMed: 31816423
Andreasen, N. C., O’Leary, D., Cizadlo, T., Arndt, S., Rezai, K.,
Watkins, G. L., Ponto, L. L. B., & Hichwa, R. D. (1995). Remem-
bering the past: Two facets of episodic memory explored with
positron emission tomography. The American Journal of Psychi-
atry, 152(11), 1576–1585. https://doi.org/10.1176/ajp.152.11
.1576, PubMed: 7485619
Andrews-Hanna, J. R., Saxe, R., & Yarkoni, T. (2014). Contributions
of episodic retrieval and mentalizing to autobiographical
thought: Evidence from functional neuroimaging, resting-state
connectivity, and fMRI meta-analyses. NeuroImage, 91, 324–335.
https://doi.org/10.1016/j.neuroimage.2014.01.032, PubMed:
24486981
Barch, D. M., Burgess, G. C., Harms, M. P., Petersen, S. E., Schlaggar,
B. L., Corbetta, M., … Essen, D. C. (2013). Function in the human
connectome: Task-fMRI and individual differences in behavior.
NeuroImage, 80, 169–189. https://doi.org/10.1016/j.neuroimage
.2013.05.033, PubMed: 23684877
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bennett, C. M., & Miller, M. B. (2010). How reliable are the results
from functional magnetic resonance imaging? Annals of the New
York Academy of Sciences, 1191(1), 133–155. https://doi.org/10
.1111/j.1749-6632.2010.05446.x, PubMed: 20392279
Birn, R. M., Cornejo, M. D., Molloy, E. K., Patriat, R., Meier, T. B.,
Kirk, G. R., … Prabhakaran, V. (2014). The influence of physio-
logical noise correction on test–retest reliability of resting-state
functional connectivity. Brain Connectivity, 4(7), 511–522.
https://doi.org/10.1089/brain.2014.0284, PubMed: 25112809
Birn, R. M., Murphy, K., & Bandettini, P. A. (2008). The effect of res-
piration variations on independent component analysis results of
resting state functional connectivity. Human Brain Mapping,
29(7), 740–750. https://doi.org/10.1002/hbm.20577, PubMed:
18438886
Brooks, J. O., & Vizueta, N. (2014). Diagnostic and clinical impli-
cations of functional neuroimaging in bipolar disorder. Journal of
Psychiatric Research, 57, 12–25. https://doi.org/10.1016/j
.jpsychires.2014.05.018, PubMed: 25015683
Buxton, R. B. (2013). The physics of functional magnetic resonance
imaging (fMRI). Reports on Progress in Physics, 76(9), 096601.
https://doi.org/10.1088/0034-4885/76/9/096601, PubMed:
24006360
Network Neuroscience
783
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
.
t
Resting-state versus task fMRI
Calhoun, V. D., Kiehl, K. A., & Pearlson, G. D. (2008). Modulation
of temporally coherent brain networks estimated using ICA at
rest and during cognitive tasks. Human Brain Mapping, 29(7),
828–838. https://doi.org/10.1002/hbm.20581, PubMed: 18438867
Carter, C. S., Heckers, S., Nichols, T., Pine, D. S., & Strother, S.
(2008). Optimizing the design and analysis of clinical functional
magnetic resonance imaging research studies. Biological Psychi-
atry, 64(10), 842–849. https://doi.org/10.1016/j.biopsych.2008
.06.014, PubMed: 18718572
Castelli, F., Happé, F., Frith, U., & Frith, C. (2000). Movement and
mind: A functional imaging study of perception and interpreta-
tion of complex intentional movement patterns. NeuroImage,
12(3), 314–325. https://doi.org/10.1006/nimg.2000.0612,
PubMed: 10944414
Cole, M. W., Bassett, D. S., Power, J. D., Braver, T. S., & Petersen,
S. E. (2014). Intrinsic and task-evoked network architectures of
the human brain. Neuron, 83(1), 238–251. https://doi.org/10
.1016/j.neuron.2014.05.014, PubMed: 24991964
Dubois, J., & Adolphs, R. (2016). Building a science of individual
differences from fMRI. Trends in Cognitive Sciences, 20(6),
425–443. https://doi.org/10.1016/j.tics.2016.03.014, PubMed:
27138646
Ekstrom, A. (2010). How and when the fMRI BOLD signal relates to
underlying neural activity: The danger in dissociation. Brain
Research Reviews, 62(2), 233–244. https://doi.org/10.1016/j
.brainresrev.2009.12.004, PubMed: 20026191
Finn, E. S., Scheinost, D., Finn, D. M., Shen, X., Papademetris, X., &
Constable, R. T. (2017). Can brain state be manipulated to
emphasize individual differences in functional connectivity? Neu-
roImage, 160, 140–151. https://doi.org/10.1016/j.neuroimage
.2017.03.064, PubMed: 28373122
Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal
modelling. NeuroImage, 19(4), 1273–1302, https://doi.org/10
.1016/S1053-8119(03)00202-7, PubMed: 12948688
Friston, K. J., Kahan, J., Biswal, B., & Razi, A. (2014). A DCM for
resting state fMRI. NeuroImage, 94(100), 396–407. https://doi.org
/10.1016/j.neuroimage.2013.12.009, PubMed: 24345387
Friston, K. J., Litvak, V., Oswal, A., Razi, A., Stephan, K. E., van
Wijk, B. C. M., Ziegler, G., & Zeidman, P. (2016). Bayesian model
reduction and empirical Bayes for group (DCM) studies. Neuro-
Image, 128, 413–431. https://doi.org/10.1016/j.neuroimage
.2015.11.015, PubMed: 26569570
Frässle, S., & Stephan, K. E. (2022). Test-retest reliability of regres-
sion dynamic causal modeling. Network Neuroscience, 6(1),
135–160. https://doi.org/10.1162/netn_a_00215, PubMed:
35356192
Gaut, G., Turner, B., Lu, Z.-L., Li, X., Cunningham, W. A., &
Steyvers, M. (2019). Predicting task and subject differences with
functional connectivity and blood-oxygen-level-dependent
variability. Brain Connectivity, 9(6), 451–463. https://doi.org/10
.1089/brain.2018.0632, PubMed: 30957523
Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,
Fischl, B., Andersson, J. L., Xu, J., … Jenkinson, M. (2013). The
minimal preprocessing pipelines for the Human Connectome
Project. NeuroImage, 80, 105–124. https://doi.org/10.1016/j
.neuroimage.2013.04.127, PubMed: 23668970
Greene, A. S., Gao, S., Scheinost, D., & Constable, R. T. (2018).
Task-induced brain state manipulation improves prediction of
individual traits. Nature Communications, 9(1), 2807. https://
doi.org/10.1038/s41467-018-04920-3, PubMed: 30022026
Greicius, M. D., Krasnow, B., Reiss, A. L., & Menon, V. (2003).
Functional connectivity in the resting brain: A network analysis of
the default mode hypothesis. Proceedings of the National Academy
of Sciences of the United States of America, 100(1), 253–258.
https://doi.org/10.1073/pnas.0135058100, PubMed: 12506194
Joyce J. M. (2011) Kullback-Leibler divergence. In M. Lovric (Ed.),
International encyclopedia of statistical science (pp. 720–722).
Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3-642
-04898-2_327
Kass, R. E., & Raftery, A. E. (1995). Bayes factors. Journal of the
American Statistical association, 90(430), 773–795. https://doi
.org/10.1080/01621459.1995.10476572
Kelly, C., Biswal, B. B., Craddock, R. C., Castellanos, F. X., &
Milham, M. P. (2012). Characterizing variation in the functional
connectome: Promise and pitfalls. Trends in Cognitive Sciences,
16(3), 181–188. https://doi.org/10.1016/j.tics.2012.02.001,
PubMed: 22341211
Kieliba, P., Madugula, S., Filippini, N., Duff, E. P., & Makin, T. R.
(2019). Large-scale intrinsic connectivity is consistent across
varying task demands. PLoS One, 14(4), e0213861. https://doi
.org/10.1371/journal.pone.0213861, PubMed: 30970031
Kiviniemi, V., Starck, T., Remes, J., Long, X., Nikkinen, J., Haapea,
M., … Tervonen, O. (2009). Functional segmentation of the brain
cortex using high model order group PICA. Human Brain Map-
ping, 30(12), 3865–3886. https://doi.org/10.1002/hbm.20813,
PubMed: 19507160
Kristo, G., Rutten, G.-J., Raemaekers, M., de Gelder, B., Rombouts,
S. A. R. B., & Ramsey, N. F. (2014). Task and task-free fMRI repro-
ducibility comparison for motor network identification. Human
Brain Mapping, 35(1), 340–352. https://doi.org/10.1002/ hbm
.22180, PubMed: 22987751
Leuthardt, E. C., Allen, M., Kamran, M., Hawasli, A. H., Snyder,
A. Z., Hacker, C. D., Mitchell, T. J., & Shimony, J. S. (2015).
Resting-state blood oxygen level-dependent functional MRI: A
paradigm shift in preoperative brain mapping. Stereotactic and
Functional Neurosurgery, 93(6), 427–439. https://doi.org/10
.1159/000442424, PubMed: 26784290
Liu, T. T. (2016). Noise contributions to the fMRI signal: An over-
view. NeuroImage, 143, 141–151. https://doi.org/10.1016/j
.neuroimage.2016.09.008, PubMed: 27612646
Lurie, D. J., Kessler, D., Bassett, D. S., Betzel, R. F., Breakspear, M.,
Kheilholz, S., … Calhoun, V. D. (2020). Questions and controver-
sies in the study of time-varying functional connectivity in resting
fMRI. Network Neuroscience, 4(1), 30–69. https://doi.org/10
.1162/netn_a_00116, PubMed: 32043043
Mars, R. B., Neubert, F.-X., Noonan, M. P., Sallet, J., Toni, I., &
Rushworth, M. F. S. (2012). On the relationship between the
“default mode network” and the “social brain.” Frontiers in
Human Neuroscience, 6, 189. https://doi.org/10.3389/fnhum
.2012.00189, PubMed: 22737119
McCormick, E. M., Arnemann, K. L., Ito, T., Hanson, S. J., & Cole
M. W. (2022). Latent functional connectivity underlying multiple
brain states. Network Neuroscience, 6(2), 570–590. https://doi
.org/10.1162/netn_a_00234, PubMed: 35733420
McDermott, T. J., Kirlic, N., & Aupperle, R. L. (2018). Roadmap
for optimizing the clinical utility of emotional stress paradigms
Network Neuroscience
784
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Resting-state versus task fMRI
in human neuroimaging research. Neurobiology of Stress, 8,
134–146. https://doi.org/10.1016/j.ynstr.2018.05.001, PubMed:
29888309
Mwansisya, T. E., Hu, A., Li, Y., Chen, X., Wu, G., Huang, X., … Liu,
Z. (2017). Task and resting-state fMRI studies in first-episode
schizophrenia: A systematic review. Schizophrenia Research, 189,
9–18. https://doi.org/10.1016/j.schres.2017.02.026, PubMed:
28268041
Noble, S., Scheinost, D., & Constable, R. T. (2019). A decade of
test-retest reliability of functional connectivity: A systematic
review and meta-analysis. NeuroImage, 203, 116157. https://doi
.org/10.1016/j.neuroimage.2019.116157, PubMed: 31494250
Raichle, M. E. (2009). A paradigm shift in functional brain imaging.
Journal of Neuroscience, 29(41), 12729–12734. https://doi.org
/10.1523/JNEUROSCI.4366-09.2009, PubMed: 19828783
Razi, A., Kahan, J., Rees, G., & Friston, K. J. (2015). Construct val-
idation of a DCM for resting state fMRI. NeuroImage, 106, 1–14.
https://doi.org/10.1016/j.neuroimage.2014.11.027, PubMed:
25463471
Reid, A. T., Headley, D. B., Mill, R. D., Sanchez-Romero, R.,
Uddin, L. Q., Marinazzo, D., … Cole, M. W. (2019). Advancing
functional connectivity research from association to causation.
Nature Neuroscience, 22(11), 1751–1760. https://doi.org/10
.1038/s41593-019-0510-4, PubMed: 31611705
Rosazza, C., Aquino, D., D’Incerti, L., Cordella, R., Andronache,
A., Zacà, D., … Minati, L. (2014). Preoperative mapping of the
sensorimotor cortex: Comparative assessment of task-based and
resting-state fMRI. PLoS One, 9(6), e98860. https://doi.org/10
.1371/journal.pone.0098860, PubMed: 24914775
Schilbach, L., Eickhoff, S. B., Rotarska-Jagiela, A., Fink, G. R., &
Vogeley, K. (2008). Minds at rest? Social cognition as the default
mode of cognizing and its putative relationship to the “default
system” of the brain. Consciousness and Cognition, 17(2),
457–467. https://doi.org/10.1016/j.concog.2008.03.013,
PubMed: 18434197
Schurz, M., Radua, J., Aichhorn, M., Richlan, F., & Perner, J. (2014).
Fractionating theory of mind: A meta-analysis of functional brain
imaging studies. Neuroscience & Biobehavioral Reviews, 42,
9–34. https://doi.org/10.1016/j.neubiorev.2014.01.009,
PubMed: 24486722
Schurz, M., Wimmer, H., Richlan, F., Ludersdorfer, P., Klackl, J., &
Kronbichler, M. (2015). Resting-state and task-based functional
brain connectivity in developmental dyslexia. Cerebral Cortex,
25(10), 3502–3514. https://doi.org/10.1093/cercor/ bhu184,
PubMed: 25169986
Sjuls, G. S., & Specht, K. (2022). Variability in resting-state func-
tional magnetic resonance imaging: The effect of body mass,
blood pressure, hematocrit and Glycated hemoglobin on hemo-
dynamic and neuronal parameters. Brain Connectivity, 12(10),
870–882. https://doi.org/10.1089/ brain.2021.0125, PubMed:
35473334
Smith, S. M., Beckmann, C. F., Andersson, J., Auerbach, E. J.,
Bijsterbosch, J., Douaud, G., … Glasser, M. F. (2013). Resting-
state fMRI in the Human Connectome Project. NeuroImage,
80, 144–168. https://doi.org/10.1016/j.neuroimage.2013.05
.039, PubMed: 23702415
Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M.,
Mackay, C. E., … Beckmann, C. F. (2009). Correspondence of
the brain’s functional architecture during activation and rest.
Proceedings of the National Academy of Sciences of the United
States of America, 106(31), 13040–13045. https://doi.org/10
.1073/pnas.0905267106, PubMed: 19620724
Specht, K. (2020). Current challenges in translational and clinical
fMRI and future directions. Frontiers in Psychiatry, 10, 924.
https://doi.org/10.3389/fpsyt.2019.00924, PubMed: 31969840
Specht, K., Willmes, K., Shah, N. J., & Jäncke, L. (2003). Assessment
of reliability in functional imaging studies. Journal of Magnetic
Resonance Imaging, 17(4), 463–471. https://doi.org/10.1002
/jmri.10277, PubMed: 12655586
Spreng, R. N., & Grady, C. L. (2010). Patterns of brain activity sup-
porting autobiographical memory, prospection, and theory of
mind, and their relationship to the default mode network. Journal
of Cognitive Neuroscience, 22(6), 1112–1123. https://doi.org/10
.1162/jocn.2009.21282, PubMed: 19580387
Spreng, R. N., Mar, R. A., & Kim, A. S. N. (2009). The common neu-
ral basis of autobiographical memory, prospection, navigation,
theory of mind, and the default mode: A quantitative meta-
analysis. Journal of Cognitive Neuroscience, 21(3), 489–510.
https://doi.org/10.1162/jocn.2008.21029, PubMed: 18510452
Uddin, L., Clare Kelly, A., Biswal, B., Xavier Castellanos, F., &
Milham, M. (2009). Functional connectivity of default mode net-
work components: Correlation, anticorrelation, and causality.
Human Brain Mapping, 30(2), 625–637. https://doi.org/10.1002
/hbm.20531, PubMed: 18219617
Vaisvilaite, L., Hushagen, V., Grønli, J., & Specht, K. (2022).
Time-of-day effects in resting-state functional magnetic reso-
nance imaging: Changes in effective connectivity and blood
oxygenation level dependent signal. Brain Connectivity, 12(6),
515–523. https://doi.org/10.1089/ brain.2021.0129, PubMed:
34636252
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E. J.,
Yacoub, E., & Ugurbil, K. (2013). The WU-Minn Human Connec-
tome Project: An overview. NeuroImage, 80, 62–79. https://doi
.org/10.1016/j.neuroimage.2013.05.041, PubMed: 23684880
Van Essen, D. C., Ugurbil, K., Auerbach, E., Barch, D., Behrens,
T. E. J., Bucholz, R., … Yacoub, E. (2012). The Human Connec-
tome Project: A data acquisition perspective. NeuroImage, 62(4),
2222–2231. https://doi.org/10.1016/j.neuroimage.2012.02.018,
PubMed: 22366334
Wang, J., Ren, Y., Hu, X., Nguyen, V. T., Guo, L., Han, J., & Guo,
C. C. (2017). Test-retest reliability of functional connectivity net-
works during naturalistic fMRI paradigms: Test-retest reliability of
naturalistic fMRI. Human Brain Mapping, 38(4), 2226–2241.
https://doi.org/10.1002/hbm.23517, PubMed: 28094464
Weber, M. J., Detre, J. A., Thompson-Schill, S. L., & Avants, B. B.
(2013). Reproducibility of functional network metrics and net-
work structure: A comparison of task-related BOLD, resting ASL
with BOLD contrast, and resting cerebral blood flow. Cognitive,
Affective, & Behavioral Neuroscience, 13(3), 627–640. https://doi
.org/10.3758/s13415-013-0181-7, PubMed: 23813017
Weissenbacher, A., Kasess, C., Gerstl, F., Lanzenberger, R., Moser,
E., & Windischberger, C. (2009). Correlations and anticorrela-
tions in resting-state functional connectivity MRI: A quantitative
comparison of preprocessing strategies. NeuroImage, 47(4),
1408–1416. https://doi.org/10.1016/j.neuroimage.2009.05.005,
PubMed: 19442749
Network Neuroscience
785
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Resting-state versus task fMRI
Welvaert, M., & Rosseel, Y. (2013). On the definition of signal-to-
noise ratio and contrast-to-noise ratio for fMRI data. PLoS One,
8(11), e77089. https://doi.org/10.1371/journal.pone.0077089,
PubMed: 24223118
Wheatley, T., Milleville, S. C., & Martin, A. (2007). Understand-
ing animate agents: Distinct roles for the social network and
mirror system. Psychological Science, 18(6), 469–474. https://
doi.org/10.1111/j.1467-9280.2007.01923.x, PubMed:
17576256
Wise, R. G., Ide, K., Poulin, M. J., & Tracey, I. (2004). Resting
fluctuations in arterial carbon dioxide induce significant low
frequency variations in BOLD signal. NeuroImage, 21(4),
1652–1664. https://doi.org/10.1016/j.neuroimage.2003.11.025,
PubMed: 15050588
Xie, H., Calhoun, V. D., Gonzalez-Castillo, J., Damaraju, E., Miller,
R., Bandettini, P. A., & Mitra, S. (2018). Whole-brain connectivity
dynamics reflect both task-specific and individual-specific
modulation: A multitask study. NeuroImage, 180(Pt B), 495–504.
https://doi.org/10.1016/j.neuroimage.2017.05.050, PubMed:
28549798
Yang, Z., Craddock, R. C., & Milham, M. P. (2015). Impact of
hematocrit on measurements of the intrinsic brain. Frontiers in
Neuroscience, 8, 452. https://doi.org/10.3389/fnins.2014
.00452, PubMed: 25653582
Yoo, K., Rosenberg, M. D., Hsu, W.-T., Zhang, S., Li, C.-S. R.,
Scheinost, D., Constable, R. T., & Chun, M. M. (2018). Connec-
tome-based predictive modeling of attention: Comparing differ-
ent functional connectivity features and prediction methods
across datasets. NeuroImage, 167, 11–22. https://doi.org/10
.1016/j.neuroimage.2017.11.010, PubMed: 29122720
Zeidman, P., Jafarian, A., Corbin, N., Seghier, M. L., Razi, A., Price,
C. J., & Friston, K. J. (2019a). A guide to group effective connec-
tivity analysis, part 1: First level analysis with DCM for fMRI.
NeuroImage, 200, 174–190. https://doi.org/10.1016/j
.neuroimage.2019.06.031, PubMed: 31226497
Zeidman, P., Jafarian, A., Seghier, M. L., Litvak, V., Cagnan, H.,
Price, C. J., & Friston, K. J. (2019b). A guide to group effective
connectivity analysis, part 2: Second level analysis with PEB.
NeuroImage, 200, 12–25. https://doi.org/10.1016/j.neuroimage
.2019.06.032, PubMed: 31226492
Zeidman, P., Kazan, S. M., Todd, N., Weiskopf, N., Friston, K. J., &
Callaghan, M. F. (2019c). Optimizing data for modeling neuronal
responses. Frontiers in Neuroscience, 12, 986. https://doi.org/10
.3389/fnins.2018.00986, PubMed: 30686967
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
7
6
9
2
1
1
8
3
3
9
n
e
n
_
a
_
0
0
3
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
786