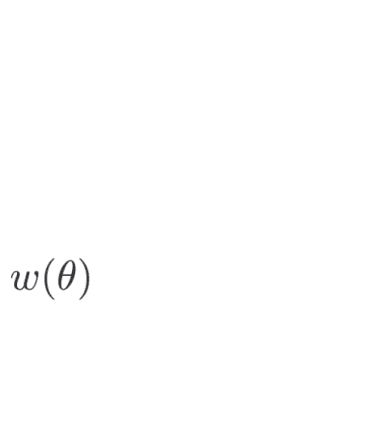研究 - 麻省理工学院人工智能研究专业

研究

Pattern forming mechanisms of color vision

Zily Burstein1, 大卫·D.. Reid1, 彼得·J. Thomas2, and Jack D. Cowan3

1Department of Physics, 芝加哥大学, 芝加哥, 伊尔, 美国
2Department of Mathematics, 应用数学, 和统计; Department of Biology;
Department of Cognitive Science, 凯斯西储大学, 克利夫兰, 哦, 美国
3Department of Mathematics, 芝加哥大学, 芝加哥, 伊尔, 美国

关键词: Color vision, V1, Pattern formation, Turing mechanism

抽象的

While our understanding of the way single neurons process chromatic stimuli in the early
visual pathway has advanced significantly in recent years, we do not yet know how these cells
interact to form stable representations of hue. Drawing on physiological studies, we offer a
dynamical model of how the primary visual cortex tunes for color, hinged on intracortical
interactions and emergent network effects. After detailing the evolution of network activity
through analytical and numerical approaches, we discuss the effects of the model’s cortical
parameters on the selectivity of the tuning curves. 尤其, we explore the role of the
model’s thresholding nonlinearity in enhancing hue selectivity by expanding the region of
稳定, allowing for the precise encoding of chromatic stimuli in early vision. 最后, 在里面
absence of a stimulus, the model is capable of explaining hallucinatory color perception via a
Turing-like mechanism of biological pattern formation.

作者总结

We present a model of color processing in which intracortical neuronal dynamics within the
visual cortex serve as the substrate for hue perception. Our analytical and numerical treatments
of the emergent behavior seek to characterize the population dynamics underlying chromatic
processing within the visual cortex, as well the roles of the various cortical parameters in
determining the selectivity of the steady-state network response. We show that the system is
self-organizing, capable of encoding stable representations of hue regardless of the stimulus
strength, and generating spontaneous color hallucinations in the absence of any input.

介绍

Our experience of color begins in the early visual pathway, 在哪里, from the moment light
strikes the retina, cone-specific neuronal responses set off the mechanisms by which the pho-
tons’ chromatic information is converted to the hues we ultimately see. While color vision
scientists agree that the single-cell processing of chromatic stimuli occurs along the two inde-
pendent cone-opponent L–M and S–(L+M) pathways (康威, Eskew, 马丁, & Stockman,
2018; Kaiser & Boynton, 1996), there is yet no consensus as to how and where the divergent
signals are synthesized to encode hue. To complicate matters, cone-opponency, observed in
electrophysiological recordings of single neurons (Shapley & Hawken, 2011), is often con-
founded with hue-opponency, a phenomenon first theorized by Ewald Hering in the 19th

开放访问

杂志

引文: Burstein, Z。, 里德, D. D .,
托马斯, 磷. J。, & 考恩, J. D. (2023).
Pattern forming mechanisms of color
想象. 网络神经科学, 7(2),
679–711. https://doi.org/10.1162/netn_a
_00294

DOI:
https://doi.org/10.1162/netn_a_00294

已收到: 19 八月 2022
公认: 17 十一月 2022

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
Zily Burstein
ceburst@gmail.com

处理编辑器:
Gustavo Deco

版权: © 2023
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Pattern forming mechanisms of color vision

Cone-opponency:
Receptive field property of neurons
in the early visual pathway, by which
chromatic stimuli are processed
through the comparison of the
relative L, 中号, and S cone responses.

Stimulus space:
A geometrical construct in which
chromatic stimuli are represented by
the relative cone responses they yield.

Color-opponent theory:
Theory of color appearance that
postulates that the four unique hues—
红色的, 绿色的, 蓝色的, and yellow—are
perceived antagonistically. 那是,
there is no such thing as a reddish
green or a bluish yellow.

century and later mapped out in clinical studies by Jameson and Hurvich (De Valois, Cottaris,
Elfar, Mahon, & Wilson, 2000; Jameson & Hurvich, 1955; Shevell & 马丁, 2017).

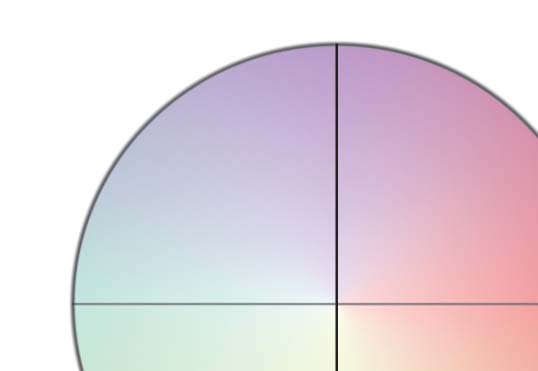
Best depicted in the Derrington-Krauskopf-Lennie (DKL) stimulus space (数字 1), cone-
opponency predicts that neurons tuned to either the L–M or S–(L+M) pathway will not respond
to light whose wavelengths isolate the other (Derrington, Krauskopf, & Lennie, 1984). 这是
tempting to equate these null responses to the four unique hues of color-opponent theory, 在
which unique blue, 例如, is observed when the “redness” and “greenness” of a per-
ceived color exactly cancel. But the wavelengths of the unique hues specified by perceptual
学习 (Jameson & Hurvich, 1955) only roughly match the wavelengths isolating either cone-
opponent pathway (Wool et al., 2015; Wuerger, Atkinson, & Cropper, 2005; Xiao, 2014), 和,
more fundamentally, we do not yet understand the mechanisms behind the processing that the
analogy implies (Mollon & 约旦, 1997; Stoughton & 康威, 2008; Valberg, 2001). 那是,
how do we get from the single neurons’ chromatic responses to our perception of color?

The necessary processing has often been attributed to higher-level brain function (De Valois
& De Valois, 1993; Lennie, Krauskopf, & Sclar, 1990; 中号. 李, 刘, Juusola, & 唐, 2014;
Mehrani, Mouraviev, & Tsotsos, 2020; Zaidi & 康威, 2019) or yet unidentified higher order
mechanisms (Valberg, 2001; Wuerger et al., 2005). A central question of color vision research
is whether these mechanisms rely on parallel or modular processing to encode stimulus
chromaticity (康威, 2009; Garg, 李, Rashid, & Callaway, 2019; 刘等人。, 2020; Nauhaus,
Nielsen, Disney, & Callaway, 2012; Schluppeck & 恩格尔, 2002; Shapley & Hawken, 2011).
If signaling about chromaticity is transmitted with information about other visual features,
such as brightness, orientation, and spatial frequency, how do these features get teased apart?
如果不, where is the purported color center of the brain (康威, Moeller, & Tsao, 2007;
Gegenfurtner, 2003)?

Several authors have addressed these questions through combinatorial models that param-
eterize the weights of the L, 中号, and S cones contributing to successive stages of processing
(De Valois & De Valois, 1993; Gegenfurtner & Ennis, 2015; Judd, 1949; Mehrani et al., 2020;
Stockman & Brainard, 2010). Though differing in their assumptions of modularity, the theories
share a mechanistic framework for the transition of single-cell receptive field properties

数字 1. The DKL space maps chromatic stimuli onto a circle with two “cardinal” axes represent-
ing the L–M and S–(L+M) pathways. The excitatory or inhibitory effect of a stimulus on cone-
opponent cells tuned to either pathway can be thought of as a projection of its location in DKL
space onto the relevant axis. Stimuli isolating the two pathways correspond roughly to wavelengths
associated with the red, 绿色的, 蓝色的, and yellow unique hues of color-opponent theory, 导致
the common, but mistaken, conflation of chromatic stimulus and color perception.

网络神经科学

680

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Pattern forming mechanisms of color vision

(棕色的, 2014). Starting with cells in the retina and lateral geniculate nucleus (LGN) known to
be tuned broadly to the cone-opponent axes, these proposed mechanisms build up to cells in
various cortical areas more narrowly tuned to divergent (and debated) chromatic directions in
DKL space. While parsimonious, this formalism comes at the cost of tuning the cone weights
arbitrarily, disregarding specific properties of real neurons’ receptive fields (Eskew, 2009;
Kaiser & Boynton, 1996; Stockman & Brainard, 2010). 此外, the linear combinatorial
mechanism is not, on its own, able to account for the variety of color cells observed in the visual
cortex (Garg et al., 2019; 约翰逊, Hawken, & Shapley, 2001; Shapley & Hawken, 2011). 在
addition to the forward flow of chromatic information through the successive stages of
加工, the encoding of color reflects the neuronal dynamics within each. Modelers
agree that the next forays into a mechanistic theory of color vision should consider these
intracortical circuits, but disagree about where such interactions first become important
(De Valois & De Valois, 1993; Hanazawa, Komatsu, & 村上, 2000; 刘等人。, 2020;
Wachtler, Sejnowski, & Albright, 2003).

Electrophysiological studies of macaque visual cortex have shed some light on this ques-
的, showing that the processing of individual hues previously associated with higher level
mechanisms has its origins in the primary visual cortex ( V1) (Garg et al., 2019; Gegenfurtner,
2003; Hanazawa et al., 2000; 李等人。, 2022; Wachtler et al., 2003; Xiao, 2014; Xiao, Casti,
Xiao, & 卡普兰, 2007). These experiments have identified the emergence of neurons in V1
tuned to the gamut of hues in DKL space, as well as to the role of processing nonlinearities
in determining their tuning curves (De Valois et al., 2000; Hanazawa et al., 2000; Lennie et al.,
1990; Wachtler et al., 2003). Puzzlingly, these cells mainly inhabit the so-called CO “blobs,”
patchy regions rich in cytochrome oxidase that display a sensitivity to stimuli modulating
either of the cone-opponent axes rather than the full set of hues (Landisman & Ts’o, 2002乙;
李等人。, 2022; Livingstone & Hubel, 1984; Salzmann, Bartels, Logothetis, & Schüz, 2012).
Some have speculated that this colocalization stems from a mixing of cell populations
encoding the two cardinal pathways (李等人。, 2022; Xiao, 2014) while others indicate a
distinct population of hue-sensitive neurons in the “interblob” regions, more conclusively
associated with orientation tuning (Garg et al., 2019; Landisman & Ts’o, 2002A). As a whole,
然而, these studies point to the need for a population theory of chromatic processing
remarkably early in the visual pathway.

在本文中, we present a model of color processing in which intracortical neuronal
dynamics within V1 serve as the substrate for hue perception. Drawing on the canonical
Wilson-Cowan neural field equations and the ring model of orientation tuning, we show
that this population approach allows us to account for cells responsive to the full range
of DKL directions without the need to fine-tune input parameters (Ben-Yishai, Bar-Or, &
Sompolinsky, 1995; Burstein, 2022; Hansel & Sompolinksy, 1998; Wilson & 考恩,
1972, 1973). The threshholding we employ bears in mind the input-response nonlinearities
of previous combinatorial models, but zooms out of the single-cell, feedforward interpreta-
tion of input as the stimulus-driven LGN afferents to individual neurons. 相当, we model
input as the total synaptic current into a population of cells, taking into account both the
cone-opponent LGN afferents as well as the hue-dependent connectivity between distinct
神经元群.

The resulting demarcation between the cone-opponent and the hue-selective mechanisms
in the same population of cells points to the importance of V1 in the transition from chromatic
stimulus to color perception. To characterize this role, we study the effects of the model’s con-
nectivity parameters and processing nonlinearities on the narrowness and stability of the hue
tuning curves. In the final part of the paper, we show that the model is able to explain color

Cardinal pathways:
In DKL space, the two orthogonal
axes representing stimuli isolating the
L–M and S–(L+M) cone-opponent
pathways.

Wilson-Cowan neural field equations:
Coupled set of partial differential
equations describing the network
dynamics of excitatory and inhibitory
神经群体.

网络神经科学

681

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Pattern forming mechanisms of color vision

Spontaneous pattern formation:
A system’s ability to self-generate
new symmetries in the absence of
external input.

responses in the absence of LGN input, evoking color hallucinations via a Turing-like mech-
anism of spontaneous pattern formation in DKL space.

MODEL

In light of the patchy distribution of color-sensitive cells reported in Landisman and Ts’o (2002乙),
李等人. (2022), Livingstone and Hubel (1984), and Salzmann et al. (2012), we model the color
map of V1 as a set of neuronal networks, each encoding the chromaticity of its corresponding
region of the visual field. This organization brings to mind the hypercolumnar structure of ori-
entation preference within V1 (Hubel & Wiesel, 1974), 哪个, on the basis of its feature-based
connectivity properties, allows for the representation of network activity as a function of a local-
ized feature space. 这里, we assume a mean hue-dependent activity a(我, t) where θ represents a
direction in the DKL stimulus space, a strictly physiological conception of “hue” from the hues
categorizing color perception, as explained above. In drawing this distinction, and in agreement
with Wool et al. (2015) and Li et al. (2022), we give no special status to V1 cells tuned to the DKL
directions associated with the unique hues of color-opponent theory, while simultaneously
emphasizing the cone-opponent nature of feedforward afferents from the LGN.

The resulting activity a(我, t) of a network of hue-preferring cells, expressed as a firing rate in
units of spikes/second, is dominated by the membrane properties of its constituent cells, 谁的
potential variations occur on the order of the membrane time constant τ0, taken to be 10 毫秒
(Ben-Yishai et al., 1995; Carandini & Ringach, 1997; Izhikevich, 2010). In the vein of previous
neural mean field models of feature detection (Bressloff & 考恩, 2002, 2003乙; Bressloff,
考恩, Golubitsky, 托马斯, & Wiener, 2001; Dayan, Abbott, & Labahn, 2001; Ermentrout,
1998; Gutkin, Pinto, & Ermentrout, 2003), and in close analogy to the ring model of orien-
tation tuning (Ben-Yishai et al., 1995; Hansel & Sompolinksy, 1998), we let a (我, t ) 发展
according to the single-population firing-rate formulation of the Wilson-Cowan equations:

t 0

da θ; t
ð
dt

¼ −a θ; t
ð

Þ þ g h θ; t
½

(西德:2);

(1)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

Activation function:
A function mapping the afferent
input into a population of neurons
(expressed as a current or membrane
潜在的) to the population’s firing
rate or probability of firing.

where h(我, t ), the synaptic input, takes into account both excitatory and inhibitory afferents into
a population of cells preferring hue θ, and g(H) is an activation function, 如下所述.

To analyze the relationships between feedforward and recurrent processing and to distin-
guish between their respective effects on a(我, t ), we write h(我, t ) as a sum of the stimulus-driven
synaptic input from the LGN and the intracortical input resulting from the hue-dependent
network connectivity within V1:

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

h θ; t
ð

Þ ¼ hctx θ; t

Þ þ hlgn θð Þ:

(2)

We express the input as the average effect of the net synaptic current on the membrane
potential of a cell, following the conventions of Ermentrout (1998) and Carandini and Ringach
(1997). 因此, H(我, t ) has units of mV and can take on both positive and negative values, 选择的
here so that a(我, t ) typically ranges from 0 到 60 spikes/sec, consistent with electrophysiological
experiments penetrating individual color-responsive cells (康威, 2001; Johnson et al.,
2001; Landisman & Ts’o, 2002A; Wachtler et al., 2003).

The input is converted to a firing rate according to the nonlinear activation function

g hð Þ ¼ β ⋅ h − T

Þ ⋅ H h −T
ð

Þ;

(3)

where H(X) is the Heaviside step function defined as H(X) = 1 for x > 0 and zero for x ≤ 0. 笔记
that in the context of machine learning, this form of activation is also known as the rectified

网络神经科学

682

Pattern forming mechanisms of color vision

linear unit function, or ReLU for short. By constraining the network activity to levels below
60 spikes/sec, we ignore the effects of neuronal saturation commonly implemented in models
of g(H) (Ben-Yishai et al., 1995; Ermentrout, 1998). 这里, T is the threshold potential of a
neuron, below which the synaptic input has no effect on the mean firing rate of the network.
有趣的是, as a processing feature, this thresholding nonlinearity has been speculated to
account for the chromatic responses of individual neurons in V1 (Hanazawa et al., 2000).
The amplification of these responses, and thus the mean network response, is modulated by
β, the neural gain measured in spikes · sec−1/mV. We assume that β is determined by
far-ranging internal and external influences, from attentional mechanisms to hallucinogenic
输入 (Ferguson & Cardin, 2020; Michaiel, 派克, & Niell, 2019).

Feedforward Input

To parameterize the input, prior work has relied on the direct relationship between cortical
feature preferences and properties of the visual stimulus (Ben-Yishai et al., 1995; Bressloff &
考恩, 2003乙). Cells in the cortex labeled, 例如, by their spatial frequency preferences
can be mapped directly onto a visual space parameterized by the same variable. 因此, 这
activity of each neuronal population is no longer labeled purely by its position on the cortical
sheet, but also by its preferred stimulus in an analogous feature space.

The corresponding network topology may be modeled on the cortical histology, 例如
orientation map of Bosking, 张, Schofield, and Fitzpatrick (1997) or spatial frequency
maps addressed in Bressloff and Cowan (2002), Bressloff and Cowan (2003A), and Bressloff
and Cowan (2003乙). 反过来, it may be based entirely on functional considerations, 作为,
例如, in the orientation tuning model of Sompolinksy et al. (Ben-Yishai et al., 1995;
Hansel & Sompolinksy, 1998), also known as the “ring model,” which posits a topology based
on the experimentally motivated assumption that populations with similar orientation prefer-
ences are maximally connected (Ben-Yishai et al., 1995) and on the argument that the impor-
tant features of such a connectivity are captured by its first-order Fourier components (Hansel
& Sompolinksy, 1998).

Our model deviates in this regard by emphasizing that the stimulus’s chromatic information
is first discretized along the two cone-opponent pathways. We incorporate this aspect of early
processing by projecting the stimulus’s DKL space position θ(西德:1)onto the two cardinal axes:

l ¼ cos θ(西德:1)
s ¼ sin θ(西德:1):
The magnitudes of l and s are thus taken to represent the normalized strengths of the L–M and
S–(L+M) cone-opponent signals respectively. The feedforward input is then given by

(4)

hlgn ¼ c l cos θ þ s sin θ

Þ;

(5)

where c is the signal strength, or contrast, expressed as the mean postsynaptic coarse mem-
brane potential (in units of mV) of the target hue population generated by the presynaptic LGN
神经元 (Carandini & Ferster, 2000). Formulated in this way, the input captures the colocali-
zation of cone-opponency and hue selectivity in the activity of V1 cells as observed in Li et al.
(2022) and Xiao et al. (2007). The hue tuning networks, parameterized by θ, are not only
responsive to the individual cone-opponent stimulus signals, l and s, but also implement
the combinatorial mechanisms by which they are first mixed (De Valois et al., 2000). Substitut-
ing the expressions for l and s into Equation 5, we obtain

hlgn ¼ c cos θ − θ(西德:1)
Þ:

(6)

683

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Pattern forming mechanisms of color vision

With this form, we point out the similarity of our combinatorial scheme to that of Mehrani et al.
(2020), in which the input from cone-opponent V2 cells into hue tuning V4 cells is weighted
as a function of the difference in their preferred hue angles. Most evidently, we differ from this
model by first combining the cone-opponent signals in V1 rather than V4, in accordance with
the above-mentioned studies. But beyond pointing to V1 as the origin of mixing, these exper-
iments indicate that the combinatorial feedforward scheme is not sufficient to account for
the variability of neuronal hue preferences. 李等人. (2022) 显示, 例如, that the con-
tribution of signals isolating the S–(L+M) pathway is too small to explain the shifting of hue
preferences away from the L–M axis by purely combinatorial means. As put forward by
Shapley and Hawken (2011), Wachtler et al. (2003), and Lehky and Sejnowski (1999), A
more complete understanding of neuronal hue encoding within V1 requires us to consider
the nonlinear population dynamics therein.

Recurrent Interactions

We begin by characterizing the connectivity of the target hue tuning populations with a trans-
lation invariant cortical connectivity function w(|x − x0|), such that the interactions between
neurons in a single CO blob (length scale ∼0.5 mm) depend only on the cortical distance
它们之间 (布莫尔 & 斯波恩斯, 2012; Salzmann et al., 2012). The network’s connectivity
comprises the interactions of both its excitatory and inhibitory populations,

each of which we model as a sum of an isotropic and distance-dependent term:

w x − x 0
j

Þ ¼ wexc þ winh;

wexc ¼ E0 þ E1 cos x − x 0
winh ¼ −I0 − I1 cos x − x 0

ð
j

Þ
j
Þ:
j

(7)

(8)

We set E0 ≥ E1 > 0 and I0 ≥ I1 > 0 so that wexc and winh are purely excitatory and inhibitory,
分别, in accordance with Dale’s law (Ben-Yishai et al., 1995; Dayan et al., 2001).

下一个, we map the weighting function onto hue space, drawing from the hue tuning micro-
architecture revealed by the imaging studies of Liu et al. (2020) and Xiao et al. (2007). 这些
studies point to a linear relationship between distance and hue angle difference, which min-
imizes the wiring length of cells tuned to similar hues (刘等人。, 2020). The hue-preferring
cells inhabit the so-called “color regions,” defined as such for their activation by red-green
grating stimuli (刘等人。, 2020). These regions predominantly overlap with the V1 CO blobs
(Landisman & Ts’o, 2002乙; 李等人。, 2022) and are responsive to the full range of hues, much
like the patchy distribution of orientation maps within the V1 hypercolumns. 因此, in a similar
manner to the local feature processing models of Bressloff and Cowan (2003乙) and Ben-Yishai
等人. (1995), we model the CO blob as a single color-processing unit consisting of N neurons
labeled by the continuous hue preference variable θ 2 [-p, 圆周率] (Bressloff & 考恩, 2003乙).

数字 2 shows the distribution of hue-responsive neurons within a typical color region
(图2A) as well as a more coarse-grained demarcation of peak activity within several of
these regions (图2B). To describe the spatial organization of their hue preference data,
Xiao et al. (2007) and Liu et al. (2020) applied a linear fit to the cortical distance between
two cell populations as a function of the difference in their preferred hue stimuli Δθ ≡ |θ −
我 0| apart in DKL space. 笔记, this implies a discontinuity between θ = 0 and θ = 2π, allowing
for the 2π periodicity of the hue preference label. 刘等人. (2020) report that the linear fit was
able to capture the micro-organization of 42% of their tested hue maps, and a regression per-
formed by Xiao et al. (2007) on an individual hue map gave a squared correlation coefficient
of R2 = 0.91.

网络神经科学

684

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Pattern forming mechanisms of color vision

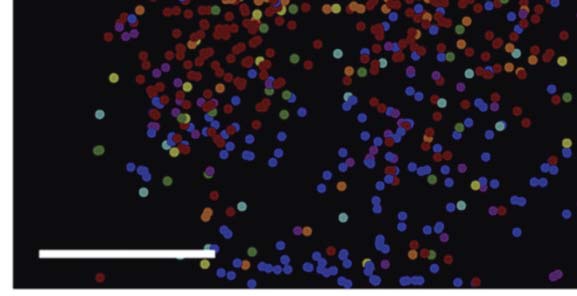
(A) Hue map of individual hue-selective cells obtained by 2-photon calcium imaging of neuronal responsiveness to seven test hues.
数字 2.
Scale bar: 200 μm. (乙) Regions of peak response to test hues (solid contours). The dashed white lines demarcate the color-preferring regions,
colocalized with the CO blobs. Scale bar: 0.5 毫米. Modified with permission from Liu et al. (2020).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

In agreement with these findings, we let |x − x 0| = |θ − θ 0|, absorbing the regression param-
eters into the connectivity strength values E0, E1, I0, and I1 in Equation 8. Substituting this
change of variables and setting J0 = E0 − I0, J1 = E1 − I1 (measured in mV/spikes · sec−1) gives

w θ − θ0

Þ ¼ J0 þ J1 cos θ − θ0

Þ:

(9)

As detailed in Figure 3, for J1 > 0, this functional form captures the local excitation and lateral
inhibition connectivity ansatz typically assumed in neural field models as an analogy to
diffusion-driven pattern formation (Amari, 1977; Bressloff, 2003; Hoyle, 2006; Kim, Rouault,
Druckmann, & Jayaraman, 2017; 图灵, 1952). 尤其, neurons in close proximity in both
cortical and hue space maximally excite each other, and those separated by Δθ = π maximally
inhibit each other, evoking the hue-opponency of perception on a cellular level. We empha-
尺寸, 然而, that this choice of metric is guided by our physiological definition of hue and
does not associate a perceived color difference to measurements in hue space.

这里, it is also important to distinguish between the connectivity function and the center-
surround receptive fields of single- and double-opponent color cells (Shapley & Hawken,
2011). While the structures of both can be approximated by the same functional form, 这
resemblance is superficial: the former characterizes the interactions between different neuro-
nal populations, and the latter is a property of single cells, often adapted for computer vision
算法 (Somers, 纳尔逊, & 在, 1995; 车工, 施瓦茨, & Rieke, 2018).

最后, we weigh the influence of the presynaptic cells by convolving the connectivity
function with the network activity, arriving at the cortical input to the target hue population
at time t:

hctx θ; t
ð

Þ ¼

Z π

-p

w θ − θ 0

Þa θ 0; t
ð

Þdθ 0:

(10)

The recurrent input is thus a continuous function in θ, derived from the population-level inter-
行动. As put forward by the above-mentioned imaging studies, these interactions are colo-
calized with the cone-opponent feedforward input, hlgn, within the same CO blob regions of

网络神经科学

685

Pattern forming mechanisms of color vision

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

数字 3. Cortical connectivity functions. (A) A difference of two Gaussians, one characterizing
the excitatory interactions (here with σE = 40°) and the other the inhibitory interactions (σI =
90°). This is the connectivity typically assumed in mean field models of cortical processing. (乙)
The difference of cosines formulation (方程 9), with J0 = −2 and J1 = 3, captures the local exci-
tation and lateral inhibition assumed in panel A.

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

V1. Collectively, our formulation of h(我, t ) implements the mixing rules posited by these
实验, without requiring us to arbitrarily fine-tune the relative weights of the afferent
signals.

结果

Evolution of Network Activity
We start by observing that by virtue of the invariance of w(θ − θ 0) under translations of θ, 这
R π
convolution operator Tw → w * F (我 ) =
−π w(θ − θ 0)F (我 0)dθ 0 is diagonalizable by the Fourier
eigenfunction basis

^eμ θð Þ ¼

1ﬃﬃﬃﬃﬃﬃ
p eiμθ
2圆周率

(11)

with μ 2  and êμ normalized to integrate to 1 在 [-p, 圆周率]. To calculate the eigenvalues λμ of the
corresponding linear transformations,

Z π

-p

w θ − θ 0

1ﬃﬃﬃﬃﬃﬃ
p eiμθ 0
2圆周率

dθ 0 ¼ λμ

1ﬃﬃﬃﬃﬃﬃ
p eiμθ;
2圆周率

(12)

686

网络神经科学

Pattern forming mechanisms of color vision

we make the change of variables θ − θ 0 = ϕ, so that the left-hand side of Equation 12 可
rewritten as

Z θ−π

θþπ

w ϕð Þe−iμϕ 1ﬃﬃﬃﬃﬃﬃ
2圆周率

p eiμθdϕ ¼

Z π

-p

w ϕð Þe−iμϕ 1ﬃﬃﬃﬃﬃﬃ
2圆周率

p eiμθdϕ:

The eigenvalues are thus:

λμ ¼

Z π

-p

w ϕð Þe−iμϕdϕ:

(13)

(14)

下一个, we assume a(我, t ) is separable in t and θ and bounded on [-p, 圆周率] so that we may

expand it in the eigenbasis of the convolution operator as:

a θ; t
ð

Þ ¼

cμ tð Þ^eμ θð Þ:

Substituting the expansion into Equation 10, we have for Equation 2
(西德:3)

(西德:4)

h θ; t
ð

Þ ¼

w θ − θ0

Þ^eμ θ0ð Þdθ0

þ hlgn θð Þ;

Z π

cμ tð Þ

-p

where w(θ − θ 0) is our choice for the connectivity function (方程 9) and hlgn(我) is defined as
in Equation 6. Evaluating the integrals, we obtain

h θ; t
ð

Þ ¼ λ−1c−1 tð Þ^e−1 θð Þ þ λ0c0 tð Þ^e0 θð Þ þ λ1c1 tð Þ^e1 θð Þ þ c cos θ − θ(西德:1)
Þ;

(17)

with λ0 = 2πJ0 and λ1 = λ−1 = πJ1. Note here that only the zeroth and first-order complex
Fourier components remain.

Substituting the expansion Equation 15 and the explicit form of the activation function

方程 3 into Equation 1 yields:

t 0

X∞

μ¼−∞

dcμ tð Þ
dt

X∞

^eμ θð Þ ¼ −

cμ tð Þ^eμ θð Þ þ β h θ; t

Þ − T

ÞH h θ; t
ð
ð

Þ − T

Þ:

(18)

μ¼−∞

In the absence of the nonlinearity, each of the eigenmodes êμ(我) would evolve indepen-
dently of the others, and a complete analysis of the time-dependent system would seek to
solve a set of equations for cμ(t ) (参见方法: Linear Solution). 然而, in our setup, 这
thresholding introduces a coupling of these coefficients, as the critical hue angles, δ1 and
δ2, at which the input is cut off and is determined by the combined cμ(t ) at each point in time.
While an analytical solution to this system is in most cases intractable, it is nonetheless infor-
mative to break down the rate equation to a coupled system of equations for the evolution of
the coefficients cμ(t ). Taking the inner product of Equation 18 with êν and using <êν|êμ> = δμν,
we obtain:

t 0

dcν tð Þ
dt

¼ −cν tð Þ þ ^eνβ h − T

ÞH h − T
ð

¼ −cν tð Þ þ β

h ϕ; t
ð

Þ^e(西德:3)

ν ϕð Þdϕ

(19)

ð
Z δ2 tð Þ

δ1 tð Þ

where the Heaviside restricts the domain of the inner product to [δ1(t ), δ2(t )]. The time depen-
dence of the cutoff angles reflects the evolution of this curve, which requires that the thresh-
olding be carried out continuously throughout the duration of the dynamics.

网络神经科学

687

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

(15)

(16)

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Pattern forming mechanisms of color vision

To determine δ1 and δ2, we reformulate the Heaviside as a function of θ. Given that the
−1. For mathematical convenience,

input h(我, t) is a real-valued function, c0 2 ℝ and c1 = c(西德:3)
we then rewrite Equation 17 in terms of c0, 关于(c−1) ≡ cR

−1, and Im(c−1) ≡ cI
−1 as
!
ﬃﬃﬃ
2
圆周率

λ−1cI

−1 tð Þ

sin θð Þ:

cos θð Þ þ cs þ

h θ; t
ð

Þ ¼

λ0c0 tð Þ
ﬃﬃﬃﬃﬃﬃ
p
2圆周率

þ cl þ

ﬃﬃﬃ
2
圆周率

λ−1cR

−1 tð Þ

Setting

qR ¼ cl þ

qI ¼ cs þ

ﬃﬃﬃ
2
圆周率
ﬃﬃﬃ
2
圆周率

λ−1cR

−1 tð Þ

λ−1cI

−1 tð Þ

q0 ¼

λ0c0 tð Þ
ﬃﬃﬃﬃﬃﬃ
p
2圆周率

the input takes the form

h θ; t
ð

Þ ¼ q0 tð Þ þ ch tð Þ cos θ þ γ tð Þ
(西德:2)

where tan(C) = − qI
qR

and ch(t) =

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
R þ q2
q2
我

The Heaviside can then be expressed as

H h − T

(西德:2) ¼ H q0 þ ch cos θ þ γ
¼ H cos θ þ γ
ð

ð
Þ − α

(西德:2)

Þ − T

(西德:2)

(20)

(21)

(22)

(23)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

where α ≡ T −q0
, and the time arguments are suppressed for simplicity. In this formulation, 这
ch
Heaviside sets the limits of integration in Equation 19 as the angles θ = δ1, δ2 where α intersects
with cos(我 + C), 如图 4.

数字 4. The limits of integration δ1 and δ2 in Equation 19 are the angles corresponding to the
intersection of α (in gray) and cos(我 + C) (in black). 这里, c = 1, β = 1, and T = −1. 我(西德:1) = π/8. J0 and J1
are as in Figure 3.

网络神经科学

688

Pattern forming mechanisms of color vision

With this reformulation, the system of equations for the evolution of the coupled cν

(方程 19) takes the more explicit form:

t 0

dcν tð Þ
dt

¼ −cν tð Þ þ β

Z δ2

δ1

(西德:2)^e(西德:3)
q0 tð Þ þ ch tð Þ cos ϕ þ γ tð Þ
(西德:2)
½

ν ϕð Þdϕ:

(24)

注意, for all cν, the integrand of Equation 24 is a function of q0(t ), ch(t ), and γ(t ) 和
所以, implicitly, only of the coefficients c0(t ), c−1(t ), and c1(t ). 因此, the dynamics are
determined in full by the evolution of c|ν|≤1(t ):

t 0

dc0 tð Þ
dt

t 0

dc1 tð Þ
dt

¼ −c0 tð Þ þ

¼ −c1 tð Þ þ

β
ﬃﬃﬃﬃﬃﬃ
p
2圆周率

h ϕ; t
½
ð

(西德:2)dϕ
Þ

Z δ2

δ1
Z δ2

δ1

t 0

dc−1 tð Þ
dt

¼ −c−1 tð Þ þ

β
ﬃﬃﬃﬃﬃﬃ
p
2圆周率

with h(ϕ, t ) as in Equation 22.

h ϕ; t
½
ð

(西德:2)eiθ ϕð Þdϕ;
Þ

h ϕ; t
½
ð

(西德:2)e−iθ ϕð Þdϕ
Þ

(25)

Separating Equation 25 into its real and imaginary parts, and noting that a real-valued
−1, reduces the system to a set of equations

activity profile a(我, t ) requires c0 2 ℝ and c1 = −c(西德:3)
for c0(t ), cR
−1(t ).

−1(t ), and cI

Evaluating the integrals, we obtain:

t 0

dc0 tð Þ
dt

t 0

dcR
−1 tð Þ
dt

t 0

dcI

−1 tð Þ
dt

¼ −c0 tð Þ þ

β
ﬃﬃﬃﬃﬃﬃ
p
2圆周率

ch sin δ2 þ γ
ð
F

Þ − sin δ1 þ γ
ð

(西德:2) þ T − q0
ð
Þ

Þ δ1 − δ2
ð

¼ −cR

−1 tð Þ þ

(西德:5)

ch
2

β
ﬃﬃﬃﬃﬃﬃ
p
2圆周率

cosγ δ2 − δ1
Þ þ cos γ þ δ1 þ δ2
ð
(西德:6)

Þ sin δ2 − δ1
ð

(西德:2)
Þ

þ T − q0
(西德:5)

β
ﬃﬃﬃﬃﬃﬃ
p
2圆周率

Þ sinδ1 − sinδ2
ð

ch
2

sinγ δ1 − δ2
ð

¼ −cI

−1 tð Þ þ

þ T − q0

Þ cosδ2 − cosδ1
ð

Þ þ sin γ þ δ1 þ δ2
(西德:6)
;

Þ sin δ2 − δ1
ð

(西德:2)
Þ

ð26Þ

where the time arguments of q0, ch, C, δ1, and δ2 are suppressed for clarity.

Written in this form, the system provides a representation of the time evolution of a(我, t ) 在
terms of the coupled evolution of the constants c|ν|≤1. It is important to note that these equa-
tions are nonlinear due to the implicit Heaviside in our determination of δ1(t ) and δ2(t ). 尽管
our reformulation of the right-hand side of Equation 24 allows for the explicit representation of
the coupling of cν via the nonlinearity, it is also this coupling that proves the analytical solution
of the trajectories intractable. 因此, to describe the behavior of the time-dependent solution,
we turn next to a numerical analysis of the system’s phase portrait—that is, to an exploration of
the features and stability of the system’s emergent steady states.

Steady-State Solution

We approach the solution to Equation 1 with a Forward Euler method, propagating the activity
from a random array of spontaneous initial values between 0 和 0.2 spikes/sec to its steady-

网络神经科学

689

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Pattern forming mechanisms of color vision

state value. Within each time step (typically chosen to be 1 毫秒), we coarse-grain the net-
work into n = 501 populations with hue preferences separated evenly across the DKL angle
domain [-p, 圆周率]. The choice of an odd n allows us to numerically integrate Equation 10 使用
the Composite Simpson’s Rule, whereupon we rectify {H(我, t ) − T } and evaluate the right-hand
side of Equation 1. 以下, we use the term tuning curve only in reference to the emergent
steady-state activity profiles.

数字 5 shows an example of a hue tuning curve obtained with this method. Note that the
peak of the tuning curve is located at the LGN hue input angle (西德:2)(西德:1), which is equivalent to the
steady-state value of −γ in Equation 26 (参见方法: Evolution of Peak Angle). 此外,
the steady-state solution requires da∞ θð Þ

dt = 0 so that Equation 1 becomes

(西德:2):
a∞ θð Þ ¼ g h∞ θð Þ

(27)

因此, the shape of the activity profile at the steady state is equivalent to the net cortical input,
cut off by g at δ1 ≡ θ⋆
c1 and θ⋆
c2. 这里, θ⋆
c2 are the critical cutoff angles for the steady-
state activity profile, beyond which a∞(我) would take on negative values.

c1 and δ2 ≡ θ⋆

We emphasize that the values of the cortical parameters J0, J1, C, 时间, and β are bounded by
the physiological properties of V1. Varying these parameters in the subsequent analysis is
therefore an investigation of their relative effects on hue processing, and we are not fine-tuning
their weights to obtain specific hue tuning curves.

这里, we explore a range of values for the cortical and stimulus parameters under the con-
straint that the network activity remains between 0 和 60 spikes/sec, as motivated above. 我们
further restrict J1 > 0 and J0 < 0 to elicit the local excitation and global inhibition connectivity ansatz of previous neural field models. Our main aim is to graphically characterize the relative c1, and peak height, a∞(θ(cid:1)), of the network effects of the parameters on the width, Δc = θ⋆ c2 tuning curves. Together, these two properties reflect the network selectivity and emergent sig- nal strength, respectively. Note that these effects are robust to small additive white noise and may also be gleaned from the net input, expressed as in Equation 20 and evaluated at the steady-state values of the coefficients. − θ⋆ Steady-state activity profile for a neuronal network encoding stimulus θ(cid:1) = π/8. Parameters Figure 5. are as in Figure 4. Network Neuroscience 690 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Pattern forming mechanisms of color vision It is also important to note here the difference between a network tuning curve and a single- neuron tuning curve. The former is a coarse-grained representation of the CO blob response, with the horizontal axis representing the gamut of hue preferences within a single network. A relatively large tuning width would therefore indicate considerable responses from a wide range of hue tuning cells and poor network selectivity. The single-neuron tuning curve, on the other hand, is an electrophysiological recording of an individual cell’s response to a set of hue stimuli, with the horizontal axis representing the range of stimulus hue angles used in the experiment. The peak location of the single-neuron tuning curve would therefore indicate the hue preference of the individual neuron, while the width would represent its selectivity for that specific hue. Thus, though the two types of tuning curves are labeled and shaped similarly, the latter is only useful to characterize our network’s constituent neurons and not the emergent properties of the population as a whole (Bressloff & Cowan, 2003b). Roles of the stimulus strength and cortical threshold. We begin by considering the role of the stimulus signal strength c on the hue tuning width and peak height. Figure 6 shows typical tuning curves for two values of J1. We find that the stimulus strength has a quickly saturating effect on Δc for all J1 > 0, which is more pronounced at lower values of c as J1 → 0. Above
saturation, the main contribution of the chromatic signal is to increase the network response,
那是, to increase a∞(我(西德:1)).

We also note that at T = 0, the trend reverses, such that increasing c has no effect on the
tuning width at T = 0 and a widening effect for T > 0. 数字 7 illustrates this reversal with four
tuning curves of matched parameters and varying values of T. The coupling of c and T must be
considered because some neural field models (see Amari, 1977; Carandini & Ringach, 1997;
Dayan et al., 2001) take T = 0 for mathematical simplicity. 的确, we might expect that there
is no more physiological significance to choosing a threshold potential of T = 0 mV than any
other value, beyond their relative magnitudes to h(我, t). 然而, the independence of c and
Δc at T = 0 and the significance of the relative signs of c and T elsewhere suggest quite the
opposite. The effect of the chromatic input on tuning the network hue selectivity weakens not
only once the anisotropic strength parameter, J1, is large enough to predominate, but also as
T → 0.

The coupling of c and T is equally significant to the effects of T on the tuning curve prop-
erties. 数字 8 shows that below a certain value, T primarily modulates a∞(我(西德:1)). 然而, 为了

数字 6. Effect of c on the tuning curve properties. The tuning role of c quickly saturates, while its effect on the network response rate grows
without bound. For θ(西德:1) = 0, β = 1, T = −1, and J0 = −1. (A) J1 = 0.2. (乙) J1 = 0.7.

网络神经科学

691

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Pattern forming mechanisms of color vision

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 7. Effect of c on the tuning curve for varying values of T with β = 1, J0 = −1, J1 = 0.2, and θ(西德:1) = 0. Note that the small network response
rates are due to the low values of c chosen here. (A) T = −5. (乙) T = −1. (C) T = 0. (D) T = 0.5.

数字 8.

Effect of T on the tuning curve properties. 我(西德:1) = 0, β = 1, J0 = −3, J1 = 2, and c = 10.

网络神经科学

692

Pattern forming mechanisms of color vision

comparable magnitudes of the stimulus strength and threshold, |C| ～ |时间 |, we see a transition in
which T also begins to sharpen the tuning curve and continues to do so until the threshold
surpasses h(我, t ) for all θ (IE。, for δ⋆
2 = 0). 因此, for higher stimulus strengths,
the thresholding nonlinearity plays a greater role in modulating the network selectivity at lower
and a wider range of T values.

1 = δ⋆

Roles of the cortical weights. The anisotropic connectivity strength J1 exhibits similar relation-
ships to the tuning curve properties to those of c. 那是, for T < 0, a∞(θ(cid:1)) grows and Δc narrows with increasing J1 (see Figure 9A). The trend with respect to Δc reverses for T > 0 (Figure 9B),
whereas the trend with respect to a∞(我(西德:1)) remains unaffected.

These similarities are a mark of the competition between the external input and the cortical
parameters in driving the network selectivity and reflect the fact that both parameters modulate
the anisotropic terms of the model. This means that the role of J1 in driving network selectivity
becomes more significant with decreasing stimulus strength (见图 10). 然而, 一个大的
external input does not suppress the contribution of J1 to the overall network activity. 那是,
increasing J1 results in raising a∞(我(西德:1)), regardless of the strength of the stimulus. 相似地, A

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

数字 9. Effect of J1 on the tuning curve properties for varying values of T. β = 1, c = 0.3, J0 = −10, and θ(西德:1) = 0. (A) T = −1. (乙) T = 0.2.

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 10.

Effect of J1 on the tuning curve properties for different stimulus strengths. β = 1, T = −5, J0 = −9, and θ(西德:1) = 0. (A) c = 1. (乙) c = 3.

网络神经科学

693

Pattern forming mechanisms of color vision

relatively large value of J1 does not restrict the growth of the network response with increasing
stimulus strength. 因此, the anisotropic tuning introduced by the external input and the recur-
rent interactions act cooperatively to raise the network’s response to the stimulus hue, 和
competitively to tune its selectivity.

相比之下, J0 acts cooperatively with the external stimulus to sharpen the curves. As shown
图中 11, the tuning curves narrow with decreasing values of J0, 那是, with an increase in
the relative strength of global inhibition to global excitation, a trend which is conserved for
various stimulus strengths. 此外, there is no trend reversal at T = 0. 相当, for much of
the parameter space, J0 acts with the thresholding to sharpen the tuning curves, as is illustrated
图中 12. This could be expected from the fact that at each point throughout the dynamics,
both T and J0 act isotropically on all hue preferences, lowering or raising the input for all con-
tributing neurons. 然而, this commonality also means that for |时间 | >> |C| (where the effect
of T on Δc saturates, as explained above), the thresholding suppresses the role of J0, analogous
to the competition between c and J1. 最后, 人物 11 和 12 also show that increasing the
global inhibition acts to reduce the value of a∞(我(西德:1)) for all c and T.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

数字 11. Effect of J0 on the tuning curve properties for varying stimulus strengths. β = 1, T = −2, J1 = 2, and θ(西德:1) = 0. (A) c = 1. (乙) c = 6.

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 12. Effect of J0 on the tuning curve properties for varying values of T. β = 1, c = 1, J1 = 2, and θ(西德:1) = 0. (A) T = −5. (乙) T = 0.2.

网络神经科学

694

Pattern forming mechanisms of color vision

We thus conclude that the emergent hue curves in V1 are both inherited from the LGN and
built on the recurrent interactions. The competition between J1 and c points to a continuum of
regimes in which either hlgn or hctx dominates. 然而, in all regimes, J0 works cooperatively
with c to narrow the curves, and all the parameters work together to raise the network
response. 同样地, the competition between J0 and T (both cortical parameters) is modulated
by the value of c, and the location of the peak is always completely determined by the LGN
signal, regardless of the relative magnitudes of the cortical and stimulus strength parameters
(参见方法: Evolution of Peak Angle).

Comparisons with the orientation tuning ring model. 最后, we seek to compare the emergent
properties of the hue tuning model with those of the orientation tuning ring model (Ben-Yishai
等人。, 1995; Hansel & Sompolinksy, 1998). This leads us to separate the analysis into two
地区: one corresponding to the analytical regime with J0 < 1 πβ, and the other to the extended regime with J1 ≥ 1 πβ and J0 constrained as described in the section Stability Analysis. As detailed in Methods: Linear Solution, the former regime defines the (J0, J1) param- eter space wherein the model permits a closed-from stable solution for cases in which the input into all cells is above threshold. By contrast, the dynamics in the latter, extended regime always implement thresholding and thus do not permit the linear closed-form solution. For comparison purposes, note that these parameter regimes are analogous to the orientation model’s homogeneous and marginal regimes, respectively, labels which refer to the system’s responses to unoriented stimuli. 2πβ and J1 < 1 An important difference between our two models is our choice to assume modularity for the color vision pathway. As described above, there is no consensus as to when and how the var- ious visual features are separated along the visual pathway. That is, we do not yet understand how the brain recognizes the extent to which an activated color- and orientation-preferring neuron is signaling for a stimulus’s color or orientation. And moreover, we do not know at which point of the visual pathway the differentiation becomes important. We have therefore chosen to emphasize the unoriented color selective cells localized in the CO blob regions of V1, though the model is intended to describe the color-processing pathway broadly, for any color-preferring neurons regardless of other feature tuning capabilities. Thus, the choice of modularity is not to reject the possibility of joint feature processing, but rather to parse out the color mechanism for a separate analysis. Furthermore, it is in keeping with perceptual studies which indicate that the red-green and blue-yellow color-opponent systems are only responsive to color stimuli and not to broadband, white light (Stockman & Brainard, 2010). The difference between our two models thus comes to our choice to consider the purely chro- matic component of the input afferent from the LGN, whereas the orientation model incorpo- rates external inputs with varying degrees of anisotropy, that is, hext θð Þ ¼ c 1 − (cid:3) þ (cid:3) cos 2θð ½ (cid:2); 0 ≤ (cid:3) ≤ 1=2 Þ (28) where (cid:3) represents the degree of anisotropy. The differing assumptions underlying the formulation of h(θ, t ) have important implications for the subsequent parameter analyses adopted by our two models. In the orientation tuning model, the authors detail the pronounced shift in the relative roles of the cortical and stimulus parameters in narrowing the tuning curve. In this setup, for (cid:3) → 0.5, an increase in c widens the tuning curve, whereas for (cid:3) → 0, the tuning curve selectivity is completely determined by the cortical parameters. The latter scenario constrains the value of the analogous anisotropic cortical parameter, J2, to the marginal regime. Network Neuroscience 695 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Pattern forming mechanisms of color vision In contrast, our model does not apportion separate regions of the parameter space to exter- nal and recurrent mechanisms. Rather, in both the analytical and extended regimes, the roles of c and J1 exist on a spectrum, where the effect of each parameter is suppressed by larger values of the other. Of course, this suppression is more stark in the extended regime because it covers larger values of J1. In this sense, our color model draws a similar conclusion to that of the orientation model: when the anisotropic tuning provided by the recurrent interactions is large, the tuning from the stimulus is negligible, and vice versa. However, we emphasize that the transition is not sharp and that c does have an effect on the tuning curve selectivity in the extended regime (see Figure 6B), as does J1 in the analytical regime. In this regard, the two models are more consistent in their interpretations of J0’s contribution to the selectivity of the tuning curves. That is, in the two regimes of each model, the inhibition acts cooperatively with the thresholding to sharpen the tuning curves. Here again, the orien- tation model makes a distinction between the marginal phase (i.e., (cid:3) = 0 and J2 2 marginal regime), wherein the tuning curve width is completely determined by the cortical anisotropy, and all other cases, where the isotropic inhibition and stimulus come into play. For these cases, the authors argue, J0 does not act alone to narrow the curve: though J0 may sharpen the tuning curves, it is the anisotropy from the input or cortical interactions which acts as the source of the orientation selectivity. Although our color model’s tuning mechanism, too, requires a source of anisotropy, we have emphasized above that there is no single source of hue selectivity. When J1 is small, in either regime, both the stimulus and the uniform inhibition are significant to the hue tuning mechanism. Ultimately, the orientation model sets up a dichotomy between two specific regions of parameter space. In the nonmarginal case, c is the primary player in the tuning mechanism, and in the marginal case, this role belongs to J2. The uniform inhibition is thus given a sec- ondary “sharpening” role. By contrast, in choosing a fully anisotropic hlgn, our color model does not encompass an analogous marginal phase with an always dominating J1. Rather, even for large J1, the uniform inhibition is at least equally important to the modulation of the tuning width. In fact, as we have shown above, for larger values of c, J0 is more effective than J1 in narrowing the tuning curves, for both the analytical and extended regimes. We thus stress that the two regimes, though analogous to those of the orientation model, do not constitute a division in the hue processing mechanism. Rather, we define the boundary between the analytical and extended regimes solely by whether or not the linear case exists. It is therefore determined by the values of J0 and J1 for which the linear solution applies, given that the values of c, T, and β keep the input above threshold throughout the dynamics (Methods: Linear Solution). We note that for each combination of J0 and J1 within the analytical regime there exists also a nonlinear case, in which h(θ, t) is cut off by the thresholding non- linearity and, thereby, the linear solution does not apply. Our definition differs from that of the orientation model, which demarcates the boundary between the homogeneous and marginal phases based on the emergent steady-state tuning curves alone. For more on this approach, see the discussion of the broad and narrow profiles in Hansel and Sompolinksy (1998). As we will show next, the boundary is integral to the corresponding stability analysis of the steady- state tuning curves. Stability Analysis To analyze the stability of the emergent tuning curves, we turn once more to our separable activity ansatz assumed in the eigenfunction decomposition of Equation 15. This means that we are faced again with a nonlinearity induced coupling of the time-dependent coefficients Network Neuroscience 696 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Pattern forming mechanisms of color vision and, consequently, the analytical intractability of the associated stability analysis. We therefore set up the Jacobian matrix for a numerical analysis of the local stability. We begin by adding a small perturbation of the form δa θ; t ð Þ ¼ X Dμ tð Þ^eμ θð Þ μ (29) and substituting the resulting activity into Equation 1. The eigenmodes then evolve according to the following equation for the coefficients Dμ (see Methods: Linear Stability Analysis): τ 0 dDν tð Þ dt ¼ −Dν tð Þ þ β Z δ⋆ 2 δ⋆ 1 δq0 tð Þ þ δqR tð Þ cos ϕð Þ þ δqI tð Þ sin ϕð Þ ½ (cid:2)^e(cid:3) ν ϕð Þdϕ; (30) 1 and δ⋆ where δ⋆ 2 are the critical cutoff angles of the steady-state solution, obtained numerically. We observe that the integrand of Equation 30 is a function of D0, DR −1 alone, and, as such, the stability of the steady-state tuning curve is completely determined by the stability of these first-order coefficients. −1, and DI Evaluating the integrals for ν = 0 and ν = −1, and noting from Equation 21 that J0δc0 ≡ J0D0 p δq0 ¼ p δqR ¼ p δqI ¼ ﬃﬃﬃﬃﬃﬃ 2π ﬃﬃﬃﬃﬃﬃ 2π ﬃﬃﬃﬃﬃﬃ 2π J1δcR −1 ≡ J1δcI −1 ≡ p p p ﬃﬃﬃﬃﬃﬃ 2π ﬃﬃﬃﬃﬃﬃ 2π ﬃﬃﬃﬃﬃﬃ 2π J1DR −1 J1DI −1 ; (31) we obtain the following system of equations for the evolution of the characteristic coefficients: τ 0 dD0 dt τ 0 dDR −1 dt τ 0 dDI −1 dt (cid:8) (cid:9) (cid:7) (cid:9) − δ⋆ 1 ¼ βJ0 δ⋆ 2 (cid:9) (cid:7) þ βJ1 sinδ⋆ 2 (cid:7) þ βJ1 cosδ⋆ 1 (cid:9) (cid:7) ¼ βJ0 sinδ⋆ (cid:3) 2 (cid:10) D0 − 1 (cid:8) − sinδ⋆ 1 (cid:10) (cid:8) − cosδ⋆ 2 DR −1 (cid:10) DI −1 − sinδ⋆ 1 (cid:8) (cid:10) D0 2δ⋆ 2 − 2δ⋆ 1 þ sin 2δ⋆ 2 (cid:7) (cid:8) (cid:7) − sin 2δ⋆ 1 (cid:8) (cid:8) (cid:4) − 1 DR −1 (cid:7) βJ1 4 þ þ (cid:3) βJ1 4 (cid:7) (cid:8) (cid:7) cos 2δ⋆ 1 (cid:7) − cos 2δ⋆ 2 (cid:4) (cid:8) (cid:8) DI −1 (cid:9) (cid:7) ¼ βJ0 cosδ⋆ (cid:3) 1 − cosδ⋆ 2 (cid:8) (cid:10) D0 (cid:7) (cid:7) cos 2δ⋆ 1 (cid:8) (cid:7) − cos 2δ⋆ 2 (cid:4) (cid:8) (cid:8) DR −1 βJ1 4 (cid:7) 2δ⋆ 2 βJ1 4 (cid:7) − 2δ⋆ 1 þ sin 2δ⋆ 1 (cid:8) (cid:7) − sin 2δ⋆ 2 (cid:8) (cid:8) (cid:4) − 1 DI −1 þ þ (cid:3) Network Neuroscience l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 (32) 697 Pattern forming mechanisms of color vision Bifurcation curve: A curve in parameter space defining a transition in the system’s dynamics and stability. The entries of the corresponding Jacobian matrix consist of the bracketed prefactors, and may equally be obtained from the general system of equations for the global network dynamics, as follows: J ¼ 2 6 6 6 6 6 6 6 6 6 4 ∂f1 ∂c0 ∂f2 ∂c0 ∂f3 ∂c0 ∂f1 ∂cR −1 ∂f2 ∂cR −1 ∂f3 ∂cR −1 3 7 7 7 7 7 7 7 7 7 5 ∂f1 ∂cI −1 ∂f2 ∂cI −1 ∂f3 ∂cI −1 c⋆ 0 ;cR⋆ −1 ;cI⋆ −1 (33) where f1, f2, and f3 are the right-hand sides of the equations in Equation 26 and the first-order partial derivatives are evaluated at the steady-state values of c0, cR −1. The stability of the tuning curve is then determined by the eigenvalues of J. −1, and cI We note that the existence of a steady state is a function of the cortical strengths J0 and J1. By fixing the values of β, c, θ(cid:1), and T, we are left with a two-parameter family of differential equations, allowing us to analyze this dependence numerically in the associated ( J0, J1) parameter space. Carrying out a parameter sweep across this space, we find that the system features a bifurcation curve, below which the model permits steady-state solutions and above which no equilibrium exists. To determine stability within the former region, we compute J at the emergent steady-state tuning curves of various points in the parameter space. Solving the associated characteristic equations, we observe that the eigenvalues are always real and negative, and thus conclude that all emergent steady-state tuning curves are stable. Figure 13 shows the bifurcation diagrams for two families of equations, distinguished by their values for T. Most notable is the extended regime, which permits stable steady-state solu- tions beyond the boundary set by the linear case (Methods: Linear Solution). As this parameter regime is not accessible to the linear solution, the tuning curves in this regime are necessarily a product of the thresholding nonlinearity and are thus always cut off below |θ| = π. The thresh- olding nonlinearity therefore not only expands the region of stability, but also ensures that the tuning curves emerging within the extended regime are selective for hue. As we have seen, this expansion is pivotal when the external input is weak and the anisotropic cortical strength plays the larger role in narrowing the tuning curves. Furthermore, regardless of input strength, it allows for a larger overall network response, as the peak activity, a∞(θ(cid:1)), grows with increasing J1. Finally, as we will see in the following section, in the absence of any stimulus (i.e., for c = 0), the extended regime features the spontaneous generation of stable tuning curves and may thus serve as the bedrock for color hallucinations. However, looking back at Figure 13, perhaps most striking is the horizontal portion of the bifurcation curve at J0 = 1 πβ, which sets the same stability conditions on J0 and J1 as in the linear case. This is despite the fact that many of the points in the analytical regimes of the two featured families correspond to solutions that implement thresholding, thus signifying that the analytical regime is not an exclusively linear one. 2πβ for J1 < 1 The key to understanding the shape of this region lies in noticing that the bifurcation dia- gram does not change for varying values of c, T, and θ(cid:1), as shown in Figure 13 for the two values Network Neuroscience 698 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Pattern forming mechanisms of color vision Figure 13. Bifurcation diagram for β = 1 and c = 1 for two values of threshold (shown in the leg- end). The gray and white regions correspond to the analytical and extended regimes, respectively. The black dashed line is the bifurcation curve, above which the tuning curves grow without bound. The overlaid symbols correspond to points tested in a parameter sweep over the extended regime. Notably, the parameter sweep produces the same bifurcation curve for both values of T. Here, we must note that for critical values of T, for which the input is not large enough to generate activity, the model permits the trivial a(θ) = 0 steady-state solution in both the analytical and extended regimes. This solution, however, is unstable to perturbations large enough to make the input cross the thresh- old. For more on bifurcation theory in the context of neural fields, see Gross (2021) and Hesse and Gross (2014). See also Hansel and Sompolinksy (1998) for an analogous “phase diagram” analysis of the orientation ring model. of T. The stability conditions on J0 and J1 are thus uniquely determined by β alone. Further- more, for the general diagram (i.e., with β fixed and c, T unfixed), each point of the analytical regime permits linear solutions, in addition to the ones that implement thresholding. Accord- ingly, the uniqueness of the bifurcation diagram implies that at each point of the analytical ( J0, J1) subspace, the stability of the latter, nonlinear solutions is equivalent to that of the linear solutions. This means that the boundary at J0 = 1 2πβ set by the linear case (Methods: Linear Solution) applies to the full, nonlinear model as well. A Turing Mechanism for Color Hallucinations Biological Turing patterns. Underpinning our hue tuning model is the mathematics of reaction- diffusion systems, for which, in particular, Alan Turing’s treatment of biological pattern forma- tion offers many valuable insights (Turing, 1952). The general Turing mechanism assumes a system of two interacting chemicals, whose local reaction and long-range diffusion properties govern the dynamics of their relative concentrations. In the original framework these chemi- cals are termed “morphogens” to elicit their form-producing capabilities within a developing embryo, whose anatomical structure emerges as a result of their underlying concentration dynamics. This, for instance, may be attributed to the morphogens’ catalysis of organ forma- tion in different parts of the developing organism. Most analogous to our model is the formulation which distributes the morphogens across a continuous ring of tissue, parameterized by the cellular position θ. Assuming that the system Reaction-diffusion system: Mathematical model of two or more interacting substances consisting of local dynamics (via the reaction terms) and spatial dynamics (via the diffusion terms). Network Neuroscience 699 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Pattern forming mechanisms of color vision never deviates far from the underlying homogeneous steady state, the two dynamical state equations for their concentrations, X and Y, take the linear form Þ dX θ; t ð dt Þ dY θ; t ð dt ¼ aX θ; t ð Þ þ bY θ; t ð Þ þ DX ∇2X θ; t ð Þ ¼ cX θ; t ð Þ þ dY θ; t ð Þ þ DY ∇2Y θ; t ð Þ; (34) where a, b, c, and d represent the chemical reaction rates, and DX and DY are the diffusion rates of X and Y, respectively. Here, we set a, c > 0, so that increasing the concentration of X
activates the production of both X and Y, and b, d < 0 so that Y has an inhibitory effect on the production of both chemicals (Hoyle, 2006). (cid:3) In the absence of diffusion (i.e., with DX = DY = 0), the system has a homogeneous steady- state solution, (X, Y ) = 0, whose stability is determined by a Jacobian composed of the reaction (cid:4) , and hence by the system’s local chemical properties alone (Hoyle, 2006). Note rates, that at this point the system is circularly symmetric with respect to interchanging any two cells on the ring. a b c d Assuming the existence of a stable steady-state solution, and the corresponding require- ments on the rate parameters a–d, we next set the diffusive terms DX, DY > 0, taking the sep-
arable ansatz for the general solution:

X∞

X ¼

Aμeλμt eiμθ

μ¼−∞

X∞

Y ¼

Bμeλμt eiμθ:

μ¼−∞

(35)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

此外, we set DX < DY to generate the local excitation and lateral inhibition of the mor- phogen concentrations (Hoyle, 2006; Murray, 2003), evoking the connectivity function ansatz Equation 9. The underlying steady state then remains stable if the real parts of the eigenvalues λμ, obtained from the modified Jacobian, are negative. With the reaction rates fixed from the stability conditions above, these eigenvalues are functions of the diffusion parameters alone. Thus, the conditions for stability may be thought of in terms of a bifurcation diagram in the (DX, DY ) phase space, comparable to Figure 13. From here, a set of additional conditions may be placed on DX and DY so that the system undergoes a Turing bifurcation, wherein at least one λμ becomes positive and the homoge- neous steady state loses its stability. With the addition of a small random perturbation, the instability results in the growth of the corresponding eigenmodes eiμθ, such that, over time, Equation 35 is dominated by the eigenmodes with largest λμ. These represent stationary waves whose wavelengths are set by the circumference of the ring (i.e., by the spatial properties of the medium) and whose growth is bounded by the higher order terms that had been initially ignored in the near-equilibrium formulation (Murray, 2003; Scholz, 2009; Turing, 1952). The underlying circular symmetry is thus broken and a spatial pattern is formed. In his seminal paper, Turing extrapolated this mechanism to explain various biological phe- nomena, such as the development of petals on a flower, spotted color patterns, and the growth Network Neuroscience 700 Pattern forming mechanisms of color vision of an embryo along various directions from an original spherical state. A hallmark of each of these examples is that there is no input into the system, so the emergent patterns reflect a mechanism of spontaneous symmetry breaking, onset by a perturbation of “some influences unspecified” (Turing, 1952). In light of this, we ask, can the visual cortex self-generate the perception of hue? Spontaneous symmetry breaking and color hallucinations. To assess our model’s ability to self- organize in the absence of visual input, we set c = 0 and seek to establish the presence of a Turing mechanism marked by the following three features: 1. A system comprised of local excitation and long-range inhibition. 2. Spontaneous symmetry breaking in the absence of input within a region of a parameter space defined by the relevant bifurcation parameter(s). 3. The emergence of patterns that are bounded by the system’s nonlinearities. As noted above, requiring DX < DY in Equation 34 sets up the diffusion-driven activator- inhibitor dynamics governing the evolution of the morphogen concentration across the ring of cells. With these assumptions, Turing’s reaction-diffusion equations bear a strong resem- blance to our one-population generalization of the excitatory and inhibitory color cell dynam- ics in the absence of LGN input: τ 0 Þ da θ; t ð dt ¼ −a θ; t ð Þ þ g (cid:3) Z π −π J0 þ J1 cos θ − θ0 ð ð Þa θ0; t ð Þ Þdθ0 ; (36) (cid:4) where the local excitation and long-range inhibition are incorporated in the anisotropic inter- action term J1 cos(θ − θ 0), and the reaction terms aX(θ, t ), bY(θ, t ), cX(θ, t ), and dY(θ, t ) find their neural analogue in the term −a(θ, t ). Importantly, the notions of “local” and “long-range” here describe interactions in the DKL space, and not in the physical cortical space correlate to Turing’s ring of tissue. Accordingly, we treat J1 as the Turing bifurcation parameter and look for spontaneous color tuning beyond a bifurcation point J1 = JT 1 . Additionally, we observe that the onset of pattern formation is determined by a critical value of T, so that the relevant parameter space for our exploration is (J1, T ) (Figure 14). This analysis is summarized in Figure 15. Figure 14. The onset of color hallucinations in the (J1, T ) parameter space. The model generates ≡ 1 spontaneous hue tuning curves beyond J1 = JT 1 πβ and below T = 0. Network Neuroscience 701 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Pattern forming mechanisms of color vision l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 15. Spontaneous pattern formation in the absence of input (c = 0). β = 1. (A–B): J0 = −2, J1 = 0.1 (A) T = 0 (B) For T < 0, the homo- geneous steady-state value increases. Here, T = −10. (C–D): Pattern formation in the extended regime for J0 = −2, J1 = 0.4. (C) No hue tuning curve emerges for T ≥ 0. Here, T = 0. (D) T = −10. A hue tuning curve is generated in the absence of external input. (E–F): T = −10, J0 = −7, J1 = 6. The emergent tuning curve is more selective for larger values of J1. For each run, the activity is peaked about a different angle, set by the random initial conditions. The peak value and tuning width are consistent between trials. Network Neuroscience 702 Pattern forming mechanisms of color vision We observe that within the analytical regime, the system generates a stable homogeneous steady-state solution a∞(θ) = const ≥ 0 for all values of the parameters β, T, J0, and J1 (Figure 15A–B). As such, from the closed-form linear steady-state solution (Methods: Linear Solution), we obtain 8 < : a∞ θð Þ ¼ − βT 1 − 2πβJ0 for T ≤ 0 0 for T > 0:

(37)

We further observe that beyond J1 = 1

πβ, a stable homogeneous steady-state solution
remains at a∞(我) = 0 for T ≥ 0 (Figure 15C). 然而, at T = 0, this radial symmetry is broken,
and the cortex generates spontaneous tuning curves with peak locations determined by
the random initial conditions (Figure 15D–F). 因此, the system bifurcates when J1 = 1
πβ and
T = 0, permitting the onset of color hallucinations in a region defined by these two values
(数字 14). Note that the unimodal tuning curves predict stationary, single-hued phosphenes.
Extension to other CO blob networks would therefore indicate a hallucination comprised of
multiple phosphenes of varied hues, each determined by the local cortical activity at hallu-
cinatory onset.

Bearing these predictions in mind, we point to a recent functional MRI study of blind
patients experiencing visual hallucinations (Hahamy, Wilf, Rosin, Behrmann, & 马拉奇,
2021). The study attributes these visions to the activation of the neural networks underlying
normal vision, precipitated by the hyper-excitability of the cortex to spontaneous resting-state
activity fluctuations when it is deprived of external input. This is suggestive of the required
lowering of neuronal threshold at the onset of color hallucinations predicted here. 尤其,
a reduction in membrane potential threshold has also been attributed to the action of
hallucinogens (De Vos, 石匠, & Kuypers, 2021; Varley, Carhart-Harris, Roseman, Menon, &
Stamatakis, 2020).

最后, we note that the stability of the emergent tuning curves is determined by the bifur-
cation diagram of Figure 13. 这意味着, in addition to expanding the region of stability in
the presence of chromatic stimuli, the model’s nonlinearity allows for stable, spontaneous
color hallucinations in their absence.

Having thus established a Turing-like mechanism for our model’s self-organization, we end
with an analogy to Turing’s original diffusion-driven formulation. In his concluding example,
Turing applies the mechanism to explain the growth of an embryo along various axes of its
original spherical state. This growth is driven by diffusion, directed by the “disturbing influ-
恩塞斯,” shaped by the system’s chemical and physical properties, and bounded by the sys-
tem’s nonlinearities. It is all too clear to see the parallels with our hue tuning model, wherein
a hallucination is driven by the anisotropy of the cortical interactions, its hue determined by
the initial conditions, its selectivity shaped by the cortical parameters, and its stability ensured
by the thresholding nonlinearity.

讨论

This paper presents a neural field model of color vision processing that reconceptualizes the
link between chromatic stimuli and our perception of hue. It does so guided by the premise
that the visual cortex initiates the mixing of the cardinal L–M and S–(L+M) pathways and

网络神经科学

703

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Pattern forming mechanisms of color vision

thereby transforms the discrete cone-opponent signals to a continuous representation of
chromatic information. Such mixing mechanisms have been implemented by previous com-
binatorial models of color processing, though through a largely feedforward approach or at
the level of the single neuron.

Our theory bears in mind the mixing mechanism, but reframes the stage-wise combina-
torial scheme to one based on the nonlinear population dynamics within the visual cortex.
因此, we propose a hue-based cortical connectivity, built upon the cortical hue map
micro-architecture revealed by recent optical imaging studies of V1. By considering the
intracortical network interactions, we have accounted for V1 cells responsive to the gamut
of DKL directions without the need to fine-tune the cortical parameters. We do so without
restricting to a particular category of V1 neuron, as both single-opponent and double-
opponent, and altogether novel types of cells, have been suggested as the primary messen-
gers of chromatic information. 相当, we zoom out from the individual neuron’s receptive
field to model the aggregate, population-level properties and, 尤其, the stable repre-
sentation of hue. We thereby offer that chromatic processing in the visual cortex is, 在其
essence, a self-organizing system of neuronal-activity pattern formation, capable of encoding
chromatic information in the presence of visual stimuli and generating information in their
缺席.

更远, in assuming modularity for chromatic processing, we have not ruled out a mech-
anism for joint feature processing. Our choice to focus on the unoriented color cells within
the CO blob regions allowed us to parse out the chromatic pathway for an independent
分析, but should not be interpreted as a claim about its functional independence. 我们
leave open the question of the functional and anatomical separation of the various visual
溪流.

Equally unsettled is the question of how much S cone input contributes to the mixing of the
cone-opponent channels, with some studies showing a relatively weak S cone input into
the neurons of V1, compared to its L and M cone counterparts (李等人。, 2022; Xiao, 2014).
The variations across these experiments may stem, 部分地, from differences in optical imaging
and electrode penetration techniques, including the particulars of the chromatic stimulus used
(李等人。, 2022; 刘等人。, 2020; 波利梅尼, Granquist-Fraser, Wood, & 施瓦茨, 2005;
Salzmann et al., 2012). 总体上, 然而, single-cell recordings have identified two
main types of color-responsive regions: color patches that contain neurons tuned exclusively
to stimuli modulating either of the cone-opponent pathways, and patches with neurons exhi-
biting a mixed sensitivity to a combination of the two (Landisman & Ts’o, 2002A; 李等人。,
2022; Livingstone & Hubel, 1984). Further experiments on the connectivity between these
地区, and among the single- and double-opponent color cell populations of which they
consist, may point to added micro-architectures for the hue maps, along the lines of the geo-
metric orientation models of Bressloff and Cowan (2003A) and Bressloff et al. (2001).

最后, we emphasize that the mechanism we offer departs from previous combinatorial
color models that predict hue sensation at the final stage of processing (De Valois & De Valois,
1993; Mehrani et al., 2020), as well as neural field models that conflate cone- and color-
opponency in their interpretations (Faugeras, 歌曲, & Veltz, 2022; Smirnova, Chizhkova, &
Chizhov, 2015; 歌曲, Faugeras, & Veltz, 2019). The emergent hue tuning curves we have
characterized are a network property reflective of the physiological neuronal responses, 和
should not be confounded with our perception of hue. A photon of wavelength 700 nm strik-
ing a retina is no more “red” than any other particle—color is a perceptual phenomenon not
yet represented in these first stages of vision. By recognizing that the hue tuning mechanism of

网络神经科学

704

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

7
2
6
7
9
2
1
1
8
5
0
1
n
e
n
_
A
_
0
0
2
9
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Pattern forming mechanisms of color vision

the visual cortex is an early stop in the visual pathway, we point to the need for further field
theory approaches to our understanding of color perception.

方法

Linear Solution
We assume in the linear case that the net input h(我, t ) is above threshold throughout the
dynamics such that the activity profile is never cut off and H(H(我, t ) – T ) = 1 ∀ θ 2 {-p, 圆周率}.
方程 18 therefore takes the linear form:

t 0

X∞

μ¼−∞

dcμ tð Þ
dt

X∞

^eμ θð Þ ¼ −

cμ tð Þ^eμ θð Þ þ β h θ; t

Þ − T

(38)

μ¼−∞

Taking the inner product of Equation 38 with êν on the full domain ≡ {-p, 圆周率}, we obtain the

system of equations for all the coefficients cν:

t 0

dc0 tð Þ
dt

t 0

dc1 tð Þ
dt

t 0

dc−1 tð Þ
dt

t 0

dcν tð Þ
dt

¼ 2πβJ0 − 1

Þc0 tð Þ −

ﬃﬃﬃﬃﬃﬃ
2圆周率

βT

ﬃﬃﬃ
圆周率

βc l − is
ð

2
ﬃﬃﬃ
r
圆周率
βc l þ is
Þ
ð

¼ πβJ1 − 1

Þc1 tð Þ þ

¼ πβJ1 − 1

Þc−1 tð Þ þ

¼ −cν tð Þ ∀ νj

j > 1

(39)

We may thus solve for each of the coefficients independently, yielding equations for the
evolution of each. Substitution into the activity expansion of Equation 15 then gives the
closed-form solution for the evolution of the activity:

(西德:5)

a θ; t
ð

Þ ¼ K0e− 1−2πβJ0

Þt=τ 0 -

(西德:6)

ﬃﬃﬃﬃﬃﬃ
2圆周率
βT
1 − 2πβJ0

(西德:5)

1ﬃﬃﬃﬃﬃﬃ
p þ K−1e− 1−πβJ1
2圆周率

Þt=τ 0 þ

ﬃﬃﬃ
圆周率

cβ l þ is
ð
1 − πβJ1

(西德:6)
Þ

1ﬃﬃﬃﬃﬃﬃ
p e−iθ
2圆周率

(西德:5)

þ K1e− 1−πβJ1

Þt=τ 0 þ

(西德:6)

ﬃﬃﬃ
圆周率

cβ l − is
Þ
ð
1 − πβJ1

1ﬃﬃﬃﬃﬃﬃ
p eiθ
2圆周率

(西德:5)

þ Kν

1ﬃﬃﬃﬃﬃﬃ
p e−t
2圆周率

(西德:6)

eiνθj νj

j>1

(40)

where the constants Kν are determined by the Fourier coefficients cν(0) of the initial activity
A(我, 0).

For J0 < 1 tuning curve 2πβ and J1 < 1 πβ, the solution approaches the globally asymptotic stable steady-state a∞ θð Þ ¼ − βT 1 − 2πβJ0 þ cβ cos θ − θ(cid:1) Þ ð 1 − πβJ1 : We call the corresponding ( J0, J1) parameter space the analytical regime. (41) 705 Globally asymptotic stable steady state: A system’s equilibrium solution which attracts all other solutions regardless of initial conditions. Network Neuroscience l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Pattern forming mechanisms of color vision Evolution of Peak Angle We first assume that upon receiving a stimulus θ(cid:1) at time t = 0, the network has a random spon- taneous firing rate a(θ, 0). Using Equation 15, with c0 2 ℝ and cμ = c(cid:3) −μ, we expand the activity profile in terms of the initial values of the corresponding coefficients cμ(0): X a θ; 0ð Þ ¼ cμ 0ð Þ^eμ θð Þ μ ( ¼ 1ﬃﬃﬃﬃﬃﬃ p 2π ¼ 1ﬃﬃﬃﬃﬃﬃ p 2π ( X (cid:11) 2cR −μ 0ð Þ cos μθð c0 0ð Þ þ Þ þ 2cI −μ 0ð Þ sin μθð ) (cid:12) Þ μ≥1 X c0 0ð Þ þ μ≥1 (cid:9) (cid:8) (cid:7) 2 rμ 0ð Þ cos μθ − ϕμ 0ð Þ ) (cid:10) (42) with tan(ϕμ) = cI −μ cR −μ and r 2 μ = (cI −μ )2 + (cR −μ )2 such that ϕμ(0) are completely determined by the initial conditions. Thus, at t = 0 the activity profile is composed of an infinite sum of cosine functions, each peaked about a corresponding disparate angle ϕμ, and therefore has no dis- cernible peak. To characterize the evolution of the network activity from these initial condi- tions to its hue tuning profile at t → ∞, we seek to obtain the steady-state values of ϕμ and the corresponding tuning curve peak inductively as follows. Let us first take μ = 1. As seen in Figure 4, we note that δ1(t ) and δ2(t ) are symmetric about γ(t ) such that δ2 + γ = 2π − (δ1 + γ ). Using this symmetry, we factor out cos(γ ) and sin(γ ), respectively, in the equations for cR −1 and cI −1 in Equation 26: β ﬃﬃﬃﬃﬃﬃ 2π p F1 cosγ −1 þ ¼ −cR ¼ −cI −1 − p F1 sinγ β ﬃﬃﬃﬃﬃﬃ 2π τ 0 τ 0 dcR −1 dt dcI −1 dt with F1 ¼ ch 2 δ2 − δ1 ½ ð Þ þ sin δ2 − δ1 ð (cid:2) þ 2 T − q0 ð Þ Þ sin γ þ δ1 ð Þ (44) and time arguments suppressed. We let F ⋆ and γ⋆ denote the steady-state values of F and γ, respectively, allowing for the following expressions for the steady-state values of cR −1: −1 and cI cR⋆ −1 ¼ 1 cosγ⋆ β p F ⋆ ﬃﬃﬃﬃﬃﬃ 2π β p F ⋆ ﬃﬃﬃﬃﬃﬃ 2π cI⋆ −1 ¼ − 1 sinγ⋆: Thus, we have (cid:8) (cid:7) tan ϕ⋆ 1 ¼ cI⋆ −1 cR⋆ −1 ¼ − tan γ⋆ ð Þ: (45) (46) Similar calculations for the steady-state values of the higher order coefficients yield the general equations τ 0 dcR −μ tð Þ dt τ 0 dcI −μ tð Þ dt ¼ −cR −μ tð Þ þ ¼ −cI −μ tð Þ − Network Neuroscience p Fμ tð Þ cos γ tð Þ ð Þ β ﬃﬃﬃﬃﬃﬃ 2π p Fμ tð Þ sin γ tð Þ ð β ﬃﬃﬃﬃﬃﬃ 2π Þ: (47) 706 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 (43) Pattern forming mechanisms of color vision As before, we note that the evolution of cμ(t ), and therefore of Fμ(t ), ∀ μ 2 ℤ depends only on the first-order coefficients c|μ|≤1(t ). Therefore, the steady-state values of the higher order coefficients cR⋆ −μ ¼ β p F ⋆ ﬃﬃﬃﬃﬃﬃ 2π μ cos μγ⋆ ð Þ cI⋆ −μ ¼ − β p F ⋆ ﬃﬃﬃﬃﬃﬃ 2π μ sin μγ⋆ ð Þ and the corresponding ϕμ, that is, (cid:11) (cid:12) tan ϕ⋆ μ ¼ cI⋆ −μ cR⋆ −μ ¼ − tan μγ⋆ ð Þ; are fully determined by the solution to Equation 26. Substitution of Equation 48 into Equation 15 then gives: a∞ θð Þ ¼ 1ﬃﬃﬃﬃﬃﬃ p c⋆ 2π 0 þ ¼ 1ﬃﬃﬃﬃﬃﬃ p c⋆ 2π 0 þ β π β π X (cid:11) μ cos μγ⋆ F ⋆ ð μ≥1 Þ cos μθð Þ − F ⋆ μ sin μγ⋆ ð Þ sin μθð (cid:12) Þ X μ cos μ θ þ γ⋆ F ⋆ ð ð Þ; Þ μ≥1 so that θ = −γ⋆ represents the peak angle of the steady-state profile a∞(θ). Further, from Equation 22, we have tan γ⋆ð Þ ¼ − q⋆ I q⋆ R ¼ − c sin θ(cid:1) − c cos θ(cid:1) þ β π β π λ−1F ⋆ sinγ⋆ λ−1F ⋆ cosγ⋆ which requires γ⋆ ¼ − θ(cid:1): That is, the steady-state peak −γ⋆ is equivalent to the LGN hue input θ(cid:1). (48) (49) (50) (51) (52) Linear Stability Analysis This section presents the mathematical details for obtaining Equation 30. Adding a small perturbation δa(θ, t ) to the steady-state tuning curve and substituting the resulting network activity into Equation 1, we obtain: a θ; t ð Þ ¼ a∞ θð Þ þ δa θ; t ð Þ (53) τ 0 dδa θ; t ð dt Þ Network Neuroscience ¼ − a∞ θð Þ þ δa θ; t ð ð Þ þ β h∞ θð Þ þ δh θ; t Þ ð ð Þ − T ÞH h∞ θð Þ þ δh θ; t ð ð Þ − T Þ; (54) 707 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Pattern forming mechanisms of color vision where δh(θ, t ) is a perturbation to the input due to δa(θ, t ). Taylor expanding the right-hand side of Equation 54 in h(θ, t ) ≡ h∞(θ ) + δh(θ, t ) about h(θ, t ) = h∞(θ) then yields τ 0 dδa θ; t ð dt Þ ¼ − a∞ θð Þ þ δa θ; t ð ð þ β h∞ θð Þ − T ð (cid:13) Þ Þ ÞH h∞ θð Þ − T ð Þ þ δh θ; t ð ÞH h∞ θð Þ − T ð (cid:7) Þ þ O δh2 (cid:8) (cid:14) : (55) For small perturbations, the higher order terms in δh(θ, t ) are negligible, and, using a∞(θ) = β(h∞(θ) – T )H(h∞(θ) – T ), we rewrite Equation 55 as τ 0 dδa θ; t ð dt Þ ¼ −δa θ; t ð Þ þ βδh θ; t ð ÞH h∞ θð Þ − T ð Þ: (56) Next, expanding δa(θ, t ) as in Equation 29, we obtain τ 0 X∞ μ¼−∞ dDμ tð Þ dt X∞ ^eμ θð Þ ¼ − Dμ tð Þ^eμ θð Þ þ βδh θ; t ð ÞH h∞ θð Þ − T ð Þ; (57) μ¼−∞ wherein we express δh(θ, t ) in terms of Equation 21 to yield: X∞ X∞ τ 0 μ¼−∞ dDμ tð Þ dt ^eμ θð Þ ¼ − Dμ tð Þ^eμ θð Þ μ¼−∞ þ β δq0 tð Þ þ δqR tð Þ cos θð Þ þ δqI tð Þ sin θð Þ ½ (cid:2)H h∞ θð Þ − T ð Þ: (58) Finally, taking the inner product of Equation 58 with êν(θ), and reformulating the thresh- olding nonlinearity in terms of the critical cutoff angles δ1 and δ2 as in section Evolution of Network Activity, we arrive at τ 0 dDν tð Þ dt ¼ −Dν tð Þ þ β Z δ⋆ 2 δ⋆ 1 δq0 tð Þ þ δqR tð Þ cos ϕð Þ þ δqI tð Þ sin ϕð Þ ½ (cid:2)^e(cid:3) ν ϕð Þdϕ; (59) where δ⋆ 1 and δ⋆ 2 are the steady-state values of the cutoff angles. ACKNOWLEDGMENTS The authors acknowledge the fruitful and stimulating discussions with Wim van Drongelen and Graham Smith, and research support from the Oberlin College libraries. AUTHOR CONTRIBUTIONS Zily Burstein: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Project administration; Resources; Software; Supervision; Validation; Visualization; Writing – original draft; Writing – review & editing. David D. Reid: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Project administration; Software; Supervision; Validation; Visualization; Writing – review & editing. Peter J. Thomas: Conceptualization; Methodology; Resources; Writing – review & editing. Jack D. Cowan: Conceptualization; Methodology; Project administration; Resources; Writing – review & editing. FUNDING INFORMATION Peter J. Thomas, Directorate for Mathematical and Physical Sciences (https://dx.doi.org/10 .13039/100000086), Award ID: DMS-2052109. Peter J. Thomas, Office of Research Infrastruc- ture Programs, National Institutes of Health (https://dx.doi.org/10.13039/100016958), Award ID: R01 NS118606. Network Neuroscience 708 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Pattern forming mechanisms of color vision REFERENCES Amari, S.-I. (1977). Dynamics of pattern formation in lateral- inhibition type neural fields. Biological Cybernetics, 27(2), 77–87. https://doi.org/10.1007/BF00337259, PubMed: 911931 Ben-Yishai, R., Bar-Or, R. L., & Sompolinsky, H. (1995). Theory of orientation tuning in visual cortex. Proceedings of the National Academy of Sciences, 92(9), 3844–3848. https://doi.org/10 .1073/pnas.92.9.3844, PubMed: 7731993 Bosking, W. H., Zhang, Y., Schofield, B., & Fitzpatrick, D. (1997). Orientation selectivity and the arrangement of horizontal con- nections in tree shrew striate cortex. Journal of Neuroscience, 17(6), 2112–2127. https://doi.org/10.1523/ JNEUROSCI.17-06 -02112.1997, PubMed: 9045738 Bressloff, P. C. (2003). Spatially periodic modulation of cortical patterns by long-range horizontal connections. Physica D: Non- linear Phenomena, 185(3–4), 131–157. https://doi.org/10.1016 /S0167-2789(03)00238-0 Bressloff, P. C., & Cowan, J. D. (2002). The visual cortex as a crystal. Physica D: Nonlinear Phenomena, 173(3–4), 226–258. https://doi.org/10.1016/S0167-2789(02)00677-2 Bressloff, P. C., & Cowan, J. D. (2003a). The functional geometry of local and horizontal connections in a model of V1. Journal of Physiology-Paris, 97(2–3), 221–236. https://doi.org/10.1016/j .jphysparis.2003.09.017, PubMed: 14766143 Bressloff, P. C., & Cowan, J. D. (2003b). A spherical model for ori- entation and spatial-frequency tuning in a cortical hypercolumn. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences, 358(1438), 1643–1667. https://doi.org/10 .1098/rstb.2002.1109, PubMed: 14561324 Bressloff, P. C., Cowan, J. D., Golubitsky, M., Thomas, P. J., & Wiener, M. C. (2001). Geometric visual hallucinations, Euclidean symmetry and the functional architecture of striate cortex. Philo- sophical Transactions of the Royal Society of London. Series B: Biological Sciences, 356(1407), 299–330. https://doi.org/10 .1098/rstb.2000.0769, PubMed: 11316482 Brown, J. W. (2014). The tale of the neuroscientists and the computer: Why mechanistic theory matters. Frontiers in Neuroscience, 8, 349. https://doi.org/10.3389/fnins.2014.00349, PubMed: 25400544 Bullmore, E., & Sporns, O. (2012). The economy of brain network organization. Nature Reviews Neuroscience, 13(5), 336–349. https://doi.org/10.1038/nrn3214, PubMed: 22498897 Burstein, Z. (2022). Pattern forming mechanisms of color vision. (Publication No. 29259093) [Doctoral dissertation, University of Chicago]. ProQuest Dissertations & Theses Global. Carandini, M., & Ferster, D. (2000). Membrane potential and firing rate in cat primary visual cortex. Journal of Neuroscience, 20(1), 470–484. https://doi.org/10.1523/ JNEUROSCI.20-01-00470 .2000, PubMed: 10627623 Carandini, M., & Ringach, D. L. (1997). Predictions of a recurrent model of orientation selectivity. Vision Research, 37(21), 3061–3071. https://doi.org/10.1016/S0042-6989(97)00100-4, PubMed: 9425519 Conway, B. R. (2001). Spatial structure of cone inputs to color cells in alert macaque primary visual cortex ( V-1). Journal of Neurosci- ence, 21(8), 2768–2783. https://doi.org/10.1523/JNEUROSCI.21 -08-02768.2001, PubMed: 11306629 Conway, B. R. (2009). Color vision, cones, and color-coding in the cortex. The Neuroscientist, 15(3), 274–290. https://doi.org/10 .1177/1073858408331369, PubMed: 19436076 Conway, B. R., Eskew, R. T., Jr., Martin, P. R., & Stockman, A. (2018). A tour of contemporary color vision research. Vision Research, 151, 2–6. https://doi.org/10.1016/j.visres.2018.06 .009, PubMed: 29959956 Conway, B. R., Moeller, S., & Tsao, D. Y. (2007). Specialized color modules in macaque extrastriate cortex. Neuron, 56(3), 560–573. https://doi.org/10.1016/j.neuron.2007.10.008, PubMed: 17988638 Dayan, P., Abbott, L. F., & Labahn, G. (2001). Theoretical neuro- science: Computational and mathematical modeling of neural systems. Cambridge, MA: MIT Press. Derrington, A. M., Krauskopf, J., & Lennie, P. (1984). Chromatic mechanisms in lateral geniculate nucleus of macaque. The Journal of Physiology, 357(1), 241–265. https://doi.org/10.1113 /jphysiol.1984.sp015499, PubMed: 6512691 De Valois, R. L., Cottaris, N. P., Elfar, S. D., Mahon, L. E., & Wilson, J. A. (2000). Some transformations of color information from lateral geniculate nucleus to striate cortex. Proceedings of the National Academy of Sciences, 97(9), 4997–5002. https://doi .org/10.1073/pnas.97.9.4997, PubMed: 10781111 De Valois, R. L., & De Valois, K. K. (1993). A multi-stage color model. Vision Research, 33(8), 1053–1065. https://doi.org/10 .1016/0042-6989(93)90240-W, PubMed: 8506645 De Vos, C. M., Mason, N. L., & Kuypers, K. P. (2021). Psychedelics and neuroplasticity: A systematic review unraveling the biologi- cal underpinnings of psychedelics. Frontiers in Psychiatry, 12, 724606. https://doi.org/10.3389/fpsyt.2021.724606, PubMed: 34566723 Ermentrout, B. (1998). Neural networks as spatio-temporal pattern-forming systems. Reports on Progress in Physics, 61(4), 353–430. https://doi.org/10.1088/0034-4885/61/4/002 Eskew, R. T., Jr. (2009). Higher order color mechanisms: A critical review. Vision Research, 49(22), 2686–2704. https://doi.org/10 .1016/j.visres.2009.07.005, PubMed: 19616020 Faugeras, O., Song, A., & Veltz, R. (2022). Spatial and color hallu- cinations in a mathematical model of primary visual cortex. Comptes Rendus Mathématique, 360, 59–87. https://doi.org/10 .5802/crmath.289 Ferguson, K. A., & Cardin, J. A. (2020). Mechanisms underlying gain modulation in the cortex. Nature Reviews Neuroscience, 21(2), 80–92. https://doi.org/10.1038/s41583-019-0253-y, PubMed: 31911627 Garg, A. K., Li, P., Rashid, M. S., & Callaway, E. M. (2019). Color and orientation are jointly coded and spatially organized in pri- mate primary visual cortex. Science, 364(6447), 1275–1279. https://doi.org/10.1126/science.aaw5868, PubMed: 31249057 Gegenfurtner, K. R. (2003). Cortical mechanisms of colour vision. Nature Reviews Neuroscience, 4(7), 563–572. https://doi.org/10 .1038/nrn1138, PubMed: 12838331 Gegenfurtner, K. R., & Ennis, R. (2015). Color vision II: Higher-order color processing. In A. J. Elliot, M. D. Fairchild, & A. Franklin (Eds.), Handbook of color psychology (pp. 70–109). Network Neuroscience 709 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Pattern forming mechanisms of color vision Cambridge, UK: Cambridge University Press. https://doi.org/10 .1017/CBO9781107337930.005 Gross, T. (2021). Not one, but many critical states: A dynamical sys- tems perspective. Frontiers in Neural Circuits, 15, 614268. https://doi.org/10.3389/fncir.2021.614268, PubMed: 33737868 Gutkin, B., Pinto, D., & Ermentrout, B. (2003). Mathematical neu- roscience: From neurons to circuits to systems. Journal of Physiology-Paris, 97(2–3), 209–219. https://doi.org/10.1016/j .jphysparis.2003.09.005, PubMed: 14766142 Hahamy, A., Wilf, M., Rosin, B., Behrmann, M., & Malach, R. (2021). How do the blind ‘see’? The role of spontaneous brain activity in self-generated perception. Brain, 144(1), 340–353. https://doi.org/10.1093/brain/awaa384, PubMed: 33367630 Hanazawa, A., Komatsu, H., & Murakami, I. (2000). Neural selectivity for hue and saturation of colour in the primary visual cortex of the monkey. European Journal of Neuroscience, 12(5), 1753–1763. https://doi.org/10.1046/j.1460-9568.2000.00041.x, PubMed: 10792452 Hansel, D., & Sompolinksy, H. (1998). Modeling feature selectivity in local cortical circuits. In C. Koch & I. Segev (Eds.), Methods in neu- ronal modeling: From ions to networks (2nd ed.) (pp. 499–567). Cambridge, MA: MIT Press. Hesse, J., & Gross, T. (2014). Self-organized criticality as a funda- mental property of neural systems. Frontiers in Systems Neuro- science, 8, 166. https://doi.org/10.3389/fnsys.2014.00166, PubMed: 25294989 Hoyle, R. (2006). Pattern formation: An introduction to methods. Cambridge, UK: Cambridge University Press. https://doi.org/10 .1017/CBO9780511616051 Hubel, D. H., & Wiesel, T. N. (1974). Uniformity of monkey striate cortex: A parallel relationship between field size, scatter, and magnification factor. Journal of Comparative Neurology, 158(3), 295–305. https://doi.org/10.1002/cne.901580305, PubMed: 4436457 Izhikevich, E. M. (2010). Hybrid spiking models. Philosophical Transactions of the Royal Society A: Mathematical, Physical, and Engineering Sciences, 368(1930), 5061–5070. https://doi .org/10.1098/rsta.2010.0130, PubMed: 20921012 Jameson, D., & Hurvich, L. M. (1955). Some quantitative aspects of an opponent-colors theory. I. Chromatic responses and spectral saturation. Journal of the Optical Society of America, 45(7), 546–552. https://doi.org/10.1364/JOSA.45.000546 Johnson, E. N., Hawken, M. J., & Shapley, R. (2001). The spatial transformation of color in the primary visual cortex of the macaque monkey. Nature Neuroscience, 4(4), 409–416. https:// doi.org/10.1038/86061, PubMed: 11276232 Judd, D. B. (1949). Response functions for types of vision according to the Müller theory. Journal of Research of the National Bureau of Standards, 42(1), 1–16. https://doi.org/10.6028/jres.042.001, PubMed: 18113662 Kaiser, K. K., & Boynton, R. M. (1996). Human color vision (2nd ed.). Washington, DC: Optical Society of America. Kim, S. S., Rouault, H., Druckmann, S., & Jayaraman, V. (2017). Ring attractor dynamics in the Drosophila central brain. Science, 356(6340), 849–853. https://doi.org/10.1126/science.aal4835, PubMed: 28473639 Landisman, C. E., & Ts’o, D. Y. (2002a). Color processing in macaque striate cortex: Electrophysiological properties. Journal of Neurophysiology, 87(6), 3138–3151. https://doi.org/10.1152 /jn.00957.1999, PubMed: 12037214 Landisman, C. E., & Ts’o, D. Y. (2002b). Color processing in macaque striate cortex: Relationships to ocular dominance, cytochrome oxidase, and orientation. Journal of Neurophysiology, 87(6), 3126–3137. https://doi.org/10.1152/jn.2002.87.6.3126, PubMed: 12037213 Lehky, S. R., & Sejnowski, T. J. (1999). Seeing white: Qualia in the context of decoding population codes. Neural Computation, 11(6), 1261–1280. https://doi.org/10.1162/089976699300016232, PubMed: 10423495 Lennie, P., Krauskopf, J., & Sclar, G. (1990). Chromatic mechanisms in striate cortex of macaque. Journal of Neuroscience, 10(2), 649–669. https://doi.org/10.1523/ JNEUROSCI.10-02-00649 .1990, PubMed: 2303866 Li, M., Liu, F., Juusola, M., & Tang, S. (2014). Perceptual color map in macaque visual area V4. Journal of Neuroscience, 34(1), 202–217. https://doi.org/10.1523/ JNEUROSCI.4549-12.2014, PubMed: 24381282 Li, P., Garg, A. K., Zhang, L. A., Rashid, M. S., & Callaway, E. M. (2022). Cone opponent functional domains in primary visual cortex combine signals for color appearance mechanisms. Nature Communications, 13(1), 6344. https://doi.org/10.1038/s41467 -022-34020-2, PubMed: 36284139 Liu, Y., Li, M., Zhang, X., Lu, Y., Gong, H., Yin, J., … Wang, W. (2020). Hierarchical representation for chromatic processing across macaque V1, V2, and V4. Neuron, 108(3), 538–550. https://doi .org/10.1016/j.neuron.2020.07.037, PubMed: 32853551 Livingstone, M. S., & Hubel, D. H. (1984). Anatomy and physiology of a color system in the primate visual cortex. Journal of Neuro- science, 4(1), 309–356. https://doi.org/10.1523/JNEUROSCI.04 -01-00309.1984, PubMed: 6198495 Mehrani, P., Mouraviev, A., & Tsotsos, J. K. (2020). Multiplicative modulations enhance diversity of hue-selective cells. Scientific Reports, 10(1), 8491. https://doi.org/10.1038/s41598-020 -64969-3, PubMed: 32444800 Michaiel, A. M., Parker, P. R., & Niell, C. M. (2019). A hallucino- genic serotonin-2a receptor agonist reduces visual response gain and alters temporal dynamics in mouse V1. Cell Reports, 26(13), 3475–3483. https://doi.org/10.1016/j.celrep.2019.02.104, PubMed: 30917304 Mollon, J. D., & Jordan, G. (1997). On the nature of unique hues. In C. Dickinson, I. Murray, & D. Carden (Eds.), John Dalton’s colour vision legacy (pp. 381–392). London, UK: Taylor and Francis. Murray, J. D. (2003). Mathematical biology II: Spatial models and biomedical applications (3rd ed.). Berlin, Germany: Springer. https://doi.org/10.1007/b98869 Nauhaus, I., Nielsen, K. J., Disney, A. A., & Callaway, E. M. (2012). Orthogonal micro-organization of orientation and spatial fre- quency in primate primary visual cortex. Nature Neuroscience, 15(12), 1683–1690. https://doi.org/10.1038/nn.3255, PubMed: 23143516 Polimeni, J. R., Granquist-Fraser, D., Wood, R. J., & Schwartz, E. L. (2005). Physical limits to spatial resolution of optical recording: Clarifying the spatial structure of cortical hypercolumns. Proceedings of the National Academy of Sciences, 102(11), 4158–4163. https://doi.org/10.1073/pnas.0500291102, PubMed: 15746240 Network Neuroscience 710 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Pattern forming mechanisms of color vision Salzmann, M. F. V., Bartels, A., Logothetis, N. K., & Schüz, A. (2012). Color blobs in cortical areas V1 and V2 of the new world monkey Callithrix jacchus, revealed by non-differential optical imaging. Journal of Neuroscience, 32(23), 7881–7894. https:// doi.org/10.1523/ JNEUROSCI.4832-11.2012, PubMed: 22674264 Schluppeck, D., & Engel, S. A. (2002). Color opponent neurons in V1: A review and model reconciling results from imaging and single-unit recording. Journal of Vision, 2(6), 480–492. https:// doi.org/10.1167/2.6.5, PubMed: 12678646 Scholz, C. (2009). Morphology of experimental and simulated Turing patterns [Unpublished master’s thesis]. FAU Erlangen- Nürnberg. Shapley, R., & Hawken, M. J. (2011). Color in the cortex: Single- and double-opponent cells. Vision Research, 51(7), 701–717. https:// doi.org/10.1016/j.visres.2011.02.012, PubMed: 21333672 Shevell, S. K., & Martin, P. R. (2017). Color opponency: Tutorial. Journal of the Optical Society of America, 34(7), 1099–1108. https://doi.org/10.1364/JOSAA.34.001099, PubMed: 29036118 Smirnova, E. Y., Chizhkova, E. A., & Chizhov, A. V. (2015). A mathematical model of color and orientation processing in V1. Biological Cybernetics, 109(4–5), 537–547. https://doi.org/10 .1007/s00422-015-0659-1, PubMed: 26330361 Somers, D. C., Nelson, S. B., & Sur, M. (1995). An emergent model of orientation selectivity in cat visual cortical simple cells. Jour- nal of Neuroscience, 15(8), 5448–5465. https://doi.org/10.1523 /JNEUROSCI.15-08-05448.1995, PubMed: 7643194 Song, A., Faugeras, O., & Veltz, R. (2019). A neural field model for color perception unifying assimilation and contrast. PLOS Com- putational Biology, 15(6), e1007050. https://doi.org/10.1371 /journal.pcbi.1007050, PubMed: 31173581 Stockman, A., & Brainard, D. H. (2010). Color vision mechanisms. In M. Bass et al. (Eds.), The optical society of America handbook of optics (3rd ed.), Volume III: Vision and vision optics. New York, NY: McGraw Hill. Stoughton, C. M., & Conway, B. R. (2008). Neural basis for unique hues. Current Biology, 18(16), R698–R699. https://doi.org/10 .1016/j.cub.2008.06.018, PubMed: 18727902 Turing, A. M. (1952). The chemical basis of morphogenesis. Philo- sophical Transactions of the Royal Society of London. Series B, Biological Sciences, 237, 37–72. https://doi.org/10.1098/rstb .1952.0012 Turner, M. H., Schwartz, G. W., & Rieke, F. (2018). Receptive field center-surround interactions mediate context-dependent spatial contrast encoding in the retina. Elife, 7, e38841. https://doi.org /10.7554/eLife.38841, PubMed: 30188320 Valberg, A. (2001). Unique hues: An old problem for a new gener- ation. Vision Research, 41(13), 1645–1657. https://doi.org/10 .1016/S0042-6989(01)00041-4, PubMed: 11348647 Varley, T. F., Carhart-Harris, R., Roseman, L., Menon, D. K., & Stamatakis, E. A. (2020). Serotonergic psychedelics LSD & psilo- cybin increase the fractal dimension of cortical brain activity in spatial and temporal domains. NeuroImage, 220, 117049. https:// doi.org/10.1016/j.neuroimage.2020.117049, PubMed: 32619708 Wachtler, T., Sejnowski, T. J., & Albright, T. D. (2003). Representa- tion of color stimuli in awake macaque primary visual cortex. Neuron, 37(4), 681–691. https://doi.org/10.1016/S0896 -6273(03)00035-7, PubMed: 12597864 Wilson, H. R., & Cowan, J. D. (1972). Excitatory and inhibitory interactions in localized populations of model neurons. Biophys- ical Journal, 12(1), 1–24. https://doi.org/10.1016/S0006 -3495(72)86068-5, PubMed: 4332108 Wilson, H. R., & Cowan, J. D. (1973). A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik, 13(2), 55–80. https://doi.org/10.1007/BF00288786, PubMed: 4767470 Wool, L. E., Komban, S. J., Kremkow, J., Jansen, M., Li, X., Alonso, J.-M., & Zaidi, Q. (2015). Salience of unique hues and implica- tions for color theory. Journal of Vision, 15(2), 10. https://doi.org /10.1167/15.2.10, PubMed: 25761328 Wuerger, S. M., Atkinson, P., & Cropper, S. (2005). The cone inputs to the unique-hue mechanisms. Vision Research, 45(25–26), 3210–3223. https://doi.org/10.1016/j.visres.2005.06.016, PubMed: 16087209 Xiao, Y. (2014). Processing of the S-cone signals in the early visual cortex of primates. Visual Neuroscience, 31(2), 189–195. https:// doi.org/10.1017/S0952523813000278, PubMed: 23941664 Xiao, Y., Casti, A., Xiao, J., & Kaplan, E. (2007). Hue maps in pri- mate striate cortex. NeuroImage, 35(2), 771–786. https://doi.org /10.1016/j.neuroimage.2006.11.059, PubMed: 17276087 Zaidi, Q., & Conway, B. (2019). Steps towards neural decoding of colors. Current Opinion in Behavioral Sciences, 30, 169–177. https://doi.org/10.1016/j.cobeha.2019.10.011 Network Neuroscience 711 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 2 6 7 9 2 1 1 8 5 0 1 n e n _ a _ 0 0 2 9 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 研究形象

下载pdf