研究
Larger lesion volume in people with multiple
sclerosis is associated with increased
transition energies between brain states
and decreased entropy of brain activity
Ceren Tozlu1
, Sophie Card2, Keith Jamison1, Susan A. Gauthier1,3,4, and Amy Kuceyeski1,5
1放射科, Weill Cornell Medicine, 纽约, 纽约, 美国
2Horace Greeley High School, Chappaqua, 纽约, 美国
3Judith Jaffe Multiple Sclerosis Center, Weill Cornell Medicine, 纽约, 纽约, 美国
4神经内科, Weill Cornell Medical College, 纽约, 纽约, 美国
5Brain and Mind Research Institute, Weill Cornell Medicine, 纽约, 纽约, 美国
关键词: Multiple sclerosis, Brain activity dynamics, Network control theory, Entropy
抽象的
Quantifying the relationship between the brain’s functional activity patterns and its structural
backbone is crucial when relating the severity of brain pathology to disability in multiple
sclerosis (MS). Network control theory (NCT) characterizes the brain’s energetic landscape
using the structural connectome and patterns of brain activity over time. We applied NCT
to investigate brain-state dynamics and energy landscapes in controls and people with MS
(pwMS). We also computed entropy of brain activity and investigated its association with
the dynamic landscape’s transition energy and lesion volume. Brain states were identified
by clustering regional brain activity vectors, and NCT was applied to compute the energy
required to transition between these brain states. We found that entropy was negatively
correlated with lesion volume and transition energy, and that larger transition energies were
associated with pwMS with disability. This work supports the notion that shifts in the pattern of
brain activity in pwMS without disability results in decreased transition energies compared to
controls, 但, as this shift evolves over the disease, transition energies increase beyond controls
and disability occurs. Our results provide the first evidence in pwMS that larger lesion volumes
result in greater transition energy between brain states and decreased entropy of brain activity.
作者总结
We investigated the brain-state dynamic and energy landscapes in healthy individuals and
people with multiple sclerosis (pwMS). We also investigated the entropy of brain activity and its
association with transition energy between brain states and lesion volume. We clustered regional
brain activity time series to identify the brain states. 然后, we applied network control theory
using structural connectivity network to identify the minimum required energy to transition
between brain states. We observed the pwMS without disability showed decreased transition
活力, while pwMS with evidence of disability showed increased transition energy compared to
healthy individuals. Lower entropy of brain activity was associated with greater lesion load and
larger transition energy. This study provides a possible mechanism of how MS-related damage
to the brain’s structural backbone can impact brain dynamics, entropy, and energetics.
开放访问
杂志
引文: Tozlu, C。, Card, S。, Jamison,
K., Gauthier, S. A。, & Kuceyeski, A.
(2023). Larger lesion volume in people
with multiple sclerosis is associated
with increased transition energies
between brain states and decreased
entropy of brain activity. 网络
神经科学, 7(2), 539–556. https://
doi.org/10.1162/netn_a_00292
DOI:
https://doi.org/10.1162/netn_a_00292
支持信息:
https://doi.org/10.1162/netn_a_00292
已收到: 1 七月 2022
公认: 7 十一月 2022
利益争夺: 作者有
声明不存在竞争利益
存在.
通讯作者:
Amy Kuceyeski
amk2012@med.cornell.edu
处理编辑器:
Shella Keilholz
版权: © 2023
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
A
_
0
0
2
9
2
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Network control theory in MS
Functional connectivity:
Temporal coactivation of the brain’s
neural activity between different
brain regions of interest.
Network control theory:
An approach to identify the brain’s
energetic landscape using the
structural connectome and patterns
of brain activity over time.
Brain state:
The recurring patterns of the brain’s
dynamic neural activity.
Entropy:
A measure indicating the complexity
and predictability of a dynamic
系统.
Transition energy:
The minimum energy required to
transition between pairs of brain
states or to remain in the same state
over some time.
网络神经科学
介绍
Multiple sclerosis (MS) is a chronic disease characterized by neuroinflammation and, eventu-
盟友, neurodegeneration in the central nervous system (CNS). The size and location of the
lesions in the CNS are very heterogeneous (Barkhof, 2002), resulting in different patterns of
structural damage among people with MS (pwMS). Structural damage to the brain may result
in changes to its functional activity patterns (Tommasin et al., 2018); 然而, how different
patterns of structural damage can modify dynamics of functional activity have not been fully
characterized in pwMS.
Functional MRI (功能磁共振成像) measures functional brain activity patterns over time, 信息
which can be used to quantify brain activity dynamics or to estimate patterns of regional
co-activation, 那是, 功能连接 (FC). Both increased or decreased fMRI-based
activity/connectivity has been observed in pwMS, where increases are often interpreted as a
compensatory mechanism serving to limit clinical disability (Buyukturkoglu et al., 2020;
Filippi et al., 2013; Sbardella et al., 2015). FMRI in pwMS has largely been used to investigate
the association between the brain’s static and/or dynamic FC and motor/cognitive impairment.
(Buyukturkoglu et al., 2020; Tozlu et al., 2021A; Tozlu et al., 2021乙). Most FC studies in pwMS
have been static in nature (Filippi et al., 2013; Sbardella et al., 2015), ignoring shorter scale
changes in FC that have been shown to occur (Calhoun et al., 2014). These shorter scale
changes in FC can be captured via dynamic FC (dFC) analysis that involves clustering FC
matrices computed via sliding windows of the fMRI time series data (Allen et al., 2014). 这
approach was previously used to differentiate between the pwMS and healthy controls (HC)
(Leonardi et al., 2013; Rocca et al., 2019; Tozlu et al., 2021A), to compare the dynamics
between cognitively impaired versus preserved pwMS (d’Ambrosio et al., 2019), and to inves-
tigate the relationship between alterations in dFC dynamics and cognition in MS (Fuchs et al.,
2022; van Geest et al., 2018A; van Geest et al., 2018乙). 然而, calculating dFCs with a
sliding-window approach is not straightforward since the estimation of the window length
and shift size of the sliding windows is required; 而且, correlations are still used to
describe coactivations of pairs of regions as in static FC. As an alternative approach, clustering
can be directly applied to the time series of regional activity to define distinct brain activity
状态. This approach was successfully used in HC to identify brain activity states that occur
while performing a working memory task, quantify the effects of psychedelics, and identify
changing dynamics of activity patterns in stroke patients (Cornblath et al., 2020; Olafson
等人。, 2022; Singleton et al., 2022). In addition to the identification of the brain’s dynamic
状态, the same studies used network control theory (NCT) 方法 (Gu et al., 2015; Stiso
等人。, 2019; 乙. Tang et al., 2017) to identify the minimum energy required to transition
between these dynamic brain states. 然而, no study to date has applied brain activity clus-
tering or NCT in a population of pwMS, let alone investigate differences in brain dynamics and
energetics across disability subgroups in MS.
In terms of capturing brain activity dynamics, entropy is also an important metric with
which to quantify the amount of regularity/unpredictability in brain activity time series (Pincus,
1991). Higher entropy of brain activity has been associated with a larger repertoire of available
brain states (Carhart-Harris et al., 2014), and decreased NCT-based transition energy under
psychedelics compared to placebo was found to be associated with greater increases in
entropy of brain states (Singleton et al., 2022). Studies in disease/disorders have shown (A)
greater entropy in controls compared to people with attention-deficit/hyperactivity disorder
(ADHD) as well as a correlation between lower entropy and more severe ADHD symptom
scores (Sokunbi et al., 2013) 和 (乙) decreased entropy in regions containing a stroke lesion
and their contralesional hemisphere homologues (Saenger et al., 2018). One study in
540
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
A
_
0
0
2
9
2
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Network control theory in MS
Transition probability:
The probability that a brain switches
to a different state or remains in
the same state (IE。, persistence
probability) at the next time point.
Fractional occupancy:
The number of TRs (repetition time)
assigned to each cluster out of the
total number of TRs.
EDSS:
Expanded Disability Status Scale that
measures the disability level in
people with multiple sclerosis. EDSS
ranges between 0 和 10, 在哪里 0
means that the subject does not have
a disability and 10 means death due
to multiple sclerosis.
relapsing-remitting MS (RRMS) showed entropy was associated with an individual’s disability
等级, where more disability was related to increased entropy (Sokunbi et al., 2013; Zhou et al.,
2016). 然而, no study to date has investigated the link between the entropy of brain activ-
ity and (A) lesion volume or (乙) NCT-based transition energy between brain states in MS.
In this study, we first aimed to identify recurrent dynamic brain states in both HC and pwMS
by unsupervised clustering of regional resting-state fMRI activity. 注意, although related
(see Olafson et al., 2022), this approach differs from dFC (sliding-window FC) in that instead of
clustering dFC matrices we are clustering the brain activity vectors from each TR to identify
commonly occurring patterns of brain activation (not FC). We calculated metrics quantifying
the dynamics of these brain activity states, including transition probability and fractional occu-
pancy, and used NCT and individuals’ structural connectomes (SC) to compute the energy
required to transition between pairs of brain states. We hypothesized that greater energy is
required for brain-state transitions in pwMS with disability compared to both controls and
pwMS with no evidence of disability. 最后, we investigated the association between overall
transition energy and the information contained in the brain activity signal, as captured by
entropy. We calculated the entropy of each region’s activity over the entire fMRI scan and
summarized the global entropy by taking the average of the regional measures. Our hypothesis
was that decreased global entropy is associated with both increased transition energy and
lesion load. This paper is the first to quantify MS-related shifts in the brain’s energetic land-
scape and to link entropy/energetic demand of brain activity to lesion burden in pwMS.
MATERIAL AND METHODS
Subjects
One hundred pwMS (年龄: 45.5 [36.7, 56.0], 66% 女性) with a diagnosis of clinically iso-
lated syndrome (CIS)/MS (CIS = 7, RRMS = 88, primary/secondary progressive primary pro-
gressive MS [PPMS] and secondary progressive MS [SPMS] = 5) 和 19 HC (年龄: 45 [35,
49], 55% 女性) were included in our study. All MS subgroups were included in the analyses
as we wanted to investigate these imaging biomarkers across the spectrum of disability sever-
实体, which are often related to disease subtype. All subjects who had preprocessed imaging
data available included in our study. MRIs and demographic data were collected (年龄, 性别,
and race for both HC and pwMS, clinical phenotype and disease duration for pwMS). 这
expanded disability status scale (EDSS) was used to quantify disability in pwMS, where an
EDSS of 2 was used as a threshold to categorize the pwMS into no disability (EDSS < 2) or
evidence of disability (EDSS ≥ 2) groups. An EDSS of greater than or equal to 2 is the cutoff
for clinical definitions of “disability,” whereas scores below that are not considered to be dis-
abled and scores above it correspond to minimal, moderate, or severe disability. All studies
were approved by an ethical standards committee on human experimentation and written
informed consent was obtained from all patients. Participants were excluded if they had con-
traindications to MRI, and controls were further excluded if they had ever been diagnosed with
or were currently on medication for a neurological or psychological disorder.
Image Acquisition, Processing, and Structural Connectome Extraction
MRI data were acquired on a 3T Siemens Skyra scanner (Siemens, Erlangen, Germany) with a
20-channel head-neck coil. Anatomical MRI (T1/T2/T2-FLAIR, 1-mm3 isovoxel), resting-state
fMRI (6 min, TR = 2.3 s, 3.75 × 3.75 × 4 mm voxels) and diffusion MRI (55 directions HARDI,
b = 800, 1.8 × 1.8 × 2.5 mm voxels) acquisitions were performed. Multi-echo 2D GRE field
Network Neuroscience
541
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
a
_
0
0
2
9
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network control theory in MS
maps were collected for use with both fMRI and diffusion MRI (0.75 × 0.75 × 2 mm voxels,
TE1 = 6.69 ms, ΔTE = 4.06 ms, number of TEs = 6).
White matter ( WM) and gray matter (GM) were segmented and GM further parcellated into
86 FreeSurfer-based regions (68 cortical and 18 subcortex/cerebellum) (Fischl & Dale, 2000)
and a fine-grained atlas cc400 (321 cortical and 71 subcortex/cerebellum) using FreeSurfer
(Craddock et al., 2012). The white and gray matter surfaces were manually checked and hand
edited with control points and reconstruction editing if necessary. As described elsewhere
(Kuceyeski et al., 2016), fMRI preprocessing included simultaneous nuisance regression and
removal of WM and cerebrospinal fluid (CSF) effects (Hallquist et al., 2013), followed by high-
pass filtering (≥0.008) using the CONN v18b toolbox (Whitfield-Gabrieli & Nieto-Castanon,
2012) and SPM12 in Matlab. Nuisance regressors included 24 motion parameters (6 rotation
and translation, temporal derivatives, and squared version of each) and the top 5 eigenvectors
from eroded masks of both WM and cerebro-spinal fluid. The mean fMRI signal over all voxels
in each of the 86 regions for each TR was calculated to obtain a regional time series matrix of
BOLD activity.
Diffusion MRI was interpolated to isotropic 1.8-mm voxels, and then corrected for eddy
current, motion, and EPI distortion with the eddy command from FSL 5.0.11 (Andersson &
Sotiropoulos, 2016) using the outlier detection and replacement option (Andersson et al.,
2016). MRtrix3Tissue (https://3tissue.github.io), a fork of Mrtrix3 (Tournier et al., 2019), was
used to estimate a voxel-wise single-shell, three-tissue constrained spherical deconvolution
model (SS3T-CSD) and then compute whole-brain tractography for each subject. We per-
formed deterministic (sd-stream) tractography with MRtrix3 (Tournier et al., 2010; Tournier
et al., 2012) with uniform seeding at each white matter voxel, after which the SIFT2 global
filtering algorithm (Smith et al., 2015) was applied to account for bias that exists in greedy,
locally optimal streamline reconstruction algorithms. The SC matrix was constructed by taking
the sum of the SIFT2 weights of streamlines connecting pairs of regions and then dividing by
the sum of the two regions’ volumes.
Lesion masks were produced for each pwMS in a semiautomated process. The WM hyper-
intensity lesion masks were created by running the T2 FLAIR images through the lesion seg-
mentation tool (LST) and were further hand edited as needed. T2 FLAIR-based lesion masks
were transformed to the individual’s T1 native space using the inverse of the T1 to GRE trans-
form and nearest neighbor interpolation. Individual T1 images were then normalized to MNI
space using FSL’s linear (FLIRT) and nonlinear (FNIRT) transformation tools (https://www.fmrib
.ox.ac.uk/fsl/index.html); transformations with nearest neighbor interpolation were then
applied to transform the native anatomical space T2FLAIR lesion masks to MNI space. The
transformations were concatenated (T2FLAIR to T1 to MNI) to minimize interpolation effects.
Lesions were manually inspected after the transformation to MNI space to verify the accuracy
of coregistration and lesion volume (in mm3) calculated.
Brain-State Identification
K-means clustering was used to identify commonly recurring brain states (see Figure 1 for the
workflow of the study) over all subjects’ normalized regional brain activity time series. We used
both the elbow criterion and the gain in explained variance to identify the optimal number of
clusters, which we identified to be six (see Supporting Information Figure S2). Once the optimal
number of clusters was identified, clustering was run 10 times. Within each of the 10 runs, clus-
tering was restarted 50 times with different random initializations to identify the final clusters
having the best separation, that is, those that minimized the Pearson correlation between pairs
Network Neuroscience
542
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
a
_
0
0
2
9
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network control theory in MS
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
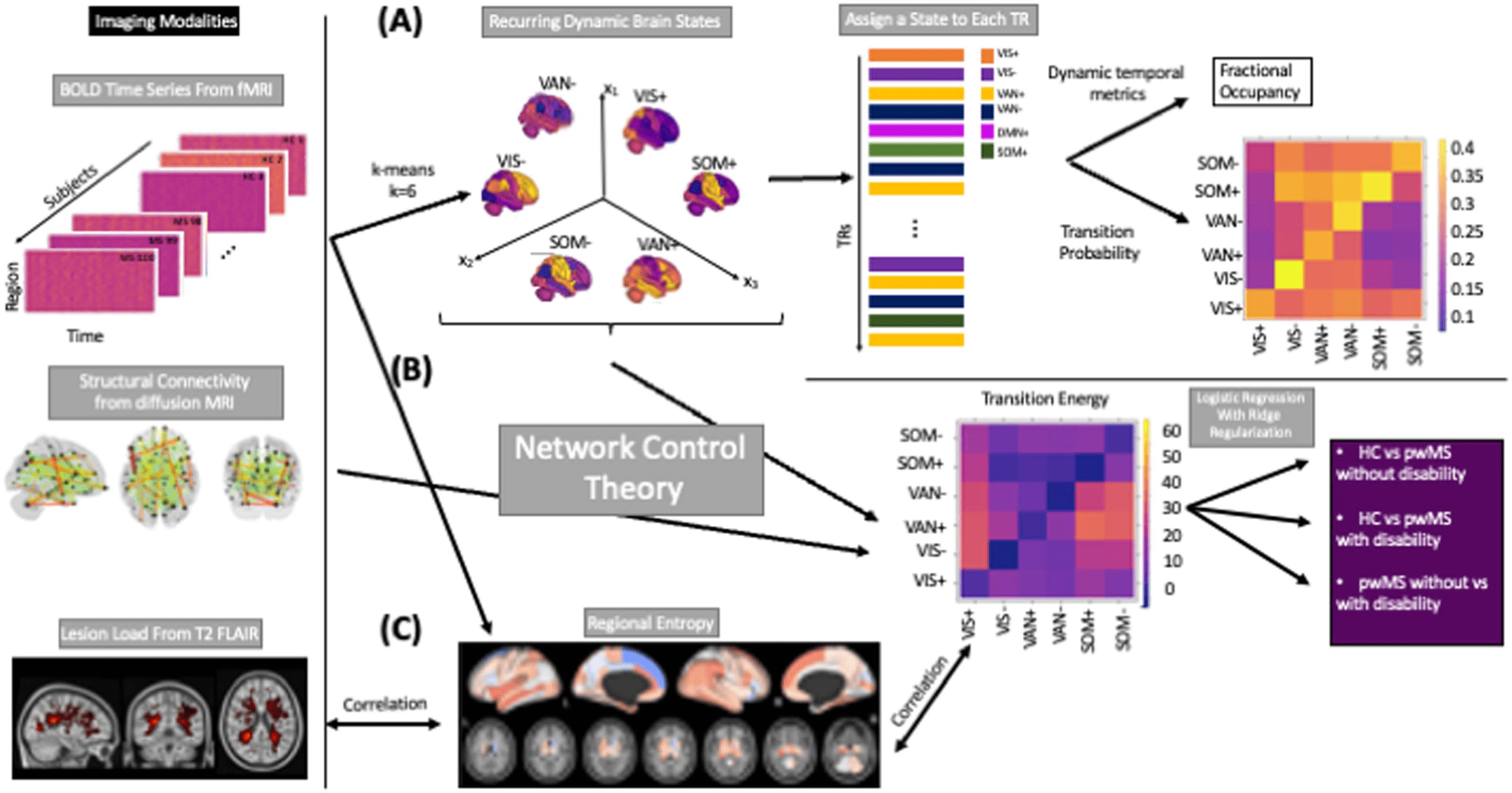
Figure 1. The workflow of the study. (A) Regional BOLD time series for all subjects (19 HC and 99 pwMS) were collected and k-means was
applied to identify commonly occurring brain states. This approach allows us to assign a state to each TR in each individual’s scan. Metrics
such as fractional occupancy and transition probability for each state were then calculated. (B) Network control theory was applied to compute
the minimum energy required to transition between pairs of brain states or to remain in the same state. Logistic regression with ridge regu-
larization was used to predict class (HC, pwMS with no disability, pwMS with disability) using state transition/persistence energy. (C) Entropy of
regional BOLD time series were also computed, compared across the three groups and global entropy was associated with global transition
energy and global disease burden (log lesion volume).
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
a
_
0
0
2
9
2
p
d
.
t
of cluster centroids. Adjusted mutual information (AMI) (Nguyen, 2021) was computed to assess
the stability of the clustering results over the 10 repetitions; AMI was greater than 0.89 for all
pairs of repetitions indicating robust cluster assignment (see Supporting Information Figure S1).
Finally, we replicated the cluster analysis using a higher dimensional atlas (cc400), where
optimal k was identified as 5 (see Supporting Information Figure S7). The results obtained with
the cc400 atlas were interpreted in the main text and the figures associated with those results
were given in the supplementary materials.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Each of the 86 regions was assigned to one of nine networks, including the seven Yeo func-
tional networks, a subcortical and a cerebellar network (Yeo et al., 2011). The network-level
contributions of the six centroids were characterized by calculating the cosine similarity of
each state’s centroid (positive and negative parts were analyzed separately) and nine binarized
vectors representing each of the networks. Because the mean signal from each scan’s regional
time series was removed during high-pass filtering, positive values reflect signal intensity
above the mean (high-amplitude) and negative values reflect signal intensity below the mean
(low-amplitude). The brain states were named by identifying the network with the largest mag-
nitude activation (either high+ or low- amplitude). The following dynamic brain-state metrics
were calculated: (a) transition probability between pairs of states and the persistence proba-
bility of remaining in the same state and (b) fractional occupancy, defined as the number of
TRs assigned to each cluster out of the total number of TRs (see Table 1).
Network Neuroscience
543
Network control theory in MS
Table 1.
The MRI-based metrics used in the study
Metric
Transition probability
Definition
The probability that a brain switches to a different
state or remains in the same state (i.e., persistence
probability) at the next time point
Interpretation
A higher transition probability between two
states means this transition is more likely to
occur than others.
Fractional occupancy
Number of TRs assigned to each state out of the total
Higher fractional occupancy in a specific state
number of TRs
Transition energy
The minimum energy required to transition between
pairs of brain states or to remain in the same state
over some time
means more time is spent in this state
compared to another states.
Higher transition energy means the transition
requires more energy to complete. Transition
energy is highly negatively correlated with
transition probability.
Entropy
A measure indicating the complexity and
predictability of a dynamic system
Higher entropy means increased complexity
and decreased predictability of a system.
Transition Energy Calculations
As previously described (Cornblath et al., 2020; Singleton et al., 2022), NCT can be used to
understand how the structural (white matter) connectome constrains dynamic brain-state
changes. Specifically, it can be used to compute the minimum energy (Em) required to transi-
tion between pairs of brain states or to remain in the same state (see Table 1). To begin, we
employed a time-invariant model:
_s tð Þ ¼ As tð Þ þ Bu tð Þ
Structural connectivity:
Strength of the anatomical
connections between different brain
regions of interest.
where A is the structural connectivity matrix with a dimension of 86 × 86, s(t ) is a vector of
length 86 containing the regional activity at time t, and u(t ) is the external input to the system.
In our case, B is an identity matrix with a dimension of 86 × 86 that indicates each region has
uniform control over the system.
When computing the transition energy (Em) from the initial activity s0 to final activity sf over
some time T, we use an invertible controllability Gramian W to control the structural connec-
tivity network A from the set of network nodes B. The invertible controllability Gramian W is
defined as
ZT
W ¼
ð
eA T −τ
Þ B Btr eAtr T −τ
ð
Þ dτ
0
Optimal T was identified by grid searching between 0.001 and 10 and identifying the value
that maximized the magnitude of the Spearman correlation between the entries in the transi-
tion probability matrix and the entries in the transition energy matrix. The correlation between
transition probability and energy is expected to be negative since the brain prefers trajectories
through state space requiring minimal input energy given structural constraints, therefore
the brain tends to change less between states if the minimum required energy is greater. Here,
we identified an optimal T of 1, which yielded a correlation of −0.83 (p value < 0.001) (see
Supporting Information Figure S5), while the optimal T was 0.5 for the cc400 atlas with a
correlation coefficient of −0.91 (see Supporting Information Figure S12).
After computing the invertible controllability Gramian W and optimizing T, the transition
energy (Em) is then calculated as the quadratic product between the inverted controllability
Network Neuroscience
544
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
a
_
0
0
2
9
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network control theory in MS
Gramian W and the difference between eAT s0, which represents the activation at time T assum-
ing brain activity spreads in a network diffusion manner over the SC from the initial state s0,
and the final state sT:
(cid:2)
Em ¼ eAT s0 − sT
(cid:3)tr
(cid:2)
W −1 eAT s0 − sT
(cid:3)
:
Since there were six brain states, the transition energy matrix is of size 6 × 6 where off-diagonal
entries contain the energy required to transition between each pair of unique states s0 and sT,
where s0 ≠ sT, and diagonal entries contain persistence energy required to stay in the same
state (s0 = sT).
Entropy of Brain Activity
To investigate how disease burden (lesion load) and disability level in pwMS were related to
the amount of information contained in the brain activity signal, regional entropy was calcu-
lated directly on the BOLD time series. Denoting the regional BOLD time series in a region by
s(t) = (s(1),…,s(n)) where n is the number of the BOLD time series acquisition. We define two
template vectors of length m such as sm,i = (s(i), s(i + 1), …, s(i + m − 1)) and sm, j = (s(j), s(j + 1),…,
s(j + m − 1)). Entropy was calculated as the negative logarithm of the probability that if two
template vectors of length m have distance less than r (i.e., d[sm,i, sm,j] < r ) then two template
vectors of length m + 1 also have distance less than r (i.e., d[sm +1,i, sm +1,j] < r ) such as
− ln F m rð Þ
Gm rð Þ
where Fm(r ) is the number of template vector pairs having d[sm +1,i, sm +1,j ] < r, Gm(r ) is the
number of template vector pairs having d[sm,i, sm,j ] < r, and where d was the Euclidean dis-
tance (Richman & Moorman, 2000) (see Table 1). In our study, m = 3, as suggested in two
previous studies that computed entropy from resting-state fMRI data in controls (Z. Wang
et al., 2014) and in pwMS (Zhou et al., 2016). The parameter r was defined as 0.2 sd(s) where
sd(s) is the standard deviation of the time series (s), as recommended by previous work
(Tomčala, 2020). An individual’s global entropy was calculated as the average of their regional
entropies.
Mass Univariate Analysis
First, demographics and clinical variables were tested for differences between the three groups
(HC, pwMS who had no disability, and pwMS who had disability) using Chi-squared test for
qualitative variables and permutation test (David, 2008) for quantitative variables. Second,
fractional occupancy of and transition probabilities between brain states and regional entropy
were compared between groups via permutation test. P values from permutation test were
computed as the number of permutations that had a difference in means bigger than the orig-
inal difference. Group differences were considered significant when p < 0.05 after Benjamini–
Hochberg (BH) correction (Benjamini & Hochberg, 1995) for multiple comparisons. Finally,
the association between average regional (global) entropy and average (global) transition
energy was computed using Spearman’s rank correlation, while the association between
global entropy and log of lesion volume (transformed to ensure normality) was computed using
Pearson’s correlation. All statistical analyses and graphs were performed using R (https://www.r
-project.org) version 3.4.4 and Matlab (https://www.mathworks.com/) version R2020a.
Network Neuroscience
545
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
a
_
0
0
2
9
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network control theory in MS
Classification Analysis
Logistic regression with ridge regularization was used to classify (a) HC and pwMS without
disability, (b) HC versus pwMS with disability, and (c) pwMS without versus with disability,
using demographics/clinical information (age for HC vs. pwMS classification and age and
disease duration only for the classification of pwMS subgroups) and vectorized transition
energy matrices.
The models were trained with outer and inner loops of k-fold cross-validation (k = 5) to
optimize the hyperparameter (λ) and test model performance. The folds for both inner and
outer loops were stratified to ensure that each fold contained the same proportion of subjects
in the two classes as the original dataset. The inner loop (repeated over five different partitions
of the training dataset only) optimized the set of hyperparameters that maximized the valida-
tion set area under curve (AUC). A model was then fitted using the entire training dataset and
the optimal hyperparameters, which was then assessed on the hold-out test set from the outer
loop. The outer loop was repeated for 100 different random partitions of the data. The median
AUC (over all 5 folds × 100 iterations = 500 test sets) was calculated to assess the performance
of the models.
When the data contains class imbalance, models tend to favor the majority class. Due to
the class imbalance in our data (66 vs. 33 pwMS with no disability vs. evidence of disability),
the oversampling approach synthetic majority oversampling technique (SMOTE) (Chawla
et al., 2002) was used to obtain a balanced training dataset during cross-validation. SMOTE
compensates for imbalanced classes by creating synthetic examples using nearest neighbor
information and has been shown to be among the most robust and accurate methods with
which to control for imbalanced data (Santos et al., 2018).
The interpretation of the parameter coefficients from linear models is difficult when there
are colinearities in the data (Haufe et al., 2014). To mitigate this problem, we applied the
Haufe transform to the model coefficients estimated in each outer loop. Specifically, solving
logistic regression with ridge regularization yields model coefficient estimates
ð
wridge ¼ (cid:2)x þ λI
(cid:2)
Þ−1 μþ
x
− μ−
x
(cid:3)
where (cid:2)x is the covariance matrix of the input variables x in the training dataset, λ is the hyper-
parameter of the ridge classifier optimized in the inner loop for the training dataset, I is the
identity matrix with the same dimension as (cid:2)x, μþ
x are the average of the input variables
for the positive and negative classes in the training dataset. The Haufe transform for these
model coefficients is thus
x , and μ−
(cid:2)x (cid:2)x þ λI
ð
(cid:2)
Þ−1 μþ
x
− μ−
x
(cid:3)
var ^yð Þ
where ^y is the output of the model for the training dataset. The Haufe-transformed model
coefficients were averaged over all 5 folds × 100 iterations = 500 training sets, and the result
was used to interpret the relationship between TE and the three groups of individuals.
Data/Code Availability Statement
The de-identified data that support the findings of this study are available upon reasonable
request from the corresponding author. The codes that were used to generate the results
and figures are publicly available. Please see (a) https://github.com/cerent/MS-NCT/ for the
codes that were used for the classification analysis and figures and (b) the paper of Cornblath
Network Neuroscience
546
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
a
_
0
0
2
9
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network control theory in MS
et al. (2020) for the codes that were used for the clustering and network control theory
approach.
RESULTS
Patient Characteristics
Table 2 shows the subjects’ demographic and clinical information including sex, age, disease
duration, EDSS, MS phenotype, and lesion volume. Unsurprisingly, pwMS with disability were
older than both HCs and pwMS without disability (corrected p < 0.05) and had a trend toward
shorter disease duration compared to pwMS without disability (corrected p = 0.161). Sex was
not different across any of the groups. Phenotype and disability groups were not independent
(corrected p < 0.05), where CIS individuals were included in the without disability group and
PPMS individuals were included in the with disability group. The MS subgroups did not have a
significant difference in lesion volume (corrected p value > 0.05).
Brain States and Comparison of Dynamics
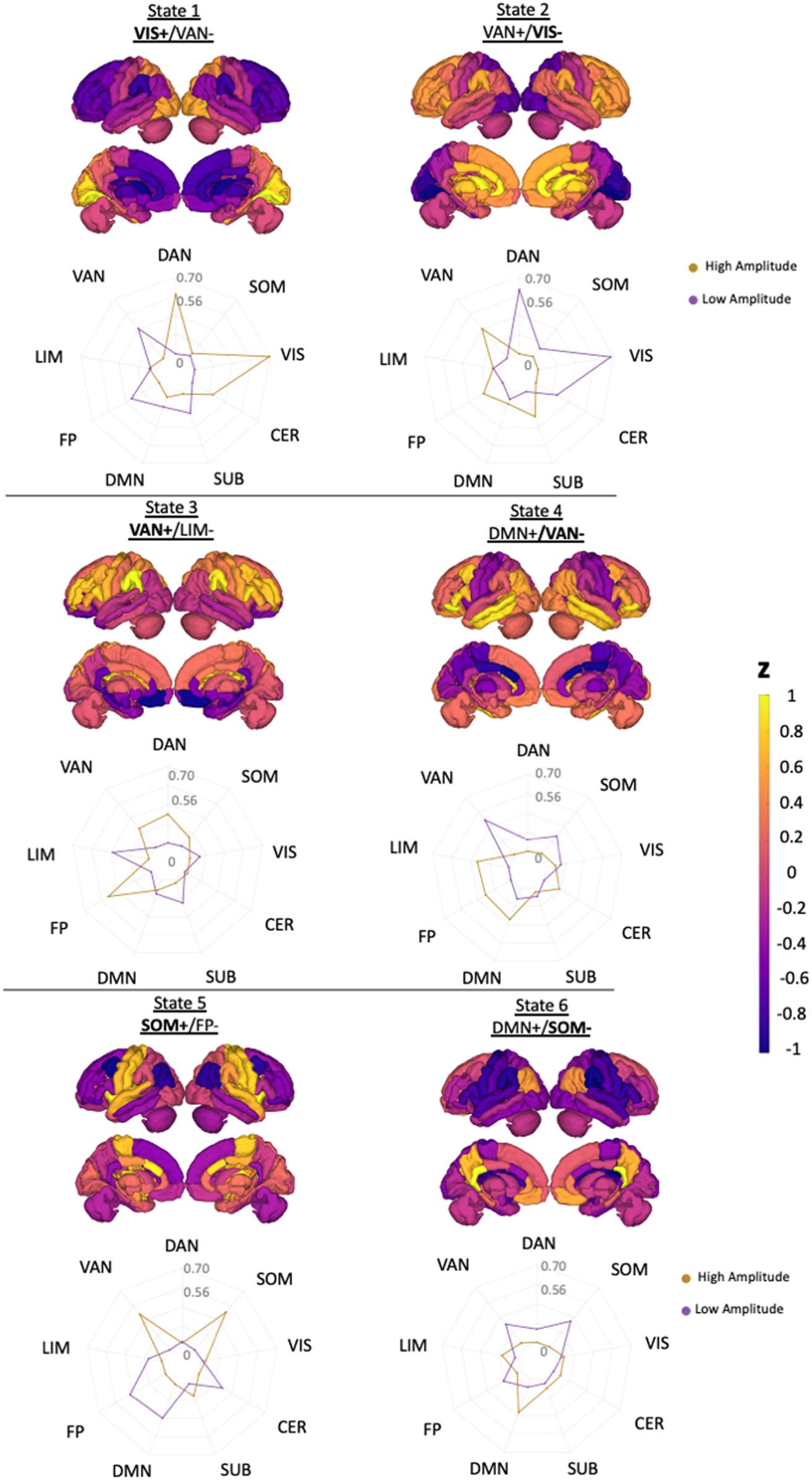
数字 2 shows the six brain states, consisting of three pairs of anticorrelated states with
high/low-amplitude activity in the visual network (VIS+/−), ventral attention network ( VAN+/−),
and somatomotor network (SOM+/−). The transition probability between dynamic states was not
significantly different between HC and any MS subgroup or between MS subgroups (corrected
p value > 0.05) (see Supporting Information Figure S3). The pwMS subgroups had a trend toward
shorter fractional occupancy in the SOM+ and longer fractional occupancy in the VAN+/− and
SOM− compared to HC. The pwMS with evidence of disability had a trend toward greater
fractional occupancy in the VIS+/−, VAN+, and SOM+ compared to those without disability.
然而, the differences were not significant for all comparisons (corrected p value > 0.05)
(see Supporting Information Figure S4).
Entropy of Brain Activity
数字 3 shows the t-statistics comparing regional entropy between HC and both MS subgroups
and between MS subgroups. There was no significant difference in regional entropy between
桌子 2.
Subject demographics and clinical information
Variable
年龄
HC (n = 19)
45 [35.55, 49.50]
女性 (%)
11 (55%)
Disease duration
EDSS
Phenotype
Lesion volume
(mm3)
pwMS without
失能 (n = 66)
40.50 [35, 50]
p value vs. HC = 0.88
pwMS with
失能 (n = 33)
56 [46, 58]
p value vs. HC = 0.005*
46 (70%)
p value vs. HC = 0.41
20 (61%)
p value vs. HC = 0.96
10 [7,14.75]
0 [0, 1]
13 [9, 17]
2 [2, 3]
7 CIS, 59 RRMS
28 RRMS, 5 PPMS
1,904 [726, 4111]
2,482 [453, 7788]
P value (pwMS without
disability vs. pwMS
with disability)
0.0001*
0.49
0.161
<2.2e−16*
<0.001*
0.0948
Note. Values are presented as median [1st, 3rd quantile] for the continuous variables and as number (percent) for sex. The HC versus pwMS without and with
disability as well as the two groups of pwMS were tested for differences; p values shown are corrected for multiple comparisons; * indicates significance.
Network Neuroscience
547
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
a
_
0
0
2
9
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network control theory in MS
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
a
_
0
0
2
9
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Brain states are visualized using glass brain and radial plots. The radial plots show the
mean of the positive and negative brain-state values over the Yeo functional network; DAN = dorsal
attention; VAN = ventral attention; LIM = limbic; FP = fronto-parietal; DMN = default-mode net-
work; SUB = subcortex; CER = cerebellum; VIS = visual; SOM = somatomotor. States were named
based on the network having the maximum magnitude in the radial plot.
Network Neuroscience
548
Network control theory in MS
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
a
_
0
0
2
9
2
p
d
.
t
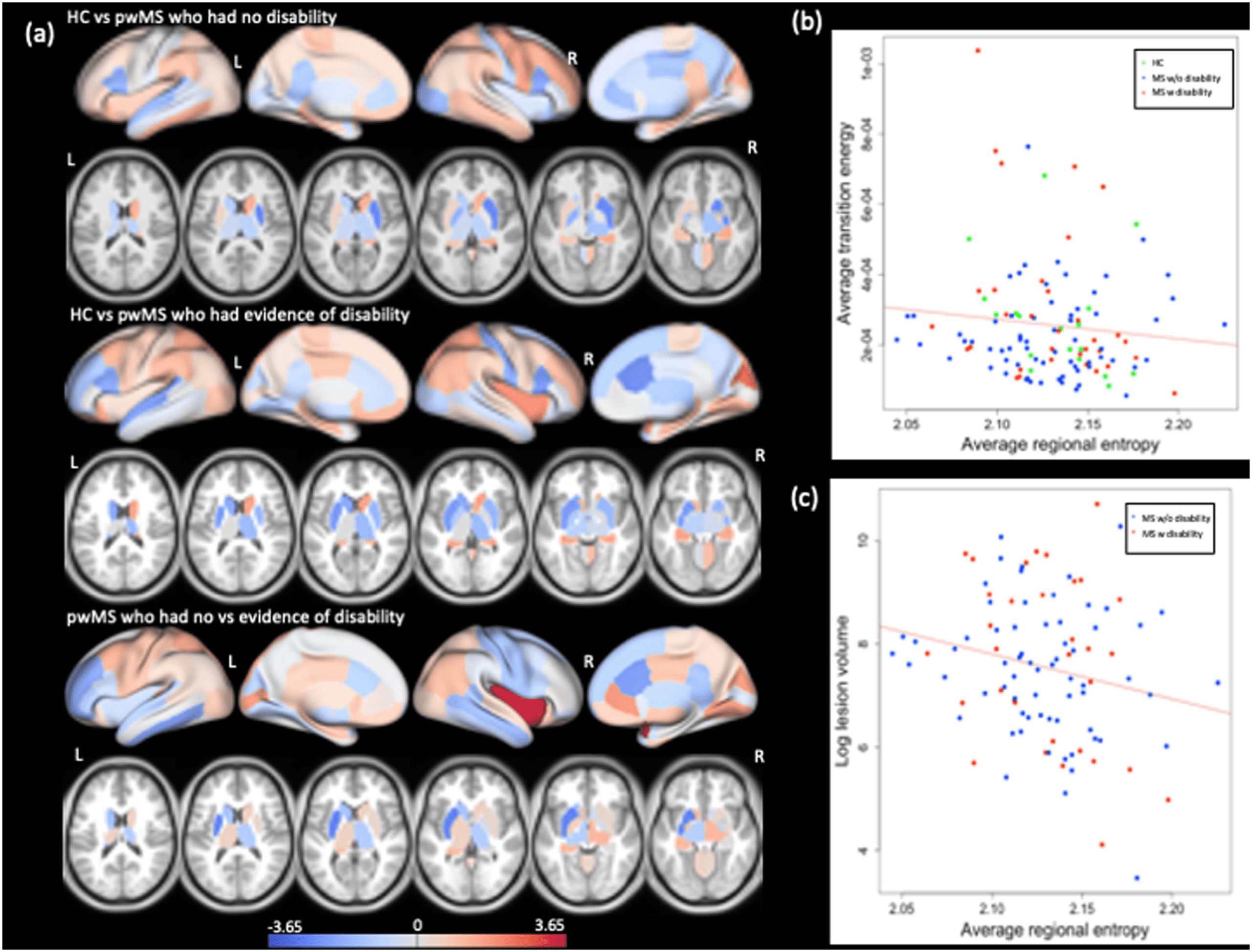
Figure 3. Group difference in entropy and correlation between entropy versus transition energy and lesion load. (A) Group differences in
regional entropy between HC versus pwMS without disability (top panel), HC versus pwMS with evidence of disability (middle panel), and
between two MS subgroups (bottom panel). The positive t statistics presented on the figure indicate greater average entropy in HC compared to
MS subgroups as well as greater average entropy in the pwMS with no disability compared to those with evidence of disability. The scatterplot
of global entropy versus (A) global transition energy and (B) log of lesion volume (in mm3). The entropy and energy were negatively correlated
with average transition energy (r = −0.17, p value = 0.04) and lesion volume (r = −0.20, p value = 0.03). Green points represent HC (only
present in the global energy plot), blue dots represent pwMS without disability, and red dots represent the pwMs with evidence of disability.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
HC and either MS subgroup (corrected p value > 0.05). 然而, entropy in the right insula,
which is in the VAN network, was significantly decreased in the pwMS with disability com-
pared to those without disability (corrected p value = 0.003). 数字 3 also shows the scatter
plot of global entropy and (A) global transition energy (average across all entries in the transi-
tion energy matrix) 和 (乙) log of lesion volume. Lower entropy was significantly correlated
with greater transition energy (r = −0.17, p value = 0.04) and greater lesion volume (r = −0.20,
p value = 0.03). The number of state transitions and overall transition energy are inversely
有关的 (higher transition energy demand = fewer transitions), 所以, unsurprisingly, lower entropy
was also significantly correlated with fewer overall state transitions (r = 0.30, p = 0.0003) (看
Supporting Information Figure S6).
网络神经科学
549
Network control theory in MS
数字 4. Assessing the relationship between transition energy and disability. Haufe-transformed coefficients for the logistic regression with
ridge regularization models classifying HC versus pwMS without disability, HC versus pwMS with disability, and pwMS without disability
versus pwMS with disability. VIS = visual; VAN = ventral attention network; SOM = somatomotor.
Group Classification Using State Transition Energies
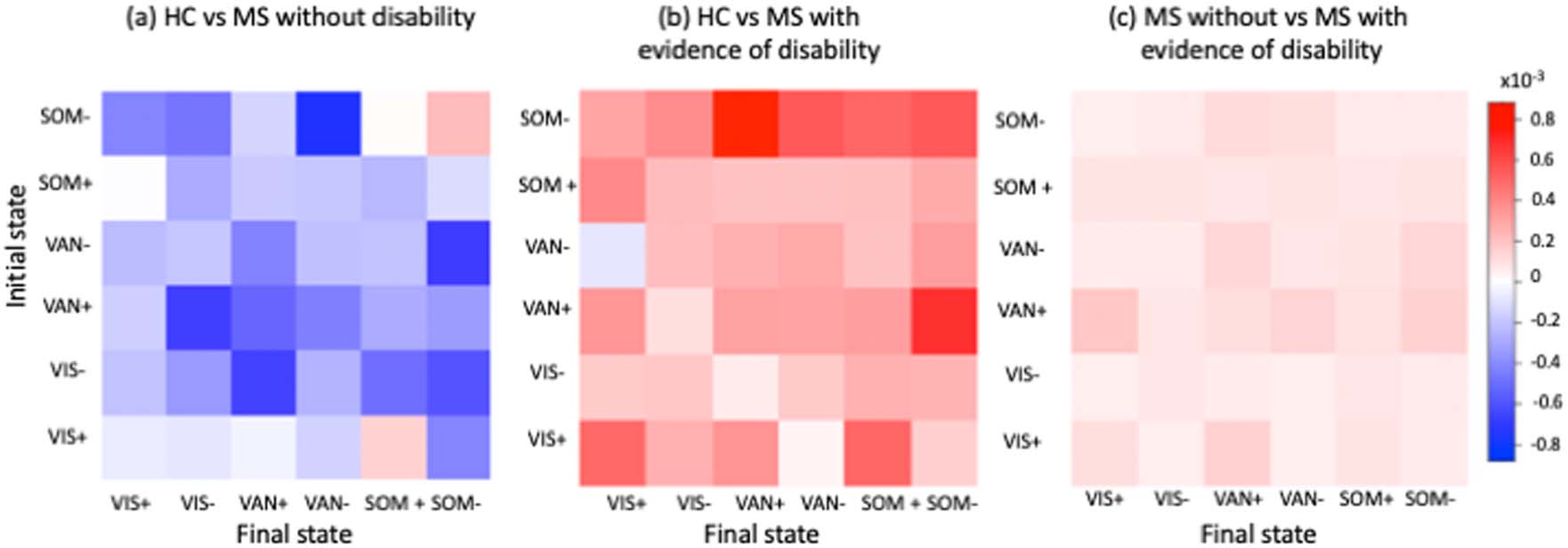
数字 4 shows the Haufe-transformed logistic regression model coefficients for classifying HC
versus pwMS without disability, HC versus pwMS with disability, and pwMS without versus
pwMS with disability; the models had an average AUC of 0.63, 0.62, 和 0.62, 分别.
全面的, greater transition energy was associated with pwMS with disability compared to both
HC and pwMS without disability, while lower transition energy was associated with pwMS
without disability compared to HC. Greater transition energies between VAN+ and SOM−
were associated with pwMS with disability compared to HC, while smaller transition energies
between SOM− and VAN− as well as between VIS− and VAN+ was associated with pwMS
without disability compared to HC. Greater transition energy out of VAN+ was most associated
with disability in pwMS compared to those without disability.
Robustness of Results
The analysis was replicated using the cc400 atlas; five optimal states were found: VIS+/−,
SOM+/−, and VAN− (see Supporting Information Figure S8), which were overlapping with
4/5 states found with the 86 region atlas. Like the original results, there was no significant differ-
ence in fractional occupancy between groups (corrected p value > 0.05) (see Supporting Infor-
mation Figure S9). There was a significant negative correlation between global transition energy
and global entropy (r = −0.16, p value = 0.03), while the correlation between global entropy and
lesion load was not significant. Results for the classification model were similar to those obtained
with the 86-region atlas include the following: (A) greater overall transition energy was associated
with pwMS who had evidence of disability compared to HC and (乙) greater transition energies
between SOM− and FP+ were associated with pwMS who had disability compared to HC.
讨论
In this study, we identified commonly occurring brain states in a group of HC and pwMS indi-
个人, investigated the energy required to transition between them using the NCT approach,
和, furthermore, associated these energetic measurements with lesion load and brain activity
entropy. Our main findings are (A) there were no group differences (HC vs. pwMS) 在里面
dynamics of the six recurring brain states, made up of high- and low-amplitude activity in
visual, ventral attention, and somatomotor networks; (乙) lower entropy of global brain activity
was associated with greater lesion load and larger global transition energy; 和 (C) pwMS
网络神经科学
550
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
A
_
0
0
2
9
2
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Network control theory in MS
without disability had decreased transition energies compared to controls, while pwMS with
disability had increased transition energy compared to both controls and pwMS without
失能. We hypothesized that this latter finding may indicate a shift in the patterns of brain
activity in the pwMS without disability that decreases transition energies, but as shift evolves
over the disease course, transition energies increase and disability occurs.
A recent study showed HCs had greater brain activity entropy than people with ADHD,
和, furthermore, that lower entropy in people with ADHD was related to worse symptom
scores (Sokunbi et al., 2013). 此外, decreased entropy was found in the activity of
regions containing a stroke lesion and their contralesional hemisphere homologues (Saenger
等人。, 2018). Our findings are consistent with these previous findings in that increased lesion
体积, and likely a weaker structural backbone that may contribute to increased state tran-
sition energy, relates to a decrease in the entropy of brain activity. One study found decreased
entropy in the right precentral and left parahippocampus and increased entropy in the left
superior temporal, right postcentral, and right transverse temporal in RRMS compared to
HC compared to controls, which is largely consistent with our regional results (Zhou et al.,
2016). 然而, the same study showed no significant correlation between overall lesion
volume and the averaged entropy computed for each voxel. The difference in our global
findings could be due to several factors, including differences in the pwMS cohort character-
主义, MRI acquisition and processing differences, and differences in the calculation of entropy
(voxel-wise as opposed to region-wise entropy in our study). 最后, greater reductions in
global transition energy from the placebo to psychedelic state (in controls) were shown to
be associated with larger increases in brain-state entropy (Singleton et al., 2022), which is con-
sistent with our findings of negative correlation between global entropy and transition energy
across HC and pwMS.
The brain dynamics have previously been studied by clustering regional fMRI time series
directly or sliding-window dynamic functional connectivity in HC (科恩, 2018; Cornblath
等人。, 2020; Zalesky et al., 2014) and in patient populations such as stroke (Bonkhoff et al.,
2021; L. 王等人。, 2010), schizophrenia (Braun et al., 2021; Damaraju et al., 2014; Rashid
等人。, 2016), and MS (d’Ambrosio et al., 2019; Rocca et al., 2019; Tozlu et al., 2021A). 尽管
many studies investigated the dynamics of sliding-window functional connectivity networks in
MS (d’Ambrosio et al., 2019; Rocca et al., 2019; Tozlu et al., 2021A), this approach has some
limitations as the window length and shift size need to be selected in a somewhat ad hoc
方式. In this study, we use an alternative approach to identify the dynamic brain states in
pwMS, 首次, by clustering the regional time series activity directly. 这种方法
has an advantage compared to other techniques as it is easy to implement, no ad hoc param-
eter estimation is required, and it uses each of the TRs as an individual data point which is
especially helpful with short scans where dFC/FC estimates may be unreliable. NCT and the
associated transition energy analysis has been applied previously in HC (Cornblath et al.,
2020; Cui et al., 2020; Deng et al., 2022; Gu et al., 2022), in pharmacological states, 和
in neurological/neuropsychiatric disorders such as schizophrenia and stroke (Braun et al.,
2021; Olafson et al., 2022; 乙. Tang et al., 2022). Using the NCT approach for the pwMS
allowed us to jointly capture the effects of MS pathology on SC and co-occurring shifts in
brain-state dynamics.
It has been shown in early MS there may be an upregulation of functional activity that ini-
tially acts to limit disability, followed by exhaustion of this functional compensation mecha-
nism as disability increases (Tommasin et al., 2018). Previous studies showed these adaptive
changes might be most prominent in motor and cognition-related networks, thus limiting clin-
ical measures of disability (李等人。, 2000) as well as cognitive impairment (Audoin et al.,
网络神经科学
551
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
A
_
0
0
2
9
2
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Network control theory in MS
2005) in MS. 而且, the extent of the compensatory mechanism was found to be nega-
tively correlated with the degree of tissue damage (Audoin et al., 2005; Rocca et al., 2002),
such that more damage was related to decreased compensation. Our study’s finding of overall
lower energetic demand in pwMS without disability compared to controls could be reflective
of this previously identified compensation mechanism, and our finding of higher energetic
demand in pwMS with disability compared to controls could be reflective of the previously
identified decrease in compensation mechanism with increased damage (and/or increased
damage to SCs).
The SOM and VAN states appeared to be the most important in the three classification
型号, with largest decreases in transition energy between SOM− and VAN− for pwMS with-
out disability compared to controls and largest decreases in transition energies between SOM−
and VAN+ for pwMS with disability compared to controls, and into/out of VAN+ for pwMS
without disability versus those with disability. The biggest contributions to the HC versus
pwMS with disability classification task were transitions between SOM− and VAN+. 我们的
recent study showed that greater functional connectivity in the SOM and VAN states was asso-
ciated with pwMS who had no disability compared to those with disability (Tozlu et al.,
2021A). In our current study, the SOM− state also had the highest amplitude default mode
网络 (DMN) 活动. The VAN and DMN are known to be highly anticorrelated since
the DMN is task-negative and the VAN is a task-positive network. Decreased anticorrelation
between DMN and attention networks was related to worse behavioral performance in HC
(Clare Kelly et al., 2008); 而且, increased functional connectivity between VAN and
DMN was observed in pwMS who had cognitive impairment compared to those without cog-
nitive impairment and HC (Huiskamp et al., 2021). Even though we did not have cognitive
scores for our cohort, previous studies have identified a strong association between disability
and cognitive impairment in MS (Lynch et al., 2005). Our results suggest that dysfunction of
the interaction between the VAN and DMN states may result in greater energetic demand
between these states in pwMS with evidence of disability compared to the other groups.
最后, our results also showed that greater transition energy between SOM+ and VIS− was
associated with pwMS who had disability. The most frequently observed disturbances are the
motor and visual impairments in pwMS, which are reflected in worse (更高) EDSS (Fuhr
等人。, 2001; Jasse et al., 2013). Our study shows, 首次, greater energetic demand
to transition between the motor and visual states compared to HC is associated with disability
in MS.
Limitations
One of the limitations of the study was in the quality of the MRI collected, as the fMRI acqui-
sition time was relatively short and had a longer TR (6 min, TR = 2.3 s) and the dMRI acqui-
sition had only a single b-value of 800 并且只有 55 方向. A longer fMRI acquisition may
result in finding other, less prevalent, dynamic states. 然而, Cornblath et al. (2020) applied
the same clustering method to 15-min fMRI scans and found five optimal states that all had an
appearance rate of approximately 2 per minute; 因此, we believe our relatively shorter scan
still represents the underlying state space well. Another limitation was the relatively low num-
ber of HCs compared to pwMS, which could result in an imbalance of the dynamic states. 我们
used a permutation test when comparing HC and pwMS to minimize the effect of this group
size imbalance. Larger lesion volume in some subjects may negatively impact coregistration to
MNI space, which is where the FCs were calculated. In our cohort, lesions were generally on
the small side, but we did visually inspect the MNI coregistration for quality and adjust if
需要的. Another limitation of the study was that most of the MS patients used in our study
网络神经科学
552
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
A
_
0
0
2
9
2
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Network control theory in MS
were of the RRMS phenotype, therefore the results may mostly represent disease processes
within this subtype. A future study that includes a similar number of all MS phenotypes such
as CIS, RRMS, PPMS, and SPMS is needed to capture the variability due to different level of
disability in MS. 最后, this study was cross-sectional; future studies will investigate how brain
dynamics change over time and relate to physical and cognitive decline.
结论
This is the first study using NCT to investigate how dynamic brain states and their associated
transition energies change in MS and, furthermore, to associate brain activity entropy with
lesion load and NCT-derived brain-state transition energies. As hypothesized, 我们发现
global brain activity entropy decreased with increasing lesion load and increasing transition
energies. Greater overall transition energies were associated with pwMS who had evidence of
disability compared to both HC and pwMS without disability, while decreased overall transi-
tion energies were associated with pwMS without disability compared to the other two groups.
Transition energies in ventral attention and somatomotor networks largely drove the group
classifications. This study, through NCT, sheds light on a possible mechanism of how
MS-related damage to the brain’s structural backbone can impact brain activity dynamics,
entropy and energetics.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00292.
作者贡献
Ceren Tozlu: 数据管理; 调查; 可视化; Writing – original draft. Sophie Card:
验证. Keith Jamison: 数据管理; 写作——复习 & 编辑. Susan Gauthier: Concep-
实体化; 数据管理; 监督; 写作——复习 & 编辑. Amy Kuceyeski: Concep-
实体化; 监督; 写作——复习 & 编辑.
资金信息
Amy Kuceyeski, NIH, 奖项ID: NS104634-01. Amy Kuceyeski, NIH, 奖项ID: NS102646-
01A1. Susan Gauthier, Weill Cornell Medicine, 奖项ID: TR000456-06. Ceren Tozlu,
National Multiple Sclerosis Society (https://dx.doi.org/10.13039/100000890), 奖项ID: FG-
2008-36976.
参考
艾伦, 乙. A。, Damaraju, E., Plis, S. M。, Erhardt, 乙. B., Eichele, T。, &
Calhoun, V. D. (2014). Tracking whole-brain connectivity
dynamics in the resting state. 大脑皮层, 24(3), 663–676.
https://doi.org/10.1093/cercor/bhs352, 考研: 23146964
安德森, J. L. R。, Graham, 中号. S。, Zsoldos, E., & 索蒂罗普洛斯, S. 氮.
(2016). Incorporating outlier detection and replacement into a
non-parametric framework for movement and distortion correc-
tion of diffusion MR images. 神经影像, 141, 556–572. https://
doi.org/10.1016/j.neuroimage.2016.06.058, 考研: 27393418
安德森, J. L. R。, & 索蒂罗普洛斯, S. 氮. (2016). An integrated
approach to correction for off-resonance effects and subject move-
ment in diffusion MR imaging. 神经影像, 125, 1063–1078.
https://doi.org/10.1016/j.neuroimage.2015.10.019, 考研:
26481672
Audoin, B., Van Au Duong, M。, Ranjeva, J. P。, Ibarrola, D ., Malikova, 我。,
Confort-Gouny, S。, Soulier, E., Viout, P。, Ali-Chérif, A。, Pelletier, J。, &
Cozzone, 磷. J. (2005). Magnetic resonance study of the influence of
tissue damage and cortical reorganization on PASAT performance at
网络神经科学
553
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
A
_
0
0
2
9
2
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Network control theory in MS
the earliest stage of multiple sclerosis. 人脑图谱, 24(3),
216–228. https://doi.org/10.1002/hbm.20083, 考研: 15543553
Barkhof, F. (2002). The clinico-radiological paradox in multiple scle-
rosis revisited. Current Opinion in Neurology, 15(3), 239–245.
https://doi.org/10.1097/00019052-200206000-00003, 考研:
12045719
Benjamini, Y。, & Hochberg, 是. (1995). Controlling the false discov-
ery rate: A practical and powerful approach to multiple testing.
Journal of the Royal Statistical Society: Series B (Methodological),
57(1), 289–300. https://doi.org/10.1111/j.2517-6161.1995
.tb02031.x
Bonkhoff, A. K., Schirmer, 中号. D ., Bretzner, M。, Etherton, M。,
多纳休, K., Tuozzo, C。, Nardin, M。, Giese, A.-K., 吴, 奥。,
Calhoun, V. D ., Grefkes, C。, & Rost, 氮. S. (2021). Abnormal
dynamic functional connectivity is linked to recovery after acute
ischemic stroke. 人脑图谱, 42(7), 2278–2291.
https://doi.org/10.1002/hbm.25366, 考研: 33650754
布劳恩, U。, Harneit, A。, Pergola, G。, Menara, T。, Schäfer, A。, 贝策尔,
右. F。, Zang, Z。, Schweiger, J. 我。, 张, X。, 施瓦茨, K., 陈, J。,
Blasi, G。, Bertolino, A。, Durstewitz, D ., Pasqualetti, F。, 施瓦茨,
E., Meyer-Lindenberg, A。, Bassett, D. S。, & Tost, H. (2021). Brain
network dynamics during working memory are modulated by
dopamine and diminished in schizophrenia. Nature Communi-
阳离子, 12(1), 3478. https://doi.org/10.1038/s41467-021-23694-9,
考研: 34108456
Buyukturkoglu, K., 曾, D ., Bharadwaj, S。, Tozlu, C。, Mormina, E.,
Igwe, K. C。, 李, S。, Habeck, C。, Brickman, A. M。, Riley, C. S。,
De Jager, 磷. L。, Sumowski, J. F。, & Leavitt, V. 中号. (2020). Classifying
multiple sclerosis patients on the basis of SDMT performance
using machine learning. Multiple Sclerosis Journal, 27(1),
107–116. https://doi.org/10.1177/1352458520958362,
考研: 33146069
Calhoun, V. D ., 磨坊主, R。, Pearlson, G。, & Adali, 时间. (2014). 这
chronnectome: Time-varying connectivity networks as the next
frontier in fMRI data discovery. 神经元, 84(2), 262–274.
https://doi.org/10.1016/j.neuron.2014.10.015, 考研:
25374354
Carhart-Harris, 右. L。, 水蛭, R。, Hellyer, 磷. J。, Shanahan, M。,
Feilding, A。, Tagliazucchi, E., Chialvo, D. R。, & Nutt, D.
(2014). The entropic brain: A theory of conscious states informed
by neuroimaging research with psychedelic drugs. Frontiers in
Human Neuroscience, 8, 20. https://doi.org/10.3389/fnhum
.2014.00020, 考研: 24550805
Chawla, 氮. 五、, Bowyer, K. W., 大厅, L. 奥。, & Kegelmeyer, 瓦. 磷.
(2002). SMOTE: Synthetic minority over-sampling technique.
Journal of Artificial Intelligence Research, 16, 321–357. https://
doi.org/10.1613/jair.953
Clare Kelly, A. M。, Uddin, L. Q., Biswal, 乙. B., Castellanos, F. X。, &
Milham, 中号. 磷. (2008). Competition between functional brain
networks mediates behavioral variability. 神经影像, 39(1),
527–537. https://doi.org/10.1016/j.neuroimage.2007.08.008,
考研: 17919929
科恩, J. 右. (2018). The behavioral and cognitive relevance of
time-varying, dynamic changes in functional connectivity. Neuro-
图像, 180(Pt B), 515–525. https://doi.org/10.1016/j.neuroimage
.2017.09.036, 考研: 28942061
Cornblath, 乙. J。, Ashourvan, A。, Kim, J. Z。, 贝策尔, 右. F。, Ciric, R。,
Adebimpe, A。, Baum, G. L。, 他, X。, Ruparel, K., 摩尔, 时间. M。,
Gur, 右. C。, Gur, 右. E., 筱原, 右. T。, Roalf, D. R。, Satterthwaite,
时间. D ., & Bassett, D. S. (2020). Temporal sequences of brain
activity at rest are constrained by white matter structure and
modulated by cognitive demands. Communications Biology,
3(1), 261. https://doi.org/10.1038/s42003-020-0961-x, 考研:
32444827
Craddock, 右. C。, James, G. A。, Holtzheimer, 磷. E., 胡, X. P。, &
Mayberg, H. S. (2012). A whole brain fMRI atlas generated via
spatially constrained spectral clustering. 人脑图谱,
33(8), 1914–1928. https://doi.org/10.1002/hbm.21333, 考研:
21769991
Cui, Z。, Stiso, J。, Baum, G. L。, Kim, J. Z。, Roalf, D. R。, 贝策尔,
右. F。, Gu, S。, 鲁, Z。, Xia, C. H。, 他, X。, Ciric, R。, Oathes,
D. J。, 摩尔, 时间. M。, 筱原, 右. T。, Ruparel, K., Davatzikos,
C。, Pasqualetti, F。, Gur, 右. E., Gur, 右. C。, … Satterthwaite,
时间. D. (2020). Optimization of energy state transition trajectory
supports the development of executive function during youth.
亿生活, 9, e53060. https://doi.org/10.7554/eLife.53060, 考研:
32216874
Damaraju, E., 艾伦, 乙. A。, Belger, A。, Ford, J. M。, McEwen, S。,
Mathalon, D. H。, Mueller, 乙. A。, Pearlson, G. D ., Potkin, S. G。,
Preda, A。, 车工, J. A。, Vaidya, J. G。, van Erp, 时间. G。, & Calhoun,
V. D. (2014). Dynamic functional connectivity analysis reveals
transient states of dysconnectivity in schizophrenia. 神经影像:
Clinical, 5, 298–308. https://doi.org/10.1016/j.nicl.2014.07.003,
考研: 25161896
d’Ambrosio, A。, Valsasina, P。, Gallo, A。, De Stefano, N。, Pareto, D .,
Barkhof, F。, Ciccarelli, 奥。, Enzinger, C。, Tedeschi, G。, Stromillo,
中号. L。, Arévalo, 中号. J。, Hulst, H. E., Muhlert, N。, Koini, M。, Filippi,
M。, & Rocca, 中号. A. (2019). Reduced dynamics of functional
connectivity and cognitive impairment in multiple sclerosis.
Multiple Sclerosis Journal, 26(4), 476–488. https://doi.org/10
.1177/1352458519837707, 考研: 30887862
大卫, H. A. (2008). The beginnings of randomization tests. 阿梅尔-
ican Statistician, 62(1), 70–72. https://doi.org/10.1198
/000313008X269576
Deng, S。, 李, J。, 杨, 乙. 时间. T。, & Gu, S. (2022). Control theory illus-
trates the energy efficiency in the dynamic reconfiguration of
功能连接. Communications Biology, 5(1), 295.
https://doi.org/10.1038/s42003-022-03196-0, 考研:
35365757
Filippi, M。, Agosta, F。, 斯皮内利, 乙. G。, & Rocca, 中号. A. (2013). 图像-
ing resting state brain function in multiple sclerosis. 杂志
Neurology, 260(7), 1709–1713. https://doi.org/10.1007/s00415
-012-6695-z, 考研: 23052604
菲舍尔, B., & 戴尔, A. 中号. (2000). Measuring the thickness of the
human cerebral cortex from magnetic resonance images. Pro-
ceedings of the National Academy of Sciences of the United
States of America, 97(20), 11050–11055. https://doi.org/10
.1073/pnas.200033797, 考研: 10984517
Fuchs, 时间. A。, Schoonheim, 中号. M。, Broeders, 时间. A. A。, Hulst, H. E.,
Weinstock-Guttman, B., Jakimovski, D ., Silver, J。, Zivadinov, R。,
Geurts, J. J. G。, Dwyer, 中号. G。, & Benedict, 右. H. 乙. (2022). Func-
tional network dynamics and decreased conscientiousness in mul-
tiple sclerosis. Journal of Neurology, 269(5), 2696–2706. https://
doi.org/10.1007/s00415-021-10860-8, 考研: 34713325
Fuhr, P。, Borggrefe-Chappuis, A。, Schindler, C。, & Kappos, L.
(2001). Visual and motor evoked potentials in the course of
网络神经科学
554
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
A
_
0
0
2
9
2
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Network control theory in MS
multiple sclerosis. Brain, 124(11), 2162–2168. https://doi.org/10
.1093/brain/124.11.2162, 考研: 11673318
Gu, S。, Fotiadis, P。, Parkes, L。, Xia, C. H。, Gur, 右. C。, Gur, 右. E.,
Roalf, D. R。, Satterthwaite, 时间. D ., & Bassett, D. S. (2022). 网-
work controllability mediates the relationship between rigid
structure and flexible dynamics. 网络神经科学, 6(1),
275–297. https://doi.org/10.1162/netn_a_00225, 考研:
36605890
Gu, S。, Pasqualetti, F。, Cieslak, M。, Telesford, 问. K., 于, A. B., 卡恩,
A. E., Medaglia, J. D ., Vettel, J. M。, 磨坊主, 中号. B., Grafton, S. T。, &
Bassett, D. S. (2015). Controllability of structural brain networks.
Nature Communications, 6(1), 8414. https://doi.org/10.1038
/ncomms9414, 考研: 26423222
Hallquist, 中号. N。, Hwang, K., & 露娜, 乙. (2013). The nuisance of
nuisance regression: Spectral misspecification in a common
approach to resting-state fMRI preprocessing reintroduces noise
and obscures functional connectivity. 神经影像, 82, 208–225.
https://doi.org/10.1016/j.neuroimage.2013.05.116, 考研:
23747457
Haufe, S。, Meinecke, F。, Görgen, K., Dähne, S。, Haynes, J. D .,
Blankertz, B., & Bießmann, F. (2014). On the interpretation of
weight vectors of linear models in multivariate neuroimaging.
神经影像, 87, 96–110. https://doi.org/10.1016/j.neuroimage
.2013.10.067, 考研: 24239590
Huiskamp, M。, Eijlers, A. J. C。, Broeders, 时间. A. A。, Pasteuning, J。,
Dekker, 我。, Uitdehaag, 乙. 中号. J。, Barkhof, F。, Wink, A.-M.,
Geurts, J. J. G。, Hulst, H. E., & Schoonheim, 中号. 中号. (2021). 朗-
gitudinal network changes and conversion to cognitive impair-
ment in multiple sclerosis. Neurology, 97(8), e794–e802.
https://doi.org/10.1212/ WNL.0000000000012341, 考研:
34099528
Jasse, L。, Vukusic, S。, Durand-Dubief, F。, Vartin, C。, Piras, C。,
Bernard, M。, Pélisson, D ., Confavreux, C。, Vighetto, A。, &
Tilikete, C. (2013). Persistent visual impairment in multiple
sclerosis: Prevalence, mechanisms and resulting disability.
Multiple Sclerosis, 19(12), 1618–1626. https://doi.org/10.1177
/1352458513479840, 考研: 23462348
Kuceyeski, A。, Shah, S。, Dyke, J. P。, Bickel, S。, Abdelnour, F。, Schiff,
氮. D ., Voss, H. U。, & Raj, A. (2016). The application of a math-
ematical model linking structural and functional connectomes in
severe brain injury. 神经影像: Clinical, 11, 635–647. https://
doi.org/10.1016/j.nicl.2016.04.006, 考研: 27200264
李, M。, Reddy, H。, Johansen-Berg, H。, Pendlebury, S。, 詹金森,
M。, 史密斯, S。, Palace, J。, & Matthews, 磷. 中号. (2000). The motor
cortex shows adaptive functional changes to brain injury from
multiple sclerosis. Annals of Neurology, 47(5), 606–613. https://
doi.org/10.1002/1531-8249(200005)47:5<606::AID-ANA8>3.0
.一氧化碳;2-L, 考研: 10805331
Leonardi, N。, Richiardi, J。, Gschwind, M。, Simioni, S。, Annoni,
J.-M。, Schluep, M。, Vuilleumier, P。, & Van De Ville, D. (2013).
Principal components of functional connectivity: A new
approach to study dynamic brain connectivity during rest. 新-
roImage, 83, 937–950. https://doi.org/10.1016/j.neuroimage
.2013.07.019, 考研: 23872496
林奇, S. G。, Parmenter, 乙. A。, & Denney, D. 右. (2005). The asso-
ciation between cognitive impairment and physical disability in
multiple sclerosis. Multiple Sclerosis, 11(4), 469–476. https://土井
.org/10.1191/1352458505ms1182oa, 考研: 16042232
阮, X. V. (2021). The Adjusted Mutual Information. MATLAB
Central File Exchange. https://www.mathworks.com/matlabcentral
/fileexchange/33144-the-adjusted-mutual-information
Olafson, E., Russello, G。, Jamison, K. W., 刘, H。, 王, D ., Bruss,
J. E., Boes, A. D ., & Kuceyeski, A. (2022). Frontoparietal network
activation is associated with motor recovery in ischemic stroke
患者. Communications Biology, 5(1), 993. https://doi.org/10
.1038/s42003-022-03950-4, 考研: 36131012
Pincus, S. 中号. (1991). Approximate entropy as a measure of system
复杂. 美国国家科学院院刊,
88(6), 2297–2301. https://doi.org/10.1073/pnas.88.6.2297,
考研: 11607165
Rashid, B., Arbabshirani, 中号. R。, Damaraju, E., Cetin, 中号. S。, 磨坊主,
R。, Pearlson, G. D ., & Calhoun, V. D. (2016). Classification of
schizophrenia and bipolar patients using static and dynamic
resting-state fMRI brain connectivity. 神经影像, 134,
645–657. https://doi.org/10.1016/j.neuroimage.2016.04.051,
考研: 27118088
Richman, J. S。, & Moorman, J. 右. (2000). Physiological time-series
analysis using approximate and sample entropy. American Jour-
nal of Physiology: Heart and Circulatory Physiology, 278(6),
H2039–H2049. https://doi.org/10.1152/ajpheart.2000.278.6
.H2039, 考研: 10843903
Rocca, 中号. A。, Falini, A。, Colombo, B., Scotti, G。, Comi, G。, &
Filippi, 中号. (2002). Adaptive functional changes in the cerebral
cortex of patients with nondisabling multiple sclerosis correlate
with the extent of brain structural damage. Annals of Neurology,
51(3), 330–339. https://doi.org/10.1002/ana.10120, 考研:
11891828
Rocca, 中号. A。, Hidalgo de La Cruz, M。, Valsasina, P。, Mesaros, S。,
Martinovic, 五、, Ivanovic, J。, Drulovic, J。, & Filippi, 中号. (2019).
Two-year dynamic functional network connectivity in clinically iso-
lated syndrome. Multiple Sclerosis Journal, 26(6), 645–658. https://
doi.org/10.1177/1352458519837704, 考研: 30887875
Saenger, V. M。, Ponce-Alvarez, A。, Adhikari, M。, 哈格曼, P。,
德科, G。, & 科尔贝塔, 中号. (2018). Linking entropy at rest with
the underlying structural connectivity in the healthy and lesioned
脑. 大脑皮层, 28(8), 2948–2958. https://doi.org/10
.1093/cercor/bhx176, 考研: 28981635
Santos, 中号. S。, Soares, J. P。, Abreu, 磷. H。, Araujo, H。, & Santos, J.
(2018). Cross-validation for imbalanced datasets: Avoiding over-
optimistic and overfitting approaches [Research Frontier]. IEEE
Computational Intelligence Magazine, 13(4), 59–76. https://土井
.org/10.1109/MCI.2018.2866730
Sbardella, E., Petsas, N。, Tona, F。, & Pantano, 磷. (2015). Resting-
state fMRI in MS: General concepts and brief overview of its
应用. BioMed Research International, 2015, 212693.
https://doi.org/10.1155/2015/212693, 考研: 26413509
Singleton, S. P。, Luppi, A. 我。, Carhart-Harris, 右. L。, Cruzat, J。,
Roseman, L。, Nutt, D. J。, 德科, G。, 克林格尔巴赫, 中号. L。,
Stamatakis, 乙. A。, & Kuceyeski, A. (2022). Receptor-informed
network control theory links LSD and psilocybin to a flattening
of the brain’s control energy landscape. Nature Communications,
13(1), 5812. https://doi.org/10.1038/s41467-022-33578-1,
考研: 36192411
史密斯, 右. E., 图尔尼耶, J. D ., 卡拉曼特, F。, & 康纳利, A. (2015).
SIFT2: Enabling dense quantitative assessment of brain white
matter connectivity using streamlines tractography. 神经影像,
网络神经科学
555
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
A
_
0
0
2
9
2
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Network control theory in MS
119, 338–351. https://doi.org/10.1016/j.neuroimage.2015.06
.092, 考研: 26163802
Sokunbi, 中号. 奥。, Fung, W., Sawlani, 五、, Choppin, S。, 林登, D. 乙. J。,
& Thome, J. (2013). Resting state fMRI entropy probes complexity
of brain activity in adults with ADHD. Psychiatry Research: 新-
roimaging, 214(3), 341–348. https://doi.org/10.1016/j
.pscychresns.2013.10.001, 考研: 24183857
Stiso, J。, Khambhati, A. N。, Menara, T。, 卡恩, A. E., 斯坦因, J. M。, 这,
S. R。, Gorniak, R。, Tracy, J。, 一点, B., 戴维斯, K. A。, Pasqualetti, F。,
Lucas, 时间. H。, & Bassett, D. S. (2019). White matter network archi-
tecture guides direct electrical stimulation through optimal state
transitions. Cell Reports, 28(10), 2554–2566. https://doi.org/10
.1016/j.celrep.2019.08.008, 考研: 31484068
唐, B., 张, W., Deng, S。, 刘, J。, 胡, N。, 锣, Q., Gu, S。, &
Lui, S. (2022). Age-associated network controllability changes in
first episode drug-naïve schizophrenia. BMC Psychiatry, 22(1),
26. https://doi.org/10.1186/s12888-021-03674-5, 考研:
35012507
唐, E., Giusti, C。, Baum, G. L。, Gu, S。, Pollock, E., 卡恩, A. E.,
Roalf, D. R。, 摩尔, 时间. M。, Ruparel, K., Gur, 右. C。, Gur, 右. E.,
Satterthwaite, 时间. D ., & Bassett, D. S. (2017). Developmental
increases in white matter network controllability support a grow-
ing diversity of brain dynamics. Nature Communications, 8(1),
1252. https://doi.org/10.1038/s41467-017-01254-4, 考研:
29093441
Tomčala, J. (2020). New fast ApEn and SampEn entropy algorithms
implementation and their application to supercomputer power
consumption. Entropy, 22(8), 863. https://doi.org/10.3390
/e22080863, 考研: 33286634
Tommasin, S。, de Giglio, L。, Ruggieri, S。, Petsas, N。, Giannì, C。,
Pozzilli, C。, & Pantano, 磷. (2018). Relation between functional
connectivity and disability in multiple sclerosis: A non-linear
模型. Journal of Neurology, 265(12), 2881–2892. https://土井
.org/10.1007/s00415-018-9075-5, 考研: 30276520
图尔尼耶, J.-D., 史密斯, R。, Raffelt, D ., Tabbara, R。, 多霍兰德, T。,
Pietsch, M。, Christiaens, D ., 约里森, B., Yeh, C. H。, & 康纳利,
A. (2019). MRtrix3: A fast, flexible and open software framework
for medical image processing and visualisation. 神经影像, 202,
116137. https://doi.org/10.1016/j.neuroimage.2019.116137,
考研: 31473352
图尔尼耶, J.-D., 卡拉曼特, F。, & 康纳利, A. (2010). Improved prob-
abilistic streamlines tractography by 2nd order integration over
fibre orientation distributions. 国际会议录
Society for Magnetic Resonance in Medicine, 抽象的 1670.
图尔尼耶, J.-D., 卡拉曼特, F。, & 康纳利, A. (2012). MRtrix: Diffu-
sion tractography in crossing fiber regions. International Journal
of Imaging Systems and Technology, 22(1), 53–66. https://doi.org
/10.1002/ima.22005.
Tozlu, C。, Jamison, K., Gauthier, S. A。, & Kuceyeski, A. (2021A).
Dynamic functional connectivity better predicts disability than
structural and static functional connectivity in people with mul-
tiple sclerosis. Frontiers in Neuroscience, 15, 763966. https://土井
.org/10.3389/fnins.2021.763966, 考研: 34966255
Tozlu, C。, Jamison, K., Gu, Z。, Gauthier, S. A。, & Kuceyeski, A.
(2021乙). Estimated connectivity networks outperform observed
connectivity networks when classifying people with multiple
sclerosis into disability groups. 神经影像: Clinical, 32, 102827.
https://doi.org/10.1016/j.nicl.2021.102827, 考研: 34601310
van Geest, Q., Douw, L。, van ‘t Klooster, S。, Leurs, C. E., Genova,
H. M。, Wylie, G. R。, Steenwijk, 中号. D ., Killestein, J。, Geurts,
J. J. G。, & Hulst, H. 乙. (2018A). Information processing speed in
multiple sclerosis: Relevance of default mode network dynamics.
神经影像: Clinical, 19, 507–515. https://doi.org/10.1016/j
.nicl.2018.05.015, 考研: 29984159
van Geest, Q., Hulst, H. E., Meijer, K. A。, Hoyng, L。, Geurts, J. J. G。,
& Douw, L. (2018乙). The importance of hippocampal dynamic
connectivity in explaining memory function in multiple sclerosis.
Brain and Behavior, 8(5), e00954. https://doi.org/10.1002/brb3
.954, 考研: 29761008
王, L。, 于, C。, 陈, H。, Qin, W., 他, Y。, Fan, F。, 张, Y。,
王, M。, 李, K., Zang, Y。, 伍德沃德, 时间. S。, & 朱, C. (2010).
Dynamic functional reorganization of the motor execution net-
work after stroke. Brain, 133(Pt 4), 1224–1238. https://doi.org
/10.1093/brain/awq043, 考研: 20354002
王, Z。, 李, Y。, Childress, A. R。, & Detre, J. A. (2014). Brain
entropy mapping using fMRI. 公共图书馆一号, 9(3), e89948. https://
doi.org/10.1371/journal.pone.0089948, 考研: 24657999
Whitfield-Gabrieli, S。, & Nieto-Castanon, A. (2012). Conn: A func-
tional connectivity toolbox for correlated and anticorrelated
brain networks. Brain Connectivity, 2(3), 125–141. https://土井
.org/10.1089/brain.2012.0073, 考研: 22642651
杨, 乙. 时间. T。, 克里宁, F. M。, 墓, J。, 肥皂, 中号. R。, 军队, D .,
霍林斯黑德, M。, 罗夫曼, J. L。, 斯莫勒, J. W., Zöllei, L。, 波利梅尼,
J. R。, 菲舍尔, B., 刘, H。, & 巴克纳, 右. L. (2011). The organization of
the human cerebral cortex estimated by intrinsic functional
连接性. 神经生理学杂志, 106(3), 1125–1165.
https://doi.org/10.1152/jn.00338.2011, 考研: 21653723
扎莱斯基, A。, 假如, A。, Cocchi, L。, Gollo, L. L。, & Breakspear, 中号.
(2014). Time-resolved resting-state brain networks. 会议记录
of the National Academy of Sciences of the United States of
美国, 111(28), 10341–10346. https://doi.org/10.1073/pnas
.1400181111, 考研: 24982140
周, F。, Zhuang, Y。, 锣, H。, Zhan, J。, Grossman, M。, & 王, Z.
(2016). Resting state brain entropy alterations in relapsing remit-
ting multiple sclerosis. 公共图书馆一号, 11(1), e0146080. https://土井
.org/10.1371/journal.pone.0146080, 考研: 26727514
网络神经科学
556
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
2
5
3
9
2
1
1
8
4
4
2
n
e
n
_
A
_
0
0
2
9
2
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3