研究
Nonoptimal component placement of the human
connectome supports variable brain dynamics
Christopher James Hayward1,2, Siyu Huo3, Xue Chen4,5,6, and Marcus Kaiser7,8
1Leeds Institute for Data Analytics, University of Leeds, Leeds, 英国
2Leeds Institute of Cardiovascular and Metabolic Medicine, University of Leeds, Leeds, 英国
3State Key Laboratory of Precision Spectroscopy and School of Physics and Electronic Science,
East China Normal University, 磷. 右. 中国
4Institute for Digital Medicine and Computer-Assisted Surgery, Qingdao University, Qingdao, 中国
5Shandong Provincial Key Laboratory of Digital Medicine and Computer-Assisted Surgery,
Affiliated Hospital of Qingdao University, Qingdao, 中国
6Shandong College Collaborative Innovation Center of Digital Medicine in Clinical Treatment and Nutrition Health,
Qingdao, 中国
7NIHR Nottingham Biomedical Research Centre, School of Medicine, University of Nottingham, 英国
8Rui Jin Hospital, Shanghai Jiao Tong University, Shanghai, 中国
关键词: Component placement optimization, Spatial networks, Wiring minimization, 结构性
连接性, Macroconnectome, Metastability, 认识
抽象的
Neural systems are shaped by multiple constraints, balancing region communication with
the cost of establishing and maintaining physical connections. It has been suggested that the
lengths of neural projections be minimized, reducing their spatial and metabolic impact on
有机体. 然而, long-range connections are prevalent in the connectomes across
various species, 因此, rather than rewiring connections to reduce length, an alternative
theory proposes that the brain minimizes total wiring length through a suitable positioning
of regions, termed component placement optimization. Previous studies in nonhuman
primates have refuted this idea by identifying a nonoptimal component placement, 在哪里
a spatial rearrangement of brain regions in silico leads to a reduced total wiring length.
这里, for the first time in humans, we test for component placement optimization. 我们
show a nonoptimal component placement for all subjects in our sample from the Human
Connectome Project (N= 280; aged 22–30 years; 138 女性), suggesting the presence
of constraints—such as the reduction of processing steps between regions—that compete
with the elevated spatial and metabolic costs. 此外, by simulating communication
between brain regions, we argue that this suboptimal component placement supports
dynamics that benefit cognition.
作者总结
The anatomical organization of the brain is shaped by competing constraints for improving
brain function while reducing the costs for connectome wiring. Concerning this trade-off,
we find that regions within the human brain are not positioned to minimize the total length
of their connections. This nonoptimal organization is mainly attributed to frontal and
occipital/parietal lobes, with connections between them acting as shortcuts allowing distant
brain areas to communicate. By using a model of brain activity, we argue that this suboptimal
spatial arrangement of the connectome promotes fluctuations in brain activity, 使能
the brain to undertake flexible behavioral responses. Altogether, this highlights that brain
开放访问
杂志
引文: Hayward, C. J。, Huo, S。, 陈,
X。, & Kaiser, 中号. (2023). Nonoptimal
component placement of the human
connectome supports variable brain
dynamics. 网络神经科学, 7(1),
254–268. https://doi.org/10.1162/netn_a
_00282
DOI:
https://doi.org/10.1162/netn_a_00282
支持信息:
https://doi.org/10.1162/netn_a_00282
已收到: 12 可能 2022
公认: 28 九月 2022
利益争夺: 作者有
声明不存在竞争利益
存在.
通讯作者:
Marcus Kaiser
Marcus.Kaiser@nottingham.ac.uk
处理编辑器:
莎拉·马尔登
版权: © 2022
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
A
_
0
0
2
8
2
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Nonoptimal component placement of the human connectome
Connectome:
The network of neural connections in
大脑.
Component placement optimization
(CPO):
The theory that brain regions are
positioned to minimize total wiring
length.
结构, while spatially suboptimal, may offer dynamic advantages that support effective
认识.
介绍
The brain consists of numerous spatially distributed, functionally distinct regions. The map of
structural connections between brain regions—the human connectome (斯波恩斯, 托诺尼, &
Kötter, 2005)—encompasses long-range links between distant regions, supporting integration,
and short-range links mainly within network modules supporting local processing (Watts &
Strogatz, 1998). Such an arrangement reduces both the transmission time in terms of the num-
ber of intermediate regions on pathways and the total wiring length of the network (Bassett &
布莫尔, 2006; 布莫尔 & 斯波恩斯, 2009; 哈格曼等人。, 2008; 希尔格塔格 & Kaiser, 2004;
Seguin, van den Heuvel, & 扎莱斯基, 2018; 斯波恩斯, Chialvo, Kaiser, & 希尔格塔格, 2004), 奥尔加-
nization thought to facilitate effective cognition (科恩 & D’Esposito, 2016; 斯波恩斯, 2013).
Brain network structure and dynamics are strongly linked with different hierarchical organiza-
的 (Huo, Zou, Kaiser, & 刘, 2022) or different topologies (Muldoon et al., 2016) leading to a
wide variability in oscillation and synchronization patterns. 然而, further research is
needed on the interaction between spatial and topological features of the brain, and the influ-
ence of spatial features on neural communication.
Concerning the network’s spatial organization, there is a trade-off between the physical and
metabolic costs of long-range connections and their benefits for distribution, robustness after
network perturbations, and modular/segregated processing (布莫尔 & 斯波恩斯, 2012). 的确,
there are more long-distance connections than would be expected in the case where wiring
is strictly minimized. 因此, rather than rewiring projections to minimize their lengths, 一个
alternative perspective is that the brain minimizes wiring lengths through a suitable spatial
arrangement of brain regions, termed component placement optimization (CPO). Under such
状况, any other arrangement of the spatial position of brain regions would always result
in a longer total wiring length. 换句话说, it would be impossible to reduce the total wiring
length by swapping regions (Cherniak, 1994; Cherniak, Mokhtarzada, Rodriguez-Esteban, &
Changizi, 2004). This idea, 然而, has been refuted in the case of Caenorhabditis elegans
(a nematode 1 mm in length) and the rhesus monkey (Kaiser & 希尔格塔格, 2006).
这里, we test for component placement optimization for the first time in humans, and offer
a novel insight into the relationship between the spatial arrangement of connectome regions
and neural dynamics. Using the method described in Kaiser and Hilgetag (2006), we swap the
positions of brain regions in silico in an attempt to identify arrangements that reduce the total
wiring length. Using the structural connectivity of 280 subjects from the Human Connectome
项目 (Van Essen et al., 2012) (aged 22–30 years; 138 女性), we find that the human con-
nectome, as previously found for the rhesus monkey (Kaiser & 希尔格塔格, 2006), shows nonop-
timal component placement—a reduction in total wiring length is possible by rearranging
regions while maintaining the connectome topology. Some regions affected the change in total
wiring length more than others; regions in the frontal, 枕骨, and parietal lobes could be
relocated to significantly reduce the length of their connections to other regions, while on the
另一方面, connections from subcortical regions and the insular cortex showed fewer
changes during optimization. In addition to providing direct communication between distant
地区, we argue that this suboptimal arrangement supports dynamics that are associated with
optimal network performance (弗里斯顿, 1997). By modeling the effects of suboptimal arrange-
ments on neural activity within the brain, we observe changes in synchronization between
网络神经科学
255
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
A
_
0
0
2
8
2
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Nonoptimal component placement of the human connectome
桌子 1.
Connectome features across age groups and sex
Edge density
年龄: 22–25 years (N= 91)
0.308 ± 0.021
年龄: 26–30 years (N= 189)
0.304 ± 0.02
Mean wiring length
0.409 ± 0.015
Relative wiring length
0.451 ± 0.034
0.408 ± 0.013
0.449 ± 0.03
Males (N= 142)
Females (N= 138)
Edge density
0.302 ± 0.02
Mean wiring length
0.406 ± 0.013
Relative wiring length
0.443 ± 0.033
0.308 ± 0.02
0.411 ± 0.014
0.456 ± 0.029
页
0.10
0.61
0.29*
Psex
0.009
0.002
0.52*
笔记. P values are calculated using a two-tailed permutation test (one million permutations). The mean wiring
length uses the Euclidean distance, normalized using the maximum Euclidean distance across all regions (= 1).
* Because of the interaction between relative wiring length and edge density (Supporting Information Figure S1),
the relative wiring length P values are corrected using edge density. Values are mean ± SD.
regions—a suggested mechanism of communication (薯条, 2015; 从 马尔斯堡, 1995)—
highlighting a novel relationship between region placement and dynamics. Altogether, 这
suggests that the spatial organization of the human connectome is shaped by multiple con-
菌株: balancing the spatial and metabolic costs of white matter connections between
地区, while ensuring the emergence of metastable dynamics that are necessary for effective
认识 (德科, Rolls, & 罗莫, 2009).
结果
Reduction in Total Wiring Length by Swapping Brain Regions
Each connectome consisted of 82 regions—34 cortical and 7 subcortical regions per hemi-
sphere (Desikan et al., 2006)—with 1,012 ± 67 connections on average (edge density equal
到 0.31 ± 0.02), and an average normalized straight-line wiring length of 0.41 ± 0.01 (分为
by the maximum Euclidean distance across each connectome). 桌子 1 displays the differences
in connectome structure between age groups and sex. Compared with males, females had a
greater edge density (磷 < 0.01, permutation test) and longer normalized wiring (P < 0.01).
To assess whether the human brain displays component placement optimization, we iter-
atively swapped the positions of random pairs of regions for each subject individually, with the
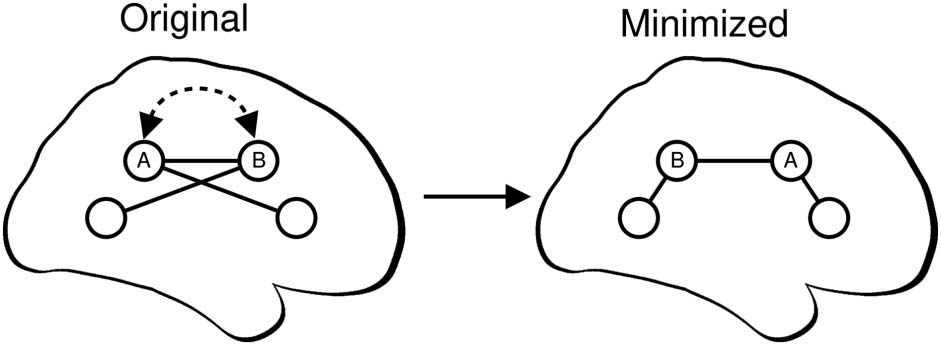
goal of reducing the total wiring length for each subject as much as possible (Figure 1; see the
Figure 1. Overview of component placement optimization procedure. Brain regions within each
connectome (circles) are swapped to reduce the total wiring length (the sum of the length of all
edges—straight black lines). Here, regions A and B are swapped (curved, dashed arrow), resulting
in the “minimized” connectome. The network topology does not change during this process. For
each subject, we identify a minimized arrangement by sampling from ≈4.8 × 10122 possible
arrangements of 82 regions (see the Materials and Methods section).
Network Neuroscience
256
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonoptimal component placement of the human connectome
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
.
t
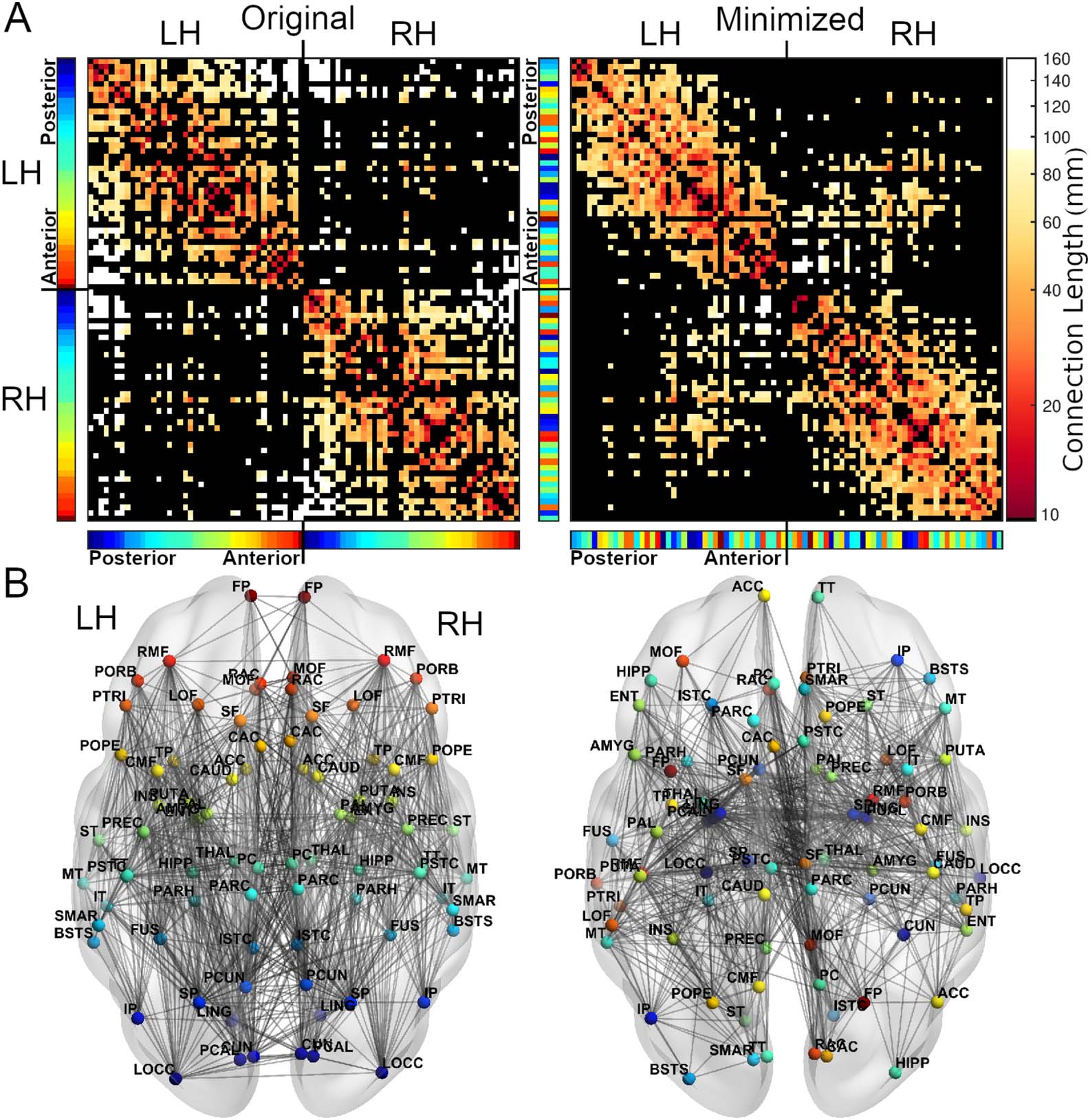
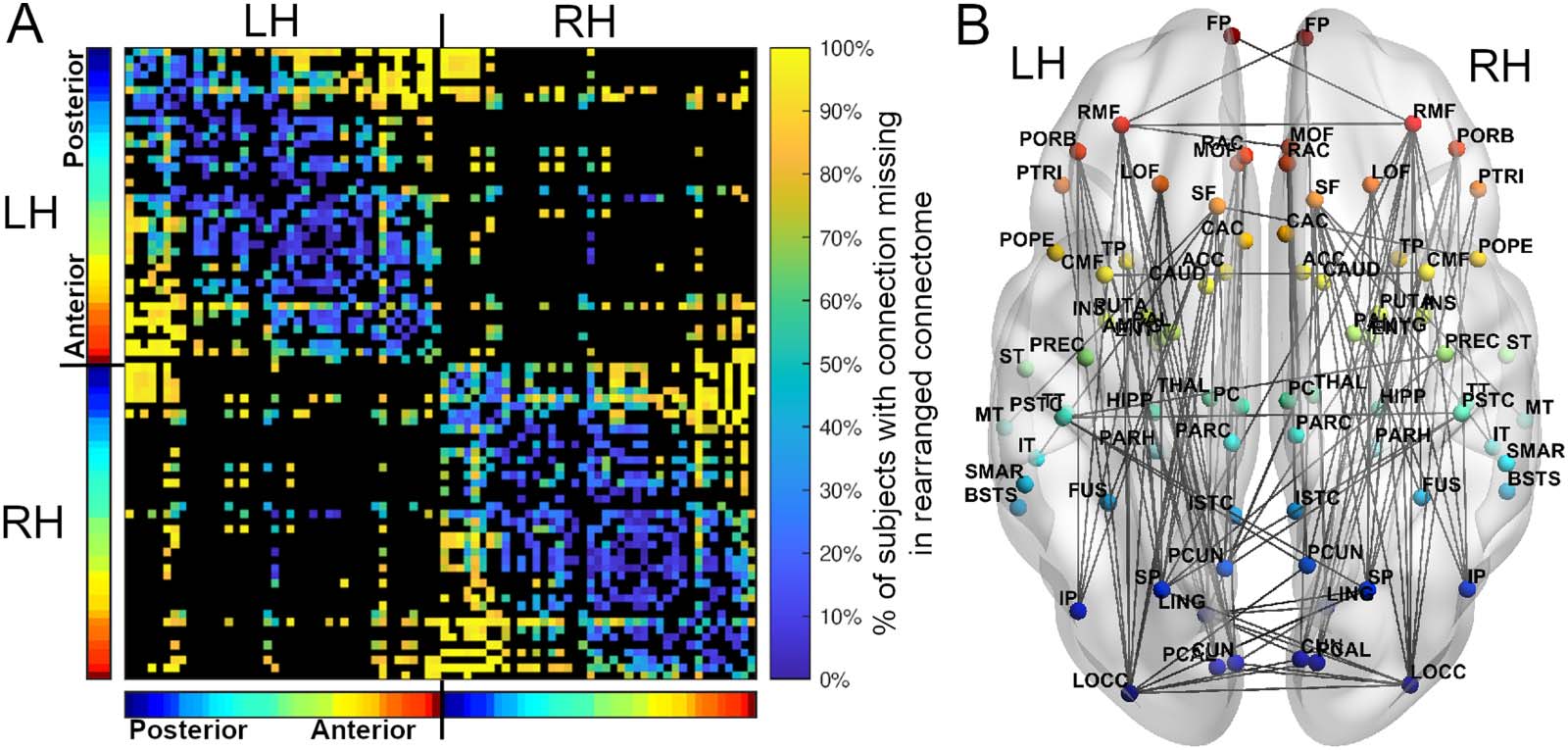
Figure 2. For an example subject, the adjacency matrices (A) and axial views (B) of the original (left) and minimized (right) arrangement of
regions. In the minimized arrangement, the spatial positions of regions are swapped to reduce the total wiring length. Regions are colored
based on their anterior-posterior position in the original arrangement, displayed in the color bars next to the adjacency matrices (red = anterior,
blue = posterior). The topology of the connectome is preserved in both arrangements, but the positions of regions often differ. White connec-
tions in the adjacency matrices are those with lengths greater than 80% of connections in the original arrangement. See Supporting Information
Table S1 for full region names. L/RH = left/right hemisphere.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Materials and Methods section). Alongside the “original” arrangement, this process converged
to produce a “minimized” spatial arrangement for each subject (Figure 2; see Supporting Infor-
mation Table S1 for full names of each region). As a result, we were able to reduce the total
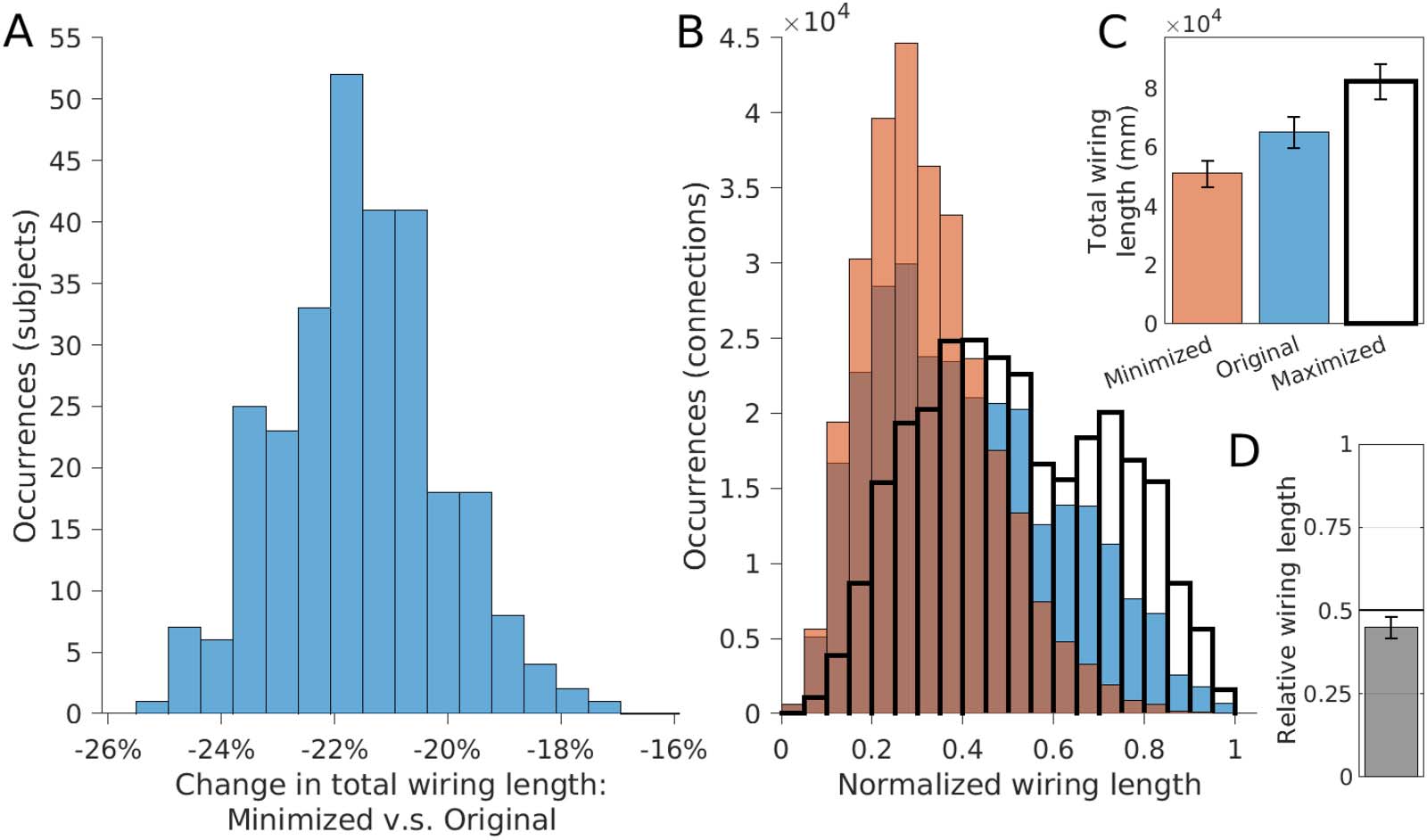
wiring length for all 280 subjects, with an average reduction in wiring length of 21.6 ± 1.4%
(Figure 3A); that is, the original arrangement was spatially suboptimal for all subjects. Mini-
mized arrangements displayed fewer long-distance connections (Figure 3B). While searching
for a reduced wiring length would be the best-case scenario of saving wiring, we also looked
at the worst-case scenario of increasing the total wiring length as much as possible. Using such
“maximized” networks, we calculated the relative total wiring length of the original network
where a value of 0 represents the best case (minimal wiring length) and a value of 1 represents
the worst case (maximal wiring length). The mean relative wiring length equated to 0.45 ±
Network Neuroscience
257
Nonoptimal component placement of the human connectome
For all 280 subjects: changes in wiring length distribution between original, minimized, and maximum arrangements. (A) The
Figure 3.
distribution of wiring length changes, from original to minimized arrangements (mean reduction of 21.6 ± 1.4%. (B) The distribution of wiring
lengths for original (blue), minimized (orange), and maximized (transparent, bold) spatial arrangements. (C) The mean wiring lengths for
minimized, original, and maximized arrangements. (D) The mean relative wiring lengths—original lengths relative to the minimized and
maximized wiring lengths (mean 0.45 ± 0.03) (error bars = 1 SD).
0.03, with 265 subjects (95%) having a value under 0.5 (ranging from 0.33 to 0.54), indicating
the original spatial arrangement of regions tended to align more closely with the best-case
scenario of minimizing the wiring length (Figure 3D). The relative wiring length was reduced
for connectomes with fewer connections (Supporting Information Figure S1), but did not differ
between sex or age groups, or between isolated hemispheres (Supporting Information Figure S2).
Regarding the connections that were most often missing between spatial positions in the
minimized arrangements, and thus the most suboptimal connections in the connectome (those
that no longer existed between spatial positions in the minimized connectomes), missing
connections were often inter- and intrahemispheric between anterior and posterior positions
(Figure 4, Supporting Information Table S2). Spatial positions in the occipital and frontal lobes
saw the greatest number of missing connections in the minimized arrangements, losing on
average 83 ± 24% and 74 ± 30% of their original projections, while subcortical positions lost
the fewest (48 ± 34%). Longer connections disappeared more frequently (Supporting Informa-
tion Figure S3), and interhemispheric versus intrahemispheric connections were more likely to
disappear, with a mean percentage of disappearance of 77 ± 18% and 29 ± 25% respectively.
Our approach of swapping regions assumed that any region could be swapped with any
other, irrespective of volume differences. In reality, swapping regions of different volumes will
alter the positions of neighboring regions, affecting the overall reduction in wiring length. We
therefore checked to see whether reductions in wiring length were still possible when only
regions with similar volume were allowed to swap positions (Supporting Information Figure
S4). Even when two regions can only swap positions if their volumes differ by no more than
±5%, a total wiring length reduction still occurred for all subjects, reducing by 3.4 ± 1.2%
compared with 21.6 ± 1.4% when swapping without volume constraints. Moreover, reduc-
tions in wiring length were still possible after removing weak connections, that is, those with
Network Neuroscience
258
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonoptimal component placement of the human connectome
Figure 4. Across all 280 subjects, the connections that disappeared after rearranging regions. (A) For the connections that were present in at
least 50% of subjects, an adjacency matrix depicting the percentage of subjects that had a connection between two positions in the original
arrangement but did not have the same connection between the same two positions in the minimized arrangement. Black regions represent
connections appearing in fewer than 50% of subjects. (B) Of the connections shown in A, an axial view of the connections that disappeared in
more than 90% of subjects. Note that connection lengths between hemispheres are scaled to pass through the center-of-mass of the connec-
tome, and are therefore longer than shown here (see the Materials and Methods section). Regions are colored based on their anterior-posterior
position in the original arrangement, displayed in the color bars next to the adjacency matrix (red = anterior, blue = posterior). L/RH = left/right
hemisphere.
few streamlines (Supporting Information Figure S5). In fact, as more connections were
removed and the rearrangement procedure became less constrained, a greater reduction in
total wiring length was observed.
Changes in Wiring Length for Individual Regions
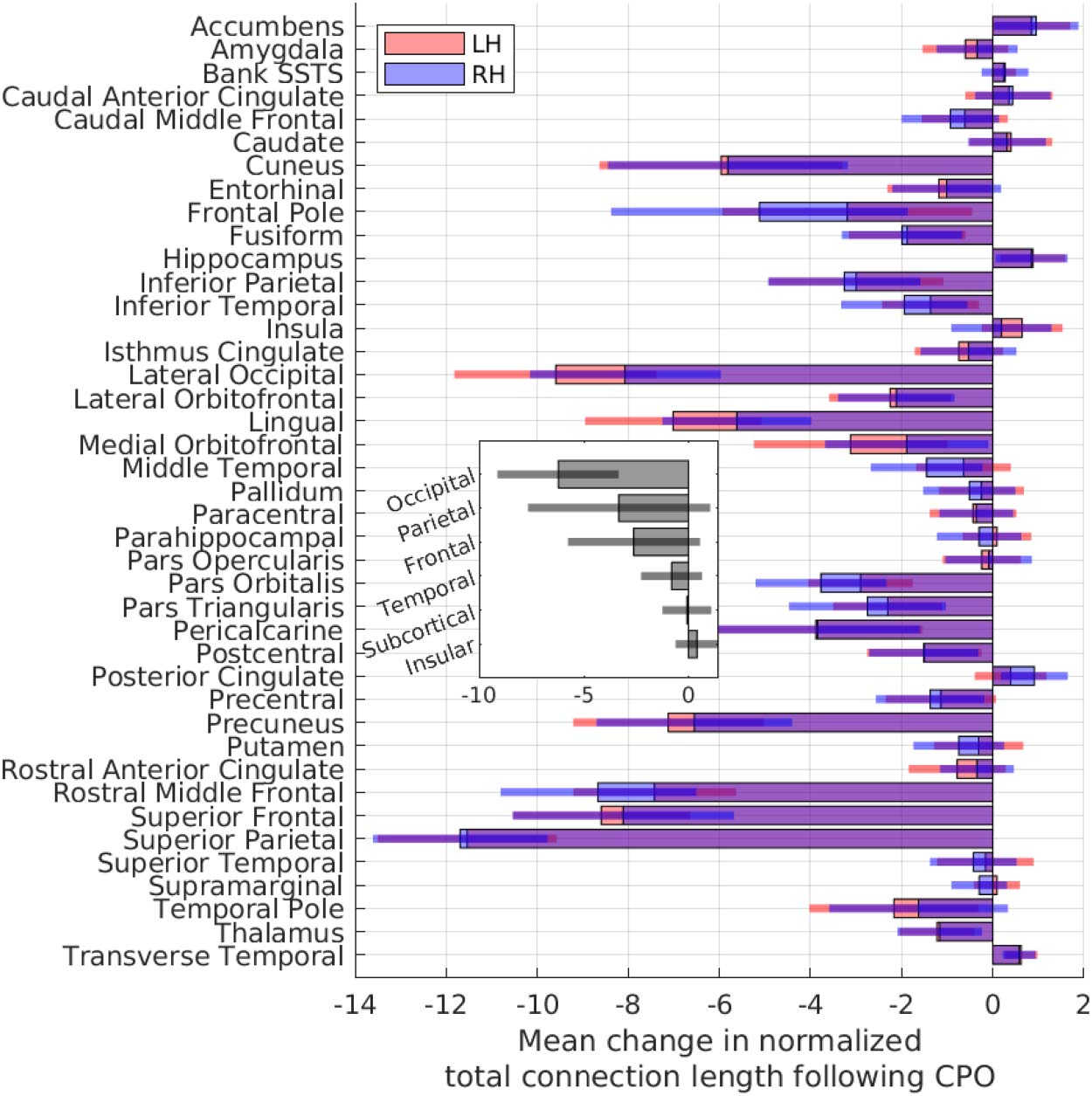
To further our analysis of the minimized arrangements, we explored the extent to which individ-
ual brain regions contribute towards reducing the wiring length in the minimized arrangements.
Comparing the wiring length of each region’s connections before and after rearrangement, we
found that wiring lengths reduced for almost all regions in the minimized arrangements, with
changes broadly consistent across hemispheres (Figure 5). Regions in the extreme anterior
and posterior areas experienced the greatest reduction in wiring length, particularly the lateral
occipital and superior parietal regions. The occipital lobe experienced the greatest reduction in
wiring length, while insular and subcortical regions contributed the least towards changes in the
wiring length. Interestingly, connection lengths increased for some regions, in particular the
nucleus accumbens, hippocampus, and transverse temporal areas. These regions often moved
to positions that increased the total wiring length, likely replaced by regions that made more
efficient use of the spatial position. Regions with longer connections, as well as those on the
periphery of the connectome, experienced a greater reduction in wiring length following rear-
rangement (Supporting Information Figure S6).
Functional Implications of Suboptimal Arrangements
Having identified that optimal positioning of regions with respect to wiring length does not
occur in the human connectome, we lastly explored the functional implications for suboptimal
arrangements by hypothesizing that such arrangements act as a structural foundation support-
ing beneficial neural dynamics. To assess changes in dynamics for each connectome, we
Network Neuroscience
259
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonoptimal component placement of the human connectome
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
Figure 5. For all 280 subjects, the change in total connection length per region (sum of lengths of
all connections attached to a region) after repositioning into the minimized arrangements (i.e., fol-
lowing component placement optimization: CPO). The lengths of connections are normalized using
the maximum Euclidean distance [= 1] between all regions, per subject. Inset: mean per lobe. Error
bars = 1 SD. L/RH = left/right hemisphere.
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
.
t
Metastability:
Variation in mean global
synchronization over time.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
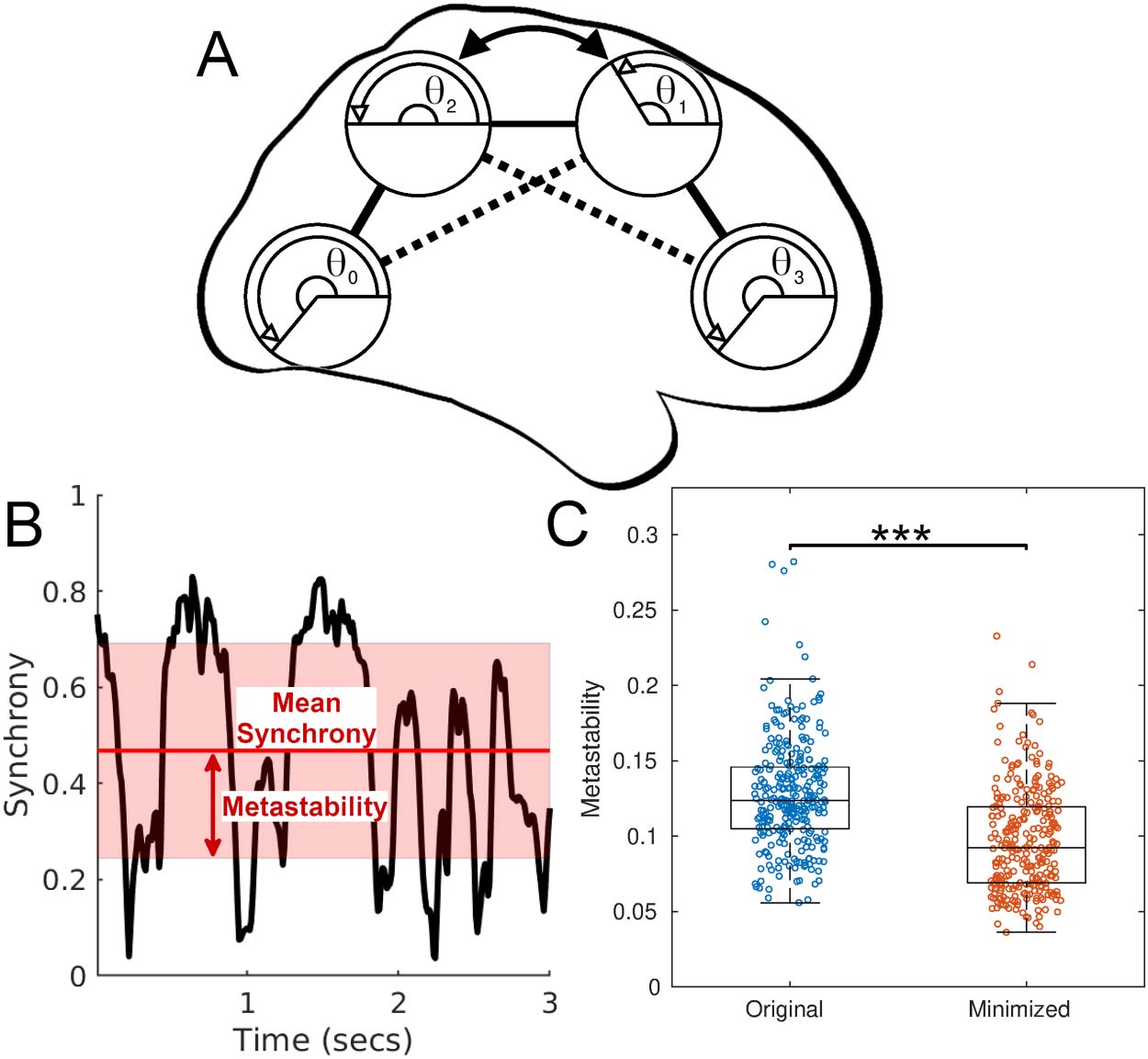
replicated neural dynamics in silico using models composed of 82 Kuramoto coupled oscil-
lators (Kuramoto, 1975). Kuramoto oscillators are commonly used to simulate interactions
between neural populations (Cabral, Hugues, Sporns, & Deco, 2011; Hellyer, Scott, Shana-
han, Sharp, & Leech, 2015; Váša et al., 2015). Here, each oscillator represents the neural
dynamics of an individual brain region, connected to one another according to the connec-
tivity defined by each subject’s connectome (Figure 6A). Between all regions, we measured
mean synchronization (correlated oscillatory neural activation across all regions) as well as
metastability (variance in mean synchronization across the duration of the simulation—
Figure 6B). Synchronization is suggested to underpin communication between regions (Fries,
2015), while high metastability reflects regular transitions between segregation and integration
of neural populations, dynamics necessary for flexible coordination between neural processes
(Deco, Rolls, & Romo, 2009; Friston, 1997) and task switching (Hellyer et al., 2015). We mea-
sured synchronization as the difference in phase between all oscillators within each connec-
tome; two oscillators are synchronized (synchronization equals 1) when their phase difference
is 0. Conduction velocities (speed of propagation of action potentials between regions) and
coupling strengths (the weight of influence that each oscillator has on their connected oscilla-
tors) were selected by comparing the model’s activity with functional connectivity obtained
from empirical resting-state fMRI data per subject (see the Supporting Information). We used
a 30 × 30 parameter space to select the parameters that best matched the empirical data
Network Neuroscience
260
Nonoptimal component placement of the human connectome
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Simulating changes in neural activity for original and minimized connectomes. (A) A
Figure 6.
simplified overview of the model setup: The dynamics of brain regions are modeled using Kuramoto
oscillators (phase θ), connected by edges, displayed here in a minimized arrangement, sagittal view
(the original arrangement is obtained by swapping regions 1 and 2—indicated by the arrow and
dashed lines). (B) A snippet of example activity showing the change in synchrony over all 82 regions
(black line) and the corresponding mean synchrony (red line) and metastability (variance of
synchrony, shaded red). (C) Across all subjects, metastability for the original and minimized
arrangements at 60 Hz (*** = P < 0.001, Wilcoxon signed-rank; Cohen’s d = 0.81). Seventy-
eight percent of subjects displayed reduced metastability for their minimized arrangements.
(velocities ranging from 1 to 30 m/s, and strengths from 1 to 30). We repeated our analyses for
three gamma-band frequencies—40 Hz, 60 Hz, and 80 Hz—corresponding to the natural fre-
quency of oscillation for each region.
Across all subjects, for 60 Hz, the fMRI-validated mean conduction velocities and coupling
strengths were 12.9 ± 3.9 m/s and 13.5 ± 4.3, respectively (see Supporting Information Figures S7
and S9 for 40 Hz and 80 Hz). At 60 Hz, the mean values of synchrony and metastability were
0.51 ± 0.04 and 0.13 ± 0.04, respectively (for metastability, this equated to 59 ± 15% of the
maximum metastability achieved over the parameter space). Because simulated activity gen-
erated from the minimized arrangements cannot be validated against empirical fMRI data, we
calculated the corresponding metastability for the minimized arrangements by identifying the
velocity/strength parameters, per subject, which gave rise to a level of synchronization com-
parable to that of the models validated against the original arrangements (Fukushima & Sporns,
2020; Váša et al., 2015) (Supporting Information Figures S7–S9). This approach meant that
synchronization was restricted to be as similar as possible between spatial arrangements,
enabling a comparison in metastability (see the Supporting Information).
Minimized arrangements displayed significantly reduced metastability compared with the
original arrangements—at 60 Hz, metastability was lower for the minimized arrangements for
Network Neuroscience
261
Nonoptimal component placement of the human connectome
217 out of the 280 subjects (78%) (P < 0.001, Wilcoxon signed-rank; Cohen’s d = 0.81;
Figure 6C). Metastability also decreased for minimized arrangements at 40 Hz (P < 0.001;
Cohen’s d = 0.76; reduced in 222 subjects [79%]) and 80 Hz (P < 0.001; Cohen’s d =
0.76; reduced in 220 subjects [79%]) (Supporting Information Figure S10). Metastability
reduced on average by 19 ± 28%, 20 ± 29%, and 19 ± 27%, for 40 Hz, 60 Hz, and
80 Hz, respectively. When considering the top 50% of subjects with the closest match with
the fMRI data, significant reductions in metastability for the minimized arrangements were
observed across all three frequencies (P < 0.001, Wilcoxon signed-rank; Cohen’s d =
0.84 [40 Hz], 0.93 [60 Hz], 1.02 [80 Hz]), reducing in 81%, 83%, and 83% of subjects for
40 Hz, 60 Hz, and 80 Hz, respectively (Supporting Information Figure S11). Significant overall
reductions in metastability still occurred (P < 0.001) irrespective of differences in mean syn-
chronization between arrangements (Supporting Information Figure S12).
DISCUSSION
In this study we explored the extent to which the human brain minimizes wiring length
through a suitable spatial arrangement of regions, a theory termed component placement opti-
mization. By analyzing wiring length distributions and rearranging regions within the connec-
tome, we have provided evidence for the existence of a suboptimal arrangement of brain
regions with respect to minimizing the total length of projections. In an attempt to identify a
reason for why this suboptimal arrangement exists, we found reduced variation in the dynam-
ics produced by the minimized arrangements compared with the original arrangements. The
overarching result is that a suboptimal arrangement may offer functional benefits by supporting
dynamics that facilitate flexible coordination between neural processes, despite the increased
spatial and metabolic costs.
Component Placement Is Suboptimal in the Human Connectome
Alongside the longer connections and increased connectivity in females, the lack of difference
in relative wiring length between sexes implies a similar suboptimal connectivity in both males
and females, and where the additional connectivity in females does not affect optimal wiring
configurations. Similar levels of optimization were also found in both age groups, demon-
strating that suboptimal wiring persists across age, albeit across the limited age range and
coarse age categories used in this study.
Our work extends the findings of other studies (Chen, Hall, & Chklovskii, 2006; Kaiser &
Hilgetag, 2006) by identifying nonoptimal component placement in the human connectome.
Long-distance connections contributed to the nonoptimal wiring in the original placement,
often attributed to connections between occipital/parietal and frontal regions. Long-range
connections have been observed across a variety of neural systems (Bassett & Bullmore,
2006), but here we find that the spatial arrangement of regions is not organized to minimize
these projections, suggesting the presence of constraints that oppose the need to minimize
spatial and metabolic costs of connections. A possible benefit of long-range connections is
to allow direct connectivity to distant regions, bypassing processing steps, reducing commu-
nication delays (Kaiser & Hilgetag, 2006), and supporting integration between regions (Samu,
Seth, & Nowotny, 2014).
In the minimized arrangements, the connection lengths decreased for almost all regions,
suggesting an overall suboptimal positioning of brain regions. This reduction was dominated
by connections emanating from peripheral regions, particularly from the lateral occipital,
superior parietal, and rostral middle frontal areas. In particular, the lengths of connections from
Network Neuroscience
262
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonoptimal component placement of the human connectome
the occipital lobe could be greatly reduced in the rearranged networks. This included anterior-
directed projections, coinciding with the inferior fronto-occipital fasciculus, superior longitu-
dinal fasciculus, and cingulum. The suboptimal placement of the occipital lobe, given its
connections, suggests a need for uninterrupted communication with distant regions, despite
the increased wiring costs. The importance of maintaining direct connectivity is supported
by the quantity of anterior-directed streamlines from the occipital lobe, more than would be
expected based on connection length alone (Roberts et al., 2016). From an evolutionary per-
spective, the occipital lobe versus other lobes is comparatively old and may have to compen-
sate for its position with the use of long-distance connections to regions that show greater
changes during evolution such as the frontal lobe (Hill et al., 2010).
Suboptimal Placement of Regions May Support Variable Brain Dynamics
While reducing the length of connections may reduce the amount of resources needed for
connection establishment and maintenance, our dynamical model suggests that a suboptimal
arrangement of regions, which includes long-range connectivity—in particular, emanating
from frontal and occipital/parietal lobes—offers functional advantages by supporting transi-
tions between synchronized and desynchronized states. Such states correspond to periods
of integration and segregation between regions (Fries, 2015), features that are crucial for
healthy brain function (Deco, Rolls, & Romo, 2009). Many of the regions with missing con-
nections overlapped with those implicated in task performance (Jung & Haier, 2007), partic-
ularly frontal and parietal areas, regions that are prone to disconnection under cost-preserving
rewirings of the connectome (Gollo et al., 2018). Metastable dynamics have been attributed to
lateral regions of the connectome in other studies (Váša et al., 2015), aligning with not only our
finding of the spatial influence on dynamics, but also with the suboptimal placement of
regions—those on the periphery of the connectome. Our results suggest that regions on the
periphery of the connectome may be critical to maintaining variable brain dynamics.
The perceived effects of long-range connectivity coincides with the metastable dynamics of
small-world networks that naturally consist of connections of different lengths (Wildie &
Shanahan, 2012). While other studies have highlighted the importance of network features
such as clusters and hub nodes in supporting integrated and segregated activity (Sporns,
2013), our results emphasize that spatial features may also contribute towards such dynamics
(Fukushima & Sporns, 2020; Seguin et al., 2018), and that minimizing wiring length may be
detrimental to healthy brain function.
Similar in nature to pipelining in semiconductor processors where initial and subsequent
instructions are processed concurrently (Shen & Lipasti, 2013), a mixture of long- and short-
range connections, giving rise to a temporal staggering of processing steps, may promote
binding between distant regions (von der Malsburg, 1995). Changes in the distribution of com-
munication delays between regions, caused by swapping regions, may be driving the changes
in dynamics (Deco, Jirsa, McIntosh, Sporns, & Kötter, 2009). The level of synchronization
enabled by a suboptimal spatial arrangement may support a broader exploration of system
states, and a wider repertoire of behavioral responses.
The rearrangement method used in this study is analytic in nature, limited in its level of
biological realism. Indeed, regions often moved far from their original position, with a median
[Q1, Q3] displacement of 54 mm [37 mm, 71 mm] (Supporting Information Figure S13). Many
features that are known to affect wiring length are missing from this analysis, particularly the
shape of regions and their connections. In our analysis, we used the Euclidean distance
between regions to analyze wiring lengths, whereas real fiber tracts will deviate from a straight
Network Neuroscience
263
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonoptimal component placement of the human connectome
line. For our subjects, subsequent analysis revealed that fiber tracts were on average 78 ±
100% longer than their Euclidean approximation. Moreover, conduction speeds will be
affected by varying amounts of myelination (Doron & Gazzaniga, 2008; Waxman, 1977), a
feature that is not accounted for in our model and one that may influence synchronization
(Park & Lefebvre, 2020). Consideration of the volume occupied by myelinated axons may lead
to further reductions inspatial costs, caused by a reduced reliance on myelination in the
minimized arrangements. Future studies could consider axon diameter and the physical shape
of fiber tracts when testing CPO and the effect on metastable dynamics. Nonetheless, by
constraining regions to stay within their hemispheres, lengthening interhemispheric connec-
tions (Supporting Information Figures S14 and S15), and considering differences across region
volumes in a separate analysis, we have attempted make our findings more biologically plau-
sible, but further work is needed to develop a more detailed swapping method that takes into
account the shape of regions and the meandering of their connections.
In summary, our results suggest that the arrangement of regions within the human connec-
tome does not minimize the total wiring length. This is the first time that component placement
optimization has been performed in the human connectome. In our sample of subjects from
the Human Connectome Project, locations of brain regions could be rearranged to reduce the
total wiring length; the human connectome allows for specific long-distance connections, in
particular fiber tracts connecting frontal and occipital/parietal regions. Using the novel
approach of pairing a model of neural oscillations with different spatial arrangements of the
connectome, we found that the connections involved in nonoptimal component placement
appear to enable bouts of integrated and segregated activity through changes in synchroniza-
tion between regions. Combined with previous studies (Kaiser & Hilgetag, 2006), our results
lend support for a universal law of connectome organization across species, contrasting with
suggestions of wiring optimization in neural systems (Cherniak, 1994). Overall, despite the
increased wiring cost, a suboptimal arrangement may be beneficial for maintaining activity
that supports flexible communication between regions, and subsequently, increased cognitive
processing performance (Fries, 2015; von der Malsburg, 1995).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MATERIALS AND METHODS
Data
Our study consisted of 280 healthy adults aged between 22 and 30. Structural, diffusion, and
functional data were obtained from the Human Connectome Project (Van Essen et al., 2012;
HCP; https://www.humanconnectome.org; S1200 release). For structural and diffusion data,
we used T1-weighted 3T MRI and diffusion imaging preprocessed data. Preprocessed data
included a FreeSurfer parcellation of each subject’s T1 image into 34 cortical and seven sub-
cortical regions (amygdala, caudate, hippocampus, nucleus accumbens, pallidum, putamen,
and thalamus) (Fischl et al., 2002) per hemisphere, based on the Desikan atlas (Desikan et al.,
2006). This resulted in a parcellation of 82 brain regions per subject. The rs-fMRI BOLD data
were obtained from the ICA-FIX denoised dataset (see the Supporting Information).
We assessed wiring length optimization by swapping brain regions and testing whether the
total length of all connections—estimated by the sum of the Euclidean distance of connections
between regions—could be reduced (Figure 1). The topology of the connectome does not
change during this rearranging process, but connections between spatial positions will often
differ between arrangements in such a way that reduces the total connection length in the
connectome. As in the previous study (Kaiser & Hilgetag, 2006), we identified these arrange-
ments using simulated annealing (see the Supporting Information).
BOLD fMRI:
Blood oxygen level–dependent
functional magnetic resonance
imaging; a method of observing
neural activity in the brain.
Network Neuroscience
264
Nonoptimal component placement of the human connectome
While fiber tracts are approximated as straight lines, this is unrealistic for connections
between hemispheres that primarily pass through the corpus callosum. To mimic the presence
of interhemispheric constraints and thus improve our approximation of the change in total
wiring length, we changed the lengths of interhemispheric connections as if they passed
through the center-of-mass of the network (Supporting Information Figures S14 and S15).
Moreover, regions are relocated only within their containing hemisphere so that arrangements
were more biologically plausible.
Age and Sex Comparison
To compare differences in network features across sexes and age groups, we conducted
nonparametric permutation testing. We computed the network feature for all subjects,
followed by interchanging subjects between either sex or age groups based on a random per-
mutation, preserving the original sizes of the groups. We then compared the mean difference
between the original groups with that of one million permutations, and computed the propor-
tion of shuffled mean differences exceeding the original mean difference. The null hypothesis
was rejected—there was no difference in the means between groups—at the 5% significance
level if this ratio was less than 0.05.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Component Placement Optimization
We used custom MATLAB code to conduct simulated annealing (Hastings, 1970), which iden-
tified an approximate optimal component placement of brain regions (Kaiser & Hilgetag,
2006). Each step of the simulated annealing process involves swapping the spatial position
of a random pair of regions and recomputing the total wiring length. The topology of the
network is maintained throughout this process. Regions are kept within their respective hemi-
sphere to make the arrangements more biologically plausible. We repeated this search 100 times
for each subject, creating 100 minimized arrangements per subject. For a given subject, the
minimized arrangement used in our analyses corresponded to that with the greatest per-
centage reduction in wiring length across the 100 repetitions. For the maximal (worst-case)
network scenario, we applied the same simulated annealing method with the goal of finding
an arrangement that maximizes the total wiring length (see the Supporting Information).
Kuramoto Model
To simulate neural activity, we used a model consisting of 82 Kuramoto oscillators (one per
region). For each oscillator, the phase θ of oscillator i at time t + 1 is determined by the fol-
lowing equation:
dθi
dt
¼ ωi þ
Xn
j¼1
(cid:2)
KAij sin θj
(cid:3)
(cid:2)
t − τ i;j
(cid:3)
− θi tð Þ
þ η
i tð Þ;
where ωi is the fixed natural frequency for oscillator i (equal to frequency in hertz multiplied by
2π), K is the global coupling strength, Aij is the binary connection between oscillators i and j, θi
(t ) is the phase of oscillator i at time t, and τi,j is the conduction delay between oscillators i and
j. The matrix A is symmetric—communication between oscillators is bidirectional. The delay
τi,j is defined by τi,j = Li,j /V, where Li,j is the length of the connection between the two regions
and V is the global conduction velocity (in meters per second). Uncorrelated Gaussian white
noise ηi (t) helps to ensure nonstationary dynamics, with zero mean and variance ≈2.5, 3.8,
and 5.0 rad/s, for 40 Hz, 60 Hz, and 80 Hz, respectively (variance equal to 1% of natural
frequency).
Network Neuroscience
265
Nonoptimal component placement of the human connectome
To calculate mean synchrony and metastability within the model, we use the instantaneous
synchronization ϕ at time t, defined as (Shanahan, 2010):
(cid:4)
(cid:4)
(cid:4)
ϕ tð Þ ¼ eiθj tð Þ
(cid:4)
D
(cid:4)
(cid:4)
(cid:4)
(cid:4);
E
j
p
ffiffiffiffiffiffi
−1
where i ¼
, j is an oscillator, and hij denotes the mean over all oscillators/regions. Synchrony is
calculated as the mean of ϕ over time, and metastability as the standard deviation of ϕ over time.
Selection of the appropriate K and V was obtained by comparing each subject’s simulated
functional connectivity (in the original arrangement) with that of the empirical resting-state
fMRI BOLD signal. For this validation process, K ranged from 1 to 30 (in steps of 1) and V from
1 to 30 m/s (in steps of 1 m/s). To enable a comparison in metastability between original
and minimized arrangements, we matched the level of synchrony produced by Kuramoto
models running on both arrangements (Fukushima & Sporns, 2020; Váša et al., 2015; see
the Supporting Information). Subsequently, for these two separate searches, conduction veloc-
ities were reduced by 3.1 ± 1.0 m/s (reduced to 6.0 ± 2.7 m/s), 4.6 ± 1.5 m/s (reduced to 8.3 ±
3.7 m/s), and 6.1 ± 1.7 m/s (reduced to 10.8 ± 4.0 m/s), for 40 Hz, 60 Hz, and 80 Hz, respec-
tively. For coupling strengths, these were reduced by 3.2 ± 1.4 (reduced to 5.3 ± 2.8), 5.0 ± 1.7
(reduced to 8.4 ± 3.9), and 7.0 ± 2.1(reduced to 11.1 ± 4.4). We used custom C (MEX) code
within a MATLAB framework to speed up our dynamical simulations.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00282.
AUTHOR CONTRIBUTIONS
Christopher Hayward: Data curation; Investigation; Methodology; Software; Writing—Original
draft. Siyu Huo: Software; Writing—Review & editing. Xue Chen: Data curation; Methodology;
Software. Marcus Kaiser: Conceptualization; Funding acquisition; Methodology; Software;
Supervision; Writing—Review & editing.
FUNDING INFORMATION
Christopher James Hayward, SAgE Doctoral Training Award, Newcastle University, UK. Marcus
Kaiser, Medical Research Council (https://dx.doi.org/10.13039/501100000265), Award ID:
MR/T004347/1, MR/T004347/2. Marcus Kaiser, Engineering and Physical Sciences Research
Council (https://dx.doi.org/10.13039/501100000266), Award ID: NS/A000026/1, EP/N031962/1,
EP/ W004488/1. Marcus Kaiser, Wellcome Trust, Award ID: 102037. Marcus Kaiser, Guangci
Professorship Program of Ruijin Hospital, Shanghai Jiao Tong University. Xue Chen, Natural
Science Foundation of Shandong Province (https://dx.doi.org/10.13039/501100007129),
Award ID: ZR2018MF017. Xue Chen, China Scholarship Council, Award ID: 201706450045.
Xue Chen, Fundamental Research Funds for the Central Universities, Award ID: 16CX06050A.
Xue Chen, The Natural Science Foundation of Shandong Province (Grant No. ZR2019PF004).
REFERENCES
Bassett, D. S., & Bullmore, E. (2006). Small-world brain networks.
The Neuroscientist, 12(6), 512–523. https://doi.org/10.1177
/1073858406293182, PubMed: 17079517
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038
/nrn2575, PubMed: 19190637
Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
https://doi.org/10.1038/nrn3214, PubMed: 22498897
Network Neuroscience
266
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonoptimal component placement of the human connectome
Cabral, J., Hugues, E., Sporns, O., & Deco, G. (2011). Role of local
network oscillations in resting-state functional connectivity. Neu-
roImage, 57(1), 130–139. https://doi.org/10.1016/j.neuroimage
.2011.04.010, PubMed: 21511044
Chen, B. L., Hall, D. H., & Chklovskii, D. B. (2006). Wiring optimi-
zation can relate neuronal structure and function. Proceedings of
the National Academy of Sciences, 103(12), 4723–4728. https://
doi.org/10.1073/pnas.0506806103, PubMed: 16537428
Cherniak, C. (1994). Component placement optimization in the
brain. Journal of Neuroscience, 14(4), 2418–2427. https://doi.org
/10.1523/JNEUROSCI.14-04-02418.1994, PubMed: 8158278
Cherniak, C., Mokhtarzada, Z., Rodriguez-Esteban, R., & Changizi, K.
(2004). Global optimization of cerebral cortex layout. Proceedings
of the National Academy of Sciences, 101(4), 1081–1086. https://
doi.org/10.1073/pnas.0305212101, PubMed: 14722353
Cohen, J. R., & D’Esposito, M. (2016). The segregation and integra-
tion of distinct brain networks and their relationship to cognition.
Journal of Neuroscience, 36(48), 12083–12094. https://doi.org
/10.1523/JNEUROSCI.2965-15.2016, PubMed: 27903719
Deco, G., Jirsa, V., McIntosh, A. R., Sporns, O., & Kötter, R. (2009).
Key role of coupling, delay, and noise in resting brain fluctuations.
Proceedings of the National Academy of Sciences, 106(25),
10302–10307. https://doi.org/10.1073/pnas.0901831106,
PubMed: 19497858
Deco, G., Rolls, E. T., & Romo, R. (2009). Stochastic dynamics as a
principle of brain function. Progress in Neurobiology, 88(1),
1–16. https://doi.org/10.1016/j.pneurobio.2009.01.006,
PubMed: 19428958
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson,
B. C., Blacker, D., … Killiany, R. J. (2006). An automated labeling
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. NeuroImage, 31(3), 968–980.
https://doi.org/10.1016/j.neuroimage.2006.01.021, PubMed:
16530430
Doron, K. W., & Gazzaniga, M. S. (2008). Neuroimaging tech-
niques offer new perspectives on callosal transfer and interhemi-
spheric communication. Cortex, 44(8), 1023–1029. https://doi
.org/10.1016/j.cortex.2008.03.007, PubMed: 18672233
Fischl, B., Salat, D. H., Busa, E., Albert, M., Dieterich, M.,
Haselgrove, C., … Dale, A. M. (2002). Whole brain segmenta-
tion: Automated labeling of neuroanatomical structures in the
human brain. Neuron, 33(3), 341–355. https://doi.org/10.1016
/S0896-6273(02)00569-X, PubMed: 11832223
Fries, P. (2015). Rhythms for cognition: Communication through
coherence. Neuron, 88(1), 220–235. https://doi.org/10.1016/j
.neuron.2015.09.034, PubMed: 26447583
Friston, K. J. (1997). Transients, metastability, and neuronal dynam-
ics. NeuroImage, 5(2), 164–171. https://doi.org/10.1006/nimg
.1997.0259, PubMed: 9345546
Fukushima, M., & Sporns, O. (2020). Structural determinants of
dynamic fluctuations between segregation and integration on the
human connectome. Communications Biology, 3(1), 606. https://
doi.org/10.1038/s42003-020-01331-3, PubMed: 33097809
Gollo, L. L., Roberts, J. A., Cropley, V. L., Di Biase, M. A., Pantelis,
C., Zalesky, A., & Breakspear, M. (2018). Fragility and volatility
of structural hubs in the human connectome. Nature Neurosci-
ence, 21(8), 1107–1116. https://doi.org/10.1038/s41593-018
-0188-z, PubMed: 30038275
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6(7), e159. https://doi
.org/10.1371/journal.pbio.0060159, PubMed: 18597554
Hastings, W. K. (1970). Monte Carlo sampling methods using
Markov chains and their applications. Biometrika, 57(1), 97–109.
https://doi.org/10.1093/biomet/57.1.97
Hellyer, P. J., Scott, G., Shanahan, M., Sharp, D. J., & Leech, R.
(2015). Cognitive flexibility through metastable neural dynamics
is disrupted by damage to the structural connectome. Journal of
Neuroscience, 35(24), 9050–9063. https://doi.org/10.1523
/JNEUROSCI.4648-14.2015, PubMed: 26085630
Hilgetag, C. C., & Kaiser, M. (2004). Clustered organization of cor-
tical connectivity. Neuroinformatics, 2(3), 353–360. https://doi
.org/10.1385/NI:2:3:353, PubMed: 15365196
Hill, J., Inder, T., Neil, J., Dierker, D., Harwell, J., & Van Essen, D.
(2010). Similar patterns of cortical expansion during human
development and evolution. Proceedings of the National Acad-
emy of Sciences, 107(29), 13135–13140. https://doi.org/10
.1073/pnas.1001229107, PubMed: 20624964
Huo, S., Zou, Y., Kaiser, M., & Liu, Z. (2022). Time-limited
self-sustaining rhythms and state transitions in brain networks.
Physical Review Research, 4(2), 023076. https://doi.org/10.1103
/PhysRevResearch.4.023076
Jung, R. E., & Haier, R. J. (2007). The Parieto-Frontal Integration
Theory (P-FIT) of intelligence: Converging neuroimaging evi-
dence. Behavioral and Brain Sciences, 30(2), 135–154. https://
doi.org/10.1017/S0140525X07001185, PubMed: 17655784
Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component place-
ment, but short processing paths, due to long-distance projec-
tions in neural systems. PLoS Computational Biology, 2(7), e95.
https://doi.org/10.1371/journal.pcbi.0020095, PubMed:
16848638
Kuramoto, Y. (1975). Self-entrainment of a population of coupled
non-linear oscillators. In International symposium on mathemat-
ical problems in theoretical physics (pp. 420–422). https://doi.org
/10.1007/BFb0013365
Muldoon, S. F., Pasqualetti, F., Gu, S., Cieslak, M., Grafton, S. T.,
Vettel, J. M., & Bassett, D. S. (2016). Stimulation-based control of
dynamic brain networks. PLoS Computational Biology, 12(9),
e1005076. https://doi.org/10.1371/journal.pcbi.1005076,
PubMed: 27611328
Park, S. H., & Lefebvre, J. (2020). Synchronization and resilience in
the Kuramoto white matter network model with adaptive
state-dependent delays. Journal of Mathematical Neuroscience,
10(1), 16. https://doi.org/10.1186/s13408-020-00091-y,
PubMed: 32936367
Roberts, J. A., Perry, A., Lord, A. R., Roberts, G., Mitchell, P. B.,
Smith, R. E., … Breakspear, M. (2016). The contribution of geom-
etry to the human connectome. NeuroImage, 124:379–393.
https://doi.org/10.1016/j.neuroimage.2015.09.009, PubMed:
26364864
Samu, D., Seth, A. K., & Nowotny, T. (2014). Influence of wiring
cost on the large-scale architecture of human cortical connectivity.
PLoS Computational Biology, 10(4), e1003557. https://doi.org/10
.1371/journal.pcbi.1003557, PubMed: 24699277
Seguin, C., van den Heuvel, M. P., & Zalesky, A. (2018). Navigation
of brain networks. Proceedings of the National Academy of
Network Neuroscience
267
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonoptimal component placement of the human connectome
Sciences, 115(24), 6297–6302. https://doi.org/10.1073/pnas
.1801351115, PubMed: 29848631
Shanahan, M. (2010). Metastable chimera states in community-
structured oscillator networks. Chaos: An Interdisciplinary Journal
of Nonlinear Science, 20(1), 013108. https://doi.org/10.1063/1
.3305451, PubMed: 20370263
Shen, J. P., & Lipasti, M. H. (2013). Modern processor design: Fun-
damentals of superscalar processors. Waveland Press, p. 20.
Sporns, O. (2013). Network attributes for segregation and integra-
tion in the human brain. Current Opinion in Neurobiology, 23(2),
162–171. https://doi.org/10.1016/j.conb.2012.11.015, PubMed:
23294553
Sporns, O., Chialvo, D. R., Kaiser, M., & Hilgetag, C. C. (2004).
Organization, development and function of complex brain net-
works. Trends in Cognitive Sciences, 8(9), 418–425. https://doi
.org/10.1016/j.tics.2004.07.008, PubMed: 15350243
Sporns, O., Tononi, G., & Kötter, R. (2005). The human connec-
tome: A structural description of the human brain. PLoS Compu-
tational Biology, 1(4), e42. https://doi.org/10.1371/journal.pcbi
.0010042, PubMed: 16201007
Van Essen, D. C., Ugurbil, K., Auerbach, E., Barch, D., Behrens,
T. E. J., Bucholz, R., … WU-Minn HCP Consortium. (2012). The
Human Connectome Project: A data acquisition perspective.
NeuroImage, 62(4), 2222–2231. https://doi.org/10.1016/j
.neuroimage.2012.02.018, PubMed: 22366334
Váša, F., Shanahan, M., Hellyer, P. J., Scott, G., Cabral, J., & Leech,
R. (2015). Effects of lesions on synchrony and metastability in
cortical networks. NeuroImage, 118, 456–467. https://doi.org
/10.1016/j.neuroimage.2015.05.042, PubMed: 26049146
von der Malsburg, C. (1995). Binding in models of perception and
brain function. Current Opinion in Neurobiology, 5(4), 520–526.
https://doi.org/10.1016/0959-4388(95)80014-X, PubMed:
7488855
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of
“small-world” networks. Nature, 393(6684), 440–442. https://
doi.org/10.1038/30918, PubMed: 9623998
Waxman, S. G. (1977). Conduction in myelinated, unmyelinated, and
demyelinated fibers. Archives of Neurology, 34(10), 585–589.
https://doi.org/10.1001/archneur.1977.00500220019003,
PubMed: 907529
Wildie, M., & Shanahan, M. (2012). Metastability and chimera
states in modular delay and pulse-coupled oscillator networks.
Chaos: An Interdisciplinary Journal of Nonlinear Science, 22(4),
043131. https://doi.org/10.1063/1.4766592, PubMed: 23278066
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
5
4
2
0
7
2
0
7
9
n
e
n
_
a
_
0
0
2
8
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
268