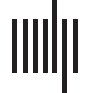研究
Functional coordinates: Modeling interactions
between brain regions as points in a
function space
Craig Poskanzer1,2
and Stefano Anzellotti2
1心理学系, 哥伦比亚大学, New York City, 纽约, 美国
2Department of Psychology and Neuroscience, Boston College, 波士顿, 嘛, 美国
关键词: Nonlinear, Connectivity, Functional coordinates
开放访问
杂志
抽象的
这里, we propose a novel technique to investigate nonlinear interactions between brain
regions that captures both the strength and type of the functional relationship. Inspired by the
field of functional analysis, we propose that the relationship between activity in separate brain
areas can be viewed as a point in function space, identified by coordinates along an infinite set
of basis functions. Using Hermite polynomials as bases, we estimate a subset of these values
that serve as “functional coordinates,” characterizing the interaction between BOLD activity
across brain areas. We provide a proof of the convergence of the estimates in the limit, 和我们
validate the method with simulations in which the ground truth is known, additionally
showing that functional coordinates detect statistical dependence even when correlations
(“functional connectivity”) approach zero. We then use functional coordinates to examine
neural interactions with a chosen seed region: the fusiform face area (FFA). Using k-means
clustering across each voxel’s functional coordinates, we illustrate that adding nonlinear basis
functions allows for the discrimination of interregional interactions that are otherwise grouped
together when using only linear dependence. 最后, we show that regions in V5 and medial
occipital and temporal lobes exhibit significant nonlinear interactions with the FFA.
作者总结
在本文中, we introduce a new method to investigate not only whether a set of brain areas
相互影响, but also how the activity in those regions is related. 要做到这一点, we model the functional
relationships between activity in distinct brain areas as points in a function space that can be
described by “functional coordinates” along multiple basis functions. 第一的, we demonstrate the
efficacy of this novel method on simulated data; 下一个, we apply it to real neural data, reporting
evidence of nonlinear interactions. Functional coordinates can serve as a tool in future studies
to further our understanding of the complex interactions across the brain.
介绍
The use of linear and nonlinear models for the analysis of neuroimaging data is at the center of
a lively debate (Ivanova et al., 2021). 一方面, proponents of linear models argue that
nonlinear models can lead to overfitting issues given the amount of data that is typically
引文: Poskanzer, C。, & Anzellotti, S.
(2022). Functional coordinates:
Modeling interactions between brain
regions as points in a function
空间. 网络神经科学, 6(4),
1296–1315. https://doi.org/10.1162
/netn_a_00264
DOI:
https://doi.org/10.1162/netn_a_00264
支持信息:
https://doi.org/10.1162/netn_a_00264
已收到: 2 十一月 2021
公认: 22 六月 2022
利益争夺: 作者有
声明不存在竞争利益
存在.
通讯作者:
Craig Poskanzer
craigposkanzer@gmail.com
处理编辑器:
Daniele Marinazzo
版权: © 2022
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
A
_
0
0
2
6
4
p
d
t
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Functional coordinates
Functional connectivity:
The correlation between the neural
responses in two brain regions.
Function estimation:
Identifying a function that
approximates another function.
网络神经科学
可用的 (Misaki et al., 2010). Linear models have been found empirically to yield insights
about the brain when used for pattern classification (Anzellotti, Fairhall, & Caramazza,
2014), representational similarity analysis (Kriegeskorte, 穆尔, & Bandettini, 2008), and func-
tional connectivity (Biswal et al., 1995). 另一方面, proponents of nonlinear models
argue that linear models are not biologically plausible: firing rates of single neurons are inte-
grated nonlinearly within dendrites (Beniaguev, Segev, & 伦敦, 2021; 徐等人。, 2012), 和
nonlinear transformations are essential to perform many of the tasks humans need to solve.
因此, while linear models might be effective to test whether a brain region encodes a given
set of features, they might fall short of capturing interactions between brain regions with a
complexity sufficient to enable the understanding of cognitively relevant computations.
More broadly, research on the statistical dependence between the responses in different
地区 (“functional connectivity”) has focused on studying whether given pairs of brain
regions interact; 然而, there is a need for methods that can be used to investigate how they
interact—to distinguish between different kinds of mappings that transform information from
brain region to brain region. Even interactions between brain regions displaying similar
strengths of functional connectivity could belie very different nonlinear computations.
A recurring criticism of nonlinear models is based on the difficulty to interpret them. 在
decoding analyses, linear models make it easier to distinguish the contribution of neural
information processing up to the brain region whose responses are being measured from
the contribution of the decoder applied to extract information from that brain region (看
Kamitani & Tong, 2005; Norman et al., 2006). 相比之下, nonlinear decoders can transform
the neural responses they receive as inputs to an extent that might lead to ambiguity about
the nature of representations in the brain region that is being investigated. To illustrate this
point with an example, if we could use any nonlinear decoder, and we had noiseless data
from every single neuron in early visual cortex, we should be able to use these data to per-
form view-invariant object classification. 毕竟, the brain itself can perform view-invariant
object classification using early visual cortex responses as input. 然而, this finding would
not support the conclusion that early visual cortex encodes view-invariant representations of
物体, because the nonlinearities in the decoder would have likely been necessary for view
invariance to occur.
This criticism of nonlinear decoders is largely motivated by the “standard” analysis strategy
used in the literature. This standard strategy consists of training one model to achieve the high-
est possible decoding accuracy, given the responses from a brain region as input, and inter-
preting decoding with significantly-above-change accuracy as evidence that the brain region
encodes information about the property that was successfully decoded (Anzellotti et al., 2014).
相似地, in the field of functional connectivity, the best estimate of the statistical dependence
between the responses in two different regions is calculated, and significance is interpreted as
evidence for the dependence between those regions’ responses (Anzellotti, Caramazza, &
Saxe, 2017A; Greicius et al., 2003).
在本文中, we introduce a new perspective. We suggest that nonlinear models should
not be used to replace linear models—instead, information about the relative contributions of
linear and nonlinear models should be preserved. Rather than selecting a single model and
using its performance to determine the strength of the interaction between two regions, 我们
propose to use a family of models and to treat the respective contributions of different models
as a set of “functional coordinates” that characterizes not just the strength, but also the type of
interaction between regions. From a mathematical perspective, the proposed approach is
rooted in seeing the problem of connectivity as function estimation, and it is inspired by the
1297
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
A
_
0
0
2
6
4
p
d
t
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Functional coordinates
Hilbert space:
A vector space with an inner product
that defines a distance with respect to
which the vector space is a complete
metric space.
Basis functions:
A set of functions in a function space
such that any function in the space
can be expressed as a linear
combination of the functions in
that set.
Dynamic causal modeling:
A technique used to infer the strength
and directions of interregional
interactions and their fluctuations.
Granger causality:
A method that determines the
influence of x on y by using past
x-values to predict future y-values.
Mutual information:
A measurement of how much
information one variable gives about
其他.
Multivariate pattern dependence:
A technique to study the multivariate
interactions between brain areas.
Hermite polynomials:
A group of polynomials that are a
basis set for a Hilbert space;
orthogonal with respect to the
normal distribution.
idea that a function can be expressed as a point in a Hilbert space, having as coordinates its
projections on a (infinite) set of basis functions.
Previous research has introduced nonlinear approaches to the study of connectivity using
Dynamic Causal Modeling (DCM; Stephan et al., 2008), Granger causality (Marinazzo, Pellicoro,
& Stramaglia, 2008), mutual information (Lizier et al., 2011), and Multivariate Pattern Depen-
登塞 (MVPD; Anzellotti et al., 2017乙). 然而, by and large these methods have followed
the traditional approach of building one model that performs as accurately as possible and
interpreting the quality of fit, parameter values, or accuracy as evidence for the existence of
互动. The approach we propose in this article, 反而, focuses on distinguishing
between different kinds of interactions between regions, offering a new technique that can
reveal differences even between region pairs whose overall correlations or statistical depen-
dencies are comparable in strength.
方法
The study of univariate statistical dependence between pairs of brain regions offers an ideal
test case for the use of functional coordinates. The univariate nature of the problem prevents a
combinatorial growth in the number of nonlinear terms, and the continuous (rather than dis-
crete) nature of the outputs makes it possible to use a simple basis set such as Hermite poly-
nomials (Hermite, 1864; Szeg, 1939). We used Hermite polynomials in this work as they are
defined on all ℝ and have a natural multivariate extension, but the same logic can be applied
to other basis sets such as Fourier basis functions or Legendre polynomials. For additional con-
to render
venience, in this study we divide each Hermite polynomial of order n by
them an orthonormal basis (see Van Eijndhoven & Meyers, 1990; 支持信息, 这
first five normalized Hermite polynomials; see also Figure 1A).
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
p
ffiffiffiffiffiffi
n!
2圆周率
理论
Expressing functions with a truncated orthonormal Hermite basis. We will consider the average
response in a predictor region at time t (which we will denote with xt) and the average
response in a target region also at time t (which we will denote with yt). Modeling the depen-
dence between xt and yt as yt = f (xt) + (西德:1)t, we will aim to characterize the function f that
t . 为了方便 (and without loss of generality), 我们将
minimizes the error E ( F ) =
normalize the inputs and outputs to have mean 0 and standard deviation 1. We will make the
assumption that the function f is in the Hilbert space of functions from the interval ℝ to ℝ
satisfying
t (西德:1)2
磷
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
A
_
0
0
2
6
4
p
d
t
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
在哪里
−∞
Z ∞
f xð Þ
j
j2
p xð Þdx < ∞;
p xð Þ ¼
1
p e−1
ffiffiffiffiffiffi
2π
2x 2 :
(1)
(2)
This is a large space of functions, and it should be sufficient to approximate well the rela-
tionship between the predictors and the targets of prediction.
The inner product between any two functions g1, g2 defined as
g1; g2
h
i ¼
Z þ∞
−∞
g1 xð Þg2 xð Þp xð Þdx:
(3)
1298
Network Neuroscience
Functional coordinates
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
/
t
.
Figure 1. Validation with synthetic data. (A) The first five Hermite polynomials. (B) Functional coordinates identify the underlying relationship
between two sets of simulated data. We generated five sets of x-y pairs where the true relationship between each subsequent pair of x and y is
one of the first five Hermite polynomials (ex. y1 = H1(x1)). As expected, the coordinate estimates assign coefficients near 1 to the polynomial in
the basis set that defines the relationship between x and y, and coefficients near 0 to all others. (C) When the simulated data are generated
using a linear combination of two basis functions (ex. y1 = H1(x1) + H2(x1)), the resulting functional coordinates reveal loadings near 1 for each
contributing basis function, and loadings near zero for all other basis functions. (D) Nonlinear coordinates can approximate U-shaped inter-
actions that would be indistinguishable using standard correlation analysis. We generated synthetic data where the relationship between activ-
ity in Region A and activity in Region B have a symmetric relationship ( y = 1 + noise, y = x2 + noise, and y = x4 + noise). A range of noise was
simulated by drawing from two normal distributions with mean 0 and standard deviation 1 and 5, respectively. The estimated function is
plotted in red and the loadings on the functional coordinates are illustrated in radar plots alongside each graph.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Hermite polynomials are a basis set of the Hilbert space. If we knew the function f that
minimizes the error E ( f ), we could express it as an infinite set of coordinates ci such that
f xð Þ ¼
X∞
cihi xð Þ;
i¼0
where hi is the ith Hermite polynomial (normalized to have norm 1). Thus
Z þ∞
−∞
ci ¼
f xð Þhi xð Þp xð Þdx ∀ i 2 ;
(4)
(5)
1299
Network Neuroscience
Functional coordinates
To make this strategy applicable in practice, we need to address two challenges. First, we
cannot calculate an infinite number of coordinates; therefore, we will truncate Hermite poly-
nomials to a specified order. The optimal order at which to truncate the polynomials can
depend on the amount of data and the nature of the interactions between the regions studied.
In the present article, the main focus is not to determine the optimal number of polynomials.
Therefore, we will use polynomials up to the fifth order (future studies can use variance
explained in independent data as a metric for the selection of the number of polynomials).
Second, we do not know the function f, we only have a training dataset containing pairs of
observations (x1, y1), …, (xT, yT). To address this second challenge, for each Hermite polyno-
mial hi we will estimate the corresponding coordinate as
^ci ¼ argmin
!
yt − cihi xtð
Þ2
Þ
:
XT
ð
t¼1
(6)
The coordinates ^ci approximately characterize the function f (up to the precision afforded
by the truncation).
If ^ci is a “good” estimate of ci, as the number of obser-
Convergence of the coordinate estimates.
vations grows the estimate should converge to the true value ci. We demonstrate this property
in the following Lemma.
We will assume that the data-generating process is approximately Normal, and since we
normalize our input data to have mean μ = 0 and standard deviation σ = 1 we have approx-
imately that x ∼ N (0, 1) (see Supporting Information, Normality of the Data; Figure S7). Since
the error function is convex, we can calculate ^ci by setting
d
dci
XT
ð
yt − cihi xtð
Þ2 ¼ 0
Þ
t¼1
which yields
^ci ¼
P
T
P
t¼1 yt hi xtð
Þ
Þ2
t¼1 hi xtð
T
¼
P
T
t¼1 f xtð
P
T
t¼1 hi xtð
Þhi xtð
Þ2
(7)
(8)
Þ
:
As the number of observations increases, taking into account the fact that x ∼ N (0, 1), we
have that
lim
T →∞
P
T
t¼1 f xtð
P
T
t¼1 hi xtð
Þhi xtð
Þ2
Þ
¼
R þ∞
−∞ f xð Þhi xð Þp xð Þdx
R þ∞
−∞ hi xð Þ2
p xð Þdx
(9)
and since we have used normalized Hermite polynomials that form an orthonormal basis,
Z þ∞
−∞
hi xð Þ2
p xð Þdx ¼ 1:
In conclusion,
Z þ∞
lim
T →∞
^ci ¼
−∞
f xð Þhi xð Þp xð Þdx ¼ ci:
(10)
(11)
1300
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional coordinates
Note that based on this observation, in the presence of nonnormally distributed data, it
might be possible to estimate the probability density of the data q(x) and develop a basis
set of polynomials that are orthonormal with respect to the inner product defined by
Z
h
g1; g2
i ¼
g1 xð Þg2 xð Þq xð Þdx
(12)
where the integral is computed over the domain of q.
Application
In order to validate the performance of the functional coordinates on
Generating synthetic data.
data in which the true relationship between datasets is known, we generated synthetic data in
which we could define normally distributed vectors of x (mean = 0, standard deviation = 1).
Next, we created a vector of y values such that
y ¼ f xð Þ;
(13)
where f is the explicit relationship that we will seek to approximate using functional
coordinates.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Participants and stimuli. All data used in this study were made publicly available as part of the
StudyForrest dataset (Hanke et al., 2016). The study procedures were approved by the Ethics
Committee of Otto-von-Guericke University, and all participants provided informed consent
(for more details, see Hanke et al., 2016). These data consist of fMRI scans of 15 subjects
(6 female, ages 21–39, mean = 29.4) as they watched the movie Forrest Gump. Data from one
subject were removed from the analyses after a technical error caused a failure in the fMRIPrep
preprocessing procedure in multiple attempts (see also Li, Saxe, & Anzellotti, 2019).
After providing consent, participants watched the movie in the scanner over the course of
eight functional runs (approximately 15 minutes each). Additionally, subjects performed a
localizer task incorporating 24 grayscale images from each of the following six categories:
faces, bodies (without heads), small objects, houses, outdoor scenes of nature and streets,
and phase scrambled images; for more information about the localizer task, please see
Sengupta et al. (2016).
All scans were performed in a 3T Philips Achieva dStream MRI scanner with a 32-channel
head coil. BOLD responses were recorded at 3 × 3 × 3 mm resolution with T2*-weighted
echo-planar (2 sec-repetition time (TR)) imaging sequence. See Hanke et al. (2016) for more
details on image acquisition.
Data preprocessing. Data were preprocessed according to the fMRIPrep pipeline described in
Esteban et al. (2019). This procedure combines the following steps: T1-weighted anatomical
images were smoothed and skull-stripped using advanced normalization tools; brain images
were segmented into white matter ( WM), gray matter, and cerebrospinal fluid (CSF) using FSL-
FAST (Zhang, Brady, & Smith, 2001); FSL-MCFLIRT (Jenkinson et al., 2002) was used to correct
functional scans for head movement; functional scans were aligned with the corresponding
anatomical image using boundary-based coregistration implemented in FSL-FLIRT.
Connectivity analyses are particularly susceptible to fluctuations in the BOLD signal as the
result of motion and respiration; in order to effectively examine the interactions between the
activity across regions, it is necessary to incorporate denoising approaches that take measures
to remove signal of no interest. To this end, after preprocessing, the data were additionally
denoised using CompCor (Behzadi et al., 2007). In this method, noise is removed from the
Network Neuroscience
1301
Functional coordinates
Seed region:
A region of interest chosen in order
to study its interactions with the rest
of the brain.
functional data by regressing out the first five principal components extracted from the com-
bined WM and CSF data. The central assumption of CompCor is that the signal extracted from
the WM and CSF is uninformative, and thus by using these anatomically defined sources of non-
neural signal, one can predict and remove fluctuations in the neural data that are of no interest.
Although this method may not be able to perfectly distinguish the signal of interest from noise, it
has been shown to effectively remove spurious signal in studies examining multivariate and non-
linear interactions (Li et al., 2019; Poskanzer et al., 2022; Power et al., 2012).
Localization of the region of interest. To define the region of interest (ROI), data from the initial
run of the functional localizer task were modeled using a standard GLM in FEAT (Woolrich
et al., 2001), which included each object category from the task as a predictor. All predictors
were convolved with a gamma hemodynamic response function. The fusiform face area (FFA)
was located among the regions maximizing the contrast in activity for faces compared with all
other stimuli. Next, we selected the single voxel within the FFA with the maximum t-value for
the contrast of faces over all other categories. We then created a 9-mm sphere surrounding this
voxel and selected the 80 voxels within this sphere with the largest t-values for faces > 非-
faces. 这些 80 voxels served as the FFA ROI for our analyses. This procedure has additionally
been reported in Fang et al. (2019) and Poskanzer et al. (2022).
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
A
_
0
0
2
6
4
p
d
.
/
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数据分析. Let’s consider an fMRI dataset, and a seed region. In this study, we used the FFA
as the seed region. We then used functional coordinates to characterize the relationship
between the normalized responses in FFA and the normalized responses in each other voxel
v in gray matter. For each participant, and for each voxel in gray matter (normalized to MNI
空间), we applied the method described in the previous section using as xt the average
response in FFA at time t, and as yt the response in the voxel v at time t. This procedure yielded
a five-dimensional vector of the estimated coordinates ^c 1, ……, ^c 5 along the first five Hermite
polynomials. 下一个, we used k-means clustering with the Akaike information criterion (AIC) 到
identify clusters of voxels using the five-dimensional vectors from all participants. 这
approach identified the optimal number of clusters from the data by balancing complexity
and quality of fit. Each cluster corresponded to a distinct kind of nonlinear interaction between
brain regions. 最后, clustering was visualized by color coding each voxel in gray matter by
the cluster to which it is assigned most often, with saturation increasing as a function of the
proportion of participants for whom the voxel was assigned to the most frequent cluster.
It is important to note that because functional coordinates describe the function that trans-
forms BOLD responses in region A into responses in region B, it is necessary for a researcher
interested in the relationship between two brain areas to select which area is region A (预-
dictor) and which is region B (the target of prediction). In the case in which a researcher does not
have an a priori hypothesis about direction of the relationship between these brain areas, 这是
recommended to calculate functional coordinates to estimate the relationship in both directions.
To test our model’s ability to distinguish between voxels based on their nonlinear interac-
tions with the FFA, we compared clustering solutions for the five-dimensional functional coor-
dinates with the optimal clustering solution across the loadings for only the linear basis vector.
这样, we were able to determine the subsets of voxels with similar linear loadings that
were differentiated by their nonlinear components. This analysis clusters voxels according to
the type of interaction between the voxel’s activity and the activity in the seed region, 因此
highlighting brain areas with distinct functional relationships to the FFA. 最后, using Statis-
tical Non-Parametric Mapping (SnPM; SnPM, 2013), which uses permutation tests in order to
determine the significance (p values), we tested whether the magnitude of the nonlinear basis
vector loadings for all voxels (using a cluster forming threshold of 0.0001) were significantly
网络神经科学
1302
Functional coordinates
nonzero to determine where neural interactions with the FFA were significantly nonlinear in
自然.
Testing statistical significance for each of the higher order coordinates requires controlling
for multiple comparisons. We suggest two possible approaches to mitigate the challenges asso-
ciated with multiple comparison correction. A first approach consists in computing the
explained variance for groups of loadings of interest. 例如, the contribution of nonlin-
ear components could be tested by comparing the explained variance including Hermite poly-
nomials of order greater than 1 to the explained variance using polynomials of order up to 1.
This approach could be also used to test other questions, 例如, it could be used to
investigate the contribution of polynomials with even order to that of polynomials with odd
order to evaluate the extent to which the response of the target region is symmetrical around
the average response of the seed region. Symmetrical effects could capture interpretable rela-
tionships between brain areas—such as cases in which the responses in one region might be
driven by both increases and decreases in the response in another region compared to
基线.
A second approach entails using part of the data as a functional localizer. 例如, 一
experimental run could be used to identify particular polynomial orders that show effects of
兴趣. 然后, independent data could be used to test specifically the significance of the
effects for those polynomial orders, much like regions of interest are used to tackle multiple
comparison issues in the spatial domain.
结果
Estimated Coordinates Match the Ground Truth in Simulated Data
In order to test the efficacy of our novel analysis to detect the functional relationship between
two patterns of activity, we used simulated data to model a series of potential interactions
between generated seed-target datasets. By manipulating the function used to create target
data from a set of simulated seed data, we can test the ability of the functional coordinate
analysis to correctly model the selected relationship. Our results illustrate that through estimat-
ing loadings on the first five basis vectors of our selected functional space, we can accurately
characterize the generative function of the target data for the functions tested (见图 1;
more complex functions might require a higher number of polynomials).
Individual polynomials. Starting with a seed sample of 10,000 normally distributed data points
(mean = 0, 标准差= 1), we defined five sets of target data as H1–5(seed ) where H1–5 represents
each of the first five normalized Hermite polynomials. Given that the interactions between the
seed and target data were selected to be the five basis vectors by which we are measuring
functional space, if our analysis correctly identifies the underlying computation that generates
the target data, we would expect to see a loading of 1 on the relevant basis vector and loadings
的 0 on all other basis vectors. For each set of target data, we found a five-dimensional set of
functional coordinates with a loading of 1.00 for the basis vector governing the underlying
relationship between the seed and target data, as well as loadings with an absolute value
< 0.12 for all other basis vectors (see Figure 1B).
Combinations of polynomials. To further probe the ability of functional coordinates to capture
more complex relationships between seed and target data, we next generated target data using
a linear combination of multiple Hermite polynomials. Assuming the underlying function that
describes the interaction between the seed and target data is an unweighted combination of a
subset of Hermite polynomials, the resulting functional coordinates should consist of a vector
Network Neuroscience
1303
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional coordinates
of loadings with values of 1 for the given subset of polynomials and loadings of 0 for all other
basis vectors. In our validation, we demonstrate in three cases (H2 + H3, H1 + H4, and H1 +
H2) that these functional coordinates capture the selective loadings on the relevant basis
vectors (see Figure 1C).
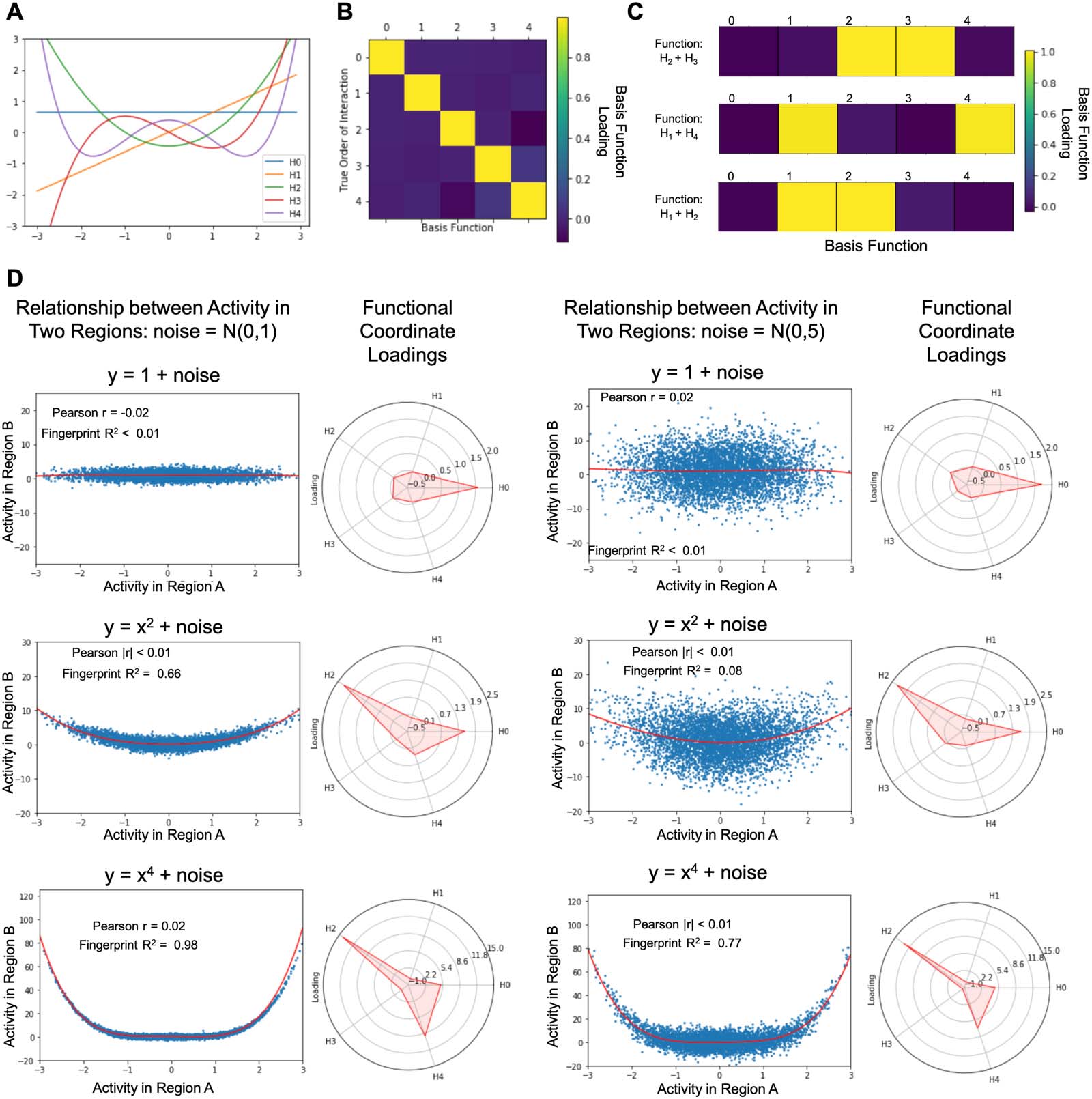
Nonlinear Coordinates Can Capture U-Shaped Dependencies
One key benefit of characterizing functional interactions using nonlinear functional coordi-
nates is that they offer considerably more explanatory power than a standard Pearson corre-
lation. One illustrative example in which our functional coordinate analysis outperforms
correlation tests arises in the instance when interactions are governed by a symmetrical under-
lying function. In the case of a U-shaped relationship, the magnitude of activity in a seed
region, either negative or positive, results in a proportional positive response in the target
ROI. This type of relationship could be particularly useful to understand brain regions that
might show greater sensitivity to the magnitude of the deviation from baseline of the responses
in another brain region, as opposed to its direction (positive/negative).
Importantly, testing for these patterns of related activity using Pearson’s correlation will
result in null findings for any significant interactions between the symmetrical data. Because
Pearson’s “r” is a measure of the linear correlation of variables, it is not especially informative
when seeking to explore nonlinear relationships between sets of data. In contrast to the inability
of correlation coefficients to distinguish between null relationships and U-shaped dependen-
cies, estimating a functional coordinate to map interactions provides a much more informative
model of any symmetrical dependencies (see Figure 1D).
In our simulated experiments, we show that not only do functional coordinate estimations
tightly track the shape of nonlinear functions (e.g., x2 and x4), but also, that these functional
coordinates are able to differentiate between dependencies that would otherwise be indistin-
guishable using measures of linear correlation (see Figure 1D). To highlight the explanatory
power of our functional coordinate analysis, we generated three sample dependencies where
Pearson r ≈ 0: y = 1 + ε, y = x2 + ε, and y = x4 + ε, where ε represents a random amount of
noise. In each case, x was defined as a normally distributed vector of 5,000 values (mean = 0,
SD = 1). In order to demonstrate the robustness of functional coordinates we used simulated
two distinct sets of noise by selecting 5,000 values from a normal distribution mean = 0, SD =
1, and mean = 0, SD = 5. Importantly, while all three of these interactions show |r| <= 0.02,
each relationship is described by a unique functional coordinate: for noise with standard devi-
ation of 1 (y = 1: [1.56, −0.02, −0.01, 0.02, −0.05]; y = x2: [1.51, 0.00, 2.26, −0.03, 0.36]; y =
x4: [5.05, 0.21, 14.26, 0.62, 9.06]) and for noise with standard deviation = 5 (y = 1: [1.63,
0.25, 0.07, 0.13, 0.10]; y = x2: [1.59, −0.03, 2.23, 0.19, 0.01]; y = x4: [4.71, 0.08, 13.07,
−0.56, 6.99]). In this way, these functional coordinates allow for the identification and model-
ing of U-shaped dependencies that could otherwise be overlooked in a standard correlation
analysis.
Nonlinear Coordinates Identify More Clusters Than Linear Coordinates
Exploring neural data using functional coordinates provides unique insight into the types of
interactions between brain regions. Moreover, using additional, nonlinear basis vectors to esti-
mate interregional dependencies allows for a heightened sensitivity to more complex interac-
tions. Other approaches like mutual information can be used to capture nonlinear dependence
between brain regions (Lizier et al., 2011; Wang et al., 2015). However, functional coordinates
are unique in that they do not characterize the interaction between two brain regions using a
Network Neuroscience
1304
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional coordinates
single value that reflects the strength of the dependence; instead, functional coordinates char-
acterize the interaction between two regions with a multidimensional vector encoding the
contributions of different Hermite basis functions. We used these multidimensional vectors
to subdivide cortex into distinct clusters of voxels with different types of interactions with
the FFA. To quantify the advantage of using multidimensional functional coordinates, we com-
pared the optimal clustering solutions for voxels across participants using five-dimensional
functional coordinates (leveraging the first five normalized Hermite polynomials as basis
vectors) and one-dimensional functional coordinates (using only the first order, linear polyno-
mial). In both cases, we calculated the AIC for clustering solutions ranging from 1 to 10 clus-
ters. In order to counterbalance the increased explained variance of more clusters with the
potential to overfit the data with too many clusters, the optimal number of clusters is deter-
mined by locating the “elbow” of the plotted AIC values—where an increase in the number of
clusters no longer corresponds with a substantial decrease in information lost. Importantly, for
the linear functional coordinate analysis, the optimal number of k-clusters was found at k = 2,
while for the nonlinear functional coordinate analysis, the best solution existed at k = 5 (see
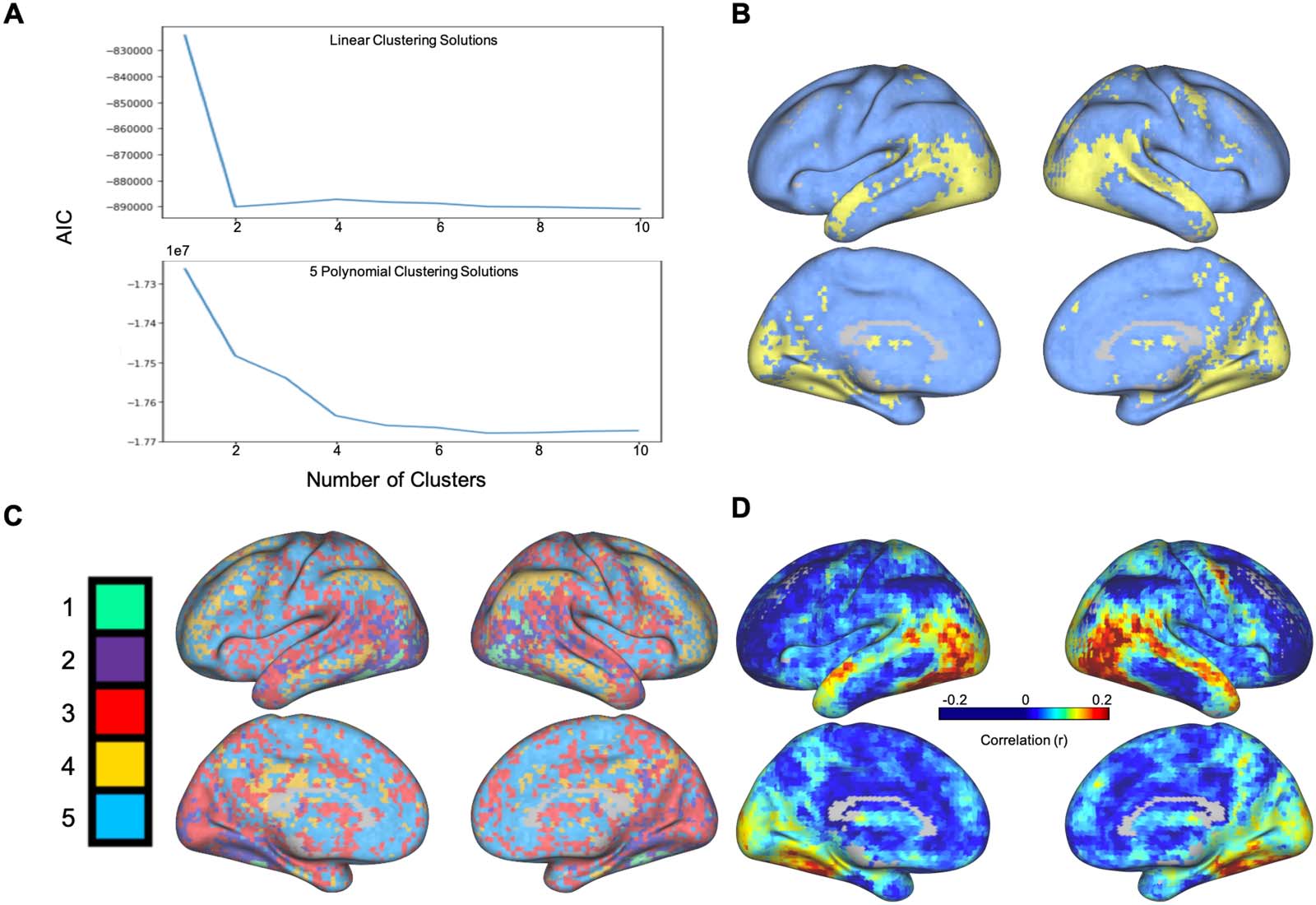
Figure 2A and C).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(A) Using k-means clustering, as the number of clusters (k value) increases, the Akaike information criterion (AIC) values decrease.
Figure 2.
The optimal clustering solution occurs when the AIC stops substantially decreasing. Top: Linear functional coordinates (Hermite polynomials
of degree 1). The elbow occurs at k = 2 clusters, meaning the optimal number of clusters across linear coordinates is 2. Bottom: Nonlinear
functional coordinates (Hermite polynomials of degree 0 through 4). The elbow occurs at k = 5 clusters. (B) Visualization of the cluster assign-
ments of different voxels based on the linear functional coordinates. For each voxel, we used the mode cluster assignment across subjects to
determine that voxel’s final cluster value. Each cluster is represented by a different color, and the intensity of the color represents the percent-
age of subjects sharing that voxel’s cluster assignment (lighter colors denote a higher percentage). (C) Visualization of the cluster assignments of
different voxels based on the nonlinear functional coordinates (generated with the same approach described in panel B). There was no dif-
ference in the clustering solution using all five basis vectors and when excluding the 0th-order basis vector. (D) Functional connectivity was
calculated between the FFA and each individual voxel for all subjects. After averaging the correlation values across all subjects, we plotted the
resulting average correlation values across the cortex. The pattern of functional connectivity with the FFA illustrates the highest correlations
with regions spanning the ventral, and dorsal temporal lobe and much of the visual cortex. These results parallel clustering solution using
linear coordinates.
Network Neuroscience
1305
Functional coordinates
After determining the ideal k value for the linear and nonlinear analyses, we used k-means to
group voxels by their linear coordinates and nonlinear coordinates across all subjects (see
Figure 2B and C). Our analysis of the linear coordinates yielded two distinct clusters across
the brain. The smaller (yellow in Figure 2B) of the two clusters encompasses the dorsal and ven-
tral temporal lobes bilaterally, as well as large sections of the bilateral visual cortex. The larger
cluster (blue in Figure 2B), comparatively, sprawls across the frontal and parietal lobes, as well as
the lateral temporal lobes in both hemispheres. In contrast, the five clusters generated from the
nonlinear coordinates show a unique division of the cerebral cortex (Figure 2C). The green clus-
ter is concentrated around a series of face selective regions, including the FFA (our seed region),
the superior temporal sulcus, and the occipital face area. The purple cluster covers the majority
of the visual cortex as well as the lateral and ventral temporal lobes. The red cluster is more
distributed, encompassing bilateral sections of the lateral temporal lobes, early visual cortex,
as well as sparse sections of the prefrontal cortex (PFC) and medial frontal lobe. The yellow clus-
ter is located in four distinct areas associated with the default mode network: the PFC, the pre-
cuneus, the angular gyrus, and the lateral temporal cortex. Finally, the blue cluster spans large
sections of the frontal and parietal lobes, as well as more sporadic areas in the anterior and lateral
temporal lobes. Since the 0th-order basis vector is a constant term, and the associated loadings
are noninterpretable, we also repeated the clustering procedure excluding them from the anal-
ysis, but found no changes in any of the clusters. This is expected, as the data were normalized
and thus the loadings on the 0th-order basis vector were close to zero for all voxels.
Comparison to Functional Connectivity
In order to facilitate the comparison with traditional analyses of the interactions between brain
areas, we additionally calculated the functional connectivity between the FFA and all gray
matter voxels by taking the correlation of activity in the FFA with the activity in each individual
voxel. After averaging the correlation coefficients across all subjects, we were able to map the
average functional connectivity of the FFA across the brain. Using a functional connectivity
analysis, we were able to determine that the areas showing the strongest correlation with activ-
ity in the FFA were the ventral and dorsal temporal lobe, as well as the visual cortex (see
Figure 2D). These results highlight a matching set of regions to those identified by the cluster-
ing of the linear functional coordinates (Figure 2D).
Distinct Clusters Are Associated With Unique Functional Relations to the FFA
One of the central advantages of the functional coordinate analysis is an enhanced interpretability
of nonlinear dependencies. Because the nonlinear components of the estimated function are
quantified as loadings on basis vectors, we can calculate the interaction between two regions
as a weighted sum of the normalized Hermite polynomials. To this end, we can observe the unique
computational relationship that defines a given cluster, by taking the loadings from the k-means
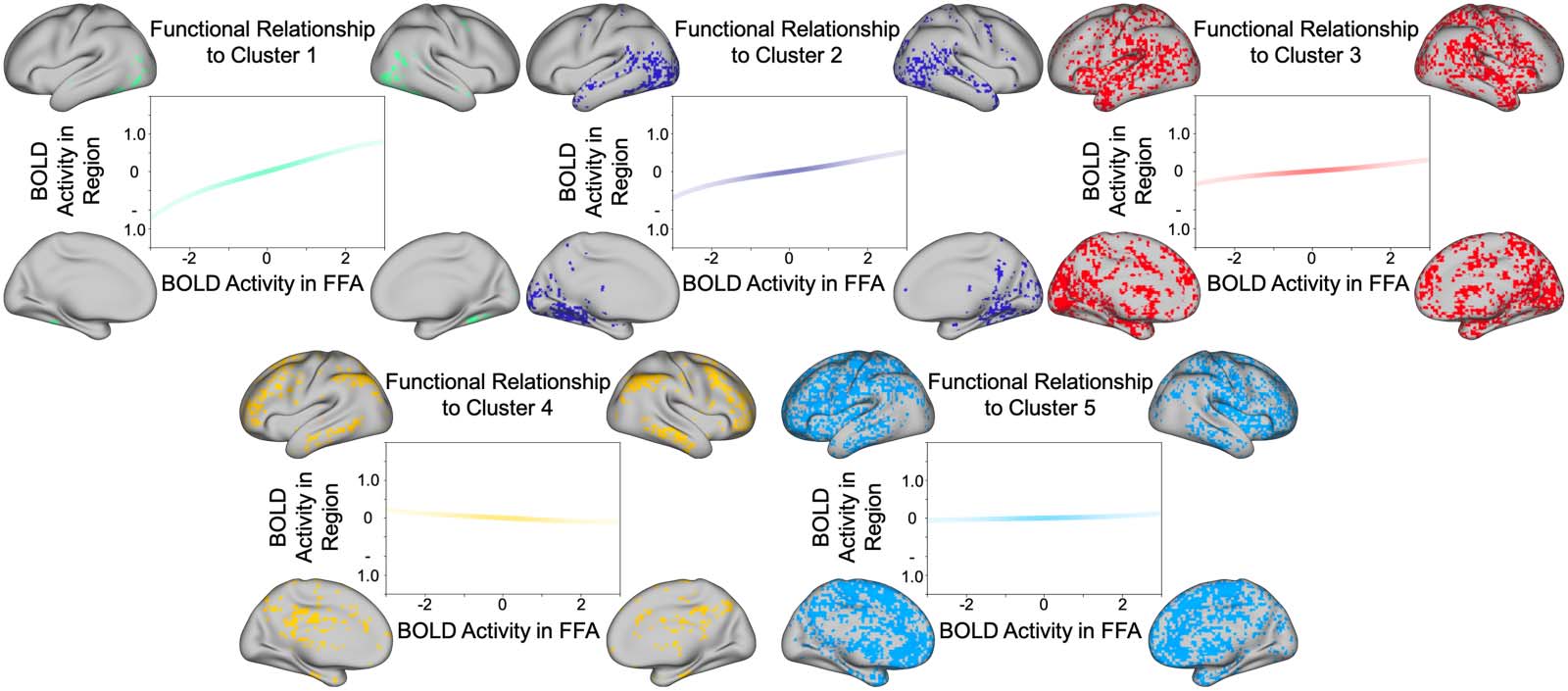
defined cluster center (see Figure 3). After segmenting the gray matter voxels using k-means clus-
tering, we identified five distinct clusters with centers at: [4.78e − 01, −3.34e − 02, 2.23e − 02,
−2.87e − 02], [2.61e − 01, −9.47e − 03, 2.43e − 02, −1.30e − 02], [1.35e − 01, −6.60e − 04, 1.51e
− 02, −4.85e − 03], [−8.28e − 02, 8.20e − 03, −7.01e − 05, 6.32e − 03], [3.40e − 02, 6.56e − 03,
5.40e − 03, 1.46e − 03]. For each cluster, we calculated the defining function using the respective
central functional coordinates as the loadings on the first- through fourth-order basis vectors.
Clustering Solutions Show Anatomical Consistency With the Increase in the Number of Clusters
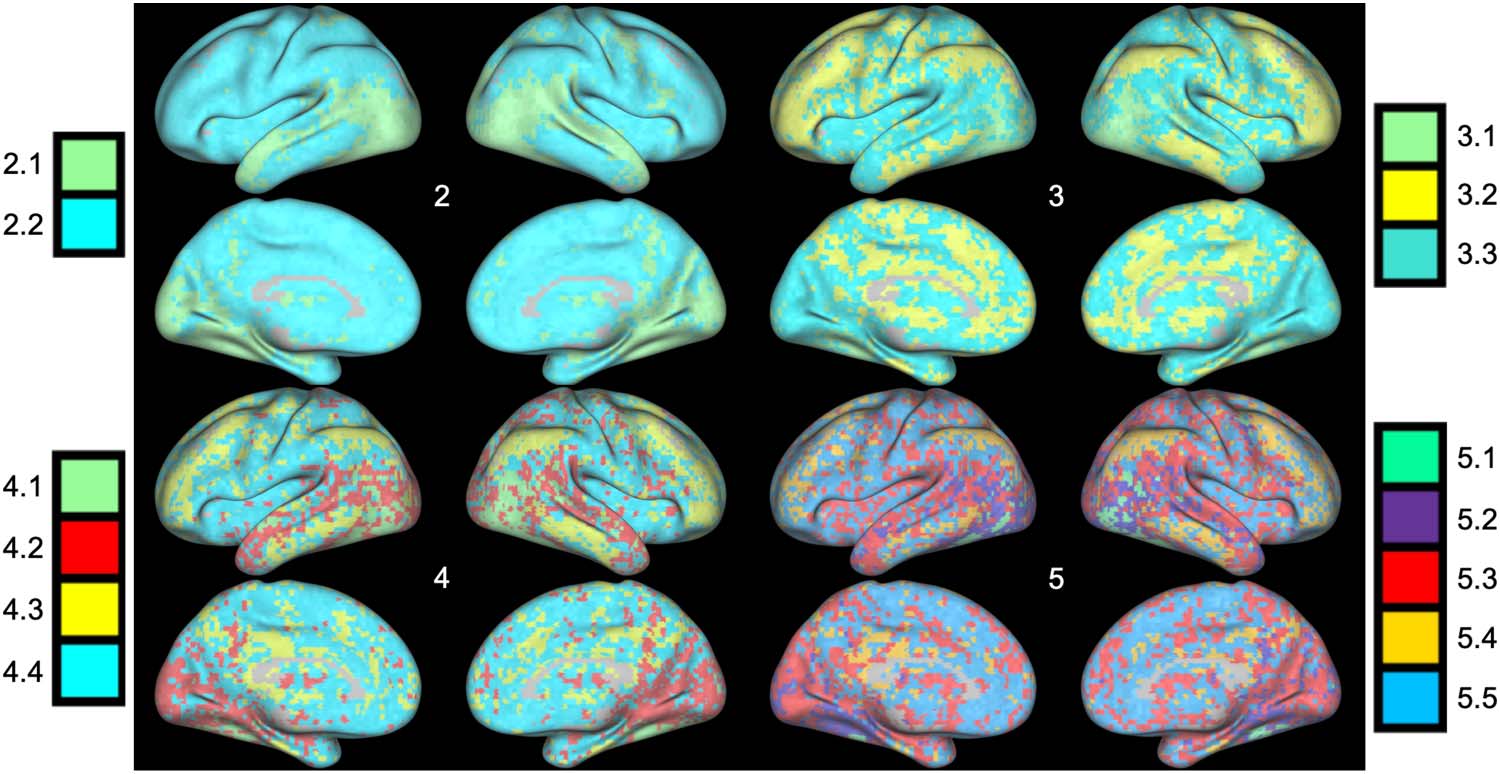
In order to test the impact of selecting different k values on the spatial layout of the resulting
clusters, we reran the k-means clustering using k values ranging from 2 to 5 (see Figure 4).
Network Neuroscience
1306
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional coordinates
Figure 3. K-means clustered voxels. Each plot represents the relationship between (z-scored) activity in the FFA (seed region) and the (z-
scored) activity in the highlighted region. Because the coordinate loadings are defined with respect to the normal probability density function
(see formula 11), the intensity of the line color is weighted by the normal probability density function in order to illustrate how the confidence
in the prediction of estimated activity varies as activity in the seed region varies. The strongest positive relationship is observed in ventral and
lateral posterior temporal regions (green cluster). Note a negative relationship with a cluster of regions in the vicinity of the default mode
network (yellow cluster).
Importantly, we found that the clustering solutions were consistent in their groupings of key
areas across the inferior and superior temporal lobe, the visual cortex, as well as the PFC. This
consistent anatomical grouping across clustering solutions suggests that our findings are robust
across clustering solutions and not dependent on the selection of a distinct number of clusters.
Coordinates Along Dimensions of the Hilbert Space Reveal the Distribution of Nonlinearities
Across Cortex
In order to observe the distribution of nonlinear interactions across the cortex, we next plotted
the loadings for each of the individual basis vectors for each voxel (see Figure 5) for the
Figure 4. K-means clustering of voxels based on five-dimensional functional coordinates, for
values of K ranging from two to five clusters. As the number of clusters increases, the spatial layout
of the new clusters provide a more detailed parcellation of the cortex, but highlight a strikingly
similar set of regions.
Network Neuroscience
1307
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional coordinates
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
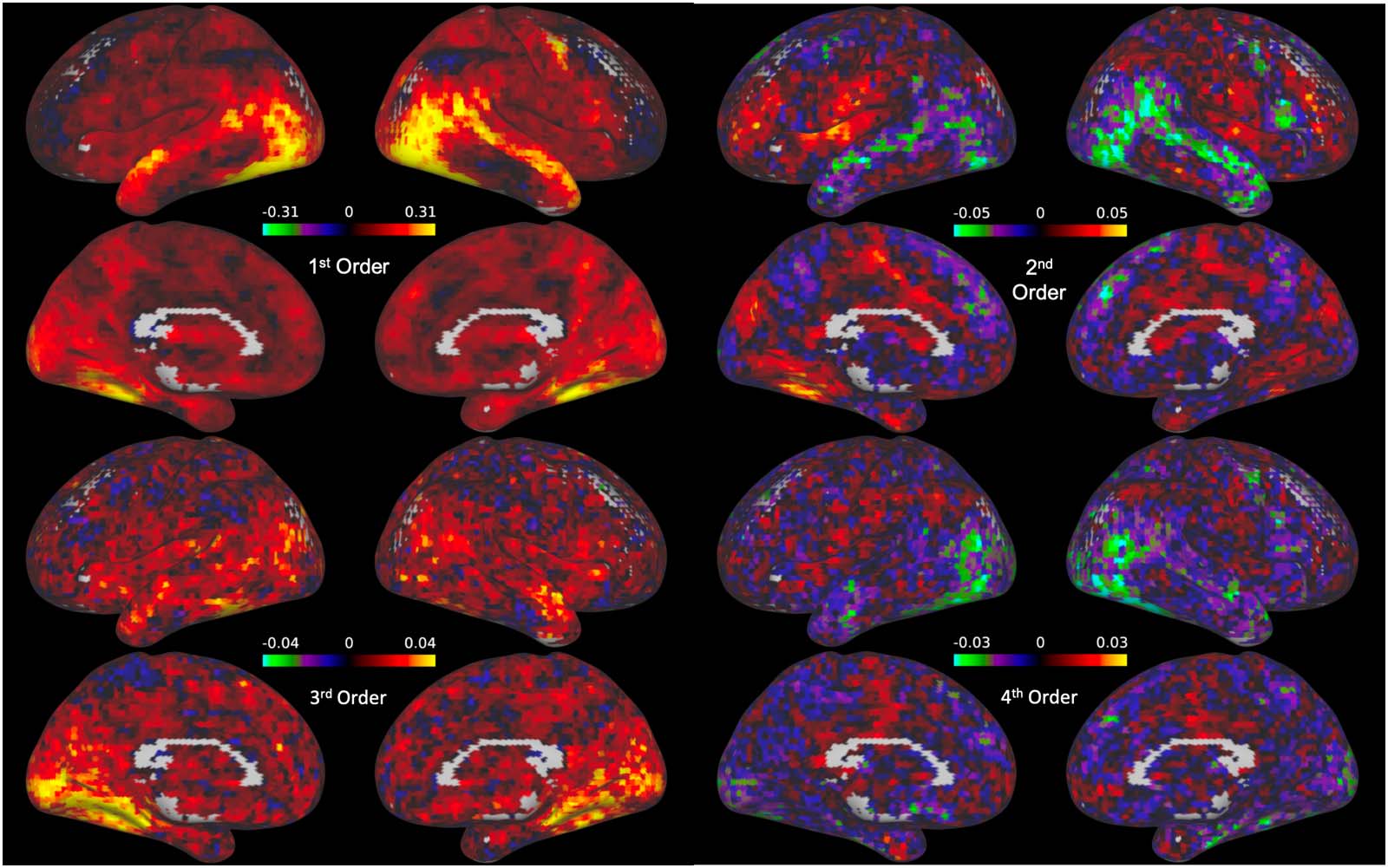
Figure 5. Whole-brain maps of the coefficient estimates for the Hermite polynomials in the basis set (excluding the constant 0th-order poly-
nomial, which captures the baseline signal and thus is not interpretable). Each polynomial in the basis set is associated with a unique cortical
map of coefficients. The magnitude of the loadings on the second-order and fourth-order basis vectors are largest in the superior temporal lobe
and medial frontal lobe, as well as the face selective visual cortex.
loadings on the first basis vector). Interestingly, while the loadings for the linear basis vectors
were highest in the regions surrounding the face selective cortical regions and dorsal temporal
lobe (Figure 5, first order), nonlinear loadings, particularly in in the second and fourth order
basis vectors, were highest in frontal and medial regions, with negative loadings in the face
selective cortex and lateral temporal regions. It is worth noting that the magnitude of the basis
vector loading reflects the contribution of that basis vector to the overall relationship between
the given voxel and the FFA. For this reason, larger loadings on nonlinear polynomials reveal
stronger nonlinear components within the given interaction.
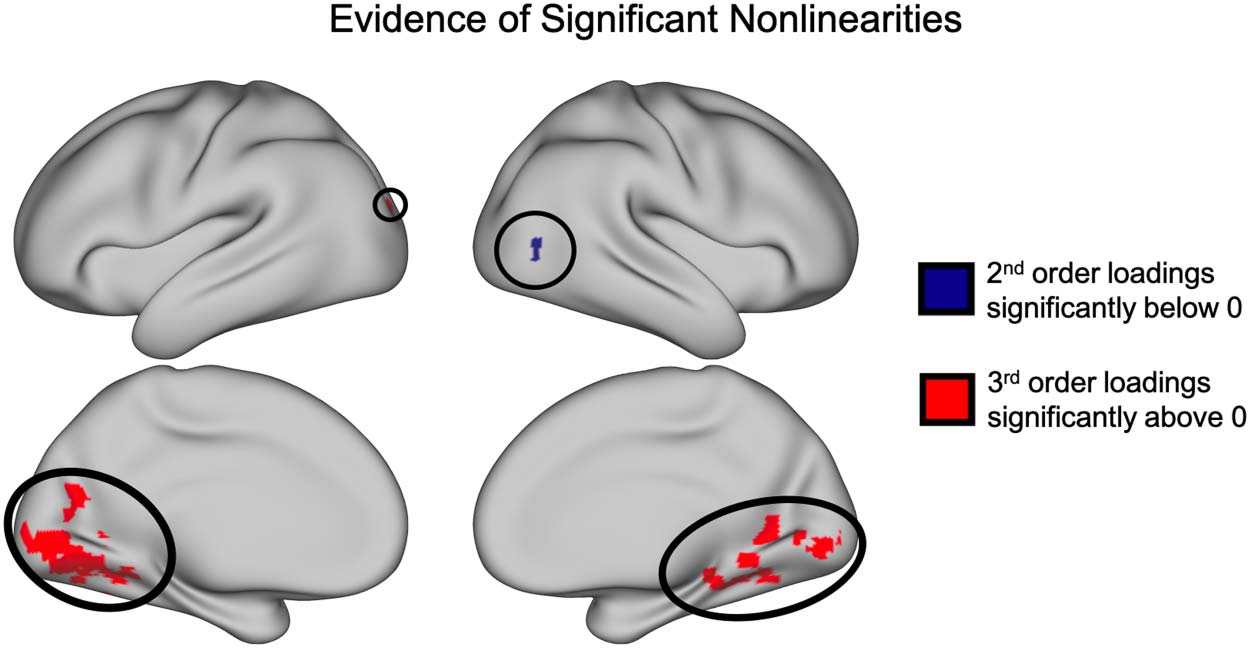
Figure 6. Significant clusters of nonzero loadings (SnPM t(13) ≥ 5.59, p < 0.05 FWE corrected).
Nonparametric pseudo t tests revealed a significant cluster of voxels with negative loadings on the
second-order basis vector as well as a collection of clusters in the medial occipital lobe and ventral
temporal lobe with positive loadings on the third-order basis vector.
Network Neuroscience
1308
Functional coordinates
To further test the significance of these nonlinear interactions across the cortex, we per-
formed across-subject one-tailed nonparametric pseudo t tests using SnPM to highlight any
clusters of voxels with significantly nonzero loadings on each of the nonlinear basis vectors
(i.e., the second-, third-, and fourth-order basis vectors; Figure 6). These tests revealed one
cluster of voxels in area V5 with significantly negative loadings on the second-order basis vec-
tor (cluster threshold p = 0.0001, p (FWE corrected) < .025; see Supporting Information section
“Variation in the cluster forming threshold” for additional analyses). Additionally, we found 24
clusters in the early visual cortex and ventral temporal lobe with positive loadings on the third-
order basis vector (cluster threshold p = .0001; all p values (FWE corrected) < .025). We found
no significant clusters with nonzero loadings on the fourth-order basis vector.
DISCUSSION
Functional Coordinates: A Novel Method to Study Neural Interactions
The major contribution of this research is a novel method to investigate nonlinear interactions
between brain regions: “functional coordinates.” Understanding the complexity of interre-
gional connectivity is an important objective within the landscape of current neuroscience
research (Anzellotti & Coutanche, 2018; Anzellotti et al., 2017b; Stephan et al., 2008). Impor-
tantly, functional coordinates allow for a balance between the interpretability of linear models
of connectivity (Friston et al., 1994) and the increased explanatory power and biological plau-
sibility of nonlinear models (Anzellotti et al., 2017b). Moreover, our method offers the ability
to characterize how the responses in different cortical regions are related, and not just whether
they are related.
Here, we demonstrated the capacity of the functional coordinate model to capture various
types of nonlinearities using synthetic data. Importantly, functional coordinates were able to
identify and distinguish between complex nonlinear relationships between data including
symmetric (U-shaped) functions, which are particularly difficult to identify using only linear
methods. This success on artificial data is an important indicator of the model’s potential to
identify the existing nonlinear interactions in real functional data.
Common methods used to study cortical networks rely on linear tools that are incapable of
capturing the wide array of potential interactions between brain regions. Functional coordi-
nates can capture the same linear interactions as methods like functional connectivity (Biswal
et al., 1995; Rogers et al., 2007). Indeed, the results of our functional connectivity analysis
illustrated a high degree of overlap with the clusters defined by the linear functional coordi-
nates. Importantly, however, adding a greater number of functional coordinates captures a
greater degree of variability in the statistical dependence across the cortex and allows for
an increased level of understanding of the functional relationship to the FFA. Moreover, using
the loadings from the nonlinear basis vectors, it is additionally possible to extract the nonlinear
components of a given relationship.
While the current study used functional coordinates to examine neural interactions of par-
ticipants during naturalistic movie watching, they can also be used to investigate statistical
dependence in resting state data. In addition, this method might be particularly useful for
examining task-evoked interactions between areas of interest. For example, in order to detect
brain areas that might respond to the emotional arousal of an image regardless of its
positive/negative affect, one could perform a searchlight analysis for a region with a U-shaped
relationship with regions that respond specifically to the emotional valence of an image. In this
way, functional coordinates could play a key role in elucidating complex cortical interactions
related to behavior. Some methods capable of capturing nonlinear interactions do exist (Lizier
Network Neuroscience
1309
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional coordinates
et al., 2011; Wang et al., 2015); however, they often focus on quantifying the strength of sta-
tistical dependence, rather than studying the type of dependence. Importantly, the responses in
different target brain regions could be predicted equally well by a given predictor region, yet at
the same time, be related to the predictor region via different functions. Functional coordinates
are able to quantify the contribution of each nonlinear component of the overall functional
relationship, allowing (unlike mutual information) for the explicit definition of the function
as a whole (see Figure 3).
One assumption when using functional coordinates is an implied directionality when cal-
culating the nonlinear transformations between brain regions. Importantly, this does not pre-
clude exploratory research into the nonlinear interactions between two brain regions without
an explicit hypothesis of which regional activity will be nonlinearly transformed. On the con-
trary, in this case, calculating functional coordinates bidirectionally may generate novel insight
into the reciprocal interactions between these brain areas.
In some respects, functional coordinates are related to estimating a polynomial fit of the
interaction between two brain regions and using the vectors of coefficient estimates to
characterize the interaction (to our knowledge, this approach has not been proposed in the
previous literature). However, functional coordinates offer a key advantage over using the
coefficients from a polynomial fit. This is because in a polynomial fit, including higher order
nonlinear terms would also lead to changes in the coefficient estimates for the lower order
polynomials, making it difficult to compare the results across different studies that used models
of different order. By contrast, due to the orthogonality of Hermite polynomials, functional
coordinates are such that the estimates of the coefficients of lower order basis functions do
not change when the model is expanded with the addition of higher order basis functions.
Moreover, functional coordinates can also be scaled up to take multidimensional patterns
of activity as input, much like existing methods such as MVPD (Anzellotti et al., 2017a) and
Informational Connectivity (Coutanche & Thompson-Schill, 2013), through the use of multi-
variate Hermite polynomials. This advantage allows for an examination of the rich high-
dimensional nature of neural data and provides the opportunity to incorporate a wider array
of neural response patterns into the study of nonlinear interactions between brain regions.
One potential future adaptation of functional coordinates might be to expand their use in
order to examine the relationship between neural activity across individuals. Functional coor-
dinates could be leveraged to contribute to the existing work on intersubject correlation
(Hasson et al., 2004), which examines the correlation of brain activity between two subjects.
Intersubject correlation provides a method to study a proxy measure of how much information
is encoded in a given voxel across multiple brains (Nastase et al., 2019); by calculating a set of
functional coordinates to characterize the interaction of neural activity across individuals, one
might gain further insight into the relationship between the amount of information encoded
across these distinct brains.
Evidence of Nonlinear Interactions Between Brain Regions
In this work, we also demonstrate the existence of distinct nonlinear interactions that charac-
terize the relationships between the FFA and other regions across the brain. After first defining
a set of functional coordinates to describe the relationship of the average FFA activity with the
activity in each other gray matter voxel, we were able to cluster the functional coordinates
across all voxels to identify five distinct sets of voxels with different functional interactions
(see Figures 2C and 3). Importantly, these clusters differ from those identified with a linear
Network Neuroscience
1310
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional coordinates
model of connectivity (see Figure 2B) highlighting the increased ability to discriminate
between voxels based on their relationship to the seed region.
Upon mapping out the functions associated with each cluster (Figure 3), we were able to
determine the functional forms of the relationships between activity in the FFA and activity
across the rest of the brain. A key feature of these relationships is their nonlinear components.
While the loadings on the linear basis vectors are, indeed, still the predominant component in
the defined clusters, the loadings on the nonlinear component are also important for differen-
tiating the patterns of connectivity across voxels. This is apparent in the increase in the optimal
number of clusters calculated for the five-dimensional functional coordinates (five clusters) as
compared to the clusters for the linear loadings only (two clusters). Noticeably, voxels sur-
rounding face selective regions and those in the anterior temporal lobe were grouped into a
single cluster when only including the linear component; in contrast, when clustering across
all five basis vectors, this same group of voxels was, instead, classified into separate, function-
ally distinct clusters. It is worth noting, that although we would expect the optimal number of
clusters to increase with additional basis vectors (because they provide additional information
regarding higher order nonlinearities), the number of clusters is not necessarily equal to the
number of Hermite polynomials used. For example, clustering across only the linear basis vec-
tor resulted in an optimal solution with two clusters.
Moreover, we report additional evidence for the importance of discovered nonlinearites in
the significant clusters of positive loadings on the third-order basis function and negative load-
ings on the second-order basis function (Figure 6). These clusters demonstrate specific areas in
both early visual cortex as well as downstream visual processing regions with which the FFA
has significant nonlinear interactions. In a follow-up analyses (see Supporting Information,
Regressed Nonlinear Loadings) we regressed out the linear basis vector loadings from those
of the nonlinear basis vectors in order to discover any nonlinearities whose spatial distribution
across cortical voxels is decoupled from that of linear interactions. With this analysis, we
found two additional clusters that were trending toward significance in the posterior superior
temporal sulcus (pSTS) and the anterior temporal lobe (Supporting Information, Figure S13),
two regions previously implicated in face perception (Anzellotti & Caramazza, 2017; Rajimehr
et al., 2009).
These clusters suggest the possible presence of very localized, anatomically specific non-
linear interactions between FFA and other regions in the face network, but additional studies
will be needed to evaluate the robustness of this finding.
Potential Pitfalls in the Search for Nonlinearities
Although, in this work, we present evidence of significant nonlinear interactions between
brain regions, it is important to note that the linear components of these interactions were still
an order of magnitude larger than the nonlinear loadings. Moreover, while we did find signif-
icant clusters of nonzero nonlinearities, these regions were particularly small and highly
localized.
This development in our understanding of nonlinear cortical interactions is intriguing, in
part, because existing computational and biological evidence suggests that nonlinearities
are a key part of neural information processing. Indeed, at the level of individual neurons,
dendrites perform nonlinear integration of signals (Lafourcade et al., 2022; Tran-Van-Minh
et al., 2015; Xu et al., 2012). One recent study found that approximating the input/output
relationship of a single pyramidal neuron requires using a deep recurrent neural network with
five to eight layers (Beniaguev et al., 2021). Other computational evidence has shown that
Network Neuroscience
1311
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional coordinates
nonlinearities are a key feature of models (like deep artificial neural networks) that approximate
human behavior (Yamins et al., 2014). Although previous research has not been able to identify
substantial nonlinear interactions (Hlinka et al., 2011), the advancement of fMRI preprocessing
and denoising techniques in the past 15 years could have revealed more evidence of nonline-
arities. The results of the current study are therefore surprising in two key ways: first, they do not
demonstrate widespread nonlinear cortical interactions, in apparent contrast with the existing
biological and theoretical evidence. Second, however, we do detect evidence of some non-
linearities, which suggests that there is promise for future research studying the nonlinear inter-
actions between brain regions in fMRI data. This pattern of results raises an important question
for research moving forward: why do nonlinear interactions not account for a greater propor-
tion of the variance in the interactions between brain regions?
The first potential explanation of the dearth of significant nonlinear interactions is that our
model is incapable of identifying the full extent of the existing nonlinearities in the relation-
ships between BOLD activity in different regions. However, our simulation data show that the
method is able to accurately capture nonlinearities, at least within the set of cases we tested. In
addition, it is important to note that we do report evidence of significant nonlinearities
between the FFA and early visual cortex, V5, and medial temporal areas (see Results; Coordi-
nates Along Dimensions of the Hilbert Space Reveal the Distribution of Nonlinearities Across
Cortex section). This suggests that our model is capable of capturing existing nonlinear inter-
actions, but that the magnitude of these interactions in the fMRI data we analyzed is small.
Additionally, our current model has outperformed previous models attempting to capture
the nonlinear interactions with the FFA within this same dataset (Poskanzer et al., 2022). In
sum, the small effect size of the nonlinearities appears to be a feature of the data, and not a
consequence of the chosen model.
Another possibility that could explain the difficulty in discovering nonlinear interactions is
that fMRI data, in particular, is not suitable to measure them. Previous work in this area has dem-
onstrated that contributions of nonlinear models of functional connectivity in resting-state fMRI
have been relatively minor when compared to their linear counterparts (Hlinka et al., 2011). This
result could be, in part, due to a number of underlying limitations of fMRI data, including spatial
resolution, temporal resolution, and hemodynamic smoothing. A further difficulty in the effort to
examine nonlinear interactions in fMRI data may be the difficulty in separating out the signal of
interest from nonneural sources of fluctuations in the data. Although, CompCor has been shown
to effectively remove signals of no interest, future denoising techniques may be better equipped
to reveal the underlying complexities of neural activity.
When considering the mechanics of connectivity at a neural level, it is entirely possible that
the nonlinear dynamics that we might expect to see are evident at a spatial scale that is too
fine-grained for the millimeter resolution of an MRI scanner. At the cellular level, neurons are
able to nonlinearly integrate signals from multiple synapses (Beniaguev et al., 2021; Xu et al.,
2012). In contrast, BOLD signal at the voxel level reflects the activity of hundreds of thousands
of neurons. In this way, spatial smoothing might “blur” the complex interactions occurring at
the neuronal level and, thus, minimize the underlying nonlinear interactions. In a similar fash-
ion to the spatial smoothing, fMRI data also suffers from temporal smoothing: our data might
not be sampled at a high enough rate to map any nonlinear interactions that occur on the order
of milliseconds. However, the averaging of a large number of nonlinear functions does not
generally produce a linear function. If the loss of nonlinear information in fMRI signal is
due to averaging over space and time, this would suggest that the amount and type of non-
linear interactions between neurons in different brain regions are such that their average is
approximately linear.
Network Neuroscience
1312
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional coordinates
Finally, another complicating factor of fMRI data is smoothing as the result of the hemody-
namic function. Neural activity is nonlinearly related to the BOLD signal (de Zwart et al.,
2009). This proxy measurement of the underlying activity of cortical neurons can serve, in this
case, as an additional smoothing function that might decrease the detectability of any nonlin-
ear neural interactions.
Despite the possibility that the BOLD signal may not be the optimal tool for the study of the
fine-grained nonlinear interactions between brain areas, it is also distinctly possible that it not
the quality but the quantity of data that is at issue. Hlinka et al. (2011) only reported finding
“subtle” nonlinear effects by “testing across many pairs or even across many sessions.” In this
study, we also found “subtle” yet significant nonlinear interactions by testing across a series of
subjects. One potential avenue for future research might be to examine datasets comprising
extensive scans of small numbers of participants (Allen et al., 2022). Using many runs of single
subject data and avoiding the averaging across subjects could increase the chances of iden-
tifying more subtle effects.
Although it is not currently clear why the scale of nonlinear interactions between brain
regions is comparatively much smaller than the scale of linear interactions, we believe that
solving this problem is essential for progress in the field of computational neuroscience. It is
clear that nonlinear computations are crucial for models that approach human behavior on
cognitive tasks (Yang et al., 2019) and for models that capture the behavior of biological neu-
rons (Beniaguev et al., 2021). Applying methods such as functional coordinates to very large
fMRI datasets, or to datasets acquired with more direct measures of neural activity (i.e., neu-
ropixels; Steinmetz et al., 2018), is likely to shed new light onto the neural bases of cognitive
computations.
ACKNOWLEDGMENTS
This work was funded by the Department of Psychology and Neuroscience at Boston College.
SUPPORTING INFORMATION
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
.
/
t
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00264.
AUTHOR CONTRIBUTIONS
Craig Poskanzer: Data curation; Formal analysis; Investigation; Methodology; Writing –
original draft; Writing – review & editing. Stefano Anzellotti: Conceptualization; Funding
acquisition; Methodology; Supervision; Writing – review & editing.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
FUNDING INFORMATION
Stefano Anzellotti, Simons Foundation Autism Research Initiative (https://dx.doi.org/10.13039
/100014370), Award ID: 614379.
REFERENCES
Allen, E. J., St-Yves, G., Wu, Y., Breedlove, J. L., Prince, J. S., Dowdle,
L. T., … Kay, K. (2022). A massive 7T fMRI dataset to bridge cogni-
tive neuroscience and artificial intelligence. Nature Neuroscience,
25(1), 116–126. https://doi.org/10.1038/s41593-021-00962-x,
PubMed: 34916659
Anzellotti, S., & Caramazza, A. (2017). Multimodal representations of
person identity individuated with fMRI. Cortex, 89, 85–97. https://
doi.org/10.1016/j.cortex.2017.01.013, PubMed: 28242496
Anzellotti, S., Caramazza, A., & Saxe, R. (2017a). Multivariate pat-
tern dependence. PLoS Computational Biology, 13(11),
Network Neuroscience
1313
Functional coordinates
e1005799. https://doi.org/10.1371/journal.pcbi.1005799,
PubMed: 29155809
Anzellotti, S., & Coutanche, M. N. (2018). Beyond functional con-
nectivity: Investigating networks of multivariate representations.
Trends in Cognitive Sciences, 22(3), 258–269. https://doi.org/10
.1016/j.tics.2017.12.002, PubMed: 29305206
Anzellotti, S., Fairhall, S. L., & Caramazza, A. (2014). Decoding
representations of face identity that are tolerant to rotation. Cere-
bral Cortex, 24(8), 1988–1995. https://doi.org/10.1093/cercor
/bht046, PubMed: 23463339
Anzellotti, S., Fedorenko, E., Kell, A. J. E., Caramazza, A., & Saxe,
R. (2017b). Measuring and modeling nonlinear interactions
between brain regions with fMRI. bioRxiv. https://doi.org/10
.1101/074856
Behzadi, Y., Restom, K., Liau, J., & Liu, T. T. (2007). A component
based noise correction method (CompCor) for BOLD and perfu-
sion based fMRI. NeuroImage, 37(1), 90–101. https://doi.org/10
.1016/j.neuroimage.2007.04.042, PubMed: 17560126
Beniaguev, D., Segev, I., & London, M. (2021). Single cortical
neurons as deep artificial neural networks. Neuron, 109(17),
2727–2739. https://doi.org/10.1016/j.neuron.2021.07.002,
PubMed: 34380016
Biswal, B., Yetkin, F. Z., Haughton, V. M., & Hyde, J. S. (1995).
Functional connectivity in the motor cortex of resting human
brain using echo-planar MRI. Magnetic Resonance in Medicine,
34(4), 537–541. https://doi.org/10.1002/mrm.1910340409,
PubMed: 8524021
Coutanche, M., & Thompson-Schill, S. (2013). Informational con-
nectivity: Identifying synchronized discriminability of
multi-voxel patterns across the brain. Frontiers in Human Neuro-
science, 7, 15. https://doi.org/10.3389/fnhum.2013.00015,
PubMed: 23403700
de Zwart, J. A., van Gelderen, P., Jansma, J. M., Fukunaga, M.,
Bianciardi, M., & Duyn, J. H. (2009). Hemodynamic nonlinear-
ities affect bold fmri response timing and amplitude. Neuro-
Image, 47(4), 1649–1658. https://doi.org/10.1016/j.neuroimage
.2009.06.001, PubMed: 19520175
Esteban, O., Markiewicz, C. J., Blair, R. W., Moodie, C. A., Isik,
A. I., Erramuzpe, A., … Gorgolewski, K. J. (2019). fMRIPrep: A
robust preprocessing pipeline for functional MRI. Nature
Methods, 16(1), 111–116. https://doi.org/10.1038/s41592-018
-0235-4, PubMed: 30532080
Fang, M., Aglinskas, A., Li, Y., & Anzellotti, S. (2019). Category-
selective neural responses are integrated in a topographically
organized hub in the angular gyrus. PsyArXiv. https://doi.org/10
.31234/osf.io/qbx4m
Friston, K. J., Holmes, A. P., Worsley, K. J., Poline, J.-P., Frith, C. D.,
& Frackowiak, R. S. J. (1994). Statistical parametric maps in func-
tional imaging: A general linear approach. Human Brain Map-
ping, 2(4), 189–210. https://doi.org/10.1002/hbm.460020402
Greicius, M. D., Krasnow, B., Reiss, A. L., & Menon, V. (2003).
Functional connectivity in the resting brain: A network analysis
of the default mode hypothesis. Proceedings of the National
Academy of Sciences, 100(1), 253–258. https://doi.org/10.1073
/pnas.0135058100, PubMed: 12506194
Hanke, M., Adelhöfer, N., Kottke, D., Iacovella, V., Sengupta, A.,
Kaule, F. R., … Stadler, J. (2016). A studyforrest extension, simul-
taneous fMRI and eye gaze recordings during prolonged natural
stimulation. Scientific Data, 3, 160092. https://doi.org/10.1038
/sdata.2016.92, PubMed: 27779621
Hasson, U., Nir, Y., Levy, I., Fuhrmann, G., & Malach, R. (2004).
Intersubject synchronization of cortical activity during natural
vision. Science, 303(5664), 1634–1640. https://doi.org/10.1126
/science.1089506, PubMed: 15016991
Hermite, M. (1864). Sur un nouveau développement en série des
fonctions. Imprimerie de Gauthier-Villars.
Hlinka, J., Paluš, M., Vejmelka, M., Mantini, D., & Corbetta, M.
(2011). Functional connectivity in resting-state fMRI: Is linear
correlation sufficient? NeuroImage, 54(3), 2218–2225. https://
doi.org/10.1016/j.neuroimage.2010.08.042, PubMed:
20800096
Ivanova, A. A., Schrimpf, M., Anzellotti, S., Zaslavsky, N.,
Fedorenko, E., & Isik, L. (2021). Is it that simple? Linear mapping
models in cognitive neuroscience. bioRxiv. https://doi.org/10
.1101/2021.04.02.438248
Jenkinson, M., Bannister, P., Brady, J. M., & Smith, S. M. (2002).
Improved optimisation for the robust and accurate linear registra-
tion and motion correction of brain images. NeuroImage, 17(2),
825–841. https://doi.org/10.1006/nimg.2002.1132, PubMed:
12377157
Kamitani, Y., & Tong, F. (2005). Decoding the visual and subjective
contents of the human brain. Nature Neuroscience, 8(5), 679–685.
https://doi.org/10.1038/nn1444, PubMed: 15852014
Kriegeskorte, N., Mur, M., & Bandettini, P. A. (2008). Representa-
tional similarity analysis-connecting the branches of systems
neuroscience. Frontiers in Systems Neuroscience, 2, 4. https://
doi.org/10.3389/neuro.06.004.2008, PubMed: 19104670
Lafourcade, M., van der Goes, M.-S. H., Vardalaki, D., Brown, N. J.,
Voigts, J., Yun, D. H., … Harnett, M. T. (2022). Differential den-
dritic integration of long-range inputs in association cortex via
subcellular changes in synaptic AMPA-to-NMDA receptor ratio.
Neuron, 110(9), 1532–1546. https://doi.org/10.1016/j.neuron
.2022.01.025, PubMed: 35180389
Li, Y., Saxe, R., & Anzellotti, S. (2019). Intersubject MVPD: Empir-
ical comparison of fMRI denoising methods for connectivity
analysis. PLoS One, 14, e0222914. https://doi.org/10.1371
/journal.pone.0222914, PubMed: 31550276
Lizier, J. T., Heinzle, J., Horstmann, A., Haynes, J.-D., & Prokopenko,
M. (2011). Multivariate information-theoretic measures reveal
directed information structure and task relevant changes in fMRI
connectivity. Journal of Computational Neuroscience, 30(1),
85–107. https://doi.org/10.1007/s10827-010-0271-2, PubMed:
20799057
Marinazzo, D., Pellicoro, M., & Stramaglia, S. (2008). Kernel
method for nonlinear Granger causality. Physical Review Letters,
100(14), 144103. https://doi.org/10.1103/ PhysRevLett.100
.144103, PubMed: 18518037
Misaki, M., Kim, Y., Bandettini, P. A., & Kriegeskorte, N. (2010).
Comparison of multivariate classifiers and response normaliza-
tions for pattern-information fMRI. NeuroImage, 53(1), 103–118.
https://doi.org/10.1016/j.neuroimage.2010.05.051, PubMed:
20580933
Nastase, S. A., Gazzola, V., Hasson, U., & Keysers, C. (2019). Measur-
ing shared responses across subjects using intersubject correlation.
Social Cognitive and Affective Neuroscience, 14(6), 667–685.
https://doi.org/10.1093/scan/nsz037, PubMed: 31099394
Network Neuroscience
1314
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional coordinates
Norman, K. A., Polyn, S. M., Detre, G. J., & Haxby, J. V. (2006).
Beyond mind-reading: Multi-voxel pattern analysis of fMRI data.
Trends in Cognitive Sciences, 10(9), 424–430. https://doi.org/10
.1016/j.tics.2006.07.005, PubMed: 16899397
Poskanzer, C., Fang, M., Aglinskas, A., & Anzellotti, S. (2022).
Controlling for spurious nonlinear dependence in connectivity
analyses. Neuroinformatics, 20(3), 599–611. https://doi.org/10
.1007/s12021-021-09540-9, PubMed: 34519963
Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., &
Petersen, S. E. (2012). Spurious but systematic correlations in
functional connectivity MRI networks arise from subject motion.
NeuroImage, 59, 2142–2154. https://doi.org/10.1016/j
.neuroimage.2011.10.018, PubMed: 22019881
Rajimehr, R., Young, J. C., & Tootell, R. B. (2009). An anterior
temporal face patch in human cortex, predicted by macaque
maps. Proceedings of the National Academy of Sciences, 106(6),
1995–2000. https://doi.org/10.1073/pnas.0807304106, PubMed:
19179278
Rogers, B. P., Morgan, V. L., Newton, A. T., & Gore, J. C. (2007).
Assessing functional connectivity in the human brain by fMRI.
Magnetic Resonance Imaging, 25(10), 1347–1357. https://doi
.org/10.1016/j.mri.2007.03.007, PubMed: 17499467
Sengupta, A., Kaule, F. R., Guntupalli, J. S., Hoffmann, M. B.,
Häusler, C., Stadler, J., & Hanke, M. (2016). A studyforrest exten-
sion, retinotopic mapping and localization of higher visual areas.
Scientific Data, 3, 160093. https://doi.org/10.1038/sdata.2016
.93, PubMed: 27779618
SnPM. (2013). Statistical non parametric mapping toolbox (SNPM)
2013. https://warwick.ac.uk/tenichols/snpm
Steinmetz, N. A., Koch, C., Harris, K. D., & Carandini, M. (2018).
Challenges and opportunities for large-scale electrophysiology
with neuropixels probes. Current Opinion in Neurobiology, 50,
92–100. https://doi.org/10.1016/j.conb.2018.01.009, PubMed:
29444488
Stephan, K. E., Kasper, L., Harrison, L. M., Daunizeau, J., den
Ouden, H. E., Breakspear, M., & Friston, K. J. (2008). Nonlinear
dynamic causal models for fMRI. NeuroImage, 42(2), 649–662.
https://doi.org/10.1016/j.neuroimage.2008.04.262, PubMed:
18565765
Szeg, G. (1939). Orthogonal polynomials (Vol. 23). New York, NY:
American Mathematical Society.
Tran-Van-Minh, A., Cazé, R. D., Abrahamsson, T., Cathala, L.,
Gutkin, B. S., & DiGregorio, D. A. (2015). Contribution of sub-
linear and supralinear dendritic integration to neuronal compu-
tations. Frontiers in Cellular Neuroscience, 9, 67. https://doi.org
/10.3389/fncel.2015.00067, PubMed: 25852470
Van Eijndhoven, S., & Meyers, J. (1990). New orthogonality
relations for the Hermite polynomials and related Hilbert spaces.
Journal of Mathematical Analysis and Applications, 146(1),
89–98. https://doi.org/10.1016/0022-247X(90)90334-C
Wang, Z., Alahmadi, A., Zhu, D., & Li, T. (2015). Brain functional con-
nectivity analysis using mutual information. In 2015 IEEE global
conference on signal and information processing (GlobalSIP)
(pp. 542–546). https://doi.org/10.1109/GlobalSIP.2015.7418254
Woolrich, M. W., Ripley, B. D., Brady, M., & Smith, S. M. (2001).
Temporal autocorrelation in univariate linear modeling of fMRI
data. Neuroimage, 14(6), 1370–1386. https://doi.org/10.1006
/nimg.2001.0931, PubMed: 11707093
Xu, N.-L., Harnett, M. T., Williams, S. R., Huber, D., O’Connor,
D. H., Svoboda, K., & Magee, J. C. (2012). Nonlinear dendritic
integration of sensory and motor input during an active sensing
task. Nature, 492(7428), 247–251. https://doi.org/10.1038
/nature11601, PubMed: 23143335
Yamins, D. L. K., Hong, H., Cadieu, C. F., Solomon, E. A., Seibert,
D., & DiCarlo, J. J. (2014). Performance-optimized hierarchical
models predict neural responses in higher visual cortex. Proceed-
ings of the National Academy of Sciences, 111(23), 8619–8624.
https://doi.org/10.1073/pnas.1403112111, PubMed: 24812127
Yang, G. R., Joglekar, M. R., Song, H. F., Newsome, W. T., & Wang,
X. J. (2019). Task representations in neural networks trained to
perform many cognitive tasks. Nature Neuroscience, 22(2),
297–306. https://doi.org/10.1038/s41593-018-0310-2, PubMed:
30643294
Zhang, Y., Brady, M., & Smith, S. (2001). Segmentation of brain MR
images through a hidden Markov random field model and the
expectation-maximization algorithm. IEEE Transactions on
Medical Imaging, 20(1), 45–57. https://doi.org/10.1109/42
.906424, PubMed: 11293691
Network Neuroscience
1315
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
6
4
1
2
9
6
2
0
5
9
7
9
8
n
e
n
_
a
_
0
0
2
6
4
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3