研究

A mixed-modeling framework for whole-brain
dynamic network analysis

Mohsen Bahrami1,2 , Paul J. Laurienti1,2, Heather M. Shappell1,3,
Dale Dagenbach1,4, and Sean L. Simpson1,3

1Laboratory for Complex Brain Networks, Wake Forest School of Medicine, Winston-Salem, NC, 美国
2放射科, Wake Forest School of Medicine, Winston-Salem, NC, 美国
3Department of Biostatistics and Data Science, Wake Forest School of Medicine, Winston-Salem, NC, 美国
4心理学系, Wake Forest University, Winston-Salem, NC, 美国

关键词: Mixed models, 功能磁共振成像, Dynamic brain networks, Multivariate, Simulation

开放访问

杂志

抽象的

The emerging area of dynamic brain network analysis has gained considerable attention in
最近几年. 然而, development of multivariate statistical frameworks that allow for
examining the associations between phenotypic traits and dynamic patterns of system-level
properties of the brain, and drawing statistical inference about such associations, has largely
lagged behind. To address this need we developed a mixed-modeling framework that
allows for assessing the relationship between any desired phenotype and dynamic patterns
of whole-brain connectivity and topology. This novel framework also allows for simulating
dynamic brain networks with respect to desired covariates. Unlike current tools, 哪个
largely use data-driven methods, our model-based method enables aligning neuroscientific
hypotheses with the analytic approach. We demonstrate the utility of this model in identifying
the relationship between fluid intelligence and dynamic brain networks by using resting-state
功能磁共振成像 (rfMRI) 数据来自 200 participants in the Human Connectome Project (HCP) 学习. 我们
also demonstrate the utility of this model to simulate dynamic brain networks at both group
and individual levels. To our knowledge, this approach provides the first model-based
statistical method for examining dynamic patterns of system-level properties of the brain and
their relationships to phenotypic traits as well as simulating dynamic brain networks.

作者总结

最近几年, a growing body of studies have aimed at analyzing the brain as a complex
dynamic system by using various neuroimaging data. This has opened new avenues to answer
compelling questions about the brain function in health and disease. 然而, methods that
allow for providing statistical inference about how the complex interactions of the brain are
associated with desired phenotypes are to be developed for a more profound insight. 这
study introduces a promising regression-based model to relate dynamic brain networks to
desired phenotypes and provide statistical inference. 而且, it can be used for simulating
dynamic brain networks with respect to desired phenotypes at the group and individual levels.

引文: Bahrami, M。, Laurienti, 磷. J。,
Shappell, H. M。, Dagenbach, D ., &
辛普森, S. L. (2022). A mixed-
modeling framework for whole-brain
dynamic network analysis. 网络
神经科学, 6(2), 591–613. https://土井
.org/10.1162/netn_a_00238

DOI:
https://doi.org/10.1162/netn_a_00238

支持信息:
https://doi.org/10.1162/netn_a_00238

已收到: 22 九月 2021
公认: 9 二月 2022

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
Mohsen Bahrami
mbahrami@wakehealth.edu

处理编辑器:
Vince Calhoun

版权: © 2022
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

t

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

.

t

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

Dynamic brain networks:
Large-scale brain networks that vary
over short periods of time on the
order of seconds.

介绍

The past two decades have witnessed an explosion of studies aimed at examining the brain as
a complex system through analysis of neuroimaging data, particularly data from functional
MRI (功能磁共振成像). Complex functional systems of the brain are often analyzed through graph
theoretical measures of the brain’s functional networks (布莫尔 & 斯波恩斯, 2009). Nodes
in brain networks often represent brain regions, and edges represent functional connections
(statistical associations) between the blood oxygen level–dependent (大胆的) signals in differ-
ent brain regions. Until recent years, most network studies of the brain focused on static func-
tional networks, in which the functional connections between brain regions were defined
over the entire scanning period or condition. Although such studies have provided promising
insights into functional organization and abnormalities of the brain (Bassett & 布莫尔,
2009; 公园 & 弗里斯顿, 2013), recent studies indicate that functional connectivity patterns
are not stationary and fluctuate over very short periods of time on the order of seconds
(张 & Glover, 2010; Handwerker, Roopchansingh, Gonzalez-Castillo, & Bandettini,
2012; Hutchison et al., 2013; Parr, Rees, & 弗里斯顿, 2018). This has resulted in a new and
rapidly evolving line of studies examining dynamic networks or time-varying functional con-
nectivity patterns of the brain.

Studies of brain dynamics are critical for establishing a profound understanding of the brain
given that the brain is a complex multiscale dynamic system rather than a stationary one (Lurie
等人。, 2020). As noted in Breakspear (2017), analytical frameworks that allow for examining
the dynamical systems of the brain, from differential equations and state space analyses of
populations of neurons to larger scale network science methods, are essential for understanding
how behavioral and cognitive processes emerge from neural activities. Dynamic brain networks
have been associated with a wide range of cognitive and behavioral responses (Cole, Bassett,
力量, Braver, & 彼得森, 2014; Shine et al., 2016; Vidaurre, Abeysuriya, 等人。, 2018). 更多的
具体来说, they have been used to determine the engagement of a participant in a specific cog-
nitive task (Gonzalez-Castillo et al., 2015; Shirer, Ryali, Rykhlevskaia, Menon, & Greicius,
2012), and have been associated with consciousness (Barttfeld et al., 2015; Godwin, Barry, &
Marois, 2015), 学习 (Bassett et al., 2011), and various neuropsychiatric and neurological
disorders, such as schizophrenia (Rashid et al., 2016; Sakoglu et al., 2010), depression (长的
等人。, 2020; Martinez, 德科, Ter Horst, & Cabral, 2020), 阿尔茨海默氏病 (Gu et al.,
2020; Jones et al., 2012), and Parkinson’s disease (Diez-Cirarda et al., 2018; Zhu et al.,
2019). New studies indicate that dynamic brain networks may provide more sensitive biomark-
ers for detecting differences between study populations or individuals than static networks
(Rashid et al., 2016). 例如, dynamic patterns of brain connectivity at rest have been
shown to better characterize people with post-traumatic stress disorder (Jin et al., 2017) or pre-
dict weight loss among older adults (Mokhtari, Laurienti, Rejeski, & Ballard, 2019).

Despite such insights, substantial challenges remain to enable more accurate analysis of
dynamic brain networks and accurate interpretation of results. Dynamic changes in the sys-
temic organization of brain networks confers much of our brains’ functional abilities (Bressler
& Menon, 2010; Buzsaki & Draguhn, 2004). If functional connections are lost or rendered
dynamically rigid due to an adverse health condition, compensatory connections may develop
to maintain organizational consistency and functional abilities. 最后, brain network
analysis necessitates a suite of tools including a multivariate modeling framework for dynamic
brain network data to assess effects of multiple variables of interest and topological network
features on the overall network structure. 然而, most current methods rudimentarily com-
pare the dynamic patterns of connection strength or networks measures across study popula-
系统蒸发散 (Elton & 高, 2015; Fukushima et al., 2018; Sizemore & Bassett, 2018), failing to fully

网络神经科学

592

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

t

/

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

t

.

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

System-level properties:
Properties of the brain as a system
comprising multiple interacting
地区.

harness the wealth of information about dynamics of system-level properties of the brain,
which can be obtained via a validated multivariate statistical method.

迄今为止, despite having a broad range, most analytical approaches have aimed at identify-
ing similar FC patterns (例如, through clustering methods; Allen et al., 2014) or hidden brain
状态 (often through hidden Markov models; Shappell, Caffo, Pekar, & Lindquist, 2019;
Vidaurre, 打猎, 等人。, 2018) with respect to desired outcomes. Although such methods have
provided useful insights, there remain many gaps in the suite of analytic methods available,
including the following. (1) One gap is the lack of a well-defined statistical framework to align
the neuroscientific hypothesis with the analytical approach and to assess the effects of multiple
phenotypes of interest simultaneously. As pointed out earlier, most current methods use
clustering-based approaches on FC patterns or hidden Markov models on time series to iden-
tify brain states and their transitions with respect to behavioral and cognitive outcomes. 这样的
data-driven methods have allowed for identifying complex patterns of dynamic changes in the
脑, providing profound insight into dynamic brain networks. 因此, they may still be the
most appropriate methods for studies aimed at examining state-based changes in dynamic
brain networks or for comparing study populations in the absence of a well-defined hypoth-
埃西斯. 然而, to conduct statistical inference (IE。, hypothesis testing) on a well-posited neu-
roscientific hypothesis about dynamic brain networks, a model-based method that allows
selectively incorporating the desired topological properties of the brain or FC patterns as well
as combinations of desired variables, will provide a more fruitful framework. Other gaps in the
suite of analytic methods include (2) difficulty in controlling for confounding effects, 例如
age and gender (this often requires matching the study populations, which is a daunting task
for most neuroimaging studies); (3) the limitation of examining fluctuations of single network
measures instead of capturing the complex dynamics of brain networks as a system; 和 (4)
inability to simulate dynamic brain networks with respect to changes in system-level properties
of the brain and desired covariates. Such critical methodological gaps may be addressed
through parsimonious multivariate statistical frameworks.

As noted by Shine et al. (2019), the neurobiological mechanisms underlying brain network
dynamics (dynamic changes in functional architecture) remain poorly understood; 并作为
pointed out in Liu (2017), “novel methods are urgently needed for a better quantification of
temporal dynamics in resting-state fMRI.” The development of rigorous statistical methods
within a multivariate framework are among such urgent needs. Developing and disseminating
explainable, validated multivariate statistical methods are paramount for relating phenotypic
traits to dynamic changes in network properties of the brain, which will greatly aid in provid-
ing profound insights into normal and abnormal brain function.

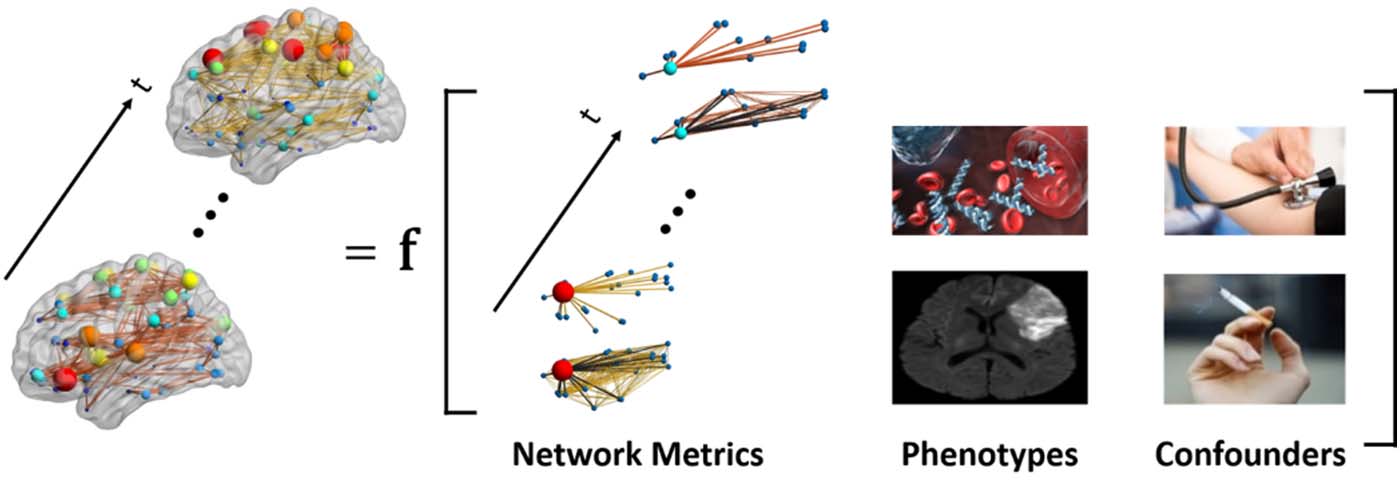
For the modeling framework, if we have

(西德:1)

数据

Y it :network of participant i at time point t
X it :covariate information

we wish to accurately estimate the probability density function of the networks given the
covariates P(Yit|Xit, βit), where βit are the parameters that relate the covariates to the network
structure as shown in Figure 1. 然而, the development of such methods has vastly lagged
behind, mainly due to the same challenges which exist in developing multivariate statistical
tools for static networks (Bahrami, Laurienti, & 辛普森, 2019A; Shehzad et al., 2014; 辛普森
& Laurienti, 2016). Here we introduce a novel multivariate statistical framework for assessing
phenotype-dynamic brain network pattern relationships and drawing inference from such
关系.

网络神经科学

593

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

t

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

t

.

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

数字 1. Dynamic brain networks as a function of endogenous and exogenous variables of interest.
Dynamic patterns of brain connectivity (presence/absence and strength) is modeled as a function of
(dynamic) nodal and global network metrics (例如, clustering coefficient, global efficiency, ETC。) 和
exogenous covariates, including phenotypes (例如, blood measurements and brain damage) 和
possible confounding effects (例如, hypertension and smoking).

This model-based framework is a fundamentally different approach toward analyzing
dynamic brain networks when compared to current approaches, which often use data-driven
methodologies to identify “brain states” and their transitions with respect to health and behav-
ioral outcomes (Allen et al., 2014; Shappell et al., 2019; Shine & Poldrack, 2018; Vidaurre,
史密斯, & 伍尔里奇, 2017). We develop this method by advancing a promising statistical
mixed-modeling framework for static networks (辛普森 & Laurienti, 2015). Several exten-
sions of the original framework (Bahrami et al., 2019A; 辛普森, Bahrami, & Laurienti,
2019), as well as a MATLAB toolbox (Bahrami, Laurienti, & 辛普森, 2019乙) have recently
been introduced. 然而, it has yet to be extended to the dynamic network context. 到
our knowledge, this proposed extension will be the first to allow relating group- 和
individual-level characteristics to time-varying changes in spatial and topological brain
network properties while also maintaining the capabilities of the original model, 例如
accounting for variance associated with confounders.

We will demonstrate the utility of this framework by identifying the relationship between
fluid intelligence and dynamic brain network patterns by using data from 200 participants from
the Human Connectome Project (HCP) (Van Essen et al., 2013) 学习. Fluid intelligence (gF)
refers to reasoning ability and the capacity of an individual to discern patterns or solve prob-
lems when that individual doesn’t have or has minimal resources or acquired knowledge to act
之上 (Cattell, 1987). Understanding the neurobiological underpinnings of gF is of great inter-
东方, as it has been associated with a variety of cognitive abilities (Colom & Flores-Mendoza,
2007; Unsworth, Fukuda, Awh, & 沃格尔, 2014; Ye et al., 2019). We also demonstrate the utility
of this new framework for simulating dynamic brain networks, which can be critical for a
better understanding of topological variability in time and across individuals with respect to
desired covariates. To our knowledge, this simulation capability is also the first to enable
simulating representative group-level dynamic networks from an array of desired global/local
network measures and phenotypic characteristics.

材料和方法

Motivating Data

We used the rich dataset provided by the HCP study (Van Essen et al., 2013) to be able to
explore dynamic functional brain network differences in cognitively variable populations as
a function of phenotype, while maintaining continuity with previous analyses to contrast and
clearly distinguish the novel utilities of our proposed method. We specifically focused on

网络神经科学

594

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

t

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

.

t

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

demonstrating the utility of our framework in assessing the relationship between dynamic
functional networks and intelligence due to the great interest in identifying such relationship.
The HCP data released to date include 1,200 个人. Of those, 1,113 (606 女性; 283
minority) have complete MRI images, cognitive testing, and detailed demographic informa-
的. Participants in the HCP were screened to rule out neurological and psychiatric disorders.
All data were collected on 3T Siemens MRI scanners located at Washington University or the
University of Minnesota, using identical scanning parameters. The HCP performed extensive
testing and development to ensure comparable imaging at the two sites. The BOLD-weighted
images were collected using the following parameters: TR = 720 多发性硬化症, = 33.1 多发性硬化症, voxel size
2 mm3, 72 slices, 和 1,200 volumes. In this study, we selected a subsample comprising 389
individuals with unique family identification numbers that also passed our image processing
quality control assessments. For multiple individuals with the same family identification num-
误码率, one individual was selected randomly. We initially used the entire 389 个人, but we
further reduced this to 200 个人 (randomly chosen from our subsample) after we faced
convergence issues in modeling one of the two-part mixed-effect models. We have provided
the HCP identification numbers for the 200 individuals used in this study in Supporting Infor-
mation Appendix S1 (Table S1). The HCP analyses are an exemplar; 重要的是, our methods
can be applied to any network-based neuroimaging study.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

t

/

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

.

t

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Dynamic Networks Generation

We used minimally preprocessed resting fMRI (rfMRI) data from HCP (Glasser et al., 2013). 我们
used two scans for each individual, the left-to-right (LR) and right-to-left (RL). For each scan,
we used ICA-AROMA (Pruim et al., 2015) to correct for any motion artifact in the rfMRI data. A
band-pass filter (0.009–0.08 Hz) was applied to each scan. The LR and RL scans for each indi-
vidual were then concatenated temporally, and transient artifacts were removed using a win-
dowed wavelet transformation. Then a regression was performed with the mean tissue signals
(GM, WM, and CSF), the six movement parameters and derivatives, as well as a binary regres-
sor to account for any mean signal differences between the two scan conditions (LR and RL
scans). Our quality control process removed 116 individuals from the analysis. QC included
manually checking the rfMRI for warping irregularities as well as remaining motion artifact
after the above processing steps. For the remaining individuals, among those with the same
family identification number, one individual was selected randomly. This provided a final
dataset comprising 389 individuals with unique family identification numbers. For all 389
个人, we divided the brain into 268 regions based on a functional atlas (沉, Tokoglu,
Papademetris, & Constable, 2013) and averaged all time series within each region to create a
single time series for that region. We used a continuous wavelet transform to filter artifact
resulting from the LR and RL concatenation with a window size of 30 s (covering 15 s from
the ending and starting points of LR and RL time series, 分别). We then prewhitened the
time series to avoid undesired autocorrelation effects for our regression analyses and as rec-
ommended by (Honari, Choe, Pekar, & Lindquist, 2019) for dynamic network analyses by
using a sliding window correlation approach.

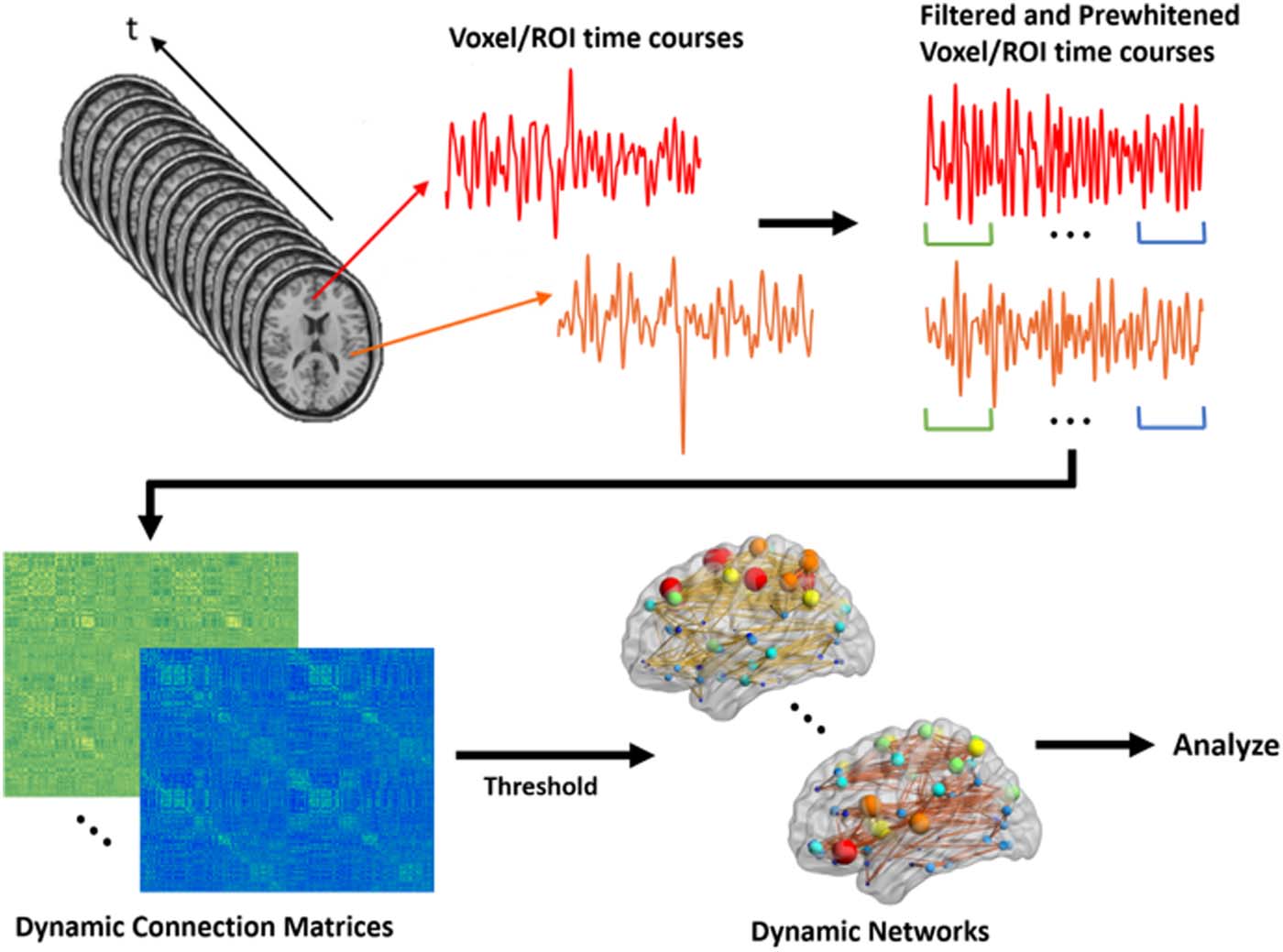
Dynamic brain networks for each participant were constructed through a sliding window
correlation approach. We used a modulated rectangular window (Mokhtari, Akhlaghi, 辛普森,
吴, & Laurienti, 2019) with a length of 120 volumes and the same shift size (IE。, 120 volumes)
to generate windows with no overlap between consecutive networks. We understand that
this is not a commonly used shift size as most studies use overlapping windows with 1 TR
shift size; 然而, unlike other methods, we subsequently use the dynamic networks in a
regression framework, thus we used windows with no overlap to further reduce temporal

网络神经科学

595

A mixed model for dynamic brain networks

autocorrelation. 然而, in an additional analysis provided in Supporting Information
Appendix S2, we used windows with 50% overlap between consecutive networks, 那是,
using a shift size of 60 volumes, which yielded similar results. Since at least one other study
that uses dynamic networks in a regression framework has used windows with 50% 重叠
between consecutive networks (张, 刘, 陈, 刘, & Duyn, 2013), we conducted this
additional analysis to see how our reported results would be affected when using this
方法. Despite similar results, we present results for windows with no overlap between
consecutive networks to ensure that temporal autocorrelation effects are minimized. The rea-
sons and implications of our choices for window type, window length, and shift size will be
further explained in the Discussion. The dynamic networks for each participant were gener-
ated by moving the window across the time series and computing the Pearson’s correlation
between time series of all pairs of 268 regions at each shift. This yielded 19 dynamic net-
works for each participant. We then thresholded all dynamic networks to remove negative
correlations as multiple network measures, particularly clustering, remain poorly understood
in networks with negative correlations (弗里德曼, Landsberg, 欧文, 李, & Mukherjee, 2014;
Telesford, 辛普森, Burdette, Hayasaka, & Laurienti, 2011). 此外, distributions of net-
work variables (such as degree) and the neurobiological interpretation of positive and nega-
tive edges are different (Parente et al., 2018; A. J. 施瓦茨 & McGonigle, 2011). 什么时候
including positive and negative edges in an analysis, networks should be generated and
assessed separately (A. J. 施瓦茨 & McGonigle, 2011). 数字 2 shows a schematic exhibit-
ing this dynamic network generation process.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

t

/

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

.

t

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

数字 2. Schematic for generating dynamic brain networks from fMRI time series. Time series are
first filtered and prewhitened to remove the undesired undershoots/overshoots in the middle as well
as undesired effects of autocorrelation. 然后, using a sliding window correlation approach, func-
tional connectivity between brain areas is estimated between all time series pairs at each shift to
produce a connection matrix at that shift. By moving the window across the entire length of time
系列, a series of dynamic connection matrices will be produced for each participant. A threshold is
applied to the matrix to remove negative connections. These networks are subsequently used for
分析.

网络神经科学

596

A mixed model for dynamic brain networks

Mixed-effects (or mixed) 型号:
Statistical regression models that
include both fixed (IE。, 人口-
等级) and random (IE。, 个人-
等级) 参数.

We also used the original models (辛普森 & Laurienti, 2015) to conduct the same analyses
but with static networks to further examine whether/how dynamic and static networks provide
different insight into fluid intelligence–brain network associations (see Supporting Information
Appendix S3).

Mixed-Effects Modeling Framework for Weighted Dynamic Brain Networks

Given that we have sparse weighted networks, a two-part mixed-effects model will be
employed to model both the probability of a connection (presence/absence) and the strength
of a connection, if it exists (辛普森 & Laurienti, 2015). The model includes the entire brain
connectivity matrix of each participant, endogenous covariates, and exogenous covariates (看
数字 1). The endogenous covariates are summary variables extracted from the network to
summarize global topology. The exogenous covariates are the biologically relevant pheno-
typic variables (例如, for our data, fluid intelligence, 性别, 种族, and education among others).
This statistical framework allows for the evaluation of group and individual effects. 其他
key feature of the model is the multivariate nature of the statistics. Inclusion of the actual con-
nectivity matrices allows the statistics to be performed on the entire network simultaneously,
rather than performing edge-by-edge analyses in a massively univariate fashion.

进一步来说, let Yijkt represent the strength of the connection (quantified as the corre-
lation in our case) and Rijkt indicate whether a connection is present (presence variable)
between node j and node k for the ith participant at time t. 因此, Rijkt = 0 if Yijkt = 0, and Rijkt =
1 if Yijkt > 0 with conditional probabilities:
(西德:4)

(西德:5)

(西德:6)

(西德:3)
P Rijkt ¼ rijktjβ

; bri; C

r

; d ri

r

¼

ð
1 − pijkt β
r
ð
; bri; C
pijkt β
r

; bri; C
r
; d ri
r

; d ri
Þ if

rijkt ¼ 0

Þ if
rijkt ¼ 1

;

(1)

where pijkt( βr; bri; γr; dri) is the probability of a connection between nodes j and k for partic-
ipant i at time t. We then have the following logistic mixed model (part I model) for the prob-
ability of this connection:

(西德:3)
logit pijkt β
ð
r

; bri ; C

r

; d ri

(西德:4)
Þ

¼ X

0
ijkt

β
r

þ

Xn

o¼1

!

!

C

ros oð Þ Xtð

Þ

þ Z

0

ijktbri þ

drios oð Þ Ztð

Þ

;

(2)

Xn

o¼1

Fixed effects:
Variables in the mixed models whose
effects are constant across all
个人.

Random effects:
Variables in the mixed models whose
effects change across individuals.

Orthonormal polynomials:
A family of orthogonal polynomials
where the inner product of the same
polynomials is one.

n

磷

where βr (note that r and s subscripts simply denote the probability and strength models in
Equations 2 和 3, 分别, and have no relationship with Rijkt or Sijkt in the next equation)
is a vector of population parameters (fixed effects) that relate the probability of a connection to
a set of covariates (Xijkt) for each participant and nodal pair (dyad), bri is a vector of participant-
and node-specific parameters (random effects) that capture how this relationship varies about
the population average (βr) by participant and node (Zijkt), Zijkt is the design matrix for the ran-
o¼1 γros(哦)(Xt) corresponds to a population-level nth-order orthonormal polyno-
dom effects,
磷
n
mial model capturing the dynamic trend in the presence of connections across time, 和
o¼1
drios(哦)(Zt) corresponds to an individual-level nth-order orthonormal polynomial model capturing
how much the participant-specific trends deviate from the population trend. s(哦) is the value of
the oth degree polynomial generated from a set of orthonormal polynomials with maximum degree
poynomial of n, Xt is the design matrix for the population-level orthonormal polynomials at time t,
and Zt is the deisgn matrix for the individual-level orthonormal polynomials at time t (see Supporting
Information Appendix S4 for a simple example of defining the design matrix and orthonormal poly-
nomials). Employing an orthonormal polynomial model in this manner has been shown to accu-
rately represent the trend in time series data while avoiding the computational issues resulting from
the use of natural polynomials (爱德华兹 & 辛普森, 2014; 辛普森 & 爱德华兹, 2013). 注意
our βr and βs are population estimates showing if/how the desired covariates are associated with

网络神经科学

597

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

/

t

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

.

t

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

dynamic networks, 那是, after accounting for the dynamic trends through incorporating ortho-
normal polynomials, βr and βs, show if/how the relationships between desired covariates and
dynamic networks, 一般, 是重要的.

For the part II model, which aims to model the strength of a connection given that there is
一, we let Sijkt = [Yijkt|Rijkt = 1]. In our case, the Sijkt will be the values of the correlation
coefficients between nodes j and k for participant i at time t. We can then use Fisher’s
Z-transform, denoted as FZT, to induce normality for the following mixed model (part II model)

(西德:3)
FZT Sijkt β
ð
s

; bsi; C

; d ri

s

(西德:4)
Þ

¼ X

0
ijkt

β
s

þ

Xn

o¼1

!

C

sos oð Þ Xtð

Þ

þ Z

0

ijktbsi þ

!

Xn

o¼1

dsios oð Þ Ztð

Þ

þ eijkt;

(3)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

t

/

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

t

.

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

where βs is a vector of population parameters that relate the strength of a connection to the
same set of covariates (Xijkt) for each participant and nodal pair (dyad), bsi is a vector of
参与者- and node-specific parameters that capture how this relationship varies about
the population average (βs) by participant and node (Zijkt),
o¼1 γsos(哦)(Xt) corresponds to a
population-level nth-order orthonormal polynomial model capturing the dynamic trend in
n
o¼1 dsios(哦)(Zt) corresponds to an individual-level
the strength of connections across time,
nth-order orthonormal polynomial model capturing how much the participant-specific trends
deviate from the population trend, and eijkt accounts for the random noise in the connection
strength of nodes j and k for participant i at time t.

磷

磷

n

In this study, the covariates (Xijkt) used to explain and predict both the presence and strength
of connection include the following. (1) 网: the average of the following network variables
(categorized and further detailed in Table 1 and in Rubinov and Sporns [2010] and Simpson,
Bowman, and Laurienti [2013]) in each dyad: Clustering Coeficient (C ), Global Efficiency
(Eglob), Degree (k) (difference between connected nodes instead of average to capture “assor-
tativity”), 模块化 (问), and Leverage Centrality (Joyce, Laurienti, Burdette, & Hayasaka, 2010)
(我 ). Clustering coefficient and global efficiency have been widely used as hallmark measures
of segregation (presence of highly interconnected regions supporting regional specialization)
and integration (widespread connectivity interconnecting specialized regions) in the brain,
分别 (鲁比诺夫 & 斯波恩斯, 2010).

We have used degree difference to capture assortativity, which provides a profound character-
ization of network resilience (鲁比诺夫 & 斯波恩斯, 2010). Leverage centrality measures the extent of
connectivity of a node relative to its neighbors’ connectivity (Joyce, Laurienti, Burdette, &
Hayasaka, 2010). This characterizes the importance of each node for information flow in the
脑. Modularity is a hallmark measure of community structure in the brain which has been
associated with cognitive performance and intelligence as will be discussed in more detail in
the Discussion. (2) COI: Covariates of Interest (fluid intelligence (gF) in our study – we modeled

桌子 1. Network measures by category

类别
Functional segregation

Measure(s)
Clustering coefficient

Type
Local measure

Functional integration

Global efficiency

全球的(/当地的) 措施

弹力

Degree difference

Local measure

Centrality and information flow

Leverage centrality

Local measure

Community structure

模块化

Global measure

网络神经科学

598

A mixed model for dynamic brain networks

gF as a continuous covariate to maximize power, 然而, in separate analysis, we used gF as a
median split binary variable (low/high) which yielded similar results. The binary results can be
found in the Supporting Information Appendix S5). gF in the HCP protocol has been assessed
using the Raven’s progressive matrices with 24 items with scores being integers representing num-
ber of correct items (Bilker et al., 2012); (3) Int: Interactions of the Covariate of Interest with the
variables in 1; 和 (4) 骗局: Confounders (for our data: 性别 (binary), 年龄 (continuous), years of
教育 (categorical with three levels − level 1 (≤11), 等级 2 (12–16), 和水平 3 (≥17)),
BMI (continuous), 种族 (categorical with six categories − cat 1 (是. Indian/Alaskan Nat.), 猫 2
(Asian/Nat. Hawaiian/Other Pacific Is.), 猫 3 (Black or African Am.), 猫 4 (白色的), 猫 5 (更多的
than one), 猫 6 (Unknown or Not Reported)), 种族 (categorical with three categories − cat 1
(Hispanic/Latino), 猫 2 (Not Hispanic/Latino), 猫 3 (Unknown or Not Reported)), Handedness
(continuous − ranging from −100 to +100, with negative and positive numbers indicating whether
participants were more left- or right-handed, 分别, assessed using the Edinburgh
Handedness Inventory (Oldfield, 1971), 收入 (Continuous − Total household income),
Alcohol abuse (Binary − Indicating whether participant met DSM4 criteria for alcohol abuse),
Alcohol dependence (Binary − Indicating whether participant met DSM4 criteria for alcohol
dependence), Smoking status (Binary − Indicating whether participant smoked or not), 空间
distance between nodes (importance of spatial distance as potential geometric confounders has
been discussed in Friedman et al. (2014), and square of spatial distance between nodes). We used
these confounding variables given their widely studied effects on intelligence. 因此, 我们可以
decompose βr and βs into βr = [βr,0 βr,net βr,coi βr,int βr,骗局] and βs = [βs,0 βs,net βs,coi βs,int βs,骗局] 到
correspond with the population intercepts and these covariates. For the random-effects vectors we
have that bri = [bri,0 bri,net bri,dist δri,jδri,k] and bsi = [bsi,0 bsi,net bsi,dist δsi,jδsi,k], where bri,0 and bsi,0
quantify the deviation of participant-specific intercepts from the population intercepts (βr,0 和
βs,0), bri,网, and bsi,net contain the participant-specific parameters that capture how much the
relationships between the network variables in (1) and the presence and strength of a
connection vary about the population relationships (βr,net and βs,网), 分别, bri,dist and bsi,dist
contain the participant-specific parameters that capture how much the relationship between
spatial distance (and square of spatial distance) and the presence and strength of a connection vary
about the population relationships, 分别, δri,j and δsi,j contain nodal-specific
parameters that represent the propensity for node j (of the given dyad) to be connected and the
magnitude of its connections, 分别, and δri,k and δsi,k contain nodal-specific parameters
that represent the propensity for node k (of the given dyad) to be connected and the magnitude
of its connections, 分别. Parameters for all 19 time points (number of networks per
个人) (t = 1, 2, ……, 19) are estimated or predicted simultaneously from the model. 在
一般的, additional covariates can also be incorporated as guided by the biological context.

Specifying a reasonable covariance model (balancing appropriate complexity with parsi-
mony and computational feasibility) is paramount for a unified dynamic model such as the
one developed here. Toward this end, we assume that bri, dri, bsi, dsi, and ei are normally
distributed and mutually independent, with variance component covariance structures for
bri, dri, bsi, and dsi, and the standard conditional independence structure for ei. 那是, bri ∼
(西德:3)
br;node2 , ……,
氮(0, Σ b r i(τ b r) = diag (τ b r)), where τbr ¼
dr;n)0, bsi ∼ N(0,
σ2
, 和

, dri ∼ N(0, Σdri(τdr) = diag (τdr)), where τdr = (σ2
dr;1, ……, σ2
(西德:3)
bs;网 , σ2
bs;0, σ2
σ2
bs;node2, ……, σ2
Σbsi(τbs) = diag (τbs)), where τbs ¼
(西德:3)
(西德:4)0—yielding (276 + (n + 1))
ds;0, σ2
σ2
dsi ∼ N(0, Σdsi(τds) = diag (τds)) where τds ¼
random effects variance parameters for both the presence and strength models—and ei ∼
氮(0, Σei = σ 2I). These variance and covariance parameters will provide insight into whether
individual and group differences in variability in dynamics relate to health and behavioral

dr;0, σ2
bs;node1, σ2

br;node1 , σ2

ds;1, ……, σ2

br;dist , σ2

br ;0 , σ2
σ2

br ;网 , σ2

bs;dist, σ2

br;node268

bs;node268

ds;n

(西德:4)0

(西德:4)0

网络神经科学

599

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

t

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

.

t

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

结果. Parameter estimation is conducted via restricted pseudo-likelihood (Wolfinger &
Oconnell, 1993) with the residual approximation of the F test for a Wald statistic employed
for inference.

We implemented the models (Equations 2 和 3) above to describe and compare brain net-
work dynamics as a function of fluid intelligence. For both models, we started model fitting
with the entire set of random effects, 那是, random effects for intercept, nodal network mea-
确定 (clustering, global efficiency, 程度, and leverage centrality), distance, and nodal pro-
pensities. 然而, after facing convergence issues, we dropped nodal propensities from our
random effects. We assessed model goodness-of-fit (GOF) and consistency of estimates (到
further avoid overfitting) to determine the orthonormal polynomial degree yielding the best
model fits. We fit the two-part model defined above with the mentioned fixed- and random-
effect parameters by using orthonormal polynomial models of degrees ranging from 3–18
(giving 16 model fits), and determined the “best” model based on a composite approach
employing the Akaike information criterion (AIC) (Akaike, 1981), Bayesian information crite-
rion (施瓦茨, 1978), modified AIC (AICc) (Hurvich & Tsai, 1989), Hannan–Quinn informa-
tion criterion (Hannan & 奎因, 1979), and consistent AIC (CAIC) (Bozdogan, 1987) GOF
measures as well as the consistency of the obtained parameter estimates and p values
to further avoid overfitting. We used MATLAB to generate the appropriate data frame for
our framework and used SAS v9.4 on a Linux operating system with 330 GB of RAM and
2.60 GH processor to perform the model fitting. We have provided the essential SAS macro
employed in fitting the statistical mixed models for both Equations 2 和 3 in Supporting
Information Appendix S6.

Simulations

Bernoulli distribution:
Discrete probability distribution for a
random variable with binary (IE。, 0
或者 1) outcome.

We used the fitted models from Equations 2 和 3 to simulate dynamic brain networks. 我们
used covariates from 50 参与者 (selected randomly from 200) 和 10 dynamic networks
(selected randomly from 19), and simulated 10 realizations for each dynamic network of each
参与者. This yielded a total of 5,000 simulated dynamic networks. To simulate each
dynamic network, we first simulated the existence of edges (presence/absence) 对全部
35,778 node pairs (vectorized symmetric network with 268 节点) from a Bernoulli distribution
with the probability from the fitted model (pijkt(βr; bri; γr; dri) from Equation 2 and the covariates
used for each participant’s dynamic network. We simulated the random-effect coefficients
(γr, dri) for each participant from a normal distribution with mean zero and the covariance matrix
obtained from the estimated parameters for random effects in Equation 2. To simulate the strength
价值观, we first simulated continuous values from a normal distribution with the mean and covari-
ance obtained from the fitted model in Equation 3 and the covariates for each dynamic network
(西德:7)
(西德:7)
氮; μ
. 我们
then used the inverse Fisher’s Z-transform to get the untransformed values, and finally multiplied
the resulting vector by the simulated binary vector to get the simulated strength values for the
weighted network. We then calculated several (weighted) descriptive measures often used in
analyzing brain networks to compare the simulated and observed networks with respect to such
topological measures as this provides the most appropriate way to assess the GOF of statistical
models in the network context (猎人, Goodreau, & Handcock, 2008). All simulations were
done in MATLAB. The MATLAB script is provided in the Supporting Information Appendix S7.
We have also provided the HCP identification numbers for the 50 randomly chosen participants
used in our simulation along with the numbers of their 10 randomly chosen dynamic networks
in Supporting Information Appendix S8.

¼ Z ijktΣbsi τbs

þ Z t Σdsi τds

sos oð Þ Xtð

þ σ2I

o¼1 γ

¼X 0

ÞZ0
t

ÞZ0

; σ2

(西德:4)
Þ

β
s

磷

þ

模拟

模拟

ijkt

ijkt

(西德:8)

(西德:8)

(西德:3)

ð

ð

n

网络神经科学

600

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

t

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

.

t

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

结果

这里, we show our framework’s ability in identifying the relationship between fluid intelligence
and dynamic brain networks and its utility for simulating dynamic brain networks. For orthonormal
polynomial models of degrees ranging from 3 到 18, all GOF measures for the strength model
(方程 3) slightly improved with increasing degree, providing good fits for almost all degrees.
然而, the models with polynomial degrees ranging from 9 到 16 provided the most consistent

桌子 2.

Fixed-effect estimates, SEs, and p values for 12th degree orthonormal polynomial fit

Parameters Ortho Poly Degree

楷模
Probability Model

Strength Model

γr,0

γr,1

γr,2

γr,3

γr,4

γr,5

γr,6

γr,7

γr,8

γr,9

γr,10

γr,11

γr,12

γs,0

γs,1

γs,2

γs,3

γs,4

γs,5

γs,6

γs,7

γs,8

γs,9

γs,10

γs,11

γs,12

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

/

t

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

.

t

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Intercept

1

2

3

4

5

6

7

8

9

10

11

12

Estimate
−0.13770

SE
0.02022

*P Value
<.0001 0.00121 0.004361 0.7817 −0.01694 0.004914 0.0021 0.02394 0.004304 <.0001 −0.00593 −0.00508 −0.01185 0.004641 0.3805 0.004429 0.4498 0.004382 0.0232 0.00794 0.004019 0.1259 0.00392 0.004106 0.4716 −0.00433 −0.01063 0.004443 0.4716 0.004236 0.0374 0.00774 0.004203 0.1583 −0.00481 0.004897 0.4716 Intercept 0.31190 0.00786 <.0001 1 2 3 4 5 6 7 8 9 10 11 12 0.00148 0.00214 0.4906 −0.01415 0.00221 <.0001 0.01782 0.00203 <.0001 −0.00110 −0.00057 −0.01012 0.00197 0.5785 0.00214 0.7917 0.00211 <.0001 0.01077 0.00226 <.0001 0.00388 0.00228 0.1106 −0.00440 −0.00726 0.00204 0.0426 0.00200 0.0005 0.00134 0.00199 0.5007 −0.00907 0.00257 0.0007 * Adjusted using the adaptive false discovery rate procedure described in Benjamini and Hochberg (2000). Network Neuroscience 601 A mixed model for dynamic brain networks estimates and p values. Thus, to avoid overfitting while still using a model with a relatively good fit as indicated by the GOF measures, we used the model with polynomial degree of 12 as a middle ground between 9 and 16. For the probability model, although all GOF measures slightly improved with increasing degree too, the differences were negligible. Thus, we used the same polynomial degree (12) for consistency. The estimates, standard errors, and p values for the poly- nomial parameters are presented in Table 2 ( p values presented in this table and other tables are corrected for multiple comparison using an adaptive false discovery rate procedure detailed in Benjamini & Hochberg, 2000). The parameter estimates, standard errors, and p values (based on the residual approximation of the F test for a Wald statistic) associated with the important fixed-effect covariates are presented in Table 3. The estimates for other parameters (e.g., gender, age, etc.) are fully explained in the Supporting Information (Table S6). The estimates quantify the relationship between dynamic patterns of probability (presence/absence) and strength of (present) connections between nodes (brain regions), as dependent variables, and the previously men- tioned sets of covariates, including (dynamic patterns of ) endogenous network measures, fluid intelligence as our covariate of interest, and confounders. The estimates for confounding covari- ates, including sex, age, education, BMI, race, ethnicity, handedness, income, DSM4 alcohol abuse, DSM4 alcohol dependence, smoking status, spatial distance, and square of spatial distance between nodes are fully explained in the Supporting Information as pointed out above. The estimates for interaction covariates shows if (and how) the relationship between dynamic patterns of probability/strength of connections and dynamic patterns of endogenous network measures are affected by fluid intelligence. Notable results are detailed in the following sections. Dynamic Network Analysis As Table 3 presents, dynamic changes of clustering (functional segregation), global efficiency (functional integration), degree difference (functional resilience), and leverage centrality Table 3. Parameter estimates, standard errors, and p values for dynamic networks Parameter βr,0 βr,COI βr,C βr,Eglob βr,D βr,L βr,Q βr,COI×C βr,COI×Eglob βr,COI×D βr,COI×L βr,COI×Q Probability Model Outputs Estimate −0.1377 0.00319 −7.22530 12.5799 −0.07686 0.04332 2.10910 0.10290 0.24720 −0.00140 −0.01690 −0.02684 SE 0.02022 0.00295 0.11490 0.43460 0.00389 0.02006 0.01471 0.11500 0.43470 0.00389 0.02006 0.01514 *P value <.0001 Parameter βs,0 Strength Model Outputs SE Estimate 0.00786 0.31190 0.4716 <.0001 <.0001 <.0001 0.0872 <.0001 0.4836 0.5696 0.7177 0.4836 0.1619 βs,COI βs,C βs,Eglob βs,D βs,L βs,Q βs,COI×C βs,COI×Eglob βs,COI×D βs,COI×L βs,COI×Q −0.00086 3.07330 3.86090 −0.07111 −0.21300 −1.35550 −0.02418 −0.00301 −0.00002 0.00127 0.03078 0.00115 0.02008 0.04105 0.00672 0.00273 0.00241 0.02009 0.04106 0.00672 0.00273 0.00248 *P value <.0001 0.4540 <.0001 <.0001 <.0001 <.0001 <.0001 0.2478 0.9416 0.9978 0.6423 <.0001 * Adjusted using the adaptive false discovery rate procedure described in Benjamini and Hochberg (2000). Bold values show fluid intelligence–related inferential results discussed here. Network Neuroscience 602 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 6 2 5 9 1 2 0 2 8 1 1 3 n e n _ a _ 0 0 2 3 8 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 A mixed model for dynamic brain networks (information flow) all play important roles in explaining dynamic patterns of both connection probability and strength, but with leverage centrality having a marginal effect on dynamic pat- terns of connection probability. Fluid intelligence, our covariate of interest (COI), is neither directly related to dynamic pat- terns of connection probability (presence/absence) nor connection strength as indicated by the p values associated with βr,COI (p value = 0.4716) and βs,COI (p value = 0.4540), respectively. However, it has a significant effect on the relationship between dynamic changes of connec- tion strength and dynamic changes of whole-brain modularity as indicated by the p value asso- ciated with βs,COI ×Q (p value < 0.0001), while having no effect on other relationships (using the gF as a median split binary [low/high] variable rather than a continuous one, provided the same results as shown in Supporting Information Appendix S5). Dynamic changes of whole-brain modularity and connection strength are negatively associated with each other (βs,Q), which implies the dominance of between-community (rather than within-community) connections in driving the dynamic changes of whole-brain modularity. Fluid intelligence interacts with this relationship—as intelligence increases, dynamic changes of modularity are less driven by dynamic changes in between-community (and more by within-community) connectivity as indicated by the positive and significant estimate for βs,COI ×Q. (However, the dynamics of between-community connections are still the dominant factor in driving the dynamic changes of whole-brain modularity.) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 6 2 5 9 1 2 0 2 8 1 1 3 n e n _ a _ 0 0 2 3 8 p d . 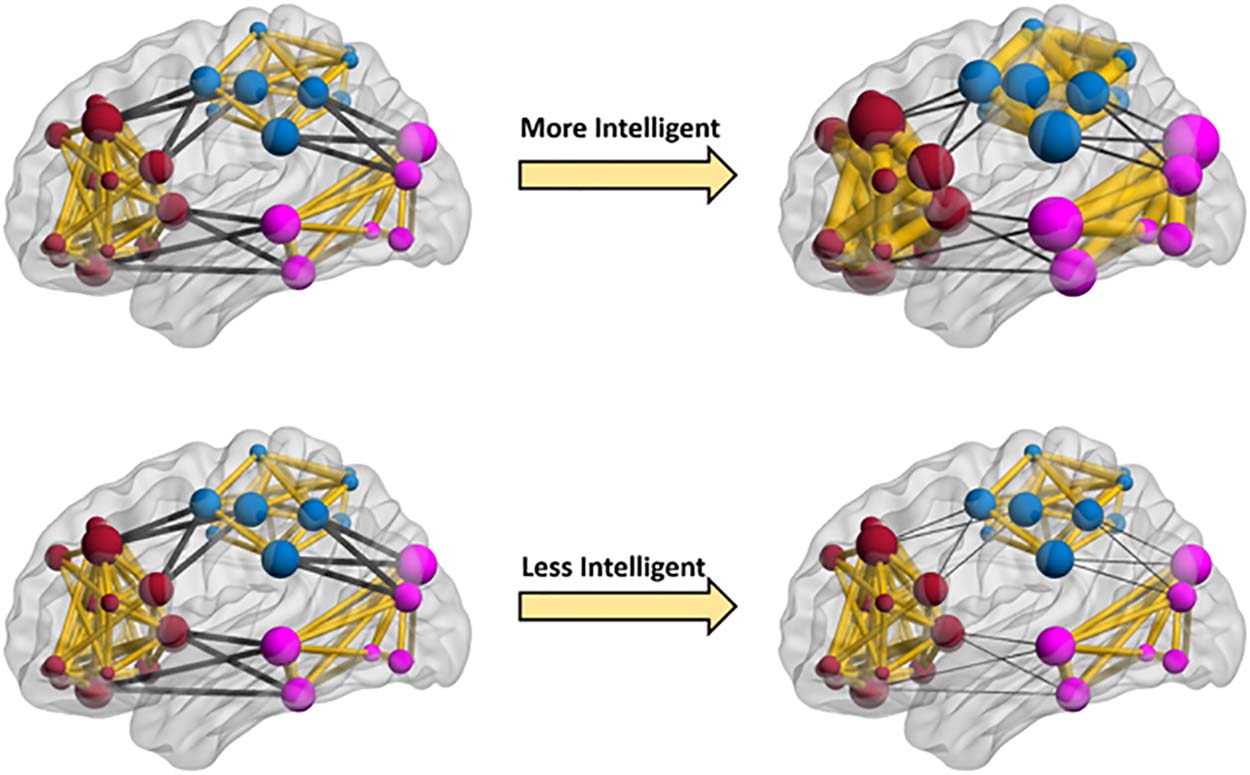t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 3. Cartoon depiction of fluid intelligence effects on dynamic brain networks. The nodes represent brain regions, and edges represent dynamic functional connections. To illustrate the effects of fluid intelligence on dynamic changes of modularity as interpreted from Table 3, three artificial communities marked with separate colors (dark red, light blue, and purple) are shown in this figure. The within- and between-community connections are shown with the yellow and black colors, respectively. As this figure illustrates, dynamic changes of modularity are predomi- nantly determined by between-community connections for any level of intelligence (here two levels are shown: low and high). However, when comparing the more and less intelligent participants (networks on the right), in more intelligent participants, dynamic changes of modularity are less determined by between-community connections (thicker dark edges in top right), and dynamic changes of within-community connections also play more important roles in changing the modu- larity (thicker yellow edges in top right network). We should note that fluid intelligence was mod- eled as a continuous variable, but for illustrative purposes we show higher and lower intelligence levels. We have made a movie that better illustrates how dynamic patterns of whole-brain modu- larity are affected across a range of fluid intelligence values (Supporting Information Movie S1). Network Neuroscience 603 A mixed model for dynamic brain networks Table 4. Weighted network measures of observed and simulated dynamic networks Observed (N = 50 × 10) Simulated (N = 50 × 10 × 10) Metric Clustering coefficient (C) Mean 0.1778 Global efficiency (Eglob) 0.2948 Degree (K) 39.229 SD 0.0217 0.0096 2.8391 Mean 0.1463 0.3263 40.847 SD 0.0296 0.0517 7.3629 Our results might imply that brain networks in people with higher fluid intelligence are more flexible with respect to changes in their modularity at rest. These changes are associated with both stronger within-community connections (more specialized neural communities) and weaker between-community connections (more segregated neural communities). This is illus- trated in Figure 3 and Supporting Information Movie S1. We provide more detail on possible l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 6 2 5 9 1 2 0 2 8 1 1 3 n e n _ a _ 0 0 2 3 8 p d t . 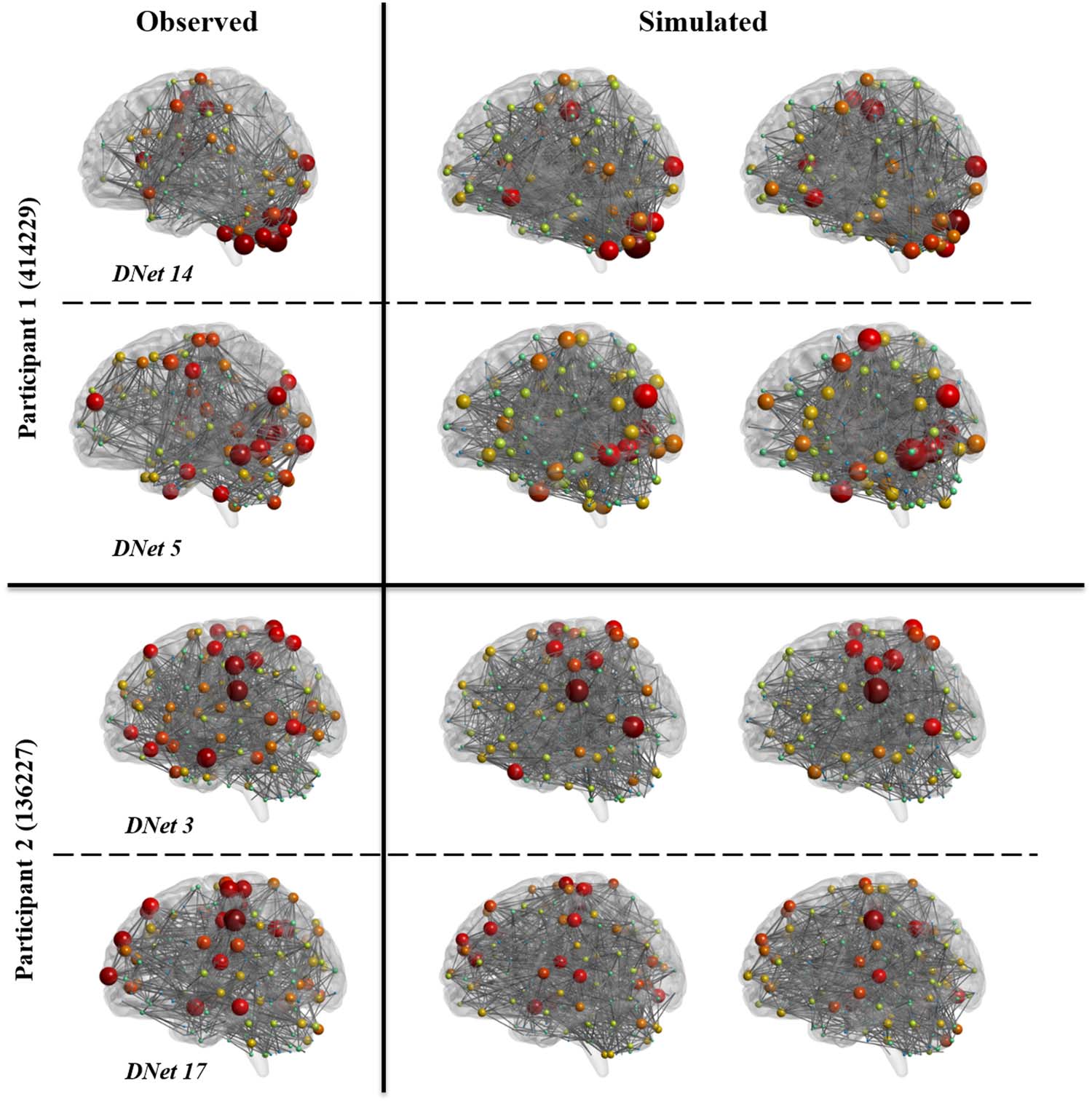f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 4. Observed and simulated dynamic networks for two randomly selected participants. For each participant, two randomly selected dynamic networks (DNet #) are shown on the left, and for each dynamic network, two randomly selected simulated networks (from the 10 simulation reali- zations) are shown on the right. We have shown the HCP individual IDs on the left. All networks are thresholded to maintain the top 5% of strongest connections. The size and color of each node rep- resent the degree of that node. Network Neuroscience 604 A mixed model for dynamic brain networks interpretations and implications of this result in the Discussion. The results for using windows with 50% overlap between consecutive networks were similar, but with gF modifying the rela- tionship between dynamic patterns of whole-brain modularity and connection probability as well. For more detail and a brief interpretation see Supporting Information Appendix S2. Dynamic Network Simulation Using the estimated parameters from fitted models in Equations 2 and 3, we simulated 5,000 dynamic networks: 10 realizations for each one of 10 (randomly selected) dynamic networks from 50 (randomly selected) individuals. We then calculated descriptive graph measures including: C, Eglob, and k. Table 4 presents the average values across all dynamic networks and all regions for both observed and simulated networks. As evidenced by Table 4, average network measures are very close between simulated and observed networks, indicating the ability of this model to simulate representative group-level dynamic networks. However, to further illustrate that simulated networks represent observed dynamic networks at multiple resolutions beyond average values, that is, at the individual and nodal level, in Figure 4, we have shown two realizations of two dynamic networks for two participants (all chosen randomly from the 5,000 simulated networks). Networks in this figure represent the top 5% of strongest connections. As this figure shows, even after thresholding the networks, the simulated networks well represent the observed networks. DISCUSSION As the interest in dynamic brain networks continues to grow, new methods are needed to enable gleaning neurobiological insight into this complex and big data. Development of mul- tivariate statistical methods, particularly model-based ones, which allow quantifying relation- ships between phenotypic traits and dynamic patterns of brain connectivity and topology, as well as drawing inference from such relationships, is among the urgent needs. Development of such methods even for static networks has remained a challenge given the size, complexity, and multiscale dependence inherent in brain network data. However several model-based methods (Shehzad et al., 2014; Simpson, Hayasaka, & Laurienti, 2011; Simpson & Laurienti, 2015) and various data-driven multivariate methods (Allen et al., 2011; Beckmann & Smith, 2004; Calhoun, Adali, Pearlson, & Pekar, 2001; Smith, Hyvarinen, Varoquaux, Miller, & Beckmann, 2014) have been introduced and extensively used for static networks. Dynamic changes in the systematic organization of our brain networks confer much of our brains’ functions abilities due to the fact that our brain is a complex multiscale dynamic system with known and unknown compensatory mechanisms at multiple scales. Thus, methods that allow analyzing the brain within a multivariate framework can provide much deeper insights into dynamic patterns of brain networks in health and disease. In addition, multivariate model- based tools enable aligning neuroscientific hypotheses with the analytic approach, which is ideal for dynamic brain network analysis (Preti, Bolton, & Van De Ville, 2017). Nevertheless, no model-based multivariate method has been introduced for dynamic network analyses to our knowledge. Here we provided a model-based multivariate method to relate phenotypic traits to dynamic patterns of brain connectivity and topology. We developed this model by advancing a two-part mixed-effects regression framework for static brain networks (Simpson & Laurienti, 2015). Our proposed model allows accounting for the connectivity/network dynamics when assessing group differences and phenotype-health outcome relationships, to avoid confound- ing and drawing erroneous conclusions. The incorporation of endogenous network measures Network Neuroscience 605 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 6 2 5 9 1 2 0 2 8 1 1 3 n e n _ a _ 0 0 2 3 8 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 A mixed model for dynamic brain networks such as clustering coefficient and global efficiency, as independent variables, allows simulta- neous analyses of connectivity and topology dynamics. There is a long history of modeling a network as a function of endogenous network metrics to identify how nodal properties are related to the probability (and strength) of connections (O’Malley, 2013; Robins, Pattison, Kalish, & Lusher, 2007; Simpson et al., 2011, 2012). Part of the motivation for our modeling framework was the desire to port this approach into the time-varying multiple-network context and blend it with the more standard exogenous covariate approach to create a hybrid method that allows examining and accounting for both an individual’s endogenous network structure and exog- enous phenotypic characteristics in a manner suitable for dynamic brain network analyses. The topological network covariates allow examining how nodal properties influence the con- nection between two brain areas. Having both the endogenous and exogenous covariates in the model allows us to assess how these topology-connection relationships vary by individual and group characteristics. Additionally, it allows simulating more realistic dynamic networks by incorporating the dynamics of an array of explanatory network measures and their interplay with desired covariates. Most current methods used to assess dynamic brain networks reduce this data into dynamic patterns of individual brain connections (Schmlazle et al., 2017; Simony et al., 2016; Tewarie et al., 2019) or commonly used topological summary variables, such as node degree or mod- ularity (Jones et al., 2012; Kabbara et al., 2019), rather than analyzing the systemic dynamics of the brain networks. Such methods not only fail to model the brain as a multiscale dynamic system (Lurie et al., 2020), but often entail matching study populations to perform group com- parisons, which is a daunting task for most neuroimaging studies. Our model provides a frame- work to assess the systemic dynamics of brain networks and thus to account for complex dynamics of the brain via the simultaneous modeling of brain connectivity and topological network variables. The multivariate nature of this framework reduces demands for matching study populations as any number of confounding effects can be incorporated as covariates, and the effects of multiple covariates of interest can be studied in a single model. Another important utility of this model is its ability to simulate dynamic brain networks, which is critical for a better understanding of brain function in health and disease (Tikidji-Hamburyan, Narayana, Bozkus, & El-Ghazawi, 2017). To our knowledge, our framework is the first model that allows simulating dynamic brain networks from system-level properties of the brain, and with respect to desired covariates. An important utility of the simulation capability of this model is to generate representative group-level dynamic networks. The need for reliably generating representative group-level networks has been well documented (Jirsa, Sporns, Breakspear, Deco, & McIntosh, 2010; Meunier, Achard, Morcom, & Bullmore, 2009; Valencia et al., 2009; Zuo et al., 2012). Additionally, the simulation capability also provides a scientif- ically appropriate way to assess GOF (as shown in the Dynamic Network Simulation section) and simulate individual-level networks. It is important to note that our framework itself, which aims to account for continuous time- varying network changes when relating covariates to topology, is not designed to identify latent states like hidden Markov models are, for example. But adding a latent state analysis to the preprocessing steps prior to implementing our model would provide a complementary and insightful extension to our overall approach. Our method will work for many approaches used to generate the networks, allowing for great flexibility in the network generation method that one chooses to use. A standard approach for assessing the performance of regression- based methods is through examining the quality of model fit. Since our method is also a regression-based framework, we used different GOF measures to examine the performance of our method. More importantly, our simulation analyses allowed for a more profound Network Neuroscience 606 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 6 2 5 9 1 2 0 2 8 1 1 3 n e n _ a _ 0 0 2 3 8 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 A mixed model for dynamic brain networks assessment of the performance of our method as the most appropriate method to assess the GOF of statistical methods in the network context is through simulation analyses (Hunter et al., 2008). In addition, with respect to identifying the association between phenotypic traits and dynamic brain networks, our method uses a fundamentally different approach, and pro- vides different (complementary) insight, than current data-driven methods, and thus a compar- ison between our model and current data-driven models would not be appropriate. We demonstrated the utility of our model in identifying the relationship between fluid intel- ligence and dynamic patterns of brain connectivity and topological network variables by using the rich data set provided by the HCP study (Van Essen et al., 2013). Our model allowed accounting for various sources of potential confounding effects, such as sex, education, age, and alcohol abuse, among others. Our results indicated that dynamic patterns of whole-brain modularity and connection strength are significantly affected by fluid intelligence. More specifically, our results showed that for any level of fluid intelligence, dynamic patterns of modularity are predominantly associated with between-community, rather than within- community, connections. However, fluid intelligence modulates this trend such that, across an entire spectrum of fluid intelligence, dynamics of whole-brain modularity play a less impor- tant role in driving changes in between-community connections for higher fluid intelligence values (with dynamics of within-community connections probably being affected more). While the ultimate neurobiological interpretations of such effects is speculative at this point, our results may suggest that at lower levels of intelligence, distinct network modules necessary for cognition (such as the module comprised of areas forming the central executive attention network, or CEN) are formed primarily by segregating information. Thus, distinct subnetworks are formed by decreasing connectivity to other subnetworks, which could result in relatively poor distribution of information between subnetworks. As intelligence increases, the formation of distinct modules is driven more by strengthening connections within the module and less by segregating modules. Increased intramodular connectivity could enhance processing within subnetworks like the CEN while maintaining communication between subnetworks for opti- mal information distribution. Other studies have reported associations between brain modu- larity and intelligence (Chaddock-Heyman et al., 2020), as well as significant correlations between creativity and learning and dynamic patterns of brain modularity (Bassett et al., 2011; Kenett, Betzel, & Beaty, 2020). In the absence of a “gold standard” in sliding window approach, the optimal choice for window type, window length, and step size is challenging. We used a modulated rectangular window due to its superior performance in examining dynamic brain networks when com- pared to other conventional window types (Mokhtari, Akhlaghi et al., 2019). We used 120 volumes for our window length for multiple reasons, including (1) to provide more stabilized correlation values while not losing the variability of the brain dynamics, (2) due to its wider use which makes comparing and contrasting our method with currently used methods easier, and (3) model fit and convergence considerations of our proposed method. It is also important to note that no commonly used window length can accurately identify different states of corre- lation (Shakil, Lee, & Keilholz, 2016), and that the sliding window correlation approach is only used to demonstrate the utility of our method rather than to provide comprehensive analyses of fluid intelligence-dynamic brain network associations. Also, typical shift sizes used in the lit- erature range from 1 TR to 50% of the window length (Chang et al., 2013; Kucyi & Davis, 2014; Shakil, Magnuson, Keilholz, & Lee, 2014), with the 1 TR being the most commonly used shift size (Shakil et al., 2016). However, as our proposed method subsequently uses the dynamic networks in a regression framework, we used a shift size of 120 volumes, equal to the window length, to create nonoverlapping windows and thus further reduce Network Neuroscience 607 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 6 2 5 9 1 2 0 2 8 1 1 3 n e n _ a _ 0 0 2 3 8 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 A mixed model for dynamic brain networks autocorrelation. Additionally, using nonoverlapping windows allowed using a smaller, but suf- ficient number of dynamic networks for each participant and thus helped avoiding possible convergence issues. Nevertheless, for windows with 50% overlap between consecutive net- works, our modeling framework yielded similar outcomes. Incorporating all brain connections and modeling the dependence among multiple vari- ables across time is computationally time intensive and can lead to convergence issues for datasets with large numbers of participants and regions of interest. This prevented us from using more complex variance-covariance structures for the random effects that could, in turn, yield even more accurate estimates and better simulations of dynamic brain networks. We plan to develop complementary data reduction methods to address this in future work. More- over, there is no agreement on a well-accepted atlas for functional connectivity studies. While many studies have used clustering-based methods or canonical correlation analysis to define nodes for their own data (Allen et al., 2014), other studies have used publicly available par- cellation schemes generated from rich datasets with higher reproducibility across individuals (Glasser et al., 2016). Even newer studies indicate that using an individual atlas rather than a group-level parcellation may provide more reliable results (Salehi et al., 2020). However, as with the parameters used for generating the dynamic networks (sliding window type, length, etc.), our method is independent of the parcellation scheme used for defining the brain regions. The sensitivity to the method used to generate dynamic networks as well as the par- cellation scheme (Bahramf & Hossein-Zadeh, 2014; Glasser et al., 2016; Power et al., 2011) will be assessed in future studies as for each parameter, multiple models should be run to find the best orthonormal polynomial degree for that particular parameter, and thus, a composite grid search over all combinations of such parameters and polynomial degrees will be required, which is beyond the scope of this paper. The proposed mixed-effects framework can be used for predicting dynamic networks based on participant characteristics as well. However, we didn’t demonstrate this capability here. These capabilities will be demonstrated in future work, given that they require extensive analytical assessment and exposition, which lie beyond the scope of this paper. We have also made our proposed framework accessible to neuroimaging researchers by incorporating new graphical user interfaces into WFU_MMNET (https://www .nitrc.org/projects/wfu_mmnet), the software developed for the application of the original static model (Bahrami et al., 2019b). This study is not without limitations. Incorporating all brain connections as well modeling the dependence structure between multiple variables across individuals’ brain connections and network metrics (e.g., clustering coefficient, global efficiency) across time is computation- ally intensive and can lead to convergence issues (particularly for the probability model; Equa- tion 2) for datasets with large numbers of participants and network nodes. This precludes using our method for studies analyzing voxel level dynamic networks and limits its utility for studies with very large numbers of subjects or very spatially resolved (>1,000 节点) brain networks.
We have developed a clustering-based data reduction method to resolve this issue for the orig-
inal model for static networks and are currently working on extending it to be applicable for
dynamic brain networks as well. This will greatly aid in resolving the convergence issue. 还,
parcellation schemes generated from a clustering or canonical correlation analysis approach
with a fewer number of regions of interest are also appealing alternatives to be used within our
框架. Interpreting the results produced by our method may not always be straightfor-
病房, as both connectivity and network topology dynamics should be considered simulta-
neously. This can complicate interpretation of the results for continuous variables and when
particular network metrics with both local and global implications are examined, such as clus-
tering coefficient. Another limitation of our method is that its only applicable for whole-brain

网络神经科学

608

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

t

/

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

t

.

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

networks at present, and not for analyzing dynamics of local brain networks or subnetworks
(例如, the default mode network) unless they are extracted from the whole-brain network. 如何-
曾经, we are working on devising a procedure to allow for analyzing dynamics of local brain
networks within the context of their whole networks as was done for the original framework for
static networks in Bahrami et al. (2019A). 最后, future studies should conduct a thorough
sensitivity analysis of our framework with respect to the parameters used in generating the
dynamics networks and the parcellation scheme used.

SUPPORTING INFORMATION

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00238.

作者贡献

Mohsen Bahrami: 数据管理; 形式分析; 方法; 验证; 可视化;
Writing – original draft; 写作——复习 & 编辑. Paul J. Laurienti: 概念化; 基金-
ing acquisition; 验证; 写作——复习 & 编辑. Heather M. Shappell: Conceptualiza-
的; 写作——复习 & 编辑. Dale Dagenbach: 概念化; 写作——复习 &
编辑. Sean L. 辛普森: 概念化; 资金获取; 方法; 监督;
验证; Writing – original draft; 写作——复习 & 编辑.

资金信息

Sean L. 辛普森, National Institute of Biomedical Imaging and Bioengineering (https://
grantome.com/grant/NIH/R01-EB024559-04), 奖项ID: R01EB024559.

参考

Akaike, H. (1981). A new look at the statistical-model identification.
Current Contents/Engineering Technology & Applied Sciences,
12(51), 22.

艾伦, 乙. A。, Damaraju, E., Plis, S. M。, Erhardt, 乙. B., Eichele, T。, &
Calhoun, V. D. (2014). Tracking whole-brain connectivity
dynamics in the resting state. 大脑皮层, 24(3), 663–676.
https://doi.org/10.1093/cercor/bhs352, 考研: 23146964

艾伦, 乙. A。, Erhardt, 乙. B., Damaraju, E., Gruner, W., Segall, J. M。,
席尔瓦, 右. F。, … Calhoun, V. D. (2011). A baseline for the multivar-
iate comparison of resting-state networks. Frontiers in Systems
神经科学, 5, 2. https://doi.org/10.3389/fnsys.2011.00002,
考研: 21442040

Bahramf, M。, & Hossein-Zadeh, G.-A. (2014). Functional parcellations
affect the network measures in graph analysis of resting-state fMRI.
Paper presented at the 2014 21st Iranian Conference on Biomed-
ical Engineering (ICBME). https://doi.org/10.1109/ICBME.2014
.7043933

Bahrami, M。, Laurienti, 磷. J。, & 辛普森, S. L. (2019A). Analysis of
brain subnetworks within the context of their whole-brain net-
作品. 人脑图谱, 40(17), 5123–5141. https://土井
.org/10.1002/hbm.24762, 考研: 31441167

Bahrami, M。, Laurienti, 磷. J。, & 辛普森, S. L. (2019乙). A MATLAB
toolbox for multivariate analysis of brain networks. 人脑
测绘, 40(1), 175–186. https://doi.org/10.1002/hbm.24363,
考研: 30256496

Barttfeld, P。, Uhrig, L。, Sitt, J. D ., Sigman, M。, Jarraya, B., &
德阿内, S. (2015). Signature of consciousness in the dynamics
of resting-state brain activity. 国家科学院院刊
of Sciences of the United States of America, 112(3), 887–892.
https://doi.org/10.1073/pnas.1418031112, 考研: 25561541
Bassett, D. S。, & 布莫尔, 乙. 时间. (2009). Human brain networks in
health and disease. Current Opinion in Neurology, 22(4), 340–347.
https://doi.org/10.1097/wco.0b013e32832d93dd, 考研:
19494774

Bassett, D. S。, Wymbs, 氮. F。, Porter, 中号. A。, Mucha, 磷. J。, 卡尔森,
J. M。, & Grafton, S. 时间. (2011). Dynamic reconfiguration of human
brain networks during learning. 国家会议录
美国科学院, 108(18),
7641–7646. https://doi.org/10.1073/pnas.1018985108,
考研: 21502525

贝克曼, C. F。, & 史密斯, S. A. (2004). Probabilistic independent
component analysis for functional magnetic resonance imaging.
IEEE Transactions on Medical Imaging, 23(2), 137–152. https://
doi.org/10.1109/TMI.2003.822821, 考研: 14964560

Benjamini, Y。, & Hochberg, 是. (2000). On the adaptive control of
the false discovery rate in multiple testing with independent
统计数据. Journal of Educational and Behavioral Statistics, 25(1),
60–83. https://doi.org/10.3102/10769986025001060

Bilker, 瓦. B., 汉森, J. A。, Brensinger, C. M。, 理查德, J。, Gur,
右. E., & Gur, 右. C. (2012). Development of abbreviated

网络神经科学

609

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

t

/

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

t

.

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

nine-item forms of the Ravenʼs Standard Progressive Matrices
测试. Assessment, 19(3), 354–369. https://doi.org/10.1177
/1073191112446655, 考研: 22605785

Bozdogan, H. J. 磷. (1987). Model selection and Akaikeʼs information
criterion (AIC): The general theory and its analytical extensions. Psy-
chometrika, 52(3), 345–370. https://doi.org/10.1007/BF02294361
Breakspear, 中号. (2017). Dynamic models of large-scale brain activ-
性. 自然神经科学, 20(3), 340–352. https://doi.org/10
.1038/nn.4497, 考研: 28230845

Bressler, S. L。, & Menon, V. (2010). Large-scale brain networks in
认识: Emerging methods and principles. Trends in Cognitive
科学, 14(6), 277–290. https://doi.org/10.1016/j.tics.2010.04
.004, 考研: 20493761

布莫尔, 乙. T。, & 斯波恩斯, 氧. (2009). 复杂的大脑网络:
Graph theoretical analysis of structural and functional systems.
自然评论神经科学, 10(3), 186–198. https://doi.org
/10.1038/nrn2575, 考研: 19190637

Buzsaki, G。, & Draguhn, A. (2004). Neuronal oscillations in cortical
网络. 科学, 304(5679), 1926–1929. https://doi.org/10
.1126/science.1099745, 考研: 15218136

Calhoun, V. D ., Adali, T。, Pearlson, G. D ., & Pekar, J. J. (2001). A
method for making group inferences from functional MRI data
using independent component analysis. 人脑图谱,
14(3), 140–151. https://doi.org/10.1002/ hbm.1048, 考研:
11559959

Cattell, 右. 乙. (1987). 智力: Its structure, growth and action.

阿姆斯特丹, 荷兰人: 爱思唯尔.

Chaddock-Heyman, L。, 翁, 时间. 中号. B., Kienzler, C。, Weisshappel,
R。, Drollette, 乙. S。, Raine, L. B., … Kramer, A. F. (2020). Brain net-
work modularity predicts improvements in cognitive and scho-
lastic performance in children involved in a physical activity
干涉. Frontiers in Human Neuroscience, 14. https://土井
.org/10.3389/fnhum.2020.00346, 考研: 33100988

张, C。, & Glover, G. H. (2010). Time-frequency dynamics of
resting-state brain connectivity measured with fMRI. Neuro-
图像, 50(1), 81–98. https://doi.org/10.1016/j.neuroimage.2009
.12.011, 考研: 20006716

张, C。, 刘, Z. M。, 陈, 中号. C。, 刘, X。, & Duyn, J. H. (2013).
EEG correlates of time-varying BOLD functional connectivity.
神经影像, 72, 227–236. https://doi.org/10.1016/j.neuroimage
.2013.01.049, 考研: 23376790

Cole, 中号. W., Bassett, D. S。, 力量, J. D ., Braver, 时间. S。, & 彼得森,
S. 乙. (2014). Intrinsic and task-evoked network architectures of
the human brain. 神经元, 83(1), 238–251. https://doi.org/10
.1016/j.neuron.2014.05.014, 考研: 24991964

Colom, R。, & Flores-Mendoza, C. 乙. (2007). Intelligence predicts
scholastic achievement irrespective of SES factors: 证据来自
巴西. 智力, 35(3), 243–251. https://doi.org/10.1016/j
.intell.2006.07.008

Diez-Cirarda, M。, Strafella, A. P。, Kim, J。, Pena,

J。, Ojeda, N。,
Cabrera-Zubizarreta, A。, & Ibarretxe-Bilbao, 氮. (2018). 动态的
functional connectivity in Parkinsonʼs disease patients with mild
cognitive impairment and normal cognition. 神经影像 –
Clinical, 17, 847–855. https://doi.org/10.1016/j.nicl.2017.12
.013, 考研: 29527489

爱德华兹, L. J。, & 辛普森, S. L. (2014). An analysis of 24-h ambulatory
blood pressure monitoring data using orthonormal polynomials
in the linear mixed model. Blood Pressure Monitoring, 19(3),

153–163. https://doi.org/10.1097/ MBP.0000000000000039,
考研: 24667908

Elton, A。, & 高, 瓦. (2015). Task-related modulation of functional
connectivity variability and its behavioral correlations. 人类
Brain Mapping, 36(8), 3260–3272. https://doi.org/10.1002/hbm
.22847, 考研: 26015070

弗里德曼, 乙. J。, Landsberg, A. S。, 欧文, J. P。, 李, Y.-O., & Mukherjee,
磷. (2014). Stochastic geometric network models for groups of
functional and structural connectomes. 神经影像, 101,
473–484. https://doi.org/10.1016/j.neuroimage.2014.07.039,
考研: 25067815

Fukushima, M。, 贝策尔, 右. F。, 他, Y。, de Reus, 中号. A。, van den
爬坡道, 中号. P。, Zuo, X. N。, & 斯波恩斯, 氧. (2018). Fluctuations
between high- and low-modularity topology in time-resolved
功能连接. 神经影像, 180, 406–416. https://土井
.org/10.1016/j.neuroimage.2017.08.044, 考研: 28823827
Glasser, 中号. F。, Coalson, 时间. S。, 罗宾逊, 乙. C。, Hacker, C. D ., Harwell,
J。, Yacoub, E., … Van Essen, D. C. (2016). A multi-modal parcellation
of human cerebral cortex. 自然, 536(7615), 171–178. https://土井
.org/10.1038/nature18933, 考研: 27437579

Glasser, 中号. F。, 索蒂罗普洛斯, S. N。, Wilson, J. A。, Coalson, 时间. S。,
菲舍尔, B., 安德森, J. L。, … for the WU-Minn HCP Consortium.
(2013). The minimal preprocessing pipelines for the Human
Connectome Project. 神经影像, 80, 105–124. https://doi.org
/10.1016/j.neuroimage.2013.04.127, 考研: 23668970

Godwin, D ., Barry, 右. L。, & Marois, 右. (2015). Breakdown of the
brainʼs functional network modularity with awareness. 会议记录
of the National Academy of Sciences of the United States of
美国, 112(12), 3799–3804. https://doi.org/10.1073/pnas
.1414466112, 考研: 25759440

Gonzalez-Castillo, J。, Hoy, C. W., Handwerker, D. A。, 罗宾逊,
中号. E., 布坎南, L. C。, Saad, Z. S。, & Bandettini, 磷. A. (2015).
Tracking ongoing cognition in individuals using brief, whole-brain
functional connectivity patterns. 国家会议录
美国科学院, 112(28),
8762–8767. https://doi.org/10.1073/pnas.1501242112,
考研: 26124112

Gu, Y。, 林, Y。, 黄, L. L。, Ma, J. J。, 张, J. B., Xiao, Y。, ……
Alzheimer’s Disease Neuroimaging Initiative. (2020). Abnormal
dynamic functional connectivity in Alzheimerʼs disease. CNS
神经科学 & Therapeutics, 26(9), 962–971. https://doi.org
/10.1111/cns.13387, 考研: 32378335

Handwerker, D. A。, Roopchansingh, 五、, Gonzalez-Castillo, J。, &
Bandettini, 磷. A. (2012). Periodic changes in fMRI connectivity.
神经影像, 63(3), 1712–1719. https://doi.org/10.1016/j
.neuroimage.2012.06.078, 考研: 22796990

Hannan, 乙. J。, & 奎因, 乙. G. (1979). Determination of the order of
an autoregression. Journal of the Royal Statistical Society Series
B-Methodological, 41(2), 190–195. https://doi.org/10.1111/j
.2517-6161.1979.tb01072.x

Honari, H。, Choe, A. S。, Pekar, J. J。, & Lindquist, 中号. A. (2019).
Investigating the impact of autocorrelation on time-varying con-
nectivity. 神经影像, 197, 37–48. https://doi.org/10.1016/j
.neuroimage.2019.04.042, 考研: 31022568

猎人, D. R。, Goodreau, S. M。, & Handcock, 中号. S. (2008). 好的-
ness of fit of social network models. Journal of the American
Statistical Association, 103(481), 248–258. https://doi.org/10
.1198/016214507000000446

网络神经科学

610

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

t

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

t

.

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

Hurvich, C. M。, & Tsai, C. L. (1989). Regression and time-series
model selection in small samples. Biometrika, 76(2), 297–307.
https://doi.org/10.1093/biomet/76.2.297

和记黄埔, 右. M。, Womelsdorf, T。, 艾伦, 乙. A。, Bandettini, 磷. A。,
Calhoun, V. D ., 科尔贝塔, M。, … Chang, C. (2013). 动态的
功能连接: Promise, 问题, and interpretations.
N e u ro I m a g e , 8 0 , 3 6 0 – 3 7 8 . h t t p s : / / d o i . o rg / 1 0 . 1 0 1 6 / j
.neuroimage.2013.05.079, 考研: 23707587

Jin, C. F。, Jia, H。, 兰卡, P。, Rangaprakash, D ., 李, L. J。, 刘, 时间. M。, ……
德什潘德, G. (2017). Dynamic brain connectivity is a better
predictor of PTSD than static connectivity. 人脑
测绘, 38(9), 4479–4496. https://doi.org/10.1002/ hbm
.23676, 考研: 28603919

Jirsa, V. K., 斯波恩斯, 奥。, Breakspear, M。, 德科, G。, & McIntosh, A. 右.
(2010). Towards the virtual brain: Network modeling of the intact
and the damaged brain. Archives Italiennes de Biologie, 148(3),
189–205. https://doi.org/10.4449/aib.v148i3.1223, 考研:
21175008

琼斯, D. T。, Vemuri, P。, 墨菲, 中号. C。, Gunter, J. L。, Senjem, 中号. L。,
Machulda, 中号. M。, … Jack, C. 右. (2012). Non-stationarity in the
“resting brainʼs” modular architecture. 公共图书馆一号, 7(6). https://
doi.org/10.1371/journal.pone.0039731, 考研: 22761880
Joyce, K. E., Laurienti, 磷. J。, Burdette, J. H。, & Hayasaka, S. (2010). A
new measure of centrality for brain networks. 公共图书馆一号, 5(8).
https://doi.org/10.1371/journal.pone.0012200, 考研:
20808943

Kabbara, A。, Khalil, M。, OʼNeill, G。, Dujardin, K., El Traboulsi, Y。,
Wendling, F。, & Hassan, 中号. (2019). Detecting modular brain
states in rest and task. 网络神经科学, 3(3), 878–901.
https://doi.org/10.1162/netn_a_00090, 考研: 31410384

Kenett, 是. N。, 贝策尔, 右. F。, & Beaty, 右. 乙. (2020). Community struc-
ture of the creative brain at rest. 神经影像, 210. https://doi.org
/10.1016/j.neuroimage.2020.116578, 考研: 31982579

Kucyi, A。, & 戴维斯, K. D. (2014). Dynamic functional connectivity
of the default mode network tracks daydreaming. 神经影像,
100, 471–480. https://doi.org/10.1016/j.neuroimage.2014.06
.044, 考研: 24973603

刘, X. (2017). Dynamic fcMRI: Approaches. Sunrise Educational
Session: Dynamic Functional Connectivity MRI: Approaches &
Mechanisms. Proceedings of the International Society for
Magnetic Resonance in Medicine.

长的, 是. C。, 曹, H. Y。, 严, C. G。, 陈, X。, 李, L。, Castellanos,
F. X。, … Liu, Z. 氮. (2020). Altered resting-state dynamic func-
tional brain networks in major depressive disorder: Findings from
the REST-meta-MDD consortium. 神经影像: Clinical, 26.
https://doi.org/10.1016/j.nicl.2020.102163, 考研: 31953148
Lurie, D. J。, Kessler, D ., Bassett, D. S。, 贝策尔, 右. F。, Breakspear, M。,
Kheilholz, S。, … Calhoun, V. D. (2020). Questions and controver-
sies in the study of time-varying functional connectivity in resting
功能磁共振成像. 网络神经科学, 4(1), 30–69. https://doi.org/10
.1162/netn_a_00116, 考研: 32043043

Martinez, S. A。, 德科, G。, Ter Horst, G. J。, & Cabral, J. (2020).
The dynamics of functional brain networks associated with
depressive symptoms in a nonclinical sample. Frontiers in Neural
Circuits, 14. https://doi.org/10.3389/fncir.2020.570583, 考研:
33071760

莫尼耶, D ., Achard, S。, Morcom, A。, & 布莫尔, 乙. 时间. (2009).
Age-related changes in modular organization of human brain

functional networks. 神经影像, 44(3), 715–723. https://土井
.org/10.1016/j.neuroimage.2008.09.062, 考研: 19027073
Mokhtari, F。, Akhlaghi, 中号. 我。, 辛普森, S. L。, 吴, G. R。, & Laurienti,
磷. J. (2019). Sliding window correlation analysis: 调制
window shape for dynamic brain connectivity in resting state.
神经影像, 189, 655–666. https://doi.org/10.1016/j
.neuroimage.2019.02.001, 考研: 30721750

Mokhtari, F。, Laurienti, 磷. J。, Rejeski, 瓦. J。, & Ballard, G. (2019).
Dynamic functional magnetic resonance imaging connectivity
tensor decomposition: A new approach to analyze and interpret
dynamic brain connectivity. Brain Connectivity, 9(1), 95–112.
https://doi.org/10.1089/brain.2018.0605, 考研: 30318906
Oldfield, 右. C. (1971). The assessment and analysis of handedness:
The Edinburgh Inventory. Neuropsychologia, 9(1), 97–113. https://
doi.org/10.1016/0028-3932(71)90067-4, 考研: 5146491
O’Malley, A. J. (2013). The analysis of social network data: 一个
exciting frontier for statisticians. Statistics In Medicine, 32(4),
539–555. https://doi.org/10.1002/sim.5630, 考研: 23023735
Parente, F。, Frascarelli, M。, Mirigliani, A。, Di Fabio, F。, Biondi, M。, &
Colosimo, A. (2018). Negative functional brain networks. Brain
Imaging and Behavior, 12(2), 467–476. https://doi.org/10.1007
/s11682-017-9715-x, 考研: 28353136

公园, H.-J., & 弗里斯顿, K. J. (2013). Structural and functional brain
网络: From connections to cognition. 科学, 342(6158).
https://doi.org/10.1126/science.1238411, 考研: 24179229
Parr, T。, Rees, G。, & 弗里斯顿, K. J. (2018). Computational neuropsy-
chology and Bayesian inference. Frontiers in Human Neurosci-
恩斯, 12. https://doi.org/10.3389/fnhum.2018.00061, 考研:
29527157

力量, J. D ., 科恩, A. L。, 纳尔逊, S. M。, 假发, G. S。, 巴恩斯, K. A。,
教会, J. A。, … Petersen, S. 乙. (2011). Functional network orga-
nization of the human brain. 神经元, 72(4), 665–678. https://土井
.org/10.1016/j.neuron.2011.09.006, 考研: 22099467

Preti, 中号. G。, Bolton, 时间. A. W., & Van De Ville, D. (2017). 这
dynamic functional connectome: State-of-the-art and perspec-
特维斯. 神经影像, 160, 41–54. https://doi.org/10.1016/j
.neuroimage.2016.12.061, 考研: 28034766

Pruim, 右. H. R。, Mennes, M。, van Rooij, D ., Llera, A。, Buitelaar, J. K.,
& 贝克曼, C. F. (2015). ICA-AROMA: A robust ICA-based
strategy for removing motion artifacts from fMRI data. Neuro-
图像, 112, 267–277. https://doi.org/10.1016/j.neuroimage
.2015.02.064, 考研: 25770991

Rashid, B., Arbabshirani, 中号. R。, Damaraju, E., Cetin, 中号. S。, 磨坊主,
R。, Pearlson, G. D ., & Calhoun, V. D. (2016). Classification of
schizophrenia and bipolar patients using static and dynamic
resting-state fMRI brain connectivity. 神经影像, 134, 645–657.
https://doi.org/10.1016/j.neuroimage.2016.04.051, 考研:
27118088

Robins, G. L。, Pattison, 磷. E., 卡利什, Y。, & Lusher, D. (2007). 一个
introduction to exponential random graph (p*) models for social
网络. Social Networks, 29(2), 173–191. https://doi.org/10
.1016/j.socnet.2006.08.002

鲁比诺夫, M。, & 斯波恩斯, 氧. (2010). 复杂的网络措施
大脑连接: 用途和解释. 神经影像, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
考研: 19819337

Sakoglu, U。, Pearlson, G. D ., Kiehl, K. A。, 王, 是. M。, 迈克尔,
A. M。, & Calhoun, V. D. (2010). A method for evaluating

网络神经科学

611

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

/

t

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

.

t

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

dynamic functional network connectivity and task-modulation:
application to schizophrenia. Magnetic Resonance Materials in
Physics Biology and Medicine, 23(5–6), 351–366. https://土井
.org/10.1007/s10334-010-0197-8, 考研: 20162320

Salehi, M。, Greene, A. S。, Karbasi, A。, 沉, X. L。, Scheinost, D ., &
Constable, 右. 时间. (2020). There is no single functional atlas even
for a single individual: Functional parcel definitions change with
任务. 神经影像, 208. https://doi.org/10.1016/j.neuroimage
.2019.116366, 考研: 31740342

Schmlazle, R。, OʼDonnell, 中号. B., 加西亚, J. 奥。, Cascio, C. N。,
Bayer, J。, Bassett, D. S。, … Falk, 乙. 乙. (2017). Brain connectivity
dynamics during social interaction reflect social network struc-
真实. 美国国家科学院院刊
美国, 114(20), 5153–5158. https://doi.org
/10.1073/pnas.1616130114, 考研: 28465434

施瓦茨, A. J。, & McGonigle, J. (2011). Negative edges and soft
thresholding in complex network analysis of resting state func-
tional connectivity data. 神经影像, 55(3), 1132–1146.
https://doi.org/10.1016/j.neuroimage.2010.12.047, 考研:
21194570

施瓦茨, G. (1978). Estimating the dimension of a model. Annals of
统计数据, 6(2), 461–464. https://doi.org/10.1214/aos/1176344136
Shakil, S。, 李, C. H。, & Keilholz, S. D. (2016). Evaluation of sliding
window correlation performance for characterizing dynamic
functional connectivity and brain states. 神经影像, 133,
111–128. https://doi.org/10.1016/j.neuroimage.2016.02.074,
考研: 26952197

Shakil, S。, 马格努森, 中号. E., Keilholz, S. D ., & 李, C. H. (2014).
Cluster-based analysis for characterizing dynamic functional
连接性. Annual International Conference of the IEEE Engi-
neering in Medicine and Biology Society, 2014, 982–985.
https://doi.org/10.1109/ EMBC.2014.6943757, 考研:
25570125

Shappell, H。, Caffo, 乙. S。, Pekar, J. J。, & Lindquist, 中号. A. (2019).
Improved state change estimation in dynamic functional connec-
tivity using hidden semi-Markov models. 神经影像, 191,
243–257. https://doi.org/10.1016/j.neuroimage.2019.02.013,
考研: 30753927

Shehzad, Z。, 凯莉, C。, Reiss, 磷. T。, Craddock, 右. C。, Emerson, J. W.,
麦克马洪, K., … Milham, 中号. 磷. (2014). A multivariate
distance-based analytic framework for connectome-wide associ-
ation studies. 神经影像, 93, 74–94. https://doi.org/10.1016/j
.neuroimage.2014.02.024, 考研: 24583255

沉, X。, Tokoglu, F。, Papademetris, X。, & Constable, 右. 时间. (2013).
Groupwise whole-brain parcellation from resting-state fMRI data
for network node identification. 神经影像, 82, 403–415.
https://doi.org/10.1016/j.neuroimage.2013.05.081, 考研:
23747961

Shine, J. M。, Bissett, 磷. G。, 钟, 磷. T。, Koyejo, 奥。, Balsters, J. H。,
Gorgolewski, K. J。, … Poldrack, 右. A. (2016). The dynamics of
functional brain networks: Integrated network states during cog-
nitive task performance. 神经元, 92(2), 544–554. https://doi.org
/10.1016/j.neuron.2016.09.018, 考研: 27693256

Shine, J. M。, Breakspear, M。, 钟, 磷. T。, Martens, K. A. E., Shine, R。,
Koyejo, 奥。, … Poldrack, 右. A. (2019). Human cognition involves
the dynamic integration of neural activity and neuromodulatory
系统. 自然神经科学, 22(6), 1036–1036. https://doi.org
/10.1038/s41593-019-0347-x, 考研: 30792538

Shine, J. M。, & Poldrack, 右. A. (2018). Principles of dynamic net-
work reconfiguration across diverse brain states. 神经影像,
180, 396–405. https://doi.org/10.1016/j.neuroimage.2017.08
.010, 考研: 28782684

Shirer, 瓦. R。, Ryali, S。, Rykhlevskaia, E., Menon, 五、, & Greicius, 中号. D.
(2012). Decoding subject-driven cognitive states with whole-brain
connectivity patterns. 大脑皮层, 22(1), 158–165. https://土井
.org/10.1093/cercor/bhr099, 考研: 21616982

Simony, E., 蜂蜜, C. J。, 陈, J。, Lositsky, 奥。, Yeshurun, Y。, Wiesel, A。,
& Hasson, U. (2016). Dynamic reconfiguration of the default mode
network during narrative comprehension. Nature Communications,
7. https://doi.org/10.1038/ncomms12141, 考研: 27424918
辛普森, S. L。, Bahrami, M。, & Laurienti, 磷. J. (2019). A
mixed-modeling framework for analyzing multitask whole-brain
network data. 网络神经科学, 3(2), 307–324. https://土井
.org/10.1162/netn_a_00065, 考研: 30793084

辛普森, S. L。, Bowman, F. D ., & Laurienti, 磷. J. (2013). Analyzing
complex functional brain networks: Fusing statistics and network
science to understand the brain. Statistics Surveys, 7, 1–36.
https://doi.org/10.1214/13-SS103, 考研: 25309643

辛普森, S. L。, & 爱德华兹, L. J. (2013). A circular LEAR correlation
structure for cyclical longitudinal data. Statistical Methods in
Medical Research, 22(3), 296–306. https://doi.org/10.1177
/0962280210395741, 考研: 21216801

辛普森, S. L。, Hayasaka, S。, & Laurienti, 磷. J. (2011). Exponential
random graph modeling for complex brain networks. 公共图书馆一号,
6(5). https://doi.org/10.1371/journal.pone.0020039, 考研:
21647450

辛普森, S. L。, & Laurienti, 磷. J. (2015). A two-part mixed-effects
modeling framework for analyzing whole-brain network data.
神经影像, 113, 310–319. https://doi.org/10.1016/j
.neuroimage.2015.03.021, 考研: 25796135

辛普森, S. L。, & Laurienti, 磷. J. (2016). Disentangling brain graphs:
A note on the conflation of network and connectivity analyses.
Brain Connectivity, 6(2), 95–98. https://doi.org/10.1089/ brain
.2015.0361, 考研: 26414952

辛普森, S. L。, Moussa, 中号. N。, & Laurienti, 磷. J. (2012). An exponen-
tial random graph modeling approach to creating group-based
representative whole-brain connectivity networks. 神经影像,
60(2), 1117–1126. https://doi.org/10.1016/j.neuroimage.2012
.01.071, 考研: 22281670

Sizemore, A. E., & Bassett, D. S. (2018). Dynamic graph metrics:
Tutorial, toolbox, and tale. 神经影像, 180, 417–427. https://
doi.org/10.1016/j.neuroimage.2017.06.081, 考研: 28698107
史密斯, S. M。, Hyvarinen, A。, Varoquaux, G。, 磨坊主, K. L。, & 贝克曼,
C. F. (2014). Group-PCA for very large fMRI datasets. 神经影像,
101, 738–749. https://doi.org/10.1016/j.neuroimage.2014.07.051,
考研: 25094018

Telesford, 问. K., 辛普森, S. L。, Burdette, J. H。, Hayasaka, S。, &
Laurienti, 磷. J. (2011). The brain as a complex system: 使用
network science as a tool for understanding the brain. Brain
Connectivity, 1(4), 295–308. https://doi.org/10.1089/brain.2011
.0055, 考研: 22432419

Tewarie, P。, Liuzzi, L。, OʼNeill, G. C。, 奎因, A. J。, Griffa, A。, 伍尔里奇,
中号. W., … Brookes, 中号. J. (2019). Tracking dynamic brain networks
using high temporal resolution MEG measures of functional con-
nectivity. 神经影像, 200, 38–50. https://doi.org/10.1016/j
.neuroimage.2019.06.006, 考研: 31207339

网络神经科学

612

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

t

/

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

.

t

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A mixed model for dynamic brain networks

Tikidji-Hamburyan, 右. A。, Narayana, 五、, Bozkus, Z。, & El-Ghazawi,
时间. A. (2017). Software for brain network simulations: A compar-
ative study. 神经信息学前沿, 11. https://doi.org/10
.3389/fninf.2017.00046, 考研: 28775687

Unsworth, N。, Fukuda, K., Awh, E., & 沃格尔, 乙. K. (2014). Working
memory and fluid intelligence: Capacity, attention control, and sec-
ondary memory retrieval. 认知心理学, 71, 1–26. https://
doi.org/10.1016/j.cogpsych.2014.01.003, 考研: 24531497
Valencia, M。, Pastor, 中号. A。, Fernandez-Seara, 中号. A。, Artieda, J。,
马蒂内里, J。, & Chavez, 中号. (2009). Complex modular structure
of large-scale brain networks. Chaos, 19(2). https://doi.org/10
.1063/1.3129783, 考研: 19566254

Van Essen, D. C。, 史密斯, S. M。, Barch, D. M。, 贝伦斯, 时间. 乙. J。,
Yacoub, E., Ugurbil, K., & WU-Minn HCP Consortium. (2013).
The WU-Minn Human Connectome Project: 概述. 新-
roImage, 80, 62–79. https://doi.org/10.1016/j.neuroimage.2013
.05.041, 考研: 23684880

Vidaurre, D ., Abeysuriya, R。, Becker, R。, 奎因, A. J。, Alfaro-Almagro,
F。, 史密斯, S. M。, & 伍尔里奇, 中号. 瓦. (2018). Discovering dynamic
brain networks from big data in rest and task. 神经影像,
180(Pt B), 646–656. https://doi.org/10.1016/j.neuroimage.2017
.06.077, 考研: 28669905

Vidaurre, D ., 打猎, L. T。, 奎因, A. J。, 打猎, 乙. A。, 布鲁克斯, 中号. J。,
高贵, A. C。, & 伍尔里奇, 中号. 瓦. (2018). Spontaneous cortical
activity transiently organises into frequency specific phase-

coupling networks. Nature Communications, 9(1), 1–13. https://
doi.org/10.1038/s41467-018-05316-z, 考研: 30061566

Vidaurre, D ., 史密斯, S. M。, & 伍尔里奇, 中号. 瓦. (2017). Brain net-
work dynamics are hierarchically organized in time. 会议记录
of the National Academy of Sciences of the United States of
美国, 114(48), 12827–12832. https://doi.org/10.1073/pnas
.1705120114, 考研: 29087305

Wolfinger, R。, & Oconnell, 中号. (1993). Generalized linear mixed
models a pseudo-likelihood approach. Journal of Statistical Com-
putation and Simulation, 48(3–4), 233–243. https://doi.org/10
.1080/00949659308811554

叶, T。, 李, P。, 张, Q., Gu, Q., 鲁, X. Q., 高, Z. F。, & 沉,
中号. 瓦. (2019). Relation between working memory capacity of
biological movements and fluid intelligence. Frontiers in Psy-
chology, 10. https://doi.org/10.3389/fpsyg.2019.02313,
考研: 31749726

朱, H。, 黄, J。, Deng, L. F。, 他, 氮. Y。, Cheng, L。, Shu, P。, … Ling,
H. 瓦. (2019). Abnormal dynamic functional connectivity associ-
ated with subcortical networks in Parkinsonʼs disease: A tempo-
ral variability perspective. Frontiers in Neuroscience, 13. https://
doi.org/10.3389/fnins.2019.00080, 考研: 30837825

Zuo, X. N。, Ehmke, R。, Mennes, M。, Imperati, D ., Castellanos, F. X。,
斯波恩斯, 奥。, & Milham, 中号. 磷. (2012). Network centrality in the human
functional connectome. 大脑皮层, 22(8), 1862–1875.
https://doi.org/10.1093/cercor/bhr269, 考研: 21968567

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

t

/

/

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

6
2
5
9
1
2
0
2
8
1
1
3
n
e
n
_
A
_
0
0
2
3
8
p
d

.

t

F

乙
y
G
你
e
s
t

t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

网络神经科学

613

下载pdf