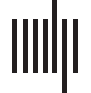研究
Braiding Braak and Braak: Staging patterns and
model selection in network neurodegeneration
Prama Putra
, Travis B. 汤普森
for the Alzheimer’s Disease Neuroimaging Initiative
, Pavanjit Chaggar, and Alain Goriely
,
Mathematical Institute, 牛津大学, 牛津, 英国
关键词: Braak, Staging, Tau, 网络, Neurodegeneration, Diffusion-reaction
抽象的
A hallmark of Alzheimer’s disease is the aggregation of insoluble amyloid-beta plaques and
tau protein neurofibrillary tangles. A key histopathological observation is that tau protein
aggregates follow a structured progression pattern through the brain. Mathematical network
models of prion-like propagation have the ability to capture such patterns, but a number of
factors impact the observed staging result, thus introducing questions regarding model
选择. 这里, we introduce a novel approach, based on braid diagrams, for studying the
structured progression of a marker evolving on a network. We apply this approach to a
six-stage ‘Braak pattern’ of tau proteins, in Alzheimer’s disease, motivated by a recent
observation that seed-competent tau precedes tau aggregation. We show that the different
modeling choices, from the model parameters to the connectome resolution, play a significant
role in the landscape of observable staging patterns. Our approach provides a systematic way
to approach model selection for network propagation of neurodegenerative diseases that
ensures both reproducibility and optimal parameter fitting.
作者总结
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
A
_
0
0
2
0
8
p
d
.
t
Network diffusion models of neurodegenerative diseases are a class of dynamical systems that
simulate the evolution of toxic proteins on the connectome. These models predict, from an
initial seed, a pattern of invasion called staging. The generalized staging problem seeks to
systematically study the effect of various model choices on staging. We introduce methods
based on braid diagrams to test the possible staging landscape of a model and how it depends
on the choice of connectome, as well as the model parameters. Our primary finding is that
connectome construction, the choice of the graph Laplacian, and transport models all have
an impact on staging that should be taken into account in any study.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
介绍
The term ‘neurodegenerative disease’ refers to a family of maladies primarily affecting the
brain’s neurons; many neurodegenerative diseases result in cognitive decline and, 最终,
a diagnosis of dementia. A hallmark of such diseases is a large concentration of toxic protein
aggregates throughout the brain. These toxic proteins interfere with normal brain functions and
are associated with neuronal impairment, neuronal loss, brain atrophy, and overall cognitive
开放访问
杂志
引文: Putra, P。, 汤普森, 时间. B.,
Chaggar, P。, & Goriely, A. (2021).
Braiding Braak and Braak: Staging
patterns and model selection in
network neurodegeneration. 网络
神经科学, 5(4), 929–956. https://土井
.org/10.1162/netn_a_00208
DOI:
https://doi.org/10.1162/netn_a_00208
支持信息:
https://doi.org/10.1162/netn_a_00208
已收到: 4 二月 2021
公认: 25 八月 2021
利益争夺:
The authors have declared that
no competing interests exist.
通讯作者:
Travis B. 汤普森
thompsont@maths.ox.ac.uk
处理编辑器:
Bratislav Misic
版权: © 2021
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
Braiding Braak and Braak
Prion-like:
A prion-like biological agent is one
that replicates an undesirable state
through an autocatalytic process.
Nonlinearity:
A nonlinearity is any mathematical
expression that does not satisfy
F (ax + y) = af (X) + F (y) 在哪里
a is a real number and x and y
are input vectors.
Simplicial mesh:
A, often complex, mesh whose
elements are triangles (2D) 或者
tetrahedra (3D); widely used to solve
partial differential equations on
complex domains.
Model selection:
The process of arriving at the set of
features that determine the model
used to study a process of interest.
Parameter inference:
Typically refers to mathematical
approaches to deduce distributions
for the parameters of a model, 从
observed data, using statistical
paradigms such as Bayesian
inference.
Structural connectome:
A structural connectome is a graph
representation G = (V, 乙 ) of the brain
where the vertices V are anatomical
regions of interest and the edges
represent connections between
regions of interest via axonal
bundles.
Graph Laplacian:
The graph Laplacian is a matrix
representation of a transport process
on a, often weighted and undirected,
network graph.
网络神经科学
衰退. 这里, we address questions related to model selection for computational studies of
阿尔茨海默氏病 (广告); AD is the most contemporarily prevalent cause of dementia. 这
practical constraints of clinical AD experiments, most especially in humans, have lead to
an interest in the development of mathematical models of pathology evolution, 特别
those that can accurately capture large-scale features of AD. Many of these models take ad-
vantage of the prion hypothesis which asserts that the progression of proteopathy, in AD, 遵循-
lows from a prion-like mechanism.
Prion-like mathematical models can be broadly characterized as either probabilistic (沃格尔
等人。, 2020, 2021) or as continuous (Fornari, Schäfer, Goriely, & Kuhl, 2019A; Raj, Kuceyeski,
& 韦纳, 2012; 汤普森, Chaggar, Kuhl, & Goriely, 2020). Both model types often invoke
nonlinearity and are typically discretized, and solved, on either a simplicial mesh
(Weickenmeier, Kuhl, & Goriely, 2018), or on the network defined by the brain’s connectome
(Fornari et al., 2019A; Raj et al., 2012; Schäfer, Mormino, & Kuhl, 2020; Thompson et al.,
2020). Probabilistic and continuous models have their individual advantages. The former
can often reveal unique insights in complex datasets while the mathematical structure of
the latter can be rigorously analyzed or, in some simple cases, closed form solutions can be
derived. Misfolded protein aggregates, in neurodegenerative diseases, often display structured
patterns of progression, and reproducing these staging patterns is a desirable trait for any math-
ematical model. 这里, we will discuss the impact of model selection, for continuous prion-like
mathematical models, with respect to an observed structured staging sequence. As a case
学习, we will consider the network progression of misfolded tau protein (τP) in AD. 我们com-
pare results to staging patterns motivated by a recent study (DeVos et al., 2018) that uses a six-
stage Braak pattern for τP in AD. 然而, our braid surface approach is generalizable to
more complex hierarchical patterns (Cho et al., 2016; Delacourte et al., 1999) and well suited
to broader investigations, including applications to the study of staging phenomena in other
neurodegenerative diseases.
The primary contribution of this manuscript is a methodical, quantitative study of model
selection features, as they pertain to structured staging, in the setting of a continuous mathe-
matical model of a prion-like proteopathy processes defined on structural networks. This man-
uscript introduces two novel investigative tools, braid diagrams and braid surfaces, facilitating
这个流程. Our approach is of practical interest for neurodegenerative diseases for two main
原因. 第一的, there is often a lack of the longitudinal radiotracer data, in which staging would
be evident, that would provide for accurate, automatic model selection via, 例如, A
parameter inference approach. Such studies are important for short-term predictions, 但他们
may make model choices based on a limited number of time points and arrive at a model that
does not capture a long-term expected staging progression. 第二, we show that there are
several other factors of a network neurodegeneration model, beyond mathematical parame-
特尔斯, which are not always considered in the model selection process and can play a significant
role in staging. 尤其, we show that the choice of structural connectome scale, tracto-
graphy method, thresholding method, graph Laplacian weights and, sometimes slight, varia-
tion in model parameters can significantly alter the landscape of observed, even accessible,
staging patterns.
Our study highlights the nuanced role played by each choice in the network neurodegen-
eration modeling pipeline, providing important insight, and quantitative tools, that inform
model selection. Even though we choose a particular example of an AD staging as a point
of study, the methods and observations are general and can be applied to the study of any
hierarchical staging process that can appear in the study of neurodegenerative diseases or other
dynamical process on networks. The source code, and connectomes, to create the braid
930
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
A
_
0
0
2
0
8
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Braiding Braak and Braak
diagrams and braid surfaces discussed in the manuscript are freely available online (Putra,
Chaggar, 汤普森, & Goriely, 2021).
THEORY AND MODEL
The Staging Problem
The central problem discussed here is the generalized staging problem. We consider a general
dynamical system with form
_p tð Þ ¼ f t; p; Θ
ð
Þ;
p 0ð Þ ¼ p0;
(1A)
(1乙)
where p(t) = ( pi, ……, pN) denotes a normalized and dimensionless quantity, 例如, A
normalized concentration 0 ≤ pi(t) ≤ 1, evolving on a network G = (V, 乙 ) with nodes V and
edge set E. The quantity pi(t) corresponds to the observed concentration in node vi and pi(0) 是
the initial concentration at that node. The quantity Θ represents the parameters of the model.
在实践中, Θ represents the parameters of differential Equation 1a in addition to other model
selection choices such as the edge weighting scheme, the choice of tractography method,
which determines graph connectivity and properties that also influence edge weights, 或者
edge weight thresholding method used to construct the network G. We further assume that the
dynamics of the system are such that starting from an initial condition, where all concentra-
tions are taken to vanish except one, the system will evolve asymptotically to a state where all
concentrations reach their maximal value. It is the spatiotemporal sequence of invasion that
we want to characterize.
Let Ω
j, for j = 1, 2, … J be a nonoverlapping collection of nodes; 那是, Ω
k are
disjoint subsets of V when j 6¼ k. Let T 2 [0, 1] be an arbitrary, 但固定, threshold value.
As p evolves, according to Equation 1a, the average concentration is computed in each region
Ω
j and the time when Ω
j first reaches the threshold T is recorded. This process produces an
ordering of the regions Ωj and the ordered sequence Ωj1, Ωj2, ……, ΩjJ is called an observed
staging pattern. The generalized staging problem is to ascertain the scope of observable
staging patterns, subject to variations in Θ. The observed staging patterns can then be com-
pared to one or more desirable staging patterns.
j and Ω
A Continuous Model of τPAD Proteopathy on a Structural Connectome
For our particular application, we model the disease progression on a structural connectome
G = (V, 乙 ) with node set V given by anatomical regions of interest (ROIs) and edge set E repre-
senting white matter connectivity between these regions. At each node, we define a tau protein
concentration, pi, as well as a marker of neurofibirlary tangle (NFT) pathology, qi, and assume
the following dynamics:
¼ −β
XN
Lijpj þ pi 1 − pi
ð
Þ;
i ¼ 1; ……; 氮
i=1
¼ δpi 1 − qi
ð
Þ;
i ¼ 1; ……; 氮:
dpi
dt
dqi
dt
(2A)
(2乙)
In Equation 2a the variables Lij represents the entries of a weighted graph Laplacian L, pi
denotes the concentration of seed-competent tau, in node i, and β a scaled ratio of transmis-
sion versus growth (the scaling is chosen so that the coefficient in front of the nonlinear term in
网络神经科学
931
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
A
_
0
0
2
0
8
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Braiding Braak and Braak
Diffusion-reaction:
A partial differential equation
describing the simultaneous diffusion
and reactive production of an agent
through a medium.
Fisher-Kolmogorov:
A class of diffusion-reaction
方程, that admit traveling wave
solutions, where the reaction term
satisfies a set of conditions. This class
includes Fisher’s equation as a
special case.
Eq. 2a is one). The system Eq. 2a is said to be growth dominated when β (西德:2) 1 and diffusion
dominated when β (西德:3) 1. The seed model Eq. 2a is a network diffusion-reaction equation, 的
Fisher-Kolmogorov type, and has been considered in several previous studies (Fornari et al.,
2019A; Goriely, Kuhl, & Bick, 2020; Kevrekidis, 汤普森, & Goriely, 2020; Schäfer et al.,
2020; Weickenmeier, Jucker, Goriely, & Kuhl, 2019; Weickenmeier et al., 2018). In Eq. 2b the
variables qi represent a marker for the local concentration NFT, in an ROI, while δ is a coef-
ficient representing an NFT accumulation rate in the presence of τP. This damage model has
also been used previously (Goriely et al., 2020; Raj et al., 2012; Raj et al., 2015). 自从
available staging patterns, observed in clinical imaging data, do not necessarily have a reso-
lution at the level of a single connectome node, we consider J regions Ω
J. In each of
these regions, 我们定义
1, ……, Ω
Pj tð Þ ¼
Qj tð Þ ¼
1
氮
1
氮
X
pi tð Þ;
i2Vj
X
qi tð Þ;
i2Vj
j ¼ 1; ……; J
j ¼ 1; ……; J;
(3)
(4)
where Vj is the set of nodes defining region Ω
region Ω
状况
j with Nj nodes. In all computations, the first
1 is defined as the bilateral entorhinal cortex with N1 nodes and we choose for initial
(西德:2)
pi 0ð Þ ¼
0:005=N1;
0;
我 2 V1
i =2 V1
qi 0ð Þ ¼ 0;
i ¼ 1; ……; 氮:
(5)
(6)
The Choice of Graph Laplacian
The graph Laplacian used in this work is the standard graph Laplacian for an undirected network:
L ¼ D − W:
(7)
where W is the weighted adjacency matrix associated and D is the degree matrix, a diagonal
matrix with entries
Dii ¼
XN
Wij;
j¼1
i ¼ 1; ……; 氮
We note that other authors (Abdelnour, Voss, & Raj, 2014; Pandya, Mezias, & Raj, 2017;
Pandya et al., 2019; Raj et al., 2012, 2015) have used normalized forms of the graph
Laplacian for their models of neurodegenerative disease progression and a natural question
for model selection is the choice of a suitable Laplacian for the underlying process.
A parametrized family of graph Laplacians, encompassing both the standard and normal-
ized forms, is given by
L
A;乙
¼ D1−a−b − D−aWD−b;
(8)
where a, 乙 2 [0, 1] and a + b ≤ 1, the choice a = b = 0, yielding the standard graph Laplacian
and other popular choices include a = −1, b = 0, a = 0, b = 1 and the normalized graph
Laplacian with a = b = 1/2. The question is to choose, within this family, a graph Laplacian
that respects some desirable properties of the transport it is supposed to model. While it is clear
网络神经科学
932
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
A
_
0
0
2
0
8
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Braiding Braak and Braak
that the dynamics, of tau proteins, do not conserve mass overall, since toxic proteins can be
either created through aggregation or removed through clearance, the transport part of the
model should preserve mass. 否则, it would require a model assumption to explain
how tau proteins are created or removed simply by being transported from one node to the
next and how this creation or removal process depend on the degrees of the two nodes and no
other mechanism. 自从, there is no known such physical mechanism, we are therefore forced
to insist on mass conservation by the diffusion part of the model, whereas growth and clear-
ance should be modeled by other terms in the model as shown in previous studies (Fornari
等人。, 2019A; Fornari, Schäfer, Goriely, & Kuhl, 2019乙; Thompson et al., 2020; 汤普森,
Meisl, & Goriely, 2021). We show in the Supporting Information S1 that the mass-conservation
condition is equivalent to the requirement 1 · La,b = 0 在哪里 1 = (1, 1, ……, 1).
A second condition that we impose on the transport is that transport is driven by difference
in concentrations. If the concentration is equal at two nodes, there is no driving force to create
an imbalance between these nodes. By analogy with diffusion processes based on Fick’s law,
we call this condition the Fick’s condition. In terms of the graph Laplacian on an undirected
网络, it reads simply La,b · 1 = 0. We note that there are other possible assumptions when
the transport process is viewed as a probabilistic event as shown in Masuda, Porter, 和
兰比奥特 (2017).
We show in Supporting Information S1 that the only possible graph Laplacian, in the class
defined by La,乙, that satisfies both mass conservation and the Fick’s condition is the standard
graph Laplacian L = L0,0. We also show how to generalize this result when regions of different
volumes are considered and Fick’s condition suitably generalized.
We want to emphasize that this unavoidable constraint on a physical model of transport
does not invalidate previous studies based on the normalized graph Laplacian as these have
shown great predictive and explanatory powers when applied to actual patient data. 然而, 这
choice of using a normalized graph Laplacian is not innocent and should be fully justified as it
has some direct implications on the assumptions used in the model, even if these assumptions
are not usually given explicitly.
Graph Laplacian Weightings
We consider networks G = (V, 乙 ) based on two families of multiresolution structural connec-
tomes generated from Human Connectome Project (HCP) 数据 (参见方法, Structural con-
nectomes). Each edge, eij, is associated with two values: the number of fibers nij constituting
the connection between (anatomical region) nodes i and j; and the fiber length ℓ
ij. We consider
the choice of weights as part of the model selection and study three possible weights based
on the literature: the length-free weighting (Abdelnour et al., 2014; Raj et al., 2012, 2015), 这
ballistic weighting (Fornari et al., 2019A, 2019乙), and the diffusive weighting (Thompson et al.,
2020). The formulas for these three weighting schemes are listed in Table 1.
桌子 1. Graph Laplacian weightings for model selection
Weighting
Length-free weighting (LW)
Ballistic weighting (BW)
Diffusive weighting (DW)
Formula for Wij
nij
ij
nij /ℓ
nij /ℓ2
ij
网络神经科学
933
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
A
_
0
0
2
0
8
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Braiding Braak and Braak
Braid Diagrams and Braid Surfaces
1, Ω
2, ……, Ω
A primary contribution of this manuscript is the introduction of braid diagrams and braid sur-
faces; these powerful tools present a direct and visual assessment of an otherwise complex,
nonlinear process evolving in time. We begin by describing a braid diagram. Let G = (V, 乙 ) 是
a fixed network and suppose that Ω
J are a fixed set of nonoverlapping node regions.
Suppose further that T1, T2, ……, TN are (biomarker) threshold values in the unit interval [0, 1]. A
braid diagram is a graph whose abscissa is the index of the regions Ω
j and whose ordinate
corresponds to the threshold values Tk. As a dynamical system, such as Eq. 2A, evolves on
G, the time tj,k at which each region, Ωj, first achieves each threshold, Tk, is recorded. If a given
threshold is never achieved in a particular region, the recorded time is prescribed as tj,k = ∞.
The collection of time values, for a fixed threshold index, establishes an ordering of the regions
Ωj. For each threshold, the ordering can then be visualized as a braid diagram.
An illustrative example of a braid diagram is shown in Figure 1. 这里, the graph consists of
four nodes and the regions are simply Ω
i = {我} for i = 1, 2, 3, 4. The threshold values are T1 =
1%, T2 = 5%, T3 = 40%, and T4 = 80%. Staging was determined from solving Eq. 2a with ln(β) =
3.897 and a synthetic weighting matrix:
2
6
6
4
W ¼
0
3:125 (西德:4) 10−7
5 (西德:4) 10−6
0
3:125 (西德:4) 10−7
0
0
1 (西德:4) 10−5
5 (西德:4) 10−6
0
0
1:5 (西德:4) 10−4
0
1 (西德:4) 10−5
1:5 (西德:4) 10−4
0
3
7
7
5;
which corresponds to the DW scheme (桌子 1) for illustrative edge lengths ℓ
2,1 = 40 和
all other edge lengths equal to 20. This simple example shows, 例如, that the regions
achieve the threshold T = 5% in the order Ω
4. 然而, for the threshold
2
T = 40%, the observed ordering of regions changes to Ω
→ Ω
2. These two
observed staging patterns can be expressed by the abbreviated notation I → III → II → IV
and I → III → IV → II, 分别. A braid diagram is useful for considering observed staging
for a fixed set of model parameters, 例如, for a fixed value of β in Eq. 2A.
1,2 = ℓ
→ Ω
→ Ω
→ Ω
→ Ω
→ Ω
1
1
4
3
3
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
A
_
0
0
2
0
8
p
d
.
t
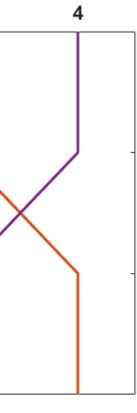
We are also interested in staging outcomes as the system parameters are varied. This infor-
mation is contained in a braid surface that generalizes a braid diagram. For each possible
staging, we assign a color. The braid surface is a two-dimensional plot that assigns for each
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 1. A network with 4 regions of interest (左边). A braid diagram (正确的) generated from an
illustrative configuration of fibers (nij), edge lengths (ℓ
ij), DW scheme, and dynamics (β).
网络神经科学
934
Braiding Braak and Braak
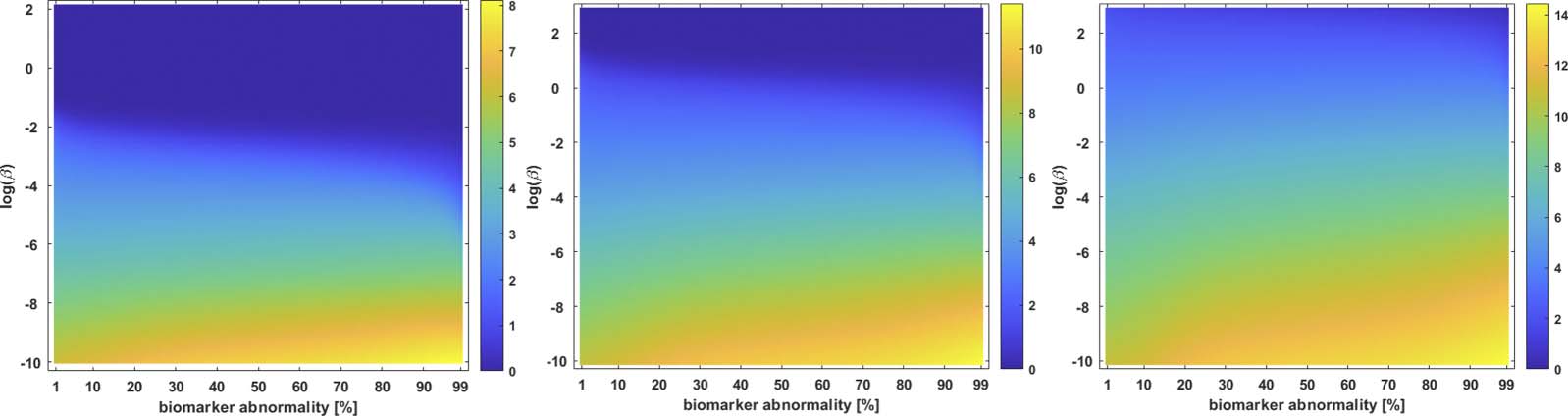
value of one parameter and one biomarker the corresponding staging color. Computationally,
this surface is generated by a simple algorithm. 第一的, one discretizes the continuous values of
a parameter, such as β in Eq. 2A, of interest. 然后, for each discretized parameter, the under-
lying system (例如, Eq. 2A) is solved, a braid diagram is constructed and the observed staging
pattern is determined for each threshold value; if an observed staging pattern has not yet been
encountered, it is added to a list. At the end of the process, every pairing of discrete parameter
and threshold has been assigned to an observed staging pattern. The set of observed staging
patterns are assigned to colors, and these colors are plotted to visualize the braid surface. 这
τP seed staging braid surface for the example network, and weighting matrix, of Figure 1 是
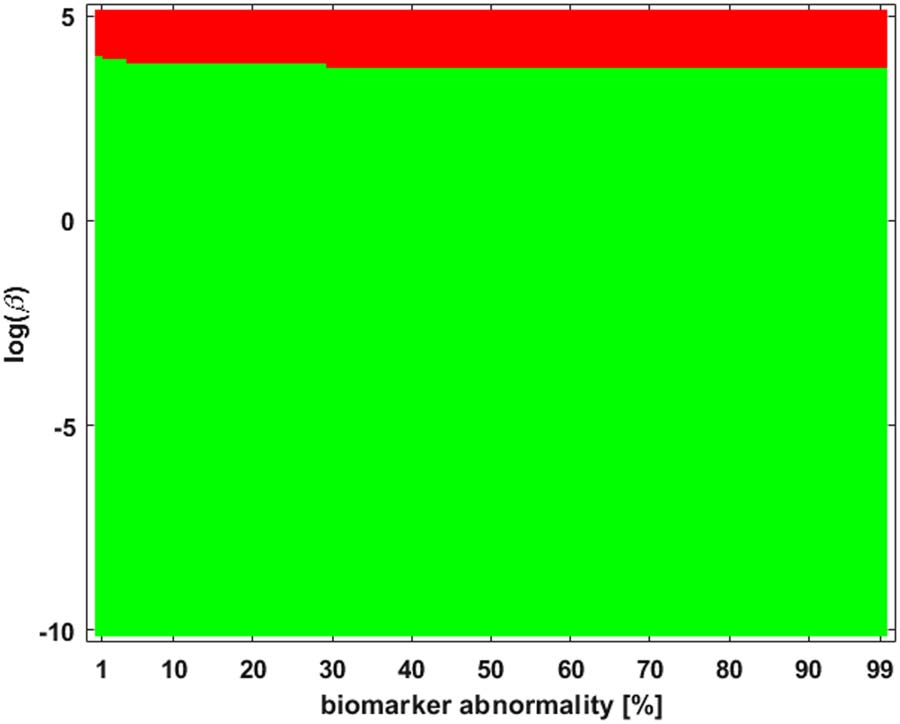
shown in Figure 2. The green corresponds to the β-parameter, and threshold, region where
a I → III → II → IV staging pattern is observed while the red corresponds to the parameter
region where a I → III → IV → II is produced. The braid surface shows that the staging
dynamics, for the four-vertex system with diffusive weights, are simple; we will observe complex
staging dynamics on structural connectome graphs of the brain.
Hierarchical Staging of τP in AD
The problem of the structured staging of τP NFT in AD has been well studied. The most famous
study being the seminal work of Braak and Braak (Braak, Alafuzoff, Arzberger, Kretzschmar, &
Del Tredici, 2006; Braak & Braak, 1991) that looked at the progression through six regions.
The six-region progression view is still in contemporary use (DeVos et al., 2018; Vogel et al.,
2020), though some authors have also proposed refinements to ten regions (Delacourte et al.,
1999). 最近, the hierarchical progression of flortaucipir tracer has also been studied
for progression patterns; authors have studied standardized uptake value ratio (SUVR) progres-
sion using a canonical 6-region (Schöll et al., 2016) and an extensive 25-region (Cho et al.,
2016) pattern.
Much of the staging literature refers to the evolution of τP NFT or of SUVR quantities,
though a recent study (DeVos et al., 2018) has advanced the notion that τP seeds precede
NFT pathology in a similar structured manner. The model that we study, 那是, Eq. 2A, 曲目
the progression of both τP seeds (via Eq. 2A) and τP NFT (via Eq. 2乙). 所以, we adopt the
staging regions given by DeVos et al. (2018); we will observe how the many, 有时
数字 2. A braid surface showing the τP seed staging dynamics for the simple network of Figure 1
as β varies. Two distinct staging patterns are produced for the (diffusive) weights considered.
网络神经科学
935
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
A
_
0
0
2
0
8
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Braiding Braak and Braak
桌子 2.
Connectome regions used in the staging problem
Stage
Region I
Connectome ROI
entorhinal cortex
Stage
Region II
Connectome ROI
hippocampus
Region III
parahippocampal gyrus
Region IV
rostral anterior cingulate,
caudal anterior cingulate
Region V
cuneus, pericalcarine cortex, lateral occipital cortex, lingual gyrus
surprising, aspects of model selection can strongly influence the set of observed regional pro-
gressions for a computational model of proteopathic τP staging in AD. The same method can
easily be generalized to the study of other staging regions such as those advanced in Cho et al.
(2016), Schöll et al. (2016), Vogel et al. (2020), or Delacourte et al. (1999).
结果
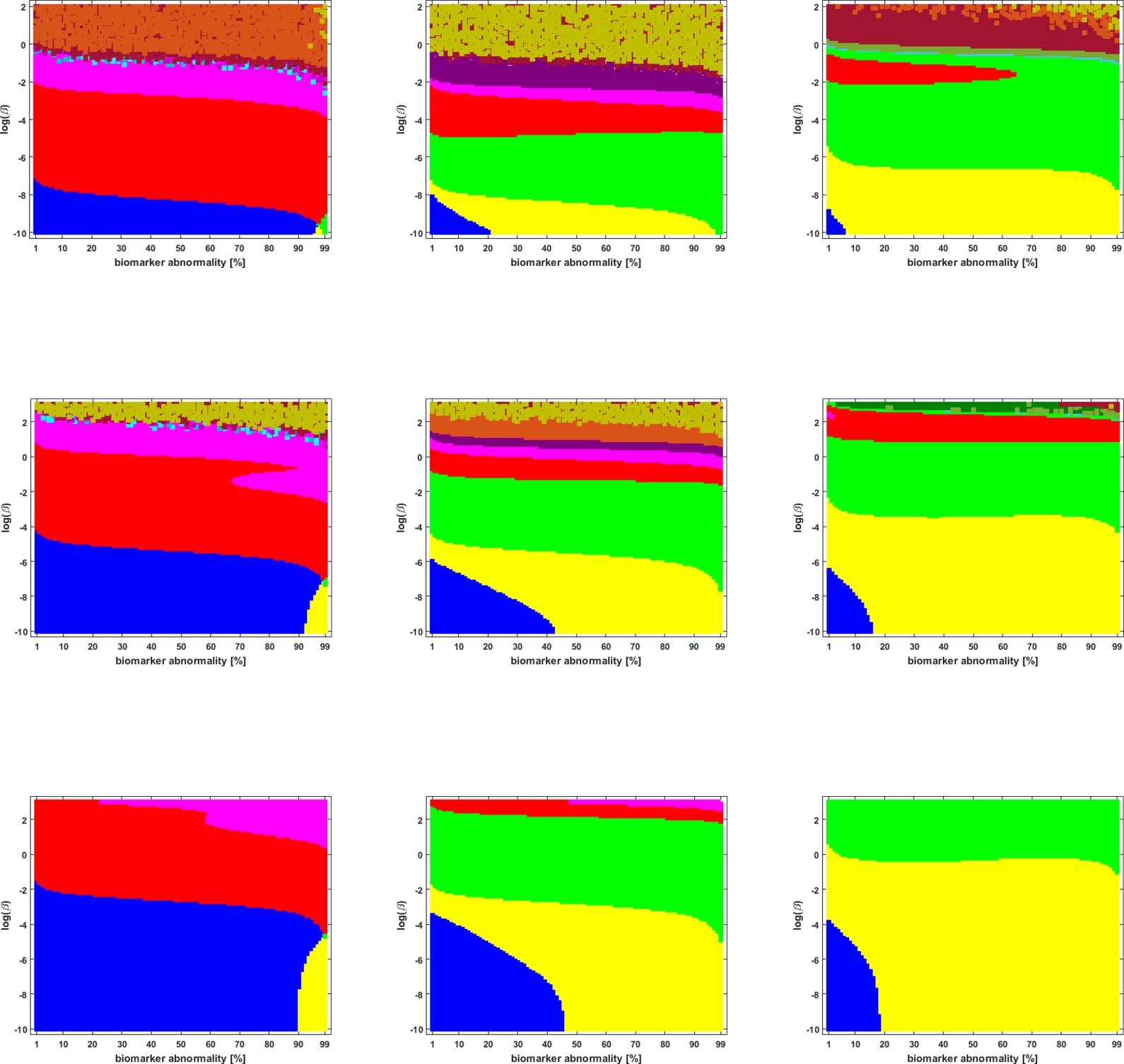
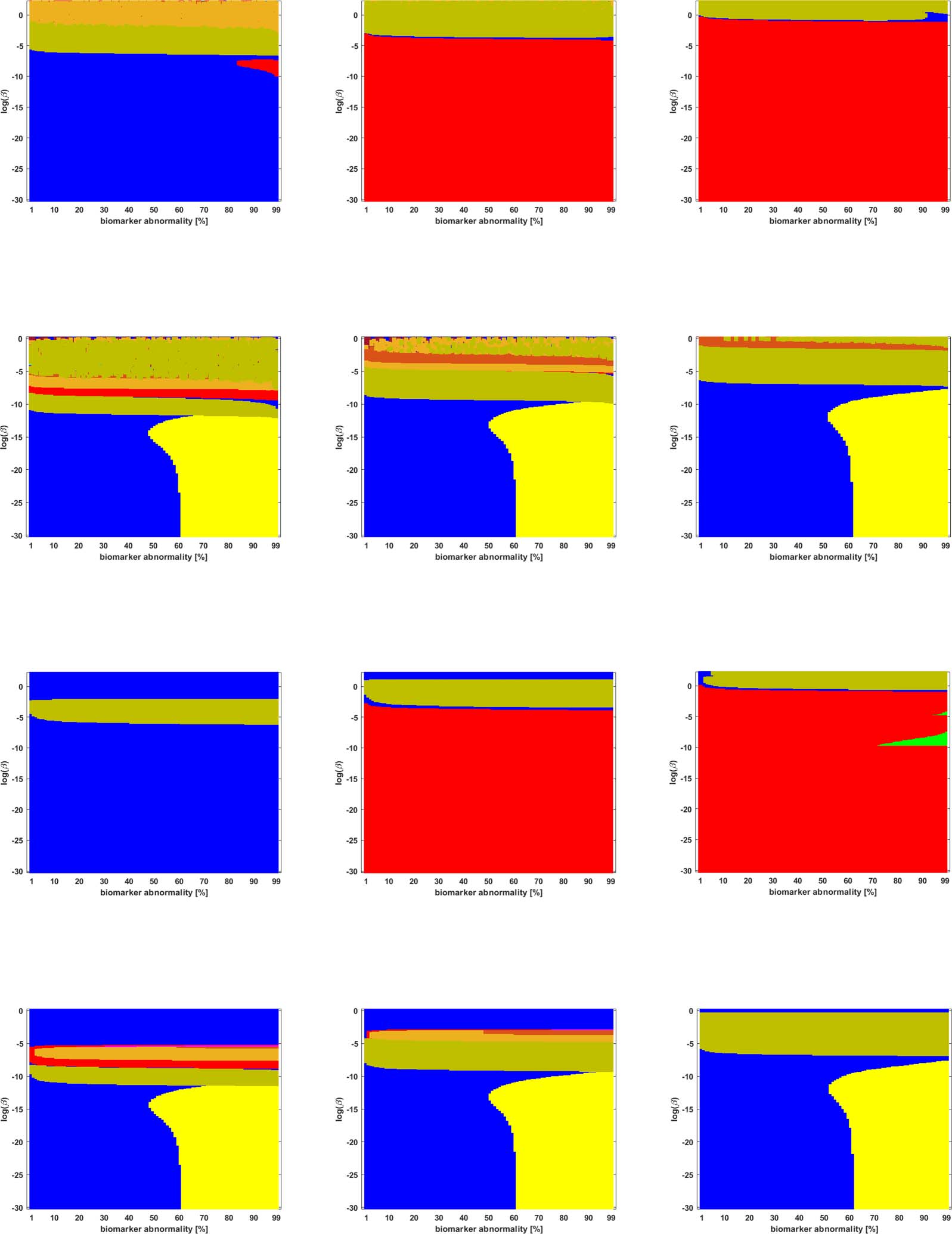
We studied the staging problem for the model (Equation 2a) of τP proteopathy in AD, using the
braid surface approach. To study this problem, a five-region adaptation, to match the structural
connectome ROI, of the six regions used in DeVos et al. (2018) was adopted and is shown in
桌子 2.
We refer to staging progression, determined by a concentration threshold 0% < T ≤ 100%, through these five regions with Roman numerals and use the I → II notation. To present the braid surface results, we first enumerate all observed regional staging patterns and assign each one a color as shown in Table 3. From the original point of view (Braak & Braak, 1991) of τP Table 3. Color coding for braid surfaces l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 4 9 2 9 1 9 7 5 2 1 3 n e n _ a _ 0 0 2 0 8 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 * Progressive computational Braak staging. † ‡ Computational staging suggested by SUVR data. Additional potential computational staging, τP seeding. Network Neuroscience 936 Braiding Braak and Braak Braak staging, one would expect that the I → II → III → IV → V progression is a likely can- didate of interest, at least for NFT. However, based on Alzheimer’s Disease Neuroimaging Initiative (ADNI) data, we also identified three other observed progression sequences that may be of interest for both τP seeds and NFT. The set of identified staging patterns of potential interest are called Suggested Patterns and summarized in Table 3 (top). Connectome Preparation Significantly Alters Observed Staging Patterns We compared two different types of connectome tractography methods: both deterministic tractography, prepared by The PIT Bioinformatics Group (2019) using the MRtrix software, and probabilistic tractography, prepared for this study using the FSL software. These generating methods used parcellation ROIs defined by the Lausanne multiresolution atlas and constructed from HCP data. The braid surfaces for the deterministic connectomes and the probabilistic connectomes are, in general, quite different. However, there are some notable similarities. For instance, both connectome types show great sensitivity as the parameter β increases to large values. In this diffusion-dominated regime, the observed staging pattern becomes non- distinct with multiple overlap for small changes of parameters. Another common feature is that there are large areas, of T and β parameter space, where the τP seed staging and τP NFT staging are consistent, meaning that both display the same staging pattern. A final notable similarity is that both connectome types are able to produce the progressive Braak ( ) pattern for NFT staging. Despite these similarities, there are also clear differences between the staging behavior ob- served on the deterministic and probabilistic connectomes. In particular, we examined ADNI SUVR data subject to an ROI selection from a recently published study (DeVos et al., 2018) on τP seeding along the Braak pathway. The SUVR staging pattern suggested ( ) by our analysis appears prominently on the deterministic connectomes (Figure 3 and Figure 4) but is nearly absent on the probabilistic connectome counterparts (Figure 5, Figure 6, Figure 7, Figure 8, and Figure 9). In fact, the deterministic connectomes can express all four suggested staging , and ) at high resolution for both τP seeds (Figure 3) and NFT (Figure 4) patterns ( while the probabilistic connectomes almost always express fewer patterns. , , We also observed (Figures 5 through 9 and Supporting Information S2) significant qualita- tive differences in the braid surface landscapes when various thresholding methods were used in preparing the probabilistic connectomes (Table 4). Therefore, we conclude that connec- tome preparation plays an important role in all downstream results and is an integral part of model selection. The Graph Laplacian Weighting Scheme Modifies Observed Staging Paradigms Several graph Laplacian weighting schemes have been suggested to model disease dynamics. But, it remains unclear as to which of these weighting choices is most biologically sound. Our results suggest that this choice also affects the observed computational staging patterns in two ways. The first of these concerns τP seed staging within the parameter regime where diffusion takes a more prominent role (i.e., large values of β). The move from length-free (LW) to ballistic (BW) weights tends to decrease the surface area where the observed computational staging is sensitive to small changes in the biomarker abnormality threshold; this surface area is again reduced when moving from BW to diffusive (DW) weights. This can be seen in both the de- terministic (Figure 3) and probabilistic (Figures 5 through 9, top two rows) braid surface results. In this sense, the length dependence in the weights ‘stabilizes’ the τP seed staging, appearing with an increase in β, in Eq. 2a. Network Neuroscience 937 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 4 9 2 9 1 9 7 5 2 1 3 n e n _ a _ 0 0 2 0 8 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Braiding Braak and Braak l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 4 9 2 9 1 9 7 5 2 1 3 n e n _ a _ 0 0 2 0 8 p d . t Figure 3. Observed computational (deterministic) connectome τP seed staging. Length-free (top), ballistic (middle), and diffusive (bottom) weighting schemes. The x-axis determines the biomarker abnormality threshold 1% < T ≤ 100%, and the y-axis corresponds to −10 ≤ ln(β) ≤ 2 for the parameter β in Eq. 2a. f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The second general observation concerns the prevalence of the progressive Braak ( ) and SUVR-suggested ( ) staging patterns. In the former case, the general trend is that the choice of a DW graph Laplacian tends to increase the prevalence of the progressive Braak ( ) NFT staging (Figure 4 and Figures 6 through 9, bottom two rows). However, we remark that this observation can depend on the choice of thresholding technique as we observed in the case of the density filtered probabilistic connectome where the LW had this effect (Figure 5, bottom two rows and Supporting Information S2 Figure S3, bottom two rows). However, if one were comparing computational results directly to SUVR staging (e.g., Schöll et al., 2016; Vogel et al., 2020), using the ROI of DeVos et al. (2018), the observation is more complex. In the case of deterministic streamlining, the prevalence of the observed SUVR-suggested staging ( ) can decrease, within the ranges of β we considered, as one moves from LW to BW and again to DW (Figure 4, right-most column). However, we do note that a number of undesirable staging patterns are observed, for LW, when ln(β) > 0 on the highest resolution connectome
网络神经科学
938
Braiding Braak and Braak
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
A
_
0
0
2
0
8
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
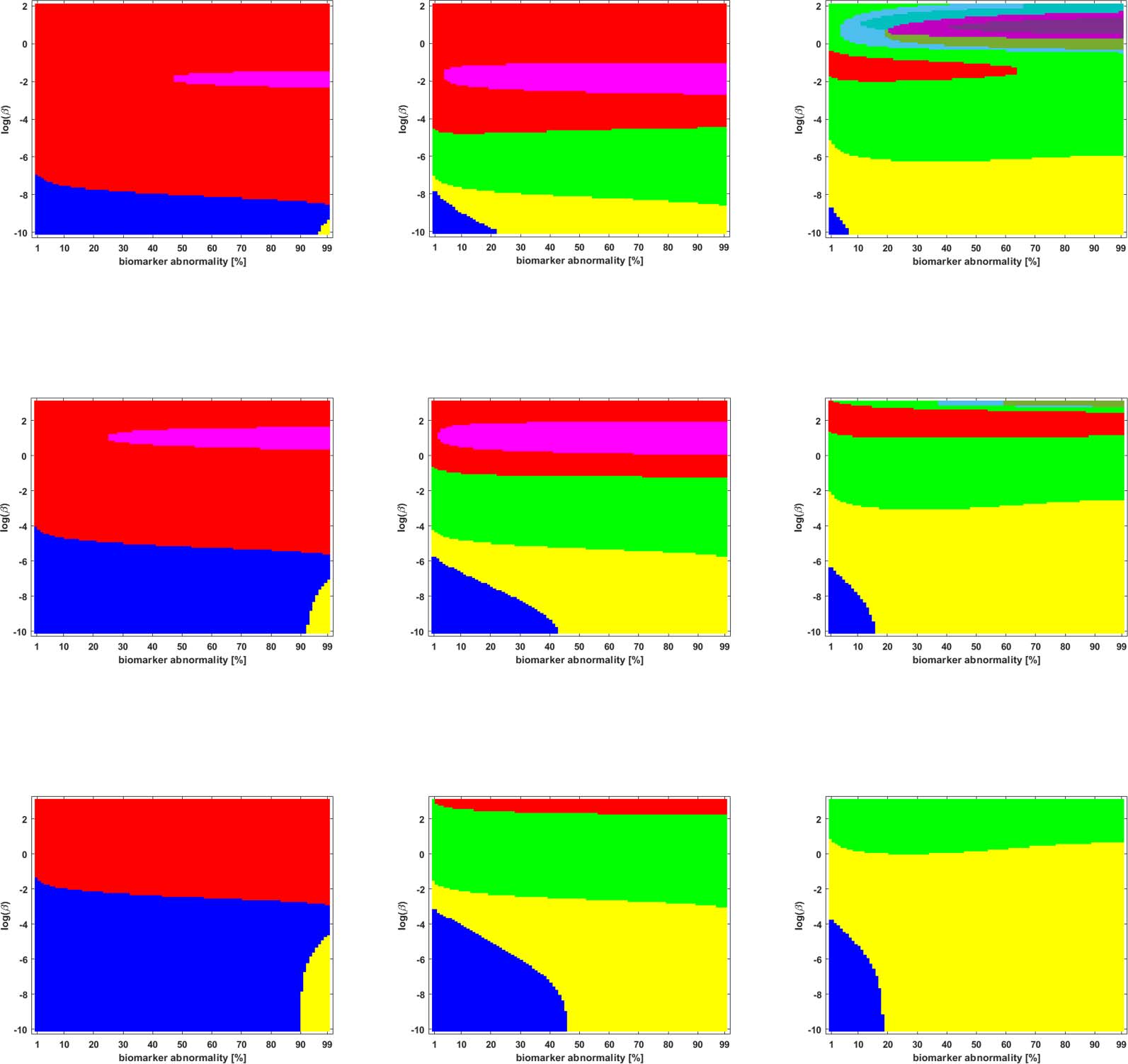
数字 4. Observed computational (确定性的) connectome τP NFT staging with δ = 1 in Eq. 2乙. Figure order, axis labels, and axis ranges
are identical to those of Figure 3.
(Figure 4C); 因此, extra consideration should be given to the mathematical model parameters
在这种情况下. For probabilistic connectomes, the appearance of the SUVR-suggested staging
pattern (
) depends more, 一般来说, on thresholding technique and the parcellation resolu-
的; the choice of weights had only a weak impact in this specific regard. Our results suggest
那, in the absence of a clear biological impetus for selecting particular graph Laplacian
重量, a braid surface analysis can play an important, practical role in selecting amenable
weights for a particular study.
Connectome Resolution Has Variable Effects on Observed Staging
Network neurodegeneration studies have evolved systems, such as Eq. 2A, on both low-
resolution (Fornari et al., 2019A; Goriely et al., 2020; Raj et al., 2012, 2015; Schäfer et al.,
2020) and high-resolution (Thompson et al., 2020) connectomes. We studied how connec-
tome resolution alters observed computational staging patterns. In the case of connectomes
网络神经科学
939
Braiding Braak and Braak
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
A
_
0
0
2
0
8
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
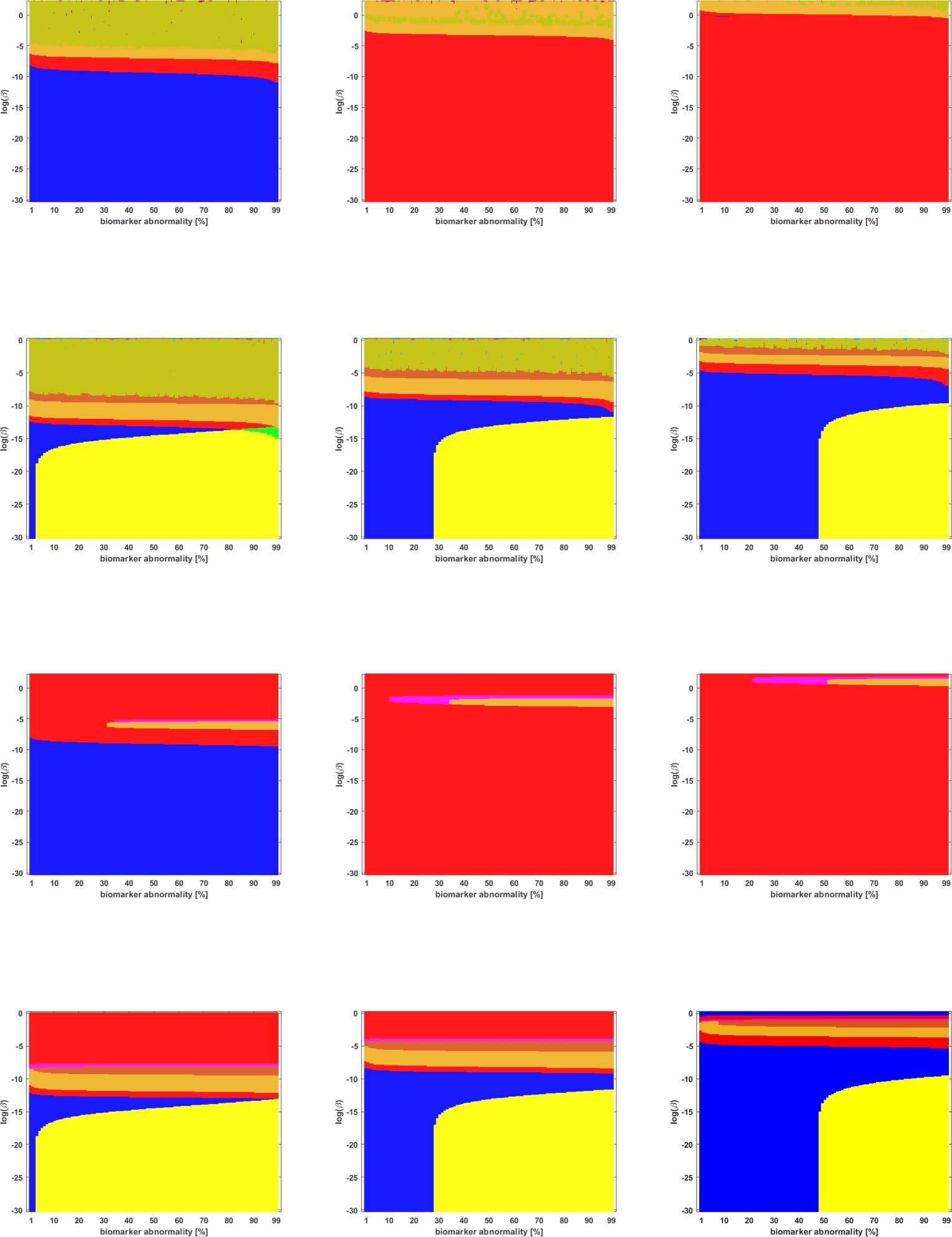
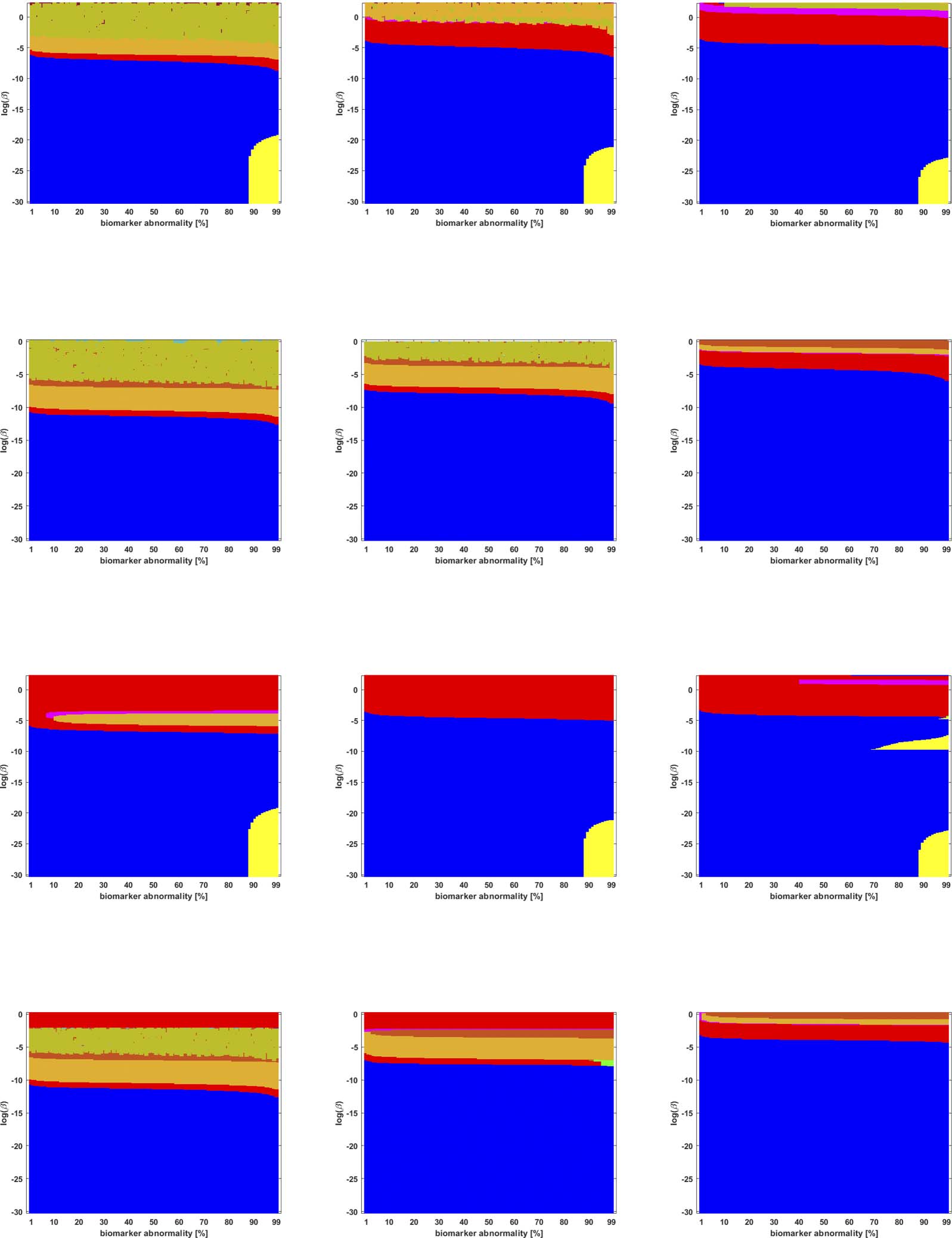
数字 5. Observed computational (概率性的) connectome τP seed staging (top two rows) and τP NFT staging (δ = 1, bottom two rows).
−1. The x-axis determines the biomarker abnormality threshold 1% ≤ T ≤ 100% 和
Density filter (DF) thresholding at a threshold of 2 × 10
y-axis corresponds to −30 ≤ ln(β) ≤ 0 for the parameter β in Eq. 2A.
generated with deterministic streamlining, increasing the connectome resolution improved the
overall observed staging results. 例如, we see a stabilizing effect on τP seed staging,
when ln(β) > 0, (columns of Figure 3) with increased connectome resolution. 而且, 这
combined area of the progressive and SUVR-suggested staging patterns of interest (
和 ,
分别) tend to increase in prominence with increased resolution; 反过来, 这
网络神经科学
940
Braiding Braak and Braak
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
A
_
0
0
2
0
8
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 6. Observed computational (概率性的) connectome τP seed staging (top two rows) and τP NFT staging (δ = 1, bottom two rows).
Doubly stochastic thresholding at a threshold of 1 × 10
−2. Axes coincide with those of Figure 5.
transposed prefix stagings ( 和 ) are more pronounced at lower resolutions. This observa-
tion also holds for NFT staging (数字 4).
In the case of probabilistic streamlined connectomes, the thresholding method and the
is invariably clear that
effect of resolution are intertwined (人物 5 通过 9).
它
网络神经科学
941
Braiding Braak and Braak
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
A
_
0
0
2
0
8
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 7. Observed computational (概率性的) connectome τP seed staging (top two rows) and τP NFT staging (δ = 1, bottom two rows).
High salience skeleton at a threshold of 1 × 10
−1. Axes coincide with those of Figure 5.
resolution has a pronounced effect on observed staging, but those effects varied depending
on the thresholding method. 一般来说, the low-resolution connectomes consisted primarily of
) when growth was sufficiently strong (circa ln(β)
a single staging pattern (typically either
< −5) and increasing the connectome resolution increased heterogeneity in addition to intro-
ducing the progressive Braak staging pattern (
).
or
Network Neuroscience
942
Braiding Braak and Braak
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. Observed computational (probabilistic) connectome τP seed staging (top two rows) and τP NFT staging (δ = 1, bottom two rows).
Noise-corrected backbone at a threshold of 2.32. Axes coincide with those of Figure 5.
Together, our results show that connectome resolution plays a deciding role in the land-
scape of observable staging patterns. In particular, the seemingly ubiquitous practice of the use
of low-resolution connectomes may partially explain discrepancies between modeling results
and comparisons to imaging data in the latter Braak regions (e.g., IV and V).
Network Neuroscience
943
Braiding Braak and Braak
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. Observed computational (probabilistic) connectome τP seed staging (top two rows) and τP NFT staging (δ = 1, bottom two rows).
Naive thresholding at a threshold of 1 × 10
−2. Axes coincide with those of Figure 5.
Braid Surfaces for Deterministic Connectomes
Deterministic connectomes were constructed using deterministic streamlining (see Methods).
We report the observed staging for both τP seeds (Figure 3) and for NFT (Figure 4). We present
these results for the lowest (Scale-33), median (Scale-125), and highest (Scale-500) resolution
Network Neuroscience
944
Braiding Braak and Braak
Connectivity thresholding
Disparity filtering
Doubly stochastic DF
High salience skeleton
Noise-corrected backboning
Naive cutoff
Table 4.
Thresholding methods for probabilistic connectomes
Abbreviation
DF
Citation
(Serrano, Boguna, & Vespignani, 2009)
DS
HSS
NC
NV
(Slater, 2009)
(Grady, Thiemann, & Brockmann, 2012)
(Coscia & Neffke, 2017)
N/A
Results
Figure 5
Figure 6
Figure 7
Figure 8
Figure 9
connectomes in addition to all three graph Laplacian weighting schemes. Both figures sum-
marize results for the model parameter value β in the range −10 ≤ ln(β) ≤ 2. Further results are
reported in the Supporting Information (S2).
Braid Surfaces for Probabilistic Connectomes
Probabilistic connectomes were constructed from HCP data. We focus on the effects of the
parameter β and of several connectivity thresholding methods on observed staging results.
For brevity, we present only one thresholding level per thresholding method, but other thresh-
olding levels are presented in the Supporting Information (S2).
DISCUSSION
In the context of studying prion-like spreading of misfolded proteins in AD, different studies
have made use of different model choices. For instance, within the class of reaction-diffusion
models such as Eq. 2a, several types of graph Laplacian weights have been used; including
those that are free of the influence of length (Pandya, Kuceyeski, & Raj, 2017; Raj et al., 2012,
2015), weights that model prion-like transport as a velocity (Fornari et al., 2019a, 2019b), or as
diffusive (Thompson et al., 2020) in nature. Various connectome resolutions, for the Lausanne
parcellation, have also been used, both low resolution (Fornari et al., 2019a, 2019b; Goriely
et al., 2020; Pandya, Kuceyeski, & Raj, 2017; Raj et al., 2012, 2015; Schäfer et al., 2020) and
high resolution (Thompson et al., 2020). Several works have compared, or fitted, spreading
models to atrophy (Raj et al., 2015) and SUVR data (Pandya, Kuceyeski, & Raj, 2017;
Schäfer et al., 2020; Vogel et al., 2020, 2021). However, to our knowledge, a systematic me-
thodical investigation into the general staging problem for AD has not been advanced, even
for the simpler class of prion-like progression models such as Eq. 2a.
In this manuscript we have undertaken a methodical investigation of the generalized stag-
ing problem for a simple network model of AD; this important problem concerns the ordered
progression of a marker of interest propagating over a network. Using an adaptation of a six-
stage sequence of ROIs (DeVos et al., 2018) along the Braak pathway, we have systematically
investigated how various aspects of model selection, including those mentioned above, may
alter the progression of τP seeds and NFT across the connectome. To do so, we have intro-
duced, and applied, the novel tools of braid diagrams and braid surfaces. Though we have
focused on a continuous network neurodegeneration model, our method also applies to prob-
abilistic spreading models as well (Iturria-Medina et al., 2014; Vogel et al., 2020).
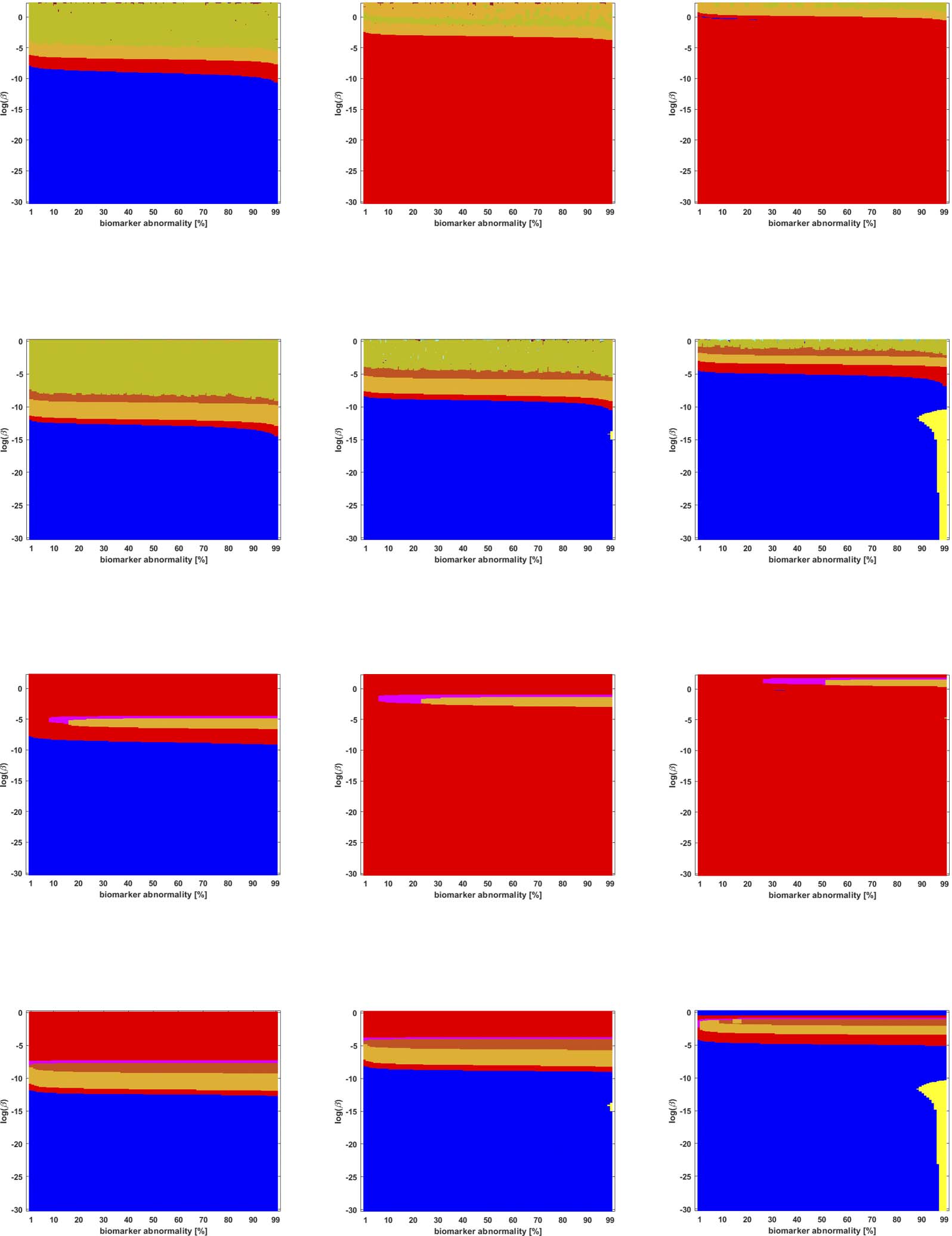
Connectome Construction Limits Realizable Staging Patterns
Our findings have several implications for model selection. The most surprising is that the par-
ticulars of the connectome itself play an important role in the staging problem. That is, when
Network Neuroscience
945
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Braiding Braak and Braak
) versus the SUVR-suggested (
) and the staging pattern suggested (
studying τP progression, the construction of the structural connectome should be considered
as an inextricable part of the model. To illustrate this, consider two particular staging patterns:
the progressive Braak pathway NFT staging pattern (
)
by our ADNI flortaucipir data analysis. It is worth noting that the difference between the progres-
sive Braak (
) staging is whether a biomarker first appears in
the hippocampus (II) or the posterior parahippocampal gyrus (III). In DeVos et al. (2018), the
histopathologically identified Braak stage II brains expressed τP seeding in the parahippocampal
gyrus (III) at a slightly higher average level than in the hippocampus, potentially explaining the dif-
ference between the SUVR-suggested (
)
) and (
) and progressive (
may essentially reflect the same effective staging but from two different points of view. Only the (
)
pattern was reliably expressed on the often-used, low-resolution (Scale-33) structural connectome
constructed with deterministic streamlining. However, both patterns appeared in the high-
resolution (Scale-500) case (Figures 3 and 4, left column vs. right column). Conversely, the
high-resolution connectomes generated with probabilistic tractography, and subsequently thre-
sholded for sparsity, almost never produced the (
) pattern suggested by our ADNI data analysis
(Figures 5 through 9, second and fourth rows), though they did produce the progressive staging (
).
The SUVR pattern (
) did, however, appear robustly for the Scale-33 connectome when naive
thresholding was used (Figure 4). For the Scale-500 naively thresholded connectome, the (
) pat-
tern does appear but is only consistent with seed staging in a very small region of parameter and
threshold space (see Figure 4, second and last rows). Figure 4 suggests that naive thresholding may
be a promising strategy for probabilistic connectomes; however, we found that the (
)
patterns were sensitive to the threshold used (see Supporting Information S2) and were almost
completely absent, at both scales, for the nearby thresholds we examined.
) staging patterns. That is, (
) and (
The consequences of these observations are nontrivial. For instance, a study comparing the
NFT model Eq. 2b to ADNI flortaucipir data on the low-resolution probabilistic tractography
connectomes, thresholded with a density filter, would not be capable of achieving the staging
pattern (
) obtained by our SUVR analysis (see Figure 5, third row), invariably leading to a
misfit between model and data. Overall, our observations imply that the methods used to con-
struct the structural connectome, for example, the choice of tractography method, parcellation
resolution, and any subsequent thresholding, can affect all downstream results and limit the
landscape of realizable staging patterns.
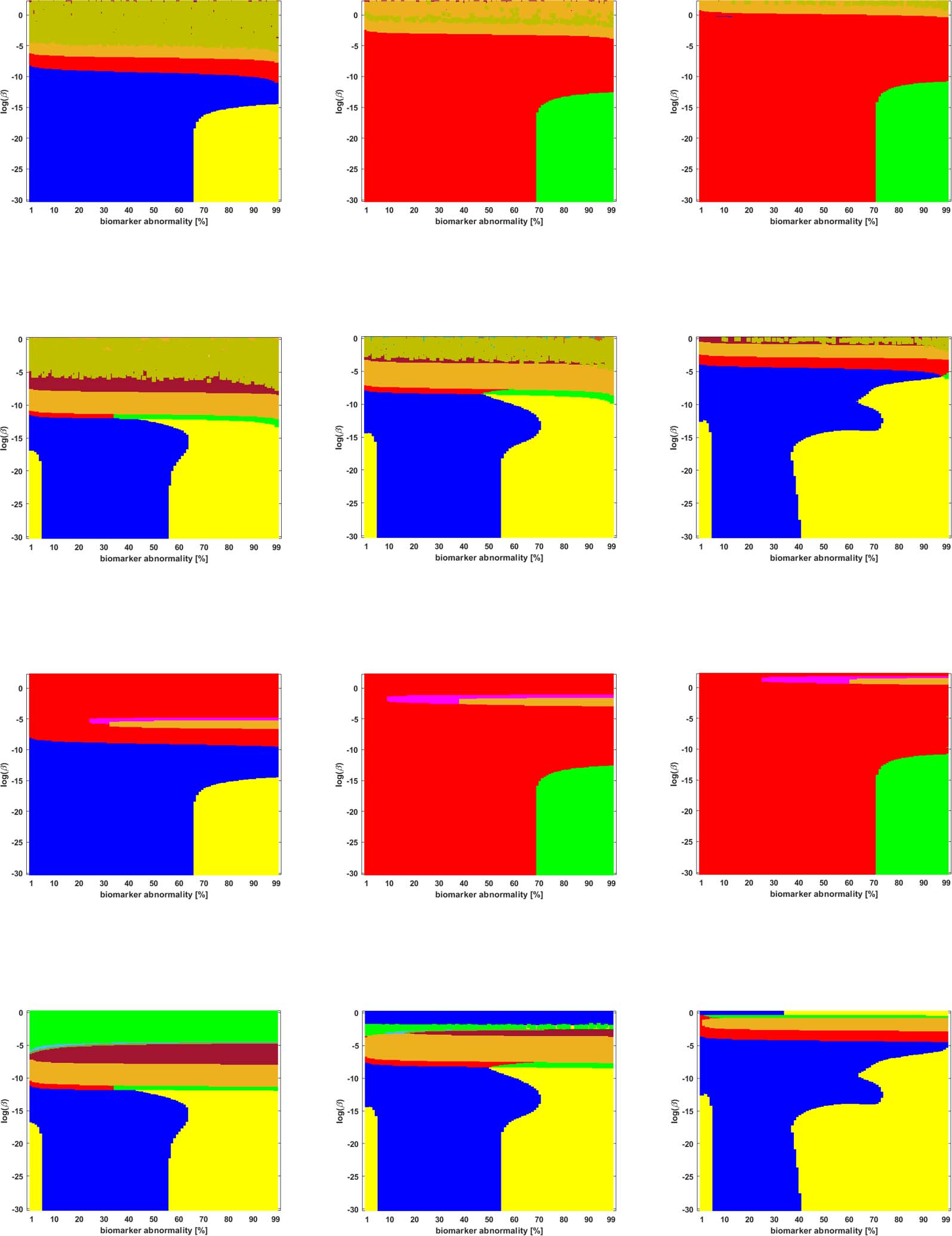
The Graph Laplacian Weight and the Characteristics of Growth versus Diffusion
The graph Laplacian plays a distinctive role in reaction-diffusion models of prion-like propa-
gation such as Eq. 2a; it provides the mechanism for the transport of misfolded proteins over
the brain’s structural network. As such, the choice of graph Laplacian weights has varied in the
literature; particular weight selections are often motivated by a biological argument or an
appeal to data fit. Overall, our results suggest that, while the choice of weights often has a
minimal impact on the number of observable staging patterns of interest (
), they
did affect the prevalence of those patterns, in particular, the diffusive weights (DW) scheme
tended to favor the expression of the progressive Braak (
) staging pattern over the options of
length-free weigt (LW) and ballsitic weights (BW).
,
,
,
In the case of τP seed staging, LW and BW showed significantly more sensitivity, in the
observed staging, than the DW scheme as ln(β) drew nearer to zero. The staging sensitivity
to the weighting scheme can be illustrated by computing the standard deviation of the staging
time series. Plots of these standard deviations, for τP seeding on the Scale-500 deterministic
connectomes (see Figure 3) are shown in Figure 10. Regions, in Figure 3, where the staging is
Network Neuroscience
946
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Braiding Braak and Braak
Figure 10.
weighting schemes.
Standard deviation of the staging time series for τP seeds on the high-resolution (S-500) deterministic connectome of Figure 3; all
sensitive to small perturbations in β or T are precisely those where the standard deviation of the
staging time series is low. This implies that the observed sensitivity is a race condition where
the differences in threshold-attainment time are nearly identical.
As length plays a more dominant role in the weighting scheme, the standard deviation of
the staging time series increases, staging patterns are no longer sensitive to small perturbations
and τP seed staging becomes pronounced. However, it is not currently known if τP seeds
should follow a clear hierarchical progression, though the appearance of τP seeds have been
shown to proceed NFT pathology (DeVos et al., 2018). In the case of NFT staging, the DW
scheme generally promoted the progressive Braak pathway NFT staging pattern (
) across all
connectomes. This pattern, however, was not the SUVR-suggested (
) pattern according to our
analysis. It is worth noting that the patient data necessary to achieve more statistically signif-
icant results, for latter stages, was not present (see Methods, Data preparation and Methods,
Identifying additional computational staging patterns of interest). Moreover, as we mentioned
previously, the II → III versus III → II paradigm, differentiating the progressive staging (
) from
the SUVR-suggested staging (
), may be related to the prevalence of seeds (DeVos et al., 2018)
in the posterior parahippocampus at histopathological Braak classification stage II.
Nevertheless, our results suggest that direct comparisons to flortaucipir data, at least for the
ROI we considered, may be best conducted (see Figures 3F and 4F) with the BW scheme
and on high-resolution connectomes created with deterministic streamlining and with a
choice of mathematical parameters given by −2 ≲ ln(β) ≲ 1.
Conversely, if a progressive Braak pattern (
) is desirable, this can most reliably be
achieved, in general, on high-resolution connectomes with the DW scheme, sufficiently dom-
inant growth (i.e., β sufficiently small) and a typical biomarker threshold of at least 50%. As a
point of practice, this should be checked with a braid surface analysis, as we did observe that
thresholding methods can perturb this trend on the probabilistic connectomes that we consid-
ered. For example, Figure 5 shows that the density filter threshold favors the LW and BW
schemes over the DW scheme for the progressive staging (
); likewise, Figure 7 shows that
the high-salience scheme more readily expresses the progressive staging (
) on lower resolution
connectomes.
Conclusion
Investigations of τP staging have been carried out histopathologically (Braak et al., 2006; Braak
& Braak, 1991; Delacourte et al., 1999), using SUVR (Cho et al., 2016; Schöll et al., 2016),
and in fitting models of spreading to SUVR data (Schäfer et al., 2020; Vogel et al., 2020, 2021).
Network Neuroscience
947
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Braiding Braak and Braak
As computational power is readily available, the prion-like hypothesis has enabled a new gen-
eration of mathematical models facilitating the latter types of studies. However, it is currently
not known how various model selection choices may promote, or limit, the expression of par-
ticular staging patterns. We have found that every aspect of model selection can alter the over-
all progression of τP staging. This includes parcellation resolution, tractography method,
choice of thresholding method, choice of threshold, graph Laplacian weights, and the math-
ematical model parameters. We have shown that the the generalized staging problem couples
the global topology of the structural connectome to the mathematical model governing the
local dynamics of a biomarker evolving on that network and that comprehensive model se-
lection cannot, in general, be ensured from a decoupled perspective. We have introduced
braid diagrams and braid surfaces as a means to investigate the complex staging landscape,
and changes thereto, for this coupled problem and to observe the implications of model se-
lection choices.
The generalized staging problem in AD reveals the need for more experimental data and
poses new theoretical questions. We propose that further study into the progression patterns of
τP seed staging, extending the results of DeVos et al. (2018), could promote a more reliable
selection of parameter ranges for the balance of growth and diffusion (β) for τP seeds and, due
to the consistency we observed, for τP NFT. Moreover, an increased number of SUVR data for
patients in the latter Braak stages would help to belay uncertainty in determining the progres-
sion patterns suggested by data studies. Mathematically, the study of the coupling between the
connectome topology, the weighted distances between ROIs, and the model parameters is a
promising candidate for theoretical research.
METHODS
Structural Connectomes
Braid surfaces have been introduced to facilitate model selection, in the context of staging
patterns developing on two sets of undirected, multiresolution structural connectomes; both
sets of connectomes were originally constructed from the data of participants in the HCP.
All of the structural connectomes considered in this manuscript were constructed using the
Lausanne multiresolution atlas parcellation (Daducci et al., 2012) with five levels of potential
resolution: the coarsest scale (Scale-33), three intermediate scales (Scale-60, Scale-125, Scale-
250), and a fine scale (Scale-500). The edges, at all scales, include information regarding the
number of fibers (nij) and fiber length (ℓ
ij) associated to each edge (eij) connecting region i to
region j. The first set of connectomes (see Figure 11) were constructed using MRtrix (Kerepesi,
Szalkai, Varga, & Grolmusz, 2017; Tournier, Calamante, & Connelly, 2012) and a determin-
istic streamlining with 20,000 streamlines and randomized seeding. These connectomes span
five scales; the lowest and highest scales are shown in Figure 11. These connectomes are pub-
licly available, as the dataset named ‘Full set, 426 brains, 20,000 streamlines’, from The PIT
Bioinformatics Group (2019).
The second set of connectomes were constructed for this study in order to assess degrees of
certitude regarding observations for the deterministic connectomes mentioned above. The
Connectome Mapping Toolkit (Daducci et al., 2012) was used to parcellate a high-resolution
MNI reference template; the FSL (Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012;
Smith et al., 2004; Woolrich et al., 2009) PROBTRACKX algorithm was employed, for the pro-
bablistic tractography, with 10,000 streamlines per voxel. The sparsity of the resulting connec-
tivity matrices was low (approximately 7–12%); these matrices are commonly thresholded
before use in computational models. To study the effect of thresholding, we considered five
Network Neuroscience
948
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Braiding Braak and Braak
Figure 11.
Lowest (left) and highest (right) connectome resolutions. Node colors signify the 83 disjoint anatomical parcellation regions.
different thresholding techniques in our comparative analysis. The thresholding techniques
used are summarized in Table 4, and a description of the method can be found in the corre-
sponding citation. The naive thresholding method removes edge eij if the corresponding con-
nectivity coefficient (nij) is below a prescribed threshold value.
For comparison, we have constructed connectomes for the lowest (Scale-33, 50 patients)
and highest scale (Scale-500, 25 patients) resolutions of the Lausanne multiresolution atlas.
The braid surface source code, and the full set of thresholded connectomes, used in this study
is available online (Putra et al., 2021).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Staging for (cid:2)P Seeds on Structural Connectomes
We have discussed several hierarchical staging patterns for τP progression in AD. As our math-
ematical model accounts for both τP seeds and τP NFT, we selected a six-stage model that has
been related to both quantities (DeVos et al., 2018). These six regions, along the Braak path-
way, are enumerated in Table 5.
The regions in Table 5 can be mapped to anatomical ROI of the Lausanne atlas used in the
construction of the structural connectomes for this study. We therefore adapt the stages of
Table 5 to the Lausanne atlas by considering the staging process of Table 2. The primary dif-
ference is that stages V and VI, of Table 5, are combined into a single terminal stage and ap-
proximated by the presence of deposition in the cuneus, pericalcarine cortex, lateral occipital
cortex, and lingual gyrus.
Staging Sequences for (cid:2)P Pathology on Computational Connectomes
In order to assess the implications of various model parameters on observed computational
staging patterns, thus facilitating model selection, a choice of preferable staging patterns must
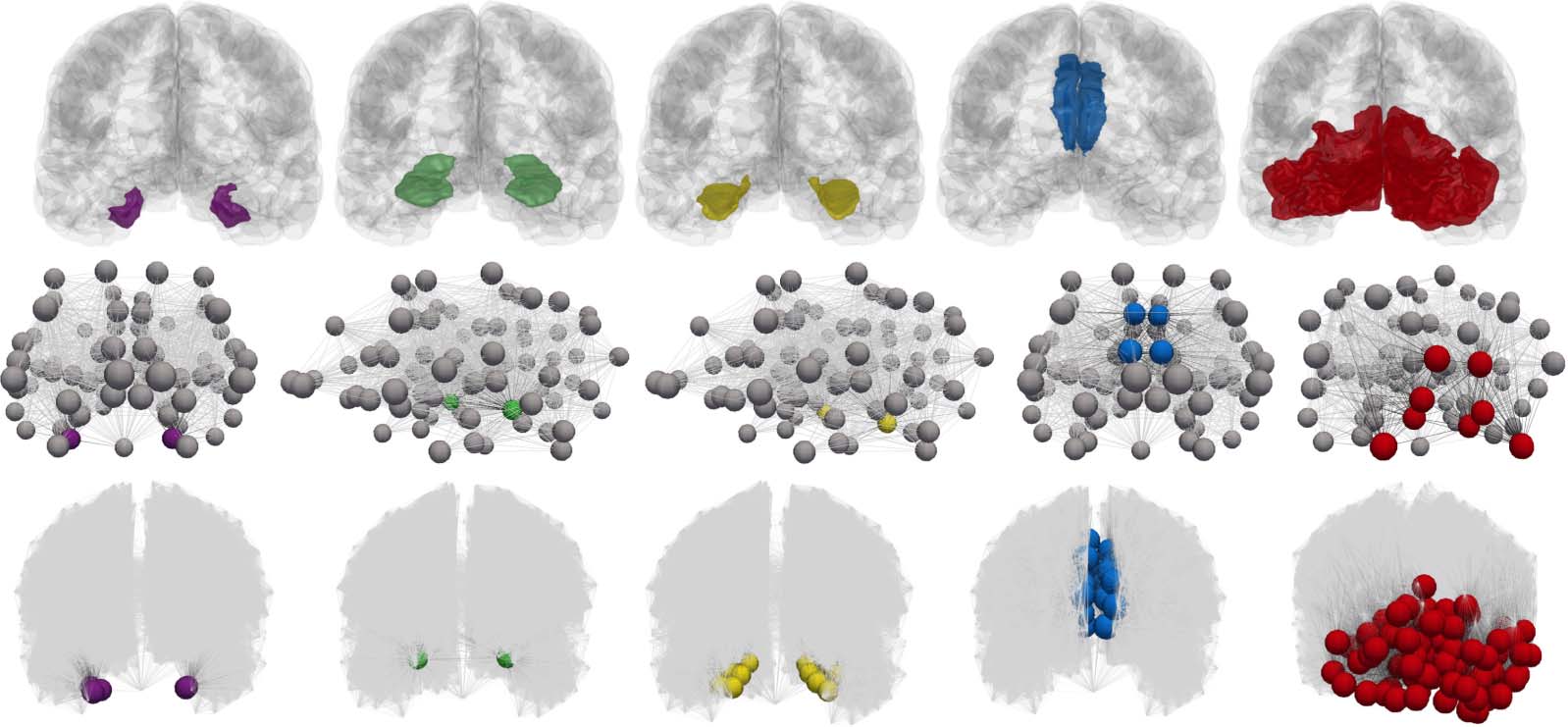
be identified. We select five collections of nodes, Ωi for i = 1, 2, …, 5, such that Ωk is the set of
nodes of the computational connectomes whose anatomical ROI labels are given by the kth
stage of Table 2; thus Ω
1 contains all nodes labeled as belonging to the left and right entorhinal
cortices, etc. The staging regions, Ωi, for the coarsest (top row) and finest (bottom row) con-
nectome resolutions are shown in Figure 12.
Table 5.
Anatomical staging regions for τP seeds as reported in DeVos et al. (2018)
Region I
Region III
Region V
entorhinal cortex
posterior parahippocampal gyrus
visual association cortex
Region II
Region IV
Region VI
Network Neuroscience
hippocampus
anterior cingulate
primary visual cortex
949
Braiding Braak and Braak
Figure 12. Connectome Braak staging regions, Ω
cellation, middle) and finest resolution (Scale-500 parcellation, bottom, additional nodes suppressed) connectomes.
i. Anatomical regions in a glass brain (top). Coarsest connectome resolution (Scale-33 par-
The work of DeVos et al. (2018) assessed τP seed staging along the Braak tau pathway and
found that tau seeding precedes the presence of NFT pathology. A clear candidate for both τP
seed and NFT staging is therefore the progressive regional staging I → II → III → IV → V. To
assess other potential staging sequences we used flortaucipir (AV-1451) data from the ADNI;
the data was fully preprocessed at the Helen Wills Neuroscience Institute at the University of
California, Berkeley, and the compiled results are freely available through the ADNI website.
The preprocessed dataset contains 1,184 records; each record corresponds to a subject struc-
tural MRI scan and tau PET scan, and the preprocessing steps are explained in the companion
document available through the ADNI website.
Data preparation The Berkeley preprocessing pipeline is as follows: each patient T1 MRI was
segmented using FreeSufer 7.1.1; each subject’s normalized-intensity flortaucipir scan was
coregistered to their bias-corrected T1 image; partial volume effects were corrected for using
the geometric transfer matrix approach (Baker, Maass, & Jagust, 2017; Baker et al., 2017); and
mean flortaucipir uptake is reported, in the dataset, for each region of the FreeSurfer segmen-
tation. We further normalized each subject’s regional SUVR score using the inferior cerebellar
gray matter as the reference region, as suggested in the dataset documentation.
We proceeded to create two datasets using this preprocessed dataset. For the first set, we
computed the volume-weighted SUVR average for each patient record over the whole brain to
compute a global score (GS) and for each region of Table 2. Thus, each ADNI patient visit
record was assigned a global volume-averaged SUVR score along with five volume-averaged
regional scores corresponding to the regions of Table 2. We refer to this dataset as the ‘base
dataset’.
We then created a second dataset we refer to as the ‘partitioned dataset’ by following the
methodology of Schöll et al. (2016). An overview of the creation process follows: First, the GS
was used as a decision variable, in a conditional inference tree (CIT) algorithm. Second, the
CIT algorithm was used to compare the GS to the BraakV regional volume-weighted SUVR,
Network Neuroscience
950
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Braiding Braak and Braak
Table 6. Conditional inference-based partitioning of ADNI flortaucipir data into the stages of
Table 2
Stage group
classification
I
II
III
IV
V
Volume-averaged
global SUVR (GS)
1.266 ≤ GS
1.266 < GS ≤ 1.392
1.392 < GS ≤ 1.52
1.52 < GS ≤ 2.365
GS > 2.365
Subject records
in group
36
248
443
416
41
producing a GS threshold. This GS threshold was used to separate patient records into two
groups who differed significantly based on their BraakV score. The BraakV patient records
were then moved, out of the full dataset, into a new data file. This process was then repeated,
once again applying the CIT algorithm and using the GS as a decision variable, but now com-
paring to the BraakIV regional volume-weight SUVR score, thus creating a BraakIV group of
patient records, 等等. This process resulted in five separate files, 那是, the partitioned
dataset, corresponding to a patient record classification according to the regions of Table 2.
The thresholds produced by the CIT algorithm can be seen in Table 6. Our application of CITs
follows the identical approach of previous authors (Schöll et al., 2016), in a similar SUVR
学习, to categorize each patient record into the discrete groups corresponding to a predefined
set of regional stages.
Identifying additional computational staging patterns of interest Our next goal was to see if ADNI
flortaucipir data may suggest alternatives to the progressive I → II → III → IV → V (computa-
的) Braak-like sequence, in particular for NFT due to the binding of flortaucipir to paired
helical filaments. Our objective here is not to rigorously study hierarchical SUVR behavior as
in Cho et al. (2016). 相当, our goal is to conduct a simple inquiry as to whether the ADNI
data may suggest alternative staging patterns of potential interest for the computational staging
problem and model selection, especially as it pertains to observed NFT staging.
Our first investigation used the partitioned dataset. 第一的, we checked that the CIT algorithm
separated the data in such a way that all of regional mean SUVR values, across all possible
group-region pairings, were significantly ( p < 0.05) different, using a Welch’s t test; this was
the case, as expected by an application of CIT-based separation. Next, we computed the
Pearson correlation between each stage group’s primary stage and all other stages within that
group; the results are reported in Table 7.
Assuming that overt NFT pathology originates in region I, Table 7 suggests that staging se-
quences with I → III may also be of interest for NFT. Assuming that III proceeds I, the next
suggested progression would be III → II. This observation suggests that sequences starting with
the prefix I → III → II could be of interest alongside the more progressive stage prefix I → II →
III. Finally, likely due to the sparsity of patient records assigned to Group V, none of the cor-
relations of Group V were significant.
Our next investigation uses the base dataset. The primary motivation was to ensure that
patient gender and age were not confounding our partitioning-based strategy. Starting with
the base dataset, we cross-referenced ADNI patient data and augmented the base set with
Network Neuroscience
951
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Braiding Braak and Braak
Table 7.
Pearson correlation between a stage group’s primary region and all other regions within the group
Patient group and region
Group I, Region I
Group II, Region II
Group III, Region III
Group IV, Region IV
Group V, Region V
Region I
1.0*
0.34*
0.69*
0.11*
−0.13
Connectome Braak regional SUVR correlation
Region III
0.53*
Region IV
0.14
Region II
0.26
1.0*
0.32*
0.28*
−0.03
0.31*
1.0*
0.32*
0.16
0.14*
0.06
1.0*
−0.08
Region V
0.04
−0.29*
−0.09
−0.13*
1.0*
Note. A * denotes a statistically significant correlation ( p < 0.05) between regions.
the age, at the time of scan, in addition to the patient’s gender. We then used regression
models covarying for age and gender. We compared each regional volume-averaged SUVR
score to that of the other regions; the results are shown in Table 8. Evidence for influence was
evaluated using standardized factor scores when the influence was significant. Region III was
most affected by Region I (R2 = 0.775, B = 0.613, p < 0.001), further supporting interest in the
I → III staging prefix. Region II was also most influenced by Region I (R2 = 0.486, B = 0.486, p <
0.001) but at a lower value of both B and R2. Removing Region I from the model decreased the
variational fidelity (R2) of the Region III model by 24.8% and the Region II model fidelity by
13.6%; in the latter case, the Region II score was most affected by the Region III score (R2 =
0.42, B = 0.5). Supposing that pathology begins in the entorhinal cortex (Region I), these ob-
servations suggest, again, that a I → III → II prefix is also of interest for evaluating computa-
tional staging.
Next, we take a second look at the staging suffix options IV → V versus V → IV. To do so,
we regressed the Region IV and Region V scores in terms of the first three regional scores, once
more covarying for age and gender. The Region IV model identified Region III as the most
influential (R2 = 0.43, B = 0.75, p < 0.001). The Region V model was only marginally ex-
plained by the data (R2 = 0.22), but the most influential factor was, again, the Region III score
(B = 0.38, p < 0.001), but with a substantially lower influence than in the Region IV model.
Table 8.
Regression models, covarying for age and gender, of regional influence
Regression
model
Region II
Region III
Region IV
Region V
Influential model
region(s)
Region I
Model R2
0.486
Region III
Region I
Region IV
Region II
Region III
Region III
0.42
0.78
0.58
0.43
0.22
B
0.49
0.5
0.61
0.39
0.36
0.75
0.38
p-value
p < 0.001
p < 0.001
p < 0.001
p < 0.001
p < 0.001
p < 0.001
p < 0.001
952
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Braiding Braak and Braak
Table 9.
Spreading order of τP (SUVR) for Region I involved patient records
Region
Region I
Region III
Region II
Region IV
Region V
% Involved
100.0
55.1
46.94
22.45
22.45
Z
3.24
2.55
1.81
1.43
1.17
These latter observations suggest that a IV → V may be more desirable than a V → IV suffix.
We have therefore corroborated, and extended, the conclusions suggested by the partitioning
strategy (Table 7).
Next, we corroborate our previous SUVR findings by following a similar approach to Cho
et al. (2016) and considering z-scores, computed from the base dataset, for the regions defined
in Table 2. First, all of the regional mean SUVR scores were individually standardized. Similar
to Cho et al. (2016), we considered a particular region to be ‘involved’ in a fixed patient record
if that region’s Z score satisfied Z ≥ 2. We then selected all patient records with an involved
Region I (entorhinal cortex). Continuing within this subset of data, we counted the frequency
of all other involved regions and computed their mean z score. The results are reported in
Table 9. Once more, we see that progression sequences starting with I → III → II may also
be of computational interest and, further, that the staging suffix IV → V appears more prefer-
able, for SUVR, than the V → IV alternative.
Finally, we compared the ADNI data findings, above, to the results for τP seeds reported in
DeVos et al. (2018) where Braak II brains (classified postmortem) also showed a slight average
increase of τP seeds in physiological region III (i.e., region III, Table 5) over that of physiolog-
ical region II; further suggesting that a computational I → III → II pattern may be of interest for
τP seeds. If one considers post-mortem Braak classification as a pseudo-time then, from DeVos
et al. (2018, Fig. 3), it is tempting to suggest a computational I → III → II → IV → V pattern of
interest for τP seeds. However, the differential between seeding levels in the latter stages is
slight. In summary, ADNI SUVR data, and results from DeVos et al. (2018), suggest a broader
set, beyond the choice of a strictly ascending progression, of potentially interesting computa-
tional staging patterns for the choice of regions in Table 2. These staging patterns are reported
in Table 10. We note that either more late stage data (i.e., Group V, Table 6), a finer SUVR
staging sequence, such as that of Cho et al. (2016), or both is needed to ascertain a higher
degree of certainty in the latter τP computational staging patterns for AD.
Table 10.
Computational staging patterns of potential interest for τP seeds and NFT
Computational staging patterns (see Table 2)
Canonical late staging
Uncertain late staging
I → II → III → IV → V*
I → II → III → V → IV
‡
†
I → III → II → IV → V
‡
I → III → II → V → IV
†
Note. *Progressive Braak staging,
potential interest pertaining to uncertain τP seed staging prefixes.
Suggested by SUVR data,
‡
Additional connectome computational stagings of
Network Neuroscience
953
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Braiding Braak and Braak
ACKNOWLEDGMENTS
Data used in the preparation of this article were obtained from the Alzheimer’s Disease
Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in
2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD.
The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI),
positron emission tomography (PET), other biological markers, and clinical and neuropsycho-
logical assessment can be combined to measure the progression of mild cognitive impairment
(MCI) and early Alzheimer’s disease. For up-to-date information, see www.adni-info.org. A
complete listing of ADNI investigators can be found at: https://adni.loni.usc.edu/wp-content
/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00208.
AUTHOR CONTRIBUTIONS
Prama Putra: Conceptualization; Formal analysis; Investigation; Software; Visualization;
Writing – review & editing. Travis B. Thompson: Conceptualization; Data curation; Formal
analysis; Investigation; Methodology; Project administration; Software; Supervision;
Visualization; Writing – original draft; Writing – review & editing. Alain Goriely:
Conceptualization; Formal analysis; Funding acquisition; Methodology; Project administra-
tion; Resources; Software; Supervision; Writing – original draft; Writing – review & editing.
Pavanjit Chaggar: Data curation; Formal analysis; Software; Writing – review & editing.
FUNDING INFORMATION
Alain Goriely, Engineering and Physical Sciences Research Council (https://dx.doi.org/10
.13039/501100000266), Award ID: EP/ R020205/1. Travis B. Thompson, John Fell Fund,
University of Oxford (https://dx.doi.org/10.13039/501100004789), Award ID: 000872.
Pavanjit Chaggar, Engineering and Physical Sciences Research Council (https://dx.doi.org/10
.13039/501100000266), Award ID: EP/L016044/1.
REFERENCES
Abdelnour, F., Voss, H., & Raj, A. (2014). Network diffusion accu-
rately models the relationship between structural and functional
brain connectivity networks. NeuroImage, 90, 335–347. https://
doi.org/10.1016/j.neuroimage.2013.12.039, PubMed:
24384152
Baker, S., Lockhart, S., Price, J., He, M., Huesman, R., Schonhaut,
D., … Jagust, W. (2017). Reference tissue-based kinetic evalua-
tion of 18F-AV1451 for tau imaging. Journal of Nuclear
Medicine, 58(2), 332–338. https://doi.org/10.2967/jnumed.116
.175273, PubMed: 27587706
Baker, S., Maass, A., & Jagust, W. (2017). Considerations and code
for partial volume correcting [(18F)]-AV-1451 tau PET data. Data
Brief, 15, 648–657. https://doi.org/10.1016/j.dib.2017.10.024,
PubMed: 29124088
Braak, H., Alafuzoff, I., Arzberger, T., Kretzschmar, H., & Del
Tredici, K. (2006). Staging of Alzhimer disease-associated
neurofibrillary pathology using paraffin sections and immunocy-
tochemistry. Acta Neuropathologica, 112(4), 389–404. https://
doi.org/10.1007/s00401-006-0127-z, PubMed: 16906426
Braak, H., & Braak, E. (1991). Neuropathological stageing of
alzheimer-related changes. Acta Neuropathologica, 82(4),
239–259. https://doi.org/10.1007/ BF00308809, PubMed:
1759558
Cho, H., Choi, J., Hwang, M., Kim, Y., Lee, H.-M., Lee, H.-S., …
Lyoo, C. (2016). In vivo cortical spreading pattern of tau and
amyloid in the Alzheimer disease spectrum. Annals of Neurology,
80(2), 247–258. https://doi.org/10.1002/ana.24711, PubMed:
27323247
Coscia, M., & Neffke, F. (2017). Network backboning with noisy
data. In 2017 IEEE 33rd International Conference on Data
Engineering (ICDE) (pp. 425–436). https://doi.org/10.1109
/ICDE.2017.100
Network Neuroscience
954
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Braiding Braak and Braak
Daducci, A., Gerhard, S., Griffa, A., Lemkaddem, A., Cammoun, L.,
Gigandet, X., … Thiran, J.-P. (2012). The Connectome Mapper:
An open-source processing pipeline to map connectomes with
MRI. PLoS One, 7(12), e48121. https://doi.org/10.1371/journal
.pone.0048121, PubMed: 23272041
Delacourte, A., David, J.-P., Sergeant, N., Buee, L., Wattez, A.,
Vermersch, P., … Di Menza, C. (1999). The biochemical
pathway of neurofibrillary degeneration in aging and Alzheimer’s
disease. Neurology, 52(6), 1158–1158. https://doi.org/10.1212
/wnl.52.6.1158, PubMed: 10214737
DeVos, S.-L., Corjuc, B.-T., Oakley, D.-H., Nobuhara, C.-K.,
Bannon, R., Chase, A., … Hyman, B. (2018). Synaptic tau
seeding precedes tau pathology in human Alzheimer’s disease
brain. Frontiers in Neuroscience, 12, 267. https://doi.org/10
.3389/fnins.2018.00267, PubMed: 29740275
Fornari, S., Schäfer, A., Goriely, A., & Kuhl, E. (2019a). Prion-like
spreading of Alzheimer’s disease within the brain’s connectome.
Journal of the Royal Society Interface. https://doi.org/10.1098/rsif
.2019.0356, PubMed: 31615329
Fornari, S., Schäfer, A., Goriely, A., & Kuhl, E. (2019b). Spatially-
extended nucleation-aggregation-fragmentation models for the
dynamics of prion-like neurodegenerative protein-spreading in
the brain and its connectome. Journal of Theoretical Biology.
https://doi.org/10.1016/j.jtbi.2019.110102, PubMed: 31809717
Goriely, A., Kuhl, E., & Bick, C. (2020). Neuronal oscillations on
evolving networks: Dynamics, damage, degradation, decline,
dementia, and death. Physical Review Letters, 125(12), 128102.
https://doi.org/10.1103/ PhysRevLett.125.128102, PubMed:
33016724
Grady, D., Thiemann, C., & Brockmann, D. (2012). Robust classifica-
tion of salient links in complex networks. Nature Communications,
3(864). https://doi.org/10.1038/ncomms1847, PubMed: 22643891
Iturria-Medina, Y., Sotero, R., Toussant, P., & Alan, C. (2014).
Epidemic spreading model to characterize misfolded proteins
propagation in aging and associated neurodegenerative disor-
ders. PLoS Computational Biology, 10(11), e1003956. https://
doi.org/10.1371/journal.pcbi.1003956, PubMed: 25412207
Jenkinson, M., Beckmann, C., Behrens, T., Woolrich, M., & Smith,
S. (2012). FSL. NeuroImage, 62, 782–790. https://doi.org/10
.1016/j.neuroimage.2011.09.015, PubMed: 21979382
Kerepesi, C., Szalkai, B., Varga, B., & Grolmusz, V. (2017). The
braingraph.org database of high resolution structural connec-
tomes and the brain graph tools. Cognitive Neurodynamics, 11,
483–486. https://doi.org/10.1007/s11571-017-9445-1, PubMed:
29067135
Kevrekidis, P., Thompson, T., & Goriely, A. (2020). Anisotropic dif-
fusion and traveling waves of toxic proteins in neurodegenerative
diseases. arXiv:2007.02421.
Masuda, N., Porter, M. A., & Lambiotte, R. (2017). Random walks
and diffusion on networks. Physics Reports, 716, 1–58. https://
doi.org/10.1016/j.physrep.2017.07.007
Pandya, S., Kuceyeski, A., & Raj, A. (2017). The brain’s structural
connectome mediates the relationship between regional neuro-
imaging biomarkers in Alzheimer’s disease. Journal of
Alzheimer’s Disease, 55(4), 1639–1657. https://doi.org/10.3233
/JAD-160090, PubMed: 27911289
Pandya, S., Mezias, C., & Raj, A. (2017). Predictive model of spread
of progressive supranuclear palsy using directional network
diffusion. Frontiers in Neurology, 8, 692. https://doi.org/10
.3389/fneur.2017.00692, PubMed: 29312121
Pandya, S., Zeighami, Y., Freeze, B., Dadar, M., Collins, D., & Raj,
A. (2019). Predictive model of spread of Parkinson’s pathology
using network diffusion. NeuroImage, 192, 178–194. https://doi
.org/10.1016/j.neuroimage.2019.03.001, PubMed: 30851444
Putra, P., Chaggar, P., Thompson, T., & Goriely, A. (2021). Oxford
Mathematical Brain Modelling group: Braid surface Matlab
source code and master connectome graphs, Github, https://
github.com/OxMBM/Connectome-Staging
Raj, A., Kuceyeski, A., & Weiner, M. (2012). A network diffusion
model of disease progression in dementia. Neuron, 73(6),
1204–1215. https://doi.org/10.1016/j.neuron.2011.12.040,
PubMed: 22445347
Raj, A., LoCastro, E., Kuceyeski, A., Tosun, D., Relkin, N., &
Weiner, M. (2015). Network diffusion model of progression pre-
dicts longitudinal patterns of atrophy and metabolism in
Alzheimer’s disease. Cell Reports, 10(3), 359–369. https://doi
.org/10.1016/j.celrep.2014.12.034, PubMed: 25600871
Schäfer, A., Mormino, E., & Kuhl, E. (2020). Network diffusion
modeling explains longitudinal tau PET data. Frontiers in
Neuroscience, 14, 1370. https://doi.org/10.3389/fnins.2020
.566876, PubMed: 33424532
Schöll, M., Lockhart, S., Schonhaut, D., O’Neil, J., Janabi, M.,
Ossenkoppele, R., … Jagust, W. (2016). PET imaging of tau de-
position in the aging human brain. Neuron, 89(5), 971–982.
https://doi.org/10.1016/j.neuron.2016.01.028, PubMed:
26938442
Serrano, M., Boguna, M., & Vespignani, A. (2009). Extracting the
multiscale backbone of complex weighted networks. PNAS,
106(16), 6483–6488. https://doi.org/10.1073/pnas.0808904106,
PubMed: 19357301
Slater, P. (2009). A two-stage algorithm for extracting the multiscale
backbone of complex weighted networks. PNAS, 106(26), E66.
https://doi.org/10.1073/pnas.0904725106, PubMed: 19549841
Smith, S., Jenkinson, M., Woolrich, M., Beckmann, C., Behrens, T.,
Johansen-Berg, H., … Matthews, P. (2004). Advances in func-
tional and structural MR image analysis and implementation as
FSL. NeuroImage, 23(S1), 208–219. https://doi.org/10.1016/j
.neuroimage.2004.07.051, PubMed: 15501092
The PIT Bioinformatics Group. (2019). Connectomes: The
Braingraph.org public website. Braingraph.org. https://
braingraph.org/cms/download-pit-group-connectomes/
Thompson, T., Chaggar, P., Kuhl, E., & Goriely, A. (2020). Protein-
protein interactions in neurodegenerative diseases: A conspiracy
theory. PLoS Computational Biology, 16(10), e1008267. https://
doi.org/10.1371/journal.pcbi.1008267, PubMed: 33048932
Thompson, T., Meisl, G., & Goriely, A. (2021). The role of clear-
ance mechanisms in the kinetics of toxic protein aggregates
involved in neurodegenerative diseases. Journal of Chemical
Physics, 154, 125101. https://doi.org/10.1063/5.0031650,
PubMed: 33810689
Tournier, J.-D., Calamante, F., & Connelly, A. (2012). MRtrix:
Diffusion tractography in crossing fiber regions. International
Journal of Imaging Systems and Technology, 22(1), 53–66.
https://doi.org/10.1002/ima.22005
Vogel, J., Itturia-Medina, Y., Strandberg, O., Smith, R., Levitis, E.,
Evans, A., & Hansson, O. (2020). Spread of pathological tau
Network Neuroscience
955
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Braiding Braak and Braak
proteins through communicating neurons in human Alzheimer’s
disease. Nature Medicine, 11(2612). https://doi.org/10.1038
/s41467-020-15701-2, PubMed: 32457389
Vogel, J., Young, A., Oxtoby, N., Smith, R., Ossenkoppele, R.,
Strandberg, O., … Hansson, O. (2021). Four distinct trajectories
of tau deposition identified in Alzheimer’s disease. Nature
Communications, 27, 871–881. https://doi.org/10.1038/s41591
-021-01309-6, PubMed: 33927414
Weickenmeier, J., Jucker, M., Goriely, A., & Kuhl, E. (2019). A
physics-based model explains the prion-like features of neuro-
degeneration in Alzheimer’s disease, Parkinson’s disease, and
amyotrophic lateral sclerosis. Journal of the Mechanics and
Physics of Solids, 124, 264–281. https://doi.org/10.1016/j.jmps
.2018.10.013
Weickenmeier, J., Kuhl, E., & Goriely, A. (2018). Multiphysics of
prionlike diseases: Progression and atrophy. Physical Review
Letters, 121(15), 158101. https://doi.org/10.1103/ PhysRevLett
.121.158101, PubMed: 30362787
Woolrich, M., Jbabdi, S., Patenaude, B., Chappell, M., Makni, S.,
Behrens, T., … Smith, S. (2009). Bayesian analysis of neuroim-
aging data in FSL. NeuroImage, 45, S173–S186. https://doi.org
/10.1016/j.neuroimage.2008.10.055, PubMed: 19059349
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
4
9
2
9
1
9
7
5
2
1
3
n
e
n
_
a
_
0
0
2
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
956