报告 - 麻省理工学院人工智能研究专业

报告

Metacognitive Information Theory

Peter Dayan1,2

1Max Planck Institute for Biological Cybernetics, 蒂宾根, 德国
2University of Tübingen, 蒂宾根, 德国

关键词: metacognition, information theory, signal detection theory, scoring rules, m-ratio

开放访问

杂志

抽象的

The capacity that subjects have to rate confidence in their choices is a form of metacognition, 和
can be assessed according to bias, sensitivity and efficiency. Rich networks of domain-specific and
domain-general regions of the brain are involved in the rating, and are associated with its quality
and its use for regulating the processes of thinking and acting. Sensitivity and efficiency are often
measured by quantities called meta–d 0 and the M-ratio that are based on reverse engineering the
potential accuracy of the original, primary, choice that is implied by the quality of the confidence
judgements. 这里, we advocate a straightforward measure of sensitivity, called meta–I , 哪个
assesses the mutual information between the accuracy of the subject’s choices and the confidence
报告, and two normalized versions of this measure that quantify efficiency in different regimes.
Unlike most other measures, meta–I -based quantities increase with the number of correctly
assessed bins with which confidence is reported. We illustrate meta–I on data from a perceptual
decision-making task, and via a simple form of simulated second-order metacognitive observer.

介绍

The confidence that we apportion to our recollections, cognitions, decisions and actions can
play a critical role in the preparations we make for success or failure; in determining whether
we need to collect more external information or more samples of internal information before
committing ourselves; in regulating the learning that we should do when outcomes are, or are
不是, as expected; and in communicating with others, for instance when engaging in collective
决策 (Bahrami et al., 2010; De Martino et al., 2013; Fleming, 2021; Fleming et al.,
2012; Kepecs & Mainen, 2012; 纳尔逊 & Narens, 1990; Schulz et al., 2020). Confidence, 作为
one of the simplest forms of higher-order or self-reflective assessment about one’s own cogni-
主动过程, has also been (sometimes controversially) influential in modern theories of
意识 (Fernandez-Duque et al., 2000; Lau, 2022; Lau & 罗森塔尔, 2011). 此外,
various impairments of metacognition are central in a number of psychiatric conditions, 为了
实例, with possibly exorbitant requirements for confidence helping underpin excessive
checking in forms of obsessive compulsive disorder; or substantial over-confidence helping
reinforce the persistent apparently erroneous conclusions drawn by those suffering from delu-
sional disorders (Hoven et al., 2019; Rouault et al., 2018; Seow et al., 2021; 孙等人。, 2017).
Various regions of the prefrontal cortex, anterior cingulate cortex, insular cortex and the
precuneus have been implicated in making such judgements and using them to control our
认识 (for a meta-analysis of a wealth of studies, see Vaccaro & Fleming, 2018).

It has therefore long been recognized that is critical to measure the nature and quality of
confidence judgements. At stake are three, related quantities: bias, 灵敏度, and efficiency

引文: Dayan, 磷. (2023).
Metacognitive Information Theory.
开放的心态: 认知方面的发现
科学, 7, 392–411. https://doi.org/10
.1162/opmi_a_00091

DOI:
https://doi.org/10.1162/opmi_a_00091

补充材料:
https://doi.org/10.1162/opmi_a_00091

已收到: 24 十月 2022
公认: 25 六月 2023

利益争夺: 作者
声明不存在利益冲突.

通讯作者:
Peter Dayan
dayan@tue.mpg.de

版权: © 2023
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

(Fleming & Lau, 2014; Galvin et al., 2003; Maniscalco & Lau, 2012; 纳尔逊, 1984). For con-
creteness, consider a simple perceptual decision-making problem: judging whether a Gabor
patch is tilted left (L) or right (右) of vertical. The sensory input α can abstractly be regarded as a
noisy version of d = −1 (L) or d = 1 (右). On each trial, subjects report their decision (the ‘action’
A) about the tilt—this is often called a type 1 judgement—and also their degree of confidence
in the rectitude or accuracy of that decision (the ‘rating’)—a type 2 judgement. For conve-
nience, we consider the original report as coming from an ‘actor’, and the confidence judge-
ment from a ‘rater’; although these are, 当然, the same individual (Schulz et al., 2023).
The type 1 judgement is the topic of conventional signal detection theory (绿色的 & Swets,
1966), with accuracy being quantified by such measures as type 1 sensitivity or d 0. If the rating
is interpreted as just the probability that the type 1 decision is correct (Pouget et al., 2016),
then metacognitive bias measures the overall calibration of the rating—whether subjects tend
to think that they are more or less accurate than they actually are. 当然, a subject could
be metacognitively unbiased if she reported the correct overall probability of being correct on
every trial, independent of the actual observation (like a well-calibrated, but useless, weather
forecaster reporting on every day of the year, the overall mean probability of rain; Dawid,
1982). 因此, metacognitive sensitivity measures the adaptability of the rating to the actual rec-
titude on a trial-by-trial basis—an ideal rater would have perfectly predictive error monitoring,
rating correctly on a trial-by-trial basis whether the type 1 decision is going to be proved cor-
rect or incorrect. 然而, metacognitive sensitivity is not the whole story—the rater has a
particularly easy job if the type 1 action is generally correct—it would be hard for the rater
to be incorrect. Thus metacognitive efficiency attempts to correct the sensitivity for the quality
of inference. 当然, metacognitive bias also has an impact: a thoroughly metacognitively
biased rater who declares themselves fully confident on every trial, even when she in fact errs,
would necessarily be fully insensitive and inefficient.

It might seem obvious, at least to the Bayesian decision theorists amongst us, that sensible
observers would use all the information available to make their type 1 choice on a trial (a = 1 如果
磷 (d = 1|A) > 0.5), and the same information to make their type 2 rating (磷 (d = 1|A)) 关于
their type 1 选择. This would be bias-free, and would leave sensitivity and efficiency at max-
imal values given the decision-maker’s perceptual capacities (d 0). This would render nugatory
the metacognitive measures. 然而, empirical findings do not accord with this expectation
(例如, it is impossible for the rating to be of a less than 50% chance of being correct;
whereas subjects can actually be aware of upcoming errors before they occur (Gehring et al.,
1993); also evident in signals that likely emanate from the anterior cingulate cortex (博特维尼克
等人。, 2004; Carter et al., 1998; Dehaene et al., 1994; Kerns et al., 2004). 因此, 有
various accounts in which, 例如, in a so-called second order model, the internal rater
has access to both additional information after the type 1 decision has been made (例如
from so-called post-decisional information, which we later call γ, that has not been processed
at the time that the decision is registered), and/or only a noisy internal report (β) of the infor-
mation α that the actor used in making the type 1 decision in the first place (Fleming & Daw,
2017; Jang et al., 2012). The rater could also suffer from noise in their metacognitive judge-
ment or report (Guggenmos, 2022, Shekhar & Rahnev, 2021). In cases such as this, it is pos-
sible to have metacognitive hypo- or hyper-sensitivity, and for the rater to predict errors.

When the type 2 decision is not a trivial function of type 1 信息, much effort has
gone into determining useful measures of metacognitive sensitivity and efficiency (埃文斯 &
Azzopardi, 2007; Ferrell & McGoey, 1980; Fleming & Lau, 2014; Galvin et al., 2003;
Guggenmos, 2021; Kunimoto et al., 2001; Maniscalco & Lau, 2012; 纳尔逊, 1984). One influ-
ential and attractive idea has been to imagine the type 1 decisions that the rater would have

开放的心态: 认知科学的发现

393

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

been able to make, and assess the notional type 1 sensitivity of this rater (Maniscalco & Lau,
2012, 2014). This value is called meta–d 0, and has the attractive characteristic of being directly
comparable to the actual type 1 灵敏度. Meta–d 0 can be assessed by fitting the actual con-
fidence statistics to the confidence statistics that would have been predicted by the imaginary
类型 1 choices of the rater. It is then possible to create a metacognitive efficiency measure that
adjusts for the underlying ease of the decision-making problem by comparing meta–d 0 to d 0
either subtractively (meta–d 0 — d 0) or divisively (the so-called M-ratio, which is meta–d 0/d 0).

Meta–d 0 and the M-ratio are widely used as measures of meta-cognitive effectiveness (Barrett
等人。, 2013). 然而, along with some obvious assumptions (such as that ratings are monotonic
in expected accuracy), they have some less desirable characteristics, including remaining depen-
dency of the M-ratio on type 1 表现 (Guggenmos, 2021, at least some aspects of which
是, as noted above, 不可避免的), and on metacognitive bias (Xue et al., 2021, which is arguably
less so). 这里, along with the common observation that there is no reason to expect subjects’
empirical confidence judgements to fit an assumed type 1 decision-process exactly, 哪个
means that the assessment of metacognitive efficiency could be inaccurate, we focus on the fact
that the M-ratio does not take explicit account of the number of levels of confidence rating that
subjects might be able to provide. A rater who can make a fine discrimination between being
correct within the intervals [80, 85)% 或者 [85, 90)% might reasonably demand to be considered
more sensitive (and more efficient) than one with a single rating ‘bucket’ for the whole range [80,
90)%. Given a rater whose confidence is perfectly consistent with a type 1 决定, this excess
discriminability will normally have no benefit from the perspective of meta–d 0.

1 and meta–I r

这里, we introduce and explore a natural alternative to meta–d 0 and the M-ratio, 即
meta–I and two forms of a meta–I -ratio (called meta–I r
2), which are based on the
mutual information between the rectitude of the actor and the confidence ratings. The mutual
information is straightforward to compute for conventional rating buckets, makes fewer
assumptions about the ratings, other than that they are distinct and, 理想地, suitably predictive
of differences in accuracy, and increases naturally with the granularity of the ratings. 这
mutual information is related to measures that are based on the correlation between accuracy
and confidence (纳尔逊, 1984), although it is, 例如, completely agnostic to any bias. 我们
first illustrate meta–I -based measures on confidence data from Shekhar and Rahnev (2021).
然后, to examine their properties in detail, we use a simple realization of a second-order rater
(Fleming & Daw, 2017; Guggenmos, 2022; Jang et al., 2012; Mamassian & de Gardelle, 2022;
Schulz et al., 2023), for which we can precisely unpick the nature of metacognitive sensitivity.

META–IIIIII

Consider a simple perceptual decision-making task such as that reported in Shekhar and
Rahnev (2021). 这里, on each of 2800 trials t, participants saw for just 100 ms a noisy Gabor
patch (of one of three different contrasts, defining three conditions) that was tilted either to the
left or right of vertical (we write this as d t = ±1), and used a single scale to report the direction
of the tilt (at = ±1) and a continuous confidence rating (c t ) about the accuracy of their choices
(whose true value is r t = d t × at ). Confidence reporting in this experiment restricted ct to being
之间 0.5 和 1.

To illustrate the issues for measuring the quality of metacognition, 数字 1 shows violin
plots of the distributions of confidence reports for three selected subjects for incorrect (红色的)
and correct (绿色的) choices and for the three contrast conditions (1 is hardest; 3 is easiest).
主题 5 is biased to report low confidence; 主题 18 to report high confidence; 主题
1 is in the middle. We can see the reduction in incorrect responses with higher contrast

开放的心态: 认知科学的发现

394

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

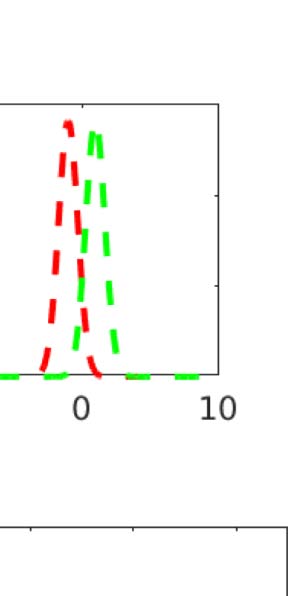
数字 1. Confidence and accuracy for three selected subjects (‘sub’). Each plot shows the distribu-
tion of confidence reports for incorrect (红色的) and correct (绿色的) choices for each of the three contrast
状况 (‘con’). The total area of the violin plots is normalized, so the overall accuracy is evident in
the sizes of the green areas. The magenta bars show the division of confidence ratings into two bins that
approximately maximize meta–I ; the lower and upper triangles show the same for three bins. 这
table provides the numerical values of the various sensitivity and efficiency measures for these subjects.
md 0 is meta–d 0, mR is the M-ratio, mI [n] is meta–I for n, approximately optimally-positioned, confi-
dence bins, mI r

1 for those same bins. Data from Shekhar and Rahnev (2021).

1[n] is meta–I r

(IE。, higher condition number); but also additional facets such as the spikes of very high con-
fidence reports. Since confidence should provide information about accuracy, measures of
meta-cognitive sensitivity report how closely related are c t and r t. In terms of the plots in
数字 1, we would seek the mass of the green distributions to be higher than those of the
red ones, with higher confidence ratings when the answer is actually correct.

As mentioned above, there is a wide variety of such measures, some of which are based on
process models of the way that participants make decisions and rate confidence (例如, Desender
等人。, 2021; Maniscalco & Lau, 2012; Shekhar & Rahnev, 2021), whereas others are agnostic to
the process by which confidence judgements are made, and depend on some form of correla-
tion between accuracy and confidence (纳尔逊, 1984). In both cases, raw assessments are
influenced by the absolute accuracy, 自从, 例如, if the decision-making task is very

开放的心态: 认知科学的发现

395

Metacognitive Information Theory Dayan

easy, there is little uncertainty to which confidence could be sensitive. The table below the
figure indicates d 0, meta–d 0 (written as md 0) and the M-ratio (mR). 这里, these quantities were
calculated using maximum likelihood fitting routines from Maniscalco and Lau (2012, 2014), 在
which the parameters of a naïve first order Bayesian rater are fit so that the distribution of its
confidence ratings match those of each subject. From the M-ratio, we can see that, 在这种情况下,
the order of the efficiency of these subjects is opposite to the order of their metacognitive bias.

Figure 2A and B show meta–d 0 and the M-ratio for all the subjects in Shekhar and Rahnev
(2021), in the three contrast condition. The subjects are sorted differently in each figure in
decreasing order of the sensitivity (图2A) or efficiency (图2B) for the most difficult
状况 (蓝色的). We see that both measures tend to decrease together for all the contrast con-
版本, confirming past observations that there something generalizable about sensitivity and
efficiency, at least for such closely related problems. Figure 2A also shows the dependence of
meta–d 0 on d 0: as noted, these values are distinctly greater for the higher contrast conditions.
Figure 2B shows that this characteristic is largely abolished for the M-ratio, in which the rater’s
meta–d 0 is normalized by the actor’s d 0.

The measure meta–d 0 (along with others mentioned above) is a model-based measure of
灵敏度, in that one imagines that the confidence reports are the first order judgements
for an actor with some particular, parametrized characteristics. 相比之下, meta–I is a
model-agnostic measure of metacognitive sensitivity which quantifies the mutual information
between r t and ct. Take the case that confidence is discrete (in Shekhar and Rahnev (2021), 这是
measured in 1/1000ths) and that we had been able to measure the full joint distribution of

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 2. Metacognition in Shekhar and Rahnev (2021). (A) meta–d 0 across the 20 subjects for the three contrast conditions (in order of
对比, 蓝色的, 红色的, 黄色的), with the subjects sorted by the lowest contrast. (乙) The M-ratio for the subjects, again sorted by the value in
the lowest contrast condition. (C) meta–I for the subjects in the same sort order as in (A) for two (lower envelope in magenta) 或三个 (upper
envelope in green) confidence bins with optimized thresholds. The lozenges fill the areas between lower and upper envelope in the colours for
the condition. (D) The two normalizers for assessing efficiency: meta–I (d 0) (绿色的; right axis, used to define meta–I r
1) and H2(r) (黑色的; left axis,
used to define meta–I r
1 for the subjects in the same sort order as in (乙) with the same plotting
conventions as in (C). (F) The relationship between the M-ratio and meta–I r
1 为了 60 combinations of subjects and conditions, for two
(magenta) 和三个 (绿色的) confidence bins, joined by thin black lines for clarity. (G) The average across subjects of the ratio between
meta–I (or equivalently meta–I r
2) 为了 2 …… 10 confidence bins to meta–I for just 2 confidence bins, for the three conditions. 这
shows that the subjects are, 一般, able to use multiple bins to some good effect. (H) meta–I r
2 for the subjects in the same sort order as in
(乙) with the same plotting conventions as in (C).

2) as a function of the actor’s d 0. (乙) meta–I r

1 or meta–I r

开放的心态: 认知科学的发现

396

Metacognitive Information Theory Dayan

rating and confidence, 磷 (r, C ), with P (r ) = (西德:1)c P (r, C ); 磷 (C ) = (西德:1)r P (r, C ). 然后, the mutual infor-
mation is the difference between two entropies (测量的, for convenience, in bits). 一
entropy, which we write as H2(r), is the overall uncertainty about the accuracy of the actor.
For binary choice, this quantity varies between 0 bits, if the actor is perfectly accurate, as d 0 →
∞ (or indeed if the actor is perfectly inaccurate; always getting the answer wrong) 和 1 bit, 如果
the action a is completely uncorrelated with the truth d, which happens as d 0 → 0. 第二
entropy, H2(r |C) is the weighted average uncertainty about the accuracy that remains after
observing the confidence rating c, where the weights come from the probability of seeing that
rating c. The confidence judgement is very sensitive and efficient if most of the initial uncer-
tainty about the accuracy is removed by the rating, making this last term near 0.

更正式一点,

meta–I ¼ H2 rð Þ−H2 rjcð

在哪里

H2 rð Þ ¼ h2 P rð Þ
(西德:2)

is the entropy of the accuracy;

(1)

(2)

H2 rjcð

Þ ¼

P cð Þh2 P rjcð
½

(西德:2)
Þ

is the conditional entropy of accuracy given confidence;

h2 P xð Þ
½

(西德:2) ¼

x¼0;1

−P xð Þ log2 P xð Þ

is the entropy of a Bernoulli random variable

(3)

(4)

Mutual information is symmetric, so one can also write meta–I = H2(C) − H2(C|r). As is some-
times common, one could condition all these quantities on the action, and so report response-
specific meta–I (a = 1) and meta–I (a = −1).

桌子 1 provides an illustration of the way that one can calculate mutual information. 这里,
we show the four combinations of correct (r = 1) and incorrect (r = 0) and high (c = h) and low
(c = l ) confidence for condition 3 for subject 5 (see the rightmost violin plot in the first row of
数字 1). We binarized the subject’s nearly continuous report of confidence at the optimal
point shown by the magenta bar in the figure (IE。, a threshold of 0.72). 在这种情况下, 问题-
ability of being correct is P (r = 1) = 855/998, with an entropy of H2(r ) = 0.593 bits; 问题-
ability of high and low confidence are P (c = h) = 420/998 和P (c = l ) = 578/998 分别;
the conditional probability of being correct given high confidence is P (r = 1|c = h) = 415/420
with an entropy of h2[磷 (r |c = h)] = 0.093 bits; and the conditional probability of being correct

桌子 1. Calculation tableau for meta–I for condition 3 for subject 5 (另请参见图 1). 这里, 我们
see the prevalence of the four combinations of being correct (r = 1) or incorrect (r = 0) and having
高的 (c = h) or low (c = l ) confidence, dividing the subject’s judgement at the single threshold of
0.72 shown by the magenta line in Figure 1

rectitude
r = 0

r = 0

r = 1

confidence
c = l

c = h

c = l

c = h

开放的心态: 认知科学的发现

prevalence
138

440

415

397

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

given low confidence is P (r = 1|c = l ) = 440/548 with an entropy of h2[磷 (r|c = l )] = 0.793 bits.
Thus the full mutual information is

meta–I ¼ H2 rð Þ − P c ¼ h

(西德:2) − P c ¼ l
Þ (西德:3) h2 P rjc ¼ h
ð
Þ
ð

Þ (西德:3) h2 P rjc ¼ l
ð

(西德:2)
Þ

- 420
998

(西德:3) 0:093

- 578
998

(西德:3) 0:793

¼ 0:593

¼ 0:094

as in the figure.

Figure 2C generalizes this to show meta–I for two ways of turning the (几乎) continuous
measure of confidence that the subjects reported into a set of mutually exclusive bins.1 The
降低 (magenta) border of the lozenge for each condition (distinguished by the fill colour) 是
the result of choosing the best binarization of confidence (something that Shekhar and Rahnev
(2021) explored explicitly). The short horizontal magenta lines on the violin plots of Figure 1
show where this binary separation falls for those three subjects—trying to separate green and
red masses vertically. These thresholds are ultimately an expression of the bias in confidence
reporting of the subjects—we see their levels roughly reflecting how the subjects employ the
confidence scale. 上层 (绿色的) border of each lozenge shows the case of three optimized
levels of confidence arising from the two thresholds shown as lower and upper triangles in
数字 1. 第一的, note that meta–I values are (by construction) higher for the extra bins—a phe-
nomenon we explore further below. 第二, the subjects are sorted as in Figure 2A (经过
meta–d 0 in the lowest contrast condition); however the lozenge for this condition is almost
monotonic; and the lozenges for the higher contrasts have a similar degree of monoticity to
those in meta–d 0, suggesting that meta–I is somewhat consistent with meta–d 0. Along with
这, we see that meta–I also increases with d 0—although we will later qualify this
finding—it arises here partly because of the rather modest levels of the actors’ d 0s in this study
(with most M-ratios being less than 1).

meta–I is a measure of metacognitive sensitivity. As for the relationship between meta–d 0
and the M-ratio, measuring metacognitive efficiency requires normalizing for a quantification
of potentially available information about confidence. Guggenmos (personal communication)
thus suggested taking the analagous step of calculating a meta–I -ratio by normalizing meta–I .
One possible normalizer would be a quantity we write as meta–I (d 0) that would arise as the
value of meta–I for a first-order rater following a conventional signal detection theory analysis
based on the actor’s d 0 在哪里

α ∼ N d; 4
Þ2
d 0ð

a ¼ sign αð Þ

c ¼

1
1 þ exp −d 0jαj
Þ
ð

The green curve in Figure 2D shows meta–I (d 0) as a function of d 0. For relatively low values of
d 0, as seen in Shekhar and Rahnev (2021), this increases with d 0. 然而, for large d 0, 它
decreases again, since meta–I is bounded above by the entropy of the accuracy H2(r )—and
as d 0 rises, the actor becomes increasingly accurate, and so this entropy decreases.

1 See Shekhar and Rahnev (2021) for their analysis of the quantization of the continuous confidence report.
They also performed a sophisticated examination of different models of metacognitive rating based on this
(notably suggesting the influence of a particular sort of noise). 然而, for our present purpose of analyzing
our model-free construct meta–I , we will make a simple comparison with a binarized estimate of meta–d 0.

开放的心态: 认知科学的发现

398

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

This manoeuvre of normalizing meta–I by meta–I (d 0) parallels the M-ratio’s use of d 0 本身
to normalize meta–d 0. It captures the inability of a first order actor with poor perceptual abil-
ities to judge confidence well; and the consequences for metacognitive sensitivity of the
lack of variability in the rectitude of an actor with excellent perceptual abilities. We write
meta–I r
1 = meta–I /meta–I (d 0), and show it in Figure 2E for the two and three confidence bins
of Figure 2C, but now sorted by the M-ratio of the lowest contrast condition (IE。, the sort used
in Figure 2B). As for the M-ratio, we see that this normalization has more nearly equated the
estimates of meta-cognitive efficiency for the three conditions, to a roughly equivalent degree
to the M-ratio.

Figure 2F shows the relationship between the M-ratio and meta–I r

1 for all subjects and all
conditions for the case of two (magenta) 和三个 (绿色的) confidence bins (with the cases
joined by vertical lines). We can see that there is a very close relationship between the M-ratio
and meta–I r
1, at least in this regime of actors and raters, confirming the impression from com-
paring Figures 1B and 1D.

如何, 尽管, should we think about the fact that there are apparently different values of
meta–I for different numbers of confidence bins? All else being equal, a rater that can accu-
rately distinguish a larger number of levels of accuracy should reasonably be considered to be
more metacognitively sensitive and efficient—since this rater can offer a finer perspective on
the chance of failure. Equivalently, meta–I will benefit from the deblurring of the ratings that
occurs when they are split into more levels, at least provided that these levels are used well.
This is not a property of meta–d 0 or the M-ratio—the main consequence of increasing the
granularity of the confidence report is to affect the fitting process for estimating the rater’s
equivalent d 0—it has no direct bearing on that version of sensitivity or efficiency.

To assess the consequence of increasing granularity, we evaluated the average across the
subjects in Shekhar and Rahnev (2021) of the ratio of meta–I for between two and ten con-
fidence bins and for just two bins. 这里, we approximately optimized the thresholds on a
主题- and condition-specific basis (Figure 2G). From the increase with the number of bins,
it is apparent that the subjects are able on average to report confidence at at relatively fine
granularity—particularly in the most difficult (蓝色的) contrast condition—but that this ultimately
saturates (with many fewer than the ∼500 confidence bins of the experimental report). 一
wrinkle here is that we calculated the efficiency normalizer, meta–I (d 0), assuming continuous
confidence judgements can be made by a first-order rater (IE。, with an infinite number of
correctly-employed confidence bins). This is reasonable, because this estimate is based on
a model that allows calculation to arbitrary accuracy. 然而, it could be questioned as a
comparator, and it would also be possible to normalize by a version of meta–I(d 0, 乙) that uses
to optimal effect the same number (乙) of confidence bins as the empirical rater.

Figure 2H reports the result of normalizing meta–I by the theoretical upper bound H2(r) 我们
mentioned above rather than meta–I (d 0). We call the resulting measure of metacognitive effi-
ciency meta–I r
2. H2(r) is shown as a function of d 0 in the black curve in Figure 2D. This also
accounts well for the fact that, for high d 0 for the actor, metacognitive sensitivity cannot be
高的, 自从, as we noted, there is little entropy in H2(r) to reduce by H2(r |C). 然而, in cases
such as the second order model we consider later in which the rater can have access to much
better information than the actor, it allows us to assess the efficiency in absolute term. 这
data in Figure 2H suggest that this regime is not relevant for the data in Shekhar and Rahnev
(2021), in that the raters appear to be generally rather worse than the actors.

A final issue with information theoretic measures concerns estimation of entropies and con-
ditional entropies. The mutual information associated with continuous variables, 例如

开放的心态: 认知科学的发现

399

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

confidence in some experiments, is known to be hard to estimate, because of biases, 所以
care is necessary (Kozachenko & Leonenko, 1987; Paninski, 2003; Panzeri & Treves, 1996;
Witter & Houghton, 2021). Biases are typically weaker for discrete variables, 哪个是
employed in many experiments on confidence. 这里, we use randomized or exact permuta-
tion methods as a simple way to correct for biases.

A SECOND-ORDER DECISION-MAKER

1;2F

In order to examine meta–I and meta–I r
g in more detail, we turned to a simulation which
allows us to abstract the relevant factors away from the noise associated with the ratings of
个人. We simulate choices and ratings from a simple, realized form of a second-order
决策 (Fleming & Daw, 2017; Jang et al., 2012; Mamassian & de Gardelle, 2022).
On any trial, the actor and rater collectively receive three Gaussian distributed signals that
bear on a true underlying quantity d = ±1 (Figure 3A–C); the actor generates a binary choice
A (Figure 3A); and the rater generates one of a number of discrete confidence values c
(Figure 3E and 3H). 这里:

α ¼ d þ A(西德:2)A

is the primary decision variable with type-1 sensitivity d 0 ¼ 2=A

(5)

β ¼ α þ B(西德:2)β

allows the rater partial insight into the basis of the actor’s decision

(6)

γ ¼ d þ G(西德:2)C

provides the rater with independent or unique information about d (7)

在哪里 {(西德:2)A, (西德:2)β, (西德:2)C} are independent standard N (0, 1) distributed random variables. 我们
assume that d = ±1 with equal probability, and that the actor is unbiased, and so makes
a decision based on the sign of α, with a = −1 if α < 0, a = 1 if α > 0 and is indifferent if
α = 0. The rater bases its choice on the observation of the action a and the random var-
iables β and γ, whose combination arranges for potentially partial correlation between the
actor’s and rater’s information about the true state of the stimulus, d, as in the standard
second order model. 这里, the rater’s confidence c = P (a = d |A, β, C) is the probability
that the actor’s action a was correct given all the information that the rater possesses.

Although for didactic convenience, the realization of the information structure relating
actor and rater is different here from the canonical stochastic detection and retrieval model
of Jang et al. (2012), the ultimate statistical relationships are the same; we provide a translation
in the Supplement. 因此, briefly, and as discussed at length in Fleming and Daw (2017), 这
model has various natural limits of metacognitive interest. In the case that B → 0; G → ∞, 这
rater has exactly the same information as the actor, and so could act like the naive Bayesian
decision theorist above. 然后, meta–d 0 would be the same as d 0, and the M-ratio would be 1.
In the opposite case, B → ∞; G → 0, the rater would have perfect knowledge about the rec-
titude of the actor’s choice (based on the equivalent of perfect post-decisional information,
also known as a confidence ’boost’; Mamassian and de Gardelle (2022)) and so could be
as sensitive as it is possible to be. If B → ∞; G → ∞, then the rater has no specific information
about the basis of the actor’s choice on a trial, 所以, like the incompetent weather forecaster,
could do no better than reporting the overall expected accuracy on each trial (which here is
Φ(d 0/2), where Φ is the cumulative distribution function for a normal distribution). In non-
limiting cases, β provides the rater with information about the data on which the actor based
their choice, which she has to combine with her private, 例如, post-decisional, 信息
about d.

It is didactically convenient to consider response-specific confidence, although here, 这
symmetry of the problem means that all the measures will be the same for a = −1 and a = 1.

开放的心态: 认知科学的发现

400

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

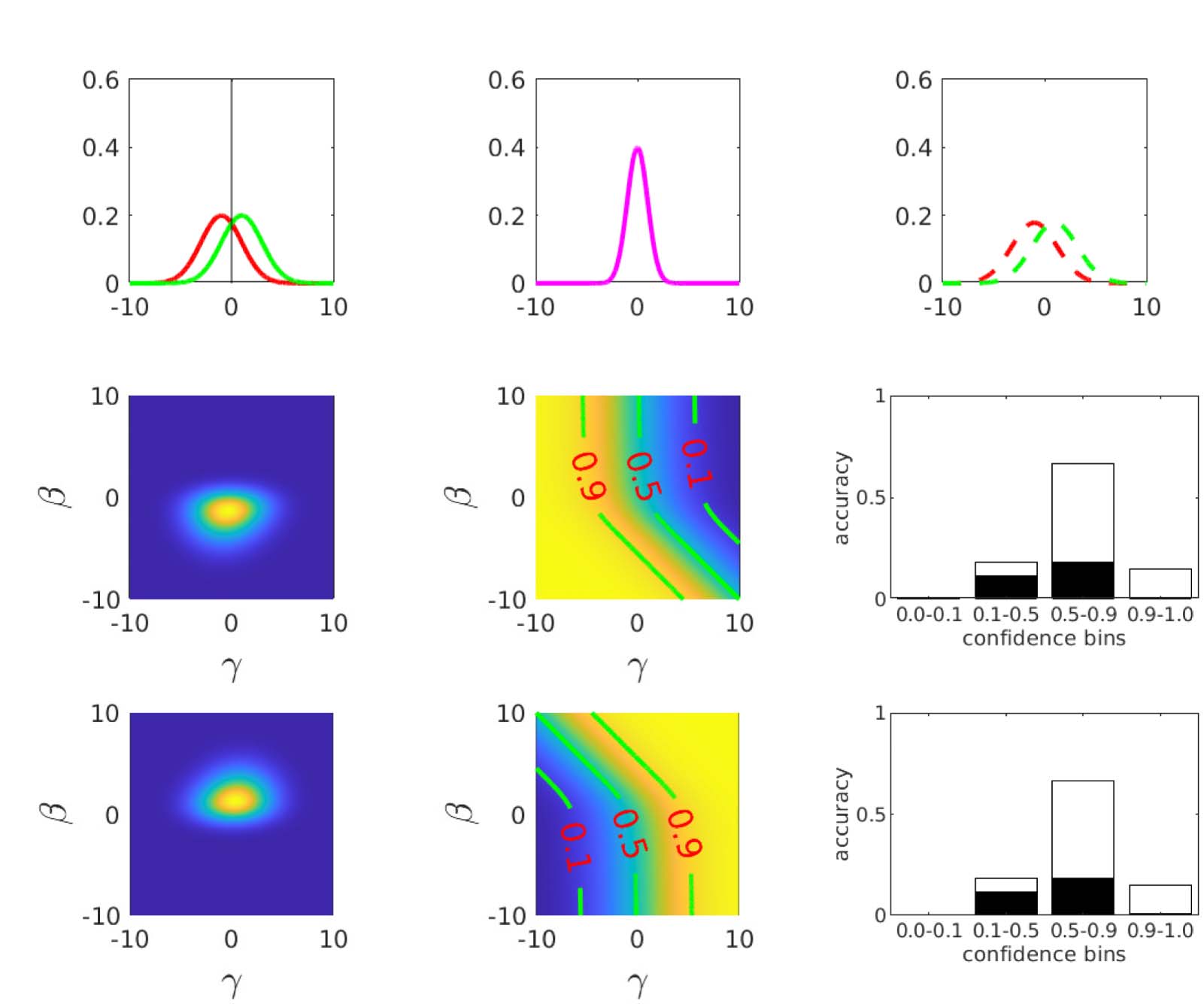
数字 3. Mutual information calculations for a realized second-order model. (A) the actor observes a signal α = d + (2/d 0)(西德:2)A (red for L: d =
−1; green for R: d = +1) and makes an unbiased decision a for d = ±1 at the boundary α = 0. (乙, C) The rater receives two pieces of information:
β = α + 乙(西德:2)β; γ = d + G(西德:2)γ where all (西德:2) are standard N (0, 1) and independent. γ is called unique since it contains information about d that is not
ﬃﬃﬃ
. (D) The density P (β, C |a = −1) slightly favours the lower left quadrant, but with substantial
shared with the actor. Here d 0 = 1; B = 1; G =
5
noise. The distribution integrates to 1; color scale not shown for convenience. (乙) The conditional probability P (d = −1 | a = −1, β, C) 是个
accuracy afforded by the rater’s information set (a = −1, β, C). If β, γ ≪ 0, then the decision a = −1 is likely to be true. The contour lines show
the boundaries where this objective confidence crosses the values shown—the enclosed regions are where objective confidence ratings would
be provided. (F) If we consider the regions of β, γ that define these bins of confidence, we can assess the expected accuracy—defined by the
combination of the probability of ending up in one of the confidence bins c (a = −1, β, C) and the chance of being correct (白色的) or incorrect
(黑色的) in that bin. The mutual information I (r, C) between being correct and c (given a = −1) 是 0.104 bits. (G–I) The same as (D–F) 除了
the case that a = 1. Since the problem is symmetric, this is essentially the same as for a = −1.

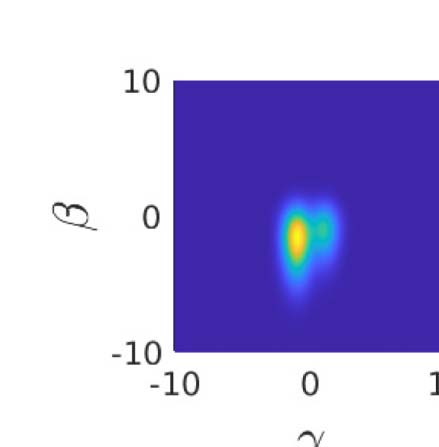
Figure 3D and 3E show the two critical quantities that govern confidence judgements for a =
ﬃﬃﬃ
−1 (for the case that d 0 = 1; B = 1, G =
). 第一的, Figure 3D shows the posterior density that the
5
rater will observe β and γ given that a = −1. These values slightly favour the lower left quadrant
(β < 0; γ < 0), since a = −1 implies that the actor saw α < 0. Note that this preference is stronger as a function of β than γ; this is because B is quite small, and we know that α < 0 (since a = −1). Second, Figure 3E shows the optimal confidence P (d = −1|a = −1, β, γ) that the rater would have about d = −1 given all the information in her possession. The plot shows contours at {0.1, 0.5, 0.9} to indicate more precisely the shape of this distribution. Coarsely, if β is very negative, which, because B is small, likely means that α was very negative, then the rater is rather con- fident that a = −1 is correct, unless γ is very large and positive, to counteract this. The slopes of the contours for negative β largely reflect the relative information about d in α and γ. If β is very positive, then since a = −1, it can only be that α is very close to 0, and so the rater has to rely on γ, implying that the contours run largely perpendicular to the γ axis. 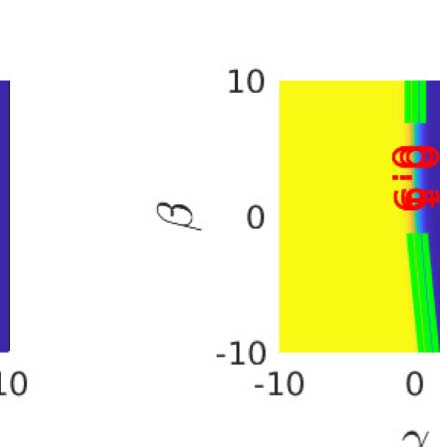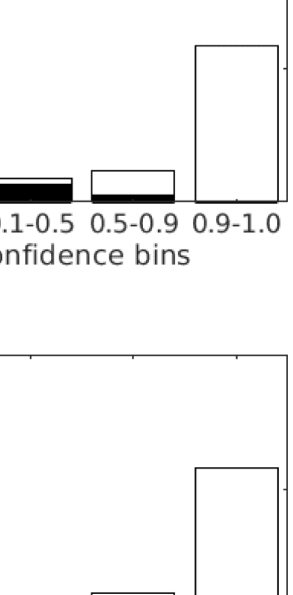OPEN MIND: Discoveries in Cognitive Science 401 Metacognitive Information Theory Dayan Figure 3F shows the consequence for the confidence ratings. Here, we consider the four bins implied by the contours in Figure 3E): {[0, 0.1), [0.1, 0.5), [0.5, 0.9)[0.9, 1.0]}. These bins were chosen to keep them separated on the plot; we consider issues of the nature of the bins later. The total height of each bar integrates the total probability mass (from Figure 3D) that ends up in each of the regions delineated in Figure 3E. This quantifies the fraction of confi- dence reports that will end up in each confidence bin. For each of these confidence reports, the actor could be correct or incorrect; we show the expected proportion of correct reports in white; and incorrect reports in black. If the confidence bins were very narrow, then since all calculations are probabilistically correct, the relative heights of black and white parts of a bar would be given by just the confidence level associated with this bar (since this is exactly what the confidence quantifies). However, since the confidence regions are rather wide, we have to calculate a weighted average, where the weights are purely determined by the probability mass in Figure 3D and the quantity that is averaged is the precise confidence in Figure 3E. Thus, for instance, the mean accuracy in the [0.5, 0.9) bin is slightly less than the centre of this internal (0.75). In this instance, we can calculate meta–d 0 = M-ratio = 1.7 based on the statistics in these confidence bins. Figure 3G–H show exactly the same as Figure 3D–F, but for the case that a = 1 instead. The distributional plots are mirror symmetric, favouring positive rather than negative values of β, γ. The confidence values in Figure 3H are exactly the same as in Figure 3F, since this rater is just as good for a = 1 as for a = −1. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u o p m i / l a r t i c e - p d f / d o i / 1;2f We now consider meta–I and meta–I r g for this case. First, the actor is 69% accurate (with d 0 = 1), making the unconditional entropy H2(r |a = −1) = 0.89 bits. Second, P (c |a = −1) is the total height of the bars in Figure 3F for confidence rating c 2 {[0, 0.1), [0.1, 0.5), [0.5, 0.9)[0.9, 1.0]}, and P (r |c, a = −1) is the ratio between the black and white portions of those bars. The individual entropy terms for the bars in Figures 3F (defined by H2[P (r |c 2 bini, a = −1)]) are 0.42, 0.95, 0.84, 0.34 bits respectively for the four bins, making the total remaining uncertainty about the accuracy as H2(r |c, a = −1) = 0.79. This leaves meta–I = 0.89 − 0.79 = 0.1 bit, and, since meta–I(d 0 = 1) = 0.052 bits, we have meta–I r 1 = 2. Here, although the rater is therefore more accurate than the actor (as similarly reflected by the M-ratio), 2 = 0.12 is rather low, since the rater’s unique information γ is her absolute efficiency meta–I r subject to quite some noise, with G being large. p ﬃﬃﬃﬃﬃﬃﬃ 0:5 Figure 4 shows the same as Figure 3, but for the case that the rater enjoys a much greater ; Figure 4C). Figure 4D now amount of unique, post-decisional, information (with G = shows bimodality, since γ is only likely to be near d = ±1, and less likely to take a value near 0. The mode associated with γ = −1 has a greater mass than that for γ = 1, since a = −1. The conditional distribution in Figure 4E now shows a much starker contrast—with the highly accurate γ being the main determinant of the confidence in the actor’s choice (so if γ > 0, 然后
the rater is rather confident that the actor erred). Figure 4F shows the consequence of this for
the rating buckets. 现在, the extreme values are much more likely—and are duly more pure in
the sense that the rater can be rather sure about the rectitude of the actor. 这里, meta–d 0 =
M-ratio = 4.5, showing the benefit of the well-informed rater. 再次, the case for a = 1
(Figure 4G–H) is the mirror image of the case for a = −1.

If we carry out the same calculations of meta–I and meta–I r

g for this case, we observe
that the individual entropy terms for the bars in Figure 4F are 0.15, 0.84, 0.82, 0.11 重新指定-
主动地. 然而, the fact that most of the weight in the average is on the outer two bars means
that the total remaining uncertainty about the accuracy as I 2(r |C, a = −1) = 0.27. 这使得
meta–I = 0.62 bits, and meta–I r
1 diverge.

1 = 12. In this regime, the M-ratio and meta–I r

1;2F

开放的心态: 认知科学的发现

402

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 4. Mutual information calculations for a realized second-order model. This figure is the same as Figure 3, except that the standard
. The bimodal distributions in (D, G) come from the two narrow possibilities for γ, 和
deviation of the rater’s unique information γ is G =
the weight on γ being near to −1 being higher in (D), because a = −1 there. Now the confidence contours are defined almost exclusively by γ
(the near vertical arrangements in E and H); and the accuracy bins are nearly exclusively one colour (when the rater’s confidence is 0–0.1, 这
actor is almost always incorrect.

ﬃﬃﬃﬃﬃﬃﬃ
0:5

然而, the actor’s performance is not a good yardstick for the rater, since the rater has sub-
stantially more information. 因此, meta–I r
2 = 0.7 is a more useful measure of the high absolute
efficiency of the rater, which reflects the high signal to noise ratio of the rater’s unique infor-
运动, with G being small.

数字 5 compares the various metacognitive sensitivity and efficiency measures for various
values of the actor’s type 1 sensitivity d 0, and for different qualities of the unique information of
the rater G2. 这里, as in Figures 3 和 4, B = 1. By contrast with the earlier figures, 然而,
the rater optimally deployed four confidence bins.

1 (D) largely agree (虽然, as we will see later, meta–I r

These plots cover the two regimes discussed earlier. In one, where G 2 is not too small, 这
rater is at least co-dependent on the information that the actor used. Here the M-ratio (乙) 和
meta–I r
1 correctly exploits extra con-
fidence bins). 然而, in the other regime, where the rater is mostly dependent on its own
source of information (G2 is small), and the actor’s performance is poor, then both the M-ratio
and meta–I r
2 (乙), of the rater is more relevant.
的确, we can see that meta–I r
2 is largely constant as a function of d 0 for very low G2. 这
property is shared by meta–d 0; however meta–d 0 lacks an appropriate scale (since the actor’s
d 0 is not an appropriate baseline).

1 diverge. 这里, the absolute efficiency, meta–I r

开放的心态: 认知科学的发现

403

Metacognitive Information Theory Dayan

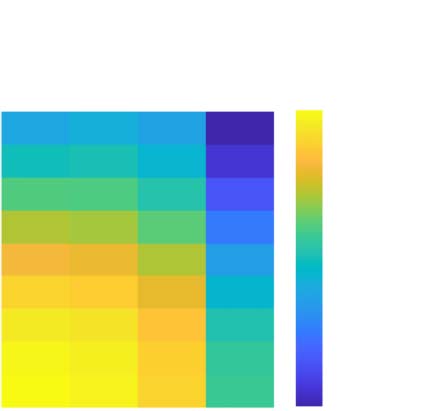
数字 5. Meta-cognitive sensitivities and efficiencies for the second order observer as a function of d 0 and log10
G2 for the case that B = 1
and there are four confidence bins that are optimized to maximize meta–I (and so differ for each combination of d 0 and G2). (A, 乙) meta–d 0
and the M-ratio, with the latter suggesting that the increase in meta–d 0 for larger d 0 is not a sign of efficiency. (C) meta–I , showing that as d 0 gets
大的, the mutual information decreases, since the entropy of accuracy, H2(r ), decreases. (D) Normalizing meta–I by the mutual information
meta–I (d 0) leads to values that are close to the M-ratio (乙) away from the regime in which G2 is small so the rater has access to higher quality
information than the actor. (乙) Normalizing meta–I by the entropy of the accuracy H2(r ) provides a measure of absolute efficiency which is
roughly constant for small G2, as the rater’s unique information dominates.

As we saw in Figure 2F and 2G, one particular issue that spurs the use of meta–I is the
effect of increasing the granularity of the confidence rating. 数字 6 examines this issue from
the perspective of our second-order rater, showing how meta–I (the same would be true of the
efficiency measures) increases with the number of confidence levels for different qualities of
actor and different amounts of independent information provided to the rater (quantified as by
G2). 这里, the thresholds defining the levels were again set to optimize meta–I . In this ideal-
ized case, the extra levels are never harmful, but the degree to which they are helpful varies
quite substantially. As we saw in Figure 2G, the increase is greater for lower d 0 (状况 1 在
that figure); it also grows with G2. Various factors are involved: for instance whether there is
such certainty of the actor (d 0 = 4) or the rater (G2 ≃ 0.1) that two levels suffice. Note that these

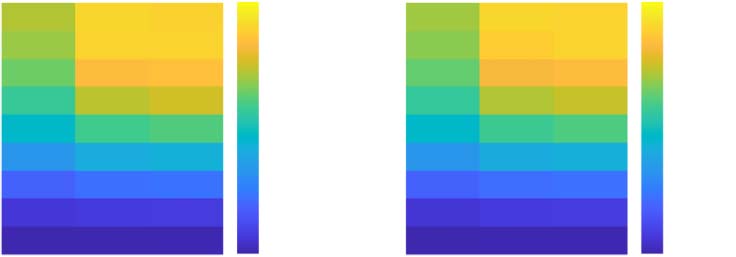
数字 6. The effect of the number of levels of confidence. The ratio between meta–I (or equivalently meta–I r
g values) 为了 4, 8, 16
confidence bins to that for 2 confidence bins for d 0 = 0.5 (A), d 0 = 1 (乙) and d 0 = 2 (C) 为了 4, 8, 或者 16 levels of confidence (all optimized)
and for values of G2 between 0.1 和 10. The scales are set to be the same for all three heatmaps. Here B = 1.

1;2F

开放的心态: 认知科学的发现

404

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 7. Hypo and hyper-sensitivity. The continuous lines show meta–I (A), log meta–I r
2 (C) for the naive first order
Bayesian case with continuous confidence levels across different values of d 0 for the case of standard signal detection theory (绿色的; discrim-
inating two Gaussian distributions with means d = ±1 and standard deviation σ = 2/d 0) and for the extreme mixture case (cyan; with an actor
那是 50% correct with probability 2(1 − Φ(d 0/2)) 和 100% correct otherwise). The magenta points are from the second order model with the
three values of B shown in the titles and the values of G 2 = {10, 3.7, 1, 0.27, 0.1}, from bottom to (顶部) for the case of 16, optimally-spaced
confidence levels. Points for the same value of G are connected by dotted lines for graphical convenience.

1 (乙) and log meta–I r

plots show the benefit as the ratios between 4, 8, 16 levels and 2 级别; as expected the total
meta–I decreases as G2 gets larger.

Even for a given number of levels, the mutual information can vary as a function of the
actual confidence intervals. 例如, for the cases of Figures 3 和 4, if we use four evenly
spaced levels (C 2 {[0, 0.25), [0.25, 0.5), [0.5, 0.75), [0.75, 1.0]}) rather than the uneven ones
(C 2 {[0, 0.1), [0.1, 0.5), [0.5, 0.9)[0.9, 1.0]}) in the figures, meta–I increases to 0.12 bits for the
case of Figure 3, and decreases to 0.60 bits for the case of Figure 4.

The efficiency measures meta–I r

2 are ways of measuring the hypo- and hyper-
metacognitive sensitivity for meta–I . 图中 7, we compare meta–I (A) and the efficiency
比率 (乙, C) for particular idealized actors and raters (green and cyan lines) with the same
measures for the actual second order rater of the previous figures for the maximum number

1 and meta–I r

开放的心态: 认知科学的发现

405

Metacognitive Information Theory Dayan

(16) of optimized confidence bins (magenta points). The green line comes from the same rater
that defined meta–I(d 0), IE。, the case of standard signal detection theory in which the actor
discriminates two Gaussian distributions with means d = ±1 and common standard deviation
σ = 2/d 0, and the rater acts as a naive Bayesian type 1 rater with a continuous range of
confidence levels. 因此, the green lines in Figure 7A are the same as in Figure 2D; 和
green lines in Figure 7B are flat at 0, since meta–I r
1 is defined as the ratio between meta–I for
a rater and meta–I (d 0) 本身. The absolute efficiency of this idealized rater decreases as d 0
gets smaller, since the actor makes more errors, but the rater lacks the information to discrim-
inate them.

1;2F

The cyan lines show meta–I and meta–I r

g for the less standard model of actor and type 1
rater that was considered as a reductio ad absurdum by Rahnev and Fleming (2019), for which
the error rate associated with a conventional d 0 (which is perr = 1 − Φ(d 0/2)) comes from a
mixture model in which the actor and rater are either completely guessing (with actual and
believed probability of error 50%); happening with a mixture proportion of 2perr; and actual
and believed probability of error 0%, with a mixture proportion of 1 − 2perr. The values of
meta–I and meta–I r
g for this rater are higher than for the standard one, since there is extra
information about the source of errors. This reminds us that d 0 is an incomplete measure of the
actor’s process, again making it important to interpret cautiously measures such as the M-ratio
and meta–I r

1 that use it directly for normalization.

1;2F

One could consider meta–I and meta–I r

g values lower than these numbers to be
hypo-efficient; and ones larger than these to be hyper-efficient—at least relative to these raters.
The magenta points show that as G2 decreases (bottom to top), the second order model gen-
erally goes from hypo to hyper-efficiency; but B also plays a role. This is clearest for the
meta–I r
1, where for intermediate values of G, the rater becomes hypo-efficient as d 0 grows
for large B, when the rater cannot prosper from the extra information the actor enjoys.

1;2F

讨论

1;2F

Fleming and Lau (2014) noted that standard ways of quantifying metacognition are based on
distributions such as those in Figures 1 and 3F, 3H (at least if extra factors such as the time
participants take to rate confidence are not taken into account; Desender et al., 2022). 的确,
纳尔逊 (1984) listed eight such measures, which do not include meta–d 0 or meta–I or
meta–I r
G, being measures of metacognitive sensitivity and efficiency that we advocate here.
meta–I is the mutual information between the actual accuracy of the choices of the actor and
the confidence ratings produced by the rater about those choices. This is a simple function of
the same statistics used to calculate meta–d 0 and the M-ratio, and shares some of the desirable
properties of those quantities (沿着, 当然, with the less desirable ones rooted in assump-
tions such as that the decision-making process is stationary, with a fixed strength of evidence;
Rahnev & Fleming, 2019). 然而, like correlation measures (纳尔逊, 1984), meta–I has the
additional benefit of not depending on a potentially imperfect fit to a model of type 1 选择
that might not be exactly appropriate, and it also scales appropriately with such factors as the
number of levels of confidence. Note that Bowman et al. (2022) suggested using the mutual
information to measure a form of type 1 sensitivity in a study of awareness rather than
confidence.

That apparent metacognitive efficiency can increase with the number of levels with which
subjects rate confidence suggests that in experiments collecting confidence ratings, 它会
be worth paying some extra attention to the way that reports are solicited. In the data from

开放的心态: 认知科学的发现

406

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

Shekhar and Rahnev (2021), metacognitive efficiency increased up to 10 levels of
reporting—at least on average—something we could observe clearly by looking at alternative
quantizations of the nearly continuous confidence data they had collected. It would be inter-
esting to carry out this exercise on other data. It should be noted that evaluating mutual infor-
mation measures for a truly continuous confidence report is tricky from modest amounts of
数据, because of known biases (Kozachenko & Leonenko, 1987; Paninski, 2003, Panzeri &
Treves, 1996; Witter & Houghton, 2021); and so further study in particular cases would be
most valuable.

We illustrated meta–I and meta–I r

G, and compared them with the other measures, 使用
both data from Shekhar and Rahnev (2021) and a simple case of a second order rater (Fleming
& Daw, 2017), which is not restricted to having confidence at least as large as 50% (as would
be true of a naive type 1 Bayesian), and can be either hypo- or hyper-metacognitively efficient.

1;2F

The evaluation of the mutual information is completely bias-free. 当然, as noted in the
介绍, bias can affect the mutual information, by affecting the utilitization of the con-
fidence levels, thereby increasing the conditional entropy of the accuracy given the rating
(H(r|C, A)). 然而, like all information theoretic quantities (though unlike the M-ratio; 薛
等人。, 2021), meta–I is completely unaffected by the labels that are given to the confidence
levels—it is only influenced by the conditional accuracy that these levels afford. 的确,
meta–I would be unaffected if the labels were scrambled, so that subjects notionally reported
‘high confidence’ in the actor’s choice to mean that an error was likely, and ‘low confidence’
when an error was not. This is also unlike meta–d 0, which makes assumptions about the appro-
priate monotonicity of the reporting levels in order to be able to calculate a notional type 1 d 0.
It might be possible to include in the optimization process that leads to the evaluation of
meta–d 0 an additional reordering of the confidence levels—although this would then create
a complex combinatorial optimization problem (with n! possible orders for n levels). 它会
be interesting to examine other information theoretic mechanisms that might preserve at least
the order of the levels. 例如, one might imagine the act of reporting as being like a
noisy channel, in which subjects can stochastically report levels that are somewhat different
from their true confidence. A treatment that would have this effect (甚至, technically, by vary-
ing the confidence criteria rather than the confidence signal) is exactly what was suggested by
Shekhar and Rahnev (2021) as a process model for metacognitive inefficiency in the data that
we analyzed above (see also Guggenmos, 2022). One limit of such noisy processes might offer
a good formalization of the common empirical practice of recording confidence on a contin-
uous scale (例如, using a slider), but then for the experimenter to create a set of bins whose
width would be determined by the structure of the stochastic report.

We noted that different positioning of the bins of confidence (even keeping the number
持续的) could lead to different values of meta–I. We approximately optimized the bins on
a case by case basis,2 a bit like efficient coding of sensory information (Laughlin, 1981;
Zhaoping, 2006), where coding levels are adjusted to reflect the ‘natural’ statistics of the infor-
mation that is being coded. In the context of social inference, Bang et al. (2017) suggested
maximising the entropy of confidence reports. The mutual information of Equation 1 能
equivalently be written as the difference between the unconditional entropy of the confidence
报告 (given the action) and the conditional entropy given the accuracy (and the action).
Thus maximizing the entropy can be beneficial for improving meta–I . 然而, the conse-
quences for the second term of the mutual information, namely the conditional entropy of

2 Although in future work, it would also be worth using cross validation methods to estimate thresholds for
discretizing confidence judgments.

开放的心态: 认知科学的发现

407

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

the confidence reports given the accuracy (and the action), also need to be taken into account.
It would certainly be interesting to examine the optimal meta–I solutions in more detail. 如果, 作为
in Bang et al. (2017), the confidence regions change over time (例如, to optimize their
utilization), then metacognitive effectiveness and meta–I will change too, and would need to
be tracked in an appropriately dynamic manner, something that poses potential statistical
问题. It has been noted that the test-retest reliability of the M-ratio is compromised when
the number of rating levels increases, suggesting that it would be important to investigate the
equivalent for meta–I and meta–I r

1;2F

There is much discussion of the need for meta–d 0 to be corrected by the type 1 sensitivity d 0
in order to assess metacognitive efficiency—since cases with high d 0 are intrinsically easier.
This has some undesirable consequences—for instance if d 0 is very low, then even a modest
meta–d 0 can lead to an extremely large M-ratio, something that has inspired the use of the
difference (meta–d 0 − d 0) rather than the M-ratio, or the logarithm of the M-ratio in such cir-
情况. We showed that meta–I r
1 has a similar issue and suggested that in the regime for
the second-order model in which the rater is replete with its own sources of information that
exceed those of the actor, it is more appropriate to consider the absolute efficiency of meta-
认识, normalizing meta–I instead by the unconditional entropy of the accuracy H2(r ),
which is an upper bound to the mutual information, and is the total available variability that
confidence could potentially rate. This alternative ratio meta–I r
2 assesses just how little of the
available unconditional entropy of the accuracy is lost to a high conditional entropy (H2(r |C,
a = −1)) in the mutual information equation.

One might look at both meta–I or the meta–I -ratio as potential correlates of brain
structure and function (Baird et al., 2015; Fleming & Dolan, 2012; Fleming et al., 2010).
Note that the informational quantities can formally also accommodate tasks which use
multiple d 0 价值观 (例如, if the quality of sensory information is different from trial to
审判, as in the mixture curve of Figure 7). 然而, interpretative care is necessary (Rahnev &
Fleming, 2019).

1;2F

Like other information theoretic proposals in neuroscience, meta–I arguably offers more
insight into bounds on the nature and quality of the computations involved in metacognition
than into the neural realization of these computations. Process models such as those in
Desender et al. (2022), Guggenmos (2022), and Shekhar and Rahnev (2021) or even the
simple second order model that we considered (Fleming & Daw, 2017; Jang et al., 2012)
are an attractive alternative, albeit adopting far stronger assumptions. 尽管如此,
meta–I or meta–I r
g would be drop-in replacements for other measures such as the
M-ratio for such assessments as volume-based morphometry for regions whose size is
correlated with the quality of metacognition (Fleming et al., 2010). 当然, 尽管
attractive theoretical properties of information theoretic measures, they are far from unique in
measuring the quality of raters. 的确, so-called skill scores (a term of art in assessing the sort
of probabilistic forecasters with which metacognition is concerned) can be based on (strictly)
proper scoring rules (Gneiting & 椽子, 2007) (a class including the famous quadratic Brier
分数; Brier (1950); and the logarithmic scoring rule that underpins meta–I ). Correcting the
evaluation of forecasters to reflect the difficulty of their forecasting tasks is also a concern in
that literature.

总共, the problem of confidence is inherently one of information—that the actor has
about the true state of the stimulus; and that the rater has about the same quantity and about
what the actor used. It therefore seems appropriate to use the methods of information theory to
judge the relationship between the stimulus, the actor and the rater.

开放的心态: 认知科学的发现

408

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

致谢

I am very grateful to Dan Bang, Stephen Fleming, Liam Paninski and Lion Schulz for most
helpful discussions and comments on earlier versions of the manuscript, and particularly to
Matthias Guggenmos for an extensive discourse and him and Li Zhaoping for suggestions
about normalization of meta–I . Funding was from the Max Planck Society and the Humboldt
基础. PD is a member of the Machine Learning Cluster of Excellence, EXC number
2064/1—Project number 39072764 and of the Else Kröner Medical Scientist Kolleg
“ClinbrAIn: Artificial Intelligence for Clinical Brain Research.”

DATA AVAILABILITY STATEMENT

This study reused data that had been made publicly available based on the study of Shekhar
and Rahnev (2021).

Data and code for reproducing the figures are available at https://github.com/Peter-Dayan

-TN/metainf.git.

参考

Bahrami, B., Olsen, K., Latham, 磷. E., Roepstorff, A。, Rees, G。, &
Frith, C. D. (2010). Optimally interacting minds. 科学,
329(5995), 1081–1085. https://doi.org/10.1126/science
.1185718, 考研: 20798320

Baird, B., Cieslak, M。, Smallwood, J。, Grafton, S. T。, & Schooler,
J. 瓦. (2015). Regional white matter variation associated with
domain-specific metacognitive accuracy. 认知杂志
神经科学, 27(3), 440–452. https://doi.org/10.1162/jocn_a
_00741, 考研: 25313660

Bang, D ., Aitchison, L。, Moran, R。, Herce Castanon, S。, Rafiee, B.,
Mahmoodi, A。, Lau, J. 是. F。, Latham, 磷. E., Bahrami, B., &
Summerfield, C. (2017). Confidence matching in group decision-
制作. Nature Human Behaviour, 1(6), 文章 0117. https://土井
.org/10.1038/s41562-017-0117

Barrett, A. B., Dienes, Z。, & 赛斯, A. K. (2013). Measures of meta-
cognition on signal-detection theoretic models. Psychological
方法, 18(4), 535–552. https://doi.org/10.1037/a0033268,
考研: 24079931

博特维尼克, 中号. M。, 科恩, J. D ., & Carter, C. S. (2004). Conflict
monitoring and anterior cingulate cortex: An update. 趋势
认知科学, 8(12), 539–546. https://doi.org/10.1016/j
.tics.2004.10.003, 考研: 15556023

Bowman, H。, 琼斯, W., Pincham, H。, Fleming, S。, Cleeremans, A。, &
史密斯, 中号. (2022). Modelling the simultaneous encoding/serial
experience theory of the perceptual moment: A blink of
meta-experience. Neuroscience of Consciousness, 2022(1), 文章
niac003. https://doi.org/10.1093/nc/niac003, 考研: 35242362
Brier, G. 瓦. (1950). Verification of forecasts expressed in terms of
probability. Monthly Weather Review, 78(1), 1–3. https://doi.org
/10.1175/1520-0493(1950)078<0001:VOFEIT>2.0.一氧化碳;2

Carter, C. S。, Braver, 时间. S。, Barch, D. M。, 博特维尼克, 中号. M。, Noll, D .,
& 科恩, J. D. (1998). Anterior cingulate cortex, error detection,
and the online monitoring of performance. 科学, 280(5364),
747–749. https://doi.org/10.1126/science.280.5364.747,
考研: 9563953

Dawid, A. 磷. (1982). The well-calibrated Bayesian. Journal of the
American Statistical Association, 77(379), 605–610. https://土井
.org/10.1080/01621459.1982.10477856

De Martino, B., Fleming, S. M。, Garrett, N。, & Dolan, 右.

J.
(2013). Confidence in value-based choice. 自然神经科学,

16(1), 105–110. https://doi.org/10.1038/nn.3279, 考研:
23222911

德阿内, S。, Posner, 中号. 我。, & Tucker, D. 中号. (1994). Localization of
a neural system for error detection and compensation. 心理-
logical Science, 5(5), 303–305. https://doi.org/10.1111/j.1467
-9280.1994.tb00630.x

Desender, K., 唐纳, 时间. H。, & Verguts, 时间. (2021). Dynamic expres-
sions of confidence within an evidence accumulation frame-
工作. 认识, 207, 文章 104522. https://doi.org/10.1016/j
.cognition.2020.104522, 考研: 33256974

Desender, K., Vermeylen, L。, & Verguts, 时间. (2022). Dynamic influ-
ences on static measures of metacognition. Nature Communica-
系统蒸发散, 13(1), 文章 4208. https://doi.org/10.1038/s41467-022
-31727-0, 考研: 35864100

埃文斯, S。, & Azzopardi, 磷. (2007). Evaluation of a ‘bias-free’ mea-
sure of awareness. Spatial Vision, 20(1–2), 61–77. https://doi.org
/10.1163/156856807779369742, 考研: 17357716
我.

(2000).
Awareness and metacognition. Consciousness and Cognition,
9(2), 324–326. https://doi.org/10.1006/ccog.2000.0449, 考研:
10924252

Fernandez-Duque, D ., Baird,

J. A。, & Posner, 中号.

Ferrell, 瓦. R。, & McGoey, 磷. J. (1980). A model of calibration for
subjective probabilities. Organizational Behavior and Human
Performance, 26(1), 32–53. https://doi.org/10.1016/0030
-5073(80)90045-8

Fleming, S. 中号. (2021). Know thyself: The science of self-awareness.

基础书籍.

Fleming, S. M。, & Daw, 氮. D. (2017). Self-evaluation of decision-
制作: A general Bayesian framework for metacognitive com-
putation. 心理评论, 124(1), 91–114. https://doi.org
/10.1037/rev0000045, 考研: 28004960

Fleming, S. M。, & Dolan, 右. J. (2012). The neural basis of metacog-
nitive ability. Philosophical Transactions of the Royal Society of
伦敦, Series B: Biological Sciences, 367(1594), 1338–1349.
https://doi.org/10.1098/rstb.2011.0417, 考研: 22492751
Fleming, S. M。, Dolan, 右. J。, & Frith, C. D. (2012). Metacognition:
计算, biology and function. Philosophical Transactions
of the Royal Society of London, Series B: Biological Sciences,
367(1594), 1280–1286. https://doi.org/10.1098/rstb.2012.0021,
考研: 22492746

开放的心态: 认知科学的发现

409

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

Fleming, S. M。, & Lau, H. C. (2014). How to measure metacogni-
的. Frontiers in Human Neuroscience, 8, 文章 443. https://土井
.org/10.3389/fnhum.2014.00443, 考研: 25076880

Fleming, S. M。, 韦尔, 右. S。, Nagy, Z。, Dolan, 右. J。, & Rees, G.
(2010). Relating introspective accuracy to individual differences
in brain structure. 科学, 329(5998), 1541–1543. https://土井
.org/10.1126/science.1191883, 考研: 20847276

Galvin, S. J。, Podd, J. 五、, Drga, 五、, & Whitmore, J. (2003). Type 2
tasks in the theory of signal detectability: Discrimination between
correct and incorrect decisions. Psychonomic Bulletin & 审查,
10(4), 843–876. https://doi.org/10.3758/BF03196546, 考研:
15000533

Gehring, 瓦. J。, 戈斯, B., Coles, 中号. G。, 迈耶, D. E., & Donchin, 乙.
(1993). A neural system for error detection and compensation.
心理科学, 4(6), 385–390. https://doi.org/10.1111/j
.1467-9280.1993.tb00586.x

Gneiting, T。, & 椽子, A. 乙. (2007). Strictly proper scoring rules,
prediction, and estimation. Journal of the American Statistical
协会, 102(477), 359–378. https://doi.org/10.1198
/016214506000001437

绿色的, D. M。, & Swets, J. A. (1966). Signal detection theory and

psychophysics. 约翰·威利.

Guggenmos, 中号. (2021). Measuring metacognitive performance:
Type 1 performance dependence and test-retest reliability. 新-
roscience of Consciousness, 2021(1), Article niab040. https://土井
.org/10.1093/nc/niab040, 考研: 34858637

Guggenmos, 中号. (2022). Reverse engineering of metacognition.
电子生活, 11, Article e75420. https://doi.org/10.7554/eLife.75420,
考研: 36107147

Hoven, M。, Lebreton, M。, Engelmann, J. B., Denys, D ., Luigjes, J。, &
van Holst, 右. J. (2019). Abnormalities of confidence in psychia-
尝试: An overview and future perspectives. Translational Psychia-
尝试, 9(1), 文章 268. https://doi.org/10.1038/s41398-019-0602
-7, 考研: 31636252

Jang, Y。, Wallsten, 时间. S。, & Huber, D. 乙. (2012). A stochastic detec-
tion and retrieval model for the study of metacognition. 心理-
逻辑审查, 119(1), 186–200. https://doi.org/10.1037
/a0025960, 考研: 22059901

Kepecs, A。, & Mainen, Z. F. (2012). A computational framework for
the study of confidence in humans and animals. 哲学
Transactions of the Royal Society of London, Series B: Biological
科学, 367(1594), 1322–1337. https://doi.org/10.1098/rstb
.2012.0037, 考研: 22492750

Kerns, J. G。, 科恩, J. D ., MacDonald III, A. W., 给, 右. Y。, Stenger,
V. A。, & Carter, C. S. (2004). Anterior cingulate conflict monitor-
ing and adjustments in control. 科学, 303(5660), 1023–1026.
https://doi.org/10.1126/science.1089910, 考研: 14963333
Kozachenko, L. F。, & Leonenko, 氮. 氮. (1987). Sample estimate of
the entropy of a random vector. Problemy Peredachi Informatsii,
23(2), 9–16.

Kunimoto, C。, 磨坊主, J。, & Pashler, H. (2001). Confidence and
accuracy of near-threshold discrimination responses. 有意识的-
ness and Cognition, 10(3), 294–340. https://doi.org/10.1006
/ccog.2000.0494, 考研: 11697867

Lau, H. (2022). In consciousness we trust: The cognitive neurosci-
ence of subjective experience. 牛津大学出版社. https://
doi.org/10.1093/oso/9780198856771.001.0001

Lau, H。, & 罗森塔尔, D. (2011). Empirical support for higher-order
theories of conscious awareness. 认知科学的趋势,
15(8), 365–373. https://doi.org/10.1016/j.tics.2011.05.009,
考研: 21737339

Laughlin, S. (1981). A simple coding procedure enhances a neu-
ron’s information capacity. Zeitschrift für Naturforschung, 部分

C: Biosciences, 36(9–10), 910–912. https://doi.org/10.1515/znc
-1981-9-1040, 考研: 7303823

Mamassian, P。, & de Gardelle, V. (2022). Modeling perceptual
confidence and the confidence forced-choice paradigm. 心理-
逻辑审查, 129(5), 976–998. https://doi.org/10.1037
/rev0000312, 考研: 34323580

Maniscalco, B., & Lau, H. (2012). A signal detection theoretic
approach for estimating metacognitive sensitivity from confidence
ratings. Consciousness and Cognition, 21(1), 422–430. https://土井
.org/10.1016/j.concog.2011.09.021, 考研: 22071269

Maniscalco, B., & Lau, H. (2014). Signal detection theory analysis
of type 1 and type 2 数据: Meta–d 0, response-specific meta–d 0,
and the unequal variance SDT model. 在S. 中号. Fleming &
C. D. Frith (编辑。), The cognitive neuroscience of metacognition
(PP. 25–66). 施普林格. https://doi.org/10.1007/978-3-642-45190
-4_3

纳尔逊, 时间. 氧. (1984). A comparison of current measures of the
accuracy of feeling-of-knowing predictions. Psychological
Bulletin, 95(1), 109–133. https://doi.org/10.1037/0033-2909.95
.1.109, 考研: 6544431

纳尔逊, 时间. 奥。, & Narens, L. (1990). Metamemory: A theoretical
framework and new findings. In G. H. Bower (埃德。), 心理学
of learning and motivation (卷. 26, PP. 125–173). Academic
按. https://doi.org/10.1016/S0079-7421(08)60053-5

Paninski, L. (2003). Estimation of entropy and mutual information.
神经计算, 15(6), 1191–1253. https://doi.org/10.1162
/089976603321780272

Panzeri, S。, & Treves, A. (1996). Analytical estimates of limited
sampling biases in different information measures. 网络:
Computation in Neural Systems, 7(1), 87–107. https://doi.org
/10.1080/0954898X.1996.11978656, 考研: 29480146

Pouget, A。, Drugowitsch, J。, & Kepecs, A. (2016). Confidence and
肯定: Distinct probabilistic quantities for different goals.
自然神经科学, 19(3), 366–374. https://doi.org/10.1038
/nn.4240, 考研: 26906503

Rahnev, D ., & Fleming, S. 中号. (2019). How experimental proce-
dures influence estimates of metacognitive ability. 神经科学
of Consciousness, 2019(1), Article niz009. https://doi.org/10
.1093/nc/niz009, 考研: 31198586

Rouault, M。, Seow, T。, Gillan, C. M。, & Fleming, S. 中号. (2018). Psy-
chiatric symptom dimensions are associated with dissociable
shifts in metacognition but not task performance. Biological Psy-
chiatry, 84(6), 443–451. https://doi.org/10.1016/j.biopsych.2017
.12.017, 考研: 29458997

Schulz, L。, Fleming, S. M。, & Dayan, 磷. (2023). Metacognitive com-
putations for information search: Confidence in control. 心理-
逻辑审查, 130(3), 604–639. https://doi.org/10.1037
/rev0000401, 考研: 36757948

Schulz, L。, Rollwage, M。, Dolan, 右. J。, & Fleming, S. 中号. (2020).
Dogmatism manifests in lowered information search under
uncertainty. 美国国家科学院院刊,
117(49), 31527–31534. https://doi.org/10.1073/pnas.2009641117,
考研: 33214149

Seow, 时间. X. F。, Rouault, M。, Gillan, C. M。, & Fleming, S. 中号. (2021).
How local and global metacognition shape mental health. Bio-
logical Psychiatry, 90(7), 436–446. https://doi.org/10.1016/j
.biopsych.2021.05.013, 考研: 34334187

Shekhar, M。, & Rahnev, D. (2021). The nature of metacognitive
inefficiency in perceptual decision making. Psychological
审查, 128(1), 45–70. https://doi.org/10.1037/rev0000249,
考研: 32673034

Sun, X。, 朱, C。, & 所以, S. H. 瓦. (2017). Dysfunctional metacogni-
tion across psychopathologies: A meta-analytic review. 欧洲的

开放的心态: 认知科学的发现

410

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d

F
/

d
哦

我
/

我

1
0
1
1
6
2
哦
p
米
_
A
_
0
0
0
9
1
2
1
4
8
1
4
0
哦
p
米
_
A
_
0
0
0
9
1
p
d

我

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Metacognitive Information Theory Dayan

Psychiatry, 45, 139–153. https://doi.org/10.1016/j.eurpsy.2017
.05.029, 考研: 28763680

Vaccaro, A. G。, & Fleming, S. 中号. (2018). Thinking about thinking:
A coordinate-based meta-analysis of neuroimaging studies of
metacognitive judgements. Brain and Neuroscience Advances, 2,
A r t i c l e 2 3 9 8 2 1 2 8 1 8 8 1 0 5 9 1 . h t t p s : / / d o i . o rg / 1 0 . 11 7 7
/2398212818810591, 考研: 30542659

Witter, J。, & Houghton, C. (2021). A note on the unbiased estima-
tion of mutual information. arXiv:2105.08682. https://doi.org/10
.48550/arXiv.2105.08682

薛, K., Shekhar, M。, & Rahnev, D. (2021). Examining the robust-
ness of the relationship between metacognitive efficiency and
metacognitive bias. Consciousness and Cognition, 95, 文章
103196. https://doi.org/10.1016/j.concog.2021.103196,
考研: 34481178

Zhaoping, L.

the early
(2006). Theoretical understanding of
visual processes by data compression and data selection.
网络: Computation in Neural Systems, 17(4), 301–334.
https://doi.org/10.1080/09548980600931995, 考研:
17283516

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
哦
p
米

我
/

我

A
r
t
我
C
e
–
p
d