PERSPECTIVE - 麻省理工学院人工智能研究专业

PERSPECTIVE

Columnar connectome: toward a mathematics
of brain function

Anna Wang Roe

Institute of Interdisciplinary Neuroscience and Technology, Zhejiang University, 杭州, 中国

关键词: Primate, Cerebral cortex, 功能网络, Functional tract tracing, Matrix mapping,
Brain theory, Artiﬁcial intelligence

抽象的

Understanding brain networks is important for many ﬁelds, including neuroscience,
心理学, medicine, and artiﬁcial intelligence. To address this fundamental need, 有
multiple ongoing connectome projects in the United States, 欧洲, and Asia producing
brain connection maps with resolutions at macro- and microscales. 然而, still lacking is
a mesoscale connectome. This viewpoint (1) explains the need for a mesoscale connectome
in the primate brain (the columnar connectome), (2) presents a new method for acquiring
such data rapidly on a large scale, 和 (3) proposes how one might use such data to achieve
a mathematics of brain function.

THE COLUMNAR CONNECTOME

The Cerebral Cortex Is Composed of Modular Processing Units Termed “Columns”

In humans and nonhuman primates, the cerebral cortex occupies a large proportion of brain
体积. This remarkable structure is highly organized. 解剖学上, it is a two-dimensional
(2D) sheet, roughly 2mm in thickness, and divided into different cortical areas, each specializ-
ing in some aspect of sensory, motor, cognitive, and limbic function. There is a large literature,
especially from studies of the nonhuman primate visual cortex, to support the view that the
cerebral cortex is composed of submillimeter modular functional units, termed “columns”
(Mountcastle, 1997). Columns span the 2-mm thickness of cortex and are characterized by
six input/output layers (laminae) linked together via interlaminar circuits (数字 1). The tens of
thousands of neurons within a single column are not functionally identical but share a common
functional preference such that single stimuli maximally activate the population and produce a
coherent columnarresponse. These coherent responses can be visualized using multiple methods,
including electrophysiology (例如, Hubel & Wiesel, 1977; Mountcastle, 1997; Katzner et al.,
2009), 2-deoxyglucose (例如, Tootell et al., 1988), optical imaging (例如, Blasdel & Salama,
1986; Grinvald et al., 1986), and high spatial resolution fMRI methods (例如, Cheng, 2012;
Nasr et al., 2016; 李等人。, 2019). More in-depth and scholarly articles about the deﬁnition and
existence of the column are available (例如, Horton & Adams, 2005; Rakic, 2008; Ts’o et al.,
2009; da Costa & 马丁, 2010; Rockland, 2010).

In nonvisual cortical areas, data on columnar organization is more limited (DeFelipe et al.,
1986; Lund et al., 1993; 克里策尔 & Goldman-Rakic, 1995; Friedman et al., 2004; Gharbawie
等人。, 2014). 然而, there is accumulating evidence, as well as compelling genetic de-
velopmental (Rakic, 1988; Torii et al., 2009; 李等人。, 2012), and computational reasons
(Swindale, 2004; Schwalger et al., 2017; Berkowitz & Sharpee, 2018) to believe that columnar

开放访问

杂志

引文: Roe, A. 瓦. (2019). Columnar
connectome: toward a mathematics of
brain function. 网络神经科学,
3(3), 779–791. https://doi.org/10.1162/
netn_a_00088

DOI:
https://doi.org/10.1162/netn_a_00088

已收到: 26 十月 2018
公认: 14 四月 2019

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
Anna Wang Roe
annawang@zju.edu.cn

处理编辑器:
Pedro Valdes-Sosa

版权: © 2019
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Columnar connectome: mathematics of brain function

Column:
A modular functional unit of cerebral
cortex.

organization may be a fundamental feature throughout cortex. Pasko Rakic (2008) writes: “这
neurons within a given column are stereotypically interconnected in the vertical dimension,
share extrinsic connectivity, and hence act as basic functional units subserving a set of common
static and dynamic cortical operations that include not only sensory and motor areas but also
association areas subserving the highest cognitive functions.” For the purposes of this view-
观点, the term “column” refers to a unit of information integration and functional speciﬁcity.

Why a Columnar Connectome Is Needed

Columns come in different ﬂavors and have very speciﬁc connections with other columns.
例如 (数字 2), in primary visual cortex (V1, dotted lines divide V1, V2, and V4),
different functional columns focus on visual features such as eye speciﬁcity (ocular dominance
columns, 图2B), 颜色 (blobs; Figure 1C: dark dots in V1 are color “blobs,” red dot overlies
a blob), and orientation (orientation columns; Figure 1D dark and light domains in V1, 黄色的
dot overlies a horizontal orientation domain). In the second visual area (V2), columns within
the thin stripe (green dots) and thick/pale stripe (blue dots) types integrate columnar informa-
tion from V1 to generate higher order parameters of color (thin stripes: hue), 形式 (thick/pale
stripes: cue-independent orientation response), and depth (thick stripes: near to far binocular
disparity) (for review see Roe et al., 2009). Columns in V4 are hypothesized to perform fur-
ther abstractions such as color constancy (Kusunoki et al., 2006), invariance of shape position
and size (Rust & Dicarlo, 2010; Sharpee et al., 2013), and relative (与. absolute) 深度 (Shiozaki
等人。, 2012; Fang et al., 2019) (for review see Roe et al., 2012).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

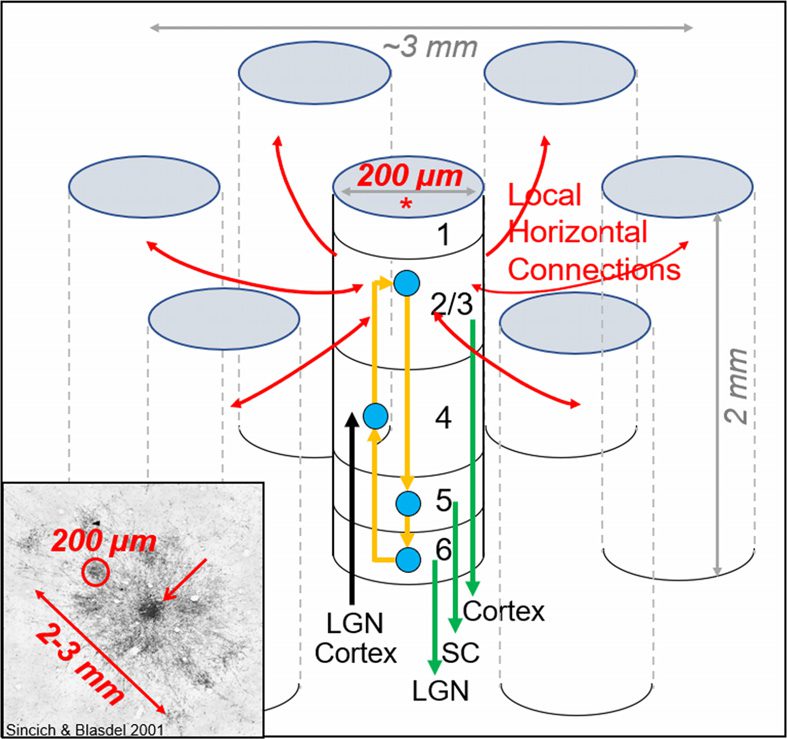
数字 1. The canonical cortical column and its connections (based on nonhuman primate cortex).
The cortical column (*) is a very organized input/output device, ∼200 µm in size and comprising
6 layers. Layer 4 receives inputs (black arrow, 例如, from thalamus or other visual areas). Layers 2
和 3 provide outputs to other cortical columns within the same cortical area (red arrows) 还有
as to other cortical areas (green arrow from layer 2/3). Layers 5 和 6 provide outputs to subcortical
targets (green arrows, 例如, LGN: lateral geniculate nucleus; SC: superior colliculus). 全部 6 layers
share information via interlaminar connections (yellow arrows). Through these connections, 这
thousands of cells in each column share similar function; 所以, each column is functionally
speciﬁc. Bottom left inset provides example of one such network (adapted from Sincich & Blasdel,
2001). Star-like arrangement of connections between columns within a local network (top down
view from surface of cortex). Labeled orientation columns (∼200 µm in size, one circled in red) 有
orientation preference similar to the injected column (red arrow). This local anatomical network
embodies the concept of orientation selectivity.

网络神经科学

780

Columnar connectome: mathematics of brain function

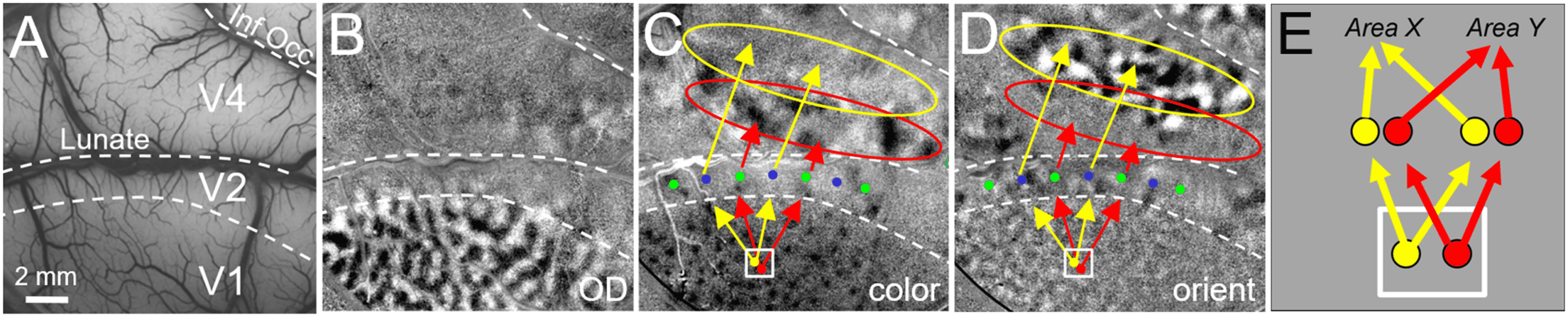
数字 2. Organization of columnar connections in visual cortex. (A) Cortical surface vasculature of visual areas V1, V2, and V4 in macaque
monkey brain. (乙) optical image obtained by a CCD camera through window on the brain reveals ocular dominance map in V1 of macaque
猴 (dark and light columns activated by left eye and right eye, 分别). (C) When monkey views a color (red/green isoluminant)
grating on a monitor, this optical image reveals activated color columns (V1: dark “blobs”; V2: dark “thin stripes” indicated by green dots; V4:
domains in “color band” indicated by red oval). (D) When monkey views an achromatic grating, orientation columns are revealed (垂直的
minus horizontal gratings). V1: orientation columns; V2: orientation domains in “thick/pale” stripes indicated by blue dots; V4: 域
in “orientation band” indicated by yellow oval. Arrows are schematics of connectivity between columns in V1, V2, and V4. Red arrows:
connectivity between blobs in V1, thin stripes in V2, and color bands in V4. Yellow arrows: connectivity between orientation domains in V1,
thick/pale stripes in V2, and orientation bands in V4 (for review see Roe et al., 2012). (乙) Yellow column projects to Area X, and Red column
projects to Area Y. If connections are traced via a large anatomical tracer injection or large voxel (represented by white box), the result will
展示, incorrectly, that each of the yellow and red columns project to both Area X and Area Y. 笔记: for simplicity, feedback connections, 例如,
from V4 to V2 and from V2 to V1, are not depicted.

A key aspect of cortical columns is their highly speciﬁc connections with other columns
(Figure 2C and 2D, red and yellow arrows). This has been demonstrated from studies using
focal injections of tracers targeted to single columns. Such studies have revealed sets of patchy
连接, both intra-areal (数字 1, inset) and inter-areal (数字 2, arrows) (例如, Livingstone
& Hubel, 1984; Sincich & Horton, 2005; Shmuel et al., 2005; Federer et al., 2013). Column-
speciﬁc connection patterns thus embody a functionally speciﬁc (例如, orientation or color)
网络. 然而, 迄今为止, because of the demanding nature of these experiments, 有
only a small number of such studies. 到目前为止, there has not been a method that permits system-
atic large-scale study of columnar connectivity. 实际上, 超过 40 years after Hubel and Wiesel’s
(1977) description of the organization of functional columns in V1, little is known about the
organization of cortical connectivity at the columnar level. I propose that we extend the con-
cept of the hypercolumn (all the machinery required to represent a single point in space) 到
the connectional hypercolumn (all the connections of that unit of representation).

A New Mapping Method

The primary limitation of current methods are the following. (A) Lack of spatial resolution: 最多
anatomical mapping methods employ tracer injections 2−5 mm in size. Human connectomes
are based on resting-state or diffusion methods, which typically are mapped at 2−3 mm voxel
resolution. These volumes (white rectangle in Figure 2E) encompass multiple columns and
therefore reveal connections of a population of multiple functionally distinct columns. 自从
individual nearby columns can exhibit quite distinct connectivity patterns (例如, Figure 2C
and 2D: color blobs to thin stripes vs. orientation columns to pale/thick stripes), 连接
arising from such averages are inaccurate and misleading (Figure 2E). (乙) Slow and expensive:
traditional anatomical tract tracing typically requires 2 到 3 weeks for tracer transport, 动物
sacriﬁce to acquire tissue, and time-consuming weeks to map label locations and 3D recon-
struction. (C) Not large scale: anatomical studies are limited to several tracers, 因此
the connections of only a handful of nodes can be studied in any single brain. Other methods
such as electrophysiological stimulation with fMRI mapping have elegantly revealed networks

网络神经科学

781

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Columnar connectome: mathematics of brain function

Optogenetics:
A method of controlling neurons by
light by viral transfection of
rhodopsin proteins.

underlying speciﬁc behaviors (例如, Tolias et al., 2005); 然而, electrical methods can suf-
fer from current spread, leading to lack of spatial speciﬁcity, as well as inability to map local
connections because of signal dropout near the electrode. Optogenetic stimulation with fMRI
mapping is a powerful cell-type speciﬁc approach (例如, Gerits et al., 2012); 然而, in pri-
伙伴, it takes weeks for viral expression and has thus far been limited by the small number
of transfected nodes, making large-scale mapping of connections in the primate brain chal-
lenging. (d) Correlation based functional connectivity: fMRI BOLD signal correlation (resting
state studies) noninvasively probes networks in human and animal brains, but are limited to
inference about correlation rather than connectivity. Such limitations also exist with neuro-
physiological cross-correlation studies of spike timing coincidence.

To overcome some of these limitations, we have developed a new rapid in vivo mapping
技术. This method combines an optical stimulation method, termed pulsed infrared neu-
ral stimulation (INS), with high-ﬁeld fMRI (徐等人。, 2019A). INS is a method that uses pulsed
trains of light (1,875 nm) to induce heat transients in tissue (Wells et al., 2005; Cayce et al.,
2014; Chernov & Roe, 2014). Although the mechanism underlying INS is still under study, 这
leading theory is that the heat transients lead to membrane capacitance change, which leads
to induction of neuronal ﬁring. When INS is delivered with a ﬁne ﬁber optic (例如, 200-µm
diameter) to the cerebral cortical surface, the light distribution is highly focal (roughly the
same diameter as the ﬁber optic) and roughly ∼300 µm in penetration depth; this penetration
reaches cells in the superﬁcial layers (2/3) and apical dendrites of pyramidal cells in deep lay-
呃 (5/6). Such neuronal activation, 反过来, is propagated to downstream neurons at connected
站点. Similar activation can be achieved by inserting the ﬁber optic into deep brain sites (徐
等人。, 2019乙). The resulting BOLD responses associated with this activation constitutes a map
of cortico-cortical connectivity arising from a single site. 例如, when INS is applied to
区域 17 with ﬁne 200-µm optic ﬁbers in a high-ﬁeld MRI, INS evokes focal activations in areas
18 和 19, the ipsilateral LGN, and contralateral 17/18 (徐等人。, 2019A). This activation is
robust, intensity dependent, and safe for long-term use (Chernov et al., 2014). One can also
use high-resolution mapping to examine BOLD activation in different cortical lamina. This re-
veals local connections that distinguish between feedforward (层 4 activation) and feedback
(superﬁcial and deep laminae) 连接 (徐等人。, 2019A). 重要的, as no animal sac-
riﬁce is required for large dataset collection, the brain can be probed systematically with ﬁber
optic bundles applied to windows on the brain, across multiple sessions. It is also compati-
ble with other imaging, electrophysiological, and behavioral methods for multimodal dataset
correlation (Chernov & Roe, 2014; 徐等人。, 2019A).

COLUMNAR MOTIFS

The long-standing notion that cortical columns perform common functional transformations
would be further bolstered by the presence of columnar connectivity motifs. The existence of
motifs would suggest that there are indeed common modes of information distribution and
一体化. The true value of such motifs is the possibility of identifying a small set of gen-
eral motifs to characterize cortical function (数字 3). This would provide basis vectors for
constructing biological representation of information.

One could wonder why it matters what the underlying anatomical motif is. For some com-
putational neuroscientists, it matters not what the brain circuit is, as long as a circuit can
achieve the desired functional output. 然而, it is a fact that our brain contains organized
anatomical constructs, and these constructs perform some pretty sophisticated functions that
so far have been difﬁcult to mimic with other architectures. Although the brain may not be the

网络神经科学

782

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Columnar connectome: mathematics of brain function

Mesoscale:
The submilleter scale, columnar
规模.

only architecture capable of intelligent behavior, perhaps it is one optimal architecture given
existing biological and physical constraints.

以下, I present two possible motifs: an intra-areal motif (Motif1, binding) and an inter-
areal motif (Motif2, 转型). The basis for these motifs comes from prevous studies of
mesoscale anatomical connections.

Motif1: Intra-Areal Networks (捆绑)

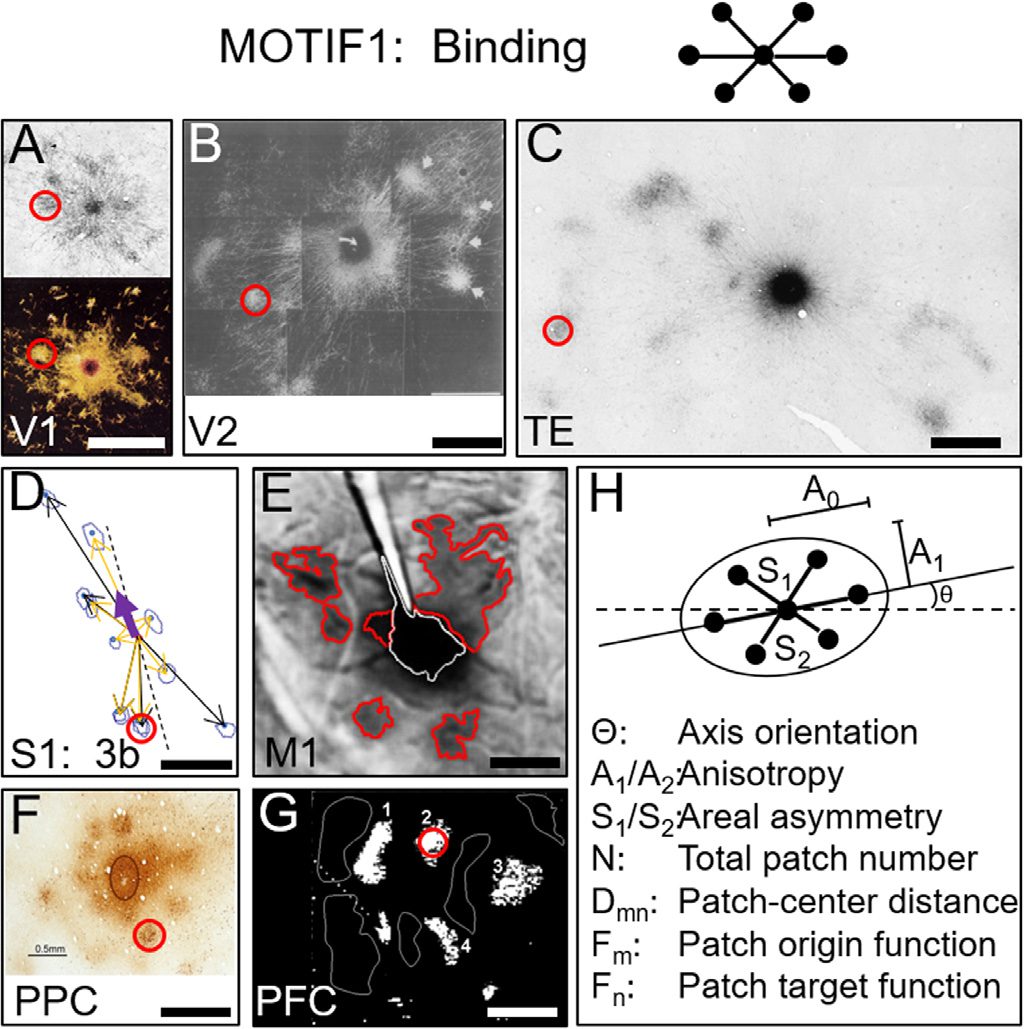
如图 3, many cortical areas contain striking local “star-like” topologies in which
a central column is linked to nearby columns of similar functional preference. The columns
within these networks are typically 200–300 µms in size (red circles) (Amir et al., 1993). A
few examples from the literature illustrate the ubiquity of these constructs; areas include vi-
sual (A–C), sensorimotor (D–E), 顶叶 (F), and prefrontal (G) 地区. In V1, injection of tracer
into an orientation column labels nearby columns of similar orientation preference, 从而
forming an orientation selective network (Figure 3A, 顶部). Color blobs in V1 also form star-like
网络 (Figure 3A, 底部). In V2, 颜色, 形式, and disparity columns lie within separate
functional streams but are linked via interstripe connections to form single multifeature net-
作品 (Figure 3B). Similar networks are seen in temporal cortex (Figure 3C). In area 3b of
体感皮层, columns subserving digits D1 to D5 are linked in interdigit networks
and are hypothesized to underlie sensory co-activation during power grasp (Figure 3D). 其他
star-like networks are observed in primary motor (Figure 3E), 后顶叶 (Figure 3F), 和
prefrontal (Figure 3G) 地区.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 3. Examples of Intra-areal connection motifs. Motif1: Intra-areal circuits serve binding func-
tion and display “star-like” pattern (cartoon at top). This is exempliﬁed by anatomical tract tracing.
Labeled patches are 200 µm in size (red circles). (A) V1, 顶部: Sincich & Blasdel, 2001; 底部:
Livingstone & Hubel, 1984. (乙) V2, Malach et al., 1993. (C) TE, inferotemporal; Tanigawa et al.,
2005. (D) S1; Pálﬁ et al., 2018, 王等人。, 2013. (乙) M1, motor; Gharbawie et al., 2014. (F) 个人电脑,
顶叶; Stepniewska et al., 2016. (G) 全氟碳化物, prefrontal; Sawaguchi, 1994. (H) Motif parameters.

网络神经科学

783

Columnar connectome: mathematics of brain function

Connectome:
A complete map of neural
connections in the brain, 或其
“wiring diagram.”

In Motif1, the central node integrates inputs from a subset of surrounding nodes, 从而
performing a “binding” function. In some areas, nodes of similar functionality (例如, V1; Ts’o
等人。, 1986) are linked, 然而, in others, nodes bind different modalities into a coherent
multimodal representation (例如, orientation, 颜色, and disparity via interstripe connections in
V2; Levitt et al., 1994). Note that opposing networks of complementary function are similarly
“bound” via inhibitory relationships. 一起, these interdigitated networks underlie push-pull
功能 (例如, white vs. outlined domains in Figure 3G; Cayce et al., 2014; Chernov et al.,
2018; 比照. Sawaguchi, 1994; Weliky et al., 1995; Sato et al., 1996; Toth et al., 1996).

The speciﬁc characteristics of these networks (such as overall size, number of nodes, 轴,
anisotropy; Figure 3H) may be tailored to the functional/computational purpose of each area
and may be inﬂuenced by more global factors, such as size of the cortical area or by the
number of other linked cortical areas. These possibilities remain to be explored and tested via
mesoscale connectome data.

Motif2: Inter-Areal Networks (Transformation)

This motif captures the anatomical connections underlying transformations from one cortical
area to another. It is well known that representation becomes increasingly abstract with cortical
等级制度. 然而, it is unknown whether the connections from one area to the next that
mediate functional transformations are in any way systematic or standard. 如果是这样, one might be
able to systematize the transformations into functional classes, potentially reducing all cortico-
cortical projections into a small set of functions. In addition to providing a mathematical way
to represent the brain concisely, it would provide insight into the function of areas for which
there is as yet little understanding.

The idea that there are common functional transformations derives from studies in early
sensory cortical areas. Vision: From studies that simultaneously monitor responses of V2 and
V1 function to single “illusory” stimuli, we have shown that neurons in V2 domains respond to
the illusory aspect, whereas neurons in V1 respond to the “real” aspect (Roe, 2009, for review).
This “real-to-illusory” higher order transformation must be mediated by the anatomical connec-
tivity between V1 and V2. Speciﬁcally, we observe establishment of modality-speciﬁc higher
order properties in different stripes of V2: (A) thin stripes: color representation in V1 blobs,
which is dominated by red-green/blue-yellow axes, transforms to a multicolor map of hue
columns in V2 (康威, 2001; Xiao et al., 2003); (乙) thin stripes: luminance encoding in V1
transforms to brightness encoding in V2 (Roe et al., 2005); (C) thick/pale stripes: encoding of
simple contour orientation transforms to higher order cue-invariant orientation representation
in V2 (Rasch et al., 2013); (d) thick stripes: simple motion direction detection transforms to
the detection of coherent motion in V2 (useful for ﬁgure-ground segregation, Peterhans and
von der Heydt) and to motion contrast deﬁned borders (Hu et al., 2018); 和 (e) thick stripes:
segregated representation of left and right eyes in V1 to maps of near-to-far binocular disparity
columns in V2 (陈等人。, 2008, 2017). Touch: 与此相类似, in somatosensory cortex, 在-
tegration of tactile pressure domains in area 3b (Friedman et al., 2004) are hypothesized to gen-
erate motion selectivity domains in area 1 (Pei et al., 2010; 王等人。, 2013; Roe et al., 2017).
These modality-speciﬁc transformations could be achieved by integrating across multiple uni-
modal inputs in V1 and in S1.

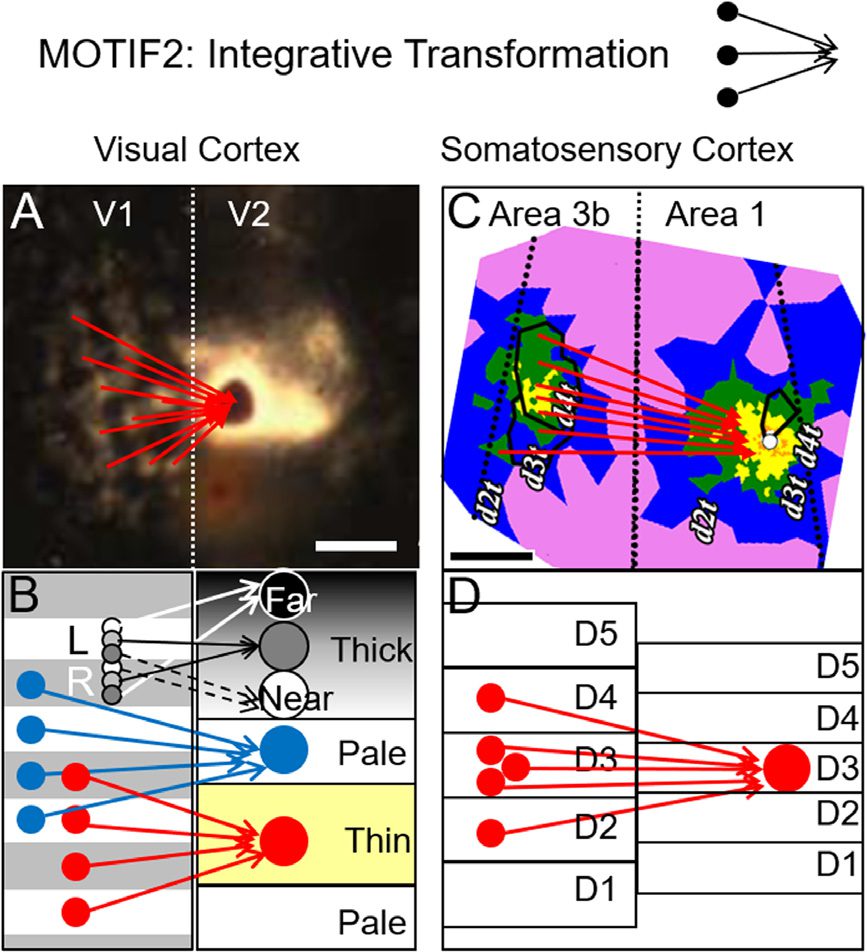
值得注意的是, common anatomical motifs underlie these functional computations. Injection
of tracer into V2 labels multiple columns in V1 (数字 4). These motifs are observed follow-
ing injections into thin stripes (Figure 4B, 红色的), pale stripes (Figure 4B, 蓝色的), and thick stripes
(Figure 4B, grays). 相似地, injection of tracer into a single digit location in area 1 labels

网络神经科学

784

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Columnar connectome: mathematics of brain function

数字 4. Examples of Interareal connection motifs. Motif2: interareal circuits serve to transform
representation by integration of inputs from multiple columns. (A) Image of labeled blobs in V1
following injection of tracer in V2 (Sincich & Horton, 2005). Red arrows: interblob inputs from V1
converge onto a single pale stripe in V2. Vertical dotted line: V1/V2 border. (乙) This motif is observed
从 (红色的) V1 blobs to V2 thin stripes, (蓝色的) V1 interblobs to V2 pale/thick stripes, 和 (grays) 从
V1 ocular dominance columns to V2 thick stripes. (C, D) Red arrows: converging digit tip inputs
from Area 3b to Area 1 in somatosensory cortex (王等人。, 2013).

多种的 (presumed) columns in area 3a (Figure 4C and 4D). Although it remains to be seen
whether such proposed transformations are also found in other sensory, motor, and cogni-
tive systems, identiﬁcation of such common motifs (along with characteristic integration size,
数字, and functional type) would be important for generating an understanding of how the
anatomy of brain connections leads to and limits brain function.

SOME THOUGHTS ABOUT MATHEMATICAL FORMULATION

There is a very large gap between what is known about cortico-cortical connection patterns and
what we need to know to guide concepts about mappings in mathematical terms. 最终
we should like to know what are the organizational principles underlying cortical connec-
tion patterns. The work of investigators such as Obermayer and Blasdel (1993), Goodhill and
Cimponeriu (2000), Carreira-Perpiñán et al. (2005), Swindale (2004, 2007), 和其他人有
beautifully demonstrated that the arrangement of multiple maps within an area arises largely
through maximizing parameters of continuity and coverage. Similar constraints need to be
identiﬁed and modelled for cortico-cortical connectivity. Progress on this front will be greatly
aided by availability of data on columnar connectivity. There are numerous efforts to char-
acterize connectomes by using mathematical topology (比照. 斯波恩斯, 2011). 然而, greater
attention needs to be focused at the columnar scale.

这里, I propose one possible view of modelling cortical connections. Although represen-
tation of some parameters is continuous (例如, continuously shifting orientation preference), A
“binned” representation is valid from the view of functional organization; 那是, continuity

网络神经科学

785

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Columnar connectome: mathematics of brain function

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

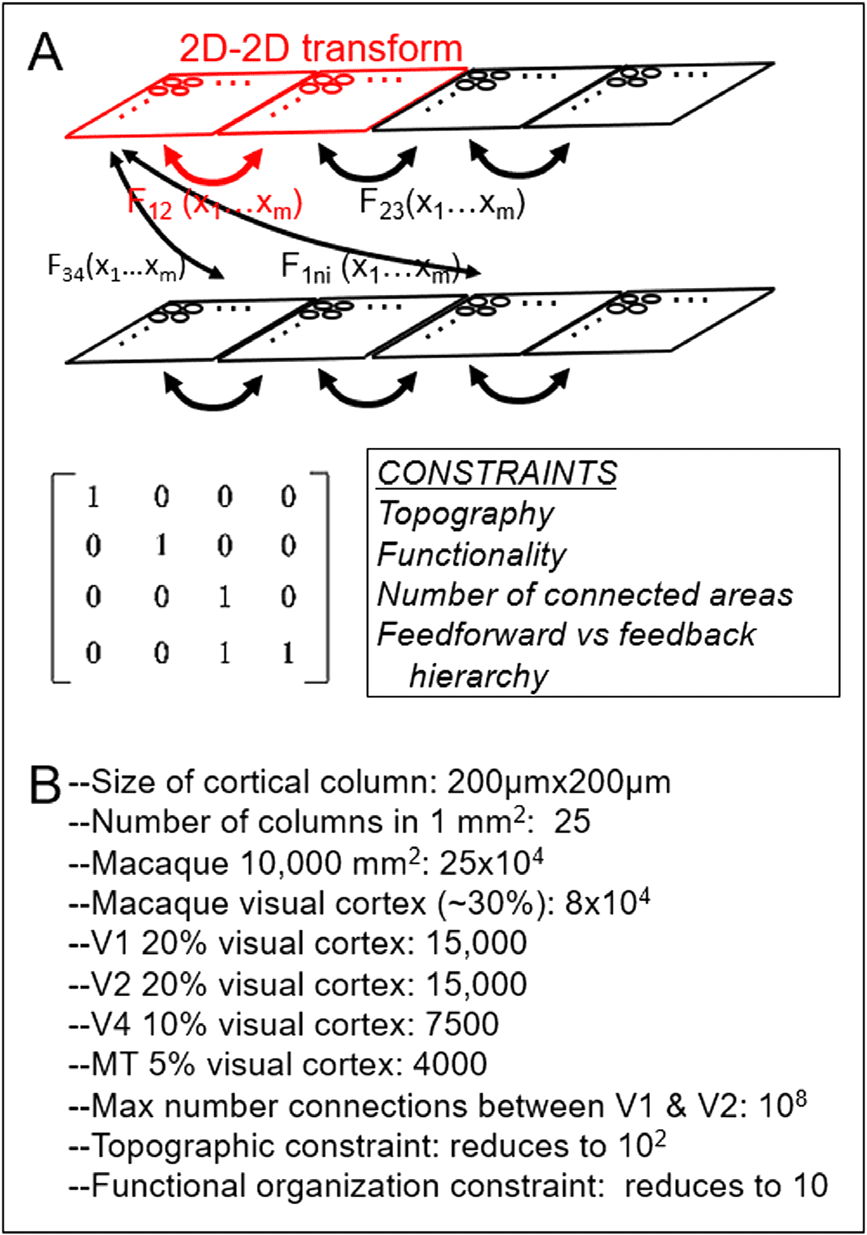
数字 5. 数字 5. 2D-to-2D matrix representation of cortico-cortical mapping. (A) Each cortical
区域 (rectangle) is represented as a 2D array of columns (circles). Red outlined portion: 映射
between a single pair of areas. This 2D-2D mapping can be expressed as a matrix transformation
(以下) with identiﬁed constraints such as topography and functional selectivity. The hope is that
one can reduce the mappings to a small number of motifs (Fij). (乙) Some rough numbers used to
suggest that computation is manageable.

gets broken up into columnar representations by the constraint of mapping multiple parameters
within a single sheet (Obermayer & Blasdel, 1993; Swindale, 2004).

Matrix Mapping

If one views the cortical sheet as a 2D array of columns, then connections between cortical
areas can be viewed as 2D-to-2D mappings (数字 5, red outlined portion). The challenge
to characterize connectional motifs may then be expressed as identifying generalized 2D-2D
matrix mappings that govern how two cortical areas connect (Figure 5A, Fij). For any pair of
地区, such mappings would be constrained by anatomical and functional constraints such as
continuity (topography) and functional speciﬁcity. One additional constraint to be considered
might include the number of areas with which a single area directly connects (typically this is a
small number). Once an anatomical scaffold is constructed, column-speciﬁc feedforward and
feedback modulation could be implemented to model circuit dynamics. From such treatment
of connectivity, general patterns of mappings (motifs) may emerge. Although the problem may,
at ﬁrst glance appear formidable, 在我看来, constraints of anatomical architecture dictate
that each cortical area maps only a few (例如, 3 到 4) key parameters in a continuous and
complete fashion. I make an argument below that this matrix representation may help reduce
the complexity.

网络神经科学

786

Columnar connectome: mathematics of brain function

Computational Feasibility

A few back-of-the-envelope estimates suggest that this mapping problem may be computa-
tionally manageable (Figure 5B). These estimates are based on published neuroanatomical
studies and inferred order-of-magnitude calculations. We use 200 µm as the dimension of a
2
cortical column in macaque monkey (size of orientation domains and blobs in V1); each mm
2
,
then contains 25 columns. The macaque neocortex has an area of about 10,000–15,000 mm
roughly a third of which is visual cortex (比照. Van Essen et al., 1984; Purves & LaMantia, 1993;
Sincich et al., 2003). This means that there are on the order of 25 × 10
columns total and
关于 (a third) 8 × 10
columns in visual cortex. [笔记: 在人类中, although visual cortex is
3 times as large, due to larger column size (roughly double), there are a comparable number
of columns (Horton & Hedley-Whyte, 1984; Adams et al., 2007).] Out of this total of 80,000
columns, V1, V2, and V4 occupy roughly 20%, 20%, 和 10% of visual cortical area, 或者
15,000, 15,000, 和 7,500 columns, 分别 (Weller et al., 1983; Sincich et al., 2003).
This is likely an underestimate as it assumes square columnar packing.

If all columns in V1 mapped to all columns in V2, the number of single node-to-single node
(15,000 × 15,000) (Figure 5B). From neuroanatom-
connections would be on the order of 10
ical studies, we estimate that a single node in V1 connects to on the order of 10 nodes in V2
(Livingstone & Hubel, 1984; Federer et al., 2013; Sincich et al., 2010). This small number is
due to (A) constraints of topography: a single point in visual space takes up roughly 2 mm of
cortical space (Hubel & Wiesel, 1977), 或者 4 × 25 = 100 columns (10
); 和 (乙) constraints
of functional speciﬁcity (数字 4), which further reduces this number by a ﬁfth or a tenth the
number of nodes from a single topographic point. 举个例子, if a full 180
cycle of orien-
tations is represented in 1-mm distance (Hubel & Wiesel, 1977) 或者 5 (200 µm-sized) columns,
area there may be 5 在......之外 25 columns that represent a single orien-
then within a 1-mm
站. This reduces the total number of target nodes from 100 to 10–20 or on the order of
10. This potentially reduces a problem that is on the order of 10
到 10. Such a 1:10 conver-
gence/divergence could underlie a basic architectural motif of interareal connectivity, or an
“interareal connectional hypercolumn.”

○

Such connectional hypercolumns may be replicated at a higher level, albeit with distinct
convergence/divergence ratios and functional constraints. 例如, from V2 to V4, 这
number of connections decreases (15,000 × 7,500, 或者 10
), producing a correspondingly
smaller cortical area (V4 is roughly half the size of V2). An area such as MT, which is only
5% the size of V1, is likely to have a greater convergence/divergence ratio from V1 to MT; 这
would be consistent with the large receptive ﬁeld sizes and comparatively spatially broad inte-
grations for computation of motion direction. 因此, interareal connectivity would be speciﬁed
by parameters such as unique topographical constraints, convergence/divergence ratios, 和
functional selectivities. This set of relationships would be represented as a set of connectional
hypercolumns: F1 (x1…xm) …Fn(x1…xm). Solving how multiple connectional hypercolumns
mutually constrain the entire set of mappings will lead to a representation of total cortical
connectivity in a brain.

Columnar Organization Constrains the Global Network

到目前为止, topological treatment of brain networks has been based on parameters such as connec-
tion number, connectional distance, routing efﬁciency (例如, Young, 1993; Avena-Koenigsberger
等人。, 2019; Chaudhuri et al., 2015). These approaches have provided important advances in
our understanding of brain networks and information ﬂow at an areal level (typically with each

网络神经科学

787

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Columnar connectome: mathematics of brain function

cortical area treated as a single node). 然而, what is lacking is the concept of spatial loca-
tion within each area. 那是, the X,Y coordinate in the matrix deﬁnes a node’s topographical
location and its functionality. Each node’s position is not independent of another nodes posi-
的; neighbors constrain neighbors, and this impacts the organization of the global network.
Studies that address issues of multiscale constraints (例如, Jeub et al., 2018) could incorporate
such spatial information to further specify the resulting architecture.

结论

总结一下, I have described a column-based view of the cerebral cortex and presented a
new methodology (INS-fMRI) to map column-based networks in vivo. I suggest that acquisition
of such large-scale connectivity data may demand new ways of representing cortical networks
(例如, 2D-2D matrix transformations). From such data, patterns or motifs of cortical connectivity
may emerge, and give rise to basic connectivity units termed connectional hypercolumns.

My goal in this viewpoint is to encourage the connectomics ﬁeld to capture columnar con-
nectivity. New representations and mathematics need to be developed for multidimensional
treatment of nodes, one that incorporates the spatial and functional relationships between
neighboring nodes. Such representations may simplify the apparently complex connectional
relationships in the global network. Although we do not yet have enough columnar data to do
this on a large scale, one could start by using available data to generate prototype solutions.
I list a few questions here to motivate future studies. For a given cortical area, how does the
number of directly connected areas affect motif architecture? How do the number of total areas
affect the total possible mappings? Is there a general solution to the mappings of smaller brains
with fewer cortical areas versus larger brains with many? What aspects of cortical architecture
produce and simultaneously constrain our behavioral repertoire? Can one design mappings to
generate alternative artiﬁcial intelligences?

最终, I envision a general connectional theory of brain function, complete with a
system of theorems, derivations, and corollaries (Sporns et al., 2000; 斯波恩斯, 2011). Such a
rule-based representation will lead to new understandings of brain construction and brain
evolution, and will inform our understanding of biological intelligence as well as bio-inspired
人工智能.

致谢

Thanks to Charles Gilbert and Akshay Edathodathil for useful discussions.

资金信息

Anna Wang Roe, National Natural Science Foundation of China (http://dx.doi.org/10.13039/
501100001809), 奖项ID: 81430010. Anna Wang Roe, National Natural Science Foundation
of China (http://dx.doi.org/10.13039/501100001809), 奖项ID: 31627802. Anna Wang Roe,
National Hi-Tech Research and Development Program Grant, 奖项ID: 2015AA020515.

参考

Adams, D. L。, Sincich, L. C。, & Horton, J. C. (2007). Complete pat-
tern of ocular dominance columns in human primary visual cor-
tex. 神经科学杂志, 27(39), 10391–10403. https://土井.
org/10.1523/JNEUROSCI.2923-07.2007

Amir, Y。, 哈雷尔, M。, & 马拉奇, 右. (1993). Cortical hierarchy re-
ﬂected in the organization of intrinsic connections in macaque

monkey visual cortex. Journal of Comparative Neurology, 334(1),
19–46. https://doi.org/10.1002/cne.903340103

Avena-Koenigsberger, A。, 严, X。, Kolchinsky, A。, van den Heuvel,
中号. P。, 哈格曼, P。, & 斯波恩斯, 氧. (2019). A spectrum of routing
strategies for brain networks. 公共科学图书馆计算生物学, 15(3),
e1006833. https://doi.org/10.1371/journal.pcbi.1006833

网络神经科学

788

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Columnar connectome: mathematics of brain function

Berkowitz, J。, & Sharpee, 时间. (2018). Decoding neural responses
with minimal information loss. BioRxiv. https://doi.org/10.1101/
273854

Blasdel, G. G. (1992). Orientation selectivity, preference, 和骗局-
tinuity in monkey striate cortex. 神经科学杂志, 12(8),
3139–3161.

Blasdel, G. G。, & Salama, G. (1986). Voltage-sensitive dyes reveal
a modular organization in monkey striate cortex. 自然,
321(6070), 579–85. https://doi.org/10.1038/321579a0

Carreira-Perpiñán, 中号. A。, Lister, 右. J。, & Goodhill, G. J. (2005). A
computational model for the development of multiple maps in
primary visual cortex. 大脑皮层, 15(8), 1222–1233. https://
doi.org/10.1093/cercor/bhi004

Cayce, J. M。, 弗里德曼, 右. M。, 陈, G。, Jansen, 乙. D ., Mahadevan-
Jansen, A。, & Roe, A. 瓦. (2014). Infrared neural stimulation of
primary visual cortex in non-human primates. Neuroimage, 84,
181–190. https://doi.org/10.1016/j.neuroimage.2013.08.040
Chaudhuri, R。, Knoblauch, K., Gariel, M.-A., 肯尼迪, H。, &
王, X.-J.
(2015). A large-scale circuit mechanism for
hierarchical dynamical processing in the primate cortex. 新-
ron, 88(2), 419–431. https://doi.org/10.1016/j.neuron.2015.09.
008

陈, G。, 鲁, H. D ., & Roe, A. 瓦. (2008). A map for horizontal
disparity in monkey v2. 神经元, 58(3), 442–450. https://doi.org/
10.1016/j.neuron.2008.02.032

陈, G。, 鲁, H. D ., Tanigawa, H。, & Roe, A. 瓦. (2017). Solv-
ing visual correspondence between the two eyes via domain-
based population encoding in nonhuman primates. 会议记录
of the National Academy of Sciences of the United States of
美国, 114(49), 13024–13029. https://doi.org/10.1073/pnas.
1614452114

Cheng, K. (2012). Revealing human ocular dominance columns
using high-resolution functional magnetic resonance imag-
英. Neuroimage, 62(2), 1029–1034. https://doi.org/10.1016/j.
neuroimage.2011.08.086

Chernov, M。, & Roe, A. 瓦. (2014). Infrared neural stimulation: A
new stimulation tool for central nervous system applications.
Neurophotonics, 1(1), 011011. https://doi.org/10.1117/1.NPh.1.
1.011011

Chernov, 中号. M。, 弗里德曼, 右. M。, 陈, G。, Stoner, G. R。, & Roe,
A. 瓦. (2018). Functionally speciﬁc optogenetic modulation in
primate visual cortex. 美国国家科学院院刊
Sciences of the United States of America, 115(41), 10505–10510.
https://doi.org/10.1073/pnas.1802018115

Chernov, 中号. M。, 陈, G。, & Roe, A. 瓦. (2014). Histological as-
sessment of thermal damage in the brain following infrared neu-
ral stimulation. Brain Stimulation, 7(3), 476–482. https://doi.org/
10.1016/j.brs.2014.01.006

康威, 乙. 右. (2001). Spatial structure of cone inputs to color cells
in alert macaque primary visual cortex (V-1). Journal of Neuro-
科学, 21(8), 2768–2783.

da Costa, 氮. M。, & 马丁, K. A. C. (2010). Whose cortical column
would that be? Frontiers in Neuroanatomy, 4, 16. https://doi.org/
10.3389/fnana.2010.00016

DeFelipe, J。, Conley, M。, & 琼斯, 乙. G. (1986). Long-range focal
collateralization of axons arising from corticocortical cells in

monkey sensory-motor cortex. 神经科学杂志, 6(12),
3749–3766.

Fang, Y。, 陈, M。, 徐, H。, 李, P。, Han, C。, 胡, J。, . . . 鲁, H. D.
(2019). An orientation map for disparity-deﬁned edges in area v4.
大脑皮层, 29(2), 666–679. https://doi.org/10.1093/cercor/
bhx348

Federer, F。, 威廉姆斯, D ., Ichida, J. M。, Merlin, S。, & Angelucci, A.
(2013). Two projection streams from macaque v1 to the pale
神经科学杂志,
cytochrome oxidase stripes of v2.
33(28), 11530–11539. https://doi.org/10.1523/JNEUROSCI.5053-
12.2013

弗里德曼, 右. M。, 陈, L. M。, & Roe, A. 瓦. (2004). Modality
maps within primate somatosensory cortex. 诉讼程序
美国国家科学院,
101(34),12724–12729. https://doi.org/10.1073/pnas.0404884101
Gerits, A。, Farivar, R。, 罗森, 乙. R。, Wald, L. L。, Boyden, 乙. S。,
& Vanduffel, 瓦. (2012). Optogenetically induced behavioral
and functional network changes in primates. 现代生物学:
CB, 22(18), 1722–1726. https://doi.org/10.1016/j.cub.2012.07.
023

Gharbawie, 奥。, 弗里德曼, 右. M。, & Roe, A. 瓦. (2014). Localization
of grasp domains in frontal and parietal cortex with intrinsic op-
tical imaging in behaving monkeys. 华盛顿, 直流: Society of
神经科学.

锣, H。, 徐, D ., Yuan, J。, 李, X。, Guo, C。, 彭, J。, . . . Luo, 问.
(2016). High-throughput dual-colour precision imaging for
brain-wide connectome with cytoarchitectonic landmarks at the
cellular level. Nature Communications, 7, 12142. https://doi.org/
10.1038/ncomms12142

Goodhill, G. J。, & Cimponeriu, A. (2000). Analysis of the elastic net
model applied to the formation of ocular dominance and orien-
tation columns. 网络 (布里斯托尔, England), 11(2), 153–168.
Grinvald, A。, Lieke, E., Frostig, 右. D ., 吉尔伯特, C. D ., & Wiesel,
时间. 氮. (1986). Functional architecture of cortex revealed by op-
tical imaging of intrinsic signals. 自然, 324(6095), 361–364.
https://doi.org/10.1038/324361a0

Horton, J. C。, & Hedley-Whyte, 乙. 时间. (1984). Mapping of cytochrome
oxidase patches and ocular dominance columns in human vi-
sual cortex. Philosophical Transactions of the Royal Society
of London. Series B, Biological Sciences, 304(1119), 255–272.
https://doi.org/10.1098/rstb.1984.0022

Horton, Jonathan C., & Adams, D. L. (2005). The cortical column:
A structure without a function. 哲学, Transactions of
the Royal Society of London. Series B, Biological Sciences, 360,
837–862. https://doi.org/10.1098/rstb.2005.1623

胡, J。, Ma, H。, 朱, S。, 李, P。, 徐, H。, Fang, Y。, 陈, M。, Han, C。,
Fang, C。, Cai, X。, 严, K., & 鲁, H. D. (2018). Visual Motion Pro-
cessng in Macaque V2. Cell Rep., 25(1), 157–167.e5. https://土井.
org/10.1016/j.celrep.2018.09.014

Hubel, D. H。, & Wiesel, 时间. 氮. (1977). Ferrier lecture. Functional
architecture of macaque monkey visual cortex. 会议记录
of the Royal Society of London. Series B, Biological Sciences,
198(1130), 1–59. https://doi.org/10.1098/rspb.1977.0085

Jeub, L. G. S。, 斯波恩斯, 奥。, & Fortunato, S. (2018). Multiresolution
consensus clustering in networks. 科学报告, 8(1). https://
doi.org/10.1038/s41598-018-21352-7

网络神经科学

789

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Columnar connectome: mathematics of brain function

Katzner, S。, Nauhaus, 我。, Benucci, A。, Bonin, 五、, Ringach, D. L。, &
Carandini, 中号. (2009). Local origin of ﬁeld potentials in visual
cortex. 神经元, 61(1), 35–41. https://doi.org/10.1016/j.neuron.
2008.11.016

克里策尔, 中号. F。, & Goldman-Rakic, 磷. S. (1995). Intrinsic circuit
organization of the major layers and sublayers of the dorsolat-
eral prefrontal cortex in the rhesus monkey. Journal of Compar-
ative Neurology, 359(1), 131–143. https://doi.org/10.1002/cne.
903590109

Kusunoki, M。, Moutoussis, K., & Zeki, S. (2006). Effect of back-
ground colors on the tuning of color-selective cells in monkey
area v4. 神经生理学杂志, 95(5), 3047–3059. https://
doi.org/10.1152/jn.00597.2005

莱维特, J. B., Yoshioka, T。, & Lund, J. S. (1994). Intrinsic cortical con-
nections in macaque visual area v2: Evidence for interaction be-
tween different functional streams. Journal of Comparative Neurology,
342(4), 551–570. https://doi.org/10.1002/cne.903420405

李, X。, 朱, Q., Janssens, T。, Arsenault, J. T。, & Vanduffel, 瓦. (2019).
In vivo identiﬁcation of thick, thin, and pale stripes of macaque
area v2 using submillimeter resolution (F)MRI at 3 时间. Cerebral
Cortex, 29(2), 544–560. https://doi.org/10.1093/cercor/bhx337
李, Y。, 鲁, H。, Cheng, P。, 锗, S。, 徐, H。, Shi, S.-H., & Dan, 是. (2012).
Clonally related visual cortical neurons show similar stimulus
feature selectivity. 自然, 486(7401), 118–121. https://doi.org/
10.1038/nature11110

Livingstone, 中号. S。, & Hubel, D. H. (1984). Anatomy and physiology
of a color system in the primate visual cortex. Journal of Neuro-
科学, 4(1), 309–356.

Lund, J. S。, Yoshioka, T。, & 莱维特, J. 乙. (1993). Comparison of intrin-
sic connectivity in different areas of macaque monkey cerebral
cortex. 大脑皮层, 3(2), 148–162.

马拉奇, R。, Amir, Y。, 哈雷尔, M。, & Grinvald, A. (1993). Relation-
ship between intrinsic connections and functional architecture
revealed by optical imaging and in vivo targeted biocytin in-
jections in primate striate cortex. 国家会议录
美国科学院, 90(22),
10469–10473. https://doi.org/10.1073/pnas.90.22.10469

Mountcastle, V. 乙. (1997). The columnar organization of the neo-
cortex. Brain: A Journal of Neurology, 120(Pt. 4), 701–722.
Nasr, S。, 波利梅尼, J. R。, & Tootell, 右. 乙. H. (2016). Interdigitated
颜色- and disparity-selective columns within human visual corti-
cal areas v2 and v3. 神经科学杂志, 36(6), 1841–1857.
https://doi.org/10.1523/JNEUROSCI.3518-15.2016

Obermayer, K., & Blasdel, G. G. (1993). Geometry of orientation
and ocular dominance columns in monkey striate cortex. 杂志
of Neuroscience, 13(10), 4114–4129.

Pálﬁ, E., Zalányi, L。, Ashaber, M。, 帕尔默, C。, Kántor, 奥。, Roe,
A. W., . . . Négyessy, L. (2018). Connectivity of neuronal popula-
tions within and between areas of primate somatosensory cortex.
Brain Structure & Function, 223(6), 2949–2971. https://doi.org/
10.1007/s00429-018-1671-8

裴, Y.-C., Hsiao, S. S。, Craig, J. C。, & Bensmaia, S. J. (2010). Shape
invariant coding of motion direction in somatosensory cortex.
公共科学图书馆生物学, 8(2), e1000305. https://doi.org/10.1371/journal.
pbio.1000305

Rakic, 磷. (1988). Speciﬁcation of cerebral cortical areas. 科学,

241(4862), 170–176.

Rakic, Pasko (2008). Confusing cortical columns. 会议记录
the National Academy of Sciences of the United States of
美国, 105(34), 12099–12100. https://doi.org/10.1073/pnas.
0807271105

Rasch, 中号. J。, 陈, M。, 吴, S。, 鲁, H. D ., & Roe, A. 瓦. (2013).
Quantitative inference of population response properties across
eccentricity from motion-induced maps in macaque v1. Jour-
nal of Neurophysiology, 109(5), 1233–1249. https://doi.org/10.
1152/杰恩.00673.2012

Rockland, K. S. (2010). Five points on columns. Frontiers in Neu-
roanatomy, 4, 22. https://doi.org/10.3389/fnana.2010.00022
Roe, A. W., Chelazzi, L。, Connor, C. E., 康威, 乙. R。, Fujita, 我。,
Gallant, J. L。, . . . Vanduffel, 瓦. (2012). Toward a uniﬁed theory
of visual area v4. 神经元, 74(1), 12–29. https://doi.org/10.1016/
j.neuron.2012.03.011

Roe, A. W., 陈, G。, & 鲁, H. D.

(2009). Visual System:
Functional architecture of Area V2. 在: Squire L. 右. (编辑。) Encyclo-
pedia of Neuroscience, 卷. 10, PP. 331–349. 牛津: Academic
按

Roe, A. W., 鲁, H. D ., & Hung, C. 磷. (2005). Cortical processing
of a brightness illusion. 美国国家科学院院刊
Sciences of the United States of America, 102(10), 3869–3874.
https://doi.org/10.1073/pnas.0500097102

Roe, A. W., Winberry, J. E., & 弗里德曼, 右. 中号. (2017). Study of
single and multidigit activation in monkey somatosensory cor-
tex using voltage-sensitive dye imaging. Neurophotonics, 4(3),
031219. https://doi.org/10.1117/1.NPh.4.3.031219

Rust, 氮. C。, & Dicarlo, J. J. (2010). Selectivity and tolerance (“in-
variance”) both increase as visual information propagates from cor-
tical area v4 to IT. 神经科学杂志, 30(39), 12978–12995.
https://doi.org/10.1523/JNEUROSCI.0179-10.2010

Sato, H。, Katsuyama, N。, Tamura, H。, Hata, Y。, & Tsumoto, 时间. (1996).
Mechanisms underlying orientation selectivity of neurons in the
primary visual cortex of the macaque. 生理学杂志,
494(Pt. 3), 757–771.

Sawaguchi, 时间.

(1994). Modular activation and suppression of
neocortical activity in the monkey revealed by optical imaging.
NeuroReport, 6(1), 185–189.

Schwalger, T。, Deger, M。, & Gerstner, 瓦. (2017). Towards a the-
ory of cortical columns: From spiking neurons to interacting neu-
ral populations of ﬁnite size. 公共科学图书馆计算生物学, 13(4),
e1005507. https://doi.org/10.1371/journal.pcbi.1005507

Sharpee, 时间. 奥。, Kouh, M。, & Reynolds, J. H. (2013). Trade-off be-
tween curvature tuning and position invariance in visual area
v4. 美国国家科学院院刊
美国, 110(28), 11618–11623. https://土井.
org/10.1073/pnas.1217479110

Shiozaki, H. M。, Tanabe, S。, Doi, T。, & Fujita, 我. (2012). Neural ac-
tivity in cortical area v4 underlies ﬁne disparity discrimination.
神经科学杂志, 32(11), 3830–3841. https://doi.org/10.
1523/JNEUROSCI.5083-11.2012

Purves, D ., & LaMantia, A. (1993). Development of blobs in the
visual cortex of macaques. Journal of Comparative Neurology,
334(2), 169–175. https://doi.org/10.1002/cne.903340202

Shmuel, A。, Korman, M。, Sterkin, A。, 哈雷尔, M。, Ullman, S。, 马拉奇,
R。, & Grinvald, A. (2005). Retinotopic axis speciﬁcity and selec-
tive clustering of feedback projections from v2 to v1 in the owl

网络神经科学

790

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

3
3
7
7
9
1
0
9
2
4
4
9
n
e
n
_
A
_
0
0
0
8
8
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Columnar connectome: mathematics of brain function

猴. 神经科学杂志, 25(8), 2117–2131. https://土井.
org/10.1523/JNEUROSCI.4137-04.2005

Sincich, L. C。, & Blasdel, G. G. (2001). Oriented axon projections
in primary visual cortex of the monkey. 神经科学杂志,
21(12), 4416–4426.

Sincich, Lawrence C., Adams, D. L。, & Horton, J. C. (2003). 康姆-
plete ﬂatmounting of the macaque cerebral cortex. Visual Neuro-
科学, 20(6), 663–686.

Sincich, Lawrence C., & Horton, J. C. (2005). Input to v2 thin
stripes arises from v1 cytochrome oxidase patches. 杂志
神经科学, 25(44), 10087–10093. https://doi.org/10.1523/
JNEUROSCI.3313-05.2005

Sincich, Lawrence C., Jocson, C. M。, & Horton, J. C.

(2010). V1
interpatch projections to v2 thick stripes and pale stripes. Jour-
nal of Neuroscience, 30(20), 6963–74. https://doi.org/10.1523/
JNEUROSCI.5506-09.2010

斯波恩斯, 氧. (2011). Networks of the Brain. 剑桥, 嘛: 与新闻界.
斯波恩斯, 奥。, 托诺尼, G。, & Edelman, G. 中号. (2000). Theoretical neuro-
anatomy: Relating anatomical and functional connectivity in graphs
and cortical connectionmatrices. 大脑皮层, 10(2), 127–141.
Stepniewska, 我。, Cerkevich, C. M。, & Kaas, J. H. (2016). Cortical
connections of the caudal portion of posterior parietal cortex in
prosimian galagos. 大脑皮层, 26(6), 2753–2777. https://
doi.org/10.1093/cercor/bhv132

Swindale, 氮. V. (2004). How different feature spaces may be rep-

resented in cortical maps. 网络, 15(4), 217–242.

Swindale, 氮. V. (2007). A model for the thick, thin and pale stripe

organization of primate v2. 网络, 18(4), 327–342.

Tanigawa, H。, 王, Q., & Fujita,

(2005). Organization of
horizontal axons in the inferior temporal cortex and primary vi-
sual cortex of the macaque monkey. 大脑皮层, 15(12),
1887–1899. https://doi.org/10.1093/cercor/bhi067

我.

Tolias, A. S。, Sultan, F。, Augath, M。, Oeltermann, A。, Tehovnik,
乙. J。, Schiller, 磷. H。, & Logothetis, 氮. K. (2005). Mapping corti-
cal activity elicited with electrical microstimulation using fMRI in
the macaque. 神经元, 48(6), 901–911. https://doi.org/10.1016/
j.neuron.2005.11.034

Tootell, 右. B., Silverman, 中号. S。, 汉密尔顿, S. L。, De Valois, 右. L。, &
Switkes, 乙. (1988). Functional anatomy of macaque striate cortex.
三、. 颜色. 神经科学杂志, 8(5), 1569–1593.

Torii, M。, Hashimoto-Torii, K., 莱维特, P。, & Rakic, 磷. (2009). Integra-
tion of neuronal clones in the radial cortical columns by EphA
and ephrin-A signalling. 自然, 461(7263), 524–528. https://
doi.org/10.1038/nature08362

Toth, L. J。, 饶, S. C。, Kim, D. S。, Somers, D ., & 在, 中号. (1996). Sub-
threshold facilitation and suppression in primary visual cortex

revealed by intrinsic signal imaging. 国家会议录
美国科学院, 93(18),
9869–9874. https://doi.org/10.1073/pnas.93.18.9869

Ts’o, D. Y。, 吉尔伯特, C. D ., & Wiesel, 时间. 氮. (1986). Relationships be-
tween horizontal interactions and functional architecture in cat
striate cortex as revealed by cross-correlation analysis. 杂志
神经科学, 6(4), 1160–1170.

Ts’o, D. Y。, Zarella, M。, & Burkitt, G. (2009). Whither the hypercol-
umn? 生理学杂志, 587(Pt 12), 2791–2805. https://土井.
org/10.1113/jphysiol.2009.171082

Van Essen, D. C。, Newsome, 瓦. T。, & Maunsell, J. H. (1984). 这
visual ﬁeld representation in striate cortex of the macaque mon-
钥匙: Asymmetries, anisotropies, and individual variability. Vision
研究, 24(5), 429–448.

王, Z。, 陈, L. M。, Négyessy, L。, 弗里德曼, 右. M。, Mishra, A。,
Gore, J. C。, & Roe, A. 瓦. (2013). The relationship of anatomical
and functional connectivity to resting-state connectivity in pri-
mate somatosensory cortex. 神经元, 78(6), 1116–1126. https://
doi.org/10.1016/j.neuron.2013.04.023

Weliky, M。, Kandler, K., Fitzpatrick, D ., & Katz, L. C. (1995). Pat-
terns of excitation and inhibition evoked by horizontal connec-
tions in visual cortex share a common relationship to orientation
columns. 神经元, 15(3), 541–552.

Weller, 右. E., & Kaas, J. H. (1983). Retinotopic patterns of con-
nections of area 17 with visual areas V-II and MT in macaque
猴子. Journal of Comparative Neurology, 220(3), 253–279.
https://doi.org/10.1002/cne.902200302

韦尔斯, J。, Kao, C。, Mariappan, K., Albea, J。, Jansen, 乙. D ., Konrad,
P。, & Mahadevan-Jansen, A. (2005). Optical stimulation of neural
tissue in vivo. Optics Letters, 30(5), 504–506.

Xiao, Y。, 王, Y。, & Felleman, D. J. (2003). A spatially organized
representation of colour in macaque cortical area v2. 自然,
421(6922), 535–539. https://doi.org/10.1038/nature01372

徐, A. G。, Qian, M。, Tian, F。, 徐, B., 弗里德曼, 右. M。, 王,
J. B., 歌曲, X。, Sun, Y。, Chernov, 中号. M。, Cayce, J. M。, Jansen,
乙. D ., Mahadevan-Jansen, A。, 张, X. T。, 陈, G。, & Roe,
A. 瓦. (2019A). Focal infrared neural stimulation with high-ﬁeld
functional MRI: A rapid way to map mesoscale brain con-
nectomes. Science Advances, 5(4):eaau7046. https://doi.org/10.
1126/sciadv.aau7046

徐, A. G。, Rui, 是. Y。, 王, J. B., 歌曲, X. M。, Gothard, K., & Roe,
A. 瓦. (2019乙). INS-fMRI reveals functional connections of amyg-
dalar subnuclei in the Macaque monkey. SPIE Photonics West.
旧金山, CA.

Young, 中号. 磷. (1993). The organization of neural systems in the pri-
mate cerebral cortex. 会议记录. Biological Sciences, 252(1333),
13–18. https://doi.org/10.1098/rspb.1993.0040

网络神经科学

791

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我