PERSPECTIVE - 麻省理工学院人工智能研究专业

PERSPECTIVE

The global neuronal workspace as a
broadcasting network

Abel Wajnerman Paz1,2

1Department of Philosophy, Universidad Alberto Hurtado, 圣地亚哥, 智利
2Neuroethics Buenos Aires, Buenos Aires, 阿根廷

关键词: 意识, Global neuronal workspace, Broadcasting, Functional connectivity

抽象的

A new strategy for moving forward in the characterization of the global neuronal workspace
(GNW) is proposed. According to Dehaene, 尚古克斯, and colleagues (德阿内, 2014,
PP. 304, 312; 德阿内 & 尚古克斯, 2004, 2005), broadcasting is the main function of the
GNW. 然而, the dynamic network properties described by recent graph theoretic GNW
models are consistent with many large-scale communication processes that are different from
broadcasting. We propose to apply a different graph theoretic approach, originally developed
for optimizing information dissemination in communication networks, which can be used to
identify the pattern of frequency and phase-specific directed functional connections that the
GNW would exhibit only if it were a broadcasting network.

介绍

德阿内, 尚古克斯, and colleagues postulate the existence of a global network or a “global
neuronal workspace” (GNW) constituted by a set of cortical neurons that send projections to
many distant areas through long-range excitatory axons. The main function of this network is
to make the information encoded in a given specialized processor globally available by
broadcasting it to all brain systems, a process that constitutes the neural basis of access to
consciousness (德阿内, 2014, PP. 304, 312; 德阿内 & 尚古克斯, 2004, 2005).

Although the model has been supported through the detection of key neural signatures
associated with GNW broadcasting, these are not substantially different from those that could
be associated with alternative large-scale processes. Perhaps the more precise characterization
of these signatures has been provided by recent models describing graph theoretic properties
that were found in transient undirected functional GNW networks. These properties indicate a
high degree of “integration” between network components and therefore contribute to moving
forward in our understanding of the connection between GNW signatures and broadcasting.
尽管如此, integration only entails efficient communication between GNW nodes and is
therefore consistent with very different communication processes. 相比之下, a GNW broad-
casting model entails dynamic network properties uniquely tied to broadcasting. The next sec-
tion characterizes the mentioned ambiguity of the GNW model. We then present a framework
that can be used to depict a set of neural signatures exclusively associated with a GNW broad-
casting process and a possible approach to experimentally detect them. A GNW broadcasting
scheme is constituted by a specific pattern of frequency and phase-specific directed functional

开放访问

杂志

引文: Wajnerman Paz, A. (2022).
The global neuronal workspace as
a broadcasting network. 网络
神经科学, 6(4), 1186–1204.
https://doi.org/10.1162/netn_a_00261

DOI:
https://doi.org/10.1162/netn_a_00261

已收到: 23 十二月 2021
公认: 13 六月 2022

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
Abel Wajnerman Paz
awajnerman@uahurtado.cl

处理编辑器:
Alex Fornito

版权: © 2022
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

Broadcasting:
A one-to-all process dissemination
process in a communication network
G = (V, 乙 ) in which a message m (或者
set of messages M ) originated by one
root node u 2 V is transmitted to all
nodes in G.

connections that could be detected through the application of phase transfer entropy (PTE) 到
the EEG signals that pick up the GNW’s “ignition.”

GNW SIGNATURES

The Four Original Signatures

According to the workspace model, the GNW breaks the modularity of the cortex by making
the information encoded within any given specialized (and otherwise encapsulated) processor
globally available, 那是, by broadcasting it to all the other processors (德阿内 & 尚古克斯,
2004). This broadcasting process was originally associated with four predicted neural “signa-
特雷斯,“ 那是, neural markers that reliably indicate that the stimulus was consciously
perceived.

The first two signatures describe, 分别, the spatial and temporal properties of a large-
scale activity pattern that characterizes conscious states. 第一的, conscious perception is an “ava-
lanche” in which signals pick up strength as they progress forward into the cortex and are
finally spread throughout parietal and prefrontal lobes, resulting in a sustained large-scale igni-
tion reaching and connecting distant processors (德阿内, 2014, PP. 223–225). 第二
signature characterizes the temporal properties of the conscious avalanche. Only for con-
scious stimuli, a late (300 ms after stimulus onset) slow wave of activity is amplified and flows
into the prefrontal cortex and many other associative regions, and then back to visual areas
(德阿内, 2014, PP. 334, 335). 最后, two additional signatures provide a more precise char-
acterization of the GNW global activity pattern: the active units exhibit high-frequency
(gamma-band) oscillations and a massive long-distance phase synchrony between them
(德阿内, 2014, PP. 216, 262; 德阿内 & 纳克卡什, 2001; Mashour, 罗尔夫塞玛, 尚古克斯,
& 德阿内, 2020).

These last two signatures are associated with the specific mechanism through which com-
munication between GNW modules occurs. Dehaene suggests that the GNW implements Pas-
cal Fries’s communication through coherence (CTC) 机制 (德阿内, 2014, PP. 255 ff.;
薯条, 2005, 2015). This is the proposal that gamma-band phase synchronization can have an
essential role in communication between neural populations.

The basic idea is that rhythmic modulations of postsynaptic activity in a given neuron or set
of neurons constitute rhythmic modulations in synaptic input gain or excitability. Presynaptic
inputs that consistently arrive at moments of high postsynaptic input gain will be more effec-
tive than those arriving at random phases of the excitability cycle. When a postsynaptic neu-
ronal group receives inputs from several different presynaptic groups, it will respond primarily
to the presynaptic group to which it is coherent. 因此, effective communication requires rhyth-
mic synchronization between pre- and postsynaptic neurons (薯条, 2005, 2009, 2015). 这
mechanism will be crucial for the discussion of our graph theoretic approach.

Graph Theoretic Signatures

A key development in the characterization of GNW signatures comes from recent graph the-
oretic studies on dynamic functional brain networks. These explore the idea that cognitive
tasks result from transient functional networks, established and dissolved on the timescale
of milliseconds (Bola & Borchardt, 2016; Braun et al., 2015; Gonzalez-Castillo & Bandettini,
2018; Gonzalez-Castillo et al., 2012; Hutchison et al., 2013; Kucyi & 戴维斯, 2014; Kucyi,
Hove, Esterman, 和记黄埔, & Valera, 2017; Simony et al., 2016). Some of these studies char-
acterize the GNW theory as implying such functional reorganization. These approaches offer a
graph theoretic interpretation of the GNW’s ignition in terms of a transient functional network

网络神经科学

1187

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

exhibiting forms of integration that maximize intermodular communication. I will mention
three representative examples of this trend spanning the past decade.

Kitzbichler, Henson, 史密斯, Nathan, and Bullmore (2011) interpret the network organization
predicted by workspace theory as a shift toward small-worldness in which the performance of
tasks that require conscious access reduces minimum path length (maximizing integration) 和
reduces clustering or modularity (thus minimizing segregation). 反过来, Godwin, Barry, 和
Marois (2015) argued that GNW ignition is associated with a degradation of modularity via
an increase in the participation coefficient, 那是, an increase in functional connectivity across
modules rather than within modules. 最后, 德科, Vidaurre, and Kringelbach (2021) argue
that GNW intermodular integration must be characterized through the concept of a functional
rich club. During GNW global ignition, specialized modules tend to be more densely function-
ally connected among themselves than to other brain regions (for complementary GNW anal-
yses, see also Finc et al., 2019; Finc et al., 2017; and Vatansever, Menon, Manktelow, Sahakian,
& Stamatakis, 2015).

These findings constitute a crucial step toward a mechanistic understanding of the GNW.
A key insight is that the large-scale communication between any given pair of GNW nodes
depends not only on a mechanism involving those two nodes (such as CTC) but also on the
global pattern of functional connections between all network nodes. 那是, 沟通
between any pair of GNW modules is facilitated by the transient functional connectivity of
the whole network.

然而, a key assumption of the GNW theory is underdetermined by the predictions pro-
vided by these network models. All the mentioned graph theoretic measures account for the
“integration” of information by the GNW, which in this context is equivalent to a general
notion of communication. Network properties such as reduced average path length, reduced
模块化, and increased rich-club connectivity are used to indicate how communication
between specialized modules is facilitated. In the same way as in the anatomical network
型号, these measures are employed in dynamic models to explain (following Sporns,
Chialvo, Kaiser, & 希尔格塔格, 2004) how a network solves the trade-off between time and
metabolic cost required for communication between a relevant set of nodes (布莫尔 &
斯波恩斯, 2012; Chklovskii & Koulakov, 2004; Kaiser & 希尔格塔格, 2006; 斯波恩斯, 2016; 英镑
& Laughlin, 2015, Chapter 13). 尽管如此, efficient communication is consistent with many
different large-scale processes that may be different from broadcasting. This is why focusing on
network properties uniquely tied to broadcasting is an appealing strategy for exploring the
GNW further.

Broadcasting Versus Alternative Communication Processes

A notion of broadcasting was developed within a graph theory research program that origi-
nated in the 1950s. It is focused on problems concerning information dissemination in com-
munication networks with multiple sources and/or destinations (例如, Bavelas, 1950; Landau,
1954; Shimbel, 1951). A communication network is presented as a graph G = (V, 乙 ) 其中
the set V of vertices or nodes corresponds to the members or processors of the network, 和
set E of edges corresponds to the communication lines connecting pairs of members. A subset
U of nodes are identified as the originators that introduce a set M of messages into G. 期间
each communication round, each informed node makes a call (represented by a directed
边缘); 那是, it sends a message to an uninformed node. During a series of rounds in which
each node is either a message sender or a receiver, a communication task is completed
(数字 1).

Communication network:
A graph G = (V, 乙 ) representing
information dissemination with
multiple sources and/or destinations.

圆形的:
The time unit used to measure calls.
Whereas in some networks each call
takes one round, in a weighted
communication network a weight
can represent the number of rounds
required to make a call through a
given edge.

Call:
The process, represented by a
directed edge, of sending a message
from one informed node to an
adjacent uniformed node through a
direct communication line,
represented by an undirected edge.

Communication task:
Sending a set M of messages in a
communication network G from a set
of informed nodes U ⊆ V to a set of
uniformed nodes by placing a series
of calls over the communication lines
of a network, represented by G’s
边缘.

网络神经科学

1188

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

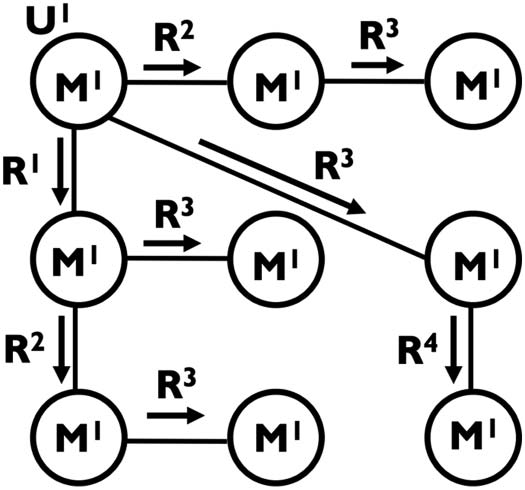
数字 1. A communication network. Node U1 is the originator introducing message M1 to the
网络. Undirected edges represent communication lines between nodes. Directed edges repre-
sent the propagation of M1 from one node to another (IE。, a call) during one of the communication
rounds R1–R4. 在这种情况下, the network is performing a broadcasting process.

例如, Hajnal, Milner, and Szemeredi (1972) considered the so-called gossip prob-
莱姆, which can be characterized as follows: There is a scandal, which can be divided into n
different pieces of information, and there are n people, each of whom knows one piece of
scandal that is not known to any of the others. The problem is to determine how many calls
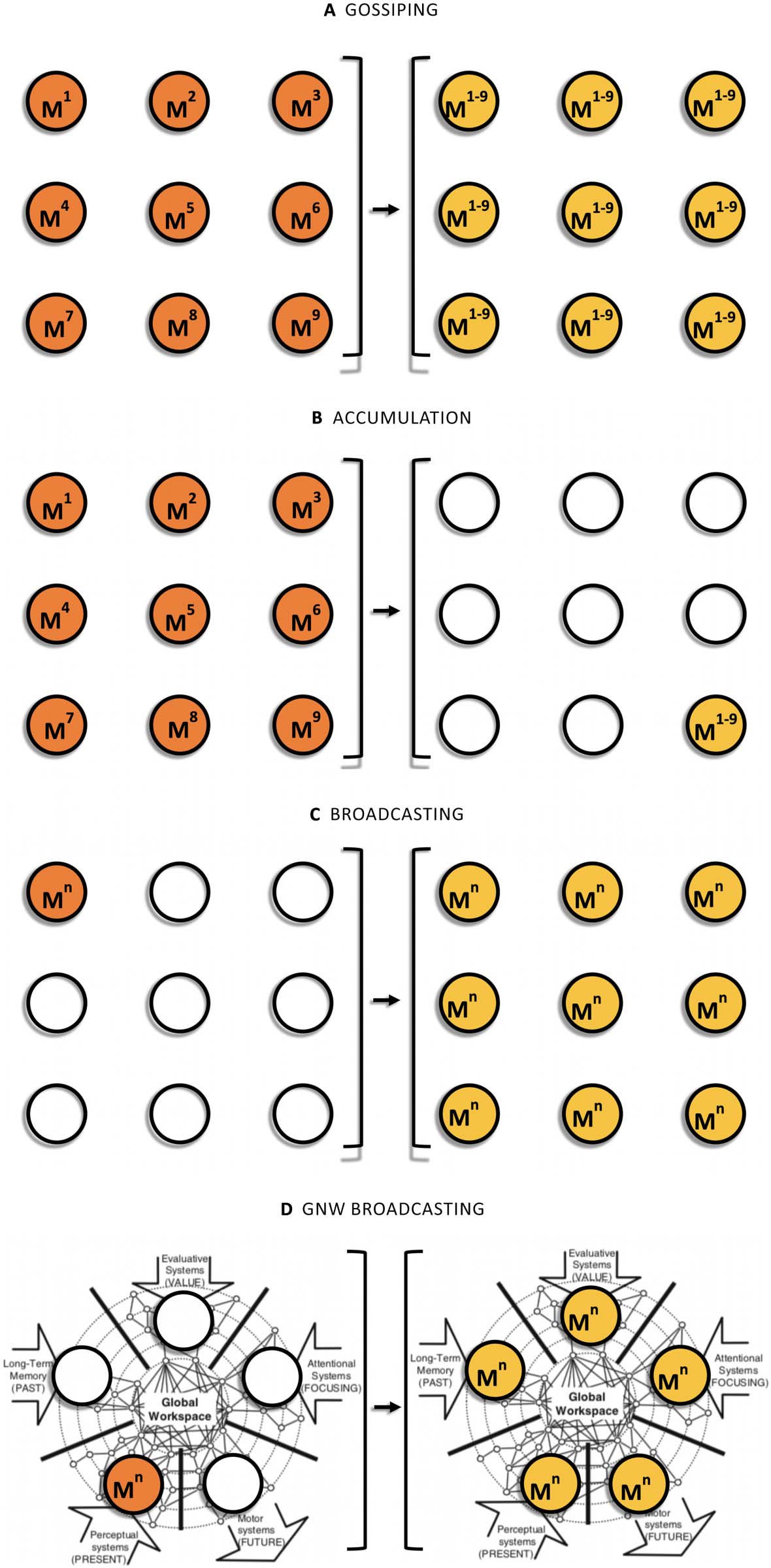
are needed before all the people know all the scandal (图2A). The accumulation problem
is a second task. 在这种情况下, we have the same initial conditions but the task is to accumulate
or send the n pieces of information from all the sources to a single receiver in the network
(Hromkovič et al., 2005, p. 26; 图2B).

A major variant of the gossip problem is the broadcasting problem. Whereas gossiping is an
all-to-all information dissemination process and accumulation is an all-to-one process, broad-
casting is a one-to-all process. Broadcasting is the process in a communication network G = (V,
乙 ), whereby a message m (or set of messages M ) originated by one root or source node u 2 V
is transmitted to all the nodes of the network (Hedetniemi, Hedetniemi, & Liestman, 1988;
Figure 2C).

These tasks define different optimization problems that will have different solutions for a
given number n of nodes. 所以, if the GNW can be characterized as an efficient broad-
casting system (Figure 2D), we should be able to identify signatures that are different from
those it would exhibit if it were dedicated to an alternative communication process. In the next
section the kinds implications that a broadcasting model entails will be articulated.

Broadcast problem:
An optimization problem that
consists of finding the scheme that
has b (你) in a graph G with n nodes.

TAKING BROADCASTING SERIOUSLY

Broadcast scheme:
The specification of a set of calls in a
graph G originating from a node u to
be made during successive rounds
until all network nodes receive a
given message m.

Broadcast tree:
A spanning tree of a graph G rooted
at the source u of a given broadcast
scheme s for G that includes only the
set of communication lines required
to execute s.

The Broadcast Problem
Broadcasting is accomplished by placing a series of “calls” over the communication lines of a
网络. According to the original version of the problem, the main goal is to complete this
task as quickly as possible (for further discussion, see the section below entitled Neural Broad-
casting Design Variables). In order to achieve this, a broadcast algorithm or scheme must be
设计的. A broadcasting scheme for a message m is the specification of a set of calls in a
graph G originating from a vertex u to be made during successive time steps or rounds until
all network nodes receive m (Farley, 2004). The broadcast scheme generates a broadcast tree,
which is a spanning tree of the graph rooted at the originator (Harutyunyan, 2014; Harutyunyan
& 李, 2017, 2020; Harutyunyan, Liestman, Peters, & Richards, 2013). The broadcast tree is sim-
ply the set of communication lines required to execute a given scheme.

网络神经科学

1189

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 2. An input-output representation of three communication tasks: gossiping (A), 积累
(乙), and broadcasting (C). Nodes on the left side represent the initial state of the network (the initial
distribution of messages M1–Mn), whereas nodes on the right side represent the result of the relevant
communication algorithm. A GNW broadcasting model (D) can be used to determine what network
properties the GNW would have if it were exclusively dedicated to solve this third problem.

网络神经科学

1190

The global neuronal workspace as a broadcasting network

Broadcast graph problem:
The optimization problem that
requires finding n schemes for
broadcasting in an n node network,
each of which has its root in a
different node and minimal b (你).

Broadcast time:
The minimum time, 乙 (你), 为了
broadcasting from u in a given graph
G with n nodes.

Minimum broadcast tree:
A subgraph containing only the edges
necessary to implement a broadcast
scheme with minimal b (你).

Broadcast time of a graph G:
The time equal to the maximum
broadcast time of any source node u
in G, 那是, 乙 (G) = max {乙 (你) | u 2
V (G)}.

Broadcast graph:
The graph that results from
combining the minimum broadcast
trees for the schemes that solve a
broadcast graph problem.

Minimum broadcast graph:
A graph on n nodes with optimal
乙 (G) and the minimum number of
边缘, determined by a broadcast
function B (n).

The original formulation of the broadcast problem involved a set of restrictions for calls.
These represent constraints imposed by some of the systems to which the framework was orig-
inally applied (例如, people communicating by telephone). 所以, they may have to be
revised if we want to apply this approach to a brain system (see the section below entitled
Neural Restrictions on the Broadcast Model). The original rules determined that (A) each call
involves only two nodes (a sender and a receiver), (乙) each call requires one round or unit of
时间, (C) a node can participate in only one call per unit of time, (d) a node can only call its
neighbors (IE。, its adjacent nodes), 和 (e) many calls can be performed in parallel (例如, Farley,
Hedetniemi, 米切尔, & Proskurowski, 1979; Harutyunyan, 2014; Hedetniemi et al., 1988).

The basic broadcasting optimization problem is to find the scheme that minimizes the num-
ber of rounds required to complete broadcasting from a message originator, node u, in a con-
nected graph with n nodes. The minimum time for broadcasting from u in a given graph G with
n nodes is called the broadcast time b (你) of a vertex u in G. The task is to find the graph that
can implement a scheme with minimal b (你), which is a minimum broadcast tree (a tree for
which b (你) = ⌈log2n⌉ in networks constrained by the rules mentioned above; Proskurowski,
1981).

A more complex version of this problem is to determine how efficient a network is in broad-
casting from any of its nodes. The broadcast time of the whole graph G, 乙 (G), is defined as
equal to the maximum broadcast time of any vertex u in G, 那是, 乙 (G) = max {乙 (你) | 你 2 V
(G)} (例如, Harutyunyan & 李, 2017). 在这种情况下, the optimization problem is to find n schemes
for broadcasting in an n node network, each of which determines a minimal broadcast tree
with its root in a different node. The graph that results from combining these trees is a broad-
cast graph. The broadcast time of the graph b (G) seems a plausible design variable for the
GNW. This is because all the specialized processors must be able to make their outputs glob-
ally accessible. 最后, efficient broadcasting may also be required to minimize wiring cost.
The minimum broadcast graph (数字 3) is a graph on n vertices with optimal b (G) and min-
imum number of edges, determined by a broadcast function B (n) (Farley, 1979; Harutyunyan
& 李, 2017).

The present framework entails that if the GNW is an efficient broadcasting network con-
necting n nodes, it will exhibit very specific structural and functional properties (IE。, its broad-
cast graph and broadcast schemes, 分别).

A Neural Broadcast Model

Characterizing the specific predictions that a GNW broadcasting model entails (IE。, 这
GNW’s broadcast graph and schemes) requires experimentally determining the value of some
key network parameters (见下文), and therefore it is beyond the scope of this perspective.
然而, this section and the two that follow will conceptualize the kinds of predictions that
the framework can make (例如, explain what a GNW broadcasting scheme is); identify the
parameters that must be experimentally determined for computing the specific GNW broad-
cast graph and schemes; and propose a possible approach for experimentally testing these
specific predictions.

The first step in the characterization of the GNW as a broadcast network is finding an
adequate parcellation scheme. Given that the function of the GNW is to broadcast signals
from any given specialized module to all the others, the natural choice is to characterize these
modules as the nodes of the GNW broadcast network. 至关重要的是, unlike nodes in alternative
macroscale parcellation strategies (例如, sensor-based schemes), modules may define actual
anatomical and functional neural boundaries that can be detected through graph theoretic

网络神经科学

1191

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

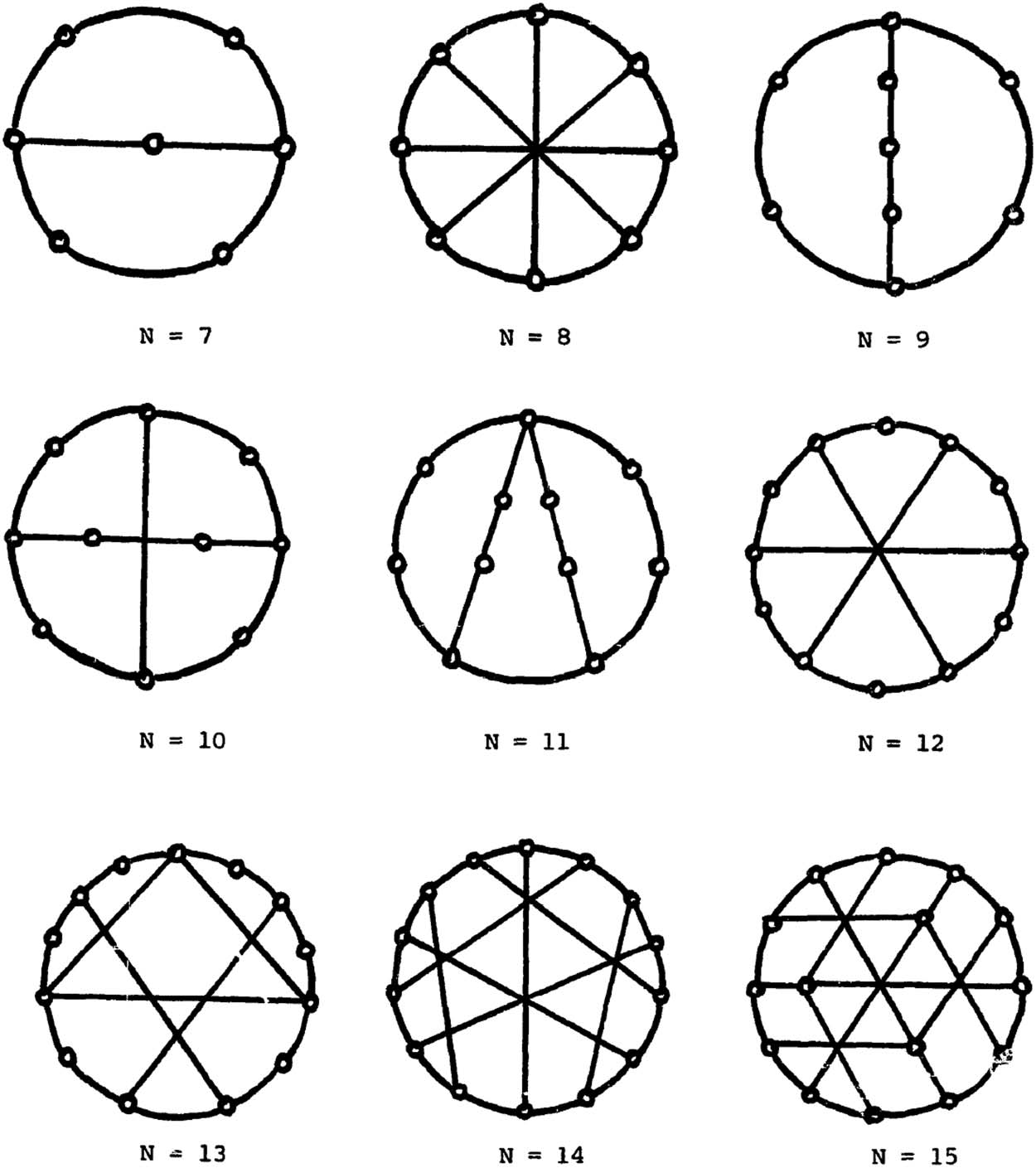
数字 3.

From Farley et al. (1979). Minimum broadcast graphs for n = 7–15 nodes.

方法. In graph theoretic terms, a module (also called “community”) is a subset of nodes
within a network that exhibit dense internal connections between them but weak or sparse
connections with nodes that do not belong to that subset. These are often considered the
building blocks in the organization of brain networks and are detected through different
方法, of which the most widely applied is modularity maximization. This method aims
to maximize a modularity quality function Q (纽曼 & Girvan, 2004), where a partition
of a network into different communities has a high Q value when its communities are more
internally dense than would be expected by chance (for a technical and methodological anal-
ysis of this approach, see Betzel, 2020; 斯波恩斯 & 贝策尔, 2016).

This notion is different from the characterization of modules in cognitive science as systems
specialized for realizing particular cognitive functions (福多尔, 1983), often defined by a set of
special features such as informational encapsulation and inaccessibility, fast and mandatory
加工, fixed neural architecture, and/or domain specificity, 除其他外. As we saw,
the GNW presupposes a modular architecture in this last sense: The GNW is supposed to
diminish the modules’ informational encapsulation. 然而, the connection between graph
theoretic and cognitive modules has been explored in both structural and functional brain net-
作品. 例如, the community structure that was discovered in the C. elegans network
through different methods (Bassett et al., 2010; Sohn, Choi, Ahn, 李, & Jeong, 2011; Towlson,
Vértes, Ahnert, Schafer, & 布莫尔, 2013) seems to line up with the organization of its func-
tionally specialized structures (例如, Jarrell et al., 2012; Pan, Chatterjee, & Sinha, 2010; Sohn

网络神经科学

1192

The global neuronal workspace as a broadcasting network

等人。, 2011). Other examples of anatomical modules that map onto known cognitive modules
include Drosophila (Shih et al., 2015), 老鼠 (王, 斯波恩斯, & Burkhalter, 2012), 和老鼠
(丢弃, 斯波恩斯, & 斯旺森, 2015) 脑. In the human brain, Crossley et al. (2013) associated
modules defined by functional connectivity with specific cognitive domains. 更普遍,
it has been shown that functional modules identified through community detection methods
line up with specialized modules with proprietary cognitive domains (贝策尔, 2020; 莫尼耶,
兰比奥特, & 布莫尔, 2010; 斯波恩斯 & 贝策尔, 2016).

If the cognitive modules in Dehaene’s model also line up with community analysis, then its
application as a parcellation scheme entails that the GNW has a relatively small number of
节点. This means that the task of finding the GNW broadcast graph and schemes is a rela-
tively simple computational problem. The problem of finding the optimal broadcast algorithm
for a network with an arbitrary number n of nodes is a hard problem (更确切地说, an NP-
complete problem; Farley et al., 1979; Garey & 约翰逊, 1979, Problem ND4). This is why
minimum broadcast graphs have been determined for specific and relatively low values of n
(见图 3). Global accessibility only involves perceptual, motor, long-term memory, eval-
uation, and attention systems (德阿内 & 纳克卡什, 2001). By identifying GNW nodes with
cognitive modules, we know that in this network n is low and its minimum broadcast graph is
plausibly already known or easily determinable.

The next step is to understand how a broadcasting scheme (IE。, a sequence of calls) 是
accomplished between such set of nodes. We saw that a call is the process, represented by
a directed edge, of sending a message from one node to another through a direct communi-
cation line, represented by an undirected edge. At the neural level, this could be understood as
the propagation of an electrical (or electrochemical) signal from one neural structure to
another through the fiber tract directly connecting them (假如, 扎莱斯基, & 布莫尔,
2016, Chapter 7). In network neuroscience terms, identifying signal propagation requires
determining edge direction, which can be accomplished through different approaches, 这样的
as Granger causality (例如, 德什潘德, Santhanam, & 胡, 2011; Goebel, Roebroeck, Kim, &
Formisano, 2003), dynamic causal modeling (例如, 弗里斯顿, Moran, & 赛斯, 2013; Kahan &
Foltynie, 2013), and lagged correlations (米特拉 & Raichle, 2016).

A call is not only defined by a directed functional connection between two nodes. 这也是
constituted by the specific communication line or anatomical edge underlying this functional
联系. Calls bridge structural and functional connectivity. Different approaches are being
developed for determining the relationship between functional and structural connections
(例如, Avena-Koenigsberger, Misic, & 斯波恩斯, 2018; Griffa et al., 2017; Mišić et al., 2016;
Suárez et al., 2020; see Sadaghiani & Wirsich, 2020, for a review). 因此, a neural call will
be a directed functional connection between two nodes depending on a direct anatomical con-
nection between them. 反过来, a broadcast scheme will be a sequence of such calls. 那是, A
scheme describes the trajectory or temporal pattern of signal propagation through a structural
网络.

Having identified the elements of neural broadcasting, we can now specify what kind of
predictions the model will make regarding GNW structural and functional properties. A first
prediction is that the anatomical connections between n GNW modules will resemble the
broadcast graph for n nodes. Assuming that the GNW has the anatomical structure of a
small-world network, the broadcast model would describe the pattern of long-range intermod-
ular connections (those reducing average path length) that specifically facilitates broadcasting.
A second prediction is related to how the GNW broadcasting schemes will shape dynamical
功能连接. During its ignition, the GNW will exhibit a specific pattern of directed

网络神经科学

1193

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

functional dependencies between its nodes, which will have the form of a minimum spanning
tree with its root at the originator module. 最后, given that broadcasting is accomplished
through neural calls, a further prediction is that each functional edge between GNW nodes
will depend on a structural edge belonging to the GNW broadcast graph.

How can these predictions be experimentally assessed? Regarding the anatomical proper-
ties associated with the broadcasting model, a first possibility is to explore them by employing
any of the different methods for identifying structural macroscopic connectivity (anatomically
segregated brain regions connected by interregional pathways), including invasive (例如, 他的-
tological dissection and staining, degeneration methods, or axonal tracing) and noninvasive
in vivo mapping (例如, diffusion MRI and tractography). 例如, by applying white matter
tractography to diffusion MRI data, we can produce a structural connectivity matrix, represent-
ing connectivity between GNW nodes.

然而, these matrices describe only direct connections between regions, and identifying
and characterizing indirect polysynaptic connections may be crucial for computing the opti-
mal GNW broadcasting schemes that will be executed over its structural connections. 为了
实例, we will see in the next section (Neural Restrictions on the Broadcast Model) 那
broadcasting rounds can probably be implemented in the GNW by the oscillation cycles of
the CTC mechanism. These cycles determine the time window during which communication
between a pair of directly connected pre- and postsynaptic neurons is possible. 因此, 社区-
nication through a path with n synaptic crossings will require n broadcasting rounds. 给定
that directly connected regions are generally sparse (there are no white matter tracts between
many pairs of regions), the optimal strategy minimizing GNW broadcasting time should prob-
ably be computed over a weighted structural matrix including information about the time costs
of indirect connections.

In a recent study, Seguin, Tian, and Zalesky (2020) analyzed polysynaptic neural signaling
by transforming structural connectivity matrices into communication matrices that quantified
the efficiency of communication between indirectly as well as directly connected regions
under different network communication models, defined by different kinds of schemes or
算法. 有趣的是, the assessment of communication efficiency relied on applying these
different optimization strategies to matrices with different kinds connectivity weights that oper-
ationalize metabolic factors shaping large-scale signaling (布莫尔 & 斯波恩斯, 2012; 假如
等人。, 2016; 鲁比诺夫 & 斯波恩斯, 2010). Efficient communication will privilege high-volume
white matter projections that may enable fast and reliable signal propagation, 连接
with a lower number of synaptic crossings, and connections with less physical length. Follow-
ing this approach, the optimal GNW broadcasting schemes can be computed for a weighted
structural graph representing some of these parameters. 至关重要的是, the binary weight represent-
ing the number of synaptic crossings of a given edge connecting two GNW nodes can be used
to measure its time cost in terms of broadcasting rounds (see the next section).

反过来, the assessment of the functional properties described by the broadcasting model
presents different challenges. Functional connectivity is very often measured from functional
magnetic resonance imaging (功能磁共振成像) data that, having a spatial resolution of the order of some
millimeters, can be employed for reliably mapping large-scale functional networks (狐狸 &
Raichle, 2007; Gillebert & Mantini, 2013). 然而, despite a number of technical issues,
the higher temporal resolution electroencephalography (EEG) or magnetoencephalography
(乙二醇) makes them potentially better suited than fMRI to capture the dynamics of GNW broad-
casting, which is characterized by functional connections that rely on the CTC mechanism,
那是, on the phase alignment of oscillations with specific frequencies.

网络神经科学

1194

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

Perhaps the main technical issue related to EEG spatiotemporal mapping is that at each
channel, the signal is the result of the contributions from an unknown number of different
来源, including distant neural and nonneural sources (Lopes da Silva, 2013). 最后,
sensor-level data cannot provide the information required to identify the spatial origin, trajec-
保守党, and destination of a neural broadcasting call. This is why source modeling is necessary to
resolve (to some degree) the ambiguity of sensor-level analysis (巴耶莱特, 2017; Lopes da Silva,
2013; Michel et al., 2004; Stropahl, Bauer, Debener, & Bleichner, 2018). 例如, 刘,
Farahibozorg, Porcaro, Wenderoth, and Mantini (2017) 和刘, Ganzetti, Wenderoth, 和
Mantini (2018) have recently proposed the use of independent component analysis (ICA),
which performs a blind decomposition of different spatiotemporal patterns that are mixed in
数据, assuming that these patterns are mutually and statistically independent in time or
空间. ICA identifies a number of independent components, each of which consists of a spatial
map and an associated time course (Calhoun, Adali, Pearlson, & Pekar, 2001). The IC spatial
map reveals brain regions that have a similar response pattern, and are therefore considered to
be functionally connected (布鲁克斯等人。, 2011; Mantini et al., 2007).

然而, we saw that GNW broadcasting schemes are constituted by directed functional
connections that depend on the phase alignment of oscillations with specific frequencies. A
number of very recent EEG-based network analyses use phase transfer entropy (PTE) for iden-
tifying phase-specific directed functional connectivity as part of the biomarkers of different
psychiatric disorders. PTE was presented by Paluš and Stefanovska (2003) and evaluated by
洛比尔, 七只母鸡, 崇拜, and Palva (2014), and is a reformulation of Granger’s causality
principle mentioned above (Granger, 1969; Wiener, 1956). Unlike other phase synchrony
指标 (Rosenblum, Pikovsky, & Kurths, 1996; 斯塔姆, 诺尔特, & Daffertshofer, 2007; Vinck,
Oostenveld, van Wingerden, Battaglia, & Pennartz, 2011), PTE allows identification of the
direction of information flow. Unlike other directed functional connectivity metrics, it allows
identification of frequency and phase-specific information flow. 例如, Hasanzadeh,
Mohebbi, and Rostami (2020) used PTE to discover patterns of directed connectivity associ-
ated with major depressive disorder. In addition to local and global efficiency, they calculated
node degree (number of links connected to a node) and node strength (the sum of link weights
connected to a node), separately computing inward and outward links (in-degree, in-strength,
and out-degree and out-strength, 分别). 反过来, Ekhlasi, Nasrabadi, and Mohammadi
(2021) investigated directed functional connections in attention-deficit/hyperactivity disorder
(ADHD) patients with EEG by using PTE in each frequency band during an attentional task.
Among other findings, they showed that the posterior to anterior pattern of connectivity com-
monly seen in the control group is disturbed in the ADHD patients in the theta band during
visual tasks. 最后, Al-Ezzi, Al-Shargabi, Al-Shargie, and Al-Shargabi (2022) developed an
EEG study of functional directed connectivity for assessing the severity of social anxiety disor-
这 (SAD) in different patients. They identified the direction of functional connections by using
partial directed coherence (PDC) at four frequency bands (delta, theta, alpha, and beta). PDC
is a frequency-domain metric similar to PTE that is also based on the Granger causality
方法. In addition to other network properties, they also used in-degree, in-strength, 和
out-degree and out-strength for assessing the severity of SAD.

因此, PTE or PDC could constitute a possible approach for assessing the direction of EEG-
detected functional connections in the GNW. The GNW model predicts an intense propaga-
tion or ignition of neural activity particularly toward the prefrontal and parietal cortex at 200 到
300 ms after stimulus onset on trials with conscious perception. This is a robust signature that
can be detected through EEG independently of stimulus modality or paradigm used to manip-
ulate consciousness (Mashour et al., 2020). Given a GNW ignition originated from a specific

网络神经科学

1195

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

module u, we can examine whether the system implements a broadcasting process by deter-
mining whether the direction of each gamma-band functional connection between GNW
modules during this process is consistent with the direction of the calls that constitute the
GNW scheme for broadcasting from u.

然而, computing the GNW broadcasting schemes with which PTE analysis will be
matched may require introducing a number of biologically plausible constraints and param-
eters that were not considered in the more basic versions of the broadcast model. 这些骗局-
straints will be examined in the next section.

Neural Restrictions on the Broadcast Model

Calls (and consequently schemes) are also defined by the restrictions of the original version of
the broadcast problem, which specify how they work in some of the systems to which the
framework was originally applied (例如, communication by telephone). These constraints
strongly shape the predictions of our network model. 因此, it is crucial to assess whether they
apply to neural processing. 在这个部分, we will focus on what we take to be the most prob-
lematic constraints on calls.

第一的, we have to assess the constraints prohibiting that a given node has simultaneous rela-
tions with n > 1 节点. These are the conditions that a node can participate in only one call
per round and that each call involves only two nodes.

Telesford, 辛普森, Burdette, Hayasaka, and Laurienti (2011) have analyzed information
flow in brain networks by following a characterization of different flow types provided by
Borgatti (2005). There are at least two classification parameters that are relevant for neural
沟通. 第一的, nodes can communicate with each other via transfer (IE。, the message
remains at only one node at a time) or via replication (IE。, the message is copied at each
node). If a system communicates through replication, we should determine whether informa-
tion is duplicated at one node at a time (serial) or simultaneously duplicated at several nodes
(parallel). Telesford et al. (2011) claim that the brain uses parallel duplication. This is implied
by how signal propagation works in divergent connections (IE。, multiple synaptic outputs from
a single source). Activation of multiple synapses from a single terminal occurs simultaneously
(例如, Shepherd, 2003, p. 10). A neuron can send signals simultaneously to different postsyn-
aptic neurons and, 最后, through different neural paths.

幸运的是, broadcasting processes with one-to-many relations have been considered in
the literature. There are two different approaches to this form of broadcasting. In “radio broad-
casting,” each node makes simultaneous calls to all of its neighboring nodes. In broadcasting
with “conference calls,” each node makes one call per round but each call can involve n ≥ 2
节点. A question for further research is to determine which, if either, of these approaches
would be suitable for modeling the GNW. (例如, Telesford et al., 2011, affirms that
the firing neuron typically activates approximately 30% of all synapses in a stochastic manner.
This seems to favor conference calls, in which not all of the postsynaptic neurons would be
activated.)

第二, we have to examine the rule that each call requires one unit of time. 这需要
determining first whether there is a GNW round. Although the idea that neural processes in
general can be parsed into regular and functionally relevant time intervals seems implausible
(Piccinini & Bahar, 2013), it is possible that the GNW is an exception.

The idea that the CTC mechanism underlies communication in the GNW suggests a can-
didate for a GNW round. As we saw, synchronization between pre- and postsynaptic neurons

网络神经科学

1196

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

determines the time window in which effective communication between them is possible.
CTC demands that information is only sent at moments of high input gain in the postsynaptic
oscillation cycle. This cycle is a possible candidate for a GNW communication round
因为, as we saw, the network produces a large-scale synchrony between its active units.
This suggests that all of the GNW active units have a regular and shared series of time windows
in which communication between them can occur. (Recall that within this context neural syn-
chrony refers to phase alignment.) The identification between broadcasting rounds and oscil-
lation cycles is a possibility that could be experimentally and theoretically explored.

Assuming that these cycles do constitute GNW rounds, what about the condition that each
call occurs in one round? It seems that this condition should be revised. As we suggested,
many edges in the GNW network are probably polysynaptic paths connecting two processors
and therefore communication between processors could take more than one round. A possible
way to address the broadcasting problem in a network not satisfying this one-round condition
is by using a weighted graph in which each weight represents the time cost (IE。, 的数量
rounds) of communicating through a given edge. We saw that binary weights have been used
to represent the number of synaptic crossings of a given edge (Seguin et al., 2020). In a broad-
casting model the same weights could stand for the number of rounds required for sending a
message through a given edge. 因此, the tree representing an optimal GNW broadcast scheme
would be a weighted minimum spanning tree. The algorithm for developing a minimum span-
ning tree in a weighted graph was developed by Prim (1957).

An additional key constraint that a broadcasting model of neural signal propagation should
account for is related to recent discussions on neural routing. Routing involves the control of
paths that information can take across a network. Given that physical networks have limited
资源, the role of routing is to allocate signal paths in a way that optimizes relevant com-
munication goals, such as those defining the broadcasting problem (IE。, time and wire mini-
mization). 在这个意义上, a scheme constituting the optimal solution to a given broadcasting
problem represents an efficient routing strategy. 然而, we still need to assess whether it
lines up with the general strategies that are plausibly implemented by neural communication.

Daniel Graham distinguishes three different routing models that have been employed in
神经科学 (例如, Graham, 2014; Graham & Rockmore, 2011). According to a message-
switched routing model, each message is passed along in its entirety from node to node.
Graham suggests that it is implausible that this strategy is implemented by brain networks
because message-switched routing requires memory buffers to store messages in a queue in
which they wait their turn to be passed along. 反过来, in circuit-switched routing an exclusive
path is established between the nodes that send and receive a given message. 然而, 这样的
systems are plausibly not implemented by the brain, 因为, among other reasons, 它不是
have the resources for the all-to-all connectivity that exclusive paths between each sender and
each receiver would require. 最后, in packet switching routing (the scheme used on the
internet), messages at a source are chopped into small packets and then reassembled at their
destination. As Graham and Rockmore (2011) point out, packet switching has several appeal-
ing parallels with cortical signaling. They emphasize that this strategy entails (A) an ability to
dynamically reroute traffic, as cortex does following lesion; (乙) a capacity for different appli-
阳离子 (例如, 电子邮件, http) to run concurrently on the same system, as distinct modalities and
signaling systems do in cortex; 和 (C) an inherent hierarchy of the network protocol stack,
which mirrors hierarchical organization within and across cortex.

How would a GNW scheme look if it performed broadcasting by using packet switching
routing? There is a version of the broadcasting problem, first studied by Chinn, Hedetniemi,

网络神经科学

1197

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

and Mitchell (1979) and Farley (1980), in which the broadcasted message at an originator
node can be represented as being chopped into different sub-messages. Given that each
sub-message is broadcasted to all network nodes, all sub-messages will be reunited at each
destination to be assembled, as packet switching requires. Multiple message broadcasting is
the process of multiple message dissemination in a communication network in which n mes-
sages, originated by one vertex, are transmitted to all vertices of the network (Harutyunyan,
2006). 在这种情况下, the optimization problem requires finding, for m nodes, the graph and
scheme with the minimum number of time units necessary to broadcast n messages to all ver-
tices from any given originator.

此外, the fact that GNW broadcasting depends on CTC could also contribute to
understanding how routing may work in this system. In CTC models of visual processing,
the feedforward propagation of signals is modulated by top-down signals. If CTC also controls
signals within the GNW, then their propagation schemes would also be regulated by feedback
signals from receptor units. Graham (2014) has pointed out that neural feedback from higher
levels in a processing hierarchy could be a fundamental aspect of neural routing. The optimi-
zation of GNW schemes predicted by the broadcasting model could be the result of signal
routing through the CTC mechanisms.

最后, there is an additional restriction that did not affect the original broadcasting model
but may nonetheless be required for its neural implementation. We need to assess whether, 为了
each node, sending a message (or a number of messages) can be a function of a number of
inputs defining a transmission threshold. Very often neural communication depends on the
summation of presynaptic potentials in a shared post postsynaptic neuron within a time win-
dow (例如, the kind of integration performed by simple cells in the visual cortex). This kind of
restriction would obviously affect broadcasting schemes, as a given node would make a call
(or a number of simultaneous calls) 什么时候 (and only when) a given number of signals have
arrived from other nodes. 然而, the fact that GNW communicates through the CTC mech-
anism suggests that its broadcasting scheme will possibly not involve a fixed or general input-
output rule of this kind. Recall that CTC’s main function is to modulate input gain or excitability,
thus making possible to route neural signals in a flexible way by affecting the sensitivity of a given
node to specific input signals (薯条, 2015). In CTC communication, postsynaptic units can selec-
tively modulate which presynaptic are effective in producing postsynaptic activation and which
不是. 此外, GNW feedback projections act as distributed routers through which sig-
nals can be amplified, sustained, and spread (Mashour et al., 2020), modulating the strength of
the input signals themselves. This routing is plausibly a form of balanced amplification that
depends not only on interareal excitatory feedback connections but also on intra-areal lateral
inhibition, so that the facilitation of signal propagation between weakly connected areas does
not undermine the stability of more strongly connected areas (Joglekar, Mejias, 哪个, & 王,
2018). These top-down routing mechanisms can be used to adapt input-output relations at each
GNW node to fit an optimal broadcasting scheme.

Neural Broadcasting Design Variables

In addition to constraints, we must also consider whether the design variables that define the
broadcasting problem (time and wiring costs) also require adjustment or reinterpretation in
order to represent plausible GNW demands.

The idea that brain networks evolved to solve the trade-off between wiring cost and
processing speed can be traced back to Ramón y Cajal’s time and space conservation laws
(布莫尔 & 斯波恩斯, 2012; Chklovskii & Koulakov, 2004; Kaiser & 希尔格塔格, 2006; 斯波恩斯,

网络神经科学

1198

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

2016; 英镑 & Laughlin, 2015, Chapter 13). In network neuroscience, small-world networks
have been proposed as a possible solution to this trade-off. Regular clustering minimizes
wiring cost, whereas short average path length produced by random long-range connections
minimizes conduction delay, thus increasing the speed at which information can be
exchanged. 因此, the broadcast approach can be considered a development of small-world
GNW models in the following sense: 如果 (as Kitzbichler et al., 2011, argue) the GNW exhibits a
small-world structure, then the communication processes it performs are plausibly optimized
for minimizing time and wiring cost. The broadcast model then shows how the optimization of
those specific parameters would affect the pattern of intermodular connections of this small-
world network if it were dedicated exclusively to broadcasting.

Another possible worry is related to a design variable that seems to be crucial to neural
设计, 即, energy cost. In very early studies of neural information transmission, it has
been suggested that because the brain is one of the metabolically most active organs of the
身体 (Sokoloff, 1989), optimizing neural processing would require a compromise between
energy and informational efficiency (例如, 征收 & Baxter, 1996). 例如, a long-standing
hypothesis affirms that the visual system optimizes information processing by implementing
sparse coding, which basically consists of representing each environmental condition by using
very few active units (巴洛, 1961). This is why it is reasonable to ask whether and how the
demand for energy cost minimization shapes a broadcast network. Calls seem to be a key
component of broadcasting energy cost. A GNW call is a signaling process, and neural sig-
naling has been considered a major element in the brain’s energy budget (Attwell & Laughlin,
2001). 因此, it is plausible that the cost of a broadcasting process is at least partially deter-
mined by the total number of calls required by the implemented algorithm or scheme.

尽管如此, once we identify the number of calls as one of the key elements for estimating
broadcasting energy cost, it becomes clear why this variable has not been considered in the
文学. The main reason is that this number is constant, 那是, alternative algorithms for
broadcasting to a given number of nodes require the same amount of calls. Although the pos-
sibility of having simultaneous calls makes broadcasting time much smaller, n - 1 calls are
always required to broadcast in graphs with n nodes (Richards & Liestman, 1988). For broad-
casting in k-uniform hypergraphs (the kind of graph required by conference calls) with n
节点, n - 1 / k − 1 calls will be required.

当然, energy cost makes no difference regarding algorithm choice only if we assume
that all calls have the same cost. 然而, we saw that this is plausibly not the case for the
GNW. Many GNW edges may be polysynaptic paths that require more than one round to
make a call. Part of the energy cost of a particular call may be given by the n consecutive
synapses that a signal has to pass through in order to go from one processor to another. If n
is different for different GNW edges, then the broadcasting scheme could be optimized by
using only the cheapest paths. 然而, notice that an energy weight of this kind would be
redundant. If these weights are determined by the number of synaptic crossings of a given
小路, they will be equal to the time weight mentioned in the previous section.

结论

The graph theoretic characterization of the GNW theory’s key assumption, 那是, that the GNW
is a broadcasting network, can contribute to the development of its model. It predicts fine-
grained network properties that are uniquely tied to broadcasting. Unlike current GNW network
型号, which focus exclusively on undirected functional connectivity associated with efficient
沟通, the broadcast model entails signal propagation hypotheses characterized in

网络神经科学

1199

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

terms of directed functional connectivity. GNW broadcasting schemes are constituted by fre-
quency and phase-specific directed functional connections that could be detected through
the application of phase transfer entropy (PTE) to the EEG signals that pick up the GNW’s igni-
的. The computation of these schemes requires experimentally determining time weights for
each GNW path through the detection of polysynaptic connections and theoretically determin-
ing a communication strategy (例如, multiple vs. single message broadcasting and radio broad-
casting vs. conference calls). 最后, the model is not an alternative to but a development of
previous ones in that it abstracts away from intramodular connectivity and explores the specific
pattern of long-range intermodular connections described by small-world GNW models.

致谢

The author thanks researchers that discussed previous versions of this manuscript, 包括
Nicolás Serrano, Sabrina Haimovici, Arleen Salles, Francisco Pereira, Juan Manuel Garrido,
Rodolfo Aldea, Gabriel Reyes, Ignacio Cea, Mazviita Chirimuuta, Alfredo Vernazzani, Daniel
Burnston, and Julieta Picasso Cazón.

作者贡献

Abel Wajnerman Paz: 概念化; 调查; Writing – original draft; Writing –
review & 编辑.

资金信息

PI: Abel Wajnerman Paz, Funding Agency: Agencia Nacional de Investigación y Desarrollo,
奖项ID: FONDECYT INICIACIÓN 11220327.

PI: Juan Manuel Garrido, Funding Agency: Fondo Nacional de Desarrollo Científico y

Tecnológico, 奖项ID: FONDECYT REGULAR 1210091.

PI: Francisco Pereira, Funding Agency: Agencia Nacional de Investigación y Desarrollo,

奖项ID: FONDECYT REGULAR 1200197.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

参考

Al-Ezzi, A。, Al-Shargabi, A. A。, Al-Shargie, F。, and Al-Shargabi, A.
(2022). Machine learning for the detection of social anxiety dis-
order using effective connectivity and graph theory measures.
CMPBUP-D-22-00033. https://ssrn.com/abstract=4030605

Attwell, D ., & Laughlin, S. 乙. (2001). An energy budget for signaling
in the grey matter of the brain. Journal of Cerebral Blood Flow
and Metabolism, 21(10), 1133–1145. https://doi.org/10.1097
/00004647-200110000-00001, 考研: 11598490

Avena-Koenigsberger, A。, Misic, B., & 斯波恩斯, 氧. (2018). Commu-
nication dynamics in complex brain networks. 自然评论
神经科学, 19(1), 17–33. https://doi.org/10.1038/nrn.2017
.149, 考研: 29238085

巴耶莱特, S. (2017). Magnetoencephalography for brain electrophys-
iology and imaging. 自然神经科学, 20(3), 327–339.
https://doi.org/10.1038/nn.4504, 考研: 28230841

巴洛, H. 乙. (1961). Possible principles underlying the transforma-

tion of sensory messages. Sensory Communication, 1(1).

Bassett, D. S。, Greenfield, D. L。, Meyer-Lindenberg, A。, 温伯格,
D. R。, 摩尔, S. W., & 布莫尔, 乙. 时间. (2010). Efficient physical

embedding of topologically complex information processing
networks in brains and computer circuits. 公共科学图书馆计算
生物学, 6(4), e1000748. https://doi.org/10.1371/journal.pcbi
.1000748, 考研: 20421990

Bavelas, A. (1950). Communication patterns in task-oriented
团体. Journal of the Acoustical Society of America, 22, 725–730.
https://doi.org/10.1121/1.1906679

贝策尔, 右. F. (2020). Community detection in network neuroscience.
arXiv:2011.06723. https://doi.org/10.48550/arXiv.2011.06723
Bola, M。, & Borchardt, V. (2016). Cognitive processing involves
dynamic reorganization of the whole-brain network’s functional
community structure. 神经科学杂志, 36(13), 3633–3635.
https://doi.org/10.1523/ JNEUROSCI.0106-16.2016, 考研:
27030750

Borgatti, S. 磷. (2005). Centrality and network flow. Social Networks,

27(1), 55–71. https://doi.org/10.1016/j.socnet.2004.11.008

丢弃, M。, 斯波恩斯, 奥。, & 斯旺森, L. 瓦. (2015). Architecture of the
cerebral cortical association connectome underlying cognition.
美国国家科学院院刊, 112(16),

网络神经科学

1200

The global neuronal workspace as a broadcasting network

E2093–E2101. https://doi.org/10.1073/pnas.1504394112,
考研: 25848037

布劳恩, U。, Schäfer, A。, Walter, H。, Erk, S。, Romanczuk-Seiferth, N。,
Haddad, L。, … Bassett, D. S. (2015). Dynamic reconfiguration of
frontal brain networks during executive cognition in humans.
美国国家科学院院刊, 112(37),
11678–11683. https://doi.org/10.1073/pnas.1422487112,
考研: 26324898

布鲁克斯, 中号. J。, 黑尔, J. R。, Zumer, J. M。, 史蒂文森, C. M。, Francis,
S. T。, 巴恩斯, G. R。, … Nagarajan, S. S. (2011). Measuring func-
tional connectivity using MEG: Methodology and comparison
with fcMRI. 神经影像, 56(3), 1082–1104. https://doi.org/10
.1016/j.neuroimage.2011.02.054, 考研: 21352925

布莫尔, E., & 斯波恩斯, 氧. (2012). The economy of brain network
组织. 自然评论神经科学, 13, 336–349.
https://doi.org/10.1038/nrn3214, 考研: 22498897

Calhoun, V. D ., Adali, T。, Pearlson, G. D ., & Pekar, J. J. (2001). A
method for making group inferences from functional MRI data
using independent component analysis. 人脑图谱,
14(3), 140–151. https://doi.org/10.1002/ hbm.1048, 考研:
11559959

Chinn, P。, Hedetniemi, S。, & 米切尔, S. (1979). Multiple-message
broadcasting in complete graphs. In Proceedings of the 10th SE
conference on Combinatorics, Graph Theory and Computing
(PP. 251–260). Utilitas Mathematica.

Chklovskii, D. B., & Koulakov, A. A. (2004). Maps in the brain:
What can we learn from them? Annual Review of Neuroscience,
27, 369–392. https://doi.org/10.1146/annurev.neuro.27.070203
.144226, 考研: 15217337

Crossley, 氮. A。, Mechelli, A。, Vértes, 磷. E., Winton-Brown, 时间. T。,
Patel, A. X。, Ginestet, C. E., McGuire, P。, & 布莫尔, 乙. 时间.
(2013). Cognitive relevance of the community structure of the
human brain functional coactivation network. 会议记录
the National Academy of Sciences, 110(28), 11583–11588.
https://doi.org/10.1073/pnas.1220826110, 考研: 23798414
德科, G。, Vidaurre, D ., & 克林格尔巴赫, 中号. L. (2021). Revisiting the
global workspace orchestrating the hierarchical organization of
the human brain. Nature Human Behaviour, 5(4), 497–511.
https://doi.org/10.1038/s41562-020-01003-6, 考研: 33398141
德阿内, S. (2014). Consciousness and the brain: Deciphering how

the brain codes our thoughts. 企鹅.

德阿内, S。, & 尚古克斯, J. 磷. (2004) Neural mechanisms for
access to consciousness. 在米. S. Gazzaniga (埃德。), The cognitive
neurosciences (PP. 1145–1157). 与新闻界.

德阿内, S。, & 尚古克斯, J. 磷. (2005). Ongoing spontaneous activ-
ity controls access to consciousness: A neuronal model for inat-
tentional blindness. 公共科学图书馆生物学, 3(5), e141. https://doi.org/10
.1371/journal.pbio.0030141, 考研: 15819609

德阿内, S。, & 纳克卡什, L. (2001). Towards a cognitive neurosci-
ence of consciousness: Basic evidence and a workspace frame-
工作. 认识, 79, 1–37. https://doi.org/10.1016/S0010-0277
(00)00123-2, 考研: 11164022

德什潘德, G。, Santhanam, P。, & 胡, X. (2011). Instantaneous and
causal connectivity in resting state brain networks derived from
functional MRI data. 神经影像, 54, 1043–1052. https://doi.org
/10.1016/j.neuroimage.2010.09.024, 考研: 20850549

Ekhlasi, A。, Nasrabadi, A. M。, & Mohammadi, 中号. 右. (2021). Direc-
tion of information flow between brain regions in ADHD and

healthy children based on EEG by using directed phase transfer
entropy. 认知神经动力学, 15(6), 975–986. https://土井
.org/10.1007/s11571-021-09680-3, 考研: 34790265

Farley, A. (1979). Minimal broadcast networks. 网络, 9(4),

313–332. https://doi.org/10.1002/net.3230090404

Farley, A. (1980). Broadcast time in communication networks.
SIAM Journal on Applied Mathematics, 39(2), 385–390. https://
doi.org/10.1137/0139032

Farley, A. (2004). Minimal path broadcast networks. 网络, 43(2),

61–70. https://doi.org/10.1002/net.10104

Farley, A。, Hedetniemi, S。, 米切尔, S。, & Proskurowski, A. (1979).
Minimum broadcast graphs. Discrete Mathematics, 25, 189–193.
https://doi.org/10.1016/0012-365X(79)90022-0

Finc, K., Bonna, K., 他, X。, Lydon-Staley, D. M。, Kühn, S。, Duch,
W., & Bassett, D. S. (2019). Dynamic reconfiguration of
functional brain networks during working memory training.
bioRxiv:685487. https://doi.org/10.1101/685487

Finc, K., Bonna, K., Lewandowska, M。, Wolak, T。, Nikadon, J。,
Dreszer, J。, … Kühn, S. (2017). Transition of the functional brain
network related to increasing cognitive demands. 人脑
测绘, 38(7), 3659–3674. https://doi.org/10.1002/ hbm
.23621, 考研: 28432773

福多尔, J. A. (1983). The modularity of mind: An essay on faculty
心理学. 与新闻界. https://doi.org/10.7551/mitpress/4737
.001.0001

假如, A。, 扎莱斯基, A。, & 布莫尔, 乙. (2016). Fundamentals of

brain network analysis. 学术出版社.

狐狸, 中号. D ., & Raichle, 中号. 乙. (2007). Spontaneous fluctuations in
brain activity observed with functional magnetic resonance
成像. 自然评论神经科学, 8(9), 700–711. https://
doi.org/10.1038/nrn2201, 考研: 17704812

薯条, 磷. (2005). A mechanism for cognitive dynamics: Neuronal
communication through neuronal coherence. Trends in Cogni-
tive Sciences, 9, 474–480. https://doi.org/10.1016/j.tics.2005.08
.011, 考研: 16150631

薯条, 磷. (2009). Neuronal gamma-band synchronization as a funda-
mental process in cortical computation. Annual Review of Neu-
roscience, 32(1), 209–224. https://doi.org/10.1146/annurev
.神经的.051508.135603, 考研: 19400723

Fries P. (2015). 认知节奏: 沟通通过
连贯性. 神经元, 88(1), 220–235. https://doi.org/10.1016/j
.neuron.2015.09.034, 考研: 26447583

弗里斯顿, K., Moran, R。, & 赛斯, A. K. (2013). Analysing connectivity
with Granger causality and dynamic causal modelling. 当前的
Opinion in Neurobiology, 23, 172–178. https://doi.org/10.1016
/j.conb.2012.11.010, 考研: 23265964

Garey, 中号. R。, & 约翰逊, D. S. (1979). Computers and intractability:
A guide to the theory of NP-completeness (with an addendum,
1991). 弗里曼.

Gillebert, C. R。, & Mantini, D. (2013). Functional connectivity in the
normal and injured brain. The Neuroscientist, 19(5), 509–522.
https://doi.org/10.1177/1073858412463168, 考研: 23064084
Godwin, D ., Barry, 右. L。, & Marois, 右. (2015). Breakdown of the
brain’s functional network modularity with awareness. Proceed-
ings of the National Academy of Sciences, 112(12), 3799–3804.
https://doi.org/10.1073/pnas.1414466112, 考研: 25759440
Goebel, R。, Roebroeck, A。, Kim, D. S。, & Formisano, 乙. (2003).
Investigating directed cortical interactions in time resolved fMRI

网络神经科学

1201

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

data using vector autoregressive modeling and Granger causality
映射. Magnetic Resonance Imaging, 21, 1251–1261. https://
doi.org/10.1016/j.mri.2003.08.026, 考研: 14725933

Gonzalez-Castillo, J。, & Bandettini, 磷. A. (2018). Task-based
dynamic functional connectivity: Recent findings and open ques-
系统蒸发散. 神经影像, 180, 526–533. https://doi.org/10.1016/j
.neuroimage.2017.08.006, 考研: 28780401

Gonzalez-Castillo, J。, Saad, Z. S。, Handwerker, D. A。, Inati, S. J。,
Brenowitz, N。, & Bandettini, 磷. A. (2012). Whole-brain,
time-locked activation with simple tasks revealed using massive
averaging and model-free analysis. 国家会议录
Academy of Sciences, 109(14), 5487–5492. https://doi.org/10
.1073/pnas.1121049109, 考研: 22431587

Graham, D. J. (2014). Routing in the brain. Frontiers in Computa-
tional Neuroscience, 8, 44. https://doi.org/10.3389/fncom.2014
.00044, 考研: 24782752

Graham, D ., & Rockmore, D. (2011). The packet switching brain.
认知神经科学杂志, 23(2), 267–276. https://土井
.org/10.1162/jocn.2010.21477, 考研: 20350173

Granger, C. 瓦. (1969). Investigating causal relations by economet-
ric models and cross-spectral methods. Econometrica, 37(3),
424–438. https://doi.org/10.2307/1912791

Griffa, A。, Ricaud, B., Benzi, K., Bresson, X。, Daducci, A。,
Vandergheynst, P。, … Hagmann, 磷. (2017). Transient networks of
spatio-temporal connectivity map communication pathways in
brain functional systems. 神经影像, 155, 490–502. https://土井
.org/10.1016/j.neuroimage.2017.04.015, 考研: 28412440
Hajnal, A。, Milner E. C。, & Szemeredi, 乙. (1972). A cure for the tele-
phone disease. Canadian Mathematical Bulletin, 15, 447–450.
https://doi.org/10.4153/CMB-1972-081-0

Harutyunyan, H. A. (2006). Minimum multiple message broadcast
图表. 网络, 47(4), 218–224. https://doi.org/10.1002/net
.20110

Harutyunyan, H. A. (2014). Broadcast networks with near optimal
成本. In International conference on algorithmic applications in
管理 (PP. 312–322). 施普林格. https://doi.org/10.1007
/978-3-319-07956-1_28

Harutyunyan, H. A。, & 李, Z. (2017). Broadcast graphs using new
dimensional broadcast schemes for Knödel graphs. In Conference
on algorithms and discrete applied mathematics (PP. 193–204).
施普林格. https://doi.org/10.1007/978-3-319-53007-9_18

Harutyunyan, H. A。, & 李, Z. (2020). A new construction of broad-
cast graphs. Discrete Applied Mathematics, 280, 144–155.
https://doi.org/10.1016/j.dam.2018.09.015

Harutyunyan, H. A。, Liestman, A. L。, Peters, J. G。, & Richards, D.
(2013). Broadcasting and gossiping. In Handbook of graph theory
(PP. 1477–1494). Chapman and Hall. https://doi.org/10.1201
/b16132-87

Hasanzadeh, F。, Mohebbi, M。, & Rostami, 右. (2020). Graph theory
analysis of directed functional brain networks in major depres-
sive disorder based on EEG signal. Journal of Neural Engineering,
17(2), 026010. https://doi.org/10.1088/1741-2552/ab7613,
考研: 32053813

Hedetniemi, S. M。, Hedetniemi, T。, & Liestman, A. L. (1988). A sur-
vey of gossiping and broadcasting in communication networks.
网络, 18, 319–349. https://doi.org/10.1002/net.3230180406
Hromkovič, J。, Klasing, R。, Pelc, A。, Ruzicka, P。, & Unger, 瓦.
(2005). Dissemination of information in communication

网络: Broadcasting, gossiping, leader election, and fault-
宽容. Springer Science and Business Media.

和记黄埔, 右. M。, Womelsdorf, T。, 艾伦, 乙. A。, Bandettini, 磷. A。,
Calhoun, V. D ., 科尔贝塔, M。, … Chang, C. (2013). 动态的
功能连接: Promise, 问题, and interpretations.
N e u ro I m a g e , 8 0 , 3 6 0 – 3 7 8 . h t t p s : / / d o i . o rg / 1 0 . 1 0 1 6 / j
.neuroimage.2013.05.079, 考研: 23707587

Jarrell, 时间. A。, 王, Y。, Bloniarz, A. E., Brittin, C. A。, 徐, M。,
Thomson, J. N。, … Emmons, S. 瓦. (2012). The connectome of a
decision-making neural network. 科学, 337(6093), 437–444.
https://doi.org/10.1126/science.1221762, 考研: 22837521
Joglekar, 中号. R。, Mejias, J. F。, 哪个, G. R。, & 王, X. J. (2018). 国际米兰-
areal balanced amplification enhances signal propagation in a
large-scale circuit model of the primate cortex. 神经元, 98(1),
222–234. https://doi.org/10.1016/j.neuron.2018.02.031,
考研: 29576389

Kahan, J。, & Foltynie, 时间. (2013). Understanding DCM: Ten simple
rules for the clinician. 神经影像, 83, 542–549. https://土井
.org/10.1016/j.neuroimage.2013.07.008, 考研: 23850463
Kaiser, M。, & 希尔格塔格, C. C. (2006). Nonoptimal component place-
蒙特, but short processing paths, due to long-distance projections
in neural systems. 公共科学图书馆计算生物学, 2(7), e95. https://
doi.org/10.1371/journal.pcbi.0020095, 考研: 16848638
Kitzbichler, 中号. G。, Henson, 右. N。, 史密斯, 中号. L。, Nathan, 磷. J。, &
布莫尔, 乙. 时间. (2011). Cognitive effort drives workspace config-
uration of human brain functional networks. Journal of Neurosci-
恩斯, 31(22), 8259–8270. https://doi.org/10.1523/JNEUROSCI
.0440-11.2011, 考研: 21632947

Kucyi, A。, & 戴维斯, K. D. (2014). Dynamic functional connectivity
of the default mode network tracks daydreaming. 神经影像,
100, 471–480. https://doi.org/10.1016/j.neuroimage.2014.06
.044, 考研: 24973603

Kucyi, A。, Hove, 中号. J。, Esterman, M。, 和记黄埔, 右. M。, & Valera,
乙. 中号. (2017). Dynamic brain network correlates of spontaneous
fluctuations in attention. 大脑皮层, 27(3), 1831–1840.
https://doi.org/10.1093/cercor/bhw029, 考研: 26874182
Landau, H. G. (1954). The distribution of completion times for
random communication in a task- oriented group. Bulletin of
Mathematical Biophysics, 16, 187–201. https://doi.org/10.1007
/BF02478413

征收, 瓦. B., & Baxter, 右. A. (1996). Energy efficient neural codes.
神经计算, 8(3), 531–543. https://doi.org/10.1162
/neco.1996.8.3.531, 考研: 8868566

刘, Q., Farahibozorg, S。, Porcaro, C。, Wenderoth, N。, & Mantini,
D. (2017). Detecting large-scale networks in the human brain
using high-density electroencephalography. 人脑图谱-
平, 38(9), 4631–4643. https://doi.org/10.1002/ hbm.23688,
考研: 28631281

刘, Q., Ganzetti, M。, Wenderoth, N。, & Mantini, D. (2018). Detect-
ing large-scale brain networks using EEG: Impact of electrode
density, head modeling and source localization. Frontiers in Neu-
roinformatics, 12, 4. https://doi.org/10.3389/fninf.2018.00004,
考研: 29551969

洛比尔, M。, 七只母鸡, F。, 崇拜, S。, & 崇拜, J. 中号. (2014). Phase
transfer entropy: A novel phase-based measure for directed con-
nectivity in networks coupled by oscillatory interactions. Neuro-
图像, 85, 853–872. https://doi.org/10.1016/j.neuroimage.2013
.08.056, 考研: 24007803

网络神经科学

1202

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

Lopes da Silva, F. (2013). 脑电图和脑磁图: Relevance to neuroscience.
神经元, 80(5), 1112–1128. https://doi.org/10.1016/j.neuron
.2013.10.017, 考研: 24314724

Mantini, D ., 佩鲁奇, 中号. G。, Cugini, S。, Ferretti, A。, 罗马尼人, G. L。,
& Del Gratta, C. (2007). Complete artifact removal for EEG
recorded during continuous fMRI using independent component
分析. 神经影像, 34(2), 598–607. https://doi.org/10.1016/j
.neuroimage.2006.09.037, 考研: 17112747

Mashour, G. A。, 罗尔夫塞玛, P。, 尚古克斯, J. P。, & 德阿内, S.
(2020). Conscious processing and the global neuronal work-
space hypothesis. 神经元, 105(5), 776–798. https://doi.org/10
.1016/j.neuron.2020.01.026, 考研: 32135090

莫尼耶, D ., 兰比奥特, R。, & 布莫尔, 乙. 时间. (2010). Modular and
hierarchically modular organization of brain networks. Frontiers
in Neuroscience, 4, 200. https://doi.org/10.3389/fnins.2010
.00200, 考研: 21151783

Michel, C. M。, 穆雷, 中号. M。, Lantz, G。, 冈萨雷斯, S。, 斯皮内利, L。,
& de Peralta, 右. G. (2004). EEG source imaging. Clinical Neuro-
physiology, 115(10), 2195–2222. https://doi.org/10.1016/j.clinph
.2004.06.001, 考研: 15351361

Mišić, B., 贝策尔, 右. F。, de Reus, 中号. A。, van den Heuvel, 中号. P。,
Berman, 中号. G。, McIntosh, A. R。, & 斯波恩斯, 氧. (2016). 网-
work-level structure-function relationships in human neocortex.
大脑皮层, 26(7), 3285–3296. https://doi.org/10.1093
/cercor/bhw089, 考研: 27102654

米特拉, A。, & Raichle, 中号. 乙. (2016). How networks communicate:
Propagation patterns in spontaneous brain activity. Philosophi-
cal Transactions of the Royal Society B: Biological Sciences,
371(1705), 20150546. https://doi.org/10.1098/rstb.2015.0546,
考研: 27574315

纽曼, 中号. E., & Girvan, 中号. (2004). Finding and evaluating com-
munity structure in networks. Physical Review E, 69(2), 026113.
https://doi.org/10.1103/PhysRevE.69.026113, 考研: 14995526
Paluš, M。, & Stefanovska, A. (2003). Direction of coupling from
phases of interacting oscillators: An information-theoretic
方法. Physical Review E, 67(5), 055201. https://doi.org/10
.1103/PhysRevE.67.055201, 考研: 12786211

Pan, 右. K., Chatterjee, N。, & Sinha, S. (2010). Mesoscopic organi-
zation reveals the constraints governing Caenorhabditis elegans
nervous system. PLoS ONE, 5(2), e9240. https://doi.org/10
.1371/journal.pone.0009240, 考研: 20179757

Piccinini, G。, & Bahar, S. (2013). Neural computation and the
computational theory of cognition. 认知科学, 37(3),
453–488. https://doi.org/10.1111/cogs.12012, 考研:
23126542

Prim, 右. C. (1957). Shortest connection networks and some gener-
alizations. Bell System Technical Journal, 36(6), 1389–1401.
https://doi.org/10.1002/j.1538-7305.1957.tb01515.x

Proskurowski, A. (1981). Minimum broadcast trees. IEEE Transac-
tions on Computers, 30, 363–366. https://doi.org/10.1109/ TC
.1981.1675796

Richards, D ., & Liestman, A. L. (1988). Generalizations of broad-
casting and gossiping. 网络, 18(2), 125–138. https://土井
.org/10.1002/net.3230180205

Rosenblum, 中号. G。, Pikovsky, A. S。, & Kurths, J. (1996). Phase
synchronization of chaotic oscillators. 物理评论快报,
76(11), 1804–1807. https://doi.org/10.1103/ PhysRevLett.76
.1804, 考研: 10060525

鲁比诺夫, M。, & 斯波恩斯, 氧. (2010). 复杂的网络措施
大脑连接: 用途和解释. 神经影像, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
考研: 19819337

萨达吉亚尼, S。, & Wirsich, J. (2020). Intrinsic connectome organiza-
tion across temporal scales: New insights from cross-modal
方法. 网络神经科学, 4(1), 1–29. https://doi.org
/10.1162/netn_a_00114, 考研: 32043042

Seguin, C。, Tian, Y。, & 扎莱斯基, A. (2020). Network communication
models improve the behavioral and functional predictive utility
of the human structural connectome. 网络神经科学,
4(4), 980–1006. https://doi.org/10.1162/netn_a_00161, 考研:
33195945

Shepherd, G. 中号. (埃德。). (2003). The synaptic organization of the
脑. 牛津大学出版社. https://doi.org/10.1093/acprof:
oso/9780195159561.001.1

Shih, C.-T., 斯波恩斯, 奥。, Yuan, S.-L., Su, T.-S., 林, Y.-J., Chuang,
C.-C., … Chiang, A.-S. (2015). Connectomics-based analysis of
information flow in the Drosophila brain. 现代生物学, 25(10),
1249–1258. https://doi.org/10.1016/j.cub.2015.03.021,
考研: 25866397

Shimbel, A. (1951). Applications of matrix algebra to communica-
tion nets. Bulletin of Mathematical Biophysics, 13, 165–178.
https://doi.org/10.1007/BF02478225

Simony, E., 蜂蜜, C. J。, 陈, J。, Lositsky, 奥。, Yeshurun, Y。, Wiesel,
A。, & Hasson, U. (2016). Dynamic reconfiguration of the default
mode network during narrative comprehension. Nature Commu-
nications, 7(1), 1–13. https://doi.org/10.1038/ncomms12141,
考研: 27424918

Sohn, Y。, Choi, 中号. K., Ahn, 是. Y。, 李, J。, & Jeong, J. (2011). Topo-
logical cluster analysis reveals the systemic organization of the
Caenorhabditis elegans connectome. PLoS Computational Biol-
奥吉, 7(5), e1001139. https://doi.org/10.1371/journal.pcbi
.1001139, 考研: 21625578

Sokoloff, L. (1989). Measurement of regional hemodynamic and
metabolic changes in the central nervous system with imaging
技巧. In Regulatory mechanisms of neuron to vessel com-
munication in the brain (PP. 345–392). 施普林格. https://doi.org
/10.1007/978-3-642-74152-4_17

斯波恩斯, 氧. (2016). Networks of the brain. 与新闻界.
斯波恩斯, 奥。, & 贝策尔, 右. F. (2016). 模块化大脑网络. Annual
Review of Psychology, 67, 613–640. https://doi.org/10.1146
/annurev-psych-122414-033634, 考研: 26393868

斯波恩斯, 奥。, Chialvo, D. R。, Kaiser, M。, & 希尔格塔格, C. C. (2004).
组织, development and function of complex brain net-
作品. 认知科学的趋势, 8(9), 418–425. https://土井
.org/10.1016/j.tics.2004.07.008, 考研: 15350243

斯塔姆, C. J。, 诺尔特, G。, & Daffertshofer, A. (2007). Phase lag index:
Assessment of functional connectivity from multi channel EEG
and MEG with diminished bias from common sources. 人类
Brain Mapping, 28(11), 1178–1193. https://doi.org/10.1002
/hbm.20346, 考研: 17266107

英镑, P。, & Laughlin, S. (2015). Principles of neural design. 和
按. https://doi.org/10.7551/mitpress/9780262028707.001.0001
Stropahl, M。, Bauer, A. K. R。, Debener, S。, & Bleichner, 中号. G.
(2018). Source-modeling auditory processes of EEG data using
EEGLAB and brainstorm. Frontiers in Neuroscience, 12, 309.
https://doi.org/10.3389/fnins.2018.00309, 考研: 29867321

网络神经科学

1203

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
1
1
8
6
2
0
5
9
7
5
1
n
e
n
_
A
_
0
0
2
6
1
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The global neuronal workspace as a broadcasting network

Suárez, L. E., Markello, 右. D ., 贝策尔, 右. F。, & Misic, 乙. (2020). Link-
ing structure and function in macroscale brain networks. Trends
in Cognitive Sciences, 24(4), 302–315. https://doi.org/10.1016/j
.tics.2020.01.008, 考研: 32160567

Telesford, 问. K., 辛普森, S. L。, Burdette, J. H。, Hayasaka, S。, &
Laurienti, 磷. J. (2011). The brain as a complex system: 使用
network science as a tool for understanding the brain. Brain
Connectivity, 1(4), 295–308. https://doi.org/10.1089/brain.2011
.0055, 考研: 22432419

Towlson, 乙. K., Vértes, 磷. E., Ahnert, S. E., Schafer, 瓦. R。, &
布莫尔, 乙. 时间. (2013). The rich club of the C. elegans neuronal
connectome. 神经科学杂志, 33(15), 6380–6387.
https://doi.org/10.1523/ JNEUROSCI.3784-12.2013, 考研:
23575836

Vatansever, D ., Menon, D. K., Manktelow, A. E., Sahakian, 乙. J。, &
Stamatakis, 乙. A. (2015). Default mode dynamics for global

一体化.

functional
神经科学杂志, 35(46),
15254–15262. https://doi.org/10.1523/ JNEUROSCI.2135-15
.2015, 考研: 26586814

Vinck, M。, Oostenveld, R。, van Wingerden, M。, Battaglia, F。, &
Pennartz, C. 中号. (2011). An improved index of phase-
synchronization for electrophysiological data in the presence of
volume-conduction, noise and sample-size bias. 神经影像,
55(4), 1548–1565. https://doi.org/10.1016/j.neuroimage.2011
.01.055, 考研: 21276857

王, Q., 斯波恩斯, 奥。, & Burkhalter, A. (2012). Network analysis of
corticocortical connections reveals ventral and dorsal processing
streams in mouse visual cortex. 神经科学杂志, 32(13),
4386–4399. https://doi.org/10.1523/JNEUROSCI.6063-11.2012,
考研: 22457489

Wiener, 氮. (1956). The theory of prediction. 在E中. Beckenbach (埃德。),

Modern mathematics for engineers. 麦格劳-希尔.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我