Morphological Computation
and Morphological Control:
Steps Toward a Formal
Theory and Applications
Abstract Morphological computation can be loosely defined as the
exploitation of the shape, material properties, and physical dynamics
of a physical system to improve the efficiency of a computation.
Morphological control is the application of morphological computing
to a control task. In its theoretical part, this article sharpens and
extends these definitions by suggesting new formalized definitions
and identifying areas in which the definitions we propose are still
inadequate. We go on to describe three ongoing studies, in which we
are applying morphological control to problems in medicine and in
化学. The first involves an inflatable support system for patients
with impaired movement, and is based on macroscopic physics and
concepts already tested in robotics. The two other case studies (自己-
assembly of chemical microreactors; models of induced cell repair
in radio-oncology) describe processes and devices on the micrometer
规模, in which the emergent dynamics of the underlying physical system
(例如, phase transitions) are dominated by stochastic processes such
as diffusion.
Rudolf M. Füchslin*,**
Zurich University of Applied Sciences
Andrej Dzyakanchuk†
Bern University of Applied Sciences
Dandolo Flumini
Zurich University of Applied Sciences
‡
Helmut Hauser§
苏黎世大学
Kenneth J. Hunt¶
Bern University of Applied Sciences
Rolf H. Luchsinger#
Empa—Center for Synergetic
结构
††
Benedikt Reller
European Center for Living
技术
Stephan Scheidegger**
Zurich University of Applied Sciences
Richard Walker
Blue Brain Project
‡‡
关键词
Morphological computation, embodiment,
analogue computation, systems medicine,
prosthetics
A version of this paper with color figures is
available online at http://dx.doi.org/10.1162/
artl_a_00079. Subscription required.
* Contact author.
** Center for Applied Mathematics and Physics, School of Engineering, Zurich University of Applied Sciences, Tecnikumstr. 9, CH-8400,
Winterthur, 瑞士. 电子邮件: rudolf.fuechslin@zhaw.ch (R.M.F.); stephan.scheidegger@zhaw.ch (S.S.)
† Institute for Rehabilitation and Performance Technology, Division of Mechanical Engineering, Department of Engineering and
信息技术, Bern University of Applied Sciences, CH-3400 Burgdorf, 瑞士. 电子邮件: andrei.dzyakanchuk@bfh.ch
‡ School of Engineering, Zurich University of Applied Sciences, Lagerstrasse 41 8004 苏黎世, 瑞士. 电子邮件: dandolo.
flumini@zhaw.ch
§ Artificial Intelligence Laboratory, Department of Informatics, 苏黎世大学, Andreasstrasse 15, CH-8050 Zurich, 瑞士.
电子邮件: hhauser@ifi.uzh.ch
¶ Institute for Rehabilitation and Performance Technology, Division of Mechanical Engineering, Department of Engineering and
信息技术, Bern University of Applied Sciences, CH-3400 Burgdorf, 瑞士. 电子邮件: kenneth.hunt@bfh.ch
# Empa—Center for Synergetic Structures, Ueberlandstrasse 129, CH-8600 Dübendorf, 瑞士. 电子邮件: Rolf.Luchsinger@empa.ch
†† European Centre for Living Technology, Caʼ Minich, S. Marco 2940, 30124 Venezia, 意大利. 电子邮件: bene.reller@gmail.com
‡‡ Blue Brain Project, EPFL, QIJ 3 115.6 CH-1015 Lausanne, 瑞士. 电子邮件: richard.walker@epfl.ch
© 2013 麻省理工学院
人工生命 19: 9–34 (2013)
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
1 介绍
Some of the most important current applications of morphological computing are in robotics, a field
in which it is widely accepted that the intrinsic dynamics of a physical system (the robot body) need
not be regarded only as a potential source of perturbations, but can be exploited to facilitate the
control of the system [28]. Control implies computation. The use of the dynamics of the robot body
to facilitate control can thus be interpreted as an outsourcing of computational tasks to the body. 在
this interpretation, the body is performing morphological computation [25].
In robotics, the concept of morphological computing has been around for some time, though the
term itself is relatively recent (看 [17] 和, for a broader presentation, [27]). 今天, 然而, 这是
clear that the concept of morphological computing can be applied not just to systems such as robots,
whose dynamics are governed by classical mechanics, but also to systems, such as self-assembling
and/or chemical systems, that are better described in terms of statistical physics [29].
在 2007, a workshop at the first International Conference on Morphological Computing in Venice,
意大利, led by Norman Packard, informally defined morphological computing as “any process that
(A) serves for a computational purpose, (乙) has clearly assignable input and output states and (C) 是
programmable, where ‘programmable’ is understood in the broad sense that a programmer can vary
the behavior of the system by varying a set of parameters.” This definition implies that conventional
digital computing systems are instances of morphological computing. 然而, many researchers
require that at least part of the computation should rely in a significant way on the physical dynamics
of the system implementing the computation, which should be entirely defined by the “program.” By
this definition, the execution of a conventional computer program that completely specifies the trans-
formation of an input to an output cannot be classed as morphological computation. The formaliza-
tion we propose in Section 2.2 casts new light on this issue.
The rest of the article will be structured as follows. We begin by discussing conceptual aspects of
morphological computation and morphological control. We then examine how these concepts apply
to robotics and to more general computational applications. 以这个为基础, we suggest a more for-
malized definition. Our definition is a suggestion and reflects our point of view; in what follows
“morphological computation” should be interpreted as “the view of morphological computation
held by the authors.” The article concludes with three case studies, two of which go beyond robotics
and the underlying classical mechanics to consider systems whose dynamics are governed by statis-
tical mechanics.
2 Morphological Computation and Control
开始, we would like to clarify a number of issues that often arise in discussions.
1. The concept of morphological computation, as we understand it, does not imply
any notion of “hypercomputation.” All the computational and/or control problems we
discuss in our case studies are computable by a conventional Turing machine. 不像
Turing machine, morphological computation does not define a class of computational
问题. Rather it provides a method for solving such problems: In Marrʼs terminology,
the concept belongs not to the “computational level” (the level of the Turing machine)
but to the “implementation level” [22].
2. In our work we use “morphology” to mean the combination of shape and material
properties—elasticity, friction coefficients and so on; by this definition, morphology
includes material as well as geometrical properties.
3. 下文中, we distinguish between computation and control. In our terminology,
“morphological control” means “control achieved via morphological computation.”
10
人工生命量 19, 数字 1
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
4. The concepts of morphological computation and control overlap to some extent with
control theory. 然而, in control theory, the crucial notion is that of the reference,
which provides an exact specification of the way system parameters should behave.
In morphological control, as we will see, no reference is explicitly required.
5. Morphological computing also overlaps to a large extent with what has previously
been called natural computing [15], the attempt to implement conventional computation
processes using non-electronic means, 例如, DNA computation or membrane
计算. 然而, the two fields have different emphases. Much of the literature
on natural computing is dedicated to demonstrations that a specific system of natural
computing is universal, in the sense that it can compute all problems that can be computed
by a Turing machine. The literature on morphological computation attaches much less
importance to this concept. 在多数情况下, the goal of morphological computing is to
control specific devices in potentially broad but specified contexts, which may or may
not allow the representation of a particular class of mathematical problem (例如, a Hamiltonian
graph problem). A second difference in emphasis is in the role of electronics. Most of
the natural computing techniques reported in the literature do not use electronics at all.
Many morphological computing and control systems continue to use some kind of
conventional control unit.
6. In the view we present here, the main goal of morphological control is to perform control
tasks in a more efficient manner than would be possible with conventional computing
技术, where efficiency is understood in in terms of time, 记忆, 力量, 空间, 和
other costly resources. This is a tradeoff: The gain in efficiency is achieved by abandoning
the strict separation of hardware and software, one of the fundamental characteristics
of conventional control. Morphological control may also provide looser control than
conventional computing technologies.
2.1 From Robotics to General Models of Morphological Computation
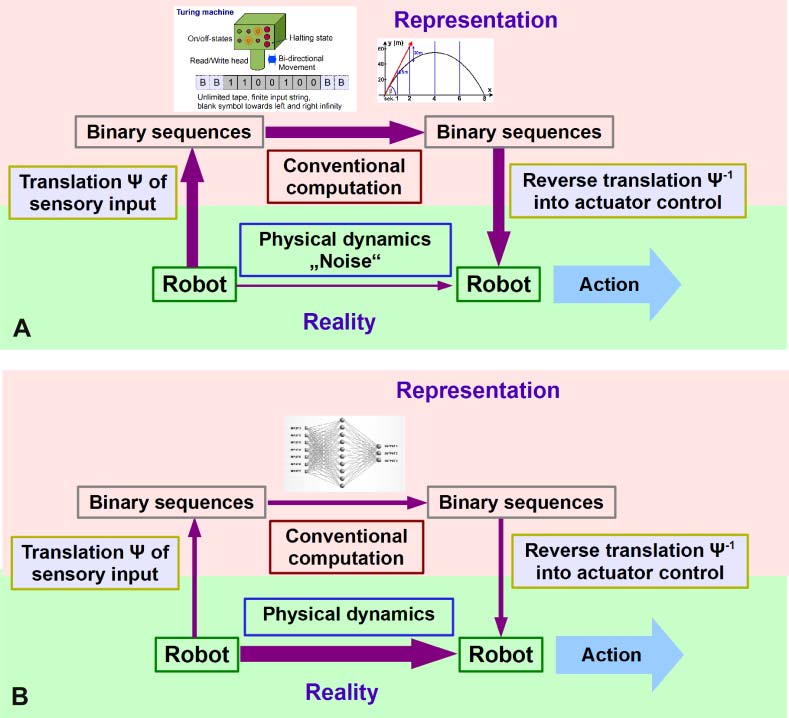
Conventionally, the control of a robot follows the scheme given in Figure 1A. 这里, a robot gets
information from the environment via a sensory system. These signals are then transformed into a
binary representation, which is processed by a conventional computer. The result of this computa-
tion is used to determine the action of the robot. 在多数情况下, the conventional computation is
based on a kinematic model of the robot and uses classical mechanics to evaluate relevant aspects of
the robot dynamics. The kinematic model requires knowledge of the state of the robot. 鉴于
the free parameters of the robot (angles of joints, velocities, ETC。) can only be determined with finite
accuracy and with a finite sampling rate, the control unit has to deal with physical noise. 因此, to keep
the computation as simple and reliable as possible, control systems are designed to minimize the
undesirable influence of the robotʼs morphology (seen as a source of physical noise). One strategy
is to keep the number of degrees of freedom as low as possible. From a physical point of view, 这是
one of the reasons why most robots are heavy and stiff. Under these conditions, a limited number of
system parameters can give an account of the state of the robot (例如, its posture and velocities) 那
is sufficiently complete and accurate to allow effective control.
Morphological control pursues an alternative strategy, described in Figure 1B. Now the control
system is designed not to dampen the robotʼs natural dynamics, but to exploit them. As we will dis-
坏话, it is no longer necessary to represent the complete state of the robot in the control unit. 作为一个
consequence, robots with morphological control can use soft materials with many internal degrees of
freedom. Using soft and lightweight materials offers many benefits. In health care, 例如, 他们
usually raise fewer safety concerns than harder, heavier materials.
Although biological systems usually involve more sophisticated control schemes, the way the
physical dynamics of a system can be used for control can best be explained by a simple example
(见图 2). Assume a (子)system determined by two parameters. These parameters are subject
人工生命量 19, 数字 1
11
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
数字 1. (A) Conventional control scheme, (乙) control scheme using morphological control. The lower panel refers to
the physical realization of the systems under consideration. The upper panel refers to the digital representation of the
same system. The width of the arrows represents the relative importance of different flows of information. In conven-
国家控制, the ideal situation is achieved when all relevant information is passed through the digital control, 那是,
when the control unit (implemented by a conventional digital computer ) has complete information about the state of the
系统, and the system performs its commands with maximal precision. 事实上, this ideal situation is never reached,
but good engineering aims to minimize the non-controlled aspects of the system. 因此, the lower horizontal arrow in
(A) is as thin as possible. (乙) Illustrates morphological control. The amount of information passed through the digital
control is as small as possible and the conventional computation is as simple as possible (例如, a feed-forward neural net).
As far as possible, the computation exploits the physical dynamics of the system.
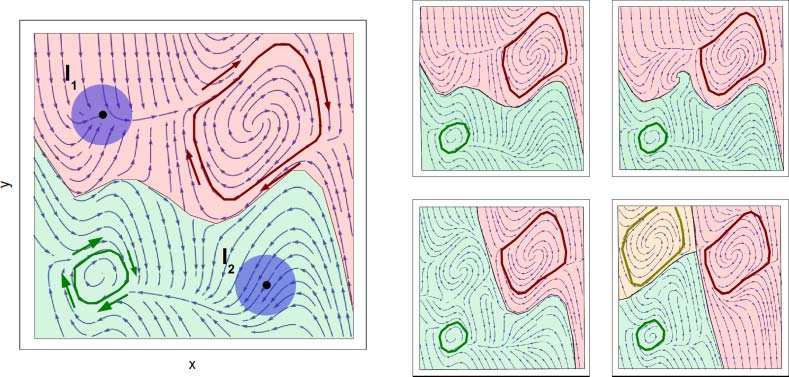
to dynamics that create two limit cycles, each with its own basin of attraction. (Note that the dy-
namical systems under consideration are usually dissipative, meaning they take up energy.) 这
means they can display limit cycles, despite the presence of friction. To move between the two ba-
sins of attraction, the control unit does not need to regulate every detail of the systemʼs trajectory.
All it has to do is choose some initial (x0, y0) lying in the right basin of attraction. Small perturbations
are corrected naturally by the tendency of the system to choose one of the two limit cycles. 其他
字, the limit cycles significantly simplify the computational task for the control unit. In classical
控制, the controller needs to generate every detail of a trajectory and to handle perturbations. 在
morphological control, all it has to do is choose a basin of attraction. 当然, there is a price to pay:
While conventional control allows a large variety of different trajectories (and gives complete control
over transients), the simple system in the left panel of Figure 2 is only able to produce two loosely
defined oscillatory movements.
12
人工生命量 19, 数字 1
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
事实上, the concept of morphological control means much more than simply exploiting the
self-stabilizing properties of dynamical systems (standard practice in good engineering). Control sys-
tems can also change the properties of a system, altering the structure of its attractor landscape. 这样的
changes can result in a modification of the limit cycle, the basins of attraction, and even the number
and structure of attractors (见图 2, right side). In more general terms, we can construct the
system in such a way that a small number of internal system parameters (such as internal tension) 能
generate a rich variety of movement patterns. The control unit basically performs two tasks: 第一的, 它
shapes the attractor landscape of the dynamical system it controls; 第二, it initiates jumps from
one basin of attraction to another. 这样, the calibration and stabilization of a movement pat-
tern are outsourced to the dynamics of the system.
Moving from robotics to physiology, we can use similar concepts to interpret the behavior of natural
系统. 例如, consider the way one changes oneʼs posture when carrying a heavy load. 尽管
we have no strict proof, we interpret the change as a reshaping of the bodyʼs attractor landscape. 这
human body is a dynamical system that is optimized for walking under normal conditions. A heavy load
changes the properties of the system. To readjust we alter the positions of some of our joints and change
the tension on some of our muscles. This seems to be a form of morphological control.
Another example of the interplay between physiological dynamics, control by the brain, 和科技-
nology is downhill skiing. Skiers continuously adjust their posture to the terrain in order to gain
stability against perturbations (without losing the ability to steer ). 同时, the choice of
the mechanical properties of skis and boots influences the dynamical behavior of the “skier,” con-
sidered as an integrated system [2, 24]. We hypothesize that these changes represent forms of mor-
phological control. 例如, certain types of skis (carving skis) are generally regarded as easier to
use than the skis used by athletes. 换句话说, they reduce the complexity of the control problem
posed by downhill skiing. 然而, they also offer less precise control. This explains why racers choose
不同的, harder-to-use models.
We hypothesize that, in the two cases we have just considered (步行, downhill skiing), 这
brain plays an important role not just in choosing between preexisting basins of attraction, but in
reshaping the attractor landscape (例如, when a skier needs to change direction or vary speed). It does
not need to control all of the bodyʼs free parameters to achieve this. 相当, it learns to control a small
number of parameters governing posture and internal tension, thereby altering the overall dynamics of
数字 2. 左边: Schematic example of self-regulation of a dynamical system. Two system parameters x and y are subject to
a dynamics that leads to limit cycles, sketched together with their respective basins of attraction. I1 and I2 denote initial
状况: An observer is not able to prepare a system in an exactly specified initial state, but may guarantee to choose a
point within a certain finite part of the parameter space. 正确的: Dynamic attractor landscape. Upon change of a system
parameter, the basins of attraction, the shape of the limit cycles, and even the number of attractors is altered.
人工生命量 19, 数字 1
13
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
the body and drastically reducing the complexity of the control task. The hypothesis that the brain be-
haves in this way is supported by psychological findings showing that humans organize complex move-
ments into subtasks, represented in memory by morphologies [35].
A further layer of sophistication can be added by reading out certain system parameters and pro-
cessing the results. 例如, it is well established that the dynamics of artificial neural networks
can be used to perform complex computations [14, 20]. Hauser et al. have recently demonstrated
[10] that similar results hold for compliant bodies: A (sufficiently complex) mass-spring system
coupled to a feed-forward neural network can, 原则, approximate a large class of input-output
关系 (time-invariant filters with fading memory) with arbitrary precision.
总之, we can establish a hierarchy of different forms of morphological computation:
1. Switching between basins of attraction under the control of a simple control signal.
2. Control of the attractor landscape by a simple control system.
3. Postprocessing of the state of a dynamical system to obtain a computational result.
This last level is particularly interesting when the system in question is an animal or a robot. 在这个
案件, the information gained by postprocessing can be translated into control signals and fed back
into the system as input signals.
One may also extend this hierarchy to take account of learning: changes in the program of the
conventional controller. 迄今为止, 然而, we have yet to achieve a theory of learning that combines
abstracted and physical aspects of control.
2.2 Morphological Computation in General: Toward a Definition
So far we have based our discussion on an informal definition of morphological computation. 在这个
section we take a more formal approach, 哪个, while not directly applicable to all aspects of our case
学习, establishes a connection to theoretical computer science.
As we saw earlier, the Venice definition states that a natural system is a morphological computing
system if and only if
1.
2.
it converts reproducible input into a reproducible output;
it is programmable in the sense that the map between input and output is parameterized
in such a way that a wide variety of outputs can be produced;
3.
it has a sort of teleological embedding.
Requirement 1 has three important consequences. 第一的, the notion of a “conversion” implies that
the system under consideration is a dynamical system. 第二, reproducibility requires that the sys-
tem should be deterministic in the strong sense. 第三, the same condition requires that it should be
possible to tune the system so that two indistinguishable input states lead to the same output state.
Note that “indistinguishable” does not mean “identical.” In the example of a dynamical system with
different basins of attraction, it is sufficient that the observer should be able to start the system in a
given basin of attraction. This condition rules out continuous chaotic systems, whose behaviors can
be completely different for arbitrarily similar inputs.
Requirement 2 requires that a computational system should be programmable at least to some
extent. While equivalence to a universal Turing machine is not required, the system should be adapt-
有能力的. Take as an example a passive dynamic walker [23]. The dynamics of the system should spon-
taneously compensate for small perturbations. 然而, programmability implies that it should be
possible to adapt the system to different types of terrain (perhaps by adjusting spring constants, fric-
tion coefficients, ETC。). Note that in this case, programmability does not require a formal programming
语言. The “program” may be a set of parameters.
14
人工生命量 19, 数字 1
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
The third requirement protects the concept of morphological computation from the trivial observa-
tion that any dynamical system is a “simulation” of itself and can thus be regarded as computing its own
defining equations.
In order to develop a theory of morphological computation, formalized definitions are a necessity. 作为
will be discussed, the definitions we suggest do not yet capture the whole range of processes one might
consider as morphological computations. Part of the motivation for presenting our definition is that we
claim to have worked out what is lacking to get a more comprehensive definition. 此外, 我们的
definition does not require the system to be discrete (as a conventional computer is).
2.2.1 Formalizing Morphological Computation
Our first task is to elaborate a suitable way to assign functions to dynamical systems. 换句话说,
we have to give them a denotational semantics. A natural approach to this problem is to assign each
system to the (部分的) function that maps any initial state x to some state y, where y is the fixed point
one reaches starting from x. 然而, we want to be more liberal in what we will allow as an out-
put value, not restricting ourselves to fixed points. As output values, we will therefore admit forward
invariant state sets that we call terminations.
Definition: A dynamical system G is a triple G = (S, 中号, F ) consisting of a set of states S, a partially
ordered monoid (中号, <), and a transition function f : S × M → S such that:
(cid:129) f(s, x + y) = f( f (s, x), y).
(cid:129) The set M is linearly ordered by <.
(cid:129) In order to guarantee that the addition of times in the first requirement is compatible with
the monoid, we have to require that ( p, t 2 M ) ∧ ( p < t) ⇒ ∃q 2 M( p + q = t).
The set M is nothing else than the set of time values. In what follows, it will always hold that M ¼ R.
Definition: Given a dynamical system G = (S, M, f ), the forward orbit OG
the set of states OG
+(x) = { p|p 2 S, ∃t > 0 ( F(t, X) = p)}.
+(X) of x 2 S is defined as
Definition: Given a dynamical system G = (S, 中号, F ), let T be a subset of S.
(西德:129) T is called forward closed if a 2 T ⇒ OG
+(A) ⊂ T.
(西德:129) T is called forward connected if a, 乙 2 T ⇒ a 2 OG
那是, it implicitly holds that b 2 OG
+(A).
+(乙). Note that this definition is symmetric,
(西德:129) T is called a termination if it is both forward closed and forward connected.
The set of all terminations of G will be denoted by Q(G).
Accepting terminations as output values makes it possible to have a sequences of states as output—
例如, in robotics, the sequence of states representing a movement.
Definition: The functional dynamics of a dynamical system G = (S, 中号, F ) 是个 (部分的) function dG that
sends, 如果可能的话, 一个 (最初的) state x to a termination T if OG
+(X) has a nontrivial intersection with T.
Note that if the system G starting with initial condition x after a transient eventually stabilizes in
an oscillatory movement given by the termination T, then we have dG(X) = T.
现在, we introduce the concept of a programmable dynamical system.
Definition: A programmable dynamical system is a triple C = (S, 中号, ( fj )j 2 J), where for each j 2 J the
triple (S, 时间, fj ) is a dynamical system. An element j 2 J is a program for P.
人工生命量 19, 数字 1
15
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
The definitions given up to this point help us to discuss morphological control. 他们 (and the con-
cept of an observer to be detailed below) will be used in the discussion of the case studies. In what
如下, we extend our formalization to treat morphological computations that map natural numbers
onto other natural numbers, establishing contact with the theory of conventional computation, 和
showing how the concept of a programmable dynamical system can represent the first step toward
a theory of morphological computation oriented toward computation in general. A future article will
examine this possibility in greater depth.
First of all, we introduce the concept of an observer and specify what we mean when we say that
a specific observer can use a system to compute a given function from the natural numbers to the
natural numbers. The interpretation of such natural numbers as reals representing positions, angles,
and so on is regarded as unproblematic.
We observe that there are three possible kinds of interaction between an observer and a compu-
特尔: programming, setting input, and reading output. To formalize the notion of an observer of a
given programmable dynamical system C = (S, 中号, ( fj )j 2 J), we define a triple (IC, RC, p). 在这个
环境, IC are input states (a subset of S), and RC is a binary relation defined on S with a value of 0
when two states cannot be distinguished and 1 否则. We impose the requirement that, for each
pair x, y 2 IC, we have RC (X, y) = 0. This allows us to handle the problem that the initial states of a
continuous physical system can only be prepared with finite precision. 最后, the partial function p
maps a number-theoretic function B to the set J, the index set of the transition functions. (注意
each element j of J corresponds to a parameter setting.) The partial function p models the ability of
the observer to set up the parameters of the system such that the system computes the function B
(见下文). The situation is visualized in Figure 2. The set IC = {i1, i2} consists of representatives (例如,
the centers, black dots) from each of the surrounding shaded regions. When preparing the system in
state in the observer chooses a state in the surround of in. The condition that any two elements of IC
can be distinguished ensures that the observer is able to check the input for correctness.
Before we can say under which conditions an observer is able to compute a given number-
theoretic function, we have to connect the functional dynamics of a system with number-theoretic
功能. We call this link a computational interpretation.
Definition: A computational interpretation (西德:2)G of a dynamical system G = (S, 中号, F ) is a pair (CG, DG)
that consists of a coding function CG : N→S that maps natural numbers to initial states of G and a
decoding function DG : QðGÞ→N that maps terminations of G to the natural numbers.
现在, we can define what it means when we say that an observer can use a dynamical system to
compute a partial number-theoretic function B.
Definition: Given a programmable dynamical system C = (S, 中号, ( fj )j 2 J) and a computational
解释 (西德:2)C= (CC, 直流), the observer (IC, RC, p) can use C to compute the partial function
乙 : N → N relative to the computational interpretation (西德:2)C if for each natural number n:
(西德:129) The function p is defined on B.
Remark: The purpose of this condition is to make sure that there is a program to implement B.
(西德:129) CC(n) is an element of IC.
Remark: The purpose of this condition is to make sure that the observer is capable of
setting up the system so that it computes the function for all desired values.
(西德:129) For any natural number k, if dC, p(乙) (CC(n)) is different from dC, p(乙) (CC(k)), 那里
exist two states q 2 dC, p(乙) (CC(n)) and s 2 dC, p(乙) (CC(k)), 分别, 这样
RC (q, s) = 1.
Remark: This condition allows an observer to use a system to compute two different
values of the function B only in the case that the observer is capable of distinguishing the
two related outputs.
16
人工生命量 19, 数字 1
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
(西德:129) 乙(n) = DC (dC, p(乙) (CC(n))).
Remark: This last item connects the functional dynamics of Ci with the function B
via the interpretation (CC, 直流).
The computation of B using the dynamics of C is called a morphological computation.
基本上, the definition of morphological computation states that the diagram
S →dC;j QðCi Þ
↑CC
↓DC
乙
氮
N →
ð1Þ
is commutative and that all information processing required is accessible to the observer. Note that the
coding and the decoding function do not depend on the program j, whereas the functional dynamics is
determined by the parameter setting.
It is crucial to understand the relationship between the function B, a conventional program, 这
functional dynamics dC, p(乙), and the program p(乙) determining the functional dynamics given the
dynamical system C.
The function B is a mathematical object that does not describe how its output B(n) is generated
from an input n. A conventional program is a string over a certain alphabet and describes an algo-
rithm that makes it possible to compute B(n) on a standardized device such as a universal Turing
机器. This string, together with the description of a Turing machine, contains all the information
necessary for the evaluation of B(n). The program contains no reference to the physical properties of
the device that actually performs the computation. In the case of the functional dynamics of a pro-
grammable dynamical system, the program consists of a set of parameter values. This set, 一起
with the dynamical system and the computational interpretation (CC, 直流), makes it possible to com-
pute B(n). Whereas in the case of a conventional computation an abstract description is sufficient, 这
morphological computation requires an actual physical system. Note that it may well be the case that
the dynamical system can be simulated; the morphological computation can then be replaced by a
conventional computation. 尽管如此, such a virtualization requires a complete description of the
physics governing the dynamical system. One important aspect of morphological computation is that
we do not necessarily need to understand the complete physics of the system we use for computation;
all we need is a phenomenological description of its functional dynamics.
There are still a number of important open problems:
(西德:129) In our definition of a termination, we compared states and asked whether they are equal.
This is not critical as long as these states are discrete; for a continuous system our naı̈ve
usage of the equal sign is not satisfactory.
(西德:129) The restriction to deterministic dynamical systems is, in a strict sense, too narrow.
Already in the case studies, we will present systems with stochastic properties. As long
as one neglects fluctuations, the dynamics of mean values can often be regarded as
确定性的. A valid definition of morphological computation should, 然而, 包括
systems that are governed by statistical physics.
It may also be valuable to clarify another point that sometimes comes up in discussion. 到底, A
computation performed on a digital, electronic device relies on the physics of the hardware and can
thus be interpreted as a special instance of morphological computation. 然而, it is also possible to
consider morphological and conventional computation as constituting a dichotomy. According to this
看法, the main difference between morphological and conventional computing is that conventional
computers are designed to minimize the influence of the hardware on which they are implemented,
ensuring that programs can be written independently of direct physical considerations; in morphological
computing this is not required and is not usually possible.
人工生命量 19, 数字 1
17
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
On these grounds, many researchers define morphological computation in such a way that it has to
depend significantly on the physical dynamics of the system on which it is implemented. We agree with
this position. The definitions presented earlier allow us to specify what we mean by “significantly.” In
our formalized definition of morphological computation, we defined the concept of a programmable
dynamical system in a very broad sense. Additional restrictions allow us to define subcategories of mor-
phological computation. 尤其, we can define the class of non-portable morphological computa-
系统蒸发散. The corresponding requirement is that the program for the computation (in the sense defined
多于) should not contain all the information necessary to perform a desired computational task on a
Turing machine. In this category of morphological computation, part of the information determining
the computation is given by the physical structure of the device performing the computation. Non-
portable morphological and conventional computation constitutes a true dichotomy that matches
intuitive ideas about morphological computation. All instances of morphological computation we
discuss here are of the non-portable type.
The formalization we have presented matches the Venice definition of morphological computa-
的, providing a formal interpretation for each of its terms. Although we are aware that our for-
malization may rule out some systems one would like to regard as performing morphological
计算, we believe that it can provide clarification for future theoretical studies.
The first requirement in the definition was that reproducible input should be converted into repro-
ducible output. With the concept of a termination, we can cover a broad range of outputs, 包括
oscillatory movements. We observe that the notion of reproducibility is closely related to the ability of
the observer to distinguish states. A morphological computation is regarded as reproducible as long as
the outputs cannot be distinguished by the observer. 所以, an asymptotic transient toward a limit
cycle may at some point no longer be recognized as being different from the limit cycle itself. Two such
transients may differ in an absolute sense for all times; our framework captures the notion that if they are
sufficiently close to each other, 他们是, from the observerʼs perspective, identical.
The second requirement in the Venice definition is that morphological computing systems should
be programmable. We give a precise definition of what is understood by programming that includes
parameter tuning.
最后, the Venice definition requires that the computations performed by a morphological com-
puting system should have some sort a sort of teleological embedding. In our framework, this em-
bedding is understood and specified as a computational interpretation.
2.2.2 Formalizing Morphological Control
出于本文的目的, we define morphological control as a control process that relies at least
partially on morphological computation. Since we have defined the functional dynamics of systems liberally
enough to allow all sorts of terminations as possible outputs, we can regard instances of morphological
control tasks as special cases of morphological computation in the absence of an observer or computational
解释. We should nonetheless stress that there is a basic distinction between control and computa-
的, be it conventional or morphological: A computation maps an input onto an output, with the input
completely given at the start of the process. 控制, 相比之下, generates a stream of output signals from a
stream of input signals. The input at any given time depends on previous outputs. 因此, 完整的
stream of input signals is not known at the start of the computation. As a consequence the relation between
input and output is much more intricate than in a computation involving a permanent interplay between
morphological and conventional control, 如图 1. We are currently preparing a more elaborate
definition of morphological control that takes account of sequences of input signals. When inputs are dis-
cretized, the problem is rather easy from a formal point of view. 然而, coping with nondiscrete input
that is not generically discretized as in a conventional computation offers a considerable challenge.
2.3 Programming Morphological Computation and Control
When we perform a computation, morphological or conventional, we perform it on the representation
of a system. It follows that the difficulty (we deliberately avoid the term complexity) of a computation
18
人工生命量 19, 数字 1
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
may well depend on the properties of the state space for the system, and not on the intrinsic difficulty of
the computation. A binary representation of a computational task (例如, a simulation on a universal com-
电脑) is a case in point. The intrinsic structure of the computerʼs state space (理想地, a long sequence
of bits) is completely independent of the physics of the process to be simulated. 此外, 这
representation is largely independent of the physics of the device performing the binary computation
except for the fact that it needs to provide a sufficiently large set of discrete states and the ability to
switch between them. Whether a representation is binary is not of importance as such; what is important
is the use of a finite alphabet of some fixed size. It is a key property of modern computer programs that
they are device independent. This has (至少) two important advantages: 第一的, 普遍性 (the ideal
computer is an abstract Turing machine whose capabilities encompass everything we deem as compu-
站), 第二个, portability—the ability to run the same program on different machines. To ensure
portability, it is necessary to minimize the influence of the physics of specific machines (their specific
embodiments).
That embodiment may yield considerable efficiency gains is nothing new to digital computer en-
gineers. 实际上, embedded systems quite often profit from wiring topologies that reflect properties
of the space to be simulated. 例如, FPGA-based customizable machines have been used to
simulate spatially heterogeneous chemistries [5, 40]. The embodiment—the morphology given by the
wiring of the processors—facilitates computation by making it unnecessary to explicitly encode com-
plete spatial information for the molecules in the simulation. At least part of this information is im-
plicitly given by the position of the processor that hosts the data representing the molecule under
consideration. Morphological computation extends this idea by avoiding explicit coding of more gen-
eral physical information. In the case of a system governed by classical mechanics, one way to achieve
morphological programmability is to construct a dynamical system with a parameterized attractor
景观. A (possibly digital) controller moves the system from one basin of attraction to another,
without coordinating the details of the movement. The pattern itself is realized and stabilized by the
吸引子. The parameterization of the attractor landscape provides a certain degree of programmability.
重要的, this form of programmability does not require the programmer to encode the physics of
系统, as would be necessary for a controller simulating Newtonʼs laws, but only to know (或许
only roughly) the arrangement of the basins of attraction. The downside of such a program is that its
portability is limited: It only works for a given physical system.
What are underlying reasons for these gains in efficiency? We claim that there are at least four:
1. Nature is not susceptible to the problems of numerical analysis.
2. In a morphological computation, the physics is already there; there is no need to encode it.
3. Nature is inherently parallel.
4. Instances of morphological computation are proven to be evolvable.
As far as concerns the first point, it is well known that some problems are numerically more dif-
ficult than others and that this difficulty may have nothing to do with the intrinsic properties of the
问题. One argument in favor of morphological computation is that the translation of the physical
reality into strings adds complexity to the problem. 举个例子, consider collisions among hard
物体. If the objects are rotating, simulating their collision dynamics is demanding, even if they are
convex [4]. Morphological computation offers a far easier solution, significantly enhancing the effi-
ciency of the control process.
更普遍, conventional computing requires the encoding of the whole of the relevant physics.
A morphological control process, 相比之下, can exploit the fact that the physical system used to per-
form the computation already incorporates the physics (the second point). 当然, a conventional
computer is also a physical system. 然而, it is designed in such a way that the computation as such is
device independent. We can illustrate this point with the example of a recipe. 今天, it is not possible to
use a simulation to control the cooking of potato soup. Such a simulation would need to include the
人工生命量 19, 数字 1
19
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
complex chemistry and convection dynamics of highly viscous fluids near phase transitions. 然而,
with loosely standardized pots, potatoes, ovens, and spices, a recipe for potato soup takes only a single
页. The recipe qualifies as a program, but one that relies on the embodiment of the cooking process.
In this way it avoids the need to program the dynamics under consideration. The EU-funded project
MATCH-IT (http://fp7-matchit.eu/) is currently applying a similar idea to chemistry, examining how
far morphological computing can be used to facilitate chemical process management.
With respect to the third point, we note that in general the computational cost of simulating the
interaction among n particles is O(n2) in CPU time and O(n) in memory. In morphological computa-
的, 相比之下, the inherent parallelism of the interactions means that the time necessary for com-
putation is basically independent of the number of particles. Time is only needed for the preparation
输入的; this time usually scales linearly with n. 此外, general costs (材料, 活力) 为了
the production of the particles are also linear in n.
As far as concerns the fourth point, our own existence proves that some kinds of morphological
control are evolvable (看, 例如, the discussion about the human leg in [27]). 然而, our claim goes
further than this. The evolvability of a system depends critically on the representation of the control
问题. Since physical systems can be constructed such that their behavior is a smooth function of
their morphology, evolutionary methods provide a good solution for parameter tuning. Note that this
is not necessarily the case for control programs represented by strings of characters. Here slight var-
iations may have a large impact. For a detailed discussion of this point, 看 [30].
The program for a conventional control device consists of a syntactically correct string of char-
acters representing a sequence of semantically meaningful functions. 相比之下, current methods for
programming morphological control involve tuning parameters and designing systems so that they
can generate a large variety of dynamical structures. Even if further formalization is possible, 这是
unlikely we will ever be able to construct a context-free language for morphological computing. 如何-
曾经, it may be possible to identify primitives for specific classes of system and combine them into
larger process chains. Developing a methodology to identify and combine functional primitives is a
对未来工作的挑战. 迄今为止, we know quite well how to program a number of specific systems,
but a unifying view is still lacking.
2.4 Statistical Physics for Morphological Control
The dynamics of robots is governed by classical, deterministic mechanics. The system parameters
are positions, angles, and their respective velocities. This is the context in which the notion of mor-
phological control was originally developed. 然而, one of the goals of our work is to enlarge the
scope of morphological control to systems that are subject to statistical physics and to exploit the
specific properties of their dynamics. Examples of such systems include chemical reactions, functional
many-particle systems (such as membranes), and self-assembling systems. These systems are character-
ized by diffusive transport and phase transitions—two categories of processes absent in classical
mechanics. 在这个设置下, system parameters are no longer (仅有的) positions and velocities, 但是也
chemical and thermodynamic properties such as densities, temperature, or entropy.
下文中, we will focus on self-assembly in chemical systems, showing how we can use the
morphological properties of a system to control a construction process, while simultaneously profiting
from statistical physics. In a self-assembly process, two components connect only if their shapes match.
On its own, 然而, this is a necessary but not a sufficient condition. They also have to encounter each
other when they are in a proper configuration (例如, when they have matching orientations). In the realm
of statistical physics, a system can operate on timescales where such encounters are highly probable. 作为
previously discussed for the case of asymmetric diffusion [39], shape-dependent interactions and appro-
priate timescales can play a dynamic role in the control of sorting processes.
We mentioned that in order to take a statistical perspective, it is necessary to adopt appropriate
timescales. If diffusive transport plays a role, there is a fundamental relation between scales for time
and length, which limits the size of systems that can be used for practical applications (though size is
no fundamental barrier [43].) A rough estimate of these scales can be obtained by calculating the
20
人工生命量 19, 数字 1
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
average time tdiam to transport an object of diameter d over a distance d. Using ðr→ðt1Þ − r→ðt0ÞÞ2
¼
6Dðt1 − t0Þ for the expected squared distance traveled by a particle immersed in a fluid with diffusion
− t0 and the Einstein-Smoluchowski relation D = kBT/
constant D during a time interval of length t1
(3kDd ), we obtain
(西德:1)
(西德:3)
tdiam ≈
kDd 3
2kBT
ð2Þ
(viscosity is denoted by D). 例如, in the case of a particle of a diameter d = 1 是, we have tdiam = 0.4 s.
One could argue that this limit to length scales and timescales is a somewhat negative statement:
在实践中, exploiting the combination of statistical physics and morphology is only possible on
small length scales. 然而, there is also a positive perspective. Not only is morphological control
based on statistical physics possible only at small length scales, it is probably the only possibility for
控制. As demonstrated by Rothemund, who introduced DNA origami, our present technology
does not allow molecule-by-molecule construction [34].
今天, programming morphological control in the context of self-assembly consists of choosing
appropriate shapes and/or selective linkers (例如, DNA strands). Self-assembly, 然而, offers more
opportunities for the application of morphological control than just matching linkers. One possibility is
hierarchical self-assembly, a process in which a first set of building blocks assemble into compounds,
which then become the building blocks for a second-order self-assembly process (more levels can be
added). This kind of multi-order process may be difficult to set up. 然而, it also offers advantages.
尤其, we interpret the process as implicit, morphology-determined quality control: Only properly
assembled building blocks will match on the next level of self-assembly.
A second opportunity offered by morphological control is the possibility of combining self-assembly
with evolvable hardware. 在之前的工作中, one of the authors (R.M.F.) demonstrated that a combina-
tion of genetic algorithms, self-assembly, and a novel scheme for evolving test problems can generate
scalable multipliers [6]. This was possible because parts of the problem were solved implicitly by the
geometry of self-assembling digital components.
3 Case Studies
下文中, we present three case studies illustrating applications of morphological control and
the relation between these applications and the definitions developed earlier in this article.
3.1 Tensairity-Based Support Systems for Patients with Movement Impairments
3.1.1 动机
One effect of aging is the gradual loss of control over complex movement patterns. This loss may have
many causes, one of them being reduced sensory and neural performance. The notion of morphological
computation suggests another possible explanation. Aging changes the mechanical properties of the
身体, altering its attractor landscape and thereby reducing the bodyʼs ability to contribute to control
任务. Viewed from this perspective, the difficulty many elderly people experience in controlling their
movements is not due (at least not exclusively) to poor performance by their brains, but to changes in
their body that make the morphological control problem harder. 下文中, we describe the use of
a novel technology, tensairity [19], to reshape the bodyʼs attractor landscape so as to restore morpholo-
gical control. The system we have in mind is not some kind of machinery that physically moves the
patient as though he or she were a passive object. Rather it modulates the patientʼs own actions.
3.1.2 Implementation
The term tensairity brings together tensegrity with air; inflatable elements play a crucial role.
Tensairity has made it possible to build inflatable bridges that can carry a car using pressures of only
人工生命量 19, 数字 1
21
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
300 mbar. 最近, it has been demonstrated that tensairity can also be used to implement
actuated structures [18]. In therapeutic contexts, such structures offer a variety of benefits, 包括
low weight and cost, high intrinsic safety, and high adaptability. 然而, their softness means they
cannot be programmed in the same way as, 说, an exoskeleton.
Work by one of the authors (K.J.H.) has shown that the tensairity actuator systems can be used to
provide soft support to patients undergoing rehabilitation following stroke, spinal cord injuries, 和
other conditions leading to partial paralysis. The idea is to provide additional support during standing
向上, 常设, 步行, and sitting down. Similar techniques can also be useful for elderly people with
weak lower-limb musculature.
Several systems to support walking are already in widespread use for clinical rehabilitation. One such
system is the Lokomat (Hocoma AG, Volketswil, 瑞士), a device that combines a treadmill with
powered, rigid walking orthoses and an overhead body-weight unloading system. The G-EO System
(Reha Technology AG, Olten, 瑞士) offers an alternative approach based on endpoint control:
The patientʼs feet are attached to an external powered actuator system that allows simulation of walking
on the level, upstairs, and downstairs. Other powered exoskeleton devices to support walking are under
发展 (例如, eLEGS, Berkeley Bionics, 加利福尼亚州, 美国; ReWalk, Argo Medical Technologies,
Haifa, 以色列).
Compared to these systems, tensairity actuators offer several potential advantages. The key dif-
ferentiating feature is that the actuator provides lightweight soft support to patients suffering from
partial paralysis or muscle weakness due to injury, 疾病, or aging. The idea is to supplement joint
supports and orthoses with customized tensairity actuators, or to integrate the actuators into wearable
garments. The actuators would not replace the action of the patient but would help the patient to
regain control over his or her movements.
To evaluate the potential of tensairity actuators, two of the authors (K.J.H., A.D.) have con-
structed and tested a biomechanical prototype system that mechanically simulates the human thigh,
calf (shank), and knee joint, allowing the integration of different tensairity support actuators (数字 3).
The actuators themselves were custom designed and manufactured to fit the mechanical con-
struction. They were then positioned on each side of the artificial knee joint, and the joint angle
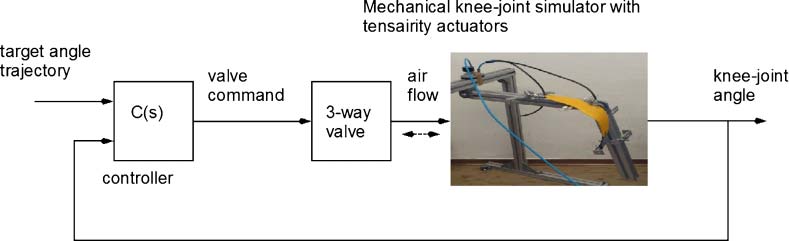
was measured using a digital encoder. This setup made it possible to implement a feedback control
system so that the knee-joint angle could follow arbitrary, prespecified trajectories (数字 4). 这
feedback controller drives a three-way valve, which bidirectionally supplies air to the actuators.
In a real-life implementation, the feedback system would take its target angle trajectory from
values corresponding to physiological knee-joint motion during functional tasks such as standing up
or walking.
Tests showed that the system can lift a 3-kg mass at the notional ankle joint (IE。, at the bottom of
the shank) from the vertical to the horizontal, using a pressure of less than 1 bar. The torque generated
in this way is 15 N m. This suggests that the system could provide useful joint support at low cost, 低的
重量, and low pressure. The next phase of the study will investigate combinations of controlled
数字 3. Biomechanical test bed simulating the knee joint, thigh, and shank. The knee joint is supported by a pair of
feedback-controlled tensairity actuators. The picture shows a knee-joint extension sequence (left to right).
22
人工生命量 19, 数字 1
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
数字 4. Feedback control system for knee-angle trajectory tracking, with tensairity actuators supporting the knee joint.
tensairity actuators with existing or custom-built joint supports and orthoses. The resulting systems
will be tested first with healthy people and then in people with lower-limb impairments.
3.1.3 Interpretation in Terms of the Formal Framework
In terms of the concepts introduced earlier, the patientʼs body is a compliant, multi-joint mechanical
系统, which we can consider as a programmable dynamical system C = (S, 中号, ( fj )j 2 J). 这
monoid M represents time and is equal to R. The set S represents the states of the body, 给定
by geometry as well as internal physical parameters such as muscle tension. The terminations one
seeks are self-stabilizing gait patterns that are stable on slightly uneven terrain. The transition func-
tions fj represent the morphology-dependent temporal dynamics of the body; the index j refers to the
different morphologies a human being can distinguish and attain. The function of the tensairity
actuators is to alter the dynamics of at least one morphology so that the functional dynamics leading
to the desired termination becomes as stable and easy to enter (large basin of attraction) 尽可能.
As mentioned earlier, movement control is the result of the interplay between morphological
control and, in the case of a human being, the control exerted by the brain on the body. The cali-
bration of the actuator has to take into account of the patientʼs physiology as well as his or her neural
control capabilities.
3.2 Programmable Self-Assembly of Spatially Heterogeneous Microreactors
3.2.1 动机
The synthesis of complex branched molecules (例如, oligosaccharides for glycol conjugates with med-
ical applications) is still a demanding task. One of the important tasks is controlling potential side
reactions [16]. Whereas the synthesis of a linear chain molecule can happen in a template-based
manner and the reaction, 至少在理论上, leads to an unambiguously defined end product, 不
comparable technique is available for branched structures. Without a template, the only way to
achieve unambiguously defined end products would be to use addresses specific to each connection.
Unique addressing based on strands of DNA or related chain molecules has previously been used to
construct large supramolecular structures [34, 41] and even for the construction of self-assembled
compounds of vesicles [8]. 然而, large linkers are not always suitable for the connection of small
molecules. Using small linker structures means that, instead of being able to exploit a combinatorial
variety of addresses, one has only a small number of linkers at hand, and that it may be necessary to
use the same linker more than once. With one-pot reactions, the multiplicity of reaction pathways lowers
the yield [16].
3.2.2 Spatially Heterogeneous Microreactors
The synthesis of branched molecules is a control problem. Given the many types of chemical bond
available in the lab (例如, so-called click chemistries [38]), building arbitrarily branched structures is not a
人工生命量 19, 数字 1
23
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
significant problem in itself. The challenge is controlling the reaction pathways. This is one of the ques-
tions addressed by the European research project MATCHIT (Matrix for Chemical IT), coordinated by
Steen Rasmussen at The Center for Fundamental Living Technology (FLinT), University of Southern
丹麦. The work presented here was funded by the MATCHIT project. For implementations of spa-
tially resolved chemistries, readers should consult the MATCHIT Web site http://fp7-matchit.eu/.
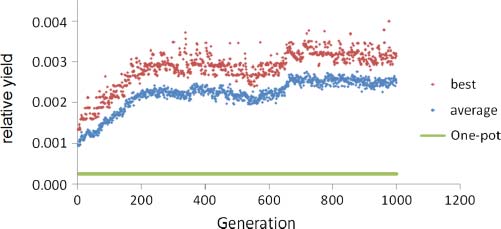
In our study, we demonstrated in silico [32] that it is possible to create a spatially heterogeneous
reaction environment with a bias toward specific reaction channels that increases the yield from the
reaction (for details of the rather intricate implementation, 看 [32]). 重要的, this increase is purely
due to spatial organization and happens without any kind of interference with the kinetic constants for
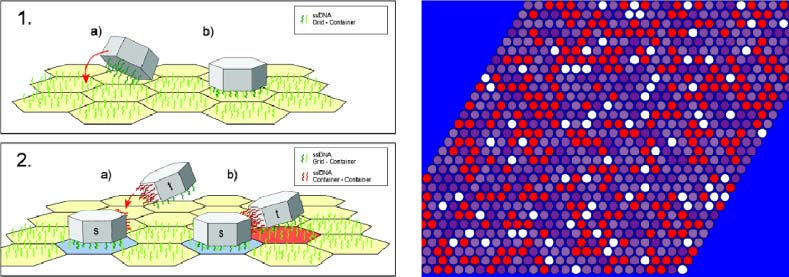
the reactions. Briefly, we combined two self-assembly processes: 第一的, we used self-assembly to con-
struct a two-dimensional microreactor from what we call chemtainers (see details below). 第二, 我们
used the microreactor as a platform for the self-assembly of branched oligomers from monomeric
building blocks. 下文中, we will limit our discussion to the spatial structure of the microreactor
and the way we exploited it to modulate the self-assembly process. Other important aspects of our work
(such as the methods used to transport molecules from one chemtainer to the next and the implemen-
tation of selective linkers between chemtainers) are not discussed here, but are investigated in the
MATCHIT project by other groups.
The self-assembly processes we employed both use selective linkers. Both are reversible (the im-
portance of reversibility is discussed in [42].) Our primary aim was to synthesize branched goal struc-
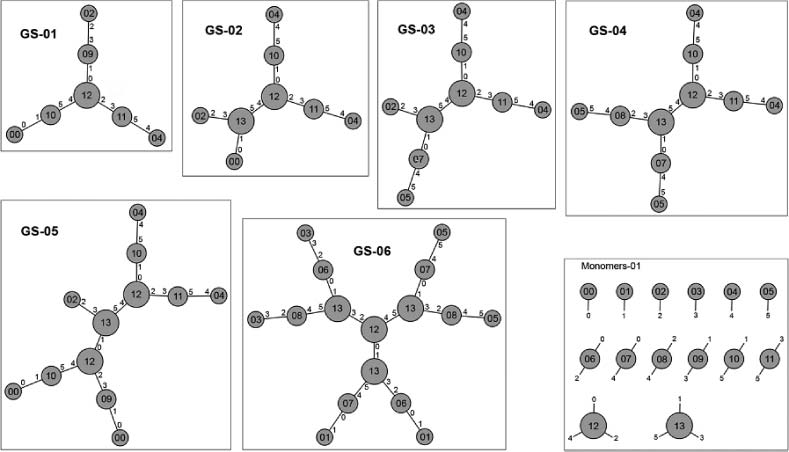
tures as shown in Figure 5. Goal structures are composed of monomers, each equipped with up to three
linkers. As described in the figure caption, we used three types of linker. Whether or not the bonds
determined by these linkers can be established depends on chemical conditions in the environment,
such as the presence of catalysts and whether the linkers match. The reactions required to match linkers
take place in chemtainers: potentially microscopic reaction containers that can be linked to other chem-
tainers to build spatially heterogeneous reaction environments. In the first self-assembly process, 这
chemtainers self-assemble to form the reaction environment for the second self-assembly process,
namely the formation of the branched molecules (the goal structures).
数字 5. Various goal structures synthesized in spatially heterogeneous microreactors. Each structure is composed of
some of the building blocks (monomers) given in the inset in the lower right corner. A monomer is equipped with up to
three linkers, making it possible to establish a link between linker pairs 0-1, 2-3, 和 4-5. During synthesis, monomers or
compounds of monomers can be coupled, as long as a pair of linkers is matching and the chemical environment is such
that the coupling can be established.
24
人工生命量 19, 数字 1
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
数字 6. 左边: Self-assembly of the 2D grid of containers via specific linker molecules (ssDNA). The upper part (1) 节目
the association of a container to the grid; (2) illustrates the specific association between two containers (s, t). 正确的:
Example of a spatially heterogeneous microreactor. In the electronic version, a circle indicates a single container, 和
the colors indicate the different container types.
To obtain a spatially heterogeneous reaction environment, we assumed hexagonal chemtainers of
various types, whose type was specified first by their internal chemistry (to be discussed below) 和
second by selective linkers on their edges (例如, DNA-based addresses). The chemtainers self-assemble
on a two-dimensional substrate. Their bindings to the substrate are nonselective and relatively weak.
Where they are available, bindings to neighbors are reversible and selective. The chemtainers are mod-
eled as freely floating above the substrate, binding to the ground and to already bound adjacent chem-
tainers. For an illustration see Figure 6. 重要的, bonds between chemtainers are reversible: A bound
chemtainer can be released again. If a chemtainer is connected to six matching neighbors, the total
binding energy is tuned so that release is no longer probable. 这 (reversible) self-assembly process
is run long enough to ensure the emergence of a structure with a defined neighborhood correlation,
though not a spatially regular pattern (数字 6, 正确的).
Different types of chemtainers provide chemical environments capable of catalyzing the estab-
lishing or breaking of some of the possible links between the molecular monomers depicted in
数字 5. Monomers and oligomers are assumed to diffuse between chemtainers. 然而, the func-
tionality of the chemtainers is maintained. One way of realizing this is by anchoring catalysts to the
walls of the chemtainers. If these walls are scaffolds with sufficiently large holes, oligomers can be
transported via ordinary diffusion.
If one uses only a small number of different types of linkers (a realistic assumption in glycochem-
istry), then the chemical functionality of the chemtainers is determined exclusively by the type of link
and not by the molecules that are linked. 然而, it is also possible to link two oligomers if their
respective linkers match. This is what makes it so difficult to control the process: The limited num-
ber of linkers means that the combination of intermediates (oligomers or monomers) is not suffi-
ciently specific, and therefore many side reactions are possible.
In a one-pot reaction, all oligomers may be connected, always provided that they are equipped
with matching linkers. In our system, 然而, the spatial arrangement of the chemtainers implicitly
biases some reaction channels, leading to an increase in yield. 例如, our method offers a
tenfold increase in yield for the synthesis of oligomer GS-04 (见图 5) 图中 7 we show
the results of an evolutionary optimization of the properties of the chemtainer. As explained above,
chemtainers are characterized first by their linkers and second by their functionality. It was these
properties we attempted to optimize. For each set of parameters, we performed 20 runs, each simu-
lating the self-assembly of the spatially heterogeneous microreactor and the subsequent synthesis of
the goal oligomer (GS-04). We then compared the results with those for a one-pot reaction. 数字 7
shows the average yield (as a percentage of the total number of molecules synthesized) and the yield
of the best run. 有趣的是, the best result was not far from the average. This indicates that our
procedure is rather robust.
人工生命量 19, 数字 1
25
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
数字 7. Development of the yield of the goal structure GS-04 期间 1,000 generations of the evolutionary algorithm.
The lower line indicates the expected yield of polymerization in a homogeneous reaction environment. Chemtainers are
characterized first by their linkers to other chemtainers on their edges, and second by their chemical functionality,
即, the ability of their content to influence the links between the building blocks of the oligomers to be synthesized.
We evolved these properties using an evolutionary algorithm. For each combination of properties, we performed 20
complete simulations of the self-assembly process.
The arrangement of the chemtainers biases certain reaction pathways by enhancing the probabil-
ity of some sequences of additions or removals of parts of an intermediate molecule. 举个例子,
consider a chemtainer with functionality A, surrounded by chemtainers with functionality B and C,
but not D. When an intermediate molecule M reaches chemtainer A, it undergoes reactions in the
order A-B or A-C but not A-D, except for the case in which M travels through chemtainers B or C
unaffected and somehow reaches a chemtainer with functionality D. In a spatially homogeneous
环境, it would be possible to obtain the same effect by varying kinetic constants and reaction
rates with respect to time, perhaps by transferring intermediates from one chemical environment to
其他. 然而, this transfer would require external control. The system we used here makes it
possible to remain homogeneous with respect to time and to delegate the creation of specific, TEM-
porarily ordered sequences of reaction environments to the interplay between diffusion and the pat-
terned reaction environment.
3.2.3 Interpretation in Terms of the Formal Framework
It is well established that self-assembly can be used in order to implement computation [21]. Inde-
pendent of the interpretation of the outcome, we thus regard self-assembly as an instance of mor-
phological control. This is because it is the dynamics of the system itself that defines the outcome,
which is potentially highly specific. The decision of whether two components can be linked is
determined locally by the morphology of the linkers without any reference to external control.
In terms of our formalism, the solution containing the chemtainers constitutes a programmable
dynamical system C = (S, 中号, ( fj )j 2 J). 再次, the monoid M represents time and is equal to R. 这
set S stands for the arrangement of chemtainers on the substrate, the concentration of chemtainers
in the solution, and the content of the chemtainers. The transition functions fj represent the dynam-
ics of the solution, which are basically determined by the choice of matching linkers, the relative
concentration of chemtainers in the solution, and the initial content of the chemtainer.
It must be emphasized that in this case, we need to extend the definitions given in Section 2.2. 在
the stochastic system we consider here, the input is the distribution of chemtainers at the start of the
self-assembly process; the program is given by the choice of the chemical functionalities of the build-
ing blocks and the structure of their linkers; the terminations are an arrangement of chemtainers with
given neighborhood correlations or a given distribution of oligomers (subject to fluctuations). The role
of the observer is a trivial one; his or her only role is to run the experiment.
3.2.4 Potential Application
What is the interest of self-assembled microreactors? In the last analysis, a tenfold increase in yield
is interesting but not spectacular. One possibility is that our technique could allow us to implement
26
人工生命量 19, 数字 1
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
the production of chemicals on a very small scale. Perhaps more significantly, we hypothesize that
spatially heterogeneous microreactors could provide opportunities to use types of catalysts not used
in conventional process management. Assume that one does not synthesize oligomers, but some
sort of catalyst that is used in a subsequent step. It may well be the case that the environment in
which this catalyst is synthesized (or activated) is different from the environment in which the cat-
alyst has to act. In a macroscopic laboratory, this implies that the catalyst has to be transferred from
one environment to the other, a process that takes time. This means that catalysts have to fulfill two
要求: 第一的, they have to be efficient, 第二个, they have to be stable. On a microscopic
length scale, where transport involves diffusion over micrometers, 10 s is quite a long time. 这
means that in microscopic reactors, catalysts, if they are produced in situ, only have to be efficient
but no longer need to be particularly stable (an average lifetime of minutes is sufficient). 因此,
many more molecules qualify as potential catalysts. The possibility that microreactors could enable
the use of metastable catalysts in a technically feasible manner is more than sufficient justification
for the study of such systems.
3.3 Multi-Scale Approaches in Systems Medicine and Oncology
3.3.1 The General Systems Perspective in Medicine
Systems approaches are becoming increasingly popular in applied oncology [3] and other medical
settings [1]. 今天, many authors combine a molecular perspective with approaches that rely on the
dynamics of intracellular structures on larger size and timescales or that rely on the way whole cells
are organized in tissues. The list of cellular processes relying on the interplay of molecular kinetics with
physical aspects of mesoscopic structures such as membranes [33] includes endocytosis, aspects of the
cytoskeleton, and macromolecular crowding. The way the physics of the cytoskeleton interacts with
cellular information processing is discussed in [12] 和 [13]. Interpreting the behavior of cells, aggregates
of cells, and whole tissues in terms of a dynamical system with chemical and physical components acting
on different length scales and timescales opens new perspectives on phenomena that are already familiar
in medical practice.
If a biological system is regarded as a network of interacting components, the network constitutes
a dynamical system. Such a system can misbehave for one of two fundamentally different reasons:
Either (1) one or several components cease to operate in the way necessary to maintain the overall
functionality of the network, 或者 (2) the individual components continue to operate correctly, 但是
network as a whole exhibits undesired dynamics. There are many therapeutic measures for tackling
medical problems due to the failure of system components, which we can repair or replace. 然而,
dysfunctions caused when an otherwise healthy system exhibits pathological self-stabilizing dynamics
(when it falls into the wrong basin of attraction) are less well understood. One possible example is
ventricular fibrillation.
Possible therapies can again be divided into two groups. The first group aims at pushing the
system from the wrong into the right basin of attraction (as probably occurs in defibrillation).
The second group tries to reduce the probability of accidental transitions from one basin into the
其他. From the perspective of morphological control, the existence of these basins of attraction is
no accident, but the result of an evolutionary process that benefits from this form of control scheme
(probably in combination with others that rely purely on chemical kinetics). We argue that concepts
from morphological control can contribute to the design of novel therapeutic strategies, 尤其
for dysfunctions of the wrong-basin-of-attraction type. Possible strategies could combine molecular
with physical measures.
3.3.2 An Example of the Systems Perspective in Oncology
In radio-oncology, tumors are treated by irradiating the tumor tissue with ionizing radiation. 在
添加, moderate heating (up to 43°C) of the tumors (hyperthermia) results in a synergistic cell-
killing effect. 有趣的是, heating alone (below 45°C) does not kill cells. The mechanism behind
人工生命量 19, 数字 1
27
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
the synergistic effect is poorly understood, but it is known that heat and ionizing radiation both have an
effect on a wide variety of intracellular processes and structures as well as on the whole tissue. 最多
existing radiobiological models cannot really explain the response of the tumor system to hyperthermia
and radiotherapy. Most prominently, such models do not properly explain the nonmonotonic dose-
response behavior of the tumor cells in the case of low-dose hypersensitivity (LDHS). One would
assume that if low doses of ionizing radiation kill tumor cells, increasing the dose would produce a
larger effect. 然而, this assumption is not corroborated by the experimental results (见图 8).
We start from the observation that tumor dynamics are well described by a class of rather simple
型号, based on a quantity G, called the dose equivalent [37]. 重要的, this quantity is an emergent
property of the cell. The model template describing the structure of the class of models is given by a
set of differential equations:
dNi
dt
dNk
dt
d G
dt
¼ f ðNi ; Nk; …… ; GÞ
¼ gðNi ; Nk; …… ; GÞ
¼ R − hðGÞ
(3)
where Ni denotes the number of tumor cells that are not damaged by heat or radiation, Nk denotes
the number of tumor cells with lethal or sublethal damage, the dose rate R is the absorbed radiation
energy per unit mass, and G denotes the dose equivalent. 在这个设置下, the functions f and g de-
termine the rates of damage induction, repair, and cell killing on the population level, whereas the
function h describes the (average) repair of cellular damage (changes of the repair capacity of a single
cell). Specific choices for the functions f, G, h lead to different types of models, described in detail in
[37]. These choices are justified by explicit assumptions about cellular processes, such as the repair
kinetics. 在之前的工作中, Scheidegger et al. reported at least two types of models (the G-LQ and
the G-IR model) that are able to reproduce biological observations (见图 8 for the G-IR model
as presented in [36].)
数字 8. Comparison of the proposed G-IR model (方程 4) with the model of [7], the IR model, and experimental
数据 (irradiated multicellular spheroids of breast cancer MCF-7 cell line). S denotes the fraction of surviving cells as a
function of the absorbed dose D.
28
人工生命量 19, 数字 1
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
数字 9. 左边: Logarithm of surviving fraction as a function of the time gap between HT and RT fraction (solid: 模拟
of an HT-RT model according to the model structure of variant 1 多于; dashed: results corresponding to the experimental
observations). 正确的: Schematic illustration of the underlying dynamic process; the effect strengths of heat (solid) and radia-
的 (dashed) can be described by a dose equivalent for radiation and the fraction of thermally affected cells for heat.
For the purposes discussed here, it is important to note that the dose equivalent is an input for
the functions f, g in the equations. This indicates that the dose equivalent is more than a purely
descriptive quantity, and can be used as a true parameter of the system.
Further developments have made it possible to understand the synergistic effect of hyperthermia
and radiotherapy (HT-RT model). Following the concept of a dose equivalent, the thermal effect can
be summarized by a second, heat-related dose equivalent, which we call (西德:3). We are currently con-
sidering two extensions to our previous system of equations (2) that allow us to model how heat-
induced denaturation of proteins can contribute to or interfere with cellular repair:
(西德:129) Variant 1:
dNi
dt
d G
dt
¼ f ðNi ; Nk; …… ; G; LÞ;
dNk
dt
¼ gðNi ; Nk; …… ; G; LÞ
¼ R − hðGÞ;
d L
dt
¼ uðLÞ − wðLÞ
(西德:129) Variant 2:
dNi
dt
d G
dt
¼ f ðNi ; Nk; …… ; GÞ;
dNk
dt
¼ gðNi ; Nk; …… ; GÞ
¼ R − hðG; LÞ;
d L
dt
¼ uðLÞ − wðLÞ
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
ð4Þ
ð5Þ
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Up to now, it is not clear which of the two variants offers a better explanation for the behavior we
observe in Figure 9.
The observation that a low-dimensional parameterization is capable of explaining the dynamics of
a system at least to some degree of accuracy brings up three questions:
1. 第一的, why is it possible to map a generically high-dimensional system to a low-dimensional one?
2. 第二, what is the interpretation of the observed parameters?
3. 第三, how can we interpret and control the dynamics of the observed parameters?
人工生命量 19, 数字 1
29
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
With respect to the first question, the engineerʼs perspective offers a hypothesis for the explana-
tion of the low dimensionality. Biological systems have evolved to be robust, 和, at least in tech-
科学, robust behavior is much easier to realize in low- than in high-dimensional systems.
Before answering the second question, one should consider a mathematical fact: A single curve
(or higher-dimensional attractor ) can be parameterized in many ways, using coordinates that may or
may not have an obvious physical foundation. In the case discussed here, the dose equivalent may be
justified using considerations of statistical mechanics and cellular structures. Since a cell is not an
ideal gas or crystal and there is no well-defined equilibrium, the exact calculation of the dose equiva-
lent seems to be impossible, and we treat it in a phenomenological manner. But though our present
understanding of the dose equivalent is incomplete, this does not affect its usefulness as a parameter.
Given that we have discovered a parameterization that effectively describes cellular dynamics, 这
second question addresses the task of finding a physical interpretation for the parameters—for ex-
充足, of explaining them in terms of appropriate system-specific functional primitives.
The third, quite different task is to explore the attractor landscape in terms of the observed param-
eterization: We hypothesize that the attractor landscape of the tumor system is related to the malig-
nancy of tumors and also to its response to cancer treatment.
The genetic instability of malignant tumors leads to a diverse collection of a number of subclones,
each of which is equipped with a slightly different, mutated genome. It is at least plausible to assume
that the corresponding biochemical attractor landscape resulting from the mutated genomes is less
well suited for controlling cell function and that the barriers between different attractors are lowered.
In consequence, it may be more difficult to trigger a specific cellular process—a possible reason for
the low efficacy of so-called magic bullets (cancer treatments using a specific key molecule). 在阿迪-
的, the fact that a malignant tumor contains subclones with differing attractor landscapes renders
the task of finding a specific magic bullet even more demanding. 相比之下, the success of treat-
ments combining ionizing radiation and heat could depend on a system-level effect on the whole
attractor landscape, not relying on details of specific attractors.
These dynamics, connecting different length scales and timescales, form the dynamical system we
are trying to control. 在这个设置下, the terminations are cellular processes, ranging from the syn-
thesis of linear polymers through protein sorting, to cell division. 然而, there is no observer in
the sense of Section 2.2 and consequently no input. The role of the observer is interpreted as an
intervention in an otherwise autonomous system.
然而, the cellular dynamics that interest us do not depend just on molecular kinetics, 但是也
on the physics of mesoscopic structures, which combine the mechanics of soft matter with elements of
statistical mechanics. This means that our current understanding of cellular processes is not sufficient to
establish a connection to each of the terms in our formal definition of morphological computation.
进一步来说, the determination of program and input would require the identification of cell process
primitives that could be taken as building blocks for the construction of larger process chains. 今天,
然而, we lack a complete list of such building blocks and their potential combinations.
4 Summary and Discussion
在本文中, we have discussed the concept of morphological computation and control, a concept
already in use in robotics and related fields. The case studies we present show that the concept of
morphological computing can easily be extended from classical mechanics to systems governed by
statistical physics and chemistry. They also suggest that exploiting the physical dynamics of a system
can lead to major improvements in computational efficiency (reduced use of costly resources), not least
because it is no longer necessary to encode all the relevant physics. 当然, there is a price to pay:
Morphological programs are not portable, and morphological computing devices are not universal. 在
一些案例, they may also offer less precise control than classical control systems. 然而, precise
control may not be necessary so long as the qualitative aspects of the dynamics are sufficiently robust
against perturbations.
30
人工生命量 19, 数字 1
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
These advantages and disadvantages are illustrated by the case studies. In the first study, we are
using morphological control to change the dynamics of a physical system (the patientʼs body) 在这样的
a way that it is easier for the patient to control. Experiments planned for the near future will test the
effectiveness of this approach. If it is shown to be valid, it should be relatively easy to further im-
prove the stability of the control mechanism, to make it easier to use, and to use it as a complement
to existing therapeutic schemes.
Recent results indicate that there is a subtle interplay between the dynamics of the body and
sensory functions [9, 31], especially for the elderly. The theoretical framework presented by Hauser
等人. [10] goes far beyond the simple picture of a body as a dynamical system with different attractors,
describing a feedback system in which an electronic control unit (a feed-forward neural network) 和
a body constitute a feedback system. It may be possible to use such a system to test learning strategies,
and use the results to design more efficient therapeutic strategies.
The second case study discusses morphological control in the context of chemical self-assembly.
In the case we describe, it is the morphology that controls which building blocks are connected, A
process that is technically too difficult to be executed by a central control unit. 这, 然而, 是一个
relatively trivial example of morphological control. Future studies should also consider dynamical
forms of self-assembly, which can form self-healing systems (看, 例如, http://www.math.udel.
edu/MECLAB/Projects/SelfAssembly/selfassembly1.htm). In this kind of system, which is also
discussed in [26], removing components only temporarily limits the functionality of the system.
The dynamic self-assembly process and the morphology of the building blocks allow it to recon-
struct itself. This is a good example of a kind of dynamics that is not covered by our formaliza-
tion of morphological computation and control in Section 2.2 and points to the need for a more
extensive definition.
The third case study suggests that the concept of morphological control can help us to under-
stand the response of tumors to treatment or, 更普遍, to understand the dynamic response
of the human body, 器官, or tissues. The idea of implicitly encoding a behavior instead of encoding
details of cellular processes explicitly leads to the concept of summarizing radiation-induced or thermal
damage by dose equivalent quantities. First results in the field of radiation oncology are promising. 这
suggests it could be useful to focus future research on the development of adequate but accessible
descriptions of the dynamics of biological systems.
合在一起, the case studies and the theoretical definitions proposed earlier suggest the
existence of a hierarchy of control:
1. Conventional electronic control: Based on universal computers and string manipulation;
precision limited only by the size of available memory; can be implemented on many
different classes of hardware; no implicit robustness; need to handle physical noise.
2. Systems in which parts of the program of a conventional computer are replaced by a physical system:
Domain restricted (no universal computation); precision restricted (the properties of the
physical part may be subject to changes, 例如, elasticity may depend on temperature); 仅有的
one implementation; implicitly robust; implicitly resistant to noise.
3. Systems in which conventional computers and physical systems mutually interact: For a discussion
看 [11].
4. Purely non-conventional computation and control: No classical control involved. Examples are
almost all biological information-processing systems.
For engineering, the most interesting systems are those belonging to classes 2 和 3. 调查
aiming at a better understanding of biological systems and their potential dysfunctions will mostly
deal with controllers in class 4, taking into account that morphological control can be, and in actual
biological systems is, nested. Nesting here means that cell function and the way cells form tissues and
organs are both subject to morphological control.
人工生命量 19, 数字 1
31
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
原则, we can extend this hierarchy further, by taking account of learning processes. 在这个
框架, learning may involve changes in the program of the conventional controller as well as in
the morphology of the body. 然而, a mathematized theory of learning that combines abstracted
and physical aspects of control is not yet available. Work by Thomas Schack and his collaborators in
the EU-funded project AMARSi (http://www.amarsi-project.eu/) promises a conceptual, 理论-
伊卡尔, and experimental framework applicable to human motor skills, but also in a more general set-
ting [35]. It has been claimed that such a theory could have useful applications in physiotherapy
and rehabilitation.
To conclude, our case studies suggest that morphological computing and control have the po-
tential to open up new application domains where conventional computing solutions would be com-
putationally expensive or infeasible. To realize this potential, it will be necessary to turn what is
basically a set of engineering concepts into a true conceptualization of morphological computation.
明显地, this will require much theoretical and experimental research. 在本文中, we have at-
tempted to take a step along this road. We make no claim that our formalization of morphological
computing and control is complete or that our case studies prove its value. What we hope is that we
have demonstrated sufficient progress to justify further research in the future.
Acknowledgment
The work presented in Section 3.2 was supported by the EU FP7 project MATCHIT.
参考
1. Ahn, A. C。, Tewari, M。, 胡桐, C。, & Phillips, 右. S. (2006). The limits of reductionism in medicine: 可以
systems biology offer an alternative? PLoS Medicine, 3(6), e208, 710; DOI 10.1371/journal.pmed.0030208.
2. Burtscher, M。, Gatterer, H。, Flatz, M。, Sommersacher, R。, Woldrich, T。, Ruedl, G。, Hotter, B., 李, A。, &
Nachbauer, 瓦. (2008). Effects of modern ski equipment on the overall injury rate and the pattern of injury
location in alpine skiing. Clinical Journal of Sport Medicine, 18(4), 355–357.
3. Costa, J. (2008). Systems medicine in oncology. Nature Clinical Practice Oncology, 5(3), 117.
4. Donev, A。, Torquato, S。, & Stillinger, F. H. (2005). Neighbor list collision-driven molecular dynamics
simulation for nonspherical hard particles. 二. Applications to ellipses and ellipsoids. 杂志
Computational Physics, 201, 765–793.
5. Füchslin, 右. M。, & McCaskill, J. S. (2001). Evolutionary self-organization of cell-free genetic coding.
Proceedings of the National Academy of Science of the U.S.A., 98(16), 9185–9190.
6. Füchslin, 右. M。, Maeke, T。, Tangen, U。, & McCaskill, J. S. (2006). Evolving inductive generalization via
genetic self-assembly. Advances in Complex Systems, 9, 1–29.
7. Guirado Llorente, D ., Aranda, M。, Ortiz Seidel, M。, Mesa Perez, J. A。, Vega Fernandez, J. 中号. D. L。,
Martinez Luna, 右. J。, Zamora Ardoy, L. 我。, Villalobos Torres, M。, & Lallena, A. 中号. (2010). Low dose
hypersensitivity in multicellular tumour spheroids. Radiotherapy & Oncology, 96(Suppl. 1), 607–608.
8. Hadorn, M。, & Eggenberger Hotz, 磷. (2010). DNA-mediated self-assembly of artificial vesicles. 公共图书馆一号,
5(3), e9886; DOI 10.1371/journal.pone.0009886.
9. Harry, J. D ., Niemi, J. B., Priplata, A. A。, & 柯林斯, J. J. (2005). Balancing act. IEEE Spectrum, 42(4), 36.
10. Hauser, H。, Ijspeert, A. J。, Füchslin, 右. M。, 普法伊费尔, R。, & Maass, 瓦. (2011). Towards a theoretical
foundation for morphological computation with compliant bodies. Biological Cybernetics, 105(5–6), 355–370.
11. Hauser, H。, Ijspeert, A. J。, Füchslin, 右. M。, 普法伊费尔, R。, & Maass, 瓦. (2012). The role of feedback
in morphological computation with compliant bodies. Biological Cybernetics, 106(10), 595–613;
DOI 10.1007/s004-22-012-0516-4.
12. Ingber, D. 乙. (2003). Tensegrity I. Cell structure and hierarchical systems biology. Journal of Cell Science,
116, 1157–1173.
13. Ingber, D. 乙. (2003). Tensegrity II. How structural networks influence cellular information processing
网络. Journal of Cell Science, 116, 1397–1408.
14. Jaeger, H。, & Haas, H. (2004). Harnessing nonlinearity: Predicting chaotic systems and saving energy in
wireless communication. 科学, 78–80; DOI:10.1126/science.1091277.
32
人工生命量 19, 数字 1
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
15. 卡里, L。, & Rozenberg, G. (2008). The many facets of natural computing. ACM 通讯,
51(10), 72–83.
16. Koeller, K. M。, & 黄, C. H. (2000). Complex carbohydrate synthesis tools for glycobiologists:
Enzyme-based approach and programmable one-pot strategies. Glycobiology, 10(11), 1157–1169.
17. Lichtensteiger, L。, & Eggenberger Hotz, 磷. (1999). Evolving the morphology of a compound eye on a
robot. In Proceedings of the Third European Workshop on Advanced Mobile Robots (Eurobot 99) (PP. 127–134).
皮斯卡塔韦, 新泽西州: IEEE.
18. Luchsinger, 右. H。, & Bräker, 中号. (2010). A novel pneumatic actuator with tensairity. 在C中. A. Brebbia (埃德。),
Design and nature V. 南安普敦: WIT Press.
19. Luchsinger, 右. H。, Pedretti, A。, Pedretti, M。, & Steingruber, 磷. (2004). The new structural concept tensairity:
Basic principles. 在一个. von Zingoni (埃德。), Progress in structural engineering, mechanics and computation.
伦敦: A. A. Balkema.
20. Maass, W., Natschläger, T。, & Markram, H. (2002). Real-time computing without stable states: A new
framework for neural computation based on perturbations. 神经计算, 14(11), 2531–2560.
21. Mao, C。, LaBean, 时间. H。, Reif, J. H。, & Seeman, 氮. C. (2000). Logical computation using algorithmic
self-assembly of DNA triple-crossover molecules. 自然, 407, 493–496.
22. 马尔, D. (1969). A theory of cerebellar cortex. 生理学杂志, 202, 437–470.
23. McGeer, 时间. (1993). Dynamics and control of bipedal locomotion. 理论生物学杂志, 16(3),
277–314.
24. Mildner, E., Lembert, S。, & Raschner, C. (2010). Influence of ski boots on balance performance.
Sportverletzung-Sportschaden, 24(1), 31–35.
25. 保罗, C. (2004). Morphology and computation. 在S. Schaal, A. Ijspeert, A. Billard, S. Vijayakkumar,
J. Hallam, & J.-A. 迈耶 (编辑。), Proceedings of the Eighth Conference on the Simulation of Adaptive Behavior:
From Animals to Animats 8 (PP. 33–38). 剑桥, 嘛: 与新闻界.
26. Pelesko, J. A. (2007). Self assembly: The science of things that put themselves together. Boca Raton, FL:
Chapman & Hall/CRC Press.
27. 普法伊费尔, R。, & 邦加德, J. (2007). How the body shapes the way we think. 剑桥, 嘛: Bradford Books,
与新闻界.
28. 普法伊费尔, R。, Lungarella, M。, & Iida, F. (2007). Self-organization, embodiment, and biologically inspired
机器人技术. 科学, 318(5853), 1088–1093; DOI:10.1126/science.1145803.
29. 普法伊费尔, R。, 帕卡德, N。, 巴杜, M。, & Iida, F. (编辑。). (2007). Proceedings of the First International Conference on
Morphological Computation.
30. 波利, R。, Langdon, 瓦. B., McPhee, 氮. F。, & Koza, J. 右. (2008). A field guide to genetic programming.
Published via http://lulu.com; freely available at http://www.gp-field-guide.org.uk.
31. Priplata, A. A。, Niemi, J. B., Harry, J. D ., Lipsitz, L. A。, & 柯林斯, J. J. (2003). Vibrating insoles and balance
control in elderly people. The Lancet, 362, 1123–1124.
32. Reller, 乙. (2010). Programmable self-assembling spatially heterogeneous micro-reactors. Master thesis, Universität Zürich.
33. Reynwar, 乙. J。, Illya, G。, Harmandaris, V. A。, 穆勒, 中号. M。, Kremer, K., & Desorno, 中号. (2007).
Aggregation and vesiculation of membrane proteins by curvature-mediated interactions. 自然, 447,
461–464.
34. Rothemund, 磷. 瓦. K. (2006). Folding DNA to create nanoscale shapes and patterns. 自然, 440(16),
297–302.
35. Schack, T。, & 里特尔, H. (2009). The cognitive nature of action—Functional links between cognitive
心理学, movement science and robotics. 在米. Raab, J. 约翰逊, & H. Heekeren, Progress in
brain research: Mind and motion—The bidirectional link between thought and action (PP. 231–252).
伯灵顿, 嘛: 爱思唯尔.
36. Scheidegger, S。, & Füchslin, 右. 中号. (2011). Kinetic model for dose equivalent—An efficient way to predict
systems response of irradiated cells. In W. Maurer (埃德。), Proceedings of ASIM 2011.
37. Scheidegger, S。, Lutters, G。, & Bodis, S. (2011). A LQ-based kinetic model formulation for exploring
dynamics of treatment response of tumours in patients. Zeitschrift für Medizinische Physik, 21, 164–173.
人工生命量 19, 数字 1
33
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
右. 中号. Füchslin et al.
Morphological Computation and Morphological Control
38. Sharpless, K. B., Kolb, H. C。, & 芬恩, 中号. G. (2001). Click chemistry: Diverse chemical function from a few
good reactions. Angewandte Chemie, International Edition, 40(11), 2004–2021.
39. Shaw, 右. S。, 帕卡德, N。, Schröter, M。, & Swinney, H. L. (2007). Geometry-induced asymmetric diffusion.
美国国家科学院院刊, 104(23), 9580–9584.
40. Tangen, U. (2010). Enzyme-like replication de novo in a microcontroller environment. 人工生命, 16(4),
311–328.
41. von Kiedrowski, G。, Eckhardt, L. H。, Naumann, K., Pankau, 瓦. M。, Raimold, M。, & Rein, 中号. (2003).
Toward replicatable, multifunctional, nanoscaffolded machines. A chemical manifesto. Pure and Applied
Chemistry, 75(5), 609–619.
42. Whitesides, G. M。, & Boncheva, 中号. (2002). Beyond molecules: Self-assembly of mesoscopic and
macroscopic components. 美国国家科学院院刊, 99(8), 4769–4774.
43. Whitesides, G. M。, & Grzybowski, 乙. (2002). Self-assembly at all scales. 科学, 295, 2418–2421;
DOI:10.1126/science.1070821.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
9
1
9
1
6
6
7
5
1
4
A
r
t
我
/
_
A
_
0
0
0
7
9
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
34
人工生命量 19, 数字 1