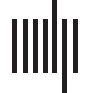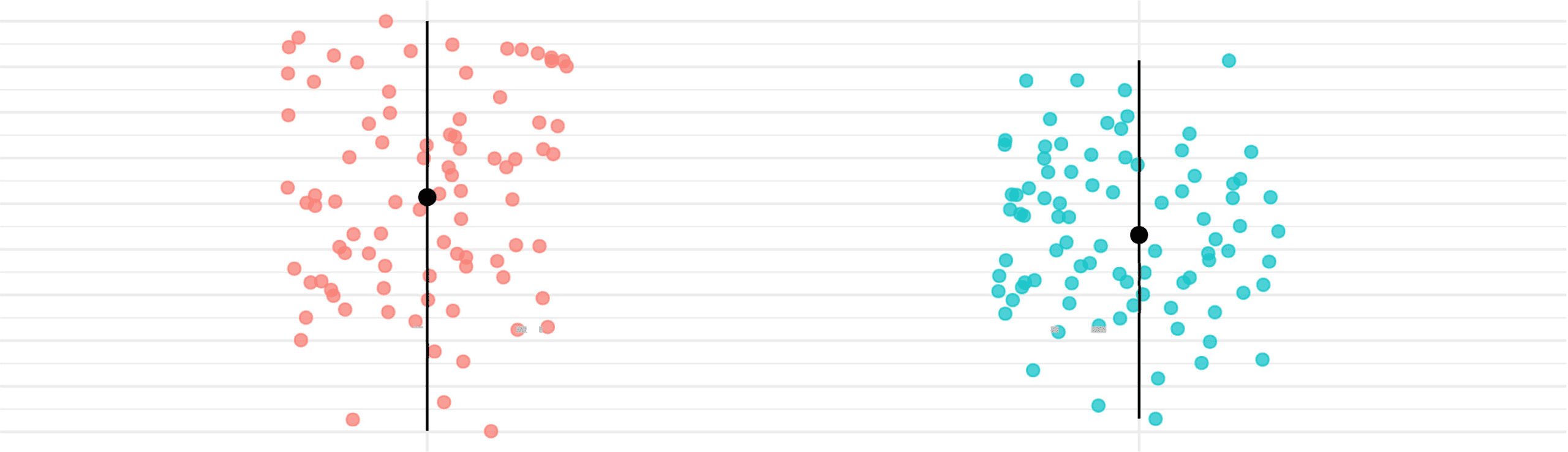方法
Connectome sorting by consensus
clustering increases separability
in group neuroimaging studies
Javier Rasero
Daniele Marinazzo
, Ibai Diez
, Jesus M. 科尔特斯
, and Sebastiano Stramaglia
7
1
2,3,4
1,5,6
,
8,9,10
1Biocruces Health Research Institute, Hospital Universitario de Cruces, Barakaldo, 西班牙
2Functional Neurology Research Group, 神经内科, Massachusetts General Hospital,
哈佛医学院, 波士顿, 嘛, 美国
3Gordon Center, Department of Nuclear Medicine, Massachusetts General Hospital,
哈佛医学院, 波士顿, 嘛, 美国
4Neurotechnology Laboratory, Tecnalia Health Department, Derio, 西班牙
5Department of Cell Biology and Histology, University of the Basque Country, Leioa, 西班牙
6Ikerbasque, The Basque Foundation for Science, Bilbao, 西班牙
7Faculty of Psychology and Educational Sciences, Department of Data Analysis, Ghent University, Ghent, 比利时
8Dipartimento di Fisica, Universitá degli Studi “Aldo Moro” Bari, 意大利
Istituto Nazionale di Fisica Nucleare, Sezione di Bari, 意大利
10TIRES-Center of Innovative Technologies for Signal Detection and Processing, Universitá degli Studi “Aldo Moro” Bari, 意大利
9
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
A
_
0
0
0
7
4
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
关键词: Unsupervised learning, Consensus clustering, Brain connectivity, Classification
抽象的
A fundamental challenge in preprocessing pipelines for neuroimaging datasets is to increase
the signal-to-noise ratio for subsequent analyses. In the same line, we suggest here that the
application of the consensus clustering approach to brain connectivity matrices can be a
valid additional step for connectome processing to find subgroups of subjects with reduced
intragroup variability and therefore increasing the separability of the distinct subgroups when
connectomes are used as a biomarker. 而且, by partitioning the data with consensus
clustering before any group comparison (例如, between a healthy population vs. A
pathological one), we demonstrate that unique regions within each cluster arise and bring
new information that could be relevant from a clinical point of view.
介绍
In the supervised classification of human connectome data (斯波恩斯, 2011), subjects are usu-
ally grouped based on high-level clinical categories (例如, patients and controls, early vs. 晚的
cognitive impairment, ETC。), and typical approaches aim at deducing a decision function from
the labeled training data (看, 例如, 假如 & 布莫尔, 2010). 同样地, unsupervised anal-
ysis is also usually performed with the researcher being blind to any phenotypic factors and
aiming to find subgroups of subjects/features with similar characteristics. The existing litera-
ture reports several clustering algorithms dealing with these issues (看, 例如, 徐 & Wunsch,
2005, and references within). The emergence of substructures underlying the data is very often
due to the fact that the populations to be studied (healthy subjects, 患者, ETC。) are usually
highly heterogeneous. 最后, stratification of groups may be a useful preliminary step,
allowing the subsequent supervised analysis to exploit the knowledge of the data’s structure.
A convenient strategy for group stratification involves using subjects’ phenotypic variables
when available (例如, the presence or absence of one specific gene mutation). 更多的
开放访问
杂志
引文: Rasero, J。, Diez, 我。, 科尔特斯,
J. M。, Marinazzo, D ., & Stramaglia, S.
(2019). Connectome sorting by
consensus clustering increases
separability in group neuroimaging
学习. 网络神经科学, 3(2),
325–343. https://doi.org/10.1162/
netn_a_00074
DOI:
https://doi.org/10.1162/netn_a_00074
支持信息:
https://doi.org/10.1162/netn_a_00074
已收到: 18 六月 2018
公认: 9 十一月 2018
利益争夺: 作者有
声明不存在竞争利益
存在.
通讯作者:
Sebastiano Stramaglia
sebastiano.stramaglia@ba.infn.it
处理编辑器:
奥拉夫·斯波恩斯
版权: © 2018
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
Connectome sorting by consensus clustering
Brain connectivity network
(connectome):
A network in which the nodes are
brain regions and the links are
anatomical connections
(“anatomical/structural connectivity”)
or statistical dependencies
(“functional connectivity”).
Distance matrix:
For each node, a distance matrix for
the set of subjects is constructed as
如下. For each pairs of subjects,
the corresponding distance is
(西德:2)
2(1 − r), where r is the Pearson
correlation between the nodal
connectivity patterns of the given
node in the two subjects.
Consensus matrix:
Given several partitions of a given set
of nodes, for each pair of nodes the
consensus matrix assumes, 作为
corresponding entry, the fraction of
partitions in which the two nodes
belong to the same subset.
interestingly, stratification may also rely on the measured variables, like the human connec-
tome data itself, applying clustering algorithms to find natural groupings in the data.
An effective supervised approach, named multivariate distance matrix regression (MDMR),
has been proposed in Zapala & Schork (2006) for the analysis of gene expression patterns;
it tests the relationship between variation in a distance matrix and predictor information col-
lected on the samples whose gene expression levels have been used to construct the matrix.
The same method was also applied to the cross-group analysis of brain connectivity matrices
(Shehzad et al., 2014), as an alternative to the very commonly used method of connectome-
wide association, 那是, mass-univariate statistical analyses, in which the association with
a phenotypic variable of each entry of the brain connectivity matrix across subjects is tested.
While MDMR has found wide application (看, 例如, Rasero et al., 2017), these findings
may be certainly affected by the heterogeneity of classes.
Recently an unsupervised method (Rasero et al., 2017), rooted on the notion of consensus
clustering (Lancichinetti & Fortunato, 2012), has been developed for community detection in
复杂网络 (Barabasi & Frangos, 2002), when a connectivity matrix is associated with
each item to be classified. In this method, the different features, extracted from connectivity
matrices, are not combined into a single vector to feed the clustering algorithm; 相当, 这
information coming from the various features is combined by constructing a consensus network
(Lancichinetti & Fortunato, 2012). Consensus clustering is commonly used to generate stable
results out of a set of partitions delivered by different clustering algorithms (and/or parameters)
applied to the same data (Strehl & 戈什, 2002). In the method developed in Rasero et al.
(2017), instead the consensus strategy was used to combine the information about the data
structure arising from different features so as to summarize them in a single consensus matrix.
此外, such a matrix not only provides a partition of subjects in communities, but also a
geometrical representation of the set of subjects. It has been shown that this technique can be
effective in disentangling the heterogeneity of a population. The main similarity with MDMR
is that in both methods a distance matrix in the space of subjects is introduced.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
A
_
0
0
0
7
4
p
d
t
.
The purpose of this work is to propose the consensus clustering approach from Rasero et al.
(2017) as a step to perform prior to MDMR in exploratory analysis, so as to cope with the het-
erogeneity present in user-defined groups. 第一的, we will test the robustness of our consensus
clustering by using noise to introduce heterogeneity in the data. 第二, we will show that
extracting the natural classes present in the user-defined groups and subsequently performing
the supervised analysis between the subgroups found by consensus clustering allows us to
identify variables whose patterns are altered in group comparisons, which are not identified
when the groups are used as a whole. 因此, the proposed approach leads to an increase
in separability.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
材料和方法
Materials
The robustness of the consensus clustering algorithm to disentangle the real structure of data
was tested using simulated data for two groups of 15 subjects each, generated using simTB
(Erhardt, 艾伦, Wei, Eichele, & Calhoun, 2012), a toolbox written in MATLAB that allows sim-
ulation of functional magnetic resonance imaging (功能磁共振成像) datasets under a model of spatiotem-
poral separability. Given the number of sources/components (nC), repetition time (TR), and a
hemodynamic model, the program yields the time course profile subject to the experimental
= 20 成分
设计 (block- and/or event-related) 假如. Our scenario consists of nC
网络神经科学
326
Connectome sorting by consensus clustering
and TR = 2s, such that in an event-related experiment the first 10 components of the co-
hort of group 1 have high probability (90%) of becoming activated, whereas for the remaining
components the activation is rare (10 %). For subjects of group 2 the situation is the opposite.
This scenario could be then considered as the same group of subjects performing two orthog-
onal tasks, where different components get involved. The length of the simulated time series is
148 点.
The advantages of using the consensus clustering method as a sorting preliminary step were
explored on two real and public neuroimaging datasets. The first dataset comprises healthy
controls (HC) and individuals diagnosed with three pathologies: attention-deficit hyperactivity
紊乱 (ADHD), bipolar disorder (BD), and schizophrenia (SCH). This dataset is provided
by the Consortium for Neuropsychiatric Phenomics LA5C Study and was downloaded from
the OpenfMRI database with accession number ds000030 (Poldrack et al., 2016). We used
resting functional MRI (rfMRI) 的 255 subjects: 40 ADHD, 47 BD, 50 SCH, 和 118 HC. Dem-
ographics information about this cohort can be found in Table 1. Data were preprocessed with
FSL (FMRIB Software Library v5.0). All volume images were corrected for motion, 之后
slice timing correction was applied to correct for temporal alignment. All voxels were spatially
smoothed with a 6-mm full width at half-maximum isotropic Gaussian kernel, and a band-
pass filter was applied between 0.01 和 0.08 Hz after intensity normalization. 此外,
linear and quadratic trends were removed. We next regressed out the motion time courses, 这
average CSF signal and the average white matter signal. Global signal regression was not per-
形成的. Data were transformed to the MNI152 template, such that a given voxel had a volume
的 3 mm × 3 mm × 3 毫米. 最后, 我们得到了 278 time series, each corresponding to an
anatomical region of interest by averaging the voxel signals according to the functional atlas
described in (沉, Tokoglu, Papademetris, & Constable, 2013). 最后, A 278 × 278 matrix of
Pearson coefficients among time series for each subject was obtained.
As for the second dataset, it contains resting-state fMRI scans from a population of autism
spectrum disorder (自闭症谱系障碍) subjects and a population of typically developing (TD) 那些, 从
the Autism Brain Imaging Data Exchange (ABIDE) repository (Di Martino et al., 2014), 一个
initiative that aims at collecting data from laboratories around the world to accelerate the
understanding of the neural bases of this disorder. Since it is unclear what effect that different
scanner machines can have on the observable results, we decided to avoid this additional
possible confounder by considering only a sample of 75 subjects for each group acquired at
the same site (NYU). For this subset, we matched age and sex between samples (Wilcoxon rank
sum p = 0.27 and χ2
test p = 0.29, 分别). Preprocessing of the data was done using FSL,
AFNI, and MATLAB. 第一的, slice-time correction was applied. 然后, each volume was aligned
to the middle volume to correct for head motion artifacts followed by intensity normalization.
We next regressed out 24 motion parameters, the average cerebrospinal fluid (CSF) 和
average white matter signal. A band-pass filter was applied between 0.01 和 0.08 赫兹, 和
桌子 1. Demographic information for LA5C dataset
Resting-state fMRI:
Functional magnetic resonance
imaging acquired while the subject
is simply instructed to stay awake.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
A
_
0
0
0
7
4
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
HC (N= 118)
ADHD (N= 40)
BD (N= 47)
SCH (N= 50)
笔记. FWD = framewise displacement; HC = healthy controls; ADHD = attention-deficit hyper-
activity disorder; BD = bipolar disorder; SCH = schizophrenia.
年龄
31.56 ± 8.83
32.05 ± 10.4
35.47 ± 9.16
36.46 ± 8.88
FWD
0.17 ± 0.15
0.15 ± 0.11
0.19 ± 0.13
0.25 ± 0.20
性别 (M/F)
64/54
21/19
26/21
38/12
网络神经科学
327
Connectome sorting by consensus clustering
linear and quadratic trends were removed. All voxels were spatially smoothed with a 6-mm
FWHM. 最后, FreeSurfer software was used for brain segmentation and cortical parcellation.
一个 86 region atlas was generated with 68 cortical regions from the Desikan-Killiany Atlas (34
in each hemisphere) 和 18 subcortical regions (9 in each hemisphere: thalamus, caudate,
putamen, pallidum, hippocampus, amygdala, accumbens, ventralDC and cerebellum). 每个
subject parcellation was projected to individual functional data, and the mean functional time
series of each region was computed.
Consensus clustering method
Given a set of matrices of distance among subjects, the consensus clustering proposed in
(Rasero, Pellicoro, 等人。, 2017) can be summarized as follows: (我) cluster each distance matrix
using a known clustering algorithm, (二) build the consensus network from the correspond-
ing partitions and (三、) extract groups of subjects by finding the communities of the consensus
network thus obtained.
Regarding the distance matrices calculation in the case of fMRI data, let us consider m
subjects such that each one has a N × N matrix of features, which can for example represent
the brain functional connectivity matrix. We will denote this matrix as {A(我, j)A}, where α =
1, . . . , m and i, j = 1, . . . , 氮. For each row i, we build a distance matrix for the set of subjects as
如下. Consider a pair of subjects α and β, and consider the corresponding patterns {A(我, :)A}
和 {A(我, :)β}; let r be their Pearson correlation. As the distance between the two subjects,
for the node i we take dαβ = 1 − r; other choices for the distance can be used, 喜欢, 为了
2(1 − r), where r is the Pearson correlation. The m × m distance matrix dαβ
例子, dαβ =
corresponding to row i will be denoted by Di, with i = 1, . . . , 氮. The set of D matrices may
be seen as corresponding to layers of a multilayer network (Boccaletti et al., 2014), each brain
node representing a layer.
(西德:2)
Each distance matrix Di is then partitioned into k groups of subjects using the k-medoids
方法 (Brito, Bertrand, Cucumel, & Carvalho, 2007), and this cluster information is encoded
into an adjacency matrix among subjects. 随后, an m × m consensus matrix C is evalu-
ated by averaging this different information across the nodes. 因此, the entries of Cαβ indicate
the number of partitions in which subjects α and β are assigned to the same group, divided by
the number of partitions N. 最终, the consensus matrix is averaged over k ranging in the
间隔 (2-20) so as to combine, in the final consensus matrix, information about structures at
different resolutions (for more details, see Rasero, Pellicoro, 等人。, 2017).
The consensus matrix obtained as explained before provides a weighted graph that contains
all the community information, whose structure can be further examined by an appropriate
方法. Following Rasero, Pellicoro, 等人. (2017), we perform this by modularity optimiza-
的, for which we compared this consensus matrix with the ensemble of all consensus matri-
ces that one may obtain randomly and independently by permuting the cluster labels obtained
after applying the k-medoids algorithm to each of the set of distance matrices. 更确切地说,
a modularity matrix is evaluated as
B = C − γ · P,
(1)
K-medoids algorithm:
A classical partitioning technique of
clustering that groups the data set of
n objects into k clusters known
a priori. Like the k-means, k-medoids
algorithms attempts to minimize the
distance between points labeled to
be in a cluster and a point designated
as the center of that cluster; 在
contrast to the k-means algorithm,
k-medoids chooses data points as
中心 (medoids).
Modularity matrix:
For each entry in the consensus
矩阵, the null ensemble of all
possible configurations by label
permutation at a given resolution
is subtracted.
where P is the expected co-assignment matrix, uniform as a consequence of the null ensemble
here chosen, obtained repeating many times the permutation of labels, and γ is the resolution
parameter that all modularity matrices implicitly or explicitly carry. As in the Newman and
Girvan scenario, we hereafter set this parameter to be 1, which corresponds to the maximum
modularity case (Reichardt & Bornholdt, 2006).
网络神经科学
328
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
A
_
0
0
0
7
4
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Connectome sorting by consensus clustering
A modularity matrix of this kind encodes all the information at different levels about the
interaction strength among subjects. 因此, one could now just as easily define a distance
matrix based on this matrix by computing any metric distance between pairs of rows and
follow with k-medoids to perform a clustering analysis. We instead submitted this matrix to a
modularity optimization algorithm, which does not require a predefined number of clusters,
to obtain the output partition by the proposed approach (we used the Community Louvain
routine in the Brain Connectivity Toolbox (鲁比诺夫 & 斯波恩斯, 2010), which admits modularity
matrices instead of connectivity matrices as input.
Multivariate Distance Matrix Regression
The cross-group analysis of brain connectivity matrices has been performed using the MDMR
approach as described in Shehzad et al. (2014) and Zapala & Schork (2006). This method
allows for an identification of voxels/regions whose whole-brain connectivity patterns vary
significantly with a given set of regressor variables. In contrast to the usual general linear re-
gression model, the variation on the total sum of squares here is tested on the Distance matrix,
constructed from the connectivity patterns for each node, rather than directly on the observed
数据. This approach can assess significance of multiple connections at the same time and is
especially useful when the number of dependent variables—in this case, the entries of the
connectivity matrices—exceeds the number of observations.
For a fixed brain node i, the distance between connectivity patterns of i with the rest of
the brain was calculated per pair of subjects (你,v), by calculating Pearson correlation between
connectivity vectors of subject pairs, thus leading to a distance matrix in the subject space for
each i investigated. 尤其, the following formula was applied
(西德:3)
(西德:4)
2
(西德:5)
1 − ri
紫外线
的
紫外线
=
(2)
where ri
uv is the Pearson correlation between connectivity patterns of node i for subjects u and
v. 下一个, MDMR was applied to perform cross-group analysis as implemented in R (McArtor,
日期不详。).
MDMR yielded a pseudo-F estimator (analogous to that F estimator in standard ANOVA
分析), which addresses significance due to between-group variation as compared with
within-group variations (McArdle & 安德森, 2001) on a distance matrix calculated from
a set of variables. In the particular case when the only regressor variable is categorical (IE。,
the group label), given a distance matrix for a certain node, one can calculate the total sum of
squares as
=
SST
1
n
氮
∑
u=1
氮
∑
v=u+1
2
紫外线
d
(3)
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
A
_
0
0
0
7
4
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
with N being the total number of subjects. 相似地, the within-group sum of squares can be
written as
SSW
= ∑ 1
ng
∑
u=1
n
∑
v=u+1
2
紫外线
(西德:6)G
紫外线
d
(4)
where ng is the number of subjects per group and (西德:6)G
uv a variable equal to 1 if subjects u and v
belong to group g and 0 否则. The between-group variation is simply SSB = SST − SSW,
which leads to a pseudo-F statistic as follows
F = (N − 1) SSA
SSW
,
(5)
329
网络神经科学
Connectome sorting by consensus clustering
where m is the number of groups. As it was acknowledged in Zapala & Schork (2006), 这
pseudo-F statistic is not distributed like the usual Fisher’s F-distribution under the null hy-
pothesis. 因此, we randomly shuffled the subject indexes and computed the pseudo-F
statistic each time. A p value is computed by counting those pseudo-F statistic values from per-
muted data greater than that from the original data respect to the total number of performed
permutations.
尽管如此, in our cross-group analyses, in addition to group label, 年龄, 性别, and mean
framewise displacement (FWR) were also considered as covariates because of their possible
confounding effect in distance variation between subjects. 最后, we controlled for I errors
by false discovery rate corrections and set significance threshold at 1%.
The proposed approach
The application of MDMR to identify altered patterns is hampered by the heterogeneity of
subjects in the same group (healthy controls or patients). 所以, we propose here the use
of the consensus clustering approach as a sorting preliminary tool. In a first step, the consensus
clustering is to be applied to extract the natural classes present in the group of controls (和/或
in the group of patients). In a subsequent step, the supervised analysis of MDMR is to be
performed between the pairs of subgroups found by consensus clustering. In this way one can
identify variables whose pattern is altered in subgroups comparisons, but not in the whole
团体.
结果
Simulated data
Our approach aims to use cluster information from each node instead of using the whole set
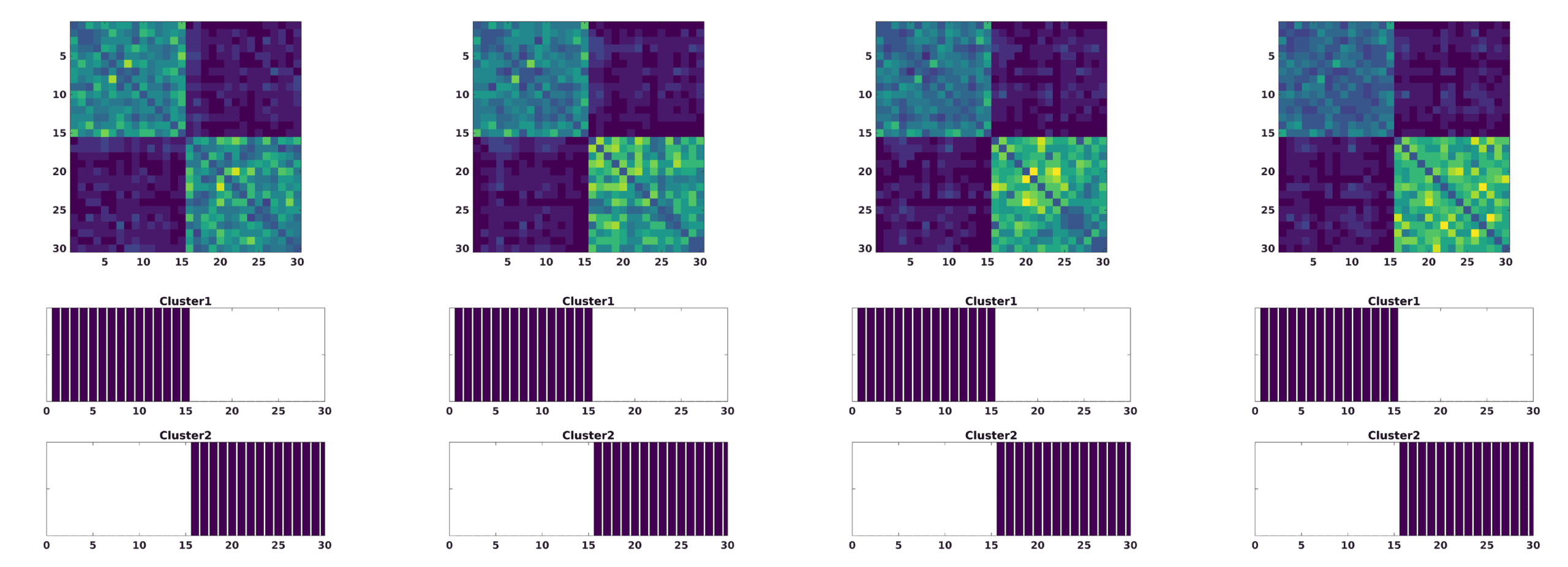
of nodes across the brain. We can visualize this in Figure 1, where the group reconstruction
provided by our method is compared with the one yielded by considering the whole corre-
lation matrix as pattern connectivity from which one calculates the distance matrix, 所以
average is only carried out over different resolutions κ when applying k-medoids. 所以,
the introduction of a clustering step at a node-level resolution seems to permit a better cluster
reconstruction, confirming the findings in Rasero et al. (2017).
We also assessed the robustness of our method in group reconstruction when Gaussian
noise is added to the time series of group 1 (TS1) 和组 2 (TS2) as follows:
TS
ij
1 = TS
TS
ij
2 = TS
1 + (西德:6)ij
ij
1 · A · N ij
1 (0, 1)
2 + (西德:6)ij
ij
2 · A · N ij
2 (0, 1),
(6)
for i = 1 . . . 15 subjects and j = 1 . . . 20 成分. A is the amplitude of the perturbations
和 (西德:6)ij
1,2 is a binary matrix allowing us to play with different noise configuration scenarios. 在
our notation, subscript index represents group label and superscript indices i, j subject and
成分, 分别.
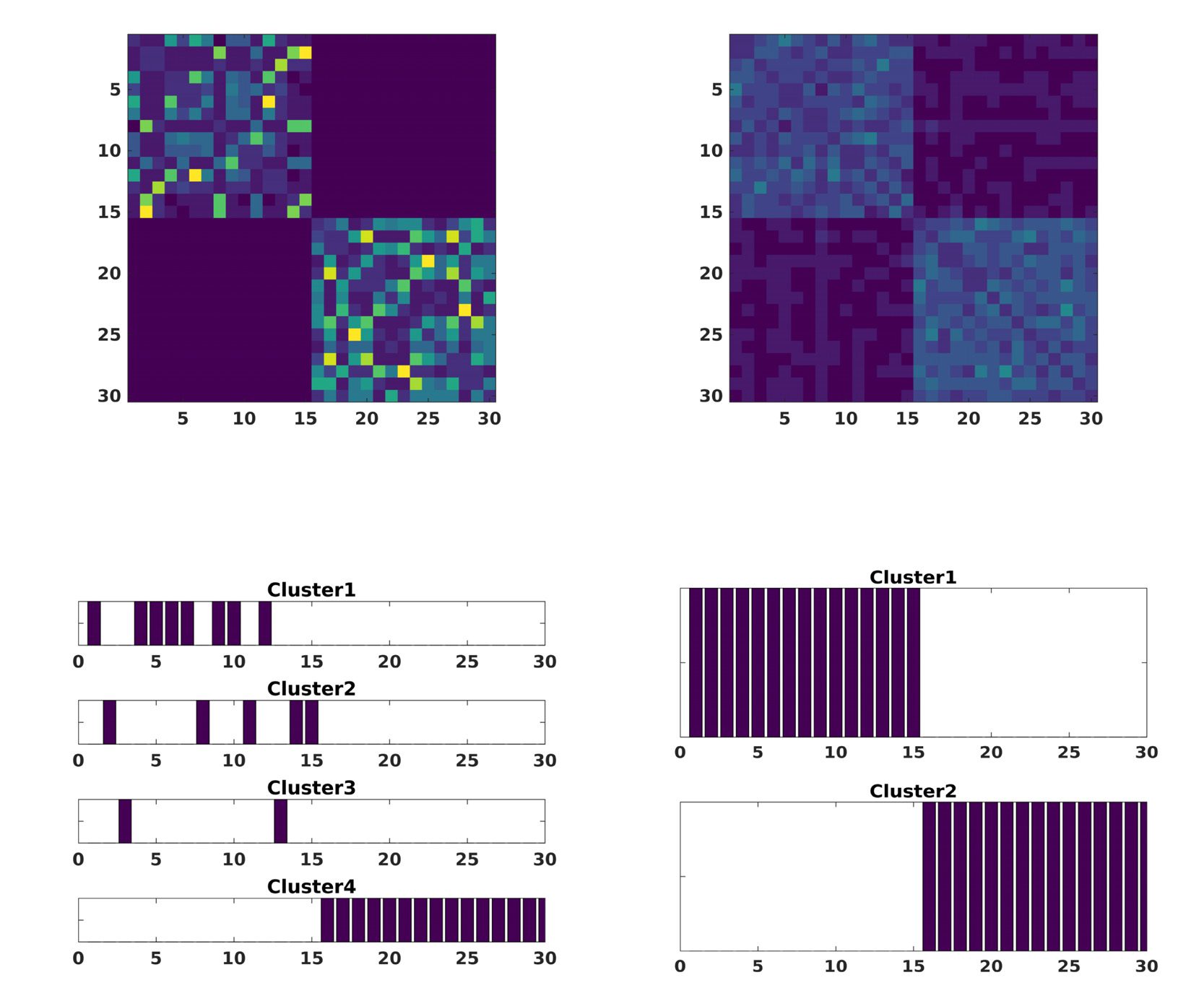
In a first scenario, different values of the noise amplitude A = {0.1, 0.3, 0.5} were applied to
all components and subjects (西德:6)i=1..15,j=1..20
= 1. As we can see in Figure 2, only for large ampli-
tude, noise starts to dominate so much that the consensus algorithm renders group more com-
pact and mix them together making it incapable of distinguishing between groups perfectly.
1,2
网络神经科学
330
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
A
_
0
0
0
7
4
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Connectome sorting by consensus clustering
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
A
_
0
0
0
7
4
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
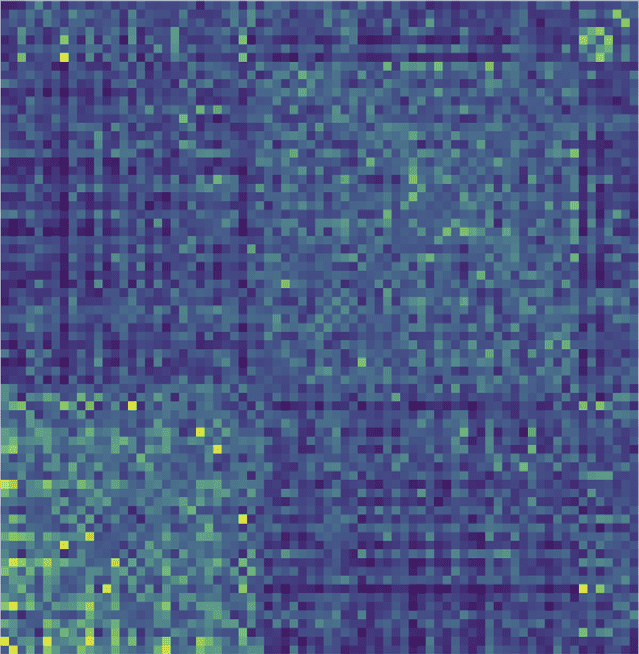
数字 1. The modularity matrix among subjects of both groups and its cluster structure reconstruc-
tion provided by the Louvain community detection algorithm on this matrix is depicted in two
different scenarios: Application of the consensus clustering to the distance matrix from the whole
pattern connectivity matrix (A) or to the set of distance matrices from each node pattern connec-
活力 (乙).
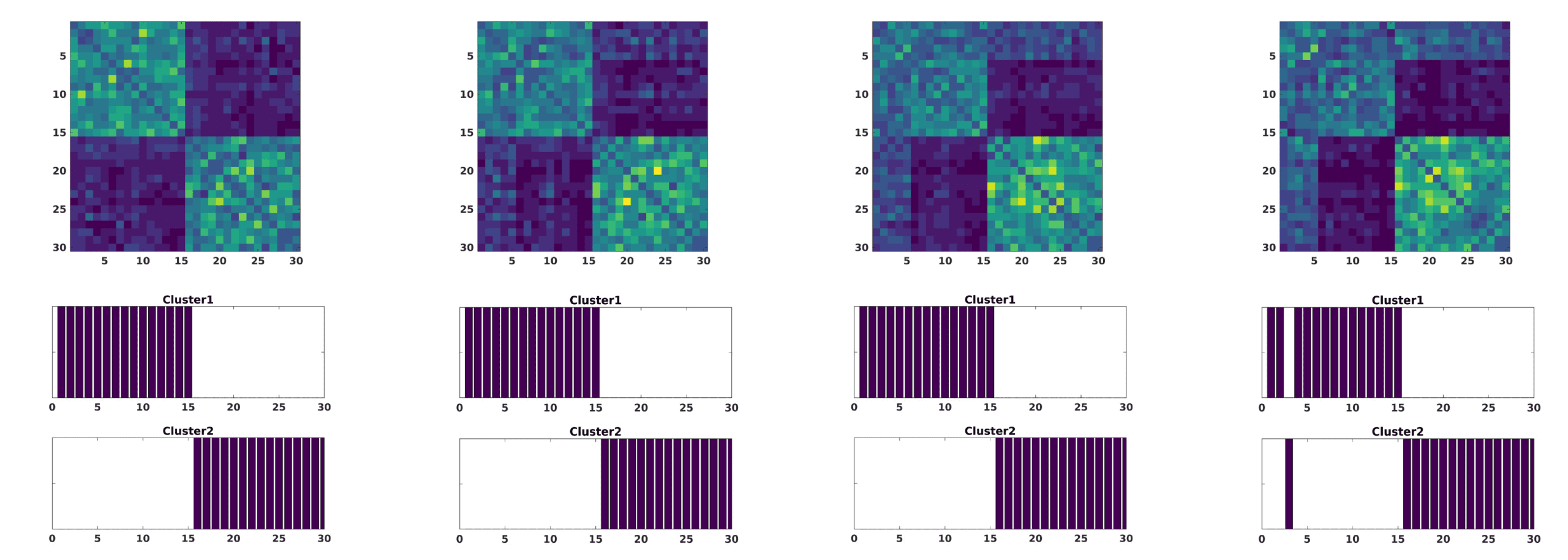
In a second scenario, variation of noise across subsets of components was studied. To am-
plify this effect, we restrict noise amplitudes to a fixed large value A = 0.5. Four subsets of
components affected by noise were taken j = {(1), (1 . . . 3), (1 . . . 6), (1 . . . 10)}. 此外, 在
order to add more complexity, we considered the application of noise to five subjects of group 1
和 10 of group 2, 分别. 作为结果, this effect is stronger in group 2, since for the
首先 10 components the activity is lower and therefore more sensitive to noise. When applied to
a different number of components, this leads to a decrease of intragroup distance of subjects
做作的 (yellowish areas in the modularity matrices of Figure 3) and also a slight approxi-
mation between groups as a consequence of the synchronization among the noised compo-
尼特. 尽管如此, the consensus clustering is pretty robust when reconstructing both groups.
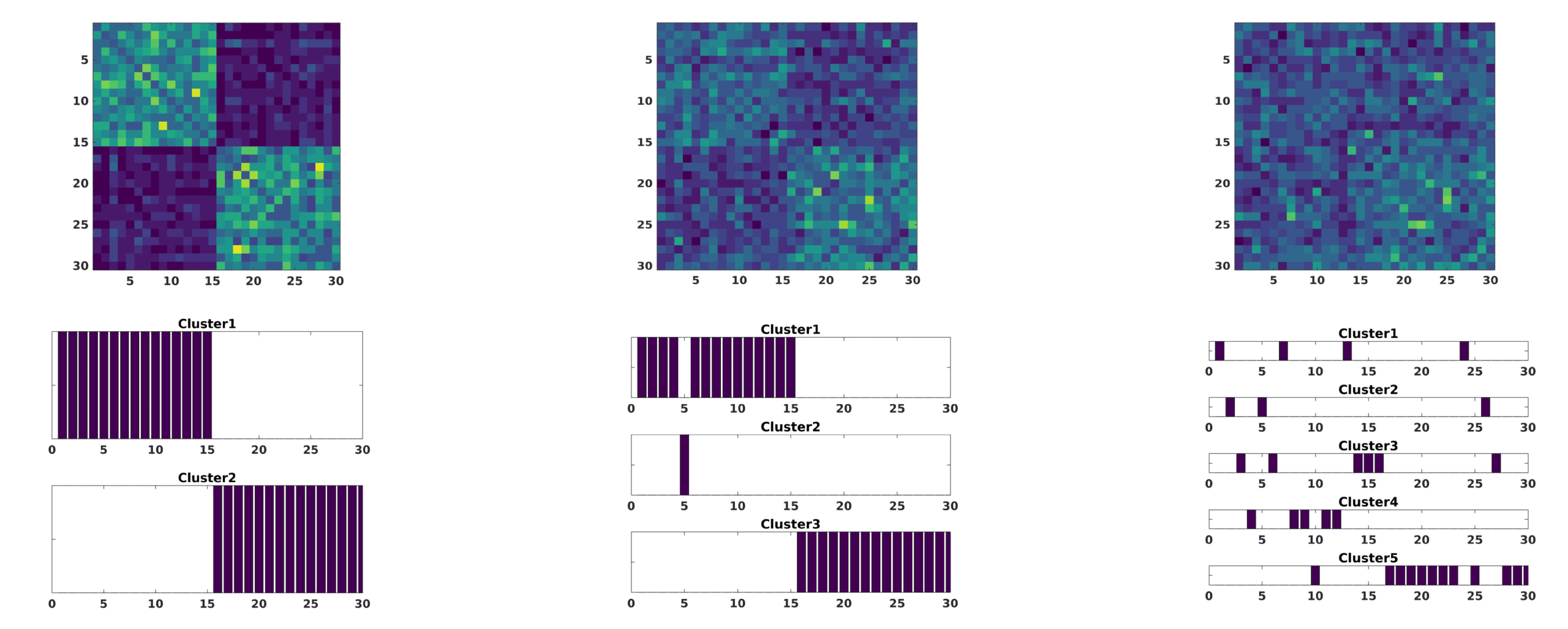
最后, variation of number of subjects was taken into account (见图 4). To simplify
this scenario, we considered that noise only affected group 2 and the first 10 components with
a large amplitude A = 0.5. The subset of number of subjects are i = {(1), (1 . . . 5), (1 . . . 10),
(1 . . . 15)}. The consensus turns out to be again robust when reconstructing both groups. 为了
这个案例, the effect of changing the number of subjects of group 2 affected by noise makes
this group more compact as more subjects are involved since noise makes them look more
相似的. This also makes these subjects of group 2 more similar with those of group 1 为了
网络神经科学
331
Connectome sorting by consensus clustering
数字 2. The modularity matrix among subjects of both groups and its cluster structure reconstruction provided by a Louvain community
detection algorithm on this matrix is depicted when changing the amplitude noise A in Equation 6, that affects all the simulated time series
for both groups: A = 0.1 (A), A = 0.3 (乙), A = 0.5 (C).
首先 10 成分, but not enough to mix them together to make them indistinguishable by
the consensus method.
LA5C dataset
The application of the consensus clustering method to the brain matrices in the four groups
yields the modularity matrices depicted in Figure 5, which have been ordered according to the
数字 3. The modularity matrix among subjects of both groups and its cluster structure reconstruction provided by a Louvain community
detection algorithm on this matrix is depicted when changing the number of components, IE。, the index j of (西德:6)ij in Equation 6 affected by large
amplitude noise (A = 0.5): j = (1) (A), j = (1 . . . 3) (乙), j = (1 . . . 6) (C), j = (1 . . . 10) (D).
网络神经科学
332
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
A
_
0
0
0
7
4
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Connectome sorting by consensus clustering
数字 4.
The modularity matrix among subjects of both groups and its cluster structure reconstruction provided by a Louvain community
detection algorithm on this matrix is depicted when changing the subjects affected, IE。, the index i of (西德:6)ij in Equation 6 affected by large
amplitude noise (A = 0.5): i = (1) (A), i = (1 . . . 5) (乙), i = (1 . . . 10) (C), i = (1 . . . 15) (D).
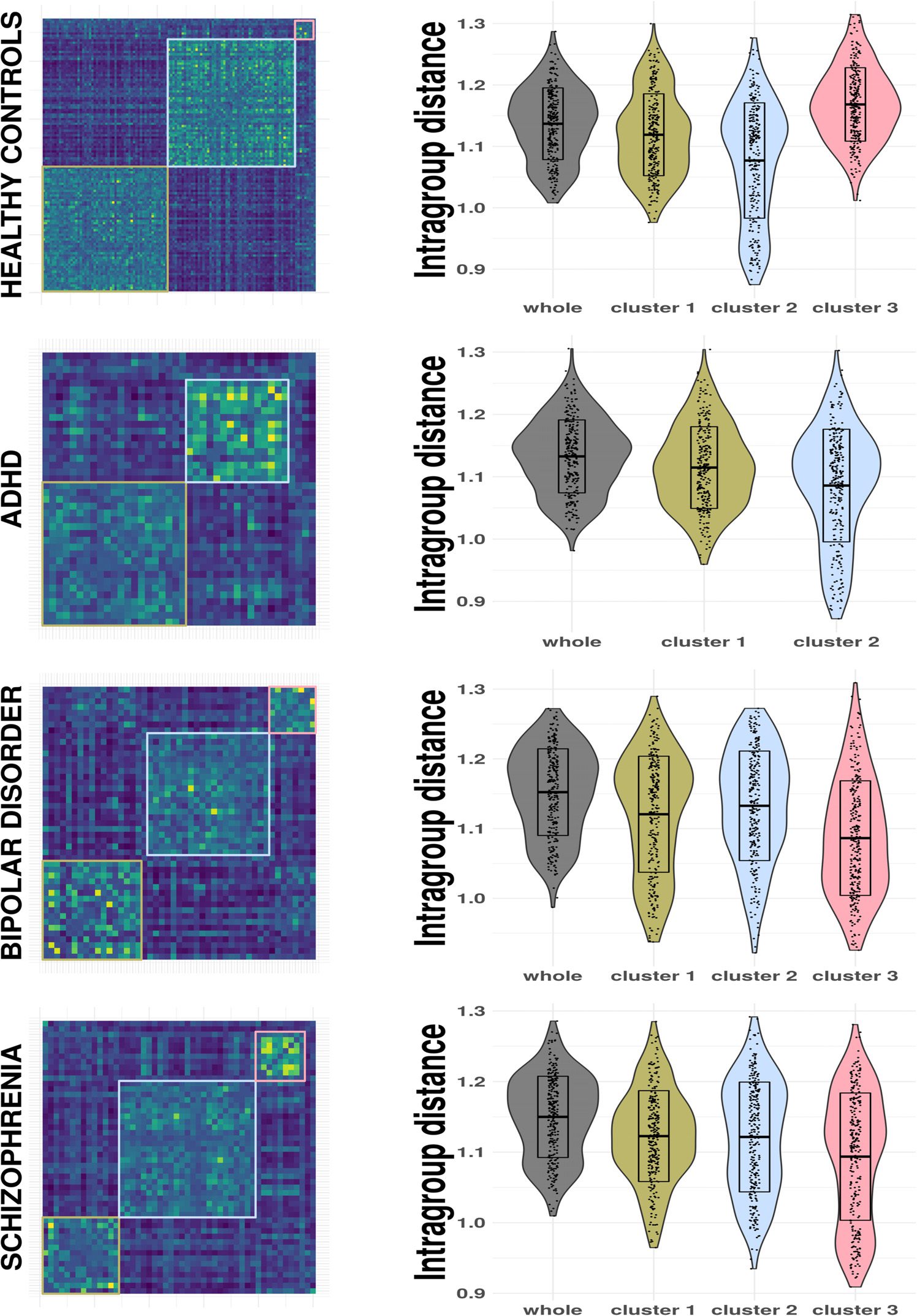
membership configuration found by the community Louvain routine. For the healthy group,
this algorithm detects three communities of 55, 54, 和 8, 分别. Such clusters are sta-
tistically differentiated by FWD (Kruskal-Wallis test, p < 0.0001) and sex (χ2
test, p = 0.0201).
For the ADHD group, it finds two clusters of 21 and 15 subjects. For the BD group it detects
three communities of 17, 21, and 8 subjects, and for the SCH group, three clusters of 14, 25,
and 9, these SCH clusters being statistically different with respect to FWD ( Kruskal-Wallis test,
p = 0.0003). In all cases, communities with fewer subjects than five have been considered as
outliers.
Likewise, the consensus clustering algorithm allows extraction of more homogeneous sub-
groups of subjects, as can be noticed from Figure 5, where the mean intragroup distance distri-
bution produced by the collection of distance matrix for each pattern connectivity is exhibited.
We stress that the intersubjects distance is highly and significantly smaller for the clusters with
respect to the whole groups, as estimated pairwise by means of a Wilcoxon signed-rank test.
2
Furthermore, having more homogeneous clusters is translated into a variability decrease,
leading in some cases to a gain in separability, when clusters are introduced in between-group
comparison studies. As can be seen in Figure 6, the partition of individual groups by consensus
clustering in general enhances the effect size (here evaluated through the pseudo-R
measure
in MDMR) per node associated with class difference. Furthermore, this also allows us to reject
the null model even though the sample size decreases when a partitioned group is involved,
providing a better control for type I errors compared with the unpartitioned case (see p values
distribution Supporting Information Figure S2, Rasero, Diez, Cortes, Marinazzo, & Stramaglia,
2019). Concerning partition of the healthy group, such an enhancement is notorious, showing,
for example, that a procedure selecting and recruiting subjects with similar characteristics of
those subjects within the cluster 2 in our healthy control sample would optimize the node
association with the pathology. In addition, for the ADHD group, which lacks of significant
results when being involved in group comparisons as a whole, size effect amplification leads to
development of a significant gain improvement when clustered using the consensus algorithm.
In contrast, for both BD and SCH clusters such an improvement takes place specially in some
2
measure:
Pseudo-R
Measure that accounts for the
proportion of sum of squared
pairwise distances explained by the
predictors and that can be therefore
used to assess the effect size of
association between the dependent
and independent variables in the
multivariate distance matrix
regression.
Network Neuroscience
333
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
a
_
0
0
0
7
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectome sorting by consensus clustering
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
a
_
0
0
0
7
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Modularity matrix and the reduction of the mean intragroup distance per node after
applying the consensus clustering method for each group in the LA5C dataset.
of their clusters and as a consequence, the consensus algorithm can also help filter out “noisy”
subjects, which have less in common with the pathology in study.
On the other hand, application of consensus clustering to brain connectivity matrices of
pathologies can also help unmask substructures whose underlying properties are unique and
Network Neuroscience
334
Connectome sorting by consensus clustering
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
a
_
0
0
0
7
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. The change in the effect size measure R
provided by MDMR across nodes, where subscript term “whole” involves both whole
groups comparison and “cluster” one partitioned group by consensus clustering. An enhancement is developed above zero, here displayed
by a gray thick line. Median value point reaching the maximum and minimum values are depicted here in black.
2
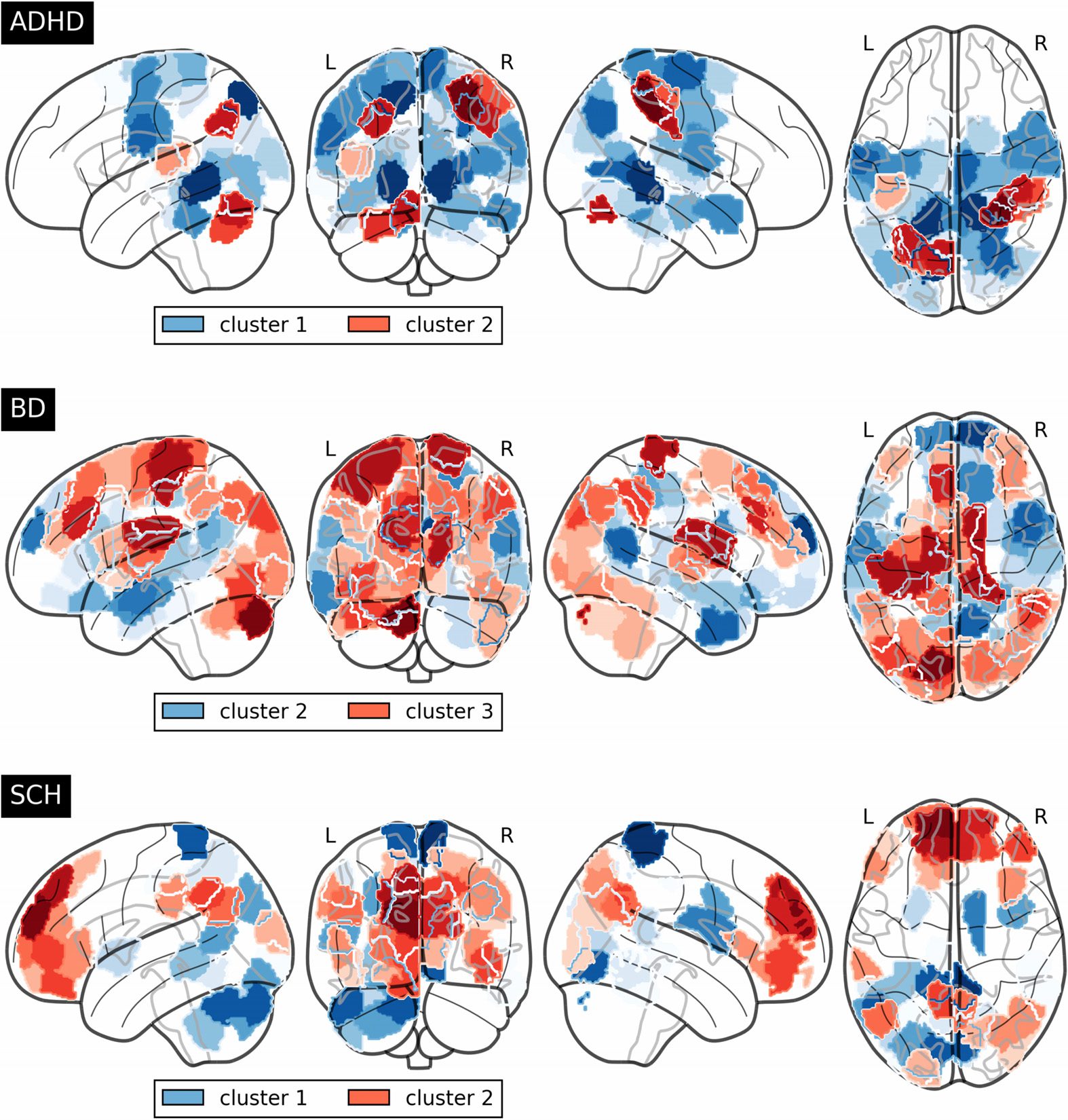
that might be worth studying. For example, concerning the comparisons with healthy subjects
of the ADHD group after having been partitioned, we obtain for cluster 1, 59 significant nodes
that are present neither in cluster 2 nor when this group is taken as a whole. We will here-
after denote these nodes as unique nodes for cluster 1, meaning that only the comparison with
cluster 1 leads one to point out their altered pattern with respect to pathological conditions.
Likewise, seven nodes are unique for cluster 2 of the same disorder group. Regarding compar-
ison with the BD group, there are 61 unique nodes that are recognized as significant for cluster
1 and 46 for cluster 2. Finally, 113 nodes arise as being significantly associated with the whole
group of schizophrenia, whereas substructure inspection increases this number to 128 and
132 for clusters 1 and 2, exhibiting both 27 different unique nodes. Both cluster 1 of BD and
cluster 3 of SCH keep subjects associated with both pathologies, and therefore no association
is found whatsoever. Regions affected by unique nodes in each pathology are represented in
Figure 7.
Higher significant regions for cluster 1 of ADHD lie in cortical regions from the lateral
occipital cortex, superior division, the cingulate gyrus, posterior division and lingual gyrus,
Network Neuroscience
335
Connectome sorting by consensus clustering
and involve functions from the visual and dorsal attention system. Cluster 2 has also incidence
from parts of the lingual gyrus in addition to postcentral gyrus, the superior parietal lobule and
the supramarginal gyrus, anterior division—all associated with the dorsal attention system—
and a small portion of the cerebellum.
On the other hand, regarding the BD group, the default mode system fundamentally emerges
in cluster 2 with cortical regions in the frontal pole, temporal pole, inferior temporal gyrus,
anterior division and the precuneus. Cluster 3 includes the postcentral gyrus and the left thala-
mus, which take part in sensorimotor functions, and parts of the cerebellum and the occipital
fusiform gyrus.
Finally, SCH community representation obtained through the consensus algorithm exhibits
a well-differentiated structure, with cluster 1 focusing mainly on the posterior parts of the brain
with the postcentral gyrus, precuneus and lingual gyrus, somatosensory, and visual systems;
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
a
_
0
0
0
7
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Unique nodes for each cluster within the disorder groups, i.e., significant nodes not
presented in the whole group or the rest of cluster comparisons, which emerge when confronting
with the whole healthy control group.
Network Neuroscience
336
Connectome sorting by consensus clustering
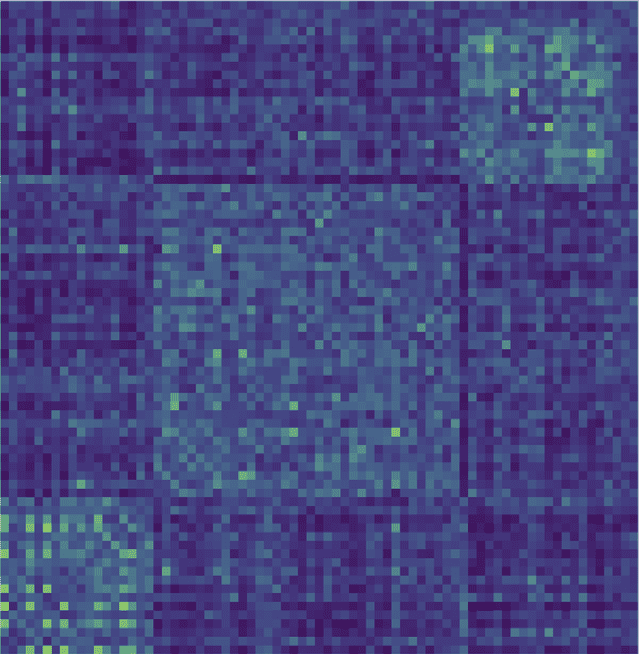
Figure 8. The modularity matrix B ordered after label structure provided by community detection
is depicted for typically developing (left) and autism spectrum disorder (right) group in the ABIDE
dataset considered.
and cluster 2 involving basically the prefrontal cortex and some parts of the superior frontal
gyrus (mainly associated to the default mode network).
ABIDE dataset
Application of the consensus clustering algorithm and subsequent community detection al-
gorithm to both groups leads to the ordered community structure provided by the modularity
matrices in Figure 8. For the TD group, the modularity matrix B yields three modules of 18, 36,
and 19 subjects, respectively. In contrast, division of the ASD group consists of two modules
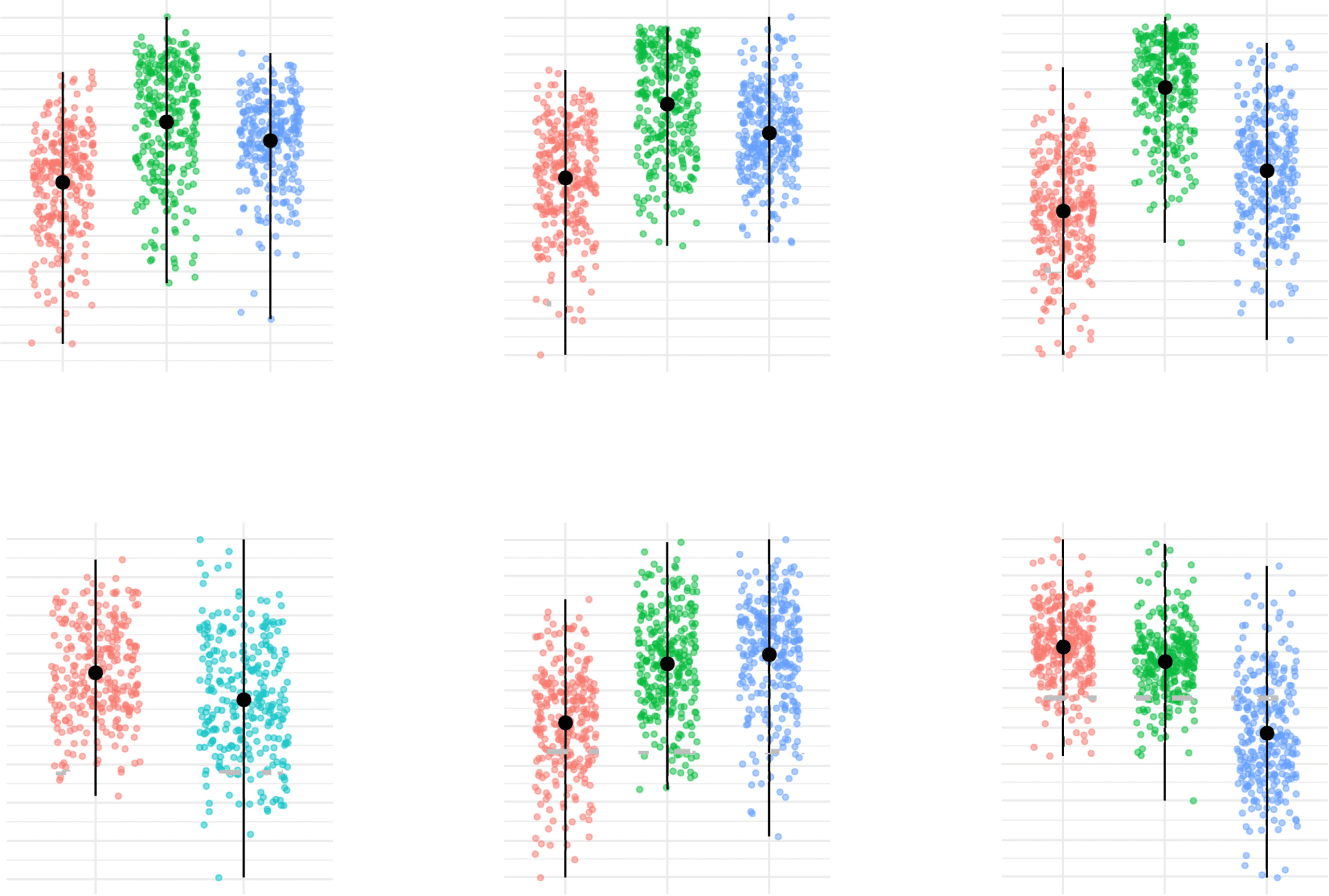
of 30 and 38 patients, respectively. Moreover, a Wilcoxon rank sum test performed on ASD
community partition separates subjects statistically by age (p = 0.0028) and framewise dis-
placement (p < 0.0001) (see Figure 9).
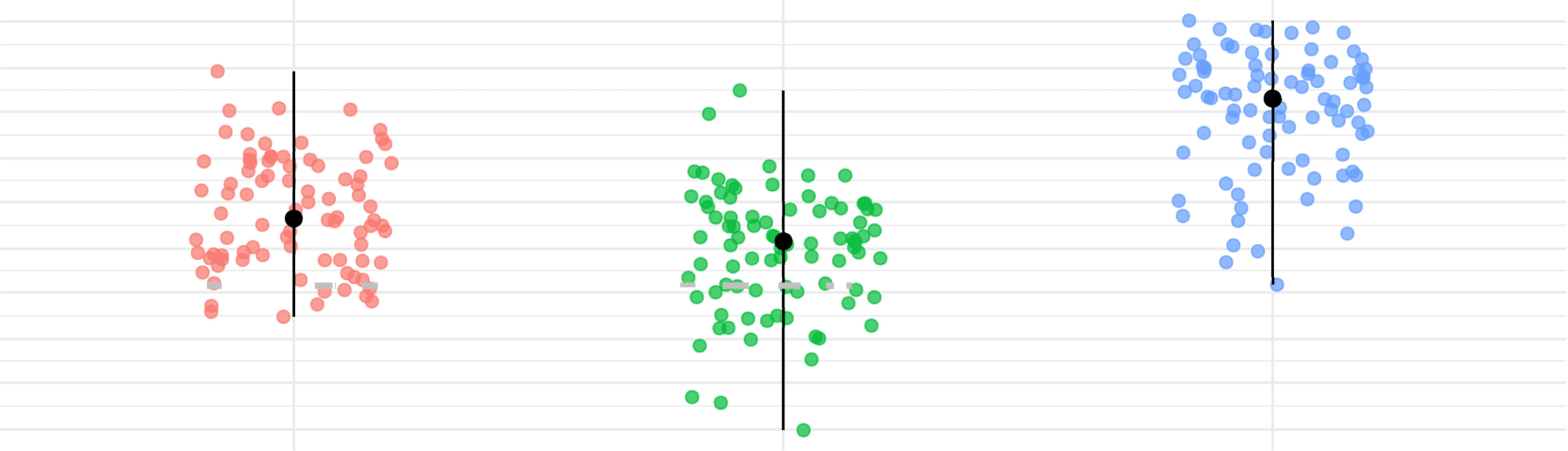
Figure 9. Age and FWD points distribution for the subjects within the clusters of ASD group
found by the consensus clustering algorithm. In red, the dot displays the median, and the vertical
lines reach the maximum and minimum dispersion of the points in each case.
Network Neuroscience
337
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
a
_
0
0
0
7
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectome sorting by consensus clustering
On the other hand, we can see in Figure 10 that overall, the effect size of each node pattern
connectivity for distinguishing between both group labels is larger when a partitioned case
is involved. This is also translated into an increase of statistical significance (see Supporting
Information Figure S3, Rasero et al., 2019). In particular, it is notable how cluster 3 of the
TD population shows all the benefits of applying the consensus clustering method since it
gathers the TD subjects with the highest connectome difference in comparison with the ASD
subjects. Moreover, this pronounced case corresponds to the scenario where the decrease of
intragroup distance (cluster is more homogeneous) also follows an increase of the intergroup
distance (left panel of Figure 11). This effect is not reproduced in the rest of the cases, even
though clusters become more compact. We are indeed clustering each group separately, thus
maximum separation between classes does not need to be guaranteed. Likewise, the intragroup
distance reduction also yields an effect size enhancement in both autistic subpopulations, more
clearly for cluster 1 where this reduction is more pronounced. Consequently, the increase in
effect size and the subsequent gain in statistical significance for some of the cases might allow
to unmask regions not observed significantly different at first and therefore be further exploited
by a more thorough exploratory analysis.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
a
_
0
0
0
7
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 10. The change in the effect size measure R
provided by MDMR across nodes, where subscript term “whole” involves both whole
groups comparison and “cluster” one partitioned group. An enhancement is developed above zero, here displayed by a gray thick line. Median
value point reaching the maximum and minimum values are depicted here in black.
2
Network Neuroscience
338
Connectome sorting by consensus clustering
Figure 11. Mean intra- and intergroup distance distribution provided by the collection of distance matrices per each node. On the left, this
is shown for the TD group, and on the right for the ASD subjects. The intergroup distance is always evaluated considering the other group as
a whole.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
a
_
0
0
0
7
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
When considering both groups each as a whole, MDMR yields only two significant regions
(region 57 and 83) as explained by group label variation between subjects, whereas this num-
ber increases to 13 and 70 for age and FWR, respectively, showing an important effect of the
observed variance based on these last covariates. However, applying first consensus cluster-
ing to the TD group produces three clusters such that when comparing with the ASD group,
one cluster yields 52 significant nodes, with 48 nodes uniquely assigned to it. Likewise, both
clusters obtained by partitioning the ASD group lead to 16 and 9 significant nodes when com-
pared with the group of typically developing subjects and, most importantly, 14 and 6 of them,
respectively, only observable in each cluster. Therefore, not only we do gain separability by
means of an increase of significant nodes, but also our approach allows us to unmask unique
regions not visible whatsoever when using standard whole groups comparisons.
From a clinical point of view the emergence of unique nodes can evidence brain regions
whose implications on the development of the pathology should be further examined. In our
case, concentrating on the ASD case, cluster 1 has 14 regions not present neither in clus-
ter 2 versus TD, nor in whole group comparison. These regions are prominently localized
on the right brain hemisphere with the highest overall significance in the pars triangularis of
fdr = 0.0004). Areas in the same hemisphere involving the frontal
the inferior frontal gyrus (p
fdr = 0.0014) and
fdr = 0.0036) and postcentral (p
pole (p
fdr = 0.0019) in the opposite hemisphere are also associated to greater
paracentral regions (p
separation. On the other hand, the six unique significant nodes of cluster 2 belong to areas in
fdr = 0.0021 in the left
both hemispheres involving the banks of the superior temporal sulcus (p
fdr = 0.0085
hemisphere and p
fdr = 0.0069) and
and p
the supramarginal (p
fdr = 0.0075, respectively), and regions in the inferior temporal lobe (p
fdr = 0.0079) in the right hemisphere.
fdr = 0.0078 in the right one) and the superior temporal lobe (p
fdr = 0.0018) and the precuneus (p
DISCUSSION
New techniques aimed to increase group separability in neuroimaging studies are constantly
being developed to gain deeper and better insight on brain function and malfunctioning. The
use of connectomes as a biomarkers is also increasingly prominent. Our clustering method
Network Neuroscience
339
Connectome sorting by consensus clustering
is naturally located in this latter field and helps unveil more compact subclasses beyond the
group labels. In addition, the application of consensus clustering to different regions of the
brain allows us to capture differences in the groups unseen when the whole connectivity matrix
is used. To our best knowledge, such an approach has not been yet explored in neuroimaging.
Additionally, the consensus matrix gathers information from different resolutions and nodes
and encodes them into the consensus matrix. As a consequence, some possible arbitrariness
such as choosing a priori the number of clusters to be obtained disappears. Moreover, clusters
found by our method are fairly robust with respect to moderate changes in amplitude noise. Of
note, clinical and control groups have been shown to share functional connectivity patterns
(Easson, Fatima, & McIntosh, in press; Spronk et al., 2018). Here we do not go after a wholly
data driven clustering of subjects irrespective of their main clinical label, but rather on refining
these user-defined groups based on their FC patterns.
Preliminary analysis of groups of labeled subjects by consensus clustering leads to more
compact partitions and a subsequent increase in separability of classes when performing group
comparisons. This effect can be simply understood by looking at the comparison of two uni-
variate distributions, where the separability of both groups can be expressed in terms of the
mean difference (intergroup distance) divided by the variability of both groups (intragroup dis-
tance). As a consequence, a reduction of the intragroup distance can help increase separability.
Nonetheless, it is important to note that application of our clustering method to an individual
group only optimizes the intragroup distance, and therefore it might happen that for some parti-
tions the intergroup distances also decrease, compensating the benefit of having more compact
groups. Different strategies to preprocess the data and to address motion confounders mod-
ify to some extent the output of virtually any subsequent analysis. One of the most debated
choices in this respect, and likely one of the most influential on the results, is global signal
regression. In our original analyses we decided not to apply global signal regression because
of the expected network-specific differential effects evidenced in Gotts et al. (2013). On the
other hand, there are also reasons to use global signal regression (Murphy & Fox, 2017), and
this choice was made in a recent paper proposing a similar subgroup classification strategy
(Easson et al., in press). We repeated our analysis after regressing the global signal out, and
found that the results were qualitatively similar (see Supporting Information Figure S4, Rasero
et al., 2019 for the ABIDE dataset).
In addition to variability reduction that allows us to elucidate regions with distinctive con-
nectivity patterns in group comparisons, each cluster found also provides unique information.
In particular, we have shown this for two different datasets that include four different mental
disorders: ADHD, BD, SCH, and ASD.
Most of the studies aimed at finding brain alterations in ADHD subjects have been focused
on children, since the symptoms related to this disorder such as inattention and/or hyperactiv-
ity/impulsivity need to be treated at the beginning of their appearance. In our case, however,
our cohort consists of adult subjects, among which we have found two different clusters car-
rying both different and unique information. The first cluster comprises a vast anterior brain
area, in addition to the lateral occipital cortex and the lingual gyrus, mainly associated with
visual attention. Similar results were reported using structural data (Ahrendts et al., 2011). The
second one covers a small portion of the brain associated with the dorsal attention and the
cerebellum, possibly capturing the cognitive functions of the latter in attention tasks (Berquin
et al., 1998).
Network Neuroscience
340
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
a
_
0
0
0
7
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectome sorting by consensus clustering
Our clustering method clearly evidences the default mode network as one of the relevant
systems in one of the subgroups in bipolar disorder and schizophrenia. Such a fundamental
network is likely very sensitive to most modulations and already reported to be affected in
both mental disorders (V. Calhoun et al., 2012; Ongür et al., 2010). In our specific clusters,
regions with a disrupted connectivity pattern concentrate in the frontal cortex (Deakin et al.,
1989; Johnston-Wilson et al., 2000), with also some areas in the temporal lobe, which may
account for differences between bipolar disorder and schizophrenia (Altshuler et al., 2000;
V. D. Calhoun, Maciejewski, Pearlson, & Kiehl, 2008; Johnstone et al., 1989).
The present study evidenced areas involved in different functional systems, such as the
cerebellum (DelBello, Strakowski, Zimmerman, Hawkins, & Sax, 1999; Forlim et al., 2017;
McDonald et al., 2005), and the postcentral gyrus was connected to the appearance of delusion
and hallucinations associated with a dysfunction of the sensory system (Song et al., 2015), and
the bilateral lingual gyrus, whose hyperactivation has been connected to lack of empathy in
schizophrenic subjects (Kühn & Gallinat, 2013).
On the other hand, two clear macroregions characterize our results on ASD subjects. The
first one has a clear right asymmetry, with the participation of areas around the pars opercu-
laris and pars triangularis in the inferior frontal gyrus, usually connected to lack of emotions
(Dapretto et al., 2005; De Foss et al., 2004; Herbert et al., 2002). This domain also includes
sensorimotor areas such as the postcentral and paracentral gyrus and precuneus and confirm
the results observed in a larger ABIDE cohort of subjects when comparing ASD with typically
developing controls (Lee, Kyeong, Kim, & Cheon, 2016). The second set of regions comprises
some parts of the temporal lobe that, in addition to regions in the orbitofrontal cortex and the
amygdala, define the “social brain.” In this case, autistic subjects develop abilities for verbally
labeling complex visual stimuli and processing faces and eyes, to compensate for amygdala
abnormality (Baron-Cohen et al., 1999).
It is worth stressing that the connectivity patterns among brain regions are influenced by
respiration, movement, cardiac phase, and other physiological variables, and what we observe
and can infer here (and in most fMRI studies) is just a higher level view in which the effects of
all these actors are conflated.
CONCLUSIONS
In this work we have proposed the use of the consensus clustering approach for exploratory
analysis in order to cope with the heterogeneity of subjects. Extracting the natural classes
present in data and subsequently performing the supervised analysis by MDMR on these al-
lows us to identify variables whose adjacency pattern is altered in group comparisons, and
which are not highlighted when considering the groups as a whole. As a result, the proposed
approach leads to an increase in the effect sizes. We presented an application to public fMRI
data, evidencing groups of subjects in which specific regions contributed to a higher separa-
bility between classes. In sum, we have shown an additional benefit of using the consensus
clustering algorithm developed in Rasero et al. (2017). Such an algorithm is based on the idea
of condensing information on structure at different levels, which in general works well when
extracting the inherent data subclasses. Future studies could test alternative strategies when
this is not the case.
AUTHOR CONTRIBUTIONS
Javier Rasero: Conceptualization; Data curation; Formal analysis; Investigation; Methodology;
Software; Validation; Visualization; Writing – original draft. Ibai Diez: Data curation. Jesus
Network Neuroscience
341
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
a
_
0
0
0
7
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectome sorting by consensus clustering
M Cortes: Conceptualization; Methodology; Supervision; Writing – original draft. Daniele
Marinazzo: Conceptualization; Data curation; Formal analysis; Investigation; Methodology;
Supervision; Visualization; Writing – original draft. Sebastiano Stramaglia: Conceptualization;
Formal analysis; Investigation; Methodology; Supervision; Writing – original draft.
FUNDING INFORMATION
Sebastiano Stramaglia, University of Bari “Aldo Moro” (http://doi.org/10.13039/501100005362),
Award ID: “Progetti di Ricerca su base competitiva, f.di ex 60% - residuo 2015.” Javier Rasero,
Department of Education (Basque Country Government), Award ID: Doctoral Research Staff
Improvement Programme.
REFERENCES
Ahrendts, J., Rüsch, N., Wilke, M., Philipsen, A., Eickhoff, S. B.,
Glauche, V., . . . van Elst, L. T. (2011). Visual cortex abnormal-
ities in adults with ADHD: A structural MRI study. The World
Journal of Biological Psychiatry, 12(4), 260–270. https://doi.org/
10.3109/15622975.2010.518624
Altshuler, L. L., Bartzokis, G., Grieder, T., Curran, J., Jimenez, T.,
Leight, K., . . . Mintz, J. (2000). An MRI study of temporal lobe
structures in men with bipolar disorder or schizophrenia. Biolog-
ical Psychiatry, 48(2), 147–162. https://doi.org/10.1016/S0006-
3223(00)00836-2
Barabasi, A.-L., & Frangos, J. (2002). Linked: The New Science of
Networks (1st ed.). New York: Perseus Books Group.
Baron-Cohen, S., Ring, H. A., Wheelwright, S., Bullmore, E. T.,
Brammer, M. J., Simmons, A., & Williams, S. C. R. (1999). So-
cial intelligence in the normal and autistic brain: An fMRI study.
European Journal of Neuroscience, 11(6), 1891–1898. http://
doi.org/10.1046/j.1460-9568.1999.00621.x
Berquin, P. C., Giedd, J. N., Jacobsen, L. K., Hamburger, S. D.,
Krain, A. L., Rapoport, J. L., & Castellanos, F. X. (1998). Cerebel-
lum in attention-deficit hyperactivity disorder. Neurology, 50(4),
1087–1093. http://n.neurology.org/content/50/4/1087
Boccaletti, S., Bianconi, G., Criado, R., del Genio, C., Gómez-
Gardeñes, J., Romance, M., . . . Zanin, M. (2014). The structure
and dynamics of multilayer networks. Physics Reports, 544(1),
1–122. http://doi.org/10.1016/j.physrep.2014.07.001
Brito, P., Bertrand, P., Cucumel, G., & Carvalho, F. D. (2007). Clus-
tering by Means of Medoids. Selected Contributions in Data
Analysis and Classification. Berlin: Springer Science & Business
Media.
Calhoun, V., Sui, J., Kiehl, K., Turner, J., Allen, E., & Pearlson, G.
(2012). Exploring the psychosis functional connectome: Aber-
rant intrinsic networks in schizophrenia and bipolar disorder.
Frontiers in Psychiatry, 2, 75. https://www.frontiersin.org/article/
10.3389/fpsyt.2011.00075
Calhoun, V. D., Maciejewski, P. K., Pearlson, G. D., & Kiehl,
K. A. (2008). Temporal lobe and default hemodynamic brain
modes discriminate between schizophrenia and bipolar dis-
order. Human Brain Mapping, 29(11), 1265–1275. http://doi.org/
10.1002/hbm.20463
Dapretto, M., Davies, M. S., Pfeifer, J. H., Scott, A. A., Sigman, M.,
Bookheimer, S. Y., & Iacoboni, M. (2005). Understanding emo-
tions in others: Mirror neuron dysfunction in children with autism
spectrum disorders. Nature Neuroscience, 9(1), 2830. https://doi.
org/10.1038/nn1611
Deakin, J. F. W., Slater, P., Simpson, M. D. C., Gilchrist, A. C., Skan,
W. J., Royston, M. C., . . . Cross, A. J. (1989). Frontal cortical
and left temporal glutamatergic dysfunction in schizophrenia.
Journal of Neurochemistry, 52(6), 1781–1786. http://doi.org/
10.1111/j.1471-4159.1989.tb07257.x
De Foss, L., Hodge, S. M., Makris, N., Kennedy, D. N., Caviness,
V. S., McGrath, L., . . . Harris, G. J. (2004). Language-association
cortex asymmetry in autism and specific language impairment.
Annals of Neurology, 56(6), 757–766. http://doi.org/10.1002/
ana.20275
DelBello, M. P., Strakowski, S. M., Zimmerman, M. E., Hawkins,
J. M., & Sax, K. W. (1999). MRI analysis of the cerebellum in bipo-
lar disorder: A pilot study. Neuropsychopharmacology, 21(1),
63–68. https://doi.org/10.1016/S0893-133X(99)00026-3
Di Martino, A., Yan, C. G., Li, Q., Denio, E., Castellanos, F. X.,
Alaerts, K., . . . Milham, M. P. (2014). The autism brain imag-
ing data exchange: Towards a large-scale evaluation of the in-
trinsic brain architecture in autism. Molecular Psychiatry, 19(6),
659–667. http://doi.org/10.1038/mp.2013.78
Easson, A. K., Fatima, Z., & McIntosh, A. R. (in press). Func-
tional connectivity-based subtypes of individuals with and with-
out autism spectrum disorder. Network Science. Retrieved from
https://doi.org/10.1162/netn_a_00067
Erhardt, E. B., Allen, E. A., Wei, Y., Eichele, T., & Calhoun, V. D.
(2012). SimTB, a simulation toolbox for fmri data under a model
of spatiotemporal separability. NeuroImage, 59(4), 4160–4167.
https://doi.org/10.1016/j.neuroimage.2011.11.088
Forlim, C., Klock, L., Bchle, J., Stoll, L., Giemsa, P., Fuchs, M.,
. . . Kühn, S. (2017). Disrupted cerebrum-cerebellum network
in schizophrenia revealed by network-based statistics and graph
theory. BMC Neuroscience, 18(1), 138.
Fornito, A., & Bullmore, E. T. (2010). What can spontaneous fluc-
tuations of the blood oxygenation-level-dependent signal tell us
about psychiatric disorders? Current Opinion in Psychiatry, 23(3),
239–249. http://doi.org/10.1097/yco.0b013e328337d78d
Gotts, S., Saad, Z., Jo, H. J., Wallace, G., Cox, R., & Martin, A.
(2013). The perils of global signal regression for group com-
parisons: A case study of autism spectrum disorders. Frontiers
Network Neuroscience
342
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
a
_
0
0
0
7
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Connectome sorting by consensus clustering
in Human Neuroscience, 7, 356. https://www.frontiersin.org/
article/10.3389/fnhum.2013.00356
Herbert, M. R., Harris, G. J., Adrien, K. T., Ziegler, D. A., Makris, N.,
Kennedy, D. N., . . . Caviness, V. S. (2002). Abnormal asymmetry
in language association cortex in autism. Annals of Neurology,
52(5), 588–596. http://doi.org/10.1002/ana.10349
Johnstone, E. C., Owens, D. G., Crow, T.
J., Frith, C. D.,
Alexandropolis, K., Bydder, G., & Colter, N. (1989). Temporal
lobe structure as determined by nuclear magnetic resonance in
schizophrenia and bipolar affective disorder. Journal of Neurol-
ogy, Neurosurgery & Psychiatry, 52(6), 736–741. http://jnnp.bmj.
com/content/52/6/736
Johnston-Wilson, N. L., Sims, C. D., Hofmann, J.-P., Anderson, L.,
Shore, A. D., Torrey, E. F., & Yolken, R. H. (2000). Disease-specific
alterations in frontal cortex brain proteins in schizophrenia, bipo-
lar disorder and major depressive disorder. Molecular Psychiatry,
5(2), 142149. https://doi.org/10.1038/sj.mp.4000696
Kühn, S., & Gallinat, J. (2013). Resting-state brain activity in schizo-
phrenia and major depression: A quantitative meta-analysis.
Schizophrenia Bulletin, 39(2), 358–365. http://doi.org/10.1093/
schbul/sbr151
Lancichinetti, A., & Fortunato, S. (2012). Consensus clustering in
complex networks. Scientific Reports, 2:336. http://doi.org/10.
1038/srep00336
Lee, J. M., Kyeong, S., Kim, E., & Cheon, K.-A. (2016). Abnormalities
of inter- and intra-hemispheric functional connectivity in autism
spectrum disorders: A study using the autism brain imaging data
exchange database. Frontiers in Neuroscience, 10, 191. https://
www.frontiersin.org/article/10.3389/fnins.2016.00191
McArdle, B. H., & Anderson, M. J. (2001). Fitting multivariate
models to community data: A comment on distance-based re-
dundancy analysis. Ecology, 82(1), 290–297. http://doi.org/10.
1890/0012-9658(2001)082[0290:FMMTCD]2.0.CO;2
McArtor, D. B. (n.d.). MDMR: Multivariate distance matrix re-
gression R package. Retrieved from https://CRAN.R-project.org/
package=MDMR
McDonald, C., Bullmore, E., Sham, P., Chitnis, X., Suckling, J.,
Maccabe, J., . . . Murray, R. M.
(2005). Regional volume de-
viations of brain structure in schizophrenia and psychotic bipo-
lar disorder: Computational morphometry study. British Journal of
Psychiatry, 186(5), 369377. https://doi.org/10.1192/bjp.186.5.369
Murphy, K., & Fox, M. D. (2017). Towards a consensus regard-
ing global signal regression for resting state functional connec-
tivity MRI. NeuroImage, 154, 169–173. https://doi.org/10.1016/
j.neuroimage.2016.11.052
Ongür, D., Lundy, M., Greenhouse, I., Shinn, A. K., Menon, V.,
Cohen, B. M., & Renshaw, P. F. (2010). Default mode network
abnormalities in bipolar disorder and schizophrenia. Psychia-
try Research: Neuroimaging, 183(1), 59–68. https://doi.org/10.
1016/j.pscychresns.2010.04.008
Poldrack, R. A., Congdon, E., Triplett, W., Gorgolewski, K. J.,
Karlsgodt, K. H., Mumford, J. A., . . . Bilder, R. M. (2016). A
phenome-wide examination of neural and cognitive function.
Sci Data, 3, 160110.
Rasero,
J., Alonso-Montes, C., Diez,
Remaki, L., Escudero,
I.,
.
.
I., Olabarrieta-Landa, L.,
. Alzheimer’s Disease Neuro-
imaging Initiative. (2017). Group-level progressive alterations in
brain connectivity patterns revealed by diffusion-tensor brain net-
works across severity stages in Alzheimer’s disease. Frontiers in
Aging Neuroscience, 9, 215. https://www.frontiersin.org/article/
10.3389/fnagi.2017.00215
Rasero, J., Diez, I., Cortes, J. M., Marinazzo, D., & Stramaglia, S.
(2019). Supporting Information for “Connectome sorting by con-
sensus clustering increases separability in group neuroimaging
studies.” Network Neuroscience, 3(2), 325–343. https://doi.org/
10.1162/netn_a_00074
Rasero, J., Pellicoro, M., Angelini, L., Cortes, J. M., Marinazzo,
D., & Stramaglia, S.
(2017). Consensus clustering approach to
group brain connectivity matrices. Network Neuroscience, 1(3),
242–253. https://doi.org/10.1162/NETN_a_00017
Reichardt, J., & Bornholdt, S. (2006). Statistical mechanics of com-
munity detection. Physics Review E, 74, 016110. https://link.aps.
org/doi/10.1103/PhysRevE.74.016110
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003
Shehzad, Z., Kelly, C., Reiss, P. T., Craddock, R. C., Emerson, J. W.,
McMahon, K., . . . Milham, M. P. (2014). A multivariate distance-
based analytic framework for connectome-wide association
studies. NeuroImage, 93(Part 1), 74–94. https://doi.org/10.1016/
j.neuroimage.2014.02.024
Shen, X., Tokoglu, F., Papademetris, X., & Constable, R. (2013).
Groupwise whole-brain parcellation from resting-state fMRI data
for network node identification. NeuroImage, 82(Supplement C),
403–415. https://doi.org/10.1016/j.neuroimage.2013.05.081
Song, J., Han, D., Kim, S., Hong, J., Min, K. J., Cheong, J., & Kim,
B.
(2015). Differences in gray matter volume corresponding
to delusion and hallucination in patients with schizophrenia
compared with patients who have bipolar disorder. Neuropsy-
chiatric Disease and Treatment, 1211. https://doi.org/10.2147/
ndt.s80438
Sporns, O. (2011). Networks of the Brain. Cambridge, MA: MIT
Press.
Spronk, M., Kulkarni, K., Ji, J. L., Keane, B., Anticevic, A., & Cole,
M. W. (2018). A whole-brain and cross-diagnostic perspective on
functional brain network dysfunction. bioRxiv, 326728. https://
doi.org/10.1101/326728
Strehl, A., & Ghosh, J. (2002). Cluster ensembles - A knowledge
In Eighteenth
reuse framework for combining partitionings.
National Conference On Artificial Intelligence (AAAI-02)/Fourteenth
Innovative Applications of Artificial
Intelligence Conference
(IAAI-02), Proceedings (p. 93–98). Cambridge, MA: MIT PRESS.
Xu, R., & Wunsch, D. (2005). Survey of clustering algorithms. IEEE
Transactions on Neural Networks, 16(3), 645–678. https://doi.
org/10.1109/TNN.2005.845141
Zapala, M. A., & Schork, N. J. (2006). Multivariate regression
analysis of distance matrices for testing associations between
gene expression patterns and related variables. Proceedings
of the National Academy of Sciences of the United States of
America, 103(51), 19430–19435. http://www.pnas.org/content/
103/51/19430.abstract
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
2
5
1
0
9
2
6
2
6
n
e
n
_
a
_
0
0
0
7
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
343