方法 - 麻省理工学院人工智能研究专业

方法

Large-scale DCMs for resting-state fMRI

1,2,3

Adeel Razi

, Mohamed L. Seghier

, Yuan Zhou

, Peter McColgan

, Peter Zeidman

7
Hae-Jeong Park

8
, 奥拉夫·斯波恩斯

, Geraint Rees

, and Karl J. 弗里斯顿

1,9

1,4

1,5

1The Wellcome Trust Centre for Neuroimaging, 伦敦大学学院, 伦敦, 英国
2Monash Biomedical Imaging and Monash Institute of Cognitive and Clinical Neurosciences, Monash University,
克莱顿, 澳大利亚
3Department of Electronic Engineering, NED University of Engineering and Technology, Karachi, 巴基斯坦
Cognitive Neuroimaging Unit, 阿布扎比, United Arab Emirates
5CAS Key Laboratory of Behavioral Science and Magnetic Resonance Imaging Research Center, Institute of Psychology,
Chinese Academy of Sciences, 北京, 中国
6Huntington’s Disease Centre, Institute of Neurology, 伦敦大学学院, 伦敦, 英国
7Department of Nuclear Medicine and BK21 PLUS Project for Medical Science, Yonsei University College of Medicine, Seoul,
Republic of Korea
8Department of Psychological and Brain Sciences, 印第安纳大学, 布卢明顿, 印第安纳州
9Institute of Cognitive Neuroscience, 伦敦大学学院, 伦敦, 英国.

关键词: Dynamic causal modeling, Effective connectivity, Functional connectivity, Resting state,
功能磁共振成像, Graph theory, Bayesian inference, Large-scale networks

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

1
3
2
2
2
1
0
9
2
0
5
0
n
e
n
_
A
_
0
0
0
1
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

抽象的

This paper considers the identiﬁcation of large directed graphs for resting-state brain
networks based on biophysical models of distributed neuronal activity, 那是, effective
连接性. This identiﬁcation can be contrasted with functional connectivity methods
based on symmetric correlations that are ubiquitous in resting-state functional MRI (功能磁共振成像).
We use spectral dynamic causal modeling (DCM) to invert large graphs comprising dozens of
nodes or regions. The ensuing graphs are directed and weighted, hence providing a
neurobiologically plausible characterization of connectivity in terms of excitatory and
inhibitory coupling. 此外, we show that the use of Bayesian model reduction to
discover the most likely sparse graph (or model) from a parent (例如, fully connected) 图形
eschews the arbitrary thresholding often applied to large symmetric (功能连接)
图表. Using empirical fMRI data, we show that spectral DCM furnishes connectivity
estimates on large graphs that correlate strongly with the estimates provided by stochastic
DCM. 此外, we increase the efﬁciency of model inversion using functional
connectivity modes to place prior constraints on effective connectivity. 换句话说, 我们
use a small number of modes to ﬁnesse the potentially redundant parameterization of large
DCMs. We show that spectral DCM—with functional connectivity priors—is ideally suited
for directed graph theoretic analyses of resting-state fMRI. We envision that directed graphs
will prove useful in understanding the psychopathology and pathophysiology of
neurodegenerative and neurodevelopmental disorders. We will demonstrate the utility of
large directed graphs in clinical populations in subsequent reports, using the procedures
described in this paper.

介绍

Dynamic causal modeling is a Bayesian framework that allows one to make inferences about
the causal (指导的) interactions between the nodes (例如, brain regions) of a coupled sys-
TEM; 即, effective connectivity (Razi & 弗里斯顿, 2016). Effective connectivity contrasts with
correlation-based functional connectivity that is inherently undirected. 通常, DCM is used
to test hypotheses about subgraphs or brain networks that contain a relatively small number of

开放访问

杂志

引文: Razi, A. Seghier, 中号. L。, 周,
Y。, McColgan, P。, Zeidman, P。, 公园,
H.-J., 斯波恩斯, 奥。, Rees, G。, & 弗里斯顿, K.
J. (2017). Large-scale DCMs for
resting-state fMRI. 网络
神经科学, 1(3), 222–241.
https://doi.org/10.1162/netn_a_00015

DOI:
https://doi.org/10.1162/netn_a_00015

支持信息:
http://www.ﬁl.ion.ucl.ac.uk/spm
http://fcon_1000.projects.nitrc.org/
fcpClassic/FcpTable.html

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
Adeel Razi
a.razi@ucl.ac.uk

处理编辑器:
Michael Breakspear

版权: © 2017
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

Large-scale spectral DCMs

Dynamic causal modeling:
A Bayesian framework that is used to
infer causal interaction between
coupled or distributed neuronal
系统.

Effective connectivity:
A measure of the directed (causal)
inﬂuence of one neural system over
another using a model of neuronal
互动.

Functional connectivity:
A (undirected) measure of the
statistical dependencies between
spatially remote neurophysiological
事件.

Generative model:
A model for randomly generating
observable data values, typically
given some hidden parameters.

Bayesian model selection:
Procedure to determine the most
likely among a set of competing
hypotheses (or models) 关于
mechanisms that generated observed
数据.

nodes that are of speciﬁc interest in the context of an experimental manipulation. 然而, 在
最近几年, there has been a marked increase in research that combines resting-state fMRI
with large-scale, big-data network analyses (Nakagawa, Jirsa, Spiegler, McIntosh, & 德科,
2013; 史密斯等人。, 2013; 斯波恩斯, 2014). Resting-state fMRI allows one to study connectiv-
ity in the brain through the acquisition of fMRI data, as participants lie at rest in an MRI
scanner. Analyzing large-scale resting-state functional brain networks using graph theory
has become a popular approach to these data (for reviews see Bullmore & 斯波恩斯, 2009;
假如, 扎莱斯基, & Breakspear, 2015). Graph theoretic characterizations generally rest upon
the statistics of the edges, using descriptive statistics like degree, path lengths and clustering
coefﬁcients, or community detection methods to extract densely coupled clusters or mod-
ules (鲁比诺夫 & 斯波恩斯, 2010; 斯波恩斯 & 贝策尔, 2016). There are several international efforts
in place to characterize brain connectivity and its variability in healthy adults. 例如,
the Human Connectome Project has collected a rich set of large data (> 1,200 参与者)
and the UK Biobank project aims to scan 100,000 参与者, using several neuroimaging
modalities—including resting-state fMRI—to compute functional and effective connectivity
and diffusion weighted MRI for estimating anatomical connectivity. While the structural
connectome can be characterized using a variety of computational approaches including
probabilistic ﬁber tracking, resting-state fMRI has a complementary role in characterizing
the “functional connectome”—through a detailed mapping of functional integration. 不像
structural networks, functional networks refer to statistical constructs that express substantial
variability on short timescales—in response to either external inputs or endogenous (sponta-
尼厄斯) activity—as in the case of resting-state fMRI. This means that functional connections
are time and context sensitive, unlike anatomical connectivity which is conserved over shorter
timescales. 至关重要的是, these functional links exist without mandating any direct (monosynap-
tic) connection between neuronal populations; 例如, polysynaptic connections that
mediate functional coupling vicariously, such as through transitive closure.

Functional connectivity reﬂects the statistical dependencies between spatially remote
neurophysiological events (Razi & 弗里斯顿, 2016). These correlations are inherently undi-
rected and—as the statistical dependencies are “model-free”—do not support any inference
关于 (指导的) causal interactions between neuronal systems. 相比之下, effective con-
nectivity measures the directed (causal) inﬂuence of one neural system over another us-
ing a model of neuronal interactions that best explains the observed signal ﬂuctuations
(Breakspear, 2004; 弗里斯顿, Frith, Liddle, & Frackowiak, 1993). Dynamic causal modeling
(弗里斯顿, Harrison, & 一分钱, 2003) is the most widely adopted framework to estimate effective
连接性. The key concept underlying DCM is to treat the brain as a nonlinear dynamic
system that accepts multiple inputs and produces multiple outputs (IE。, MIMO model). 这
neuronal MIMO model is augmented with a regionally speciﬁc hemodynamic forward model
that describes the mapping from neuronal activity to observed (功能磁共振成像) responses. 一起, 这
neuronal and observation model comprise a full generative model.

This paper demonstrates that a recent variant of DCM (弗里斯顿, Kahan, Biswal, & Razi,
2014)—namely, spectral DCM that was designed to model resting-state fMRI—can be used to
invert large-scale graphs. We show that spectral DCM can handle graphs comprising dozens
of nodes and may therefore contribute to a mechanistic understanding of large-scale connec-
活力. 传统上, DCM has been used to test competing hypothesis that embody a priori
hypotheses about networks comprising only a few regions. Several competing hypotheses
(that constitute a model space) are speciﬁed in the form of subgraphs, which are then com-
pared using Bayesian model selection. 然而, increasing the number of regions or nodes
in a DCM presents some challenges. 例如, the number of extrinsic (between-node)

网络神经科学

223

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

1
3
2
2
2
1
0
9
2
0
5
0
n
e
n
_
A
_
0
0
0
1
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Large-scale spectral DCMs

Bayesian model reduction:
A Bayesian inversion and
comparison of models that are
reduced (or sparsed) forms of a full
(or parent) 模型.

Thresholding:
A procedure applied to adjacency
matrix of a graph to induce sparsity
by removing connections above or
below a certain value.

Neural ﬂuctuations:
Refers to the random intrinsic (或者
spontaneous) ﬂuctuations within
神经元网络.

connections or edges increases with the square of the number of nodes. This can lead to
models with an enormous number of free parameters and profound conditional dependencies
among the parameters. 此外, the computational time required to invert these mod-
els grows exponentially with the number of free parameters. Because stochastic DCM has to
estimate both hidden (神经元的) states and parameters, it is computationally more intensive
and—in its current form—unable to invert models with more than 10 nodes within pragmatic
time frames. 相比之下, spectral DCM has a much lower computational complexity and is
ideally suited to invert large-scale models comprising in the order of 32 到 64 brain regions.

在这项工作中, we used empirical data to invert graphs comprising 36 brain regions and
establish the construct validity of the ensuing parameter estimates using two inversion schemes:
stochastic DCM that inverts models in the time domain and spectral DCM, which is based on
inversion in the frequency domain. Razi, Kahan, Rees, and Friston (2015) established in silico
construct validation of spectral DCM against stochastic DCM. These analyses showed that
spectral DCM was not only computationally efﬁcient but also more accurate in terms of root
mean squared error and sensitivity to group differences. 在本文中, we use empirical data to
show that spectral DCM is a computationally viable method for inferring large directed graphs
of effective connectivity.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

This paper comprises three sections. The ﬁrst describes the requisite background for dynam-
ical causal modeling of resting-state fMRI data and the model reduction procedures that can
be used to place prior constraints on large networks for efﬁcient inference. We then present
the empirical data, attending model speciﬁcation, and inversion procedures.
In the subse-
quent section, we present the results of model inversion using two (stochastic and spectral)
inversion schemes. We also describe the use of Bayesian model reduction procedures that are
analogous to thresholding in graph theoretic analyses. The implicit induction of sparsity can be
very useful for subsequent graph theoretical analysis, 解释, and reducing the multiple
comparisons problem. The ﬁnal section concludes with a discussion of future applications and
implications of the procedures described in this paper.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

1
3
2
2
2
1
0
9
2
0
5
0
n
e
n
_
A
_
0
0
0
1
5
p
d

METHODS AND MATERIALS

Dynamic Causal Modeling for Resting-State fMRI

Resting-state fMRI is a paradigm that has become very popular during the past decade or so.
This is largely because the data are easy to acquire and they disclose the intrinsic architecture
of the brain in the absence of experimental or exogenous inputs. In the absence of external
输入, neuronal dynamics are driven by intrinsic activity, known as endogenous or neural
ﬂuctuations that are internal to the system. The generative models for resting-state fMRI time
series have the same form as DCMs of task fMRI but discount exogenous modulatory inputs.
These models can be formulated as a Taylor expansion, retaining only the linear terms; 即,

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

˙x(t) = Ax(t) + Cu(t) + v(t)

y(t) = h (X(t), 我) + e(t).

Adjacency matrix:
Square matrix representation of graph
that is either binary (presence or
absence of connections) or weighted
(showing strength of connections).

The matrix A is known as the adjacency matrix or Jacobian describing the behavior—that
是, the effective connectivity—of the system near its ﬁxed point ( F (xo) = 0), in the absence
of the neuronal ﬂuctuations v(t) and the experimental inputs u(t).
In fMRI, the mapping
from hidden neuronal states, X(t), to the observed blood oxygenation level dependent (大胆的)
fMRI data y(t) is based on a hemodynamic model, which transforms hidden neuronal states
of each population or region into predicted BOLD responses, using a previously established

网络神经科学

224

Large-scale spectral DCMs

Cross spectral density:
A frequency domain transformation
of the cross-correlation or
cross-covariance between two time
series signals.

biophysical model (K. J. Friston et al., 2003). Here e(t) represents the measurement error and
θ are parameters of the hemodynamic response function or convolution kernel h(X(t), 我).

There are currently two schemes for inverting models of resting fMRI. Although both schemes
use the same variational Bayes procedures for model inversion, they differ in the data fea-
tures they use for parameter estimation. The ﬁrst scheme inverts data in the time domain and
the model is used to predict the time series per se. This is referred to as stochastic DCM
(弗里斯顿, Stephan, 李, & Daunizeau, 2010; 李等人。, 2011). This requires estimation of not only
the model parameters, but also the hidden states that become random variables. 按照
temporal characteristics, the hidden states are time-variant, whereas the model parameters are
time-invariant. This poses a difﬁcult inverse problem that is computationally demanding, 埃斯佩-
cially when the number of hidden states (IE。, the graph) becomes too large. To ﬁnesse this prob-
莱姆, we proposed a DCM based upon a deterministic model (弗里斯顿, Kahan, Biswal, 等人。,
2014; Razi et al., 2015). This scheme provides a constrained inversion of the stochastic model
by parameterizing the cross spectral density of neuronal ﬂuctuations; 即,

gv (ω, 我) = αααvω−β

ge (ω, 我) = αeω−β

e .

Here gx(ω) = X (ω) X(ω)†
represents the complex cross spectra, 其中 X(ω) is the Fourier
transform of the x(t), {A, β} ⊂ θ are the parameters controlling the amplitudes and expo-
nents of the spectral density of the neural ﬂuctuations, and ω = 2π f is the angular frequency.
The implicit parameterization of endogenous ﬂuctuations means that the states are no longer
概率性的 (in contrast to stochastic DCM). This means the inversion is signiﬁcantly simpler,
requiring estimation of only the (time-invariant) parameters of the endogenous ﬂuctuations and
the effective connectivity. 换句话说, spectral DCM estimates the time-invariant parame-
ters of models that generate observed (复杂的) cross spectra. In an earlier study (Razi et al.,
2015), we compared and contrasted spectral and stochastic DCM with endogenous ﬂuctua-
系统蒸发散 (also known as state noise) on hidden states of models with a small number of nodes (IE。,
a four-node graph). We showed that spectral DCM was not only more accurate and compu-
tationally efﬁcient, but also more sensitive to group differences. This makes spectral DCM an
ideal method for inferring effective connectivity in large brain networks. 然而, 有一个
potential to invert large-scale network models even more quickly, by calling on a previously
established device that uses a prior constraint to reduce the effective number of free parameters
(Seghier & 弗里斯顿, 2013).

Parameter Constraints Under Functional Connectivity Priors

如上所述, large-scale networks entail many free parameters, which make inference on
large graphs computationally slow, precluding their use in large-scale studies. 此外,
the large number of connectivity parameters can inﬂate model complexity, leading to potential
problems with overﬁtting. 然而, it is possible to ease this problem via a simple trick;
即, by using plausible priors to constrain the number of extrinsic coupling parameters.
这里, we applied the procedure detailed in Seghier and Friston (2013). In brief, this procedure
involves using functional connectivity to furnish priors on effective connectivity. 虽然
absence of an effective connection does not preclude a functional connection (that can be
mediated vicariously through other nodes), the absence of a functional connection means
that the effective connection is, a priori, 不太可能. This means that we can use functional
connectivity to place shrinkage priors on implausible effective connections. 此外, 一
can substantiate these priors by evaluating the increase in model evidence as one increases the

网络神经科学

225

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

1
3
2
2
2
1
0
9
2
0
5
0
n
e
n
_
A
_
0
0
0
1
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Large-scale spectral DCMs

Singular value decomposition:
A procedure in linear algebra that
factorizes a matrix into simpler and
meaningful pieces.

number of prior constraints. 在实践中, we do not consider each connection individually but
deal with mixtures of effective connectivity that can be regarded as coupling different patterns
of nodes. These patterns are referred to as modes. 有效地, this means that we can test the
hypothesis that distributed brain responses are mediated by directed coupling among spatial
patterns or modes (弗里斯顿, 2009; Seghier & 弗里斯顿, 2013).

总之, the problem of overparameterization can be ﬁnessed by replacing priors on
coupling among nodes with priors on coupling among modes—where modes correspond to
the principal components of the functional connectivity matrix. This provides an efﬁcient and
informed dimension reduction of the (priors over the parameters of a) large graph, based on the
functional connectome. Formally—following the formulation provided in Seghier and Friston
(2013)—the priors used in DCM on the exogenous connections are given by

(西德:2)

Aij

(西德:4)

(西德:3)
(西德:3) 中号

(西德:2)

= N

(西德:4)

μij, vij

which leads to the diagonal form for prior covariance over extrinsic connectivity parameters:

Σ = diag (vec (v)) ∈ Rn2

x n2.

这里, n is the number of nodes in the model. This diagonal form means that we have no
prior beliefs about dependencies among various parameters. 换句话说, the parameters
are assumed to be conditionally independent. 然而, if we introduce some conditional
dependencies then we can decrease the effective number of parameters (IE。, rank of the prior
covariance matrix). An informed way of introducing dependencies is to use the functional
connectivity as a prior constraint: 例如, by decomposing the BOLD signal using singular
value decomposition (SVD) and then using its eigenvectors to reduce the rank of the prior
covariance matrix Σ. 从数学上来说, let Y be the set of BOLD responses in nodes:

Y= [y1, y2, . . .yn] ∈ Rn x t,

where y1, y2, . . ., yn are the regional time series in regions 1, 2, …n. By using singular value
分解, we can ﬁnd the principal modes:

Y=USVT ,

is the unitary matrix containing the modes or eigenvectors, S∈ Rnx t

where U∈ Rn x n
是一个
diagonal matrix of singular values, and V∈ Rt x t
is the unitary matrix of eigenvariates. 我们
then select the modes m with the largest singular values to remove minor modes from the prior
covariance as follows:

在哪里

Σm = KmΣKT
米

(西德:5)

(西德:6)

(西德:5)

(西德:6)

⊗

Km=

UmUT
米

UmUT
米
Here ⊗ denotes the Kronecker product. With this formulation, we have effectively used
Km to introduce prior correlations so that Σm is no longer diagonal (for an illustration see
Seghier & 弗里斯顿, 2013). 换句话说, we have reduced the rank of the prior covariance
matrix and the effective number of connectivity parameters. The best number of principal
modes m can then be optimized using Bayesian model selection (or reduction), thereby pro-
viding evidential support for the hypothesis that functional connectivity provides useful priors
on effective connectivity.

网络神经科学

226

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

1
3
2
2
2
1
0
9
2
0
5
0
n
e
n
_
A
_
0
0
0
1
5
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Large-scale spectral DCMs

Empirical Data and Model Speciﬁcation

We used the open-access Oxford dataset from the FC1000 project. This dataset contains
22 adults (12 males) with a mean age of 29 年. Scanning was performed at the University
of Oxford Centre for Clinical Magnetic Resonance Research using a 3-T Siemens Trio scanner
with a 12-channel head coil. Whole-brain functional imaging was performed using a gradient
○
echo EPI sequence (repetition time (TR) = 2,000 多发性硬化症, echo time (TE) = 28 多发性硬化症, ﬂip angle = 89
,
ﬁeld of view = 224 毫米, voxel dimension = 3 × 3 × 3.5 毫米, acquisition time = 6 min 4 s).
High-resolution anatomical 3D T1-weighted MRI scans were acquired using a magnetization-
prepared rapid gradient echo sequence (TR = 2,040 多发性硬化症, = 4.7 多发性硬化症, ﬂip angle = 8
, ﬁeld of
view = 192 毫米, voxel dimension = 1 mm isotropic, acquisition time = 12 min). 参加者
were instructed to lie in dimmed light with their eyes open, think of “nothing in particular,”
and not fall asleep. From the functional data containing 180 consecutive image volumes per
参与者, the ﬁrst ﬁve volumes (dummy scans) from each participant were removed.

○

Data were preprocessed using standard procedures in SPM (一分钱, 弗里斯顿, Ashburner,
Kiebel, & Nichols, 2011) as follows: data were realigned, normalized to Montreal Neurolog-
ical Institute (MNI) 空间, and spatially smoothed using a 6 mm full width at half maximum
(FWHM) Gaussian kernel. A general linear model (GLM) containing only movement (骗局-
成立) regressors was constructed and inverted. An adjusted time series from the lateral ven-
tricle was included in subsequent GLMs as an additional confound. To identify nodes, 这
resting state was modeled using a GLM containing a discrete cosine basis set with frequencies
范围从 0.0078 到 0.1 赫兹 (Fransson, 2005; Kahan et al., 2014), in addition to the afore-
mentioned nuisance regressors. Data were high-pass ﬁltered to remove any slow frequency
drifts (< 0.0078 Hz) in the normal manner. An F contrast was speciﬁed across the discrete cosine transformation, producing an SPM that identiﬁed regions exhibiting BOLD ﬂuctuations within the modeled frequencies of interest. We used the 36 regions of interest (ROI) with coordinates from Raichle (2011) representing seven resting-state networks: default mode network, dorsal attention network, executive con- trol network, salience network, sensorimotor system, and visual and auditory networks. The principal eigenvariate from a (8 mm radius) sphere centered on the peak F value from each region was computed for each region and adjusted for confounds. Table 1 gives the ROI names and their respective MNI coordinates. DCM Speciﬁcation, Inversion, and Reduction We proceeded to specify a fully connected 36-node DCM, without exogenous inputs, for each of the 22 participants separately. We inverted these speciﬁed DCMs using both stochastic and spectral DCM. For 3 participants stochastic DCM failed to converge after 128 iterations, so we discarded those participants from subsequent analysis, yielding a set of 38 inverted DCMs altogether (i.e., 2 DCM schemes × 19 subjects). In terms of computational time, a graph with 36 nodes takes about 200 min per iteration for stochastic DCM and around 20 min per iteration for spectral DCM with convergence achieved within 64–128 iterations. This means that spectral DCM is considerably more efﬁcient than stochastic DCM (around 10 times faster). It is also more robust as it successfully inverted all models, whereas stochastic DCM failed to invert 3 DCMs (see above). We then used Bayesian model reduction (Seghier & Friston, 2013) to optimize the num- ber of prior modes in the DCMs, based on the modes (i.e., eigenvectors) of the functional Network Neuroscience 227 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Large-scale spectral DCMs Table 1. This table shows the 36 ROIs (names and MNI coordinates) that we adopted from Raichle (2011). The selected 36 regions belong to seven large-scale networks. Region name Posterior cingulate/Precuneus Medial Prefrontal Left lateral parietal Right lateral parietal Left inferior temporal Right inferior temporal Medial dorsal thalamus Left posterior cerebellum Right posterior cerebellum Default mode network 1 2 3 4 5 6 7 8 9 Dorsal attention network Left frontal eye ﬁeld 10 Right frontal eye ﬁeld 11 Left posterior IPS 12 Right posterior IPS 13 Left anterior IPS 14 Right anterior IPS 15 Left MT 16 Right MT 17 Control executive network 18 Dorsal medial PFC 19 20 21 22 Left anterior PFC Right anterior PFC Left superior parietal Right superior parietal Region name Salience network 23 Dorsal anterior cingulate Left anterior PFC 24 Right anterior PFC 25 Left insula 26 Right insula 27 Left lateral parietal 28 29 Right lateral parietal Sensorimotor network Left motor cortex 30 Right motor cortex 31 32 Supplementary motor area Visual network 33 34 Auditory network Left A1 35 Right A1 36 Left V1 Right V1 Coordinates (in mm) 0 21 36 -35 45 30 32 45 30 -41 3 6 41 3 6 -62 -45 30 62 -45 30 -39 -26 51 38 -26 48 0 -21 48 -7 83 2 7 83 2 -62 -30 12 59 -27 15 Coordinates (in mm) 0 -52 7 -1 54 27 -46 -66 30 49 -63 33 -61 -24 -9 58 -24 -9 0 -12 9 -25 -81 -33 25 -81 -33 -29 -9 54 29 -9 54 -26 -66 48 26 -66 48 -44 -39 45 41 -39 45 -50 -66 -6 53 -63 -6 0 24 46 -44 45 0 44 45 0 -50 -51 45 50 -51 45 Free energy: A lower bound on model evidence typically used for model selection; higher free energy indicates better ﬁt of data. connectivity matrix as described above. Bayesian model reduction enables the experimenter to analytically derive the free energy(as a proxy for log-model evidence) and parameters for in- verted DCM with modiﬁed prior covariance matrices. We therefore inverted a fully connected DCM (using spectral and stochastic schemes) for each subject, without any constraints on the prior covariance matrix. We then used Bayesian model reduction to calculate the free energy for variants of the DCM with a different number of prior modes. This means that the constraints on the prior covariance are data driven (see deﬁnition of Km and Σm above) and varied from subject to subject. In routine analyses, we envisage that the initial (fully connected) inversion would start with a relatively small number of modes (e.g., m = 10: see below), which reduces computation time considerably. 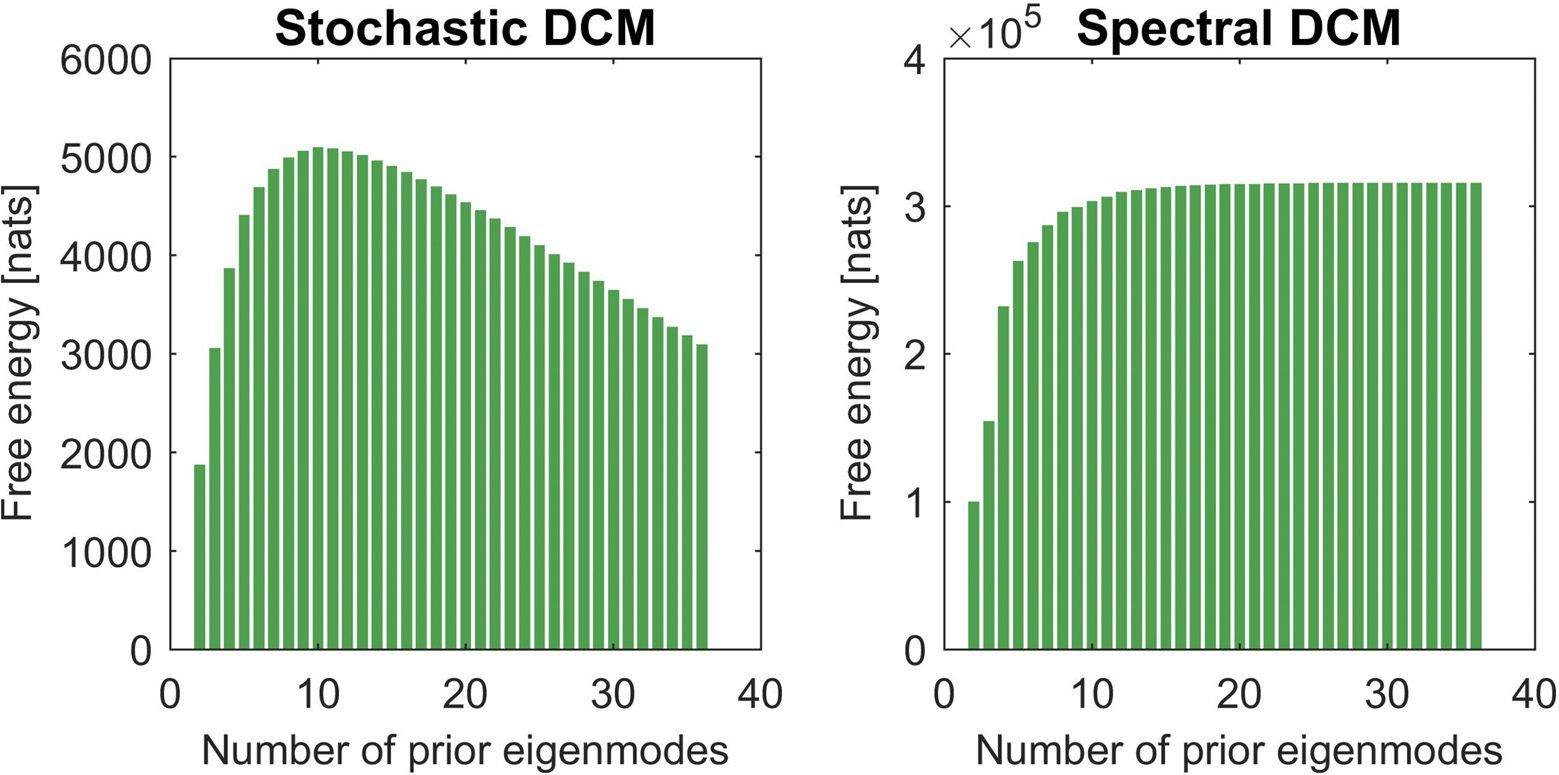RESULTS Effective connectivity was computed using both inversion schemes; namely, stochastic and spectral DCM. Figure 1 (left panel) shows the average free energy (log evidence), in nats, over 19 participants over the number of modes m relative to the free energy at m = 1 using stochastic DCM. The plot shows that free energy ﬁrst increases and then systematically decreases with increasing number of modes (peak at m = 10). The right panel shows results when the inver- sion was performed using spectral DCM. We again see a similar trend, but this time the free energy reached a plateau at around m = 10 modes. Thus, in contrast to stochastic DCM, the uncertainty about the exact number of modes is not a critical issue for spectral DCM, because any intermediate number of modes (within the plateau in Figure 1) would yield the same (high) In summary, this analysis shows that by replacing connections between model evidence. Network Neuroscience 228 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Large-scale spectral DCMs Figure 1. This ﬁgure shows the plots of the averaged free energy over participants as we increase the number of prior eigenmodes m. The left panel shows the proﬁle of free energy (as a proxy for log-model evidence) for stochastic DCM. One can see that free energy ﬁrst increases with a peak at m = 10 and then decreases. Using 36 modes (equal to the number of nodes) means that there are effectively no prior constraints. In the right panel, we show a similar plot for spectral DCM. We now see that the free energy plateaus at around m = 10. many nodes with connections between a small number of modes (here m = 10), effective connectivity of large graphical models can be optimally estimated with both spectral and stochastic DCM. 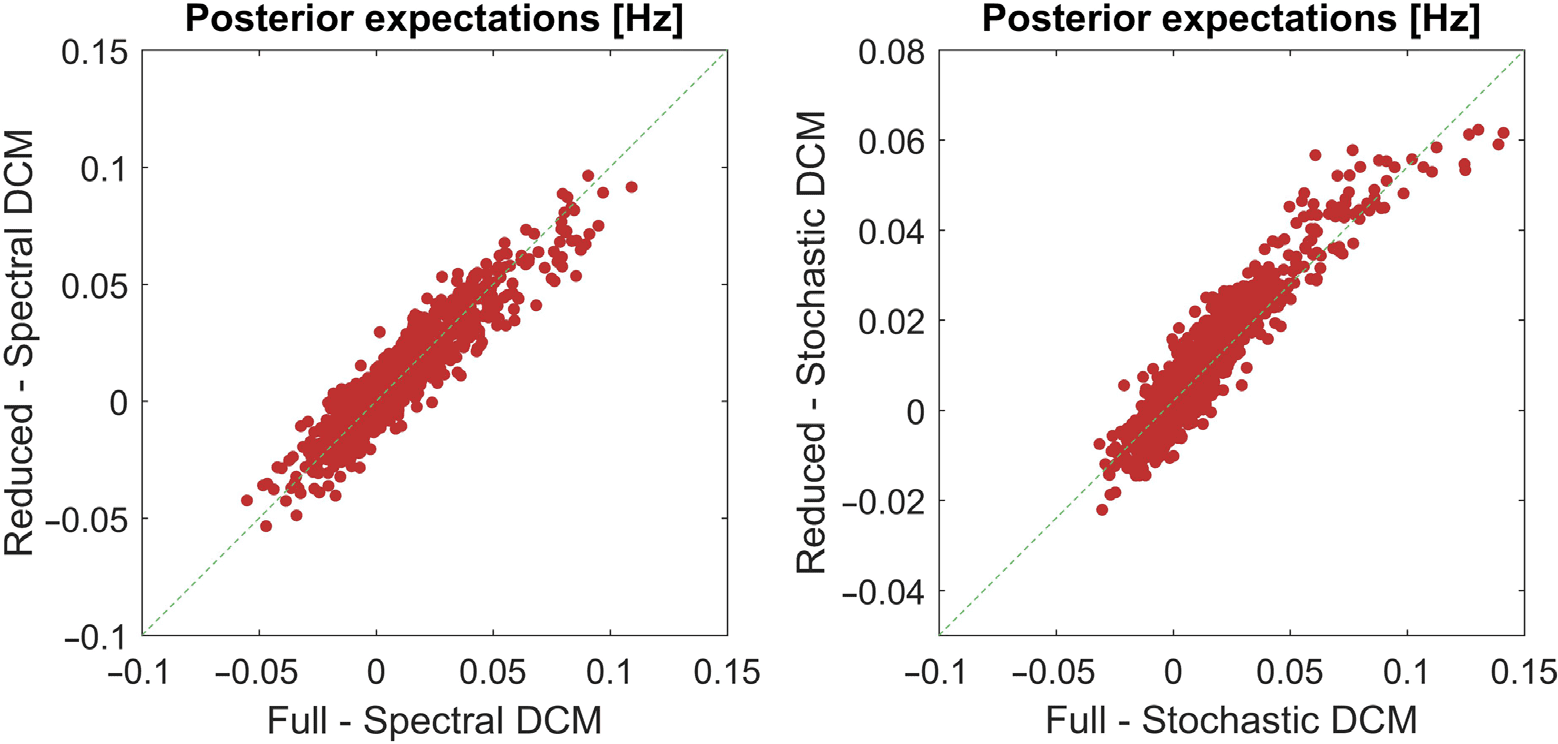Figure 2 presents regression plots that compare the posterior estimates (i.e., expectations of effective connectivity parameters) from the two inversion schemes. The left panel shows the parameter estimates, averaged over participants, from the two inversion schemes when all modes were used; that is, no post hoc model reduction is employed and the number of modes was equal to the number of nodes (m = n = 36). Here, we see the parameter estimates from the two schemes are highly correlated (rho = 0.67). The right panel shows the regression plot when we used the optimal number of modes for each subject for both inversion schemes (m = 10). The two inversion schemes still return highly correlated parameters (rho = 0.65). 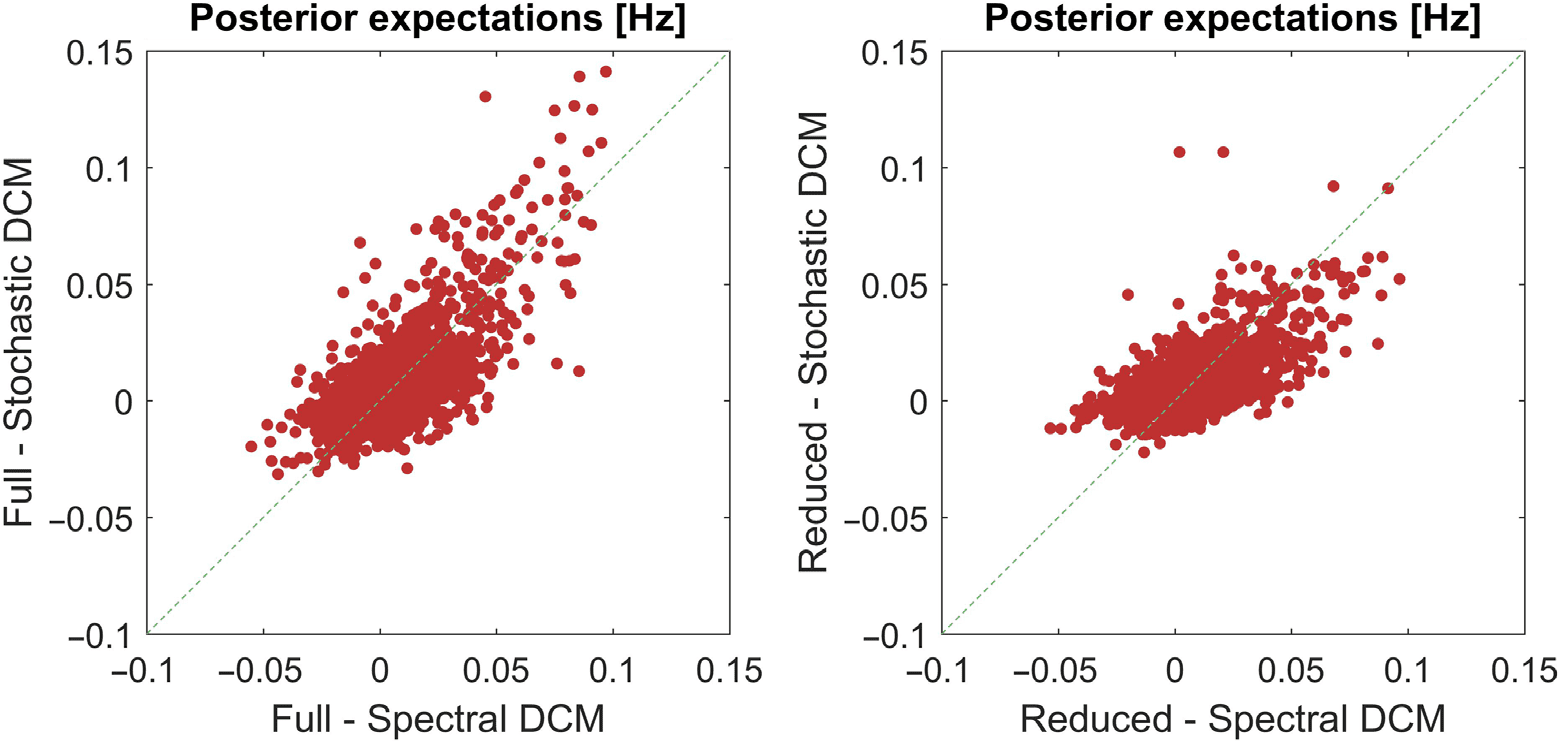In Figure 3 we again show the regression plots, but this time we were interested in compar- ing the validity of parameter estimates for each scheme separately. The left panel shows the spectral DCM results, when we plot the parameter estimates, averaged over participants, when no reduction was performed against the parameter estimates when using the optimal number of modes for each subject. This reveals a very high conformance between the parameter esti- mates (rho = 0.93). The right panel shows the equivalent plot for stochastic DCM. We again see highly correlated parameter estimates (rho = 0.94). 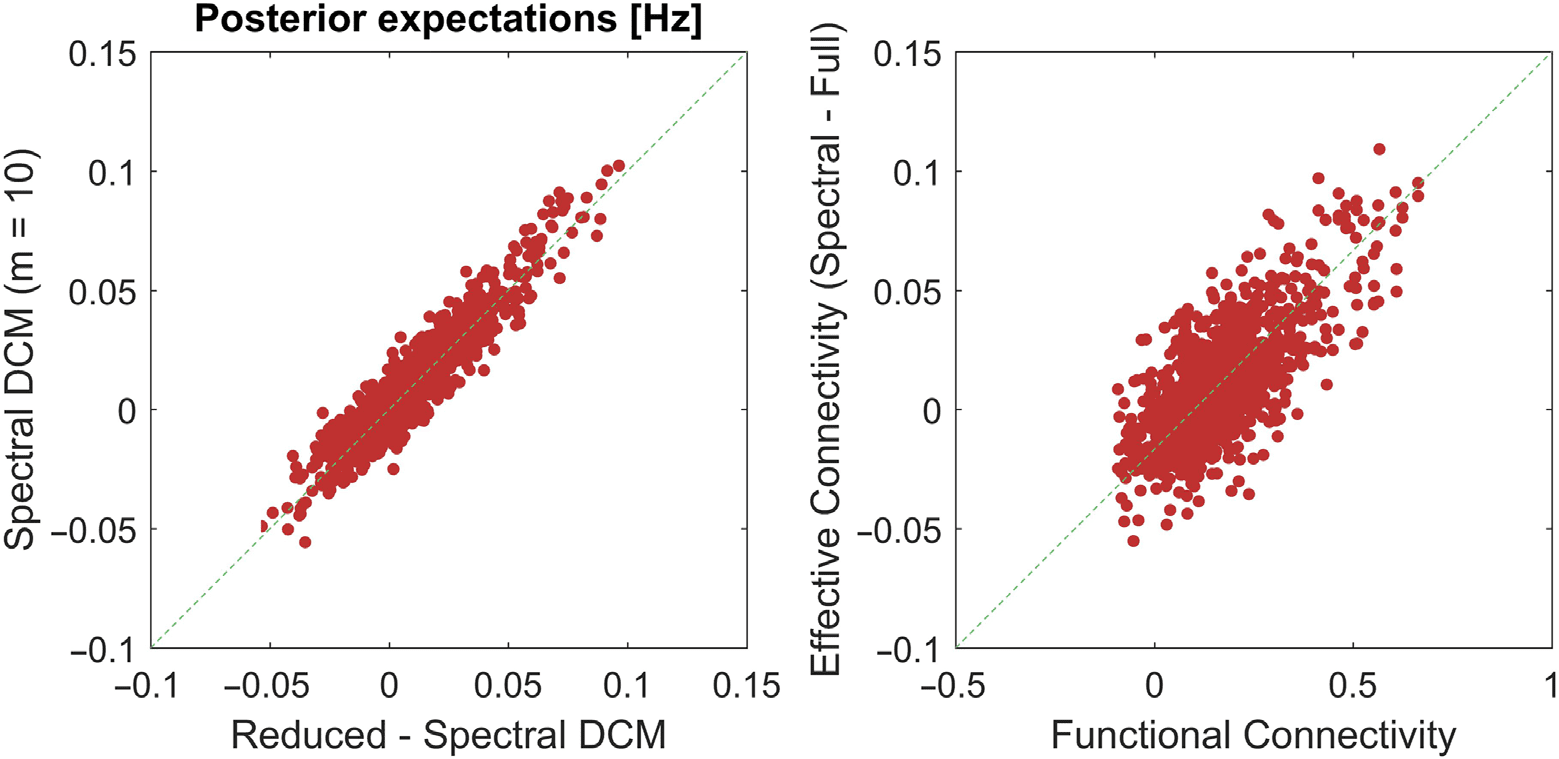Figure 4 uses the same format but this time only for the spectral DCM (left panel). Here, we were interested in the consistency of parameter estimates when ﬁxing m to 10 modes for all subjects, against using the optimal number of modes for each subject. Pleasingly, we see that there was very high correlation between the parameter estimates (rho = 0.94). For completeness, we also plot (on the right panel) the high conformance between effective (using spectral DCM) and functional connectivity (rho = 0.70), which is not surprising as the effective connectivity are the causes that engender the observations or the functional connectivity. The Network Neuroscience 229 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Large-scale spectral DCMs Figure 2. This ﬁgure uses regression plots to illustrate the correspondence between the averaged parameter estimates over participants from two (stochastic and spectral) inversion schemes. The left panel shows the relationship in the absence of any prior constraint. We see that the parameter estimates are highly correlated (rho = 0.67). The plot on the right shows the equivalent results when we used an optimal number of prior modes, in terms of those that maximizes the free energy, for each subject and then averaged the parameter estimates over participants. We again see that there is high correlation between the parameter estimates of the two inversion schemes (rho = 0.65). We excluded the self-connections (diagonal entries) when doing this analysis as they are scaled parameters. results shown in Figures 3 and 4 demonstrate the construct validity of stochastic and spectral DCM. Furthermore, they show that the functional connectivity priors have empirical validity. This is because their application increases model evidence—and that the number of linear prior constraints (functional connectivity modes) is roughly the same for spectral and stochastic l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 3. This ﬁgure shows the regressions comparing the parameter estimates for each inversion scheme separately. On the left, we compare the averaged parameter estimate from spectral DCM when we used no prior constraint (full) and when we used an optimal number of modes, selected on the basis of free energy, for each subject (reduced). We see that the parameter estimates are highly correlated (rho = 0.93). The right-hand plot shows the parameter estimates for stochastic DCM, which also evidence high correlations (rho = 0.94). Network Neuroscience 230 Large-scale spectral DCMs Figure 4. This ﬁgure shows the regression of parameter estimates from spectral DCM (left panel) and the high conformance between functional and effective connectivity (spectral DCM with all modes). The plot in the left panel illustrates the validity of parameter estimates when we used m = 10 modes for every participant, relative to using an optimal number of modes for each subject. We again see a high correlation between the estimated connectivity parameters (rho = 0.94). The right panel plots functional connectivity against effective connectivity, which unsurprisingly showed a strong correlation (rho = 0.70). models. Finally, the underlying posterior estimates of effective connectivity do not depend sensitively on the number of prior constraints. In the next analyses, we used Bayesian model reduction to examine the contribution of individual connections to model evidence, as op- posed to modes or patterns of connections illustrated above. This application of Bayesian model reduction to individual connections aims to discover the structure of the optimal sparse graph. 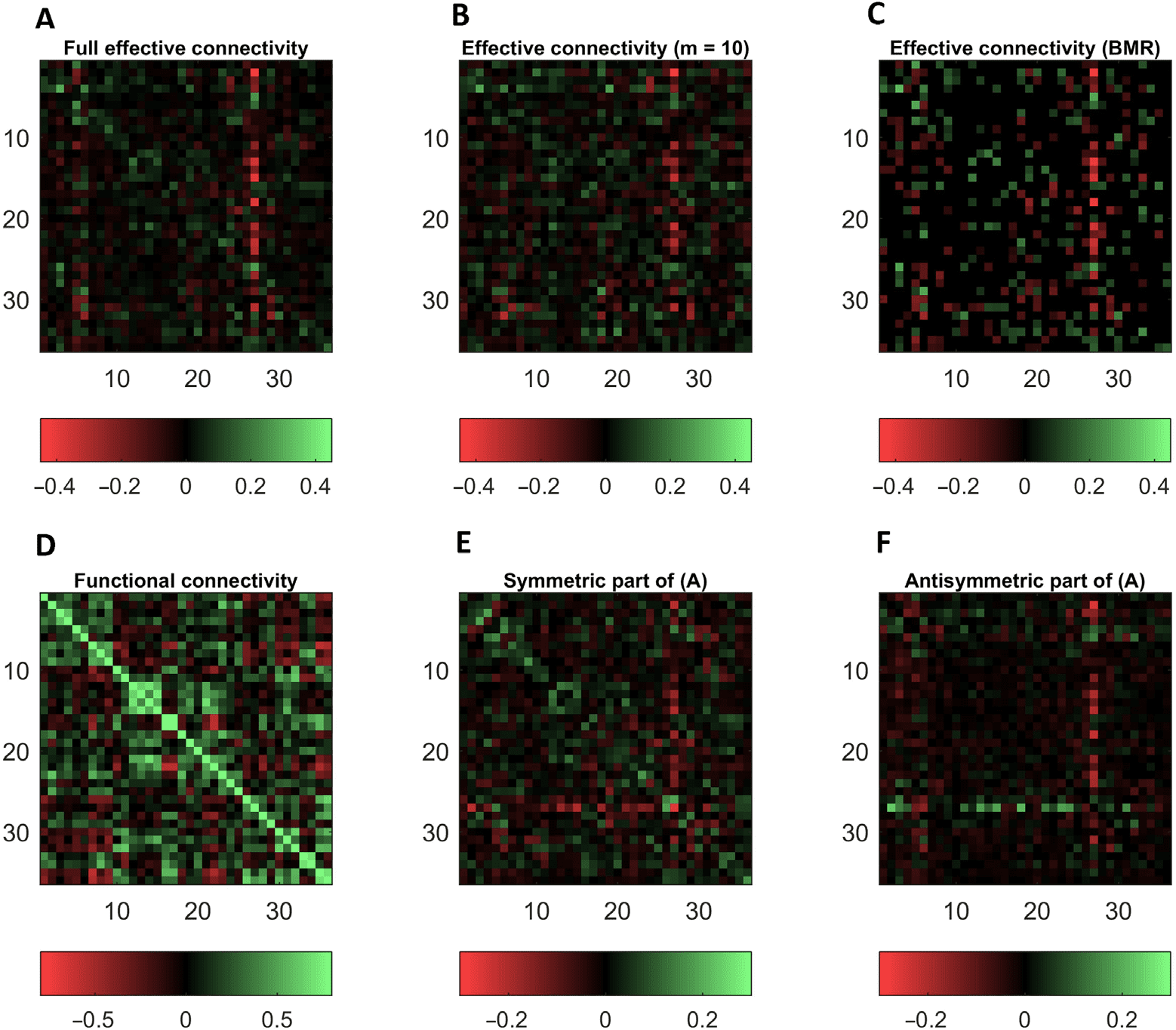Figure 5 (A, upper left panel) shows the posterior expectations, for a typical subject, after Bayesian model reduction (Friston, Li, Daunizeau, & Stephan, 2011; Friston et al., 2016) was applied to each connection in turn. We used two-tone color map throughout with excita- tory connections shown as green (go) and inhibitory as red (stop). This involves comparing models with and without each connection in terms of their (reduced) free energies or model evidence. Bayesian model reduction eliminates redundant connections (shown as (dark) black on panel C), when the evidence for the sparser model exceeds that of the model that retains each connection. This represents a principled way of thresholding or eliminating connections that are not necessary to explain the fMRI data. Heuristically, redundant connections are pa- rameters whose complexity cost exceeds the increase in accuracy or goodness of ﬁt (noting that model evidence is equal to accuracy minus complexity). Figure 5 also shows the effect of Bayesian model reduction at the level of functional connectivity priors (upper middle panel) and at the level of individual connections (upper right panel). Crucially, the resulting extrinsic connectivity (adjacency) matrix is very sparse compared with the fully connected architecture that constitutes the parent model. The lower panels in Figure 5 show different characterizations of connectivity. The left panel (D) shows the functional connectivity matrix associated with (or generated by) the (reduced) effective connectivity on the upper right. Note the sparse nature of effective connectivity, in relation to functional connectivity (when comparing the lower left and middle panels). Network Neuroscience 231 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Large-scale spectral DCMs l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 5. This ﬁgure illustrates the sparse structure of effective connectivity after applying Bayesian model reduction to eliminate redundant connections. Top row: These three effective connectivity matrices correspond to the full or parent estimate for this particular subject (A), the equivalent ma- trix following Bayesian model reduction with 10 prior modes (B), and, ﬁnally (on the right) after eliminating redundant connections (shown in dark black, which are the majority of the connec- tions here) with Bayesian model reduction (C). Lower row: These show different characterizations of symmetric and asymmetric connectivity. The left panel (D) shows the functional connectivity matrix associated with (or generated by) the (reduced) effective connectivity on the upper right. The effective connectivity has been separated into symmetric (E) and antisymmetric components (F), in the lower middle and right panels respectively. Note the sparse nature of effective connectivity, in relation to functional connectivity (when comparing the lower left and middle panels). This differ- ence illustrates the general phenomena that functional connections can be mediated vicariously via indirect effective connections. This difference illustrates the general phenomena that functional connections can be mediated vicariously via indirect effective connections. The remaining panels in Figure 5 highlight the asymmetry of effective connectivity by showing the symmetric part (E, lower middle panel) and antisymmetric part (F, lower right panel). These are obtained simply by transposing the adjacency matrices and taking the sum and difference respectively (see discussion for the importance of this decomposition). In summary, this application of Bayesian model reduction (BMR) ﬁnds the best model struc- ture by removing the edges from the large (parent) graph by comparing models with and with- out each connection. The resulting BMR is particularly useful for large graphs and serves to prune connections and reveal any underlying sparsity. 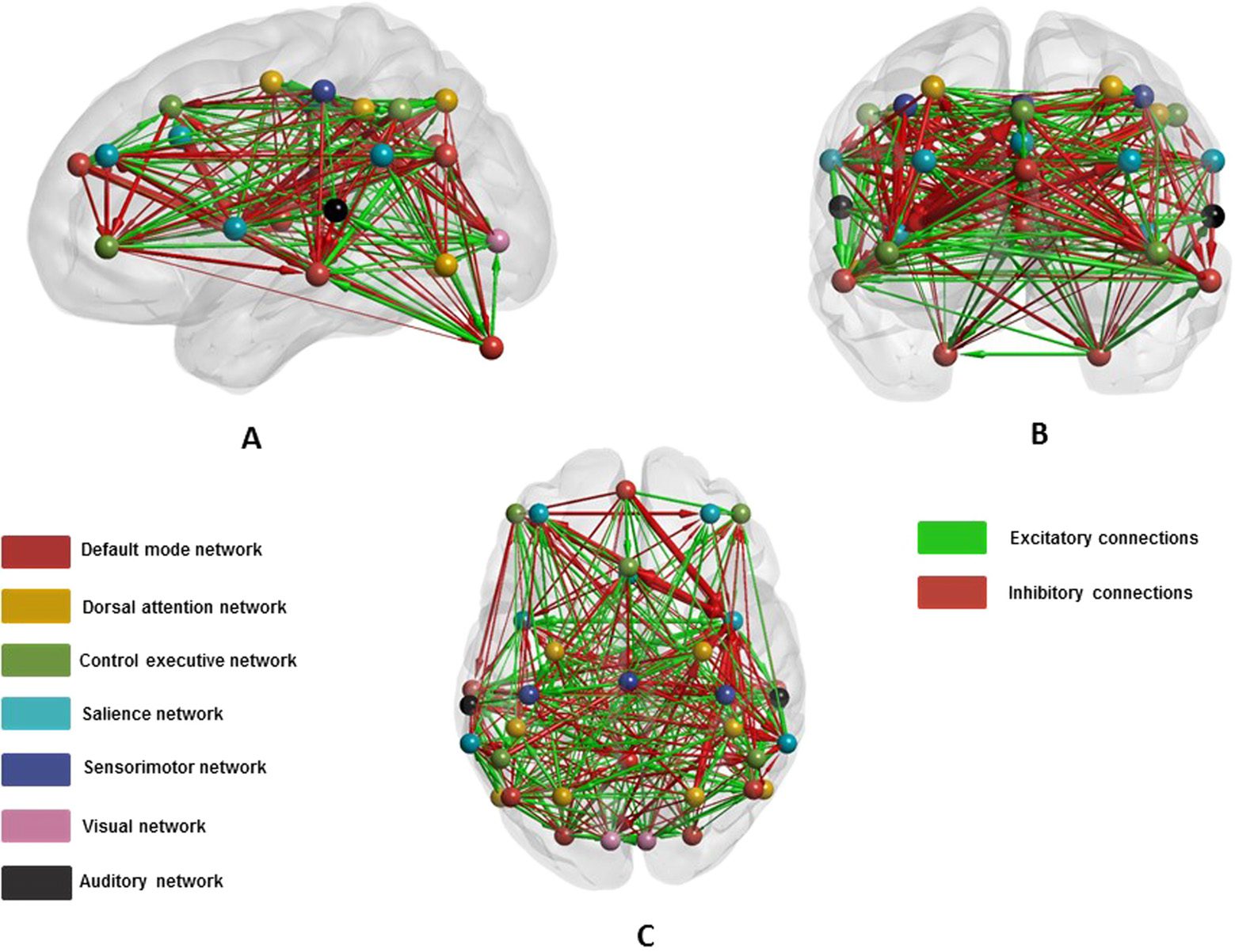This BMR form of model selection offers Network Neuroscience 232 Large-scale spectral DCMs a principled alternative to the arbitrary thresholding strategies common in the graph theoretic literature. Figure 6 shows one such subject’s (the same subject as in Figure 5) graph. Note that the edges on this graphic are directed and signed, where green arrows denote excitatory (positive) connections and red arrows are inhibitory (negative) connections. The width of each connection represents coupling strength (in hertz). We have suppressed self or recurrent con- nections, which are—by construction—inhibitory in DCM (to model intrinsic inhibition that precludes runaway excitation). 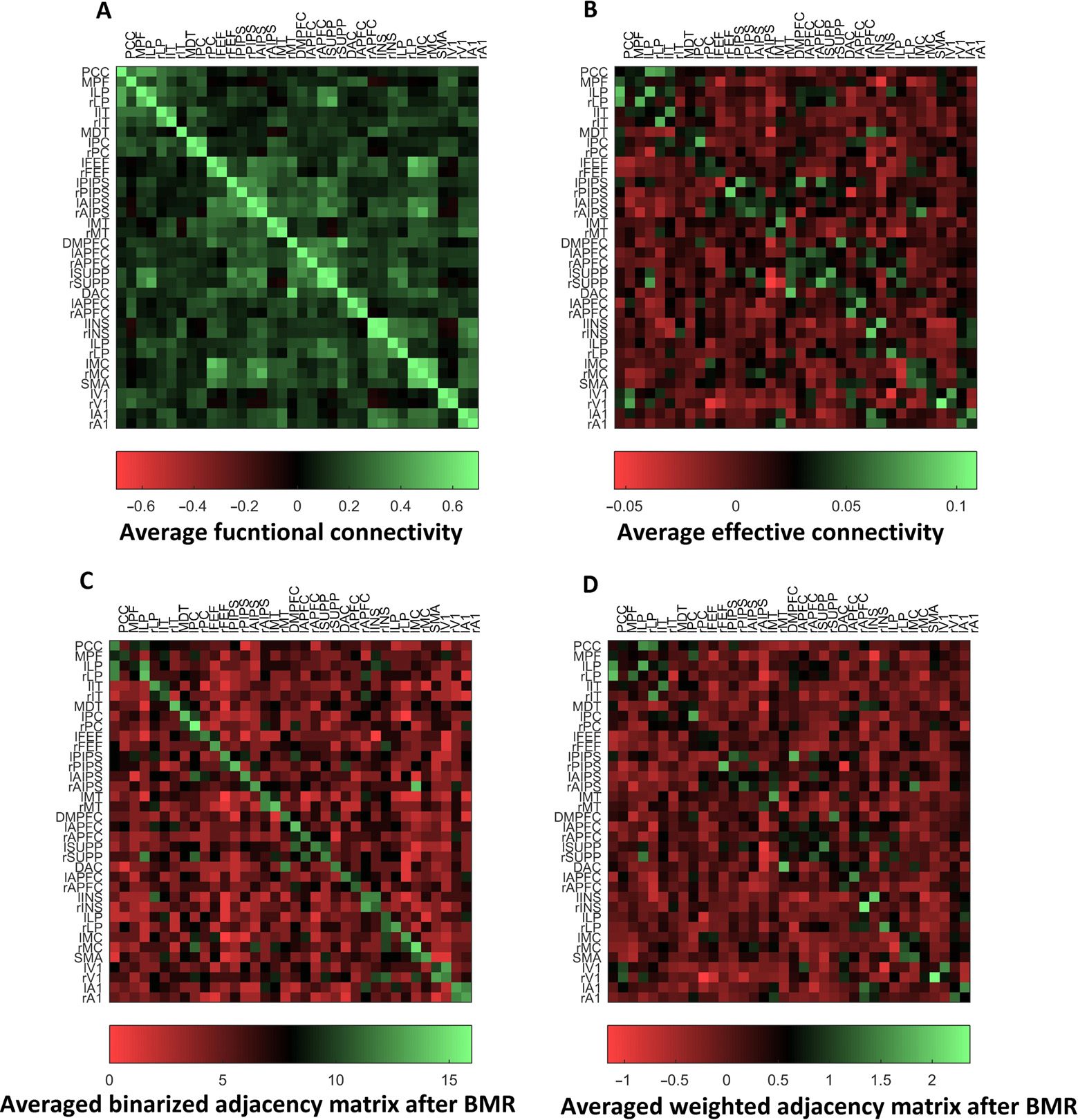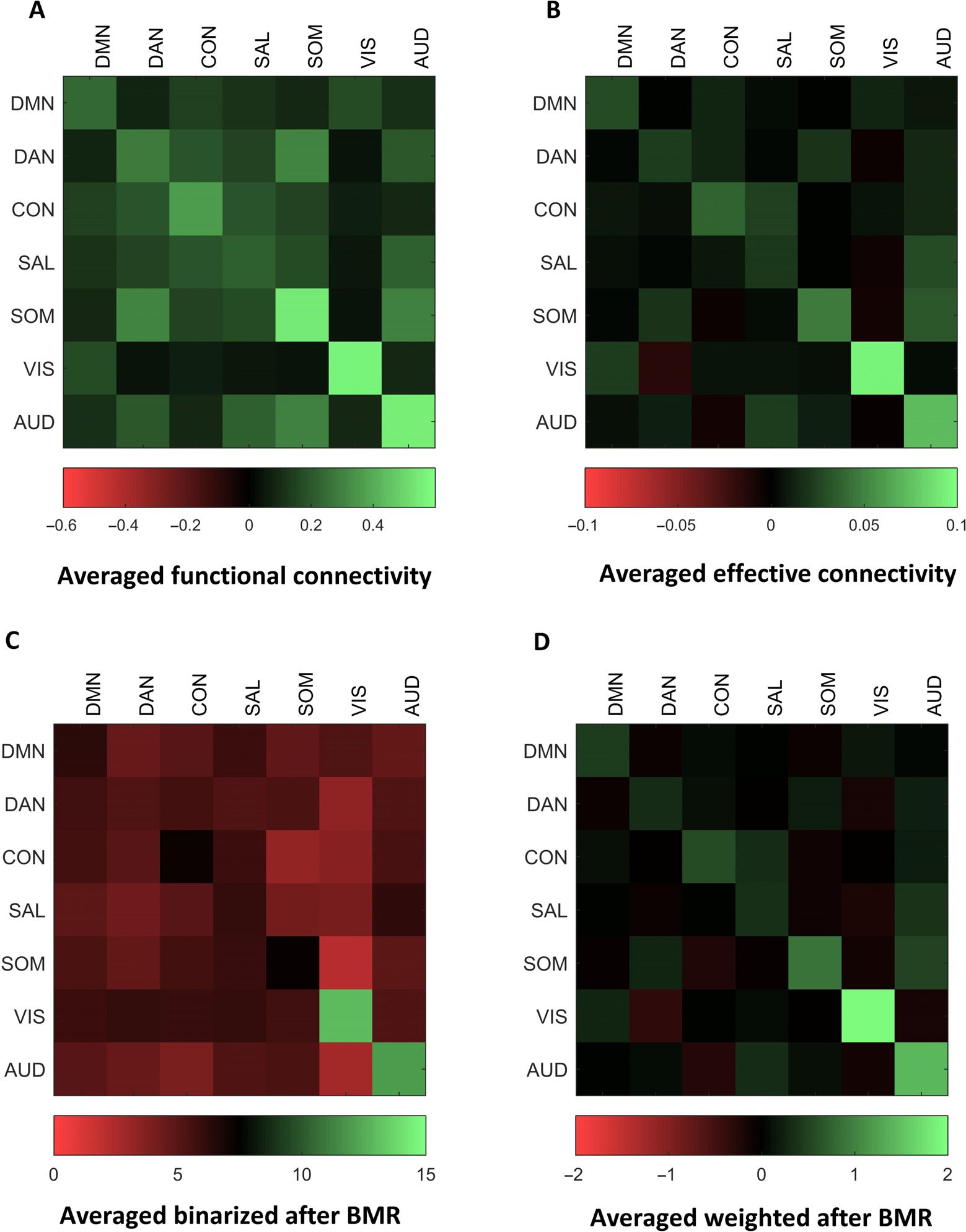Figure 7 shows the averaged functional (A) and effective connectivity (B) over subjects. The diagonal terms in the effective connectivity matrix show self-connections that are mod- eled as inhibitory connections. It is interesting to compare the functional connectivity with that reported in Raichle (2011) for a single subject (but for a much longer time series of around 30 min). Different modes or networks are relatively easy to identify visually as they are grouped in terms of functional connectivity. This structure is less obvious with effective connectivity, which is asymmetric. Note that functional connectivity is based on sampled time series and is therefore confounded by the observation (or thermal) noise. We have also plotted aver- aged effective connectivity after removing redundant connections with Bayesian model reduc- tion and binarizing the effective connectivity (i.e., setting the adjacency matrix to one if the l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 6. This ﬁgure shows the 36 ROIs (Raichle, 2011) that form seven large-scale brain modes or intrinsic networks. The graphics show a typical participants (same as in Figure 5) inverted graph after applying Bayesian model reduction to connections. The brain regions, represented as balls, are color-coded for various networks. The edges or connections are shown by directed arrows where the width of the arrows reﬂects the strength of the coupling. The color of the arrows represents the excitatory (green) and inhibitory (red) coupling among neuronal populations. We show the brain in sagittal (A), coronal (B), and axial (C) views. Network Neuroscience 233 Large-scale spectral DCMs l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 7. This ﬁgure shows the averaged functional (A) and effective connectivity (B) over 19 subjects. The diagonal for the functional connectivity represents the correlation of each region with itself. The correlations within each network are quite distinctive, and the relationship between networks is visually evident. We see similar patterns in the effective connectivity matrix but there are clear asymmetries in the connectivity. We have also shown averaged effective connectivity matrix after Bayesian reduction and binarization (C) and when the weights are retained (D). connection exists for each subject) (C); the ensuing average reﬂects the number of times a connection is evident over subjects. Finally, we present the associated (averaged effective connectivity) matrix after Bayesian model reduction (D) for comparison with (B). To illustrate how different brain networks or modes are functionally integrated, Figure 8 shows the connectivity matrices from Figure 7 but after down-sampling to connect the con- stituent modes. This down-sampling entails averaging effective connectivity strengths among the sets of regions that constitute each node. It is interesting to note that the functional connec- tivity, as plotted in (A), between modes is exclusively positive whereas there are both excitatory (positive) and inhibitory (negative) inﬂuences among different modes in the effective connec- tivity matrix (B). These are even more pronounced in the averaged connectivity matrix after Bayesian model reduction (D). Network Neuroscience 234 Large-scale spectral DCMs l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 8. This ﬁgure is in the same format as Figure 7. The graphics show the averaged functional (A) and effective connectivity (B) over 19 subjects after down-sampling the 36 ROIs to the seven networks or modes. For the seven modes, we have also plotted averaged effective connectivity matrix after Bayesian reduction and binarization (C) and when the weights are retained (D). In our ﬁnal analysis, we looked more closely at asymmetric nature of the effective con- nectivity afforded by the spectral DCM. These asymmetries are fundamental to characterize the organization of the cortex—in terms of hierarchies or lateralization—that cannot be dis- closed with undirected measures of connectivity. 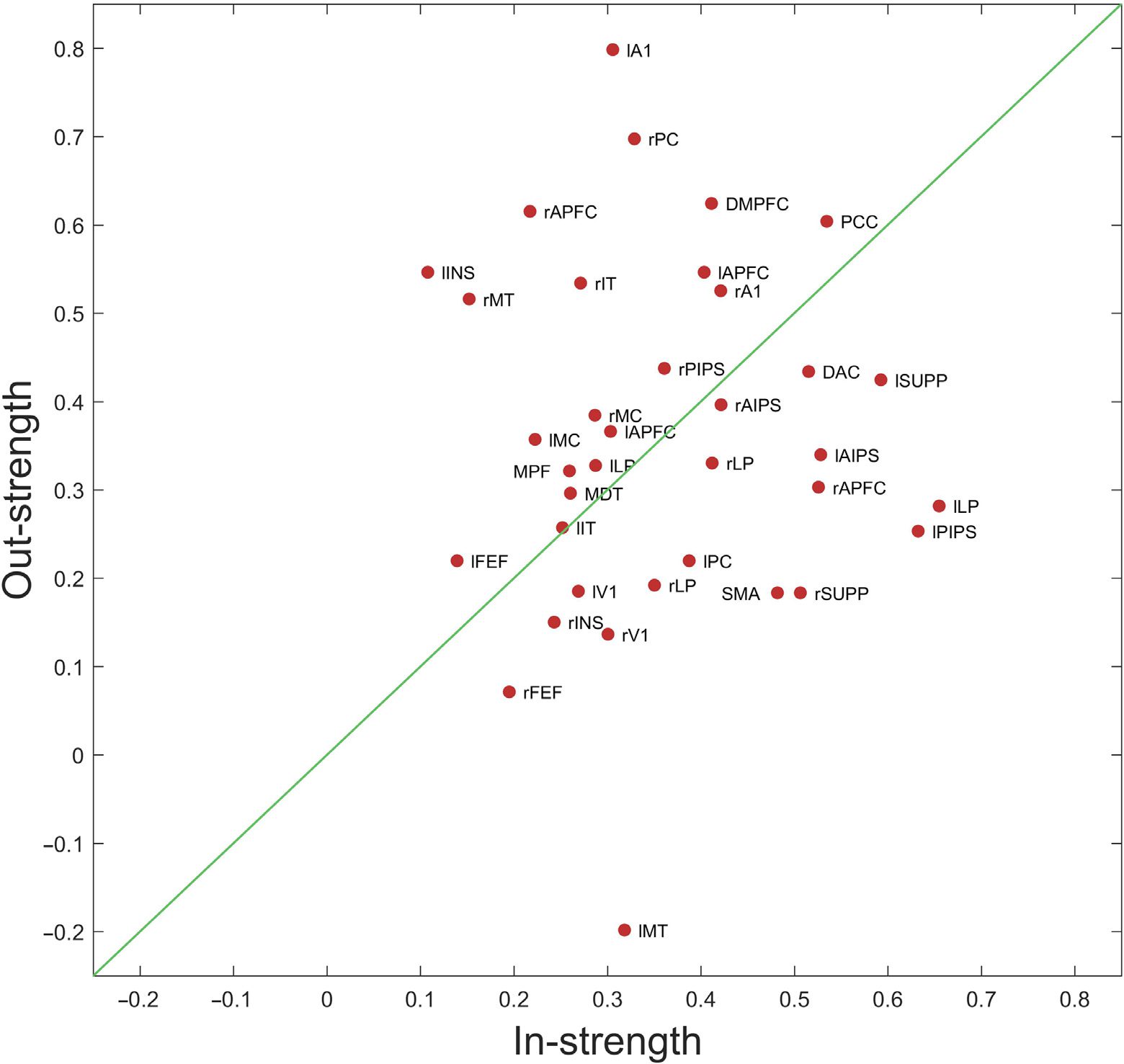As an example, we examine the hemispheric asymmetries in Figure 9, which shows these asymmetries as scatter plot using the averaged effective connectivity matrix from Figure 7B. The scatter plot shows the nodal in-strength versus out-strength such that the regions that lie above the line are net senders or sources, Network Neuroscience 235 Large-scale spectral DCMs l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 9. This ﬁgure shows the hemispheric asymmetries as a scatter plot, using the averaged effective connectivity estimates as shown in Figure 7B. We used nodal in-strengths and out-strengths to identify these asymmetries. The in-strength summarizes the sum of all weighted connections entering the node, while the out-strength is the sum of all the weighted connections going out from a particular node. On the scatter plot, regions that lie above the diagonal line are net senders or sources, whereas regions that lie below the diagonal line are the net receivers or sinks. that is, they have greater out than in-strength, whereas the regions that are below the diago- nal line are the net receivers or sinks. 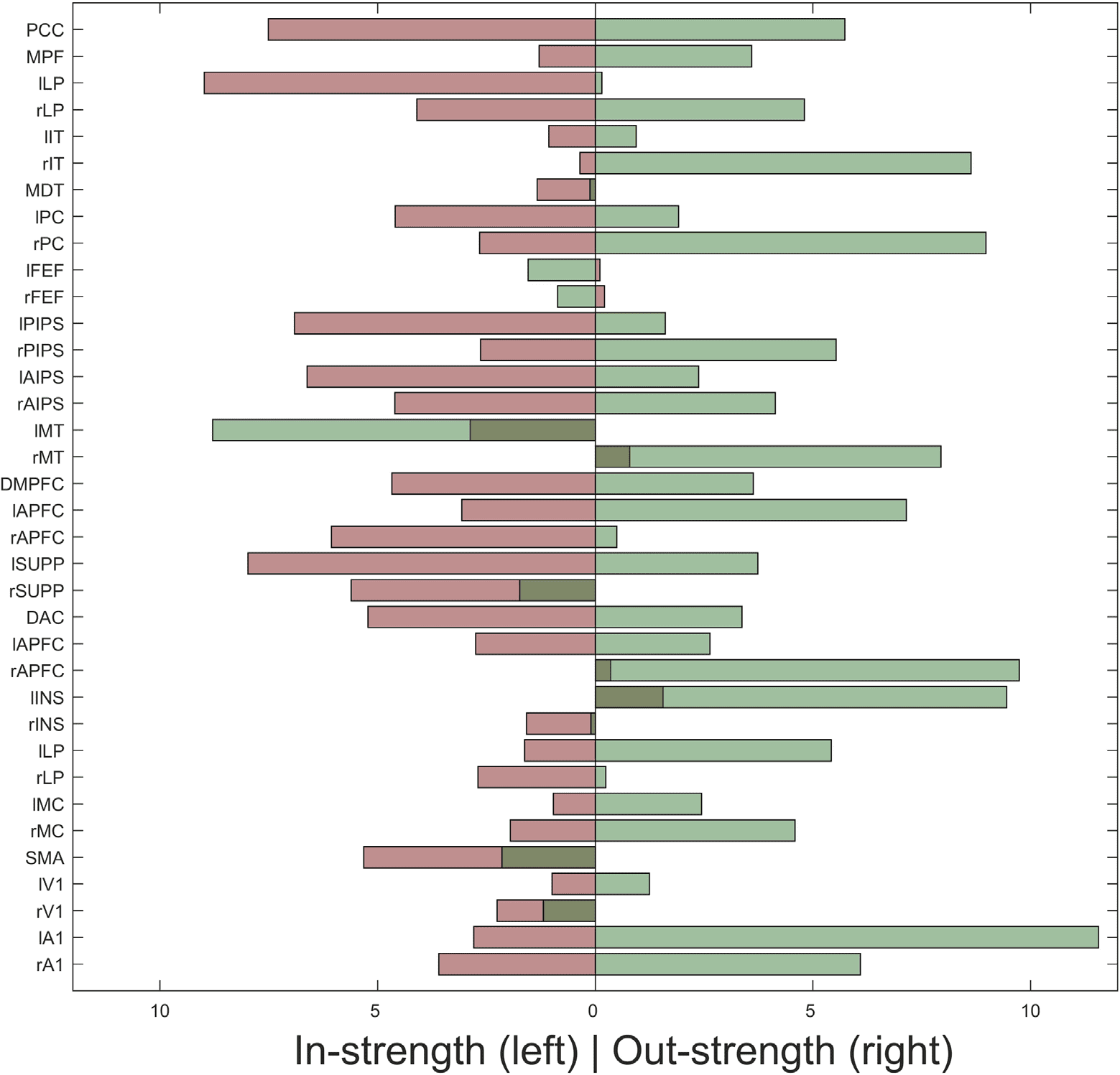There are very notable hemispheric asymmetries; for example, notice the difference between left and right fontal eye ﬁeld (FEF) or left and right insula (INS). The hemispheric asymmetries are even clearer when we used the averaged effec- tive connectivity matrix in Figure 10, after Bayesian model reduction, as shown in Figure 7D, using a bar plot. The bar plot shows the nodal in-strength (light red bars) and out-strength (light green bars). There are notable hemispheric asymmetries: for example, the difference between left and right lateral parietal lobules or left and right insula (INS). These are interesting obser- vations attesting the utility of spectral DCM for characterizing large-scale brain networks at a level not accessible previously. It is important to remember that these results are based upon one dataset and are just used to illustrate the sorts of analyses that can be performed. DISCUSSION In this paper, we have described a framework for estimating effective connectivity from fMRI data collected at rest. Our framework builds upon three recent developments: (a) a robust Network Neuroscience 236 Large-scale spectral DCMs l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 10. This ﬁgure shows the hemispheric asymmetries as a bar plot based on the effective connectivity estimates after Bayesian model reduction as shown in Figure 7D. The nodal in-strength and out-strength are calculated as in Figure 9. and fast inversion scheme called spectral DCM (Friston, Kahan, Biswal, et al., 2014), (b) an in- formed data-driven procedure to reduce the effective number of parameters in large DCMs (Seghier & Friston, 2013), and (c) a principled network discovery procedure that produces sparse graphs using Bayesian model reduction (Friston et al., 2016). We have demonstrated the construct validity of this framework using empirical fMRI data with large DCMs (36-node graphs). Speciﬁcally, we have shown that one can use spectral DCM to infer large-scale networks describing whole-brain connectivity efﬁciently from resting-state fMRI. We have demonstrated that the connectivity estimates from two (stochastic and spectral) inversion schemes for resting- state fMRI are internally consistent, in terms of high correlations, when averaged over par- ticipants. However, spectral DCM is computationally much more efﬁcient (approximately 10 times faster in this study) by virtue of using a deterministic generative model of spec- tral data, obtained after transformation of time series to the spectral domain (Friston, Kahan, Biswal, et al., 2014). This spectral formulation eludes the computational burden of estimating hidden states per se, hence speeding up model inversion. It is noteworthy that the inversion of spectral DCM is even faster than conventional deterministic DCM, since it does not require the integration of differential equations. Network Neuroscience 237 Large-scale spectral DCMs In principle, there are no limits on the size of the graph, given sufﬁcient memory and com- putational power. However, there are practical limitations: inverting a large model with many parameters can entail slow convergence—taking around 64 to 128 iterations—where each iteration takes longer as the graph size increases. The bottleneck here becomes memory size, which may require use of high-performance computing facilities (that are available at some institutions). Practically speaking, we have inverted graphs as large as 64 nodes. One can invert larger graphs; for example, by splitting the graphs into two (e.g., for each hemisphere). One can then use the posterior estimates of subgraphs as the initial values for inverting a full graph, that then converge more quickly. There are several advantages such large graphs bring to the table. First, they are inherently directed. Here, causality is deﬁned in control theoretic terms. In other words, causality is em- bedded in the generative model via differential equations that model interactions and evolution of latent neural states that cause the measured BOLD responses. This is in contrast to directed measures of functional connectivity; for example, Granger causal modeling that is based on temporal precedence (Friston, Moran, & Seth, 2013; Razi & Friston, 2016). Second, the edges or connections of these graphs are weighted, representing the coupling strengths between regions. Third, they are signed, where the positive and negative edges model excitatory and inhibitory inﬂuences on neuronal populations. The potential asymmetry between reciprocal connections is of fundamental importance for brain connectivity. For example, neurobiological formulations of cortical hierarchies in terms of feedforward (usually excitatory) and feedback (usually inhibitory) connections rest on asymmetric directed connectivity. Finally, the diagonal entries on the adjacency matrix are also weighted, representing the self-connections or activity within region that is modeled as self or recurrent inhibition. The proposed framework can be usefully employed to address some of the methodolog- ical challenges faced by the (functional) connectomics. We note one of the limitations of graphs based on functional (and structural) connectivity; while some techniques use the full connectivity matrix, such as for community detection (Rubinov & Sporns, 2011), most extant network studies have employed thresholding to remove spurious connections and to sup- press negative correlations in functional networks (hence functional connectomes are usually unsigned). There are several ways to threshold (i.e., absolute, proportional, or based on group thresholding methods) and little consensus on the best way to threshold (Qi, Meesters, Nicolay, Romeny & Ossenblok, 2013; Simpson et al., 2013). Furthermore, thresholding removes many (functional connectivity) data features. This is potentially important because the metrics calcu- lated from the ensuing sparse graphs are sensitive to the amount and the method of threshold- ing (usually requiring the computation of graph theoretic descriptors over several thresholding levels). The Bayesian framework used by DCM allows for an informed and graceful way of per- forming “network inference” via Bayesian model reduction to select or threshold out redundant edges (Friston et al., 2016). This model reduction procedure, now in wide use, allows one to infer the best model that is nested within the parent or fully connected model. In summary, Bayesian model reduction can be used to disclose the underlying sparsity by comparing the evidence for models with and without particular connections, and thus enables a principled way to perform graph-based functional network analysis. Another interesting issue in this ﬁeld is the availability of tools to analyze directed graphs. Although there has been a huge interest and increasing sophistication in the use of graph theoretic summary measures (for example clustering coefﬁcient, path length, efﬁciency, and modularity), most of the existing literature (at least within human neuroimaging) is based on undirected and unsigned anatomical and functional connectivity. However, as empirical work Network Neuroscience 238 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Large-scale spectral DCMs Spectral graph theory: A study of the relationship between a graph and the eigenvalues and eigenvectors of its Laplacian matrix. Graph Laplacian: A matrix representation of graph that combines node adjacency and node degree in mathematical formulation and belongs to spectral graph theory. in animal models amply demonstrates, anatomical neural projections and their physiological interactions are fundamentally directed and weighted, rendering binary and undirected graphs relatively poor approximations. One interesting aspect of directed graphs or adjacency matri- ces is that they cannot be embedded in metric spaces. For example, several procedures (e.g., multidimensional scaling and spectral embedding) are based upon the eigenvectors of the ad- jacency matrix that assume the adjacency matrix is symmetric. Put simply, this means that the coupling between two nodes can be treated as a distance in some metric space, thereby affording the opportunity to understand the relationship between nodes in terms of distances between them. This facility disappears in the context of weighted and directed graphs. For example, it is impossible to have a negative distance in signed graphs. A more subtle point is that weighted graphs mean that node A can be close (or similar) to node B, while node B can be distant (or dissimilar) from node A. So what are the emerging tools for characterizing weighted graphs in functional connectomics? Spectral graph theory has not attracted much attention in neuroimaging but may be an emerging candidate. For example, Raj, Kuceyeski, & Weiner (2012) use spectral graph theory through the properties of the graph Laplacian and its eigenspectrum. Spectral graph theory can be a useful tool because the Laplacian—and its eigenspectrum—contains all the information necessary to characterize a graph. Developing efﬁcient algorithms for ﬁnding community structure and modules via the Laplacian of directed (hyper)graphs is still a nascent ﬁeld (Chung, 2005). We have previously proposed a variant of DCM (Friston, Kahan, Razi, Stephan, & Sporns, 2014) using a generative model that used the eigen- modes and associated eigenspectrum to parameterize the effective connectivity. However, this formulation rests upon a symmetry constraint—and therefore deals with real eigenvalues—to provide estimates of (symmetric) connectivity and the underlying topology, where the con- nectivity between nodes depends upon their location in a multidimensional scaling space. Although this approach is mathematically elegant, it would be nice to have equivalent proce- dures for directed graphs whose Laplacian has complex eigenvalues (with imaginary parts). It is interesting to note that state-of-the-art functional connectivity studies appeal to the notion of hierarchies in understanding principal modes of functional connectivity (e.g., Margulies et al., 2016), despite the fact that the asymmetries in connectivity that deﬁne hierarchies are pre- cluded in undirected (functional connectivity) graphs. Although convenient, the symmetry of undirected graphs compromises their biological plausibility by denying asymmetries; for example, in terms of feedforward (e.g., targeting excit- atory spiny stellate neurons) and feedback (e.g., targeting inhibitory interneurons) connections in the brain. With this limitation in mind, it may be possible to relax the symmetry constraint by parameterizing a DCM with complex eigenvalues by splitting (effective) connectivity into sym- metric and antisymmetric components (see the lower row of Figure 6; see also Carlson, 1999; Chung, 2005; Donetti, Neri, & Munoz, 2006). We hope to explore these avenues in future work with the ultimate aim of characterizing network architectures in clinical populations. ACKNOWLEDGMENTS We would like to thank Ric Davis for providing extensive computational resources for the inversion of large stochastic DCMs. SUPPORTING INFORMATION The two DCM schemes described in this paper are implemented in MATLAB code and are available freely as part of the open-source software package SPM12 (Penny et al., 2011) and its Network Neuroscience 239 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Large-scale spectral DCMs website (http://www.ﬁl.ion.ucl.ac.uk/spm). The raw data used in this paper are openly acces- sible and can be downloaded from the 1000 Functional Connectomes Project (Biswal et al., 2010) and its website (http://fcon_1000.projects.nitrc.org/fcpClassic/FcpTable.html). AUTHOR CONTRIBUTIONS Adeel Razi: Conceptualization; Data curation; Formal analysis; Methodology; Visualization; Writing – original draft. Mohamed Seghier: Conceptualization: Supporting; Methodology: Supporting; Writing – review & editing: Supporting. Yuan Zhou: Contributor Information: Writing – review & editing: Supporting. Peter McColgan: Writing – review & editing: Supporting. Peter Zeidman: Writing – review & editing: Supporting. Hae-Jeong Park: Writing – review & editing: Supporting. Olaf Sporns: Visualization: Supporting; Writing – review & editing: Supporting. Geraint Rees: Conceptualization: Equal; Writing – review & editing: Supporting. Karl Friston: Conceptualization: Equal; Formal analysis: Supporting; Methodol- ogy: Supporting; Writing – original draft: Supporting; Writing – review & editing: Supporting. FUNDING INFORMATION This work was funded by the Wellcome Trust (AR, GR, KJF), CHDI Foundation (AR, GR), NIHR UCLH Research Capability Funding Award (AR), China Scholarship Council, grant no. 201504910067 (YZ), and the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI) funded by the Ministry of Health & Welfare, Republic of Korea (HI14C2444) (HJP). REFERENCES Biswal, B. B., Mennes, M., Zuo, X.-N., Gohel, S., Kelly, C., Smith, S. M., . . . Milham, M. P. (2010). Toward discovery science of human brain function. Proceedings of the National Academy of Sciences, 107, 4734–4739. Breakspear, M. (2004). “Dynamic” connectivity in neural sys- tems: Theoretical and empirical considerations. Neuroinformat- ics, 2(2), 205–226. https://doi.org/10.1385/NI:2:2:205 Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat Rev Neurosci, 10(3), 186–198. https://doi.org/10.1038/ nrn2575 Carlson, R. Inverse eigenvalue problems on directed graphs. Transactions of the American Mathematical Society, 351(10), 4069–4088. https://doi.org/10.1090/s0002-9947-99- 02175-3 (1999). Chung, F. (2005). Laplacians and the Cheeger inequality for di- rected graphs. Annals of Combinatorics, 9(1), 1–19. https://doi. org/10.1007/s00026-005-0237-z Donetti, L., Neri, F., & Munoz, M. A. (2006). Optimal network topologies: Expanders, cages, Ramanujan graphs entangled net- works and all that. Journal of Statistical Mechanics. https://doi. org/10.1088/1742-5468/2006/08/p08007 Fornito, A., Zalesky, A., & Breakspear, M. (2015). The connec- tomics of brain disorders. Nature Reviews Neuroscience, 16(3), 159–172. https://doi.org/10.1038/nrn3901 of brain function hypothesis. Human Brain Mapping, 26(1), 15– 29. https://doi.org/10.1002/hbm.20113 Friston, K., Moran, R., & Seth, A. K. (2013). Analysing connectiv- ity with Granger causality and dynamic causal modelling. Cur- rent Opinion in Neurobiology, 23(2), 172–178. https://doi.org/ 10.1016/j.conb.2012.11.010 Friston, K. J. (2009). Modalities, modes, and models in functional neuroimaging. Science, 326(5951), 399–403. https://doi.org/10. 1126/science.1174521 Friston, K. J., Frith, C. D., Liddle, P. F., & Frackowiak, R. S. (1993). Functional connectivity: The principal-component anal- Journal of Cerebral Blood Flow ysis of large (PET) data sets. and Metabolism, 13(1), 5–14. https://doi.org/10.1038/jcbfm. 1993.4 Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal modelling. Neuroimage, 19(4), 1273–1302. Friston, K. J., Kahan, J., Biswal, B., & Razi, A. (2014). A DCM for resting state fMRI. NeuroImage, 94, 396–407. https://doi.org/10. 1016/j.neuroimage.2013.12.009 Friston, K. J., Kahan, J., Razi, A., Stephan, K. E., & Sporns, O. (2014). On nodes and modes in resting state fMRI. NeuroImage. https:// doi.org/10.1016/j.neuroimage.2014.05.056 Friston, K. J., Li, B., Daunizeau, J., & Stephan, K. E. (2011). Network discovery with DCM. NeuroImage, 56(3), 1202–1221. https:// doi.org/10.1016/j.neuroimage.2010.12.039 Fransson, P. (2005). Spontaneous low-frequency BOLD signal ﬂuc- tuations: An fMRI investigation of the resting-state default mode Friston, K. J., Litvak, V., Oswal, A., Razi, A., Stephan, K. E., van (2016). Bayesian model Wijk, B. C. M., . . . Zeidman, P. Network Neuroscience 240 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Large-scale spectral DCMs reduction and empirical Bayes for group (DCM) studies. Neuro- Image, 128, 413–431. https://doi.org/10.1016/j.neuroimage. 2015.11.015 Friston, K. J., Stephan, K., Li, B. J., & Daunizeau, J. (2010). Gen- eralised ﬁltering. Mathematical Problems in Engineering, Article ID 621670. https://doi.org/10.1155/2010/621670 Kahan, J., Urner, M., Moran, R., Flandin, G., Marreiros, A., Mancini, L., . . . Foltynie, T. (2014). Resting state functional MRI in Parkinson’s disease: The impact of deep brain stimulation on “effective” connectivity. Brain, 137(4), 1130–1144. https:// doi.org/10.1093/brain/awu027 Li, B., Daunizeau, J., Stephan, K. E., Penny, W., Hu, D., (2011). Generalised ﬁltering and stochastic DCM & Friston, K. for fMRI. NeuroImage, 58(2), 442–457. https://doi.org/10.1016/ j.neuroimage.2011.01.085 Margulies, D. S., Ghosh, S. S., Goulas, A., Falkiewicz, M., Huntenburg, J. M., Langs, G., . . . Smallwood, J. (2016). Situating the default-mode network along a principal gradient of macro- scale cortical organization. Proceedings of the National Acad- emy of Sciences. https://doi.org/10.1073/pnas.1608282113 Nakagawa, T. T., Jirsa, V. K., Spiegler, A., McIntosh, A. R., & Deco, G. (2013). Bottom up modeling of the connectome: Link- ing structure and function in the resting brain and their changes in aging. NeuroImage, 80, 318–329. https://doi.org/10.1016/j. neuroimage.2013.04.055 Penny, W. D., Friston, K. J., Ashburner, J. T., Kiebel, S. J., & Nichols, (2011). Statistical parametric mapping: The analysis of T. E. functional brain images. London: Academic Press. Qi, S. L., Meesters, S., Nicolay, K., Romeny, B. M. T., & Ossenblok, P. (2015). The inﬂuence of construction method- ology on structural brain network measures: A review. Journal of Neuroscience Methods, 253, 170–182. https://doi.org/10.1016/ j.jneumeth.2015.06.016 Raichle, M. E. (2011). The restless brain. Brain Connect, 1(1), 3–12. https://doi.org/10.1089/brain.2011.0019 Raj, A., Kuceyeski, A., & Weiner, M. (2012). A network diffu- sion model of disease progression in dementia. Neuron, 73(6), 1204–1215. https://doi.org/10.1016/j.neuron.2011.12.040 Razi, A., & Friston, K. J. (2016). The connected brain causality, models, and intrinsic dynamics. IEEE Signal Processing Magazine, 33(3), 14–35. https://doi.org/10.1109/Msp.2015.2482121 Razi, A., Kahan, J., Rees, G., & Friston, K. J. (2015). Construct vali- dation of a DCM for resting state fMRI. NeuroImage, 106, 1–14. https://doi.org/10.1016/j.neuroimage.2014.11.027 Rubinov, M., & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52(3), 1059–1069. https://doi.org/10.1016/j.neuroimage.2009. 10.003 Rubinov, M., & Sporns, O. (2011). Weight-conserving charac- terization of complex functional brain networks. NeuroImage, (56), 42068–2079. https://doi.org/10.1016/j.neuroimage.2011. 03.069 Seghier, M. L., & Friston, K. J. (2013). Network discovery with large DCMs. NeuroImage, 68, 181–191. https://doi.org/10.1016/j. neuroimage.2012.12.005 Simpson, S. L., Bowman, F. D., & Laurienti, P. J. (2013). Ana- lyzing complex functional brain networks: Fusing statistics and network science to understand the brain. Statistics Surveys, 7, 1–36. https://doi.org/10.1214/13-SS103 Smith, S. M., Vidaurre, D., Beckmann, C. F., Glasser, M. F., Jenkinson, M., Miller, K. L., . . . Van Essen, D. C. (2013). Func- tional connectomics from resting-state fMRI. Trends Cognitive Sciences, 17(12), 666–682. https://doi.org/10.1016/j.tics.2013. 09.016 Sporns, O. (2014). Contributions and challenges for network models in cognitive neuroscience. Nature Neuroscience, 17(5), 652–660. https://doi.org/10.1038/nn.3690 Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual Review of Psychology, 67, 613–640. https://doi.org/10. 1146/annurev-psych-122414-033634 Network Neuroscience 241 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 3 2 2 2 1 0 9 2 0 5 0 n e n _ a _ 0 0 0 1 5 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 METHODS image

下载pdf