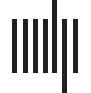方法 - 麻省理工学院人工智能研究专业

方法

Bridging global and local topology in whole-brain
networks using the network statistic jackknife

Teague R. 亨利

1, Kelly A. Duffy1, Marc D. Rudolph1, Mary Beth Nebel2,3,

Stewart H. Mostofsky2,3,4, and Jessica R. Cohen1

1Department of Psychology and Neuroscience, University of North Carolina at Chapel Hill, 教堂山, NC, 美国
2Center for Neurodevelopmental and Imaging Research, Kennedy Krieger Institute, 巴尔的摩, 医学博士, 美国
3神经内科, Johns Hopkins School of Medicine, 巴尔的摩, 医学博士, 美国
4Department of Psychiatry and Behavioral Science, Johns Hopkins School of Medicine, 巴尔的摩, 医学博士, 美国

关键词: 网络, 统计数据, 功能磁共振成像, Functional connectivity, Graph theory, Whole-brain
分析, Jackknife

开放访问

杂志

抽象的

Whole-brain network analysis is commonly used to investigate the topology of the brain
using a variety of neuroimaging modalities. This approach is notable for its applicability to a
large number of domains, such as understanding how brain network organization relates to
cognition and behavior and examining disrupted brain network organization in disease. A
beneﬁt to this approach is the ability to summarize overall brain network organization with a
single metric (例如, global efﬁciency). 然而, important local differences in network
structure might exist without any corresponding observable differences in global topology,
making a whole-brain analysis strategy unlikely to detect relevant local ﬁndings. 反过来,
using local network metrics can identify local differences, but are not directly informative of
differences in global topology. 这里, we propose the network statistic (NS) jackknife
框架, a simulated lesioning method that combines the utility of global network analysis
strategies with the ability to detect relevant local differences in network structure. 我们
evaluate the NS jackknife framework with a simulation study and an empirical example
comparing global efﬁciency in children with attention-deﬁcit/hyperactivity disorder (ADHD)
and typically developing (TD) 孩子们. The NS jackknife framework has been implemented
in a public, open-source R package, netjack, 可以在
https://cran.r-project.org/package=netjack.

介绍

Describing the brain as a network, an approach termed network neuroscience (Bassett &
斯波恩斯, 2017), is a powerful method that allows regions distributed across the entire brain
to be incorporated into a single model describing overall brain topology. This method has pro-
vided insights into whole-brain disruption in neurological and psychiatric diseases (假如,
布莫尔, & 扎莱斯基, 2017; 假如, 扎莱斯基, & Breakspear, 2015), the dynamic processes
underlying cognition (科恩 & D’Esposito, 2016; Kucyi, Tambini, 萨达吉亚尼, Keilholz, &
科恩, 2018), and changes across development (Baum et al., 2017; Grayson & Fair, 2017).
Researchers using a network neuroscience framework can draw upon the rich methodological
and statistical literature in graph theory and network analysis, grounding the approach in a
well-established mathematical framework.

然而, whole-brain analysis methods, as commonly applied in network neuroscience,
often fail at what Hallquist and Hillary (Hallquist & Hillary, 2018) refer to as “matching theory

引文: 亨利, 时间. R。, Duffy, K. A。,
Rudolph, 中号. D ., Nebel, 中号. B.,
Mostofsky, S. H。, & 科恩, J. 右. (2020).
Bridging global and local topology in
whole-brain networks using the
network statistic jackknife. 网络
神经科学, 4(1), 70–88. https://
doi.org/10.1162/netn_a_00109

DOI:
https://doi.org/10.1162/netn_a_00109

支持信息:
https://doi.org/10.1162/netn_a_00109
https://CRAN.R-project.org/
package=netjack

已收到: 4 六月 2019
公认: 12 九月 2019

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
Teague Rhine Henry
trhenry@email.unc.edu

处理编辑器:
Richard Betzel

版权: © 2019
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The network statistic jackknife

Jackknife:
A nonparametric statistical technique
that involves repeatedly reestimating
a parameter value after the removal
of single observations.

Whole-brain (全球的)
network statistic:
A statistic derived from a whole-brain
network that describes an aspect of
global topology.

Global topology:
The overall shape and structure of a
网络.

to scale.” This refers to the fact that whole-brain network analysis methods operate at a global
resolution, while relevant differences might be very localized. 换句话说, there may be
differences at a local scale (IE。, within a single subnetwork) that would be missed when cal-
culating a single, whole-brain summary measure that describes global topology. 反过来,
observed global differences in topology could be driven by a speciﬁc local difference (IE。, 一个
observed overall difference in network integration could be driven by a difference limited to
a single subnetwork). This mismatch in resolution, 所以, could obscure meaningful differ-
ences in network structure. While local network statistics, such as participation coefﬁcient of
a single node, can be used to identify local differences of interest, these local statistics do not
directly assess a localized difference in global topology, and as such are not ideal for matching
a global theory to a local scale. In the present manuscript, we develop the network statistic
(NS) jackknife as a general method to localize global network statistics across a variety of
network metrics and brain features of interest, thus allowing researchers to better address this
resolution issue.

The NS jackknife method (available for use at https://cran.r-project.org/package=netjack)
proposed here allows researchers to identify speciﬁc brain regions, 连接, or subnet-
作品 (IE。, local features) that drive global network analysis results or, 反过来, that are not
detected by global network analysis. 通过这样做, our method can detect local differences in
network structure using the same summary metrics that a global analysis would use, as op-
posed to relying on local metrics that do not explicitly link to the global metrics in question.
This approach bridges the gap between a global and a local scope of analysis by allowing
researchers to apply global analysis strategies in a way that reveals differences at local scopes,
even when those differences would not be detected with the global analysis method. We eval-
uate the performance of the NS jackknife with a simulation study and demonstrate the utility
of this method with an empirical example comparing resting-state brain network organization
in children with attention-deﬁcit/hyperactivity disorder (ADHD) and age-matched typically
developing (TD) 孩子们.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Global Versus Local Topology

There are many network statistics that can be used to analyze the global topology of a network;
for simplicity we focus on two widely used network statistics as examples. 第一的, we use mod-
独特性, or a measure of a network’s segregation into multiple communities (or subnetworks;
纽曼, 2006). 第二, we use global efﬁciency, a statistic that assesses the overall inte-
gration of a network (Latora & Marchiori, 2001). These two statistics have led to great insight
regarding brain organization, in particular for supporting the hypothesis that the balance be-
tween network segregation (dense, within-subnetwork connectivity) and network integration
(communication across distinct subnetworks) is critical for cognition (for reviews and canon-
ical articles, see the following: 科恩 & D’Esposito, 2016; Shine & Poldrack, 2017; 斯波恩斯,
2013; 斯波恩斯, Chialvo, Kaiser, & 希尔格塔格, 2004).

然而, a key issue for whole-brain analysis is its poor detection of local differences in
topology. 例如, if a whole-brain analysis produces differences in overall network topol-
ogy between groups or conditions, it does not provide insight into where in the brain these
differences might arise. 更远, if a whole-brain analysis produces no differences in overall
network topology, that does not preclude the existence of important local differences. 这
property of whole-brain network analysis is less than ideal as it ignores local features, 哪个
can include speciﬁc brain regions, speciﬁc connections between brain regions, or speciﬁc
subnetworks. A local topological difference arising from one region/connection/subnetwork

网络神经科学

The network statistic jackknife

Speciﬁcity:
When differences in global topology
are being driven by speciﬁc
differences in local topology, 作为
opposed to globally distributed
差异.

Equiﬁnality:
When different network
conﬁgurations can lead to the same
global network statistic.

versus another could have vastly different implications for empirical inferences and resultant
clinical applications.

There are several existing graph theory metrics that operate on a local scale. 考试用-
普莱, within-module degree indicates which nodes are more central to their communities, 和
participation coefﬁcient indicates which nodes connect different communities (Guimerà &
Nunes Amaral, 2005). 此外, there are a variety of statistical models for identifying
nodes and other network features of importance. One of the most widely used is the network-
based statistic method (NBS; 扎莱斯基, 假如, & 布莫尔, 2010), which identiﬁes differences
between groups by examining maximally different sets of edges. The degree-based statistic
method of Yoo and colleagues (Yoo et al., 2017) is more focused than that of the NBS method,
and identiﬁes highly central nodes that are related to a hypothesis of interest. Another recent
方法, that of screen ﬁltering (Meskaldji et al., 2015), allows researchers to analyze group
differences in nodal and edge-wise metrics; 然而, this method as currently implemented
is restricted to nodal, edge-wise or subnetwork statistics as it relies on correcting a collection
of statistical tests. All of these methods allow researchers to assess local differences between
groups and thus are powerful tools for understanding different features of network organi-
扎化, but none of these methods assess local drivers of global topological properties of a
网络. 例如, a common method for examining group differences in local modular
structure is examining differences in participation coefﬁcient for individual nodes or subsets
of nodes. While nodes that exhibit a participation coefﬁcient difference might correspond to
nodes that are relevant to differences in global modularity, this is by no means assured. 当地的
metrics and tests can be related to global metrics (IE。, participation coefﬁcient can be related
to whole-brain modularity), but these relations are not one-to-one, and a difference in local
properties does not necessarily imply a difference in global properties. 相似地, previous sta-
tistical models that identify network elements of importance do not identify these elements
based on their relative contribution to global topology, but rather based on their impacts on
local topology. These properties of local metrics and existing local statistical models suggest
a need for a framework that can assess differences in global topology and directly link these
global differences to local structures.

The disconnect that arises between the global and the local scope can be due to speciﬁcity,
in which whole-brain network results are driven by speciﬁc connections, 地区, or subnet-
作品; or to equiﬁnality, in which strikingly different network conﬁgurations can lead to the
same whole-brain summary metric values. These two concepts can be related, as equiﬁnality
can be caused by speciﬁc differences in local topology that do not lead to differences in sum-
mary metrics describing global topology. The NS jackknife, proposed here, provides a solution
to these issues. This statistical approach allows researchers to simultaneously analyze differ-
ences in global topology and localize these differences to speciﬁc brain regions, 连接,
or subnetworks.

Network Speciﬁcity and Equiﬁnality

Speciﬁcity is the network principle whereby differences in observed whole-brain or whole-
network topology can be driven by speciﬁc differences in local topology, as opposed to glob-
ally distributed differences. A whole-brain network difference can be speciﬁc if, 例如,
one group of interest has greater connectivity within one speciﬁc functional subnetwork than
a different group, and this increase in connectivity is substantial enough that it alone drives a
signiﬁcant difference in global modularity. 反过来, a whole-brain network difference can
be nonspeciﬁc if the difference in topology is due to a diffuse pattern of local differences.

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The network statistic jackknife

例如, if one group has higher connectivity between all pairs of subnetworks, this can
result in a difference in global efﬁciency that cannot be localized to any given subset of net-
作品. One key issue with whole-brain network analysis is that it is not capable of determining
whether an observed topological difference is speciﬁc or nonspeciﬁc. This property has been
termed the theory-to-scale issue (Hallquist & Hillary, 2018).

This lack of speciﬁcity is complicated by the fact that, when calculating various summary
statistics for brain networks, typical approaches in network neuroscience can produce the
same network statistics for different network conﬁgurations. Equiﬁnality, a term borrowed from
system theory (Bertalanffy, 1950), is the network principle whereby the same result can be
achieved by many different means. 这里, we use it to emphasize the fact that the same in-
ference can result from different global network conﬁgurations. 例如, 数字 1 节目
two networks, each consisting of two subnetworks. The difference between these networks is
in how these subnetworks are connected. In Network A, the communities are connected via a
hub node (dotted circle), while for Network B the subnetworks are connected more diffusely.
Whole-network modularity of the two networks in Figure 1 is identical, yet this result masks
the fact that the local structure of the inter-subnetwork connections in the two networks is quite
不同的. This demonstrates the possible disconnect between whole-brain ﬁndings (IE。, 全球的
范围) and speciﬁc local differences in topology (IE。, local scope).

Speciﬁc versus nonspeciﬁc whole-brain ﬁndings occur with regularity in neuroimaging re-
搜索. 例如, individuals suffering from Alzheimer’s disease exhibit reductions in de-
fault mode network connectivity as well as global loss of a small-world network structure
(Pievani, de Haan, 吴, Seeley, & Frisoni, 2011). This analysis of whole-brain small-world
structure differentiates patients with Alzheimer’s disease from healthy control participants but
provides no information as to the role default mode network connectivity plays in that global
ﬁnding. The NS jackknife method has the ability to quantify whether reductions of whole-brain
small-world structure in Alzheimer’s disease are driven by the default mode network alone, 是
widely distributed across all subnetworks in the brain, or are driven by a small number of sub-
网络.

数字 1. Two networks with the same value of modularity yet very different inter-subnetwork
patterns of connectivity. Note that Network A contains a single connector hub, or a node that links
two communities (dashed circle), while Network B does not.

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The network statistic jackknife

Virtual/simulated lesioning:
A technique in neuroimaging that
removes components of a network
during analysis to examine the
impact of those components on
global topology.

Network robustness:
How much a network’s global
topology changes when nodes/edges
are removed. This removal is
typically done in a random or
semirandom fashion to assess the
network’s robustness to attack or
damage.

These speciﬁc local differences with prominent global differences found in Alzheimer’s
disease can be contrasted with the ﬁnding that individuals with autism spectrum disorder
(自闭症谱系障碍) tend to exhibit increased whole-brain integration, as assessed with global efﬁciency,
as compared with healthy control participants (Lewis, Theilmann, Townsend, & 埃文斯, 2013;
Rudie & Dapretto, 2013). While other research has shown speciﬁc differences between indi-
viduals with ASD and healthy control participants, for example within the salience network
(Di Martino et al., 2009), the ﬁnding of increased functional integration appears be a result of
more diffuse and weaker functional connections distributed across the entire brain, and thus a
whole-brain phenomenon (Roine et al., 2015; Rudie & Dapretto, 2013). While a whole-brain
network analysis would accurately detect this group difference, it would give no indication
whether the difference was due to a widely distributed whole-brain difference or driven by
speciﬁc subnetworks or connections, a conclusion that could be made with use of the NS jack-
knife. These examples emphasize that whole-brain network analysis strategies are designed to
examine a global scope but lack the ability to determine the speciﬁcity of any given ﬁnding
(Hallquist & Hillary, 2018).

Localization of Whole-Brain Analysis Using the NS Jackknife

The NS jackknife localizes whole-brain network analyses by iteratively removing elements of
网络, such as edges, 节点, or subnetworks, and recalculating the target network statis-
tic without those elements. By sweeping through the whole network, as well as assessing the
impact of the removal across subjects, the NS jackknife creates an empirical distribution of
network element effects, allowing a researcher to localize speciﬁc features of brain network
organization that contribute most strongly to a given whole-brain network statistic. The NS
jackknife was inspired by the traditional jackknife estimator used extensively in nonparametric
statistics and can be considered a virtual lesioning technique. We are using the term “jackknife”
not only because the NS jackknife relies on the leave-one-out approach of the traditional jack-
knife, but also because like the traditional jackknife, the NS jackknife is a general statistical
technique that can be applied to any question that entails localizing a global network statistic.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

A jackknife in statistics is a resampling technique used to adjust for outliers using a leave-
one-out approach (Efron, 1982; Tukey, 1958). This procedure removes a single observation,
such as a single subject’s data, from a sample, recalculates the effect estimate, then adds the
removed observation back into the sample and removes another; it iterates through the sample
in this fashion. In standard sampling situations, in which each observation is the behavioral data
of a single individual, this method is useful for detecting potential outliers. Jackknife techniques
have been previously used in network science to assess the overall robustness of a network
statistic to node removal (Snijders & Borgatti, 1999). 然而, previous uses of this technique
have focused on single instances of a network (IE。, one social network) and on obtaining
estimates of a network statistic, rather than on assessing the importance of particular network
structures in a set of multiple networks (IE。, multiple brain networks).

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

While a standard jackknife procedure removes individual subjects in turn from an analysis,
we are proposing here to remove elements of a graph, such as nodes, 边缘, or subnetworks.
Here for the sake of example, we focus on the removal of entire functional subnetworks, 或者
tightly interconnected sets of regions of interest (ROIs) thought to underlie various aspects of
认识, such as the default mode network (Greicius, Krasnow, Reiss, & Menon, 2003) 或者
salience network (Seeley et al., 2007). Once a subnetwork is removed, the network statistic is
recalculated, and the procedure continues with the removal of another subnetwork. Speciﬁc
versions of this procedure have been used in previous neuroimaging research (例如, Achard,

网络神经科学

The network statistic jackknife

Salvador, Whitcher, Suckling, & 布莫尔, 2006; 亨利, Dichter, & Gates, 2018); we develop
a general framework here. Critically, while our NS jackknife estimator is based on previous
work in simulated lesioning, and at its core is a simulated lesioning method (Achard et al.,
2006; Alstott, Breakspear, 哈格曼, 卡蒙, & 斯波恩斯, 2009; Crucitti, Latora, Marchiori,
& Rapisarda, 2004), it is focused on localization of network effects rather than the overall
robustness of a network. 更具体地说, while robustness focuses on understanding the
overall resiliency of a network to attack, localization attempts to understand the impact of the
removal of speciﬁc elements on the network. Robustness and localization are highly related,
and the NS jackknife differs from previous simulated lesioning methods mainly in interpretation
and in its speciﬁc focus on understanding group differences. 此外, while the focus here
is on testing group differences without subject- or network-level covariates, the NS jackknife
framework can be extended to more complex models that can account for covariates and
other design factors. 在这个意义上, the NS jackknife is an extension of the simulated lesioning
technique into a general testing framework for localizing global network statistics. 最后, 我们
provide an easily accessible implementation of the NS jackknife in the netjack package.

The NS Jackknife

To describe the NS jackknife in more precise terms, 让 {G1, . . . Gn} be the observed networks
of n subjects. Let f (·) be the functional form of some network statistic, such as modularity,
and let k be the indicator of a feature of interest (such as a subnetwork), taken from some set
K of size |K|. Gi[−k] is the network of individual i with feature k removed. More concretely, 如果
we were analyzing functional connectivity networks, then Gi would be the whole-brain func-
tional connectivity network of individual i, and Gi[−DMN] would be the functional connectivity
network of individual i with all the nodes of the default mode network removed.

The set of original network statistics is f (·) applied to all G1, . . . Gn, and this n-length vector
is denoted as ˆf . The jackknife estimate with regard to feature k is then f (·) applied to all
G1[−k], . . . , Gn[−k]; this length n vector is denoted as ˆf−k. 最后, the difference between the
original network statistic and the jackknife estimator with regard to structure k is denoted as
ˆd−k.

Applying this procedure to the |K| features of interest (例如, all functional subnetworks) leads
到 |K| jackknife estimate vectors and |K| difference vectors for each subject. If subjects are
(乙)
divided between Groups A and B, we denote the estimate and difference vectors as ˆf
−k
and ˆd

(A)
−k

, ˆf

(A)

−k , ˆd

(乙)
−k .

There are several methodological considerations when using the NS jackknife. The ﬁrst is
that network statistics are a priori dependent on network size and density (van Wijk, 斯塔姆,
& Daffertshofer, 2010); comparing network statistics across different subsets of networks of
different sizes can lead to spurious ﬁndings. In the NS jackknife framework, this issue is handled
by comparing networks of the same size (as in the group test) or changes in network statistics
(as in the differential impact test).

此外, the NS jackknife produces a series of dependent multiple comparisons. In tra-
ditional jackknife settings, observations removed at each iteration are independent of all other
observations. 然而, in the NS jackknife the removal of individual elements from every sub-
ject’s network and the subsequent reestimation of network statistics results in a series of depen-
dent statistical tests. Because of the dependent nature of these tests, and the risk for inﬂation
because of multiple comparisons, the Benjamani-Hochberg (BH) procedure is an appropriate
false discovery rate (FDR) correction for multiple comparisons (Benjamini & Hochberg, 1995).

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The network statistic jackknife

Other multiple comparisons corrections that allow for dependent tests, such as the Benjamani-
Yekutieli (BY; Benjamini & Yekutieli, 2001) correction, are also appropriate, while the Bonfer-
roni correction would not be, as it does not account for the presence of dependent tests. 如果
network components of interest are nodes or edges, and the subnetwork membership of these
components is known, the screen ﬁltering approach of Meskaldji et al. (2015) provides a way
of correcting for multiple comparisons that results in more power to detect effects than the BH
or BY corrections, and should be preferentially used.

All analyses and graphical outputs in this manuscript use the netjack open source R pack-
年龄 (亨利, 2018), a package tailor-made for performing the NS jackknife in a simple to use,
customizable fashion.

Localizing Group Differences and Differential Impact

The primary use of the NS jackknife is to localize global network statistic differences be-
tween groups to speciﬁc subnetworks, 节点, or edges. Consider the example of comparing
the whole-brain modularity for a given set of subnetworks between two clinical groups. 在广告中-
dition to quantifying differences across the groups in global modularity using standard network
统计数据, the NS jackknife allows for two additional questions of substantive interest:

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

1. Group differences: Given the removal of a subnetwork, are the two groups’ mean global
values signiﬁcantly different from each other? This corresponds to a hypothesis of the
following:

(A)
ˆf
−k i 6= E h
2. Differential impact: Is there a differential impact of the removal of a subnetwork between

(乙)
ˆf
−k i .

E h

the two groups? This corresponds to a hypothesis of the following:

E h

(A)
ˆd
−k i 6= E h

(乙)
ˆd
−k i .

We illustrate the use of these two tests in the following simulated example.

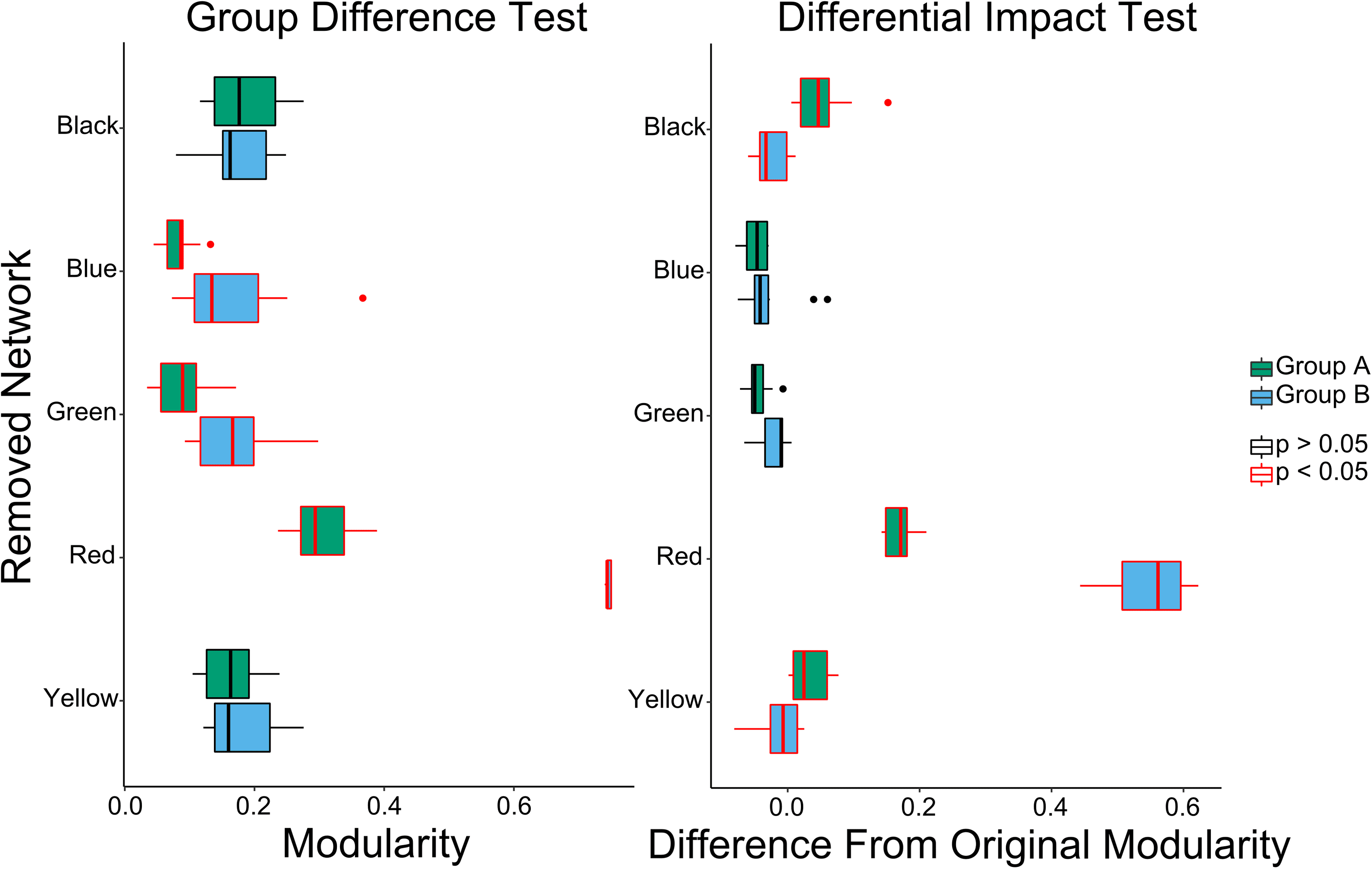
Data generation. For Group A, the sample of networks was generated using a stochastic
block model for binary undirected networks (Nowicki & Snijders, 2001), with probabilities set
to create the observed community structure (0.9 之内, 0.5 之间). The sample contained
10 “subjects.” For Group B, data generation used the same procedure and the same base prob-
能力 (0.9 之内, 0.5 之间), with additional connections between the yellow and black
groups set to 0.5 probability (见图 2).Group B, like Group A, contained 10 “subjects.”

分析. The NS jackknife was used to quantify the effect of the removal of each of the ﬁve
subnetworks on each subject’s overall network modularity. For the group differences analysis,
a two-sample t test was conducted to determine whether the updated modularity due to the
removal of any given subnetwork was signiﬁcantly different across groups. For the differential
impact analysis, a two-sample t test was conducted on the difference in modularity due to the
removal of any given subnetwork to determine whether there was a differential impact across
the groups in removing each subnetwork. For the differential impact analysis, p values were
corrected for ﬁve tests using the BH correction for dependent multiple comparisons. 团体
difference test p values are uncorrected.

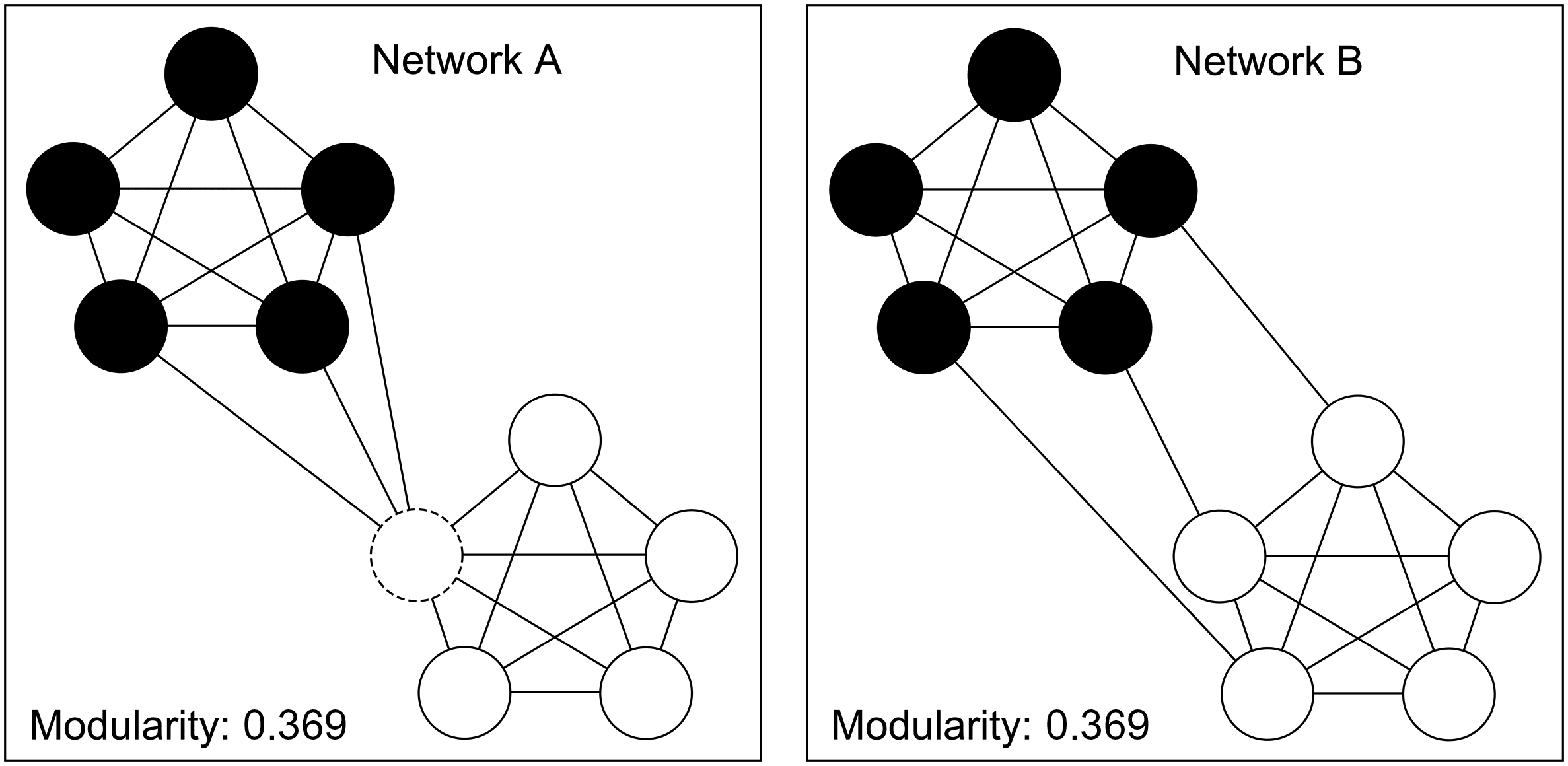
结果. Whole-brain modularity was signiﬁcantly higher in Group B than in Group A
(t(13.41) = 2.9288, p < 0.05; average modularity 0.1974 and 0.1332, respectively). For the group differences analysis, the whole-brain group difference (B > A) remained after removal of

网络神经科学

The network statistic jackknife

数字 2. Two modular networks. The red module acts as a central hub for both networks, 尽管
in Network A the black and yellow modules are directly interconnected.

the blue, 绿色的, or red subnetworks, while removal of the black or yellow subnetworks resulted
in no group difference in modularity (数字 3, left panel). For the differential impact analysis,
removal of the black and yellow subnetworks resulted in an increased change in modularity for
Group A as compared with Group B. Removal of the red subnetwork resulted in an increased
change in modularity for Group B as compared with Group A (although modularity increased

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 3. Group differences (left ﬁgure) and differential impact (right ﬁgure) of subnetwork removal
on modularity of Network A (in blue) and Network B (绿色) from Figure 2. Central line is the
median, box is the interquartile range (IQR), and whiskers represent 1.5 ∗ IQR. Points represent
values greater than 2 SD from the mean. Both group difference and differential impact tests suggest
that the red network is signiﬁcantly more centrally integrated in Group B than in Group A. 这
differential impact tests additionally show that removal of the black or yellow network causes more
of an increase in modularity for Group A than Group B, suggesting that these subnetworks are more
integrated into the whole network in Group A.

网络神经科学

The network statistic jackknife

for both groups), and removal of the blue and green subnetworks resulted in a comparable
(and near-zero) change in modularity across the groups (数字 3, right panel).

Interpretation. The red subnetwork was highly integrated in both Group A and Group B;
然而, its removal led to less of an impact on modularity in Group A than Group B. 这
black and yellow subnetworks were more integrated into the rest of the network in Group A
than Group B.

Comparing group differences with differential impact analysis permits one to directly assess
the impact that local differences can have on global ﬁndings. 总结一下, the removal of
the red subnetwork corresponded to a signiﬁcant group difference as well as a signiﬁcant
differential impact, suggesting that its removal led to the networks becoming more different
from each other. 相比之下, the removal of the yellow or black subnetworks led to signiﬁcant
differential impact but no signiﬁcant group differences, indicating that the removal of either of
these subnetworks led to the networks becoming more similar to one another.

Simulation Study: Speciﬁcity and Sensitivity of the NS Jackknife

A simulation study assessing the speciﬁcity and sensitivity of the NS jackknife to the magni-
tude of group differences, sample size, and network size was conducted. Results show that NS
jackknife has good sensitivity to detect small group differences in the generating model at mod-
erate sample sizes (50 subjects per group) and larger networks (250 节点) and shows excel-
lent sensitivity for larger group differences across multiple conditions. In a condition in which
groups had different whole-network statistics that were driven by speciﬁc local differences,
NS jackknife detected differences in differential impact across all subnetworks (Condition 4,
Supplementary Figure 5), and an examination of effect sizes correctly identiﬁed which subnet-
works had the most impact on the network statistic (Supplementary Figure 6). In all conditions
经测试, network size was an important predictor of power, with larger networks demonstrating
greater power to detect small effects.

One key conclusion from this simulation study regards the interpretation of NS jackknife
results when the tested groups are signiﬁcantly different in their whole-brain statistic. 在这个
案件, the NS jackknife tends to detect differences upon the removal of all the network elements
being jackknifed on. 在这种情况下, two routes of interpretation are viable. The ﬁrst is to examine
the effect sizes of differences to determine which component of the network contributes most
to the differences between the groups (IE。, which has the largest effect size). The second is to
determine whether any subnetwork was not found to have a signiﬁcant differential impact, 在
which case it can be concluded that those subnetworks were not signiﬁcant contributors to
the observed group difference.

For full details of this simulation study, see the Supporting Information.

Empirical Example: Reduced Integration of Subnetworks in ADHD

This empirical example is a proof of concept demonstrating how the use of the NS jackknife
provides important information about differences in functional brain network organization in
children with ADHD and TD children. ADHD is a neurodevelopmental disorder characterized
by difﬁculty with sustaining attention, as well as excessive impulsive or hyperactive behavior
(American Psychiatric Association, 2013). Existing research indicates that whole-brain func-
tional and structural topology are disrupted in individuals with ADHD, as are speciﬁc local
differences in connectivity (for reviews, see the following: 曹, Shu, 曹, 王, & 他, 2014;

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The network statistic jackknife

亨利 & 科恩, 2019). Individuals with ADHD exhibit higher whole-brain functional segrega-
tion than healthy control participants (林等人。, 2014; 王等人。, 2009). In terms of speciﬁc
local differences, there appears to be disruptions in networks such as the default mode, fron-
toparietal, 注意力, visual, and motor subnetworks (Castellanos & Proal, 2012). Given these
ﬁndings at the global and local level, a comparison of individuals with ADHD and healthy
control participants is a useful test case for the NS jackknife. In the following analyses, 我们
examine global efﬁciency (Latora & Marchiori, 2001) of resting-state functional MRI scans in
children with ADHD as compared with TD children. Global efﬁciency is a measure of func-
tional integration. Previous studies have mixed ﬁndings with regard to differences in global
efﬁciency, either showing that individuals with ADHD have slightly lower global efﬁciency
than healthy control participants (林等人。, 2014) or no differences in global efﬁciency (王
等人。, 2009). 在这个例子中, we attempt to localize potential differences in global efﬁciency
to speciﬁc functional subnetworks in an effort to learn more about these inconsistencies in the
prior literature.

方法

Sample Characteristics and Data Acquisition

Participants included 80 children with ADHD between 8 和 12 年龄 (male N = 55
and female N = 25) 和 208 age-matched TD children (male N = 150 and female N = 58).
For details on study inclusion criteria, see Barber and colleagues (2015).

All data were collected at the Kennedy Krieger Institute (巴尔的摩, 医学博士) using a Philips
3T Achieva MRI scanner. High-resolution T1-weighted 3D MPRAGE images were acquired
with the following parameters: repetition time (TR) = 8.05 多发性硬化症, echo time (TE) = 3.76 多发性硬化症, ﬂip
angle = 8◦, 矩阵 256 × 256, ﬁeld of view (FOV) = 200 毫米, and slice thickness 1 毫米. 为了
resting-state data, 21 participants had 128 T2*-weighed echoplanar images (EPIs), 尽管 167
participants had 156, both collected with the following parameters: TR = 2.5 s, = 30 多发性硬化症,
ﬂip angle = 70◦, 矩阵 96 × 96, and FOV = 256 毫米.

预处理

The resting-state images were preprocessed using FMRIPREP version 1.0.7 (Esteban et al.,
2018), a Nipype-based tool (戈尔戈莱夫斯基等人。, 2011). Each T1-weighted volume was cor-
rected for intensity nonuniformity using N4BiasFieldCorrection v2.1.0 (塔斯蒂森等人。, 2010)
and skull-stripped using antsBrainExtraction.sh v2.1.0 (using the OASIS template). Brain sur-
faces were reconstructed using recon-all from FreeSurfer v6.0.1 (戴尔, 菲舍尔, & Sereno, 1999),
and the brain mask estimated previously was reﬁned with a custom variation of the method
to reconcile ANTs-derived and FreeSurfer-derived segmentations of the cortical graymatter of
Mindboggle (Klein et al., 2017). Spatial normalization to the ICBM 152 Nonlinear Asymmet-
ric template version 2009c (Fonov, 埃文斯, McKinstry, Almli, & 柯林斯, 2009) was performed
through nonlinear registration with the antsRegistration tool of ANTs v2.1.0 (Avants, 爱泼斯坦,
Grossman, & Gee, 2008), using brain-extracted versions of both the T1-weighted volume
and template. Brain tissue segmentation of cerebrospinal ﬂuid (CSF), whitematter (WM), 和
graymatter (GM) was performed on the brain-extracted T1-weighted image using FAST
(张, 布雷迪, & 史密斯, 2001).

Functional data were slice time corrected using 3dTshift from AFNI v16.2.07 (考克斯, 1996)
and motion corrected using mcﬂirt (FSL v5.0.9; 詹金森, 栏干, 布雷迪, & 史密斯, 2002).

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The network statistic jackknife

This was followed by coregistration to the corresponding T1-weighted image using boundary-
based registration (Greve & 菲舍尔, 2009) 和 9 degrees of freedom, using bbregister (FreeSurfer
v6.0.1). Motion-correcting transformations, BOLD-to-T1-weighted transformation, and T1-
weighted-to-template (MNI) warp were concatenated and applied in a single step using
antsApplyTransforms (ANTs v2.1.0) using Lanczos interpolation. Frame-wise displacement
(FD) (Power et al., 2013) was calculated for each functional run using the implementation
of Nipype.

Many internal operations of FMRIPREP use Nilearn (Abraham et al., 2014), principally
within the BOLD-processing workﬂow. For more details of the pipeline see https://fmriprep.
readthedocs.io/en/latest/workﬂows.html. This description of the preprocessing pipeline was
generated at http://fmriprep.readthedocs.io/en/latest/citing.html.

Motion Processing and Spectral Filtering

Following preprocessing with FMRIPREP, the resting-state scans were corrected for nuisance
变量, including motion, WM signal, and CSF signal. This correction proceeded in the
following steps. Timepoints that exceeded 0.3mm FD (力量, 巴恩斯, 斯奈德, 施拉加尔, &
彼得森, 2012) were ﬂagged, as were the timepoints immediately preceding and following the
ﬂagged timepoint. Interpolation across these ﬂagged timepoints was conducted using spectral
interpolation (Ciric et al., 2017). Following the spectral interpolation, a high-pass ﬁlter at 0.008
MHz was applied to the voxel time series containing the interpolated timepoints. The ﬂagged
timepoints were then set to missing for all voxels. A nuisance regression set consisting of the 6
degrees of motion and mean WM and CSF signal, as well as the temporal derivatives, quadratic
扩展, and the quadratic expansions of the temporal derivatives of these 8 regressors, 曾是
high-pass ﬁltered at 0.008 MHz, as per the suggestion of Ciric, Satterthwaite, and colleagues
(Ciric et al., 2017; Satterthwaite et al., 2013). The ﬁltered nuisance regressors were used to
regress out nuisance signal from the scrubbed and ﬁltered voxel time series. 最后, subjects
that had more than 30% of their data lost because of scrubbing were removed from the analysis,
as were subjects who exceeded 0.2 mm mean FD overall. This resulted in a ﬁnal sample of
34 children with ADHD and 121 TD children, with mean percentage timepoints lost 8% 和
10% 分别. This difference in percentage timepoints lost was nonsigniﬁcant (t(48.423) =
−1.47, p = 0.14). 此外, the mean FD in the ﬁnal sample was not signiﬁcantly different
between children with ADHD and TD children (t(49.902) = 1.27, p = 0.21, ADHD mean =
0.131, TD mean = 0.121).

ROI Extraction and Network Construction

From the preprocessed and motion-corrected resting-state images, ROI time series were
extracted using a commonly used functional brain atlas (Power et al., 2011). This atlas
consists of 264 ROIs, 234 of which are classiﬁed into 13 functional subnetworks. 这些
functional subnetworks and abbreviations are as follows: auditory (AUD), cerebellar (CER),
cingulo-opercular (一氧化碳), default mode (DMN), dorsal attention (DAN), frontoparietal (FP),
记忆 (MEM), salience (SAL), somatomotor hand (SM Hand), somatomotor mouth (SM
嘴), subcortical (SUB), ventral attention (VAN), and visual (VIS). From these ROI time series,
234 × 234 correlation matrices were computed. These correlation matrices were then con-
verted to absolute values and thresholded at a correlation magnitude of 0.35 to create binary
connectivity networks. The pattern of ﬁndings below was consistent for a band of thresholds
从 0.25 到 0.4.

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The network statistic jackknife

Network Statistics and Jackknife

In this application, we use global efﬁciency as our network statistic. Global efﬁciency is de-
ﬁned as the average of the inverse shortest path length between all nodes in the network (Latora
& Marchiori, 2001), and can be thought of as a measure of global integration. We applied the
jackknife over the 13 functional subnetworks in the functional brain atlas. The two tests previ-
ously described were then applied to the jackknifed data. This allowed us to assess (A) 无论
the removal of a functional subnetwork led to a signiﬁcant difference in global efﬁciency be-
tween children with ADHD and TD children; 和 (乙) whether the impact of the removal of
a functional subnetwork on functional integration was different for children with ADHD as
compared with TD children.

Jackknife Estimate and Group Comparisons

Independent two-sample t tests were conducted to compare global efﬁciency values across the
entire sample, and to compare global efﬁciency values and differential impacts across groups.
Differential impact results were corrected for multiple dependent comparisons using the BH
correction, as described in the above simulations.

结果

Group differences in whole-brain global efﬁciency: There was no group difference in global
efﬁciency for children with ADHD and TD children (t(5037) = 0.99, p = 0.32; ADHD
mean = 0.29, TD mean = 0.28).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

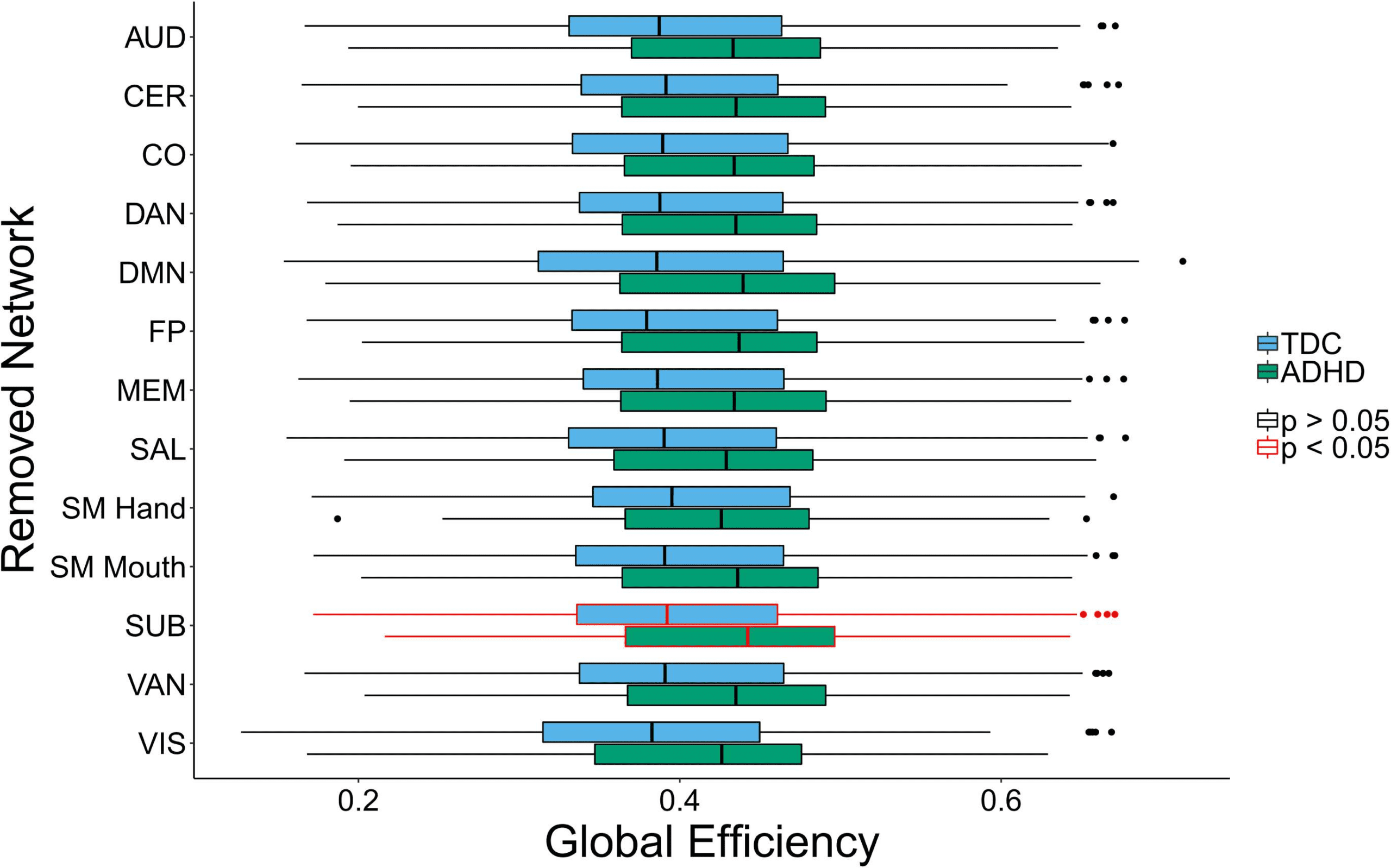
数字 4. Group differences in global efﬁciency between children with ADHD and TD children
after the removal of a given subnetwork. Networks are presented here in alphabetical order. 中央
line is the median, box is the interquartile range (IQR), and whiskers represent 1.5 ∗ IQR. Points
represent values more than 2 SD away from the mean. Removal of the SUB network resulted in
children with ADHD having signiﬁcantly higher global efﬁciency than TD children.

网络神经科学

The network statistic jackknife

Group differences by subnetwork removal: 下一个, we examined group differences in global
efﬁciency between children with ADHD and TD children after removing each functional
subnetwork.

Removal of the SUB subnetwork led to a signiﬁcant difference between children with ADHD
and TD children with respect to global efﬁciency (数字 4). Speciﬁcally, children with ADHD
had greater global efﬁciency than TD children after SUB subnetwork removal. 桌子 1 在里面
Supporting Information contains the numerical differences and p values. It should be noted that
these results are best interpreted when combined with the differential impact results below.

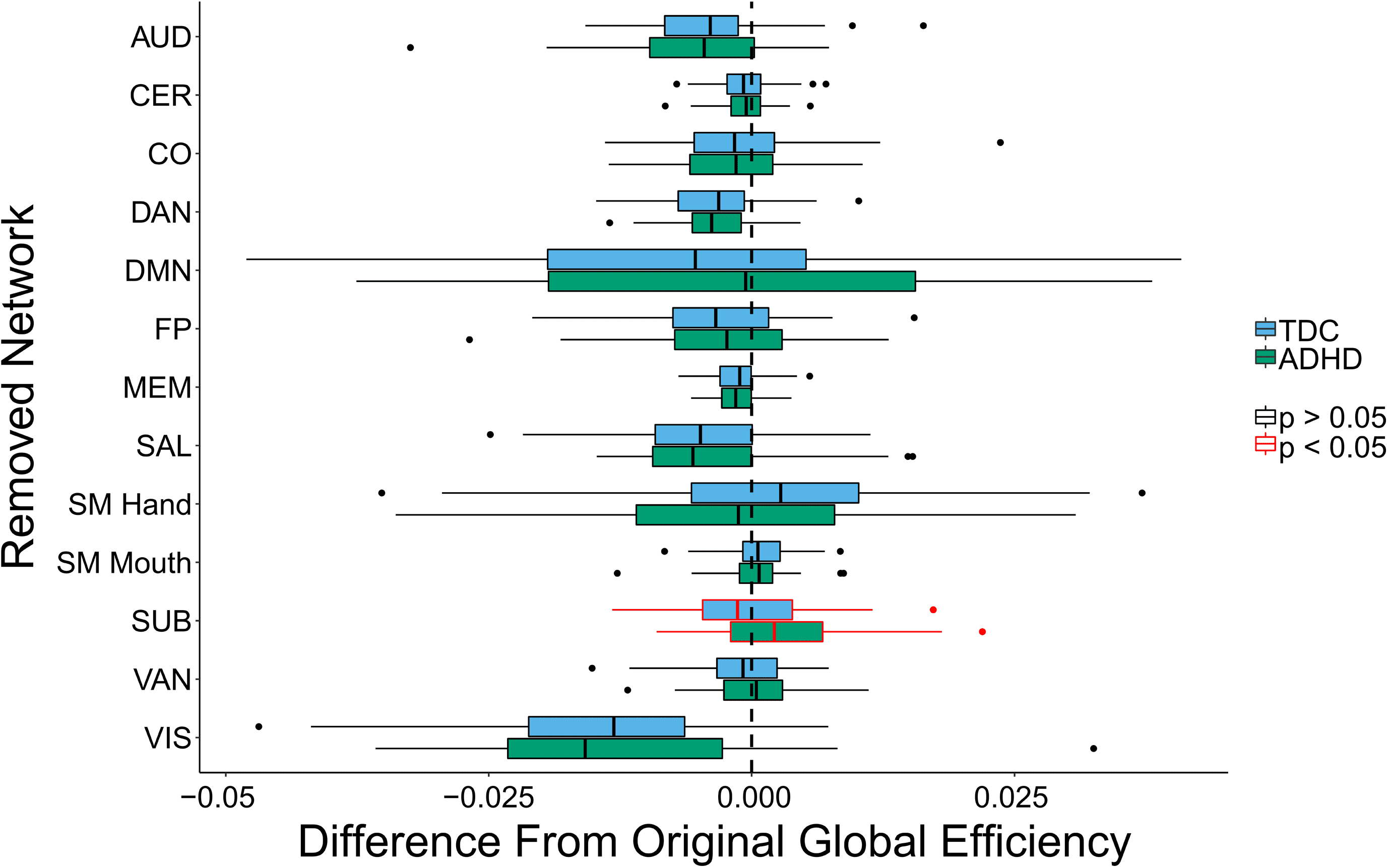
Differential impact of subnetwork removal: 最后, we examined whether the removal of
any of the functional subnetworks led to a differential change in global efﬁciency for children
with ADHD as compared with TD children.

The only subnetwork that exhibited signiﬁcant differential impact after adjusting for mul-
tiple comparisons was the SUB subnetwork. Children with ADHD exhibited an increase in
global efﬁciency after SUB subnetwork removal, while TD children exhibited a slight decrease
(数字 5). These ﬁndings suggest that the SUB subnetwork has lower integration with the global
network in children with ADHD. The lower integration of the SUB subnetwork in children with
ADHD is consistent with prior ﬁndings of disruptions in cortico-striatal-thalamic-cortical loops
in ADHD (for a review, see Posner, 公园, & 王, 2014). 重要的, this ﬁnding is an ex-
ample of equiﬁnality, as the difference in the local topology of the subcortical network did
not lead to an observed difference in whole-brain global efﬁciency. 桌子 3 in the Supporting
Information contains the numerical differences and p values for this analysis.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 5. Differential impact on global efﬁciency when removing subnetworks between children
with ADHD and TD children. Central line is the median, box is the interquartile range (IQR), 和
whiskers represent 1.5 ∗ IQR. Points represent values more than 2 SD away from the mean. Removal
of the subcortical subnetwork (SUB) led to a greater increase in global efﬁciency in children with
ADHD as compared with TD children, suggesting that the SUB subnetwork is less integrated into the
whole-brain network in children with ADHD. Signiﬁcant differences were based on BH corrected
p values.

网络神经科学

The network statistic jackknife

讨论

Whole-brain network analysis is a powerful tool for assessing brain topology, yet it lacks the
ability to localize ﬁndings related to global topology to a speciﬁc location. This issue, com-
bined with the fact that robust local differences do not necessarily result in observable global
differences in topology, suggests that whole-brain network analysis has a substantial blind
spot. Local graph theory analysis metrics can alleviate this but lack the ability to directly relate
local ﬁndings to global topology. 在本文中, we introduced the NS jackknife, a ﬂexible tool
for localizing global differences in network topology. Our framework links the global scope to
the local scope (Hallquist & Hillary, 2018) and is ﬂexible enough to operate on any global
network statistic. We implemented this framework in an open source R package, netjack
to make it accessible to re-
(亨利, 2018; https://CRAN.R-project.org/package=netjack)
searchers. Our simulation study evaluating the performance of the NS jackknife showed that
the method has excellent sensitivity to local differences in network topology across a variety of
状况, while keeping the false discovery rate at a nominal level (0.05; see the Supporting
信息).

The NS jackknife is an extension of the simulated lesioning approach that offers a variety of
advantages to neuroimaging researchers interested in examining group differences in network
topology. The NS jackknife extends the simulated lesioning approach beyond its most common
应用, examining the robustness of a network to attack, thus enabling researchers to
examine how individual elements of a given network contribute to a global network statistic.
It can be applied to any global network statistic under study, which allows researchers to extend
existing analysis pipelines rather than requiring implementation of a new set of analyses. 这
speciﬁcity of a global analysis can be tested at any level of resolution (subnetwork, node,
边缘), and resulting signiﬁcance tests are appropriately corrected for multiple comparisons,
making this an easy tool to implement and interpret. 最后, while the focus here was on binary
networks derived from functional MRI data, the NS jackknife can easily be applied to weighted
functional networks or to structural networks derived from diffusion-weighted imaging.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

There are several further methodological developments for the NS jackknife. While we fo-
cused on comparisons between two groups of subjects, future versions of the NS jackknife
toolbox will allow for within-subject across-time comparisons, testing covariates and control-
ling for potential confounds, and analyzing factorial grouping structures. The NS jackknife
framework can be extended to generalized linear regression approaches as well as to allow
for dependencies, such as those that arise from multiple collection sites. This is an active area
of development, with implementations being introduced in the near future. Although the NS
jackknife as currently presented examines network statistics as the outcome, it is likewise nat-
ural to consider network statistics as predictors of some distal outcome, such as behavior or
symptomology. Our framework can be extended to handle cases where some distal outcome
is of interest and would allow an assessment of the importance of local differences in network
topology with regard to that distal outcome.

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

最后, our empirical example produced results that were consistent with prior results
suggesting little difference in global metrics of functional integration (IE。, global efﬁciency)
between children with ADHD and TD children. 重要的, our use of the NS jackknife un-
covered an occurrence of equiﬁnality, in which a local group difference did not lead to a
global group difference. Speciﬁcally, an analysis of group differences and differential impact of
subnetwork removal showed that the subcortical subnetwork was less integrated into the whole-
brain network in children with ADHD, consistent with prior literature (Hong et al., 2014).

网络神经科学

The network statistic jackknife

Limitations and Considerations

A key consideration for the use of the NS jackknife is in the use of weighted networks or
networks formed from white matter tractography. The NS jackknife is agnostic to the type of
网络 (weighted vs. binary, undirected vs. 指导的), but special care needs to be taken
when using weighted networks to ensure that the appropriate network statistics are used. 为了
例子, when global efﬁciency is computed on correlation networks, it often exhibits scaling
issues due to taking the inverse of correlations that are close to zero. If those correlations are
removed during the NS jackknife, the resulting difference in global efﬁciency could simply be
due to that scaling, and not due to any true difference in network structure. This is an issue for
any weighted graph analysis and is not limited to the NS jackknife approach.

NS jackknife as a general framework has a limitation that users need to consider. As most
tests of interest involve multiple comparisons, a multiple comparison correction is necessary to
reduce the false discovery rate. Because of this, as the number of network features jackknifed
增加, power to detect any given difference due to the removal of a single network feature
decreases. This therefore limits the scope of an NS jackknife application. In smaller samples,
NS jackknife is likely best applied to questions regarding functional subnetworks, 其中
the number of subnetworks is relatively small and potential impacts are large. For larger
学习, particularly studies utilizing public datasets such as the Human Connectome Project
(Van Essen et al., 2013) or the Autism Brain Imaging Data Exchange (ABIDE) datasets
(Di Martino et al., 2017; Di Martino et al., 2014), it becomes more feasible to examine dif-
ferences at the level of nodes or even edges. Another strategy that researchers with smaller
samples can employ is examining more localized networks with the NS jackknife. 对于前-
充足, conducting an analysis limiting the network under consideration to the default mode
network and removing nodes and edges of that smaller network rather than of the whole-brain
网络. This particular limitation, 然而, is inherent to neuroimaging analysis given the
high-dimensional nature of the data. This speaks to a general need for the development of
analytic methods of high-dimensional data dealing with issues of global to local scoping as
discussed above. One potential solution to this problem is to use the screen ﬁltering method
of Meskaldji and colleagues (2015) to adjust the p values for tests of difference at the node or
edge level with respect to subnetwork groupings.

For pedagogical purposes the manuscript focused on detecting local differences in single
canonical functional subnetworks; 然而, the NS jackknife can be applied to combinations
of canonical subnetworks as well combinations of nodes or edges. One key consideration
here is that of combinatoric complexity. When using the NS jackknife to test removal of com-
binations of multiple subnetworks or nodes, the number of possible combinations increases
factorially. To avoid this, the NS jackknife can be used in a conﬁrmatory way, with researchers
specifying a set of combinations of network structures informed by previous literature or a pre-
vious exploratory application of NS jackknife, then testing for local differences with that set
of combinations. 最后, the NS jackknife does not require the use of canonical subnetworks
as demonstrated here. Sample-speciﬁc parcellations derived from some other method can be
used instead. The only requirement here is that a given network is deﬁned on the same nodes
for all subjects.

There are two additional considerations for researchers interested in using the NS jackknife
框架. The ﬁrst is that of network construction. The NS jackknife assumes a ﬁxed network
结构, and that the only changes that are occurring are due to the removal of speciﬁc
网络特性. This means that network estimation techniques, such as regularized partial
correlations, are to be used before the NS jackknife is applied, and not applied to the jackknifed

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The network statistic jackknife

networks themselves. This ensures that any localized effect can be interpreted as due to the
removal of the speciﬁc structure only, and not an analytical artifact caused by a reestimation
of the network.

The second consideration is that of the density/strength dependency. As mentioned earlier,
network statistics (such as average degree) are dependent on the size and density of the network
(van Wijk et al., 2010). 像这样, it is expected that the network statistics would change when
structures are removed. This potentially causes issues with interpretation, where an observed
group difference might simply be due to differences in density of the removed component
rather than any topological difference. One potential solution to this interpretational concern
is to add the network element’s density or strength as a covariate to the jackknife models.
Research into adjustments for density/strength dependency is ongoing.

结论

In closing, the NS jackknife framework bridges the gap between global network analysis and
local differences in topology, making it an ideal tool with which to investigate the speciﬁcity
of observed differences in whole-brain topology. 此外, it allows researchers to explore
local network features in the absence of a global result while still using the tools, terminology,
and interpretation of network neuroscience at the global level. 最后, future developments will
extend the NS jackknife to more complex modeling frameworks and settings, further extending
its utility within the neuroimaging community.

SUPPORTING INFORMATION

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00109.
The NS jackknife method is available at https://cran.r-project.org/package=netjack (亨利,
2018).

作者贡献

Teague Henry: 形式分析; 调查; 方法; 软件; 可视化; Writing –
Original Draft; Writing – Review & Editing. Kelly A. Duffy: 数据管理; 资源; Writing –
审查 & Editing. Marc D. Rudolph: Writing – Original Draft; Writing – Review & Editing. Mary
Beth Nebel: 数据管理; Writing – Review & Editing. Stewart H. Mostofsky: 数据管理;
资金获取; Writing – Review & Editing. Jessica R. 科恩: 概念化; 资金
acquisition; 资源; 监督; Writing – Original Draft; Writing – Review & Editing.

资金信息

Jessica R. 科恩, National Institute of Mental Health (我们), 奖项ID: R00MH102349. 斯图尔特
H. Mostofsky, National Institute of Mental Health (我们), 奖项ID: R01MH085328. 斯图尔特
H. Mostofsky, National Institute of Mental Health (我们), 奖项ID: R01MH078160. Mary Beth
Nebel, National Institute of Mental Health (我们), 奖项ID: K01MH109766.

参考

Abraham, A。, Pedregosa, F。, Eickenberg, M。, Gervais, P。, Mueller,
A。, Kossaiﬁ, J。, . . . Varoquaux, G. (2014). Machine learning for
neuroimaging with scikit-learn. 神经信息学前沿, 8.
https://doi.org/10.3389/fninf.2014.00014

Achard, S。, Salvador, R。, Whitcher, B., Suckling, J。, & 布莫尔,
乙. (2006). A resilient, low-frequency, small-world human brain
functional network with highly connected association cortical

枢纽. 神经科学杂志, 26(1), 63–72. https://doi.org/10.
1523/JNEUROSCI.3874-05.2006

Alstott, J。, Breakspear, M。, 哈格曼, P。, 卡蒙, L。, & 斯波恩斯,
氧. (2009). Modeling the impact of lesions in the human brain.
公共科学图书馆计算生物学, 5(6), e1000408. https://doi.org/10.
1371/journal.pcbi.1000408

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The network statistic jackknife

American Psychiatric Association. (2013). Diagnostic and statistical
manual of mental disorders (5第三版。). Arlington, VA: 美国人
Psychiatric Publishing.

Avants, 乙. B., 爱泼斯坦, C. L。, Grossman, M。, & Gee, J. C. (2008). Sym-
metric diffeomorphic image registration with cross-correlation:
Evaluating automated labeling of elderly and neurodegenerative
脑. Medical Image Analysis, 12(1), 26–41. https://doi.org/10.
1016/j.media.2007.06.004

Barber, A. D ., Jacobson, L. A。, Wexler, J. L。, Nebel, 中号. B., Caffo,
乙. S。, Pekar, J. J。, & Mostofsky, S. H. (2015). Connectivity support-
ing attention in children with attention deﬁcit hyperactivity dis-
命令. 神经影像: Clinical, 7, 68–81. https://doi.org/10.1016/j.
nicl.2014.11.011

Bassett, D. S。, & 斯波恩斯, 氧. (2017). Network neuroscience. 自然
神经科学, 20(3), 353–364. https://doi.org/10.1038/nn.4502
Baum, G. L。, Ciric, R。, Roalf, D. R。, 贝策尔, 右. F。, 摩尔, 时间. M。,
(2017). Modular
筱原, 右. T。,
segregation of structural brain networks supports the develop-
ment of executive function in youth. 现代生物学, 27(11),
1561–1572.e8. https://doi.org/10.1016/j.cub.2017.04.051

. Satterthwaite, 时间. D.

Benjamini, Y。, & Hochberg, 是. (1995). Controlling the false discov-
ery rate: A practical and powerful approach to multiple testing.
Journal of the Royal Statistical Society. Series B (Methodological),
57(1), 289–300. https://doi.org/10.2307/2346101

Benjamini, Y。, & Yekutieli, D. (2001). The control of the false discov-
ery rate in multiple testing under dependency. Annals of Statistics,
29(4), 1165–1188. https://doi.org/10.1214/aos/1013699998
Bertalanffy, L. Von. (1950). An outline of general system theory.
British Journal for the Philosophy of Science, 1(2), 134–165. https://
doi.org/10.1093/bjps/I.2.134

曹, M。, Shu, N。, 曹, Q., 王, Y。, & 他, 是. (2014). 图像-
ing functional and structural brain connectomics in attention-
deﬁcit/hyperactivity disorder. Molecular Neurobiology, 50(3),
1111–1123. https://doi.org/10.1007/s12035-014-8685-x

Castellanos, F. X。, & Proal, 乙. (2012). Large-scale brain systems in
ADHD: Beyond the prefrontal-striatal model. Trends in Cogni-
tive Sciences, 16(1), 17–26. https://doi.org/10.1016/j.tics.2011.
11.007

Ciric, R。, Wolf, D. H。, 力量, J. D ., Roalf, D. R。, Baum, G. L。,
Ruparel, K., . . . Satterthwaite, 时间. D. (2017). Benchmarking of
participant-level confound regression strategies for the control
of motion artifact in studies of functional connectivity. Neuro-
图像,154, 174–187. https://doi.org/10.1016/j.neuroimage.2017.
03.020

科恩, J. R。, & D’Esposito, 中号. (2016). The segregation and integra-
tion of distinct brain networks and their relationship to cognition.
神经科学杂志, 36(48), 12083–12094. https://doi.org/
10.1523/JNEUROSCI.2965-15.2016

考克斯, 右. 瓦. (1996). AFNI: Software for analysis and visualization
of functional magnetic resonance neuroimages. Computers and
Biomedical Research, 29(3), 162–173. https://doi.org/10.1006/
cbmr.1996.0014

Crucitti, P。, Latora, 五、, Marchiori, M。, & Rapisarda, A. (2004). Error
and attack tolerance of complex networks. Physica A: Statistical
Mechanics and Its Applications, 340(1–3), 388–394. https://土井.
org/10.1016/j.physa.2004.04.031

戴尔, A. M。, 菲舍尔, B., & Sereno, 中号. 我. (1999). Cortical surface-
based analysis:
我. Segmentation and surface reconstruction.
神经影像, 9(2), 179–194. https://doi.org/10.1006/nimg.1998.
0395

Di Martino, A。, O’Connor, D ., 陈, B., Alaerts, K., 安德森, J. S。,
Assaf, M。, . . . Milham, 中号. 磷. (2017). Enhancing studies of the
connectome in autism using the autism brain imaging data ex-
change II. Scientiﬁc Data, 4(170010). https://doi.org/10.1038/
sdata.2017.10

Di Martino, A。, Shehzad, Z。, 凯莉, C。, Roy, A. K., Gee, D. G。, Uddin,
L. Q., . . . Milham, 中号. 磷. (2009). Relationship between cingulo-
insular functional connectivity and autistic traits in neurotypical
adults. American Journal of Psychiatry, 166(8), 891–899. https://
doi.org/10.1176/appi.ajp.2009.08121894

Di Martino, A。, 严, C. G.-G., 李, Q., Denio, E., Castellanos,
F. X。, Alaerts, K., . . . Milham, 中号. 磷. (2014). The autism brain
imaging data exchange: Towards a large-scale evaluation of the
intrinsic brain architecture in autism. Molecular Psychiatry, 19(6),
659–667. https://doi.org/10.1038/mp.2013.78

Efron, 乙. (1982). The jackknife, the bootstrap and other resampling
计划. 费城, PA: Society for Industrial and Applied Math-
信息学. https://doi.org/10.1137/1.9781611970319

Esteban, 奥。, Markiewicz, C。, 布莱尔, 右. W., Moodie, C。, Isik, A. 我。,
Aliaga, A. E., . . . Gorgolewski, K. J. (2018). FMRIPrep: A ro-
bust preprocessing pipeline for functional MRI. BioRxiv, 306951.
https://doi.org/10.1101/306951

Fonov, 五、, 埃文斯, A。, McKinstry, R。, Almli, C。, & 柯林斯, D. (2009).
Unbiased nonlinear average age-appropriate brain templates
from birth to adulthood. 神经影像, 47(1), S102. https://土井.
org/10.1016/S1053-8119(09)70884-5

假如, A。, 布莫尔, 乙. T。, & 扎莱斯基, A. (2017). Opportunities and
challenges for psychiatry in the connectomic era. Biological Psy-
chiatry: Cognitive Neuroscience and Neuroimaging, 2(1), 9–19.
https://doi.org/10.1016/j.bpsc.2016.08.003

假如, A。, 扎莱斯基, A。, & Breakspear, 中号. (2015). The connectomics of
brain disorders. 自然评论神经科学, 16(3), 159–172.
https://doi.org/10.1038/nrn3901

Gorgolewski, K., Burns, C. D ., 麦迪逊, C。, 克拉克, D ., Halchenko,
是. 奥。, Waskom, 中号. L。, & 戈什, S. S. (2011). Nipype: A ﬂexible,
lightweight and extensible neuroimaging data processing frame-
work in Python. 神经信息学前沿, 5(13). https://土井.
org/10.3389/fninf.2011.00013

Grayson, D. S。, & Fair, D. A. (2017). Development of large-scale
functional networks from birth to adulthood: A guide to the neu-
roimaging literature. 神经影像, 160, 15–31. https://doi.org/
10.1016/j.neuroimage.2017.01.079

Greicius, 中号. D ., Krasnow, B., Reiss, A. L。, & Menon, V. (2003).
Functional connectivity in the resting brain: A network analy-
sis of the default mode hypothesis. 国家会议录
Academy of Sciences, 100(1), 253–258. https://doi.org/10.1073/
普纳斯.0135058100

Greve, D. N。, & 菲舍尔, 乙. (2009). Accurate and robust brain image
alignment using boundary-based registration. 神经影像, 48(1),
63–72. https://doi.org/10.1016/j.neuroimage.2009.06.060

Guimerà, R。, & Nunes Amaral, L. A. (2005). Functional cartography
of complex metabolic networks. 自然, 433(7028), 895–900.
https://doi.org/10.1038/nature03288

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The network statistic jackknife

Hallquist, 中号. N。, & Hillary, F. G. (2018). Graph theory approaches
to functional network organization in brain disorders: A critique
for a brave new small-world. 网络神经科学, 1(八月),
243741. https://doi.org/10.1101/243741

亨利, 时间. 右.

(2018). Netjack: Tools for working with samples
of networks. Retrieved from https://cran.r-project.org/package=
netjack

亨利, 时间. R。, & 科恩, J. 右. (2019). Dysfunctional brain network
organization in neurodevelopmental disorders. 在P. J. Laurienti,
乙. Munsell, & G. 吴 (编辑。), Connectomics: 方法, mathemat-
ical models and applications. 爱思唯尔.

亨利, 时间. R。, Dichter, G. S。, & Gates, K. (2018). Age and gender
effects on intrinsic connectivity in autism using functional in-
tegration and segregation. Biological Psychiatry: Cognitive Neu-
roscience and Neuroimaging, 3(5), 414–422. https://doi.org/10.
1016/j.bpsc.2017.10.006

洪, S. B., 扎莱斯基, A。, 假如, A。, 公园, S。, 哪个, 是. H。, 公园,
中号. H。, . . . Kim, J. 瓦. (2014). Connectomic disturbances in
attention-deﬁcit/hyperactivity disorder: A whole-brain tractogra-
phy analysis. Biological Psychiatry, 76(8), 656–663. https://土井.
org/10.1016/j.biopsych.2013.12.013

詹金森, M。, 栏干, P。, 布雷迪, M。, & 史密斯, S. (2002). 改进
optimization for the robust and accurate linear registration and
motion correction of brain images. 神经影像, 17(2), 825–841.
https://doi.org/10.1016/S1053-8119(02)91132-8

克莱因, A。, 戈什, S. S。, Bao, F. S。, Giard, J。, Häme, Y。, Stavsky,
E., . . . Keshavan, A. (2017). Mindboggling morphometry of hu-
man brains. 公共科学图书馆计算生物学, 13(2). https://doi.org/
10.1371/journal.pcbi.1005350

Kucyi, A。, Tambini, A。, 萨达吉亚尼, S。, Keilholz, S。, & 科恩, J. 右.
(2018). Spontaneous cognitive processes and the behavioral vali-
dation of time-varying brain connectivity. 网络神经科学,
1–57. https://doi.org/10.1162/NETN_a_00037

Latora, 五、, & Marchiori,中号. (2001). Efficient behavior of small-worldnet-
作品. 物理评论快报, 87(19), 198701-1-198701–198704.
https://doi.org/10.1103/PhysRevLett.87.198701

Lewis, J. D ., Theilmann, 右. J。, Townsend, J。, & 埃文斯, A. C. (2013).
Network efﬁciency in autism spectrum disorder and its relation to
brain overgrowth. Frontiers in Human Neuroscience, 7. https://
doi.org/10.3389/fnhum.2013.00845

林, P。, Sun, J。, 于, G。, 吴, Y。, 哪个, Y。, 梁, M。, & 刘, X. (2014).
Global and local brain network reorganization in attention-
deﬁcit/hyperactivity disorder. Brain Imaging and Behavior, 8(4),
558–569. https://doi.org/10.1007/s11682-013-9279-3

Meskaldji, D. E., Vasung, L。, Romascano, D ., Thiran, J. P。, 哈格曼,
P。, Morgenthaler, S。, & Van De Ville, D. (2015). Improved stat-
istical evaluation of group differences in connectomes by
screening-ﬁltering strategy with application to study matura-
tion of brain connections between childhood and adolescence.
神经影像,108, 251–264. https://doi.org/10.1016/j.neuroimage.
2014.11.059

纽曼, 中号. 乙. J. (2006). Modularity and community structure in
网络. 美国国家科学院院刊, 103(23),
8577–8582. https://doi.org/10.1073/pnas.0601602103

Nowicki, K., & Snijders, 时间. A. 乙. (2001). Estimation and predic-
tion for stochastic blockstructures. Journal of the American Statis-

tical Association, 96(455), 1077–1087. https://doi.org/10.1198/
016214501753208735

Pievani, M。, de Haan, W., 吴, T。, Seeley, 瓦. W., & Frisoni, G. 乙.
(2011). Functional network disruption in the degenerative de-
mentias. The Lancet Neurology, 10(9), 829–843,. https://doi.org/
10.1016/S1474-4422(11)70158-2

Posner, J。, 公园, C。, & 王, Z. (2014). Connecting the dots: A
review of resting connectivity MRI studies in attention-deﬁcit/
hyperactivity disorder. Neuropsychology Review, 24(1), 3–15.
https://doi.org/10.1007/s11065-014-9251-z

力量, J. D ., 巴恩斯, K. A。, 斯奈德, A. Z。, 施拉加尔, 乙. L。, &
彼得森, S. 乙. (2012). Spurious but systematic correlations in
functional connectivity MRI networks arise from subject mo-
的. 神经影像, 59(3), 2142–2154. https://doi.org/10.1016/j.
neuroimage.2011.10.018

力量, J. D ., 科恩, A. L。, 纳尔逊, S. M。, 假发, G. S。, 巴恩斯, K. A。,
教会, J. A。, . . . 彼得森, S. 乙. (2011). Functional network or-
ganization of the human brain. 神经元, 72(4), 665–678. https://
doi.org/10.1016/j.neuron.2011.09.006

力量, J. D ., 米特拉, A。, 劳曼, 时间. 奥。, 斯奈德, A. Z。, 施拉加尔,
乙. L。, & 彼得森, S. 乙. (2013). Methods to detect, characterize,
and remove motion artifact in resting state fMRI. 神经影像, 84,
320–341. https://doi.org/10.1016/j.neuroimage.2013.08.048
Roine, U。, Roine, T。, Salmi, J。, Nieminen-von Wendt, T。, Tani,
P。, Leppämäki, S。, . . . Sams, 中号. (2015). Abnormal wiring of
the connectome in adults with high-functioning autism spectrum
紊乱. Molecular Autism, 6(1), 65. https://doi.org/10.1186/
s13229-015-0058-4

Rudie,

J. D ., & Dapretto, 中号.

(2013). Convergent evidence of
brain overconnectivity in children with autism? Cell Reports, 5(3),
565–566. https://doi.org/10.1016/j.celrep.2013.10.043

J。, Calkins, 中号. E.,

Satterthwaite, 时间. D ., Elliott, 中号. A。, Gerraty, 右. T。, Ruparel, K.,
Loughead,
(2013). 一个
.
improved framework for confound regression and ﬁltering for
control of motion artifact in the preprocessing of resting-state
functional connectivity data. 神经影像, 64(1), 240–256. https://
doi.org/10.1016/j.neuroimage.2012.08.052

. Worf, D. H.

Seeley, 瓦. W., Menon, 五、, Schatzberg, A. F。, 凯勒, J。, Glover, G. H。,
Kenna, H。, . . . Greicius, 中号. D. (2007). Dissociable intrinsic con-
nectivity networks for salience processing and executive control.
神经科学杂志, 27(9), 2349–2356. https://doi.org/10.
1523/JNEUROSCI.5587-06.2007

Shine, J. M。, & Poldrack, 右. A. (2017). Principles of dynamic
network reconﬁguration across diverse brain states. NeuroIm-
年龄, 180(Pt. 乙), 396–405. https://doi.org/10.1016/j.neuroimage.
2017.08.010

Snijders, 时间. A. B., & Borgatti, S. 磷. (1999). Non-parametric standard
errors and tests for network statistics. 连接, 22(2), 1–10.
斯波恩斯, 氧. (2013). Network attributes for segregation and integra-
tion in the human brain. 神经生物学的当前观点, 23(2),
162–171. https://doi.org/10.1016/j.conb.2012.11.015

斯波恩斯, 奥。, Chialvo, D. R。, Kaiser, M。, & 希尔格塔格, C. C. (2004).
组织, development and function of complex brain net-
作品. 认知科学的趋势, 8(9), 418–425. https://土井.
org/10.1016/j.tics.2004.07.008

Tukey, J. 瓦. (1958). Bias and conﬁdence in not-quite large sample.

Annals of Mathematical Statistics, 29, 614.

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

The network statistic jackknife

Tustison, 氮.

J。, Avants, 乙. B., 厨师, 磷. A。, 郑, Y。, Egan,
A。, Yushkevich, 磷. A。, & Gee, J. C. (2010). N4ITK: 改进
N3 bias correction. IEEE Transactions on Medical Imaging, 29(6),
1310–1320. https://doi.org/10.1109/TMI.2010.2046908

Van Essen, D. C。, 史密斯, S. M。, Barch, D. M。, 贝伦斯, 时间. 乙. J。,
Yacoub, E., & Ugurbil, K. (2013). The WU-minn human connec-
tome project: 概述. 神经影像, 80, 62–79. https://土井.
org/10.1016/j.neuroimage.2013.05.041

van Wijk, 乙. C. M。, 斯塔姆, C. J。, & Daffertshofer, A. (2010). 康姆-
paring brain networks of different size and connectivity density
using graph theory. PLoS ONE, 5(10), e13701. https://doi.org/10.
1371/journal.pone.0013701

王, L。, 朱, C。, 他, Y。, Zang, Y。, 曹, Q., 张, H。, . . . 王,
是. (2009). Altered small-world brain functional networks in chil-

dren with attention-deﬁcit/hyperactivity disorder. 人脑
测绘, 30(2), 638–649. https://doi.org/10.1002/hbm.20530
Yoo, K., 李, P。, 钟, 中号. K., Sohn, 瓦. S。, 钟, S. J。, Na, D. L。,
. . . Jeong, 是. (2017). Degree-based statistic and center persistency
for brain connectivity analysis. 人脑图谱, 38(1),
165–181. https://doi.org/10.1002/hbm.23352

扎莱斯基, A。, 假如, A。, & 布莫尔, 乙. 时间. (2010). 基于网络
statistic: Identifying differences in brain networks. 神经影像,
53(4), 1197–1207. https://doi.org/10.1016/j.neuroimage.2010.
06.041

张, 是. J。, 布雷迪, M。, & 史密斯, S. 乙. (2001). Segmentation of brain
MR images through a hidden Markov random ﬁeld model and the
expectation-maximization algorithm. IEEE Transactions on Med-
ical Imaging, 20, 45–57.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
1
7
0
1
9
2
0
5
3
8
n
e
n
_
A
_
0
0
1
0
9
p
d