信 - 麻省理工学院人工智能研究专业

信

Communicated by Si Wu

Progressive Interpretation Synthesis: Interpreting
Task Solving by Quantifying Previously Used
and Unused Information

Zhengqi He
zhengqi.he@riken.jp
Lab for Neural Computation and Adaptation, 日本理化学研究所脑科学中心,
埼玉 351-0198, 日本

Taro Toyoizumi
taro.toyoizumi@riken.jp
Lab for Neural Computation and Adaptation, 日本理化学研究所脑科学中心,
埼玉 351-0198, 日本, and Department of Mathematical Informatics, Graduate
School of Information Science and Technology, the University of Tokyo,
东京 113-8656, 日本

A deep neural network is a good task solver, but it is difficult to make
sense of its operation. People have different ideas about how to interpret
its operation. We look at this problem from a new perspective where the
interpretation of task solving is synthesized by quantifying how much
and what previously unused information is exploited in addition to the
information used to solve previous tasks. 第一的, after learning several
任务, the network acquires several information partitions related to each
任务. We propose that the network then learns the minimal information
partition that supplements previously learned information partitions to
more accurately represent the input. This extra partition is associated
with unconceptualized information that has not been used in previous
任务. We manage to identify what unconceptualized information is used
and quantify the amount. To interpret how the network solves a new task,
we quantify as meta-information how much information from each par-
tition is extracted. We implement this framework with the variational in-
formation bottleneck technique. We test the framework with the MNIST
and the CLEVR data set. The framework is shown to be able to com-
pose information partitions and synthesize experience-dependent inter-
pretation in the form of meta-information. This system progressively
improves the resolution of interpretation upon new experience by con-
verting a part of the unconceptualized information partition to a task-
related partition. It can also provide a visual interpretation by imaging
what is the part of previously unconceptualized information that is
needed to solve a new task.

神经计算 35, 38–57 (2023)
https://doi.org/10.1162/neco_a_01542

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Progressive Interpretation Synthesis

1 介绍

Deep neural networks (DNNs) have made great achievements in fields
such as image recognition (克里热夫斯基, 吸勺, & 欣顿, 2017), speech
认出 (Hinton et al., 2012), natural language processing (Vaswani
等人。, 2017), and game playing beyond human-level performance (Silver
等人。, 2016). DNNs, 然而, are famous black-box models. That they
fail under certain circumstances, such as adversarial attack (好人,
Shlens, & 塞格德, 2014), motivates increasing research into understanding
how DNNs solve tasks or model interpretation. More recent research also
suggests that better model interpretation can be useful to, 例如,
explanation about model behavior, knowledge mining, 伦理, and trust.
(Doshi-Velez & Kim, 2017; Lipton, 2018)

Researchers have proposed different approaches to proceed with model
解释; 例如, concerning the interpretation style, the post
hoc style tries to separate the model training step and model interpreta-
tion step, and the concurrent style aims simultaneously for task perfor-
mance as well as interpretation (Lipton, 2018). As for the applicability of
interpretation methods, the model-specific type targets a certain class of
型号, and with the model-agnostic type, the interpretation method does
not depend on the model (Arrieta et al., 2020). Considering the scope of in-
terpretation, global interpretation gives information about how the task is
solved from a broader view, and local interpretation is more focused on cer-
tain examples or parts of the model (Doshi-Velez & Kim, 2017). 有
also diverse forms of interpretation, such as the information feature (陈,
歌曲, Wainwright, & 约旦, 2018), the relevance feature (Bach et al., 2015),
a hot spot of attention (哈德逊 & 曼宁, 2018), or gradient informa-
的 (Sundararajan, Taly, & 严, 2017). Another stream of research proposes
that interpretable models are usually simple ones: 例如, 离散的-
state models (Hou & 周, 2018), shallower decision trees (Freitas, 2014;
Wu et al., 2017), graph models (张, 曹, Shi, 吴, & 朱, 2017), 或一个
small number of neurons (Lechner et al., 2020). (See Arrieta et al., 2020, 为了
a more detailed overview.)

One particular dimension for model interpretation related to our let-
ter is how much preestablished human knowledge is needed. 方法
that require high human involvement, such as interpretation with human
predefined concepts (Koh et al., 2020; 陈, Bei, & Rudin, 2020) 或与
large human-annotated data sets (Kim, Tapaswi, & Fidler, 2018), implicitly
assume the background knowledge of an average human to make sense
of the interpretation, which is hard to define rigorously. Contrarily, 存在-
ing human-agnostic methods transfer interpretation into some measurable
形式, such as the depth of the decision tree (Freitas, 2014; Wu et al., 2017).
然而, how well this kind of measure is related to human-style interpre-
tation is under debate.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Z. He and T. Toyoizumi

Within the human-agnostic dimension of interpretation, we extend the
discussion with two new perspectives. One perspective starts with the sim-
ple idea that interpretation should be experience dependent. Motivated by
this idea, we focus on the situation where the model learns a sequence of
tasks by assuming that later tasks can be explained using earlier experi-
恩塞斯. 换句话说, model interpretation in our framework is defined
as meta-information describing how the information used to solve the new
task is related to previous ones. The second perspective is motivated by the
idea that interpretation should be able to handle the out-of-experience situ-
化. In a situation where a new task cannot be fully solved by experience,
the model interpretation method should be able to report new knowledge,
mimicking a human explaining what is newly learned. We demonstrate that
this framework can cast insight into how later tasks can be solved based on
previous experience on MNIST and CLEVR data sets (Johnson et al., 2017)
and express ignorance when experience is not applicable.

Our work is related to the concept bottleneck model (CBM) 和骗局-
cept whitening model (CWM; Koh et al., 2020; 陈等人。, 2020) 在
the sense that meaningful interpretation of the current task depends on
previously learned knowledge. 然而, these methods do not capture
reasonable interpretation when the human-defined concepts alone are in-
sufficient to solve downstream tasks (Margeloiu et al., 2021). In our frame-
工作, we add the unconceptualized region to take care of information not
yet associated with tasks. 而且, a recent study also shows that contam-
ination of concept-irrelevant information in the predefined feature space
can hamper interpretation (Mahinpei et al., 2021). We implement infor-
mation bottleneck (IB; 蒂什比, 佩雷拉, & Bialek, 2000) as a remedy to this
information leak problem. Our method also shares similarities with varia-
tional information bottleneck for interpretation (VIBI) 方法 (Bang, Xie,
李, 吴, & Xing, 2019) and the multiview information bottleneck method
(王, Boudreau, Luo, Tan, & 周, 2019) in the sense that these methods
use IB to obtain minimal latent representation from previously given repre-
句子. 然而, unlike the multiview IB method for problem solving,
the goal of our framework is to synthesize interpretation. 此外, 我们的
framework does so using macroscopic task-level representations, 这是
different from microscopic input-level representations used in VIBI.

2 Insight into Interpretation

This section discusses the intuition behind our framework for model inter-
预谋.

2.1 Interpretation as Meta-Information. To quantify how a new task
is solved using the experience of previous tasks, we evaluate meta-
信息. We define meta-information as a vector of mutual information,

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Progressive Interpretation Synthesis

where each element of the vector describes how much the corresponding
information partition is used for the new task.

2.1.1 Interpreting Using the Right Level. 在这项工作中, a machine learns a
series of different tasks. The aim is to ascribe an interpretation of how the
model solves the new task based on previous experience. If we did this us-
ing low-level features, such as the intensity and color of each pixel, the task
description would become complicated. 反而, we aim to give an inter-
pretation at a more abstract level—for example, “This new task is solved by
combining the knowledge about tasks 2 and 4.” To achieve this goal, infor-
mation about the input is partitioned at the task level. We therefore prepare
information partitions that encode useful features for each task.

2.1.2 Inducing Independence. These partitions have to satisfy certain con-
版本. If these information partitions are redundant, we will have arbi-
trariness in assigning meta-information since a task can equally be solved
using different partitions (Wibral, Priesemann, Kay, Lizier, & Phillips, 2017).
所以, inducing independence among partitions is preferred for hav-
ing unambiguous meta-information. Useful methods are widely available
in machine learning fields such as independent component analysis (钟
& Sejnowski, 1995; Hyvärinen & Oja, 2000) and variational autoencoders
(Kingma & Welling, 2013).

2.1.3 Meaning Assignment. We have defined meta-information meta-
information as a vector of Shannon information measured in bits (IE。, 如何
much each information partition is used). Although the number of bits itself
has no meaning, each entry of the vector is linked to a corresponding task.
因此, the meta-information can be mapped to the relevance of previous
任务.

2.2 Progressive Nature of Interpretation.

2.2.1 Progressive Interpretation. One important but usually ignored prop-
erty of interpretation is that we interpret based on experience (国家的
Research Council, 2002; Bada & Olusegun, 2015). Progressively learning
multiple tasks is not a rare setting in machine learning (Andreas, Rohrbach,
Darrell, & 克莱因, 2016; Rusu et al., 2016; 帕里西, Kemker, 部分, Kanan, &
Wermter, 2019), which is usually referred to as “lifelong learning,” “sequen-
tial learning,” or “incremental learning.” However, these studies usually
focus on avoiding catastrophic forgetting and do not investigate how pro-
gressiveness contributes to interpretation. In one example, Kim et al. (2018),
point out that interpretability emerges when lower-level modules are pro-
gressively made use of. We propose that interpretation should be synthe-
sized in a progressive manner, where the model behavior is interpreted by
how much the current task is related to previously experienced tasks.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Z. He and T. Toyoizumi

2.2.2 Knowing You Don’t Know. An experience-based progressive in-
terpretation framework may inevitably encounter the situation when its
previous experience does not help interpret the current task. To solve this
问题, we introduce an unconceptualized partition, storing information
not yet included in the existing information partitions. We noticed that
this unconceptualized partition generates a “knowing you don’t know”
type of interpretation—a meta-cognition ability that allows a person to re-
flect on their knowledge, including what they don’t know (Glucksberg &
McCloskey, 1981). Under this situation, the design of the framework should
be able to interpret knowing you don’t know when faced with out-of-
experience tasks.

We now formalize our insights in the language of information theory in

the following sections.

3 The Progressive Interpretation Framework

Assume we have a model with stochastic input X, which is statistically the
same regardless of a task. Task i is defined as predicting a series of stochastic
labels Zi. Its corresponding internal representation is Yi. The progressive
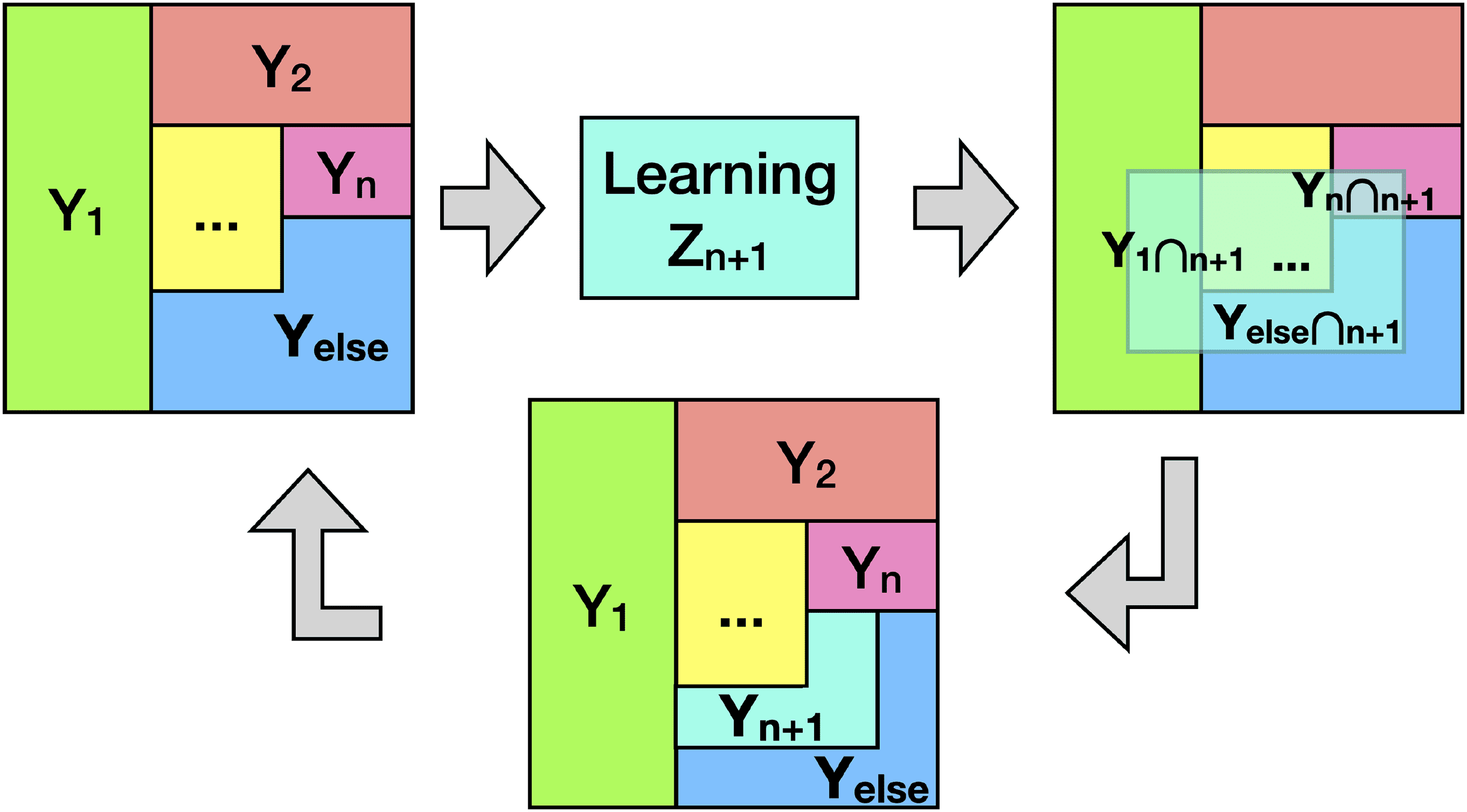
interpretation framework is formalized iteratively as follows:

, Y2

, . . . , Yn, Yelse

1. Assume that after task n, a model has a minimal internal representa-
tion Y = {Y1
} that encodes input X. Yi describes the
internal representation learned to solve task i. Yelse describes inter-
nal representation encoding X that is not yet used to solve and task.
The optimization in the ideal case yields independence among the
previous task-relevant partitions:

我(Yi

; Yj ) = 0, (我 (西德:2)= j ∈ [1, n] ∪ else).

这里, we define the notation [1, n] 成为 {1, 2, 3, . . . , n}.

2. Then the model is faced with the new task n + 1 and learns to predict
Zn+1. After learning Zn+1, the model distills the necessary part Y(i∩n+1)
from each partition Yi(i = [1, n] ∪ else) for solving task n + 1. 这是
achieved by minimizing

我(是(i∩n+1)

; Yi), (i ∈ [1, n] ∪ else)

while maintaining the best task performance, 那是, by maintaining
ideally all task-relevant information:

我(∪n,别的

i=1 Yi

; Zn+1) = I(∪n,别的

i=1 Y(i∩n+1)

; Zn+1).

3. The interpretation is defined as the meta-information of how much
the individual partitions {Yi
} for previous tasks i ∈ [1, n] ∪ else are
used to solve task n + 1. 即, the composition of the mutual

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Progressive Interpretation Synthesis

数字 1: A schematic plot showing the intuition of the progressive inter-
pretation framework. Interpretation in our framework is based on the meta-
information that specifies from which partitions the needed information comes
to solve a new task, Zn+1. The map has the resolution in the level of task par-
titions Yi, where partitions are made independent of each other. Independence
among task partitions ensures the uniqueness of the needed information. 任何-
thing the model has not yet learned to use would stay in the unconceptualized
Yelse region. The more tasks the model has encountered, the smaller the uncon-
ceptualized region would be. 因此, later tasks lead to better interpretation.

; Yi) over the different partitions i = [1, n] ∪ else
information I(是(i∩n+1)
is the meta-information we use to interpret the global operation of
the neural network. Then the local interpretation for each example is
available from {是(i∩n+1)

4. After task n + 1, the model updates the representation partition by
splitting Yelse into the newly added representation Y(else∩n+1) 和它的
\是(else∩n+1). Then the former is denoted as Yn+1 and
complement, Yelse
the latter as new Yelse. The model would continue for further iteration
and interpretation of the tasks.

The process is shown in Figure 1.

4 Implementation

Our particular interest is in the system involving neural networks. Since our
framework is information-theoretic, all types of neural networks are treated
equally as segments of information processing pipelines. Which type of
neural network to choose depends on the specific problem.

Neural network implementation of progressive interpretation can be im-
plemented as loops over the four steps set out in section 3. In step 1, 我们
assume a network already has information maps for task 1-to-n. Then we
extract the unconceptualized partition that is unrelated to task 1-to-n by

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Z. He and T. Toyoizumi

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

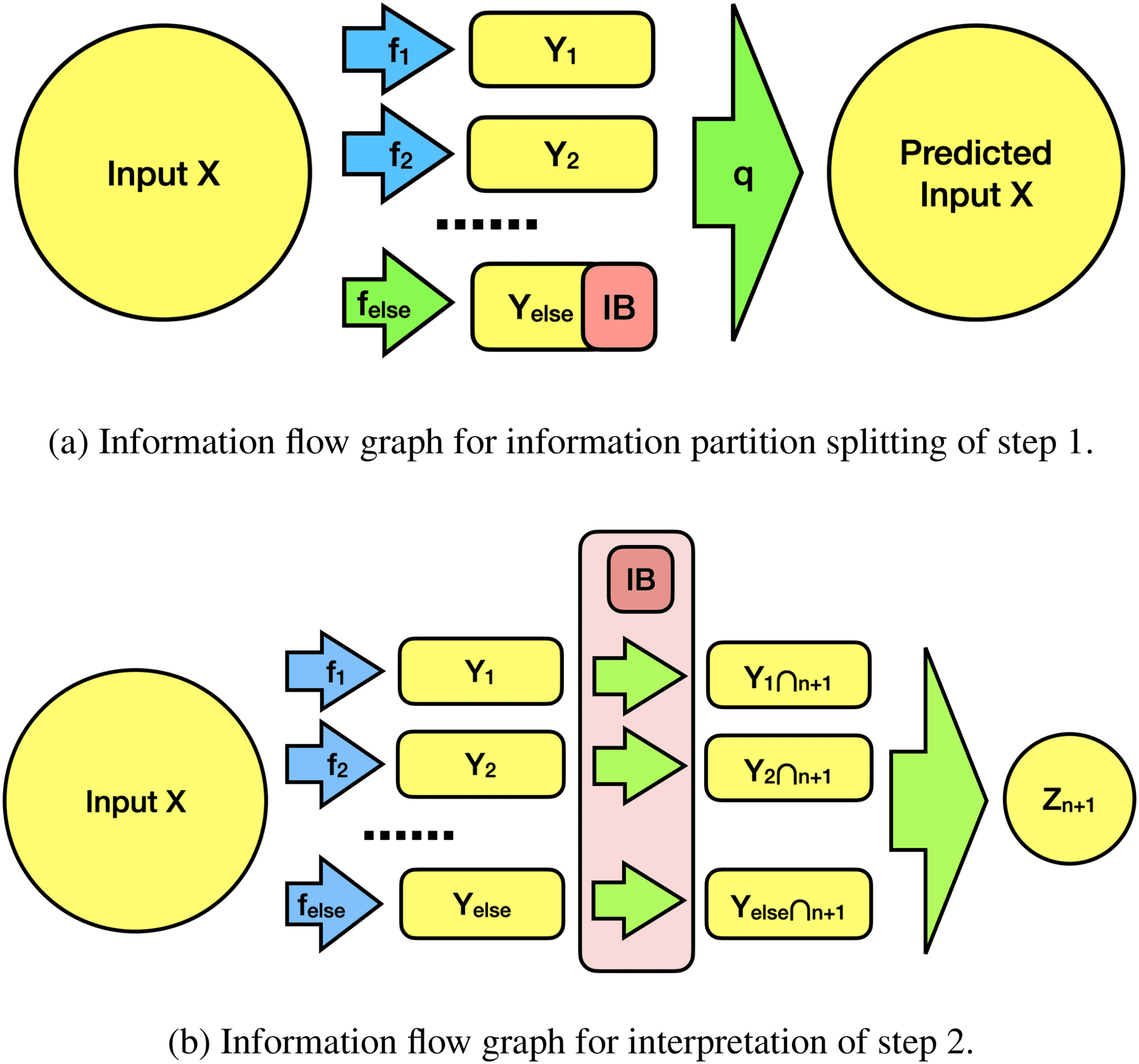
数字 2: Information flow graph of the progressive interpretation framework.
Yellow areas are representations, and green and blue arrows represent neural
网络. Green ones are put under training while blue ones are fixed. The red
square with IB represents the information bottleneck.

IB. In step 2, the model learns a new task, n + 1. Then the interpretation
is gained by knowing how much information is needed from each subre-
gion as in step 3. In step 4, we repeat step 1 with a new map for task n + 1
and prepare for the next loop. By adding new tasks and looping over the
脚步, a progressively more informative interpretation can be gained. 这
information flow chart implemented in the following sections is shown in
数字 2.

4.1 Information Bottleneck. In our framework, IB plays an important
role in manipulating information flow. To predict label Z from statistical
input X with inner representation Y, IB would maximize

[我(是; Z) − γ I(是; X )], Y = fθ (X, (西德:4)),

max
我

(4.1)

where γ ∈ [0, 1] is the scaling factor controlling the balance between the
task performance (when γ is small) and having nonredundant information
表示 (when γ is large). f is a neural network parameterized by

Progressive Interpretation Synthesis

the parameter θ , 和 (西德:4) is a noise term that is important to suppress task-
irrelevant information out of X.

We choose the variational information bottleneck (VIB) implementation
(Alemi, Fischer, Dillon, & 墨菲, 2016; Chalk, Marre, & Tkacik, 2016; 李 &
艾斯纳, 2019) with loss function

L(p, q, r) = E

是,Z

(西德:2)
− log q (Z | 是)

(西德:3)

+ γ EX{吉隆坡

(西德:2)

(西德:3)
p (是 | X ) , r(是)

}

(4.2)

to optimize the encoding distribution p(是|X ), decoding distribution q(Z|是),
and prior distribution r(是) for p. EX describes taking the expectation over
random variable X. Note that E
EZ|X. During the optimization,
= EXE
EXEZ|X is computed by averaging over N training samples of input {x j
| j =
1, . . . , 氮} and label {z j
是|X is the average over the encoding
distribution p(是|X ), which is computed using the mapping Y = fθ (X, (西德:4)) 的
the encoding neural network. Y can be a vector of either continuous or dis-
crete variables (李 & 艾斯纳, 2019) (see appendix section 3 欲了解详情). 为了
clarity, we further simplify the notation of loss function to be

| j = 1, . . . , 氮}. 乙

是|X

是,Z

L = Q(Z|是) + γ KL(是)

(4.3)

for future use, where the Q term corresponds to the log-likelihood term
trying to approximate Z from internal representation Y. The KL term cor-
responds to the KL-divergence term trying to control the expressiveness
of Y.

4.2 Task Training and Information Partition Splitting. Suppose a
new model with task input X learns its first task to predict label Z1. 它
is not difficult to train a neural network for this task by optimization:
minθ D( f1,θ (X )||Z1), where D is a distance function, such as KL divergence
or mean-square error, which is decided by the problem. f1,θ is an encoder
network parameterized by θ . After training, we will be able to obtain
= f1(X, (西德:4)), where f1 indicates a neural
the representation of task 1 as Y1
network f1,θ after optimizing θ .

Our next problem is how to obtain task 1 unrelated representation Yelse,
; Yelse) = 0, to complement the intermediate rep-
which ideally satisfies I(Y1
resentation about the input. 这里, we propose that Yelse can be obtained via
the implementation of IB on an autoencoding task:

max
我

[我(Y1

, Yelse

; X ) − γ I(Yelse

; X )],

Yelse

= felse,我 (X, (西德:4)),

(4.4)

where γ is again the scaling factor controlling the trade-off between in-
cluding and excluding different information. Note that the learned f1
function is fixed while felse,θ is trained. The intuition behind equation

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Z. He and T. Toyoizumi

; Yelse) > 0 implies redundant information
4.4 描述如下. 我(Y1
about Y1 contained in Yelse. This redundant information would not improve
; X ). 然而, removing this redundant information can decrease
我(Y1
; X ), thus contributing to our optimization goal. Note that we assume
我(Yelse
γ is less than one.

, Yelse

With the simplified notation of the VIB introduced above, the loss

function

L = Q(X|Y1

, Yelse) + γ KL(Yelse)

(4.5)

is minimized. The loss function seeks to autoencode X given previously
learned Y1 (which is fixed) together with Yelse, while controlling expressive-
ness of Yelse.

4.3 New Task Interpretation. Now assume the model has internal rep-
resentation Y = {Y1
} after learning tasks 1 to n. 当。。。的时候
new task n + 1 is introduced, the model learns to predict Zn+1. Task n + 1
relevant information can be extracted from Y by the IB as follows:

, . . . , Yn, Yelse

, Y2

(西德:4)
我(∪n,别的

i=1 Y(i∩n+1)

max
我

; Zn+1) − γ

(西德:6)

我(是(i∩n+1)

; Yi)

n,别的(西德:5)

我=1

是(i∩n+1)

= f(i∩n+1),我 (Yi

, (西德:4)),

(4.6)

, (i ∈ [1, n] ∪ else) is the information needed from Yi to solve
where Y(i∩n+1)
task n + 1. 再次, (西德:4) is the noise term required to eliminate information irrel-
evant to task n + 1. Since Y(i∩n+1)
, (西德:4)) depends on Yi, 一起
with IB, 是(i∩n+1) is then a minimum subpartition of Yi required for task
n + 1. We again implement the variational IB loss function with simplified
notation:

= f(i∩n+1),我 (Yi

L = Q(Zn+1

| ∪n,别的

i=1 Y(i∩n+1)) +

C
n + 1

n,别的(西德:5)

我=1

吉隆坡(是(i∩n+1)).

(4.7)

After getting {是(i∩n+1)

The loss function seeks to maximize the prediction of Zn+1 while controlling
the needed information from Yi. Index i specifies a representation partition.
}, we can derive an interpretation as the meta-
; Yi) needed from each partition Yi as defined in sec-
information I(是(i∩n+1)
的 3. We can also look into the representations of Y(i∩n+1) to gain insight
into how task n + 1 is solved for each example.

是(else∩n+1) is the information needed from the unconceptualized partition
Yelse to solve task n + 1. We can rewrite this to be Yn+1 and define the new
\是(别的;n+1). We can then go back
unconceptualized partition as Yelse
to step 1 and continue the iteration for task n + 2.

← Yelse

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Progressive Interpretation Synthesis

5 实验

5.1 MNIST Data Set. We first illustrate our progressive interpretation
framework on the MNIST data set (60,000/10,000 train/test splits). We set
任务 1 as digit recognition. For task 2, we propose three kinds of tasks: 阻止-
mining if a number is even or odd (parity task), predicting the sum of pixel
intensities (ink task), or a task that involves both digit information and pixel
intensity information with a certain resolution (见下文). 第一的, we train a
network f1 to perform digit recognition, and then we train an autoencoder
with IB to train a network felse to obtain a digit-independent partition. 然后
we extend the network to train on a second task and obtain interpretation
from the information flow. We choose continuous latent representation for
this section. (See appendix sections 1 和 2 for implementation details.)

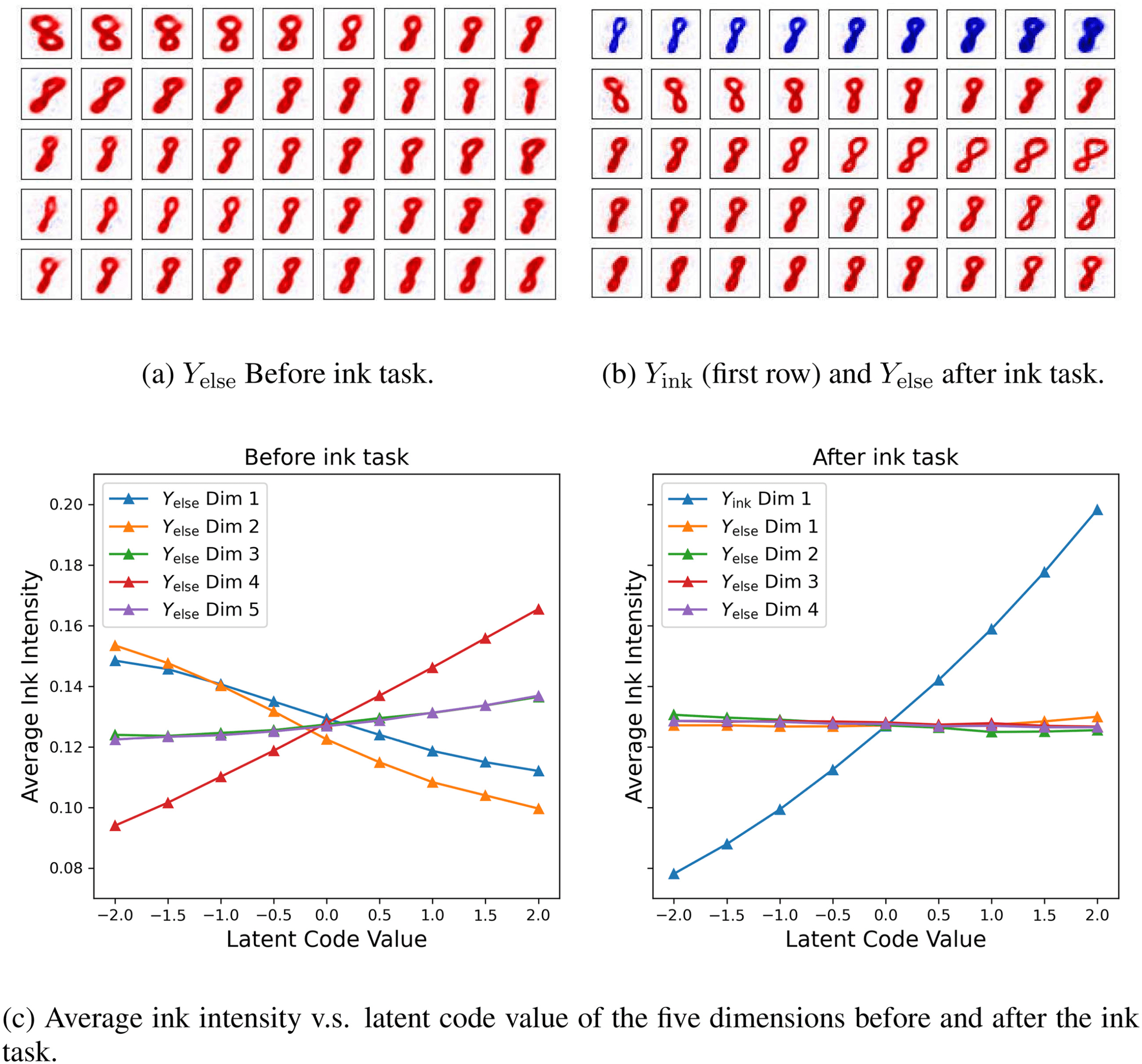
5.1.1 IB Removes Task-Relevant Information from the Unconceptualized Re-
只园. Unconceptualized representation can be obtained after the autoen-
coding step. We can check what has been learned by scanning this latent
代码. Figure 3a shows the scanning result of the top five latent represen-
tation units, ordered by descending mutual information with X. 注意
changing these features does not change the digit. 而且, mutual infor-
mation between Ydigit and Yelse is estimated by training a neural network
that predicts Ydigit from Yelse. The estimated information is smaller than 0.1
Nat when γ is larger than 5e-4, which indicates that digit information is
removed from the un-conceptualized region by IB.

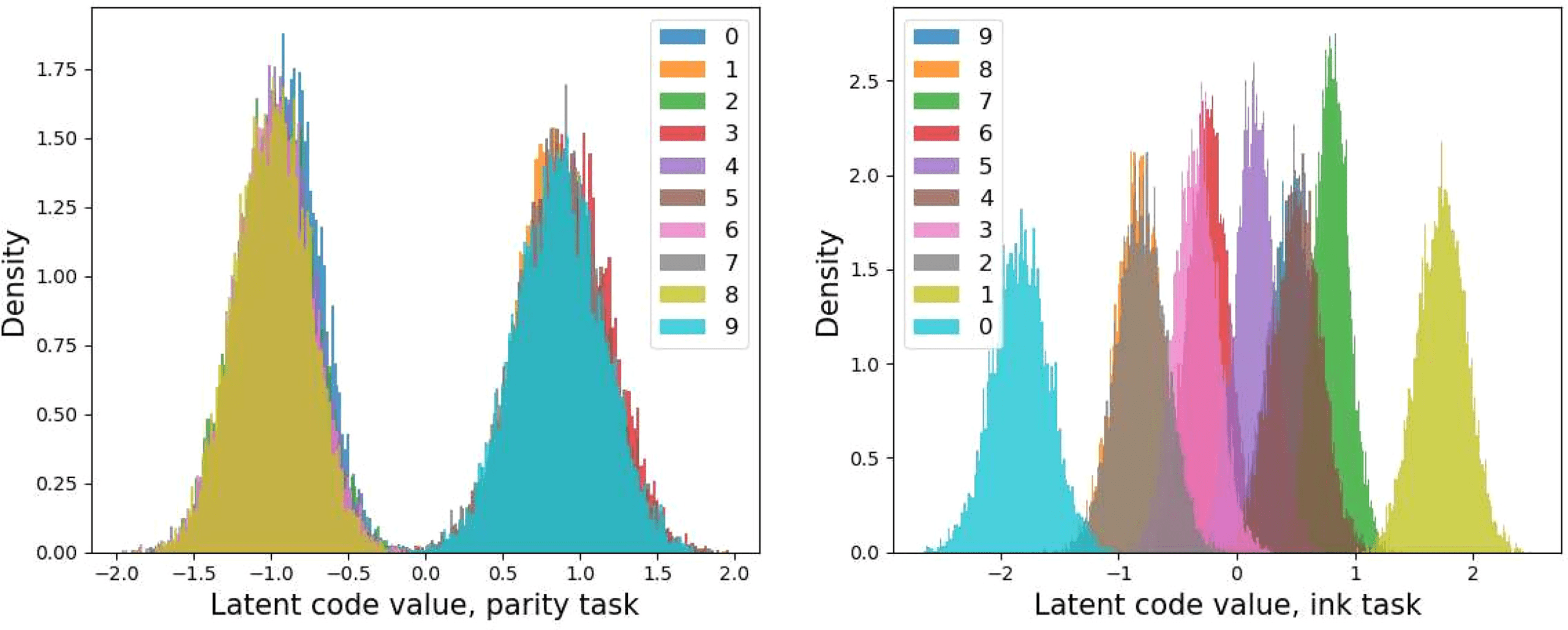
5.1.2 The Framework Explains How a New Task is Solved. After the auto-
encoding step, we proceed to solve either the parity task or ink task to
study the interpretation that the framework provides. For the parity task,
mutual information from Ydigit and Yelse are 0.702 Nat and 0.002, Nat re-
spectively, and for the ink task, 1.498 Nat and 2.045 Nat. The result shows
that the parity task doesn’t need information from Yelse, while the ink task
做. Clues of how the tasks are solved can also be found by looking into
the representation obtained after IB. For the parity task, different digits are
clustered into two groups according to their parity. For the ink task, digits
are aligned in an order corresponding to their actual average ink amount
(0 > 8 > 2 > 3 > 6 > 5 > 9 > 4 > 7 > 1), as Figure 4 节目.

5.1.3 Experience-Dependence of the ELSE Partition. After learning the digit
and the ink tasks, we can update the autoencoder felse to exclude the ink-
task-related information. 一方面, Yink (the first row of Figure 3b)
represents the average pixel intensity. 另一方面, this information
is suppressed in Yelse (rows 2–5). The suppression can be measured by fea-
ture correlation between Yink and Yelse. Before the ink task, the correlations
是 (0.295, 0.414, 0.080, 0.492, 0.100) for the five units visualized, but after
the ink task, the correlation becomes (0.030, 0.194, 0.019, 0.028, 0.001). 我们

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Z. He and T. Toyoizumi

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 3: Latent code scanning of unconceptualized representation after au-
toencoding, 前 (A) and after (乙) ink task (except the first row). The recon-
structed images plotted as the activity (columns) of one of the coding units
(rows) are varied with others fixed. (C) Shows how the average ink intensity
varies when we scan the latent code of the same five units as in panels a and b.

also present the result of the average ink intensity versus the latent code
of the five units. It can clearly be seen that before the ink task, the knowl-
edge of average intensity is distributed across all five units. 然而, 后
the ink task, the knowledge of average intensity is extracted as Yink and
removed from Yelse (see Figure 3c). The result indicates that the unconcep-
tualized region is experience dependent, and information about the already
learned task is excluded. Unlike other frameworks such as variational au-
toencoder (Kingma & Welling, 2013) and infoGAN (陈等人。, 2016), 哪个
usually have no explicit control over partitioning latent representation, 我们的
framework allows latent representation reorganization through progressive
任务.

Progressive Interpretation Synthesis

数字 4: VIB latent code distribution of different digits for the parity task
Ydigit∩parity (左边) and ink task Ydigit∩ink (正确的). The x-axis shows the code value,
and the y-axis shows the code density; different colors represent different digits
范围从 0 到 9. For the parity task, the latent code formed two clusters,
one for even numbers and one for odd numbers. And for the ink task, digits are
aligned in the order of the average amount of ink.

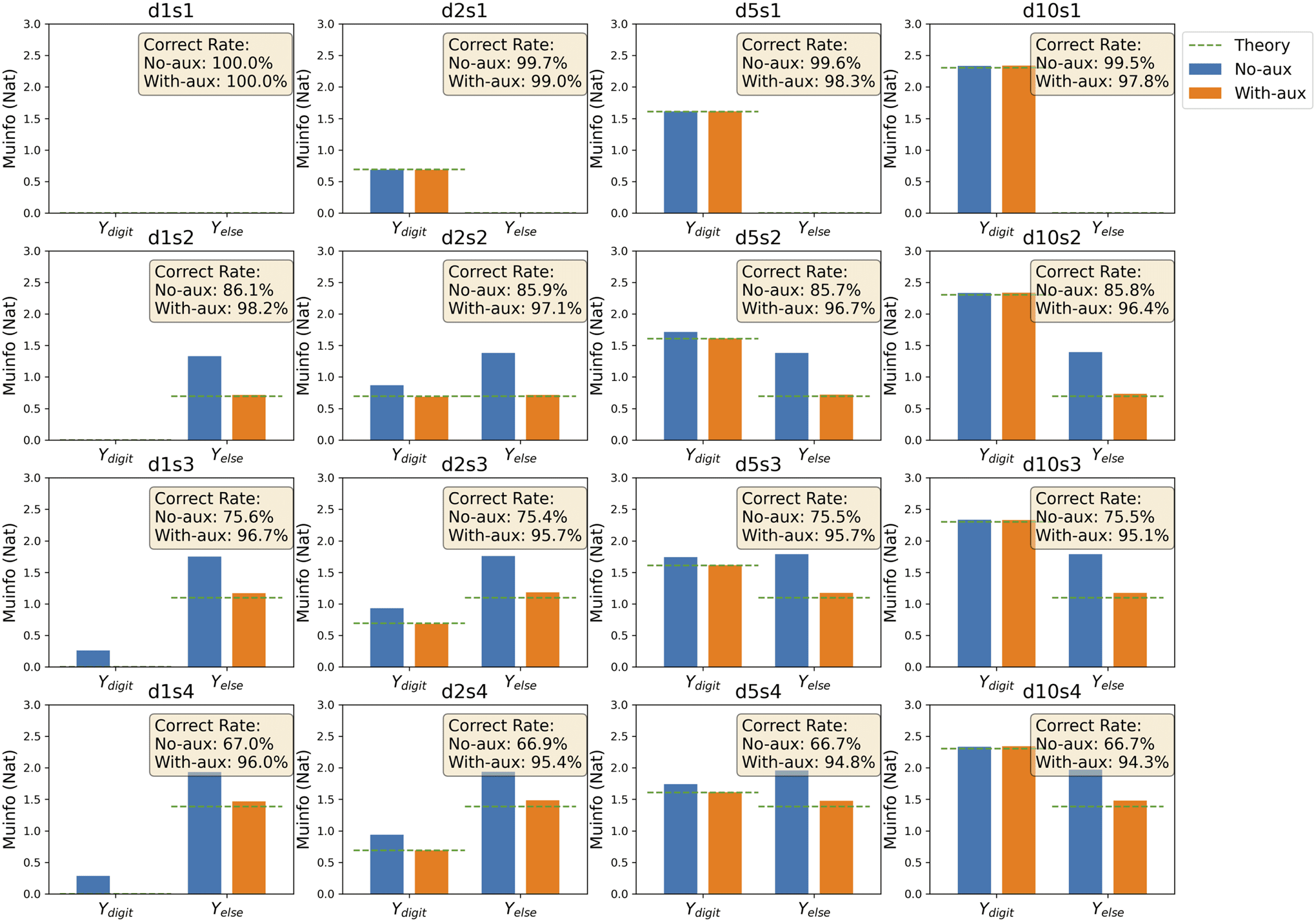
5.1.4 Quantitative Benchmark of Interpretation. 下一个, we ask if our pro-
posed interpretation is quantitatively useful. Because we are not aware of
task-level, human-agnostic interpretation algorithms directly comparable
to ours, we study how the interpretation changes as we systematically mod-
ify the required type of information for task 2. 任务 2 is designed to require
both digit information and digit-independent ink information involving
different resolutions. For digit information, we have four resolutions: d1,
d2, d5, and d10. 例如, d5 means that 10 digits are separated into five
equally sized groups, and the task is to tell which group the image belongs
到. 因此, (0, 0.693, 1.609, 2.303) Nat of information about digits is the-
oretically needed, 分别. For digit-independent ink information, 我们
also have four resolutions (according to the percentile-based grouping for
each digit by the amounts of ink used): s1, s2, s3, and s4, which theoretically
require (0, 0.693, 1.099, 1.386) Nat of information. By combining them, 我们
get 16 possibilities for task 2; the interpretation measured as mutual infor-
mation and the corresponding theoretical values are shown in Figure 5. 这
; Ydigit), 可
figure shows that information needed from Ydigit, 我(Ydigit∩2
; Yelse) 从
precisely predicted. The required nondigit information I(Yelse∩2
Yelse via autoencoding correlates with the required amount to solve the task.
然而, due to the imperfection of the variational IB algorithm to purely
extract relevant information, more than the theoretically required amount
of information from Yelse is used for good performance. This problem can
be practically remedied by allowing Yelse to be retrained by adding an aux-
iliary autoencoding task when learning task 2. Since input data are avail-
able during task 2, adding an auxiliary autoencoding task during task 2

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Z. He and T. Toyoizumi

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

数字 5: Mutual information from Ydigit and Yelse used to solve the benchmark
任务. Blue/orange bars are mutual information without/with auxiliary autoen-
编码, and the theory indicating the required amount of information is plot-
ted with the green dotted line. Inside text boxes are task-correct rates without/
with auxiliary autoencoding. The title of each panel represents different task
types combining four digit resolutions—d1, d2, d5, and d10—and four digit-
independent ink resolution—s1, s2, s3, and s4—forming a 4-by-4 matrix.

training increases task performance without needing extra data. (看
appendix section 9 for further discussion.)

5.2 CLEVR Data Set. 在这个部分, we demonstrate the progressive
interpretation framework on the CLEVR data set (Johnson et al., 2017), A
large collection of 3D-rendered scenes (70,000/15,000 train/test splits) 和
multiple objects with compositionally different properties. The CLEVR data
set was originally designed for a visual question-answering task, but we
train the model without using natural language. 例如, we train the
model to classify the color of an object or conduct a multiple-choice (MC)
task using only pictures. For the MC task, the model is trained on a large set
of four pictures and learns to choose one of the four pictures that includes
a target object (100,000/20,000 train/test splits).

在这个部分, we divide the tasks into two groups. In task group 1, 这
model that is pretrained to tell objects apart learns to recognize three of
the important properties, 位置, 颜色, and material, among shape, 尺寸,

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Progressive Interpretation Synthesis

颜色, 材料, and position. In task group 2, the model is asked to perform
an MC task selecting a picture according to a specific context, 例如,
“Choose the picture with red cubes,” which needs information learned or
not yet learned in task 1. For task group 1, we first use convolutional neu-
ral networks (CNNs) to report the image properties by supervised learning
and then obtain the unconceptualized region via autoencoding. After that,
task group 2 is performed with interpretation synthesized. We choose dis-
crete latent representation for this section. (See appendix sections 1 和 2
for implementation details.)

5.2.1 Interpretation by Information Flow. The result of interpretation by in-
; Yi)
formation flow is shown in Table 1. The mutual information I(是(i∩MC)
for i ∈ {posi, 颜色, 材料, 别的} is measured in Nat per object, where MC
represents the multiple-choice task. Different rows represent different ques-
tion types. We sample five random initializations of the networks for each
task and present both the average and standard deviations. The theoretical
amount of information required for feature i is shown in parentheses. 我们
can interpret how the model is solving the task by calculating mutual infor-
mation coming from each information partition. 例如, the task to
“choose the picture with green metal” needs 0.345 Nat of information from
the color domain and 0.686 Nat from the material domain. 正如预期的那样, 在-
formation coming from other domains is judged as irrelevant to this task. 如果
the task is to “choose the picture with a small yellow object,” the model then
需要 0.343 Nat from the color domain, 加 0.70 Nat of information from
the unconceptualized region since the model has not yet explicitly learned
about object size. If the task is “choose the picture with a large sphere,“ 这
model finds out that all previously learned properties are useless and has
to pick 0.31 Nat of information from the unconceptualized region. 这是
because neither size nor shape information has been used in previous tasks.

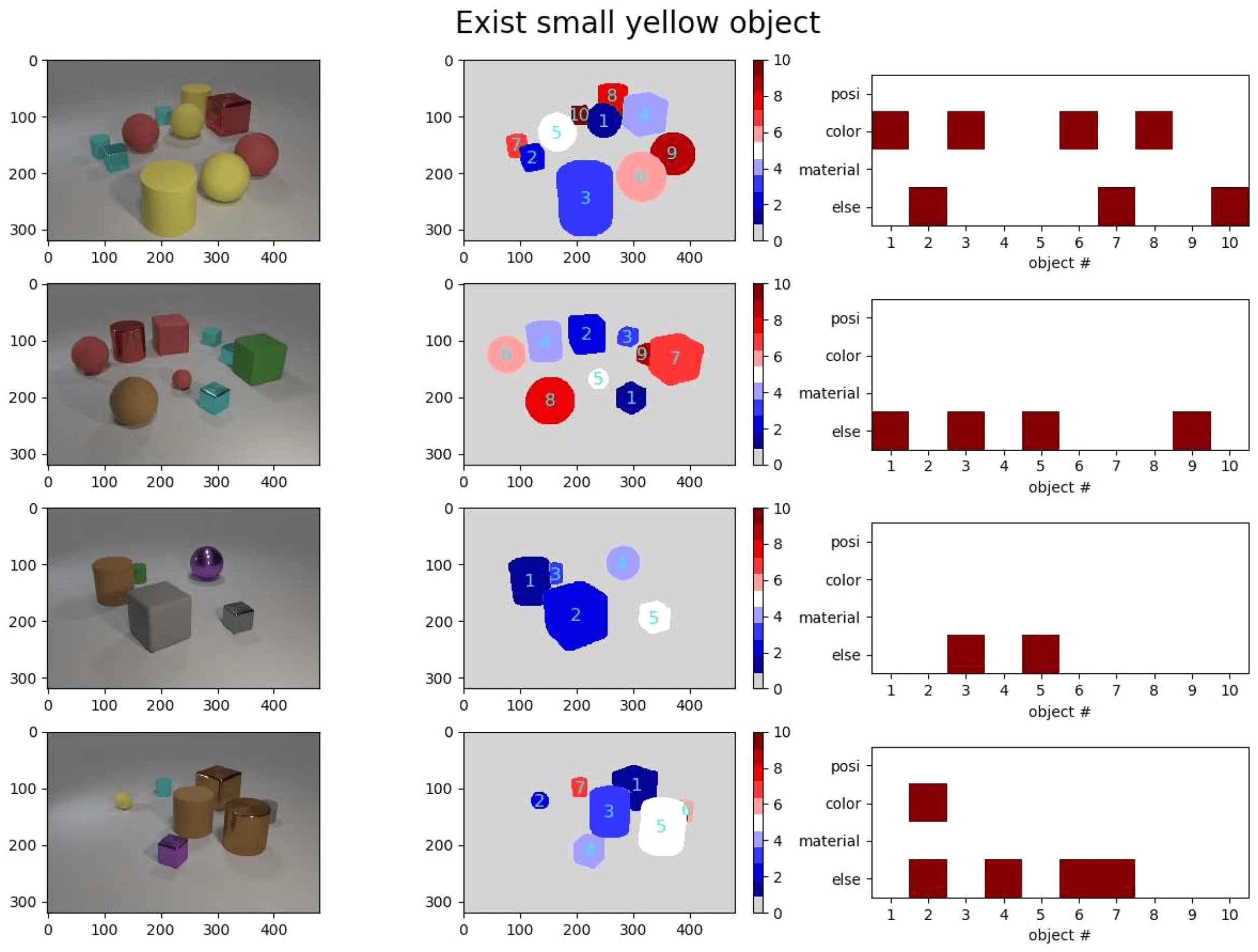
5.2.2 Single-Example Interpretation and Unconceptualized Representation.
After getting the model, it is also possible to synthesize interpretation for
a single example by looking into the discrete representation Y(i∩MC) 为了
i ∈ {posi, 颜色, 材料, 别的}. A typical example is shown in Figure 6. 这
example corresponds to a “small yellow object.” We can see the model dis-
criminates if the object has the color “yellow” while neglecting position
and material information. 解决问题, the model also needs in-
formation from the unconceptualized partition, which is representing the
size “small.” The behavior of the model is consistent with the expectation
of the question regarding the “small yellow object.”

We examine the correctness of the unconceptualized representation by
comparing it with the true label. 例如, if the task is “choose the
small yellow object,” the unconceptualized region should represent the
size “small.” We can cross-check by calculating their mutual information,
这是 0.662 Nat per object. For the case “choosing a red cube,” mutual

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
1
3
8
2
0
7
5
4
4
0
n
e
C
哦
_
A
_
0
1
5
4
2
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Z. He and T. Toyoizumi

9
9

)
1
5
4
.
0
(
1
0

%
1

%
7

%
1

%
4

%
7

%
1

0
±
3

0
±
0

0
±
2

0
±
8

0
±
4

9
9

7
9

9
9

5
9

4
9

)
0
(
1
0
0

0
< ) 0 ( 2 0 . 0 ± 1 0 . 0 ) 3 9 6 . 0 ( 1 0 ) 7 3 6 . 0 ( 6 0 ) 7 3 6 . 0 ( 6 0 . . . . 0 ± 0 7 0 ± 9 8 0 ± 8 8 0 ± 1 3 . . . . 0 0 0 0 ) 3 9 6 . 0 ( 8 0 0 ) 3 9 6 . 0 ( 1 0 0 . . 0 ± 6 8 6 0 ± 8 8 6 . . 0 0 ) 0 ( 1 0 0 ) 0 ( 1 0 0 ) 0 ( 1 0 0 ) 0 ( 1 0 0 . . . . 0 < 0 < 0 < 0 < ) 7 7 3 . 0 ( 1 0 0 . 0 ± 5 4 3 . 0 ) 0 ( 1 0 0 . 0 < ) 7 7 3 . 0 ( 2 0 0 ) 7 7 3 . 0 ( 2 0 0 . . 0 ± 3 4 3 0 ± 1 8 3 . . 0 0 ) 0 ( 1 0 0 ) 0 ( 1 0 0 . . 0 < 0 < ) 0 ( 1 0 0 . 0 < . ) 2 5 0 ( 2 0 . 0 ± 6 5 . 0 ) 0 ( 1 0 0 ) 0 ( 1 0 0 . . 0 < 0 < ) 1 5 . 0 ( 3 0 . 0 ± 9 5 . 0 ) 0 ( 1 0 0 . 0 < l a t e M n e e r G r e b b u R t f e L w o l l e Y l l a m S e b u C d e R r e d n i l y C t h g i R e r e h p S e g r a L e t a r t c e r r o C n w o n k n U l a i r e t a M r o l o C n o i t i s o P e p y T n o i t s e u Q . n o i t a t e r p r e t n I 2 k s a T r o f e l b a T : 1 e l b a T l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 3 8 2 0 7 5 4 4 0 n e c o _ a _ 0 1 5 4 2 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 . e u l a v l a c i t e r o e h t e h t s i , s e s e h t n e r a p e d i s n i j , ) t c e b o / t a N ( t i n u n o i t a m r o f n i e h T : e t o N Progressive Interpretation Synthesis 53 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 3 8 2 0 7 5 4 4 0 n e c o _ a _ 0 1 5 4 2 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 6: Single-example interpretation of the task “choose the small yellow object.” The left column shows input pictures, and the middle column shows masks colored according to object IDs. We overlaid the masks with the object IDs for visual aid. The right column shows the binary activity summarizing the information at layer Y(i∩MC). The x-axis corresponds to object ID, and the y-axis represents four kinds of representations: position Y(posi∩MC), color Y(color∩MC), ma- terial Y(material∩MC), and else Y(else∩MC), where the dimension with highest mutual information is plotted. The red square represents the lower frequency binary representation, and the white space represents the counterpart. information with the label “cube” is 0.432 Nat per object. For the case “choosing cylinder on the right side,” mutual information with the label “cylinder” is 0.408 Nat per object. All of these numbers exceed the chance level (the 99, 95, and 90 percentile by chance are 0.637, 0.495, and 0.368 Nat, respectively, for balanced binary random variables like size, and 0.583, 0.449, 0.332 Nat for cases with three alternatives like shape). 5.2.3 Visualizing the Unconceptualized Representation. After getting the un- conceptualized representation useful for the new task, we can continue the framework by splitting that representation into the learned useful part and its complement. Separating this new useful representation is nontriv- ial because labels of the MC task jointly depend on multiple image prop- erties. While previous methods (Koh et al., 2020; Chen et al., 2020) need feature-specific labels to learn a new property, the proposed framework 54 Z. He and T. Toyoizumi Figure 7: Visualizing the newly learned YMC about size after learning the task “choose the picture with a small yellow object.” As can be seen from the result, changing YMC of a small object renders a big counterpart of the same object, and changing YMC of a big object renders a small counterpart of the same object. automatically segregates a new, useful representation from previously learned representations. Furthermore, the proposed system can visualize what new representation has just been learned. Here, we demonstrate the result after learning the task “choose the pic- ture with a small yellow object. We have mentioned that after learning this new task, the model is expected to learn a new concept about size as the = Y(else∩MC). Note, again, that we never provided new representation YMC the model labels specifically about size. Then we can continue the frame- work by performing another round of autoencoding, which splits Yelse into \YMC. After that, the model explains what property is newly YMC and Yelse learned by generating the image of an object and changing its size as the newly latent representation YMC is altered (see Figure 7). This visualization also helps humans interpret the operation of the model. Information about other studies on the CLEVR data set can be found in appendix sections 4 to 8. We also offer more discussion about our method in appendix section 9 and discuss limitations of our method in appendix sec- tion 10. The source code of this project can be found at https://github.com/ hezq06/progressive_interpretation. 6 Conclusion This letter proposes a progressive framework based on information the- ory to synthesize interpretation. We show that interpretation involves independence, is progressive, and can be given at a macroscopic level l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 3 8 2 0 7 5 4 4 0 n e c o _ a _ 0 1 5 4 2 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Progressive Interpretation Synthesis 55 using meta-information. Changing the receiver of the interpretation from a human to a target model helps define interpretation clearly. Our inter- pretation framework divides the input representations into independent partitions by tasks and synthesizes interpretation for the next task. This framework can also visualize what conceptualized and unconceptualized partitions code by generating images. The framework is implemented with a VIB technique and is tested on the MNIST and the CLEVR data sets. The framework can solve the task and synthesize nontrivial interpretation in the form of meta-information. The framework is also able to progressively form meaningful new representation partitions. Our information-theoretic framework capable of forming quantifiable interpretations is expected to inspire future understanding-driven deep learning. Acknowledgments We thank Ho Ka Chan, Yuri Kinoshita, and Qian-Yuan Tang for useful dis- cussions about the work. This study was supported by Brain/MINDS from the Japan Agency for Medical Research and Development (AMED) under grant JP15dm0207001, Japan Society for the Promotion of Science (JSPS) un- der KAKENHI grant JP18H05432, and the RIKEN Center for Brain Science. References Alemi, A. A., Fischer, I., Dillon, J. V., & Murphy, K. (2016). Deep variational information bottleneck. arXiv:1612.00410. Andreas, J., Rohrbach, M., Darrell, T., & Klein, D. (2016). Neural module networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 39–48). Arrieta, A. B., Díaz-Rodríguez, N., Del Ser, J., Bennetot, A., Tabik, S., Barbado, A., . . . Herrera, F. (2020). Explainable artificial intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Information Fusion, 58, 82– 115. 10.1016/j.inffus.2019.12.012 Bach, S., Binder, A., Montavon, G., Klauschen, F., Müller, K.-R., & Samek, W. (2015). On pixel-wise explanations for non-linear classifier decisions by layer-wise rele- vance propagation. PLOS One, 10(7), e0130140. Bada, S. O., & Olusegun, S. (2015). Constructivism learning theory: A paradigm for teaching and learning. Journal of Research and Method in Education, 5(6), 66–70. Bang, S., Xie, P., Lee, H., Wu, W., & Xing, E. (2019). Explaining a black-box using a deep variational information bottleneck approach. arXiv:1902.06918. Bell, A. J., & Sejnowski, T. J. (1995). An information-maximization approach to blind separation and blind deconvolution. Neural Computation, 7(6), 1129–1159. 10.1162/neco.1995.7.6.1129 Chalk, M., Marre, O., & Tkacik, G. (2016). Relevant sparse codes with variational in- formation bottleneck. In D. Lee, M. Sugiyama, U. Luxburg, I. Guyon, & R. Garnett (Eds.), Advances in neural information processing systems, 29. Curran. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 3 8 2 0 7 5 4 4 0 n e c o _ a _ 0 1 5 4 2 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 56 Z. He and T. Toyoizumi Chen, J., Song, L., Wainwright, M. J., & Jordan, M. I. (2018). Learning to explain: An information-theoretic perspective on model interpretation. arXiv:1802.07814. Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. (2016). InfoGAN: Interpretable representation learning by information maximizing gen- erative adversarial nets. In D. Lee, M. Sugiyama, U. Luxburg, I. Guyon, & R. Gar- nett (Eds.), Advances in neural information processing systems, 29 (pp. 2180–2188). Curran. Chen, Z., Bei, Y., & Rudin, C. (2020). Concept whitening for interpretable im- age recognition. Nature Machine Intelligence, 2(12), 772–782. 10.1038/s42256-020 -00265-z Doshi-Velez, F., & Kim, B. (2017). Towards a rigorous science of interpretable machine learning. arXiv:1702.08608. Freitas, A. A. (2014). Comprehensible classification models: A position paper. ACM SIGKDD Explorations Newsletter, 15(1), 1–10. 10.1145/2594473.2594475 Glucksberg, S., & McCloskey, M. (1981). Decisions about ignorance: Knowing that you don’t know. Journal of Experimental Psychology: Human Learning and Memory, 7(5), 311. 10.1037/0278-7393.7.5.311 Goodfellow, I. J., Shlens, J., & Szegedy, C. (2014). Explaining and harnessing adversarial examples. arXiv:1412.6572. Hinton, G., Deng, L., Yu, D., Dahl, G. E., Mohamed, A.-r., Jaitly, N., . . . Kingsbury, B. (2012). Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Processing Magazine, 29(6), 82– 97. 10.1109/MSP.2012.2205597 Hou, B.-J., & Zhou, Z.-H. (2018). Learning with interpretable structure from RNN. arXiv:1810.10708. Hudson, D. A., & Manning, C. D. (2018). Compositional attention networks for machine reasoning. arXiv:1803.03067. Hyvärinen, A., & Oja, E. (2000). Independent component analysis: Algorithms and applications. Neural Networks, 13(4–5), 411–430. Johnson, J., Hariharan, B., van der Maaten, L., Fei-Fei, L., Lawrence Zitnick, C., & Girshick, R. (2017). CLEVR: A diagnostic dataset for compositional language and elementary visual reasoning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 2901–2910). Kim, S. W., Tapaswi, M., & Fidler, S. (2018). Visual reasoning by progressive module networks. arXiv:1806.02453. Kingma, D. P., & Welling, M. (2013). Auto-encoding variational Bayes. arXiv:1312.6114. Koh, P. W., Nguyen, T., Tang, Y. S., Mussmann, S., Pierson, E., Kim, B., & Liang, P. (2020). Concept bottleneck models. In Proceedings of the International Conference on Machine Learning (pp. 5338–5348). Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2017). ImageNet classification with deep convolutional neural networks. Communications of the ACM, 60(6), 84–90. 10.1145/3065386 Lechner, M., Hasani, R., Amini, A., Henzinger, T. A., Rus, D., & Grosu, R. (2020). Neural circuit policies enabling auditable autonomy. Nature Machine Intelligence, 2(10), 642–652. 10.1038/s42256-020-00237-3 Li, X. L., & Eisner, J. (2019). Specializing word embeddings (for parsing) by information bottleneck. arXiv:1910.00163. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 3 8 2 0 7 5 4 4 0 n e c o _ a _ 0 1 5 4 2 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Progressive Interpretation Synthesis 57 Lipton, Z. C. (2018). The mythos of model interpretability. Queue, 16(3), 31–57. 10.1145/3236386.3241340 Mahinpei, A., Clark, J., Lage, I., Doshi-Velez, F., & Pan, W. (2021). Promises and pitfalls of black-box concept learning models. arXiv:2106.13314. Margeloiu, A., Ashman, M., Bhatt, U., Chen, Y., Jamnik, M., & Weller, A. (2021). Do concept bottleneck models learn as intended? arXiv:2105.04289. National Research Council. (2002). Learning and understanding: Improving advanced study of mathematics and science in US high schools. National Academies Press. Parisi, G. I., Kemker, R., Part, J. L., Kanan, C., & Wermter, S. (2019). Continual lifelong learning with neural networks: A review. Neural Networks, 113, 54–71. 10.1016/ j.neunet.2019.01.012 Rusu, A. A., Rabinowitz, N. C., Desjardins, G., Soyer, H., Kirkpatrick, J., Kavukcuoglu, K., . . . Hadsell, R. (2016). Progressive neural networks. arXiv:1606. 04671. Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., Van Den Driessche, G., . . . Hassabis, D. (2016). Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587), 484–489. 10.1038/nature16961 Sundararajan, M., Taly, A., & Yan, Q. (2017). Axiomatic attribution for deep networks. arXiv:1703.01365. Tishby, N., Pereira, F. C., & Bialek, W. (2000). The information bottleneck method. arXiv:0004057. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, . . . Polosukhin, I. (2017). Attention is all you need. In I. Guyon, Y. V. Luxburg, S. Bengio, H. Wal- lach, R. Fergus, S. Vishwanathan, & R. Garnett (Eds.), Advances in neural informa- tion processing systems, 30 (pp. 5998–6008). Curran. Wang, Q., Boudreau, C., Luo, Q., Tan, P.-N., & Zhou, J. (2019). Deep multi-view in- formation bottleneck. In Proceedings of the 2019 SIAM International Conference on Data Mining (pp. 37–45). Wibral, M., Priesemann, V., Kay, J. W., Lizier, J. T., & Phillips, W. A. (2017). Partial information decomposition as a unified approach to the specification of neural goal functions. Brain and Cognition, 112, 25–38. 10.1016/j.bandc.2015.09.004 Wu, M., Hughes, M. C., Parbhoo, S., Zazzi, M., Roth, V., & Doshi-Velez, F. (2017). Be- yond sparsity: Tree regularization of deep models for interpretability. arXiv:1711.06178. Zhang, Q., Cao, R., Shi, F., Wu, Y. N., & Zhu, S.-C. (2017). Interpreting CNN knowledge via an explanatory graph. arXiv:1708.01785. Received May 24, 2022; accepted August 10, 2022. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 3 8 2 0 7 5 4 4 0 n e c o _ a _ 0 1 5 4 2 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 字母图像

下载pdf