信 - 麻省理工学院人工智能研究专业

信

由 Peer Neubert 传达

模拟和预测动力系统
使用空间语义指针

亚伦·R. 沃尔克
arvoelke@uwaterloo.ca
彼得·布劳
peter.blouw@appliedbrainresearch.com
朱轩
xuan.choo@appliedbrainresearch.com
应用脑研究, 滑铁卢, ON N2L 3G1, 加拿大

妮可·桑德拉·雅法·杜蒙
ns2dumont@uwaterloo.ca
切里顿计算机科学学院, 滑铁卢大学,
滑铁卢, 安大略省, N2L 3G1, 加拿大

泰伦斯·C. 斯图尔特
terrence.stewart@nrc-cnrc.gc.ca
加拿大国家研究委员会, 滑铁卢大学
协作中心, 滑铁卢, ON N2L 3G1 加拿大

克里斯·埃利亚史密斯
celiasmith@uwaterloo.ca
理论神经科学中心, 滑铁卢大学,
滑铁卢, 安大略省, N2L 3G1, 加拿大

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

虽然神经网络在学习与任务相关的代表方面非常有效-
数据的反感, 他们通常不会学习表征
假设支持高层的那种符号结构
认知过程, 他们也不自然地在内部建模此类结构
在空间和时间上连续的问题域. 填补这些空白,
这项工作利用了一种定义绑定向量表示的方法
离散的 (类似符号的) 连续拓扑空间中的实体到点
为了模拟和预测一系列动态系统的行为-
特姆斯. 这些向量表示是空间语义指针 (SSP),
我们证明他们可以 (1) 用于模拟动力系统-
涉及以类似符号的方式表示的多个对象的项目
和 (2) 与深度神经网络集成来预测未来

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

音视频. 和P.B. 同等贡献.

神经计算 33, 2033–2067 (2021) © 2021 麻省理工学院
https://doi.org/10.1162/neco_a_01410

2034

A. 沃尔克等人。.

物理轨迹. 这些结果有助于统一传统应用程序的内容-
机器学习中的不同方法.

1 介绍

人工智能研究近期取得了大量进展
事实上，人工神经网络是高效的函数 ap-
经过足够多的数据训练后的接近器. 然而, 这是
人们普遍认为，智能仍然存在重要的方面
应用于 dis 的静态函数不能自然描述的行为-
具体的输入集. 例如, 乐存, 本吉奥, 和辛顿 (2015) 有
谴责缺乏将表征学习与
复杂的推理 (另见博图, 2014), 一种研究途径
传统上激励研究人员提出结构化符号的需要-
折线表示法 (马库斯, 1998; 斯摩棱斯基 & 勒让德, 2006; 哈德利,
2009). 其他人指出，此类方法不能有效捕获 dy-
连续时空认知信息处理的动力学
(埃利亚史密斯, 2013; 更美丽, 2014). 最后, 扩展神经网络
在任务上下文中操纵结构化符号表示-
连续空间和时间上的旋转动力学是一个重要的统一
场上的目标.

在这项工作中, 我们通过开发一种方法朝着这个目标迈出了一步
定义对连续和离散的混合进行编码的向量表示-
混凝土结构，以模拟和预测一系列的行为
多个物体连续运动的动力系统
空间和时间. 这些向量表示是空间语义指针
(SSP), 我们对他们代表 com 的能力进行了分析-
复杂的空间地形及其学习和建模任意能力的能力
根据这些地形定义的动力学. 进一步来说, 我们
展示 SSP 如何用于 (1) 模拟连续轨迹，涉及
多个对象, (2) 模拟这些物体和墙壁之间的相互作用,
和 (3) 了解控制这些相互作用的动态以便预测
未来物体位置.

从数学上来说, SSP 建立在矢量符号 ar 的概念之上-
建筑 (VSA; 盖勒, 2004), 其中一组代数运算是
用于将向量表示绑定到角色填充对中并对此类进行分组
配对成组 (斯摩棱斯基, 1990; 盘子, 2003; 希瑟, 2009; 弗拉迪, 克莱科,
& 索默, 2020; 施莱格尔, 诺伯特, & 挥霍, 2020). 传统上, VSA
已被描述为捕获类似符号的离散表示的手段-
使用向量空间的情感结构. 最近对 VSA 的扩展
引入了将 SSP 定义为分布式的分数绑定操作
角色和填充符都可以编码连续量的表示-
乳头 (腰部, 斯图尔特, 沃尔克, & 埃利亚史密斯, 2019; 弗拉迪, 希瑟, & 作为-
梅尔, 2018). SSP 之前曾被用来模拟空间推理

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2035

任务 (鲁, 沃尔克, 腰部, & 埃利亚史密斯, 2019; 韦斯, 张, & 奥尔斯豪森,
2016), 模型路径规划和导航 (腰部 & 埃利亚史密斯, 2020),
并在 spik 的背景下对网格单元进行建模并放置单元放电模式-
神经网络 (杜蒙 & 埃利亚史密斯, 2020). 存储容量分析-
还进行了 SSP 实验 (死后, 斯图尔特, & 康拉特, 2020).
这里, 我们将之前的工作扩展到连续动力系统建模
与 SSP 合作，从而整合人工智能的观点，或者关注
关于深度学习 (乐存, 本吉奥, 和辛顿, 2015; 好人, 本吉奥,
& 考维尔, 2016; 施米德胡贝尔, 2015), 符号结构 (马库斯, 1998,
2019; 哈德利, 2009), 和时间动态 (埃利亚史密斯, 2013; 沃尔克, 2019;
麦克莱兰等人。, 2010).

我们首先介绍 VSA 和分数结合. 然后我们使用这些
定义 SSP 的概念并讨论可视化它们的方法. 我们不-
讨论它们与神经生物学表征的相关性 (IE。, 网格单元) 和
深度学习中的特征表示. 看完本介绍性材料后,
我们转向我们的贡献, 揭示了新的表示方法
以及学习神经网络中的任意轨迹. 然后我们演示
如何动态模拟单个和任意轨迹
多个对象. 下一个, 我们推导出偏微分方程 (偏微分方程) 那
可以通过线性变换模拟连续时间轨迹
嵌入循环尖峰神经网络. 我们还介绍两款
模拟多个对象的方法, 并对它们进行比较和对比.
最后, 我们展示了 SSP 如何与 Legendre 内存单元相结合
(LMU; 沃尔克, 卡吉茨, & 埃利亚史密斯, 2019) 来预测未来的轨迹
沿着运动不连续变化的路径移动的物体.

2 结构化向量表示

2.1 矢量符号架构. 矢量符号架构
(VSA) 是在长期争论的背景下制定的-
解决如何用 dis 编码符号结构的问题-
由神经网络操纵的那种致敬表示 (福多尔
& 对不起, 1988; 马库斯, 1998; 斯摩棱斯基 & 勒让德, 2006). 提供
这个问题的答案, VSA 首先定义一组映射
d 维空间中一组向量的原始符号, V ⊆ 路. 这
映射通常被称为 VSA 的“词汇”。通常是向量-
选择词汇表中的tors，以便通过使用的相似性度量
在VSA中, 每个向量都是不同的，因此可以与每个向量区分开来
词汇表中的其他向量. 生成随机数的常用方法
d 维向量涉及从正态分布中采样每个元素-
贡献的平均值为 0 方差为 1/d (穆勒, 1959). 选择
以这种方式的向量元素确保了预期的 L2 范数
向量是 1 以及执行离散傅立叶变换 (密度泛函理论) 在
向量导致傅里叶系数均匀分布在周围 0 和
所有频率分量的方差相同.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2036

A. 沃尔克等人。.

此外, VSA 定义了可以执行的代数运算
启用符号操作的词汇项. 这些操作可以是
分为五种类型: (1) 计算标量的相似性运算
衡量两个向量的相似程度; (2) 一个集合操作-
将两个向量合并为一个与两个输入相似的新向量; (3) A
绑定操作将两个向量压缩为一个新向量，即
与两个输入不同; (4) 解压缩 vec 的逆运算-
tor 撤消一个或多个绑定操作; 和 (5) 清理操作
将噪声或解压缩向量映射到最相似的“干净”向量-
VSA 词汇中的 tor. 我们依次讨论每项操作并
重点关注使用矢量加法进行收集和循环的特定 VSA
卷积结合, 其向量通常称为
全息简化表示 (心率; 盘子, 2003):

相似. 衡量相似度 (s) 两个向量之间, VSA 类型-
特别使用欧氏空间中的内积运算 (又名, 这
点积):

s = A · B = ATB.

(2.1)

当两个向量都是单位长度时, 这变得与
“余弦相似度”度量. 当使用该措施时, 两个身份-
cal 向量的相似度为 1, 而两个正交向量将
有相似之处 0. 我们注意到，当维数, d, 是
大的, 那么两个随机生成的单位向量预计是
近似正交, 或不相似, 彼此 (戈斯曼,
2018).

收藏. 集合操作被定义为映射任意一对输入
向量到与两个输入相似的输出向量. 这是
对于表示无序符号集很有用. 矢量叠加-
的 (IE。, 逐元素加法) 通常用来实现这个
手术.

捆绑. 定义绑定操作来映射任意一对输入向量-
到与两个输入向量都不相似的输出向量.
这对于表示多个符号的连接很有用.
绑定操作的常见选择包括循环卷积-
的 (盘子, 2003), 逐元素乘法 (盖勒, 2004), 向量-
派生转换结合 (戈斯曼 & 埃利亚史密斯, 2019), 和
异或 (希瑟, 2009), 尽管其中一些选择强加
对它们所适用的词汇向量的要求. 带圆形
卷积 ((西德:2)), 可以有效地计算 A 和 B 的结合
作为

A (西德:2) B = F −1{F{A} (西德:3) F{乙}},

(2.2)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2037

其中 F{·} 是 DFT 算子并且 (西德:3) 表示按元素求和-
两个复向量的倒数. 一起, 通过加法收集
并且通过循环卷积进行绑定遵守 com 的代数定律-
变异性, 关联性, 和分配性 (戈斯曼, 2018).

此外, 因为循环卷积产生输出 vec-
tor，其中每个元素都是一个输入向量之间的点积-
tor 和另一个输入向量中元素的排列, 它
可以排列 A 的元素以构建固定的“绑定”
矩阵,” T(A) ε Rd×d 可用于实现此绑定操作-
进化 (盘子, 2003):

A (西德:2) B=T(A)乙.

(2.3)

进一步来说, 时间(A) 是一种特殊的矩阵，称为“循环矩阵”
矩阵”，由向量 A 完全指定. 它的第一列是 A, 和
其余列是 A 的循环排列，偏移量等于
列索引.

逆. 反之, 或“解除约束,” 操作可以被认为是
创建一个向量来消除绑定操作的影响, 这样的
如果 ∼A 是 A 的逆, 然后将~A结合到一个结合的载体上
A 和 B 一起返回 B. 对于使用循环卷积的 VSA-
溶液, 向量的逆是通过计算 com 来计算的-
其傅立叶系数的复共轭. 有趣的是, 执行
傅里叶域中的复共轭相当于执行-
对向量的各个元素进行求和运算.
由于向量的精确逆必须考虑 mag-
其傅里叶系数的个数, 而复杂的共轭物则
不是, 逆运算一般只计算一个近似值
向量的逆, 那是, ∼A ≈ A−1, 其中 A−1 是精确的逆
A.2的

清理. 当逆运算近似时, 绑定 vec-
tor 及其逆向结果中引入了噪声. 执行
对集合了多个向量的绑定操作
其他向量也引入了潜在不需要的输出项3

求和运算保留了向量中第一个元素的顺序，并重新-
与剩余元素的顺序相反. 举个例子, 向量的对合
[0, 1, 2, 3] 是 [0, 3, 2, 1].

计算向量的精确逆有时会导致较大的傅立叶值
系数大小, 因为输入向量的傅立叶系数均匀分布-
周围致敬 0. 大傅里叶系数幅度因此生成向量
向量幅度“行为不当” (IE。, 他们不符合这样的假设
矢量幅度应约为 1).

这些无关符号术语的代数类比是考虑使用 (A + 乙)2
计算a2 + b2. 在这个类比中, 的扩展形式 (A + 乙)2 包含“想要的”
a2 和 b2 项以及“无关”2ab 项.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2038

A. 沃尔克等人。.

进入符号计算. 因此, VSA 定义清理
操作可用于减少通过累积的噪音
应用绑定和解除绑定操作并删除
这些运算结果中不需要的向量项. 至每-
形成清理行动, 将输入向量与所有向量进行比较
所需词汇表内的向量, 与清理的输出
操作是词汇表中具有高值的向量-
与输入向量的 est 相似度. 这个操作可以借鉴
使用深度神经网络的数据 (腰部 & 埃利亚史密斯, 2020) 或者我-
直接通过组合矩阵乘法来实现 (计算
点积) 具有阈值函数 (斯图尔特, 唐, & 埃利亚-
史密斯, 2011) 或赢家通吃机制 (戈斯曼, 沃尔克, &
埃利亚史密斯, 2017).

直到最近, VSA 已广泛用于绘制离散结构
使用创建的槽填充表示进入高维向量空间
通过应用绑定和集合操作. 这样的代表-
语句非常通用，捕获各种熟悉的数据类型
神经和认知建模者, 包括列表, 树, 图表, 语法,
和规则. 然而, 有许多自然任务需要离散代表-
怨恨结构不合适. 考虑一个例子
代理在非结构化空间环境中移动 (例如, 一片森林).
理想情况下, 代理对环境的内部表示是
能够合并任意对象 (例如, 著名的树木或岩石) 绑定时-
将这些对象移动到任意空间位置或区域. 为了实施这样的
与 VSA 的陈述, 理想情况下，槽应该是连续的 (IE。,
映射到连续的空间位置) 即使填充物不是. 骗局-
这种连续的槽将允许绑定特定的表示
物体 (例如, 一棵大橡树的类似符号的表示) 到特别的
空间位置. 开发这种连续的空间表示,
利用使用循环的 VSA 的某些附加属性是有用的
卷积作为绑定算子.

2.1.1 酉向量. 在循环操作的向量集中
卷积, 存在“单一”向量的子集 (盘子, 2003) 那个前任-
禁止以下两个属性: 他们的 L2 范数恰好是 1, 和
它们的傅里叶系数的大小也恰好是 1. 重要的, 这些
属性确保 (1) 酉向量的近似逆是
等于它的精确倒数, 因此我们可以互换使用 A−1 = ∼A,
(2) 两个酉向量之间的点积变得等于它们的
余弦相似度, 和 (3) 将一个酉向量与另一个酉向量结合-
tary 向量产生另一个酉向量; 因此, 酉向量是
与循环卷积绑定下的“闭合”.

由于这些向量的近似逆是精确的, 绑定一个uni-
tary 向量及其逆不会在结果中引入噪声. 因此,

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2039

酉向量支持无损绑定和解除绑定操作. 阿比-
这些操作的三元序列是完全可逆的，无需使用
只要需要反转的操作数是
预先知道.

2.1.2 迭代绑定. 酉式的一个特别有用的应用
向量涉及迭代特定的绑定操作以生成一组
线性变换下闭合的点 (腰部, 2020). 典型-
卡莉, 这涉及将给定向量与其自身绑定一定次数
使得如果 k 是自然数并且 A 是向量, 然后

AK=A (西德:2) A (西德:2) A . . . (西德:2) A
(西德:5)

(西德:2)

(西德:3)(西德:4)
A出现k次

(2.4)

这个过程有时被称为重复的“自动卷积”
(盘子, 2003).

这个定义的意义在于，当 A 是酉时, 它-
迭代绑定创建近似正交向量的闭合序列-
可以轻松穿越的路径. 例如, 从向量 Ak 移动
向量 Ak+1 的序列与执行绑定一样简单
和 (西德:2) A; 从 Ak+1 返回到 Ak 就像执行绑定一样简单-
Ak+1 (西德:2) A−1 因为酉向量的逆元是精确的.
+k2 = Ak1 (西德:2) Ak2 对于所有整数 k1 和 k2, 一个单一的
更普遍, 因为Ak1
绑定操作足以在闭合向量中的任意两个向量之间移动
对应于A下自结合的序列.

因为可以使用进一步的绑定操作来关联中的点
该序列与其他表示, 编码变得非常自然
使用这些技术的单个向量中的元素列表. 例如, 到
对列表 X 进行编码, 是, Z . . ., 可以将这个列表中的每个向量绑定到邻居-
荷兰国际集团点如下: A1 (西德:2) X + A2 (西德:2) 是 + A3 (西德:2) Z . . . 具体检索
然后可以通过移动到所需的提示来执行此列表中的元素
在由 A 定义的向量集合中，在自绑定下闭合 (例如, A2), 和
然后解除绑定此提示以从 en 中提取相应的元素-
编码列表 (例如, 是). 该方法已在多个神经模型中得到应用
工作记忆 (秋, 2010; 埃利亚史密斯等人。, 2012; 戈斯曼 & 埃利亚史密斯,
2020).

2.1.3 分数结合. 可以进一步推广迭代绑定-
允许 k 为实数值而不是整数. 马特-
机械地, 绑定迭代的分数可以表示为
傅立叶域为

Ak DEF= F −1

(西德:6)

(西德:7)

F{A}k

(2.5)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2040

A. 沃尔克等人。.

其中 F{A}k 是一组复数傅里叶的逐元素取幂
系数. 这个定义等价于方程 2.4 当 k 为正数时
整数，但将其概括为允许 k 为实数.

假设A是酉的, 我们经常发现重述这个定义很方便-
通过使用欧拉公式以及对单位长度求幂的事实
复数相当于缩放其极角,

Ak = F −1

(西德:7)

(西德:6)
eikφ

(2.6)

其中 φ 是 F 的极角 {A}. 同样地, 绑定两个酉向量-
tors 相当于将它们的极角相加, as 隐含在 equal 中-
的 2.2.

这个定义的一个结果是对于任何 k1

代数性质成立:

, k2

ε R, 下列

AK1 (西德:2) Ak2 = Ak1

+k2 .

(2.7)

因此, 分数结合可用于生成 vec 的闭合序列-
可以很容易地通过或连续移动任何 (西德:3)k. 如何-
曾经, 这些向量并非全部彼此近似正交. 相当,
对于附近的 k 值, 指针 Ak 将与一个高度相似-
其他 (腰部, 2020). 尤其, 当维度变得足够时-
古代高, 预期相似度接近:

Ak1·Ak2 = sinc(k2

− k1)

(2.8)

对于具有独立 φ ∼ U 的酉 A (-p, 圆周率 ) (沃尔克, 2020). 我们解决
A.1 节中的后面几点.

能够执行分数的最重要的结果
使用 k 的实值进行绑定是 Ak 形式的向量可以编码 con-
连续数量. 然后可以将这些连续的数量绑定到其他数量中
陈述, 从而允许对任意混合进行编码的向量
连续和离散元素. 例如, 离散对连续-
(西德:2) AK2 . 相似地, 一个连续-
的值可以表示为 P1
三维值可以表示为 Ak1 (西德:2) 黑2 (西德:2) CK3 . 这
从这些例子中得出的一点是，使用分数绑定 sig-
显着扩展了可编码和可编辑的数据结构类别-
使用矢量符号架构进行 nipulated, 即, 对于那些可定义的
在连续空间上 (IE。, 具有连续槽).

(西德:2) AK1 + P2

2.2 空间语义指针. 为了最好地利用上述功能
VSA 在空间推理任务中的应用, 我们合并分数
将操作绑定到称为 se 的认知建模框架中-
Mantic指针架构 (温泉; 埃利亚史密斯, 2013). SPA 提供

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2041

整合认知的架构和方法, 感性的, 和
尖峰神经网络中的运动系统. SPA 定义向量表示-
句子, 命名语义指针 (SP), 那 (1) 通过 com 生成-
涉及任意表示的压缩和集合操作
方式, (2) 表达语义特征, (3) “指向”附加表示-
通过解压缩操作访问的语句, 和 (4) 可
神经执行的 (埃利亚史密斯, 2013). 通过整合符号结构
具有更丰富感觉形式的传统 VSA 定义的类型-
托尔数据, SPA 创造了至今仍然是世界上最先进的技术
人类大脑最大的功能模型 (埃利亚史密斯等人。, 2012; 秋,
2018), 以及专注于更具体认知的各种其他模型-
主动功能 (拉斯穆森 & 埃利亚史密斯, 2011; 斯图尔特, 秋, & 埃利亚史密斯,
2014; 克劳福德, 金格里奇, & 埃利亚史密斯, 2015; 布劳, 索洛德金, 萨加德, &
埃利亚史密斯, 2016; 戈斯曼 & 埃利亚史密斯, 2020).

SSP 扩展了内部定义的表征结构类别
SPA 通过将离散对象的任意复杂表示绑定到
连续拓扑空间中的点 (科梅尔等人。, 2019; 鲁, 沃尔克,
腰部, & 埃利亚史密斯, 2019; 腰部 & 埃利亚史密斯, 2020). 水疗中心提供
在尖峰中实现和操纵这些表示的方法
(和非尖峰) 神经网络.

为了方便, 我们引入了编码 a 的简写符号

位置 (X, y) 在连续的空间里,

磷(X, y)

防御= Xx (西德:2) 是,

(2.9)

其中 X, Y ∈ V 是随机生成的, 但固定, 酉向量表示-
在欧几里得空间中发送两个轴. 我们的定义自然地概括了
到多维拓扑空间, 但我们的重点仅限于
用于实际说明目的的二维欧几里得空间.

从数学上来说, 编码平面上 m 个对象的集合的 SSP 可以是

定义为

米=

米(西德:8)

我=1

OBJ

(西德:2) 和

(2.10)

在等式中 2.10, OBJ

ε V 是代表第 i 个对象的任意 SP, 和

和

=P(希

, 做),

在哪里 (希, 做) 是它在空间中的位置, 或者

(西德:9)

和

磷(X, y) dx dy,

(X,y)εRi

里里在哪里

⊆ R2 是其在二维空间中的区域.

(2.11)

(2.12)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2042

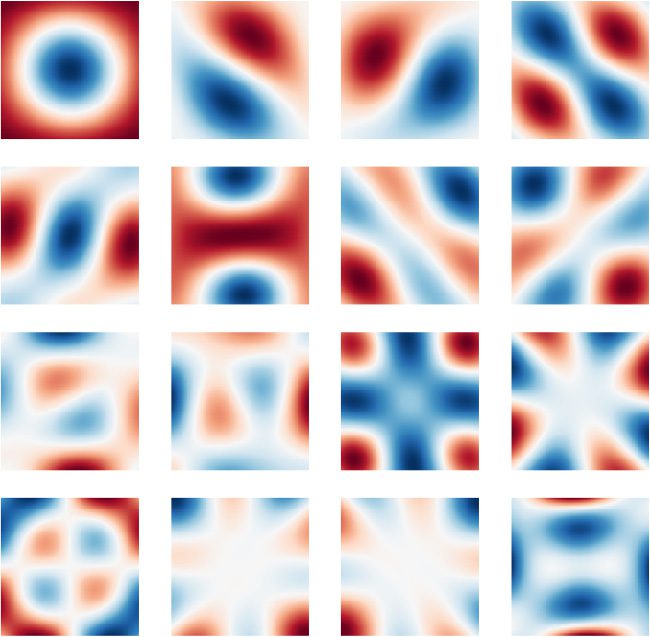
A. 沃尔克等人。.

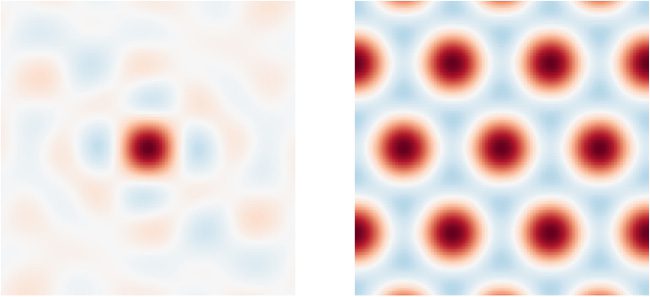
数字 1: 两个不同 SSP 的相似性图示例, 每个编码一个罪恶-
目标位置处的gle对象 (0, 0) 在一张大小为正方形的地图上 6
2. 左边: 512维
SSP 使用随机生成的酉轴向量构建. 正确的: A
7-维度 SSP 是使用产生六边形的轴向量构建的
格子 (参见部分 2.2.2).

√

定义 Si 的积分可以在一组点上变化, 在这种情况下阿比-
二进制区域可以被编码到SSP中 (另请参阅部分 2.2.1); 否则,
Si 编码平面上的单个点. 总和范围为 1 to m 可以毛皮-
其中包括空实体和空间表示 (IE。, 身份语义-
抽动指针) 使得 SSP 能够包含不包含实体表示
与空间中的特定位置相关, 以及空间表示-
与特定实体无关的系统蒸发散. 定义的这些特征
允许 SSP 灵活地编码有关广泛空间的信息 (和
其他连续) 环境.

SSP 可以被操纵, 例如, 移动或定位多个对象
在太空 (科梅尔等人。, 2019) 并查询之间的空间关系
物体 (鲁, 沃尔克, 腰部, & 埃利亚史密斯, 2019). 提供简单的考试-
普莱, 一个物体位于 (X, y) 可以通过计算从 SSP 中检索
中号 (西德:2) 磷(X, y)−1，然后将结果清理为最相似的 SP
词汇 {OBJ
}米
我=1. 同样地, 空间中的第 i 个点或区域, 和, 可
−1
通过计算M检索 (西德:2) OBJ
, 对结果进行可选的清理.
我
作为最后一个例子, 方程 2.7 可以用来移动所有坐标
M 相同数量, ((西德:3)X, (西德:3)y), 与绑定M (西德:2) 磷((西德:3)X, (西德:3)y).

2.2.1 使用相似性图可视化 SSP. 可视化某些物体的
空间中的点或区域 (和, 从方程 2.11 或者 2.12), 我们经常策划什么
我们称之为“相似度图” (见图 1). 这是通过 se 计算的-
选择一些想要评估的二维坐标-
吃然后每 (X, y) 按值对相应像素着色

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2043

的 P(X, y)硅钛矿, 那是, 指针与对应的相似度-
空间中的编码点. 通常，颜色是从不同的颜色中选择的-
调色板, 标准化为 [−1, 1], 之间的相似性极限
两个酉向量.

更正式一点, 相似度图是一个线性算子，它消耗
固相磷酸盐, S, 并产生一个函数 (X, y) 对于特定的 SSP, 我们
可以在数学上表示为

中号(S) =P(X, y)TS.

(2.13)

数字 1 说明了两种不同选择的示例相似性图
轴向量 (X, 是), 给予不同的P(X, y). 在每种情况下, 我们正在密谋
中号 (磷(0, 0)), 在哪里 (X, y) 均匀地平铺在大小为正方形的网格上 6
2,
以 (0, 0).

√

这些插图对于理解和形象化什么是有用的
特定的SSP代表. 值得注意的是，SSP 本身
不是离散的像素集; 它们本质上是压缩的代表-
使用傅里叶基函数对其进行计算. 相似度图是主要的-
是一个可视化工具.

那就是说, 相似性图确实提供了重要的见解: 平等-
系统蒸发散 2.11 或者 2.12 是构建 SSP 的充分但不是必要的方法
对空间点或区域进行编码. 那是, S 可以是任何向量，使得
中号(S) 近似某些所需的函数 (X, y), 使得相似度
S 和 P 之间(X, y) 表示该空间地图. 我们提供一个例子
A.1 节中这一见解的有趣应用.

相似度图还有一些重要的属性. 第一的,
移动 A 的相似度图相当于将 A 移动相同的距离
数量, 自从

磷(X + X

(西德:8), y + y

(西德:8)

)T S =

(西德:10)

磷(X, y) (西德:2) 磷(X
(西德:10)

=P(X, y)时间
(西德:10)
= 米

S (西德:2) 磷(X

时间

(西德:8)

(西德:8), y

(西德:11)
)
(西德:8), y
S (西德:2) 磷(X
(西德:11)
(西德:8), y
.
)

(西德:8)

S
(西德:11)
)

(2.14)

第二, 因为点积是线性算子, 产生的函数
相似度图, 中号(·), 实际上是一个线性函数; 采取线性组合-
相似图国家相当于取该国家的相似图
向量的相同线性组合. 第三, 峰值(s) 在情节中, 超过一些
空间域, 对应理想目标(s) 进行清理-
把最相似的P(X, y) 给定该域作为其词汇表.

2.2.2 SSP 与神经生物学表征的相关性. SSP 也可以是
用于重现相同的网格单元放电模式 (杜蒙 & 埃利亚史密斯,
2020) 众所周知，它们被认为是大脑空间的基础

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2044

A. 沃尔克等人。.

代表制度 (莫塞尔, 克罗普夫, & 莫塞尔, 2008). 这样就完成了
通过生成轴向量, (X, 是), 通过以下方式.

考虑代表单个 d 维 SSP 的相似度图
观点, 注意到两个向量之间的点积相等 (最多一个
持续的) 到它们的傅里叶变换的点积,

中号(磷(x0

, y0)) =P(X, y)TP(x0

, y0) ∝

d(西德:8)

j=1

不(Kj,1(x+x0 )+Kj,2(y+y0 )),

(2.15)

其中 Kj,1 是傅立叶变换第 j 个分量的极角
轴向量 X, 和 Kj,2 是轴向量 Y 的极角.

索舍尔, 梅尔, 甘古利, 和奥科 (2019, 参见方程 2.10) 和杜蒙
和埃利亚史密斯 (2020, 参见方程 2.11–2.13) 提供条件
这些相使得相似图是正六边形格子图案-
燕鸥横跨 (X, y) 飞机. 核心构建块是矩阵 K ∈ R3×2
保存等边三角形的三个二维坐标
内接于单位圆:
⎛

⎞

⎟
⎠ .

(2.16)

⎜
⎝

K =

√

0
3/2 −1/2
√
3/2 −1/2

在方程中使用这些值作为极角 2.15 产生六边形-
仅平铺相似性图. 然而, 确保得到的轴向量
是真实且单一的, 需要额外的极角. 尤其, 这
轴向量的傅立叶变换必须具有埃尔米特对称性 (IE。,
包含 K 给出的系数的复共轭) 和一个零-
一的频率项. 这会产生七维轴向量.

K 矩阵的缩放和/或旋转版本可用于设置
分辨率和方向, 分别, 由此产生的六边形图案.
这里, 缩放意味着将 K 乘以固定标量, 和旋转装置
将 2D 旋转矩阵应用于 K 的列. 例如, 生产
放置或网格单元凸块的直径为
2 (见图 1, 正确的), 这
缩放因子的平均值应为 2π/
6.4

√

虽然这些 7 维 SSP 可用于创建尖峰神经网络-
使用类似网格单元的发射模式, 这种模式相似意味着
此类 SSP 只能唯一地代表一小部分区域 (X, y) 价值观.
为了增加 SSP 的代表性能力并产生位置细胞 –
像相似度图, 维数必须通过组合来增加

利用六方晶格中峰之间的距离为 4π 的事实 /

在哪里 |k| 是 K 上的比例因子 (杜蒙 & 埃利亚史密斯, 2020).

(西德:18)√

(西德:19)
3|k|

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2045

具有不同分辨率和方向的各种网格. 缩放和
K 的旋转版本可以在傅里叶域中堆叠 n 次以生成-
评价 x- 和 y 轴向量. 轴向量的最终维度
是 d = 6n + 1 (6 来自不同尺度/旋转的每个 3 维 K 块
及其复杂的共轭体, 和 1 从零频率项). SSP
使用此类轴向量的结构将被称为六边形 SSP. 神经元
在代表六边形 SSP 的网络中可以挑选出不同的网格
包含. 这再现了类似网格单元的调谐分布并提供
在尖峰神经网络中使用 SSP 更准确地定位细胞表示-
作品 (杜蒙 & 埃利亚史密斯, 2020).

2.2.3 SSP 作为深度学习的特征. SSP, 在更大的 SPA 中使用
框架, 提供一种编码连续变量的通用方法
在代数运算具有se的高维向量空间中-
曼蒂克解释. 因此, 这些向量和运算可用于
制定复杂的认知模型. 超出此, SSP 是深入研究的有用工具
学习作为一种将数据嵌入到具有所需特征空间的方法
特性.

用于创建特征的数据以及特征的表示方式-
怨恨可能会对神经元的性能产生很大的影响
网络 (腰部, 2020). 这里, “features”指的是初始向量输入
提供给网络. 网络的每一层接收信息代表-
重新作为向量并将其投影到另一个向量空间. 神经元
在一个层中可以被认为是其空间的基础. 如果一半 (或者更多) 的
神经元活跃, 这意味着向量的大部分维度
需要空间来表示信息. 这样的层将包含
输入信息的密集编码. 如果只有一个神经元活跃-
分层, 它将代表本地编码. One-hot 编码和
特征散列是用于编码离散数据的启发式示例
对应于局部密集编码, 分别. 介于两者之间的任何东西
密集且局部的代码称为稀疏代码. 稀疏代码是一个优点-
两个极端之间的微妙平衡; 他们有较高的代表性-
比本地代码具有更强的能力和更好的通用性，并且是通用的-
与密集代码相比，更容易学习函数 (褶皱, 2003).
换句话说, 这样的特征向量具有合理的维数并且
在下游任务中使用时可以获得更好的性能.

特征学习 (例如, 使用自动编码器) 可以用来学习有用的
陈述, 但, 正如深度学习中常见的情况, 结果是usu-
盟友无法解释. 一个著名的词嵌入模型是 word2vec,
它采用一个单词的单热编码并输出一个较低维的
向量. 所得向量的一个重要属性是它们的余弦
相似度对应于编码词的语义相似度. 清楚的
输入的相似度接近于零. 当词嵌入用这个
财产被使用, 使用单层学习稀疏编码很容易
神经元.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2046

A. 沃尔克等人。.

如何从连续的特征中构造具有这些属性的特征
变量, 尤其, 低维变量? 连续数字
值可以直接输入神经网络, 但这个原始输入是在
密集编码的形式, 所以通常更大/更深的网络是
精确函数逼近所需. 获得稀疏编码
从连续数据, 它必须映射到更高维的向量-
托空间. 这正是将变量编码为 SSP 时所做的事情. A
简单的自动编码器无法解决这个问题; 自动编码器的工作原理是使用
信息瓶颈, 如果它们的嵌入有更高的维度-
比输入, 它只会学习将输入传递给. 冰毒-
可以使用瓦片编码和径向基函数表示等ods
在高维空间中编码连续变量, 但 SSP 有
被发现比在数组上进行此类编码具有更好的性能
深度学习任务 (腰部, 2020). 很像 word2vec 嵌入, SSP
欧几里德空间中距离较长的变量将具有较低的余弦值
相似, 因此可以从中获得稀疏代码. 此外,
SSP 可以与离散数据的表示绑定，而无需增加
它们的维度来创建结构化的符号表示
易于解释和操作. SSP 的这些特性激发了扩展-
使用 SSP 理论来表示轨迹和动态变量. 这
将填补结构化方法的空白, 动态特征表示.

3 使用 SSP 模拟动力学的方法

先前关于 SSP 的工作主要集中于表示二维空间
地图 (科梅尔等人。, 2019; 卢等人。, 2019; 腰部 & 埃利亚史密斯, 2020; 杜蒙
& 埃利亚史密斯, 2020; 腰部, 2020). 其中一些工作还表明
关于需要连续表示的机器学习问题, SSP
最常应该是首选. 具体来说, 腰部 (2020) com-
将 SSP 与其他四种标准编码方法进行比较 122 不同的
任务并证明 SSP 在以下方面优于所有其他方法 65.7%
的回归和 57.2% 分类任务的数量. 这里, 我们延续过去的工作
通过引入表示任意单对象轨迹的方法
以及模拟一个或多个物体跟随的动力学的方法
独立轨迹.

3.1 表示任意轨迹. 对于很多问题, 一
需要对动态数据进行编码, 不是静态的. 时间是一个连续变量-
有能力的, 很像太空, 因此它也可以作为附加项包含在 SSP 中-
轴,

磷(X, y, t) = CT (西德:2) xx (西德:2) 是,

(3.1)

其中 C 是随机选择的单一 SP. 这个时间指针可以是manip-
与任何其他 SSP 的计算和解码方式相同.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2047

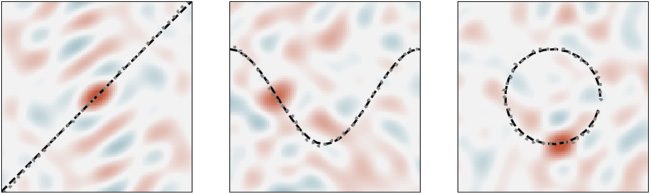
数字 2: 解码 SSP 代表的轨迹 (左边: 线性; 中间: 余弦;
正确的: 圆圈). 连续轨迹的二十五个采样点 (显示为
黑色虚线) 与“提示”轨迹绑定 (例如, 时间) 并总结
一起作为 SSP. 解码来自 SSP 的内插位置, 144 提示
使用积分. 这些解码后的位置 (清理程序后) 是情节-
带有灰色虚线的 ted. 使用计算的相似性图的快照
解码位置绘制在下面.

这种时间相关的 SSP 序列是整个 ar 的编码-

位轨迹. 编码此类轨迹的方程是

米(西德:8)

我=1

Cti (西德:2) 和

(3.2)

它是 m 个点的离散集合的总和, 其中 Si 是编码
ti 是该点在空间上的相对时间
弹道. 如果我们想对 SSP 的有序序列进行编码, 订单可以
被用作“时间,”，ti 是空间 SSP 的位置
列表.

连续轨迹也可以用自然概括来编码-

方程的重刑 3.2:

(西德:9)

t (西德:2) S(t ) dτ,
C

(3.3)

哪里(t ) 生成某个轨迹内每个点的编码
在连续时间间隔内定义的点, τ ε [0, t].

实现平稳推进转型的 SSP
然后可以使用该轨迹来解码插值的信息-
调整原始非线性轨迹中的点. 当人少而遥远的时候
使用样本点, 该插值类似于线性插值,
尽管解码结果超出了样本点的时间范围
(IE。, 推断) 衰减到零. 数字 2 显示三个连续轨迹-
从 SSP 解码的历史. 第一个描绘出线性 y = x 函数,
第二个追踪余弦函数, 第三次画出一个圆.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2048

A. 沃尔克等人。.

回放的流畅度取决于采样点的数量
用于学习轨迹, 样本点之间的距离, 迪-
SSP的重要性, 以及时间和空间变量的缩放. 这
可视化中的噪声量也取决于这些因素，因为, 为了
例子, 低维 SSP 将无法编码大数字-
轨迹采样点的误码率，而不会产生大量的
压缩损失.

这里介绍的方法用于对整个动态序列进行编码
作为固定长度向量的变量可以在许多领域中使用. 科雷耶斯
等人. (2018) 提供连续状态下性能的示例
和行动强化学习问题可以使用tra来改善-
投影编码. 他们使用经过训练的自动编码器来编码序列
状态空间观察并生成动作轨迹. 对轨迹进行编码-
拥有 SSP 的知识不需要任何学习. 尽管没有学到,
研究发现，与 SSP 相比，SSP 在导航任务上表现更好
学习到的编码 (腰部 & 埃利亚史密斯, 2020).

3.2 模拟任意轨迹. 在这个部分, 我们从
使用以下方法对特定轨迹进行编码以在线模拟这些轨迹
控制每个对象的动力学的一些规范由
一个SSP.

3.2.1 使用连续偏微分方程模拟单个对象. 第一的, 我们举例说明
如何通过应用来模拟 SSP 空间中的偏微分方程
转换为在特定位置对单个对象进行编码的初始 SSP
空间中的点. 在离散时间情况下, 变换将应用于
每个时间步的 SSP 来解释它所代表的对象的运动-
怨恨. 从数学上来说, 对初始 SSP 的这些更新采用以下内容
随着时间的推移形成.

山+(西德:3)t =

(西德:10)

(西德:3)xt (西德:2) 是

(西德:3)yt

(西德:11)

(西德:2) 山=P((西德:3)xt, (西德:3)yt ) (西德:2) 公吨,

(3.4)

在哪里 (西德:3)xt 和 (西德:3)yt 是从将 x 和
以某种方式 y 到 t. 例如, 如果潜在的动态是线性的, 我们
有 (西德:3)x = dx
(西德:3)t. 假设 Mt = Xxt (西德:2) 耶 , 那么代数性质
dt
SSP 确保 Xxt (西德:2) 耶 (西德:2) X(西德:3)xt (西德:2) 是(西德:3)yt = Xxt +(西德:3)xt (西德:2) 耶 +(西德:3)yt = Mt+(西德:3)t, 作为
必需的.

一个重要的观察结果是与 P 的结合((西德:3)xt, (西德:3)yt ) 相当于-
能够将矩阵变换应用于 SSP (参见方程 2.3).
具体来说,

山+(西德:3)t = T (磷((西德:3)xt, (西德:3)yt )) 公吨,

(3.5)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2049

其中T(·) 是产生结合矩阵的线性算子
给定SP (IE。, 时间(A)乙=甲 (西德:2) 乙). 尽管我们上面假设
微分方程在离散时间上表达, 我们还可以做
在连续时间内相同. 我们省略证明并简单地陈述结果,
使用 ln 表示矩阵对数的主分支:

dM
dt

(西德:20)

磷

dx
, 迪
dt
dt
温度(X ) + 迪
dt

温度

dx
dt

(西德:21)(西德:21)(西德:21)

中号

(西德:21)

温度(是)

中号.

(3.6)

所以, 演化出的连续时间偏微分方程
SSP 随着时间的推移相对于 dx/dt 和 dy/dt 是两个固定值相加
SSP 的矩阵变换，每个变换都按各自的比例缩放
衍生品. 方程 3.6 因此相当于线性动力系统,
用两个时变积分时间常数控制速度
x 和 y 的系统——可以通过以下方式准确有效地实现的系统：
循环尖峰神经网络 (埃利亚史密斯 & 安德森, 2003; 沃尔克,
2019).

我们也可以将上述连续时间线性系统表示为
绑定, 首先引入以下定义, 这是类似的
方程 2.5:

熔点

dM
dt

(西德:20)

DEF=F-1{lnF{A}}.
lnX + 迪
dt

dx
dt

(西德:21)

(西德:2) 中号.

(3.7)

(3.8)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

方程组 3.6 直接映射到循环神经网络
有两个循环权重矩阵, 温度(X ) 和 T(是), 与增益因子
dx/dt 和 dy/dt 独立缩放各自的矩阵向量 mul-
提示. 在我们的例子中, 我们模拟方程的动力学 3.8 我们-
构建尖峰神经网络. 使用尖峰神经元进行模拟时, 这
突触前活动必须经过过滤才能产生突触后电流.
必须在循环网络中考虑这种过滤.

神经工程框架 (NEF; 埃利亚史密斯 & 安德森, 2003)
提供了一种通过集体活动表示向量的方法
一群尖峰神经元并通过 re 实现动力学-
当前连接. 假设使用一阶低通滤波器, 一个神经元
代表向量 M 的群体可以根据某种动态演化-
ICS dM
dt 通过循环连接并设置权重来执行传输-
+ 中号, 其中 τ 是滤波器时间常数. 最佳权重
形成 τ dM
dt
可以通过最小二乘法找到用一层进行变换
优化.

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2050

A. 沃尔克等人。.

数字 3: 实现等式动力系统的神经网络-
的 3.8 使用 Stewart 中描述的绑定网络, 贝科莱, 和埃利亚史密斯
(西德:11) + 1) 神经群体 (其中 d
(2011). 绑定网络包括 4((西德:10) d
2
是SSP的大小). 将输入连接到这些总体的权重
设置为计算傅立叶变换. 每个群体执行其中一项
傅里叶域中两个输入的逐元素乘法. 重量
从这些群体传出到网络的输出执行以下操作-
逆傅立叶变换.

数字 4: 使用尖峰神经网络来模拟连续时间部分
映射到单个物体的振动的微分方程. 新的-
ral 网络由单个循环连接层组成 30,400 尖峰
神经元.

dt ln X + 迪

之前的工作已经使用 NEF 构建了一个神经网络，可以预-
形成循环卷积 (斯图尔特, 贝科莱等人。, 2011). 该系统的
方程 3.8 映射到这样的网络, 如图 3. 网络
绑定输入向量 dx
dt y (通过连接传入 1 在
图表) 具有表示 SSP M 的内部状态向量. 使用
两个循环连接, 提供绑定缩放结果的一个
由 τ 返回网络作为输入 (联系 2) 和另一个喂养
内部表示的 M (预绑定) 也到输入 (联系
3), 方程的动力学 3.8 被实现. 因此, 提出的方法
这里可用于构建在空间中移动任何 SSP 的神经网络
通过随时间积分 dx/dt 和 dy/dt, 类似于路径的神经模型-
整合 (康克林 & 埃利亚史密斯, 2005).

举个例子, 我们使用这些方法来模拟 SSP 振荡-
二维空间中的延迟 (见图 4), 类似于受控循环
吸引子 (埃利亚史密斯, 2005). 六方固相聚合物 (节中描述 2.2.2) 是

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2051

数字 5: 模拟由微分方程和弹性控制的轨迹
碰撞. 每个轨迹都是通过绑定编码对象的 SSP 来生成的
在每个时间步将状态转换为“转换”SSP，对其瞬时进行编码
速度根据初始速度的影响, 重力, 和碰撞
与飞机底部.

与 n = 一起使用 25 (具有五个统一的 K 缩放范围 0.9
到 1.5, 和五次旋转; 这导致 d = 151) 和 100 尖峰积分-
并激发傅里叶域中每个元素乘积的神经元 (30,400
神经元总数). 在这个例子中, 偏导数 dx/dt 和 dy/dt 为
由一个决定 0.2 Hz 振荡，半径为 5 个空间单位.

每当模拟时，也可以施加碰撞动力学
所表示物体的轨迹遇到固体表面 (例如, 一层楼或
一堵墙). 具体来说, 由给定的反式施加的瞬时速度-
地层在与表面撞击时被倒转并按比例缩放
具有弹性碰撞物理的简单模型. 换句话说, 这
((西德:3)xt, (西德:3)yt) 或者 (dx/dt, dy/dt) 对应于碰撞发生的时间
可以以上下文相关的方式确定. 图中 5, 快照
来自对球掉落的模拟 (左边) 并扔掉 (正确的) 与差异-
显示了在硬表面上弹跳之前的不同初始条件. 这里,
转化 SSP 的序列是在假设下推导出来的 (1) 一个初始对象
位置和速度, (2) 重力效应的微分方程, 和
(3) 一个简单的弹性碰撞模型，可以反转并缩放物体的
当到达所表示的底部时沿 y 轴的移动
飞机.

总结一下, 我们可以对离散时间和连续时间进行建模
使用线性变换求解空间微分方程 (见平等-
系统蒸发散 3.5 和 3.6) 或绑定 (方程 3.4 和 3.8) 那些应用于
SSP随时间的变化. 请注意，动态本身是由
速度输入. 这里提出的方法的目的是模拟
SSP 空间中的这种动态并证明这是可能的-
尖峰神经网络. 这些方法可以以多种方式使用.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2052

A. 沃尔克等人。.

如果动力学是动物的自我运动, 这个模拟-
化是一种生物学上合理的路径整合模型, 其结果
可用于下游认知任务. 当六角形 SSP 为
用过的, 该模型将具有类似网格单元的发射模式, 与新一致-
生物学发现. 此外, 模拟 SSP 空间中的动力学
规避了神经网络表征半径的限制问题
人口, 这会阻止欧几里得空间中的动力学被模拟-
直接与此类网络相关. 此外, 动态编码
不断变化的量可以用作深度学习网络中的特征. A
动态编码对于某些问题非常有用, 比如一个在-
线强化学习任务, 跟踪移动障碍物
可能很重要, 或涉及预测未来轨迹的问题.

3.2.2 预测未来物体位置. 在模拟动态时
系统可用于执行预测, 我们也可以直接解决
通过训练一个不使用潜在动力学知识的问题
网络输出移动物体未来状态的预测. 这里,
我们简要描述了一种利用 SSP 表示来实现的技术
预测方形环境中的弹跳球. 具体来说, 为了这
网络, 我们提供了球绕着物体弹跳的 SSP 表示
square 环境作为最近开发的在线输入时间序列
称为勒让德记忆单元的循环神经网络类型 (慕尼黑大学;
沃尔克, 卡吉茨, & 埃利亚史密斯, 2019).

LMU 已被证明优于其他类型的循环网络-
适用于时间序列处理的各种基准任务. 它有
也被证明在压缩连续信号方面是最佳的-
比特时间窗, 这非常适合动态预测. 这
LMU 通过使用线性时不变系统来工作 (由矩阵定义
A Î Rn×n 且 B Î Rn×1) 在滑动时间内正交化输入信号
某个固定长度 θ 的窗口 . 加窗信号投影到基
类似于前 n 个勒让德多项式 (那些被转移的, 普通的-
化的, 并离散化).

假设我们的 SSP 随时间变化, Mt ∈ Rd, 然后让 [公吨] j 是它的
第 j 个分量. 在每个时间步, LMU 将更新其内部存储器,
米( j)
t

, 对于 SSP 的每个组件如下:

米( j)
t

= 上午( j)
t−1

+ 乙 [公吨] j

定义 LTI 系统的矩阵由下式给出

(西德:22)

[A]我j

= (2我 + 1)
我

−1
(−1)i−j+1

如果 i ≤ j

别的

= (2我 + 1)(−1)我
我

[乙]我

(3.9)

(3.10)

(3.11)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2053

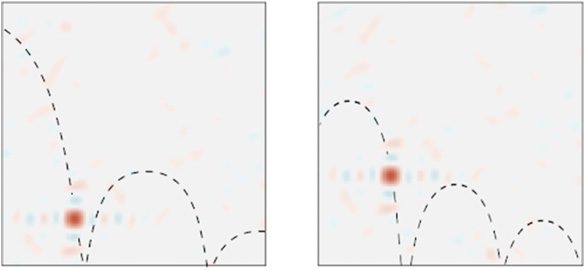
数字 6: 弹跳球历史总和的相似度图 (一次
SSP 窗口) 和 (正确的) 它的未来或 (左边) 对这个未来com的预测-
使用勒让德内存单元 (慕尼黑大学) 和历史. 绘制的是
虚线表示这些时间窗口所代表的位置
SSP, 这是使用清理程序计算的.

我们在这里使用的 LMU 的历史窗口 θ 为 4 的用途
12 勒让德基地 (例如, n = 12). 使用六边形 541 维 SSP
和 10 K 的缩放均匀范围为 0.9 到 3.5, 和 9 旋转.

该模型预测相同的时间窗口，但是 6 走向未来
(因此, 有一个 2 s 当前时间与预训练开始时间之间的差距-
预测未来状态). LMU 的输出被输入神经网络
具有三个致密层. 网络的输入是 d 个记忆向量
ε Rn×1, SSP 的每个维度都有一个, 作为
通过 LMU 计算, 米( j)
t
具有大小的单个展平向量 6492. 前两层有一个隐藏层
大小 1024 后面是 ReLU 激活函数. 最后一层
隐藏尺寸为 6492. 该网络的输出被投影到 n Leg-
endre 多项式以获得 SSP 的预测 10 时间点均等
与未来窗口间隔开. 该网络共有 14,352,732 火车-
可用参数.

该网络经过训练 4000 s 内的弹跳动态 1 经过
1 盒子. 训练数据是编码球的 PO 的 SSP 时间序列-
位于 0.4 s 间隔. 球的轨迹是通过模拟生成的
具有随机初始条件 (盒子内的位置和速度) 和
边界碰撞动力学.

仿真示例如图所示 6, 其中LMU预-
措辞和实际的未来 SSP 表示进行比较. 我们发现
它能够准确地表示球历史的滑动窗口
同时预测其未来的滑动窗口. 我们骗-
认为这是一个原理证明，展示了成功的潜力

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2054

A. 沃尔克等人。.

将 SSP 与深度学习方法结合起来，进行动态仿真和预测-
措辞. 作为演示, 我们留下定量分析和比较
与其他深度网络集成以进行未来的工作 (见科梅尔, 2020,
证明 SSP 在回归和分类方面的通用性
问题).

3.3 模拟多个对象. 而方程 2.10 确定
单个SSP可用于对多个ob的位置进行编码和解码-
项目, 需要进一步的步骤来模拟定义的连续动态
对于这些物体. 这里, 我们说明可以-
同时模拟动态的精细独特运算符或函数
多个对象的, 这样每个对象都遵循自己独立的tra-
猜测. 具体来说, 我们描述了一种模拟动力学的方法
代数上的多个对象, 以及模拟此类 dy 的方法-
使用经过训练的函数逼近器进行动力学.

在编码多个对象的 SSP 上下文中, 至关重要的是
考虑到每当特定对象的位置
从 SSP 中提取, 提取的位置将是一个有损的近似值-
−1
真实位置的图像, 自从 M (西德:2) OBJ
≈ Xxi (西德:2) 做吧 . 而且, 这
我
在这种情况下观察到的压缩损失量将成正比
编码对象的数量, 进行transforma的应用-
SSP 编码多个对象的困难. 然而, 通过杠杆-
了解用于生成这些 SSP 的具体方法, 它
可以定义显着改善这些的清理方法
挑战.

−1 返回点 (希

3.3.1 清理方法. 本节我们介绍两种清理方法-
SSP 的 ods. 第一种方法涉及预先计算 Xxi (西德:2) Yyi 处于离散状态
沿固定网格的点数, 然后取每个的点积
向量与 M (西德:2) OBJ
, 做) 最大余弦模拟-
给定 SSP 的稀有性. 这可以通过神经网络中的单层来实现
网络, 其权重为 Xxi (西德:2) 做吧 , 随后是 argmax, 临界点, 或者
其他一些赢家通吃的机制. 该应用程序的主要缺点-
Proach 的缺点是它不能自然地处理连续输出, 虽然
人们可以权衡相邻点积的相似性来进行插值
网格点之间.

第二种清理方法利用了这样一个事实：它通常是
只对检索 Xxi 重要 (西德:2) yyi 也不一定 (希
, 做). 具体来说,
我们需要学习一个函数 f 来获取解除绑定的噪声结果
来自 SSP 的对象作为输入并输出“干净”的 SSP:

−1
F (中号 (西德:2) OBJ
) = Xxi (西德:2) 做吧 ,
我
−1
其中 M (西德:2) OBJ
我

−1
= Xxi (西德:2) 做吧 + 这 (西德:2) OBJ
我

(3.12)

(3.13)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2055

和 η 是一些“嘈杂”向量，代表所有其他 ob 的叠加-
解除绑定操作适用的 SSP 中的项目. 这个函数f
可以以与自动编码降噪器相同的方式进行训练, 与平均值
平方误差 (均方误差) 损耗和高斯噪声 (σ = 0.1/天) 包含在
培训投入 (腰部 & 埃利亚史密斯, 2020). 我们发现有一个网络com-
奖励一层 ReLU, 有多少个维度就有多少个神经元
在SSP中, 足够了. 我们还将清理的输出标准化为强制
它保持单一. 这种方法的好处是它可以连续
输出 (与一组离散的可能输出相反). 清理工作可以
还可以接受训练以返回连续的 (希

, 做) 与 Xxi 相反 (西德:2) 做吧 .

3.3.2 以代数方式模拟多个对象. 代数性质
SSP 引入了多种应用转换的可能性
多个物体的空间位置. 回忆部分 2.2 对于
编码一组对象位置的 SSP, 可以改变所有这些
职位由 (西德:3)x 和 (西德:3)y 如下:

中号=中号 (西德:2) X

(西德:3)X (西德:2) 是

(西德:3)y.

(3.14)

这种方法的缺点是无法应用差异化-
对每个对象位置的不同更新, 因为没有办法区分
哪个更新应该应用于哪个位置 (由于广告-
条件是可交换的).

另一种方法是用一个标签来标记每对坐标
相应对象的表示，然后应用变换-
系统蒸发散独立更新每个对象的位置. 标签的使用
允许单独提取和更新每个对象位置, 后
这些更新后的位置可以反弹到其对应的对象
并汇总在一起生成新的 SSP. 从数学上来说, 这个流程
描述如下,

中号←

米(西德:8)

我=1

OBJ

−1
(西德:2) F (中号 (西德:2) OBJ
我

) (西德:2) X

(西德:3)希 (西德:2) 是

(西德:3)做 ,

(3.15)

其中 f 是方程的清理结果 3.12. 我们发现这个方法有效
只要清理功能足够准确. 主要抽签-
后面是每个时间步骤都需要 m 次清理应用,
尽管这些可以并行应用并相加.

更有效的方法是标记每组坐标
具有相应对象的表示，然后应用 addi-
tive 移位独立更新每个对象的位置，如下所示:

中号←中号 (西德:2) OBJ

(西德:2) (西德:3)圆周率

(3.16)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2056

A. 沃尔克等人。.

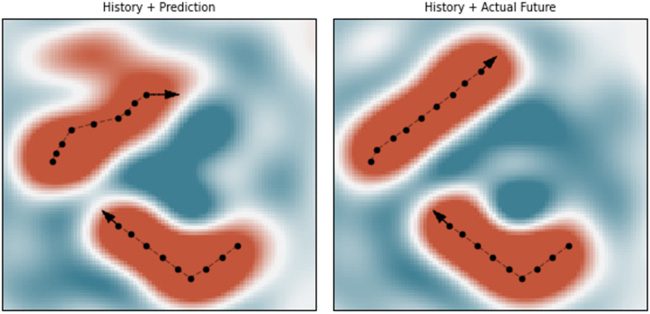
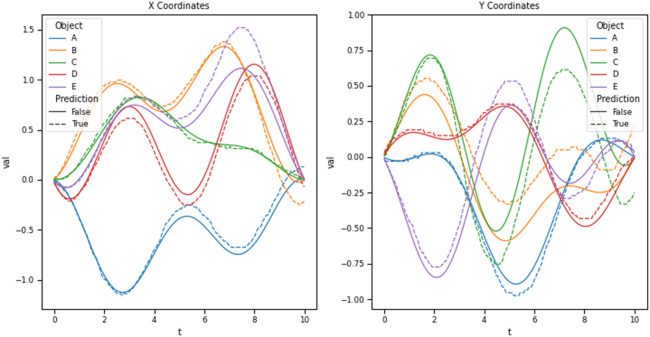
数字 7: 使用单独的代数更新 (参见方程 3.16) 与第一个
cleanup 方法来模拟一个物体内五个不同物体的轨迹
单固相聚合. 首先是所有五个对象初始 po 的 SSP 表示-
地点. 在每一个 0.05 s 时间步长, SSP 进行代数更新以模拟
物体的运动. 虚线代表解码的物体轨迹
从这个模拟, 而实线代表真实对象
轨迹.

在哪里

(西德:3)圆周率

= Xxi

+(西德:3)希 (西德:2) 做吧

+(西德:3)yi − f (中号 (西德:2) OBJ

−1
我

这有效是因为

OBJ
= 对象

(西德:2) 二十一 (西德:2) 做吧 + OBJ
+(西德:3)希 (西德:2) 做吧

(西德:2) 二十一

+(西德:3)做 .

(西德:2) (二十一

+(西德:3)希 (西德:2) 做吧

−1
+(西德:3)yi − f (中号 (西德:2) OBJ
我

))

(3.17)

(3.18)

这种方法的缺点是需要多次操作
更新 SSP (每个编码对象一个). 否则，方法是
与之前的方法类似, 虽然这里定义的更新是 itera-
主动的 (一次减去每个过去的位置), 与 hav 相比-
将所有过去的位置信息立即替换为新的总和. 两个都
代数方法可以自然地实现为神经网络. 如图-
乌尔 7 演示了如何使用加法位移来沿着dis移动五个物体-
SSP 内的色调轨迹. 解码的轨迹是准确的
时间跨度短，但最终由于误差的积累而漂移. 给定
其良好的性能特点, 我们使用这种加性位移方法
作为我们最喜欢的模拟多个运动的代数方法
物体 (请参阅下面描述的基准测试结果).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2057

3.3.3 使用学习模型模拟多个对象. 替代方案
依赖于 SSP 的代数性质涉及近似一个函数-
通过将 SSP 映射到新的 SSP 相关性来重复转换 SSP-
沿着某个轨迹响应下一个点:

中号←克(中号, (西德:3)中号),

(3.19)

其中 g 是经过训练以最小化等式中的 MSE 损失的神经网络-
的 3.19 来自单独的训练数据, 和 (西德:3)M 对所有对象 ve 进行编码-
地点如下:

(西德:3)米=

米(西德:8)

我=1

OBJ

(西德:2) X

(西德:3)希 (西德:2) 是

(西德:3)做 .

(3.20)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

(西德:24)

(西德:23)

中号
(西德:3)中号

在本质上, 这种方法相当于学习代数位移 de-
如上所述，更新可以在单个“步骤”中执行。我们
使用 g 的线性模型模拟轨迹 (例如, G(中号, (西德:3)中号) =A
+
b 矩阵 A ∈ Rd×2d 且偏置向量 b ∈ Rd×1), g 是一个 mul-
层感知器 (多层线性规划). MLP的第一层有许多神经元
等于 SSP 维度的四倍，后跟 ReLU 非线性-
性, 第二层神经元数量等于SSP维度.
包含五个对象并使用 MLP 进行模拟的示例轨迹
五个轨迹上的训练如图所示 8. 第一个清理程序
用于每个时间步 MLP 的输出. 如果清理失败 (IE。,
解码对象的位置与检查区域中的所有 SSP 不同),
然后继续前一个时间步的位置估计. 这
方法在训练数据上表现良好. 然而, 即使在这里, 德-
编码位置有时呈直线. 对于一些输入, 解除对象 SP 的绑定
从模型的输出结果得到一个不在空间中的向量
SSP.

3.3.4 模拟多个对象的结果. 执行 SSP 分析
模拟多对象动力学时容量和精度的权衡,
我们重点关注执行的代数方法之间的比较
涉及函数逼近器的加性位移和学习方法,
G(中号, (西德:3)中号).

模型经过训练 100 随机轨迹, 每个都有 200 时间
步骤并由一系列 SSP 和速度 SSP 表示 (山和
(西德:3)公吨). 准确地说, 这些随机轨迹是二维带-
位于二乘二框中的有限白噪声信号. 测试性能
报告为代表 SSP 的真实时间序列之间的 RMSE
轨迹和使用代数方法模拟的轨迹或
G, 平均超过 50 随机测试轨迹.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2058

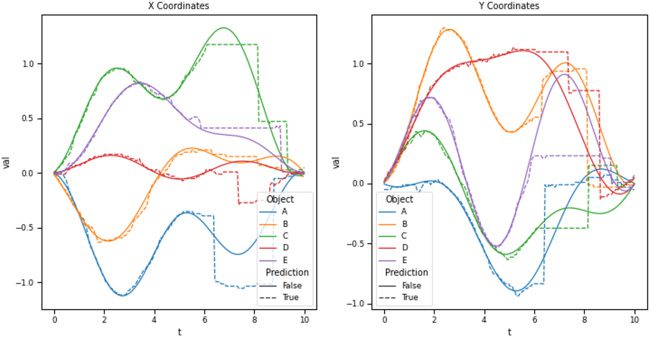
A. 沃尔克等人。.

数字 8: 使用多层感知器 (多层线性规划) 与第一个结合
cleanup 方法来模拟一个物体内五个不同物体的轨迹
单固相聚合. MLP 接收 SSP 和物体速度的最新估计值
表示为单个 SSP 作为输入，并估计下一个时间步的 SSP.
从初始 SSP 开始, 在每一个 0.05 s 时间步长, SSP 使用更新
MLP，然后“清理”以模拟物体的运动. 虚线
表示从该模拟中解码的对象轨迹, 而固体
线代表真实物体轨迹.

数字 9 显示了代数和
学习函数逼近器方法同时改变数量
编码对象的数量，同时保持 SSP 的维数固定, 和
改变 SSP 的维数，同时保持 en 的数量-
编码对象固定. 线性模型和 MLP 都在以下方面表现良好
小训练集但不能推广到测试数据. 有趣的是, 这
当维度的情况下，线性模型比 MLP 表现得更好
SSP足够高.

全面的, 这表明代数方法比
从 MSE 角度学习模型. 海藻的另一个优点-
braic 方法的特点是它是组合的, 这对于灵活性至关重要
扩展到更大的问题. 具体来说, 一旦任何一条轨迹被
学到了, 它可以与其他轨迹并行组合, 同时添加
将 SSP 表示放在一起. 对组合性的唯一限制
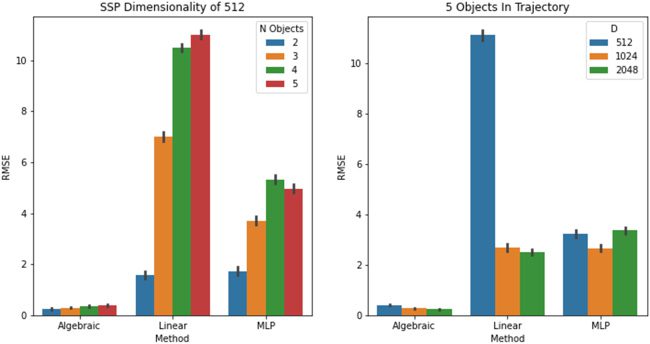
由 SSP 的维数决定. 如图 9, 512
维度可以有效处理至少五个物体.

综上所述, 通过使用 SSP, 结构化的, 类似符号的表示,
可以构建神经网络来执行使用的代数运算
这种结构可以准确地执行计算. 由此产生的网络
是完全可以解释的; 这不是黑匣子. 结构化表示

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2059

数字 9: 对单独动态轨迹的模拟进行基准测试-
应用于单个 SSP 中编码的多个对象. 代数方法
(IE。, 加法位移) 与几种学习模型的方法进行比较
的轨迹的. 左边: 模型误差作为对象数量的函数
固相磷酸盐. 正确的: 模型误差与 SSP 维数的函数关系.

矢量形式, 像 SSP, 允许这种象征式推理的结合
深层网络.

4 结论

空间语义指针 (SSP) 是构建con的有效手段-
连续的空间表示，可以自然地扩展到表示-
动力系统的状态. 我们将最近的 SSP 方法扩展到
捕捉更大的空间细节并编码由 diff 定义的动力系统-
微分方程或任意轨迹. 我们应用了这些方法
模拟具有多个对象的系统并预测轨迹的未来-
运动不连续变化.

进一步来说, 我们表明可以代表并继续-
使用以下方法以最小的误差巧妙地更新多个对象的轨迹
使用适当的代数 con 更新 SSP 时的单个 SSP-
建设和清理. 此外, 我们表明，将 SSP 与
LMU 可以预测移动物体的未来轨迹
正如被观察到的那样.

有几种方法可以扩展这些结果. 对于在-
姿态, 尝试定义的动力学会很有趣
更高维的空间和更复杂的表示
位于这些空间中的物体. 例如, 可能可以定义在-
决定特定对象类型动态的贡品, 这样的小说

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2060

A. 沃尔克等人。.

可以仅根据这些属性来预测物体动力学.
将我们预测对象交互的工作扩展到
提高可预测的不同交互类型的范围
以及预测的准确性.

在更理论的层面上, SSP 有助于统一当前不同的应用程序-
在通用数学模型中对智能行为进行建模的方法
框架. 尤其, 支持的绑定操作的组合-
带有神经网络的端口连续角色填充结构提供了一个点
专注于机器学习的人工智能方法之间的共同点-
英, 动力系统, 和符号处理. 利用这个共同点
为了在该领域取得持续进展，可能需要奠定基础
长期.

软件包

用于生成和操作空间语义指针的实用程序 (SSP)
内置于软件包 NengoSPA 中 (应用脑研究,
2020), 它支持许多 VSA 的神经实现，并且
是 Nengo 生态系统的一部分 (贝科莱等人。, 2014), 一个通用的
用于构建和模拟尖峰和尖峰的 Python 软件包
非尖峰神经网络.

将 Nengo 模型与深度学习相结合, 和深度学习 (拉斯穆森,
2019) 提供了一个TensorFlow (阿巴迪等人。, 2016) 后端使
使用反向传播训练 Nengo 模型, 在 GPU 上运行, 和
与其他网络（例如勒让德内存单元）接口 (LMU;
沃尔克等人。, 2019). 我们利用 Nengo, 能戈SPA, TensorFlow, 和
整个 LMU.

用于重现报告结果的软件和数据可在

https://github.com/abr/neco-dynamics.

附录: 额外的模拟实验

A.1 递归空间语义指针 (重组SSP). 一个重要的限制-
-
SSP 的设置是 P(x1
y1)2 ≤ 2, 那是, 附近点的点积接近于一 (腰部,
2020). 无论维度如何，都会发生这种情况 (d) SP 的.

, y1) 类似于P(x2

, y2) 什么时候 (x2

− x1)2 + (y2

更普遍, 种类有一个根本的限制
可以通过生成的函数表示的相似性图
通过方程 2.13, 由向量的线性组合确定
(西德:7)
(西德:6)
, R ⊆ R2; 这组向量不一定跨越
磷(X, y) : (X, y) ε R
所有路. 换句话说, 因为编码不同部分的向量
空间通常是线性相关的, 少于 d 度
决定可以表示的空间地图类型的自由度
给定有限空间区域内的固定轴向量.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2061

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

数字 10: 第一的 16 Xx的主要成分 (西德:2) Yy 为 x2 + y2≤ 2. 这些巴-
sis 向量与维度无关并且与绝对值无关
空间位置. 只有第一个 21 向量的奇异值大于
一.

√

是,
√

那
(西德:7)
. 半径为一个圆

数字 10 通过绘制主成分使其变得精确
在一个半径的圆内
的左奇异向量
(西德:6)
磷(X, y) : x2 + y2≤ 2
2 近似可逆 do-
主要的正弦(X) 正弦(y) (沃尔克, 2020; 另见科梅尔, 2020, 数字 3.21).
直观地, 任意P(X, y) 在这个圆内可以准确地表示为
该空间基础的线性组合. 我们发现——假设 d 是 suf-
足够大——仅需要 ≈21 个主成分就可以准确地
表示这个子空间 (奇异值大于 1); 数量要少得多
自由度大于 SSP 中的维度 (例如, d = 1024 在
数字 10), 和, 最重要的, 增加 d 不会创建任何新的 de-
自由的格力.

2062

A. 沃尔克等人。.

√

一种解决方案是简单地重新调整所有 (X, y) 坐标使得点
必须彼此几乎正交并由欧几里德分隔
距离至少
2. 然而, 如果 SSP 已经
已编码 (没有已知的方法可以在不改变坐标的情况下重新调整坐标
首先清理 SSP 中的某些特定词汇) 并通向 UNFA-
通过低效使用，对某些类型的空间地图进行 d 的大幅缩放
连续曲面的.

另一种解决方案是改变轴向量, (X, 是), 作为一个函数
(X, y). 一种便捷的方法是使用 SSP 代替每个轴向量.
我们将其称为递归空间语义指针 (重组SSP). 一般来说, 一个
rSSP使用以下公式对位置进行编码:

磷(X, y) = (西德:9)(X, y; X )X (西德:2) (西德:9)(X, y; 是)y,

(A.1)

在哪里 (西德:9)(X, y ; A) 是一些产生 SSP 的函数. (西德:9)(·) 可能是预-
由神经网络确定或计算——前馈或循环——
可以选择通过反向传播进行训练. 例如,

(西德:9)(X, y ; A) =A

|H(X,y)|/3+2

(A2)

使用六方晶格生成在 A2 和 A3 之间振荡的轴
从方程 2.15 和 2.16, 然后用于编码 (X, y) 照常
通过方程 A.1. 我们发现这增加了自由度
半径范围内 ≈21 至 ≈36
2, 给定相同的维度, 地图比例尺,
和奇异值截止.

√

在本质上, 该公式使编码能够使用不同的轴
空间不同部分的向量. 自从 (氨基酸)乙 (西德:14)= Aab 一般用于 a, b ε
右, 这与重新缩放不同 (X, y). 相当, 自从 (西德:9)(·) 是一个非线性的
具有潜在无限复杂分支的操作, 这增加了
通过减少线性依赖来提高表面的表示灵活性-
P 中的密度(X, y) 从而允许 rSSP 捕获精细尺度的空间结构-
通过额外的自由度来实现.

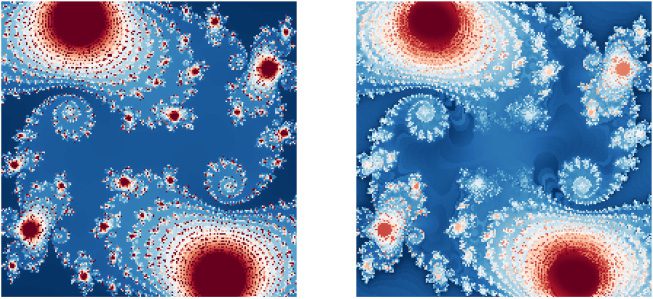
我们通过对 Julia 的分形进行编码来说明 (1918) 设置——一个com-
复杂动力系统——使用单个 rSSP (d = 1,024). 具体来说我们
定义 (西德:9)(X, y ; A) = 阿杰(x+iy) 其中 J(z) 是一个仿射变换
z ← z2 所需的迭代次数 + c 转义集合 |z| ≤ R (c =
−0.1 + 0.65我, R ≈ 1.4527, 1000 迭代). 然后我们求解向量
最佳重建 J(X + 我) 通过优化正则化在其相似度图中
最小二乘问题, 这是可能的，因为方程 2.13 是一个线性的
操作员. 该解决方案生成的地图在感知上非常相似
到理想的分形 (见图 11), 从而证明了有效性
rSSP 使用相对较少的数据来表示复杂的空间结构
方面.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2063

(A) 理想朱莉娅集分形

(乙) 递归空间语义
指针 (重组SSP)

数字 11: 表示相似度图中 Julia 集中的分形
递归生成的 SSP (d = 1,024). 渲染图像是 501 × 501 (IE。,
251,001 像素). 详情请见文字.

A.2 轴特定代数 SSP 更新. 应用 diff 的一种选择-
对 SSP 中编码的不同对象的不同更新涉及表示
每个对象的平面轴分别如下:

SSP = Xx1
1

(西德:2) yy1
1

+ xx2
2

(西德:2) 是2
2

. . .

(A.3)

有了这个表示, 可以定义一个转换SSP

分别作用于每个对象:

(西德:3)x1
固相磷酸 = 固相磷酸 (西德:2) (X
1

(西德:3)y1
(西德:2) 是
1

(西德:3)x2
+ X
2

(西德:3)y2
(西德:2) 是
2

. . .).

(A.4)

应用此转换的效果是生成更新的 SSP
如果 m 是编码对象的数量，则使用 m2 − m 噪声项, 因为每个
括号内的术语将适用于 SSP 中的相应术语，并且
与其他 m 结合 - 1 SSP 中的项会产生噪声. 有米
括号内的总和项, 所以创建 m - 1 噪声项出现 m
次, 导致总共 O(平方米) 总体噪声项. 这种扩展是不可能的
允许成功操纵编码大量的 SSP
物体, 即使噪声是零均值.

正式地, 我们可以如下描述噪声项随时间的增长:
正如刚才提到的, 上述括号内总和中的每一项均适用
到 SSP 中的一个对应项并与其他 m 结合 - 1 条款
在 SSP 中产生噪声. 括号内的和有 m 项, 所以创作

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2064

A. 沃尔克等人。.

的 m - 1 噪声项出现 m 次, 导致总共 m2 − m 个噪声项
在单个时间步之后. 在下一个时间步, 括号中的每个术语
总和适用于 SSP 中的一项对应项, 然后与
m - 1 其他编码项和 m2 − m 噪声项
前一个时间步; 再次, 这些组合出现 m 次. 这产生
总共米(米 - 1 + m2 − m = O(立方米) 第二个时间步长的噪声项.
经过 t 个时间步后, 噪声项的数量为 O(MT+1).

全面的, 在没有清理的情况下，特定于轴的偏移不能令人满意
方法, 因为噪声项在每个时间步复合, 快推-
使信噪比接近于零.

参考

阿巴迪, M。, 巴勒姆, P。, 陈, J。, 陈, Z。, 戴维斯, A。, 院长, J。, . . . 郑, X. (2016).
TensorFlow: 大规模机器学习系统. 在第 12 届会议记录中
USENIX 操作系统设计与实现研讨会 (PP. 265–283),
同行杂志.

应用脑研究. (2020). 水疗中心参观. https://www.nengo.ai/nengo-spa/.
贝科莱, T。, 贝格大街, J。, 洪斯伯格, E., 德沃尔夫, T。, 斯图尔特, 时间. C。, 拉斯穆森, D .,
& 埃利亚史密斯, C. (2014). 我曾是: 一个用于构建大规模函数式的Python工具
大脑模型. 神经信息学前沿, 7, 48.

布劳, P。, 索洛德金, E., 萨加德, P。, & 埃利亚史密斯, C. (2016). 作为语义的概念
指针: 框架和计算模型. 认知科学, 40(5), 1128–
1162.

波图, L. (2014). 从机器学习到机器推理: 一篇作文. 机器

学习, 94(2), 133–149.

秋, X. (2010). 序数串行编码模型: 尖峰神经元中的串行记忆. 但-

第三者的论文, 滑铁卢大学.

秋, X. (2018). 斯潘 2.0: 扩展世界上最大的功能性大脑模型. 博士

指责。, 滑铁卢大学.

科雷耶斯, J. D ., 刘, Y。, 古普塔, A。, 艾森巴赫, B., 阿贝尔, P。, & 莱文, S. (2018). 自己-
一致轨迹自动编码器: 带轨迹的分层强化学习
嵌入. arXiv:1806.02813.

康克林, J。, & 埃利亚史密斯, C. (2005). 路径的受控吸引子网络模型-

大鼠体内的整合. 计算神经科学杂志, 18(2), 183–203.

克劳福德, E., 金格里奇, M。, & 埃利亚史密斯, C. (2015). 生物学上合理的, 人类-

尺度知识表示. 认知科学, 40, 782–821.

杜蒙, 氮. S.-Y。, & 埃利亚史密斯, C. (2020). 空间齿轮的准确表示-
使用网格单元的概念. 第 42 届认知科学年会论文集
科学社. 红钩, 纽约: 柯兰.

埃利亚史密斯, C. (2005). 构建和控制尖峰吸引子的统一方法

网络. 神经计算, 17(6), 1276–1314.

埃利亚史密斯, C. (2013). 如何构建大脑: 生物认知的神经架构.

纽约: 牛津大学出版社.

埃利亚史密斯, C。, & 安德森, C. H. (2003). 神经工程: 计算, 代表-

的, 和神经生物学系统动力学. 剑桥, 嘛: 与新闻界.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2065

埃利亚史密斯, C。, 斯图尔特, 时间. C。, 秋, X。, 贝科莱, T。, 德沃尔夫, T。, 唐, Y。, & 拉斯-
必须, D. (2012). 大脑功能的大型模型. 科学, 338, 1202–
1205.

福多尔, J。, & 对不起, Z. (1988). 联结主义和认知架构: 一个批评的

分析. 认识, 28(1–2), 3–71.

褶皱, 磷. (2003). 灵长类动物皮层的稀疏编码. 在米. A. 阿尔比布 (埃德。), 这

脑理论和神经网络手册. 剑桥, 嘛: 与新闻界.

弗拉迪, 乙. P。, 克莱科, D ., & 索默, F. (2020). 稀疏分布式的变量绑定

陈述: 理论与应用. arXiv:绝对/2009.06734.

弗拉迪, P。, 希瑟, P。, & 索默, F. (2018). 链接计算的框架
和基于节奏的神经放电计时模式, 例如相位进动
海马位置细胞. 认知计算会议论文集
神经科学.

盖勒, 右. (2004). 矢量符号架构回答了 Jackendoff 的认知挑战

神经科学. arXiv 预印本 cs/0412059.

好人, 我。, 本吉奥, Y。, & 考维尔, A. (2016). 深度学习, 卷. 1. 剑桥,

嘛: 与新闻界.

戈斯曼, J. (2018). 上下文的集成模型, 短期, 和长期记忆.

博士论文。, 滑铁卢大学.

戈斯曼, J。, & 埃利亚史密斯, C. (2019). 载体衍生的转化结合: 开启于-
经证明的神经网络中深度类符号处理的绑定操作.
神经计算, 31(5), 849–869.

戈斯曼, J。, & 埃利亚史密斯, C. (2020). 提示: 统一的短脉冲神经元模型-

短期记忆和长期记忆. 心理. 审查, 128, 104–124.

戈斯曼, J。, 沃尔克, A. R。, & 埃利亚史密斯, C. (2017). 一个尖峰独立acc-
用于赢家通吃计算的仿真器模型. 第 39 届年会论文集
认知科学学会会议. 伦敦, 英国: 认知科学学会.
哈德利, 右. (2009). 快速变量创建的问题. 神经计算, 21,

510–532.

朱莉娅, G. (1918). 有理函数迭代回忆录. J. 数学. 纯的

应用。, 8, 47–245.

希瑟, 磷. (2009). 超维计算: 计算简介
具有高维随机向量的分布式表示. 认知的
计算, 1(2), 139–159.

腰部, 乙. (2020). 受生物学启发的空间表征. 博士论文。, 大学

滑铁卢.

腰部, B., & 埃利亚史密斯, C. (2020). 使用可扩展的高效导航, 生物学上
受启发的空间表现. 在第 42 届年会记录中
认知科学学会. 伦敦, 英国: 认知科学学会.

腰部, B., 斯图尔特, T。, 沃尔克, A. R。, & 埃利亚史密斯, C. (2019). 神经表征
使用分数绑定的连续空间. 第 41 届年会论文集
认知科学学会会议. 伦敦, 英国: 认知科学学会.
乐存, Y。, 本吉奥, Y。, & 欣顿, G. (2015). 深度学习. 自然, 521(7553), 436–

444.

鲁, T。, 沃尔克, A. R。, 腰部, B., & 埃利亚史密斯, C. (2019). 表示空间关系
具有分数结合. 第 41 届认知科学年会论文集
科学社. 伦敦, 英国: 认知科学学会.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2066

A. 沃尔克等人。.

马库斯, G. (1998). 重新思考取消联结主义. 认知心理学, 37,

243–282.

马库斯, G. F. (2019). 代数思维: 整合联结主义和认知科学.

剑桥, 嘛: 与新闻界.

麦克莱兰, J。, 博特维尼克, M。, 诺艾尔, D ., 普劳特, D ., 罗杰斯, T。, 塞登伯格, M。, &
史密斯, L. (2010). 让结构浮现出来: 联结主义和动力系统-
认知建模的 tems 方法. 认知科学的趋势, 14(8), 348–
356.

死后, F。, 斯图尔特, T。, & 康拉特, J. (2020). 分布式容量分析
用于编码空间信息的向量表示. 在诉讼程序中 2020
国际神经网络联合会议 (PP. 1–7). 皮斯卡塔韦, 新泽西州: IEEE.
莫塞尔, 乙. 我。, 克罗普夫, E., & 莫塞尔, M.-B. (2008). 放置单元格, 网格单元, 和大脑的

空间表示系统. 安努. 牧师. 神经科学。, 31, 69–89.

穆勒, 中号. 乙. (1959). 关于在n上均匀生成点的方法的注释-

维度球体. 通讯. 副会长. 电脑. 马赫。, 2(1–2), 19–20.

盘子, 时间. (2003). 全息简化表示: Cog 的分布式表示-

本质结构. 斯坦福大学, CA: CSLI出版物.

拉斯穆森, D. (2019). 和深度学习: 结合深度学习和神经形态模型-

埃林方法. 神经信息学, 17(4), 611–628.

拉斯穆森, D ., & 埃利亚史密斯, C. (2011). 归纳规则生成的神经模型

推理. 认知科学主题, 3(1), 140–153.

施莱格尔, K., 诺伯特, P。, & 挥霍, 磷. (2020). 矢量符号架构的比较-

特雷斯. arXiv:2001.11797.

施米德胡贝尔, J. (2015). 神经网络中的深度学习: 概述. 神经网络-

作品, 61, 85–117.

更美丽, G. (2014). 具身认知, 的神经场模型. 在百科全书中

计算神经科学 (PP. 1084–1092). 柏林: 施普林格.

斯摩棱斯基, 磷. (1990). 张量积变量绑定和表示
联结主义系统中的符号结构. 人工智能, 46(1–2), 159–
216.

斯摩棱斯基, P。, & 勒让德, G. (2006). 和谐的心灵: 从神经计算到

最优理论语法. 剑桥, 嘛: 与新闻界.

索舍尔, B., 梅尔, G。, 甘古利, S。, & 爸爸, S. (2019). 起源的统一理论
通过图案形成透镜的网格单元. 在H. 瓦拉赫, H. 拉罗谢尔,
A. 贝格尔齐默, F. 阿尔谢比克, 乙. 狐狸, & 右. 加内特 (编辑。), 神经方面的进展
信息处理系统, 32 (PP. 10003–10013). 红钩, 纽约: 柯兰.
斯图尔特, T。, 贝科莱, T。, & 埃利亚史密斯, C. (2011). 复合的神经表征-
国家结构: 用尖峰 neu 表示和操作向量空间-
罗恩. 连接科学, 23, 145–153.

斯图尔特, 时间. C。, 秋, X。, & 埃利亚史密斯, C. (2014). spiking neu 中的句子处理-
罗恩: 生物学上合理的左角解析器. 第 36 届年会论文集
认知科学学会会议 (PP. 1533–1538). 伦敦, 英国。: 认知的
科学社.

斯图尔特, 时间. C。, 唐, Y。, & 埃利亚史密斯, C. (2011). 生物学上真实的清理记忆-
奥里: 尖峰神经元的自动关联. 认知系统研究, 12(2), 84–92.
沃尔克, A. 右. (2019). 尖峰神经形态硬件中的动力系统. 博士论文。,

滑铁卢大学.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
3
8
2
0
3
3
1
9
3
0
8
6
7
n
e
C
哦
_
A
_
0
1
4
1
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

具有空间语义指针的动力系统

2067

沃尔克, A. 右. (2020). 旋转傅里叶变换之间的点积上的短字母.

arXiv:2007.13462.

沃尔克, A. R。, 卡吉茨, 我。, & 埃利亚史密斯, C. (2019). 勒让德内存单元: 连续的-
循环神经网络中的时间表示. 在H. 瓦拉赫, H. 拉罗谢尔,
A. 贝格尔齐默, F. 阿尔谢比克, 乙. 狐狸, & 右. 加内特 (编辑。), 神经方面的进展
信息处理系统, 32 (PP. 15544–15553). 红钩, 纽约: 柯兰.
韦斯, E., 张, B., & 奥尔斯豪森, 乙. (2016). 表示的神经架构-
关于空间关系的分析和推理. 国际会议录
学习表征会议——研讨会轨道. 拉霍亚, CA: ICLR.

11月收到 4, 2020; 接受三月 15, 2021.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d