Justin Smith

经济系

University of Manitoba

648 Fletcher Argue Building

Winnipeg MB R3T 5V5

加拿大

smith44@cc.umanitoba.ca

HOW VALUABLE IS THE GIFT

OF TIME? THE FACTORS

THAT DRIVE THE BIRTH DATE

EFFECT IN EDUCATION

抽象的
The age at which students enter school is increasing.
More parents are delaying their child’s entry, 和美国.
states are moving school entry cutoffs earlier, mainly be-
cause older students outperform younger ones on many
educational outcomes. Much of the literature interprets
advantages held by older students as beneﬁts to entering
school older, but because entering older means being
older when students take tests, it is unknown if perfor-
mance differences are attributable to entry age or test
年龄. Policy and parent behavior depend on which age ef-
fect matters more. Using a natural experiment from the
province of British Columbia, 加拿大, that temporarily
altered entry dates, I estimate an upper bound of the
test age effect and a lower bound of the entry age effect.
Results show that the upper bound of the test age effect
is much larger than the lower bound of the entry age
影响.

This article is part of a series invited by this journal, in which authors present results of dissertation
research receiving the Jean Flanigan Outstanding Dissertation Award from the American Education
Finance Association.

C(西德:2) 2010 American Education Finance Association

247

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

HOW VALUABLE IS THE GIFT OF TIME?

介绍

1.
A large amount of recent research has shown that older students outperform
younger students by a considerable amount along a variety of dimensions in
early elementary school, persisting into late high school and into the labor
市场. The belief that students who enter school older will perform better is
partly responsible for a developing trend in education that has been coined the
“graying of kindergarten”—the increase in the age of the average student on
his or her ﬁrst day of school. 在美国, the increase in age at entry
is being driven by a rise in the number of parents enrolling their children one
year later than normal and by states that have moved their school entry dates
earlier in the year.1

Even though policy and parental decisions about school entry dates are be-
ing made under the belief that when students are older at entry they perform
better on average in school, we do not know for sure whether estimated age
effects are due to the effect of entering older or the effect of being one year
older when tested. These effects are difﬁcult to separate empirically because
students who enter school one year older are almost always one year older
when they take tests, making it impossible to know whether any estimated
effect represents entry age, test age, or a combination of both. Knowing the
relative magnitudes of entering older versus being older when tested is impor-
tant because policy may differ depending on which effect is responsible for the
advantages held by older students. 例如, ﬁnding a large difference in
student performance attributable to entry age could imply adjustments to the
current school entry structure. 另一方面, ﬁnding a large difference in
performance attributable to test age suggests ﬁnding alternatives to the com-
mon practice of testing all students in the same grade at the same time, 但它
does not necessarily have direct implications for school entry policy.

Given the importance of separating entry age from test age, this article
attempts to disentangle the two effects by exploiting a natural experiment that
temporarily changed the school entry laws for students in British Columbia
(B.C.), 加拿大. To address the issue of school readiness, in the early 1990s
the B.C. Ministry of Education switched from a single-date entry system to
a dual-date entry system. Prior to 1990 under the single-date entry system,
all students who turned ﬁve years old in a given calendar year began school
in September of that year. Under dual entry, 然而, children turning ﬁve

1. Deming and Dynarski (2008) note that in 1968, 96 占美国的百分比. six-year-olds were in grade 1
相对 84 百分比在 2005, with much of the difference being enrolled in kindergarten. 此外,
Bedard and Dhuey (2007) note that in 1985, seventeen states required a child to be ﬁve in September
of the ﬁrst year of school, whereas twenty years later that number jumped to thirty-six states. 更多的
最近, four states have introduced legislation to move the cutoff earlier in the calendar year (韦尔
2007).

248

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Justin Smith

years old between May 1990 and October 1990 began school in September
1990, and children turning ﬁve between November 1990 and April 1991 began
school in January 1991.

Due to strong opposition by teachers and parents, the dual entry system
was repealed almost immediately in June 1991. As part of the annulment
of this policy, students born in November and December 1990 were moved
ahead to ﬁrst grade without having completed a full year of kindergarten, 尽管
those born in January–April 1991 were required to repeat kindergarten. 这
effectively placed students in the grade level they would have been in under
the old single-date entry system.

This policy had the effect of breaking the direct link that normally exists
between entry age and test age for students who were part of dual entry. 平杆-
针状的, students turning ﬁve years old around 1 十一月 1990 started school
at different ages, but because of the reshufﬂing of students after the cancel-
lation of dual entry they were approximately the same age when they began
all future grades. 此外, students turning ﬁve years old around 1 一月
1991 all began kindergarten at the same time, but due to the reshufﬂing they
entered all future grades at different times. For these groups of children, entry
age and test age do not move together, making it possible to separate the two
effects empirically.

Using data from the B.C. Ministry of Education on the group of children
affected by dual entry, I empirically separate the entry age from the test age
影响. What I provide is an upper bound estimate of the test age effect and
a lower bound estimate of the entry age effect because neither effect can be
completely disentangled from a schooling effect. If the true estimates are
close to the bounds, the estimates indicate that test age has a negative effect
on the probability of repeating third grade and a positive effect on grade
10 math and reading test scores. 另一方面, entry age has a relatively
small effect on grade repetition and grade 10 test scores. 在某种程度上
the estimates deviate from the bounds due to positive schooling effects, 这
true test age effect will be lower than reported, and the true entry age effect
will be higher. The empirical results are robust to adding controls for baseline
student characteristics and a polynomial in day of birth, which accounts for
any effect of season of birth on outcomes.

I show that important heterogeneity in the effect exists across gender. Per-
haps the most interesting result is that the effect of test age on the probability
that a student repeats grade 3 is more than twice as large for boys than for
girls. This result may derive from maturity differences between boys and girls
at young ages and suggests that if lowering the amount of grade repetition
is important from a policy perspective, increasing the age at which students
enter school for the ﬁrst time (which will also increase their age when they

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

249

HOW VALUABLE IS THE GIFT OF TIME?

enter each grade) may have an especially pronounced effect on boys. Given the
higher effect on boys, such a policy could also reduce the gap in the amount
of grade repetition between boys and girls.

Using long-term test scores as the outcome, I ﬁnd that being younger has
a disproportionately larger effect on girls, especially in reading. The lower
bound of the entry age effect continues to be relatively small for both genders.
This result suggests that the policy described above, while helping boys more
relative to girls in short-term outcomes, could help girls more relative to boys
in terms of long-run test outcomes.

黑色的, Devereux, and Salvanes (2008) and Crawford, Dearden, and Meghir
(2007) have also recently produced research directly separating these two ef-
fects empirically.2 My contribution over and above their strong research is that
I separate entry age from test age for grade repetition, which neither work
examines as an outcome. 此外, while I use a similar estimation method,
the identifying variation comes from an entirely different and unique source.
Using variation from a different source will help either conﬁrm existing ﬁnd-
ings or highlight important differences. 最后, I use data from the province
of British Columbia, which has a school system that is very typical of the av-
erage Canadian or U.S. school system. These estimates can be applied more
directly to a North American context as compared with the other two articles,
which use European data from countries with very different school systems
than those typical in North America.

I proceed by discussing the main identiﬁcation problem faced by re-
searchers in this ﬁeld. I next review what has been researched up to now
in terms of estimating age effects in general, and more speciﬁcally in terms
of separating entry age and test age. I then discuss my identiﬁcation and es-
timation strategy, followed by a presentation of the results and concluding
remarks.

2. ENTRY AGE OR TEST AGE? THE IDENTIFICATION PROBLEM
Researchers are interested in estimating the effect of both entry age (AEi) 和
test age (ATig) on some outcome (Oig). One way to estimate this relationship
is with the following linear equation:

Oig = β0 + β1 AEi + β2 ATig + εig,

(1)

where i indexes students and g indexes the grade level. The available data are
usually observations on a group of students in a particular grade taking a test
同时. Using such data means that the level of schooling is constant

I discuss a broader set of papers in the literature review section.

250

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Justin Smith

for all students, and its effect is absorbed into the intercept. As several recent
articles have highlighted, there are at least two important problems with trying
to estimate equation 1 using this kind of data.3

The ﬁrst is that both AEi and ATig are endogenous because parents can
usually defer entry of their child into school by one year and because a nontrivial
number of students either repeats or skips a grade at some point in their
schooling career. The students whose age is manipulated in this way are
typically a nonrandom group, so without any further control variables ordinary
least squares (OLS) estimates of equation 1 will be biased. All the research cited
in the following section has solved this problem easily by instrumenting AEi
and ATig with variation in age derived from the interaction of date of birth and
school entry laws. Identiﬁcation comes from the fact that given ﬁxed school
entry dates, date of birth is correlated highly with age but is expected to have
no independent effect on outcomes.

The second problem has received relatively less attention. For any child

that is in school, the following identity always holds:

ATig ≡ AEi + 说.

(2)

Using a sample of children who are in the same grade, Sig is held constant,
meaning that any change in AEi must be accompanied by an equal change
in ATig. It is therefore impossible to estimate equation 1 in most situations
because of a perfect collinearity between the two independent variables.

Most of the previous research has instead estimated

Oig = β∗

+ β∗

1 AEi + εig.

(3)

The problem with this approach is that because of the collinearity problem
noted above, students who enter older will always be older when they take
测试, meaning that what equation 3 identiﬁes is some combination of the
entry and test age effects. Many researchers have found that the estimate of
β∗
1 tends to decline in higher grade levels, and this is sometimes used to argue
indirectly that test age is responsible for the majority of the effect because a
one-year age difference for older children translates into a smaller maturity
difference than for younger children. The problem is that not all researchers
ﬁnd a declining age effect over time, and furthermore the fact still remains
that they cannot directly separate either effect.

3. A third problem that is not covered here is that the effects of chronological age cannot be separated
from relative age—the effect of being the oldest in the class. Some researchers have tackled this
问题: see Fredriksson and Ockert 2006, Elder and Lubotsky 2009, Cascio and Schanzenbach 2007,
and Kawaguchi 2006. The general consensus seems to be that the relative age effect is small and
likely very close to zero.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

251

HOW VALUABLE IS THE GIFT OF TIME?

In this article I focus on providing a direct solution to the second iden-
tiﬁcation problem by using a policy change that helped remove the direct
collinearity between AEi and ATig. It is important to keep in mind, 如何-
曾经, that while I can separate AEi from ATig, a ﬁnal identiﬁcation problem
precludes separating either effect from Sig. While children are in school, 它
is fundamentally impossible to independently identify all three effects be-
cause holding one of the three variables constant and manipulating one of
the other two implies that the third variable must also change by the same
数量. 例如, holding AEi constant means that (西德:4)ATig = (西德:4)说. Like-
明智的, when ATig is kept constant, (西德:4)AEi = −(西德:4)说. Given that test age varies
directly with schooling while entry age varies inversely with schooling, 测试
age effects are upper bounds while entry age effects are lower bounds. I dis-
cuss the implications of this fact in the context of the empirical estimates
以下.

3. EXISTING LITERATURE
Most of the articles in the age effects literature have estimated that younger
students perform worse than older students on a variety of educational out-
来了. In early elementary school, researchers ﬁnd that older students have
a test score advantage between 0.3 和 0.8 standard deviations (σ ) (Bedard
and Dhuey 2006; Elder and Lubotsky 2009; McEwan and Shapiro 2008;
史密斯 2009; Fredriksson and Ockert 2006; Datar 2006; Puhani and Weber
2006), are less likely to repeat a grade by up to 15 百分点 (Elder and
Lubotsky 2009), and are less likely to be diagnosed with a learning disability
by up to 3 百分点 (Elder and Lubotsky 2009; Dhuey and Lipscomb
2007). Toward the end of compulsory schooling and beyond, researchers show
that the test score advantage held by older students persists at a lesser magni-
tude of roughly 0.1–0.2σ (Bedard and Dhuey 2006; Elder and Lubotsky 2009;
McEwan and Shapiro 2008; 史密斯 2009; Fredriksson and Ockert 2006) 和
that other outcomes such as being university bound and wages may also be
affected by age (Bedard and Dhuey 2006; Fredriksson and Ockert 2006; Datar
2006; Puhani and Weber 2006). While most of these studies interpret their
estimates as the effect of starting school later, the identiﬁcation problem out-
lined above suggests that they cannot separate it from the effect of being one
year older when tested.

Even though these articles cannot directly separate the two effects, 一些
conclusions about the relative magnitudes of entry age versus test age have
been advanced based on their ﬁndings. One argument is that since the age ef-
fect falls over time (for most studies), test age effects might be dominating.
另一方面, McEwan and Shapiro (2008) ﬁnd an increasing age effect

252

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Justin Smith

over time for Chile, suggesting possible entry age effects.4 Further evidence
in favor of test age is given by Elder and Lubotsky (2009), who estimate the
age effect in early kindergarten and argue that there has not been sufﬁcient
exposure to schooling for an entry age effect to affect students.

A small handful of articles have made direct attempts to separate entry
and test age. An early attempt is Datar (2006), who uses the Early Childhood
Longitudinal Study of Kindergarten, Class of 1998–99 (ECLS-K), sample to
estimate the entry age effect for a group of children in kindergarten and grade
1. Assuming that test age is linear in time, it is differenced out by using test
score gains as the dependent variable, leaving only entry age. She ﬁnds a
signiﬁcant positive entry age effect. This work is somewhat limited by the fact
that it cannot provide test age effects and because the data allow a focus only
on very young students. 此外, it is unclear whether test age effects are
linear over time, which is crucial to the identiﬁcation strategy.

Fredriksson and Ockert (2006) also provide an early attempt to identify
the effect of entry age on educational attainment and earnings for a sample of
individuals from Sweden who have ﬁnished their schooling. When individuals
are outside the school system, entry age and test age are no longer directly
链接的, and the effects of entry age can be identiﬁed. 此外, in Sweden
graduates typically all have the same amount of schooling, so that is also
removed as a confounder. The authors ﬁnd a small positive effect of starting
school later on attainment and a small negative effect on earnings overall.

最近, 黑色的, Devereux, and Salvanes (2008) estimate the effects of
entry age and test age on IQ scores for a sample of eighteen-year-old Norwegian
男人. Identiﬁcation is possible because the IQ tests are not part of the school
系统, and therefore no exact linear dependence between entry age, test age,
and schooling exists.5 They conclude that the bulk of the age-related differences
in test scores are attributable to test age. Using a larger sample that includes
女性, they also look at the effect of entry age on longer-term outcomes
such as educational attainment, earnings, and early fertility using the same
identiﬁcation strategy as Fredriksson and Ockert (2006). They ﬁnd no effect
on educational attainment, a small negative effect on early fertility, and a small
positive effect on earnings.

4. Test age is generally thought to be related to maturity. As children age, the maturity gap between
two students who are one year apart in age gets smaller and smaller, hence the shrinking age effect.
Entry age effects are expected to grow over time as the skills of older students who perform better
initially are reinforced through placement in advanced streams, 例如.

5. While the authors are able to separate entry age from test age, they are not able to separate either
effect from schooling for their main sample because most students take the IQ test while they
are still in school. Using a sample of school ﬁnishers, they do show that this does not bias their
estimates much.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

253

HOW VALUABLE IS THE GIFT OF TIME?

A slight limitation is that their data force them to focus entirely on post-
schooling outcomes. While long-term outcomes are certainly important eco-
nomically, providing estimates of entry age and test age early in school is
equally important for education authorities and parents who may base policy
and school entry decisions on these early differences. A secondary limitation
is that IQ scores are available only for males, so heterogeneity across gender
cannot be examined. This is important because the effect may differ quite
substantially across gender. 最后, it is unclear whether differences in the
Norwegian education system would affect generalizability of their results to
other countries.

克劳福德, Dearden, and Meghir (2007) identify entry age and test age
effects for test scores using a sample of English schoolchildren. They sepa-
rate the effects with geographic variation in the structure of the school entry
规则: some jurisdictions have multiple entry points, while others do not. 这
creates a sample in which some children who start school at the same time
are tested at different times, and some children who are tested at the same
time started school at different times. The authors ﬁnd that most of the age
effect is attributable to test age, which is large in early elementary school and
diminishes thereafter.6

I contribute to the literature in several ways. The main contribution is that
I directly identify lower bound entry age and upper bound test age effects for a
sample of in-school children using a completely new source of identifying vari-
化. The studies by Black, Devereux, and Salvanes (2008) and Fredriksson
and Ockert (2006) consider only outcomes post schooling. 此外, 最多
of the previous literature that has identiﬁed age effects for in-school children
has only been able to speculate on the relative strength of these two effects
based on how the age effect evolves over time. While Crawford, Dearden,
and Meghir (2007) also directly separate these effects for in-school children, 我
add to their work by considering an additional outcome (grade repetition),
considering a different source of identifying variation, and using a Canadian
sample from a jurisdiction typical of any Canadian or U.S. educational sys-
TEM, which will highlight any differences in these effects across European and
North American education systems.

IDENTIFICATION AND ESTIMATION

4.
A recent policy experiment in British Columbia creates a unique way to sep-
arate entry age from test age effects. For many years up to 1990, 英国人
Columbia had a single-date school entry system. Under this system, 学生
turning ﬁve years old in a given calendar year would start school in September

Like Black, Devereux, and Salvanes (2008), they cannot separate the effect of schooling from entry
age or test age while children are in school.

254

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Justin Smith

of that year. This effectively meant that all students born within a calendar year
started school together in September ﬁve years later.

As part of a larger education reform initiative called the Year 2000 Edu-
cation Plan, the B.C. Ministry of Education mandated a “dual entry” system
into kindergarten in school year 1990–91.7 Unlike the previous system, 和-
der dual entry students turning ﬁve years old between 1 May and 31 十月
1990 began school in September 1990, while students turning ﬁve years old
之间 1 十一月 1990 和 30 四月 1991 began school in January 1991.
Equivalently, students born within the six-month span between November and
April would start school ﬁve years later in January, while those not born within
that span started a few months earlier in September.8

Under considerable criticism, dual entry was quickly repealed at the end of
the school year in June 1991 and replaced with the old single-entry system. 作为
part of the change back to the single-entry system, the government mandated
that the children born in November and December be moved ahead to grade
1 without completing a full year of kindergarten, and the children born in
January–April repeat kindergarten, putting them into the cohort they would
have been in if dual entry had never existed.

The existence of multiple entry dates and the subsequent reshufﬂing of
students had a signiﬁcant impact on student entry age and test age, breaking
the perfect collinearity that normally exists between these two variables. 这
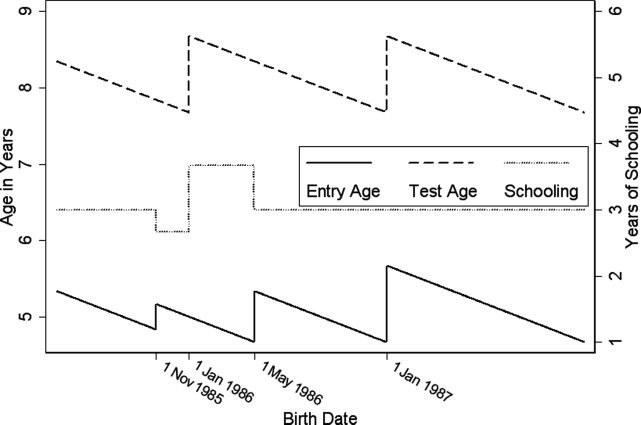
effect is most easily understood by examining the graph in ﬁgure 1. This graph
plots entry age and test age against date of birth for a group of grade 3 学生
whose birth dates put them among the cohorts of students subjected to dual
entry. The exact linear relationship is broken at three distinct discontinuity
点. Students born near 1 十一月 1985 entered grade 3 at approximately
the same time but began school at different times. While students born just
after that date were legislated to start school slightly older, the fact that the
government forced them ahead to grade 1 upon cancellation of dual entry
meant that they entered grade 3 at roughly the same age as those born just
前 1 十一月 1985. Thus we have a group of students who started school
at different ages but whose test age is held constant. An identical relationship
exists for students born near 1 可能 1986.

7. Dual entry was piloted in select school districts in 1989–90 that opted into the program. Because I
cannot identify which districts opted in, I focus on analyzing students who were born in the time
period when this policy was speciﬁcally legislated and mandatory for all districts. See Glegg (1995).
8. The Year 2000 plan was intended to establish broad goals for learning among B.C. 青年. 最多
important for this analysis is that there were no changes implemented by this plan that would
have affected cohorts of children differently, particularly those in the immediate vicinity of entry
cutoffs. 此外, at the time these children were being born, this plan was not yet in effect, 所以
parents could not have sorted in response to its anticipation. For a brief discussion of the plan, 看
Gammage (1991).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

255

HOW VALUABLE IS THE GIFT OF TIME?

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

数字 1. Predicted Entry and Test Ages under Dual Entry in British Columbia

Students born just before 1 一月 1986 were legislated to start school at
roughly the same time as students born just after that date, but again, 因为
they were forced to skip ahead to grade 1 while students born just after were
forced to repeat kindergarten, the two groups entered grade 3 at different times.
The key here is that there is now a group of students who all began school at
the same age but entered grade 3 at different ages.

The existence of these three discontinuities breaks the direct linear rela-
tionship between entry age and test age and thus makes it possible to separate
these two effects from each other. Empirically, I make use of this identifying
variation by estimating the following instrumental variables (IV) model using
two-stage least squares (2SLS):

Oig = β0 + β1 AEi + β2 ATig + εig

AEi = θ0 + θ1 AEp
我
ATig = γ0 + γ1 AEp
我

+ θ2 ATp
IG
+ γ2 ATp
IG

+ ν1ig

+ ν2ig.

(4)

(5)

(6)

In this model, Oig is an indicator for either grade 3 repetition or grade 10 测试
scores, AEi is actual student entry age, and ATig is actual student test age. 我
treat both AEi and ATig as endogenous and instrument them with predicted
entry age AEp
IG. Predicted entry age is derived as
the age a student should have been had she begun school according to the
entry rules, while predicted test age is the age a student should have been
had she entered grade 3 (or taken the grade 10 测试) according to the rules.

i and predicted test age ATp

256

Justin Smith

Discrepancies between predicted and actual entry and test age arise when
students delay entry or repeat or skip grades.

Recall that although the procedure statistically separates the effects of entry
age from test age, due to the identity in equation 2, it cannot separate either
effect from schooling (and it is impossible to do so while children are in
学校). Holding entry age constant, increases in test age will be accompanied
by increases in schooling, whereas when holding test age constant, 增加
in entry age will be accompanied by decreases in schooling. Thus we must
think of β1 as a lower bound estimate of the entry age effect and β2 as an upper
bound estimate of the test age effect.

Both predicted test age and entry age are piecewise linear functions of birth
日期, where discontinuities arise at the school entry cutoff points. Because both
instruments are deterministic functions of birth date, internal validity depends
entirely on whether the birth date is correlated with factors that determine
student outcomes. The most obvious violation of this restriction would be
if a nonrandom group of parents could somehow plan their child’s date of
birth to be at a speciﬁc time. Season of birth in particular has been linked
with observable parent factors in the existing literature (例如, Bound and Jaeger
2000; Buckles and Hungerman 2009), but as I show later, the results are
generally robust to including a third-order polynomial in day of birth, 哪个
should account for any relationship that might exist between the outcomes
and the time of year that a student was born.

Birth date planning of a more precise nature around the discontinuity
点, perhaps through Cesarean sections or induced labor, may also create
an internal validity problem. While there is no direct evidence that parents plan
births according to school entry laws (Dickert-Conlin and Elder 2009), 有
evidence that they plan births precisely according to tax rules (Dickert-Conlin
and Chandra 1999). I show that there is no evidence in the B.C. data of such
行为, suggesting that internal validity is not compromised by this type of
行为.

The unique nature of the policy experiment used in this article creates
some additional ways in which the exclusion restriction may be violated. 这样的
a violation could occur, 例如, if students entering school in January
were streamed into separate classes. If this were the case, students entering
in January and September may have experienced different classroom environ-
评论, in particular with respect to class size. The exclusion restriction may
also fail if teachers treated January entrants differently. 最后, if there were
any other provision in the Year 2000 Education Plan that is related to date of
birth, internal validity would be compromised.

There is some evidence that the inﬂuence of confounding factors like those
suggested above are minimal. I have not been able to ﬁnd any speciﬁc policy in

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

257

HOW VALUABLE IS THE GIFT OF TIME?

the Year 2000 Education Plan that might be related to a student’s date of birth,
meaning that the problem of confounding policies is likely minimal or nonex-
istent. With respect to classroom streaming, the direct implementation of this
policy was very abrupt, such that schools were generally unprepared to make
special arrangements for the cohort of January entrants. According to a recent
article in the Victoria Times Colonist (Knox 2008), more often than not these
students were placed in existing classrooms with their peers who had entered
four months earlier in September. This means that classroom assignment is
likely not related to date of birth and would therefore not confound estimates.
One effect I cannot directly rule out is that some students were treated
differently by teachers. Teachers in particular may have given the January
entrants some special treatment because they were the ﬁrst cohort that did
not enter in September. 再次, 然而, the abruptness of the policy may
act to mitigate any inﬂuence this might have had. While teachers would have
liked to alter lesson plans and treat these students differently, they may not
have had enough time to implement such a strategy. 当然, this does not
preclude students being treated differently on a day-to-day basis, but it may
have prevented something more systematic and planned.

Assuming heterogeneous treatment effects, the question of external valid-
ity arises because the IV model above identiﬁes a local average treatment effect
(LATE) of entry age and test age on outcomes. This local estimator applies to
people whose actual entry and test age are determined by the school entry laws
and the government’s subsequent reshufﬂing of students between kinder-
garten and grade 1. For most cohorts in the sample, the fraction of students
who start school in accordance with the laws is over 90 百分, suggesting
that for many people entry age is directly inﬂuenced by the laws.9 If most
people in the sample are affected by the instrument, the LATE may be a good
approximation to the average treatment effect (ATE).

笔记, 然而, that the cohort born in November–December 1985 节目
considerably more slippage than other cohorts, 仅与 46 percent of student
starting in accordance with the laws. For this cohort, it is perhaps less plausible
that the LATE and ATE are close to one another. To get a handle on whether
this is true, I assume that the entry age of all students who start on time has
been manipulated by the instruments (thereby making them “compliers” in
the treatment effects sense), and I then compare personal characteristics of
these students across cohorts. Evidence based on this exercise indicates that

It is technically not possible to tell whether older students who start on time are affected by the
laws or whether they would have started at that time in the absence of the laws. It seems reasonable
to assume that many of these students would not have started school at the exact time predicted
by the entry laws had they not been forced to do so. Note that increasing predicted entry age must
be associated with increasing actual entry age or no change in entry age for the monotonicity
assumption of LATE to be valid.

258

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Justin Smith

these complying students may not be different across the cohorts in terms of
baseline characteristics, implying that the LATE could indeed be generalizable
to the average person in the sample.

The uniqueness of the policy that induced the age variation also raises some
questions about external validity. Dual entry and its cancellation altered entry
and test age but also made the overall schooling experience quite different
from past and future cohorts. 例如, this cohort may have been treated
不同地, perhaps even developing a stigma. Thus increasing entry or test
age in a different context could lead to different results. While this is entirely
可能的, in defense of the generalizability of the estimates I obtain, 他们的
sign and magnitude are generally comparable to other research (尤其
黑色的, Devereux, and Salvanes 2008 and Crawford, Dearden, and Meghir
2007). Because of this, I believe that my estimates are at least as good an
approximation of what might happen if the same treatment were applied
outside the sample, but I certainly do not rule out the possibility that the
results are not completely generalizable.

5. DATA AND ANALYSIS SAMPLE
The data used for analysis are derived from administrative records collected
once yearly by the B.C. Ministry of Education. They contain information on all
students attending any public or private school in British Columbia between
1990 和 2004. Students are tracked across time, 学校, and grades using a
unique identiﬁcation number as long as they stay in the B.C. school system; 不
information is collected if they exit the system. A small set of baseline personal
characteristics is known for each student, such as gender, home language,
English as a second language (ESL) 地位, and an Aboriginal identiﬁer, 但
no parental background variables are available.

I use the data to construct three outcomes. 第一的, a forward-looking measure
for repeating grade 3 is derived by tracking students across time: if a student is
observed in grade 3 this year and next, that student is identiﬁed as a repeater.10
In this case the interpretation of the coefﬁcient on test age is the effect of
increasing age at the beginning of grade 3 on the probability of staying in the
same grade next year.11

10. While it is technically possible to study repetition of other grades, I focus only on grade 3 因为
the structure of the B.C. school system creates a situation with very few repeaters in the surrounding
grades. The curriculum is separated into three stages: the primary years (K − 3), the intermediate
年 (4–10), and the graduation years (11–12). Because there is a natural transition point between
the primary and intermediate years, in the sample I use for analysis I observe 2.67 percent repeating
年级 3 相对 0.5 percent or less repeating the surrounding grades.

11. Using a cumulative measure indicating whether a student has repeated any grade prior to grade 3
as the outcome would be problematic for this analysis. The coefﬁcient on test age would then have
the awkward interpretation as the impact of being one year older at the beginning of grade 3 在
having repeated at least one grade in the past. 为此原因, I focus only on the forward-looking

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

259

HOW VALUABLE IS THE GIFT OF TIME?

Grade 10 reading and numeracy test scores come from British Columbia’s
annual standardized test, the Foundation Skills Assessment (FSA). All stu-
dents are required to write the test, but a small subsample of about 5 百分
are excused if they cannot write due to learning disabilities or if their English
skills are not adequate. Only the grade 10 test scores are used as outcomes be-
cause the test was initiated in 1999, and this is the only test students entering
school around 1990 are observed writing. This variable is standardized to have
a mean of zero and standard deviation of one for each test in each year.

Because exact birth date is known, test age and entry age can be computed
precisely for each student. I construct test age as 1 September of the beginning
of grade 3 when repetition is the outcome or the exact day of the standardized
test for the grade 10 sample. Since all schools in British Columbia start at
the same time each year (the day following Labor Day), 环境 1 九月
as the test age should not cause problems. Entry age is constructed as either
1 September or 1 January of the year students are observed in kindergarten,
whichever entry date is appropriate under the entry laws.12

Analysis focuses on two subsamples of a universe of 120,108 students born
between May 1985 and December 1987 who were observed at kindergarten
entry. The ﬁrst subsample is a set of 109,956 students from the universe who
are observed each year after entry until grade 3 and who are not missing grade
information in the year after grade 3 (thereby allowing me to tell whether
they actually repeated that grade). The second subsample consists of 94,478
students who are observed in each year after entry until they take the grade 10
standardized test and who are observed writing the test.13

桌子 1 presents basic summary statistics for variables used in the analysis
for the grade 3 和 10 subsamples. In table 1 I show means for each subsample
as a whole, and then separately for a one-month range around each entry

measure of grade repetition as the outcome. To control for past repetitions, I added an indicator for
repeating prior grades (other than kindergarten) to the right-hand side of the IV model, which did
not change the results.

12. Note that one ambiguity in entry dates arose because of British Columbia’s practice of collecting
data once every October. Most students born between January and April 1986 began school in
一月 1991, but they could have delayed entry until September of that year. When dual entry
was canceled, this group of students was forced to repeat kindergarten, meaning that a January
entrant who started in January cannot be identiﬁed separately from a January entrant who delayed
entry until September. To solve this ambiguity, I assume that all January–April students observed
for the ﬁrst time in kindergarten in October 1991 began school on 1 一月 1991. This introduces
measurement error into entry age (but not test age), which may bias coefﬁcients toward zero.
13. Though the loss of students from the universe is not trivial (关于 20 percent for the grade 10
sample), students in each subsample remain comparable to the universe itself along baseline
特征, so I do not expect that the attrition will cause selection problems. As one robustness
查看, I ran the regressions for grade 3 students using the grade 10 subsample and the results were
very similar, further bolstering the notion that the attrition does not cause problems. The results
should be interpreted as holding only for those students who stay in the B.C. school system through
grades 3 或者 10.

260

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Justin Smith

桌子 1. Average Student Characteristics

全部

1 十一月 85
+1

−1

1 Jan 86
+1

−1

1 可能 86
+1

−1

1 Jan 87
+1

−1

Panel A: Grade 3

Entry age

Test age

Repeated grade

男性

Aboriginal

Non-English

Panel B: Grade 10

Entry age

Test age

Numeracy

Reading

男性

Aboriginal

Non-English

5.09

8.15

2.63

4.92

7.9

3.52

5.15

7.92

5.46

5.12

7.91

6.32

4.96

8.56

1.07

4.72

8.36

1.7

5.3

8.31

1.42

4.83

7.83

7.05

5.63

8.63

0.91

51.14

51.04

51.43

52.4

49.85

53.71

50.53

50.89

52.11

9.86

9.79

10.01

9.58

9.95

9.11

9.43

10.46

11.53

11.71

11.61

12.78

12.9

12.15

10.15

11.03

11.46

12.95

5.09

4.92

5.14

5.11

4.96

4.72

5.3

4.83

5.62

15.84

15.63

15.65

15.66

16.07

15.96

15.98

15.58

16.31

0.08

0.16

0.01

0.09

0.02

0.1

0.04

0.09

0.07

0.15

0.12

0.19

0.13

0.2

0.05

0.13

0.11

0.21

50.48

50.58

51.35

51.77

49.62

52.93

50.6

50.57

51.44

8.15

9.77

8.1

9.61

8.74

9.33

7.99

8.73

10.58

10.01

7.96

8.15

8.36

8.66

9.01

9.39

9.46

11.07

Notes: +1 indicates that students are born one month after the listed cutoff, whereas −1 indicates
they are born one month before the cutoff. Age is in years; Repeated grade, 男性, Aboriginal,
and Non-English are all percentages; Numeracy and Reading scores are z-scores with mean 0 和
标准差 1. “All” refers to the entire sample of students, and the dates listed in the
header refer to a school entry cutoff point.

age or test age discontinuity. The reason for focusing on the area around the
discontinuity is that this is where the identifying variation arises, and this is
thus the most important subgroup of students to analyze.

Column 1 presents means for all variables using each subsample as a
whole. On average the grade 3 students are just over ﬁve years old at entry and
eight years old at the beginning of grade 3, while the grade 10 students are just
under sixteen years old at the time they are tested. 关于 2.6 percent of grade 3
students repeat, and the mean numeracy and reading test scores for the grade
10 students are slightly above zero, meaning that students in the birth cohorts
I choose to analyze are above average. Just over half of the students are male,
8–10 percent are Aboriginal, and 10–12 percent speak a non-English language
at home.

Columns 2–9 present the same averages for subgroups of students born
on either side of the ﬁve relevant school entry cutoff dates. I focus in particular
on grade repetition, test scores, and the age variables because these are the
main factors in the estimating equations. Variation in entry age and test age
are consistent with previous descriptions. There are notable discontinuities

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

261

HOW VALUABLE IS THE GIFT OF TIME?

in test age near both of the January entry cutoff dates, but there is much
less variation around the November and May cutoffs. 反过来, entry age
varies signiﬁcantly at all cutoffs except January 1986. Note that there is some
variation at this discontinuity, and this is the result of parents reshufﬂing
after the policy was canceled. 最后, there are notable differences in grade
repetition at all the cutoff points. More often than not, people born just before
a cutoff point are much more likely to repeat a grade. Generally speaking, 测试
scores are higher for students born just after each discontinuity, but normally
少于 5 percent of a standard deviation.

The patterns of entry age, test age, and outcomes across each of the dis-
continuity points provide some intuition behind the results to come. 在 1
十一月 1985 discontinuity, notice that to the right of the cutoff the average
entry age increases, but so does grade repetition. On its own, this implies that
entering older increases grade repetition, but recall that increases in grade rep-
etition are associated with declines in schooling. Thus this pattern suggests
that there may be a schooling effect overriding any entry age effect among
these students. Looking across to the 1 一月 1986 cutoff, students born
just after the cutoff are younger at entry but older at the beginning of grade 3
and have a much lower probability of repeating grade 3. Those born just af-
ter the cutoff also have more schooling, suggesting that when test age and
schooling effects work together, the result is quite a large change in outcomes.
有趣的是, with a large increase in entry age to the right of the 1 可能 1986
discontinuity there is very little change in grade repetition, which is consistent
with offsetting entry age and schooling effects. These preliminary summary
statistics suggest that both entry age and test age effects are likely to be positive,
but both are inﬂuenced by the associated change in schooling.

桌子 2 outlines the fraction of students who enter school on time (在
compliance with school entry laws) for different subgroups of students deﬁned
over birth date ranges for the entire sample universe. For nearly all cohorts, 出色地
超过 90 percent enter on time, with most closer to 100 百分. Among those
students who enter one year early or late, it appears as though the slippage
occurs mostly due to starting school late. One cohort stands out in particular:
those born between November and December 1985. These students were the
ﬁrst cohort slated to start in January under mandated dual entry. 由于
parental reluctance to have children begin school halfway through the school
年, many parents opted to have their children start four months early, 和
a slightly smaller fraction postponed entry to the following September. 这
explains the large amount of slippage for that particular cohort.14

14. The values for the January–April 1986 cohort are measured with error because all students born in

this range were assigned a 1 January entry date. See note 11 for an explanation of this issue.

262

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Justin Smith

桌子 2. School Start Times for Students Born 1985–87

Expected
Start Date

Birth Date

Panel A: All Students

全部的

% on Time

% Late

% 早期的

May–Oct 85

Nov–Dec 85

Jan–Apr 86

May–Dec 86

Jan–Dec 87

Panel B: Males

May–Oct 85

Nov–Dec 85

Jan–Apr 86

May–Dec 86

Jan–Dec 87

Panel C: Females

May–Oct 85

Nov–Dec 85

Jan–Apr 86

May–Dec 86

Jan–Dec 87

九月 90

Jan 91

九月 91

九月 92

九月 90

Jan 91

九月 91

九月 92

九月 90

Jan 91

九月 91

九月 92

24,328

7,188

14,363

29,708

44,521

11,502

1,722

7,330

14,512

22,259

11,855

3,456

6,934

14,577

21,718

92.96

48.86

98.48

96.99

98.20

92.22

46.14

98.67

95.91

97.77

93.75

51.79

98.27

98.11

98.66

6.99

21.59

0.32

2.90

1.68

5.24

16.82

0.17

1.46

1.18

6.22

16.46

0.26

1.77

1.18

0.05

29.55

1.20

0.11

0.12

0.06

27.52

0.96

0.11

0.07

0.03

31.74

1.47

0.12

0.17

Notes: Expected start date is derived from B.C. law and is based on when the student turns ﬁve
years old. On time refers to the percentage of students who begin at the assigned entry date, 晚的
refers to students who postpone entry by one or two entry dates, and early refers to students who
begin one or two entry dates before their normal entry date.

While this slippage does not affect the internal validity of the LATE esti-
伙伴, it may affect their interpretation. The IV estimator is deﬁned over those
people who comply with the rules, and if this is a select subset, 结果
may not be that generalizable. 尤其, one worry is that the November–
December compliers discussed above are a very select subgroup. To assess the
validity of this claim, 桌子 3 computes means of baseline characteristics for
students who start school on time, separated by the time period in which they
were born. The idea behind this table is that if students who start on time rep-
resent compliers (in the treatment effects sense) sufﬁciently well, 比较
their baseline characteristics gives us some idea of whether the November–
December students are a select subgroup. There are only slight differences
between the November–December cohort and the rest of the cohorts in terms
of gender and whether they speak English at home, indicating that they are
not an overly select subgroup of students. This supports the notion that the
LATE estimates may be generalizable to the average student in the sample.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

263

HOW VALUABLE IS THE GIFT OF TIME?

桌子 3. Average Baseline Characteristics of Compliers

Birth Date Range

男性

Aboriginal

Non-English

May–Oct 1985

Nov–Dec 1985

Jan–Apr 1986

May 1986–Dec 1987

50.9

51.8

50.7

9.3

9.6

9.5

10.1

14.5

14.6

10.5

11.4

Notes: The percentages generated in this table use only the sample of
students who start on time (those who follow school entry rules strictly).
Non-English refers to the student’s home language being anything other
than English.

6. 结果
First-Stage Estimates
In table 4, I show the ﬁrst-stage estimates of actual entry age and test age
regressed on the instruments—predicted entry age and test age. Odd columns
present speciﬁcations without any controls, whereas even columns add school
ﬁxed effects, baseline covariates, and a cubic in day of birth. Panel A presents
the estimates for the grade 3 subsample, and panel B presents those for the
年级 10 subsample.

Due to the inclusion of both predicted entry age and test age in each
speciﬁcation, the coefﬁcients can be slightly confusing to interpret. In column 1
of panel A, which uses entry age as the dependent variable, the coefﬁcient on
predicted entry age suggests that for students who are supposed to start grade
3 同时 (IE。, holding predicted test age constant), those who are
predicted to enter one year older are actually 0.982 years older when they enter.
The fact that the coefﬁcient on predicted entry age is not identically equal to
1 reﬂects the effects of delayed entry, as some parents will postpone entry of
their child by up to one year. The coefﬁcient on predicted test age in column 1
implies that among students who are supposed to enter school at the same
时间, those with a higher predicted test age actually enter slightly younger.
This coefﬁcient can be interpreted as a measure of the nonrandomness of
the group of parents that choose to delay entry. According to these estimates,
holding constant predicted kindergarten entry age, those who are predicted to
have a lower test age will be those who delay entry.

In column 3 of panel A, I run a similar regression except with test age
as the dependent variable. The coefﬁcient on predicted test age means that
among students who are supposed to start school at the same time, 那些
with a predicted test age that is one year older actually take the test 0.831 年
较老的. The slippage here results from the effects of both delayed entry and
grade repetition. 最后, the coefﬁcient on predicted entry age means that

264

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

5
3
2
4
7
1
6
8
9
1
9
8
e
d
p
_
A
_
0
0
0
0
1
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Justin Smith

桌子 4. First-Stage Estimates

Panel A: Grade repetition

Expected entry age

Expected test age

氮

Panel B: Test scores

Expected entry age

Expected test age

氮

Controls

Baseline
School FE
Day of birth

Entry Age

Test Age

0.982∗∗
(0.003)

−0.067∗∗
(0.003)

0.675

45,679

0.983∗∗
(0.003)

−0.068∗∗
(0.003)

0.682

14,216

0.072∗∗
(0.005)

0.831∗∗
(0.007)

0.656

16,881

0.073∗∗
(0.005)

0.830∗∗
(0.007)

0.663

6,907

109,956

0.996∗∗
(0.003)

−0.052∗∗
(0.004)

0.740

50,843

94,478

不
不
不

0.997∗∗
(0.003)

−0.053∗∗
(0.004)

0.742

16,185

94,478

是的
是的
是的

0.235∗∗
(0.010)

0.625∗∗
(0.009)

0.366

6,794

94,478

不
不
不

0.239∗∗
(0.009)

0.622∗∗
(0.009)

0.391

2,715

94,478

是的
是的
是的

Notes: Estimates are in years. Grade repetition refers to the grade 3 sample, while test score
refers to the grade 10 sample. Standard errors are clustered on birth date. Baseline controls
include a dummy for male, Aboriginal, and whether the student speaks a language other than
English at home. Day of birth refers to a cubic polynomial in day of birth.
∗∗p < 0.05. among students who were supposed to start grade 3 at the same time, those who are predicted to be one year older at entry are 0.072 years older when they actually enter grade 3. Again, this can be interpreted as a measure of the nonrandom group of parents that choose not to follow the rules: children who have an older predicted entry age are slightly more likely to have been held back and start grade 3 later. While this result seems counterintuitive, I believe it is driven by the large number of students born in November–December 1985 who started school late, since they tended to be older at entry than the students born just prior to November, with whom they were supposed to begin grade 3. A similar set of results follows in panel B, using the grade 10 sample. The noticeable difference from panel A is that in the equation with test age as the dependent variable, increases in expected test age lead to a much smaller increase in actual test age. In addition, among those who are supposed to take the grade 10 test at the same time, those expected to be one year older at entry are 0.235 years older when they sit for the test. This suggests the same pattern l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d f . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 265 HOW VALUABLE IS THE GIFT OF TIME? Table 5. OLS and 2SLS Estimates Grade Repetition Numeracy Reading OLS 2SLS 2SLS OLS 2SLS 2SLS OLS 2SLS 2SLS Entry age Test age 0.001 −0.007∗∗ −0.006∗∗ 0.231∗∗ −0.022 −0.040∗∗ 0.245∗∗ −0.02 −0.040∗∗ (0.017) (0.020) (0.003) (0.020) (0.017) (0.020) (0.002) (0.020) (0.003) −0.054∗∗ −0.060∗∗ −0.058∗∗ −0.369∗∗ 0.090∗∗ 0.109∗∗ −0.375∗∗ 0.107∗∗ 0.124∗∗ (0.019) (0.022) (0.003) (0.022) (0.015) (0.019) (0.002) (0.015) (0.003) Under-id F-Stat Weak-id F-Stat 32014 67025 32238 69584 8809 6695 9383 7271 8809 6695 9383 7271 N 109,956 109,956 109,914 94,478 94,478 94,428 94,478 94,478 94,428 Controls Baseline No School FE No Day of birth No No No No Yes Yes Yes No No No No No No Yes Yes Yes No No No No No No Yes Yes Yes Notes: The critical values for the under-identiﬁcation and weak identiﬁcation statistics can be found in Stock and Yogo (2002). Standard errors on coefﬁcients are clustered on birth date. The under- and weak identiﬁcation statistics are unclustered. The small drop in sample size as the controls are added is due to the addition of school ﬁxed effects; there were a few observations with one student per school. Baseline controls include a dummy for male, Aboriginal, and whether the student speaks a language other than English at home. Day of birth refers to a cubic polynomial in day of birth. ∗∗p < 0.05. as above, except much stronger, perhaps reﬂecting the additional inﬂuence of grade repetition occurring between grades 3 and 10. It is important to keep in mind, however, that this does not invalidate the identiﬁcation strategy in any way. Table 4 also presents the R2 and F-statistic as measures of the validity of the instruments. The R2 is between 0.391 and 0.742 across regressions, indicating that the instruments explain a large amount of the variation in both entry age and test age. The F-test of joint signiﬁcance of both of the instruments is extremely high, which, according to the Staiger-Stock rule of thumb of 10, is preliminary evidence in favor of strong instruments. Note that because there are two endogenous variables, the ﬁrst-stage F-statistic could be misleading if one instrument is a strong predictor of both endogenous variables. In this case, however, it is clear that predicted entry age is a strong predictor of actual entry age and predicted test age is a strong predictor of actual test age, meaning that the ﬁrst-stage F is not likely giving misleading results. Nevertheless, I present the results from a more appropriate test developed by Stock and Yogo (2002) in the next section. Baseline 2SLS Estimates I now turn to the baseline 2SLS estimates of both the entry age and test age effects, which are located in table 5. In this section I focus on the ﬁrst two columns for each outcome: an OLS estimate for comparison and the 266 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Justin Smith 2SLS baseline estimates. The third column contains 2SLS speciﬁcations with covariates, which I discuss in the next section. When grade repetition is an outcome, the OLS estimate of test age is strongly negative, while the entry age effect is mildly positive. OLS estimates are presented only for comparative purposes; due to potential endogeneity of entry and test age, 2SLS coefﬁcients are more reliable. In terms of 2SLS, I estimate a large and signiﬁcant effect of test age and a much smaller negative effect of entry age. Quantitatively, increasing test age by one year leads to a 6.0 percentage point decline in the probability of repeating grade 3. Comparatively, McEwan and Shapiro (2008) estimate that increasing age leads to a more modest 2 percentage point decline in the probability of repeating ﬁrst grade, and Elder and Lubotsky (2009) estimate a much higher 13–15 percentage point decline. Compared with both those estimates, the coefﬁcient estimated here is still large but somewhere in the middle of the range. Looking now at column 5, which uses the grade 10 numeracy test as an outcome, 2SLS estimates reveal a pattern of small negative entry age effects but large positive and signiﬁcant test age effects. The 2SLS estimates imply that increasing test age by one year will increase numeracy test scores by 9.0 percent of a standard deviation (σ ). This estimate is slightly smaller than other estimates in the literature using data near the same grade but somewhat similar to the estimate from Black, Devereux, and Salvanes (2008), which was around 0.10σ for their Norwegian sample. Moving to column 8 in table 5, the 2SLS estimates suggest a slightly higher effect of test age on reading scores than that obtained using numeracy as an outcome but a similar effect for entry age. Quantitatively, increasing test age by one year leads to a 0.107σ increase in reading scores. Table 5 presents two instrument tests to supplement the ﬁrst-stage F- statistics already presented. First is an under-identiﬁcation test intended to check whether the 2SLS system passes the “rank” test with a null of full rank, while the second is a weak instrument test based on the Cragg-Donald statistic, where the null is either that 2SLS is less biased than OLS by a given fraction or that the size of the 2SLS tests does not exceed some given threshold. The cutoff values for these tests using different such thresholds are located in Stock and Yogo (2002), and I will note here that the values of the test statistics exceed all possible critical values by a large amount, indicating strong instruments. Recall that the test age effect is an upper bound, whereas the entry age effect is a lower bound. The small size, and sometimes “wrong” sign, on entry age suggests that schooling does exert some inﬂuence over students’ outcomes that is about as large as the entry age effect. Given a schooling effect, the true test age effect is therefore lower than the upper bound estimate in this article. Unfortunately I cannot directly assess the size of this schooling effect with any l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . f / / e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d f . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 267 HOW VALUABLE IS THE GIFT OF TIME? sort of certainty using the B.C. data. Black, Devereux, and Salvanes (2008), however, are able to address this issue directly; when they restrict their sample of Norwegian males to those who have ﬁnished schooling, they ﬁnd that both the entry age and test age effects shrink toward zero. Interestingly, the entry age effect shrinks much more than the test age effect does, suggesting that schooling and test age are likely playing the largest roles, and entry age is playing a relatively smaller role, in determining school outcomes. To the extent that the variation used in this study and in Black, Devereux, and Salvanes (2008) is similar, one might expect a similar pattern using the B.C. sample. The variation used in this article, however, does have one unique aspect that implies a potentially different impact of schooling. Whereas the confounding inﬂuence of schooling in Black, Devereux, and Salvanes (2008) arises because some students have been exposed to extra schooling at the end of their school- ing career, the confounding inﬂuence in this article arises due to extra time in kindergarten at the beginning of their schooling career. If one believes that the impact of extra kindergarten fades by the time students enter grade 3 or grade 10, the confounding impact of schooling may not be that large. There is some support for this idea in the literature on early childhood interventions, though overall the evidence appears to be mixed on whether such interven- tions persist.15 Even so, it is still likely to be the case that schooling exerts some inﬂuence over these outcomes, and this must be kept in mind when interpreting the coefﬁcients. Robustness Since both instruments are derived from piecewise linear functions of date of birth, it is crucial to identiﬁcation that date of birth is not correlated with the error term in the main structural equation. There is evidence that season of birth is correlated with many of the predictors of school outcomes (Buckles and Hungerman 2009), so when using an IV strategy based on birth dates one must control for such effects. Furthermore, it is possible that precise timing of birth around speciﬁc key dates might cause a relationship between birth date and outcomes at the discontinuities that generate the main identifying variation. While there is no evidence that parents plan births around dis- continuities speciﬁcally for school entry purposes (Dickert-Conlin and Elder 2009), there is evidence that they target birth dates just before the calendar year for tax purposes (Dickert-Conlin and Chandra 1999). Because one of the main discontinuities occurs on 1 January, such tax planning may also induce a 15. For example, DeCicca (2007) shows that the effects of attending full day versus half day kindergarten fade out within a couple of years. But Currie (2001) and Currie, Garces, and Thomas (2002) suggest that impacts of Head Start (and other programs) may actually carry over to medium- and long-term outcomes. 268 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Justin Smith correlation between date of birth and unobserved parental characteristics that would work against the identiﬁcation strategy. To check robustness to season of birth effects I include a series of control variables for baseline characteristics, school ﬁxed effects, and a cubic polyno- mial in day of birth. The school ﬁxed effects are designed to proxy for any school and neighborhood characteristics such as income and education that may be correlated with both date of birth and school outcomes. The cubic in day of birth is meant to absorb any relationship that might exist between the time of the year a student is born and grade 3 repetition or test scores. Speciﬁcations including these controls are reported in columns 3, 6, and 9 of table 5. The general pattern is that the effects are robust to the inclusion of these controls. In particular, the coefﬁcients on both test age and entry age for grade repetition differ minimally. The test age and entry age coefﬁcients on both numeracy and reading scores increase in magnitude but not by enough to cause serious concern. Another check on the robustness to season of birth effects is to limit the sample to those located around the discontinuities, because this is where all the identifying variation occurs and because the inﬂuence of season of birth factors should be eliminated by considering such a small subset of the population born around the same time. Black, Devereux, and Salvanes (2008) and Elder and Lubotsky (2009) implement this strategy under the as- sumption that it eliminates the potential for bias stemming from birth date timing or the seasonality of births described above. One potential problem with this strategy that must be kept in mind is that if treatment effects are heterogeneous, different estimates could arise if this speciﬁc subpopulation responded to the age change differently from the average individual in the population. Table 6 presents the results from limiting the sample to those born one month on either side of the school entry cutoffs. The results are very similar to the baseline results, except that the magnitudes of the test age effects have increased. The standard errors also increase signiﬁcantly due to a large loss of sample size; it is approximately one-twelfth the size. In spite of this, the test age effects still remain highly statistically signiﬁcant. The overall conclusion from this exercise is that the estimates are robust to limiting the sample to those near the identifying variation. To address issues of precise birth timing, I look for evidence that parents precisely time births to one side of each of the discontinuities. The only really concerning cutoff is the one at 1 January 1986; since the dual entry policy came into effect several years after any of the children in the sample were born, parents could not have sorted around the 1 November or 1 May cutoffs. They may, however, have sorted around the 1 January cutoff based on tax l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 269 HOW VALUABLE IS THE GIFT OF TIME? Table 6. 2SLS Estimates: Discontinuity Sample Grade Repetition Numeracy Reading 2SLS 2SLS 2SLS 2SLS 2SLS 2SLS 0.001 (0.004) −0.082∗ (0.005) 6860 13747 0.001 (0.004) −0.079∗ (0.004) 6508 13094 −0.025 (0.028) 0.131∗ (0.032) 4183 2791 −0.038 (0.025) 0.154∗ (0.030) 4459 3107 −0.02 (0.027) 0.157∗ (0.031) 4183 2791 −0.023 (0.025) 0.176∗ (0.029) 4459 3107 23,605 23,534 20,707 20,644 20,707 20,644 Entry age Test age Under-id F-Stat Weak-id F-Stat N Controls Baseline School FE Day of birth No No No Yes Yes Yes No No No Yes Yes Yes No No No Yes Yes Yes Notes: The discontinuity sample includes those born one month on either side of the discontinuities generating the identifying variation. The critical values for the under-identiﬁcation and weak identi- ﬁcation statistics can be found in Stock and Yogo (2002). Standard errors are clustered on birth date. The under- and weak identiﬁcation statistics are unclustered. The small drop in sample size as the controls are added is due to the addition of school ﬁxed effects; there were a few observations with one student per school. Baseline controls include a dummy for male, Aboriginal, and whether the student speaks a language other than English at home. Day of birth refers to a cubic polynomial in day of birth. ∗p < 0.01. incentives. One method to assess birth date targeting is to take the population of all births between 1 May 1985 and 31 December 1987 and look at a frequency histogram of the number of births per day to see if there is any clustering near 1 January. Unfortunately, disaggregated vital statistics data on births for British Columbia are not readily available, so as a second-best alternative I look at the sample of all 120,108 kindergarten entrants from the B.C. data during the relevant time period. The frequency histogram of number of births using the kindergarten entry cohort is plotted in ﬁgure 2. Dips on weekends and key holidays are clearly evident in the graph, as is a distinct seasonal pattern, but there does not appear to be any obvious clustering around any of the discontinuities. To support this claim further, I regressed the natural logarithm of counts of the number of students born on each day (and the raw counts in a separate regression) on a second order spline function of birth date, allowing changes in the intercept at each of the key cutoff points and for different slopes between any two adjacent cutoff points. Table 7 shows that there are only tiny changes in the intercept as the spline function crosses each of the cutoffs, supporting the notion that parents have not precisely timed births around any of the discontinuities. For visual reference, ﬁgure 3 plots student counts and the associated predicted values from the regression against date of birth. 270 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d f . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Justin Smith Figure 2. Frequency Histogram of Number of Students Born per Day, May 1985–December 1987 Table 7. Discontinuities in Number of Students Born at School Entry Cutoffs Dependent Variable ln(# students) # students School Entry Cutoff Point 1 Nov 85 1 Jan 86 1 May 86 1 Jan 87 N −0.02 (0.061) −0.015 (0.067) 0.04 (0.047) −0.008 (0.035) 975 −2.911 (7.274) −2.532 (8.043) 4.795 (5.653) −0.778 (4.165) 975 Notes: This table presents regressions of either the logarithm of the number of students or the number of students born on each day on a quadratic spline function of date of birth, allowing for breaks at each school entry cutoff point. Subgroup Analysis Perhaps more interesting than the effect of entry age and test age on the average individual is the difference in these effects across gender. Some researchers argue that the brains of boys and girls develop at different rates when they are young (Sax 2007), so there is an a priori reason to believe that both entry age and test age would have different effects across gender. If the effect of entry age is seen to be different by gender, and if reducing gender gaps in both the outcomes analyzed in this article is policy relevant, it raises the possibility of a l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 271 HOW VALUABLE IS THE GIFT OF TIME? l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 3. Actual and Predicted Number of Births per Day “genderized” school entry policy where boys enter at one time and girls enter at another. If test age effects differ by gender, some may suggest the same policy, as changing entry age normally changes test age at the same time. It also raises the possibility of an alternative policy that tests boys and girls at different times. Table 8 replicates the baseline estimates with covariates for males and females. Interestingly, the effect of test age on grade repetition is much higher for males than for females. Being one year older when starting grade 3 reduces the probability of repeating that grade by about 8.2 percentage points for males and 3.4 percentage points for females. This result is perhaps unsurprising given that males are thought to be less mature than females at younger ages, so allowing them to be one year older would have a much stronger effect. The entry age effects are near zero for both genders, indicating a lack of such an effect or an offsetting schooling effect. For test scores, the test age effects are roughly similar between males and females, with females showing slightly larger effects in both numeracy and reading. What is much different is the size of the entry age effect. Recall that the entry age effect is a lower bound, being pulled down by a schooling effect. If this is true, it appears that females are much more negatively affected by the loss of schooling that accompanies entering school one year older. Quantitatively, entering one year older tends to reduce female test scores by about 0.068σ in numeracy and 0.052σ in reading. For males, the effects are much smaller and statistically insigniﬁcant. 272 Justin Smith Table 8. 2SLS Estimates: Females and Males Grade Repetition Numeracy Reading Females Males Females Males Females Males Entry age Test age −0.006∗∗ (0.003) −0.034∗ (0.003) −0.008∗∗ (0.003) −0.082∗ (0.004) −0.068∗ (0.026) 0.117∗ (0.027) Under-id F-Stat Weak-id F-Stat 19645 39344 14661 26684 4024 3024 −0.012 (0.024) 0.100∗ (0.027) 5476 4344 −0.052∗∗ (0.026) 0.137∗ (0.028) 4024 3024 −0.025 (0.023) 0.109∗ (0.025) 5476 4344 N Controls 53,670 56,176 46,737 47,625 46,737 47,625 Baseline School FE Day of birth Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Notes: The critical values for the under-identiﬁcation and weak identiﬁcation statistics can be found in Stock and Yogo (2002). Standard errors are clustered on birth date. The under- and weak identiﬁcation statistics are unclustered. The small drop in sample size as the controls are added is due to the addition of school ﬁxed effects; there were a few observations with one student per school. Baseline controls include a dummy for male, Aboriginal, and whether the student speaks a language other than English at home. Day of birth refers to a cubic polynomial in day of birth. ∗p < 0.01; ∗∗p < 0.05. There has been a large amount of media coverage in the past few years about the relatively poor performance of boys in terms of school outcomes, which continues to plague boys today. The results of this research suggest that at least in terms of grade repetition, one potential cause of this problem may be that young boys are simply not mature enough at the time they start grade 3. Allowing them one extra year before beginning that grade may lead to a large decrease in the number of boys that end up repeating a given elementary grade. As Sax (2007) suggests, one way to accomplish this is to have boys enter school when they are one year older than girls. Such a policy would have the effect of increasing both entry age and test age and could allow the gap between boys’ and girls’ performance to be closed somewhat. Even given the potential beneﬁts in the reduction of grade repetition, it is unclear whether parents would accept a policy that discriminates only on the basis of gender. A potentially more viable alternative would be to direct extra school or parent resources toward boys to compensate for their relative disadvantages in terms of maturity. 7. CONCLUSIONS AND POLICY IMPLICATIONS Disentangling the entry age from the test age effect is important for parental behavior and policy. Most of the existing research that estimates the relation- ship between age and student outcomes has not been able to separate these distinct effects. In this article I solve this identiﬁcation problem by comparing l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d f . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 273 HOW VALUABLE IS THE GIFT OF TIME? the outcomes of children enrolled in B.C. schools around the time of the dual entry experiment. By decoupling entry age from test age, this policy allowed me to provide estimates of the two independent effects (but not independent of schooling) on grade repetition and test scores. Estimating the relevant parameters using an IV model, I reach several interesting conclusions. The ﬁrst is that the upper bound test age effect is large for both grade repetition and test scores, suggesting a strong test age effect bolstered by a schooling effect. Second, I ﬁnd small negative lower bound entry age effects, which are suggestive of a positive entry age effect being offset by an equally large schooling effect. Generally speaking, these results are quite similar to other European estimates that have been put forth recently. I show further that the effects of test age are different by gender, with males showing a stronger effect on grade repetition and females showing a slightly stronger effect on grade 10 reading scores. The qualitative predictions of the IV model used are robust to inclusions of a set of controls that accounts for the effects of season of birth in particular. How can these results help inform parental decisions and policy? Interest- ingly, increasing the current school entry age from, say, ﬁve to six years of age may help students greatly if both entry and test age effects are positive, since such a policy would make students older at entry and when they are tested. Thus, had the policy not been canceled so quickly after implementation, a pol- icy such as B.C.’s dual entry experiment may have beneﬁted students in terms of increasing both entry age and test age. Changing the school entry structure, however, can be confusing and controversial. In fact, the major reason that B.C.’s dual entry program failed was the opposition of parents to the change away from the single-entry system. It was seen as confusing and was certainly not fully understood (see Ungerleider 2003). An alternative method would improve the outcomes of the youngest children without manipulating their entry ages. If entry age effects are small and test age effects are large, some student outcomes can be improved if we alter the way students are tested. In most jurisdictions, all students are tested at the same time of year, creating a large variance in test age at the time of the test. As an alternative, students could be tested at the same age, which would eliminate the maturity advantage held by older students at test time. This type of policy, however, would be difﬁcult to implement and is likely to be unpopular with parents and possibly educators. As an alternative, one might also consider age adjusting test scores to reﬂect the relative maturity disadvantages. Yet another, more feasible, option would be to direct extra resources at the youngest students in a class with the intention of providing compensation for the age disadvantage they face. Examples of such investments include extra 274 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Justin Smith books, after-school programs, or teaching assistants that focus their attention on the younger students. It is also important to keep in mind the variation in these effects across gender. Males are currently lagging behind females based on several educa- tional outcome measures. The results of this research show that part of the reason could be that test age affects males more strongly than females. Thus, if an alternative entry age policy were to be considered, deﬁning entry dates by gender could be a feasible option if parents were not too opposed. A slightly more feasible policy would be to pinpoint younger males and help by directing more resources toward them. Thanks to Abigail Payne, Tom Crossley, and Phil DeCicca for many valuable discus- sions. Thanks also to Jan Brenner, David Card, Elizabeth Dhuey, Fabian Waldinger, and participants of the Berkeley Labor “therapy” group and McMaster Seminar Series for their helpful input. REFERENCES Bedard, Kelly, and Elizabeth Dhuey. 2006. The persistence of early childhood maturity: International evidence of long-run age effects. Quarterly Journal of Economics 121(4): 1437–72. Bedard, Kelly, and Elizabeth Dhuey. 2007. Is September better than January? The effect of minimum school entry age laws on adult earnings. Unpublished paper, University of California, Santa Barbara. Black, Sandra E., Paul J. Devereux, and Kjell G. Salvanes. 2008. Too young to leave the nest: The effects of school starting age. NBER Working Paper No. 13969. Bound, John, and David Jaeger. 2000. Do compulsory school attendance laws alone explain the association between quarter of birth and earnings? Worker Well-Being 19: 83–108. Buckles, Kasey, and Daniel Hungerman. 2009. Season of birth and later outcomes: Old questions, new answers. NBER Working Paper No. 14573. Cascio, Elizabeth, and Diane Whitmore Schanzenbach. 2007. First in the class? Age and the education production function. NBER Working Paper No. 13661. Crawford, Claire, Lorraine Dearden, and Costas Meghir. 2007. When you are born matters: The impact of date of birth on child cognitive outcomes in England. London: Institute for Fiscal Studies. Currie, Janet. 2001. Early childhood intervention programs: What do we know? Journal of Economic Perspectives 15(2): 213–38. Currie, Janet, Eliana Garces, and Duncan Thomas. 2002. Longer term effects of Head Start. American Economic Review 92(4): 999–1012. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . f / / e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d f . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 275 HOW VALUABLE IS THE GIFT OF TIME? Datar, Ashlesha. 2006. Does delaying kindergarten entrance give children a head start? Economics of Education Review 25(1): 43–62. DeCicca, Philip. 2007. Does full-day kindergarten matter? Evidence from the ﬁrst two years of schooling. Economics of Education Review 26: 67–82. Deming, David, and Susan Dynarski. 2008. The lengthening of childhood. Journal of Economic Perspectives 22(3): 71–92. Dhuey, Elizabeth, and Stephen Lipscomb. 2007. Disabled or young? Relative age and special education diagnoses in schools. Unpublished paper, University of Toronto. Dickert-Conlin, Stacey, and Amitabh Chandra. 1999. Taxes and the timing of births. Journal of Political Economy 107(1): 161–77. Dickert-Conlin, Stacey, and Todd Elder. 2009. Suburban legend: School cutoff dates and the timing of births. SSRN Working Paper No. 1342520. Elder, Todd E., and Darren H. Lubotsky. 2009. Kindergarten entrance age and chil- dren’s achievement: Impacts of state policies, family background, and peers. Journal of Human Resources 44(3): 641–83. Fredriksson, Peter, and Bjorn Ockert. 2006. Is early learning really more productive? The effect of school starting age on school and labor market performance. Institute for Labour Market Policy Evaluation Paper No. 2006:12. Gammage, Philip. 1991. Changing ideologies and provision in western Canadian pri- mary education. Comparative Education 27(3): 311–23. Glegg, Alastair R. 1995. Inquest on a failure: The dual entry kindergarten exper- iment in British Columbia. International Journal of Educational Reform 4(1): 18– 24. Kawaguchi, Daiji. 2006. The effect of age at school entry on education and income. ESRI Discussion Paper No. 162. Knox, Jack. 2008. Being born at “wrong” time of year hurting students’ success. Victoria Times Colonist, 30 December. McEwan, Patrick, and Joseph Shapiro. 2008. The beneﬁts of delayed primary school enrollment: Discontinuity estimates using exact birth dates. Journal of Human Resources 93(1): 1–29. Puhani, Patrick A., and Andrea M. Weber. 2006. Does the early bird catch the worm? Instrumental variable estimates of educational effects of age of school entry in Ger- many. Diskussionspapiere der Wirtschaftswissenschaftlichen Fakult¨at der Universit¨at Hannover No. 332. Sax, Leonard. 2007. Boys adrift: The ﬁve factors driving the growing epidemic of unmotivated boys and underachieving young men. New York: Basic Books. Smith, Justin. 2009. Can regression discontinuity help answer an age-old question in education? The effect of age on elementary and secondary school outcomes. Unpub- lished paper, University of Manitoba. 276 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . f / / e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Justin Smith Stock, James H., and Motohiro Yogo. 2002. Testing for weak instruments in linear IV regression. NBER Technical Working Paper No. 0284. Ungerleider, Charles. 2003. Failing our kids: How we are ruining our public schools. Toronto: McClelland and Stewart Limited. Weil, Elizabeth. 2007. When should a kid start kindergarten? New York Times, 3 June. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / / 5 3 2 4 7 1 6 8 9 1 9 8 e d p _ a _ 0 0 0 0 1 p d f . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 277 Justin Smith image

下载pdf