Impulsivity and Active Inference
中号. Berk Mirza, Rick A. Adams, Thomas Parr, and Karl Friston
抽象的
■ This paper characterizes impulsive behavior using a patch-
leaving paradigm and active inference—a framework for
describing Bayes optimal behavior. This paradigm comprises
different environments (patches) with limited resources that
decline over time at different rates. The challenge is to decide
when to leave the current patch for another to maximize
reward. We chose this task because it offers an operational
characterization of impulsive behavior, 即, maximizing
proximal reward at the expense of future gain. We use a Markov
decision process formulation of active inference to simulate be-
havioral and electrophysiological responses under different
models and prior beliefs. Our main finding is that there are at
least three distinct causes of impulsive behavior, 我们
demonstrate by manipulating three different components of
the Markov decision process model. These components com-
prise (我) the depth of planning, (二) the capacity to maintain
and process information, 和 (三、) the perceived value of
immediate (relative to delayed) rewards. We show how these
manipulations change beliefs and subsequent choices through
variational message passing. 此外, we appeal to the
process theories associated with this message passing to simu-
late neuronal correlates. In future work, we will use this scheme
to identify the prior beliefs that underlie different sorts of
impulsive behavior—and ask whether different causes of
impulsivity can be inferred from the electrophysiological
correlates of choice behavior. ■
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
介绍
Our everyday lives present us with different paths that
lead to different outcomes. When choosing among alter-
native courses of action, we take into account the overall
reward we are likely to get if we were to follow a certain
path—and the time it would take to obtain the reward.
Although some of us care more about long-term goals,
others have a tendency to act for immediate gratification,
even when the latter is less beneficial in the long run
(Logue, 1995; Strotz, 1955). This sort of behavior can
be characterized as impulsive. 更确切地说, impulsive
behavior can be operationally defined as seeking proxi-
mal rewards over distal rewards. A common theme in
many impulsivity scales ( Whiteside & Lynam, 2001;
Patton, 斯坦福大学, & Barratt, 1995; Eysenck & Eysenck,
1978) is a failure to plan ahead. 在本文中, we show
that at least three different factors can lead to impulsive
行为. To show this formally, we use a Markov deci-
sion process (MDP) formulation of active inference in a
patch-leaving paradigm.
Under active inference, both perception and action
serve to minimize variational free energy (Friston et al.,
2015). Variational free energy is an upper bound on neg-
ative Bayesian model evidence, such that minimizing var-
iational free energy means maximizing model evidence.
This single imperative can account for a wide range of
感性的, cognitive, and executive processes in cog-
伦敦大学学院
nitive neuroscience and can be summarized as follows:
Perception minimizes surprise (例如, prediction errors),
whereas action minimizes expected surprise or uncer-
污点 (例如, epistemic foraging while avoiding sur-
prising absence of reward). Variational free energy is
a formal measure of surprise: It is a function of beliefs
about unobserved or hidden variables (that can be
subdivided into “states” of the world and “policies”)
and observed sensations they cause. The hidden states
define the unknown aspects of an environment that
generate observable outcomes. In active inference,
the transitions between the hidden states depend upon
the policies pursued. 换句话说, policies dictate
sequences of actions or state transitions. This means
that we have (一些) control over the environment through
our actions, and we can act to produce the outcomes
that we desire.
In the patch-leaving paradigm (Charnov, 1976;
MacArthur & Pianka, 1966; Gibb, 1958), the problem is
deciding when to leave an environment with exhaustible
资源. In our version of this task, there are several
patches with unique reward–probability decay rates. 铝-
though a general notion, we can make it more intuitive
with an example. A patch can be thought of as a bag of
chocolates and stones, where chocolate is a rewarding
and stone is a nonrewarding outcome. One can succes-
sively draw single items from the bag. 至关重要的是, 有
a hole at the bottom of the bag, and the chocolates are
falling from the bag faster than the stones. This means
that the probability of drawing a chocolate decreases with
© 2018 麻省理工学院. Published under a
Creative Commons Attribution 4.0 国际的 (抄送 4.0) 执照.
认知神经科学杂志 31:2, PP. 202–220
土井:10.1162/jocn_a_01352
时间. At each time point, one is presented with the
choices “stay” and “leave.” Choosing to stay entails
drawing a chocolate from the same bag that one has
been foraging in. Choosing to leave entails moving onto
a new bag that might have more chocolates. 然而,
leaving has a cost—and the cost (IE。, switching penalty)
is to forfeit attempts at drawing a chocolate for the time
taken to find the new bag. The new bag can be a new
kind of bag or the same kind of bag as the previous.
至关重要的是, the holes at the bottom of each kind of bag
have different sizes. This means that the chocolates are
dropping from each kind of bag with a different rate.
This task requires one to decide when to leave a patch
to maximize reward. In this task, we equate staying
longer in a patch (compared with a simulated reference
主题) with more impulsive behavior. 直观地, A
greater emphasis on proximal outcomes means a
greater reluctance to accept the switching penalty com-
pared with accepting a small probability of immediate
reward.
In the next section, we describe the MDP used to de-
fine the patch-leaving paradigm, and the active inference
scheme used to solve it. Through simulation, we illus-
trate the different deficits that can lead to impulsive
行为. This illustration entails manipulating how
deeply a synthetic subject looks into the future (前任-
pressed in terms of her “policy depth”), her capacity to
maintain and process sequential information (expressed
in terms of the “precision” of beliefs about transitions),
and how much immediate rewards and penalties are
discounted compared with distant ones (expressed in
terms of a “discount slope” of preferences over time).
These manipulations may correspond to different cogni-
tive and psychological processes. We use policy depth in
a sense that it is analogous to processes such as planning
ahead or planning horizons (Huys et al., 2012). Manipu-
lating the precision of beliefs about transitions may cor-
respond to forgetting rate ( Wickens, 1998) or working
记忆 (Baddeley, 1992). Discount slope can be seen
as a time preference over utilities, and varying it changes
how much distant rewards are discounted (Frederick,
Loewenstein, & O’Donoghue, 2002). These manipula-
tions will be unpacked in subsequent sections, 和他们的
effects on the simulated responses will be compared with
an MDP model that serves as a point of reference (A
“canonical” model).
This paper comprises three sections. The first de-
scribes an MDP formulation of active inference for the
patch-leaving task. In the second, we manipulate three
components of the MDP, 一次一个, to produce im-
pulsive behaviors. These manipulations will underline the
prior beliefs that can lead to impulsive behaviors. 我们
present the associated (simulated) electrophysiological
responses and how these responses change with the
above manipulations. We conclude with a discussion of
how this paradigm could be used in an empirical setup
in the future.
方法
Active Inference
In the active inference framework, everything is de-
scribed in terms of minimizing variational free energy.
Minimizing variational free energy is equivalent to maxi-
mizing the evidence for a subject’s generative model in
actively sampled observations or outcomes.
F ¼ EQ − ln P ~o; ~xð
Þ
½
(西德:2)− H Q ~xð Þ
½
(西德:2)
¼ − ln P ~o mj
ð
Þ þ DKL Q ~xð Þ P ~x ~oj Þ
k
ð
½
(1)
(2)
(西德:2)
这里, F is the variational free energy, which is expressed
as the expected energy under a generative model and the
entropy of the approximate posterior. Rearranging this
expression shows that the variational free energy is an
upper bound on the negative Bayesian model evidence
−lnP(õ|米) (Beal, 2003). m is the generative model,
and Q and P are the approximate and true posterior
distributions over the hidden variables, 分别. 最小-
imizing the KL divergence minimizes the divergence be-
tween Q and P, making Q an approximate distribution
over the true distribution, Q ~xð Þ ≈ P ~x ~oj Þ
. 这里, õ is
series of observations over time õ = [o1, o2, …… ,oT]时间. ~x ¼
½
x1; x2; ……; xT
(西德:2)T denotes a sequence of hidden variables.
ð
The process of free energy minimization can be inter-
preted as maximization of an agent’s evidence for its own
存在 (弗里斯顿, 2010) or their avoidance of states that
puts their existence at risk (IE。, states they are unlikely to
be found in). Minimizing variational free energy restricts
an agent to a set of states in which it is characteristically
found and, by definition, can exist (弗里斯顿, Kilner, &
哈里森, 2006).
In active inference, an agent is defined in terms of a
generative model of its observed outcomes. 属-
tive model can be thought of as what an agent believes
the structure of the world is like. These models usually
use a discrete state space that map onto observations
at each discrete time step or epoch (Parr & 弗里斯顿,
2018乙). The real structure of the environment is called
the generative process. The structure of the world is de-
fined through initial state vectors, transition matrices,
and likelihood matrices. The initial state vectors D define
beliefs about the initial states the world is in. The transi-
tion matrix B is a probabilistic mapping from the current
state to the next state. The likelihood matrix A is a map-
ping from hidden states to outcomes. In addition to
these vectors and matrices, the generative model also
embodies an agent’s goals (卡普兰 & 弗里斯顿, 2018) 在
the form of prior preferences C over outcomes. 这些
prior preferences indicate how much an outcome is
expected relative to another in the form of log probabil-
实体. These goals can be achieved by sampling the ac-
tions that would realize an agent’s preferred outcomes
(see Figure 1A for the form of generative model used
在本文中).
Mirza et al.
203
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
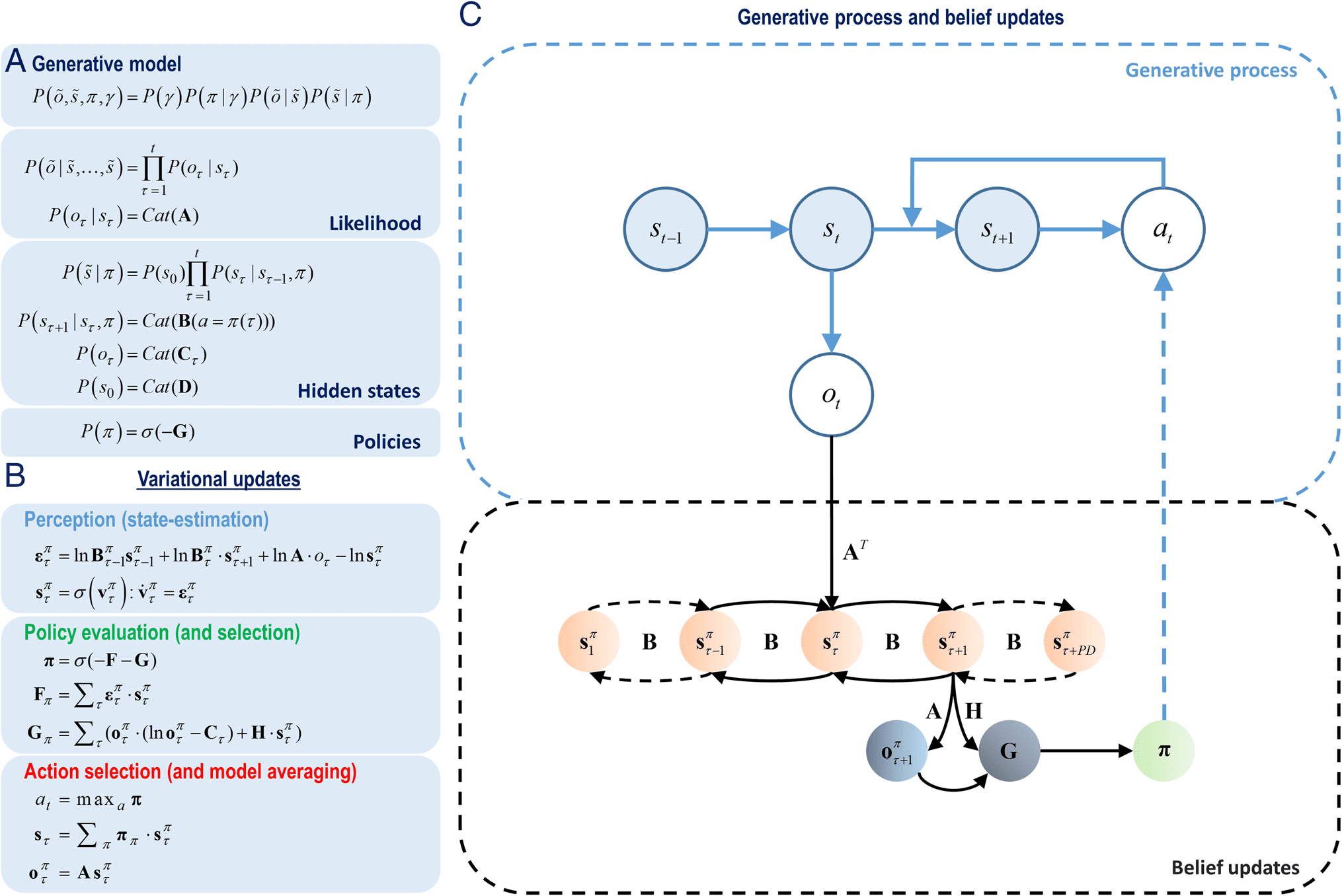
数字 1. Markovian generative model and variational message passing. (A) The equations specify the form of the Markovian generative model.
This generative model is a joint probability of outcomes and their hidden causes. This model constitutes a likelihood mapping (A) from hidden
states to outcomes and the transitions among hidden states are expressed in terms of transition matrices (乙). The transitions among states
depend on actions (A), which are sampled from the posterior beliefs about the policies (圆周率). Precision term γ (or inverse temperature 1/β) 报告
a confidence in beliefs about policy selection. A policy is more likely if it minimizes the path integral of expected free energy (G). The prior
preference matrix (C) defines how much one outcome is expected relative to another outcome. The initial state probability vector (D) defines
the probability of each state in the beginning. (乙) These equations summarize the variational message passing shown at the right. 在里面
perception phase, the most likely states are estimated using a gradient descent on the variational free energy. Here ετ
derivative of the variational free energy with respect to the hidden states) and vτ
in terms of their expected free energies and the posterior distributions over the policies are obtained by applying a softmax function to the
expected free energies under all policies. In the action selection phase, an action is sampled from the posterior distribution over the policies.
这里, π corresponds to the beliefs about the policies. See the Appendix for details. (C) The top half shows the generative process. 这
process specifies that the hidden state of the world in the current epoch (st) depends on the hidden state in the previous epoch
(st−1) and the action (在). The hidden state in the current epoch then produces a new observation (ot). The bottom half shows the
Bayesian belief updates (variational message passing). The new observations are used to infer the most likely causes (sτ) 的
observations. The beliefs about the hidden states (sτ) are then projected backward (sτ−1, ……, s1) and forward (sτ+1, ……, sτ+PD) in time.
这里, PD is a variable that specifies how far into the future these beliefs should be projected. This term will be used later in our
simulations. The expected hidden states in the future (sτ+1, ……, sτ+PD) are used to specify expected observations in the future
(oτ+1, ……, oτ+PD). Only sτ+1 and oτ+1 are shown for simplicity. Then these expectations are used along with the entropy of the
likelihood matrix (H) to compute the (path integral of ) expected free energy (G) under all policies. A softmax function of expected
free energies under all policies provides the posterior distribution over policies. 最后, an action is sampled from the posterior
distribution over the policies. The conditional dependencies in the generative process are shown with blue arrows, whereas the message
passing—implementing belief updates—is shown with black arrows.
圆周率 (the negative
圆周率. In the policy evaluation phase, the policies are evaluated
π ¼ −dF/dsτ
π = lnsτ
至关重要的是, in active inference, the state transitions are a
function of action. The sequences of actions are referred
to as policies. This means that outcomes do not only de-
pend on the hidden states but also on the actions that
control state transitions. Prior beliefs about policies are
defined such that an agent believes that it will minimize
expected free energy in the future. This means that an
agent is more likely to follow a path (IE。, 政策) 那
returns the lowest expected free energy (or greatest
Bayesian model evidence). A softmax function (IE。, 普通的-
ized exponential) of the expected free energies under com-
peting policies can then be used to define the posterior
204
认知神经科学杂志
体积 31, 数字 2
expectations over the policies—from which an action can
be selected. The expected free energy can be written as
G πð Þ ¼
X
ð
G π; t
Þ
ð
G π; t
t
Þ ¼ E ~Q
½ ln QðsτjπÞ− ln Qðsτjoτ; πÞ− ln P oτð
Þ(西德:2)
¼ − E ~Q
½ ln Qðsτjoτ; πÞ− ln QðsτjπÞ(西德:2)
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
epistemic value
− E ~Q
½ ln PðoτÞ(西德:2)
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
extrinsic value
¼ EQðsτjπÞ½H½ PðoτjsτÞ(西德:2)(西德:2)
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Ambiguity
þ D½ QðoτjπÞ‖ PðoτjmÞ(西德:2)
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
风险
where ~Q ¼ Q oτ; sτ πj Þ ¼ P oτ sτj ÞQ sτ πj Þ ≈ P oτ; sτ ~o; πj
ð
ð
ð
ð
(3)
(4)
Þ
.
The expected free energy comprises two terms, 即,
epistemic and extrinsic value. Epistemic value expresses
how much uncertainty can be resolved about the hidden
states of the world if a particular policy is pursued (Mirza,
Adams, Mathys, & 弗里斯顿, 2018; Parr & 弗里斯顿, 2017A).
Extrinsic value expresses the expected utility under a
政策 (Friston et al., 2013), 那是, outcomes with high
extrinsic value are those of high probability in the agent’s
prior preferences (C). These terms can be regarded as
contributing to expected surprise or uncertainty that
has both epistemic, information-seeking and pragmatic,
goal-seeking aspects. Rearranging the expected free
energy shows that it can be written in terms of ambiguity
and risk. Ambiguity is the expected uncertainty in the
mapping from hidden states to observations, 然而
risk is the expected divergence from preferred outcomes.
Policies that minimize both ambiguity and risk are more
likely to be chosen.
Given the definitions above, 洞察力, policy eval-
uation, and action selection can be explicitly formulated
as minimizing variational free energy via a gradient
flow—that can be implemented by neuronal dynamics
(Figure 1B). In the perception phase, the most likely
(隐) states causing observed outcomes are inferred
under a generative model. The perceptual flow is based
on the derivative of the variational free energy with re-
spect to the hidden states (first equation), which can be
interpreted as a state prediction error (弗里斯顿, FitzGerald,
Rigoli, Schwartenbeck, & Pezzulo, 2017). 第二
equation in Figure 1B shows that the most likely states
can then be inferred via a gradient descent on state pre-
diction errors.
In the policy evaluation phase, expectations about the
hidden states are used to evaluate the policies π in terms
of their expected free energies (policy evaluation: 第一的
方程). Please see the Appendix for more details.
Computing the variational free energy, under competing
政策, requires an agent to have expectations about the
past and future states of the world. Optimizing these
(后部) expectations entails minimizing the varia-
tional free energy under a policy, given the current
observations. These posterior expectations are then
projected into the future to obtain the expected states
(and outcomes). How far into the future the posterior
expectations are projected depends on the “policy
depth.”
In the action selection phase, the action that is the
most probable under posterior beliefs about policies is
selected (see Figure 1B). An agent’s interaction with its
environment through action generates a new observa-
的, and a new cycle begins. A graphical representation
of this cycle is shown in Figure 1C.
The policy depth (shown with the subscript PD in
圆周率
sτ+PD
in the lower half of Figure 1C) determines how
many epochs beliefs about hidden states are projected
into the future. An important feature of this scheme is
that a synthetic subject holds beliefs about “epochs” in
both the past and the future. This means that there are
two sorts of times. The first is the actual time that pro-
gresses as the subject samples new observations. 这
第二 (epoch) time is referenced to the onset of a
trial and can be in the past or future, 根据
the actual time. Posterior expectations about the hid-
den states of the world can change as the actual time
progresses and are projected to both future and past
纪元. 在这个 (variational message passing) scheme,
it is assumed that beliefs at the current epoch are pro-
jected: (我) back in time to all epochs from the current
epoch to the initial epoch and (二) forward in time (到
form future beliefs) to a number of epochs correspond-
ing to the policy depth.
The ensuing belief updates are used to mimic electro-
physiological responses obtained in empirical studies.
We have previously used a similar approach to simulate
electrophysiological responses during a scene construc-
tion task (Mirza, Adams, Mathys, & 弗里斯顿, 2016). 我们将
use the example shown in Figure 2 to explain these re-
响应. The left panel in Figure 2A shows how beliefs
about hidden states change at different epochs as new
observations are made, and how these beliefs are passed
to other epochs. The actual time that progresses as new
observations are made is shown on the x-axis. After each
观察, expectations about the hidden states are op-
timized. 在这种情况下, there are four hidden states. 每个
set of four units on the y-axis corresponds to expecta-
tions about these hidden states on different epochs
(例如, 第一的, fifth, 9th and 13th rows show the expectations
about the first hidden state in epochs one to four). Ex-
pectations about hidden states in each epoch are up-
dated as new observations are made. In the left panel
of Figure 2A, the current time is shown on the diagonal
(with red squares), and the past and future epochs are
shown above and below the diagonal, 分别. 在
this example the policy depth is 1, which means that
expectations about hidden states at the current time
are projected one epoch into the future (IE。, there is only
one epoch represented below the diagonal in each
Mirza et al.
205
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
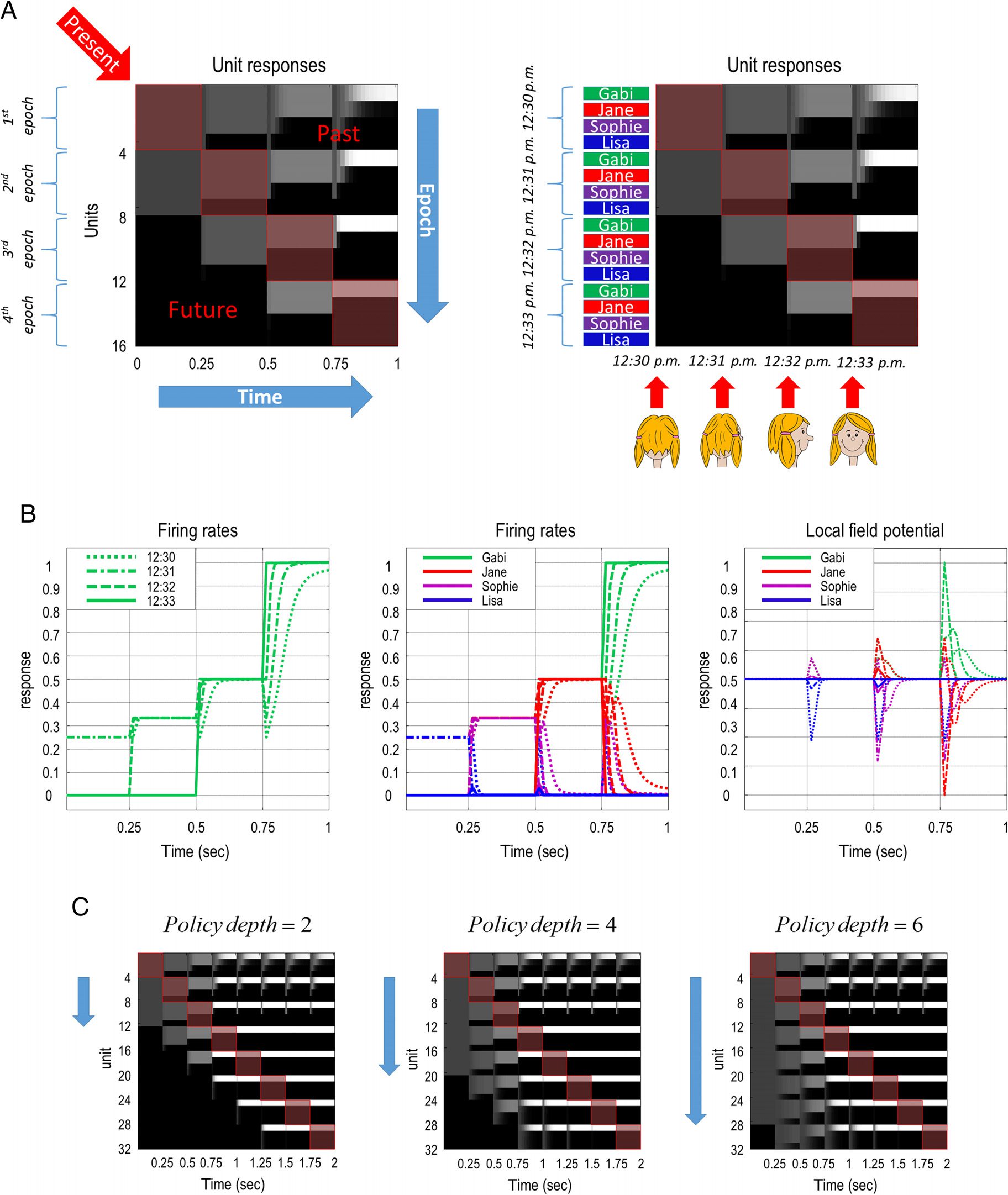
数字 2. Simulated electrophysiological responses. (A) The left shows how the expectations about hidden states are optimized at the current
time and projected to (past and future) 纪元. The actual time—that progresses as new observations are made—is shown on the x-axis.
Epochs occupy a fixed time frame of reference and are shown along the y-axis. 在这个例子中, there are four hidden states that repeat over
epochs on the y-axis. This figure shows that expectations about hidden states at the present time (shown on the diagonal in red squares) 是
projected backward to the past (above diagonal) and forward into the future (below the diagonal) 纪元. The right shows the variational
message passing in the context of identifying someone by accumulating evidence in a sequential manner across different epochs. 这里,
one sees someone that resembles one of four people at 12:30 下午. These four identities are Gabi, Jane, 苏菲, and Lisa. 随着时间的推移, the identity
is disclosed as one gets a better view of the person. Finally at 12:33 p.m., the person that was seen is identified as Gabi. 在这个例子中,
the policy depth is one. This means that expectations about hidden states are projected one epoch into the future. (乙) The left shows the
expectations of hidden state that encodes the identity of Gabi over different epochs, using curves rather than using a raster plot (as shown
多于). These epochs correspond to 12:30, 12:31, 12:32, 和 12:33 下午. The middle shows this for all possible identities. Each color in
the legend corresponds to the identity of each person. The right shows the LFPs, defined in terms of rate of change of expectations about
hidden states, 那是, the gradient of each curve in the middle. (C) These show that using different policy depths project expectations about
hidden states to n number of epochs in the future, where n is chosen as 2, 4, 和 6 from left to right, 分别.
206
认知神经科学杂志
体积 31, 数字 2
柱子). This shows that beliefs about hidden states
reach one epoch into the future.
the expectations about the hidden states (shown in the
middle panel of Figure 2B).
To gain further intuition about this way of how we
might model sequences of states and actions, consider
the example on the right panel of Figure 2A. Assume that
you are walking behind someone who you think you rec-
ognize. 在 12:30 p.m., you can only see this person from
behind—and she resembles one of four people you
知道, 例如, Gabi, Jane, 苏菲, and Lisa. 这些
identities are the four hidden states in this case. 在
12:31 下午. you get closer, and now, you are sure that
she is not Lisa. 在 12:32 下午. you catch up and see her
from the side. 现在, you are convinced this person is not
Sophie either. 在 12:33 下午. you finally see the person’s
脸, and you recognize her as Gabi. This resolves all
uncertainty over the identity of the person. The belief
that the person you see at 12:33 下午. is projected back-
ward in time to 12:30 p.m.—this can be seen clearly in
the final column. 直观地, 在 12:33 p.m., you know that
the person you saw at 12:30 下午. was Gabi.
The left panel of Figure 2B shows the same expecta-
tions about the hidden states that encode Gabi’s identity
as in the right panel of Figure 2A over all epochs (看到
1st, 5th, 9th, and 13th rows in the right panel of
图2A). The figure in the middle panel of Figure 2B
shows the same as the left panel, but for each identity.
The right panel of Figure 2B shows the simulated local
field potentials (LFPs) in terms of the rate of change in
The panels in Figure 2C show how far the beliefs are
projected into the future when different policy depths
被使用. 从左到右, the policy depths are two,
四, and six. One can see that the number of epochs
current beliefs are projected to is two, 四, and six from
left to right, 分别. 之后, we will show how the
policy depth changes the simulated electrophysiological
responses mentioned above—and can have a substan-
tial effect on policy evaluation and subsequent choice
行为.
MDP Model of the Patch-leaving Paradigm
This section describes an MDP model of active inference
for the patch-leaving paradigm. The model is used to sim-
ulate behavioral responses (IE。, choosing to stay or
leave) when the reward probability in a patch declines
exponentially as one stays in a patch. In this paradigm,
there are several patches with their own unique reward
probability decay rates. Choosing to leave a patch war-
rants one epoch to be spent in a reward-free state (IE。,
a switch state). In the next epoch, one enters a patch ran-
domly, and all reward probabilities reset to their initial
价值观. This means one needs to consider how many
epochs to spend in a patch before leaving to realize prior
优先, 那是, being rewarded as much as possible.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
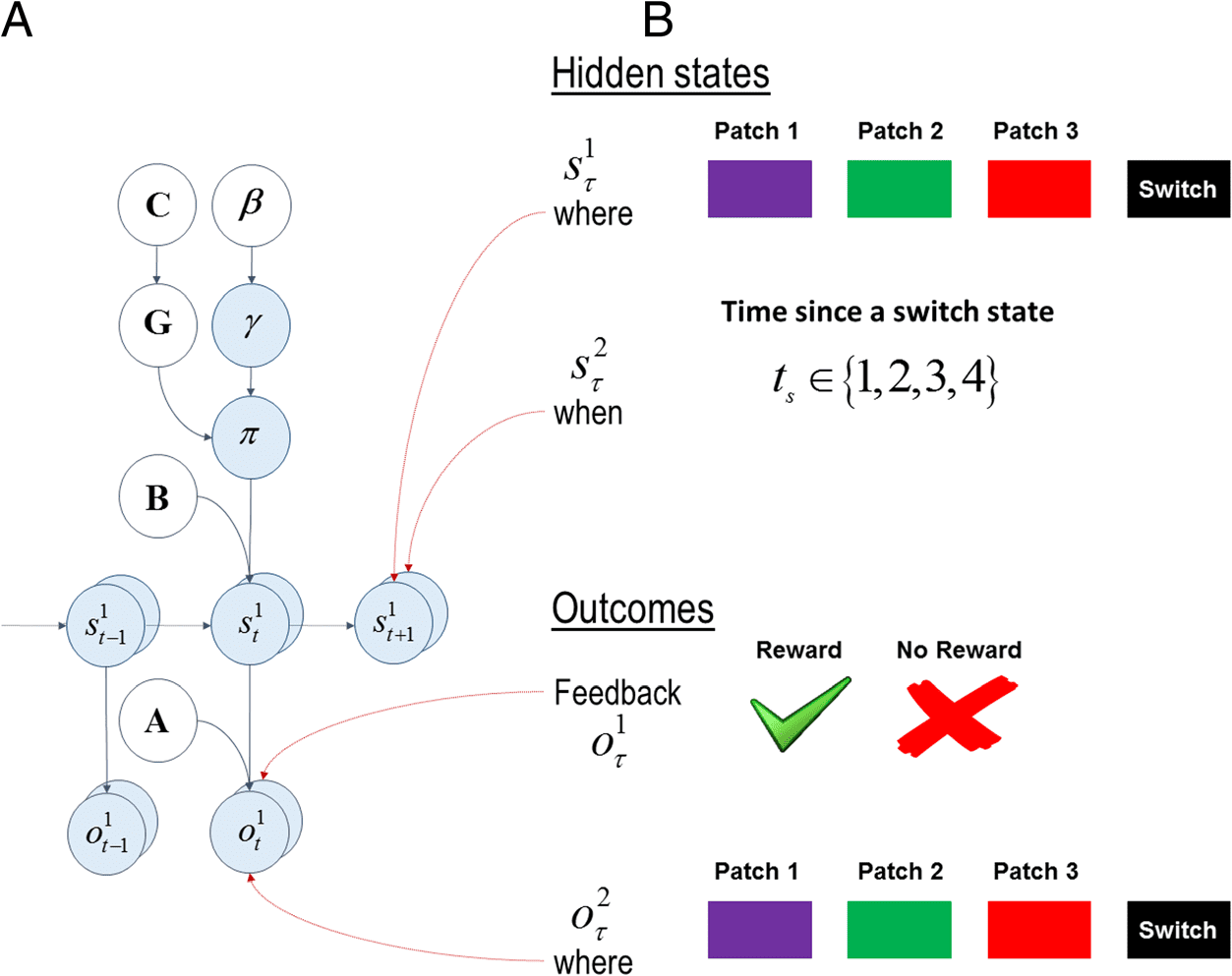
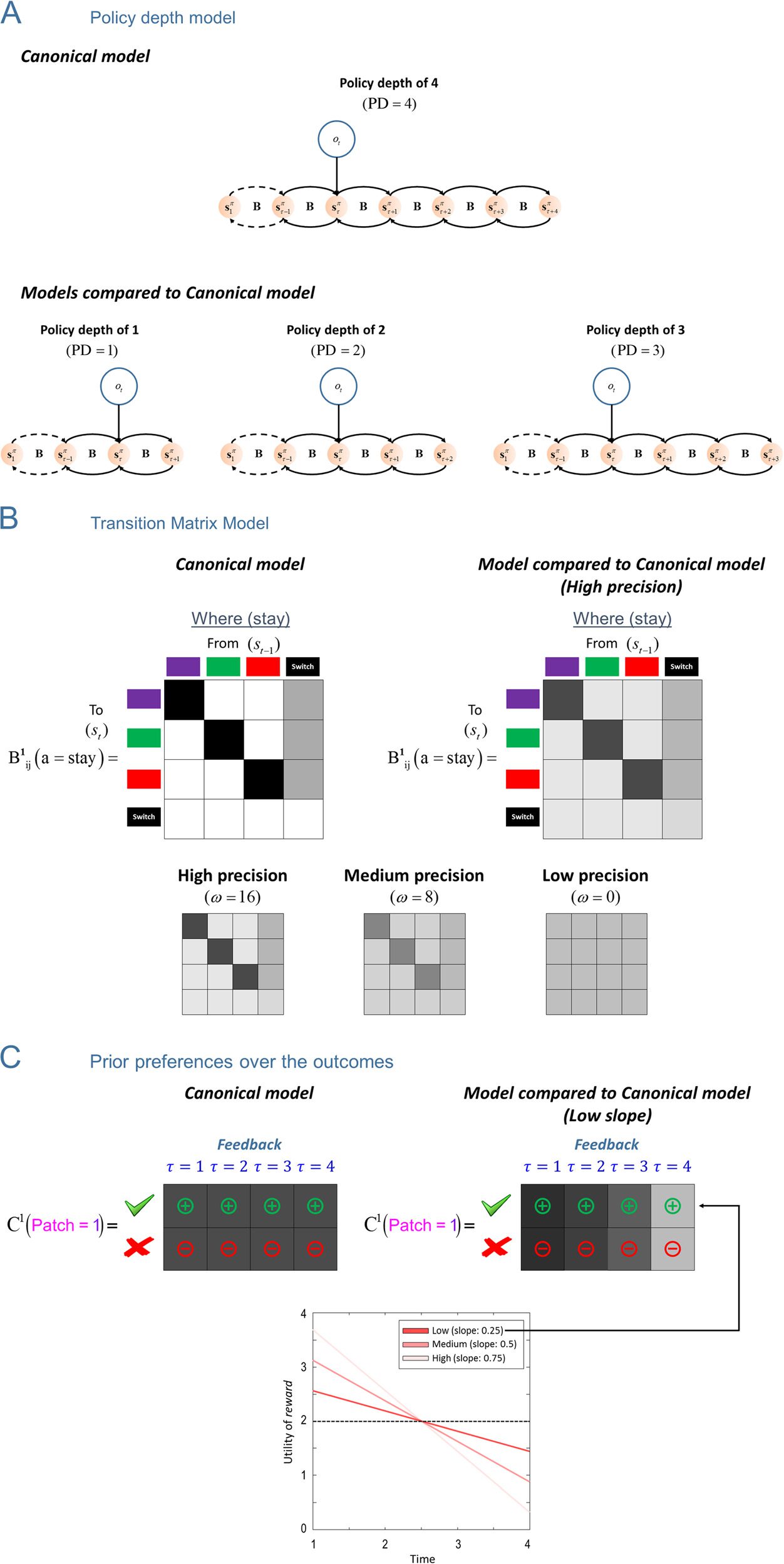
数字 3. Graphical
representation of the generative
模型. (A) The left shows the
set of transition matrices
(shown with B) 和
likelihood matrices (shown with
A) that define the structure of
an environment. The transition
matrices specify the transition
probabilities between hidden
states and the likelihood
matrices specify how likely
outcomes are given the hidden
状态. An agent’s prior
preferences over outcomes are
encoded in the C matrix. A
precision term γ (or inverse
temperature 1/β) reflects the
confidence in policy selection.
本质上, the belief about
policies is a softmax function of
(negative) expected free
energies under all policies
divided by β. A smaller β can be
interpreted as an agent being
more confident about what
policy is selected. The expected free energy, G, has two components, 即, extrinsic value and epistemic value. Extrinsic value is the expected
公用事业 (pragmatic value) expected under a policy, whereas epistemic value is the expected information gain about the hidden causes of observations
under a policy. The state transitions among hidden states s depend on two things, the hidden state and the action in the previous epoch. (乙) 这
right shows different sets of hidden states and outcome modalities in the patch-leaving task. There are two sets of hidden states, 即, the patch
identity and the time since a switch state ts (where and when, 分别). There are two outcome modalities, 即, the feedback and where. 这
feedback modality signals whether an agent receives a reward or not, whereas the where modality signals on which patch an agent is in.
Mirza et al.
207
In this MDP (见图 3), we considered two dimen-
sions of hidden states, 即, “where” and “when.” The
first hidden dimension, 在哪里, corresponds to the “patch
identity.” There are four hidden states under this di-
mension, 即, Patch 1, Patch 2, Patch 3, and a “switch”
状态. Under the action stay, the where state does not
change unless it is in the switch state. Under the action
leave, the where state changes to the switch state, 除了
for the switch state itself. Under both stay and leave, 这
switch state transitions to one of the first three patches
with equal probabilities. The second hidden state dimen-
锡安, 什么时候, keeps track of the number of time steps
since a switch state. The time since a switch state is rep-
resented by ts. This state ts increases by 1 up to a maxi-
mum of 4. The hidden state associated with the fourth
epoch since a switch state ts ¼ 4 is an absorbing state
and does not change over subsequent epochs. 那里-
ward probability in a given patch declines with ts and
does not change after ts ¼ 4, even if one chooses to stay
after the fourth epoch, 那是, reward probability under a
patch is the same for ts > 4 as ts ¼ 4. Choosing to leave at
any point in time resets ts to 1, 那是, ts ¼ 1.
There are two outcome modalities. The first modality
signals the “feedback” (reward or no reward). The prob-
ability of reward declines exponentially under all patches
as ts increases (up to a maximum of 4). There are three
different patches with unique rates of decline in reward
probability. The rate at which the reward probability de-
clines under the first patch exp((1 − ts)/16) is slower than
the second exp((1 − ts)/8) and the third exp((1 − ts)/4)
patches, where ts 2 {1, 2, 3, 4}, 分别. The reward
probabilities under different patches are shown on the
left panel in Figure 4A. The second outcome modality,
在哪里, signals the patch identity. Notice that the patch
身份 (在哪里) appears both as an outcome and as a
hidden state. This is because where (patch identity) 作为
an outcome is used to inform the agent about the where
hidden state.
In this MDP scheme, we consider prior preferences
over only the feedback modality, such that the agent ex-
pects reward (utility or relative log probability of 2 nats)
more than no reward (utility of −2 nats). We defined no
prior preferences over the where modality, 意思是
that there were no preferences over patch identity. 看
数字 4 for the likelihood transition and prior preference
matrices provide a complete specification of this patch-
leaving paradigm.
结果
Simulating Impulsivity
Impulsivity can be characterized as a tendency to act to
require immediate rewards, rather than planning to se-
cure rewards in the long run. In the patch-leaving para-
digm, one is always presented with the choices stay and
leave. The experimental design for this paradigm is such
that it requires one to spend one epoch in a reward-free
switch state upon leaving a patch (IE。, switching penalty).
然而, staying in a patch always has the prospect of
reward. Acting on the proximal reward requires one to
choose stay, whereas acting on the distal reward requires
one to choose leave at some point. 这里, we operation-
ally define “impulsivity” as staying longer in a patch be-
cause only stay has the prospect of an immediate—if
less likely—reward. This raises the question, “longer than
什么?” To address this, we introduce an agent who serves
as a reference or “canonical” model.
在这个部分, we show how impulsive behavior can
be underwritten by changes in prior beliefs about the dif-
ferent aspects of the MDP model. For this purpose, 我们
use the MDP described in Figure 4 as a canonical model.
The simulated responses obtained under the canonical
model will be compared with the models that deviate
from this reference, in terms of the policy depth, 这
precision of the transition matrices, and the discount
slope of the prior preferences over time (IE。, 时间
discounted reward sensitivity). These models will be
compared with the canonical model in terms of dwell
次. “Dwell time” is the average time spent in a patch
upon entering it. The models that induce an agent to stay
longer than the canonical model are considered to exhib-
it impulsive behavior. The models we entertained are as
如下:
• Varying the policy depth. The policy depth of the
canonical model is 4. This model is compared with
the models where the policy depth is varied over
三个级别, 即, PD ¼ 3 (deep policy), PD ¼ 2
(intermediate policy), and PD ¼ 1 (shallow policy)
型号. See Figure 5A for a comparison between
the canonical model and the models above. The pol-
icy depth for all remaining models was PD ¼ 4.
• Varying the precision of the transition matrices.
这里, the precisions of state transitions were ren-
dered less precise. 换句话说, we modeled a loss
of confidence in beliefs about the future. Operation-
盟友, this is implemented by multiplying the columns
的 (日志) transition matrices (shown on Figure 4B)
with a constant, bij ¼ ωlnBij and then applying a soft-
max function. This ensures each column corresponds
to a probability distribution, Bij ¼ ebij =
ebkj . 这
X
k
precision, also known as an inverse temperature,
was varied over three levels: ω ¼ 16 (high precision),
ω ¼ 8 (medium precision), and ω ¼ 0 (low precision).
The lower the precision, the more uniform the dis-
tributions over state transitions become from any
given state. This manipulation is only applied to the
transition matrices in the generative model (IE。, 这
subject’s beliefs about transitions) and not to the gen-
erative process (that actually generates the data
presented to the subject). See Figure 5B for the dif-
ference between an example transition matrix with a
208
认知神经科学杂志
体积 31, 数字 2
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
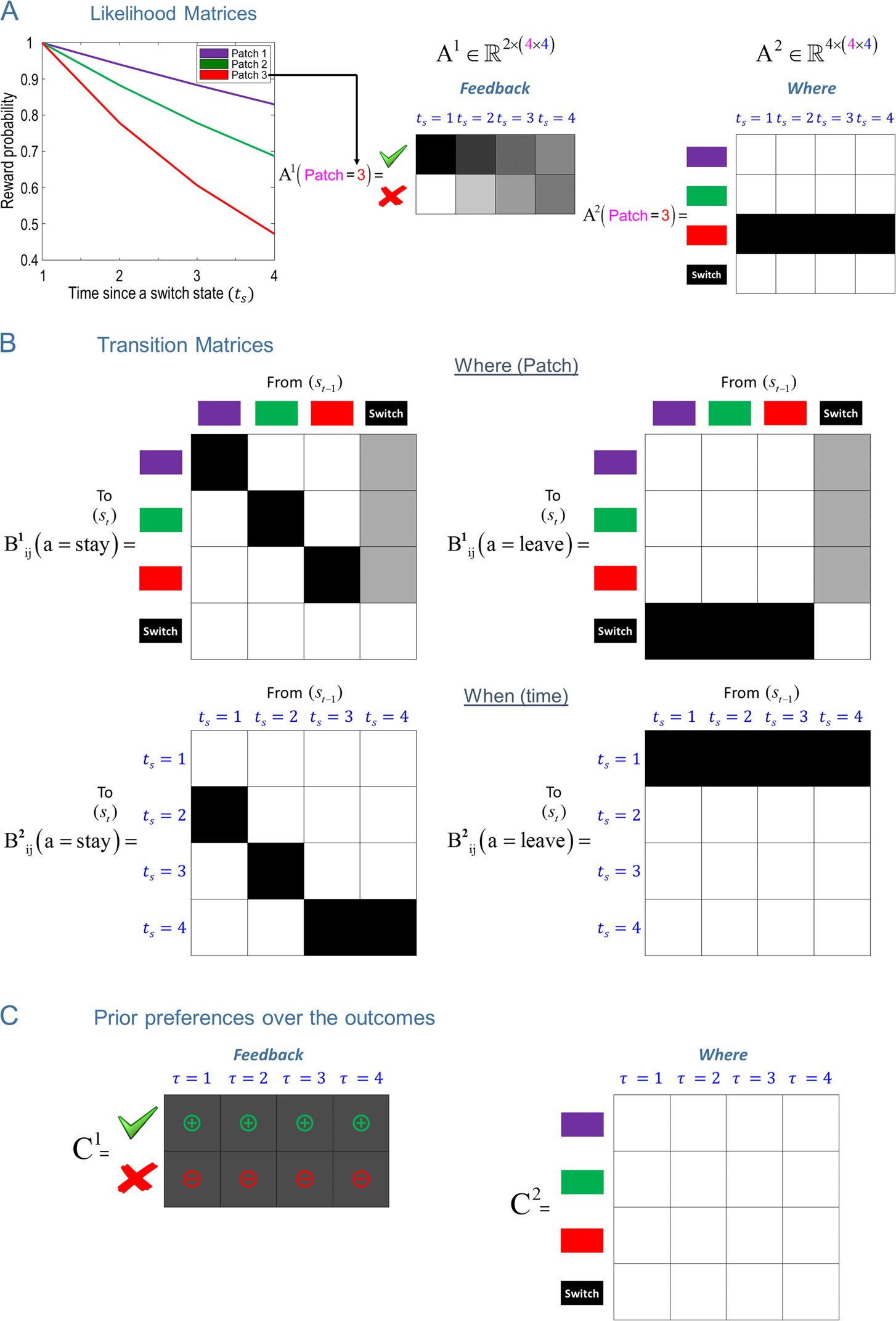
数字 4. ABC of generative model. (A) The left shows how the reward probability decreases in different patches as a function of time since a
switch state ts. The subsequent two panels show the likelihood (A) matrices. The likelihood matrices specify the probability of outcomes given two
sets of hidden states, 即, 在哪里 (the patch the agent is in, shown with magenta color) 什么时候 (ts is shown with blue color). 这里, 这
likelihood matrices are shown for Patch 3 (shown with red color) as a function of when hidden state ts. The first likelihood matrix A1 shows
that the probability of reward (shown with green tick) decreases as ts increases. The second likelihood matrix A2 signals the patch the agent is in
(in this case Patch 3) with respect to the when hidden state. (乙) This shows the transition matrices for where and when (ts) dimensions of
hidden states. The state transitions depend on the actions. 首先 (在哪里) transition matrix shows that, under the action stay B1(a = stay), 这
agent stays in the same patch it is in currently, except when the agent is in the switch state. Under the action leave B1(a = leave), the agent enters
the switch state, given that the agent is not in the switch state. The probability of entering one of the three patches is equally likely when
the agent takes the actions stay or leave given it is in the switch state. 第二 (什么时候) transition matrix under a stay B2(a = stay) 增加
by 1—up to a maximum of 4. The fourth epoch is an absorbing state—and an agent would have to take the action leave to leave this state.
Under a leave B2(a = leave), ts is reset to one (IE。, ts = 1). (C) This shows the prior preferences over outcomes as a function of time (关系到
the current time). We only define a prior preference over reward and no reward outcomes under the feedback modality and do not define
any preference over the patches (where modality). Plus and minus signs show the valence of the utilities, whereas different shades of gray indicate
their magnitude. The model described in this figure is the canonical model. The policy depth in this model is chosen as 4.
Mirza et al.
209
数字 5. MDP models that
were compared with the
canonical model. This figure
shows the difference between
the canonical model and
models in which the certain
model components are
改变了. These elements are
the policy depth, the precision
of the transition matrices,
and the slope of the prior
preference matrices. (A) 这
shows the difference between
the canonical model and the
model in which the policy
depth is changed. The policy
depth in the canonical model is
四. The policy depths in the
models that are compared with
the canonical are one, 二,
和三个. (乙) This shows
the difference between the
canonical model and the model
in which the precision of
transition matrices is changed.
For illustrative purposes only,
the transition matrix for where
under the action stay is used;
然而, the changes are
applied to all transition matrices
under all actions. The precision
of the transition matrices are
changed over three levels.
These are high, medium, 和
low levels of precisions. 这
higher the precision, the more
similar the transition matrices
approach those of the canonical
模型. With lower precisions,
the uncertainty in the
probability distributions over
the columns of the transition
matrices increases. (C) 这
shows the difference between
the canonical model and the
model in which the discount
slope is changed. 在里面
canonical model, the prior
preferences over a reward and
no reward are fixed at 2 和
−2 (IE。, they are not time
sensitive). 然而, 该模型
in which the discount slope is
changed is subject to the
following equation Creward(t) =
2 + slope × x(t) and CNo reward
(t) = −2 − slope × x(t), 在哪里
x = [2.25, 0.75, −0.75, −2.25]
and τ 2 {1, 2, 3, 4}. 这里, t
represents the future epochs,
例如, τ = 1 方法 1
epoch into the future. 这
intercepts of these equations are set to the prior preferences over reward (and no reward) in the canonical model, 这是 2 (and −2). The slope
term endows prior preferences with time sensitivity, when planning future actions. The slope is changed over three levels, 即, high slope (0.75),
medium slope (0.5), and low slope (0.25). The bottom shows how the utility of reward changes over future epochs with different slopes. The utility of
no reward (under different slopes) is just a mirrored version of this figure (since the utility of no reward is negative). With these equations, the agent
discounts the utility of reward and no reward outcomes as it plans further into the future.
210
认知神经科学杂志
体积 31, 数字 2
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
low precision. In this figure, although only one tran-
sition matrix is shown (transition matrix for where
under the action stay), the precision of all transition
matrices under all actions are subject to the same
manipulation. The precision was ω ≫ 16 in all other
型号.
• Varying the discount slope. In this model, the prior
preferences over outcomes are equal to the prior pref-
erences in the canonical model on average. 在里面
canonical model, the utilities for reward and no reward
are fixed at 2 and −2, 分别. These utilities are
not discounted as the agent plans into the future. 如何-
曾经, in models where we manipulate the slope of prior
优先, they change in the following way:
Creward τð Þ ¼ 2 þ slope (西德:3) x τð Þ and
CNo reward τð Þ ¼ − 2 − slope (西德:3) x τð Þ
where x ¼ [2.25, 0.75, −0.75, −2.25] and τ 2 {1, 2, 3,
4}. Here τ represents the future epochs, 例如,
τ ¼ 1 方法 1 epoch in the future. These equations
show that the agent discounts utilities as it plans into
未来. The term “slope” took the following values:
0.75 (high slope), 0.5 (medium slope), 或者 0.25 (低的
slope). Manipulating the slope makes the utility of re-
ward in the near future appear larger (and no reward
较小) and the opposite effect for the distant future.
This means that proximal rewards will always be re-
garded as more valuable and distal rewards as less
valuable, compared with the canonical model (这
comparison is illustrated in Figure 5C). The slope term
was slope = 0 in all other models.
We have chosen the policy depth in the canonical
model such that the model can look ahead long enough
to see how the reward probabilities under different
patches change as a function of time since a switch state.
至关重要的是, the reward probabilities changed in the first
four time steps after entering a patch and staying in it.
Precision of the transition matrix in the canonical model
was very high. This allowed the canonical model to main-
tain its confidence about the future. 最后, the discount
slope in the canonical model was flat. This meant that the
agent’s preference for immediate and future rewards were
equal. These parameters were chosen such that the agent
would not discount the future abnormally. These choices
are somewhat arbitrary, and we do not assume that the
reference model represents neurotypical behavior. 作为
这样的, we are unable to categorize impulsive versus non-
impulsive behavior according to any objective threshold.
We are only able to describe more or less impulsive
行为.
Comparing the simulated behavior of the canonical
model and the above models shows that all manipula-
tions resulted in longer dwell times. 换句话说, 全部
of the above manipulations induced more impulsive,
short-term behavior, in which synthetic subjects found it
difficult to forego the opportunity for an immediate
reward—and overcome the switching cost of moving to
a new patch. The bar plots in Figure 6 show the increase
in dwell times under the three models (over three differ-
ent levels of each model) compared with the canonical
模型. The average increase in dwell times over all
patches is shown on the left panel of Figure 6. The subse-
quent three panels show the same results for each patch
separately.
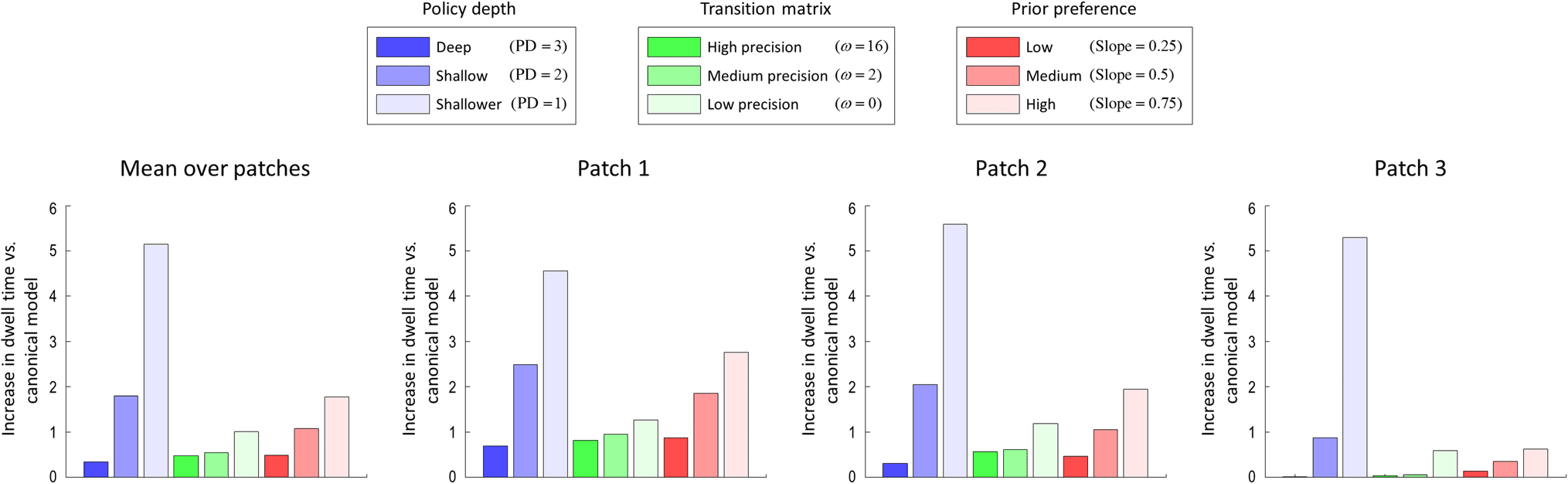
数字 6. Average time spent in patches under different models. This figure show the increase in dwell time under the alternative models,
compared with the canonical model. In the alternative models, the policy depth, the precision of transition matrices, and the slope of prior
preference matrices are changed (over three levels) with respect to the canonical model. The policy depth in the canonical model is chosen as four.
In the models compared with the canonical model, the policy depth is varied over three levels, 即, 深的 (PD = 3), intermediate (PD = 2),
and shallow (PD = 1), 分别. The precision of the transition matrices is varied over three levels, 即, 高的 (ω = 16), medium (ω = 8), 和
低的 (ω = 0). The discount slope are changed over three levels, 即, 高的 (slope = 0.75), medium (slope = 0.5), and low (slope = 0.25). 这
leftmost panel shows the increase in dwell time, averaged over patches, whereas the subsequent three panels show the increase in dwell times
in each patch separately. This figure shows that manipulating the policy depth, the precision of the transition matrices, and the discount slope all
cause the dwell time (our metric of impulsivity) to increase.
Mirza et al.
211
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
The policy depth, the precision of the transition
matrices, and the slope of the prior preference matrix
have similar kinds of effects on dwell times. With deeper
政策, the agent leaves the patches earlier to exploit
the distal rewards. With shallow policies, the agent stays
longer in the patches and exploits proximal rewards (看
blue bars in Figure 6). With less precise transition ma-
trices, the agent remains longer in any patch. This is be-
cause imprecise transition matrices mean that the further
one looks ahead, the less precise one’s beliefs become
and the future becomes uncertain. These beliefs are
about both where (which patch) and when ts the agent
是. With uncertainty over where and when, the agent pre-
fers proximal rewards, rather than risking leaving a patch
for an uncertain outcome (see green bars in Figure 6).
With more time-sensitive prior preferences, the agent
discounts the utility of reward more steeply over time.
This means that the agent prefers proximal rewards, 如何-
ever unlikely they may be over distal rewards; 因此, 这
agent stays longer in each patch to exploit rewards in the
near future (see the red bars in Figure 6).
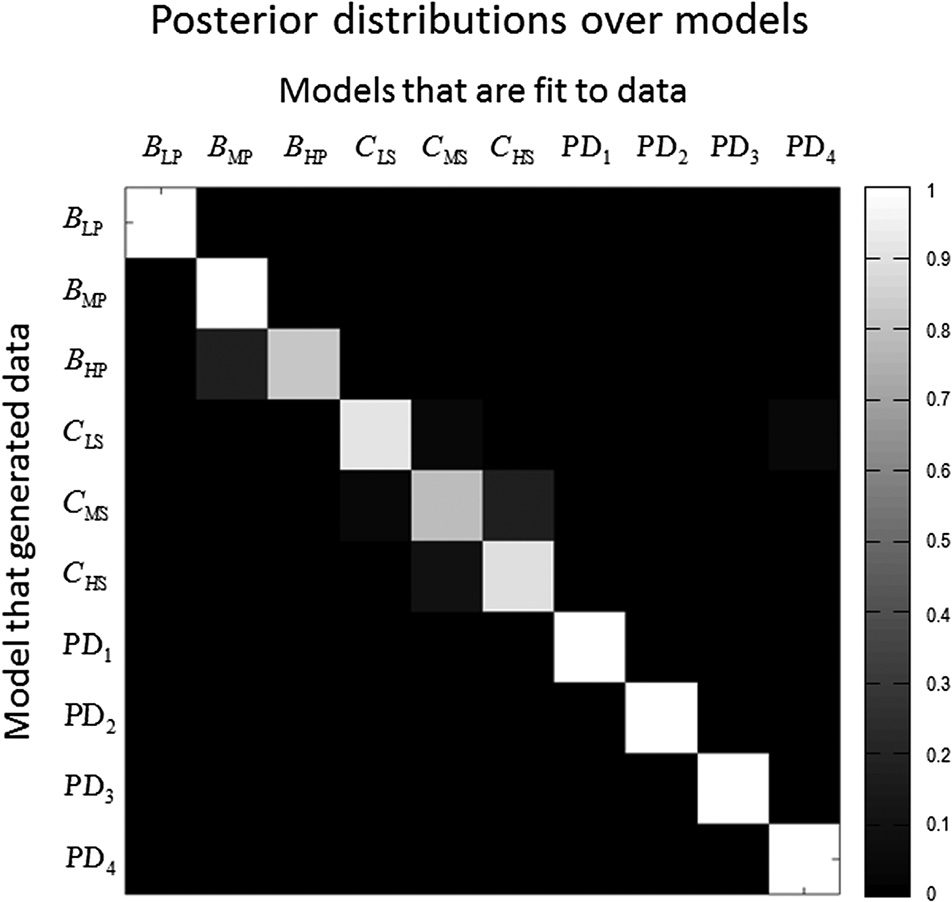
In the following, we ask whether the different models
examined above can be distinguished by observing their
choice behavior. This entails fitting models to the simu-
lated choice behavior and using the resulting Bayesian
model evidence to perform Bayesian model selection
(assuming uniform priors over models; Mirza et al.,
2018; Schwartenbeck & 弗里斯顿, 2016; 弗里斯顿, Mattout,
Trujillo-Barreto, Ashburner, & 一分钱, 2007). The models
that were used to generate (synthetic) behavioral data
were the above models, in which the policy depth, 这
precision of the transition matrices, and the discount
slope varied over three levels (见图 5) and the ca-
nonical model (10 models in total). 这些 10 型号
were then fit to the data generated with each model to
create a confusion matrix of model evidences (IE。, 这
probability that any one model was evidenced by the data
from itself or another). The posterior distributions over
the models suggest that these models can indeed be dis-
ambiguated in terms of their Bayesian model evidence
(见图 7). This shows that, although the resulting
behavior under these models looks similar—namely,
staying longer in patches (greater dwell times)—subtle
differences in choice behavior can still inform model
比较.
总之, we have shown distinct differences in the
form and nature of prior beliefs that underlie generative
models of active inference can all lead to impulsive
行为. In the next section, we will simulate and
characterize the electrophysiological responses we
would expect to observe under these distinct causes
of impulsivity.
Simulated Electrophysiological Responses
在这个部分, we show how simulated electrophysiolog-
ical responses vary with the policy depth, the precision of
数字 7. Model inversion and parameter estimation. This figure shows
the posterior distribution over models, when these models are
fit to data generated by the same models. The simulated data are
generated with the models on the y-axis. The models shown on the top
are fit to the data to estimate the log evidence for each model. 这些
simulations show that these models considered (see previous figures)
can be distinguished in terms of their model evidence. In this figure
BLP, BMP, and BHP correspond to low, medium, and high precision
transition matrices, 分别. CLS, CMS, and CHS correspond to low,
medium, and high slopes over the prior preferences, 分别. PD1,
PD2, and PD3 correspond to Policy Depths 1, 2, 和 3, 分别. 这
canonical model PD4 is included in these simulations.
the transition matrix, and the slope of prior preferences.
The simulated responses under question are LFPs. 作为
new observations are made, evidence for the competing
hypotheses (hidden states) is acquired. Variational mes-
sage passing that mediates belief updates over these hy-
potheses, where we assume that activity in different
neural populations reflects belief updating over different
hypotheses. The simulated depolarization of these “neu-
ral populations” is combined to simulate LFPs. The deriv-
ative of the free energy (with respect to the sufficient
statistics of a posterior belief ) can be expressed as a pre-
diction error (比照. ε in Figure 1B). One can think of this
prediction error as driving fluctuations in an auxiliary
圆周率 (log beliefs about the hidden states)
variable vτ
that plays the role of a membrane potential. It is this
depolarization that we associate with the generation of
π through a softmax
LFPs (see Figure 1B). By passing vτ
function (that we can think of as a sigmoid firing rate
function of depolarization), we obtain the sufficient sta-
圆周率, putatively encoded by firing rates (please see
tistics sτ
Friston et al., 2017, 欲了解详情). 有 16 epochs in
每次试验, and on each epoch, the expectations are up-
dated with 16 variational iterations of the above gradient
血统. 我们有 (arbitrarily) chosen the time scale of
each decision point to fit within the theta rhythm
π = lnsτ
212
认知神经科学杂志
体积 31, 数字 2
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 8. Simulated LFPs under different models. This figure represents simulated LFPs. 这里, LFP is defined as the rate of change in the beliefs about
圆周率 (see Figure 1B). (A) This shows the updates over expectations about (在哪里) 隐
the hidden states. This is basically the rate of change in vτ
states when the agent stays in different patches for four consecutive epochs. As the reward probability decreases faster with ts the LFP peaks are
attenuated and it takes longer for them to converge. The inconsistency in the degree of belief updating in later epoch—in Patch 3 compared with the
other patches—is because the agent expects to leave this patch; 然而, it ends up staying in it due to an unlucky sampling of the action stay
(sampling low probability stay rather than high probability leave), which induces more belief updating in later epochs. (乙) This shows the effect of the
policy depth on LFPs: With deeper policies, the LFPs peak less, and it takes longer for them to converge. (C) The LFPs obtained with different
precisions of transition matrices are shown: With more precise transition matrices, the LFPs peak higher and converge more quickly. (D) This shows
how the LFPs change when the discount slope varies over three levels while keeping the average utilities over time fixed. With higher slopes, the LFPs
peak at higher levels, whereas the convergence does not appear to be sensitive to the different slopes.
Mirza et al.
213
(≈0.25 sec). 理论上, one can estimate the time scale of
the temporal dynamics in the real brain by finding the
time scale in which the simulated behavioral responses
and the behavioral responses in empirical studies are
comparable.
The LFPs can be characterized by their amplitude and
convergence time. Higher amplitudes are associated with
greater belief updates that can be thought of in terms of
larger state prediction errors. Convergence time can be
defined as the time it takes before the LFPs returned to
零, as belief updating converges on a new posterior
信仰. These two characterizations speak to the confi-
dence in beliefs about hidden states and how quickly that
confidence is manifest.
We characterized the responses of units encoding the
hidden state dimension where (patch identity). 第一的, 我们
examined belief updates when the agent stays in the
three patches for four consecutive epochs. The corre-
sponding LFPs are shown in Figure 8A. Smaller LFPs
are generated when the reward probability decreases at
a greater rate with ts (compare Patches 1–3 from left to
right in Figure 8A). This follows because the subject’s
belief about staying in a patch reaches a higher level of
confidence when the reward probability declines at a
slower rate (例如, Patch 1). This results in larger LFPs be-
ing generated under that patch. A second observation
here is that the LFPs at the first epoch are greater than
the LFPs in the subsequent epochs under all patches.
这是因为, before entering a patch, the agent has
uniform beliefs about what patch it will end up in. 这
means that once a patch is entered, there will be more
belief updates initially, whereas later epochs just modify
those beliefs already held.
第二, we examined how the LFPs change with differ-
ent policy depths. The LFPs have higher peaks, 当。。。的时候
agent entertains a shallow representation of the future
(PD = 2) and peak less when it looks deeper into the
未来 (PD = 4; see Figure 8B. With deeper policies,
the beliefs (expectations) about the hidden states are
projected further into the future, causing future epochs
to be informed by the expectations over the hidden
states at the present time. This causes the beliefs about
being in a certain patch during an epoch to change less
随着时间的推移. A second observation here is that the expecta-
tions converge faster under shallow policies. Before these
expectations are projected to any future epochs, 这
agent maintains uniform distributions over the hidden
状态. The further the expectations about the hidden
states in the current epoch are projected to future, 这
more imprecise these expectations become, 采取
longer to converge, especially in the epochs in the distant
未来. This is why deeper policies require longer for
expectations to converge.
第三, the effect of the precision of the transition
matrices on the LFPs is characterized. With precise tran-
sition matrices, the LFPs have greater amplitude—and it
takes less time for these expectations to converge (看
Figure 8C). This follows because—with precise transition
matrices—the expectations about the hidden states in
the current epoch are projected forward with greater
fidelity than with less precise transition matrices. 这
induces large updates over expectations and more rapid
convergence.
最后, the effect of the discount slope on the LFPs is
shown on Figure 8D. As shown in Figure 5C, the utility
over reward declines at different rates under different
slopes, whereas the average over future times is con-
服务. When the discount slope is high, the agent values
rewards in the immediate future more than the distant
未来. With a high slope over the prior preferences,
the agent believes that it will stay in the same patch with
a greater degree of confidence than with lower slopes.
This causes the LFPs to peak higher. 然而, 这确实
not affect the convergence time.
讨论
在这项工作中, our objective was to show that there are
different computational mechanisms that can lead to im-
pulsive behavior by abnormal temporal discounting
(Story, Moutoussis, & Dolan, 2015). For this purpose,
we introduced an MDP formulation of active inference
for the patch-leaving paradigm. We defined three compu-
tational mechanisms that may lead to abnormal temporal
discounting, 即, lower depth of planning (Patton
等人。, 1995), poor maintenance of information (Hinson,
Jameson, & Whitney, 2002), and preference for imme-
diate rewards (Lejuez et al., 2002; Leigh, 1999). 每一个
these may be interpreted in relation to other established
concepts in the impulsivity literature. 例如, pref-
erences are defined in terms of a distribution over pre-
ferred outcomes, so they incorporate both the cost of
different policies (in terms of expectations) and also
the risk preferences associated with this (in terms of
the spread of the distribution over different outcomes).
一个可以, 当然, propose an alternative “motor”
definition of impulsivity in which the subject is always
more likely to change patch, irrespective of the reward
statistics of the patches. We defined impulsivity as acting
to gain temporally proximal rewards at the expense of
more distal rewards. The patch-leaving task allows us to
address impulsivity, as it places proximal and distal re-
wards in conflict. Although the reward probability de-
clines as one stays in the same patch, only choosing to
stay can deliver an immediate reward, however unlikely
可能是. This means that acting to secure proximal re-
wards requires one to stay in a patch for longer.
We have suggested that staying in a patch is analogous
to acting on proximal rewards, whereas leaving corre-
sponds to acting for delayed rewards. This is a common
theme in delay discounting paradigms. Under this inter-
预谋, overstaying can be considered as impatient,
whereas leaving can be seen as patient behavior. Having
said this, there is still some controversy—especially in
214
认知神经科学杂志
体积 31, 数字 2
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
animal studies—about whether the accepted impulsive
behaviors in intertemporal choice paradigms have ex-
ternal validity (Blanchard & Hayden, 2015). Ecological
rationality hypothesis reconciles this by stating that the
same short-sighted impulsive decision rule can lead to
poor performance by choosing smaller-sooner rewards
in delay discounting paradigms and better performance
by staying longer in patch foraging tasks (Stephens,
2008; Stephens, Kerr, & Fernández-Juricic, 2004). 这
is because the patch foraging paradigms bear more re-
semblance to the real situations the animals encounter
in their habitats, and this short-sighted decision rule
works well in those situations.
It is important to note that there are several possible
definitions of impulsivity. We have chosen an operational
definition that can be precisely (mathematically) articu-
lated and is consistent with previous accounts of the
话题 (Stephens, 2008). The motivation for the definition
in this paper is as follows. For our account of impulsivity
to hold, the following conditions need to be met. 第一的,
one should know the reward probabilities under different
patches and how they change over time. Possessing
imprecise knowledge about patches may lead to under-
estimating (or overestimating) the reward in the environ-
蒙特. An agent that underestimates background reward
would be more likely to stay in a patch. 第二, we as-
sumed that there could be only one forager in the envi-
ronment at a time. Staying longer in the current patch
can be advantageous and would not be considered im-
pulsive if there is a competitor that depletes the reward
in the environment (IE。, other patches) rapidly. 那里
may be other cases in which repetitive exploitation of a
patch can be considered as impulsive behavior, 为了
例子, overfishing can reduce the replenishment rate
of marine life and decrease the amount of fish caught in
the long run.
We introduced a canonical model that serves as a point
of reference for the dwell time in various patches. 这
model was compared with deviant models in which the
policy depth, the precision of the transition matrix, 和
the discount slope were manipulated. With shallow poli-
化学系, the agent stays longer in each patch (see the light
blue bars in Figure 6). An agent that uses deep policies
realizes how quickly (或慢慢地) the reward probabilities
衰退 (see dark blue bars in Figure 6). This realization
causes the agent to leave before the reward probability
declines a great deal under the prospective belief it will
secure rewards elsewhere.
With imprecise beliefs about probability transitions,
the agent places less confidence in its beliefs about future
hidden states and outcomes. This means that it is difficult
to infer what might happen after leaving a patch, 因为
this requires the subject to look at least two epochs into
the future to see if reward can be obtained. 相比之下-
儿子, the expected outcome of staying in the same patch
requires the agent to consider only one epoch into the
未来 (anticipating the reward probability in the very
next outcome). Because the agent is relatively more con-
fident about the outcome of staying in a patch (因此
more certain about getting a reward upon staying in a
patch), it chooses to stay for longer under less precise
transition matrices than more precise transition matrices
(see light and dark green bars in Figure 6). This result
suggests that impulsivity can result from not being able
to anticipate the future confidently.
最后, manipulating the discount slope over time
proves to have a profound effect on dwell times as well.
When the time sensitivity of preferences is high, 这
agent values the immediate future much more—and
hence dwells longer—than when the slope is low (看
the light and dark red bars in Figure 6). This causes the
agent to value proximal rewards more, even when they
are less likely.
The underlying causes of impulsivity under the three
models mentioned above speak to different personality
特质. The explanation for impulsivity under shallow pol-
icies is due to steep discounting of the future (Alessi &
Petry, 2003), which may be due to a lack of planning
(Patton et al., 1995). Imprecise beliefs about environ-
mental transitions impair an agent’s ability to maintain
and process information when planning its future actions
(Parr & 弗里斯顿, 2017乙). The kind of response obtained
here is similar to acting impulsively due to high working
memory load (Hinson, Jameson, & Whitney, 2003) 或者
poor working memory (Hinson et al., 2002). The high
temporal sensitivity of prior preferences causes the agent
to act impulsively, despite an ability to plan deep into the
未来. This is because it prefers immediate rewards
more than rewards in the distant future. These prior pref-
erences can lead to risk-taking behavior (Lejuez et al.,
2002; Leigh, 1999) or “venturesomeness” (Eysenck,
1993; Eysenck, 皮尔逊, Easting, & Allsopp, 1985), 作为
the perceived risk decreases with discounting of prefer-
ences in the distant future.
There are other personality traits that we have not
considered in our paradigm but may lead to varieties of
impulsivity (Evenden, 1999), such as lack of inhibitory
控制, lack of persistence, sensation seeking (Buss &
Plomin, 1975), high novelty seeking, low harm avoidance,
low reward dependence (Cloninger, 1987), inability to
maintain attention (Dickman, 1993), and positive and
negative urgency (Lynam, 史密斯, Whiteside, & Cyders,
2006). Although some of these personality traits may
predict similar behaviors as above, others may predict
different behaviors in the patch-foraging paradigm. 为了
例子, people who find it difficult to wait (IE。, inhibi-
tory control) may avoid leaving a patch, as leaving can be
interpreted as waiting for the new patch. 相似地, 人-
ple who are less sensitive to negative outcomes (IE。, 低的
harm avoidance) may stay longer in a patch, 即使
staying is more likely to result in a nonrewarding out-
come. 相比之下, people who tend to jump between dif-
ferent interests (IE。, lack of persistence), who get bored
easily (IE。, sensation seeking), or who want to try new
Mirza et al.
215
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
事物 (IE。, novelty seeking) may leave patches earlier
than expected. These traits could be modeled within this
framework as a loss of precision over policies, 这样
an agent becomes less likely to consistently choose the
same policy (and instead, choose either exploitative or
exploratory policies). Being less able to focus (IE。, 在-
注意力) on different aspects of the patch-leaving task
makes mixed predictions about behavior. The extent to
which one focuses on the current patch relative to the
other patches in the environment may cause one to
either overestimate or underestimate the reward in the
environment and may lead to overharvesting or under-
harvesting. 相似地, overreacting to positive and negative
情怀 (positive/negative urgency) can make mixed
预测.
One of the key advantages of adopting an active infer-
ence framework, as opposed to approaches based upon
the marginal value theorem (MVT), is that the imperative
to minimize expected free energy forces us to define ex-
ploration and exploitation in the same (概率性的)
currency and reveals the interplay between the two. 作为
这样的, any disruption to goal-directed planning (在里面
sense of trying to obtain preferential outcomes) 将要
lead to more exploratory, novelty seeking (克拉克, 2018;
Schwartenbeck, FitzGerald, Dolan, & 弗里斯顿, 2013) 是-
haviors. 此外, flatter distributions over prefer-
ences would lead to behaviors less constrained by the
threat of surprising (昂贵) outcomes and might appear
to an observer as riskier behavior.
We have also shown how the belief updates relate to
(simulated) LFPs under these different models. Compar-
ing the LFPs obtained with the canonical model on the
first and subsequent epochs, we showed that the LFPs
peak less as time progresses (see Figure 8A). Comparing
different patches, the LFPs peak less as the reward prob-
ability declines faster in a patch (compare Patches 1–3 in
Figure 8A). This suggests that the amplitude of the LFPs
correlate positively with the reward probability. Compar-
ing different policy depths, the LFPs peak less with shal-
low policies (compare PD = 2 with PD = 4 in Figure 8B).
The LFPs peak higher with more precise transition ma-
trices than less precise transition matrices (compare high
to low precision in Figure 8C). 最后, with high slopes
over the prior preferences, the LFPs peak higher (com-
pare high to low slope in Figure 8D). The findings in
the ERP literature show that the different components
of ERPs can indeed be manipulated by reward probability
( Walsh & 安德森, 2012; Eppinger, Kray, Mock, &
Mecklinger, 2008; 科恩, Elger, & Ranganath, 2007)
and reward magnitude (Meadows, Gable, Lohse, & 磨坊主,
2016; Bellebaum, Polezzi, & Daum, 2010; Goldstein et al.,
2006). Using the simulated LFPs, 我们已经证明
similar reward probability and magnitude effects are an
emergent property of belief updating and neuronal (var-
iational) message passing in synthetic brains.
These simulated electrophysiological responses show
那, although the observed behaviors under different
型号 (IE。, staying longer in a patch) are similar, 差异-
ferent LFPs are generated. Comparing a shallow policy
模型 (see the left panel of Figure 8B) with the model
in which the slope of the preferences is high (see the left
panel of Figure 8D), the amplitude of the LFPs looks
相似的; 然而, the LFPs in the model with shallow pol-
icies converge sooner. Comparing the model with low
precision transition matrices (see the right panel of
Figure 8C) with the above two models, the LFPs neither
peak as high nor do they converge as quickly.
The MVT represents the “standard model” in the opti-
mal foraging literature (Charnov, 1976). 在此之下
theorem, the time spent in a patch is optimal when the
average rate of reward in a patch is equal to the long-term
average rate of reward everywhere. 还有其他的
models that define optimal foraging in particular ex-
perimental paradigms, largely based on the MVT. 这些
foraging decisions involve learning average reward rates
in the environment (Constantino & Daw, 2015; Ward,
奥斯汀, & Macdonald, 2000; Bernstein, Kacelnik, &
Krebs, 1988), inferring patch type using Bayes’ theorem
(McNamara, 1982), describing patch-leaving time
in terms of a hazard function (Tenhumberg, 凯勒, &
Possingham, 2001), and model free reinforcement learn-
ing approaches that learn state–action values (Constantino
& Daw, 2015).
The solution offered by active inference complements
the MVT. Our model evaluates the expected utility it
would acquire under each policy and is more likely to
choose the policy it expects to yield the greatest utility
(IE。, extrinsic value). Comparing a policy comprising se-
quential stay actions with a policy that starts with a leave
action and followed by sequence of stays is very similar to
comparing the average rate of reward in a patch with the
average reward in the environment. Our repertoire of
policies includes all possible combinations of stay and
leave actions across time, where time is determined by
how deeply into the future the agent plans, 即, 政策
深度.
Computational modeling is used increasingly in psy-
chiatry to provide computational accounts of behaviors
seen in psychiatric disorders (Addicott, 皮尔逊, Sweitzer,
Barack, & Platt, 2017; Rutledge & Adams, 2017; Montague,
Dolan, 弗里斯顿, & Dayan, 2012). In the context of im-
pulsivity, aberrant temporal discounting has been a prev-
alent explanation for impulsive behavior (Story et al.,
2015). Computational methods provide different expla-
nations for temporal discounting, including uncertainty
about acquiring a promised delayed reward or missed op-
portunity of reinvesting a smaller-sooner reward (Story
等人。, 2015; Cardinal, 2006; Sozou, 1998). Other compu-
tational accounts of impulsivity emphasize parameters
encoding the degree to which actions are chosen based
on previous outcomes, preference for action over inac-
的, and learning rate ( 威廉姆斯 & Dayan, 2005). 这
three parameters that we considered in our model
generate impulsive behavior mainly through temporal
216
认知神经科学杂志
体积 31, 数字 2
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
discounting. Although varying the discount slope changes
the degree to which the future rewards are discounted,
the policy depth controls how much the future itself is
discounted. Varying the precision of the transition matrix
can be interpreted as inducing uncertainty about acquir-
ing a future reward.
Our model differs from the above models and decision
rules in a number of ways. 第一的, our model makes a
distinction between the beliefs about the patchy environ-
蒙特 (IE。, generative model) and the real-world dynam-
ics that describe the patchy environment (IE。, generative
过程). This allows for different optimal policies de-
pending on prior beliefs, making our framework more
suitable to studying individual differences and psycho-
pathologies. 举个例子, the MVT cannot make behav-
ioral predictions in regard to different prior beliefs about
the policy depth, the precision of the transition matrices,
and the discount slope—as these quantities are not rep-
resented in the MVT. An agent with shallow planning
would not infer what might happen after leaving a patch,
which would cause the agent to leave unrewarding
patches later than MVT. An agent with imprecise transi-
tion matrices would leave poorly rewarding patches later
than MVT, because the rewards in the distant future
would become more ambiguous. An agent that discounts
the utility of future rewards steeply would stay longer in
poorly rewarding patches than MVT due to a high pre-
ference over proximal rewards (and low preference over
distant ones). 第二, our objective function can be
reformulated in terms of ambiguity and risk (see Equa-
的 4), where policies that lead to more ambiguous, 和-
certain outcomes are less likely to be chosen. The risk
term means that the policies that are less likely to fulfill
an agent’s prior preferences are less likely to be chosen
(Parr & 弗里斯顿, 2018A). This means that the agent not
only acts to maximize reward (as in MVT) 但是也
resolves uncertainty. This means that an agent is more
likely to leave the patches sooner than MVT-like ap-
proaches, if uncertainty about outcomes increases with
the time a patch is occupied. 更普遍, policy selec-
tion in active inference is equipped with epistemic value.
Although epistemic value does not play a crucial role in
the patch-leaving paradigm described in this work, it can
easily come into play if the second outcome modality
在哪里, which signals the patch identity, is withdrawn.
Removing this source of information means that patch
身份 (IE。, the where hidden state) can only be in-
ferred by observing a rewarding or nonrewarding out-
come under the feedback modality. Because active
inference tries to resolve uncertainty about hidden
状态, epistemic behavior corresponds to staying in
patches longer to acquire information about patch
身份.
An influential model (Gläscher, Daw, Dayan, &
O’Doherty, 2010) assesses the degree to which subjects
are “model based” (IE。, learn the transition matrix and
then use it to plan) versus “model free” (IE。, just repeat-
ing previously rewarded actions). It has been shown that
various disorders of compulsivity (例如, obsessive compul-
sive disorder, binge eating, drug addiction) are less
“model based” in this task (Voon et al., 2015), as are high
impulsivity subjects (Deserno et al., 2015), and that com-
pulsivity in a large population sample also relates to this
task measure (Gillan, Kosinski, Whelan, Phelps, & Daw,
2016). 然而, this model does not explain why the
subjects are less model based. Our formulation suggests
that one possibility for this is a less precise transition
matrix and another is lower policy depth.
The policy depth, the precision of the transition ma-
trices, and the discount slope can be manipulated in dif-
ferent ways in an experimental paradigm. 例如,
previous work—investigating the depth of planning—
used a sequential decision-making task that is entailed
searching through subbranches of a decision tree. Sub-
jects were asked to find the optimal sequence of choices
that would yield the greatest reward (Huys et al., 2012).
This study showed that subjects performed poorly when
the decision tree was deeper. This task was adapted to
manipulate the policy depth in an experimental setup.
In the same task, some sequential decisions involved
an early large loss, which was compensated with a large
reward further down the decision tree. Although accept-
ing the large loss would eventually yield larger reward
than other sequences of decisions with smaller losses
early on, subjects tended to choose the latter. A similar
approach could be taken to manipulate the discount
slope empirically. 最后, by varying the transition matri-
ces over time, the precision of the transition matrices
may be manipulated in an empirical setup.
In the context of the patch-leaving paradigm, 这些
manipulations are more difficult to induce. 然而,
the fact that we can recover the policy depth, 迪斯-
count slope, and the precision of transitions used by
our synthetic subjects from their behavioral choices sug-
gests that we could disambiguate between these causes
of impulsivity in a between-subject study, comparing a
临床 (or subclinical) population to neurotypicals or un-
理解, at an individual level, the causes of impul-
sive behaviors among neuropsychiatric populations
(例如, impulsive behavior associated with Parkinson’s
medication). Classifying such patients according to their
individual phenotypes could help to direct the develop-
ment of individualized therapies. 换句话说, 反而
of inducing the above changes experimentally, we would
aim to discover the differences that give rise to distinct
behavioral phenotypes.
This work has some limitations. The policy depth, 这
precision of the transition matrices, and the discount
slope cannot be manipulated experimentally in a straight-
forward way. This means model selection given empirical
choice behavior can only be validated in relation to in-
dependent variables, 例如, correlations between
working memory measures and transition matrix preci-
锡安. 此外, we have only looked at model features
Mirza et al.
217
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
that explain impulsivity relating to depth of planning, 工作-
ing memory, and value discounting: We have not con-
sidered other causes, 例如, motor disinhibition or
effort cost (Klein-Flugge, Kennerley, Saraiva, 一分钱, &
Bestmann, 2015).
结论
This theoretical work has demonstrated several possible
causes for impulsive behavior. 至关重要的是, we have also
shown that it is possible to disambiguate between these
causes using choice behavior. 最后, we showed that
there is a distinct (simulated) electrophysiological profile
associated with each putative explanation for impulsive
行为. Formally speaking, we have provided proof of
principle of a degenerate (IE。, many to one) 映射
between the structure of generative models and the func-
tional or impulsive aspects of behavior. This degeneracy
is potentially important in the sense that any etiological
or remedial approach to impulsive behavior needs to
accommodate a plurality of underlying causes—both at
the level of pathophysiology and belief updating—even
if the resulting psychopathology looks very similar.
In future work, we intend to leverage the theoretical
findings in an empirical setup. 原则, one can fit
different models (like the ones introduced in this paper)
to the observed responses (series of stay and leave but-
ton presses on a button box) of the subjects and estimate
subject-specific priors. Our objective is to search for
evidence that there are distinct electrophysiological pro-
files associated with these computational phenotypes as
predicted by our model.
Data Accessibility
The simulations in this paper have been generated using
the spm software routine spm_MDP_VB_X.m. The simu-
lated responses shown in this paper can be reproduced
by invoking DEM_demo_MDP_patch.m.
APPENDIX
The variational free energy for MDP model described in
the text is as follows:
F ¼ −EQ ~s ;πð
Þ ln P ~o ; ~s; 圆周率
½
ð
(西德:2) − H Q ~s; πð
½
Þ
Þ
(西德:2)
¼ −EQ ~s;πð
Þ½ ln Pð~o; ~sjπÞ(西德:2) − H½ Qð~sjπÞ(西德:2) þ DKL½ QðπÞ‖ PðπÞ(西德:2)
½
¼ EQ πð Þ F πð Þ
(西德:2) þ DKL½ QðπÞ‖ PðπÞ(西德:2)
¼ π⋅ ln π þ F þ G
ð
Þ þ lnZ
Rearranging the first equation shows that the varia-
tional free energy comprises three terms, 即, F(圆周率),
问(圆周率), 和P(圆周率), and a normalization constant lnZ =
(西德:2)πexp(−Gπ).
F(圆周率) is the free energy of hidden states
F ¼ F πð Þ
X
F πð Þ ¼
ð
F π; t
Þ
t
ð
F π; t
Þ ¼ E ~Q
½DKL½QðsτjπÞ jjPðsτjsτ−1πÞ(西德:2)(西德:2)
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
复杂
− E ~Q
½ ln PðoτjsτÞ(西德:2)
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
准确性
¼ sπ
τ−1sπ
τ − ln Bπ
(西德:3)
τ ⋅ ln sπ
τ−1
G(圆周率) is the expected free energy
G ¼ G πð Þ
X
G πð Þ ¼
ð
G π; t
Þ
t
ð
G π; t
Þ ¼ D½ QðoτjπÞ‖ PðoτÞ(西德:2)
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
expected cost
(西德:3)
τ ⋅ ln oπ
τ − Cτ
¼ oπ
(西德:4)
þ sπ
τ ⋅H
(西德:4)
− ln A⋅oτ
þ E ~Q
½H½PðoτjsτÞ(西德:2)(西德:2)
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
expected ambiguity
这里, H is the entropy over each outcome under the like-
lihood matrix for each hidden state combination. 问(圆周率) 是
the posterior distribution over the policies. This term can
be obtained by setting the derivative of the variational
free energy with respect to this term, 那是, solving
for ∂F(圆周率, t)/∂π = 0.
致谢
This work was part of Innovative Training Network Perception
and Action in Complex Environments (PACE), supported by
the European Union’s Horizon 2020 research and innovation
program under the Marie Sklodowska-Curie grant agreement
不. 642961. 中号. 乙. 中号. is a member of PACE network. 右. A. A. 是
funded by the Academy of Medical Sciences (AMS-SGCL13-
Adams) and the National Institute of Health Research (CL-2013-
18-003). 时间. 磷. is supported by the Rosetrees Trust (奖
不. 173346). K. F. is funded by a Wellcome Trust Principal
Research Fellowship (ref. 088130/Z/09/Z). This paper reflects
only the authors’ view and the Research Executive Agency of
the European Commission is not responsible for any use that
may be made of the information it contains.
Reprint requests should be sent to M. Berk Mirza, The Wellcome
Trust Centre for Neuroimaging, Institute of Neurology, 大学
College London, 12 Queen Square, 伦敦, 英国,
WC1N 3BG, or via e-mail: muammer.mirza.15@ucl.ac.uk.
参考
Addicott, M。, 皮尔逊, J。, Sweitzer, M。, Barack, D ., & Platt, 中号.
(2017). A primer on foraging and the explore/exploit trade-off
for psychiatry research. Neuropsychopharmacology, 42,
1931–1939.
Alessi, S. M。, & Petry, 氮. 中号. (2003). Pathological gambling
severity is associated with impulsivity in a delay discounting
procedure. Behavioural Processes, 64, 345–354.
Baddeley, A. (1992). Working memory. 科学, 255, 556–559.
Beal, 中号. J. (2003). Variational algorithms for approximate
Bayesian inference. 伦敦: 伦敦大学.
Bellebaum, C。, Polezzi, D ., & Daum, 我. (2010). It is less than you
预期的: The feedback-related negativity reflects violations
218
认知神经科学杂志
体积 31, 数字 2
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
of reward magnitude expectations. Neuropsychologia, 48,
3343–3350.
Bernstein, C。, Kacelnik, A。, & Krebs, J. 右. (1988). 个人
decisions and the distribution of predators in a patchy
环境. Journal of Animal Ecology, 57, 1007–1026.
Blanchard, 时间. C。, & Hayden, 乙. 是. (2015). Monkeys are more
patient in a foraging task than in a standard intertemporal
choice task. 公共图书馆一号, 10, e0117057.
Buss, A. H。, & Plomin, 右. (1975). A temperament theory of
personality development. 纽约: Wiley-Interscience.
Cardinal, 右. 氮. (2006). Neural systems implicated in delayed
and probabilistic reinforcement. Neural Networks, 19,
1277–1301.
Charnov, 乙. L. (1976). Optimal foraging, the marginal value
theorem. Theoretical Population Biology, 9, 129–136.
克拉克, A. (2018). A nice surprise? Predictive processing and the
active pursuit of novelty. Phenomenology and the Cognitive
科学, 17, 521–534.
Cloninger, C. 右. (1987). A systematic method for clinical description
and classification of personality variants: A proposal.
Archives of General Psychiatry, 44, 573–588.
科恩, 中号. X。, Elger, C. E., & Ranganath, C. (2007). Reward
expectation modulates feedback-related negativity and EEG
spectra. Neuroimage, 35, 968–978.
Constantino, S. M。, & Daw, 氮. D. (2015). Learning the
opportunity cost of time in a patch-foraging task. 认知的,
Affective, & Behavioral Neuroscience, 15, 837–853.
Deserno, L。, Wilbertz, T。, 赖特, A。, Horstmann, A。, 诺伊曼,
J。, 狂野的召唤者, A。, 等人. (2015). Lateral prefrontal model-based
signatures are reduced in healthy individuals with high trait
impulsivity. Translational Psychiatry, 5, e659.
Dickman, S. J. (1993). Impulsivity and information processing.
In W. G. McCown, J. L. 约翰逊, & 中号. 乙. Shure (编辑。),
The impulsive client: 理论, 研究, and treatment
(PP. 151–184). 华盛顿, 直流: 美国心理学
协会.
Eppinger, B., Kray, J。, Mock, B., & Mecklinger, A. (2008). 更好的
or worse than expected? 老化, 学习, and the ERN.
Neuropsychologia, 46, 521–539.
Evenden, J. L. (1999). Varieties of impulsivity. Psychopharmacology,
146, 348–361.
Eysenck, S. (1993). The I7: Development of a measure of
impulsivity and its relationship to the superfactors of
性格. In W. G. McCown, J. L. 约翰逊, & 中号. 乙. Shure
(编辑。), The impulsive client: 理论, research and treatment
(PP. 141–149). 华盛顿, 直流: 美国心理学
协会.
Eysenck, S. B., & Eysenck, H. J. (1978). Impulsiveness and
venturesomeness: Their position in a dimensional system of
personality description. Psychological Reports, 43, 1247–1255.
Eysenck, S. 乙. G。, 皮尔逊, 磷. R。, Easting, G。, & Allsopp, J. F.
(1985). Age norms for impulsiveness, venturesomeness and
empathy in adults. Personality and Individual Differences, 6,
613–619.
Frederick, S。, Loewenstein, G。, & O’Donoghue, 时间. (2002). 时间
discounting and time preference: A critical review. 杂志
Economic Literature, 40, 351–401.
弗里斯顿, K. (2010). The free-energy principle: A unified brain
理论? 自然评论神经科学, 11, 127–138.
弗里斯顿, K., FitzGerald, T。, Rigoli, F。, Schwartenbeck, P。, &
Pezzulo, G. (2017). Active inference: A process theory.
神经计算, 29, 1–49.
弗里斯顿, K., Kilner, J。, & 哈里森, L. (2006). A free energy
principle for the brain. Journal of Physiology-Paris, 100,
70–87.
弗里斯顿, K., Mattout, J。, Trujillo-Barreto, N。, Ashburner, J。, &
一分钱, 瓦. (2007). Variational free energy and the Laplace
approximation. Neuroimage, 34, 220–234.
弗里斯顿, K., Rigoli, F。, Ognibene, D ., Mathys, C。, Fitzgerald, T。, &
Pezzulo, G. (2015). Active inference and epistemic value.
Cognitive Neuroscience, 6, 187–214.
弗里斯顿, K., Schwartenbeck, P。, Fitzgerald, T。, Moutoussis, M。,
贝伦斯, T。, & Dolan, 右. (2013). The anatomy of choice:
Active inference and agency. Frontiers in Human
神经科学, 7, 598.
Gibb, J. A. (1958). Predation by tits and squirrels on the
eucosmid Ernarmonia conicolana (Heyl.). Journal of Animal
Ecology, 27, 375–396.
Gillan, C. M。, Kosinski, M。, Whelan, R。, Phelps, 乙. A。, & Daw, 氮. D.
(2016). Characterizing a psychiatric symptom dimension
related to deficits in goal-directed control. Elife, 5, e11305.
Gläscher, J。, Daw, N。, Dayan, P。, & O’Doherty, J. 磷. (2010).
States versus rewards: Dissociable neural prediction error
signals underlying model-based and model-free reinforcement
学习. 神经元, 66, 585–595.
戈德斯坦, 右. Z。, Cottone, L. A。, Jia, Z。, Maloney, T。, Volkow,
氮. D ., & Squires, 氮. K. (2006). The effect of graded monetary
reward on cognitive event-related potentials and behavior
in young healthy adults. International Journal of
Psychophysiology, 62, 272–279.
Hinson, J. M。, Jameson, 时间. L。, & Whitney, 磷. (2002). Somatic
标记, 工作记忆, and decision making. 认知的,
Affective, & Behavioral Neuroscience, 2, 341–353.
Hinson, J. M。, Jameson, 时间. L。, & Whitney, 磷. (2003). Impulsive
decision making and working memory. 杂志
实验心理学: 学习, 记忆, 和
认识, 29, 298–306.
Huys, 问. J. M。, Eshel, N。, O’Nions, E., Sheridan, L。, Dayan, P。, &
Roiser, J. 磷. (2012). Bonsai trees in your head: How the
Pavlovian system sculpts goal-directed choices by pruning
decision trees. 公共科学图书馆计算生物学, 8, e1002410.
卡普兰, R。, & 弗里斯顿, K. (2018). Planning and navigation as
active inference. Biological Cybernetics, 112, 323–343.
Klein-Flugge, 中号. C。, Kennerley, S. W., Saraiva, A. C。, 一分钱,
瓦. D ., & Bestmann, S. (2015). Behavioral modeling of human
choices reveals dissociable effects of physical effort and
temporal delay on reward devaluation. 公共科学图书馆计算
生物学, 11, e1004116.
Leigh, 乙. C. (1999). Peril, 机会, adventure: Concepts of
风险, alcohol use and risky behavior in young adults.
Addiction, 94, 371–383.
Lejuez, C. W., Read, J. P。, Kahler, C. W., Richards, J. B., Ramsey,
S. E., Stuart, G. L。, 等人. (2002). Evaluation of a behavioral
measure of risk taking: The Balloon Analogue Risk Task
(捷运). 实验心理学杂志: Applied, 8,
75–84.
Logue, A. 瓦. (1995). Self-control: Waiting until tomorrow for
what you want today. 恩格尔伍德悬崖, 新泽西州: 普伦蒂斯霍尔,
Inc.
Lynam, D. R。, 史密斯, G. T。, Whiteside, S. P。, & Cyders, 中号. A.
(2006). The UPPS-P: Assessing five personality pathways to
impulsive behavior. West Lafayette, 在: Purdue University.
MacArthur, 右. H。, & Pianka, 乙. 右. (1966). On optimal use of a
patchy environment. American Naturalist, 100, 603–609.
McNamara, J. (1982). Optimal patch use in a stochastic
环境. Theoretical Population Biology, 21, 269–288.
Meadows, C. C。, Gable, 磷. A。, Lohse, K. R。, & 磨坊主, 中号. 瓦.
(2016). The effects of reward magnitude on reward
加工: An averaged and single trial event-related
potential study. Biological Psychology, 118, 154–160.
Mirza, 中号. B., Adams, 右. A。, Mathys, C。, & 弗里斯顿, K. J. (2018).
Human visual exploration reduces uncertainty about the
sensed world. 公共图书馆一号, 13, e0190429.
Mirza, 中号. B., Adams, 右. A。, Mathys, C. D ., & 弗里斯顿, K. J. (2016).
Scene construction, visual foraging, and active inference.
Frontiers in Computational Neuroscience, 10, 56.
Mirza et al.
219
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Montague, 磷. R。, Dolan, 右. J。, 弗里斯顿, K. J。, & Dayan, 磷. (2012).
Computational psychiatry. 认知科学的趋势, 16,
72–80.
Parr, T。, & 弗里斯顿, K. J. (2017A). Uncertainty, epistemics and
active inference. Journal of The Royal Society Interface, 14,
20170376.
Parr, T。, & 弗里斯顿, K. J. (2017乙). Working memory, 注意力,
and salience in active inference. Scientific Reports, 7, 14678.
Parr, T。, & 弗里斯顿, K. J. (2018A). Generalised free energy and
active inference: Can the future cause the past? bioRxiv.
土井:10.1101/304782.
Parr, T。, & 弗里斯顿, K. J. (2018乙). The computational anatomy of
visual neglect. 大脑皮层, 28, 777–790.
Patton, J. H。, 斯坦福大学, 中号. S。, & Barratt, 乙. S. (1995). Factor
structure of the Barratt Impulsiveness Scale. 杂志
Clinical Psychology, 51, 768–774.
Rutledge, 右. B., & Adams, 右. A. (2017). 计算型
psychiatry. 在一个. Moustafa (埃德。), Computational models of
brain and behavior (PP. 29–42). 霍博肯, 新泽西州: 威利
布莱克威尔.
Schwartenbeck, P。, FitzGerald, T。, Dolan, R。, & 弗里斯顿, K.
(2013). Exploration, 新奇, surprise, and free energy
minimization. 心理学前沿, 4, 710.
Schwartenbeck, P。, & 弗里斯顿, K. (2016). 计算型
phenotyping in psychiatry: A worked example. eNeuro, 3.
土井:10.1523/ENEURO.0049-16.2016.
Sozou, 磷. D. (1998). On hyperbolic discounting and uncertain
hazard rates. Proceedings of the Royal Society of London,
Series B, Biological Sciences, 265, 2015.
Stephens, D. 瓦. (2008). Decision ecology: Foraging and the
ecology of animal decision making. 认知的, Affective, &
Behavioral Neuroscience, 8, 475–484.
Stephens, D. W., Kerr, B., & Fernández-Juricic, 乙. (2004).
Impulsiveness without discounting: The ecological rationality
假设. Proceedings of the Royal Society of London,
Series B, Biological Sciences, 271, 2459–2465.
Story, G. W., Moutoussis, M。, & Dolan, 右. J. (2015). A
computational analysis of aberrant delay discounting in
psychiatric disorders. 心理学前沿, 6, 1948.
Strotz, 右. H. (1955). Myopia and inconsistency in dynamic
utility maximization. Review of Economic Studies, 23,
165–180.
Tenhumberg, B., 凯勒, 中号. A。, & Possingham, H. 磷. (2001).
Using Cox’s proportional hazard models to implement
optimal strategies: An example from behavioural ecology.
Mathematical and Computer Modelling, 33, 597–607.
Voon, 五、, Derbyshire, K., Rück, C。, 尔湾, 中号. A。, Worbe, Y。,
Enander, J。, 等人. (2015). Disorders of compulsivity: A
common bias towards learning habits. Molecular Psychiatry,
20, 345.
Walsh, 中号. M。, & 安德森, J. 右. (2012). Learning from
经验: Event-related potential correlates of reward
加工, neural adaptation, and behavioral choice.
Neuroscience and Biobehavioral Reviews, 36, 1870–1884.
Ward, J. F。, 奥斯汀, 右. M。, & Macdonald, D. 瓦. (2000). A
simulation model of foraging behaviour and the effect of
predation risk. Journal of Animal Ecology, 69, 16–30.
Whiteside, S. P。, & Lynam, D. 右. (2001). The Five Factor Model
and impulsivity: Using a structural model of personality to
understand impulsivity. Personality and Individual
Differences, 30, 669–689.
Wickens, 时间. D. (1998). On the form of the retention function:
Comment on Rubin and Wenzel (1996): A quantitative
description of retention. 心理评论, 105, 379–386.
威廉姆斯, J。, & Dayan, 磷. (2005). Dopamine, 学习, 和
impulsivity: A biological account of attention-deficit/
hyperactivity disorder. Journal of Child and Adolescent
Psychopharmacology, 15, 160–179; discussion 157–169.
220
认知神经科学杂志
体积 31, 数字 2
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
j
/
哦
C
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
1
2
2
0
2
1
7
8
8
2
4
7
/
j
哦
C
n
_
A
_
0
1
3
5
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3