焦点功能:
Bridging Scales and Levels
Mapping hybrid functional-structural connectivity
traits in the human connectome
Enrico Amico
1,2
and Joaquín Goñi
1,2,3
1School of Industrial Engineering, Purdue University, West-Lafayette, 在, 美国
2Purdue Institute for Integrative Neuroscience, Purdue University, West-Lafayette, 在, 美国
3Weldon School of Biomedical Engineering, Purdue University, West-Lafayette, 在, 美国
关键词: Brain connectivity, Human connectome, Structural/functional patterns, Task-sensitive
连接性
开放访问
杂志
抽象的
One of the crucial questions in neuroscience is how a rich functional repertoire of brain
states relates to its underlying structural organization. How to study the associations between
these structural and functional layers is an open problem that involves novel conceptual ways
of tackling this question. We here propose an extension of the Connectivity Independent
Component Analysis (connICA) framework to identify joint structural-functional connectivity
特质.
这里, we extend connICA to integrate structural and functional connectomes by merging
them into common “hybrid” connectivity patterns that represent the connectivity
fingerprint of a subject. We tested this extended approach on the 100 unrelated subjects
from the Human Connectome Project. The method is able to extract main independent
structural-functional connectivity patterns from the entire cohort that are sensitive to the
realization of different tasks.
The hybrid connICA extracts two main task-sensitive hybrid traits. The first trait
encompasses the within and between connections of dorsal attentional and visual
地区, as well as frontoparietal circuits. The second trait mainly encompasses the
connectivity between visual, attentional, default mode network (DMN), and subcortical
网络. 全面的, these findings confirm the potential of the hybrid connICA for the
compression of structural/functional connectomes into integrated patterns from a set of
individual brain networks.
引文: Amico, E., & 戈尼, J. (2018).
Mapping hybrid functional-structural
connectivity traits in the human
connectome. 网络神经科学,
2(3), 306–322. https://doi.org/10.1162/
netn_a_00049
DOI:
https://doi.org/10.1162/netn_a_00049
支持信息:
https://doi.org/10.1162/netn_a_00049
https://engineering.purdue.edu/
CONNplexityLab
已收到: 4 十月 2017
公认: 14 二月 2018
利益争夺: 作者有
声明不存在竞争利益
存在.
作者总结
通讯作者:
Joaquín Goñi
jgonicor@purdue.edu
处理编辑器:
Fabrizio De Vico Fallani
版权: © 2018
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
A crucial question in neuroscience is how a rich functional repertoire of brain states relates
to its underlying structural organization. How to study the associations between structural
and functional layers is an open problem that requires novel conceptual frameworks. 我们
here propose an extension of our connectivity independent component analysis (connICA)
framework to integrate structural and functional connectomes and obtain hybrid connectivity
fingerprints.
We use this method to extract two task-sensitive independent structural-functional
connectivity patterns. The first encompasses the within and between connections of
dorsal attentional and visual areas, as well as frontoparietal circuits. The second mainly
encompasses the connectivity between visual, attentional, DMN, and subcortical networks.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Mapping hybrid functional-structural connectivity traits
These findings confirm the potential of hybrid connICA for the compression of
structural/functional connectomes into integrated patterns.
介绍
Brain connectomics is a rapidly growing area of research (布莫尔 & 斯波恩斯, 2009; 假如,
扎莱斯基, & 布莫尔, 2016). It is based on the investigation of functional and structural con-
nections in the human brain, modeled as networks (布莫尔 & 斯波恩斯, 2009; Fornito et al.,
2016; 斯波恩斯, 2011). In large-scale brain network models, nodes correspond to gray matter
地区 (based on brain atlases or parcellations), whereas links or edges correspond to
connections between the nodes. Structural connections are modeled from diffusion-weighted
成像 (DWI) data by inferring the main white matter axonal pathways between brain region
pairs through tractography algorithms (Fornito et al., 2016), normally denominated by struc-
tural connectome or connectivity (SC; 斯波恩斯, 2011). Functional connections are modeled
from functional magnetic resonance imaging (功能磁共振成像) data by measuring temporal statistical
dependences between the estimated neural activity of brain region pairs while subjects are
either at rest or performing a task in the scanner, usually defined as functional connectivity of
connectome (FC; 狐狸 & Raichle, 2007; 弗里斯顿, 2011).
The exponential growing of publicly available neuroimaging datasets in recent years has
allowed researchers to make inferences on the different organization of brain networks in
clinical and healthy populations, and to identify changes in these cohorts (假如, 扎莱斯基,
& Breakspear, 2015; Fornito et al., 2016), both at the structural and functional level. 期间
the past few years, many efforts have also been made to address one of the crucial questions
in brain connectomics. 那是, how a rich functional repertoire of brain states relates to its
underlying structural organization, especially at the large scale of cortical/subcortical gray
matter modules and white matter fiber bundles (Falcon, Jirsa, & 索洛德金, 2016; Goñi et al.,
2014; Honey et al., 2009; 蜂蜜, Kötter, Breakspear, & 斯波恩斯, 2007; 蜂蜜, Thivierge, &
斯波恩斯, 2010).
The study of the associations between these structural and functional layers (Miši´c et al.,
2016) is difficult to accomplish because of several factors. One factor is related to obtaining
individual accurate connectivity patterns. This involves the following: the design of MRI se-
quences for structural imaging, DWI, and fMRI; the development of processing pipelines to
process MRI data; and a brain parcellation or atlas to reduce the dimensionality from gray mat-
ter voxels to brain regions and criteria to estimate levels of structural and functional coupling.
Another aspect relates to the intersubject variability of these two modalities. The identifi-
cation of group-level structure-function relationships (Miši´c et al., 2016) may become an
even more powerful approach if individual estimations were taken into account. As a matter
事实上, it has recently been shown that the “individual fingerprint” of a functional connec-
tome (Finn et al., 2015) is a key property for investigating further inferences and links between
connectomics and genetic, demographic, or clinical variables (Shen et al., 2017). 最近的
trend goes, 所以, toward working at the single-subject level and toward the refinement
and improvement of this individual signature in an individual human connectome (Amico &
在这个意义上, providing not only group-level SC or covarying SC/FC patterns
戈尼, 2017).
but also their individual estimations is an important step forward. 最后, the vast amount
of information contained in both functional and structural connectomes is problematic for
In this scenario, the researcher has to extract
the investigation of joint FC and SC patterns.
网络:
an ordered pair formed by a set of
nodes and a set of edges (哪个
represent connections between
pairs of nodes). Nodes are usually
represented by circles, 然而
edges are represented by lines or
arcs connecting pairs of nodes.
Diffusion-weighted imaging (DWI):
a magnetic resonance imaging (MRI)
technique based on measuring the
random Brownian motion of water
molecules within a voxel based
on sampling 3D directions. 这
technique allows for estimating
white matter streamlines and fiber
bundles connecting brain regions.
纤维束成像术:
computational reconstruction
procedure that may be used to
obtain, from DWI data, 白色的
matter streamlines or fiber tracts
connecting different brain regions.
Connectome or structural
连接性 (SC) 矩阵:
a network representation of the
physical connections in the brain.
Nodes represent brain regions,
whereas edges represent physical
connections of pairs of brain regions
through the white matter. 重量
typically denote the density or also
the integrity of the connections.
Functional magnetic resonance
成像 (功能磁共振成像):
a noninvasive technique that
estimates brain activity by detecting
changes associated with blood flow.
The rationale of this technique relies
on the fact that there is a positive
association between cerebral blood
flow and neuronal activation.
网络神经科学
307
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Mapping hybrid functional-structural connectivity traits
Functional connectome/connectivity
(FC) 矩阵:
a network representation of the
functional coupling between
brain regions. Such coupling is
usually measured by quantifying
the statistical dependencies
between time series of brain
地区 (例如, pairwise Pearson’s
correlation, mutual information)
as obtained by functional magnetic
resonance imaging (功能磁共振成像).
Independent component analysis
(ICA):
a computational method for
disentangling the independent
additive subcomponents of a
multivariate input signal, under the
assumption that the subcomponents
are non-Gaussian signals and that
they are statistically independent
from each other.
and compress informative features from hundreds of functional and structural connectomes
separately, from either healthy or clinical populations, and then come up with creative ways
to merge the extracted functional information with its structural counterpart, or find ways to
compress them in some integrative framework.
We here define an extension of our recently proposed connectivity-based independent com-
ponent analysis (IE。, connICA; Amico et al., 2017) 技术, to overcome the aforementioned
问题. The connICA methodology implements independent component analysis (ICA) 为了
extraction of robust independent functional connectivity patterns from a set of individual func-
tional connectomes, without imposing any a priori data stratification into groups (Amico et al.,
2017). 这里, we extend connICA to include both structural and functional connectomes by
merging them into a common “hybrid” matrix (see scheme in Figure 1) that includes both
the structural and functional fingerprint of each subject (Amico & 戈尼, 2018). We tested
this extended approach on the 100 unrelated subjects taken from the Human Connectome
项目 (details on the project available at http://www.humanconnectome.org/) and evaluated
it for two brain parcellations. We here show how this method is able to extract main indepen-
dent structure-function couplings with individual estimations for the entire population of sub-
项目, and to disentangle the joint functional-structural subsystems that are sensitive to different
functional tasks (including also resting state).
These findings confirm the potential of the hybrid connICA for the compression of mean-
ingful information out of a set of heterogeneous brain networks based on both functional and
structural connectomes while capturing individual differences. We conclude by discussing
limitations and potential future directions for this methodology.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
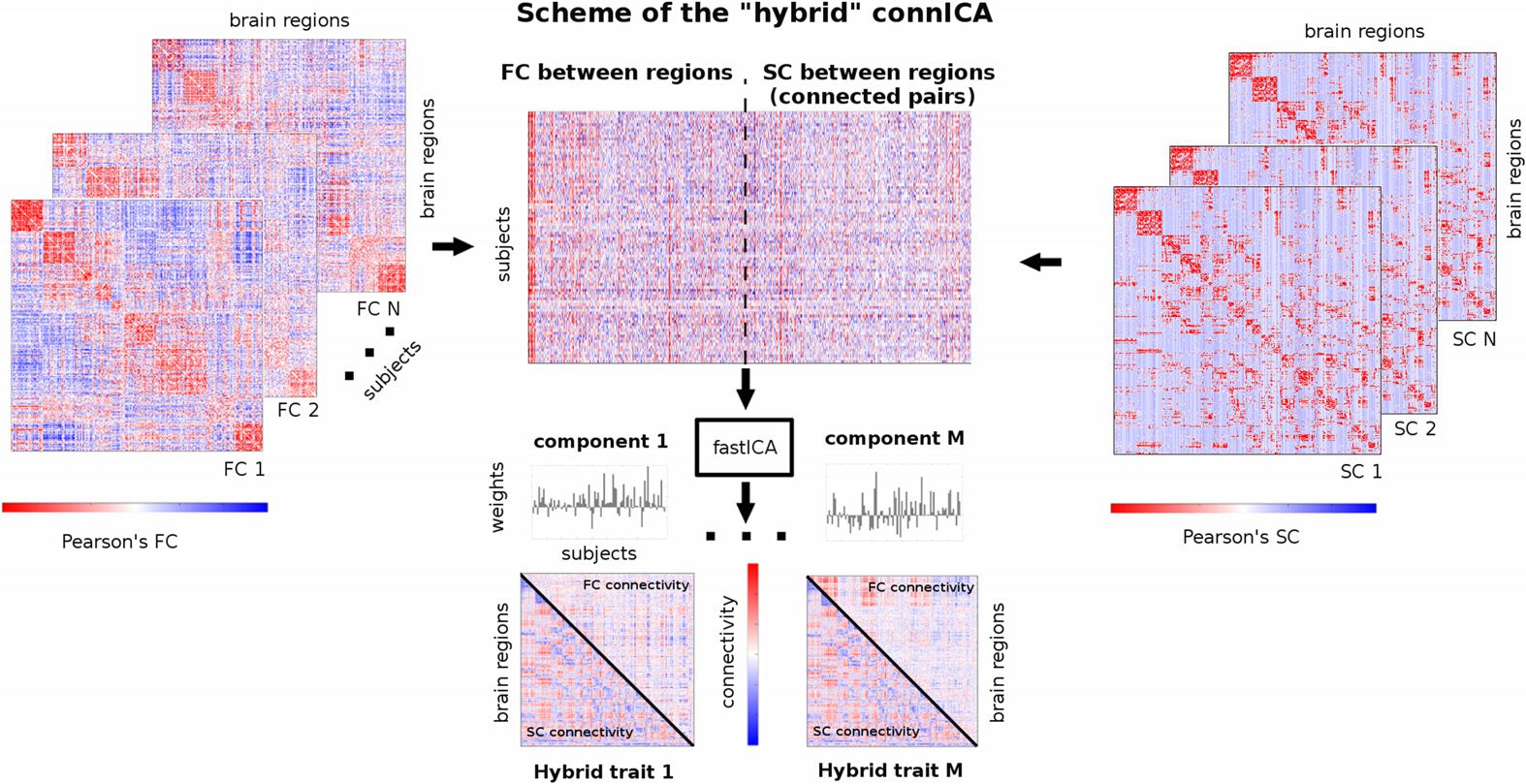
数字 1. Workflow scheme of the hybrid connICA. The upper triangular of each individual func-
tional connectivity (FC) 矩阵 (左边) and lower triangular of each correspondent structural connec-
tivity profile (SC) are added to a matrix where rows are the subjects and columns are their vectorized
hybrid (structural-functional) connectivity patterns. Note that for SC, only connected pairs across all
subjects were included (see Materials and Methods section for details). The ICA algorithm extracts
the M independent components (IE。, hybrid traits) associated to the whole population and their
relative weights across subjects. Colorbars indicate positive (红色的) and negative (蓝色的) 连接性
价值观: Pearson’s correlation coefficient values in the case of individual FC and SC matrices (左边
and right side of scheme), and unitless connectivity weights in the case of hybrid traits (bottom of
the scheme).
网络神经科学
308
Mapping hybrid functional-structural connectivity traits
材料和方法
数据集
The functional and structural dataset used in this work is from the Human Connectome Project
(HCP; http://www.humanconnectome.org/), Release Q3. Per HCP protocol, all subjects gave
written, informed consent to the Human Connectome Project consortium. Below is the full
description of the acquisition protocol and processing steps.
HCP: Functional Data
We used fMRI runs from the 100 unrelated subjects of the HCP 900 subjects data release
(Van Essen et al., 2012; Van Essen et al., 2013). The fMRI resting-state runs (HCP filenames:
rfMRI_REST1 and rfMRI_REST2) were acquired in separate sessions on two different days, 和
two different acquisitions (left to right, or LR, and right to left, or RL) per day (Glasser et al.,
2013; Van Essen et al., 2012; Van Essen et al., 2013). The seven fMRI tasks were the follow-
英: gambling (tfMRI_GAMBLING), relational (tfMRI_RELATIONAL), 社会的 (tfMRI_SOCIAL),
工作记忆 (tfMRI_WM), motor (tfMRI_MOTOR), 语言 (tfMRI_LANGUAGE, 包括-
ing both a story-listening and arithmetic task), and emotion (tfMRI_EMOTION). The working
记忆, gambling, and motor task were acquired on the first day, and the other tasks were
acquired on the second day (Barch et al., 2013; Glasser et al., 2013). The HCP scanning
protocol was approved by the local Institutional Review Board at Washington University in
英石. 路易斯. For all sessions, data from both the LR and RL phase-encoding runs were used
to calculate connectivity matrices. Full details on the HCP dataset have been published pre-
viously (Barch et al., 2013; Glasser et al., 2013; S. 中号. 史密斯等人。, 2013).
HCP: Structural Data
2
We used DWI data from the same 100 unrelated subjects of the HCP 900 subjects data release
(Van Essen et al., 2012; Van Essen et al., 2013). The diffusion acquisition protocol is covered in
detail elsewhere (Glasser et al., 2013; Sotiropoulos et al., 2013; U˘gurbil et al., 2013). 以下
we mention the main characteristics. Very high resolution acquisitions (1.25 mm isotropic)
were obtained by using a Stejskal-Tanner (monopolar) (Stejskal & Tanner, 1965) 扩散-
encoding scheme. Sampling in q-space was performed by including three shells at b = 1,000,
2,000 和 3,000 s/mm
. For each shell corresponding to 90 diffusion gradient directions and
5 b = 0’s acquired twice were obtained, with the phase-encoding direction reversed for
each pair (IE。, LR and RL pairs). Directions were optimized within and across shells (IE。,
staggered) to maximize angular coverage by using the approach of Caruyer et al.
(2011;
http://www-sop.inria.fr/members/Emmanuel.Caruyer/q-space-sampling.php) and to form a to-
tal of 270 noncollinear directions for each phase-encoding direction. Correction for EPI and
eddy current–induced distortions in the diffusion data was based on manipulation of the ac-
quisitions so that a given distortion manifested itself differently in different images (安德森,
Skare, & Ashburner, 2003). To ensure better correspondence between the phase-encoding
reversed pairs, the whole set of diffusion-weighted (DW) volumes was acquired in six separate
系列. These series were grouped into three pairs, and within each pair the two series contained
the same DW directions but with reversed phase encoding (IE。, a series of Mi DW volumes with
RL phase encoding is followed by a series of Mi volumes with LR phase encoding, i = [1,2,3]).
Brain Atlases
We employed a cortical parcellation into 360 brain regions as recently proposed by Glasser
等人. (2016). For completeness, 14 subcortical regions were added, as provided by the HCP
网络神经科学
309
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Mapping hybrid functional-structural connectivity traits
发布 (filename “Atlas_ROI2.nii.gz”). 这样做, this file was converted from NIFTI to CIFTI for-
mat by using the HCP workbench software (Glasser et al., 2013; Marcus et al., 2011) (command
-cifti-create-label; http://www.humanconnectome.org/software/connectome-workbench.html).
An additional parcellation scheme was also evaluated (德斯特里厄, 164 brain regions; 德斯特里厄,
菲舍尔, 戴尔, & 哈尔格伦, 2010; Fischl et al., 2004; as available in FreeSurfer).
HCP Preprocessing: Functional Data
The HCP functional preprocessing pipeline (Glasser et al., 2013; S. 中号. 史密斯等人。, 2013) 曾是
used for the employed dataset. This pipeline included artefact removal, motion correction,
and registration to standard space. Full details on the pipeline can be found in Glasser et al.
(2013) 和S. 中号. Smith et al. (2013). The main steps were the following: 空间的 (“minimal”)
preprocessing, in both volumetric and grayordinate forms (IE。, where brain locations are stored
as surface vertices; S. 中号. 史密斯等人。, 2013); weak high-pass temporal filtering (>2,000 s full
width at half maximum) applied to both forms, achieving slow drift removal; MELODIC ICA
(詹金森, 贝克曼, 贝伦斯, 伍尔里奇, & 史密斯, 2012) applied to volumetric data; artifact
components identified using FIX (Salimi-Khorshidi et al., 2014). Artifacts and motion-related
time courses were regressed out (IE。, 这 6 rigid-body parameter time series, their backward-
looking temporal derivatives, plus all 12 resulting regressors squared) of both volumetric and
grayordinate data (S. 中号. 史密斯等人。, 2013).
For the resting-state fMRI data, we also added the following steps: global gray matter sig-
nal was regressed out of the voxel time courses (Power et al., 2014); a band-pass first-order
Butterworth filter in forward and reverse directions [0.001 赫兹, 0.08 赫兹] (Power et al., 2014)
was applied (Matlab functions butter and filtfilt); the voxel time courses were z scored and
then averaged per brain region, excluding outlier time points outside of 3 标准差
from the mean, using the workbench software (Marcus et al., 2011) (workbench command
-cifti-parcellate). For task fMRI data, we applied the same above mentioned steps, with a less
restrictive range for the band-pass filter [0.001 赫兹, 0.25 赫兹].
Pearson correlation coefficients between pairs of nodal time courses were calculated
(MATLAB command corr), resulting in a symmetric connectivity matrix for each fMRI ses-
sion of each subject. Functional connectivity matrices from the LR and RL phase-encoding
runs were averaged to improve signal-to-noise ratio. The functional connectomes were kept
in their signed weighted form, hence neither thresholded nor binarized. This was done for the
two parcellations described above, namely Glasser with subcortical regions added (giving a
total of 374 brain regions) and Destrieux (164 brain regions).
最后, the resulting individual functional connectivity matrices were ordered (rows and
columns) according to seven resting-state cortical subnetworks (RSNs) as proposed by
Yeo et al. (2011). For completeness, an eighth subnetwork including the 14 HCP subcorti-
cal regions was added (as analogously done in a recent paper; Amico et al., 2017).
HCP Preprocessing: Structural Data
The HCP DWI data were processed following the MRtrix3 (图尔尼耶, 卡拉曼特, & 康纳利,
2012) guidelines (http://mrtrix.readthedocs.io/en/latest/tutorials/hcp_connectome.html). 总共-
mary, we first generated a tissue-segmented image appropriate for anatomically constrained
tractography (ACT; 右. 乙. 史密斯, 图尔尼耶, 卡拉曼特, & 康纳利, 2012; MRtrix command
5ttgen); we then estimated the multishell multitissue response function (Christiaens et al.,
2015), MRtrix command dwi2response msmt_5tt) and performed the multishell, multitissue
网络神经科学
310
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Mapping hybrid functional-structural connectivity traits
约束球形反卷积 (约里森, 图尔尼耶, 多霍兰德, 康纳利, & 西贝尔斯, 2014;
MRtrix dwi2fod msmt_csd); 之后, we generated the initial tractogram (MRtrix command
tckgen, 10 million streamilines, maximum tract length = 250, FA cutoff = 0.06) and applied
the successor of spherical-deconvolution informed filtering of tractograms (SIFT2; 右. 乙. 史密斯,
图尔尼耶, 卡拉曼特, & 康纳利, 2015) 方法论 (MRtrix command tcksift2). Both SIFT
(右. 乙. 史密斯, 图尔尼耶, 卡拉曼特, & 康纳利, 2013) and SIFT2 (右. 乙. 史密斯等人。, 2015,
p. 2) methods provide more biologically meaningful estimates of structural connection density.
SIFT2 allows for a more logically direct and computationally efficient solution to the stream-
lines connectivity quantification problem: by determining an appropriate cross-sectional area
multiplier for each streamline rather than removing streamlines altogether, biologically accu-
rate measures of fiber connectivity are obtained while making use of the complete streamlines
reconstruction (右. 乙. 史密斯等人。, 2015). 然后, we mapped the SIFT2 outputted streamlines
onto the 374 chosen brain regions (360 from Glasser et al., 2016, brain atlas plus 14 subcorti-
cal regions; see Brain Atlases section) to produce a structural connectome (MRtrix command
tck2connectome). 最后, a log10 transformation (Fornito et al., 2016) was applied on the
structural connectomes to better account for differences at different magnitudes. 最后,
SC values ranged between 0 和 5 on this dataset. To test the method with a different par-
cellation scheme, we performed the same mapping steps from the streamlines to a second
分割 (德斯特里厄, 164 brain regions; Destrieux et al., 2010; Fischl et al., 2004; 作为
available in FreeSurfer).
Hybrid connICA: Independent Component Analysis of Joint Functional and Structural Connectomes
The potential of multidimensional feature extraction from different neuroimaging modalities
has been already introduced and explored (Calhoun et al., 2006A, 2006乙; Calhoun, 刘, &
Adali, 2009) in the fMRI domain. 最近, applications of ICA (Hyvärinen & Oja, 2000) 在里面
functional connectome domain (Amico et al., 2017; Kessler, Angstadt, & Sripada, 2016) 和
in joint patterns of functional connectomes and gray/white matter volumes (Kessler, Angstadt,
Welsh, & Sripada, 2014) have been investigated. Here we propose a framework that allows for
the extraction of joint connectivity traits from a set of functional and structural connectomes
based on the extension of our recently proposed connICA (Amico et al., 2017), here named
“hybrid connICA.” Below is the detailed description of the hybrid connICA scheme.
The first step relates to uniforming the different distributions of FC values (Pearson’s cor-
relation values ranging between −1 and 1) and SC values (after log10 transformation, 测距
之间 0 和 5). There are several options to normalize FC and SC connections in the same
范围: here we proceeded as follows. For each pair of nodes i and j directly connected in the
SC matrix, we evaluated their “structural correlation,“ 那是, the Pearson’s correlation coeffi-
cient between the ith and jth row of the structural connectome. Iterating this procedure over
all connected pairs gives a correlation matrix of a structural connectome (see Figure S2 of
the Supplemental Material, Amico & 戈尼, 2018). The values in this matrix range between
between −1 and 1, with negative values indicating two nodes that are connected antago-
nistically to the rest of the network, and positive indicating high similarity in their structural
connections with the rest of the brain network. This solution, similarly to matching index
(鲁比诺夫 & 斯波恩斯, 2010), provides several advantages: it does not change the general prop-
erties of the SC (Figure S2) and it also allows to have functional and structural connectomes in
the same range between −1 and 1. 然而, this transformation also changes the SC matrix
structure from sparse to full. 所以, in order for this correlation matrix to be representative
of the real structural architecture of a human brain, we only considered the correlation values
corresponding to structurally connected pairs of brain regions (IE。, edges with nonzero values
网络神经科学
311
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Mapping hybrid functional-structural connectivity traits
Principal component analysis (PCA):
a statistical procedure that uses an
orthogonal transformation to convert
a set of observations of possibly
correlated variables into a set of
values of linearly uncorrelated
variables called principal
成分.
in all the SCs of the population; this corresponds to approximately 21% of all possible pairs;
see Figure S2).
The second step is similar to the standard connICA approach (Amico et al., 2017): 输入
of the hybrid connICA consists of all the individual FC and SC profiles embedded into a
“hybrid” dataset matrix where each row contains all the edges of the upper triangular part
of an individual FC matrix (first half) and the correspondent lower triangular part of the SC
matrix from the same individual (second half; see scheme at Figure 1). Note that due to
symmetry of Pearson’s correlations on FC and SC, taking the upper or the lower part of both
matrices is just conventional. In this cross-sectional study, we selected 10 different subjects
per task (7 tasks and 1 resting state; see HCP: Functional Data section), ending up with a
hybrid matrix of 80 hybrid connectivity profiles. Each profile represents the unique hybrid
connectivity signature (both structural and functional) of a human brain (数字 1). 注意
this method is insensitive to the ordering of the columns on the input hybrid matrix (IE。, 它
does not affect the results obtained).
Before running the ICA algorithm, dimensionality reduction on the dataset was obtained
by applying principal component analysis (PCA; Jolliffe, 2014) on the hybrid matrix. The ad-
vantage of applying PCA before ICA for noise filtering and dimensionality reduction in order
to avoid overfitting has already been shown, both by the machine learning (Särelä & Vigário,
2003) and neuroimaging communities (Calhoun et al., 2006A; Kessler et al., 2014). 最近,
we also showed that PCA decomposition and subsequent reconstruction of functional con-
nectomes can increase individual identifiability in a population by retaining an optimal
number of principal components (which usually explained the 90% of the variance in the
functional data employed; see Amico & 戈尼, 2017). 这里, we applied PCA to compress and
reduce the dimensionality of the data by keeping the principal components explaining 90% 的
the variance of the initial hybrid data. 的确, since the hybrid input matrix is highly redundant
(due to high similarity in structural healthy connectomes, as well as task-based FCs), 40 com-
ponents explained 90% of variance in the data (see Figure S1 of the Supplemental Material,
Amico & 戈尼, 2018).
下一个, ICA decomposition of the PCA-reconstructed hybrid matrix was applied by running
the FastICA algorithm (Hyvarinen, 1999). Similarly to connICA (Amico et al., 2017), the output
of the hybrid connICA consists of two vectors per component. The first output vector will be
referred to as hybrid trait, which represents an independent pattern of joint functional-structural
连接性, common to the whole population. The second output vector is the weight of
the hybrid trait on each subject, which quantifies the prominence or presence of the trait in
each individual connectivity hybrid profile (both functional and structural). This methodology
allows for compressing the information contained in a population of structural and functional
connectomes into a few connectivity traits and unique individual weights associated to them.
This can greatly ease the process of making inferences between the hybrid connectivity sub-
systems present in a single-subject structural-FC profile and genetic, demographic, or clinical
variables at hand.
Given the nondeterministic nature of
the FastICA decomposition into components
(Hyvarinen, 1999), it is very important to run it several times and only select the most robust
结果, in this case hybrid traits. We evaluated the robustness of the traits over 100 FastICA
runs, 如 (Amico et al., 2017). A bootstrap technique was used to accurately estimate the
hybrid traits from the 100 subjects pool of the HCP dataset (see Hybrid connICA: Independent
Component Analysis of Joint Functional and Structural Connectomes section for details). 在
网络神经科学
312
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Mapping hybrid functional-structural connectivity traits
Intraclass correlation (ICC):
an inferential statistic for quantitative
measurements that are organized
into groups. It describes how strongly
units in the same group resemble
彼此. A typical application
consists of the assessment of
consistency or reproducibility of
quantitative measurements made by
different observers measuring the
same quantity.
every run, random samples comprising hybrid profiles from 80 different subjects (10 subjects
per task and resting state) were performed. This was meant to avoid results driven by a small
subset of the population. 最后, a hybrid trait was considered robust when it appeared (科尔-
relation of 0.5 or higher across runs) in at least 50% of the runs and its representation consisted
of the average across all its appearances over the 100 runs.
The last point worth mentioning about the procedure relates to the number of independent
components chosen. There is not a gold standard for this choice: it usually depends on heuristic
measures and the dataset at hand (Calhoun et al., 2009; Hyvärinen & Oja, 2000). Since here
the main aim of the study was to investigate joint FC-SC task-dependent hybrid traits, 我们
assessed the number of ICA components (范围从 2 up to the dimension of the hybrid
matrix after PCA reconstruction; see Figure S1) that would maximize both the number of robust
hybrid traits and task-based intraclass correlation (ICC) on their weights (see next section for
细节). This heuristic measure resulted in an optimal choice of 10 independent components
(see Figure S1).
Task-Based Sensitivity
We quantified whether a hybrid trait was task sensitive by using intraclass correlation (Bartko,
1966; Shrout & 弗莱斯, 1979). ICC is a widely used measure in statistics, normally to assess
the percent of agreement between units (or ratings/scores) of different groups (or raters/judges)
(麦格劳 & 黄, 1996). It describes how strongly units in the same group resemble each
其他. The stronger the agreement, the higher its ICC value. We used ICC to quantify to what
extent the individual values of the weights of an hybrid trait could separate between subjects
performing different tasks. Following this rationale, the different tasks are “raters” and “scorers”
given by the individual hybrid weights of the subjects.
在这种情况下, the higher the ICC, 这
more separable the different tasks across subjects and consequently the more task dependent
(IE。, higher changes in the weights) in the correspondent hybrid traits.
Structural Connectome Randomization
To avoid the possibility that the hybrid patterns were only driven by the functional profiles,
we ran the hybrid connICA with randomized structural connectomes. The edges of each in-
dividual SC were swapped 50,000 次, following the randomization technique proposed in
(戈尼, 科罗米纳斯-穆特拉, 唯一, & 罗德里格斯-卡索, 2010). This randomization preserves the
main topological properties of the structural connectomes, such as size, density and degree
顺序 (and hence degree distribution; Goñi et al., 2010). The chosen number of swaps
(50,000) represents the best trade-off for this data between minimum number of swaps and
maximum gain in dissimilarity of the randomized connectomes with respect to the original
SCs (see Figure S2).
结果
The dataset used for this study consisted of structural and functional data from the 100 unre-
lated subjects in the Q3 release of the HCP (Van Essen et al., 2012, 2013). For each subject,
we estimated eight functional connectivity matrices, one corresponding to resting state (经过
averaging the REST1_LR and REST1_RL FCs), seven corresponding to each of the seven tasks (经过
averaging LR and RL corresponding FCs; see Materials and Methods); and one structural con-
nectome, corresponding to the HCP DWI acquisition S1 (see Materials and Methods). The mul-
timodal parcellation used here, as proposed by Glasser et al. (2016), includes 360 cortical
网络神经科学
313
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Mapping hybrid functional-structural connectivity traits
brain regions. 我们添加了 14 subcortical regions, hence producing functional connectome
matrices (square, symmetric) 的 374 × 374 (see Materials and Methods for details).
From the test-retest pool of 100 unrelated subjects (total of 800 FC matrices and 100 SC
matrices), a bootstrap technique was used to accurately estimate the task-dependent hybrid
特质. 那是, for each run of hybrid connICA, a random cross-sectional sample comprising the
functional-structural connectomes pairs of 80 subjects (10 subjects per task and resting state)
was considered. This was meant to avoid results driven by a small subset of the population and
to minimize redundancy in the SCs due to including the same subjects performing different
任务.
The hybrid connICA procedure can be summarized as follows (数字 1; see also
Amico et al., 2017): 第一的, the upper and lower triangular parts of each individual FC and
SC were vectorized and added to a matrix where rows are the subjects and columns are their
full connectivity pattern; 第二, the ICA algorithm was run (100 runs, number of IC = 10; 看
Materials and Methods) to extract the main hybrid (joint FC-SC) traits associated to the whole
人口; 第三个, the most robust (appearing at least 50% of the times with correlation
higher than 0.5; see Materials and Methods) and task-dependent components (测量的
by intraclass correlation on the weights per different task/resting session; see Materials and
方法) were selected.
The hybrid connICA procedure resulted in two main task-sensitive hybrid traits (数字 2).
The frequency of the averaged hybrid traits across runs were 90% 和 89% 分别. 那
是, the main functional-structural patterns, common to the whole population, which weights
change depending on the task that is being performed (high values of task-based intraclass
correlation: 0.65 和 0.70; see Figure 2A1 and 2A2). A third robust averaged hybrid trait
(64% frequency across runs) was obtained through hybrid connICA (Figure S4), 哪个, 如何-
曾经, was not task sensitive (ICC = 0.16). 有趣的是, this trait encompasses the main resting-
state networks and corresponding within-network structural connections (Figure S4).
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
.
t
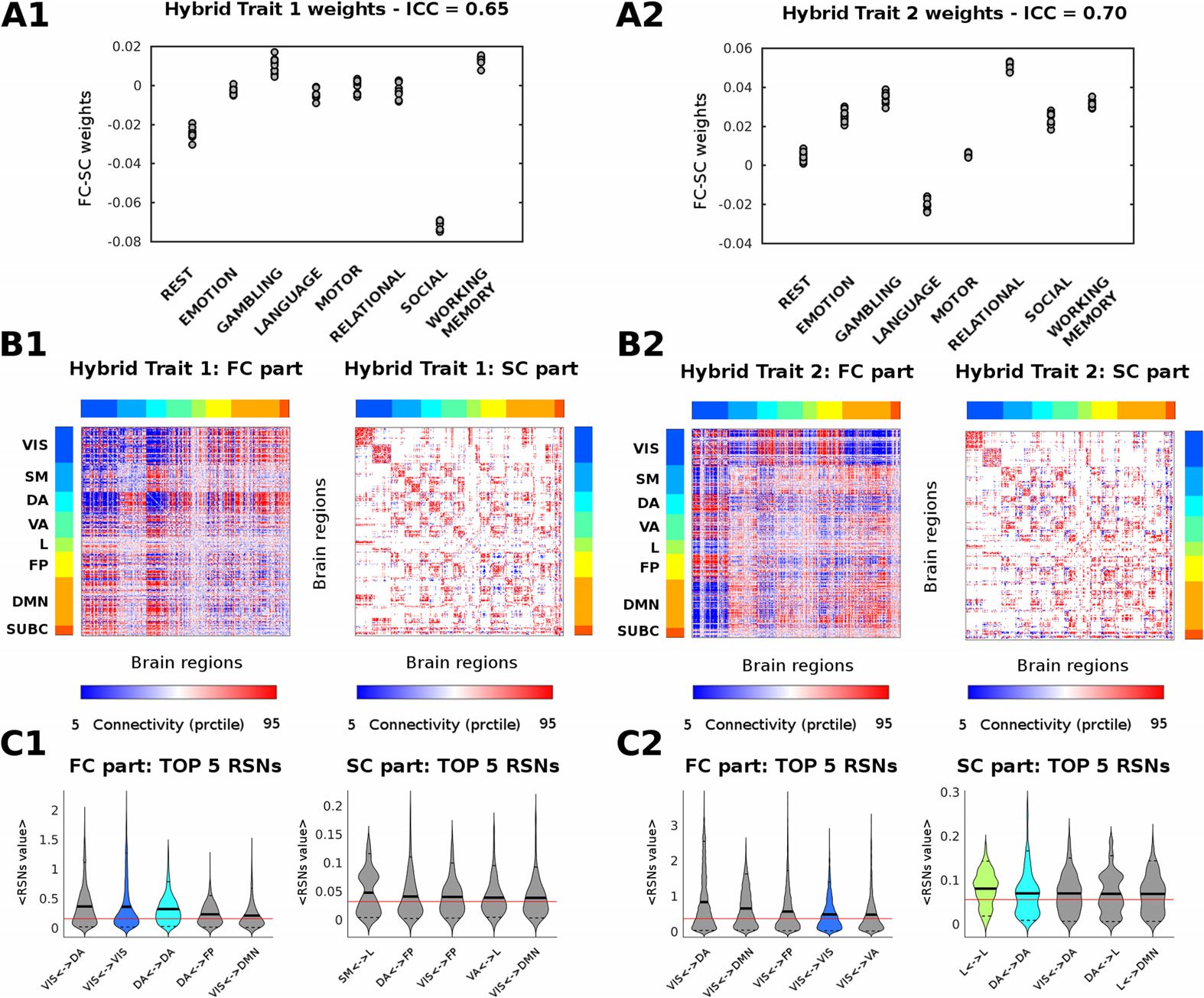
Among the task-dependent hybrid traits, the functional part of the first trait mainly cap-
tures the within-connectivity of dorsal and visual networks, as well as interconnections among
dorsal attentional, visual, and subcortical networks (数字 2). The structural part mainly
evidences the within-network connectivity between these aforementioned three networks.
The functional part of the second trait mainly represents the connectivity between the visual,
attentional (dorsal and ventral), DMN, frontoparietal (FP), and subcortical networks (数字 2).
The structural part mainly captures the within-network connectivity between those and the
limbic system.
It is worth mentioning here one of the advantages of the hybrid connICA
procedure: The hybrid traits represent joint structural-functional profiles learned from the
whole population at the same time (the subject weights corresponding to the FC or SC are
相同).
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
To assess the generalization of these results with respect to the gray matter parcellation
用过的, we ran the same analyses with a lower resolution parcellation, namely Destrieux atlas
(Destrieux et al., 2010; Fischl et al., 2004; as available in FreeSurfer software) which includes
164 brain regions. The two most frequent averaged hybrid traits (92% 和 97%, 分别)
are shown in Figure S5. Both hybrid traits were task sensitive (ICC being 0.60 和 0.58, 关于-
spectively). When comparing the hybrid traits obtained from both parcellations (数字 2
and Figure S5), we observed a high resemblance from the perspective of an RSN (within and
之间).
网络神经科学
314
Mapping hybrid functional-structural connectivity traits
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 2. Mapping of the main task-sensitive hybrid traits. (A1 and A2) Quantified presence of
each hybrid trait on each individual functional connectome. Subject weights are grouped according
to each of the seven tasks and resting state (10 subjects per task and resting state; see Materials and
方法). Task-based intraclass correlation values are reported on top. (B1 and B2) 可视化
of the two hybrid traits associated to significant changes (as measured by ICC) between tasks and
resting state. For ease of visualization, the hybrid traits are split in two matrices, corresponding to the
功能连接 (FC) and structural connectivity (SC) 图案. The brain regions are ordered
according to functional RSNs (Yeo et al., 2011): visual (VIS), somatomotor (SM), dorsal attention
(DA), ventral attention (VA), limbic system (L), frontoparietal (FP), default mode network (DMN),
and for completeness, also subcortical regions (SUBC). (C1 and C2) Violin plot of hybrid trait values
for the top five RSNs. The top five edge distributions per within or between RSNs interaction are
shown separately for the FC and SC profiles. Each color indicates a different within-RSN (如
B and C RSN colorbars), whereas gray indicates edge values between RSN networks. The solid
black lines of the violins depict the mean value of the distribution; the dashed black lines the 5
和 95 percentiles; the solid red line indicates the whole-brain mean value.
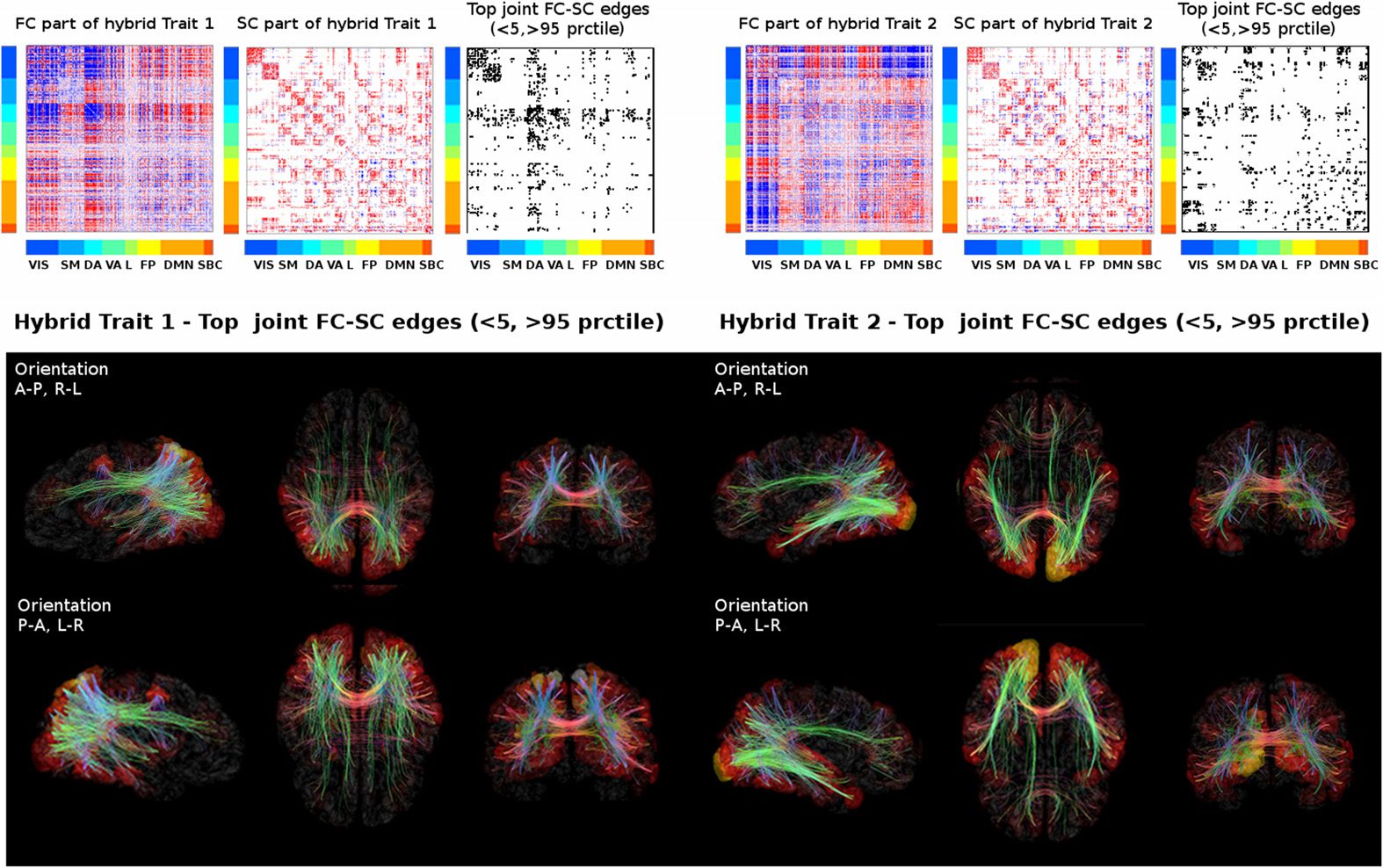
We then mapped each resulting hybrid connectivity profile onto a brain cortical surface
(数字 3). First we created a “hybrid mask” by taking only the most extreme edges in the FC
and SC parts of the two hybrid traits (outside the 5th and 95th percentile of each distribution
of values; 见图 3). That binary mask was then mapped onto a brain cortical mesh to
visualize the main hybrid circuitry involved in task switching (数字 3). This allows to examine
simultaneously functional nodes and structural pathways that are sensitive (IE。, 不同地
In the case of the first trait, the dorsal cortical regions are more
engaged) along the tasks.
著名的, as expected, as are their interhemispheric structural connections, as well as the
fibers projecting from these regions to subcortices and frontal areas (数字 3). For the second
trait, visual cortices are the most prominent functionally, as well as the pathways connecting
网络神经科学
315
Mapping hybrid functional-structural connectivity traits
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Nodal strength:
In a weighted graph (IE。, 在哪里
edges have assigned numerical
价值观) node strength represents
the total sum of the edge weights
attached to the node.
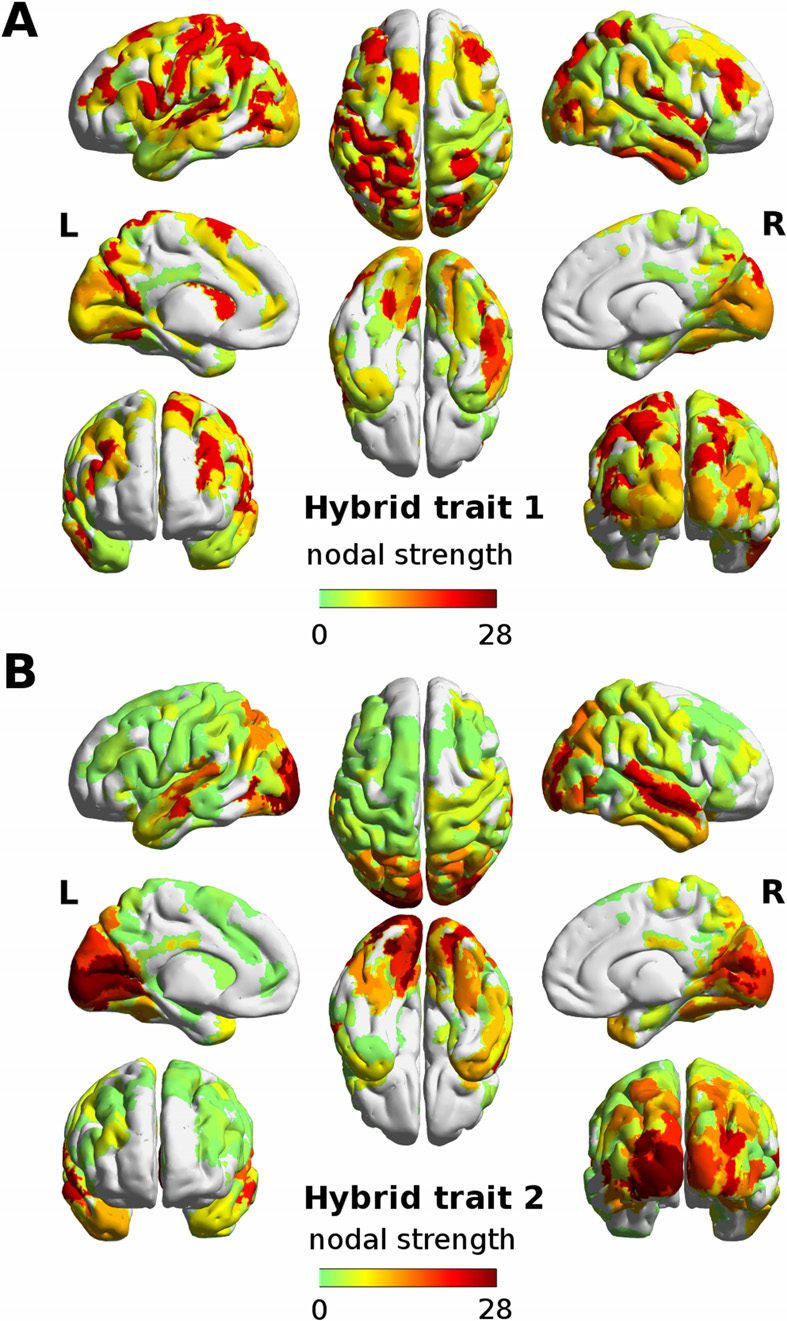
数字 3. Visualizing task-sensitive joint functional-structural circuits in the human brain. Top:
The hybrid traits (split in functional and structural patterns) shown in Figure 2 and the joint mask
obtained from the product of the more extreme values (outside the [5 95] percentile range) 在里面
corresponding FC and SC profiles. Bottom: The joint masks are projected onto brain renders, 在哪里
tracts (color coded by direction; 红色的: left-right; 绿色的: anterior-posterior; 蓝色的: superior-inferior)
represent nonzero edges in the masks, and nodal strength (sum over columns of the masks) 是
mapped onto the cortical meshes, from low strength (黑色的) to high nodal strength (bright yellow).
The brain renders were obtained with MRtrix3 (Tournier et al., 2012).
DMN and FP regions (数字 3). 尤其, none of these task-switching circuits (IE。, the joint
masks in Figure 3) were found when robust hybrid traits were obtained from the randomi-
zation of the SCs (see Materials and Methods for details and Figure S2). 的确, it is noteworthy
that the number of hybrid edges found in the joint FC-SC masks were significantly lower after
randomization (see Figure S3).
The analysis of the nodal strength on the joint mask allows for an assessment of the overall
centrality of each region on the hybrid task-sensitive traits (数字 4). In the first hybrid trait,
the main areas involved are the dorsal and ventral lobes, associated to attentional network
连接性, as expected. 另一方面, the left and right visual cortices dominate the
nodal strength overview of the second hybrid trait (数字 4).
讨论
The investigation of the interaction between structural and FC layers in large-scale human brain
networks is one of the current challenges in brain connectomics (Falcon et al., 2016; 假如
等人。, 2016; Honey et al., 2010; Miši´c et al., 2016). The difficulty of addressing this problem is
manifold: from the different data processing to the huge amount of information of difficult inter-
预谋, to the necessity of estimating individual weights of group-level structural-functional
circuits.
Here we proposed a framework, named hybrid connICA (which expands on connICA;
Amico et al., 2017), that allows to extract, in a data-driven fashion, the most representa-
tive joint functional-structural (IE。, hybrid) patterns from a set of individual joint connectivity
网络神经科学
316
Mapping hybrid functional-structural connectivity traits
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 4. Node centrality of the hybrid task-sensitive traits. The strength per region computed as
sum of nonzero values in the joint FC-SC mask, 为了 (A) first and (乙) second hybrid trait. The mask
was obtained by taking only the most extreme edges in the FC and SC parts of the two hybrid traits
(outside the 5th and 95th percentile of each distribution of values). Note how the first trait mainly
involves attentional-related areas in the dorsal and ventral lobes lobe, whereas both left and right
visual cortices dominate in the second trait. The brain renders were obtained with BrainNet Viewer
(Xia, 王, & 他, 2013).
profiles (见图 1). We tested this methodology on the HCP data benchmark to retrieve
the hybrid connectivity subsystem related to changes in functional tasks and resting state
(人物 2 和 3).
The hybrid connICA extracted two main task-dependent traits; 第一个, encompassing the
之内- and between-network connections of dorsal attentional and visual areas, 也
subcortical structures (数字 2). The second hybrid trait associated to task switching mainly
specializes in the connectivity between the visual and frontoparietal, DMN, and subcortical
网络 (数字 2). These findings are in line with previous research showing that these are
the main areas (attentional cortices, DMN, visual, and subcortical regions) undergoing major
changes when passing from rest to task sessions (Cole, Bassett, 力量, Braver, & 彼得森, 2014;
狐狸 & Raichle, 2007; Hasson, Nusbaum, & 小的, 2009; Hermundstad et al., 2013; Tavor et al.,
2016). Recent studies also reported the existence of an “intrinsic functional architecture” (Cole
等人。, 2014) that shapes the brain’s functional network architecture during task performance
(Tavor et al., 2016). These findings suggest that a set of small but consistent changes in FC
across tasks might distinguish task states from rest (Cole et al., 2014), and it might also allow
us to predict task states from the intrinsic resting-state organization (Tavor et al., 2016). 我们
also assessed the reproducibility of the results by evaluating the two most frequent hybrid traits
网络神经科学
317
Mapping hybrid functional-structural connectivity traits
at a coarser grain resolution (Figure S5). 有趣的是, a high resemblance from the perspective
of an RSN (within and between) was found, suggesting that the method presented here shows
consistency in the results across brain spatial scales and resolutions.
这里, we took one step forward in this direction by using a hybrid connICA approach
to map the main joint FC-SC circuitry involved in task switching (数字 3). 有趣的是, 这
intrinsic resting-state organization of a human brain both at the functional and structural level
was also recovered, even though it was not associated to changes across tasks. 的确, 一
robust trait captured all the main functional and structural connections of RSN blocks (hybrid
trait 3; Figure S4).
One benefit of this methodology resides in the possibility to extract and visualize “cities”
(cortical functional nodes) 和高速公路 (structural connections) corresponding to specific
subsystems simultaneously (数字 3). In the case of this work, functional-structural patterns
that change depending on whether the subject is at rest or performing a specific task (数字 3).
尤其, both hybrid traits capture two main aspects of brain network connectivity: integra-
的 (in the sense of functional interaction between networks) and segregation (expressed as
main within-network connectivity between structural circuits; 数字 2 and Figure S4; 托诺尼,
斯波恩斯, & Edelman, 1994). It is worth stressing here that the resulting hybrid patterns are by
all means entangled together. 尤其, it is not likely to retrieve the same joint subsystems with-
out the real connectivity structure (Figure S3). When the SCs were randomized (see Figure S3
and Materials and Methods), it was not possible to retrieve any of the hybrid joint pathways
presented in Figure 3 (IE。, the number of nonzero values in the FC-SC mask significantly low-
ered after randomization; see Figure S3).
There are several advantages in applying a data-driven procedure such as hybrid connICA.
The compression of the meaningful information into a few hybrid connectivity layers that are
robust, 独立的, and task sensitive is one of the major points.
此外, the subject
weights associated to each hybrid trait are unique, meaning that there are single individual
weights that allow us to recover the structural-functional subsystem at the single-subject level
(例如, the ICA procedure was performed at once by concatenating structural and functional
profiles, hence it provided unique sets of weights associated to the FC and SC connectomes).
This might ease inferences at the individual level with cognitive, genetic variables directly
on the weights, and avoid multiple comparisons when working with multidimensional matri-
ces. Our approach based on independent group-level hybrid traits with associated individual
weights adds to recently proposed data-driven methods, where group-level orthogonal covary-
ing structural-functional patterns are extracted based on singular value decomposition (Miši´c
等人。, 2016). Although these approaches are focused on the integration of different modali-
领带, frameworks such as canonical correlation analysis (Irimia & Van Horn, 2013) allow us to
disentangle which modalities are responsible for associations between different brain regions.
Here we showed an application of the hybrid connICA in disentangling task-dependent joint
FC-SC circuits in healthy young adults. Next steps for using this framework will involve the
investigation of hybrid patterns in clinical populations where heterogeneous individual struc-
tural damage is usually associated with a rich repertoire of different functional responses (这样的
as in Parkinson’s disease, 阿尔茨海默氏病, traumatic brain injury, disorders of conscious-
内斯, ETC。). This method can then provide a data-driven way to disentangle the main circuits
associated with the disease (similarly to the functional connICA; Amico et al., 2017; Contreras
等人。, 2017), while assessing structural and functional changes at the same time. This might
also allow researchers to investigate and make inferences on the structural and functional
网络神经科学
318
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Mapping hybrid functional-structural connectivity traits
circuitries involved by compressing them into a few hybrid traits. The flexibility of the method
enables for extending the approach to layers other than the structural ones. 例如, 一
may substitute the SC layer proposed in this work with other network measures such as mod-
独特性, efficiency, or search information. 还, one may assess the multimodal integration of
different functional modalities such as electroencephalography at different frequency bands,
or magnetoencephalography, 除其他外.
This study has several limitations. The optimal size of the cohort for the extraction of the
hybrid connICA components needs to be further investigated. 相似地, the best choice of
the starting number of ICA components (here set to 10; see Figure S1) and the threshold for
the final selection of the most frequent components over multiple ICA runs (here set to 50%)
depends on the research question at hand.
It is important to have a priori hypotheses for
filtering the robust traits for analyses. 例如, here we used intraclass correlation among
tasks as a criterion. 还, in recent clinical studies, multilinear models were used to asso-
ciate the connectivity traits to crucial behavioral and/or clinical variables (Amico et al., 2017;
Contreras et al., 2017). Despite that a state-of-the-art tractography (SIFT2, MRtrix3) algorithm
was used in this study, further exploration of the sensitivity and specificity of the hybrid traits
to different tractography could be performed. 最后, for the ICA extraction to work properly,
we also strongly recommend for the range of the two connectivity profiles concatenated to
be consistent across edges. Here we proposed the use of SC-based correlations. 然而,
different normalizations could be applied for making SC and FC magnitudes comparable or at
least more homogeneous (例如, using absolute values, dividing by the maximum value, or by
applying L1 and L2 norms (Calhoun et al., 2006A; Kessler et al., 2014).
综上所述, we here proposed a novel data-driven approach, hybrid connICA (succes-
sor of connICA; Amico et al., 2017), to disentangle the most influential functional-structural
connectivity patterns related to changes in brain networks across tasks and resting state. 我们的
results shed light on the key hybrid circuitry (both functional and structural) involved in
the differentiation of connectivity profiles across different tasks. By simultaneously extracting
structural-functional subsystems, the proposed methodology might improve our understanding
of connectivity changes associated to brain pathologies.
作者贡献
Enrico Amico: 概念化; 数据管理; 方法; Writing – original draft;
写作——复习 & 编辑. Joaquín Goñi: 概念化; 数据管理; 形式分析;
资金获取; 调查; 方法; 监督; 验证; 写作——原创
草稿; 写作——复习 & 编辑.
资金信息
Data were provided, 部分地, by the Human Connectome Project, WU-Minn Consortium
(Principal Investigators: David Van Essen and Kamil U˘gurbil; 1U54MH091657) funded by the
16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; 和
by the McDonnell Center for Systems Neuroscience at Washington University. This work
was partially supported by NIH Grants R01EB022574 and by NIH R01MH108467 and by the
Indiana Clinical and Translational Sciences Institute (Grant UL1TR001108) from the National
Institutes of Health, National Center for Advancing Translational Sciences, Clinical and
Translational Sciences Award.
网络神经科学
319
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Mapping hybrid functional-structural connectivity traits
SUPPORTING INFORMATION
The code used for extract hybrid connICA traits from joint FC-SC data is available on the
CONNplexity lab website (https://engineering.purdue.edu/ConnplexityLab).
参考
Amico, E., & 戈尼, J.
(2018). The quest for identifiability in hu-
man functional connectomes. Scientific Report. Accepted for
出版物.
Amico, E., & 戈尼, J. (2018). Supplemental Material for “Mapping
hybrid functional-structural connectivity traits in the human con-
nectome.” Network Neuroscience, 2(3), 306–322. https://土井.
org/10.1162/netn_a_00049
Amico, E., Marinazzo, D ., Di Perri, C。, Heine, L。, Annen, J。, Martial,
C。, . . . 戈尼, J. (2017). Mapping the functional connectome traits
of levels of consciousness. 神经影像, 148, 201–211. https://
doi.org/10.1016/j.neuroimage.2017.01.020
安德森, J. L. R。, Skare, S。, & Ashburner, J. (2003). How to cor-
rect susceptibility distortions in spin-echo echo-planar images:
Application to diffusion tensor imaging. 神经影像, 20(2),
870–888. https://doi.org/10.1016/S1053-8119(03)00336-7
Barch, D. M。, 伯吉斯, G. C。, Harms, 中号. P。, 彼得森, S. E.,
施拉加尔, 乙. L。, 科尔贝塔, M。, . . . Van Essen, D. C. (2013). Func-
tion in the human connectome: Task-fMRI and individual dif-
ferences in behavior. 神经影像, 80, 169–189. https://doi.org/
10.1016/j.neuroimage.2013.05.033
Bartko, J. J.
(1966). The intraclass correlation coefficient as a
measure of reliability. Psychological Reports, 19(1), 3–11. https://
doi.org/10.2466/pr0.1966.19.1.3
布莫尔, E., & 斯波恩斯, 氧. (2009). 复杂的大脑网络: 图形
结构和功能系统的理论分析. 自然
评论 神经科学, 10(3), 186–198. https://doi.org/10.1038/
nrn2575
Calhoun, V. D ., Adali, T。, Giuliani, 氮. R。, Pekar, J. J。, Kiehl, K. A。,
& Pearlson, G. D.
(2006A). Method for multimodal analysis of
independent source differences in schizophrenia: Combining
gray matter structural and auditory oddball functional data.
人脑图谱, 27(1), 47–62. https://doi.org/10.1002/
hbm.20166
Calhoun, V. D ., Adali, T。, Kiehl, K. A。, Astur, R。, Pekar, J. J。, &
Pearlson, G. D. (2006乙). A method for multitask fMRI data
fusion applied to schizophrenia. 人脑图谱, 27(7),
598–610. https://doi.org/10.1002/hbm.20204
Calhoun, V. D ., 刘, J。, & Adali, 时间. (2009). A review of group ICA
for fMRI data and ICA for joint inference of imaging, genetic,
and ERP data. 神经影像, 45(1), S163–S172. https://doi.org/
10.1016/j.neuroimage.2008.10.057
Caruyer, E., Cheng, J。, Lenglet, C。, Sapiro, G。, Jiang, T。, & Deriche,
右. (2011). Optimal Design of Multiple Q-shells experiments for
弥散磁共振成像. Presented at the MICCAI Workshop on Compu-
tational Diffusion MRI – CDMRI’11. Retrieved from https://hal.
inria.fr/inria-00617663/文档
weighted imaging data using a multi-tissue model. 神经影像,
123, 89–101. https://doi.org/10.1016/j.neuroimage.2015.08.008
Cole, 中号. W., Bassett, D. S。, 力量, J. D ., Braver, 时间. S。, & 彼得森,
S. 乙. (2014). Intrinsic and task-evoked network architectures of
the human brain. 神经元, 83(1), 238–251. https://doi.org/10.
1016/j.neuron.2014.05.014
CONNplexity Lab.
网络.
ConnplexityLab
Retrieved
(2018). Brain Connectomics & Complex
来自 https://engineering.purdue.edu/
Contreras, J. A。, 戈尼, J。, Risacher, S. L。, Amico, E., Yoder, K.,
Dzemidzic, M。, . . . Saykin, A. J. (2017). Cognitive complaints
in older adults at risk for Alzheimer’s disease are associated
with altered resting-state networks. Alzheimer’s and Dementia:
Diagnosis, Assessment, and Disease Monitoring, 6, 40–49.
https://doi.org/10.1016/j.dadm.2016.12.004
德斯特里厄, C。, 菲舍尔, B., 戴尔, A。, & 哈尔格伦, 乙. (2010). 汽车-
matic parcellation of human cortical gyri and sulci using
standard anatomical nomenclature. 神经影像, 53(1), 1–15.
https://doi.org/10.1016/j.neuroimage.2010.06.010
Falcon, 中号. 我。,
Jirsa, 五、, & 索洛德金, A. (2016). A new neuro-
informatics approach to personalized medicine in neurology:
The virtual brain. Current Opinion in Neurology, 29(4), 429–436.
https://doi.org/10.1097/WCO.0000000000000344
芬恩, 乙. S。, 沉, X。, Scheinost, D ., Rosenberg, 中号. D ., 黄, J。,
Chun, 中号. M。, . . . Constable, 右. 时间. (2015). Functional connec-
tome fingerprinting:
Identifying individuals using patterns of
大脑连接. 自然神经科学, 18(11), 1664–1671.
https://doi.org/10.1038/nn.4135
菲舍尔, B., 范德库韦, A。, 德斯特里厄, C。, 哈尔格伦, E., Ségonne,
F。, 礼拜, D. H。, . . . 戴尔, A. 中号.
(2004). Automatically parcel-
lating the human cerebral cortex. 大脑皮层, 14(1), 11–22.
https://doi.org/10.1093/cercor/bhg087
假如, A。, 扎莱斯基, A。, & Breakspear, 中号.
(2015). The connec-
tomics of brain disorders. 自然评论神经科学, 16(3),
159–172. https://doi.org/10.1038/nrn3901
假如, A。, 扎莱斯基, A。, & 布莫尔, 乙. (2016). Fundamentals of
Brain Network Analysis. 阿姆斯特丹, 荷兰人: Academic
按.
狐狸, 中号. D ., & Raichle, 中号. 乙.
(2007). Spontaneous fluctuations
in brain activity observed with functional magnetic resonance
成像. 自然评论神经科学, 8(9), 700–711. https://
doi.org/10.1038/nrn2201
弗里斯顿, K. J. (2011). Functional and effective connectivity: A review.
Brain Connectivity, 1(1), 13–36. https://doi.org/10.1089/brain.
2011.0008
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Christiaens, D ., 旅行过, M。, 多霍兰德, T。, Sunaert, S。, Suetens, P。,
& Maes, F. (2015). Global tractography of multi-shell diffusion-
Glasser, 中号. F。, Coalson, 时间. S。, 罗宾逊, 乙. C。, Hacker, C. D .,
Harwell, J。, Yacoub, E., . . . Van Essen, D. C. (2016). A multi-modal
网络神经科学
320
Mapping hybrid functional-structural connectivity traits
parcellation of human cerebral cortex. 自然, 536(7615), 171–
178. https://doi.org/10.1038/nature18933
103, 411–426. https://doi.org/10.1016/j.neuroimage.2014.07.
061
Glasser, 中号. F。, 索蒂罗普洛斯, S. N。, Wilson, J. A。, Coalson, 时间. S。,
. . . 詹金森, 中号. (2013). 这
菲舍尔, B., 安德森,
minimal preprocessing pipelines for the Human Connectome
项目. 神经影像, 80, 105–124. https://doi.org/10.1016/j.
neuroimage.2013.04.127
J. L。,
戈尼,
J。, 科罗米纳斯-穆特拉, B., 唯一, 右. 五、, & Rodríguez-
Caso, C. (2010). Exploring the randomness of directed acyclic
网络. Physical Review E, 82(6), 066115. https://doi.org/10.
1103/PhysRevE.82.066115
戈尼,
J。, 爬坡道, 中号. 磷. van den, Avena-Koenigsberger, A。,
Mendizabal, 氮. V. 的, 贝策尔, 右. F。, Griffa, A。, . . . 斯波恩斯, 氧.
(2014). Resting-brain functional connectivity predicted by ana-
lytic measures of network communication. 诉讼程序
美国国家科学院, 111(2), 833–838. https://doi.org/
10.1073/pnas.1315529111
Hasson, U。, Nusbaum, H. C。, & 小的, S. L. (2009). Task-dependent
organization of brain regions active during rest. 会议记录
of the National Academy of Sciences, 106(26), 10841–10846.
https://doi.org/10.1073/pnas.0903253106
Hermundstad, A. M。, Bassett, D. S。, 棕色的, K. S。, Aminoff, 乙. M。,
Clewett, D ., 弗里曼, S。, . . . 卡尔森, J. 中号.
(2013). 结构性
foundations of resting-state and task-based functional connec-
tivity in the human brain. 国家科学院院刊
科学系, 110(15), 6169–6174. https://doi.org/10.1073/pnas.
1219562110
蜂蜜, C. J。, Kötter, R。, Breakspear, M。, & 斯波恩斯, 氧. (2007). 网-
work structure of cerebral cortex shapes functional connectivity
on multiple time scales. 美国国家科学院院刊
科学, 104(24), 10240–10245. https://doi.org/10.1073/pnas.
0701519104
蜂蜜, C. J。, 斯波恩斯, 奥。, 卡蒙, L。, 巨人, X。, Thiran, J. P。,
买, R。, & 哈格曼, 磷. (2009). Predicting human resting-state
functional connectivity from structural connectivity. 会议记录
of the National Academy of Sciences, 106(6), 2035–2040. https://
doi.org/10.1073/pnas.0811168106
蜂蜜, C. J。, Thivierge, J.-P., & 斯波恩斯, 氧. (2010). Can structure pre-
dict function in the human brain? 神经影像, 52(3), 766–776.
https://doi.org/10.1016/j.neuroimage.2010.01.071
Hyvarinen, A. (1999). Fast ICA for noisy data using Gaussian mo-
评论. 在诉讼程序中 1999 IEEE International Symposium
on Circuits and Systems, 1999. ISCAS ’99 (卷. 5, PP. 57–61).
https://doi.org/10.1109/ISCAS.1999.777510
Hyvärinen, A。, & Oja, 乙. (2000). Independent component analysis:
Algorithms and applications. Neural Networks, 13(4), 411–430.
https://doi.org/10.1016/S0893-6080(00)00026-5
Irimia, A。, & Van Horn, J. D. (2013). The structural, connectomic
and network covariance of the human brain. 神经影像, 66,
489–499. https://doi.org/10.1016/j.neuroimage.2012.10.066
詹金森, M。, 贝克曼, C. F。, 贝伦斯, 时间. 乙. J。, 伍尔里奇, 中号. W.,
& 史密斯, S. 中号. (2012). FSL. 神经影像, 62(2), 782–790. https://
doi.org/10.1016/j.neuroimage.2011.09.015
约里森, B., 图尔尼耶, J.-D., 多霍兰德, T。, 康纳利, A。, & 西贝尔斯,
J.
(2014). Multi-tissue constrained spherical deconvolution for
improved analysis of multi-shell diffusion MRI data. 神经影像,
Jolliffe, 我. (2014). Principal component analysis. In Wiley Statsref:
Statistics Reference Online. 约翰·威利 & Sons. https://doi.org/
10.1002/9781118445112.stat06472
Kessler, D ., Angstadt, M。, & Sripada, C.
(2016). Growth charting
of brain connectivity networks and the identification of attention
impairment in youth. JAMA Psychiatry, 73(5), 481–489. https://
doi.org/10.1001/jamapsychiatry.2016.0088
Kessler, D ., Angstadt, M。, Welsh, 右. C。, & Sripada, C. (2014).
Modality-spanning deficits
in attention-deficit/hyperactivity
disorder in functional networks, gray matter, and white matter.
神经科学杂志, 34(50), 16555–16566. https://doi.org/
10.1523/JNEUROSCI.3156-14.2014
马库斯, D ., Harwell, J。, Olsen, T。, 霍奇, M。, Glasser, M。, 事先的,
F。, . . . Van Essen, D. (2011). Informatics and data mining tools
and strategies for the Human Connectome Project. Frontiers in
神经信息学, 5. https://doi.org/10.3389/fninf.2011.00004
(1996). Forming inferences about
some intraclass correlation coefficients. Psychological Methods,
1(1), 30–46. https://doi.org/10.1037/1082-989X.1.1.30
麦格劳, K. 奥。, & 黄, S. 磷.
Miši´c, B., 贝策尔, 右. F。, Reus, D ., A, M。, 爬坡道, V. D ., 磷, M。, . . .
斯波恩斯, 氧.
(2016). Network-level structure-function relation-
ships in human neocortex. 大脑皮层, 26(7), 3285–3296.
https://doi.org/10.1093/cercor/bhw089
力量, J. D ., 米特拉, A。, 劳曼, 时间. 奥。, 斯奈德, A. Z。, 施拉加尔,
乙. L。, & 彼得森, S. 乙. (2014). Methods to detect, characterize,
and remove motion artifact in resting state fMRI. 神经影像,
84, 320–341. https://doi.org/10.1016/j.neuroimage.2013.08.048
鲁比诺夫, M。, & 斯波恩斯, 氧. (2010). 复杂的网络措施
大脑连接: 用途和解释. 神经影像, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003
Salimi-Khorshidi, G。, Douaud, G。, 贝克曼, C. F。, Glasser, 中号. F。,
Griffanti, L。, & 史密斯, S. 中号. (2014). Automatic denoising of func-
tional MRI data: Combining independent component analysis
and hierarchical fusion of classifiers. 神经影像, 90, 449–468.
https://doi.org/10.1016/j.neuroimage.2013.11.046
S ä r e l ä,
J。, & Vig ário, 右.
(2003). Overlearning in marginal
distribution-basedICA: Analysis and solutions. Journal of Machine
Learning Research, 4(Dec), 1447–1469.
沉, X。, 芬恩, 乙. S。, Scheinost, D ., Rosenberg, 中号. D ., Chun, 中号. M。,
Papademetris, X。, & Constable, 右. 时间. (2017). Using connectome-
based predictive modeling to predict individual behavior from
大脑连接. Nature Protocols, 12(3), 506–518. https://
doi.org/10.1038/nprot.2016.178
Shrout, 磷. E., & 弗莱斯, J. L. (1979). Intraclass correlations: Uses in
assessing rater reliability. Psychological Bulletin, 86(2), 420–428.
https://doi.org/10.1037/0033-2909.86.2.420
史密斯, 右. E., 图尔尼耶, J.-D., 卡拉曼特, F。, & 康纳利, A. (2012).
Anatomically-constrained tractography: Improved diffusion MRI
streamlines tractography through effective use of anatomical
信息. 神经影像, 62(3), 1924–1938. https://doi.org/
10.1016/j.neuroimage.2012.06.005
史密斯, 右. E., 图尔尼耶,
J.-D., 卡拉曼特, F。, & 康纳利, A.
(2013). SIFT:
spherical-deconvolution informed filtering of
tractograms. 神经影像, 67, 298–312. https://doi.org/10.1016/
j.neuroimage.2012.11.049
网络神经科学
321
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Mapping hybrid functional-structural connectivity traits
史密斯, 右. E., 图尔尼耶, J.-D., 卡拉曼特, F。, & 康纳利, A. (2015).
SIFT2: Enabling dense quantitative assessment of brain white
matter connectivity using streamlines tractography. 神经影像,
119, 338–351. https://doi.org/10.1016/j.neuroimage.2015.06.
092
史密斯, S. M。, 贝克曼, C. F。, 安德森, J。, 奥尔巴赫, 乙. J。,
Bijsterbosch, J。, Douaud, G。, . . . Glasser, 中号. F. (2013). Resting-
state fMRI in the Human Connectome Project. 神经影像, 80,
144–168. https://doi.org/10.1016/j.neuroimage.2013.05.039
索蒂罗普洛斯, S. N。, Jbabdi, S。, 徐, J。, 安德森, J. L。, Moeller, S。,
奥尔巴赫, 乙. J。, . . . 贝伦斯, 时间. 乙. J. (2013). Advances in diffu-
sion MRI acquisition and processing in the Human Connectome
项目. 神经影像, 80, 125–143. https://doi.org/10.1016/j.
neuroimage.2013.05.057
斯波恩斯, 氧. (2011). The human connectome: a complex network.
Annals of the New York Academy of Sciences, 1224(1), 109–125.
https://doi.org/10.1111/j.1749-6632.2010.05888.x
Stejskal, 乙. 奥。, & Tanner, J. 乙. (1965). Spin diffusion measurements:
Spin echoes in the presence of a time-dependent field gradient.
The Journal of Chemical Physics, 42(1), 288–292. https://doi.org/
10.1063/1.1695690
Tavor, 我。, 琼斯, 氧. P。, 火星, 右. B., 史密斯, S. M。, 贝伦斯, 时间. E., &
Jbabdi, S. (2016). Task-free MRI predicts individual differences
in brain activity during task performance. 科学, 352(6282),
216–220. https://doi.org/10.1126/science.aad8127
托诺尼, G。, 斯波恩斯, 奥。, & Edelman, G. 中号. (1994). A measure for
brain complexity: relating functional segregation and integration
in the nervous system. 美国国家科学院院刊
科学, 91(11), 5033–5037.
图尔尼耶, J.-D., 卡拉曼特, F。, & 康纳利, A. (2012). MRtrix: Diffu-
sion tractography in crossing fiber regions. International Journal
of Imaging Systems and Technology, 22(1), 53–66. https://土井.
org/10.1002/ima.22005
U˘gurbil, K., 徐, J。, 奥尔巴赫, 乙. J。, Moeller, S。, Vu, A. T。, Duarte-
Carvajalino, J. M。, . . . Yacoub, 乙. (2013). Pushing spatial and
在里面
temporal resolution for functional and diffusion MRI
Human Connectome Project. 神经影像, 80, 80–104. https://
doi.org/10.1016/j.neuroimage.2013.05.012
Van Essen, D. C。, 史密斯, S. M。, Barch, D. M。, 贝伦斯, 时间. 乙. J。,
Yacoub, E., & Ugurbil, K. (2013). The WU-Minn Human Con-
nectome Project: 概述. 神经影像, 80, 62–79. https://
doi.org/10.1016/j.neuroimage.2013.05.041
Van Essen, D. C。, Ugurbil, K., 奥尔巴赫, E., Barch, D ., 贝伦斯,
时间. 乙. J。, Bucholz, R。, . . . WU-Minn HCP Consortium.
(2012).
The Human Connectome Project: A data acquisition perspec-
主动的. 神经影像, 62(4), 2222–2231. https://doi.org/10.1016/j.
neuroimage.2012.02.018
Xia, M。, 王, J。, & 他, 是.
(2013). BrainNet Viewer: A network
visualization tool for human brain connectomics. PloS one, 8(7),
e68910. https://doi.org/10.1371/journal.pone.0068910
杨, 乙. 时间. T。, 克里宁, F. M。, 墓, J。, 肥皂, 中号. R。, 军队,
D ., 霍林斯黑德, M。, . . . 巴克纳, 右. L. (2011). The organization
of the human cerebral cortex estimated by intrinsic functional
神经生理学杂志, 106(3), 1125–1165.
连接性.
https://doi.org/10.1152/jn.00338.2011
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
2
3
3
0
6
1
0
9
2
1
0
3
n
e
n
_
A
_
0
0
0
4
9
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
网络神经科学
322