焦点功能: - 麻省理工学院人工智能研究专业

焦点功能:
Connectivity, 认识, and Consciousness

Benchmarking functional connectivity by the
structure and geometry of the human brain

Zhen-Qi Liu1

, Richard F. Betzel2

, and Bratislav Misic1

1McConnell Brain Imaging Centre, Montréal Neurological Institute, 麦吉尔大学, 蒙特利尔, 加拿大
2Psychological and Brain Sciences, 印第安纳大学, 布卢明顿, 在, 美国

关键词: Connectome, Functional connectivity, 结构连接, Geometry, 嵌入,
Gradient, Hierarchy, Transmodal

开放访问

杂志

抽象的

The brain’s structural connectivity supports the propagation of electrical impulses, manifesting
as patterns of coactivation, termed functional connectivity. Functional connectivity emerges
from the underlying sparse structural connections, particularly through polysynaptic
沟通. 因此, functional connections between brain regions without direct
structural links are numerous, but their organization is not completely understood. Here we
investigate the organization of functional connections without direct structural links. 我们
develop a simple, data-driven method to benchmark functional connections with respect to
their underlying structural and geometric embedding. We then use this method to reweigh and
reexpress functional connectivity. We find evidence of unexpectedly strong functional
connectivity among distal brain regions and within the default mode network. We also find
unexpectedly strong functional connectivity at the apex of the unimodal-transmodal hierarchy.
Our results suggest that both phenomena—functional modules and functional hierarchies—
emerge from functional interactions that transcend the underlying structure and geometry.
These findings also potentially explain recent reports that structural and functional
connectivity gradually diverge in transmodal cortex. Collectively, we show how structural
connectivity and geometry can be used as a natural frame of reference with which to study
functional connectivity patterns in the brain.

作者总结

The structural connectivity of the brain supports interregional signaling, manifesting as highly
organized patterns of functional connectivity. 重要的, structural and functional
connectivity are fundamentally constrained by the spatial embedding of brain regions, 这样的
that proximal regions are more likely to exhibit stronger connectivity. Here we develop a
simple method that uses robust relationships between geometry, 结构, and function as the
baseline to reweigh and reexpress functional connectivity. We use the method to identify
functional connections that are greater than expected given their structural and geometric
embedding. We then show that the arrangement of these connections systematically follows
the functional modules and the putative unimodal-transmodal hierarchy of the brain.
Collectively, our findings demonstrate highly organized patterns of polysynaptic functional
connections that support the emergence of canonical features of functional connectivity
网络, including modules and hierarchies.

引文: 刘, Z.-Q., 贝策尔, 右. F。, &
Misic, 乙. (2022). Benchmarking
functional connectivity by the structure
and geometry of the human brain.
网络神经科学, 6(4), 937–949.
https://doi.org/10.1162/netn_a_00236

DOI:
https://doi.org/10.1162/netn_a_00236

支持信息:
https://doi.org/10.1162/netn_a_00236

已收到: 12 十月 2021
公认: 18 一月 2022

利益争夺: 作者有
声明不存在竞争利益
存在.

通讯作者:
Bratislav Misic
bratislav.misic@mcgill.ca

处理编辑器:
Sean Hill

版权: © 2022
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Structure- and geometry-informed functional connectivity

介绍

结构连接:
Anatomical projections between
neural elements.

Functional connectivity:
Temporal coactivation among neural
元素.

Axonal wiring among neurons and neuronal populations promotes signal exchange and informa-
tion integration. At the mesoscale, signaling via the complex network of structural connectivity
(SC) manifests as patterns of temporal correlations, termed functional connectivity (FC).
Functional connectivity is highly organized (Bellec, Rosa-Neto, Lyttelton, Benali, & 埃文斯,
2010; Damoiseaux et al., 2006; Yeo et al., 2011), reproducible (Gordon et al., 2017; 高贵,
Scheinost, & Constable, 2019), and related to individual differences in behaviour (Mišić &
斯波恩斯, 2016; 史密斯等人。, 2015).

Monosynaptic:
Communication between neural
elements via a direct anatomical
投影.

Polysynaptic:
Communication between neural
elements via a sequence of multiple
anatomical projections and
intermediate neural elements.

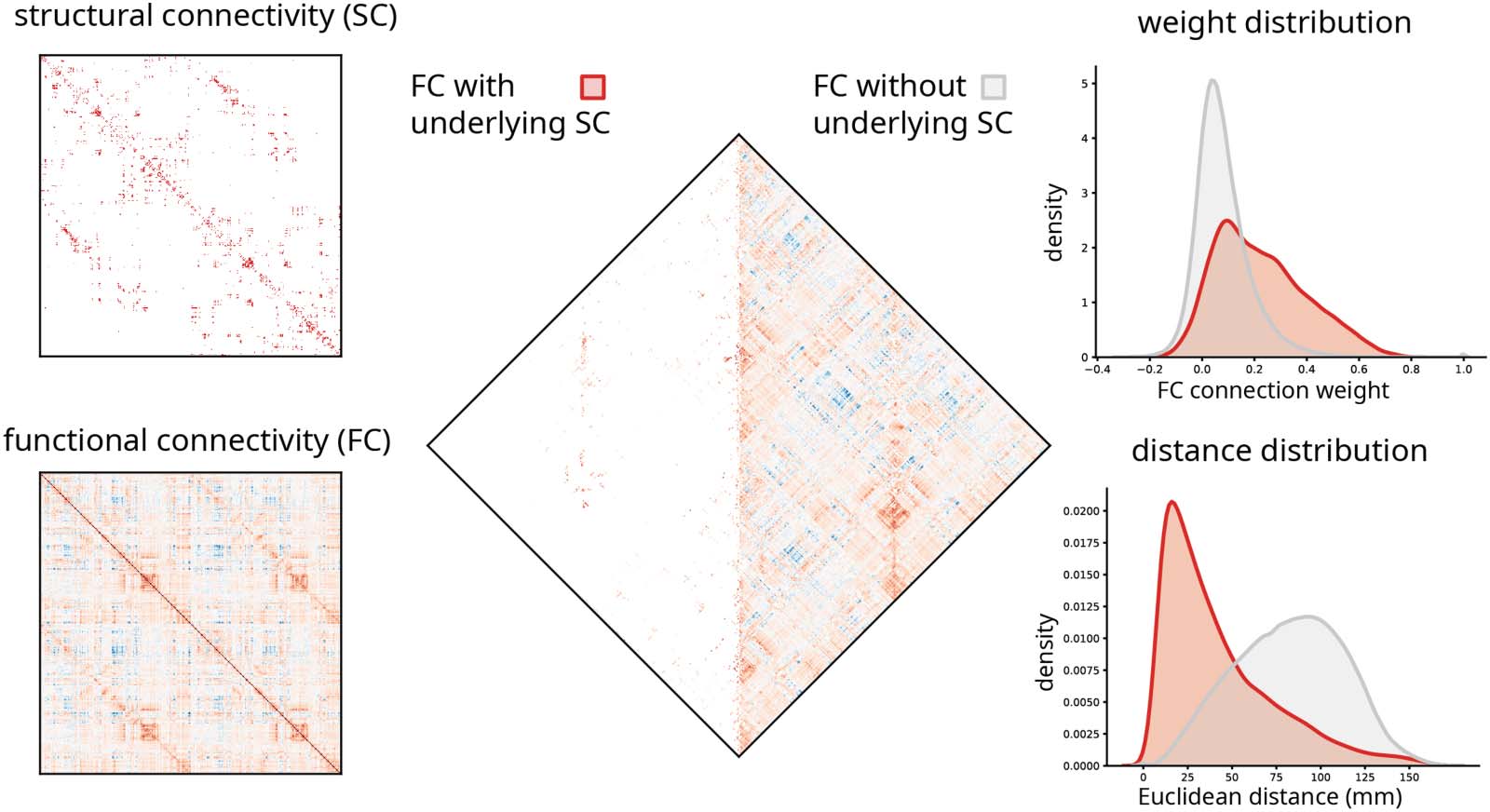
Most pairwise functional connections are not supported by a direct structural connection.
By definition, functional networks are fully connected, while structural networks are sparse
(数字 1). Across species, reconstruction techniques, and spatial scales, structural connection
density is typically reported to be between 2% 和 40% (Van den Heuvel, 布莫尔, & 斯波恩斯,
2016) (but see also Markov et al., 2013), meaning that the majority of functional connections
between two regions are not accompanied by a corresponding monosynaptic structural con-
nection. These “indirect” functional connections are thought to emerge from polysynaptic
communication in the structural network (Bazinet, Vos de Wael, 哈格曼, Bernhardt, &
Misic, 2021; Suárez, Markello, 贝策尔, & Misic, 2020).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

重要的, structural and functional connectivity are fundamentally constrained by the
spatial embedding of brain regions (Stiso & Bassett, 2018). Structural connection probability
is inversely correlated with spatial separation, such that proxmimal neural elements are more
likely to be structurally connected, while distant neural elements are less likely to be con-
nected (Horvát et al., 2016; 马尔可夫等人。, 2013; Roberts et al., 2016). A similar distance
dependence is also observed for functional connectivity (Margulies et al., 2016; Mišić et al.,
2014; Salvador et al., 2005; Sepulcre et al., 2010). The overrepresentation of low-cost, short-
range connections is thought to reflect finite material and metabolic resources (数字 1)
(布莫尔 & 斯波恩斯, 2012). Altogether, structural connectivity and spatial proximity constitute
a natural frame of reference for understanding and interpreting functional connectivity.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Functional connections with and without direct structural links. 左边: 结构连接 (SC) and functional connectivity (FC)
数字 1.
matrices in the 1,000-node Lausanne parcellation (Cammoun et al., 2012). 中间: Functional connections with and without underlying struc-
tural connections. 正确的: The weight and anatomical (Euclidean) distance distribution of the two types of functional connections.

网络神经科学

938

Structure- and geometry-informed functional connectivity

Intrinsic networks:
Subnetworks of brain areas with
coherent time courses, identified by
clustering, independent component
分析, or community detection.

Cortical hierarchy:
A continuous axis separating
unimodal sensory-motor cortex from
transmodal association cortex.

Here we investigate the organization of functional connections without direct structural
links (数字 1). We develop a simple method that uses robust relationships between geometry,
结构, and function as the baseline to reweigh and reexpress functional connectivity. 我们
use the method to identify functional connections that are greater than expected given their
structural and geometric embedding. We then show that the arrangement of these connections
systematically follows the functional modules (intrinsic networks) (Yeo et al., 2011) 和
putative unimodal-transmodal hierarchy of the brain (Margulies et al., 2016).

结果

The results are organized as follows. We first establish a method to quantify how unexpectedly
strong a functional connection is given the physical Euclidean distance between its connected
地区. We then describe the organizational principles of these structurally unconnected func-
tional connections by characterizing their (1) statistical properties, (2) correspondence with
intrinsic networks, 和 (3) correspondence with the cortical hierarchy. Data sources include
(see Materials and Methods for detailed procedures):

▪ Structural connectivity. Structural and functional connectivity were derived from N = 66
healthy control participants (来源: Lausanne University Hospital; https://doi.org/10
.5281/zenodo.2872624) using the 1,000-node Lausanne parcellation (Cammoun et al.,
2012). Participants were randomly divided into a Discovery and Validation cohort (N=
33 each). Structural connectivity was reconstructed using diffusion spectrum imaging
and deterministic streamline tractography. A consistency- and length-based procedure
was then used to assemble a group-representative structural connectivity matrix (贝策尔,
Griffa, 哈格曼, & Mišić, 2018; Mišić et al., 2015, 2018).

▪ Functional connectivity. Functional connectivity was estimated in the same individuals
by using resting-state functional MRI (rs-fMRI). A functional connectivity matrix was con-
structed using pairwise Pearson correlations among regional time courses. A group-
average functional connectivity matrix was then estimated as the mean connectivity of
pairwise connections across individuals.

Long-Range Functional Connections Are Unexpectedly Strong

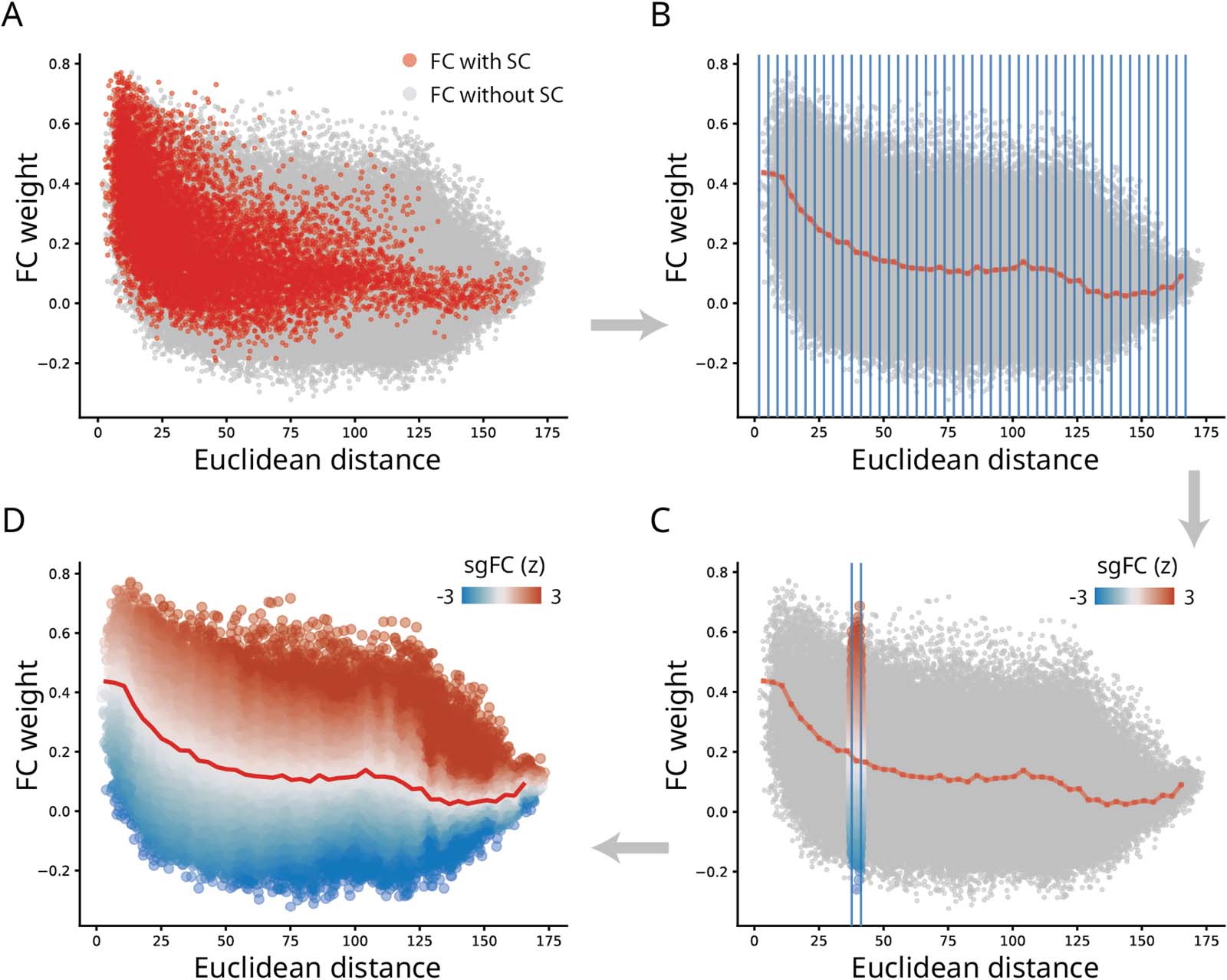
To quantify how unexpectedly strong a functional connection is, we first seek to establish a
基线 (for a conceptually similar approach, see Roberts et al., 2016). Figure 2A shows the
relationship between the spatial separation of two nodes (横坐标) and the functional con-
nectivity between them (纵坐标). Functional connections that are supported by an under-
lying structural connection are shown in red, and all other functional connections, 我们
refer to as indirect or structurally unconnected FCs, are shown in gray. We note the classical
exponential decrease in magnitude with increasing spatial separation (Roberts et al., 2016;
Stiso & Bassett, 2018). We also note that connected (monosynaptic) and unconnected (poly-
synaptic) FCs have similar distributions at short distances, but that they diverge considerably
at long distances. 即, when the spatial separation between two regions is greater than
大约 125 毫米, there is greater variability among unconnected FCs, with many
unconnected FCs marked by greater magnitude than connected FCs spanning comparable
distances.

We therefore set the magnitude of connected FCs at a given distance as the baseline for
unconnected FCs at a comparable distance. The goal is to identify unconnected FCs that
are unexpectedly large relative to connected FCs. To operationalize this intuition, we first

网络神经科学

939

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Structure- and geometry-informed functional connectivity

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

数字 2. Benchmarking functional connectivity by structure and geometry. (A) FC connection weight-to-distance relationship shown for FC
和 (红色的) and without (gray) direct SC connections, 分别. (乙) FCs grouped into distances bins (blue lines), and the mean value within
each bin of those with direct SCs (dotted red line). (C) Within a sample bin, unconnected (polysynaptic) FCs are expressed as a z-score relative
to connected (monosynaptic) FCs. We refer to this z-score as structure- and geometry-informed FC (sgFC). (D) sgFCs shown as a smoothly-
transitioning spectrum after the procedure is applied for each distance bin. See Methods for more technical details and Supporting Information
Figure S2 for details about smoothing and bin size selection.

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

bin FCs according to their spatial proximity (图2B). Within each bin, we record the dis-
tribution of connected FCs, including their mean and standard deviation. 最后, we express
each unconnected FC as a z-score relative to the distribution of connected FCs in the same
distance bin (Figure 2C). This measure reflects how unexpectedly strong a functional connec-
化是, given its length. 重要的, z-scores for unconnected FCs are estimated based on
moments of a distribution estimated for connected FCs. For simplicity, we term the reexpressed
unconnected FCs as structure- and geometry-informed FC (sgFC).

Figure 2D shows the reweighing of unconnected FCs. Across the entire range of distances,
there exist many unconnected FCs that are disproportionately strong relative to their length. A
population of unconnected positive FCs spanning distances greater than 125 mm are partic-
ularly prominent, suggesting the existence of multiple strong functional interactions above and
beyond what would be expected on the basis of their length. Values of sgFC have a distribution
centered around zero, with a long positive tail (Supporting Information Figure S1). 在里面
following sections we explore the organization of these connections in greater detail. 为了
sensitivity analyses regarding bin sizes, preprocessing choices and validation, please see
Control Analyses section and Supporting Information Figures S2 and S3. For replication in
individual participants, see Supporting Information Figure S4.

网络神经科学

940

Structure- and geometry-informed functional connectivity

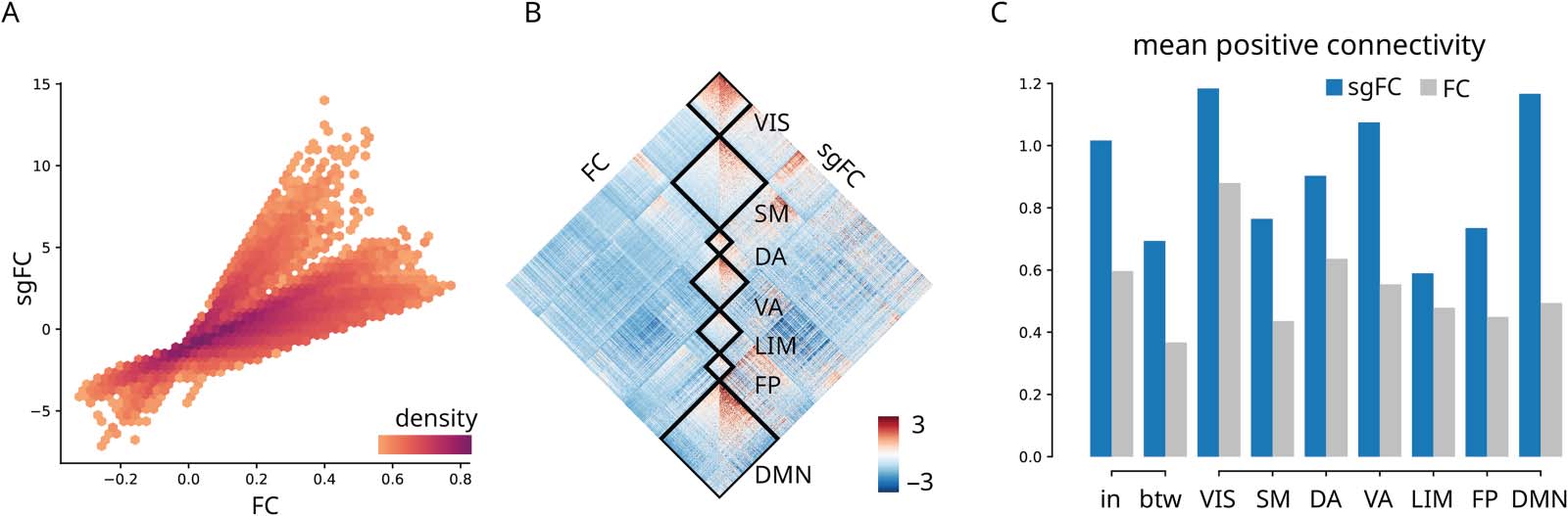
数字 3. Contribution to intrinsic network architecture. (A) sgFC correlated with FC, colored by scatter density. Only polysynaptic FCs are
显示. (乙) FC and sgFC shown side-by-side, reordered according intrinsic networks (Yeo et al., 2011). VIS = visual; SM = somatomotor; DA =
dorsal attention; VA = ventral attention; LIM = limbic; FP = frontoparietal; DMN = default mode. (C) Comparison of within- 和之间-
network mean positive-valued connectivity with a dissection of within-network connectivity for intrinsic networks. (sgFC to FC ratios: in =
1.70; betw = 1.89; VIS = 1.35; SM = 1.75; DA = 1.42; VA = 1.94; LIM = 1.23; FP = 1.63; DMN = 2.36). In panels B and C, polysynaptic FCs are
standardized by the overall average and standard deviation of FCs with direct SCs to facilitate comparison.

Contribution to Intrinsic Network Architecture

We first ask how conventional FC and sgFC are related to each other and how they are dis-
tributed within and between intrinsic functional networks (Yeo et al., 2011). Figure 3A shows
the correlation between FC and sgFC connection weights. 正如预期的那样, the reweighing of FCs
accentuates some connections and attenuates others. Supporting Information Figure S5 shows
that long-distance connections tend to be stronger than expected, confirming the intuition
developed in the previous subsection (数字 2).

To investigate whether the reweighing of FCs reflects any organizational features of the
脑, we first display FC and sgFC, now reordered by the canonical intrinsic networks
(Figure 3B) (Yeo et al., 2011). To facilitate comparison, we standardize polysynaptic FCs by
the overall average and standard deviation of FCs with direct SCs, which can be seen as FC
informed by structure but not by geometry or distance. 有趣的是, the largest differences
between uncorrected and corrected FCs are observed within transmodal networks (default
mode and ventral attention), while more modest differences are observed in the unimodal net-
作品 (visual and somatomotor) (Figure 3C). This suggests that unexpectedly strong FCs may
occur more frequently between brain regions at the apex of the unimodal-transmodal cortical
等级制度. We investigate this possibility in the next section.

Contribution to the Cortical Hierarchy

We next investigate the arrangement of unconnected FCs in macroscale cortical hierarchies.
Recent work suggests that the functional architecture of human brain networks can be sum-
marized by a small number of smooth topographic gradients, with the most prominent such
gradient spanning unimodal to transmodal cortex (Margulies et al., 2016). This putative hier-
archy is thought to support a sensory-fugal representational hierarchy (Mesulam, 1998) 和
correlates with spatial variation in cytoarchitecture (Paquola et al., 2019), myelination
(Huntenburg et al., 2017), and gene expression (Burt et al., 2018).

To place each cortical node along this putative hierarchy, we adapted the diffusion embed-
ding method described by Margulies and colleagues (Coifman et al., 2005; Margulies et al.,
2016; Vázquez-Rodríguez et al., 2019) (see Materials and Methods for more detail). Figure 4A
shows the topography of the first gradient, differentiating primary sensory and transmodal cor-
泰斯, replicating the original report (Margulies et al., 2016).

网络神经科学

941

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Structure- and geometry-informed functional connectivity

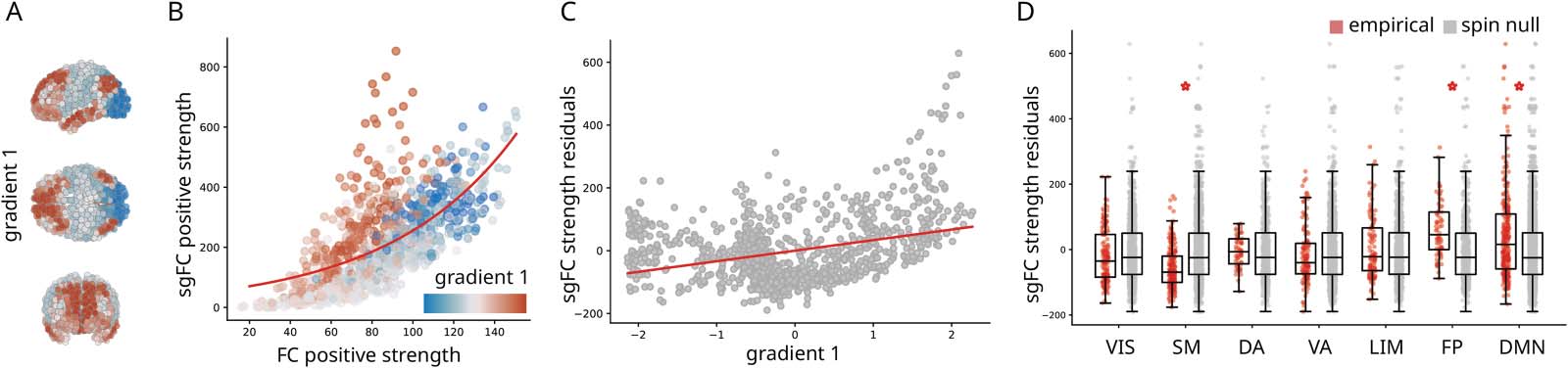
数字 4. Contribution to the cortical hierarchy. (A) First principal connectivity gradient estimated using diffusion map embedding applied to
the FC matrix (Margulies et al., 2016). Cold colors indicate unimodal regions and warmer colors indicate transmodal regions. (乙) Correlation of
positive strengths (sum of all weights incident on a given node) between sgFC and FC. Points are regions and are colored by their position in
the unimodal-transmodal gradient. An exponential curve is fitted to the points (红线). (C) Residuals of the fitted curve in panel B correlated
with gradient 1. (D) Residuals grouped by intrinsic networks and benchmarked against spatial autocorrelation-preserving null models
(Alexander-Bloch et al., 2018; Markello & Misic, 2021). Statistically significant differences (with Bonferroni correction) are marked with a
red asterisk.

To assess the hypothesis that unexpectedly strong FCs are more concentrated in transmodal
cortex, we first compare node strengths (the sum of all weights incident on a given region)
computed using FC and sgFC. Figure 4B shows the relationship between node strength for
the original FC matrix and for the sgFC matrix. Nodes are coloured by their position in the
等级制度 (gradient 1; red = transmodal, blue = unimodal). The relationship is well-fit by an
exponential function ( y = ex; R2 = 0.44). 重要的, a cloud of red points are consistent out-
绑定, residing above the curve. 换句话说, brain regions at the apex of the hierarchy are
more likely to participate in unexpectedly strong functional interactions.

We further confirm the link between the cortical hierarchy and unexpectedly strong FCs by
computing the residual of each node relative to the exponential trend shown in Figure 4C
(皮尔逊 r = 0.34). Large positive residuals indicate that the node is disproportionately central
in the sgFC functional network. Mean residuals for each intrinsic network, ordered by the
unimodal-transmodal hierarchy, are shown in Figure 4D. The greatest increases appear in
额顶叶 (T = 5.96, p = 1.26 × 10−7, d = 0.62) and default mode networks (T =
5.45, p = 1.13 × 10−7, d = 0.42), when compared to a null model that permutes region labels
while preserving their spatial autocorrelation (Alexander-Bloch et al., 2018; Markello & Misic,
2021). Collectively, these results show that transmodal cortex participates in polysynaptic FCs
that are stronger than expected given their length.

Control Analyses

The results presented in the preceding subsections are potentially contingent on a number of
methodological choices, which we explore in detail here. We first replicate the major
findings—the distribution of sgFC weights and their involvement in cortical hierarchies—in
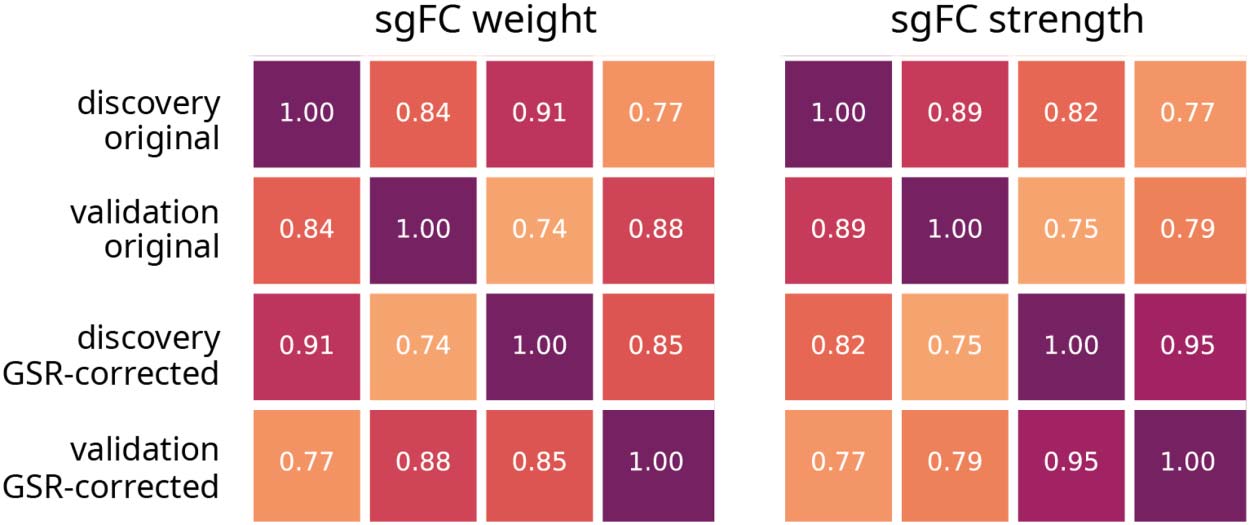
a validation cohort constructed from N = 33 参与者. 数字 5 shows the Pearson corre-
lation of the two results in the Discovery and Validation cohorts (see Supporting Information
Figure S3 for reproduced result figures). The correlation coefficients for both measures are
greater than 0.8 in all cases.

We next seek to determine the extent to which global signal regression could influence the
发现. This particular preprocessing step induces negative correlations in FC, profoundly
changing the distribution of weights (Aquino, Fulcher, Parkes, Sabaroedin, & 假如, 2020;
墨菲 & 狐狸, 2017). We regenerated regional time series, correcting for fluctuations in
the global signal, and repeated the analysis. 数字 5 shows the effects of the procedure, 在
both the Discovery and Validation cohorts (Supporting Information Figure S3). As before, 那里

Global signal:
The mean time course computed
over all voxels within the brain.

网络神经科学

942

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Structure- and geometry-informed functional connectivity

数字 5. Validation and global signal removal. Correlation matrices shown for sgFC weight
(values in Figure 2D) and sgFC positive node strength (values in Figure 4B) between controls. Values
of sgFC are calculated from Discovery and Validation datasets, with and without global signal
regression (GSR). Reproduced Figure 2D and Figure 4B with these values are shown in Supporting
Information Figure S3.

appears to be minimal change in the results, with correlations at approximately 0.9 (为了
重量) 和 0.8 (for strength). 此外, correlations between data cohorts with different
加工 (例如, Discovery set with no global signal regression correlated with Validation
set with global signal regression) were also greater than 0.75.

讨论

In the present report we introduce a simple data-driven method to benchmark functional
connections with respect to their underlying structural and geometric embedding. We find
evidence for unexpectedly strong functional connectivity among transmodal brain regions.
These results suggest a hidden but highly organized pattern among polysnaptic FCs.

Our findings build on an emerging literature about the importance of geometry and struc-
tural connectivity for functional connectivity in the brain. Although the effect of spatial prox-
imity on the probability and weight of connections is well known (Horvát et al., 2016; 罗伯茨
等人。, 2016), in practice it is less obvious how this information should be taken into account
when representing functional connectivity. 同样地, multiple studies report significant corre-
lations between structural and functional connectivity between regions that share direct struc-
tural links (Honey et al., 2009), but how polysynaptic or multihop structural connectivity
shapes functional connectivity is less well known. 的确, computational models of
structure-function coupling tend to perform more poorly when predicting functional connec-
tions between regions that are not structurally connected (Goñi et al., 2014). More recent
communication models of structure-function coupling explicitly account for polysynaptic
沟通 (Seguin, Tian, & 扎莱斯基, 2020; Vázquez-Rodríguez, 刘, 哈格曼, & Misic,
2020). Here we show that information about structural connectivity and spatial proximity can
be naturally used as a frame of reference to describe functional connectivity between regions
without direct structural connections.

有趣的是, we find that unexpectedly strong FCs are highly organized with respect to the
modular (斯波恩斯 & 贝策尔, 2016) and hierarchical (Huntenburg et al., 2017) organization of
大脑. Although both modules and hierarchies or “gradients” are robust and well-studied
features of functional networks, their anatomical origin is less clear (Suárez et al., 2020). 我们的
results suggest that both phenomena emerge from functional interactions or coactivations that
transcend the underlying structure and geometry. 换句话说, this class of polysynaptic

网络神经科学

943

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Structure- and geometry-informed functional connectivity

functional connections may be physiologically unique, and future empirical and theoretical
studies could potential stratify direct and indirect FCs prior to analysis.

The fact that unexpectedly strong FCs are overrepresented in transmodal cortex may poten-
tially explain recent reports that structure-function relationships are regionally heterogeneous.
即, multiple reports have found that structure-function coupling is greater in unimodal
cortex and smaller in transmodal cortex (Baum et al., 2020; Bazinet et al., 2021; Esfahlani,
Faskowitz, Slack, Mišić, & 贝策尔, 2021; Gu, Jamison, 肥皂, & Kuceyeski, 2021; Preti &
Ville, 2019; Vázquez-Rodríguez et al., 2019; 王等人。, 2019). Our results suggest that the
reason for this heterogeneity is that regions in transmodal cortex tend to participate in poly-
synaptic functional connections that are much stronger than expected given the underlying
anatomical constraints. 因此, models relating structural and functional connectivity
may be disadvantaged when applied to transmodal cortex relative to unimodal cortex.

更普遍, the present framework is part of an emerging literature on simultaneously
representing and modeling brain geometry, structure and function. A natural extension of sgFC
is in the domain of spatially embedded null models that generate surrogate structural or func-
tional networks to benchmark the presence of specific network attributes (Esfahlani, Bertolero,
Bassett, & 贝策尔, 2020; Roberts et al., 2016). 而且, sgFC may also serve as a quality func-
tion for generative models of connectivity (Akarca, Vértes, 布莫尔, & Astle, 2021; 贝策尔
等人。, 2016; Oldham et al., 2021; Shinn et al., 2021; Vértes et al., 2012). 最后, we envision
sgFC as the basis for more sophisticated network communication models that consider spatial
proximity as a constraint for routing signals (Seguin, Razi, & 扎莱斯基, 2019; Seguin, van den
爬坡道, & 扎莱斯基, 2018; Vázquez-Rodríguez et al., 2020). While these models traditionally
focus only on spatial proximity, sgFC opens the possibility for a hybrid approach that takes into
account structural connectivity and geometry.

The present results also need to be interpreted with respect to several methodological con-
siderations. Despite the fact that we adopted a robust dataset and included a replication sec-
的, methodological choices including MRI acquisition scheme, processing pipeline, 网络
reconstruction, and group consensus algorithm may still be susceptible to false positives and
negatives (Jiang et al., 2021; 科尔霍宁, Zanin, & Papo, 2021; Maier-Hein et al., 2017; 萨瓦尔,
你的兄弟, & 扎莱斯基, 2021). 尤其, the deterministic tractography procedure
yields relatively sparse connectomes, and future work should consider the effect of connec-
tome reconstruction and sparsity on the definition of polysynaptic FCs. 此外, systematic
false positives or false negatives in connectome reconstruction could potentially emphasize or
mask some classes of connections, such as long-distance connections. 在这个意义上, the sgFC
procedure developed here presents a framework to comprehensively compare multiple trac-
tography pipelines with each other.

总之, we show how fundamental structural and geometric priors can be used to
reweigh and re-represent the functional connectivity matrix. Our results show that the canonical
features of functional connectivity—modules and hierarchies—are delineated by unexpectedly
strong functional connections between nodes without underlying structural links. The biological
origin of this class of connections remains an exciting question for future research.

材料和方法

Data Acquisition

A total of N = 66 healthy young adults (16 女性, 25.3 ± 4.9 years old) were scanned at the
放射科, University Hospital Center and University of Lausanne. The scans

网络神经科学

944

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Structure- and geometry-informed functional connectivity

were performed in 3-Tesla MRI scanner (Trio, Siemens Medical, 德国) using a 32-channel
head-coil. The protocol included (1) a magnetization-prepared rapid acquisition gradient echo
(MPRAGE) sequence sensitive to white/gray matter contrast (1-mm in-plane resolution,
1.2-mm slice thickness), (2) a diffusion spectrum imaging (DSI) 顺序 (128 扩散-
weighted volumes and a single b0 volume, maximum b-value 8,000 秒/毫米2, 2.2 × 2.2 ×
3.0 mm voxel size), 和 (3) a gradient echo EPI sequence sensitive to BOLD contrast
(3.3-mm in-plane resolution and slice thickness with a 0.3-mm gap, TR 1,920 多发性硬化症, resulting
在 280 images per participant). Participants were not subject to any overt task demands during
the fMRI scan.

Structural Network Reconstruction
Gray matter was parcellated into 68 cortical nodes according to the Desikan–Killiany atlas
(Desikan et al., 2006). These regions of interest were then further divided into four additional,
increasingly finer grained resolutions, comprising 114, 219, 448, 和 1,000 大约
equally-sized nodes (Cammoun et al., 2012). Structural connectivity was estimated for indi-
vidual participants by using deterministic streamline tractography. The procedure was imple-
mented in the Connectome Mapping Toolkit (Daducci et al., 2012), initiating 32 streamline
propagations per diffusion direction for each white matter voxel.

To mitigate concerns about inconsistencies in reconstruction of individual participant con-
nectomes (琼斯, 克诺舍, & 车工, 2013; 托马斯等人。, 2014), as well as the sensitive
dependence of network measures on false positives and false negatives (Zalesky et al.,
2016), we adopted a group-consensus approach (Betzel et al., 2018; de Reus & van den
爬坡道, 2013; 罗伯茨, Perry, 罗伯茨, 米切尔, & Breakspear, 2017). In constructing a con-
sensus adjacency matrix, we sought to preserve (1) the density and (2) the edge length distri-
bution of the individual participants matrices (Betzel et al., 2016, 2018; Mišić et al., 2015). 我们
first collated the extant edges in the individual participant matrices and binned them according
to length. The number of bins was determined heuristically, as the square root of the mean
binary density across participants. The most frequently occurring edges were then selected
for each bin. If the mean number of edges across participants in a particular bin is equal to
k, we selected the k edges of that length that occur most frequently across participants. 到
ensure that interhemispheric edges are not under-represented, we carried out this procedure
separately for inter- and intrahemispheric edges. The binary density for the final whole-brain
matrix was around 2.1%.

Functional Network Reconstruction

Functional MRI data were preprocessed using procedures designed to facilitate subsequent
network exploration (力量, 巴恩斯, 斯奈德, 施拉加尔, & 彼得森, 2012). fMRI volumes were
corrected for physiological variables, including regression of white matter, cerebrospinal fluid,
as well as motion (three translations and three rotations, estimated by rigid body coregistra-
的). BOLD time series were then subjected to a low-pass filter (temporal Gaussian filter with
full width half maximum equal to 1.92 s). The first four time points were excluded from sub-
sequent analysis to allow the time series to stabilize. Motion “scrubbing” was performed as
described by Power and colleagues (Power et al., 2012). The data were parcellated according
to the same atlas used for structural networks (Cammoun et al., 2012). Individual functional
connectivity matrices were defined as zero-lag Pearson correlation among the fMRI BOLD
time series. A group-consensus functional connectivity matrix was estimated as the mean
connectivity of pairwise connections across individuals.

网络神经科学

945

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Structure- and geometry-informed functional connectivity

Structure- and Geometry-Informed Indirect FC Modeling

To construct the structure- and geometry-informed FC (sgFC), we apply equally spaced bins to
the dimension of Euclidean distance. In each bin, we acquire the mean and standard deviation
of those FCs with direct SC link. Then we take the z-score of FCs without direct SC link using
the acquired statistics. The final z-scores are smoothed to get a robust representation by
averaging over a spectrum of bin numbers (±25%) centering the optimal bin size decided
by Freedman Diaconis Estimator shown in Supporting Information Figure S2. The resulting
sgFC values corresponding to those without direct SC link are mapped back to a 1,000-by-
1,000 matrix and used for network analysis through the article.

Diffusion Map Embedding

Diffusion map embedding is a nonlinear dimensionality reduction algorithm (Coifman et al.,
2005). The algorithm seeks to project a set of embeddings into a lower dimensional Euclidean
空间. Briefly, the similarity matrix among a set of points (in our case, the correlation matrix rep-
resenting functional connectivity) is treated as a graph, and the goal of the procedure is to iden-
tify points that are proximal to one another on the graph. 换句话说, two points are close
together if there are many relatively short paths connecting them. A diffusion operator, represent-
ing an ergodic Markov chain on the network, is formed by taking the normalized graph Lapla-
cian of the matrix. The new coordinate space is described by the eigenvectors of the diffusion
操作员. We set the diffusion rate α = 1 and the variance of the Gaussian used in affinity com-
putation σ = 1. The procedure was implemented using the Dimensionality Reduction Toolbox
(https://lvdmaaten.github.io/drtoolbox/) (Van Der Maaten, Postma, & Van den Herik, 2009).

致谢

We thank Justine Hansen, Vincent Bazinet, Golia Shafiei, Estefany Suarez, Andrea Luppi, 和
Filip Milisav for their comments and suggestions on the manuscript.

SUPPORTING INFORMATION

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00236.

作者贡献

Zhen-Qi Liu: 概念化; 形式分析; 方法; 可视化; Writing—Original
草稿. Richard F. 贝策尔: 形式分析; Writing—Review & 编辑. Bratislav Misic: Concep-
实体化; 方法; 监督; Writing—Original draft; Writing—Review & 编辑.

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

资金信息

Bratislav Misic, Canada First Research Excellence Fund (https://dx.doi.org/10.13039
/501100010785). Bratislav Misic, Natural Sciences and Engineering Research Council of
加拿大 (NSERC Discovery Grant), 奖项ID: 017-04265. Bratislav Misic, Canada Research
Chairs (https://dx.doi.org/10.13039/501100001804). 奖项ID: SFB 936/Z3.

参考

Akarca, D ., Vértes, 磷. E., 布莫尔, 乙. T。, & Astle, D. 乙. (2021). A gen-
erative network model of neurodevelopmental diversity in struc-
tural brain organization. Nature Communications, 12(1), 4216.
https://doi.org/10.1038/s41467-021-24430-z, 考研: 34244490

Alexander-Bloch, A. F。, Shou, H。, 刘, S。, Satterthwaite, 时间. D .,
Glahn, D. C。, 筱原, 右. T。, … Raznahan, A. (2018). 在
testing for spatial correspondence between maps of human
brain structure and function. 神经影像, 178, 540–551.

网络神经科学

946

Structure- and geometry-informed functional connectivity

https://doi.org/10.1016/j.neuroimage.2018.05.070, 考研:
29860082

Aquino, K. M。, Fulcher, 乙. D ., Parkes, L。, Sabaroedin, K., & 假如,
A. (2020). Identifying and removing widespread signal deflec-
tions from fMRI data: Rethinking the global signal regression
问题. 神经影像, 212, 116614. https://doi.org/10.1016/j
.neuroimage.2020.116614, 考研: 32084564

Baum, G. L。, Cui, Z。, Roalf, D. R。, Ciric, R。, 贝策尔, 右. F。, Larsen, B.,
… Satterthwaite, 时间. D. (2020). Development of structure–function
coupling in human brain networks during youth. 会议记录
the National Academy of Sciences of the United States of Amer-
伊卡, 117(1), 771–778. https://doi.org/10.1073/pnas.1912034117,
考研: 31874926

Bazinet, 五、, Vos de Wael, R。, 哈格曼, P。, Bernhardt, 乙. C。, &
Misic, 乙. (2021). Multiscale communication in cortico-cortical
网络. 神经影像, 243, 118546. https://doi.org/10.1016/j
.neuroimage.2021.118546, 考研: 34478823

Bellec, P。, Rosa-Neto, P。, Lyttelton, 氧. C。, Benali, H。, & 埃文斯, A. C.
(2010). Multi-level bootstrap analysis of stable clusters in
resting-state fMRI. 神经影像, 51(3), 1126–1139. https://土井
.org/10.1016/j.neuroimage.2010.02.082, 考研: 20226257
贝策尔, 右. F。, Avena-Koenigsberger, A。, 戈尼, J。, 他, Y。, De Reus,
中号. A。, Griffa, A。, … Sporns, 氧. (2016). Generative models of the
human connectome. 神经影像, 124, 1054–1064. https://土井
.org/10.1016/j.neuroimage.2015.09.041, 考研: 26427642
贝策尔, 右. F。, Griffa, A。, 哈格曼, P。, & Mišić, 乙. (2018). Distance-
dependent consensus thresholds for generating group-
representative structural brain networks. 网络神经科学,
3(2), 475–496. https://doi.org/10.1162/netn_a_00075, 考研:
30984903

布莫尔, E., & 斯波恩斯, 氧. (2012). The economy of brain network
组织. 自然评论神经科学, 13(5), 336–349.
https://doi.org/10.1038/nrn3214, 考研: 22498897

Burt, J. B., Demirtaş, M。, Eckner, 瓦. J。, Navejar, 氮. M。, 吉, J. L。,
马丁, 瓦. J。, … Murray, J. D. (2018). Hierarchy of transcriptomic
specialization across human cortex captured by structural neuro-
imaging topography. 自然神经科学, 21(9), 1251–1259.
https://doi.org/10.1038/s41593-018-0195-0 , 考研:
30082915

卡蒙, L。, 巨人, X。, Meskaldji, D ., Thiran, J. P。, 斯波恩斯, 奥。,
做, K. Q., … Hagmann, 磷. (2012). Mapping the human connec-
tome at multiple scales with diffusion spectrum MRI. 杂志
Neuroscience Methods, 203(2), 386–397. https://doi.org/10.1016
/j.jneumeth.2011.09.031, 考研: 22001222

Coifman, 右. R。, Lafon, S。, 李, A. B., Maggioni, M。, Nadler, B.,
华纳, F。, & Zucker, S. 瓦. (2005). Geometric diffusions as a tool
for harmonic analysis and structure definition of data: Diffusion
地图. 美国国家科学院院刊
美国, 102(21), 7426–7431. https://doi.org
/10.1073/普纳斯.0500334102, 考研: 15899970

Daducci, A。, Gerhard, S。, Griffa, A。, Lemkaddem, A。, 卡蒙, L。,
巨人, X。, … Thiran, J.-P. (2012). The connectome mapper: 一个
open-source processing pipeline to map connectomes with MRI.
公共图书馆一号, 7(12), e48121. https://doi.org/10.1371/journal.pone
.0048121, 考研: 23272041

Damoiseaux, J。, Rombouts, S。, Barkhof, F。, Scheltens, P。, 斯塔姆, C。,
史密斯, S. M。, & 贝克曼, C. (2006). Consistent resting-state
networks across healthy subjects. 国家会议录

美国科学院, 103(37),
13848–13853. https://doi.org/10.1073/pnas.0601417103,
考研: 16945915

de Reus, 中号. A。, & van den Heuvel, 中号. 磷. (2013). Estimating false
positives and negatives in brain networks. 神经影像, 70,
402–409. https://doi.org/10.1016/j.neuroimage.2012.12.066,
考研: 23296185

Desikan, 右. S。, Ségonne, F。, 菲舍尔, B., 奎因, 乙. T。, Dickerson,
乙. C。, Blacker, D ., … Killiany, 右. J. (2006). An automated labeling
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. 神经影像, 31(3), 968–980.
https://doi.org/10.1016/j.neuroimage.2006.01.021, 考研:
16530430

Esfahlani, F. Z。, Bertolero, 中号. A。, Bassett, D. S。, & 贝策尔, 右. F. (2020).
Space-independent community and hub structure of functional
brain networks. 神经影像, 211, 116612. https://doi.org/10
.1016/j.neuroimage.2020.116612, 考研: 32061801

Esfahlani, F. Z。, Faskowitz, J。, Slack, J。, Mišić, B., & 贝策尔, 右. F.
(2021). Local structure-function relationships in human brain
networks across the human lifespan. bioRxiv. https://doi.org/10
.1101/2021.05.23.445128

戈尼, J。, van den Heuvel, 中号. P。, Avena-Koenigsberger, A。, 的
Mendizabal, 氮. 五、, 贝策尔, 右. F。, Griffa, A。, … Sporns, 氧.
(2014). Resting-brain functional connectivity predicted by ana-
lytic measures of network communication. 诉讼程序
美国国家科学院,
111(2), 833–838. https://doi.org/10.1073/pnas.1315529111,
考研: 24379387

Gordon, 乙. M。, 劳曼, 时间. 奥。, Gilmore, A. W., Newbold, D. J。,
Greene, D. J。, 伯格, J. J。, … Dosenbach, 氮. U. F. (2017). Precision
functional mapping of individual human brains. 神经元, 95(4),
791–807. https://doi.org/10.1016/j.neuron.2017.07.011,
考研: 28757305

Gu, Z。, Jamison, K. W., 肥皂, 中号. R。, & Kuceyeski, A. (2021).
Heritability and interindividual variability of regional structure-
function coupling. Nature Communications, 12(1), 4894. https://
doi.org/10.1038/s41467-021-25184-4, 考研: 34385454

蜂蜜, C. J。, 斯波恩斯, 奥。, 卡蒙, L。, 巨人, X。, Thiran, J. P。,
买, R。, & 哈格曼, 磷. (2009). Predicting human resting-state
functional connectivity from structural connectivity. 会议记录
of the National Academy of Sciences of the United States of
美国, 106(6), 2035–2040. https://doi.org/10.1073/pnas
.0811168106, 考研: 19188601

Horvát, S。, Gămănut, R。, Ercsey-Ravasz, M。, Magrou, L。, Gămănut,
B., Van Essen, D. C。, … Kennedy, H. (2016). Spatial embedding
and wiring cost constrain the functional layout of the cortical net-
work of rodents and primates. 公共科学图书馆生物学, 14(7), e1002512.
https://doi.org/10.1371/journal.pbio.1002512, 考研:
27441598

Huntenburg, J. M。, Bazin, P.-L., Goulas, A。, Tardif, C. L。, 狂野的召唤者,
A。, & 马古利斯, D. S. (2017). A systematic relationship between
functional connectivity and intracortical myelin in the human
cerebral cortex. 大脑皮层, 27(2), 981–997. https://doi.org
/10.1093/cercor/bhx030, 考研: 28184415

Jiang, C。, 贝策尔, R。, 他, Y。, 王, Y.-S., Xing, X.-X., & Zuo, X.-N.
(2021). Toward reliable network neuroscience for mapping indi-
vidual differences. bioRxiv. https://doi.org/10.1101/2021.05.06
.442886

网络神经科学

947

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Structure- and geometry-informed functional connectivity

琼斯, D ., 克诺舍, T。, & 车工, 右. (2013). White matter integrity,
fiber count, and other fallacies: The do’s and don’ts of diffusion
MRI. 神经影像, 73, 239–254. https://doi.org/10.1016/j
.neuroimage.2012.06.081, 考研: 22846632

科尔霍宁, 奥。, Zanin, M。, & Papo, D. (2021). Principles and open
questions in functional brain network reconstruction. 人类
Brain Mapping, 42(11), 3680–3711. https://doi.org/10.1002
/hbm.25462, 考研: 34013636

迈尔-海因, K. H。, Neher, 磷. F。, Houde, J.-C., Côté, M.-A., Garyfallidis,
E., Zhong, J。, … Descoteaux, 中号. (2017). The challenge of mapping
the human connectome based on diffusion tractography. 自然
通讯, 8(1), 1349. https://doi.org/10.1038/s41467-017
-01285-X, 考研: 29116093

马古利斯, D. S。, 戈什, S. S。, Goulas, A。, Falkiewicz, M。, Huntenburg,
J. M。, Langs, G。, … Smallwood, J. (2016). Situating the default-mode
network along a principal gradient of macroscale cortical organiza-
的. 美国国家科学院院刊
美国, 113(44), 12574–12579. https://doi.org
/10.1073/pnas.1608282113, 考研: 27791099

Markello, 右. D ., & Misic, 乙. (2021). Comparing spatial null models
for brain maps. 神经影像, 236, 118052. https://doi.org/10
.1016/j.neuroimage.2021.118052, 考研: 33857618

Markov, 氮. T。, Ercsey-Ravasz, M。, Van Essen, D. C。, Knoblauch, K.,
Toroczkai, Z。, & 肯尼迪, H. (2013). Cortical high-density coun-
terstream architectures. 科学, 342(6158), 1238406. https://土井
.org/10.1126/science.1238406, 考研: 24179228

Mesulam, M.-M. (1998). From sensation to cognition. Brain, 121(6),
1013–1052. https://doi.org/10.1093/brain/121.6.1013, 考研:
9648540

Mišić, B., 贝策尔, 右. F。, Griffa, A。, De Reus, 中号. A。, 他, Y。, Zuo, X.-N.,
… Zatorre, 右. J. (2018). Network-based asymmetry of the human
auditory system. 大脑皮层, 28(7), 2655–2664. https://土井
.org/10.1093/cercor/bhy101, 考研: 29722805

Mišić, B., 贝策尔, 右. F。, Nematzadeh, A。, Goni, J。, Griffa, A。,
哈格曼, P。, … Sporns, 氧. (2015). Cooperative and competitive
spreading dynamics on the human connectome. 神经元, 86(6),
1518–1529. https://doi.org/10.1016/j.neuron.2015.05.035,
考研: 26087168

Mišić, B., Fatima, Z。, Askren, 中号. K., Buschkuehl, M。, 丘吉尔, N。,
Cimprich, B., … Berman, 中号. G. (2014). The functional connec-
tivity landscape of the human brain. 公共图书馆一号, 9(10), e111007.
https://doi.org/10.1371/journal.pone.0111007, 考研:
25350370

Mišić, B., & 斯波恩斯, 氧. (2016). From regions to connections and
网络: New bridges between brain and behavior. 当前的
Opinion in Neurobiology, 40, 1–7. https://doi.org/10.1016/j
.conb.2016.05.003, 考研: 27209150

墨菲, K., & 狐狸, 中号. D. (2017). Towards a consensus regarding
global signal regression for resting state functional connectivity
MRI. 神经影像, 154, 169–173. https://doi.org/10.1016/j
.neuroimage.2016.11.052, 考研: 27888059

高贵, S。, Scheinost, D ., & Constable, 右. 时间. (2019). A decade of
test-retest reliability of functional connectivity: A systematic
review and meta-analysis. 神经影像, 203, 116157. https://
doi.org/10.1016/j.neuroimage.2019.116157, 考研:
31494250

Oldham, S。, Fulcher, 乙. D ., Aquino, K. M。, Arnatkeviciute, A. M。,
Paquola, C。, Shishegar, R。, & 假如, A. (2021). Modeling

空间的, 发展性的, 生理, and topological con-
straints on human brain connectivity. bioRxiv. https://doi.org/10
.1101/2021.09.29.462379

Paquola, C。, Wael, 右. V. D ., Wagstyl, K., Bethlehem, 右. A. 我。, 洪,
S.-J., Seidlitz, J。, … Bernhardt, 乙. C. (2019). Microstructural and
functional gradients are increasingly dissociated in transmodal
cortices. 公共科学图书馆生物学, 17(5), e3000284. https://doi.org/10
.1371/journal.pbio.3000284, 考研: 31107870

力量, J. D ., 巴恩斯, K. A。, 斯奈德, A. Z。, 施拉加尔, 乙. L。, & 彼得森,
S. 乙. (2012). Spurious but systematic correlations in functional
connectivity MRI networks arise from subject motion. Neuro-
图像, 59(3), 2142–2154. https://doi.org/10.1016/j.neuroimage
.2011.10.018, 考研: 22019881

Preti, 中号. G。, & Ville, D. V. D. (2019). Decoupling of brain function
from structure reveals regional behavioral specialization in
人类. Nature Communications, 10(1), 1–7. https://doi.org/10
.1038/s41467-019-12765-7, 考研: 31628329

罗伯茨, J. A。, Perry, A。, Lord, A. R。, 罗伯茨, G。, 米切尔, 磷. B., 史密斯,
右. E., … Breakspear, 中号. (2016). The acontribution of geometry to
the human connectome. 神经影像, 124, 379–393. https://土井
.org/10.1016/j.neuroimage.2015.09.009, 考研: 26364864
罗伯茨, J. A。, Perry, A。, 罗伯茨, G。, 米切尔, 磷. B., & Breakspear,
中号. (2017). Consistency-based thresholding of the human con-
nectome. 神经影像, 145, 118–129. https://doi.org/10.1016/j
.neuroimage.2016.09.053, 考研: 27666386

Salvador, R。, Suckling, J。, Coleman, 中号. R。, Pickard, J. D ., Menon,
D ., & 布莫尔, 乙. (2005). Neurophysiological architecture of
functional magnetic resonance images of human brain. Cerebral
Cortex, 15(9), 1332–1342. https://doi.org/10.1093/cercor
/bhi016, 考研: 15635061

萨瓦尔, T。, 你的兄弟, K., & 扎莱斯基, A. (2021). 一个批评的
review of connectome validation studies. NMR in Biomedicine,
34(12), e4605. https://doi.org/10.1002/nbm.4605, 考研:
34516016

Seguin, C。, Razi, A。, & 扎莱斯基, A. (2019). Inferring neural signalling
directionality from undirected structural connectomes. 自然
通讯, 10(1), 1–13. https://doi.org/10.1038/s41467
-019-12201-w, 考研: 31537787

Seguin, C。, Tian, Y。, & 扎莱斯基, A. (2020). Network communication
models improve the behavioral and functional predictive utility
of the human structural connectome. 网络神经科学,
4(4), 980–1006. https://doi.org/10.1162/netn_a_00161,
考研: 33195945

Seguin, C。, van den Heuvel, 中号. P。, & 扎莱斯基, A. (2018). Navigation
of brain networks. 美国国家科学院院刊-
美利坚合众国, 115(24), 6297–6302.
https://doi.org/10.1073/pnas.1801351115, 考研: 29848631
墓, J。, 刘, H。, Talukdar, T。, Martincorena, 我。, 杨, 乙. T。, &
巴克纳, 右. L. (2010). The organization of local and distant
functional connectivity in the human brain. 公共科学图书馆计算
生物学, 6(6), e1000808. https://doi.org/10.1371/journal.pcbi
.1000808, 考研: 20548945

Shinn, M。, 胡, A。, 车工, L。, 高贵, S。, Achard, S。, Anticevic, A。, ……
穆雷, J. D. (2021). Spatial and temporal autocorrelation weave
human brain networks. bioRxiv. https://doi.org/10.1101/2021.06
.01.446561

史密斯, S. M。, Nichols, 时间. E., Vidaurre, D ., Winkler, A. M。, 贝伦斯,
时间. E., Glasser, 中号. F。, … Miller, K. L. (2015). A positive-negative

网络神经科学

948

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

6
4
9
3
7
2
0
5
6
2
8
0
n
e
n
_
A
_
0
0
2
3
6
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Structure- and geometry-informed functional connectivity

mode of population covariation links brain connectivity, demo-
graphics and behavior. 自然神经科学, 18(11), 1565–1567.
https://doi.org/10.1038/nn.4125, 考研: 26414616

斯波恩斯, 奥。, & 贝策尔, 右. F. (2016). 模块化大脑网络. Annual
Review of Psychology, 67(1), 613–640. https://doi.org/10.1146
/annurev-psych-122414-033634, 考研: 26393868

Stiso, J。, & Bassett, D. S. (2018). Spatial embedding imposes con-
straints on neuronal network architectures. Trends in Cognitive
科学, 22(12), 1127–1142. https://doi.org/10.1016/j.tics.2018
.09.007, 考研: 30449318

Suárez, L. E., Markello, 右. D ., 贝策尔, 右. F。, & Misic, 乙. (2020). Link-
ing structure and function in macroscale brain networks. Trends
in Cognitive Sciences, 24(4), 302–315. https://doi.org/10.1016/j
.tics.2020.01.008, 考研: 32160567

托马斯, C。, Frank, 问. Y。, Irfanoglu, 中号. 奥。, Modi, P。, Saleem, K. S。,
Leopold, D. A。, & 皮尔保利, C. (2014). Anatomical accuracy of
brain connections derived from diffusion MRI tractography is
inherently limited. 美国国家科学院院刊-
美利坚合众国, 111(46), 16574–16579.
https://doi.org/10.1073/pnas.1405672111, 考研: 25368179
Van den Heuvel, 中号. P。, 布莫尔, 乙. T。, & 斯波恩斯, 氧. (2016).
Comparative connectomics. 认知科学的趋势, 20(5),
345–361. https://doi.org/10.1016/j.tics.2016.03.001, 考研:
27026480

Van Der Maaten, L。, Postma, E., & Van den Herik, J. (2009). Dimen-
sionality reduction: A comparative review. Journal of Machine
Learning Research, 10, 66–71.

Vázquez-Rodríguez, B., 刘, Z.-Q., 哈格曼, P。, & Misic, 乙.
(2020). Signal propagation via cortical hierarchies. 网络

神经科学, 4(4), 1072–1090. https://doi.org/10.1162/netn_a
_00153, 考研: 33195949

Vázquez-Rodríguez, B., Suárez, L. E., Markello, 右. D ., Shafiei, G。,
Paquola, C。, 哈格曼, P。, … Misic, 乙. (2019). Gradients of
structure–function tethering across neocortex. 诉讼程序
美国国家科学院,
11 6 ( 4 2 ) , 2 1 21 9 – 2 1 2 2 7 . h t t p s : / / d o i . o rg / 1 0 . 1 0 7 3 / p n a s
.1903403116, 考研: 31570622

Vértes, 磷. E., Alexander-Bloch, A. F。, Gogtay, N。, Giedd, J. N。,
Rapoport, J. L。, & 布莫尔, 乙. 时间. (2012). Simple models of
human brain functional networks. 国家会议录
美国科学院, 109(15),
5868–5873. https://doi.org/10.1073/pnas.1111738109,
考研: 22467830

王, P。, 孔, R。, 孔, X。, Liégeois, R。, Orban, C。, 德科, G。, ……
杨, 乙. 时间. 时间. (2019). Inversion of a large-scale circuit model
reveals a cortical hierarchy in the dynamic resting human brain.
Science Advances, 5(1), eaat7854. https://doi.org/10.1126/sciadv
.aat7854, 考研: 30662942

杨, 乙. 时间. T。, 克里宁, F. M。, 墓, J。, 肥皂, 中号. R。, 军队,
D ., 霍林斯黑德, M。, … Buckner, 右. L. (2011). The organization of
the human cerebral cortex estimated by intrinsic functional con-
nectivity. 神经生理学杂志, 106(3), 1125–1165.
https://doi.org/10.1152/jn.00338.2011, 考研: 21653723

扎莱斯基, A。, 假如, A。, Cocchi, L。, Gollo, L. L。, van den Heuvel,
中号. P。, & Breakspear, 中号. (2016). Connectome sensitivity or spec-
ificity: Which is more important? 神经影像, 142, 407–420.
https://doi.org/10.1016/j.neuroimage.2016.06.035, 考研:
27364472