Commonalities for Numerical and Continuous Quantity - 麻省理工学院人工智能研究专业

Commonalities for Numerical and Continuous Quantity
Skills at Temporo-parietal Junction

Marinella Cappelletti1,3, Rebecca Chamberlain1, Elliot D. Freeman2,
Ryota Kanai1, Brian Butterworth1, Cathy J. Price1, and Geraint Rees1

抽象的

■ How do our abilities to process number and other continu-
ous quantities such as time and space relate to each other?
Recent evidence suggests that these abilities share common
magnitude processing and neural resources, although other
findings also highlight the role of dimension-specific processes.
To further characterize the relation between number, 时间,
and space, we first examined them in a population with a devel-
opmental numerical dysfunction (developmental dyscalculia)
and then assessed the extent to which these abilities correlated
both behaviorally and anatomically in numerically normal partic-
爱普茨. We found that (1) participants with dyscalculia showed
preserved continuous quantity processing and (2) in numeri-

cally normal adults, numerical and continuous quantity abilities
were at least partially dissociated both behaviorally and anato-
mically. 具体来说, gray matter volume correlated with both
measures of numerical and continuous quantity processing in
the right TPJ; 相比之下, individual differences in number pro-
ficiency were associated with gray matter volume in number-
specific cortical regions in the right parietal lobe. 一起,
our new converging evidence of selective numerical impair-
ment and of number-specific brain areas at least partially dis-
tinct from common magnitude areas suggests that the human
brain is equipped with different ways of quantifying the outside
世界. ■

介绍

Philosophers, neurologists, 教育工作者, and psychologists
have long pondered the relation between number and con-
连续数量, such as space and time (see Dehaene
& Brannon, 2011): Are these dimensions built on one com-
mon system for quantification, or do they stand indepen-
dently from each other? The first hypothesis derives from
the popular idea that number, 时间, and space all depend
on shared magnitude processing (Bueti & Walsh, 2009;
Cantlon, Platt, & Brannon, 2009; Walsh, 2003). 然而,
evidence for this common processing is mixed. 为了
例子, supporting data come from the similarity of
performance in number, 时间, or space processing (例如,
Brannon, Suanda, & Libertus, 2007; Zorzi, Priftis, & Umiltà,
2002), but the opposite possibility—that number, 时间,
and space may each be fully independent—is supported
by TMS and lesion studies showing dissociations among
these dimensions (例如, Aiello et al., 2012; Dormal,
Seron, & Pesenti, 2006; Doricchi, Guariglia, Gasparini, &
Tomaiuolo, 2005). A third, intermediate, possibility is that
数字, 时间, and space are only partly independent (例如,
Walsh, 2003). This is suggested by interactions between
方面: 例如, large numbers can be perceived
as longer than veridical in physical size or duration (例如,
Dormal et al., 2006), even when number or time are selec-

1伦敦大学学院, 2City University London, 3金子-
smiths College, 伦敦大学

tively impaired by brain lesions (Cappelletti, 弗里曼, &
Cipolotti, 2009, 2011).

Previous studies investigated the relationship between
数字, 时间, and space by examining performance either
averaged across groups or in single cases, but here we
complemented this approach by focusing on individual
differences in task performance and in brain anatomy. 在-
dividual differences were assessed within the normal and
abnormal spectrum of numerical skills, the latter consisting
of participants whose numerical abilities are developmen-
tally impaired, 那是, dyscalculia (Butterworth, 2003). 我们的
reasoning for including participants with dyscalculia was
that they offer a unique perspective on the relation be-
tween number, 时间, and space and in particular, 因为
number skills are by diagnosis impaired in dyscalculia, 在
possible associations or dissociations between number,
时间, and space.

The above three hypotheses on the link between num-
误码率, 时间, and space predict different patterns of results.
The proposal of a common magnitude system predicts
that numerical proficiency will be associated with perfor-
mance in continuous quantity discrimination in numeri-
cally normal and in participants with dyscalculia and also
a possible correlation of number, 时间, and space measures
with the volume of common brain regions. 相比之下, 这
second hypothesis of fully independent magnitude dimen-
sions predicts dissociation between behavioral measures
and independent correlations of each measure with the

认知神经科学杂志 26:5, PP. 986–999
土井:10.1162/jocn_a_00546

D
哦
w
n
我
哦
A
d
e
d

F
r
哦
米

我

/
j

t
t

F
/

我
t
.

:
/
/

H
t
t
p
:
/
D
/
哦
米
w
我
n
t
哦
p
A
r
d
C
e
.
d
s
F
我
r
哦
我
米
v
e
H
r
C
p
H
A
d
我
我
r
r
e
.
C
C
t
.
哦
米
米
/
j
e
d
哦
你
C
n
哦
/
C
A
n
r
A
t
r
我
t
我
C
C
我
e
e
–
p
–
d
p
d
2
F
6
/
5
2
6
9
/
8
5
6
/
1
9
9
8
4
6
7
/
3
1
3
7
3
8
哦
1
C
2
n
0
_
0
A
/
_
j
0
哦
0
C
5
n
4
6
_
A
p
_
d
0
0
乙
5
y
4
G
6
你
.
e
p
s
t
d
哦
F
n
乙
0
y
8
S
中号
e
我
p
时间
e
米
L
我
乙
乙
e
r
r
A
2
r
0
我
2
3
e
s

/
j

你
s
e
r

哦
n

1
7

中号
A
y

2
0
2
1

volume of distinct brain regions. Dyscalculicsʼ performance
may provide converging evidence of independent rather
than shared processes among dimensions if number pro-
cessing dissociate from maintained continuous quantity
加工. The third hypothesis of partial independence
of number and continuous quantity processing predicts a
partial correlation between behavioral measures, 哪个
may be associated with both common and distinct brain
地区.

We first tested whether continuous quantity process-
ing was maintained in participants with dyscalculia; 拥有
found a dissociation between impaired numerical abilities
and preserved continuous quantity skills in dyscalculia,
we then measured correlations between individual differ-
ences in number, 时间, and space performance in another
non-dyscalculic sample for whom numeracy skills varied
within the normal range. In the same sample, we used
voxel-based morphometry ( VBM; Ashburner & 弗里斯顿,
2000), optimized for neurologically normal brains, to test
whether our behavioral measures each correlated with
anatomical differences in common and/or distinct brain
地区.

方法

For all participants, we administered a series of carefully
selected numerical and arithmetical tasks, as well as psy-
chophysical tasks measuring continuous quantity dis-
crimination in space and time. Our choice of tasks and
stimuli was motivated by the aim of measuring numerical/
arithmetical and continuous quantity skills as indepen-
dently as possible. This independence was essential to
obtain an unbiased measure of how these cognitive abil-
ities correlate with each other. We reasoned that if ex-
perimental paradigms that are different but more suited
to test each individual magnitude dimension result in
similar behavioral and anatomical responses in processing
数字, 时间, and space, then such similarities are more
likely to be accounted for by a common magnitude system
or other processes shared between number and continuous
quantity. We used symbolic numbers (1–9), typically em-
ployed to test numerical proficiency (Butterworth, 2010)
independently from nonsymbolic continua (水平的
lines changing in length or duration), such that numbers
were never manipulated along continuous dimensions
and nonsymbolic continua were never presented with
symbolic numbers.

who were age- and gender-matched to the previous group
(Control Group 1: mean age = 23 年, range = 19–35,
23 女性) but with numerical abilities within the normal
范围. All participants performed the numerical and con-
tinuous quantity tasks, and we obtained brain scans from
37 nondyscalculic participants only. Two additional groups
of numerically normal participants performed two sup-
plementary control tasks (Supplementary Task 1 in Con-
trol Group 2: n = 18, mean age = 26.1 年, range =
20–35 years, 8 女性; Supplementary Task 2 in Control
团体 3: n = 22, mean age = 24.6 年, range = 20–
34 年, 13 女性). The study was approved by the local
research ethics committee.

Participants with Dyscalculia

Dyscalculia was diagnosed before participants were invited
to take part in the study. The diagnosis was based on (1)
the Dyscalculia Screener (Butterworth, 2003); (2) a stan-
dardized arithmetical task, 那是, the Graded Difficulty
Arithmetic Task ( Jackson & Warrington, 1986); (3) 这
arithmetic subtest of WAIS-R ( Wechsler, 1986); 和
(4) a task consisting of discriminating the numerosity of
clouds of dots, which allows the calculation of the Weber
fraction, an index of accuracy sensitive to dyscalculia
(Mazzocco, Feingenson, & Halberda, 2011; Piazza et al.,
2010; Halberda, Mazzocco, & Feigenson, 2008). General
intelligence was also assessed (Wechsler, 1986).

In the Dyscalculia Screener, 全部 16 participants with
dyscalculia obtained a score below the cutoff point in
either the capacity or the achievement scale, thereby ful-
filling the criteria for dyscalculia. They were also impaired
in the other numerical or arithmetical tasks consistent
with their diagnosis. IQ was average or high average, 苏格-
gesting preserved intellectual functioning (见表 1).

Experimental Tasks

There were two sets of experimental tasks, one testing con-
tinuous quantity discrimination and the other testing
numerical competence. Stimulus presentation and data col-
lection were controlled using the Cogent Graphics toolbox
(www.vislab.ucl.ac.uk/Cogent/) and MATLAB 7.3 软件
on a Sony S2VP laptop computer with video mode of
640 × 480 像素, screen dimensions of 20.8° horizontal
by 15.83° vertical and 60 Hz refresh rate. Participants placed
their head on a chin rest positioned 50 cm from the screen.

参加者

Ninety-three right-handed, neurologically normal adults
with normal or corrected-to-normal vision gave written
informed consent to take part in the study. The main sam-
ple consisted of 16 参与者 (mean age = 34.7 年,
range = 22–38 years, 15 女性, 1 男人) who had been
diagnosed with dyscalculia (见下文) 和 37 参与者

Continuous Quantity Tasks

Two tasks were used, which have been extensively
employed in neurologically normal and brain-lesioned
参与者 (Cappelletti, 弗里曼, & Butterworth,
2011; Cappelletti, 弗里曼, & Cipolotti, 2011; Cappelletti
等人。, 2009). The two tasks required comparing visual
stimuli along the dimension of length or the orthogonal
dimension of time.

Cappelletti et al.

987

D
哦
w
n
我
哦
A
d
e
d

F
r
哦
米

我

/
j

F
/

t
t

我
t
.

:
/
/

/
j

你
s
e
r

哦
n

1
7

中号
A
y

2
0
2
1

桌子 1. Performance of Numerically Normal Participants and of Participants with Dyscalculia in IQ and in Number Tasks (Stanine
分数, Percentile, or Weber Fraction and Standard Deviation in Brackets)

Tasks Performed

IQa

Number tasks

Dyscalculia Screenerb

Capacity subscale

Dot–number matching

Number Stroop

Achievement subscale

Addition

Multiplication

Graded Difficulty Arithmetic Testc

Arithmetic subtest of WAIS-R

Number discrimination (wf )e

Numerically Normal Participants

Participants with Dyscalculia (n = 16)

112.7 (14.06)

2.36 (0.56)

2.5 (0.8)

2.69 (0.7)

2.0 (0.97)

2.38 (0.7)

2.56 (0.8)

2.03 (0.94)

18d (17.5)

15d (16.1)

0.47 (0.16)

≥3

25–75d

0.27 (0.04)

Impaired performance is shown in bold. Independent sample t tests were used to analyze performance of the group with dyscalculia relative to
numerically normal age-matched participants (n = 50, 33 女性, mean age = 35.6 年, 标准差= 9.43) who took part in a previous study (Cappelletti
等人。, in press); performance of individual dyscalculic was analysed with Crawford et al. (1998) t test.
aWAIS-3 (Wechsler, 1986). Full IQ calculated disregarding performance in the arithmetic subtask.
bDyscalculia Screener expressing performance as stanine score ranging from 1 到 9 where ≤3 indicate an impairment (see Butterworth, 2003).
cJackson and Warrington (1986).
dPercentile.
ePerformance expressed as Weber fraction (wf, Halberda et al., 2008), an index sensitive to dyscalculia (例如, Mazzocco et al., 2011; Piazza et al., 2010).
Participants with dyscalculia were significantly impaired relative to a sample of numerically normal participants who took part in previous studies
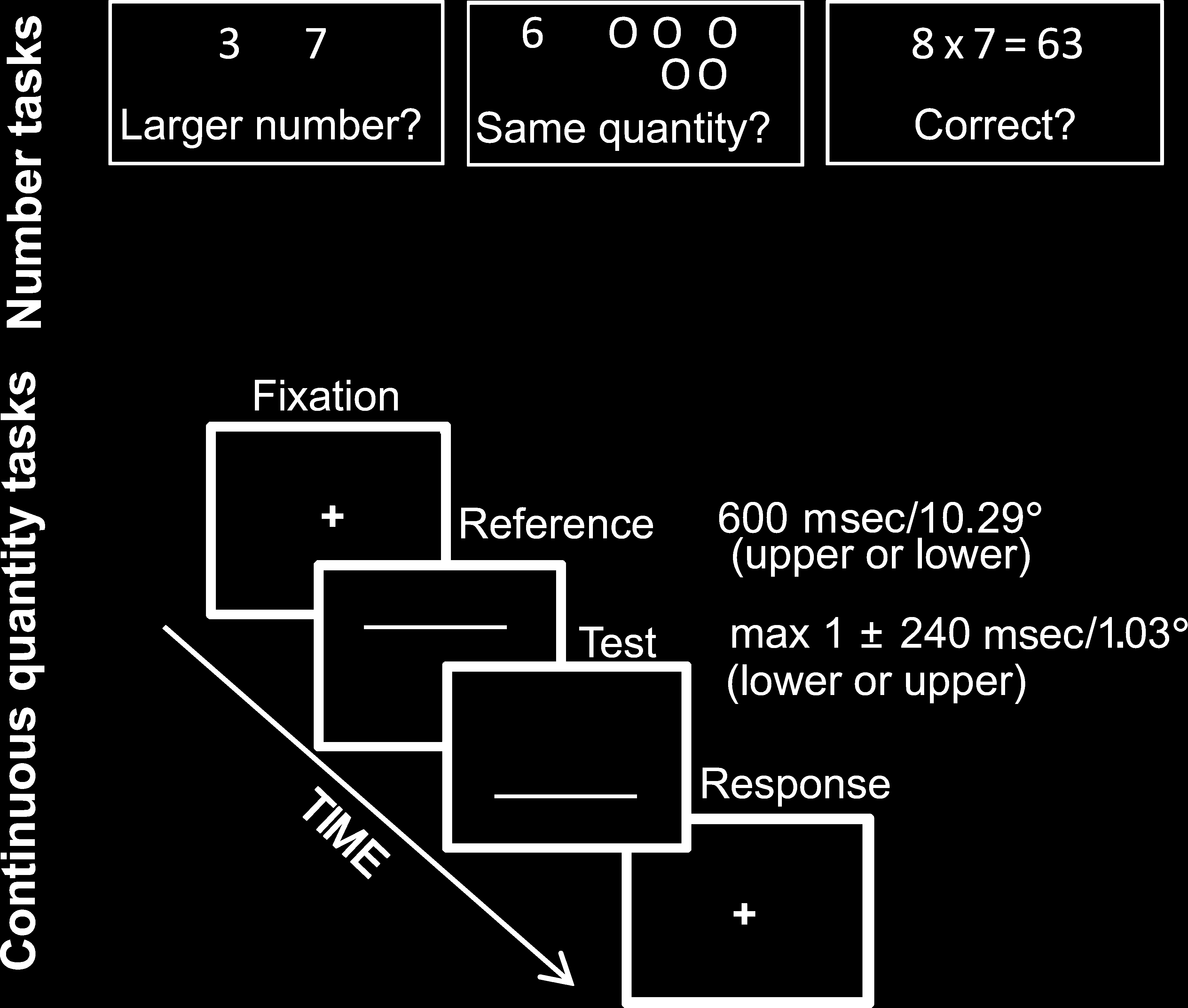
[t(64) = 5.3, p < .001]. Stimuli. These consisted of two horizontal white lines (thickness = 0.17°) centered on the vertical meridian on a black background and presented sequentially in a two-interval discrimination paradigm, one line 5.07° above the horizontal meridian and the other 5.07° below in random order. Design. The first line stimulus (the Reference) was fixed (length of 10.29° and duration of 600 msec), whereas the second line (the Test) could vary according to the method of constant stimuli either in length or duration, depending on the dimension to be judged (the irrelevant dimension always matched the Reference). For each di- mension, the ratio between the smaller and the larger stimulus could vary unpredictably over five levels: 1.06, 1.13, 1.2, 1.26, and 1.33 for time and 1.025, 1.05, 1.075, 1.10, and 1.25 for length, selected from previous studies (Cappelletti, Freeman, & Cipolotti, 2011; Cappelletti et al., 2009). Test stimulus values were randomly sampled without replacement from a set of five equally spaced values for each dimension (steps of 0.257° for length and 40 msec for time) with equal frequency. There were five blocks of 40 observations for each level of the test stim- ulus (total 200 observations for each task). The time and space discrimination tasks were run independently from each other in counterbalanced order across participants to avoid order effects. Procedure. Each trial began with a centrally displayed fixation point (diameter = 0.17°), which remained visible until a key-press from the participant. The reference line was then immediately displayed followed by the test line and an interstimulus interval of 100 msec. The screen then remained blank with a fixation cross in the middle until a response from the participant. The next trial im- mediately followed the response (see Figure 1, bottom). In each task, participants made unspeeded responses by pressing either the “up” or “down” cursor arrow keys of the computer keyboard if either the upper or the lower line appeared the longest, either in duration or in spatial extent. Correct answers were equally assigned to the “up” or “down” keys in each task. For each task, before the first experimental block participants had at least 20 practice trials, which were not included in analysis. Number Tasks To test numerical and arithmetical competence, three tasks were devised (see Figure 1, top), for which par- ticipants were instructed to make speeded answers; 988 Journal of Cognitive Neuroscience Volume 26, Number 5 D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 6 / 5 2 6 9 / 8 5 6 / 1 9 9 8 4 6 7 / 3 1 3 7 3 8 o 1 c 2 n 0 _ 0 a / _ j 0 o 0 c 5 n 4 6 _ a p _ d 0 0 b 5 y 4 g 6 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 i 2 3 e s / j f / t . u s e r o n 1 7 M a y 2 0 2 1 6 = 13” or “7 − 2 = 3”) or 2 units apart for multiplication problems (e.g., “6 × 3 = 16”). PROCEDURE. Following a 500-msec central fixation cross, each operation was presented for up to 7 sec during which participants could provide an answer. Number comparison. This asked participants to indi- cate as fast as possible the larger of two Arabic numbers. STIMULI AND DESIGN. Thirty-six pairs of single-digit Arabic numbers (1–9) were individually presented. Using a de- sign similar to previous studies (e.g., Cappelletti, Didino, Stoianov, & Zorzi, in press), the following numerical dis- tances were used: 1 (e.g., 7 vs. 6 or 4 vs. 5; eight trials), 2 (e.g., 3 vs. 1 or 7 vs. 9; eight trials), 3 (e.g., 5 vs. 8 or 4 vs. 1; eight trials), 4 (e.g., 6 vs. 2 or 3 vs. 7; eight trials), 5 (e.g., 9 vs. 4 or 1 vs. 6; four trials). Within each numerical distance, there was an equal number of trials where the smaller digit was displayed on the left or on the right of fixation. PROCEDURE. Stimulus pairs were centered along the horizontal line of the computer screen and each displayed for 500 msec to the left or the right of the fixation cross. Stimuli were then replaced by a black screen for a maxi- mum of 4 sec during which participants made an answer. After this, the following trial started immediately. Partici- pants were required to make speeded answer by pressing one of two predefined keys. Dot–number matching. This required participants to indicate as fast as possible with a finger press whether or not an Arabic number presented in one hemifield matched the number of dots presented in the other hemifield. STIMULI AND DESIGN. Thirty-six pairs of stimuli ranging from 1 to 9 were used. When the stimuli did not match, they could differ by 1, 2, 3 or 4 units, for instance, 6 dots presented with the Arabic number 5, or 7 dots with number 8, or 5 dots with number 2. PROCEDURE. Each pair of stimuli was presented for 500 msec with hemifield assignment of the dot and number stimuli counterbalanced between trials. Control Tasks Two control tasks were designed to match either the behavioral measures (accuracy and speeded RTs) or the experimental paradigm (line stimuli presented above and below fixation) of the number and continuous quan- tity tasks, respectively. However, these control tasks did not measure number, time, or space processing and as such allowed us to distinguish effects reflecting number and continuous quantity processing from other effects reflecting generic aspects of performance such as compar- ing stimuli or stimulus and response selection processes. Cappelletti et al. 989 Figure 1. Experimental tasks. Schematic depiction of the number/ arithmetic and the continuous quantity discrimination tasks. In the number tasks, participants had to decide (from left: the larger among two numbers; whether a number and a set of dots indicated the same quantity; whether the result of arithmetical operations was correct). In the continuous quantity tasks, participants indicated whether the upper or the lower line was longer in either duration or length, in different blocks. accuracy and RTs were collected. These tasks were similar but not identical to those used to diagnose dyscalculia: For instance, the Screener uses a “Number Stroop” task where numbers change in value as well as physical size (e.g., 1 vs. 3) because this task is sensitive to dyscalculia (e.g., Rubinsten & Henik, 2005); moreover, the Screener is based on addition and multiplication problems only. In contrast, our experimental tasks used a number com- parison task where the numbers changed only in value but not physical size; our tasks also included subtraction problems besides addition and multiplication to better capture the cognitive processes underlying different arithmetical operations because subtractions are thought to rely on quantity-based processes, whereas multiplica- tions and additions on verbal memory processes (Dehaene, Piazza, Pinel, & Cohen, 2003). Arithmetical verification. This task required partici- pants to indicate as fast as possible using predefined re- sponse keys whether an arithmetic problem displayed the correct or incorrect answer. Twenty single-digit pro- blems for each type of operation (addition, subtraction, and multiplication) were presented in separate blocks. STIMULI AND DESIGN. Single-digit and two-digit Arabic num- bers were presented as operands or as possible results of the arithmetical operations. For instance, participants were presented with problems such as “9 + 6 = 13,” “7 − 2 = 3,” or “6 × 3 = 16.” When results were incor- rect, these were either 1 or 2 units apart from the correct result for addition and subtraction problems (e.g., “9 + D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 6 / 5 2 6 9 / 8 5 6 / 1 9 9 8 4 6 7 / 3 1 3 7 3 8 o 1 c 2 n 0 _ 0 a / _ j 0 o 0 c 5 n 4 6 _ a p _ d 0 0 b 5 y 4 g 6 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 i 2 3 e s / j t f / . u s e r o n 1 7 M a y 2 0 2 1 Location discrimination. This control task consisted of 40 trials each displaying a dot for 200 msec in random locations on the left or right of a computer monitor and following an ISI randomly selected between 500 msec and 2 sec. Similar to the number tasks, participants were instructed to make speeded responses identifying the location of each stimulus (left or right of fixation) by pressing one of two predefined keys. Accuracy and RTs were recorded similarly to the number tasks. Luminance discrimination. In this second control task, participants made unspeeded responses indicating which of two horizontal lines was brighter by pressing either the “up” or “down” arrow key. The same design, procedure, and number of trials as the other continuous quantity tasks were used, except that the line stimuli varied along the dimension of luminance, whereas time and space were both kept constant (600 msec and 10.29°). The first line stimulus remained constant in luminance (40 cd m−2, 50% of maximum display luminance), whereas the second line could have one of five linearly spaced input values, from 50% to 58% of maximum luminance, re- sulting in minimum and maximum luminances of 40 and 55.5 cd m−2, respectively (i.e., a max increase of 38.75%). Supplementary Control Tasks There were two sets of supplementary control tasks: the first set aimed to control for the possible impact of vari- ables that were unmatched between the continuous quan- tity and the number/arithmetic tasks, for instance, task instructions. Participants (Control Group 2) performed the same time and space discrimination tasks twice in ran- domized order, once following the identical instructions as previous participants and once under time pressure, similar to the number and arithmetic tasks. To make the number/arithmetic and the continuous quantity tasks as similar as possible, we also increased the amount of trials of the number/arithmetical tasks (from 132 to 324 trials) to equate it to the continuous quantity task (400 trials). A second supplementary control task tested whether nonsymbolic discrete quantity may be linked to continu- ous quantity or number/arithmetic. We compared perfor- mance in the number/arithmetic and continuous quantity tasks with performance in another nonsymbolic task (i.e., numerosity discrimination), using the same design and procedure of an established paradigm (Halberda et al., 2008; Cappelletti et al., 2013) in a new group of numeri- cally normal participants (Control Group 3). MRI Imaging and Data Preprocessing High-resolution anatomical images were acquired using a T1-weighted 3-D Modified Driven Equilibrium Fourier Transform (MDEFT) sequence (repetition time = 12.24 msec, echo time = 3.56 msec, field of view = 256 × 256 mm, voxel size = 1 × 1 × 1 mm) on a 1.5-T Siemens Sonata MRI scanner (Siemens Medical Systems, Erlangen, Germany). Analyses used SPM8 ( Wellcome Trust Centre for Neuroimaging, www.fil.ion.ucl.ac.uk/spm) running under MATLAB 7.3 (MathWorks, Natick, MA). The images were spatially normalized to Montreal Neurological Insti- tute space (MNI) and segmented into gray and white matter using the unified segmentation algorithm (Ashburner & Friston, 2005). Subsequently, a Diffeomorphic Anatomical Registration through Exponentiated Lie Algebra was per- formed for intersubject registration of the gray matter images. To ensure that the total gray matter volume was re- tained before and after spatial transformation, the image intensity was modulated by the Jacobian determinants of the deformation fields. The registered images were then smoothed with a Gaussian kernel (FWHM = 8 mm) and were then affine transformed to MNI stereotactic space using affine and nonlinear spatial normalization for multiple regression analysis. Data Analysis Behavioral Data Performance in the continuous quantity discrimination tasks was expressed as the difference in duration or length that could be discriminated at 75% accuracy (Just Notice- able Difference, JND). The JND was calculated by plotting the percentage of “Test longer” (or “Test brighter”) re- sponses to the actual Test magnitude for each participant and each continuous quantity task. These percentages (typically from floor to ceiling performance, i.e., near 50% to near 100%) were then interpolated by a logistic function using a maximum-likelihood algorithm imple- mented by PSIGNIFIT toolbox for MATLAB ( Wichmann & Hill, 2001). The JND was read off from the interpolated psychometric function as the line length, duration, or luminance at which 75% of the responses were “Test longer.” For the number and arithmetical tasks, an effi- ciency score was calculated, that is, accuracy divided by mean RT for the correct answers for each task (Machizawa & Driver, 2011). JNDs and efficiency scores were normal- ized to produce z scores so that performance could be compared across tasks in planned two-tailed t tests. Behavioral data were also included in a principal com- ponent analysis (PCA) based on the normalized efficiency scores and JNDs. Four components with eigenvalues higher than 1 were extracted and then Varimax rotated (Wood, Tataryn, & Gorsuch, 1996), and these values were used as a behavioral index for the VBM analysis. Correlation analysis was used to test the relation between performance in numerical/arithmetical and continuous quantity tasks. MRI Data VBM analyses of structural MRI images were performed in SPM8 on each voxel in the spatially normalized gray 990 Journal of Cognitive Neuroscience Volume 26, Number 5 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 6 / 5 2 6 9 / 8 5 6 / 1 9 9 8 4 6 7 / 3 1 3 7 3 8 o 1 c 2 n 0 _ 0 a / _ j 0 o 0 c 5 n 4 6 _ a p _ d 0 0 b 5 y 4 g 6 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 i 2 3 e s / j t . / f u s e r o n 1 7 M a y 2 0 2 1 matter images (see above) using behavioral measures as the independent variable and the gray matter volume in each voxel as the dependent variable. Global signal intensity differences were removed using proportional scaling. For these analyses, we report regions that showed significant effects at a threshold p < .05, corrected for multiple comparisons (using family-wise error correction) across the whole brain. We used cluster level statistics with a nonstationary correction, which is essential to adjust cluster sizes according to local “roughness” (Hayasaka, Phan, Liberzon, Worsley, & Nichols, 2004). Three analyses were performed: Two were based on examination of the whole-brain volume and one on predefined ROIs in accordance with our prior hypotheses (see below). Analysis 1: Gray matter volumes associated with perfor- mance on both number and continuous quantity tasks. This analysis introduced the two PCA rotated values cor- responding to numerical/arithmetical and continuous quan- tity performance as behavioral regressors in the VBM analysis, controlling for age, sex, and intracranial volume, fol- lowing an approach used successfully in previous VBM stu- dies (e.g., Garrido et al., 2009). Statistical contrasts identified brain areas where there was a correlation between gray mat- ter increase and (1) the main effect of each PC component, (2) any common effect between the first and second prin- ciple component (PC1 and PC2), and (3) any effect that was higher for one component over the other, that is, an interaction. Analysis 2: Gray matter volumes associated with perfor- mance on number/arithmetic and continuous quantity tasks relative to control tasks. This analysis included the normalized raw values corresponding to performance in the number/arithmetic, the continuous quantity, and the two control tasks (individual tasks for number/arithmetic and for continuous quantity averaged together). It tested whether any gray matter change in areas previously iden- tified (Analysis 1) remained significant after controlling for any effect related to the control tasks. Analysis 3: Predefined ROIs. This analysis was restricted to brain regions identified by a previous functional im- aging study we conducted (Cappelletti, Lee, Freeman, & Price, 2010) and by meta-analyses of functional results based on behavioral tasks similar to those used here ( Wiener, Turkeltaub, & Coslett, 2010; Cohen Kadosh, Lammertyn, & Izard, 2008; Dehaene et al., 2003). Specifi- cally, it included the bilateral intraparietal sulcus (IPS), superior parietal lobe, and left angular gyrus for numbers and the left SMA, right inferior parietal lobe and supra- marginal gyrus, and the left frontal gyrus for continuous quantity. For these areas, we used small spheres of 8-mm radius placed in the anatomical ROIs and reported effects at a threshold of p < .05 after correction. RESULTS Comparison of Behavioral Performance in Participants with Dyscalculia and in Numerically Normal Participants In participants with dyscalculia, we found individual variability in performing number and arithmetic tasks, con- sistent with previous studies looking at dyscalculic per- formance (Cappelletti & Price, 2014; Rubinsten & Henik, 2009). For instance, accuracy across number tasks ranged from 50% (chance) to 68% correct, and the mean RT varied from about 760 msec to over 4 sec. We also found a large and not previously reported variability in performing the continuous quantity tasks such that, for example, accuracy for discriminating the smallest increment ranged from 50% (chance) to 90% correct for length discrimination from 50% to 73% correct for time. Moreover, in adults with dyscalculia, performance in the number/arithmetic tasks correlated significantly with a measure of nonsymbolic numerosity discrimination [i.e., indicating the set with the larger number of items, see Halberda et al., 2008, r = 0.56, F(1, 15) = 6.6, p = .02] and consistent with previous reports (e.g., Mazzocco et al., 2011; Piazza et al., 2010). Performance in time and space discrimination tasks also correlated significantly [r = 0.79, F(1, 15) = 21.3, p < .001]. Critically, continuous quantity and number performance did not correlate signif- icantly [time vs. mean number tasks: r = 0.25, F(1, 15) = 0.8, p = .36, ns; space vs. mean number tasks: r = 0.29, F(1, 15) = 1.2, p = .29, ns], similar to numerically normal participants (see below). To examine the extent to which performance in par- ticipants with dyscalculia was outside the normal range, we compared them to our sample of numerically normal participants (Control Group 1). An ANOVA based on the normalized raw data of the number/arithmetic tasks and of the time and space discrimination tasks was used with Task (number/arithmetic vs. continuous quantity) as within factor and Group (dyscalculic vs. numerically nor- mal participants) as between factor. 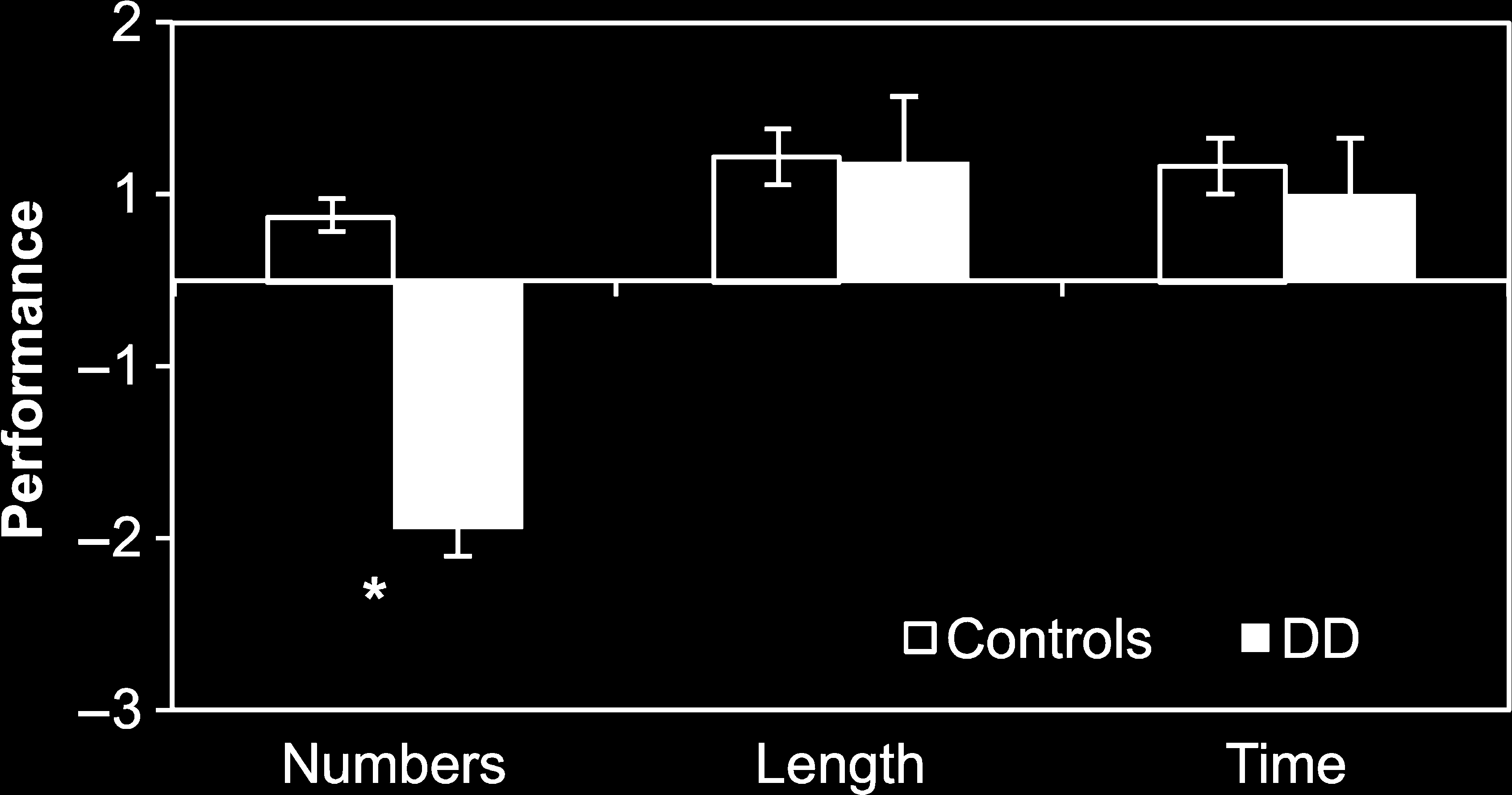The interaction of Task and Group was the only significant effect found [F(1, 51) = 49.1, p < .001], and post hoc tests indicated a significant numerical impairment in participants with dyscalculia relative to numerically normal participants [t(51) = 20.9, p < .001], but normal performance in the continuous quantity tasks [space: t(51) = 1.8, p > .08, ns;
时间: t(51): 1.7, p = .1, ns; 见图 2]. These effects
were significant even when the dyscalculic sample was
compared with a subsample of numerically normal partici-
pants more closely matched for sex and age within Con-
trol Group 1 [n = 16: 15 女性, 1 男人; mean age =
32.0 年, range = 22–37 years; F(1, 30) = 5.7, p < .02]. Post hoc comparisons based on this subsample con- firmed that participants with dyscalculia were impaired in the number and arithmetic tasks [t(30) = 11.3, p < .001], but not the continuous quantity ones [space: t(30) = 0.8, p < .09, ns; time: t(30): 2.3, p = .2, ns]. Cappelletti et al. 991 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 6 / 5 2 6 9 / 8 5 6 / 1 9 9 8 4 6 7 / 3 1 3 7 3 8 o 1 c 2 n 0 _ 0 a / _ j 0 o 0 c 5 n 4 6 _ a p _ d 0 0 b 5 y 4 g 6 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 i 2 3 e s / j / . t f u s e r o n 1 7 M a y 2 0 2 1 compared with just RTs in the number tasks, which may be more sensitive than accuracy to quantify number performance (all p > .3).

In the control tasks, participants also showed large
variability in performance: In the location discrimination
任务, RTs ranged from about 250 到 680 毫秒; 在里面
luminance task, accuracy for discriminating the smallest
increment ranged from chance to 84% 正确的, 和
JNDs ranged from 2.6% 到 10.5%. Neither of the control
tasks correlated with the number or continuous quantity
任务, with the exception of number comparison and the
location discrimination task [r = 0.6, F(1, 36) = 20.5,
p < .001; see Table 2]; this may be because these tasks were both defined in terms of speed of response rather than accuracy, which was at ceiling or close to ceiling in both cases. To establish potential overlap of function and to re- duce the dimensionality of the behavioral data for fur- ther analyses, we performed a PCA on the data from the 37 numerically normal participants (Control Group 1; see Methods). Four orthogonal factors emerged, overall accounting for about 81% of the variance (40.8%, 16.2% 13.1%, and 10.6%, respectively; see Table 3). PC factor 1 was characterized by tasks that despite several methodolo- gical differences were all defined in terms of numerical/ arithmetical processing (i.e., arithmetical verification, num- ber comparison and dot-number matching). PC factor 2 contained just the space and time discrimination tasks, and PC factor 3 was associated with luminance dis- criminability, despite the time, space, and luminance tasks all employing similar stimuli and experimental paradigms. Hence, commonalities between space and time (PCA 2) are likely to be driven by the processing of some continuous quantity rather than similarities in the paradigm used. PC D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 6 / 5 2 6 9 / 8 5 6 / 1 9 9 8 4 6 7 / 3 1 3 7 3 8 o 1 c 2 n 0 _ 0 a / _ j 0 o 0 c 5 n 4 6 _ a p _ d 0 0 b 5 y 4 g 6 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 i 2 3 e s / j t / . 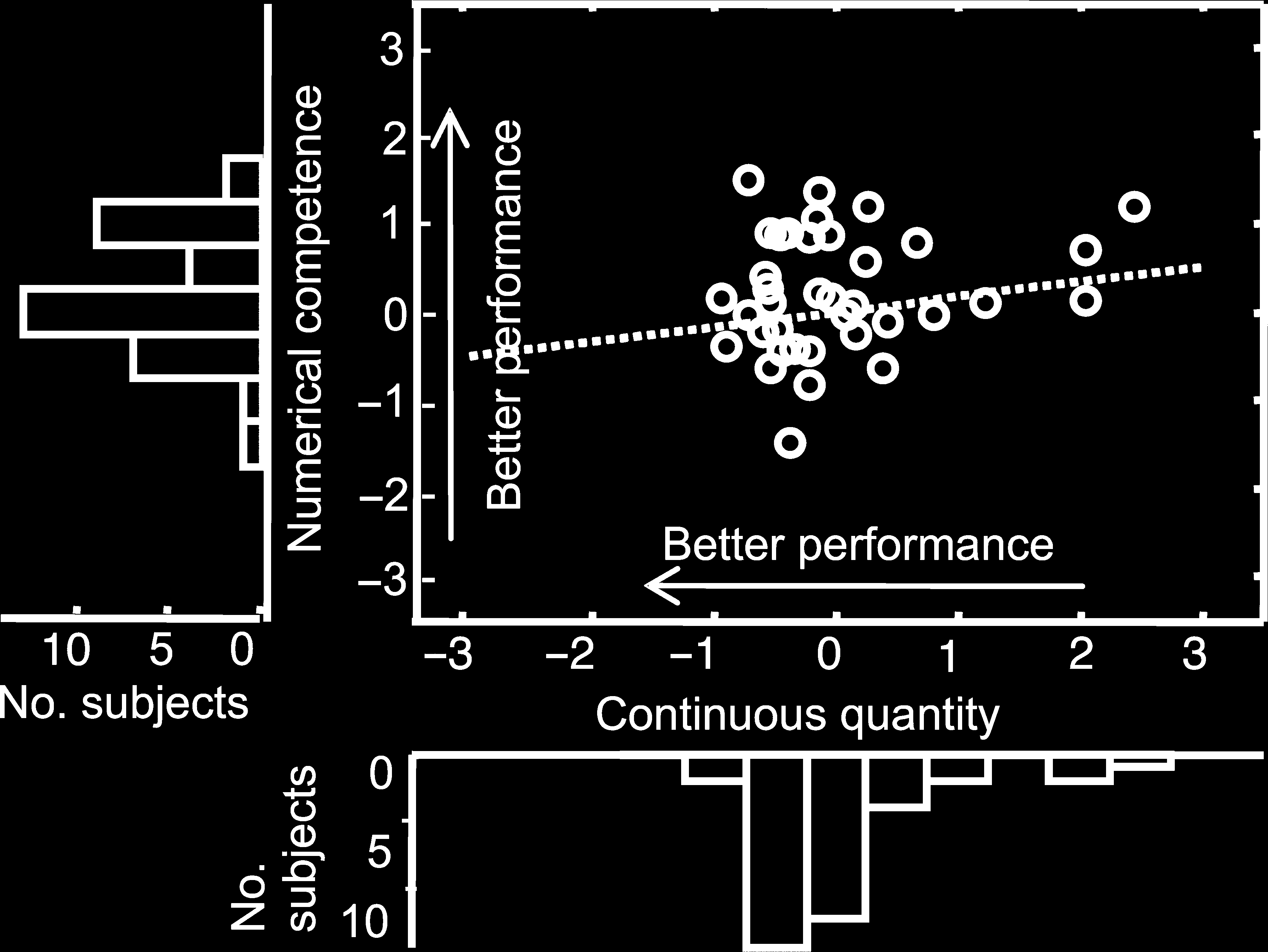f u s e r o n 1 7 M a y 2 0 2 1 Figure 3. Behavioral results of numerically normal participants. Scatterplot (with marginal histograms), plotting normalized measures of efficiency in numerical tasks ( y axis), and JND for continuous quantity discrimination (x axis) in the numerically normal participants (Control Group 1). Symbols represent results from individual participants, with superimposed line of best fit revealing no significant correlation. Figure 2. Behavioral results. Mean performance across participants with dyscalculia (DD, n = 16; black bars) versus numerically normal participants included in the VBM analysis (Control Group 1, n = 37; white bars). Dyscalculia show impaired performance on numerical tasks but preserved JNDs for time and space discrimination (normalized values). Asterisk indicates a significant in the two groups ( p < .001). The dissociation between number/arithmetic and con- tinuous quantity performance in participants with dys- calculia as well as the lack of correlation between these tasks suggests that atypical number development leaves spared other types of quantity processing like time and space (see also Cappelletti, Freeman, & Butterworth, 2011; Rubinsten et al., 2005). Behavioral Performance in Numerically Normal Participants Given the dissociation between number/arithmetic and continuous quantity tasks in dyscalculicsʼ performance, we examined whether or not there was a similar disso- ciation in numerically normal healthy adults or whether such dissociation may reflect peculiarities of the dyscalculic sample. In numerically normal participants (Control Group 1), we found remarkably large individual variability in performing number and arithmetic tasks, consistent with previous studies (Halberda et al., 2008). For instance, accuracy across these tasks ranged from about 70% cor- rect to 100% and mean RT varied from about 300 msec to 1.9 sec. We also found a similar variability in the con- tinuous quantity tasks, which has not previously been documented (see Figure 3). Hence, accuracy for discrimi- nating the smallest increment ranged from 50% (chance) to 88% correct for space discrimination and from 50% to 78% correct for time; for both space and time, averaged JNDs ranged from 1.5% to 14% increments. JNDs for space and time correlated [Pearsonsʼ r = 0.48, F(1, 36) = 10.7, p = .002] and similarly performance in number/arithmetic tasks expressed as efficiency score correlated (Table 2). Nonetheless, there was no significant correlation between performance in the continuous quantity and the number/ arithmetic tasks neither when performance was compared on the basis of efficiency scores and JNDs (all p > .1, 看
数字 3, 桌子 2) nor when compatible measures of
accuracy were considered (JNDs and percent correct only;
all ps > .2), or when JNDs in continuous quantity were

992

认知神经科学杂志

体积 26, 数字 5

桌子 2. Correlations between Tasks and between Behavior and Gray Matter Volume

Brain Area

任务

Numbera

1 D-N matching

2 Number comparison

3 Arithmetics

Continuous Quantityb

4 空间

5 时间

Control Tasks

6 Location detectiona

7 Luminanceb

8 IPS

9 Cuneus

10 TPJ

–

.37*

–

.54**

.31*

–

.48**

–

.57**

–

.6**

.29*

.5**

.65**

.37*

.59**

–

.48**

–

.36*

.46*

.42*

.48**

–

Significant correlations (indicated by asterisks) between performance in number/arithmetic, continuous quantity, control tasks (expressed as effi-
ciency scores or JNDs), and gray matter volume in the IPS, cuneus, and TPJ regions.
D-N matching = dot–number matching; ns = not significant.
aEfficiency score = accuracy/mean RT of correct answers only.
bJNDs.

*p < .05. **p < .001. factor 4 was associated with the location discrimination task. In summary, the PCA (1) confirmed our initial hypoth- esis that our tasks probe distinct versus common resources and (2) allowed us to reduce the number of behavioral di- mensions used in the VBM analyses, as done in previous studies (see Garrido et al., 2009). Our behavioral data showed a dissociation between number/arithmetic and continuous quantity tasks in par- ticipants with dyscalculia and no evidence for a correla- tion between these tasks in numerically normal participants. This was also the case when we controlled for variables that were unmatched between the con- tinuous quantity and the number/arithmetic tasks, for in- stance, task instructions (Supplementary Control Task 1). Indeed, when task instructions were similar, we found that performance in the time and space discrimination indexed by JNDs correlated irrespective of whether the tasks were performed under time pressure [r(16) = .53, p < .04] or with no time pressure [r(16) = .72, p < .003], consistent with our previous results. How- ever, performance in time and space discrimination did not correlate with number and arithmetic proficiency whether this was measured in terms of accuracy ( p >
.09) or RTs ( p > .8).

而且, proficiency in the numerosity task (事物-
sured in Supplementary Control Task 1) correlated with
accuracy in arithmetic verification [r = 0.45, p = .03] 和
dot–number matching tasks [r = 0.43, p = .04], 但不是
number comparison [r = 0.3, p < .1, ns]. Critically, per- formance in the numerosity discrimination task did not correlate with performance in either the time [r = 0.33, p = .1, ns] or the space discrimination tasks [r = 0.26, p = .7, ns]. VBM of Regional Gray Matter Volume A dissociation and no correlation between number/ arithmetic and continuous quantity tasks might indicate their independence or alternatively the presence of additional uncontrolled variables. To test such possible independence, we used VBM with the prediction that independence in our experimental tasks might result in different brain regions being associated with number/ arithmetic and continuous quantity. In contrast, com- monality in number/arithmetic and continuous quantity processing might be reflected in commonality in the brain regions associated with these processes. Cappelletti et al. 993 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 6 / 5 2 6 9 / 8 5 6 / 1 9 9 8 4 6 7 / 3 1 3 7 3 8 o 1 c 2 n 0 _ 0 a / _ j 0 o 0 c 5 n 4 6 _ a p _ d 0 0 b 5 y 4 g 6 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 i 2 3 e s / j / . t f u s e r o n 1 7 M a y 2 0 2 1 Table 3. PCA for Numerically Normal Participants Revealing Four Independent Factors Accounting for Performance in Number/ Arithmetic Tasks (Factor 1), Time and Space Discrimination (Factor 2), Luminosity Discrimination (Factor 3), and Location Discrimination (Factor 4), Respectively Factor Task Number and Arithmetic Dot–number matching Number comparison Arithmetics Addition problems Subtraction problems Multiplication problems Continuous Quantity Space discrimination Time discrimination Control Tasks Luminosity discrimination Location discrimination 1 0.860 0.843 0.824 0.890 0.825 0.822 0.190 −0.151 0.114 −0.360 2 0.230 −0.106 −0.047 −0.195 −0.170 0.115 0.740 0.799 −0.003 −0.158 3 0.037 0.007 0.091 0.079 0.038 0.300 −0.287 0.235 0.940 0.232 4 −0.147 0.264 0.165 −0.108 0.032 0.096 −0.209 0.107 −0.061 0.823 We first assessed whether normal individual differ- ences in number/arithmetic competence and in continu- ous quantity discrimination correlated with individual differences in gray matter volume (for Control Group 1, see Methods). 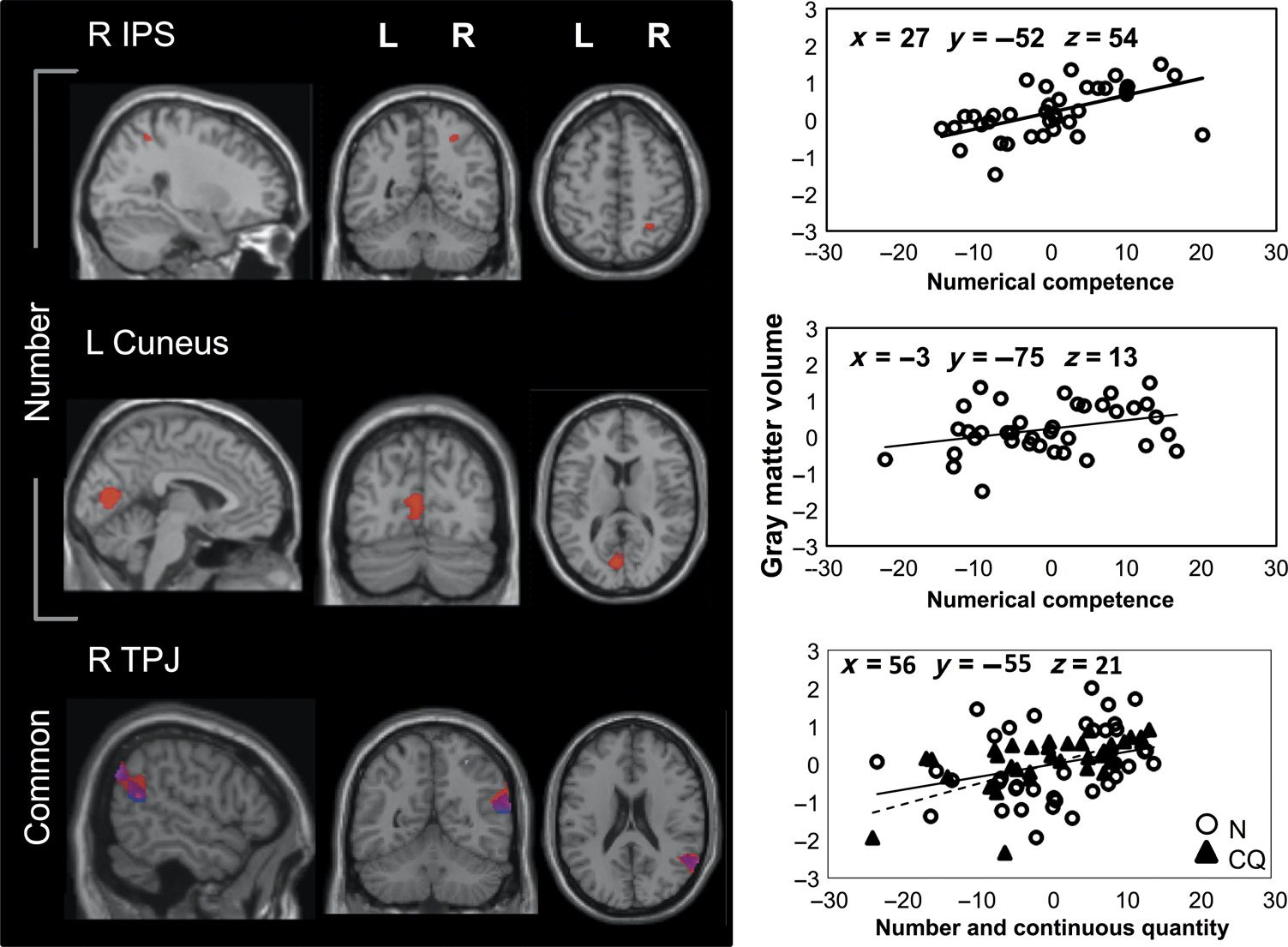Using PCA Rotated Factors 1 and 2 as indices of behavior (see Table 3), we found significant relationships between gray matter volume and per- formance measures on both number/arithmetic and con- tinuous quantity in the right TPJ [r = 0.62, p < .001; see Table 4]. Yet, there were significantly greater associations (i.e., significant interaction) between gray matter volume and number/arithmetic relative to continuous quantity Table 4. Brain Areas of Increased Gray Matter Volume Associated with Performance in Number/Arithmetic and in Continuous Quantity Tasks (Space and Time) Coordinates Number Continuous Quantitya Interaction Number–control Taskb Continuous Quantity–Control Taskc Area Cuneus IPSd TPJ H L R R x 3 27 56 y −75 −52 −55 z 13 54 21 Z Score (No. of Voxels) 4.3 (596) 4.1 (56) 3.1 (33) ns ns 4.1 (505) 3.2 4.3 (1027) ns 3.3 (16) 2.8 (22) 3.2 (10)e 3.6 (94) Only areas significant ( p < .001) after correcting for multiple comparisons are reported. H = hemisphere; L = left; R = right; ns = not significant. aSpace and time. bLocation discrimination. cLuminosity discrimination. dROI based on functional data obtained in similar number tasks (Cappelletti et al., 2010) and consistent with previous studies (Cohen Kadosh et al., 2008; Dehaene et al., 2003). eWithin 6-mm radius. 994 Journal of Cognitive Neuroscience Volume 26, Number 5 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 6 / 5 2 6 9 / 8 5 6 / 1 9 9 8 4 6 7 / 3 1 3 7 3 8 o 1 c 2 n 0 _ 0 a / _ j 0 o 0 c 5 n 4 6 _ a p _ d 0 0 b 5 y 4 g 6 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 i 2 3 e s / j t f . / u s e r o n 1 7 M a y 2 0 2 1 Figure 4. Neuroanatomical results. Left column shows structural MRI sections from a standard T1 template in MNI stereotactic space in sagittal, coronal, and axial view. Each row highlights a different cortical locus where correlation between gray matter volume and PCA-rotated behavioral measures was significant in numerically normal participants of Control Group 1 ( p < .05 for multiple comparisons across the whole brain using family- wise error correction, see also Table 2; red = numerical competence, blue = continuous quantity). Each graph on the right plots normalized gray matter volume ( y axes) sampled from the corresponding highlighted region on its left (with Talairach coordinates), against the behavioral measure with which it was found to correlate (x axes, in z scores). In the bottom graph, circle symbols (and continuous line of best fit) represent numerical/arithmetical competence (N), and triangles represent performance on continuous quantity tasks (CQ, with dotted line of best fit). Note that, for convenience of comparison with numerical competence, the continuous quantity JNDs have been sign-inverted (i.e., negative values transformed to positive and vice versa), so that higher values correspond on the graph to better rather than poorer performance. performance in the right IPS [r = 0.56, p < .001] and in the left cuneus [r = 0.19, p < .05; see Table 4 and Figure 4]. One possibility is that gray matter volume in the re- gions identified simply reflected a correlation with any measure of RT or accuracy respectively. In this case, gray matter volume in the right IPS, cuneus, and TPJ regions should also correlate with the control tasks, which shared the same behavioral measures with the experimental tasks. However, we found that performance in neither the location discrimination nor in the luminance discrimi- nation (expressed as efficiency scores or JNDs) correlated with gray matter volume in any of these brain regions (all ps > .18; 见表 2), therefore suggesting that
the effect of number/arithmetic and continuous quantity
did not simply reflect the type of behavioral measure
用过的 (RTs vs. 准确性). We also tested whether the link
between gray matter volume and behavior was driven
by any specific task grouped within each PCA factor.
We therefore looked at correlations between gray matter
volume and each individual task used (而不是
PCA factors). We used the estimates of gray matter vol-
ume extracted from the significant clusters identified in
分析 1 and the normalized raw scores of the number/
arithmetic and continuous quantity tasks. Besides cor-
relating with the PCA factors, gray matter volume in the
right IPS and cuneus correlated with all the number tasks

(with the exception of a marginal correlation for the
number comparison task, p = .07) and in TPJ regions
with both continuous quantity tasks used, after correct-
ing for multiple comparisons. This indicates that all
the tasks included in the PCA factors contributed to the
correlation between gray matter volume and behavior.

最后, we examined whether there was any effect of
number/arithmetic or continuous quantity in a set of pre-
defined ROIs (参见方法). These ROI analyses indicated
that our number/arithmetic-specific parietal effects corre-
sponded to the same right IPS number area reported in
previous functional imaging studies (Cappelletti et al.,
2010; Wiener et al., 2010; Cohen Kadosh et al., 2008;
Dehaene et al., 2003). No further brain regions reached
significance.

讨论

Our study aimed to investigate the relation between
numerical/arithmetical abilities and other continuous
quantity abilities, such as those involved in time and space
加工. 具体来说, we used neuropsychology, psy-
chophysics, and VBM to test whether the ability to process
continuous quantities was maintained when numerical
processes are developmentally impaired (IE。, in dys-
calculia) and whether number and continuous quantity

Cappelletti et al.

995

D
哦
w
n
我
哦
A
d
e
d

F
r
哦
米

我

/
j

t
t

F
/

我
t
.

:
/
/

/
j

你
s
e
r

哦
n

1
7

中号
A
y

2
0
2
1

correlated behaviorally and anatomically in numerically
normal participants. Our results indicate that proficiency
in numerical and continuous quantity tasks dissociated
in dyscalculia (IE。, impaired number but spared time
and space processing). 而且, performance in these
tasks did not correlate in numerically normal partici-
pants, although individual differences in performing
numerical and continuous quantity tasks both correlated
with increased gray matter volume in the right TPJ. 经过
using several control measures, we also established that
these results did not just depend on generic aspects
of our behavioral measures but appeared specific for
numerical and continuous quantity tasks. 此外,
gray matter in right IPS and left cuneus was more closely
related to numerical/arithmetical than continuous quantity
任务.

Numerical Proficiency Dissociates from Time
and Space Processing

Our two main findings of behavioral independence de-
spite anatomical association of numerical and continuous
quantity skills provide a deeper understanding of the rela-
tion between these skills. The independence of number
and continuous quantity was supported by their disso-
ciation in dyscalculia, the lack of behavioral correlation in
numerically normal participants, and the number-specific
anatomical correlations in right IPS and cuneus. This in-
dependence may reflect some intrinsic differences in pro-
cessing number and continuous quantity. 例如,
unlike continuous quantity, number has discrete referents
and is based on enumeration and arithmetical principles
rather than approximation as in time and space processing
(Henik, Leibovich, Naparstek, Diesendruck, & Rubinsten,
2011; Castelli, Glaser, & Butterworth, 2006). Critically,
the dissociation between numerical and continuous quan-
tity skills in dyscalculia suggests that contrary to nu-
merical skills, continuous quantity processing develops
adequately and is adequately maintained in dyscalculia
(see also Cappelletti, 弗里曼, & Butterworth, 2011).
然而, it is currently unknown whether in dyscalculia
number processing is independent and dysfunctional
from birth or whether numerical and continuous quan-
tity skills correctly develop together with number skills
deteriorating later.

Besides the IPS, increased gray matter volume associ-
ated with RTs but not accuracy in number tasks was
shown in the cuneus, a brain area frequently reported in
relation to working memory (Slotinick & Schacter, 2006),
suggesting that this area may be sensitive to task difficulty
in the context of number processing.

A recent study indicated a link between performing
continuous quantity tasks (spatial extent), numerosity dis-
定罪, and arithmetical abilities. 具体来说, 空间
and numerosity processing were shown to be linked and
foundational to arithmetical proficiency (Lourenco, Bonny,

Fernandez, & 饶, 2012). This is different to what we
成立, although a closer look at these recent data shows
only an apparent discrepancy with ours: 的确, 缺点-
tribution of space processing to arithmetical abilities was
actually only indirect, with a much stronger role in per-
forming geometry rather than arithmetical tasks (Lourenco
等人。, 2012).

One or Multiple Quantity Systems?

Our second finding is of an association between number/
arithmetical and continuous quantity tasks, 哪些是
both related to an increase in gray matter volume in
TPJ. The anatomical association between these tasks
could reflect magnitude processes (Cantlon et al., 2009;
Walsh, 2003) or alternatively the cognitive resources
needed to judge magnitude, which could include deci-
锡安, 刺激, response selection, or attentional pro-
过程 (Cappelletti et al., 2010; Cohen Kadosh et al.,
2008). The contribution of attentional processes may
be suggested by the involvement of the right TPJ region,
a brain area part of a stimulus-driven attention system
that detects relevant stimuli or changes in their status
(Kincade, Abrams, Astafiev, 舒尔曼, & 科尔贝塔, 2005;
科尔贝塔 & 舒尔曼, 2002) also on dimensions such as
duration, 地点, and numerosity (Coull, Cheng, & Meck,
2011; Vetter, Butterworth, & Bahrami, 2011; Ansari, Lyons,
van Eimeren, & 徐, 2007). Our data indicate that such
processes can also be associated with symbolic numbers,
in line with lesion data showing that right TPJ lesions
affect attention-related processes. These processes, 甚至
not always in the context of TPJ lesions, are known to
interfere with number ( Vuilleumier, Ortigue, & Brugger,
2004) or with continuous quantity manipulation (Danckert
等人。, 2007).

Attentional processes associated with right TPJ may
subserve different functions on which different tasks may
rely. 例如, separate processes may be needed to
maintain attention up to the end of the stimulus presen-
站 (in the time task) to respond to a change in the
刺激 (in both the time and space tasks) or to extract
the meaning of symbols or retrieve the correct result of
the arithmetical operations (in the arithmetic tasks). 这
hypothesis of multiple types of attention converging in
the right TPJ may explain the apparent similarity of perfor-
mance in number and continuous quantity tasks previously
报道 (Vetter et al., 2011; Brannon et al., 2007; Zorzi
等人。, 2002) and may be the reason why performance on
number and continuous quantities tasks did not correlate
在我们的研究中. 或者, the right TPJ might support the
same function in all number and continuous quantity
任务, 例如, comparison processes may be a point
of convergence between these tasks (Cantlon et al.,
2009). 进一步来说, the number and the continuous
quantity tasks imply the preparation and maintenance of
a target-stimulus template to be compared with the actual

996

认知神经科学杂志

体积 26, 数字 5

D
哦
w
n
我
哦
A
d
e
d

F
r
哦
米

我

/
j

F
/

t
t

我
t
.

:
/
/

/
j

你
s
e
r

哦
n

1
7

中号
A
y

2
0
2
1

目标, 那是, a matching or mismatching process, 这是
linked to the left and right TPJ area (DiQuattro & Geng,
2011; Doricchi, Macci, Silvetti, & Macaluso, 2010; Kincade
等人。, 2005). This comparison or matching process may
be different in the luminance task, possibly because infor-
mation about luminance could be obtained directly from
every local part of the stimulus line (Gilchrist & Radonjić,
2009). 所以, participants did not need to build up
and keep active the whole line stimulus template to
perform the luminance comparison, as they would do for
time and space. This may explain why discriminating lumi-
南斯, arguably another quantity dimension (Pinel et al.,
2004), did not correlate with gray matter volume in the
right TPJ, which was linked to number, 时间, and space.
同样地, in the other control task used, location discrimi-
国家, there was no reference–template matching or
mismatching a stimulus target, a process linked to the
TPJ area (Doricchi et al., 2010; Kincade et al., 2005). 因此,
although luminance discrimination and location detection
tasks aimed respectively to control for response and stim-
ulus selection processes in common with the time and
space discrimination tasks and to match the behavioral
measure used with the number tasks, they differed sub-
stantially in other underlying cognitive processes. 这
may explain the lack of anatomical overlap with the
数字, 时间, and space tasks.

It may be surprising that common resources were not
detected in the IPS, a region previously hypothesized to
host a shared magnitude representation ( Walsh, 2003)
and that functional imaging studies often report as
involved in number processing (例如, Cappelletti et al.,
2010; Dehaene et al., 2003; Dormal et al., 2012; Fias et al.,
2003). This may be because functional and structural
imaging studies measure different things, and currently
the relationship between function and structure is only
poorly understood (然而, see Song, 施华蔻, &
Rees, 2013, for a study on the relation between brain
function and structure in primary visual cortex). Functional
imaging looks at neural responses averaged across indi-
个人 (IE。, activations common across many participants),
and it measures current involvement in a task, with more
activation for more involvement (less with practice and
efficiency). 相比之下, in structural imaging measures
are derived from differences across individuals, 和他们
reflect many different factors including a lifetime of re-
sponses and efficiency (more with practice and efficiency;
Kanai & Rees, 2011). As many different activations can
engage the same process (例如, 空间注意力), 那里
may be no correlation with performance of a single task
(例如, numerical processing), but a correlation might
arise with a measure that encompasses process rather
than task.

综上所述, we report novel evidence that charac-
terizes the relation between number and continuous quan-
tity processing. 第一的, in a population with a developmental
numerical dysfunction, 那是, dyscalculia, continuous
quantity processing was well maintained; 第二, 在

numerically normal people, numerical/arithmetical and
continuous quantity skills were at least partially dissoci-
ated, both behaviorally and anatomically. Despite no cor-
relation between behavioral measures, both number/
arithmetic and continuous quantity correlated with struc-
tural changes in right TPJ, whereas the right IPS and the
cuneus were distinguished by their correlation with the
number/arithmetic tasks only. 一起, our new evidence
of a number-specific impairment and of number-specific
brain areas distinct from common magnitude areas sug-
gests that the human brain is equipped with different
ways of quantifying the outside world.

致谢
This work was supported by the Wellcome Trust (G. R。, C. J. P。);
a Royal Society Dorothy Hodgkin Fellowship, Royal Society, 和
British Academy Research Grants (中号. C。); and the Japan Society
for the Promotion of Science and Japan Science and Technology
机构 (右. K.). We would like to thank two anonymous reviewers
for their helpful comments.

Reprint requests should be sent to Marinella Cappelletti, 大学
College London, Institute of Cognitive Neuroscience, 17 Queen
Square, 伦敦, WC1N 3AR, 英国, or via e-mail: m.cappelletti@
ucl.ac.uk.

参考

Aiello, M。, Jacquin-Courtois, S。, Merola, S。, Ottaviani, T。,

Tomaiuolo, F。, Bueti, D ., 等人. (2012). No inherent left
and right side in human “mental number line”: 证据
from right brain damage. Brain, 135, 2492–2505.

Ansari, D ., Lyons, 我. M。, van Eimeren, L。, & 徐, F. (2007).

Linking visual attention and number processing in the brain:
The role of the temporo-parietal junction in small and large
symbolic and nonsymbolic number comparison. 杂志
of Cognitive Neuroscience, 19, 1845–1853.
Ashburner, J。, & 弗里斯顿, K. J. (2000). Voxel-based

morphometry. The methods. Neuroimage, 11, 805–821.
Ashburner, J。, & 弗里斯顿, K. J. (2005). Unified segmentation.

Neuroimage, 26, 839–851.

Brannon, 乙. M。, Suanda, S。, & Libertus, K. (2007). Temporal

discrimination increases in precision over development and
parallels the development of numerosity discrimination.
Developmental Science, 10, 770–777.

Bueti, D ., & Walsh, V. (2009). The parietal cortex and

the representation of time, 空间, number and other
幅度. Phil Trans of Royal Society, Series B,
Biological Science, 364, 1831–1840.

Butterworth, 乙. (2003). Dyscalculia screener. 伦敦:

Nelson Publishing Company Ltd.

Butterworth, 乙. (2010). Foundational numerical capacities

and the origins of dyscalculia. Trends in Cognitive
科学, 14, 534–541.

Cantlon, J. F。, Platt, 中号. L。, & Brannon, 乙. 中号. (2009). 超过
the number domain. Trends in Cognitive Science, 13,
83–91.

Cappelletti, M。, Didino, D ., Stoianov, 我。, & Zorzi, 中号.

(in press). Number skills are maintained in healthy
老化. 认知心理学.

Cappelletti, M。, 弗里曼, E., & Butterworth, 乙. (2011). 时间
perception in dyscalculia. Frontiers in Cognitive Science,
2, 364.

Cappelletti et al.

997

D
哦
w
n
我
哦
A
d
e
d

F
r
哦
米

我

/
j

F
/

t
t

我
t
.

:
/
/

/
j

你
s
e
r

哦
n

1
7

中号
A
y

2
0
2
1

Cappelletti, M。, 弗里曼, 乙. D ., & Cipolotti, L. (2009).

Fias, W., Lammertyn, J。, Reynvoet, B., Dupont, P。, & Orban,

Dissociations and interactions between time, numerosity
and space processing. Neuropsychologia, 47, 2732–2748.

Cappelletti, M。, 弗里曼, 乙. D ., & Cipolotti, L. (2011).

Numbers and time doubly dissociate. Neuropsychologia,
49, 3078–3092.

Cappelletti, M。, Gessaroll, E., Hithersay, R。, Mitolo, M。,

Didino, D ., Kanai, R。, 等人. (2013). Neuroenhancement:
Greatest, long-term and transferable quantity judgement
induced by brain stimulation combined with cognitive
训练. The Journal of Neuroscience, 33, 14899–17907.
Cappelletti, M。, 李, H. L。, 弗里曼, 乙. D ., & Price, C. J. (2010).
Dissociating number selectivity and response-times in the
parietal lobes. 认知神经科学杂志, 22,
331–346.

Cappelletti, M。, & Price, C. J. (2014). Residual number

skills in adults with dyscalculia. Neuroimage Clinical, 4,
18–28.

Castelli, F。, Glaser, D. E., & Butterworth, 乙. (2006). Discrete
and analogue quantity processing in the parietal lobe:
A functional MRI study. 国家会议录
Academy of Sciences, 美国。, 103, 4693–4698.

Cohen Kadosh, R。, Lammertyn, J。, & Izard, V. (2008).
Are numbers special? An overview of chronometric,
neuroimaging, developmental and comparative studies
of magnitude representation. Progress in Neurobiology,
84, 132–147.

科尔贝塔, M。, & 舒尔曼, G. L. (2002). Control of goal-directed
and stimulus-driven attention in the brain. Nature Review
神经科学, 3, 215–229.

Coull, J. T。, Cheng, R。, & Meck, 瓦. H. (2011). Neuroanatomical

and neurochemical substrates of timing.
Neuropsychopharmacology, 36, 3–25.

克劳福德, J. R。, 豪厄尔, D. C。, & Garthwaite, 磷. H. (1998).
Payne and Jones revisited: Estimating the abnormality of
test score differences using a modified paired samples
t test. Journal of Clinical and Experimental
Neuropsychology, 20, 898–905.

G. A. (2003). Parietal representation of symbolic
and nonsymbolic magnitude. 认知杂志
神经科学, 15, 47–56.

Garrido, L。, Furl, N。, Draganski, B., Weiskopf, N。, Stevens, J。,
Tan, G. C。, 等人. (2009). VBM reveals reduced gray matter
volume in the temporal cortex of developmental
prosopagnosics. Brain, 132, 3443–3455.

Gilchrist, A. L。, & Radonjić, A. (2009). Anchoring of lightness
values by relative luminance and relative area. 杂志
Vision, 9, 1–10.

Halberda, J。, Mazzocco, 中号. 中号. M。, & Feigenson, L. (2008).

Individual differences in nonverbal number acuity predict
maths achievement. 自然, 455, 665–668.

Hayasaka, S。, Phan, K. L。, Liberzon, 我。, Worsley, K. J。, & Nichols,

时间. 乙. (2004). Non-stationary cluster-size inference with
random field and permutation methods. Neuroimage, 22,
676–687.

Henik, A。, Leibovich, T。, Naparstek, S。, Diesendruck, L。, &
Rubinsten, 氧. (2011). 数量, 金额, 和
numerical core system. Frontiers in Human Neuroscience,
5, 186.

Jackson, M。, & Warrington, 乙. K. (1986). Arithmetic skills
in patients with unilateral cerebral lesions. Cortex, 22,
611–620.

Kanai, R。, & Rees, G. (2011). The structural basis of inter-

individual differences in human behaviour and cognition.
自然评论神经科学, 12, 231–242.

Kincade, J. M。, Abrams, 右. A。, Astafiev, S. 五、, 舒尔曼, G. L。, &
科尔贝塔, 中号. (2005). An event-related functional magnetic
resonance imaging study of voluntary and stimulus-driven
orienting of attention. 神经科学杂志, 25,
4593–4604.

Lourenco, S。, Bonny, J。, Fernandez, E., & 饶, S. (2012).

Nonsymbolic number and cumulative area representations
contribute shared and unique variance to symbolic math
competence. 美国国家科学院院刊
科学, 109, 18737–18742.

Danckert, J。, Ferber, S。, Pun, C。, Broderick, C。, Striemer, C。,

Machizawa, M。, & Driver, J. (2011). Principal component

Rock, S。, 等人. (2007). Neglected time: Impaired
temporal perception of multisecond intervals in
unilateral neglect. 认知神经科学杂志,
19, 1706–1720.

德阿内, S。, & Brannon, 乙. 中号. (2011). 空间, time and number
in the brain: Searching for evolutionary foundations of
mathematical thought. 伦敦: 爱思唯尔.

德阿内, S。, Piazza, M。, Pinel, P。, & 科恩, L. (2003).

Three parietal circuits for number processing.
Cognitive Neuropsychology, 20, 487–506.

DiQuattro, 氮. E., & Geng, J. J. (2011). Contextual knowledge

configures attentional control networks. 杂志
神经科学, 31, 18026–18035.

Doricchi, F。, Guariglia, P。, Gasparini, M。, & Tomaiuolo, F.

(2005). Dissociation between physical and mental number
line bisection in right hemisphere brain damage. 自然
神经科学, 12, 1663–1665.

Doricchi, F。, Macci, E., Silvetti, M。, & Macaluso, 乙. (2010).

Neural correlates of the spatial and expectancy
components of endogenous and stimulus-driven
orienting of attention in the Posner task. Cerebral
Cortex, 20, 1574–1585.

Dormal, 五、, Dormal, G。, Joassin, F。, & Pesenti, 中号. (2012).
A common right fronto-parietal network for numerosity
and duration processing: An fMRI study. 人脑
测绘, 33, 1490–1501.

Dormal, 五、, Seron, X。, & Pesenti, 中号. (2006). Numerosity-duration

干涉: A Stroop experiment. 心理学学报
(阿姆斯特丹), 121, 109–124.

analysis of behavioural individual differences suggests that
particular aspects of visual working memory may relate to
specific aspects of attention. Neuropsychologia, 49,
1518–1526.

Mazzocco, M。, Feingenson, L。, & Halberda, J. (2011). Impaired

acuity of the approximate number system underlies
mathematical learning disability (dyscalculia). Child
发展, 82, 1224–1237.

Piazza, M。, Facoetti, A。, Trussardi, A. N。, Berteletti, 我。, Conte, S。,
Lucangeli, D ., 等人. (2010). Developmental trajectory of
number acuity reveals a severe impairment in developmental
dyscalculia. 认识, 116, 33–41.

Pinel, P。, Piazza, M。, LeBihan, D ., & 德阿内, S. (2004).

Distributed and overlapping cerebral representations of
number size and luminance during comparative judgements.
神经元, 41, 983–993.

Rubinsten, 奥。, & Henik, A. (2005). Automatic activation of

internal magnitudes: A study of developmental dyscalculia.
Neuropsychology, 19, 641–648.

Rubinsten, 奥。, & Henik, A. (2009). Developmental dyscalculia:
Heterogeneity may not mean different mechanisms. Trends
in Cognitive Science, 13, 92–99.

Slotinick, S。, & Schacter, D. (2006). The nature of memory

related activity in early visual areas. Neuropsychologia, 44,
2874–2886.

歌曲, C。, 施华蔻, D. S。, & Rees, G. (2013). Variability in
visual cortex size reflects tradeoff between local orientation
sensitivity and global orientation modulation. 自然
通讯, 4, 2201.

998

认知神经科学杂志

体积 26, 数字 5

D
哦
w
n
我
哦
A
d
e
d

F
r
哦
米

我

/
j

t
t

F
/

我
t
.

:
/
/

/
j

你
s
e
r

哦
n

1
7

中号
A
y

2
0
2
1

Vetter, P。, Butterworth, B., & Bahrami, 乙. (2011). A candidate
for the attentional bottleneck: Set-size specific modulation of
right TPJ during attentive enumeration. 认知杂志
神经科学, 23, 728–736.

Vuilleumier, P。, Ortigue, S。, & Brugger, 磷. (2004). The number

space and neglect. Cortex, 40, 399–410.

Walsh, V. (2003). A theory of magnitude: Common cortical
metrics of time, space and quantity. Trends in Cognitive
科学, 7, 483–488.

Wichmann, F. A。, & 爬坡道, 氮. J. (2001). The psychometric

function: 我. Fitting, sampling and goodness-of-fit. 洞察力
and Psychophysics, 63, 1293–1313.

Wiener, M。, Turkeltaub, P。, & Coslett, H. 乙. (2010). 这

image of time: A voxel-wise meta-analysis. Neuroimage,
49, 1728–1740.

Wood, D. J。, Tataryn, R。, & Gorsuch, L. (1996). Effects of under

and overextraction on principal axis factor analysis with
varimax rotation. Psychological Methods, 14, 354–365.

Wechsler, D. (1986). Wechsler Adult Intelligence Scale-Revised.

Zorzi, M。, Priftis, C。, & Umiltà, C. (2002). Neglect disrupts the

纽约: The Psychological Corporation.