Bill Alves
Harvey Mudd College
301 乙. 12th St.
Claremont, 加利福尼亚州 91711
alves@hmc.edu
Digital Harmony of Sound
and Light
In the late 1980s and early 1990s I was privileged to
work with the computer animation pioneer John
Whitney Sr. and was profoundly influenced by his
ideas on how to apply musical concepts of harmony
to visual arts of motion. At the time of his death in
1995, he and I were planning composition software
in which an artist could apply these concepts to cre-
ate harmonic patterns simultaneously in sound and
animation.
Though this idea was never realized beyond cer-
tain tests, I have taken this step in my subsequent
work in computer-generated music and video in
ways inspired by, if distinct from, Whitney’s early
artworks. This article examines ways in which
Whitney’s ideas can be applied to musical composi-
的, and in particular to ways in which I have ex-
trapolated principles from these ideas to create an
artistic correspondence between abstract animation
and computer music.
Visual Harmony
We use the word harmony today to refer not just to
the vertical dimension of music, but also a general
sense of agreement or peace—the original meaning
of harmonia to the ancient Greeks (Franklin 2002).
Pythagoras was credited with defining this equilib-
rium in mathematical terms, as whole number pro-
portions that represented an ideal not just in musical
scales, but in sculpture and architecture. Indeed the
same mathematical proportions formed the very
fabric of Platonic universe (Cornford 1937).
This close connection between music and visual
art remained a vital force in European and Islamic
art well into the Renaissance period. One does not
have to subscribe to Pythagorean numerology to
feel the arresting impact of the pure and crystalline
harmonies created by musical tunings based on in-
teger ratios, or Just intonation, as well as the beau-
ties of proportional symmetries in visual design.
电脑音乐杂志, 29:4, PP. 45–54, 冬天 2005
© 2005 麻省理工学院.
The sounds and compositional resources available
in Just intonation first attracted me as a composer.
Though the Pythagorean tradition receded with
the adoption of musical temperament and other
compositional structures for visual arts and archi-
结构, Sir Isaac Newton and others proposed a
connection of sound and vision through the wave
properties of color in light and pitch in music (琼斯
1972). Arguably the first efforts to use technology to
apply concepts of musical composition to abstract
arts of motion came with a series of experimental
devices from the 18th through the 20th centuries
generally called “color organs.” Most famously, 这
composer Aleksandr Skryabin’s Prométhée includes
a part for such an instrument which would project
the colors of Skryabin’s synesthetic associations.
然而, the technology these innovators used al-
lowed only poor and vague definition of visual form
(Collopy 2000).
The technology of filmed animation offered much
greater control over form and direct synchroniza-
tion to music. The great abstract animator Oskar
Fischinger created a remarkable series of films in
the first half of the twentieth century in which he
represented the sounds of accompanying music of-
ten with delicately fluid forms (莫里茨 2004). 许多
of his films are a kind of supple choreography dis-
tilled to abstraction, but relying on an intuitive
sense of connection to musical form.
Mapping Vision to Sound
Distinct approaches to the correspondences be-
tween sound and light are at least as important as
differences in technique in distinguishing the work
of artists in this tradition. Many artists, 从
18th-century inventor of a “color harpsichord,”
Louis-Bertrand Castel, to modern creators of music
visualizer software, have attempted to directly illus-
trate music, mapping pitch to spatial height or color
hue, 例如 (克莱因 1937). The Music Anima-
tion Machine (www.musanim.com/) of Stephen Ma-
linowski is especially interesting in this approach.
Alves
45
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
2
9
4
4
5
1
8
5
4
4
8
4
0
1
4
8
9
2
6
0
5
7
7
5
1
7
9
9
8
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
然而, though artists often speak of “color har-
金钱,” attempts to create a direct mapping of color
relationships to the immediacy of musical conso-
nance and dissonance have largely failed.
To Whitney, such a direct, synesthetic mapping of
music’s most basic parameters (沥青, 响度, 和
so forth) failed to capture the expressive vision of
great works of music, 哪个, to him, depended more
directly on multidimensional interplay of tension
and resolution. 而且, he advocated an approach
in which animation, instead of being a direct repre-
sentation of music, corresponds to this higher level
of aesthetic intention, creating what he termed
“complementarity” (Whitney 1984).
Whitney’s Differential Dynamics
John Whitney recognized that digital computers
could uniquely and directly realize in animated
form the same kind of harmonic movement found
in music in ways never imagined by the Greeks. 是-
ginning in the 1960s, Whitney created a series of ex-
traordinary films of abstract animation that used
computers to create a harmony not of color, 空间,
or musical intervals, but of motion.
在他的 1980 book Digital Harmony: On the Com-
plementarity of Music and Visual Art, Whitney hy-
pothesized that Pythagorean harmony could be
matched in visual art: “This hypothesis assumes
the existence of a new foundation for a new art. 它
assumes a broader context in which Pythagorean
laws of harmony operate. . . . 换句话说, the hy-
pothesis assumes that the attractive and repulsive
forces of harmony’s consonant/dissonant patterns
function outside the dominion of music” (p. 5).
More particularly, Whitney discovered that if he set
a large number of elements into repetitive motion
such that the motion of the second was two times
the speed of the first, the third three times the speed
of the first, 等等, the animation that would re-
sult would demonstrate beautiful patterns of sym-
metry at points corresponding to the same ratios
that define musical consonances.
ferent senses throughout history. 尤其, 我们
must be careful to distinguish between consonance
as a psychoacoustical phenomenon, which may de-
pend in large part on the closeness of the frequency
proportions to ratios of relatively small whole num-
bers, my focus here, and consonance in a more gen-
eral sense as harmonic stasis or resolution, 哪个
may be created in many different ways.)
Though Whitney’s films brilliantly demonstrate
how computer animation can effectively create a
temporal sensation of attraction and repulsion, 的
tension and resolution, he was never able to take
the next step of creating music to correspond di-
rectly to those visual images.
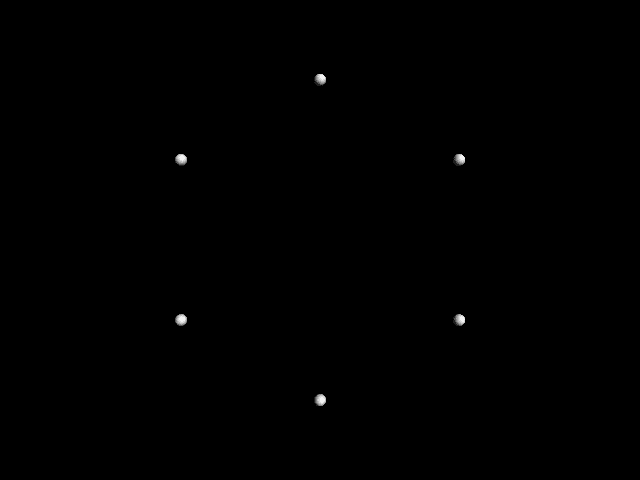
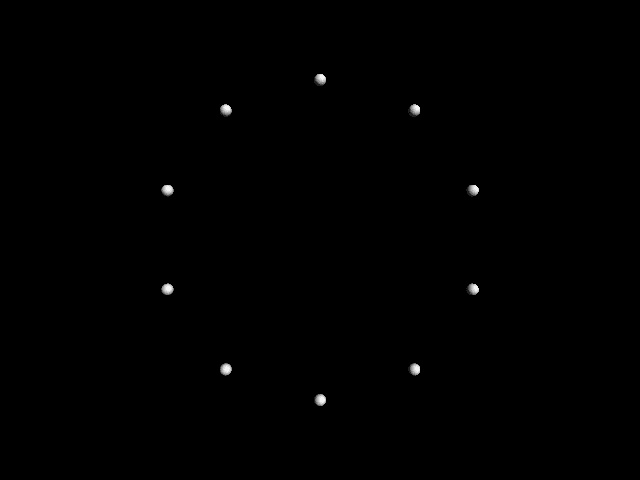
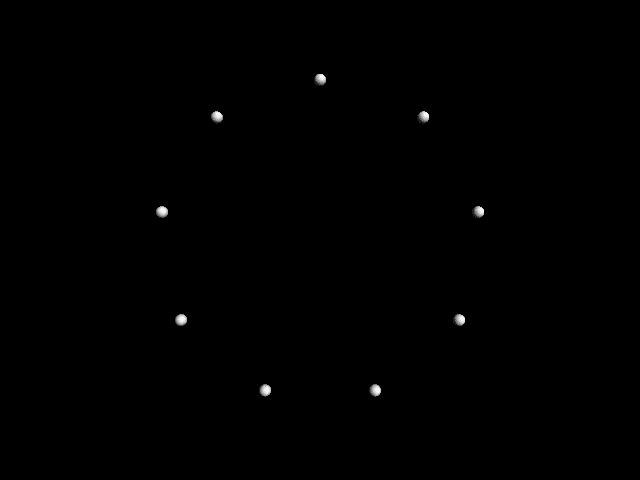
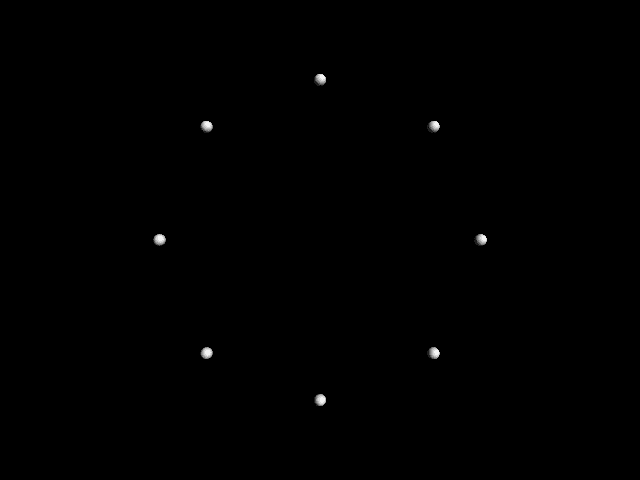
To take a very simple example of what Whitney
called “differential dynamics,” imagine a set of
points going around a circle, the second traveling
twice the speed of the first, the third three times the
speed of the first, 等等, all starting together at
the twelve o’clock position. By the time the slowest
point reaches halfway around the circle, all the points
will align with either the six or twelve o’clock posi-
的. If the slowest point is at either the one-third or
two-thirds position, all points will line up at the
thirds: twelve, 四, or eight o’clock. When the slow-
est point is at a position around the circle which is
not a very clear integer divisor of the circle’s perime-
特尔, the points will appear scattered somewhat ran-
domly, and the eye will not detect a clear pattern.
Whitney’s Works
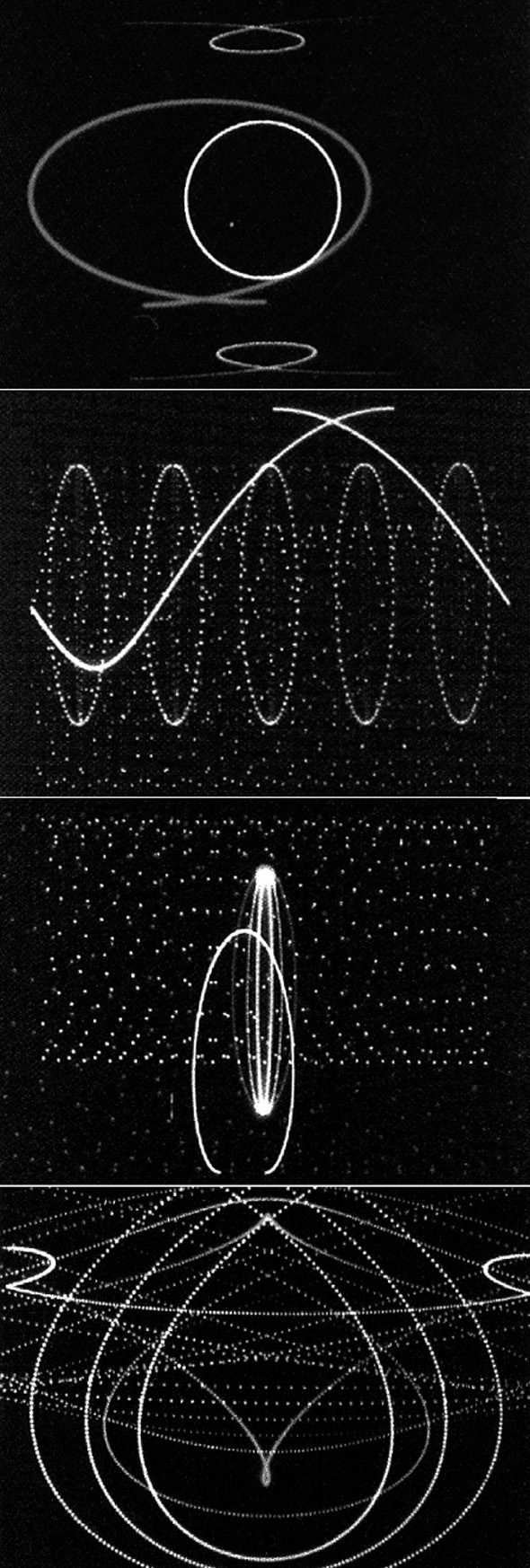
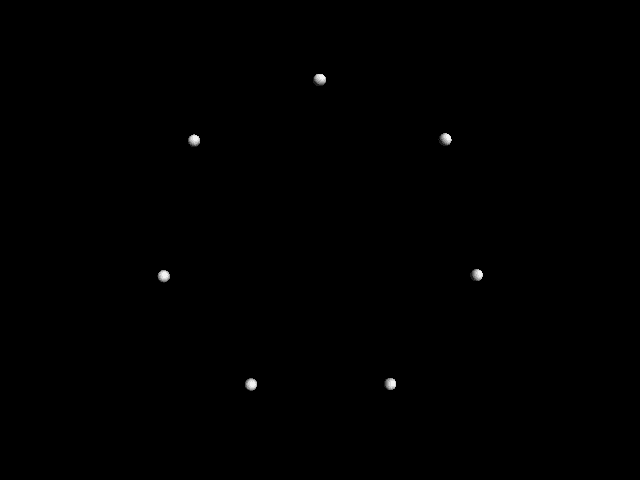
Of course points moving around a circle is a very
simple example. In his films Matrix I and III (1970
和 1972), Whitney had points or other shapes
move around parametric curves. In Permutations
(1968), the points move in various rose curves (sine
functions in polar coordinates), and in Arabesque
(1973) points initially arranged in a circle move
linearly but wrap around at the edge of the screen
(见图 1). In all of these examples, 相同
points of resonance, of striking symmetry, occur at
the same points of harmonic proportions.
(Tenney [1988] reminds us that the terms conso-
nance and dissonance have been used in many dif-
Each of these early films, created by photograph-
ing frames from a CRT monitor with an animation
46
电脑音乐杂志
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
2
9
4
4
5
1
8
5
4
4
8
4
0
1
4
8
9
2
6
0
5
7
7
5
1
7
9
9
8
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
数字 1. Images from John
Whitney’s 1973 film
Arabesque. Images repro-
duced with the permission
of the Estate of John and
James Whitney.
camera and then combining them and adding color
with an optical printer, is an intricate composition
arranged in sections in which various themes are
发达. Most distinctively, these films create
form through the manipulation of expectation, reso-
溶液, and surprise, mostly achieved through the
technique of differential dynamics. 然而, 和
the exception of Matrix I, Whitney avoided sound-
tracks with conventional tonal harmonic progres-
西翁, whose sequences of harmonic tension and
resolution might conflict with those he was pre-
senting visually.
An effort to move to an interactive compositional
system led him to create works of very low color
and spatial resolution on an IBM PC in the 1980s.
Although not nearly as immediately attractive as
his earlier works, these pieces, collected as Moon
Drum (1991), allowed him to develop works of com-
positional complexity and nuance. With this soft-
器皿, developed by Jerry Reed, he was also able to
send out MIDI messages at keyframes, creating his
own soundtrack of non-metrical FM tones and
drum machine crashes. Whereas this approach al-
lowed for musical articulation of important points
of the animation, it hardly demonstrated the possi-
bilities of a true complementarity, to use Whitney’s
学期, of visual and musical composition.
Differential Dynamics in Music
In the composing software that Whitney and I
planned, he envisioned multitudes of sine waves
rising and falling in correspondence to the spatial
motion of the elements on the screen. 然而, 我
soon realized that a literal mapping of pitch space to
height on the screen was only intuitive because our
culture has adopted that particular arbitrary meta-
phor of “low” and “high” to describe pitch. 尽管
other pioneers of connections between music and
the visual arts have explored such a mapping, 它
does not retain the possibility of musical conso-
nance resulting in visually “consonant” patterns.
The fact that whole number proportions create
these arresting patterns of visual resonance suggest
a correspondence, or complementarity, to conso-
nant musical sonorities created by whole number
frequency ratios, 那是, Just intonation. Seeing that
Just musical intervals occur naturally in the har-
monic series, many Just intonation composers, 这样的
as La Monte Young, have focused on the composi-
tional resources of frequency ratios related implic-
itly to a common fundamental, a relationship
Partch (1974) terms an otonality.
然而, the proportions of Whitney’s differential
Alves
47
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
2
9
4
4
5
1
8
5
4
4
8
4
0
1
4
8
9
2
6
0
5
7
7
5
1
7
9
9
8
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
dynamics suggest a different kind of relationship.
In the example of points moving around a circle,
when the first point reaches the one-third point in
the circle, all the points are aligned to the 12:00,
4:00, 和 8:00 positions. By treating the 12:00 posi-
tion as the fundamental, the one-third point would
represent a 3/1 frequency ratio and the two-thirds
point the 3/2 frequency ratio. (Just intonation ratios
are conventionally notated with the larger number
in the numerator. I have adopted this convention for
ratios of both frequencies and visual proportions, 作为
in this example.)
Similar patterns would occur at other whole-
number divisions, but with increasing complexity
as that whole number increases. Thus a five-fold di-
vision of the circle would correspond to frequency
的比率 5/5 (那是, 1/1, 基本的), 5/4, 5/3,
5/2, 和 5/1. Unlike the harmonic series, this set of
musical intervals has a constant factor in the nu-
merator. This set defines what Partch called an
utonality and what others have called a subhar-
monic series (那是, the inversion of the harmonic
系列). Subharmonic series occur with combina-
tions of any integer divisions of a whole, as with di-
visions of string lengths or evenly spaced holes on
aerophones, 例如.
The higher the numerator, or number of divi-
西翁, what Partch calls the numerary nexus, 这
further along the spectrum we are towards disso-
南斯. The smaller this common factor or numer-
ary nexus, the more stable but less dynamic the
sound and image. Thus the frequency ratio of 2:1 是
the octave, 哪个, as with the differential dynamics
例子, results in a profoundly stable but not very
interesting consonance. Somewhat more complex
factors such as 5 或者 7, which offer more interesting
musical consonances, result in fascinating symmet-
rical patterns that catch the eye’s attention when
applied the differential dynamics system.
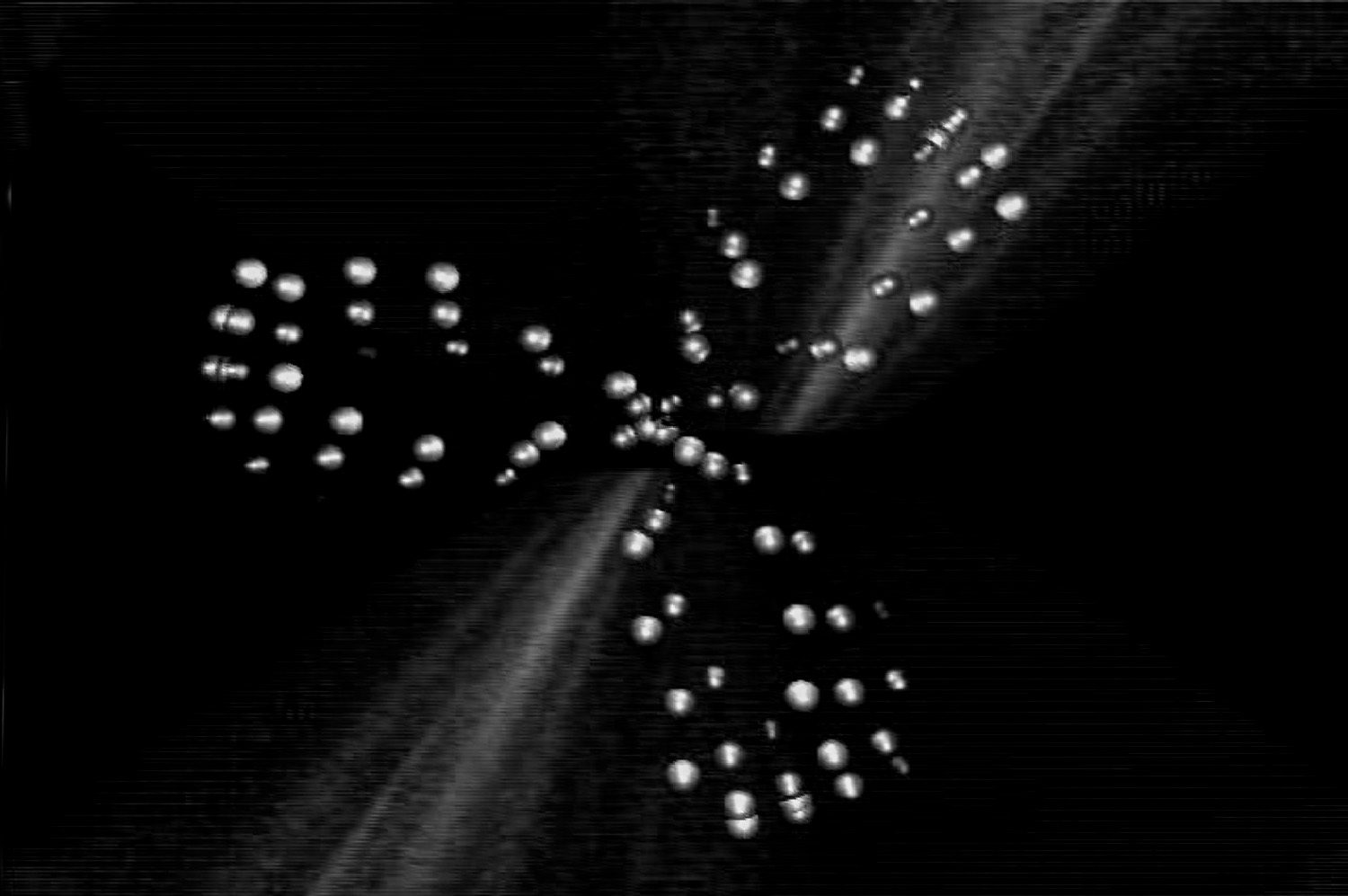
数字 2 demonstrates examples of these points of
consonance, first in the simple example of points
moving in a circle, then in a more complex rose-
curve pattern, and finally as a set of tones in the
same proportions. The number in the first column
represents the proportion that the slowest element
has traversed through the entire cycle, 因此
the common factor or numerary nexus of all the ele-
评论. At points where this number represents a ra-
tio of relatively small whole numbers, symmetrical
patterns emerge.
The right-hand column of Figure 2 shows the
chords that would result if a set of sixteen pitches
went through the same differential cycle. The be-
ginning position (12:00 in circular motion), the fun-
damental, is here set to C2. One quarter through the
循环, 例如, would represent a 4/1 比率, 或一个
frequency four times C2. To represent some of the
pitches poorly approximated by twelve-tone nota-
的, I have used an accidental of an arrow up or
down to represent a pitch inflection of about 33
cents and a plus sign to indicate raising the pitch
关于 15 cents. The final row is an example of how
both visual and aural dissonance results when the
common factor is irrational or sufficiently complex.
Artists such as Ronald Pellegrino have discovered
similar points of correspondence between Just into-
nation and visual symmetry through the use of ana-
log electronics, especially the oscilloscope (Pellegrino
1983). When two tones of relatively simple whole
number frequency relationships are connected to
the x and y inputs of an oscilloscope (or the vibrat-
ing mirrors of a laser scanner), the resulting visual
form will be a Lissajou figure of relative stability
and symmetry. The algorithms of Monro and Press-
英 (1998) demonstrate similar relationships between
Just intonation harmonies and visual symmetries in
more extensible and elaborate ways. 然而,
Whitney intended differential dynamics to provide a
set of principles which could be applied composi-
tionally in many different forms, rather than algo-
rithms for visualization.
New Explorations
In my first video based on these principles, Hiway
70 (1997), I extended the polar coordinate curves of
Whitney’s Permutations to three-dimensional
图形. But the most important way in which my
work was distinguished from his is that, 方法-
ing this work as a composer, I created a soundtrack
in tandem with the visual composition, 小心
synchronizing movement between points of tension
and dissonance and points of stability and tonal
48
电脑音乐杂志
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
2
9
4
4
5
1
8
5
4
4
8
4
0
1
4
8
9
2
6
0
5
7
7
5
1
7
9
9
8
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
数字 2. Correspondences
between points of visual
resonance in two examples
of differential motion and
musical pitches (see text).
Common
因素
Differential dynamics
example—spheres moving
in a circle
Differential dynamics
example—spheres moving
in a rose curve pattern
Musical correspondence
pitches are approximate
1
2
3
4
5
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
2
9
4
4
5
1
8
5
4
4
8
4
0
1
4
8
9
2
6
0
5
7
7
5
1
7
9
9
8
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
continued
Common
因素
Differential dynamics
example—spheres moving
in a circle
Differential dynamics
example—spheres moving
in a rose curve pattern
Musical correspondence
pitches are approximate
6
7
8
9
10
8.45
50
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
2
9
4
4
5
1
8
5
4
4
8
4
0
1
4
8
9
2
6
0
5
7
7
5
1
7
9
9
8
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
电脑音乐杂志
数字 3. Still from
Hiway 70.
数字 4. Still from
Hiway 70.
consonance. I created the music entirely in Just in-
tonation, using harmonies which were often direct
analogues of the patterns of visual symmetry (看
人物 3 和 4).
Just as digital technology allowed me to control
the visual elements with precision necessary for dif-
ferential dynamics, so did Csound realization of the
music allow me to create a Just intonation system
which could freely modulate between tonal centers.
(The Csound code for Hiway 70 is on the CD-ROM
accompanying Boulanger 2000. See also Alves 2000
in the same volume.) I mostly used POV-ray to real-
ize the images. Csound and POV-ray are comparable
in that they are languages freely available for a vari-
ety of platforms that allow the power and speci-
ficity to implement my vision of differential
dynamics and dynamic Just intonation, 之中
many other advantages, 当然.
Static Cling (2000) explores the ways in which
harmonic patterns can emerge from visual or audi-
tory chaos. The video begins with television static
accompanied by multiple tracks of overlapping
chatter of news anchors resynthesized through lin-
ear prediction and then driven with noise. Gradu-
ally the noisy chatter is resonated into specific
harmonic frequencies emphasizing prime relation-
ships of 7 和 11 while the random fluctuations of
the video static align themselves into particular
shapes and grids.
The principles of differential motion can also be
reflected the rhythmic dimension of the music. 在
Static Cling sets of vertical lines flash in correspon-
dence to several layers of repetitive polyrhythmic
图案. Each set of lines moves in harmonic pro-
portion with the others, so that they line up at met-
rically important points. The lines and other shapes
which follow in this work move in a wider variety
of curve types than in previous works, but the prin-
ciple is the same. The elements line up into sym-
metrical patterns at points of stability in the
作品, reflecting the simultaneously conso-
nant Just ratios in the music (see Figures 5 和 6).
aleph
In my next work, aleph (2002), I explored the ways
in which Whitney’s principles of patterned motion
creating and resolving expectation could be extrapo-
lated to approaches sometimes not involving differ-
ential dynamics at all. I was inspired by ancient
Islamic arts of geometric abstraction that find their
high point in the intricate tessellations of the Al-
hambra in Spain or the Isfahan mosque in Iran, 前任-
quisite frozen examples of Whitney’s points of
visual resonance. In aleph, I “unfroze” those elabo-
rate patterns so that they could reform into new
ones at points of tonal stability in the accompany-
ing music.
The great philosophical schools of medieval Bagh-
dad and elsewhere in the Islamic world deeply felt
the influence of Pythagoreanism and Platonism, 在-
testing to the power of number in music, 艺术, callig-
拉菲, and religious symbolism. Critchlow (1976)
Alves
51
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
2
9
4
4
5
1
8
5
4
4
8
4
0
1
4
8
9
2
6
0
5
7
7
5
1
7
9
9
8
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
数字 5. Still from Static
Cling.
数字 6. Still from Static
Cling.
showed how Islamic art is built up through patterns
of number, starting with the monad, unity, 哪个
symbolically recapitulates creation when it is ex-
tended into two dimensions into the circle, the tes-
sellating polygons of the triangle, square, 和
hexagon, and finally more ornate manifestations.
He relates this extension of unity to the first letter
of the Arabic alphabet, aleph, as the “creative ray
which initiates existence at the diacritical point of
bey [the second character] and thence proceeds to
expand horizontally with the lateral gesture of the
second character. By this the fundamental three-fold
nature of reality is established—the descent of the
光, the expansion into creation and (in the sym-
bolism of the written words of the Quran) the means
whereby the ‘light’ returns to its source” (p. 8).
Rather than relying on harmonics or subharmon-
ics to form the basis for the Just intonation, I in-
stead turned to structures known as “hexanies” to
establish points of musical repose and stasis in the
soundtrack. Hexanies, a type of “combination prod-
uct set” invented by the visionary tuning theorist
Ervin Wilson, are sets of six pitches created through
the various possible pairings of four selected integer
因素 (Wilson 1989; Grady 1991). A characteristic
of combination product sets that distinguishes
them from traditional approaches to Just intonation
is that no one pitch in the set necessarily has prior-
ity over the others. Like ever-expanding tessellation
patterns that offer multiple perspectives of what
functions as a center, this approach allows pitch
sets to retain the integrity of Just harmonic struc-
ture together with the ability to float free.
In the beginning of aleph, a formlessness gradu-
ally coalesces into visual and musical patterns. Res-
onant drones are eventually replaced with bell-like
tones that follow the mathematical patterns of
change-ringing. In this English folk art, groups of
bell ringers follow strict permutations of the order
of a set of bells, so that each ringer follows a “path”
through the successive orders that I envision rather
like the paths that the eye may traverse in following
the interlocking weaves of Islamic design. In my
version other attributes such as octave, density, 和
pitch sets gradually shift together with the changes
of bells. The frequencies of the bell partials are
tuned to the same pitches in the hexany then in use,
so that the timbres will retain a consonant relation-
ship in the context of the pitch sets (塞塔雷斯 1999).
By the time the visual patterns coalesce into
striking symmetries, so too do the pitch sets arrive
at stable hexanies (see Figures 7 和 8). In between
pitches change gradually from one set to the next,
reflecting the visual disorder as one pattern slowly
transforms into the next. 再次, the flexibility of
the Csound language enabled me to freely shift be-
tween pitch sets without having to establish a
single fixed gamut of pitches. (This approach con-
trasts with that of some other composers who prefer
to explore the structure of a single combination
52
电脑音乐杂志
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
2
9
4
4
5
1
8
5
4
4
8
4
0
1
4
8
9
2
6
0
5
7
7
5
1
7
9
9
8
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
数字 7. Still from aleph.
数字 8. Still from aleph.
all kinds. . . . That partnership will be grounded on
valid harmonic interrelationships equally applicable
to sound and image” (Whitney 1980, p. 18). Even as
he predicted the digital computer and video tech-
nology would launch a new golden age of artistic
可能性, he remained convinced that the suc-
cess of a new art of visual motion would depend on
its basis in fundamental principles extending from
the canon of Pythagoras to the artful play of tension
and resolution in European musical harmonies.
This article illustrates some new possibilities
that creatively apply Whitney’s ideas as a founda-
tion to achieve a complementarity of music and
visual art in motion. Within the psychologically
powerful but indefinitely flexible applications of
these general principles lie boundless opportunities
for new visions of a fluid architecture of form, mo-
的, and music.
参考
Alves, Bill. 2000. “Using Alternate Tunings in Csound.”
In CD-ROM accompanying Boulanger, 理查德, 编辑. 这
Csound Book. 剑桥, 马萨诸塞州: MIT Univer-
城市出版社.
Boulanger, 理查德, 编辑. 2000. The Csound Book. 凸轮-
桥, 马萨诸塞州: MIT University Press.
Collopy, Fred. 2000. “Color, Form, and Motion: Dimen-
sions of a Musical Art of Light.” Leonardo 33(5):
355–360.
Cornford, Francis Macdonald. 1937. Plato’s Cosmology.
伦敦: K. 保罗, Trench, Trubner & 钴.
Critchlow, 基思. 1976. Islamic Patterns: An Analytical
and Cosmological Approach. 伦敦: 泰晤士河 &
哈德逊.
Franklin, John Curtis. 2002. “Harmony in Greek and
Indo-Iranian Cosmology.” The Journal of Indo-
European Studies 30(1/2):1–25.
Grady, Kraig. 1991. “Ervin Wilson’s Hexanies.” 1/1: Jour-
nal of the Just Intonation Network 7(1):8–15.
琼斯, Tom Douglas. 1972. The Art of Light and Color.
纽约: Van Nostrand Reinhold.
克莱因, Adrian Bernard. 1937. Coloured Light: An Art
中等的. 伦敦: The Technical Press.
Monro, G。, 和 J. Pressing. 1998. “Sound Visualization
Using Embedding: The Art and Science of Auditory
Autocorrelation.” Computer Music Journal 22(2):
20–34.
Alves
53
数字 7
数字 8
product set within a particular composition. Among
the composers who have explored combination
product sets in their works are Warren Burt, Kraig
Grady, Greg Schiemer, and Stephen James Taylor.)
Future Harmony
John Whitney recognized that his work represented
the infancy of an art form, but suggested that,
“Composers will discover a congruence of aural-
visual partnership as productive as that which they
found for centuries in writing for combinations of
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
2
9
4
4
5
1
8
5
4
4
8
4
0
1
4
8
9
2
6
0
5
7
7
5
1
7
9
9
8
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
莫里茨, 威廉. 2004. Optical Poetry: The Life and
Work of Oskar Fischinger. 布卢明顿: Indiana Uni-
大学出版社.
Whitney, 约翰. 1980. Digital Harmony: On the Comple-
mentarity of Music and Visual Art. 纽约: Byte
图书.
Partch, Harry. 1974. Genesis of a Music. 2ND版. 新的
Whitney, 约翰. 1984. “To Paint on Water: The Audiovi-
约克: Da Capo.
Pellegrino, Ronald. 1983. The Electronic Arts of Light and
sual Duet of Complementarity.” Computer Music Jour-
纳尔 18(3):44–52.
Sound. 纽约: Van Nostrand Reinhold.
Wilson, Ervin. 1989. “D’Alessandro, Like a Hurricane.”
塞塔雷斯, William A. 1999. Tuning, 音色, Spectrum,
Xenharmonikon XII:1–39.
Scale. 伦敦: Springer Verlag.
Tenney, James. 1988. A History of Consonance and Dis-
sonance. 纽约: Excelsior.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
2
9
4
4
5
1
8
5
4
4
8
4
0
1
4
8
9
2
6
0
5
7
7
5
1
7
9
9
8
2
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
54
电脑音乐杂志