文章 - 麻省理工学院人工智能研究专业

文章

Communicated by Tim Verbelen

Reward Maximization Through Discrete Active Inference

Lancelot Da Costa
l.da-costa@imperial.ac.uk
Department of Mathematics, Imperial College London, London SW7 2AZ, U.K.

Noor Sajid
noor.sajid.18@ucl.ac.uk
Thomas Parr
thomas.parr.12@ucl.ac.uk
Karl Friston
k.friston@ucl.ac.uk
Wellcome Centre for Human Neuroimaging, 伦敦大学学院,
伦敦, WC1N 3AR, U.K.

Ryan Smith
rsmith@laureateinstitute.org
Laureate Institute for Brain Research, Tulsa, OK 74136, 美国.

Active inference is a probabilistic framework for modeling the behavior
of biological and artificial agents, which derives from the principle of
minimizing free energy. 最近几年, this framework has been applied
successfully to a variety of situations where the goal was to maximize re-
病房, often offering comparable and sometimes superior performance to
alternative approaches. 在本文中, we clarify the connection between
reward maximization and active inference by demonstrating how and
when active inference agents execute actions that are optimal for max-
imizing reward. 恰恰, we show the conditions under which active
inference produces the optimal solution to the Bellman equation, A
formulation that underlies several approaches to model-based rein-
forcement learning and control. On partially observed Markov decision
流程, the standard active inference scheme can produce Bellman
optimal actions for planning horizons of 1 but not beyond. 相比之下,
a recently developed recursive active inference scheme (sophisticated
inference) can produce Bellman optimal actions on any finite tempo-
ral horizon. We append the analysis with a discussion of the broader
relationship between active inference and reinforcement learning.

1 介绍

1.1 Active Inference. Active inference is a normative framework for
modeling intelligent behavior in biological and artificial agents. It simulates

神经计算 35, 807–852 (2023)
https://doi.org/10.1162/neco_a_01574

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

808

L. Da Costa et al.

behavior by numerically integrating equations of motion thought to de-
scribe the behavior of biological systems, a description based on the free
energy principle (Barp et al., 2022; Friston et al., 2022). Active inference com-
prises a collection of algorithms for modeling perception, 学习, 和的-
cision making in the context of both continuous and discrete state spaces
(Barp et al., 2022; Da Costa et al., 2020; Friston et al., 2021, 2010; 弗里斯顿,
Parr, 等人。, 2017). Briefly, building active inference agents entails (1) equip-
ping the agent with a (generative) model of the environment, (2) fitting the
model to observations through approximate Bayesian inference by mini-
mizing variational free energy (IE。, optimizing an evidence lower bound
Beal, 2003; Bishop, 2006; Blei et al., 2017; Jordan et al., 1998) 和 (3) 和-
lecting actions that minimize expected free energy, a quantity that that can
be decomposed into risk (IE。, the divergence between predicted and pre-
ferred paths) and ambiguity, leading to context-specific combinations of ex-
ploratory and exploitative behavior (Millidge, 2021; Schwartenbeck et al.,
2019). This framework has been used to simulate and explain intelligent be-
havior in neuroscience (Adams et al., 2013; Parr, 2019; Parr et al., 2021; Sajid
等人。, 2022), psychology and psychiatry (史密斯, Khalsa, 等人。, 2021; 史密斯,
Kirlic, 斯图尔特, Touthang, Kuplicki, Khalsa, 等人。, 2021; 史密斯, Kirlic, Stew-
艺术, Touthang, Kuplicki, 麦克德莫特, 等人。, 2021; 史密斯, Kuplicki, Feinstein,
等人。, 2020; 史密斯, Kuplicki, Teed, 等人。, 2020; 史密斯, Mayeli, 等人。, 2021;
史密斯, Schwartenbeck, 斯图尔特, 等人。, 2020; 史密斯, 泰勒, 等人。, 2022), 嘛-
chine learning (Çatal et al., 2020; 丰塔斯等人。, 2020; Mazzaglia et al., 2021;
Millidge, 2020; Tschantz et al., 2019; Tschantz, Millidge, 等人。, 2020), 和
机器人技术 (Çatal et al., 2021; Lanillos et al., 2020; Oliver et al., 2021; Pezzato
等人。, 2020; Pio-Lopez et al., 2016; Sancaktar et al., 2020; Schneider et al.,
2022).

1.2 Reward Maximization through Active Inference? 相比之下, 这
traditional approaches to simulating and explaining intelligent behavior—
stochastic optimal control (Bellman, 1957; Bertsekas & Shreve, 1996) 和
reinforcement learning (RL; Barto & Sutton, 1992)—derive from the nor-
mative principle of executing actions to maximize reward scoring the util-
ity afforded by each state of the world. This idea dates back to expected
utility theory (Von Neumann & Morgenstern, 1944), an economic model of
rational choice behavior, which also underwrites game theory (Von Neu-
mann & Morgenstern, 1944) and decision theory (Berger, 1985; Dayan &
Daw, 2008). Several empirical studies have shown that active inference can
successfully perform tasks that involve collecting reward, 经常 (but not al-
方法) showing comparative or superior performance to RL (Cullen et al.,
2018; Markovi´c et al., 2021; Mazzaglia et al., 2021; Millidge, 2020; Paul et al.,
2021; Sajid, Ball, 等人。, 2021; 史密斯, Kirlic, 斯图尔特, Touthang, Kuplicki,
Khalsa, 等人。, 2021; 史密斯, Kirlic, 斯图尔特, Touthang, Kuplicki, 麦克德莫特,
等人。, 2021; 史密斯, Schwartenbeck, 斯图尔特, 等人。, 2020; 史密斯, 泰勒, 等人。,
2022; van der Himst & Lanillos, 2020) and marked improvements when

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

809

interacting with volatile environments (Markovi´c et al., 2021; Sajid, Ball,
等人。, 2021). Given the prevalence and historical pedigree of reward maxi-
mization, we ask: How and when do active inference agents execute actions that
are optimal with respect to reward maximization?

1.3 Organization of Paper. 在本文中, 我们解释 (and prove)
how and when active inference agents exhibit (Bellman) optimal reward-
maximizing behavior.

为了这, we start by restricting ourselves to the simplest problem: max-
imizing reward on a finite horizon Markov decision process (MDP) 和
known transition probabilities—a sequential decision-making task with
complete information. 在这个设置下, we review the backward-induction al-
gorithm from dynamic programming, which forms the workhorse of many
optimal control and model-based RL algorithms. This algorithm furnishes a
Bellman optimal state-action mapping, which means that it provides prov-
ably optimal decisions from the point of view of reward maximization
(参见部分 2).

We then introduce active inference on finite horizon MDPs (参见部分
3)—a scheme consisting of perception as inference followed by planning
as inference, which selects actions so that future states best align with pre-
ferred states.

In section 4, we show how and when active inference maximizes reward
in MDPs. 具体来说, when the preferred distribution is a (uniform mix-
ture of) Dirac distribution(s) over reward-maximizing trajectories, selecting
action sequences according to active inference maximizes reward (see sec-
的 4.1). Yet active inference agents, in their standard implementation, 能
select actions that maximize reward only when planning one step ahead
(参见部分 4.2). It takes a recursive, sophisticated form of active inference
to select actions that maximize reward—in the sense of a Bellman optimal
state-action mapping—on any finite time-horizon (参见部分 4.3).

In section 5, we introduce active inference on partially observable
Markov decision processes with known transition probabilities—a se-
quential decision-making task where states need to be inferred from
observations—and explain how the results from the MDP setting generalize
to this setting.

In section 6, we step back from the focus on reward maximization and
briefly discuss decision making beyond reward maximization, learning un-
known environments and reward functions, and outstanding challenges
in scaling active inference. We append this with a broader discussion of
the relationship between active inference and reinforcement learning in
appendix A.

Our findings are summarized in section 7.
All of our analyses assume that the agent knows the environmental dy-
namics (IE。, transition probabilities) and reward function. In appendix A,
we discuss how active inference agents can learn their world model and

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

810

L. Da Costa et al.

rewarding states when these are initially unknown—and the broader rela-
tionship between active inference and RL.

2 Reward Maximization on Finite Horizon MDPs

在这个部分, we consider the problem of reward maximization in Markov
decision processes (MDPs) with known transition probabilities.

2.1 Basic Definitions. MDPs are a class of models specifying environ-
mental dynamics widely used in dynamic programming, model-based RL,
and more broadly in engineering and artificial intelligence (Barto & Sutton,
1992; Stone, 2019). They are used to simulate sequential decision-making
tasks with the objective of maximizing a reward or utility function. An MDP
specifies environmental dynamics unfolding in discrete space and time un-
der the actions pursued by an agent.

Definition 1 (Finite Horizon MDP). A finite horizon MDP comprises the fol-
lowing collection of data:

• S, a finite set of states.
• T = {0, . . . , 时间}, a finite set that stands for discrete time. T is the temporal

horizon (a.k.a. planning horizon).

• A, a finite set of actions.
• P(st = s(西德:2) | st−1
= s, at−1

= a), the probability that action a ∈ A in state s ∈
S at time t − 1 will lead to state s(西德:2) ∈ S at time t. st are random variables over
S that correspond to the state being occupied at time t = 0, . . . , 时间.

= s), the probability of being at state s ∈ S at the start of the trial.

• P(s0
• R(s), the finite reward received by the agent when at state s ∈ S.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

The dynamics afforded by a finite horizon MDP (见图 1) can be written glob-
ally as a probability distribution over state trajectories s0:时间 := (s0
, . . . , sT ), 给定
, . . . , aT−1), which factorizes as
a sequence of actions a0:T−1 := (a0

磷(s0:时间 | a0:T−1) =P(s0)

时间(西德:2)

τ =1

磷(sτ | sτ −1

, aτ −1).

Remark 1 (On the Definition of Reward). 更普遍, the reward func-
tion can be taken to be dependent on the previous action and previous state:
Ra (s(西德:2) | s) is the reward received after transitioning from state s to state s(西德:2)
到期的
to action a (Barto & Sutton, 1992; Stone, 2019). 然而, given an MDP with
such a reward function, we can recover our simplified setting by defining
a new MDP where the new states comprise the previous action, previous
状态, and current state in the original MDP. By inspection, the resulting re-
ward function on the new MDP depends only on the current state (IE。, 右(s)).

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

811

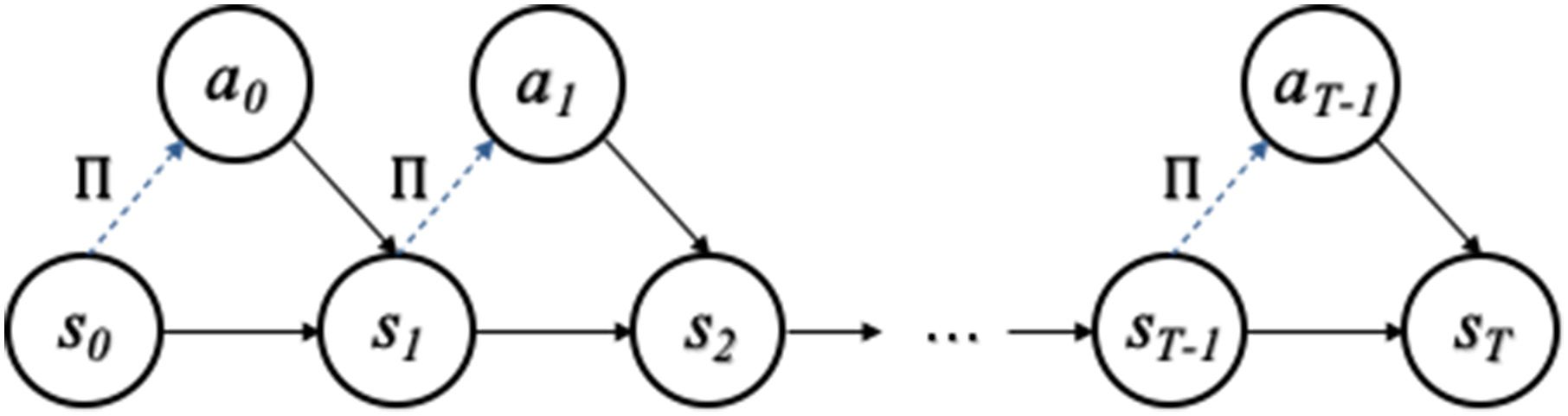
数字 1: Finite horizon Markov decision process. This is a Markov decision
process pictured as a Bayesian network (Jordan et al., 1998; Pearl, 1998). A finite
horizon MDP comprises a finite sequence of states, indexed in time. The transi-
tion from one state to the next depends on action. 像这样, for any given action
顺序, the dynamics of the MDP form a Markov chain on state-space. 在这个
fully observed setting, actions can be selected under a state-action policy, (西德:3), 在-
dicated with a dashed line: this is a probabilistic mapping from state-space and
time to actions.

Remark 2 (Admissible Actions). 一般来说, it is possible that only some ac-
tions can be taken at each state. 在这种情况下, one defines As to be the finite set
的 (allowable) actions from state s ∈ S. All forthcoming results concerning
MDPs can be extended to this setting.

To formalize what it means to choose actions in each state, we introduce

the notion of a state-action policy.
Definition 2 (State-action Policy). A state-action policy (西德:3) is a probability dis-
tribution over actions that depends on the state that the agent occupies, and time.
Explicitly,

(西德:3) : A × S × T → [0, 1]

(A, s, t) (西德:5)→ (西德:3)(A | s, t)
(西德:3)

∀(s, t) ∈ S × T :

(西德:3)(A | s, t) = 1.

a∈A

When st = s, we will write (西德:3)(A | st ) := (西德:3)(A | s, t). Note that the action at the
temporal horizon T is redundant, as no further can be reaped from the environ-
蒙特. 所以, one often specifies state-action policies only up to time T − 1, 作为
(西德:3) : A × S × {0, . . . , T − 1} → [0, 1]. The state-action policy—as defined here—
can be regarded as a generalization of a deterministic state-action policy that as-
signs the probability of 1 to an available action and 0 否则.

Remark 3 (Time-Dependent State-Action Policies). The way an agent
chooses actions at the end of its life is usually going to be very different from
the way it chooses them when it has a longer life ahead of it. In finite horizon
decision problems, state-action policies should generally be considered to
be time-dependent, as time-independent optimal state-action policies may
not exist. To see this, consider the following simple example: S = Z/5Z

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

812

L. Da Costa et al.

(integers mod 5), T = {0, 1, 2}, A = {−1, 0, +1}, 右(0) = R(2) = R(3) =
0, 右(1) = 1, 右(4) = 6. Optimal state-action policies are necessarily time-
dependent as the reward-maximizing trajectory from state 2 at time 0
consists of reaching state 4, while the optimal trajectory from state 2 at time
1 consists of reaching state 1. This is particular to finite-horizon decisions,
作为, in infinite-horizon (discounted) 问题, optimal state-action policies
can always be taken to be time-independent (Puterman, 2014, theorem
6.2.7).

Remark 4 (Conflicting Terminologies: Policy in Active Inference). In active
inference, a policy is defined as a sequence of actions indexed in time.1 To
avoid terminological confusion, we use action sequences to denote policies
under active inference.

At time t, the goal is to select an action that maximizes future cumulative

reward:

右(st+1:时间 ) :=

时间(西德:3)

τ =t+1

右(sτ ).

具体来说, this entails following a state-action policy (西德:3) that maximizes

the state-value function:

v(西德:3)(s, t) := E(西德:3)[右(st+1:时间 ) | st = s]

for any (s, t) ∈ S × T. The state-value function scores the expected cumula-
tive reward if the agent pursues state-action policy (西德:3) from the state st = s.
When the state st = s is clear from context, we will often write v(西德:3)(st ) :=
v(西德:3)(s, t). Loosely speaking, we will call the expected reward the return.
Remark 5 (Notation E(西德:3)). While standard in RL (Barto & Sutton, 1992;
Stone, 2019), the notation E(西德:3)[右(st+1:时间 ) | st = s] can be confusing. It denotes
the expected reward, under the transition probabilities of the MDP and a
state-action policy (西德:3), 那是,

乙

磷(st+1:时间 |在:T−1

,st =s)(西德:3)(在:T−1

|st+1:T−1

,st =s)[右(st+1:时间 )].

It is important to keep this correspondence in mind, as we will use both
notations depending on context.

Remark 6 (Temporal Discounting). In infinite horizon MDPs (IE。, when T
is infinite), RL often seeks to maximize the discounted sum of rewards,

These are analogous to temporally extended actions or options introduced under the

options framework in RL (Stolle & Precup, 2002).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

813

v(西德:3)(s, t) := E(西德:3)

(西德:4)

∞(西德:3)

(西德:5)
γ τ −tR(sτ +1) | st = s

τ =t

for a given temporal discounting term γ ∈ (0, 1) (Barto & Sutton, 1992; Bert-
sekas & Shreve, 1996; Kaelbling et al., 1998). 实际上, temporal discounting is
added to ensure that the infinite sum of future rewards converges to a finite
价值 (Kaelbling et al., 1998). In finite horizon MDPs, temporal discounting
is not necessary so we set γ = 1 (see Schmidhuber, 2006, 2010).

To find the best state-action policies, we would like to rank them in terms
of their return. We introduce a partial ordering such that a state-action pol-
icy is better than another if it yields a higher return in any situation:

(西德:3) ≥ (西德:3)(西德:2) ⇐⇒ ∀(s, t) ∈ S × T : v(西德:3)(s, t) ≥ v(西德:3)(西德:2) (s, t).

相似地, a state-action policy (西德:3) is strictly better than another (西德:3)(西德:2)
strictly higher returns:

if it yields

(西德:3) > (西德:3)(西德:2) ⇐⇒ (西德:3) ≥ (西德:3)(西德:2)

and ∃(s, t) ∈ S × T : v(西德:3)(s, t) > v(西德:3)(西德:2) (s, t).

2.2 Bellman Optimal State-Action Policies. A state-action policy is

Bellman optimal if it is better than all alternatives.
Definition 3 (Bellman Optimality). A state-action policy (西德:3)∗ is Bellman optimal
if and only if it is better than all other state-action policies:

(西德:3)∗ ≥ (西德:3), ∀(西德:3).

换句话说, it maximizes the state-value function v(西德:3)(s, t) for any state s at
time t.

It is important to verify that this concept is not vacuous.

Proposition 1 (Existence of Bellman Optimal State-Action Policies). 给定
a finite horizon MDP as specified in definition 1, there exists a Bellman optimal
state-action policy (西德:3)∗.

A proof is found in appendix B.1. Note that the uniqueness of the
Bellman optimal state-action policy is not implied by proposition 1; 在-
契据, multiple Bellman optimal state-action policies may exist (Bertsekas
& Shreve, 1996; Puterman, 2014).

Now that we know that Bellman optimal state-action policies exist, 我们
can characterize them as a return-maximizing action followed by a Bellman
optimal state-action policy.

Proposition 2 (Characterization of Bellman Optimal State-Action Policies).
For a state-action policy (西德:3), the following are equivalent:

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

814

L. Da Costa et al.

1. (西德:3) is Bellman optimal.
2. (西德:3) is both

A. Bellman optimal when restricted to {1, . . . , 时间}. 换句话说, ∀ state-

action policy (西德:3)(西德:2) 和 (s, t) ∈ S × {1, . . . 时间}

v(西德:3)(s, t) ≥ v(西德:3)(西德:2) (s, t).

乙. At time 0, (西德:3) selects actions that maximize return:

(西德:3)(A | s, 0) > 0 ⇐⇒ a ∈ arg max
a∈A

乙(西德:3)[右(s1:时间 ) | s0

= s, a0

= a],

∀s ∈ S.

(2.1)

A proof is in appendix B.2. Note that this characterization offers a recur-
sive way to construct Bellman optimal state-action policies by successively
selecting the best action, as specified by equation 2.1, starting from T and
inducting backward (Puterman, 2014).

2.3 Backward Induction. Proposition 2 suggests a straightforward re-
cursive algorithm to construct Bellman optimal state-action policies known
as backward induction (Puterman, 2014). Backward induction has a long his-
保守党. It was developed by the German mathematician Zermelo in 1913 到
prove that chess has Bellman optimal strategies (Zermelo, 1913). In stochas-
tic control, backward induction is one of the main methods for solving the
Bellman equation (Adda & 库珀, 2003; Miranda & Fackler, 2002; Sargent,
2000). In game theory, the same method is used to compute subgame perfect
equilibria in sequential games (Fudenberg & Tirole, 1991).

Backward induction entails planning backward in time, from a goal state
at the end of a problem, by recursively determining the sequence of actions
that enables reaching the goal. It proceeds by first considering the last time
at which a decision might be made and choosing what to do in any situa-
tion at that time in order to get to the goal state. Using this information, 一
can then determine what to do at the second-to-last decision time. This pro-
cess continues backward until one has determined the best action for every
possible situation or state at every point in time.

Proposition 3 (Backward Induction: Construction of Bellman Optimal
State-Action Policies). Backward induction

(西德:3)(A | s, T − 1) > 0 ⇐⇒ a ∈ arg max
a∈A
(西德:3)(A | s, T − 2) > 0 ⇐⇒ a ∈ arg max
a∈A

乙[右(sT ) | sT−1

= s, aT−1

= a],

∀s ∈ S

乙(西德:3)[右(sT−1:时间 ) | sT−2

= s, aT−2

= a],

∀s ∈ S
…

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

815

(西德:3)(A | s, 0) > 0 ⇐⇒ a ∈ arg max
a∈A

乙(西德:3)[右(s1:时间 ) | s0

= s, a0

= a],

∀s ∈ S

(2.2)

defines a Bellman optimal state-action policy (西德:3). 此外, this characterization
is complete: all Bellman optimal state-action policies satisfy the backward induction
关系, 方程 2.2.

A proof is in appendix B.3.
直观地, the backward induction algorithm 2.2 consists of planning
落后, by starting from the end goal and working out the actions
needed to achieve the goal. To give a concrete example of this kind of plan-
ning, backward induction would consider the following actions in the order
显示:

1. Desired goal: I would like to go to the grocery store.
2. Intermediate action: I need to drive to the store.
3. Current best action: I should put my shoes on.

Proposition 3 tells us that to be optimal with respect to reward maxi-
mization, one must plan like backward induction. This will be central to
our analysis of reward maximization in active inference.

3 Active Inference on Finite Horizon MDPs

We now turn to introducing active inference agents on finite horizon MDPs
with known transition probabilities. We assume that the agent’s generative
model of its environment is given by the previously defined finite horizon
MDP (see definition 1). We do not consider the case where the transitions
have to be learned but comment on it in appendix A.2 (see also Da Costa
等人。, 2020; Friston et al., 2016).

下文中, we fix a time t ≥ 0 and suppose that the agent has been
, . . . , st. To ease notation, we let (西德:2)s := st+1:时间 ,(西德:2)A := at:T be the future
in states s0
states and future actions. We define Q to be the predictive distribution, 哪个
encodes the predicted future states and actions given that the agent is in
state st:

问((西德:2)s,(西德:2)A | st ) :=

T−1(西德:2)

τ =t

问(sτ +1

| aτ , sτ )问(aτ | sτ ).

3.1 Perception as Inference. In active inference, perception entails in-
ferences about future, 过去的, and current states given observations and a se-
quence of actions. When states are partially observed, this is done through
variational Bayesian inference by minimizing a free energy functional also
known as an evidence bound (Beal, 2003; Bishop, 2006; Blei et al., 2017;
Wainwright & 约旦, 2007).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

816

L. Da Costa et al.

In the MDP setting, past and current states are known, so it is necessary
only to infer future states given the current state and action sequence P((西德:2)s |
(西德:2)A, st ). These posterior distributions P((西德:2)s | (西德:2)A, st ) can be computed exactly in
virtue of the fact that the transition probabilities of the MDP are known;
因此, variational inference becomes exact Bayesian inference:

问((西德:2)s | (西德:2)A, st ) :=P((西德:2)s | (西德:2)A, st ) =

T−1(西德:2)

τ =t

磷(sτ +1

| sτ , aτ ).

(3.1)

3.2 Planning as Inference. Now that the agent has inferred future states
given alternative action sequences, we must assess these alternative plans
by examining the resulting state trajectories. The objective that active in-
ference agents optimize—in order to select the best possible actions—is the
expected free energy (Barp et al., 2022; Da Costa et al., 2020; Friston et al.,
2021). Under active inference, agents minimize expected free energy in or-
der to maintain themselves distributed according to a target distribution C
over the state-space S encoding the agent’s preferences.

Definition 4 (Expected Free Energy on MDPs). On MDPs, the expected free
energy of an action sequence (西德:2)a starting from st is defined as (Barp et al., 2022, 看
部分 5):

G((西德:2)A | st ) = DKL[问((西德:2)s | (西德:2)A, st ) | C((西德:2)s)],

(3.2)

where DKL is the KL-divergence. 所以, minimizing expected free energy cor-
responds to making the distribution over predicted states close to the distribution
C that encodes prior preferences. Note that the expected free energy in partially
observed MDPs comprises an additional ambiguity term (参见部分 5), 这是
dropped here as there is no ambiguity about observed states.

Since the expected free energy assesses the goodness of inferred fu-
ture states under a course of action, we can refer to planning as inference
(Attias, 2003; 博特维尼克 & Toussaint, 2012). The expected free energy may
be rewritten as

G((西德:2)A | st ) = E
(西德:6)

问((西德:2)s|(西德:2)A,st )[− log C((西德:2)s)]
(西德:9)
(西德:7)(西德:8)

− H[问((西德:2)s | (西德:2)A, st )]
(西德:9)

(西德:7)(西德:8)

(西德:6)

(3.3)

Expected surprise

Entropy of future states

因此, minimizing expected free energy minimizes the expected surprise
of states2 according to C and maximizes the entropy of Bayesian beliefs over

The surprise (also known as self-information or surprisal) of states—log C((西德:2)s) 是
information-theoretic nomenclature (Stone, 2015) that scores the extent to which an

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

817

future states (a maximum entropy principle (Jaynes, 1957A), which is some-
times cast as keeping options open (Klyubin et al., 2008)).

Remark 7 (Numerical Tractability). The expected free energy is straight-
forward to compute using linear algebra. Given an action sequence (西德:2)A, C((西德:2)s)
and Q((西德:2)s | (西德:2)A, st ) are categorical distributions over ST−t. Let their parameters
|S|(T−1), 在哪里 | · | denotes the cardinality of a set. Then the
be c, s(西德:2)A
expected free energy reads

∈ [0, 1]

G((西德:2)A | st ) = sT

(西德:2)A (log s(西德:2)A

− log c).

(3.4)

Notwithstanding, 方程 3.4 is expensive to evaluate repeatedly when
all possible action sequences are considered. 在实践中, one can adopt a
temporal mean field approximation over future states (Millidge, Tschantz,
& Buckley, 2020):

问((西德:2)s | (西德:2)A, st ) =

时间(西德:2)

τ =t+1

问(sτ | (西德:2)A, sτ −1) ≈

时间(西德:2)

τ =t+1

问(sτ | (西德:2)A, st ),

which yields the simplified expression

G((西德:2)A | st ) ≈

时间(西德:3)

τ =t+1

DKL[问(sτ | (西德:2)A, st ) | C(sτ )].

(3.5)

Expression 3.5 is much easier to handle: for each action sequence (西德:2)A, 一
evaluates the summands sequentially τ = t + 1, . . . , 时间, and if and when
the sum up to τ becomes significantly higher than the lowest expected
free energy encountered during planning, G((西德:2)A | st ) is set to an arbitrarily
high value. Setting G((西德:2)A | st ) to a high value is equivalent to pruning away
unlikely trajectories. This bears some similarity to decision tree pruning
procedures used in RL (Huys et al., 2012). It finesses exploration of the deci-
sion tree in full depth and provides an Occam’s window for selecting action
序列.

Complementary approaches can help make planning tractable. 对于前-
充足, hierarchical generative models factorize decisions into multiple lev-
这. By abstracting information at a higher-level, lower levels entertain
fewer actions (Friston et al., 2018), which reduces the depth of the decision
tree by orders of magnitude. Another approach is to use algorithms that
search the decision tree selectively, such as Monte Carlo tree search (占婆-
pion, Bowman, 等人。, 2021; Champion, Da Costa, 等人。, 2021; 丰塔斯等人。,

observation is unusual under C. It does not imply that the agent experiences surprise
in a subjective or declarative sense.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

818

L. Da Costa et al.

2020; Maisto et al., 2021; Silver et al., 2016) and amortizing planning using
artificial neural networks (IE。, learning to plan) (Çatal et al., 2019; Fountas
等人。, 2020; Millidge, 2019; Sajid, Tigas, 等人。, 2021).

4 Reward Maximization on MDPs through Active Inference

这里, we show how active inference solves the reward maximization
问题.

4.1 Reward Maximization as Reaching Preferences. From the defini-
tion of expected free energy, 方程 3.2, active inference on MDPs can
be thought of as reaching and remaining at a target distribution C over
state-space.

The basic observation that underwrites the following is that the agent
will maximize reward when the stationary distribution has all of its mass on
reward maximizing states. To illustrate this, we define a preference distri-
bution Cβ , β > 0 over state-space S, such that preferred states are rewarding
状态:3

Cβ (σ ) :=

exp βR(σ )
ς ∈S exp βR(ς )
⇐⇒ − log Cβ (σ ) = −βR(σ ) − c(β ),

(西德:10)

∝ exp(βR(σ )),

∀σ ∈ S

∀σ ∈ S, for some c(β ) ∈ R constant w.r.t σ.

这 (inverse temperature) parameter β > 0 scores how motivated the
agent is to occupy reward-maximizing states. Note that states s ∈ S that
maximize the reward R(s) maximize Cβ (s) and minimize − log Cβ (s) for any
β > 0.

Using the additive property of the reward function, we can extend Cβ to a
, . . . , σT ) ∈ ST . 具体来说,

probability distribution over trajectories (西德:2)σ := (σ
Cβ scores to what extent a trajectory is preferred over another trajectory:

Cβ ((西德:2)σ ) :=

(西德:10)

exp βR((西德:2)σ )
(西德:2)ς∈ST exp βR((西德:2)ς )

时间(西德:2)

τ =1

(西德:10)

exp βR(στ )
ς ∈S exp βR(ς )

时间(西德:2)

τ =1

Cβ (στ ),

∀(西德:2)σ ∈ ST

⇐⇒ − log Cβ ((西德:2)σ ) = −βR((西德:2)σ ) − c

(西德:2)

(β ) = −

时间(西德:3)

τ =1

βR(στ ) − c

(西德:2)

(β ),

∀(西德:2)σ ∈ ST ,

(4.1)

where c(西德:2)(β ) := c(β )T ∈ R is constant with regard to (西德:2)σ .

Note the connection with statistical mechanics: β is an inverse temperature parame-
特尔, −R is a potential function, and Cβ is the corresponding Gibbs distribution (Pavliotis,
2014; Rahme & Adams, 2019).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

819

When preferences are defined in this way, the preference distribution
assigns exponentially more mass to states or trajectories that have a higher
reward. Put simply, for trajectories (西德:2)σ , (西德:2)ς ∈ ST with reward R((西德:2)σ ) > R((西德:2)ς ), 这
ratio of preference mass will be the exponential of the weighted difference
in reward, where the weight is the inverse temperature:

Cβ ((西德:2)σ )
Cβ ((西德:2)ς )

= exp(βR((西德:2)σ ))
经验值(βR((西德:2)ς ))

= exp(β(右((西德:2)σ ) − R((西德:2)ς ))).

(4.2)

As the temperature tends to zero, the ratio diverges so that Cβ ((西德:2)σ ) becomes
infinitely larger than Cβ ((西德:2)ς ). As Cβ is a probability distribution (with a max-
β→+∞
imal value of one), we must have Cβ ((西德:2)ς )
−→ 0 for any suboptimal trajec-
保守党 (西德:2)ς and positive preference for reward maximizing trajectories (所有
preferences must sum to one). 此外, all reward maximizing trajecto-
ries have the same probability mass by equation 4.2. 因此, in the zero tem-
perature limit, preferences become a uniform mixture of Dirac distributions
over reward-maximizing trajectories:

lim
β→+∞

Cβ ∝

(西德:3)

(西德:2)σ ∈IT−t

Dirac(西德:2)σ ,

我 := arg max
s∈S

右(s).

(4.3)

当然, the above holds for preferences over individual states as it does
for preferences over trajectories.

We now show how reaching preferred states can be formulated as reward

maximization:
Lemma 1. The sequence of actions that minimizes expected free energy also max-
imizes expected reward in the zero temperature limit β → +∞ (参见方程 4.3):

lim
β→+∞

arg min

(西德:2)A

G((西德:2)A | st ) ⊆ arg max

(西德:2)A

乙

问((西德:2)s|(西德:2)A,st )[右((西德:2)s)].

此外, of those action sequences that maximize expected reward, the expected
free energy minimizers will be those that maximize the entropy of future states
H[问((西德:2)s | (西德:2)A, st )].

A proof is in appendix B.4. In the zero temperature limit β → +∞,
minimizing expected free energy corresponds to choosing the action se-
序列 (西德:2)a such that Q((西德:2)s | (西德:2)A, st ) has most mass on reward-maximizing states
or trajectories (见图 2). Of those reward-maximizing candidates, 这
minimizer of expected free energy maximizes the entropy of future states
H[问((西德:2)s | (西德:2)A, st )], thus keeping options open.

4.2 Reward Maximization on MDPs with a Temporal Horizon of 1.
在这个部分, we first consider the case of a single-step decision problem
(IE。, a temporal horizon of T = 1) and demonstrate how the standard active

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

820

L. Da Costa et al.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

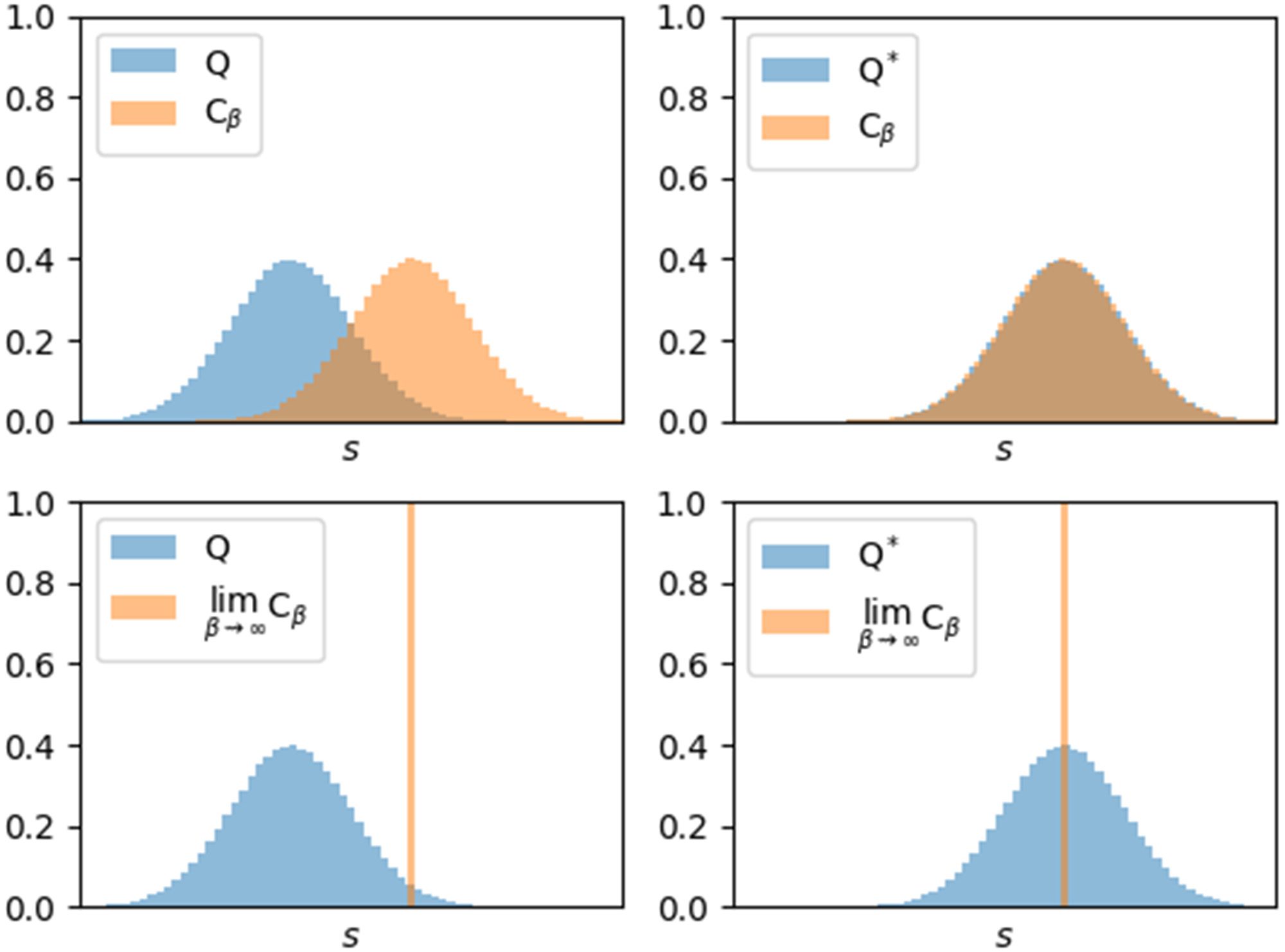
数字 2: Reaching preferences and the zero temperature limit. We illustrate
how active inference selects actions such that the predictive distribution Q((西德:2)s |
(西德:2)A, st ) most closely matches the preference distribution Cβ ((西德:2)s) (top right). We il-
lustrate this with a temporal horizon of one, so that state sequences are states,
which are easier to plot, but all holds analogously for sequences of arbitrary
finite length. 在这个例子中, the state-space is a discretization of a real inter-
val, and the predictive and preference distributions have a gaussian shape. 这
predictive distribution Q is assumed to have a fixed variance with respect to
action sequences, such that the only parameter that can be optimized by ac-
tion selection is its mean. In the zero temperature limit, 方程 4.3, Cβ be-
comes a Dirac distribution over the reward-maximizing state (底部). 因此,
minimizing expected free energy corresponds to selecting the action such that
the predicted states assign most probability mass to the reward-maximizing
状态 (bottom-right). 这里, Q∗ := Q((西德:2)s | (西德:2)a∗, st ) denotes the predictive distribu-
tion over states given the action sequence that minimizes expected free energy
(西德:2)a∗ = arg min(西德:2)a G((西德:2)A | st ).

inference scheme maximizes reward on this problem in the limit β → +∞.
This will act as an important building block for when we subsequently con-
sider more general multistep decision problems.

The standard decision-making procedure in active inference consists of
assigning each action sequence with a probability given by the softmax of
the negative expected free energy (Barp et al., 2022; Da Costa et al., 2020;
弗里斯顿, FitzGerald, 等人。, 2017):

问((西德:2)A | st ) ∝ exp(−G((西德:2)A | st )).

Reward Maximization Active Inference

821

桌子 1: Standard Active Inference Scheme on Finite Horizon MDPs (Barp et al.,
2022, 部分 5).

Process

Perceptual inference
Planning as inference
Decision making
Action selection

计算

(西德:11)

(西德:10)

| sτ , aτ )

(西德:2)a Q(at = a | (西德:2)A)问((西德:2)A | st )

(西德:13)

Agents then select the most likely action under this distribution:

at ∈ arg max
a∈A

问(A | st ) = arg max
a∈A

问(A | (西德:2)A) 经验值(−G((西德:2)A | st )) = arg max
a∈A

= arg max
a∈A

(西德:3)

(西德:2)A

问(A | (西德:2)A)问((西德:2)A | st )

经验值(−G((西德:2)A | st )).

(西德:3)

(西德:2)A
(西德:3)

(西德:2)A
=a
((西德:2)A)t

总之, this scheme selects the first action within action sequences
那, 一般, maximize their exponentiated negative expected free
energies. As a corollary, if the first action is in a sequence with a very
low expected free energy, this adds an exponentially large contribution
to the selection of this particular action. We summarize this scheme in
桌子 1.

Theorem 1. In MDPs with known transition probabilities and in the zero tem-
perature limit β → +∞ (4.3), the scheme of Table 1,

at ∈ lim
β→+∞

arg max
a∈A

(西德:3)

(西德:2)A
=a
((西德:2)A)t

经验值(−G((西德:2)A | st )),

G((西德:2)A | st ) = DKL[问((西德:2)s | (西德:2)A, st ) | Cβ ((西德:2)s)],

(4.4)

is Bellman optimal for the temporal horizon T = 1.

A proof is in appendix B.5. 重要的, the standard active inference
scheme, 方程 4.4, falls short in terms of Bellman optimality on planning hori-
zons greater than one; this rests on the fact that it does not coincide with
backward induction. Recall that backward induction offers a complete de-
scription of Bellman optimal state-action policies (see proposition 3). 在骗子-
特拉斯特, active inference plans by adding weighted expected free energies of
each possible future course of action. 换句话说, unlike backward in-
归纳法, it considers future courses of action beyond the subset that will
subsequently minimize expected free energy, given subsequently encoun-
tered states.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

822

L. Da Costa et al.

4.3 Reward Maximization on MDPs with Finite Temporal Hori-
zons. To achieve Bellman optimality on finite temporal horizons, we turn
to the expected free energy of an action given future actions that also mini-
mize expected free energy. 要做到这一点, we can write the expected free energy
recursively, as the immediate expected free energy, plus the expected free
energy that one would obtain by subsequently selecting actions that mini-
mize expected free energy (Friston et al., 2021). The resulting scheme con-
sists of minimizing an expected free energy defined recursively, 从
last time step to the current time step. In finite horizon MDPs, this reads

G(aT−1

| sT−1) = DKL[问(sT | aT−1

G(aτ | sτ ) = DKL[问(sτ +1

, sT−1) | Cβ (sT )]
| aτ , sτ ) | Cβ (sτ +1)]

+ 乙

问(aτ +1

,sτ +1

|aτ ,sτ )[G(aτ +1

| sτ +1)],

τ = t, . . . , T − 2,

在哪里, at each time step, actions are chosen to minimize expected free
活力:

问(aτ +1

| sτ +1) > 0 ⇐⇒ aτ +1

∈ arg min
a∈A

G(A | sτ +1).

(4.5)

To make sense of this formulation, we unravel the recursion,

G(在 | st ) = DKL[问(st+1
= DKL[问(st+1

| 在, st ) | Cβ (st+1)] + 乙
| 在, st ) | Cβ (st+1)]

问(at+1

,st+1

|在 ,st )[G(at+1

| st+1)]

(西德:12)

+ 乙

问(at+1

,st+1

|在 ,st )

DKL[问(st+2

问(at+1:t+2

,st+1:t+2

|在 ,st )[G(at+2
T−1(西德:3)

| at+1
| st+2)]

(西德:13)
, st+1) | Cβ (st+2)]

= . . . = E

问((西德:2)A,(西德:2)s|在 ,st )

DKL[问(sτ +1

| aτ , sτ ) | Cβ (sτ +1)]

τ =t
问((西德:2)A,(西德:2)s|在 ,st )DKL[问((西德:2)s | (西德:2)A, st ) | Cβ ((西德:2)s)],

= E

(4.6)

which shows that this expression is exactly the expected free energy under
action at, if one is to pursue future actions that minimize expected free en-
ergy, 方程 4.5. We summarize this “sophisticated inference” scheme in
桌子 2.

The crucial improvement over the standard active inference scheme (看
桌子 1) is that planning is now performed based on subsequent counterfac-
tual actions that minimize expected free energy as opposed to considering
all future courses of action. Translating this into the language of state-action
policies yields ∀s ∈ S:

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

823

桌子 2: Sophisticated active inference scheme on finite horizon MDPs (弗里斯顿
等人。, 2021).

Process

计算

Perceptual inference
Planning as inference

Decision making
Action selection

问(aτ +1

aT−1(s) ∈ arg min
a∈A
aT−2(s) ∈ arg min
a∈A

G(A | sT−1

= s)

G(A | sT−2

= s)

…
a1(s) ∈ arg min
a∈A
a0(s) ∈ arg min
a∈A

G(A | s1

= s)

G(A | s0).

(4.7)

方程 4.7 is strikingly similar to the backward induction algorithm
(主张 3), and indeed we recover backward induction in the limit β →
+∞.

Theorem 2 (Backward Induction as Active Inference). In MDPs with known
transition probabilities and in the zero temperature limit β → +∞, 方程 4.3,
the scheme of Table 2,

问(aτ | sτ ) > 0 ⇐⇒ at ∈ lim
β→+∞

G(aτ | sτ ) = DKL[问(sτ +1

G(A | sτ )

arg min
a∈A
| aτ , sτ ) | Cβ (sτ +1)]

+ 乙

问(aτ +1

,sτ +1

|aτ ,sτ )[G(aτ +1

| sτ +1)],

(4.8)

is Bellman optimal on any finite temporal horizon as it coincides with the back-
ward induction algorithm from proposition 3. 此外, if there are multiple
actions that maximize future reward, those that are selected by active inference also
maximize the entropy of future states H[问((西德:2)s | (西德:2)A, A, s0)].

Note that maximizing the entropy of future states keeps the agent’s op-
tions open (Klyubin et al., 2008) in the sense of committing the least to a
specified sequence of states. A proof of theorem 2 is in appendix B.6.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

824

L. Da Costa et al.

5 Generalization to POMDPs

Partially observable Markov decision processes (POMDPs) generalize
MDPs in that the agent observes a modality ot, which carries incomplete
information about the current state st, as opposed to the current state itself.

Definition 5 (Finite Horizon POMDP). A finite horizon POMDP is an MDP
(see definition 1) with the following additional data:

• O is a finite set of observations.
• P(ot = o | st = s) is the probability that the state s ∈ S at time t will lead to
the observation o ∈ O at time t. ot are random variables over O that corre-
spond to the observation being sampled at time t = 0, . . . , 时间.

5.1 Active Inference on Finite Horizon POMDPs. We briefly introduce
active inference agents on finite horizon POMDPs with known transition
probabilities (for more details, see Da Costa et al., 2020; Parr et al., 2022;
史密斯, 弗里斯顿, 等人。, 2022). We assume that the agent’s generative model of
its environment is given by POMDP (see definition 5).4

Let (西德:2)s := s0:时间 ,(西德:2)A := a0:T−1 be all states and actions (过去的, 展示, 和福-
真实), let ˜o := o0:t be the observations available up to time t, 然后让(西德:2)哦 := ot+1:时间
be the future observations. The agent has a predictive distribution over
states given actions

问((西德:2)s | (西德:2)A, ˜o) :=

T−1(西德:2)

τ =0

问(sτ +1

| aτ , sτ , ˜o),

which is continuously updated following new observations.

5.1.1 Perception as Inference. In active inference, perception entails in-
ferences about (过去的, 展示, and future) states given observations and a
sequence of actions. When states are partially observed, the posterior distri-
bution P((西德:2)s | (西德:2)A, ˜o) is intractable to compute directly. 因此, one approximates
it by optimizing a variational free energy functional F(西德:2)A (also known as an
evidence bound; Beal, 2003; Bishop, 2006; Blei et al., 2017; Wainwright &
约旦, 2007) over a space of probability distributions Q(· | (西德:2)A, ˜o) 叫做
variational family:

磷((西德:2)s | (西德:2)A, ˜o) = arg min
问

F(西德:2)A[问((西德:2)s | (西德:2)A, ˜o)] = arg min
问

DKL[问((西德:2)s | (西德:2)A, ˜o) | 磷((西德:2)s | (西德:2)A, ˜o)]

F(西德:2)A[问((西德:2)s | (西德:2)A, ˜o)] := E

问((西德:2)s|(西德:2)A, ˜o)[log Q((西德:2)s | (西德:2)A, ˜o) − log P( ˜o,(西德:2)s | (西德:2)A)].

(5.1)

We do not consider the case where the model parameters have to be learned but com-

ment on it in appendix A.2 (details in Da Costa et al., 2020; Friston et al., 2016).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

825

这里, 磷( ˜o,(西德:2)s | (西德:2)A) is the POMDP, which is supplied to the agent, 和P((西德:2)s | (西德:2)A, ˜o).
When the free energy minimum (参见方程 5.1) is reached, the inference
is exact:

问((西德:2)s | (西德:2)A, ˜o) =P((西德:2)s | (西德:2)A, ˜o).

(5.2)

For numerical tractability, the variational family may be constrained to a
parametric family of distributions, in which case equality is not guaranteed:

问((西德:2)s | (西德:2)A, ˜o) ≈ P((西德:2)s | (西德:2)A, ˜o).

(5.3)

5.1.2 Planning as Inference. The objective that active inference minimizes
in order the select the best possible courses of action is the expected free energy
(Barp et al., 2022; Da Costa et al., 2020; Friston et al., 2021). In POMDPs, 这
expected free energy reads (Barp et al., 2022, 部分 5)

G((西德:2)A | ˜o) = DKL[问((西德:2)s | (西德:2)A, ˜o) | Cβ ((西德:2)s)]
(西德:9)

(西德:7)(西德:8)

(西德:6)

+ 乙
(西德:6)

问((西德:2)s|(西德:2)A, ˜o)H[磷((西德:2)哦 | (西德:2)s)]
(西德:9)
(西德:7)(西德:8)

风险

Ambiguity

The expected free energy on POMDPs is the expected free energy on MDPs
plus an extra term called ambiguity. This ambiguity term accommodates the
uncertainty implicit in partially observed problems. The reason that this
resulting functional is called expected free energy is because it comprises
a relative entropy (风险) and expected energy (ambiguity). The expected
free energy objective subsumes several decision-making objectives that pre-
dominate in statistics, 机器学习, and psychology, which confers it
with several useful properties when simulating behavior (见图 3 为了
细节).

5.2 Maximizing Reward on POMDPs. 至关重要的是, our reward maxi-
mization results translate to the POMDP case. To make this explicit, 我们
rehearse lemma 1 in the context of POMDPs.

Proposition 4 (Reward Maximization on POMDPs). In POMDPs with
known transition probabilities, provided that the free energy minimum is reached
(参见方程 5.2), the sequence of actions that minimizes expected free energy also
maximizes expected reward in the zero temperature limit β → +∞ (参见方程
4.3):

lim
β→+∞

arg min

(西德:2)A

G((西德:2)A | ˜o) ⊆ arg max

(西德:2)A

乙

问((西德:2)s|(西德:2)A, ˜o)[右((西德:2)s)].

此外, of those action sequences that maximize expected reward, 前任-
pected free energy minimizers will be those that maximize the entropy of future

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

826

L. Da Costa et al.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

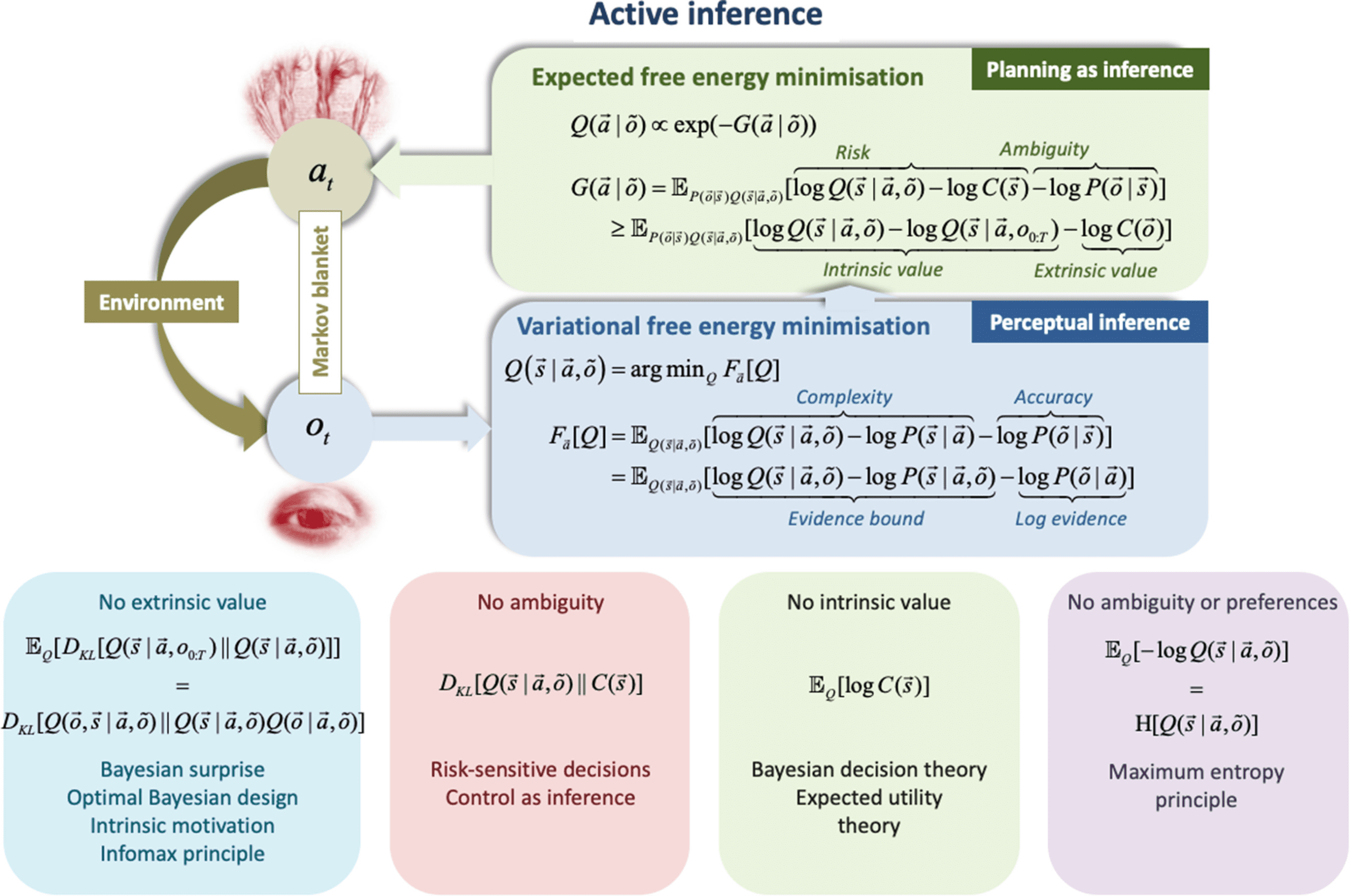
数字 3: Active inference. The top panels illustrate the perception-action loop
in active inference, in terms of minimization of variational and expected free en-
ergy. The lower panels illustrate how expected free energy relates to several de-
scriptions of behavior that predominate in the psychological, 机器学习,
and economics. These descriptions are disclosed when one removes particular
terms from the objective. 例如, if we ignore extrinsic value, we are left
with intrinsic value, variously known as expected information gain (Lindley,
1956; MacKay, 2003). This underwrites intrinsic motivation in machine learning
and robotics (Barto et al., 2013; Deci & Ryan, 1985; Oudeyer & 卡普兰, 2007) 和
expected Bayesian surprise in visual search (Itti & Baldi, 2009; 孙等人。, 2011)
and the organization of our visual apparatus (巴洛, 1961, 1974; Linsker, 1990;
Optican & Richmond, 1987). In the absence of ambiguity, we are left with mini-
mizing risk, which corresponds to aligning predicted states to preferred states.
This leads to risk-averse decisions in behavioral economics (Kahneman & Tver-
天空, 1979) and formulations of control as inference in engineering such as KL
控制 (van den Broek et al., 2010). If we then remove intrinsic value, we are left
with expected utility in economics (Von Neumann & Morgenstern, 1944) 那
underwrites RL and behavioral psychology (Barto & Sutton, 1992). Bayesian for-
mulations of maximizing expected utility under uncertainty are also the basis
of Bayesian decision theory (Berger, 1985). 最后, if we only consider a fully
observed environment with no preferences, minimizing expected free energy
corresponds to a maximum entropy principle over future states (Jaynes, 1957乙,
1957A). Note that here C(哦) denotes the preferences over observations derived
from the preferences over states. These are related by P(哦 | s)C(s) =P(s | 哦)C(哦).

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

827

states minus the (预期的) entropy of outcomes given states H[问((西德:2)s | (西德:2)A, ˜o)] -
乙
问((西德:2)s|在 , ˜o)H[磷((西德:2)哦 | (西德:2)s)]].

From proposition 4, we see that if there are multiple maximize reward

action sequences, those that are selected maximize

H[问((西德:2)s | (西德:2)A, ˜o)]
(西德:9)
(西德:7)(西德:8)
(西德:6)

乙
(西德:6)

问((西德:2)s|在 , ˜o)[H[磷((西德:2)哦 | (西德:2)s)]]
(西德:9)
(西德:7)(西德:8)

Entropy of future states

Entropy of observations given future states

换句话说, they least commit to a prespecified sequence of future
states and ensure that their expected observations are maximally informa-
tive of states. 当然, when inferences are inexact, the extent to which
主张 4 holds depends on the accuracy of the approximation, 平等-
的 5.3. A proof of proposition 4 is in appendix B.7.

The schemes of Tables 1 和 2 exist in the POMDP setting, (例如, Barp
等人。, 2022, 部分 5, and Friston et al., 2021, 分别). 因此, 在
POMDPs with known transition probabilities, provided that inferences are
exact (参见方程 5.2) and in the zero temperature limit β → +∞ (看
方程 4.3), standard active inference (Barp et al., 2022, 部分 5) max-
imizes reward on temporal horizons of one but not beyond, and a recursive
scheme such as sophisticated active inference (Friston et al., 2021) max-
imizes reward on finite temporal horizons. Note that for computational
易处理性, the sophisticated active inference scheme presented in Friston
等人. (2021) does not generally perform exact inference; 因此, the extent to
which it will maximize reward in practice will depend on the accuracy of
its inferences. 尽管如此, our results indicate that sophisticated active
inference will vastly outperform standard active inference in most reward-
maximization tasks.

6 讨论

在本文中, we have examined a specific notion of optimality, 即,
Bellman optimality, defined as selecting actions to maximize future ex-
pected rewards. We demonstrated how and when active inference is Bell-
man optimal on finite horizon POMDPs with known transition probabilities
and reward function.

These results highlight important relationships among active inference,
stochastic control, and RL, as well as conditions under which they would
and would not be expected to behave similarly (例如, environments with
multiple reward-maximizing trajectories, those affording ambiguous ob-
servations). We refer readers to appendix A for a broader discussion of the
relationship between active inference and reinforcement learning.

6.1 Decision Making beyond Reward Maximization. More broadly,
it is important to ask if reward maximization is the right objective

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

828

L. Da Costa et al.

underwriting intelligent decision making. This is an important question for
decision neuroscience. 那是, do humans optimize a reward signal, 前任-
pected free energy, or other planning objectives? This can be addressed by
comparing the evidence for these competing hypotheses based on empirical
数据 (史密斯, Kirlic, 斯图尔特, Touthang, Kuplicki, Khalsa, 等人。, 2021; 史密斯,
Kirlic, 斯图尔特, Touthang, Kuplicki, 麦克德莫特, 等人。, 2021; 史密斯,
Schwartenbeck, 斯图尔特, 等人。, 2020; 史密斯, 泰勒, 等人。, 2022). Current em-
pirical evidence suggests that humans are not purely reward-maximizing
代理人; they also engage in both random and directed exploration (Daw
等人。, 2006; 格什曼, 2018; Mirza et al., 2018; Schulz & 格什曼, 2019;
Wilson et al., 2021, 2014; 徐等人。, 2021) and keep their options open
(Schwartenbeck, FitzGerald, Mathys, Dolan, Kronbichler, 等人。, 2015). 作为
we have illustrated, active inference implements a clear form of directed
exploration through minimizing expected free energy. Although not cov-
ered in detail here, active inference can also accommodate random explo-
ration by sampling actions from the posterior belief over action sequences,
as opposed to selecting the most likely action as presented in Tables 1
和 2.

Note that behavioral evidence favoring models that do not solely maxi-
mize reward within reward-maximization tasks—that is, where “maximize
reward” is the explicit instruction—is not a contradiction. 相当, 搜集
information about the environment (勘探) generally helps to reap
more reward in the long run, as opposed to greedily maximizing reward
based on imperfect knowledge (Cullen et al., 2018; Sajid, Ball, 等人。, 2021).
This observation is not new, and many approaches to simulating adaptive
agents employed today differ significantly from their reward-maximizing
antecedents (see appendix A.3).

6.2 学习. When the transition probabilities or reward function are
unknown to the agent, the problem becomes one of reinforcement learning
(RL; Shoham et al., 2003 as opposed to stochastic control. Although we did
not explicitly consider it above, this scenario can be accommodated by ac-
tive inference by simply equipping the generative model with a prior and
updating the model using variational Bayesian inference to best fit observed
数据. Depending on the specific learning problem and generative model
结构, this can involve updating the transition probabilities and/or the
target distribution C. In POMDPs it can also involve updating the prob-
abilities of observations under each state. We refer to appendix A.2 for
discussion of reward learning through active inference and connections to
representative RL approaches, and Da Costa et al. (2020) and Friston et al.
(2016) for learning transition probabilities through active inference.

6.3 Scaling Active Inference. When comparing RL and active inference
approaches generally, one outstanding issue for active inference is whether
it can be scaled up to solve the more complex problems currently handled

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

829

by RL in machine learning contexts (Çatal et al., 2020, 2021; 丰塔斯等人。,
2020; Mazzaglia et al., 2021; Millidge, 2020; Tschantz et al., 2019). This is an
area of active research.

One important issue along these lines is that planning ahead by evaluat-
ing all or many possible sequences of actions is computationally prohibitive
in many applications. Three complementary solutions have emerged:
(1) employing hierarchical generative models that factorize decisions into
multiple levels and reduce the size of the decision tree by orders of magni-
tude (Çatal et al., 2021; Friston et al., 2018; Parr et al., 2021); (2) efficiently
searching the decision tree using algorithms like Monte Carlo tree search
(Champion, Bowman, 等人。, 2021; Champion, Da Costa, 等人。, 2021; Foun-
tas et al., 2020; Maisto et al., 2021; Silver et al., 2016); 和 (3) amortizing
planning using artificial neural networks (Çatal et al., 2019; 丰塔斯等人。,
2020; Millidge, 2019; Sajid, Tigas, 等人。, 2021).

Another issue rests on learning the generative model. Active inference
may readily learn the parameters of a generative model; 然而, 更多的
work needs to be done on devising algorithms for learning the structure of
generative models themselves (弗里斯顿, 林, 等人。, 2017; 史密斯, Schwarten-
beck, Parr, 等人。, 2020). This is an important research problem in generative
造型, called Bayesian model selection or structure learning (格什曼
& 尼夫, 2010; Tervo et al., 2016).

Note that these issues are not unique to active inference. Model-based
RL algorithms deal with the same combinatorial explosion when evaluat-
ing decision trees, which is one primary motivation for developing efficient
model-free RL algorithms. 然而, other heuristics have also been devel-
oped for efficiently searching and pruning decision trees in model-based RL
(Huys et al., 2012; Lally et al., 2017). 此外, model-based RL suffers
the same limitation regarding learning generative model structure. Yet RL
may have much to offer active inference in terms of efficient implementa-
tion and the identification of methods to scale to more complex applications
(丰塔斯等人。, 2020; Mazzaglia et al., 2021).

7 结论

总之, we have shown that under the specification that the active
inference agent prefers maximizing reward, 方程 4.3:

1. On finite horizon POMDPs with known transition probabilities, 这
objective optimized for action selection in active inference (IE。, 前任-
pected free energy) produces reward-maximizing action sequences
when state estimation is exact. When there are multiple reward-
maximizing candidates, this selects those sequences that maximize
the entropy of future states—thereby keeping options open—and
that minimize the ambiguity of future observations so that they are
maximally informative. 更普遍, the extent to which action

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

830

L. Da Costa et al.

sequences will be reward maximizing will depend on the accuracy
of state estimation.

2. The standard active inference scheme (例如, Barp et al., 2022, 部分
5) produces Bellman optimal actions for planning horizons of one
when state estimation is exact but not beyond.

3. A sophisticated active inference scheme (例如, Friston et al., 2021) 亲-
duces Bellman optimal actions on any finite planning horizon when
state estimation is exact. 此外, this scheme generalizes the
well-known backward induction algorithm from dynamic program-
ming to partially observed environments. Note that for computa-
tional efficiency, the scheme presented in Friston et al. (2021), 做
not generally perform exact state estimation; 因此, the extent to which
it will maximize reward in practice will depend on the accuracy of its
inferences. 尽管如此, it is clear from our results that sophisticated
active inference will vastly outperform standard active inference in
most reward-maximization tasks.

Note that for computational tractability, the sophisticated active infer-
ence scheme presented in Friston et al. (2021) does not generally perform
exact inference; 因此, the extent to which it will maximize reward in prac-
tice will depend on the accuracy of its inferences. 尽管如此, it is clear
from these results that sophisticated active inference will vastly outperform
standard active inference in most reward-maximization tasks.

综上所述, the sophisticated active inference scheme should be the
method of choice when applying active inference to optimally solve the
reward-maximization problems considered here.

附录A: Active Inference and Reinforcement Learning

This article considers how active inference can solve the stochastic control
问题. In this appendix, we discuss the broader relationship between ac-
tive inference and RL.

Loosely speaking, RL is the field of methodologies and algorithms that
learn reward-maximizing actions from data and seek to maximize reward
从长远来看. Because RL is a data-driven field, algorithms are selected
based on how well they perform on benchmark problems. This has pro-
duced a plethora of diverse algorithms, many designed to solve specific
问题, each with its own strengths and limitations. This makes RL dif-
ficult to characterize as a whole. Thankfully, many approaches to model-
based RL and control can be traced back to approximating the optimal
solution to the Bellman equation (Bellman & Dreyfus, 2015; Bertsekas &
Shreve, 1996) (although this may become computationally intractable in
high dimensions; Barto & Sutton, 1992). Our results showed how and when
decisions under active inference and such RL approaches are similar.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

831

This appendix discusses how active inference and RL relate and differ
更普遍. Their relationship has become increasingly important to
understand, as a growing body of research has begun to (1) compare the
performance of active inference and RL models in simulated environments
(Cullen et al., 2018; Millidge, 2020; Sajid, Ball, 等人。, 2021), (2) apply active
inference to model human behavior on reward learning tasks (史密斯, Kir-
利克, 斯图尔特, Touthang, Kuplicki, Khalsa, 等人。, 2021; 史密斯, Kirlic, Stew-
艺术, Touthang, Kuplicki, 麦克德莫特, 等人。, 2021; 史密斯, Schwartenbeck,
斯图尔特, 等人。, 2020; 史密斯, 泰勒, 等人。, 2022), 和 (3) consider the comple-
mentary predictions and interpretations each offers in computational neu-
roscience, 心理学, and psychiatry (Cullen et al., 2018; Huys et al., 2012;
Schwartenbeck, FitzGerald, Mathys, Dolan, & 弗里斯顿, 2015; Schwartenbeck
等人。, 2019; Tschantz, 赛斯, 等人。, 2020).

A.1 Main Differences between Active Inference and Reinforcement

学习.

A.1.1 Philosophy. Active inference and RL differ profoundly in their phi-
losophy. RL derives from the normative principle of maximizing reward
(Barto & Sutton, 1992), while active inference describes systems that main-
tain their structural integrity over time (Barp et al., 2022; Friston et al., 2022).
Despite this difference, these frameworks have many practical similarities.
例如, recall that behavior in active inference is completely deter-
mined by the agent’s preferences, determined as priors in their generative
模型. 至关重要的是, log priors can be interpreted as reward functions and vice
versa, which is how behavior under RL and active inference can be related.

A.1.2 Model Based and Model Free. Active inference agents always em-
body a generative (IE。, 向前) model of their environment, while RL
comprises both model-based and simpler model-free algorithms. In brief,
“model-free” means that agents learn a reward-maximizing state-action
映射, based on updating cached state-action pair values through ini-
tially random actions that do not consider future state transitions. 在
对比, model-based RL algorithms attempt to extend stochastic control
approaches by learning the dynamics and reward function from data. 关于-
call that stochastic control calls on strategies that evaluate different actions
on a carefully handcrafted forward model of dynamics (IE。, known transi-
tion probabilities) to finally execute the reward-maximizing action. 在下面
this terminology, all active inference agents are model-based.

A.1.3 Modeling Exploration. Exploratory behavior—which can improve
reward maximization in the long run—is implemented differently in the
two approaches. 在多数情况下, RL implements a simple form of explo-
ration by incorporating randomness in decision making (Tokic & Palm,
2011; Wilson et al., 2014), where the level of randomness may or may not

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

832

L. Da Costa et al.

change over time as a function of uncertainty. 在其他情况下, RL incorpo-
rates ad hoc information bonuses in the reward function or other decision-
making objectives to build in directed exploratory drives (例如, upper-
confidence-bound algorithms or Thompson sampling). 相比之下, 指导的
exploration emerges naturally within active inference through interactions
between the risk and ambiguity terms in the expected free energy (Da Costa
等人。, 2020; Schwartenbeck et al., 2019). This addresses the explore-exploit
dilemma and confers the agent with artificial curiosity (弗里斯顿, 林, 等人。,
2017; 施米德胡贝尔, 2010; Schwartenbeck et al., 2019; 仍然 & Precup, 2012),
as opposed to the need to add ad hoc information bonus terms (Tokic &
Palm, 2011). We expand on this relationship in appendix A.3.

A.1.4 Control and Learning as Inference. Active inference integrates state
estimation, 学习, decision making, and motor control under the single
objective of minimizing free energy (Da Costa et al., 2020). 实际上, 积极的
inference extends previous work on the duality between inference and con-
控制 (Kappen et al., 2012; Rawlik et al., 2013; Todorov, 2008; Toussaint, 2009)
to solve motor control problems via approximate inference (IE。, 规划
as inference: Attias, 2003; 博特维尼克 & Toussaint, 2012; Friston et al., 2012,
2009; Millidge, Tschantz, 赛斯, 等人。, 2020). 所以, some of the clos-
est RL methods to active inference are control as inference, 也称为
maximum entropy RL (莱文, 2018; Millidge, Tschantz, 赛斯, 等人。, 2020;
Ziebart, 2010), though one major difference is in the choice of decision-
making objective. Loosely speaking, these aforementioned methods min-
imize the risk term of the expected free energy, while active inference also
minimizes ambiguity.

Useful Features of Active Inference

1. Active inference allows great flexibility and transparency when mod-
eling behavior. It affords explainable decision making as a mixture of
信息- and reward-seeking policies that are explicitly encoded
(and evaluated in terms of expected free energy) in the generative
model as priors, which are specified by the user (Da Costa, Lanillos,
等人。, 2022). As we have seen, the kind of behavior that can be pro-
duced includes the optimal solution to the Bellman equation.

2. Active inference accommodates deep hierarchical generative models
combining both discrete and continuous state-spaces (弗里斯顿, Parr,
等人。, 2017; Friston et al., 2018; Parr et al., 2021).

3. The expected free energy objective optimized during planning sub-
sumes many approaches used to describe and simulate decision mak-
ing in the physical, 工程, and life sciences, affording it various
interesting properties as an objective (见图 3 and Friston et al.,
2021). 例如, exploratory and exploitative behavior are canon-
ically integrated, which finesses the need for manually incorporating

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

833

ad hoc exploration bonuses in the reward function (Da Costa, Tenka,
等人。, 2022).

4. Active inference goes beyond state-action policies that predominate
in traditional RL to sequential policy optimization. In sequential pol-
icy optimization, one relaxes the assumption that the same action is
optimal given a particular state and acknowledges that the sequen-
tial order of actions may matter. This is similar to the linearly solvable
MDP formulation presented by Todorov (2006, 2009), where transi-
tion probabilities directly determine actions and an optimal policy
specifies transitions that minimize some divergence cost. 这边走
of approaching policies is perhaps most apparent in terms of explo-
配给. Put simply, it is clearly better to explore and then exploit than
the converse. Because expected free energy is a functional of beliefs,
exploration becomes an integral part of decision making—in contrast
with traditional RL approaches that try to optimize a reward function
of states. 换句话说, active inference agents will explore until
enough uncertainty is resolved for reward-maximizing, goal-seeking
imperatives to start to predominate.

Such advantages should motivate future research to better characterize
the environments in which these properties offer useful advantages—such
as where performance benefits from learning and planning at multiple tem-
poral scales and from the ability to select policies that resolve both state and
parameter uncertainty.

A.2 Reward Learning. Given the focus on relating active inference to
the objective of maximizing reward, it is worth briefly illustrating how ac-
tive inference can learn the reward function from data and its potential con-
nections to representative RL approaches. One common approach for active
inference to learn a reward function (史密斯, Schwartenbeck, 斯图尔特, 等人。,
2020; 史密斯, 泰勒, 等人。, 2022) is to set preferences over observations rather
than states, which corresponds to assuming that inferences over states given
outcomes are accurate:

DKL [问 ((西德:2)s | (西德:2)A, ˜o) | C ((西德:2)s)]
(西德:9)
(西德:7)(西德:8)
(西德:6)

= DKL [问 ((西德:2)哦 | (西德:2)A, ˜o) | C ((西德:2)哦)]
(西德:9)
(西德:7)(西德:8)

(西德:6)

风险 (状态)

+ 乙
(西德:6)

(西德:6)

风险 (结果)

那是, equality holds whenever the free energy minimum is reached
(参见方程 5.2). Then one sets the preference distribution such that the

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

834

L. Da Costa et al.

observations designated as rewards are most preferred. In the zero tem-
perature limit (see eqnarray 4.3), preferences only assign mass to reward-
maximizing observations. When formulated in this way, the reward signal
is treated as sensory data, as opposed to a separate signal from the envi-
罗门特. When one sets allowable actions (controllable state transitions)
to be fully deterministic such that the selection of each action will transi-
tion the agent to a given state with certainty, the emerging dynamics are
such that the agent chooses actions to resolve uncertainty about the prob-
ability of observing reward under each state. 因此, learning the reward
probabilities of available actions amounts to learning the likelihood matrix
磷((西德:2)哦 | (西德:2)s) := ot · Ast, where A is a stochastic matrix. This is done by setting a
prior a over A, 那是, a matrix of nonnegative components, the columns
of which are Dirichlet priors over the columns of A. The agent then learns
by accumulating Dirichlet parameters. Explicitly, at the end of a trial or
episode, one sets (Da Costa et al., 2020; Friston et al., 2016)

a ← a +

时间(西德:3)

τ =0

oτ ⊗ Q(sτ | o0:时间 ).

(A.1)

In equation A.1, 问(sτ | o0:时间 ) is seen as a vector of probabilities over the state-
space S, corresponding to the probability of having been in one or another
state at time τ after having gathered observations throughout the trial. 这
rule simply amounts to counting observed state-outcome pairs, 这是
equivalent to state-reward pairs when the observation modalities corre-
spond to reward.

One should not conflate this approach with the update rule consisting of

accumulating state-observation counts in the likelihood matrix,

A ← A +

时间(西德:3)

τ =0

oτ ⊗ Q(sτ | o0:时间 ),

(A2)

and then normalizing its columns to sum to one when computing proba-
能力. The latter simply approximates the likelihood matrix A by accumu-
lating the number of observed state-outcome pairs. This is distinct from the
approach outlined above, which encodes uncertainty over the matrix A, 作为
a probability distribution over possible distributions P(ot | st ). The agent
is initially very unconfident about A, which means that it doesn’t place
high-probability mass on any specification of P(ot | st ). This uncertainty is
gradually resolved by observing state-observation (or state-reward) 对.
Computationally, it is a general fact of Dirichlet priors that an increase
in elements of a causes the entropy of P(ot | st ) to decrease. As the terms
added in equation A.1 are always positive, one choice of distribution

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

835

磷(ot | st )—which best matches available data and prior beliefs—is ulti-
mately singled out. 换句话说, the likelihood mapping is learned.

The update rule consisting of accumulating state-observation counts in
the likelihood matrix (see equation A.2) (IE。, not incorporating Dirichlet
priors) bears some similarity to off-policy learning algorithms such as Q-
学习. In Q-learning, the objective is to find the best action given the cur-
rent observed state. 为了这, the Q-learning agent accumulates values for
state-action pairs with repeated observation of rewarding or punishing ac-
tion outcomes—much like state-observation counts. This allows it to learn
the Q-value function that defines a reward maximizing policy.

As always in partially observed environments, we cannot guarantee that
the true likelihood mapping will be learned in practice. Smith et al. (2019)
provides examples where, although not in an explicit reward-learning con-
文本, learning the likelihood can be more or less successful in different sit-
uations. Learning the true likelihood fails when the inference over states
is inaccurate, such as when using too severe a mean-field approximation
to the free energy (Blei et al., 2017; Parr et al., 2019; Tanaka, 1999), 哪个
causes the agent to misinfer states and thereby accumulate Dirichlet param-
eters in the wrong locations. 直观地, this amounts to jumping to conclu-
sions too quickly.

Remark 8. If so desired, reward learning in active inference can also be
| st, 在 ).
equivalently formulated as learning transition probabilities P(st+1
In this alternative setup (as exemplified in Sales et al. (2019)), mappings
between reward states and reward outcomes in A are set as identity matri-
ces, and the agent instead learns the probability of transitioning to states
that deterministically generate preferred (rewarding) observations given
the choice of each action sequence. The transition probabilities under each
action are learned in a similar fashion as above (see equation A.1), by accu-
| st, 在 ). See Da Costa et al.,
mulating counts on a Dirichlet prior over P(st+1
2020, appendix, 欲了解详情.

Given the model-based Bayesian formulation of active inference, 更多的
direct links can be made between the active inference approach to reward
learning described above and other Bayesian model-based RL approaches.
For such links to be realized, the Bayesian RL agent would be required to
have a prior over a prior (例如, a prior over the reward function prior or
transition function prior). One way to implicitly incorporate this is through
Thompson sampling (Ghavamzadeh et al., 2016; Russo & Van Roy, 2014,
2016; Russo et al., 2017). While that is not the focus of this article, 未来
work could further examine the links between reward learning in active
inference and model-based Bayesian RL schemes.

A.3 Solving the Exploration-Exploitation Dilemma. An important
distinction between active inference and reinforcement learning schemes
is how they solve the exploration-exploitation dilemma.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

836

L. Da Costa et al.

The exploration-exploitation dilemma (Berger-Tal et al., 2014) arises
whenever an agent has incomplete information about its environment, 这样的
as when the environment is partially observed or the generative model has
to be learned. The dilemma is then about deciding whether to execute ac-
tions aiming to collect reward based on imperfect information about the
environment or to execute actions aiming to gather more information—
allowing the agent to reap more reward in the future. 直观地, it is al-
ways best to explore and then exploit, but optimizing this trade-off can be
difficult.

Active inference balances exploration and exploitation through mini-
mizing the risk and ambiguity inherent in the minimization of expected
free energy. This balance is context sensitive and can be adjusted by mod-
ifying the agent’s preferences (Da Costa, Lanillos, 等人。, 2022). 反过来,
the expected free energy is obtained from a description of agency in bi-
ological systems derived from physics (Barp et al., 2022; Friston et al.,
2022).

Modern RL algorithms integrate exploratory and exploitative behavior
in many different ways. One option is curiosity-driven rewards to en-
courage exploration. Maximum entropy RL and control-as-inference make
decisions by minimizing a KL divergence to the target distribution (Eysen-
bach & 莱文, 2019; Haarnoja et al., 2017, 2018; 莱文, 2018; Todorov, 2008;
Ziebart et al., 2008), which combines reward maximization with maximum
entropy over states. This is similar to active inference on MDPs (Millidge,
Tschantz, 赛斯, 等人。, 2020). 相似地, the model-free Soft Actor-Critic
(Haarnoja et al., 2018) algorithm maximizes both expected reward and
entropy. This outperforms other state-of-the-art algorithms in continuous
control environments and has been shown to be more sample efficient than
its reward-maximizing counterparts (Haarnoja et al., 2018). Hyper (Zintgraf
等人。, 2021) proposes reward maximization alongside minimizing uncer-
tainty over both external states and model parameters. Bayes-adaptive
RL (Guez et al., 2013A, 2013乙; Ross et al., 2008, 2011; Zintgraf et al., 2020)
provides policies that balance exploration and exploitation with the aim
of maximizing reward. Thompson sampling provides a way to balance
exploiting current knowledge to maximize immediate performance and ac-
cumulating new information to improve future performance (Russo et al.,
2017). This reduces to optimizing dual objectives, reward maximization and
information gain, similar to active inference on POMDPs. Empirically, Sajid,
Ball, 等人. (2021) demonstrated that an active inference agent and a Bayesian
model-based RL agent using Thompson sampling exhibit similar behavior
when preferences are defined over outcomes. They also highlighted that
when completely removing the reward signal from the environment, 这
two agents both select policies that maximize some sort of information
gain.

一般来说, the way each of these approaches the exploration-exploitation

dilemma differs in theory and in practice remains largely unexplored.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

837

附录B: Proofs

B.1 Proof of Proposition 1. Note that a Bellman optimal state-action
政策 (西德:3)∗
is a maximal element according to the partial ordering ≤. Exis-
tence thus consists of a simple application of Zorn’s lemma. Zorn’s lemma
states that if any increasing chain

(西德:3)

≤ (西德:3)

≤ . . .

(B.1)

has an upper-bound that is a state-action policy, then there is a maximal
element (西德:3)∗.

Given the chain equation B.1, we construct an upper bound. We enumer-
, t1), . . . ,(αN, σN, tN ). Then the state-action policy

, σ

ate A × S × T by (A
1
顺序

(西德:3)n(A
1

| σ

, t1),

n = 1, 2, 3, . . .

| σ

is bounded within [0, 1]. By the Bolzano-Weierstrass theorem, there ex-
ists a sub-sequence (西德:3)nk (A
, t1), k = 1, 2, 3, . . . that converges. 相似地,
(西德:3)nk (A
, t2) is also a bounded sequence, and by Bolzano-Weierstrass, 它
has a sub-sequence (西德:3)nk j
, t2) that converges. We repeatedly take sub-
sequences until N. To ease notation, call the resulting sub-sequence (西德:3)米,
m = 1, 2, 3, . . .

(a2

| σ

With this, we define ˆ(西德:3) = limm→∞ (西德:3)米. It is straightforward to see that ˆ(西德:3)

is a state-action policy:

ˆ(西德:3)(A | σ, t) = lim
m→∞

(西德:3)

α∈A

(西德:3)米(A | σ, t) ∈ [0, 1],
(西德:3)

(西德:3)米(A | σ, t) = 1,

α∈A

∀(A, σ, t) ∈ A × S × T,

∀(σ, t) ∈ S × T.

To show that ˆ(西德:3) is an upper bound, take any (西德:3) in the original chain of
state-action policies, equation B.1. Then by the definition of an increasing
sub-sequence, there exists an index M ∈ N such that ∀k ≥ M: (西德:3)
≥ (西德:3). 自从
k
limits commute with finite sums, we have v ˆ(西德:3)(s, t) = limm→∞ v(西德:3)米 (s, t) ≥
v(西德:3)
k (s, t) ≥ v(西德:3)(s, t) for any (s, t) ∈ S × T. 因此, by Zorn’s lemma, there ex-
ists a Bellman, optimal state-action policy (西德:3)∗
(西德:2)

B.2 Proof of Proposition 2. 1) ⇒ 2) : We only need to show assertion
(乙). By contradiction, suppose that ∃(s, A) ∈ S × A such that (西德:3)(A | s, 0) > 0
和

乙(西德:3)[右(s1:时间 ) | s0

= s, a0

= α] < max a∈A E(cid:3)[R(s1:T ) | s0 = s, a0 = a]. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 5 8 0 7 2 0 7 9 4 7 3 n e c o _ a _ 0 1 5 7 4 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 838 We let α(cid:2) be the Bellman optimal action at state s and time 0 defined as L. Da Costa et al. α(cid:2) := arg max a∈A E(cid:3)[R(s1:T ) | s0 = s, a0 = a]. Then we let (cid:3)(cid:2) assigns α(cid:2) deterministically. Then be the same state-action policy as (cid:3) except that (cid:3)(cid:2) (· | s, 0) (cid:3) v(cid:3)(s, 0) = E(cid:3)[R(s1:T ) | s0 = s, a0 = a](cid:3)(a | s, 0) a∈A < max a∈A E(cid:3)[R(s1:T ) | s0 = s, a0 = a] = E(cid:3)(cid:2) [R(s1:T ) | s0 = (cid:3) E(cid:3)(cid:2) [R(s1:T ) | s0 = s, a0 = s, a0 = α(cid:2) ](cid:3)(cid:2) = a](cid:3)(cid:2) (α(cid:2) | s, 0) (a | s, 0) a∈A = v(cid:3)(cid:2) (s, 0). So (cid:3) is not Bellman optimal, which is a contradiction. 1) ⇐ 2) : We only need to show that (cid:3) maximizes v(cid:3)(s, 0), ∀s ∈ S. By and a state s ∈ S such that contradiction, there exists a state-action policy (cid:3)(cid:2) v(cid:3)(s, 0) < v(cid:3)(cid:2) (s, 0), (cid:3) ⇐⇒ E(cid:3)[R(s1:T ) | s0 = s, a0 = a](cid:3)(a | s, 0) < a∈A (cid:3) a∈A E(cid:3)(cid:2) [R(s1:T ) | s0 = s, a0 = a](cid:3)(cid:2) (a | s, 0). By a, the left-hand side equals E(cid:3)[R(s1:T ) | s0 = s, a0 = a]. max a∈A Unpacking the expression on the right-hand side, (cid:3) E(cid:3)(cid:2) [R(s1:T ) | s0 = s, a0 = a](cid:3)(cid:2) (a | s, 0) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 5 8 0 7 2 0 7 9 4 7 3 n e c o _ a _ 0 1 5 7 4 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 a∈A (cid:3) = = = (cid:3) E(cid:3)(cid:2) [R(s1:T ) | s1 = σ ]P(s1 = σ | s0 = s, a0 = a)(cid:3)(cid:2) (a | s, 0) a∈A (cid:3) σ ∈S (cid:3) a∈A (cid:3) σ ∈S (cid:3) a∈A σ ∈S (cid:14) E(cid:3)(cid:2) [R(s2:T ) | s1 (cid:15) = σ ] + R(σ ) P(s1 = σ | s0 = s, a0 = a)(cid:3)(cid:2) (a | s, 0) (cid:14) v(cid:3)(cid:2) (σ, 1) + R(σ )] P(s1 = σ | s0 = s, a0 = a)(cid:3)(cid:2) (a | s, 0). (B.2) Reward Maximization Active Inference 839 Since (cid:3) is Bellman optimal when restricted to {1, . . . , T}, we have v(cid:3)(cid:2) (σ, 1) ≤ v(cid:3)(σ, 1), ∀σ ∈ S. Therefore, (cid:3) (cid:3) (cid:14) v(cid:3)(cid:2) (σ, 1) + R(σ )] P(s1 = σ | s0 = s, a0 = a)(cid:3)(cid:2) (a | s, 0) a∈A σ ∈S (cid:3) (cid:3) ≤ (cid:14) v(cid:3)(σ, 1) + R(σ )] P(s1 = σ | s0 = s, a0 = a)(cid:3)(cid:2) (a | s, 0). a∈A σ ∈S Repeating the steps above equation B.2, but in reverse order, yields (cid:3) a∈A E(cid:3)(cid:2) [R(s1:T ) | s0 = s, a0 = a](cid:3)(cid:2) (a | s, 0) ≤ (cid:3) a∈A E(cid:3)[R(s1:T ) | s0 = s, a0 = a](cid:3)(cid:2) (a | s, 0). However, (cid:3) a∈A E(cid:3)[R(s1:T ) | s0 = s, a0 = a](cid:3)(cid:2) (a | s, 0) < max a∈A E(cid:3)[R(s1:T ) | s0 = s, a0 = a], which is a contradiction. (cid:2) B.3 Proof of Proposition 3. We first prove that state-action policies (cid:3) defined as in equation 2.2 are Bellman optimal by induction on T. T = 1 : (cid:3)(a | s, 0) > 0 ⇐⇒ a ∈ arg max

乙[右(s1) | s0

= s, a0

= a],

∀s ∈ S

is a Bellman optimal state-action policy as it maximizes the total reward
possible in the MDP.

Let T > 1 be finite and suppose that the proposition holds for MDPs with

a temporal horizon of T − 1. 这意味着

(西德:3)(A | s, T − 1) > 0 ⇐⇒ a ∈ arg max

乙[右(sT ) | sT−1

= s, aT−1

= a],

∀s ∈ S,

(西德:3)(A | s, T − 2) > 0 ⇐⇒ a ∈ arg max

A
∀s ∈ S,
…

乙(西德:3)[右(sT−1:时间 ) | sT−2

= s, aT−2

= a],

(西德:3)(A | s, 1) > 0 ⇐⇒ a ∈ arg max

乙(西德:3)[右(s2:时间 ) | s1

= s, a1

= a],

∀s ∈ S,

is a Bellman optimal state-action policy on the MDP restricted to times 1 到
时间. 所以, 自从

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

840

L. Da Costa et al.

(西德:3)(A | s, 0) > 0 ⇐⇒ a ∈ arg max

乙(西德:3)[右(s1:时间 ) | s0

= s, a0

= a],

∀s ∈ S.

Proposition 2 allows us to deduce that (西德:3) is Bellman optimal.

We now show that any Bellman optimal state-action policy satisfies the

backward induction algorithm equation 2.2.

Suppose by contradiction that there exists a state-action policy (西德:3) 那是
Bellman optimal but does not satisfy equation 2.2. Say, ∃(A, s, t) ∈ A × S ×
时间, t < T, such that (cid:3)(a | s, t) > 0 and a /∈ arg max
α∈A

乙(西德:3)[右(st+1:时间 ) | st = s, at = α].

This implies

乙(西德:3)[右(st+1:时间 ) | st = s, at = a] < max α∈A E(cid:3)[R(st+1:T ) | st = s, at = α]. Let ˜a ∈ arg maxα E(cid:3)[R(st+1:T ) | st = s, at = α]. Let ˜(cid:3) be a state-action pol- icy such that ˜(cid:3)(· | s, t) assigns ˜a ∈ A deterministically and such that ˜(cid:3) = (cid:3) otherwise. Then we can contradict the Bellman optimality of (cid:3) as follows: v(cid:3)(s, t) = E(cid:3)[R(st+1:T ) | st = s] (cid:3) = E(cid:3)[R(st+1:T ) | st = s, at = α](cid:3)(α | s, t) α∈A < max α∈A E(cid:3)[R(st+1:T ) | st = s, at = α] = E(cid:3)[R(st+1:T ) | st = s, at = ˜a] = E ˜(cid:3)[R(st+1:T ) | st = s, at = ˜a] = (cid:3) E ˜(cid:3)[R(st+1:T ) | st = s, at = α] ˜(cid:3)(α | s, t) α∈A = v ˜(cid:3)(s, t). B.4 Proof of Lemma 1. lim β→+∞ arg min (cid:2)a DKL[Q((cid:2)s | (cid:2)a, st ) | Cβ ((cid:2)s)] = lim β→+∞ arg min (cid:2)a = lim β→+∞ arg min (cid:2)a = lim β→+∞ arg max (cid:2)a −H[Q((cid:2)s | (cid:2)a, st )] + E Q((cid:2)s|(cid:2)a,st )[− log Cβ ((cid:2)s)] −H[Q((cid:2)s | (cid:2)a, st )] − βE Q((cid:2)s|(cid:2)a,st )[R((cid:2)s)] H[Q((cid:2)s | (cid:2)a, st )] + βE Q((cid:2)s|(cid:2)a,st )[R((cid:2)s)] l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 5 5 8 0 7 2 0 7 9 4 7 3 n e c o _ a _ 0 1 5 7 4 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 (cid:2) Reward Maximization Active Inference 841 ⊆ lim β→+∞ arg max βE Q((cid:2)s|(cid:2)a,st )[R((cid:2)s)] = arg max (cid:2)a E (cid:2)a Q((cid:2)s|(cid:2)a,st )[R((cid:2)s)]. The inclusion follows from the fact that, as β → +∞, a minimizer of the expected free energy has to maximize E Q((cid:2)s|(cid:2)a,st )[R((cid:2)s)]. Among such action se- quences, the expected free energy minimizers are those that maximize the entropy of future states H[Q((cid:2)s | (cid:2)a, st )]. (cid:2) B.5 Proof of Theorem 1. When T = 1, the only action is a0. We fix an = s ∈ S. By proposition 2, a Bellman optimal state- 0 that maximizes immedi- arbitrary initial state s0 action policy is fully characterized by an action a∗ ate reward: ∗ 0 a ∈ arg max a∈A E[R(s1) | s0 = s, a0 = a]. Recall that by remark 5, this expectation stands for return under the transi- tion probabilities of the MDP: ∗ 0 a ∈ arg max a∈A E P(s1 |a0 =a,s0 =s)[R(s1)]. Since transition probabilities are assumed to be known (see equation 3.1), this reads ∗ a 0 ∈ arg max a∈A E Q(s1 |a0 =a,s0 =s)[R(s1)]. On the other hand, a0 ∈ lim β→+∞ arg max a∈A exp(−G(a | st )) = lim β→+∞ arg min a∈A G(a | st ). By lemma 1, this implies a0 ∈ arg max a∈A E Q(s1 |a0 =a,s0 =s)[R(s1)], which concludes the proof. (cid:2) B.6 Proof of Theorem 2. We prove this result by induction on the tem- poral horizon T of the MDP. The proof of the theorem when T = 1 can be seen from the proof of the- orem 1. Now suppose that T > 1 is finite and that the theorem holds for
MDPs with a temporal horizon of T − 1.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

842

L. Da Costa et al.

Our induction hypothesis says that Q(aτ | sτ ), as defined in equation 4.8,
is a Bellman optimal state-action policy on the MDP restricted to times τ =
1, . . . , 时间. 所以, by proposition 2, we only need to show that the action
a0 selected under active inference satisfies

∈ arg max
a∈A

乙

问[右((西德:2)s) | s0

, a0

= a].

This is simple to show as

乙

问[右((西德:2)s) | s0

, a0

= a]

arg max
a∈A
= arg max
a∈A
= arg max
a∈A

乙

磷((西德:2)s|a1:时间 ,a0

=a,s0 )问((西德:2)A|s1:时间 )[右((西德:2)s)]

(by remark 4)

问((西德:2)s,(西德:2)A|a0

=a,s0 )[右((西德:2)s)]

(as the transitions are known)

= lim
β→+∞

arg max
a∈A

⊇ lim
β→+∞

arg max
a∈A

乙

问((西德:2)s,(西德:2)A|a0

=a,s0 )[βR((西德:2)s)]

问((西德:2)s,(西德:2)A|a0

=a,s0 )[βR((西德:2)s)] − H[问((西德:2)s | (西德:2)A, a0

= a, s0)]

= lim
β→+∞

arg min
a∈A

乙

问((西德:2)s,(西德:2)A|a0

=a,s0 )[− log Cβ ((西德:2)s)] − H[问((西德:2)s | (西德:2)A, a0

= a, s0)]

(通过方程 4.1)

= lim
β→+∞

arg min
a∈A

= lim
β→+∞

arg min
a∈A

乙

问((西德:2)s,(西德:2)A|a0

=a,s0 )DKL[问((西德:2)s | (西德:2)A, a0

= a, s0) | Cβ ((西德:2)s)]

G(a0

= a | s0)

(通过方程 4.6).

所以, an action a0 selected under active inference is a Bellman optimal
state-action policy on finite temporal horizons. 此外, the inclusion
follows from the fact that if there are multiple actions that maximize ex-
pected reward, that which is selected under active inference maximizes the
(西德:2)
entropy of beliefs about future states.

B.7 Proof of Proposition 4. Unpacking the zero temperature limit,

lim
β→+∞

arg min

(西德:2)A

G((西德:2)A | ˜o)

= lim
β→+∞

arg min

(西德:2)A

= lim
β→+∞

arg min

(西德:2)A

= lim
β→+∞

arg min

(西德:2)A

DKL[问((西德:2)s | (西德:2)A, ˜o) | Cβ ((西德:2)s)] + 乙

问((西德:2)s|(西德:2)A, ˜o)H[磷((西德:2)哦 | (西德:2)s)]

−H[问((西德:2)s | (西德:2)A, ˜o)] + 乙

问((西德:2)s|(西德:2)A, ˜o)[− log Cβ ((西德:2)s)] + 乙

问((西德:2)s|(西德:2)A, ˜o)H[磷((西德:2)哦 | (西德:2)s)]

−H[问((西德:2)s | (西德:2)A, ˜o)] − βE

问((西德:2)s|(西德:2)A, ˜o)[右((西德:2)s)] + 乙

问((西德:2)s|(西德:2)A, ˜o)H[磷((西德:2)哦 | (西德:2)s)]

(通过方程 4.1)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

843

⊆ lim
β→+∞

arg max

βE

问((西德:2)s|(西德:2)A, ˜o)[右((西德:2)s)]

= arg max

(西德:2)A

乙

(西德:2)A
问((西德:2)s|(西德:2)A, ˜o)[右((西德:2)s)].

The inclusion follows from the fact that as β → +∞, a minimizer of
the expected free energy has first and foremost to maximize E
问((西德:2)s|(西德:2)A, ˜o)[右((西德:2)s)].
Among such action sequences, the expected free energy minimizers are
those that maximize the entropy of (beliefs about) future states H[问((西德:2)s | (西德:2)A, ˜o)]
and resolve ambiguity about future outcomes by minimizing E
问((西德:2)s|(西德:2)A, ˜o)H[磷((西德:2)哦 |
(西德:2)s)].

致谢

We thank Dimitrije Markovic and Quentin Huys for providing helpful feed-
back during the preparation of the manuscript.

Funding Information

L.D. is supported by the Fonds National de la Recherche, 卢森堡
(Project code: 13568875). N.S. is funded by the Medical Research Coun-
cil (MR/S502522/1) 和 2021-2022 Microsoft PhD Fellowship. K.F. is sup-
ported by funding for the Wellcome Centre for Human Neuroimaging
(Ref: 205103/Z/16/Z), a Canada-U.K. Artificial Intelligence Initiative (Ref:
ES/T01279X/1), and the European Union’s Horizon 2020 Framework Pro-
gramme for Research and Innovation under the Specific Grant Agreement
945539 (Human Brain Project SGA3). R.S. is supported by the William K.
Warren Foundation, the Well-Being for Planet Earth Foundation, the Na-
tional Institute for General Medical Sciences (P20GM121312), and the Na-
tional Institute of Mental Health (R01MH123691). This publication is based
on work partially supported by the EPSRC Centre for Doctoral Training
in Mathematics of Random Systems: 分析, Modelling and Simulation
(EP/S023925/1).

Author Contributions

L.D.: conceptualization, proofs, 写作: first draft, review and editing. N.S.,
T.P., K.F., R.S.: conceptualization, 写作: review and editing.

参考

Adams, 右. A。, Stephan, K. E., 棕色的, H. R。, Frith, C. D ., & 弗里斯顿, K. J. (2013).
The computational anatomy of psychosis. Frontiers in Psychiatry, 4. 10.3389/
fpsyt.2013.00047

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

844

L. Da Costa et al.

Adda, J。, & 库珀, 右. 瓦. (2003). Dynamic economics: Quantitative methods and appli-

阳离子. 与新闻界.

Attias, H. (2003). Planning by probabilistic inference. In Proceedings of the 9th Int.

Workshop on Artificial Intelligence and Statistics.

巴洛, H. 乙. (1961). Possible principles underlying the transformations of sensory mes-

sages. 与新闻界.

巴洛, H. 乙. (1974). Inductive inference, 编码, 洞察力, 和语言. Percep-

的, 3(2), 123–134. 10.1068/p030123, 考研: 4457815

Barp, A。, Da Costa, L。, França, G。, 弗里斯顿, K., Girolami, M。, 约旦, 中号. 我。, & Pavli-
otis, G. A. (2022). Geometric methods for sampling, optimisation, inference and
adaptive agents. 在F中. Nielsen, A. S. 右. Srinivasa Rao, & C. 饶 (编辑。), Geometry
and statistics. 爱思唯尔.

Barto, A。, Mirolli, M。, & Baldassarre, G. (2013). Novelty or surprise? Frontiers in Psy-

chology, 4. 10.3389/fpsyg.2013.00907

Barto, A。, & Sutton, 右. (1992). Reinforcement learning: An introduction. 与新闻界.
Beal, 中号. J. (2003). Variational algorithms for approximate Bayesian inference. 博士论文。,

伦敦大学.

Bellman, 右. 乙. (1957). Dynamic programming. 普林斯顿大学出版社.
Bellman, 右. E., & Dreyfus, S. 乙. (2015). Applied dynamic programming. 普林斯顿大学-

大学出版社.

Berger, J. 氧. (1985). Statistical decision theory and Bayesian analysis (2nd 版。). 施普林格-

Verlag.

Berger-Tal, 奥。, Nathan, J。, Meron, E., & Saltz, D. (2014). The exploration-exploitation
dilemma: A multidisciplinary framework. PLOS One, 9(4), e95693. 10.1371/
journal.pone.0095693

Bertsekas, D. P。, & Shreve, S. 乙. (1996). Stochastic optimal control: The discrete time case.

Athena Scientific.

Bishop, C. 中号. (2006). Pattern recognition and machine learning. 施普林格.
Blei, D. M。, Kucukelbir, A。, & McAuliffe, J. D. (2017). Variational inference: A review
for statisticians. Journal of the American Statistical Association, 112(518), 859–877.
10.1080/01621459.2017.1285773

博特维尼克, M。, & Toussaint, 中号. (2012). Planning as inference. Trends in Cognitive Sci-

恩塞斯, 16(10), 485–488. 10.1016/j.tics.2012.08.006, 考研: 22940577

Çatal, 奥。, Nauta, J。, Verbelen, T。, Simoens, P。, & Dhoedt, 乙. (2019). Bayesian policy

selection using active inference. http://arxiv.org/abs/1904.08149

Çatal, 奥。, Verbelen, T。, Nauta, J。, Boom, C. D ., & Dhoedt, 乙. (2020). Learning per-
ception and planning with deep active inference. In Proceedings of the IEEE In-
ternational Conference on Acoustics, Speech and Signal Processing (PP. 3952–3956).
10.1109/ICASSP40776.2020.9054364

Çatal, 奥。, Verbelen, T。, Van de Maele, T。, Dhoedt, B., & Safron, A. (2021). Robot nav-
igation as hierarchical active inference. Neural Networks, 142, 192–204. 10.1016/
j.neunet.2021.05.010

Champion, T。, Bowman, H。, & Grz´s, 中号.

(2021). Branching time active infer-
恩斯: Empirical study and complexity class analysis. http://arxiv.org/abs/2111
.11276

Champion, T。, Da Costa, L。, Bowman, H。, & Grze´s, 中号. (2021). Branching time active

inference: The theory and its generality. http://arxiv.org/abs/2111.11107

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

845

Cullen, M。, Davey, B., 弗里斯顿, K. J。, & Moran, 右. J. (2018). Active inference in
OpenAI Gym: A paradigm for computational investigations into psychiatric ill-
内斯. Biological Psychiatry: Cognitive Neuroscience and Neuroimaging, 3(9), 809–818.
10.1016/j.bpsc.2018.06.010, 考研: 30082215

Da Costa, L。, Lanillos, P。, Sajid, N。, 弗里斯顿, K., & 汗, S. (2022). How active infer-
ence could help revolutionise robotics. Entropy, 24(3), 361. 10.3390/e24030361
Da Costa, L。, Parr, T。, Sajid, N。, Veselic, S。, Neacsu, 五、, & 弗里斯顿, K. (2020). Active
inference on discrete state-spaces: A synthesis. Journal of Mathematical Psychology,
99, 102447. 10.1016/j.jmp.2020.102447

Da Costa, L。, Tenka, S。, 赵, D ., & Sajid, 氮. (2022). Active inference as a model
of agency. Workshop on RL as a Model of Agency. https://www.sciencedirect
.com/science/article/pii/S0022249620300857

Daw, 氮. D ., O’Doherty, J. P。, Dayan, P。, Seymour, B., & Dolan, 右. J. (2006). Corti-
cal substrates for exploratory decisions in humans. 自然, 441(7095), 876–879.
10.1038/nature04766, 考研: 16778890

Dayan, P。, & Daw, 氮. D. (2008). Decision theory, reinforcement learning, 和
脑. 认知的, Affective, and Behavioral Neuroscience, 8(4), 429–453. 10.3758/
CABN.8.4.429

Deci, E., & Ryan, 右. 中号. (1985). Intrinsic motivation and self-determination in human be-

行为. 施普林格.

艾森巴赫, B., & 莱文, S. (2019). If MaxEnt Rl is the answer, what is the question?

arXiv:1910.01913.

Fountas, Z。, Sajid, N。, Mediano, 磷. A. 中号. Deep active inference agents using Monte-Carlo

方法. http://arxiv.org/abs/2006.04176

弗里斯顿, K., Da Costa, L。, Sajid, N。, Heins, C。, Ueltzhöffer, K., Pavliotis, G. A。, & Parr,
时间. (2022). The free energy principle made simpler but not too simple. http://arxiv.org/
abs/2201.06387

弗里斯顿, K., Da Costa, L。, Hafner, D ., Hesp, C。, & Parr, 时间. (2021). Sophis-
ticated inference. 神经计算, 33(3), 713–763. 10.1162/neco_a_01351,
考研: 33626312

弗里斯顿, K., FitzGerald, T。, Rigoli, F。, Schwartenbeck, P。, O’Doherty, J。, & Pezzulo, G.
(2016). Active inference and learning. Neuroscience and Biobehavioral Reviews, 68,
862–879. 10.1016/j.neubiorev.2016.06.022, 考研: 27375276

弗里斯顿, K., FitzGerald, T。, Rigoli, F。, Schwartenbeck, P。, & Pezzulo, G. (2017). 乙酰胆碱-
tive inference: A process theory Neural Computation, 29(1), 1–49. 10.1162/NECO_a
_00912, 考研: 27870614

弗里斯顿, K., Samothrakis, S。, & Montague, 右. (2012). Active inference and agency:
Optimal control without cost functions. Biological Cybernetics, 106(8), 523–541.
10.1007/s00422-012-0512-8, 考研: 22864468

弗里斯顿, K. J。, Daunizeau, J。, & Kiebel, S. J. (2009). Reinforcement learning or active

inference? PLOS One, 4(7), e6421. 10.1371/journal.pone.0006421

弗里斯顿, K. J。, Daunizeau, J。, Kilner, J。, & Kiebel, S. J. (2010). Action and behav-
ior: A free-energy formulation. Biological Cybernetics, 102(3), 227–260. 10.1007/
s00422-010-0364-z, 考研: 20148260

弗里斯顿, K. J。, 林, M。, Frith, C. D ., Pezzulo, G。, Hobson, J. A。, & Ondobaka, S. (2017).
Active inference, curiosity and insight. 神经计算, 29(10), 2633–2683.
10.1162/neco_a_00999, 考研: 28777724

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

846

L. Da Costa et al.

弗里斯顿, K. J。, Parr, T。, & de Vries, 乙. (2017). The graphical brain: Belief propaga-
tion and active inference. 网络神经科学, 1(4), 381–414. 10.1162/NETN_a
_00018, 考研: 29417960

弗里斯顿, K. J。, Rosch, R。, Parr, T。, Price, C。, & Bowman, H. (2018). Deep temporal
models and active inference. Neuroscience and Biobehavioral Reviews, 90, 486–501.
10.1016/j.neubiorev.2018.04.004, 考研: 29747865
Fudenberg, D ., & Tirole, J. (1991). Game theory. 与新闻界.
格什曼, S. J. (2018). Deconstructing the human algorithms for exploration. 齿轮-

尼尼申, 173, 34–42. 10.1016/j.cognition.2017.12.014, 考研: 29289795

格什曼, S. J。, & 尼夫, 是. (2010). Learning latent structure: Carving nature at its
joints. 神经生物学的当前观点, 20(2), 251–256. 10.1016/j.conb.2010.02.008,
考研: 20227271

Ghavamzadeh, M。, Mannor, S。, Pineau, J。, & 添马舰, A. (2016). Bayesian reinforcement

学习: 一项调查. arXiv:1609.04436.

Guez, A。, Silver, D ., & Dayan, 磷. (2013A). Scalable and efficient Bayes-adaptive rein-
forcement learning based on Monte-Carlo tree search. Journal of Artificial Intelli-
gence Research, 48, 841–883. 10.1613/jair.4117

Guez, A。, Silver, D ., & Dayan, 磷. (2013乙). Efficient Bayes-adaptive reinforcement learning

using sample-based search. http://arxiv.org/abs/1205.3109

Haarnoja, T。, 唐, H。, 阿贝尔, P。, & 莱文, S. (2017). Reinforcement learning with deep

energy-based policies. arXiv:1702.08165.

Haarnoja, T。, 周, A。, 阿贝尔, P。, & 莱文, S. (2018). Soft actor critic: Off-
policy maximum entropy deep reinforcement learning with a stochastic actor. CoRR,
abs/1801.01290. http://arxiv.org/abs/1801.01290

Huys, 问. J. M。, Eshel, N。, O’Nions, E., Sheridan, L。, Dayan, P。, & Roiser, J. 磷. (2012).
Bonsai trees in your head: How the Pavlovian system sculpts goal-directed
choices by pruning decision trees. PLOS Computational Biology, 8(3), e1002410.
10.1371/journal.pcbi.1002410

Itti, L。, & Baldi, 磷. (2009). Bayesian surprise attracts human attention. 视觉研究,

49(10), 1295–1306. 10.1016/j.visres.2008.09.007, 考研: 18834898

Jaynes, 乙. 时间. (1957A). Information theory and statistical mechanics. 物理评论,

106(4), 620–630. 10.1103/PhysRev.106.620

Jaynes, 乙. 时间. (1957乙). Information theory and statistical mechanics. 二. 物理评论,

108(2), 171–190. 10.1103/PhysRev.108.171

约旦, 中号. 我。, Ghahramani, Z。, Jaakkola, 时间. S。, & Saul, L. K. (1998). An introduction to
variational methods for graphical models. 在米. 我. 约旦 (埃德。), Learning in graph-
ical models (PP. 105–161). Springer Netherlands. 10.1007/978-94-011-5014-9_5
Kaelbling, L. P。, Littman, 中号. L。, & Cassandra, A. 右. (1998). Planning and acting
in partially observable stochastic domains. 人工智能, 101(1), 99–134.
10.1016/S0004-3702(98)00023-X

Kahneman, D ., & Tversky, A. (1979). Prospect theory: An analysis of decision under

风险. Econometrica, 47(2), 263–291. 10.2307/1914185

切, H. J。, Gómez, 五、, & Opper, 中号. (2012). Optimal control as a graphical model
inference problem. Machine Learning, 87(2), 159–182. 10.1007/s10994-012-5278-7
Klyubin, A. S。, Polani, D ., & Nehaniv, C. L. (2008). Keep your options open: 一个
information-based driving principle for sensorimotor systems. PLOS One, 3(12),
e4018. 10.1371/journal.pone.0004018

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

847

Lally, N。, Huys, 问. J. M。, Eshel, N。, Faulkner, P。, Dayan, P。, & Roiser, J. 磷.
(2017). The neural basis of aversive Pavlovian guidance during planning
神经科学杂志, 37(42), 10215–10229. 10.1523/JNEUROSCI.0085-17.2017,
考研: 28924006

Lanillos, P。, Pages, J。, & Cheng, G. (2020). Robot self/other distinction: Active infer-
ence meets neural networks learning in a mirror. In Proceedings of the European
Conference on Artificial Intelligence.

莱文, S. (2018, 可能 20). Reinforcement learning and control as probabilistic inference:

tutorial and review. http://arxiv.org/abs/1805.00909

Lindley, D. V. (1956). On a measure of the information provided by an ex-
periment. Annals of Mathematical Statistics, 27(4), 986–1005. 10.1214/aoms/
1177728069

Linsker, 右. (1990). Perceptual neural organization: Some approaches based on net-
work models and information theory. Annual Review of Neuroscience, 13(1), 257–
281. 10.1146/annurev.ne.13.030190.001353, 考研: 2183677

MacKay, D. J. C. (2003, 九月 25). Information theory, inference and learning algo-

rithms. 剑桥大学出版社.

Maisto, D ., Gregoretti, F。, 弗里斯顿, K., & Pezzulo, G. (2021, 行进 25). Active tree search

in large POMDPs. http://arxiv.org/abs/2103.13860

Markovi´c, D ., Stoji´c, H。, Schwöbel, S。, & Kiebel, S. J. (2021). An empirical evalua-
tion of active inference in multi-armed bandits. Neural Networks, 144, 229–246.
10.1016/j.neunet.2021.08.018

Mazzaglia, P。, Verbelen, T。, & Dhoedt, 乙. (2021). Contrastive active inference. https://

openreview.net/forum?id=5t5FPwzE6mq

Millidge, 乙. (2019, 行进 11). Implementing predictive processing and active inference:

Preliminary steps and results. PsyArXiv. 10.31234/osf.io/4hb58

Millidge, 乙. (2020). Deep active inference as variational policy gradients. 杂志

Mathematical Psychology, 96, 102348. 10.1016/j.jmp.2020.102348

Millidge, 乙. (2021). Applications of the free energy principle to machine learning and neu-

roscience. http://arxiv.org/abs/2107.00140

Millidge, B., Tschantz, A。, & Buckley, C. L. (2020, 四月 21). Whence the expected free

活力? http://arxiv.org/abs/2004.08128

Millidge, B., Tschantz, A。, 赛斯, A. K., & Buckley, C. L. (2020). On the relationship
between active inference and control as inference. 在T. Verbelen, 磷. Lanillos, C. L.
Buckley, & C. De Boom (编辑。), Active inference (PP. 3–11). 施普林格.

Miranda, 中号. J。, & Fackler, 磷. L. (2002, 九月 1). Applied computational economics

and finance. 与新闻界.

Mirza, 中号. B., Adams, 右. A。, Mathys, C。, & 弗里斯顿, K. J. (2018). Human visual explo-
ration reduces uncertainty about the sensed world. PLOS One, 13(1), e0190429.
10.1371/journal.pone.0190429

Oliver, G。, Lanillos, P。, & Cheng, G. (2021). An empirical study of active inference
on a humanoid robot. IEEE Transactions on Cognitive and Developmental Systems
PP(99), 1–1. 10.1109/TCDS.2021.3049907

Optican, L. M。, & Richmond, 乙. J. (1987). Temporal encoding of two-dimensional
patterns by single units in primate inferior temporal cortex. 三、. Information theo-
retic analysis. 神经生理学杂志, 57(1), 162–178. 10.1152/jn.1987.57.1.162,
考研: 3559670

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

848

L. Da Costa et al.

Oudeyer, P.-Y., & 卡普兰, F. (2007). What is intrinsic motivation? A typology of
computational approaches. Frontiers in Neurorobotics, 1, 6. 10.3389/neuro.12.006
.2007

Parr, 时间. (2019). The computational neurology of active vision (博士论文。). University Col-

lege London.

Parr, T。, Limanowski, J。, Rawji, 五、, & 弗里斯顿, K. (2021). The computational neurology
of movement under active inference. Brain, 144(6), 1799–1818. 10.1093/brain/
awab085, 考研: 33704439

Parr, T。, Markovic, D ., Kiebel, S. J。, & 弗里斯顿, K. J. (2019). Neuronal message pass-
ing using mean-field, Bethe, and marginal approximations. Scientific Reports, 9(1),
1889. 10.1038/s41598-018-38246-3

Parr, T。, Pezzulo, G。, & 弗里斯顿, K. J. (2022, 行进 29). Active inference: The free energy

principle in mind, 脑, and behavior. 与新闻界.

保罗, A。, Sajid, N。, Gopalkrishnan, M。, & Razi, A. (2021, 八月 27). Active inference

for stochastic control. http://arxiv.org/abs/2108.12245

Pavliotis, G. A. (2014). Stochastic processes and applications: Diffusion processes, 这

Fokker-Planck and Langevin equations. 施普林格.

Pearl, J. (1998). Graphical models for probabilistic and causal reasoning. 在P.
Smets (埃德。), Quantified representation of uncertainty and imprecision (PP. 367–389).
Springer Netherlands.

Pezzato, C。, Ferrari, R。, & Corbato, C. H. (2020). A novel adaptive controller for robot
manipulators based on active inference. IEEE Robotics and Automation Letters, 5(2),
2973–2980. 10.1109/LRA.2020.2974451

Pio-Lopez, L。, Nizard, A。, 弗里斯顿, K., & Pezzulo, G. (2016). Active inference and
robot control: 案例研究. Journal of the Royal Society Interface, 13(122), 20160616.
10.1098/rsif.2016.0616

Puterman, 中号. L. (2014, 八月 28). Markov decision processes: Discrete stochastic dy-

namic programming. 威利.

Rahme, J。, & Adams, 右. 磷. (2019, 六月 24). A theoretical connection between statistical

physics and reinforcement learning. http://arxiv.org/abs/1906.10228

Rawlik, K., Toussaint, M。, & Vijayakumar, S. (2013). On stochastic optimal con-
trol and reinforcement learning by approximate inference. 在诉讼程序中
the Twenty-Third International Joint Conference on Artificial Intelligence. https://
www.aaai.org/ocs/index.php/IJCAI/IJCAI13/paper/view/6658

Ross, S。, Chaib-draa, B., & Pineau, J. (2008). Bayes-adaptive POMDPs. 在J. C.
Platt, D. Koller, 是. 歌手, & S. 时间. Roweis (编辑。), Advances in neural informa-
tion processing systems, 20 (PP. 1225–1232). 柯兰. http://papers.nips.cc/paper/
3333-bayes-adaptive-pomdps.pdf

Ross, S。, Pineau, J。, Chaib-draa, B., & Kreitmann, 磷. (2011). A Bayesian approach for
learning and planning in partially observable Markov decision processes. 杂志
of Machine Learning Research, 12 (2011).

Russo, D ., & Van Roy, 乙. (2014). Learning to optimize via posterior sampling. 数学-

ematics of Operations Research, 39(4), 1729–1770. 10.1287/moor.2014.0650

Russo, D ., & Van Roy, 乙. (2016). An information-theoretic analysis of Thompson sam-

pling. Journal of Machine Learning Research, 17(1), 2442–2471.

Russo, D ., Van Roy, B., Kazerouni, A。, Osband, 我。, & Wen, Z. (2017). A tutorial on

Thompson sampling. arXiv:1707.02038.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

849

Sajid, N。, Ball, 磷. J。, Parr, T。, & 弗里斯顿, K. J. (2021). Active inference: Demysti-
fied and compared. 神经计算, 33(3), 674–712. 10.1162/neco_a_01357,
考研: 33400903

Sajid, N。, Holmes, E., Costa, L. D ., Price, C。, & 弗里斯顿, K. (2022). A mixed generative

model of auditory word repetition. 10.1101/2022.01.20.477138

Sajid, N。, Tigas, P。, Zakharov, A。, Fountas, Z。, & 弗里斯顿, K. (2021, 七月 18). Explo-
ration and preference satisfaction trade-off in reward-free learning. http://arxiv.org/
abs/2106.04316

Sales, A. C。, 弗里斯顿, K. J。, 琼斯, 中号. W., 皮克林, A. E., & Moran, 右. J. (2019). Lo-
cus Coeruleus tracking of prediction errors optimises cognitive flexibility: 一个
active inference model. PLOS Computational Biology, 15(1), e1006267. 10.1371/
journal.pcbi.1006267

Sancaktar, C。, van Gerven, M。, & Lanillos, 磷. (2020, 可能 29). End-to-end pixel-based
deep active inference for body perception and action. http://arxiv.org/abs/2001.05847
Sargent, 右. 瓦. H. (2000). Optimal control. Journal of Computational and Applied Math-

信息学, 124(1), 361–371. 10.1016/S0377-0427(00)00418-0

施米德胡贝尔, J. (2006). Developmental robotics, optimal artificial curiosity, cre-
ativity, 音乐, and the fine arts. 连接科学, 18(2), 173–187. 10.1080/
09540090600768658

施米德胡贝尔, J. (2010). Formal theory of creativity, fun, and intrinsic motivation
(1990–2010). IEEE Transactions on Autonomous Mental Development, 2(3), 230–247.
10.1109/TAMD.2010.2056368

施耐德, T。, Belousov, B., Abdulsamad, H。, & Peters, J. (2022, 六月 1). Active infer-

ence for robotic manipulation. 10.48550/arXiv.2206.10313

Schulz, E., & 格什曼, S. J. (2019). The algorithmic architecture of explo-
ration in the human brain. 神经生物学的当前观点, 55, 7–14. 10.1016/
j.conb.2018.11.003, 考研: 30529148

Schwartenbeck, P。, FitzGerald, 时间. H. B., Mathys, C。, Dolan, R。, & 弗里斯顿, K.
(2015). The dopaminergic midbrain encodes the expected certainty about
desired outcomes. 大脑皮层, 25(10), 3434–3445. 10.1093/cercor/bhu159,
考研: 25056572

Schwartenbeck, P。, FitzGerald, 时间. H. B., Mathys, C。, Dolan, R。, Kronbichler, M。, &
弗里斯顿, K. (2015). Evidence for surprise minimization over value maximization
in choice behavior. Scientific Reports. 5, 16575. 10.1038/srep16575

Schwartenbeck, P。, Passecker, J。, Hauser, 时间. U。, FitzGerald, 时间. H。, Kronbichler, M。, &
弗里斯顿, K. J. (2019). Computational mechanisms of curiosity and goal-directed
勘探. 电子生活, 45.

Shoham, Y。, 权力, R。, & Grenager, 时间. (2003). Multi-agent reinforcement learning: A

critical survey. Computer Science Department, 斯坦福大学.

Silver, D ., 黄, A。, Maddison, C. J。, Guez, A。, Sifre, L。, van den Driessche, G。, . . .
Hassabis, D. (2016). Mastering the game of Go with deep neural networks and
tree search. 自然, 529(7587), 484–489. 10.1038/nature16961, 考研: 26819042
史密斯, R。, 弗里斯顿, K. J。, & Whyte, C. J. (2022). A step-by-step tutorial on active infer-
ence and its application to empirical data. Journal of Mathematical Psychology, 107,
102632. 10.1016/j.jmp.2021.102632

史密斯, R。, Khalsa, S. S。, & Paulus, 中号. 磷. (2021). An active inference approach to
dissecting reasons for nonadherence to antidepressants. Biological Psychiatry.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

850

L. Da Costa et al.

Cognitive Neuroscience and Neuroimaging, 6(9), 919–934. 10.1016/j.bpsc.2019.11
.012, 考研: 32044234

史密斯, R。, Kirlic, N。, 斯图尔特, J. L。, Touthang, J。, Kuplicki, R。, Khalsa, S. S. F。, . . .
Aupperle, 右. L. (2021). Greater decision uncertainty characterizes a transdiagnos-
tic patient sample during approach-avoidance conflict: A computational mod-
eling approach. Journal of Psychiatry an Neuroscience, 46(1), E74–E87. 10.1503/
jpn.200032

史密斯, R。, Kirlic, N。, 斯图尔特, J. L。, Touthang, J。, Kuplicki, R。, 麦克德莫特, 时间. J。, . . .
Aupperle, 右. L. (2021). Long-term stability of computational parameters during
approach-avoidance conflict in a transdiagnostic psychiatric patient sample. Sci-
entific Reports, 11(1), 11783. 10.1038/s41598-021-91308-x

史密斯, R。, Kuplicki, R。, Feinstein, J。, Forthman, K. L。, 斯图尔特, J. L。, Paulus, 中号. P。,
. . . Khalsa, S. S. (2020). A Bayesian computational model reveals a failure to
adapt interoceptive precision estimates across depression, anxiety, eating, 和
substance use disorders. PLOS Computational Biology, 16(12), e1008484. 10.1371/
journal.pcbi.1008484

史密斯, R。, Kuplicki, R。, Teed, A。, Upshaw, 五、, & Khalsa, S. S. (2020, 九月 29).
Confirmatory evidence that healthy individuals can adaptively adjust prior expectations
and interoceptive precision estimates. 10.1101/2020.08.31.275594

史密斯, R。, Mayeli, A。, 泰勒, S。, Al Zoubi, 奥。, Naegele, J。, & Khalsa, S. S. (2021). Gut
inference: A computational modeling approach. Biological Psychology, 164 108152.
10.1016/j.biopsycho.2021.108152

史密斯, R。, Schwartenbeck, P。, Parr, T。, & 弗里斯顿, K. J. (2019). An active inference model

of concept learning. bioRxiv:633677. 10.1101/633677

史密斯, R。, Schwartenbeck, P。, Parr, T。, & 弗里斯顿, K. J. (2020). An active inference ap-
proach to modeling structure learning: concept learning as an example case. Fron-
tiers in Computational Neuroscience, 14. 10.3389/fncom.2020.00041

史密斯, R。, Schwartenbeck, P。, 斯图尔特, J. L。, Kuplicki, R。, Ekhtiari, H。, & Paulus, 中号. 磷.
(2020). Imprecise action selection in substance use disorder: evidence for active
learning impairments when solving the explore-exploit dilemma. Drug and Alco-
hol Dependence, 215, 108208. 10.1016/j.drugalcdep.2020.108208

史密斯, R。, 泰勒, S。, 斯图尔特, J. L。, Guinjoan, S. M。, Ironside, M。, Kirlic, N。, . . . Paulus,
中号. 磷. (2022). Slower learning rates from negative outcomes in substance use dis-
order over a 1-year period and their potential predictive utility. 计算型
Psychiatry, 6(1), 117–141. 10.5334/cpsy.85

仍然, S。, & Precup, D. (2012). An information-theoretic approach to curiosity-
driven reinforcement learning. Theory in Biosciences, 131(3), 139–148. 10.1007/
s12064-011-0142-z, 考研: 22791268

Stolle, M。, & Precup, D. (2002). Learning options in reinforcement learning. 演讲

计算机科学笔记, 212–223. 施普林格. 10.1007/3-540-45622-8_16

Stone, J. V. (2015, 二月 1). Information theory: A tutorial introduction. Sebtel Press.
Stone, J. V. (2019). Artificial intelligence engines: A tutorial introduction to the mathematics

of deep learning. Sebtel Press.

Sun, Y。, Gomez, F。, & 施米德胡贝尔, J. (2011, 行进 29). Planning to be surprised: Opti-
mal Bayesian exploration in dynamic environments. http://arxiv.org/abs/1103.5708
Tanaka, 时间. (1999). A theory of mean field approximation. 在S. Solla, 时间. Leen, & K.
穆勒 (编辑。), Advances in neural information processing systems, 11. 与新闻界.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

Reward Maximization Active Inference

851

Tervo, D. G. R。, Tenenbaum, J. B., & 格什曼, S. J. (2016). Toward the neural im-
plementation of structure learning. 神经生物学的当前观点, 37, 99–105.
10.1016/j.conb.2016.01.014, 考研: 26874471

Todorov, 乙. (2006). Linearly-solvable Markov decision problems. In Advances in neu-
ral information processing systems, 19. 与新闻界. https://papers.nips.cc/paper/
2006/hash/d806ca13ca3449af72a1ea5aedbed26a-Abstract.html

Todorov, 乙. (2008). General duality between optimal control and estimation. 在
Proceedings of the 47th IEEE Conference on Decision and Control (PP. 4286–4292).
10.1109/CDC.2008.4739438

Todorov, 乙. (2009). Efficient computation of optimal actions. In Proceedings of the Na-

美国科学院, 106(28), 11478–11483. 10.1073/普纳斯.0710743106

Tokic, M。, & Palm, G. (2011). Value-difference based exploration: Adaptive Con-
trol between epsilon-greedy and Softmax. 在J. 巴赫 & S. Edelkamp (编辑。),
智力 (PP. 335–346). 施普林格. 10.1007/
KI 2011: Advances in artificial
978-3-642-24455-1_33

Toussaint, 中号. (2009). Robot trajectory optimization using approximate inference. 在
Proceedings of the 26th Annual International Conference on Machine Learning (PP.
1049–1056). 10.1145/1553374.1553508

Tschantz, A。, Baltieri, M。, 赛斯, A. K., & Buckley, C. L. (2019, 十一月 24). 缩放

active inference. http://arxiv.org/abs/1911.10601

Tschantz, A。, Millidge, B., 赛斯, A. K., & Buckley, C. L. (2020). Reinforcement learning

through active inference. http://arxiv.org/abs/2002.12636

Tschantz, A。, 赛斯, A. K., & Buckley, C. L. (2020). Learning action-oriented models
through active inference. PLOS Computational Biology, 16(4), e1007805. 10.1371/
journal.pcbi.1007805

van den Broek, B., Wiegerinck, W., & 切, 乙. (2010). Risk sensitive path integral

控制. https://arxiv.org/ftp/arxiv/papers/1203/1203.3523.pdf

van der Himst, 奥。, & Lanillos, 磷. (2020). Deep active inference for partially observable

MDPs. 10.1007/978-3-030-64919-7_8

Von Neumann, J。, & Morgenstern, 氧. (1944). Theory of games and economic behavior.

普林斯顿大学出版社.

Wainwright, 中号. J。, & 约旦, 中号. 我. (2007). Graphical models, exponential families,
and variational inference. Foundations and Trend in Machine Learning, 1(1–2), 1–
305. 10.1561/2200000001

Wilson, 右. C。, Bonawitz, E., Costa, V. D ., & Ebitz, 右. 乙. (2021). Balancing exploration
and exploitation with information and randomization. Current Opinion in Behav-
ioral Sciences, 38, 49–56. 10.1016/j.cobeha.2020.10.001, 考研: 33184605

Wilson, 右. C。, Geana, A。, 白色的, J. M。, Ludvig, 乙. A。, & 科恩, J. D. (2014). 人类
use directed and random exploration to solve the explore–exploit dilemma. Jour-
nal of Experimental Psychology. General, 143(6), 2074–2081. 10.1037/a0038199
徐, H. A。, Modirshanechi, A。, Lehmann, 中号. P。, Gerstner, W., & Herzog, 中号. H.
(2021). Novelty is not surprise: Human exploratory and adaptive behavior in se-
quential decision-making. PLOS Computational Biology, 17(6), e1009070. 10.1371/
journal.pcbi.1009070

Zermelo, 乙. (1913). Über eine Anwendung der Mengenlehre auf die Theorie des
https://www.mathematik.uni-muenchen.de/∼spielth/artikel/

Schachspiels.
Zermelo.pdf

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

852

L. Da Costa et al.

Ziebart, 乙. (2010). Modeling purposeful adaptive behavior with the principle of maximum

causal entropy. 卡内基梅隆大学.

Ziebart, 乙. D ., Maas, A. L。, Bagnell, J. A。, & Dey, A. K. (2008). Maximum entropy
inverse reinforcement learning. In Proceedings of the AAAI Conference on Artificial
智力.

Zintgraf, L。, Shiarlis, K., Igl, M。, Schulze, S。, Gal, Y。, Hofmann, K., & Whiteson, S.
(2020, 二月 27). VariBAD: A very good method for Bayes-adaptive deep RL via
meta- 学习. http://arxiv.org/abs/1910.08348

Zintgraf, L. M。, 冯, L。, 鲁, C。, Igl, M。, Hartikainen, K., Hofmann, K., & Whiteson,
S. (2021). Exploration in approximate hyper-state space for meta reinforcement
学习. International Conference on Machine Learning (PP. 12991–13001).

Received September 13, 2022; accepted December 17, 2022.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
5
5
8
0
7
2
0
7
9
4
7
3
n
e
C
哦
_
A
_
0
1
5
7
4
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

下载pdf