文章 - 麻省理工学院人工智能研究专业

文章

Communicated by Shigehiro Namiki

A Neural Model for Insect Steering Applied to Olfaction
and Path Integration

Andrea Adden
andrea.adden@crick.ac.uk
Vision Group, Department of Biology, Lund University, 221 00 Lund, 瑞典

泰伦斯·C. 斯图尔特
terrence.stewart@nrc-cnrc.gc.ca
加拿大国家研究委员会, University of Waterloo Collaboration Centre,
滑铁卢, N2L 3G1 Canada

Barbara Webb
B.Webb@ed.ac.uk
Insect Robotics Group, School of Informatics, University of Edinburgh EH8 9YL,
爱丁堡, U.K.

Stanley Heinze
stanley.heinze@biol.lu.se
Vision Group, Department of Biology, Lund University, Lund, 瑞典; 和
NanoLund, Lund University, 221 00 Lund, 瑞典

Many animal behaviors require orientation and steering with respect to
环境. For insects, a key brain area involved in spatial orien-
tation and navigation is the central complex. Activity in this neural cir-
cuit has been shown to track the insect’s current heading relative to its
environment and has also been proposed to be the substrate of path inte-
gration. 然而, it remains unclear how the output of the central com-
plex is integrated into motor commands. Central complex output neurons
project to the lateral accessory lobes (LAL), from which descending neu-
rons project to thoracic motor centers. 这里, we present a computational
model of a simple neural network that has been described anatomically
and physiologically in the LALs of male silkworm moths, in the context
of odor-mediated steering. We present and analyze two versions of this
网络, one rate based and one based on spiking neurons. The mod-
eled network consists of an inhibitory local interneuron and a bistable
descending neuron (flip-flop) that both receive input in the LAL. 这
flip-flop neuron projects onto neck motor neurons to induce steering. 我们
show that this simple computational model not only replicates the basic

Andrea Adden is now at the Francis Crick Institute, 伦敦, U.K.

神经计算 34, 2205–2231 (2022) © 2022 麻省理工学院.
https://doi.org/10.1162/neco_a_01540
在知识共享下发布
归因 4.0 国际的 (抄送 4.0) 执照.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2206

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

parameters of male silkworm moth behavior in a simulated odor plume
but can also take input from a computational model of path integration
in the central complex and use it to steer back to a point of origin. 毛皮-
瑟莫雷, we find that increasing the level of detail within the model im-
proves the realism of the model’s behavior, leading to the emergence of
looping behavior as an orientation strategy. Our results suggest that de-
scending neurons originating in the LALs, such as flip-flop neurons, 是
sufficient to mediate multiple steering behaviors. This study is therefore
a first step to close the gap between orientation circuits in the central com-
plex and downstream motor centers.

1 介绍

Insects display an astonishing range of behaviors that include highly di-
rected movements. 例如, male moths navigate toward females
emitting pheromones (沼泽, 肯尼迪, & Ludlow, 1978; Obara, 1979) 和
female crickets move toward singing males (Simmons, 1988; Balakrishnan
& 波拉克, 1996). Other insects use visual cues to maintain a straight head-
ing over short or long distances (dung beetle: Dacke, Nordström, & Scholtz,
2003; Baird, Byrne, Smolka, Warrant, & Dacke, 2012; monarch butterfly:
Mouritsen & Frost, 2002; bogong moth: Dreyer et al., 2018) and can even
rely purely on memory to navigate home (斯里尼瓦桑, 2015; Honkanen,
Adden, da Silva Freitas, & Heinze, 2019). While the cues used for naviga-
tion are different in these examples, they elicit very similar behaviors: 之上
encountering an appropriate stimulus, the animal chooses a direction with
respect to that stimulus and begins moving in that direction. If the stimulus
is temporarily lost, searching behavior is initiated. 因此, the motor patterns
elicited by different kinds of stimuli can be remarkably similar.

The spatial context for orientation and navigation is computed in the cen-
tral complex (CX), the only unpaired and midline-spanning neuropil in the
insect brain (见图 1; Heinze, 2017). 最近几年, progress has been
made in understanding and modeling this “compass system” of insects.
Neurons in the CX integrate external inputs with self-generated angular ve-
locity cues, thus providing a reliable internal representation of the animal’s
heading (Green et al., 2017; Kakaria & de Bivort, 2017). An extended model
of the CX network furthermore showed that the CX is a possible substrate
for path integration (Stone et al., 2017), continuously integrating velocity to
maintain an estimate of the direction and distance to a reference location.
This model also demonstrates how CX output can serve directly as a steer-
ing command: the summed activity of columnar output neurons in each
hemisphere is compared, and any imbalance between the two hemispheres
should produce a turn toward the relevant side, while a balanced output
results in straight movement. 然而, the model does not postulate a bio-
logically plausible mechanism to achieve steering and instead summarizes

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2207

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

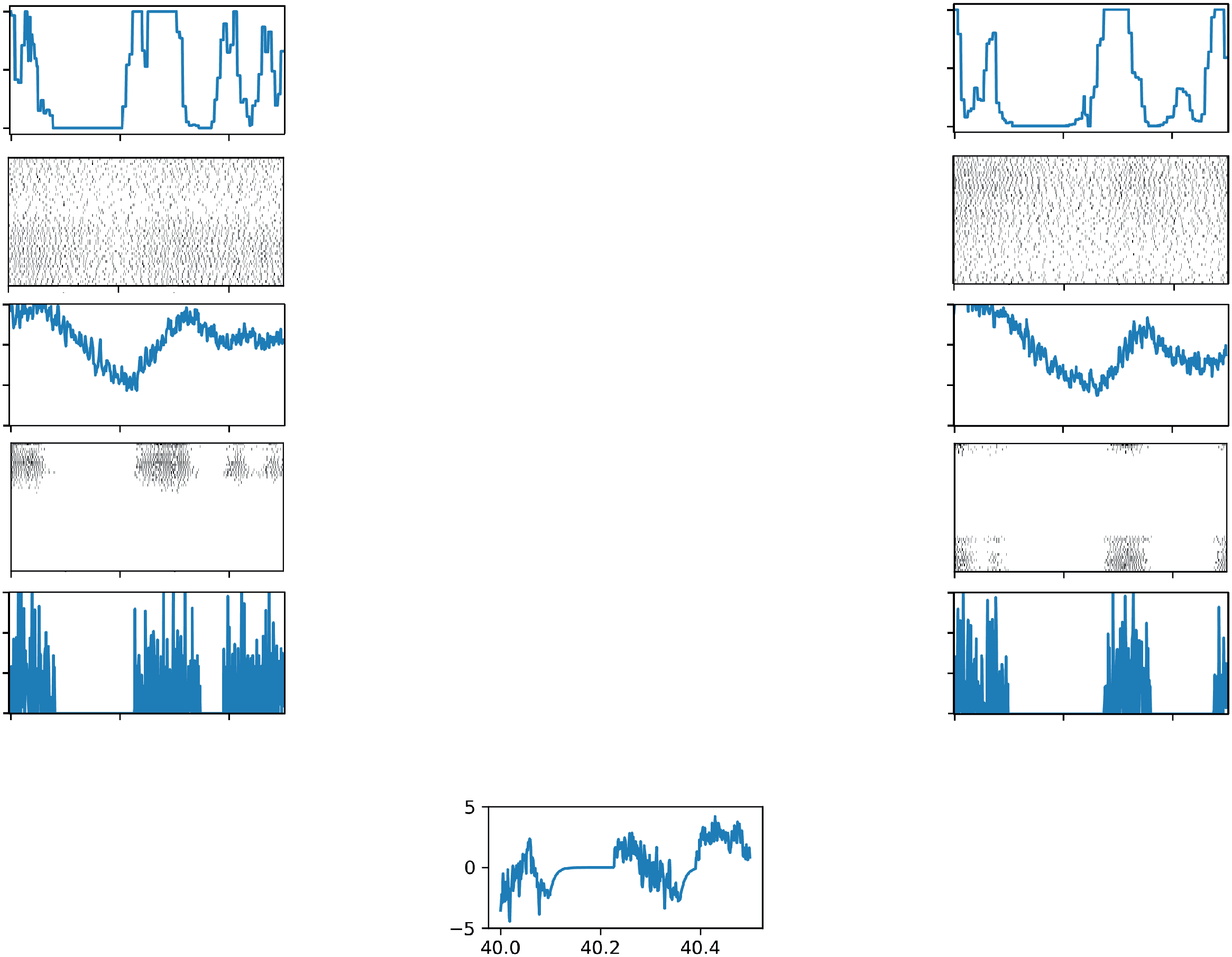
数字 1: The flip-flop network. Protocerebral bilateral neurons (PBN) and flip-
flop neurons (FF) both get input directly from the ipsilateral sensor. PBNs in-
hibit the contralateral FF. FF neurons activate the motor. For the spiking model,
each neuron comprises 100 spiking components, recurrently connected so as to
achieve an approximation of the rate-based model. The output from each neu-
ron is a weighted sum of the output of its components. The final output controls
the turning rate of the moth and is computed as the left FF output minus the
right FF output times a fixed scaling factor. Activity shown here is for the spik-
ing network. See Figure S1 for a comparison of activity propagation through the
rate-based versus spiking model given artificial input. See the supplementary
video for an animated version of this figure.

the entire steering system as one theoretical motor command. Despite our
increasingly complete understanding of CX networks, a question that re-
mains unanswered is how CX output is translated into motor control—that
是, how it is transmitted to thoracic motor centers to influence behavioral
决定.

The answer likely lies in the lateral accessory lobes (LAL), a paired neu-
ropil flanking the CX. The LAL forms part of the pheromone-processing
pathway that has been described in detail in the silkworm moth (Namiki,
Iwabuchi, Pansopha Kono, & Kanzaki, 2014; Kymre et al., 2021). While the
CX integrates information from modalities such as vision and mechanore-
it does not appear to process olfactory information. Odors,
塞申斯,

2208

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

including pheromones, are integrated in higher-order neuropils including
the lateral horn, mushroom bodies, and finally the LAL. The LAL has been
described as a premotor center, as several types of descending neurons that
project to thoracic motor centers have postsynaptic endings in the LAL
(Namiki, 狄金森, 黄, Korff & Card, 2018). It has been suggested that
interactions between the two LALs are sufficient to mediate search behav-
iors triggered by, 例如, pheromone input, but that goal-oriented be-
haviors require CX input into the LAL network (Namiki & Kanzaki, 2016;
Álvarez-Salvado et al., 2018). 的确, CX output neurons project to the
LALs, but how they interact with the LAL circuitry is currently unknown.
此外, how descending neurons encode motor commands on a pop-
ulation level is currently not well understood, although multiple recent
studies have been able to dissect single neural circuits that underlie spe-
cific behaviors (Schnell, Ros, & 狄金森, 2017; Cande et al., 2018; Namiki,
Wada, & Kanzaki, 2018).

One such behavior, which has been examined in detail,

是个
pheromone-following behavior of silkworm moths. Male silkworm moths
display a highly stereotyped behavioral sequence when following a fe-
male’s pheromone plume. Upon first contact with the plume, the moth re-
sponds with a “surge,“ 那是, a straight movement toward the source of the
odor. When the odor plume is lost, several ways of reacquiring the plume
have been described; most notably casting, during which the moths walks
in a zig-zag pattern until it finds a new odor pocket, and looping downwind
(Cardé & 威利斯, 2008). Early studies have identified several descending
neuron types whose activity correlates with turning behavior when a male
moth orients in a pheromone plume (Mishima & Kanzaki, 1999). Among
这些, the most notable are “flip-flop” neurons, which are bistable neurons
that switch between a high-activity and a low-activity state in response to a
trigger stimulus (Olberg, 1983; Kanzaki, Ikeda, & Shibuya, 1994; Mishima &
Kanzaki, 1999). 那是, the same stimulus can cause the neuron to increase
or decrease its firing, depending on whether it is in the low or high activity
状态, 分别, when that stimulus occurs.

These neurons have postsynaptic terminals in the LALs, and their ax-
ons descend through the ventral nerve cord and synapse onto neck motor
神经元, which in turn activate neck muscles that control head movements
(Kanzaki & Mishima, 1996; Mishima & Kanzaki, 1998). 因此, if the left-
descending flip-flop neuron is in its high-activity state, the left neck motor
neuron and the left neck muscle are also active, causing the head and con-
sequently the moth to turn left. Although this network has been described
in the context of pheromone following, other studies have shown that flip-
flop neurons can also be triggered by light flashes (Olberg, 1983) and sound
(Zorovic & Hedwig, 2011). It therefore seems likely that flip-flop neuron-
mediated steering may constitute a general form of targeted steering, 在-
dependent of the stimulus modality that drives the behavior (Steinbeck,
Adden, & Graham, 2020).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2209

In this study, we aim to evaluate whether a basic flip-flop neuron net-
work can produce naturalistic steering in a simulated odor plume and when
presented with compass input via a neural model of the central complex.
为此, we present a rate-based and a spiking computational model
of a simple flip-flop network. The two models presented here allow us to
compare two different implementations of the same network, where both
models follow the same connectivity pattern. The rate-based model uses
continuous-valued sigmoid neurons, while the spiking model uses leaky
integrate-and-fire (LIF) spiking neurons. Both models are effective at nav-
igating in the simulated olfactory and visual tasks; 然而, the spiking
model produces more realistic trajectories. Comparing the behavior of our
models to behavioral data from male silkworm moths, we find that this sim-
ple flip-flop-based neural circuit is sufficient to replicate the basic character-
istics of the moths’ paths. 此外, we describe looping behavior as an
emerging orientation strategy when sensory input is directionally ambigu-
乌斯. 最后, we demonstrate for the first time that the flip-flop network can
work as a general steering network when combined with a computational
model of the CX (Stone et al., 2017). This study is therefore a step toward
closing the gap between higher processing centers in the brain that make
navigational decisions, such as the CX, and the thoracic motor circuits that
ultimately move the insect.

2 Materials and Methods

The neurons modeled here were physiologically and anatomically de-
刻写的 (Olberg, 1983; Kanzaki, Sugi, & Shibuya, 1992; Mishima & Kanzaki,
1999; Kanzaki et al., 1994). We infer input and output regions of neurons
from their anatomical appearance, 那是, smooth terminals are assumed to
be inputs, while varicose terminals are assumed to be outputs. Two neurons
are assumed to be connected if the input region of one neuron overlaps with
the second neuron’s output region. The model connections are furthermore
based on the network proposed in Mishima and Kanzaki (1999) 和一些
small modifications.

The network consists of two pairs of neurons: one flip-flop neuron (FF)
and one protocerebral bilateral neuron (PBN; see Figure 1A) per hemi-
sphere. Both cell types receive input directly from the plume or from the
output neurons of the central complex (CPU1/PFL neurons) when con-
nected to the path integration network (PI). PBN neurons were proposed
to provide bilateral inhibition between the two LALs (Mishima & Kanzaki,
1999; Kanzaki, Nagasawa, & Shimoyama, 2005) and are therefore mod-
eled to inhibit the contralateral FF neuron. FF neurons have excitatory con-
nections directly onto the contralateral motor, based on the finding that
FF neuron activity correlates with neck motor neuron activity (Kanzaki &
Mishima, 1996).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2210

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

We present two implementations of this network, which we call the rate-
based model and the spiking model. The rate-based model uses continuous-
valued sigmoid neurons, the most common neural model used in insect
brain network models. 然而, while such neurons are easier to work
with and build models from, they abstract away many of the underlying bi-
ological details. To complement this, we also present a spiking model built
from leaky integrate-and-fire (LIF) 神经元, bringing richer temporal dy-
namics to the model. While this is still abstracted, we show that the spiking
model leads to more realistic behavior.

The general approach for creating the spiking model is known as the neu-
ral engineering framework (NEF; 埃利亚史密斯 & 安德森, 2003). This allows
us to take any particular desired dynamics (such as the dynamics of a flip-
flop neuron) and construct it using more basic components (such as a group
of spiking LIF neurons). 尤其, here we approximate one FF neuron
使用 100 recurrently connected spiking LIF neurons. The NEF treats this
as an optimization problem and finds the ideal connection weights among
those components, such that the overall system produces behavior that is
as close as possible to the desired rate-based description of an FF neuron.
Our interpretation of the model is that this is one flip-flop neuron with 100
internal components, and the flip-flop behavior arises out of these internal
互动.

Both models are described in detail below. The source code is available
在https://github.com/stanleyheinze/insect_steering. The spiking model
was implemented using the software toolkit Nengo (贝科莱等人。, 2014).

3 楷模

3.1 Rate-Based Model. For the rate-based model, we use continuous-
valued sigmoid neurons, with one addition described below for the FF neu-
罗恩. If the total input to the neuron is J, then the output r from the neuron
is generally defined as

r = 1/(1 + e

−aJ−b),

(3.1)

where a and b are the gain and bias constants for the neuron, 分别.
The total input to the neuron is the weighted sum of the rates of all incoming
连接:
(西德:2)

J j

i jri

(3.2)

The weights w are either 0 (no connection), 1 (excitation), or −1 (inhibi-
的), with gaussian noise of standard deviation 0.01 added when the model
is created. We also add random noise (西德:2) (西德:3)→ N (0, σ 2) with σ 2 = 0.02 到
input to each neuron on every time step. These two sources of randomness

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2211

are meant to give some individual variation to the models. For both PBN
and FF neurons, we also add the neurons’ previous output to its own input
to allow for the sustained activity that has been described for these neurons.
This gives them the following equation, where rt is the output for time step
t, which is what we use in our model:

rt = 1/(1 + e

−a(J+rt−1

+(西德:2))−b).

(3.3)

For the FF neurons, we added a mechanism to produce flip-flop behav-
ior, where an input stimulus will switch a neuron from a high state to a low
state and vice versa, depending on the state of the neuron preceding the
刺激. Since sigmoid neurons by themselves are too simple to produce
this behavior, we added a feature to the rate-based model where if the cur-
rent output r is large (>0.8) and the input is large (>0.5), then the output of
this FF neuron is reduced by 0.5 and the opposite FF is increased by 0.5. 这
produces the required flip-flop behavior (see Figure S1), but does not postu-
late a plausible mechanism whereby this behavior is produced. We present
a more realistic mechanism in the next section on the spiking model.

3.2 Spiking Model. 如上所述, each neuron in the spiking
model is represented by a group of 100 LIF neurons. The NEF approach
to doing this is to start by writing out the particular desired dynamics as a
= f (X, 你), where x is the internal state and u is the
differential equation dx
dt
输入. In the case of our flip-flop neuron, we can write the flip-flop mecha-
nism as given in equation 3.4:

⎧

1 − x,
⎪⎪⎪⎪⎨
0 − x,
⎪⎪⎪⎪⎩
0 − x,
1 − x,

dx
dt

if x > 0.5 and u < 0.2 (if FF is high and no input, stay high) if x > 0.5 and u > 0.2 (if FF is high and input, go low)
if x < 0.5 and u < 0.2 (if FF is low and no input, stay low) if x < 0.5 and u > 0.2 (if FF is low and input, go high).

(3.4)

This differential equation will give similar behavior to the sigmoid FF
neuron described above. 尤其, note that if a differential equation is
outputting a value of the form T − x, then the value x will move toward
T until T = x. This means that in the first and last cases above, the state of
the FF neuron will go to 1 (IE。, the FF is high), and in the second and third
案例, the FF neuron will go to 0 (低的). This gives us a differential equation
approximation of the sigmoid FF.

The next step is to train a feedforward single-hidden-layer neural net-
work that approximates y = τ f (X, 你) + X. 重要的, we use LIF neurons
in the hidden layer, but we have no nonlinearity at all in the input and out-
put layers. These hidden layer neurons will eventually become the recur-
rently connected internal components that will approximate a FF neuron.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2212

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

To train this network, the training data are a set of randomly generated x
values and the y values are generated using equation 3.4. The τ parameter
is the time constant of the postsynaptic currents that will be used in the next
step, which we choose here to be 100 多发性硬化症. While any neural network train-
ing approach can be used (例如, backpropagation of error), here we take the
simple approach of randomly generating the first layer of weights and us-
ing regularized least-squares minimization (IE。, ridge regression) to find the
second layer of weights. This is a fast approach that works for any neuron
model and avoids the difficulties of applying backpropagation to spiking
神经元 (埃利亚史密斯 & 安德森, 2003).

Given this network, we now connect the output of the network back to
its own input and include an exponential synapse model: H(t) = e−t/τ /τ for
t > 0; 那是, every time a neuron spikes, the current it produces in the neu-
rons it is connected to follows an exponential decay. 出奇, the result-
= f (X, 你). 到
ing recurrent neural network will approximate the desired dx
dt
prove this, we note that the synapse will have the effect of convolving the
output of the network with h(t). Since this output is also the input to the
网络, we have x(t) = (τ f (X(t)) + X(t)) ∗ h(t). Taking the Laplace trans-
形式, X(s) = (τ F(s) + X(s))H(s). Since the Laplace transform of the synapse
model is H(s) = 1/(1 + sτ ), this gives

X(s) = (τ F(s) + X(s))/(1 + sτ )

X(s)(1 + sτ ) = τ F(s) + X(s)
X(s) + sτ X(s) = τ F(s) + X(s)
sX(s) = F(s).

最后, converting back to the time domain, we get dx
dt

= f (X, 你). 那
是, this recurrently connected set of LIF neurons will approximate the de-
sired flip-flop dynamics. 此外, since our feedforward network has
no nonlinearity at the input or output, we can convert the system into a sin-
gle pool of 100 LIF neurons whose recurrent connection weights are given
by W = WoutWin, where Win is the weights from the input to the hidden layer
and Wout is the weights from the hidden layer to the output.

This overall method (埃利亚史密斯 & 安德森, 2003) lets us take any de-
sired dynamics (written as a differential equation) and convert it into a pool
of basic components (here we use 100 LIF neurons) that are connected to
each other using exponential synapses. As the number of components in-
creases, the accuracy of this approximation will improve, up to the limit of
how well the feedforward neural network approximates y = τ f (X, 你) + X.
We can think of the resulting system as defining a spiking attractor network
whose dynamics are governed by that function.

Note that we are not suggesting the flip-flop neurons must have recur-
rent connections, but rather that these neurons have a sufficiently complex

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2213

internal state that such feedback is necessary to capture their properties.
The resulting spiking model produces a notably different time course of
response compared to the rate-based model, although the key qualitative
characteristics are maintained. One crucial difference between the rate-
based and spiking models is in how synchronization between the two FF
cells is achieved. In the rate-based model, we have explicitly added a rule
that forces the contralateral flip-flip to its up-state when an input pushes the
ipsilateral flip-flop to the down-state, and vice versa. This is not necessary
in the spiking model, as the internal components of a FF neuron can success-
fully switch the activity state of the neuron. 然而, there is no way for the
internal components of one FF neuron to directly affect the contralateral FF
neuron. 有, 然而, an inhibitory connection between the PBN and
the contralateral FF, so this allows the system to push the contralateral FF
to a low state when the ipsilateral FF and PBN get input from the sensor.
This allows for some asynchrony to emerge in the spiking model rather than
forcing it as in the rate-based model. Note that this type of asynchronous
flip-flopping behavior can be most easily observed when using artificial in-
放 (see Figure S1A). It becomes less obvious when the agent is exposed to
a naturalistic stimulus, such as the simulated odor plume (见图 1). 在
this more complex scenario, it is evident that the spiking model is only an
approximation of the ideal equations given, and as such it is possible for
both FFs to be high or low at the same time.

3.3 Experimental Situation 1: Following an Odor Plume. Our model
is directly inspired by the flip-flop neurons that have been implicated in
pheromone tracking in moths; 因此, we first evaluate its ability to con-
trol the behavior of a simulated agent in an odor plume (see Figure 2A).
To simulate a realistic plume, we use an efficient model of odor dispersion
in a turbulent medium (Farrell, Murlis, 长的, 李, & Cardé, 2002), as im-
plemented with the Python-based module pompy (https://github.com/
InsectRobotics/pompy, by Matthew Graham, Insect Robotics Group, Ed-
inburgh University). This model was validated against measured gypsy
moth plume data (琼斯, 1983) and generates meandering plumes (Far-
rell et al., 2002), while still being efficient enough to be run at a very fine
timescale (5 多发性硬化症) to capture the high-frequency changes observed in moth
plumes (≈0.1 s; Mafra-Neto & Cardé, 1994; Vickers, Christensen, 贝克, &
Hildebrand, 2001; Levakova, Kostal, Monsempès, 雅各布, & Lucas, 2018).
The plume was dispersed by a weak constant wind (2 m/s) flowing from
the direction of the odor plume source toward the agent’s starting point.
The agent was equipped with two frontolateral sensors designed to mimic
antennas. The antenna size and angle (away from the center line) 从
each other were adjusted to match real moths (Loudon & Koehl, 2000; 看
桌子 1 for moth parameters). We set a maximum antenna sensitivity, 多于
which the response is saturated (IE。, any higher concentration does not
elicit a stronger response). We then chose a maximum response value to

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2214

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

数字 2: Overview over the odor plume experiment. (A) The pheromone
plume is released from the source and dispersed by wind. Shown is one frame
of the plume, with the gray value reflecting the pheromone concentration on a
scale from 0 到 1, 在哪里 0 translates into no input to the agent’s sensor and 1 进入
maximal sensory input. The agent is expected to navigate toward the source us-
ing the odor plume. In the absence of input, the agent turns upwind. (乙) Typical
path of the rate-based model, with right turns indicated by filled gray circles and
left turns indicated by empty black circles. (C) The rotation rate defines whether
a rotation is classified as a turn. Detected turns are marked: right turn = gray,
left turn = black. Definition as in Ando et al. (2013).

桌子 1: Simulation Parameters.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

范围

Number of LIF components to implement one neuron
Random noise added to neurons
Wind speed
Plume puff release rate
Plume puff initial radius
Antenna size
Antenna angle
Antenna maximum sensitivity
Antenna maximum output value
Moth maximum rotation speed
Moth acceleration
Moth drag
Moth turn-into-wind rate

Value

100
氮 (0, 0.02)
2 m/s
50 赫兹
0.1 米
7.5 毫米
○
45
100
3.0
8.0 rad/s
0.2 m/s2
0.5 m/s
0.1 rad/s

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2215

correspond to this level of concentration and scaled the response linearly
between this value and 0 for lower concentrations. These two parameters
were adjusted manually. At each point in time, the network processes the
input and makes a steering decision, which is applied to the center of mass
of the agent and scaled by the maximum rotation speed (见表 1), anal-
ogous to Stone et al. (2017). The agent’s walking speed was determined by
an acceleration and a drag parameter, analogous to Stone et al. (2017; 看
桌子 1). The agent’s acceleration setting in the simulation was adjusted
to match the actual walking speed of moths (Loudon & Koehl, 2000). 这
resulting forward speed was not influenced by the headwind, but agents
were given a weak tendency to turn upwind in the absence of plume input,
in accordance with observations in silkworm moths (Cardé & 威利斯, 2008).
Unless otherwise specified, all parameters were tuned manually to match
the behavior of real moths as closely as possible. Certain arbitrary parame-
ters of the models, such as the maximum output value for the antennas and
the maximum rotation speed, were set such that the resulting tracks ap-
proximated the tracks of silkworm moths as reported in Ando, Emoto, 和
Kanzaki (2013).

Ando et al. (2013) presented a robot that was steered through an odor
plume by an on-board moth walking on a trackball. The moth’s movement
on the trackball was translated into wheel speeds for the robot. 作者
presented trajectories for both the moth-controlled robot and the moth only
in the odor plume. 这里, we adjusted the parameters of this model such that
the agent’s trajectories were similar to the moths’ trajectories presented in
Ando et al. (2013), based not only on the trajectories but also quantitatively
on the turn duration, turn angle, and turn velocity.

Using their robot, Ando and colleagues performed further experiments
where they added a bias to the turning of the robot. 那是, a constant signal
was added to the left (or right) wheel while the moth was controlling the
robot. This causes the moth to drift to the edge of the pheromone plume, 但
they show the moth is able to compensate for this and continue to follow
the plume. We performed the same experiment in our simulation by adding
a constant bias (in rad/s) to the moth rotation, causing the simulated agent
to have an extra tendency to turn in a particular direction. Ando and col-
leagues show that moths’ plume-following behavior is robust to this sort of
manipulation and that the resulting paths tend to follow along the edge of
the plume.

Behavioral measurement thresholds were defined in accordance with
Ando et al. (2013) to allow for comparing the models to data from male silk-
worm moths. A turn was identified if the agent’s turn duration was larger
比 0.5 s, the turn angular velocity was larger than 5 deg/s, and the turn
angle was larger than 30◦
(see Figures 2B and 2C; Ando et al., 2013). Loops
were detected based on their high rotation rate, 多于 30 deg/s for at least
5 s. An experiment was considered successful if the agent arrived within
5 cm of the goal. All data were analyzed in Python 3.5.5.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2216

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

3.4 Experimental Situation 2: Path Integration. A second motivation
for our model was to understand how output from the central complex is
translated to steering behavior. 具体来说, we connected our steering sys-
tem to a previously developed CX path integrator model using sigmoid
神经元 (Stone et al., 2017). This model is based on the neuroanatomy
of the central complex, and we take the output neurons from the model
(CPU1/PFL; see Figure 6A) and project them to the lateral accessory lobes
in our model, where they may interact with the flip-flop descending neu-
rons as well as the protocerebral bilateral neurons modeled here. 从那里
are eight CPU1 cells per hemisphere whose summed activity is thought to
activate the motor but only one flip-flop neuron in our model, the activity of
all eight neurons was summed by projecting onto the same flip-flop cell.

In the plume experiments, the value of each sensor was between 0 和
1, so that the absolute difference between the two sensors could also fall be-
补间 0 和 1. 然而, the output from the path integrator had a narrower
传播 (0.5 到 1). While our models worked with that smaller difference, 我们
also rescaled the path integrator output to a scale of 0 到 1 to test whether
this would improve the models’ behaviors.

To evaluate the behavior in this situation, we used exactly the same sim-
ulator as before (pompy) but removed the odor plume. We then caused the
agent to take a random exploratory path by setting its rotation rate to be
a gaussian white noise process with σ = 0.1 rad/s while moving forward
at a constant speed (见表 1), 为了 15 seconds in total. The agent then at-
tempted to return directly home using the CX output combined with our
steering model. The simulation was continued for another 40 seconds. 一个
experiment was considered successful if the agent arrived within 5 cm of
the starting location.

4 结果

In order to determine how realistic the behavior of our model is, we com-
pared the simulated tracks quantitatively to data from silkworm moths
(Bombyx mori, originally published in Ando et al. 2013; 见图 3). 这
total turn duration of the rate-based model falls within the standard devi-
ation of real moth data but was slightly higher for the spiking model (看
Figure 3A). The total turn angle of both models fell within the standard de-
viation of real moth data (see Figure 3C), while the mean turn velocity of
both models was 10% 到 15% lower compared to real moths (see Figure 3B).
然而, both models performed well with respect to finding the origin
of the plume, with a success probability of 0.84 到 1.0 (see Figure 3D). 这
tracks of both models display cross-wind zigzagging and straight surges,
as well as loops (see Figures 3E and 3F), with the rate-based model having
straighter paths than the spiking model. 全面的, when comparing the rate-
based and spiking models to moth data, we find that both models replicate
real moth data reasonably well.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2217

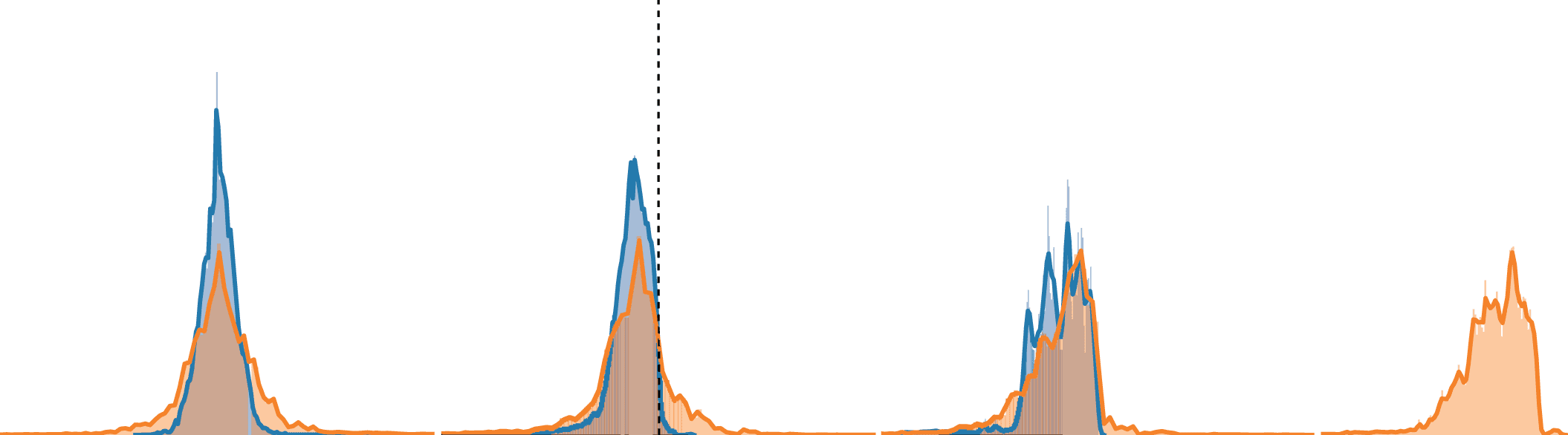
数字 3: Behavior of both models in a simulated odor plume. (A–D) Compari-
son of the rate-based and spiking model to data from silkworm moths. Bar plots
represent the median, with the error bar giving the bootstrapped 95% confi-
dence interval. The moth median ± median absolute deviation (dark blue line
and blue area) are given for comparison. Moth data reproduced with permission
from Ando et al. (2013). (E–F) Example trajectories for the rate-based (乙) 和
尖峰 (F) 型号, with different colors denoting individual trials. For addi-
tional paths, see Figure S2.

A further way of testing how well our models replicate real moth behav-
ior was to add a turn bias to the simulation. When given a turn bias, silk-
worm moths were shown to track the edges of the odor plume instead of the
中心 (Ando et al., 2013). This was also the case for our models (见图
4). When analyzing the angle between the current position of the agent and
the source of the odor plume, we found that the models shift away from
the center of the plume already at a turn bias of 1 rad/s (see Figures 4A and
4乙). With increasing turn bias, the models’ success rates decrease, and at
a turn bias of 3 rad/s, no agent simulated by the rate-based model reaches
the goal. The spiking model is more robust but starts failing at a turn bias of
5 rad/s (data not shown). While these results are more difficult to compare
quantitatively to real moth data owing to the different ways of implement-
ing the turn bias, it is clear that qualitatively, the models behave similar to
real moths, as they track the edge of the plume rather than the center when
given a turn bias.

有趣的是, looping behavior emerges from the spiking model but is
only rarely observed in the rate-based model (see Figures 5A and 5B). 在
事实, we were unable to find ways of modifying the rate-based model to cre-
ate these tight loops while still being able to successfully follow the plume
(see Figures S3 and S4). It should be noted that while it is possible to ob-
serve clean flip-flop behavior in ideal circumstances (see Figure S1A), 和

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2218

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

数字 4: Turn bias. (A) Proportion of time the agent spent at a specific angle
relative to the source of the odor plume. Only successful trials were included.
When a turn bias was added to the left motor, the agents shifted away from
the center of the plume toward the plume’s edge. At a turn bias of 3 rad/s,
the rate-based model failed consistently. (乙) Paths of the rate-based and spiking
models with increasing turn bias. N= 40 per condition. Dotted line = center
of the odor plume; dashed outline = area of odor concentration of at least 10%
of the maximum detectable level, averaged across 3000 time steps; blue dot =
plume origin; gray circle = area around plume origin that needs to be reached
in order to count as success.

more realistic input, the model exhibits a much richer array of behaviors
(see Figure S1B), including times where both flip-flops are active and times
when neither is active. This is due to the fact that the spiking model uses
internal components to approximate the ideal flip-flop algorithm, 但是这个
approximation is imperfect. 因此, the spiking model may be able to get
into a transient stable state where both flip-flops are on but one is slightly
stronger, causing a long turn in one direction. 或者, there may be
other low-level differences between the components used for the two sides
of the model, leading to subtle asymmetries in the model. With this in mind,
further examination of the looping behavior is warranted. Since moths have

A Neural Model for Insect Steering

2219

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

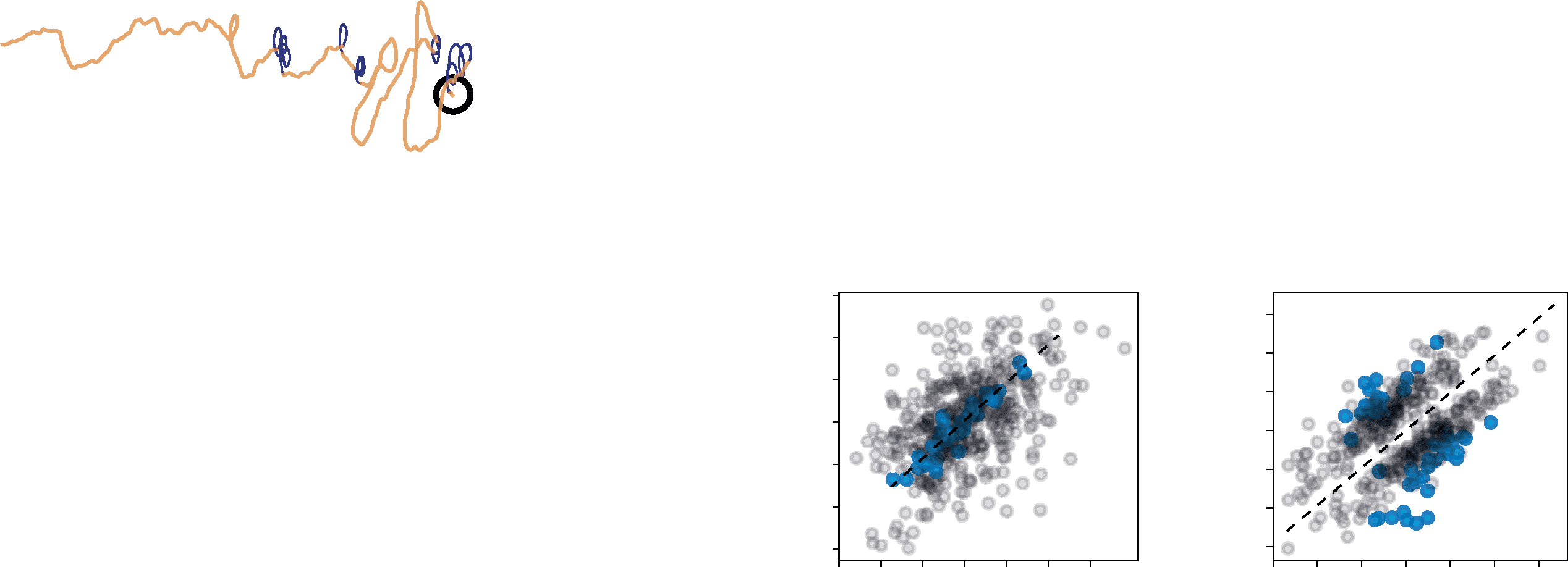
数字 5: Looping behavior of the spiking model. (A) Example track of a spik-
ing model agent orienting in an odor plume, with loops highlighted in purple.
(乙) During tracks lasting on average 253 s, the spiking model spends over 20 s
looping, while loops almost never occur in the rate-based model. (C, D) 差异-
ference in sensor input is consistently lower during a loop than during a turn.
(乙) Z-score of the sensor activity and FF neuron output during loops (蓝色的) 版本-
sus turns (gray). Sensor activity is substantially more similar during a loop than
during a turn, while FF neuron output tends to remain on one side. (F) Compar-
ison of the spiking FF brain to a control brain in which the sensors are directly
connected to the motor, at starting angles of 0 degrees and 90 degrees relative
to the origin of the plume. The spiking FF model is significantly more robust to
increasingly sparse plumes, with a high success rate down to a puff release rate
的 10 puffs per second, independent of starting angle.

been described to perform loops when they lose the odor plume (贝克 &
Haynes, 1996), we analyzed the sensor values during looping. Loops were
detected automatically based on their high rotation rates, allowing us to di-
vide the trajectory into looping and nonlooping stretches (see Figure 5A).
Analyzing the difference in value between the two sensors during looping,
we find that looping occurs proportionally more often when the two sen-
sors have similar or equal values (see Figures 5C and 5E), suggesting that
looping emerges from the model when the sensor data are nondirectional.
此外, the average difference in sensor values is consistently lower
during a loop than during a turn, and both terminate when the difference
between left and right sensor increases (see Figure 5C). During a loop, FF

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2220

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

neurons switch activity state less, and their output tends to remain stable
on one side as compared to a turn (see Figure 5E).

To investigate what a possible advantage of looping could be, we com-
pared the spiking FF network to a control agent in which the sensors were
connected directly to the motor and showed no looping behavior. We re-
moved the tendency to turn upwind in the absence of sensory input to sim-
ulate a situation in which the agent solely relies on the odor plume, 和
we tested both agents in successively sparser plumes. Under these condi-
系统蒸发散, the spiking FF agent had a significantly higher success rate than the
control brain (see Figure 5F). 出奇, at very low plume concentra-
系统蒸发散, the control brain had a high success rate. We suspected that this may
be a side effect of the agent pointing toward the odor source at the start of
the simulation and simply walking straight in the absence of sensor input.
的确, when we changed the starting angle such that the agent faced 90
degrees to the right of the odor source, the success rate of the control brain
was reduced to almost 0, while the spiking FF agent remained successful
at finding the source of the plume. This indicates that looping is indeed an
orientation strategy that in the absence of all other sensory information can
aid in locating the target.

Having established that the simple flip-flop networks are able to reli-
ably replicate several characteristics of male silkworm moth behavior, 我们
proceeded to test whether the models could also take CX output as in-
put signals. For this experiment, we used a computational model of the
CX that computes path integration in an anatomically constrained network
(see Figure 6A; Stone et al., 2017). 简而言之, path integration is a compu-
tation that combines, at each time step, the current heading of the animal
(represented in TB1/delta7 neurons; see Figure 6A) with its forward speed
(represented in TN/LNO neurons; see Figure 6A). The resulting vector (向上-
dated in the CPU4/PFN memory loop; see Figure 6A) points in the direc-
tion of the path’s origin, and the length of the vector represents the distance
of the animal from that origin. 因此, an animal that continuously updates
this vector during an outbound path has the possibility to return to its
origin in a straight line. Once the animal decides to return, the desired head-
英 (encoded in the CPU4/PFN vector) is compared to the current head-
英 (TB1/delta7 neurons), and mismatches between the two are transferred
to an unspecified motor via CPU1/PFL neurons. As CPU1 neurons project
from the CX to the LAL, it is plausible that they interact with flip-flop neu-
rons there. 重要的, steering signals are encoded as an imbalance be-
tween the summed activity of all CPU1 neurons in the right hemisphere
and those in the left hemisphere. We therefore used the summed CPU1 ac-
tivity as input to the flip-flop network. Using the same model parameters
as for odor-plume experiments, both the rate-based and the spiking model
steer an agent back to its origin based on path integrator output (见图
6乙), albeit with a lower success rate than the ideal path integrator (见图-
ure 6C). We assessed the accuracy of homing by analyzing the orientation

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2221

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

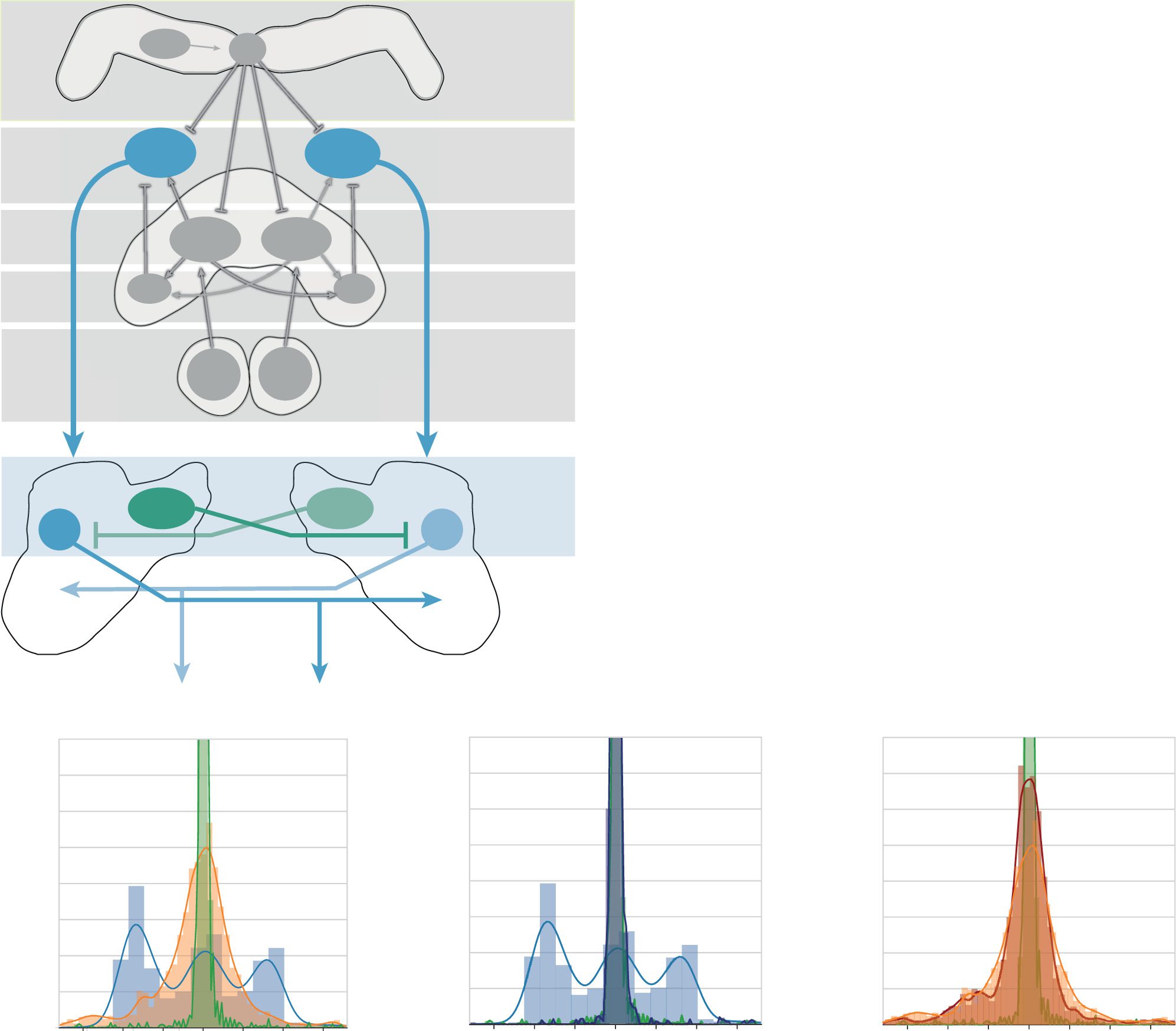
数字 6: (A) Schematic of the integrated network. The path integrator receives
compass input via CL1a neurons and speed input via TN neurons. TB1 neu-
rons compute the current heading direction. CPU4 and pontine (Pon) 神经元
form a memory loop that integrates the current heading direction with the cur-
rent speed, resulting in a vector that points to the path’s origin. When the agent
wants to return home, CPU1 neurons compare the current heading (代表
in TB1 neurons) to the desired heading given by the CPU4 home vector. CPU1
neuron output is then fed directly into the flip-flop networks, with the same in-
put driving both the inhibitory protocerebral bilateral neurons (PBN) 和
flip-flop neurons (FF). (乙) Example paths of the path integrator without a steer-
ing network (ideal), with the rate-based model and with the spiking model.
(C) Success rate of the integrated models compared to the ideal path integra-
托尔. The success probability of both models increases when the CPU1 output is
rescaled to a range of 0 到 1. Error bars represent the bootstrapped 95% 骗局-
fidence interval around the median. (D) Proportion of time the models spend
at a certain angle relative to the path’s origin. (乙) With rescaled input, 迪斯-
tribution of the rate-based model becomes almost identical to that of the ideal
path integrator. (F) With rescaled input, the distribution of the spiking model
has a smaller spread around 0◦ and becomes more similar to the ideal path in-
tegrator. N= 50 for all path integrator experiments. Only successful trials were
considered in panels D–F.

2222

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

○
of the agent relative to the origin, 在哪里 0
indicates that the agent is per-
fectly tracking along the straight line between the end of the outbound
path and its origin (see Figure 6D). Without any connections to the steer-
○
ing model, the ideal path integrator peaks at an orientation of 0
并且有
○
a standard deviation of 15.4
but has a
. The spiking model also peaks at 0
wider standard deviation of 67.9
. 有趣的是, the rate-based model has
○
one peak at 0
, and two additional peaks
○
at ±90
.

, a standard deviation of 50.2

○

Due to this odd distribution of orientations and the relatively low success
rate for the two models (0.7 和 0.57, 分别), we examined different
ways of connecting the path integrator to our steering system. There is no a
priori reason for expecting an output value of 0.5 from the path integrator
to mean the same thing as a 0.5 from the odor detection system. 然而,
we do not want to postulate complex neural mechanisms between these
two systems. Two simple things to adjust are the gain of this connection
(which would correspond to increasing the number of synapses or mov-
ing the synapse closer to the spike initiation zone) and the bias current
(which would correspond to changing the threshold at which the neuron
will fire). While neither of these on their own significantly improved behav-
ior, we found that adjusting both gain and bias such that a path integrator
value of 0.5 is mapped to a 0 input to the steering system and a value of
1.0 stays at 1.0 (and intermediate values are linearly interpolated between
这些) greatly improved performance while keeping the same qualitative
effects (见图 6). When rescaling the path integrator output to a scale
之间 0 和 1, we find that both models are significantly more successful
as well as more accurate in tracking along a straight line back to the origin
(see Figures 6C to 6F). At a sensor difference of 0.5 or above, the rate-based
model’s percentage of successful runs increases from 0.7 到 0.78, 和
spiking model increases from 0.57 到 0.92 (see Figure 6C). 因此, the flip-
flop circuit can be used to steer using multiple input sources, with minimal
modifications.

5 讨论

We modeled a simple flip-flop network based on neurons that have been de-
scribed in detail in the silkworm moth. The computational model has only
two pairs of neurons: the flip-flop neurons (FF), which are bistable neu-
罗恩, and the PBNs, which provide inhibition between the two flip-flops
and thereby synchronize the two hemispheres. Note that in our model, 那里
are no other connections between the two hemispheres; 因此, this synchro-
nization is entirely mediated by the PBNs. This network was modeled as
both a rate-based model and a spiking model. 出奇, 两种型号
were able to replicate the behavior of real moths in an odor plume reliably,
despite their simplicity. We found that additional neurons were not neces-
sary to produce the behavior presented in this article (see Figure S2).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2223

We also tested whether this simple steering network could serve as an
interface between the CX and downstream motor centers by combining it
with the CX path integrator network (Stone et al., 2017). We could show
that both the rate-based and the spiking model can take input from the path
integrator and use it for steering toward a target and that the efficiency of
steering depends on the scaling of the input into the system.

We next discuss our findings with respect to the models, their be-
haviors, and the predictions and conclusions we can draw from these
实验.

5.1 Rate-Based versus Spiking Model. When comparing the rate-
based and the spiking models, both produced similar overall plume-
following behaviors despite the difference in complexity. This reflects that
rate-based models are, to a certain degree, a valid way of modeling neu-
ral networks, despite the many simplifications they involve. 然而, 这
more subtle behaviors of the system seem to be more realistic in the spiking
version, in particular for looping behavior and for the influence of turning
bias. 有趣的是, when a turning bias is introduced (see Figure 4B), 这
spiking model produces the same edge-following behavior observed in the
original experiment (Ando et al., 2013), while the rate-based model exhibits
some shift but with a wider spread. 全面的, this indicates that the spiking
model produces more realistic behavior.

A major open question is how flip-flopping can be achieved in a real
neuron. In the spiking model presented here, we combine low-level com-
ponents, which consist of voltage buildup and spikes, to approximate the
flip-flop behavior. While this produces more realistic behavior than the rate-
based approach, more details could be added. 尤其, various models
of neural bistability exist (Camperi & 王, 1998; Gruber, Solla, Surmeier,
& Houk, 2003) that might serve as the basis for a more accurate model of
flip-flop neurons.

5.2 Model Behavior. When evaluating the behavior of both models, 这
turn angle, turn angular velocity, and turn duration agree well with val-
ues reported for male silkworm moths and fall within the mean ± 1 斯坦-
dard deviation of moths (Ando et al., 2013). The high positive deviation of
the spiking model’s turn duration (see Figure 3A) can be explained by this
model’s tendency to loop, leading to more and longer turns. The rate-based
model also produced looping behavior but at a much lower rate than the
spiking model. Loops occurred when the difference between the two sen-
sors’ values was very low and the directional information of the sensory
input was therefore ambiguous. We could show that looping conferred a
distinct advantage in sparser odor plumes, leading to significantly higher
success rates as compared to a nonlooping control agent. This suggests that
looping is a basic orientation strategy that allows an insect to sample its
entire local environment and may be especially useful if the insect orients

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2224

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

relative to an external cue or toward the source of an intermittent cue such
as an odor plume. As an orientation strategy, looping has been described in
several insects; 例如, fruit moths perform a loop as a search mecha-
nism when they lose the odor plume (贝克 & Haynes, 1996); dung beetles
perform a circular dance on their dung ball to take a “snapshot” of skylight
cues before rolling their dung ball in a straight line relative to these cues
(Baird et al., 2012; el Jundi, 促进, Khaldy, Byrne, Dacke, & Baird, 2016)
and perform another dance after losing their bearing; and desert ants use
a similar strategy to learn their visual surroundings during learning walks
(Fleischmann, Grob, Wehner, & Rössler, 2017). Looping therefore appears
to be a robust strategy to sample and learn the local sensory environment,
as well as to reacquire a sensory signal that has been lost. Note that this ori-
entation strategy would not be expected in simple taxis behaviors, 其中
the animal navigates purposefully toward or away from a sensory cue. 在
this situation, a very small difference between the two sensor values would
be expected to elicit a straight walk, with the aim of keeping the difference
as small as possible.

5.3 Central Complex Output Can Be Used for Steering. 此外
to steering toward the source of an odor plume, we have shown that the
models also steer well when getting input from the CX path integrator (PI)
network published in Stone et al. (2017). The output from this network is in
essence a steering signal that represents the difference between the intended
heading and the current heading. This signal is asymmetric between the
right and left hemisphere, depending on whether the agent needs to correct
to the right or the left.

Our steering models can take this input and steer the agent toward its
point of origin, using the same parameters that were used for odor-based
steering. This was surprising, considering that the sensory input experi-
enced in an odor plume is quite different from the input provided by the
PI. Odor plume input is intermittent and varies at a high temporal fre-
quency, whereas PI output is constant, changes smoothly without sudden
jumps, and ideally varies within a relatively small range around the in-
tended heading. Rescaling the PI output to match the range given by the
odor plume resulted in successful control behavior without necessitating
fundamental changes to the model. Biologically, this rescaling could be
achieved by the presence of interneurons or neuromodulators or both, 在
the inputs to the flip-flop system and facilitate adapting to new sensory
环境.

Our results suggest that the flip-flop system can take and integrate in-
put signals from multiple modalities, including the CX, to generate down-
stream steering commands. One important limitation is that the multimodal
input signals need to be directional, 那是, there must be an imbalance be-
tween the signals in the right and left hemispheres. 这里, we tested input

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2225

signals that are derived from visual cues, but there is no reason to assume
that the input should be restricted to olfactory and visual cues alone (斯坦因-
beck et al., 2020). Silkworm moth flip-flop neurons are known to switch
state in response to odor cues as well as light flashes, and bistable neurons
of a similar morphology were found to switch state in response to auditory
input in the cricket (Zorovic & Hedwig, 2011). Our data therefore support
the idea that this neural network may work as a general-purpose steering
network at least in the context of targeted orientation behaviors (excluding
taxis behaviors).

5.4 Purpose of the Flip-Flop System. One important question is
whether the flip-flop neurons convey any actual advantage to the steering
circuit. 的确, the path integrator model without a flip-flop steering com-
ponent works perfectly well (Stone et al., 2017; see also the “ideal” model in
数字 6). 相似地, pheromone plumes could be followed by directly con-
necting the left and right sensor data to downstream motor neurons, 经过-
passing the flip-flop network altogether (see Figures 5F and S3). 然而,
we have shown that one advantage of using the flip-flop network when
following an odor plume is the emergence of looping behaviors, which in-
crease the robustness of the behavior to disturbances such as intermittent
loss of sensory input. 此外, the flip-flop models produce paths that
cover a wider part of the available space while still successfully finding
the plume source. We thus conclude that one purpose of the flip-flop sys-
tem is to support reliable goal-directed behaviors while also facilitating ex-
ploratory behaviors that cause the insect to vary its position and orientation
rather than following a direct path.

5.5 预测. Our analysis generates several testable predictions.
First and foremost, CPU1 neurons that project from the CX to the LAL
are expected to have either direct or indirect excitatory synaptic connec-
tions with flip-flop neurons. To our knowledge, only two similar connec-
tions have been described so far. In the fruit fly, CPU1 neurons (PFL in
Drosophila nomenclature) were shown to synapse onto bilateral LAL in-
terneurons (Franconville, Beron, & Jayaraman, 2018; see also Hulse et al.,
2021), as well as the ipsilaterally descending LAL neuron DNa02 (Rayshub-
skiy et al., 2020). 然而, whether CX output neurons also project onto
contralaterally descending neurons in the LAL remains unknown. Finding
the interaction sites between CX output neurons and LAL descending neu-
罗恩, such as the flip-flop neurons modeled here, will be an important step
toward understanding how the CX controls behavior.

第二, our findings support that the flip-flop network does not only un-
derlie olfactory steering, but that it can be a multimodal steering network.
If this is correct across insects, we would expect flip-flop neurons to switch
state in response to any stimulus that elicits targeted locomotion (excluding

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2226

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

taxis behaviors). 这里, we discuss three examples of targeted locomotion:
straight line orientation, 移民, and path integration.

Dung beetles perform short-distance, straight-line orientation when
rolling their ball away from the dung pile (Dacke, Nilsson et al., 2003). 到
keep their path straight, they rely on skylight cues such as the position of
the sun, the polarization pattern of the sky, and the sky’s spectral gradi-
耳鼻喉科 (Dacke, Nordström et al., 2003; Dacke, Byrne, Scholtz, & Warrant, 2004;
Dacke, Baird, Byrne, Scholtz, & Warrant, 2013; el Jundi et al., 2014). 这些
cues are integrated in the CX to generate a current heading (el Jundi et al.,
2016), which can be used to steer the animal along its straight path and ad-
just for deviations. We therefore expect that dung beetle flip-flop neurons
should respond to a change of the skylight cue, such as a sudden rotation
of the polarization pattern, with a state change.

When it comes to long-distance migration, the monarch butterfly and the
bogong moth are well-known insect models for diurnal and nocturnal mi-
gration, 分别 (Reppert, Guerra, & Merlin, 2016; Warrant et al., 2016).
The monarch butterfly uses a time-compensated sun compass, as well as the
geomagnetic field to migrate from its breeding grounds in North America to
overwintering regions in central Mexico (Mouritsen & Frost, 2002; Guerra,
Gegear, & Reppert, 2014). The bogong moth uses the geomagnetic field in
combination with visual landmarks to migrate from its breeding grounds in
southern Queensland and western New South Wales (澳大利亚) to its over-
wintering sites in the Australian Alps (Dreyer et al., 2018). The CX path inte-
gration network processes sun compass information and has been proposed
to be a possible substrate for computing long-distance migration (Heinze &
Reppert, 2011; Honkanen et al., 2019), thus making it likely that the resulting
steering commands are passed on to LAL descending neurons. 我们会
expect flip-flop neurons in the monarch butterfly and the bogong moth to
switch state in response to sudden changes in the skylight cues or landmark
configuration that they use to orient. 此外, many flying insects use
optic flow for flight control, including moths (Fry, Rohrseitz, Straw, & 迪克-
inson, 2009; Weir, Schnell, & 狄金森, 2014; Stöckl & Kelber, 2019; Mauss
& Borst, 2020). One might therefore expect flip-flop neurons to also respond
to a change in the rotational component of optic flow with a state change.
最后, path-integrating ants and bees are obvious targets for measuring
flip-flop neuron responses, considering that we use the PI network as an
input for our steering models. 然而, since the flip-flop neurons are not
driven directly by sensory input that can be controlled in an experimental
situation, but rather by a memory state, it is more difficult to test how flip-
flop neurons respond during homing. 一个可以, 然而, test optic flow
cues and compass cues separately to dissect how the different components
of the path integrator drive the flip-flop neurons. 或者, 可能是
possible to perform extracellular tetrode recordings from flip-flop neurons
during natural homing on a trackball (Dahmen, Wahl, Pfeffer, Mallot, &
Wittlinger, 2017).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2227

6 Conclusions and Outlook

当然, motor control mediated by descending neurons is much more
complex than the simple model presented here. In the silkworm moth,
several other neuron types were described to play a role in pheromone-
mediated steering, which can be added to the model for increased complex-
ity and biological relevance. 此外, complex motor patterns are most
likely mediated by not just one cell type but by a population code across a
number of descending neurons (Namiki, Dickinson et al., 2018). Creating
larger and more integrated models of this form is a useful tool for a fuller
understanding of these complex interactions.

We believe that the model we have developed and presented here is one
small step toward understanding the connection between the heading di-
rection system in the CX and downstream motor centers. 重要的, 这
approach we have taken to develop this model is flexible and suitable for a
wide range of model features. 迄今为止, this is the most complex insect-based
model developed using the Nengo neural modeling software. 然而,
Nengo has also been used for a wide variety of mammal-based models,
including Spaun, a large-scale model of the human brain (埃利亚史密斯等人。,
2012). While modeling insect brains offers different challenges than mam-
malian brains, we believe our work has shown that this sort of large-scale
model is possible and can lead to more realistic behavior than some tradi-
tional modeling approaches.

Developing a more complete model cannot be done by a single group
of researchers. We have made our model freely available at https://
github.com/stanleyheinze/insect_steering, and we hope that a community
of researchers can, 随着时间的推移, add neuron types and neural systems to in-
crease the complexity of the model and advance our understanding of this
general steering system in insects.

致谢

We thank the organizers and participants of the 2016 Nengo summer school,
in particular Ben Morcos and Xuan Choo, for contributing to the initial moth
model and for helpful discussions. We are also grateful to Noriyasu Ando
for sharing his data with us.

参考

Álvarez-Salvado, E., Licata, A. M。, Connor, 乙. G。, McHugh, 中号. K., 国王, 乙. M。,
Stavropoulos, N。, . . . Nagel, K. 我. (2018). Elementary sensory-motor transforma-
tions underlying olfactory navigation in walking fruit-flies. 电子生活, 7, 1–38.

Ando, N。, Emoto, S。, & Kanzaki, 右. (2013). Odour-tracking capability of a silk-
moth driving a mobile robot with turning bias and time delay. Bioinspiration and
Biomimetics, 8(1). 10.1088/1748-3182/8/1/016008

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2228

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

Baird, E., Byrne, 中号. J。, Smolka, J。, Warrant, 乙. J。, & Dacke, 中号. (2012). The dung beetle

dance: An orientation behaviour? PLOS One, 7(1), 1–6.

贝克, 时间. C。, & Haynes, K. F. (1996). Pheromone-mediated optomotor anemotaxis and
altitude control exhibited by male oriental fruit moths in the field. Physiological
Entomology, 21(1), 20–32. 10.1111/j.1365-3032.1996.tb00831.x

Balakrishnan, R。, & 波拉克, G. S. (1996). Recognition of courtship song in the
field cricket, Teleogryllus oceanicus. 动物行为, 51(2), 353–366. 10.1006/
anbe.1996.0034

贝科莱, T。, 贝格大街, J。, 洪斯伯格, E., 德沃尔夫, T。, 斯图尔特, 时间. C。, 拉斯穆森,
D ., . . . 埃利亚史密斯, C. (2014). 我曾是: A Python tool for building large-scale
functional brain models. 神经信息学前沿, 7(一月), 1–13. 10.3389/
fninf.2013.00048

Camperi, M。, & 王, X. J. (1998). A model of visuospatial working memory in pre-
frontal cortex: Recurrent network and cellular bistability. Journal of Computational
神经科学, 5(4), 383–405. 10.1023/A:1008837311948, 考研: 9877021

Cande, J。, Namiki, S。, Qiu, J。, Korff, W., Card, G. M。, Shaevitz, J. W., . . . . Berman, G.
J. (2018). Optogenetic dissection of descending behavioral control in Drosophila.
电子生活, 7, 1–23. 10.7554/eLife.34275

Cardé, 右. T。, & 威利斯, 中号. A. (2008). Navigational strategies used by insects to find
distant, wind-borne sources of odor. Journal of Chemical Ecology, 34(7), 854–866.
Dacke, M。, Baird, E., Byrne, M。, Scholtz, C. H。, & Warrant, 乙. J. (2013). Dung bee-
tles use the milky way for orientation. 现代生物学, 23(4), 298–300. 10.1016/
j.cub.2012.12.034, 考研: 23352694

Dacke, M。, Byrne, 中号. J。, Scholtz, C. H。, & Warrant, 乙. J. (2004). Lunar orientation in a
beetle. In Proceedings of the Royal Society B: Biological Sciences, 271(1537), 361–365.
10.1098/rspb.2003.2594

Dacke, M。, Nilsson, D.-E., Scholtz, C. H。, Byrne, M。, & Warrant, 乙. J. (2003). Insect
orientation to polarized moonlight. 自然, 424(6944), 33–33. 10.1038/424033A,
考研: 12840748

Dacke, M。, Nordström, P。, & Scholtz, C. H. (2003). Twilight orientation to polarised
light in the crepuscular dung beetle Scarabaeus zambesianus. 实验杂志
生物学, 206(9), 1535–1543. 10.1242/jeb.00289, 考研: 12654892

Dahmen, H。, Wahl, V. L。, Pfeffer, S. E., Mallot, H. A。, & Wittlinger, 中号. (2017).
Naturalistic path integration of Cataglyphis desert ants on an air-cushioned
lightweight spherical treadmill. Journal of Experimental Biology, 220(4), 634–644.
10.1242/jeb.148213, 考研: 28202651

Dreyer, D ., Frost, B., Mouritsen, H。, Günther, A。, 绿色的, K., Whitehouse, M。, . . . 战争-
rant, 乙. (2018). The earth’s magnetic field and visual landmarks steer migratory
flight behavior in the nocturnal Australian bogong moth. 现代生物学, 28, 1–7.
10.1016/j.cub.2018.05.030, 考研: 29937347

el Jundi, B., 促进, J. J。, Khaldy, L。, Byrne, 中号. J。, Dacke, M。, & Baird, 乙. (2016). A
snapshot-based mechanism for celestial orientation. 现代生物学, 26(11), 1456–
1462. 10.1016/j.cub.2016.03.030, 考研: 27185557

el Jundi, B., Smolka, J。, Baird, E., Byrne, 中号. J。, & Dacke, 中号. (2014). Diurnal dung
beetles use the intensity gradient and the polarization pattern of the sky for ori-
entation. Journal of Experimental Biology, 217(13), 2422–2429. 24737763

埃利亚史密斯, C。, & 安德森, C. H. (2003). 神经工程: 计算, 代表-

的, 和神经生物学系统动力学. 剑桥, 嘛: 与新闻界.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2229

埃利亚史密斯, C。, 斯图尔特, 时间. C。, 秋, X。, 贝科莱, T。, 德沃尔夫, T。, 唐, Y。, & 拉斯穆森,
D. (2012). 大脑功能的大型模型. 科学, 338(6111), 1202–
1205. 10.1126/science.1225266, 考研: 23197532

Farrell, J. A。, Murlis, J。, 长的, X。, 李, W., & Cardé, 右. 时间. (2002). Filament-based atmo-
spheric dispersion model to achieve short time-scale structure of odor plumes.
Environmental Fluid Mechanics, 2(1–2), 143–169. 10.1023/A:1016283702837

Fleischmann, 磷. N。, Grob, R。, Wehner, R。, & Rössler, 瓦. (2017). Species-specific differ-
ences in the fine structure of learning walk elements in Cataglyphis ants. 杂志
Experimental Biology, 220(13), 2426–2435. 10.1242/jeb.158147, 考研: 28679795
Franconville, R。, Beron, C。, & Jayaraman, V. (2018). Building a functional connectome

of the drosophila central complex. 电子生活, 7, 1–25. 10.7554/eLife.37017

Fry, S. N。, Rohrseitz, N。, Straw, A. D ., & 狄金森, 中号. H. (2009). Visual control of
flight speed in Drosophila melanogaster. Journal of Experimental Biology, 212, 1120–
1130. 10.1242/jeb.020768, 考研: 19329746

绿色的, J。, Adachi, A。, Shah, K. K., Hirokawa, J. D ., Magani, 磷. S。, & Maimon, G.
(2017). A neural circuit architecture for angular integration in Drosophila. 自然,
546(7656), 101–106. 10.1038/nature22343, 考研: 28538731

Gruber, A. J。, Solla, S. A。, Surmeier, D. J。, & Houk, J. C. (2003). Modulation
of striatal single units by expected reward: A spiny neuron model display-
ing dopamine-induced bistability. 神经生理学杂志, 90(2), 1095–1114.
10.1152/杰恩.00618.2002, 考研: 12649314

Guerra, 磷. A。, Gegear, 右. J。, & Reppert, S. 中号. (2014). A magnetic compass aids
monarch butterfly migration. Nature Communications, 5. 10.1038/ncomms5164
Heinze, S. (2017). Unraveling the neural basis of insect navigation. Current Opinion

in Insect Science, 24, 58–67. 10.1016/j.cois.2017.09.001, 考研: 29208224

Heinze, S。, & Reppert, S. 中号. (2011). Sun compass integration of skylight cues in mi-
gratory monarch butterflies: Supplemental information. 神经元, 69(2), 345–358.
10.1016/j.neuron.2010.12.025, 考研: 21262471

Honkanen, A。, Adden, A。, da Silva Freitas, J。, & Heinze, S. (2019). The insect central
complex and the neural basis of navigational strategies. 实验杂志
生物学, 222. 10.1242/jeb.188854, 考研: 30728235

Hulse, 乙. K., Haberkern, H。, Franconville, R。, Turner-Evans, D. B., Takemura, S.
Y。, Wolff, T。, . . . Jayaraman, V. (2021). A connectome of the drosophila central
complex reveals network motifs suitable for flexible navigation and context-
dependent action selection. 电子生活, 10, 1–180. 10.7554/eLife.66039

琼斯, C. D. (1983). On the structure of instantaneous plumes in the atmosphere.

Journal of Hazardous Materials, 7(2), 87–112. 10.1016/0304-3894(83)80001-6

Kakaria, K. S。, & de Bivort, 乙. L. (2017). Ring attractor dynamics emerge from a spik-
ing model of the entire protocerebral bridge. Frontiers in Behavioral Neuroscience,
11. 10.3389/fnbeh.2017.00008, 考研: 28261066

Kanzaki, R。, Ikeda, A。, & Shibuya, 时间. (1994). Morphological and physiological prop-
erties of pheromone-triggered flipflopping descending interneurons of the male
silkworm moth, Bombyx mori. Journal of Comparative Physiology A, 175, 851–851.
10.1007/BF00217431

Kanzaki, R。, & Mishima, 时间. (1996). Pheromone-triggered “flipflopping” neural sig-
nals correlate with activities of neck motor neurons of a male moth, Bombyx mori.
Zoological Science, 13(1), 79–87. 10.2108/zsj.13.79

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

2230

A. Adden, 时间. 斯图尔特, 乙. Webb, 和S. Heinze

Kanzaki, R。, Nagasawa, S。, & Shimoyama, 我. (2005). Neural basis of odor-source
searching behavior in insect brain systems evaluated with a mobile robot. Chem-
ical Senses, 30(补充. 1), 285–286. 10.1093/chemse/bjh226

Kanzaki, R。, Sugi, N。, & Shibuya, 时间. (1992). Self-generated zigzag turning of Bombyx
mori males during pheromone-mediated upwind walking. Zoological Science, 9(3),
515–527.

Kymre, J. H。, 刘, X. L。, Ian, E., Berge, C. N。, 王, G. R。, 伯格, 乙. G。, . . . Chu, X.
(2021). Distinct protocerebral neuropils associated with attractive and aversive
female-produced odorants in the male moth brain. 电子生活, 10, 1–27. 10.7554/电子生活
.65683

Levakova, M。, Kostal, L。, Monsempe‘s, C。, 雅各布, 五、, & Lucas, 磷. (2018). Moth ol-
factory receptor neurons adjust their encoding efficiency to temporal statistics
of pheromone fluctuations. PLOS Computational Biology, 14(11), 1–17. 10.1371/
journal.pcbi.1006586

Loudon, C。, & Koehl, 中号. (2000). Sniffing by a silkworm moth: Wing fanning
enhances air penetration through and pheromone interception by antennae.
Journal of Experimental Biology, 203(Pt. 19), 2977–2990. 10.1242/jeb.203.19.2977,
考研: 10976034

Mafra-Neto, A。, & Cardé, 右. 时间. (1994). Fine-scale structure of pheromone plumes
modulates upwind orientation of flying moths. Letters to Nature, 369(可能), 142–
144. 10.1038/369142a0

沼泽, D ., 肯尼迪, J. S。, & Ludlow, A. 右. (1978). An analysis of anemotactic zigzag-
ging flight in male moths stimulated by pheromone. Physiological Entomology, 3,
221–240. 10.1111/j.1365-3032.1978.tb00152.x

Mauss, A. S。, & Borst, A. (2020). Optic flow-based course control in insects. 当前的
Opinion in Neurobiology, 60, 21–27. 10.1016/j.conb.2019.10.007, 考研: 31810007
Mishima, T。, & Kanzaki, 右. (1998). Coordination of flipflopping neural signals and
head turning during pheromone-mediated walking in a male silkworm moth
Bombyx mori. J. 比较. Physiol. A, 183, 273–282. 10.1007/s003590050255

Mishima, T。, & Kanzaki, 右. (1999). Physiological and morphological characterization
of olfactory descending interneurons of the male silkworm moth, Bombyx mori.
Journal of Comparative Physiology A, 184(2), 143–160. 10.1007/s003590050314
Mouritsen, H。, & Frost, 乙. J. (2002). Virtual migration in tethered flying monarch
butterflies reveals their orientation mechanisms. PNAS, 99(15), 10162–10166.
10.1073/pnas.152137299, 考研: 12107283

Namiki, S。, 狄金森, 中号. H。, 黄, A. M。, Korff, W., & Card, G. 中号. (2018). 这
functional organization of descending sensory-motor pathways in drosophila.
电子生活, 7, 1–50. 10.7554/eLife.34272

Namiki, S。, Iwabuchi, S。, Pansopha Kono, P。, & Kanzaki, 右. (2014). Information flow
through neural circuits for pheromone orientation. Nature Communications, 5,
5919. 10.1038/ncomms6919, 考研: 25533353

Namiki, S。, & Kanzaki, 右. (2016). The neurobiological basis of orientation in insects:
Insights from the silkmoth mating dance. Current Opinion in Insect Science, 15,
16–26. 10.1016/j.cois.2016.02.009, 考研: 27436728

Namiki, S。, Wada, S。, & Kanzaki, 右. (2018). Descending neurons from the lateral ac-
cessory lobe and posterior slope in the brain of the silkmoth Bombyx mori. Scientific
报告, 8(1), 1–26. 10.1038/s41598-018-27954-5, 考研: 29941958

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d

我

F
/

3
4
1
1
2
2
0
5
2
0
8
6
5
0
0
n
e
C
哦
_
A
_
0
1
5
4
0
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

A Neural Model for Insect Steering

2231

Obara, 是. (1979). Bombyx mori mating dance: An essential in locating the female. 应用程序-

plied Entomology and Zoology, 14(1), 130–132. 10.1303/aez.14.130

Olberg, 右. 中号. (1983). Pheromone-triggered flip-flopping interneurons in the ventral
nerve cord of the silkworm moth, Bombyx mori. Journal of Comparative Physiology,
152(3), 297–307. 10.1007/BF00606236

Rayshubskiy, A。, Holtz, S。, D’Alessandro, 我。, 李, A。, Vanderbeck, Q., Haber, 我。, . . .
Wilson, 右. (2020). Neural circuit mechanisms for steering control in walking Drosophila.
bioRxiv: 2020.04.04.024703.

Reppert, S. M。, Guerra, 磷. A。, & Merlin, C. (2016). Neurobiology of monarch butter-
fly migration. Annual Review of Entomology, 61(1), 25–42. 10.1146/annurev-ento
-010814-020855, 考研: 26473314

Schnell, B., Ros, 我. G。, & 狄金森, 中号. H. (2017). A descending neuron correlated
with the rapid steering maneuvers of flying drosophila. 现代生物学, 27(8),
1200–1205. 10.1016/j.cub.2017.03.004, 考研: 28392112

Simmons, L. 瓦. (1988). The calling song of the field cricket, Gryllus bimaculatus (的
Geer), constraints on transmission and its role in intermale competition and fe-
male choice. 动物行为, 36(2), 380–394. 10.1016/S0003-3472(88)80009-5
斯里尼瓦桑, 中号. V. (2015). Where paths meet and cross: navigation by path integration
in the desert ant and the honeybee. Journal of Comparative Physiology A, 201(6),
533–546. 10.1007/s00359-015-1000-0

Steinbeck, F。, Adden, A。, & Graham, 磷. (2020). Connecting brain to behaviour: A role
for general purpose steering circuits in insect orientation? 实验杂志
生物学, 223(4). 10.1242/jeb.212332, 考研: 32161054

Stöckl, A. L。, & Kelber, A. (2019). Fuelling on the wing: Sensory ecology of hawkmoth
觅食. Journal of Comparative Physiology A: Neuroethology, Sensory, Neural, 和
Behavioral Physiology, 205(3), 399–413.

Stone, T。, Webb, B., Adden, A。, Weddig, 氮. B., Honkanen, A。, Templin, . . . Heinze, S。,
(2017). An anatomically constrained model for path integration in the bee brain.
现代生物学, 27(20), 3069–3085. 10.1016/j.cub.2017.08.052, 考研: 28988858
Vickers, 氮. J。, Christensen, 时间. A。, 贝克, 时间. C。, & Hildebrand, J. G. (2001). Odour-
plume dynamics influence the brain’s olfactory code. 自然, 410(行进).
11260713

Warrant, E., Frost, B., 绿色的, K., Mouritsen, H。, Dreyer, D ., Adden, A。, . . . Heinze,
S. (2016). The Australian bogong moth Agrotis infusa: A long-distance noctur-
nal navigator. Frontiers in Behavioral Neuroscience, 10(四月). 10.3389/fnbeh.2016
.00077

Weir, 磷. T。, Schnell, B., & 狄金森, 中号. H. (2014). Central complex neurons exhibit
behaviorally gated responses to visual motion in Drosophila. Journal of Neuro-
physiology, 111(1), 62–71. 10.1152/杰恩.00593.2013, 考研: 24108792

Zorovic, M。, & Hedwig, 乙. (2011). Processing of species-specific auditory patterns
in the cricket brain by ascending, 当地的, and descending neurons during standing
and walking. 神经生理学杂志, 105(5), 2181–2194. 10.1152/杰恩.00416.2010,
考研: 21346206

Received September 7, 2021; accepted July 14, 2022.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d