文章
Communicated by Terrence Sejnowski
Disentangled Representation Learning and Generation
With Manifold Optimization
Arun Pandey
arun.pandey@esat.kuleuven.be
KU Leuven, Department of Electrical Engineering, STADIUS Center for Dynamical
系统, Signal Processing and Data Analytics, B-3001 Leuven, 比利时
Michaël Fanuel
michael.fanuel@univ-lille.fr
Université de Lille, 法国国家科学研究中心, Centrale Lille, F-59000 Lille, 法国
Joachim Schreurs
joachim.schreurs@esat.kuleuven.be
Johan A. K. Suykens
johan.suykens@esat.kuleuven.be
KU Leuven, Department of Electrical Engineering, STADIUS Center for Dynamical
系统, Signal Processing and Data Analytics, Kasteelpark Arenberg 10,
B-3001 Leuven, 比利时
Disentanglement is a useful property in representation learning, 哪个
increases the interpretability of generative models such as variational
autoencoders (VAE), generative adversarial models, and their many vari-
蚂蚁. Typically in such models, an increase in disentanglement perfor-
mance is traded off with generation quality. In the context of latent
space models, this work presents a representation learning framework
that explicitly promotes disentanglement by encouraging orthogonal
directions of variations. The proposed objective is the sum of an autoen-
coder error term along with a principal component analysis reconstruc-
tion error in the feature space. This has an interpretation of a restricted
kernel machine with the eigenvector matrix valued on the Stiefel man-
ifold. Our analysis shows that such a construction promotes disentan-
glement by matching the principal directions in the latent space with
the directions of orthogonal variation in data space. In an alternating
minimization scheme, we use the Cayley ADAM algorithm, a stochastic
optimization method on the Stiefel manifold along with the Adam opti-
悲惨的. Our theoretical discussion and various experiments show that the
proposed model is an improvement over many VAE variants in terms of
both generation quality and disentangled representation learning.
神经计算 34, 2009–2036 (2022) © 2021 麻省理工学院.
https://doi.org/10.1162/neco_a_01528
在知识共享下发布
归因 4.0 国际的 (抄送 4.0) 执照.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
2010
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
1 介绍
Latent space models are popular tools for sampling from high-dimensional
分布. 经常, only a small number of latent factors are sufficient
to describe data variations. These models exploit the underlying struc-
ture of the data and learn explicit representations that are faithful to the
data-generating factors. Popular latent space models are variational autoen-
coders (VAEs; Kingma & Welling, 2014), restricted Boltzmann machines
(RBMs; Salakhutdinov & 欣顿, 2009), normalizing flows (Rezende &
Mohamed, 2015), and their many variants.
In latent variable models, one is often interested in modeling the data in
terms of uncorrelated or independent components, yielding a so-called dis-
entangled representation (本吉奥, 考维尔, & Vincent, 2013), which is of-
ten studied in the context of VAEs. Generative adversarial networks (GAN)
have also been extended to perform disentangled representation learning,
例如, with Info-GANs. It is a GAN that also maximizes the mutual
information between a small subset of the discrete latent codes and the
true images. 原则, disentanglement corresponds to identifying the
underlying factors that generate the data. Components corresponding to
the orthogonal directions in latent space may be interpreted as generating
distinct factors in the input space (例如. lighting conditions, style, 颜色).
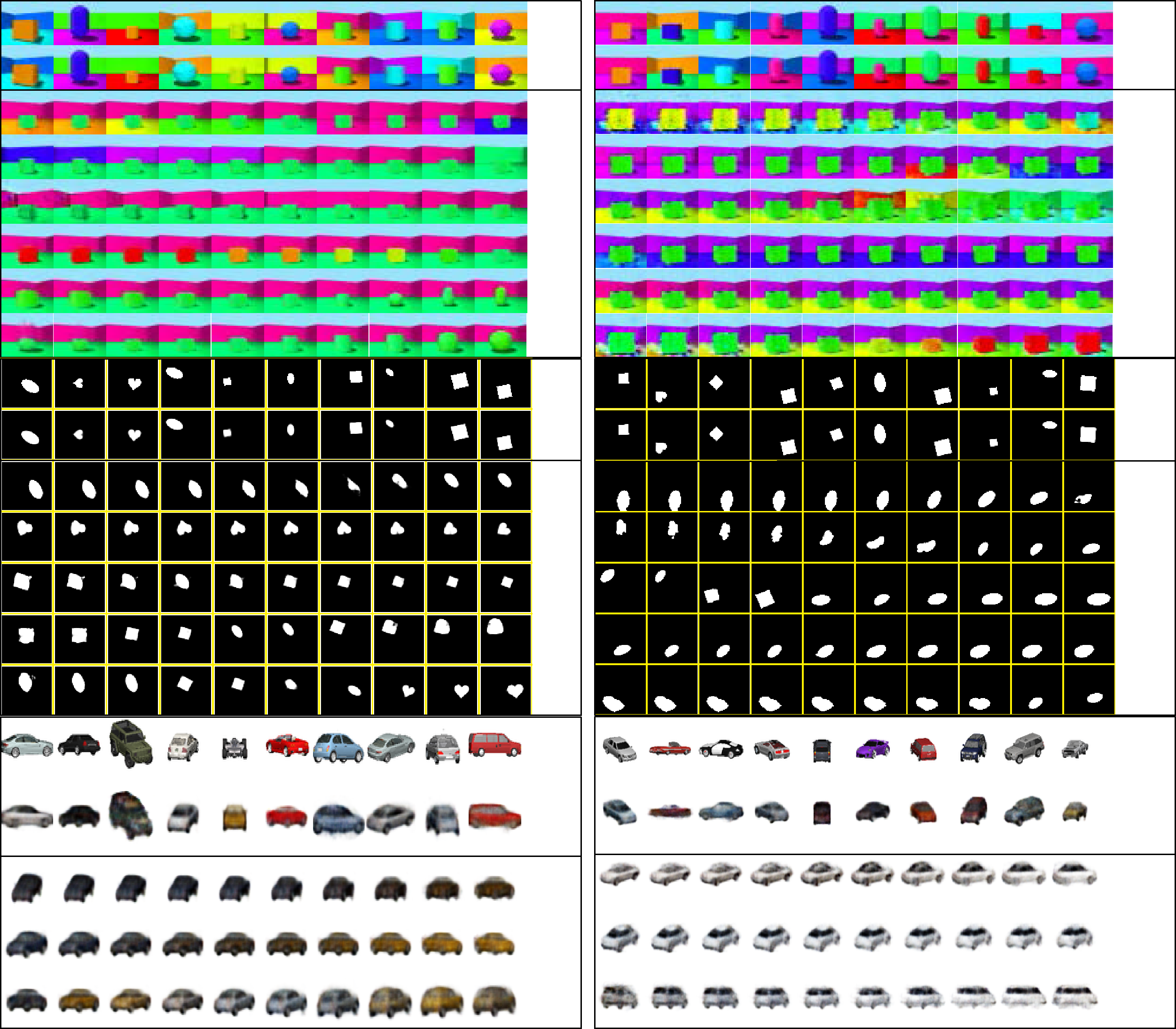
An illustration of a latent traversal is shown in Figure 1, where one ob-
serves that only one specific feature of the image is changing as one moves
along a component in the latent space. 例如, 图中 1, we ob-
serve that moving along the first component (vector u1) generates images
where only floor color is varying, 尽管, all other features, such as shape,
规模, wall color, and object color, are constant, whereas traversing along
the sixth component (vector u6), 例如, generates images where only
the object scale changes as shown in the second row. As we explain later,
the components here refer to the principal components given by the princi-
pal component analysis (PCA). 所以, these principal directions encode
the directions of maximum variance. Since the floor color is encoded by the
largest number of pixels, it gets represented by the first principal compo-
nent u1. 相似地, the other components correspond to the directions with
smaller variance. An advantage of such a representation is that the different
latent units impart more interpretability to the model. Disentangled models
are useful for the generation of plausible pseudo-data with certain desir-
able properties (例如, generating new car designs with a predefined color or
height).
Now we introduce the mathematical setting to formalize our discussion
throughout the paper. We start by introducing a VAE (Kingma & Welling,
2014). Let p(X) be the distribution of the data x ∈ Rd and consider latent
vectors z ∈ R(西德:2)
with the prior distribution p(z), typically a standard nor-
mal distribution. 然后, one defines an encoder q(z|X) that can be deter-
ministic or probabilistic, 例如, given by N (z|φθ (X), γ 2I), 哪里的
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Stiefel-Restricted Kernel Machine
2011
数字 1: Images by the decoder of the latent space traversal: ψξ (tui) for t ∈
[A, 乙] 与一个 < b and for some i ∈ {1, . . . , m}. Green and black dashed lines repre-
sent the walk along u1 and u6, respectively. At every step of the walk, the output
of the decoder generates the data in the input space. The images were generated
by St-RKM with σ = 10−3 on 3Dshapes dataset. See Figure 5 for traversal along
other components.
mean1 is given by the neural network φθ parametrized by θ. A random de-
coder p(x|z) = N (x|ψξ (z), σ 2
I) is associated with the decoder neural net-
0
work ψξ, parameterized by ξ, which maps latent codes to the data points.
A VAE is trained by maximizing the lower bound to the idealized log-
likelihood as:
E
z∼q(z|x)[log(p(x|z))] − βKL(q(z|x), p(z)) ≤ log p(x).
(1.1)
This lower bound is often called as the evidence lower bound (ELBO) when
β = 1. Higgins et al. (2017) show that the larger values of β > 1 promote
more disentanglement but at the expense of generation quality. In this arti-
克莱, we attempt to reconcile the generation quality with disentanglement. 到
introduce the model, we first make explicit the connection between β-VAEs
and standard autoencoders (AEs). Let the data set be {希
∈ Rd.
Let q(z|X) = N (z|φθ (X), γ 2I) be an encoder, where z ∈ R(西德:2)
. For a fixed γ > 0,
the maximization problem 1.1 is then equivalent to the minimization of the
regularized AE,
}n
i=1 with xi
min
我,ξ
(西德:3)
乙(西德:6)(西德:5)希
1
n
n(西德:2)
我=1
− ψξ (φθ (希) + (西德:6))(西德:5)2
2
+ A(西德:5)φθ (希)(西德:5)2
2
(西德:4)
,
(1.2)
where α = βσ 2
0 , (西德:6) ∼ N (0, γ 2I) and additive constants depending on γ have
been omitted. The first term in equation 1.2 can be interpreted as an AE loss,
whereas the second term can be viewed as a regularization. This regularized
AE interpretation motivates our method as introduced in section 3.
1
A typical implementation of VAE includes another neural network (after the primary
网络) for parametrizing the covariance matrix. To simplify this introductory discus-
锡安, this matrix is here chosen as a constant diagonal γ 2I.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
2012
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
本文的其余部分组织如下. In section 2 we discuss the
closely related work on disentangled representation learning and genera-
tion in the context of autoencoders. Further in section 3, we describe the
proposed model along with the connection between PCA and disentangle-
蒙特. In section 3.2, we discuss our contributions. In section 4, we derive
the evidence lower bound of the proposed model and show connections
with the probabilistic models. In section 5, we describe our experiments
and discuss the results.
2 相关工作
Related works can be broadly classified into two categories: Variational au-
toencoders (VAE) in the context of disentanglement and Restricted Kernel
Machines (RKM), a recently proposed modeling framework that integrates
kernel methods with deep learning.
2.1 VAE. As discussed in the section 1 (Higgins et al., 2017) suggested
that a stronger emphasis on the posterior to match the factorized unit gaus-
sian prior puts further constraints on the implicit capacity of the latent bot-
tleneck. Burgess et al. (2017) further analyzed the effect of the β term in
深度. 之后, 陈, 李, Grosse, and Duvenaud (2018) showed that the KL
term includes the mutual information gap, which encourages disentangle-
蒙特. 最近, several variants of VAEs promoting disentanglement have
been proposed by adding extra terms to the ELBO. 例如, FactorVAE
(Kim & Mnih, 2018) augments the ELBO by a new term enforcing factoriza-
tion of the marginal posterior (or aggregate posterior). Rolínek et al. (2019)
analyzed the reason for the alignment of the latent space with the coor-
dinate axes, as the design of VAE itself does not suggest any such mech-
万物有灵论. The authors argue that due to the diagonal approximation in the
encoder, together with the inherent stochasticity, forces the local orthogo-
nality of the decoder. Locatello et al. (2020) considered adding an extra term
that accounts for the knowledge of some partial label information to im-
prove disentanglement. 之后, 戈什, Sajjadi, Vergari, 黑色的, and Schölkopf
(2020) studied the deterministic AEs, where another quadratic regulariza-
tion on the latent vectors was proposed. In contrast to Rolínek et al. (2019),
where the implicit orthogonality of VAE was studied, our proposed model
has orthogonality by design due to the introduction of the Stiefel manifold.
2.2 RKM. Restricted kernel machines (RKM; Suykens, 2017) 提供了一个
representation of kernel methods with visible and hidden variables sim-
ilar to the energy function of restricted Boltzmann machines (RBM; Le-
Cun, 黄, & 波图, 2004; 欣顿, 2005), thus linking kernel methods
with RBMs. Training and prediction schemes are characterized by the sta-
tionary points for the unknowns in the objective. The equations in these
stationary points lead to solving a linear-system or matrix decomposition
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Stiefel-Restricted Kernel Machine
2013
数字 2: Schematic illustration of St-RKM training problem. The length of the
dashed line represents the reconstruction error (see the autoencoder term in
方程 3.3) and the length of the vector projecting on hyperplane represents
the PCA reconstruction error. After training, the projected points tend to be dis-
tributed normally on the hyperplane.
for the training. Suykens (2017) shows various RKM formulations for
doing classification, regression, kernel PCA, and singular value decompo-
位置. Later the kernel PCA formulation of RKM was extended to a mul-
tiview generative model called generative-RKM (Gen-RKM) which uses
convolutional neural networks as explicit feature maps (Pandey, Schreurs,
& Suykens, 2020, 2021). For the joint feature selection and subspace learn-
英, the proposed training procedure performs eigendecomposition of the
kernel/covariance matrix in every minibatch of the optimization scheme.
直观地, the model could be seen as learning an autoencoder with ker-
nel PCA in the bottleneck part. 因此, the computational complexity
scales cubically with the minibatch size and is proportional to the number of
minibatches. 而且, backpropagation through the eigendecomposition
could be numerically unstable due to the possibility of small eigenvalues.
All such limitations are addressed by our proposed model.
3 Proposed Mechanism
The main idea of this article consists of learning an autoencoder, along with
finding an optimal linear subspace of the latent space such that the vari-
ance of the training set in latent space is maximized within this space. (看
数字 2 to follow the discussion below.) Note the distinction with linear au-
toencoders, which also project the data into the low-dimensional subspace
although via nonorthogonal transformations. 作为结果, the latent
variables are not guaranteed to be uncorrelated. The encoder φθ : Rd → R(西德:2)
typically sends input data to a latent space, while the decoder ψξ : 右(西德:2) → Rd
goes in the reverse direction and constitutes an approximate inverse. 两个都
the encoder and decoder are neural networks parameterized by vectors θ
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
2014
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
and ξ. 然而, it is unclear how to define a parameterization or an archi-
tecture of these neural networks so that the learned representation is disen-
tangled. 所以, in addition to these trained parameters, we also jointly
find an m-dimensional linear subspace range(U ) of the latent space R(西德:2)
, 这样的
that the encoded training points mostly lie within this subspace. This linear
subspace is given by the span of the orthonormal columns of the (西德:2) × m ma-
trix U = [u1
, . . . , um]. The set of such matrices with m orthonormal columns
在R中(西德:2)
和 (西德:2) ≥ m defines the Stiefel manifold St((西德:2), 米). For a reference about
optimization on Stiefel manifold, we refer to Absil, Mahony, and Sepulchre
(2008). Input data are then encoded into a subspace of the latent space by
(西德:9)
X (西德:8)→ PU φθ (X) = u
1
φθ (X) ×
⎤
⎦ + . . . + 你
(西德:9)
米
φθ (X) ×
⎡
⎣
|
u1
|
⎤
⎦ ,
⎡
⎣
|
um
|
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
where the orthogonal projector onto range(U ) is simply PU = UU (西德:9)
.
Orthogonal latent directions. Naturally, given an m × m orthogonal matrix
O and a matrix U ∈ St((西德:2), 米), 我们有
范围(U ) = range(UO).
n
我=1
φθ (希)φ(西德:9)
, . . . , 你(西德:7),m to be the eigenvectors of the matrix Cθ = 1
n
, . . . , 你(西德:7),米] ∈ St((西德:2), 米), we choose
To select a specific matrix U(西德:7) = [你(西德:7),1
(西德:9)
我 (希),
你(西德:7),1
associated with the m largest eigenvalues sorted in descending order. 为了
simplicity, we assume that the m largest eigenvalues of Cθ are distinct,
whereas the general case involves minor technicalities. Here the feature
map is assumed to be centered, 乙
x∼p(X)[φθ (X)] = 0, so that Cθ is interpreted
as a covariance matrix. 下一个, we state a result that we will use extensively
之后.
Proposition 1. Let M be an (西德:2) × (西德:2) symmetric matrix. Let ν
, . . . , νm be its m
1
smallest eigenvalues, possibly including multiplicities, with associated orthonor-
mal eigenvectors v
, . . . , vm. Let V be a matrix whose columns are these eigenvec-
托尔斯. Then the optimization problem minU∈St((西德:2),米) Tr(U (西德:9)MU ) has a minimizer at
MU(西德:7) = diag(ν), with ν = (ν
U(西德:7) = V and we have U(西德:7)
1
, . . . , νm)
(西德:9).
(西德:9)
1
(西德:7) MU (西德:10)
A few remarks follow. 第一的, if U(西德:7) is a minimizer of the optimization prob-
lem in proposition 1 then U (西德:10)
(西德:7) = U(西德:7)O with O orthogonal is also a minimizer,
but U (西德:10)(西德:9)
(西德:7) is not necessarily diagonal. 第二, notice that if the eigen-
values of M in proposition 1 have a multiplicity larger than 1, there can
exist several sets of eigenvectors v
, . . . , vm, associated with the m smallest
eigenvalues, spanning distinct linear subspaces. 尽管如此, 在实践中,
the eigenvalues of the matrices considered in this article are numerically
distinct.
1
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Stiefel-Restricted Kernel Machine
2015
We now use proposition 1. For a given positive integer m ≤ (西德:2), the sub-
space spanned by the eigenvectors of Cθ with the m largest eigenvalues is
obtained by solving
min
U∈St((西德:2),米)
Tr (Cθ − PUCθPU ) = 1
n
n(西德:2)
我=1
(西德:5)磷
U⊥ φθ (希)(西德:5)2
2
,
where P
U⊥ = I − PU , as it is explained, 例如, in section 4.1 of Avron,
阮, and Woodruff (2014). The above objective corresponds to the re-
construction error of kernel PCA, for the kernel kθ (X, y) = φ(西德:9)
我 (X)φθ (y). 作为
described earlier, we choose a specific U(西德:7) ∈ St((西德:2), 米) by requiring that the
following matrix is diagonal,
(西德:9)
(西德:7) CθU(西德:7) = diag(λ),
U
(3.1)
where λ is a vector containing the m largest eigenvalues sorted in de-
creasing order. If these eigenvalues are distinct, then the U(西德:7) is essentially
独特的, up to sign flip of each of its columns. Notice that Tr(U(西德:9)
(西德:7) CθU(西德:7)) =
Tr(U(西德:7)U (西德:9)
(西德:7) CθU(西德:7)U (西德:9)
(西德:7) ).
Orthogonal directions of variation in input space. We want the lines defined
by the orthonormal vectors {你(西德:7),1
, . . . , 你(西德:7),米} to provide directions associated
with different generative factors of our model. 换句话说, we conjec-
ture that a possible formalization of disentanglement is that the principal
directions in latent space match orthogonal directions of variation in the
data space (见图 2). 那是, we would like that
(西德:9)
U
(西德:7)
d(西德:2)
(西德:10)
a=1
(西德:9)
∇ψa(做)∇ψa(做)
(西德:11)
U(西德:7) is diagonal,
(3.2)
= PU φθ (希) for i = 1, . . . , n. 在等式中
for all the points in latent space yi
3.2, ψa(y) refers to the ath component of the image ψ(y) ∈ Rd. To sketch this
主意, we study the local motions in the latent space.
= ∇ψ(y)(西德:9)你(西德:7),k
∈ Rd be the directional derivative of ψ at point y
in the direction u(西德:7),k with 1 ≤ k ≤ m. 然后, as one moves in the latent space
from a point y in the direction of u(西德:7),k, the generated data change by
Let (西德:9)
k
ψ(y + tu(西德:7),k) − ψ(y) = t(西德:9)
k
+ 氧(t2),
∈ Rd and t ∈ R. Consider now a different direction, k(西德:10) (西德:13)= k. 作为
和 (西德:9)
k
latent point moves along u(西德:7),k or along u(西德:7),k(西德:10) , we expect the decoder output to
vary in a significantly different manner, (西德:9)(西德:9)
k(西德:10) = 0. We presume this inter-
k
pretation to model the change in floor color and object scale in Figure 1 为了
实例. More explicitly, we can expect uk and uk(西德:10) to model, 分别,
the change of colors of the floor and of the main object while leaving the
color of the other objects unchanged. Since the floor and the main object
(西德:9)
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
2016
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
(西德:9)
do not overlap, 那是, they are different regions in pixel space, we would
有 (西德:9)(西德:9)
k(西德:10) = 0. 诚然, the change in object shape in Figure 1 is less
k
obviously interpreted. 现在, denote by (西德:9) the matrix obtained by stacking
(西德:9)U(西德:7).
the vector (西德:9)
因此, for all y in the latent space, we expect the Gram matrix (西德:9)(西德:9)(西德:9) 成为
diagonal (参见方程 3.2). We now discuss how this idea might be realized
by minimizing specific objective functions.
k as columns for 1 ≤ k ≤ m. Explicitly, 我们有 (西德:9) = ∇ψa(y)
3.1 Objective Function. 在本文中, we propose to train an objective
function which is composed of an AE loss and a PCA loss. 因此, 专业人士-
posed model is given by
min
U∈St((西德:2),米)
我,ξ
n(西德:2)
我=1
λ 1
n
(西德:12)
Lξ,PU (希
(西德:13)(西德:14)
, φθ (希))
(西德:15)
,
+ Tr (Cθ − PUCθPU )
(西德:15)
(西德:13)(西德:14)
(西德:12)
PCA objective
Autoencoder objective
(3.3)
(西德:9)
n
我=1
φθ (希)φ(西德:9)
where λ > 0 is a trade-off parameter and Cθ = 1
我 (希). Natu-
n
集会, the above objective is invariant if U is replaced by UO with O an or-
thogonal matrix. Given a local minimizer, we select U(西德:7) ∈ St((西德:2), 米) 这样
U (西德:9)
(西德:7) CθU(西德:7) is diagonal as in equation 3.1, to identify the principal directions in
the latent space. This last step is conveniently done with a singular value
分解 (see step 10 of algorithm 1). In the proposed model, recon-
struction of an out-of-sample point x is given by ψξ
. We call the
procedure to
(西德:11)
PU φθ (X)
(西德:10)
find a triplet (U(西德:7), 我, ξ) solving (5) s.t. U
(西德:9)
(西德:7) CθU(西德:7) is diagonal,
St-RKM
the training of a Stiefel-restricted kernel machines, 方程 3.3, in view of
our discussion in section 2. The basic idea is to design different AE losses
with a regularization term that penalizes the feature map in the orthogonal
subspace U ⊥
. The choice of the AE losses is motivated by the expression
of the regularized AE in equation 1.2 and by the following lemma, 哪个
extends the result of Rolínek et al. (2019). Here we adapt it in the context of
optimization on the Stiefel manifold (see appendix for the proof).
Lemma 1. Let (西德:6) ∼ N (0, 我是) a random vector and U ∈ St((西德:2), 米). Let ψa(·) ∈
C2(右(西德:2)
a has La-Lipschitz continuous Hes-
sian for all a ∈ [d], 我们有
) with a ∈ [d]. If the function [ψ(·) − x]2
乙(西德:6)(西德:5)x − ψ(y + σU(西德:6))(西德:5)2
2
= (西德:5)x − ψ(y)(西德:5)2
2
(西德:10)
+ σ 2Tr
U
(西德:9)
(西德:9)∇ψ(y)∇ψ(y)
U
(西德:11)
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
− σ 2
d(西德:2)
(西德:10)
[x − ψ(y)]aTr
U
(西德:9)
Hessy[ψa]U
d(西德:2)
(西德:11)
+
a=1
Ra(σ ),
(3.4)
2(m+1)(西德:11)((m+1)/2)
(西德:11)(m/2)
在哪里 (西德:11) is Euler’s gamma function.
a=1
√
和 |Ra(σ )| ≤ 1
6
σ 3La
Stiefel-Restricted Kernel Machine
2017
In lemma 1, the first term on the right-hand side in equation 3.4 戏剧
the role of the classical AE loss. The second term is proportional to the trace
of equation 3.2. This is related to our discussion above where we argue that
jointly diagonalizing both U(西德:9)∇ψ(y)∇ψ(y)
(西德:9)U and U (西德:9)CθU helps to enforce
角度. 然而, determining the behavior of the third term in
方程 3.4 is difficult. 这是因为, for a typical neural network archi-
结构, it is unclear in practice if the function [x − ψ(·)]2
a has La-Lipschitz
continuous Hessian for all a ∈ [d]. Hence we propose another AE loss (split-
ted loss) in order to cancel the third term in equation 3.4. 尽管如此,
the assumption in lemma 1 is used to provide a meaningful bound on the
remainder in equation 3.4. In the light of these remarks, we propose two
stochastic AE losses.
3.1.1 AE Losses. In analogy with the VAE objective equation 1.2, the first
AE encoder loss function can be chosen as
L(σ )
ξ,PU
(X, z) = E(西德:6)∼N (0,我是 )
(西德:16)
(西德:16)
x − ψξ
(西德:10)
PU z + σU(西德:6)
(西德:11)(西德:16)
(西德:16)2
2
, with σ > 0.
As motivated by lemma 1, the noise term σU(西德:6) above promotes a smoother
decoder network. To further promote disentanglement, we propose a split
AE loss
L(σ ),sl
ξ,PU
(X, z) =
(西德:16)
(西德:16)
x − ψξ
(西德:10)
PU z
(西德:11)(西德:16)
(西德:16)2
2
+ 乙(西德:6)
(西德:16)
(西德:16)ψξ
(西德:11)
(西德:10)
PU z
(西德:10)
− ψξ
PU z + σU(西德:6)
(西德:11)(西德:16)
(西德:16)2
2
,
(3.5)
和 (西德:6) ∼ N (0, 我是). The first term in equation 3.5 is the classical AE loss while
the second term promotes orthogonal directions of variations. 因此, by re-
lating lemma 1 方程 3.5 we see that
L(σ ),sl
ξ,PU
(X, z) =
(西德:16)
(西德:16)
x − ψξ
(西德:10)
PU z
(西德:11)(西德:16)
(西德:16)2
2
(西德:10)
+ σ 2Tr
U
(西德:9)
(西德:9)∇ψ(y)∇ψ(y)
U
d(西德:2)
(西德:11)
+
a=1
Ra(σ ).
简而言之, the optimization over U in equation 3.3 with the splitted loss aims
to promote a U(西德:7) 这样
(西德:9)
(西德:9)
(西德:7) CθU(西德:7) and U
(西德:7)
U
(西德:17)
n(西德:2)
我=1
(西德:18)
(西德:9)
∇ψ(做)∇ψ(做)
U(西德:7) are jointly diagonal.
数字 3 gives a visualization of the diagonal form of
1
|C|
(西德:2)
i∈C
(西德:9)
(西德:9)
(西德:7) ∇ψ(做)∇ψ(做)
U
U(西德:7), with yi
= PU φθ (希)
(3.6)
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
2018
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 3: Visualizing the matrix, 方程 3.6 for St-RKM models after train-
ing on three data sets. The first two rows show, 方程 3.6, where U =
U(西德:7) ∈ St((西德:2), 米) is the output of algorithm 1. These matrices are effectively close
to being diagonal and especially for St-RKM-sl, as expected. 相比之下, 这
third row shows the same matrix, 方程 3.6, with U ∈ St((西德:2), 米) sampled uni-
formly at random (见表 6 for the corresponding normalized diagonalization
错误).
obtained after training; where C contains the indices of a subset of 50 im-
ages sampled uniformly at random. (For numerical values, 桌子 6 在里面
appendix shows the normalized diagonalization errors.)
Note that we do not simply propose another encoder-decoder architec-
真实, given by U (西德:9)φθ (·) and ψξ (U·). 反而, our objective assumes that the
neural network defining the encoder provides a better embedding if we im-
pose that it maps training points on a linear subspace of dimension m < (cid:2)
in the (cid:2)-dimensional latent space. In other words, the optimization of the
parameters in the last layer of the encoder does not play a redundant role,
since the second term in equation 3.3 clearly also depends on P
U⊥ φθ (·). The
full training involves an alternating minimization procedure, which is de-
scribed in algorithm 1.
Stiefel-Restricted Kernel Machine
2019
3.2 Contributions. Here is a summary of our contributions. We propose
three main changes with respect to the related works. First, to promote dis-
entangled representation learning, we propose orthogonal projection in the
latent space via a rectangular matrix that is valued on the Stiefel manifold.
Then for the training, we use the Cayley ADAM algorithm of Li, Li, and
Todorovic (2020) for stochastic optimization on the Stiefel manifold and call
our proposed model St-RKM. Second, we propose several objective func-
tions to learn the feature map and the pre-image map networks in the form
of an encoder and a decoder, respectively. The best configuration for pro-
moting a disentangled representation is
λ
n
n(cid:2)
i=1
min
U∈St((cid:2),m)
θ,ξ
(splitted) AE loss(xi
, PU , θ, ξ) + PCA objective(Cθ, PU ),
(cid:9)
n
i=1
φθ (xi)φ(cid:9)
θ (xi) and PU = UU (cid:9)
where the covariance matrix reads Cθ = 1
n
with U an (cid:2) × m matrix with orthonormal columns. Here λ > 0 is a trade-
off parameter. The final parameters (U(西德:7), 我, ξ) give a local minimizer of this
objective with U(西德:7) chosen such that U (西德:9)
(西德:7) CθU(西德:7) is diagonal. 第三, we validate
through experiments the following statement: The combination of a split
AE loss with a PCA objective by using an explicit optimization on the Stiefel
manifold promotes disentanglement. 在本文中, disentanglement is in-
terpreted as jointly diagonalizing the matrix representing variations in the
(西德:9)U(西德:7) 在哪里
input space with respect to latent motions
φθ (希) and the covariance matrix of the data set in the latent space
做
U (西德:9)
(西德:7) ∇ψξ (做)∇ψξ (做)
= PU(西德:7)
(西德:7) CθU(西德:7).
i U (西德:9)
(西德:9)
4 Connections with the Evidence Lower Bound
We now discuss the interpretation of the proposed model in the probabilis-
tic setting and the independence of latent factors. In order to formulate an
ELBO, consider the following random encoders,
q(z|X) = N (z|φθ (X), γ 2I(西德:2)) and qU (z|X) = N (z|PU φθ (X), σ 2PU + δ2P
U⊥ ),
where φθ has zero mean on the data distribution. 这里, σ 2 plays the role
of a trade-off parameter, while the regularization parameter δ is introduced
for technical reasons and is put to a numerically small absolute value (看
the appendix for details). Let the decoder be p(X|z) = N (X|ψξ (z), σ 2
我) 和
0
the latent space distribution is parameterized by p(z) = N (0, (西德:13)) 在哪里
(西德:13) ε R(西德:2)×(西德:2)
is a covariance matrix. We treat (西德:13) as a parameter of the opti-
mization problem that is determined at the last stage of the training. 然后
the minimization problem 3.3 with stochastic AE loss is equivalent to the
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
2020
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
maximization of
(西德:3)
n(西德:2)
1
n
我=1
乙
(西德:12)
qU (z|希 )[日志(p(希
(西德:13)(西德:14)
|z))]
(西德:15)
− KL(qU (z|希), q(z|希))
(西德:15)
(西德:13)(西德:14)
(西德:12)
− KL(qU (z|希), p(z))
(西德:15)
(西德:13)(西德:14)
(西德:12)
(我)
(二)
(三、)
(西德:4)
,
(4.1)
which is a lower bound to the ELBO, since the KL divergence in term II
in equation 4.1 is positive. For details of the derivation, see the appendix.
The hyperparameters γ , σ, σ
0 take a fixed value. Up to additive constants,
the terms I and II of equation 4.1 match the objective, 方程 3.3. The third
学期 (三、) in equation 4.1 is optimized after the training of the first two terms.
It can be written as
1
n
n(西德:2)
我=1
吉隆坡(qU (z|希), p(z)) = 1
2
Tr[(西德:13)
0
(西德:13)−1] + 1
2
日志(这 (西德:13)) + constants,
= PUCθPU + σ 2PU + δ2P
和 (西德:13)
0
matrix is diagonalized (西德:13) = U(diag(λ) + σ 2Im)U (西德:9) + δ2PU⊥
the principal values of the PCA.
U⊥ . In that case, the optimal covariance
, with λ denoting
Now we briefly discuss the factorization of the encoder. Let h(X) =
U (西德:9)φθ (X) and let the effective latent variable be z(U ) = U (西德:9)z ∈ Rm. Then the
probability density function of qU (z|X) 是
fqU (z|X)(z) = e
√
-
(西德:5)U
(西德:9)
⊥ z(西德:5)2
2
2δ2
2πδ2)(西德:2)−m
(z
-
e
√
(U )
j
−h j (X))2
2σ 2
2πσ 2
,
米(西德:19)
j=1
(
where the first factor is approximated by a Dirac delta if δ → 0. 因此, 这
factorized form of qU shows the independence of the latent variables z(U ).
This factorization is used as a regularization term in the objective by Kim
and Mnih (2018) to promote disentanglement. 尤其, term II in equa-
的 4.1 is analogous to a “total correlation” loss (陈等人。, 2018).
5 实验
在这个部分, we investigate if St-RKM2 can simultaneously achieve ac-
curate reconstructions on training data, good random generations, 和
good disentanglement performance. We use the standard data sets: MNIST
(乐存 & 科尔特斯, 2010), Fashion-MNIST (fMNIST; Xiao, Rasul, & Vollgraf,
2017), and SVHN (Netzer et al., 2011). To evaluate disentanglement, 我们
use data sets with known ground-truth generating factors such as dSprites
2
The source code is available at http://bit.ly/StRKM_code.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Stiefel-Restricted Kernel Machine
2021
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
(Matthey, 希金斯, Hassabis, & Lerchner, 2017), 3DShapes (伯吉斯 & Kim,
2018), and 3D cars (芦苇, 张, 张, & 李, 2015). 更远, all fig-
ures and tables report average errors with 1 standard deviation over 10
实验.
5.1 Algorithm. We use an alternating-minimization scheme as shown
in algorithm 1. 第一的, the Adam optimizer with a learning rate 2 × 10−4 is
used to update the encoder-decoder parameters; 然后, the Cayley Adam
optimizer (李等人。, 2020) with a learning rate 10−4 is used to update U. Fi-
nally, at the end of the training, we recompute U from the singular value
分解 (SVD) of the covariance matrix as a final correction-step of
the kernel PCA term in our objective (step 10 of algorithm 1). 自从 (西德:2) × (西德:2)
covariance matrix is typically small, this decomposition is fast (见表 3).
在实践中, our training procedure only marginally increases the computa-
tion cost, which can be seen from training times in Table 1.
5.2 实验装置. We consider four baselines for comparison:
VAE, β-VAE, FactorVAE, and Info-GAN. An ablation study with the
2022
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
桌子 1: Training Time in Minutes (为了 1000 Epochs, Mean with 1 Standard De-
viation over 10 Runs) and the Number of Parameters (Nb) of the Generative
Models on the MNIST Data Set.
模型
St-RKM
(β)-VAE
FactorVAE
Info-GAN
Nb parameters
Training time
4164519
21.93 (1.3)
4165589
19.83 (0.8)
8182591
33.31 (2.7)
4713478
45.96 (1.6)
Gen-RKM is shown in section A.4 in the appendix. Extensive experimen-
tation was not computationally feasible since the evaluation and decompo-
sition of kernel matrices scales O(n2) 和O(n3) with the data set size (看
the discussion in section 2).
5.3 Inductive Biases. To be consistent in evaluation, we keep the same
encoder (discriminator) and decoder (发电机) architecture and the same
latent dimension across the models. We use convolutional neural networks
due to the choice of image data sets for evaluating generation and disentan-
glement. In the case of Info-GAN, batch normalization is added for training
稳定 (see section A.3 in the appendix for details). For the determination
of the hyperparameters of other models, we start from values in the range of
the parameters suggested in the authors’ reference implementation. 后
trying various values, we noticed that β = 3 and γ = 12 seem to work well
across the data sets that we considered for β-VAE and FactorVAE, 重新指定-
主动地. 此外, in all the experiments on St-RKM, we keep the recon-
struction weight λ = 1. All models are trained on the entire data set. 笔记
that for the same encoder-decoder network, the St-RKM model has the least
number of parameters compared to any VAE variants and Info-GAN (看
桌子 1).
To evaluate the quality of generated samples, we report the Fréchet in-
ception distance (FID; Heusel et al., 2017) and the sliced Wasserstein dis-
坦斯 (SWD; Karras, Aila, Laine, & Lehtinen, 2017) scores with mean and
standard deviation in Figure 4. Note that FID scores are not necessarily
appropriate for dSprites since this data set is significantly different from Im-
ageNet on which the Inception network was originally trained. (Randomly
generated samples are shown in Figure 8 in the appendix). To generate sam-
ples from the deterministic St-RKM (σ = 0), we sample from a fitted normal
distribution on the latent embedding of the data set; for a similar procedure,
see Ghosh et al., 2020). 数字 4 shows that the St-RKM variants perform
更好的 (lower mean scores) on most data sets, and within them, the stochas-
tic variants with σ = 10−3 perform best. This can be attributed to a better
generalization of the decoder network due to the addition of noise term on
latent variables (see lemma 1). The training times for St-RKM variants are
shorter compared to FactorVAE and Info-GAN due to a significantly small
number of parameters.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Stiefel-Restricted Kernel Machine
2023
数字 4: Fréchet inception distance (FID; Heusel, Ramsauer, Unterthiner,
Nessler, & Hochreiter, 2017) and sliced Wasserstein distance (SWD) scores
(mean and 1 标准差) 为了 8000 randomly generated samples (较小
is better).
To evaluate the disentanglement performance, various metrics have
been proposed. A comprehensive review by Locatello et al. (2019) 节目
that the various disentanglement metrics are correlated, albeit with a dif-
ferent degree of correlation across data sets. 在本文中, we use three
metrics to evaluate disentanglement: Eastwood’s framework (Eastwood &
威廉姆斯, 2018), mutual information gap (MIG; 陈等人。, 2018), and sep-
arated attribute predictability (SAP; Kumar et al., 2018) scores. Eastwood’s
框架 (Eastwood & 威廉姆斯, 2018) further proposes three metrics: 迪斯-
entanglement: the degree to which a representation factorizes the underlying
factors of variation, with each variable capturing at most one generative fac-
托尔; completeness: the degree to which each underlying factor is captured by
a single code variable; and informativeness: the amount of information that
a representation captures about the underlying factors of variation. 毛皮-
瑟莫雷, we use a slightly modified version of MIG score as proposed by
Locatello et al. (2019). 数字 6 shows that St-RKM variants have better dis-
entanglement and completeness scores (higher mean scores). 然而, 这
informativeness scores are higher for St-RKM when using a lasso-regressor
in contrast to mixed scores with a random forest regressor. 数字 7 更远
complements these observations by showing MIG and SAP scores. 这里,
the St-RKM-sl model has the highest mean scores for every data set. Qual-
itative assessment can be done from Figure 5, which shows the generated
images by traversing along the principal components in the latent space.
In the 3DShapes data set, the St-RKM model captures floor hue, wall hue,
and orientation perfectly but has a slight entanglement in capturing other
因素. This is worse in β-VAE, which has entanglement in all dimensions
except the floor hue, along with noise in some generated images. 相似的
trends can be observed in the dSprites and 3D cars data sets.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
2024
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 5: Traversals along the principal components. The first two rows show
the ground-truth and reconstructed images. Each subsequent row shows the
generated images by traversing along a principal component in the latent space.
The last column in each subimage indicates the dominant factor of variation.
6 结论
This article proposes he St-RKM model for disentangled representation
learning and generation based on manifold optimization. For the train-
英, we use the Cayley Adam algorithm of Li et al. (2020) for stochastic
optimization on the Stiefel manifold. Computationally, St-RKM increases
the training time by only a reasonably small amount compared to β-VAE,
例如. 此外, we propose several autoencoder objectives and
discuss that the combination of a stochastic AE loss with an explicit opti-
mization on the Stiefel manifold promotes disentanglement. 此外, 我们
establish connections with probabilistic models, formulate an evidence
lower bound, and discuss the independence of latent factors. Where the
considered baselines have a trade-off between generation quality and dis-
entanglement, we improve on both of these aspects as illustrated through
Stiefel-Restricted Kernel Machine
2025
数字 6: Eastwood framework’s (Eastwood & 威廉姆斯, 2018) disentangle-
ment metric with Lasso and random forest (RF) regressor. The plot shows
mean and 1 standard deviation of scores over 10 迭代. For disentangle-
ment and completeness, a higher score is better; for informativeness, lower is
更好的. “Info.” indicates (average) root-mean-square error in predicting z.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 7: MIG (陈等人。, 2018; Locatello et al., 2019) and SAP (Kumar, Sat-
tigeri, & Balakrishnan, 2018) scores to evaluate disentanglement performance
showing the mean (标准差) 超过 10 random seeds.
various experiments. The proposed model has some limitations. A first limi-
tation is hyperparameter selection: the number of components in the KPCA,
neural network architecture, and the final size of the feature map. When ad-
ditional knowledge on the data is available, we suggest that the user selects
the number of components close to the number of underlying generating
2026
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
因素. The final size of the feature map should be large enough so that
KPCA extracts meaningful components. 第二, we interpret the disentan-
glement as the two orthogonal changes in the latent space corresponding to
two orthogonal changes in input space. Although not perfect, we believe it
is a reasonable mathematical approximation of the loosely defined notion
of disentanglement. 而且, experimental results confirm this assump-
的. Among the possible regularizers on the hidden features, 该模型
associated with the squared Euclidean norm was analyzed in detail, 尽管
a deeper study of other regularizers is a prospect for further research, 在
particular for the case of spherical units.
附录
A.1 Proof of Lemma 1. We first quote a result that is used in the context
of optimization (Nesterov, 2014, 引理 1.2.4). Let f be a function with La-
Lipschitz continuous Hessian. 然后,
(西德:20)
(西德:20)
(西德:9)
(西德:20) F (y1) − f (y) − ∇ f (y)
(西德:12)
(y1
(y1
(西德:9)
− y)
Hessy[ F ](y1
(西德:20)
(西德:20)
(西德:20)
− y)
(西德:15)
− y) - 1
2
(西德:13)(西德:14)
−y)
r(y1
≤ La
6
(西德:5)y1
− y(西德:5)3
2
.
(A.1)
Then we calculate the power series expansion of f (y) = [x − ψ(y)]2
a and
take the expectation with respect to (西德:6) ∼ N (0, 我). 第一的, we have ∇ f (y) =
−2[x − ψ(y)]a∇ψa(y) 和
Hessy[ F ] = 2∇ψa(y)∇ψa(y)
(西德:9) - 2[x − ψ(y)]aHessy[ψa].
Then we use equation A.1 with y1
超过 (西德:6), notice that the order 1 term in σ vanishes since E(西德:6)[(西德:6)] = 0. We find
− y = σU(西德:6). By taking the expectation
乙(西德:6)[x − ψ(y + σU(西德:6))]2
A
= [x − ψ(y)]2
A
(西德:10)
+ σ 2Tr
U
(西德:10)
− σ 2[x − ψ(y)]aTr
U
(西德:9)∇ψa(y)∇ψa(y)
Hessy[ψa]U
(西德:11)
(西德:9)
(西德:9)
(西德:11)
U
+ 乙(西德:6)r(σU(西德:6)),
where we used that E(西德:6)[(西德:6)(西德:9)中号(西德:6)] = Tr[中号] for any symmetric matrix M since
乙(西德:6)[(西德:6)
我j. 下一个, denote Ra(σ ) = E(西德:6)r(σU(西德:6)); we can use the Jensen in-
我
equality and subsequently equation A.1:
j] = δ
(西德:6)
|Ra(σ )| = |乙(西德:6)r(σU(西德:6))| ≤ E(西德:6)|r(σU(西德:6))| ≤ La
6
乙(西德:6)(西德:5)σU(西德:6)(西德:5)3
2
.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Stiefel-Restricted Kernel Machine
2027
= σ ((西德:6)(西德:9)U (西德:9)U(西德:6))1/2 = σ (西德:5)(西德:6)(西德:5)
2. It is useful to notice
2 is distributed according to a chi distribution. By using this remark,
2
下一个, we notice that (西德:5)σU(西德:6)(西德:5)
那 (西德:5)(西德:6)(西德:5)
我们发现
|Ra(σ )| ≤ σ 3 这
6
乙(西德:6)(西德:5)(西德:6)(西德:5)3
2
= σ 3 这
6
√
2(米 + 1)(西德:11)((米 + 1)/2)
(西德:11)(m/2)
,
where the last equality uses the expression for the third moment of the chi
distribution and where the gamma function (西德:11) is the extension of the facto-
rial to the complex numbers.
A.2 Details on Evidence Lower Bound for St-RKM model. Now we
discuss the details of ELBO given in section 4. The first term in equation 4.1
是
乙
qU (z|希 )[日志(p(希
|z))] = − 1
2σ 2
0
乙(西德:6)∼N (0,我)
(西德:5)希
− ψξ (PU φθ (希) + σ PU (西德:6) + δP
U⊥ (西德:6))(西德:5)2
2
− d
2
日志(2πσ 2
0 ),
where we used the following reparameterization following Kingma and
(西德:22)
Welling (2014): 乙
U⊥ )(西德:15))
,
with p(X|z) = N (X|ψξ (z), σ 2
U⊥ ).
0
清楚地, the above expectation can be written as
我), and qU (z|X) = N (z|PU φθ (X), σ 2PU + δ2P
F (PU φθ (X) + (σ PU + δP
qU (z|希 )[ F (z)] = E(西德:6)∼N (0,我)
(西德:21)
乙(西德:6)乙(西德:6)⊥
(西德:5)希
− ψξ (PU φθ (希) + σU(西德:6) + δU⊥(西德:6)⊥)(西德:5)2
2
,
和 (西德:6) ∼ N (0, 我是) 和 (西德:6)⊥ ∼ N (0, 我(西德:2)−m). 因此, we fix σ 2
= 1/2 and take δ >
0
0 to a numerically small value. For the other terms of equation 4.1, 我们用
the formula giving the KL divergence between multivariate normals. Let N
0
and N
1 and covariance
(西德:13)
, (西德:13)
0
1 是 (西德:2)-variate normal distributions with mean μ
0
1, 分别. 然后,
, μ
(西德:23)
吉隆坡(氮
0
, 氮
1) = 1
2
Tr((西德:13)−1
1
(西德:13)
0) + (μ
1
− μ
0)
(西德:9)(西德:13)−1
1 (μ
1
− μ
0) - (西德:2) + 日志
(西德:24)
这 (西德:13)
1
这 (西德:13)
0
(西德:25)(西德:26)
.
By using this identity, we find the second term of equation 4.1,
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
吉隆坡[qU (z|希), q(z|希)] = 1
2
(西德:23)
mσ 2 + ((西德:2) − m)δ2
C 2
(西德:24)
+ 1
C 2
(西德:25)(西德:26)
C 2(西德:2)
σ 2mδ2((西德:2)−m)
,
- (西德:2) + 日志
(西德:5)φθ (希) − PU φθ (希)(西德:5)2
2
2028
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
桌子 2: Data Sets and Hyperparameters Used for the Experiments.
Data Set
氮
d
MNIST
fMNIST
SVHN
dSprites
3DShapes
3D cars
60,000
60,000
73,257
737,280
480,000
17,664
28 × 28
28 × 28
32 × 32 × 3
64 × 64
64 × 64 × 3
64 × 64 × 3
米
10
10
10
5
6
3
中号
256
256
256
256
256
256
笔记: N is the number of training samples, d
the input dimension (resized images), m the sub-
space dimension, and M the minibatch size.
where q(z|X) = N (z|φθ (X), γ 2I(西德:2)). For the third term in equation 4.1, 我们发现
(西德:3)
Tr((σ 2PU + δ2P
吉隆坡[qU (z|希), p(z)] = 1
2
(西德:4)
+ log det((西德:13)) - (西德:2) − log(σ 2mδ2((西德:2)−m))
,
U⊥ )(西德:13)−1) + (PU φθ (希))
(西德:9)(西德:13)−1(PU φθ (希))
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
with p(z) = N (0, (西德:13)). By averaging over i = 1, . . . , n, we obtain
1
n
n(西德:2)
我=1
吉隆坡[qU (z|希), p(z)] = 1
2
(西德:3)
Tr((σ 2PU + δ2P
U⊥ )(西德:13)−1) + Tr(PUCθPU (西德:13)−1)
(西德:4)
+ log det((西德:13)) - (西德:2) − log(σ 2mδ2((西德:2)−m))
,
where we used the cyclic property of the trace and Cθ = 1
φθ (希)
n
φθ (希)(西德:9). This proves the analogous expression in section 4. 最后, the esti-
mation of the optimal (西德:13) can be done in parallel to the maximum likelihood
estimation of the covariance matrix of a multivariate normal.
n
我=1
(西德:9)
A.3 Data Sets and Hyperparameters. We refer to Tables 2 和 3 为了
specific details on the model architectures, data sets, and hyperparameters
used in this article. All models were trained on full data sets and for a maxi-
mum of 1000 纪元. 此外, all data sets are scaled between [0-1] 和
are resized to 28 × 28 dimensions except dSprites and 3D cars. The PyTorch
library (single precision) in Python was used as the programming language
在 8 GB NVIDIA QUADRO P4000 GPU. See algorithm 1 for training the
St-RKM model. In the case of FactorVAE, the discriminator architecture is
same as proposed in the original paper (Kim & Mnih, 2018).
A.3.1 Disentanglement Metrics. MIG was originally proposed by Chen
等人. (2018); 然而, we use the modified metric as proposed in Locatello
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Stiefel-Restricted Kernel Machine
2029
桌子 3: Model Architectures.
Data Set
Architecture
MNIST/fMNIST/
φθ (·) =
/SVHN/3DShapes/
sDprites/3Dcars
⎧
⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎩
Conv [C] × 4 × 4;
Conv [c × 2] × 4 × 4;
Conv [c × 4] × ˆk × ˆk;
FC 256;
FC 50 (Linear)
ψζ (·) =
⎧
⎪⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎪⎩
FC 256;
FC [c × 4] × ˆk × ˆk;
Conv [c × 2] × 4 × 4;
Conv [C] × 4 × 4;
Conv [C] (Sigmoid)
Notes: All convolutions and transposed convolutions are with stride 2 and padding 1. 和-
less stated otherwise, layers have parametric-RELU (α = 0.2) activation functions, 除了
output layers of the preimage maps, which have sigmoid activation functions (since in-
put data are normalized [0, 1]). Adam and Cayley ADAM optimizers have learning rates
−4, 分别. The preimage map/decoder network is always taken as
2 × 10
transposed of the feature map/encoder network. c = 48 for 3D cars; and c = 64 for all oth-
呃. 更远, ˆk = 3 and stride 1 for MNIST, fMNIST, SVHN and 3DShapes; and ˆk = 4 为了
其他的. SVHN and 3DShapes are resized to 28 × 28 input dimensions.
−4 and 10
等人. (2019). We evaluate this score on 5000 test points across all the con-
sidered data sets. SAP and Eastwood’s metrics use different classifiers to
compute the importance of each dimension of the learned representation
for predicting a ground-truth factor. For these metrics, we randomly sam-
普莱 5000 和 3000 training and testing points, 分别. To compute
these metrics, we use the open source library available at github.com/
google-research/disentanglement_lib.
A.4 Ablation Studies.
A.4.1 Significance of the KPCA Loss. 在这个部分, we show an ablation
study on the KPCA loss and evaluate its effect on disentanglement. We re-
peat the experiments of section 5 on the mini-3DShapes data set (floor hue,
wall hue, object hue, and scale: 8000 样品), where we consider three dif-
ferent variants of the proposed model:
1. St-RKM (σ = 0): The KPCA loss is optimized in a stochastic manner
using the Cayley ADAM optimizer, as proposed in this article.
2. Gen-RKM: The KPCA loss is optimized exactly at each step by per-
forming an eigendecomposition in each minibatch (this corresponds
to the algorithm in Pandey et al., 2021).
3. AE-PCA: A standard AE is used, and a reconstruction loss is mini-
mized for the training. As a postprocessing step, a PCA is performed
on the latent embedding of the training data.
The encoder/decoder maps are the same across all the models, and for the
AE-PCA model, additional linear layers are used to map the latent space to
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
2030
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
桌子 4: Training Timings per Epoch (in minutes) and Disentanglement Scores
(Heusel et al., 2017) for Different Variants of RKM When Trained on the mini-
3Dshapes Data Set.
St-RKM (σ = 0) Gen-RKM AE-PCA
Training time
Disentanglement score
Compliance score
Information score
Lasso
RF
Lasso
RF
Lasso
RF
3.01 (0.71)
0.40 (0.02)
0.27 (0.01)
0.64 (0.01)
0.67 (0.02)
1.01 (0.02)
0.98 (0.01)
9.21 (0.54)
0.44 (0.01)
0.31 (0.02)
0.51 (0.01)
0.58 (0.01)
1.11 (0.02)
1.09 (0.01)
2.87 (0.33)
0.35 (0.01)
0.22 (0.02)
0.42 (0.01)
0.45 (0.02)
1.20 (0.01)
1.17 (0.02)
Notes: Gen-RKM has the worst training time but gets the highest disentangle-
ment scores. This is due to the exact eigendecomposition of the kernel matrix at
every iteration. This computationally expensive step is approximated by the St-
RKM model, which achieves significant speed-up and scalability to large data
套. 最后, the AE-PCA model has the fastest training time due to the absence
of eigendecompositions in the training loop. 然而, using PCA in the post-
processing step alters the basis of the latent space. This basis is unknown to the
decoder network, resulting in degraded disentanglement performance.
桌子 5: FID Scores Computed on Randomly Generated 8000 Images When
Trained with Architecture and Hyperparameters.
St-RKM
VAE
β-VAE
FactorVAE
InfoGAN
MNIST
fMNIST
24.63 (0.22)
61.44 (1.02)
36.11 (1.01)
73.47 (0.73)
42.81 (2.01)
75.21 (1.11)
35.48 (0.07)
69.73 (1.54)
45.74 (2.93)
84.11 (2.58)
Notes: Lower is better with standard deviations. Adapted from Dupont (2018).
the subspace. From Table 4, we conclude that optimizing the KPCA loss
during training improves disentanglement. 而且, using a stochastic
algorithm improves computation time and scalability with only a slight
decrease in disentanglement score. Note that calculating the exact eigen-
decomposition at each step (Gen-RKM) comes with numerical difficul-
领带. 尤其, double floating-point precision has to be used together
with a careful selection of the number of principal components to avoid
ill-conditioned kernel matrices. This problem is not encountered when us-
ing the St-RKM training algorithm.
A.4.2 Smaller Encoder/Decoder Architecture. 在这个部分, we analyze the
impact of the encoder/decoder architecture on the generation quality of
considered models. The generation quality experiment of section 5 is re-
peated on the fMNIST and MNIST data set, where the architecture and hy-
perparameters are adapted from Dupont (2018). From Table 5 和图 9,
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Stiefel-Restricted Kernel Machine
2031
桌子 6: Computing the Diagonalization Scores (见图 3).
楷模
dSprites
3DShapes
3D cars
St-RKM-sl (σ = 10
St-RKM (σ = 10
St-RKM (σ = 10
−3, U(西德:7))
−3, random U)
−3, U(西德:7))
0.17 (0.05)
0.26 (0.05)
0.61 (0.02)
0.23 (0.03)
0.30 (0.10)
0.72 (0.01)
0.21 (0.04)
0.31 (0.09)
0.69 (0.03)
(西德:9)
i∈C U
φθ (希 ) (比照.
Notes: Denote M = 1
|C|
F , 在哪里
方程 3.6). Then we compute the score as
diag : Rm×m (西德:8)→ Rm×m sets the off-diagonal elements of matrix to zero. 这
scores are computed for each model over 10 random seeds and show the mean
(标准差). Lower scores indicate better diagonalization.
(西德:9)
U(西德:7), with yi
(西德:7) ∇ψ(做 )∇ψ(做 )
(西德:16)
(西德:16)
(西德:16)
(西德:16)
M − diag(中号)
=P
U
/ (西德:5)中号(西德:5)
(西德:9)
F
we see that the overall FID scores and generation quality have improved;
然而, the relative scores among the models did not change significantly.
A.4.3 Analysis of St-RKM with a Fixed U. We discuss here the role of the
optimization of St((西德:2), 米) on disentanglement in the case of a classical AE
loss (σ = 0). 这样做, a matrix ˜U ∈ St((西德:2), 米) is generated randomly3 and
kept fixed during the training of the following optimization problem,
min
我,ξ
λ 1
n
n(西德:2)
我=1
L(0)
ξ, ˜U (希
, φθ (希)) + 1
n
(西德:12)
n(西德:2)
我=1
(西德:5)磷(ε)
,
˜U⊥ φθ (希)(西德:5)2
2
(西德:15)
(西德:13)(西德:14)
(A2)
regularized PCA objective
˜U⊥ = ε( ˜U ˜U (西德:9) + εI(西德:2))
with λ = 1 and where ε ≥ 0 is a regularization constant and where the reg-
ularized (or mollified) projector P(ε)
−1 is used in order to
prevent numerical instabilities. 的确, if ε = 0, the second term in equation
A2 (PCA term) is not strictly convex as a function of φθ, since this quadratic
form has flat directions along the column subspace of ˜U. Our numerical
simulations in single-precision PyTorch with ε = 0 exhibit instabilities, 那
是, the PCA term in equation A.2 takes negative values during the training.
因此, the regularized projector is introduced so that the PCA quadratic
is strongly convex for ε > 0. This instability is not observed in the training
of equation 3.3 where U is not fixed. This is one asset of our training pro-
cedure using optimization over Stiefel manifold. Explicitly, the regularized
projector satisfies the following properties:
˜U⊥ u⊥ = u⊥ for all u⊥ ∈ (范围(U ))
˜U⊥ u = εu for all u ∈ range(U ).
• P(ε)
• P(ε)
⊥
,
3
Using a random ˜U ∈ St((西德:2), 米) can be interpreted as sketching the encoder map in the
spirit of randomized orthogonal systems (ROS) sketches (see Yang, Pilanci, & Wainwright,
2017).
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
2032
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
数字 8: Samples of randomly generated batch of images used to compute FID
scores and SWD scores (见图 4).
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Thanks to the push-through identity, we have the alternative expression
磷(ε)
磷(ε)
˜U⊥ = I − U(U (西德:9)U + εIm)
˜U⊥ = P ˜U⊥ , as it
−6, the regularized
应该. In our experiments, we set ε = 10
PCA objective in equation A.2 takes negative values after a few epochs due
to the numerical instability as mentioned above.
−1U (西德:9). 所以, it holds limε→0
−5. If ε ≤ 10
Stiefel-Restricted Kernel Machine
2033
数字 9: Samples of randomly generated images used to compute the FID
scores. 见表 5.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
数字 10: (A) Loss evolution (log plot) during the training of equation A.2 over
1000 epochs with ε = 10−5 once with Cayley ADAM optimizer (green curve)
and then without (blue curve). (乙) Traversals along the principal components
when the model was trained with a fixed U, 那是, with the objective given by
equation A.2 and ε = 10−5. There is no clear isolation of a feature along any of
the principal components, indicating further that optimizing over U is key to
better disentanglement.
In Figure 10a, the evolution of the training objective A.2 is displayed.
It can be seen that the final objective has a lower value [经验值(6.78) ≈ 881]
when U is optimized compared to its fixed counterpart [经验值(6.81) ≈ 905],
showing the merit of optimizing over Stiefel manifold for the same parame-
ter ε. 因此, the subspace determined by range(U ) has to be adapted to the
encoder and decoder networks. 换句话说, the training over θ, ξ is not
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
2034
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
sufficient to minimize the St((西德:2), 米) objective with Adam. Figure 10b further
explores the latent traversals in the context of this ablation study. In the top
row of Figure 10b (latent traversal in the direction of u1), both the shape of
the object and the wall hue are changing. A coupling between wall hue and
shape is also visible in the bottom row of this figure.
致谢
Most of this work was done when M.F. was at KU Leuven.
欧洲联盟: The research leading to these results received funding from the Euro-
pean Research Council under the European Union’s Horizon 2020 研究
and innovation program/ERC Advanced Grant E-DUALITY (787960). 这
article reflects only the authors’ views, and the EU is not liable for any use
that may be made of the contained information.
Research Council KUL: Optimization frameworks for deep kernel ma-
chines C14/18/068.
Flemish government: (A) FWO: 项目: GOA4917N (Deep Restricted
Kernel Machines: Methods and Foundations), PhD/postdoc grant. (乙) 这
research received funding from the Flemish government (AI Research Pro-
公克). We are affiliated with Leuven.AI-KU Leuven institute for AI, B-3000,
Leuven, 比利时.
Ford KU Leuven Research Alliance Project: KUL0076 (stability analysis
and performance improvement of deep reinforcement learning algorithms).
Vlaams Supercomputer Centrum: The computational resources and ser-
vices used in this work were provided by the VSC (Flemish Supercomputer
中心), funded by the Research Foundation–Flanders (FWO) and the Flem-
ish government department EWI.
参考
Absil, P.-A., Mahony, R。, & Sepulchre, 右. (2008). Optimization algorithms on matrix
manifolds. 普林斯顿大学, 新泽西州: 普林斯顿大学出版社.
Avron, H。, 阮, H。, & Woodruff, D. (2014). Subspace embeddings for the poly-
nomial kernel. In Z. Ghahramani, 中号. Welling, C. 科尔特斯, 氮. 劳伦斯, & K. 问.
温伯格 (编辑。), Advances in neural information processing systems, 27 (PP. 2258–
2266). 红钩, 纽约: 柯兰.
本吉奥, Y。, 考维尔, A。, & Vincent, 磷. (2013). Representation learning: A review and
new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence,
35(8), 1798–1828. 10.1109/TPAMI.2013.50, 考研: 23787338
伯吉斯, C。, & Kim, H. (2018). 3Dshapes dataset. https://github.com/deepmind/
3dshapes-dataset/
伯吉斯, C. P。, 希金斯, 我。, 朋友, A。, Matthey, L。, Watters, N。, Desjardins, G。, & Ler-
chner, A. (2017). Understanding disentangling in β-VAE. In NIPS 2017 工作-
shop on Learning Disentangled Representations: From Perception to Control. https:
//sites.google.com/view/disentanglenips2017
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Stiefel-Restricted Kernel Machine
2035
陈, 右. 时间. Q., 李, X。, Grosse, 右. B., & Duvenaud, D. K. (2018). Isolating sources
of disentanglement in variational autoencoders. 在S. 本吉奥, H. 瓦拉赫, H.
拉罗谢尔, K. Grauman, 氮. Cesa-Bianchi, & 右. 加内特 (编辑。), Advances in neu-
ral information processing systems, 31 (PP. 2610–2620). 红钩, 纽约: 柯兰.
Dupont, 乙. (2018). Learning disentangled joint continuous and discrete representa-
系统蒸发散. 在S. 本吉奥, H. 瓦拉赫, H. 拉罗谢尔, K. Grauman, 氮. Cesa-Bianchi, & 右.
加内特 (编辑。), Advances in neural information processing systems, 31 (PP. 708–718).
红钩, 纽约: 柯兰.
Eastwood, C。, & 威廉姆斯, C. K. 我. (2018). A framework for the quantitative evalua-
tion of disentangled representations. In Proceedings of the International Conference
on Learning Representations.
戈什, P。, Sajjadi, 中号. S。, Vergari, A。, 黑色的, M。, & Schölkopf, 乙. (2020). From varia-
tional to deterministic autoencoders. In Proceedings of the International Conference
on Learning Representations.
Heusel, M。, Ramsauer, H。, Unterthiner, T。, Nessler, B., & Hochreiter, S. (2017). GANs
trained by a two time-scale update rule converge to a local Nash equilibrium. 在
我. Guyon, 是. V. Luxburg, S. 本吉奥, H. 瓦拉赫, 右. 弗格斯, S. Vishwanathan, &
右. 加内特 (编辑。), Advances in neural information processing systems, 30 (PP. 6629–
6640). 红钩, 纽约: 柯兰.
希金斯, 我。, Matthey, L。, 朋友, A。, 伯吉斯, C。, Glorot, X。, 博特维尼克, M。, . . . Lerchner, A.
(2017). Beta-VAE: Learning basic visual concepts with a constrained variational
框架. In Proceedings of the International Conference on Learning Representations
(卷. 2, p. 6).
欣顿, G. 乙. (2005). What kind of a graphical model is the brain? In Proceed-
ings of the 19th International Joint Conference on Artificial Intelligence (PP. 1765–
1775).
Karras, T。, Aila, T。, Laine, S。, & Lehtinen, J. (2017). Progressive growing of GANs
for improved quality, 稳定, and variation. 国际会议录
Conference on Learning Representations.
Kim, H。, & Mnih, A. (2018). Disentangling by factorising. In Proceedings of the Thirty-
Fifth International Conference on Machine Learning (卷. 80, PP. 2649–2658).
Kingma, D. P。, & Welling, 中号. (2014). Auto-encoding variational Bayes. In Proceedings
of the International Conference on Learning Representations.
Kumar, A。, Sattigeri, P。, & Balakrishnan, A. (2018). Variational inference of disen-
tangled latent concepts from unlabeled observations. In Proceedings of the Interna-
tional Conference on Learning Representations. https://openreview.net/forum?id=
H1kG7GZAW
乐存, Y。, & 科尔特斯, C. (2010). MNIST handwritten digit database. http://yann.lecun
.com/exdb/mnist/
乐存, Y。, 黄, F. J。, & 波图, L. (2004). Learning methods for generic object
recognition with invariance to pose and lighting. In Proceedings of the Conference
on Computer Vision and Pattern Recognition.
李, J。, 李, F。, & Todorovic, S. (2020). Efficient Riemannian optimization on the Stiefel
manifold via the Cayley transform. In Proceedings of the International Conference on
Learning Representations.
Locatello, F。, Bauer, S。, Luˇci´c, M。, Rätsch, G。, Gelly, S。, Schölkopf, B., & Bachem,
氧. F. (2019). Challenging common assumptions in the unsupervised learning of
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
2036
A. Pandey, 中号. Fanuel, J. Schreurs, 和 J. Suykens
disentangled representations. In Proceedings of the International Conference on Ma-
chine Learning.
Locatello, F。, Tschannen, M。, Bauer, S。, Rätsch, G。, Schölkopf, B., & Bachem, 氧. (2020).
Disentangling factors of variations using few labels. In International Conference on
Learning Representations.
Matthey, L。, 希金斯, 我。, Hassabis, D ., & Lerchner, A. (2017). dSprites: Disentanglement
testing Sprites dataset. https://github.com/deepmind/dsprites-dataset/
Nesterov, 是. (2014). Introductory lectures on convex optimization: A basic course. 柏林:
施普林格.
Netzer, Y。, 王, T。, Coates, A。, Bissacco, A。, 吴, B., & 的, A. 是. (2011). Reading
digits in natural images with unsupervised feature learning. In NIPS Workshop
on Deep Learning and Unsupervised Feature Learning. http://ufldl.stanford.edu/
housenumbers/nips2011_housenumbers.pdf
Pandey, A。, Schreurs, J。, & Suykens, J. A. K. (2020). Robust generative restricted
kernel machines using weighted conjugate feature duality. 在诉讼程序中
the Sixth International Conference on Machine Learning, Optimization, and Data
科学.
Pandey, A。, Schreurs, J。, & Suykens, J. A. (2021). Generative restricted kernel
machines: A framework for multi-view generation and disentangled feature
学习. Neural Networks, 135, 177–191. 10.1016/j.neunet.2020.12.010, 考研:
33395588
芦苇, S。, 张, Y。, 张, Y。, & 李, H. (2015). Deep visual analogy-making. 在C中.
科尔特斯, 氮. 劳伦斯, D. 李, 中号. Sugiyama, & 右. 加内特 (编辑。), 神经方面的进展
信息处理系统, 28. 红钩, 纽约: 柯兰.
Rezende, D. J。, & Mohamed, S. (2015). Variational inference with normalizing flows.
In Proceedings of the International Conference on Machine Learning.
Rolínek, M。, Zietlow, D ., & Martius, G. (2019). Variational autoencoders pursue PCA
方向 (by accident). 在诉讼程序中 2019 IEEE/CVF conference on Computer
Vision and Pattern Recognition (PP. 12398–12407).
Salakhutdinov, R。, & 欣顿, G. (2009). Deep Boltzmann machines. 在诉讼程序中
the Twelfth International Conference on Artificial Intelligence and Statistics.
Suykens,
J. A. K.
(2017). Deep restricted kernel machines using conjugate
feature duality. 神经计算, 29(8), 2123–2163. 10.1162/neco_a_00984,
考研: 28562217
Xiao, H。, Rasul, K., & Vollgraf, 右. (2017). Fashion-MNIST: A novel image dataset for
benchmarking machine learning algorithms. arXiv:1708.07747.
哪个, Y。, Pilanci, M。, & Wainwright, 中号. J. (2017). Randomized sketches for kernels:
Fast and optimal nonparameteric regression. Annals of Statistics, 45(3), 991–1023.
10.1214/16-AOS1472
Received October 4, 2021; accepted May 24, 2022.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
1
0
2
0
0
9
2
0
4
2
4
5
4
n
e
C
哦
_
A
_
0
1
5
2
8
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3