文章
Communicated by Ben Tsuda
Recurrent Connections in the Primate Ventral Visual Stream
Mediate a Trade-Off Between Task Performance and Network
Size During Core Object Recognition
Aran Nayebi
anayebi@stanford.edu
Javier Sagastuy-Brena
jvrsgsty@stanford.edu
Daniel M. Bear
dbear@stanford.edu
斯坦福大学, 斯坦福大学, CA 94305, 美国.
Kohitij Kar
kohitij@mit.edu
和, 剑桥, 嘛 02139, 美国.
Jonas Kubilius
qbilius@gmail.com
和, 剑桥, 嘛 02139, 美国。, and KU Leuven, Leuven 3000, 比利时
Surya Ganguli
sganguli@stanford.edu
David Sussillo
sussillo@stanford.edu
斯坦福大学, 斯坦福大学, CA 94305, 美国.
詹姆斯·J. DiCarlo
dicarlo@mit.edu
和, 剑桥, 嘛 02139, 美国.
Daniel L. K. Yamins
yamins@stanford.edu
斯坦福大学, 斯坦福大学, CA 94305, 美国.
The computational role of the abundant feedback connections in the ven-
tral visual stream is unclear, enabling humans and nonhuman primates
to effortlessly recognize objects across a multitude of viewing condi-
系统蒸发散. Prior studies have augmented feedforward convolutional neural
Aran Nayebi is the corresponding author.
神经计算 34, 1652–1675 (2022) © 2022 麻省理工学院
https://doi.org/10.1162/neco_a_01506
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
C
哦
_
A
_
0
1
5
0
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Recurrent Connections in the Primate Ventral Visual Stream
1653
网络 (CNNs) with recurrent connections to study their role in vi-
sual processing; 然而, often these recurrent networks are optimized
directly on neural data or the comparative metrics used are undefined
for standard feedforward networks that lack these connections. 在这个
工作, we develop task-optimized convolutional recurrent (ConvRNN)
network models that more correctly mimic the timing and gross neu-
roanatomy of the ventral pathway. Properly chosen intermediate-depth
ConvRNN circuit architectures, which incorporate mechanisms of feed-
forward bypassing and recurrent gating, can achieve high performance
on a core recognition task, comparable to that of much deeper feedfor-
ward networks. We then develop methods that allow us to compare both
CNNs and ConvRNNs to finely grained measurements of primate cat-
egorization behavior and neural response trajectories across thousands
of stimuli. We find that high-performing ConvRNNs provide a better
match to these data than feedforward networks of any depth, predict-
ing the precise timings at which each stimulus is behaviorally decoded
from neural activation patterns. 而且, these ConvRNN circuits con-
sistently produce quantitatively accurate predictions of neural dynamics
from V4 and IT across the entire stimulus presentation. 实际上, 我们发现
that the highest-performing ConvRNNs, which best match neural and be-
havioral data, also achieve a strong Pareto trade-off between task perfor-
mance and overall network size. 合在一起, our results suggest the
functional purpose of recurrence in the ventral pathway is to fit a high-
performing network in cortex, attaining computational power through
temporal rather than spatial complexity.
1 介绍
The visual system of the brain must discover meaningful patterns in a com-
plex physical world (James, 1890). 之内 200 多发性硬化症, primates can quickly
identify objects despite changes in position, 姿势, 对比, background,
foreground, and many other factors from one occasion to the next, a be-
havior known as “core object recognition” (Pinto, 考克斯, & Dicarlo, 2008;
DiCarlo, Zoccolan, & Rust, 2012). It is known that the ventral visual stream
(VVS) underlies this ability by transforming the retinal image of an object
into a new internal representation, in which high-level properties, 例如
object identity and category, are more explicit (DiCarlo et al., 2012).
Nontrivial dynamics result from a ubiquity of recurrent connections in
the VVS, including synapses that facilitate or depress dense local recur-
rent connections within each cortical region and long-range connections
between different regions, such as feedback from higher to lower visual
cortex (吉尔伯特 & 吴, 2013). 此外, the behavioral roles of recur-
rence and dynamics in the visual system are not well understood. 一些
conjectures are that recurrence “fills in” missing data, (Spoerer, McClure, &
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
C
哦
_
A
_
0
1
5
0
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
1654
A. Nayebi et al.
Kriegeskorte, 2017; Michaelis, Bethge, & Ecker, 2018; Rajaei, Mohsenzadeh,
Ebrahimpour, & Khaligh-Razavi, 2019; Linsley, Kim, Veerabadran, Windolf,
& Serre, 2018) such as object parts occluded by other objects; that it “sharp-
ens” representations by top-down attentional feature refinement, allowing
for easier decoding of certain stimulus properties or performance of certain
任务 (吉尔伯特 & 吴, 2013; Lindsay, 2015; McIntosh, Maheswaranathan, Sus-
sillo, & Shlens, 2018; 李, Jie, 冯, 刘, & 严, 2018; Kar, Kubilius, 施密特,
Issa, & DiCarlo, 2019); that it allows the brain to “predict” future stimuli,
such as the frames of a movie (饶 & Ballard, 1999; Lotter et al., 2017; Issa,
Cadieu, & DiCarlo, 2018); or that recurrence “extends” a feedforward com-
putation, reflecting the fact that an unrolled recurrent network is equivalent
to a deeper feedforward network that conserves on neurons (and learnable
参数) by repeating transformations several times (Liao & Poggio,
2016; Zamir et al., 2017; Leroux et al., 2018; Rajaei et al., 2019; Kubilius et al.,
2019; Spoerer, Kietzmann, Mehrer, Charest, & Kriegeskorte, 2020). 正式的
computational models are needed to test these hypotheses: if optimizing a
model for a certain task leads to accurate predictions of neural dynamics,
then that task may be a primary reason those dynamics occur in the brain.
We therefore broaden the method of goal-driven modeling from solving
tasks with feedforward CNNs (Yamins & DiCarlo, 2016) or recurrent neu-
ral networks (RNNs) (Mante, Sussillo, 谢诺伊, & Newsome, 2013) 给前任-
plain dynamics in the primate visual system, building convolutional RNNs
(ConvRNNs), 如图所示 1. There has been substantial prior work
in this domain (Liao & Poggio, 2016; McIntosh et al., 2018; Zamir et al., 2017;
Kubilius et al., 2019; Kietzmann et al., 2019; Spoerer et al., 2020), 我们
go beyond in several important ways.
We show that with a novel choice of layer-local recurrent circuit and
long-range feedback connectivity pattern, ConvRNNs can match the per-
formance of much deeper feedforward CNNs on ImageNet but with far
fewer units and parameters, as well as a more anatomically consistent
number of layers, by extending these computations through time. 实际上,
such ConvRNNs most accurately explain neural dynamics from V4 and IT
across the entirety of stimulus presentation with a temporally fixed linear
mapping compared to alternative recurrent circuits. 此外, 我们发现
that these suitably chosen ConvRNN circuit architectures provide a better
match to primate behavior in the form of object solution times compared
to feedforward CNNs. We observe that ConvRNNs that attain high task
performance but have small overall network size, as measured by num-
ber of units, are most consistent with these data, while even the highest-
performing but biologically implausible deep feedforward models are
overall a less consistent match. 实际上, we find a strong Pareto trade-off
between network size and performance, with ConvRNNs of biologically
plausible intermediate depth occupying the sweet spot with high perfor-
mance and a (comparatively) small overall network size. Because we do not
fit neural networks end-to-end to neural data (see Kietzmann et al., 2019),
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
C
哦
_
A
_
0
1
5
0
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Recurrent Connections in the Primate Ventral Visual Stream
1655
数字 1: ConvRNNs as models of
the primate ventral visual stream.
Performance-optimized recurrence: Convolutional recurrent networks (骗局-
vRNNs) have a combination of local recurrent circuits (绿色的) and long-range
feedback connections (红色的) added on top of a feedforward CNN BaseNet back-
骨 (蓝色的). Feedforward CNNs are therefore a special case of ConvRNNs, 和
we consider a variety of CNNs of varying depths, trained on the ImageNet cat-
egorization task. We also perform large-scale evolutionary searches over the
local and long-range feedback connections. 此外, we consider particu-
lar choices of lightweight (in terms of parameter count) decoding strategy that
determines the final object category of that image. In our implementation dis-
played on the top, propagation along each arrow takes one time step (10 多发性硬化症)
to mimic conduction delays between cortical layers. Measurements: From each
network class, we measure categorization performance and its size in terms of
its parameter and neuron count. Comparison to neural and behavioral data: 每个
stimulus was presented for 100 多发性硬化症, followed by a mean gray stimulus inter-
leaved between images, lasting a total of 260 多发性硬化症. All images were presented to
the models for 10 time steps (对应于 100 多发性硬化症), followed by a mean
gray stimulus for the remaining 15 time steps, to match the image presentation
to the primates. We stipulated that units from each multiunit array must be fit
by features from a single model layer, detailed in Section A.6.2. Model features
produce a temporally varying output that can be compared to primate neural
dynamics in V4 and inferior temporal cortex (它), as well as temporally varying
behaviors in the form of object solution times (OST).
but instead show that these outcomes emerge naturally from task perfor-
曼斯, our approach enables a normative interpretation of the structural
and functional design principles of the model.
Our work is also the first to develop large-scale, task-optimized
ConvRNNs with biologically plausible temporal unrolling. Unlike most
studies of combinations of convolutional and recurrent networks, 哪个
posit a recurrent subnetwork concatenated onto the end of a convolutional
backbone (McIntosh et al., 2018), we model local recurrence implanted
within ConvRNN layers, and allow long-range feedback between layers.
而且, we treat each connection in the network, whether feedforward
or feedback, as a real temporal object with a biophysical conduction delay
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
C
哦
_
A
_
0
1
5
0
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
1656
A. Nayebi et al.
(set at ∼10 ms), rather than the typical procedure (例如, as in McIntosh et al.,
2018; Zamir et al., 2017; and Kubilius et al., 2019) in which the feedforward
component of the network (no matter now deep) operates in one time step.
因此, our networks can be directly compared with neural and behav-
ioral trajectories at a fine-grained scale limited only by the conduction delay
本身.
This level of realism is especially important for establishing what
we have found appears to be the main real quantitative advantage of
ConvRNNs as biological models as compared to very deep feedforward
网络. 尤其, we can define an improved metric for assessing the
correctness of the match between a ConvRNN network, thought of as a dy-
namical system, and the actual trajectories of real neurons. By treating such
feedforward networks as ConvRNNs with recurrent connections set to 0,
we can map these networks to temporal trajectories as well. 因此, 我们
can directly ask how much of the neural-behavioral trajectory of real brain
data is explicable by very deep feedforward networks. This is an important
question because implausibly deep networks have been shown in the litera-
ture to achieve not only the highest categorization performance (他, 张,
Ren, & Sun, 2016) but also competitive results on matching static (tempo-
rally averaged) neural responses (Schrimpf et al., 2018). Due to nonbiolog-
ical temporal unrolling, previous work with comparing such networks to
temporal trajectories in neural data (Kubilius et al., 2019) has been forced to
unfairly score feedforward networks as total failures, with temporal match
score artificially set at 0. With our improved realism, 我们发现 (参见部分
2) that deep feedforward networks actually make quite nontrivial temporal
predictions that do explain some of the reliable temporal variability of real
神经元. 在此背景下, our finding that plausibly deep ConvRNNs in turn
meaningfully outperform these deep feedforward networks on this more
fair metric is a strong and nontrivial signal of the actually better biological
match of ConvRNNs as compared to deep feedforward networks.
2 结果
2.1 An Evolutionary Architecture Search Yields Specific Layer-Local
Recurrent Circuits and Long-Range Feedback Connectivity Patterns That
Improve Task Performance and Maintain Small Network Size. We first
tested whether augmenting CNNs with standard RNN circuits from the
machine learning community, SimpleRNNs and LSTMs, could improve
performance on ImageNet object recognition (see Figure 2a). We found that
these recurrent circuits added a small amount of accuracy when introduced
into the convolutional layers of a shallow, six-layer feedforward backbone
(FF in Figure S1) based off the AlexNet (克里热夫斯基, 吸勺, & 欣顿,
2012) 建筑学, which we refer to as a “BaseNet” (see section A.3
for architecture details). 然而, there were two problems with these
resultant recurrent architectures. 第一的, these ConvRNNs did not perform
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
C
哦
_
A
_
0
1
5
0
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Recurrent Connections in the Primate Ventral Visual Stream
1657
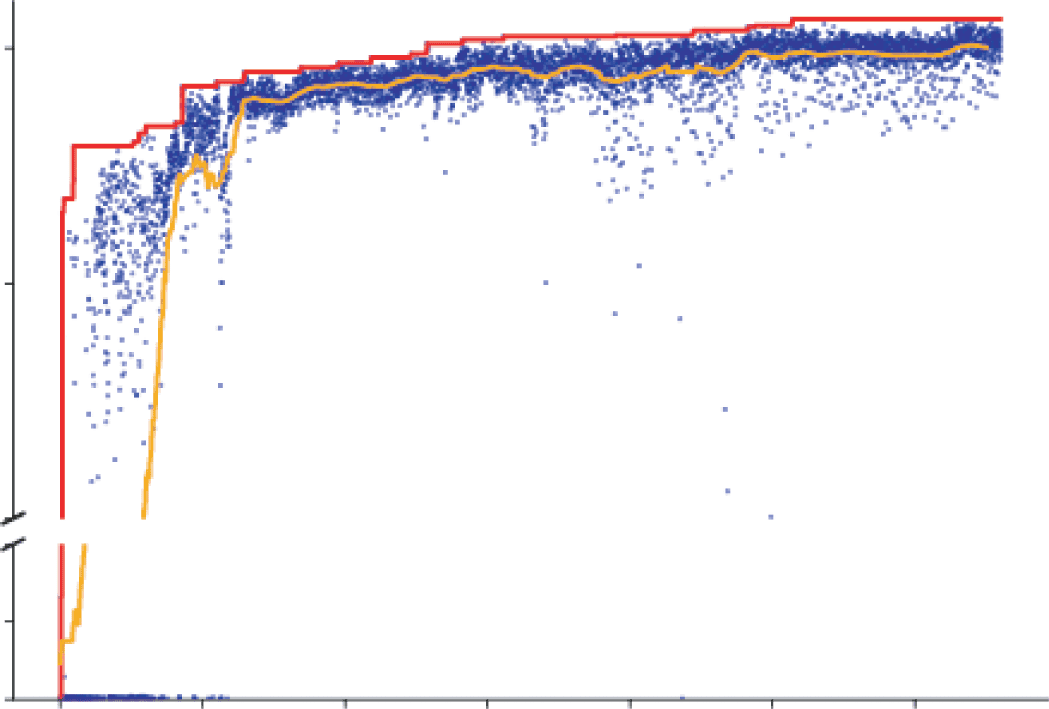
数字 2: Suitably chosen intermediate ConvRNN circuits can match the ob-
ject recognition performance of much deeper feedforward models. (A) Archi-
tectural differences between ConvRNN circuits: Standard ResNet blocks and
SimpleRNN circuits have direct passthrough but not gating. 即, 在
first time step, the output of a given ConvRNN layer is directly a single linear-
nonlinear function of its input, equivalent to that of a feedforward CNN layer
+ 乙), where f is a nonlinear function such as ELU/ReLU and xt is
( F (W ∗ xt
输入). The LSTM circuit has gating, denoted by T-junctions, but not direct
passthrough. The reciprocal gated circuit (RGC) has both. (乙) ConvRNN circuit
搜索: Each blue dot represents a model, sampled from hyperparameter space,
trained for five epochs. The orange line is the average performance of the last 50
models up to that time. The red line denotes the top-performing model at that
point in the search. Search space schematic: Question marks denote optional con-
连接, which may be conventional or depth-separable convolutions with a
choice of kernel size. (C) Performance of models fully trained on ImageNet. 我们
compared the performance of an 11-layer feedforward base model (BaseNet)
modeled after ResNet-18, a control ConvRNN model with trainable time con-
stants (Time Decay), along with various other common RNN architectures im-
planted into this BaseNet, as well as the median reciprocal gated circuit (RGC)
model from the search (RGC Median) with or without global feedback connec-
活力, and its minimally unrolled control (see the first table in section A.3 for the
exact time step values). The RGC Random model was selected randomly from
the initial, random phase of the model search. Parameter and unit counts (全部的
number of neurons in the output of each layer) in millions are shown on top of
each bar.
substantially better than parameter-matched, minimally unrolled controls,
defined as the minimum number of time steps after the initial feedforward
pass whereby all recurrence connections were engaged at least once. 这
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
C
哦
_
A
_
0
1
5
0
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
1658
A. Nayebi et al.
control comparison suggested that the observed performance gain was due
to an increase in the number of unique parameters added by the implanted
ConvRNN circuits rather than temporally extended recurrent computation.
第二, making the feedforward model wider or deeper yielded an even
larger performance gain than adding these standard RNN circuits, but with
fewer parameters. This suggested that standard RNN circuits, 虽然
well suited for a range of temporal tasks, are less well suited for inclusion
within deep CNNs to solve challenging object recognition tasks.
We speculated that this was because standard circuits lack a combination
of two key properties, each of which on their own have been successful
either purely for RNNs or for feedforward CNNs: (1) direct passthrough,
where at the first time step, a zero-initialized hidden state allows feedfor-
ward input to pass on to the next layer as a single linear-nonlinear layer
just as in a standard feedforward CNN layer (see Figure 2a, top left); 和
(2) Gating, in which the value of a hidden state determines how much of
the bottom-up input is passed through, retained, or discarded at the next
time step (see Figure 2a, top right). 例如, LSTMs employ gating
but not direct passthrough, as their inputs must pass through several non-
linearities to reach their output, whereas SimpleRNNs do pass through a
zero-initialized hidden state but do not gate their input (see Figure 2a; 看
section A.3 for cell equations). 此外, each of these computations has
direct analogies to biological mechanisms: direct passthrough would corre-
spond to feedforward processing in time, and gating would correspond to
adaptation to stimulus statistics across time (Hosoya, Baccus, & Meister,
2005; McIntosh et al., 2016).
We thus implemented recurrent circuits with both features to determine
whether they function better than standard circuits within CNNs. One ex-
ample of such a structure is the reciprocal gated circuit (RGC; Nayebi et al.,
2018), which passes through its zero-initialized hidden state and incorpo-
rates gating (see Figure 2a, bottom right; see section A.3.7 for the circuit
方程). Adding this circuit to the six-layer BaseNet (FF) increased accu-
racy from 0.51 和 0.53 (RGC Minimal, the minimally unrolled, parameter-
matched control version) 到 0.6 (RGC Extended). 而且, the RGC used
substantially fewer parameters than the standard circuits to achieve greater
准确性 (see Figure S1).
然而, it has been shown that different RNN structures can succeed or
fail to perform a given task because of differences in trainability rather than
differences in capacity (柯林斯, Sohl-Dickstein, & Sussillo, 2017). 所以,
we designed an evolutionary search to jointly optimize over both discrete
choices of recurrent connectivity patterns and continuous choices of learn-
ing hyperparameters and weight initializations (search details are in sec-
tion A.4). While a large-scale search over thousands of convolutional LSTM
architectures did yield a better purely gated LSTM-based ConvRNN (LSTM
Opt), it did not eclipse the performance of the smaller RGC ConvRNN. 在
事实, applying the same hyperparameter optimization procedure to the RGC
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
C
哦
_
A
_
0
1
5
0
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
Recurrent Connections in the Primate Ventral Visual Stream
1659
ConvRNNs equally increased that architecture class’s performance and fur-
ther reduced its parameter count (see Figure S1, RGC Opt).
所以, given the promising results with shallower networks, 我们
turned to embedding recurrent circuit motifs into intermediate-depth feed-
forward networks at scale, whose number of feedforward layers corre-
sponds to the timing of the ventral stream (DiCarlo et al., 2012). We then
performed an evolutionary search over these resultant intermediate-depth
recurrent architectures (see Figure 2b). If the primate visual system uses
recurrence in lieu of greater network depth to perform object recognition,
then a shallower recurrent model with a suitable form of recurrence should
achieve recognition accuracy equal to a deeper feedforward model, 甚至
with temporally fixed parameters (Liao & Poggio, 2016). We therefore tested
whether our search had identified such well-adapted recurrent architec-
tures by fully training a representative ConvRNN, the model with the me-
甸 (across 7000 sampled models) validation accuracy after five epochs of
ImageNet training. This median model (RGC Median) reached a final Ima-
geNet top-1 validation accuracy nearly equal to a ResNet-34 model with
nearly twice as many layers, even though the ConvRNN used only ap-
近似地 75% as many parameters. The fully unrolled model from the
random phase of the search (RGC Random) did not perform substantially
better than the BaseNet, though the minimally unrolled control did (见图-
ure 2c). We suspect the improvement of the base intermediate feedforward
model over using shallow networks (as in Figure S1) diminishes the dif-
ference between the minimal and extended versions of the RGC compared
to suitably chosen long-range feedback connections. 然而, compared
to alternative choices of ConvRNN circuits, even the minimally extended
RGC significantly outperforms them with fewer parameters and units, 在-
dicating the importance of this circuit motif for task performance. This ob-
servation suggests that our evolutionary search strategy yielded effective
recurrent architectures beyond the initial random phase of the search.
We also considered a control model (Time Decay) that produces tempo-
ral dynamics by learning time constants on the activations independently
at each layer rather than by learning connectivity between units. 在这个
ConvRNN, unit activations have exponential rather than immediate falloff
once feedforward drive ceases. These dynamics could arise, 例如,
from single-neuron biophysics (例如, synaptic depression) rather than in-
terneuronal connections. 然而, this model did not perform any better
than the feedforward BaseNet, implying that ConvRNN performance is
not a trivial result of outputting a dynamic time course of responses. 我们
further implanted other more sophisticated forms of ConvRNN circuits
into the BaseNet, and while this improved performance over the Time
Decay model, it did not outperform the RGC Median ConvRNN despite
having many more parameters (see Figure 2c). 一起, these results
demonstrate that the RGC Median ConvRNN uses recurrent computations
to subserve object recognition behavior and that particular motifs in its
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
n
e
C
哦
A
r
t
我
C
e
–
p
d
/
我
F
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
C
哦
_
A
_
0
1
5
0
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
1660
A. Nayebi et al.
recurrent architecture (see Figure S2), found through an evolutionary
搜索, are required for its improved accuracy. 因此, given suitable local
recurrent circuits and patterns of long-range feedback connectivity, A
physically more compact, temporally extended ConvRNN can do the same
challenging object recognition task as a deeper feedforward CNN.
2.2 ConvRNNs Better Match Temporal Dynamics of Primate Behav-
ior Than Feedforward Models. To address whether recurrent processing
is engaged during core object recognition behavior, we turn to behavioral
data collected from behaving primates. There is a growing body of evi-
dence that current feedforward models fail to accurately capture primate
行为 (Rajalingham et al., 2018; Kar et al., 2019). We therefore reasoned
that if recurrence is critical to core object recognition behavior, then recur-
rent networks should be more consistent with suitable measures of primate
behavior compared to the feedforward model family. Since the identity of
different objects is decoded from the IT population at different times, 我们
considered the first time at which the IT neural decoding accuracy reaches
这 (pooled) primate behavioral accuracy of a given image, known as the
object solution time (OST) (Kar et al., 2019). Given that our ConvRNNs also
have an output at each 10 ms time bin, the procedure for computing the OST
for these models is computed from its IT-preferred layers, and we report the
OST consistency, which we define as the Spearman correlation between the
model OSTs and the IT population’s OSTs on the common set of images
solved by the given model and IT under the same stimulus presentation
(see sections A.6.1 and A.8 for more details).
Unlike our ConvRNNs, which exhibit more biologically plausible tem-
poral dynamics, evaluating the temporal dynamics in feedforward models
poses an immediate problem. Given that recurrent networks repeatedly ap-
ply nonlinear transformations across time, we can analogously map the lay-
ers of a feedforward network to time points, observing that a network with
k distinct layers can produce k distinct OSTs in this manner. 因此, 最多
direct definition of a feedforward model’s OST is to uniformly distribute
the time bins between 70 和 260 ms across its k layers. For very deep feed-
forward networks such as ResNet-101 and ResNet-152, this number of dis-
tinct layers will be as fine-grained as the 10 ms time bins of the IT responses;
然而, for most other shallower feedforward networks, this will be much
coarser. Therefore to enable these feedforward models to be maximally tem-
porally expressive, we additionally randomly sample units from consec-
utive feedforward layers to produce a more graded temporal mapping,
depicted in Figure 3a. This graded mapping is ultimately what we use for
the feedforward models in Figure 3c, providing the highest OST consistency
for that model class.1 Note that for ConvRNNs and very deep feedforward
1
Mean OST difference 0.0120 and standard error of the mean (s.e.m.) 0.0045, Wilcoxon
test on uniform versus graded mapping OST consistencies across feedforward models,
p < 0.001; see also Figure S3.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Recurrent Connections in the Primate Ventral Visual Stream
1661
Figure 3: Intermediate ConvRNNs best explain the object solution times (OST)
of IT across images. (a) Comparing to primate OSTs. Mapping model layers to time
points: In order to compare to primate IT object solution times (namely, the first
time at which the neural decode accuracy for each image reached the level of
the (pooled) primate behavioral accuracy), we first need to define object solu-
tion times for models. This procedure involves identification of the IT-preferred
layer(s) via a standard linear mapping to temporally averaged IT responses.
Choosing a temporal mapping gradation: These IT-preferred model layer(s) are then
mapped to 10 ms time bins from 70 to 260 ms in either a uniform or graded fash-
ion, if the model is feedforward. For ConvRNNs, this temporal mapping is al-
ways one-to-one with these 10 ms time bins. (b) Defining model OSTs. Once the
temporal mapping has been defined, we train a linear SVM at each 10 ms model
time bin and compute the classifier’s d(cid:4) (displayed in each of the black dots for
a given example image). The first time bin at which the model d(cid:4) matches the
primate’s accuracy is defined as the Model OST for that image (obtained via
linear interpolation), which is the same procedure previously used (Kar et al.,
2019) to determine the ground truth IT OST (Primate OST vertical dotted line).
(c) Proper choices of recurrence best match IT OSTs. Mean and s.e.m. are com-
puted across train/test splits (N = 10) when that image (of 1320 images) was a
test set image, with the Spearman correlation computed with the IT object solu-
tion times (analogously computed from the IT population responses) across the
image set solved by both the given model and IT, constituting the Fraction of
IT Solved Images on the x-axis. We start with either a shallow base feedforward
model consisting of 5 convolutional layers and 1 layer of readout (BaseNet in
blue) as well as an intermediate-depth variant with 10 feedforward layers and 1
layer of readout (BaseNet in purple), detailed in section A.2.1. From these base
feedforward models, we embed recurrent circuits, resulting in either Shallow
ConvRNNs or Intermediate ConvRNNs, respectively.
models (ResNet-101 and ResNet-152) whose number of IT-preferred layers
matches the number of time bins, then the uniform and graded mappings
are equivalent, whereby the earliest (in the feedforward hierarchy) layer is
matched to the earliest 10 ms time bin of 70 ms, and so forth.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1662
A. Nayebi et al.
With model OST defined across both model families, we compared vari-
ous ConvRNNs and feedforward models to the IT population’s OST in Fig-
ure 3c. Among shallower and deeper models, we found that ConvRNNs
were generally able to better explain IT’s OST than their feedforward
counterparts. Specifically, we found that ConvRNN circuits without any
multiunit interaction such as the Time Decay ConvRNN only marginally,
and not always significantly, improved the OST consistency over its
respective BaseNet model.2 On the other hand, ConvRNNs with multiunit
interactions generally provided the greatest match to IT OSTs than even the
deepest feedforward models,3 where the best feedforward model (ResNet-
152) attains a mean OST consistency of 0.173 and the best ConvRNN
(UGRNN) attains an OST consistency of 0.237.
Consistent with our observations in Figure 2 that different recurrent cir-
cuits with multiunit interactions were not all equally effective when em-
bedded in CNNs (despite outperforming the simple Time Decay model),
we similarly found that this observation held for the case of matching IT’s
OST. Given recent observations (Kar & DiCarlo, 2021) that inactivating parts
of macaque ventrolateral PFC (vlPFC) results in behavioral deficits in IT
for late-solved images, we reasoned that additional decoding procedures
employed at the categorization layer during task optimization might have
a meaningful impact on the model’s OST consistency, in addition to the
choice of recurrent circuit used. We designed several decoding procedures
(defined in section A.5), motivated by prior observations of accumulation
of relevant sensory signals during decision making in primates (Shadlen
& Newsome, 2001). Overall, we found that ConvRNNs with different de-
coding procedures but with the same layer-local recurrent circuit (RGC
Median) and long-range feedback connectivity patterns yielded significant
differences in final consistency with the IT population OST (see Figure S4;
Friedman test, p < 0.05). Moreover, the simplest decoding procedure of
outputting a prediction at the last time point, a strategy commonly em-
ployed by the computer vision community, had a lower OST consistency
than each of the more nuanced Max Confidence4 and Threshold decoding
2
3
4
Paired t-test with Bonferroni correction: shallow Time Decay versus BaseNet in blue,
mean OST difference 0.101 and s.e.m. 0.0313, t(9) ≈ 3.23, p < 0.025; intermediate Time
Decay versus BaseNet in purple, mean OST difference 0.0148 and s.e.m. 0.00857, t(9) ≈
1.73, p ≈ 0.11.
Paired t-test with Bonferroni correction: shallow RGC versus BaseNet in blue, mean
OST difference 0.153 and s.e.m. 0.0252, t(9) ≈ 6.08, p < 0.001; intermediate UGRNN ver-
sus ResNet-152, mean OST difference 0.0652 and s.e.m. 0.00863, t(9) ≈ 7.55, p < 0.001;
intermediate GRU versus ResNet-152, mean OST difference 0.0559 and s.e.m. 0.00725,
t(9) ≈ 7.71, p < 0.001; RGC Median versus ResNet-152, mean OST difference 0.0218 and
s.e.m. 0.00637, t(9) ≈ 3.44, p < 0.01.
Paired t-test with Bonferroni correction, mean OST difference 0.0195, and s.e.m.
0.00432, t(9) ≈ −4.52, p < 0.01.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Recurrent Connections in the Primate Ventral Visual Stream
1663
procedures5 that we considered. Taken together, our results suggest that the
type of multiunit layer-wise recurrence and downstream decoding strategy
are important features for OST consistency with IT, suggesting that spe-
cific, nontrivial connectivity patterns farther downstream of the ventral vi-
sual pathway may be important to core object recognition behavior over
timescales of a couple hundred milliseconds.
2.3 Neural Dynamics Differentiate ConvRNN Circuits. ConvRNNs
naturally produce a dynamic time series of outputs given an unchanging in-
put stream, unlike feedforward networks. While these recurrent dynamics
could be used for tasks involving time, here we optimized the ConvRNNs
to perform the static task of object classification on ImageNet. It is possi-
ble that the primate visual system is optimized for such a task, because
even static images produce reliably dynamic neural response trajectories
at temporal resolutions of tens of milliseconds (Issa et al., 2018). The object
content of some images becomes decodable from the neural population sig-
nificantly later than the content of other images, even though animals rec-
ognize both object sets equally well. Interestingly, late-decoding images are
not well characterized by feedforward CNNs, raising the possibility that
they are encoded in animals through recurrent computations (Kar et al.,
2019). If this were the case, we reason then that recurrent networks trained
to perform a difficult but static object recognition task might explain neural
dynamics in the primate visual system, just as feedforward models explain
time-averaged responses (Yamins et al., 2014; Khaligh-Razavi & Kriegesko-
rte, 2014).
Prior studies (Kietzmann et al., 2019) have directly fit recurrent param-
eters to neural data, as opposed to optimizing them on a task. While it is
natural to try to fit recurrent parameters to the temporally varying neural
responses directly, this approach naturally has a loss of normative explana-
tory power. In fact, we found that this approach suffers from a fundamen-
tal overfitting issue to the particular image statistics of the neural data
collected. Specifically, we directly fit these recurrent parameters (implanted
into the task-optimized feedforward BaseNet) to the dynamic firing rates
of primate neurons recorded during encoding of visual stimuli. However,
while these nontask optimized dynamics generalized to held-out images
and neurons (see Figures S5a and S5b), they had no longer retained per-
formance to the original object recognition task that the primate itself is
able to perform (see Figure S5c). Therefore, to avoid this issue, we instead
asked whether fully task-optimized ConvRNN models (including the ones
introduced in section 2.1) could predict these dynamic firing rates from
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
5
Paired t-test with Bonferroni correction, mean OST difference 0.0279, and s.e.m.
0.00634, t(9) ≈ −4.41, p < 0.01.
1664
A. Nayebi et al.
multielectrode array recordings from the ventral visual pathway of rhesus
macaques (Majaj, Hong, Solomon, & DiCarlo, 2015).
We began with the feedforward BaseNet and added a variety of
ConvRNN circuits, including the RGC Median ConvRNN and its counter-
part generated at the random phase of the evolutionary search (RGC Ran-
dom). All of the ConvRNNs were presented with the same images shown to
the primates, and we collected the time series of features from each model
layer. To decide which layer should be used to predict which neural re-
sponses, we fit linear models from each feedforward layer’s features to the
neural population and measured where explained variance on held-out im-
ages peaked (see section A.6 for more details). Units recorded from distinct
arrays—placed in the successive V4, posterior IT (pIT), and central/anterior
IT (cIT/aIT) cortical areas of the macaque—were fit best by the successive
layers of the feedforward model, respectively. Finally, we measured how
well ConvRNN features from these layers predicted the dynamics of each
unit. In contrast with feedforward models’ fit to temporally averaged neu-
ral responses, the linear mapping in the temporal setting must be fixed at
all time points. The reason for this choice is that the linear mapping yields
“artificial units” whose activity can change over time (just like the real tar-
get neurons), but the identity of these units should not change over the
course of 260 ms, which would be the case if instead a separate linear map-
ping was fit at each 10 ms time bin. This choice of a temporally fixed linear
mapping therefore maintains the physical relationship between real neu-
rons and model neurons.
As can be seen from Figure 4a, with the exception of the RGC Random
ConvRNN, the ConvRNN feature dynamics fit the neural response trajec-
tories as well as the feedforward baseline features on early phase responses
(see Wilcoxon test p-values in Table 1 in the online Extended Data section)
and better than the feedforward baseline features for late phase responses
(Wilcoxon test with Bonferroni correction p < 0.001), across V4, pIT, and
cIT/aIT on held-out images. For the early phase responses, the ConvRNNs
that employ direct passthrough are elaborations of the baseline feedforward
network, although the ConvRNNs that only employ gating are still a non-
linear function of their input, similar to a feedforward network. For the late
phase responses, any feedforward model exhibits similar “square wave”
dynamics as its 100 ms visual input, making it a poor predictor of the subset
of late responses that are beyond the initial feedforward pass (see Figure S6,
purple lines). In contrast, the activations of ConvRNN units have persistent
dynamics, yielding predictions of the entire neural response trajectories.
Crucially, these predictions result from the task-optimized nonlinear dy-
namics from ImageNet, as both models are fit to neural data with the same
form of temporally fixed linear model with the same number of parame-
ters. Since the initial phase of neural dynamics was well fit by feedforward
models, we asked whether the later phase could be fit by a much simpler
model than any of the ConvRNNs we considered, namely, the Time Decay
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Recurrent Connections in the Primate Ventral Visual Stream
1665
Figure 4: Suitably chosen intermediate ConvRNN circuits provide consistent
predictions of primate ventral stream neural dynamics. (a) The y-axis indicates
the median across neurons of the explained variance between predictions and
ground-truth responses on held-out images divided by the square root of the in-
ternal consistencies of the neurons, defined in section A.6.3. Error bars indicates
the s.e.m. across neurons (N = 88 for V4, N = 88 for pIT, N = 80 for cIT/aIT)
averaged across 10 ms time bins (N = 4 each for the Early and Late designa-
tions). As can be seen, the intermediate-depth feedforward BaseNet model (first
bars) is a poor predictor of the subset of late responses that are beyond the feed-
forward pass, but certain types of ConvRNN circuits (such as RGC Median,
UGRNN, and GRU) added to the BaseNet are overall best predictive across vi-
sual areas at late time points (Wilcoxon test, with Bonferroni correction with
feedforward BaseNet, p < 0.001 for each visual area). See Figure S6 for the full
time courses at the resolution of 10 ms bins. (b) For each ConvRNN circuit, we
compare the average neural predictivity (averaged per neuron across early and
late timepoints) averaged across areas, to the OST consistency. The ConvRNNs
that have the best average neural predictivity also best match the OST consis-
tency (RGC Median, UGRNN, and GRU).
ConvRNN with ImageNet-trained time constants at convolutional layers. If
the Time Decay ConvRNN were to explain neural data as well as the other
ConvRNNs, it would imply that interneuronal recurrent connections are
not needed to account for the observed dynamics; however, this model did
not fit the late phase dynamics of intermediate areas (V4 and pIT), as well
as the other ConvRNNs.6 The Time Decay model did match the other
ConvRNNs for cIT/aIT, which may indicate some functional differences in
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
6
Wilcoxon test with Bonferroni correction p < 0.001 for each ConvRNN versus Time
Decay, except for the SimpleRNN p ≈ 0.46 for pIT.
1666
A. Nayebi et al.
the temporal processing of this area versus V4 and pIT. Thus, the more com-
plex recurrence found in ConvRNNs is generally needed to improve object
recognition performance over feedforward models and to account for neu-
ral dynamics in the ventral stream, even when animals are only required
to fixate on visual stimuli. However, not all forms of complex recurrence
are equally predictive of temporal dynamics. As depicted in Figure 4b, we
found among these that the RGC Median, UGRNN, and GRU ConvRNNs
attained the highest median neural predictivity for each visual area in both
early and late phases, but they significantly outperformed the SimpleRNN
ConvRNN at the late phase dynamics of these areas,7 and these models in
turn were among the best matches to IT object solution times (OST) from
section 2.2.
A natural follow-up question to ask is whether a lack of recurrent pro-
cessing is the reason for the prior observation that there is a drop in ex-
plained variance for feedforward models from early to late time bins (Kar
et al., 2019). In short, we find that this is not the case and that this drop
likely has to do with task-orthogonal dynamics specific to individual pri-
mates, which we examine below.
It is well known that recurrent neural networks can be viewed as very
deep feedforward networks with weight sharing across layers that would
otherwise be recurrently connected (Liao & Poggio, 2016). Thus, to ad-
dress this question, we compare feedforward models of varying depths to
ConvRNNs across the entire temporal trajectory under a varying linear
mapping at each time bin, in contrast to the above. This choice of linear map-
ping allows us to evaluate how well the model features are at explaining
early compared to late time dynamics without information from the early
dynamics influencing the later dynamics, and also more crucial, to allow
the feedforward model features to be independently compared to the late
dynamics. Specifically, as can be seen in Figure S7a, we observe a drop in ex-
plained variance from early (130–140 ms) to late (200–210 ms) time bins for
the BaseNet and ResNet-18 models, across multiple neural data sets. Mod-
els with increased feedforward depth (such as ResNet-101 or ResNet-152),
along with our performance-optimized RGC Median ConvRNN, exhibit a
similar drop in median population explained variance as the intermediate
feedforward models. The benefit of model depth with respect to increased
explained variance of late IT responses might be noticeable only while com-
paring shallow models (less than 7 nonlinear transforms) to much deeper
(more than 15 nonlinear transforms) models (Kar et al., 2019). Our results
suggest that the amount of variance explained in the late IT responses is not
a monotonically increasing function of model depth.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
7
Wilcoxon test with Bonferroni correction between each of these ConvRNNs versus
the SimpleRNN on late phase dynamics, p < 0.001 per visual area.
Recurrent Connections in the Primate Ventral Visual Stream
1667
As a result, an alternative hypothesis is that the drop in explained
variance from early to late time bins could instead be attributed to task-
orthogonal dynamics specific to an individual primate as opposed to iter-
ated nonlinear transforms, resulting in variability unable to be captured by
any task-optimized model (feedforward or recurrent). To explore this pos-
sibility, we examined whether the model’s neural predictivity at these early
and late time bins was relatively similar in ratio to that of one primate’s IT
neurons mapped to that of another primate (see section A.7 for more de-
tails, where we derive a novel measure of the neural predictivity between
animals, known as the “interanimal consistency”).
As shown in Figure S7b, across various hyperparameters of the linear
mapping, we observe a ratio close to one between the neural predictivity (of
the target primate neurons) of the feedforward BaseNet to that of the source
primate mapped to the same target primate. Therefore, as it stands, tempo-
rally varying linear mappings to neural responses collected from an animal
during rapid visual stimulus presentation (RSVP) may not sufficiently sepa-
rate feedforward models from recurrent models any better than one animal
to another, though more investigation is needed to ensure tight estimates of
the interanimal consistency measure we have introduced here with neural
data recorded from more primates. Nonetheless, this observation further
motivates our earlier result of additionally turning to temporally varying
behavioral metrics (such as the OST consistency) in order to be able to sep-
arate these model classes beyond what is currently achievable by neural
response predictions.
2.4 ConvRNNs Mediate a Trade-Off between Task Performance and
Network Size. Why might a suitably shallower feedforward network with
temporal dynamics be desirable for the ventral visual stream? We reasoned
that recurrence mediates a trade-off between network size and task perfor-
mance, a trade-off that the ventral stream also maintains. To examine this
possibility, in Figure 5, we compare each network’s task performance versus
its size, measured by either parameter count or unit count. Across models,
we found unit count (related to the number of neurons) to be more consis-
tent with task performance than parameter count (related to the number of
synapses). In fact, there are many models with a large parameter count but
not very good task performance, indicating that adding synapses is not nec-
essarily as useful for performance as adding neurons. For shallow recurrent
networks, task performance seemed to be more strongly associated with
OST consistency than network size. This trade-off became more salient for
deeper feedforward models and the intermediate ConvRNNs, as the very
deep ResNets (ResNet-34 and deeper) attained an overall lower OST con-
sistency compared to the intermediate ConvRNNs, using both many more
units and parameters compared to small relative gains in task performance.
Similarly, intermediate ConvRNNs with high task performance and mini-
mal unit count, such as the UGRNN, GRU, and RGCs, attained both the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1668
A. Nayebi et al.
Figure 5: Intermediate ConvRNN circuits with highest OST consistency con-
serve on network size while maintaining task performance. Across all models
considered, the intermediate ConvRNNs (denoted by ×) that attain high cat-
egorization performance (x-axis) while maintaining a low unit count (panel B)
rather than parameter count (panel A) for their given performance level, achieve
the highest mean OST consistency (Spearman correlation with IT population
OST, averaged across N = 10 train/test splits). The color bar indicates this mean
OST consistency (monotonically increasing from purple to red), binned into six
equal ranges. Models with a larger network size at a fixed performance level
are less consistent with primate object recognition behavior (e.g., deep feedfor-
ward models, denoted by boxes), with recurrence maintaining a fundamental
trade-off between network size and task performance.
highest OST consistency overall (see Figures 3 and 5), along with providing
the best match to neural dynamics among ConvRNN circuits across visual
areas (see Figure 4b). This observation indicates that suitably chosen recur-
rence can provide a means for maintaining this fundamental trade-off.
Given our finding that specific forms of task-optimized recurrence are
more consistent with IT’s OST than iterated feedforward transformations
(with unshared weights), we asked whether it was possible to approxi-
mate the effect of recurrence with a feedforward model. This approximation
would allow us to better describe the additional “action” that recurrence
is providing in its improved OST consistency. In fact, one difference
between this metric and the explained variance metric evaluated on neural
responses in the prior section is that the latter uses a linear transform from
model features to neural responses, whereas the former operates directly
on the original model features. Therefore, a related question is whether the
(now standard) use of a linear transform for mapping from model units
to neural responses can potentially mask the behavioral improvement that
suitable recurrent processing has over deep feedforward models in their
original feature space.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Recurrent Connections in the Primate Ventral Visual Stream
1669
To address these questions, we trained a separate linear mapping (PLS
regression) from each model layer to the corresponding IT response at the
given time point, on a set of images distinct from those on which the OST
consistency metric is evaluated on (see section A.8.2 for more details). The
outputs of this linear mapping were then used in place of the original model
features for both the uniform and graded mappings, constituting PLS Uni-
form and PLS Graded, respectively. Overall, as depicted in Figure S3, we
found that models with less temporal variation in their source features
(namely, those under a uniform mapping with less IT-preferred layers than
the total number of time bins) had significantly improved OST consistency
with their linearly transformed features under PLS regression (Wilcoxon
test, p < 0.001; mean OST difference 0.0458 and s.e.m. 0.00399). On the other
hand, the linearly transformed intermediate feedforward models were not
significantly different from task-optimized ConvRNNs that achieved high
OST consistency,8 suggesting that the action of suitable task-optimized re-
currence approximates that of a shallower feedforward model with linearly
induced ground-truth neural dynamics.
3 Discussion
The overall goal of this study is to determine what role recurrent circuits
may have in the execution of core object recognition behavior in the ven-
tral stream. By broadening the method of goal-driven modeling from solv-
ing tasks with feedforward CNNs to ConvRNNs that include layer-local
recurrence and feedback connections, we first demonstrate that appropri-
ate choices of these recurrent circuits that incorporate specific mechanisms
of direct passthrough and gating lead to matching the task performance of
much deeper feedforward CNNs with fewer units and parameters, even
when minimally unrolled. This observation suggests that the recurrent
circuit motif plays an important role even during the initial time points
of visual processing. Moreover, unlike very deep feedforward CNNs,
the mapping from the early, intermediate, and higher layers of these
ConvRNNs to corresponding cortical areas is neuroanatomically consis-
tent and reproduces prior quantitative properties of the ventral stream. In
fact, ConvRNNs with high task performance but small network size (as
measured by number of neurons rather than synapses) are most consis-
tent with the temporal evolution of primate IT object identity solutions.
We further find that these task-optimized ConvRNNs can reliably produce
8
Paired t-test with Bonferroni correction: RGC Median versus PLS Uniform BaseNet,
mean OST difference −0.0052 and s.e.m. 0.0061, t(9) ≈ −0.86, p ≈ 0.41; RGC Median with
Threshold Decoder versus PLS Uniform ResNet-18, mean OST difference 0.00697 and
s.e.m. 0.0085, t(9) ≈ 0.82, p ≈ 0.43; RGC Median with Max Confidence Decoder versus
PLS Uniform ResNet-34, mean OST difference 0.0001 and s.e.m. 0.0079, t(9) ≈ 0.02, p ≈
0.99.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1670
A. Nayebi et al.
quantitatively accurate dynamic neural response trajectories at temporal
resolutions of tens of milliseconds throughout the ventral visual hierarchy.
Taken together, our results suggest that recurrence in the ventral stream
extends feedforward computations by mediating a trade-off between task
performance and neuron count during core object recognition, suggesting
that the computer vision community’s solution of stacking more feedfor-
ward layers to solve challenging visual recognition problems approximates
what is compactly implemented in the primate visual system by leveraging
additional nonlinear temporal transformations to the initial feedforward IT
response. This work therefore provides a quantitative prescription for the
next generation of dynamic ventral stream models, addressing the call to
action in a recent previous study (Kar et al., 2019) for a change in architec-
ture from feedforward models.
Many hypotheses about the role of recurrence in vision have been put
forward, particularly in regard to overcoming certain challenging image
properties (Spoerer et al., 2017; Michaelis et al., 2018; Rajaei et al., 2019; Lins-
ley et al., 2018; Gilbert & Wu, 2013; Lindsay, 2015; McIntosh et al., 2018; Li
et al., 2018; Kar et al., 2019; Rao & Ballard, 1999; Lotter, Kreiman, & Cox,
2017; Issa et al., 2018). We believe this is the first work to address the role
of recurrence at scale by connecting novel task-optimized recurrent mod-
els to temporal metrics defined on high-throughput neural and behavioral
data, to provide evidence for recurrent connections extending feedforward
computations. Moreover, these metrics are well defined for feedforward
models (unlike prior work; Kubilius et al., 2019) and therefore meaning-
fully demonstrate a separation between the two model classes.
Though our results help to clarify the role of recurrence during core
object recognition behavior, many major questions remain. Our work ad-
dresses why the visual system may leverage recurrence to subserve visu-
ally challenging behaviors, replacing a physically implausible architecture
(deep feedforward CNNs) with one that is ubiquitously consistent with
anatomical observations (ConvRNNs). However, our work does not ad-
dress gaps in understanding either the loss function or the learning rule
of the neural network. Specifically, we intentionally implant layer-local re-
currence and long-range feedback connections into feedforward networks
that have been useful for supervised learning via backpropagation on Im-
ageNet. A natural next step would be to connect these ConvRNNs with
unsupervised objectives, as has been done for feedforward models of the
ventral stream in concurrent work (Zhuang et al., 2021). The question of bi-
ologically plausible learning targets is similarly linked to biologically plau-
sible mechanisms for learning such objective functions. Recurrence could
play a separate role in implementing the propagation of error-driven learn-
ing, obviating the need for some of the issues with backpropagation (such
as weight transport), as has been recently demonstrated at scale (Akrout,
Wilson, Humphreys, Lillicrap, & Tweed, 2019; Kunin et al., 2020). There-
fore, building ConvRNNs with unsupervised objective functions optimized
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Recurrent Connections in the Primate Ventral Visual Stream
1671
with biologically plausible learning rules would be essential toward a more
complete goal-driven theory of visual cortex.
High-throughput experimental data will also be critical to further sepa-
rate hypotheses about recurrence. While we see evidence of recurrence as
mediating a trade-off between network size and task performance for core
object recognition, it could be that recurrence plays a more task-specific role
under more temporally dynamic behaviors. Not only would it be an inter-
esting direction to optimize ConvRNNs on more temporally dynamic vi-
sual tasks than ImageNet, but to compare to neural and behavioral data
collected from such stimuli, potentially over longer timescales than 260 ms.
While the RGC motif of gating and direct passthrough gave the highest task
performance among ConvRNN circuits, the circuits that maintain a trade-
off between number of units and task performance (RGC Median, GRU,
and UGRNN) had the best match to the current set of neural and behav-
ioral metrics, even if some of them do not employ passthroughs. How-
ever, it could be the case that with the same metrics we develop here but
used in concert with such stimuli over potentially longer timescales, we can
better differentiate these three ConvRNN circuits. Therefore, such models
and experimental data would synergistically provide great insight into how
rich visual behaviors proceed, while also inspiring better computer vision
algorithms.
Acknowledgments
We thank Tyler Bonnen, Eshed Margalit, and the anonymous reviewers for
comments on this article. We thank the Google TensorFlow Research Cloud
team for generously providing TPU hardware resources for this project.
D.L.K.Y. is supported by the James S. McDonnell Foundation (Understand-
ing Human Cognition Award, grant 220020469), the Simons Foundation
(Collaboration on the Global Brain, grant 543061), the Sloan Foundation
(fellowship FG-2018-10963), the National Science Foundation (RI 1703161
and CAREER Award 1844724), the DARPA Machine Common Sense pro-
gram, and hardware donation from the NVIDIA Corporation. This work
is also supported in part by Simons Foundation grant SCGB-542965 (J.J.D.
and D.L.K.Y.). This project has received funding from the European Union’s
Horizon 2020 research and innovation programme under grant agreement
70549 (J.K.). J.S. is supported by the Mexican National Council of Science
and Technology (CONACYT).
Author Contributions
A.N. and D.L.K.Y. designed the experiments. A.N., J.S., and D.B. conducted
the experiments, and A.N. analyzed the data. K.K. contributed neural data,
and J.K. contributed to initial code development. K.K. and J.J.D. provided
technical advice on neural predictivity metrics. D.S. and S.G. provided
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1672
A. Nayebi et al.
technical advice on recurrent neural network training. A.N. and D.L.K.Y.
interpreted the data and wrote the article.
Competing Interest Declaration
The authors declare no competing interests.
References
Akrout, M., Wilson, C., Humphreys, P., Lillicrap, T., & Tweed, D. B. (2019). Deep
learning without weight transport. In H. Wallach, H. Larochelle, A. Beygelzimer,
F. d’Alché-Buc, E. Fox, & R. Garnett (Eds.), Advances in neural information process-
ing systems, 32. Red Hook, NY: Curran. https://proceedings.neurips.cc/paper/
2019/file/f387624df552cea2f369918c5e1e12bc-Paper.pdf
Collins, J., Sohl-Dickstein, J., & Sussillo, D. (2017). Capacity and trainability in re-
current neural networks. In Proceedings of the International Conference on Learning
Representations.
DiCarlo, J. J., Zoccolan, D., & Rust, N. C. (2012). How does the brain solve vi-
sual object recognition? Neuron, 73(3), 415–434. 10.1016/j.neuron.2012.01.010,
PubMed: 22325196
Gilbert, C. D., & Wu, L. (2013). Top-down influences on visual processing. Nat. Rev.
Neurosci., 14(5), 350–363. 10.1038/nrn3476, PubMed: 23595013
He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recog-
nition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recog-
nition (pp. 770–778). Piscataway, NJ: IEEE.
Hosoya, T., Baccus, S. A., & Meister, M. (2005). Dynamic predictive coding by the
retina. Nature, 436(7047), 71–77. 10.1038/nature03689, PubMed: 16001064
Issa, E. B., Cadieu, C. F., & DiCarlo, J. J. (2018). Neural dynamics at successive stages
of the ventral visual stream are consistent with hierarchical error signals. Elife, 7,
e42870. 10.7554/eLife.42870, PubMed: 30484773
James, W. (1890). The principles of psychology (vol. 1). New York: Holt.
Kar, K., & DiCarlo, J. J. (2021). Fast recurrent processing via ventrolateral prefrontal
cortex is needed by the primate ventral stream for robust core visual object recog-
nition. Neuron, 109(1), 164–176. 10.1016/j.neuron.2020.09.035, PubMed: 33080226
Kar, K., Kubilius, J., Schmidt, K., Issa, E. B., & DiCarlo, J. J. (2019). Evidence that re-
current circuits are critical to the ventral stream’s execution of core object recog-
nition behavior. Nature Neuroscience, 22(6), 974–983. 10.1038/s41593-019-0392-5,
PubMed: 31036945
Khaligh-Razavi, S.-M., & Kriegeskorte, N. (2014). Deep supervised, but not unsuper-
vised, models may explain it cortical representation. PLOS Computational Biology,
10(11), e1003915. 10.1371/journal.pcbi.1003915, PubMed: 25375136
Kietzmann, T. C., Spoerer, C. J., Sörensen, L. K., Cichy, R. M., Hauk, O., & Kriegesko-
rte, N. (2019). Recurrence is required to capture the representational dynamics of
the human visual system. In Proceedings of the National Academy of Sciences, 116(43),
21854–21863. 10.1073/pnas.1905544116
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Recurrent Connections in the Primate Ventral Visual Stream
1673
Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). ImageNet classification with
deep convolutional neural networks. In F. Pereira, C. J. C. Burges, L. Bottou,
& K. Q. Weinberger (Eds.), Advances in neural information processing systems,
25. Red Hook, NY: Curran. https://proceedings.neurips.cc/paper/2012/file/
c399862d3b9d6b76c8436e924a68c45b-Paper.pdf
Kubilius, J., Schrimpf, M., Kar, K., Rajalingham, R., Hong, H., Majaj, N.,
.
DiCarlo, J. J. (2019). Brain-like object recognition with high-performing shallow
recurrent ANNs. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc,
E. Fox, & R. Garnett (Eds.), Advances in neural in- formation processing systems,
32. Red Hook, NY: Curran. https://proceedings.neurips.cc/paper/2019/file/
7813d1590d28a7dd372ad54b5d29d033-Paper.pdf
.
.
Kunin, D., Nayebi, A., Sagastuy-Brena, J., Ganguli, S., Bloom, J., & Yamins, D. (2020).
Two routes to scalable credit assignment without weight symmetry. In Proceedings
of the International Conference on Machine Learning (pp. 5511–5521).
Leroux, S., Molchanov, P., Simoens, P., Dhoedt, B., Breuel, T., & Kautz, J. (2018).
IAMNN: iterative and adaptive mobile neural network for efficient image clas-
sification. In International Conference on Learning Representations Workshop. https:
//openreview.net/forum?id=BkG3_ykDz
Li, X., Jie, Z., Feng, J., Liu, C., & Yan, S. (2018). Learning with rethinking: Recurrently
improving convolutional neural networks through feedback. Pattern Recognition,
79, 183–194. 10.1016/j.patcog.2018.01.015
Liao, Q., & Poggio, T. (2016). Bridging the gaps between residual learning, recurrent neural
networks and visual cortex. arXiv:1604.03640.
Lindsay, G. W. (2015). Feature-based attention in convolutional neural networks.
arXiv:1511.06408.
Linsley, D., Kim, J., Veerabadran, V., Windolf, C., & Serre, T. (2018). Learning long-
range spatial dependencies with horizontal gated recurrent units. In S. Bengio,
H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, & R. Garnett (Eds.),
Advances in neural information processing systems, 31. Red Hook, NY: Curran.
https://proceedings.neurips.cc/paper/2018/file/ec8956637a99787bd197eacd7
7acce5e-Paper.pdf
Lotter, W., Kreiman, G., & Cox, D. (2017). Deep predictive coding networks for video
prediction and unsupervised learning. In Proceedings of the International Conference
on Learning Representations.
Majaj, N. J., Hong, H., Solomon, E. A., & DiCarlo, J. J. (2015). Simple learned
weighted sums of inferior temporal neuronal firing rates accurately predict hu-
man core object recognition performance. Journal of Neuroscience, 35(39), 13402–
13418. 10.1523/JNEUROSCI.5181-14.2015, PubMed: 26424887
Mante, V., Sussillo, D., Shenoy, K. V., & Newsome, W. T. (2013). Context-dependent
computation by recurrent dynamics in prefrontal cortex. Nature, 503, 78–84.
10.1038/nature12742, PubMed: 24201281
McIntosh, L., Maheswaranathan, N., Nayebi, A., Ganguli, S., & Baccus, S. (2016).
Deep learning models of the retinal response to natural scenes. In D. Lee,
M. Sugiyama, U. Luxburg, I. Guyon, & R. Garnett (Eds.), Advances in neu-
ral information processing systems, 29 (pp. 1369–1377). Red Hook, NY: Curran.
28729779
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1674
A. Nayebi et al.
McIntosh, L., Maheswaranathan, N., Sussillo, D., & Shlens, J. (2018). Recurrent seg-
mentation for variable computational budgets. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition Workshops (pp. 1648–1657).
Piscataway, NJ: IEEE.
Nayebi, A., Bear, D., Kubilius,
Michaelis, C., Bethge, M., & Ecker, A. (2018). One-shot segmentation in clutter. In
Proceedings of the International Conference on Machine Learning (pp. 3549–3558).
.
.
Yamins, D. L. (2018). Task-driven convolutional recurrent models of the vi-
sual system. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-
Bianchi, & R. Garnett (Eds.), Advances in neural information processing systems,
31. Red Hook, NY: Curran. https://proceedings.neurips.cc/paper/2018/file/
6be93f7a96fed60c477d30ae1de032fd-Paper.pdf
J., Kar, K., Ganguli, S., Sussillo, D.,
.
Pinto, N., Cox, D. D., & DiCarlo, J. J. (2008). Why is real-world visual object recog-
nition hard? PLOS Computational Biology, 4(1), e27. 10.1371/journal.pcbi.0040027,
PubMed: 18225950
Rajaei, K., Mohsenzadeh, Y., Ebrahimpour, R., & Khaligh-Razavi, S.-M. (2019).
Beyond core object recognition: Recurrent processes account for object recog-
nition under occlusion. PLOS Computational Biology, 15(5), e1007001. 10.1371/
journal.pcbi.1007001, PubMed: 31091234
Rajalingham, R., Issa, E. B., Bashivan, P., Kar, K., Schmidt, K., & DiCarlo, J. J. (2018).
Large-scale, high-resolution comparison of the core visual object recognition be-
havior of humans, monkeys, and state-of-the-art deep artificial neural networks.
Journal of Neuroscience, 38(33), 7255–7269. 10.1523/JNEUROSCI.0388-18.2018,
PubMed: 30006365
Rao, R. P., & Ballard, D. H. (1999). Predictive coding in the visual cortex: A functional
interpretation of some extra-classical receptive-field effects. Nature Neuroscience,
2(1), 79–87. 10.1038/4580, PubMed: 10195184
Schrimpf, M., Kubilius, J., Hong, H., Majaj, N. J., Rajalingham, R., Issa, E. B., . . . others
(2018). Brain-score: Which artificial neural network for object recognition is most brain-
like? BioRxiv:407007.
Shadlen, M. N., & Newsome, W. T. (2001). Neural basis of a perceptual decision in
the parietal cortex (area LIP) of the rhesus monkey. Journal of Neurophysiology,
86(4), 1916–1936. 10.1152/jn.2001.86.4.1916, PubMed: 11600651
Spoerer, C. J., Kietzmann, T. C., Mehrer, J., Charest, I., & Kriegeskorte, N. (2020).
Recurrent neural networks can explain flexible trading of speed and accu-
racy in biological vision. PLOS Computational Biology, 16(10), e1008215. 10.1371/
journal.pcbi.1008215, PubMed: 33006992
Spoerer, C. J., McClure, P., & Kriegeskorte, N. (2017). Recurrent convolutional neural
networks: A better model of biological object recognition. Front. Psychol., 8, 1–14.
10.3389/fpsyg.2017.01551, PubMed: 28197108
Yamins, D. L., & DiCarlo, J. J. (2016). Using goal-driven deep learning models to
understand sensory cortex. Nature Neuroscience, 19(3), 356. 10.1038/nn.4244
Yamins, D. L. K., Hong, H., Cadieu, C. F., Solomon, E. A., Seibert, D., & DiCarlo,
J. J. (2014). Performance-optimized hierarchical models predict neural responses
in higher visual cortex. In Proceedings of the National Academy of Sciences, 111(23),
8619–8624. 10.1073/pnas.1403112111
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Recurrent Connections in the Primate Ventral Visual Stream
1675
Zamir, A. R., Wu, T.-L., Sun, L., Shen, W. B., Shi, B. E., Malik, J., & Savarese, S. (2017).
Feedback networks. In Proceedings of the Conference on Computer Vision and Pattern
Recognition. Piscataway, NJ: IEEE. 10.1109/CVPR.2017.196
Zhuang, C., Yan, S., Nayebi, A., Schrimpf, M., Frank, M. C., DiCarlo, J. J., & Yamins,
D. L. (2021). Unsupervised neural network models of the ventral visual stream.
In Proceedings of the National Academy of Sciences, 118(3).
Received July 28, 2021; accepted February 17, 2022.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
8
1
6
5
2
2
0
3
4
9
0
4
n
e
c
o
_
a
_
0
1
5
0
6
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3