Amine Ouazad

INSEAD

经济系

77300 Fontainebleau

法国

amine.ouazad@insead.edu

ASSESSED BY A TEACHER LIKE

ME: RACE AND TEACHER

ASSESSMENTS

抽象的
Do teachers assess same-race students more favorably?
This paper uses nationally representative data on teacher
assessments of student ability that can be compared with
test scores to determine whether teachers give better as-
sessments to same-race students. The data set follows
students from kindergarten to grade 5, a period dur-
ing which racial gaps in test scores increase rapidly.
Teacher assessments comprise up to twenty items mea-
suring specific skills. Using a unique within-student
and within-teacher identification and while controlling
for subject-specific test scores, I find that teachers do
assess same-race students more favorably. Effects ap-
pear in kindergarten and persist thereafter. Robustness
checks suggest that: student behavior does not explain
this effect; same-race effects are evident in teacher as-
sessments of most of the skills; grading “on the curve”
should be associated with lower assessments; and mea-
surement error in assessments or test scores does not
significantly affect the estimates.

334

土井:10.1162/EDFP_a_00136
© 2014 Association for Education Finance and Policy

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

F

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

F

.

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Amine Ouazad

1. 介绍
A growing body of research in education and psychology argues that minority
students receive less favorable feedback and less praise than do their white
同行 (Meier, 斯图尔特, and England 1989; 马库斯, 总的, and Seefeldt 1991;
Casteel 1998; Van Ewijk 2011). The research is usually conducted on small
样品, which may cast doubt on the wider applicability of results obtained
for particular schools or school districts (IE。, on whether results are externally
valid; Carpenter, 哈里森, and List 2005). In this paper I use a longitudinal
and nationally representative data set to measure whether or not teachers
assess same-race students more favorably. Field experiments with nationally
representative European data sets have recently measured whether teachers
assess minority students more favorably (Hinnerich, H¨oglin, and Johannesson
2011). 在美国, 然而, there are no nationally representative
data on teachers’ perceptions of same-race students’ skills. Analysis of the
National Educational Longitudinal Study of 1988 suggests that teachers have
more favorable perceptions of same-race students (Dee 2005), but in that study
the variables used to capture those perceptions (例如, “constantly inattentive,”
“frequently disruptive,” “rarely completes homework”) are measures more of
student behavior than of student performance. Hence these data cannot be
used to infer a same-race effect because such teacher perceptions are not
comparable to test scores.

There is another reason why it is so difficult to measure whether teachers
assess same-race students more highly. Even if the researcher has comparable
teacher assessments of students and test scores, a finding that teachers give
better assessments to same-race students (conditional on test scores) 可以
not be given a causal interpretation owing to possible confounding factors.
Causal effects can be estimated if the researcher randomizes the assignment
of teachers to students, but such randomization is a long and costly process
that is usually performed only for small, nonrepresentative samples.

These considerations leave the researcher in a quandary. 一方面,
randomized samples with comparable teacher assessments and test scores
provide convincing evidence that teachers have more favorable perceptions
of same-race students’ skills, but randomized estimates are typically available
only for nonrepresentative samples of students. 另一方面, 国家-
ally representative samples usually lack two important features: teacher as-
sessments of student performance that are comparable to test scores, 和
randomized assignment of teachers to students.1

1. Lavy (2004) uses a nationally representative sample to estimate the impact of student gender on
grades at the high-school matriculation exam in Israel, but teacher assignments are not randomized.
Adding unique teacher identifiers to Lavy (2004) would also allow an identification strategy based
on comparisons of teacher assessments and test scores while controlling for teacher effects.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

F

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

.

F

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

335

ASSESSED BY A TEACHER LIKE ME

This paper uses a longitudinal, nationally representative data set, the Early
Childhood Longitudinal Study, Kindergarten Class of 1998–1999, which in-
cludes detailed teacher assessments and test scores—in both mathematics
and English—in each wave of data collection from kindergarten to grade 5.
The teacher assessments are available for both subjects, and there are as
many as ten questions on specific skills within each subject in each follow-up
(Tourangeau et al. 2009). Given these data, continuous teacher assessments
can be compared with test scores.2 Teachers are not randomly assigned to
学生. Because the data set follows students through five follow-ups (从
kindergarten to grade 5) and includes teacher and student identifiers, 如何-
曾经, I am able to estimate the same-race effect on teacher assessments by
using a unique within-student (IE。, across grades3) and within-teacher iden-
tification strategy that controls for student- and teacher-specific confounding
因素. The paper also describes several robustness checks, which indicate
那: (1) behavior does not explain the reported estimate of the same-race effect
on teacher assessments; (2) the same-race effect appears in kindergarten for
most skills that are assessed by the teacher; (3) grading on the curve within a
classroom would result in lower teacher assessments for same-race students;
和 (4) measurement error in teacher assessments or in test scores has no
significant effect on the point estimates.

The within-student identification strategy yields the following result: A
student who moves from a same-race teacher in one grade to a different-race
teacher in the next grade encounters a significant drop in teacher assessments.4
Our second, within-teacher identification strategy compares the teacher as-
sessment of same-race students to the average teacher assessment in the
student’s classroom. I combine the within-student and within-teacher iden-
tification strategies and condition the results on student test scores: 存在
assessed by a same-race teacher increases teacher assessments of student per-
formance by 4 percent of a standard deviation in English and by 7 的百分比
a standard deviation in mathematics.

I design robustness checks to assess whether these results are consistent
with a teacher bias in favor of same-race students. One might object that
higher teacher assessments for same-race students reflect behavioral differ-
恩塞斯. 毕竟, teacher assessments of student performance do reflect, 部分地,

2. Tourangeau et al. (2009) mention that teacher assessments and test scores measure students’ skills
within the same broad curricular domains. 部分 4 examines teachers’ perceptions of students
skill by skill—and as early as in kindergarten—for skills that are the most likely to be assessed by
test scores; the results are similar (if not stronger) same-race effects.

3. 还, the survey is designed in a way that facilitates test score comparisons across grades. The tests
consist of two stages: an initial routing test for student ability, and second-stage tests that include
questions common to multiple grades (Tourangeau et al. 2009).

4. All of these results are conditional on student test scores.

336

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

/

F

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

F

.

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Amine Ouazad

student behavior (Sherman and Cormier 1974). The within-student identifica-
tion strategy used here neutralizes the effect of permanent student behavioral
差异, but it cannot control for changes in student behavior that could
affect teacher assessments. Because the allocation of teachers to students is
not random,5 behavioral changes that raise teacher assessments may correlate
with being assigned to a same-race teacher in the subsequent grade. The data
set includes four reliable measures of student behavior that are based on the
Social Skills Rating System (Gresham and Elliott 1990). These measures vary
both across students and across grades. I do not find that behavioral differ-
ences between same-race and other-race students explain the within-student
and within-teacher estimates of same-race effects on teacher assessments. Nei-
ther do I find that changes in behavior from one grade to the next are associated
with the student moving from a same-race (other-race) teacher to an other-race
(same-race) teacher.

A second possible objection is that, as measures of student performance,
test scores are noisy and therefore may not fully condition for student per-
formance when assessing same-race effects on teacher assessments. 在那里面
案件, teacher assessments could be higher for same-race students simply be-
cause same-race students perform better. Test scores and teacher assessments
are highly reliable, but the question is whether a small amount of measure-
ment error would be sufficient to confound the estimate of a same-race effect.
This paper calculates the impact of a given amount of measurement error in
test scores on the derived estimate of the same-race effect. A test score mea-
surement error of 50 percent would be required to account for the estimated
same-race effect.

The third major objection to this paper’s findings is that teacher assess-
ments may be an implicit ranking of students within a given classroom rather
than measures (例如, test scores) based on a common scale. I have used a
simple statistical framework to show that, because minority students have (在
average) lower test scores than white students and because minority and white
students tend to be in different classrooms, grading on a curve would lead
to higher teacher assessments for minority students—even though minority
students have significantly (最多 40 percent of a standard deviation) 降低
teacher assessments. Grading on a curve also would affect estimates of the
same-race effect if peer group composition were correlated with assignment
to a same-race teacher. Controlling for peers’ average test score in the main
specification does not affect my estimate of the same-race effect on teacher

5. For some evidence of nonrandom allocation of teachers to students, see Clotfelter, Ladd, and Vigdor

(2005).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

/

F

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

.

F

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

337

ASSESSED BY A TEACHER LIKE ME

assessment. 而且, assignment to a same-race teacher is not significantly
correlated with peers’ average test score.

My main finding—that students are assessed more highly by teachers of
their own race—is robust to the three objections just detailed. That finding is
of particular relevance if teacher assessments are shown to have an effect on
student achievement. Identifying the impact of teacher perceptions of student
skills on later test scores is difficult, and it has led to a large and somewhat
controversial literature in psychology and education (Rosenthal and Jacobson
1968; Jussim 1989; Jussim and Harber 2005). In the so-called Pygmalion
实验, a random subset of students in a small sample of participating
schools is typically labeled “bloomers,” and the research focus is on estimat-
ing the effect of such information on student performance. In this paper’s
nationally representative data set, I find that previous assessments have a
significant impact on later test scores (after conditioning for student effects,
teacher effects, and grade effects).6 实际上, previous teacher assessments are
more strongly correlated with later test scores than are previous test scores.

The paper contributes to two separate literatures. 第一的, it belongs to the
growing literature that documents same-race effects in a number of other
上下文. Price and Wolfers (2010) provide statistical evidence that National
Basketball Association referees favor players of their own race. In firms, Giu-
liano, 莱文, and Leonard (2009) found that white, Hispanic, and Asian
managers hire more whites and fewer blacks than do black managers. 在里面
data set of Giuliano, 莱文, and Leonard (2011), employees have better out-
comes when they are the same race as their manager. The main contribution
of this paper to that literature is providing evidence of same-race effects on
perceptions in education while using a nationally representative data set and
novel robustness checks.

In studying teacher perceptions of student skills from kindergarten to
年级 5, this paper adds also to the literature on teachers’ perceptions of
minority students during their early years of schooling. The previous literature
on race and student assessment has used data for no earlier than grade 8 (Dee
2004). Racial test score gaps expand rapidly much sooner, 然而; Fryer and
莱维特 (2004) document that, between the start of kindergarten and the end
of first grade, black students’ scores fall by 20 percent of a standard deviation
relative to white students with otherwise similar characteristics.

The conclusions reported in this paper should be of particular interest to
policy makers. 第一的, teachers as a group are less diverse than the U.S. student
人口. 有, 尤其, a persistent gap between the percentage of

6.

I also instrument the previous test score by lagged test scores to avoid biases stemming from
regression to the mean (看, 例如, Arellano and Bond 1991).

338

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

F

/

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

F

.

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Amine Ouazad

minority teachers and the percentage of minority students. Numerous papers
and reports have suggested improvements in the recruitment and retention
of minority teachers (Kirby, Berends, and Naftel 1999; Achinstein et al. 2010;
Ingersoll and May 2011). 第二, the paper’s results suggest that involving
teachers in student assessments7 may affect those assessments in ways that
reflect racial perceptions. To ensure fairness, 所以, an assessment system
that involves teachers should exhibit an appropriate racial balance among
graders. Note also that an interesting area of research suggests that racial
perceptions are not fixed and can be significantly altered.8

The paper is structured as follows. 部分 2 presents the data set and
descriptive evidence for higher teacher assessments of same-race students
(conditional on test scores). 部分 3 presents the within-student and within-
teacher identification strategies separately before combining them to obtain
the paper’s baseline estimate. 部分 4 discusses the three major objections as
well as two policy implications of our results on teacher assessments. 部分 5
concludes.

2. DATA SET AND DESCRIPTIVE EVIDENCE
Structure of the Data Set

The data set is the Early Childhood Longitudinal Study, Kindergarten cohort
的 1998 (ECLS-K) from the National Center for Education Statistics, 我们.
教育部. The data follow a nationally representative sam-
的 20,000 kindergarten students in fall and spring kindergarten 1998,
spring grade 1, spring grade 3, and spring grade 5. About a thousand schools
participated.

全面的, the design of the experiment is such that observations are mostly
missing at random. Follow-ups have combined procedures to reduce costs
and maintain the sample’s representativeness. Students who move to an-
other school are randomly subsampled to reduce costs, and new schools and
children have been added to the data set to strengthen the survey’s repre-
sentativeness. In the spring of 1999, some of the schools that had previ-
ously declined participation were included. The new participating children
rendered the cross-sectional sample representative of first-grade children, 全部
of whom were followed in the spring of grades 3 和 5. This paper uses weights

7. 例如, Darling-Hammond and Pecheone (2010) argue that teachers should be integrally

involved in the scoring of assessments.

8. Stangor, Sechrist, and Jost (2001) show how informing participants that others hold different be-
liefs about African Americans changes their beliefs about that group. Lyons and Kashima (2003)
suggest that interpersonal communication figures strongly in maintaining stereotypes. An inter-
esting avenue for future research involves examining how colleagues’ perceptions may affect a
teacher’s perceptions—using data as in Jackson and Bruegmann (2009) but instead with teachers’
perceptions of student performance.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

/

F

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

.

F

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

339

ASSESSED BY A TEACHER LIKE ME

桌子 1. Descriptive Statistics

Observations per Student

Observations per Teacher

Test Score

英语
Mathematics

Teacher Assessment

英语
Mathematics

Teacher Racea

白色的, non-Hispanic
黑色的, non-Hispanic
Asian, non-Hispanic
Hispanic, any race
Other race, non-Hispanic

Student Racea

白色的, non-Hispanic
黑色的, non-Hispanic
Asian, non-Hispanic
Hispanic, any race
Other race, non-Hispanic

Same-race Teacher by Student Raceb

白色的, non-Hispanic
黑色的, non-Hispanic
Asian, non-Hispanic
Hispanic, any race
Other race, non-Hispanic

意思是

6.991

8.198

50.00
50.00

50.00
50.00

0.809
0.063
0.019
0.052
0.057

0.587
0.137
0.057
0.157
0.062

0.436
0.683
0.188
0.069
0.163
0.056

标清

(2.020)

(5.914)

(10.00)
(10.00)

(10.00)
(10.00)

(0.393)
(0.244)
(0.135)
(0.221)
(0.232)

(0.492)
(0.344)
(0.232)
(0.364)
(0.241)

(0.496)
(0.465)
(0.391)
(0.253)
(0.369)
(0.230)

观察结果

115,950

115,950

67,885
48,065

67,885
48,065

115,950
115,950
115,950
115,950
115,950

115,950
115,950
115,950
115,950
115,950

115,950

115,950
115,950
115,950
115,950
115,950

aOther race, non-Hispanic includes Pacific Islanders, 美洲印第安人, and non-Hispanic students
reporting multiple races.
bBoth of the same race, non-Hispanic, or Hispanic, any race.

provided by the survey’s designers to estimate representative effects, 尽管
the analysis is robust to changes in weights.

Observations that lacked data on basic variables (test scores, subjective
assessments, teachers’ and children’s race and gender) were deleted.9 The
analysis in this paper is based on 48,065 observations in mathematics and
67,885 in English, numbers that are similar to Fryer and Levitt (2006).

The restricted-use version of the data set includes both student and teacher
identifiers. 因此, students can be followed across grades. Within each follow-
向上, observations can be grouped by classroom using the teacher identifiers.
桌子 1 shows that data set includes about 6.9 observations per student (3.45

9. Results are robust to an alternative specification where missing observations are present with a

dummy variable indicating that the data are missing.

340

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

F

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

.

F

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Amine Ouazad

on average per student in each subject); the data set includes 8.2 observations
per teacher.

Test Scores and Teacher Assessments

Test scores are based on answers to multiple-choice questionnaires conducted
by external assessors. They conform to national and state standards.10 Overall,
tests ask more than seventy questions in English, and more than sixty questions
in mathematics. Skills covered by the English assessments from kindergarten
to fifth grade include: print familiarity, letter recognition, and beginning and
ending sounds; recognition of common words (sight vocabulary) and decod-
ing multisyllabic words; vocabulary knowledge, such as receptive vocabulary
and vocabulary in context; and passage comprehension. Skills covered by the
mathematics assessment include: number sense, 特性, and operations;
measurement; geometry and spatial sense; data analysis, 统计数据, and proba-
能力; and patterns, algebra, and functions. Test scores were standardized to a
mean of 50 and a standard deviation of 10 (桌子 1). Reliability measures based
on repeated estimates of test scores indicate that the tests are highly reliable;
Rasch coefficients range between 0.88 和 0.95, 包括的.

Teacher assessments of student skills11 are collected at approximately the
same time as the tests are taken. Up to the spring of grade 3, the same teacher
in English and in mathematics assesses students. A different teacher assesses
students in each grade. Teachers do not see the test results, so that test score
results do not directly affect teacher assessments. The user guide specifies that
“This is not a test and should not be administered directly to the child” (看,
例如, the Spring 2004 Fifth Grade questionnaire12). Teachers complete
one questionnaire per student. There are three different teacher assessments:
for language and literacy, mathematical thinking, and general knowledge.
The current paper uses the English (language and literacy) and mathematics
(mathematical thinking) assessments, as there is no corresponding test score
for general knowledge. The instructions make it clear that these assessments
should not be administered as a test directly to the student. For English and
for mathematics, teachers answer seven to nine questions, for a total number
of fourteen to eighteen questions. Answers are on a 5-point scale: Not Yet,

10. These include the National Assessment for Educational Progress, the National Council of Teachers
of Mathematics, the American Association for the Advancement of Science, and the National
Academy of Sciences.
11.
In the ECLS-K user guide, teacher assessments are also known as the academic rating scale.
12. 页 3 的 2004 Grade 5 mathematics form: “Please rate this child’s skills, 知识, 和
behaviors in mathematics based on your experience with the child identified on the cover of this
questionnaire. This is NOT a test and should not be administered directly to the child. Each question
includes examples that are meant to help you think of the range of situations in which the child
may demonstrate similar skills and behaviors.”

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

F

/

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

.

F

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

341

ASSESSED BY A TEACHER LIKE ME

Beginning, In Progress, Intermediate, and Proficient. An overall assessment
is computed for English and for mathematics. Teacher assessments, like test
scores, were standardized to a mean of 50 and a standard deviation of 10
(桌子 1). Reliability measures suggest that teacher assessments are highly
可靠的; Rasch coefficients range between 0.87 和 0.94.

Descriptive Evidence of Same-Race Effects on Teacher Assessments

The restricted-use version of the ECLS-K reports teachers’ and students’ race
和性别. The survey combines race and ethnicity for teachers. “Hispanic,
any race” is one category, and others are “White, any race,” “Black, any race,”
等等. The survey does distinguish race and ethnicity for students, 如何-
曾经. The two variables for students’ race and ethnicity were hence com-
bined to match the single teacher’s race and ethnicity variable. Hence “same
race” should be read as “same race (non-Hispanic) or both Hispanic (任何
种族).”13

The data set oversamples students from racial and ethnic minorities to
increase the precision of the estimates. In the data set, 14 percent are black
学生, 16 percent are Hispanic students, 和 6 percent are Asian students.
There are significantly more white teachers than white students as a fraction of
the observations, and significantly fewer black, Hispanic, and Asian teachers
compared with the corresponding fractions of black, Hispanic, and Asian
学生. Hence a white student is significantly more likely to be assessed by
a same-race teacher than a black, Hispanic, or Asian student.

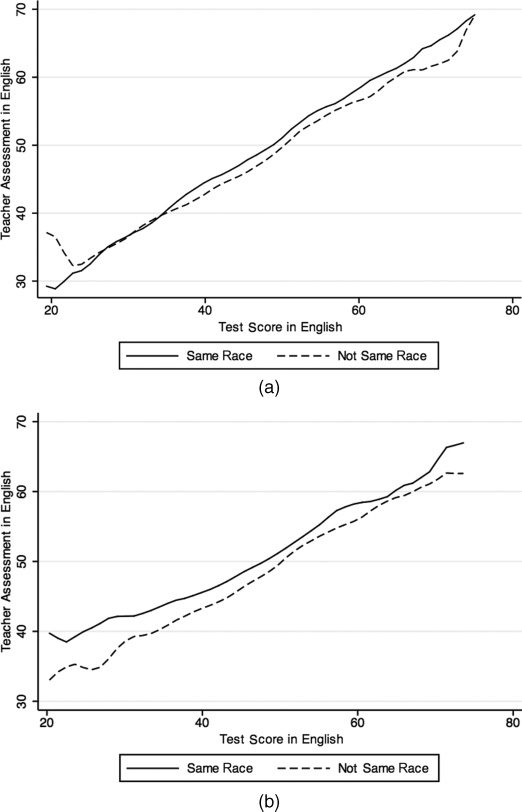
数字 1 presents the average teacher assessments at each test score level,
for students assessed by a same-race teacher and for students assessed by a
teacher of another race. Each line is a local polynomial regression of teacher
assessments on test scores;14 the solid line (the dashed line) is estimated on
observations for students assessed by a same-race teacher (a teacher of another
种族). The two graphs suggest that, at most test score levels, students have on
average higher teacher assessments when assessed by a same-race teacher.
The gap appears larger for Hispanic students (bottom graph) than for black
学生 (top graph).

13. Also the student’s race variable follows the 1997 我们. Revisions to the Standards for the Classifica-
tion of Federal Data on Race and Ethnicity published by the Office for Management and Budget,
which allow for the possibility of specifying “more than one race.” However, the share of multira-
cial students is small. Multiracial students are classified as “Other race,” but results are robust to
alternative classifications.

14. Figure generated with local mean smoothing with 500 点, Epanechnikov kernel, and optimal
half-width. The gap is robust to a variety of number of points, kernels, and half-width sizes.

342

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

F

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

.

F

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Amine Ouazad

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

F

/

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

.

F

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 1. Descriptive Evidence of the Same-Race Effect in (A) Black Students and (乙) Hispanic
Students. Notes: Each panel plots a local polynomial regression of teacher assessments on test
scores, using an Epanechnikov kernel, 500 点, and optimal half-width. The gap between the two
curves is present even when changing the type of the kernel, number of points, and the half-width.

An ordinary least squares (OLS) regression estimates the average effect of
same race teachers on the difference between teacher assessments and test
scores, and provides confidence intervals:

TAi, F,t − TSi, F,t = constant + δ · Same Race i, F,t

+ StudentChar acter is tics i β

+ Teacher Char acter is tics i, F,t γ

+ Gr ade t + εi, F,t

(1)

343

ASSESSED BY A TEACHER LIKE ME

where i indexes students, f the subject area (mathematics or English), and t
the wave of the longitudinal data (t = {Fall kindergarten, spring kindergarten,
spring grade 1, spring grade 3, spring grade 5}). TAi,F,t is the standardized
teacher assessment, TSi,F,t represents the standardized test score. Same Racei,F,t
is a dummy set to 1 if student i in subject f in wave t was assessed by a same-
race teacher. Student characteristicsi is a vector of dummies for the student’s
gender and race. Teacher Characteristicsi,F,t is a vector of dummies for student
i’s teacher in subject f in wave t. Gradet is a grade effect, and εi,F,t is the residual,
clustered by student.15

The regression is performed separately for English and for mathematics.
Throughout the paper, I also present the regression with the teacher assess-
ment as the dependent variable, and the test score as a control. While the
regression with the test score as an explanatory variable corresponds to the
concept of conditional bias (Ferguson 2003), putting the test score on the right-
hand side means that the estimate of the coefficient of the same-race dummy
may capture measurement error in test scores. Specification 1 has both teacher
assessment and test score on the left-hand side, which substantially alleviates
any bias caused by measurement error.

The OLS regression suggests that a student assessed by a same-race teacher
gets a teacher assessment that is about 2.8 百分比到 5.7 percent of a standard
deviation higher in mathematics, 和 4.3 百分比到 6.7 percent of a standard
deviation higher in English (桌子 2). In this specification, the test score as an
explanatory variable explains only 34.8 到 44 percent of the variance of teacher
assessments.

3. IDENTIFICATION STRATEGY
Within-Student Identification: Using Student Mobility

from/to a Same-Race Teacher

In the descriptive evidence that was presented in the previous section, 这
OLS estimate of the same-race effect may be biased because a number of
student-specific variables are omitted from the regression.

例如, literature suggests that teacher perceptions of student per-
formance might depend on a number of characteristics other than student
种族: student behavior (Sherman and Cormier 1974), 语言 (Gluszek and
Dovidio 2010), parental involvement (Wilson and Martinussen 1999), student
academic engagement (Hughes and Kwok 2007), and other factors. Neither of
these variables is measured by test scores nor reflects racial perceptions per se.

15. Clustering by classroom, by student, or two-clustering (Cameron, Gelbach, and Miller, 2011) 经过
both student and classroom has little impact on the standard errors. Because two-way clustering
with two-way fixed effect (used later in section 3) does not yet exist in the literature, I chose to
present standard errors clustered by student. Clustering by classroom yields very similar standard
errors in all specification.

344

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

F

/

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

.

F

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Amine Ouazad

桌子 2. OLS Regressions

Mathematics

英语

(1)

(2)

(3)

(4)

Teacher
Assessment

Teacher Assessment
– Test Score

Teacher
Assessment

Teacher Assessment
– Test Score

Same-Race

Test Score

0.281∗
(0.118)

0.591∗∗
(0.004)

0.566∗∗
(0.131)

–

0.428∗∗
(0.093)

0.659∗∗
(0.003)

Controls

Student and teacher race and gender, grade effects

观察结果

48,065

Students

教师

R2

20,252

5,297

0.348

F Statistic

1,218.5

48,065

20,252

5,297

0.034

85.3

67,855

20,252

5,496

0.436

2,501.1

0.665∗∗
(0.122)

–

67,855

20,252

5,496

0.029

68.9

Notes: Standard errors clustered by student. Clustering by classroom yields similar significance
级别. Test scores and teacher assessments are standardized to a mean of 50 and a standard
deviation of 10.
∗Statistically significant at the 5% 等级; ∗∗statistically significant at the 1% 等级.

Identifying the specific effect of the student’s race requires a more complete
specification than equation 1, one that at least controls for student-specific
omitted variables. Such omitted variables will confound the estimate of the
same-race effect if teachers and students are non-randomly matched.

Assume that the teacher assessment incorporates a measure of the test

分数, captures a same-race bias, and also student-specific omitted variables:

TAi, F,t = constant + δ · Same Race i, F,t + αTes t Scor e i, F,t + Gr ade t

+ Contr ol s i, F,t + Student Omitted Var iabl e i, F,t + Res idual i, F,t

(2)

with the same notations as in specification 1, and εi,F,t = Student Omitted
Variablei,F,t + Residuali,F,t. Controlsi,F,t is a set of dummies for the teacher’s
race and gender. If student-specific omitted variables that have a positive im-
pact on the teacher assessment are correlated with assignment to a same-race
teacher, the effect δ of a same-race teacher on assessments is overestimated.
换句话说, if assignment to teachers depends on unobservables that affect
teacher assessments, the same-race effect is biased. Student-specific omitted
variables that are not correlated with same-race assignments will also imply a
(西德:3)) 是
correlation of residuals common to a given student, 那是, Corr(εi,F,t,εi,F

,t

(西德:3)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

/

F

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

F

.

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

345

ASSESSED BY A TEACHER LIKE ME

not equal to 0, and standard errors will need to be corrected for student-level
clustering.16

If student-specific omitted variables do not vary across grades,17 specifica-

的 2 can be estimated using a student fixed effect Studenti,F:

T Ai, F,t = constant + δ · Same Race i, F,t + α · Tes t Scor e i, F,t + Contr ol si, F,t

+Student i, F + Gr ade t + Res idual i, F,t

(3)

which is estimated using either a set of student dummies, or in first-difference.
A major advantage of the dummy variable approach is that it allows us to
recover an estimate of the student unobservables Studenti; using this estimate
we can check whether there is a significant correlation between assignment
to a same-race teacher and student unobservables. Specification 3 can also be
estimated in first-difference,18 那是, using a within-student regression:

T Ai, F,t+1 − T Ai, F,t = δ(Same Race i, F,t+1 − Same Race i, F,t )

+ (Contr ol s i, F,t+1 − Contr ol s i, F,t )

+ A(Tes t Scor e i, F,t+1 − Tes t Scor e i, F,t )

+ (Gr ade t+1 − Gr ade t ) + (Res idual i, F,t+1

− Res idual i, F,t ).

(4)

The first-differenced specification makes clear that the identification of
the same-race effect δ relies on student mobility from/to a same-race teacher.
The effect of a same-race teacher is estimated without bias if the mobility
of a student from a teacher of the same-race (another-race) in one grade to
a teacher of another race (the same race), in the next grade, is uncorrelated
with time varying student unobservables that have an impact on test scores,
那是, Corr((Same Racei,F,t + 1 − Same Racei,F,t), (Residuali,F,t + 1 – Residuali,F,t)) =
0. Student behavior is one such time varying unobservable that may affect
teacher assessments and is potentially correlated with student mobility to/from

16. Specifically, Cov(εi,F,t,εi,F (西德:3),t(西德:3) ) = Cov(Student Omitted Variablei,F,t,Student Omitted Variablei,F (西德:3),t(西德:3) ) for f (西德:4)=
F (西德:3) and for t (西德:4)= t(西德:3). If student-specific omitted variables are constant across grades, then Cov(εi,F,t,
εi,F,t (西德:3) ) = Var(Student Omitted Variablei,F) and the correlation of residuals for a given student across
grades will be equal to the ratio of the variance of student unobservables to the overall variance of
the residuals (Moulton 1990).

17. Student Omitted Variablei,F,t = Student Omitted Variablei,F,t (西德:3) for any t, t (西德:3).
18. Both approaches (student dummies and first-differenced specification) are equivalent with a large
number of observations as long as the strict exogeneity assumption is satisfied (Baltagi 2008), 那
是, 乙(Residuali,F,t|席,F,1,席,F,2,…,席,F,5) = 0, where 1,2,…,5 indexes waves of the survey, and Xi,F,t denotes
the vector of explanatory variables for student i in subject area f, in grade t (常数, same race
dummy, test score, and grade dummies).

346

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

/

F

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

F

.

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Amine Ouazad

a teacher of the same race. I discuss the impact of behavior on estimates in
部分 4.

Because identification relies on student mobility across teachers, it is im-
portant to check that a sufficient number of students move to teachers of
different races. Otherwise identification would rely on a small number of stu-
dents who move from/to a teacher of the same race.19 There are a large number
of such moves: 51 percent of students experience mobility from/to a same-race
teacher at some point between kindergarten and grade 5, and the sample of
movers is balanced in terms of race, 性别, and parental income.20

Columns (1) 和 (4) of table 3 present the estimation of the first-differenced
specification 4 in mathematics and in English, with standard errors clustered
by student.21 Being assessed by a teacher of the same race raises teacher assess-
ments by 3.5 percent of a standard deviation in mathematics and by 4.3 百分
in English. The specification has fewer observations because the number of
observations is equal to the number of first-differenced teacher assessments.
Columns (2) 和 (5) present results of the estimation of specification 3, 哪个
includes a student fixed effect. Being assessed by a teacher of the same race
raises assessments by 7 percent of a standard deviation in mathematics and
经过 4.8 percent of a standard deviation in English. The regression is strongly
significant with an F statistic of 82.6. 重要的, there is a significantly pos-
itive correlation between the estimated student effects and assignment to a
same race teacher both in mathematics and in English, which indicates that
the regression without student fixed effects underestimates the impact of a
same-race teacher on assessments. Columns (3) 和 (6) regress the difference
between the teacher assessment and the test score on the explanatory variables.
Estimates of the same race effect are comparable to columns (2) 和 (5) 的
same table.

Within-Classroom Identification

Teacher-specific omitted variables may also confound the estimate of the same-
race effect. Although OLS specification 1 controls for teachers’ race and gender,
other teacher characteristics, imperfectly correlated with race and gender, 影响
teacher assessments. 例如, Figlio and Lucas (2004) find that some
teachers give higher average grades regardless of their students’ ability, 种族,
or gender. Such variation in average assessments across classrooms should

19.

一般来说, if a covariate does not vary for a given student in a panel data regression with student
fixed effects, the student’s observation will not contribute to the estimation of the effect (Wooldridge
2002).

20. At each parental income level, 从 41 百分比到 52 percent of students experience a transition

from/to a same race teacher. Statistics available on request.

21. Clustering either by classroom, by student, or clustering by both classroom and student (Cameron,

Gelbach, and Miller 2011) does not significantly affect the estimated standard errors.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

/

F

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

F

.

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

347

ASSESSED BY A TEACHER LIKE ME

)
6
(

)
5
(

)
4
(

)
3
(

)
2
(

)
1
(

e
r
哦
C
S
t
s
e
时间

–

t
n
e
米
s
s
e
s
s
A

t
n
e
米
s
s
e
s
s
A

e
r
哦
C
S
t
s
e
时间

–

t
n
e
米
s
s
e
s
s
A

t
n
e
米
s
s
e
s
s
A

t
n
e
米
s
s
e
s
s
A
r
e
H
C
A
e
时间

r
e
H
C
A
e
时间

r
e
H
C
A
e
时间

d
e
C
n
e
r
e
F
F
我

D
–
t
s
r
我

F

t
n
e
米
s
s
e
s
s
A
r
e
H
C
A
e
时间

r
e
H
C
A
e
时间

r
e
H
C
A
e
时间

d
e
C
n
e
r
e
F
F
我

D
–
t
s
r
我

F

H
s
我
我

G
n
乙

s
C
我
t
A
米
e
H
t
A
中号

s
t
C
e
F
F
乙

d
e
X
我
F

t
n
e
d
你
t
S
H
t
我

w
d
n
A

n
哦
我
t
A
C
fi
我
C
e
p
S
d
e
C
n
e
r
e
F
F
我

D

–
t
s
r
我
F

H
t
我

w
s
t
我
你
s
e
右

.

我

3
e
乙
A
时间

348

∗
∗
3
8
4
0

.

)
6
7
1
0
(

.

–

s
e
是

哦
氮

s
e
是

5
5
8
,
7
6

0
3
4
0

.

6
4
6
1

.

)
0
0
0
0
(

.

∗
∗
6
9
0
0
-

.

)
0
0
0
0
(

.

∗
∗
3
1
4
0

.

)
3
1
1
0
(

.

∗
∗
6
1
3
0

.

)
6
0
0
0
(

.

s
e
是

哦
氮

s
e
是

5
5
8
,
7
6

9
9
6
0

.

4
2
0
2

.

)
0
0
0
0
(

.

∗
∗
5
6
0
0

.

)
0
0
0
0
(

.

∗
∗
9
2
4
0

.

∗
∗
4
8
7
0

.

∗
∗
4
0
7
0

.

∗
∗
1
4
2
0

.

)

4
5
1
0

(

.

)

7
0
0
0

(

.

哦
氮

s
e
是

s
e
是

A
2
9
4

,

4
4

6
3
0
0

.

–

–

)

9
7
1
0

(

.

–

s
e
是

哦
氮

s
e
是

5
6
0

,

8
4

0
4
0
0

.

∗
∗
3
6
2
0

.

)

2
6
1
0

(

.

)

9
0
0
0

(

.

s
e
是

哦
氮

s
e
是

5
6
0

,

8
4

5
6
6
0

.

2
7
3
2

.

8
0
1
3

.

)

0
0
0
0

(

.

)

0
0
0
0

(

.

∗
∗
5
4
1
0
-

.

∗
∗
2
4
0
0

.

)

0
0
0
0

(

.

)

0
0
0
0

(

.

+
0
5
3
0

.

)
1
1
2
0
(

.

∗
∗
9
2
1
0

.

)
1
1
0
0
(

.

哦
氮

s
e
是

s
e
是

A
9
8
0
,
2
2

0
1
0
0

.

–

–

r
e
d
n
e
G
d
n
A

e
C
A
右
r
e
H
C
A
e
时间

d
n
A

t
n
e
d
你
t
S

s
t
C
e
F
F
乙

e
d
A
r
G

s
n
哦
我
t
A
v
r
e
s
乙
氧

2
右

)
e
你
A
v

我

p
(

s
t
C
e
F
F
乙

t
n
e
d
你
t
S
r
哦
F

C
我
t
s
我
t
A
t
S
F

)
s
t
C
e
F
F
乙

t
n
e
d
你
t
S

,

e
C
A
右
e
米
A
S
(
r
r
哦
C

–

e
C
A
右
e
米
A
S

e
r
哦
C
S
t
s
e
时间

t
C
e
F
F
乙

t
n
e
d
你
t
S

d
r
A
d
n
A
t
s

A

d
n
A

0
5

F
哦

n
A
e
米
A

哦
t

d
e
z
我
d
r
A
d
n
A
t
s

s
t
n
e
米
s
s
e
s
s
A

r
e
H
C
A
e
t

d
n
A

s
e
r
哦
C
s

t
s
e
时间

.

米
哦
哦
r
s
s
A
C

我

y
乙

G
n
我
r
e
t
s
你
C

我

哦
t

t
s
你
乙
哦
r

s
t
我
你
s
e
右

.
t
n
e
d
你
t
s

y
乙

d
e
r
e
t
s
你
我
C

s
r
哦
r
r
e

d
r
A
d
n
A
t
S

:
s
e
t
哦
氮

.
0
1

F
哦

n
哦
我
t
A
我
v
e
d

.
我
e
v
e

我

%
0
1
e
H
t

t
A

t
n
A
C
fi
n
G
s

我

我

y
我
我

A
C
我
t
s
我
t
A
t
s
+

;
我
e
v
e

我

%
1

e
H
t

t
A

t
n
A
C
fi
n
G
s

我

我

y
我
我

A
C
我
t
s
我
t
A
t
s
∗
∗

;
我
e
v
e

我

%
5

e
H
t

t
A

t
n
A
C
fi
n
G
s

我

我

.
G
n
我
C
n
e
r
e
F
F
我
d

t
s
r
fi

哦
t

e
你
d

s
n
哦
我
t
A
v
r
e
s
乙
哦

F
哦

r
e
乙
米
你
n

y
我
我

A
C
我
t
s
我
t
A
t
S
∗

r
e

我
我

A
米
S
A

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

F

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

F

.

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Amine Ouazad

be controlled for in specification 1 as the nonrandom sorting of teachers to
students implies that the teacher’s average assessment may be correlated with
assignment to a same-race student.

All these teacher-specific omitted variables enter in the determination of

teacher assessments:

T Ai, F,t = constant + δ · Same Racei, F,t + αT es t Scor ei, F,t

+ T eacher Omitted Var iabl ei, F,t + Contr ol si, F,t

+ Gr adet + Res iduali, F,t .

(5)

Teacher omitted variables (Teacher Omitted Variablei,F,t), if correlated posi-
tively with assignment to a same race teacher (Same Racei,F,t), lead to an upward
bias in the estimate δ of the same-race effect. The presence of teacher-specific
omitted variables also imply a correlation of residuals in the OLS specification
across observations of the same classroom, and standard errors should be
corrected for clustering at the classroom level.22 Because of the large number
of fixed effects (6,093 教师), a specification like specification 5 is usually
estimated by taking the within-classroom difference of teacher assessments,
test scores, and each covariate of the specification

T Ai, F,t − E (T A., F,t |cl as s r oom)

= δ · (Same Racei, F,t − E (Same Racei, F,t |cl as s r oom)

+ α · (硅钛矿, F,t − E (T S., F,t |cl as s r oom))

+ Contr ol si, F,t − E (Contr ol si, F,t |cl as s r oom))

+ Res idual

(西德:3)
我, F,t

.

(6)

where E(x.,f,t|classroom) is the average of covariate x in the classroom of student
i in subject f in year t. The within-classroom specification makes it clear that
the identification relies on comparing the teacher assessment TAi,F,t of a stu-
dent to the average teacher assessment E(TA .,f,t|classroom) in the classroom. A
classroom contributes to the identification of the same-race effect if it has both
same-race and other-race students.23 Fortunately, 97.2 percent of the class-
rooms of the sample have observations of same-race and other-race students,
和 44 percent of students are of the same race as teacher on average.

22. Throughout the paper I cluster standard errors at the student level, but clustering at the classroom
level or two-way clustering at the student and classroom levels (Cameron, Gelbach, and Miller 2011)
yields similar significance levels.

23. 正式地, if the value of Same Racei,F,t – E(Same Race.,f,t|classroom) changes within a classroom.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

F

/

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

F

.

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

349

ASSESSED BY A TEACHER LIKE ME

Specification 5 can also be estimated by including a set of teacher fixed

effects, 即, one dummy of each teacher of the sample.

T Ai, F,t = constant + δ · Same Race i, F,t + αTes t Scor e i, F,t

+ Teacher E f f ect i, F,t

+ Gr ade t + Res idual i, F,t .

(7)

Both approaches (specifications 6 和 7) yield the same estimate with
a large number of observations (Baltagi 2008).24 The advantage of such a
specification is that it allows us to recover an estimate of the teacher effect. In all
waves except the spring grade 5 后续行动, the same teacher assesses students
in English and mathematics, but separate teacher effects are estimated for
English and for mathematics.

Columns (1) 和 (4) of table 4 show the results of the within-classroom
specification 6. Students assessed by a teacher of the same race have higher
teacher assessments, 经过 4.1 percent of a standard deviation in English and 5.5
percent in mathematics. All results are significant at 1 百分. 有趣的是,
test scores and observable controls explain 34 percent of the variance of teacher
assessments. Columns (2) 和 (5) present results of the estimation of speci-
fication 7, which includes teacher effects. The point estimates are larger than
in the within-teacher approach, but they are not statistically different from the
estimates of columns (1) 和 (4). Having a same-race teacher raises teacher
assessments by 6.9 percent of a standard deviation in English and 7.0 百分
of a standard deviation in mathematics. The specification allows us to estimate
that teacher effects are significant (the null hypothesis that teacher effects are
equal to zero is rejected), indicating that teacher unobservables play a role in
assessments. 而且, being assessed by a same-race teacher is negatively
correlated with the teacher effect (especially in mathematics), and we indeed
observe a downward bias: The OLS estimation of the same-race effect without
teacher effects in columns (1) 和 (3) of table 2 is lower than the estimates
of columns (2) 和 (5) of table 4. 最后, results available on request show
that teacher unobservables are not accounted for by the teacher’s race, 性别,
经验, or tenure.

Combining the Within-Student and Within-Classroom Identification Strategies

最后, I combine both the former two identification strategies to control
for both student-specific and teacher-specific omitted variables. My preferred

24. 那是, both estimators converge in probability to the same estimate. Under the assumption that
residuals are strictly exogenous within each classroom, 那是, 乙(Residual(西德:3)我,F,t|X·,F,t) = 0, 在哪里
席,F,t is the vector of explanatory (right-hand side) variables in specification 6.

350

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

F

/

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

.

F

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Amine Ouazad

)
6
(

)
5
(

)
4
(

)
3
(

)
2
(

)
1
(

t
n
e
米
s
s
e
s
s
A

t
n
e
米
s
s
e
s
s
A

A
时间

e
G
A
r
e
v
A
–

t
n
e
米
s
s
e
s
s
A

t
n
e
米
s
s
e
s
s
A

A
时间

e
G
A
r
e
v
A
–

r
e
H
C
A
e
时间

r
e
H
C
A
e
时间

t
n
e
米
s
s
e
s
s
A
r
e
H
C
A
e
时间

r
e
H
C
A
e
时间

r
e
H
C
A
e
时间

t
n
e
米
s
s
e
s
s
A
r
e
H
C
A
e
时间

H
s
我
我

G
n
乙

s
C
我
t
A
米
e
H
t
A
中号

s
t
C
e
F
F
乙

d
e
X
我
F

r
e
H
C
A
e
时间

d
n
A

t
n
e
d
你
t
S
H
t
哦
乙

我

我

G
n
n
乙
米
哦
C
d
n
A

,
n
哦
我
t
A
C
fi
我
C
e
p
S
s
t
C
e
F
F
乙
d
e
X
我
F

–

r
e
H
C
A
e
时间

e
H
t

F
哦

,
n
哦
我
t
A
米

我
t
s
乙

r
e
H
C
A
e
时间
n
H
t
我

我

–

瓦
e
H
t

F
哦

s
t
我
你
s
e
右

.

我

4
e
乙
A
时间

∗
∗
5
3
4
0

.

)
4
1
1
0
(

.

∗
∗
3
1
3
0

.

)
5
0
0
0
(

.

s
e
是

s
e
是

哦
氮

5
5
8
,
7
6

3
7
7
.
0

6
8
7
2

.

)
0
0
0
0
(

.

∗
∗
3
1
0
0

.

)
0
0
0
0
(

.

2
5
1
2

.

)
0
0
0
0
(

.

∗
∗
8
5
0
0

.

)
0
0
0
0
(

.

∗
∗
2
0
7
0

.

)
4
9
0
0
(

.

∗
∗
9
6
6
0

.

)
3
0
0
0
(

.

s
e
是

哦
氮

s
e
是

5
5
8
,
7
6

3
5
5
.
0

6
3
8
2

.

)
0
0
0
0
(

.

∗
∗
7
1
0
0
–

.

)
0
0
0
0
(

.

–

–

∗
∗
9
4
5
0

.

∗
∗
1
1
7
0

.

∗
∗
4
9
6
0

.

)

8
9
0
0

(

.

)

0
9
1
0

(

.

)

0
2
1
0

(

.

∗
∗
4
5
6
0

.

∗
∗
1
4
2
0

.

∗
∗
8
8
5
0

.

)

4
0
0
0

(

.

)

9
0
0
0

(

.

)

4
0
0
0

(

.

哦
氮

哦
氮

s
e
是

5
5
8
7
6

,

8
3
4

.

0

–

–

–

–

s
e
是

s
e
是

哦
氮

5
6
0

,

8
4

6
8
7

.

0

6
9
9
2

.

s
e
是

哦
氮

s
e
是

5
6
0

,

8
4

0
4
5

.

0

1
9
2
3

.

)

0
0
0
0

(

.

)

0
0
0
0

(

.

)

0
0
0
0

(

.

4
9
7
1

.

)

0
0
0
0

(

.

∗
∗
0
3
0
0

.

–

–

∗
∗
0
2
0
0

.

∗
∗
1
1
0
0
–

.

)

0
0
0
0

(

.

)

8
1
0
0

(

.

∗
∗
6
0
4
0

.

)
9
1
1
0
(

.

∗
∗
5
6
5
0

.

)
5
0
0
0
(

.

哦
氮

哦
氮

s
e
是

5
6
0
,
8
4

8
3
3
.
0

–

–

–

–

我

s
e
乙
A
v
r
e
s
乙
氧

r
e
H
C
A
e
时间

d
n
A

t
n
e
d
你
t
S

)
e
你
A
v

我

p
(

.
t
A
t
S
F

s
t
C
e
F
F
乙

r
e
H
C
A
e
时间

)
s
t
C
e
F
F
乙

r
e
H
C
A
e
时间

,

e
C
A
右
e
米
A
S
(
r
r
哦
C

)
e
你
A
v

我

p
(

.
t
A
t
S
F

s
t
C
e
F
F
乙

t
n
e
d
你
t
S

)
s
t
C
e
F
F
乙

t
n
e
d
你
t
S

,

e
C
A
右
e
米
A
S
(
r
r
哦
C

s
n
哦
我
t
A
v
r
e
s
乙
氧

2
右

e
C
A
右
e
米
A
S

e
r
哦
C
S
t
s
e
时间

s
t
C
e
F
F
乙

r
e
H
C
A
e
时间

s
t
C
e
F
F
乙

t
n
e
d
你
t
S

.
t
n
e
米
s
s
e
s
s
A

r
e
H
C
A
e
t

=

A
时间

.
s
e
t
A
米

我
t
s
e

r
A

我
我

米
s

我

我

s
d
e
我
y
米
哦
哦
r
s
s
A
C

我

y
乙

G
n
我
r
e
t
s
你
C

我

.
t
n
e
d
你
t
s

y
乙

d
e
r
e
t
s
你
C

我

s
r
哦
r
r
e

d
r
A
d
n
A
t
S

.
s
t
C
e
F
F
e

e
d
A
r
G

e
d
你
我
C
n

我

.
我
e
v
e

我

%
1
e
H
t

t
A

s
n
哦
我
t
A
C
fi
我
C
e
p
s

我
我

A

:
s
e
t
哦
氮

t
n
A
C
fi
n
G
s

我

我

y
我
我

A
C
我
t
s
我
t
A
t
S
∗
∗

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

F

/

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

F

.

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

351

ASSESSED BY A TEACHER LIKE ME

estimate is thus the same-race δ coefficient in the regression that controls for
both teacher effects and student effects:

T Ai, F,t = constant + δSame Race i, F,t + αTes t Scor e i, F,t

+ Teacher E f f ect i, F,t
+ Gr ade t + Res idual i, F,t

+ Student E f f ect i

(8)

where the teacher effect (Teacher Effecti,F,t) and the student effect (Student Effecti)
are estimated by including a set of dummies for teachers and a set of dum-
mies for students as controls. The large number of students (21,409) 和
large number of teachers (6,093) make it necessary to estimate the model
using econometric techniques pioneered by Abowd, Creecy, and Kramarz
(2002) and Abowd, Kramarz, and Margolis (1999) in the labor economics
employer–employee literature. The technique provides estimates for all stu-
dent effects, teacher effects, grade effects, and same-race and test score co-
efficients. Standard errors are clustered at the student level; clustering by
classroom yields similar standard errors.

Columns (3) 和 (6) present the estimates. Teachers give better assess-
ments to students of their own race; the effect is 7.1 percent of a standard
deviation in mathematics and 4.4 of a standard deviation in English. Teacher
and student effects are significant.

4. DISCUSSION OF THE FINDINGS
Behavior and Assessments

Teacher assessments of student performance are partly determined by student
行为 (Sherman and Cormier 1974). Column (1) (分别, Column (2))
of table 5 shows a regression of mathematics teacher assessments (分别,
English teacher assessments) on four behavioral measures.

The four behavioral measures come from a separate questionnaire of each
wave of the study. Teachers reported the measures in terms of the social rat-
ing scale: approaches to learning, interpersonal skills, externalizing problems
行为, internalizing problems behavior. The scale for approaches to learn-
ing measures the ease with which children can benefit from their learning
环境. The interpersonal skills scale rates the child’s skill in forming
and maintaining friendships; getting along with people who are different;
comforting or helping other children; expressing feelings, ideas, and opinions
in positive ways; and showing sensitivity to the feelings of others. The exter-
nalizing problem behaviors scale (IE。, impulsive/overactive scale) addresses
acting-out behaviors, and the internalizing problem behavior scale addresses
evidence of anxiety, loneliness, low self-esteem, or sadness.

352

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

/

/

F

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

.

F

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Amine Ouazad

桌子 5. Behavior and Assessments

(1)

(2)

(3)

(4)

Mathematics Teacher
Assessment

English Teacher
Assessment

Same Race

Same Race

Same Race

Test Score

Approaches

to Learning

Interpersonal

Skills

Externalizing

Problem Behavior

Internalizing

Problem Behavior

Student and Teacher
Race and Gender

Student Effects

Teacher Effects

F Statistic

R2

0.707∗∗
(0.199)

0.207∗∗
(0.008)

0.267∗∗
(0.008)

0.042∗∗
(0.007)

0.045∗∗
(0.012)

−0.040∗∗
(0.006)

不

是的

是的

4.62

0.73

观察结果

48,065

0.419∗∗
(0.134)

0.265∗∗
(0.006)

0.298∗∗
(0.004)

0.035∗∗
(0.004)

0.035∗∗
(0.003)

−0.058∗∗
(0.005)

不

是的

是的

0.80

67,855

–0.001
(0.001)

0.001∗∗
(0.001)

−0.001
(0.001)

−0.001
(0.001)

−0.001∗∗
(0.000)

是的

不

不

4,249.2

0.59

0.001
(0.000)

−0.001+
(0.000)

0.000
(0.000)

0.001
(0.001)

0.001∗∗
(0.000)

是的

是的

不

26.66

0.79

67,855A

67,855A

aRegression performed using English observations. Students are assessed by the same teacher in
English and mathematics from kindergarten to grade 3, and different teachers in grade 5. 相似的
results hold when estimating the regression with mathematics observations.
∗∗Statistically significant at the 1% 等级. All specifications include grade effects. Standard errors
clustered by student. Clustering by classroom yields similar estimates.

The measures of behavior vary substantially, both across students and for a
given student, across time. On the interpersonal skills scale, 50.1 的百分比
variance is explained by within-student variance, and the behavioral measure
in the previous wave of the study explains about 31 percent of the variance of
the behavioral measure of the next grade.

In Column (1) of table 5, the teacher assessment in mathematics is re-
gressed on the mathematics test score, the same-race dummy, the four behav-
ioral measures, a student effect, and a teacher effect.

The first noticeable fact is the impact of behavior on assessment. Smaller
values indicate stronger behavioral problems. A one standard deviation in-
crease in the approaches to learning scale raises teacher assessments by 3
percent of a standard deviation. A one standard deviation increase in the inter-
personal skills measure raises teacher assessments by 0.4 percent of a standard

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

F

/

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

F

.

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

353

ASSESSED BY A TEACHER LIKE ME

deviation. Externalizing behavior problems has a similar positive effect. 国际米兰-
nalizing behavior problems has a negative impact on teacher assessments.
That last result is consistent with the finding (Rutherford, 奎因, and Mathur
2004) that students with internalizing behavior problems (social withdrawal,
anxiety, depression) are harder to identify than students with externalizing
behavior problems (noncompliance, aggression, disruption).

How behavior affects the baseline estimate of the same-race effect in speci-
fication 8 depends on whether students are partly matched to teachers based on
their behavior. Because I am using a student fixed-effect regression, 行为
is a confounding factor in the regression if changes in behavior across grades
are significantly correlated with the probability of being assigned a same-race
teacher. If students whose behavior improves are more likely to be assigned to
a same-race teacher, the same-race effect δ in specification 8 will be overesti-
mated. Column (3) regresses the same-race dummy on the test score, the four
behavioral measures, and student and teacher race and gender dummies. 这
effect of behavior on same-race assignments is either nonsignificant or very
小的. Column (4) confirms the finding when including student fixed effects.
不出所料, 所以, behavioral controls leave the same-race effect
(0.707 compared with 0.702 in mathematics, 0.420 compared with 0.435 在
英语) virtually unchanged compared with the estimate with a student effect
and a teacher effect in table 4.

Same-Race Effects Skill by Skill

桌子 6 presents results of baseline regression for English, considering only
kindergarten fall semester observations. The novelty is that the dependent
variable is the teacher assessment broken down into eight separate skills.
The results are informative with regard to the likelihood of a bias for two
原因: 第一的, it is unlikely that students benefit from the better teaching of
a same-race teacher (Dee 2005) only a few weeks after the start of school and
hence better teacher assessments for same-race students are more likely to
represent perceptions rather than actual skills. 第二, same-race assessment
gaps appear also for the least abstract questions—in other words, 问题
that address the skills that are most likely to be captured by achievement tests.
拿, 例如, the statement: “This child easily and quickly names all
upper- and lower-case letters of the alphabet.” In the fall semester of kinder-
garten, teachers assess students of their own race 4 percent of a standard
deviation higher than children of other races. This English skill is measured
in the kindergarten test and is measured early in the curriculum. And similar
regressions in grade 5 present similar positive same-race effects.

The same-race effect can also be estimated separately for each grade by in-
cluding interactions between the grade dummies and the same-race dummy.

354

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

p

:
/
/

d
我
r
e
C
t
.

米

我
t
.

F

/

/

e
d
你
e
d
p
A
r
t
我
C
e
–
p
d

我

F
/

/

/

/

/

9
3
3
3
4
1
6
9
1
3
8
7
e
d
p
_
A
_
0
0
1
3
6
p
d

.

F

F

乙
y
G
你
e
s
t

t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Amine Ouazad

s
t
n
e
米
s
s
e
s
s
A
r
e
H
C
A
e
时间

H
s
我
我

G
n
乙

n
e
t
r
A
G
r
e
d
n
K

我

我
我

A
F

∗
6
9
1
0

.

)
7
7
0
0
(

.

4
6
8
,
6
1

1
9
.
0

3
.
8
8
3

6
3
1
0

.

)
8
9
0
0
(

.

4
6
8
,
6
1

5
8
.
0

9
.
5
4
0
,
1

r
e
t
你
p
米
哦
C

s
n
哦
我
t
n
e
v
n
哦
C

G
n
我
t
我
r

瓦

8
1
0
0

.

)

8
0
1
0

(

.

s
d
A
e
右

0
8
0
0

.

我

G
n
米
y
H
右

∗
∗
4
7
6
0

.

s
e
米
A
氮

∗
∗
7
9
3
0

.

)

4
0
1
0

(

.

)

6
0
1
0

(

.

)

7
2
1
0

(

.

s
t
C
e
F
F
乙

r
e
H
C
A
e
时间

d
n
A

s
e
r
哦
C
S
t
s
e
时间

H
s

我
我

G
n
乙

4
6
8

,

6
1

4
6
8

,

6
1

2
8

.

0

3
8

.

0

4
6
8

,

6
1

2
8
0

.

4
6
8

,

6
1

4
7

.

0

.

9
9
2
5

,

1

.

4
3
2
1

,

1

.

2
7
2
8

,

.

3
5
6
5

,

4

1

我

s
哦
r
t
n
哦
C

s
d
n
A
t
s
r
e
d
n
U

我

X
e
p
米
哦
C

∗
∗
5
3
0
1

.

)
6
4
1
0
(

.

4
6
8
,
6
1

5
6
.
0

.

3
2
9
1
,
2

∗
∗
7
5
2
1

.

)
2
4
1
0
(

.

4
6
8
,
6
1

7
6
.
0

7
.
9
3
0
,
2

r
e
H
C
A
e
时间

–

e
C
A
右
e
米
A
S

r
e
H
C
A
e
时间

–

e
C
A
右
e
米
A
S

s
n
哦
我
t
A
v
r
e
s
乙
氧

我

s
哦
r
t
n
哦
C

C
我
t
s
我
t
A
t
S
F

2
右

我
我
我

k
S
y
乙

我
我
我

k
S
s
t
C
e
F
F
乙

e
C
A
右
e
米
A
S

.

我

6
e
乙
A
时间

e
H
t

r
哦
F

我

s
哦
r
t
n
哦
C

e
d
你
我
C
n

我

我

s
哦
r
t
n
哦
C

r
e
H
C
A
e
t

;
r
e
d
n
e
G

d
n
A

e
C
A
r

r
哦
F

我

s
哦
r
t
n
哦
C

e
d
你
C
n

我

我

d

我
我

H
C

;
0
5

F
哦

n
A
e
米
A

d
n
A

0
1

F
哦

n
哦
我
t
A
我
v
e
d

d
r
A
d
n
A
t
s

A

e
v
A
H

s
e
r
哦
C
s

t
s
e
时间

:
s
e
t
哦
氮

.
e
C
n
e
我
r
e
p
X
e

d
n
A

,
e
r
你
n
e
t

,
r
e
d
n
e
G

,
e
C
A
r

s
’
r
e
H
C
A
e
t

s
e
米
A
氮

我

.
r
e
H
/
米
H
哦
t
d
A
e
r

t
X
e
t

r
e
H
t
哦
r
哦
y
r
哦
t
s
A
s
t
e
r
p
r
e
t
n

我

d
n
A
s
d
n
A
t
s
r
e
d
n
你
d

我
我

我

H
C
s
H
时间
=
s
d
n
A
t
s
r
e
d
n
U

.
s
e
r
你
t
C
你
r
t
s
e
C
n
e
t
n
e
s
X
e
p
米
哦
C
s
e
s
你
d

我

我
我

我

H
C
s
H
时间
=
X
e
p
米
哦
C

我

:
s
n
哦
我
t
我
n
fi
e
D

我

e
p
米
s

我

s
d
A
e
r

d

我
我

H
C

我

s
H
时间
=
s
d
A
e
右

.
s
d
r
哦
w
G
n
米
y
H
r

我

s
e
C
你
d
哦
r
p

d

我
我

H
C

我

s
H
时间
=
G
n
米
y
H
右

我

.
t
e
乙
A
H
p
A

我

e
H
t

F
哦

s
r
e
t
t
e

我

e
s
A
C
–
r
e
w
哦

我

d
n
A

–
r
e
p
p
你

我
我

A

s
e
米
A
n

y
我
k
C
我
你
q

d
n
A

y
我
我

s
A
e

d

我
我

H
C

我

s
H
时间
=

s
n
哦
我
t
n
e
v
n
哦
C

e
H
t

F
哦

e
米
哦
s

F
哦

我

G
n
d
n
A
t
s
r
e
d
n
你

n
A

s
e
t
A
r
t
s
n
哦
米
e
d

d

我
我

H
C

我

s
H
时间
=

s
n
哦
我
t
n
e
v
n
哦
C

.
s
r
哦
我
v
A
H
e
乙

G
n
我
t
我
r

w
y
我
r
A
e

s
e
t
A
r
t
s
n
哦
米
e
d