Alastair Channon
Keele University
School of Computing and
Mathematics
a.d.channon@keele.ac.uk
关键词
Open-ended evolution, biotic selection,
ongoing growth of complexity, diversity,
indefinite scalability
Maximum Individual Complexity
is Indefinitely Scalable in Geb
Abstract Geb was the first artificial life system to be classified as
exhibiting open-ended evolutionary dynamics according to Bedau and
Packardʼs evolutionary activity measures and is the only one to have
been classified as such according to the enhanced version of that
classification scheme. Its evolution is driven by biotic selection, 那是
(大约), by natural selection rather than artificial selection.
Whether or not Geb can generate an indefinite increase in maximum
individual complexity is evaluated here by scaling two parameters:
world length (which bounds population size) and the maximum
number of neurons per individual. Maximum individual complexity is
found to be asymptotically bounded when scaling either parameter
独自的. 然而, maximum individual complexity is found to be
indefinitely scalable, to the extent evaluated so far (with run times
in years and billions of reproductions per run), when scaling both
world length and the maximum number of neurons per individual
一起. 更远, maximum individual complexity is shown to scale
logarithmically with (the lower of ) maximum population size and
maximum number of neurons per individual. This raises interesting
questions and lines of thought about the feasibility of achieving
complex results within open-ended evolutionary systems and how to
improve on this order of complexity growth.
1 介绍
Perhaps the most important outcome of the First Workshop on Open-Ended Evolution (OEE) 曾是
the distillation of previously disparate thoughts about OEE into something close to a consensus
about what the term OEE should mean: “Loosely defined, an open-ended evolutionary system is
one that is capable of producing a continual stream of novel organisms rather than settling on some
quasi-stable state beyond which nothing fundamentally new occurs. Some definitions of OEE fur-
ther require that the maximum complexity of organisms in the system increases over time, 或者那个
ecosystem complexity increases” [27, p. 409]. Crucial in arriving at and refining this loose definition
was recognition of “the importance of distinguishing observable behavioral hallmarks of systems un-
dergoing OEE from hypothesized underlying mechanisms that explain why a system exhibits those hall-
marks” [ 27, p. 407]. While there are a range of opinions about what underlying mechanisms may be
necessary or sufficient for a system to exhibit OEE, there is something close to a consensus about
the observable behavioral hallmarks of OEE: “ongoing adaptive novelty” [ p. 415] (例如, 新的
adaptations, new kinds of entities, major transitions, or the evolution of evolvability) 和 (一些
definitions of OEE further require) “ongoing growth of complexity” [p. 416] of the most complex entities
in the evolving population, or of interactions among entities [27].
© 2019 by the Massachusetts Institute of Technology. 根据知识共享署名发布 4.0
人工生命 25: 134–144 (2019) 土井:10.1162/artl_a_00285
国际的 (抄送 4.0) 执照.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
2
5
2
1
3
4
1
8
9
6
6
8
6
A
r
t
我
/
_
A
_
0
0
2
8
5
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
A. Channon
Maximum Individual Complexity is Indefinitely Scalable in Geb
2 Ongoing Adaptive Novelty and the Accumulation of Adaptive Success
At the core of open-ended evolution is the ongoing evolution of adaptive novelty: “new components
flowing into the system and proving their adaptive value through their persistent activity” [5, p. 230]
(components could be, 例如, 基因, 有机体, or species). 然而, an evolutionary pro-
cess could continue to generate adaptive novelty but lose what had previously been evolved at the
same or a faster rate, cycling or idling with a limited extent of adaptive success. Ongoing adaptive
novelty alone would provide for a poor definition of OEE, for a trivial system could generate ever
more novel components. Ongoing progress, an unbounded accumulation in adaptive success, is also
core to OEE.
2.1 Unbounded Accumulation of Adaptive Success
Logically, unbounded accumulation of adaptive success can occur in an evolutionary system
through an unbounded increase in either (minimum, 意思是, median, or maximum) adaptive success
per component or the diversity of adaptive components, 或两者. In a system of evolving entities
(有机体, 生物, 代理人, ETC。) and considering lower-level components (for example genes), 一个
increase in the diversity of adaptive components (IE。, the number of different adaptive compo-
尼特) can occur through an increase in either the number of different adaptive components
per entity (a simple measure of entity complexity) or the number of different entities (IE。, the diver-
sity of entities), 或两者.
巴杜, 斯奈德, and Packardʼs classification of long-term evolutionary dynamics [5] provided the
fieldʼs first “objective, quantitative test of success” [5, p. 236]: a means to distinguish those systems
that exhibit unbounded evolutionary dynamics according to this classification scheme from those
that do not, rather than a definitive definition of open-ended evolution. The classification scheme
is based on elegantly simple evolutionary activity statistics that can be computed for any evolving
system with an available record of its componentsʼ existence times, making the scheme widely appli-
cable across artificial and natural systems. It uses cumulative evolutionary activity, based on adaptive persis-
张力 (具体来说, the length of time that a component has existed, discounting any periods of absence),
as “a measure of the continual adaptive success of the components in the system” [5, p. 230], 那是, 作为
a measure of the accumulation of a componentʼs adaptive success; and it uses the sum of component
活动 (for those components present that are in use) as a measure of the systemʼs accumulation of
adaptive success, termed total cumulative evolutionary activity. Ongoing adaptive novelty is determined
through new activity: the sum of newly adaptively significant componentsʼ activities, divided by the compo-
nent diversity (the number of components present that are in use). A component is considered adap-
tively significant if its activity is above a threshold that screens out most non-adaptive activity, 作为
determined through the use of a shadow system that mirrors the real system in every detail except that
where selection (artificial or natural) operates in the real system, neutral (random) selection is employed
in the shadow. In line with the logic above, total cumulative evolutionary activity can be considered as
the product of component diversity and mean evolutionary activity per component. The classification
scheme requires ongoing adaptive novelty and unbounded total cumulative evolutionary activity (和-
bounded component diversity or unbounded mean evolutionary activity per component) for a clas-
sification of unbounded evolutionary dynamics.
Earthʼs biosphere was classified, through fossil record data on taxonomic families, as exhibiting
open-ended evolutionary dynamics according to Bedau, 斯奈德, and Packardʼs classification scheme
[5]. Bedau et al. reasoned that it was not necessary to include a shadow mechanism in this analysis;
they considered “this normalization to be accomplished de facto by the fossil record itself,” arguing
that “the mere fact that a family appears in the fossil record is good evidence that its persistence
reflects its adaptive significance” (添加了强调), as “[s]ignificantly maladaptive taxonomic
families would likely go extinct before leaving a trace in the fossil record” [5, p. 229].
人工生命量 25, 数字 2
135
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
2
5
2
1
3
4
1
8
9
6
6
8
6
A
r
t
我
/
_
A
_
0
0
2
8
5
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
A. Channon
Maximum Individual Complexity is Indefinitely Scalable in Geb
2.2 Component Activity Normalization and an Enhanced Classification Scheme
for Unbounded Evolutionary Dynamics
Channon [8, 9] presented improvements to Bedau et al.ʼs classification scheme. Resetting the sys-
temʼs shadow (including components and activity history) to be identical to the real run immediately
after each snapshot (when an entry is made in the component existence record) allows us to com-
pare inter-snapshot changes in activity in the real run with changes we would expect from neutral
(random) 选择, the result being an improved generic shadowing mechanism. The shadow can
then be used to normalize (exclude non-adaptive) evolutionary activity at the component level
(“component activity normalization” [p. 253]), giving a measure of each componentʼs adaptive evo-
lutionary activity and so also component-normalized (adaptive) measures of both ongoing adaptive
novelty and total (and mean or, 更好的, median) cumulative evolutionary activity.
Stout and Spector [26] attempted to “break” the original and enhanced classification schemes by
achieving a classification of unbounded dynamics in “intuitively unlifelike” [p. 137] 系统. 他们
concluded that component activity normalization is “of particular importance to the schemeʼs ro-
bustness … canceling out the potential for spurious results arising from the (random) divergence of
the real and shadow populations” [ p. 141]. Bedau et al.ʼs reasoning that “the mere fact that a
family appears in the fossil record is good evidence that its persistence reflects its adaptive signif-
icance” [5, p. 229] is generally accepted. But for artificial systems, Stout and Spectorʼs findings
support the argument for employing the enhanced classification scheme, at least for cases (choices
of component class) in which components can be maladaptive.
Geb is a two-dimensional environment populated with agents that move around and interact with
彼此. Its evolution is driven by biotic selection, with no (or negligible) abiotic selection [11, 12].
It was designed following the principles of Harveyʼs Species Adaptation Genetic Algorithms
(SAGA) framework for incremental evolution [15–18], but with coevolutionary feedback arising
(rather than being specified: 比照. ‘get cube’ [24]) via biotic selection rather than abiotic fitness
functions—that is (大约), via natural selection rather than artificial selection. In Geb,
selection results from interactions that are activated by the agentsʼ genetically specified neuro-
controllers. So selection varies as the population and environment of individuals evolve. This allows
for the possibility of feedback in selection, and of that driving the ongoing evolution of adaptive
新奇. Novel adaptations reported include behaviors such as following, fighting, fleeing, mimick-
英, and novel artifacts such as matching input and output channels in agentsʼ neurocontrollers. Geb
was the first artificial life system to be classified as exhibiting open-ended evolutionary dynamics
according to Bedau and Packardʼs evolutionary activity measures [5, 7] and is the only one to have
been classified as such according to the enhanced classification scheme [8, 9, 27]. It was shown to
exhibit ongoing adaptive novelty (positive component-normalized new activity per component) 和
unbounded component-normalized median component evolutionary activity.
3 Ongoing Growth of Complexity
One of the most interesting questions that OEE systems can address is whether or not OEE can be
the cause of an unbounded increase in maximum individual (or group or system) 复杂. 这,
当然, requires a definition of complexity, and also that our definition of OEE not already
include ongoing growth of complexity [27], which would prevent us from being able to address
(or even ask) this important question.
This is closely related to the open question: Can or under what conditions does biotic (natural)
selection lead to a sustained increase in maximum entity complexity? In particular this is relevant to
the debate as to whether or not it is natural selection that led to the increase in maximum organism
complexity observed in nature. Within both biology and artificial life, doubts have been raised as to
natural selectionʼs role as the drive for increasing complexity, and arguments have been made on
both sides [4, 10, 20, 21, 28, 29], with the suggestion put forward that non-adaptive evolutionary
136
人工生命量 25, 数字 2
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
2
5
2
1
3
4
1
8
9
6
6
8
6
A
r
t
我
/
_
A
_
0
0
2
8
5
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
A. Channon
Maximum Individual Complexity is Indefinitely Scalable in Geb
军队 (such as mutation, recombination, and genetic drift) or mathematical/statistical constraints
may be the primary drives, through either a passive increase in the variance of complexity in the
presence of a lower bound, or a constraint-driven drive toward complexity.
One unsatisfactory general measure of complexity is the number of components in an entity. A
more satisfactory one is the number of different components, sometimes referred to as the diversity
of components. The number of different components is still not a very satisfactory measure of
复杂, just as it is not a very satisfactory measure of diversity, but it does lead us toward
the general idea that complexity at one level of analysis (例如, 个人, 物种, or system)
can be considered as the diversity of components at the level(s) 以下 (例如, 基因, genes or
个人, genes or individuals or species). The same desirable tweaks to discount redundancy
(such as counting only adaptive components or measuring information content), and to include be-
haviors and interactions as well as artifacts, apply to both. 还, considering diversity at only some
component levels (例如, just at a very low level: diversity of atoms in a biological organism,
logic gates in a computerʼs processors, neuron types in a neurocontroller, ETC。) risks missing other
diversity in a system and correspondingly underestimating the systemʼs complexity; 再次, 两个都
diversity and complexity suffer from the same problem.
Within biology, it has long been understood that eukaryotic genome size (length) does not cor-
relate with organism complexity [22], but assumed that the number of distinct genes (IE。, the diver-
sity of genes) that an organism makes use of is a valid measure of its complexity [6]. 这个假设
was called into doubt [14] following the first complete sequencing and analysis of plant and human
基因组. 然而, subsequently Schad, Tompa, and Hegyi [23] demonstrated that organism com-
plexity correlates significantly with gene number (and more closely with proteome information con-
帐篷) in the absence of plant genomes. More recently still, 陈, 衬套, 等人. [13] reached the same
finding. They also found that specific protein-protein interaction and alternative splicing indices were
better predictors; these have no analogue in Geb.
In line with the logic above (部分 2.1), in Bedau, 斯奈德, and Packardʼs classification of long-
term evolutionary dynamics [5], the class of systems with unbounded evolutionary dynamics can be
divided into three subclasses: (A) those with unbounded diversity of adaptive components but
bounded adaptive success (cumulative evolutionary activity, based on adaptive persistence) per com-
波南特; (乙) those with bounded diversity but unbounded adaptive success per component; 和 (C)
those with unbounded diversity and unbounded adaptive success per component.
然而, while adaptive success per component can be truly unbounded (if measured based on adap-
tive persistence and over unbounded time), the diversity of adaptive components (both the number
of different components per entity and the diversity of entities) is necessarily bounded: in artificial
systems by unavoidable physical limits such as computer memory, and in nature (whether consid-
ering the biosphere or the universe) again by physical limits such as number of atoms. A claim of
unbounded diversity in the biosphere is really a claim that diversity is not practically bounded, 或者
that it has not reached the upper bound yet. A more precise notion than “unbounded” diversity
(of entities or of adaptive components per entity) is needed.
3.1 Indefinite Scalability
Ackleyʼs concept of indefinite scalability, “defined as supporting open-ended computational growth with-
out requiring substantial re-engineering” [1, p. 606], now enables us to address this. The key criterion
for indefinite scalability is that, should an upper bound be reached, increasing the values of physical
局限性 (such as available matter, population size, or memory) should enable an unbounded
sequence of greater upper bounds to be achieved (after sufficient increases in the limitations); 在
the case of diversity this means an unbounded sequence of greater upper bounds on diversity.
然而, 这不可能 (in finite system time) to establish that a metric (例如, a mea-
sure of adaptive success per component) is truly unbounded. And it is not possible (over a finite
number of increases in system parameter(s)) to establish that a metric (例如, a measure of
人工生命量 25, 数字 2
137
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
2
5
2
1
3
4
1
8
9
6
6
8
6
A
r
t
我
/
_
A
_
0
0
2
8
5
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
A. Channon
Maximum Individual Complexity is Indefinitely Scalable in Geb
diversity) is infinitely scalable. 更远, an increase in parameter(s) may require a longer system (跑步)
time before a greater scale (higher-value metric) is achieved.
A practical (and the most literal) interpretation of indefinite scalability is that the sequence of
greater upper bounds (on increasing the values of physical limitations) continues to an unknown
length, 那是, that no end to it has been been found. It is therefore best to qualify any empirical
claims by quantifying the extent to which indefinite scalability has been established. Claims about
systems can be expressed and evaluated in terms such as a metric (例如, a measure of adap-
tive success per component) increasing apparently without bound up to a certain system time (或者
number of generations, ETC。); or a metric (例如, diversity) increasing up to certain value(s)
of system parameter(s) being reached, where it was necessary to increase these to establish increases
in scale (for example of diversity) over successive runs.
3.2 Indefinitely Scalable Complexity
If the diversity of adaptive components is accepted as a simple measure of system complexity, 和
the number of different adaptive components per entity as a simple measure of entity complexity,
then it follows trivially from the logic above (部分 2.1) 第一的, that indefinitely scalable system
complexity can occur through indefinite scalability in either entity complexity or entity diversity, 或者
两个都; 第二个, that indefinite scalability in the accumulation of adaptive success can occur
through indefinite scalability in either adaptive success per component or system complexity, 或者
两个都.
The above reasoning follows only for the case of complexity equating to diversity of adaptive
成分 (in the system or per entity). It would be perfectly reasonable to use alternative com-
plexity metrics, and to then ask such questions as under what conditions OEE systems exhibit
indefinitely scalability in those measures of entity complexity. Likewise it is reasonable to ask under
what conditions OEE systems evolve (日益) interesting, surprising (not predictable), 或者我-
pressive artifacts and behaviors [19]. Complexity metrics include simple counts of the number of
bases (genome size), 基因, cell types, 神经元, synapses, 物种, 和行为; and measures of
information content, again genetic, cellular, neural (例如 [29]), ecological, and behavioral.
4 Evaluating Indefinite Scalability in Geb
This work investigates whether or not the observed maximum complexity of any individual is in-
definitely scalable in Geb [7–9], where an individualʼs complexity is measured as the diversity of
components in it. Note that if the diversity of components in an individual is indefinitely scalable,
then so is the diversity of components in the system, so the question of which subclass (A, 乙, or c)
Geb is in is also being addressed.
As in previous work analyzing Gebʼs long-term evolutionary dynamics, a component is, in loose
条款, an active gene: a gene involved in the agentʼs neural development; 看 [9] 欲了解详情. 所以, 这里,
an individualʼs complexity is measured as the number of different genes involved in its neural
发展.
Two parameters cause diversity to be bounded in Geb: (1) a limit on the maximum number of
neurons an agent can have, 和 (2) the 2D worldʼs length L, as there can be at most L2 individuals
in the population at any one time. These are the two parameters that are scaled. Results are reported
below for world lengths 10, 20 (the original systemʼs value for this parameter ), 40, 和 80; and with
the maximum numbers of neurons per individual set at 20 (the original systemʼs value for that
parameter ), 40, 80, 和 160. These ranges avoid edge effects that arise from smaller values of these
参数. 20 runs were carried out for each combination (value pair ) of these parameters, 和
average (超过 20 runs) maximum individual complexity recorded and graphed using a running
average of length 100 to reveal underlying trends.
138
人工生命量 25, 数字 2
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
2
5
2
1
3
4
1
8
9
6
6
8
6
A
r
t
我
/
_
A
_
0
0
2
8
5
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
A. Channon
Maximum Individual Complexity is Indefinitely Scalable in Geb
数字 1. Results when scaling the maximum number of neurons per individual (at different world lengths).
5 Results and Analysis
The basic plots of maximum individual complexity against time indicate that maximum individual
complexity may be asymptotically bounded when scaling just the maximum number of neurons per
个人 (数字 1). 同样地, maximum individual complexity appears to be asymptotically
bounded when scaling just world length (数字 2).
数字 3 gives the first indication that maximum individual complexity may be indefinitely
scalable—that is, scalable to the extent evaluated so far (with run times in years and billions
of reproductions per run)—when scaling both the maximum number of neurons per individual
and the world length together.
数字 2. Results when scaling world length (at different maximum numbers of neurons per individual).
人工生命量 25, 数字 2
139
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
2
5
2
1
3
4
1
8
9
6
6
8
6
A
r
t
我
/
_
A
_
0
0
2
8
5
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
A. Channon
Maximum Individual Complexity is Indefinitely Scalable in Geb
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
2
5
2
1
3
4
1
8
9
6
6
8
6
A
r
t
我
/
数字 3. Results when scaling both world length and maximum number of neurons per individual, 一起.
_
A
_
0
0
2
8
5
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
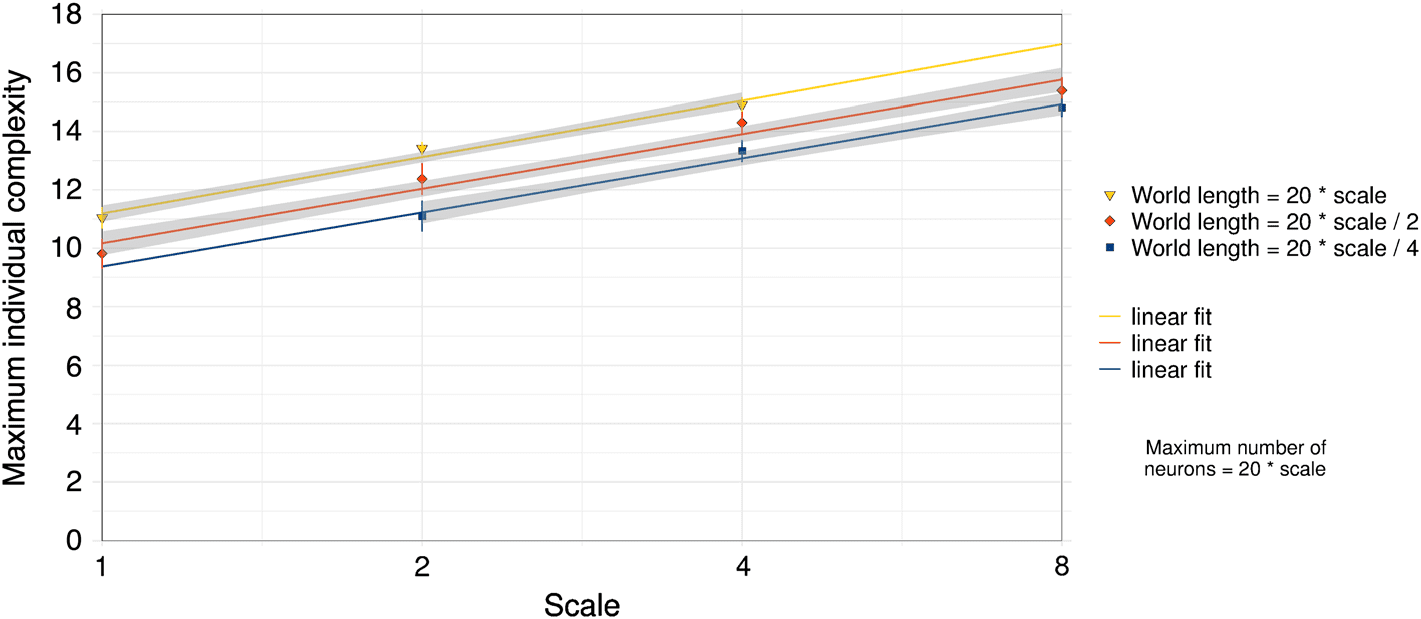
数字 4 demonstrates this more conclusively. It shows maximum individual complexity averaged over
time steps 2 百万至 3 million and over 20 runs, with world lengths scaling in conjunction with the
maximum number of neurons per individual as shown. The fitted lines are the result of linear regression
−15
on the logarithm of scale (see horizontal axes), with resulting R2 = 0.855, F1,58
−15 (中间: world length = 20 ×
(顶部: world length = 20 × scale); R2 = 0.794, F1,78
scale/2); and R2 = 0.741, F1,58
−15 (底部: world length = 20 × scale/4).
= 166, 磷 < 10
= 341, P < 10
= 301, P < 10
The simplest function of two variables (x and y) that is bounded when each is increased alone but
unbounded when both are increased together is min(x, y): the minimum (lower ) of the two values.
−y) is a smooth approximation to this. It is bounded within
The function softmin(x, y) = −log(e
[min(x, y) − log(2), min(x, y)).
−x + e
Figure 5 confirms that maximum individual complexity is asymptotically bounded when scaling
just the maximum number of neurons per individual. At each constant world length, the observed
140
Artificial Life Volume 25, Number 2
A. Channon
Maximum Individual Complexity is Indefinitely Scalable in Geb
Figure 4. Indefinite scalability of maximum individual complexity (averaged over time steps 2 million to 3 million of
20 runs) when scaling both world length and maximum number of neurons per individual together, through their
common dependence on the variable scale graphed on the x-axis, as indicated in the legend. Error bars show 95%
confidence intervals based on the replicate populations. Shown with linear-fit model and 95% confidence regions for
the regression fit.
maximum individual complexities are fitted very closely by the model a + b softmin(lw, lm), where a
and b are the regression parameters, lw = log(worldlength), and lm = log(maxneurons). That complexity
is bounded when scaling just the maximum number of neurons per individual rules out the possi-
bility that the key finding (that complexity is indefinitely scalable when scaling both the maximum
number of neurons per individual and the maximum population size, together ) is due to increases in
this resource constraint allowing for drift to increasing levels of noise in the neural development
process and so to unbounded individual complexity (number of different genes involved in neural
development).
Figure 6 confirms that maximum individual complexity is asymptotically bounded when scaling
just world length. At each constant maximum number of neurons, the results are fitted very closely
by the model b softmin(lw + c, lm), where b and c are the regression parameters. That complexity is
bounded when scaling just maximum population size (world length squared) rules out the possibility
that the key finding is due to increasing the sample size over which maximum individual complexity
is measured.
Figure 5. Bounded maximum individual complexity (averaged over time steps 2 million to 3 million of 20 runs) when
scaling just the maximum number of neurons per individual (at different world lengths). Error bars show 95% confidence
intervals based on the replicate populations. Shown with softmin-fit model.
Artificial Life Volume 25, Number 2
141
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
2
1
3
4
1
8
9
6
6
8
6
a
r
t
l
/
_
a
_
0
0
2
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A. Channon
Maximum Individual Complexity is Indefinitely Scalable in Geb
Figure 6. Bounded maximum individual complexity (averaged over time steps 2 million to 3 million of 20 runs) when
scaling just world length (at different maximum numbers of neurons per individual). Error bars show 95% confidence
intervals based on the replicate populations. Shown with softmin-fit model.
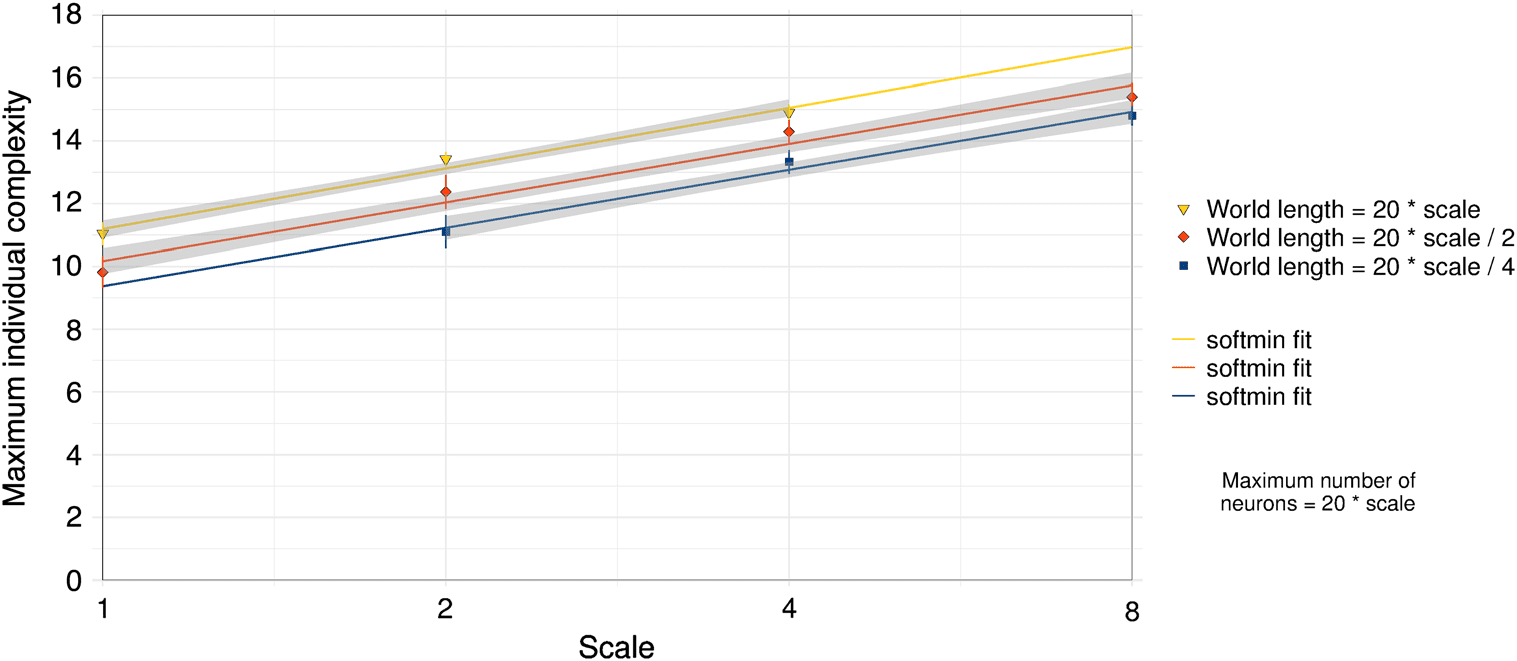
Figure 7 shows that when scaling both the maximum number of neurons per individual and the
world length together, the maximum individual complexity is again closely fitted (residual standard
error and R2 equal to those from the linear model above, to at least eleven significant figures) by the
model a + b softmin(lw, lm), which is unbounded. Unsurprisingly, this resembles the linear model
very closely: softmin(x, y) = x − log(2) when y = x, and in the more general case y = cx (for some
constant c within (0, 1]), softmin(x, y) is bounded within [ y − log(2), y) and can be empirically shown
to be within y (cid:1) 1−10−5; 1
2. Indeed, the linear and softmin regression
curves are indistinguishable to the human eye.
Þ for x≥20, y≥1 and c≤ 1
ð
6 Conclusions and Discussion
According to this analysis, the only bounds to complexity and diversity are time and computer mem-
ory (similarly to nature), and, taking this finding in combination with those from the analysis of
evolutionary activity in [9], Geb is in subclass c.
Figure 7. Indefinite scalability of maximum individual complexity (averaged over time steps 2 million to 3 million of 20 runs)
when scaling both world length and maximum number of neurons per individual, together. Shown with softmin-fit model.
The softmin-fit curves are indistinguishable (to the human eye) from the those of the linear-fit model (Figure 4).
142
Artificial Life Volume 25, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
2
1
3
4
1
8
9
6
6
8
6
a
r
t
l
/
_
a
_
0
0
2
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A. Channon
Maximum Individual Complexity is Indefinitely Scalable in Geb
The order of complexity growth has significant implications for the prospects of achieving com-
plex results from an open-ended evolutionary system within feasible time scales. The analysis above
shows that, in Geb, maximum individual complexity scales logarithmically with (the lower of ) max-
imum population size and maximum number of neurons per individual. This would be sufficient for
achieving the evolution of more complex artifacts and behaviors (arising from evolutionary changes
rather than from a very small number of mutations from a hard-coded ancestor ) than have been seen
(evidenced by phenotypes rather than by metrics) to date. It would also be sufficient to achieve
nontrivial long (evolutionary) sequences of evolved artifacts or behaviors. Again, we have not seen these
yet, evidenced by phenotypes evolved within an ALife system. In terms of these two goals, Geb is
lacking in its behavioral transparency, preventing the direct observation of artifacts and behaviors
much beyond those noted in Section 2.2, as discussed in [9]. This highlights the need to develop
future systems such that behavioral descriptions are as easy to generate as possible, for example by
constructing systems such that behaviors will be transparent to human observers.
The evolution of artifacts and behaviors of much greater complexity, for example comparable to
those in nature, within feasible time scales, will almost certainly require a higher order of complexity
scaling. How to achieve this is an open question. Perhaps the most promising line of thought here
relates to establishing the requirements for evolution to itself generate (perhaps an open sequence
of ) major transitions. Following its very earliest phases, our universe has evolved from a sparse fog
of hydrogen and helium atoms. Its history includes the emergence of complex molecules, replicators,
single-cell and multicellular life, brains, sociality, users and manufacturers of simple and compound
tools, cultural learning, and technology, to highlight just a few of the major transitions [2, Table 1].
Aunger divides big history into four eras: material, biological, cultural, and technological [3, Table 2].
Some evolutionary innovations increase the evolvability (capacity for adaptive evolution) of their
lineages [25]. It is not computationally feasible (even if we knew how) for an OEE simulation to
start from a sparse fog of hydrogen and helium and transition to a biological-level era, so it is clearly
necessary to skip over or engineer in at least some complex features that arose through major tran-
sitions in our universe. Geb can be used as an example to inform decisions about engineering in such
features, through its demonstration of a feature set that is sufficient for achieving open-ended evo-
lutionary dynamics and indefinitely scalable complexity.
References
1. Ackley, D. H., & Small, T. R. (2014). Indefinitely scalable computing = artificial life engineering. In H.
Sayama, J. Rieffel, S. Risi, R. Doursat, & H. Lipson (Eds.), Artificial life XIV (pp. 606–613). Cambridge,
MA: MIT Press.
2. Aunger, R. (2007). Major transitions in ‘big’ history. Technological Forecasting and Social Change, 74(8),
1137–1163.
3. Aunger, R. (2007). A rigorous periodization of ‘big’ history. Technological Forecasting and Social Change, 74(8),
1164–1178.
4. Bedau, M. A. (2009). The evolution of complexity. In A. Barberousse, M. Morange, & T. Pradeu
(Eds.), Mapping the future of biology: Evolving concepts and theories ( pp. 111–130). Dordrecht: Springer
Netherlands.
5. Bedau, M. A., Snyder, E., & Packard, N. H. (1998). A classification of long-term evolutionary dynamics. In
C. Adami, R. K. Belew, H. Kitano, & C. E. Taylor (Eds.), Artificial life VI (pp. 228–237). Cambridge, MA:
MIT Press.
6. Bird, A. P. (1995). Gene number, noise reduction and biological complexity. Trends in Genetics, 11(3),
94–100.
7. Channon, A. (2001). Passing the ALife test: Activity statistics classify evolution in Geb as unbounded. In
J. Kelemen & P. Sosík (Eds.), Advances in artificial life: Proceedings of the Sixth European Conference on Artificial
Life (pp. 417–426). Berlin, Heidelberg: Springer-Verlag.
8. Channon, A. (2003). Improving and still passing the ALife test: Component-normalised activity statistics
classify evolution in Geb as unbounded. In R. K. Standish, M. A. Bedau, & H. A. Abbass (Eds.), Artificial
life VIII (pp. 173–181). Cambridge, MA: MIT Press.
Artificial Life Volume 25, Number 2
143
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
2
1
3
4
1
8
9
6
6
8
6
a
r
t
l
/
_
a
_
0
0
2
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A. Channon
Maximum Individual Complexity is Indefinitely Scalable in Geb
9. Channon, A. (2006). Unbounded evolutionary dynamics in a system of agents that actively process and
transform their environment. Genetic Programming and Evolvable Machines, 7(3), 253–281.
10. Channon, A. (2008). A measure for natural selectionʼs contribution to the origins and maintenance of
organismal complexity. In S. Bullock, J. Noble, R. Watson, & M. A. Bedau (Eds.), Artificial life XI (p. 758).
Cambridge, MA: MIT Press.
11. Channon, A., & Damper, R. I. (1998). Perpetuating evolutionary emergence. In R. Pfeifer, B. Blumberg,
J.-A. Meyer, & S. W. Wilson (Eds.), From animals to animats 5: Proceedings of the Fifth International Conference on
Simulation of Adaptive Behavior (pp. 534–539). Cambridge, MA: MIT Press.
12. Channon, A., & Damper, R. I. (2000). Towards the evolutionary emergence of increasingly complex
advantageous behaviours. International Journal of Systems Science, 31(7), 843–860.
13. Chen, L., Bush, S. J., Tovar-Corona, J. M., Castillo-Morales, A., & Urrutia, A. O. (2014). Correcting for
differential transcript coverage reveals a strong relationship between alternative splicing and organism
complexity. Molecular Biology and Evolution, 31(6), 1402–1413.
14. Hahn, M. W., & Wray, G. A. (2002). The g-value paradox. Evolution & Development, 4(2), 73–75.
15. Harvey, I. (1992). Species adaptation genetic algorithms: A basis for a continuing SAGA. In F. J. Varela &
P. Bourgine (Eds.), Towards a practice of autonomous systems: Proceedings of the First European Conference on Artificial
Life (pp. 346–354). Cambridge, MA: MIT Press.
16. Harvey, I. (1993). Evolutionary robotics and SAGA: The case for hill crawling and tournament selection.
In C. G. Langton (Ed.), Artificial life III (pp. 299–326). Reading, MA: Addison-Wesley Longman.
17. Harvey, I. (1997). Artificial evolution for real problems. In T. Gomi (Ed.), Evolutionary robotics: From intelligent
robots to artificial life (ERʼ97), proceedings of the 5th International Symposium on Evolutionary Robotics (pp. 127–149).
Ontario, Canada: AAI Books.
18. Harvey, I. (1997). Cognition is not computation; evolution is not optimisation. In W. Gerstner, A.
Germond, M. Hasler, & J.-D. Nicoud (Eds.), Proceedings of the 7th International Conference on Artificial Neural
Networks (ICANNʼ97) (pp. 685–690). Berlin, Heidelberg: Springer-Verlag.
19. Lehman, J., & Stanley, K. O. (2012). Beyond open-endedness: Quantifying impressiveness. Artificial Life,
13, 75–82.
20. Lynch, M. (2007). The frailty of adaptive hypotheses for the origins of organismal complexity. Proceedings of
the National Academy of Sciences of the U.S.A., 104, 8597–8604.
21. Miconi, T. (2008). Evolution and complexity: The double-edged sword. Artificial Life, 14(3), 325–344.
22. Moore, G. P. (1984). The c-value paradox. BioScience, 34(7), 425–429.
23. Schad, E., Tompa, P., & Hegyi, H. (2011). The relationship between proteome size, structural disorder and
organism complexity. Genome Biology, 12(12), R120.
24. Sims, K. (1994). Evolving 3D morphology and behavior by competition. In R. A. Brooks & P. M. Maes
(Eds.), Artificial life IV (pp. 28–39). Cambridge, MA: MIT Press.
25. Sterelny, K. (2011). Evolvability reconsidered. In B. Calcott & K. Sterelny (Eds.), The major transitions in
evolution revisited (pp. 83–100). Cambridge, MA: MIT Press.
26. Stout, A., & Spector, L. (2005). Validation of evolutionary activity metrics for long-term evolutionary
dynamics. In H.-G. Beyer, U.-M. OʼReilly, D. V. Arnold, W. Banzhaf, C. Blum, E. W. Bonabeau,
E. Cantu-Paz, D. Dasgupta, K. Deb, J. A. Foster, E. D. de Jong, H. Lipson, X. Llora, S. Mancoridis,
M. Pelikan, G. R. Raidl, T. Soule, A. M. Tyrrell, J.-P. Watson, & E. Zitzler (Eds.), Proceedings of the 2005
Genetic and Evolutionary Computation Conference (GECCO 2005) (pp. 137–142). New York: ACM.
27. Taylor, T., Bedau, M., Channon, A., Ackley, D., Banzhaf, W., Beslon, G., Dolson, E., Froese, T.,
Hickinbotham, S., Ikegami, T., McMullin, B., Packard, N., Rasmussen, S., Virgo, N., Agmon, E., Clark, E.,
McGregor, S., Ofria, C., Ropella, G., Spector, L., Stanley, K. O., Stanton, A., Timperley, C., Vostinar, A., &
Wiser, M. (2016). Open-ended evolution: Perspectives from the OEE workshop in York. Artificial Life,
22(3), 408–423.
28. Yaeger, L. S. (2009). How evolution guides complexity. HFSP Journal, 3(5), 328–339.
29. Yaeger, L. S. (2014). Evolution of complexity and neural topologies. In M. Prokopenko (Ed.), Guided
self-organization: Inception ( pp. 415–454). Berlin, Heidelberg: Springer-Verlag.
144
Artificial Life Volume 25, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
2
1
3
4
1
8
9
6
6
8
6
a
r
t
l
/
_
a
_
0
0
2
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3