UNRAVELING AMBIGUITY AVERSION∗ - IA de Investigación especializada en el MIT

Desentrañando la aversión a la ambigüedad ∗

Ilke Aydogan†

Lo¨ıc Berger‡

Valentina Bosetti§

Abstracto

We report the results of two experiments designed to better understand the

mechanisms driving decision-making under ambiguity. Provocamos individuo preferir-

ences over diﬀerent sources of uncertainty, entailing diﬀerent degrees of complexity,

from subjects with diﬀerent sophistication levels. Nosotros mostramos que (1) ambiguity

aversion is robust to sophistication, but the strong relationship previously reported

between attitudes toward ambiguity and compound risk is not. (2) Ellsberg am-

biguity attitude can be partly explained by attitudes toward complexity for less

∗We thank Mohammed Abdellaoui, Aur´elien Baillon, Laure Cabantous, Thomas Ep-
por, Helena Hauser, Chen Li, Massimo Marinacci, Sujoy Mukerji, Vincent Th´eroude,
Uyanga Turmunkh, and Peter Wakker for helpful comments and suggestions. Nosotros también
thank seminar and conference participants at D-TEA, FUR, MUSEES, Bocconi Uni-
versity, Ghent University, and LMU for insightful comments and discussions. Somos
grateful to Hans-Joachim Zwiesler for the opportunity to run the experiment at ICA
2018 and thank the organizing committee for their help with the experiment. Nosotros
also thank Diana Valerio for her help with the laboratory experiment. This project
has received funding from the European Union’s Horizon Europe research and innova-
tion programme under grant agreement (No 101056891 CAPABLE), the Agence Na-
tionale de la Recherche (ANR-17-CE03-0008-01 INDUCED and ANR-21-CE03-0018
ENDURA), the Region Hauts-de-France (2021.00865 CLAM), and the I-SITE UNLE
(project IBEBACC). Logistic support from the Bocconi Experimental Laboratory for
the Social Sciences (BELSS) and from the Anthropo-Lab (ETHICS EA 7446) is kindly
acknowledged.

†IESEG School of Management, Univ. Lille, CNRS, UMR 9221 – LEM – Lille ´Economie
Gestión, F-59000 Lille, Francia; and iRisk Research Center on Risk and Uncertainty
(i.aydogan@ieseg.fr).

‡Corresponding author. Univ. Lille, CNRS, IESEG School of Management, UMR
9221 – LEM – Lille ´Economie Management, F-59000 Lille, Francia; iRisk Research Cen-
ter on Risk and Uncertainty; RFF-CMCC European Institute on Economics and the
Environment (EIEE), and Centro Euro-Mediterraneo sui Cambiamenti Climatici, Italia
(loic.berger@cnrs.fr). Phone: +33 320 545 892.

§Department of Economics and IGIER, Bocconi University, and RFF-CMCC Euro-
pean Institute on Economics and the Environment (EIEE), Centro Euro-Mediterraneo
sui Cambiamenti Climatici, Italia (valentina.bosetti@unibocconi.it).

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 por el presidente y becarios de Harvard College y el Instituto de Tecnología de Massachusetts. Published under a Creative Commons Attribution 4.0 Internacional (CC POR 4.0) licencia.

sophisticated subjects only. En general, regardless of the subject’s sophistication level,

the main driver of Ellsberg ambiguity attitude is a speciﬁc treatment of unknown

probabilities.

Palabras clave: Ambiguity aversion, reduction of compound risk, model uncertainty, com-

plejidad

JEL Classiﬁcation: C91-C93-D81

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 Internacional (CC POR 4.0) licencia.

Introducción

For several decades, the standard way to make rational decisions under uncertainty has

been to follow Savage’s (1954) subjective expected utility (SEU) theory. En 1961, Ellsberg

proposed several experiments challenging canonical axioms of SEU. These experiments

have given rise to a vast literature studying the phenomenon of ambiguity aversion (es decir.,

the preference for known probabilities, or risk, over unknown probabilities, or ambiguity)

at both theoretical and empirical levels. Sin embargo, whether this deviation from SEU

constitutes an irrational response to uncertainty or not remains an open question (Gilboa

et al., 2009, 2010, 2012; Gilboa and Marinacci, 2013). As ambiguity is present and plays an

important role in most real-life decision problems,1 such a question is critical for normative

interpretations of ambiguity attitudes and for the use of ambiguity models in applications

with prescriptive purposes. Por eso, it has profound implications for policymaking (Berger

et al., 2021). Our goal, in this paper, is to clarify the extent to which ambiguity aversion

is tied to an arguable mistake, such as the failure to reduce compound lotteries, y

study its relationship with the decision-makers’ potential limitations or the complexity

of a situation.

We explore experimentally decision-making under uncertainty along three dimensions.

(1) The ﬁrst dimension concerns the sources of uncertainty.2 We investigate attitudes

1Por ejemplo, in ﬁnancial economics, Mukerji and Tallon (2001) show how ambiguity

aversion may lead to incompleteness of ﬁnancial markets, while Easley and O’Hara (2009)

show how it can explain low participation in the stock market despite the potentially high

beneﬁts. In the health domain, Berger et al. (2013) show that ambiguity aversion aﬀects

treatment decisions. In climate change economics, Drouet et al. (2015) and Berger et al.

(2017) show how ambiguity aversion aﬀects optimal emission policies.

2Sources of uncertainty are deﬁned as “groups of events that are generated by the

same mechanism of uncertainty, which implies that they have similar characteristics”

(Abdellaoui et al., 2011, pag. 696).

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

toward diﬀerent sources of risk (presented in simple or compound forms) and ambiguity

(presented in the form of model ambiguity `a la Marinacci (2015)3 or ambiguity `a la

Ellsberg (1961)). Under SEU, the distinction between these sources is irrelevant: todo

ambiguous sources are treated as risks through the assignment of subjective probabilities,

whereas compound risks are reduced to simple risks in accordance with the reduction

of compound lotteries axiom.

(2) The second dimension concerns the subjects’ level

of sophistication. We investigate the preferences of a unique pool of risk professionals

(working in insurance related jobs and possessing a high level of education in the ﬁelds of

matemáticas, Estadísticas, or actuarial science) and compare them to those of a convenience

sample of university students. Given their background and their training in dealing

with computationally complex problems requiring proﬁciency in probabilistic reasoning,

risk professionals can be considered as being more quantitatively “sophisticated” than

estudiantes. (3) Finalmente, the third dimension relates to the complexity of the problem. Por

proposing tasks with varying degrees of complexity within the same source, we are able

to isolate the role of complexity in decision-making under risk and ambiguity.

We elicit individual preferences using a two-color Ellsberg-type setting. The large

body of existing empirical literature using such a setting has so far highlighted two stylized

hechos:

SF1: Individuals are ambiguity averse.

SF2: There exists a strong relationship between attitudes towards ambiguity and com-

pound risk.

SF1 results from the many experiments that have formally tested Ellsberg’s (1961) idea,

typically using student subjects (L’Haridon et al., 2018; see also the reviews of Machina

3Model ambiguity arises when the decision-maker is not able to identify a single proba-

bility distribution (among a set of probability models) corresponding to the phenomenon

de interés (Hansen, 2014; Marinacci, 2015).

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

and Siniscalchi, 2014; Trautmann and van de Kuilen, 2015).4 It also typically generalizes

to alternative subject pools, including risk professionals (Cabantous, 2007; Cabantous

et al., 2011; Hogarth and Kunreuther, 1989). While ambiguity and compound risks have

distinct properties, SF2 has been put forward by Halevy (2007), who documented strong

similarities in attitudes towards Ellsberg ambiguity and compound risks among student

sujetos. Based on his ﬁndings, Halevy wrote “The results suggest that failure to reduce

compound (objetivo) lotteries is the underlying factor of the Ellsberg paradox.” (halevy,

2007, pag. 532). Such ﬁndings have been replicated on other student samples (p.ej., Masticar

et al., 2017; Dean and Ortoleva, 2019; Gillen et al., 2019), and on a representative sample

of the U.S. población (Chapman et al., 2018). Whether explicitly or implicitly, SF2

has been invoked to challenge the normative status of ambiguity aversion. Específicamente,

if non-reduction of compound (o, more generally, of complex) risks is considered as a

mistake (possibly related to computational diﬃculties), and if the subjects making this

“mistake” are mainly those who are ambiguity non-neutral, there would be little room

for using ambiguity models for normative purposes.

Although results in line with SF1 and SF2 have consistently emerged from the lit-

erature, their relationship with the subjects’ level of sophistication has received little

attention so far. Exceptions are the studies of Chew et al. (2018), who investigate the

role of subjects’ level of comprehension for SF1; and Abdellaoui et al. (2015), and Berger

and Bosetti (2020), who report somewhat weaker relationships between ambiguity and

compound risk attitudes among engineering students and climate policymakers respec-

activamente. Además, the role of complexity as a factor contributing to explain SF1 and SF2

remains largely understudied, with the exceptions of Armantier and Treich (2016), y

Kov´aˇr´ık et al. (2016). Our paper attempts to ﬁll these gaps by examining two research

4We note that ambiguity seeking is also common for ambiguous events with low like-

medios de vida. This local ambiguity seeking attitude is shown to be due to an ambiguity-

generated likelihood insensitivity (Dimmock et al., 2015). Our study focuses on proba-

bilities around 50% and does not consider this other component of ambiguity attitudes.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

preguntas:

RQ1: Are SF1 & SF2 robust to sophistication?

RQ2: What are the main drivers of ambiguity attitude?

To answer these questions, we speciﬁcally targeted a sample of risk professionals, OMS

possess a high level of sophistication in probabilistic reasoning. Hasta donde sabemos, we are

the ﬁrst to study the preferences of such a unique pool of subjects in an incentivized ex-

periment with a simple, context-free, design allowing us to make direct comparisons with

other subject pools. Although focusing on such a unique sample necessarily sacriﬁces

representativeness, it enables us to answer our ﬁrst research question and to bring novel

insights on the role of sophistication. Our second research question aims at disentangling

the driving mechanisms of the Ellsberg paradox. Diﬀerent explanations have been pro-

posed in the literature: Following theories that equate ambiguity to compound risk (p.ej.,

Segal, 1987; SEO, 2009), the driving factor of the Ellsberg paradox is the failure to reduce

compound risks.5 Along similar lines, some recent studies have suggested that ambiguity

aversion can be related to an aversion towards complex risks (p.ej., Armantier and Treich,

2016; Kov´aˇr´ık et al., 2016). Alternativamente, according to a variety of theoretical models

with normative underpinnings (see Gilboa and Marinacci, 2013, para una revisión), Ellsberg-

type behaviors are primarily driven by a speciﬁc attitude towards unknown probabilities.

En lo que sigue, we analyze the eﬀect of these factors to understand their respective roles

in explaining SF1 and SF2, and relate them to the subjects’ sophistication level.

2 experimentos

We report the results of two experiments. The data were collected in the context

of a broad research project investigating the layers of uncertainty (see Aydogan et al.,

5Segal (1987, pag. 179) wrote: “In other words, risk aversion and ambiguity aversion

are two sides of the same coin, and the rejection of the Ellsberg urn does not require a

new concept of ambiguity aversion, or a new concept of risk aversion.”

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

2023). Específicamente, Aydogan et al. (2023) proposed and experimentally tested the layer

hypothesis by comparing attitudes towards the layers of risk, model ambiguity, and model

misspeciﬁcation. They reported behavioral diﬀerences across the three layers based on a

main experiment conducted with university students, which was supplemented by robust-

ness experiments conducted with diﬀerent subject pools (including risk professionals). En

el estudio actual, we use a subset of the same data to address the distinct research ques-

tions RQ1 and RQ2.6 In particular, the current study focuses on the contrast between

two speciﬁc subject pools with distinct characteristics and documents new results on the

relationship between uncertainty, sophistication, and the level of complexity.

2.1 Samples

We consider two distinct samples. The main experiment in this study is an artefactual

ﬁeld experiment run on a unique pool of risk professionals (actuaries). The control

experiment is a standard laboratory experiment with university students.

Actuaries at ICA We collected data from 84 risk professionals during the 31st Inter-

national Congress of Actuaries (ICA).7 The average age was around 40 y 44% del

subjects were female. The subjects were highly educated: 58 sujetos (69%) reported

a master’s degree as the highest level of education completed and 18 sujetos (21%) re-

ported a PhD degree. 46 subjects reported that their highest degree was obtained in a

ﬁeld related to mathematics and statistics, mientras 17 subjects reported it related to actu-

6More speciﬁcally in the current study, we leave out the treatments involving model

misspeciﬁcation and report on the standard Ellsberg treatment, which is diﬀerent from

the Extended Ellsberg treatment reported in the main analysis of Aydogan et al. (2023).
7ICA is a conference organized by the International Actuarial Association every four

años. It gathers more than 2,500 actuaries, academics, and high-ranking representatives

from the international insurance and ﬁnancial industry. The 31st congress was held from

Junio 4 a 8, 2018, in Berlin, Alemania.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

arial sciences. The remaining subjects reported diplomas in physics (2), engineering (1),

ﬁnance (1), economics and management (3), or did not report anything (14). Finalmente, el

subjects had an average of 13 years of relevant work experience.

University students We collected data from 125 social science students at Bocconi

Universidad, Italia. At the time of the experiment, 80 de ellos (64%) were in a bachelor’s

program while 34 (27%) were in a master’s program, y el resto (9%) were in a PhD

programa. 42% of the subjects were female, and the average age was 20.5.

En lo que sigue, we characterize sophistication by the background of the subjects.

En ese sentido, actuaries are considered as more “sophisticated” than students. Such a

distinction is justiﬁed on the ground that actuaries are experts in decision-making under

uncertainty and experienced risk evaluators, who are used to make decisions in situations

of ambiguity in their professional roles. They also possess a high training in statistics,

probability and decision theory. debería, sin embargo, be clear that diﬀerent dimensions may

arguably contribute to making the pool of actuaries diﬀerent than that of students. En

particular, the two samples diﬀer in the following dimensions: (1) Curriculum: 79% del

actuaries possess a training in STEM (ciencia, tecnología, engineering, y matemáticas),

while the students are in social science programs; (2) Level of education: 90% del

actuaries reported to hold at least a master’s degree, while this is the case for only 9%

of the students; (3) Experience: actuaries reported an average 13 years of relevant work

experiencia, whereas most students had no work experience at all. Además, the age

diﬀerence between the two groups could be seen as a confounder to what precedes. Nosotros

report the results of a within-sample heterogeneity analysis in the Online Appendix.

2.2 Diseño

Sources of uncertainty We use a within subject design to study individual choices

under risk and ambiguity. The experiment entails betting on the color of a card drawn

from a deck in diﬀerent situations. We consider the following four distinct sources of

uncertainty that are constructed in a two-color Ellsberg-type setting (Ver también Figura 1

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

(a)).

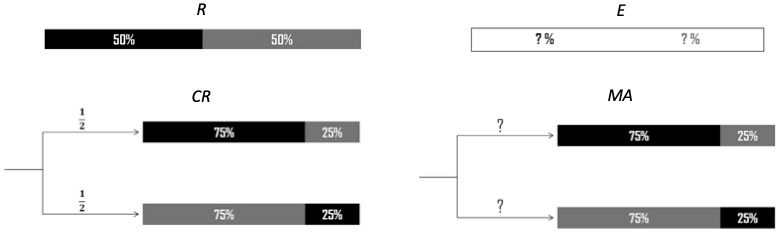
1. (R) Risk entails a deck that contains equal proportions of black and red cards.

2. (CR) Compound Risk entails, with equal probabilities, either a deck that contains

p% red and (1 − p)% black cards, or a deck that contains p% black and (1 − p)%

red cards.

3. (M A) Model Ambiguity entails, with unknown probabilities, either a deck that

contains p% red and (1 − p)% black cards, or a deck that contains p% black and

(1 − p)% red cards.

4. (mi) Ellsberg ambiguity entails a deck of 100 cards that contains an unknown pro-

portion of black and red cards.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

(a) Illustration of the four sources of uncertainty (here p = 25 in CR and M A)

(b)

(C)

Cifra 1: Sources of uncertainty and their characteristics

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

RiskAmbiguityRECRMANon compoundCompound1.a1.b1.cGlobal attitudes towards sourcesCR0MA0CR25MA25Less complexMore complex3223Attitudes CompoundriskModelambiguityReview of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 Internacional (CC POR 4.0) licencia.

The sources R and CR are two sources of risk (known probabilities), mientras que el

sources M A and E are ambiguous (unknown probabilities). The sources CR and M A are

compounded as they explicitly entail two stages, with two potential deck compositions.

They diﬀer from each other in the type of uncertainty they entail in the ﬁrst stage.

Específicamente, the two possible deck compositions are unambiguously assigned an objective

50% probability under CR, whereas these probabilities are unknown in the case of M A.

On the basis of a symmetry argument, a 50% probability could be assigned to the two

possible deck compositions under M A, but these probabilities would then necessarily be

subjectively determined.8 E is the standard ambiguous source originally proposed by

Ellsberg (1961).

Complexity We consider a notion of complexity related to the number of stages of

uncertainty a situation features. Respectivamente, for each source CR and M A, we propose

two distinct cases that are characterized by diﬀerent levels of complexity. In the ﬁrst case,

we consider p = 0 so that the deck features a degenerate distribution: it contains either

100% black or 100% red cards. We denote the corresponding situations CR0 and M A0.9

This case is of minimal complexity: although the situation is presented in two stages, él

entails only one stage of uncertainty (as all the uncertainty stems from the ﬁrst stage).

The second case considers p = 25, so that the deck contains either 25% rojo (y 75%

8In our experiment, symmetry in the prior distribution stems from the indiﬀerence

between betting on a red or black card. The symmetry condition can also be justiﬁed

on the grounds of a general symmetry of information argument: given the information

disponible, there is a priori no reason to believe that one composition deserves more weight

than another.

9In the literature, CR0 has also been used to study the hypothesis of time neutrality

(Segal, 1987, 1990; Dillenberger, 2010; Nielsen, 2020), es decir., the indiﬀerence between early

and late resolution of risk. It should be clear that the time dimension is not considered

in our experiment.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

negro) cards or 25% negro (y 75% rojo) cards. We denote the corresponding situations

CR25 and M A25.10

Procedure Our experiments measure individual preferences over the situations R, CR0,

CR25, M A0, M A25, y e. For each of them, the subjects faced a bet on the color of a

card randomly drawn from a deck. For every bet, the winning color was determined by

the subjects themselves. We elicited the certainty equivalents (CEs) of the bets using a

choice-list design. We use the midpoint of an indiﬀerence interval implied by a switching

point as a proxy for the CE of a bet. In view of the stark income gap between risk pro-

fessionals and students (see Online Appendix), we adjusted the stakes oﬀered to the two

groups by a factor of 10. Específicamente, bets yielded either e200 or e0 in the experiment

with actuaries and either e20 or e0 in the experiment with students. We used a standard

prior within-subject random incentive mechanism in the lab (es decir., all students were paid

based on one of their choices) but adopted a between-subject random incentive system in

the ﬁeld (es decir., one-in-ten actuaries was paid) due to budgetary and logistical constraints.11

The details of the experimental procedures are provided in the Online Appendix.

10Note that our characterization of complexity can also be seen as referring to the

number of branches of a lottery. It is consistent with Chew et al. (2017, Ver nota al pie 20)

in the case of compound risk, and with the notion of complexity under simple risk, cual

is typically assessed by the number of diﬀerent outcomes of the lottery (Sonsino et al.,

2002; Moﬀatt et al., 2015).

11Previous literature has reported no systematic diﬀerence between paying all subjects

or paying one-of-N (Beaud and Willinger 2015; Clot et al. 2018; Berlin et al. 2022). Nota

also that to further encourage risk professionals to reveal their preferences conditional on

being selected for payment, we carried out the between-subject randomization prior to the

experimento, thus enhancing the isolation assumption of Kahneman and Tversky (1979)

(see Johnson et al., 2021 for more discussion on the prior random incentive mechanisms).

Under the isolation assumption, the higher stakes oﬀered to actuaries compensate for the

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

3 A relative premium measure

To examine attitudes toward the diﬀerent sources of uncertainty, we introduce the

following premia measure relative to risk (R).

Definición 1. The relative premium ΠR,j is the diﬀerence between the CE of the bet on

R (CER) and the CE of the bet on j (CEj), expressed in % of the CE of the bet on the

most preferred situation:

ΠR,j ≡

CER − CEj
máximo {CER, CEj}

∀j ∈ {CR0, CR25, M A0, M A25, mi} .

(1)

Intuitivamente, two cases can be distinguished. If the individual is relatively more averse to

the uncertainty present in situation j, the preferred bet is the one on R, and the relative

premium represents the percentage of extra money that an individual would be ready to

sacriﬁce to avoid betting on j, relative to the value of the bet on R. Symmetrically, si

the preferred situation is j, the relative premium ΠR,j represents the extra money that

would be sacriﬁced to avoid betting on R, relative to the value of the bet on j. This index

possesses some desirable properties. Primero, ΠR,j is symmetric around zero across relatively

more or less averse preferences. Segundo, ΠR,j belongs to the interval [−1; 1], which also

makes it easy to interpret in terms of percentages. Por último, the normalization with respect

to the maximum CE allows more robust comparisons among subject pools by controlling

for diﬀerences in payoﬀs and subjects’ overall level of uncertainty attitudes.12

In the literature, ΠR,E has been commonly referred to as the Ellsberg-ambiguity pre-

mium (ver, p.ej., Berger, 2011; Maccheroni et al., 2013), and ΠR,CR as the compound risk

large income gap between risk professionals and students (see Online Appendix).

12In the Online Appendix, discutimos

some alternative measures

that have

been proposed in the literature, such as ΠR,j ≡ (CER − CEj)/CER or ΠR,j ≡

(CER − CEj)/(CER + CEj) (Sutter et al., 2013; Trautmann and van de Kuilen, 2015).

Our conclusions do not diﬀer when using these alternative deﬁnitions.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

premium (ver, p.ej., Abdellaoui et al., 2015).

En la misma vena, ΠR,M A represents the

model ambiguity premium. These premia are represented by the arrows 1.a-c in Figure

1(b). The relative premium can furthermore be used to measure the eﬀects of complexity

and of a speciﬁc attitude toward unknown probabilities (in the ﬁrst stage), as illustrated

by arrows 2 y 3 En figura 1(C). Específicamente, as the sources CR and M A both present

a relatively less and more complex case (es decir., one stage of uncertainty when p = 0 vs.

two stages of uncertainty when p = 25), the eﬀect of complexity, within each source, poder

be examined by (ΠR,CR25 − ΠR,CR0) y (ΠR,M A25 − ΠR,M A0). These diﬀerences indicate

whether the compound risk or model ambiguity premia are larger in more complex cases

than in less complex ones. Similarmente, (ΠR,M A0 − ΠR,CR0) y (ΠR,M A25 − ΠR,CR25) gorra-

ture the eﬀect of the distinct treatment of known and unknown probabilities in the ﬁrst

stage within situations entailing the same degree of complexity.

4 Resultados

Our data consist of six choice lists per subject. Observations with multiple-switching,

reverse-switching, or no-switching patterns are not included in the analysis as they do

not provide clear measurements of the CEs.13 We do not detect any order eﬀect on

tratos (see Online Appendix).

13The proportions of subjects aﬀected by such inconsistencies in at least one of the

choice lists are 11.9% for actuaries (10 fuera de 84) y 10.4% for students (13 fuera de 125)

and do not diﬀer across the two samples (two-sample Z-test of proportions, p=0.73).

Discarding four actuaries who show inconsistent patterns in all lists, suggesting a lack of

attention to the experiment, inconsistencies were present in 16 fuera de 480 liza (3.3%) para

actuaries and in 25 fuera de 750 liza (3.3%) for students. These proportions are notably

lower than what is typically observed in the literature (Yu et al., 2021).

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
/
r
mi
s
t
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
/
r
mi
s
t
_
a
_
0
1
3
5
8
2
1
5
6
1
6
6
/
r
mi
s
t
_
a
_
0
1
3
5
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

4.1 General attitudes toward diﬀerent sources of uncertainty

Mesa 1 presents the mean relative premia. We observe that both groups of subjects

are comparable in terms of ambiguity premia, exhibiting aversion toward the sources M A

y e (t-tests, pag<0.001).14 This suggests that ambiguity aversion (SF1) is robust to the subjects’ level of sophistication. Regarding the source CR, the average relative premium for CR25 is positive for students (p<0.001), indicating aversion toward compound risk, but we cannot reject the null hypothesis that ΠR,CR25 = 0 for actuaries (t-test, p=0.03 but p=0.17 after Bonferroni correction15). The diﬀerence between actuaries and students is particularly marked for this premium (t-test, p<0.001). In contrast, the average relative premium for the less complex case CR0 does not diﬀer from zero for both groups (t-test, p=0.59 for actuaries, and p=0.55 for students). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / . / 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 14Testing multiple hypotheses (e.g., testing H0 : ΠR,j = 0 for all j ∈ {CR0, CR25, M A0, M A25, E}) may require Bonferroni corrections. To allow for direct comparisons with previous literature, we report the original p-values, together with Bon- ferroni corrections when these aﬀect the results. 15The minimum detectable diﬀerence from zero mean premium for 5% level of signiﬁ- cance (with Bonferroni correction) and a power of 90% is 0.043. 15 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. Table 1: Average premia relative to risk Actuaries Students ΠR,CR0 ΠR,CR25 -0.007 (0.0127) 0.023∗ (0.0108) 0.010 (0.0171) 0.136∗∗∗ (0.0216) Two-sample tests (p-value) 0.472 <0.001 ΠR,M A0 ΠR,M A25 ΠR,E Notes: Standard errors in parentheses. The tests are based on two-sided t-tests. 0.121∗∗∗ (0.0324) 0.106∗∗∗ (0.0227) 0.190∗∗∗ (0.0316) 0.130∗∗∗ (0.0219) 0.181∗∗∗ (0.0227) 0.191∗∗∗ (0.0249) 0.814 0.027 0.982 ∗∗∗ signiﬁcant at 0.001, ∗∗ signiﬁcant at 0.01, ∗ signiﬁcant at 0.05. Signiﬁcance stars are based on p-values before Bonferroni correction. Values that are signiﬁcant at 0.05 after Bonferroni correction are bolded. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / / . 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 16 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. 4.2 The relationship between ambiguity and compound risk at- titudes Following the existing literature, we investigate the relationship between attitudes towards ambiguity and compound risk within our two subject pools and test the robust- ness of SF2 to sophistication. Table 2 reports the Pearson correlation coeﬃcients between compound risk premia and ambiguity premia.16 In line with SF2, we observe a signiﬁcant correlation between attitudes toward ambiguity and compound risk for students (except between ΠR,CR0 and ΠR,E, p=0.475). However, such a relationship is absent in the case of actuaries.17 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / . / 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 16The same conclusions are obtained with Spearman rank correlations, which measure monotonic –rather than linear– relationships between premia (see Online Appendix). 17We also analyzed correlations based on the method of obviously related instrumen- tal variables (ORIV) developed by Gillen et al. (2019) to correct for measurement errors. ORIV uses an instrumental variable approach to compute correlations when there are multiple measurements of behavioral variables. We used ORIV in our data by using multiple elicitations of preferences under compound risk and model ambigu- ity (i.e., with p = 0 and p = 25). We observe that, although the correlations be- tween compound risk and ambiguity using ORIV are consistently high for students: corr(ΠR,CR, ΠR,M A)=0.988 and corr(ΠR,CR, ΠR,E)=0.916, they remain remarkably low for actuaries: corr(ΠR,CR, ΠR,M A)=0.369 and corr(ΠR,CR, ΠR,E)=0.057. 17 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. Table 2: Pearson correlations between compound risk and ambiguity pre- mia Actuaries Students ΠR,M A0 ΠR,M A25 ΠR,E ΠR,M A0 ΠR,M A25 ΠR,E 0.169 0.135 -0.033 -0.078 ΠR,CR0 ΠR,CR25 Notes: ∗∗∗ signiﬁcant at 0.001, ∗∗ signiﬁcant at 0.01, ∗ signiﬁcant at 0.05. Signiﬁcance stars are based on p-values before Bonferroni correction. Values that are signiﬁcant at 0.05 after Bonferroni correction are bolded. 0.315∗∗∗ 0.344∗∗∗ 0.407∗∗∗ 0.652∗∗∗ 0.475∗∗∗ ΠR,CR0 ΠR,CR25 0.067 0.107 0.109 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / / . 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 18 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. Next, we examine the links between ambiguity neutrality and reduction of compound risk. We adopted a comprehensive deﬁnition of ambiguity neutrality according to which a subject is considered as ambiguity neutral if ΠR,E = ΠR,M A0 = ΠR,M A25 = 0.18 Similarly, a subject is said to be reducing compound risk if ΠR,CR0 = ΠR,CR25 = 0. The proportion of ambiguity non-neutrality among subjects who do not reduce com- pound risk is 95% (=20/21) for actuaries and 94% (=77/82) for students. These propor- tions, which are in line with the literature, suggest that non-reduction of CR is suﬃcient for ambiguity non-neutrality, irrespective of the subjects’ sophistication level. Turning to necessity, we ﬁnd that 80% (=77/96) of ambiguity non-neutral students are also not re- ducing CR. However, this proportion is 57% (=20/35) for actuaries, which is signiﬁcantly less than for students (two-sample test of proportions, p=0.008). This result indicates that, although compound risk non-reduction appears to be also necessary for ambiguity non-neutrality when less sophisticated subjects are considered, this is not the case for more sophisticated ones. Overall, this ﬁrst set of results enables us to answer RQ1. Result 1 (a) Ambiguity aversion is robust to the subjects’ sophistication level, but (b) the strong relationship between attitudes toward ambiguity and compound risk is not. 4.3 Complexity and ambiguity We now focus on compound sources to examine the eﬀects of complexity and ambiguity in diﬀerent subject pools. For this, we run a regression analysis with random eﬀects at individual level, where the relative premia ΠR,j for j ∈ {CR0, CR25, M A0, M A25} are regressed on a dummy for complexity (taking value 1 if j ∈ {CR25, M A25}), a dummy for the presence of ambiguity (taking value 1 if j ∈ {M A0, M A25}), and their interaction. The baseline is the behavior in a compound risk situation with minimal complexity. To test the eﬀect of sophistication, we run a regression by pooling data from the two samples and using a dummy for actuaries. 18Our conclusions are robust to the use of alternative deﬁnitions of ambiguity neutrality under M A and E separately (see Online Appendix). 19 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / . / 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. Table 3 reports the results. We observe positive coeﬃcients for complexity and model ambiguity, indicating that the relative premia are higher when the situation is more complex or does not entail objective probabilities, in comparison to the less complex situation with objective probabilities (i.e., CR0). Therefore, both students and actuaries can be said to be averse to complexity and unknown probabilities in the ﬁrst-stage. However, the eﬀect of complexity is signiﬁcantly lower among actuaries than among students, although there is no diﬀerence between the two groups regarding the eﬀect of unknown probabilities. We also observe a negative interaction between the variables, suggesting that the eﬀect of complexity is less pronounced in the presence of model ambiguity. This interaction is signiﬁcant for students but not for actuaries. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / . / 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 20 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. Table 3: Random Effects Regressions of Relative Premia Complexity Model ambiguity Complexity × Model ambiguity Constant Actuaries Students 0.031∗ (0.015) 0.128∗∗∗ (0.033) -0.046 (0.031) 0.123∗∗∗ (0.023) 0.120∗∗∗ (0.023) -0.075∗∗ (0.026) -0.006 (0.013) 299 0.010 (0.017) 471 Eﬀect of sophistication (pooled data) -0.092∗∗∗ (0.027) 0.008 (0.040) 0.028 (0.040) -0.016 (0.021) 770 Observations Notes: Cluster-robust standard errors in parentheses. ∗∗∗ signiﬁcant at 0.001, ∗∗ signiﬁcant at 0.01, ∗ signiﬁcant at 0.05. Similar results are obtained when controling for age, gender, income, and education (see Online Appendix). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / . / 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 21 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. 4.4 Explaining Ellsberg ambiguity Based on what precedes, we now investigate the roles of attitudes toward complex- ity and unknown probabilities, together with the failure of the reduction principle in explaining Ellsberg-ambiguity attitude. We use the following OLS regression: E-AM Bi = β0 + β1COM P Xi + β2U N KN OW Ni + β3REDi + εi, (2) where Ellsberg ambiguity attitude (E-AM B) for subject i is computed by ΠR,E. At- titudes toward complexity and unknown probabilities (COM P X and U N KN OW N , respectively) are both measured with respect to ΠR,CR0 to isolate their pure eﬀects and avoid interactions between them. Speciﬁcally, complexity attitude is captured by (ΠR,CR25 − ΠR,CR0), which computes the diﬀerence between the compound risk premia under diﬀerent degrees of complexity.19 Attitude toward unknown probabilities is mea- sured by (ΠR,M A0 − ΠR,CR0), which captures the diﬀerence in relative premia between two compound situations presenting the same degree of complexity, but diﬀerent type of probabilities in their ﬁrst stage.20 Finally, the measure of reduction (RED) is based on ΠR,CR0: As CR0 is arguably the most easily reducible compound risk situation, its non-reduction shows a clear failure of the reduction principle (rather than a failure to deal with complexity). The dummy for (non-) reduction takes 1 if ΠR,CR0 (cid:54)= 0 and 0 otherwise. Table 4 reports the results of the regressions. We ﬁnd that attitude toward un- known probabilities has a positive and signiﬁcant impact for both actuaries and stu- 19Note that the alternative, which is to use (ΠR,M A25 − ΠR,M A0), could be confounded by ambiguity attitudes because M A0 may also be seen as being more ambiguous than M A25 due to a larger spread of ﬁrst stage probabilities (see Jewitt and Mukerji, 2017; Berger, 2022). 20The alternative, which is to use (ΠR,M A25 − ΠR,CR25) could be confounded by risk attitudes because of the presence of risk in the second stage (see the discussion in Berger and Bosetti, 2020). 22 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / / . 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. dents. The magnitudes of the coeﬃcients indicate that one percentage point increase in (ΠR,M A0 − ΠR,CR0) leads to 0.74 percentage points increase in ΠR,E for actuaries, and to 0.43 percentage points increase for students. The diﬀerence in this coeﬃcient between the two groups is signiﬁcant (p = 0.03), indicating a stronger eﬀect of attitude toward unknown probabilities for actuaries. In contrast, complexity attitude has a positive and signiﬁcant impact for students only. The diﬀerence in the magnitude of the coeﬃcients between the groups suggests that the eﬀect of complexity is also more pronounced for students (p=0.04). Finally, the positive coeﬃcients of the reduction variable suggest that failure of the reduction principle increases the ambiguity premium, although the coeﬃ- cients are neither signiﬁcant nor diﬀerent in the two groups. Overall, this second set of results enables us to answer RQ2. Result 2: (a) For both actuaries and students, the main driver of Ellsberg-ambiguity attitude is a speciﬁc treatment of unknown probabilities. (b) A speciﬁc attitude toward complexity is found to play a signiﬁcant role in explaining Ellsberg-ambiguity attitude for students only. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / / . 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 23 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. Table 4: OLS Regressions of Ellsberg Ambiguity Premium COM P X U N KN OW N RED Constant Actuaries Students -0.170 (0.167) 0.735∗∗∗ (0.091) 0.137 (0.074) 0.079∗∗ (0.026) 0.253∗ (0.116) 0.434∗∗∗ (0.106) 0.036 (0.048) 0.091∗∗∗ (0.024) Diﬀerence between groups (pooled data) -0.423∗ (0.203) 0.302∗ (0.140) 0.101 (0.088) -0.012 (0.036) Observations Notes: Robust standard errors in parentheses, ∗∗∗ signiﬁcant at 0.001, ∗∗ signif- 188 114 74 icant at 0.01, ∗ signiﬁcant at 0.05. Simlar results are obtained when controling for age, gender, income, and education. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / . / 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 24 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. 5 Concluding remarks Decisions made by unusual subject pools, such as climate policymakers (Berger and Bosetti, 2020), professional traders (Fox et al., 1996), professional chess players (Levitt et al., 2011), or golf players (Pope and Schweitzer, 2011) have been the focus of stud- ies trying to explain important behavioral phenomena. Following this line of research, we focus on a unique pool of risk professionals to re-examine two stylized facts about ambiguity attitudes, which have emerged in the literature. Because these professionals routinely price risk and uncertainty at work, their occupational practice makes them of special interest for studying decision-making under uncertainty. Our results show that this selected group of subjects is as much aﬀected by ambi- guity as a standard pool of university students. However, attitudes towards ambiguity and compound risk are less closely related for risk professionals than for students. In particular, compound risk non-reduction is found suﬃcient but not necessary for am- biguity non-neutrality for these more sophisticated subjects. We argue that attitudes toward complexity may explain these ﬁndings. Indeed, if ambiguity is viewed as a com- pound source of uncertainty, or presented as such (as in model ambiguity situations), non-reduction of compound risk can be suﬃcient for ambiguity non-neutrality. On the other hand, if complexity makes compound risk situations being perceived as ambiguous by some subjects, those who are ambiguity non-neutral will also exhibit compound risk non-reduction (and hence the necessity). Interestingly, this eﬀect is signiﬁcantly weaker for more sophisticated subjects, who are less aﬀected by the complexity of a situation. Consistent with this interpretation, we observe that a non-negligible proportion of ambi- guity non-neutral actuaries do actually reduce compound risk. The paper closest to ours is Abdellaoui et al. (2015), who compared two student samples diﬀering in their training (engineering vs. non-engineering ﬁelds). While they also report a somewhat weaker link between compound risk and ambiguity for more quantitatively sophisticated students, the diﬀerences they ﬁnd between their two student samples are not as stark as those between students and actuaries. By studying a pool of 25 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / . / 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. risk professionals, whose contrast with students is more extreme, our study may be seen as more revealing for the role of sophistication in decision-making. Yet we also note that diﬀerences in sophistication might exist within the populations studied. An additional analysis of our data indeed indicates some heterogeneity among students but not among risk professionals (for the details, see Online Appendix). For example, undergraduate students are found to be more aﬀected by complexity than graduate ones, whereas work experience (or age) is not found to play any role among actuaries. We argue that our ﬁndings may have important implications for diﬀerent ambiguity models. Overall, by suggesting that ambiguity aversion is mainly driven by a genuine preference for known probabilities over unknown ones, but not necessarily by an inabil- ity/aversion to deal with the compoundness or complexity of a situation, the results we report in this paper are more consistent with the predictions of ambiguity theories with normative underpinnings. Thus, they leave room for using ambiguity models in applications with prescriptive purposes. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / . / 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 26 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. References Abdellaoui, Mohammed, Aur´elien Baillon, Laetitia Placido, and Peter P Wakker (2011) “The rich domain of uncertainty: Source functions and their experimental implemen- tation,” The American Economic Review, 101 (2), 695–723. Abdellaoui, Mohammed, Peter Klibanoﬀ, and Lætitia Placido (2015) “Experiments on Compound Risk in Relation to Simple Risk and to Ambiguity,” Management Science, 61 (6), 1306–1322. Armantier, Olivier and Nicolas Treich (2016) “The Rich Domain of Risk,” Management Science, 62, 1954–1969. Aydogan, Ilke, Lo¨ıc Berger, Valentina Bosetti, and Ning Liu (2023) “Three Layers of Uncertainty,” Journal of the European Economic Association. Beaud, Mickael and Marc Willinger (2015) “Are people risk vulnerable?” Management Science, 61 (3), 624–636. Berger, Lo¨ıc (2011) “Smooth Ambiguity Aversion in the Small and in the Large,” Working Papers ECARES 2011-020, ULB – Universit´e libre de Bruxelles. Berger, Lo¨ıc (2022) “What is Partial Ambiguity?” Economics and Philosophy, 38 (2), 206–220. Berger, Lo¨ıc, Nicolas Berger, Valentina Bosetti, Itzhak Gilboa, Lars Peter Hansen, Christopher Jarvis, Massimo Marinacci, and Richard D. Smith (2021) “Rational Pol- icymaking during a Pandemic,” Proceedings of the National Academy of Science, 118 (4), e2012704118. 27 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / . / 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. Berger, Lo¨ıc, Han Bleichrodt, and Louis Eeckhoudt (2013) “Treatment decisions under ambiguity,” Journal of Health Economics, 32 (3), 559–569. Berger, Lo¨ıc and Valentina Bosetti (2020) “Are Policymakers Ambiguity Averse?” The Economic Journal, 130, 331–355. Berger, Lo¨ıc, Johannes Emmerling, and Massimo Tavoni (2017) “Managing Catastrophic Climate Risks Under Model Uncertainty Aversion,” Management Science, 63 (3), 749– 765. Berlin, Noemie, Emmanuel Kemel, Vincent Lenglin, and Antoine Nebout-Javal (2022) “A convenient truth : between-subject random incentives and preferences towards risk and time,” mimeo. Cabantous, Laure (2007) “Ambiguity aversion in the ﬁeld of insurance: Insurers’ attitude to imprecise and conﬂicting probability estimates,” Theory and Decision, 62 (3), 219– 240. Cabantous, Laure, Denis Hilton, Howard Kunreuther, and Erwann Michel-Kerjan (2011) “Is imprecise knowledge better than conﬂicting expertise? Evidence from insurers’ decisions in the United States,” Journal of Risk and Uncertainty, 42 (3), 211–232. Chapman, Jonathan, Mark Dean, Pietro Ortoleva, Erik Snowberg, and Colin Camerer (2018) “Econographics,”Technical report, National Bureau of Economic Research. Chew, Soo Hong, B. Miao, and S. Zhong (2017) “Partial Ambiguity,” Econometrica, 85 (4), 1239–1260. Chew, Soo Hong, Mark Ratchford, and Jacob S. Sagi (2018) “You Need to Recognise Ambiguity to Avoid It,” The Economic Journal, 128 (614), 2480–2506. 28 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / . / 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. Clot, Sophie, Gilles Grolleau, and Lisette Ibanez (2018) “Shall we pay all? An experi- mental test of Random Incentivized Systems,” Journal of Behavioral and Experimental Economics, 73, 93–98. Dean, Mark and Pietro Ortoleva (2019) “The empirical relationship between nonstan- dard economic behaviors,” Proceedings of the National Academy of Sciences, 116 (33), 16262–16267. Dillenberger, David (2010) “Preferences for one-shot resolution of uncertainty and Allais- type behavior,” Econometrica, 78 (6), 1973–2004. Dimmock, Stephen G, Roy Kouwenberg, and Peter P Wakker (2015) “Ambiguity Atti- tudes in a Large Representative Sample,” Management Science, null. Drouet, Laurent, Valentina Bosetti, and Massimo Tavoni (2015) “Selection of Climate Policies under the uncertainties in the Fifth Assessment Report of the IPCC,” Nature Climate Change, 5, 937–940. Easley, David and Maureen O’Hara (2009) “Ambiguity and nonparticipation: The role of regulation,” The Review of Financial Studies, 22 (5), 1817–1843. Ellsberg, Daniel (1961) “Risk, ambiguity, and the Savage axioms,” The Quarterly Journal of Economics, 75, 643–669. Fox, Craig R, Brett A Rogers, and Amos Tversky (1996) “Options traders exhibit sub- additive decision weights,” Journal of Risk and uncertainty, 13 (1), 5–17. Gilboa, Itzhak, Fabio Maccheroni, Massimo Marinacci, and David Schmeidler (2010) “Objective and subjective rationality in a multiple prior model,” Econometrica, 78 (2), 755–770. 29 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / / . 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. Gilboa, Itzhak and Massimo Marinacci (2013) “Ambiguity and the Bayesian paradigm,” in Advances in Economics and Econometrics: Theory and Applications, Tenth World Congress of the Econometric Society.: D. Acemoglu, M. Arellano, and E. Dekel (Eds.). New York: Cambridge University Press. Gilboa, Itzhak, Andrew Postlewaite, and David Schmeidler (2009) “Is it always rational to satisfy Savage’s axioms?” Economics and Philosophy, 25 (3), 285–296. (2012) “Rationality of belief or: why Savage’s axioms are neither necessary nor suﬃcient for rationality,” Synthese, 187 (1), 11–31. Gillen, Ben, Erik Snowberg, and Leeat Yariv (2019) “Experimenting with measurement error: Techniques with applications to the caltech cohort study,” Journal of Political Economy, 127 (4), 1826–1863. Halevy, Yoram (2007) “Ellsberg revisited: An experimental study,” Econometrica, 75 (2), 503–536. Hansen, Lars Peter (2014) “Nobel Lecture: Uncertainty Outside and Inside Economic Models,” Journal of Political Economy, 122 (5), 945–987. Hogarth, Robin M and Howard Kunreuther (1989) “Risk, ambiguity, and insurance,” Journal of Risk and Uncertainty, 2 (1), 5–35. Jewitt, Ian and Sujoy Mukerji (2017) “Ordering Ambiguous Acts,” Journal of Economic Theory, 171, 213–267. Johnson, Cathleen, Aur´elien Baillon, Han Bleichrodt, Zhihua Li, Dennie Van Dolder, and Peter P Wakker (2021) “Prince: An improved method for measuring incentivized preferences,” Journal of Risk and Uncertainty, 1–28. 30 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / . / 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. Kahneman, Daniel and Amos Tversky (1979) “Prospect theory: An analysis of decision under risk,” Econometrica, 47 (2), 363–391. Kov´aˇr´ık, Jarom´ır, Dan Levin, and Tao Wang (2016) “Ellsberg paradox: Ambiguity and complexity aversions compared,” Journal of Risk and Uncertainty, 52 (1), 47–64. Levitt, Steven D, John A List, and Sally E Sadoﬀ (2011) “Checkmate: Exploring back- ward induction among chess players,” American Economic Review, 101 (2), 975–90. L’Haridon, Olivier, Ferdinand M Vieider, Diego Aycinena, Agustinus Bandur, Alexis Belianin, Lubomir Cingl, Amit Kothiyal, and Peter Martinsson (2018) “Oﬀ the charts: Massive unexplained heterogeneity in a global study of ambiguity attitudes,” Review of Economics and Statistics, 100 (4), 664–677. Maccheroni, Fabio, Massimo Marinacci, and Doriana Ruﬃno (2013) “Alpha as Ambigu- ity: Robust Mean-Variance Portfolio Analysis,” Econometrica, 81 (3), 1075–1113. Machina, Mark J and Marciano Siniscalchi (2014) “Ambiguity and ambiguity aversion,” in Handbook of the Economics of Risk and Uncertainty, 1, 729–807: Elsevier. Marinacci, Massimo (2015) “Model Uncertainty,” Journal of the European Economic Association, 13 (6), 1022–1100. Moﬀatt, Peter G, Stefania Sitzia, and Daniel John Zizzo (2015) “Heterogeneity in pref- erences towards complexity,” Journal of Risk and Uncertainty, 51 (2), 147–170. Mukerji, Sujoy and Jean-Marc Tallon (2001) “Ambiguity aversion and incompleteness of ﬁnancial markets,” The Review of Economic Studies, 68 (4), 883–904. Nielsen, Kirby (2020) “Preferences for the resolution of uncertainty and the timing of information,” Journal of Economic Theory, 189, 105090. 31 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / / . 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. Pope, Devin G and Maurice E Schweitzer (2011) “Is Tiger Woods loss averse? Persistent bias in the face of experience, competition, and high stakes,” American Economic Review, 101 (1), 129–57. Savage, Leonard J (1954) The Foundations of Statistics, New York: J. Wiley, Second revised edition, 1972. Segal, Uzi (1987) “The Ellsberg paradox and risk aversion: An anticipated utility ap- proach,” International Economic Review, 175–202. (1990) “Two-stage lotteries without the reduction axiom,” Econometrica, 349– 377. Seo, Kyoungwon (2009) “Ambiguity and Second-Order Belief,” Econometrica, 77 (5), 1575–1605. Sonsino, Doron, Uri Benzion, and Galit Mador (2002) “The complexity eﬀects on choice with uncertainty–Experimental evidence,” The Economic Journal, 112 (482), 936–965. Sutter, Matthias, Martin G Kocher, Daniela Gl¨atzle-R¨utzler, and Stefan T Trautmann (2013) “Impatience and uncertainty: Experimental decisions predict adolescents’ ﬁeld behavior,” American Economic Review, 103 (1), 510–31. Trautmann, Stefan T. and Gijs van de Kuilen (2015) Ambiguity Attitudes, Chap. 3, 89– 116: The Wiley Blackwell Handbook of Judgment and Decision Making, John Wiley & Sons, Ltd. Yu, Chi Wai, Y Jane Zhang, and Sharon Xuejing Zuo (2021) “Multiple switching and data quality in the multiple price list,” Review of Economics and Statistics, 103 (1), 136–150. 32 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / r e s t / l a r t i c e - p d f / d o i / / . 1 0 1 1 6 2 / r e s t _ a _ 0 1 3 5 8 2 1 5 6 1 6 6 / r e s t _ a _ 0 1 3 5 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Review of Economics and Statistics Just Accepted MS. https://doi.org/10.1162/rest_a_01358 © 2023 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. UNRAVELING AMBIGUITY AVERSION∗ image

Descargar PDF