Esteban Bilbao,∗ Charlotte Desvages,†
Michele Ducceschi,∗ Brian Hamilton,∗
Reginald Harrison-Harsley,∗∗
Alberto Torin,∗ and Craig Webb††
∗Acoustics and Audio Group
University of Edinburgh
Room 2.10, Alison House
12 Nicolson Square
Edinburgh EH8 9DF, Reino Unido
†School of Mathematics
University of Edinburgh
Room 5313, James Clerk Maxwell
Edificio
Mayfield Road
Edinburgh EH9 3JZ, Reino Unido
∗∗i4 Product Design
Suite 3
Broomhills Business Centre
49 Frogston Road East
Edinburgh EH17 8RT, Reino Unido
††Physical Audio
15 Heath Park Road
Romford RM2 5UB, Reino Unido
{sbilbao, charlotte.desvages,
michele.ducceschi,
brian.hamilton}@ed.ac.uk,
rharrison@i4pd.co.uk,
alberto.torin@gmail.com,
craig@physicalaudio.co.uk
Physical Modeling,
Algorithms, and Sound
Synthesis: The NESS Project
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
Abstracto: Synthesis using physical modeling has a long history. As computational costs for physical modeling synthesis
are often much greater than for conventional synthesis methods, most techniques currently rely on simplifying
suposiciones. These include digital waveguides, as well as modal synthesis methods. Although such methods are
efficient, it can be difficult to approach some of the more detailed behavior of musical instruments in this way, incluido
strongly nonlinear interactions. Mainstream time-stepping simulation methods, despite being computationally costly,
allow for such detailed modeling. In this article, the results of a five-year research project, Next Generation Sound
Synthesis, are presented, with regard to algorithm design for a variety of sound-producing systems, including brass
and bowed-string instruments, guitars, and large-scale environments for physical modeling synthesis. Además, 3-D
wave-based modeling of large acoustic spaces is discussed, as well as the embedding of percussion instruments within
such spaces for full spatialization. This article concludes with a discussion of some of the basics of such time-stepping
methods, as well as their application in audio synthesis.
Digital sound synthesis has, por supuesto, a long
history—too long to recount here in detail, pero
easily found in standard references (Roads 1996)
and the pages of this Journal. The most well-known
Computer Music Journal, 43:2/3, páginas. 15–30, Summer/Fall 2019
doi:10.1162/COMJ a 00516
C(cid:2) 2020 Instituto de Tecnología de Massachusetts.
técnicas, including additive synthesis, frequency
modulation, wavetable methods, and granular
synthesis have reached a certain level of maturity;
practitioners of electronic music are familiar with
a ellos, and real-time implementations abound.
Synthesis with physical modeling is somewhat
younger. En principio, the idea is straightforward:
Starting from a target system, which is often—but
Bilbao et al.
15
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
not always—an acoustic instrument or analog elec-
tronic device from the real world, develop a physical
modelo, which is invariably a system of equations
describing the input, the system dynamics, y el
producción. From the model, one then proceeds to a
discrete-time simulation algorithm that can be im-
plemented as a sound-producing computer program.
The earliest roots of physical modeling synthesis
are in speech synthesis (Kelly and Lochbaum 1962),
followed by early attempts at string simulation
(Ruiz 1969; Hiller and Ruiz 1971a,b). The first truly
sophisticated use of principles of physical modeling
for musical purposes was certainly the CORDIS sys-
tema, developed by Cadoz and associates (Cadoz 1979;
Cadoz, Luciani, and Florens 1983) in the late 1970s
and early 1980s. Many varieties of simulation algo-
rithms have emerged, most notably modal synthesis
(Morrison and Adrien 1993) and digital waveguides
(Herrero 1992), both of which will be described in
more detail in the next section. The most important
benefit of physical modeling synthesis is that, en
theory, it should be possible to generate sound of
a genuinely acoustic character. Además, ambos
instruments and control are parameterized in terms
of physical quantities and constants, which should
ideally be intuitive and approachable for the end
user.
It is interesting that physical modeling synthesis
has not been as widely adopted as earlier conven-
tional synthesis techniques. There are a few good
reasons for this:
1. Model choice: There are different levels at
which an acoustic system such as a musical
instrument may be modeled. In many cases,
a complete model of the system is not yet
disponible, and model simplifications can lead
to sound output of an unnatural or synthetic
personaje.
2. Algorithm design: The step from a model to
a sound-producing algorithm operating at an
audio rate is nontrivial, with many concerns.
Chief among these are avoiding perceptual
artefacts and ensuring numerical stability.
3. Computational cost: The operation count
and memory requirements for physical
modeling synthesis can be much larger than
for conventional synthesis algorithms.
4. Instrument design and control: Aprendiendo
to design and play a physical model is
not straightforward, and requires a lengthy
acclimatization process for the eventual user,
much as in the case of learning an acoustic
instrument.
The Next Generation Sound Synthesis (NESS)
project was a recent five-year effort devoted to
addressing the difficulties above. Work on the first
two, at the level of models and algorithm design,
and across a wide variety of instrument types,
is described in this article. Work on the third
difficulty, through implementation strategies in
parallel hardware and, to a much more tentative
nivel, the fourth, is detailed in a companion article
in this Journal (Bilbao et al. 2020). This article is
intended for a relatively nontechnical audience.
For a more detailed overview, see the conference
proceedings articles (Bilbao et al. 2013, 2014).
A complete repository for all publications that
have been produced during the NESS Project, tutorial
material, as well as links to musical works and the
NESS interface are available at the project Web site,
www.ness-music.eu.
State of the Art
Most approaches to physical modeling synthesis
are grounded in the theory of linear systems and
the powerful simplifications it engenders. Este
is not to say that a physical model of a musical
instrument is a linear system; en efecto, it virtually
never is. The standard model coalesced with the
landmark work of McIntyre, Schumacher, y
Woodhouse (1983), which cemented the critical
notion that a musical instrument can be divided
into an excitation mechanism and a resonator. Para
the purposes of sound synthesis, the excitation
mechanism, driven by an external signal supplied
by the player, is strongly nonlinear but assumed
to be pointlike, or “lumped.” Examples are the
interactions of the bow with the string, the hammer
with the string, and the lip with the reed. El
resonator is modeled as a linear system of finite
spatial extent—examples are strings, barras, plates,
16
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
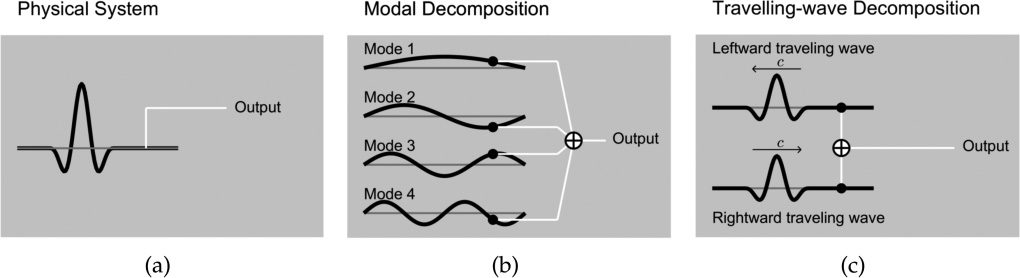
Cifra 1. Physical system
in 1-D (a), modal
decomposition (b), y un
traveling-wave
decomposition (C).
and acoustic tubes. It is the linear character of
the resonator that has been fruitfully exploited in
modern physical modeling synthesis.
A linear—more precisely, linear and time-
invariant—representation of a distributed system
leads naturally to a description in terms of modes
of vibration; with each such mode is associated a
forma, frequency, and damping factor. In isolation,
the dynamics of such a system may be expressed
completely in terms of its modes, and synthesis
becomes similar to additive approaches—one con-
structs a sound from sinusoidal components, dónde,
in contrast to additive synthesis, there are precise
physical constants determining the weightings of
the various components. In implementation, a lin-
ear system representation is attractive because the
various modes evolve independently (ver figura 1).
Modal approaches have been used for some time,
particularly in the successful Mosaic synthesis envi-
ambiente (more recent updates have been distributed
under the name Modalys; for more information, ver
Adrien 1991; Morrison and Adrien 1993), desarrollado
at the Institut de Recherche et Coordination Acous-
tique/Musique (IRCAM). These approaches have
also been developed independently elsewhere (p.ej.,
Bruyns 2006; van den Doel and Pai 2007).
Under further restrictions, a saber, that the
distributed object is uniform (es decir., spatially homoge-
neous), with constant wave speed, and well-modeled
in one dimension (such as a simplified string model,
or cylindrical or conical acoustic tubes), then an-
other useful characterization is in terms of traveling
ondas. Under such conditions, the vibration of such
an object may be described completely in terms of
so-called wave components, which travel through
the medium without change in shape. Such a wave
decomposition leads immediately to a highly ef-
ficient discrete-time implementation in terms of
delay lines, como en la figura 1. Waveguide techniques
were developed by Julius O. Smith at Stanford Uni-
versity’s Center for Computer Research in Music
and Acoustics (CCRMA) from the starting point of
the nonphysical Karplus-Strong algorithm (Jaffe and
Herrero 1983; Karplus and Strong 1983). The first pub-
lication on the use of digital waveguides for sound
synthesis was presented at the 1986 Internacional
Computer Music Conference (Herrero 1986), a pesar de
they had been proposed a year earlier in the con-
text of artificial reverberation (Herrero 1985). Digital
waveguides have since seen enormous application
to physical modeling synthesis for stringed and
wind instruments (for an early overview of digital
waveguides, see Smith 1992).
Such methods are undeniably powerful; and yet,
there are underlying limitations to their use. A
major roadblock is the presence of nonlinear effects
in the resonator itself. The perceptual effects of
such nonlinearities range from the relatively minor
as in, p.ej., the case of phantom partials in heavy-
gauge strings (Conklin 1999) to dominant, as in
the case of crashes in gongs and cymbals (Rossing
and Fletcher 1983), and rattling in instruments
such as the snare drum (Rossing et al. 1992) o
fretted string instruments (Bilbao and Torin 2015).
But there are other limitations even in the linear
caso. Modal methods rely on the availability of
Bilbao et al.
17
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
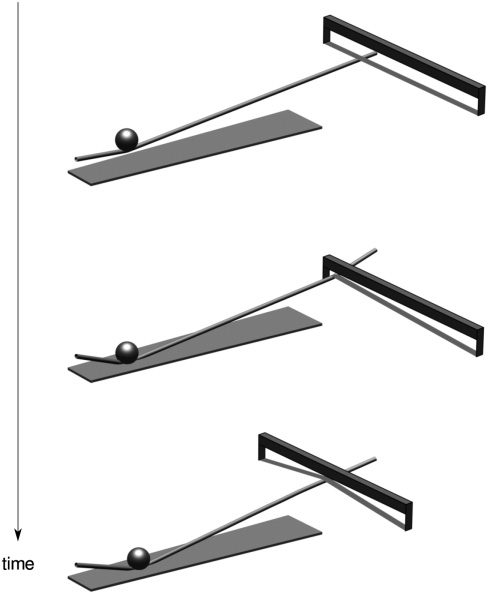
Cifra 2. Time stepping
method in 1-D. At left: el
initial state of a system, en
time step n = 0, como
represented over a grid
(and sampled from an
underlying continuous
distribución, indicated as
a solid line), and then as
time progresses at
subsequent iterations
norte = 1, . . . , 4.
modal shapes and frequencies. In certain simplified
casos, these are available in closed form; in most,
sin embargo, they are not, and must be computed
numerically, and stored—potentially an enormous
undertaking, particularly in the 3-D setting. El
efficiency advantage of digital waveguides is limited
to linear 1-D systems, y, more strictly to those
with low dispersion—restrictions that rule out
various musical components of interest such as
vibrating bars, or tubes of variable cross section. (Para
more on the limitations of such methods, see Bilbao
2009b.)
Time-stepping methods, whereby the various
components of a musical instrument are represented
over grids, and then advanced over discrete time
intervals, are a mainstream simulation technique
with an extensive history. Fleetingly used for string
synthesis (Ruiz 1969; Hiller and Ruiz 1971a,b),
they were later adopted as a brute force tool for
the scientific study of musical instruments (Bacon
and Bowsher 1978; Boutillon 1988; Chaigne and
Askenfelt 1994), and finally again for synthesis
purposes (Kurz and Feiten 1996; Bensa et al. 2003).
Independently, time-stepping methods for lumped
mass-spring networks were developed by Cadoz and
colegas, leading to the first modular physical
modeling synthesis environment, Cordis (Cadoz
1979; Cadoz, Luciani, and Florens 1983). Such time-
stepping methods consume more computational
resources than methods such as digital waveguides,
but are more general, and are able to deal directly
with complex nonlinearities, as well as time-
varying behavior through player interaction. Allá
are many varieties of such methods; under the NESS
Proyecto, relatively simple finite-difference (FD,
see Strikwerda 2004) and finite-volume methods
(Leveque 2002) have been used (ver figura 2).
One useful feature of standard FD methods is
that updating at a given grid point is local—
only neighboring grid values need be used. Este
leads to great simplifications, especially when
dealing with connections between objects, y
also yields computational structures suitable for
parallelization. For more on parallelization aspects
of the sound synthesis methods presented here, ver
the companion article (Bilbao et al. 2020).
Modelos
En esta sección, a variety of models of musical
instruments of distinct types are presented, con
an emphasis on detailed modeling of both highly
nonlinear behavior, as well as time-varying control.
Brass Instruments
The acoustics of a brass instrument are determined
primarily by the bore profile (ver, p.ej. Causs ´e,
Kergomard, and Lurton 1984). A note is generated
by buzzing the lips to set up oscillations within the
tube, the fundamental frequency of which is close
to one of the natural resonant frequencies of the
bore. To modify the resonant frequencies, adicional
lengths of tubing can be introduced, such as those
in the valve sections of a trumpet. Cifra 3 muestra
a hypothetical brass instrument with additional
lengths of tubing, to be activated by valves (no
pictured).
The synthesis of brass instrument sounds has
been approached using several methods—from the
early AM synthesis of Risset (1965) to frequency
modulation synthesis (Morrill 1977) and then later
physical modeling work using digital waveguides
(Cocinar 1991). Under the NESS project, a fully
18
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 3. Three-valved
brass instrument model,
excited with an impulse
under partial valved
condiciones. Light-colored
regions indicate high
pressure, and dark-colored
regions indicate low
pressure.
articulated brass instrument environment has been
developed using FD methods (Bilbao and Harrison
2016), and the algorithm design resembles seminal
speech synthesis work by Kelly and Lochbaum
(1962). The user has complete control over the
instrument design, including the specification of
the bore profile, valve positions and lengths of
valve sections, and lip parameters. The instrument
can be played through the manipulation of several
time-varying control streams, including mouth pres-
sure, lip frequency, and multiple valve depression
positions. In addition to generating note transi-
ciones, this model can also produce sounds with
multiphonic timbre caused by partially open valve
configuraciones, a novel feature of this work. Porque
execution times are relatively small, brass synthesis
has been a mainstay for composers using the NESS
sistema (cf. Bilbao et al. 2020).
Additional information on the brass instrument
environment can be found in an earlier publication
in this Journal that also documents its implemen-
tation in the Composers Desktop Project (harrison
et al. 2015). Además, a multiplatform software
release and tutorial files are available at www.ness
-music.eu.
Bowed String Instruments
The oscillations of a bowed string arise from the
strongly nonlinear friction interaction between the
bow hair, coated in rosin, and the string surface
at the bowing point. Under certain excitation pa-
rameter choices (p.ej., bow force, posición, velocity),
the string vibrations settle into a periodic stick-slip
regime, known as Helmholtz motion (McIntyre and
Woodhouse 1979). Otro, less musically pleasant os-
cillation regimes are found elsewhere in the playing
parameter space, some of which are characterized by
screeching noise or overtone jumps. The left-hand
fingers of the musician are used to clamp the string
against the fingerboard and to transition between
stopped notes, often with added effects (vibrato
being the most well-known example).
Existing bowed-string physical models have
relied on traveling-wave representations that go
back to work by Smith (1986; see also Mansour,
Woodhouse, and Scavone 2016). In this framework,
sin embargo, the implementation of time-varying or
distributed nonlinear interactions is nontrivial,
thus drastically restricting the range of reproducible
bowing gestures.
An FD scheme for the bowed-string system is
presented in Desvages and Bilbao (2016). An example
of a bowed-string system is shown in Figure 4. A two-
polarization linear string is coupled to a stopping
finger, which allows users to play different notes
along the neck, and to execute certain gestures, semejante
as glissando, legato, or vibrato. The fingerboard is
modeled as a rigid barrier underneath the string.
Other gestures (Por ejemplo, spiccato bowing) son
made possible by a dynamic nonlinear bow model,
which can bounce against the simulated string. El
nonlinear friction force applied transversally by the
bow onto the string depends on the relative velocity
between string and bow (Smith and Woodhouse
2000).
Guitars
Like bowed string instruments, guitar-like instru-
ments are enormously complex constructions,
consisting of a set of strings coupled via a bridge
to a body, which then radiates acoustic energy to
the listener. The linear behavior of the body and
Bilbao et al.
19
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 4. A bow is lowered
onto a string, cual es
pinned between a finger
and the fingerboard. El
bow is then pushed across
the string to set it into
movimiento.
sliding barre chords, as well as the ability to play
harmonics when fingers touch the string lightly.
For a visualization of some of these gestures, ver
Cifra 5.
A complete system for the interactions between
fingers, strings, and fretboard has been developed
using FD methods, allowing for an arbitrary number
of strings, a user-defined fretboard, and stopping
fingers, all with independent time-varying control
over finger positions and forcing. The details of
the model and algorithm are presented in Bilbao
and Torin (2015). Nota, sin embargo, that the body
and radiation are not implemented in the current
modelo.
3-D Wave-Based Simulation of Room Acoustics
One important target system in the NESS project has
been 3-D room acoustics, with the overarching goal
of full-wave simulations at audio rates. As opposed
to image source and ray tracing techniques (Savioja
and Svensson 2015), which are high-frequency ap-
proximations based on geometrical acoustics, ola
simulation is valid across all audible frequencies
and can be viewed as a complete approach to room
acoustics simulation.
Wave simulations of room acoustics were first
attempted in the 1990s using finite difference
methods (Chiba et al. 1993; Botteldooren 1994, 1995)
as well as the digital waveguide-mesh paradigm
applied in an equivalent finite-difference form
(Savioja, Rinne, and Takala 1994). In the NESS
proyecto, the main developments were with respect to
the modeling of complex geometries and frequency-
dependent boundaries (Bilbao et al. 2016), aire
absorption effects and acceleration over parallel
computing hardware (Webb and Bilbao 2011), y
the use of non-Cartesian spatial grids (hamilton
and Bilbao 2013) for computational efficiency. Semejante
wave-based simulations can typically be parallelized
over the underlying spatial grid. Este, with the help
of modern parallel computing hardware—such as
graphics processing unit (GPU) devices—has made
it possible to carry out large-scale wave simulations
of room acoustics at audio rates such as 44.1 kHz
(Webb and Bilbao 2011). This is illustrated here
radiation characteristics has undergone intensive
numerical investigation through time-stepping
methods (Derveaux et al. 2003; Bader 2005). Synthe-
sis methods for linear guitar-string models include
digital waveguides, often accompanied by a filter
summarizing the effects of the body and radiation
(Laurson et al. 2001).
The strongly nonlinear collision interaction
between the strings and fretboard, particularly
under the action of stopping or tapping fingers, tiene
not been investigated as thoroughly as body and
radiation characteristics. Such nonlinear behavior
leads to delicate twanging and rattling effects,
particularly when the fingers are able to move.
Under simple plucked and unstopped conditions,
the strings will bounce off the raised frets, leading
to highly amplitude-dependent timbres (Rabenstein
and Trautmann 2004; Evangelista and Eckerholm
2010). The dynamics of the stopping fingers may
be modeled separately. When these dynamics are
present, it is possible to emulate chord changes,
20
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 5. Six-string guitar
modelo, in the course of a
time-varying gesture
including fretboard and
finger interactions.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
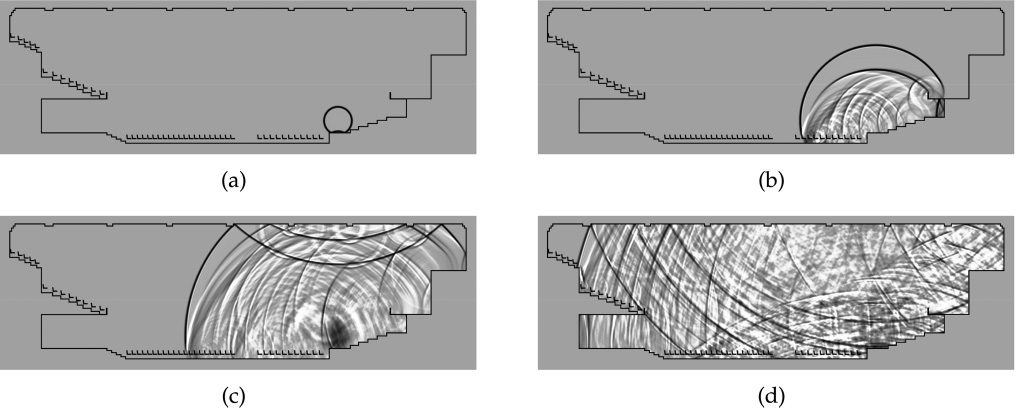
in the case of a concert hall approximately 14,000
cubic meters in volume (ver figura 6). En figura 7,
snapshots of the time evolution of the acoustic field
in response to a point-source excitation are shown.
What is notable in these images is the diffraction
that is faithfully reproduced at many points in the
scene (p.ej., steps, balcony, and seats). Es generalmente
impractical to reproduce such effects within the
paradigm of geometrical acoustics.
Percussion Instruments
Timpani are an example of percussion instruments
that are well-suited to the type of large-scale 3-D
simulations attempted in NESS. By combining the
room models detailed in the previous section with
embedded membranes and shells, it is possible to
create a complete simulation of multiple timpani in
a virtual space (Bilbao and Webb 2013).
Bilbao et al.
21
Cifra 6. Model of a 3-D
concert hall model; axis
units in meters.
Cifra 7. Snapshots of a
simulated 3-D acoustic
field within large concert
hall as 2-D x–z slices (en
y = 8.5 metro) at times: 5 mseg
(a), 25 mseg (b), 50 mseg
(C), y 100 mseg (d).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 6
Cifra 7
The time-stepping model used here is similar
to that used by Rhaouti, Chaigne, and Joly (1999),
consisting of a simplified nonlinear membrane and
boundary reflection from the body of the instrument.
The instrument is played by applying a time-varying
force at a point on the membrane, representing
22
Computer Music Journal
Cifra 8. A 2-D slice of the
acoustic field from a
simulation of four timpani
drums being played in a
room model.
a mallet or drumstick strike. The position of the
strike leads to variations in timbre, and higher
amplitudes lead to characteristic pitch glide effects.
Cifra 8 shows a slice of a full simulation using four
timpani being played in a room. Audio output can
be drawn from any location (or multiple locations
for spatialized output).
Snare drums are another interesting application
of time-stepping methods. Estos, En realidad, are able
to capture all the complex interactions (Rossing
et al. 1992) that take place among the different
components of the system, as already anticipated
in the Introduction. The snare drum model devel-
oped during the NESS project is composed of two
membranes, connected together by a rigid cavity.
The bottom membrane is in contact with a set of
stiff snares and the drum is embedded in a 3-D
habitación. Here the excitation mechanism is a drum-
stick, explicitly included as a lumped object. Torin,
hamilton, and Bilbao (2014) provide details of the
modelo.
Cifra 9 shows the typical initial excitation phase
of a snare drum. In the first instant, cuando el
drumstick travels against the membrane, the drum
and the surrounding acoustic field are at rest. During
the interaction with the membrane, there is a build-
up of positive pressure inside the cavity that pushes
the bottom membrane and the snares downwards.
When the snares collide against the membrane,
a wave front is created, which propagates inside
the cavity and excites the upper membrane. Este
behavior continues until all the energy of the system
is dissipated. These repeated collisions give the snare
drum its characteristic rattling sound, cual, como
the rest of the instruments presented here, can be
captured at any of the points inside the virtual room.
Finalmente, another drum model that has been
created is the bass drum. This model shares many
similarities with the snare drum, but apart from
lacking the snares, it has one fundamental difference:
both membranes include nonlinearities, in the form
described by the F ¨oppl–von K ´arm ´an equations.
This virtual model allows composers to produce
the dramatic attacks and the pitch glide effects
typical of bass drums and has been used in several
compositions during the NESS project.
Modular Synthesis Environments
Beyond modeling real-world instruments, or variants
de ellos, an ultimate goal of physical modeling
synthesis is to model instruments that behave
according to physical principles despite the lack of
real-world counterparts. In this way, it is hoped,
the door may be opened to new classes of synthetic
sound with an acoustic character.
One approach is through the use of modular
constructions: An instrument may be assembled
given a set of elementary objects that obey certain
physical laws, as well as connections between
a ellos. Such ideas have a long history, and were first
Bilbao et al.
23
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 9. Evolution of the
snare drum simulation
(arriba) and corresponding
2-D slice of the acoustic
field (abajo), at four
different time steps. El
arrows next to the
drumstick indicate the
direction of travel.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
explored by Claude Cadoz, leading ultimately to the
Cordis-Anima environment (Cadoz, Luciani, y
Florens 1993), for which the canonical elements are
masses and springs. Modal synthesis environments
also allow for modular instrument construction, y
other modular formalisms have also been proposed
(Rabenstein et al. 2007).
In the NESS Project, distributed canonical ele-
mentos, such as strings, barras, or plates have been
utilized. Each instance can be represented over a
grid, and then advanced in time using an FD method.
A connection, in the simplest case, can be idealized
as a pointwise link between two given elements
at given locations. A given connection element
may have its own internal dynamics, and may be
characterized by its mass, damping, and stiffness,
which could be nonlinear—reflecting hardening
spring behavior or even intermittent loss of contact,
leading to highly nonlinear responses.
Input to such an instrument can take a variety
of forms. Perhaps the simplest form of excitation
is a series of plucks or strikes, in which case for a
given component, and at a given location, a pulse-
like force input signal is sent, where the user has
control over the duration of the pulse (cual es
generally short, on the order of 1 a 5 milisegundos),
as well as the amplitude (in Newtons). Otro
approach is to treat the instrument as an effect, y
to send in audio input. In either case, for a nonlinear
instrument design, the resulting timbres will be
highly dependent on the input amplitude.
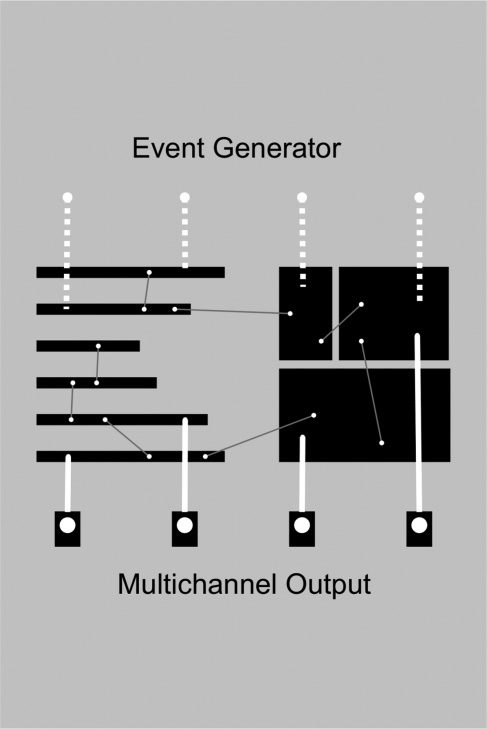
There are great opportunities for multichannel
synthesis from such modular constructions. Para
a given instrument, which will in general consist
of multiple interacting components, outputs may
be drawn simultaneously from “virtual pickups”
placed at different locations on distinct components.
For a given input, entonces, there will be a natural degree
of coherence among the various outputs, y por lo tanto
a holistic approach to spatialization is possible (ver
Cifra 10). For more on the use of such environments
in a multichannel setting, see the companion article
in this issue of Computer Music Journal (Bilbao
et al. 2020).
Various modular frameworks have emerged
throughout the course of the NESS Project. El
first complete environment that was ported to a
GPU was called Zero Code, which allowed for
the nonlinear interconnection of plates and for
percussive input. The Zero Code environment was
later refined to allow audio input (ver figura 11).
A later iteration, called Net1 Code, involved the
24
Computer Music Journal
Cifra 10. Funcional
diagram of a modular
network constructed from
interconnected bar and
plate elements, subject to
input excitations from an
event generator (puntaje) y
yielding multichannel
producción.
interconnections of strings and bars, using “rattling”
nonlinear connections. Both have been used in a
multichannel setting to generate complete pieces of
music by various artists. For more on the technical
considerations of designing such modular synthesis
sistemas, see Bilbao (2009a) and Bilbao, Ducceschi,
and Webb (2019).
Time-stepping Algorithms: Basics
The main advantage of time-stepping methods rel-
ative to other sound-synthesis techniques based on
physical modeling is generality; such methods are
able to handle a large variety of types of musical
instruments, including the emulation of strongly
nonlinear effects. One price to be paid for such gen-
erality is computational cost—always a concern, pero
perhaps currently less of one due to the availability
of fast parallel hardware. Deeper concerns are at the
algorithmic level—poorly designed time-stepping
methods can produce sound of poor quality, due to
perceptual artefacts and, en algunos casos, may not
produce a meaningful solution. A major part of the
algorithm design effort under the NESS Project has
been concerned with attacking such difficulties.
A Simple Example: An FD Scheme for the 1-D
Wave Equation
Perhaps the very simplest system of interest in
physical modeling, and one which may be familiar
to the reader, is the 1-D wave equation:
∂ 2u
∂t2
= c2
∂ 2u
∂ x2
.
(1)
Aquí, the function u(X, t), for a spatial coordinate
x ∈ [0, l], for some length L, and for time t ≥ 0
represents an unknown of interest, and Equation 1
describes its time evolution. If Equation 1 is intended
to represent the dynamics of an ideal string, entonces
tu(X, t) represents string displacement; in the case of a
lossless cylindrical acoustic tube, it could represent
the pressure field. In either case, c is the wave speed
and is assumed constant. The 1-D wave equation
must be supplemented by two initial conditions,
as well as a boundary condition at each end—for
simplicity, assume that u(0, t) = u(l, t) = 0, cual
has the interpretation of a “fixed” termination in
the case of a string. The 1-D wave Equation 1 es
the starting point for digital waveguide-synthesis
methods (Herrero 1992).
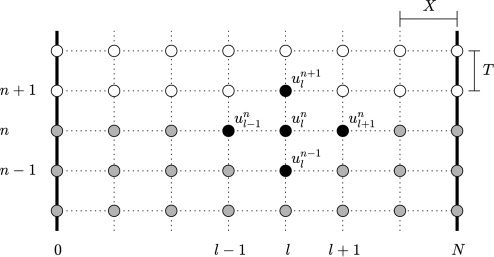
The first step in the design of a time-stepping
method is the definition of a grid. The numerical
solution will be calculated at multiples of a given
time step T (in seconds), or at times tn = nT, para
integer n ≥ 0; in audio applications, Fs = 1/T is the
sample rate. In space, the solution is approximated
at spatial intervals of X (in meters), or at locations
xl = lX, for integer l. Because the spatial domain is
of finite extent, it is simplest to set l = 0, . . . , norte, para
Bilbao et al.
25
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 11. Snapshots of the
time evolution of a
connected network of
plates.
Cifra 12. Spatiotemporal
grid for scheme in
Ecuación 3 for the 1-D
wave equation. Given
values of the grid function
y
yo , known through time
step n (shown in gray),
values at time step n + 1
may be updated, at a given
spatial index l, con
reference to neighboring
valores (shown in black).
an integer N such that L/ X = N. The grid function
y
yo , entonces, represents an approximation to u(SG, tn).
Consider the following approximations:
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
∂ 2u
∂t2
∂ 2u
∂ x2
(cid:2) 1
T2 (tu(SG, tn+1) − 2u(SG, tn) + tu(SG, tn−1)) ,
(2a)
x=xl,t=tn
x=xl,t=tn
(cid:2) 1
X2 (tu(xl+1, tn) − 2u(SG, tn) + tu(xl−1, tn)) .
(2b)
Identifying u(SG, tn) with un
yo
difference scheme
leads to the finite
un+1
yo
= 2un
yo
− un−1
yo
+ l2
(cid:3)
y
l+1
− 2un
yo
+ y
l−1
(cid:4)
,
(3)
yo
yo
which approximates Equation 1. The parameter
λ = cT/ X, sometimes referred to as the Courant
number (Strikwerda 2004) plays an important role
in the eventual behavior of the scheme, as will be
discussed momentarily. Given values un−1
and un
yo ,
the scheme computes an update to the values at the
next time step un+1
, a process that will be repeated
within a run-time loop operating at sample rate Fs
(ver figura 12). This update holds for values of l with
l = 1, . . . , N − 1. At the endpoints l = 0 and l = N,
it appears to require values of the grid function
from outside the domain; this can be addressed
by imposing the boundary conditions un
0
corresponding to fixed termination. This basic
scheme was used to generate the numerical results
como se muestra en la figura 2.
= un
norte
= 0,
Cifra 12
Dispersion and Band Limiting
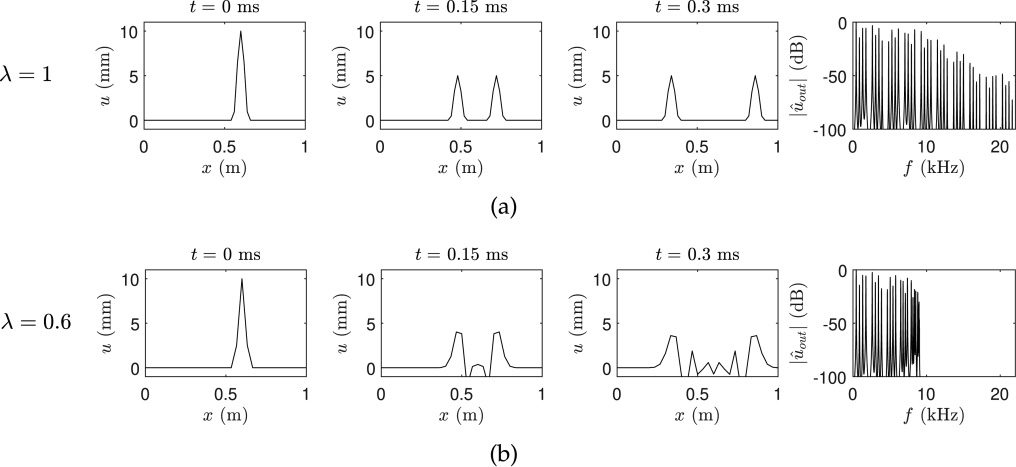
Consider first the operation of the scheme in
Ecuación 3 subject to a static initial condition in the
form of a peaked distribution. Assume L = 1 m y
c = 882 m/sec, and that Fs = 44,100 Hz. In the ideal
caso, one should expect the distribution to split
into two wave-like solutions, traveling to the left
and right with speed c, and maintaining the initial
forma. This is indeed what the scheme in Equation 3
yields, when the Courant number λ is set to 1. Ver
Figure 13a. If one reads, decir, an output displacement
anywhere along the string, one should expect,
también, that the frequency response will consist of
equally spaced frequencies, up to the Nyquist limit,
at multiples of c/2L = 441 Hz, the fundamental;
this is also true for scheme given in Equation 3
cuando λ = 1. The same is not true if λ is chosen
differently: See Figure 13b, where results are plotted
for scheme given in Equation 3 with λ = 0.6. El
26
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 13. Time evolution
of an initial distribution
according to the scheme
given in Equation 3, y
resulting output
magnitude spectrum ˆuout,
in dB for λ = 1 (a) y
λ = 0.6 (b).
initial distribution no longer travels coherently—it
is dispersed. Accompanying this is a great reduction
in bandwidth (down to approximately one-third of
the Nyquist limit), y, furthermore, the partials
are no longer equally spaced (es decir., they are now
inharmonic). Such anomalous behavior (known as
numerical dispersion) is a major difficulty in the
design of time-stepping methods, and can lead to a
great reduction in sound quality, through the loss of
bandwidth, smearing of responses, as well as other
perceptually undesirable features, such as chirps.
The scheme in Equation 3 possesses a similar
conserved quantity, E n+1/2, which may be defined as
E n+ 1
2 =
(cid:9)
norte(cid:8)
l=0
X
2T2
(cid:10)
2
un+1
yo
− un
yo
+
(cid:9)
N−1(cid:8)
l=0
c2
2X
un+1
l+1
− un+1
yo
(cid:10) (cid:3)
y
l+1
(cid:4)
− un
yo
= constant.
(5)
Numerical Stability and Energy Balances
One property of the 1-D wave equation under fixed
termination is that it is lossless; eso es, it possesses a
conserved quantity E(t), defined to within a constant
multiplicative factor as
mi(t) =
(cid:7)
2
(cid:6)
(cid:5)
l
0
1
2
∂u
∂t
+ c2
2
(cid:6)
∂u
∂ x
(cid:7)
2
dx(cid:5) = constant ≥ 0.
(4)
The total energy of the system remains constant;
furthermore, it is nonnegative, providing for bounds
on the state itself.
This quantity is clearly a discrete approximation
to the total energy of the system, from Equation 4.
It may be shown that this quantity is nonnegative
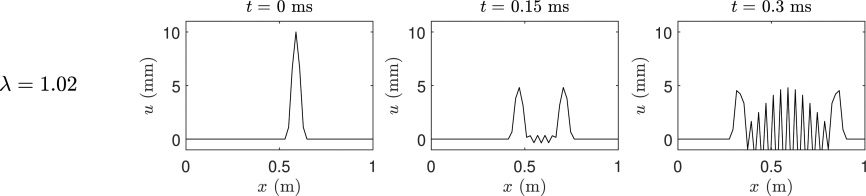
only under the condition λ ≤ 1, which is sometimes
referred to as the Courant-Friedrichs-Lewy condi-
ción. En efecto, when λ > 1, the scheme is numerically
unstable—spurious oscillations, usually at the res-
olution of the grid itself, grow exponentially (ver
Cifra 14).
The numerical energy conservation property is
a useful one for two reasons: Primero, it allows the
determination of conditions for numerical stability;
y segundo, it provides a useful debugging tool—by
monitoring the numerical energy in the run-time
loop, any deviations on the order of more than
Bilbao et al.
27
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 14. Time evolution
of an initial distribution
according to Equation 3,
illustrating numerical
instability when λ = 1.02.
machine precision indicate a programming error.
The same ideas extend to the notion of an energy
balance, dónde, for more realistic models of musical
instruments, stored energy is related to integrated
power loss and supplied power. It is also possible to
approach stability for relatively complex systems,
involving strongly nonlinear and coupled systems
in this way, and thus the numerical energy balance
has been used as a design principle for all computer
code in the NESS project.
Concluding Remarks
Mainstream techniques for numerical simulation
in the time domain offer a general approach to
the simulation of complex musical instruments
for physical modeling synthesis, allowing for the
simulation of a system according to the most
basic laws of physics, and without recourse to
simplifying assumptions (which may be unphysical
and ultimately degrade sound quality). Y todavía, two
major challenges remain. One is the step to real-time
actuación: Although already possible for some
of the systems described here (in particular brass
instruments and modular networks, depending on
their complexity), the remainder of the algorithms
are available only in offline mode. Aquí, código
parallelization, either on a GPU or in a multicore
CPU, offers a partial solution—provided that the
underlying operations can be parallelized, forming
an additional design constraint not discussed here.
Otro, deeper, issue is that of learning to play these
instruments, a process that can be very difficult,
just as learning to play an acoustic instrument is. En
este caso, the experience of the musician, informing
control strategies and user interface design, is an
essential step towards the mature musical use of
these synthesis algorithms. Both of these challenges
are discussed in detail in the companion article in
this issue of Computer Music Journal.
Expresiones de gratitud
This work was supported by the European Research
Council, under grants 2011-StG-279068-NESS and
2016-PoC-737574-WRAM. Michele Ducceschi was
supported by the Newton International Fellow
programa, through the Royal Society and British
Academia, and a Early Career Fellowship from the
Leverhulme Trust.
Referencias
Adrien, J.-M. 1991. “The Missing Link: Modal Synthesis.”
In G. DePoli, A. Picialli, and C. Roads, eds. representar-
tations of Musical Signals. Cambridge, Massachusetts:
CON prensa, páginas. 269–297.
Bacon, r., y j. Bowsher. 1978. “A Discrete Model of a
Struck String.” Acustica 41:21–27.
Bader, R. 2005. Computational Mechanics of the Classical
Guitar. Berlina: Saltador.
Bensa, J., et al. 2003. “The Simulation of Piano String
Vibration: From Physical Models to Finite Difference
Schemes and Digital Waveguides.” Journal of the
Acoustical Society of America 114(2):1095–1107.
Bilbao, S. 2009a. “A Modular Percussion Synthesis
Environment.” In Proceedings of the International
Conference on Digital Audio Effects, páginas. 321–328.
Bilbao, S. 2009b. Numerical Sound Synthesis: Finite Dif-
ference Schemes and Simulation in Musical Acoustics.
Chichester, Reino Unido: wiley.
Bilbao, S., METRO. Ducceschi, and C. Webb. 2019. “Large-
Scale Real-Time Modular Physical Modeling Sound
28
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Synthesis.” In Proceedings of the International Con-
ference on Digital Audio Effects. Available online at
dafx.de/paper-archive/2019/DAFx2019 paper 22.pdf.
Accessed February 2019.
Bilbao, S., y r. harrison. 2016. “Passive Time-Domain
Numerical Models of Viscothermal Wave Propagation
in Acoustic Tubes of Variable Cross Section.” Journal
of the Acoustical Society of America 140:728–740.
Bilbao, S., y un. Torin. 2015. “Numerical Modeling
and Sound Synthesis for Articulated String–Fretboard
Interactions.” Journal of the Audio Engineering Society
63(5):336–347.
Bilbao, S., and C. j. Webb. 2013. “Physical Modeling of
Timpani Drums in 3-D on GPGPUs.” Journal of the
Audio Engineering Society 61(10):737–748.
Bilbao, S., et al. 2013. “Large Scale Physical Modeling
Synthesis.” In Proceedings of the Stockholm Musical
Acoustics Conference, páginas. 593–600.
Bilbao, S., et al. 2014. “Modular Physical Modeling
Synthesis Environments on GPU.” In Proceedings
of the International Computer Music Conference,
páginas. 1396–1403.
Bilbao, S., et al. 2016. “Finite Volume Time Domain
Room Acoustics Simulation under General Impedance
Boundary Conditions.” IEEE/ACM Transactions on
Audio Speech and Language Processing 24(1):161–173.
Bilbao, S., et al. 2020. “Large-Scale Physical Modeling
Synthesis, Parallel Computing, and Musical Experi-
mentation: The NESS Project in Practice.” Computer
Music Journal 43(2–3):31–47.
Botteldooren, D. 1994. “Acoustical Finite-Difference
Time-Domain Simulation in a Quasi-Cartesian Grid.”
Journal of the Acoustical Society of America 95(5):2313–
2319.
Botteldooren, D. 1995. “Finite-Difference Time-Domain
Simulation of Low-Frequency Room Acoustic Prob-
lems.” Journal of the Acoustical Society of America
98(6):3302–3308.
Boutillon, X. 1988. “Model for Piano Hammers: Experi-
mental Determination and Digital Simulation.” Journal
of the Acoustical Society of America 83(2):746–754.
Bruyns, C. 2006. “Modal Synthesis for Arbitrarily Shaped
Objects.” Computer Music Journal 30(3):22–37.
Cadoz, C. 1979. “Synth `ese sonore par simulation
de m ´ecanismes vibratoires: Applications aux sons
musicaux.” PhD dissertation, Grenoble Institute of
Tecnología.
Cadoz, C., A. Luciani, and J.-L. Florens. 1983. “Responsive
Input Devices and Sound Synthesis by Simulation of
Instrumental Mechanisms.” Computer Music Journal
8(3):60–73.
Cadoz, C., A. Luciani, and J.-L. Florens. 1993. “CORDIS-
ANIMA: A Modeling and Simulation System for
Sound and Image Synthesis.” Computer Music Journal
17(1):19–29.
Causs ´e, r., j. Kergomard, and X. Lurton. 1984. “Input
Impedance of Brass Musical Instruments: Comparison
between Experiment and Numerical Models.” Journal
of the Acoustical Society of America 75(1):241–
254.
Chaigne, A., y un. Askenfelt. 1994. “Numerical Simula-
tions of Struck Strings: (I) A Physical Model for a Struck
String Using Finite Difference Methods.” Journal of the
Acoustical Society of America 95(2):1112–1118.
Chiba, o., et al. 1993. “Analysis of Sound Fields in
Three Dimensional Space by the Time-Dependent
Finite-Difference Method Based on the Leap Frog
Algorithm.” Journal of the Acoustical Society of Japan
49(8):551–562.
Conklin, h. 1999. “Generation of Partials Due to Non-
linear Mixing in a Stringed Instrument.” Journal of the
Acoustical Society of America 105(1):536–545.
Cocinar, PAG. 1991. “Tbone: An Interactive Waveguide Brass
Instrument Synthesis Workbench for the NeXT Ma-
chine.” In Proceedings of the International Computer
Music Conference, páginas. 297–299.
Derveaux, GRAMO., et al. 2003. “Time-Domain Simulation of a
Guitar: Model and Method.” Journal of the Acoustical
Society of America 114(6):3368–3383.
Desvages, C., and S. Bilbao. 2016. “Two-Polarisation
Physical Model of Bowed Strings with Nonlinear
Contact and Friction Forces, and Application to
Gesture-Based Sound Synthesis.” Applied Sciences
6(5):135.
Evangelista, GRAMO., and F. Eckerholm. 2010. “Player In-
strument Interaction Models for Digital Waveguide
Synthesis of Guitar: Touch and Collisions.” IEEE
Transactions on Audio Speech and Language Process-
En g 18(4):822–832.
hamilton, B., and S. Bilbao. 2013. “On Finite Difference
Schemes for the 3-D Wave Equation Using Non-
Cartesian Grids.” In Proceedings of the Sound and
Music Computing Conference, páginas. 592–599.
harrison, R. l., et al. 2015. “An Environment for Physical
Modeling of Articulated Brass Instruments.” Computer
Music Journal 29(4):80–95.
Hiller, l., y P. Ruiz. 1971a. “Synthesizing Musical
Sounds by Solving the Wave Equation for Vibrating
Objects: Part I.” Journal of the Audio Engineering
Sociedad 19(6):462–470.
Hiller, l., y P. Ruiz. 1971b. “Synthesizing Musical
Sounds by Solving the Wave Equation for Vibrating
Bilbao et al.
29
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Objects: Part II.” Journal of the Audio Engineering
Sociedad 19(7):542–550.
Roads, C. 1996. The Computer Music Tutorial. Cambridge,
Massachusetts: CON prensa.
Jaffe, D., y j. oh. Herrero. 1983. “Extensions of the Karplus-
Strong Plucked String Algorithm.” Computer Music
Diario 7(2):56–68.
Rossing, T., y N. Fletcher. 1983. “Nonlinear Vibrations
in Plates and Gongs.” Journal of the Acoustical Society
de América 73(1):345–351.
Karplus, K., y un. Strong. 1983. “Digital Synthesis of
Plucked-String and Drum Timbres.” Computer Music
Diario 7(2):43–55.
Rossing, t. D., et al. 1992. “Acoustics of Snare Drums.”
Journal of the Acoustical Society of America 92(1):84–
94.
Kelly, J., and C. Lochbaum. 1962. “Speech Synthesis.” In
Proceedings of the International Congress on Acoustics,
paper G42.
Ruiz, PAG. 1969. “A Technique for Simulating the Vibrations
of Strings with a Digital Computer.” Master’s thesis,
University of Illinois, School of Music.
Kurz, METRO., y B. Feiten. 1996. “Physical Modeling of a
Stiff String by Numerical Integration.” In Proceedings
of the International Computer Music Conference,
páginas. 361–364.
Laurson, METRO., et al. 2001. “Methods for Modeling Realistic
Playing in Acoustic Guitar Synthesis.” Computer
Music Journal 25(3):38–49.
Leveque, R. 2002. Finite Volume Methods for Hyperbolic
Problems. Cambridge, Reino Unido: Prensa de la Universidad de Cambridge.
Mansour, h., j. Woodhouse, y G. PAG. Scavone. 2016.
“Enhanced Wave-based Modelling of Musical Strings:
Parte 2, Bowed Strings.” Acta Acustica united with
Acustica 102(6):1082–1093.
McIntyre, METRO., R. Schumacher, y j. Woodhouse. 1983.
“On the Oscillations of Musical Instruments.” Journal
of the Acoustical Society of America 74(5):1325–1345.
McIntyre, METRO. MI., y j. Woodhouse. 1979. “On the
Fundamentals of Bowed-String Dynamics.” Acustica
43(2):93–108.
Morrill, D. 1977. “Trumpet Algorithms for Computer
Composition.” Computer Music Journal 1(1):46–52.
Morrison, D., and J.-M. Adrien. 1993. “MOSAIC: A
Framework for Modal Synthesis.” Computer Music
Diario 17(1):45–56.
Savioja, l., t. j. Rinne, and T. Takala. 1994. “Simulation
of Room Acoustics with a 3-D Finite Difference Mesh.”
In Proceedings of the International Computer Music
Conferencia, páginas. 463–466.
Savioja, l., and U. PAG. Svensson. 2015. “Overview of
Geometrical Room Acoustic Modeling Techniques.”
Journal of the Acoustical Society of America 138(2):708–
730.
Herrero, j. h., y j. Woodhouse. 2000. “The Tribology of
Rosin.” Journal of the Mechanics and Physics of Solids
48:1633–1681.
Herrero, j. oh. 1985. “A New Approach to Digital Re-
verberation Using Closed Waveguide Networks.” In
Proceedings of the International Computer Music
Conferencia, páginas. 47–53.
Herrero, j. oh. 1986. “Efficient Simulation of the Reed-
Bore and Bow-String Mechanisms.” In Proceedings
of the International Computer Music Conference,
páginas. 275–280.
Herrero, j. oh. 1992. “Physical Modelling Using Digital
Waveguides.” Computer Music Journal 16(4):74–91.
Strikwerda, j. 2004. Finite Difference Schemes and Partial
Differential Equations. Filadelfia, Pensilvania:
Society for Industrial and Applied Mathematics.
Rabenstein, r., y yo. Trautmann. 2004. “Multirate
Torin, A., B. hamilton, and S. Bilbao. 2014. “An Energy
Simulations of String Vibrations Including Nonlinear
Fret-String Interactions Using the Functional Transfor-
mation Method.” EURASIP Journal on Advances in
Signal Processing 2004(7):949–963.
Rabenstein, r., et al. 2007. “Block-based Physical Model-
ing for Digital Sound Synthesis.” IEEE Signal Processing
Magazine 24(2):42–54.
Rhaouti, l., A. Chaigne, y P. Joly. 1999. “Time-
Domain Modeling and Numerical Simulation of a
Kettledrum.” Journal of the Acoustical Society of
America 105(6):3545–3562.
Risset, J.-C. 1965. “Computer Study of Trumpet Tones.”
Journal of the Acoustical Society of America 38(5):912.
Conserving Finite Difference Scheme for the Simulation
of Collisions in Snare Drums.” In Proceedings of the
International Conference on Digital Audio Effects,
páginas. 145–152.
van den Doel, K., y D. Pai. 2007. “Modal Synthesis for
Vibrating Objects.” In K. Greenebaum and R. Barzel,
eds. Audio Anecdotes III. Wellesley, Massachusetts: A.
k. Peters, páginas. 99–120.
Webb, C., and S. Bilbao. 2011. “Computing Room
Acoustics with CUDA: 3D FDTD Schemes with
Boundary Losses and Viscosity.” In Proceedings of the
IEEE International Conference on Acoustics, Discurso
y procesamiento de señales, páginas. 317–320.
30
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
4
3
2
–
3
1
5
2
0
0
5
6
5
5
/
C
oh
metro
_
a
_
0
0
5
1
6
pag
d
.
j
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3