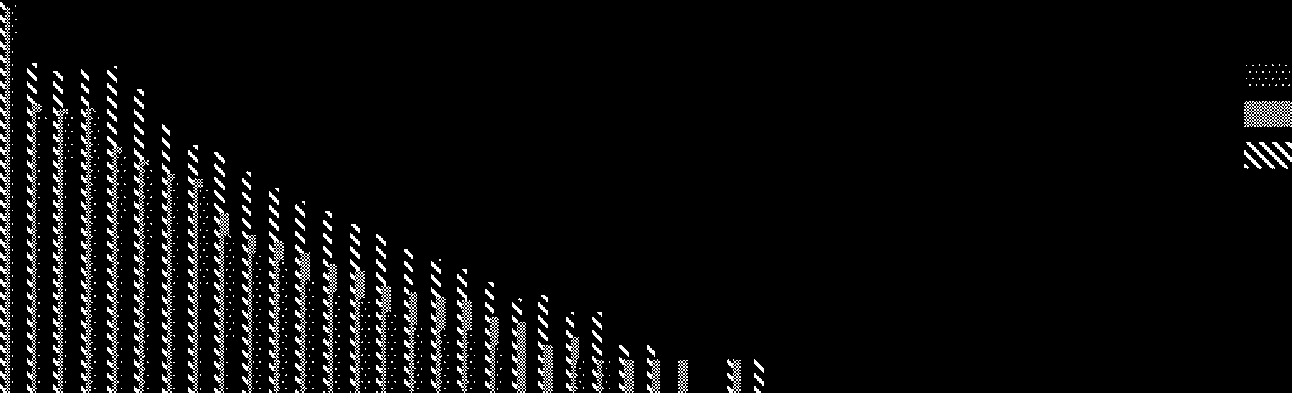Spatial-Pattern-Induced Evolution
of a Self-Replicating Loop Network
Abstract We study a system of self-replicating loops in which
interaction rules between individuals allow competition that leads
to the formation of a hypercycle-like network. The main feature
of the model is the multiple layers of interaction between loops,
which lead to both global spatial patterns and local replication.
The network of loops manifests itself as a spiral structure from
which new kinds of self-replicating loops emerge at the boundaries
between different species. In these regions, larger and more complex
self-replicating loops live for longer periods of time, managing
to self-replicate in spite of their slower replication. Of particular
interest is how micro-scale interactions between replicators lead to
macro-scale spatial pattern formation, and how these macro-scale
patterns in turn perturb the micro-scale replication dynamics.
Keisuke Suzuki*
Takashi Ikegami
Department of General Systems
Ciencias
The Graduate School of Arts
and Sciences
University of Tokyo
3-8-1 Komaba
Tokio 153-8902, Japón
ksk@sacral.c.u-tokyo.ac.jp
ikeg@sacral.c.u-tokyo.ac.jp
Palabras clave
Self-replication, cellular automata,
evolution, hypercycle, evoloop
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1 Introducción
Open-ended evolution is one of the challenging problems of artificial life studies [1]. It is simply
defined as the continuing generation by evolutionary systems of novel phenotypic characteristics. En
particular, the necessary conditions for open-ended evolution remain to be understood.
Desafortunadamente, only a few examples of open-ended evolution are available, such as open-endedness
in forms, (p.ej., [20, 8]) and in programs (p.ej., [4, 12, 7, 10]). One of the earliest examples is Lindgren’s
model of evolutionary game dynamics. He showed that the memory strategies of the iterated
prisoner’s dilemma game lead to continuous growth of memory size. Such growth is supported by the
duplication dynamics of binary strings that encode a game strategy [10]. Sims’ artificial creatures give
another example of evolution of diversified forms. The underlying mechanism can be thought as a
mixture of physical embodiment and internal logical circuitry [20]. These two examples certainly show
increasing complexity of replicating systems, but whether they are truly open-ended or not is still
unknown. This is also true for the Tierra system of artificial creatures.
We focus on the open-ended properties of a simple replicating system. En particular, we study an
extension of Langton’s loops (p.ej., [22, 9, 6, 21, 11, 3, 17]) to explore the properties of open-ended
evolution. Langton’s original loop lacks a universal capability for replicating forms. Morita and Imai
designed a new loop model that has such a universal capability. Tempesti also extended Langton’s
model to make it universal. But from the point of view of open-ended evolution, the interactions
between loops are important and need to be investigated. Sayama designed a new replicating loop
* Autor correspondiente.
norte 2006 Instituto de Tecnología de Massachusetts
Artificial Life 12: 461 – 485 (2006)
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
sistema [17], where collisions between loops generated novel species, which is a first step in this
direction. In Sayama’s earlier work, the size of loops was found to gradually decrease on average, y
thus they cannot exhibit open-ended evolution. Further investigations showed that certain loop
configurations can sustain and develop complexity of the loops [13, 14].
We extend these studies by introducing a food-web structure between loops. For the basic model,
we extended Sayama’s shape-encoding worm system [18] to make it a universal replicator. Species are
simply distinguished by an extra tag, and the transition rules may be a function of such additional
species bits. Those with the same tag have no way of distinguishing whether objects undergoing
replication are part of their own structure or that of another replicator. The distinction between
organism and environment is thus blurred, enabling replicators to mutate and create novel structural
variants. Como resultado, spatiotemporal patterns constructed by the loops can lead to new types of loops.
Our simulation results yield two observations. En primer lugar, we report the micro dynamics by which
new replicators emerge. Some statistical analysis shows that there are four micro-mutation types, y
the mutation event caused by fusion processes among loops is the most frequently observed.
En segundo lugar, we show that populations of self-replicating loops can generate macro-scale spatial
patrones, such as spirals, that are distinct from the micro-scale behavior of the individual replicators
ellos mismos. Larger loops with longer life spans emerge and breed locally at the boundary regions
between different species in these spiral formations.
En la sección 2, we introduce the design of the present model. The assumed food-web structure is
detailed in Section 3, and we study the effect of mutations in Section 4. The relationship between
macroscopic structures and micro-level mutations is discussed in Section 5.
2 Modelo
There are two main aspects of the design in our model: the design of the self-replicating patterns
ellos mismos, and the interactions between them. We use a shape-encoding method originally
introduced by Morita and Imai [11] to design a program of self-replicating loops. In their model,
the self-replicating patterns’ genetic information encodes their own shapes. Sayama introduced a
variant of such a shape-encoding self-replicator, a worm, introducing interactions among replicators.
Our self-replicating structure follows Sayama’s ‘‘shape-encoding worm,’’ but the rules that govern
the process of self-replication are new.
También, we introduce interactions between replicators. In Sayama’s evoloop system, the dissolving
loop resulting from the interaction leads to natural selection related to their replication rates. Nosotros
designed several types of dissolving interactions between replicators to construct food-web networks.
Such ecological relationships, which have not been studied in self-replicating cellular automata (CAs),
can exhibit interesting relationships between global and local behaviors.
We now describe the model in terms of its (i) cell states, (ii) self-replication mechanisms, y (iii)
interaction mechanisms.
2.1 Description of Cell States and Functional Roles
To aid intuition we use biological terminology throughout. Sin embargo, we have the following
definitions. A cell is defined as a minimal square in the two-dimensional space. A loop is a spatial
entity specified by the connected cell states. A gene represents the shape of a loop that is given by a set
of gene fields of the connected cells. A species is a special state value of the cell. The cells with
different species indexes don’t communicate with each other, so that a set of cells that constitutes a
loop has a common species index. Como resultado, a loop is now characterized by the shape and the
species index, and the loop-loop interaction can be twofold: interspecific and intraspecific.
Using this terminology, we give a detailed instruction of the CA rule. Each cell takes 128n + 1
different possible states, where n specifies the number of species; each species identifies a way of
response when interacting with other cells of the same or a different species (mira la sección 2.3). Allá
is a unique quiescent (inactive) cell state that constitutes the background state. The remaining 128n
462
Artificial Life Volume 12, Número 4
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
states constitute structure states, and they are classified into three main fields according to their
functional roles (Cifra 1). We can independently design and execute the three fields, so that it is easy
to designate a transition rule for self-replication dynamics.
Details of the three fields and one species field are given in Table 1. The link field constitutes a
phenotypic structure (forma) of the organism that determines the path where genetic signals (genes)
propagate. The gene field stores directional information (C, R, l) that is later translated into the
direction of link fields in newly created cells. Finalmente, the mode field identifies the current functional
role of a cell in the context of a self-replication process. En mesa 2, each functional role associated
with the mode fields is summarized briefly.
2.2 Self-replication Cycle
In what follows, rather than describing each state transition rule in detail, we instead outline a single
self-replication cycle. The complete cycle is given in Appendix 1.
A self-replicator in our model is represented as a closed loop structure of connected structure
cells. The directions of the link fields determine the connectivity between cells. The loop’s shape is
defined by the sequential values in link fields of cells constituting a loop.
The gene field in one cell stores information about the direction to take in creating a new cell in
constructing a new loop structure (l, C, or R). The entire self-replication process is directed by the
shape information coded in the gene fields (p.ej., CLCLCLC) of all connected cells.
In contrast to Langton’s SR loop [9], shape information is generated dynamically during the
replication process. When phenotypic changes occur, the corresponding shape information is also
automatically altered. Then the self-replication continues according to the new genetic information.
Por lo tanto, self-replicators are easier to be modify stably, which may lead to an increase in structural
complejidad. Each step of the self-replication cycle (encoding and propagation of genes, construction
of new cells) is governed by the status of the mode field. At the beginning of the self-replication
proceso, one cell is in the EXPLORE mode and all others are in the NORMAL mode.
Cells that have different values in their species field cannot constitute a same loop structure,
because they do not interact with each other except in special cases (as will be discussed later in this
artículo). During a normal self-replication cycle, all the cells forming one loop structure are thus
assured of having the same values in the species fields.
Cifra 1. An illustration of cell states, classified into four different fields according to functional roles. The link field (four
estados) specifies cell direction (drawn as a black trapezoid). The gene field (four states) stores shape information for
constructing new loop structures (drawn as a square in one of three locations). The mode field (eight states) stores special
functional information to be used in the self-replication process (drawn as the fill patterns of the squares). The species
field stores an index that identifies which interaction rules to use (drawn as the color of loops in selected figures; ver,
p.ej., Cifra 4). The design of the cell is based on the ‘‘shape-encoding worm’’ created and studied by Sayama [18].
Artificial Life Volume 12, Número 4
463
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
Mesa 1. Roles of the four different fields that together describe each multilayered state. For a detailed description
of the mode field, ver tabla 2.
Campos
link
gene
mode
No.
Nombre
Role
4
4
4
TOP, BOTTOM, RIGHT, LEFT
Specifies the direction of propagation of genes through
the cell.
C, R, l, ninguno
Stores genetic information that is translated into the
shape of the new loop structure.
NORMAL, DECODE, ENCODE I, ENCODE II,
Describes the functional mode (ver tabla 2).
BRANCH, EXPLORE, WITHDRAW, DESTROY
species
norte
S1,S2,
. . . Sn
Identifies the species, which determines the appropriate
interaction rules (mira la sección 2.3).
En figura 2, the four processes constituting a normal self-replication cycle are shown: corner
positioning, shape encoding, arm extension, and arm withdrawal. Tenga en cuenta que, with the exception of arm
withdrawal, these processes work in parallel in time and occur concurrently at the various stages of
the self-replication cycle.
Corner positioning (t=0–3). This phase commences the self-replication cycle. The configuration
of the parent loop consists of one cell in EXPLORE mode and all others in NORMAL mode. El
EXPLORE mode is transferred counterclockwise through neighboring cells until it reaches the
branch corner, where it switches to DECODE mode in preparation for the arm extension phase
(Cifra 2, t=2). The cell in DECODE mode then switches to BRANCH mode, a new cell is created
in the arm, and its counterclockwise neighbor switches to ENCODE I mode, triggering the shape
encoding phase (Cifra 2, t=3).
Shape encoding (t=3– 13). This phase is initiated with the last step of the corner positioning
phase, at which point an ENCODE I mode cell has just been created next to the BRANCH mode
Mesa 2. Functions of the different mode fields.
Mode name
Functions
NORMAL
Propagates genetic information towards the leading cell.
DECODE
Translates genetic information into new cells at the end
of the arm.
ENCODE I
ENCODE II
Encodes the direction of the leading cell.
BRANCH
Marks the starting point from which the arm extends.
EXPLORE
Cycles around the loop until reaching the branching
corner.
WITHDRAW
Destroys all structure cells not in the BRANCH mode.
DESTROY
Destroys all structure cells (structural dissolution).
464
Artificial Life Volume 12, Número 4
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
Cifra 2. Self-replication mechanisms of a six-cell loop. Replication of arbitrary loop structures proceeds by the same
basic steps. For the meaning of each symbol refer to Figure 1.
cell (Cifra 2, t=3). The ENCODE I mode cell switches to the ENCODE II mode cell, storing
a connecting direction to the next cell into the gene field (Cifra 2, t=4). Entonces, un nuevo
ENCODE I mode cell is created next to the ENCODE II mode cell (Cifra 2, t=5). Este
process of alternating between two encode modes is propagated counterclockwise around
the loop, encoding the phenotypic structure of the whole loop (connectivity of link field
valores) into the gene fields of the encode-mode cell; these field values are then propagated
forward through the neighboring cells. The replicator’s shape information is thus stored
throughout the loop structure, in the propagating values stored in gene fields. Por ejemplo,
En figura 2 (t=11), the shape information is read as CLLCCCC. At the corner BRANCH
mode cell, the encoded shape information is propagated into the extending arm (see ‘‘Arm
extension’’ below). Genes reentering the loop structure from the branch, sin embargo, are reset
to the C gene. This is done to assure that, prior to the propagation of shape information,
an arm of the sufficient length must be constructed, preventing collisions between parent
and daughter loops (see ‘‘Arm extension’’ below).
Arm extension (t=2 –26). This phase is initiated with the creation of a DECODE mode cell at
the corner of the parent loop (Cifra 2, t=3). Shape information encoded in the gene field
values of cells is propagated through the corner BRANCH mode cell into the extending arm.
When the gene information reaches the DECODE mode cell at the tip of the arm (Cifra 2,
t=16), this information is translated into a new loop structure (a new cell in the NORMAL
mode oriented in the direction specified by the gene: Cifra 2, t=17). In the next time step,
this cell in NORMAL mode switches to DECODE mode, and the process is repeated (Cifra 2,
t=18). Construction of the new loop is completed when the tip of the arm encounters an
earlier portion of its own structure (Cifra 2, t=24), at which point the arm is cut to create
a separate daughter loop. The cell connecting the parent to the daughter loop switches to
EXPLORE mode, initiating the corner positioning phase in the daughter loop (Cifra 2, t=25).
This EXPLORE mode changes the tip of the parent loop to WITHDRAW mode in preparation
Artificial Life Volume 12, Número 4
465
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
for the arm withdrawal phase (Cifra 2, t=26). In a normal (unperturbed) self-replication cycle,
the daughter loop inherits the same structure as that of the parent loop.
Arm withdrawal (t=27 – 31). This phase begins when the daughter loop is completed, and does
not overlap in time with the other phases discussed above. Withdrawal of the arm begins
when the tip of the arm of the parent loop switches to WITHDRAW mode (Cifra 2, t=26).
The effect of this mode is to sequentially remove cells of the extended arm, stopping only
when it reaches the first corner cell (Cifra 2, t=30). When it reaches this cell, it switches the
corner BRANCH mode state into EXPLORE mode, initiating the next corner positioning phase
in the parent loop (Cifra 2, t=31).
We didn’t mention the role of the DESTROY mode. This last mode is used only for implementing the
interaction process between different species. We come back to the process in the next subsection.
2.3 Competitive Interaction Process
The self-replication process described in the last section works correctly when there is only a single
loop in the CA space. Sin embargo, with other loops competing for space to self-replicate,
local
intercellular interactions become critical. Following the Evoloop modeling approach, we classified the
interaction types according to the idea of structural dissolution discussed and implemented by Sayama
[15, 16]. Structural dissolution is one aspect of ‘‘death of life.’’ It enables damaged organisms not just
to stop their function like a crystal, but to dissolve to make space for healthy organisms. Él
introduced an extra state into Langton’s original loop system for dissolution of damaged loops.
For structural dissolution, we use the DESTROY mode, which is not used in the basic self-replicating
mechanisms described in the last subsection. This DESTROY mode only emerges at sites where collisions
occur between neighboring loops. Unlike WITHDRAW mode, which only dissolves cells of the loop arm,
DESTROY mode dissolves any of the cell types that constitute the basic loop structure.
We used a food-web structure to organize loop species according to their interactions with other
species. These interactions, which decide the relative ‘‘superiority’’ or ‘‘inferiority’’ of competing
species, together constitute a hypercycle-like network as shown in Figure 3. There are four basic
types of interaction in this network:
Inroad. When the expanding arm of one loop collides with any part of the other loop, el
first loop destroys the second loop, and the arm continues extending.
Counter. When the expanding arm of one loop collides with any part of the other loop, el
first loop is destroyed, but the second loop is unaffected by the collision.
Defensive. When the expanding arm of one loop collides with any part of the other loop, el
first loop retracts its extending arm, leaving the second loop unaffected by the collision. El
two loops may thus coexist.
Cancel. When the expanding arm of one loop collides with the other loop, both loops are
destroyed.
Examples of these four types of interaction are illustrated in Figure 3. The complete state
transition table is given in Appendix 2. Note that genes are lost in the inroad interactions, porque
the decoding process of the left-hand loop is disturbed by the cells of the right-hand loop that are
undergoing structural dissolution.
With these four interactions, a cycle of competitive relationships can be designed between
multiple species. Por ejemplo, the species S2 is made superior to S1 but inferior to S3 by using the
inroad interaction between S2 and S1 and the counter interaction between S2 and S3. Interactions
between loops of the same species are made to be symbiotic by using the defensive interaction,
which leaves both loops unaffected by the collision. The remaining interaction between species,
which we call the cancel interaction, is symmetric: it destroys both loops in the collision (Cifra 3).
466
Artificial Life Volume 12, Número 4
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
Cifra 3. Relative strengths of the four different interaction types are illustrated in the collision processes depicted on the
izquierda. When the arm of a loop on the left side collides with a loop on the right, only the right-hand loop is destroyed by an
inroad interaction, only the left loop is destroyed by a counter interaction, both of them survive following a defensive
interacción, and both of them are destroyed following a cancel interaction. Competitive interaction-based relationships
between species are illustrated in the food web shown on the right. Each species has exactly one superior and exactly
one inferior species.
In collisions between the arm of one loop and any part of another loop, there is only one special
case in which the above rules are not used. As mentioned in Section 2.2, the head of the construction
arm encounters its own structure when the construction process of the daughter loop is reaching
completion (arm bonding). Simply applying the above defensive rule to this case would thus disable
the self-replication process. We therefore distinguish between two types of interaction in the case
where cells of the same species index and of different species indexes collide with each other. Cuando
cells of the same species index come together, the collision of a constructing arm with another arm
from the left-hand side is identified as the arm-bonding step of the self-replication process and is
therefore allowed to occur. When cells of different species index collide, we apply the defensive rule
so that the extending arm is withdrawn.
The structure of interactions between different species described above allows a variety of
different self-replicators to coexist in the CA space. Dynamics of this kind have not been studied in
the previous CA models of self-replicators, and will be the focus of this article.
3 Spatiotemporal Pattern of a Loop Ensemble
We study a simple food-web structure, eso es, a hypercycle type of the linear case; eso es, the network
is expressed as S1 ! S2 ! (cid:2) (cid:2) (cid:2) ! Sn(cid:3)1 ! Sn ! S1. It should be noted here that those different
interaction types are defined between cell sites, not between loop units.
As visualized in Figure 4, the spatial region of Si is invaded by that of Si+1 and in turn invades that
of Si(cid:3)1. This chain relationship generates a spiral or strip waveform from most initial configurations.
Generally, the pattern fluctuates between spiral and strip patterns.
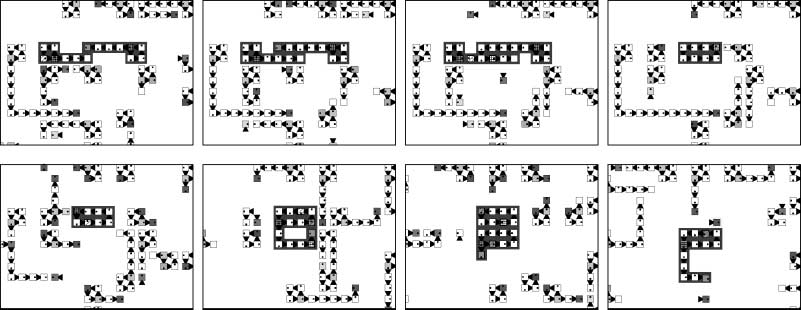
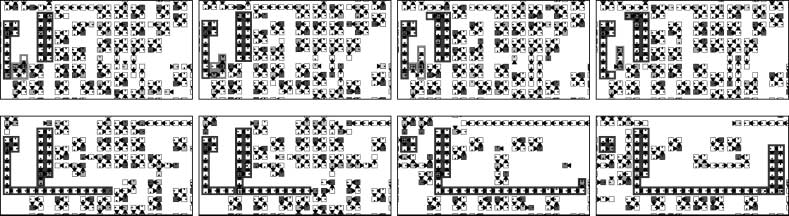
In the upper series of snapshots of Figure 4, the dynamics of a system of five species is shown.
The initial configuration of this system consists of loops of length 4, randomly distributed in the
periodic domain. Different colors in these snapshots denote different species. The white species
overwhelms the black species, the black species overwhelms the gray species, etcétera [en el
grayscale bar at the base of each snapshot, the order of colors goes from inferior (left-hand side) a
superior (lado derecho)]. The center of a spiral can be seen at the bottom left of these snapshots,
where black, white, and gray stripes are chasing each other.
Artificial Life Volume 12, Número 4
467
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
Cifra 4. A spiral structure produced by five interacting species in a 400 (cid:4) 400 cell space. The different species
are illustrated with grayscales. The spiral rotates in a counterclockwise direction (upper series). The lifetimes of loops
are shown as grayscale gradations in the lower series of snapshots, which represent the same run as the upper hand
snapshots. In the lower series, light gray indicates loops that have lived more than 1000 time steps, whereas black
indicates loops that are newly born. At the center of the spiral shown at the bottom left of the snapshots there are
many new loops. Alternation of generations is faster in this region than in other regions (lower series).
The lower four images of Figure 4 show the lifetimes of loops as a grayscale gradation. Lighter
gray represents older loops, whereas black represents younger loops. In the central region of the
spiral at the bottom left of each snapshot, younger loops appear in greater numbers. New replicators
are frequently born in these regions when a spiral structure is formed.
Populations of each species vary over time as they cycle around the center of the spiral. El
periodicity of the variation is determined by the number of species in the food-web chain. Spirals
consist of unstable oscillatory waves. In the case of less than four species, moving wavefronts are
observado, but these fronts do not form complete spiral patterns. The reason appears to be that the
length of the boundary between species is greater in this case, enabling loops from one species to
more easily encroach on regions of an inferior species. This frequent encroachment prevents the
formation of spiral patterns. Note that a similar result is found in more traditional spatially extended
models of hypercycles,
in which the minimum number of species for spiral formation is five.
Ocasionalmente, all loops of a species are destroyed, preventing the spiral structure from organizing,
and leading eventually to dominance by a single species.
This type of spatiotemporal pattern, a spiral, is expected from former studies of, Por ejemplo,
spatially extended BZ reactions, prey-predator models, and hypercycles (ver, p.ej., [2]). It is thus not
surprising that a food-web chain produces spiral or strip patterns. Sin embargo, there are significant
differences from those pattern formation studies. The spatiotemporal pattern in our case constitutes
a source for intraspecific variation in new replicators. Differences between our model and a mere
hypercycle system originate in the following characteristics of our loop replicators:
1. Replication speed. An offspring of a loop is not generated instantly. A finite number of time
steps are required to replicate new generations. Within this period of offspring construction,
an arm is extended from a parental loop to the position where the daughter loop will be
creado. Loop replicators are therefore fragile with respect to perturbations during this period.
Such fragility has never been modeled in spatially extended hypercycles. Note also that there
will be a natural selection of smaller loop replicators, as they breed more quickly.
468
Artificial Life Volume 12, Número 4
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
2. Internal degrees of freedom of replicators. When Si interacts with Si(cid:3)1, the latter loop is destroyed,
but at the same time the invading loop Si is modified in some complicated ways (descrito
en la sección 4). This naturally introduces mutation in the arm (gene) part of the replicator (Y),
so that variants will be generated during the interacting process.
3. Long arm intrusion. As a consequence of interspecies interaction, arms of loops may be
extended abnormally far from the original parent structure. As can be seen in Figure 4,
such species intrude tongue-like arms into the populations of neighboring species. Estos
extended arms destabilize the spiral and strip structures.
As a consequence of these new features, variant replicating structures evolve depending on the
spatiotemporal patterns. En particular, larger or non-square-shaped loops appear at the boundaries of
spirals or strips. These larger loops can sometimes self-reproduce, and a colony of larger loop
variants is generated. In the following two sections, we describe micro mechanisms of these variant
replicating structures and analyze how they are controlled by the spatiotemporal patterns.
4 Mutational Dynamics
Various shapes and sizes of loops are deterministically generated by the interactions between
individual loops. A variety of shapes and sizes arise from interaction-based mutations that cause
irregular loop reproduction. Such irregular processes occasionally fail to replicate loops but
sometimes generate new replication patterns.
In the following figures, we depict snapshots of irregular reproducing processes, taken from
evolutions of minimal-sized loops in a five-species food-web chain replicating in the 400(cid:4)400 cell
espacio. The number of species in the food web may not be the significant parameter, at least if it is set
larger than three.
4.1 Basic Mutation Processes
There are two major mutation patterns; (1) a point mutation in the gene entity and (2) intraspecific
fusion of more than two loops. We report concrete examples of these and analyze the statistical
significance.
4.1.1 Point Mutation of Genes
Self-replication of loops proceeds according to the gene sequence pattern coded in the gene fields of
loops. Those genes are forwarded through the connecting cells that reproduce a new daughter loop
at the tip of the arm. Without any perturbation, genetic information is transferred through a self-
replication process forever. Sin embargo, they may be lost during the replication process via interactions
with other loops. In more detail, a gene loss occurs when the decoding process controlled by the
DECODE mode cell at the tip of the arm is interrupted by the neighboring processes.
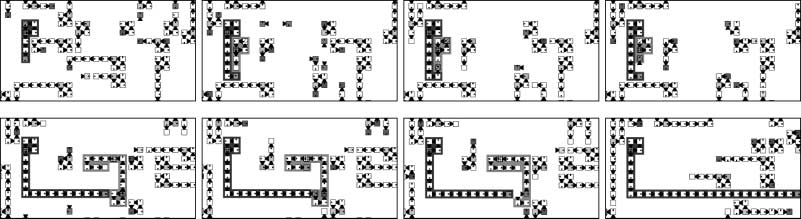
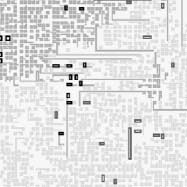
Cifra 5 shows one example in which genes may be lost during the self-replication processes.
This figure depicts the case in which interactions with inferior species cause a loss of genes. Nosotros
also found that even the interaction between two loops of the same species often cause a loss of
genes in similar ways (not shown here). By the gene loss processes, a daughter loop has a different
shape from the parent loop. In the presented example, the daughter loop becomes smaller than
el padre.
4.1.2 Intraspecific Fusion
Normal completion of the replication process occurs when the extended arm makes contact with its
own structure. Sin embargo, in general the arm may connect with itself or with the arm of a different
loop of the same species. When two loops happen to collide with each other in specific ways, una novela
shape may be created, as shown in the example of Figure 6. Because the new shape is encoded to
Artificial Life Volume 12, Número 4
469
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
Cifra 5. A smaller daughter loop is created by interaction-based mutation with a loop of an inferior species. A loop of
species Si (dark gray) collides with another loop of an inferior species Si(cid:3)1 (light gray) via the inroad interaction. En esto
proceso, the tip of the Si loop is not able to decode certain genes, because there exist cells of the Si(cid:3)1 loop in the target
site (t=525, t=526). Because of the loss of the two C genes, the daughter loop that is constructed becomes smaller than
the original parent loop (t=536).
genes via the normal encoding mechanism, the emergent loop is also capable of replicating itself,
as well as the parent loop. A veces, emergent loops have irregular internal states, Por ejemplo,
containing multiple ENCODE-mode cells or multiple BRANCH-mode cells. This abnormal situation
causes irregular replication and reduces the accuracy of self-replication.
To investigate the statistical nature of such processes in our system, we classified the mutation
processes into four types: (1) normal self-replication events, (2) mutation events involving no other
loops than the parent (point mutation), (3) intraspecific fusion with other loops, y (4) other types
of mutation events (Cifra 7).
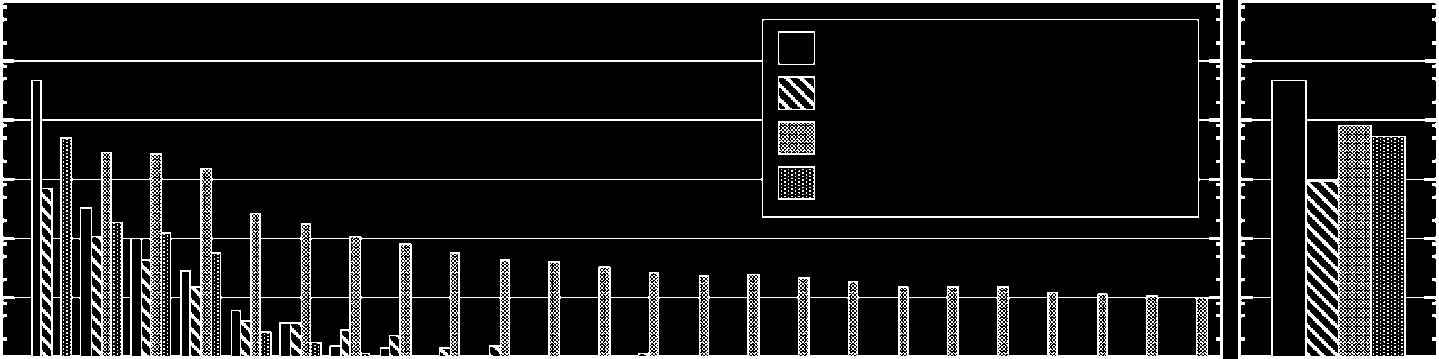
Frequencies are counted over 10,000 time steps and averaged over 10 different runs. In the case
of the smallest (four-cell) loop, a normal replication is the dominant event. Both mutations and
normal replication frequencies tend to increase on increasing the loop size. De hecho, the frequency of
the normal replication events roughly obeys a power law. Loops of a size larger than 30 are created
exclusively via fusion. Finalmente, one example of the fourth type of mutation event [tipo (4) arriba]
occurs when the fragments of partially dissolved loops are arranged into a loop shape accidentally. Si
this loop has appropriate modes (p.ej., one BRANCH mode), it can self-replicate. This particular event
is only observed in the smallest four-cell loops.
Cifra 6. When two loop arms connect as they are each making the first left turn in the arm extension phase of the self-
replication process, the arms become merged together, often leading to the emergence of a new loop. This type of event
was frequently observed in our simulations and was found to lead to an increase in the overall variation of loop shapes
within a population.
470
Artificial Life Volume 12, Número 4
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
Cifra 7. The frequency of four different types of replication events (log scale): (1) normal self-replication events, (2)
mutation events originated by gene losses, (3) mutation events by fusion of other loops, y (4) other atypical mutation
events. The left-hand graph shows the frequency of loops for different loop sizes, and the right-hand graph shows the
total frequency summed over all loop sizes. Initially, four-cell loops are randomly distributed in the 400(cid:4)400 espacio.
Frequencies are summed over 10,000 time steps and are averaged over ten different runs.
4.2 Open Extended Arm Structures and Irregular Self-replication
The irregular behaviors of loops provide functional changes to loop replication.
One example is that gene loss in point mutation causes the loop arms to extend abnormally. Este
situation occurs if the L gene is lost that is responsible for a left turn in the extended arm. If this gene
is lost, the extended arm continues to create new cells in the forward direction rather than closing
and completing the replication process (Cifra 8). Such open extended arms act as a part of the
ambiente, and make the global spiral pattern unstable (as mentioned earlier in Section 3).
Open extended arms can also provide another source of irregular behavior. Cifra 9 shows two
loops fusing to produce one daughter loop. In cases such as this one, the shape of the daughter
loop is the same as that of the parent. Sin embargo, because fusion occurs with the operation arm
extended abnormally far from the parent, the arm becomes a conduit through which genes can
travel a long distance across the CA domain. It enables loops of a superior species to advance deeply
and rapidly into the territory of an inferior species, extending the region of S1 into the adjacent
region of S2.
In order to investigate the above-mentioned irregular self-replicating process, we further classified
fusion-based mutation into four categories with respect to size changes: (1) no size change (irreg-
ular replication), (2) smaller size change, (3) larger size change, y (4) unidentified size change
(Cifra 10). Because the operation arm may merge several times during the fusion process, el
parent loop is often difficult to identify. We here define a parent loop as the loop connected to the
operation arm when construction of the daughter loop is completed. Still, en algunos casos, it is difficult
Cifra 8. Collision with a loop of an inferior species (light gray) triggers indefinite extension of the operation arm of
the superior species (dark gray). The arm continues to extend until it contacts the loop of a superior species or one
of the same species.
Artificial Life Volume 12, Número 4
471
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
Cifra 9. An example of fusion between two colliding loop structures. A four-cell loop (marked A) collides with a loop of
an inferior species (marked B). The result is that two L genes in loop A are not decoded (t=845, t=846), and thus the
loop, rather than constructing a square-shaped offspring as it otherwise would,
instead extends its operation arm
indefinitely. A twelve-cell loop on the right, of the same species as loop A (marked C), collides with loop A and interrupts
this indefinite arm extension, fusing the two arms together. With arms fused together, genes of loop C are redirected
through the arm structure constructed by loop A. Loop C utilizes this extended arm structure to replicate itself, causing
the daughter loop to be constructed a great distance away from the parent.
to identify a parent loop. Such an example can be found in Figure 6. When a large loop fuses with
other loops, the resulting loops tend to get larger. En particular, almost all loops of size greater than
acerca de 20 increase their size after the fusion process. Sin embargo, small loops not only change their size,
but also replicate themselves, even through fusion. This indicates that the fusion process results not
only in change of size, but also in gene transportation, as illustrated in Figure 9.
Mutation events such as the ones described so far generate a variety of variant replicating
estructuras. Interactions between loops cause the loss of some genes, leading to the generation of
different shapes of loops. En particular, the fusion of multiple loops into a single daughter generates a
number of larger loops. It is worth noting that the mutation may affect not only the shape of the
loop, but also the replication process itself. The long extending arm, formed by loss of genes, can be
used as a path for information on the shape of a parent loop. Como resultado, a daughter loop can be
generated at a distance (Cifra 9). When the place where the daughter loop is created is suitable for
replication, such as a region of inferior species, the loop can survive longer than when the daughter
loop is created near the parent. De este modo, how the loop replicates itself in an advantageous space may be
an important criterion for survival.
With interaction-based mutation, loops have the potential to produce a variety of larger repli-
cators. Sin embargo, that such larger loops can survive for extended periods of time in competition with
other loops has not yet been established. In the next section, we will demonstrate the survivability
and robustness of these larger variant loops.
Cifra 10. The frequency of mutation events involving fusion of other loops, categorized with respect to change in
the loop size. The left-hand graph shows the frequency of loops of different sizes, and the right-hand graph shows the
total frequency summed over all loop sizes. Initially, four-cell loops are randomly distributed in the 400(cid:4)400 espacio.
Frequencies are summed over 10,000 time steps and are averaged over ten different runs.
472
Artificial Life Volume 12, Número 4
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
5 A Mechanism for Synthesizing Larger Loops
The mutational dynamics discussed so far does not directly lead to the emergence and reproduction
of larger loops. Large loops are disadvantaged in that they require more time steps than smaller
loops to carry out self-replication. Therefore larger loops generally disappear soon after they appear.
The CA space will finally be dominated by the smallest, size-4 loops. We have observed that the
larger loops do, sin embargo, sometimes manage to replicate themselves at the boundary between
different species.
En esta sección, we report successful replication of larger loops on the boundary, and quantify the
proceso. Más, the population dynamics of the large loops is investigated. In the following sub-
sección, we construct genealogy trees of loop replicators to study their lifetimes and diversification. A
system with an initial random distribution of four-cell loops is simulated on the 400(cid:4)400 cell space.
5.1 Emergence of Larger Loops at the Boundary between Species
A main reason for the generation of large loops at a boundary is that the boundary is the interface
between superior and inferior species in the spiral hypercycle formation. While intraspecific collisions
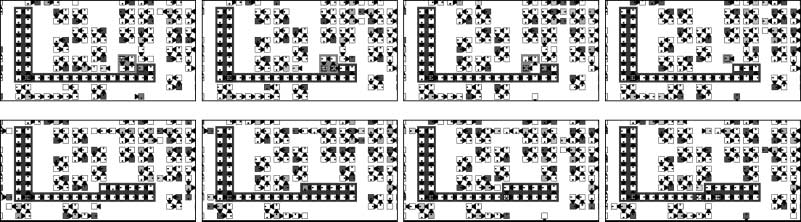
occur within a region, as we see in Figure 11, at the boundary between regions, large loops form
colonies and outperform the minimal-loop population.
Primero, at the boundary between species, superior loops frequently collide with inferior loops by
using the inroad interaction. Mutations of genes leading to variant loops occur much more frequently
by this type than by the other types of interaction classified in Section 2.3. Segundo, the region of
inferior species along the boundary provides a vacant space for the superior species, where their
larger loops will be bred. Además, as shown in Section 4.2, fusion often creates abnormally long
arms that fail to close to form daughter loops, instead extending indefinitely into the region of
inferior species. These extended arms occasionally generate variant daughter loops in the middle of
the population of inferior loops (Cifra 11). When this happens, such larger loops rapidly increase
their numbers. Creation of these variant loops perturbs the spiral structure and makes it unstable.
This never occurs in hypercycle models of replicators with no internal structural dynamics [2].
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
a
r
t
yo
/
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
1
2
4
4
6
1
1
6
6
2
3
4
8
a
r
t
yo
.
/
.
.
2
0
0
6
1
2
4
4
6
1
pag
d
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 11. An example of the emergence of larger loops inside the population of inferior loops at the boundary between
species. The loops of size greater than 6 are highlighted in darker shades. A colony of mainly size-6 loops appears and
grows as loops of the superior (S3) species invade the population of loops of the inferior (S2) species. Sin embargo, el
larger loops are destroyed by the invasion of S4 species (superior to S3) and cannot survive for a long period of time.
Después, larger loops from the S4 species emerge and grow in this region.
Artificial Life Volume 12, Número 4
473
k. Suzuki and T. Ikegami
Spatial-Pattern-Induced Evolution of a Self-Replicating Loop Network
To quantify how the larger loops replicate and interact with each other, we introduce a new
quantifier, which measures the spatial density of the neighboring loop sizes. By using the loop size i
and the distance rij between two loops, we calculate the measure as follows:
B ¼
1
2norte 2
X
X
i
j