Sectoral Infrastructure Investments in an
Unbalanced Growing Economy:
The Case of Potential Growth in India
CHETAN GHATE, GERHARD GLOMM, AND JIALU LIU STREETER
∗
We construct a two-sector (agriculture and modern) overlapping generations
growth model calibrated to India to study the effects of sectoral tax rates, sectoral
infrastructure investments, and labor market frictions on potential growth in
India. Our model is motivated by the idea that because misallocation depends on
distortions, policies that reduce distortions raise potential growth. Nosotros mostramos que
the positive effect of a variety of policy reforms on potential growth depends on
the extent to which public and private capital are complements or substitutes.
We also show that funding more infrastructure investments in both sectors by
raising labor income taxes in the agriculture sector raises potential growth.
Palabras clave: Indian economic growth, misallocation, public capital, structural
transformación, two-sector OLG growth models, unbalanced growth
JEL codes: H21, O11, O20, O41
I. Introducción
How do sectoral tax policies and labor laws distort the sectoral allocation
of labor and capital to prevent developing economies from realizing their growth
potencial? Luis (1954) famously argued that economic development means growth
of the modern sector. En ese caso, what prevents the development and expansion of the
modern sector in growing economies? What are the impediments to the reallocation
of labor to sectors of high productivity? Will a tax on agriculture income that funds
higher public investment inhibit the rise of the modern sector? These questions have
policy importance as distortions in the agriculture and the nonagriculture (modern)
sectors constrain growth in developing economies by preventing the full productivity
effect of factor reallocation.
∗Chetan Ghate (Autor correspondiente): Economics and Planning Unit, Indian Statistical Institute Delhi. Correo electrónico:
cghate@isid.ac.in; Gerhard Glomm: Departamento de Economía, Universidad de Indiana, Indiana. Correo electrónico: gglomm
@indiana.edu; Jialu Liu Streeter: Departamento de Economía, Allegheny College, Pensilvania. Correo electrónico: jstreeter
@allegheny.edu. The authors would like to thank Partha Sen, k. PAG. Krishnan, Pawan Gopalakrishnan, Pedro de
Araujo, participants at the Asian Development Outlook–Asian Development Review Conference held in Seoul in
Noviembre 2015, the managing editor, and an anonymous referee for helpful comments. Gerhard Glomm gratefully
acknowledges very generous hospitality from the Indian Statistical Institute Delhi, especially the Policy and Planning
Research Unit for financial assistance related to this project. The usual disclaimer applies.
Asian Development Review, volumen. 33, No. 2, páginas. 144–166
C(cid:3) 2016 Asian Development Bank
and Asian Development Bank Institute
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
SECTORAL INFRASTRUCTURE INVESTMENTS IN INDIA 145
eso
We address these questions within the context of an unbalanced growing
is undergoing fundamental changes in the structure of
economía, India,
production and employment. We build a two-sector overlapping generations (OLG)
neoclassical growth model calibrated to India. The two sectors are an agriculture
sector and a modern (nonagriculture) sector that merges the manufacturing and
service sectors together.1 In our model, all individuals work when young and retire
when old. Individuals pay taxes on their labor income in both sectors, and receive
an excise subsidy for the consumption of agriculture products. The remaining tax
revenues are allocated as infrastructure investments across both sectors. In each
sectoral production technology, the stock of public infrastructure is a productive
aporte, and is combined with sector specific capital and labor in accordance with a
constant elasticity of scale (CES) production function. Public and private capital
can be complements or substitutes. To incorporate the drag on modern sector
output because of the presence of labor laws, we subtract a term that increases
proportionately with the amount of labor employed in the modern sector. We think
of this loss occurring because of bureaucratic problems related to a large labor force
in the modern sector. Labor and capital are assumed to be perfectly mobile across
sectors.
Given this setup, we show that exogenous fiscal policies (sectoral taxes and
subsidies) and labor market frictions can play an important role in misallocating
factors of production, which affects potential growth. Since less misallocation would
suggest that the economy can produce more with the same factors of production
and production technology, policy reforms that induce greater efficiency are key to
understanding India’s growth and growth potential.
A.
India’s Pattern of Structural Transformation
Most economies have undergone substantial structural changes that involved
shifts of resources across the agriculture, manufacturing, and service sectors, y
very large changes in the capital–output ratios of all three sectors. In the context of
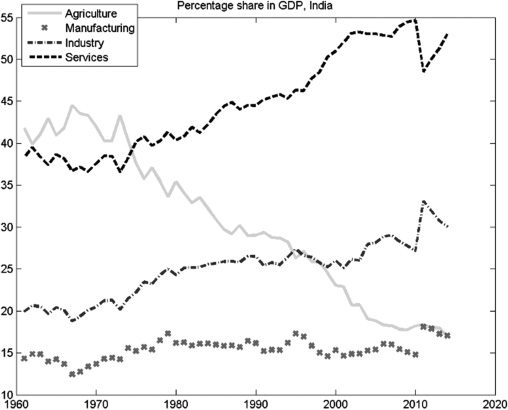
the development process, India stands out for three reasons.2 As can be seen from
Cifra 1, India’s service sector has grown rapidly in the last 3 décadas, constituting
55% of the gross domestic product (PIB) en 2010, with a share close to 53% en
2015.3 The large size of the service sector in India is comparable to the size of the
service sector in developed economies where services often provide more than 60%
of total output and an even larger share of employment. Since many components
1This identification is not necessary as we just need two sectors whose output and employment shares in the
total economy rise and fall, respectivamente, and whose capital–output ratios are not constant over relatively long time
horizons.
2These structural shifts are documented in Verma (2012).
3Industry comprises value added in mining, manufacturing, construction, electricidad, and water and gas.
En 2014, value added in industry was 30% of GDP. Manufacturing value added was 17% of GDP, comprising
aproximadamente 57% of industry’s share.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
146 ASIAN DEVELOPMENT REVIEW
Cifra 1. Structural Transformations in India
GDP = gross domestic product.
Fuente: Banco mundial. World Development Indicators. http://data.worldbank.org/indicator/
of services (p.ej., financial services, business services, hotels, and restaurants) son
income related and increase only after a certain stage of development, the fact that
India’s service sector is very large relative to its level of development is puzzling.
Segundo, the entire decline in the share of agriculture in India’s GDP in the last 2
decades has been accounted for by an expanding service sector. The manufacturing
sector’s share of GDP has stayed constant at around 15% of GDP over the past
30 years.4 In general, such a trend is experienced by high-income economies and
not by developing economies. In developing economies, the typical pattern is for
the manufacturing sector to replace the agriculture sector’s declining share of GDP
initially. Only at higher levels of aggregate income does the service sector play an
increasingly large role. Además, in spite of the rising share of services in both
GDP and trade, there has not been a corresponding rise in the share of services
in India’s total employment. En otras palabras, India’s service sector has not been
sufficiently employment generating.5
4En comparación, en 2010, manufacturing value added as a percentage of GDP was 29.5% in the People’s
República de China, 24.8% in Indonesia, 24.5% in Malaysia, y 33.6% in Thailand (UN National Account Statistics
2015). Gupta and Kumar (2012) provide a comprehensive review of the factors inhibiting India’s manufacturing sector
in the postreform period. Hsieh and Klenow (2009) show that firm heterogeneity in productivity and distortions have
led to misallocation in Indian firms.
5While there will always be issues with modeling three disparate sectors such as services, manufacturing, y
agricultura, one can think of agriculture in our model—and other models of economic transformation—as being the
one truly traditional sector and the rest of the economy as the more modern sector. These models typically capture
the shrinking of the agriculture sector as the economy develops.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
SECTORAL INFRASTRUCTURE INVESTMENTS IN INDIA 147
Mesa 1. Data on Structural Transformation in India, 1970–2000
Variable
Employment
Shar e
Agriculture Agriculture Manufacturing Manufacturing Services Services
1970
77%
2000
62%
1970
12%
2000
19%
1970
12%
2000
20%
48%
3.3
18%
G D P
Shar e
K/Y Ratio
Gr oss
Capital For mation
GDP = gross domestic product.
Nota: “K/Y Ratio” refers to the capital–output ratio.
Fuente: Verma. 2012. Structural Transformation and Jobless Growth in the Indian Economy. In C. Ghate, ed. El
Oxford Handbook of the Indian Economy. prensa de la Universidad de Oxford: Nueva York.
48%
1.8
61%
29%
11.0
49%
27%
4.3
30%
23%
0.6
33%
25%
0.9
9%
Tercero, unlike the case of aggregate data in advanced economies where
capital–output ratios are often constant over time, the sectoral capital–output ratios in
India exhibit large changes over time (Mesa 1).6 While agriculture’s capital–output
ratio fell from 3.3 a 0.9 entre 1970 y 2000, the manufacturing sector’s
capital–output ratio rose from 0.6 a 4, and the service sector’s capital–output ratio
fell from 11 a 1.8.
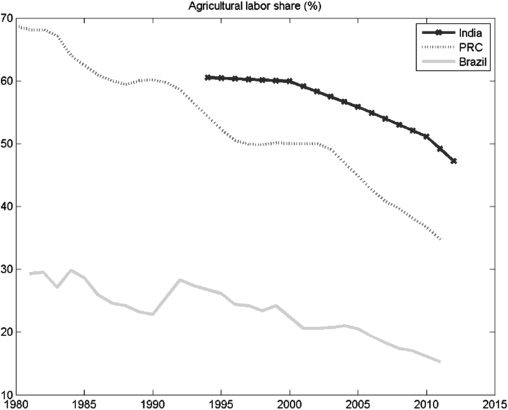
Cifra 2 shows agriculture employment in Brazil, the People’s Republic of
Porcelana, and India during 1980–2015. What is apparent is that the relative decline of
agriculture’s share of employment is slower in India than in these economies. Tomando
Cifra 1 y figura 2 together, what stands out is that the changes in India’s GDP
structure are asymmetric to its sectoral employment intensity.
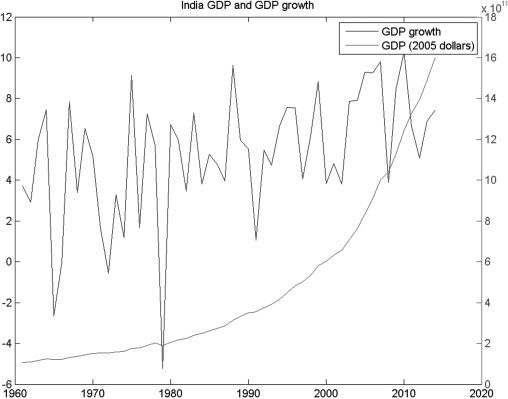
Cifra 3 shows that when measured in constant 2005 United States dollars,
the growth of India’s GDP has risen persistently since 1980.
B.
Description of the Main Results
The observations in the previous section suggest that, in the context of India
over the last 50 años, the balanced growth assumption does not seem appropriate.
Primero, the growth rate of GDP seems to be increasing over the sample period.
Además, the transition out of agriculture seems to have accelerated after 1975. Nosotros
therefore abandoned the strategy of balanced growth and instead pursued a strategy
of matching the transition out of agriculture with growth in the modern sector
(manufacturing and services).7 In our model, growth will not be balanced since
the production technologies do not exhibit constant returns in all the augmentable
6See Verma (2012).
7In models of capital accumulation, balanced growth typically prevails when there are constant returns to
all augmentable factors. In such a case, all variables that can grow will grow at the same constant rate forever, y
all variables that are bounded are constant over time. In growth models of structural transformation such as Gollin,
Parente, and Rogerson (2002), balanced growth in the sense defined above typically is not obtained since the perpetual
shifting of resources from the traditional to the modern sector prevents the growth rate of GDP from being constant
con el tiempo. It is still possible, sin embargo, to define something like balanced growth in terms of a constant rate of labor
migration from the traditional to the modern sector.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
148 ASIAN DEVELOPMENT REVIEW
Cifra 2. Agriculture Employment in Select Emerging Market Economies
PRC = People’s Republic of China.
Fuente: Banco mundial. World Development Indicators. http://data.worldbank.org/indicator/
Cifra 3. Indian GDP and GDP Growth (Constant 2005 Prices)
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
GDP = gross domestic product.
Fuente: Banco mundial. World Development Indicators. http://data.worldbank.org/indicator/
factores. In our model, both physical and infrastructure capital are augmentable.
The labor’s share of value added differs across the two sectors, so the returns to
the two augmentable factors differ across the two sectors as well. It is this difference
in the returns to augmentable factors that helps us match the transition out of
SECTORAL INFRASTRUCTURE INVESTMENTS IN INDIA 149
agriculture into the modern sector. This transition will generally be neither constant
nor balanced.
Our baseline calibrations capture some of the observations discussed in
Figures 1–3 for India fairly closely over a 30-year period. Por ejemplo, GDP per
capita increases persistently, as is shown in Figure 3. Segundo, consistent with the
observations in Table 1, the agriculture sector is shrinking over time: its employment
share drops from 67% a 40%. The drop in agriculture’s share of GDP is relatively
larger from 56% a 30%. These drops are largely consistent with the asymmetry in
the data in Table 1, which show that agriculture’s share of GDP in the Indian data
falls more rapidly than its employment share.
Given that
the baseline model captures unbalanced growth in India
qualitatively, we use the calibrated version of the model to conduct a variety
of counterfactual policy experiments on (i) the sectoral allocation of public
infrastructure investment between the agriculture and modern sectors, (ii) changes in
sectoral tax rates and subsidies, y (iii) changes in the drag created by labor market
friction to increase potential growth. Our first result addresses how public capital
should be allocated between the agriculture and modern sectors to influence India’s
growth potential. We show that a major policy reform that increases the sectoral
allocation of public capital to the agriculture sector leads to smaller effects on overall
GDP when public and private capital are substitutes, rather than complements. Cuando
public and private capital are substitutes, an increase (decrease) in public capital is
followed by a decrease (increase) in private capital, thus undoing the effects of policy
cambiar. In the case of complements, a reinforcing effect takes place that magnifies
the policy effects.
Segundo, we show that increasing the agricultural income tax rate and using the
extra tax revenue to fund increased investment in infrastructure in both sectors leads
to a large and persistent increase in GDP. When the same experiment is conducted
with an identical rise in the modern sector’s tax rate, the substitutability between
private and public capital induces larger shifts in labor across the sectors, cual
translates into a larger decline in modern sector output, which in turn, causes a
larger decline in overall GDP.
Tercero, we find that an increase in the subsidies for the agriculture goods shifts
demand away from the modern sector to the agriculture sector. This shift drags down
potential growth and decreases overall GDP.
To incorporate the drag on the modern sector’s output caused by the presence
of labor laws, following Das and Saha (2015), we subtract a term that increases
proportionately with the amount of labor employed in the modern sector. We think
of this loss occurring because of bureaucratic problems related to a large labor
force in the modern sector. We show that increasing the regulatory drag—or labor
market frictions—decreases wages in the modern sector and this shifts employment
to agriculture. There is a drop in output in both the modern and the agriculture
sectors, with the drop in the modern sector being larger. Since both sectoral outputs
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
150 ASIAN DEVELOPMENT REVIEW
decline, overall GDP declines as well. These results are very similar when public
and private capital are substitutes. This is a new interpretation of the effect of labor
market frictions on sectoral infrastructure investments. Typically in the literature,
labor market frictions are seen to employ inefficient labor in the modern sector (ver,
Por ejemplo, Gupta and Kumar 2012) or to constrain growth by deterring entry
and skewing firm-size distribution (ver, Por ejemplo, Alfaro and Chari 2014). En
our model, labor market frictions depress potential output by pulling productive
resources out of the modern sector. A lower value of the labor market friction
parameter leads to higher efficiency, suggesting that policies that diminish labor
market distortions can affect potential growth.
C.
Literature Review
Our paper builds on the literature in the field of growth and development.
There is a large body of literature that studies how structural change and growth are
related in the development process, including Caselli and Coleman (2001); Glomm
(1992); Gollin, Parente, and Rogerson (2002); Laitner (2000); and Lucas (2004).
Sin embargo, there has been relatively little work within this literature focusing on
developing economies in general and India in particular.
There is also a large body of literature studying the effects of infrastructure
investment on economic growth. Usually these types of analyses are carried out
in a one-sector growth model with an aggregate production function, often of
the Cobb–Douglas kind. Examples here include Barro (1990); Turnovsky and
pescador (1995); Turnovsky (1996); Glomm and Ravikumar (1994, 1997); Eicher
(2000); Ag´enor and Moreno-Dodson (2006); Ag´enor (2008); Ott and Turnovsky
(2006); and Angelopoulos, Economides, and Kammas (2007); among others.
There are also many empirical studies to go along with the above theoretical
investigations. Examples of such empirical papers include Barro (1990), Ai and
Cassou (1995), Holtz-Eakin (1994), and Lynde and Richmond (1992).8 To the extent
that infrastructure is often seen as being strategic to development, these papers do
not discuss how infrastructure spending should be financed across sectors or whether
the agriculture sector should be taxed.
II. The Model
The economy in our model is populated by an infinite number of generations.
Each generation is alive for two periods, young age and old age, and each accounts for
8Combining these two areas of growth and development research, there is a smaller body of literature that
analyzes the effects of infrastructure investment in economies undergoing structural changes such as large shifts of
productive activity from agriculture to manufacturing and then to services. Examples include Arcalean, Glomm, y
Schiopu (2012); Carrera, Freire-Seren, and Manzano (2009); de la Fuente et al. (1995); Caminal (2004); and Ott and
Soretz (2010).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
SECTORAL INFRASTRUCTURE INVESTMENTS IN INDIA 151
25 años. All individuals work when young and retire when old. Within a generation,
all individuals are identical. Por simplicidad, we assume that all individuals consume
only in the second period of life.9 Thus, all income from the first period is saved
for consumption when old. There are two sectors: one we call “agriculture” and a
second sector we call “modern,” although the names are not crucial. What is crucial
is that there are two sectors, with one sector declining and one sector increasing
along the development path. The utility function for all households is given
abajo:
tu(cm,t+1, ca,t+1) = lncm,t+1 + φlnca,t+1,
φ > 0
(1)
where cm,t+1 denotes household consumption of the modern sector good and ca,t+1
the consumption of the agriculture good.
Households working in the agriculture and modern sectors solve the following
problema:
máximo
cm ,ca
s.t.
lncm,t+1 + φlnca,t+1
cm,t+1 + (1 − ξ ) pt+1ca,t+1 = (1 − τa)wa,t (rt + 1 − d) Agriculture
cm,t+1 + (1 − ξ ) pt+1ca,t+1 = (1 − τm)wm,t (rt + 1 − d) Modern
(2)
dónde 0 < ξ < 1 is a government subsidy on agriculture goods consumption and τa ∈ [0, 1] and τm ∈ [0, 1] are tax rates levied on labor income in the agriculture and modern sectors, respectively. rt represents the rental price of capital. d is the depreciation rate of capital, wa,t is the wage rate in the agriculture sector, and wm,t is the wage rate in the modern sector. We assume that the modern sector good is the numeraire, and so pt denotes the relative price of the agriculture good relative to the modern sector good.10 Since households only consume in the second period, aggregate consumption for the agriculture good, ca,t+1, and the modern sector good, cm,t+1, satisfies ca,t+1 cm,t+1 = φ (1 − ξ ) pt+1 (3) Following Getachew and Turnovsky (2015), we assume output in each sector is produced by the production functions specified in equations (4) and (5), in 9We make the assumption that consumption only takes place when individuals are old. In that case, all income earned by the young is saved. This assumption generates results that are very similar to more general models where utility is derived from consumption in both periods of life, preferences are homothetic, and, as a result, savings are a constant fraction of income. With our assumption, the savings rate happens to be constant at 100%. 10We assume that wa,t is inclusive of the relative price, pt, as shown in equation (10). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u a d e v / a r t i c e - p d l f / / / / 3 3 2 1 4 4 1 6 4 3 3 9 7 a d e v _ a _ 0 0 0 7 6 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 152 ASIAN DEVELOPMENT REVIEW which private capital and public capital are combined in accordance with the CES production function, with elasticity of substitution being (cid:5) = 1/(1 − ρ): ρa Ya,t = Aa,t [a1 K at ρm Ym,t = Am,t [a2 K mt Yt = Ya,t pt + Ym,t a ]θa /ρa L 1−θa + (1 − a1)Gρa ρm mt ]θm /ρm L 1−θm + (1 − a2)G mt at 0 < a1 < 1 − γ L m,t 0 < a2 < 1 (4) (5) (6) Here, Aa,t and Am,t are total factor productivity (TFP) in the agriculture and modern sectors, respectively. Ka,t and Km,t are the total amount of physical capital used in each sector, respectively, and L a,t and L m,t stand for the total amount of labor employed in each of the two sectors. Ga,t and Gm,t denote the stock of public capital in the agriculture and modern sectors, respectively. γ L mt represents the labor friction in the modern sector: we subtract a term that increases proportionately with the size of labor employed in the modern sector. We think of this loss occurring because of bureaucratic problems related to a large labor force in the modern sector. This specification follows Das and Saha (2015). We assume that investments in public infrastructure can be financed by a tax on (i) labor income in the modern sector, (ii) labor income in the agriculture sector, or (iii) both. In addition to financing the public good investment, the government also subsidizes consumption of agricultural products. The government budget constraint can be written as Ga,t + Gm,t + ξ pt ca,t = τawa,t L a,t + τmwm,t L m,t (7) where ξ is the subsidy for the consumption of the agriculture good. We do not allow public debt in our model. Letting δa ∈ [0, 1] denote the fraction of government revenue allocated to agricultural infrastructure, we can write Ga,t = δa[τawa,t L a,t + τmwm,t L m,t − ξ pt ca,t ] Gm,t = (1 − δa)[τawa,t L a,t + τmwm,t L m,t − ξ pt ca,t ] The returns to factors in the two sectors are wa,t = pt Aat [a1 K ρm wm,t = Aat [a2 K mt ra,t = pt Aat θa[a1 K ρm rm,t = Aat θm[a2 K mt ρa at + (1 − a2)G ρa at ]θa /ρa (1 − θa)L + (1 − a1)G ρm mt ]θm /ρm (1 − θm)L ρa ρa at )θa /ρa −1a1 K + (1 − a1) ∗ G at ρm mt )θm /ρm −1a2 K + (1 − a2) ∗ G −θa at −θm mt − γ ρa −1 at ρm −1 mt L 1−θa at L 1−θm mt (8) (9) (10) (11) (12) (13) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u a d e v / a r t i c e - p d l f / / / / 3 3 2 1 4 4 1 6 4 3 3 9 7 a d e v _ a _ 0 0 0 7 6 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 SECTORAL INFRASTRUCTURE INVESTMENTS IN INDIA 153 Assuming costless mobility of labor, we can equate the after tax wage rates across the two sectors (1 − τa)wa,t = wm,t (1 − τm) Similarly, we also assume perfect capital mobility, which implies ra,t = rm,t = rt (14) (15) For capital and labor markets, the aggregate capital Kt and aggregate labor Lt are both known at the beginning of time t: Kat + Kmt = Kt L at + L mt = L t (16) There is no population growth in the model: L t = L t+1. All income is saved and funds the future capital stock: Kt+1 = (1 − τa) pt wa,t L a,t + (1 − τm)wm,t L m,t For the two goods market, agriculture goods can only be used for consumption. Modern sector goods can be used as consumption or investment (see, for example, Cheremukhin et al. 2014). The market clearing condition for the two goods are cat L t = Yat cmt L t + Kt+1 − (1 − d)Kt + Gt+1 = Ymt (17) Finally, both sectors have no direct interaction with one another, the economy is closed, and prices are determined fully by domestic production. III. Calibration Parameters This section describes the parameters used in our calibration exercises. Our calibration strategy is to match the initial shares of sectoral employment rates, sectoral capital–output ratios, and sectoral GDP ratios; and the rate of decline (increase) of these shares over a 30-year period, as depicted in Table 1. The initial TFP in the agriculture sector (Aa) is set at 2, while that in the modern sector (Am) is set at 1. The growth rate of agricultural TFP is 1.4, equivalent to 1.4% annual growth; the growth rate of modern TFP is 1.3, equivalent to 1.3% annual growth. This reflects that average annual TFP growth was lower in the modern l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u a d e v / a r t i c e - p d l f / / / / 3 3 2 1 4 4 1 6 4 3 3 9 7 a d e v _ a _ 0 0 0 7 6 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 154 ASIAN DEVELOPMENT REVIEW sector in India in its earlier stages of development (Verma 2012). In the agriculture production function, a1 represents the weight of private capital when combined with public capital, and is set at 0.8. Similarly, a2 is also set at 0.8. This reflects the common observation that private capital is more important than public capital in final goods production. The CES parameters, ρa and ρm, each assume two values: 0.6 and −0.3. If ρ = 0.6, then private capital and public capital are substitutes; if ρ = −0.3, then private and public capital are complements. In the production function, labor has a power parameter (1 − θ). The crucial distinction in our model between the two sectors is capital intensity. In all the experiments below, we assume that the modern sector is more capital intensive than the agriculture sector: θm = 0.5 > θa = 0.3.
We now describe the policy parameters. The government funding share for
agricultural infrastructure, δa, is set at 0.5 in the baseline model and assumes values
de 0.2 a 0.55 in the experiment. The tax rate of agricultural income, τa, es 0.2
in the baseline and varies from 0.1 a 0.4 in the experiment. Similarmente, the tax rate
on modern sector income, τm, es 0.3 in the baseline, and varies from 0.1 a 0.4 en
the experiment. Government subsidies of agriculture goods prices, ξ , are set at 0.1
in the baseline and range from 0.01 a 0.15 in the experiment. Por último, the labor
friction parameter, γ , is set at zero in the baseline, and varies from zero to 0.1 en el
experimento. These values are summarized in Table 2.
IV. Policy Experiments
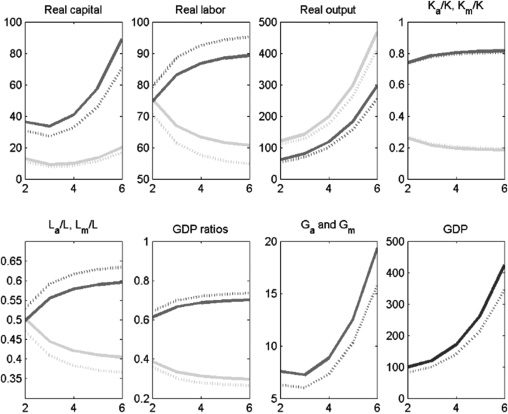
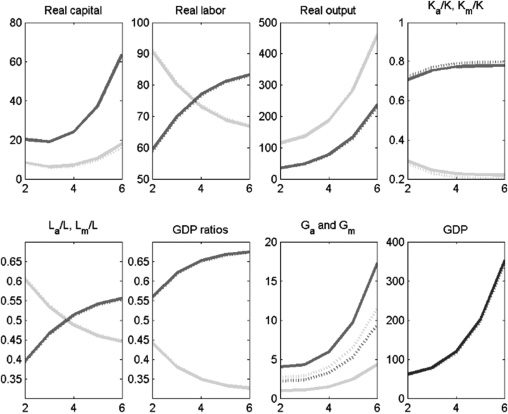
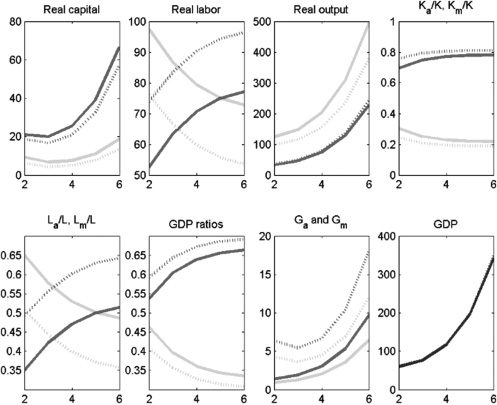
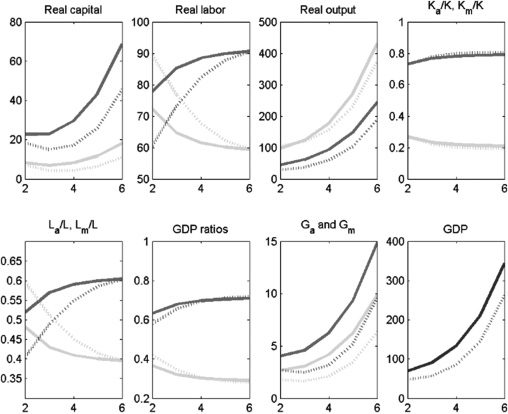
Cifra 4 depicts our calibration to Indian data, assuming no labor market
frictions and no subsidies. We refer to this as the baseline model. The dashed lines
show the results for the complementarity assumption.11 We assume that public
capital is split evenly between the two sectors. For the calibrated version with the
parameter values from Table 2, we obtain the following results. Primero, GDP per capita
grows persistently, as shown in Figure 3. Segundo, consistent with the observations
en mesa 1, the agriculture sector is shrinking over time: its employment share
drops from 67% a 40%. The decline in agriculture’s share of GDP is even larger
proportionately, dropping from 56% a 30%. These declines are largely consistent
with the asymmetry in the data in Table 1, which show that agriculture’s share of GDP
falls more rapidly than its employment share. The sizes of these relative drops are
maintained if public and private capital are substitutes, rather than complements. El
reason why overall GDP is lower when public and private capital are complements is
that a limited amount of G constrains total output as this constrains the productivity
of K. Como resultado, overall output is less than the case where K and G are substitutes.12
11In each experiment, we show two technological cases: (i) the case of private capital and public capital being
complements, which we take to be the empirically valid assumption, y (ii) the case where they are substitutes.
12An example of substitutes is government-owned machinery versus privately owned machinery. An example
of complements is private factories that rely on public infrastructure to deliver products.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
SECTORAL INFRASTRUCTURE INVESTMENTS IN INDIA 155
}
1
0
.
,
0
{
}
5
1
0
.
,
1
0
0
{
.
}
4
.
0
,
1
.
0
{
}
4
.
0
,
1
.
0
{
}
5
5
.
,
2
.
0
{
3
.
5
.
5
.
2
.
3
.
1
.
0
1
2
1
4
.
1
3
.
1
8
.
3
.
−
3
.
−
8
.
,
6
.
,
6
.
)
s
r
a
mi
y
0
2
(
PAG
F
t
gramo
norte
i
r
tu
t
C
a
F
tu
norte
a
METRO
F
oh
mi
t
a
R
h
t
w
oh
r
GRAMO
norte
oh
i
t
C
tu
d
oh
r
PAG
mi
r
tu
t
yo
tu
C
i
r
gramo
A
norte
i
r
mi
t
mi
metro
a
r
a
PAG
yo
a
t
i
pag
a
C
norte
oh
i
t
C
tu
d
oh
r
PAG
gramo
norte
i
r
tu
t
C
a
F
tu
norte
a
METRO
norte
i
r
mi
t
mi
metro
a
r
a
PAG
yo
a
t
i
pag
a
C
)
s
r
a
mi
y
0
2
(
PAG
F
t
yo
a
r
tu
t
yo
tu
C
i
r
gramo
A
F
oh
mi
t
a
R
h
t
w
oh
r
GRAMO
norte
oh
i
t
C
tu
d
oh
r
PAG
gramo
norte
i
r
tu
t
C
a
F
tu
norte
a
METRO
norte
i
r
mi
t
mi
metro
a
r
a
PAG
S
mi
C
norte
oh
i
t
C
tu
d
oh
r
PAG
mi
r
tu
t
yo
tu
C
i
r
gramo
A
norte
i
r
mi
t
mi
metro
a
r
a
PAG
S
mi
C
norte
oh
i
t
C
tu
d
oh
r
PAG
gramo
norte
i
r
tu
t
C
a
F
tu
norte
a
METRO
norte
i
r
mi
t
mi
metro
a
r
a
PAG
norte
oh
i
t
C
tu
d
oh
r
PAG
mi
r
tu
t
yo
tu
C
i
r
gramo
A
norte
i
r
mi
t
mi
metro
a
r
a
PAG
mi
r
tu
t
yo
tu
C
i
r
gramo
A
norte
i
mi
r
a
h
S
mi
r
tu
t
C
tu
r
t
s
a
r
F
norte
I
t
norte
mi
metro
norte
r
mi
v
oh
GRAMO
s
mi
C
i
r
PAG
mi
r
tu
t
yo
tu
C
i
r
gramo
A
norte
oh
y
d
i
s
b
tu
S
t
norte
mi
metro
norte
r
mi
v
oh
GRAMO
mi
metro
oh
C
norte
I
gramo
norte
i
r
tu
t
C
a
F
tu
norte
a
METRO
norte
oh
mi
t
a
R
X
a
t
mi
metro
oh
C
norte
I
mi
r
tu
t
yo
tu
C
i
r
gramo
A
norte
oh
mi
t
a
R
X
a
t
gramo
norte
i
r
tu
t
C
a
F
tu
norte
a
METRO
norte
i
PAG
F
t
yo
a
i
t
i
norte
I
mi
r
tu
t
yo
tu
C
i
r
gramo
A
norte
i
PAG
F
t
yo
a
i
t
i
norte
I
y
t
i
yo
i
t
Ud.
norte
i
r
mi
t
mi
metro
a
r
a
PAG
y
C
i
yo
oh
PAG
a
A
metro
A
a
gramo
metro
gramo
1
a
Fi
2
a
a
metro
a
metro
ρ
ρ
i
i
yo
a
C
s
i
F
a
a
metro
δ
t
t
ξ
.
y
t
i
v
i
t
C
tu
d
oh
r
pag
r
oh
t
C
a
F
yo
a
t
oh
t
=
PAG
F
t
,
norte
oh
i
t
tu
t
i
t
s
b
tu
s
F
oh
y
t
i
C
i
t
s
a
yo
mi
t
norte
a
t
s
norte
oh
C
=
S
mi
C
.
s
norte
oh
i
t
a
yo
tu
C
yo
a
C
'
s
r
oh
h
t
tu
A
:
mi
C
r
tu
oh
S
norte
oh
i
t
C
i
r
F
t
mi
k
r
a
METRO
r
oh
b
a
l
t
mi
k
r
a
METRO
r
oh
b
a
l
γ
s
r
mi
t
mi
metro
a
r
a
PAG
norte
oh
i
t
a
r
b
i
yo
a
C
.
2
mi
yo
b
a
t
s
t
norte
mi
metro
i
r
mi
pag
X
mi
mi
tu
yo
a
V
mi
norte
i
yo
mi
s
a
B
norte
oh
i
t
i
norte
fi
mi
D
r
mi
t
mi
metro
a
r
a
PAG
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
156 ASIAN DEVELOPMENT REVIEW
Cifra 4. Baseline Model: No Labor Market Frictions, No Subsidies
GDP = gross domestic product.
Notas: Solid lines denote the period before the policy experiment; dashed lines denote the period after the policy
experimento. Medium-shaded lines denote the modern sector; light-shaded lines denote the agriculture sector;
dark-shaded lines denote overall GDP.
Fuente: Authors’ calculations.
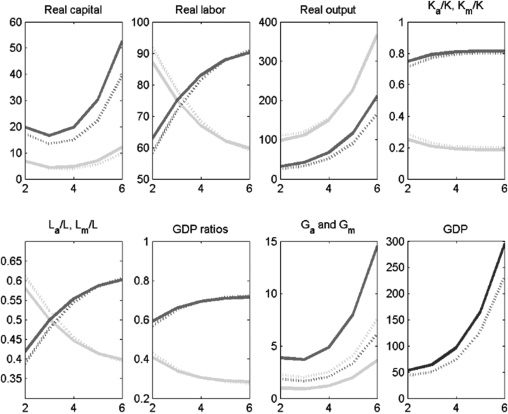
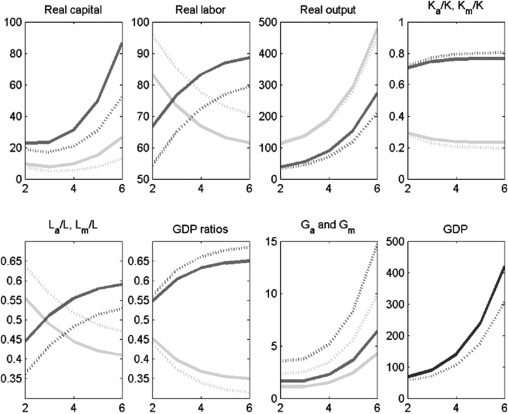
One important policy issue that can fundamentally influence the growth
potential relates to how public capital should be allocated between the agriculture
and modern sectors. It is expected that increasing the share of public capital going
to agriculture will increase agricultural output, the question is by how much. En el
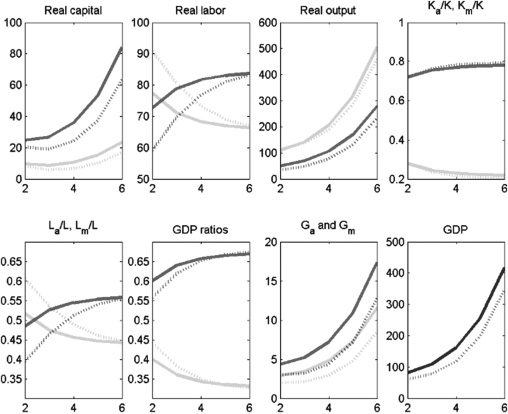
first policy experiment (Cifra 5), we increase agriculture’s share of infrastructure,
δa, de 0.2 a 0.6. This represents a very significant policy reform. An immediate
impact of an increase in the share of infrastructure in agriculture is that Ga increases
and Gm falls. Because G and K are assumed to be complements, Km also falls.
Cifra 6 reveals that GDP growth declines as more public capital is allocated to
agricultura. This is true simply because of the higher capital intensity (private and
público) of the modern sector relative to agriculture. As expected (because La also
aumenta), the relative size of the agriculture sector increases, both measured in
terms of employment and GDP share, although the effect on the labor share seems
to be larger than on the GDP share. The effect on the level of overall GDP is
persistent, while the magnitude of the effects on agriculture’s labor share and GDP
share declines over time. Finalmente, the effect on overall GDP is far smaller when public
and private capital are substitutes. This makes sense; when public and private capital
are substitutes, an increase (decrease) in public capital is followed by a decrease
(increase) in private capital, thus undoing the effect of policy change. En el caso de
complements, a reinforcing effect occurs that magnifies the policy effect.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
SECTORAL INFRASTRUCTURE INVESTMENTS IN INDIA 157
Cifra 5. Policy Experiment: Increase δa from 0.2 a 0.6; K and G complements
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
GDP = gross domestic product.
Notas: Solid lines denote the period before the policy experiment; dashed lines denote the period after the policy
experimento. Medium-shaded lines denote the modern sector; light-shaded lines denote the agriculture sector;
dark-shaded lines denote overall GDP.
Fuente: Authors’ calculations.
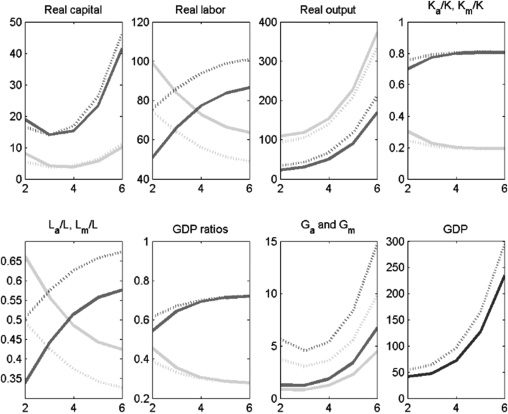
Cifra 6. Policy Experiment: Increase δa from 0.2 a 0.6; K and G substitutes
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
GDP = gross domestic product.
Notas: Solid lines denote the period before the policy experiment; dashed lines denote the period after the policy
experimento. Medium-shaded lines denote the modern sector; light-shaded lines denote the agriculture sector;
dark-shaded lines denote overall GDP.
Fuente:Authors’ calculations.
158 ASIAN DEVELOPMENT REVIEW
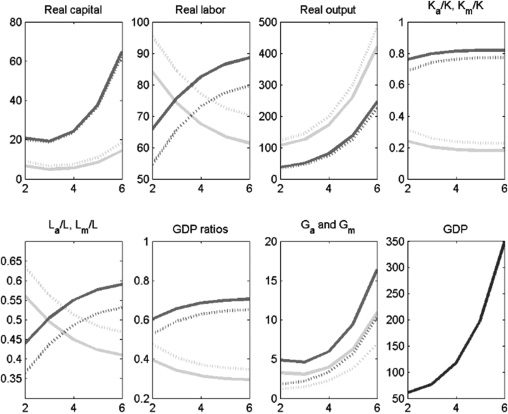
Cifra 7. Policy Experiment: Increase τa from 0.1 a 0.4; increase government expenditure
proportionately in both sectors; K and G complements
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
GDP = gross domestic product.
Notas: Solid lines denote the period before the policy experiment; dashed lines denote the period after the policy
experimento. Medium-shaded lines denote the modern sector; light-shaded lines denote the agriculture sector;
dark-shaded lines denote overall GDP.
Fuente: Authors’ calculations.
In the next policy experiment, we increase the agricultural income tax rate,
τa, de 10% a 40% and use the extra tax revenue to fund increased investment
(proportionately) in both types of infrastructure. We first consider the case of
complements (Cifra 7). This policy leads to a large and persistent increase in
GDP for two reasons. Primero, the tax increase in the agriculture sector induces a large
shift of labor (because of the reduction in the after-tax wage) out of agriculture
and into the more capital-intensive modern sector. Segundo, the increased stock of
infrastructure in both sectors increases output directly, as well as indirectly through
the productivity of capital (an augmentable factor) and labor. Por supuesto, the last effect
is not there, or is at least smaller, when public and private capital are substitutes
(Cifra 8). The massive shift of labor from agriculture to the modern sector increases
output in the modern sector and decreases output in agriculture. But the associated
change in agriculture’s share of GDP is relatively small and declines over time.
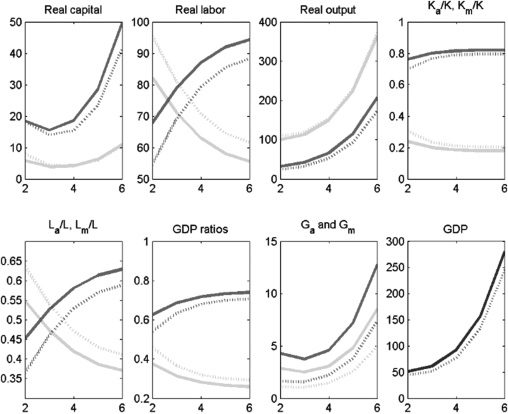
Alternatively to financing additional investment in public infrastructure, el
government could raise taxes on income, τm, in the modern sector instead. En
Cifra 9, we illustrate the economic effects of raising the income tax in the modern
sector from 10% a 40% (an identical increase compared to τa in the previous case)
and use the extra revenue to finance infrastructure investment proportionately in both
sectors. Una vez más, an immediate impact of an increase in τm is that Ga and Gm
SECTORAL INFRASTRUCTURE INVESTMENTS IN INDIA 159
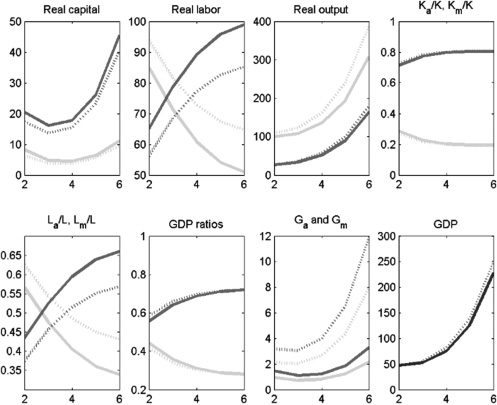
Cifra 8. Policy Experiment: Increase τa from 0.1 a 0.4; increase government expenditure
proportionately in both sectors; K and G substitutes
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
GDP = gross domestic product.
Notas: Solid lines denote the period before the policy experiment; dashed lines denote the period after the policy
experimento. Medium-shaded lines denote the modern sector; light-shaded lines denote the agriculture sector;
dark-shaded lines denote overall GDP.
Fuente: Authors’ calculations.
Cifra 9. Policy Experiment: Increase τm from 0.1 a 0.4; increase government expenditure
proportionately in both sectors; K and G complements
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
GDP = gross domestic product.
Notas: Solid lines denote the period before the policy experiment; dashed lines denote the period after the policy
experimento. Medium-shaded lines denote the modern sector; light-shaded lines denote the agriculture sector;
dark-shaded lines denote overall GDP.
Fuente: Authors’ calculations.
160 ASIAN DEVELOPMENT REVIEW
Cifra 10. Policy Experiment: Increase τm from 0.1 a 0.4; increase government
expenditure proportionately in both sectors; K and G substitutes
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
GDP = gross domestic product.
Notas: Solid lines denote the period before the policy experiment; dashed lines denote the period after the policy
experimento. Medium-shaded lines denote the modern sector; light-shaded lines denote the agriculture sector;
dark-shaded lines denote overall GDP.
Fuente: Authors’ calculations.
increase. Sin embargo, there is one basic benefit and one basic cost associated with this
política. The cost is a shift of labor to agriculture with its lower capital productivity.
The benefit is the extra infrastructure capital. Por lo tanto, when public and private
capital are complements, these two effects roughly cancel each other out and, as a
consequence, the effects on overall GDP are small; when public and private capital
are substitutes, the effect on overall GDP is negative. The substitutability induces
larger shifts in labor across the sectors, which translates into a larger decline in
modern sector output, which in turn causes a larger decline in overall GDP. Estos
results also show that funding more infrastructure investments in both sectors by
raising labor income taxes in the agriculture sector raises potential growth.
Many poor economies maintain subsidies for agricultural products, como
alimento, and India is no exception in this regard. En figura 11, we illustrate the effect
of increasing such a subsidy. As expected, we find that a higher subsidy, o un
increase in ξ , leads to a reduction in Ga and Gm. We also find that (i) the subsidy for
the agriculture good shifts demand away from the modern sector to the agriculture
sector, y (ii) this shift drags down potential growth and decreases overall GDP.
There are many reasons to believe that various regulations and labor practices
in manufacturing and the service sector (modern sector) hold back productivity at
unnecessarily low levels. We model this in the production function as a subtraction
from output by the amount, γ L m. Hasta ahora, we have assumed in all computations
SECTORAL INFRASTRUCTURE INVESTMENTS IN INDIA 161
Cifra 11. Policy Experiment: Increase ξ from 0.01 a 0.15; K and G complements
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
GDP = gross domestic product.
Notas: Solid lines denote the period before the policy experiment; dashed lines denote the period after the policy
experimento. Medium-shaded lines denote the modern sector; light-shaded lines denote the agriculture sector;
dark-shaded lines denote overall GDP.
Fuente: Authors’ calculations.
Cifra 12. Policy Experiment: Increase ξ from 0.01 a 0.15; K and G substitutes
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
GDP = gross domestic product.
Notas: Solid lines denote the period before the policy experiment; dashed lines denote the period after the policy
experimento. Medium-shaded lines denote the modern sector; light-shaded lines denote the agriculture sector;
dark-shaded lines denote overall GDP.
Fuente: Authors’ calculations.
162 ASIAN DEVELOPMENT REVIEW
Cifra 13. Policy Experiment: Increase γ from 0.0 a 0.1; K and G complements
GDP = gross domestic product.
Notas: Solid lines denote the period before the policy experiment; dashed lines denote the period after the policy
experimento. Medium-shaded lines denote the modern sector; light-shaded lines denote the agriculture sector;
dark-shaded lines denote overall GDP.
Fuente: Authors’ calculations.
that this drag is zero. To investigate the effect of this regulatory drag on economic
growth, we increase γ in equation (5) from zero to 0.1. Cifra 13 shows that
increasing the regulatory drag decreases wages in the modern sector, shifting
employment to agriculture. Because γ increases, modern sector GDP, Ym, también
falls, which leads to a reduction in Ga and Gm. This is a new interpretation of the
effect of labor market frictions on sectoral infrastructure investments. Labor market
frictions are typically seen to employ inefficient labor in the modern sector (ver, para
ejemplo, Gupta and Kumar 2012) or constrain growth by deterring entry and skewing
firm-size distribution (ver, Por ejemplo, Alfaro and Chari 2014). In our model, labor
market frictions depress potential output by pulling productive resources out of the
modern sector.
We also find that there is a drop in output in both the modern and agriculture
sectors, with the drop in the modern sector being larger. Since both sectoral outputs
decline, overall GDP declines as well. These results are very similar when public
and private capital are substitutes.
A.
Robustez
A feature of our model described in equations (1)–(17) is that the relative
price of the agriculture good falls steadily. The drop in price is a function of the
Cobb–Douglas specification, which has been used in many similar models. In effect,
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
SECTORAL INFRASTRUCTURE INVESTMENTS IN INDIA 163
Cifra 14. Policy Experiment: Increase γ from 0.0 a 0.1; K and G substitutes
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
GDP = gross domestic product.
Notas: Solid lines denote the period before the policy experiment; dashed lines denote the period after the policy
experimento. Medium-shaded lines denote the modern sector; light-shaded lines denote the agriculture sector;
dark-shaded lines denote overall GDP.
Fuente: Authors’ calculations.
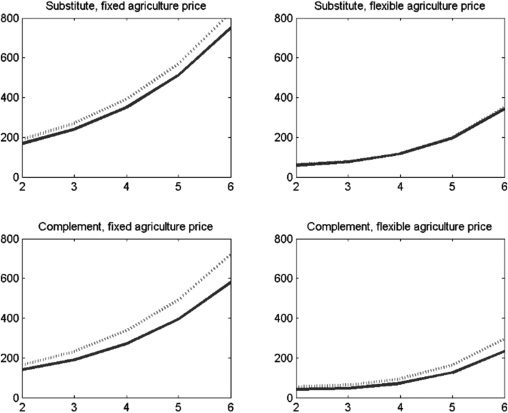
as the TFP of the agriculture sector increases, the price of the agriculture product
decreases. This offsets the increase in the agricultural product, Ya,t . To adjust for
este, instead of equation (6) we define output in constant prices, which holds the
agriculture price from the first period fixed:
Yt = p0Ya,t + Ym,t
(18)
p0 is endogenously determined from the system. In subsequent periods, it is kept
fixed.13 We consider one key policy experiment: an increase in agriculture income
taxation. In the first period, zero, Cifra 15 shows that the overall GDP level defined
by equation (18) is higher than the corresponding level of GDP from equation (6).
Under the fixed-price definition of GDP, the relative price of the agriculture good
is invariant with respect to changes in agricultural productivity. When the relative
price is flexible, it declines over time.14
13Because of parameter sensitivity, in the fixed-price definition of GDP, we change the following parameter
values in Table 2: (i) initial agricultural TFP, Aa, is set to 3; (ii) initial manufacturing TFP, Am, is set to 1;
(iii) agricultural TFP growth is set to 1.3%; y (iv) manufacturing TFP growth is set to 1.2%. To facilitate the
GDP comparison, we apply this subset of parameters for the calculation of flexible-price GDP as well.
14The comparisons between flexible-price and fixed-price GDP for the other policy experiments are available
from the authors upon request. In these, we see that the ordering of the policies that we consider by their effects on
growth are invariant to the definition we use.
164 ASIAN DEVELOPMENT REVIEW
Cifra 15. Comparison between fixed-price GDP from equation (18) (dark-shaded line)
and flexible-price GDP from equation (6) (dashed medium-shaded line) después
τa increases from 0.1 a 0.4
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
GDP = gross domestic product.
Notas: Graphs in top row correspond to K and G being substitutes; graphs in bottom row correspond to K and G
being complements.
Fuente: Authors’ calculations.
V. Conclusion and Policy Implications
We build a two-sector (agriculture and modern) OLG growth model calibrated
to India to examine the effects of sectoral tax policies, sectoral infrastructure
investments, and labor market frictions on the sectoral allocation of labor and capital
in the Indian economy. Our paper hopes to address two broad issues. Primero, how do
sectoral tax rates and labor market frictions prevent developing economies like
India from realizing their growth potential? Segundo, what prevents the development
and expansion of the modern sector in a growing economy like India? Estos
questions have policy implications as distortions in the agriculture and modern
sectors have constrained growth in India by limiting the full productivity effect of
factor reallocation.
The calibrated model yields several policy implications. We show that a major
policy reform that increases the sectoral allocation of public capital to the agriculture
sector leads to a smaller effect on overall GDP when public and private capital are
substitutes rather than complements. When public and private capital are substitutes,
an increase (decrease) in public capital is followed by a decrease (increase) in private
capital, thus undoing the effect of the policy change. In the case of complements,
a reinforcing effect takes place that magnifies the policy effect. We also show that
SECTORAL INFRASTRUCTURE INVESTMENTS IN INDIA 165
funding more infrastructure investment in both sectors by raising labor income taxes
in the agriculture sector raises potential growth. If the same policy reform is enacted
by taxing labor income in the modern sector, potential growth increases by much
menos.
Finalmente, increasing the regulatory drag—or labor market friction—decreases
wages in the modern sector and shifts employment to agriculture. This leads to a
drop in output in both the modern and agriculture sector, with the drop in the modern
sector being larger. Since both sectoral outputs decline, overall GDP declines as well.
These results are very similar when public and private capital are substitutes.
En suma, policy reforms relating to sectoral tax rates, sectoral infrastructure
investments, and labor market frictions can have a sizable effect on growth and
potential growth in the Indian context.
References∗
Ag´enor, PAG. R. 2008. Fiscal Policy and Endogenous Growth with Public Infrastructure. Oxford
Economic Papers 60 (1): 57–87.
Ag´enor, PAG. r., y B. Moreno-Dodson. 2006. Public Infrastructure and Growth: New Channels and
Policy Implications. World Bank Policy Research Working Paper No. 4064. Washington,
corriente continua: Banco mundial.
Ai, C., and S. PAG. Cassou. 1995. A Normative Analysis of Public Capital. Economía Aplicada 27
(1995): 1201–209.
Alfaro, l., y un. Chari. 2014. Deregulation, Misallocation, and Size: Evidence from India.
Journal of Law and Economics 57 (4): 897–936.
Angelopoulos, K., GRAMO. Economides, y P. Kammas. 2007. Tax-Spending Policies and Economic
Growth: Theoretical Predictions and Evidence from the OECD. European Journal of
Political Economy 23 (4): 885–902.
Arcalean, C., GRAMO. Glomm, y yo. Schiopu. 2012. Growth Effects of Spatial Redistribution Policies.
Journal of Economic Dynamic and Control 36 (2012): 998–1008.
Barro, R. j. 1990. Government Spending in a Simple Model of Endogenous Growth. Diario de
Political Economy 98 (5): S103–S125.
Caminal, R. 2004. Personal Redistribution and the Regional Allocation of Public Investment.
Regional Science and Urban Economics 34 (2004): 55–69.
Carrera, j. A., METRO. j. Freire-Seren, y B. Manzano. 2009. Macroeconomic Effects of the Regional
Allocation of Public Capital Formation. Regional Science and Urban Economics 39 (2009):
563–74.
Caselli, F., and W. j. Coleman. 2001. The US Structural Transformation and Regional Convergence:
A Reinterpretation. Journal of Political Economy 109 (3): 584–616.
Cheremukhin, A., METRO. Golosov, S. Guriev, y un. Tsyvinski. 2014. The Industrialization and
Economic Development of Russia through the Lens of a Neoclassical Growth Model.
Mimeo, Departamento de Economía, Yale University.
El, S. PAG., y un. saha. 2015. Growth of Business Services: A Supply-side Hypothesis. canadiense
Journal of Economics 48 (1): 83–109.
∗ADB recognizes “China” as the People’s Republic of China.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
166 ASIAN DEVELOPMENT REVIEW
de la Fuente, A., X. Vives, j. Dolado, y r. Faini. 1995. Infrastructure and Education as
Instruments of Regional Policy: Evidence from Spain. Economic Policy 10 (20): 13–51.
Eicher, t. S. 2000. Scale, Congestion and Growth. Economica 67 (267): 325–46.
Getachew, y., and S. j. Turnovsky. 2015. Productive Government Spending and Its Consequences
for the Growth-Inequality Trade-off. Research in Economics 69 (4): 621–40.
Glomm, GRAMO. 1992. A Model of Growth and Migration. Canadian Journal of Economics 25 (4):
901–22.
Glomm, GRAMO., y B. Ravikumar. 1994. Public Investment in Infrastructure in a Simple Growth
Modelo. Journal of Economic Dynamics and Control 18 (1994): 1173–87.
———. 1997. Productive Government Expenditures and Long-Run Growth. Journal of Economic
Dynamics and Control 21 (1997): 183–204.
Gollin, D., S. Parente, y r. Rogerson. 2002. The Role of Agriculture in Development. Americano
Economic Review 92 (2): 160–64.
Gupta, PAG., and U. Kumar. 2012. Performance of Indian Manufacturing in the Post-Reform Period.
Chapter 8. In C. Ghate, ed. The Oxford Handbook of the Indian Economy, páginas. 276–310.
Nueva York: prensa de la Universidad de Oxford.
Holtz-Eakin, D. 1994. Public-Sector Capital and the Productivity Puzzle. Review of Economics
and Statistics 76 (1): 12–21.
Hsieh, C., y P. Klenow. 2009. Misallocation and Manufacturing TFP in China and India.
Revista trimestral de economía 124 (4): 1403–48.
Laitner, j. 2000. Structural Change and Economic Growth. Review of Economic Studies 67 (3):
545–61.
Luis, A. 1954. Economic Development with Unlimited Supplies of Labor. The Manchester
School 22 (2): 139–91.
lucas, R. mi. j. 2004. Life Earnings and Rural-Urban Migration. Journal of Political Economy 112
(1): 29–59.
Lynde, C., y j. Richmond. 1992. The Role of Public Capital in Production. Review of Economics
and Statistics 74 (1): 37–44.
Ott, I., and S. Soretz. 2010. Productive Public Input, Integration and Agglomeration. Regional
Science and Urban Economics 40 (2010): 538–49.
Ott, I., and S. j. Turnovsky. 2006. Excludable and Non-Excludable Public Inputs: Consequences
for Economic Growth. Economica 73 (292): 725–48.
Turnovsky, S. 1996. Optimal Tax, Debt, and Expenditure Policies in a Growing Economy. Diario
of Public Economics 60 (1996): 21–44.
Turnovsky, S., and W. pescador. 1995. The Composition of Government Expenditure and Its
Consequences for Macroeconomic Performance. Journal of Economic Dynamics and
Control 19 (4): 747–86.
United Nations. UN National Account Statistics, December 2015. http://unstats.un.org/unsd
/snaama/Introduction.asp
Verma, R. 2012. Structural Transformation and Jobless Growth in the Indian Economy. Chapter
10. In C. Ghate, ed. The Oxford Handbook of the Indian Economy, páginas. 276–310. Nueva York:
prensa de la Universidad de Oxford.
Banco mundial. World Development Indicators. http://data.worldbank.org/indicator/
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
a
d
mi
v
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
3
2
1
4
4
1
6
4
3
3
9
7
a
d
mi
v
_
a
_
0
0
0
7
6
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
9
S
mi
pag
mi
metro
b
mi
r
2
0
2
3