Sanaz Ghasemi*
universidad de toronto
Mechanical and Industrial
Ingeniería (MIE) Departamento
universidad de toronto
5 King’s College Road
Toronto ON Canada M5S 3G8
Use of Random Dot Patterns in
Achieving X-Ray Vision for
Near-Field Applications of
Stereoscopic Video-Based
Augmented Reality Displays
Mai Otsuki
University of Tsukuba
Paul Milgram
universidad de toronto
Ryad Chellali
Nanjing Tech University
Presence, volumen. 26, No. 1, Invierno 2017, 42–65
doi:10.1162/PRES_a_00286
Abstracto
This article addresses some of the challenges involved with creating a stereoscopic
video augmented reality ‘‘X-ray vision’’ display for near-field applications, cual
enables presentation of computer-generated objects as if they lie behind a real object
surface, while maintaining the ability to effectively perceive information that might be
present on that surface. To achieve this, we propose a method in which patterns con-
sisting of randomly distributed dots are overlaid onto the real surface prior to the ren-
dering of a virtual object behind the real surface using stereoscopic disparity. Fue
hypothesized that, even though the virtual object is occluding the real object’s surface,
the addition of the random dot patterns should increase the strength of the binocular
disparity cue, resulting in improved performance in localizing the virtual object behind
the surface. In Phase I of the experiment reported here, the feasibility of the display
principle was confirmed, and concurrently the effects of relative dot size and dot den-
sity on the presence and sensitivity of any perceptual bias in localizing the virtual
object within the vicinity of a flat, real surface with a periodic texture were assessed.
In Phase II, the effect of relative dot size and dot density on perceiving the impression
of transparency of the same real surface while preserving detection of surface infor-
mation was investigated. Results revealed an advantage of the proposed method in
comparison with the ‘‘No Pattern’’ condition for the transparency ratings. Surface
information preservation was also shown to decrease with increasing dot density and
relative dot size.
1
Introducción
To enhance interactions with the real world, augmented reality (AR) dis-
plays are designed to combine computer-generated elements with real-world
elementos. One of the most intriguing applications of AR is the notion of
‘‘X-ray vision,’’ denoting the ability to virtually ‘‘see through’’ a real surface to
present information that is not otherwise visible to the user (Livingston, Dey,
Sandor, & tomás, 2013). In contrast to most AR applications, which involve
superimposing computer-generated images onto real surfaces, the present con-
text involves adding images beneath, or behind, real surfaces.
ª 2017 by the Massachusetts Institute of Technology
*Correspondence to sanaz.ghasemi@mail.utoronto.ca.
42 PRESENCE: VOLUME 26, NUMBER 1
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Ghasemi et al. 43
Generally, the technology used for X-ray applications
of AR can be placed within two categories: optical see-
a través de (OST) and video-based AR (VAR). In OST
displays, the real world is seen through an optical
combiner, which is used to reflect the virtual object into
the user’s eyes (Rolland & Fuchs, 2000). Due to the lim-
ited brightness, resolution, and contrast of these dis-
plays, virtual objects can’t completely occlude real ones
(Azuma et al., 2001). Various researchers, como
Edwards et al. (2004) and Rosenthal et al. (2002), tener
looked into the use of these displays for X-ray vision
applications of AR.
In VAR displays, por otro lado, the virtual
objects are electronically combined with images of the
real world. With this type of display, unless the virtual
and real objects are somehow modified, the virtual
objects will normally occlude the real image, cual es
likely to cause the user to perceive them as floating in
front of the real objects—even in cases where the binoc-
ular disparity cue is suggesting otherwise (Schmalstieg
& Hollerer, 2016). Many researchers have studied the
application of this notion using VAR displays in a variety
of surgical, architectural, inspection, and military set-
tings, showing promising results (p.ej., Bajura, Fuchs, &
Ohbuchi, 1992; Bichlmeier, Wimmer, Heining, &
Navab, 2007; Fuchs et al., 1998; Furmanski, Azuma, &
Daily, 2002; Kalkofen, Mendez, & Schmalstieg, 2007;
Kang et al., 2013; Lerotic, Chung, Mylonas, & Cual,
2007; Sielhorst, Bichlmeier, Heining, & Navab, 2006;
Soler et al., 2008). In the context of our research, como
reported in the present article, we use video-based dis-
plays for augmenting the real images with virtual
objects.
One of the major challenges of X-ray AR vision is the
potential perceptual ambiguity caused by simply super-
imposing a hidden virtual object onto the image of a
real object’s surface.1 The consequent blocking off of
the real surface suggests to the observer that the virtual
object must be in front of the real surface, en vez de
1. For the sake of clarity, in describing this method we use the term
surface to refer to the surface of a real object, which has been captured
by some kind of a sensor and has been reproduced in the image. El
computer-generated object, por otro lado, will be referred to as
the virtual object.
behind it, thus contradicting the notion of X-ray vision.
Even with stereoscopic (3D) displays, simply rendering
a virtual object at the correct depth ‘‘correctly’’ behind
a real object will create the perception of a floating vir-
tual object in front of the surface of the real object
(Drascic & Milgram, 1996; Johnson, Edwards, &
Hawkes, 2003). This is a consequence of the strength
of occlusion cues (Cutting & Vishton, 1995). Incluso
when the relative locations of the virtual object and
the real surface are judged correctly, research has
shown that the presence of a transparent surface can
lead to imprecise absolute depth judgments of the vir-
tual object (Edwards et al., 2004) and reduce the dis-
tance within which the virtual object can be placed
from the real surface in order to be successfully fused
(Johnson et al., 2003).
To deal with the challenges involved in the simultane-
ous presentation of overlapping surfaces, various
researchers have suggested the addition of some sort of
‘‘texture’’ to the real surface. Interrante, Fuchs, y
Pizer (1997) suggested using sparse opaque textures
that were specifically designed to convey intrinsic
surface-shape properties to improve perception of depth
and spatial understanding of the surface. By adding grid
lines or strokes to the surface of a 3D computer-
generated transparent object, Interrante et al. were able
to use a combination of the occlusion cue, the binocular
disparity cue, the relative density cue, and the kinetic
depth effect to improve depth perception. Their claim
was based on the idea that consistent depth cues rein-
force each other, leading to improved depth perception
(Interrante, 1996).2 While doing so in a completely
virtual environment is straightforward, applying such a
solution to an AR display requires precise modeling
of the real surface and its relationship to the virtual
object.
With regards to AR environments, Zollmann,
Kalkofen, Mendez, and Reitmayr (2010) have also sug-
gested adding synthetic features, based on ‘‘tonal art
maps,’’ to provide compensation for surfaces where too
few features exist. Por ejemplo, by adding a hatching
2. Note that Interrante et al.’s (1997) idea was implemented in an
application where all the objects were computer-generated.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
44 PRESENCE: VOLUME 26, NUMBER 1
pattern to the surface of the pavement in an outdoor
scene and having the pattern occlude parts of the under-
ground pipes, they provide occlusion cues, which suggest
that the virtual pipes are in fact located underneath the
pavement.3 Other X-ray vision AR researchers who sug-
gest preserving the salient features of real surfaces have
also used those features to occlude the virtual object,
allowing the observer to perceive the virtual object
behind the real object (Lerotic et al., 2007; Avery,
Sandor, & tomás, 2009). These methods are not
applicable to cases where occlusion of the virtual object
is difficult to realize, or is not desired. Además, estos
methods require the real object’s surface to possess
salient features in order for the algorithms to function
effectively. The effectiveness of these visualization tech-
niques should be reassessed without these features pres-
ent to prove their generalizability.
In this article, we propose another method of dealing
with the perceptual challenges involved in X-ray vision.
With this method, which we are proposing be used for
near-field applications of AR, an artificial texture is added
to the surface of a real object. The key differences distin-
guishing our approach from others is that: (a) our tex-
ture involves randomly distributed (negro) dots; (b) el
only depth cues that are present are the occlusion and
binocular disparity cues (which limit the application of
this method to stereoscopic displays only); y (C) el
occlusion cue is not consistent with the binocular dispar-
ity cue (the virtual object occludes the real surface). Nosotros
have also limited ourselves in the research reported here
to flat, real surfaces that have periodic 2D textures and
do not comprise 3D topological features.
Following a summary of some related research, nosotros
present an explanation of the rationale underlying our
proposed display technique, together with some of its
expected advantages. Próximo, the results of a set of experi-
ments conducted to study the feasibility and effective-
ness of this method are presented. Por último, implications of
the results and an overview of future experiments are
outlined.
3. Note that their method is applied to nonstereoscopic images,
whereas the primary justification for our method is the presence of the
binocular disparity cue.
2
Background on X-Ray Vision
To mitigate the perceptual challenges caused by
overlaying virtual images showing internal structures
onto real surfaces, a variety of techniques have been pre-
sented in the past. To assess the success of these methods
in effectively achieving X-ray vision AR, there are a few
indicators to consider. En primer lugar, an effective method must
provide the observer with the ability to understand the
depth order between the virtual and real objects. In sim-
pler terms, the observer must be able to perceive the vir-
tual image as being behind the real object’s surface (y
thus inside the real object). Además, an effective
method is one that preserves some amount of detail
about both the virtual objects and the surface of the real
objects that is sufficient for carrying out one’s intended
tarea.
No es sorprendente, achieving these two properties typi-
cally involves a compromise. If the real object’s surface is
able to occlude portions of the virtual object (permitiendo
the observer easily to infer the virtual object as being
behind the real surface), at least some details of the vir-
tual object may be lost. Por otro lado, if the virtual
object is overlaid onto the real surface without occlusion
by the real surface, in addition to losing details of the real
surface, the depth order of the virtual and real objects
may become incomprehensible. Another aspect is the
computational complexity involved in creating the final
representación. Por ejemplo, some methods require the com-
putation of an accurate 3D model of the physical envi-
ronment to create a convincing composition of virtual
and physical objects. To achieve an optimal trade-off,
various methods have been proposed. In evaluating the
strengths and weaknesses of those methods, a convincing
solution should be one that finds the best compromise
between depth perception and information preservation (de
both real and virtual objects), while minimizing computa-
tional cost.
One of the more traditional methods, referred to as
the cutaway technique, involves rendering a ‘‘synthetic
(virtual) hole’’ in the real object’s surface, within which
the virtual object is placed. This solution has been imple-
mented using both OST (Ellis & Menges, 1998; rosa-
thal et al., 2002) and VAR displays (Bajura et al., 1992).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Ghasemi et al. 45
In addition to requiring adequate information about the
real object’s surface, the major problem with that
method is that it does not preserve any information
about the surface that has been removed.
As an alternative approach, other researchers have car-
ried out a partial removal of the real object’s surface
when adding the virtual image to it, such that certain
details of the real surface are preserved. Those methods
are generally categorized as context-preserving techniques.
One example of that technique, as applied to a VAR dis-
play, involves simulating a reduction in the opacity of
the real object’s pixels using image processing, such that
the real object’s surface is depicted as being partially
transparent (Bichlmeier et al., 2007). To achieve a
‘‘natural’’-looking partial transparency, those researchers
defined an optimized opacity value that varied across the
surface as a function of the surface curvature and the
angle and distance between the observer and the image.
An important constraint of that method is that it
requires a model of the real object. In practical situa-
ciones, this model may not precisely align with the physi-
cal scene, as a consequence of either inaccuracies of the
model or imprecision of the AR tracking system (Zoll-
mann, Grasset, Reitmayr, & Langlotz, 2014).
To eliminate the need for a complete 3D model of the
real world, several other methods have been proposed,
for which partial models based on information extracted
from real object images may suffice. Such partial models
may include edges (Kalkofen et al., 2007), salient
regiones (Lerotic et al., 2007; Sandor, Cunningham,
Dey, & Mattila, 2010), or a combination of salient
regiones, bordes, and texture details (Zollmann et al.,
2010). Although shown to be beneficial, those methods
require extra rendering steps, based on which of the spe-
cific features of the real object’s images are identified,
and the overlaying of virtual objects is then done.
3
Overview of Relevant Depth
Perception Cues
Because the fundamental goal of X-ray vision in
AR is to see through a real surface and reliably observe a
virtual object behind it, we provide in the following a
brief background on depth perception, which in turn
will serve as the guiding principle for our proposed
solución.
Accurate perception of objects in depth results from
the operation of various perceptual cues. Some of these
cues provide information about the ordinal, or relative,
depth of objects (es decir., which is the farthest, cual es
nearer, etc.) while others provide absolute or metric
depth information and allow the observer to ascertain a
medición (p.ej., in cm).
Typically, real environments are rich in information,
comprising multiple depth cues that allow the observer
to make reliable judgements about the relative and abso-
lute depths of objects. Cutting and Vishton (1995)
divided the continuum of depth into three regions: por-
sonal space, action space, and vista space, terms which
are also commonly referred to respectively as near-field,
medium-field, and far-field distances (Livingston et al.,
2013). According to Cutting and Vishton, some cues
are more effective at different distances. Por ejemplo, como
distance is increased, the accommodation and binocular
disparity cues both decrease in effectiveness, whereas aer-
ial perspective starts to be used as an effective depth cue
only at far-field distances. Other cues, such as relative
size and occlusion, are effective regardless of the dis-
tance.
Because of the different relative strengths of the depth
cues within the three regions, when investigating percep-
tual challenges and solutions, it is important to consider
the specific application and depth region for which the
solution is being proposed. Since our study focuses on
X-ray vision (using stereoscopic AR displays) for near-
field applications, only the cues that are most relevant to
our study are considered.
3.1 Occlusion
Occlusion refers to the case where a closer object,
known as the occluder, prevents light rays from an object
behind it, known as the occluded, from reaching the ob-
server. The information that does arrive is limited to the
relative depth of objects rather than their absolute depth.
When occlusion is present, the contours of the closer
object obscure those of the farther object. Por lo tanto, para
this cue to work effectively, one must be able to differen-
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
46 PRESENCE: VOLUME 26, NUMBER 1
tiate between the two objects. En otras palabras, para el
visual system to detect the objects and their contours,
there must be a distinguishable difference in the bright-
ness or color of the occluder and the occluded object
(Cutting & Vishton, 1995). Despite this limitation,
occlusion is commonly recognized as the most powerful
depth cue at all distances where visual perception holds.
In the context of X-ray vision applications of AR, variar-
ous researchers have exploited the strength of this cue by
having the salient features of the real surface occlude the
virtual object, thus allowing the observer to perceive the
virtual object as being behind the real object (Lerotic
et al., 2007; Avery, Sandor, & tomás, 2009; Sandor
et al., 2010).
3.2 Binocular Disparity
The ability to perceive a scene from two eyes that
are separated by an interpupillary distance provides (95%
de) humans with one of the most important and percep-
tually acute sources of depth information (Coutant &
Westheimer, 1993).
When a scene is viewed, the fixation point (also referred
to as the focal point) will fall on a particular location on
the retina of each eye, resulting in zero disparity. One can
furthermore envisage an imaginary geometric arc called
the horopter, comprising all retinal points, including the
focal point, that also have zero retinal disparity. Otro
points that are closer or farther from this arc are mapped
onto disparate locations on the two retinas.
The horopter thus provides a reference plane from
which the relative depth of other objects can be judged.
Objects that are in front of the horopter (closer to the
observer) will result in images with crossed disparity,
whereas objects that are behind the horopter (farther
from the observer) will result in uncrossed disparity.
Based on the amount of retinal disparity in the projec-
tion of each point to each eye, the visual system is thus
able to discern the relative depths between two points in
space via the binocular disparity depth cue (Patterson,
2009).
The importance of binocular disparity in perceiving
depth was first shown through the invention of the stere-
oscope by Wheatstone (1838), where a pair of flat draw-
ings were used to achieve a three-dimensional percept of
an object. Más tarde, en 1960, by introducing the concept of
random dot stereograms, Julesz (1971) made a significant
contribution to the science behind stereo vision. A typi-
cal example of a random dot stereogram is one where
two images consist of identical randomly distributed
dots, with a central square region that is shifted horizon-
tally by a small distance relative to the other image.
When viewed individually, each image appears as a flat
field of random dots. Sin embargo, when viewed stereo-
scopically, the central square region appears at a depth
that is different from the background plane of random
dots. Random dot stereograms provided evidence that
binocular depth perception can be achieved without the
need for monocular form recognition.
Although the neurophysiological processes through
which the brain derives depth information from binocu-
lar disparity is outside the scope of this article, it is never-
theless important to note the importance of vergence
eye movements for the effectiveness of this cue. Como
mentioned, the brain uses the horizontal disparity of
objects on the retina to estimate their depth relative to
the fixation point. Since the fixation point is defined as
the intersection of the line of sight of the two eyes, es
obvious that through the use of vergence eye move-
mentos, the fixation point will change, resulting in a cor-
responding shift in the position of the horopter. Por
doing so, our visual system is able to expand the disparity
limits for which binocular fusion is possible (Yeh &
Silverstein, 1990). It is also able to increase its accuracy
in perceiving depth through binocular disparity (Foley &
Richards, 1972), due to the fact that the brain uses those
changes in ocular vergence as a depth cue in its own
bien. Por lo tanto, by providing the observer with the
means of making appropriate eye vergence movements,
it may be possible to take advantage of the benefits of
this mechanism.
Como ejemplo, in cases where a virtual object is
intended to be shown behind a real surface that lacks a
visible texture (as shown in Figure 2[a]), it may be possi-
ble to aid the observer in making proper vergence eye
movements by adding a pattern onto the real surface
(ver figura 2[b]). Such a pattern can provide observers
with distinct fixation points, guiding them in making
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Ghasemi et al. 47
vergence eye movements (between the real surface and
virtual object) which may lead to improved depth
judgments.
3.3 Integration of Depth Cues
In natural environments, multiple depth cues typi-
cally provide both consistent and complementary infor-
formación. Sin embargo, in specific cases and especially with
the use of visual displays (due to the technological limita-
tions of implementing various depth cues), cue conflicts
do arise. En otras palabras, two or more sources of depth
information can in some cases provide inconsistent
and/or discrepant information about depth. The way in
which these consistent and inconsistent cues interact
with each other to provide a single depth map or shape
estimate to the observer has been the topic of much
investigación (p.ej., Johnston, Cumming, & parker, 1993;
Joven, landy, & Maloney, 1993; landy, Maloney,
Johnston, & Joven, 1995).
En general, three models have been suggested for
explaining cue interaction (Johnston et al., 1993). El
first is ‘‘vetoing,’’ which usually occurs in cases where
two depth cues are providing strongly inconsistent
information and the stronger cue overrides the
weaker cue.
The second model of cue interaction is referred to as
‘‘weak fusion,’’ or ‘‘weighted linear combination.’’ In
this model, the so-called ‘‘weak observer’’ processes the
information provided by each depth cue separately and
then averages the separate depth estimates (from each
cue) by using different weights for each. The weighting
of each cue depends on its estimated reliability under the
circumstances (Johnston et al., 1993).
An alternative to the weak fusion model is the ‘‘strong
fusion’’ model, which involves the cooperation of depth
cues prior to obtaining depth estimates. En otras palabras,
in contrast to the weak fusion model, the depth cues are
not processed separately; bastante, they interact and pro-
vide the ‘‘strong observer’’ with the most probable
three-dimensional interpretation of the scene. Examples
of this include ‘‘promotion’’ and ‘‘disambiguation.’’ In
the former case, one cue provides compensating infor-
mation for another incomplete depth cue. In the latter,
depth information provided from an inherently ambigu-
ous cue (p.ej., kinetic depth) is disambiguated by another
depth cue (Johnston et al., 1993). Based on Landy et al.
(1995), weak and strong fusion ‘‘fall at the two ends of a
continuum of possible models of depth and shape proc-
essing.’’ In general, models that are focused on modular-
ity tend toward the weak side, whereas those that sug-
gest more holistic interactions amongst cues tend
toward the strong side.
In the same paper, Landy et al. (1995) introduce the
‘‘modified weak fusion’’ (MWF) modelo, based on which
interactions between different cues result in two types of
information for each cue: a commensurate depth map
and an estimated measure of the cue’s reliability (cual
are both based on a combination of information pro-
vided by the cue itself and those provided by other cues).
These estimates provide inputs to the final fusion (o
weighted averaging) stage, where the weights of each
cue take the estimated reliabilities and the discrepancies
between cues into account. En otras palabras, the MWF
model can be simplified to the weak fusion model and
provide a means of constraining the strong fusion model
to one that is able to be tested.
One of the most relevant aspects of the MWF model
is its ability to consider conditions under which cue
weights change due to changes in cue reliability, cue
availability, or cue inconsistency. Based on this model,
por lo tanto, it may be possible to manipulate the reliability
and weighting of cues such that, when combining infor-
mation provided by the cues, a veridical depth judgment
can be made despite the presence of discrepancies. Para
ejemplo, in Figures 2(a) y 2(b), even though the
occlusion cue (which according to Cutting & Vishton,
1995, is considered to be the strongest depth cue, para
all distances) is suggesting that the virtual object is in
front of the real surface, it is possible to reduce the
weighting of the occlusion cue by increasing the reliabil-
ity of the binocular disparity cue. In the following sec-
ción, we propose that adding a random dot pattern to a
real surface in a stereoscopic display is a potentially effec-
tive means of increasing the binocular disparity cue. Si
this is done successfully, the observer should be able
to perceive the virtual object as lying behind the real
surface.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
48 PRESENCE: VOLUME 26, NUMBER 1
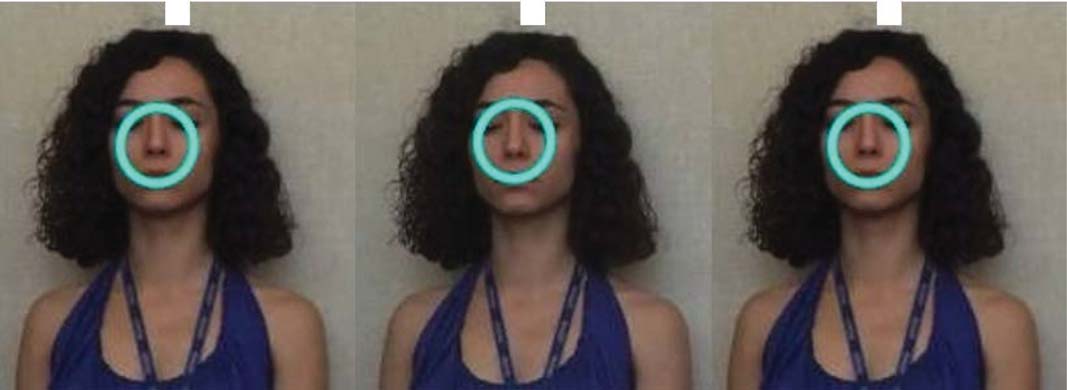
Cifra 1. Stereo pairs. The blue circle indicates a virtual object rendered in front of the surface of a real object
(the face). En este caso, the binocular disparity cue and the occlusion cue provide consistent information, permitiendo
the virtual object to be perceived unambiguously as being in front of the person’s face.
To view the image in this figure (as well as those in Figures 2, 4, y 7) in stereo without the aid of any
stereoscopic viewing equipment, the reader is advised to free fuse the images, using the white squares at the top
as a fixation point. Depending on which method the reader finds easier, either a) cover the right image and, mientras
observing the left pair, allow your eyes to relax, as if looking into the distance, until the two images fuse into one
(parallel fusing); or b) cover the left image and, while observing the right pair, cross (es decir., converge) your eyes until
the two images fuse into one (cross fusing).
4
Our X-Ray AR System
To expand the potential application areas of X-ray
vision with stereoscopic displays, while offering a viable
compromise between depth perception, información
preservación, and minimal computational expense, nosotros
propose adding random dot patterns (similar to those
used in random dot stereograms) to the surface of real
objects, as explained below.
4.1 Depth Perception and
Stereo-Translucency
In the context of stereoscopic AR displays, cuando un
virtual object is correctly rendered (stereoscopically) en
front of a real object, the binocular disparity cue and the
occlusion cue together provide consistent information,
allowing the virtual object to be perceived unambigu-
ously as being in front, as illustrated in Figure 1.4 En esto
caso, the addition of random dot patterns to the real sur-
face should have no effect on how the virtual object is
perceived relative to the real surface. Sin embargo, in cases
where the virtual image is rendered stereoscopically
behind a real object, even though the binocular disparity
cue is communicating that the virtual object is behind the
real surface, the occlusion cue nevertheless continues to
suggest that the virtual object is in front (Drascic & Mil-
gram, 1996). An example of this situation is depicted in
Cifra 2(a). We refer to this case as being incongruous, como
a consequence of the conflict between these two very im-
portant depth cues—occlusion and binocular disparity.
To aid the observer to contend with the sometimes
perplexing effects of incongruity, and to facilitate percep-
tion of the correct depth order of the virtual object and
the real surface, we propose the addition of random dot
patterns onto the real surface. By comparing Figure 2(b)
con 2(a),5 one should get the impression that perceiving
the virtual object as being behind the surface is easier
4. To view the left and right images in Figures 1, 2, 4, y 7 en
stereo, the reader is advised to free fuse the image pairs provided, como
explained in the caption of Figure 1. Another alternative is to save the
images and view them using stereo vision software and hardware.
5. Tenga en cuenta que, unless the reader is able to view these stereo pair
images stereoscopically, it will not be possible to perceive any differen-
ces with regards to where the virtual object is located relative to the real
surface.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Ghasemi et al. 49
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
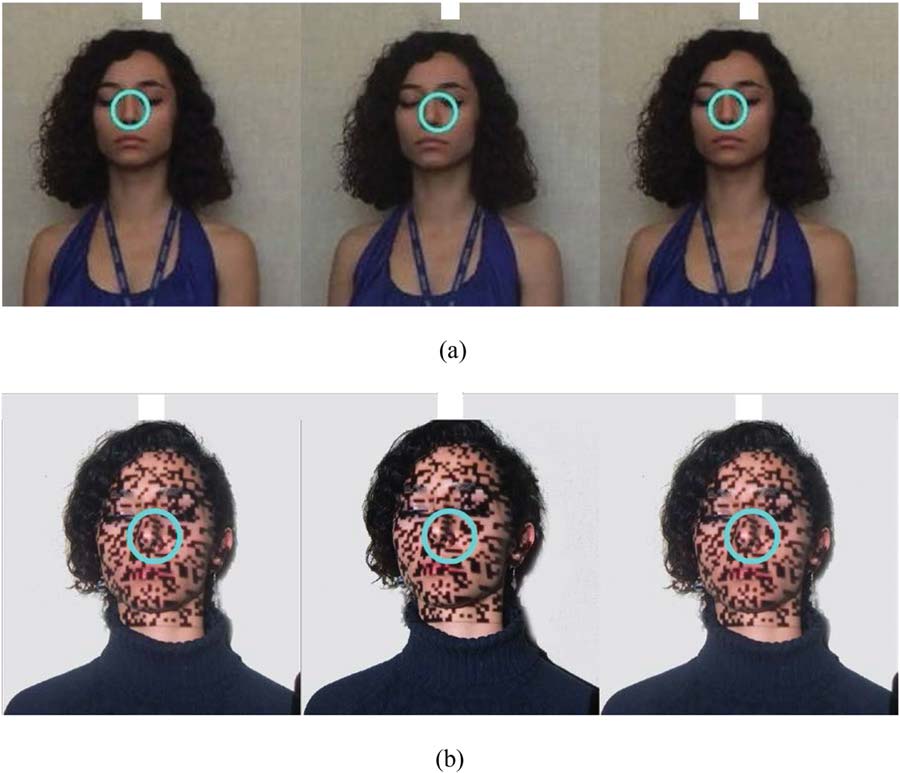
Cifra 2. In both sets of stereo pairs (a) y (b), the blue virtual circle is stereoscopically
rendered behind the face. En este caso, the binocular disparity cue and the occlusion cue provide
inconsistent information leading to a cue conflict: (a) absence of random dot pattern, (b) addition
of random dots onto the face using a projector.
when the random dot pattern is present (Cifra 2[b])
compared to when it is not (Cifra 2[a]).6
6. In addition to the visible textures of real object surfaces (which we
clearly are modifying by means of our superimposed random dot pat-
charranes), for the sake of clarity we also present a framework for categorizing
surfaces that are potentially relevant to our research focus, usando 3 sepa-
rate parameters: one that pertains to the global curvature of the surface
(p.ej., flat vs. non-flat), one that pertains to the presence or absence of
local 3D topological features, and one that pertains to the visible dimen-
sionality of the texture of the surface (p.ej., smooth surfaces vs. surfaces
with 3D elements such as bumps or ridges). The surface of the woman’s
face in Figures 1 y 2, Por ejemplo, would thus be categorized as a
smooth curved (non-flat) surface with 3D topological features (nose, lips,
etc.). Although Figure 2 is provided to demonstrate the general concept
of adding random dot patterns to an easily identifiable surface, it should
be pointed out that the experimental portion of this study (ver figura 5)
specifically focuses on flat surfaces without 3D texture elements and with-
out 3D topological features, because it was expected that adding random
dot patterns would be most effective for such surfaces. Sin embargo, as men-
tioned in Section 9, we have not yet explored whether the addition of
random dot patterns will have comparable effects for real non-flat surfaces
that comprise 3D topological features and/or 3D texture elements.
One explanation for the expected effect is that by add-
ing random dots to the real object’s surface, we can assist
observers in making vergence eye movements (entre
a virtual object and the real surface) and thereby in mak-
ing better depth judgments. By doing so, we should be
able to adjust the reliability, and thus weight, of the bin-
ocular disparity cue such that the observer is more easily
able to perceive the virtual object behind the real surface
(despite the conflicting occlusion cue). Además,
because the virtual object is perceived as being behind
the real surface, which remains visible, observers are able
to perceive the real surface as being ‘‘transparent’’—that
es, X-ray vision.
It is important to clarify the terminology we are using
aquí. Referring to an excellent summary provided by
Tsirlin, alison, and Wilcox (2008), one can consider
transparency to have three different primary manifesta-
ciones: (a) Glass-Transparency, which is essentially what is
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
50 PRESENCE: VOLUME 26, NUMBER 1
observed when light passes through clear materials such
as glass; (b) Translucency, which is what occurs when
light is diffused as it passes through a material and causes
objects to appear less clear on the other side; y (C)
Pseudo-Transparency, which is the result of light passing
through gaps in nontransparent objects, such as lace or
wire fences. Based on Julesz’s definition of Stereo-Trans-
parency, which is Pseudo-Transparency that is perceived
in surfaces defined solely by disparity (Julesz, 1971),
Tsirlin et al. (2008) investigated some of the limits of
this phenomenon, in particular the number of parallel
planes that can be distinguished in a set of overlaid ran-
dom dot stereograms.
With regards to our own research, we have hesitated
to use Julesz’s term to refer to the phenomenon
described above as Stereo-Transparency (or Stereo-
Pseudo-Transparency), due to the fact that the percept is
not due only to binocular disparity, but rather to the
conjunction of both binocular disparity and occlusion
señales. Otherwise stated, what we observe is not due to
light passing through gaps in non-transparent surfaces,
and thus does not fit the accepted constraints of Pseudo-
Transparency. One option is to label the observed phe-
nomenon as Pseudo-Translucency (or Stereo-Pseudo-
Translucency), a term that is further justified by the fact
that virtual objects that are rendered stereoscopically
behind a real surface but nevertheless occlude that sur-
face give the overall impression of a diffuse surface,
somewhat akin to frosted glass. As discussed later on in
this article, sin embargo, we have avoided using the term
‘‘translucency’’ in the subjective judgement components
of our experiments, due to our (perhaps unjustified) pre-
monition that participants would be confused by ques-
tions that are framed using that term. In the remainder
of this article we use the term ‘‘transparency’’ in our dis-
cussion, to reflect the instructions given to participants.
Another hypothesized effect of the addition of a dot
pattern onto a surface is the expected creation of ‘‘holes’’
on the surface wherever the (negro) dots are added. Nuestro
hypothesis is that, when observers are faced with the
aforementioned cue conflict, they are given the impres-
sion of looking through these holes on the real surface
(the dots being the holes) at the virtual object placed
underneath the real surface. Al mismo tiempo, sin embargo,
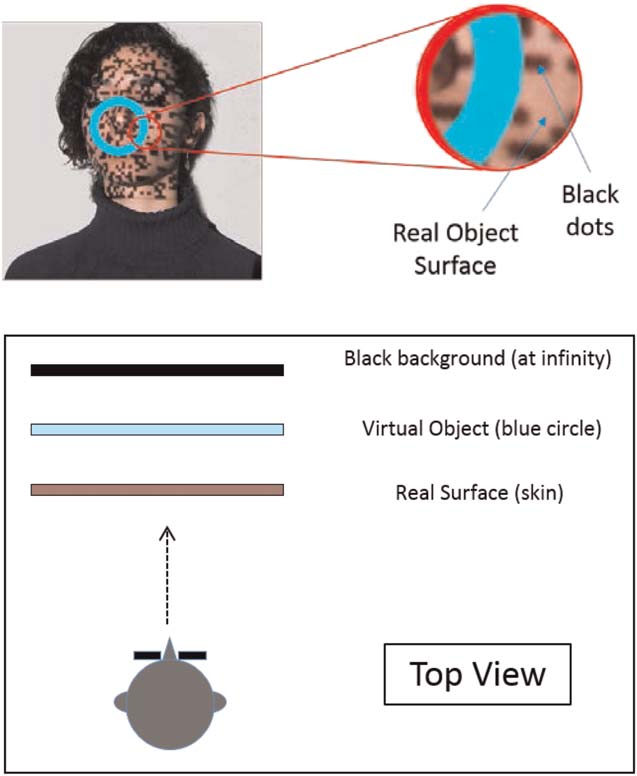
Cifra 3. Possible desired percept when using a dot pattern as a
means of surface manipulation. The top portion of the image shows a
magnified (2D) view of the real surface (skin), which has been altered by
adding a random dot pattern. The lower portion of the image shows the
top view of the observer as he/she would perceive the image once the
desired percept is achieved.
because the non-dotted parts are still occluded by the
virtual object while remaining visible, this adds to the
impression of translucency, as discussed above.
Además, by using a uniform color for the dots in the
dot pattern (as shown in Figure 2[b]), we postulate that
a potential consequence of the virtual object occluding
the dots may be the illusion of a uniform background, de
the same color as the dots,7 lying behind the virtual
object, within the real object. As explained in Figure 3,
our reasoning here is that, in contrast to the non-dot
portions of the pattern, which retain all of the original
surface information, the black dot portions contain
ninguno. Como consecuencia, it may be possible for an observer
7. En otras palabras, although our discussion here refers to a black
background caused by the addition of black dots, that background
could be any color.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Ghasemi et al. 51
to perceive all of the black dot part of the image as
belonging to a large black background. This percept is
likely to be reinforced further by the portions of the
black background that are occluded by the virtual object
that is clearly in front of that background.
4.2 Information Preservation
Although other patterns such as a checkerboard
may also achieve the impression of transparency, using a
random dot pattern allows for independent experimental
control over not only the size of the black dots but also
the density.8 Furthermore, compared to regular pat-
charranes, the randomness of these patterns is intended to
aid users in focusing their attention on the surface rather
than the pattern itself. En otras palabras, the use of promi-
nent patterns that take on a character of their own may
lead to adding visual noise rather than enhancing the
overall effectiveness of the presentation (Interrante,
1996).
4.3 Computational Costs
Since presentation of the real surface requires no
image processing steps other than the overlaying of the
random dots, computational costs can be minimized.
Eso es, unlike the use of grid lines and strokes for add-
ing texture (Interrante et al., 1997), one does not need
to have a model of the real object. The only extra step is
to render the black dots of the pattern at depths corre-
sponding to points on the real surface, which can be
done by either using a projector to project a pattern onto
the surface, or by using a depth map obtained from
stereo pair images.9
8. From a practical point of view, since the pattern is random, el
user of such a display system could be provided with the means to easily
adjust the parameters of the random-dot mask (such as dot size, dot
density, dot distribution, etc.) in order to preserve the visibility of
desired parts of the real surface.
9. It is important to distinguish between different extents to which
one can model a real object surface. In the present case, we are consider-
ing a point cloud depth map obtained from scanning a real surface, o
from performing stereo matching, to comprise a minimal extent of
modeling that surface, in contrast to more extensive models that
involve quantitative relationships among all, or most, components of
the object.
5
Experiment Hypotheses
Despite these features, our method is nevertheless
similar to the other proposed techniques in that it
involves a trade-off between depth information and sur-
face preservation. As part of our effort to explore that
trade-off, and thereby the effectiveness of this method in
dealing with the challenges of X-ray vision with stereo-
scopic AR, the following section presents the results of
an experiment to determine the effect of dot size and dot
density on both of the dependent parameters of per-
ceived transparency (related to perception of depth
información) and preservation of real object surface
información.
Our first hypothesis (H1), based on our reasoning
about the perceptual mechanisms at play, was that
when virtual objects are stereoscopically rendered
behind but very close to the real surface, the addition of
random dot patterns can lead to disambiguation of the
depth order between the virtual object and the real
surface.
Además, we hypothesized (H2) eso, whereas on
the one hand it should be easier relative to the No Pat-
tern conditions tested to perceive transparency whenever
random dots are added (H2a), on the other hand surface
information should be easier to preserve for the No Pat-
tern condition, for which there are no random dots to
interfere with examining the surface (H2b).
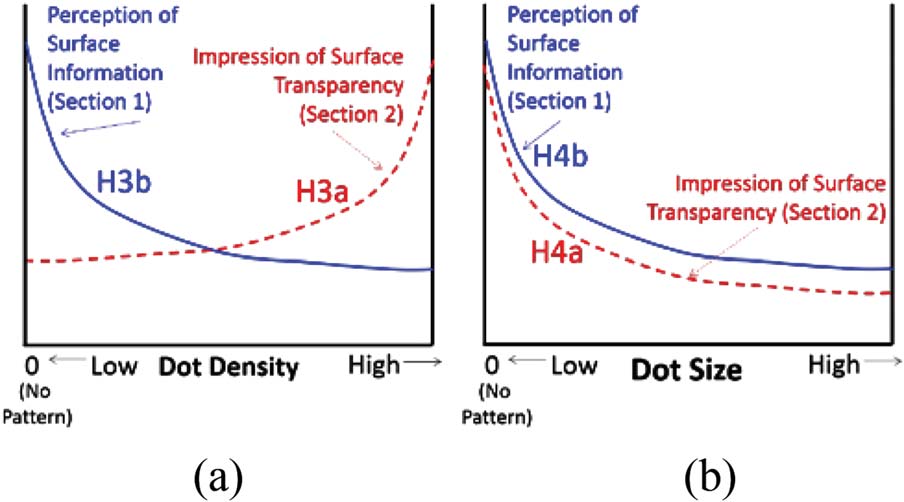
We also hypothesized (H3) that increasing the
dot density of the pattern would result in a stronger
impression of transparency (H3a) but a reduction in
preservation of surface information (H3b). La razón-
ing behind this is that, as explained above, the black
dots are expected to give the impression of there being
‘‘holes’’ in the surface, such that with more holes in the
surface, it should be easier to see through it (es decir.,
more perceived transparency) but harder to retain
information about the portions of the surface with the
black dots.
Por otro lado, it was also hypothesized (H4) eso
increasing the dot size (which is not the same as increas-
ing the dot density) should lead to a weaker sense of
transparencia (H4a), since larger dots will yield a larger
area of coherent surface information that is occluded by
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
52 PRESENCE: VOLUME 26, NUMBER 1
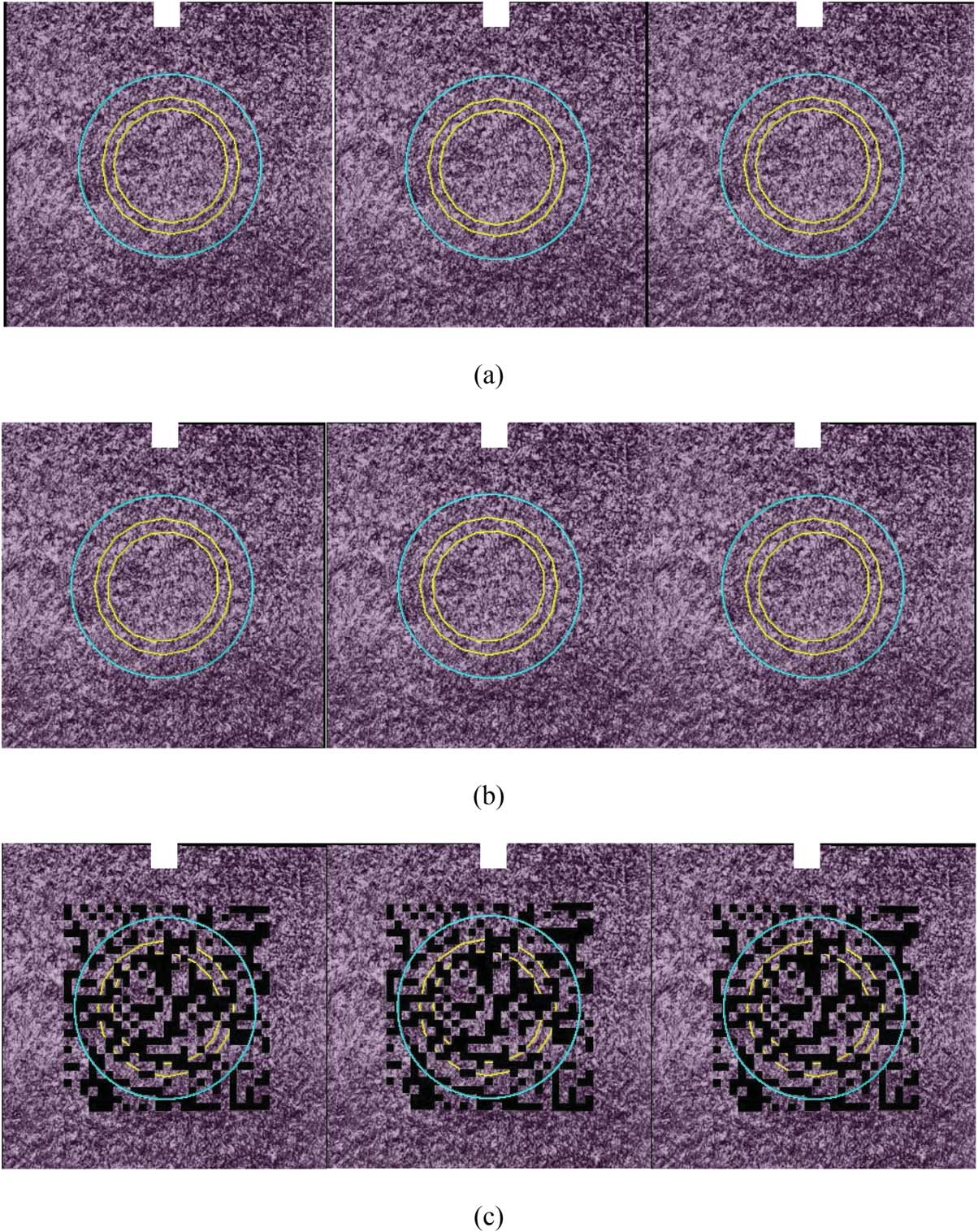
Cifra 4. Example of a stimulus used in the experiment. The blue circle indicates a virtual object rendered beneath a textured
purple surface, which has been modified through the addition of a pattern of random black dots.
the virtual object. Además, those larger chunks of
coherent surface information being occluded by the pat-
tern were expected to lead to a reduction in surface in-
formation preservation (H4b).
to investigate the trade-off involved in perceiving the
impression of transparency while also preserving surface
información.
6
Overview of Experiment
In investigating the effect of dot size and dot den-
sity on the ability to perceive both depth and surface in-
formación, it is important to use an appropriate distance
between the real surface and the virtual object, such that
the virtual object can easily be perceived as being behind
the real surface. En otras palabras, our primary objective
here was not to examine participants’ ability to discern
different distances between the virtual object and the real
object surface. Bastante, our objective was first to ensure
that participants would be able to perceive that the vir-
tual object was behind the surface (H1), and then to
explore the factors that influenced the resulting sense of
the transparency of that surface and their ability to per-
ceive information on the object surface (H3 and H4).
Por esta razón, the experiment was done in two
phases. In addition to testing our hypothesis related to
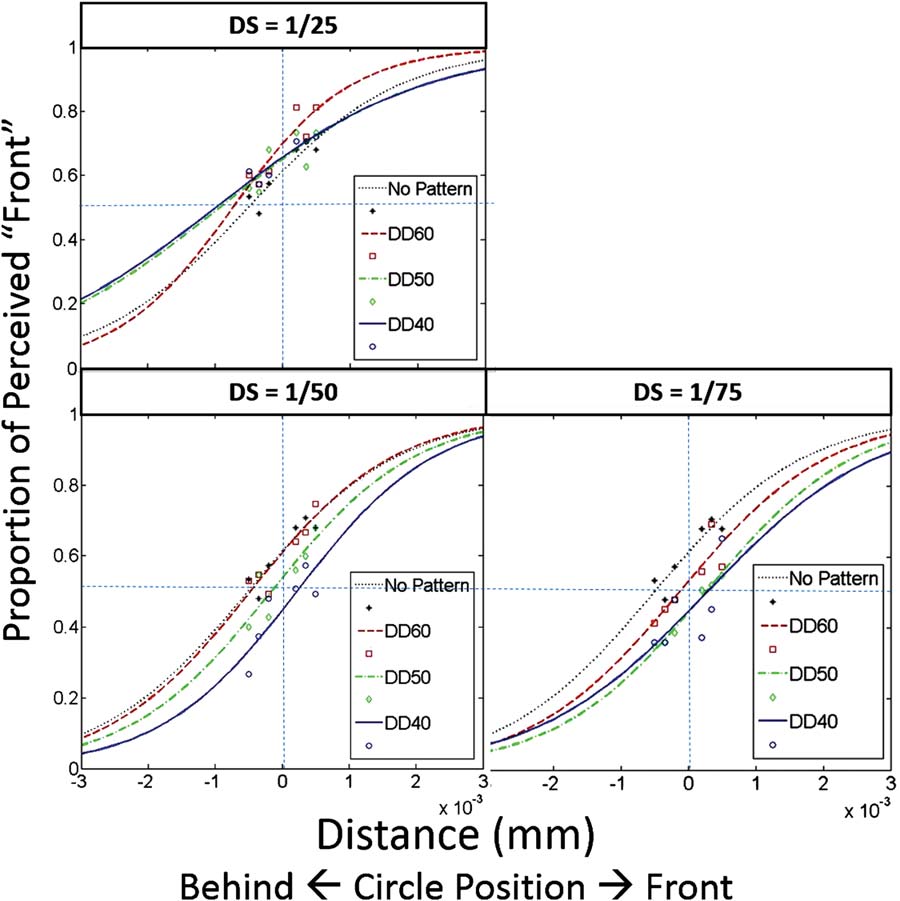
depth order perception (H1), Phase I also aimed to
determine an appropriate distance for placing the virtual
object in later experiments. Al hacerlo, we aimed to
reveal the presence and sensitivity of any perceptual bias
in localizing the virtual object within the vicinity of the
real surface. Phase II, por otro lado, was designed
6.1 Image Generation and Presentation
An example of the stimuli used in the experiment is
como se muestra en la figura 4, which is a simplified version of the
more general case depicted in Figure 2, but with the
complex 3D face shown in Figure 2 replaced by a
(purple) textured plane perpendicular to the line of
sight. With regards to the apparent similarity here to
stimuli used in an earlier experiment reported by Otsuki
and Milgram (2013), in which a non-textured virtual
surface was used, we note that a primary goal of the pres-
ent experiments was to investigate the effectiveness of
this method when applied to real surfaces (in compliance
with the definition of AR). For our real object, nosotros
employed a colored photo of a real textured surface that
was extracted from a volume of professional photographs
by P. Brodatz (Abdelmounaime & Dong-Chen, 2013;
Brodatz, 1966).10 Al hacerlo, our intention at this
point was that the surface, as shown in Figure 4, would
be flat and would comprise a visible 2D texture (bastante
than a surface comprising 3D topological features and/
or 3D texture elements). Based on the reasoning behind
our idea (as explained in Section 3.2), the absence of 3D
10. These textures are publicly available in support of research on
image processing and image analysis.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Ghasemi et al. 53
topological features and 3D texture elements on this sur-
face was intended to provide us with the means of evalu-
ating our solution for these specific surface types. Such a
surface can be considered analogous to the smooth sur-
face of organs containing 2D marks, spots or vessels.11
Once the random dot patterns were generated (como
explained below) and overlaid onto the real surface, todo
images were rendered stereoscopically using a desktop
computer (Windows 7 Professional OS with NVIDIA
Quadro 600), coded using Visual Cþþ 2010 y
OpenGL. The stimuli were presented to participants on
a 23-inch LCD screen (ASUS VG236HE, 1920 (cid:2) 1080
resolution, 120-Hz refresh rate). Stereo images were
observed using the NVIDIA 3D vision system with 3D
Vision 2 glasses.
For all trials, the real object surface with the random
dot pattern was presented at the same depth as the dis-
play surface (es decir., with zero disparity).12 The blue virtual
circle, por otro lado, was rendered at different
depths, based on an equivalent parallel camera orienta-
ción, depending on the particular stimulus presentation.
The on-screen horizontal disparities for the circle were
calculated based on a fixed viewer-to-display distance of
40 cm and an assumed average inter-pupillary distance
de 65 mm. To prevent the use of the relative size depth
cue, the diameter of the circle was kept constant, en 187
píxeles, regardless of the distance from the surface. El
line width of the circle was also kept constant, en 2 píxeles.
Together with the selection of the real surface, outlined
arriba, the color and line width of the virtual circle were
chosen such that the stimuli as a whole could be consid-
ered analogous to a partial endoscopic view of an organ
with a virtual vessel rendered beneath the surface.
In keeping with our goal of investigating the case of
incongruous AR displays in this experiment, no occlu-
sion cues were present in the stimuli. En otras palabras, como
seen in Figure 4, the blue virtual circle covered all parts
of the image—even though it was stereoscopically ren-
dered behind the surface.
11. Medical applications of X-ray vision are considered as one of the
most important application areas of near-field AR.
12. Because the real object surface was flat and was rendered with
zero disparity for the present experiment, it was functionally equivalent
to a monoscopic image.
In both phases of the experiment the random dot pat-
terns were generated using the MATLAB function
‘‘rand.’’ In all cases, the textured surface was square, con
an area of 334 (cid:2) 334 píxeles, and the area of the random
dot pattern, also square, era 148 (cid:2) 148 píxeles.
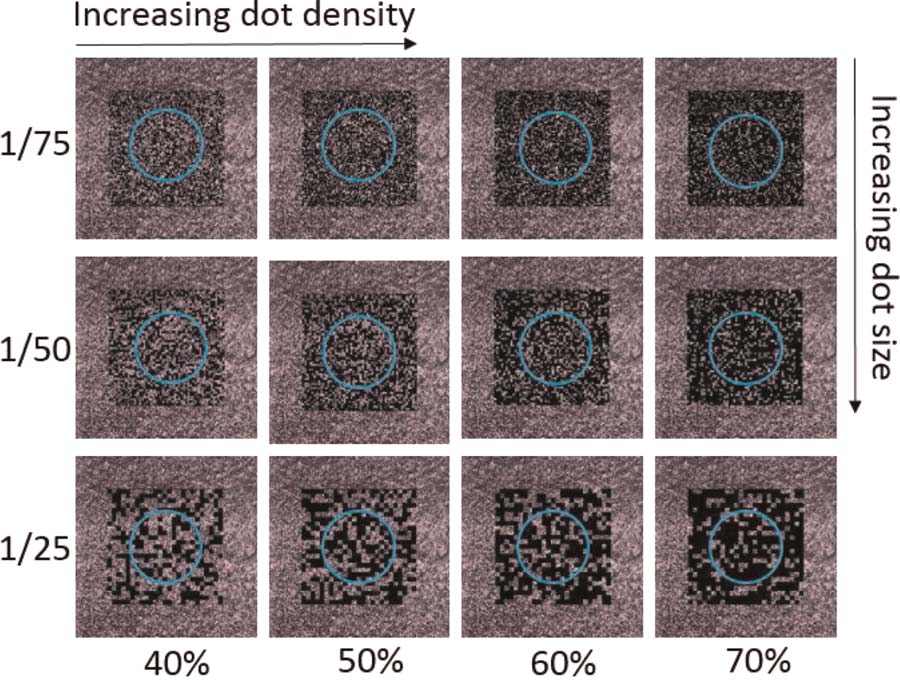
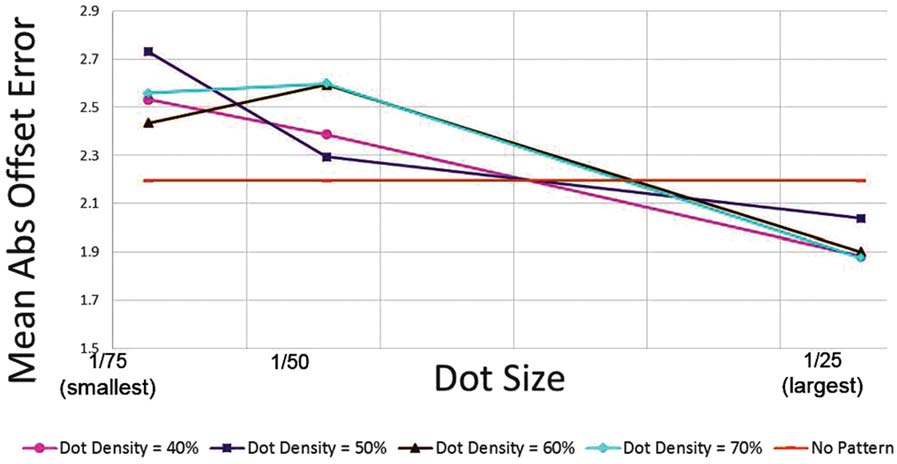
Dot size (DS) and dot density (DD) were varied
throughout both phases of the experiment, as illustrated
En figura 5. The parameter that we are calling dot size
debería, technically speaking, be referred to as ‘‘relative
dot size,’’ since it refers to the fraction into which each
dimension was divided, rather than the actual physical
size of the dots. Por ejemplo, a (relative) dot size of
1/25 means that a 25 (cid:2) 25 grid was used to generate
the random dot pattern. For our 148 (cid:2) 148 grid, a dot
tamaño de 1/25, Por ejemplo, therefore meant that each dot
had an area of 6 (cid:2) 6 píxeles. Dot density, en el otro
mano, refers to the percentage of the entire random pat-
tern area that was covered with dots. It should be noted
that these two parameters are independent of each other.
In addition to the stimuli presented in Figure 5, a ‘‘no
random dot pattern’’ condition was also presented.
6.2 Participantes
For each phase of the experiment, 15 estudiantes
from the University of Toronto were recruited, all 18–
39 years old (7 masculino y 8 female for Phase I, y 12
masculino y 3 female for Phase II). All participants either
had normal visual acuity or used corrective devices to
achieve normal visual acuity during the experiments. A
confirm the absence of any stereoscopic vision problems,
the NVIDIA 3D stereo vision test was administered.
Participants of Phase I were precluded from participating
in Phase II to prevent learning effects. As compensation,
participants were each paid $15/hour. 7 Experimento: Phase I 7.1 Objectives and Hypotheses The aim of this phase of the experiment was to test the basic premise of X-ray vision—whether adding ran- dom dot patterns is indeed able to facilitate the percep- tion of an incongruous virtual object located behind a real surface. At a more detailed level, the aim was to l D o w n o a d e d f r o m h t t p : / / directo . mi t . / e d u p v a r / a r t i c e – pdlf / / / / / 2 6 1 4 2 1 8 3 6 4 5 3 p r e s _ a _ 0 0 2 8 6 pd . f por invitado 0 7 septiembre 2 0 2 3 54 PRESENCE: VOLUME 26, NUMBER 1 Cifra 5. Stimuli used for Phase I and II. Only the 9 stimuli in the 40, 50, y 60% columns were used in Phase I. Todo 12 stimuli were used in Phase II. investigate both accuracy, in terms of determining the presence of any perceptual bias in localizing the virtual circle within the vicinity of the real surface, as well as pre- decisión, in terms of estimating the sensitivity of perceiving the location of the circle. To perform this experiment, the psychophysical method of constant stimuli was used (Gescheider, 2013), comprising a series of trials in which the virtual circle was presented at different distances both in front of and behind the real surface. Expanding further upon hypothesis H1 outlined ear- lier, it was hypothesized that, because all portions of the virtual circle were always visible in the image (as opposed to portions of it being occluded by the real object sur- rostro), the participants would be biased toward perceiving the virtual circle as being closer to the viewer in compari- son with its actual geometric location, as defined by its imposed stereoscopic disparity. En otras palabras, cuando- ever the virtual circle was presented, by means of on- screen disparity, to be in front of the real surface, it was hypothesized that this would be unambiguously per- ceived as such. Sin embargo, whenever the circle was ren- dered to be behind the real surface, we hypothesized (H1a) that it would be perceived to be closer to the sur- face than its actual distance behind it. Además, considering our postulate that the addition of random dot patterns can lead to disambiguation of the depth order between the virtual object and the real surface, we predicted that, in cases where the random dot pattern was present, participants would be more likely to determine the virtual circle’s position correctly (H1b). In addition to testing the above hypotheses, a second goal of this phase of the experiment was to determine an appropriate depth for posterior positioning of the virtual circle for Phase II of the experiment, to permit compen- sation for the predicted bias. En otras palabras, our aim was to increase the probability that participants in Phase II would consistently perceive the virtual circle as being placed behind the real surface. 7.2 Procedure After getting acquainted with the software, participar- pants were shown a series of stimuli, to each of which l D o w n o a d e d f r o m h t t p : / / directo . mi t . / e d u p v a r / a r t i c e – pdlf / / / / / 2 6 1 4 2 1 8 3 6 4 5 3 p r e s _ a _ 0 0 2 8 6 pd . f por invitado 0 7 septiembre 2 0 2 3 Ghasemi et al. 55 they responded whether they perceived the circle as being in front of or behind the surface. The virtual circle was presented at 6 distances relative to the surface, three in front and three behind. Relative to the physical setup of our experiment, the values used, all in mm, eran {þ0.2, þ0.35, þ0.5} in front and {(cid:3)0.2, (cid:3)0.35, (cid:3)0.5} behind. (These distances were equivalent to disparity angles of {(cid:3)0.24, (cid:3)0.49, (cid:3)0.7} (in front) y {þ0.24, þ0.49, þ0.7} (behind), in units of arc-minutes.13) These values were selected based on pilot studies per- formed using the three dot sizes {1/25, 1/50, 1/75} and the three dot densities {40%, 50%, 60%}, as well as the ‘‘no random dot pattern’’ condition. The objective in choosing these particular values was to maximize the sen- sitivity for identifying the associated thresholds of depth perception, while avoiding any ‘‘floor’’ and ‘‘ceiling’’ effects associated with 100% certainty judgments. Con 5 trials for each combination of conditions, this led to 300 ensayos (6 (cid:2) (3 (cid:2) 3 þ 1) (cid:2) 5) for each partici- pant. The stimuli containing the random dot patterns used are shown in the first three columns of Figure 5. The presentation order of the stimuli was randomized. Participants had 4 seconds to reply to each presentation. (This time limit was chosen through extensive pilot test- En g, to reduce speed-accuracy trade-off effects.) If partic- ipants ran out of time for a particular stimulus, the sub- sequent stimulus would appear automatically, but the missed trial would reappear, unbeknownst to partici- pants, later on in the experiment. This would occur as many times as required until the participant had success- fully replied within the time limit for that stimulus. 7.3 Results and Discussion Figure 6 shows the results obtained from Phase I, where each curve represents a psychophysical function 13. The disparity angles were obtained from the equation r ¼ (d*I)/(D*(Dþd)) where r, d, I, and D correspond respectively to dis- parity angle, predicted depth, inter-pupillary distance, and viewing dis- tance (Patterson, 2009). Note that because the units in both the nu- merator and denominator of this equation cancel each other, the disparity angle, r, expressed here in arc-minutes, is dimensionless. Note as well that reporting disparity values when presenting results has been recommended by researchers in the 3D community, since it ‘‘affords more efficient and accurate cross-study comparisons’’ (McIntire, Havig, & Geiselman, 2014). fitted to the associated set of experimental data (Gescheider, 2013). It should be recalled that only the 9 stimuli in the 40, 50, y 60% columns of Figure 5 were used in this phase of the experiment. The y-axis in Figure 6 represents the proportion of times that the circle was perceived as being in front of the surface, averaged over participants. The x-axis represents the actual position of the circle relative to the surface. The dashed vertical line indicating x ¼ 0 (mm) corresponds to the Point of Objective Equality—that is, el (hypothetical) case for which the circle would be placed exactly at the depth of the real surface.14 For comparison purposes, the same set of results for the ‘‘No Pattern’’ condition have also been included in the graphs for all three dot size conditions. Looking first at the No Pattern results, we see clearly that the Point of Subjective Equality (PSE), defined as the intersection of each fitted psychophysical function with the 0.5 proportion level (shown as a dashed hori- zontal line in Figure 6) lies at 0.493 mm behind the plane of the real surface. What this means is that if the virtual circle had been placed at this (interpolated) dis- tance behind the real surface, participants would have perceived it 50% of the time as being in front of and 50% of the time behind that location. En otras palabras, the point of subjective equality, referring to the hypothetical location at which participants believed on the average that the surface was located (the POE) was closer (more proximal) to the participants than its actual location at 0.493 mm behind the real surface. This result was thus in support of our hypothesis H1a. Referring now to the random dot pattern responses, for all relative dot sizes there does not appear to be any obvious differences among the three dot density (DD) graphs. Por otro lado, for the DS ¼ 1/25 graph, the PSE appears clearly to be behind the surface, for all three DD values. Sin embargo, for the other two DS values (1/50 y 1/75), the PSE values appear to be very close to 0. By comparing the random dot pattern psychophysical functions to those of the No Pattern condition, one can observe that the PSE values for the two dot sizes of 1/50 y 1/75 lie closer to zero than for the No Pattern condition. These observations suggest that, unless larg- 14. Note that this condition was not in fact part of the stimulus set. l D o w n o a d e desde h t t p : / / directo . mi t . / e d u p v a r / a r t i c e – pdlf / / / / / 2 6 1 4 2 1 8 3 6 4 5 3 p r e s _ a _ 0 0 2 8 6 pd . f por invitado 0 7 septiembre 2 0 2 3 56 PRESENCE: VOLUME 26, NUMBER 1 l D o w n o a d e desde h t t p : / / directo . mi t . / e d u p v a r / a r t i c e – pdlf / / / / / 2 6 1 4 2 1 8 3 6 4 5 3 p r e s _ a _ 0 0 2 8 6 pd . f por invitado 0 7 septiembre 2 0 2 3 Cifra 6. Psychophysical functions fitted to results of Phase I. est dot sizes are used, the addition of random dot patterns can help with disambiguation of the depth order between virtual objects and the real surfaces. This result thus sup- ports hypothesis H1b. To determine the minimum distance that would ensure that the participants would ‘‘reliably’’ perceive the virtual circle as being behind the real surface, a maxi- mum error frequency of 25% was chosen. Amongst the 10 condiciones, the largest distance corresponding to the intersection of the fitted psychophysical functions with the 0.25 proportion level belongs to the largest relative dot size (1/25) and smallest dot density (40%), and is equivalent to 2.68 mm behind the real surface. Allá- delantero, for the next phase of the experiment, as long as the displacement chosen places the virtual circle beyond this distance behind the real surface, one could be confident that the circle would be consistently perceived as being placed behind the real surface (with a maximum error frequency of 25%, for the DS ¼ 1/25, DD ¼ 40% condi- ción, and a much smaller error frequency for all of the other conditions. De hecho, to reduce the error frequency further, the blue virtual circle was presented even farther away, at a distance of 3 mm (equivalent to 4.16 arc- minutos) behind the screen/surface for the next phase of the experiment.15 8 Experimento: Phase II 8.1 Objectives, Hypotheses, and Procedure As explained above, the goal of this phase of the study was to investigate the trade-off involved between 15. Care was taken not to place the virtual circle too far behind the real surface, by confirming that this value was within Panum’s fusional area, to ensure that binocular fusion would be maintained. Ghasemi et al. 57 concurrently perceiving surface transparency while pre- serving the ability to discern surface information. To accomplish this, the experiment was conducted in two consecutive sections (1 y 2). For both sections, the blue virtual circle was presented at a constant disparity angle of 4.16 arc-minutes, as explained above. The inde- pendent parameters, illustrated in Figure 5, were three relative dot sizes {1/25, 1/50, 1/75} and four dot den- ciudades {40%, 50%, 60%, 70%}, as well as the ‘‘no random dot pattern’’ condition. It is worth pointing out some more of the important differences between the current experiment and an ear- lier set of related experiments reported by our team (Otsuki & Milgram, 2013). In that earlier experiment, although a similar psychophysical test was administered, there was no attempt to employ it to compute an effec- tive location for the virtual object for their subsequent investigation of perceived transparency. This resulted in their placement of the virtual object too close to the real surface to act as a reliable stimulus for exploring the transparency effect in their investigation of the incongru- ous condition. Además, the surface used in that experiment contained no texture, cual, in addition to the fact that it was simulated rather than real, made it somewhat less realistic. Finalmente, there was no attempt in that experiment to explore the ability to discern surface information, and thus to explore the hypothesized trade- off explained below. 8.1.1 Sección 1: Perception of Surface Information. Sección 1 of Phase II aimed to assess the effect of the random dot pattern parameters in terms of any potential loss of surface information. Since the sur- rostro, by itself, did not contain any specific information to be preserved, there was a need to add elements onto the surface. These additional elements were covered by the random dots just as any other surface containing such elements would be (an example of this, once again, could be the surface of an organ containing visible vessels). To investigate how much information was lost due to the addition of the random dot patterns, a shape matching task was designed, to evaluate participants’ accuracy in identifying information presented on the real object’s surface when covered by different random dot patterns. To accomplish this, each real surface was modified by adding to it a pair of concentric yellow shapes, either two circles or a circle and an ellipse, after which the ran- dom dot patterns were added.16 As shown in the exam- ple of Figure 7(C), this means that the black dots occluded different parts of the yellow shapes in different ways, depending on the particular random pattern, just as they occluded the rest of the surface. (Tenga en cuenta que, although the blue virtual circle was still present for the surface information task, and was rendered behind the real surface, it did not play any role in this task.) For all of the surface information stimuli, the outer yellow shape was a circle. Sin embargo, the inner yellow shape had a 30% probability of being also a circle (ver figura 7[a]) o un 70% probability of being an ellipse (ver figura 7[b]). The task was to determine, dentro 6 segundo- onds, whether the inner yellow shape was also a circle, like the outer circle, or whether it was an ellipse—that is, not a circle. To help participants do the shape-matching task, they were advised during their training to visually scan the whole image to examine the separation between the inner yellow shape and the outer yellow circle. En otras palabras, if the two shapes appeared to be equally separated from each other around their circumferences, it was logi- cal to conclude that they were both circles, whereas if the separations appeared to vary, the conclusion should be that one shape was an ellipse. It should be noted that, because we wanted this to be a relatively difficult task, the ellipses were designed to have very small eccentric- ities.17 As can be seen in Figures 7(a) y 7(b), la diferencia- ference between the two surface accuracy conditions was very slight. Keeping in mind our overriding goal of evaluating whether an observer would be able holistically to exam- ine large parts of a real surface while employing our ster- eoscopic AR display, we made the task even more diffi- 16. It should be noted that, although the yellow shapes were digi- tally added to the surface (and not, specifically, captured by a sensor), they were meant to be considered as a ‘‘real’’ feature present on the real object’s surface. 17. De hecho, the ellipses were not obtained according to the formal definition of eccentricity; bastante, the ‘‘ellipses’’ were obtained by multi- plying the x-axis of a corresponding circle by a factor of 0.95. l D o w n o a d e desde h t t p : / / directo . mi t . / e d u p v a r / a r t i c e – pdlf / / / / / 2 6 1 4 2 1 8 3 6 4 5 3 p r e s _ a _ 0 0 2 8 6 pd . f por invitado 0 7 septiembre 2 0 2 3 58 PRESENCE: VOLUME 26, NUMBER 1 l D o w n o a d e desde h t t p : / / directo . mi t . / e d u p v a r / a r t i c e – pdlf / / / / / 2 6 1 4 2 1 8 3 6 4 5 3 p r e s _ a _ 0 0 2 8 6 pd . f por invitado 0 7 septiembre 2 0 2 3 Cifra 7. Samples of stereo pairs illustrating the shape-matching task for assessment of surface information. (a) inner and outer yellow objects are both circles; (b) inner yellow object is ellipse; (a) y (b) constitute the No Pattern condition; (C) example of task with random dot pattern present, and where inner yellow object is an ellipse. The orientation of the major axes of the ellipses in (b) y (C) son 548 (corresponding to level 3) y 1448 (corresponding to level 8), respectivamente. Ghasemi et al. 59 cult by preventing participants from focusing on only one specific region of the stimulus. To accomplish this, the orientation of the major axis of each ellipse was var- ied randomly and, in addition to pronouncing whether any particular stimulus was an ellipse, participants were also asked to identify the direction of the major axis of that perceived ellipse. (This was also intended to reduce the likelihood of guessing the responses.) The orienta- tions could possess any value from 0 a 1808, con 188 intervals, Resultando en 10 possible orientations. If partici- pants perceived the inner yellow object as a circle, they would press the ‘‘up’’ arrow. Por otro lado, if they perceived the inner object as an ellipse, they were asked to indicate, using the numeric keypad, which of the 10 orientations of the major axis of the ellipse they had observed, according to the response selection scheme depicted in Figure 8. For each combination of dot size (DS) and dot density (DD), as well as for the No Pattern condition, 10 trials were randomly presented to each participant, of which 7 were ellipses (con un 10% chance for each orientation, unbeknownst to them) y 3 were circles. This led to a minimum of 130 ensayos ((3 (cid:2) 4 þ 1) (cid:2)10) for each par- ticipant. The presentation order of the stimuli was randomized. None of the shape-matching conditions occurred more than once. The parameter values for the experiment—namely ec- centricity, number of response angles, time limit dura- tion—were selected on the basis of extensive pilot testing. In trials where participants ran out of time, la experiencia- ment would automatically move on to the next stimulus and the missed trial would repeat itself throughout the experiment as many times as required until the partici- pant had replied to all stimuli within the time limit. To motivate participants during the experiment, a lot- tery with a $50 gift card prize was performed after all
experiments were done. The participants were informed
that the number of lottery ballots assigned to their
names would be proportional to their respective per-
formance scores.
For analysis purposes, Signal Detection Theory (SDT)
fue usado (Gescheider, 2013) for assessing performance
on distinguishing circles from ellipses. Además, el
absolute offset errors in detecting the orientation of the
Cifra 8. Options for designating the orientation of the major axis
in ellipse conditions. This image was provided as a guide for assisting
participants in selecting their numerical responses to the ellipse
axis orientation questions.
major axis of the ellipse (using the numerical responses
como se muestra en la figura 8) were averaged across each condition.
Reiterating the reasoning presented in Section 4, fue
hypothesized that as both dot density and dot size
increased, performance on the surface-identification task
would decrease. En particular, it was hypothesized that
d0 values, which are indicative of detection sensitivity,
would decrease, while average absolute offset errors
would increase. The reasoning behind these hypotheses
(H3b and H4b) was that, as relatively greater portions of
the yellow objects were covered by dots, it would be
more difficult to perform the shape-matching task. Para
obvious reasons, the No Pattern condition was expected
to result in the highest sensitivity and lowest average
offset error, since the yellow shapes were completely
unobstructed (hypothesis H2b).
8.1.2 Sección 2: Impression of Surface
Transparency. Sección 2 of the experiment, which was
administered to the same participants directly following
completion of Section 1, focused on exploring the rela-
tive effectiveness of the random dot pattern parameters
for creating the perception of transparency. Prior to
starting this section of the experiment, the purpose of
the research and the concept of ‘‘transparency’’ in the
present context were explained and demonstrated to par-
ticipants. En particular, they were instructed that they
would be shown a set of images similar to that illustrated
here in Figure 4, in each of which the blue wireframe
circle should appear to them to be located behind the
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
60 PRESENCE: VOLUME 26, NUMBER 1
portion of the textured purple surface containing a ran-
dom dot pattern. They were also told that, due to the
manner in which the display had been created, fue
likely that they would perceive the textured purple sur-
face as being transparent,18 and that the goal of this part
of the experiment was to explore the manner in which
they perceived this transparency effect.
Because we did not consider it feasible to estimate in a
direct and objective way how participants would be able
to perceive ‘‘transparency’’ in the present context, nosotros
instead deemed Thurstone’s classical method of paired
comparison scaling (Thurstone, 1927) to be the most
viable means of achieving this end. During the data gath-
ering phase, participants were presented with all possible
pairs of the images shown in Figure 5 (plus the No Pat-
tern condition), two at a time. They had unlimited time
to examine each pair of images and to respond to the
pregunta: ‘‘In which image is the impression of transpar-
ency more convincing?’’ The 13 different conditions (3
dot sizes (cid:2)4 dot densities þ no pattern condition)
resulted in 78 paired comparisons for each participant,
which were then transformed into an (equal interval)
scale of transparency ratings (TR).
It should be pointed out that the question presented
to participants was designed such that, rather than asking
directly about the perceived ‘‘degree’’ of transparency,
the relative strength of their impression about transpar-
ency was instead being questioned. It is also important to
realize that there is no real zero on the equal interval
scale of values resulting from this procedure, such that
high or low comparative impressions of transparency do
not necessarily translate to high or low absolute ratings of
degree of transparency.
Based on previous findings (Otsuki & Milgram,
2013), it was hypothesized that larger dot densities and
smaller dot sizes would lead to higher ratings for impres-
sion of transparency (hypotheses H3a and H4a, respetar-
activamente), and in addition that the No Pattern condition
would yield the lowest rating (H2a). One explanation
for this is that the black dots in the random dot pattern
were postulated to be perceived as the presence of holes
in the surface, such that, by increasing dot density, el
increased number of perceived holes should lead to a
stronger sense of transparency. Por otro lado, él
was surmised that increasing the dot size would lead to a
weaker sense of transparency, since the resulting lower
resolution of the unaffected portions of the surface (es decir.,
the non-black dot portion of the pattern) would yield a
lower number of reference points for where the virtual
object is. Based on the same reasoning, it was expected
that the control condition comprising no pattern would
result in the lowest transparency ratings (hypothesis H2a).
It should be noted that the extra 70% dot density con-
ditions that were added to this phase were a result of
pilot tests, which led to the prediction that including
these conditions would potentially provide a better man-
ifestation of the expected trade-off, explained in the next
subsection.
8.1.3 Hypothesized Trade-Offs. Before examin-
ing the results of the experiment, it is important to
understand the relationship between the various hypoth-
eses presented for the two sections. Cifra 9 resume
those respective hypotheses and illustrates our a priori
expectation about the relationship between them. El
primary message to be extracted from Figure 9(a) es el
trade-off between what we believe to be the two primary
objectives of augmented reality X-ray vision: effectively
presenting the impression of a virtual object being inside
of a real object (es decir., effectively equivalent to conveying
the impression of surface transparency) while concur-
rently maintaining the ability to observe and understand
any pertinent information on the surface of that real
object (es decir., perception of surface information). Cifra
9(b), por otro lado, suggests that having smaller
dots should always have the effect of better perceiving
surface transparency, while also retaining surface infor-
formación. The results presented in the following section
should be read in light of these two sets of hypotheses.
18. Tenga en cuenta que, as explained earlier, we avoided using the term
‘‘translucency’’ for this experiment, based on our sense that participants
might be confused by that term.
As mentioned, to assess participants’ performance
in detecting ellipses, signal detection theory (SDT) era
8.2 Results and Discussion
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Ghasemi et al. 61
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Cifra 9. Schematic illustration of hypotheses for both parts of Phase II: (a) effect of dot density
(H3); (b) effect of dot size (H4).
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 10. d0 and transparency rating (TR) results obtained from Phase II. The solid lines show
the d0 results, corresponding to the left-hand axis, while the dashed lines join the transparency
ratings (TR), corresponding to the right-hand axis. The yellow horizontal lines correspond to the
No Pattern condition.
usado, where the occurrence of an inner ellipse was con-
sidered a ‘‘signal’’ event, and a ‘‘hit’’ occurred whenever
an ellipse was correctly detected as an ellipse.19 To
19. Although there were 10 possible response angles (es decir., orienta-
ciones) for the elliptical signal conditions, it is important to note that
these were all considered as having equivalent signal strengths. En otra
palabras, our assumption was that there was one single value of d0 for the
signal present case, en vez de 10 different signal strengths.
obtain a set of average performance data over all partici-
pants, hits and false alarm rates were aggregated across
participants and then used to estimate the two collective
SDT parameters, d0 and beta, for each condition. The d0
results for different dot sizes and dot densities are shown
as solid lines in Figure 10.
The transparency rating (TR) measures are also pre-
sented in Figure 10, as dashed lines. The No Pattern
62 PRESENCE: VOLUME 26, NUMBER 1
Cifra 11. Mean absolute offset errors as a function of dot size and dot density. The orange
horizontal line corresponds to the No Pattern condition.
condition results supported our hypothesis (H2a) de
having the lowest TR value. (Por conveniencia, this value
was assigned a value of zero on the scale derived from
the paired comparison data.) Sin embargo, we were unable
to obtain a clear trend for the remaining TR values for
different dot sizes and dot densities (H3a and H4a).
Comparing these results to those of Otsuki and Milgram
(2013), who carried out an analogous test for DD ¼
25% y 50%, it is suspected that designing our experi-
ment with lower dot densities (< 40%) might have
allowed us to observe the hypothesized increasing trend
of TR values with increased dot density, as depicted in
Figure 9. Nevertheless, the substantial difference
between the TR value for the No Random Dot Pattern
condition and the TR values for the pattern conditions
in support of hypothesis H2a demonstrates at least to
some extent the potential effectiveness of this method
for creating the percept of transparency.
With regards to discerning surface information, it was
hypothesized that with increases in both dot density and
relative dot size, performance on the detection task
should decrease (hypotheses H3b and H4b). This
appears to have been supported by the results shown in
20. It is important to note that ‘‘good performance’’ is manifested
in Figure 10 by d0 values in the vicinity of 1, whereas d0 values in the vi-
cinity of 0 (and below) represent essentially chance performance. This
suggests that the difficulty of the shape-matching task may have been
too high.
Figure 10, where the d0 values do in fact decrease with
increases in both DS and DD.20 The No Random Dot
Pattern condition also conforms to the expectation of
yielding the highest d0 value (hypothesis H2b).
The averages of the absolute offset errors for the
ellipse orientation task were plotted as a function of dot
size and dot density (see Figure 11). As can be seen, the
effect of dot density does not seem to contribute much
to the variance. Dot size, however, does seems to have
had an effect on the error, with the largest dot size
(1/25) leading to smaller mean offset errors, even when
compared to the No Pattern condition. To check the
significance of this finding, a two-way ANOVA was car-
ried out, followed by post hoc tests. Results showed that
average offset errors were indeed significantly affected by
the dot size, F(2,28) ¼ 16.37, p < .0001 but not by
dot density, F(3,42) ¼ 0.329, p > .05. Contrasts
revealed that average offset errors for the 1/50 dot size,
F(1,14) ¼ 18.55, y el 1/75 dot size, F(1,14) ¼
22.34, were significantly larger than those of the 1/25
dot size.
This interesting finding may initially seem to contra-
dict the SDT results, which showed d0 values reflecting
essentially chance performance for the 1/25 y 1/50
dot size conditions. This makes sense since the larger the
dot sizes, the larger the chunks of surface information
that were being covered by the pattern and thus the
more difficult the task (leading to lower sensitivity).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Ghasemi et al. 63
Offset error results, por otro lado, reveal that in
cases where participants were correctly able to detect the
ellipse, the larger black dots, which are accompanied by
larger non-black dots, allowed for more accurate predic-
tions of the major axis orientation of the ellipses (es decir.,
lower average absolute offset errors). These findings sug-
gest that, in cases where a holistic view of the real surface
is not required, it may be better to use larger dot sizes to
enhance the percept of transparency. Además, el
presence of (grande) dot patterns may in fact prove benefi-
cial in estimating distances/shapes, considering the
smaller offset errors obtained for the 1/25 dot size con-
condición, compared to the No Pattern condition.
9
Conclusions and Limitations
Results from this set of experiments showed that
the use of random dot patterns can be effective in con-
tributing to the percept of transparency of real surfaces
in 3D AR displays, with expected relevance toward
X-ray vision applications. En particular, our results from
Phase I of the experiment were successful in demonstrat-
ing that it is indeed possible to disambiguate the depth
order between virtual objects and real surfaces by means
of using such patterns as an add-on feature to surfaces
with periodic textures that lack 3D elements. Además,
our results indicated that by appropriately controlling
the relative dot size and dot density of the patterns, él
should be possible to retain sufficient information about
the real surface to enable a user both to observe a virtual
object being presented inside of a real one, while concur-
rently examining the surface of the real object.
It is important, sin embargo, to point out that the series of
experiments presented here were limited to the use of a
flat real surface with a periodic nondirectional21 texture,
and to a 2D wireframe virtual object being presented in
profundidad. Although these are easy to manipulate digitally,
such constraints are rare in actual AR applications.
Además, an important factor to consider is the
range of distances between the virtual object and the real
surface for which this method will prove to be effective.
21. A nondirectional texture is one whose appearance does not
depend on the direction from which one is observing it.
Por lo tanto, it should be pointed out that the results pre-
sented here are intended to serve as a relatively early step
in a series of experiments that will go beyond these spe-
cific fixed conditions. In the following phase of the
investigación, the goal will be to extend the application of this
method to overlaying 3D solid objects onto stereo
images taken from different curved surfaces, while also
considering the effect of varying the distance between
the virtual object and the real surface. Doing so will
allow us to assess the generalizability of these results to
actual AR applications, both in terms of feasibility of
implementation as well as overall effectiveness. Addition-
ally, since the experiments in this article involved the use
of only one periodic surface texture without any 3D top-
ological features or 3D texture elements, it is important
to scientifically determine whether the results observed
for our flat, real surface (and for the non-flat surfaces
currently being investigated) will pertain also for real
surfaces that do comprise non-periodic textures and/or
3D topological features and/or 3D texture elements.
Expresiones de gratitud
This research was supported by the Canadian Natural Sciences
and Engineering Research Council (NSERC), as well as by the
Italian Institute of Technology (IIT), Genova, Italia.
Referencias
Abdelmounaime, S., & Dong-Chen, h. (2013). New Brodatz-
based image databases for grayscale color and multiband tex-
ture analysis. ISRN Machine Vision.
Avery, B., Sandor, C., & tomás, B. h. (2009, Marzo).
Improving spatial perception for augmented reality X-ray
visión. Proceedings of the IEEE Virtual Reality Conference,
79–82.
Azuma, r., Baillot, y., Behringer, r., Feiner, S., Julier, S., &
MacIntyre, B. (2001). Recent advances in augmented reality.
IEEE Computer Graphics and Applications, 21(6), 34–47.
Bajura, METRO., Fuchs, h., & Ohbuchi, R. (1992, Julio). Merging
virtual objects with the real world: Seeing ultrasound im-
agery within the patient. ACM SIGGRAPH Computer
Graphics, 26(2), 203–210.
Bichlmeier, C., Wimmer, F., Heining, S. METRO., & Navab, norte.
(2007, Noviembre). Contextual anatomic mimesis hybrid
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
64 PRESENCE: VOLUME 26, NUMBER 1
in-situ visualization method for improving multi-sensory
depth perception in medical augmented reality. Actas
del 2007 6th IEEE and ACM International Symposium on
Mixed and Augmented Reality (ISMAR), 129–138.
Johnson, l. GRAMO., Edwards, PAG., & Hawkes, D. (2003). Surface
transparency makes stereo overlays unpredictable: lo implícito-
cations for augmented reality. Studies in Health Technology
and Informatics, 131–136.
Brodatz, PAG. (1966). Textures: A photographic album for artists
Johnston, mi. B., Cumming, B. GRAMO., & parker, A. j. (1993).
and designers. Nueva York: Dover Publications.
Coutant, B. MI., & Westheimer, GRAMO. (1993). Population distri-
bution of stereoscopic ability. Ophthalmic and Physiological
Optics, 13(1), 3–7.
Cutting, j. MI., & Vishton, PAG. METRO. (1995). Perceiving layout and
knowing distances: The integration, relative potency, y
contextual use of different information about depth. En
W.. Epstein & S. Rogers (Editores.), Perception of space and
movimiento (páginas. 69–117). San Diego, California: Prensa académica.
Drascic, D., & Milgram, PAG. (1996). Perceptual issues in aug-
mented reality. Proceedings of SPIE: Stereoscopic Displays and
Virtual Reality Systems III, San Jose, California, 123–134.
Edwards, PAG. J., Johnson, l. GRAMO., Hawkes, D. J., Fenlon, METRO. r.,
Strong, A. J., & Gleeson, METRO. j. (2004). Clinical experience
and perception in stereo augmented reality surgical naviga-
ción. Medical Imaging and Augmented Reality, 369–376.
Berlin Heidelberg: Saltador.
Ellis, S. r., & Menges, B. METRO. (1998). Localization of virtual
objects in the near visual field. Human Factors, 40(3),
415–431.
Foley, j. METRO., & Richards, W.. (1972). Effects of voluntary eye
movement and convergence on the binocular appreciation of
profundidad. Atención, Percepción, & Psicofísica, 11(6), 423–427.
Fuchs, h., Livingston, METRO. A., Raskar, r., Keller, K., Crawford,
j. r., Rademacher, PAG., et al. (1998). Augmented Reality Vis-
ualization for Laparoscopic Surgery, 934–943. Berlin Heidel-
berg: Saltador.
Furmanski, C., Azuma, r., & Daily, METRO. (2002). Augmented-
reality visualizations guided by cognition: Perceptual heuris-
tics for combining visible and obscured information. Proceed-
ings of the 2002 International Symposium on Mixed and Aug-
mented Reality (ISMAR), 215–320.
Gescheider, GRAMO. A. (2013). Psicofísica: The fundamentals.
Londres: Routledge/Psychology Press.
Interrante, V. (1996). Illustrating transparency: Communicat-
ing the 3D shape of layered transparent surfaces via texture.
Doctoral dissertation, University of North Carolina at
Chapel Hill.
Interrante, v., Fuchs, h., & Pizer, S. METRO. (1997). Conveying
the 3D shape of smoothly curving transparent surfaces via
texture. IEEE Transactions on Visualization and Computer
Graphics, 3(2), 98–117.
Integration of depth modules: Stereopsis and texture. Vision
Investigación, 33(5), 813–826.
Julesz, B. (1971). Foundations of Cyclopean perception.
chicago: University of Chicago Press.
Kalkofen, D., Mendez, MI., & Schmalstieg, D. (2007, Novem-
ber). Interactive focus and context visualization for aug-
mented reality. Actas de la 2007 International Sympo-
sium on Mixed and Augmented Reality (ISMAR), 1–10.
Kang, X., Oh, J., wilson, MI., Yaniv, Z., kane, t. D., Peters,
C. A., & Shekhar, R. (2013). Towards a clinical stereoscopic
augmented reality system for laparoscopic surgery. Clinical
Image-Based Procedures. Translational Research in Medical
Imaging, 108–116. Nueva York: Springer International
Publishing.
landy, METRO. S., Maloney, l. T., Johnston, mi. B., & Joven, METRO.
(1995). Measurement and modeling of depth cue combina-
ción: In defense of weak fusion. Vision Research, 35(3),
389–412.
Lerotic, METRO., Chung, A. J., Mylonas, GRAMO., & Cual, GRAMO. z. (2007).
Pq-space based non-photorealistic rendering for augmented
reality. Medical Image Computing and Computer-Assisted
Intervention–MICCAI 2007, 102–109. Berlin Heidelberg:
Saltador.
Livingston, METRO. A., Dey, A., Sandor, C., & tomás, B. h.
(2013). Pursuit of ‘‘X-ray vision’’ for augmented reality,
67–107. Nueva York: Saltador.
McIntire, j. PAG., Havig, PAG. r., & Geiselman, mi. mi. (2014). Ster-
eoscopic 3D displays and human performance: A compre-
hensive review. Displays, 35(1), 18–26.
Otsuki, METRO., & Milgram, PAG. (2013, Octubre). Psychophysical
exploration of stereoscopic pseudo-transparency. Actas
del 2013 International Symposium on Mixed and Aug-
mented Reality (ISMAR), 1–6.
Patterson, R. (2009). Review paper: Human factors of stereo
displays: An update. Journal of the Society for Information
Display, 17(12), 987–996.
Rolland, j. PAG., & Fuchs, h. (2000). Optical versus video see-
through head-mounted displays in medical visualization.
Presence: Teleoperators and Virtual Environments, 9(3),
287–309.
Rosenthal, METRO., Estado, A., Sotavento, J., Hirota, GRAMO., ackerman, J.,
Keller, K., et al. (2002). Augmented reality guidance for
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Ghasemi et al. 65
needle biopsies: An initial randomized, controlled trial in
phantoms. Análisis de imágenes médicas, 6(3), 313–320.
Sandor, C., Cunningham, A., Dey, A., & Mattila, V. V.
Tsirlin, I., alison, R. S., & Wilcox, l. METRO. (2008). Stereoscopic
transparencia: Constraints on the perception of multiple sur-
faces. Revista de visión, 8(5), 5–5.
(2010, Octubre). An augmented reality X-ray system based
on visual saliency. Actas de la 2010 9th IEEE and
ACM International Symposium on Mixed and Augmented
Reality (ISMAR), 27–36.
Schmalstieg, D., & Hollerer, t. (2016). Augmented reality:
Wheatstone, C. (1838). Contributions to the physiology of
vision—Part the first. On some remarkable, and hitherto
unobserved, phenomena of binocular vision. Philosophical
Transactions of the Royal Society of London, 371–394.
Yeh, Y. y., & Silverstein, l. D. (1990). Limits of fusion and
Principles and practice. Bostón: Addison-Wesley
Professional.
Sielhorst, T., Bichlmeier, C., Heining, S. METRO., & Navab, norte.
(2006). Depth perception—A major issue in medical AR:
Evaluation study by twenty surgeons. Medical Image Com-
puting and Computer-Assisted Intervention–MICCAI 2006,
364–372. Berlin Heidelberg: Saltador.
Soler, l., Nicolau, S., Fasquel, J., Agnus, v., Charnoz, A.,
Hostettler, A. et al. (2008, Puede). Virtual reality and aug-
mented reality applied to laparoscopic and notes procedures.
Proceedings of the 5th IEEE International Symposium on
Biomedical Imaging: From Nano to Macro 1399–1402.
Thurstone, l. l. (1927). The method of paired comparisons
for social values. The Journal of Abnormal and Social Psychol-
ogia, 21(4), 384.
depth judgment in stereoscopic color displays. Human Fac-
tores, 32(1), 45–60.
Joven, METRO. J., landy, METRO. S., & Maloney, l. t. (1993). A pertur-
bation analysis of depth perception from combinations of tex-
ture and motion cues. Vision Research, 33(18), 2685–2696.
Zollmann, S., Grasset, r., Reitmayr, GRAMO., & Langlotz, t.
(2014). Image-based X-ray visualization techniques for spa-
tial understanding in outdoor augmented reality. Actas
of the 26th Australian Computer-Human Interaction Confer-
ence on Designing Futures: The Future of Design, 194–203.
Zollmann, S., Kalkofen, D., Mendez, MI., & Reitmayr, GRAMO.
(2010, Octubre). Image-based ghostings for single layer
occlusions in augmented reality. Actas de la 2002
International Symposium on Mixed and Augmented Reality
(ISMAR), 19–26.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
v
a
r
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
2
6
1
4
2
1
8
3
6
4
5
3
pag
r
mi
s
_
a
_
0
0
2
8
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3