REVISAR
Disentangling causal webs in the brain using
functional magnetic resonance imaging:
A review of current approaches
Natalia Z. Bielczyk
1,2, Sebo Uithol
1,3, Tim van Mourik
1,2, Paul Anderson 1,4,
Jeffrey C. Glennon1,2, and Jan K. Buitelaar
1,2
1Donders Institute for Brain, Cognition and Behavior, Nimega, Los países bajos
2Department of Cognitive Neuroscience, Radboud University Nijmegen Medical Centre, Nimega, Los países bajos
3Bernstein Centre for Computational Neuroscience, Charité Universitätsmedizin, Berlina, Alemania
4Faculty of Science, Radboud University Nijmegen, Nimega, Los países bajos
un acceso abierto
diario
Palabras clave: Causal inference, Effective connectivity, Functional Magnetic Resonance Imaging,
Dynamic Causal Modeling, Granger Causality, Structural Equation Modeling, Bayesian Nets,
Directed Acyclic Graphs, Pairwise inference, Large-scale brain networks
ABSTRACTO
In the past two decades, functional Magnetic Resonance Imaging (resonancia magnética funcional) has been used
to relate neuronal network activity to cognitive processing and behavior. Recently this
approach has been augmented by algorithms that allow us to infer causal links between
component populations of neuronal networks. Multiple inference procedures have been
proposed to approach this research question but so far, each method has limitations when it
comes to establishing whole-brain connectivity patterns. en este documento, we discuss eight ways
to infer causality in fMRI research: Bayesian Nets, Dynamical Causal Modelling, Granjero
Causality, Likelihood Ratios, Linear Non-Gaussian Acyclic Models, Patel’s Tau, Structural
Equation Modelling, and Transfer Entropy. We finish with formulating some recommendations
for the future directions in this area.
INTRODUCCIÓN
What is causality?
Although inferring causal relations is a fundamental aspect of scientific research, the notion
of causation itself is notoriously difficult to define. The basic idea is straightforward: Cuando
process A is the cause of process B, A is necessarily in the past from B, and without A, B would
not occur. But in practice, and in dynamic systems such as the brain in particular, the picture
is far less clear. Primero, for any event a large number of (potencial) causes can be identified. El
efficacy of certain neuronal process in producing behavior is dependent on the state of many
otro (neuronal) procesos, but also on the availability of glucose and oxygen in the brain, y
so forth. In a neuroscientific context, we are generally not interested in most of these causes,
but only in a cause that stands out in such a way that it is deemed to provide a substantial part
of the explanation, for instance causes that vary with the experimental conditions. Sin embargo,
the contrast between relevant and irrelevant causes (in terms of explanatory power) is arbitrary
and strongly dependent on experimental setup, contextual factors, Etcétera. Por ejemplo,
respiratory movement is typically considered a confound in fMRI experiments, unless the re-
search question concerns the influence of respiration speed on the dynamics of the neuronal
redes.
Citación: Bielczyk, norte. Z., Uithol, S.,
van Mourik, T., anderson, PAG.,
Glennon, j. C., & Buitelaar, j. k. (2019).
Disentangling causal webs in the brain
using functional magnetic resonance
imaging: A review of current
approaches. Neurociencia en red,
3(2), 237–273. https://doi.org/10.1162/
netn_a_00062
DOI:
https://doi.org/10.1162/netn_a_00062
Recibió: 13 Marzo 2018
Aceptado: 08 Junio 2018
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Natalia Z. Bielczyk
natalia.bielczyk@gmail.com
Editor de manejo:
Olaf Sporns
Derechos de autor: © 2018
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
norte
mi
norte
_
a
_
0
0
0
6
2
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
In dynamic systems, causal processes are unlikely to be part of a unidirectional chain
of events, but rather a causal web, with often mutual influences between process A and B
(Mannino & Bressler, 2015). Como resultado, it is hard to maintain the temporal ordering of cause
and effect and, en efecto, a clear separation between them (Schurger & Uithol, 2015).
Además, causation can never be observed directly, just correlation (Hume, 1772).
When a correlation is highly stable, we are inclined to infer a causal link. Additional in-
formation is then needed to assess the direction of the assumed causal link, as correlation
indicates for association and not for causation (Altman & Krzywi ´nski, 2015). Por ejemplo, el
motor cortex is always active when a movement is made, so we assume a causal link between
the two phenomena. The anatomical and physiological properties of the motor cortex, y
the timing of the two phenomena provide clues about the direction of causality (es decir., cortical
activity causes the movement, and not the other way around). Sin embargo, only intervention
estudios, such as delivering Transcranial Magnetic Stimulation (kim, Pesiridou, & O’Reardon,
2009), pulses over the motor cortex or lesion studies, can confirm the causal link between the
activity in the motor cortex and behavior.
Causal studies in fMRI are based on three types of correlations: correlating neuronal activity
a (1) mental and behavioral phenomena, (2) to physiological states (such as neurotransmitters,
hormones, etc.), y (3) to neuronal activity in other parts of the brain. In this review, we will
focus on the last field of research: establishing causal connections between activity in two or
more brain areas.
A Note on the Limitations of fMRI Data
fMRI studies currently use a variety of algorithms to infer causal links (Proporcionó, Brilla, &
romper la lanza, 2013; S. Smith et al., 2011). All these methods have different assumptions, anuncio-
vantages and disadvantages (ver, p.ej., Esteban & Roebroeck, 2012; Valdes-Sosa, Roebroeck,
Daunizeau, & Friston, 2011), and approach the problem from different angles. An important
reason for this variety of approaches is the complex nature of fMRI data, which imposes severe
restrictions on the possibility of finding causal relations using fMRI.
•
Temporal resolution and hemodynamics. Primero, and best known, the temporal resolution
of the image acquisition in MR imaging is generally restricted to a sampling rate < 1[Hz].
Recently, multiband fMRI protocols have gained in popularity (Feinberg & Setsompop,
2013), which increases the upper limit for the scanning frequency to up to 10[Hz], albeit
at the cost of a severely decreased signal-to-noise ratio. However, no imaging proto-
col (including multiband imaging) can overcome the limitation of the recorded signal
itself: the lagged change in blood oxygenation, which peaks 3 to 6[s] after neuronal
firing in the adult human brain (Arichi et al., 2012). The hemodynamic response thus
acts as a low-pass filter, which results in high correlations between activity in consec-
utive frames (J. D. Ramsey et al., 2010). Since the hemodynamic lags (understood as
the peaks of the hemodynamic response) are region- and subject-specific (Devonshire
et al., 2012) and vary over time (Glomb, Ponce-Alvarez, Gilson, Ritter, & Deco, 2017),
it is difficult to infer causality between two time series with potentially different hemo-
dynamic lags (Bielczyk, Llera, Buitelaar, Glennon, & Beckmann, 2017). Computational
work by Seth, Chorley, and Barnett (2013) suggests that upsampling the signal to low
repetition times (TRs) (< 0.1[s]) might potentially overcome this issue. Furthermore,
hemodynamics typically fluctuates in time. These slow fluctuations, similarly to other
low frequency artifacts such as heartbeat or body movements, should be removed from
Network Neuroscience
238
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
•
•
the datasets through high-pass filtering before the inference procedure (J. D. Ramsey,
Sanchez-Romero, & Glymour, 2014).
Signal-to-noise ratio. Second, fMRI data is characterized by a relatively low signal-to-
noise ratio.
In gray matter, the recorded hemodynamic response changes by 1 to 2%
at field strengths of 1.5 − 2.0[T] (Boxerman et al., 1995; Ogawa et al., 1993), and by 5
to 6% at field strengths of 4.0[T]. Moreover, typical fMRI protocols generate relatively
short time series. For example, the Human Connectome Project resting state datasets
(Essen et al., 2013) do not contain more than a few hundred to maximally few thou-
sand samples. The two most popular ways of improving on the signal-to-noise ratio in
fMRI datasets are averaging signals over multiple voxels (K. J. Friston, Ashburner, Kiebel,
Nichols, & Penny, 2007) and spatial smoothing (Triantafyllou, Hoge, & Wald, 2006).
Caveats associated with region definition. Third, in order to propose a causal model, one
first needs to define the nodes of the network. A single voxel does not represent a biolog-
ically meaningful part of the brain (Stanley et al., 2013). Therefore, before attempting to
establish causal connection in the network, one needs to integrate the BOLD time series
over regions of interest (ROIs): groups of voxels that are assumed to share a common sig-
nal with a neuroscientific meaning. Choosing the optimal ROIs for a study is a complex
problem (Fornito et al., 2013; Kelly et al., 2012; Marrelec & Fransson, 2011; Poldrack,
In task-based fMRI, ROIs are
2007; Thirion, Varoquaux, Dohmatob, & Poline, 2014).
often chosen on the basis of activation patterns revealed by the standard General Linear
Model analysis (K. J. Friston et al., 2007).
On the other hand, in research on resting-state brain activity, the analysis is usually
exploratory and the connectivity in larger, meso- and macroscale networks is typically
considered. In that case, a few strategies for ROI definition are possible. First, one can
define ROIs on the basis of brain anatomy. However, a consequence of this strategy
could be that BOLD activity related to the cognitive process of interest will be mixed
with other, unrelated activity within the ROIs. This is particularly likely to happen given
that brain structure is not exactly replicable across individuals, so that a specific area
cannot be defined reliably based on location alone. As indicated in the computational
study by S. Smith et al. (2011), and also in a recent study by Bielczyk, et al. (2017), such
signal mixing is detrimental to causal inference and causes all the existing methods for
causal inference in fMRI to underperform. What these studies demonstrate is that parcel-
lating into ROIs based on anatomy rather than common activity, can induce additional
scale-free background noise in the networks. Since this noise has high power in low fre-
quencies, the modeled BOLD response cannot effectively filter it out. As a consequence,
the signatures of different connectivity patterns are getting lost.
As an alternative to anatomical parcellation, choosing ROIs can be performed in a
functional, data-driven fashion. There are multiple techniques developed to reach this
goal, and to list some recent examples: Instantaneous Correlations Parcellation imple-
mented through a hierarchical Independent Component Analysis (ICP; van Oort et al.,
2017), probabilistic parcellation based on Chinese restaurant process (Janssen, Jylänki,
Kessels, & van Gerven, 2015), graph clustering based on intervoxel correlations (van den
Heuvel, Mandl, & Pol, 2008), large-scale network identification through comparison be-
tween correlations among ROIs versus a model of the correlations generated by the noise
(LSNI; Bellec et al., 2006), multi-level bootstrap analysis (Bellec, Rosa-Neto, Lyttelton,
Benali, & Evans, 2010), clustering of voxels revealing common causal patterns in terms of
Granger Causality (DSouza, Abidin, Leistritz, & Wismüller, 2017), spatially constrained
hierarchical clustering (Blumensath et al., 2013) and algorithms providing a trade-off
between machine learning techniques and knowledge coming from neuroanatomy
Causal inference:
Inferring direct causal effects within a
given network based on available
empirical data, e.g., BOLD fMRI
recordings in the nodes of
the network.
Network Neuroscience
239
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
(Glasser et al., 2016). Another possibility to reduce the effect of mixing signals is to
perform Principal Component Analysis (PCA; Jolliffe, 2002; Shlens, 2014), separate the
BOLD time series within each anatomical region into a sum of orthogonal signals (eigen-
variates) and choose only the signal with the highest contribution to the BOLD signal
(the first eigenvariate; K. J. Friston, Harrison, & Penny, 2003), instead of averaging activ-
ity over full anatomical regions. Finally, one can build ROIs on the basis of patterns of
activation only (task localizers; Fedorenko, Hsieh, Nieto-Castañón, Whitfield-Gabrieli,
& Kanwisher, 2010; Heinzle, Wenzel, & Haynes, 2012). However, this approach can-
not be applied to resting-state research. In this work, we assume that the definition of
ROIs has been performed by the researcher prior to the causal inference, and we do not
discuss it any further.
Criteria for Evaluating Methods for Causal Inference in Functional Magnetic Resonance Imaging
Given the aforementioned characteristics of fMRI data (low temporal resolution, slow hemo-
dynamics, low signal-to-noise ratio) and the fact that causal webs in the brain are likely dense
and dynamic, is it in principle possible to investigate causality in the brain by using fMRI?
Multiple distinct families of models have been developed in order to approach this problem
over the past two decades. One can look at the methods from different angles and classify
them into different categories.
One important distinction proposed by K. Friston, Moran, and Seth (2013), includes division
of methods with respect to the depth of the neuroimaging measurements at which a method
is defined. Most methods (such as the original formulation of Structural Equation Modeling
for fMRI (Mclntosh & Gonzalez-Lima, 1994) see section Structural Equation Modeling) oper-
ate on the experimental observables, that is, the measured BOLD responses. These methods
are referred to as directed functional connectivity measures. On the contrary, other methods
(e.g., Dynamic Causal Modeling) consider the underlying neuronal processes. These meth-
ods are referred to as effective connectivity measures. Mind that while some methods such
as Dynamic Causal Modeling are hardwired to assess effective connectivity (as they are built
upon a generative model), other methods can be used both as a method to assess directed
functional connectivity or effective connectivity. For example, in Granger Causality research,
a blind deconvolution is often used in order to deconvolve the observed BOLD responses
into an underlying neuronal time series (David et al., 2008; Goodyear et al., 2016; Hutcheson
et al., 2015; Ryali et al., 2016; Ryali, Supekar, Chen, & Menon, 2011; Sathian, Deshpande,
& Stilla, 2013; Wheelock et al., 2014), which allows for assessing effective connectivity. On
the contrary, when Granger Causality is used without deconvolution (Y. C. Chen et al., 2017;
Regner et al., 2016; Zhao et al., 2016), it is a directed functional connectivity method. Of
course, both scenarios have pros and cons, as blind deconvolution can be a very noisy oper-
ation (Bush et al., 2015), and for more details, please see K. Friston, Moran and Seth (2013).
Another important distinction was proposed by Valdes-Sosa et al. (2011). According to this
point of view, methods can be divided on the basis of the approach toward temporal sequence
of the samples: some of the methods are based on the temporal sequence of the signals (e.g.,
Transfer Entropy (Schreiber, 2000), see section Transfer Entropy, or Granger Causality, (Granger,
1969), see section Granger Causality), or rely on the dynamics expressed by state-space equa-
tions (so-called state-space models, e.g., Dynamic Causal Modeling), while other methods do
not draw information from the sequence in time, and solely focus on the statistical properties
of the time series (so-called structural models, e.g., Bayesian Nets (Frey & Jojic, 2005), see
section Bayesian Nets).
Directed functional connectivity:
Causal relations between nodes
of investigated network, derived
from experimental observables,
e.g., measured BOLD responses.
Effective connectivity:
Causal relations between nodes of
investigated network, derived from a
model that additionally considers
the underlying neuronal processes.
Generative model:
A model representing prior
knowledge of how underlying
causal structures are manifested
in the experimental datasets.
Network Neuroscience
240
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
In this work, we would like to propose another classification of methods for causal inference
in fMRI. First, we identify nine characteristics of models used to study causality. Then, we
compare and contrast the popular approaches to the causal research in fMRI according to
these criteria. Our list of features of causality is as follows:
1. Sign of connections: Can the method distinguish between excitatory and inhibitory
causal relations? In this context, we do not mean synaptic effects, but rather an overall
driving or attenuating impact of the activity in one brain region on the activity in another
region. Certain methods only detect the existence of causal influence from the BOLD
responses, whereas others can distinguish between these distinct forms of influence.
2. Strength of connections: Can the method distinguish between weak and strong con-
nections, apart from indicating the directionality of connections at a certain confidence
level?
3. Confidence intervals: How are the confidence intervals for the connections determined?
4. Bidirectionality: Can the method pick up bidirectional connections X (cid:2) Y, or only
indicate the strongest of the two connections X → Y and Y → X? Some methods do
not allow for bidirectional relations, since they cannot deal with cycles in the network.
Immediacy: Does the method specifically identify direct influences X → Y, or does it
→ Y? We assume that Zi represent
pool across direct and indirect influences Zi: X → Zi
nodes in the network, and the activity in these nodes is measured (otherwise Zi become
a latent confounder). While some methods aim to make this distinction, others highlight
any influence X → Y, whenever it is direct or not.
5.
6. Resilience to confounds: Does the method correct for possible spurious causal effects
from a common source (Z → X, Z → Y, so we infer X → Y and/or Y → X), or other
confounders? In general, confounding variables are an issue to all the methods for causal
inference, especially when a given study is noninterventional (Rohrer, 2017); however,
different methods can suffer from these issues to a different extent.
7. Type of inference: Does the method probe causality through classical hypothesis testing
or through model comparison? Hypothesis-based methods will test a null hypothesis H0
that there is no causal link between two variables, against a hypothesis H1 that there
is causal link between the two. In contrast, model comparison based methods do not
have an explicit null hypothesis.
Instead, evidence for a predefined set of models is
computed. In particular cases, when the investigated network contains only a few nodes
and the estimation procedure is computationally cheap, a search through all the con-
nectivity patterns by means of model comparison is possible. In all the other cases, prior
knowledge is necessary to select a subset of possible models for model comparison.
8. Computational cost: What is the computational complexity of the inference procedure?
In the case of model comparison, the computational cost refers to the cost of finding the
likelihood of a single model, as the range of possible models depends on the research
question. This can lead to practical limitations based on computing power.
9. Size of the network: What sizes of network does the method allow for? Some methods
are restricted in the number of nodes that it allows, for computational or interpretational
reasons.
In certain applications, an additional criterion of empirical accuracy in realistic simula-
tion could be of help to evaluate the method. Testing the method on synthetic, ground truth
datasets available for the research problem at hand can give a good picture on whether or
not the method gives reliable results when applied to experimental datasets. In fMRI research,
multiple methods for causal inference were directly compared with each other in a seminal
Confounder:
A node that projects information
to two other nodes in the network,
causing a spurious causal association
between them. A con founder can
be latent in the experiment.
Classical hypothesis testing:
Testing whether a given hypothesis
is plausible in the light of available
data. This approach requires the
assumption of a null distribution, i.e.,
the distribution of the values for that
variable if the hypothesis is not true.
Model comparison:
Causal inference in which one model
is selected from a set of candidate
models representing potential causal
structures in the network on the basis
of experimental evidence.
Network Neuroscience
241
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
simulation study by Smith et al. In this study, the authors employed a Dynamic Causal Model-
ing generative model (DCM; K. J. Friston et al., 2003), introduced in section Dynamic Causal
Modeling in order to create synthetic datasets with a known ground truth. Surprisingly, most
of the methods struggled to perform above chance level, even though the test networks were
sparse and the noise levels introduced to the model were low compared with what one would
expect in real recordings. In this manuscript, we will refer to this study throughout the text.
However, we will not list empirical accuracy as a separate criterion, for two reasons. First, some
of the methods reviewed here, for example, Structural Equation Modeling (SEM; Mclntosh &
Gonzalez-Lima, 1994), were not tested on the synthetic benchmark datasets. Second, the
most popular method in the field, DCM (K. J. Friston et al., 2003), builds on the same genera-
tive model that is used for comparing methods to each other in Smith’s study. Therefore, it is
hard to perform a fair comparison between DCM and other methods in the field by using this
generative model.
In the following chapters, the references to this “causality list” will be marked in the text
with subscripted indices that refer to 1–9 above.
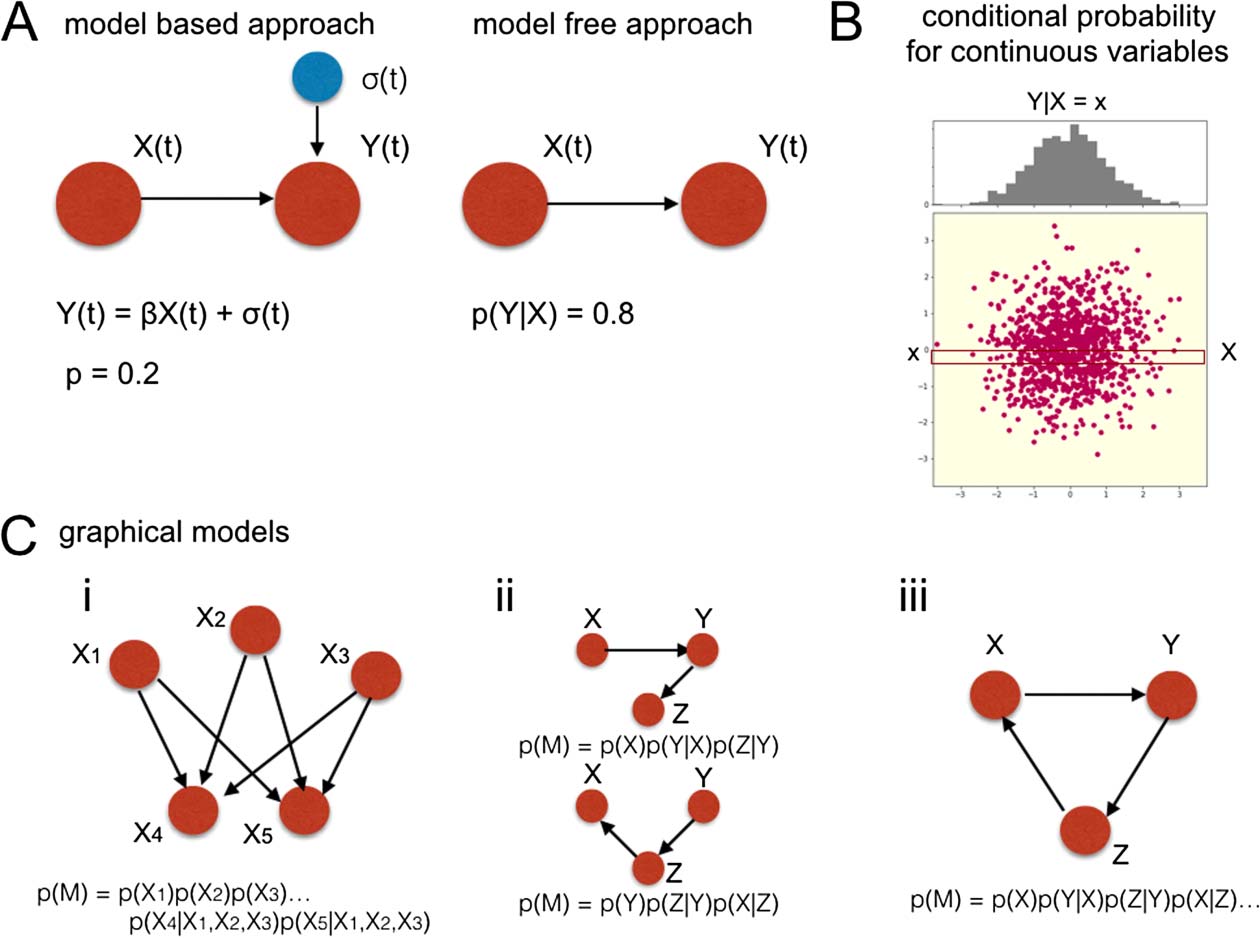
With respect to assumptions made on the connectivity structure, the approaches discussed
here can be divided into three main groups (Figure 1). The first group comprises multivariate
methods that search for directed graphs without imposing any particular structure onto the
graph: GC (Seth, Barrett, & Barnett, 2015), Transfer Entropy (TE; Marrelec et al., 2006), SEM
(Mclntosh & Gonzalez-Lima, 1994) and DCM (K. J. Friston et al., 2003). These methods will be
referred to as network-wise models throughout the manuscript. The second group of methods
is also multivariate, but requires an additional assumption of acyclicity. Models in this group
assume that information travels through the brain by feed-forward projections only. As a result,
the network can always be represented by a Directed Acyclic Graph (DAG; Thulasiraman &
Swamy, 1992). Methods in this group include Linear Non-Gaussian Acyclic Models (LiNGAM;
Directed Acyclic Graph (DAG):
A graph structure with no closed
loops (i.e., between each pair of
nodes X and Y, there is at most one
path to cross the graph from X to Y).
This property imposes a structural
hierarchy on the network.
Figure 1. Causal research in fMRI. The discussed methods can be divided into two families: Net-
work Inference Methods, which are based on a one-step multivariate procedure, and Pairwise Infer-
ence Methods, which are based on a two-step pairwise inference procedures. As pairwise methods
by definition establish causal connections on a connection-by-connection basis, they do not require
any assumptions on the structure of the network, but also do not reveal the structure of the network.
Network Neuroscience
242
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Shimizu, Hoyer, Hyvärinen, & Kerminen, 2006) and Bayesian Nets (BNs; Mumford & Ramsey,
2014), and will be referred to as hierarchical network-wise models throughout the manuscript.
The last group of methods, referred to as pairwise methods, use a two-stage procedure: first,
a map of nondirectional functional connections is rendered; and second, the directionality
in each connection is assessed. Since these methods focus on pairwise connections rather
than complete network architectures, they by definition do not impose network assumptions
like acyclicity. Patel’s tau (PT; Patel, Bowman, & Rilling, 2006) and Pairwise Likelihood Ratios
(PW-LR; Hyvärinen & Smith, 2013) are members of this group.
In this review, we do not
include studying a coupling between brain region and the rest of the brain with relation to a
particular cognitive task, The Psycho-Physiological Interactions (PPIs; K. J. Friston et al., 1997),
as we are only focused on the methods for assessing causal links within brain networks, and
we do not include brain-behavior causal interactions.
NETWORK-WISE METHODS
The first group of models that we discuss in this review involves multivariate methods: meth-
ods that simultaneously assess all causal links in the network—specifically, GC (Granger,
1969), TE (Schreiber, 2000), SEM (Wright, 1920) and DCM (K. J. Friston et al., 2003). These
methods do not pose any constraints on the connectivity structure. GC, TE, and SEM infer
causal structures through classical hypothesis testing. As there are no limits to the size of the
analyzed network, these methods allow for (relatively) hypothesis-free discovery. DCM on the
other hand, compares a number of predefined causal structures in networks of only a few
nodes. As such, it requires a specific hypothesis based on prior knowledge.
Granger Causality
Clive Granger introduced Granger Causality (GC) in the field of economics (Granger, 1969).
GC has found its way into many other disciplines, including fMRI research (Bressler & Seth,
2011; Roebroeck, Seth, & Valdes-Sosa, 2011; Seth et al., 2015; Solo, 2016). GC is based on
prediction (Diebold, 2001):
the signal in a certain region is dependent on its past values.
Therefore, a time series Y(t) at time point t can be partly predicted by its past values Y(t − i).
A signal in an upstream region is followed by the same signal in a downstream region with
a certain temporal lag. Therefore, if prediction of Y(t) improves when past values of another
signal X(t − i) are taken into account, X is said to Granger-cause Y. Time series X(t) and Y(t)
can be multivariate, therefore they will be further referred to as (cid:2)X(t), (cid:2)Y(t).
Y(t) is represented as an autoregressive process: it is predicted by a linear combination
of its past states and a Gaussian noise (there is also an equivalent of GC in the frequency
domain, spectral GC [Geweke, 1982, 1984], but this method will not be covered in this
review). This model is compared with model including the past values of X(t):
H0 : (cid:2)Y(t) =
N
∑
i=1
(cid:2)Y(t − i) +(cid:2)σ(t)
Byi
H1 : (cid:2)Y(t) =
N
∑
i=1
(cid:2)Y(t − i) +
Byi
N
∑
i=1
Bxi
(cid:2)X(t − i) +(cid:2)σ(t)
(1)
(2)
where σ(t) denotes noise (or rather, the portion of the signal not explained by the model).
Theoretically, this autoregressive (AR) model can take any order N (which can be optimized
using, e.g., Bayesian Information Criterion; Schwarz, 1978), but in fMRI research it is usually
set to N = 1 (Seth et al., 2015), that is, a lag that is equal to the TR.
Network Neuroscience
243
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
By fitting the parameters of the AR model, which include the influence magnitudes Byi, Bxi,
the sign1 as well as the strength2 of the causal direction can be readily assessed with GC. The
significance of the results is evaluated by comparing variance of the noise obtained from mod-
els characterized by Equation 1 and Equation 2. This can be achieved either by means of
F tests or by permutation testing3. Like all the methods in this chapter, GC does not impose
any constraints on the network architecture and therefore can yield bidirectional connections4.
As a multivariate method, GC fits the whole connectivity structure at once. Therefore, ideally,
it indicates the direct causal connections only5, whereas the indirect connections should be
captured only through higher order paths in the graph revealed in the GC analysis. However,
this is not enforced directly by the method. Furthermore, in the original formulation of the
problem by Granger, GC between X and Y works based on the assumption that the input of
all the other variables in the environment potentially influencing X and Y has been removed
(Granger, 1969). In theory, this would provide resilience to confounds6. However, in reality
this assumption is most often not valid in fMRI (Grosse-Wentrup, 2014b). In a result, direct
and indirect causality between X and Y are in fact pooled. In terms of the inference type, one
can look at GC in two ways. On the one hand, GC is a model comparison technique, since the
inference procedure is, in principle, based on a comparison between two models expressed by
Equations 1 and 2. On the other hand, the difference between GC and other model comparison
techniques lies in the fact that GC does not optimize any cost function, but uses F tests or
permutation testing instead, and it can therefore also be interpreted as a method for classic
hypothesis testing7. Since the temporal resolution of fMRI is so low, typically first order AR
models with a time lag equal to 1 TR are used for the inference in fMRI. Therefore, there is no
need to optimize either the temporal lag or the model order, and as such the computational
cost of GC estimation procedure in fMRI is low8. One constraint though, is that the AR model
imposes a mathematical restriction on the size of the network: the number of regions divided
by the number of shifts can never exceed the number of time points (degrees of freedom).
GC is used in fMRI research in two forms: as mentioned in section Criteria for Evaluat-
ing Methods for Causal Inference in Functional Magnetic Resonance Imaging, GC can be
either applied to the observed BOLD responses (Y. C. Chen et al., 2017; Regner et al., 2016;
Zhao et al., 2016), or to the BOLD responses deconvolved into neuronal time series (David
et al., 2008; Goodyear et al., 2016; Hutcheson et al., 2015; Ryali et al., 2016, 2011; Sathian
et al., 2013; Wheelock et al., 2014). The purpose of deconvolution is to model fMRI data
more faithfully. However, estimating the hemodynamic response from the data—a necessity to
perform this deconvolution—adds uncertainty to the results.
The applicability of GC to fMRI data has been heavily debated (Stokes & Purdon, 2017).
Firstly, the application of GC requires certain additional assumptions such as signal station-
arity (stationarity means that the joint probability distribution in the signal does not change
over time. This also implies that mean, variance and other moments of the distribution of the
samples in the signal do not change over time), which does not always hold in fMRI data. The-
oretical work by Seth et al. (2013), and work by Roebroeck, Formisano, and Goebel (2005),
suggest that despite the limitations related to slow hemodynamics, GC is still informative about
the directionality of causal links in the brain (Seth et al., 2015). In the study by S. Smith et al.
(2011), several versions of GC implementation were tested. However, all versions of GC were
characterized by a low sensitivity to false positives and low overall accuracy in the direction-
ality estimation. The face validity of GC analysis was empirically validated using joint fMRI
and magnetoencephalography recordings (Mill, Bagic, Bostan, Schneider, & Cole, 2017), with
the causal links inferred with GC matching the ground truth confirmed by MEG. On the other
hand, experimental findings report that GC predominantly identifies major arteries and veins
Network Neuroscience
244
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
as causal hubs (Webb, Ferguson, Nielsen, & Anderson, 2013). This result can be associated
with a regular pulsating behavior with different phases in the arteries across the brain. This is
a well-known effect and is even explicitly targeted with physiological noise estimates such as
RETROICOR (Glover, Li, & Ress, 2000).
Another point of concern is the time lag in fMRI data, which restricts the possible scope of
AR models that can be fit in the GC procedure. Successful implementations of GC in EEG/MEG
research typically involve lags of less than 100 ms (Hesse, Möller, Arnold, & Schack, 2003).
In contrast, for fMRI the minimal lag is one full TR, which is typically between 0.7[s] and
3.0[s] (although new acceleration protocols allow for further reduction of TR). What is more,
the hemodynamic response function (HRF) may well vary across regions (David et al., 2008;
Handwerker, Ollinger, & D’Esposito, 2004), revealing spurious causal connections: when
the HRF in one region is faster than in another, the temporal precedence of the peak will
easily be mistaken for causation. The estimated directionality can in the worst case, even be
reversed, when the region with the slower HRF in fact causes the region with the faster HRF
(Bielczyk, et al., 2017). Furthermore, the BOLD signal might be noninvertible into the neu-
ronal time series (Seth et al., 2015), which can affect GC analysis regardless of whether it is
performed on the BOLD time series or the deconvolved signal.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Transfer Entropy
Transfer Entropy (TE; Schreiber, 2000) is another data-driven technique, equivalent to Granger
Causality under Gaussian assumptions (Barnett, Barrett, & Seth, 2009), and asymptotically equiv-
alent to GC for general Markovian (nonlinear, non-Gaussian) systems (Barnett & Bossomaier,
2012a).
In other words, TE is a nonparametric form of GC (or, GC is a parametric form of
TE). It was originally defined for pairwise analysis and later extended to multivariate analysis
(J. Lizier, Prokopenko, & Zomaya, 2008; Montalto, Faes, & Marinazzo, 2014). TE is based
on the concept of Shannon entropy (Shannon, 1948). Shannon entropy H(x) quantifies the
information contained in a signal of unknown spectral properties as the amount of uncertainty,
or unpredictability. For example, a binary signal that only gets values of 0 with a probability p,
and values of 1 with a probability 1 − p, is most unpredictable when p = 0.5. This is because
there is always exactly a 50% chance of correctly predicting the next sample. Therefore, being
informed about the next sample in a binary signal of p = 0.5 reduces the amount of uncertainty
to a higher extent than being informed about the next sample in a binary signal of, say, p =
0.75. This can be interpreted as a larger amount of information contained in the first signal as
compared with the latter. The formula which quantifies the information content according to
this rule reads as follows:
H(X) = − ∑
i
P(xi)log2P(xi)
(3)
where xi denotes the possible values in the signal (for the binarized signal, there are only two
possible values: 0 and 1).
TE builds up on the concept of Shannon entropy by extension to conditional Shannon
entropy: it describes the amount of uncertainty reduced in future values of Y by knowing
the past values of X along with the past values of Y:
TEX→Y = H(Y|Yt−τ) − H(Y|Xt−τ, Yt−τ)
where τ denotes the time lag.
(4)
245
Network Neuroscience
Disentangling causal webs in the brain using fMRI
In theory, TE requires no assumptions about the properties of the data, not even signal
stationarity. However, in most real-world applications, stationarity is required to almost the
same extent as in GC. Certain solutions for TE in nonstationary processes are also avail-
able (Wollstadt, Martinez-Zarzuela, Vicente, Diaz-Pernas, & Wibral, 2014). TE does need an
a priori definition of the causal process, and it may work for both linear and nonlinear inter-
actions between the nodes.
TE can distinguish the signum of connections1, as the drop in the Shannon entropy can be
both positive and negative. Furthermore, the absolute value of the drop in the Shannon entropy
can provide a measure of the connection strength2. TE can also distinguish bidirectional con-
nections, as in this case, both TEX→Y and TEY→X will be nonzero4. In TE, significance testing
by means of permutation testing is advised (Vicente, Wibral, Lindner, & Pipa, 2011)3. Imme-
diacy and resilience to confounds in TE is the same as in GC: multivariate TE represents direct
interactions, and becomes resilient to confounds only when defined for an isolated system. The
inference in TE is performed through classical hypothesis testing 7 and is highly cost-efficient 8.
As in GC, the maximum number of regions in the network divided by the number of shifts can
never exceed the number of time points (degrees of freedom) 9.
TE is a straightforward and computationally cheap method (Vicente et al., 2011). However,
TE did not perform well when applied to synthetic fMRI benchmark datasets (S. Smith et al.,
2011). One reason for this could be the time lag embedded in the inference procedure, which
poses an obstacle to TE in fMRI research for the same reasons as to GC: it requires at least one
full TR. TE is nevertheless gaining interest in the field of fMRI (Chai, Walther, Beck, & Fei-Fei,
2009; J. T. Lizier, Heinzle, Horstmann, Haynes, & Prokopenko, 2011; Montalto et al., 2014;
Ostwald & Bagshaw, 2011; Sharaev, Ushakov, & Velichkovsky, 2016).
Structural Equation Modeling
Structural Equation Modeling (SEM; Mclntosh & Gonzalez-Lima, 1994) is a simplified version
of GC and can be considered a predecessor to DCM (K. J. Friston et al., 2003). This method was
originally applied to a few disciplines: economics, psychology and genetics (Wright, 1920),
and was only recently adapted for fMRI research (Mclntosh & Gonzalez-Lima, 1994). SEM
is used to study effective connectivity in cognitive paradigms, for example, on motor coordi-
nation (Kiyama, Kunimi, Iidaka, & Nakai, 2014; Zhuang, LaConte, Peltier, Zhang, & Hu, 2005),
as well as in search for biomarkers of psychiatric disorders (Carballedo et al., 2011; R. Schlösser
et al., 2003). It was also used for investigating heritability of large-scale resting-state connec-
tivity patterns (Carballedo et al., 2011).
The idea behind SEM is to express every ROI time series in a network by a linear com-
bination of all the time series (with the addition of noise), which implies no time lag in the
communication. These signals are combined in a mixing matrix B:
(cid:2)X(t) = B(cid:2)X(t) +(cid:2)σ(t)
(5)
where (cid:2)σ denotes the noise, and the assumption is that each univariate component Xi(t) is a
mixture of the remaining components Xj(t), j (cid:3)= i. This is a simple multivariate regression
equation. The most common strategy for fitting this model is a search for the regression coeffi-
cients that correspond to the maximum likelihood (ML) solution: a set of model parameters B
that give the highest probability of the observed data (Anderson & Gerbing, 1988; Mclntosh &
Gonzalez-Lima, 1994). Assuming that variables Xi are normally distributed, the ML function
Network Neuroscience
246
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
can be computed and optimized. This function is dependent on the observed covariance
between variables, as well as a concept of a so-called implied covariance; for the details,
see Bollen (1989), and for a practical example of SEM inference, see Ferron and Hess (2007).
Furthermore, under the assumption of normality of the noise, there is a closed-form solution to
this problem which gives the ML solution for parameters B, known as Ordinary Least Squares
(OLS) approximation (Bentler, 1985; Hayashi, 2000).
In SEM applications to fMRI datasets, it is a common practice to establish the presence of
connections with use of anatomical information derived, for example, from Diffusion Tensor
Imaging (Protzner & McIntosh, 2006). In that case, SEM inference focuses on estimating the
strength of causal effects and not on identifying the causal structure.
SEM does not constrain the weight of connections, therefore it can retrieve both excitatory
and inhibitory connections1 as well as bidirectional connections4. The connection coeffi-
cients Bij can take any values of rational numbers and as such they can reflect the strength
of the connections 2. Since OLS gives a point estimate for β, it does not provide a measure of
confidence that would determine whether the obtained β is significantly different from zero.
This issue can be overcome in multiple ways. First, one can perform parametric tests, for exam-
ple, a t test. Second, one can obtain confidence intervals through nonparametric permutation
testing (generate a null distribution of B values by the repeated shuffling of node labels across
subjects and creating surrogate subjects). Third, one can perform causal inference through
model comparison: various models are fitted one by one, and the variance of the residual
noise resulting from different model fits is compared, using either an F test, or a goodness of fit
(Zhuang et al., 2005). Highly optimized software packages such as LiSREL (Joreskög & Thillo,
1972) allow for an exploratory analysis with SEM by comparing millions of models against
each other (James et al., 2009). Last, one can fit the B matrix with new methods including reg-
ularization that enforces sparsity of the solution (Jacobucci, Grimm, & McArdle, 2016), and
therefore eliminates weak and noise-induced connections from the connectivity matrix3. As
with GC, SEM was designed to reflect direct connections5: if regions Xi and Xj are connected
only through a polysynaptic causal web, Bij should come out as zero, and the polysynaptic
connection should be retrievable from the path analysis. Again, similar to GC, SEM is resilient
to confounds only under the assumption that the model represents an isolated system, and all
the relevant variables present in the environment are taken into account6. Moreover, in order
to obtain the ML solution for B parameters, one needs to make a range of assumptions on the
properties of the noise in the network. Typically, a Gaussian white noise is assumed, although
background noise in the brain is most probably scale-free (He, 2014). Inference can be per-
formed either through the classical hypothesis testing (as the computationally cheap version)
or through model comparison (as the computationally heavier version) 7,8.
In summary, SEM is a straightforward approach: it simplifies the causal inference by reduc-
ing the complex network with a low-pass filter at the output to a very simple linear system,
but this simplicity comes at the cost of a number of assumptions. In the first decade of fMRI
research, SEM was often a method of choice (R. G. M. Schlösser et al., 2008; Zhuang, Peltier,
He, LaConte, & Hu, 2008) however recently, using DCM has become more popular in the
field. One recently published approach in this domain, by Schwab et al. (2018), extends lin-
ear models by introducing time-varying connectivity coefficients, which allows for tracking
the dynamics of causal interactions over time. In this approach, linear regression is applied
to each node in the network separately (in order to find causal influence of all the remaining
nodes in the network on that node). The whole graph is then composed from node-specific
DAGs node by node, and that compound graph can be cyclic.
Network Neuroscience
247
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Dynamic Causal Modeling
All the aforementioned network-wise methods were developed in other disciplines, and only
later applied to fMRI data. Yet, using prior knowledge about the properties of fMRI datasets can
prove useful when searching for causal interactions. Dynamic Causal Modeling (DCM; K. J.
Friston et al., 2003) is a model comparison tool that uses state space equations reflecting the
structure of fMRI datasets. This technique was also implemented for other neural recording
methods: EEG and MEG (Kiebel, Garrido, Moran, & Friston, 2008). DCM is well received
within the neuroimaging community (the original article by K. J. Friston et al. gained over
3,300 citations at the time of publishing this manuscript).
In this work, we describe the original work by (K. J. Friston et al., 2003) because, des-
pite multiple recent developments (Daunizeau, Stephan, & Friston, 2012; Frässle, Lomakina,
Razi, Friston, Buhmann, & Stephan, 2017; Frässle, Lomakina-Rumyantseva, Razi, Buhmann,
& Friston, 2016; K. J. Friston, Kahan, Biswal, & Razi, 2011; Havlicek et al., 2015; Kiebel,
Kloppel, Weiskopf, & Friston, 2007; Li et al., 2011; Marreiros, Kiebel, & Friston, 2008; Prando,
Zorzi, Bertoldo, & Chiuso, 2017; Razi & Friston, 2016; Seghier & Friston, 2013; Stephan et al.,
2008; Stephan, Weiskopf, Drysdale, Robinson, & Friston, 2007), it remains the most popular
version of DCM in the fMRI community. The idea of DCM is as follows. First, one needs to
build a generative model (Figure 2). This model has two levels of description: the neuronal
level (Figure 2, iii), and the hemodynamic level (Figure 2, v). Both of these levels contain
parameters that are not directly recorded in the experiment and need to be inferred from the
data. This model reflects scientific evidence on how the BOLD response is generated from
neuronal activity.
At the neuronal level of the DCM generative model, simple interactions between brain areas
are posited, either bilinear (K. J. Friston et al., 2003) or nonlinear (Stephan et al., 2008). In the
simplest, bilinear version of the model, the bilinear state equation reads:
˙z = (A + ∑
j
ujBj)z + Cu
(6)
Figure 2. The full pipeline for the DCM forward model. The model involves three node network
stimulated during the cognitive experiment (i). The parameter set describing the dynamics in this
network includes a fixed connectivity matrix (A), modulatory connections (B), and inputs to the
nodes (C) (ii). In the equation describing the fast neuronal dynamics, z denotes the dynamics in the
nodes, and u is an experiment-related input. Red: excitatory connections. Blue: inhibitory connec-
tions. The dynamics in this network can be described with use of ordinary differential equations.
The outcome is the fast neuronal dynamics (iii). The neuronal time series is then convolved with the
hemodynamic response function (HRF) (iv) in order to obtain the BOLD response (v), which may be
then subsampled (vertical bars). This is the original, bilinear implementation of DCM (K. J. Friston
et al., 2003). Now, more complex versions of DCM with additional features are available, such as
spectral DCM (K. J. Friston et al., 2011), stochastic DCM (Daunizeau et al., 2012), nonlinear DCM
(Stephan et al., 2008), two-state DCM (Marreiros et al., 2008), large DCMs (Frässle et al., 2018;
Frässle, Lomakina-Rumyantseva, et al., 2016; Seghier & Friston, 2013) and so on.
Network Neuroscience
248
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
where z denotes the dynamics in the nodes of the network, u denotes the experimental in-
puts, A denotes the connectivity matrix characterizing causal interactions between the nodes
of the network, B denotes the modulatory influence of experimental inputs on the connec-
tions within the network, and C denotes the experimental inputs to the nodes of the network
(Figure 2). The hemodynamic level is more complex and follows the biologically informed
Balloon-Windkessel model (Buxton, Wong, & Frank, 1998); for details please see K. J. Friston
et al. (2003). The Balloon–Windkessel model (Buxton et al., 1998) describes the BOLD sig-
nal observed in fMRI experiments as a function of neuronal activity but also region-specific
and subject-specific physiological features such as the time constant of signal decay, the rate
of flow-dependent elimination, and the hemodynamic transit time or resting oxygen fraction.
This is a weakly nonlinear model with free parameters estimated for each brain region. These
parameters determine the shape of the hemodynamic response (Figure 2, iv), which typically
peaks at 4 − 6[s] after the neuronal activity takes place, to match the lagged oxygen consump-
tion in the neuronal tissue mentioned in section A Note on the Limitation of fMRI Data. The
Balloon–Windkessel model is being iteratively updated based on new experimental findings,
for instance to mimic adaptive decreases to sustained inputs during stimulation or the post-
stimulus undershoot (Havlicek et al., 2015).
In this paper, the deterministic, bilinear single-state per region DCM will be described (K. J.
Friston et al., 2003). The DCM procedure starts with defining hypotheses based on observed
activations, which involves defining which regions are included in the network (usually on the
basis of activations found through the General Linear Model (K. J. Friston et al., 2007) and then
defining a model space based on the research hypotheses. In the latter model selection phase,
a range of literature-informed connectivity patterns and inputs in the networks (referred to as
“models”) are posited (Figure 2, i). The definition of a model space is the key to the DCM analy-
sis. The models should be considered carefully in the light of the existing literature. The model
space represents the formulation of a prior over models, therefore, it should always be con-
structed prior to the DCM analysis. Subsequently, for every model one needs to set priors on
the parameters of interest: connectivity strengths and input weights in the model (Figure 2, ii)
and the hemodynamic parameters. The priors for hemodynamic parameters are experimentally
informed Gaussian distributions (K. J. Friston et al., 2003). The priors for connectivity strengths
are Gaussian probability distributions centered at zero (which is often referred to as conserva-
tive shrinkage priors). The user usually does not need to specify the priors, as they are already
implemented in the DCM algorithms.
Next, an iterative procedure is used to find the model evidence by maximizing a cost func-
tion, a so-called negative free energy (K. J. Friston & Stephan, 2007). Negative free energy
is a particular cost function which gives a trade-off between model accuracy and complex-
ity (which accounts for correlations between parameters, and for moving away from the prior
distributions). During the iterative procedure, the prior probability distributions gradually shift
their mean and standard deviation, and converge toward the final posterior distributions. Neg-
ative free energy is a more sophisticated approximation of the model evidence when compared
to methods such as Akaike’s Information Criterion (AIC; Akaike, 1998) or Bayesian Informa-
tion Criterion (BIC; Schwarz, 1978); AIC and BIC simply count the number of free parameters
(thereby assuming that all parameters are independent), while negative free energy also takes
the covariance of the parameters into account (W. D. Penny, 2012).
In DCM, causality is modeled as a set of upregulating or downregulating connections be-
tween nodes. During the inference procedure, conservative shrinkage priors can shift towards
both positive and negative values, which can be interpreted as effective excitation or effec-
tive inhibition. The exceptions aren self-connections, which are always only negative (this
Network Neuroscience
249
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
self inhibition is mathematically motivated:
the system characterizing the fast dynamics of
the neuronal network must be stable, and this requires the diagonal terms of the adjacency
matrix A to be negative), Figure 2, ii, connections denoted in blue1. During the inference
procedure, the neural and hemodynamic parameters of all models postulated for model com-
parison are optimized2. The posterior probability distributions determine significance of all the
parameters3. The models can contain both uni- and bidirectional connections (Buijink et al.,
2015; Vaudano et al., 2013)4. The estimated model evidence can then be compared7. As such,
the original DCM (K. J. Friston et al., 2003) is a hypothesis-testing tool working only through
model comparison. However, now a linear version of DCM dedicated to exploratory research
in large networks is also available (Frässle, Lomakina-Rumyantseva, et al., 2016). Testing the
immediacy5 and resilience to confounds6 in DCM is possible through creating separate models
and comparing their evidence. For instance, one can compare the evidence for X → Y with ev-
idence for X → Z → Y in order to test whether or not the connection X → Y is direct or rather
mediated by another region Z. Note that this strategy requires an explicit specification of the
alternative models and it cannot take hidden causes into consideration (in this work, we refer
to the original DCM implementation [K. J. Friston et al., 2003], but there are also implementa-
tions of DCM involving estimation of time-varying hidden states, such as Daunizeau, Friston, &
Kiebel, 2009). However, including extra regions in order to increase resilience to confounds is
not necessarily a good idea. Considering the potentially large number of fitted parameters per
region (the minimum number of nodes per region is two hemodynamic parameters and one
input/output to connect to the rest of network), this may result in a combinatorial explosion.
Also, models with different nodes are not comparable in DCM for fMRI (K. J. Friston et al.,
2003). DCM is, in general, computationally costly. The original DCM (K. J. Friston et al., 2003)
is restricted to small networks of a few nodes9 (as mentioned previously, today, large DCMs
dedicated to exploratory research in large networks are also available; Frässle, Lomakina-
Rumyantseva, et al., 2016; Seghier & Friston, 2013).
The proper application of DCM needs a substantial amount of expertise (Daunizeau, David,
& Stephan, 2011; Stephan et al., 2010). Even though ROIs can be defined in a data-driven fash-
ion (through a preliminary classical General Linear Model analysis; K. J. Friston et al., 1995), the
model space definition requires prior knowledge of the research problem (Kahan & Foltynie,
2013).
In principle, the model space should reflect prior knowledge about possible causal
connections between the nodes in the network. If a paradigm developed for the fMRI study is
novel, there might be no reference study that can be used to build the model space. In that case,
using family-wise DCM modeling can be helpful (W. D. Penny et al., 2010). Family-wise mod-
els group large families of models defined on the same set of nodes, in order to test a particular
hypothesis. For instance, one can explore a three node network with nodes X, Y, Z and com-
pare the joint evidence behind all the possible models that contain connection X → Y with
the joint evidence behind all the possible models that contain connection Y → X (Figure 2, i).
Another solution that allows for constraining a large model space is Bayesian model averaging
(Hoeting, Madigan, Raftery, & Volinsky, 1999; Stephan et al., 2010) which explores the en-
tire model space and returns average value for each model parameter, weighted by the poste-
rior probability for each model. Finally, one can perform a Bayesian model reduction (J.Friston
et al., 2016), in which the considered models are reduced versions of a full (or “parent”) model.
This is possible when the priors can be reduced, for example, when a prior distribution of a
parameter in a parent model is set to a mean and variance of zero.
There are a few points that need particular attention when interpreting the results of the
DCM analysis. First, in case the data quality is poor, evidence for one model over another
In the worst case, it could give a preference to the simplest model
will not be conclusive.
Network Neuroscience
250
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
(i.e., the model with the fewest free parameters). In that case, simpler models will be preferred
over more complex ones regardless of the low quality of fit. It is important, therefore, to in-
clude a “null model” in a DCM analysis, with all parameters of interest fixed at zero. This null
model can then act as a baseline against which other models can be compared (W. D. Penny,
2012).
Second, the winning model might contain parameters with a high probability of being equal
to zero. To illustrate this, let us consider causal inference in a single subject (also referred to as
first level analysis). Let us assume that we chose a correct set of priors (i.e., model space). The
Variational Bayes (VB; Bishop, 2006) procedure then returns a posterior probability distribu-
tion for every estimated connectivity strength. This distribution gives a measure of probability
for the associated causal link to be larger than zero. Some parameters may turn out to have
high probability of being equal to zero in the light of this posterior distribution. This may be
due to the fact that the winning model is correct, but some of the underlying causal links are
weak and therefore hard to confirm by the VB procedure. Also, DCM requires data of high
quality; when the signal-to-noise ratio is insufficient, it is possible that the winning model
would explain a small portion of the variance in the data. In that case, getting insignificant
parameters in the winning model is likely. Therefore, it is advisable to check the amount of
variance explained by the winning model at the end of the DCM analysis.
The most popular implementation of the DCM estimation procedure is based on VB (Bishop,
2006) which is a deterministic algorithm. Recently, also Markov-Chain Monte Carlo (MCMC;
Bishop, 2006; Sengupta, Friston, & Penny, 2015) was implemented for DCM. When applied
to a unimodal free energy landscape, these two algorithms will both identify the global maxi-
mum. MCMC will be slower than VB as it is stochastic and therefore computationally costly.
However, free energy landscape for multiple-node networks is most often multimodal and
complex. In such case, VB—as a local optimization algorithm—might settle on a local max-
imum. MCMC on the other hand, is guaranteed to converge to the true posterior densities—
and thus the global maximum (given an infinite number of samples).
DCM was tailored for fMRI and, unlike other methods, it explicitly models the hemody-
namic response in the brain. The technique tends to return highly reproducible results, and
is therefore statistically reliable (Bernal-Casas et al., 2013; Rowe, Hughes, Barker, & Owen,
2010; Schuyler, Ollinger, Oakes, Johnstone, & Davidson, 2010; Tak et al., 2018). Recent
longitudinal study on spectral DCM in resting state revealed systematic and reliable patterns
of hemispheric asymmetry (Almgren et al., 2018). DCM also yielded high test-retest reliability
in an fMRI motor task study (Frässle et al., 2015) in a face perception study (Frässle, Paulus,
Krach, & Jansen, 2016), in a facial emotion perception study (Schuyler et al., 2010), and in
a finger-tapping task in a group of subjects suffering from Parkinson’s disease (Rowe et al.,
2010). It has also been demonstrated most reliable when directly compared with GC and SEM
(W. Penny, Stephan, Mechelli, & Friston, 2004). Furthermore, the DCM procedure can provide
complimentary information to GC (K. Friston, Moran, & Seth, 2013): GC models dependency
among observed BOLD responses, whereas DCM models coupling among the hidden states
generating observations. GC seems to be equally effective as DCM in certain circumstances,
such as when the HRF is deconvolved from the data (David et al., 2008; Ryali et al., 2016,
2011; Wang, Katwal, Rogers, Gore, & Deshpande, 2016).
Importantly, the face validity of
DCM was examined on experimental datasets coming from interventional study with use of
rat model of epilepsy (David et al., 2008; Papadopoulou et al., 2015).
DCM is not always a method of choice in causal studies in fMRI. Proper use of DCM re-
quires knowledge of the biology and of the inference procedure. DCM also has limitations
Network Neuroscience
251
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
in terms of the size of the possible models. Modeling a large network may run into problems
with identifiability; there will be many possible combinations of parameter settings that could
give rise to the same or similar model evidence. In other words, strong covariance between
parameters will preclude confident estimates of the strength of each connection. One possible
remedy for this, in the context of large-scale networks, is to impose appropriate prior constrains
on the connections, for example, using priors based on functional connectivity as priors (Razi
et al., 2017). Large networks may also give rise to comparisons of large number of different
models with varying combinations of connections. To reduce the possibility of overfitting at
the level of model comparison—that is, finding a model which is appropriate for one subject
or group of subjects’ data, but not for others—it can be useful to group the models into a small
number of families (W. D. Penny et al., 2010) based on pre-defined hypotheses. More infor-
mation on the limitations of DCM can be found in work by Daunizeau et al. (2011). A critical
note on limitations of DCM in terms of network size can also be found in Lohmann, Erfurth,
Muller, and Turner, 2012, and see also a response to this article, Breakspear (2013); K. Friston,
Daunizeau, and Stephan (2013).
However, to extend the scope of application of the DCM analysis to larger networks, re-
cently two approaches were developed. First, a new, large-scale DCM framework for resting-
state fMRI has been proposed (Razi et al., 2017). This framework uses the new, spectral DCM
(K. J. Friston et al., 2011) designed for resting-state fMRI and is able to handle dozens of nodes
in the network. Spectral DCM is then combined with functional connectivity priors in or-
der to estimate the effective connectivity in the large-scale resting-state networks. Second, a
new approach by Frässle et al. (2018) imposes sparsity constraints on the variational Bayesian
framework for task fMRI, which enables for causal inference on the whole-brain network level.
DCM was further developed into multiple procedures including more sophisticated gener-
ative models than the original model discussed here. The field of DCM research in fMRI is still
growing (K. J. Friston et al., 2017). The DCM generative model is continuously being updated
in terms of the structure of the forward model (Havlicek et al., 2015), the estimation procedure
(Sengupta et al., 2015), and the scope of the possible applications (K. J. Friston et al., 2017).
HIERARCHICAL NETWORK-WISE MODELS
The second group of methods involves hierarchical network-wise models: Linear Non-Gaussian
Acyclic Models (LiNGAM, Shimizu et al. (2006)) and Bayesian Nets (BNs; Frey & Jojic, 2005).
Similarly, as network-wise methods reviewed in the previous chapter, these methods are also
multivariate but with one additional constraint: the network can only include feed forward
projections (and therefore, no closed cycles). Consequently, the resulting models have a hier-
archical structure with feed forward distribution of information through the network.
LiNGAM
Linear Non-Gaussian Acyclic Models (LiNGAM; Shimizu et al., 2006) is an example of a data
driven approach working under the assumption of acyclicity (Thulasiraman & Swamy, 1992).
The model is simple: every time course within an ROI Xi(t) is considered to be a linear
combination of all other signals with no time lag:
(cid:2)X(t) = B(cid:2)X(t) +(cid:2)σ(t)
(7)
in which B denotes a matrix containing the connectivity weights, and (cid:2)σ denotes multivariate
noise. The model is in principle the same as in SEM (section Structural Equation Modeling),
Network Neuroscience
252
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
but the difference lies in the inference procedure: whereas in SEM, inference is based on
minimizing the variance of the residual noise under the assumption of independence and
Gaussianity, LiNGAM finds connections based on the dependence between residual noise
components (cid:2)σ(t) and regressors (cid:2)X(t).
The rationale of this method is as follows (Figure 3). Let us assume that the network is noisy,
and every time series within the network is associated with a background noise uncorrelated
with the signal in that node. An example of such a mixture of signal with noise is given in
Figure 3A. Then, let us assume that ˆX(t), which is a mixture of signal X(t) and noise σ
X(t),
causes Y(t). Then, as it cannot distinguish between the signal and the noise, Y becomes a
function of both these components. Y(t) is also associated with noise σ
Y(t); however, as there
is no causal link Y → X, X(t) is not dependent on the noise component σ
Y(t). Therefore, if Y
depends on the σ
Y(t) component, one can
infer projection X → Y.
X(t) component, but X does not depend on the σ
This effect is further explained on an example of a simple causal relationship between two
variables is demonstrated in Figure 3B: age versus length in a fish. If fish length is expressed
in a function of fish age (upper panel), the residual noise in the dependent variable (length)
is uncorrelated with the independent variable (age). Therefore, the noise variance is constant
over a large range of fish age. On the contrary, once the variables are flipped and fish age
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. The Linear Non-Gaussian Acyclic Model (LiNGAM). A: The noisy time series ˆX(t) con-
sists of signal X(t) and noise σ
X(t). Y(t) thus becomes a function of both the signal and the
noise in ˆX(t). B: Causal inference through the analysis of the noise residuals (figure reprinted from
http://videolectures.net/bbci2014_grosse_wentrup_causal_inference/). The causal link from age to
length in a population of fish can be inferred from the properties of the residual noise in the system.
If fish length is expressed in a function of fish age (upper panel), the residual noise in the dependent
variable (length) is uncorrelated with the independent variable (age): the noise variance is constant
over a large range of fish age (red bars). On the contrary, once the variables are flipped and fish
age becomes a function of fish length (lower panel), the noise variance becomes dependent on the
independent variable (length): it is small for small values of fish length and large for the large values
of fish length (red bars).
Network Neuroscience
253
Disentangling causal webs in the brain using fMRI
becomes a function of fish length (lower panel), the noise variance becomes dependent on
the independent variable (length): it is small for small values of fish length and large for the
large values of fish length. Therefore, the first causal model (fish age influencing fish length) is
correct.
In applications to causal research in fMRI, the LiNGAM inference procedure is often ac-
companied by an Independent Component Analysis (ICA; Hyvärinen & Oja, 2000) as follows.
The connectivity matrix B in Equation 7 describes how signals in the network mix together.
By convention, not B but a transformation of B into
A = (1 − B)−1
(8)
is used as a mixing matrix in the LiNGAM inference procedure. By using this mixing matrix A,
one can look at Equation 7 in a different way:
(cid:2)X = A(cid:2)σ
(9)
Now, the BOLD time course in the network (cid:2)X(t) can be represented as a mixture of in-
dependent sources of noise (cid:2)σ(t). This is the well-known cocktail party problem and it was
originally described in acoustics (Bronkhorst, 2000): in a crowded room, a human ear regis-
ters a linear combination of the noises coming from multiple sources. In order to decode the
components of this cacophony, the brain needs to perform a blind source separation (Comon &
Jutten, 2010): to decompose the incoming sound into a linear mixture of independent sources
of sounds. In the LiNGAM procedure, ICA (Hyvärinen & Oja, 2000) is used to approach this
issue. ICA assumes that the noise components (cid:2)σ are independent and have a non-Gaussian
distribution, and finds these components as well as the mixing matrix A through dimensionality
reduction with Principal Component Analysis (Jolliffe, 2002; Shlens, 2014). From this mixing
matrix, one can in turn estimate the desired adjacency matrix B with use of Equation 8.
Since the entries Bij of the connectivity matrix B can take any value, LiNGAM can in
principle retrieve both excitatory and inhibitory connectivity1 of any strength2. The author of
LiNGAM recommends (Shimizu, 2014) performing significance testing through either boot-
strapping (Hyvärinen, Zhang, Shimizu, & Hoyer, 2010; Komatsu, Shimizu, & Shimodaira,
2010; Thamvitayakul, Shimizu, Ueno, Washio, & Tashiro, 2012) or permutation testing
(Hyvärinen & Smith, 2013)3. However, LiNGAM makes the assumption of acyclicity, there-
fore only unidirectional connections can be picked up4. Moreover, the connectivity matrix
revealed with the use of LiNGAM is meant to pick up on direct connections5. The original for-
mulation of LiNGAM assumes no latent confounds (Shimizu et al., 2006), but the model can be
extended to a framework that can capture the causal links even in the presence of (unknown)
hidden confounds (Z. Chen & Chan, 2013; Hoyer, Shimizu, Kerminen, & Palviainen, 2008)6.
LiNGAM-ICA’s causal inference consists of ICA and a simple machine learning algorithm, and,
as such, it is a fully data-driven strategy that does not involve model comparison7. Confidence
intervals for the connections B can be found through permutation testing. ICA itself can be
computationally costly and its computational stability cannot be guaranteed (the procedure
that searches for independent sources of noise can get stuck in a local minimum). Therefore,
the computational cost in LiNGAM can vary depending on the dataset8. This also sets a limit
on the potential size of the causal network. When the number of connections approaches the
number of time points (degrees of freedom), the fitting procedure will become increasingly
unstable as it will be overfitting the data 9.
Network Neuroscience
254
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
When tested on synthetic fMRI benchmark datasets (S. Smith et al., 2011), LiNGAM-ICA
performs relatively well, but is more sensitive to confounders than several other methods dis-
cussed in this paper, such as Patel’s tau or GC. However, as LiNGAM performs particularly
well for datasets containing a large number of samples, the authors suggested that a group
analysis could resolve the sensitivity problem in LiNGAM. The concept was then picked up
and developed by at least two groups. Firstly, Ramsey et al. (J. D. Ramsey, Hanson, & Glymour,
2011) proposed LiNG Orientation, Fixed Structure technique (LOFS). The method is inspired by
LiNGAM and uses the fact that, within one graph equivalence class, the correct causal model
should return conditional probability distributions that are maximally non-Gaussian. LOFS
was tested on the synthetic benchmark datasets, where it achieved performance very close
to 100%. Second, Xu et al. published a pooling-LiNGAM technique (Xu et al., 2014), which
is a classic LiNGAM-ICA applied to the surrogate datasets. Validation on synthetic datasets
revealed that both False Positive (FP) and False Negative (FN) rates decrease exponentially
along with the length of the (surrogate) time series; however, combining time series of as
long as 5,000 samples is necessary for this method to give both FP and FN as a reasonable
level of 5%.
Despite the promising results obtained in the synthetic datasets, LiNGAM is still rarely ap-
plied to causal research in fMRI to date.
Bayesian Nets
The use of the LiNGAM inference procedures assumes a linear mixing of signals underlying a
causal interaction. Model-free methods do not make this assumption: the bare fact that one
is likely to observe Y given the presence of X can indicate that the causal link X → Y exists
(Figure 4). Let as assume the simplest example: causal inference for two binary signals X(t),
Y(t).
In a binary signal, only two values are possible: 1 and 0; 1 can be interpreted as an
“event” while 0 - as “no event.” Then, if in signal Y(t), events occur in 80% of the cases when
events in signal X(t) occur (Figure 4A), but the opposite is not true, the causal link X → Y
is likely. Computing the odds of events given the events in the other signal, is sufficient to
establish causality. In a model-based approach on the other hand, a model is fitted to the data,
in order to establish the precise form of the influence of the independent variable X on the
dependent variable Y.
Note that both model-based and model-free approaches contain a measure of uncertainty,
but this uncertainty is computed differently. In model-based approaches, p values associated
with the fitted model are a measure of confidence that the modeled causal link is a true positive
(Figure 4A, left panel). In contrast, in model-free approaches this confidence is quantified
directly by quantifying causal relationships in terms of conditional probabilities (Figure 4A,
right panel).
In practice, since the BOLD response—unlike the aforementioned example of
binary signals—takes continuous values, estimating conditional probabilities is based on the
basis of the joint distribution of the variables X and Y (Figure 4B). Conditional probability
P(Y|X) becomes a distribution of Y when X takes a given value. BNs (Frey & Jojic, 2005) are
based on such a model-free approach (Figure 4C).
The causal inference in BNs is based on the concept of conditional independency (a.k.a.
Causal Markov Condition; (Hausman & Woodward, 1999). For example, suppose there are
two events that could independently cause the grass to get wet: either a sprinkler, or rain. When
one only observes the grass being wet, the direct cause for this event is unknown. However,
once rain is observed, it becomes less likely that the sprinkler was used. Therefore, one can
Network Neuroscience
255
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Figure 4. Bayesian nets. A: Model-based versus model-free approach. β: a regressor coefficient
fitted in the modeling procedure. σ(t): additive noise. Both model-based and model-free approach
contain a measure of confidence. In a model-based approach, a model is fitted to the data, and
p-values associated with this fit are a measure of confidence that the causal link exists (i.e., is a true
positive, left panel). In a model-free approach, this confidence is quantified directly by expressing
causal relationships in terms of conditional probabilities (right panel). B: Conditional probability
for continuous variables. Since BOLD fMRI is a continuous variables, the joint probability distribu-
tion for variables X and Y is a two-dimensional distribution. Therefore, conditional probability of
P(Y|X = x) becomes a distribution. C: (i) An exemplary Bayesian Net. X1, X2, X3: parents, X4,
X5: children. (ii) Competitive Bayesian Nets: one can define competitive models (causal structures)
in the network and compare their joint probability derived from the data. (iii) Cyclic belief propa-
gation: if there was a cycle in the network, the expression for the joint probability would convert
into an infinite series of conditional probabilities.
say that the variables X1 (sprinkler) and X2 (rain) are conditionally dependent given variable
X3 (wet grass), because X1, X2 become dependent on each other after information about X3
In BNs, the assumption of conditional dependency in the network is used to
is provided.
compute the joint probability of a given model, that is, the model evidence (once variables Xi
are conditionally dependent on Xj, the joint distribution P(Xi, Xj) factorizes into a product
of probabilities P(Xj)P(Xi
|Xj).
Implementing a probabilistic BN requires defining a model: choosing a graph of “parents”
who send information to their “children.” For instance, in Figure 4C, i, node X1 is a parent
of nodes X4 and X5, and node X4 is a child of nodes X1, X2 and X3. The joint probability
of the model can then be computed as the product of all marginal probabilities of the parents
and conditional probabilities of the children given the parents. Marginal probability P(Xj)
is the total probability that the variable of interest Xj occurs while disregarding the values of
all the other variables in the system. For instance, in Figure 4C, (i), P(X1) means a marginal
|Xj) is the prob-
probability of X1 happening in this experiment. Conditional probability P(Xi
ability of a given variable (Xi) occurring given that another variable has occurred (Xj). For
|X1, X3) means a conditional probability of X5 given its parents
instance, in Figure 4C, i, P(X5
X1 and X3.
Network Neuroscience
256
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Then, once the whole graph is factorized into the chain of marginal and conditional proba-
bilities, the joint probability of the model can be computed as the product of all marginal and
conditional probabilities. For instance, in Figure 4C, i, the joint probability of the model M
yields
P(M) = P(X1)P(X2)P(X3)P(X4
|X1, X2, X3)P(X5
|X1, X2, X3)
(10)
Finally, there are at least three possible approaches to causal inference with BNs:
1. Model comparison: choosing the scope of possible models (by defining their structure
a priori), and comparing their joint probability. Mind that in this case, the algorithm
will simply return the winning graphical model, without estimation of the coefficients
representing connection weights
3.
2. Assuming one model structure a priori, and only inferring the weights. This is common
practice, related to, for example, Naive Bayes (Bishop, 2006) in which the structure is
assumed, and the connectivity weights are estimated from conditional probabilities. In
this case, the algorithm will assume that the proposed graphical model is correct, and
infer the connection weights only
Inferring the structure of the model from the data in an iterative way, by using a variety of
approximate inference techniques that attempt to maximize posterior probability of the
model by minimizing a cost function called free energy (Frey & Jojic, 2005), similar to
DCM): expectation maximization (EM; Bishop, 2006; Dempster, Laird, & Rubin, 1977),
variational procedures (Jordan, Ghahramani, Jaakkola, & Saul, 1998), Gibbs sampling
(Neal, 1993) or the sum-product algorithm (Kschischang, Frey, & Loeliger, 2001), which
gives a broader selection of procedures than in the DCM.
BNs can detect both excitatory and inhibitory connections X → Y, depending on whether
the conditional probability p(Y|X) is higher or lower than the marginal probability p(X)1.
Like LiNGAM, BNs cannot pick up on bidirectional connections in general. The assumption
of acyclicity comes from the cyclic belief propagation (Figure 4C, iii): the joint probability
of a cyclic graph would be expressed by an infinite chain of conditional probabilities, which
usually does not converge into a closed form. This restricts the scope of possible models to
DAGs (Thulasiraman & Swamy, 1992). However, there are also implementations of BNs that
cope with cyclic propagation of information throughout the network, for example, Cyclic
Causal Discovery algorithm (CCD; Richardson & Spirtes, 2001). This algorithm is not often
used in practice. However, as it works in the large sample limit, CCD requires assumption on
the graph structure and retrieves a complex output4. In BNs, the value of conditional prob-
ability P(Y|X) can be a measure of a connection strength2. We can consider conditional
probabilities significantly higher than chance as an indication for significant connections3. In
principle, BNs are not resilient to latent confounds. However, some classes of algorithms were
designed specifically to tackle this problem, such as Stimulus-based Causal Inference (SBCI;
Grosse-Wentrup, Janzing, Siegel, & Schölkopf, 2016), Fast Causal Inference (FCI; P. Spirtes,
Glymour, & Scheines, 1993; Zhang, 2008) and Greedy Fast Causal Inference (GFCI; Ogarrio,
Spirtes, & Ramsey, 2016)6. BNs can either work through model comparison or as an explor-
atory technique7. In the first case, it involves model specification that, like in DCM, requires
a priori knowledge about the experimental paradigm. In the latter case, the likelihood is in-
tractable and can only be approximated 8 (Diggle, 1984). In principle, networks of any size
can be modeled with BNs, either through a model comparison or through exploratory tech-
niques. Exploratory techniques typically minimize a cost function during the iterative search
for the best model. Since together with the growing network size, the landscape of the cost
Network Neuroscience
257
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Bayesian inference:
A probabilistic method for causal
inference, in which competitive
models representing causal structure
in the network are evaluated with
respect to evidence in the
experimental data to support
these models.
Pairwise inference:
A two-step causal inference
procedure that reduces causal
inference in a large graph to
studying two-node interactions,
in contrast to network-wise
inference and hierarchical
network-wise models.
function becomes multidimensional and complex, and the algorithm is more likely to fall into
a local minimum, exploratory techniques may become unreliable for large networks9.
What can also become an issue while using BNs in practice is that multiple BN algorithms
return an equivalence class of a graph: the set of all graphs indistinguishable from the true
causal structure on the basis of their sole probabilistic independency (Spirtes, 2010). These
structures cannot be further distinguished without further assumptions or experimental inter-
ventions. For finite data, taking even one wrong assumption upon the directionality of causal
link in the graph can be propagated through the network, and cause an avalanche of incorrect
orientations (Spirtes, 2010). One approach designed to overcome this issue is the Constraint-
In this approach, Bayesian Inference is
Based Causal Inference (Claassen & Heskes, 2012).
employed to estimate the reliability of a set of constraints. This estimation can further be used
to decide whether this prior information should be used to determine the causal structure in
the graph.
BNs cope well with noisy datasets, which makes them an attractive option for causal re-
search in fMRI (Mumford & Ramsey, 2014). S. Smith et al. (2011) tested multiple implemen-
tations of BNs, including FCI, CCD, as well as other algorithms: Greedy Equivalence Search
(GES; Chickering, 2002; Meek, 1995), “Peter and Clark” algorithm (PC; Meek, 1995) and a
conservative version of “Peter and Clark” (J. Ramsey, Zhang, & Spirtes, 2006). All these imple-
mentation performed similarly well with respect to estimating the existence of connections,
but not to the directionality of the connections.
BNs are not widely used in fMRI research up to date, the main reason being the assumption
of acyclicity. One exception is Fast Greedy Equivalence Search (FGES; J. D. Ramsey, 2015;
J. D. Ramsey, Glymour, Sanchez-Romero, & Glymour, 2017; J. D. Ramsey et al., 2014), a
variant of GES optimized to large graphs. The algorithm assumes that the network is acyclic
with no hidden confounders, and returns an equivalence class for the graph. In a recent work
by Dubois et al. (2017), FGES was applied with use of a new, computational-experimental
approach to causal inference from fMRI datasets. In the initial step, causal inference is per-
formed from large observational resting-state fMRI datasets with use of FGES in order to get the
aforementioned class of candidate causal structures. Further steps involve causal inference in
a single patient informed by the results of the initial analysis, and interventional study with use
of an electrical stimulation in order to determine which of the equivalent structures revealed
by FGES can be associated with a particular subject.
PAIRWISE INFERENCE
The last group of methods reflects the most recent trends in the field of causal inference in
fMRI. This family of methods is represented by Pairwise Likelihood Ratios (PW-LR; Hyvärinen
& Smith, 2013), and involves a two-stage inference procedure. In the first step, functional con-
nectivity is used to find connections, without assessing their directionality.Unlike network-wise
methods which eliminate insignificant connections post hoc, pairwise methods eliminate in-
significant connections prior to causal inference. In the second step, each previously found
connection is analyzed separately, and the two nodes involved are classified as an upstream or
downstream region. These methods do not involve assumptions on the global patterns of con-
nectivity at the network level (recurrent vs. feedforward). However, they involve the assump-
tion that the connections are nontransitive: if X projects to Y, and Y projects to Z, it does
not imply that X projects to Z. The causal inference is based on the pairs of nodes only, and
this has consequences for the interpretation of the network as a whole. As there is uncertainty
Network Neuroscience
258
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
associated with estimation of every single causal link, the probability that all connections
are correctly estimated decreases rapidly with the number of nodes in the network.
Pairwise Likelihood Ratios
A two-step procedure to causal inference in fMRI was first proposed by Patel et al. (2006) as
Patel’s tau (PT). The first step involves identifying the (undirected) connections by means of
functional connectivity, and is achieved on the basis of correlations between the time series in
different regions. This step results in a binary graph of connections, and the edges identified
as empty are disregarded from further considerations, because if there is no correlation, there
is no causation.
The second step determines the directionality in each one of the previously detected con-
nections. The causal inference boils down to a two-node Bayesian network as the whole
concept is based on a simple observation: if there is a causal link X → Y, Y should get a
transient boost of activity every time X increases activity. And vice versa: if there is a causal
link Y → X, X should react to the activation in Y by increasing activity. Therefore, one can
threshold the signals X(t), Y(t), and compute the difference between conditional probabilities
P(Y|X) and P(X|Y). Three scenarios are possible:
1. P(Y|X) equals P(X|Y): it is a bidirectional connection X ↔ Y (since empty connections
were sorted out in the previous step).
2. The difference between P(Y|X) and P(X|Y) is positive: the connection X → Y is likely.
3. The difference between P(Y|X) and P(X|Y) is negative: the connection Y → X is likely.
Building on the concept of PT,
the Pairwise Likelihood Ratios approach (PW-LR;
Hyvärinen & Smith, 2013) was proposed. The authors improved on the second step of the in-
ference by analytically deriving a classifier to distinguish between two causal models X → Y
and Y → X, which corresponds to the LiNGAM model for two variables. The authors com-
pared the likelihood of these two competitive models derived under LiNGAM’s assumptions
(Hyvärinen et al., 2010), and provided with a cumulant based approximation to their ratio.
In particular, the authors focused on the approximation of the likelihood ratios with third cu-
mulant for variables X and Y, which is an asymmetry between first (the mean) and second
(the variance) moment of the distributions of variables X and Y (this version of the method is
referred to by the authors as “PW-LR skew”):
C3 =
1
N
N
∑
i=1
(X(i)Y(i)2 − X(i)2Y(i))
(11)
Then, if the value of this cumulant is positive, it indicates for the connection X → Y, and back-
ward otherwise. Additionally, the authors proposed a modified version of the third cumulant,
including a nonlinear transformation of the signal to improve resilience against outliers in the
signal (and referred to this modified metric as “PW-LR r skew”). Additionally, the authors also
introduced a version based on fourth cumulant (referred to as “PW-LR kurtosis”).
PW-LR methods cannot distinguish between excitation and inhibition1, but provide with
a quantitative measure for the strength of the connection2. The authors recommended to test
significance of PW-LR results through permutation testing (Hyvärinen & Smith, 2013)3. Follow-
ing the interpretation from Patel, it is possible to distinguish between uni- and bidirectionality
(since scores close to zero might indicate the bidirectionality)4. The authors proposed using
partial correlation instead of Pearson’s correlation in the first step of the causal inference, which
Network Neuroscience
259
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
aims to find direct connections in the network5. As for the resilience to confounds, PW-LR
methods were tested on benchmark data for which common inputs to the nodes of the net-
work were introduced (S. Smith et al., 2011, simulation no. 12). PW-LR gave much better
performance than the best competitors (LiNGAM-ICA and PT) and reached as much as 84% of
correctly classified connections across all the benchmark datasets6. In the original formulation,
PW-LR involves a point estimate for the strength of effective connectivity and lacks estimation
of confidence intervals. In such cases, in fMRI studies, estimating confidence intervals is per-
formed in a data-driven fashion. This is typically achieved by means of permutation testing
(Hyvärinen & Smith, 2013; S. Smith et al., 2011), but can also be approached with use of mix-
ture modeling (Bielczyk et al., 20187). PW-LR, as a closed-form solution, is computationally
cheap8. As the pair-by-pair inferences do not require network fitting procedures, this approach
can easily be applied to larger networks9.
On the benchmark datasets, all versions of PW-LR were performing very well, as contrasted
with the best competitors: PT and LiNGAM (and, PW-LR r skew was giving the best results). In
all but one out of 28 simulations PW-LR methods were performing highly above chance, and
in a few cases they even reached 100% accuracy. However, PW-LR has not been validated on
the experimental fMRI datasets to date.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
NEW DIRECTIONS IN CAUSAL RESEARCH IN fMRI
A number of methods have been discussed, but the search for new ways of extracting causal
information from fMRI data is still on, of which we want to highlight four representatives.
Laminar Analysis
Advancements in fMRI acquisition have made it possible to scan at submillimeter resolution,
which opens up the possibility of a layer-specific examination of the BOLD signal. As the dif-
ferent layers of the cortex receive and process feedforward and feedback information largely
in different layers (Bastos et al., 2015; Felleman & Essen, 1991, e.g.), these different processes
could be visible in the laminar BOLD response. In rat studies, the BOLD response was indeed
shown to have laminar specificity and have its onset in the input layer of rat motor and so-
matosensory cortex (Yu, Qian, Chen, Dodd, & Koretsky, 2014). And also in humans, several
studies suggest laminar specificity of feedback processes (Kok, Bains, vanMourik, Norris, &
de Lange, 2016; Muckli et al., 2015).
These results suggest that human laminar BOLD signal may contain directional and causal
information. Hitherto, only single-region laminar fMRI has been employed, but it may well
be worthwhile to investigate how output layers of one region influence the input layer of the
other.
Fractional Cumulants
Certain new methods take a more statistical approach to neuroimaging data. For instance, char-
acterizing the shape of BOLD distributions by means of fractional moments of the BOLD dis-
tribution combined into cumulants (Bielczyk et al., 2016) can improve on the classification of
the two nodes within one connection into an upstream and a downstream node. Fractional
moments of a distribution are a mathematical concept with limited practical interpretation,
but could still contain valuable (causal) information.
In this method a classification procedure using fractional cumulants derived from BOLD
distribution is developed. The classifier is informed by the DCM generative model. The initial
Network Neuroscience
260
Disentangling causal webs in the brain using fMRI
results show that the causal classification scores similarly or better than competitive methods
when applied to low-noise benchmark synthetic datasets (S. Smith et al., 2011), and its perfor-
mance is, in general, similar to PW-LW r-skew. The difference shows up after imposing higher
level neuronal noise on the network: the fractional cumulant-based classifier is the most robust
approach in presence of such natural confounds. However, validation on real fMRI datasets
for this method is still pending.
Rendering Whole-Brain Effective Connectivity with Use of Covariance Matrices
Recent approach to causal inference in fMRI involves inferring directionality of information
transfer by using a set of covariance matrices with both zero and nonzero time lags (Gilson,
Moreno-Bote, Ponce-Alvarez, Ritter, & Deco, 2016). The authors build a dynamic model of the
brain network and optimize the effective connectivity (adjacency matrix) such that the model
covariances reproduce the empirical fMRI/BOLD covariance matrices. In this way, the fitted
model best matches the BOLD dynamics with respect to the second-order statistics. The authors
validate the model in synthetic datasets, and apply to experimental fMRI datasets by using
diffusion-weighted MRI imaging in order to constrain the network connectivity. The concept
of lagged covariance matrices was also used to evaluate the difference in cortical activation
between two behavioral conditions (in application to movie watching; M. Gilson et al., 2017).
As this method incorporates lags, it has similar limitations as other lagged methods (such as
GC or TE): it becomes lag-dependent. The authors theoretically demonstrate that for accuracy
of the directed connectivity estimation, time lag must be matched with the time constant of
the underlying dynamical system representing the network. How to achieve the accuracy in
order to fulfill this requirement in practice remains an open research question.
Another recent contribution in this domain by Schiefer et al. (2018) focuses on inferring
causal connections from resting-state fMRI datasets (and other continuous time series coming
from noninterventional studies), based on the assumption that the symmetric, nonlagged co-
variance matrix derived from the observed activity contains footprints of the direction and
the sign of sparse directed connections. This underlying sparse structure is found via L1-
minimization with a gradient descent, which allows for obtaining asymmetric output con-
nectivity matrix from the initial symmetric covariance structure. In the process, the method
utilizes the fact that in case of a collider present in the network (X and Y projecting to the
same node Z), projecting nodes X and Y have a positive covariance, which indicates for a
particular motif in the covariance structure. The validation on ground truth synthetic datasets
derived from a simple Ornstein–Uhlenbeck process resulted in impressive results. On the other
hand, application to the experimental fMRI datasets brought more vague results; therefore, the
method requires more exploration in the fMRI datasets.
Neural Network Models
Another recent development relevant to the problem of causal inference is the approach of
implementing neural network models to perform a complex task that is emblematic of hu-
man cognition (most commonly, visual object recognition).
It is then possible to study the
functional architecture and representational space of such models and attempt to draw insight
from optimal model parameters as to how such tasks are implemented in the human brain. In
recent years neural network models designed to recognize objects have reached human levels
of performance (Kriegeskorte, 2015; Krizhevsky, Sutskever, & Hinton, 2012), and the potential
of using these as models of how biological brains represent object space became a realizable
goal. Early studies of feedforward neural networks that has been replicated across multiple
Network Neuroscience
261
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
studies is that the closer the representational space a model uses resembles inferior temporal
cortex fMRI activity the better the model performs (Khaligh-Razavi & Kriegeskorte, 2014; D. L.
Yamins, Hong, Cadieu, & DiCarlo, 2013; D. L. K. Yamins et al., 2014). Of particular interest is
the finding that object representations in neural network models correlate with human brain
representations in a hierarchical fashion, a result shown in across both spatial and temporal
dimensions (Cichy, Khosla, Pantazis, Torralba, & Oliva, 2016). While care must be taken not to
overinterpret the generalisability of such models, these promising findings indicate that neural
network models may be able to provide insight into the fundamental constraints of certain
computational processes which in turn can be applied to determining functional (and casual)
relationships in human cognition.
SUMMARY
We sum up the characteristics of all the discussed methods in the Table 1:
DISCUSSION
In this work, we focused on discussing methods with respect to the causal structure imposed
on the brain. According to this criterion, the methods fall into three categories. Network-
wise methods, such as GC or SEM, do not restrict the connectivity patterns, whereas DAGs,
such as BNs, assume a hierarchical structure and unidirectional connections.
In the latter
category, a primary node receives input from outside the network and distributes information
downstream throughout the network. This may be a good approximation for many processes,
(see for instance recent work on the visual cortex by Michalareas et al., 2016). However, the
feed forward structure assumes a strictly hierarchical organization, which limits its capacity
to model communication between different brain networks. Under what circumstances DAGs
can be an accurate representation for causal structures in the brain remains an open question.
Next to network-wise methods and DAGs, we also discussed a third group of methods, re-
ferred to as “pairwise.” In this approach, the causal inference is done by splitting the inference
into many pairwise inferences. Prior to this, the dimensionality is reduced based on functional
Table 1.
Summary for all the methods discussed in this paper. GC: Granger causality; SEM: Struc-
tural Equation Modeling; DC: Dynamic Causal Modeling; LN: LINGaM; BN: Bayesian Nets; TE:
Transfer Entropy; PW-LR: Pairwise Likelihood Ratios; net: network-wise; dag: Directed Acyclic
Graphs only; pw: pairwise; +/-: depends on implementation; mc: model comparison; c: classical
hypothesis testing; ml: machine learning; l: low; h: high; n/a: nonapplicable. PW-LR is based on the
same concept as Patel’s tau (PT), and the inference is the same, therefore we did not add a separate
column for PT.
Feature — Method
Group of methods
Sign of connections
Directionality
Connection strength
Immediacy
Resilience to confounds
Causality through...
Computational cost
Model-free?
Prespecify the graph?
Regression in time
GC
net
+
+
+
+/−
+/−
c
l
−
−
+
SEM
net
+
+
+
+/−
+/−
mc/c
l/h
−
−
−
DCM
net
+
+
+
−
−
mc
h
−
+
−
LN
dag
+
−
+
+
+/−
ml+c
h
−
−
−
BN
dag
−
−
+
+
+/−
mc/ml
l/h
+
+/−
−
TE
net
+
+
+
+/−
+/−
c
l
+
−
+
PW-LR
pw
−
+
+
+
+
c
l
+
−
−
Network Neuroscience
262
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
connectivity, based on the idea that (partial) correlation is a good indicator for the existence
of causal links (S. Smith et al., 2011) and therefore allows for simplifying the problem, both
computationally and conceptually. Since the inference in this class of methods is split into
a set of pairwise inferences, it is important to be aware of the fact that the confidence levels
are also obtained connection by connection. Therefore, for a network represented by a set
i(1 − pi) (in
of connections with p values pi, the joint probability of the model is roughly Π
practice, confidence values for the existence of single connections are not independent, there-
fore this is only a rough approximation of the joint probability). This also means that there is
a trade-off between the joint probability of the graph and its density: the joint probability of
the whole network pattern can be increased by decreasing the threshold for connectivity at
more conservative p values. Furthermore, one can look at the pairwise inference methods as
a sort of model comparison, because in the second step of the inference, for every connection
only three options are possible to choose from. The difference with DCM procedure lies in the
fact that pairwise inference methods are based on the simple statistical properties emerging
from causation in linear systems, and do not involve minimizing the cost function—such as
negative free energy—as is done in DCM.
In the fMRI community, the DCM family (K. J. Friston et al., 2003) is currently the most
popular approach to causal inference. This is partially due to the fact that DCM was tailor-
made for fMRI, and includes a generative model based on the biological underpinnings of the
BOLD dynamics (Buxton et al., 1998). Some of the GC studies also involve estimation of the
HRF, and deconvolving the data before applying the estimation procedure (David et al., 2008;
Goodyear et al., 2016; Hutcheson et al., 2015; Ryali et al., 2016, 2011; Sathian et al., 2013;
Wheelock et al., 2014). This notion of the hemodynamics is both a strength and a weakness:
the generative model fits the data well, but only as long as the current state of knowledge is
accurate. New studies suggest that human hemodynamics are very dynamic and driven by
state-dependent processes (Handwerker, Gonzalez-Castillo, D’Esposito, & Bandettini, 2012;
Miezin, Maccotta, Ollinger, Petersen, & Buckner, 2000). The influence of this complex behav-
ior on the performance of DCM is hard to estimate.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
The DCM procedure performs causal inference through model comparison, and as such, it is
restricted to causal research in small networks containing a few nodes since the computational
costs increase like a factorial with the number of nodes. With the rise of research into resting-
state networks that contain up to 200 nodes, this may prove to be a limiting characteristic (S. M.
Smith et al., 2009a). This issue can be addressed with new methods for pairwise inference such
as PT and PW-LR, which do not impose any upper bound on the size of the network as well
as new versions of whole-brain DCMs (Frässle et al., 2016, Frässle et al., 2018).
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
It is important to remember that there are always two aspects to a method for causal infer-
ence. First, the method should have assumptions grounded in a biologically plausible frame-
work, well suited for the given dataset. For instance, a method for causal inference in fMRI
should respect (1) the confounding, region- and subject-specific BOLD dynamics (Handwerker
et al., 2004) and (2) co-occurance of cause and effect (since the time resolution of the data
is low compared with the underlying neuronal dynamics; the causes and their effects most
likely happen within the same frame in the fMRI data). The new methods for pairwise infer-
ence address this issue by (1) breaking the time order, and performing causal inference on the
basis of statistical properties of the distribution of the BOLD samples, and not from the timing
of events; and (2) using correlation in order to detect connections. A good counterexam-
ple here is GC. GC has been proven useful in multiple disciplines, and its estimation proce-
dure is impeccable: nonparametric, computationally straightforward, and it gives a unique,
Network Neuroscience
263
Disentangling causal webs in the brain using fMRI
unbiased solution. However, there is an ongoing discussion on whether or not GC is suited for
causal interpretations of fMRI data. On the one hand, theoretical work by Seth et al. (2013) and
Roebroeck et al. (2005) suggest that despite the slow hemodynamics, GC can still be informa-
tive about the directionality of causal links in the brain. On the other hand, the work by Webb
et al. (2013) demonstrates that the spatial distribution of GC corresponds to the Circle of Willis,
the major blood vessels in the brain.
Second, an estimation procedure needs to be computationally stable. Even if the generative
model faithfully describes the data, it still depends on the estimation algorithm whether the
method will return correct results. However, the face validity of the algorithms can only be
tested in particular paradigms, in which the ground truth is known. If in the given paradigm,
the ground truth is unknown, which is most often the case in fMRI experiments, only reliability
can be tested. One way of assessing reliability of the method is testing for the test-retest conver-
gence. So far, DCM is the only method that has been extensively tested in terms of test-retest
reliability in separate studies (Frässle, Paulus, et al., 2016; Frässle et al., 2015; Rowe et al.,
2010; Schuyler et al., 2010; Tak et al., 2018) and performed good overall. In general, it is de-
sirable to have more studies testing the reliability of the methods on reliability in experimental
fMRI datasets, as such validation of multiple methods such as GC or SEM, is still missing.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
One last remark about the nature of the different methods: some methods are developed for
event-related fMRI, such as DCM. Yet, new implementations of spectral DCM for the resting
state were also developed (K. J. Friston et al., 2011). As for other methods, application to
resting-state studies is relatively straightforward, while task fMRI can pose certain constraints
on the methods. For instance, lag-based methods such as GC work best when the task is
executed in a form of epochs (Deshpande, LaConte, James, Peltier, & Hu, 2008) rather than
a few second stimulus-response blocks, because it is extremely difficult to fit an AR model to
datasets of 1 to 2 frames in length. For this reason, structural methods (which do not regard
the time sequence) such as BNs or PW-LR, will be much more efficient in estimating causality
in such cases.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
Coming back to the main question posed in this review, can we hope to uncover causal
relations in the brain using fMRI? Although there are new concepts in the field, which propose
to consider causal interactions in the brain in probabilistic terms (Griffiths, 2015; Mannino &
Bressler, 2015), the “traditional,” deterministic models of causality are prevalent in neuroimag-
ing. Within these deterministic models, in the light of the existing literature, the new research
directions based on breaking the time order as the axiom of causal inference (such as PW-LR,
PT, and LiNGAM), prove more successful than the more “traditional” approaches, which take
regression in time into account (such as GC or TE; Hyvärinen & Smith, 2013; S. Smith et al.,
2011). Also, Patel’s two-step design to achieve a causal map of connections is very promis-
ing, especially once the Pearson correlation is replaced with partial correlation as is done in
PW-LR. One note to add is that “success” of any method for causal inference in fMRI de-
pends on the forward model used for generating the synthetic dataset. In the seminal paper by
S. Smith et al. (2011), multiple methods were evaluated and critically discussed on the basis of
simulations of the DCM generative model. However, there are alternatives, for example, the
generative model Seth et al. (2013), which might potentially yield other hierarchy of methods
in terms of success rate in inferring causal links from synthetic fMRI BOLD datasets.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
In this paper, we discuss the topic of inferring causal processes from fMRI datasets on the
level of individual subject. One approach that could further contribute to the development
of methods for causal inference in fMRI though, is a group inference approach. In such an
Network Neuroscience
264
Disentangling causal webs in the brain using fMRI
approach, a prior that different subjects represent similar causal structures is added to the
inference procedure. As lumping the datasets coming from different subjects increases the
amount of data to derive the causal structure from, this assumption, in general, facilitates the in-
ference. Multiple algorithms for group inference for effective connectivity in fMRI have already
been proposed, including Independent Multiple sample Greedy Equivalence Search (IMaGES;
J. D. Ramsey et al., 2010), previously mentioned LOFS algorithm (J. D. Ramsey et al., 2011)
and Group Iterative Multiple Model Estimation (GIMME; Gates & Molenaar, 2012).
Furthermore, with the current rapid growth of translational research and increase in use of
invasive and acute stimulation techniques such as optogenetics (Deisseroth, 2011; Ryali et al.,
2016) or transcranial magnetic stimulation (Kim et al., 2009), a rigid validation of methodol-
ogy for causal inference becomes feasible through interventional studies. Recently, multiple
methods for inferring causality from fMRI data were validated using a joint fMRI and MEG
experiment (Mill et al., 2017), with promising results for GC and BNs. This gives hope for
establishing causal relations in neural networks using fMRI.
ACKNOWLEDGMENTS
We thank to Lionel Barnett, Christian Beckmann, Daniel Borek, Patrick Ebel, Daniel Gomez,
Moritz Grosse-Wentrup, Max Hinne, Maciej Jedynak, Christopher Keown, S ´andor Kolumb ´an,
Vinod Kumar, Randy McIntosh, Nils Müller, Hanneke den Ouden, Payam Piray, Thomas
Rhys-Marshall, Gido Schoenmacker, Ghaith Tarawneh, Fabian Walocha, and Johannes Wilbertz
for sharing knowledge about causal inference in fMRI, and for providing a valuable content.
We further thank Martha Nari-Havenith and Peter Vavra for his contribution to the conceptual
work. In addition, we cordially thank Thomas Wolfers for encouragement and help at an early
stage.
AUTHOR CONTRIBUTIONS
Natalia Bielczyk: Conceptualization; Writing – original draft; Writing – review & editing. Sebo
Uithol: Conceptualization; Writing – original draft; Writing – review & editing. Tim van Mourik:
Conceptualization; Writing – original draft; Writing – review & editing. Paul Anderson: Con-
ceptualization; Writing – original draft; Writing – review & editing. Jeffrey Glennon: Writing –
review & editing. Jan K Buitelaar: Writing – review & editing.
FUNDING INFORMATION
European Research Council
Natalia Bielczyk, FP7 Ideas:
(http://dx.doi.org/10.13039/
100011199), Award ID: 305697. Natalia Bielczyk, FP7 Ideas: European Research Coun-
cil (http://dx.doi.org/10.13039/100011199), Award ID: 278948. Natalia Bielczyk, FP7 Ideas:
European Research Council (http://dx.doi.org/10.13039/100011199), Award ID: 603016. Sebo
Uithol, H2020 Marie Skłodowska-Curie Actions (http://dx.doi.org/10.13039/100010665),
Award ID: 657605. Jeffrey Glennon, FP7 Ideas: European Research Council (http://dx.doi.org/
10.13039/100011199), Award ID: 603016. Jeffrey Glennon, FP7 Ideas: European Research
Council (http://dx.doi.org/10.13039/100011199), Award ID: 278948. Jeffrey Glennon, FP7
Ideas: European Research Council
(http://dx.doi.org/10.13039/100011199), Award ID:
602805. Jeffrey Glennon, FP7 Ideas: European Research Council (http://dx.doi.org/10.13039/
100011199), Award ID: 305697. Jeffrey Glennon, Horizon 2020 (http://dx.doi.org/10.13039/
Jan K Buitelaar, FP7 Ideas: European Research Coun-
501100007601), Award ID: 115916.
cil (http://dx.doi.org/10.13039/100011199), Award ID: 115300.
Jan K Buitelaar, FP7 Ideas:
European Research Council (http://dx.doi.org/10.13039/100011199), Award ID: 603016. Jan
K Buitelaar, FP7 Ideas: European Research Council (http://dx.doi.org/10.13039/100011199),
Network Neuroscience
265
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Award ID: 278948. Jan K Buitelaar, FP7 Ideas: European Research Council (http://dx.doi.org/
10.13039/100011199), Award ID: 602805.
Jan K Buitelaar, FP7 Ideas: European Research
Council (http://dx.doi.org/10.13039/100011199), Award ID: 305697. Jan K Buitelaar, Horizon
2020 (http://dx.doi.org/10.13039/501100007601), Award ID: 115916.
REFERENCES
Akaike, H. (1998). Information theory and an extension of the maxi-
mum likelihood principle. In Selected papers of Hirotugu Akaike
(pp. 199–213). New York: Springer.
Almgren, H. B. J., de Steen, F. V., Kühn, S., Razi, A., Friston, K. J., &
Marinazzo, D. (2018). Variability and reliability of effective con-
nectivity within the core default mode network: A longitudinal
spectral DCM study. BioRxiV. https://doi.org/10.1101/273565
Altman, N., & Krzywi ´nski, M. (2015). Association, correlation and
causation. Nature Methods, 12(10), 899–900. https://doi.org/10.
1038/nmeth.3587
Anderson,
J. C., & Gerbing, D. W. (1988). Structural equation
modeling in practice: A review and recommended two-step ap-
proach. Psychological Bulletin, 103(3), 411–23. https://doi.org/
10.1037/0033-2909.103.3.411
Arichi, T., Fagiolo, G., Varela, M., Melendez-Calderon, A., Allievi, A.,
Merchant, N., . . . Edwards, A. D. (2012). Development of BOLD
signal hemodynamic responses in the human brain. Neuro-
Image, 63(2), 663–73. https://doi.org/10.1016/j.neuroimage.2012.
06.054
Barnett, L., Barrett, A. B., & Seth, A. K. (2009). Granger causality
and transfer entropy are equivalent for Gaussian variables. arXiv.
https://doi.org/10.1103/PhysRevLett.103.238701
Barnett, L., & Bossomaier, T. (2012). Transfer entropy as a log-
likelihood ratio. Physical Review Letters, 109(13). https://doi.org/
10.1103/PhysRevLett.109.138105
Bastos, A. M., Vezoli, J., Schoffelen, C. A. B. J.-M., Oostenveld, R.,
Dowdall, J. R., Weerd, P. D., . . . Fries, P. (2015). Visual areas
exert feedforward and feedback influences through distinct fre-
quency channels. Neuron, 85(2), 390–401. https://doi.org/10.
1016/j.neuron.2014.12.018
Bellec, P., Perlbarg, V., Jbabdi, S., Pélégrini-Issac, M., Anton, J. L.,
Doyon, J., . . . Benali, H. (2006). Identification of large-scale
networks in the brain using fMRI. NeuroImage, 29(4), 1231–43.
https://doi.org/10.1016/j.NeuroImage.2005.08.044
Bellec, P., Rosa-Neto, P., Lyttelton, O. C., Benali, H., & Evans,
A. C. (2010). Multi-level bootstrap analysis of stable clusters in
resting-state fMRI. NeuroImage, 51(3), 1126–39. https://doi.org/
10.1016/j.neuroimage.2010.02.082
Bentler, P. M. (1985). Theory and implementation of EQS, a struc-
tural equations program. BMDP Statistical Software, Pennsylvania
State University.
Bernal-Casas, D., Balaguer-Ballester, E., Gerchen, M. F., Iglesias,
S., Walter, H., Heinz, A., . . . Kirsch, P. (2013). Multi-site re-
producibility of prefrontal-hippocampal connectivity estimates
by stochastic DCM. NeuroImage, 82, 555–63. https://doi.org/10.
1016/j.NeuroImage.2013.05.120
Bielczyk, N. Z., Llera, A., Buitelaar,
J. K., Glennon,
J. C., &
Beckmann, C. F.
Increasing robustness of pairwise
methods for effective connectivity in Magnetic Resonance Imag-
(2016).
ing by using fractional moment series of BOLD signal distribu-
tions. arXiV preprint. Retrieved from https://arxiv.org/abs/1606.
08724
Bielczyk, N. Z., Llera, A., Buitelaar,
J. C., &
Beckmann, C. F. (2017). The impact of haemodynamic variabil-
ity and signal mixing on the identifiability of effective connectiv-
ity structures in BOLD fMRI. Brain and Behavior, 7(8), e00777.
https://doi.org/10.1002/brb3.777
J. K., Glennon,
Bielczyk, N. Z., Walocha, F., Ebel, P. W. J., Haak, K., Llera, A.,
Buitelaar, J. K., . . . Beckmann, C. F. (2018). Thresholding func-
tional connectomes by means of mixture modeling. NeuroImage,
171,402–414.https://doi.org/10.1016/j.neuroimage.2018.01.003
(2006). Pattern recognition and machine learning.
Bishop, C. M.
New York: Springer.
Blumensath, T.,
Jbabdi, S., Glasser, M. F., Essen, D. C. V.,
Ugurbil, K., Behrens, T. E., & Smith, S. M.
(2013). Spatially
constrained hierarchical parcellation of the brain with resting-
state fMRI. NeuroImage, 76, 313–24. https://doi.org/10.1016/
j.NeuroImage.2013.03.024
Bollen, K. (1989). Structural Equations with Latent Variables. New
York: John Wiley and Sons.
Boxerman, J. L., Bandettini, P. A., Kwong, K. K., Baker, J. R.,
Davis, T. L., Rosen, B. R., & Weisskoff, R. M. (1995). The intra-
vascular contribution to fMRI signal change: Monte Carlo
modeling and diffusion-weighted studies in vivo. Magnetic
Resonance in Medicine, 34(1), 4–10. https://doi.org/10.1002/
mrm.1910340103
Breakspear, M. (2013). Dynamic and stochastic models of neuro-
imaging data: A comment on Lohmann et al. NeuroImage, 75,
270–4. https://doi.org/10.1016/j.neuroimage.2012.02.047
Bressler, S. L., & Seth, A. K. (2011). Wiener-Granger causality:
A well established methodology. NeuroImage, 58(2), 323–9.
https://doi.org/10.1016/j.neuroimage.2010.02.059
Bronkhorst, A. W. (2000). The cocktail party phenomenon: A re-
view on speech intelligibility in multiple-talker conditions. Acta
Acustica United with Acustica, 86, 117–28. https://doi.org/10.
1121/1.1345696
Buijink, A. W. G., van der Stouwe, A. M. M., Broersma, M.,
Sharifi, S., Groot, P. F. C., Speelman, J. D., . . . van Rootselaar,
A.-F.
tremor:
A functional and effective connectivity study. Brain, 138(10),
2934–47. https://doi.org/10.1093/brain/awv225
(2015). Motor network disruption in essential
Bush, K., Cisler, J., Bian, J., Hazaroglu, G., Hazaroglu, O., & Kilts,
C. (2015). Improving the precision of fMRI BOLD signal decon-
volution with implications for connectivity analysis. Magnetic
Resonance Imaging, 33(10), 1314–23. https://doi.org/10.1016/
j.mri.2015.07.007
Buxton, R. B., Wong, E. C., & Frank, L. R.
(1998). Dynamics of
blood flow and oxygenation changes during brain activation: The
Network Neuroscience
266
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Balloon model. Magnetic Resonance in Medicine, 39(6),
855–64. https://doi.org/10.1002/mrm.1910390602
J., Meisenzahl, E., Schoepf, V.,
Carballedo, A., Scheuerecker,
(2011). Functional
.
Bokde, A., Möller, H.
Journal
connectivity of emotional processing in depression.
of Affective Disorders, 134(1-3), 272–9. https://doi.org/10.1016/
j.jad.2011.06.021
. Frodl, T.
J.,
.
Chai, B., Walther, D., Beck, D., & Fei-fei, L. (2009). Exploring func-
tional connectivities of the human brain using multivariate in-
formation analysis.
In Y. Bengio, D. Schuurmans, J. D. Lafferty,
C. K. I. Williams, & A. Culotta (Eds.), Advances in Neural Informa-
tion Processing Systems 22 (pp. 270–278). La Jolla, CA: Curran
Associates, Inc.
Chen, Y. C., Xia, W., Chen, H., Feng, Y., Xu, J. J., Gu, J. P., . . . Yin, X.
(2017). Tinnitus distress is linked to enhanced resting-state func-
tional connectivity from the limbic system to the auditory cortex.
Human Brain Mapping, 38(5), 2384–97. https://doi.org/10.1002/
hbm.23525
Chen, Z., & Chan, L. (2013). Causality in linear nongaussian acyclic
models in the presence of latent gaussian confounders. Neural
Computation, 25(6), 1605–41.
Chickering, D. M. (2002). Optimal structure identification with
greedy search. Journal of Machine Learning Research, 3, 507–54.
https://doi.org/10.1162/153244303321897717
Cichy, R. M., Khosla, A., Pantazis, D., Torralba, A., & Oliva, A.
(2016). Comparison of deep neural networks to spatio-temporal
cortical dynamics of human visual object recognition reveals
hierarchical correspondence. Scientific Reports, 6, 1–13.
Claassen, T., & Heskes, T. (2012). A Bayesian approach to constraint
based causal inference. In UAI, Proceedings of the 28th Confer-
ence on Uncertainty in Artificial Intelligence.
Comon, P., & Jutten, C. (2010). Handbook of Blind Source Sep-
Independent Component Analysis and Applications.
aration:
Academic Press.
Daunizeau, J., David, O., & Stephan, K. E. (2011). Dynamic causal
modelling: A critical review of the biophysical and statistical
foundations. NeuroImage, 58(2), 312–22. https://doi.org/10.1016/
j.neuroimage.2009.11.062
Daunizeau, J., Friston, K. J., & Kiebel, S. J. (2009). Variational
Bayesian identification and prediction of stochastic nonlinear
dynamic causal models. Physica D: Nonlinear Phenomena,
238(21), 2089–118. https://doi.org/10.1016/j.physd.2009.08.
002a
Daunizeau, J., Stephan, K. E., & Friston, K. (2012). Stochastic dy-
namic causal modelling of fMRI data: Should we care about neu-
ral noise? NeuroImage, 62(1), 464–81. https://doi.org/10.1016/
j.NeuroImage.2012.04.061
David, O., Guillemain, I., Saillet, S., Reyt, S., Deransart, C., Segebarth,
C., Depaulis, A. (2008). Identifying neural drivers with functional
MRI: An electrophysiological validation. PLoS Biology, 6(12),
e315. https://doi.org/10.1371/journal.pbio.0060315
Deisseroth, K. (2011). Optogenetics. Nature Methods, 8, 26–9.
https://doi.org/doi:10.1038/nmeth.f.324
Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum
likelihood from incomplete data via the EM algorithm. Journal of
the Royal Statistical Society. Series B, 39(1), 1–38. https://doi.org/
10.2307/2984875
Deshpande, G., LaConte, S., James, G. A., Peltier, S., & Hu, X.
(2008). Multivariate Granger causality analysis of fMRI data.
Human Brain Mapping, 30(4), 1361–73. https://doi.org/10.1002/
hbm.20606
Devonshire,
I. M., Papadakis, N. G., Port, M., Berwick,
J.,
Kennerley, A. J., Mayhew, J. E., & Overton, P. G. (2012). Neuro-
vascular coupling is brain region-dependent. NeuroImage, 59(3),
1997–2006. https://doi.org/10.1016/j.neuroimage.2011.09.050
Diebold, F. X. (2001). Elements of Forecasting (2nd ed.). Cincinnati:
South Western.
Diggle, P. J. (1984). Monte Carlo methods of inference for implicit
statistical models. Journal of the Royal Statistical Society, Series
B, 46, 193–227.
DSouza, A. M., Abidin, A. Z., Leistritz, L., & Wismüller, A.
(2017). Exploring connectivity with large-scale Granger causal-
Journal of Neuroscience
ity in resting-state functional MRI.
Methods, 287, 68–79. https://doi.org/10.1016/j.jneumeth.2017.
06.007
Dubois, J., Oya, H., Tyszka, J. M., Howard, M., Eberhardt, F., &
Adolphs, R. (2017). Causal mapping of emotion networks in
the human brain: Framework and preliminary findings. Neuro-
psychologia. https://doi.org/10.1016/j.neuropsychologia.2017.
11.015
Essen, D. C. V., Smith, S. M., Barch, D. M., Behrens, T., Yacoub, E.,
Ugurbil, K., & Consortium W.-M. H. (2013). The Human Con-
nectome Project: A data acquisition perspective. NeuroImage,
62(4), 2222–31. https://doi.org/10.1016/j.NeuroImage.2012.02.
018
Fedorenko, E., Hsieh, P.-J., Nieto-Castañón, A., Whitfield-Gabrieli,
S., & Kanwisher, N. (2010). New method for fMRI investigations
of language: Defining ROIs functionally in individual subjects.
Journal of Neurophysiology, 104(2), 1177–94. https://doi.org/
10.1152/jn.00032.2010
Feinberg, D. A., & Setsompop, K. (2013). Ultra-fast MRI of the
Journal
human brain with simultaneous multi-slice imaging.
of Magnetic Resonance, 229, 90–100. https://doi.org/10.1016/
j.jmr.2013.02.002
Felleman, D. J., & Essen, D. C. V. (1991). Distributed hierarchical pro-
cessing in the primate cerebral cortex. Cerebral Cortex, 1(1), 1–47.
Ferron, J. M., & Hess, M. R. (2007). Estimation in SEM: A concrete
example. Journal of Educational and Behavioral Statistics, 32(1),
110–20. https://doi.org/10.3102/1076998606298025
Fornito, A., Zalesky, A., & Breakspear, M. (2013). Graph analy-
sis of the human connectome: Promise, progress, and pitfalls.
NeuroImage, 80, 426–44. https://doi.org/10.1016/j.neuroimage.
2013.04.087
Frässle, S., Lomakina, E. I., Razi, A., Friston, K. J., Buhmann, J. M.,
& Stephan, K. E. (2017). Regression DCM for fMRI. NeuroImage,
155, 406–21. https://doi.org/10.1016/j.neuroimage.2017.02.090
Frässle, S., Lomakina, E. I., Kasper, L., Manjaly, Z. M., Leffe, A.,
Pruessmann, K. P., . . . Stephan, K. E. (2018). A generative model
of whole-brain effective connectivity. NeuroImage. https://doi.
org/10.1016/j.neuroimage.2018.05.058
Frässle, S., Lomakina-Rumyantseva, E., Razi, A., Buhmann, J. M., &
Friston, K. J. (2016). Whole-brain Dynamic Causal Modeling of
fMRI data. Retrieved from https://www.researchgate.net/project/
Whole-brain-dynamic-causal-modeling-of-fMRI-data
Network Neuroscience
267
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
n
e
n
_
a
_
0
0
0
6
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Frässle, S., Paulus, F. M., Krach, S., & Jansen, A. (2016). Test-
retest reliability of effective connectivity in the face perception
network. Human Brain Mapping, 37(2), 730–44. https://doi.org/
10.1002/hbm.23061
Frässle, S., Stephan, K. E., Friston, K. J., Steup, M., Krach, S., Paulus,
F. M., & Jansen, A. (2015). Test-retest reliability of dynamic causal
modeling for fMRI. NeuroImage, 117, 56–66. https://doi.org/
10.1016/j.neuroimage.2015.05.040
Frey, B. J., & Jojic, N. (2005). A comparison of algorithms for in-
ference and learning in probabilistic Graphical Models. IEEE
Transactions on Pattern Analysis and Machine Intelligence, 27(9),
1392–416. https://doi.org/10.1109/TPAMI.2005.169
Friston, K., Daunizeau, J., & Stephan, K. E. (2013). Model selection
and gobbledygook: Response to Lohmann et al. NeuroImage, 75,
275–8. https://doi.org/10.1016/j.neuroimage.2011.11.064
Friston, K., Moran, R., & Seth, A. K. (2013). Analysing connectivity
with Granger causality and dynamic causal modelling. Current
Opinion in Neurobiology, 23(2), 172–8. https://doi.org/10.1016/
j.conb.2012.11.010.
Friston, K. J., Ashburner, J., Kiebel, S. J., Nichols, T. E., & Penny,
(2007). Statistical Parametric Mapping: The Analysis of
W. D.
Functional Brain Images. Cambridge, MA: Academic Press.
Friston, K. J., Buchel, C., Fink, G. R., Morris, J., Rolls, E., & Dolan, R.
(1997). Psychophysiological and modulatory interactions in neu-
roimaging. NeuroImage, 6(3), 218–29. https://doi.org/10.1006/
nimg.1997.0291
Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal mo-
deling. NeuroImage, 19(4), 1273–302. https://doi.org/10.1016/
S1053-8119(03)00202-7
Friston, K. J., Holmes, A. P., Worsley, K. J., Poline, J.-P., Frith, C. D.,
& Frackowiak, R. S. J.
(1995). Statistical parametric maps in
functional imaging: A general linear approach. Human Brain
Mapping, 2, 189–210.
Friston, K. J., Kahan, J., Biswal, B., & Razi, A. (2011). A DCM
for resting state fMRI. NeuroImage, 94, 396–407. https://doi.org/
10.1016/j.NeuroImage.2013.12.009
Friston, K. J., Preller, K. H., Mathys, C., Cagnan, H., Heinzle, J.,
Razi, A., & Zeidman, P. (2017). Dynamic causal modelling re-
visited. NeuroImage, S1053-8119(17), 30156–8. https://doi.org/
10.1016/j.neuroimage.2017.02.045
Friston, K. J., & Stephan, K. E. (2007). Free-energy and the brain. Syn-
these,159(3),417–58. https://doi.org/10.1007/s11229-007-9237-y
Gates, K. M., & Molenaar, P. C. M. (2012). Group search algorithm
recovers effective connectivity maps for individuals in homoge-
neous and heterogeneous samples. NeuroImage, 63(1), 310–9.
https://doi.org/10.1016/j.neuroimage.2012.06.026
Geweke,
J. F. (1982). Measurement of linear dependence and
feedback between multiple time series. Journal of the American
Statistical Association, 77(378), 304–13. https://doi.org/10.1080/
01621459.1982.10477803
Geweke, J. F. (1984). Measures of linear dependence and feed-
back between multiple time series. Journal of the American
Statistical Association, 79(388), 907–15. https://doi.org/10.1080/
01621459.1984.10477110
Gilson, M., Moreno-Bote, R., Ponce-Alvarez, A., Ritter, P., & Deco,
G. (2016). Estimation of directed effective connectivity from fMRI
functional connectivity hints at asymmetries of cortical con-
nectome. PLoS Computational Biology. https://doi.org/10.1371/
journal.pcbi.1004762
Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D.,
Harwell, J., Yacoub, E., . . . Essen, D. C. V. (2016). A multi-
modal parcellation of human cerebral cortex. Nature, 536(7615),
171–8. https://doi.org/10.1038/nature18933
Glomb, K., Ponce-Alvarez, A., Gilson, M., Ritter, P., & Deco, G.
(2017). Stereotypical modulations in dynamic functional con-
nectivity explained by changes in BOLD variance. NeuroImage.
https://doi.org/10.1016/j.neuroimage.2017.12.074
(2000).
Image-based
method for retrospective correction of physiological motion ef-
fects in fMRI: RETROICOR. Magnetic Resonance in Medicine,
44(1), 162–167. https://doi.org/10.1002/1522-2594(200007)44:
1<162::AID-MRM23>3.0.CO;2-mi
guantero, GRAMO. h., li, t. P., & Ress, D.
Goodyear, K., Parasuraman, r., Chernyak, S., Madhavan, PAG.,
Deshpande, GRAMO., & krüger, F.
(2016). Advice taking from
humans and machines: An fMRI and effective connectivity
estudiar. Frontiers in Human Neuroscience, 4(10), 542. https://doi.
org/10.3389/fnhum.2016.00542
Granjero, C. W.. j. (1969). Investigating causal relations by econo-
metric models and cross-spectral methods. Econometrica, 37(3),
424–38. https://doi.org/10.2307/1912791
Griffiths, j. D. (2015). Causal influence in neural systems: Reconciling
mechanistic-reductionist and statistical perspectives. comment
on “Foundational perspectives on causality in large-scale brain
networks’’ by M. Mannino & S. l. Bressler. Physics of Life Reviews,
15, 130–2. https://doi.org/10.1016/j.plrev.2015.11.003
Grosse-Wentrup, METRO. (2014). Lecture: An introduction to causal
inference in neuroimaging. Max Planck Institute for Intelligent Sys-
tems. Retrieved from http://videolectures.net/bbci2014_grosse_
wentrup_causal_inference/
Grosse-Wentrup, METRO., Janzing, D., Siegel, METRO., & Schölkopf, B. (2016).
Identification of causal relations in neuroimaging data with la-
tent confounders: An instrumental variable approach. Neuro-
Image, 125, 825–33. https://doi.org/10.1016/j.neuroimage.2015.
10.062
Handwerker, D. A., Gonzalez-Castillo,
J., D'Esposito, METRO., &
Bandettini, PAG. A. (2012). The continuing challenge of understand-
ing and modeling hemodynamic variation in fMRI. NeuroImagen,
62(2), 1017–23. https://doi.org/10.1016/j.NeuroImage.2012.02.
015
Handwerker, D. A., Ollinger, j. METRO., & D'Esposito, METRO. (2004). Varia-
tion of BOLD hemodynamic responses across subjects and brain
regions and their effects on statistical analyses. NeuroImagen,
21(4), 1639–51. https://doi.org/10.1016/j.NeuroImage.2003.11.
029
Hausman, D. METRO., & Woodward, j.
Independence, invari-
ance, and the causal markov condition. British Journal for the
Philosophy of Science, 50(4), 521–83. https://doi.org/10.1093/
bjps/50.4.521
(1999).
Havlicek, METRO., Roebroeck, A., Friston, K., Gardumi, A., Ivanov, D.,
& Uludag, k. (2015). Physiologically informed Dynamic Causal
Modeling of fMRI data. NeuroImagen, 122, 355–72. https://10.
1016/j.NeuroImage.2015.07.078
Neurociencia en red
268
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
norte
mi
norte
_
a
_
0
0
0
6
2
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Hayashi, F. (2000). Econometría. Prensa de la Universidad de Princeton.
Él, B. Y. (2014). Scale-free brain activity: Past, present, and future.
Trends in Cognitive Neurosciences, 18(9), 480–87. https://doi.org/
10.1016/j.tics.2014.04.003
Heinzle,
J., Wenzel, METRO. A., & Haynes,
(2012). Visuo-
motor functional network topology predicts upcoming tasks.
Revista de neurociencia, 32(29), 9960–8. https://doi.org/10.1523/
JNEUROSCI.1604-12.2012
J.-D.
Hesse, w., moller, MI., arnold, METRO., & Schack, B.
(2003).
The use of time-variant EEG Granger causality for inspecting
Diario de
directed interdependencies of neural assemblies.
Neuroscience Methods, 124(1), 27–44. https://doi.org/10.1016/
S0165-0270(02)00366-7
Hoeting, j. A., Madigan, D., Raftery, A. MI., & Volinsky, C. t. (1999).
Bayesian model averaging: A tutorial. Statistical Science, 14,
382–401. https://doi.org/10.1214/ss/1009212519
Hoyer, PAG. o., Shimizu, S., Kerminen, A., & Palviainen, METRO. (2008).
Estimation of causal effects using linear non-Gaussian causal
International Journal of Approx-
models with hidden variables.
imate Reasoning, 49(2), 362–78. https://doi.org/10.1016/j.ijar.
2008.02.006
Hume, D.
(1772). Cause and effect.
In An Enquiry Concerning
Human Understanding.
Hutcheson, norte. l., Sreenivasan, k. r., Deshpande, GRAMO., Reid, METRO. A.,
Hadley, J., Blanco, D. METRO., . . . Lahti, A. C. (2015). Effective connec-
tivity during episodic memory retrieval in schizophrenia partic-
ipants before and after antipsychotic medication. Human Brain
Cartografía, 36(4), 1442–57. https://doi.org/10.1002/hbm.22714
Hyvärinen, A., & Oja, mi. (2000). Independent component analysis:
Algorithms and applications. Neural Networks, 13(4–5), 411–430.
https://doi.org/10.1016/s0893-6080(00)00026-5
Hyvärinen, A., & Herrero, S.
(2013). Pairwise likelihood ratios for
estimation of non-Gaussian structural equation models. Diario
de Investigación sobre Aprendizaje Automático, 14(1), 111–52.
Hyvärinen, A., zhang, K., Shimizu, S., & Hoyer, PAG. oh. (2010). Es-
timation of a structural vector autoregression model using non-
gaussianity. Journal of Machine Learning Research, 11, 1709–31.
j. j. (2016). Regular-
ized structural equation modeling. Structural Equation Mod-
eling, 23(4), 555–66. https://doi.org/10.1080/10705511.2016.
1154793
Jacobucci, r., Grimm, k. J., & McArdle,
James, GRAMO., kelly, METRO., Craddock, r., Holtzheimer, PAG., Dunlop, B.,
Nemeroff, C., . . . Hu, X. (2009). Exploratory structural equation
modeling of resting-state fMRI: Applicability of group models to
individual subjects. NeuroImagen, 45(3), 778–87. https://doi.org/
10.1016/j.NeuroImage.2008.12.049
Janssen, R.
J.,
Jylänki, PAG., Kessels, R. PAG., & van Gerven,
METRO. A. (2015). Probabilistic model-based functional parcellation
the striatum.
reveals a robust, fine-grained subdivision of
NeuroImagen, S1053-8119(15), 00589–3. https://doi.org/10.1016/
j.NeuroImage.2015.06.084
j. Friston, K., Litvak, v., Oswal, A., Razi, A., Esteban, k. MI., camioneta
Wijk, B. C. METRO., . . . Zeidman, PAG. (2016). Bayesian model reduction
and empirical Bayes for group (DCM) estudios. NeuroImagen, 128,
413–31. https://doi.org/10.1016/j.neuroimage.2015.11.015
Jolliffe,
I. t. (2002). Principal Component Analysis. Nueva York:
Saltador.
Jordán, METRO. I., Ghahramani, Z., Jaakkola, t. S., & Saul, l. k. (1998).
An introduction to variational methods for Graphical Models.
Jordán (Ed.), Learning in Graphical Models. Desorden
En m.
Académico.
I.
Joreskög, k. GRAMO., & Thillo, METRO. V. (1972). LISREL a general com-
puter program for estimating a linear structural equation sys-
tem involving multiple indicators of unmeasured variables. ETS
Research Bulletin Series, 2, i–71 https://doi.org/10.1002/j.2333-
8504.1972.tb00827.x
Kahan, J., & Foltynie, t. (2013). Understanding DCM: Ten simple
rules for the clinician. NeuroImagen, 83, 542–9. https://doi.org/
10.1016/j.NeuroImage.2013.07.008.
Kelly, C., Toro, r., Martino, A. D., Cox, C., Bellec, PAG., Castellanos,
F. X., & Milham, METRO. PAG. (2012). A convergent functional archi-
tecture of the insula emerges across imaging modalities. nuevo-
roImage, 61(4), 1129–42. https://doi.org/10.1016/j.neuroimage.
2012.03.021
Khaligh-Razavi, S.-M., & Kriegeskorte, norte. (2014). Deep supervised,
but not unsupervised, models may explain IT cortical represen-
tation. Biología Computacional PLoS, 10(11), e1003915–29.
Kiebel, S. J., Garrido, METRO. I., Moran, R. J., & Friston, k. j. (2008).
Dynamic causal modelling for EEG and MEG. Cognitive Neu-
rodynamics, 2(2), 121–36. https://doi.org/10.1007/s11571-008-
9038-0
Kiebel, S. J., Kloppel, S., Weiskopf, NORTE., & Friston, k. j. (2007).
Dynamic causal modeling: A generative model of slice timing
in fMRI. NeuroImagen, 34(4), 1487–96. https://doi.org/10.1016/
j.neuroimage.2006.10.026
kim, D. r., Pesiridou, A., & O’Reardon, j. PAG. (2009). Transcra-
nial magnetic stimulation in the treatment of psychiatric disor-
ders. Current Psychiatry Reports, 11(6), 447–52. https://doi.org/
10.1007/s11920-009-0068-z
Kiyama, S., Kunimi, METRO., Iidaka, T., & Nakai, t. (2014). Distant
functional connectivity for bimanual finger coordination dec-
lines with aging: An fMRI and SEM exploration. Fronteras en
Human Neuroscience, 8, 251. https://doi.org/10.3389/fnhum.
2014.00251
Kok, PAG., Bains, l., van Mourik, T., Norris, D., & el largo, F. (2016).
Selective activation of the deep layers of the human primary
visual cortex by top-down feedback. Biología actual, 26(3),
371–376. https://doi.org/10.1016/j.cub.2015.12.038
Komatsu, y., Shimizu, S., & Shimodaira, h. (2010). Assessing statis-
tical reliability of lingam via multiscale bootstrap. En procedimientos
in 20th International Conference on Artificial Neural Networks
(ICANN2010).
Kriegeskorte, norte. (2015). Deep neural networks: A new framework
for modeling biological vision and brain information processing.
Annual Review of Vision Science, 1(1), 417–446.
Krizhevsky, A., Sutskever, I., & Hinton, GRAMO. mi. (2012). Imagenet clas-
sification with deep convolutional neural networks. En curso-
ings of the 25th International Conference on Neural Information
Sistemas de procesamiento – Volumen 1 (páginas. 1097–1105). EE.UU: Curran
Associates Inc. Retrieved from http://dl.acm.org/citation.cfm?
id=2999134.2999257
Kschischang, F. r., Frey, B. J., & Loeliger, H.-A. (2001). Factor graphs
and the sum-product algorithm. Transacciones IEEE sobre información
Teoría, 47(2), 498–519. https://doi.org/10.1109/18.910572
Neurociencia en red
269
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
norte
mi
norte
_
a
_
0
0
0
6
2
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
li, B., Piriz, J., Mirrione, METRO., Chung, C., Proulx, C. D., Schulz, D.,
. . . Schulz, D. (2011). Synaptic potentiation onto habenula neu-
rons in the learned helplessness model of depression. Naturaleza,
470(7335), 535–9. https://doi.org/10.1038/nature09742
Lizier, J., Prokopenko, METRO., & Zomaya, A. (2008). Local information
transfer as a spatiotemporal filter for complex systems. Físico
Review E – Statistical, Nonlinear, and Soft Matter Physics, 77(2),
026110. https://doi.org/10.1103/PhysRevE.77.026110
Lizier,
j. T., Heinzle,
J., Horstmann, A., Haynes,
j. D.,
& Prokopenko, METRO. (2011). Multivariate information-theoretic
measures reveal directed information structure and task rele-
vant changes in fMRI connectivity. Journal of Computational
Neurociencia, 30(1), 85–107. https://doi.org/10.1007/s10827-
010-0271-2
Lohmann, GRAMO., Erfurth, K., Muller, K., & Tornero, R. (2012). Critical
comments on dynamic causal modelling. NeuroImagen, 59(3),
2322–29. https://doi.org/10.1016/j.neuroimage.2011.09.025
Mannino, METRO., & Bressler, S. l. (2015). Foundational perspectives on
causality in large-scale brain networks. Physics of Life Reviews,
15, 107–23. https://doi.org/10.1016/j.plrev.2015.09.002
Marreiros, A. C., Kiebel, S. J., & Friston, k. j. (2008). Dynamic causal
modelling for fMRI: A two-state model. NeuroImagen, 39(1),
269–78. https://doi.org/10.1016/j.NeuroImage.2007.08.019
Marrelec, GRAMO., & Fransson, PAG. (2011). Assessing the influence of
different ROI selection strategies on functional connectivity
analyses of fMRI data acquired during steady-state conditions.
Más uno, 6(4), e14788. https://doi.org/10.1371/journal.pone.
0014788
Marrelec, GRAMO., Krainik, A., Duffau, h., Pélégrini-Issac, METRO., Lehéricy,
S., Doyon, J., & Benali, h. (2006). Partial correlation for func-
tional brain interactivity investigation in functional MRI. Neuro-
Image, 32(1), 228–37. https://doi.org/10.1016/j.NeuroImage.
2005.12.057
Mclntosh, A., & Gonzalez-Lima, F. (1994). Structural equation
modeling and its application to network analysis in functional
brain imaging. Mapeo del cerebro humano, 2, 2–22. https://doi.org/
10.1002/hbm.460020104
Meek, C. (1995). Causal inference and causal explanation with back-
ground knowledge. In Proceedings of the 11th Annual Confer-
ence on Uncertainty in Artificial Intelligence 558 (páginas. 403–10).
M.Gilson, k. j. Friston, GRAMO. D., Hagmann, PAG., Mantini, D., Betti,
v., Romani, GRAMO. l., & Corbetta, METRO. (2017). Effective connec-
tivity inferred from fMRI
transition dynamics during movie
viewing points to a balanced reconfiguration of cortical inter-
comportamiento. NeuroImagen. https://doi.org/10.1016/j.neuroimage.
2017.09.061
Michalareas, GRAMO., Vezoli, J., van Pelt, S., Schoffelen, J.-M., Kennedy,
h., & Fries, PAG. (2016). Alpha-beta and gamma rhythms sub-
serve feedback and feedforward influences among human visual
cortical areas. Neurona, 89(2), 384–97. https://doi.org/10.1016/j.
neuron.2015.12.018
Miezín, F. METRO., Maccotta, l., Ollinger, j. METRO., Petersen, S. MI., &
(2000). Characterizing the hemodynamic re-
Buckner, R. l.
respuesta: Effects of presentation rate, sampling procedure, y
the possibility of ordering brain activity based on relative tim-
En g. NeuroImagen, 11(6), 735–59. https://doi.org/10.1006/nimg.
2000.0568
Mill, R. D., Bagic, A., Bostan, A., Schneider, w., & Col,
METRO. W.. (2017). Empirical validation of directed functional con-
conectividad. NeuroImagen, 146, 275–87. https://doi.org/10.1016/j.
NeuroImage.2016.11.037
Montalto, A., Faes, l., & Marinazzo, D.
(2014). Mute: A Matlab
toolbox to compare established and novel estimators of the mul-
tivariate transfer entropy. Más uno, 9(10), e109462. https://doi.
org/10.1371/journal.pone.0109462
Muckli, l., De Martino, F., Vizioli, l., Petro, l., Herrero, F., Ugurbil,
K., . . . Yacoub, mi.
(2015). Contextual feedback to superficial
layers of V1. Biología actual, 25(20), 2690–2695. https://doi.
org/10.1016/j.cub.2015.08.057
Mumford, j. A., & Ramsey, j. D. (2014). Bayesian networks for fMRI:
A primer. NeuroImagen, 86, 573–82. https://doi.org/10.1016/
j.NeuroImage.2013.10.020
Neal, R. METRO. (1993). Probabilistic inference using Markov Chain
Monte Carlo methods (Technical Report CRG-TR-93-1). Depart-
ment of Computer Science, universidad de toronto.
Ogarrio, j. METRO., Spirtes, PAG., & Ramsey, j. (2016). A hybrid causal
search algorithm for latent variable models. En procedimientos de
the Eighth International Conference on Probabilistic Graphical
Modelos, PMLR.
Ogawa, S., menón, R. S., Tank, D. w., kim, S. GRAMO., Merkle, h.,
Ellermann, j. METRO., & Ugurbil, k.
(1993). Functional brain map-
ping by blood oxygenation level-dependent contrast magnetic
resonance imaging. a comparison of signal characteristics with
a biophysical model. Biophysics Journal, 64(3), 803–12. https://
doi.org/10.1016/S0006-3495(93)81441-3
(2011).
Information theoretic
approaches to functional neuroimaging. Resonancia magnetica
Imaging, 29(10), 1417–28. https://doi.org/10.1016/j.mri.2011.
07.013
Ostwald, D., & Bagshaw, A. PAG.
Papadopoulou, METRO., Leite, METRO., van Mierlo, PAG., Vonck, K., Lemieux, l.,
Friston, K., & Marinazzo, D. (2015). Tracking slow modulations
in synaptic gain using dynamic causal modelling: Validation in
epilepsy. NeuroImagen, 107, 117–126. https://doi.org/10.1016/j.
neuroimage.2014.12.007
patel, r., Bowman, F. D., & Rilling, j. (2006). A Bayesian approach
to determining connectivity of the human brain. Human Brain
Cartografía, 27(3), 267–76. https://doi.org/10.1002/hbm.20182
Penny, w., Esteban, K., Mechelli, A., & Friston, k.
(2004). Mod-
elling functional integration: A comparison of structural equa-
tion and dynamic causal models. NeuroImagen, 23(S1), 264–74.
https://doi.org/10.1016/j.NeuroImage.2004.07.041
Penny, W.. D. (2012). Comparing dynamic causal models using AIC,
BIC and free energy. NuroImage, 59(1), 319–330. https://doi.org/
10.1016/j.neuroimage.2011.07.039
Penny, W.. D., Esteban, k. MI., Daunizeau, J., Rosa, METRO. J., Friston,
(2010). Comparing families of dynamic
k. J., & et al., t. METRO. S.
causal models. Biología Computacional PLoS, 6(3), e1000709.
https://doi.org/10.1371/journal.pcbi.1000709
Poldrack, R. A. (2007). Region of interest analysis for fMRI. Social
Cognitive and Affective Neuroscience, 2(1), 67–70. https://doi.
org/10.1093/scan/nsm006
Prando, GRAMO., Zorzi, METRO., Bertoldo, A., & Chiuso, A. (2017). Estimat-
ing effective connectivity in linear brain network models. arXiv
preprint. Retrieved from https://arxiv.org/abs/1703.10363
Neurociencia en red
270
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
norte
mi
norte
_
a
_
0
0
0
6
2
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Protzner, A. B., & McIntosh, A. R.
(2006). Testing effective con-
nectivity changes with structural equation modeling: What does
a bad model tell us? Mapeo del cerebro humano, 27(12), 935–47.
https://doi.org/10.1002/hbm.20233
Ramsey, J., zhang, J., & Spirtes, PAG. (2006). Adjacency-faithfulness and
conservative causal inference. In Proceedings of the 22nd Annual
Conference on Uncertainty in Artificial Intelligence (páginas. 401–8).
Ramsey, j. D. (2015). Scaling up Greedy Causal Search for contin-
uous variables. arXiv:1507.7749.
Ramsey, j. D., Glymour, METRO., Sanchez-Romero, r., & Glymour,
C. (2017). A million variables and more: The fast greedy equiv-
alence search algorithm for learning high-dimensional graphi-
cal causal models, with an application to functional magnetic
resonance images. International Journal of Data Science and
Analytics, 3(2), 121–9. https://doi.org/10.1007/s41060-016-
0032-z
Ramsey, j. D., Hanson, S. J., & Glymour, C. (2011). Multi-subject
search correctly identifies causal connections and most causal
directions in the DCM models of
the Smith et al. simula-
tion study. NeuroImagen, 58(3), 838–48. https://doi.org/10.1016/
j.NeuroImage.2011.06.068
Ramsey,
j. D., Hanson, S. J., Hanson, C., Halchenko, Y. o.,
Poldrack, r., & Glymour, C. (2010). Six problems for causal in-
ference from fMRI. NeuroImagen, 49(2), 1545–58. https://doi.org/
10.1016/j.NeuroImage.2009.08.065
Ramsey, j. D., Sanchez-Romero, r., & Glymour, C. (2014). No-
Gaussian methods and high-pass filters in the estimation of
effective connections. NeuroImagen, 84, 986–1006. https://doi.
org/10.1016/j.neuroimage.2013.09.062
Razi, A., & Friston, k. j. (2016). The connected brain: Causality,
modelos, and intrinsic dynamics. IEEE Signal Processing Magazine,
33(3), 14–35. https://doi.org/10.1109/MSP.2015.2482121
Razi, A., Seghier, METRO. l., zhou, y., McColgan, PAG., Zeidman, PAG., Parque,
H.-J., . . . Friston, K.-J. (2017). Large-scale DCMs for resting state
resonancia magnética funcional. Neurociencia en red, 1, 222–241.
Regner, METRO. F., Saenz, NORTE., Maharajh, K., Yamamoto, D. J., Mohl, B.,
Wylie, K., . . . Tanabe, j.
(2016). Top-down network effective
connectivity in abstinent substance dependent individuals. PLoS
Uno, 11(10), e0164818. https://doi.org/10.1371/journal.pone.
0164818
Richardson, T., & Spirtes, PAG. (2001). Automated discovery of linear
feedback models. In C. Glymour & GRAMO. Cooper (Editores.), Computa-
ción, Causation and Causality. Cambridge, MAMÁ: CON prensa.
Roebroeck, A., Formisano, MI., & Goebel, R. (2005). Cartografía
directed influence over
the brain using Granger causality
and fMRI. NeuroImagen, 25(1), 230–42. https://doi.org/10.1016/
j.NeuroImage.2004.11.017
Roebroeck, A., Seth, A. K., & Valdes-Sosa, PAG. (2011). Causal time
series analysis of functional magnetic resonance imaging data.
Journal of Machine Learning Research: Workshop and Confer-
ence Proceedings, 12, 65–94.
Rohrer, j. METRO. (2017). Clarifying the confusion surrounding correla-
ciones, statistical control and causation. PsyArXiv preprint. https://
doi.org/10.17605/OSF.IO/T3QUB
Rowe, J., abrazos, l., Pregonero, r., & Owen, A.
(2010). Dynamic
causal modelling of effective connectivity from fMRI: Are results
reproducible and sensitive to Parkinson’s disease and its treat-
mento? NeuroImagen, 52(3), 1015–26. https://doi.org/10.1016/
j.NeuroImage.2009.12.080
Ryali, S., Shih, Y. y., Chen, T., Kochalka, J., Albaugh, D., Fang, Z.,
. . . menón, V. (2016). Combining optogenetic stimulation and
fMRI to validate a multivariate dynamical systems model for es-
timating causal brain interactions. NeuroImagen, 132, 398–405.
https://doi.org/10.1016/j.NeuroImage.2016.02.067
Ryali, S., Supekar, K., Chen, T., & menón, V.
(2011). Multivari-
ate dynamical systems models for estimating causal interactions
in fMRI. NeuroImagen, 54(2), 807–23. https://doi.org/10.1016/
j.NeuroImage.2010.09.052
Sathian, K., Deshpande, GRAMO., & Stilla, R.
(2013). Neural changes
with tactile learning reflect decision-level reweighting of percep-
tual readout. Revista de neurociencia, 33(12), 5387–98. https://
doi.org/10.1523/JNEUROSCI.3482-12.2013
Schiefer, J., Niederbühl, A., Pernice, v., Lennartz, C., Hennig, J.,
LeVan, PAG., & Rotter, S. (2018). From correlation to causation:
Estimating effective connectivity from zero-lag covariances of
brain signals. Biología Computacional PLoS, 14(3), e1006056.
https://doi.org/10.1371/journal.pcbi.1006056
Schlösser, r., Gesierich, T., Kaufmann, B., Vucurevic, GRAMO.,
Hunsche, S., Gawehn, J., & Stoeter, PAG. (2003). Altered effec-
tive connectivity during working memory performance in
schizophrenia: A study with fMRI and structural equation model-
En g. NeuroImagen, 19(3), 751–63. https://doi.org/10.1016/S1053-
8119(03)00106-X
Schlösser, R. GRAMO. METRO., Wagner, GRAMO., Koch, K., Dahnke, r.,
Reichenbach, j. r., & Sauer, h. (2008). Fronto-cingulate effec-
tive connectivity in major depression: A study with fMRI and
Dynamic Causal Modeling. NeuroImagen, 43(3), 645–55.
Schreiber, t. (2000). Measuring information transfer. Physical Re-
view Letters, 85(2), 461–4. https://doi.org/10.1103/PhysRevLett.
85.461
Schurger, A., & Uithol, S. (2015). Nowhere and everywhere: The causal
origin of voluntary action. Review of Philosophy and Psychol-
ogia, 6(4), 761–78. https://doi.org/10.1007/s13164-014-0223-2
Johnstone, T., &
Davidson, R. j. (2010). Dynamic causal modeling applied to fMRI
data shows high reliability. NeuroImagen, 49(1), 603–11. https://
doi.org/10.1016/j.neuroimage.2009.07.015
Schuyler, B., Ollinger,
j. METRO., Oakes, t. r.,
Schwab, S., Harbord, r., Zerbi, v., ad S. Afyouni, l. MI., Herrero, j. P.,
lana rica, METRO. w., . . . Nichols, t. mi. (2018). Directed functional
connectivity using dynamic graphical models. NeuroImagen,
S1053–8119(18), 30284–2. https://doi.org/10.1016/j.neuroimage.
2018.03.074
Schwarz, GRAMO. mi. (1978). Estimating the dimension of a model. Annals
of Statistics, 6(2), 461–4. https://doi.org/10.1214/aos/1176344136
Seghier, METRO. l., & Friston, k. j. (2013). Network discovery with
large DCMs. NeuroImagen, 68, 181–91. https://doi.org/10.1016/
j.neuroimage.2012.12.005
Sengupta, B., Friston, k. J., & Penny, W.. D. (2015). Gradient-free
mcmc methods for dynamic causal modelling. NeuroImagen, 112,
375–81. https://doi.org/10.1016/j.NeuroImage.2015.03.008
Seth, A. K., Barrett, A. B., & barnett, l. (2015). Granger causality
analysis in neuroscience and neuroimaging. Journal of Neuro-
ciencia, 35(8), 3293–7. https://doi.org/10.1523/JNEUROSCI.
4399-14.2015
Neurociencia en red
271
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
norte
mi
norte
_
a
_
0
0
0
6
2
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Seth, A. K., Chorley, PAG., & barnett, l. C.
(2013). Granger causal-
ity analysis of fMRI BOLD signals is invariant to hemodynamic
convolution but not downsampling. NeuroImagen, 65, 540–55.
https://doi.org/10.1016/j.NeuroImage.2012.09.049
shannon, C. mi. (1948). A mathematical theory of communication.
Bell System Technical Journal, 27(4), 623–56. https://doi.org/
10.1002/j.1538-7305.1948.tb01338.x
Sharaev, METRO., Ushakov, v., & Velichkovsky, B. (2016). Causal in-
teractions within the default mode network as revealed by low-
frequency brain fluctuations and information transfer entropy. En
A. V. Samsonovich, V. V. Klimov, & GRAMO. V. Rybina (Editores.), Biologi-
cally Inspired Cognitive Architectures (bica) for Young Scientists :
Proceedings of the First International Early Research Career En-
hancement School (FIERCES 2016) (páginas. 213–18).
Shimizu, S. (2014). LiNGAM: Non-Gaussian methods for estimat-
ing causal structures. Behaviormetrika, 41(1), 65–98. https://doi.
org/10.2333/bhmk.41.65
Shimizu, S., Hoyer, PAG. o., Hyvärinen, A., & Kerminen, A. (2006). A
linear non-gaussian acyclic model for causal discovery. Diario
de Investigación sobre Aprendizaje Automático, 7, 2003–30.
Shlens, j. (2014). A tutorial on principal component analysis. arxiv.
org/abs/1404.1100
Herrero, S., Molinero, K., Salimi-Khorshidi, GRAMO., Webster, METRO., beckman,
C., Nichols, T., . . . lana rica, METRO.
(2011). Network modelling
methods for fMRI. NeuroImagen, 54(2), 875–91. https://doi.org/
10.1016/j.NeuroImage.2010.08.063
Herrero, S. METRO., Fox, PAG. T., Molinero, k. l., Glahn, D. C., Fox, PAG. METRO.,
Mackay, C. A., . . . beckman, C. F.
(2009). Correspondence
of the brain’s functional architecture during activation and rest.
procedimientos de la Academia Nacional de Ciencias, 106(31),
13040–5. https://doi.org/10.1073/pnas.0905267106
Solo, V. (2016). State-space analysis of Granger-geweke causality
measures with application to fMRI. Computación neuronal, 28(5),
914–49. https://doi.org/10.1162/NECO_a_00828
Spirtes, PAG.
(2010).
Introduction to causal
inferencia.
Diario de
Machine Learning Research, 11, 1643–62.
Spirtes, PAG., Glymour, C., & Scheines, R. (1993). Causation, Predic-
ción, and Search. Springer-Verlag Lecture Notes in Statistics.
Stanley, METRO. l., Moussa, METRO. NORTE., Paolini, B. METRO., Lyday, R. GRAMO., Burdette,
j. h., & Laurienti, PAG. j. (2013). Defining nodes in complex
redes cerebrales. Frontiers in Computational Neuroscience, 7,
169. https://doi.org/10.3389/fncom.2013.00169
Esteban, k. MI., Kasper, l., harrison, l., Deaunizeau, J., van den
(2008).
Ouden, h. mi. METRO., romper la lanza, METRO., . . . Friston, k. j.
Nonlinear dynamic causal models for fMRI. NeuroImagen, 42(2),
649–62. https://doi.org/10.1016/j.NeuroImage.2008.04.262
Esteban, k. MI., Penny, W.. D., Moran, R. J., den Ouden, h. MI.,
Daunizeau, J., & Friston, k. j. (2010). Ten simple rules for dy-
namic causal modeling. NeuroImagen, 49(4), 3099–109. https://
doi.org/10.1016/j.NeuroImage.2009.11.015
Esteban, k. MI., & Roebroeck, A. (2012). A short history of causal
modeling of fMRI data. NeuroImagen, 62(2), 856–63. https://doi.
org/10.1016/j.NeuroImage.2012.01.034
Esteban, k. MI., Weiskopf, NORTE., Drysdale, PAG. METRO., robinson, PAG. A., &
Friston, k. j.
(2007). Comparing hemodynamic models with
DCM. NeuroImagen, 38(3), 387–401. https://doi.org/10.1016/
j.neuroimage.2007.07.040
alimenta, PAG. A., & Purdon, PAG. l. (2017). A study of problems encoun-
tered in Granger causality analysis from a neuroscience perspec-
tivo. procedimientos de la Academia Nacional de Ciencias. https://
doi.org/10.1073/pnas.1704663114
Tak, S., Noh, J., Cheong, C., Zeidman, PAG., Razi, A., Penny, W.. D., &
Friston, k. j. (2018). A validation of dynamic causal modelling
for 7T fMRI. Journal of Neuroscience Methods. https://doi.org/
10.1016/j.jneumeth.2018.05.002
Thamvitayakul, K., Shimizu, S., Ueno, T., Washio, T., & Tashiro, t.
(2012). Assessing statistical reliability of LiNGAM via multiscale
En procedimientos de 2012 IEEE 12th International Con-
bootstrap.
ference on Data Mining Workshops (icdmw2012).
Thirion, B., Varoquaux, GRAMO., Dohmatob, MI., & Poline, j. B.
(2014).
Which fMRI clustering gives good brain parcellations? Fronteras en
Neurociencia, 8, 167. https://doi.org/10.3389/fnins.2014.00167
Thulasiraman, K., & Swamy, METRO. norte. S. (1992). Directed acyclic graphs.
In Graphs: Theory and Algorithms. Nueva York: John Wiley and
Hijo.
Triantafyllou, C., Hoge, R. D., & Wald, l. (2006). Effect of spa-
tial smoothing on physiological noise in high-resolution fMRI.
NeuroImagen, 32(2), 551–7. https://doi.org/10.1016/j.neuroimage.
2006.04.182
Valdes-Sosa, PAG. A., Roebroeck, A., Daunizeau, J., & Friston, k.
(2011). Effective connectivity: Influence, causality and biophys-
ical modeling. NeuroImagen, 58(2), 339–61. https://doi.org/10.
1016/j.NeuroImage.2011.03.058
van den heuvel, METRO., Mandl, r., & Pol, R. h. (2008). Normalized
cut group clustering of resting-state fMRI data. Más uno, 3(4),
e2001. https://doi.org/10.1016/j.NeuroImage.2008.08.010
van Oort, mi. S. B., Mennes, METRO., Schröder, t. NORTE., Kumar, V. J.,
Jimenez, norte. I. Z., Grodd, w., . . . beckman, C. F. (2017). Func-
tional parcellation using time courses of instantaneous connec-
actividad. NeuroImagen. https://doi.org/10.1016/j.neuroimage.2017.
07.027
Vaudano, A. MI., Avanzini, PAG., Tassi, l., Ruggieri, A., Cantalupo, GRAMO.,
Benuzzi, F., . . . Meletti, S. (2013). Causality within the epilep-
tic network: An EEG-fMRI study validated by intracranial EEG.
Frontiers in Neurology, 14(4), 185. https://doi.org/10.3389/fneur.
2013.00185
Vicente, r., Wibral, METRO., Lindner, METRO., & Pipa, GRAMO.
(2011). Transferir
entropy—A model-free measure of effective connectivity for the
Journal of Computational Neuroscience, 30(1),
neurosciences.
45–67. https://doi.org/10.1007/s10827-010-0262-3
Wang, y., Katwal, S., Rogers, B., Sangre,
J., & Deshpande, GRAMO.
(2016). Experimental validation of dynamic Granger causality for
inferring stimulus-evoked sub-100ms timing differences from
IEEE Transactions on Neural Systems and Rehabilita-
resonancia magnética funcional.
tion Engineering, PÁGINAS(99). https://doi.org/10.1109/TNSRE.2016.
2593655
Webb, j. T., Ferguson, METRO. A., Nielsen, j. A., & anderson, j. S. (2013).
BOLD Granger causality reflects vascular anatomy. Más uno,
8:e84279. https://doi.org/10.1371/journal.pone.0084279
Wheelock, METRO. D., Sreenivasan, k. r., Wood, k. h., Hoef, l. W.. v.,
Deshpande, GRAMO., & Caballero, D. C.
(2014). Threat-related learn-
ing relies on distinct dorsal prefrontal cortex network connec-
actividad. NeuroImagen, 102(2), 904–12. https://doi.org/10.1016/j.
NeuroImage.2014.08.005
Neurociencia en red
272
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
norte
mi
norte
_
a
_
0
0
0
6
2
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Disentangling causal webs in the brain using fMRI
Wollstadt, PAG., Martinez-Zarzuela, METRO., Vicente, r., Diaz-Pernas, F. J.,
& Wibral, METRO. (2014). Efficient transfer entropy analysis of non-
stationary neural time series. Más uno, 9(7), e102833. https://
doi.org/10.1371/journal.pone.0102833
Wright, S. (1920). The relative importance of heredity and environ-
ment in determining the piebald pattern of guinea-pigs. Proceed-
ings of the National Academy of Sciences, 6(6), 320–32. https://
doi.org/10.1073/pnas.6.6.320
Xu, l., Admirador, T., Wu, X., Chen, K., guo, X., zhang, J., & Yao, l.
(2014). A pooling-LiNGAM algorithm for effective connectivity
analysis of fMRI data. Frontiers in Computational Neuroscience,
8, 125. https://doi.org/10.3389/fncom.2014.00125
Yamins, D. l., hong, h., Cadieu, C., & DiCarlo, j. j. (2013). Hierar-
chical modular optimization of convolutional networks achieves
representations similar to macaque it and human ventral stream.
In C. j. C. Burges, l. Bottou, METRO. Welling, z. Ghahramani, & k. q.
Weinberger (Editores.), Avances en el procesamiento de información neuronal
Sistemas 26 (páginas. 3093–3101). Asociados Curran, Cª.
Yamins, D. l. K., hong, h., Cadieu, C. F., Solomon, mi. A.,
Seibert, D., & DiCarlo, j. j. (2014). Performance-optimized hier-
archical models predict neural responses in higher visual cortex.
Proceedings of the National Academy of Sciences of the United
States of America, 111(23), 8619–8624. https://doi.org/10.1073/
pnas.1403112111
Yu, X., Qian, C., Chen, D.-y., Dodd, S. J., & Koretsky, A. PAG. (2014).
Deciphering laminar-specific neural inputs with line-scanning
resonancia magnética funcional. Nature Methods, 11(1), 55–58.
zhang,
j. (2008). On the completeness of orientation rules for
causal discovery in the presence of latent confounders and selec-
tion bias. Artificial Intelligence, 172(16–17), 1873–96. 0.1016/
j.artint.2008.08.001
zhao, Z., Wang, X., Admirador, METRO., Yin, D., Sol, l., Jia, J., . . . Gong, j.
(2016). Altered effective connectivity of the primary motor cor-
tex in stroke: A resting-state fMRI study with Granger causality
análisis. Más uno, 11(11), e0166210. https://doi.org/10.1371/
diario.pone.0166210
Zhuang, J., LaConte, S., Peltier, S., zhang, K., & Hu, X. (2005).
Connectivity exploration with structural equation modeling: Un
fMRI study of bimanual motor coordination. NeuroImagen, 25(2),
462–70. https://doi.org/10.1016/j.NeuroImage.2004.11.007
Zhuang, J., Peltier, S., Él, S., LaConte, S., & Hu, X. (2008). Cartografía
the connectivity with structural equation modeling in an fMRI
study of shape from motion task. NeuroImagen, 42(2), 799–806.
https://doi.org/10.1016/j.neuroimage.2008.05.036
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
3
2
2
3
7
1
0
9
2
5
4
5
norte
mi
norte
_
a
_
0
0
0
6
2
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Neurociencia en red
273