RESEARCH ARTICLE - IA de Investigación especializada en el MIT

ARTÍCULO DE INVESTIGACIÓN

Impact of geographic diversity on citation
of collaborative research

Cian Naik1

, Cassidy R. Sugimoto2

, Vincent Larivière3

Chenlei Leng4,6

, and Weisi Guo4,5,6

1Universidad de Oxford, Oxford, Reino Unido
2Georgia Institute of Technology, Atlanta, Georgia, EE.UU
3University of Montreal, Montréal, Canada
4University of Warwick, Coventry, Reino Unido
5Alan Turing Institute, Londres, Reino Unido
6Cranfield University, Cranfield, Reino Unido

Palabras clave: air travel, citation, collaborative research, diversity, geography

ABSTRACTO

Diversity in human capital is widely seen as critical to creating holistic and high-quality
investigación, especially in areas that engage with diverse cultures, entornos, and challenges.
Quantification of diverse academic collaborations and their effect on research quality is
lacking, especially at international scale and across different domains. Aquí, we present the
first effort to measure the impact of geographic diversity in coauthorships on the citation of
their papers across different academic domains. Our results unequivocally show that
geographic coauthor diversity improves paper citation, but very long distance collaborations
have variable impact. We also discover “well-trodden” collaboration circles that yield much
less impact than similar travel distances. These relationships are observed to exist across
different subject areas, but with varying strengths. These findings can help academics identify
new opportunities from a diversity perspective, as well as inform funders on areas that require
additional mobility support.

INTRODUCCIÓN

International collaboration is a key part of scientific research, with the exchange of ideas from
diverse sources leading to numerous breakthroughs. A recent paper by Sugimoto, robinson-
Garcia et al. (2017) showed that researchers with affiliations to more than one country during
their career, so-called “mobile” researchers, had a significant boost in citations over their non-
mobile colleagues. En efecto, several well-established international initiatives (Marie Curie Staff
Exchange, German DAAD, Royal Society International Exchange) fund researcher mobility
between countries and across disciplines. An important facilitator in long-distance collabora-
tion is the ease of air transportation between locations.

1.1. Relevant Research

Collaboration in science is not new. Despite being often seen as a contemporary practice,
research collaboration has always existed—although many collaborators were invisible from
the authors’ lists (Shapin, 1989). Already in the early 20th century, a scientist like
Einstein—who is wrongly seen as a “lone genius”—was collaborating with colleagues on

un acceso abierto

diario

Citación: Naik, C., Sugimoto, C. r.,
Larivière, v., longitud, C., & guo, W.. (2023).
Impact of geographic diversity on
citation of collaborative research.
Estudios de ciencias cuantitativas, 4(2),
442–465. https://doi.org/10.1162/qss_a
_00248

DOI:
https://doi.org/10.1162/qss_a_00248

Revisión por pares:
https://www.webofscience.com/api
/gateway/wos/peer-review/10.1162
/qss_a_00248

Supporting Information:
https://doi.org/10.1162/qss_a_00248

Recibió: 10 Octubre 2022
Aceptado: 15 Enero 2023

Autor correspondiente:
Vincent Larivière
vincent.lariviere@umontreal.ca

Editor de manejo:
Juego Waltman

Derechos de autor: © 2023 Cian Naik, Cassidy
R. Sugimoto, Vincent Larivière, Chenlei
longitud, and Weisi Guo. Published under
a Creative Commons Attribution 4.0
Internacional (CC POR 4.0) licencia.

La prensa del MIT

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

many aspects of his research (Janssen & Renn, 2015; Pyenson, 1985). The first discipline to
exhibit collaboration in the form of coauthorship was chemistry: 34% of papers in the field
had more than one author, comparado con 10% in physics and less than 1% en matemáticas
(Gingras, 2010).

After the Second World War, the large influx of research funding and the era of “big sci-
ence” led to an important rise in collaboration activities and, as consequence, of multi-
authored papers (Wuchty, jones, & Uzzi, 2007). Since the beginning of the 1950s, most papers
in the natural and medical sciences have more than one author (Cronin, Shaw, & La Barre,
2003; Franceschet & Costantini, 2010; Galison, 2003; Persson, Glänzel, & Danell, 2004;
Wuchty et al., 2007), while single authorship remained the norm in social sciences and
humanities until the early 2000s (Larivière, Gingras et al., 2015). In the latter group of disci-
plines, social sciences and arts and humanities have distinct practices: While the majority of
papers in social sciences are the results of collaboration, single authorship remains the norm in
arts and humanities (Larivière, Gingras, & Archambault, 2006). At the other end of the spec-
trum, fields such as high-energy physics have author lists that have gone beyond 5,000 names,
a phenomenon named hyperauthorship (Cronin, 2005). Such decline in single authorship had
long been predicted (Precio, 1986), and shown empirically in the work of Harriet Zuckerman
(1967). En efecto, focusing on Nobel Laureates between 1900 y 1959, she shows that after
1920, most of the laureates’ papers are the result of collaboration. The rise in collaborative
activities can also be linked with an increase in international collaboration (Sonnenwald,
2007; Wagner & Leydesdorff, 2005), which is also observed in all fields but the arts and
humanidades (Larivière et al., 2006). Such growth is observed both in terms of the share of
papers that are in international collaboration and the number of countries involved
(Larivière et al., 2015).

1.1.1. Multifaceted nature of collaboration

Several factors can be associated with this rise in researchers’ collaborative activities. The first
factor is the ease with which technology has allowed researchers to communicate and con-
duct research (katz & Martín, 1997). Since the advent of the digital age, tecnologías, como
the Internet, email, and online communication platforms, such as Skype, Zoom, and Teams,
have allowed researchers to exchange data, meet, and write papers at a distance with much
more ease than what was previously possible. Despite these technologies, previous research
shows that there remains an effect of distance, where researchers are more likely to collaborate
with colleagues that are physically closer (Abramo, D’Angelo, & Di Costa, 2009; Catalini,
2018; Gieryn, 2002; Hoekman, Frenken, & Tijssen, 2010). Another factor is its epistemic
effect—that is, its effect on scientific impact (Wray, 2002). Science is increasingly complex,
and larger teams are therefore necessary to tackle contemporary scientific problems. Este
has been shown empirically, as collaborative research is associated with higher citation rates
(Franceschet & Costantini, 2010; Narin, stevens, & Whitlow, 1991; Wuchty et al., 2007). Este
is specifically true for international collaboration (Glänzel, 2001). This can also be associated
with infrastructure: Big science infrastructures have become so expensive that they have to
be shared, often internationally. This is particularly true for smaller countries (Luukkonen,
Persson, & Sivertsen, 1992). This positive relationship has been observed already in the early
20th century (Larivière et al., 2015). A third factor is policies from funders and universities.
En efecto, some countries have made policies that emphasized collaboration, especially interna-
tional (Abramo et al., 2009) or interdisciplinary (Academia Nacional de Ciencias, National
Academy of Engineering, and Institute of Medicine, 2005). Such policies are based on the fact
that countries’ resources are limited, and that collaboration is considered to lead to more

Estudios de ciencias cuantitativas

443

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

important scientific results. A fourth factor is specialization: In a context where researchers are
increasingly specialized, collaboration allows for researchers with complementary expertise to
work together on a research problem (Franceschet & Costantini, 2010).

1.1.2.

Importance of distance and diversity

Despite the importance of digital technology in making long-distance collaboration possible, en
person collaborations are still conducted. In this context, the possibility of traveling between
two cities can be hypothesized to have an effect on the likelihood of collaboration, and reduce
the effect of physical distance. Previous analyses (Ploszaj, yan, & Börner, 2020) have been per-
formed, using data on flight capacity and frequency, as well as collaboration. Using a sample of
four universities in the United States, they have shown that more flights between cities and the
proximity of airports to universities are linked with higher numbers of collaborations. Unsurpris-
ingly, collaboration was higher in cases where direct flights can be obtained between the cities.
Catalini, Fons-Rosen, and Gaulé (2020) also show that not only does travel cost constitute a
friction to collaboration, a reduction to this friction leads to a increase in higher-quality projects.
Sin embargo, air travel is not necessarily associated with academic success. Research by Wynes,
Donner et al. (2019) ha mostrado, using a sample of researchers from the University of British
Columbia (Canada) eso, once controlling for age and discipline, air travel emissions were
not associated with higher impact measures, although traveling was associated with higher sal-
Aries. Recent work at university level by Guo, Del Vecchio, and Pogrebna (2017) showed that
the connectivity of universities via the air transport network is an important indicator of ranking
growth for the universities, even after accounting for economic development.

1.2. Contribution

Building on these ideas, we use the air transport network to quantify the geographical diversity
in paper coauthorships. The air transport network is a network of connections between cities
(nodos) where the edges are flights. We use it to define measures of diversity between the
researchers based in these cities, with full details provided on how we do this in Section 5.
We focus on establishing a link between the geographical diversity of coauthors on a given
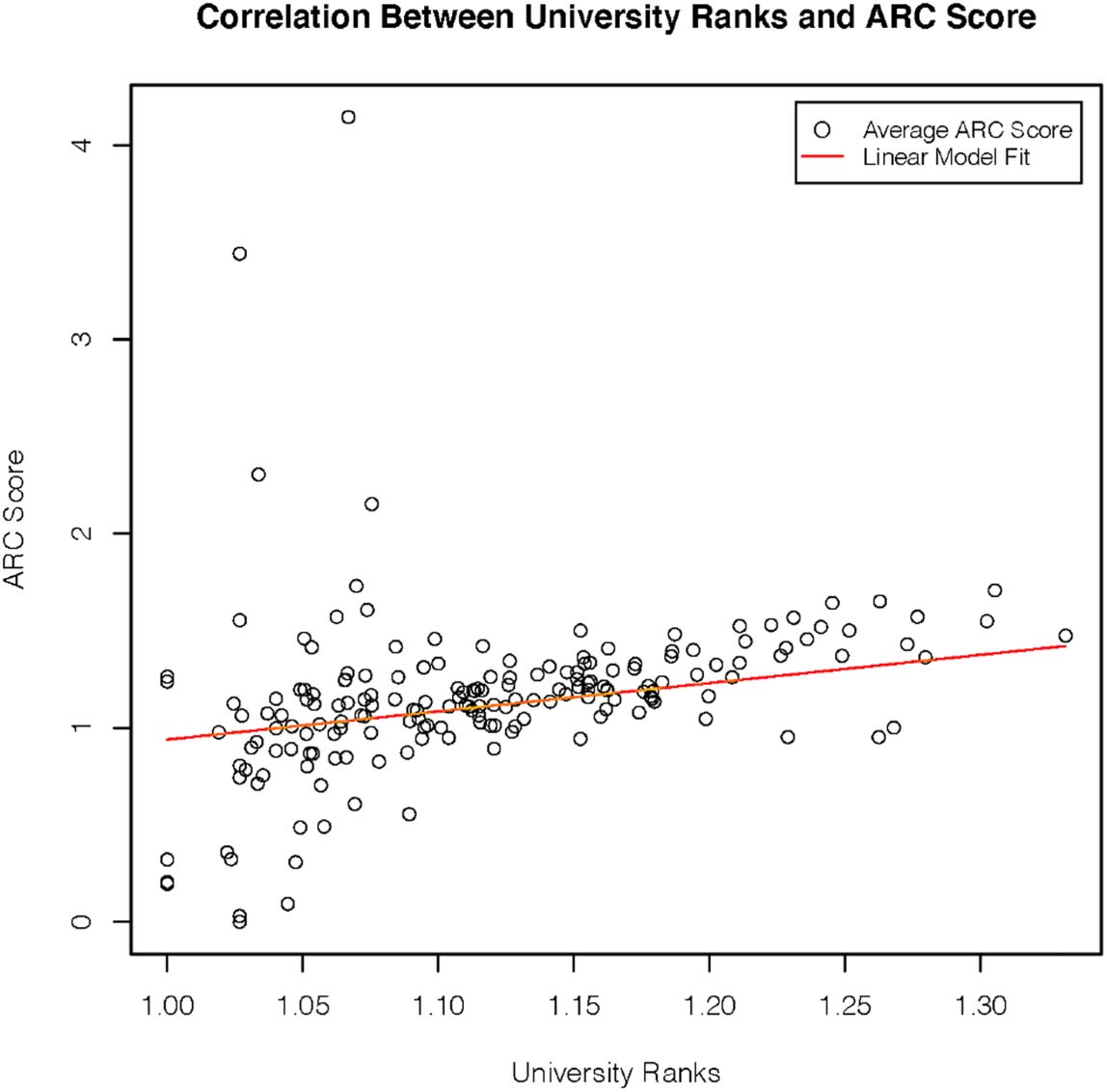
paper and the number of citations that paper receives. As shown in Figure 1, a novelty is to
develop distance and entropy measures for diversity on the coauthorship network and evalu-
ate the variation of the Average Relative Citation (ARC) score against these.

The rest of the paper is structured as follows. En la sección 2 we present the key results. En
Sección 3, we present the robustness of our results to potential confounding variables, como
the effect of university rankings. En la sección 4 we examine the results by subject area and location,
in order to examine subject and geographic specific differences. We provide details of the data
and methods we use for this analysis in Section 5. We discuss implications for individual aca-
demics, universidades, funders, and government policy in Section 6. In the Supplementary
material, we include some additional results.

2. RESULTADOS

2.1. Main Discoveries

2.1.1. Diverse collaborations lead to higher citations

Our primary main discovery is that for a relatively simple notion of diversity measured by the
entropy of the probability of forming a collaboration, the ARC score is highly correlated with
the entropy, as seen in Figure 2(a). We are aware of certain confounding variables, chiefly the

Estudios de ciencias cuantitativas

444

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

Cifra 1. Diversity analysis of coauthorship networks. En (a) we plot the global flight connections. (b) gives the corresponding plot for a
selection of academic collaborations. (C) introduces the factors that compose our distance metric. (d) introduces the corresponding factors
for the diversity metrics. (mi) lists the metrics we use.

potential effect that university rankings have on citations (cláusula, Arbesman, & Larremore,
2015). We show that this correlation persists even when accounting for this. We also reveal some
popular “well-trodden” two-, three-, and four-way collaboration paths in Figures 2(b)–(C).

2.1.2. Well-trodden paths and extreme distances lead to relatively lower citations

Our secondary main discovery is that the aforementioned “well-trodden” paths yield relatively
lower citations than similar distances and that extremely long distance collaborations have
variable or reduced citations. Using the air transport network distance metric, we show in

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 2. Headline results showing that diverse collaborations lead to greater ARC. (a) shows the relationship between weighted airport
network distance entropy and average ARC score. (b) y (C) give examples of popular collaboration routes at the country and city level
respectivamente.

Estudios de ciencias cuantitativas

445

Impact of geographic diversity on citations

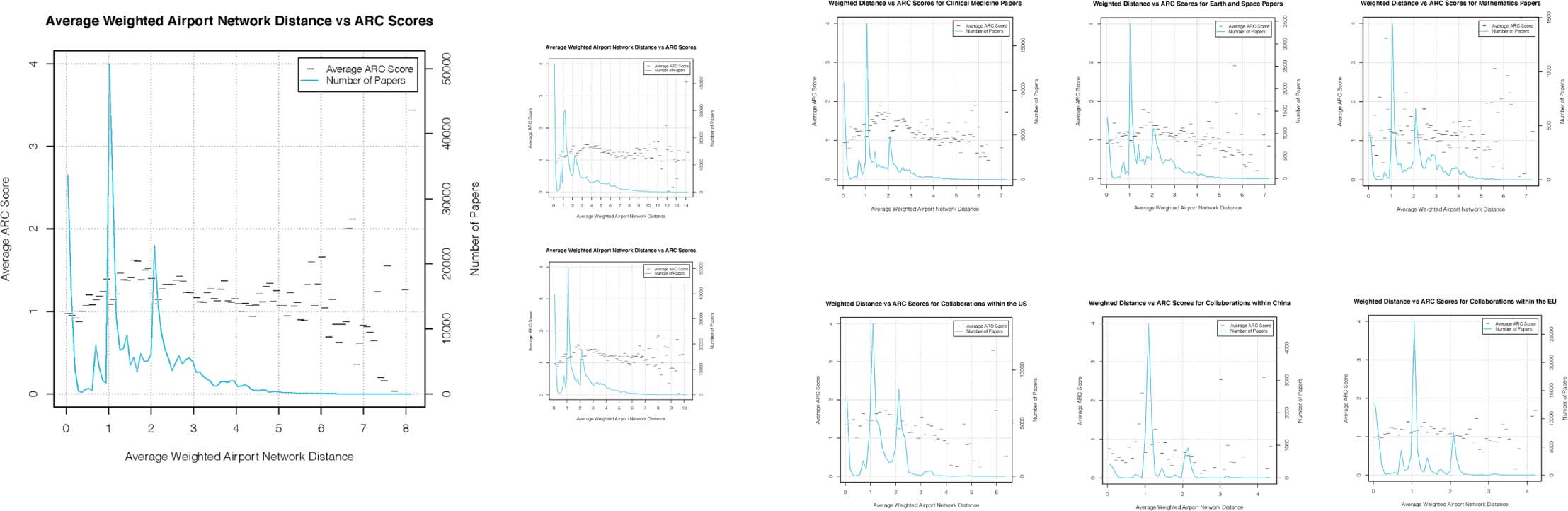
Cifra 3. Relationship between average weighted airport network distance and average ARC score, showing that well-trodden paths and
extreme long distance collaborations can reduce ARC. En (a) we look at the overall relationship, before breaking it down by (b) academic
domain and (C) country.

Cifra 3(a) how diversity initially benefits collaboration until distance takes its toll and
impedes frequent exchange of ideas. Local spikes in the number of collaborations exist in
the general data set, specific academic domains, and specific countries. These spikes corre-
spond to well-trodden collaboration paths—see Figures 2(b)–(C) (highlighted by a black box in
Cifra 3) also correspond to local “dips” in ARC scores. Es decir, well-trodden collabo-
ration paths do not yield as much citation as similar distances between other collaboration
locations. We observe this pattern across all domains and countries, but note exaggerated
effects in certain cases (p.ej., long-distance collaboration is more detrimental in clinical
medicine, possibly due to the practical and timely nature of its practice).

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

2.1.3. A north-south divide exists in collaborative research

Finalmente, our third main discovery is that a divide exists in the composition of collaborative
investigación, with most collaborations occurring between researchers located in the Global North.
When looking at pairs of collaborations (where a collaboration between more than two
authors contains multiple pairs), we see from Figure 1(b) eso 94% of collaboration pairs are
between researchers in the Global North.

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

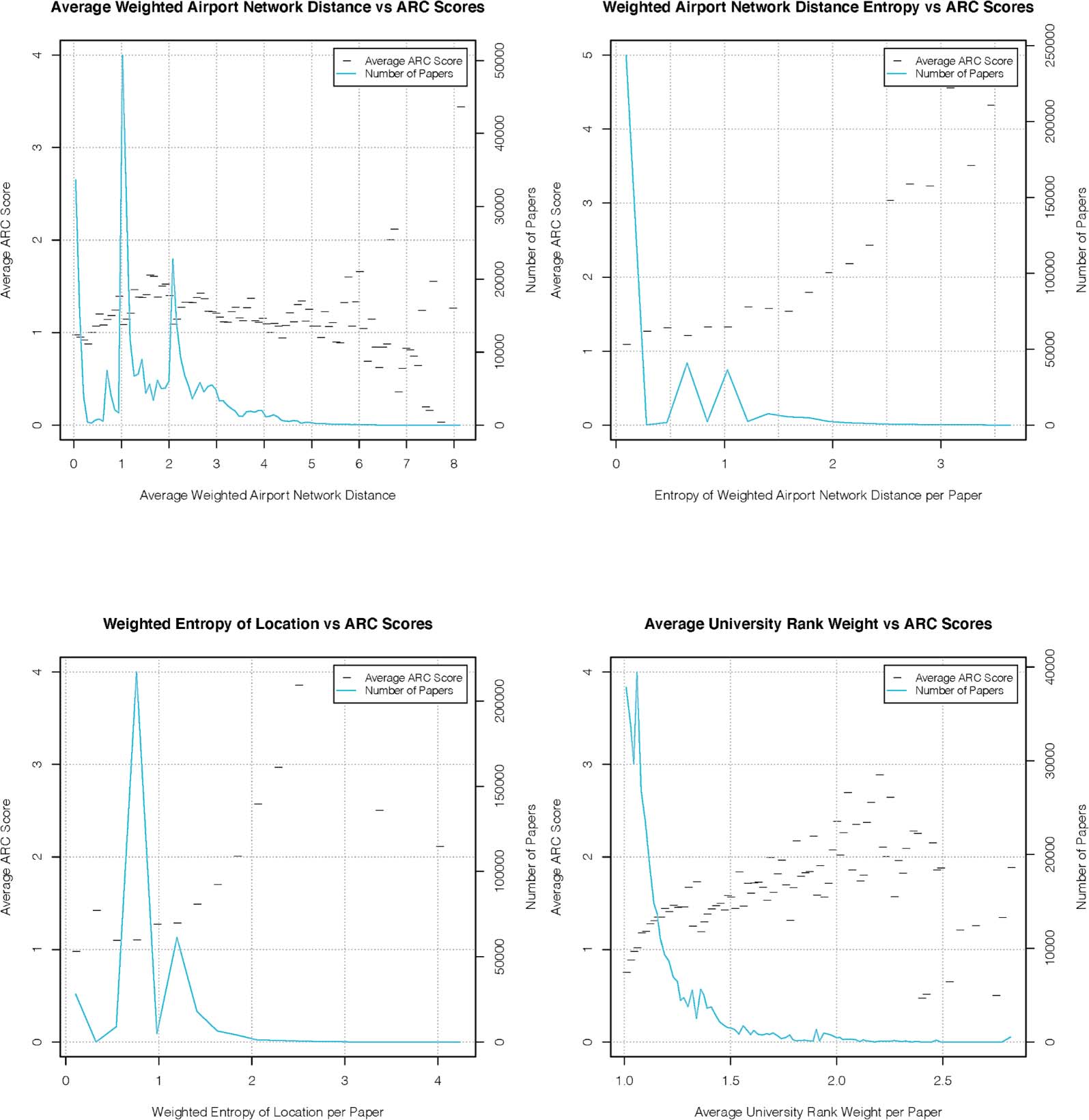
2.2. Detailed Analysis of Effect of Distance, Diversity, and University Rank on ARC Scores

En figura 1(mi), we briefly introduce four important measures whose relationship with ARC
scores we are interested in investigating. We give a more detailed explanation of these here,
with the full derivation of the measures presented in Section 5. We also identify some key
patterns we see in the relationships with ARC score, which can be seen in Figure 4.

1. Collaboration distance: average weighted airport network distance. This is a measure of
the average distance between collaborators on a given paper. The distance is the
weighted network distance on the flight network. Based on the work of Gastner and
Hombre nuevo (2006), an edge on the network is assigned a weight

effective length of edge i; j

Þ
Þ ¼ λdij þ 1 − λ

(1)

446

Estudios de ciencias cuantitativas

Impact of geographic diversity on citations

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

Cifra 4. Binned comparison of (a) average weighted airport network distance, (b) weighted airport network distance entropy, (C) weighted
entropy of coauthor location, y (d) average university rank weight against ARC score.

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

where dij is the Euclidean distance between nodes i and j, and λ is a parameter that
controls the importance of physical distance against graph distance. From Figure 4(a),
we see a positive correlation between citations and this measure of distance. Sin embargo,
past a certain point, we see that the number of citations decreases. We can conjecture
that the large average distance could mean that these coauthors are in remote areas,
geographically and in terms of transport links.

2. Collaboration diversity: weighted airport network distance entropy. This measure also
looks at the weighted network distance between coauthors. It uses a more direct
measure of diversity—the entropy of these distances. En figura 4(b) we see that as this
measure of diversity increases, the number of citations also increases consistently,
showing a clear trend between diversity and citations.

3. Alternative collaboration diversity: weighted entropy of coauthor location. En esto
alternative measure of diversity, we consider the entropy of the geographic locations

Estudios de ciencias cuantitativas

447

Impact of geographic diversity on citations

of the coauthors. In this case a weighted entropy measure is used (not to be confused
with the weighted distances introduced previously). The “weight” in this case incor-
porates the centrality of nodes on the flight network, as well as university rankings.
Again we see in Figure 4(C) that as this measure of diversity increases, the number of
citations also increases consistently, showing a clear trend between diversity and
citas.
Important confounding factor: average university rank weight. This measure weights
cities by the average world ranking of the universities located within a certain radius.
This is important to consider, as the reputation of a university can have a significant
effect on the number of citations received by papers produced by its researchers
(Clauset et al., 2015). En figura 4(d) we see a strong correlation between the university
rank weights and number of citations. This effect seems to flatten out somewhat as the
average weight increases. This could be indicating that the effect of university rankings
is less important for the top universities. Sin embargo, it could also come from our specific
choice of the construction of the weights. The exact nature of this relationship is outside
the scope of this work.

In each of the plots comprising Figure 4 the data are binned. En cada caso, we also plot the
number of papers that are in each bin. In addition to the main results already presented, we see
that the variability of the ARC score increases for large values of each of these measures. Nosotros
can see that these cases correspond to a very small number of papers, so this is not
unexpected.

2.3. Robustness of Results to Parameter Choices and Confounding Variables

There are two key situations in which we check the robustness of the results obtained. The first
of these concerns the key configuration parameter λ, which controls the balance between
Euclidean distance and flight hop distance in Eq. 1. In our case, we choose a value of λ = 1
10;000 ,
as this gives some interpretability, which we lose for larger choices, as detailed in Section 5.
Sin embargo, the results we observe can also be seen for different choices of λ. One exception to
this is that for much larger choices, such as λ = 1
5, the weighted distances are completely
dominated by the Euclidean distances. In this case we lose the interpretation of “well-trodden
paths.” Further discussion is presented in the Supplementary material.

Segundo, as noted, it is well known that there is a strong link between university rankings
and paper citations (Clauset et al., 2015). The relationship of interest in our case is therefore
the effect that our distance and diversity measures have on ARC score, specifically not occur-
ring via university rankings (as this is a relationship that is already well understood). To disen-
tangle these effects, we explicitly account for the confounding effects of unversity rankings.
We see that the patterns already observed still persist having done so. En la sección 3 we present
the full analysis controlling for this effect. En particular, the results displayed in Tables 1 y 2
give evidence to support our claims.

Mesa 1.
distancia, before and after adjusting for the effect of university rankings

Fitting a piecewise linear model for ARC score using average weighted airport network

Método
Before adjusting

After adjusting

^x*
1.60

1.65

^
b1
0.25

0.24

p-value
0.00

0.00

^
b2
−0,08

−0,04

p-value
0.00

0.00

448

Estudios de ciencias cuantitativas

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

Mesa 2.
before and after adjusting for the effect of university rankings

Fitting a linear model for ARC score using weighted airport network distance entropy,

Método
Before adjusting

After adjusting

^
b
0.69

0.66

p-value
0.00

0.00

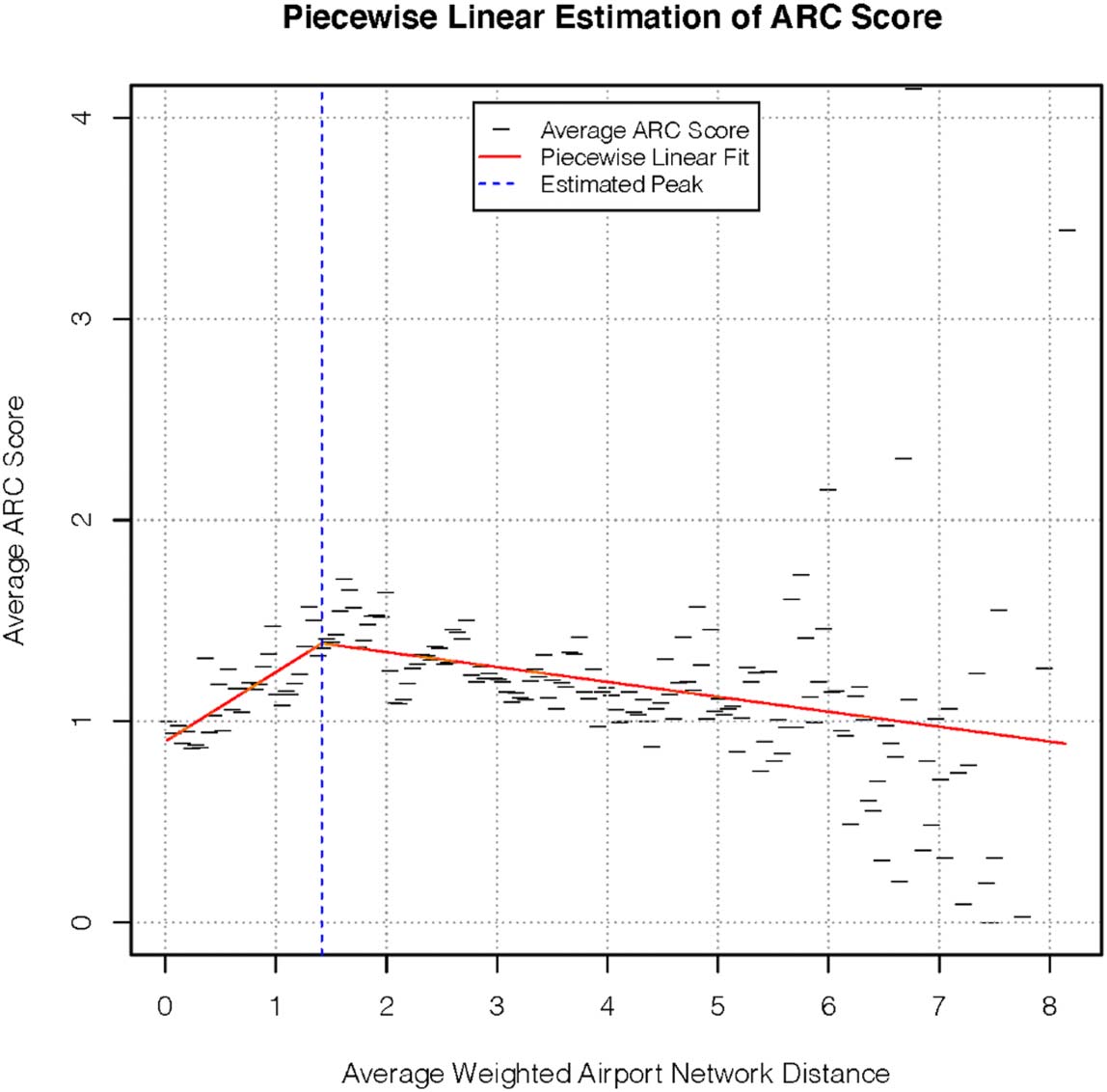
3. STATISTICAL ANALYSIS OF RESULTS

So far we have presented results that have been largely qualitative in nature. Tenemos
observed two distinct trends in the ARC score with increasing average distance and entropy
of distance between coauthors. Sin embargo, we now wish to quantify these results. Motivated by
the patterns of the points in Figure 4(a), we first define a model to check for the existence,
ubicación, and significance of the “peak” we observe in the relationship between average
weighted network distance and ARC score.

3.1. Average Weighted Airport Network Distance

To check for the existence and location of a peak, we fit a piecewise linear model, limited to
two pieces. The model can be summarized as

(cid:1)
f xð Þ ¼ a1 þ b1x
a2 þ b2x

x ≤ x (cid:2)
x > x (cid:2)

(2)

where a1, b1, a2, b2 are such that f(X) is continuous at x*. The model is fitted for a range of
values x*, and is optimized to find the value of x* for which the residual sum of squares is
lowest. The optimal value ^x* gives the estimated location of the peak. We can test whether
^
a statistically significant peak exists by checking that the corresponding gradients
b2 are
significantly ≥0 and ≤0 respectively1. En figura 5 we see an example of what this fit looks like.
Our analysis confirms what we intuitively saw in Figure 4(a), with a statistically significant
increase and decrease in ARC before and after the peak2. We emphasize that our goal here
is not to accurately model the relationship that we observe, but merely to confirm the exis-
tence of this peaked shape that we see in the data. For this purpose, a simple piecewise linear
model works well. More complicated models may capture the relationship better, but that is
outside the scope of this work.

^
b1,

This does not yet tell the full story. As before, we can test for the pattern detailed above after
removing the effect of university rankings, as mentioned in Section 2.3. The effect that they
have on citations received by papers is already well studied (Clauset et al., 2015). We can see
this clearly if we plot the (binned) university rank weights (as defined in Eq. 6) against the ARC
puntuaciones. We do this in Figure 6 and see an almost linear relationship.

Disentangling how much of the relationship between average weighted distance and ARC
score occurs via university ranks is a potentially difficult task, and we do not focus on that in
nuestro trabajo. En cambio, we take a conservative approach, removing as much of the effect of uni-
versity ranks as possible by directly fitting ARC score against average university rank weights,
and removing that effect before fitting the piecewise linear model of ARC score against average
weighted distance. Específicamente, letting yARC be the ARC score for each paper, dAV be the

1 In this case we define significance at the 5% level by checking that the p-values are ≤0.05.
2 Throughout our analysis, we fit the piecewise linear model on the raw (rather than binned) datos, but for ease
of understanding we show the fit on the binned plot. Sin embargo, in practice we find that the results are very
similar if we perform a weighted fit to the binned data using the number of data points in each bin.

Estudios de ciencias cuantitativas

449

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

Cifra 5. Piecewise linear estimation of the relationship between average weighted distance and
ARC score.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 6. Correlation between university rank score and ARC score.

Estudios de ciencias cuantitativas

450

Impact of geographic diversity on citations

average weighted airport network distance between the coauthors, and wAV the average uni-
versity rank weights of the coauthor locations, we first estimate ^y ARC from yARC ∼ wAV. Entonces
we fit our piecewise model yARC − ^y ARC ∼ f (dAV), where f (X) is defined as in Eq. 2.

We compare the unadjusted fit (as seen in Figure 5) with the corresponding fit having
adjusted for the effect of the university ranks in this way, with the results given in Table 1.
We see that the observed increase stays almost constant, as does the peak location. Sin embargo,
the decrease that we observe seems to be at least partly tied in the university ranks.

Further analysis is presented in the Supplementary material, where we use stratification to

support the results presented here.

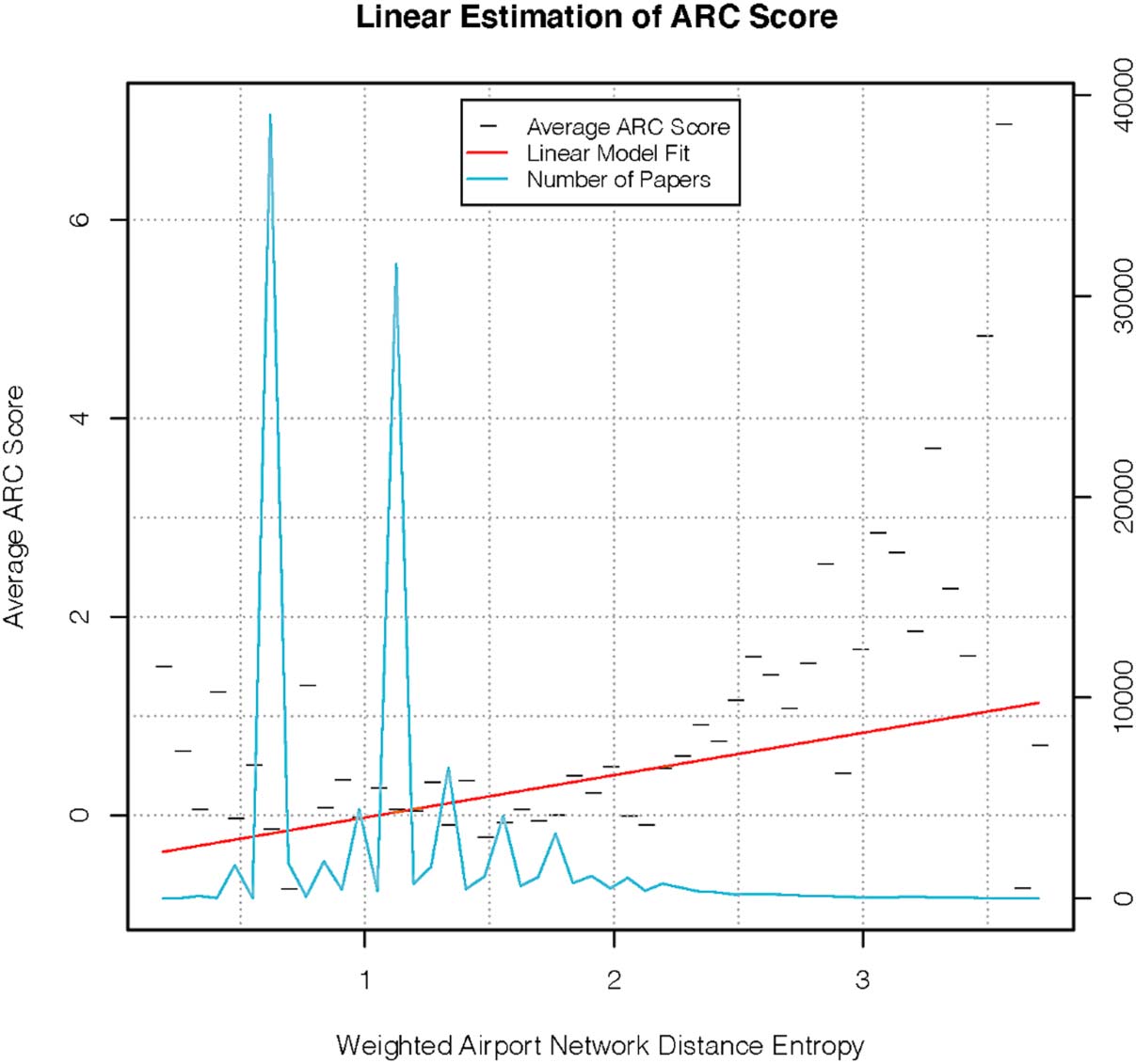
3.2. Weighted Airport Network Distance Entropy

We now investigate the relationship between weighted airport network distance entropy and
ARC score. En figura 4(b) we see that the ARC score increases as the entropy increases. To test
whether this increase is significant, the first step is to fit a linear model of ARC score against
weighted distance entropy, having accounted for university rankings. Específicamente, letting yARC
be the ARC score for each paper, dENT be the average weighted airport network distance
between the coauthors and wAV the average university rank weights of the coauthor locations,
we first estimate ^y ARC from yARC ∼ wAV. Then we fit the simple model yARC − ^y ARC ∼ dENT.
De nuevo, we emphasize that our goal here is not to accurately model the relationship that we
observe, and that other models may provide a better fit than the linear model that we use.
Sin embargo, our goal is simply to confirm the existence of a statistically significant trend.

En mesa 2 we see the estimated parameters from fitting the above model, and from fitting
the model without adjusting for university rankings. En cada caso, we see a significant increase
in ARC score as distance entropy increases. En figura 7 we see the fit of the model, teniendo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 7.

Linear estimation of ARC score using weighted distance entropy.

Estudios de ciencias cuantitativas

451

Impact of geographic diversity on citations

accounted for university rankings. A linear model does not capture the behavior of the data as
well as the piece wise linear model fit for the average weighted distance metric. De hecho, it looks
as though the ARC scores initially decrease as the entropy increases. The reason for this is that
we fit the model with the full data, but plot the binned data. As we can see from the numbers of
papers in each bin, most of the bins have very few values, and the model fit is dominated by
the two large spikes. De este modo, En figura 7, the higher ARC scores for very small values of the
distance entropy are somewhat misleading, as are the corresponding results for very large
values of the distance entropy.

4. COMPARISONS

Having defined methods to analyze our results quantitatively, and to control for the effect of
university rankings, we now break the overall results down by academic field and coauthor
ubicación, in order to gain a better insight into the trends that are occurring.

4.1. Results by Academic Field

4.1.1. Average weighted airport network distance

Primero, we compare different fields based on the location of the peak in the relationship between
average weighted network distance and ARC score. We also compare the gradients before and
después, to see how prominent the peak is. En mesa 3 we see the results. There are several inter-
esting features we notice here. En primer lugar, we see that for all the fields but one, there is a significant
positive relationship until a point. En segundo lugar, we notice that we can broadly split the different
fields into three different categories, based on the patterns exhibited:

1. Fields such as Social Sciences, Clinical Medicine and Biomedical Research, cual
exhibit the peaked form described earlier, with significant increases and decreases.

Mesa 3. Comparison of relationships between average weighted network distance and ARC score
for different fields

Field
Social Sciences

Engineering and Technology

Professional Fields

Clinical Medicine

Physics

Salud

Biomedical Research

Chemistry

Earth and Space

Psicología

Biología

Matemáticas

^x*
1.37

1.43

1.46

1.65

1.67

1.69

1.76

1.86

1.90

2.72

3.96

^
b1
0.38

0.26

0.46

0.34

0.21

0.27

0.25

0.11

0.25

0.22

0.07

0.01

p-value
0.00

0.00

0.65

^
b2
−0,10

0.01

−0.15

−0,10

−0.01

−0.07

−0,06

0.04

−0.09

−0.01

0.17

p-value
0.01

0.64

0.00

0.79

0.33

0.00

0.13

0.00

0.75

0.54

0.19

452

Estudios de ciencias cuantitativas

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

2. Fields such as Physics, Engineering and Technology and Psychology, which exhibit a
significant initial positive relationship, but subsequently plateau, with no significant
positive or negative relationship.

3. Matemáticas, which does not seem to exhibit any significant relationship.

Last, if we examine the point at which there is no longer a positive relationship (either the
peak or the start of the plateau), then we see differences between the field. En mesa 3 tenemos
sorted the fields by the estimate of ^x*, and we see that for fields such as Biology and Psy-
chology increasing the average weighted network distance has a positive effect on ARC scores
for much longer than for fields such as Social Sciences and Engineering and Technology.

4.1.2. Weighted airport network distance entropy

We can perform the same comparison for the weighted distance entropy measure. En este caso,
we rank the subjects based on their estimated coefficients. We see from Table 4 that while the
positive relationship between entropy and ARC score exists for every subject considered, el
strength of that relationship varies greatly. Mathematics and Chemistry exhibit a much weaker
relationship than the other subjects, while Social Sciences and Clinical Medicine exhibit the
strongest relationship. An important factor to consider here is the number of coauthors that
papers in each field generally have. This measure of diversity only makes sense for papers with
more than two coauthors, but we know that medical papers can sometimes have very large
numbers of authors, while mathematics papers often have only a handful. It may be valuable
to examine further how this factor impacts the differing relationships we see here.

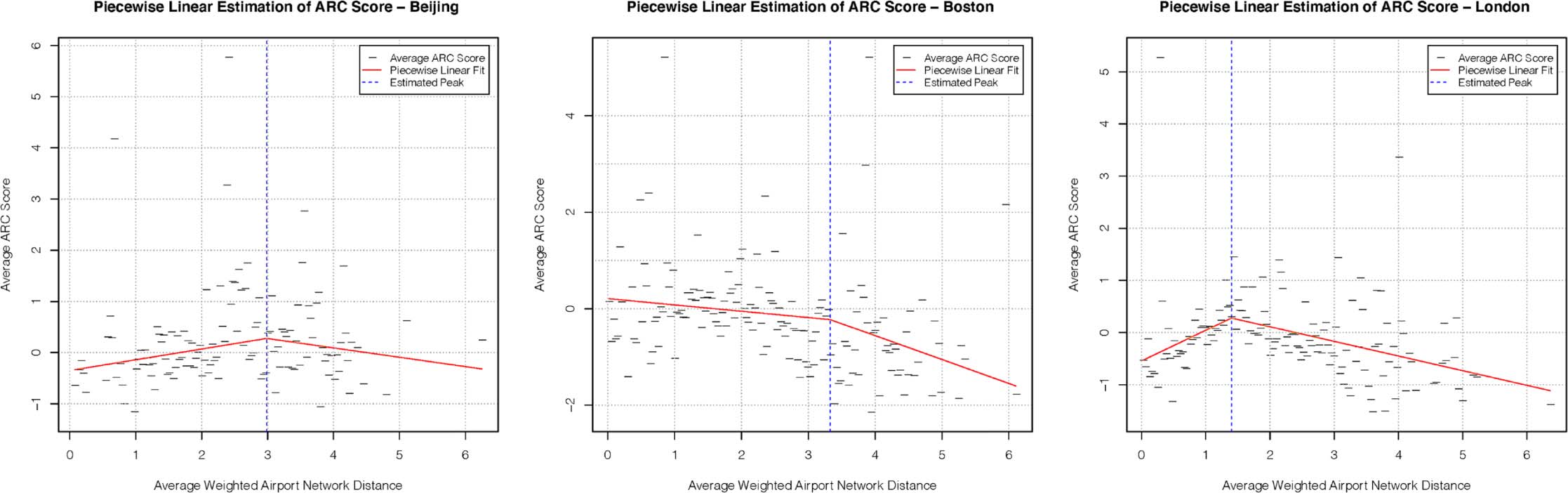
4.2. Results by City

Segundo, we compare the collaborations involving certain cities to investigate differences in the
collaboration patterns of their researchers. En figura 8(a) we see the plot of average weighted

Mesa 4. Comparison of relationships between weighted network distance entropy and ARC score
for different fields

Field
Matemáticas

Chemistry

Psicología

Professional Fields

Biología

Physics

Engineering and Technology

Salud

Earth and Space

Biomedical Research

Social Sciences

Clinical Medicine

^
b
0.15

0.18

0.26

0.28

0.29

0.30

0.35

0.38

0.43

0.56

p-value
0.00

0.00

453

Estudios de ciencias cuantitativas

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

Cifra 8. Piecewise linear estimation of ARC score using average weighted airport network distance for (a) Beijing, (b) Boston and (C)
Londres.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

network distance against ARC score for Beijing, with Figures 8(b) y 8(C) showing the
results for Boston and London respectively. The three patterns we can see are noticeably
diferente. For Beijing and London, there are clear peaks, but the peak for London occurs at
less than half that of Beijing. Mientras tanto, for Boston, it appears that there is no peak at all.
A closer examination reveals that while there does still appear to be a peaked relationship,
some collaborations only a small distance away from Boston but with very high ARC scores
are distorting this result.

This is certainly interesting in terms of understanding how these cities collaborate with
otros. Sin embargo, a slight complication arises when comparing cities in this way. A pesar de
we can see three distinct patterns here, it is not yet clear how much of these differences arises
from fundamentally different behaviors of the researchers in these cities, and how much is
simply due to the geographies of the cities. Por ejemplo, we might expect that the most pro-
ductive collaborations for researchers from Beijing are those with large American centers of
investigación, which would generally be a weighted network distance of 2–3 away. Similarmente, para
researchers from London, the weighted network distances to major European and American
centres of research will be roughly between 1.2 y 1.9. Finalmente, the highly productive collab-
orations that researchers from Boston have are often from nearby Cambridge (home to Harvard
and MIT), or other East Coast cities with large research institutions.

To try to reduce these geographical effects, we can compare cities where we imagine that
the geographical effects would be similar. We see some of these comparisons in Table 5. De
este, we can see that even between cities with similar geographical effects, there can be a sig-
nificant difference in the observed patterns, especially with regards to the magnitude of the
initial positive effect that increasing diversity has.

4.3. Further Work

En este trabajo, we focus on testing whether there is a significant increase in the ARC score as the
entropy measures increase, rather than measuring this effect. Similarmente, for the average
weighted airport network distance, we look for the existence and location of a peak using a

Estudios de ciencias cuantitativas

454

Impact of geographic diversity on citations

Mesa 5. Comparison of relationships between average weighted network distance and ARC score
for different cities

City
Bostón

Cambridge (EE.UU)

Nueva York

berkeley

Londres

Oxford

Edimburgo

Dublín

Beijing

Hong Kong

^x*
3.32

0.84

0.90

1.30

1.40

1.62

1.98

1.43

2.96

2.42

^
b1
−0,13

p-value
0.02

0.43

0.74

0.68

0.58

0.31

0.62

0.82

0.21

0.27

0.20

0.00

0.02

0.00

0.02

0.00

0.02

^
b2
−0.50

−0.23

−0.41

−0.20

−0.28

−0.20

−0.52

−0.19

−0.18

−0.24

p-value
0.11

0.03

0.00

0.10

0.00

0.15

0.00

0.20

0.57

0.33

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

piecewise linear model, without considering how well this model fits the data. While in each
caso, these models are suitable for our purposes, further work would be needed to more accu-
rately model the relationships we observe.

Hasta ahora, we have also been using fairly simple models to control for the effect of university
rankings. To better understand the results, we may want to fit more complicated models by
accounting for possible nonlinear effects of the variables involved. We may also want to inves-
tigate other factors that may affect ARC scores apart from university ranks, such as economic
desarrollo.

Finalmente, our work has been looking at a specific year of data. An interesting extension would
be to investigate if the relationships we have found differ for different years, and if so try to
measure how the changing pattern of airline travel corresponds to the change in collaboration
patrones.

5. MÉTODOS

Here we detail the data and methods that we use in our analysis. En particular, en la sección 5.1
we describe the data and in Section 5.2 we detail how the measures of diversity that we use
are constructed.

5.1. Datos

5.1.1. Coauthorship network

This network consists of collaborations between different coauthors, where for each collabo-
ration we have the location of each coauthor, an identifier for the paper, and a citation score
for the paper. The citation score relates to the number of citations the paper received, normal-
ized based on the subject area. This is the ARC score. The data consist of 352,057 documentos
published in 2005, with coauthors from 21,131 different locations. The locations of the
coauthors are given as cities rather than universities. This means that we need to construct
a mapping from universities to cities in order to incorporate university rankings into our anal-
ysis, as we shall describe.

Estudios de ciencias cuantitativas

455

Impact of geographic diversity on citations

Cifra 9. Global collaboration route plots.

5.1.2. Air transport network

We take a snapshot of the air transport network in 2005 as a representative network showing
major intercity connections. While we could have used a year-by-year analysis, we felt this
was overanalyzing the problem, as collaborations are built up over a long time period and
synchronicity with a particular year is unnecessary. The data consists of flight volumes
between airports, con 9,192 airports and 33,075 flight links between them for the year that
we focus on.

5.1.3. Comparisons

En figura 1 we see some simple comparisons between the networks of interest. We explore
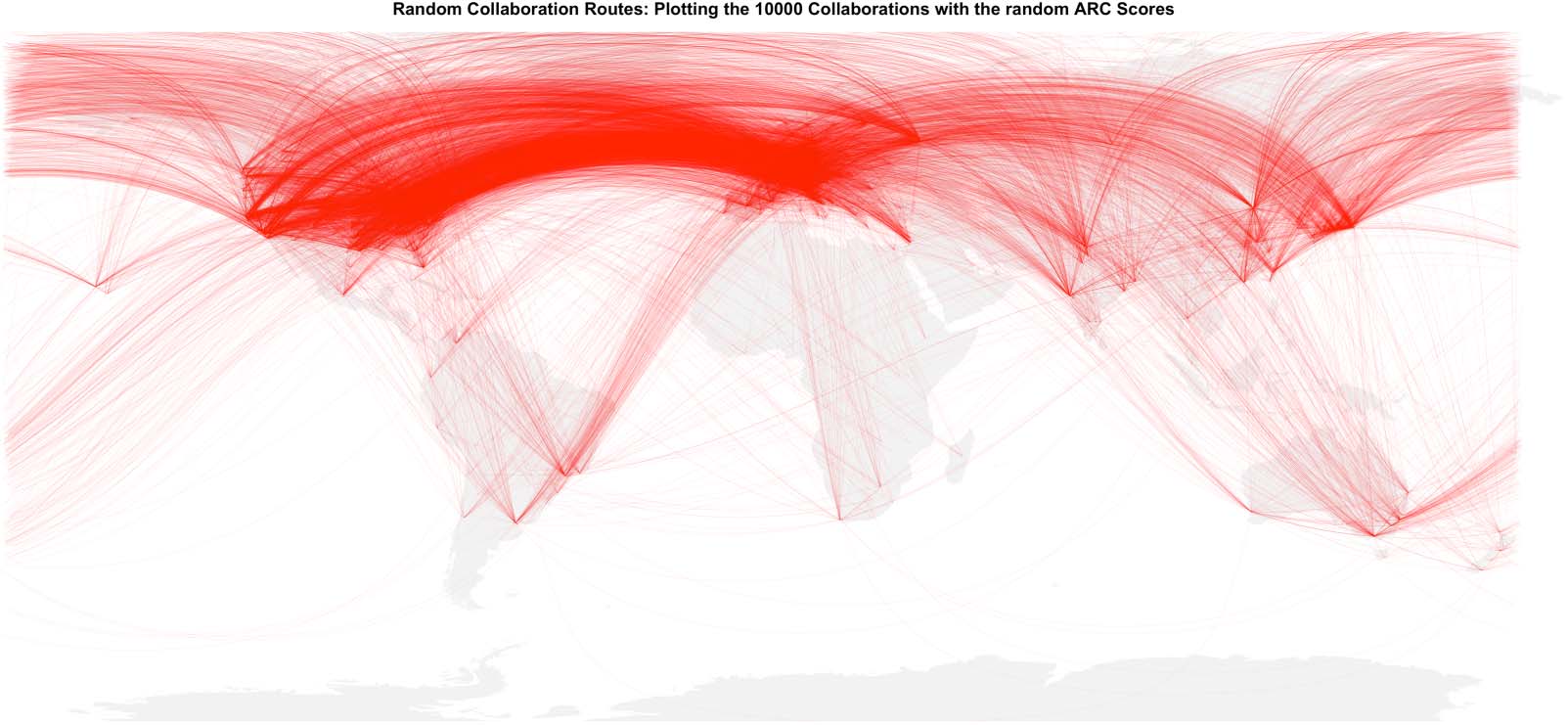
some of these in more detail here. En figura 9 we see a random sample of the collaboration
routes (the total number of routes is too large to plot clearly), while in Figure 10 we see the air
transport routes. Comparing these, we see a number of differences. Primero, we see that although
there is a strong connection between the United States and Europe in the air transport network,

Cifra 10. Global air transport route plots.

Estudios de ciencias cuantitativas

456

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

Mesa 6.

Top two- and three-way collaborations by country

Two-way collaborations

Three-way collaborations

Countries
Canada-USA

Germany-USA

UK-USA

China-USA

Japan-USA

No. of collaborations Countries

3,447

3,043

2,965

2,578

2,252

Germany-UK-USA

France-Germany-USA

Germany-Switzerland-USA

Canada-UK-USA

France-UK-USA

No. of collaborations
128

108

106

this is far more pronounced in the collaboration network. The same pattern holds true for the
connections between Europe and Asia and Asia and the United States. En efecto, if we restrict
ourselves to collaborations with coauthors from two or three different cities, we can see from
Mesa 6 that the top collaboration routes (by ARC score) follow these patterns.

As noted in Figure 1, we see a north-south divide in the data, with disproportionately many
collaborations occurring between cities in the Global North. En particular, the percentages
given in Figure 1(b) are calculated by considering every pairwise collaboration and noting
the location of the two relevant collaborators.

From this preliminary analysis, we also notice that there are a lot of long-distance collab-
orations present, in many cases between cities that do not have direct flights between them.
This raises the interesting question of how journeys with multiple flights act as a barrier to
colaboración, and what role is played by the distance on the air transport network compared
with Euclidean distance. This provides further motivation for our work.

When performing our full analysis, our focus is on linking the number of citations that each
paper receives with the relationship between the coauthors on the air transport network. Más
específicamente, we want to see if there is a link between some measure of geographical diversity
of the coauthors via the air transport network, and the ARC score for the paper. De este modo, in what
follows, we split our data by paper rather than considering summaries over all papers collab-
orated on by pairs of cities. For each paper, we then have access to a list of the coauthors on it,
their location, and the ARC score. This is what we use for our analysis.

5.1.4. University rankings

One more data set that we will make use of is the world university rankings, which comprises
the rankings of the top 500 universities each year from 2005 onwards. As before, we focus on
data from the year 2005. These data are necessary for our analysis because, as shown by
Clauset et al. (2015), there is a relationship between the reputation and ranking of a university
and the number of citations that a paper written by one of its researchers receives. When we
look for a relationship between the number of citations that a paper receives and our various
measures of diversity of the coauthors, we want to make sure that we take this effect into
cuenta.

5.2. Análisis

We now present the methods we use to investigate the link between geographical diversity of
coauthors on a paper and the number of citations it receives. A key part in this will be defining

Estudios de ciencias cuantitativas

457

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

our measures of geographical diversity. The first step towards these definitions is to connect
our coauthorship data with our air transport data.

5.2.1. Connecting cities with airports

There are a number of different ways to connect the coauthorship data with the air transport
datos. Primero, we want to find a distance measure between the cities in the coauthorship data
colocar, where this distance is linked to the air transport network. We do this in an effort to replicate
how two collaborating authors from potentially different countries could travel to meet each
otro. An initial measure of the distance between two cities is the number of flights it takes to
travel between the two. We can calculate this by mapping each city to an airport and then
finding the graph distance between the two airports on the air transport network.

We can improve upon this by incorporating Euclidean distances between the nodes of a
graph, as in Gastner and Newman (2006). This is done by assigning an effective length to each
borde

effective length of edge i; j

Þ ¼ λdij þ 1 − λ

(3)

where dij is the Euclidean distance between nodes i and j, and λ is a parameter that controls
the relative importance of physical distance against graph distance. The weighted network dis-
tance between two nodes is then given by the sum of the effective lengths on the shortest
effective path between them. Incorporating Euclidean distance into our model makes sense
intuitively because our distance measure is attempting to capture the geographical diversity
of coauthors. We believe an important part of this is the difficulty of two potential collaborators
traveling to meet each other. Teniendo esto en cuenta, a long-haul flight presents more of a barrier
than a shorter one.

It can be shown that, for the global air transport network, the value of λ that leads to the best
replication of the observed network is 0 or close to it (Gastner & Hombre nuevo, 2006). En nuestro
modelo, we choose λ = 1
10;000. This choice fits with the conclusions of Gastner and Newman
(2006), but is also useful from a practical perspective. We measure the Euclidean distances
in kilometers, and because the longest distance Euclidean distance between two nodes on
the air transport network is ∼9,000 km this means that a journey that involves multiple flights
will always be assigned a greater weighted network distance than one involving only a single
flight. De nuevo, this fits with our intuition about the difficulty of two potential collaborators
reunión, and gives some interpretability to the weighted network distances.

Using this, we calculate the weighted network distance between two cities A and B using

the air transport network as follows:

1. Mapping cities to airports: Primero, each city is mapped to one or more airports, chosen as
follows. We calculate the weighted degrees, on the air transport network, of all the
airports within 100 km of the city. The city is then mapped to the five airports with
the highest weighted degrees. If there is no airport within 100 km of the city, then it
is mapped to the nearest airport. We denote the sets of airports associated with cities
A and B as A and B respectively.

2. Calculating weighted network distances: For each pair of airports (a, b)a2A,b2B we then
calculate the weighted graph distance on the air transport network using the edge
weighting given by Eq. 3.

3. Calculate shortest route: We set the weighted network distance between A and B, cual

we denote as dAB, to be the minimum of these weighted network distances.

Estudios de ciencias cuantitativas

458

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

4. Correcting zero distances: A veces, due to the geographical proximity of two cities,
the same airport might appear in A and B. En este caso, the minimum calculated in Step
3 will be 0, even though the cities may be up to 200 km apart. To correct for this, el
distance between the two cities is set to be proportional to the Euclidean distance
between them, normalized so that the maximum value it can take is 1.

The weighted network distance between the cities A and B is thus defined as

dAB ¼ min
a2A;b2B

n¼1

λd e

ininþ1

d
þ 1 − λ

Þ þ d E
AB

1A∩B≠∅

(4)

ij is the Euclidean distance between i and j, and a = i1 → i2 → … → iN = b is the

where d e
shortest weighted path from a to b on the air transport network.

We choose to map each city to potentially multiple airports in another attempt to recreate
real-world travel situations, as the nearest airport to a city may not be the one with the best
connections to certain other cities. El 100 km limit is set as the limit that a person might be
willing to travel to an airport. Using a similar intuition to our choice of λ, setting the maximum
distance to be 1 in the case that two cities share an airport is to ensure that any journey that
contains a flight is considered “longer” than one that does not.

En mesa 7, we can see that the weighted airport network distance is quite highly correlated
with the Euclidean distance. When comparing ARC scores with average distance for different
values of λ, we will see similar patterns for varying λ. This is perhaps unsurprising given these
high correlation values.

As well as using the air transport network to calculate distances between coauthors, podemos
use it to define centrality measures for them. Following Guo et al. (2017), we want to find a
measure of connectivity for the cities in the coauthorship data set by associating them with
airports in the air transport data set. Eso es, we want to find out how connected the cities
are within the air transport network, as opposed to within the coauthorship network. Hacemos
this using the same method of calculating a weighted aggregate of the connectivities of each of
the airports associated with a city. For any particular centrality measure i, such as eigenvector
centrality or betweenness, the weighted centrality of a city A is thus given by

Ci Að Þ ¼

(cid:3)
Ci að Þ d e
aA

(cid:4)−α

(5)

a2A

where A is the set of airports within 100 km of A, como antes. Ci(a) is the centrality of airport a,
aA is the Euclidean distance between the city A and airport a, and α is a decay parameter that
d e
we set to be equal to 2 as in Guo et al. (2017).

5.2.2. Connecting cities with universities

As noted previously, the reputation of a university can have a large effect on the number of
citations a paper written by one of its researchers receives (Clauset et al., 2015). De este modo, we may

Mesa 7.

Correlations between distance measures

Airport network

Weighted airport network

Euclidean

0.96

0.62

Weighted airport network
0.96

Euclidean
0.62

0.80

459

Estudios de ciencias cuantitativas

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

want to control for university rankings in our analysis. We can use the university rankings data
set to do this, but as the nodes in the coauthorship network are cities rather than universities
we will have to use a similar method as we have done for the centrality measures to associate
the ranked universities with the cities.

We can construct a university rank weight for each city A as follows. Primero, we find all the
universities within 20 km of the city and call this set UA. Then we calculate the weight wA as
follows:

wA ¼

u2UA

1 þ 1ﬃﬃﬃﬃ
pag
ru

(6)

where ru is the rank of the university u.

There are a number of things to note about this construction. Primero, we do not use a decay
factor. This is because we are trying to replicate how the coauthorship data is aggregated into
cities. Aquí, the collaborations from a city are the collection of the collaborations from each
university associated with that city, with no dependence on how far the universities are from
the city. Because we do not know exactly which universities are associated with each city, nosotros
usar 20 km as an estimate. Empirically, this seems to include the relevant ranked universities for
the largest cities of interest. The downside of this method is that many small towns very close
to much larger cities are also given high university rank weights. This is hard to avoid with the
current method, as all we have to match cities with universities are the respective location
coordinates. Además, this will not affect our results significantly because these smaller towns
have relatively few edges in the coauthorship network, except in the case when they are home
to a large university. En este caso, the large university ranking weight will have been assigned to
them correctly.

The exact form of the weight with respect to the rankings is calculated so that the better a
ranking is, the more weight it adds, with the square root term ensuring that this effect is not too
dominant. We only have the rankings for 500 universidades, so for most cities the university set
U A will be empty. El +1 means that the baseline weight is 1 en vez de 0, because for a
specific paper, we may want to look at the product of the university rank weights for its coau-
thors. Por ejemplo, a city that did not have any top 500 universities within its radius would
have a weight of 1. Boston has the highest weight of 2.84, which is unsurprising given its
proximity to Harvard and MIT.

5.2.3. Measures of diversity

We now present the three measures that we will use to investigate the relationship between
coauthor diversity and paper citations.

5.2.3.1. Average weighted network distance We have already outlined a method for calculating
a weighted network distance between two cities. For a specific paper Pi with Ni coauthors
2 Ci we can then calculate the average weighted network distance as
from cities ci1, …, ciNi

cij ;cik 2Ci

(cid:7)

(cid:6)

1
Ci
j
2

dcij cik

(7)

which is the average of the weighted network distances between all the pairs of coauthors on
the paper. This is a simple measure, but it captures the geographical diversity of the coauthors
in a sense which takes into account the difficulty of traveling between their various locations.
The intuition behind it is also clear—a higher average weighted network distance means that

Estudios de ciencias cuantitativas

460

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

on average the coauthors are further apart both geographically and in terms of travel links, y
are thus more diverse in this sense.

Entropy of weighted network distance A related measure of diversity can be found by
5.2.3.2.
calculating the entropy of the weighted network distances between the coauthors on a paper.
We use the Shannon entropy (shannon, 1948), defined as

H ¼ −

pi log pið

(8)

where the pi in this case are the probabilities of a certain weighted network distance appearing
given the distribution of distances in our data. We can estimate these probabilities by sorting
the observed distances into bins and then using the bin counts as an empirical distribution
estimator.

This measure, also known as Shannon’s diversity index, quantifies the diversity of weighted
network distances between coauthors on a paper. It may be more difficult to see how this
measure captures diversity in a similar sense to our previous measure. En este caso, un mayor
value indicates that the distances between coauthors are more varied. From the viewpoint
of one specific coauthor, this would indicate that they collaborate with coauthors that are vary-
ing distances away from them—perhaps one international coauthor and one from a nearby
university. Conversely a smaller value would indicate several coauthors that are the same dis-
tance from each other, such as several coauthors from local universities. It is worth noting that
this measure is only meaningful for papers with more than two coauthors. With only two coau-
thors this entropy measure will always be zero, as the entropy of a single number is zero.

5.2.3.3. Weighted entropy of coauthor location An entropy-based measure that may seem more
intuitive can be found by directly calculating the entropy of the geographical locations of the
coauthors of a paper. We can calculate this as before by discretizing the locations into “bins,"
which are two-dimensional in this case. The entropy of the locations then gives a direct mea-
sure of geographical diversity, as a higher value means that the coauthors are more spread out
throughout the world, with fewer located close together in the same “bin.” This entropy mea-
sure is different to the one used previously in that it does not concern the actual (weighted
network) distances between the coauthors, just whether or not they are clustered together.

This initial construction does not involve the air transport network distances between coau-
thors or the university rank weights of their locations, both of which we have said are impor-
tant factors. Thus we can improve it by using the weighted entropy introduced by Guiaşu
(1971). This is of the form

H ¼ −

wipi log pið

(9)

where the pi are the probabilities of a certain geographic location bin. The wi are weights that
in our case take the form

wi ¼

C 0:05
eig;i
Ui

(10)

Aquí, the Ui are the averages of the university rank weights of the coauthor locations in the 2D
bin used to calculate pi. The Ceig,i are averages of the eigenvector centralities over the bins. Nosotros
“power down” Ceig by raising it to a small power because the range is huge (encima 10 órdenes de
magnitude) and we do not want it to dominate the entropy values or university rank weights.

Estudios de ciencias cuantitativas

461

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

This form for the weights associates more weight with lower ranked universities and less
connected cities. De este modo, our measure of diversity rewards papers where the coauthors are
not only spread out geographically but also not well connected on the air transport network.
This means that papers with a higher weighted diversity indicate a greater difficulty for their
coauthors to travel to each other, which is in line with our previous measures. The diversity
measure also rewards papers with coauthors from less highly ranked universities, which helps
to counteract the effect reported by Clauset et al. (2015) on the effects of university rankings
and reputation on citations.

6. DISCUSSION ON LIMITATIONS AND IMPACT

In terms of limitations, we first acknowledge that funding is a strong confounding variable in
the prominence of citation metrics for papers (zhou, Cai, & Lyu, 2020), thus skewing our
results to the importance of funded research. Tal como, heavy bias towards national-specific
funding might lead to a preference to high citation papers for shorter distances than interna-
tional distances. So, while there is supporting evidence from the literature (de Moya-Anegon,
Guerrero-Bote et al., 2018) that international collaboration does improve citation, any dimin-
ishing return results analysis might need to consider the impact that funding has and the open
challenge of disentangling causal mechanisms between funding and citation. Another consid-
eration is the relative cost of a flight as a proportion of salary for underfunded researchers,
which as a proportion of funding might be lower in the Global South, and certainly long-haul
flights to the north make the problem more severe.

We also believe that university ranking is probably the most obvious confounding variable
to check for, which indirectly includes aspects such as GDP. Por ejemplo, if you are collab-
orating with someone overseas, while GDP may affect the flight cost and frequency, the fun-
damental motivation might be more related to academic aspects or the sheer practical distance
of the flight. Certainly, there are secondary factors such as desirability of the travel location
(Caballero, 2014) and the dominance of conference locations in instigating collaborations (Fraz,
2015), and GDP may discourage early career researchers in low-income countries from
making collaboration trips out of their own pocket, or that those without family or care respon-
sibilities are more likely to form collaborations (Hu, Chen, & Liu, 2014), but we cannot dis-
tinguish this level of granularity within one paper, as there are inherent privilege issues in
research for many countries.

Another limitation is that some researchers may use ground or maritime travel, but in gen-
eral we believe air travel dominates international and long-distance national travel, or at least
has a reasonable approximation to the distance cost irrespective of modality. Therefore small
discrepancies in personal choice might not change the overall statistics much.

In terms of impact on the academic knowledge transfer and international collaboration,
there are two distinct areas to which these results can contribute. The first is exchange and
movilidad: Many bilateral schemes (p.ej., Royal Society International Exchange, German DAAD)
dictate which countries are priority countries based on largely bilateral funding agreements
and a common scientific priority agenda. Often this overlooks diversity and especially the
Global North-South divide highlighted in this paper (94% of collaborations are between
northern hemisphere universities). Beyond travel grants, domain-specific researchers can also
benefit from this work (p.ej., which countries have the greatest diversity potential for similar
distancia). En segundo lugar, this paper may inform research funding policy: Current best practice
recognizes the need to improve diversity, but lacks quantitative frameworks. While this work
only provides a single dimension of geographic diversity (though one can argue geography is

Estudios de ciencias cuantitativas

462

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

closely associated with many aspects of culture, ethnolinguistics, y practicas), it provides
domain-specific data on diversity gaps. This in turn can inform university policy as well as
adding an extra diversity dimension for international partnerships (p.ej., current GCRF funding
is only based on income).

7. CONCLUSIONS

In this paper we have investigated connections between the citations that papers receive and
how the coauthors are connected via the air transport network. En particular, we have looked
at how different measures of geographical diversity of the coauthors on a paper are related to
its ARC score. We have defined three different measures of diversity, relating to the average
weighted (air transport) network distance between coauthors, the entropy of these weighted
network distances, and the weighted entropy of the coauthors’ geographical locations. Nosotros
have seen interesting relationships in each case. For the two types of entropy, the ARC score
for a paper increases as the entropy, and thus the diversity, aumenta. As the average weighted
distance increases, the ARC scores increase up to a point, but then start to decrease. En todo
cases there appears to be a link between diversity and citations.

To ensure that there were no obvious global confounding variables that could offer an alter-
native explanation for these results, we have also investigated the effects that the university
rankings have on this relationship. We have seen that the relationship between the diversity
measures and the average university rank weights is similar to the relationship between the
diversity measures and the ARC scores. Sin embargo, we have shown that the effects discussed
above persist having controlled for the effects of university rankings. Además, tenemos
seen that different subject areas exhibit different relationships between diversity and ARC
puntuaciones. This is also true when we look at collaborations made by researchers from specific
cities.

CONTRIBUCIONES DE AUTOR

Cian Naik: Conceptualización, Curación de datos, Análisis formal, Investigación, Metodología,
Administración de proyecto, Validación, Visualización, Escritura: borrador original; Escritura: revisión &
edición. Cassidy Sugimoto: Conceptualización, Metodología, Administración de proyecto,
Escritura: revisión & edición. Vincent Larivière: Conceptualización, Curación de datos, Metodología,
Administración de proyecto, Escritura: revisión & edición. Chenlei Leng: Conceptualización, Fondos
adquisición, Metodología, Administración de proyecto, Supervisión, Escritura: revisión & edición.
Weisi Guo: Conceptualización, Curación de datos, Metodología, Administración de proyecto, Supervi-
sión, Visualización, Escritura: revisión & edición.

INFORMACIÓN DE FINANCIACIÓN

Weisi Guo was supported by H2020 Marie-Curie [778305] and EPSRC [EP/L016400/1]. Cian
Naik was supported by the EPSRC and MRC [1930478].

DISPONIBILIDAD DE DATOS

The data sets used in our analysis are available from: https://www.kaggle.com/datasets
/ciannaik/impact-of-geographic-diversity-on-citations-data.

CONFLICTO DE INTERESES

Los autores no tienen intereses en competencia.

Estudios de ciencias cuantitativas

463

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

REFERENCIAS

Abramo, GRAMO., D’Angelo, C. A., & Di Costa, F. (2009). Research collab-
oration and productivity: Is there correlation? Higher Education,
57(2), 155–171. https://doi.org/10.1007/s10734-008-9139-z

Catalini, C. (2018). Microgeography and the direction of inventive
actividad. Management Science, 64(9), 4348–4364. https://doi.org
/10.1287/mnsc.2017.2798

Catalini, C., Fons-Rosen, C., & Gaulé, PAG. (2020). How do travel costs
shape collaboration? Management Science, 66(8), 3340–3360.
https://doi.org/10.1287/mnsc.2019.3381

cláusula, A., Arbesman, S., & Larremore, D. B. (2015). Systematic
inequality and hierarchy in faculty hiring networks. Ciencia
Avances, 1(1), e1400005. https://doi.org/10.1126/sciadv
.1400005, PubMed: 26601125

Cronin, B. (2005). The hand of science: Academic writing and its

recompensas. Scarecrow Press.

Cronin, B., Shaw, D., & La Barre, k. (2003). A cast of thousands:
Coauthorship and subauthorship collaboration in the 20th
century as manifested in the scholarly journal literature of psy-
chology and philosophy. Journal of the American Society for
Information Science and Technology, 54(9), 855–871. https://
doi.org/10.1002/asi.10278

de Moya-Anegon, F., Guerrero-Bote, V. PAG., Lopez-Illescas, C., &
Moed, h. F. (2018). Statistical relationships between correspond-
ing authorship, international co-authorship and citation impact
of national research systems. Journal of Informetrics, 12(4),
1251–1262. https://doi.org/10.1016/j.joi.2018.10.004

Franceschet, METRO., & Costantini, A. (2010). The effect of scholar
collaboration on impact and quality of academic papers. Diario
of Informetrics, 4(4), 540–553. https://doi.org/10.1016/j.joi.2010
.06.003

Fraz, METRO. (2015). International academic collaboration: Why it may or
may not work? In ASEE International Forum (páginas. 19.21.1–19.21.9).
https://doi.org/10.18260/1-2–17144

Galison, PAG. (2003). The collective author. In P. Galison & METRO.
Biagioli (Editores.), Scientific authorship: Credit and intellectual
property in science (páginas. 325–353). New York and Oxford:
Routledge.

Gastner, METRO. T., & Hombre nuevo, METRO. mi. (2006). The spatial structure of
redes. European Physical Journal B: Condensed Matter and
Complex Systems, 49(2), 247–252. https://doi.org/10.1140/epjb
/e2006-00046-8

Gieryn, t. F. (2002). Three truth-spots. Journal of the History of the
Ciencias del Comportamiento, 38(2), 113–132. https://doi.org/10.1002
/jhbs.10036, PubMed: 11954037

Gingras, Y. (2010). The transformation of physics from 1900 a
1945. Physics in Perspective, 12(3), 248–265. https://doi.org/10
.1007/s00016-010-0017-6

Glänzel, W.. (2001). National characteristics in international scien-
tific co-authorship relations. cienciometria, 51(1), 69–115.
https://doi.org/10.1023/A:1010512628145

Guiaşu, S. (1971). Weighted entropy. Reports on Mathematical
Physics, 2(3), 165–179. https://doi.org/10.1016/0034
-4877(71)90002-4

guo, w., Del Vecchio, METRO., & Pogrebna, GRAMO. (2017). Global network
centrality of university rankings. Royal Society Open Science,
4(10), 171172. https://doi.org/10.1098/rsos.171172, PubMed:
29134105

Hoekman, J., Frenken, K., & Tijssen, R. j. (2010). Research collab-
oration at a distance: Changing spatial patterns of scientific col-
laboration within Europe. Política de investigación, 39(5), 662–673.
https://doi.org/10.1016/j.respol.2010.01.012

Hu, Z., Chen, C., & Liu, z. (2014). How are collaboration and
productivity correlated at various career stages of scientists?
cienciometria, 101, 1553–1564. https://doi.org/10.1007/s11192
-014-1323-6

Janssen, METRO., & Renn, j. (2015). Historia: Einstein was no lone genius.
Naturaleza, 527(7578), 298–300. https://doi.org/10.1038/527298a,
PubMed: 26581276

katz, j. S., & Martín, B. R. (1997). What is research collaboration?
Política de investigación, 26(1), 1–18. https://doi.org/10.1016/S0048
-7333(96)00917-1

Caballero,

(2014).

International education hubs: Collaboration
for competitiveness and sustainability. New Directions for
Higher Education, 2014(168), 83–96. https://doi.org/10.1002
/he.20115

Larivière, v., Gingras, y., & Archambault, É. (2006). canadiense
collaboration networks: A comparative analysis of the natural
sciences, social sciences and the humanities. cienciometria,
68(3), 519–533. https://doi.org/10.1007/s11192-006-0127-8
Larivière, v., Gingras, y., Sugimoto, C. r., & Tsou, A. (2015).
Team size matters: Collaboration and scientific impact since
1900. Journal of the Association for Information Science and
Tecnología, 66(7), 1323–1332. https://doi.org/10.1002/asi
.23266

Luukkonen, T., Persson, o., & Sivertsen, GRAMO. (1992). Comprensión
patterns of international scientific collaboration. Ciencia, Tech-
nología, & Human Values, 17(1), 101–126. https://doi.org/10
.1177/016224399201700106

Narin, F., stevens, K., & Whitlow, mi. S. (1991). Científico
co-operation in Europe and the citation of multinationally
authored papers. cienciometria, 21(3), 313–323. https://doi.org
/10.1007/BF02093973

Academia Nacional de Ciencias, National Academy of Engineering,
and Institute of Medicine. (2005). Facilitating interdisciplinary
investigación. Washington, corriente continua: National Academies Press.

Persson, o., Glänzel, w., & Danell, R. (2004). Inflationary bib-
liometric values: The role of scientific collaboration and the
need for relative indicators in evaluative studies. cienciometria,
60(3), 421–432. https://doi.org/10.1023/ B:SCIE.0000034384
.35498.7d

Ploszaj, A., yan, X., & Börner, k. (2020). The impact of air transport
availability on research collaboration: A case study of four uni-
versidades. MÁS UNO, 15(9), e0238360. https://doi.org/10.1371
/diario.pone.0238360, PubMed: 32886681

Precio, D. j. de Solla. (1986). Little science, big science … and

más allá de. Nueva York: Columbia University Press.

Pyenson, l. (1985). The young Einstein: The advent of relativity.

Bristol: Adam Hilger.

shannon, C. mi. (1948). A mathematical theory of communication.
Bell System Technical Journal, 27(3), 379–423. https://doi.org/10
.1002/j.1538-7305.1948.tb01338.x

Shapin, S. (1989). The invisible technician. American Scientist,

77(6), 554–563.

Sonnenwald, D. h. (2007). Scientific collaboration. Annual Review
of Information Science and Technology, 41(1), 643–681. https://
doi.org/10.1002/aris.2007.1440410121

Sugimoto, C. r., Robinson-Garcia, NORTE., Murray, D. S., Yegros-
Yegros, A., costas, r., & Larivière, V. (2017). Scientists have most
impact when they’re free to move. Naturaleza, 550(7674), 29–31.
https://doi.org/10.1038/550029a, PubMed: 28980663

Wagner, C. S., & Leydesdorff, l. (2005). Network structure,
self-organization, and the growth of international collaboration

Estudios de ciencias cuantitativas

464

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d

F
/

4
2
4
4
2
2
1
3
6
3
9
5
q
s
s
_
a
_
0
0
2
4
8
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Impact of geographic diversity on citations

in science. Política de investigación, 34(10), 1608–1618. https://doi.org
/10.1016/j.respol.2005.08.002

Wray, k. B. (2002). The epistemic significance of collaborative
investigación. Philosophy of Science, 69(1), 150–168. https://doi.org
/10.1086/338946

Wuchty, S., jones, B. F., & Uzzi, B. (2007). The increasing dominance of
teams in production of knowledge. Ciencia, 316(5827), 1036–1039.
https://doi.org/10.1126/science.1136099, PubMed: 17431139

Wynes, S., Donner, S. D., Tannason, S., & Nabors, norte. (2019). Aca-
demic air travel has a limited influence on professional success.

Journal of Cleaner Production, 226, 959–967. https://doi.org/10
.1016/j.jclepro.2019.04.109

zhou, PAG., Cai, X., & Lyu, X. (2020). An in-depth analysis of govern-
ment funding and international collaboration in scientific
investigación. cienciometria, 125, 1331–1347. https://doi.org/10
.1007/s11192-020-03595-2

Zuckerman, h. (1967). Nobel laureates in science: Patterns of pro-
ductivity, colaboración, and authorship. American Sociological
Revisar, 32(3), 391–403. https://doi.org/10.2307/2091086,
PubMed: 6046812

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
q
s
s
/
a
r
t
i
C
mi
–
pag
d