INVESTIGACIÓN

The R1-weighted connectome: complementing
brain networks with a myelin-sensitive measure

Tommy Boshkovski

1

2
, Ljupco Kocarev

, Julien Cohen-Adad

1,3,4

5
, Bratislav Miši´c

,

Stéphane Lehéricy

, Nikola Stikov

, and Matteo Mancini

6

1,7,∗

1,8,9,∗

1NeuroPoly Lab, Polytechnique Montreal, Montréal, QC, Canada
2Macedonian Academy of Sciences and Arts, Skopje, Macedonia
3Department of Neurosciences, Faculty of Medicine, University of Montreal, Montréal, QC, Canada
4Functional Neuroimaging Unit, Centre de recherche de l’institut universitaire de gériatrie de Montréal, Montréal, QC, Canada
5Instituto Neurológico de Montreal, Montréal, QC, Canada
6Paris Brain Institute (ICM), Centre for NeuroImaging Research (CENIR), Inserm U 1127, CNRS UMR 7225, Sorbonne
Université, F-75013, París, Francia
7Montreal Heart Institute, Montréal, QC, Canada
8Department of Neuroscience, Brighton and Sussex Medical School, University of Sussex, Brighton, Reino Unido
9CÚBRICO, Universidad de Cardiff, Cardiff, Reino Unido
*These authors contributed equally to this work.

Palabras clave: Connectome, Myelin; Diffusion MRI, Quantitative MRI

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

5
2
3
5
8
1
9
1
3
5
2
5
norte
mi
norte
_
a
_
0
0
1
7
9
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

ABSTRACTO

Myelin plays a crucial role in how well information travels between brain regions.
Complementing the structural connectome, obtained with diffusion MRI tractography,
with a myelin-sensitive measure could result in a more complete model of structural brain
connectivity and give better insight into white-matter myeloarchitecture. In this work we
weight the connectome by the longitudinal relaxation rate (R1), a measure sensitive to
mielina, and then we assess its added value by comparing it with connectomes weighted by
the number of streamlines (NOS). Our analysis reveals differences between the two
connectomes both in the distribution of their weights and the modular organization.
Además, the rank-based analysis shows that R1 can be used to separate transmodal
regiones (responsible for higher-order functions) from unimodal regions (responsible for
low-order functions). En general, the R1-weighted connectome provides a different perspective
on structural connectivity taking into account white matter myeloarchitecture.

RESUMEN DEL AUTOR

In the present work, we show that by using a myelin-sensitive measure we can complement
the diffusion MRI-based connectivity and provide a different picture of the brain
organización. We show that the R1-weighted average distribution does not follow the same
trend as the number of streamlines strength distribution, and the two connectomes exhibit
different modular organization. We also show that unimodal cortical regions tend to be
connected by more streamlines, but the connections exhibit a lower R1-weighted average,
while the transmodal regions have higher R1-weighted average but fewer streamlines. Este
could imply that the unimodal regions require more connections with lower myelination,
whereas the transmodal regions rely on connections with higher myelination.

INTRODUCCIÓN

The brain is a complex system that can be modelled as an intricate network of interconnected
elementos (Fornito et al., 2016). Using magnetic resonance imaging (resonancia magnética), connectomics aims

un acceso abierto

diario

Citación: Boshkovski, T., Kocarev, l.,
Cohen-Adad, J., Miši ´c, B., Lehéricy,
S., Stikov, NORTE., & Mancini, METRO. (2021).
The R1-weighted connectome:
complementing brain networks with a
myelin-sensitive measure. Red
Neurociencia, 5(2), 358–372.
https://doi.org/10.1162/netn_a_00179

DOI:
https://doi.org/10.1162/netn_a_00179

Supporting Information:
https://doi.org/10.1162/netn_a_00179
https://github.com/TommyBoshkovski
/The_R1-weighted_connectome

Recibió: 12 Agosto 2020
Aceptado: 11 Noviembre 2020

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autor correspondiente:
Matteo Mancini
ingmatteomancini@gmail.com

Editor de manejo:
Andrew Zalesky

Derechos de autor: © 2020
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

The R1-weighted connectome

Myeloarchitecture:
Spatial organization of myelinated
axons in the cerebral cortex.

qMRI:
Quantitative MRI, referring to the use
of MRI to measure tissue physical
and chemical properties.

Myelin:
Lipidic structure that wraps around
axons and allows faster electrical
conduction.

to characterize macroscopic connectivity by viewing the brain as a set of nodes defined by
functionally or anatomically distinguishable regions of interest (ROI) and edges that are con-
ventionally assumed to reflect the white matter tracts connecting those nodes (bassett & despreciar,
2017; Hagmann et al., 2007; van den Heuvel et al., 2008). Específicamente, the white matter tracts
can be reconstructed using diffusion MRI and tractography (Jeurissen et al., 2019; Mori & Van
Zijl, 2002). To better characterize the relationship between the nodes and edges of a brain
network, weights can be assigned to the connections, which are presumed to reflect relevant
propiedades (Rubinov & despreciar, 2010).

There is an ongoing debate as to the most appropriate choice of weighting for the con-
nectome (Yeh et al., 2020). Hasta ahora, the most widely used weight is the number of streamlines
(NOS), which counts the reconstructed streamlines, from diffusion tractography, between pairs
of ROIs (Fornito et al., 2016). Although previous work (Sinke et al., 2018; van den heuvel
et al., 2015) showed a positive correlation between NOS and tract-tracing connectivity, sug-
gesting that NOS could be used in principle as a proxy for microstructural fiber count, the use
of NOS to weight the structural connectome is still problematic (Calamante, 2019). In partic-
ular, NOS does not measure biologically meaningful properties such as conduction velocity.
Además, fiber tracking often lacks specificity as it can be affected by a number of factors,
including the tractography algorithm used (jones, 2010; Yeh et al., 2020) as well as image
acquisition parameters (Jones et al., 2013).

Another potential candidate for weighting the connections is the fractional anisotropy (FA)
that can be obtained using diffusion tensor imaging (DTI). While FA does provide more insights
into the microstructural properties of white matter, it is also influenced by numerous tissue
propiedades, including axonal diameter, fiber density, tissue geometry, as well as the degree of
mielinización (Jones et al., 2013). Another reason why FA might not be the best candidate for
weighting the connectome is because it is derived from the same diffusion-based measures that
are used to reconstruct the tractography. To gain additional insights into the myeloarchitecture
it would make sense to weight the connectome by a metric that is orthogonal to diffusion.
Many quantitative MRI (qMRI) measures (es decir., magnetization transfer ratio [MTR], longitudinal
relaxation rate [R1], myelin water fraction [MWF]) have been used to characterize myelin.
Myelin is the dielectric material that wraps around the axons to enable fast conduction in the
cerebro. The use of such metrics is particularly well suited for studies that examine activity-
dependent myelination (Sampaio-Baptista & Johansen-Berg, 2017) and pathology related to
myelin-specific changes in brain connectivity.

Several studies (Caeyenberghs et al., 2016; Kamagata et al., 2019; Mancini et al., 2018;
van den Heuvel et al., 2010) used such myelin-sensitive MR measures in brain network models.
Específicamente, in the work of Caeyenberghs et al. (2016), multiple quantitative myelin-sensitive
MRI metrics were used as weights, including the R1, which has been shown to be effective for
myelin imaging (Stüber et al., 2014). Caeyenberghs et al. analyzed the white matter plasticity
using connectomics to determine which measures best correlate with white matter plasticity
during a working memory task. To weight the connectome they used diffusion-derived mea-
sures (FA, ANUNCIO, 1/Maryland, 1/RD, TRF [total restricted fraction], TVF [tissue volume fraction], MWF),
and relaxometry measures (R1 and R2). They reported that the increased global efficiency
in the network during working memory tasks was best captured by the R1-weighted connec-
a mi. The influence of myelin on R1 values can be traced to its molecular composition. Voxels
containing more myelinated axons have an increased proportion of macromolecules, cual
increases the longitudinal relaxation rate (Yeatman et al., 2014). Although R1 is affected by
iron, calcium content, and axon size (Harkins et al., 2016) and count (Schmierer et al., 2008),

Neurociencia en red

359

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

5
2
3
5
8
1
9
1
3
5
2
5
norte
mi
norte
_
a
_
0
0
1
7
9
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The R1-weighted connectome

Flip angle (in magnetic resonance):
Angle at which an RF pulse tips the
longitudinal magnetization into the
transverse plane.

Inversion time
(in magnetic resonance):
Time between an 180° (inversion)
pulse and 90° (excitation) pulse.

Longitudinal relaxation time
(in magnetic resonance):
Time constant of the exponential
decay of the net magnetization
longitudinal component after an
excitation pulse.

a recent meta-analysis showed that R1 is comparable to other MRI techniques for quantifying
myelin content (Mancini et al., 2020).

In this article, we introduce a myelin-sensitive measure (R1) to the structural connectome.
We do this by weighting the connections in the structural connectome using the median R1
value along a bundle of streamlines connecting pairs of brain regions. We then compared the
R1-weighted connectome with the conventional NOS-weighted connectome in terms of mul-
tiple network attributes, including strength distribution and modular structure. The differences
between the R1- and NOS-weighted connectomes in terms of their overall network organiza-
tion have the potential to provide a complementary perspective on white matter myeloarchi-
tecture, as R1 is more directly sensitive to myelin compared to NOS.

MATERIALES Y MÉTODOS

Data Acquisition
Thirty-five healthy volunteers (HC) (12 female/23 male, mean age ± SD: 61.2 ± 9.16 años)
participated in the present study. Subjects were scanned at the Paris Brain Institute (ICM –
Institut du Cerveau), París, Francia. All subjects signed informed consent forms. El estudio
was approved by the local ethics committee (Ethics Committee: Comité de Protection des
Personnes [CPP] Ile de France VI – RCB: 2014-A00725-42). Scans were performed on a 3T
SIEMENS Prisma Scanner. The protocol included (i) 3-shell DWI sequence (TR = 10,400 EM,
3
, number of gradient directions per shell = 64,
TE = 59 EM, voxel size = 1.7 × 1.7 × 1.7 mm
2
32, y 8 en, respectivamente, b = 2,500, 700, y 300 s/mm
) y (ii) magnetization-prepared 2
rapid acquisition gradient echoes (MP2RAGE) sequence for R1 mapping (TR = 5,000 EM, TE =
2.98 EM, flip angles = 4◦
, TI = 700/2,700 EM, FOV = 256 × 232 mm, voxel size =
1 mm

and 5◦

).

3

Reconstruction of Quantitative R1 Maps

The MP2RAGE sequence (Marques et al., 2010) produces two T1-weighted images with differ-
ent flip angles and different inversion times (INV1 and INV2). These images are then combined
to produce a more uniform T1w image (UNI). The UNI image was used to estimate the lon-
gitudinal relaxation times (T1 maps) using qMRLab (Karakuzu et al., 2020). The longitudinal
relaxation rate (R1) was then calculated from the T1 maps as:

R1 =

1
T1

The quantitative maps were reconstructed using the qMRLab module MP2RAGE (Karakuzu
et al., 2020).

Anatomical and Diffusion Data Preprocessing

As a first step in the anatomical preprocessing pipeline, background noise removal (O'Brien
et al., 2014) was applied to the UNI images by using a combination of the two inversion time
images with a denoising regularization factor of 70. The denoised UNI images were then
processed using FreeSurfer 6.0 (pescado, 2012) to segment the different tissues and parcellate
the brain using the Desikan–Killiany Atlas (Desikan et al., 2006). To reduce the bias from
the different parcel sizes, we subdivided them into finer regions of approximately equal size
using the Lausanne 2008 parcellation (escala 125) (Cammoun et al., 2012; Hagmann et al.,
2008), which resulted in 234 brain parcels. Además, because this article focuses on the

Neurociencia en red

360

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

5
2
3
5
8
1
9
1
3
5
2
5
norte
mi
norte
_
a
_
0
0
1
7
9
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The R1-weighted connectome

Constrained spherical deconvolution:
Mathematical approach to
deconvolve the diffusion MRI signal
into fiber orientation–specific
spherical harmonics.

connectivity between cortical regions, we discarded all the subcortical regions from the anal-
ysis, which resulted in 219 regiones del cerebro.

The preprocessed anatomical images, T1w image, and parcellation; in addition the recon-
structed quantitative maps for each subject were transferred to the subject’s diffusion space
by coregistering them to the mean b0 image using FSL FLIRT (Jenkinson et al., 2002, 2012)
rigid body registration. Each registration was visually inspected to check the alignment (ver
Figure S1 in the Supporting Information). Besides the registration, all preprocessed images
were visually inspected for errors.

The preprocessing of the diffusion images was done using MRtrix3 (Tournier et al., 2019).
Primero, we applied a noise removal technique (Veraart et al., 2016a, 2016b) followed by a Gibbs
ringing artifacts removal method (Kellner et al., 2016) and a B1 field inhomogeneity correc-
ción. Entonces, the images were preprocessed for motion and inhomogeneity distortion correction
using FSL’s eddy (andersson & Sotiropoulos, 2016) and topup tools (Andersson et al., 2003), re-
spectively. Además, to increase the anatomical contrast and improve the tractography and
registration, the preprocessed images were upsampled to a 1-mm isotropic resolution. Multitis-
sue constrained spherical deconvolution (Jeurissen et al., 2014), followed by the anatomically
constrained tractography method (Smith et al., 2012), were used to reconstruct the tractogram.
We applied the SD_STREAM deterministic tracking algorithm (Tournier et al., 2012) that used
1 million seeds dynamically placed using the SIFT model (Smith et al., 2015). The tractography
procedure was set to stop either when (i) it produces 200,000 streamlines and/or (ii) the maxi-
mum number of seeds (1,000,000) se alcanza. During tracking the maximum turning angle was
set to 60
. Streamlines with length shorter than 20 mm or longer than 250 mm were discarded
from the tractogram. Additional constraints were provided by the anatomically constrained
tractography (ACT) estructura (Smith et al., 2012).

◦

Structural Connectome Reconstruction

Structural connectivity was represented using a weighted graph, where each node corresponded
to one of the 219 cortical ROIs, and each edge reflected the presence of reconstructed stream-
lines between each pair of ROIs. Two metrics were used as weights of the connections: (i) el
NOS reconstructed between two regions and (ii) the median R1 values along the bundle of re-
constructed streamlines between two regions. The same steps were followed to reconstruct the
FA-weighted connectome (see Supporting Information). We decided to use the median value
of the metric (R1 or FA) along the tract for two main reasons: (i) the median is less sensitive to
outliers and (ii) it does not assume a normal distribution of the values along the bundle.

To mitigate the problem with spurious connections reconstructed by the tractography al-
gorithm, we considered two nodes as connected only if there are at least two streamlines
connecting the specific pair of ROIs. También, a more conservative threshold (at least five connec-
ciones) was applied to test the robustness of the results.

A group consensus approach for both NOS- and R1-weighted connectomes was adopted
to reduce individual variability in the reconstructed networks. The group consensus networks
for both connectomes were constructed by taking into account only the connections that are
present in at least 50% of the subjects (de Reus & van den heuvel, 2013). The weight of a
connection in the group consensus network corresponded to the median of the connection’s
weights across subjects. We then assessed the relationship between the connection’s weights
of the R1-weighted connectome and the NOS-weighted connectome using linear regression,
as well as between the R1-weighted connectome and the FA-weighted connectome.

Neurociencia en red

361

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

5
2
3
5
8
1
9
1
3
5
2
5
norte
mi
norte
_
a
_
0
0
1
7
9
pag
d

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The R1-weighted connectome

NOS Strength and R1-Weighted Average

We chose strength as a measure of centrality because of its straightforward interpretation. Para
the NOS-weighted connectome, the strength was calculated as:

SNOS
i

=

norte
∑
j

wij

where i is a given node, and wij is the NOS connectivity between the nodes i and j.

For the R1-weighted connectome, we looked at the R1-weighted average, as it is not influ-
enced by the number of connections (Kamagata et al., 2019). The R1-weighted average was
calculated as:

SR1
i =

∑N
j wijvij
∑N
j wij

where i is a given node, wij is the number of streamlines and vij is the median R1 sampled
along the bundle of those streamlines connecting the nodes i and j.

We then looked at the distribution of the centrality measures for each weight. The nodes
were first sorted according to their NOS strength. Entonces, we defined the hubs as regions that
have NOS strength of at
el menos 2 standard deviations above the mean NOS strength
(van den heuvel & despreciar, 2013). A more conservative hub definition, al menos 3 standard
deviations above the mean NOS strength, was also used. Entonces, we highlighted the hub re-
gions, defined in the NOS-weighted connectome and in the R1-weighted connectome.

Modular Structure

To probe the modular structure of the NOS- and R1-weighted connectomes, we used a modu-
larity maximization method (Blondel et al., 2008; Rubinov & despreciar, 2011; despreciar & Betzel,
2016). This is a common method that is used to divide a network into modules/communities
with highly interconnected regions within, and less connected regions between the submod-
ules. To achieve this, the method aims to maximize a quality function given by the following
equation:

q(γ) =

Aij − γPij

(cid:3)

(cid:4)

δ

ci, cj

(cid:5)

(cid:2)

norte
∑
ij

where Aij is the empirical connectivity matrix, and Pij represents the estimated connectivity
matrix given a specific null model. The module assignment of node i is described by the
is the Kronecker function which is equal to 1 when ci = cj and
variable ci, whereby δ
0 de lo contrario.

ci, cj

(cid:4)

(cid:5)

The modularity maximization also depends on a resolution parameter (γ), which makes it
sensitive to different scales. If γ < 1, then the network is partitioned into larger modules, while for γ > 1 the method tends to find smaller modules.

To determine at which resolution the modular structure is best described, eso es, when it
maximizes the quality functions, for each connectome we iterated over γ values ranging from
0.5 a 3 with steps of 0.1. At each step, we ran the Louvain algorithm 1,000 veces (rubia
et al., 2008). Entonces, the resolution parameter (γ) with highest Q was selected on the basis of the
highest Rand index (Traud et al., 2011) similarity and created a consensus modularity using
the netneurotools package (Netneurolab, 2020).

Neurociencia en red

362

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

/

5
2
3
5
8
1
9
1
3
5
2
5
norte
mi
norte
_
a
_
0
0
1
7
9
pag
d

.

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The R1-weighted connectome

Rank-Based Analysis

To further explore the modular structure and assess the difference between weights, a rank-
based analysis (Vázquez-Rodríguez et al., 2019) was performed: the nodes were first sorted by
their strength (for the NOS-weighted connectome) and by their weighted average (for the R1-
weighted connectome) defining their nodal rank (1 meaning highest and 219 meaning lowest).
Entonces, nodal ranks in the NOS-connectome were subtracted from the corresponding nodal
ranks in the R1-weighted connectome. To normalize the difference, a z score normalization
was applied. The nodes were then grouped according to the von Economo cytoarchitectonic
parcellation (Scholtens et al., 2018) and Yeo’s functional parcellation (Yeo et al., 2011). Finalmente,
the median z score for each cytoarchitectonic and functional class was computed across the
respective nodes.

RESULTADOS

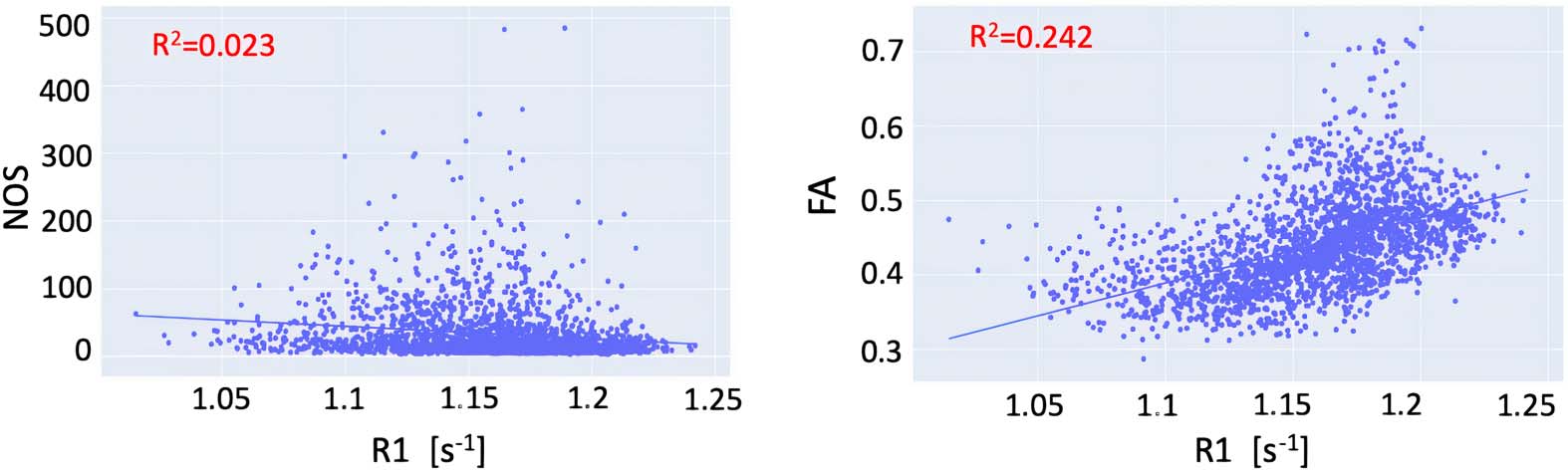
To assess the shared variance between the different connectomes, we first compared the con-
nection weights of the R1-weighted connectome with the weights obtained from the NOS-and
FA-weighted connectomes. We found that the R1 and NOS weights exhibited an R2
de 0.023
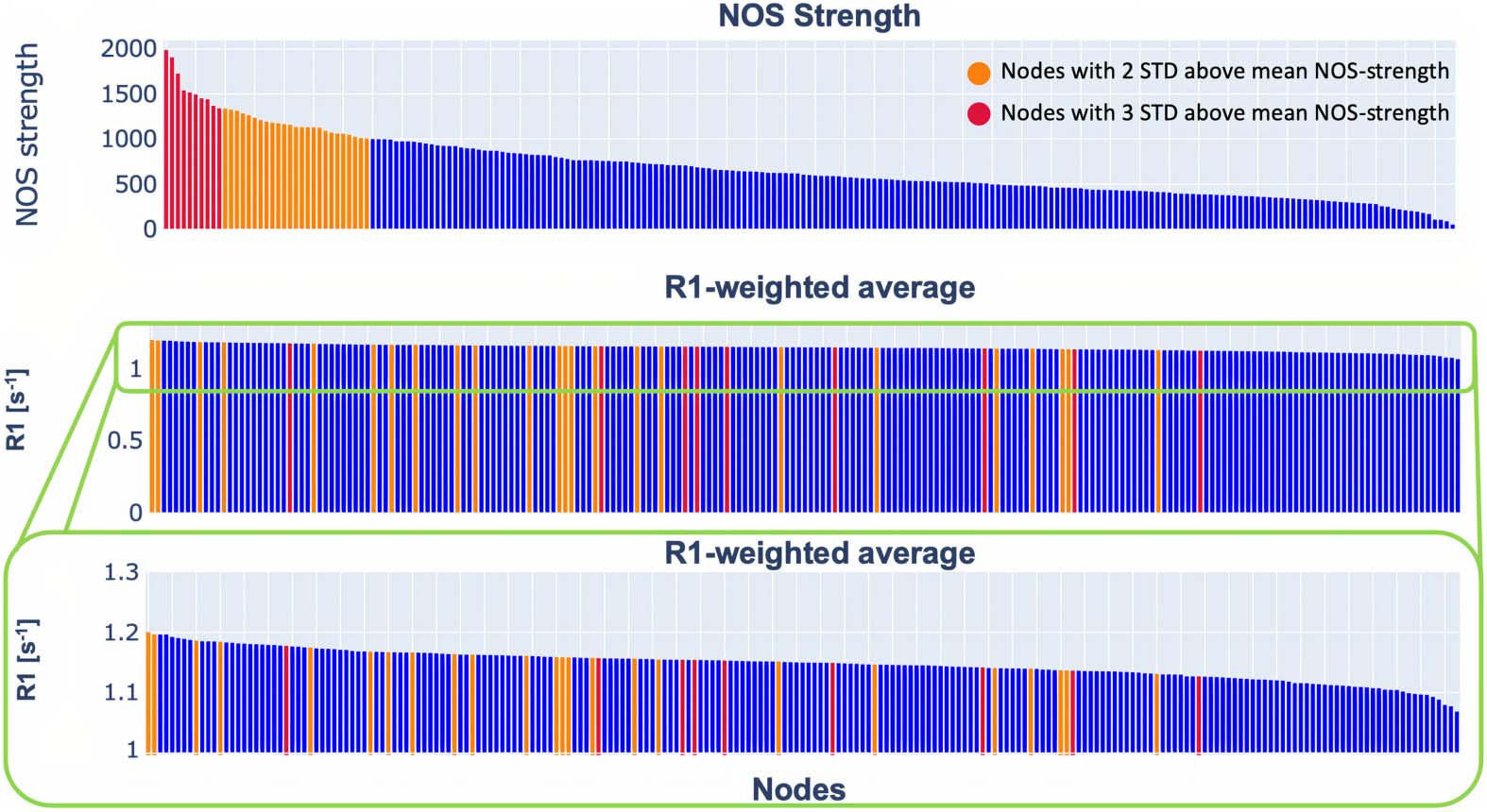
(pag < 0.01), while the R1 and the FA weights exhibited R2 of 0.24 (p < 0.01) (Figure 1). Given that R1 measures different microstructural properties compared to NOS and FA, the shared variance between the connections weighted with these measures is limited. Next, we looked at the strength distribution and weighted average for the NOS- and R1- weighted connectomes. The strength distribution of the NOS-weighted connectome is heavy tailed (Figure 2). Among the nodes with the highest strength were the superior frontal gyrus, lateral occipital, pre-, and postcentral gyrus. (Table S1 in the Supporting Information). The R1-weighted average distribution did not follow the same trend as the NOS strength distribution (Figure 2). This result indicates that a high number of streamlines is not associated with higher R1 values. Also, the hubs defined with the more conservative threshold (at least 3 standard deviations above the mean NOS strength) did not exhibit a high R1-weighted average (Figure 2). 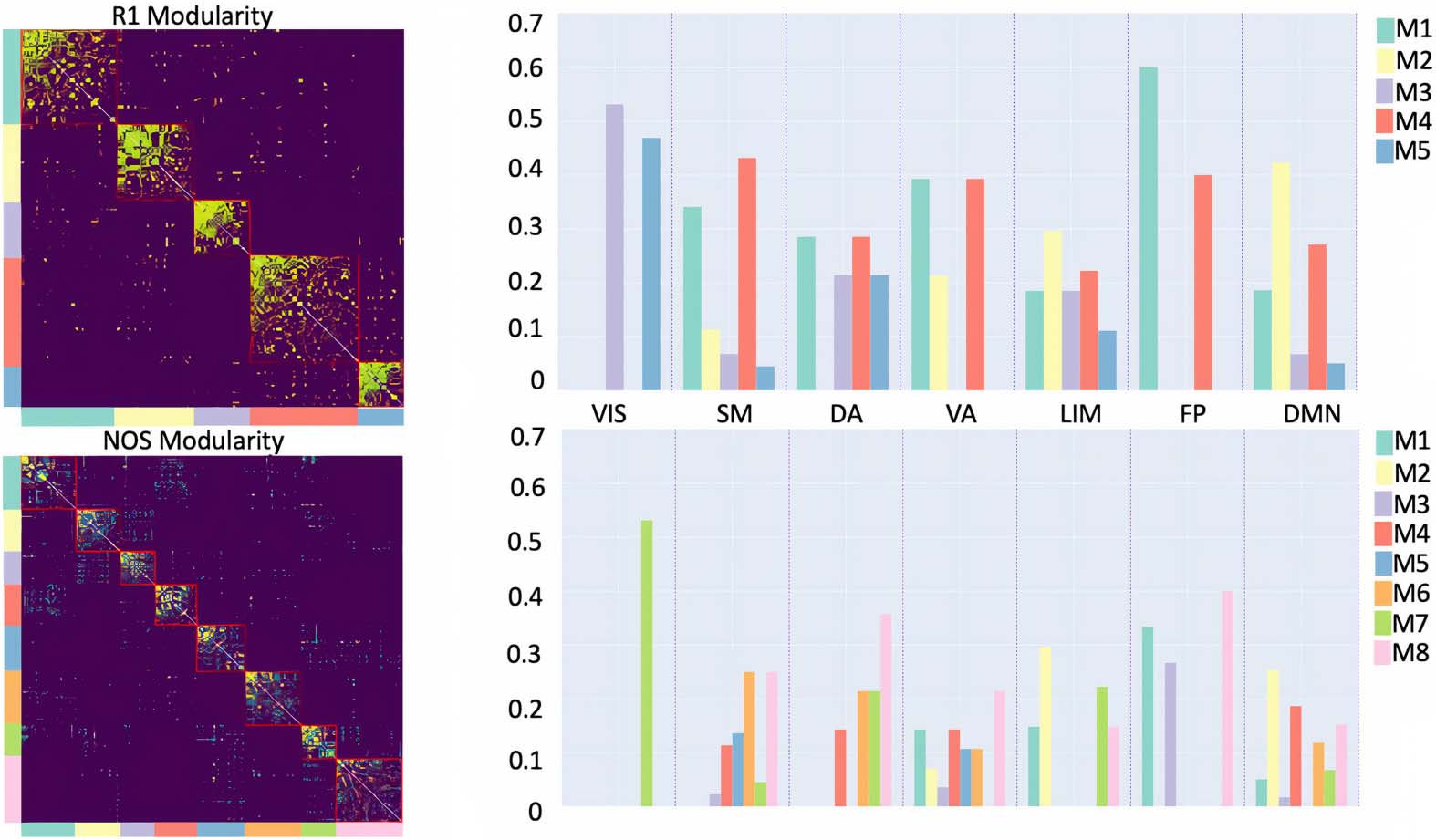As for the community structure (Figure 3), the selected resolution parameter was 0.8 for the R1-weighted, while for the NOS-weighted connectome it was 2.6. The consensus mod- ularity for the R1-weighted connectome yielded 5 modules with average modularity score Figure 1. Relationship between the connection weights in the R1-weighted and FA-weighted connectome (left) and R1-weighted and NOS-weighted (right). Network Neuroscience 363 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 2 3 5 8 1 9 1 3 5 2 5 n e n _ a _ 0 0 1 7 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The R1-weighted connectome Figure 2. Distribution of the NOS strength and R1-weighted average. The plot in the middle shows the distribution of the R1-weighted average on a scale from 0 to 1.2. To make it easier to see the trend, we showed the same data on a scale from 1 to 1.2 (bottom plot). In orange are highlighted the nodes that are 2 standard deviations above the mean NOS strength, while in red are highlighted the nodes that are 3 standard deviations above the NOS strength. The details about the nodes are provided in the Supporting Information. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 2 3 5 8 1 9 1 3 5 2 5 n e n _ a _ 0 0 1 7 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 3. Community structure of the R1- and NOS-weighted connectomes. The bar plots repre- sent the distributions of functional classes, given by Yeo et al. (2011), within the modules (denoted as M#) for the R1- and NOS-weighted connectomes, respectively. Yeo’s functional classes include the following: SM (somatomotor), VIS (visual), VA (ventral attention), FP (fronto-parietal), LIM (limbic), DA (dorsal attention), and DMN (default mode network). Q(γ) = 0.569, whereas the NOS-weighted connectome yielded 11 modules with an average modularity score of Q(γ) = 0.44. We further explored the organization of the modules by looking at the distributions of the functional classes of the nodes provided by Yeo et al. (2011). Both the NOS and R1 modules were found to include multiple functional classes. Network Neuroscience 364 The R1-weighted connectome Unimodal regions: Brain regions responsible for specific, concrete functions. G-ratio: Ratio of the inner and the outer diameters of a myelinated axon. 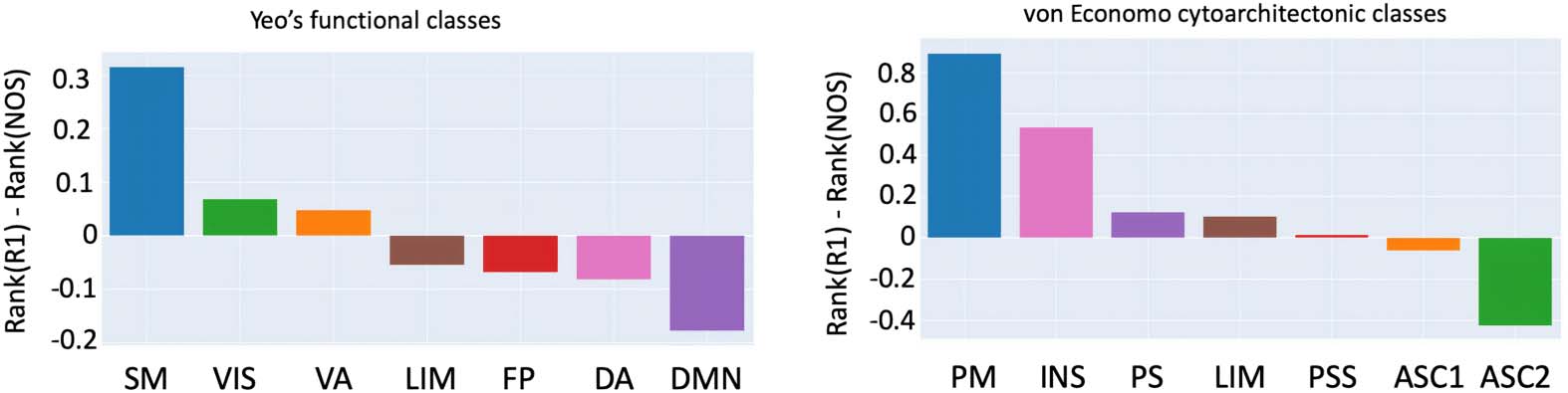Figure 4. Rank-based comparison across functional and cytoarchitectonic classes. The rank for each node was calculated by its strength (for NOS)/weighted average (for R1) and then grouped using a cytoarchitectonic parcellation and a functional one. Yeo’s functional classes include the following: SM (somatomotor), VIS (visual), VA (ventral attention), FP (fronto-parietal), LIM (limbic), DA (dorsal attention), and DMN (default mode network). Von Economo cytoarchitectonic classes include the following: PM (primary motor), INS (insular), LIM (limbic), PS (primary sensory), PSS (primary secondary sensory), ASC1 (association cortex), and ASC2 (association cortex 2). The rank-based analysis (Figure 4) shows where the functional and cytoarchitectonic classes are over- and underrepresented in terms of R1-weighted average and NOS strength. For Yeo’s functional atlas, the R1 is overrepresented (compared to NOS) in the higher-order subnetworks (transmodal) and underrepresented for function-specific subnetworks (unimodal). However, this is not the case for the cytoarchitectonic subnetworks derived using the von Economo parcellation, that is, the transmodal/unimodal distinction was less obvious, as R1 was also underrepresented for the insular and the limbic subnetworks, which are transmodal. We repeated the same analysis on the connectomes constructed with a stricter threshold, that is, two regions are connected if there are at least five streamlines reconstructed between them (see Supporting Information). The results showed that centrality measures’ distributions and rank-based analysis are consistent between the two thresholds. However, regarding the modularity, R1-based connectome yielded a different number of modules, although the com- munity structure was still different from NOS. Furthermore, the same analysis was done on the connectome constructed using probabilistic tractography and we have obtained similar results (see Supporting Information). DISCUSSION In this study, we showed that by using a myelin-sensitive measure we can complement the diffusion MRI-based connectivity and provide a different picture of the brain organization. To better characterize the myelin-weighted connectome, we decided to compare it with a connectome weighted by a diffusion-based metric. While there were several candidates for comparison, such as apparent axon density (Raffelt et al., 2012) and SIFT2 (Smith et al., 2015), we settled on NOS as it is the most commonly used approach. First, we focused on the strength distribution and compared it to the R1-weighted average. From Figure 2 one can appreciate that they do not follow the same trend. The R1-weighted average reflected a more uniform distribution. We also found that the hub regions, defined in the NOS connectome, do not necessarily have a high R1-weighted average. Similar results have been previously reported in Mancini et al. (2018) for a g-ratio-weighted connectome. Second, we observed differences in the modular structure between the NOS- and R1- weighted connectomes. The number of modules was influenced by the resolution parame- ter, and a different number of modules was expected as the most optimal parameters were Network Neuroscience 365 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 2 3 5 8 1 9 1 3 5 2 5 n e n _ a _ 0 0 1 7 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The R1-weighted connectome Transmodal regions: Brain regions involved in multiple- or higher-level functions. different for the two connectomes. However, what we wanted to highlight in this study was the different modular structure for the two weights, and to do this we partitioned the network in the most appropriate way for each weight. We also explored the distribution of the functional classes within the modules and found that there was limited agreement between the functional classes and the estimated modules, that is, the modules included multiple functional classes. This result is in agreement with results previously reported in the literature: it has been ob- served that structural and functional perspectives highlight different interregional relationships (Betzel et al., 2013; Goñi et al., 2014; Honey et al., 2010; Suárez et al., 2020). Regarding the rank-based analysis, we found that there was a good division of the unimodal versus transmodal functional classes. This pattern seems to follow the functional gradient observed in previous studies (Margulies et al., 2016; Vázquez-Rodríguez et al., 2019). An interesting result was that the unimodal regions exhibited more connections but in proportion a lower R1-weighted average, while the transmodal regions exhibited a higher R1-weighted average but less connections. A recent study has shown an opposite trend in cortical gray matter (Glasser & van Essen, 2011), but our study focuses on white matter connectivity and uses a different imaging modality (R1 versus T1w/T2w). Our results showed that differences exist between the connectome weighted with NOS and the one weighted with R1 in terms of the distribution of their weights, as well as in the modular organization. Interestingly, the rank-based analysis showed an agreement in subdivision of the regions in unimodal and transmodal functional subnetworks. Future studies could focus on the relationship between white matter myeloarchitecture and function. The use of qMRI metrics to weight the connectome could have important implications for many applications. qMRI offers several techniques that are sensitive to myelin (Laule et al., 2007; Petiet et al., 2019), such as magnetization transfer, myelin water imaging, or relaxom- etry (for extensive reviews see Heath et al., 2018, and Piredda et al., 2020). Additionally, these techniques could be used to estimate the conduction velocity and conduction delays, and to incorporate these metrics as weights in the connectome. This would potentially result in a more complete model of the structural connectome and may provide a more comprehen- sive understanding of how the structure shapes the function. In this direction, Berman and colleagues calculated the conduction delay among the fibers in the corpus callosum using MRI-derived g-ratio (Berman et al., 2019). However, to calculate the conduction velocities and delays, in addition to the information about myelin, one would also need information about the axonal diameter and potentially information about other microstructural properties not accessible from MRI (Drakesmith et al., 2019). The work of Drakesmith et al. (2019) studied the feasibility of estimating conduction velocity in vivo using MRI microstructural measures. They performed simulations and reported that most of the variance in the estimation of the conduction velocity is explained by the axonal diameter and the g-ratio. However, axonal di- ameter can be accurately measured only with high gradients (300 mT/m) (Veraart et al., 2020) and is therefore not a measure that one can have on a clinical scanner yet. Additionally, even at such high gradients, the MRI-derived axonal measure is not sensitive to small axons (1 µm or lower) (Jones et al., 2018), so there are still challenges that need to be tackled in order to compute a robust estimate of the conduction velocity or delay. There are a few methodological aspects of this work that are worth mentioning. The first is the choice of quantitative MRI metrics to weight the connectome (Collin et al., 2014, 2016; Larivière et al., 2019; Messaritaki et al., 2019; Verstraete et al., 2011). As mentioned before, the structural connectome is often weighted using diffusion-derived metrics such as NOS and Network Neuroscience 366 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 2 3 5 8 1 9 1 3 5 2 5 n e n _ a _ 0 0 1 7 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The R1-weighted connectome FA. For NOS, this stems from the assumption that streamline count is a proxy of microstruc- tural fiber count, that is, the greater the number of streamlines, the higher the connectivity between regions. This has been shown to be questionable, however, as results are influenced by the tractography algorithms and the choice of tracking parameters. Here we decided to use R1 to weight the connectome, as it has been repeatedly shown to correlate highly with myelin content (Lee et al., 2012; Lutti et al., 2014). Also, the MP2RAGE sequence, which was used to acquire the R1 maps, is a stock, relatively short protocol with open-source processing, which makes it suitable for a wide clinical application. There are several studies that demon- strated the usefulness of complementing the tractography with longitudinal relaxation time. For instance, De Santis et al. (2014) showed that to compare two groups, that is, to detect differences between groups, the longitudinal relaxation time (T1), which is just an inverse of R1, requires a smaller sample size compared to the diffusion derived metrics. Another study (De Santis et al., 2016) demonstrated that it is possible to measure tract-specific T1 relaxation, potentially leading to fiber-specific myelin metrics and more thorough network models. Another aspect is that here we weighted the connectome using the median rather than the standard approach of taking the mean along the bundle of reconstructed streamlines. This is due to the fact that the median is more robust against outliers and does not rely on the normality assumption for the R1 distribution along a fiber bundle. Relying on one measure per bundle instead of averaging a measure across streamlines also avoids biasing the results towards NOS. Furthermore, we should also mention the choice of network measures that were inves- tigated. The more canonical graph measures such as clustering coefficient and path length were not calculated. The rationale behind our choice is the consequence of the complex role of myelin in white matter pathways: myelinated axons show faster conduction than unmyeli- nated axons, but when comparing myelinated axons with different amount of myelin, the over- all effect on conduction speed, as already mentioned, depends on several factors (e.g., axon diameter, g-ratio, internodal) (Drakesmith et al., 2019). Therefore, the use of myelin measures in network models requires more careful interpretation. As the weight in network models usu- ally reflects the intensity or capacity of a connection (Barrat et al., 2004), most analyses rely on the same assumption. To take into account the myelin-specific role in conduction phenomena and to avoid the strict intensity-based interpretation of the network weight, we decided to focus on the use of R1-weighted average as a centrality measure (as previously done in Kamagata et al., 2019) and on the modular structure. The choice of tractography algorithm is also an important methodological aspect that has to be considered when reconstructing the connectome. Two main classes of tractography al- gorithms, deterministic and probabilistic, can be employed to reconstruct the connectome. There is an ongoing debate on the advantages and disadvantages of these two classes of algo- rithms for mapping the connectome (Sarwar et al., 2019). Both classes of algorithms are valid choices for performing fiber tracking but they also have some disadvantages: in recent studies (Maier-Hein et al., 2017; Sotiropoulos & Zalesky, 2019), it has been shown that the determinis- tic tractography algorithms reconstruct fewer true positive streamlines compared to probabilis- tic tractography. On the other hand, probabilistic tractography reconstructs more false positive streamlines as opposed to deterministic tractography, which further biases the reconstructed connectome by introducing spurious connections. In this study, we used both deterministic and probabilistic algorithms to double check the robustness of our results. The limitation of introducing spurious connections is particularly evident for modularity: the different results obtained for R1 using two different thresholds may imply that including spurious streamlines Network Neuroscience 367 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 2 3 5 8 1 9 1 3 5 2 5 n e n _ a _ 0 0 1 7 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The R1-weighted connectome deeply affects the R1 weight distribution and therefore the estimated modular structure. To tackle these thresholding issues, new algorithms have recently been proposed (Schiavi et al., 2020; Smith et al., 2015) that aim to reduce the number of false positive streamlines by using microstructural and anatomical priors. Future studies need to clarify how such methods could be applied to combine tractography with complementary measures. Finally, one limitation of this study is the relatively small sample size. Unfortunately, we are not aware of any publicly available dataset that includes quantitative MRI metrics (besides diffusion derived ones) that are sensitive to myelin. In conclusion, the R1-weighted connectome complements the structural connectome de- rived from dMRI and could provide new biomarkers for many pathologies that affect the brain. Further validation of this approach is required, for example, by studying demyelinating dis- eases. ACKNOWLEDGMENTS We thank the ICEBERG study group and particularly Marie Vidailhet, MD (Pitié-Salpêtrière Hospital, Paris, Principal investigator), Jean-Christophe Corvol, MD, PhD (Paris Brain Insti- tute, Paris, clinical and genetic data), Isabelle Arnulf, MD, PhD (Pitié-Salpêtrière Hospital, Paris, clinical and sleep data), Rahul Gaurav, MS, (Pitié-Salpêtrière Hospital, Paris, data analy- sis), Nadya Pyatigorskaya, MD, PhD, (Pitié-Salpêtrière Hospital, Paris, data analysis); for their help in collecting data. SUPPORTING INFORMATION Supporting information for this article is available at https://doi.org/10.1162/netn_a_00179. In the Supporting Information we provided additional results using also the FA to weight the connectome. We also reported the outcomes obtained using a more stringent threshold in the connectivity matrices as well as outcomes obtained using probabilistic tractography to recon- struct the connectomes. The code and data to reproduce the results are available on GitHub (https://github.com/TommyBoshkovski/The_R1-weighted_connectome, Boshkovski, 2020). AUTHOR CONTRIBUTIONS Tommy Boshkovski: Conceptualization; Formal analysis; Methodology; Visualization; Writing – original draft; Writing – review & editing. Ljupco Kocarev: Conceptualization; Methodology; Writing – review & editing. Julien Cohen-Adad: Conceptualization; Methodology; Writing – review & editing. Bratislav Misi´c: Conceptualization; Methodology; Writing – review & editing. Stéphane Lehéricy: Conceptualization; Data curation; Methodology; Writing – review & editing. Nikola Stikov: Conceptualization; Methodology; Supervision; Writing – review & editing. Matteo Mancini: Conceptualization; Methodology; Supervision; Writing – review & editing. FUNDING INFORMATION Stéphane Lehéricy, Investissements d’Avenir, Award ID: ANR-10-IAIHU-06. Stéphane Lehéricy, Investissements d’Avenir, Award ID: ANR-11-INBS-0006. Stéphane Lehéricy, EDF Founda- tion. Nikola Stikov, Fondation Institut de Cardiologie de Montréal (http://dx.doi.org/10.13039 /501100012651). Nikola Stikov, Canadian Open Neuroscience Platform (Brain Canada PSG). Nikola Stikov, Réseau en Bio-Imagerie du Quebec (http://dx.doi.org/10.13039/100010571), Award ID: 8436-0501. Nikola Stikov, Natural Sciences and Engineering Research Council of Network Neuroscience 368 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 2 3 5 8 1 9 1 3 5 2 5 n e n _ a _ 0 0 1 7 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The R1-weighted connectome Canada (http://dx.doi.org/10.13039/501100000038), Award ID: 2016-06774. Nikola Stikov, Fonds de Recherche du Québec - Santé (http://dx.doi.org/10.13039/501100000156), Award ID: FRSQ 36759 and FRSQ 35250. Matteo Mancini, Wellcome Trust (http://dx.doi.org/10 .13039/100004440), Award ID: 213722/Z/18/Z. Stéphane Lehéricy, Fondation Thérèse and René Planiol. REFERENCES Andersson, J. L. R., Skare, S., & Ashburner, J. (2003). How to correct susceptibility distortions in spin-echo echo-planar images: Appli- cation to diffusion tensor imaging. NeuroImage, 20(2), 870–888. DOI: https://doi.org/10.1016/s1053-8119(03)00336-7 Andersson, J. L. R., & Sotiropoulos, S. N. (2016). An integrated ap- proach to correction for off-resonance effects and subject move- ment in diffusion MR imaging. NeuroImage, 125, 1063–1078. DOI: https://doi.org/10.1016/j.neuroimage.2015.10.019, PMID: 26481672, PMCID: PMC4692656 Barrat, A., Barthélemy, M., Pastor-Satorras, R., & Vespignani, A. (2004). The architecture of complex weighted networks. Pro- ceedings of the National Academy of Sciences of the United States of America, 101(11), 3747–3752. DOI: https://doi.org/10 .1073/pnas.0400087101, PMID: 15007165, PMCID: PMC374315 Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature Neuroscience, 20(3), 353–364. DOI: https://doi.org/10.1038/nn .4502, PMID: 28230844, PMCID: PMC5485642 Berman, S., Filo, S., & Mezer, A. A. (2019). A Modeling conduc- tion delays in the corpus callosum using MRI-measured g-ratio. NeuroImage, 195, 128–139. DOI: https://doi.org/10.1016/j .neuroimage.2019.03.025, PMID: 30910729 Betzel, R. F., Avena-Koenigsberger, A., Goãi, J., Sporns, O., Griffa, A., Thiran, J. P., & Hagmann, P. (2013). Multi-scale community organization of the human structural connectome and its rela- tionship with resting-state functional connectivity. Network Sci- ence, 1(3), 353–373. DOI: https://doi.org/10.1017/nws.2013.19 Boshkovski, T. (2020). Code and data for R1-weighted connectome analysis. https://github.com/TommyBoshkovski/The_R1-weighted _connectome Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Jour- nal of Statistical Mechanics: Theory and Experiment, 2008(10), P10008. DOI: https://doi.org/10.1088/1742-5468/2008/10/P10008 Caeyenberghs, K., Metzler-Baddeley, C., Foley, S., & Jones, D. K. (2016). Dynamics of the human structural connectome underly- ing working memory training. Journal of Neuroscience, 36(14), 4056–4066. DOI: https://doi.org/10.1523/JNEUROSCI.1973-15 .2016, PMID: 27053212, PMCID: PMC4821915 Calamante, F. (2019). The seven deadly sins of measuring brain structural connectivity using diffusion MRI streamlines fibre- tracking. Diagnostics, 9(3), 115. DOI: https://doi.org/10.3390 /diagnostics9030115, PMID: 31500098, PMCID: PMC6787694 Cammoun, L., Gigandet, X., Meskaldji, D., Thiran, J. P., Sporns, O., Do, K. Q., Maeder, P., Meuli, R., & Hagmann, P. (2012). Mapping the human connectome at multiple scales with diffusion spec- trum MRI. Journal of Neuroscience Methods, 203(2), 386–397. DOI: https://doi.org/10.1016/j.jneumeth.2011.09.031, PMID: 22001222 Collin, G., Sporns, O., Mandl, R. C. W., & Van Den Heuvel, M. P. (2014). Structural and functional aspects relating to cost and benefit of rich club organization in the human cerebral cortex. Cerebral Cortex, 24(9), 2258–2267. DOI: https://doi.org/10.1093 /cercor/bht064, PMID: 23551922, PMCID: PMC4128699 Collin, G., van den Heuvel, M. P., Abramovic, L., Vreeker, A., de Reus, M. A., van Haren, N. E. M., Boks, M. P. M., Ophoff, R. A., & Kahn, R. S. (2016). Brain network analysis reveals affected connectome structure in bipolar I disorder. Human Brain Map- ping, 37(1), 122–134. DOI: https://doi.org/10.1002/hbm.23017, PMID: 26454006, PMCID: PMC5597048 de Reus, M. A., & van den Heuvel, M. P. (2013). Estimating false positives and negatives in brain networks. NeuroImage, 70, 402–409. DOI: https://doi.org/10.1016/j.neuroimage.2012.12.066, PMID: 23296185 De Santis, S., Assaf, Y., Jeurissen, B., Jones, D. K., & Roebroeck, A. (2016). T1 relaxometry of crossing fibres in the human brain. NeuroImage, 141, 133–142. DOI: https://doi.org/10.1016 /j.neuroimage.2016.07.037, PMCID: PMC5035137 27444568, PMID: De Santis, S., Drakesmith, M., Bells, S., Assaf, Y., & Jones, D. K. (2014). Why diffusion tensor MRI does well only some of the time: Variance and covariance of white matter tissue micro- structure attributes in the living human brain. NeuroImage, 89(100), 35–44. DOI: https://doi.org/10.1016/j.neuroimage.2013 .12.003, PMID: 24342225, PMCID: PMC3988851 Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C., Blacker, D., Buckner, R. L., Dale, A. M., Maguire, R. P., Hyman, B. T., Albert, M. S., & Killiany, R. J. (2006). An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage, 31(3), 968–980. DOI: https://doi.org/10.1016/j.neuroimage.2006.01.021, PMID: 16530430 Drakesmith, M., Harms, R., Rudrapatna, S. U., Parker, G. D., Evans, C. J., & Jones, D. K. (2019). Estimating axon conduction veloc- ity in vivo from microstructural MRI. NeuroImage, 203, 116186. DOI: https://doi.org/10.1016/j.neuroimage.2019.116186, PMID: 31542512, PMCID: PMC6854468 Fischl, B. (2012). Freesurfer. NeuroImage, 62(2), 774–781. DOI: https://doi.org/10.1016/j.neuroimage.2012.01.021, PMID: 22248573, PMCID: PMC3685476 Fornito, A., Zalesky, A., & Bullmore, E. T. (2016). Fundamentals of brain network analysis. Elsevier. Glasser, M. F., & van Essen, D. C. (2011). Mapping human cortical areas in vivo based on myelin content as revealed by T1- and T2- weighted MRI. Journal of Neuroscience, 31(32), 11597–11616. DOI: https://doi.org/10.1523/JNEUROSCI.2180-11.2011, PMID: 21832190, PMCID: PMC3167149 Network Neuroscience 369 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 2 3 5 8 1 9 1 3 5 2 5 n e n _ a _ 0 0 1 7 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The R1-weighted connectome Goñi, J., van den Heuvel, M. P., Avena-Koenigsberger, A., Velez de Mendizabal, N., Betzel, R. F., Griffa, A., Hagmann, P., Corominas-Murtra, B., Thiran, J.-P., & Sporns, O. (2014). Resting- brain functional connectivity predicted by analytic measures of network communication. Proceedings of the National Academy of Sciences. DOI: https://doi.org/10.1073/pnas.1315529111, PMID: 24379387, PMCID: PMC3896172 Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J., Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core of human cerebral cortex. PLoS Biology, 6(7), e159. DOI: https:// doi.org/10.1371/journal.pbio.0060159, 18597554, PMCID: PMC2443193 PMID: Hagmann, P., Kurant, M., Gigandet, X., Thiran, P., Wedeen, V. J., Meuli, R., & Thiran, J.-P. (2007). Mapping human whole-brain structural networks with diffusion MRI. PLoS ONE, 2(7), e597. DOI: https://doi.org/10.1371/journal.pone.0000597, PMID: 17611629, PMCID: PMC1895920 Harkins, K. D., Xu, J., Dula, A. N., Li, K., Valentine, W. M., Gochberg, D. F., Gore, J. C., & Does, M. D. (2016). The micro- structural correlates of T1 in white matter. Magnetic Reso- nance in Medicine, 75(3), 1341–1345. DOI: https://doi.org/10 .1002/mrm.25709, PMID: 25920491, PMCID: PMC4624612 Heath, F., Hurley, S. A., Johansen-Berg, H., & Sampaio-Baptista, C. (2018). Advances in noninvasive myelin imaging. Develop- mental Neurobiology, 78(2), 136–151. DOI: https://doi.org/10 .1002/dneu.22552, PMID: 29082667, PMCID: PMC5813152 Honey, C. J., Thivierge, J. P., & Sporns, O. (2010). Can structure pre- dict function in the human brain? NeuroImage, 52(3), 766–776. DOI: https://doi.org/10.1016/j.neuroimage.2010.01.071, PMID: 20116438 Jenkinson, M., Bannister, P., Brady, M., & Smith, S. (2002). Im- proved optimization for the robust and accurate linear registra- tion and motion correction of brain images. NeuroImage, 17(2), 825–841. DOI: https://doi.org/10.1016/S1053-8119(02)91132-8 J., Woolrich, M. W., & Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790. DOI: https://doi.org/10.1016/j.neuroimage.2011.09.015, PMID: 21979382 Jenkinson, M., Beckmann, C. F., Behrens, T. E. Jeurissen, B., Descoteaux, M., Mori, S., & Leemans, A. (2019). Dif- fusion MRI fiber tractography of the brain. NMR in Biomedicine, 32(4), e3785. DOI: https://doi.org/10.1002/nbm.3785, PMID: 28945294 Jeurissen, B., Tournier, J. D., Dhollander, T., Connelly, A., & Sijbers, J. (2014). Multi-tissue constrained spherical deconvolu- tion for improved analysis of multi-shell diffusion MRI data. NeuroImage, 103, 411–426. DOI: https://doi.org/10.1016/j .neuroimage.2014.07.061, PMID: 25109526 Jones, D. K. (2010). Challenges and limitations of quantifying brain Imaging in Medicine, connectivity in vivo with diffusion MRI. 2(3). DOI: https://doi.org/10.2217/iim.10.21 Jones, D. K., Alexander, D. C., Bowtell, R., Cercignani, M., Dell’Acqua, F., McHugh, D. J., Miller, K. L., Palombo, M., Parker, G. J. M., Rudrapatna, U. S., & Tax, C. M. W. (2018). Micro- structural imaging of the human brain with a ‘super-scanner’: 10 key advantages of ultra-strong gradients for diffusion MRI. NeuroImage, 182, 8–38. DOI: https://doi.org/10.1016/j .neuroimage.2018.05.047, PMID: 29793061 Jones, D. K., Knösche, T. R., & Turner, R. (2013). White matter integrity, fiber count, and other fallacies: The dos and dont’s of diffusion MRI. NeuroImage, 73, 239–254. DOI: https://doi.org /10.1016/j.neuroimage.2012.06.081, PMID: 22846632 Kamagata, K., Zalesky, A., Yokoyama, K., Andica, C., Hagiwara, A., Shimoji, K., Kumamaru, K. K., Takemura, M. Y., Hoshino, Y., Kamiya, K., Hori, M., Pantelis, C., Hattori, N., & Aoki, S. (2019). MR g-ratio-weighted connectome analysis in patients with multi- ple sclerosis. Scientific Reports, 9(1), 1–13. DOI: https://doi.org /10.1038/s41598-019-50025-2, PMID: 31534143, PMCID: PMC6751178 Karakuzu, A., Boudreau, M., Duval, T., Boshkovski, T., Leppert, I., Cabana, J.-F., Gagnon, I., Beliveau, P., Pike, G., Cohen-Adad, J., & Stikov, N. (2020). qMRLab: Quantitative MRI analysis, under Journal of Open Source Software, 5(53), 2343. one umbrella. DOI: https://doi.org/10.21105/joss.02343 Kellner, E., Dhital, B., Kiselev, V. G., & Reisert, M. (2016). Gibbs- ringing artifact removal based on local subvoxel-shifts. Magnetic Resonance in Medicine, 76(5), 1574–1581. DOI: https://doi.org /10.1002/mrm.26054, PMID: 26745823 Larivière, S., Vos De Wael, R., Paquola, C., Hong, S. J., Miši´c, B., Bernasconi, N., Bernasconi, A., Bonilha, L., & Bernhardt, B. C. (2019). Microstructure-informed connectomics: Enriching large- scale descriptions of healthy and diseased brains. Brain Connec- tivity, 9(2), 113–127. DOI: https://doi.org/10.1089/brain.2018 .0587, PMID: 30079754, PMCID: PMC6444904 Laule, C., Vavasour, I. M., Kolind, S. H., Li, D. K. B., Traboulsee, T. L., Moore, G. R. W., & MacKay, A. L. (2007). Magnetic reso- nance imaging of myelin. Neurotherapeutics, 4(3), 460–484. DOI: PMID: https://doi.org/10.1016/j.nurt.2007.05.004, 17599712, PMCID: PMC7479725 Lee, J., Shmueli, K., Kang, B. T., Yao, B., Fukunaga, M., Van Gelderen, P., Palumbo, S., Bosetti, F., Silva, A. C., & Duyn, J. H. (2012). The contribution of myelin to magnetic susceptibility-weighted contrasts in high-field MRI of the brain. NeuroImage, 59(4), 3967–3975. DOI: https://doi.org/10.1016/j .neuroimage.2011.10.076, PMCID: PMC3288572 22056461, PMID: Lutti, A., Dick, F., Sereno, M. I., & Weiskopf, N. (2014). Using high- resolution quantitative mapping of R1 as an index of cortical myelination. NeuroImage, 93, 176–188. DOI: https://doi.org.10 .1016/j.neuroimage.2013.06.005, PMID: 23756203 Maier-Hein, K. H., Neher, P. F., Houde, J. C., Côté, M. A., Garyfallidis, E., Zhong, J., Chamberland, M., Yeh, F. C., Lin, Y. C., Ji, Q., Reddick, W. E., Glass, J. O., Chen, D. Q., Feng, Y., Gao, C., Wu, Y., Ma, J., Renjie, H., Li, Q., . . . Descoteaux, M. (2017). The challenge of mapping the human connectome based on diffusion tractography. Nature Communications, 8(1), 1–13. DOI: https://doi.org/10.1038/s41467-017-01285-x, PMID: 29116093, PMCID: PMC5677006 Mancini, M., Giulietti, G., Dowell, N., Spanò, B., Harrison, N., Bozzali, M., & Cercignani, M. (2018). Introducing axonal myelination in connectomics: A preliminary analysis of g-ratio distribution in healthy subjects. NeuroImage, 182, 351–359. DOI: https://doi.org/10.1016/j.neuroimage.2017.09.018, PMID: 28917698 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 2 3 5 8 1 9 1 3 5 2 5 n e n _ a _ 0 0 1 7 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Mancini, M., Karakuzu, A., Cohen-Adad, M., Nichols, T. E., & Stikov, N. J., Cercignani, (2020). An interactive Network Neuroscience 370 The R1-weighted connectome meta-analysis of MRI biomarkers of myelin. ELife, 9. DOI: https://doi.org/10.7554/eLife.61523, PMID: 33084576, PMCID: PMC7647401 Margulies, D. S., Ghosh, S. S., Goulas, A., Falkiewicz, M., Huntenburg, J. M., Langs, G., Bezgin, G., Eickhoff, S. B., Castellanos, F. X., Petrides, M., Jefferies, E., & Smallwood, J. (2016). Situating the default-mode network along a principal gradient of macroscale cortical organization. Proceedings of the National Academy of Sciences of the United States of America, 113(44), 12574–12579. DOI: https://doi.org/10.1073 /pnas.1608282113, PMID: 27791099, PMCID: PMC5098630 Marques, J. P., Kober, T., Krueger, G., van der Zwaag, W., de Van Moortele, P. F., & Gruetter, R. (2010). MP2RAGE, a self bias-field corrected sequence for improved segmentation and T1-mapping at high field. NeuroImage, 49(2), 1271–1281. DOI: https://doi.org/10.1016/j.neuroimage.2009.10.002, PMID: 19819338 Messaritaki, E., Dimitriadis, S. I., & Jones, D. K. (2019). Optimiza- tion of graph construction can significantly increase the power of structural brain network studies. NeuroImage, 199, 495–511. DOI: https://doi.org/10.1016/j.neuroimage.2019.05.052, PMID: 31176831, PMCID: PMC6693529 Mori, S., & Van Zijl, P. C. M. (2002). Fiber tracking: Principles and strategies - A technical review. NMR in Biomedicine, 15(7–8), 468–480. DOI: PMID: 12489096 Netneurolab. (2020). netneurotools, GitHub. https://github.com https://doi.org/10.1002/nbm.781, /netneurolab/netneurotools O’Brien, K. R., Kober, T., Hagmann, P., Maeder, P., Marques, J., (2014). Robust T1- Lazeyras, F., Krueger, G., & Roche, A. weighted structural brain imaging and morphometry at 7T using MP2RAGE. PLoS ONE, 9(6), e99676. DOI: https://doi.org /10.1371/journal.pone.0099676, PMID: 24932514, PMCID: PMC4059664 Petiet, A., Adanyeguh, I., Aigrot, M., Poirion, E., Nait-Oumesmar, B., Santin, M., & Stankoff, B. (2019). Ultrahigh field imaging of myelin disease models: Toward specific markers of myelin in- tegrity? Journal of Comparative Neurology, 527(13), 2179–2189. DOI: https://doi.org/10.1002/cne.24598, PMID: 30520034 Piredda, G. F., Hilbert, T., Thiran, J., & Kober, T. (2020). Probing myelin content of the human brain with MRI: A review. Mag- netic Resonance in Medicine, mrm.28509. DOI: https://doi.org /10.1002/mrm.28509, PMID: 32936494 Raffelt, D., Tournier, J. D., Rose, S., Ridgway, G. R., Henderson, R., Crozier, S., Salvado, O., & Connelly, A. (2012). Apparent fibre density: A novel measure for the analysis of diffusion-weighted magnetic resonance images. NeuroImage, 59(4), 3976–3994. DOI: https://doi.org/10.1016/j.neuroimage.2011.10.045, PMID: 22036682 Rubinov, M., & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52(3), 1059–1069. DOI: https://doi.org/10.1016/j.neuroimage.2009.10 .003, PMID: 19819337 Rubinov, M., & Sporns, O. (2011). Weight-conserving character- ization of complex functional brain networks. NeuroImage, 56(4), 2068–2079. DOI: https://doi.org/10.1016/j.neuroimage .2011.03.069, PMID: 21459148 Sampaio-Baptista, C., & Johansen-Berg, H. (2017). White mat- ter plasticity in the adult brain. Neuron, 96(6), 1239–1251. DOI: PMID: https://doi.org/10.1016/j.neuron.2017.11.026, 29268094, PMCID: PMC5766826 Sarwar, T., Ramamohanarao, K., & Zalesky, A. (2019). Map- ping connectomes with diffusion MRI: Deterministic or proba- bilistic tractography? Magnetic Resonance in Medicine, 81(2), 1368–1384. DOI: https://doi.org/10.1002/mrm.27471, PMID: 30303550 Schiavi, S., Ocampo-Pineda, M., Barakovic, M., Petit, L., Descoteaux, M., Thiran, J.-P., & Daducci, A. (2020). A new method for accurate in vivo mapping of human brain con- information. nections using microstructural and anatomical Science Advances, 6(31), eaba8245. DOI: https://doi.org/10.1126 /sciadv.aba8245, PMID: 32789176, PMCID: PMC7399649 Schmierer, K., Wheeler-Kingshott, C. A. M., Tozer, D. J., Boulby, P. A., Parkes, H. G., Yousry, T. A., Scaravilli, F., Barker, G. J., (2008). Quantitative magnetic res- Tofts, P. S., & Miller, D. H. onance of postmortem multiple sclerosis brain before and after fixation. Magnetic Resonance in Medicine, 59(2), 268–277. DOI: https://doi.org/10.1002/mrm.21487, PMID: 18228601, PMCID: PMC2241759 Scholtens, L. H., de Reus, M. A., de Lange, S. C., Schmidt, R., & van den Heuvel, M. P. (2018). An MRI Von Economo – Koskinas atlas. NeuroImage, 170, 249–256. DOI: https://doi.org /10.1016/j.neuroimage.2016.12.069, PMID: 28040542 Sinke, M. R. T., Otte, W. M., Christiaens, D., Schmitt, O., Leemans, A., van der Toorn, A., Sarabdjitsingh, R. A., Joéls, M., & Dijkhuizen, R. M. (2018). Diffusion MRI-based cortical con- nectome reconstruction: Dependency on tractography proce- dures and neuroanatomical characteristics. Brain Structure and Function, 223(5), 2269–2285. DOI: https://doi.org/10.1007 /s00429-018-1628-y, PMID: 29464318, PMCID: PMC5968063 J. D., Calamante, F., & Connelly, A. (2012). Anatomically-constrained tractography: Improved dif- fusion MRI streamlines tractography through effective use information. NeuroImage, 62(3), 1924–1938. of anatomical DOI: https://doi.org/10.1016/j.neuroimage.2012.06.005, PMID: 22705374 Smith, R. E., Tournier, Smith, R. E., Tournier, J. D., Calamante, F., & Connelly, A. (2015). SIFT2: Enabling dense quantitative assessment of brain white matter connectivity using streamlines tractography. NeuroImage, 119, 338–351. DOI: https://doi.org/10.1016/j .neuroimage.2015.06.092, PMID: 26163802 Sotiropoulos, S. N., & Zalesky, A. (2019). Building connectomes using diffusion MRI: Why, how and but. NMR in Biomedicine, 32(4), e3752. DOI: https://doi.org/10.1002/nbm.3752, PMID: 28654718, PMCID: PMC6491971 Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual Review of Psychology, 67(1), 613–640. DOI: https://doi.org/10 .1146/annurev-psych-122414-033634, PMID: 26393868, PMCID: PMC4782188 Stüber, C., Morawski, M., Schäfer, A., Labadie, C., Wähnert, M., Leuze, C., Streicher, M., Barapatre, N., Reimann, K., Geyer, S., Spemann, D., & Turner, R. (2014). Myelin and iron concentra- tion in the human brain: A quantitative study of MRI contrast. NeuroImage, 93(P1), 95–106. DOI: https://doi.org/10.1016/j .neuroimage.2014.02.026, PMID: 24607447 Network Neuroscience 371 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 2 3 5 8 1 9 1 3 5 2 5 n e n _ a _ 0 0 1 7 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The R1-weighted connectome Suárez, L. E., Markello, R. D., Betzel, R. F., & Misic, B. (2020). Linking structure and function in macroscale brain net- Trends in Cognitive Sciences, 24(4), 302–315. DOI: works. https://doi.org/10.1016/j.tics.2020.01.008, PMID: 32160567 Tournier, J. D., Calamante, F., & Connelly, A. (2012). MRtrix: International Diffusion tractography in crossing fiber regions. Journal of Imaging Systems and Technology, 22(1), 53–66. DOI: https://doi.org/10.1002/ima.22005 Tournier, J. D., Smith, R., Raffelt, D., Tabbara, R., Dhollander, T., Pietsch, M., Christiaens, D., Jeurissen, B., Yeh, C. H., & Connelly, A. (2019). MRtrix3: A fast, flexible and open software image processing and visualisa- framework for medical tion. NeuroImage, 202, 116137. DOI: https://doi.org/10.1016/j .neuroimage.2019.116137, PMID: 31473352 Traud, A. L., Kelsic, E. D., Mucha, P. J., & Porter, M. A. (2011). Comparing community structure to characteristics in online col- legiate social networks. SIAM Review, 53(3), 526–543. DOI: https://doi.org/10.1137/080734315 van den Heuvel, M. P., de Reus, M. A., Feldman Barrett, L., Scholtens, L. H., Coopmans, F. M. T., Schmidt, R., Preuss, T. M., (2015). Comparison of diffusion trac- Rilling, J. K., & Li, L. tography and tract-tracing measures of connectivity strength in rhesus macaque connectome. Human Brain Mapping, 36(8), 3064–3075. DOI: https://doi.org/10.1002/hbm.22828, PMID: 26058702, PMCID: PMC6869766 van den Heuvel, M. P., Mandl, R. C. W., Stam, C. J., Kahn, R. S., & Hulshoff Pol, H. E. (2010). Aberrant frontal and temporal complex network structure in schizophre- nia: A graph theoretical analysis. The Journal of Neuro- science, 30(47), 15915–15926. DOI: https://doi.org/10.1523 /JNEUROSCI.2874-10.2010, PMCID: PMC6633761 21106830, PMID: van den Heuvel, M. P., & Sporns, O. (2013). Network hubs in the human brain. Trends in Cognitive Sciences, 17(12). DOI: https://doi.org/10.1016/j.tics.2013.09.012, PMID: 24231140 van den Heuvel, M. P., Stam, C. J., Boersma, M., & Hulshoff Pol, H. E. (2008). Small-world and scale-free organization of voxel- based resting-state functional connectivity in the human brain. NeuroImage, 43(3), 528–539. DOI: https://doi.org/10.1016/j .neuroimage.2008.08.010, PMID: 18786642 Vázquez-Rodríguez, B., Suárez, L. E., Markello, R. D., Shafiei, G., Paquola, C., Hagmann, P., Van Den Heuvel, M. P., Bernhardt, B. C., Spreng, R. N., & Misic, B. (2019). Gradients of structure– function tethering across neocortex. Proceedings of the National Academy of Sciences of the United States of America, 116(42), 21219–21227. DOI: https://doi.org/10.1073/pnas.1903403116, PMID: 31570622, PMCID: PMC6800358 Veraart, J., Fieremans, E., & Novikov, D. S. (2016a). Diffusion MRI noise mapping using random matrix theory. Magnetic Resonance in Medicine, 76(5), 1582–1593. DOI: https://doi.org/10.1002/mrm .26059, PMID: 26599599, PMCID: PMC4879661 Veraart, J., Novikov, D. S., Christiaens, D., Ades-aron, B., Sijbers, (2016b). Denoising of diffusion MRI using J., & Fieremans, E. random matrix theory. NeuroImage, 142, 394–406. DOI: https:// doi.org/10.1016/j.neuroimage.2016.08.016, PMID: 27523449, PMCID: PMC5159209 Veraart, J., Nunes, D., Rudrapatna, U., Fieremans, E., Jones, D. K., (2020). Noninvasive quan- Novikov, D. S., & Shemesh, N. tification of axon radii using diffusion MRI. ELife, 9. DOI: https://doi.org/10.7554/eLife.49855, PMID: 32048987, PMCID: PMC7015669 Verstraete, E., Veldink, J. H., Mandl, R. C. W., van den Berg, L. H., & van den Heuvel, M. P. Impaired struc- tural motor connectome in amyotrophic lateral sclerosis. PLoS ONE, 6(9). DOI: https://doi.org/10.1371/journal.pone.0024239, PMID: 21912680, PMCID: PMC3166305 (2011). Yeatman, J. D., Wandell, B. A., & Mezer, A. A. (2014). A Lifespan maturation and degeneration of human brain white matter. Nature Communications, 5(1), 4932. DOI: https://doi.org/10 .1038/ncomms5932, PMID: 25230200, PMCID: PMC4238904 Liang, X., Descoteaux, M., & Connelly, A. (2020). Mapping structural connectivity using dif- fusion MRI: Challenges and opportunities. Journal of Magnetic Resonance Imaging. DOI: https://doi.org/10.1002/jmri.27188, PMID: 32557893 Jones, D. K., Yeh, C., Yeo, B. T. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D., Hollinshead, M., Roffman, J. L., Smoller, J. W., Zöllei, L., Polimeni, J. R., Fisch, B., Liu, H., & Buckner, R. L. (2011). The organization of the human cerebral cortex estimated by intrin- sic functional connectivity. Journal of Neurophysiology, 103(3), 1125–1165. DOI: https://doi.org/10.1152/jn.00338.2011, PMID: 21653723, PMCID: PMC3174820 Network Neuroscience 372 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 2 3 5 8 1 9 1 3 5 2 5 n e n _ a _ 0 0 1 7 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3

Descargar PDF