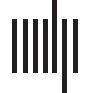INVESTIGACIÓN

Connection strength of the macaque
connectome augments topological
and functional network attributes

Siemon C. el largo

1, Dirk Jan Ardesch1, and Martijn P. van den Heuvel1,2

1Connectome Lab, Department of Complex Trait Genetics, Center for Neurogenomics and Cognitive Research, Vrije
Universiteit Amsterdam, Amsterdam Neuroscience, Ámsterdam, Los países bajos
2Department of Clinical Genetics, Amsterdam UMC, Vrije Universiteit Amsterdam, Amsterdam Neuroscience,
Ámsterdam, Los países bajos

un acceso abierto

diario

Palabras clave: Macaque, Connectome, Red, Projection strength, Functional synchronization

ABSTRACTO

Mammalian brains constitute complex organized networks of neural projections. On top of
their binary topological organization, the strength (or weight) of these neural projections can
be highly variable across connections and is thus likely of additional importance to the
overall topological and functional organization of the network. Here we investigated the
specific distribution pattern of connection strength in the macaque connectome. Nosotros
performed weighted and binary network analysis on the cortico-cortical connectivity of the
macaque provided by the unique tract-tracing dataset of Markov and colleagues (2014) y
observed in both analyses a small-world, modular and rich club organization. Además,
connectivity strength showed a distribution augmenting the architecture identified in the
binary network version by enhancing both local network clustering and the central
infrastructure for global topological communication and integration. Funcional
consequences of this topological distribution were further examined using the Kuramoto model
for simulating interactions between brain regions and showed that the connectivity strength
distribution across connections enhances synchronization within modules and between rich
club hubs. Juntos, our results suggest that neural pathway strength promotes topological
properties in the macaque connectome for local processing and global network integration.

Citación: el largo, S. C., Ardesch,
D. J., & van den heuvel, METRO. PAG. (2019).
Connection strength of the macaque
connectome augments topological and
functional network attributes. Red
Neurociencia, 3(4), 1051–1069.
https://doi.org/10.1162/netn_a_00101

DOI:
https://doi.org/10.1162/netn_a_00101

Supporting Information:
https://doi.org/10.1162/netn_a_00101

Recibió: 7 Marzo 2019
Aceptado: 14 Junio 2019

RESUMEN DEL AUTOR

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autor correspondiente:
Siemon C. el largo
s.c.de.lange@vu.nl

Editor de manejo:
Danielle Bassett

Derechos de autor: © 2019
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

High-resolution tract-tracing methods allow for the measurement of cortico-cortical
anatomical pathways and quantification of their connectivity strength. The variable strength
of neural pathways holds additional information on the complex organization of brain
redes. We studied connectivity strength in the macaque by using the open-access
connectome dataset of Markov and colleagues (2014), which contains high-resolution
information on the number of axonal projections interconnecting brain regions. Nuestros resultados
show that connectivity strength adopts a nonrandom distribution and enhances key network
features already present in the binary version of the network. Using the Kuramoto model to
simulate functional dynamics, we further demonstrated that connectivity strength enhances
local processing and global network integration. This study aids in the understanding of the
macaque connectome by clarifying the role of connectivity strength in the network topology
and functioning.

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

3
4
1
0
5
1
1
8
6
6
8
2
3
norte
mi
norte
_
a
_
0
0
1
0
1
pag
d

/

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Connection strength of the macaque brain augments network attributes

Connectome:
The comprehensive network of
neural interactions of a species
sistema nervioso.

Modular organization:
Property of network nodes to form
communities with strong within-
community connectivity but
relatively weak connectivity to nodes
of other communities.

Hubs:
Set of brain regions with high
number of connections.

Rich club:
Set of hub regions that are more
densely interconnected than
expected based on their degree
solo.

Small-world organization:
The presence of both local and
global integration in a network.

Kuramoto model:
Mathematical model describing
synchronizations between coupled
oscillators as model for the functional
dynamics between brain regions.

INTRODUCCIÓN

Brain function depends on efficient communication through a complex network of neural
connections. A species’ macroscale connectome describes the total network of all anatomi-
cal communication pathways linking brain regions (Sporns et al., 2005). Tract-tracing methods
enabled the mapping and reconstruction of comprehensive macroscale connectome maps of
several mammalian species, including that of the cat (Scannell et al., 1999), the mouse (Oh
et al., 2014; Zingg et al., 2014), the rat (Burns & Joven, 2000; Swanson, 1992; Zakiewicz
et al., 2011) and the macaque (Felleman & VanEssen, 1991; Markov et al., 2014; Métodos
& singh, 2010; Stephan et al., 2001). Comparison of neural wiring topology across species
has shown a tendency in neural networks toward modular organization providing functional
specialization, and short communication paths, hubs, and rich club organization facilitating
topological integration (van den Heuvel et al., 2016a). The connection strength of anatom-
ical projections is noted to be strongly variable across pathways (Hilgetag & Grant, 2000;
Markov et al., 2011), and graph analysis studies have shown that the connection strength
distribution enhances functional specialization and global integration in the connectome of
several mammals, including the rat (Bota et al., 2015; van den Heuvel et al., 2015), mouse
(van den heuvel & de Reus, 2014; Rubinov et al., 2015), and human brain (Grayson et al.,
2014; Hagmann et al., 2008, 2010; van den Heuvel et al., 2012; van den heuvel & despreciar,
2011).

High-resolution tract-tracing studies of the macaque have further employed systematic and
standardized mapping of cortical white matter pathways (Markov et al., 2013b, 2014). Estos
reconstructed macaque connectome maps include not only information on the presence and
absence of macroscale anatomical projections but also detailed quantitative information on the
strength of reconstructed anatomical projections. Studies investigating the dataset showed that
the connection strength distribution adheres to an exponential decay in connection strength
with connection length (Ercsey-Ravasz et al., 2013; Markov et al., 2013a) and that connec-
tions between brain regions sharing topological neighbors show high connectivity strength
(Goulas et al., 2014). Network analyses further provided insight into the macaque connec-
tome organization, elucidating a core that is important for network integration (Betzel et al.,
2018; Ercsey-Ravasz et al., 2013; Markov et al., 2013a), a small-world organization (bassett &
bullmore, 2017; Hilgetag & Goulas, 2015), and a modular organization (Song et al., 2014) pro-
viding complex functional dynamics (Honey & despreciar, 2008; Zamora-López et al., 2016). So
far, network studies have been investigating the weighted and binary versions of the macaque
connectome mostly separately, so the topological and functional consequences of the specific
connectivity strength distribution in the macaque connectome remain unclear.

We examined the contribution of connectivity strength to the topological and functional
organization of the macaque connectome. Primero, the binary macaque connectome was cha-
racterized with respect
to key network organizational principles including small-world,
modular, and rich club organization. Próximo, we tested whether the connection strength dis-
tribution enhances the identified organizational properties. Además, we related macaque
connectome organization and connectivity strength distribution to functional synchrony be-
tween brain regions simulated by the Kuramoto model (Breakspear et al., 2010; Cabral et al.,
2014; Rodrigues et al., 2016; Vlasov & Bifone, 2017; Vuksanovi´c & Hövel, 2014, 2016). Nuestro
results indicate that connection strength across connections is distributed in such a way that
it enhances the binary network organization, increasing local processing and global network
integración.

Neurociencia en red

1052

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

3
4
1
0
5
1
1
8
6
6
8
2
3
norte
mi
norte
_
a
_
0
0
1
0
1
pag
d

.

/

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Connection strength of the macaque brain augments network attributes

MATERIALES Y MÉTODOS

Macaque Connectome Data

Anatomical connectivity of the monkey cortical connectome was obtained from the study by
Markov and colleagues (2014). The macaque cortico-cortical structural connectivity dataset,
as made freely available at http://core-nets.org (Markov et al., 2014), contains information
collated from single-injection retrograde tract-tracing studies in 28 macaque specimens (27
Macaca fascicularis—left and right hemispheres intermixed—and 1 Macaca mulatta—right
hemisferio) performed by Markov and coworkers. Retrograde viral tracer experiments were
performed in 29 unique cortical regions, based on a reference atlas dividing the cortex into
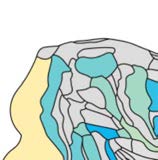
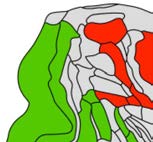
91 cortical regions. Injection site regions (illustrated in Figure 1) were distributed over 4 areas
in occipital, 6 in temporal, 6 in parietal, 5 in frontal, 7 in prefrontal and 1 area in limbic
cortical structures. The dataset describes a dense cortical network consisting of 1,615 interareal
pathways (Markov et al., 2014).

Following Markov et al. (2014), we examined the subnetwork of 29 injection sites (out of
a total of 91 defined cortical regions) for which the dataset contains complete information on
all possible axonal projections (Markov et al., 2014). The associated mathematical graph in-
cluded 29 nodos, representing brain regions, y 536 directed connections, referring to axonal
projections, forming a dense graph with 66% del 812 possible connections present. Datos
was presented in the adjacency matrix A, with entry Aij = 1 in case an axonal projection was
reported between regions i and j, and Aij = 0 if no projections were reported.

Besides information on presence or absence of pathways between brain regions, Markov
et al. report on the number of labeled neurons (pij) involved in each reported pathway. El
number of labeled neurons formed a log-normal distribution, therefore the biologically more
representative log-transformed number of labeled neurons, wij = log(pij + 1) was used as
connectivity strength in the weighted network (Hagmann et al., 2008; Honey et al., 2009).

To compensate for fluctuations in effective tracer uptakes, Markov et al. also report the more
relative measure of the extrinsic fraction of labeled neurons (FLNe), computed as the ratio

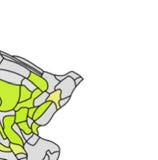
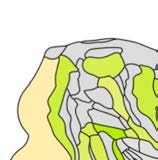
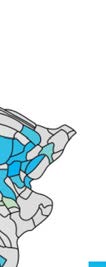
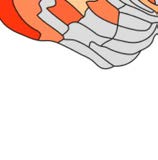
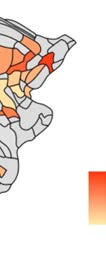
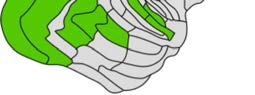
Cifra 1. El 29 injection sites of the macaque dataset. Injection sites were distributed along all
six cortical lobes, eso es, 4 in occipital (yellow), 6 in temporal (verde), 6 in parietal (naranja), 5 en
frontal (light blue), 7 in prefrontal (rojo), 1 in limbic (dark blue) cortical structures. El 29 injection
regions are highlighted. The layout is as presented by Markov et al. (2014) and made available at
core-nets.org by Markov and colleagues.

Neurociencia en red

1053

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

3
4
1
0
5
1
1
8
6
6
8
2
3
norte
mi
norte
_
a
_
0
0
1
0
1
pag
d

t

/

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Connection strength of the macaque brain augments network attributes

Clustering coefficient:
Ratio between existing and possible
number of triangle motifs in a
network. Measure of local network
circuitry.

Characteristic path length:
Average minimum number of steps
(or minimal weight) needed to travel
between any two nodes in a network.
Measure of global network
integración.

between the number of labeled neurons and the total number of reported cortical neurons
extrinsic to the injected area (Markov et al., 2014). Results from the FLNe-weighted network
are presented in the Supporting Information.

Network Measures

Network organizational characteristics were calculated for both binary and weighted networks,
including the following metrics (Rubinov & despreciar, 2010).

Clustering coefficient. In the binary network, node-wise clustering coefficient Cb was com-
puted, expressing the extent to which neighbors of a node are mutually connected (vatios &
Strogatz, 1998). In weighted networks, the clustering coefficient Cw was examined, reflecting
the strength of all closed triangles a node forms with its neighbors (Frijol, 2007). Both binary
and weighted clustering coefficient were compared with the clustering coefficients Cb
aleatorio
and Cw
random of randomized networks (10,000 randomizations examined), formed by randomly
switching connections between regions, preserving the number of in- and outgoing connec-
ciones (en- y fuera de grado), and total strength of the incoming connections (in-strength) of each
nodo (Rubinov & despreciar, 2010). The ratios between the clustering coefficients of the original
network and the clustering coefficient of randomized networks were denoted by the normal-
ized clusterings Cb
norm. To assess the effect of the connectivity strength distribution
on clustering, the weighted clustering coefficient was compared with the clustering coefficient
Cw
shu f f led of 10,000 weights-shuffled network versions in which the connection strengths, como
seen in the original network, were randomly redistributed.

norm and Cw

Shortest Path length. Network integration was assessed by examining the shortest path
length between nodes. The binary shortest path length between nodes is defined as the min-
imal number of connections needed to traverse from one node to another (vatios & Strogatz,
1998). The average binary shortest path length over all node combinations was referred to as
the binary characteristic path length Lb. The shortest path in the weighted network from node i
to j was identified as the trajectory that minimized cost, with the “cost” of traveling a path taken
as the inverse connection strength (Rubinov & despreciar, 2010). The weighted characteristic path
length Lw was measured as the average shortest path cost between all node combinations. El
weighted characteristic step length Lstepw was defined as the minimal number of connections
(es decir., discrete steps) the weighted shortest paths used and is a measure of the binary efficiency
of weighted paths. Results for the weighted characteristic step length are presented in the
Supporting Information. Both binary and weighted characteristic path lengths were compared
with the characteristic path lengths Lrand and Lw
rand of 10,000 randomized network versions,
their ratio denoted by Lb
norm. To assess the contribution of the connection strength
distribution on characteristic path length, the average characteristic path length Lw
shu f f led of
10,000 weights-shuffled network versions was examined.

norm and Lw

Modularity. Modules in the binary and weighted networks were determined by modular-
ity detection, generalized for directed and weighted networks (Leicht & Hombre nuevo, 2008). El
quality of the network division was expressed by the modularity Q (Hombre nuevo, 2006). Similar-
ity between the modularity structure of the binary and weighted network versions was quan-
tified by the Rand index, measuring the probability of both community assignments being in
agreement on grouping two regions together or apart (Rand, 1971). Statistical significance was
assessed by computing the Rand index for 10,000 permutations with randomized modular
assignments, and assigning a p value based on the proportion of permutations for which the
Rand index exceeded the Rand index of the original dataset (Scholtens et al., 2014). Basado

Neurociencia en red

1054

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

/

t

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

3
4
1
0
5
1
1
8
6
6
8
2
3
norte
mi
norte
_
a
_
0
0
1
0
1
pag
d

.

/

t

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Connection strength of the macaque brain augments network attributes

on the modules in the binary network, connections were categorized as “intramodular” when
spanning between nodes of the same module, and as “intermodular” when they connected
regions belonging to different modules. Connectivity strength of both classes was compared
and statistically evaluated by permutation testing by using random group assignment (10,000
permutations).

Rich club organization. Rich club organization of the network was assessed, exploring the
tendency of high degree nodes to be more interconnected than expected on the basis of their
individual degree alone (Colizza et al., 2006). With the Markov dataset providing information
on in-degree of 91 cortical regions, rich club analysis was based on the number of afferent
(incoming) axonal projection tracings from all 91 regions to the 29 regiones de interés, referred
to as kin. Binary rich club coefficient φb for kin was calculated as

φb (kin) =

E>kin
(cid:2)
N>kin

(cid:3) ,

− 1

N>kin

where N>kin is the number of nodes in the 29 nodes network with an in-degree greater than
kin, and E>kin is the number of directed connections between these nodes. The weighted rich
club coefficient φw (Opsahl et al., 2008) is the ratio of the total weight of connections between
highest degree nodes and the sum of the strongest connections in the network, computed as

φw (kin) =

W>kin
i=1 wrank

∑E>kin

i

,

where W>kin is the total weight of connections between nodes with in-degree greater than kin,
and wrank are the ranked connection weights.

For both binary and weighted rich club coefficients, a normalized rich club coefficient φnorm
rand of a

was derived by dividing rich club coefficients with the average rich club coefficient φ
set of randomized networks (10,000 randomized networks).

The probability that the normalized rich club coefficient φnorm(k) exceeded one due to
chance was calculated as the percentage randomized networks with rich club coefficients
exceeding the original coefficient φ(k). The resulting p values, assigned throughout the full
range of kin, were corrected for multiple testing by the false discovery rate correction procedure
(Benjamini & Hochberg, 1995).

The rich club was determined as the subset of the top 20% highest in-degree nodes (based
on tracings from all 91 regiones). Using the identified rich club, three connection classes were
identified: connections spanning between rich club nodes (rich club connections), connec-
tions between rich club and peripheral nodes (feeder connections), and connections between
peripheral nodes (local connections). Average strength of connection classes was compared
en general, and among intra- and intermodular connections specifically (modules defined by
the binary network). Statistical significance was assessed by means of permutation testing us-
ing random group assignment (10,000 permutations), false discovery rate correction was per-
formed to adjust for multiple comparisons (Benjamini & Hochberg, 1995).

Network Morphospace

In addition to comparing the observed clustering coefficient and characteristic path length with
values seen in randomized networks, we compared them with minimum and maximum pos-
sible values for networks with the same density and connection strength distribution (Avena-

Neurociencia en red

1055

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

/

t

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

3
4
1
0
5
1
1
8
6
6
8
2
3
norte
mi
norte
_
a
_
0
0
1
0
1
pag
d

/

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Connection strength of the macaque brain augments network attributes

Network morphospace:
Representation of networks in a
space with axes that represent
specific network properties.

Koenigsberger et al., 2014; Zamora-López & Brasselet, 2018). Específicamente, we focused on the
presence of large clustering and small characteristic path length that together indicates a small-
world organization (vatios & Strogatz, 1998). We followed the procedures as proposed by Goñi
et al. (2013) and Avena-Koenigsberger et al. (2014) to construct a “network morphospace” by
using an evolutionary algorithm. Iteratively generated networks were optimized to two dif-
ferent types of network tradeoffs: (1) maximizing L and minimizing C to explore networks
with weak (es decir., minimal) small-world organization and (2) minimizing L and maximizing C
to explore networks with strong (es decir., maximal) small-world organization. Simulations were
carried out on a population of 500 redes, initialized at the start with the original (binario
and weighted both examined) macaque connectome. In each iteration, networks part of the
so-called “Pareto front,” which means those networks that were most optimized, were identi-
fied as nondominated (following terminology introduced in Goñi et al., 2013), and networks
not part of the Pareto front were identified as dominated. The networks in the population were
optimized by iteratively replacing all dominated networks by (seleccionado al azar) nondomi-
nated networks and in the replacement process four randomly selected network edges were
adjusted. Networks in the morphospace of the binary network were constructed by randomly
switching the four edges while preserving the in- and out-degree distributions (Rubinov &
despreciar, 2010). We examined two types of morphospaces for the weighted network: en el
primero, the four network edges were randomly switched preserving the in- and out-degree and
in-strength distributions (Rubinov & despreciar, 2010). In the second morphospace, conectividad
strength of the four connections was randomly switched, preserving the binary topology and
the connectivity strength distribution. The algorithm was applied for 1,000 iterations and the
normalized characteristic path length and normalized clustering coefficient of the sampled
networks provided a reference space to which the observed network was compared.

Functional Dynamics

We further examined the role of connectivity strength in the macaque connectome by exam-
ining how the weights of the network shape functional dynamics. Brain network dynamics
were simulated by the Kuramoto model with oscillators representing brain regions coupled
according to structural pathways and functional dynamics estimated from the synchronization
between oscillators (Cabral et al., 2014; Kuramoto, 1975; Rodrigues et al., 2016; Vuksanovi´c
& Hövel, 2014). In the Kuramoto model, the system evolves toward a globally synchronized
sistema. With the macaque connectome involving a complex system of coupled values (es decir.,
binary and weighted topology), synchronization occurs in a nontrivial pattern that elucidates
clusters of nodes that synchronize together and sets of nodes that drive the dynamical pro-
cesses. The dynamics of the model based on the binary structural connectivity was defined
por

˙θ

i(t) = ω

i + λ

norte
∑
j=1

Aji sin(i

j(t) − yo

i(t))

where θ
i(t) is the phase of the oscillator associated with brain region i at time t, and ω
i is the
associated internal angular frequency and N is the number of brain regions. The cortical cou-
pling strength is denoted by λ and indicates how much the phase of an oscillator is influenced
by its neighbors. For the weighted structural network, coupling was described by the weighted
connectivity matrix W normalized such that the total strength of all connections was equal
to that of the binary connectivity matrix A to assure comparable coupling strength λ between
redes (Motter et al., 2005). The model started with random initial phases, distributed uni-
formly in the interval [−π, Pi] and random internal frequencies, distributed uniformly between
[0, 1]. In line with earlier studies, the evolution of the system was numerically approximated

Neurociencia en red

1056

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

t

/

/

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

yo

F
/

/

/

/

3
4
1
0
5
1
1
8
6
6
8
2
3
norte
mi
norte
_
a
_
0
0
1
0
1
pag
d

/

t

.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Connection strength of the macaque brain augments network attributes

by the Runge-Kutta method for running time T = 700, and the system was evaluated after
transient time τ = 300 (Schmidt et al., 2015). The model was evaluated for cortical coupling
strengths in the range [0, 0.1] at intervals of 0.005. For the binary and weighted structural
redes 1,000 model runs were realized for each cortical coupling strength, the functional
dynamics of weights-shuffled network versions was obtained from model realizations of 1,000
weights-shuffled network versions.

The global dynamic coherence of the system was described by two order parameters r and
rlink (Gómez-Gardeñes et al., 2007). The first order parameter r described the phase synchrony
among all oscillators and was the time average of the modulus of the complex variable z(t)
defined as,

z(t) =

1
norte

norte
∑
j=1

eiθ

j(t).

The second order parameter rlink (Gómez-Gardeñes et al., 2007) was derived from the syn-

chrony matrix C,

Cij =

1
T − τ

|∑T

t=τei(i

i(t)−θ

j(t))|,

and measures local construction of synchronization patterns by the fraction of synchronized
node pairs

rlink =

1
norte(N − 1)

Cij.

∑
i,j

The development of synchronization within the network was explored by examining the
probability of region pairs being synchronized, defined as the average of the filtered synchrony
matrix F,

(cid:4)

Fij =

1, norte (N − 1) rlink largest elements of C
0,

lower values of C

,

over all model realizations of a specific cortical coupling strength.

The role of structural modules in synchronization was measured by the dynamical mod-
ularity, being the ratio between intra- and intermodular synchrony (Gómez-Gardeñes et al.,
2010). Similarmente, the effect of anatomical rich club structure on synchronization was examined
by inspecting the ratio of synchrony among anatomical rich club regions and synchrony of
other region pairs (including the synchrony between rich club regions and peripheral regions,
and the synchronization among peripheral regions). The synchrony ratio of rich club regions
and other region pairs was further investigated among intra- and intermodular region pairs
separately.

RESULTADOS

Agrupación

The binary macaque network exhibited significantly higher clustering (Cb = 0.76) than ob-
rand = 0.73 ± 0.0017; pag = 0.021), resulting in a
served in randomized network instances (Cb
normalized clustering coefficient of Cb
norm = 1.04. Incorporating strength revealed a weighted
clustering coefficient Cw of 3.70, significantly higher than observed in weighted randomized
rand = 3.42 ± 0.011; pag < 0.001), resulting in a normalized weighted clustering networks (Cw coefficient Cw norm = 1.08. The weighted network showed significantly higher clustering coefficient (1.04×, p < 0.001) than network versions with projection strengths shuffled between connections (Cw shu f f led = 3.55 ± 0.011). In the binary network, regions expressing high clustering (examining the top Network Neuroscience 1057 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Connection strength of the macaque brain augments network attributes l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d . 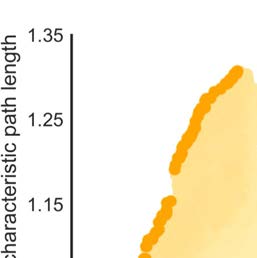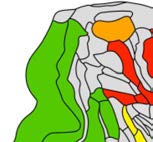t / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 2. Clustering and characteristic path length per region. Clustering in binary (A) and weighted (B) macaque connectome reconstructions. Clustering coefficient of cortical regions in the binary network ranged from 0.67 (medium clustering) to 0.87 (high clustering). In the weighted reconstruction, clustering coefficients ranged from 0.54 (medium clustering) to 0.90 (high cluster- ing). (C) Cortical regions showed characteristic path length ranging from 1.13 to 1.68 steps. (D) The path length of the weighted network ranged from 0.19 to 0.31 steps. 20%) were distributed throughout the brain (Figure 2A), including regions in the occipital (V1, V4), prefrontal (8B, 10), parietal (5), and temporal cortex (PBr), and showed high overlap with the top 20% weighted clustering regions that included regions V1, V4, 8B, 10, 5, and region F7 (Figure 2B). Path Length The characteristic path length of the binary network was short (Lb = 1.34) and not significantly rand = 1.34 ± 0.00; p = 0.86), different from the path length of the randomized networks (Lb resulting in a normalized path length of Lb norm = 1.00. The characteristic path length of the weighted macaque cerebral cortex network was Lw = 0.24 and was longer than for weighted randomized networks (Lw being 1.16. rand = 0.21 ± 0.001; p < 0.001), the normalized path length Lw norm The connection strength distribution was found to increase the characteristic path length of the network, as network versions with shuffled projection strengths showed lower average path length than the original weighted network (0.87×, p = 0.001). Examining the average path length of regions revealed the top 20% regions exhibiting shortest path length to overlap Network Neuroscience 1058 Connection strength of the macaque brain augments network attributes between binary and weighted network (top regions in the binary network: frontal (F5), pre- frontal (81, 9/46d, 8m), parietal (7A) and temporal cortex (STPc) (Figure 2C); top regions in the weighted network included areas in the prefrontal lobe (81, 9/46d, 9/46v, 8m), and two more posterior regions in the parietal (7A) and temporal lobe (STPc) (Figure 2D)). Network Morphospace The clustering and path length of the macaque brain network was further examined in com- parison with networks optimized for minimum or maximum small-world organization. 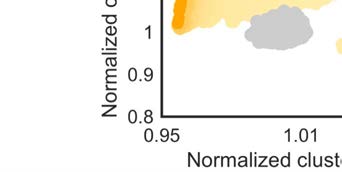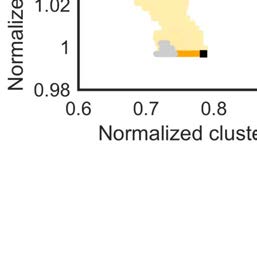All networks were graphically represented in a morphospace to elucidate the relative position of the macaque network in this network space (Figure 3). The morphospace of (degree-preserved) versions of the binary network showed normalized clustering coefficients with values between Cb min = 0.69 and Cb max = 1.05, and normalized characteristic path lengths between Lb min = 1.00 and Lb max = 1.13 (Figure 3B). The binary macaque network was located at the Pareto front of networks with optimized small-world organization and with a characteristic path length equal or lower than that of all generated networks. 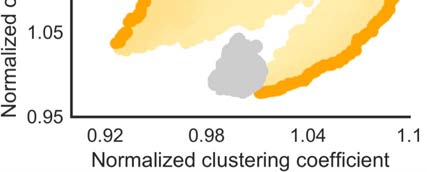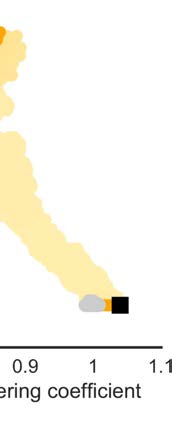The morphospace of (in- and out-degree and in-strength preserved) versions of the weighted macaque brain network showed normalized clustering coefficients with values between Cw min = max = 1.10, and normalized characteristic path lengths between Lw 0.90 and Cw min = 0.95 and Lw max = 1.50 (Figure 3C). The weighted macaque network was situated close to the Pareto front of networks with optimized small-world organization. Specifically, the macaque brain network was located on the right-side of the morphospace, indicating a relatively high cluster- ing coefficient and relatively high average shortest path length. The proximity of the weighted network to the Pareto front illustrates that the high shortest path length (relative compared with randomized networks) was partly driven by mathematical constrains on networks with high clustering coefficients. 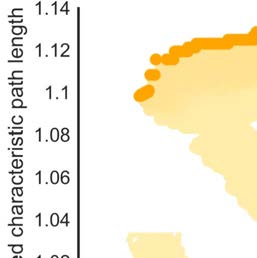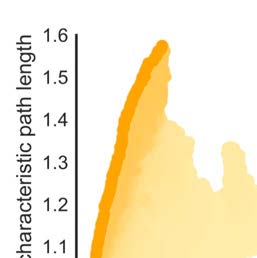The morphospace of network versions with fixed binary topology and optimized connec- tivity strength distribution showed clustering coefficients that ranged from Cw min = 0.99 to Cw max = 1.13 and normalized path lengths between Lw max = 1.60 (Figure 3D). The weighted macaque brain network was located in the middle of the Pareto fronts with mini- mum and maximum small-world organization, suggesting the connectivity strength distribution optimized small-world organization more than randomly distributed connectivity strength but that connectivity strength was not distributed to fully maximize, or minimize, the small-world organization. min = 0.87 and Lw Modular Organization Modularity detection in the binary network (i.e., identifying modules based on connection density only) revealed two modules (Q = 0.10, Figure 4A). The largest module included re- gions in the prefrontal lobe (7 regions), frontal lobe (4), parietal lobe (6), and one region in the limbic lobe. The second module spanned all regions in the occipital lobe (4 regions), all regions of the temporal lobe (6), and one region in the prefrontal lobe. Thirty-eight percent of all connections were intermodular, linking different modules (50% of the possible inter- modular node to node combinations), and 62% were intramodular (82% of the possible in- tramodular node to node combinations). Modularity detection in the weighted network (i.e., identifying modules based on connectivity strength) revealed a modularity structure consist- ing of four modules (Qw = 0.21, Figure 4B). Two of the four modules overlapped with the modules identified in the binary network. Two new modules were distinct: the first module included mostly frontal/prefrontal regions (7m (parietal), F7 (frontal), 8B (prefrontal), 9/46d Network Neuroscience 1059 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d t . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Connection strength of the macaque brain augments network attributes l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d . t / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 3. Network configurations in the small-world morphospace. (A) Schematic representation of a morphospace. The clustering coef- ficient and average shortest path length are shown for networks generated by either a small-world organization maximizing or minimizing optimization procedure (orange arrows). The black square indicates the original macaque connectome. Yellow circles indicate the generated networks, and darker shades of yellow indicate networks generated in later iterations. Network variants in the final iteration, forming the Pareto front, are indicated by orange circles. Gray circles represent the population of generated randomized networks. (B) The binary macaque network shows an as low as possible shortest path length and as high as possible clustering coefficient. (C) The weighted network shows close to the Pareto front of networks with maximum small-world organization in the morphospace of networks with similar in- and out-degree and in-strength. (D) The weighted network shows not close to either Pareto front in the space of networks with similar binary topology. 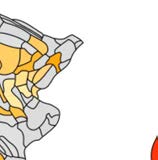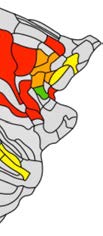Network Neuroscience 1060 Connection strength of the macaque brain augments network attributes Figure 4. Detection of modules in the macaque dataset. (A) Modularity detection in the binary network showed the presence of two modules. (B) In the weighted network version, modularity detection revealed four modules. High overlap was observed between the modules found in the binary and weighted networks (Rand index = 0.70, p < 0.001, 10,000 permutations). (prefrontal), 8m (prefrontal)) and the second included temporal/prefrontal regions (STPr (tem- poral), STPi (temporal), STPc (temporal), PBr (temporal), 10 (prefrontal), 46d (prefrontal)). Mod- ular structure of the binary and weighted network showed high overlap (Rand index = 0.70, p < 0.001, 10,000 permutations). Examining connection strength with respect to the binary modules showed stronger intramodular connections than intermodular connections (1.40×, p < 0.001), suggesting connectivity strength to enhance the modular organization of the binary network. Rich Club Organization The normalized binary rich club coefficient as a function of in-degree kin, computed on the incoming connections from all 91 regions, is shown in Figure 5. The rich club coefficient increased with kin and was significantly higher than random for 36 < kin < 56 (p < 0.05, FDR corrected). Weighted rich club analysis revealed rich club organization throughout the range of in-degree kin 25 < kin < 64 and 65 < kin < 75, p < 0.05 (FDR corrected, Figure 5). Further examining rich club organization, we selected the top 20% highest in-degree nodes ≥ 71) (Harriger et al., 2012). The selected six high in-degree as hubs forming a rich club set (kin regions included (ordered by in-degree) 81, 8m, 9/46d, 9/46v, F5, and 7m. Between these re- gions all possible binary connections were present, forming a fully connected clique. The weighted version of the rich club coefficient showed significantly higher connection strength between hub regions than expected from randomized networks (1.21×, p = 0.009), suggest- ing connection strength to underscore rich club organization. Moreover, the strength of con- nections linking rich club nodes was on average higher than strength of feeder (1.30×) and local connections (1.27×, p = 0.008 and p = 0.042, respectively, 10,000 permutations, all connection strength comparisons are FDR corrected). Strength of feeder and local connections were similar (p = 0.738). Examination of rich club organization in modules showed that intermodular rich club con- nections were on average stronger than intermodular feeder connections present in the network (1.74×, p < 0.001, Figure 6) and intermodular local pathways (1.68×, p = 0.004, no signif- icant difference was observed between strength of feeder and local connections, p = 0.738). Concerning the class of intramodular connections, rich club, feeder and local intramodular connections showed no significant strength differences (rich club–feeder: p = 0.607, rich club– local: p = 0.607, and feeder–local: p = 0.940). Network Neuroscience 1061 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d t . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Connection strength of the macaque brain augments network attributes A B Figure 5. Rich club coefficient as function of in-degree kin. (A) Curves represent the rich club coefficient in the binary connectivity network of the macaque cerebral cortex (black), averaged rich club coefficient of randomized networks (gray; 10,000 permutations) and the normalized rich club coefficient (red). Shading of the region 36 < kin < 56, indicates rich club presence where φunw significantly exceeded φnorm (p < 0.05, FDR corrected). (B) For the weighted macaque network, the normalized rich club coefficient (red) increased with kin and rich club organization was present for 25 < kin < 64 and 65 < kin < 75 (p < 0.05, FDR corrected). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d / t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 6. Comparison strength of connection groups. Average strength of inter- (A) and intramod- ular (B) connections, linking between rich club nodes (rich club connections, red), between rich club and the periphery (feeder connections, orange), or between peripheral regions (local con- nections, yellow). Among intermodular links, rich club connections exhibited on average strongest connections (rich club–feeder, p < 0.001; rich club–local, p < 0.004; feeder–local, p = 0.738; 10,000 permutations, FDR corrected), indicating the importance of rich club connections in com- munication between anatomical communities. Intramodular links showed similar strength between connection classes (all p > 0.05, FDR corrected).

Neurociencia en red

1062

Connection strength of the macaque brain augments network attributes

Functional Dynamics

The effect of the connectivity strength distribution on the modular and rich club organization
observed in the macaque structural network was further investigated by examining simulated
functional dynamics. The functional coherence of the networks was described by order pa-
rameters r and rlink and showed a critical period between λ = 0.02 and λ = 0.04 in which the
functional networks switch from asynchronous dynamics to global synchrony.

The synchronization between regions followed the structural modular organization, con
higher synchronization observed within modules (based on the binary connectivity) than
between modules for both dynamics simulated from binary and weighted structural networks
(Cifra 7). The ratio was particularly high for low cortical coupling values (maximum at λ =
0.01), suggesting synchronization within modules to precede intermodular synchronization.
Comparing the functional dynamics of the weighted structural network and the weights-shuffled
redes, showed higher intra- and intermodular synchrony ratio in the weighted network
(0.005 ≤ λ ≤ 0.055, pag < 0.001, FDR corrected), suggesting that connectivity strength in the macaque connectome endorses intramodular synchronization (Figure 7). In line with the rich club organization observed in the structural network, the simulated synchrony of both binary and weighted networks was higher among rich club regions than the synchrony between rich club regions and peripheral regions, and the synchrony among peripheral regions (Figure 7). Synchrony among rich club regions was higher in the weighted network than in weights-shuffled network versions (0.005 ≤ λ ≤ 0.045, p < 0.001, FDR corrected), suggesting the connectivity strength distribution also emphasizes functional rich club organization. Further inspection showed stronger rich club synchronization ratio between modules (maximum of 2.37) than within modules (maximum of 1.62, as shown in Figure 8). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 7. Synchrony of simulated function. (A) Computed average synchronization probability for binary, weighted, and weights-shuffled macaque networks showed a critical regime between 0.02 and 0.04. (B) Binary and weighted networks showed higher intramodular synchrony relative to intermodular synchrony, reflecting the structural organization. The intra-/intermodular synchrony ratio of the weighted network was also higher than in the weights-shuffled network, suggesting connectivity strength to increase local functional specialization. (C) The synchrony between rich club regions (RC-RC) was higher than between rich club regions and periphery (RC-P) or among peripheral regions (P-P) for the binary and weighted network. The synchrony ratio in the weighted network was higher compared with the ratio seen in the weights-shuffled network, indicating that the connectivity strength distribution increases network integration through rich club synchronization. Network Neuroscience 1063 Connection strength of the macaque brain augments network attributes Tract-tracing: Method to reconstruct axonal projections by using viral tracers. 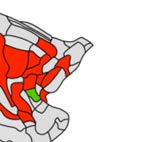Figure 8. Interaction of rich club and modular network organization on synchrony of simulated function. The ratio of synchrony between rich club regions (RC-RC) and the synchrony between rich club regions and periphery (RC-P) or among periphery (P-P) among intramodular (A) or intermodular (B) region pairs. DISCUSSION Our study provides extended evidence that the macaque connectome adheres to the gen- eral neural wiring principle of local specialization combined with systems-level topologi- cal integration. Graph analysis of the structural macaque connectome dataset obtained using tract-tracing by Markov et al. (2014) revealed that binary and weighted network versions have overlapping architectures, including a small-world, modular, and rich club organization. In- vestigation of the connectivity strength distribution showed projection strengths to enhance these network features in both structural and functional organization. The macaque connectome showed architectural characteristics present in both binary and weighted connectivity networks. First, both networks showed local clustering and relatively short path lengths, together indicating a small-world network organization. Second, both networks showed a modular organization; two modules were reported in the binary network and four modules were revealed in the weighted network. Third, both network versions showed a rich club organization, with hub nodes (selected by in-degree) forming a densely connected rich club with a higher than chance mutual connectivity strength. These observations are in line with earlier examinations of the considered macaque connectome dataset (Bassett & Bullmore, 2017; Ercsey-Ravasz et al., 2013; Goulas et al., 2014; Markov et al., 2013a) and validate network analyses on earlier binary macaque connectome reconstructions (Bassett & Bullmore, 2006; Harriger et al., 2012; Hilgetag et al., 2000). The strength placement across binary connections showed a nonrandom organization, with projection strengths increasing the binary network’s shortest path length and clustering (rela- tive to randomized weight placement), with the observed network measures compared with the minimum and maximum these measures could attain. The combined increase in shortest path length, clustering, and modularity indicates a shift toward a stronger local network organi- zation. Indeed, post hoc analysis confirmed that the characteristic step length increase resulted from stronger modular structure, with the weighted network showing lower characteristic step Network Neuroscience 1064 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d / t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Connection strength of the macaque brain augments network attributes length within communities (1.46, p = 0.029) and higher step lengths between communities (1.90, p < 0.001) in comparison with weights-shuffled networks (respectively, 1.53 and 1.75). Rich club en- hancement was significantly driven by effects in intermodular connections, suggesting that the distribution of connection strengths further boosts the rich club’s role as central infrastructure for global network integration (van den Heuvel & Sporns, 2013; Zamora-López et al., 2010). Using functional simulations, we further showed that the connectivity strength distribution increases the modular and rich club organization. In the weighted network, intramodular syn- chronization preceded intermodular synchronization more strongly than in weights-shuffled reference networks, suggesting connectivity strength to be distributed toward local functional specialization (Sporns, 2011; Sporns et al., 2005). The rich club was more pronounced in leading global network synchronization in the weighted network than in weights-shuffled net- works, suggesting connectivity strength to enhance the functional rich club as central integra- tor of neural information (Gómez-Gardeñes et al., 2010; Schmidt et al., 2015; Senden et al., 2014; Vlasov & Bifone, 2017). The role of the rich club in global functional integration was underscored by rich club regions leading intermodular synchronization more strongly than intramodular synchronization. Our study provides evidence for a characteristic wiring organization in the macaque con- nectome, but the evolutionary, developmental, and neurophysiological principles that might underlie this organization remain unclear. Multiple, likely interacting, organizational principles have been proposed that determine the organization of neural networks (Vértes et al., 2012). Comparison of brain networks across species suggest a trade-off between topolog- ical integration and minimizing wiring length (van den Heuvel et al., 2016a; Song et al., 2014). Possible spatial constraints have also been observed in the macaque connectome in the form of an exponential relation between weights and distances (Ercsey-Ravasz et al., 2013). Further- more, brain network architecture might also relate to repeated regional differentiation of brain regions during evolution, resulting in patterns of functional similarity and specialization of cor- tical areas (Ardesch et al., 2019; Betzel et al., 2015; Goulas et al., 2019; de Lange et al., 2016). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d . / t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 The following should be noted when interpreting the findings of the present study. First, the high density of the macaque connectome has a large impact on the topology of the bi- nary macaque connectome, illustrated by small differences in the network measures between the observed macaque connectome and randomized network versions. Exploring the mor- phospace of the binary network revealed that as a result of the high density and degree distri- bution, the randomized versions of the network showed nearly minimum characteristic path length. This observation is in line with studies observing that the characteristic path length in randomized versions of cortical neural networks is not only short but even ultrashort, imply- ing near-optimal efficiency of these randomized networks (Zamora-López & Brasselet, 2018). High network density also limits the possibly observable difference in normalized clustering coefficient between the binary network and randomized network versions (Cb norm = 1.04). The morphospace of the binary network showed that the clustering of the binary network was al- most the maximum possible clustering (Cb max = 1.05). This methodological limitation on the evaluation of the binary network topology has also been described and dis- cussed earlier and argues for both more fine-grain parcellations and incorporating information on connectivity strength in network analyses (Bassett & Bullmore, 2017; Hilgetag & Goulas, 2015). The benefit of weighted connectome analysis was further underscored in the modular- ity analysis, in which incorporating connectivity strength in the module detection algorithm resulted in the detection of a finer modular structure (four modules) compared with the binary networks (two modules). min = 0.69 and Cb Network Neuroscience 1065 Connection strength of the macaque brain augments network attributes Second, analyses were constrained by the methodological limitations of the connectome reconstructions based on tract-tracing. The connectome map described full connectivity of 29 regions of 91 parcellated cortical regions, and future tract-tracing might complement the dataset. Specifically, the reconstructed connectivity described intrahemispheric connections, and the inclusion of interhemispheric connections could provide more understanding of the whole-brain network organization. Variation in tracer uptake across injections might affect the number of labeled neurons reported. We validated our results to be independent of tracer uptake by repeating our analyses with connectivity strength weighted by fraction of extrin- sic labeled neurons (FLNe). The FLNe weighting provides a relative measure of connectivity strength that normalizes the total tracer uptake across injections. The FLNe connection strength showed strong correlation with the number of labeled neurons strength (ρ = 0.99, p < 0.001, Spearman’s rank correlation of raw nonzero values), and we observed in all our analyses similar results when using the FLNe measure, underlining the robustness of our results (see Supporting Information). Third, the investigated Kuramoto model for functional dynamics models all brain regions as identical oscillators. This is a simplification, with studies showing neurophysiological het- erogeneity in the cortex having clear influences on functional connectivity (Chaudhuri et al., 2015; van den Heuvel et al., 2016b; Mejias et al., 2016; Turk et al., 2016). Moreover, in the used Kuramoto model the system eventually evolves to a globally synchronized state. Future studies could incorporate global time delays to examine the effect of structural connectivity strength on meta-stable functional connectivity. Combined research into structural connec- tivity, functional connectivity, and neuroarchitecture might provide further understanding of function and organization of large scale neural networks (Wang & Kennedy, 2016). We observe that strength of connections in the macaque connectome is nonrandomly dis- tributed and enhances local processing and global network integration. Our findings elucidate the role of connectivity strength in the topology of the macaque connectome. ACKNOWLEDGMENTS We thank Fraukje Coopmans for her input on earlier versions of the manuscript. SUPPORTING INFORMATION Supporting information for this article is available at https://www.doi.org/10.1162/netn_a_00101. AUTHOR CONTRIBUTIONS Siemon C. de Lange: Investigation; Methodology; Writing - Original Draft; Writing - Review & Editing. Dirk Jan Ardesch: Methodology; Writing - Original Draft; Writing - Review & Editing. Martijn P. van den Heuvel: Conceptualization; Funding acquisition; Investigation; Methodol- ogy; Project administration; Supervision; Writing - Original Draft; Writing - Review & Editing. FUNDING INFORMATION Martijn P. van den Heuvel, MQ: Transforming Mental Health (GB). Martijn P. van den Heuvel, Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NL), Award ID: VIDI-452-16-015. Martijn P. van den Heuvel, Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NL), Award ID: ALWOP.179. Network Neuroscience 1066 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d . / t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Connection strength of the macaque brain augments network attributes REFERENCES Ardesch, D. J., Scholtens, L. H., Li, L., Preuss, T. M., Rilling, J. K., & van den Heuvel, M. P. (2019). Evolutionary expansion of connectivity between multimodal association areas in the human brain compared with chimpanzees. Proceedings of the National Academy of Sciences of the United States of America, 201818512. https:// doi.org/10.1073/pnas.1818512116 Avena-Koenigsberger, A., Goni, J., Sole, R., & Sporns, O. (2014). Network morphospace. Journal of the Royal Society Interface, 12, 20140881–20140881. https://doi.org/10.1098/rsif.2014.0881 Bassett, D. S., & Bullmore, E. T. (2006). Small-world brain net- works. Neuroscience, 12, 512–523. https://doi.org/10.1177/ 1073858406293182 Bassett, D. S., & Bullmore, E. T. (2017). Small-world brain revisited. Neuroscientist. https://doi.org/10.1177/ networks 1073858416667720 Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discov- ery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society, 57, 289–300. Betzel, R. F., Avena-Koenigsberger, A., Goñi, J., He, Y., de Reus, M. A., Griffa, A., et al. (2015). Generative models of the human connectome. NeuroImage. https://doi.org/10.1016/j. neuroimage.2015.09.041 Betzel, R. F., Medaglia, J. D., & Bassett, D. S. (2018). Diversity of meso- scale architecture in human and non-human connectomes. Nature Communications. https://doi.org/10.1038/s41467-017-02681-z Bota, M., Sporns, O., & Swanson, L. W. (2015). Architecture of the cerebral cortical association connectome underlying cogni- tion. Proceedings of the National Academy of Sciences of the United States of America, 201504394. https://doi.org/10.1073/ pnas.1504394112 Breakspear, M., Heitmann, S., & Daffertshofer, A. (2010). Gener- ative models of cortical oscillations: Neurobiological implica- tions of the Kuramoto model. Frontiers in Human Neuroscience. https://doi.org/10.3389/fnhum.2010.00190 Burns, G. A. P. C., & Young, M. P. (2000). Analysis of the con- nectional organization of neural systems associated with the hippocampus in rats. Philosophical Transactions of the Royal So- ciety of London, 355, 55–70. https://doi.org/10.1098/rstb.2000. 0549 Cabral, (2014). Exploring the network dynamics underlying brain activity during rest. Progress in Neurobiology, 114, 102–131. https://doi.org/10. 1016/j.pneurobio.2013.12.005 J., Kringelbach, M. L., & Deco, G. Chaudhuri, R., Knoblauch, K., Gariel, M.-A., Kennedy, H., & Wang, X.-J. (2015). A large-scale circuit mechanism for hierarchical dy- namical processing in the primate cortex. Neuron, 88, 419–431. https://doi.org/10.1016/j.neuron.2015.09.008 Colizza, V., Flammini, A., Serrano, M. A., & Vespignani, A. (2006). Detecting rich-club ordering in complex networks. Nature Physics, 2, 110–115. https://doi.org/10.1038/nphys209 de Lange, S. C., van den Heuvel, M. P., & de Reus, M. A. (2016). The role of symmetry in neural networks and their Laplacian spectra. NeuroImage, 141, 357–365. https://doi.org/10.1016/j. neuroimage.2016.07.051 Ercsey-Ravasz, M., Markov, N. T., Lamy, C., Van Essen, D. C., Knoblauch, K., Toroczkai, Z., et al. (2013). A predictive network model of cerebral cortical connectivity based on a distance rule. Neuron, 80, 184–97. https://doi.org/10.1016/j.neuron.2013.07. 036 Fagiolo, G. (2007). Clustering in complex directed networks. Phys- ical Review E, 76, 1–8.https://doi.org/10.1103/PhysRevE.76. 026107 Felleman, D. J., & Van Essen, D. C. (1991). Distributed hierarchi- cal processing in the primate cerebral cortex. Cerebral Cortex, 1, 1–47. https://doi.org/10.1093/cercor/1.1.1 Gómez-Gardeñes, J., Moreno, Y., & Arenas, A. (2007). Paths to syn- chronization on complex networks. Physical Review Letters, 98, 034101. https://doi.org/10.1103/PhysRevLett.98.034101 Gómez-Gardeñes, J., Zamora-López, G., Moreno, Y., & Arenas, A. (2010). From modular to centralized organization of synchro- nization in functional areas of the cat cerebral cortex. PLoS One, 5, e12313+. https://doi.org/10.1371/journal.pone.0012313 Goñi, J., Avena-Koenigsberger, A., Velez de Mendizabal, N., van den Heuvel, M. P., Betzel, R. F., & Sporns, O. (2013). Explor- ing the morphospace of communication efficiency in complex networks. PLoS One, 8, e58070. https://doi.org/10.1371/journal. pone.0058070 Goulas, A., Margulies, D. S., Bezgin, G., & Hilgetag, C. C. (2019). The architecture of mammalian cortical connectomes in light of the theory of the dual origin of the cerebral cortex. Cortex. https:// doi.org/10.1016/j.cortex.2019.03.002 Goulas, A., Schaefer, A., & Margulies, D. S. (2014). The strength of weak connections in the macaque cortico-cortical network. Brain Structure and Function, https://doi.org/10.1007/s00429- 014-0836-3 Grayson, D. S., Ray, S., Carpenter, S., Iyer, S., Dias, T. G. C., Stevens, C., et al. (2014). Structural and functional rich club organization of the brain in children and adults. PLoS One, 9, e88297. https:// doi.org/10.1371/journal.pone.0088297 Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J., Van Wedeen, J., et al. (2008). Mapping the structural core of human cerebral cortex. PLoS Biology, 6, e159. https://doi.org/ 10.1371/journal.pbio.0060159 Hagmann, P., Sporns, O., Madan, N., Cammoun, L., Pienaar, R., Wedeen, V. J., et al. (2010). White matter maturation reshapes structural connectivity in the late developing human brain. Pro- ceedings of the National Academy of Sciences of the United States of America, 107, 19067–19072. https://doi.org/10.1073/ pnas.1009073107 Harriger, L., van den Heuvel, M. P., & Sporns, O. (2012). Rich club organization of macaque cerebral cortex and its role in network communication. PLoS One, 7, e46497. https://doi.org/10.1371/ journal.pone.0046497 Hilgetag, C. C., Burns, G. A., O’Neill, M. A., Scannell, J. W., & Young, M. P. (2000). Anatomical connectivity defines the or- ganization of clusters of cortical areas in the macaque monkey and the cat. Philosophical Transactions of the Royal Society of London, 355, 91–110. https://doi.org/10.1098/rstb.2000.0551 Network Neuroscience 1067 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Connection strength of the macaque brain augments network attributes Hilgetag, C. C., & Goulas, A. (2015). Is the brain really a small- world network? Brain Structure and Function. https://doi.org/10. 1007/s00429-015-1035-6 Hilgetag, C. C., & Grant, S. (2000). Uniformity, specificity and vari- ability of corticocortical connectivity. Philosophical Transactions of the Royal Society of London, 355, 7–20. https://doi.org/10. 1098/rstb.2000.0546 Honey, C. J., & Sporns, O. (2008). Dynamical consequences of lesions in cortical networks. Human Brain Mapping, 29, 802–809. https://doi.org/10.1002/hbm.20579 Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J. P., Meuli, R., et al. (2009). Predicting human resting-state functional connectivity from structural connectivity. Proceedings of the Na- tional Academy of Sciences of the United States of America, 106, 2035–2040. https://doi.org/10.1073/pnas.0811168106 Kuramoto, Y. (1975). Lecture notes in physics. International Sympo- sium on Mathematical Problems in Theoretical Physics, 30. Leicht, E. A., & Newman, M. E. J. (2008). Community structure in directed networks. Physical Review Letters, 100, 1–4. https://doi. org/10.1103/PhysRevLett.100.118703 Markov, N. T., Ercsey-Ravasz, M., Van Essen, D. C., Knoblauch, K., Toroczkai, Z., & Kennedy, H. (2013a). Cortical high-density counterstream architectures. Science, 342, 1238406. https://doi. org/10.1126/science.1238406 Markov, N. T., Ercsey-Ravasz, M., Lamy, C., Ribeiro Gomes, A. R., Magrou, L., Misery, P., et al. (2013b). The role of long-range connections on the specificity of the macaque interareal corti- cal network. Proceedings of the National Academy of Sciences of the United States of America, 110, 5187–92. https://doi.org/ 10.1073/pnas.1218972110 Markov, N. T., Ercsey-Ravasz, M. M., Ribeiro Gomes, A. R., Lamy, C., Magrou, L., Vezoli, J., et al. (2014). A weighted and directed interareal connectivity matrix for macaque cerebral cor- tex. Cereberal Cortex, 24, 17–36. https://doi.org/10.1093/cercor/ bhs270 Markov, N. T., Misery, P., Falchier, A., Lamy, C., Vezoli, J., Quilodran, R., et al. (2011). Weight consistency specifies reg- ularities of macaque cortical networks. Cerebral Cortex, 21, 1254–1272. https://doi.org/10.1093/cercor/bhq201 Mejias, J. F., Murray, J. D., Kennedy, H., & Wang, X.-J. (2016). Feedforward and feedback frequency-dependent interactions in a large-scale laminar network of the primate cortex. Cold Spring Harbor Labs Journals. https://doi.org/10.1101/065854 Modha, D. S., & Singh, R. (2010). Network architecture of the long- distance pathways in the macaque brain. Proceedings of the Na- tional Academy of Sciences of the United States of America, 107, 13485–13490. https://doi.org/10.1073/pnas.1008054107 Motter, A. E., Zhou, C. S., & Kurths, J. (2005). Enhancing complex- network synchronization. Europhysics Letters, 69, 334–340. https://doi.org/10.1209/epl/i2004-10365-4 Newman, M. E. J. (2006). Modularity and community structure in networks. Proceedings of the National Academy of Sciences of the United States of America, 103, 8577–8582. https://doi.org/ 10.1073/pnas.0601602103 Oh, S. W., Harris, J. A., Ng, L., Winslow, B., Cain, N., Mihalas, S., (2014). A mesoscale connectome of the mouse brain. et al. Nature, 508, 207–214. https://doi.org/10.1038/nature13186 Opsahl,T., Colizza, V., Panzarasa, P., & Ramasco, J. (2008). Prominence and control:The weighted rich-club effect. Physical Review Letters, 101, 1–4. Rand, W. M. (1971). Objective criteria for the evaluation of cluster- ing methods. Journal of the American Statistical Association, 66, 846–850. https://doi.org/10.2307/2284239 Rodrigues, F. A., Peron, T. K. D. M., Ji, P., & Kurths, J. (2016). The Kuramoto model in complex networks. Physics Reports. https:// doi.org/10.1016/j.physrep.2015.10.008 Rubinov, M., & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52, 1059–69. https://doi.org/10.1016/j.neuroimage.2009.10.003 Rubinov, M., Ypma, R. J. F., Watson, C., & Bullmore, E. T. (2015). Wiring cost and topological participation of the mouse brain con- nectome. Proceedings of the National Academy of Sciences of the United States of America, 201420315. https://doi.org/10.1073/ pnas.1420315112 Scannell, J. W., Burns, G. A. P. C., Hilgetag, C. C., Neil, M. A. O., & Young, M. P. (1999). The connectional organization of the cortico-thalamic system of the cat. Cerebral Cortex, 9, 277–299. Schmidt, R., LaFleur, K. J. R., de Reus, M. A., van den Berg, L. H., van den Heuvel, M. P., Kaiser, M., et al. (2015). Kuramoto model simulation of neural hubs and dynamic synchrony in the human cerebral connectome. BMC Neuroscience, 16, 54. https://doi. org/10.1186/s12868-015-0193-z Scholtens, L. H., Schmidt, R., de Reus, M. A., & van den Heuvel, M. P. (2014). Linking macroscale graph analytical organiza- tion to microscale neuroarchitectonics in the macaque connec- tome. Journal of Neuroscience, 34, 12192–205. https://doi.org/ 10.1523/jneurosci.0752-14.2014 Senden, M., Deco, G., de Reus, M. A., Goebel, R., & van den Heuvel, M. P. (2014). Rich club organization supports a diverse set of functional network configurations. NeuroImage, 96C, 174–182. https://doi.org/10.1016/j.neuroimage.2014.03.066 Song, H. F., Kennedy, H., & Wang, X.-J. (2014). Spatial embedding of structural similarity in the cerebral cortex. Proceedings of the National Academy of Sciences of the United States of America, 111, 16580–16585. https://doi.org/10.1073/pnas.1414153111 Sporns, O. (2011). The human connectome: A complex network. Annals of the New York Academy of Sciences, 1224, 109–125. https://doi.org/10.1111/j.1749-6632.2010.05888.x Sporns, O., Tononi, G., & Kötter, R. (2005). The human connectome: A structural description of the human brain. PLoS Computational Biology, 1, e42. https://doi.org/10.1371/journal.pcbi.0010042 Stephan, K. E., Kamper, L., Bozkurt, A., Burns, G. A., Young, M. P., & Kötter, R. (2001). Advanced database methodology for the Col- lation of Connectivity data on the Macaque brain (CoCoMac). Philosophical Transactions of the Royal Society of London, 356, 1159–1186. https://doi.org/10.1098/rstb.2001.0908 Swanson, L. W. (1992). Brain Maps: Structure of the Rat Brain. Oxford: Elsevier Science. Turk, E., Scholtens, L. H., & van den Heuvel, M. P. (2016). Cor- tical chemoarchitecture shapes macroscale effective functional connectivity patterns in macaque cerebral cortex. Human Brain Mapping, 37, 1856–65. https://doi.org/10.1002/hbm.23141 van den Heuvel, M. P., Bullmore, E. T., & Sporns, O. (2016a). Comparative connectomics. Trends in Cognitive Sciences, 20, 345–361. https://doi.org/10.1016/j.tics.2016.03.001 Network Neuroscience 1068 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Connection strength of the macaque brain augments network attributes van den Heuvel, M. P., Kahn, R. S., Goñi, J., & Sporns, O. (2012). High-cost, high-capacity backbone for global brain communi- cation. Proceedings of the National Academy of Sciences of the United States of America, 109, 11372–7. https://doi.org/10. 1073/pnas.1203593109 van den Heuvel, M. P., & de Reus, M. A. (2014). Chasing the dreams of early connectionists. ACS Chemical Neuroscience, 5, 491–3. https://doi.org/10.1021/cn5000937 van den Heuvel, M. P., Scholtens, L. H., & de Reus, M. A. (2015). Topological organization of connectivity strength in the rat con- nectome. Brain Structure and Function. https://doi.org/10.1007/ s00429-015-0999-6 van den Heuvel, M. P., Scholtens, L. H., Turk, E., Mantini, D., Vanduffel, W., & Feldman Barrett, L. (2016b). Multimodal analysis of cortical chemoarchitecture and macroscale fMRI resting-state functional connectivity. Human Brain Mapping, 37, 3103–3113. https://doi.org/10.1002/hbm.23229 van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organization of the human connectome. J. Neuroscience, 31, 15775–15786. https://doi.org/10.1523/jneurosci.3539-11.2011 van den Heuvel, M. P., & Sporns, O. (2013). Network hubs in the human brain. Trends in Cognitive Sciences, 17, 683–696. https:// doi.org/10.1016/j.tics.2013.09.012 Vértes, P. E., Alexander-Bloch, A. F., Gogtay, N., Giedd, J. N., Rapoport, J. L., & Bullmore, E. T. (2012). Simple models of human brain functional networks. Proceedings of the National Academy of Sciences of the United States of America, 109, 5868–73. https://doi.org/10.1073/pnas.1111738109 Vlasov, V., & Bifone, A. (2017). Hub-driven remote synchronization in brain networks. Scientific Reports. https://doi.org/10.1038/ s41598-017-09887-7 Vuksanovi´c, V., & Hövel, P. (2014). Functional connectivity of dis- tant cortical regions: Role of remote synchronization and sym- metry in interactions. NeuroImage, 97, 1–8. https://doi.org/10. 1016/j.neuroimage.2014.04.039 Vuksanovi´c, V., & Hövel, P. (2016). Role of structural inhomo- geneities in resting-state brain dynamics. Cognitive Neurodynam- ics, 10, 361–365. https://doi.org/10.1007/s11571-016-9381-5 Wang, X.-J., & Kennedy, H. (2016). Brain structure and dynamics across scales: In search of rules. Current Opinion in Neurobiol- ogy, 37, 92–98. https://doi.org/10.1016/j.conb.2015.12.010 Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-world” networks. Nature, 393, 440–2. https://doi.org/10.1038/30918 Zakiewicz, I. M., van Dongen, Y. C., Leergaard, T. B., & Bjaalie, J. G. (2011). Workflow and atlas system for brain-wide mapping of axonal connectivity in rat. PLoS One, 6, e22669. https://doi. org/10.1371/journal.pone.0022669 Zamora-López, G., & Brasselet, R. (2018). Sizing the length of complex networks. ArXiv. Available at: http://arxiv.org/abs/ 1810.12825 [Accessed April 26, 2019] Zamora-López, G., Chen, Y., Deco, G., Kringelbach, M. L., & Zhou, C. (2016). Functional complexity emerging from anatomical con- straints in the brain: The significance of network modularity and rich-clubs. Scientific Reports, 6, 38424. https://doi.org/10.1038/ srep38424 Zamora-López, G., Zhou, C., & Kurths, J. (2010). Cortical hubs form a module for multisensory integration on top of the hierarchy of cortical networks. Frontiers in Neuroinformatics, 4, 1. https://doi. org/10.3389/neuro.11.001.2010 Zingg, B., Hintiryan, H., Gou, L., Song, M. Y., Bay, M., Bienkowski, M. S., et al. (2014). Neural networks of the mouse neocortex. Cell, 156, 1096–111. https://doi.org/10.1016/j.cell.2014.02.023 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 3 4 1 0 5 1 1 8 6 6 8 2 3 n e n _ a _ 0 0 1 0 1 p d . t / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Network Neuroscience 1069

Descargar PDF