RESEARCH - IA de Investigación especializada en el MIT

INVESTIGACIÓN

Detecting modular brain states in rest and task

Aya Kabbara

1,2,3

Youssof El Traboulsi

, Mohamad Khalil
7

, Georges O’Neill
2
, Fabrice Wendling

, and Mahmoud Hassan

, Kathy Dujardin

5,6

1,3

1Azm Center for Research in Biotechnology and Its Applications, EDST, Lebanese University, Beirut, Líbano
2University of Rennes, LTSI – U1099, Rennes, Francia
3CRSI Lab, Engineering Faculty, Lebanese University, Beirut, Líbano
4Sir Peter Mansﬁeld Imaging Centre, Escuela de Física y Astronomía, University of Nottingham,
University Park, Nottingham, Reino Unido
5INSERM, U1171, Lille, Francia
6CHU Lille, Neurology and Movement Disorders Department, Lille, Francia
7LaMA-Liban, Lebanese University, Tripoli, Líbano

un acceso abierto

diario

Palabras clave: Brain network dynamics, Conectividad funcional, M/EEG source-space networks

ABSTRACTO

The human brain is a dynamic networked system that continually reconﬁgures its functional
connectivity patterns over time. De este modo, developing approaches able to adequately detect fast
brain dynamics is critical. Of particular interest are the methods that analyze the modular
structure of brain networks, eso es, the presence of clusters of regions that are densely
interconnected. en este documento, we propose a novel framework to identify fast modular states
that dynamically ﬂuctuate over time during rest and task. We started by demonstrating the
feasibility and relevance of this framework using simulated data. Compared with other
methods, our algorithm was able to identify the simulated networks with high temporal and
spatial accuracies. We further applied the proposed framework on MEG data recorded during
a ﬁnger movement task, identifying modular states linking somatosensory and primary motor
regiones. The algorithm was also performed on dense-EEG data recorded during a picture
naming task, revealing the subsecond transition between several modular states that relate to
visual processing, semantic processing, and language. Próximo, we tested our method on a
dataset of resting-state dense-EEG signals recorded from 124 patients with Parkinson’s
enfermedad. Results disclosed brain modular states that differentiate cognitively intact patients,
patients with moderate cognitive deﬁcits, and patients with severe cognitive deﬁcits. Nuestro
new approach complements classical methods, offering a new way to track the brain
modular states, in healthy subjects and patients, on an adequate task-speciﬁc timescale.

RESUMEN DEL AUTOR

The brain is a dynamic modular network. De este modo, exploring the dynamic behavior of the brain
can reveal insights about its characteristics during rest and task, in healthy and pathological
condiciones. en este documento, we propose a new framework that aims to track the dynamic
changes of the modular brain organization. The method presents two algorithms that can be
applied during task-free or task-related paradigms. Using simulations, we demonstrated the
advantages of the proposed algorithm over existing methods. The proposed algorithm was
also tested on three datasets recorded from real EEG and MEG acquisitions. En general, resultados
showed the capacity of the proposed algorithm to track brain network dynamics with good
spatial and temporal accuracy.

Citación: Kabbara, A., Khalil, METRO.,
O’Neill, G.,Dujardin, K., El Traboulsi, y.,
Wendling, F. & Hassan, METRO. (2019).
Detecting modular brain states in rest
and task. Neurociencia en red, 3(3),
878–901. https://doi.org/10.1162/
netn_a_00090

DOI:
https://doi.org/10.1162/netn_a_00090

Supporting Information:
https://doi.org/10.1162/netn_a_00090
https://github.com/librteam/
Modularity_algorithm_NN

Recibió: 3 Enero 2019
Aceptado: 18 Abril 2019

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autor correspondiente:
Aya Kabbara
aya.kabbara7@gmail.com

Editor de manejo:
Olaf Sporns

Derechos de autor: © 2019
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
7
8
1
0
9
2
5
1
8
norte
mi
norte
_
a
_
0
0
0
9
0
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Detecting modular brain states in rest and task

INTRODUCCIÓN

The human brain is a modular dynamic system. Following fast neuronal activity (Pfurtscheller &
Aranibar, 1977; Pfurtscheller & Lopes Da Silva, 1999), the spatiotemporal organization of rest-
En g (Baker et al., 2014; Damaraju et al., 2014; de Pasquale et al., 2012; de Pasquale, Della Penna,
despreciar, Romani, & Corbetta, 2015; Kabbara, El Falou, Khalil, Wendling, & Hassan, 2017) y
task-evoked connectivity (Bola & Sabel, 2015; Hassan, Benquet, et al., 2015; Hutchison et al.,
2013; O’Neill, Tewarie, Colclough, et al., 2017) is in constant ﬂux.

Por eso, an appropriate description of time-varying connectivity is of utmost importance
to understand how cognitive and behavioral functions are supported by networks. En esto
contexto, several frameworks have been suggested to explore the time-varying nature of func-
tional brain connectivity. entre ellos, hidden Markov model approaches (Baker et al., 2014;
Vidaurre et al., 2017), K-means clustering (allen, Damaraju, Eichele, Wu, & Calhoun, 2017;
Allen et al., 2014; Damaraju et al., 2014), independent component analysis (ICA; O’Neill,
Tewarie, Colclough, et al., 2017), principal component analysis (Preti & Van De Ville, 2016),
or orthogonal connectivity factorization (Hyvärinen, Hirayama, Kiviniemi, & Kawanabe, 2016)
have been applied to identify the main brain networks shaping dynamic functional connec-
actividad. These methods consist of grouping the temporal networks into states, where each state
reﬂects a unique spatial connectivity pattern. It is important to note that in these frameworks,
states are identiﬁed without looking at the modular organization of the networks.

Sin embargo, because of the modular organization of the human brain network (despreciar &
Betzel, 2016) methods for detecting network communities (or modules) are of particular inter-
est (despreciar & Betzel, 2016). These methods decompose the network into building blocks or
modules that are internally strongly connected, often corresponding to specialized functions.
En tono rimbombante, during a learning task, Basset et al. showed that the ﬂexibility (deﬁned as how
often a given node changes its modular afﬁliation over time) of the networks facilitates the
prediction of individual future performances in next learning sessions (Bassett y cols., 2011),
remembering, atención, and integrated reasoning (Gallen et al., 2016).

To compute modularity in networks collected across multiple slices (time points), one could
simply decompose each network independently. Another algorithm proposed to link corre-
sponding nodes across slices before generating communities. This algorithm is known as
multislice modularity (also called multilayer modularity; Mucha, Richardson, Macon, Portero,
& Onnela, 2010), which has been used to follow changes of the modular architecture in differ-
ent applications (Bassett y cols., 2011; bassett, Cual, Wymbs, & Grafton, 2015). Sin embargo, el
problem with solely applying these techniques is that they may not lead to easily interpretable
results because of the particularly high number of modular structures generated. More speciﬁ-
cally, the dynamic modular structures obtained are technically difﬁcult to visualize since their
number is equal to the number of slices. Alternativamente, one could use the multislice modularity
algorithm to generate a community structure consistent over time. But such a strategy will con-
strain the dynamic analysis. Por eso, it would be very useful to ﬁnd the main modular structures
driving the dynamics of neural activity. Hasta la fecha, there is no automatic framework that is able
to decipher modular brain states, eso es, subsets of brain modules implicated in a given brain
function at a given time period.

Aquí, we propose a novel framework aiming to elucidate the main modular brain struc-
turas, called modular states (MS), that ﬂuctuate over time during rest and task. We attempt
to ﬁnd the modular structures that share the same topology by quantifying the similarity be-
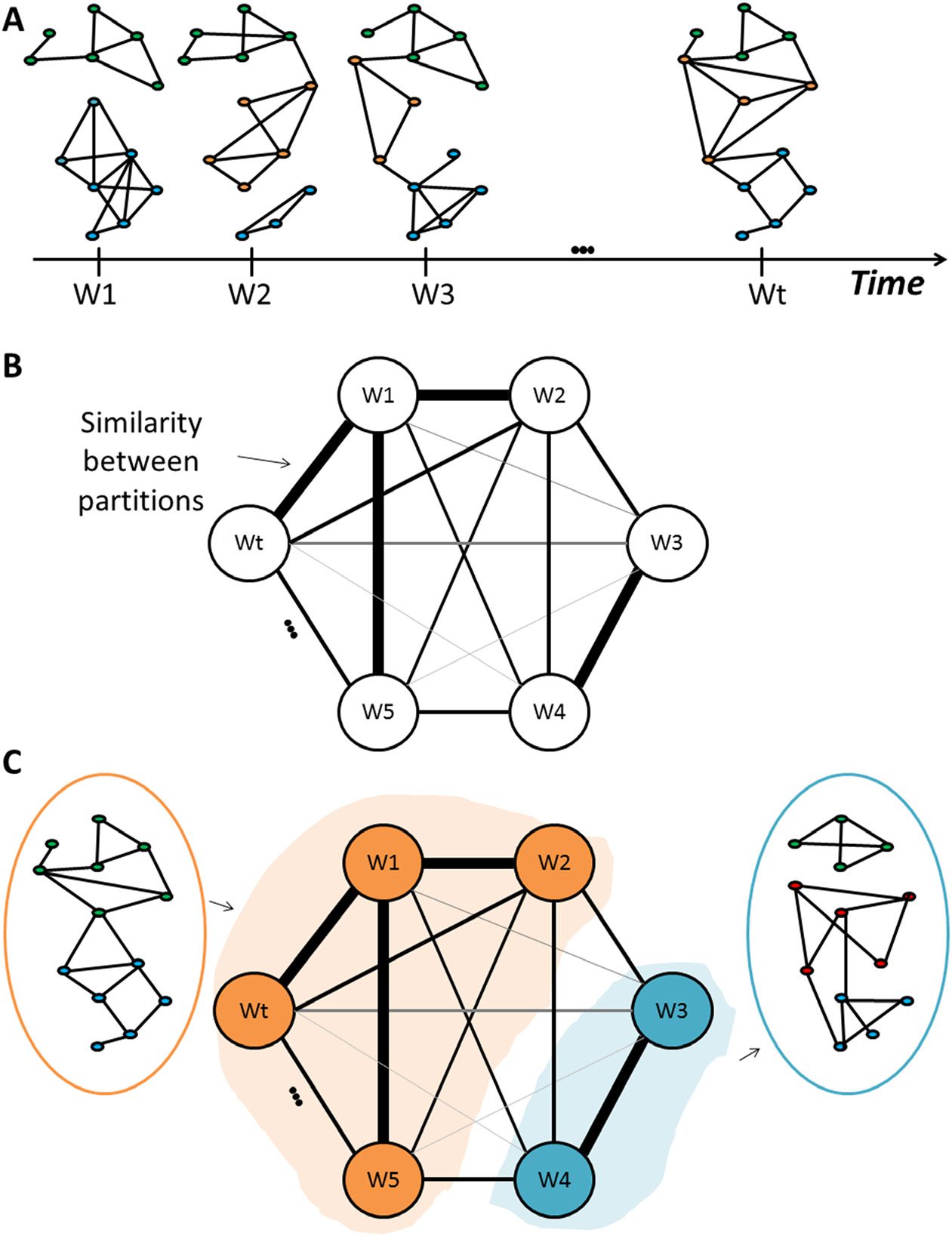
tween all the computed temporal partitions (Cifra 1). The proposed framework simply takes

Dynamic functional connectivity:
Measurement of transient changes in
the functional brain network across
tiempo.

Module:
A subnetwork composed of strongly
connected nodes that are weakly
connected to the rest of the network.

Modular structure:
The partition of the network into
nonoverlapping modules.

Brain state:
A network pattern representing time
points that share some similar
topological properties.

Neurociencia en red

879

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
7
8
1
0
9
2
5
1
8
norte
mi
norte
_
a
_
0
0
0
9
0
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Detecting modular brain states in rest and task

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
7
8
1
0
9
2
5
1
8
norte
mi
norte
_
a
_
0
0
0
9
0
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 1. The algorithm procedure. (A) Computation of modules for each temporal network (Wt).
(B) Assessment of the similarity between the dynamic modular structures. (C) Clustering the similarity
matrix into “categorical modules.”

as input a set of connectivity matrices, without making any constraint on how these matrices
are computed. This means that it is independent of the choice of the connectivity method, el
frequency range of interest, the temporal resolution of dynamic connectivity, and the regions
de interés (ROI). Connectivity matrices could be also extracted from different individuals, o
different experimental conditions. The main purpose of the framework is to ﬁnd the common
modular states between the connectivity patterns interpreted. In the paper, we used simulated
data to show the advantages of our method over other existing methods in terms of spatial and
temporal accuracy. Entonces, using three different MEG/EEG datasets, recorded in rest and task
from healthy subjects and/or patients, we demonstrate the feasibility of the method to reveal
both time-varying functional connectivity and the corresponding spatial patterns, as compared
with the state-of-the art ﬁndings. En general, ﬁndings show that the algorithm was able to track
the dynamics of brain networks in adapted timescale, offering a new way to explore the spa-
tiotemporal organization of brain function.

880

Conectividad funcional:
Statistical dependency between
spatially separated brain regional
time series.

Neurociencia en red

Detecting modular brain states in rest and task

MATERIALES Y MÉTODOS

We have developed two versions of the algorithm: (a) “categorical,” where we aim to ﬁnd the
main modular structures over time, with no interest in their sequential order; y (b) “con-
secutive,” where the objective is to ﬁnd the modular structures in a successive way. The two
versions are described hereafter.

Categorical Version

The categorical version includes three main steps:

(1) Decompose each temporal network into modules (es decir., clusters of nodes that are inter-
nally strongly connected, but externally weakly connected; Figura 1A). To do that, diferente
modularity algorithms were proposed in the literature (rubia, Guillaume, Lambiotte,
& Lefebvre, 2008; Duch & Arenas, 2005; girvan & Hombre nuevo, 2002; Guimerà & Amaral,
2005).
In our study, we adopted the consensus modularity approach that was previously used in
many studies (Bassett y cols., 2013; Kabbara et al., 2017): Given an ensemble of partitions
acquired from the Newman algorithm (girvan & Hombre nuevo, 2002) and Louvain algorithm
(Blondel et al., 2008) repeated for 200 carreras, an association matrix is obtained. This results
in an N × N matrix (N is the number of nodes), and an element Ai,j represents the
number of times the nodes i and j are assigned to the same module across all runs
and algorithms. The association matrix is then compared with a null model association
matrix generated from a permutation of the original partitions, and only the signiﬁcant
values are retained (Bassett y cols., 2013). To ultimately obtain consensus communities,
we reclustered the association matrix using the Louvain algorithm.

(2) Assess the similarity between the temporal modular structures (Figura 1B). In this context,
several methods have been suggested to compare community structures (Traud, Kelsic,
Mucha, & Portero, 2008). Aquí, we focused on the pair-counting method, which deﬁnes
a similarity score by counting each pair of nodes drawn from the N nodes of a network
according to whether the pair falls in the same or in different groups in each partition
(Traud et al., 2008). We considered the z-score of Rand coefﬁcient, bounded between
0 (no similar pair placements) y 1 (identical partitions). This yields a T × T similarity
matrix, where T is the number of time windows.

(3) Cluster the similarity matrix into “categorical” modular states (MS) using the consensus
modularity method (Figura 1C). This step combines similar temporal modular structures
in the same community. Por eso, the association matrix of each “categorical” community
is computed using the modular afﬁliations of its corresponding networks.

Consecutive Version

The difference between the two versions of the algorithm is essentially in the third step, en
which the ﬁnal communities were deﬁned. Particularly, the similarity matrix is segmented in a
sequential way using the following steps:

(1) Threshold the similarity matrix using an automatic thresholding algorithm described in
Genovese, Lázaro, and Nichols (2002). Brieﬂy the matrix was converted into a p value
map that is then thresholded based on the false discovery rate (FDR) controlling.
(2) Apply a median ﬁlter in order to get a smoother presentation of the similarity matrix.
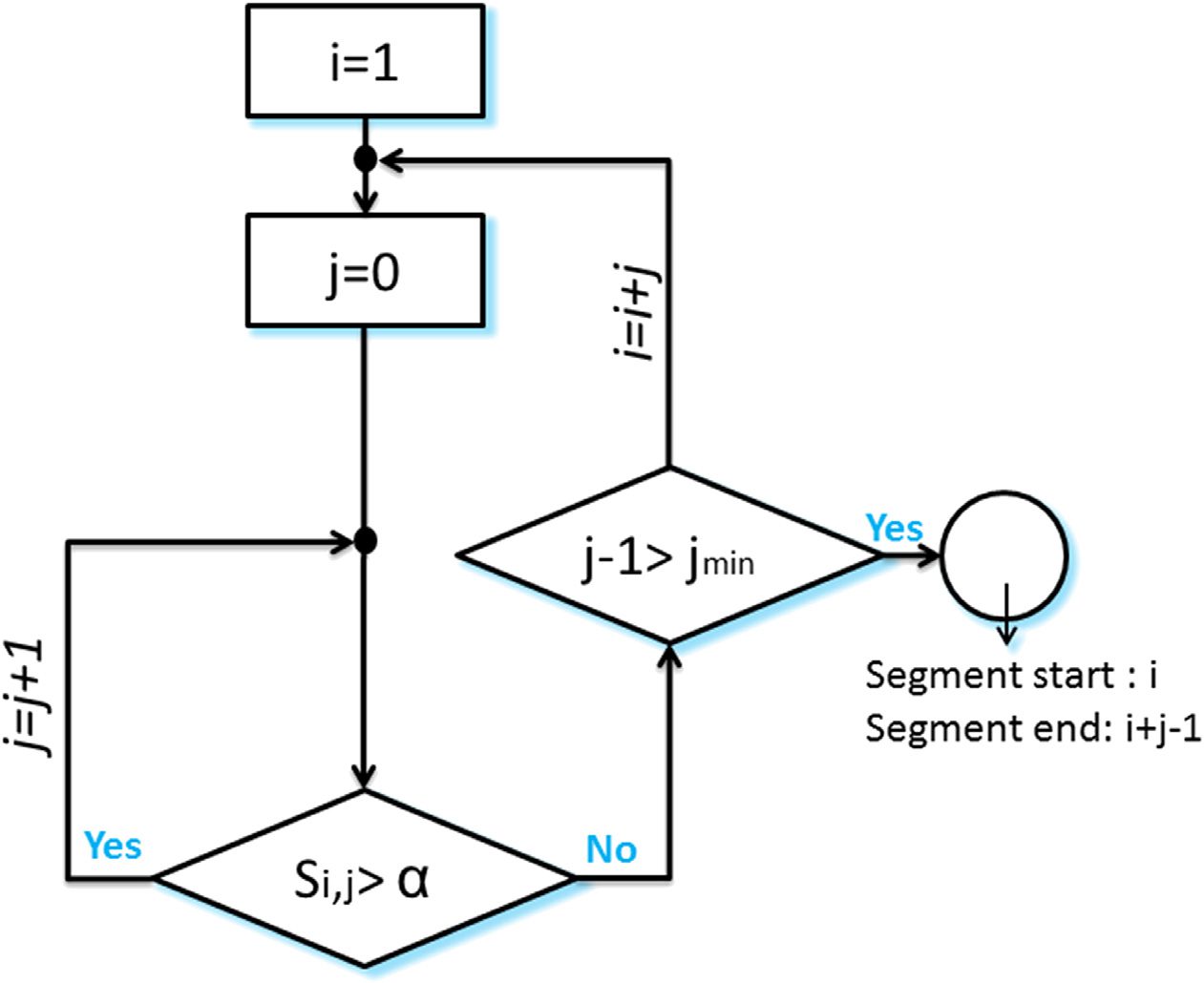
(3) Segment the matrix in a sequential way following the algorithm illustrated in the ﬂowchart
of Figure 2. In brief, the method groups similar consecutive modular structures. As these

Neurociencia en red

881

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
7
8
1
0
9
2
5
1
8
norte
mi
norte
_
a
_
0
0
0
9
0
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Detecting modular brain states in rest and task

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
7
8
1
0
9
2
5
1
8
norte
mi
norte
_
a
_
0
0
0
9
0
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 2.

Flowchart of the segmentation algorithm.

modular structures show high similarity values with each other, the algorithm detects the
squares located around the diagonal of the similarity matrix. As presented in Figure 2,
the condition for which two consecutive structures are associated with the same state is
the following:

Y,j > a,

where Si,j = ∑

j
k=0 ai+k,i+j − ai+j,i+j ; i, j ∈ [1, t], where al,m denotes the
similarity value between the modular structure corresponding to the time window l and that
corresponding to the time window m.

j
k=0 ai+j,i+k + ∑

a is the “accuracy parameter,” strictly bounded between 0 y 1. It regulates the temporal-
spatial accuracy of detected modular states. We recommend choosing an adaptive value of
a. en este documento, a equals the average of the similarity matrix. A segment is considered to be
relevant if the number of included time windows is greater than jmin (the minimal size allowed
for a segment).

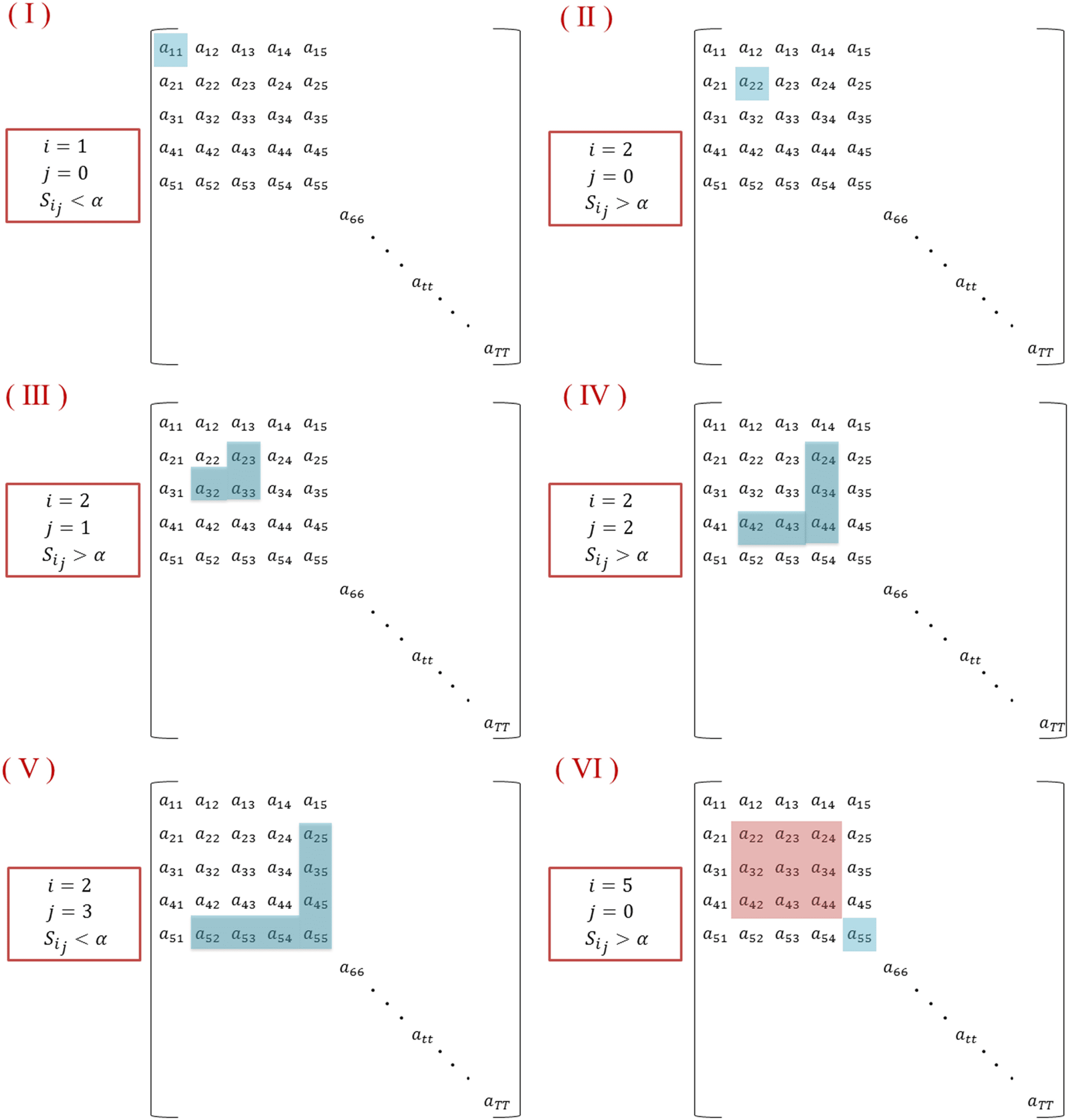
The algorithm is illustrated in Figure 3. (I): Starting with i = 1, j = 0; and considering that a11
is lower than a, we obtained S1,0 = a11 < a, and the algorithm moves to the next time window i = 2. (II): As S2,0 = a22 is greater than a, j is incremented by 1. (III): Having S2,1 = a23+a23+a33 >
a, the second and the third time windows are associated with the segment. (IV): The algorithm
succeeds to add also the fourth time window as S2,2 = a24+a42+a34+a43+a44
> a. (V): Entonces, para
j = 3, we obtain S2,3 = a25+a35+a45+a55+a52+a53+a54
< a. This means that the ﬁfth time window differs from the previous windows in its modular structure. Afterwards, the algorithm moves toward ﬁnding another segment by incrementing i and repeating the process (IV). 3 5 7 For each detected segment, the modular structure is obtained after computing the associa- tion matrix of the corresponding time windows modular afﬁliations. Network Neuroscience 882 Detecting modular brain states in rest and task l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 3. An illustrative example describing the segmentation algorithm. Network Neuroscience 883 Detecting modular brain states in rest and task The Matlab code developed to apply the algorithm in the two versions is publicly available (Kabbara et al., 2019). Simulated Data We simulated the adjacency tensor data following the methodology applied in O’Neill, Tewarie, Colclough, et al. (2017). Brieﬂy, four N × N adjacency matrices Pj were constructed, where j ∈ [1, 4] and N is the number of ROIs. We used an anatomical atlas of 221 ROIs with the mean of the Desikan-Killiany atlas (Desikan et al., 2006) subdivided by Hagmann et al. (2008), yielding to N = 221. The adjacency matrices and the 3-D visualization of the networks are presented in Figure 4A. Following this step, the time evolution of dynamic connectivity in each network is given by the following: Mj(t) = a. f1j(t) + b. f2j(t); f1j(t) is the modulation function, which was represented by the Hanning window of unit amplitude; f2j(t) represents uncorrelated Gaussian noise added to the simulated time courses; and a and b are scalar values set to 0.45 and 0.15 as in O’Neill, Tewarie, Colclough, et al. (2017). In our study, Mj(t) is sampled at 3.3 Hz (to obtain a sliding window of 0.3 s as in real data). The onset as well as the duration of each module structure is illustrated in Figure 4B. We then combined the four network matrices in order to generate a single adjacency matrix at each time point t over a time course spanning 60 s. As a ﬁnal step, we added a random Gaussian noise to the adjacency tensor, and the standard deviation of the noise was allowed to vary between 0.2 and 0.5. Validation On simulated data, we evaluated the performance of the algorithm by computing the simi- larity between the reconstructed and the simulated (reference) networks, taking into account both spatial and temporal similarities. The spatial similarity is given by the z-score of Rand coefﬁcient between the simulated and the constructed modular structures, while the temporal similarity represents the rate of the correct afﬁliation of time windows. In addition, we have compared our algorithm with three methods originally developed to identify the brain states without looking at their modular structures. The three methods are K-means clustering as applied by Allen et al. (2014), independent component analysis as suggested by O’Neill, Tewarie, Colclough, et al. (2017), and the consensus clustering algorithm proposed by Rasero et al. (2017). For each method, we followed the same pipeline adapted by the authors. To ultimately obtain the modular brain states, we preceded the analysis by decomposing each connectivity state to modules using the consensus modularity approach as detailed in the Categorial Version section. Real Data In order to track the brain network dynamics effectively, we particularly tested our method using electro- and magnetoencephalography (EEG/MEG), which allow the tracking of brain dynamics on a subsecond timescale, a resolution not reachable using other techniques such as functional magnetic resonance imaging (fMRI; Cohen, 1972; Nunez & Srinivasan, 2007; Penﬁeld & Jasper, 1954). Network Neuroscience 884 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Detecting modular brain states in rest and task l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 4. The simulation scenario. (A) Left: The adjacency matrix Pj of the constructed networks. Right: The 3-D cortical presentation of the modular structures of the simulated networks. (B) The time axis showing the beginning and the end of each network Mj (which was generated by combining Pj to uncorrelated noise). Thus, three M/EEG datasets were analyzed. Before applying the algorithm, we reconstucted the functional brain networks at the level of the cortex using an emerging technique called EEG source connectivity (Chavez et al., 2013; De Vico Fallani et al., 2008; De Vico Fallani, Latora, & Chavez, 2017; De Vico Fallani, Richiardi, Chavez, & Achard, 2014; Hassan, Shamas, Khalil, Network Neuroscience 885 Detecting modular brain states in rest and task El Falou, & Wendling, 2015; Hassan & Wendling, 2018; Kabbara et al., 2017; Lai, Demuru, Hillebrand, & Fraschini, 2018; Schoffelen & Gross, 2009). In order to remove any bias from our analysis, we have generated the dynamic functional connectivity matrices according to how they were computed in the three previous studies that interpreted the data (Hassan, Benquet, et al., 2015; Hassan et al., 2017; O’Neill, Tewarie, Colclough, et al., 2017) The aim of this work is to test whether the modular states generated by our algorithm match the ﬁndings obtained in the literature. Previously used in O’Neill Dataset 1: Self-paced motor task for healthy participants (MEG data). et al. (2015); O’Neill, Tewarie, Colclough, et al. (2017), and Vidaurre et al. (2016), this dataset includes 15 participants (9 male, 6 female) asked to press a button using the index ﬁnger of their dominant hand, once every 30 s. Using a 275-channel CTF MEG system (MISL; Coquitlam, BC, Canada), MEG data were recorded at a sampling rate of 600 Hz. MEG data were coreg- istered with a template MRI. The cortex was parcellated using the Desikan-Killiany atlas (68 regions; Desikan et al., 2006). The preprocessing, the source reconstruction, and the dynamic functional connectivity computations were performed similarly to those in O’Neill, Tewarie, Colclough, et al. (2017). Brieﬂy, the preprocessing comprises the exclusion of trials (t = −12s → 12s) contaminated by noise. Then, source time courses were reconstructed using a beamforming approach (please refer to O’Neill, Tewarie, Colclough, et al., 2017, for more details). Afterwards, the regional time series were symmetrically orthogonalized following the method proposed in Colclough, Brookes, Smith, & Woolrich (2015) to remove the effects of “signal leakage.” The amplitude envelopes of the time courses were obtained using a Hilbert transform. Finally, the dynamic connectivity was estimated by the Pearson correlation measure using a sliding window approach of 6 s of length. The sliding window was shifted by 0.5 s over time. The number of connectivity matrices obtained for each trial was then 49. A statistical threshold (FDR) approach was used to threshold the matrices (Genovese, Lazar, & Nichols, 2002). This yields to a set of connectivity matrices that are thresholded and weighted. Then, the consecutive scheme of the proposed method was tested. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Twenty-one right-handed Dataset 2: Picture naming task for healthy participants (dense-EEG data). healthy subjects (11 women and 10 men) with no neurological disease participated in this study. In a session of about 8 min, each participant was asked to name 148 displayed pictures on a screen using E-Prime 2.0 software (Psychology Software Tools, Pittsburgh, PA; Schneider, Eschman, & Zuccolotto, 2002). Oral responses were recorded to set the voice onset time. This study was approved by the National Ethics Committee for the Protection of Persons (CPP), ConneXion study, agreement number 2012-A01227-36, and promoter, Rennes University Hos- pital. All participants provide their written informed consent to participate in this study. A typi- cal trial started with the appearance of an image during 3 s followed by a jittered interstimulus interval of 2 or 3 s randomly. Errors in naming were discarded from the analysis. A total of 2,926 on 3,108 events were considered. Dense-EEG data were recorded using a system of 256 electrodes (EGI, Electrical Geodesic, Inc.). EEGs were collected at 1 kHz sampling frequency and bandpass ﬁltered between 3 and 45 Hz. The preprocessing and the computation of the functional connectivity followed the same pipeline applied in Hassan, Benquet, et al. (2015). In brief, each trial (t = 0 → 600 ms) was visually inspected, and epochs contaminated by eye blinks, muscle movements, or other noise sources were rejected. As described in the previous study (Hassan, Benquet, et al., 2015), the source connectivity method was performed using the wMNE/PLV (phase locking value) combination, and the dynamic functional connectivity was computed at each millisecond. 886 Phase locking value: A measure used to quantify the statistical coupling, in term of phase synchrony, between two time series. Network Neuroscience Detecting modular brain states in rest and task Resting state: An experimental paradigm in which the subject is asked to relax and to do nothing. Authors also used the Destrieux atlas subdivided into 959 regions (Hassan, Benquet, et al., 2015). To remove spurious connections from the dynamic connectivity matrices, we have adopted a statistical threshold based on FDR (Genovese et al., 2002). Finally, a weighted and thresholded connectivity tensor of dimension 959 × 959 × 600 was obtained and analyzed using the consecutive scheme of our algorithm. This dataset includes Dataset 3: Resting state in Parkinson’s disease patients (dense-EEG data). 124 patients with idiopathic Parkinson’s disease deﬁned according to the UK Brain Bank cri- teria for idiopathic Parkinson’s disease (Gibb & Lees, 1988). These patients were separated into three groups: (G1) cognitively intact patients (N = 63); (G2) patients with mild cognitive deﬁcits (N = 46); and (G3) patients with severe cognitive impairment (N = 15). All partic- ipants gave their informed consent to participate in the study, which had been approved by the local institutional review boards (CPP Nord-Ouest IV, 2012-A 01317-36, ClinicalTrials.gov Identiﬁer: NCT01792843). Dense-EEG were recorded with a cap (Waveguard, ANT software BV, Enschede, Netherlands) with 122 scalp electrodes distributed according to the interna- tional system 10-05 (Oostenveld & Praamstra, 2001). Electrode impedance was kept below 10 kΩ. Patients were asked to relax without performing any task. Signals were sampled at 512 Hz and bandpass ﬁltered between 0.1 and 45 Hz. The data were preprocessed according to Hassan et al. (2017) dealing with the same dataset. Brieﬂy, EOG artifact detection and correction was applied following the method developed in Gratton, Coles, & Donchin (1983). Afterwards, epochs with voltage ﬂuctuation between 90 μV and −90 μV were kept. For each participant, two artifact-free epochs of 40-s lengths were selected. This epoch length was used previously and considered as a good compromise between the needed temporal resolution and the reproducibility of the results in resting state (Kabbara et al., 2017). To compute the dynamic functional connectivity, the steps adopted here are the same used in many previous studies (Hassan et al., 2017; Kabbara et al., 2018, 2017). First, EEG data were coregistered with a template MRI through identiﬁcation of the same anatomical landmarks (left and right preauricular points and nasion). Second, the lead ﬁeld matrix was computed for a cortical mesh with 15,000 vertices using the OpenMEEG package (Gramfort, Papadopoulo, Olivi, & Clerc, 2010) available in Brainstorm. The noise covariance was estimated using a 1-min resting segment. After that, the time series of EEG sources were estimated using the wMNE algorithm where the regularization parameter was set according to the signal to noise ratio (λ = 0.1 in our analysis). An atlas-based segmentation approach was used to project EEGs onto an anatomical framework consisting of 68 cortical regions identiﬁed by means of the Desikan-Killiany atlas (Desikan et al., 2006). The dynamic functional connectivity was then computed using a sliding window over which PLV was calculated (Lachaux, Rodriguez, Martinerie, & Varela, 1999). In the previous study (Hassan et al., 2017), the disruptions of the functional connectivity were found in the alpha 2 band (10–13 Hz). For this reason, we con- sidered the same frequency band in our analysis. To obtain a sufﬁcient number of cycles at the 6 given frequency band, we chose the smallest window length that is equal to central frequency , as recommended in Lachaux et al. (1999). This yields a sliding window of 0.52 s. We then adopted a proportional threshold of 10% to maintain only the top 10% of correlation values of the connectivity matrix. These steps produce, for each epoch, a weighted thresholded con- nectivity tensor of dimension N × N × T, where N is the number of ROIs (68 regions) and T is the number of time windows (77 time windows). This tensor is formally equivalent to dynamic functional connectivity matrices, and it was analyzed using the categorical version of the proposed algorithm. Network Neuroscience 887 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Detecting modular brain states in rest and task RESULTS Having the set of connectivity matrices, we ﬁrst applied a community detection algorithm (Louvain method) to decompose each network into modules (i.e., clusters of nodes that are internally strongly connected, but externally weakly connected). The similarity between the temporal modular structures was calculated (Figure 1B). Finally, the modular states (MS) were obtained by applying a community detection algorithm to the similarity matrix (Figure 1C). We propose two different frameworks: (a) “categorical,” where the objective is to ﬁnd the main modular structures, without any interest in their sequential order; and (b) “consecutive,” where the objective is to ﬁnd the modular structures in a successive way. 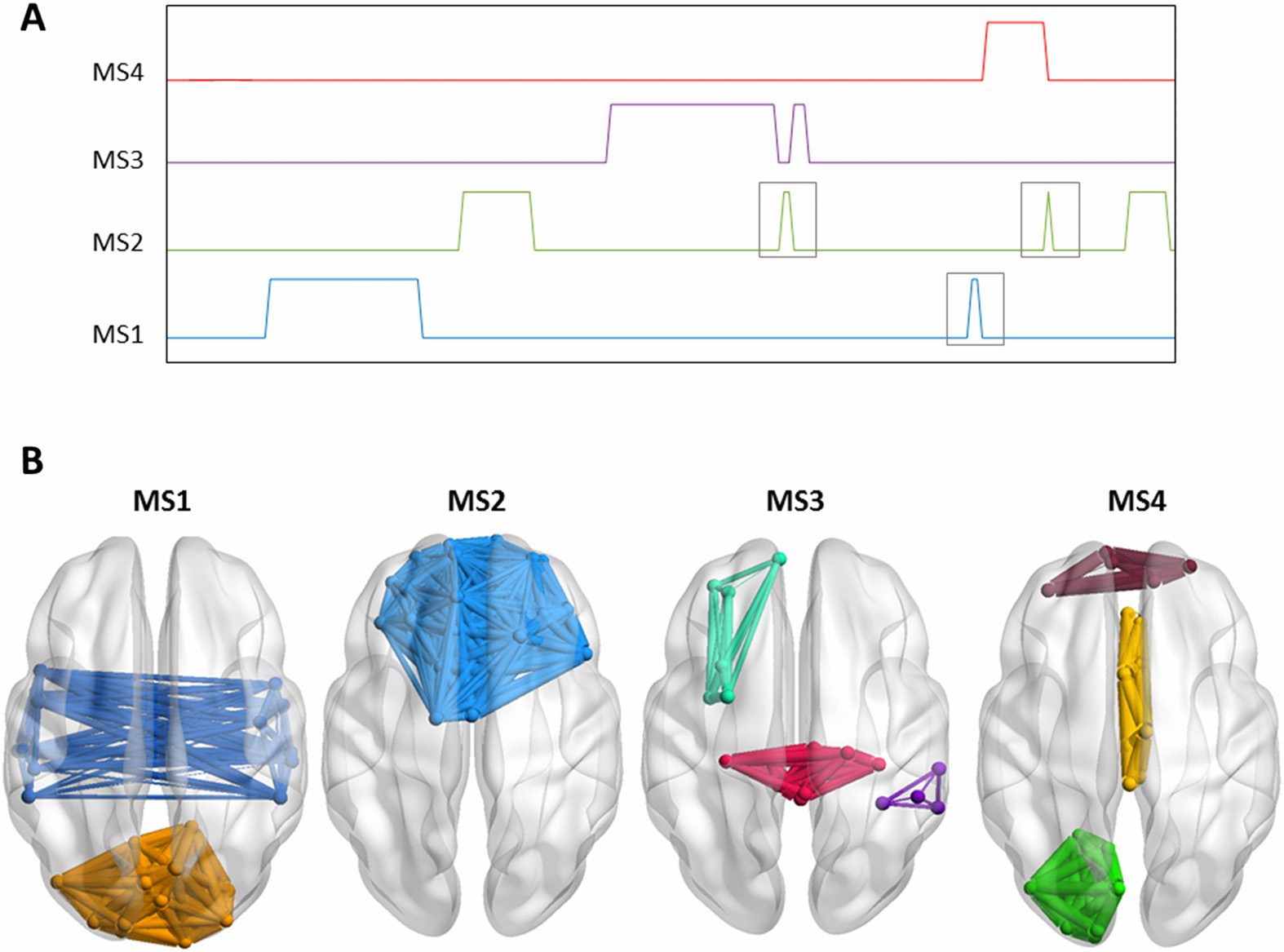Validation on Simulated Data Figure 5 shows the results of the categorical method applied on the dynamic networks gen- erated by the simulation scenario (STDnoise = 0.2). Four modular states were obtained: MS1, MS2, MS3, and MS4. Figure 5A illustrates the modular states’ time courses, showing the most likely state at each time window, while Figure 5B shows the 3-D representation of the MS. Qual- itatively, the four simulated modular structures have been successfully reconstructed. However, one time window that actually belongs to the background (i.e., random) has been wrongly afﬁliated with MS2. Moreover, the MS3 state time course presented two false time window detections: one belongs to MS4, and the other belongs to the background. To quantitatively validate the obtained results, we compared the simulated structures (M1, M2, M3, and M4) with the reconstructed structures (MS1, MS2, MS3, and MS4) in terms of spatial and temporal l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 5. Results of the categorical method applied on simulated data. (A) The time course of the four modular structures reconstructed. The gray square indicates false time window detection. (B) The 3-D representation of the four modular structures’ states. Network Neuroscience 888 Detecting modular brain states in rest and task l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d t . 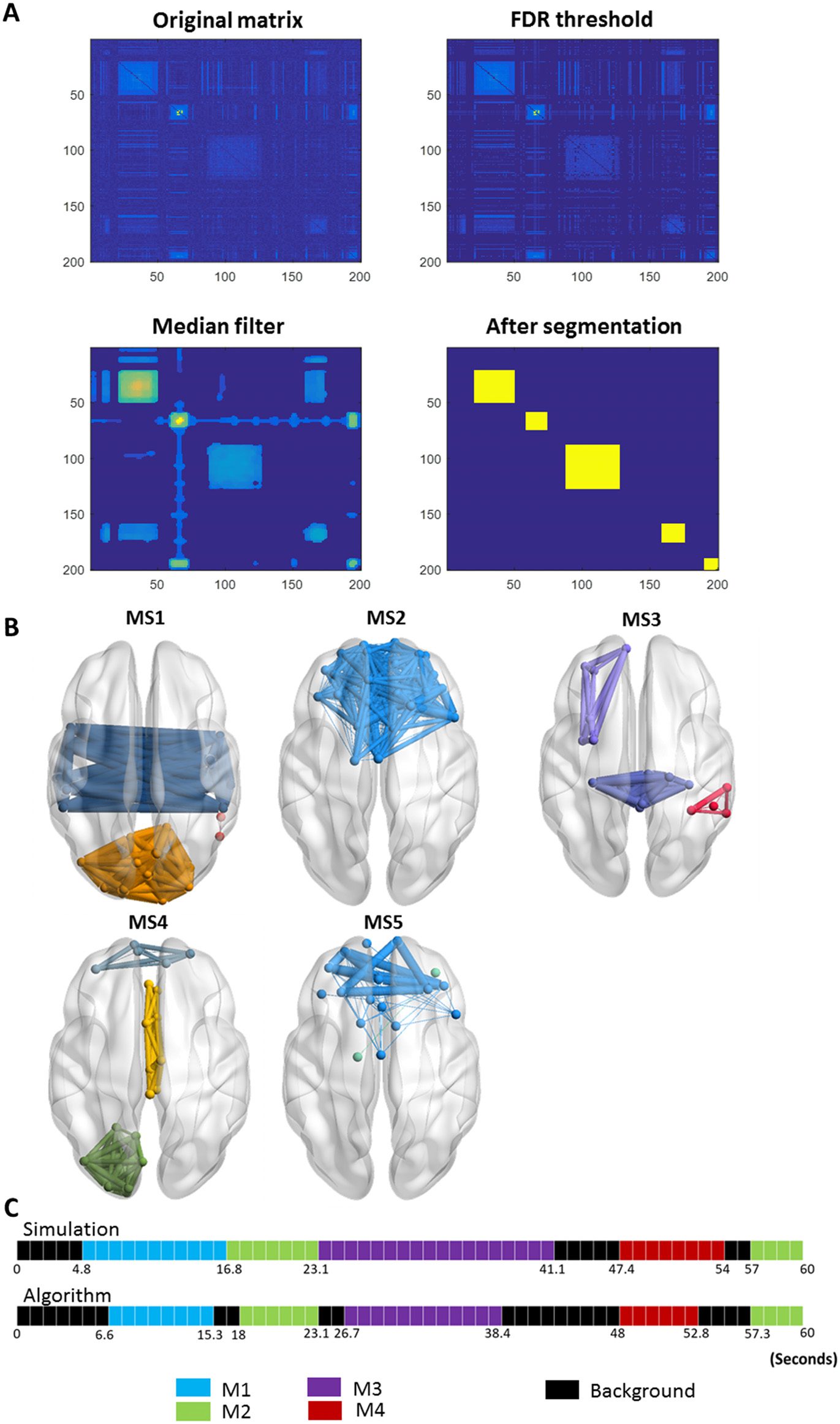f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 6. Results of the consecutive method applied on simulated data. (A) The results of the segmentation algorithm used to derive the consecutive modular structures from the similarity matrix by (1) thresholding the matrix using FDR, (2) applying a median ﬁlter on the thresholded matrix, and (3) extracting the most signiﬁcant segments. (See the Methods section for more details about the consecutive algorithm steps.) (B) The 3-D representation of the ﬁve consecutive modular structures obtained. (C) The difference between the simulated time axis and the obtained time axis. Network Neuroscience 889 Detecting modular brain states in rest and task similarities. The spatial similarities between the simulated and the reconstructed data are 0.99, 0.98, 0.99, and 0.98 for MS1, MS2, MS3, and MS4, respectively. The temporal similarities are 0.79, 0.83, 0.9, and 0.71 for MS1, MS2, MS3, and MS4, respectively. On average, the cate- gorical method achieved spatial accuracy of 98.5% and a temporal accuracy of 80.8%. Using the consecutive method, the algorithm has segmented the similarity matrix yielding to the detection of ﬁve modular states (Figure 6A). Their 3-D representations are shown in Figure 6B. One can remark that MS1 (spatial similarity = 0.94; temporal similarity = 0.88), MS2 (spatial similarity = 0.99; temporal similarity = 0.94), MS3 (spatial similarity = 0.97; temporal similarity = 0.77), MS4 (spatial similarity = 1; temporal similarity = 0.88), and MS5 (spatial similarity = 0.95; temporal similarity = 1) matched, temporally and spatially, the simulated networks generated at the corresponding time windows. In addition, one can remark that the algorithm hasn’t produced false positive results. Globally, the assessed spatial and temporal accuracies are 94% and 83%, respectively. Results corresponding to STDnoise = 0.35; STDnoise = 0.5 are illustrated in the Supporting Information. In brief, results show that using the categorical algorithm, the spatial characteriza- tions of the four modular states were successfully detected. However, the state time course of MS3 failed to detect the second corresponding segment (Figures 1 and 2 in the Supporting In- formation). Using the consecutive algorithm, the ﬁve MSs were temporally detected (Figures 3 and 4 in the Supporting Information). 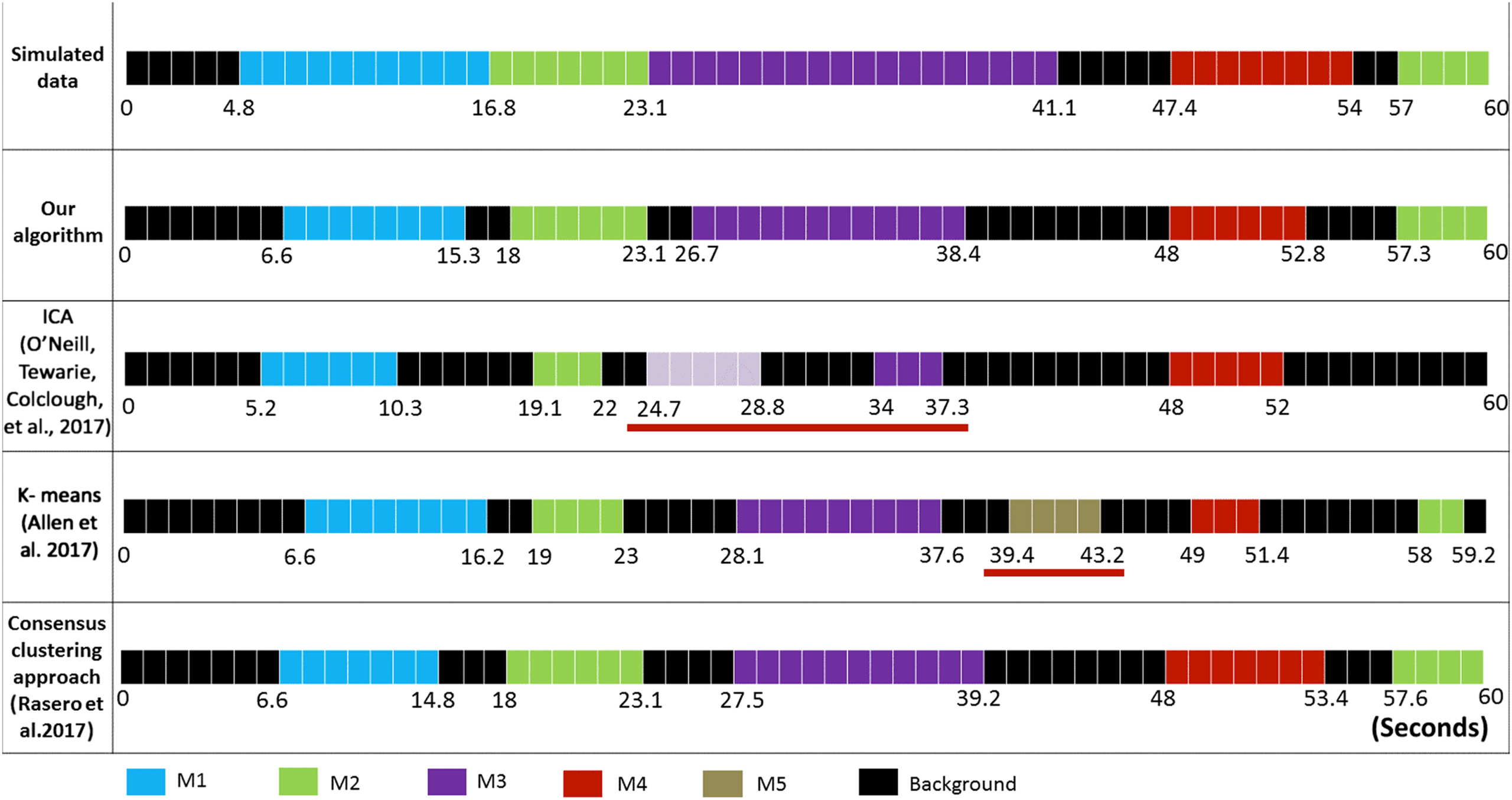The difference between the simulated time axis and the obtained time axis using other differ- ent algorithms is presented in Figure 7. Using ICA (O’Neill, Tewarie, Colclough, et al., 2017), ﬁve independent components (ICs) were detected: IC1, IC2, and IC5 correspond, respectively, l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 7. The difference between the simulated time axis and the obtained time axis using the different algorithms. Network Neuroscience 890 Detecting modular brain states in rest and task Table 1. Temporal similarities between the simulated MSs and those obtained using the different algorithms Algorithm Our algorithm ICA (O’Neill, Tewarie, Colclough, et al., 2017) K-means (Allen et al., 2017) Consensus clustering approach (Rasero et al., 2017) MS1 0.73 0.43 MS2 0.98 0.6 MS3 0.67 0.41 MS4 0.86 0.71 MS5 0.93 0 0.8 0.77 0.53 0.61 0.55 0.68 0.98 0.65 0.79 0.85 False positive rate 0 0 0.07 0 Average temporal similarity 0.83 0.43 0.58 0.79 to M1 (spatial similarity = 0.96; temporal similarity = 0.43), M2 (spatial similarity = 0.85; temporal similarity = 0.60), and M4 (spatial similarity = 0.86; temporal similarity = 0.71). However, M3 (spatial similarity = 0.94; temporal similarity = 0.42) was reﬂected by two sep- arated components: IC3 and IC4. One can realize also that the ICA algorithm failed to detect M2 spanning between 57 ms and 60 ms. Using K-means clustering (Allen et al., 2014), six brain states (BSs) were generated. BS1, BS2, BS3, BS5, and BS6 correspond, respectively, to M1 (spatial similarity = 0.96; temporal similarity = 0.8), M2 (spatial similarity = 0.94; tem- poral similarity = 0.77), M3 (spatial similarity = 0.97; temporal similarity = 0.53), M4 (spatial similarity = 1; temporal similarity = 0.61), and M5 (spatial similarity = 0.99; temporal similar- ity = 0.55). While the ﬁve simulated modular states were reconstructed, a false time win- dow detection was captured (BS4). Regarding the consensus clustering algorithm proposed by Rasero et al. (2017), the algorithm succeeded to detect the ﬁve simulated states. Tables 1 and 2 report the temporal and spatial similarities between the simulated MSs and those obtained us- ing the different algorithms. Overall, results show that our algorithm reached the highest tem- poral detection accuracy (0.83) compared with ICA (0.43), K-means clustering (0.58), and the consensus clustering (0.79). Spatially, our algorithm procured a good spatial similarity (0.97), outperforming ICA (0.72) and the consensus clustering algorithms (0.91). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d . t Task-related paradigm: An experimental paradigm in which the subject is asked to focus on a speciﬁc function. 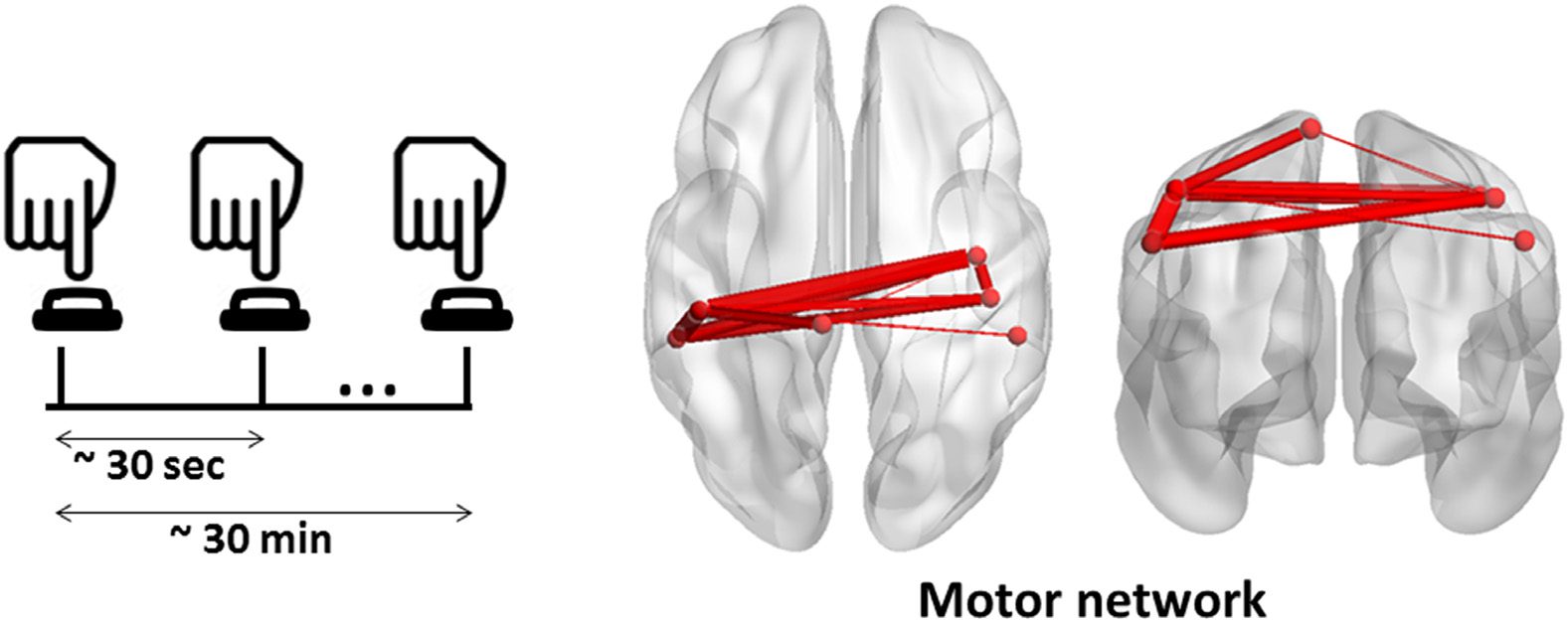Real Data As the considered dataset Dataset 1: Self-paced motor task for healthy participants (MEG data). is collected during a task-related paradigm, our objective was to follow the spatiotemporal organization of the dynamic brain networks during time (from the stimulus onset to the reaction time). Thus, we applied the consecutive algorithm to track the MSs in a successive way. The input of the algorithm is the tensor of dynamic connectivity matrices averaged over all trials and subjects. The same dataset and methods were previously used in O’Neill et al. (2015), O’Neill, Tewarie, Colclough, et al. (2017), and Vidaurre et al. (2016). The algorithm results in f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Table 2. Spatial similarities between the simulated MSs and those obtained using the different algorithms Algorithm Our algorithm ICA (O’Neill, Tewarie, Colclough, et al., 2017) K-means (Allen et al., 2017) Consensus clustering approach (Rasero et al., 2017) MS1 0.94 0.96 0.96 0.92 MS2 0.99 0.85 0.94 0.96 MS3 0.97 0.94 0.97 0.89 MS4 1 0.86 1 0.91 MS5 0.95 0 0.99 0.89 Average spatial similarity 0.97 0.72 0.99 0.91 Network Neuroscience 891 Detecting modular brain states in rest and task Figure 8. The MS of the MEG motor task obtained using the consecutive method. one signiﬁcant MS found between −0.5 s and 1.5 s (Figure 8). As illustrated, this module impli- cates the sensory motor area, the post- and precentral regions of both hemispheres. The objective of using Dataset 2: Picture naming task for healthy participants (dense-EEG data). this dataset was to track the fast space/time dynamics of functional brain networks at subsecond timescale from the onset (presentation of the visual stimuli) to the reaction time (articulation). Hence, the consecutive version was applied on the dynamic connectivity matrices averaged over subjects. 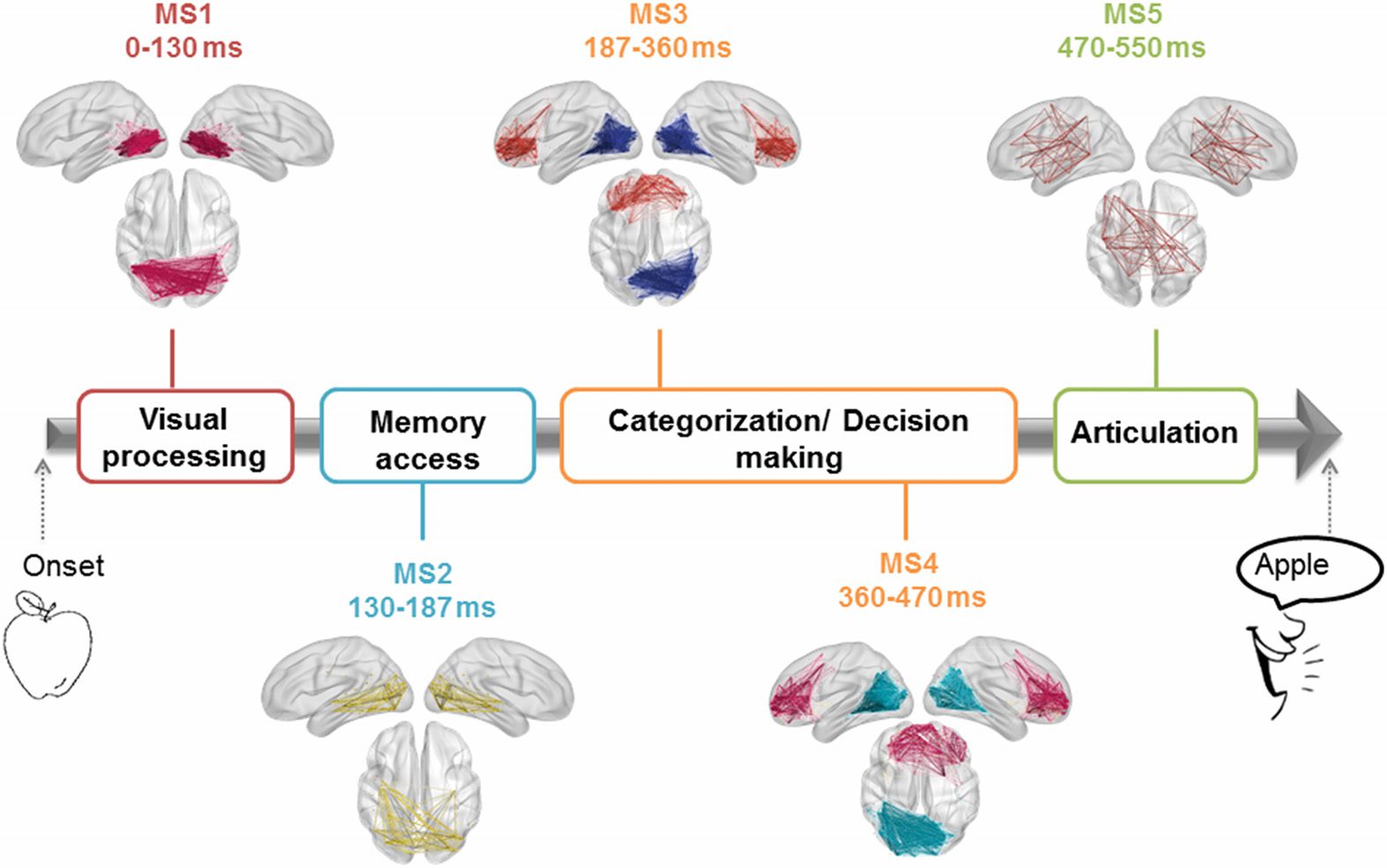Figure 9 shows the results, revealing that the cognitive process can be divided into ﬁve modular structures: The ﬁrst MS corresponds to the time period ranging from the stimulus onset l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 9. The sequential MSs of the EEG picture naming task obtained using the consecutive method and their corresponding cognitive functions. Network Neuroscience 892 Detecting modular brain states in rest and task to 130 ms and presents one module located mainly in the occipital region. The second MS is observed between 131 and 187 ms, and involves one module showing occipitotemporal connections. The third MS is identiﬁed between 188 and 360 ms, and illustrates a module located in the occipitotemporal region, and another module located in the frontocentral region. This structure was then followed by a fourth MS, found over the period 361–470 ms. MS4 was very similar to the previous MS but with additional frontocentral connections. The last MS is observed between 471 and 500 ms, and it shows a module connecting the frontal, central, and temporal regions. It is worth noting that these MSs denote the transitions from the visual processing and recognition to the semantic processing and categorization to the preparation of the articulation process (Hassan, Benquet, et al., 2015; VanRullen & Thorpe, 2001). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d t . 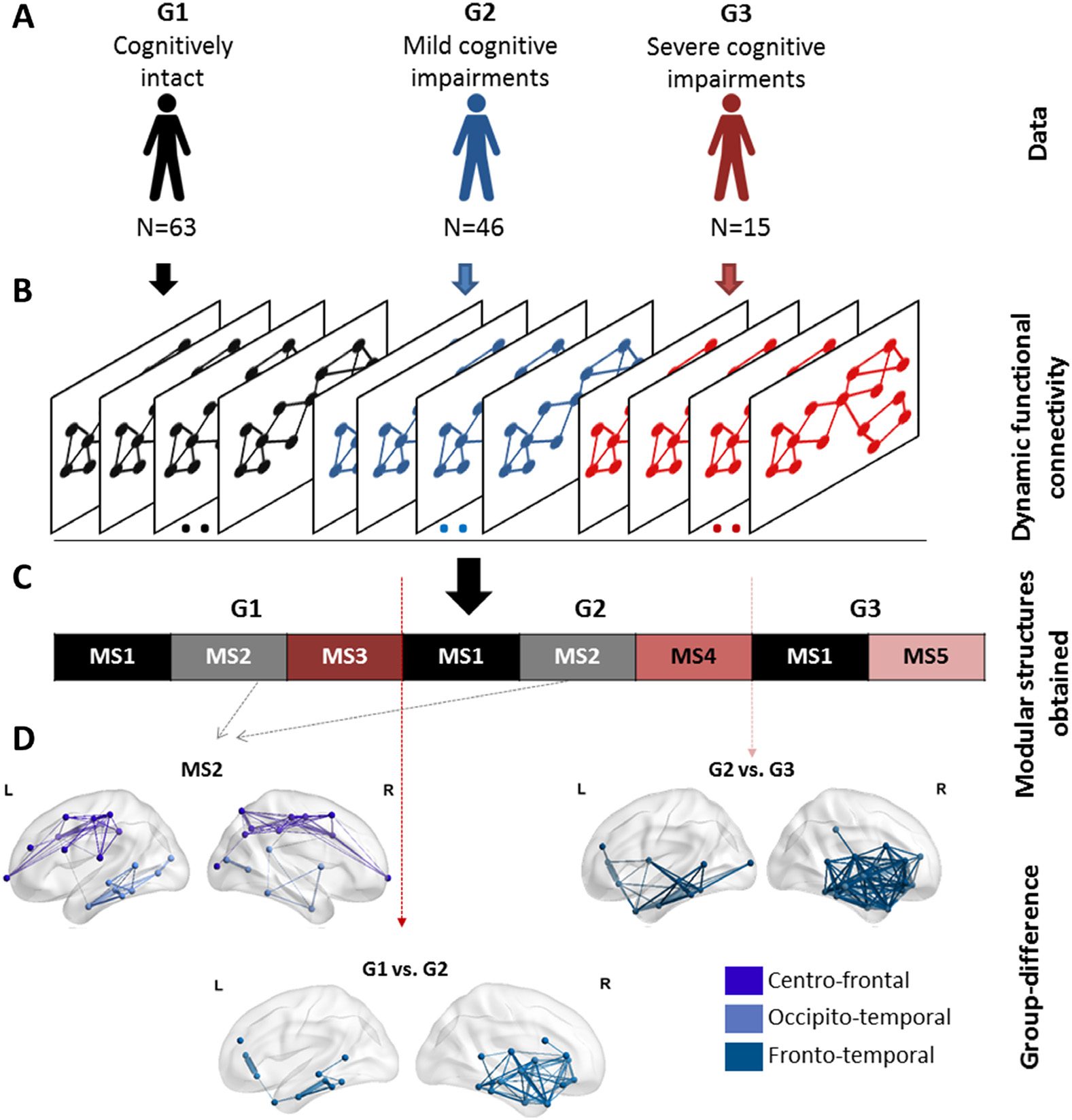f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 10. The analysis pipeline and the results of the categorical method applied on the Parkinson’s disease EEG dataset. (A) The dataset composed of 124 patients partitioned into three groups: (G1) cognitively intact patients (N = 63), (G2) patients with mild cognitive deﬁcits (N = 46), and (G3) pa- tients with severe cognitive impairment (N = 15). (B) The functional dynamic connectivity matrices of the three groups concatenated over time. (C) The ﬁve modular structures obtained after applying the categorical algorithm on the concatenated tensor. (D) The modular differences between G1 and G2, G1 and G3, and G2 and G3. Network Neuroscience 893 Detecting modular brain states in rest and task Dataset 3: Resting state in Parkinson’s disease patients (dense-EEG data). Our objective here was to identify the modular structures that are common between G1, G2, and G4, and those that are speciﬁc to each group. As the sequential order of MSs is not intended, we applied the cat- egorical version of the proposed algorithm. The latter takes as input the concatenation of the dynamic connectivity matrices of the three groups. This will form a single data tensor of dimen- sion N × N × T, where N is the number of ROIs and T is equal to the number of time windows × the number of patients (Figure 10). The algorithm was then applied to validate the usefulness of the categorical version in detecting the modular alterations between G1, G2, and G3. 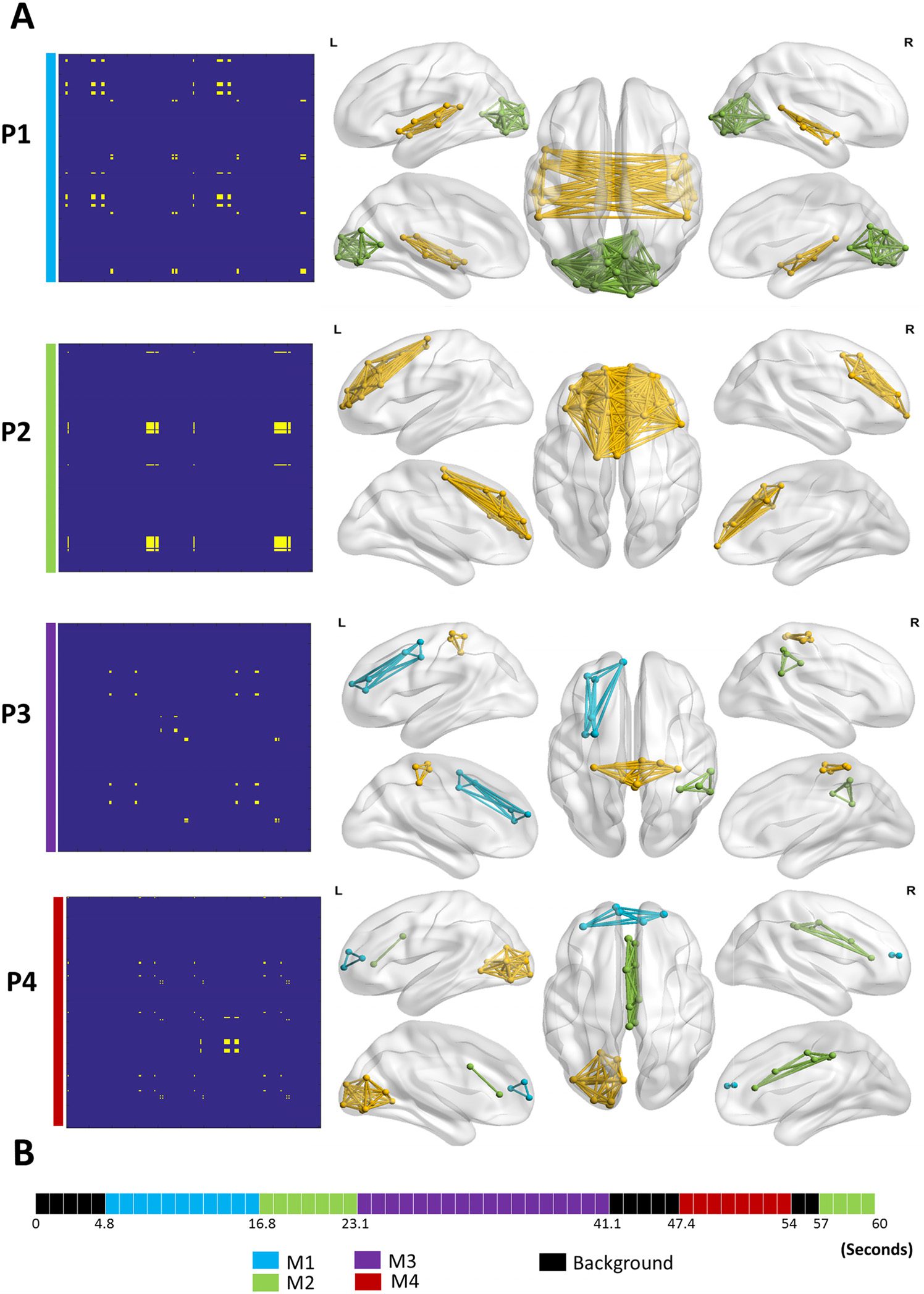Results are illustrated in Figure 10. Five modular structures were identiﬁed (MS1, MS2, MS3, MS4, and MS5). Three MSs were found for G1 and G2. However, the number of MSs decreased from three to two MSs in G3. Results revealed that MS1 was found to be present in the three groups, while MS2 was present only in G1 and G2. The modular structure MS2 (absent in G3) is illustrated in Figure 10 and includes two modules involving mainly frontocentral and occipitotemporal connections. The difference between G1 and G2 was reﬂected by the absence of the structure MS3 replaced by the structure MS4 in G2. Results in Figure 10 show that the difference concerns mainly the frontotemporal connections. The difference between G2 and G3 was reﬂected by the absence of the structure MS4 from G2 and the presence of the structure MS5 in G3. Figure 10 shows that the functional disruptions between G2 and G3 are mainly frontotemporal connections. It is worth noting that the frontotemporal disruptions were widely reported in mild cognitive impairments (Beyer, Janvin, Larsen, & Aarsland, 2007; de Haan et al., 2012; Song et al., 2011; Zhang et al., 2009), while the central disruptions are widely observed in severe cognitive impairments (Hassan et al., 2017) and dementia (Song et al., 2011). DISCUSSION In this paper, we have developed a novel framework to explore the fast reconﬁguration of the functional brain networks during rest and task. This new method can be used to track the sequential evolution of brain modules during a task-directed paradigm or to identify the modular brain states that arise at rest. The simulation-based analysis showed the ability of the method to “reestimate” the modular network structures over time. Compared with other methods, our proposed algorithm reached the highest temporal accuracy detection and a very good spatial accuracy. The new framework was validated on three different EEG/MEG datasets: (a) MEG data recorded from 15 healthy subjects during a self-paced motor task, (b) dense-EEG data recorded from 21 healthy subjects during a picture naming task, and (c) dense-EEG data recorded at rest from 124 Parkinson’s disease patients with different cognitive phenotypes. Results show that our method can track the fast modular states of the human brain network at a subsecond timescale, and also highlight its potential clinical applications, such as the detection of the cognitive decline in Parkinson’s disease. “Categorical” and “Consecutive” Processing Schemes The two processing schemes proposed here are both derived from the similarity matrix between the temporal modules (Steps 1 to 3 in the Methods section). However, each version highlights a speciﬁc characterization of the modular structures, which can then be exploited depend- ing on the application (time/condition dependent). In particular, the results of the categorical algorithm on the simulated data reveal high spatial resolution and relatively low temporal resolution compared with those obtained using the consecutive algorithm. The low temporal Network Neuroscience 894 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Detecting modular brain states in rest and task resolution of the categorical version is reﬂected by the false (Figure 5) as well as the missed time windows detection (Figures 1 and Figure 2 in the Supporting Information). In contrast, these time windows were correctly detected by the consecutive version despite their short length (Figure 6, and Supporting Information Figures 3 and 4). Yet, the low spatial resolution of the consecutive version can be illustrated by MS5 (Figure 6, and Supporting Information Figures 3 and 4) that should represent M2 (Figure 4). This is probably due to the categorical version using the maximum number of available data points to generate their corresponding MS, while the consecutive version treats each temporal segment solely. We suggest using the consecutive version where sequential order of MSs is interesting to in- vestigate, such as the tracking of cognitive tasks. When the temporal aspects are not necessary, we would recommend the categorical version. Tracking of Fast Cognitive Functions The brain dynamically reconﬁgures its functional network structure on subsecond temporal scales to guarantee efﬁcient cognitive and behavioral functions (O’Neill, Tewarie, Vidaurre, et al., 2017). Tracking the spatiotemporal dynamics of large-scale networks over this short time dura- tion is a challenging issue (Allen et al., 2014; Hutchison et al., 2013). In this paper, we aimed to examine how fast changes in the modular architecture shape information processing and distribution in (a) motor tasks and (b) picture naming tasks. Concerning the self-paced motor task, it is a simple task where only motor areas are ex- pected to be involved over time. Our results indeed showed that the motor module is clearly elucidated related to the tactile movement of the button press. The spatial and temporal fea- tures of the obtained module are very close to the signiﬁcant component obtained by O’Neill, Tewarie, Colclough, et al. (2017) using the temporal ICA method. The different MSs obtained in the EEG picture naming task are temporally and spatially anal- ogous to the network brain states detected using other approaches such as K-means clustering by Hassan, Benquet, et al. (2015). In particular, the ﬁrst MS representing the visual network is probably modulated by the visual processing and recognition processes (Thorpe, Fize, & Marlot, 1996; VanRullen & Thorpe, 2001). The second MS reﬂects the memory access re- ﬂected by the presence of the occipital-temporal connections (Martin & Chao, 2001). In other words, the brain tries to retrieve the information related to the picture illustrated from memory (Martin & Chao, 2001). In the third and the fourth MSs, we notice the implication of a sep- arated frontal module. This module may be related to the object category recognition (tools vs. animals) and the decision-making process (Andersen & Cui, 2009; Clark & Manes, 2004; Rushworth, Noonan, Boorman, Walton, & Behrens, 2011). After making the decision, speech articulation and the naming process is prepared and started (Dronkers, 1996). This is reﬂected by the MS5 that combines the frontal, the motor, and the temporal brain areas. Modular Brain States and Cognitive Phenotypes in Parkinson’s Disease Emerging evidence shows that Parkinson’s disease (PD) is associated with alteration in struc- tural and functional brain networks (Fornito, Zalesky, & Breakspear, 2015). Hence, from a clinical perspective, the demand is high for a network-based technique to identify the patho- logical networks and to detect early cognitive decline in PD. Here, we used a dataset with a large number (N = 124) of PD patients categorized into three groups in terms of their cogni- tive performance: G1, cognitively intact patients; G2, patients with mild to moderate cognitive Network Neuroscience 895 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Detecting modular brain states in rest and task deﬁcits; and G3, patients with severe cognitive deﬁcits in all cognitive domains. See Dujardin et al. (2015), Hassan et al. (2017), and Lopes et al. (2017) for more information about this database. The obtained MSs presented in Figure 10 show that while some MSs remain unchangeable during cognitive decline from G1 to G3, others are altered and replaced by new MSs. More speciﬁcally, the number of MSs detected in G3 has decreased compared with G1 and G2; MS3 in G1 was replaced by MS4 in G2, while MS4 in G2 was replaced by MS5 in G3. In addition, the alterations in G3 involve more distributed modules (central, frontotemporal) than the alterations occurring between G1 and G2 (frontotemporal modules) where the impairment still moderate. Interestingly, the underlying modular differences between the MSs of groups are con- sistent with the previously reported studies that explored the network changes in PD (Beyer et al., 2007; Bosboom, Stoffers, Wolters, Stam, & Berendse, 2009; de Haan & Pijnenburg, 2009; Hassan et al., 2017; Song et al., 2011; Zhang et al., 2009). Particularly, the loss of fron- totemporal connections in PD is supported by several EEG and MEG studies (Bosboom et al., 2009; Hassan et al., 2017; Zhang et al., 2009). Similarly, results of structural MRI studies reveal frontal and temporal atrophies in PD with mild cognitive impairment (Beyer et al., 2007; Song et al., 2011). Other functional (de Haan et al., 2012) and structural (Zhang et al., 2009) studies showed that Alzheimer’s disease networks are characterized by frontotemporal alterations. In addition, the brain regions involved in the modular alterations in G3 found in our study are in line with ﬁndings obtained by EEG edgewise analysis (Hassan et al., 2017), and by structural MRI studies showing widespread atrophy associated with PD patients’ related dementia (Song et al., 2011). Methodological Considerations First, we used a template anatomical image generated from MRIs of healthy controls for EEG/ MEG source functional connectivity analysis. The template-based method is common practice in the absence of individual anatomical images and was previously employed by multiple EEG and MEG source reconstruction studies, because of nonavailability of native MRIs (Hassan et al., 2017; Kabbara et al., 2018; Lopez et al., 2014). Furthermore, a recent study showed that there are few potential biases introduced during the use of a template MRI compared with individual MRI coregistration. Second, the connectivity matrices in Dataset 3 (Parkinson’s disease analysis) were thresh- olded by keeping the highest 10% of the edge’s weights. According to previous studies, the 10% threshold provides an optimal trade-off between retaining the true connections and reduc- ing spurious connections (Lord, Horn, Breakspear, & Walter, 2012). However, the consistency of results across a range of proportional thresholds would be interesting to consider. In con- trast, a statistical threshold (FDR) approach was used in Dataset 1 (self-paced motor tasks) and Dataset 2 (picture naming); see Methods. The reason is that in Dataset 3, three groups were compared. The proportional threshold approach, compared with other threshold approaches, ensures equal density between the analyzed groups (van den Heuvel et al., 2017). More- over, studies suggest that FDR controlling procedures are effective for the analysis of neuro- imaging data in the absence of intergroup comparison (Bassett et al., 2013; Genovese et al., 2002; Patel & Bullmore, 2016). One should also note that other strategies and criteria could be used to objectively threshold the connectivity matrices, such as the minimum spanning tree metric (Tewarie, van Dellen, Hillebrand, & Stam, 2015) and the efﬁciency cost optimization (De Vico Fallani et al., 2017). EEG/MEG source connectivity: A method used to estimate functional brain networks at the cortical level using EEG/MEG sensors. Network Neuroscience 896 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Detecting modular brain states in rest and task Third, according to the consecutive algorithm, it is noteworthy that two parameters should be adequately tuned to obtain relevant results: (a) the accuracy parameter a, and (b) the min- imal length allowed for a state jmin. In particular, the accuracy parameter a will dramatically affect the number and the temporal accuracy of detected states. Thus, it should be appropriately selected. A high value may eliminate strong and signiﬁcant similarity values in a low-average matrix, whereas a low value may overemphasize weak similarity values in high-average con- nectivity networks. Thus, we recommend choosing an adaptive value determined based on the distribution of the similarity matrix. For this reason, the use of the average value is proposed. In order to evidence our choice, we illustrate, based on simulated data with different noise levels, the number of detected MSs as well the temporal accuracy as a function of a (Figures 5, 6, and 7 in the Supporting Information). In all cases, results show that the average value of the similarity matrix provides the exact number of MSs and a good temporal accuracy. Concerning the second parameter, jmin, it will depend on the way in which the connectivity matrices are computed. In the case where the connectivity is calculated over a time window that guarantees a sufﬁcient number of data points, there is no need to set a minimal length for a state (jmin = 1). In contrast, when a connectivity matrix is computed at each millisecond, one may restrict the length of a state to be less than a speciﬁc number of milliseconds. As an example, Mheich, Hassan, Khalil, Berrou, & Wendling (2015) suggested to reject a brain state that has a time interval less than 30 ms. In our study, jmin was set to 1 time window in simulated data, Dataset 1 and Dataset 3, since an optimal sliding window was used. In Dataset 2, where a connectivity matrix based on the PLV metric was computed each millisecond, jmin was set equal to 30 ms, as proposed by Mheich et al. (2015). Fourth, we are aware that spurious correlations caused by the problem of “source leakage” should be carefully considered. Here, we have adopted in each dataset the same pipeline (from data processing to network construction) used by the previous studies dealing with the same dataset. Thus, for the MEG dataset, the correction for source leakage was performed by the symmetric orthogonalization method proposed by Colclough et al. (2015). Using the same pipeline also helps to avoid inﬂuencing factors caused by changing the source connectivity method, the number of ROIs, the connectivity measure, or the sliding window length. By rely- ing on previous studies (Hassan, Benquet, et al., 2015; Hassan et al., 2017; O’Neill, Tewarie, Colclough, et al., 2017), we provide appropriate input—already tested and validated—to the algorithm, regardless of how it was obtained. The source leakage issue was extensively dis- cussed in a very recent review about M/EEG source-space networks (Hassan & Wendling, 2018). In addition, a quantitative comparison presented in the paper was performed between our algorithm, K-means clustering as proposed by Allen et al. (2014), independent component analysis as proposed by O’Neill, Tewarie, Vidaurre, et al. (2017), and the consensus cluster- ing algorithm as proposed by Rasero et al. (2017). Nevertheless, other strategies that showed accurate results in previous studies could be also investigated and compared, such as the use of a hidden Markov model (HMM), which models the cortical time series using a probabilis- tic generative model (Vidaurre et al., 2017), or the use of a multivariate autoregressive model (De Vico Fallani et al., 2008). ACKNOWLEDGMENTS This work has received a French government support granted to the CominLabs excellence laboratory and managed by the National Research Agency in the “Investing for the Future” program under reference ANR-10-LABX-07-01. It was also ﬁnanced by the Rennes University Network Neuroscience 897 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Detecting modular brain states in rest and task Hospital (COREC Project named conneXion, 2012-14). This work was ﬁnanced by the Azm Center for Research in Biotechnology and Its Applications. GCO is funded by a Medical Research Council New Investigator Research Grant (MR/M006301/1). This study was also sup- ported by the Future Emerging Technologies (H2020-FETOPEN-2014-2015-RIA under agree- ment No. 686764) as part of the European Union’s Horizon 2020 research and training program 2014–18. The study was also funded by the National Council for Scientiﬁc Research (CNRS) in Lebanon. AUTHOR CONTRIBUTIONS Aya Kabbara: Conceptualization; Formal analysis; Methodology; Software; Validation; Visu- alization; Writing - Original Draft. Mohamad Khalil: Funding acquisition. Georges O’Neill: Data curation. Kathy Dujardin: Data curation. Youssof El Traboulsi: Methodology. Fabrice Wendling: Funding acquisition. Mahmoud Hassan: Conceptualization; Formal analysis; Super- vision; Writing - Original Draft. FUNDING INFORMATION Fabrice Wendling, Rennes University Hospital (http://dx.doi.org/10.13039/501100001665), Award ID: ANR-10-LABX-07-01. Mohamad Khalil, National Council for Scientiﬁc Research. Georges O’Neill, Medical Research Council, Award ID: MR/M006301/1. Fabrice Wendling, Hôpital de rennes1, Award ID: COREC Project named conneXion, 2012–14. REFERENCES Allen, E. A., Damaraju, E., Eichele, T., Wu, L., & Calhoun, V. D. (2017). EEG signatures of dynamic functional network connec- tivity states. Brain Topography, 1–16. https://doi.org/10.1007/ s10548-017-0546-2 Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele, T., & Calhoun, V. D. (2014). Tracking whole-brain connectivity dy- namics in the resting state. Cerebral Cortex, 24, 663–676. https:// doi.org/10.1093/cercor/bhs352 Andersen, R. A., & Cui, H. (2009). Intention, action planning, and decision making in parietal-frontal circuits. Neuron. https://doi. org/10.1016/j.neuron.2009.08.028 Baker, A. P., Brookes, M. J., Rezek, I. A., Smith, S. M., Behrens, T., Smith, P. J. P., & Woolrich, M. (2014). Fast transient networks in spontaneous human brain activity. eLife. https://doi.org/10.7554/ eLife.01867 Bassett, D. S., Porter, M. A., Wymbs, N. F., Grafton, S. T., Carlson, J. M., & Mucha, P. J. (2013). Robust detection of dynamic com- munity structure in networks. Chaos, 23. https://doi.org/10.1063/ 1.4790830 Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson, J. M., & Grafton, S. T. (2011). Dynamic reconﬁguration of hu- man brain networks during learning. Proceedings of the National Academy of Sciences, 108, 7641–7646. https://doi.org/10.1073/ pnas.1018985108 Bassett, D. S., Yang, M., Wymbs, N. F., & Grafton, S. T. (2015). Learning-induced autonomy of sensorimotor systems. Nature Neuroscience, 18, 744–751. https://doi.org/10.1038/nn.3993 Beyer, M. K., Janvin, C. C., Larsen, J. P., & Aarsland, D. (2007). A magnetic resonance imaging study of patients with parkin- son’s disease with mild cognitive impairment and dementia using voxel-based morphometry. Journal of Neurology, Neuro- surgery, and Psychiatry, 78, 254–259. https://doi.org/jnnp.2006. 093849[pii]\r10.1136/jnnp.2006.093849 Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Jour- nal of Statistical Mechanics: Theory and Experiment, 10008, 6. https://doi.org/10.1088/1742-5468/2008/10/P10008 Bola, M., & Sabel, B. A. (2015). Dynamic reorganization of brain func- tional networks during cognition. NeuroImage, 114, 398–413. https://doi.org/10.1016/j.neuroimage.2015.03.057 Bosboom, J. L. W., Stoffers, D., Wolters, E. C., Stam, C. J., & Berendse, H. W. (2009). MEG resting state functional con- Journal of nectivity in Parkinson’s disease related dementia. Neural Transmission,116,193–202. https://doi.org/10.1007/s00702- 008-0132-6 Chavez, M., De Vico Fallani, F., Valencia, M., Artieda, J., Mattia, D., Latora, V., & Babiloni, F. (2013). Node accessibility in cor- tical networks during motor tasks. Neuroinformatics. https://doi. org/10.1007/s12021-013-9185-2 Clark, L., & Manes, F. (2004). Social and emotional decision-making following frontal lobe injury. Neurocase, 10, 398–403. https:// doi.org/10.1080/13554790490882799 Cohen, D. (1972). Magnetoencephalography: Detection of the brain’s electrical activity with a superconducting magnetome- ter. Science, 175, 664–666. https://doi.org/10.1126/science.175. 4022.664 Colclough, G. L., Brookes, M. J., Smith, S. M., & Woolrich, M. W. (2015). A symmetric multivariate leakage correction for MEG connectomes. NeuroImage, 117, 439–448. https://doi.org/10. 1016/j.neuroimage.2015.03.071 Network Neuroscience 898 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Detecting modular brain states in rest and task Damaraju, E., Allen, E. A., Belger, A., Ford, J. M., McEwen, S., Mathalon, D. H., . . . Calhoun, V. D. (2014). Dynamic functional connectivity analysis reveals transient states of dysconnectivity in schizophrenia. NeuroImage: Clinical, 5, 298–308. https://doi. org/10.1016/j.nicl.2014.07.003 de Haan, W., & Pijnenburg, Y. (2009). Functional neural network analysis in frontotemporal dementia and Alzheimer’s disease us- ing EEG and graph theory. BMC Neuroscience, 10, 101. https:// doi.org/10.1186/1471-2202-10-101 de Haan, W., Van der Flier, W. M., Koene, T., Smits, L. L., Scheltens, P., & Stam, C. J. (2012). Disrupted modular brain dynamics reﬂect cognitive dysfunction in Alzheimer’s disease. NeuroImage, 59, 3085–3093. https://doi.org/10.1016/j.neuroimage.2011.11.055 de Pasquale, F., Della Penna, S., Snyder, A. Z., Marzetti, L., Pizzella, V., Romani, G. L., & Corbetta, M. (2012). A cortical core for dy- namic integration of functional networks in the resting human brain. Neuron, 74, 753–764. https://doi.org/10.1016/j.neuron. 2012.03.031 de Pasquale, F., Della Penna, S., Sporns, O., Romani, G. L., & Corbetta, M. (2015). A dynamic core network and global ef- ﬁciency in the resting human brain. Cerebral Cortex, bhv185. https://doi.org/10.1093/cercor/bhv185 De Vico Fallani, F., Latora, V., Astolﬁ, L., Cincotti, F., Mattia, D., Marciani, M. G., . . . Babiloni, F. (2008). Persistent patterns of in- terconnection in time-varying cortical networks estimated from high-resolution EEG recordings in humans during a simple motor act. Journal of Physics A: Mathematical and Theoretical. https:// doi.org/10.1088/1751-8113/41/22/224014 De Vico Fallani, F., Latora, V., & Chavez, M. (2017). A topo- logical criterion for ﬁltering information in complex brain networks. PLoS Computational Biology. https://doi.org/10.1371/ journal.pcbi.1005305 De Vico Fallani, F., Richiardi, J., Chavez, M., & Achard, S. (2014). Graph analysis of functional brain networks: Practical issues in translational neuroscience. Philosophical Transactions of the Royal Society B: Biological Sciences. https://doi.org/10.1098/ rstb.2013.0521 Desikan, R. S., Sugonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C., Blacker, D., . . . Killiany, R. J. (2006). An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage, 31, 968–980. https://doi.org/10.1016/j.neuroimage.2006.01.021 Dronkers, N. F. (1996). A new brain region for coordinating speech articulation. Nature, 384, 159–161. https://doi.org/10. 1038/384159a0 Duch, J., & Arenas, A. (2005). Community detection in complex networks using extremal optimization. Physical Review E, 72, 027104. https://doi.org/10.1103/PhysRevE.72.027104 Dujardin, K., Moonen, A. J. H., Behal, H., Defebvre, L., Duhamel, A., Duits, A. A., . . . Leentjens, A. F. G. (2015). Cognitive disor- ders in Parkinson’s disease: Conﬁrmation of a spectrum of sever- ity. Parkinsonism and Related Disorders, 21, 1299–1305. https:// doi.org/10.1016/j.parkreldis.2015.08.032 Fornito, A., Zalesky, A., & Breakspear, M. (2015). The connectomics of brain disorders. Nature Reviews Neuroscience. https://doi.org/ 10.1038/nrn3901 Gallen, C. L., Baniqued, P. L., Chapman, S. B., Aslan, S., Keebler, M., Didehbani, N., & D’Esposito, M. (2016). Modu- lar brain network organization predicts response to cognitive training in older adults. PLoS ONE, 11. https://doi.org/10.1371/ journal.pone.0169015 Genovese, C. R., Lazar, N. A., & Nichols, T. (2002). Thresholding of statistical maps in functional neuroimaging using the false dis- covery rate. NeuroImage, 15, 870–878. https://doi.org/10.1006/ nimg.2001.1037\rS1053811901910377[pii] Gibb, W. R. G., & Lees, A. J. (1988). The relevance of the Lewy body to the pathogenesis of idiopathic Parkinson’s disease. Jour- nal of Neurology, Neurosurgery, and Psychiatry. https://doi.org/ 10.1136/jnnp.51.6.745 Girvan, M., & Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences, 99, 7821–7826. https://doi.org/10.1073/ pnas.122653799 Gramfort, A., Papadopoulo, T., Olivi, E., & Clerc, M. (2010). Open- MEEG: Opensource software for quasistatic bioelectromagnetics. Biomedical Engineering Online, 9, 45. https://doi.org/10.1186/ 1475-925X-9-45 Gratton, G., Coles, M. G. H., & Donchin, E. (1983). A new method for off-line removal of ocular artifact. Electroencephalography and Clinical Neurophysiology, 55, 468–484. https://doi.org/10. 1016/0013-4694(83)90135-9 Guimerà, R., & Amaral, L. A. N. (2005). Functional cartography of complex metabolic networks. Nature, 433, 895–900. https://doi. org/10.1038/nature03288 Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J., Van Wedeen, J., & Sporns, O. (2008). Mapping the structural core of human cerebral cortex. PLoS Biology, 6, 1479–1493. https:// doi.org/10.1371/journal.pbio.0060159 Hassan, M., Benquet, P., Biraben, A., Berrou, C., Dufor, O., & Wendling, F. (2015). Dynamic reorganization of functional brain networks during picture naming. Cortex, 73, 276–288. https:// doi.org/10.1016/j.cortex.2015.08.019 Hassan, M., Chaton, L., Benquet, P., Delval, A., Leroy, C., Plomhause, L., . . . Dujardin, K. (2017). Functional connectiv- ity disruptions correlate with cognitive phenotypes in Parkinson’s disease. NeuroImage: Clinical, 14, 591–601. https://doi.org/10. 1016/j.nicl.2017.03.002 Hassan, M., Shamas, M., Khalil, M., El Falou, W., & Wendling, F. (2015). EEGNET: An open source tool for analyzing and visualiz- ing M/EEG connectome. PLoS ONE, 10. https://doi.org/10.1371/ journal.pone.0138297 Hassan, M., & Wendling, F. (2018). Electroencephalography source connectivity: Toward high time/space resolution brain networks. IEEE Signal Processing Magazine, 1–25. Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A., Calhoun, V. D., Corbetta, M., . . . Chang, C. (2013). Dynamic functional connectivity: Promise, issues, and interpretations. NeuroImage, 80, 360–378. https://doi.org/10.1016/j.neuroimage. 2013.05.079 Hyvärinen, A., Hirayama, J. I., Kiviniemi, V., & Kawanabe, M. (2016). Orthogonal connectivity factorization: Interpretable de- composition of variability in correlation matrices. Neural Com- putation. https://doi.org/10.1162/NECO_a_00810 Network Neuroscience 899 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 7 8 1 0 9 2 5 1 8 n e n _ a _ 0 0 0 9 0 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Detecting modular brain states in rest and task Kabbara, A., Eid, H., El Falou, W., Khalil, M., Wendling, F., & Hassan, M. (2018). Reduced integration and improved segrega- tion of functional brain networks in Alzheimer’s disease. Journal of Neural Engineering, 15. https://doi.org/10.1088/1741-2552/ aaaa76 Kabbara, A., El Falou, W., Khalil, M., Wendling, F., & Hassan, M. (2017). The dynamic functional core network of the human brain at rest. Scentiﬁc Reports, 7, 2936. https://doi.org/10.1038/ s41598-017-03420-6 Kabbara, A., Khalil, M., O’Neill, G., Dujardin, K., El Traboulsi, Y., Wendling, F., & Hassan, M. (2019). Modularity_algorithm_NN, GitHub, https://github.com/librteam/Modularity_algorithm_NN J. (1999). Measuring phase synchrony in brain signals. Human Brain Mapping, 8, 194–208. https://doi.org/10.1002/(SICI)1097- 0193(1999)8:4<194::AID-HBM4>3.0.CO;2-C

j. PAG., Rodriguez, MI., Martinerie,

J., & Varela, F.

Lachaux,

Dejar, METRO., Demuru, METRO., Hillebrand, A., & Fraschini, METRO. (2018). A
comparison between scalp- and source-reconstructed EEG net-
obras. Scientiﬁc Reports. https://doi.org/10.1038/s41598-018-
30869-w

Lopes, r., Delmaire, C., Defebvre, l., Moonen, A. J., Duits, A. A.,
Hofman, PAG., . . . Dujardin, k. (2017). Cognitive phenotypes in
Parkinson’s disease differ in terms of brain-network organiza-
tion and connectivity. Mapeo del cerebro humano, 38, 1604–1621.
https://doi.org/10.1002/hbm.23474

López, METRO. MI., Bruna, r., Aurtenetxe, S., Pineda-Pardo,

j. A.,
Marcos, A., Arrazola, J., . . . Maestu, F. (2014). Alpha-band hy-
persynchronization in progressive mild cognitive impairment: A
magnetoencephalography study. Revista de neurociencia, 34,
14551–14559.https://doi.org/10.1523/JNEUROSCI.0964-14.2014
Lord, A., Horn, D., romper la lanza, METRO., & walter, METRO. (2012). Changes
in community structure of resting state functional connectivity
in unipolar depression. PLoS ONE, 7(8). https://doi.org/10.1371/
diario.pone.0041282

Martín, A., & chao, l. l. (2001). Semantic memory and the brain:
Structure and processes. Opinión actual en neurobiología, 11,
194–201. https://doi.org/10.1016/S0959-4388(00)00196-3

Mheich, A., Hassan, METRO., Khalil, METRO., Berrou, C., & Wendling, F.
(2015). A new algorithm for spatiotemporal analysis of brain
conectividad funcional. Journal of Neuroscience Methods. https://
doi.org/10.1016/j.jneumeth.2015.01.002

Mucha, PAG. J., Richardson, T., Macon, K., Portero, METRO. A., & Onnela,
j. PAG. (2010). Community structure in time-dependent, multiscale,
and multiplex networks. Ciencia, 328, 876–878. https://doi.org/
10.1126/science.1184819

Núñez, PAG. l., & Srinivasan, R. (2007). Electroencephalogram. Schol-
arpedia, 2, 1348. https://doi.org/10.4249/scholarpedia.1348
O’Neill, GRAMO. C., Bauer, METRO., lana rica, METRO. w., morris, PAG. GRAMO., Barnes,
GRAMO. r., & Brookes, METRO. j. (2015). Dynamic recruitment of resting
state sub-networks. NeuroImagen, 115, 85–95. https://doi.org/10.
1016/j.neuroimage.2015.04.030

O’Neill, GRAMO. C., Tewarie, PAG. K., Colclough, GRAMO. l., Gascoyne, l. MI.,
Hunt, B. A. MI., morris, PAG. GRAMO.,
(2017).
Measurement of dynamic task related functional networks us-
ing MEG. Neuroimagen, 146, 667–678. https://doi.org/10.1016/
j.neuroimage.2016.08.061

. Brookes, METRO.

O’Neill, GRAMO. C., Tewarie, PAG. K., Vidaurre, D., Liuzzi, l., lana rica,
METRO. w., & Brookes, METRO. j. (2017). Dynamics of large-scale electro-
physiological networks: A technical review. NeuroImagen. https://
doi.org/10.1016/j.neuroimage.2017.10.003

Oostenveld, r., & Praamstra, PAG. (2001). The ﬁve percent electrode
system for high-resolution EEG and ERP measurements. Clin-
ical Neurophysiology, 112, 713–719. https://doi.org/10.1016/
S1388-2457(00)00527-7

patel, A. X., & bullmore, mi. t. (2016). A wavelet-based estima-
tor of the degrees of freedom in denoised fMRI time series for
probabilistic testing of functional connectivity and brain graphs.
NeuroImagen, 142, 14–26. https://doi.org/10.1016/j.neuroimage.
2015.04.052

Penﬁeld, w., & Jaspe, h. (1954). Epilepsy and the functional
anatomy of the human brain. JAMA, 155, 86. https://doi.org/10.
1001/jama.1954.03690190092039

Pfurtscheller, GRAMO., & Aranibar, A.

(1977). Event-related cortical
desynchronization detected by power measurements of scalp
EEG. Electroencephalography and Clinical Neurophysiology, 42,
817–826. https://doi.org/10.1016/0013-4694(77)90235-8

Pfurtscheller, GRAMO., & Lopes Da Silva, F. h. (1999). Event-related
EEG/MEG synchronization and desynchronization: Basic prin-
ciples. Clinical Neurophysiology. https://doi.org/10.1016/S1388-
2457(99)00141-8

Preti, METRO. GRAMO., & Van De Ville, D.

(2016). Eigenmaps of dy-
namic functional connectivity: Voxel-level dominant patterns
through eigenvector centrality. 2016 IEEE 13th International Sym-
posium on Biomedical
Imaging. https://doi.org/10.1109/ISBI.
2016.7493431

Rasero, J., Pellicoro, METRO., Angelini, l., Cortes, j. METRO., Marinazzo, D.,
& Stramaglia, S. (2017). Consensus clustering approach to group
brain connectivity matrices. Neurociencia en red, 1, 242–253.
https://doi.org/10.1162/NETN_a_00017

Rushworth, METRO. F. S., Noonan, METRO. A. PAG., Boorman, mi. D., Walton,
METRO. MI., & Behrens, t. mi. (2011). Frontal cortex and reward-guided
learning and decision-making. Neurona. https://doi.org/10.1016/
j.neuron.2011.05.014

Schneider, w., Eschman, A., & Zuccolotto, A. (2002). E-Prime ref-

erence guide. Psychology Software Tools, 3, 1.

Schoffelen, J., & Bruto, j. (2009). Source connectivity analysis with
MEG and EEG. Mapeo del cerebro humano. https://doi.org/10.1002/
hbm.20745

Song, S. K., Sotavento, j. MI., Parque, h. J., Sohn, Y. h., Sotavento, j. D., & Sotavento,
PAG. h. (2011). The pattern of cortical atrophy in patients with
Parkinson’s disease according to cognitive status. Movment Dis-
orders, 26, 289–296. https://doi.org/10.1002/mds.23477

despreciar, o., & Betzel, R. F. (2016). Modular brain networks. Annual
Review of Psychology, 67, 613–640. https://doi.org/10.1146/
annurev-psych-122414-033634

Tewarie, PAG., van Dellen, MI., Hillebrand, A., & estampar, C.

j.
(2015). The minimum spanning tree: An unbiased method for
brain network analysis. NeuroImagen. https://doi.org/10.1016/
j.neuroimage.2014.10.015

Thorpe, S., Fize, D., & Marlot, C. (1996). Speed of processing
in the human visual system. Naturaleza. https://doi.org/10.1038/
381520a0

Neurociencia en red

900

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
7
8
1
0
9
2
5
1
8
norte
mi
norte
_
a
_
0
0
0
9
0
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Detecting modular brain states in rest and task

Traud, A. l., Kelsic, mi. D., Mucha, PAG. J., & Portero, METRO. A. (2008). Com-
paring community structure to characteristics in online collegiate
social networks. SIAM Review, 53, 526–543. https://doi.org/10.
1137/080734315

van den heuvel, METRO. PAG., el largo, S. C., Brilla, A., Seguin, C.,
yo, B. t. T., & Schmidt, R. (2017). Proportional thresholding in
resting-state fMRI functional connectivity networks and conse-
quences for patient-control connectome studies: Issues and rec-
ommendations. NeuroImagen, 152, 437–449. https://doi.org/10.
1016/j.neuroimage.2017.02.005

VanRullen, r., & Thorpe, S. j. (2001). The time course of visual
Procesando: From early perception to decision-making. Diario de
Neurociencia Cognitiva, 13, 454–461. https://doi.org/10.1162/
08989290152001880

Vidaurre, D., Abeysuriya, r., Becker, r., quinn, A. J., Alfaro-
Almagro, F., Herrero, S. METRO., & lana rica, METRO. W.. (2017). Discovering

dynamic brain networks from big data in rest and task. Neuro-
Image. https://doi.org/10.1016/j.neuroimage.2017.06.077

Vidaurre, D., quinn, A. J., Panadero, A. PAG., Dupret, D., Tejero-Cantero,
A., & lana rica, METRO. W.. (2016). Spectrally resolved fast transient
brain states in electrophysiological data. NeuroImagen, 126,81–95.
https://doi.org/10.1016/j.neuroimage.2015.11.047

zhang, y., Schuff, NORTE., Du, A.-T., rosa, h. J., Kramer, j. h., Gorno-
Tempini, METRO. l., . . . Weiner, METRO. W.. (2009). White matter damage
in frontotemporal dementia and Alzheimer’s disease measured
by diffusion MRI. Cerebro, 132, 2579–92. https://doi.org/10.1093/
brain/awp071

zhang, y., Wang, S. J., Xing, J., Liu, B., Mamá, z. l., Cual, METRO., . . .
Teng, GRAMO. j. (2009). Detection of PCC functional connectivity
characteristics in resting-state fMRI in mild Alzheimer’s disease.
Behavioural Brain Research, 197, 103–108. https://doi.org/10.
1016/j.bbr.2008.08.012

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
7
8
1
0
9
2
5
1
8
norte
mi
norte
_
a
_
0
0
0
9
0
pag
d