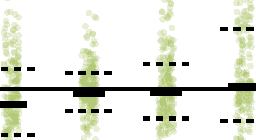RESEARCH - IA de Investigación especializada en el MIT

INVESTIGACIÓN

Functional control of electrophysiological
network architecture using direct
neurostimulation in humans

Ankit N. Khambhati

Roberto E.. Bruto

, Ari E. Kahn
10

1,3,9

, Barbara C. Jobst
15

Gregory Worrell
Richard Gorniak

, Sarah Seger
, Sandhitsu R. El

7
Timothy H. lucas

5
, Kathryn A. davis

, Bradley C. Lega

, Joel M. piedra

, Julia Costantini

, Youssef Ezzyat

, Ethan A. Solomon

, Sameer A. Sheth

, Kareem A. Zaghloul

, Shennan Weiss
8
, Daniel S.. Rizzuto

, Michael R. Sperling
4
, miguel j.. Kahana

, Joseph I. Tracy

, and Danielle S. bassett

1,2,5,6

1Department of Bioengineering, Universidad de Pennsylvania, Filadelfia, Pensilvania, EE.UU
2Department of Electrical and Systems Engineering, Universidad de Pennsylvania, Filadelfia, Pensilvania, EE.UU
3Department of Neuroscience, Universidad de Pennsylvania, Filadelfia, Pensilvania, EE.UU
4Department of Psychology, Universidad de Pennsylvania, Filadelfia, Pensilvania, EE.UU
5Department of Neurology, Hospital of the University of Pennsylvania, Filadelfia, Pensilvania, EE.UU
6Department of Physics & Astronomy, Universidad de Pennsylvania, Filadelfia, Pensilvania, EE.UU
7Department of Neurosurgery, Hospital of the University of Pennsylvania, Filadelfia, Pensilvania, EE.UU
8Department of Radiology, Hospital of the University of Pennsylvania, Filadelfia, Pensilvania, EE.UU
9Human Research and Engineering Directorate, A NOSOTROS. Army Research Laboratory, Aberdeen, Maryland, EE.UU
10Department of Neurosurgery, Emory University Hospital, Atlanta, Georgia, EE.UU
11Department of Neurology, Dartmouth-Hitchcock Medical Center, Líbano, NH, EE.UU
12Department of Neurosurgery, Baylor College of Medicine, houston, Texas, EE.UU
13Surgical Neurology Branch, Institutos Nacionales de Salud, Bethesda, Maryland, EE.UU
14Department of Neurology, Mayo Clinic, Rochester, Minnesota, EE.UU
15Department of Neurosurgery, University of Texas, Southwestern Medical Center, Dallas, Texas, EE.UU
16Department of Neurology, Thomas Jefferson University Hospital, Filadelfia, Pensilvania, EE.UU
17Department of Radiology, Thomas Jefferson University Hospital, Filadelfia, Pensilvania, EE.UU

Palabras clave: Neurostimulation, Electrocorticography, Structural controllability, Reconﬁguration

ABSTRACTO

Chronically implantable neurostimulation devices are becoming a clinically viable option
for treating patients with neurological disease and psychiatric disorders. Neurostimulation
offers the ability to probe and manipulate distributed networks of interacting brain areas
in dysfunctional circuits. Aquí, we use tools from network control theory to examine the
dynamic reconﬁguration of functionally interacting neuronal ensembles during targeted
neurostimulation of cortical and subcortical brain structures. By integrating multimodal
intracranial recordings and diffusion-weighted imaging from patients with drug-resistant
epilepsy, we test hypothesized structural and functional rules that predict altered patterns of
synchronized local ﬁeld potentials. We demonstrate the ability to predictably reconﬁgure
functional interactions depending on stimulation strength and location. Stimulation of areas
with structurally weak connections largely modulates the functional hubness of downstream
areas and concurrently propels the brain towards more difﬁcult-to-reach dynamical states.
By using focal perturbations to bridge large-scale structure, función, and markers of
comportamiento, our ﬁndings suggest that stimulation may be tuned to inﬂuence different scales
of network interactions driving cognition.

RESUMEN DEL AUTOR

Brain stimulation devices capable of perturbing the physiological state of neural systems are
rapidly gaining popularity for their potential to treat neurological and psychiatric disease.
A root problem is that underlying dysfunction spans a large-scale network of brain regions,

,
,

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
4
8
1
0
9
2
4
4
0
norte
mi
norte
_
a
_
0
0
0
8
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

un acceso abierto

diario

Citación: Khambhati, A. NORTE., Kahn, A. MI.,
Costantini, J., Ezzyat, y., Solomon, mi. A.,
Bruto, R. MI., . . . bassett, D. S. (2019).
Functional control of
electrophysiological network
architecture using direct
neurostimulation in humans. Red
Neurociencia, 3(3), 848–877.
https://doi.org/10.1162/netn_a_00089

DOI:
https://doi.org/10.1162/netn_a_00089

Supporting Information:
https://doi.org/10.1162/netn_a_00089

Recibió: 2 Enero 2019
Aceptado: 14 Abril 2019

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autor correspondiente:
Danielle S. bassett
dsb@seas.upenn.edu

Editor de manejo:
Álex Amueblado

Derechos de autor: © 2019
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

Functional control of brain networks using direct neurostimulation

requiring the ability to control the complex interactions between multiple brain areas.
Aquí, we use tools from network control theory to examine the dynamic reconﬁguration of
functionally interacting neuronal ensembles during targeted neurostimulation of cortical and
subcortical brain structures. We demonstrate the ability to predictably reconﬁgure patterns
of interactions between functional brain areas by modulating the strength and location of
stimulation. Our ﬁndings have high signiﬁcance for designing stimulation protocols capable
of modulating distributed neural circuits in the human brain.

INTRODUCCIÓN

Novel neurotechnologies capable of perturbing the physiological state of neural systems are
rapidly gaining popularity for their potential to treat neurological disease and psychiatric dis-
orders (Stacey & Litt, 2008). Chronically implantable devices that stimulate the human brain
are clinically approved to treat Parkinson’s disease, essential tremor, dystonia, epilepsy, y
obsessive-compulsive disorder and have been investigated for major depressive disorder and
Tourette syndrome (Lozano & Lipsman, 2013). Recent human studies have investigated the
ability for direct stimulation of cortical and subcortical structures to modulate biomarkers of
memory (Ezzyat et al., 2017; Inman et al., 2017), visual perception (Rangarajan et al., 2014;
Winawer & Parvizi, 2016), language production (Chang, Kurteff, & wilson, 2017), somatosen-
sory perception (Muller et al., 2018), sensorimotor function (W.. Wang y cols., 2013), y sujeto-
tive experience (Foster & Parvizi, 2017). While neurostimulation is a promising interventional
approach to modulate brain state, current practices of calibrating where, cuando, and how to
stimulate the brain are “open-loop” and limited in efﬁcacy—relying on manual and periodic
tuning of device parameters to optimize therapy (Morrell, 2011). Automated, “closed-loop”
approaches would augment the capability of current stimulation devices to dynamically ad-
just parameters based on the physiological state of the brain network, monitored in real time
(Stanslaski et al., 2012). Undoubtedly, the translational prospect of neurostimulation to ma-
nipulate brain networks that generate abnormal rhythms, dysrhythmias, or bursts of activity
associated with dysfunction is promising. Sin embargo, critical gaps in knowledge hinder the
development of a robust control policy for next-generation implantable devices.

How does the architecture of the neural system mediate the effect of neurostimulation on
neurophysiology and behavior? Network control theory (Pasqualetti, Zampieri, & Bullo, 2014)
provides a mathematical framework for mapping the inﬂuence of a control signal on the dy-
namics of an interconnected system. When combined with graph modeling tools from network
neurociencia (bassett & despreciar, 2017), where nodes represent discrete brain regions and edges
represent the structural connections between brain regions, control theoretic approaches can
elucidate how the brain’s structural architecture of white matter ﬁber pathways shapes its abil-
ity to navigate through a repertoire of dynamical states (Gu et al., 2015). Theoretical rules of
controllability prescribe the trajectories through state space elicited by a given control signal
(Betzel, Gu, Medalla, Pasqualetti, & bassett, 2016; Gu et al., 2017, 2015), and begin to ex-
plain why one brain network may be more or less inﬂuential on brain dynamics than another
(Kim y cols., 2018). Recent efforts to test control theoretic predictions of the relationship between
controllability and brain activity have relied on in silico models in which neuronal ensembles
are interlinked by structural connections measured by human neuroimaging (Muldoon et al.,
2016). Despite the promising convergence between theory and model simulation, empirical
stimulation data bridging network control and neurophysiology are lacking.

849

Direct neurostimulation:
Delivery of electrical pulses to
electrodes located on the surface or
in deep structures of the brain.

Control policy:
Rules for when, dónde, y cómo
inputs should be delivered to a
dynamical system to reach the
desired target state.

Network control theory:
Framework to model changes in the
state of a complex system under
constraints prescribed by the
structure of that system.

Graph:
Mathematical representation of a
network consisting of nodes as brain
regions and edges as structural or
functional connections between
regiones.

Controllability:
Ability to steer a dynamical system
from its current state towards a
desired target state over a ﬁnite time
horizon.

Neurociencia en red

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
4
8
1
0
9
2
4
4
0
norte
mi
norte
_
a
_
0
0
0
8
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Functional control of brain networks using direct neurostimulation

Coherence:
Functional communication capacity
(conectividad) between two brain
regions based on phase alignment of
their oscillatory activity at a speciﬁc
frequency.

Network control theory accounts for the structural connections that convey modulated brain
activity to downstream regions in the network; sin embargo, it does not account for the functional
rules that govern whether communication between brain regions can occur at a speciﬁc point
in time. At the millimeter scale, synchronous oscillations in the local ﬁeld potential are thought
to actively gate the transfer of information across the network (Bonnefond, Kastner, & Jensen,
2017; Buzsáki et al., 2012; Canolty & Caballero, 2010; Fries, 2015; Schalk, 2015) and are com-
monly observed during higher order cognitive processing (Buzsáki, 2006). A functional (en vez de
structural) network representation of the coherence between different ensembles of neurons may
capture dynamical states of communication (decoración & Kringelbach, 2016; Hutchison et al.,
2013). The neurophysiologic interpretation of these states can depend on the measured frequency
range of the functional network (bassett, Meyer-Lindenberg, Achard, Duke, & bullmore, 2006;
Solomon et al., 2017), which in turn implicates certain types of cells interacting over speciﬁc
spatial scales (Kopell, Ermentrout, Whittington, & Traub, 2000). Prior studies have examined
how these functional networks may reconﬁgure during higher order cognitive functions such
as learning new skills (bassett ,Wymbs et al., 2011; Bassett y cols., 2013; bassett, Cual, Wymbs,
& Grafton, 2015; Mattar, Col, Thompson-Schill, & bassett, 2015), forming memories (Braun
et al., 2015), attending to the environment (Brillar, Koyejo, & Poldrack, 2016), and processing
idioma (Chai, Mattar, Blank, Fedorenko, & bassett, 2016). Complimentary work also posits
that reconﬁguration of functional networks may underlie neurophysiological abnormalities in
patients with epilepsy (Khambhati et al., 2017, 2015), schizophrenia (bassett, nelson, Mueller,
Camchong, & Lim, 2012; Braun et al., 2016), Parkinson’s disease (Olde Dubbelink et al., 2014;
Sang et al., 2015), and stroke (Grefkes & Fink, 2011; l. Wang y cols., 2010). While these studies
explain changes in functional network reconﬁguration when the brain is perturbed en masse,
a rigorously quantiﬁed map of functional network reconﬁguration due to controlled, focal per-
turbation has not been attained.

Here we seek to elucidate the network control principles by which neurostimulation can
alter function and behavior based on constraints prescribed by structural connectivity and
spontaneous functional interactions. We measure the electrocorticogram (ECoG) en 94 drug-
resistant epilepsy patients undergoing neurostimulation (Figura 1A-B), and we construct
structural networks from diffusion imaging data acquired in the same individuals. We also con-
struct functional networks before and after individual stimulation trials using multitaper coher-
ence between sensors (Prieto, parker, & Vernon, 2009) in distinct frequency bands (Khambhati,
Davisa, lucas, Litt, & bassett, 2016; Kramer et al., 2011 (Figura 1C), and we deﬁne brain state
before and after stimulation using a previously validated biomarker of memory (Ezzyat et al.,
2017). We test four hypotheses. Primero, we hypothesize that the strength and location of stimula-
tion can differentially drive two separate modes of global versus local control over functional
architecture (Muldoon et al., 2016). Intuitivamente, stimulation to functional hubs—nodes that tend
to interact strongly with the rest of the network—may have swiftly attenuated effects due to sig-
nal dispersion across many downstream regions, while stimulation to nonhubs may have more
localized and targeted effects. Segundo, we hypothesize that regions with strong baseline func-
tional interaction with the stimulation site are more likely to exhibit altered hub properties
following stimulation than brain regions with weak functional interaction with the stimula-
tion site, indicating a functional conduit of stimulation. Tercero, based on prior data (Betzel,
Medalla, Kahn, et al., 2017), we hypothesize that these functional interactions—particularly
in high-frequency bands—colocalize with structural white matter networks (Figure 1D). Cuatro,
we hypothesize that neurostimulation directed towards modal control points (Gu et al., 2015;
Pasqualetti et al., 2014), which tend to be structural nonhubs of a patient’s white matter network
thereby minimizing signal dispersion, facilitate a stronger shift in dynamical state associated
with memory encoding, a function that is altered in patients with epilepsy (Aarts, Binnie, Smit,

Neurociencia en red

850

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
4
8
1
0
9
2
4
4
0
norte
mi
norte
_
a
_
0
0
0
8
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Functional control of brain networks using direct neurostimulation

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
4
8
1
0
9
2
4
4
0
norte
mi
norte
_
a
_
0
0
0
8
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

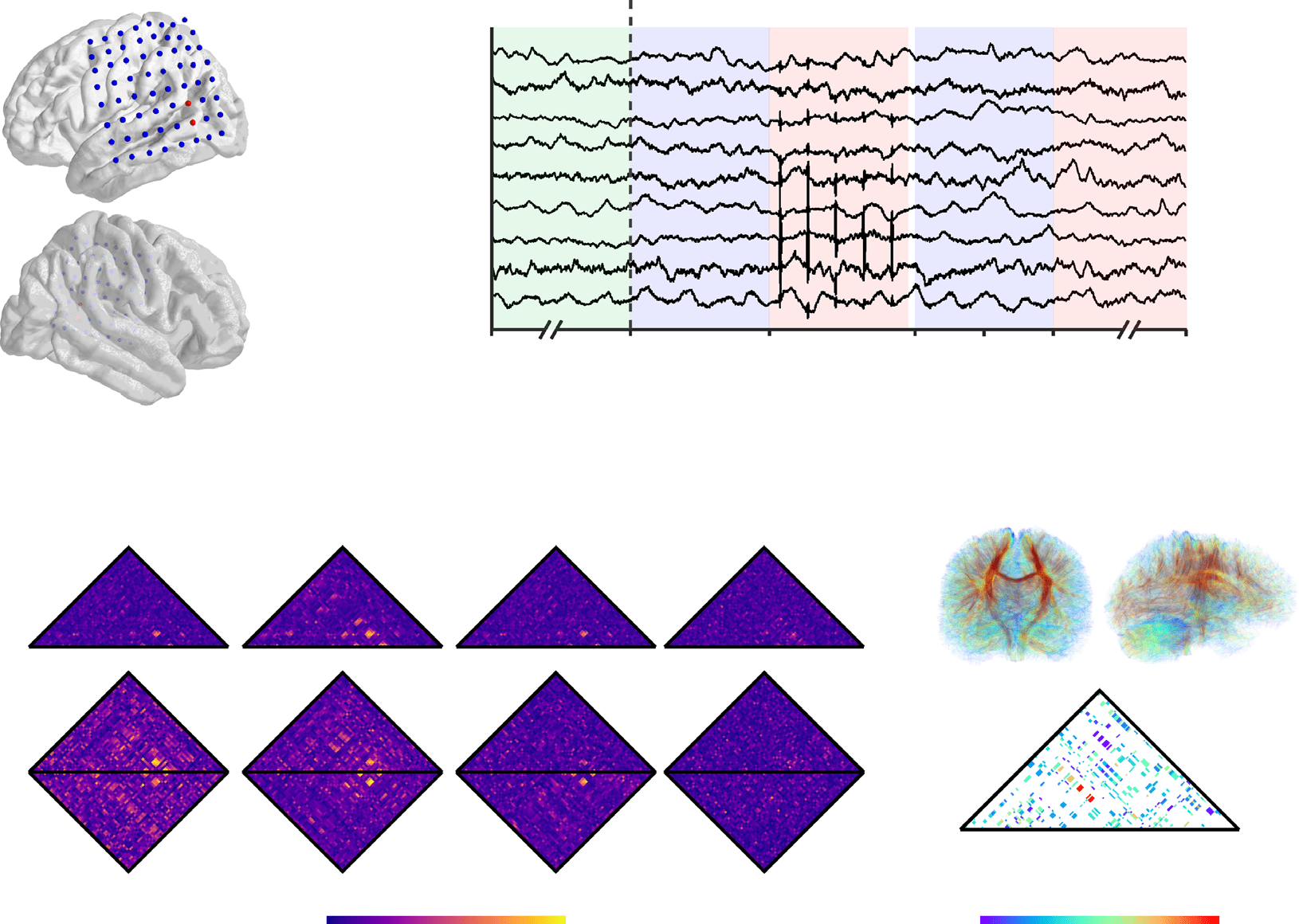
Cifra 1. Measuring network response to targeted, intracranial neurostimulation. (A) We record the electrocorticogram (ECoG) en 94 patients
with drug-resistant epilepsy across 8 clinical institutions using intracranial sensors implanted in cortical and subcortical brain structures. A
evoke a network response, we stimulate adjacent electrode pairs using a charge-balanced, biphasic current source with a square waveform
of variable amplitude, frequency, and duration. (B) For each experimental session, we select a stimulation location and collect the following
epochs of ECoG activity: (i) 30 seconds of baseline activity before any stimulation is given, (ii) one half-second of activity before a stimulation
trial, y (iii) two consecutive and nonoverlapping half-second windows of activity after a stimulation trial. A stimulation trial is deﬁned by
a combination of pulse frequency, amplitude, and duration, and consecutive stimulation trials are separated by an inter-stimulation interval
drawn from a uniform random distribution ranging from 2.75 s to 3.25 s. (C) We measure the impact of neurostimulation on functional network
architecture by constructing dynamic graph models in which intracranial sensors are represented by nodes and the functional interactions
between intracranial sensors are represented by edges. To infer functional interactions, we calculate the multitaper coherence between each
pair of ECoG signals in nonoverlapping, half-second time windows for each baseline epoch, pre-stimulation epoch, and post-stimulation epoch
in the following four frequency bands: (i) alpha/theta (5−15 Hz), (ii) beta (15−25 Hz), (iii) low gamma (30−40 Hz), y (iv) high gamma (95–
105 Hz) (Khambhati et al., 2016; Kramer et al., 2011). (D) To examine how structural connectivity constrains functional network reconﬁguration
to neurostimulation, we also construct a static graph model of the brain’s structural network by applying deterministic tractography to each
subject’s diffusion-weighted imaging data.

& Wilkins, 1984; holmes & Lenck-Santini, 2006; Uhlhaas & Cantante, 2006). Colectivamente, estos
analyses will supply a roadmap of the impact of neurostimulation on network physiology, a mí-
diated by network structure, and provide fundamental mechanistic insight into the inﬂuence
of neurostimulation on behavioral state.

MÉTODOS

Study Cohort

Ninety-four patients undergoing intracranial EEG monitoring as part of clinical treatment for
drug-resistant epilepsy were included in this study. Data were collected as part of a multicenter

Neurociencia en red

851

Functional control of brain networks using direct neurostimulation

project designed to assess the effects of electrical stimulation on memory-related brain func-
ción. Data analyzed in this study were collected at the following centers: Thomas Jefferson Uni-
versity Hospital (norte = 23), University of Texas Southwestern (norte = 23), Mayo Clinic (norte = 17),
Institutos Nacionales de Salud (norte = 11), Dartmouth-Hitchcock Medical Center (norte = 9), Hospi-
tal of the University of Pennsylvania (norte = 6), Columbia University Medical Center (norte = 4),
and Emory University Hospital (norte = 1). The research protocol was approved by the institu-
tional review board at each hospital and informed consent was obtained from each participant.

Anatomical Localization of Intracranial Electrodes

Patients undergoing surgical treatment for medically refractory epilepsy believed to be of neo-
cortical origin underwent implantation of intracranial electrodes to localize the seizure onset
zone. These procedures were applied after presurgical evaluation with scalp EEG recording
of ictal epochs, resonancia magnética, PET, and neuropsychological testing suggested that focal cortical re-
section may be a therapeutic option. Patients were then deemed candidates for implantation
of intracranial electrodes to better deﬁne epileptic networks. Electrode conﬁgurations spanned
the surface of the cortex (linear and two-dimensional arrays, each sensor is 2.3 mm diameter
spaced 10 mm apart) and subcortical depth (each sensor is 1.5–10 mm apart). All electrode
conﬁgurations were planned by a multidisciplinary team of neurologists and neurosurgeons
at each of the eight medical centers.

Electrodes were anatomically localized using separate processing pipelines for surface and
depth electrodes. To localize depth electrodes we ﬁrst labeled hippocampal subﬁelds and
medial temporal lobe cortices in a pre-implant, 2 mm thick, coronal T2-weighted MRI using
the automatic segmentation of hippocampal subﬁelds (ASHS) multiatlas segmentation method
(Yushkevich et al., 2015). We additionally used whole-brain segmentation to localize depth
electrodes not in medial temporal lobe cortices. We next coregistered a postimplant CT with
the preimplant MRI using advanced normalization tools (ANTs; Avants, Epstein, Grossman, &
Gee, 2009). Electrodes visible in the CT were then localized within subregions of the medial
temporal lobe by a pair of neuroradiologists with expertise in medial temporal lobe anatomy.
The neuroradiologists performed quality checks on the output of the ASHS/ANTs pipeline. A
localize subdural electrodes, we ﬁrst extracted the cortical surface from a pre-implant, volu-
métrico, T1-weighted MRI using FreeSurfer (Fischl et al., 2004). We next coregistered and local-
ized subdural electrodes to cortical regions using an energy minimization algorithm (Dykstra
et al., 2012). For patient imaging in which automatic localization failed, the neuroradiologists
performed manual localization of the electrodes.

Electrophysiological Data Acquisition and Stimulation Mapping Protocol

The electrocorticogram (ECoG) was recorded and digitized at 500 Hz, 512 Hz, 1,000 Hz,
1,024 Hz, o 2,000 Hz depending on clinical considerations at each medical center. Signals
were recorded using a referential montage with the reference electrode, chosen by the clinical
equipo, distant to the site of seizure onset.

To study the response of the electrocorticogram to neurostimulation, we used a mapping
procedure in which stimulation was delivered to cortical and subcortical brain regions. Patients
were not instructed to engage in any other task before or during stimulation. Prior to the start
of each mapping session, we selected a pair of adjacent electrodes for stimulation by prior-
itizing electrodes in brain regions thought to be associated with memory function. For each
mapping session, we selected a new stimulation site and patients underwent one or several
mapping sessions depending on their availability for testing and the monitoring needs of the

Neurociencia en red

852

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
4
8
1
0
9
2
4
4
0
norte
mi
norte
_
a
_
0
0
0
8
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Functional control of brain networks using direct neurostimulation

clinicians. Prior to the start of a mapping session, we recorded 30 s of ECoG activity as a
baseline epoch. During a mapping session, we performed several stimulation trials in which
a single trial consisted of the following epochs: (a) a half-second pre-stimulation epoch, (b)
a stimulation epoch with variable duration, two consecutive and nonoverlapping half-second
post-stimulation epochs, and an inter-stimulation epoch with variable duration. During each
stimulation trial, we delivered stimulation using charge-balanced, biphasic, rectangular pulses
with a pulse width of 600 μs and combinations of the following parameters: pulse frequency
(10, 25, 50, 100, 200 Hz), pulse amplitude (maximum safe amplitude minus 0, 0.5, 1 mA;
range of 0.125–3.0 mA across subjects), stimulation duration (250, 500, 1,000 EM), and inter-
stimulation interval (2,750–3,250 ms). These stimulation parameter ranges were chosen to be
well below the accepted safety limits for charge density (shannon, 1992) and ECoG was con-
tinuously monitored for afterdischarges by a trained neurologist.

We will now describe a typical stimulation experimental session in further detail. In a sin-
gle session, stimulation location was kept constant across trials, and in each trial stimulation
parámetros (pulse frequency, pulse amplitude, and duration) were each separately drawn uni-
formly at random from the aforementioned list of parameters. This procedure produced 45
possible parameter combinations. The sampling distribution of parameter combinations was
consistent across patients; sin embargo, the number of trials in a given session differed based on a
number of factors in the hospital setting of the Epilepsy Monitoring Unit, including patient fa-
tigue, availability, and willingness to participate. En general, across 94 participants we con-
ducted an average of 3 ± 2 experimental sessions (unique stimulation locations), and per
session we conducted an average of 1, 655 ± 697 trials—more than 36 times the number of
possible parameter combinations. We conﬁrmed that the full parameter space was sampled
within a session.

To eliminate confounding effects of stimulation on signal quality and saturation, we dis-
regarded ECoG data collected during the stimulation epoch and the 100 ms following stim-
ulation offset. We also employ a conservative electrode screening procedure, in which we
discard nonstimulated channels that exhibit evidence of stimulation-related artifact. Speciﬁ-
cally, before re-referencing to a common average reference, we use a paired t test to compare
the distribution of mean signal amplitude during the pre-stimulation epoch to the distribution
of mean signal amplitude during the post-stimulation epoch, for each electrode across stimu-
lation trials. Using a Bonferroni uncorrected p-value threshold of 0.05, we discard electrodes
that exhibit signiﬁcantly elevated raw, mean signal amplitude during each stimulation session.

We analyzed ECoG data collected during the baseline, pre-stimulation, and post-stimulation
epochs. The post-stimulation epoch following 100 ms of a buffer period was split into two
consecutive and nonoverlapping segments, 0.5 s in duration to assess delayed effects of
stimulation—we refer to the ﬁrst segment as the 100-ms response and the second segment
as the 600-ms response. Because of the time constraints on experimentation in the hospi-
tal setting of the Epilepsy Monitoring Unit, we utilized the 30 s of ECoG activity recorded
before the start of a stimulation session as an indicator of the patient’s baseline state. To quan-
tify the difference between the stimulation-induced effect on network topology in contrast to
the spontaneous effects over the passage of time, we constructed a surrogate distribution of
stimulation “trials” from the baseline period by sampling-with-replacement time windows
equal in duration to the true stimulation trials. En otras palabras, the surrogate distribution con-
sisted of the same number of trials as the number of trials conducted during the stimulation
session, and each surrogate baseline trial was associated with a true stimulation trial and was

Neurociencia en red

853

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
4
8
1
0
9
2
4
4
0
norte
mi
norte
_
a
_
0
0
0
8
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Functional control of brain networks using direct neurostimulation

constructed from the same duration of baseline data as its corresponding stimulation trial. Este
sampling scheme was used to mitigate the limited baseline data that were available for analysis.

Constructing Frequency-Based Functional Brain Networks

ECoG signals were divided into 0.5s, nonoverlapping, time windows—the pre-stimulation
epoch consisted of one time window per stimulation trial, and the post-stimulation epoch
consisted of two time windows per stimulation trial (100−600 ms post-stimulation and 600−
1,100 ms post-stimulation). We applied a common average reference to the artifact-free ECoG
signal before constructing functional networks (Burns, Santaniello, Yaffe, Jouny, & Crone, 2014;
Khambhati et al., 2016; Kramer et al., 2010, 2011; Towle, Carder, Khorasani, & Lindberg, 1999).

To measure functional interactions between ECoG signals in each time window, we com-
puted spectral coherence, which is a measure of correlation between the power spectra of two
signals within a frequency range. Prior studies have shown that coherence is largely indepen-
dent of the shape of the power spectrum in ECoG signals (Bullock et al., 1995a, 1995b; Towle
et al., 1999), and underlies different forms of synchronous interactions between neural popu-
laciones (Kopell et al., 2000). We constructed functional networks in each time window using
multitaper coherence estimation, which deﬁnes a graph edge between electrode pairs (graph
nodos) as the power spectral similarity of signal activity over a speciﬁc frequency band. Nosotros
applied the mtspec Python implementation (Prieto et al., 2009) of multitaper coherence es-
timation with time-bandwidth product of ﬁve and eight tapers in accord with related studies
(Kramer et al., 2011). This procedure resulted in a symmetric adjacency matrix A(t, F ) con
size N × N, where N is the number of network nodes, or electrode sensors, t is the time win-
dow, and f is the frequency band. en este estudio, we examined network activity in the following
four frequency bands: α/θ (5–15 Hz), b (15–25 Hz), low γ (30–40 Hz), and high γ (95–105 Hz).
These frequency ranges cover traditional oscillatory classes and have been previously exam-
ined for their network topology (Khambhati et al., 2016; Kramer et al., 2011).

An alternate representation of the symmetric, square adjacency matrix A(t, F ) is a conﬁg-
uration vector ˆA(t, F ), which tabulates all N × N pairwise interactions. Because of symme-
try of the adjacency matrix, we unravel the upper triangle of A, resulting in the weights of
E = N(N−1)

functional interactions. De este modo, ˆA(t, F ) is a vector of size E.

Node strength:
Measure of global inﬂuence, o
hubness, of a node based on its
average connectivity to all other
network nodes.

Metrics of Functional Network Topology

en este estudio, we investigated the effect of neurostimulation on functional network architecture
at the scale of network nodes and at the scale of network edges. At the node scale, we ﬁrst
quantiﬁed the change in the node strength—a measure of functional “hubness”—of individual
network nodes. Específicamente, we computed the node strength as ki(t, F ) = 1
N−1 ∑j∈N Aij(t, F ),
where k is the strength of node i and Aij is the edge weight between nodes i and j. Basado en el
time-dependent set of node strengths in the network, we computed the change in the mean
of node strengths between time windows and the change in the variance of node strengths
between time windows. To assess the magnitude of change in node strength for a node between
time windows tn and tm, we calculated Δki(tn,metro, F ) = abs(ki(tm, F ) − ki(tn, F )).

At the edge scale, we quantiﬁed the amount of change in the conﬁgurational pattern of the
network edges, or coherences, as described previously in Khambhati et al. (2015). Específicamente,
we computed the conﬁguration similarity between conﬁguration vectors ˆA(tn, F ) and ˆA(tm, F ),
where tn and tm are two different time windows, using the Pearson correlation test statistic. Two

Neurociencia en red

854

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
4
8
1
0
9
2
4
4
0
norte
mi
norte
_
a
_
0
0
0
8
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Functional control of brain networks using direct neurostimulation

vectors with a Pearson correlation value closer to 0 are more dissimilar in their conﬁgurational
pattern of network edges than two vectors with a Pearson correlation value closer to 1.

For the stimulation epoch, we computed global and local network metrics between the
pre-stimulation time window and the post-stimulation time window of a stimulation trial. Para
the baseline epoch, we computed global and local network metrics between time windows
separated by an equal length of time as the duration of stimulations in the associated stimula-
tion session.

Diffusion-Weighted Imaging Acquisition and Preprocessing

We collected diffusion-weighted imaging data for a subset of patients from Thomas Jefferson
University Hospital (norte = 11) and Hospital of the University of Pennsylvania (norte = 3) y
validated our analysis of the functional network response to neurostimulation.

All scans at Thomas Jefferson University Hospital were acquired with a 3T Philips Achieva
with an 8-channel head coil using an echo-planar diffusion-weighted technique. la difusion
and TE/TR = 98/7,251 EM. The matrix
scan was 62-directional with a b-value of 3,000 s/mm
size was 96 × 96 and the slice number was 52. The ﬁeld of view was 230 × 230 mm
y
the slice thickness 2.5 mm. Acquisition time was 496 s per DTI scan.

All scans at the Hospital of the University of Pennsylvania were acquired with a 3T Siemens
Tim Trio with a 32-channel head coil using an echo-planar diffusion-weighted technique. El
and TE/TR = 117/4,180 EM.
diffusion scan was 116-directional with a b-value of 2,000 s/mm
The matrix size was 96 × 96 and the slice number was 92. The ﬁeld of view was 210 ×
and the slice thickness 1.5 mm. Acquisition time was 506 s per DTI scan.
210 mm

Based on recent evidence that diffusion imaging is highly sensitive to subject movement
(Yendiki, Koldewyn, Kakunoori, Kanwisher, & pescado, 2014) and to directional eddy currents
(Jezzard, barnett, & Pierpaoli, 1998), we processed data using the FMRIB Software Library
(Jenkinson, beckman, Behrens, lana rica, & Herrero, 2012). We ﬁrst created individual masks of
the patient brain using BET (Herrero, 2002). We next simultaneously corrected for motion effects
and eddy current distortions by applying the EDDY correction tool (andersson & Sotiropoulos,
2016) to the diffusion scans and a b = 0 image collected at the beginning of the scan.

We next reconstructed orientation density functions (ODFs) of the diffusion imaging in
each voxel. Específicamente, we used DSI Studio (http://www.dsi-studio.labsolver.org) and gen-
eralized q-sampling imaging (GQI; Yeh, Wedeen, & Tseng, 2010) to compute the quantitative
anisotropía (control de calidad; Yeh, Petrificar, Wang, Fernández-Miranda, & Tseng, 2013) in each voxel. A
conduct ﬁber tractography on the reconstructed diffusion images, we used DSI Studio to gener-
ate 1,000,000 streamlines with a maximum turning angle of 35
(bassett, Marrón, Deshpande,
Carlson, & Grafton, 2011) and a maximum length of 500 mm (Cieslak & Grafton, 2014). Nosotros
next used the streamlines to deﬁne the structural brain network at the two following spatial res-
olutions of the Lausanne atlas included in the Connectome Mapping Toolkit (Cammoun et al.,
2012) consistent with previous work (bassett, Marrón, et al., 2011; Bassett y cols., 2010; Gu
et al., 2017, 2015; Hermundstad et al., 2013, 2014; Muldoon et al., 2016): (a) at the ﬁne
scale we divided the brain into N = 1, 015 cortical and subcortical regions of interest (ROI)
(average ROI volume 1.56 ± 0.06 cm
), y (b) at the coarse scale we divided the brain into
norte = 234 cortical and subcortical ROIs (average ROI volume 6.78 ± 0.02 cm
). We summarized
these measurements in a symmetric and weighted structural adjacency matrix S whose entries

◦

Neurociencia en red

855

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
4
8
1
0
9
2
4
4
0
norte
mi
norte
_
a
_
0
0
0
8
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Functional control of brain networks using direct neurostimulation

Sij reﬂect the structural connectivity (quantitative anisotropy) between region i and region j,
separately for the ﬁne-scale and coarse-scale parcellation.

We localized electrodes in native subject T1-weighted MRI space to the Lausanne anatom-
ical space by using ANTs (Avants et al., 2009) to register the subject’s T1 image to the subject’s
difusión 0 image via afﬁne transformation and also to register the subject’s T1 image to MNI
espacio (also native Lausanne space) using a nonlinear warp.

Metrics of Structural Controllability

To study the architectural constraints of the structural brain network with the functional net-
work response to neurostimulation, we adopted a control theoretic approach known as net-
work controllability. Brieﬂy, the controllability of a networked system refers to its ability to be
driven to speciﬁc dynamical states upon external input (Kalmán, 1963). Recent research efforts
have made substantial progress in the development of quantitative heuristics to characterize
different strategies for control (Pasqualetti et al., 2014; Pequito et al., 2016). These approaches
are now being applied to brain imaging data to understand how structural brain network topol-
ogy constrains function and behavior (Betzel et al., 2016; Gu et al., 2017, 2015; Kim y cols.,
2018; Tang et al., 2017).

In line with these prior studies, we employ a simpliﬁed noise-free linear discrete-time and

time-invariant model of network dynamics:

X(t + 1) = Ax(t) + BKuK(t),

(1)

where x : R≥0 → RN
describes the state (es decir., voltage, ﬁring rate, BOLD signal) of brain regions
con el tiempo. De este modo, the state vector x has length N, where N is the number of brain regions in the
connectome parcellation, and the value of xi describes the brain activity state of that region.
The diagonal elements of the matrix A satsify Aii = 0. Prior to calculating controllability
valores, we divide A by 1 + ξ0(A), where ξ0(A) is the largest singular value of A. The input
matrix BK identiﬁes the control point K in the brain, where K = k1, …, km and

BK = [ek1

· · · ekm

(2)

and ei denotes the i-th canonical vector of dimension N. The input uK : R≥0 → R M
the control strategy.

denotes

One control strategy that we investigate in this study is modal controllability—the ability of
a network region to feasibly control all the dynamical modes of a system (Pasqualetti et al.,
2014). To calculate the modal controllability of an anatomical brain region, we ﬁrst computed
the eigenvector matrix V = [vij] of the structural network adjacency matrix S—intuitively, vij
encodes the ability to control the j-th dynamical mode from region i (Kailath, 1980). Basado
on our previous work, we deﬁned φi = ∑j∈N(1 − λ2
ij as a scaled measure of the con-
trollability of all N dynamical modes λ1(S), . . . , λN(S) from brain region i (Gu et al., 2015;
Muldoon et al., 2016; Pasqualetti et al., 2014; Tang et al., 2017). Brain regions with high modal
controllability are versatile in their ability to control all dynamical modes of the network, y

j (S))v2

Neurociencia en red

856

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
4
8
1
0
9
2
4
4
0
norte
mi
norte
_
a
_
0
0
0
8
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Functional control of brain networks using direct neurostimulation

brain regions with low modal controllability are speciﬁc in their ability to control a subset of
dynamical modes of the network.

To provide additional insight into the topological properties of structural control points,
we evaluated the structural “hubness” of each brain region by computing the structural node
strength as ki = 1
N−1 ∑j∈N Sij—similar to the calculation for functional node strength speciﬁed
earlier.

Mapping Intracranial Electrodes to Anatomical Brain Regions

To relate structural controllability to functional network topology of the stimulated electrodes,
we ﬁrst computed metrics of the structural network topology for 234 o 1015 regiones del cerebro
deﬁned by the Lausanne anatomical parcellation. The advantage of computing these mea-
sures using the anatomical parcellation is the ability to account for whole-brain structural
conectividad, including areas that are not directly sampled by the intracranial electrodes. Nosotros
next assigned intracranial electrodes to the Lausanne brain regions based on a nearest voxel
acercarse. Específicamente, we identiﬁed the voxel closest to the electrode and assigned the elec-
trode to the brain region containing that voxel. Based on this assignment, we associated values
of each structural network metric to the intracranial electrodes.

Detection of Brain States Associated With Memory Encoding

We examined stimulation-driven changes in dynamical brain state using a classiﬁer of neural
activity associated with memory encoding processes that was previously validated on data
collected during behavioral experimentation with the same patients recruited in this study
(Ezzyat et al., 2017; Kragel et al., 2017). Brieﬂy, in these prior studies a logistic regression
classiﬁer was trained to discriminate memory encoding-related changes in spectral power in
eight logarithmically spaced frequency bands across intracranial electrodes that are predictive
of whether a word was later remembered or forgotten during a free-recall task (Ezzyat et al.,
2017; Kragel et al., 2017). en este estudio, we evaluated the trained memory encoding state
classiﬁer on task-free stimulation data of the same patients by measuring spectral power during
the pre-stimulation epoch and the post-stimulation epoch, and by computing the change in
probability of good memory encoding state for each stimulation trial. We next calculated the
average change in probability of good memory encoding state across all stimulation trials of
each stimulation mapping session of each patient. These data allowed us to assess the putative
effects of different dimensions of the stimulation parameter space on previously validated,
neural biomarkers of cognitive function, speciﬁcally on memory encoding.

RESULTADOS

Neurostimulation Drives Localized and Distributed Functional Network Reconﬁguration

We ﬁrst ask the question, “How does neurostimulation alter the architecture of functional brain
redes?” Based on recent theoretical insights on the costs of forming and breaking connec-
tions in structural and functional brain networks (Achard & bullmore, 2007; Betzel, Medalla,
Papadopoulos, et al., 2017; bullmore & despreciar, 2012), we expect stimulation to heteroge-
neously affect existing coherent interactions, strengthening some and weakening others. To test
these expectations, we study the average change in the following three measures of network
topology across stimulation trials per patient: two at the topological scale of nodes and one at
the topological scale of edges (Figura 2A). At the node scale, we ﬁrst compute the strength, o
average coherence, for each network node during the pre-stim epoch and post-stim epoch for
each of the four coherence frequency bands. We next examine the change in the mean of node

Memory encoding state:
Pattern of brain activity associated
with the likelihood that a subject has
successfully encoded a word into
their episodic memory.

Neurociencia en red

857

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
4
8
1
0
9
2
4
4
0
norte
mi
norte
_
a
_
0
0
0
8
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Functional control of brain networks using direct neurostimulation

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
3
8
4
8
1
0
9
2
4
4
0
norte
mi
norte
_
a
_
0
0
0
8
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 2. Control of frequency-speciﬁc functional network topology. (A) Does stimulation induce
network reconﬁguration at the scale of network nodes or at the scale of network edges? Shown here
are different forms of network reconﬁguration: two forms at the node scale and one form at the edge
escala. At the node scale, stimulation may increase or decrease the overall functional interactions of
a node with other nodes in the network, resulting in a change in the mean of node strengths and/or
a change in the variance, or heterogeneity, of node strengths in the network. At the edge scale,
stimulation may alter the conﬁgurational pattern of functional interactions underlying functional
network topology. We measure edge scale change by computing a conﬁguration similarity metric
(Khambhati et al., 2015) of the pattern of network coherences between the pre-stim trial and the
post-stim trial; values near 1 (o 0) imply a lesser (or greater) change in network conﬁguration. (B–D)
The change in network topology due to stimulation is compared with the change in network topol-
ogy due to passive changes in the brain’s internal state by subtracting the change at baseline from the
stimulation-induced change—each plot point reﬂects the average of this difference across all trials
during a single stimulation session. (B) Difference in the change in mean of node strengths between
stim epochs and baseline epochs. Change in the mean of node strengths is signiﬁcantly greater
during stimulation epochs than baseline epochs in the alpha/theta band (pag < 0.01, corrected). (C) Difference in the change in variance of node strengths between stim epochs and baseline epochs. Change in the variance of node strengths is signiﬁcantly greater during stimulation epochs than baseline epochs in the alpha/theta band (p < 0.001, corrected). Stimulation alters low-frequency organization of the functional network at the scale of network nodes. (D) Difference in the con- ﬁguration similarity of network edges between stim epochs and baseline epochs. Reconﬁguration of functional interactions is signiﬁcantly greater during stimulation epochs than baseline epochs in the high gamma band (p < 0.001, corrected). Stimulation alters high-frequency organization of the functional network at the scale of network edges. Each observation is the average across epochs within a stimulation session of a single subject. Solid lines represent the median, and dashed lines represent the ﬁrst and third quartiles. *p < 0.05, **p < 0.01, ***p < 0.001. strengths and the change in the variance of node strengths between the pre-stim epoch and the post-stim epoch. Intuitively, a change in the mean of node strengths quantiﬁes the likelihood that nodes exhibit greater frequency-speciﬁc functional interaction following stimulation, and a change in the variance of node strengths quantiﬁes the likelihood that nodes exhibit greater heterogeneity in their degree of functional interaction with other nodes in the network. At Network Neuroscience 858 Functional control of brain networks using direct neurostimulation the edge scale, we compute the conﬁguration similarity (Khambhati et al., 2015): a Pearson correlation between the vector of coherence weights during the pre-stim epoch and the vec- tor of coherence weights during the post-stim epoch. Similarity values near 0 imply a greater change in the conﬁguration of network coherences, and values near 1 imply a lesser change in the conﬁguration of network coherences. We conﬁrmed that the topological measurements at the node scale capture different reconﬁguration phenomenon than the topological measure- ments at the edge scale by observing weak relationships between changes in the mean and variance of node strengths to conﬁguration similarity (Supporting Information: Figure 1-1). Next, we test our expectation that stimulation heterogeneously affects existing coherent in- teractions, strengthening some and weakening others, by comparing the change in network topology measures during stimulation trials to passive changes in network topology that occur during the baseline period before the stimulation session begins. We ﬁrst study changes in the mean and variance of node strengths between the pre-stim epoch and post-stim epoch for each of the four coherence frequency bands (Figure 2B,C). Using a Wilcoxon rank-sum test, Bonferroni correction for multiple comparisons, and effect size based on rank correlation, we examine whether node-level changes in the network 100 ms after stimulation offset are any greater than passive changes observed over an equal duration of spontaneous activity at base- line, before any stimulation, across stimulation sessions over subjects. We ﬁnd that stimulation leads to a signiﬁcantly greater change in the mean of node strengths than expected at base- line in the alpha/theta band (Z(247) = 11, 448, p = 0.001, rank correlation = 0.63) and to a nonsigniﬁcant change in the beta band (Z(247) = 14, 006, p = 0.68), in the low gamma band (Z(247) = 13, 131, p = 0.13), and in the high gamma band (Z(247) = 14, 883, p = 1.0). We also ﬁnd that stimulation leads to a signiﬁcantly greater change in the variance of node strengths than expected at baseline in the alpha/theta band (Z(247) = 10, 660, p = 0.0001, rank correlation = 0.65) and to a non-signiﬁcant change in the beta band (Z(247) = 13, 422, p = 0.24), in the low gamma band (Z(247) = 14, 137, p = 0.84), and in the high gamma band (Z(247) = 14, 086, p = 0.76). We ﬁnd that these effects indeed persist and possibly strengthen in the beta band and low gamma band at least 600 ms after stimulation offset (Supporting Information: Figure 2-1b, c). These results demonstrate that stimulation amenably alters func- tional network organization in lower alpha/theta band frequencies (5–15 Hz) at the node scale. Speciﬁcally, we observe that nodes generally exhibit an increase in low-frequency interaction following neurostimulation. However, changes in node strengths are also heterogeneously dis- tributed across nodes in the network. We next ask whether stimulation may still alter functional network topology at the edge scale. Using a Wilcoxon rank-sum test and Bonferroni correction for multiple comparisons, we examine whether conﬁgurational changes in the network edges 100 ms after stimulation offset are any greater than the passive change observed over an equal duration of spontaneous activity at baseline, before any stimulation, across stimulation sessions over subjects. We ﬁnd that stimulation leads to a signiﬁcantly lower conﬁguration similarity (greater reconﬁguration) than expected at baseline in the high gamma band (Z(247) = 9, 252, p = 2.3 × 10−6 , rank correlation = 0.70) and to a nonsigniﬁcant change in the alpha/theta band (Z(247) = 13, 543, p = 1.0), in the beta band (Z(247) = 12, 820, p = 1.0), and in the low gamma band (Z(247) = 13, 502, p = 1.0). We ﬁnd that these effects indeed persist at least 600 ms after stimulation offset (Supporting Information: Figure 2-1d). These results demonstrate that stimulation amenably alters functional network organization in high gamma band frequencies (95–105 Hz) at the edge scale. Speciﬁcally, we observe that functional interactions undergo a change in their conﬁgurational pattern in high frequencies following neurostimulation. Network Neuroscience 859 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional control of brain networks using direct neurostimulation Input Intensity Differentially Modulates Topological Scale of Functional Network Response Building on our observations of a complex, frequency-dependent network response to stimula- tion, we next ask, “Do properties of the stimulation signal, such as amplitude, pulse frequency, and duration, inﬂuence the extent of functional network reconﬁguration?” There is a funda- mental gap in knowledge of how different parameters of direct brain stimulation inﬂuence brain networks—delaying the therapeutic beneﬁts of stimulation in the treatment of neurologi- cal and neuropsychiatric disorders by several months or years (Crowell, Garlow, Riva-Posse, & Mayberg, 2015; Fisher, 2011; Nair & Morrell, 2017). To understand how stimulation parameters inﬂuence functional network reconﬁguration, we draw stimulation parameters from a prede- ﬁned list, uniformly at random, for each consecutive trial (Figure 3A), and we compute the stimulation intensity as the product between the three parameters (Figure 3B). Based on prior observations of a relationship between stimulation intensity and volume of tissue activated (Butson & McIntyre, 2008), we hypothesize that stronger stimulation input into the functional network will lead to more widespread change in functional architecture than weaker stimula- tion input, presumably by penetrating the network along short axonal ﬁbers in the gray matter and long myelinated ﬁbers in the white matter. To test this hypothesis, we ﬁrst compute a within-session Spearman’s ρ correlation between stimulation intensity and the three measures of functional network reconﬁguration (change in mean of node strengths, change in variance of node strengths, and conﬁguration similarity) for the four coherence frequency bands (Figure 3C–E). Using a one-sample t test, Bonferroni cor- rection for multiple comparisons, and effect size based on Cohen’s d we test whether increasing stimulation intensity drives greater node-level changes in the network 100 ms after stimulation offset (Figure 3C, D). We ﬁnd that greater stimulation intensity leads to a signiﬁcant decrease in the mean of node strengths in the high gamma band (t(247) = −6.5, p = 7.0 × 10−9 , Cohen’s d = 0.41), and to a nonsigniﬁcant change in the alpha/theta band (t(247) = 1.6, p = 1.0), beta band (t(247) = 0.2, p = 1.0), and low gamma band (t(247) = −2.0, p = 0.53). We also ﬁnd that greater stimulation intensity leads to a signiﬁcant decrease in the variance of node strengths in the high gamma band (t(247) = −5.9, p = 7.5 × 10−5 , Cohen’s d = 0.40), and to a nonsigniﬁcant change in the alpha/theta band (t(247) = 1.2, p = 1.0), in the beta band (t(247) = −0.7, p = 1.0), and in the low gamma band (t(247) = −1.6, p = 1.0). We ﬁnd that these effects indeed persist in the high gamma band at least 600 ms after stimulation offset (Supporting Information: Figure 3-1c, d). Our results indicate a robust dependence of high- frequency functional reorganization at the scale of network nodes on stimulation strength. Speciﬁcally, greater stimulation intensity disrupts and decreases cohesive node-level interac- tions in high-frequency bands. We did not observe a similar disruption in node-level architec- ture in the lower frequency bands. Logically, we next ask whether stimulation intensity similarly alters the edge-level architec- ture of the network. Using a one-sample t test and Bonferroni correction for multiple compar- isons, we test whether increasing stimulation intensity drives greater conﬁgurational change in the network edges 100 ms after stimulation offset (Figure 3E). We ﬁnd that greater stimulation intensity leads to a signiﬁcant decrease in the conﬁguration similarity (greater reconﬁguration) in the high gamma band (t(247) = −2.8, p = 0.04, Cohen’s d = 0.18), and to a nonsigniﬁcant change in the alpha/theta band (t(247) = −2.8, p = 0.06), in the beta band (t(247) = −1.6, p = 1.0), and in the low gamma band (t(247) = −1.2, p = 1.0). We ﬁnd that these effects dissipate 600 ms after stimulation offset (Supporting Information: Figure 3-1e). Our results indi- cate that greater stimulation intensity drives greater reconﬁguration of the functional topology in high-frequency bands. Additionally, stimulation strength only explains immediate edge-level Network Neuroscience 860 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional control of brain networks using direct neurostimulation l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Edge reconﬁguration: Alteration in the spatial arrangement of connections in a dynamic network. 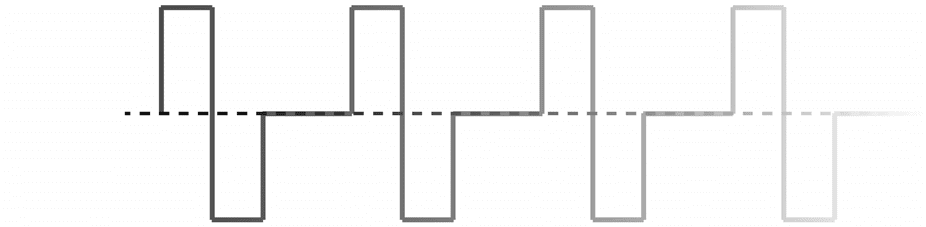Figure 3. Dose-dependent response of network reconﬁguration to stimulation. (A) To examine the effect of stimulation intensity on network reconﬁguration, we vary the amplitude, pulse frequency, and duration of the square-wave input. (B) We quantify the total input intensity delivered during a stimulation trial as the product between the amplitude, pulse frequency, and duration. Here, we show the three-dimensional plane of input parameters that contribute to the overall stimulation intensity. (C) Distribution of correlations between the stimulation intensity and the change in mean of node strengths. Correlations are signiﬁcantly negative in the low gamma band (p < 0.05, corrected) and in the high gamma band (p < 0.001, corrected). (D) Distribution of correlations between the stimulation intensity and the change in variance of node strengths. Correlations are signiﬁcantly negative in the high gamma band (p < 0.001, corrected). Greater stimulation intensity decreases node-level interactions in high-frequency networks and leads to a more homogenous distribution of node strengths in the network. (E) Distribution of correlations between the stimulation intensity and the conﬁguration similarity. Correlations are signiﬁcantly negative in the alpha/theta band (p < 0.01, corrected) and in the high gamma band (p < 0.05, corrected). Greater stimulation intensity leads to lower conﬁguration similarity (greater edge reconﬁguration) in both the low-frequency and the high-frequency networks. For high-frequency networks, the extent of edge-level reconﬁguration may subserve a ﬁner scale mechanism for node-level alterations in functional network topology. Each observation is the correlation across trials within a stimulation session of a single subject. Solid lines represent the median, and dashed lines represent the ﬁrst and third quantiles. *p < 0.05, **p < 0.01, ***p < 0.001. reconﬁguration of network topology and does not exhibit a relationship with later stage edge- level reconﬁguration. Lastly, we asked whether the observed changes in network topology were primarily driven by any single dimension of the stimulation parameter space (trial duration, pulse amplitude, pulse frequency). In contrast to stimulation duration and stimulation amplitude, we observed that changes in the frequency of stimulation signiﬁcantly drives altered network topology at the node level and at the edge level (Supporting Information: Figure 3-2g–i). Speciﬁcally, faster stimulation frequencies may disrupt high-frequency coherence between network nodes, by presumably redistributing coherent edges across the network and reducing the variance in node strengths. Conversely, slower stimulation frequencies may increase node strengths in Network Neuroscience 861 Functional control of brain networks using direct neurostimulation high-frequency networks by driving less topological reconﬁguration of the network edges and simply reinforcing existing functional interactions. 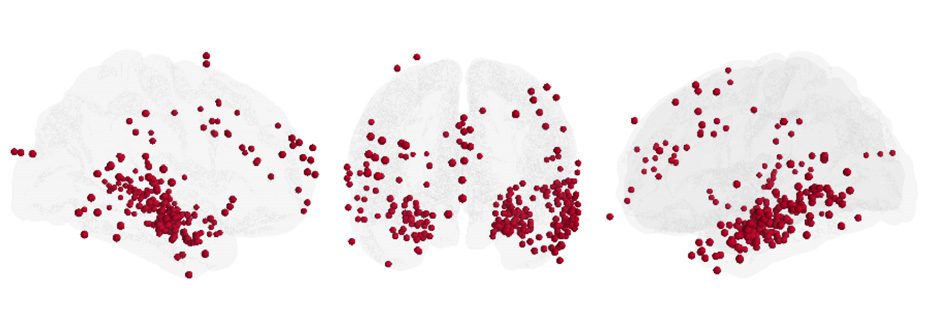Stimulation of Baseline Hubs Versus Nonhubs Has Differential Effects on the Network We next build upon our analysis of the inﬂuence of stimulation parameters on functional net- work topology by similarly investigating the role of 248 unique stimulation locations over 94 subjects in the functional brain network (83 depth locations and 165 surface locations, Figure 4A; see Supporting Information, Figure 4-1, for regional distribution of stimulation lo- cation). We speciﬁcally ask, “Do functional hubs drive more widespread reconﬁguration of the functional network than functionally isolated brain areas?” To answer this question, we measure the node strength as the mean coherence of the stimulation node to all other nodes l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 4. Functional hubs constrain topological response to stimulation. (A) Distribution of 248 stimulation locations sampled across 94 subjects. (B) To examine the effect of stimulation location on the reconﬁguration of functional network topology, we measure the node strength of the stimu- lation region during the baseline epoch—before any stimulation is delivered—for each coherence frequency band. Intuitively, nodes with low strength (left) tend to be functionally isolated and ex- hibit weak coherence with the other nodes in the network, while nodes with high strength (right) tend to be functional hubs and exhibit strong coherence with the other nodes in the network. We expect that stimulation of strong functional hubs will lead to a homogenous change in network topology, and we conversely expect that stimulation of weak functional hubs will lead to a het- erogenous change in network topology. (C) Correlation between the stimulation node strength and the change in mean of node strengths. We ﬁnd no signiﬁcant relationship between the stimulation node strength and the change in mean of node strengths in any frequency band. (D) Correlation between the stimulation node strength and the change in variance of node strengths. We ﬁnd no signiﬁcant relationship between the stimulation node strength and the change in variance of node strengths. (E) Correlation between the stimulation node strength and the conﬁguration similarity. Correlations are signiﬁcantly positive in the low gamma band (p < 0.05, corrected) and in the high gamma band (p < 0.001, corrected). Greater stimulation node strength leads to greater conﬁgura- tion similarity (lower edge reconﬁguration) in high-frequency networks. Correlations are computed over stimulation sessions across subjects. *p < 0.05, **p < 0.01, ***p < 0.001. Network Neuroscience 862 Functional control of brain networks using direct neurostimulation at baseline. We hypothesize that stimulation of a stronger functional hub will lead to greater dispersion of input intensity throughout the network, driving a homogenous network response; stimulation of a weaker functional hub will lead to more targeted dispersion of input intensity to a subset of network nodes, driving a heterogenous network response (Figure 4B). To test this hypothesis, we ﬁrst compute a Spearman’s ρ correlation between baseline node strength of the stimulation region and the average of each of the three measures of func- tional network reconﬁguration (change in the mean of node strengths, change in the variance of node strengths, and the conﬁguration similarity) for the four coherence frequency bands (Figure 4C–E). Using a Bonferroni correction for multiple comparisons, we test whether greater node strength of the stimulation region drives greater node-level changes in the network 100 ms after stimulation offset, over stimulation sessions across subjects (Figure 4C, D). We ﬁnd that stimulation node strength does not signiﬁcantly inﬂuence the mean of node strengths in the alpha/theta band (ρ(246) = −0.02, p = 1.0), in the beta band (ρ(246) = −0.02, p = 1.0), in the low gamma band (ρ(246) = −0.06, p = 1.0), or in the high gamma band (ρ(246) = −0.03, p = 1.0). We also ﬁnd that the stimulation node does not signiﬁcantly inﬂuence the vari- ance of node strengths in the alpha/theta band (ρ(246) = −0.05, p = 1.0), in the beta band (ρ(246) = −0.03, p = 1.0), in the low gamma band (ρ(246) = −0.14, p = 0.09), or in the high gamma band (ρ(246 = −0.11, p = 0.3). We also do not observe these effects after 600 ms following stimulation offset (Supporting Information: Figure 4-2c, d). Our results indicate that baseline node strength does not play an inﬂuential role in altering large-scale organization of network nodes. We next ask whether the strength of the stimulation node can differentially drive reconﬁg- uration of edge-level architecture of the network. Using a Bonferroni correction for multiple comparisons, we test whether greater node strength of the stimulation region drives greater conﬁgurational change in the network edges 100 ms after stimulation offset, over stimulation sessions across subjects (Figure 4E). We ﬁnd that greater stimulation node strength leads to a signiﬁcantly greater conﬁguration similarity (lower reconﬁguration) in the low gamma band (ρ(246) = 0.17, p = 0.03) and in the high gamma band (ρ(246) = 0.58, p = 2.2 × 10−22 ), and to a nonsigniﬁcant change in the alpha/theta band (ρ(246) = 0.01, p = 1.0) and in the beta band (ρ(246) = 0.13, p = 0.2). We ﬁnd that these effects persist in the low gamma band and in the high gamma band, and that they strengthen in the beta band at least 600 ms after stimulation offset (Supporting Information: Figure 4-1e). These results suggest that the functional topology of the stimulation region signiﬁcantly impacts the pattern of coherent in- teractions in low and high gamma coherence frequency bands. Speciﬁcally, stimulation of weaker functional hubs tends to drive a greater change in the pattern of coherent interactions in low gamma networks and in high gamma networks. We ﬁnd that a location-based rule for using stimulation to control the distributed reconﬁguration of functional interactions is most robust for high gamma networks thought to reﬂect activity associated with synaptic input and short-range interactions. Combined with our earlier ﬁndings on the negative relationship between stimulation in- tensity and edge reconﬁguration, our ﬁndings suggest that stimulation of stronger functional hubs may lead to greater attenuation of the stimulation intensity and drive less edge-level re- conﬁguration than stimulation of weaker functional hubs. Another possible explanation for our ﬁndings is that stronger coherent interactions between stimulated hub nodes and the remaining nodes in the network mechanistically constrain the network response to stimulation—which we assess next. Network Neuroscience 863 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional control of brain networks using direct neurostimulation Baseline Coherence of Stimulation Target With Other Regions Constrains Future Network Response Our ﬁndings in the previous section point to an important role of the baseline functional net- work in constraining the network response to stimulation. Logically, a stimulation node that exhibits stronger coherence with one set of brain regions may be more likely to convey the stimulation input to these brain regions than to another set of brain regions with which it ex- hibits weaker coherence. We therefore next test the hypothesis that the baseline coherence between the stimulation node and a downstream node predicts the probability that the down- stream node will be evoked during a stimulation trial (Figure 5A). In other words, a stronger baseline coherence between the stimulation node and the downstream node may facilitate a greater magnitude change in the node strength of the downstream node. To address this hypothesis, we ﬁrst compute the within-session mean and variance of the magnitude change in node strength. For each session, we next compute the Spearman’s ρ correlation between the set of baseline coherence values between the stimulation node and the downstream nodes and the mean of the magnitude changes in node strength of each l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 5. Predicting downstream modulation of regional coherence. (A) We hypothesize that the baseline strength of coherent interactions between the stimulation node (red) and network nodes away from the stimulation node (black) predicts the likelihood that these downstream nodes will be evoked because of stimulation. Intuitively, a weak baseline coherence between the stimulation node and a downstream network node is less likely to modulate the mean coherence of the down- stream node (left), and a strong baseline coherence between the stimulation node and a downstream network node is more likely to modulate the mean coherence of the downstream node (right). To test this hypothesis, we ﬁrst quantify the magnitude change in node strength within each stimulation session. We next compute Spearman’s ρ correlation between the mean (and variance) of change in downstream node strength across stimulation trials and the baseline coherence between the stimula- tion node and the downstream nodes. (B) Distribution of correlations between the mean of change in downstream node strength and the baseline coherence between the stimulation node and the downstream nodes, for each of the four coherence frequency bands. We ﬁnd a signiﬁcantly positive correlation in the alpha/theta band (p < 0.01, corrected), in the beta band (p < 0.001, corrected), and in the low gamma band (p < 0.001, corrected). These results suggest that baseline functional network topology involving the stimulation node predicts downstream modulation in node strength. (C) Distribution of correlations between the variance of change in downstream node strength and the baseline coherence between the stimulation node and the downstream nodes. We ﬁnd a sig- niﬁcantly positive correlation in the beta band (p < 0.001, corrected) and in the low gamma band (p < 0.001, corrected). These results suggest that baseline functional network topology involving the stimulation node predicts the ﬂexibility with which a downstream node may alter its interactions with other nodes in the network. Each observation is the correlation within a stimulation session of a single subject. Solid lines represent the median, and dashed lines represent the ﬁrst and third quantiles. *p < 0.05, **p < 0.01, ***p < 0.001. Network Neuroscience 864 Functional control of brain networks using direct neurostimulation downstream node (Figure 5B). Intuitively, positive correlation values imply that stronger base- line coherence between the stimulation node and the downstream nodes predicts greater mag- nitude change in node strength across stimulation epochs. Using a Wilcoxon rank-sum test, Bonferroni correction for multiple comparisons, and effect size based on rank correlation, we ﬁnd a signiﬁcant positive correlation values in the alpha/theta band (Z(247) = 4, 986, p = 0.003, rank correlation = 0.84), in the beta band (Z(247) = 2, 092, p = 5.4 × 10−15 , rank correlation = 0.93), in the low gamma band (Z(247) = 2, 355, p = 1.4 × 10−13 , rank correla- tion = 0.92), and we ﬁnd a nonsigniﬁcant positive trend in the high gamma band (Z(247) = 5, 928, p = 0.19). We also assess the Spearman’s ρ correlation between the set of baseline coherence values between the stimulation node and the downstream nodes and the variance of the magnitude changes in node strength of each downstream node (Figure 5B). We ﬁnd a signiﬁcantly positive correlation in the beta band (Z(247) = 2, 721, p = 9.9 × 0−11 , rank cor- relation = 0.91) and in the low gamma band (Z(247) = 2, 997, p = 2.0 × 10−10 , rank correlation = 0.90), and we ﬁnd a nonsigniﬁcant positive trend in the alpha/theta band (Z(247) = 5, 993, p = 0.24) and in the high gamma band (Z(247) = 6, 340, p = 0.72). We ﬁnd that these effects persist in the alpha/theta band, in the beta band, and in the low gamma band and strengthen in the high gamma band at least 600 ms after stimulation offset (Supporting Information: Figure 5-1b,c). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Our ﬁndings are consistent with the hypothesis that the baseline functional network topol- ogy involving the stimulation node may be used to predict the downstream network regions that are most inﬂuenced by stimulation. We also ﬁnd that this predictive capacity is dependent on the frequency band of the coherent measurement: The likelihood of modulating the coher- ent interactions of a downstream node is less predictable for higher frequencies. This ﬁnding suggests that the direct coherence between a stimulation node and a downstream node may be more inﬂuential in conveying stimulation input to the downstream node for lower coher- ence frequency bands. Our analysis highlights a putative mechanism of node-level ﬂexibility, or the ability for a network region to dynamically alter its level of interaction with other re- gions in the network. Speciﬁcally, stronger baseline coherence between the stimulation node and a downstream node tends to predict greater variability with which the downstream node changes its level of interaction with the rest of the network within a stimulation session. Such a rule can guide more principled targeting of network structures to amenably drive ﬂexible reconﬁguration of the functional network. Unifying Stimulation and Functional Reconﬁguration With Network Control Theory We lastly seek to integrate our observations on stimulation-driven reconﬁguration of functional brain networks with ﬁrst principles theory. Network control theory provides a mathematical framework to model changes in the state of a complex system under a set of constraints pre- scribed by the structure of that system (Pasqualetti et al., 2014; Yan et al., 2017). For brain networks, network control theory offers an opportunity to model the logical progression of a stimulus input into an anatomically deﬁned structural brain network, the traversal of that input through the network, the resulting change in interregional communication, and an ac- companying shift in the dynamical state of the brain that accommodates a change in behavior (Figure 6A; Gu et al., 2017, 2015; Kim et al., 2018; Muldoon et al., 2016; Pequito et al., 2016). The structural topology of the network may confer important control properties to a complex system such as modal controllability, which enables a system to move from its cur- rent dynamical state to more difﬁcult-to-reach dynamical states through an efﬁcient expen- diture of energy resources (Ashourvan, Gu, Mattar, Vettel, & Bassett, 2017; Gu et al., 2015; Pasqualetti et al., 2014). Recent theoretical inquiry into the relationship between brain structure Network Neuroscience 865 Functional control of brain networks using direct neurostimulation Modal controller: Network node that facilitates energetically challenging state transitions and is deﬁned based on its rigid structural connectivity with other network nodes. and function during stimulation posited that stimulation of the structural brain network’s modal controllers may drive a heterogenous change in functional architecture (Muldoon et al., 2016). However, experimental evidence linking the network control theoretic model to brain stimu- lation and its inﬂuence on functional architecture and dynamical brain state via the structural brain network is lacking. In this study, we have so far shown that stimulation drives a rich and complex functional network response that is dependent on the stimulation input intensity and the stimulation in- put location. While the input intensity drives the magnitude of functional reconﬁguration, the baseline coherence of the input location constrains the spatial speciﬁcity of the functional reconﬁguration. Yet, how does baseline network topology in the vicinity of the stimulation region relate to the modal control strategy put forth by structural control theory? To answer this question, we construct structural brain networks by applying deterministic tractography to diffusion-weighted imaging data that are parcellated into 1,015 anatomically deﬁned, cortical and subcortical regions of interest (Cammoun et al., 2012) in a subset of 14 participants (see Methods; the other participants did not have diffusion-weighted imaging data). We next assign the intracranial ECoG sensors for a subject to their nearest anatomical ROI based on the short- est spatial distance between a sensor and the ROI centroids. We then measure the structural connectivity between anatomical ROIs and the modal controllability of each anatomical ROI in the structural network, and we assign these values to the intracranial sensors based on their proximity to the nearest ROI. To establish a clear relation between structural connectivity and baseline functional con- nectivity (measured by coherence), we calculate the Pearson correlation between the pattern of structural connections and the pattern of baseline coherent interactions between intracra- nial sensors, for each coherence frequency band and each subject (Figure 6B). This proce- dure is conducted separately for connections that span the same hemisphere of the brain (intra-hemispheric connections) and for connections that span opposing hemispheres of the brain (inter-hemispheric connections), and correlation values are subsequently z-scored us- ing the Fisher transformation. Using a one-sample t test, we test the null hypothesis that the z-transformed correlation between structural connectivity and functional connectivity is equal to 0. For intra-hemispheric connections, we observe signiﬁcant negative correlation be- tween structural connectivity and baseline coherence in the low gamma band (t(13) = −3.0, p = 0.04, corrected) and in the high gamma band (t(13) = −3.6, p = 0.01, corrected), and non-signiﬁcant negative trends in the alpha/theta band (t(13) = −1.5, p = 0.64, cor- rected) and in the beta band (t(13) = −1.8, p = 0.34, corrected). For inter-hemispheric connections, we observe nonsigniﬁcant positive trends between structural connectivity and baseline coherence in the alpha/theta band (t(13) = −0.7, p = 0.48, corrected), in the beta band (t(13) = 0.9, p = 0.37, corrected), in the low gamma band (t(13) = 0.9, p = 0.39, corrected), and in the high gamma band (t(13) = 0.8, p = 0.44, corrected). Generally, inter-hemispheric connections exhibited positive trends between structural connectivity and ECoG functional connectivity, while intra-hemispheric connections exhibited negative trends between structural connectivity and ECoG functional connectivity. This observed relationship was stronger at the ﬁner scale parcellation of the brain than at the coarser scale parcellation (Supporting Information: Figure 6-1). Our results imply that weaker structural connections be- tween brain regions within the same hemisphere are generally associated with stronger coher- ent interactions in higher frequency bands, which typically reﬂect local, bottom-up processing associated with synaptic input. This divergent relationship can be explained by an expectedly strong coherence between brain regions that are in close proximity to one another, which Network Neuroscience 866 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional control of brain networks using direct neurostimulation l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 6. Using neurostimulation to bridge structure, function, and behavior. (A) Network control theory can model dynamical state changes due to external input and structural constraints on the system. Consider a stimulation input to the structural brain network (left). This input would evoke a functional response constrained by the architecture of the structural network (middle) and shift the brain from one state to another state (right). Previous studies posit that structural topology of the input region—modal controllability—may relate to the energy required to move between different dynamical states (Gu et al., 2015; Pasqualetti et al., 2014). Speciﬁcally, stronger modal controllers may lead to more distant transitions across an energy landscape than weaker modal controllers (right). Here, we demonstrate a link between stimulation of the structural brain network, the evoked functional network response, and changes in dynamical state associated with behavior. Brieﬂy, we use a previously published biomarker of brain state based on a logistic regression-based classiﬁer of neural activity associated with positive memory encoding (Ezzyat et al., 2017). (B) Distribution of Fisher z-transformed correlations between structural connectivity from DTI and baseline coherence from ECoG, across subjects. Distributions are subdivided by inter-hemispheric and intra-hemispheric connections and coherence frequency band. We ﬁnd a signiﬁcant negative correlation between structural connectivity and baseline functional connectivity in the low and high gamma bands (p < 0.05, corrected) for intra-hemispheric connections; we observed nonsigniﬁcant positive trends between structural connectivity and baseline functional connectivity for inter-hemispheric connections. (C) Correlation between the modal controllability of the stimulated brain region and the average functional conﬁguration similarity across stimulation sessions. We ﬁnd a signiﬁcant positive correlation in the beta band (p < 0.01, corrected), in the low gamma band (p < 0.01, corrected), and in the high gamma band (p < 0.01, corrected). This result implies that stimulation of modal controllers leads to less network-wide reconﬁguration of functional interactions. (D) We ﬁnd a signiﬁcant positive correlation between the average change in classiﬁer likelihood of positive memory encoding state during stimulation trials and the modal controllability of stimulated nodes based on the structural brain network (p < 0.05). This result implies that stimulation of structural brain regions that are more capable of pushing the brain to difﬁcult-to-reach dynamical states is associated with an increased likelihood of reaching a positive memory encoding state after stimulation. *p < 0.05, **p < 0.01, ***p < 0.001. are more likely to be weakly linked by structural U-shaped white matter ﬁbers (Schmahmann et al., 2007). Based on the result that structural connectivity weakly constrains baseline coherent interactions between brain regions, we ask whether a control strategy motivated by modal control- lability of the structural brain network predicts stimulation-driven reconﬁguration of the func- tional network topology. To answer this question, we ﬁrst calculate the modal controllability for Network Neuroscience 867 Functional control of brain networks using direct neurostimulation the brain region in each stimulation session across subjects. We next compute the Spearman’s ρ correlation between modal controllability of the stimulated brain region and the average, within-session conﬁguration similarity. Using Bonferroni correction for multiple comparisons, we ﬁnd a signiﬁcant positive correlation between modal controllability and conﬁguration sim- ilarity in the beta band ( ρ(24) = 0.61, p = 0.003), in the low gamma band ( ρ(24) = 0.65, p = 0.001), and in the high gamma band ( ρ(24) = 0.59, p = 0.005), and we ﬁnd a nonsignif- icant positive trend in the alpha/theta band ( ρ(24) = 0.47, p = 0.05). These effects persist at least 600 ms after stimulation offset (Supporting Information: Figure 6-2a). These results imply that stimulation of stronger modal controllers drives lower reconﬁguration of the coher- ent interactions in the functional network. To contextualize these ﬁndings, we draw upon the well-established positive relationship between modal controllability and structurally isolated brain regions (Gu et al., 2015). By targetting strong modal controllers in the structural brain network, stimulation modulates structurally isolated brain areas and drives lower functional reconﬁguration than stimulation of weak modal controllers in structurally connected brain areas. Notably, our results demonstrate a complex and frequency-speciﬁc link between structural topology and functional topology—weak structural connections tend to span between brain areas with stronger, high-frequency functional interactions, and stimulation of modal con- trollers in structurally isolated brain regions tends to limit the extent of functional network reconﬁguration. Combined with earlier ﬁndings, we put forth a putative sequence of physio- logical events associated with modal control in which stimulation of strong modal controllers activates strong, local functional hubs that drive less functional reconﬁguration of network- wide edges (Figure 4E) and greater change in the node strengths of functionally connected, downstream brain regions (Figure 5B). In contrast, stimulation of weak modal controllers acti- vates weaker, functionally isolated regions that drive distributed functional reconﬁguration of network-wide edges (Figure 4E). While these ﬁndings establish a link between network con- trol and functional reconﬁguration, they do not establish a link between network control and changes in dynamical brain state. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d t . To experimentally examine the relationship between the modal controllability of the stimu- lation region and the shift in dynamical brain state following stimulation, we leverage a previ- ously documented and validated binary classiﬁer of neural activity into good and poor episodic memory encoding states (Ezzyat et al., 2017). Speciﬁcally, we ﬁrst train the classiﬁer to dis- criminate between successful and unsuccessful word recall trials during a delayed free recall task using features based on spectral power of ECoG activity. We next evaluate the classiﬁer on ECoG activity during the pre-stim epoch and the post-stim epoch of each stimulation trial and compute the change in probability of being in a good memory encoding state. We calculate the correlation between the modal controllability of the stimulation region and the average, within-session change in probability of being in a good memory state over stimulation trials (Figure 6D). We ﬁnd a signiﬁcant positive correlation (Pearson’s r(17) = 0.49, p = 0.03). These ﬁndings imply that the push towards better memory encoding states is associated with stimulation of strong modal controllers that are theoretically positioned to push the brain to more energetically unfavorable and distant brain states. f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Collectively, our study reveals a link between brain structure and brain function that is grounded in network control theory. Using the network control framework, we uncover the important role of stimulation on reconﬁguration of functional architecture that accounts for anatomical constraints on network dynamics via the topology of structural network connectiv- ity. We ﬁnd that brain networks may use a modal control strategy during transitions between Network Neuroscience 868 Functional control of brain networks using direct neurostimulation difﬁcult-to-reach dynamical states, which is associated with a reconﬁguration in the localized coherence of individual network nodes to the broader functional brain network. DISCUSSION Here, we addressed the hypothesis that direct stimulation of cortical and subcortical struc- tures alters the architecture of functional brain networks and shifts the dynamical brain state in accord with control strategies identiﬁed by applying tools from network control theory to elec- trophysiological and structural brain imaging data. In human epilepsy patients, we measured coherent patterns of ECoG activity thought to underlie coordinated functional interactions, and we mapped how these interactions vary with neurostimulation parameters. We observed that stimulation drives two modes of functional reconﬁguration: The ﬁrst mode involves distributed changes in the pattern of functional interactions across the network, and the second mode involves preferentially localized changes in the functional interactions associated with select brain regions. Notably, the mode of reconﬁguration may be strategically selected based on the strength and location of stimulation. When we stimulated brain regions with weak structural connections to the rest of the network, we tended to invoke a modal control strategy marked by a modulation of the functional hubness of downstream brain regions and a large change in dynamical brain state. Predictors of Functional Reconﬁguration: Implications for Brain Network Control The ﬁeld of network neuroscience has long sought to understand how the rigid and inter- connected anatomy of the structural brain network shapes interactions amongst functionally specialized brain areas, which may change from moment to moment and drive cognition and behavior (Hermundstad et al., 2013, 2014; Miši´c et al., 2016; Park & Friston, 2013). Tools from network control theory (Liu, Slotine, & Barabasi, 2011; Pasqualetti et al., 2014; Tang & Bassett, 2017) have enabled researchers to identify controllability rules that prescribe how the dynam- ical state of a neural system can change based solely on the structural topology of the system (Betzel et al., 2016; Gu et al., 2017, 2015; Kim et al., 2018; Tang et al., 2017; Yan et al., 2017). Structural controllability rules account for network interactions that can occur, but they do not account for ﬁner scale functional constraints that dictate whether these interactions will occur at a point in time (Liu et al., 2011; Tang & Bassett, 2017). Previous studies have incorporated these functional constraints into the study of network control by using neurophysiologically inspired dynamical mean-ﬁeld models (Jirsa et al., 2017; Muldoon et al., 2016; Taylor et al., 2015), which require estimation of biologically plausible parameters. In contrast to these studies, we used a data-driven, perturbative approach for inferring rules of functional network reconﬁguration. By focally stimulating brain tissue at the millimeter scale, we mapped changes in the statistical interdependencies between brain regions. We note that there is a subtle distinction in the statistical methods used here to measure bidrec- tional, synchronized interactions and statistical methods used elsewhere to measure directed, effective functional interactions (Battaglia, Witt, Wolf, & Geisel, 2012; Friston, 2011; Lepage, Ching, & Kramer, 2013). We found that the observed change in statistical interdependency can be predicted by baseline levels measured before any stimulation is delivered. That is, a brain region that exhibits a strong, spontaneous functional interaction with the stimulated brain region is more likely to be modulated during stimulation than a brain region with a weak, spon- taneous functional interaction with the stimulated brain region. In the long-standing debate re- garding the validity of functional network models to explain causal dynamics (Jonas & Kording, 2017), these data provide compelling evidence in favor of a mechanism in which the functional Network Neuroscience 869 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional control of brain networks using direct neurostimulation network may causally convey the inﬂuence of stimulation on one brain region to other strongly interacting brain regions. Our ﬁndings implicate a strategy for the functional control of brain networks in which (a) stimulation of functionally isolated brain regions leads to spatially focal and strong downstream functional reconﬁguration, and (b) stimulation of functionally hub-like brain regions leads to spatially diffuse and weak downstream functional reconﬁguration. To relate rules for functional control to theoretical predictions from structural controllabil- ity, we bridged electrophysiological data with structural brain imaging data. Conﬁrming results from prior studies on controllability in healthy subjects (Gu et al., 2015; Tang et al., 2017), in epilepsy subjects we found that brain regions with structurally weak connections tend to be strong modal controllers, which facilitate more difﬁcult transitions in brain state. Stimulations of structurally weak modal control points lead to strong, local change of functional architecture in a mean-ﬁeld model of neuron population dynamics (Muldoon et al., 2016). In contrast, here we demonstrated that stimulation of modal control points leads to widespread, weak change in functional architecture because of the presence of strong functional hubs in the stimulated brain regions. We identiﬁed two potential explanations for the distinction between the model simulation and our empirical observations. First, the in silico model assumes identical bio- physical parameters across different neuronal ensembles distributed across the brain network, which may limit the reproducibility of detailed spatial and temporal dynamics that would other- wise be expressed in vivo and measured by intracranial ECoG sensors. Second, the in silico model accounts for structural connectivity between neuronal ensembles using diffusion imag- ing, which measures white matter ﬁber pathways spanning long distances but does not capture gray matter pathways spanning short distances (Thomas et al., 2014) and synaptic microarchi- tecture responsible for plasticity over varying time scales (Song, Miller, & Abbott, 2000). When combined with additional data demonstrating a moderate relationship between white matter connectivity and correlated ECoG dynamics (Betzel, Medaglia, Kahn, et al., 2017), our ﬁnd- ings suggest that non–white matter structural connectivity and other physiological factors may contribute to the reconﬁguration of functional network architecture. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t Physiological Interpretations of Altered Functional Topology Neuronal synchronization is purported to play a crucial role in facilitating interareal commu- nication between ensembles of neurons (Bonnefond et al., 2017; Buzsáki et al., 2012; Canolty & Knight, 2010; Fries, 2015; Schalk, 2015). Fries (2015) proposed that rhythmic oscillations in the local ﬁeld potential give rise to states of excitability depending on the temporal position during an oscillatory cycle—two different ensembles of neurons are able to reliably transfer information between one another when they are mutually excitable, or exhibit oscillations that are in-phase. Equally important to communication is the frequency of the oscillation— higher frequency bands (γ) are thought to facilitate communication of bottom-up input over short distances, and lower frequency bands (θ, α, β) are thought to facilitate communication of top-down processes over long distances (Fries, 2015; Kopell et al., 2000). f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Notably, we found that stimulation parameters may be tuned to selectively modulate dif- ferent regions and spatial extents of the functional network. Stimulation intensity tends to pro- vide greater control over reconﬁguration of lower frequency networks, and stimulation location tends to provide greater control over reconﬁguration of higher frequency networks. Speciﬁcally, we observed that the strength of the stimulation input has a greater effect on functional recon- ﬁguration in lower frequency bands than in higher frequency bands, suggesting that stimulation parameters such as amplitude, pulse frequency, and duration may play an important role in the modulation of long-range, top-down functional interactions. We speculate that a stronger Network Neuroscience 870 Functional control of brain networks using direct neurostimulation stimulation input may be more likely to penetrate wider spatial extent of cortex and heteroge- nously modulate network excitability at low frequencies (Fries, 2015). We also observed that the location of the stimulation input has a greater effect on functional reconﬁguration in higher frequency bands than in lower frequency bands, suggesting that the hubness of the stimu- lated brain region may play an important role in the modulation of short-range, bottom-up functional that brain regions involved in bottom-up communication associated with broadly conveying sensory input to higher order cortices might also be more sensitive to modulations via stimulation than brain regions involved in top-down communication. Intuitively, we expect interactions. Methodological Considerations and Future Work We chose to perform a network analysis of intracranial data during neurostimulation, rather than a univariate analysis of individual activations. Our decision enabled us to examine the inﬂuence of neurostimulation on the distributed and interconnected physiology of the human brain, which is in line with previous in silico modeling work (Muldoon et al., 2016). Several notable studies have teased apart the effective connectivity between brain regions using neuro- stimulation to generate cortico-cortico evoked potentials (CCEPs; Keller, Honey, Entz, et al., 2014; Keller, Honey, Me, et al., 2014; Matsumoto et al., 2004), and have more recently pre- dicted where CCEPs might occur using a combination of repetitive low-frequency stimulation and baseline connectivity (Keller et al., 2018). In a departure from these studies on effective connectivity, we test the novel hypothesis that neurostimulation can predictively perturb inter- areal statistical dependencies underlying distributed brain function. Our study is motivated by recent hypotheses regarding the role of coherent synchronization in neuronal communication. With the maturation of network analysis tools that enable simultaneous tracking of dynamic network architecture and dynamic activity (Murphy et al., 2016), we envision future studies where we investigate the potential for neurostimulation to selectively modulate brain activity or perturb functional network architecture. We also chose to examine static changes in the functional network architecture aggregated over many repeated trials of neurostimulation. This approach allowed us to examine the ability of stimulation to drive network reconﬁguration within each subject, and to evaluate the statisti- cal robustness of effects across subjects. Generally, we ﬁnd medium to large effect sizes on the order of 0.4–0.9. The advantage of our chosen approach is that the effects of stimulation are assessed separately for each patient, which enabled us to account for an individual’s stereo- typed network topology while examining generalized rules that predict the network effects of stimulation. We can thus address questions such as, “Are some brain regions more likely to change their functional interactions than other brain regions?” and “How are these brain re- gions associated with the stimulated brain region?” In future studies, we aim to understand how stimulation inﬂuences the functional brain network from one moment in time to the next, as a function of brain state. For instance, does stimulation during the beginning of a coherent oscillatory cycle inﬂuence network architecture differently than stimulation during the middle of a coherent oscillatory cycle? This temporal mapping could inform control strategies to steer functional brain network reconﬁguration in real time. One important question regarding the neural adaptation effects of stimulation is beyond the scope of this analysis and remains unanswered: “How long do stimulation-induced changes to the network last?” An answer to this valuable question could support therapeutic applica- tions of direct stimulation by reducing the need to stimulate the brain for long periods of time at high intensity—potentially improving safety, efﬁcacy, and longevity of chronically implantable Network Neuroscience 871 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional control of brain networks using direct neurostimulation devices (Fisher, 2011; Stacey & Litt, 2008). The adaptation question will be addressed in a fu- ture study by introducing longer periods of rest between consecutive stimulation trials and quantifying the duration of connectivity changes. A related consideration of this study is that a sham condition was not included during the stimulation session and changes in functional network architecture were instead compared with passive changes in network architecture at baseline. Indeed, a dedicated sham condition during stimulation would be able to dissoci- ate the effects of stimulation from natural ﬂuctation in the brain’s internal dynamics. Previous studies have emphasized that sham stimulation may be more effective at assessing behavioral, “placebo” effects of stimulation than quantifying neural effects, given the biophysical differ- ences between external input from a current source in comparison to spontaneous ﬂuctuation of endogenous neural activity (Duecker & Sack, 2015). In this study, we enforced a fairer com- parative condition to understand neural effects of stimulation by parameterically titrating the dose of stimulation via current amplitude, frequency, and duration—all likely inducing a more similar biophysical change to neural tissue than a sham condition with zero current deliv- ery. Furthermore, stimulation trials were made blind to the patient, trial durations were kept short (below 1 s), and the start of a stimulation trial was randomly jittered to mitigate neural expectation of stimulation timing. Approaches for recording and interrogating intracranial electrophysiology are inherently limited by spatial coverage of the ECoG sensors, which is determined during the management of a patient’s epilepsy. This sampling bias leads to a varied representation of the functional brain network between individual patients. While it is not yet possible to record from the entirety of the human brain using ECoG, we mitigated this shortcoming by taking key steps in our analysis. First, we used a statistically robust approach for characterizing the network impact of stimulation in individual patients. We computed separate measures of topology for each patient’s functional brain network, which enabled us to account for individual variability in sensor placement and physiological state. Our data demonstrated a set of functional rules for network reconﬁguration that fundamentally depend on topological characteristics of the stimulated brain area that can vary within and between patients. Second, we used a large dataset consisting of 94 epilepsy patients, allowing us to account for a range of individual variability in functional brain network architecture that is often not possible in studies of human electrophysiology. CONCLUSIONS Here we mapped the impact of targeted neurostimulation on distributed functional architecture in the human brain. We demonstrated that network physiology can be predictably altered based on control theoretic rules that account for structural and functional organization of the brain network. Our results provide a causal, quantiﬁed description of the inﬂuence of structure and function on dynamical brain state. Our ﬁndings have signiﬁcant translational implications in strategizing stimulation-based therapy based on a combination of behavioral biomarkers and neurophysiology. ACKNOWLEDGMENTS We thank Blackrock Microsystems for providing neural recording and stimulation equipment. The views, opinions, and/or ﬁndings contained in this material are those of the authors and should not be interpreted as representing the ofﬁcial views or policies of the Department of Defense, the U.S. government, or any of the funding agencies. Network Neuroscience 872 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional control of brain networks using direct neurostimulation AUTHOR CONTRIBUTIONS Ankit N. Khambhati: Conceptualization; Formal analysis; Investigation; Methodology; Software; Validation; Visualization; Writing – Original Draft; Writing – Review & Editing. Ari E. Kahn: Methodology. Julia Costantini: Formal analysis; Software. Youssef Ezzyat: Conceptualization; Data curation. Ethan A. Solomon: Conceptualization; Data curation. Robert E. Gross: Data cu- ration. Barbara C. Jobst: Data curation. Sameer A. Sheth: Data curation. Kareem A. Zaghloul: Data curation. Gregory Worrell: Data curation. Sarah Seger: Data curation. Bradley C. Lega: Data curation. Shennan Weiss: Data curation. Michael R. Sperling: Data curation. Richard Gorniak: Data curation. Sandhitsu R. Das: Data curation; Methodology; Software. Joel M. Stein: Data curation; Methodology; Software. Daniel S. Rizzuto: Data curation; Project administra- tion. Michael J. Kahana: Data curation; Funding acquisition; Project administration; Resources. Timothy H. Lucas: Data curation. Kathryn A. Davis: Data curation. Joseph I. Tracy: Data cura- tion. Danielle S. Bassett: Conceptualization; Funding acquisition; Methodology; Project administration; Resources; Supervision; Writing - Original Draft; Writing - Review & Editing. FUNDING INFORMATION Danielle S. Bassett, John D. and Catherine T. MacArthur Foundation (http://dx.doi.org/ 10.13039/100000870). Danielle S. Bassett, Alfred P. Sloan Foundation (http://dx.doi.org/ 10.13039/100000879). Danielle S. Bassett, Army Research Laboratory (http://dx.doi.org/10. 13039/100006754), Award ID: W911NF-10-2-0022. Danielle S. Bassett, Army Research Laboratory (http://dx.doi.org/10.13039/100006754), Award ID: W911NF-14-1-0679. Danielle Institutes of Health (http://dx.doi.org/10.13039/ S. Bassett, Foundation for the National 100000009), Award ID: 2-R01-DC-009209-11. Danielle S. Bassett, Foundation for the Na- tional Institutes of Health (http://dx.doi.org/10.13039/100000009), Award ID: 1R01HD086888-01. Danielle S. Bassett, Foundation for the National Institutes of Health (http://dx.doi.org/ 10.13039/100000009), Award ID: R01-MH107235. Danielle S. Bassett, Foundation for the Na- tional Institutes of Health (http://dx.doi.org/10.13039/100000009), Award ID: R01-MH107703. Danielle S. Bassett, Foundation for the National Institutes of Health (http://dx.doi.org/10.13039/ 100000009), Award ID: R21-M MH-106799. Danielle S. Bassett, U.S. Naval Research Labo- ratory (http://dx.doi.org/10.13039/100009917). Danielle S. Bassett, National Science Foun- dation (http://dx.doi.org/10.13039/100000001), Award ID: BCS-1441502. Danielle S. Bassett, National Science Foundation (http://dx.doi.org/10.13039/100000001), Award ID: CAREER PHY-1554488. Danielle S. Bassett, National Science Foundation (http://dx.doi.org/10.13039/ 100000001), Award ID: BCS-1631550. Michael J.Kahana, Defense Advanced Research Projects Agency (http://dx.doi.org/10.13039/100000185), Award ID: N66001-14-2-4032. REFERENCES Aarts, J. H., Binnie, C. D., Smit, A. M., & Wilkins, A. J. (1984). Selec- tive cognitive impairment during focal and generalized epilepti- form EEG activity. Brain, 107(Pt. 1), 293–308. Achard, S., & Bullmore, E. (2007). Efﬁciency and cost of economi- cal brain functional networks. PLoS Computational Biology, 3(2), e17. https://doi.org/10.1371/journal.pcbi.0030017 Andersson, J. L., & Sotiropoulos, S. N. (2016). An integrated ap- proach to correction for off-resonance effects and subject move- ment in diffusion MR imaging. NeuroImage, 125, 1063–1078. https://doi.org/10.1016/j.neuroimage.2015.10.019 in the human brain connectome. NeuroImage, 157, 364–380. https://doi.org/10.1016/j.neuroimage.2017.05.067 Avants, B. B., Epstein, C. L., Grossman, M., & Gee, J. C. (2009). Sym- metric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis, 12(1), 26–41. Bassett, D. S., Brown, J. A., Deshpande, V., Carlson, J. M., & Grafton, S. T. (2011). Conserved and variable architecture of human white matter connectivity. NeuroImage, 54(2), 1262–1279. https://doi. org/10.1016/j.neuroimage.2010.09.006 Ashourvan, A., Gu, S., Mattar, M. G., Vettel, J. M., & Bassett, D. S. (2017). The energy landscape underpinning module dynamics Bassett, D. S., Greenﬁeld, D. L., Meyer-Lindenberg, A., Weinberger, D. R., Moore, S. W., & Bullmore, E. T. (2010). Efﬁcient physical Network Neuroscience 873 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional control of brain networks using direct neurostimulation embedding of topologically complex information processing net- works in brains and computer circuits. PLoS Computational Biol- ogy, 6(4). https://doi.org/10.1371/journal.pcbi.1000748 Bassett, D. S., Meyer-Lindenberg, A., Achard, S., Duke, T., & Bullmore, E. (2006). Adaptive reconﬁguration of fractal small- world human brain functional networks. Proceedings of the National Academy of Sciences, 103(51), 19518–19523. Bassett, D. S., Nelson, B. G., Mueller, B. A., Camchong, J., & Lim, K. O. (2012). Altered resting state complexity in schizophre- nia. NeuroImage, 59(3), 2196–2207. https://doi.org/10.1016/ j.neuroimage.2011.10.002 Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature Neuroscience, 20(3), 353–364. https://doi.org/10.1038/nn.4502 Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson, J. M., & Grafton, S. T. (2011). Dynamic reconﬁguration of hu- man brain networks during learning. Proceedings of the National Academy of Sciences, 108(18), 7641–7646. https://doi.org/ 10.1073/pnas.1018985108 Bassett, D. S., Wymbs, N. F., Rombach, M. P., Porter, M. A., Mucha, P. J., & Grafton, S. T. (2013). Task-based core-periphery organi- zation of human brain dynamics. PLoS Computational Biology, 9(9), e1003171. https://doi.org/10.1371/journal.pcbi.1003171 Bassett, D. S., Yang, M., Wymbs, N. F., & Grafton, S. T. (2015). Learning-induced autonomy of sensorimotor systems. Nature Neuroscience, 18(5), 744–751. https://doi.org/10.1038/nn.3993 Battaglia, D., Witt, A., Wolf, F., & Geisel, T. (2012). Dynamic ef- fective connectivity of inter-areal brain circuits. PLoS Computa- tional Biology, 8(3), 1–20. https://doi.org/10.1371/journal.pcbi. 1002438 Betzel, R. F., Gu, S., Medaglia, J. D., Pasqualetti, F., & Bassett, D. S. (2016). Optimally controlling the human connectome: The role of network topology. Scientiﬁc Reports, 6. doi: 10.1038/srep30770 Betzel, R. F., Medaglia, J. D., Kahn, A. E., Soffer, J., Schonhaut, D. R., & Bassett, D. S. (2017). Inter-regional ECoG correlations pre- dicted by communication dynamics, geometry, and correlated gene expression. arXiv:1706.06088, 1–36. Betzel, R. F., Medaglia, J. D., Papadopoulos, L., Baum, G. L., Gur, R. C., Gur, R. E., . . . Bassett, D. S. (2017). The modular organi- zation of human anatomical brain networks: Accounting for the cost of wiring. Network Neuroscience, 1(1), 1–45. https://doi. org/10.1162/netn Bonnefond, M., Kastner, S., & Jensen, O. (2017). Communi- cation between brain areas based on nested oscillations. Neuro, 4(2), ENEURO.0153–16.2017. https://doi.org/10.1523/ ENEURO.0153-16.2017 Braun, U., Schäfer, A., Bassett, D. S., Rausch, F., Schweiger, J. I., Bilek, E., & Erk, S. (2016). Dynamic brain network recon- ﬁguration as a potential schizophrenia genetic risk mechanism modulated by NMDA receptor function. Proceedings of the National Academy of Sciences, 113(44). https://doi.org/10.1073/ pnas.1608819113 Braun, U., Schäfer, A., Walter, H., Erk, S., Romanczuk-Seiferth, N., Haddad, L., . . . Bassett, D. S. (2015). Dynamic reconﬁguration of frontal brain networks during executive cognition in humans. Proceedings of the National Academy of Sciences, 112(37), 11678–11683. https://doi.org/10.1073/pnas.1422487112 Bullmore, E., & Sporns, O. (2012). The economy of brain network organization. Nature Reviews Neuroscience, 13(May), 336–349. https://doi.org/10.1038/nrn3214 Bullock, T. H., McClune, M. C., Achimowicz, J. Z., Iragui-Madoz, V. J., Duckrow, R. B., & Spencer, S. S. (1995a). EEG coherence has structure in the millimeter domain: Subdural and hippocam- pal recordings from epileptic patients. Electroencephalography and Clinical Neurophysiology, 95(3), 161–177. https://doi.org/ 10.1016/0013-4694(95)93347-A Bullock, T. H., McClune, M. C., Achimowicz, J. Z., Iragui-Madoz, V. J., Duckrow, R. B., & Spencer, S. S. (1995b). Temporal ﬂuctu- ations in coherence of brain waves. Proceedings of the National Academy of Sciences, 92(25), 11568–11572. https://doi.org/ 10.1073/pnas.92.25.11568 Burns, S. P., Santaniello, S., Yaffe, R. B., Jouny, C. C., & Crone, N. E. (2014). Network dynamics of the brain and inﬂuence of the epileptic seizure onset zone. Proceedings of the National Academy of Sciences, 111(49), E5321–5330. https://doi.org/ 10.1073/pnas.1401752111 Butson, C. R., & McIntyre, C. C. (2008). Current steering to con- trol the volume of tissue activated during deep brain stimulation. Brain Stimulation, 1(1), 7–15. https://doi.org/10.1016/j.brs.2007. 08.004.Current Buzsáki, G. (2006). Rhythms of the brain. Oxford, United Kingdom: Oxford University Press. https://doi.org/10.1093/acprof:oso/ 9780195301069.001.0001 Buzsáki, G., Anastassiou, C. A., Koch, C., Buzsaki, G., Anastassiou, C. A., & Koch, C. (2012). The origin of extracellular ﬁelds and currents–EEG, ECoG, LFP and spikes. Nature Reviews. Neuro- science, 13(6), 407–420. https://doi.org/10.1038/nrn3241 Cammoun, L., Gigandet, X., Meskaldji, D., Thiran, J. P., Sporns, O., Do, K. Q., . . . Hagmann, P. (2012). Mapping the human con- nectome at multiple scales with diffusion spectrum MRI. Journal of Neuroscience Methods, 203(2), 386–397. https://doi.org/10. 1016/j.jneumeth.2011.09.031 Canolty, R. T., & Knight, R. T. (2010). The functional role of cross-frequency coupling. Trends in Cognitive Sciences, 14(11), 506–515. https://doi.org/10.1016/j.tics.2010.09.001 Chai, L. R., Mattar, M. G., Blank, I. A., Fedorenko, E., & Bassett, D. S. (2016). Functional network dynamics of the language sys- tem. Cerebral Cortex, 26, 112. https://doi.org/10.1093/cercor/ bhw238 Chang, E. F., Kurteff, G., & Wilson, S. M. (2017). Selective inter- ference with syntactic encoding during sentence production by direct electrocortical stimulation of the inferior frontal gyrus. Journal of Cognitive Neuroscience, Early access, 1–11. Cieslak, M., & Grafton, S. T. (2014). Local termination pattern analy- sis: A tool for comparing white matter morphology. Brain Imaging and Behavior, 8(2), 292–299. https://doi.org/10.1007/s11682- 013-9254-z Crowell, A. L., Garlow, S. J., Riva-Posse, P., & Mayberg, H. S. (2015). Characterizing the therapeutic response to deep brain stimula- tion for treatment-resistant depression: A single center long-term perspective. Frontiers in Integrative Neuroscience, 9, 41. Deco, G., & Kringelbach, M. L. (2016). Metastability and co- herence: Extending the communication through coherence hy- pothesis using a whole-brain computational perspective. Trends Network Neuroscience 874 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional control of brain networks using direct neurostimulation in Neurosciences, 39(3), 125–135. https://doi.org/10.1016/j.tins. 2016.01.001 Duecker, F., & Sack, A. T. (2015). Rethinking the role of sham TMS. Frontiers in Psychology, 6, 210. Dykstra, A. R., Chan, A. M., Quinn, B. T., Zepeda, R., Keller, C. J., Cormier, J., . . . Cash, S. S. (2012). Individualized localiza- tion and cortical surface-based registration of intracranial elec- trodes. NeuroImage, 59(4), 3563–3570. https://doi.org/10.1016/ j.neuroimage.2011.11.046.Individualized Ezzyat, Y., Kragel, J. E., Burke, J. F., Levy, D. F., Lyalenko, A., Wanda, P., . . . Kahana, M. J. (2017). Direct brain stimulation modulates encoding states and memory performance in humans. Current Biology, 27(9), 1251–1258. https://doi.org/10.1016/j.cub.2017. 03.028 Fischl, B., Kouwe, A. V. D., Destrieux, C., Halgren, E., Ségonne, F., Salat, D. H., . . . Dale, A. M. (2004). Automatically parcellating the human cerebral cortex. Cerebral Cortex, 14(1), 11–22. https:// doi.org/10.1093/cercor/bhg087 Fisher, R. S. (2011). Neurostimulation for epilepsy: Do we know the best stimulation parameters? Epilepsy Currents, 11(6), 203–204. Foster, B. L., & Parvizi, J. (2017). Direct cortical stimulation of hu- man posteromedial cortex. Neurology, 88(7), 685–691. https:// doi.org/10.1212/WNL.0000000000003607 Fries, P. (2015). Rhythms for cognition: Communication through coherence. Neuron, 88(1), 220–235. https://doi.org/10.1016/ j.neuron.2015.09.034 Friston, K. J. K. (2011). Functional and effective connectivity: A re- view. Brain Connectivity, 1(1), 13–36. https://doi.org/10.1089/ brain.2011.0008 Grefkes, C., & Fink, G. R. (2011). Reorganization of cerebral net- works after stroke: New insights from neuroimaging with con- nectivity approaches. Brain, 134(5), 1264–1276. https://doi.org/ 10.1093/brain/awr033 Gu, S., Betzel, R. F., Cieslak, M., Delio, P. R., Grafton, S. T., Pasqualetti, F., & Bassett, D. S. trajectories of brain state transitions. NeuroImage, 148(January), 305–317. https://doi.org/10.1016/j.neuroimage.2017.01.003 (2017). Optimal Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Yu, A. B., Kahn, A. E., . . . Bassett, D. S. (2015). Controllability of structural brain networks. Nature Communications, 6, 8414. https://doi.org/ 10.1038/ncomms9414 Hermundstad, A. M., Bassett, D. S., Brown, K. S., Aminoff, E. M., Clewett, D., Freeman, S., . . . Carlson, J. (2013). Structural foundations of resting-state and task-based functional connec- tivity in the human brain. Proceedings of the National Academy of Sciences, 110(15), 6169–6174. https://doi.org/10.1073/pnas. 1219562110 Hermundstad, A. M., Brown, K. S., Bassett, D. S., Aminoff, E. M., Frithsen, A., Johnson, A., . . . Carlson, J. M. (2014). Structurally constrained relationships between cognitive states in the hu- man brain. PLoS Computational Biology, 10(5). https://doi.org/ 10.1371/journal.pcbi.1003591 Holmes, G. L., & Lenck-Santini, P. P. (2006). Role of interictal epileptiform abnormalities in cognitive impairment. Epilepsy and Behavior, 8(3), 504–515. https://doi.org/10.1016/j.yebeh.2005. 11.014 Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A., Calhoun, V. D., Corbetta, M., . . . Chang, C. (2013). Dynamic functional connectivity: Promise, issues, and inter- pretations. NeuroImage, 80, 360–378. https://doi.org/10.1016/ j.neuroimage.2013.05.079 Inman, C. S., Manns, J. R., Bijanki, K. R., Bass, D. I., Hamann, S., Drane, D. L., . . . Willie, J. T. (2017). Direct electrical stimula- tion of the amygdala enhances declarative memory in humans. Proceedings of the National Academy of Sciences, 1–6. http://dx. doi.org/10.1159/000478281 Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W., & Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790. https:// doi.org/10.1016/j.neuroimage.2011.09.015 Jezzard, P., Barnett, A. S., & Pierpaoli, C. (1998). Characterization of and correction for eddy current artifacts in echo planar diffu- sion imaging. Magnetic Resonance in Medicine, 39(5), 801–812. https://doi.org/10.1002/mrm.1910390518 Jirsa, V. K., Proix, T., Perdikis, D., Woodman, M. M., Wang, H., Gonzalez-Martinez, J., . . . Bartolomei, F. (2017). The virtual epileptic patient: Individualized whole-brain models of epilepsy spread. NeuroImage, 145, 377–388. https://doi.org/10.1016/ j.neuroimage.2016.04.049 Jonas, E., & Kording, K. P. (2017). Could a neuroscientist under- stand a microprocessor? PLoS Computational Biology, 13(1), 1–24. https://doi.org/10.1371/journal.pcbi.1005268 Kailath, T. (1980). Linear systems (Vol. 156). Englewood Cliffs, NJ: Prentice-Hall. Kalman, R. E. (1963). Mathematical description of linear dynamical systems. Journal of the Society for Industrial and Applied Mathe- matics, Series A: Control, 1(2), 152–192. https://doi.org/10.1137/ 0301010 Keller, C. J., Honey, C. J., Entz, L., Bickel, S., Groppe, D. M., Toth, E., . . . Mehta, A. D. (2014). Corticocortical evoked potentials re- veal projectors and integrators in human brain networks. Journal of Neuroscience, 34(27), 9152–9163. https://doi.org/10.1523/ JNEUROSCI.4289-13.2014 Keller, C. J., Honey, C. J., Me, P., Entz, L., Ulbert, I., & Mehta, A. D. (2014). Mapping human brain networks with cortico-cortical evoked potentials. Philosophical Transactions of the Royal Soci- ety B, 369, 1–14. Keller, C. J., Huang, Y., Herrero, J. L., Fini, M. E., Du, V., Lado, F. A., . . . Mehta, A. D. (2018). Induction and quantiﬁcation of excitabil- ity changes in human cortical networks. Journal of Neuroscience, 38(23), 5384–5398. Khambhati, A. N., Bassett, D. S., Oommen, B. S., Chen, S. H., Lucas, T. H., Davis, K. A., & Liit, B. (2017). Recurring functional interactions predict network architecture of interictal and ictal states in neocortical epilepsy. eNeuro, 4(1). https://doi.org/10. 1523/ENEURO.0091-16.2017 Khambhati, A. N., Davis, K. A., Lucas, T. H., Litt, B., & Bassett, D. S. (2016). Virtual cortical resection reveals push-pull network control preceding seizure evolution. Neuron, 91(5), 1170–1182. https://doi.org/10.1016/j.neuron.2016.07.039 Khambhati, A. N., Davis, K. A., Oommen, B. S., Chen, S. H., Lucas, T. H., Litt, B., & Bassett, D. S. (2015). Dynamic network drivers of seizure generation, propagation and termination in Network Neuroscience 875 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional control of brain networks using direct neurostimulation human neocortical epilepsy. PLOS Computational Biology, 11(12), e1004608. https://doi.org/10.1371/journal.pcbi.1004608 Kim, J. Z., Soffer, J. M., Kahn, A. E., Vettel, J. M., Pasqualetti, F., & (2018). Role of graph architecture in controlling Bassett, D. S. dynamical networks with applications to neural systems. Nature Physics, 14, 91–98. Kopell, N., Ermentrout, G. B., Whittington, M. A., & Traub, R. D. (2000). Gamma rhythms and beta rhythms have different syn- chronization properties. Proceedings of the National Academy of Sciences, 97(4), 1867–1872. https://doi.org/10.1073/pnas.97. 4.1867 Kragel, J. E., Ezzyat, Y., Sperling, M. R., Gorniak, R., Worrell, G. A., Berry, B. M., . . . Kahana, M. J. (2017). Similar patterns of neural activity predict memory function during encoding and retrieval. NeuroImage, 155(February), 60–71. https://doi.org/ 10.1016/j.neuroimage.2017.03.042 Kramer, M. A., Eden, U. T., Kolaczyk, E. D., Zepeda, R., Eskandar, E. N., & Cash, S. S. (2010). Coalescence and fragmentation of cortical networks during focal seizures. Journal of Neuroscience, 30(30), 10076–10085. https://doi.org/10.1523/JNEUROSCI.6309- 09.2010 Kramer, M. A., Eden, U. T., Lepage, K. Q., Kolaczyk, E. D., Bianchi, M. T., & Cash, S. S. (2011). Emergence of persistent networks in long-term intracranial EEG recordings. Journal of Neuroscience, 31(44), 15757–15767. https://doi.org/10.1523/ JNEUROSCI.2287-11.2011 Lepage, K. Q., Ching, S., & Kramer, M. A. (2013). Inferring evoked Journal of brain connectivity through adaptive perturbation. Computational Neuroscience, 34(2), 303–318. https://doi.org/ 10.1007/s10827-012-0422-8 Liu, Y.-Y., Slotine, J.-J., & Barabasi, A.-L. (2011). Controllability of complex networks. Nature, 473(7346), 167–173. Lozano, A. M., & Lipsman, N. (2013). Probing and regulating dys- functional circuits using deep brain stimulation. Neuron, 77(3), 406–424. https://doi.org/10.1016/j.neuron.2013.01.020 Matsumoto, R., Nair, D. R., LaPresto, E., Najm, I., Bingaman, W., Shibasaki, H., & Lüder, H. O. (2004). Functional connectivity in the human language system: A cortico-cortical evoked potential study. Brain, 127(10), 2316–2330. https://doi.org/10.1093/brain/ awh246 Mattar, M. G., Cole, M. W., Thompson-Schill, S. L., & Bassett, D. S. (2015). A functional cartography of cognitive systems. PLoS Computational Biology, 11(12), 1–26. https://doi.org/10.1371/ journal.pcbi.1004533 Miši´c, B., Betzel, R. F., de Reus, M. A., van den Heuvel, M. P., Berman, M. G., McIntosh, A. R., & Sporns, O. (2016). Network- level structure-function relationships in human neocortex. Cere- bral Cortex, 26(7), 3285–3296. https://doi.org/10.1093/cercor/ bhw089 Morrell, M. J. (2011). Responsive cortical stimulation for the treatment of medically intractable partial epilepsy. Neurology, 77(13), 1295–1304. https://doi.org/10.1212/WNL.0b013e3182302056 Muldoon, S. F., Pasqualetti, F., Gu, S., Cieslak, M., Grafton, S. T., Vettel, J. M., & Bassett, D. S. (2016). Stimulation-based control of dynamic brain networks. PLoS Computational Biology, 12(9). https://doi.org/10.1109/TAC.2015.2496191 Muller, L., Rolston, J. D., Fox, N. P., Knowlton, R., Rao, V. R., & Chang, E. F. (2018). Direct electrical stimulation of human cor- tex evokes high gamma activity that predicts conscious somato- sensory perception. Journal of Neural Engineering, 15(2), 026015. Murphy, A. C., Gu, S., Khambhati, A. N., Wymbs, N. F., Grafton, S. T., Satterthwaite, T. D., & Basset, D. S. (2016). Explicitly linking regional activation and function connectivity: Commu- nity structure of weighted networks with continuous annotation. arXiv:1611.07962. Nair, D., & Morrell, M. (2017). Long-term safety and efﬁcacy of re- sponsive brain stimulation in adults with medically intractable partial onset seizures (S21.004). Neurology, 88(Suppl. 16). Olde Dubbelink, K. T. E., Hillebrand, A., Stoffers, D., Deijen, J. B., Twisk, J. W. R., Stam, C. J., & Berendse, H. W. (2014). Disrupted brain network topology in Parkinson’s disease: A longitudinal magnetoencephalography study. Brain, 137(1), 197–207. https:// doi.org/10.1093/brain/awt316 Park, H. J., & Friston, K. (2013). Structural and functional brain networks: From connections to cognition. Science, 342(6158), 1238411. https://doi.org/10.1093/brain/awt316 Pasqualetti, F., Zampieri, S., & Bullo, F. (2014). Controllability met- rics and algorithms for complex networks. IEEE Transactions on Control of Network Systems, 1(1), 40–52. https://doi.org/ 10.1109/ACC.2014.6858621 Pequito, S., Khambhati, A. N., Pappas, G. J., Siljak, D. D., Bassett, D. S., & Litt, B. (2016). Structural analysis and design of dynamic- ﬂow networks: Implications into the brain dynamics. In American Control Conference. Prieto, G. A., Parker, R. L., & Vernon, F. L. (2009). A Fortran 90 library for multitaper spectrum analysis. Computers and Geosciences, 35(8), 1701–1710. https://doi.org/10.1016/j.cageo. 2008.06.007 Rangarajan, V., Hermes, D., Foster, B. L., Weiner, K. S., Jacques, C., Grill-Spector, K., & Parvizi, J. (2014). Electrical stimulation of the left and right human fusiform gyrus causes different effects in conscious face perception. Journal of Neuroscience, 34(38), 12828–12836. https://doi.org/10.1523/JNEUROSCI.0527-14.2014 Sang, L., Zhang, J., Wang, L., Zhang, J., Zhang, Y., Li, P., . . . Qiu, M. (2015). Alteration of brain functional networks in early-stage Parkinson’s disease: A resting-state fMRI study. PLoS ONE, 10(10), 1–19. https://doi.org/10.1371/journal.pone.0141815 Schalk, G. (2015). A general framework for dynamic cortical func- tion: The function-through-biased-oscillations (FBO) hypothesis. Frontiers in Human Neuroscience, 9(June), 1–10. https://doi.org/ 10.3389/fnhum.2015.00352 J., & Weeden, V. Schmahmann, J. D., Pandya, D. N., Wang, R., Dai, G., D’arceuil, (2007). Asso- H. E., de Crespigny, A. ciation ﬁbre pathways of the brain: Parallel observations from diffusion spectrum imaging and autoradiography. Brain, 130(3), 630–653. Shannon, R. V. (1992). A model of safe levels for electrical stimulation. IEEE Transactions on Biomedical Engineering, 39(4), 424–426. https://doi.org/10.1109/10.126616 J. Shine, J. M., Koyejo, O., & Poldrack, R. A. (2016). Temporal meta- states are associated with differential patterns of time-resolved connectivity, network topology, and attention. Proceedings of the National Academy Sciences, 113(35), 9888–9891. Smith, S. M. (2002). Fast robust automated brain extraction. Human Brain Mapping, 17(3), 143–155. https://doi.org/10.1002/ hbm.10062 Network Neuroscience 876 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional control of brain networks using direct neurostimulation Solomon, E. A., Kragel, J. E., Sperling, M. R., Sharan, A., Worrell, G. A., Kucewicz, M., . . . Branch, S. N. (2017). Widespread theta synchrony and high-frequency desynchronization underlies en- hanced cognition. Nature Communications, 8. https://doi.org/ 10.1038/s41467-017-01763-2 Song, S., Miller, K. D., & Abbott, L. F. (2000). Competitive Hebbian synaptic plasticity. learning through spike-time dependent Nature Neuroscience, 3(9), 919–926. Stacey, W. C., & Litt, B. (2008). Technology insight: Neuroengineer- ing and epilepsy-designing devices for seizure control. Nature clinical practice. Neurology, 4(4), 190–201. https://doi.org/10. 1038/ncpneuro0750 Stanslaski, S., Afshar, P., Cong, P., Giftakis, J., Stypulkowski, P., Carlson, D., . . . Denison, T. (2012). Design and validation of a fully implantable, chronic, closed-loop neuromodulation device IEEE Transactions on with concurrent sensing and stimulation. Neural Systems and Rehabilitation Engineering, 20(4), 410–421. https://doi.org/10.1109/TNSRE.2012.2183617 Tang, E., & Bassett, D. S. (2017). Control of dynamics in brain net- works. arXiv:1701.01531, 1–21. Tang, E., Giusti, C., Baum, G. L., Gu, S., Pollock, E., Kahn, A. E., . . . Basset, D. S. (2017). Developmental increases in white mat- ter network controllability support a growing diversity of brain dynamics. Nature Communications, 8(1), 1252. Taylor, P. N., Thomas, J., Sinha, N., Dauwels, J., Kaiser, M., Thesen, T., & Ruth, J. (2015). Optimal control based seizure abatement using patient derived connectivity. Frontiers in Neuroscience, 9(June), 1–10. https://doi.org/10.3389/fnins.2015.00202 Thomas, C., Ye, F. Q., Irfanoglu, M. O., Modi, P., Saleem, K. S., Leopold, D. A., & Pierpaoli, C. (2014). Anatomical accuracy of brain connections derived from diffusion MRI tractography is inherently limited. Proceedings of the National Academy of Sciences, 111(46), 16574–16579. https://doi.org/10.1073/pnas. 1405672111 Towle, V. L., Carder, R. K., Khorasani, L., & Lindberg, D. (1999). Electrocorticographic coherence patterns. Journal of Clin- ical Neurophysiology, 16(6), 528–547. https://doi.org/10.1097/ 00004691-199911000-00005 Uhlhaas, P. J., & Singer, W. (2006). Neural synchrony in brain disor- ders: Relevance for cognitive dysfunctions and pathophysiology. Neuron, 52(1), 155–168. https://doi.org/10.1016/j.neuron.2006. 09.020 Wang, W., Collinger, J. L., Degenhart, A. D., Tyler-Kabara, E. C., Schwartz, A. B., Moran, D. W., . . . Boninger, M. L. (2013). An electrocorticographic brain interface in an individual with tetraplegia. PLoS ONE, 8(2), 1–8. https://doi.org/10.1371/ journal.pone.0055344 Wang, L., Yu, C., Chen, H., Qin, W., He, Y., Fan, F., . . . Zhu, C. (2010). Dynamic functional reorganization of the motor execu- tion network after stroke. Brain, 133(4), 1224–1238. https://doi. org/10.1093/brain/awq043 Winawer, J., & Parvizi, J. (2016). Linking electrical stimulation of human primary visual cortex, size of affected cortical area, neuronal responses, and subjective experience. Neuron, 92(6), 1213–1219. https://doi.org/10.1016/j.neuron.2016.11.008 Yan, G., Vértes, P. E., Towlson, E. K., Chew, Y. L., Walker, D. S., Schafer, W. R., & Barabási, A. L. (2017). Network control princi- ples predict neuron function in the Caenorhabditis elegans con- nectome. Nature, 550(7677), 519–523. https://doi.org/10.1038/ nature24056 Yeh, F. C., Verstynen, T. D., Wang, Y., Fernández-Miranda, J. C., & Tseng, W. Y. I. (2013). Deterministic diffusion ﬁber tracking improved by quantitative anisotropy. PLoS ONE, 8(11), 1–16. https://doi.org/10.1371/journal.pone.0080713 IEEE Transactions on Medical Yeh, F.-C., Wedeen, V. J., & Tseng, W.-Y. I. (2010). Generalized Imaging, q-sampling imaging. 29(9), 1626–1635. https://doi.org/10.1109/TMI.2010.2045126 Yendiki, A., Koldewyn, K., Kakunoori, S., Kanwisher, N., & Fischl, B. (2014). Spurios group differences due to head motion in a diffu- sion MRI study. Neuroimage, 88, 79–90. https://doi.org/10.1111/ obr.12065.Variation Yushkevich, P. A., Pluta, J. B., Wang, H., Xie, L., Ding, S.-L., Gertje, E. C., . . . Wolk, D. A. (2015). Automated volumetry and regional thickness analysis of hippocampal subﬁelds and medial tempo- ral cortical structures in mild cognitive impairment. Human Brain Mapping, 36(1), 258–287. https://doi.org/10.1002/hbm.22627. Automated Network Neuroscience 877 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 4 8 1 0 9 2 4 4 0 n e n _ a _ 0 0 0 8 9 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 imagen de INVESTIGACIÓN

Descargar PDF