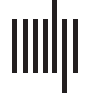RESEARCH - IA de Investigación especializada en el MIT

INVESTIGACIÓN

Evaluation of confound regression strategies for
the mitigation of micromovement artifact
in studies of dynamic resting-state functional
connectivity and multilayer network modularity

David M.. Lydon-Staley

1, Rastko Ciric

2, Theodore D. Satterthwaite

and Danielle S. bassett

1,3,4,5

1Department of Bioengineering, Universidad de Pennsylvania, Filadelfia, Pensilvania, EE.UU
2Department of Psychiatry, Perelman School of Medicine, Universidad de Pennsylvania, Filadelfia, Pensilvania, EE.UU
3Department of Electrical and Systems Engineering, Universidad de Pennsylvania, Filadelfia, Pensilvania, EE.UU
4Department of Neurology, Universidad de Pennsylvania, Filadelfia, Pensilvania, EE.UU
5Department of Physics and Astronomy, Universidad de Pennsylvania, Filadelfia, Pensilvania, EE.UU

Palabras clave: Dynamic functional connectivity, Dynamic networks, Resting-state fMRI, Motion,
Artifact, Confound

ABSTRACTO

Dynamic functional connectivity reﬂects the spatiotemporal organization of spontaneous
brain activity in health and disease. Dynamic functional connectivity may be susceptible
to artifacts induced by participant motion. This report provides a systematic evaluation of
12 commonly used participant-level confound regression strategies designed to mitigate
the effects of micromovements in a sample of 393 youths (ages 8–22 years). Each strategy
was evaluated according to a number of benchmarks, incluido (a) the residual association
between participant motion and edge dispersion, (b) distance-dependent effects of motion
on edge dispersion, (C) the degree to which functional subnetworks could be identiﬁed by
multilayer modularity maximization, y (d) measures of module reconﬁguration, incluido
node ﬂexibility and node promiscuity. Results indicate variability in the effectiveness of the
evaluated pipelines across benchmarks. Methods that included global signal regression
were the most consistently effective de-noising strategies.

RESUMEN DEL AUTOR

Dynamic functional connectivity reﬂects the spatiotemporal organization of spontaneous
brain activity in health and disease, but it can be susceptible to motion artifacts. Aquí
we provide a systematic evaluation of 12 commonly used participant-level confound
regression strategies designed to mitigate the effects of micromovements in a sample of
393 youths (ages 8–22 years). Each strategy was evaluated according to the residual
association between participant motion and edge dispersion, distance-dependent effects
of motion on edge dispersion, the degree to which functional subnetworks could be
identiﬁed by multilayer modularity maximization, and measures of module reconﬁguration,
including node ﬂexibility and node promiscuity. Results indicate variability in the
effectiveness of the evaluated pipelines across benchmarks. Methods that included
global signal regression were the most consistently effective de-noising strategies.

un acceso abierto

diario

Citación: Lydon-Staley, D. METRO., círico, r.,
Satterthwaite, t. D., & bassett, D. S.
(2019). Evaluation of confound
regression strategies for the mitigation
of micromovement artifact in studies of
dynamic resting-state functional
connectivity and multilayer network
modularity. Neurociencia en red,
3(2), 427–454. https://doi.org/10.1162/
netn_a_00071

DOI:
https://doi.org/10.1162/netn_a_00071

Supporting Information:
https://doi.org/10.1162/netn_a_00071

Recibió: 18 Puede 2018
Aceptado: 19 Septiembre 2018

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autor correspondiente:
Danielle S. bassett
dsb@seas.upenn.edu

Editor de manejo:
Andrew Zalesky

Derechos de autor: © 2018
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Motion mitigation in dynamic connectivity

Conectividad funcional:
Statistical dependence between
activity levels of brain regions.

INTRODUCCIÓN

Resting-state functional magnetic resonance imaging (rs-fMRI) has fundamentally expanded
our understanding of the spatiotemporal organization of spontaneous brain activity in health
and disease across the life span (bassett & bullmore, 2009; Betzel et al., 2014; Biswal, 2012;
van den heuvel & Pol, 2010). To quantify functional connectivity, statistical dependencies (p.ej.,
correlations, coherencia; Brilla, Proporcionó, & bullmore, 2012; z. zhang, telesford, Giusti, Lim,
& bassett, 2016) between the blood-oxygen-level-dependent (BOLD) time series of brain regions
are typically computed over entire resting-state scans. Sin embargo, in line with the increasing rec-
ognition of the time-varying nature of brain network organization (Calhoun, Molinero, Pearlson,
& Adali, 2014; Preti, Bolton, & Van De Ville, 2017), rs-fMRI has been increasingly utilized
to capture dynamics in the organization of spontaneous brain activity over time (cohen, 2018;
Hutchison et al., 2013).

Changes in the connectivity across pairs of nodes (regiones del cerebro) are investigated in studies
of dynamic rs-fMRI, rather than assuming temporal stationarity across entire resting-state scans.
This is typically achieved by decomposing the resting-state time series into temporal windows
of ﬁxed length. Functional connectivity and dynamic network indices are computed within
windows. The gathering of window-speciﬁc indices allows an examination of how connectiv-
ity changes over time (Allen et al., 2014; Sako˘glu et al., 2010). Emerging network-based tools to
describe dynamic rs-fMRI activity (Bassett y cols., 2013; Khambhati, Sizemore, Betzel, & bassett,
2018; Sizemore & bassett, 2018) have begun to provide important insights into dynamic brain
función. These insights include an appreciation for how functional connectivity among brain
regiones (Allen et al., 2014) and the organization of functional brain network architecture
(Chai et al., 2017; Smith et al., 2012) change within persons across the length of scans,
how these dynamics relate to normative development (hutchison & Morton, 2016; Medalla
et al., 2018) and cognition (bassett, Cual, Wymbs, & Grafton, 2015; Braun et al., 2015; Brillar,
Koyejo, & Poldrack, 2016), and how they are associated with healthy variations in mood
(Betzel, Satterthwaite, Gold, & bassett, 2017) as well as psychopathology (Braun et al., 2016;
Damaraju et al., 2014; Demirta¸s et al., 2016).

The Problem of Motion and Approaches to Mitigating Motion Artifact

Dynamic rs-fMRI approaches reﬂect the perspective that brain function is quintessentially time-
varying. The relatively low demands on participants during acquisition also render dynamic
rs-fMRI approaches attractive for use across diverse samples for whom performance on task-
based fMRI studies may be difﬁcult. Despite these advantages, dynamic rs-fMRI approaches—
like their stationary counterparts—are susceptible to artifacts induced by motion (Laumann
et al., 2017). Such artifacts can be mistaken for neural effects (Van Dijk, Jabonoso, & Buckner,
2012) and are particularly problematic in studies of between-person differences, because many
between-person differences of interest are correlated with motion (p.ej., edad, personality, y
clinical status; Fair et al., 2013; Satterthwaite, Lobo, et al., 2013; Siegel et al., 2016). Notablemente,
motion artifact is observed in samples free of gross motion, with micromovements as small as
0.1 mm from time point to time point capable of introducing differences in statistics derived
from rs-fMRI data (Satterthwaite et al., 2012; Yan et al., 2013).

An important aspect of motion artifact in rs-fMRI is its distance-dependence (Fuerza, Barnes,
Snyder, Schlaggar, & Petersen, 2012; Satterthwaite et al., 2012; Van Dijk et al., 2012). Higher
levels of motion are associated with greater connectivity in short-range connections and, en
some cases, weaker connectivity in long-distance connections. This ﬁnding has been of partic-
ular concern in the ﬁeld of developmental cognitive neuroscience wherein a perspective based

Neurociencia en red

428

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Motion mitigation in dynamic connectivity

on early rs-fMRI studies theorized that functional connectivity was modulated in a distance-
dependent manner across the life span (p.ej., Fair et al., 2009). Since then, it has been demon-
strated, through the use of rigorous de-noising procedures, that motion artifact substantially
inﬂated the estimates of age-related, distance-related changes in connectivity (Fair et al., 2013;
Satterthwaite, Lobo, et al., 2013).

In response to the problem of in-scanner motion for the study of functional connectiv-
idad, there has been a proliferation of techniques geared towards mitigating motion artifacts
(Caballero-Gaudes & Reynolds, 2017; Murphy, Hijo, & Bandettini, 2013). Confound regres-
sion strategies are popular and entail regressing signals thought to be of nonneural origin from
the BOLD time series. The residual time series is then used in subsequent analyses. Signals used
during confound regression (and often in combination with one another) include realignment
parámetros, tissue-speciﬁc signals, the global signal, signals derived from principal compo-
nents analysis (PCA), and signals isolated using independent components analysis (ICA).

Evaluating De-Noising Strategies in Dynamic rs-fMRI

The dizzying array of de-noising strategies provides investigators with many choices during the
preprocessing of rs-fMRI data in preparation for dynamic functional connectivity or dynamic
network analyses, especially given that the many techniques may be combined within prepro-
cessing pipelines. Recent work has systematically compared the effectiveness of many avail-
able techniques in reducing motion-related artifact in static rs-fMRI (Ciric et al., 2017; parque,
Fulcher, Yucel, & Proporcionó, 2018). These studies, including work utilizing the same dataset in-
vestigated in the present manuscript (Ciric et al., 2017), observed that pipelines with global
signal regression (GSR) were among the most effective at minimizing the relationship between
connectivity and motion. Sin embargo, these pipelines revealed a distance-dependent artifact pro-
ﬁle. Less effective de-noising pipelines in the context of static functional connectivity included
those that used 6 realignment parameter (p.ej., Yao et al., 2016), 24 realignment parameter
(Friston, williams, Howard, Frackowiak, & Tornero, 1996), and local white matter (W.M.; Jo,
Saad, Simmons, Milbury, & Cox, 2010) confound regression pipelines.

Dynamic functional connectivity:
Changes in the statistical
dependence between activity levels
of brain regions across time.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

The ﬁeld awaits an extension of this evaluative work of preprocessing strategies to dynamic
rs-fMRI. Many dynamic rs-fMRI indices are available. Indices under consideration in the cur-
rent manuscript (ver figura 1) were chosen based on their use in the existing literature and their
observed associations with cognitive processes in previous work. A commonly used measure
of dispersion (p.ej., Demirta¸s et al., 2016), capable of capturing the extent of ﬂuctuations in
connectivity between brain regions across time, acted as a dynamic counterpart to static func-
tional connectivity measures that indicate the strength of connectivity between brain regions.

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Alongside dispersion, a general measure of dynamic functional connectivity, indices spe-
ciﬁc to graph or network approaches to understanding the brain were also examined. The fo-
cus on network indices reﬂected the increasing prevalence and utility of conceptualizing the
human brain as a complex system composed of individual units (p.ej., regiones del cerebro) that are
connected with one another (bassett & despreciar, 2017; bullmore & despreciar, 2009; Calhoun et al.,
2014). An additional consideration was the availability of a formal mathematical language and
theory to accompany network conceptualizations of the brain (bullmore & bassett, 2011;
despreciar, 2015).

Layer:
An element of multilayer networks.
en este documento, layers represent
graphs in time windows of 60 s.

Within the realm of graph theory, network indices derived from multilayer modularity max-
imization are of particular interest for probing dynamic functional connectivity. Modularity
refers to the ability to decompose the large-scale network of the brain into communities of re-
gions that exhibit dense connectivity with each other and sparse connectivity with regions

Neurociencia en red

429

Motion mitigation in dynamic connectivity

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 1. An overview of the construction of time-dependent, whole-brain connectivity matrices and computation of dynamic rs-fMRI indi-
ces. Panels (a) a través de (C) provide an overview of the construction of time-dependent, whole-brain connectivity matrices and computation
of dynamic rs-fMRI indices. In panel (a), time courses of blood oxygen level-dependent (BOLD) signals from 270 brain regions were extracted.
A sampling of these time courses is plotted (abajo). For each time window (w1, w2, . . . , w11), node-by-node connectivity matrices were
estimated using Pearson correlations, the resulting r values of which were Fisher-z transformed (arriba). In panel (b), computation of the dispersion
index is illustrated. The z value of the edge connecting two nodes at each time window (outlined in red; arriba) is plotted (continuous blue line;
abajo). Dispersion was calculated by dividing the variance () del 11 z values by the mean () del 11 z values (mean is indicated by a
dotted blue line). Panel (C) illustrates time-dependent community structure over each time window as computed using a multilayer modularity
maximization algorithm. Nodes are assigned communities at each time window. A ﬂexible node (blue node) changes community many times
(pink, purple, pink, purple). A promiscuous node (red node) also changes communities many times but is marked by allegiances to many
communities (pink, purple, pink, verde).

in other communities. Modularity is a quintessential principle of brain network organiza-
tion that is thought to confer signiﬁcant advantages to cognitive functioning (Bassett y cols.,
2010; Chen, Él, Rosa-Neto, Germann, & evans, 2008; Meunier, Lambiotte, Proporcionó, Ersche, &
bullmore, 2009; despreciar & Betzel, 2016). The interrogation of modularity in dynamic networks
presents challenges that are not encountered in studies of static rs-fMRI. En particular, identify-
ing changes in modules across time requires a way of linking a module at one time point with
itself at another time point. Such a linkage is not produced by methods considering single time
points separately. Multilayer modularity maximization has emerged as a recent solution to this
challenge. In this approach, the network in one time window is linked to networks in adjacent
time windows by identity edges that connect a node in one time window to itself in neighbor-
ing time windows. Once adjacent time windows are linked, modules are identiﬁed (and their
temporal variation quantiﬁed) by maximizing a multilayer modularity function (Khambhati
et al., 2018; Mucha, Richardson, Macon, Portero, & Onnela, 2010). Multilayer modularity ap-
proaches to dynamic functional connectivity have, hasta la fecha, provided insight into a range of
cognitive and affective processes, including learning (Bassett y cols., 2011), funciones ejecutivas
(Braun et al., 2015), mood (Betzel et al., 2017), and affective disorders (Zheng et al., 2018).

Multilayer brain network:
A brain network with more than one
capa. Layers are connected to one
another via interlayer edges that link
nodes across different layers.

Neurociencia en red

430

Motion mitigation in dynamic connectivity

Edge dispersion:
Edge dispersion captures the extent
of ﬂuctuations in the functional
connectivity of an edge across time.
It is computed by dividing the
variance of an edge by the
mean value of the edge.

Node ﬂexibility:
Node ﬂexibility captures the
number of times a node changes
communities across time, normalized
by the number of times the node
could have changed communities.

Node promiscuity:
Node promiscuity captures the
number of communities in which
a node participates across time.
A node with high promiscuity
participates in many communities
a través del tiempo.

Despite the promise of multilayer modularity approaches for providing insight into the spa-
tiotemporal organization of the brain, little work has evaluated the extent to which common
preprocessing pipeline choices successfully mitigate motion artifact in the context of these
emerging methods.

The Present Study

To aid in the selection of de-noising pipelines in the study of dynamic rs-fMRI and multi-
layer network modularity, the present report compared the effectiveness of 12 preprocessing
pipelines in the construction of dynamic rs-fMRI indices using a large (norte = 393) dataset of
adolescents and young adults free of gross motion (es decir., with a focus on micromovements).
The pipelines evaluated included commonly used techniques, confound regression of varying
complejidad, PCA- and ICA-based techniques, spatially tailored local white matter regression,
and one censoring technique (despiking). GSR was also included in many of the pipelines.
Effectiveness was deﬁned by estimates of (a) the residual association between participant
motion and edge dispersion, (b) distance-dependent effects of motion on edge dispersion,
(C) the degree to which functional subnetworks could be identiﬁed by multilayer modularity
maximization, y (d) measures of module reconﬁguration such as node ﬂexibility and node
promiscuity.

MATERIALES Y MÉTODOS

Participants and Data Acquisition

The rs-fMRI data were drawn from the Philadelphia Neurodevelopmental Cohort (PNC;
Satterthwaite et al., 2016; Satterthwaite et al., 2014) on the basis of age, salud, and data qual-
idad. Participants provided signed informed consent, with assent and parental consent required
for participants under age 18. All procedures were approved by the University of Pennsylvania
and the Children’s Hospital of Philadelphia Institutional Review Boards. Selected participants
ranged in age from 8 a 22 años, were free from medical conditions that could impact brain
función (Merikangas et al., 2010), lacked gross structural brain abnormalities (Gur et al., 2013),
were not taking psychotropic medication at the time of the scan, had high-quality imaging
data that were free of gross motion (deﬁned as a mean relative root mean squared displace-
ment > 0.2 mm, or > 20 volumes with framewise relative root mean squared displace-
ment > 0.25 mm). Exclusion due to gross motion (norte = 88; 44 femenino) allowed an evaluation
of the utility of confound regression strategies for minimizing artifact associated with micro-
movimientos. Notablemente, this sample was used in a recent paper that evaluated the effectiveness
of confound regression strategies on motion artifact in studies of static functional connectivity
(Ciric et al., 2017), facilitating comparisons across static and dynamic connectivity approaches.
The sample (59% femenino) had a mean age of 16.47 (DE = 3.55) and a mean relative root mean
squared displacement of 0.07 mm (DE = 0.40).

Structural and functional data were acquired on a 3T Siemens Tim Trio scanner with a
32-channel head coil (Erlangen, Alemania). High-resolution structural images were acquired
using a magnetization-prepared, rapid-acquisition gradient-echo (MPRAGE) T1-weighted se-
quence (TR = 1, 810 EM; TE = 3.51 EM; FoV = 180 × 240 mm; resolution 1 mm isotropic).
Approximately 6 min of resting-state functional data were acquired for each subject using
a BOLD-weighted sequence (TR = 3, 000 EM; TE = 32 EM; FoV = 192 × 192 mm; resolu-
ción 3 mm isotropic; 124 spatial volumes). A mock scanning session was conducted using a
decommissioned MRI scanner and head coil prior to scanning in order to acclimatize sub-
jects to the MRI environment and to help subjects to learn to remain still during the actual

Neurociencia en red

431

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Motion mitigation in dynamic connectivity

scanning session. During the mock MRI sessions, the MoTrack motion tracking system (Psy-
chology Software Tools, Cª, Sharpsburg, Pensilvania) was used to provide feedback to subjects regard-
ing head movement. Prior to data acquisition, subjects’ heads were stabilized in the head coil
using one foam pad over each ear and a third pad over the top of the head in order to further
minimize motion during the scanning session. During the resting-state scan, a ﬁxation cross
was displayed as images were acquired. Subjects were instructed to stay awake, keep their
eyes open, ﬁxate on the displayed crosshair, and remain still.

Structural Image Processing

The “buildTemplateParallelProcedure” in ANTS (Avants, Tustison, Song et al., 2011) fue usado
to generate a study-speciﬁc template from a sample of 120 PNC subjects balanced across sex,
carrera, and age bins. Study-speciﬁc tissue priors were created using a multi-atlas segmentation
procedimiento (Wang, Cao, & Syeda-Mahmood, 2014). Each subjects’ high-resolution structural
image was then processed using the ANTs Cortical Thickness Pipeline (Tustison et al., 2014).
After bias ﬁeld correction (Tustison et al., 2010), each structural image was diffeomorphically
registered to the study-speciﬁc PNC template using the top-performing SyN deformation (Klein
et al., 2009). Study-speciﬁc tissue priors were used to guide brain extraction and segmentation
of subjects’ structural images (Avants, Tustison, Wu, Cocinar, & Gee, 2011).

BOLD Time Series Processing

Resting-state functional images were processed using the XCP Engine (Ciric et al., in press). El
XCP Engine was conﬁgured to support the pipelines evaluated in this study. Each pipeline was
based on de-noising strategies that have previously been described in the neuroimaging litera-
tura. Elements of preprocessing common to all pipelines included (a) correction for distortions
induced by magnetic ﬁeld inhomogeneity using FSL’s FUGUE utility, (b) removal of the four
initial volumes of each acquisition, (C) realignment of all volumes to a selected reference vol-
ume using MCFLIRT (Jenkinson, Bannister, Brady, & Herrero, 2002), (d) demeaning and removal
of any linear or quadratic trends, (mi) coregistration of functional data to the high-resolution
structural image using boundary-based registration (Greve & pescado, 2009), y (F ) tempo-
ral ﬁltering using a ﬁrst-order Butterworth ﬁlter with a passband between 0.01 y 0.08 Hz,
although we note that other frequency ranges may result in more reliable estimations of
static network measures (Andellini, Cannatà, Gazzellini, Bernardi, & Napolitano, 2015; Braun
et al., 2012). These common processing steps were then followed by the confound regres-
sion procedures described below. All regressors were band-pass ﬁltered to retain the same
frequency as the data. This was done to prevent frequency-dependent mismatch during con-
found regression (Hallquist, Hwang, & luna, 2013). Subject motion was captured using the
mean relative RMS (root-mean-squared; Jenkinson et al., 2002) displacement as calculated
during time series realignment using MCFLIRT (Satterthwaite, eliot, et al., 2013; Satterthwaite
et al., 2012).

Overview of Confound Regression Strategies

The pipelines evaluated in the present manuscript variably incorporated realignment param-
eters, tissue-speciﬁc signals, GSR, PCA, ICA, and censoring approaches to motion mitigation.
We provide a brief overview of these approaches before specifying the evaluated pipelines.

Realignment parameters. During the rigid body realignment of functional images to correct for
head movement (via the use of MCFLIRT in the present manuscript), 6 realignment parameters

Neurociencia en red

432

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Motion mitigation in dynamic connectivity

(3 translations and 3 rotations) are produced. Estos 6 realignment parameters are commonly
used as nuisance regressors in dynamic rs-fMRI preprocessing (p.ej., Yao et al., 2016). el primero
temporal derivatives of the 6 realignment parameters are also often included to account for
time lags in the effects of motion (p.ej., Vergara, Mayer, Damaraju, & Calhoun, 2017). Otro
expansions on realignment parameters include creating quadratic terms for the 12 parámetros
(el 6 original realignment parameters and their ﬁrst temporal derivatives), yielding 24 param-
eters in total (Friston et al., 1996).

Tissue-speciﬁc signals are also used as nuisance regressors in dynamic
Tissue-speciﬁc signals.
rs-fMRI studies and include time series from white matter and cerebrospinal ﬂuid (p.ej., Di &
Biswal, 2015). The inclusion of mean WM and CSF signals is intended to reduce the impact
of nonneural BOLD ﬂuctuations that may be attributed to motion, scanner artifacts, y
physiological signals that are typically not of interest (p.ej., respiration; Windischberger et al.,
2002). Use of local WM regressors is also possible and entails using the average signal within
an eroded WM mask within a 15 mm radius of each gray matter voxel (Jo et al., 2010).

The global signal is the time series of signal intensity averaged across
Global signal regression.
all voxels in the brain. The global signal is used in dynamic rs-fMRI studies as a nuisance regres-
sor (p.ej., Liu & duyn, 2013) as it is strongly linked to nonneuronal processes that include head
movimiento, respiratory patterns, and hardware artifacts (Fuerza, Plitt, Laumann, & Martín, 2017).
Use of GSR has been a source of debate in the rs-fMRI literature (Murphy & Fox, 2016), con
concerns that it may remove signals of interest (Schölvinck, Maier, Franco, duyn, & Leopold,
2010) and bias group comparisons (Gotts et al., 2013; Saad et al., 2012). Recent studies com-
paring a number of de-noising pipelines on motion artifact in rs-fMRI indicate that the use
of GSR in preprocessing pipelines is effective at reducing the association between motion
and functional connectivity but may have some undesirable effects on the distance-dependent
effects of motion (Ciric et al., 2017; Parkes et al., 2018).

PCA approaches have been used in the preprocessing of dy-
Principal component analysis.
namic rs-fMRI (p.ej., Verano & davis, 2014). The aim in PCA approaches is to isolate regions
of the image that are strongly driven by motion and other sources of nonneural signal, de-
rive principal components from these noise regions, and include them as nuisance regressors.
Two common variants of this approach—anatomic COMPCOR (aCOMPCOR) and temporal
COMPCOR (tCOMPCOR)—isolate noise regions of interest by either (a) performing PCA on
voxelwise CSF and eroded WM signals, o (b) identifying high-noise regions by their tempo-
ral standard deviation, respectivamente (Behzadi, Restom, Liau, & Liu, 2007; Cheng et al., 2017).
PCA has been observed to be more effective than tissue-mean signal regression approaches at
removing motion artifact from rs-fMRI data (Muschelli et al., 2014).

ICA has been used in dynamic rs-fMRI to identify distinct
Independent component analysis.
functional networks that differ based on their temporal independence (Smith et al., 2012). Como
well as being used as a technique to identify functional networks at the group level, ICA is used
in the preprocessing of dynamic rs-fMRI to identify noise time series that are then regressed
from the data (Barber, Lindquist, DeRosse, & Karlsgodt, 2018). ICA decomposes the rs-fMRI
data into multiple components, some of which will be components of interest (es decir., those re-
ﬂecting BOLD signal) and some of which will reﬂect artifactual processes. Once decomposed,
identiﬁcation of artifactual components is required. Two common approaches to noise compo-
nent identiﬁcation are ICA-FIX (Salimi-Khorshidi et al., 2014) and ICA-AROMA (Pruim et al.,

Neurociencia en red

433

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Motion mitigation in dynamic connectivity

2015). ICA-FIX requires manual labeling of the components derived from ICA in a training
conjunto de datos, whereas ICA-AROMA uses a predeﬁned set of features that are automatically extracted
from the image to identify noise. Once the data are decomposed and noise components are
identiﬁed, the noise components are regressed from the rs-fMRI data.

Beyond confound regression techniques, temporal censoring methods
Censoring methods.
are available to reduce the impact of motion. In censoring approaches, motion-corrupted vol-
umes are identiﬁed and either removed from the data or interpolated. Despiking identiﬁes
outliers on a voxelwise basis based on the intensity of each voxel’s time series, and interpo-
lates over the outliers. Scrubbing and spike regression, in contrast, censor complete volumes
based on deviation from an a priori motion threshold (Power et al., 2012; Satterthwaite, eliot,
et al., 2013). While despiking has been used in studies of dynamic rs-fMRI (p.ej., Allen et al.,
2014; Damaraju et al., 2014), more extreme censoring methods, including scrubbing, are often
explicitly avoided because of concerns over interrupting the temporal autocorrelation structure
of the data (p.ej., h. zhang, Chen, zhang, & shen, 2017) and the potential issue of resulting in
sliding windows of differing lengths (Hutchison et al., 2013).

Pipelines Used in the Present Study

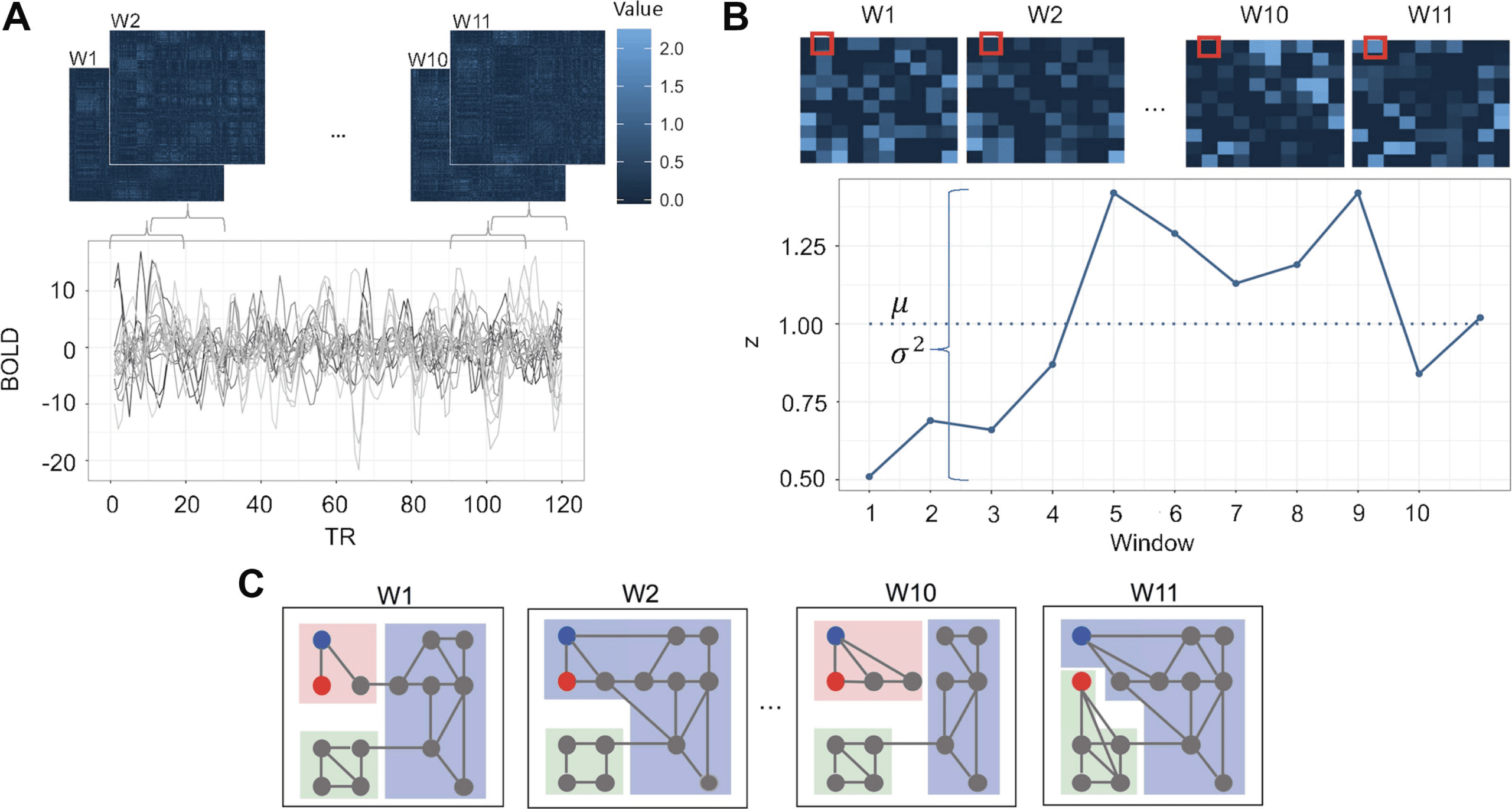
Twelve commonly used de-noising pipelines were selected for evaluation (Cifra 2; see also
Ciric et al., 2017, for more information).

Pipeline 1. Pipeline 1 (2PAG) functioned as a base pipeline for comparison with more complex
confound regression pipelines. It employed two physiological time series: mean signal
in white matter and mean signal in cerebrospinal ﬂuid.

Pipeline 2. Pipeline 2 (6PAG) used six motion estimates derived from MCFLIRT realignment as

regressors.

Pipeline 3. Pipeline 3 (9PAG) combined the two physiological time series from Pipeline 1 y

the six motion estimates from Pipeline 2 with GSR.

Pipeline 4. Pipeline 4 (24PAG) was an expansion of Pipeline 2 that included six temporal deriva-
tives, six quadratic terms, and six quadratic expansions of the derivatives of the six motion
estimados, resulting in a total of 24 regressors.

Cifra 2.
Schematic of the 12 de-noising pipelines evaluated in the present study. For each of the
12 pipelines (izquierda), the table details the included processing procedures and confound regressors
(arriba).

Neurociencia en red

434

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Motion mitigation in dynamic connectivity

Pipeline 5. Pipeline 5 (36PAG) was an expansion of Pipeline 3, incorporating derivatives, quad-
ratic terms, and squares of derivatives of six motion, two physiological time series, y
GSR.

Pipeline 6. Pipeline 6 (36P+despike) included the 36 regressors of Pipeline 5 in addition to

despiking (Cox, 1996).

Pipeline 7. Pipeline 7 (aCOMPCOR) used ﬁve principal components each from the WM and

CSF, in addition to motion estimates and their temporal derivatives.

Pipeline 8. Pipeline 8 (tCOMPCOR) used six principal components from high-variance

vóxeles.

Pipeline 9. Pipeline 9 (wmLOCAL) used a voxelwise, localized WM regressor in addition to

motion estimates, their temporal derivatives, and despiking.

Pipeline 10. Pipeline 10 (wmMEAN) used the mean signal across the WM instead of the voxel-
wise, localized WM regressor of Pipeline 9. It also included motion estimates, su
temporal derivatives, and despiking.

Pipeline 11. Pipeline 11 (ICA-AROMA) used an ICA-based procedure for removal of motion-

related variance from BOLD data, alongside mean WM and CSF regressors.

Pipeline 12. Pipeline 12 (AROMA+GSR) combined ICA-AROMA with GSR.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Análisis de los datos

Each de-noising pipeline was evaluated according to the following benchmarks: (a) the residual
association between participant motion and edge dispersion, (b) distance-dependent effects of
motion on edge dispersion, (C) the degree to which functional subnetworks could be identiﬁed
by multilayer-modularity maximization, y (d) measures of module reconﬁguration such as
node ﬂexibility and node promiscuity. En esta sección, we provide details on dynamic network
creation before providing an overview of each benchmark.

Brain networks for each de-noising pipeline were deﬁned with a
Dynamic network creation.
commonly used, whole-brain, spherical node parcellation (Power et al., 2011). For each net-
trabajar, the mean time series for each node was calculated from the de-noised residual data.
The time series was divided into T = 11 sliding time windows, cada 20 TRs (60 s) in duration,
con 50% superposición. The choice of window length was consistent with work indicating that the
majority of dynamic functional connectivity work to date has employed 30- to 60-s windows,
with most studies using 20 data points per window (Preti et al., 2017). The use of the upper
bound of 60 s and 20 TRs was chosen because evidence suggests that window lengths of 60 s
or greater may be required to balance the capacity to capture dynamics in BOLD signal and
the ability to obtain accurate connectivity estimates within windows (Leonardi & Van De Ville,
2015), although we acknowledge that shorter windows can also be useful for some questions
(Braun et al., 2016; Braun et al., 2015). An added beneﬁt of this choice was that it also al-
lowed us to achieve even window lengths across the experiment. Within each window, bordes
between all nodes were estimated via Pearson correlation. Negative correlations were set to 0,
similar to previous functional connectivity studies (p.ej., chan, Parque, Caminando, Petersen, & Peluca,
2014; grady, Sarraf, Saverino, & Campbell, 2016), to eliminate potential misinterpretation of
negative edge weights (see Supporting Information, Network Density Across Pipelines, for in-
formation on the number of negative edges, network density, and average positive edge weight
of networks across pipelines; Lydon-Staley, círico, Satterthwaite, & bassett, 2019). In additional
analiza, negative correlations were retained (see Supporting Information, Results with Neg-
ative Edge Weights Included; Lydon-Staley et al., 2019). A Fisher z-transformation was then
performed on all correlations. The result was a time-ordered set of functional connectivity

Neurociencia en red

435

Motion mitigation in dynamic connectivity

matrices for each subject and de-noising pipeline that was used in the creation of dynamic
functional connectivity and network indices (ver Figura 1A).

The extent of ﬂuctuations in connectivity between individual edges
Edge dispersion measure.
across time was assessed using a dispersion index (p.ej., Demirta¸s et al., 2016). For each
de-noising pipeline, the mean and the variance of the functional connectivity of each edge
across all sliding windows were computed for each subject. This allowed the creation of a
dispersion index

Ci =

p2
i
μ

where Ci is the dispersion of edge i based on the variance of edge i divided by the mean
value of edge i (ver Figura 1B). Dispersion values of edges that showed no ﬂuctuations across
windows were set to 0.

For each edge, we computed the cor-
Edge dispersion outcome: Dispersion-motion associations.
relation coefﬁcient between the dispersion of that edge and subject motion. To control for
the potential inﬂuence of demographic factors, partial correlations that accounted for subject
age and sex were calculated. This procedure resulted in a distribution of dispersion-motion
correlations for each pipeline. From these distributions, two outcomes of pipeline efﬁcacy in
minimizing motion artifact were computed: (a) the number of edges signiﬁcantly related to

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

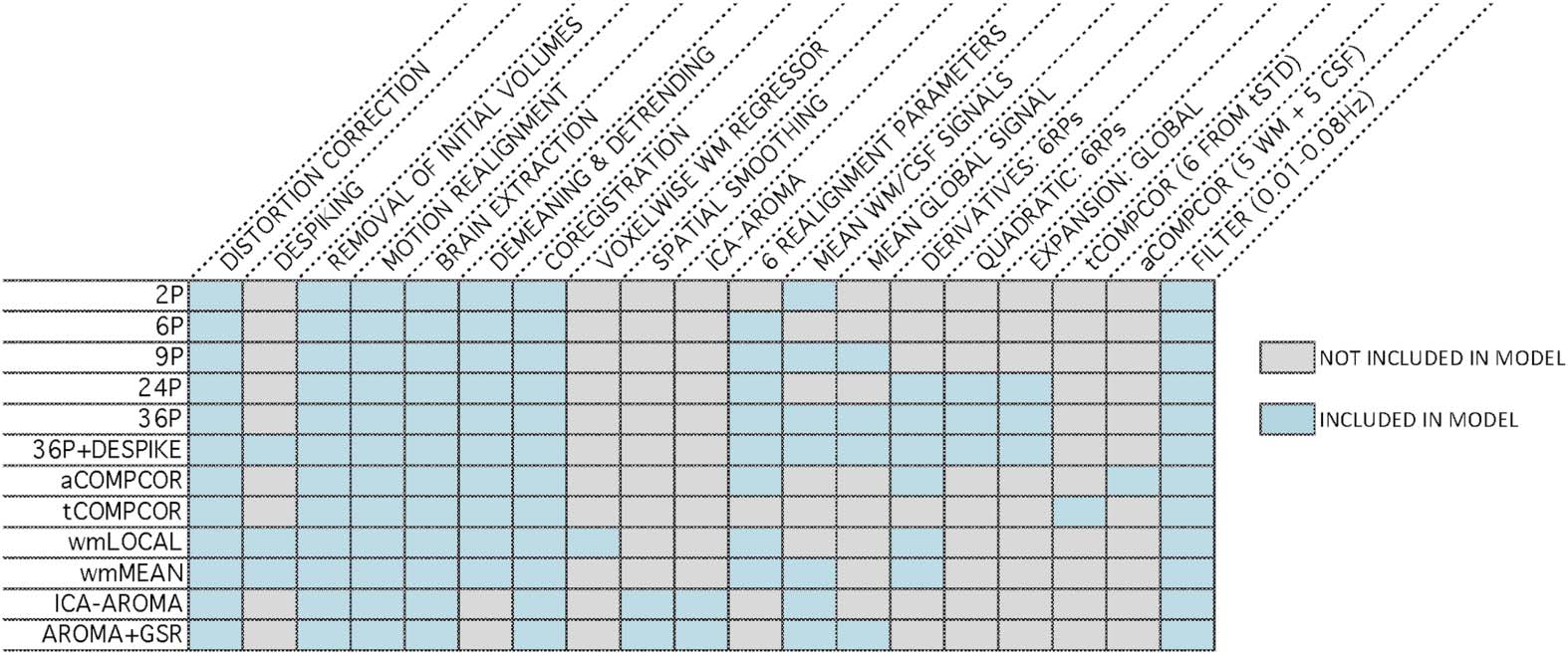
Cifra 3. Distributions of all edgewise dispersion-motion correlations after de-noising for each de-noising pipeline. The median absolute
value of the correlation and the standard deviation of the correlation are both displayed in the top right of each panel.

Neurociencia en red

436

Motion mitigation in dynamic connectivity

movimiento, computed after controlling for multiple comparisons via the false discovery rate (FDR
at α = 0.05; Benjamini & Hochberg, 1995); (b) the median absolute value of all dispersion-
motion correlations.

Edge dispersion outcome: Distance-dependent motion effects. Motion artifact has been demon-
strated to be associated with the distance between nodes (Power et al., 2012; Satterthwaite
et al., 2012). Short-distance edges exhibit stronger connectivity while long-distance edges
exhibit weaker connectivity as a result of subject motion. The center of mass of each node
was used to obtain a distance matrix D where element Dij indicated the Euclidean distance
between the centers of mass of nodes i and j. Correlations between the distance sepa-
rating each pair of nodes and the dispersion-motion correlation of the edge connecting
these nodes was then estimated to provide an outcome measure of the extent to which each
de-noising pipeline mitigated distance-dependent effects of motion. Statistical comparisons
of the distance-dependent motion effects of the pipelines were achieved using tests of the
equality of correlation coefﬁcients following Steiger ( 1980) and using the cocor package in R
(Diedenhofen & Musch, 2015).

The degree to which there were structured subnetworks in the
Network modularity measure.
connectivity matrices from each pipeline was characterized using a common dynamic
community detection technique to maximize multilayer modularity. We ﬁrst transform the
ordered set of adjacency matrices (windows 1–11 in the present case) into a multilayer net-
trabajar (Bassett y cols., 2013; Mucha et al., 2010). In this multilayer network, the graph in one time
window is linked to the graph in adjacent time windows via identity edges that connect a node
in one time window to the same node in neighboring time windows. Multilayer modularity is
deﬁned as

(cid:2)

Q =

2μ ∑

ijlr

(Aijl

− γ

l Pijl)δ

lr + δ
ij

Vaya

jlr

δ(gil, gjr),

(cid:3)

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

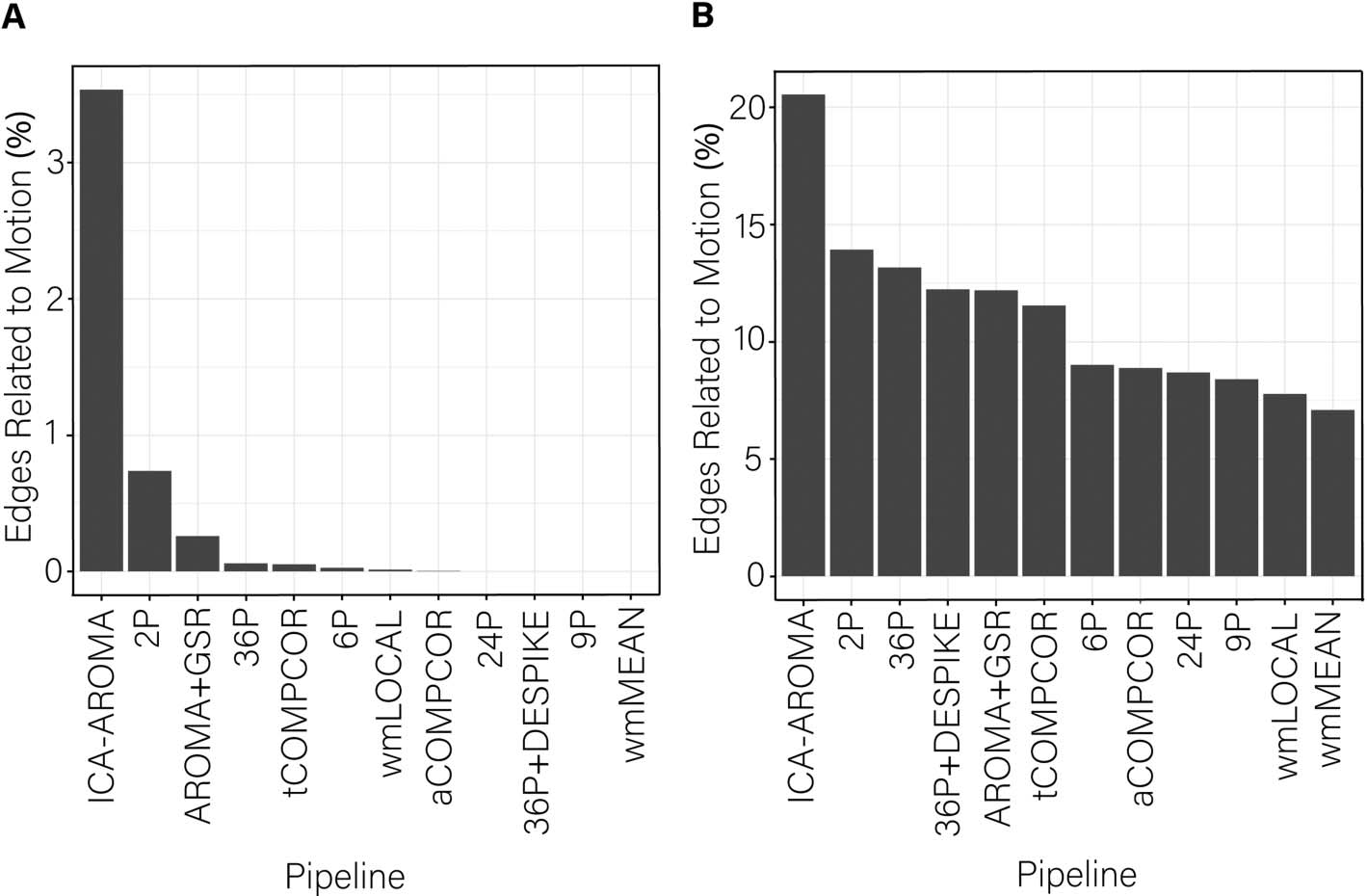
Cifra 4. Percentage of edges signiﬁcantly related to motion after de-noising for the dispersion
índice. More effective de-noising pipelines reduced the relationship between dispersion and mo-
ción. Bars are ordered such that the least effective de-noising pipelines are on the left and the most
effective are on the right. Panel A illustrates the results after correcting for multiple comparisons.
Panel B depicts the results without controlling for multiple comparisons.

Neurociencia en red

437

Motion mitigation in dynamic connectivity

where Aijl is the edge weight between nodes i and node j in time window l; Pijl is the expected
weight of the edge connecting node i and node j under a speciﬁed null model; γ
l is a structural
resolution parameter of layer l that tunes the number of communities identiﬁed; gil is the
community assignment of node i in layer l; gjr gives the community assignment of node j in
layer r; δ(gil, gjr) = 1 if gil = gjr and 0 de lo contrario; the total network edge weight is μ =
jl = κ
κ
1
jl + cjl; the intralayer strength of node j in
2
layer l is κ

jl = ∑i Aijl; and the interlayer strength of node j in layer l is cjl = ∑r

jr; the strength of node j in layer l is κ

∑jr

jlr.

Vaya

Multilayer modularity maximization was implemented in MATLAB ( Jeub, Bazzi, Jutla, &
Mucha, 2011) and was applied to each subject’s functional connectivity matrices separately
for each de-noising pipeline. The algorithm was applied with a default structural resolution
parameter, γ
jlr, de 1. As the heuristic is non-
deterministic, the algorithm was iterated 100 times for each subject for each de-noising pipeline.
This procedure resulted in 100 Q values for each subject for each de-noising pipeline as
well as 100 n × m matrices, where n is the number of nodes (264) and m is the number

yo, de 1 and an interlayer strength parameter, Vaya

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

3
2
4
2
7
1
0
9
2
6
0
9
norte
mi
norte
_
a
_
0
0
0
7
1
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

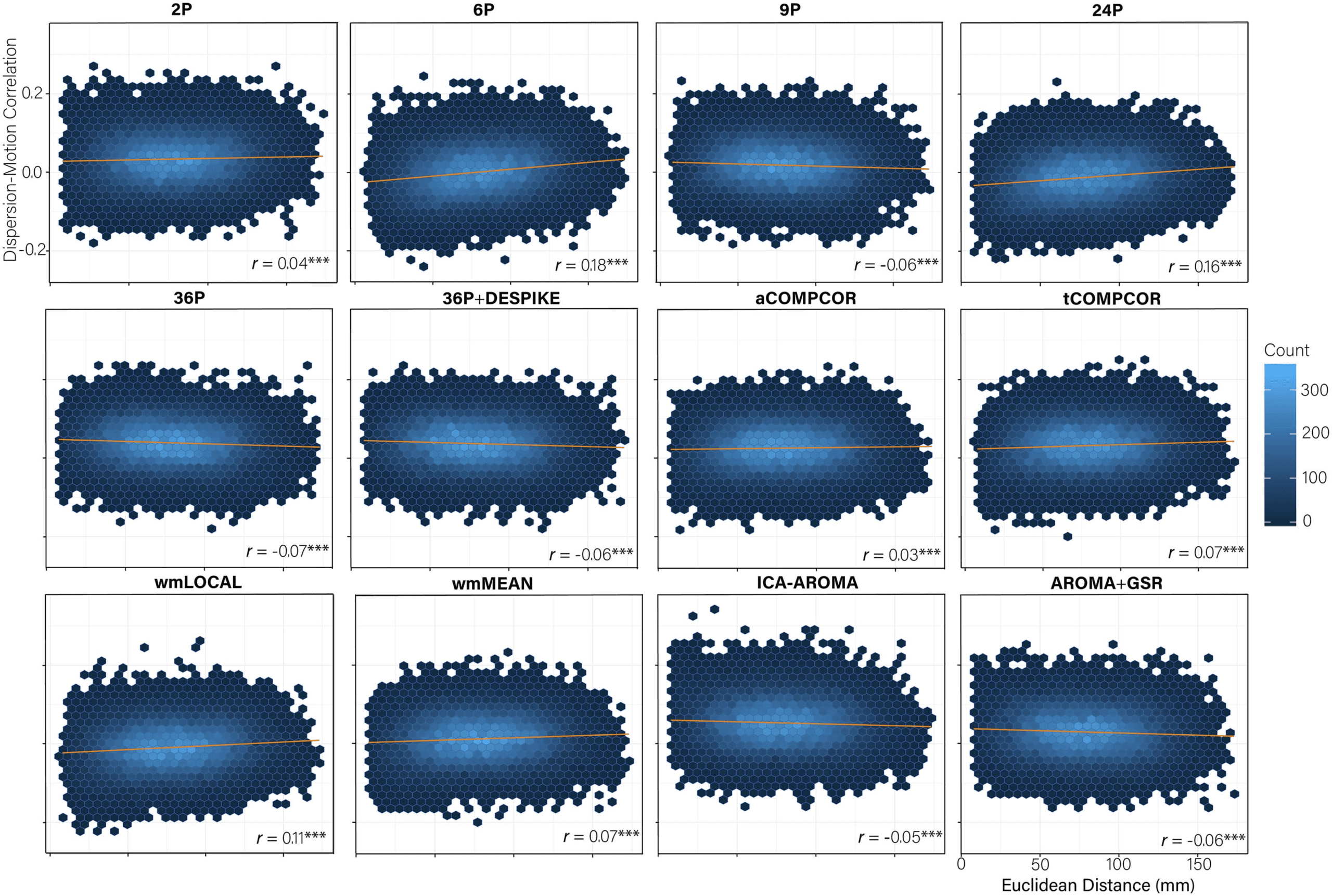
Cifra 5. Hexbin plots of the association between the Euclidean distance separating nodes (mm) and the magnitude of the dispersion-motion
correlation between the edge connecting the nodes (y-axis). A trend line for each pipeline is indicated in blue and the magnitude of the
correlation is presented in the bottom right of each panel. Nota: ***pag <0.001. Network Neuroscience 438 Motion mitigation in dynamic connectivity of sliding windows (i.e., 11), indicating the community allegiance of each node during each sliding window. The mean Q value across the 100 it- Network modularity outcome: Subnetwork identiﬁcation. erations was taken as an outcome measure of how separable the brain networks were into subnetworks after de-noising. Partial correlations between Q and partic- Network modularity outcome: Q-motion associations. ipant motion were calculated while controlling for participant age and sex in order to provide an indication of the extent to which each de-noising pipeline minimized the association be- tween motion and modularity. The matrices indicating community assignment of Node ﬂexibility and promiscuity measures. nodes across sliding windows were taken forward to create additional indices related to node ﬂexibility and node promiscuity (see Figure 1C). Node ﬂexibility captures the number of times l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d . 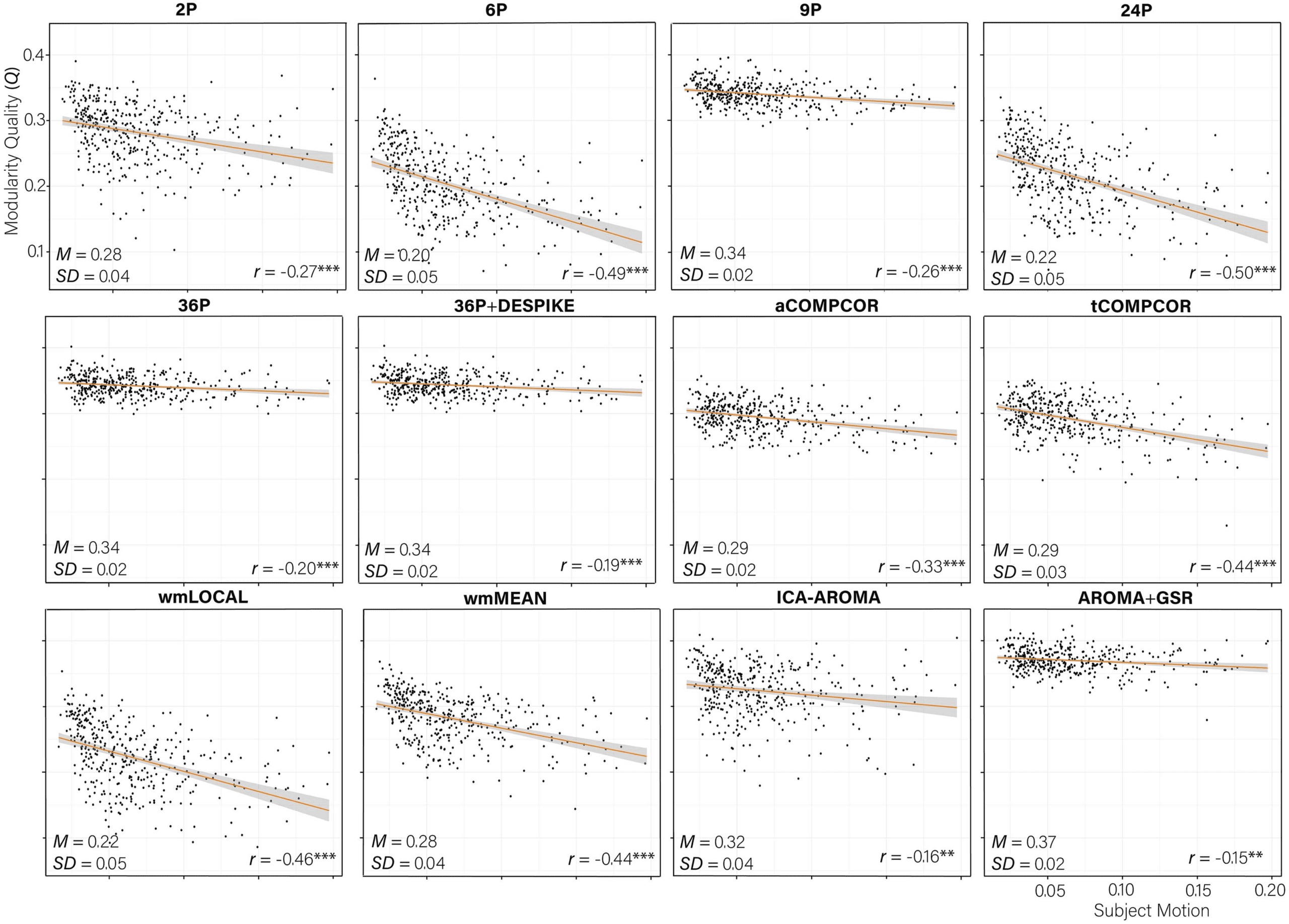t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 6. 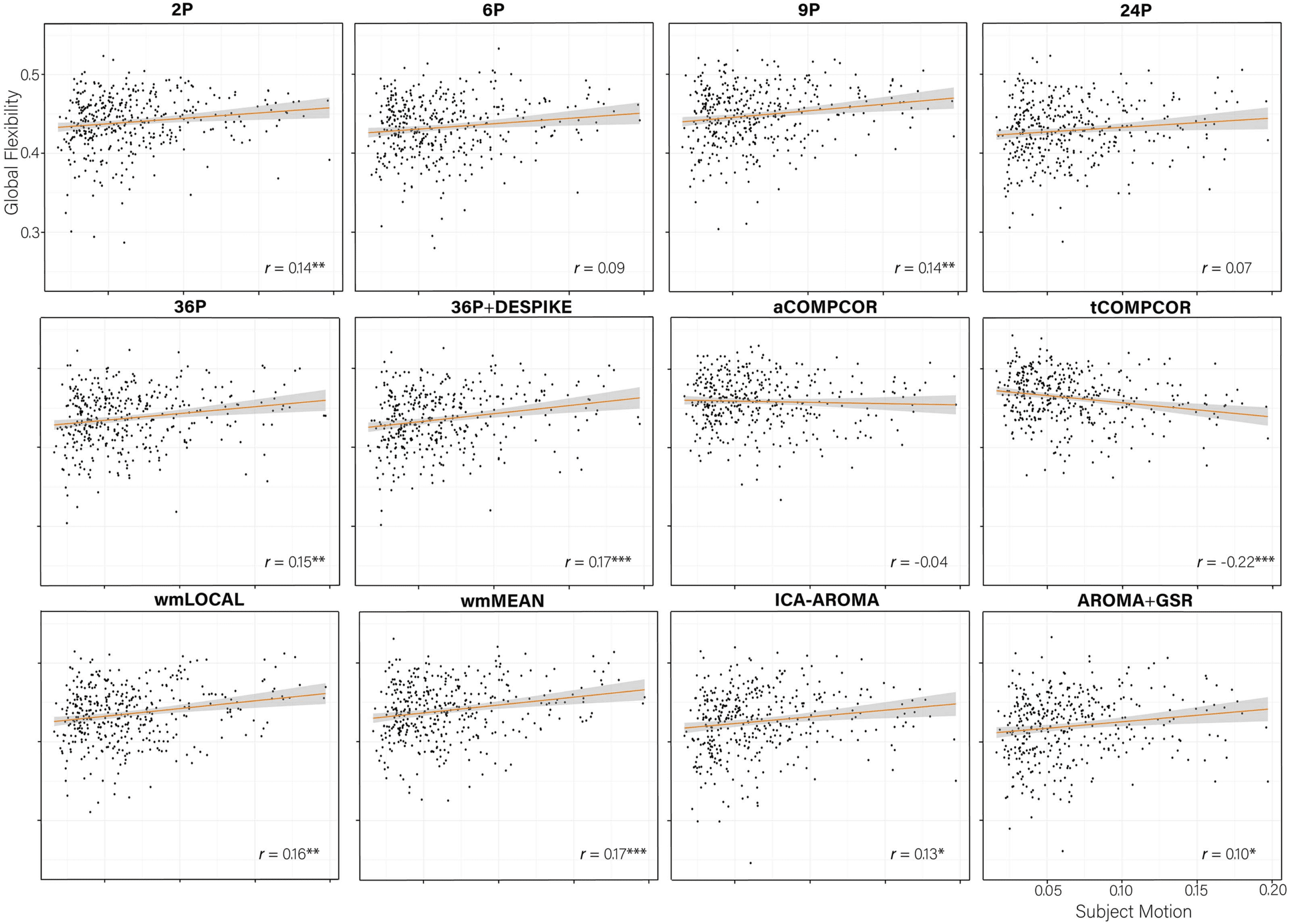Scatterplot of the association between subject motion (x-axis) and modularity quality (Q, y-axis) with trend line. The partial correla- tion between subject motion and Q controlling for age and sex is presented in the bottom right of each panel. The mean and standard deviation of the Q value for each pipeline is presented in the bottom left of each panel. ***p <0.001; **p <0.01. Network Neuroscience 439 Motion mitigation in dynamic connectivity a node changes communities across time, normalized by the number of times the node could have changed communities (Bassett et al., 2011). Formally, node ﬂexibility is deﬁned as fi = m T − 1 , where fi is the ﬂexibility of node i, m is the number of times node i changed communities, and T is the number of sliding windows. Using the Network Community Toolbox (http:// commdetect.weebly.com), node ﬂexibility was calculated for each subject across each pipeline as the average ﬂexibility value across the 100 iterations of the dynamic community detection procedure. Flexibility F of the dynamic network as a whole was calculated as the average of fi over all nodes. Node promiscuity captures additional information concerning the dynamics of network nodes and is deﬁned as ψ i = k K , l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d t . 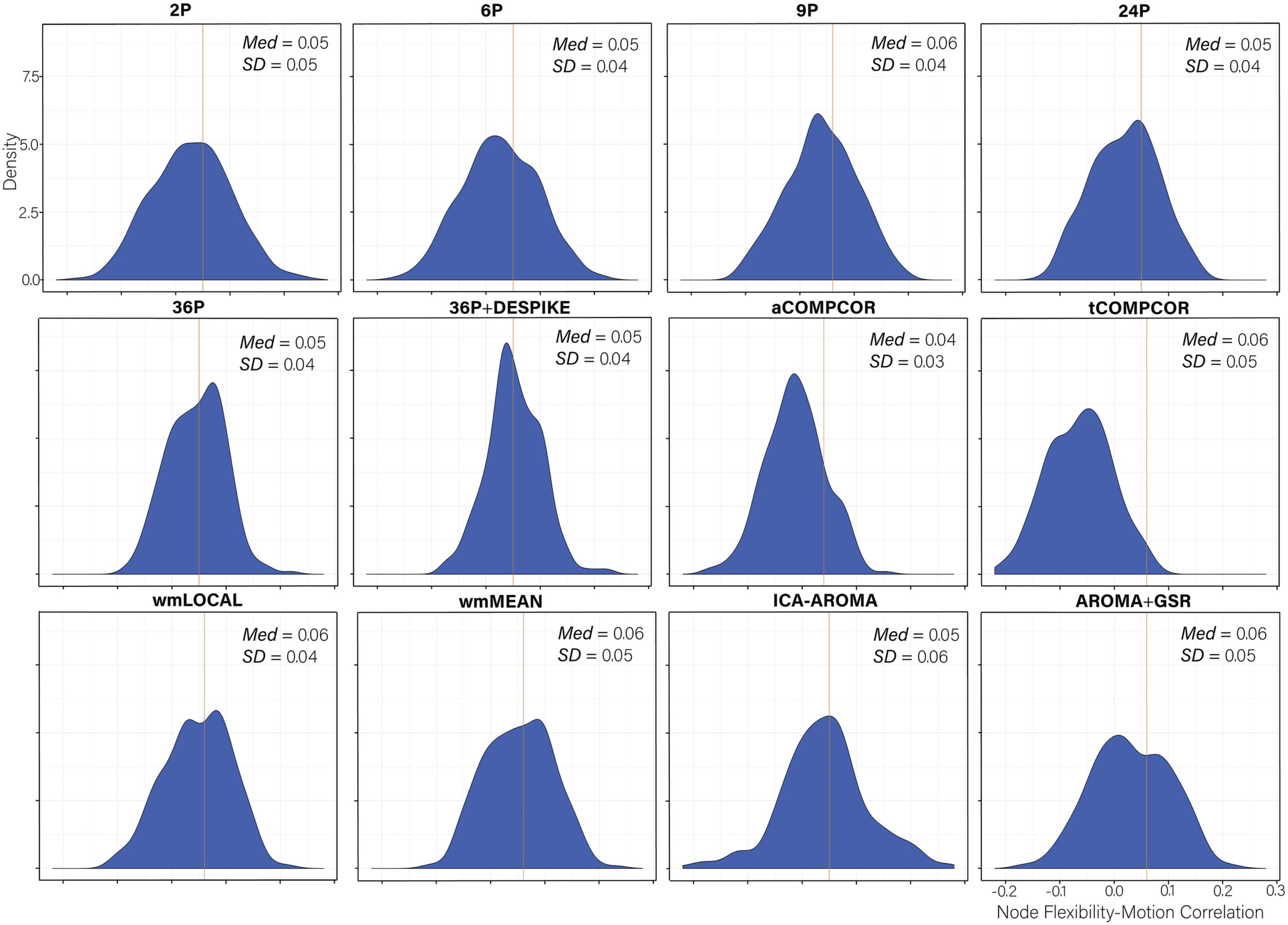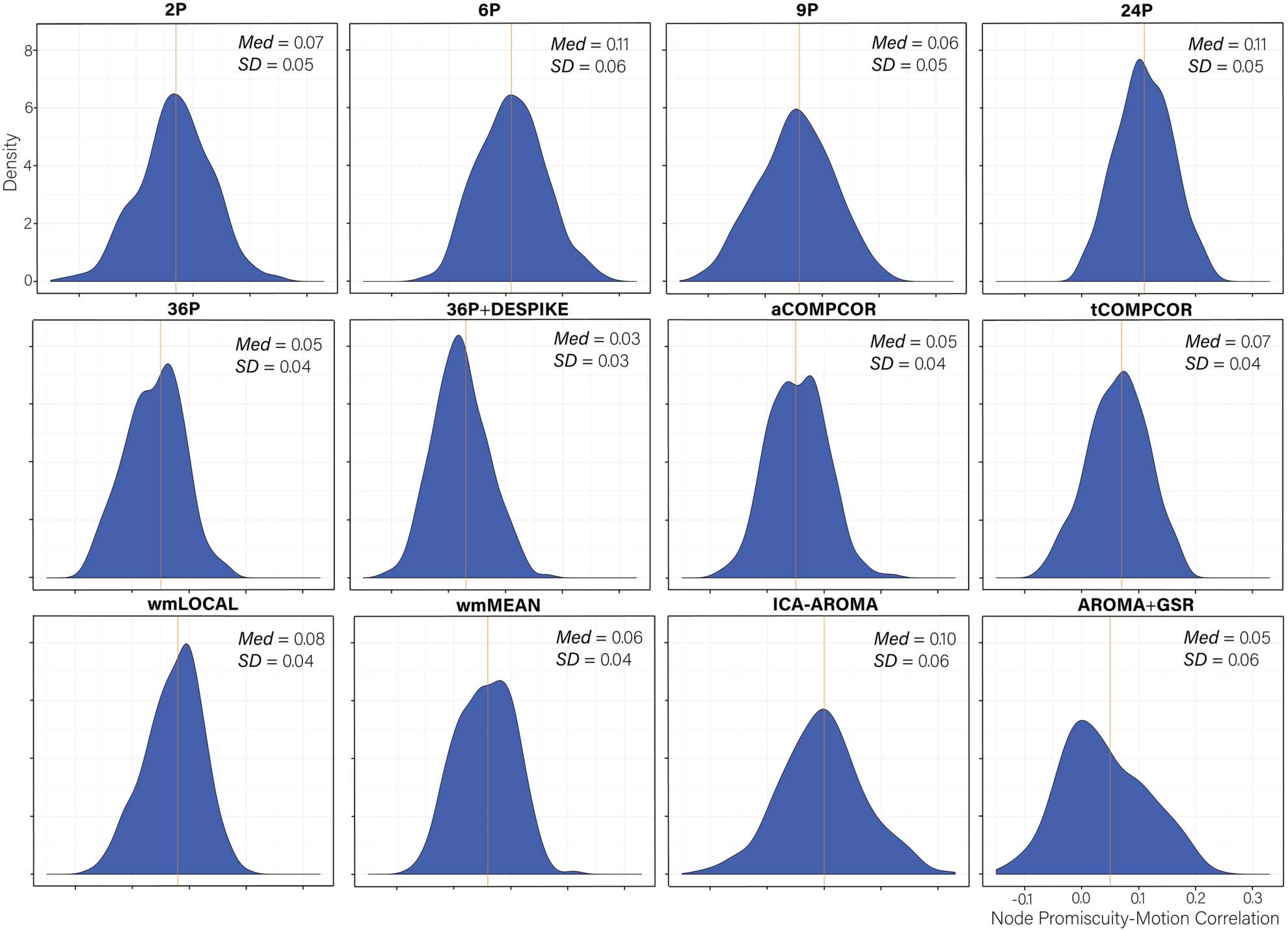f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 7. Distributions of all node ﬂexibility-motion correlations after de-noising for each pipeline. The median absolute value of the corre- lation and the standard deviation of the correlation is displayed in the top right of each panel. Panels are ordered by the magnitude of the absolute correlation. Network Neuroscience 440 Motion mitigation in dynamic connectivity where ψ i is the promiscuity of node i, k is the number of communities in which node i partic- ipates, and K is the total number of communities (Papadopoulos, Puckett, Daniels, & Bassett, 2016). A node with high promiscuity exhibits allegiances to many communities across slid- ing windows. Using the Network Community Toolbox (http://commdetect.weebly.com), node promiscuity was calculated for each subject across each pipeline as the average promiscuity value across the 100 iterations of the dynamic community detection procedure. Promiscuity Ψ of the dynamic network as a whole was calculated as the average of ψ i over all nodes. Node ﬂexibility and promiscuity outcome: Flexibility-motion and promiscuity-motion associations. For each node, a correlation was computed between the ﬂexibility of that node and participant motion. To control for the potential inﬂuence of demographic factors, partial correlations that accounted for participant age and sex were calculated. This resulted in a distribution of ﬂexibility-motion correlations for each pipeline. From these distributions, two measures of pipeline efﬁcacy in minimizing motion artifact were computed: (a) the number of nodes signiﬁcantly related to motion, computed after controlling for multiple comparisons via the false discovery rate (FDR; Benjamini & Hochberg, 1995); (b) the median absolute value of all ﬂexibility-motion correlations. Further, partial correlations between F and participant motion were calculated while controlling for participant age and sex in order to provide an indication of the extent to which each de-noising pipeline minimized the association between motion and global ﬂexibility. The analyses conducted for ﬂexibility were repeated for promiscuity. This resulted in a distri- bution of promiscuity-motion correlations for each pipeline as well as a measure of the number of nodes signiﬁcantly related to motion and the median absolute value of all ﬂexibility-motion correlations. The association between motion and global promiscuity was also computed. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 8. Percentage of nodes signiﬁcantly related to motion after de-noising for node ﬂexibility. More effective de-noising pipelines reduced the relationship between ﬂexibility and motion. Bars are ordered such that the least effective de-noising pipelines are on the left and the most effective are on the right. Panel A illustrates the results after correcting for multiple comparisons. Panel B depicts the results without controlling for multiple comparisons. Network Neuroscience 441 Motion mitigation in dynamic connectivity RESULTS In this section we present the performance of the de-noising pipelines for mitigating mo- tion artifact on (a) the residual association between participant motion and edge dispersion, (b) distance-dependent effects of motion on edge dispersion, (c) the degree to which functional subnetworks could be identiﬁed by multilayer-modularity maximization, and (d) measures of module reconﬁguration such as node ﬂexibility and node promiscuity. 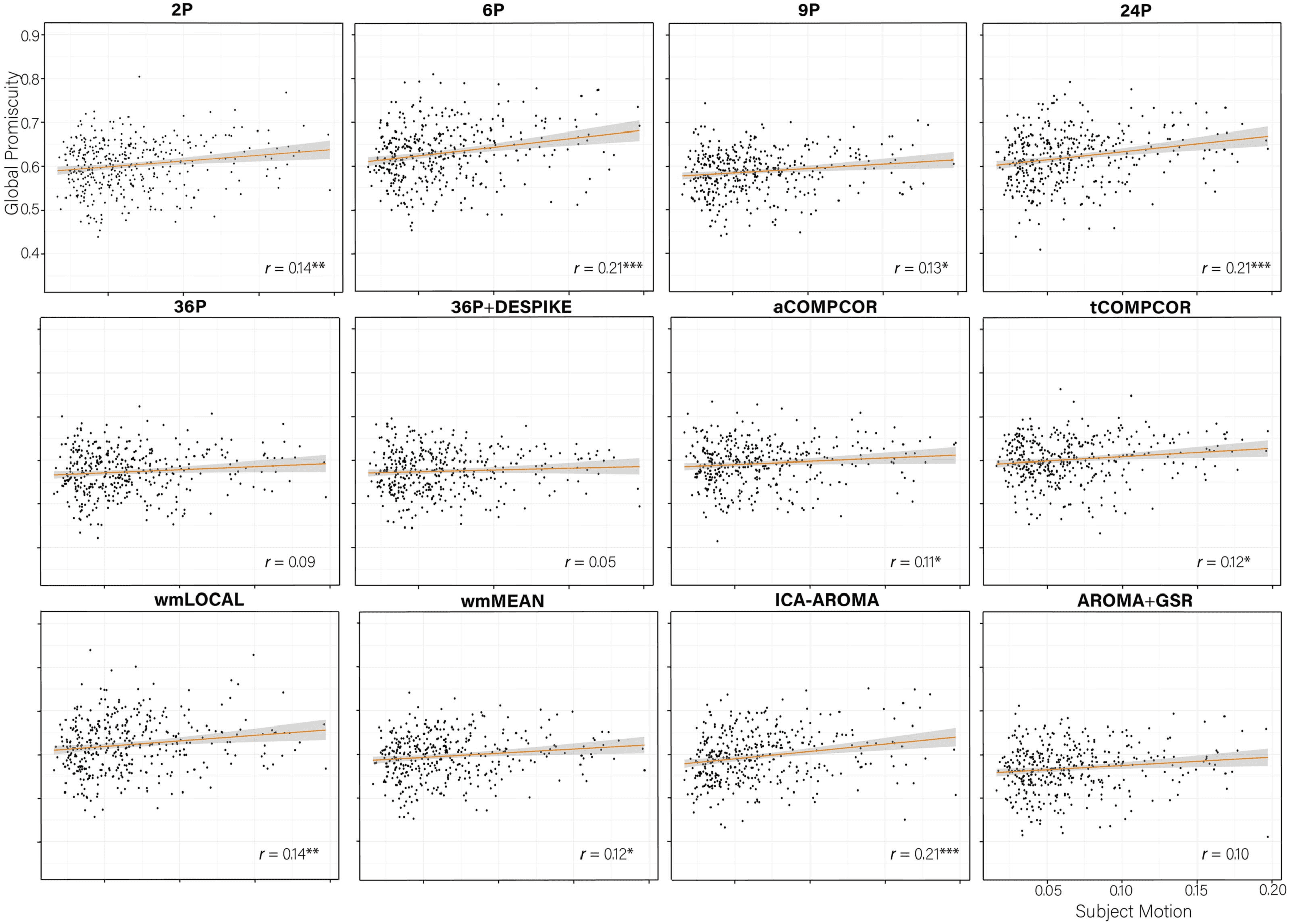Edge Dispersion–Motion Association Is Minimal Across Pipelines Distributions of dispersion-motion correlations are presented in Figure 3. Paired-sample t tests indicated signiﬁcant differences in the mean dispersion-motion correlation across all pipelines (Table S6; see Lydon-Staley et al., 2019). The median absolute dispersion-motion correlations ranged between 0.04 and 0.05, indicating small associations between dispersion and partici- pant motion following the application of the de-noising pipelines. While the range of dispersion-motion correlations was small across pipelines, there was some heterogeneity in the performance of the various pipelines. 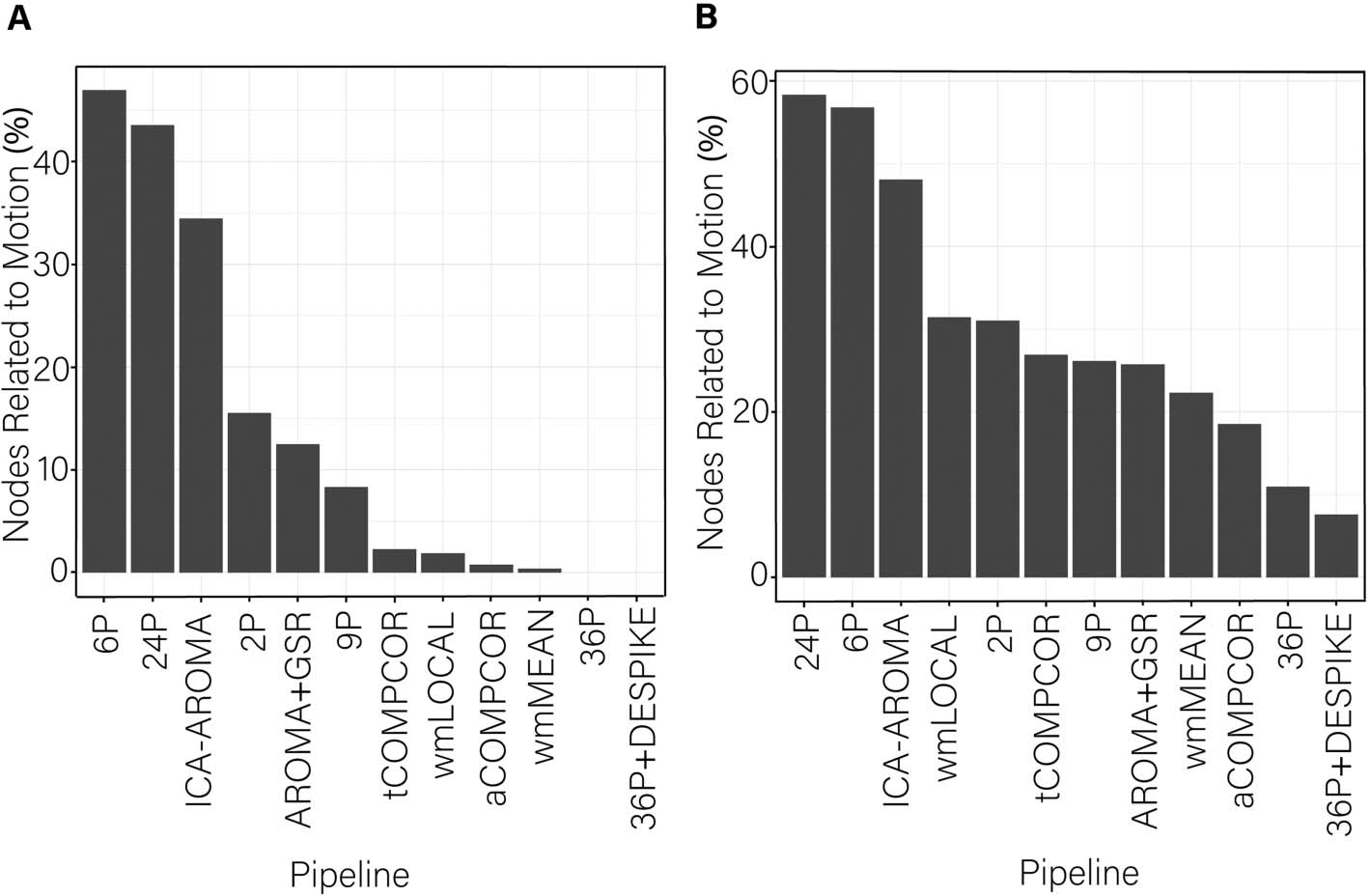This heterogeneity was most notable in the percentage of edges whose dispersion was related to motion (Figure 4A). The l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d t . 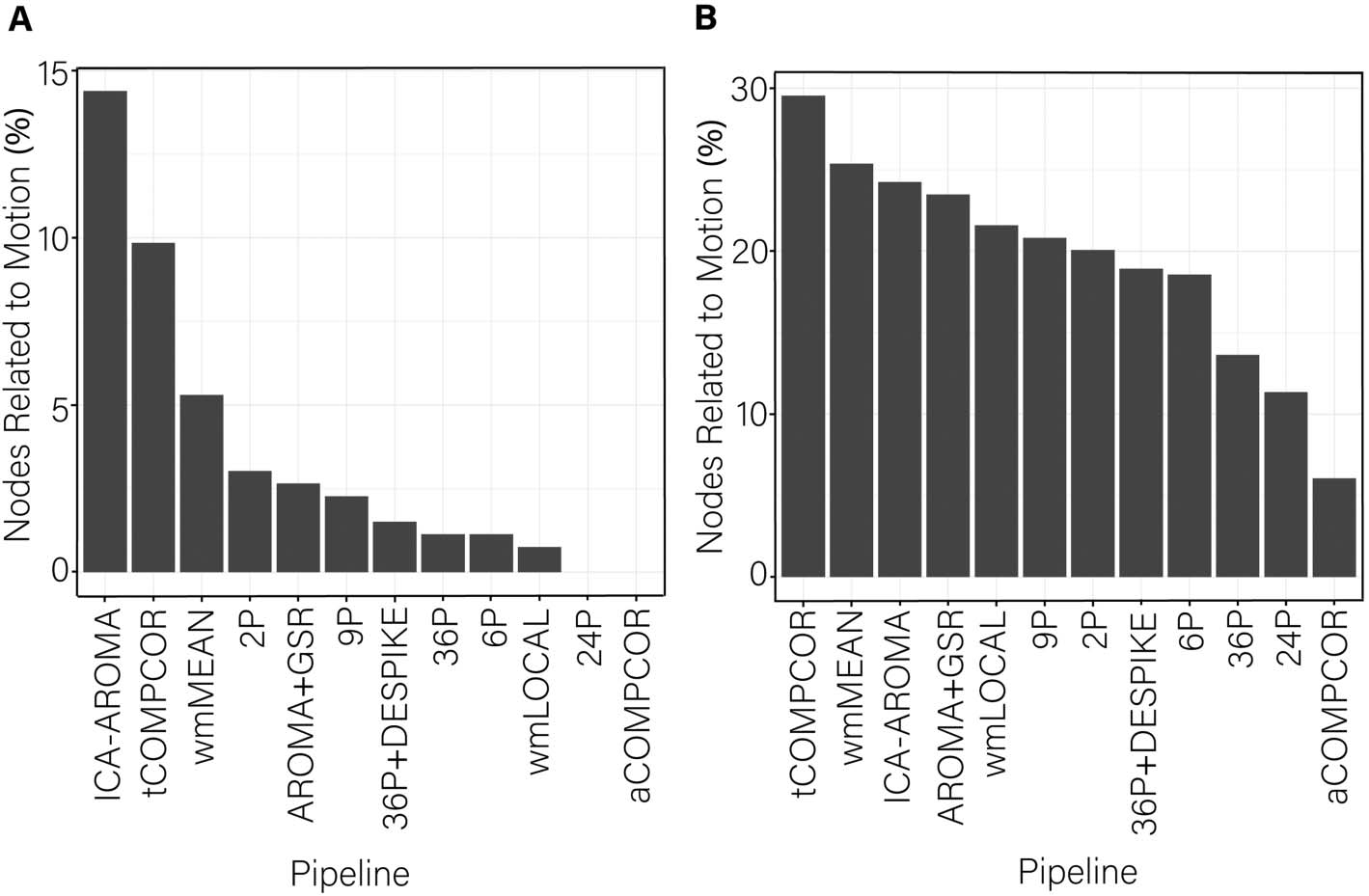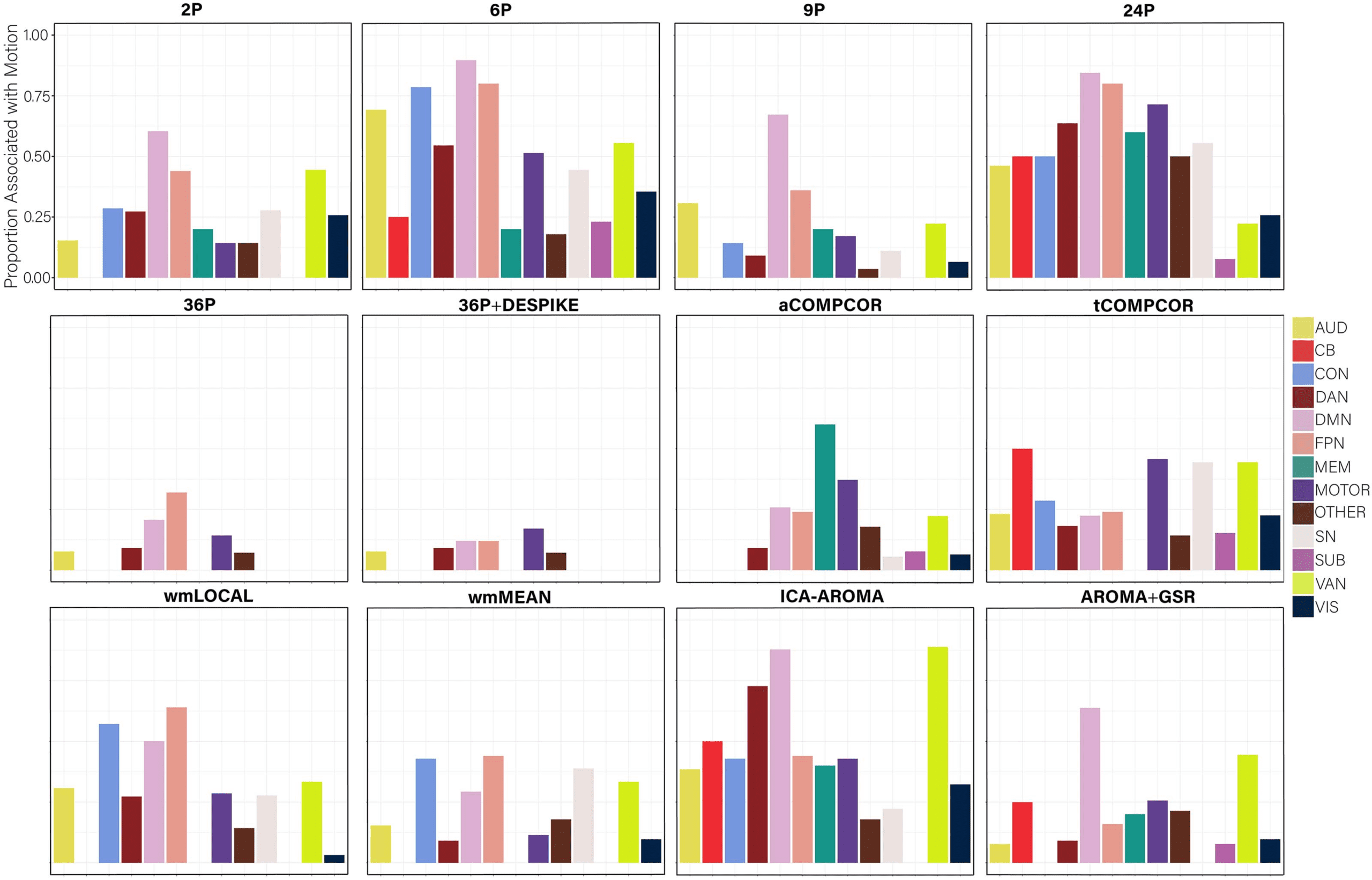f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 9. The proportion of nodes within each subnetwork of the Power et al. (2011) parcellation with ﬂexibility values signiﬁcantly re- lated to subject motion, without controlling for multiple comparisons. AUD = auditory; CB = cerebellum; CON = cingulate-opercular net- work;DAN = dorsal attention network;DMN = default mode network; FPN = frontoparietal network; MEM = memory network; SN = salience; SUB = subcortical; VAN = ventral attention network; VIS=visual network. Network Neuroscience 442 Motion mitigation in dynamic connectivity percentage of edges whose dispersion was associated with motion was generally small (i.e., < 1%). However, the ICA-AROMA pipeline emerged as a clear outlier with over 3% of edges having dispersion that remained associated with subject motion following de-noising. Minor differences among the best performing pipeline emerged when the false discovery rate to control for multiple comparisons was applied (Figure 4A) versus when it was not applied (Figure 4B). Dispersion Distance-Dependent Motion Artifact Varies Across Pipelines More marked differences emerged in the performance of the 12 pipelines for the extent to which distance-dependent effects of motion on dispersion were present following de-noising (Figure 5). Correlations between the Euclidean distance separating the nodes and the mag- nitude of the dispersion-motion correlation for the edge connecting those nodes ranged between −0.07 and 0.18. Tests of equality of correlations revealed signiﬁcant differences in the distance-dependent effects of motion across many pipelines (Table S7; Lydon-Staley et al., l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 10. Scatterplot of the association between subject motion (x-axis) and global ﬂexibility (y-axis) with trend line. The partial correlation between subject motion and global ﬂexibility controlling for age and sex is presented in the bottom right of each panel. ***p <0.001; **p <0.01; *p <0.05. Network Neuroscience 443 Motion mitigation in dynamic connectivity 2019). Little evidence for nonequivalent correlations emerged among the 9P, 36P, and 36P+DESPIKE, AROMA+GSR, ICA-AROMA pipelines (r values between −0.07 and −0.05) and the tCOMPCOR and wmMEAN pipelines (r values both equal to 0.07). Particularly poorly performing pipelines included the 6P, 24P, and wmLOCAL pipelines. Marked Heterogeneity in Subnetwork Identiﬁcation Across Pipelines There were marked differences across de-noising pipelines in the extent to which subnet- works were identiﬁable, as operationalized by the network modularity quality (Q). Paired sample t tests revealed signiﬁcant differences across the Q values of most pipelines (Table S8; Lydon-Staley et al., 2019). The difference between the Q values from the 2P and the wmMEAN pipeline was not signiﬁcant. The 6P pipeline was the least effective at allowing the identiﬁcation of subnetworks, exhibiting a mean Q value of 0.20 (see Figure 6). AROMA+GSR emerged as the most effective pipeline, with a mean Q value 0.37. Notably, of the top ﬁve pipelines, four made use of GSR. Supplementary analyses (see Supporting Information, Mean Q Across Pipelines Controlling for Graph Density; Lydon-Staley et al., 2019) examined the effect of pipeline on Q controlling for age, sex, and network density, and indicated that differences in Q values across pipelines were not simply a product of differences in network density. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 11. Distributions of all node promiscuity-motion correlations after de-noising for each pipeline. The median absolute value and the standard deviation of the correlation are both displayed in the top right of each panel. Network Neuroscience 444 Motion mitigation in dynamic connectivity Negative Q-Motion Associations Reduced by Effective Pipelines Correlations between subject motion and Q ranged between −0.50 and −0.15, with greater subject motion associated with lower Q values in all instances (Figure 6). Pipelines that were the least effective at allowing the identiﬁcation of subnetworks tended to be the pipelines that were the least effective at mitigating subject motion artifacts, r(10) = 0.89, p < 0.001. For ex- ample, pipelines 6P and 24P performed poorly across both indices. In contrast, AROMA+GSR and 36P+DESPIKE performed consistently well. Node Flexibility–Motion Correlations Generally Small Across Pipelines Distributions of node ﬂexibility–motion correlations for each pipeline are presented in Figure 7. Paired sample t tests comparing the mean node ﬂexibility–motion correlations across pipelines are presented in Table S9 (Lydon-Staley et al., 2019). Absolute median correlations were small in magnitude across pipelines and ranged between 0.04 and 0.06. Examining the percentage of nodes related to subject motion following de-noising (Fig- ure 8), there was greater variability across pipelines in the extent to which subject motion artifacts were reduced. ICA-AROMA and tCOMPCOR emerged as the least successful pipe- lines, with over 8% of nodes displaying ﬂexibility values that were signiﬁcantly associated with motion after de-noising. No nodes displayed ﬂexibility values that were signiﬁcantly as- sociated with subject motion for the 24P and aCOMPCOR pipelines. Minor differences among the best performing pipeline emerged when the false discovery rate to control for multiple comparisons was applied (Figure 8A) versus when it was not applied (Figure 8B). The pro- portion of nodes within each subnetwork of the Power et al. ( 2011) parcellation signiﬁcantly associated with subject motion are presented in Figure 9 to provide an indication of which subnetworks were most contaminated by residual motion. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 12. Percentage of nodes signiﬁcantly related to motion after de-noising for node promiscu- ity. More effective de-noising pipelines reduced the relationship between promiscuity and motion. Bars are ordered such that the least effective de-noising pipelines are on the left and the most effec- tive are on the right. Panel A illustrates the results after correcting for multiple comparisons. Panel B depicts the results without controlling for multiple comparisons. Network Neuroscience 445 Motion mitigation in dynamic connectivity When examining the association between global ﬂexibility and subject motion (Figure 10), no signiﬁcant associations between subject movement and global ﬂexibility emerged for three (6P, 24P, aCOMPCOR) of the 12 pipelines; tCOMPCOR emerged as the least effective pipeline for mitigating the association between subject motion and global ﬂexibility. Node Promiscuity–Motion Correlations Generally Small Across Pipelines Distributions of node promiscuity–motion correlations are presented in Figure 11. Paired sam- ple t tests comparing the mean node promiscuity–motion correlations across pipelines are presented in Table S10 (Lydon-Staley et al., 2019). Absolute median correlations were larger in magnitude than those observed for node ﬂexibility, but were generally small. The values across pipelines ranged between 0.03 and 0.11 with the 36P+DESPIKE exhibiting the best performance, and with both the 6P and 24P pipelines exhibiting the worst performance. 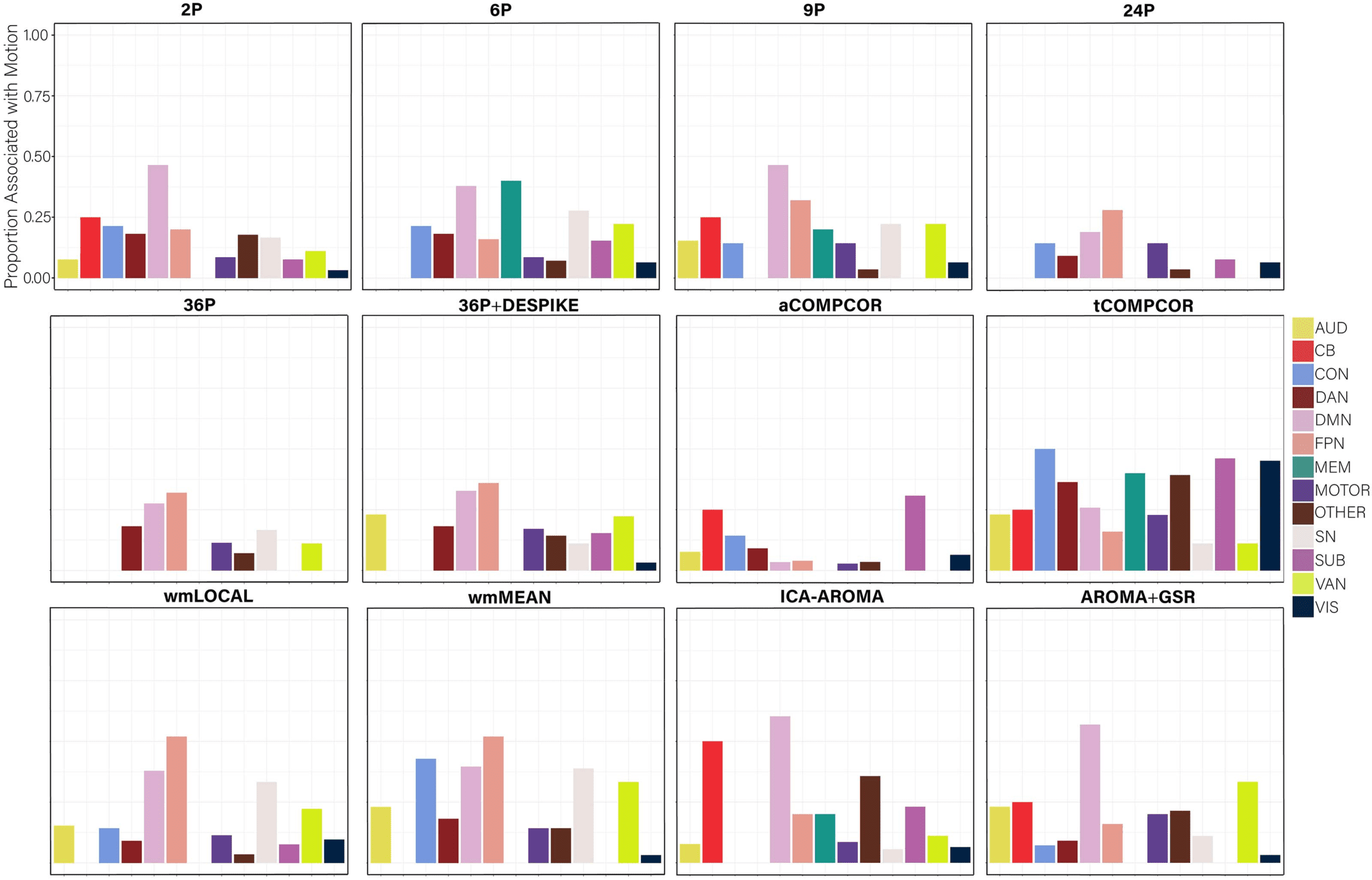Examining the percentage of nodes signiﬁcantly associated with subject motion following de-noising, there was marked variability in the effectiveness of reducing motion artifact across pipelines (Figure 12). Similar to ﬁndings for ﬂexibility, virtually no nodes displayed promiscuity values that were signiﬁcantly associated with motion after use of the aCOMPCOR pipeline. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 13. The proportion of nodes within each subnetwork of the Power et al. (2011) parcellation with promiscuity values signiﬁcantly related to subject motion, without controlling for multiple comparisons. AUD = auditory; CB = cerebellum; CON = cingulate-opercular network; DAN = dorsal attention network; DMN = default mode network; FPN = frontoparietal network; MEM = memory network; SN = salience; SUB = subcortical; VAN = ventral attention network; VIS = visual network. Network Neuroscience 446 Motion mitigation in dynamic connectivity No nodes were associated with motion in the 36P and 36P+DESPIKE pipelines. Also simi- lar was the poor performance of the ICA-AROMA pipeline. The 24P pipeline exhibited the least effectiveness at reducing the association between subject motion and node promiscuity, exhibiting the highest percentage of nodes associated with subject motion. The 6P pipeline also performed poorly. Minor differences among the best performing pipeline emerged when the false discovery rate to control for multiple comparisons was applied (Figure 12A) versus when it was not applied (Figure 12B). The proportion of nodes within each subnetwork of the Power et al. ( 2011) parcellation signiﬁcantly associated with subject motion are presented in Figure 13. When examining the association between global promiscuity and subject motion (Figure 14), pipelines exhibiting worse performance in terms of the number of nodes significantly associated with subject motion (i.e., ICA-AROMA, 6P, and 24P) also exhibited the largest correlations among subject motion and global promiscuity. Three of the four pipelines using GSR (36P, 36P+DESPIKE, AROMA+GSR) showed no signiﬁcant correlations with motion. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 14. Scatterplot of the association between subject motion (x-axis) and global promiscuity (x-axis) with trend line. The partial correla- tion between subject motion and global promiscuity controlling for age and sex is presented in the bottom right of each panel. ***p <0.001; **p <0.01; *p <0.05. Network Neuroscience 447 Motion mitigation in dynamic connectivity DISCUSSION The capacity for in-scanner participant motion to contaminate rs-fMRI data has been increas- ingly appreciated, with many de-noising strategies emerging in response (Power, Schlaggar, & Petersen, 2015; Satterthwaite et al., 2017). To aid in the selection of de-noising pipelines in the study of dynamic rs-fMRI data, the present study evaluated the performance of 12 de-noising pipelines in mitigating motion artifact associated with micromovements across a range of dy- namic (mainly multilayer) functional connectivity indices. Results indicated heterogeneity in pipeline performance according to the following benchmarks: (a) the residual association be- tween participant motion and edge dispersion, (b) distance-dependent effects of motion on edge dispersion, (c) the degree to which functional subnetworks could be identiﬁed by multi- layer modularity maximization, and (d) measures of module reconﬁguration such as node ﬂex- ibility and node promiscuity. Results also indicated that the effectiveness of the de-noising pipelines evaluated differed across dynamic functional connectivity indices. Results, implica- tions, and study limitations are discussed below. Dispersion has been used in dynamic functional connectivity studies to capture the extent to which the coupling between regions of interest ﬂuctuates at rest (e.g., Demirta¸s et al., 2016). When examining the percentage of edges signiﬁcantly related to motion, ICA-AROMA was the least successful at mitigating motion, performing worse than the base- line 2P pipeline. However, ICA-AROMA was among the most successful pipelines in terms of removing distance-dependent motion artifact, performing equivalently to the 9P, 36P, 36P+ DESPIKE, and AROMA+GSR pipelines. Notably, the dispersion-motion correlations were much lower in the current dynamic functional connectivity case than has been observed for equiva- lent edge-based indices of functional connectivity that consider the entire rs-fMRI data (e.g., Ciric et al., 2017). Given that the dispersion-motion correlation magnitudes and the percentage of edges associated with motion were generally low, one may wish to prioritize the ability for pipelines to mitigate distance-dependent motion artifacts in dispersion indices. The most consistently effective pipelines for mitigating the problem of motion for dispersion across the three performance benchmarks were pipelines including GSR and aCOMPCOR. While the majority of de-noising pipelines were effective at dealing with motion for edge dispersion, striking differences in the performance of de-noising pipelines emerged in the extent to which subnetworks could be identiﬁed in the processed data. In terms of modular- ity quality (Q), pipelines incorporating GSR (e.g., AROMA+GSR, 36P, 36P+DESPIKE) resulted in the highest Q across the board. Notable also was the reduced heterogeneity across par- ticipants in terms of Q values that resulted from pipelines incorporating GSR, with Q values for these pipelines exhibiting less variability around the mean relative to pipelines without GSR (Figure 6). Pipelines including GSR were also generally effective at mitigating participant motion–Q associations, with AROMA+GSR exhibiting the lowest correlations. The least effec- tive pipelines included 6P and 24P pipelines, which exhibited the greatest modularity-motion correlations. White matter, tissue-based regression pipelines also performed poorly. Findings are generally in accordance with de-noising pipeline performance on modularity indices in static functional connectivity (Ciric et al., 2017). Node-level dynamics were captured using ﬂexibility and promiscuity indices (Bassett et al., 2011; Papadopoulos et al., 2016). For node ﬂexibility, ICA-AROMA, tCOMPCOR, and wmMEAN pipelines exhibited the greatest percentage of nodes associated with motion and also exhibited the highest global ﬂexibility–subject motion correlations. ICA-AROMA also performed poorly for promiscuity, as did the 6P and 24P pipelines. Although 24P and 6P performed relatively well in terms of outcomes associated with ﬂexibility, we caution that Network Neuroscience 448 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Motion mitigation in dynamic connectivity ﬂexibility and promiscuity are somewhat dependent on the ability for pipelines to effectively identify subnetworks given that both ﬂexibility and promiscuity indices measure the participa- tion of nodes in communities identiﬁed via multilayer modularity. As such, when considering ﬂexibility and promiscuity, pipelines that perform consistently well in subnetwork detection as well as ﬂexibility and promiscuity (e.g., 36P, 36P+DESPIKE) are recommended. Taken together, the 12 de-noising pipelines evaluated here showed varying effectiveness across their capacity to mitigate the effect of motion and to maximize the ability to identify subnetworks in dynamic rs-fMRI. ICA-AROMA emerged as an interesting case. ICA-AROMA has performed relatively well in previous evaluations in the context of static connectivity (Ciric et al., 2017; Parkes et al., 2018), and it also performed well on a number of benchmarks in the current study (e.g., performing equivalently to pipelines using GSR in reducing distance- dependent dispersion-motion artifact). For ﬂexibility and promiscuity indices, however, ICA- AROMA performed poorly, indicating that pipelines may not perform equally well across static and dynamic functional connectivity contexts. Investigators may wish to tailor their de-noising approach to the dynamic functional con- nectivity index of most interest to them. Alternatively, de-noising approaches that show less effective performance across a range of indices (e.g., 6P, 24P, tCOMPCOR, wmLOCAL) may be avoided in favor of pipelines exhibiting more effective performance across the many different indices evaluated (e.g., 36P+DESPIKE, aCOMPCOR). We caution that, although approaches using GSR performed relatively well in the current case, there is evidence that static graph indices resulting from pipelines incorporating GSR may be less reliable (as assessed using test- retest) than those without GSR (see Andellini et al., 2015, for review). It will be important for future work to examine the extent to which limitations in reliability associated with GSR generalize from static to dynamic functional connectivity. Limitations The ﬁndings of the present report should be evaluated in light of study limitations. The choice of indices to identify effective de-noising procedures were intuitive and complemented those used in static rs-fMRI benchmarking approaches (Ciric et al., 2017). However, the lack of a ground truth remains a challenge in the evaluation of pipeline effectiveness. Although the present report included many de-noising strategies, it is not an exhaustive evaluation of all available artifact-control strategies. ICA-FIX, for example, was not evaluated. However, as it requires manual labeling and training data, it is a less common method of de-noising relative to the strategies examined in the present report. In constructing indices of dynamic functional connectivity, a sliding window approach using Pearson correlations was taken. This is a com- mon approach, but alternative approaches exist to which the current results may not generalize. These alternatives include the use of wavelet-based methods to clean the time series prior to estimating functional connectivity (Z. Zhang et al., 2016), other measures of functional con- nectivity such as coherence (Bassett et al., 2011), and approaches that do not rely on sliding windows to capture changes in functional connectivity (e.g., dynamic connectivity regression; Cribben, Haraldsdottir, Atlas, Wager, & Lindquist, 2012). Examining motion artifact in a sample free of gross motion allowed a focus on confound regression strategies for the mitigation of motion artifact introduced through micromovements. The results here may not generalize to samples with more extensive motion. The dynamic functional connectivity indices examined in the present manuscript are com- monly used, especially edge dispersion (e.g., Demirta¸s et al., 2016). The focus on graph indices Network Neuroscience 449 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Motion mitigation in dynamic connectivity (e.g., modularity, ﬂexibility) reﬂects increasing interest and utility of network indices to describe brain function and recent ﬁndings indicating their importance for understanding cognitive pro- cesses (Bassett et al., 2011; Muldoon & Bassett, 2016; Telesford et al., 2017). Dynamic network indices at smaller topological scales (e.g., temporal clustering), larger topological scales (e.g., small-worldness), and measures that may combine the two (e.g., temporal small-worldness; Sizemore & Bassett, 2018) were beyond the scope of the current manuscript and will require evaluation in future work. Finally, while the examination of dynamic connectivity has provided insight into the spatiotemporal organization of spontaneous brain activity, we direct readers to important considerations about the potential physiological underpinnings of dynamic rs-fMRI (Laumann et al., 2017; Liégeois, Laumann, Snyder, Zhou, & Yeo, 2017). Conclusion In sum, the present study highlights the varying effectiveness of commonly used de-noising pipelines in studies of dynamic functional connectivity and dynamic network architecture in rs-fMRI. By evaluating many pipelines across common indices used in dynamic functional connectivity and network neuroscience studies, the present report provides investigators with a means to evaluate the relative strengths and weaknesses of available de-noising pipelines. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 ACKNOWLEDGMENTS The content is solely the responsibility of the authors and does not necessarily represent the ofﬁcial views of any of the funding agencies. AUTHOR CONTRIBUTIONS David Martin Lydon-Staley: Formal analysis; Investigation; Methodology; Writing – original draft; Writing – review & editing. Rastko Ciric: Data curation; Formal analysis; Writing – review & editing. Theodore D. Satterthwaite: Conceptualization; Data curation; Funding acquisition; Supervision; Writing – original draft; Writing – review & editing. Danielle S. Bassett: Con- ceptualization; Funding acquisition; Investigation; Methodology; Resources; Supervision; Writing – original draft; Writing – review & editing. FUNDING INFORMATION John D. and Catherine T. MacArthur Foundation (http://dx.doi.org/ Danielle S. Bassett, 10.13039/100000870). Danielle S. Bassett, Alfred P. Sloan Foundation (http://dx.doi.org/ 10.13039/100000879). Danielle S. Bassett, ISI Foundation. Danielle S. Bassett, Paul Allen Foundation. Danielle S. Bassett, Army Research Laboratory (http://dx.doi.org/10.13039/ 100006754), Award ID: W911NF-10-2-0022. Danielle S. Bassett, Army Research Laboratory (http://dx.doi.org/10.13039/100006754), Award ID: W911NF-14-1-0679. Danielle S. Bassett, Army Research Ofﬁce (http://dx.doi.org/10.13039/100000183), Award ID: W911NF-16-1- 0474. Danielle S. Bassett, Army Research Ofﬁce (http://dx.doi.org/10.13039/100000183), Award ID: W911NF-17-2-0181. Danielle S. Bassett, Ofﬁce of Naval Research (http:// dx.doi.org/10.13039/100000006). Danielle S. Bassett, National Institute of Mental Health (http://dx.doi.org/10.13039/100000025), Award ID: 2-R01-DC-009209-11. Danielle S. Bassett, National Institute of Mental Health (http://dx.doi.org/10.13039/100000025), Award ID: R01-MH112847. Danielle S. Bassett, National Institute of Mental Health (http://dx.doi.org/ 10.13039/100000025), Award ID: R01-MH107235. Danielle S. Bassett, National Institute of Mental Health (http://dx.doi.org/10.13039/100000025), Award ID: R21-M-MH-106799. Danielle S. Bassett, National Institute of Child Health and Human Development (http:// Network Neuroscience 450 Motion mitigation in dynamic connectivity dx.doi.org/10.13039/100000071), Award ID: 1R01HD086888-01. Danielle S. Bassett, Na- tional Institute of Neurological Disorders and Stroke (http://dx.doi.org/10.13039/100000065), Award ID: R01-NS099348. Danielle S. Bassett, National Science Foundation (http://dx.doi.org/ 10.13039/100000001), Award ID: BCS-1441502. Danielle S. Bassett, National Science Foundation (http://dx.doi.org/10.13039/100000001), Award ID: BCS-1430087. Danielle S. Bassett, National Science Foundation (http://dx.doi.org/10.13039/100000001), Award ID: PHY-1554488. Danielle S. Bassett, National Science Foundation (http://dx.doi.org/10.13039/ 100000001), Award ID: BCS-1631550. Theodore D. Satterthwaite, National Institute of Mental Health (http://dx.doi.org/10.13039/100000025), Award ID: R01MH107703. Theodore D. Satterthwaite, National Institute of Mental Health (http://dx.doi.org/10.13039/ 100000025), Award ID: R21MH106799. Theodore D. Satterthwaite, National Institute of Mental Health (http://dx.doi.org/10.13039/100000025), Award ID: R01MH112847. Theodore D. Satterthwaite, Lifespan Brain Institute at Penn/CHOP. REFERENCES Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele, T., & Calhoun, V. D. (2014). Tracking whole-brain connectivity dynamics in the resting state. Cerebral Cortex, 24(3), 663–676. Andellini, M., Cannatà, V., Gazzellini, S., Bernardi, B., & Napolitano, A. (2015). Test-retest reliability of graph metrics of resting state MRI functional brain networks: A review. Journal of Neuro- science Methods, 253, 183–192. Avants, B. B., Tustison, N. J., Song, G., Cook, P. A., Klein, A., & Gee, J. C. (2011). A reproducible evaluation of ANTs similarity metric performance in brain image registration. NeuroImage, 54(3), 2033–2044. Avants, B. B., Tustison, N. J., Wu, J., Cook, P. A., & Gee, J. C. (2011). An open source multivariate framework for n-tissue segmentation with evaluation on public data. Neuroinformatics, 9(4), 381–400. Barber, A. D., Lindquist, M. A., DeRosse, P., & Karlsgodt, K. H. (2018). Dynamic functional connectivity states reﬂecting psychotic- like experiences. Biological Psychiatry: Cognitive Neuroscience and Neuroimaging, 3(5), 443–453. https://doi.org/10.1016/ j.bpsc.2017.09.008 Bassett, D. S., & Bullmore, E. T. (2009). Human brain networks in health and disease. Current Opinion in Neurology, 22(4), 340–347. Bassett, D. S., Greenﬁeld, D. L., Meyer-Lindenberg, A., Weinberger, (2010). Efﬁcient physi- D. R., Moore, S. W., & Bullmore, E. T. cal embedding of topologically complex information processing networks in brains and computer circuits. PLoS Computational Biology, 6(4), e1000748. Bassett, D. S., Porter, M. A., Wymbs, N. F., Grafton, S. T., Carlson, J. M., & Mucha, P. J. (2013). Robust detection of dynamic com- munity structure in networks. Chaos: An Interdisciplinary Journal of Nonlinear Science, 23(1), 013142. Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature Neuroscience, 20(3), 353–364. Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson, J. M., & Grafton, S. T. (2011). Dynamic reconﬁguration of hu- man brain networks during learning. Proceedings of the National Academy of Sciences, 108(18), 7641–7646. Bassett, D. S., Yang, M., Wymbs, N. F., & Grafton, S. T. (2015). Learning-induced autonomy of sensorimotor systems. Nature Neuroscience, 18(5), 744–751. Behzadi, Y., Restom, K., Liau, J., & Liu, T. T. (2007). A component based noise correction method (ComCor) for BOLD and perfu- sion based fMRI. NeuroImage, 37(1), 90–101. Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discov- ery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological), 57(1), 289–300. Betzel, R. F., Byrge, L., He, Y., Goñi, J., Zuo, X. N., & Sporns, O. (2014). Changes in structural and functional connectivity among resting-state networks across the human lifespan. NeuroImage, 102, 345–357. Betzel, R. F., Satterthwaite, T. D., Gold, J. I., & Bassett, D. S. (2017). Positive affect, surprise, and fatigue are correlates of network ﬂexibility. Scientiﬁc Reports, 7(1), 520. Biswal, B. B. (2012). Resting state fMRI: A personal history. Neuro- Image, 62(2), 938–944. Braun, U., Plichta, M. M., Esslinger, C., Sauer, C., Haddad, L., Grimm, O., . . . Walter, H. (2012). Test–retest reliability of resting- state connectivity network characteristics using fMRI and graph theoretical measures. NeuroImage, 59(2), 1404–1412. . . . Haddad, L. Braun, U., Schäfer, A., Bassett, D. S., Rausch, F., Schweiger, J. I., Bilek, E., (2016). Dynamic brain network reconﬁguration as a potential schizophrenia genetic risk mech- anism modulated by NMDA receptor function. Proceedings of the National Academy of Sciences, 113(44), 12568–12573. Braun, U., Schäfer, A., Walter, H., Erk, S., Romanczuk-Seiferth, N., Haddad, L., . . . Meyer-Lindenberg, A. (2015). Dynamic recon- ﬁguration of frontal brain networks during executive cognition in humans. Proceedings of the National Academy of Sciences, 112(37), 11678–11683. Bullmore, E. T., & Bassett, D. S. (2011). Brain graphs: Graphical models of the human brain connectome. Annual Review of Clinical Psychology, 7, 113–140. Network Neuroscience 451 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Motion mitigation in dynamic connectivity Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph theoretical analysis of structural and functional systems. Nature Reviews Neuroscience, 10(3), 186–198. Caballero-Gaudes, C., & Reynolds, R. C. (2017). Methods for cleaning the BOLD fMRI signal. NeuroImage, 154, 128–149. Calhoun, V. D., Miller, R., Pearlson, G., & Adali, T. (2014). The chronnectome: Time-varying connectivity networks as the next frontier in fMRI data discovery. Neuron, 84(2), 262–274. Chai, L. R., Khambhati, A. N., Ciric, R., Moore, T. M., Gur, R. C., Gur, R. E., . . . Bassett, D. S. (2017). Evolution of brain network dynamics in neurodevelopment. Network Neuroscience, 1(1), 14–30. Chan, M. Y., Park, D. C., Savalia, N. K., Petersen, S. E., & Wig, G. S. (2014). Decreased segregation of brain systems across the healthy adult lifespan. Proceedings of the National Academy of Sciences, 111(46), E4997–E5006. Chen, Z. J., He, Y., Rosa-Neto, P., Germann, J., & Evans, A. C. (2008). Revealing modular architecture of human brain struc- tural networks by using cortical thickness from MRI. Cerebral Cortex, 18(10), 2374–2381. Cheng, J. C., Bosma, R. L., Hemington, K. S., Kucyi, A., Lindquist, M. A., & Davis, K. D. (2017). Slow-5 dynamic functional con- nectivity reﬂects the capacity to sustain cognitive performance during pain. NeuroImage, 157, 61–68. https://doi.org/10.1016/ j.neuroimage.2017.06.005 Ciric, R., Rosen, A. F. G., Erus, G., Cook, P. A., Bassett, D. S., Davatzikos, C., . . . Satterthwaite, T. D. (in press). Mitigating head motion artifact in functional connectivity MRI. Submitted to Nature Protocols. Ciric, R., Wolf, D. H., Power, J. D., Roalf, D. R., Baum, G. L., Ruparel, K., . . . Gur, R. C. (2017). Benchmarking of participant- level confound regression strategies for the control of motion artifact in studies of functional connectivity. NeuroImage, 154, 174–187. Cohen, J. R. (2018). The behavioral and cognitive relevance of time- varying, dynamic changes in functional connectivity. Neuro- Image,180, 515–525.https://doi.org/10.1016/j.neuroimage.2017. 09.036 Cox, R. W. (1996). AFNI: Software for analysis and visualization of functional magnetic resonance neuroimages. Computers and Biomedical Research, 29(3), 162–173. Cribben, I., Haraldsdottir, R., Atlas, L. Y., Wager, T. D., & Lindquist, M. A. (2012). Dynamic connectivity regression: Determining state- related changes in brain connectivity. NeuroImage, 61(4), 907–920. Damaraju, E., Allen, E. A., Belger, A., Ford, J. M., McEwen, S., Mathalon, D. H., . . . Calhoun, V. D. (2014). Dynamic functional connectivity analysis reveals transient states of dysconnectiv- ity in schizophrenia. NeuroImage: Clinical, 5, 298–308. Demirta¸s, M., Tornador, C., Falcon, C., López-Solà, M., Hernández- Ribas, R., Pujol, J., . . . Deco, G. (2016). Dynamic functional connectivity reveals altered variability in functional connectiv- ity among patients with major depressive disorder. Human Brain Mapping, 37(8), 2918–2930. Di, X., & Biswal, B. B. (2015). Dynamic brain functional connec- tivity modulated by resting-state networks. Brain Structure and Function, 220(1), 37–46. Diedenhofen, B., & Musch, J. (2015). cocor: A comprehensive solution for the statistical comparison of correlations. PLoS ONE, 10(4), e0121945. Fair, D. A., Cohen, A. L., Power, J. D., Dosenbach, N. U., Church, J. A., Miezin, F. M., . . . Petersen, S. E. (2009). Functional brain networks develop from a “local to distributed” organization. PLoS Computational Biology, 5(5), e1000381. Fair, D., Nigg, J. T., Iyer, S., Bathula, D., Mills, K. L., Dosenbach, N. U., . . . Buitelaar, J. K. (2013). Distinct neural signatures detected for ADHD subtypes after controlling for micro- movements in resting state functional connectivity MRI data. Frontiers in Systems Neuroscience, 6, 80. Friston, K. J., Williams, S., Howard, R., Frackowiak, R. S., & Turner, (1996). Movement-related effects in fMRI time-series. Mag- R. netic Resonance in Medicine, 35(3), 346–355. Gotts, S. J., Saad, Z. S., Jo, H. J., Wallace, G. L., Cox, R. W., & Martin, A. (2013). The perils of global signal regression for group comparisons: A case study of Autism Spectrum Disorders. Frontiers in Human Neuroscience, 7. Grady, C., Sarraf, S., Saverino, C., & Campbell, K. (2016). Age differences in the functional interactions among the default, frontoparietal control, and dorsal attention networks. Neurobiol- ogy of Aging, 41, 159–172. Greve, D. N., & Fischl, B. (2009). Accurate and robust brain im- age alignment using boundary-based registration. NeuroImage, 48(1), 63–72. Gur, R. E., Kaltman, D., Melhem, E. R., Ruparel, K., Prabhakaran, K., Riley, M., . . . Gur, R. C. (2013). Incidental ﬁndings in youths volunteering for brain MRI research. American Journal of Neuroradiology, 34(10), 2021–2025. Hallquist, M. N., Hwang, K., & Luna, B. (2013). The nuisance of nuisance regression: Spectral misspeciﬁcation in a common ap- proach to resting-state fMRI preprocessing reintroduces noise and obscures functional connectivity. NeuroImage, 82, 208–225. Hutchison, R. M., & Morton, J. B. (2016). It’s a matter of time: Re- framing the development of cognitive control as a modiﬁcation the brain’s temporal dynamics. Developmental Cognitive of Neuroscience, 18, 70–77. Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A., (2013). Calhoun, V. D., Corbetta, M., . . . Handwerker, D. A. Dynamic functional connectivity: Promise, issues, and interpre- tations. NeuroImage, 80, 360–378. Jenkinson, M., Bannister, P., Brady, M., & Smith, S. (2002). Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage, 17(2), 825–841. Jeub, L. G. S., Bazzi, M., Jutla, I. S., & Mucha, P. J. (2011). A generalized Louvain method for community detection implemented in MATLAB. Retrieved from http://netwiki.amath.unc.edu/GenLouvain Jo, H. J., Saad, Z. S., Simmons, W. K., Milbury, L. A., & Cox, R. W. (2010). Mapping sources of correlation in resting state FMRI, with artifact detection and removal. NeuroImage, 52(2), 571–582. Khambhati, A. N., Sizemore, A. E., Betzel, R. F., & Bassett, (2018). Modeling and interpreting mesoscale network D. S. dynamics. NeuroImage, 180, 337–349. https://doi.org/10.1016/ j.neuroimage.2017.06.029 Klein, A., Andersson, J., Ardekani, B. A., Ashburner, J., Avants, B., Chiang, M. C., . . . Song, J. H. (2009). Evaluation of 14 Network Neuroscience 452 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Motion mitigation in dynamic connectivity nonlinear deformation algorithms applied to human brain MRI registration. NeuroImage, 46(3), 786–802. Kucyi, A., & Davis, K. D. (2014). Dynamic functional connectivity of the default mode network tracks daydreaming. NeuroImage, 100, 471–480. Laumann, T. O., Snyder, A. Z., Mitra, A., Gordon, E. M., Gratton, C., Adeyemo, B., . . . McCarthy, J. E. (2017). On the stability of BOLD fMRI correlations. Cerebral Cortex, 27(10), 4719–4732. Leonardi, N., & Van De Ville, D. (2015). On spurious and real ﬂuctuations of dynamic functional connectivity during rest. NeuroImage, 104, 430–436. Liégeois, R., Laumann, T. O., Snyder, A. Z., Zhou, J., & Yeo, B. T. T. Interpreting temporal ﬂuctuations in resting-state func- (2017). tional connectivity MRI. NeuroImage, 163, 437–455. Liu, X., & Duyn, J. H. (2013). Time-varying functional network information extracted from brief instances of spontaneous brain activity. Proceedings of the National Academy of Sciences, 110(11), 4392–4397. Lydon-Staley, D. M., Ciric, R., Satterthwaite, T. D., & Bassett, D. S. (2019). Supporting information for “Evaluation of confound re- gression strategies for the mitigation of micromovement artifact in studies of dynamic resting-state functional connectivity and multilayer network modularity.” Network Neuroscience, 3(2), 427–454. https://doi.org/10.1162/netn_a_00071 Medaglia, J. D., Satterthwaite, T. D., Kelkar, A., Ciric, R., Moore, T. M., Ruparel, K., . . . Bassett, D. S. (2018). Brain state expres- sion and transitions are related to complex executive cognition in normative neurodevelopment. NeuroImage, 166, 293–306. https://doi.org/10.1016/j.neuroimage.2017.10.048 Merikangas, K. R., He, J. P., Brody, D., Fisher, P. W., Bourdon, K., & (2010). Prevalence and treatment of mental dis- Koretz, D. S. orders among US children in the 2001–2004 NHANES. Pedi- atrics, 125(1), 75–81. Meunier, D., Lambiotte, R., Fornito, A., Ersche, K. D., & Bullmore, E. T. (2009). Hierarchical modularity in human brain functional networks. Frontiers in Neuroinformatics, 3. Mucha, P. J., Richardson, T., Macon, K., Porter, M. A., & Onnela, J. P. (2010). Community structure in time-dependent, multiscale, and multiplex networks. Science, 328(5980), 876–878. Muldoon, S. F., & Bassett, D. S. (2016). Network and multilayer network approaches to understanding human brain dynamics. Philosophy of Science, 83(5), 710–720. Murphy, K., Birn, R. M., & Bandettini, P. A. (2013). Resting-state fMRI confounds and cleanup. NeuroImage, 80, 349–359. Murphy, K., & Fox, M. D. (2016). Towards a consensus regarding global signal regression for resting state functional connectivity MRI. NeuroImage, 154, 169–173. Muschelli, J., Nebel, M. B., Caffo, B. S., Barber, A. D., Pekar, J. J., & Mostofsky, S. H. (2014). Reduction of motion-related artifacts in resting state fMRI using aCompCor. NeuroImage, 96, 22–35. Papadopoulos, L., Puckett, J. G., Daniels, K. E., & Bassett, D. S. (2016). Evolution of network architecture in a granular material under compression. Physical Review E, 94(3), 032908. Parkes, L., Fulcher, B. D., Yucel, M., & Fornito, A. (2018). An eval- uation of the efﬁcacy, reliability, and sensitivity of motion cor- rection strategies for resting-state functional MRI. NeuroImage, 171, 415–436. Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., & Petersen, S. E. (2012). Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuro- Image, 59(3), 2142–2154. Power, J. D., Cohen, A. L., Nelson, S. M., Wig, G. S., Barnes, K. A., Church, J. A., . . . Petersen, S. E. (2011). Functional network organization of the human brain. Neuron, 72(4), 665–678. Power, J. D., Plitt, M., Laumann, T. O., & Martin, A. (2017). Sources and implications of whole-brain fMRI signals in humans. Neuro- Image, 146, 609–625. Power, J. D., Schlaggar, B. L., & Petersen, S. E. (2015). Recent progress and outstanding issues in motion correction in resting state fMRI. NeuroImage, 105, 536–551. Preti, M. G., Bolton, T. A. W., & Van De Ville, D. (2017). The dy- namic functional connectome: State-of-the-art and perspectives. NeuroImage, 160, 41–54. Pruim, R. H., Mennes, M., van Rooij, D., Llera, A., Buitelaar, J. K., & ICA-based Beckmann, C. F. strategy for removing motion artifacts from fMRI data. Neuro- Image, 112, 267–277. ICA-AROMA: A robust (2015). Saad, Z. S., Gotts, S. J., Murphy, K., Chen, G., Jo, H. J., Martin, A., & Cox, R. W. (2012). Trouble at rest: how correlation patterns and group differences become distorted after global signal regression. Brain Connectivity, 2(1), 25–32. Sako˘glu, Ü., Pearlson, G. D., Kiehl, K. A., Wang, Y. M., Michael, A. M., & Calhoun, V. D. (2010). A method for evaluating dynamic functional network connectivity and task-modulation: Applica- tion to schizophrenia. Magnetic, Resonance Materials in Physics, Biology and Medicine, 23(5-6), 351–366. Salimi-Khorshidi, G., Douaud, G., Beckmann, C. F., Glasser, M. F., Griffanti, L., & Smith, S. M. (2014). Automatic denoising of func- tional MRI data: Combining independent component analysis and hierarchical fusion of classiﬁers. NeuroImage, 90, 449–468. Satterthwaite, T. D., Ciric, R., Roalf, D. R., Davatzikos, C., Bassett, in studies of D. S., & Wolf, D. H. functional connectivity: Characteristics and mitigation strategies. Human Brain Mapping. https://doi.org/10.1002/hbm.23665 Satterthwaite, T. D., Connolly, J. J., Ruparel, K., Calkins, M. E., Jackson, C., Elliott, M. A., . . . Qiu, H. (2016). The Philadelphia Neurodevelopmental Cohort: A publicly available resource for the study of normal and abnormal brain development in youth. NeuroImage, 124, 1115–1119. (2017). Motion artifact Satterthwaite, T. D., Elliott, M. A., Ruparel, K., Loughead, J., (2014). Prabhakaran, K., Calkins, M. E., . . . Mentch, F. D. Neuroimaging of the Philadelphia Neurodevelopmental Cohort. NeuroImage, 86, 544–553. Satterthwaite, T. D., Wolf, D. H., Ruparel, K., Erus, G., Elliott, M. A., Eickhoff, S. B., . . . Hakonarson, H. (2013). Heterogeneous impact of motion on fundamental patterns of developmental changes in functional connectivity during youth. NeuroImage, 83, 45–57. Satterthwaite, T. D., Elliott, M. A., Gerraty, R. T., Ruparel, K., Loughead, J., Calkins, M. E., . . . Wolf, D. H. (2013). An im- proved framework for confound regression and ﬁltering for control of motion artifact in the preprocessing of resting-state functional connectivity data. NeuroImage, 64, 240–256. Satterthwaite, T. D., Wolf, D. H., Loughead, J., Ruparel, K., Elliott, M. A., Hakonarson, H., . . . Gur, R. E. (2012). Impact of in-scanner Network Neuroscience 453 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Motion mitigation in dynamic connectivity head motion on multiple measures of functional connectiv- ity: Relevance for studies of neurodevelopment in youth. Neuro- Image, 60(1), 623–632. Schölvinck, M. L., Maier, A., Frank, Q. Y., Duyn, J. H., & Leopold, D. A. (2010). Neural basis of global resting-state fMRI activ- ity. Proceedings of the National Academy of Sciences, 107(22), 10238–10243. Shine, J. M., Koyejo, O., & Poldrack, R. A. (2016). Temporal metas- tates are associated with differential patterns of time-resolved connectivity, network topology, and attention. Proceedings of the National Academy of Sciences, 113(35), 9888–9891. Siegel, J. S., Mitra, A., Laumann, T. O., Seitzman, B. A., Raichle, M., Corbetta, M., & Snyder, A. Z. (2016). Data quality inﬂuences observed links between functional connectivity and behavior. Cerebral Cortex, 27(9), 4492–4502. Sizemore, A. E., & Bassett, D. S. (2018). Dynamic graph metrics: Tutorial, toolbox, and tale. NeuroImage, 180, 417–427. Smith, S. M., Miller, K. L., Moeller, S., Xu, J., Auerbach, E. J., Woolrich, M. W., . . . Essen, D. C. (2012). Temporally indepen- dent functional modes of spontaneous brain activity. Proceedings of the National Academy of Sciences, 109(8), 3131–3136. Sporns, O. (2015). Cerebral cartography and connectomics. Philosoph- ical Transactions of the Royal Society B, 370(1668), 20140173. Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual Review of Psychology, 67, 613–640. Steiger, J. H. (1980). Tests for comparing elements of a correlation matrix. Psychological Bulletin, 87, 245–251. Telesford, Q. K., Ashourvan, A., Wymbs, N. F., Grafton, S. T., Vettel, J. M., & Bassett, D. S. (2017). Cohesive network reconﬁguration accompanies extended training. Human Brain Mapping, 38(9), 4744–4759. Tustison, N. J., Cook, P. A., Klein, A., Song, G., Das, S. R., Duda, J. T., . . . Avants, B. B. (2014). Large-scale evaluation of ANTs and free- surfer cortical thickness measurements. NeuroImage, 99, 166–179. Tustison, N. J., Avants, B. B., Cook, P. A., Zheng, Y., Egan, A., Yushkevich, P. A., & Gee, J. C. (2010). N4ITK: Improved N3 bias correction. IEEE Transactions on Medical Imaging, 29(6), 1310–1320. van den Heuvel, M. P., & Pol, H. E. H. (2010). Exploring the brain network: A review on resting-state fMRI functional connectivity. European Neuropsychopharmacology, 20(8), 519–534. Van Dijk, K. R., Sabuncu, M. R., & Buckner, R. L. (2012). The in- ﬂuence of head motion on intrinsic functional connectivity MRI. NeuroImage, 59(1), 431–438. Vergara, V. M., Mayer, A. R., Damaraju, E., & Calhoun, V. D. (2017). The effect of preprocessing in dynamic functional network con- nectivity used to classify mild traumatic brain injury. Brain and Behavior, 7(10), e00809. https://doi.org/10.1002/brb3.809 Wang, H., Cao, Y., & Syeda-Mahmood, T. (2014). Multi-atlas seg- mentation with learning-based label fusion. Machine Learning in Medical Imaging, 35, 256–263. Windischberger, C., Langenberger, H., Sycha, T., Tschernko, E. M., Fuchsjäger-Mayerl, G., Schmetterer, L., & Moser, E. (2002). On the origin of respiratory artifacts in BOLD-EPI of the human brain. Magnetic Resonance Imaging, 20(8), 575–582. Yan, C. G., Cheung, B., Kelly, C., Colcombe, S., Craddock, R. C., Di Martino, A., . . . Milham, M. P. (2013). A comprehensive as- sessment of regional variation in the impact of head micromove- ments on functional connectomics. Neuroimage, 76(), 183–201. Yao, Z., Hu, B., Xie, Y., Zheng, F., Liu, G., Chen, X., & Zheng, W. (2016). Resting-state time-varying analysis reveals aberrant variations of func- tional connectivity in autism. Frontiers in Human Neuroscience, 10. Zalesky, A., Fornito, A., & Bullmore, E. (2012). On the use of corre- lation as a measure of network connectivity. NeuroImage, 60(4), 2096–2106. Zhang, H., Chen, X., Zhang, Y., & Shen, D. (2017). Test-retest re- liability of “high-order” functional connectivity in young healthy adults. Frontiers in Neuroscience, 11, 439. Zhang, Z., Telesford, Q. K., Giusti, C., Lim, K. O., & Bassett, D. S. (2016). Choosing wavelet methods, ﬁlters, and lengths for functional brain network construction. PloS One, 11(6), e0157243. Zheng, H., Li, F., Bo, Q., Li, X., Yao, L., Yao, Z., . . . Wu, X. (2018). The dynamic characteristics of the anterior cingulate cortex in resting-state fMRI of patients with depression. Journal of Affective Disorders, 227, 391–397. Network Neuroscience 454 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 4 2 7 1 0 9 2 6 0 9 n e n _ a _ 0 0 0 7 1 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 imagen de INVESTIGACIÓN

Descargar PDF